Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T23:17:57.695Z Has data issue: false hasContentIssue false
  • English
  • Français

FORCING QUASIRANDOMNESS WITH TRIANGLES

Part of: Graph theory

Published online by Cambridge University Press:  02 April 2019

CHRISTIAN REIHER  and
MATHIAS SCHACHT
CHRISTIAN REIHER
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Hamburg, Germany; [email protected], [email protected]
MATHIAS SCHACHT
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Hamburg, Germany; [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

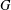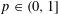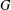We study forcing pairs for quasirandom graphs. Chung, Graham, and Wilson initiated the study of families ${\mathcal{F}}$ of graphs with the property that if a large graph $G$ has approximately homomorphism density $p^{e(F)}$ for some fixed $p\in (0,1]$ for every $F\in {\mathcal{F}}$, then $G$ is quasirandom with density 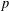$p$. Such families 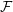${\mathcal{F}}$ are said to be forcing. Several forcing families were found over the last three decades and characterizing all bipartite graphs $F$ such that 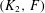$(K_{2},F)$ is a forcing pair is a well-known open problem in the area of quasirandom graphs, which is closely related to Sidorenko’s conjecture. In fact, most of the known forcing families involve bipartite graphs only.

We consider forcing pairs containing the triangle 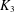$K_{3}$. In particular, we show that if 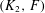$(K_{2},F)$ is a forcing pair, then so is 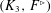$(K_{3},F^{\rhd })$, where 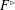$F^{\rhd }$ is obtained from 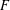$F$ by replacing every edge of 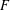$F$ by a triangle (each of which introduces a new vertex). For the proof we first show that 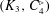$(K_{3},C_{4}^{\rhd })$ is a forcing pair, which strengthens related results of Simonovits and Sós and of Conlon et al.

MSC classification

Primary: 05C80: Random graphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e9
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Aigner-Horev, E., Conlon, D., Hàn, H., Person, Y. and Schacht, M., ‘Quasirandomness in hypergraphs’, Electron. J. Combin. 25(3) (2018), Paper 3.34, 22 pages.Google Scholar
Alon, N., ‘Eigenvalues and expanders’, Combinatorica 6(2) (1986), 83–96. Theory of Computing (Singer Island, Fla., 1984).Google Scholar
Alon, N. and Chung, F. R. K., ‘Explicit construction of linear sized tolerant networks’, inProceedings of the First Japan Conference on Graph Theory and Applications (Hakone, 1986), Discrete Mathematics, 72 (Elsevier, North-Holland, 1988), 15–19.Google Scholar
Chung, F. R. K., ‘Quasi-random classes of hypergraphs’, Random Structures Algorithms 1(4) (1990), 363–382.Google Scholar
Chung, F. R. K., ‘Quasi-random hypergraphs revisited’, Random Structures Algorithms 40(1) (2012), 39–48.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random hypergraphs’, Random Structures Algorithms 1(1) (1990), 105–124.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random tournaments’, J. Graph Theory 15(2) (1991), 173–198.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random set systems’, J. Amer. Math. Soc. 4(1) (1991), 151–196.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Maximum cuts and quasirandom graphs’, inRandom Graphs, vol. 2 (Poznań, 1989) (Wiley-Intersci. Publ., Wiley, New York, 1992), 23–33.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random subsets of Z n ’, J. Combin. Theory Ser. A 61(1) (1992), 64–86.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Sparse quasi-random graphs’, Combinatorica 22(2) (2002), 217–244, Special issue: Paul Erdős and his mathematics.Google Scholar
Chung, F. R. K., Graham, R. L. and Wilson, R. M., ‘Quasi-random graphs’, Combinatorica 9(4) (1989), 345–362.Google Scholar
Conlon, D., Fox, J. and Sudakov, B., ‘Hereditary quasirandomness without regularity’, Math. Proc. Cambridge Philos. Soc. 164(3) (2018), 385–399.Google Scholar
Conlon, D., Fox, J. and Sudakov, B., ‘An approximate version of Sidorenko’s conjecture’, Geom. Funct. Anal. 20(6) (2010), 1354–1366.Google Scholar
Conlon, D., Fox, J. and Zhao, Y., ‘Extremal results in sparse pseudorandom graphs’, Adv. Math. 256 (2014), 206–290.Google Scholar
Conlon, D., Hàn, H., Person, Y. and Schacht, M., ‘Weak quasi-randomness for uniform hypergraphs’, Random Structures Algorithms 40(1) (2012), 1–38.Google Scholar
Conlon, D., Kim, J. H., Lee, C. and Lee, J., ‘Some advances on Sidorenko’s conjecture’, J. Lond. Math. Soc. (2) 98(3) (2018), 593–608.Google Scholar
Conlon, D. and Lee, J., ‘Finite reflection groups and graph norms’, Adv. Math. 315 (2017), 130–165.Google Scholar
Cooper, J. N., ‘Quasirandom permutations’, J. Combin. Theory Ser. A 106(1) (2004), 123–143.Google Scholar
Frankl, P., Rödl, V. and Wilson, R. M., ‘The number of submatrices of a given type in a Hadamard matrix and related results’, J. Combin. Theory Ser. B 44(3) (1988), 317–328.Google Scholar
Frieze, A. and Kannan, R., ‘Quick approximation to matrices and applications’, Combinatorica 19(2) (1999), 175–220.Google Scholar
Gowers, W. T., ‘Quasirandom groups’, Combin. Probab. Comput. 17(3) (2008), 363–387.Google Scholar
Griffiths, S., ‘Quasi-random oriented graphs’, J. Graph Theory 74(2) (2013), 198–209.Google Scholar
Hàn, H., Person, Y. and Schacht, M., ‘Note on forcing pairs’, inThe Sixth European Conference on Combinatorics, Graph Theory and Applications (EuroComb 2011), Electronic Notes in Discrete Mathematics, 38 (Elsevier Science B. V., Amsterdam, 2011), 437–442.Google Scholar
Hatami, H., ‘Graph norms and Sidorenko’s conjecture’, Israel J. Math. 175 (2010), 125–150.Google Scholar
Haviland, J. and Thomason, A., ‘Pseudo-random hypergraphs’, Discrete Math. 75(1–3) (1989), 255–278, Graph Theory and Combinatorics (Cambridge, 1988).Google Scholar
He, X., ‘Linear dependence between hereditary quasirandomness conditions’, Electron. J. Combin. 25(4) (2018), Paper 4.12, 14 pages.Google Scholar
Huang, H. and Lee, C., ‘Quasi-randomness of graph balanced cut properties’, Random Structures Algorithms 41(1) (2012), 124–145.Google Scholar
Hubai, T., Král, D., Parczyk, O. and Person, Y., ‘More non-bipartite forcing pairs’, submitted.Google Scholar
Janson, S. and Sós, V. T., ‘More on quasi-random graphs, subgraph counts and graph limits’, European J. Combin. 46 (2015), 134–160.Google Scholar
Kim, J. H., Lee, C. and Lee, J., ‘Two approaches to Sidorenko’s conjecture’, Trans. Amer. Math. Soc. 368(7) (2016), 5057–5074.Google Scholar
Kohayakawa, Y. and Rödl, V., ‘Regular pairs in sparse random graphs. I’, Random Structures Algorithms 22(4) (2003), 359–434.Google Scholar
Kohayakawa, Y. and Rödl, V., ‘Szemerédi’s regularity lemma and quasi-randomness’, inRecent advances in algorithms and combinatorics, CMS Books Math./Ouvrages Math. SMC, 11 (Springer, New York, 2003), 289–351.Google Scholar
Kohayakawa, Y., Rödl, V. and Skokan, J., ‘Hypergraphs, quasi-randomness, and conditions for regularity’, J. Combin. Theory Ser. A 97(2) (2002), 307–352.Google Scholar
Krivelevich, M. and Sudakov, B., ‘Pseudo-random graphs’, inMore Sets, Graphs and Numbers, Bolyai Society Mathematical Studies, 15 (Springer, Berlin, 2006), 199–262.Google Scholar
Lenz, J. and Mubayi, D., ‘Eigenvalues and linear quasirandom hypergraphs’, Forum Math. Sigma 3(e2) (2015), 26.Google Scholar
Li, J. X. and Szegedy, B., ‘On the logarithmic calculus and Sidorenko’s conjecture’, Combinatorica to appear, Preprint, arXiv:1107.1153.Google Scholar
Lovász, L., Large Networks and Graph Limits, American Mathematical Society Colloquium Publications, 60 (American Mathematical Society, Providence, RI, 2012), xiv+475.Google Scholar
Lovász, L. and Szegedy, B., ‘Szemerédi’s lemma for the analyst’, Geom. Funct. Anal. 17(1) (2007), 252–270.Google Scholar
Reiher, C. and Schacht, M., ‘Quasirandomness from hereditary subgraph densities’. Manuscript.Google Scholar
Rödl, V., ‘On universality of graphs with uniformly distributed edges’, Discrete Math. 59(1–2) (1986), 125–134.Google Scholar
Shapira, A., ‘Quasi-randomness and the distribution of copies of a fixed graph’, Combinatorica 28(6) (2008), 735–745.Google Scholar
Shapira, A. and Yuster, R., ‘The effect of induced subgraphs on quasi-randomness’, Random Structures Algorithms 36(1) (2010), 90–109.Google Scholar
Shapira, A. and Yuster, R., ‘The quasi-randomness of hypergraph cut properties’, Random Structures Algorithms 40(1) (2012), 105–131.Google Scholar
Sidorenko, A. F., ‘Inequalities for functionals generated by bipartite graphs’, Diskret. Mat. 3(3) (1991), 50–65. (Russian); English transl., Discrete Math. Appl. 2(5) (1992) 489–504.Google Scholar
Simonovits, M., ‘Extremal graph problems, degenerate extremal problems, and supersaturated graphs’, inProgress in Graph Theory (Waterloo, Ont., 1982) (Academic Press, Toronto, ON, 1984), 419–437.Google Scholar
Simonovits, M. and Sós, V. T., ‘Szemerédi’s partition and quasirandomness’, Random Structures Algorithms 2(1) (1991), 1–10.Google Scholar
Simonovits, M. and Sós, V. T., ‘Hereditarily extended properties, quasi-random graphs and not necessarily induced subgraphs’, Combinatorica 17(4) (1997), 577–596.Google Scholar
Simonovits, M. and Sós, V. T., ‘Hereditary extended properties, quasi-random graphs and induced subgraphs’, Combin. Probab. Comput. 12(3) (2003), 319–344, Combinatorics, Probability and Computing (Oberwolfach, 2001).Google Scholar
Skokan, J. and Thoma, L., ‘Bipartite subgraphs and quasi-randomness’, Graphs Combin. 20(2) (2004), 255–262.Google Scholar
Szegedy, B., ‘An information theoretic approach to Sidorenko’s conjecture’, Preprint,arXiv:1406.6738.Google Scholar
Szemerédi, E., ‘Regular partitions of graphs’, inProblèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), Colloq. Internat. CNRS, 260 (CNRS, Paris, 1978), 399–401.Google Scholar
Thomason, A., ‘Pseudorandom graphs’, inRandom Graphs ’85 (Poznań, 1985), North-Holland Mathematics Studies, 144 (North-Holland, Amsterdam, 1987), 307–331.Google Scholar
Thomason, A., ‘Random graphs, strongly regular graphs and pseudorandom graphs’, inSurveys in Combinatorics 1987 (New Cross, 1987), London Mathematics Society Lecture Note Series, 123 (Cambridge University Press, Cambridge, 1987), 173–195.Google Scholar
Towsner, H., ‘𝜎-algebras for quasirandom hypergraphs’, Random Structures Algorithms 50(1) (2017), 114–139.Google Scholar
Wilson, Richard M., ‘Cyclotomy and difference families in elementary abelian groups’, J. Number Theory 4 (1972), 17–47.Google Scholar
Yuster, Raphael, ‘Quasi-randomness is determined by the distribution of copies of a fixed graph in equicardinal large sets’, Combinatorica 30(2) (2010), 239–246.Google Scholar