Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T23:27:07.895Z Has data issue: false hasContentIssue false
  • English
  • Français

A FILTRATION ON EQUIVARIANT BOREL–MOORE HOMOLOGY

Part of: Special varieties Cycles and subschemes

Published online by Cambridge University Press:  04 July 2019

ARAM BINGHAM ,
MAHIR BILEN CAN Open the ORCID record for MAHIR BILEN CAN [Opens in a new window]  and
YILDIRAY OZAN
ARAM BINGHAM
Affiliation:
Department of Mathematics, Tulane University, New Orleans, 70118, LA, USA; [email protected], [email protected]
MAHIR BILEN CAN
Affiliation:
Department of Mathematics, Tulane University, New Orleans, 70118, LA, USA; [email protected], [email protected]
YILDIRAY OZAN
Affiliation:
Department of Mathematics, Middle East Technical University, Ankara, Turkey; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 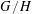$G/H$ be a homogeneous variety and let 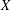$X$ be a 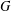$G$-equivariant embedding of 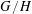$G/H$ such that the number of 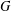$G$-orbits in 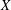$X$ is finite. We show that the equivariant Borel–Moore homology of 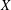$X$ has a filtration with associated graded module the direct sum of the equivariant Borel–Moore homologies of the 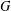$G$-orbits. If 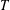$T$ is a maximal torus of 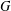$G$ such that each 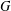$G$-orbit has a 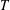$T$-fixed point, then the equivariant filtration descends to give a filtration on the ordinary Borel–Moore homology of 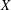$X$. We apply our findings to certain wonderful compactifications as well as to double flag varieties.

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 14M27: Compactifications; symmetric and spherical varieties
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e18
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Batyrev, V. and Moreau, A., ‘Satellites of spherical subgroups’, Preprint, 2016, ArXiv e-prints.Google Scholar
Bien, F. and Brion, M., ‘Automorphisms and local rigidity of regular varieties’, Compos. Math. 104(1) (1996), 1–26.Google Scholar
Borel, A., Linear Algebraic Groups, 2nd edn, Graduate Texts in Mathematics, 126 , (Springer, New York, 1991).Google Scholar
Brion, M., ‘Quelques propriétés des espaces homogènes sphériques’, Manuscripta Math. 55(2) (1986), 191–198.Google Scholar
Brion, M., ‘Equivariant Chow groups for torus actions’, Transform. Groups 2(3) (1997), 225–267.Google Scholar
Brion, M., ‘Equivariant cohomology and equivariant intersection theory’, inRepresentation Theories and Algebraic Geometry (Montreal, PQ, 1997), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 514 (Kluwer Academic Publishers, Dordrecht, 1998), 1–37. Notes by Alvaro Rittatore.Google Scholar
Brion, M. and Peyre, E., ‘The virtual Poincaré polynomials of homogeneous spaces’, Compos. Math. 134(3) (2002), 319–335.Google Scholar
Can, M. B., ‘The cross-section of a spherical double cone’, Adv. Appl. Math. 101 (2018), 215–231.Google Scholar
Can, M. B. and Tien, L., ‘Diagonal orbits in a double flag variety of complexity one, type A’, Preprint, 2018, arXiv:1810.06513.Google Scholar
Edidin, D. and Graham, W., ‘Characteristic classes in the Chow ring’, J. Algebraic Geom. 6(3) (1997), 431–443.Google Scholar
Edidin, D. and Graham, W., ‘Equivariant intersection theory’, Invent. Math. 131(3) (1998), 595–634.Google Scholar
Littelmann, P., ‘On spherical double cones’, J. Algebra 166(1) (1994), 142–157.Google Scholar
Luna, D. and Vust, T., ‘Plongements d’espaces homogènes’, Comment. Math. Helv. 58(2) (1983), 186–245.Google Scholar
Timashev, D. A., Homogeneous Spaces and Equivariant Embeddings, Encyclopaedia of Mathematical Sciences, 138 (Springer, Heidelberg, 2011), Invariant Theory and Algebraic Transformation Groups, 8.Google Scholar
Totaro, B., ‘The Chow ring of a classifying space’, inAlgebraic K-theory (Seattle, WA, 1997), Proc. Sympos. Pure Math., 67 (American Mathematical Society, Providence, RI, 1999), 249–281.Google Scholar
Totaro, B., ‘Chow groups, Chow cohomology, and linear varieties’, Forum Math. Sigma 2(e17) (2014), 25 pages.Google Scholar
Vinberg, È. B., ‘Complexity of actions of reductive groups’, Funktsional. Anal. i Prilozhen. 20(1) (1986), 1–13. 96.Google Scholar