Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T21:17:38.698Z Has data issue: false hasContentIssue false
  • English
  • Français

FANO HYPERSURFACES WITH ARBITRARILY LARGE DEGREES OF IRRATIONALITY

Part of: Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  08 May 2020

NATHAN CHEN  and
DAVID STAPLETON
NATHAN CHEN
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY11794, USA; [email protected]
DAVID STAPLETON
Affiliation:
Department of Mathematics, UC San Diego, La Jolla, CA92093, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that complex Fano hypersurfaces can have arbitrarily large degrees of irrationality. More precisely, if we fix a Fano index $e$, then the degree of irrationality of a very general complex Fano hypersurface of index $e$ and dimension n is bounded from below by a constant times 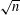$\sqrt{n}$. To our knowledge, this gives the first examples of rationally connected varieties with degrees of irrationality greater than 3. The proof follows a degeneration to characteristic 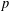$p$ argument, which Kollár used to prove nonrationality of Fano hypersurfaces. Along the way, we show that in a family of varieties, the invariant ‘the minimal degree of a dominant rational map to a ruled variety’ can only drop on special fibers. As a consequence, we show that for certain low-dimensional families of varieties, the degree of irrationality also behaves well under specialization.

MSC classification

Primary: 14E05: Rational and birational maps
Secondary: 14J45: Fano varieties
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e24
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Bastianelli, F., De Poi, P., Ein, L., Lazarsfeld, R. and Ullery, B., ‘Measures of irrationality for hypersurfaces of large degree’, Compos. Math. 153 (2017), 2368–2393.CrossRefGoogle Scholar
Beheshti, R. and Riedl, E., ‘Linear subspaces of hypersurfaces’, Preprint, 2019, arXiv:1903.02481.Google Scholar
Birkar, C., ‘The Iitaka conjecture C n, m in dimension six’, Compos. Math. 145 (2009), 1442–1446.CrossRefGoogle Scholar
Chen, N., ‘Degree of irrationality of very general abelian surfaces’, Algebra Number Theory 13 (2019), 2191–2198.CrossRefGoogle Scholar
Hassett, B., Pirutka, A. and Tschinkel, Y., ‘Stable rationality of quadric surface bundles over surfaces’, Acta Math. 220 (2018), 341–365.CrossRefGoogle Scholar
Iskovskih, V. A. and Manin, J. I., ‘Three-dimensional quartics and counterexamples to the Lüroth problem’, Mat. Sb. 86(128) (1971), 140–166.Google Scholar
de Jong, A. J. and Starr, J., ‘Cubic fourfolds and spaces of rational curves’, Illinois J. Math. 48 (2004), 415–450.CrossRefGoogle Scholar
de Jong, A. J. and Starr, J., ‘Erratum: cubic fourfolds and spaces of rational curves’, Illinois J. Math. 52 (2008), 345–346.CrossRefGoogle Scholar
Kollár, J., ‘Nonrational hypersurfaces’, J. Amer. Math. Soc. 8 (1995), 241–249.CrossRefGoogle Scholar
Kollár, J., Rational Curves on Algebraic Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete, 32 (Springer, Berlin, 1996).CrossRefGoogle Scholar
Kollár, J., Singularities of the Minimal Model Program, vol. 200. (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Kontsevich, M. and Tschinkel, Y., ‘Specialization of birational types’, Invent. Math. 217 (2019), 415–432.CrossRefGoogle Scholar
Mori, S., ‘On a generalization of complete intersections’, J. Math. Kyoto Univ. 15 (1975), 619–646.CrossRefGoogle Scholar
Nicaise, J. and Shinder, E., ‘The motivic nearby fiber and degeneration of stable rationality’, Invent. Math. 217 (2019), 377–413.CrossRefGoogle Scholar
Schreieder, S., ‘Stably irrational hypersurfaces of small slopes’, J. Amer. Math. Soc. 32 (2019), 1171–1199.CrossRefGoogle Scholar
Totaro, B., ‘Hypersurfaces that are not stably rational’, J. Amer. Math. Soc. 29 (2016), 883–891.CrossRefGoogle Scholar
Vial, C., ‘Algebraic cycles and fibrations’, Doc. Math. 18 (2013), 1521–1553.Google Scholar