Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T23:42:20.995Z Has data issue: false hasContentIssue false
  • English
  • Français

FAILURE OF THE 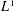$L^{1}$ POINTWISE AND MAXIMAL ERGODIC THEOREMS FOR THE FREE GROUP

Part of: Ergodic theory

Published online by Cambridge University Press:  01 December 2015

TERENCE TAO
TERENCE TAO*
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1555, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $F_{2}$ denote the free group on two generators $a$ and $b$. For any measure-preserving system 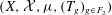$(X,{\mathcal{X}},{\it\mu},(T_{g})_{g\in F_{2}})$ on a finite measure space $X=(X,{\mathcal{X}},{\it\mu})$, any $f\in L^{1}(X)$, and any $n\geqslant 1$, define the averaging operators

$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{n}f(x):=\frac{1}{4\times 3^{n-1}}\mathop{\sum }_{g\in F_{2}:|g|=n}f(T_{g}^{-1}x), & & \displaystyle \nonumber\end{eqnarray}$$
where $|g|$ denotes the word length of 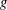$g$. We give an example of a measure-preserving system $X$ and an $f\in L^{1}(X)$ such that the sequence ${\mathcal{A}}_{n}f(x)$ is unbounded in $n$ for almost every $x$, thus showing that the pointwise and maximal ergodic theorems do not hold in 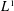$L^{1}$ for actions of $F_{2}$. This is despite the results of Nevo–Stein and Bufetov, who establish pointwise and maximal ergodic theorems in $L^{p}$ for $p>1$ and for 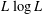$L\log L$ respectively, as well as an estimate of Naor and the author establishing a weak-type 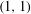$(1,1)$ maximal inequality for the action on $\ell ^{1}(F_{2})$. Our construction is a variant of a counterexample of Ornstein concerning iterates of a Markov operator.

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e27
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Bowen, L. and Nevo, A., ‘Pointwise ergodic theorems beyond amenable groups’, Ergodic Theory Dynam. Systems 33(3) (2013), 777–820.Google Scholar
Bowen, L. and Nevo, A., ‘Amenable equivalence relations and the construction of ergodic averages for group actions’, J. Anal. Math. 126 (2015), 359–388.Google Scholar
Bufetov, A., ‘Convergence of spherical averages for actions of free groups’, Ann. of Math. (2) 155(3) (2002), 929–944.Google Scholar
Bufetov, A. I. and Klimenko, A. V., ‘Maximal inequality and ergodic theorems for Markov groups’, Proc. Steklov Inst. Math. 277 (2012), 27–42.CrossRefGoogle Scholar
Bufetov, A. I., Khristoforov, M. and Klimenko, A., ‘Cesàro convergence of spherical averages for measure-preserving actions of Markov semigroups and groups’, Int. Math. Res. Not. IMRN 2012(21) (2012), 4797–4829.Google Scholar
Fujiwara, K. and Nevo, A., ‘Maximal and pointwise ergodic theorems for word-hyperbolic groups’, Ergodic Theory Dynam. Systems 18(4) (1998), 843–858.Google Scholar
Lindenstrauss, E., ‘Pointwise theorems for amenable groups’, Invent. Math. 146(2) (2001), 259–295.CrossRefGoogle Scholar
Margulis, G. A., Nevo, A. and Stein, E., ‘Analogs of Wiener’s ergodic theorems for semisimple Lie groups. II’, Duke Math. J. 103(2) (2000), 233–259.Google Scholar
Naor, A. and Tao, T., ‘Random martingales and localization of maximal inequalities’, J. Funct. Anal. 259(3) (2010), 731–779.Google Scholar
Nevo, A. and Stein, E., ‘A generalization of Birkhoff’s pointwise ergodic theorem’, Acta Math. 173(1) (1994), 135–154.Google Scholar
Nevo, A. and Stein, E., ‘Analogs of Wiener’s ergodic theorems for semisimple groups. I’, Ann. of Math. (2) 145(3) (1997), 565–595.Google Scholar
Ornstein, D., ‘On the pointwise behavior of iterates of a self-adjoint operator’, J. Math. Mech. 18 (1968/1969), 473–477.Google Scholar
Rota, G.-C., ‘An ‘Alternierende Verfahren’ for general positive operators’, Bull. Amer. Math. Soc. 68 (1962), 95–102.Google Scholar
Stein, E. M., ‘On the maximal ergodic theorem’, Proc. Natl. Acad. Sci. USA 47 (1961), 1894–1897.Google Scholar