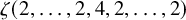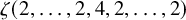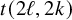1. Introduction
For any tuple
![]() $(k_1,k_2,\ldots ,k_r)$
of positive integers with
$(k_1,k_2,\ldots ,k_r)$
of positive integers with
![]() $k_r\geq 2$
, we may define a multivariable analogue of the Riemann zeta values, called a multiple zeta value (MZV) of weight
$k_r\geq 2$
, we may define a multivariable analogue of the Riemann zeta values, called a multiple zeta value (MZV) of weight
![]() $k_1+\cdots +k_r$
and depth r, by
$k_1+\cdots +k_r$
and depth r, by

These numbers arise naturally in many areas of mathematics and mathematical physics, including in connection to associators [Reference Le and Murakami30, Reference Racinet34], Feynman amplitudes [Reference Broadhurst and Kreimer3], and as periods of mixed Tate motives [Reference Brown5]. Unlike single zeta values, multiple zeta values have a rich algebraic structure, the study of which goes back to Euler Reference Euler15. Many families of relations, such as the associator relations [Reference Le and Murakami30], the double shuffle relations [Reference Racinet35], and the confluence relations [Reference Hirose and Sato22], are conjectured to exhaust all relations among MZVs. However, this is incredibly challenging and encompasses still-open questions such as the transcendence of
![]() $\zeta (2k+1)$
.
$\zeta (2k+1)$
.
One approach to make this more manageable is to consider instead motivic multiple zeta values. Via their connection to mixed Tate motives, MZVs may be lifted to formal, algebraic objects, only satisfying relations coming from the geometry of
![]() ${\mathbb {P}^1\setminus \{0,1,\infty \}}$
[Reference Brown5]. In this setting, much more is known: the ring
${\mathbb {P}^1\setminus \{0,1,\infty \}}$
[Reference Brown5]. In this setting, much more is known: the ring
![]() $\mathcal {H}$
of motivic MZVs are known to be graded by weight, with weight graded dimensions
$\mathcal {H}$
of motivic MZVs are known to be graded by weight, with weight graded dimensions
![]() $d_n$
given by
$d_n$
given by
 $$\begin{align*}\sum_{n\geq 0}d_nx^n=\frac{1}{1-x^2-x^3} .\end{align*}$$
$$\begin{align*}\sum_{n\geq 0}d_nx^n=\frac{1}{1-x^2-x^3} .\end{align*}$$
Motivic multiple zeta values have an explicit basis [Reference Brown5], given by the Hoffman zeta values
However, the question of providing a complete set of relations remains an open problem. One approach to describing all (motivic) relations among MZVs is to consider the associated graded algebra with respect to the depth filtration
Relations in
![]() $\operatorname {\mathrm {gr}}_\bullet ^{\mathcal {D}}\mathcal {H}$
are much simpler, with the stuffle product reducing to a simple shuffle product. However, this introduces additional relations [Reference Gangl, Kaneko and Zagier17],
$\operatorname {\mathrm {gr}}_\bullet ^{\mathcal {D}}\mathcal {H}$
are much simpler, with the stuffle product reducing to a simple shuffle product. However, this introduces additional relations [Reference Gangl, Kaneko and Zagier17],
and the associated Lie algebra of relations is no longer free [Reference Ihara27]
In particular, there are a family of such quadratic relations, arising from period polynomials of cusp forms [Reference Gangl, Kaneko and Zagier17]. Both the relations among multiple zeta values and among elements of the motivic Lie algebra are commonly referred to as the period polynomial relations. It is conjectured that these relations determine all additional relations among depth graded multiple zeta values – that is to say, the the associated Lie algebra of relations is the quotient of a free Lie algebra by the idea generated by these quadratic relations.
Conjecture 1.1 (Broadhurst-Kreimer, [Reference Broadhurst and Kreimer3]).
The generating series for the dimension of the depth graded multiple zeta values is given by
where
and
 $$\begin{align*}S(x)=\frac{x^{12}}{(1-x^4)(1-x^6)}\end{align*}$$
$$\begin{align*}S(x)=\frac{x^{12}}{(1-x^4)(1-x^6)}\end{align*}$$
is the generating function for the space of cusp forms of weight n for the full modular group. That is to say, that the number of linearly independent depth graded multiple zeta values of weight n and depth d is given by the coefficient of
![]() $x^ny^d$
of
$x^ny^d$
of
![]() $BK(x,y)$
, and that these dimensions are determined by the relations coming from cusp forms.
$BK(x,y)$
, and that these dimensions are determined by the relations coming from cusp forms.
However, a proof of this remains out of sight, and these additional relations make using the depth graded Lie algebra to conclude statements about ungraded MZVs challenging.
An alternative approach, first explored in [Reference Keilthy28, Reference Keilthy29] and based on results in [Reference Charlton11, Reference Charlton13], is to consider the so-called block filtration. This filtration provides a simple description of the coradical filtration associated to the motivic coaction in terms of a combinatorial degree function. Specifically
where
![]() ${\deg _{\mathcal {B}}}(w)$
counts the number of subsequences
${\deg _{\mathcal {B}}}(w)$
counts the number of subsequences
![]() $e_ie_i$
in
$e_ie_i$
in
![]() $e_0we_1$
. In [Reference Keilthy29], we see that in the associated graded algebra with respect to the block filtration, there are no additional relations, and furthermore that a complete set of relations can be given in low block degree. One might then ask how the period polynomial relations manifest in this setting.
$e_0we_1$
. In [Reference Keilthy29], we see that in the associated graded algebra with respect to the block filtration, there are no additional relations, and furthermore that a complete set of relations can be given in low block degree. One might then ask how the period polynomial relations manifest in this setting.
Lemma 1.2. The depth filtration is a subfiltration of the block filtration:
Proof. First note that the depth filtration is motivic:
As such, since the block filtration is equal to the coradical filtration, it suffices to show that
![]() $\mathcal {D}_1\mathcal {H}\subset \mathcal {B}_1\mathcal {H}$
. This is an immediate consequence of Lemma 3.2 [Reference Brown5].
$\mathcal {D}_1\mathcal {H}\subset \mathcal {B}_1\mathcal {H}$
. This is an immediate consequence of Lemma 3.2 [Reference Brown5].
As depth is a subfiltration of the block filtration, it is clear that we should be able to express double zeta values in terms of block degree 2 zeta values, and hence that all block graded relations among them, modulo products, should be determined by relations describing
![]() ${\mathfrak {bg}}$
, the associated Lie algebra of relations among block graded MZVs. However, Lemmas 1.2 and 2.8 imply that, in block degree 2 and even weight, relations among multiple zeta values modulo terms of lower block degree are genuine relations modulo products. Thus, the period polynomial relations, modulo products, should arise as a consequence of the relations among block graded MZVs introduced in [Reference Keilthy29].
${\mathfrak {bg}}$
, the associated Lie algebra of relations among block graded MZVs. However, Lemmas 1.2 and 2.8 imply that, in block degree 2 and even weight, relations among multiple zeta values modulo terms of lower block degree are genuine relations modulo products. Thus, the period polynomial relations, modulo products, should arise as a consequence of the relations among block graded MZVs introduced in [Reference Keilthy29].
And indeed, this seems to be the case. The following is a consequence of Lemma 4.1 and allows us to show that relations among double zeta values of even weight are encoded by certain explicit polynomials in
![]() ${\mathbb {Q}}[x_1,x_2,x_3]$
.
${\mathbb {Q}}[x_1,x_2,x_3]$
.
Corollary 1.3. Modulo products, the following holds for any
![]() $0\leq 2a\leq n$
,
$0\leq 2a\leq n$
,
 $$ \begin{align*} \sum_{i=a}^{n-a}{\zeta^{\mathfrak{l}}}(\{2\}^i,4,\{2\}^{n-i}) & {} = 4(-1)^{n+1}\sum_{i=a}^{n-a} {\zeta^{\mathfrak{l}}}(2i+3,2n-2i+1) \\ & {} = 4(-1)^n{\zeta^{\mathfrak{l}}}(2a+1,2n-2a+3). \end{align*} $$
$$ \begin{align*} \sum_{i=a}^{n-a}{\zeta^{\mathfrak{l}}}(\{2\}^i,4,\{2\}^{n-i}) & {} = 4(-1)^{n+1}\sum_{i=a}^{n-a} {\zeta^{\mathfrak{l}}}(2i+3,2n-2i+1) \\ & {} = 4(-1)^n{\zeta^{\mathfrak{l}}}(2a+1,2n-2a+3). \end{align*} $$
Proof. Letting ![]() in Lemma 4.1, we have
in Lemma 4.1, we have
 $$ \begin{align*} {\zeta^{\mathfrak{l}}}(\{2\}^a,4,\{2\}^b) ={} &4(-1)^{n} \bigg[ {-}{\zeta^{\mathfrak{l}}}(2a+2,2b+2) - {\zeta^{\mathfrak{l}}}(2a+3,2b+1)\\ &{} +\sum_{j=1}^{2n+3} 2^{j-4-2n}\left( \binom{2n+3-j}{2b+1}-\binom{2n+3-j}{2a+1} \right){\zeta^{\mathfrak{l}}}(j,2n+4-j) \bigg] . \end{align*} $$
$$ \begin{align*} {\zeta^{\mathfrak{l}}}(\{2\}^a,4,\{2\}^b) ={} &4(-1)^{n} \bigg[ {-}{\zeta^{\mathfrak{l}}}(2a+2,2b+2) - {\zeta^{\mathfrak{l}}}(2a+3,2b+1)\\ &{} +\sum_{j=1}^{2n+3} 2^{j-4-2n}\left( \binom{2n+3-j}{2b+1}-\binom{2n+3-j}{2a+1} \right){\zeta^{\mathfrak{l}}}(j,2n+4-j) \bigg] . \end{align*} $$
Noting that both
![]() ${\zeta ^{\mathfrak {l}}}(2a+2,2b+2)$
and
${\zeta ^{\mathfrak {l}}}(2a+2,2b+2)$
and
 $$\begin{align*}\binom{2n+3-j}{2b+1}-\binom{2n+3-j}{2a+1}\end{align*}$$
$$\begin{align*}\binom{2n+3-j}{2b+1}-\binom{2n+3-j}{2a+1}\end{align*}$$
are antisymmetric in a and b, the result immediately follows.
From this, it is possible to deduce that the dimension of double zeta values of weight
![]() $2n+2$
modulo products is bounded above by
$2n+2$
modulo products is bounded above by
![]() $\lfloor \frac {n}{3}\rfloor $
, which is precisely the dimension predicted by Conjecture 1.1. As the modulo products version of Conjecture 1.1 is known to hold in depth 2 [Reference Schneps36], we must have that all period polynomial relations can be written in terms of the block relations, defined in Section 3, and thus Proposition 3.5 holds.
$\lfloor \frac {n}{3}\rfloor $
, which is precisely the dimension predicted by Conjecture 1.1. As the modulo products version of Conjecture 1.1 is known to hold in depth 2 [Reference Schneps36], we must have that all period polynomial relations can be written in terms of the block relations, defined in Section 3, and thus Proposition 3.5 holds.
Proposition 3.5. All relations among double zeta values of weight
![]() $2n+2$
modulo products are determined by (Relation 1) and (Relation 3) via Corollary 1.3.
$2n+2$
modulo products are determined by (Relation 1) and (Relation 3) via Corollary 1.3.
Indeed, using a computer, one can easily write the period polynomial relations as linear combinations of relations coming from the dihedral symmetry of Section 8 of [Reference Keilthy29]. A more explicit connection is given in Proposition 3.7.
The structure of this paper is as follows. We first will briefly remind readers of the motivic formalism, and in particular, the use of the motivic coaction to deduce relations. We then describe the block filtration and review several of the results of [Reference Keilthy29]. In particular, we will introduce the block dihedral symmetry and the necessary framework to discuss it.
In Section 3, we then apply these results, along with a number of new evaluations to conclude that the period polynomial relations are a consequence of this block dihedral symmetry in block degree 2. The remainder of the paper is then dedicated to the necessary technical results needed for this section. Specifically, an evaluation of
![]() $\zeta (\{2\}^a,4,\{2\}^b)$
in terms of double zeta valuesFootnote
1
, and a computation of the dimension of the space cut out by the block dihedral symmetry. The latter is a straightforward argument from representation theory, while the former is a trek through the world of MZV relations and machinery, including: motivic cobracket calculations; multiple Euler sums (also called alternating MZVs) and the octagon-relation-induced dihedral symmetries thereof [Reference Glanois18, Reference Glanois19]; multiple zeta star values and the stuffle-antipode [Reference Li31, Equation 2.4],[Reference Hoffman24, Proposition 1]; Zhao’s generalised 2-1 theorem [Reference Zhao41] (and the first author’s block-decomposition description thereof [Reference Charlton12]); (alternating) multiple zeta-half values [Reference Yamamoto39]; the explicit depth-parity theory for depth 3 alternating MZVs [Reference Goncharov21, Reference Panzer33]; and a vital (and serendipitously unearthed) generalised doubling relation [Reference Zhao42, Section 14.2.5]. We divide these results between Section 4 and an appendix, according to how central they are to the main results of the article.
$\zeta (\{2\}^a,4,\{2\}^b)$
in terms of double zeta valuesFootnote
1
, and a computation of the dimension of the space cut out by the block dihedral symmetry. The latter is a straightforward argument from representation theory, while the former is a trek through the world of MZV relations and machinery, including: motivic cobracket calculations; multiple Euler sums (also called alternating MZVs) and the octagon-relation-induced dihedral symmetries thereof [Reference Glanois18, Reference Glanois19]; multiple zeta star values and the stuffle-antipode [Reference Li31, Equation 2.4],[Reference Hoffman24, Proposition 1]; Zhao’s generalised 2-1 theorem [Reference Zhao41] (and the first author’s block-decomposition description thereof [Reference Charlton12]); (alternating) multiple zeta-half values [Reference Yamamoto39]; the explicit depth-parity theory for depth 3 alternating MZVs [Reference Goncharov21, Reference Panzer33]; and a vital (and serendipitously unearthed) generalised doubling relation [Reference Zhao42, Section 14.2.5]. We divide these results between Section 4 and an appendix, according to how central they are to the main results of the article.
We end the main body of the paper with a short corollary of Proposition A.3 in relation to a variation of multiple zeta values, called multiple t values [Reference Hoffman23]

In particular, we provide an evaluation of
![]() $t(2\ell ,2k)$
, when the arguments are even, via classical double zeta values, improving upon the results of [Reference Murakami32, Theorem 1] by giving an explicit formula for the Galois descent in this case.
$t(2\ell ,2k)$
, when the arguments are even, via classical double zeta values, improving upon the results of [Reference Murakami32, Theorem 1] by giving an explicit formula for the Galois descent in this case.
2. The motivic Lie algebra and block graded multiple zeta values
An essential observation in the study of multiple zeta values is that they may be lifted to motivic periods – algebraic objects satisfying only relations coming from geometry. Because of this, motivic multiple zeta values (mMZVs) are much simpler to study. They are known to be graded by weight, and they come equipped with a coaction that encodes all motivic relations. We may consider their graded analogues with respect to a number of filtrations, or consider the associated Lie coalgebra of mMZVs modulo products, whose relations are encoded in a free Lie algebra. The theory of motivic periods is substantial [Reference Brown7], so we give only an essential overview here and refer the reader to [Reference Brown6] for more details.
2.1. Motivic multiple zeta values
The formal definition of mMZVs relies on the Tannakian formalism for the category of mixed Tate motives over
![]() $\operatorname {\mathrm {Spec}}\mathbb {Z}$
, and is intimately related to the motivic fundamental group of
$\operatorname {\mathrm {Spec}}\mathbb {Z}$
, and is intimately related to the motivic fundamental group of
![]() ${\mathbb {P}^1\setminus \{0,1,\infty \}}$
[Reference Brown5]. In brief, letting
${\mathbb {P}^1\setminus \{0,1,\infty \}}$
[Reference Brown5]. In brief, letting
![]() $\operatorname {\mathrm {MT}}(\mathbb {Z})$
denote the category of mixed Tate motives, and denoting by
$\operatorname {\mathrm {MT}}(\mathbb {Z})$
denote the category of mixed Tate motives, and denoting by
the Betti and de Rham realisation functors, the ring of motivic periods of
![]() $\operatorname {\mathrm {MT}}(\mathbb {Z})$
is the ring of functions on the scheme of tensor isomorphisms
$\operatorname {\mathrm {MT}}(\mathbb {Z})$
is the ring of functions on the scheme of tensor isomorphisms
The results of Brown [Reference Brown5] tell us that this is isomorphic to
![]() $\mathcal {H}[\mathbb {L}^{-1}]$
, where
$\mathcal {H}[\mathbb {L}^{-1}]$
, where
![]() $\mathcal {H}$
will be the algebra of motivic multiple zeta values, and
$\mathcal {H}$
will be the algebra of motivic multiple zeta values, and
![]() $\mathbb {L}$
is a motivic analogue of
$\mathbb {L}$
is a motivic analogue of
![]() $2\pi \mathrm {i}$
.
$2\pi \mathrm {i}$
.
However, for our purposes, the reader need only keep in mind the following properties.
Properties 2.1. The algebra
![]() $\mathcal {H}$
of motivic multiple zeta values is the
$\mathcal {H}$
of motivic multiple zeta values is the
![]() ${\mathbb {Q}}$
-algebra spanned by symbols
${\mathbb {Q}}$
-algebra spanned by symbols
called motivic multiple zeta values or motivic iterated integrals, satisfying the following properties:
-
i) (Equal boundaries)
 ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_0)=\delta _{n,0}$
,
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_0)=\delta _{n,0}$
, -
ii) (Reversal of paths)
 ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})=(-1)^n{\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_{n+1};a_n,\ldots ,a_1;a_0)$
,
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})=(-1)^n{\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_{n+1};a_n,\ldots ,a_1;a_0)$
, -
iii) (Functoriality)
 ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})={\operatorname {\mathrm {I}}^{\mathfrak {m}}}(1-a_0;1-a_1,\ldots ,1-a_n;1-a_{n+1})$
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})={\operatorname {\mathrm {I}}^{\mathfrak {m}}}(1-a_0;1-a_1,\ldots ,1-a_n;1-a_{n+1})$
-
iv) (Shuffle product) For
 $1<r<n$
, denote by
$1<r<n$
, denote by
 $\operatorname {\mathrm {Sh}}_{r,n-r}$
the set of permutations
$\operatorname {\mathrm {Sh}}_{r,n-r}$
the set of permutations
 $\sigma $
on n satisfying
$\sigma $
on n satisfying  $$\begin{align*}\sigma(1)<\sigma(2)<\cdots<\sigma(r)\text{ and }\sigma(r+1)<\cdots<\sigma(n).\end{align*}$$
$$\begin{align*}\sigma(1)<\sigma(2)<\cdots<\sigma(r)\text{ and }\sigma(r+1)<\cdots<\sigma(n).\end{align*}$$
Then
 $$\begin{align*}{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_1,\ldots,a_r;1){\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_{r+1},\ldots,a_n;1)=\sum_{\sigma\in\operatorname{\mathrm{Sh}}_{n,r}}{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_{\sigma^{-1}(1)},\ldots,a_{\sigma^{-1}(n)};1).\end{align*}$$
$$\begin{align*}{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_1,\ldots,a_r;1){\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_{r+1},\ldots,a_n;1)=\sum_{\sigma\in\operatorname{\mathrm{Sh}}_{n,r}}{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(0;a_{\sigma^{-1}(1)},\ldots,a_{\sigma^{-1}(n)};1).\end{align*}$$
-
v) (Period map) There is a ring homomorphism
 $\operatorname {\mathrm {per}}:(\mathcal {H},\cdot {})\to ({\mathbb {C}},{}\cdot {})$
, called the period map, sending a motivic iterated integral to the corresponding complex iterated integral when it converges.
$\operatorname {\mathrm {per}}:(\mathcal {H},\cdot {})\to ({\mathbb {C}},{}\cdot {})$
, called the period map, sending a motivic iterated integral to the corresponding complex iterated integral when it converges.
For a tuple of positive integers
![]() $(k_1,\ldots ,k_d)$
, and
$(k_1,\ldots ,k_d)$
, and
![]() $ \ell \geq 0 $
, we write
$ \ell \geq 0 $
, we write
![]() $ \zeta ^{\mathfrak {m}} = \zeta ^{\mathfrak {m}}_0 $
and
$ \zeta ^{\mathfrak {m}} = \zeta ^{\mathfrak {m}}_0 $
and
where
![]() $\{0\}^n$
denotes n repeated zeroes.
$\{0\}^n$
denotes n repeated zeroes.
Remark 2.2. In the standard definition of motivic multiple zeta values, we have that
This, combined with compatibility with the shuffle product, uniquely determines the image of motivic MZVs which do not correspond to convergent iterated integrals. This convention produces what are called shuffle regularised MZVs. It is occasionally convenient to consider other regularisations, such as stuffle regularised MZVs or MZVs regularised so that
![]() $\zeta (1)$
is regularised to a nonzero constant [Reference Ihara, Kaneko and Zagier25].
$\zeta (1)$
is regularised to a nonzero constant [Reference Ihara, Kaneko and Zagier25].
Remark 2.3. The reversal of paths property and the functoriality property give an important relation for motivic MZVs called the duality relation:
Let ![]() be the quotient by the ideal generated by
be the quotient by the ideal generated by
![]() $\zeta ^{\mathfrak {m}}(2)$
, and denote by
$\zeta ^{\mathfrak {m}}(2)$
, and denote by
![]() ${\text {I}^{\mathfrak {a}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
the image of
${\text {I}^{\mathfrak {a}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
the image of
![]() ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
. The formula given below equips
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
. The formula given below equips
![]() $\mathcal {H}$
with the structure of an
$\mathcal {H}$
with the structure of an
![]() $\mathcal {A}$
-comodule
$\mathcal {A}$
-comodule
Explicitly,
![]() $\Delta {\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
is equal to
$\Delta {\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
is equal to
 $$ \begin{align} \sum_{\substack{i_0<i_1<\cdots<i_{k+1}\\i_0=0,\, i_{k+1}=n+1}}\left(\prod_{s=0}^k{\text{I}^{\mathfrak{a}}}(a_{i_s};a_{i_s+1},\ldots,a_{i_{s+1}-1};a_{i_{s+1}})\right)\otimes{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(a_0;a_{i_1},\ldots,a_{i_k};a_{n+1}).\end{align} $$
$$ \begin{align} \sum_{\substack{i_0<i_1<\cdots<i_{k+1}\\i_0=0,\, i_{k+1}=n+1}}\left(\prod_{s=0}^k{\text{I}^{\mathfrak{a}}}(a_{i_s};a_{i_s+1},\ldots,a_{i_{s+1}-1};a_{i_{s+1}})\right)\otimes{\operatorname{\mathrm{I}}^{\mathfrak{m}}}(a_0;a_{i_1},\ldots,a_{i_k};a_{n+1}).\end{align} $$
A linear combination R of motivic multiple zeta values vanishes in
![]() $\mathcal {H}$
if and only if
$\mathcal {H}$
if and only if
-
i)
 $\operatorname {\mathrm {per}}(R)=0$
, that is, R holds numerically
$\operatorname {\mathrm {per}}(R)=0$
, that is, R holds numerically -
ii)
 $\operatorname {\mathrm {per}}(R^\prime )=0$
for all transforms
$\operatorname {\mathrm {per}}(R^\prime )=0$
for all transforms
 $R^\prime $
under the motivic coaction, that is, the relation is motivic. A transform
$R^\prime $
under the motivic coaction, that is, the relation is motivic. A transform
 $R^\prime $
of R under the motivic coaction is obtained by choosing a weight graded basis
$R^\prime $
of R under the motivic coaction is obtained by choosing a weight graded basis
 $\{a_i\}_{i\in I}$
of
$\{a_i\}_{i\in I}$
of
 $\mathcal {A}$
and writing
$\mathcal {A}$
and writing  $$\begin{align*}\Delta(R) = \sum_{i\in I} a_i\otimes R_i.\end{align*}$$
$$\begin{align*}\Delta(R) = \sum_{i\in I} a_i\otimes R_i.\end{align*}$$
Each
 $R_i$
is referred to as a transform of R.
$R_i$
is referred to as a transform of R.
As the coaction is quite combinatorially complicated, it is often convenient to instead consider the infinitesimal coactions
![]() $\operatorname {\mathrm {D}}_r$
. Define the Lie coalgebra of indecomposables
$\operatorname {\mathrm {D}}_r$
. Define the Lie coalgebra of indecomposables
where
![]() $\mathcal {A}_{>0}$
denotes the positive weight part of
$\mathcal {A}_{>0}$
denotes the positive weight part of
![]() $\mathcal {A}$
. Denote by
$\mathcal {A}$
. Denote by
![]() $I^{\mathfrak {l}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
the image of
$I^{\mathfrak {l}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
the image of
![]() ${\text {I}^{\mathfrak {a}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
in
${\text {I}^{\mathfrak {a}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
in
![]() $\mathcal {L}$
, and similarly, denote by
$\mathcal {L}$
, and similarly, denote by
![]() ${\zeta ^{\mathfrak {l}}}(k_1,\ldots ,k_r)$
the image of
${\zeta ^{\mathfrak {l}}}(k_1,\ldots ,k_r)$
the image of
![]() $\zeta ^{\mathfrak {m}}(k_1,\ldots ,k_r)$
in
$\zeta ^{\mathfrak {m}}(k_1,\ldots ,k_r)$
in
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\mathcal {L}_r$
be the weight r component of
$\mathcal {L}_r$
be the weight r component of
![]() $\mathcal {L}$
. The infinitesimal coaction is then the composition
$\mathcal {L}$
. The infinitesimal coaction is then the composition
of
![]() $\Delta -1\otimes \operatorname {\mathrm {id}}$
with the projection to
$\Delta -1\otimes \operatorname {\mathrm {id}}$
with the projection to
![]() $\mathcal {L}_r$
. Explicitly,
$\mathcal {L}_r$
. Explicitly,
![]() $\operatorname {\mathrm {D}}_r{\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
is given by
$\operatorname {\mathrm {D}}_r{\operatorname {\mathrm {I}}^{\mathfrak {m}}}(a_0;a_1,\ldots ,a_n;a_{n+1})$
is given by
 $$ \begin{align}\sum_{k=0}^{n-r}I^{\mathfrak{l}}(a_k;a_{k+1},\ldots,a_{k+r};a_{k+r+1})\otimes {\operatorname{\mathrm{I}}^{\mathfrak{m}}}(a_0;a_1,\ldots,a_k,a_{k+r+1},\ldots,a_n;a_{n+1}).\end{align} $$
$$ \begin{align}\sum_{k=0}^{n-r}I^{\mathfrak{l}}(a_k;a_{k+1},\ldots,a_{k+r};a_{k+r+1})\otimes {\operatorname{\mathrm{I}}^{\mathfrak{m}}}(a_0;a_1,\ldots,a_k,a_{k+r+1},\ldots,a_n;a_{n+1}).\end{align} $$
These infinitesimal coactions are significantly easier to compute but still encode almost all essential information surrounding motivic MZVs.
Theorem 2.4 (Brown [Reference Brown5, Theorem 3.3]).
Let
![]() $N>2$
, and denote by
$N>2$
, and denote by
![]() $\operatorname {\mathrm {D}}_{<N}=\bigoplus _{3\leq 2r+1<N}\operatorname {\mathrm {D}}_{2r+1}$
. Then in weight N, the kernel of
$\operatorname {\mathrm {D}}_{<N}=\bigoplus _{3\leq 2r+1<N}\operatorname {\mathrm {D}}_{2r+1}$
. Then in weight N, the kernel of
![]() $\operatorname {\mathrm {D}}_{<N}$
is one dimensional:
$\operatorname {\mathrm {D}}_{<N}$
is one dimensional:
Brown proves this result by considering a particular choice of isomorphism of coalgebras
which he lifts to an isomorphism of comodules over these coalgebras. We may instead consider the corresponding vector spaces of indecomposables, equipped with the structure of Lie coalgebras by defining the cobracket to be the natural cobracket coming from antisymmetrising the coproduct. We then have an isomorphism
which we use to obtain the following standard proposition.
Proposition 2.5. Denote by
the r th infinitesimal cobracket, given in weight N by
where
![]() $\tau (a\otimes b)=b\otimes a$
. Let
$\tau (a\otimes b)=b\otimes a$
. Let
![]() $\partial _{<N}=\bigoplus _{3\leq 2r+1<N}\partial _{2r+1}$
. Then, in weight N, the kernel of
$\partial _{<N}=\bigoplus _{3\leq 2r+1<N}\partial _{2r+1}$
. Then, in weight N, the kernel of
![]() $\partial _{<N}$
is at most one dimensional:
$\partial _{<N}$
is at most one dimensional:
where we note that
![]() ${\zeta ^{\mathfrak {l}}}(2n)=0$
.
${\zeta ^{\mathfrak {l}}}(2n)=0$
.
Proof. It is known
![]() $\mathcal {L}$
is isomorphic to L the Lie coalgebra of indecomposables of
$\mathcal {L}$
is isomorphic to L the Lie coalgebra of indecomposables of
![]() ${\mathbb {Q}}\langle f_3,f_5,,\ldots \rangle $
with respect to the shuffle product, which is the cofree Lie coalgebra with cogenerators
${\mathbb {Q}}\langle f_3,f_5,,\ldots \rangle $
with respect to the shuffle product, which is the cofree Lie coalgebra with cogenerators
![]() $f_3,f_5,\ldots $
. Choosing an isomorphism
$f_3,f_5,\ldots $
. Choosing an isomorphism
![]() $\phi $
, such that
$\phi $
, such that
![]() $\phi ({\zeta ^{\mathfrak {l}}}(2n+1))=f_{2n+1}$
, it suffices to show that
$\phi ({\zeta ^{\mathfrak {l}}}(2n+1))=f_{2n+1}$
, it suffices to show that
where we take ![]() .
.
As L is graded by f-degree, the vanishing of
![]() $\partial _{<N}$
is equivalent to the vanishing of the full cobracket
$\partial _{<N}$
is equivalent to the vanishing of the full cobracket
![]() $\partial $
followed by projection onto odd weight in the first component. This composition is dual to the Lie bracket
$\partial $
followed by projection onto odd weight in the first component. This composition is dual to the Lie bracket
where
![]() $L^\vee $
is the free Lie algebra on
$L^\vee $
is the free Lie algebra on
![]() $f_3^\vee ,f_5^\vee ,\ldots $
. As this map is surjective onto the f-degree at least 2 part of
$f_3^\vee ,f_5^\vee ,\ldots $
. As this map is surjective onto the f-degree at least 2 part of
![]() $L^\vee $
, this implies that
$L^\vee $
, this implies that
![]() $\partial _{<N}$
is injective on the f-degree at least 2 part of L, and hence the kernel is spanned in weight N by
$\partial _{<N}$
is injective on the f-degree at least 2 part of L, and hence the kernel is spanned in weight N by
![]() $f_N$
.
$f_N$
.
Remark 2.6. It is worth noting that this formalism for motivic multiple zeta values extends to more general motivic iterated integrals, in particular, alternating motivic MZVs [Reference Glanois19]. We will need this extension for the results of Appendix B, and will introduce the necessary results and concepts as needed.
2.2. The motivic Lie algebra
Elements of
![]() $\mathcal {L}$
may be viewed as motivic multiple zeta values, modulo products. By considering the weight graded dual, we obtain a Lie algebra
$\mathcal {L}$
may be viewed as motivic multiple zeta values, modulo products. By considering the weight graded dual, we obtain a Lie algebra
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
, called the motivic Lie algebra. From the theory of mixed Tate motives and Tannakian categories, this Lie algebra is equal to a subspace of
${\mathfrak {g}^{\mathfrak {m}}}$
, called the motivic Lie algebra. From the theory of mixed Tate motives and Tannakian categories, this Lie algebra is equal to a subspace of
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
, equipped with the Ihara bracket
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
, equipped with the Ihara bracket
![]() $\{\cdot ,\cdot \}$
[Reference Brown5, Reference Ihara and Ochiai26]. Via the pairing
$\{\cdot ,\cdot \}$
[Reference Brown5, Reference Ihara and Ochiai26]. Via the pairing
elements of
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
may be viewed as encoding relations among elements of
${\mathfrak {g}^{\mathfrak {m}}}$
may be viewed as encoding relations among elements of
![]() $\mathcal {L}$
. For example, in weight
$\mathcal {L}$
. For example, in weight
![]() $5$
,
$5$
,
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
is spanned by
${\mathfrak {g}^{\mathfrak {m}}}$
is spanned by
from which we can conclude that
As such, describing relations among motivic MZVs (up to products) is equivalent to describing the elements of
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
. In particular, to describe all such relations, it would suffice to describe explicit generators for
${\mathfrak {g}^{\mathfrak {m}}}$
. In particular, to describe all such relations, it would suffice to describe explicit generators for
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
. It is known [Reference Deligne and Goncharov14] that the motivic Lie algebra is isomorphic to a free Lie algebra
${\mathfrak {g}^{\mathfrak {m}}}$
. It is known [Reference Deligne and Goncharov14] that the motivic Lie algebra is isomorphic to a free Lie algebra
with generators
![]() $\sigma _{2k+1}$
in every odd weight greater than 1. However, this isomorphism is noncanonical, and there does not exist an explicit canonical choice of representatives of
$\sigma _{2k+1}$
in every odd weight greater than 1. However, this isomorphism is noncanonical, and there does not exist an explicit canonical choice of representatives of
![]() $\sigma _{2k+1}$
. However, we can somewhat remedy this by considering graded relations among motivic MZVs for a certain filtration.
$\sigma _{2k+1}$
. However, we can somewhat remedy this by considering graded relations among motivic MZVs for a certain filtration.
2.3. The block filtration
In [Reference Brown4], Brown proposed a new filtration on the space of convergent motivic MZVs, based on the work of the first author [Reference Charlton13]. This was expanded to a filtration on all motivic MZVs by the second author in [Reference Keilthy28, Reference Keilthy29], in which the associated graded algebra - and relations therein - is investigated. In this section, we provide a brief summary of this filtration and relations in the associated graded algebra.
Call a word in two letters
![]() $\{a,b\}$
alternating if it contains no subword of the form
$\{a,b\}$
alternating if it contains no subword of the form
![]() $aa$
or
$aa$
or
![]() $bb$
. As noted in [Reference Charlton13], every word in
$bb$
. As noted in [Reference Charlton13], every word in
![]() $\{a,b\}$
then has a unique factorisation into alternating words of maximal length. This allows us to uniquely determine a word w by its first letter and the lengths of the alternating blocks in this factorisation
$\{a,b\}$
then has a unique factorisation into alternating words of maximal length. This allows us to uniquely determine a word w by its first letter and the lengths of the alternating blocks in this factorisation
![]() $(x;\ell _1,\ldots ,\ell _n)$
,
$(x;\ell _1,\ldots ,\ell _n)$
,
![]() $x\in \{a,b\}$
. We call this sequence the block decomposition of the word w.
$x\in \{a,b\}$
. We call this sequence the block decomposition of the word w.
We define the block degree
![]() ${\deg _{\mathcal {B}}}(w)$
of a word w to be the number of instances of subwords of the form
${\deg _{\mathcal {B}}}(w)$
of a word w to be the number of instances of subwords of the form
![]() $aa$
or
$aa$
or
![]() $bb$
in w. This allows us to define the block filtration on the vector space
$bb$
in w. This allows us to define the block filtration on the vector space
![]() ${\mathbb {Q}}\langle a,b\rangle $
by defining the n
th part
${\mathbb {Q}}\langle a,b\rangle $
by defining the n
th part
to be the vector subspace spanned by words of degree at most n.
As motivic iterated integrals, and hence motivic MZVs, may be viewed as a quotient of
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
via the map
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
via the map
the space of motivic MZVs inherits the block filtration. We may also define the block degree of an iterated integral, by taking the block degree of the associated word. This turns out to be a very natural filtration to consider, satisfying a number of nice properties, the proofs of which we shall either sketch here, or may be found in [Reference Keilthy28, Reference Keilthy29].
Proposition 2.7. The block filtration is equal to the coradical filtration induced by the motivic coaction. Furthermore, when restricted to the Hoffman basis, it is the level filtration of Brown [Reference Brown5]. Hence, any MZV of block degree N may be written as a linear combination of Hoffman MZVs with at most N threes.
Lemma 2.8 [Reference Charlton13].
All MZVs of block degree b and weight N, with b and N of opposite parity, vanish.
Proof. If
![]() ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(i_0;i_1,\ldots ,i_n;i_{N+1})$
has block degree b, then the final letter of
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(i_0;i_1,\ldots ,i_n;i_{N+1})$
has block degree b, then the final letter of
![]() $e_{i_0}\ldots e_{i_{N+1}}$
must be equal to the final letter of the alternating word of length
$e_{i_0}\ldots e_{i_{N+1}}$
must be equal to the final letter of the alternating word of length
![]() $N+2-b$
, beginning with
$N+2-b$
, beginning with
![]() $e_{i_0}$
. In particular, we must have that
$e_{i_0}$
. In particular, we must have that
![]() $e_{i_{N+2-b}}=e_{i_0}$
if
$e_{i_{N+2-b}}=e_{i_0}$
if
![]() $N+2-b$
is odd, that is, N and b are off opposite parity. Hence,
$N+2-b$
is odd, that is, N and b are off opposite parity. Hence,
![]() ${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(i_0;i_1,\ldots ,i_n;i_{n+1})=0$
, as it has the same start and end points of the integral.
${\operatorname {\mathrm {I}}^{\mathfrak {m}}}(i_0;i_1,\ldots ,i_n;i_{n+1})=0$
, as it has the same start and end points of the integral.
Analogously to depth graded MZVs [Reference Brown9], we may consider the associated graded algebra
and consider relations among block graded multiple zeta values. Much like relations among motivic MZVs, modulo products, in the motivic Lie algebra
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
, relations among block graded MZVs, modulo products, are encoded in the block Lie algebra
${\mathfrak {g}^{\mathfrak {m}}}$
, relations among block graded MZVs, modulo products, are encoded in the block Lie algebra
where the filtration on
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
is induced by the filtration
${\mathfrak {g}^{\mathfrak {m}}}$
is induced by the filtration
via the embedding
![]() ${\mathfrak {g}^{\mathfrak {m}}}\hookrightarrow e_0{{\mathbb {Q}}\langle e_0,e_1\rangle } e_1$
. We denote by
${\mathfrak {g}^{\mathfrak {m}}}\hookrightarrow e_0{{\mathbb {Q}}\langle e_0,e_1\rangle } e_1$
. We denote by
![]() ${\mathfrak {bg}}_n$
the block degree n part, via the embedding into
${\mathfrak {bg}}_n$
the block degree n part, via the embedding into
![]() $\mathcal {B}^n{{\mathbb {Q}}\langle e_0,e_1\rangle }/\mathcal {B}^{n+1}{{\mathbb {Q}}\langle e_0,e_1\rangle }$
.
$\mathcal {B}^n{{\mathbb {Q}}\langle e_0,e_1\rangle }/\mathcal {B}^{n+1}{{\mathbb {Q}}\langle e_0,e_1\rangle }$
.
Proposition 2.9. As Lie algebras
![]() ${\mathfrak {g}^{\mathfrak {m}}}\cong {\mathfrak {bg}}$
. In particular, they are (noncanonically) isomorphic to
${\mathfrak {g}^{\mathfrak {m}}}\cong {\mathfrak {bg}}$
. In particular, they are (noncanonically) isomorphic to
![]() $ \operatorname {\mathrm {Lie}}[\sigma _3,\sigma _5,\ldots ]$
.
$ \operatorname {\mathrm {Lie}}[\sigma _3,\sigma _5,\ldots ]$
.
Proposition 2.10. Let
![]() $\{\sigma _{2k+1}\}_{k\geq 1}$
be a choice of generators for
$\{\sigma _{2k+1}\}_{k\geq 1}$
be a choice of generators for
![]() ${\mathfrak {g}^{\mathfrak {m}}}$
. Then the block degree
${\mathfrak {g}^{\mathfrak {m}}}$
. Then the block degree
![]() $1$
piece of the image of
$1$
piece of the image of
![]() $\{\sigma _{2k+1}\}_{k\geq 1}$
in
$\{\sigma _{2k+1}\}_{k\geq 1}$
in
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
is independent of the choice of generators. In particular, we can make a canonical identification between the image of
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
is independent of the choice of generators. In particular, we can make a canonical identification between the image of
![]() ${\mathfrak {bg}}$
in
${\mathfrak {bg}}$
in
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
and the free Lie algebra
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
and the free Lie algebra
![]() $\operatorname {\mathrm {Lie}}[\sigma _3,\sigma _5,\ldots ]$
.
$\operatorname {\mathrm {Lie}}[\sigma _3,\sigma _5,\ldots ]$
.
Remark 2.11. It is in these two results that we see a stark contrast to the case of depth graded multiple zeta values [Reference Brown9]. Analogously to the above, one can consider the associated graded Lie algebra for the depth filtration, induced by the
![]() $e_1$
-degree of words in
$e_1$
-degree of words in
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
. As for the block graded case, the image of the generators
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
. As for the block graded case, the image of the generators
![]() $\{\sigma _{2k+1}\}_{k\geq 1}$
in depth
$\{\sigma _{2k+1}\}_{k\geq 1}$
in depth
![]() $1$
is canonical. However, unlike the block graded case, the depth graded Lie algebra
$1$
is canonical. However, unlike the block graded case, the depth graded Lie algebra
![]() $\mathfrak {dg}$
is not free, having quadratic relations and extra generators in depth 4. These quadratic relations are algebraically well understood [Reference Brown9, Reference Schneps36], and give a somewhat mysterious connection to modular forms. Indeed, the quadratic relations are exactly encoded in the period polynomials of cusp forms. This is a relationship that we can discuss in a new light using the approaches of this paper.
$\mathfrak {dg}$
is not free, having quadratic relations and extra generators in depth 4. These quadratic relations are algebraically well understood [Reference Brown9, Reference Schneps36], and give a somewhat mysterious connection to modular forms. Indeed, the quadratic relations are exactly encoded in the period polynomials of cusp forms. This is a relationship that we can discuss in a new light using the approaches of this paper.
As the image of
![]() ${\mathfrak {bg}}$
in
${\mathfrak {bg}}$
in
![]() ${{\mathbb {Q}}\langle e_0,e_1\rangle }$
lies in
${{\mathbb {Q}}\langle e_0,e_1\rangle }$
lies in
![]() $e_0{{\mathbb {Q}}\langle e_0,e_1\rangle } e_1$
, the block decomposition gives an injection of vector spaces
$e_0{{\mathbb {Q}}\langle e_0,e_1\rangle } e_1$
, the block decomposition gives an injection of vector spaces
obtained by sending a word
![]() $w=e_0\ldots $
to
$w=e_0\ldots $
to
![]() $x_1^{\ell _1}\ldots x_n^{\ell _n}$
, where
$x_1^{\ell _1}\ldots x_n^{\ell _n}$
, where
![]() $(e_0;\ell _1,\ldots ,\ell _n)$
is the block decomposition of w. The image of
$(e_0;\ell _1,\ldots ,\ell _n)$
is the block decomposition of w. The image of
![]() ${\mathfrak {bg}}_n$
under this map lies in
${\mathfrak {bg}}_n$
under this map lies in
![]() $(x_1-x_{n+1})x_1\ldots x_{n+1}{\mathbb {Q}}[x_1,\ldots ,x_{n+1}]$
. We denote by
$(x_1-x_{n+1})x_1\ldots x_{n+1}{\mathbb {Q}}[x_1,\ldots ,x_{n+1}]$
. We denote by
![]() ${\mathfrak {rbg}}_n$
the image of
${\mathfrak {rbg}}_n$
the image of
![]() ${\mathfrak {bg}}_n$
divided by
${\mathfrak {bg}}_n$
divided by
![]() $(x_1-x_{n+1})x_1\ldots x_{n+1}$
, and let
$(x_1-x_{n+1})x_1\ldots x_{n+1}$
, and let ![]() . Thus, we have reduced the problem of describing relations among block graded MZVs modulo products to describing
. Thus, we have reduced the problem of describing relations among block graded MZVs modulo products to describing
![]() ${\mathfrak {rbg}}$
as a subspace of
${\mathfrak {rbg}}$
as a subspace of
![]() $\bigoplus _{n\geq 2}{\mathbb {Q}}[x_1,\ldots ,x_n]$
.
$\bigoplus _{n\geq 2}{\mathbb {Q}}[x_1,\ldots ,x_n]$
.
In [Reference Keilthy29], a number of relations are found. In particular, elements of
![]() ${\mathfrak {rbg}}$
satisfy a functional equation coming from shuffle regularisation, a differential equation, and have a dihedral symmetry.
${\mathfrak {rbg}}$
satisfy a functional equation coming from shuffle regularisation, a differential equation, and have a dihedral symmetry.
Proposition 2.12. If
![]() $f(x_1,\ldots ,x_n)\in {\mathfrak {rbg}}$
, then
$f(x_1,\ldots ,x_n)\in {\mathfrak {rbg}}$
, then
It turns out these three relations, along with Lemma 2.8, describe most relations among block graded MZVs [Reference Keilthy29]. In block degree 1, the shuffle regularisation, the differential equation, and this dihedral symmetry, along with Lemma 2.8, describe all relations among block graded motivic multiple zeta values.
Proposition 2.13. The vector space
![]() ${\mathfrak {rbg}}_1$
is the subspace of
${\mathfrak {rbg}}_1$
is the subspace of
![]() ${\mathbb {Q}}[x_1,x_2]$
given by polynomials
${\mathbb {Q}}[x_1,x_2]$
given by polynomials
![]() $f(x_1,x_2)$
, such that
$f(x_1,x_2)$
, such that
 $$ \begin{align*} f(0,x) & {} = 2f(x,-x), \\ f(-x_1,-x_2) & {}= f(x_1,x_2), && { \smash{{\displaystyle\frac{\partial^2 f}{\partial x_1^2}=\frac{\partial^2 f}{\partial x_2^2} .}} }\\ f(x_1,x_2) & {} = f(x_2,x_1), \\[-1ex] \end{align*} $$
$$ \begin{align*} f(0,x) & {} = 2f(x,-x), \\ f(-x_1,-x_2) & {}= f(x_1,x_2), && { \smash{{\displaystyle\frac{\partial^2 f}{\partial x_1^2}=\frac{\partial^2 f}{\partial x_2^2} .}} }\\ f(x_1,x_2) & {} = f(x_2,x_1), \\[-1ex] \end{align*} $$
Unfortunately, even in block degree 2, this is insufficient, leaving degrees of freedom linear in weight. While a remedy in block degree 2 was given in Proposition 2.8.7 of [Reference Keilthy28], it turns out that the failure of space cut out by the dihedral symmetry, differential equation, and shuffle regularisation to encode all relations in block degree 2 has an interesting connection to double zeta values, and gives an alternative source of the relations between double zeta values coming from period polynomials. This connection is explored in the next section.
3. Block graded relations among double zeta values
As noted above, relations among block graded motivic multiple zeta values, modulo products, are determined by the coefficients of elements of
![]() ${\mathfrak {bg}}$
. However, these relations are also genuine relations among motivic multiple zeta values mod products for motivic MZVs of block degree at most 2. Observe that
${\mathfrak {bg}}$
. However, these relations are also genuine relations among motivic multiple zeta values mod products for motivic MZVs of block degree at most 2. Observe that
and so, modulo products,
![]() $\mathcal {B}_1\mathcal {L}/\mathcal {B}_0\mathcal {L}=\mathcal {B}_1\mathcal {L}$
. Similarly, as MZVs of block degree 1 are necessarily of odd weight, and MZVs of block degree 2 are necessarily of even weight, block graded relations among motivic MZVs of block degree 2 are genuine relations, modulo products. As Corollary 1.3 defines an explicit representation of double zeta values in terms of MZVs of block degree 2, relations among double zeta values are determined, modulo products, by the coefficients of elements of
$\mathcal {B}_1\mathcal {L}/\mathcal {B}_0\mathcal {L}=\mathcal {B}_1\mathcal {L}$
. Similarly, as MZVs of block degree 1 are necessarily of odd weight, and MZVs of block degree 2 are necessarily of even weight, block graded relations among motivic MZVs of block degree 2 are genuine relations, modulo products. As Corollary 1.3 defines an explicit representation of double zeta values in terms of MZVs of block degree 2, relations among double zeta values are determined, modulo products, by the coefficients of elements of
![]() ${\mathfrak {bg}}$
. In this section, we will make this precise, and show that all relations among double zeta values are determined by the below relations.
${\mathfrak {bg}}$
. In this section, we will make this precise, and show that all relations among double zeta values are determined by the below relations.
Explicitly, following Remark 9.3 of [Reference Keilthy29], the weight
![]() $2n+2$
, block degree 2 piece of
$2n+2$
, block degree 2 piece of
![]() ${\mathfrak {bg}}$
can be identified with a subspace of
${\mathfrak {bg}}$
can be identified with a subspace of
![]() $V_n\subset {\mathbb {Q}}[x_1,x_2,x_3]$
, where
$V_n\subset {\mathbb {Q}}[x_1,x_2,x_3]$
, where
![]() $V_n$
is spanned by polynomials satisfying the following relations.
$V_n$
is spanned by polynomials satisfying the following relations.
Theorem 3.1 [Reference Keilthy29].
Define
![]() $V_n\subset {\mathbb {Q}}[x_1,x_2,x_3]$
to be the space spanned by polynomials satisfying the block relations:
$V_n\subset {\mathbb {Q}}[x_1,x_2,x_3]$
to be the space spanned by polynomials satisfying the block relations:
 $$ \begin{align} & \frac{\partial^4{f}}{\partial x_1^4}+\frac{\partial^4{f}}{\partial x_2^4}+\frac{\partial^4{f}}{\partial x_3^4}-2\frac{\partial^4{f}}{\partial x_1^2\partial x_2^2}-2\frac{\partial^4{f}}{\partial x_2^2\partial x_3^2}-2\frac{\partial^4{f}}{\partial x_3^2\partial x_1^2}=0 . \end{align} $$
$$ \begin{align} & \frac{\partial^4{f}}{\partial x_1^4}+\frac{\partial^4{f}}{\partial x_2^4}+\frac{\partial^4{f}}{\partial x_3^4}-2\frac{\partial^4{f}}{\partial x_1^2\partial x_2^2}-2\frac{\partial^4{f}}{\partial x_2^2\partial x_3^2}-2\frac{\partial^4{f}}{\partial x_3^2\partial x_1^2}=0 . \end{align} $$
Then
![]() ${\mathfrak {rbg}}_{2,2n+2}$
, the weight
${\mathfrak {rbg}}_{2,2n+2}$
, the weight
![]() $2n+2$
component of
$2n+2$
component of
![]() ${\mathfrak {rbg}}_2$
, is a subspace of
${\mathfrak {rbg}}_2$
, is a subspace of
![]() $V_n$
.
$V_n$
.
As mentioned previously, this inclusion is strict. Additional relations are necessary in order to completely describe
![]() ${\mathfrak {rbg}}_{2,2n+2}$
as a subspace of
${\mathfrak {rbg}}_{2,2n+2}$
as a subspace of
![]() ${\mathbb {Q}}[x_1,x_2,x_3]$
. A choice of such relations is given in Proposition 2.8.7 of [Reference Keilthy28]. For any
${\mathbb {Q}}[x_1,x_2,x_3]$
. A choice of such relations is given in Proposition 2.8.7 of [Reference Keilthy28]. For any
![]() $f(x_1,x_2,x_3)=\sum _{i+j+k=2n}\alpha _{i,j,k}x_1^ix_2^jx_3^k$
, define
$f(x_1,x_2,x_3)=\sum _{i+j+k=2n}\alpha _{i,j,k}x_1^ix_2^jx_3^k$
, define

One may easily check that if
![]() $f(x_1,x_2,x_3)\in V_n$
, then both
$f(x_1,x_2,x_3)\in V_n$
, then both
![]() $f_e(x_1,x_2,x_3)$
and
$f_e(x_1,x_2,x_3)$
and
![]() $f(x_1,x_2,x_3)-f_e(x_1,x_2,x_3)$
are elements of
$f(x_1,x_2,x_3)-f_e(x_1,x_2,x_3)$
are elements of
![]() $V_n$
. As such, the linear map
$V_n$
. As such, the linear map
![]() $f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
defines a projection
$f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
defines a projection
![]() $V_n\to V_n$
.
$V_n\to V_n$
.
Proposition 3.2 [Reference Keilthy28].
Let
![]() $V_n$
be as above, and let
$V_n$
be as above, and let
![]() $P_e:V_n\to V_n$
denote the projection
$P_e:V_n\to V_n$
denote the projection
![]() $f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
. Then
$f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
. Then
 $$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &\leq\Big\lfloor\frac{n}{3}\Big\rfloor\, ,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2}\, , \end{align*} $$
$$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &\leq\Big\lfloor\frac{n}{3}\Big\rfloor\, ,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2}\, , \end{align*} $$
where
![]() ${\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
denotes the vector space spanned by
${\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
denotes the vector space spanned by
![]() $\{\sigma _k,\sigma _\ell \}$
with
$\{\sigma _k,\sigma _\ell \}$
with
![]() $k+\ell =2n+2$
.
$k+\ell =2n+2$
.
We delay the proof until the following section. Denote by
the generating series of block degree n motivic MZVs modulo products. As a consequence of Lemma 7.4 [Reference Keilthy29],
for some
![]() $\phi _n\in \operatorname {\mathrm {gr}}_n^{\mathcal {B}}\mathcal {L}\otimes {\mathbb {Q}}[x_1,\ldots ,x_{n+1}]$
. This series is then given by
$\phi _n\in \operatorname {\mathrm {gr}}_n^{\mathcal {B}}\mathcal {L}\otimes {\mathbb {Q}}[x_1,\ldots ,x_{n+1}]$
. This series is then given by
where
 $$\begin{align*}F(k_1,\ldots,k_{n+1}) = -\sum_{i+j=k_1}{\text{I}^{\mathfrak{bl}}}(i+1,k_2+1,\ldots,k_n+1,k_{n+1}+j+2).\end{align*}$$
$$\begin{align*}F(k_1,\ldots,k_{n+1}) = -\sum_{i+j=k_1}{\text{I}^{\mathfrak{bl}}}(i+1,k_2+1,\ldots,k_n+1,k_{n+1}+j+2).\end{align*}$$
Conversely, we have that
Via the pairing
we can view
![]() $\Phi _n$
as a linear map
$\Phi _n$
as a linear map
the image of which is precisely the embedding described previously. We may similarly view
![]() $\phi _n$
as a linear isomorphism
$\phi _n$
as a linear isomorphism
![]() ${\mathfrak {bg}}_n\to {\mathfrak {rbg}}_n$
.
${\mathfrak {bg}}_n\to {\mathfrak {rbg}}_n$
.
Lemma 3.3. In block degree 2, the coefficients of
![]() $\phi _{3,e}(x_1,0,x_3)$
are equal to motivic double zeta values:
$\phi _{3,e}(x_1,0,x_3)$
are equal to motivic double zeta values:
for
![]() $a,b$
even nonnegative integers.
$a,b$
even nonnegative integers.
Proof. We assume, without loss of generality, that
![]() $a\leq b$
. From Lemma 4.1 and Corollary 1.3, we have that
$a\leq b$
. From Lemma 4.1 and Corollary 1.3, we have that
 $$\begin{align*}{\zeta^{\mathfrak{l}}}(2a+1,2b+3) = \frac{(-1)^{a+b}}{4}\sum_{s=a}^{b}{\zeta^{\mathfrak{l}}}(\{2\}^s,4,\{2\}^{a+b-s}).\end{align*}$$
$$\begin{align*}{\zeta^{\mathfrak{l}}}(2a+1,2b+3) = \frac{(-1)^{a+b}}{4}\sum_{s=a}^{b}{\zeta^{\mathfrak{l}}}(\{2\}^s,4,\{2\}^{a+b-s}).\end{align*}$$
The block decomposition of
is
![]() $(\ell _1,\ell _2,\ell _3)=(2s+3,1,2a+2b-2s+2)$
. Hence
$(\ell _1,\ell _2,\ell _3)=(2s+3,1,2a+2b-2s+2)$
. Hence
 $$ \begin{align*} {\zeta^{\mathfrak{l}}}(2a+1,2b+3) &= -\frac{1}{4}\sum_{s=a}^b {\text{I}^{\mathfrak{bl}}}(2s+3,1,2a+2b-2s+2)\\ &= -\frac{1}{4}\sum_{s=a}^b F(2s+1,0,2a+2b -2s +1) - F(2s+2,0,2a+2b-2s) . \end{align*} $$
$$ \begin{align*} {\zeta^{\mathfrak{l}}}(2a+1,2b+3) &= -\frac{1}{4}\sum_{s=a}^b {\text{I}^{\mathfrak{bl}}}(2s+3,1,2a+2b-2s+2)\\ &= -\frac{1}{4}\sum_{s=a}^b F(2s+1,0,2a+2b -2s +1) - F(2s+2,0,2a+2b-2s) . \end{align*} $$
The dihedral symmetry of
![]() ${\mathfrak {rbg}}_2$
implies that
${\mathfrak {rbg}}_2$
implies that
and so this sum reduces to
from which the claim follows.
Lemma 3.4. For every tuple
![]() $(a,b,c)$
of even, nonnegative integers,
$(a,b,c)$
of even, nonnegative integers,
where we denote by
the regularized iterated integral modulo products.
Proof. By viewing
![]() $\phi _2$
as a linear isomorphism
$\phi _2$
as a linear isomorphism
![]() ${\mathfrak {bg}}_2\to {\mathfrak {rbg}}_2$
, we see that we must have that the vector space
${\mathfrak {bg}}_2\to {\mathfrak {rbg}}_2$
, we see that we must have that the vector space
is dual to
![]() ${\mathfrak {rbg}}_{2,2n+2}$
, and furthermore that
${\mathfrak {rbg}}_{2,2n+2}$
, and furthermore that
is dual to
![]() $P_e({\mathfrak {rbg}}_{2,2n+2})$
.
$P_e({\mathfrak {rbg}}_{2,2n+2})$
.
Following Brown’s conventions [Reference Brown9],
![]() $\operatorname {\mathrm {gr}}_{\mathcal {D}}^1{\mathfrak {g}^{\mathfrak {m}}}$
may be identified with the space of translation invariant polynomials
$\operatorname {\mathrm {gr}}_{\mathcal {D}}^1{\mathfrak {g}^{\mathfrak {m}}}$
may be identified with the space of translation invariant polynomials
![]() $s_{2n+1}(x_0,x_1):=(x_0-x_1)^{2n}$
. By the work of the second author [Reference Keilthy29],
$s_{2n+1}(x_0,x_1):=(x_0-x_1)^{2n}$
. By the work of the second author [Reference Keilthy29],
![]() ${\mathfrak {rbg}}_1$
is spanned by polynomials
${\mathfrak {rbg}}_1$
is spanned by polynomials
Denoting by
![]() $f_e(x_0,x_1)$
the projection of a polynomial
$f_e(x_0,x_1)$
the projection of a polynomial
![]() $f(x_0,x_1)$
onto
$f(x_0,x_1)$
onto
![]() ${\mathbb {Q}}[x_0^2,x_1^2]$
, it is easy to see that
${\mathbb {Q}}[x_0^2,x_1^2]$
, it is easy to see that
The depth graded Ihara bracket
is given by
 $$ \begin{align*}\{f,g\}(x_0,x_1,x_2) & = f(x_0,x_1)\left(g(x_0,x_2)-g(x_1,x_2)\right) + f(x_1,x_2)\left(g(x_0,x_1)-g(x_0,x_2)\right)\\ &\quad + f(x_2,x_0)\left(g(x_1,x_2)-g(x_0,x_1)\right), \end{align*} $$
$$ \begin{align*}\{f,g\}(x_0,x_1,x_2) & = f(x_0,x_1)\left(g(x_0,x_2)-g(x_1,x_2)\right) + f(x_1,x_2)\left(g(x_0,x_1)-g(x_0,x_2)\right)\\ &\quad + f(x_2,x_0)\left(g(x_1,x_2)-g(x_0,x_1)\right), \end{align*} $$
which is identical to the block graded Ihara bracket
Furthermore, as all the polynomials involved are of even total degree, this commutes with projection onto polynomials even in each variable (where we have formally extended the Ihara bracket to all polynomials of even total degree). Thus, we obtain a surjective map
 $$ \begin{gather*} \operatorname{\mathrm{gr}}_{\mathcal{D}}^2{\mathfrak{g}^{\mathfrak{m}}} \to P_e({\mathfrak{rbg}}_2),\\ \{s_{2k+1},s_{2\ell+1}\} \mapsto 4\{p_{2k+1,e},p_{2\ell+1,e}\}. \end{gather*} $$
$$ \begin{gather*} \operatorname{\mathrm{gr}}_{\mathcal{D}}^2{\mathfrak{g}^{\mathfrak{m}}} \to P_e({\mathfrak{rbg}}_2),\\ \{s_{2k+1},s_{2\ell+1}\} \mapsto 4\{p_{2k+1,e},p_{2\ell+1,e}\}. \end{gather*} $$
Dualising this, we obtain an injective map
 $$ \begin{gather*} \langle F(a,b,c)\mid a,b,c\geq 0\text{ and even}\rangle_{\mathbb{Q}}\to \operatorname{\mathrm{gr}}_2^{\mathcal{D}}\mathcal{L},\\ F(a,b,c)\mapsto 4{\zeta^{\mathfrak{l}}}_a(b+1,c+1). \end{gather*} $$
$$ \begin{gather*} \langle F(a,b,c)\mid a,b,c\geq 0\text{ and even}\rangle_{\mathbb{Q}}\to \operatorname{\mathrm{gr}}_2^{\mathcal{D}}\mathcal{L},\\ F(a,b,c)\mapsto 4{\zeta^{\mathfrak{l}}}_a(b+1,c+1). \end{gather*} $$
Since this map is injective, and
![]() $\{{\zeta ^{\mathfrak {l}}}(b+1,c+1)\}_{b+c=2n}$
spans
$\{{\zeta ^{\mathfrak {l}}}(b+1,c+1)\}_{b+c=2n}$
spans
![]() $\operatorname {\mathrm {gr}}_2^{\mathcal {D}}\mathcal {L}$
in weight
$\operatorname {\mathrm {gr}}_2^{\mathcal {D}}\mathcal {L}$
in weight
![]() $2n+2$
, we must have that if
$2n+2$
, we must have that if
![]() $(a,b,c)$
are even nonnegative integers, such that
$(a,b,c)$
are even nonnegative integers, such that
then, by Lemma 3.3,
and hence
Proposition 3.5. All relations among double zeta values of weight
![]() $2n+2$
modulo products are determined by (Relation 1) and (Relation 3) via Corollary 1.3.
$2n+2$
modulo products are determined by (Relation 1) and (Relation 3) via Corollary 1.3.
Proof. By corollary 4.2 of [Reference Schneps36], we have that the dimension of the space of motivic multiple zeta values of weight
![]() $2n+2$
modulo products is equal to the dimension of
$2n+2$
modulo products is equal to the dimension of
![]() $\operatorname {\mathrm {gr}}_2^{\mathcal {D}}{\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
, which is given by
$\operatorname {\mathrm {gr}}_2^{\mathcal {D}}{\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
, which is given by
where
![]() $S_{2n+2}$
is the space of cusp forms of weight
$S_{2n+2}$
is the space of cusp forms of weight
![]() $2n+2$
. It is known that
$2n+2$
. It is known that
 $$\begin{align*}\dim S_{2n+2} =\begin{cases} \frac{n}{6}-1 & \text{if}\ n\equiv 0\quad\pmod{6} \\ \frac{n}{6} & \text{if}\ n\equiv 1,2,3,4\quad\pmod{6} \\ \frac{n}{6}+1 & \text{if}\ n\equiv 5\quad\pmod{6}. \\ \end{cases} \end{align*}$$
$$\begin{align*}\dim S_{2n+2} =\begin{cases} \frac{n}{6}-1 & \text{if}\ n\equiv 0\quad\pmod{6} \\ \frac{n}{6} & \text{if}\ n\equiv 1,2,3,4\quad\pmod{6} \\ \frac{n}{6}+1 & \text{if}\ n\equiv 5\quad\pmod{6}. \\ \end{cases} \end{align*}$$
Checking each case, we see
By Proposition 4.3,
As
![]() $\operatorname {\mathrm {gr}}^{\mathcal {D}}_2\mathcal {L}$
is spanned by motivic double zetas, Lemma 3.4 implies that
$\operatorname {\mathrm {gr}}^{\mathcal {D}}_2\mathcal {L}$
is spanned by motivic double zetas, Lemma 3.4 implies that
Hence, the surjection of Lemma 3.4 is an isomorphism
for every
![]() $n>0$
. Following Theorem 3.1, we have that
$n>0$
. Following Theorem 3.1, we have that
![]() $P_e{\mathfrak {rbg}}_{2,2n+2}\subset P_eV_n$
. But
$P_e{\mathfrak {rbg}}_{2,2n+2}\subset P_eV_n$
. But
and hence
As such, all relations in
are determined by the relations defining
![]() $V_n$
. In fact, as (Relation 2) has no even part, all weight graded relations among
$V_n$
. In fact, as (Relation 2) has no even part, all weight graded relations among
![]() $F(a,b,c)$
with
$F(a,b,c)$
with
![]() $a,b,c$
even are determined by (Relation 1) and (Relation 3).
$a,b,c$
even are determined by (Relation 1) and (Relation 3).
Notably, Proposition 3.5 tells us that the period polynomial relations among double zetas are a consequence of the dihedral symmetry of the block graded motivic Lie algebra. Using the surjection of Lemma 3.4, we can, in fact, make this quite explicit.
Remark 3.6. Note that this also shows that we can upgrade the results of Proposition 3.2 to
 $$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &=\Big\lfloor\frac{n}{3}\Big\rfloor,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2} , \end{align*} $$
$$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &=\Big\lfloor\frac{n}{3}\Big\rfloor,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2} , \end{align*} $$
with equalities in both cases.
3.1. An explicit connection to period polynomials
Recall that the space of even period polynomials
![]() $W_{2n}^+$
of degree
$W_{2n}^+$
of degree
![]() $2n$
is defined as the subspace of
$2n$
is defined as the subspace of
![]() ${\mathbb {Q}}[x_1,x_2]$
consisting of polynomials that are homogeneous of degree
${\mathbb {Q}}[x_1,x_2]$
consisting of polynomials that are homogeneous of degree
![]() $2n$
, even in each variable, and satisfy
$2n$
, even in each variable, and satisfy
 $$ \begin{align*} P(x_1,0)&=P(0,x_2)=0,\\ P(x_1,x_2)&+P(x_2,x_1)=0,\\ P(x_1,x_2)+P(x_1,x_1+x_2)&+P(x_1+x_2,x_2)=0\, \end{align*} $$
$$ \begin{align*} P(x_1,0)&=P(0,x_2)=0,\\ P(x_1,x_2)&+P(x_2,x_1)=0,\\ P(x_1,x_2)+P(x_1,x_1+x_2)&+P(x_1+x_2,x_2)=0\, \end{align*} $$
See, for example, section 8 of [Reference Brown8] for more detail.
Proposition 3.7. Denote by
![]() $e_{2k+1}$
the projection of the image of the Lie algebra generator
$e_{2k+1}$
the projection of the image of the Lie algebra generator
![]() $\sigma _{2k+1}$
in
$\sigma _{2k+1}$
in
![]() ${\mathfrak {rbg}}_1$
to
${\mathfrak {rbg}}_1$
to
![]() ${\mathbb {Q}}[x_1^2,x_2^2]$
. The kernel
${\mathbb {Q}}[x_1^2,x_2^2]$
. The kernel

is isomorphic to the space of even period polynomials
Proof. Define a pair of linear maps
 $$ \begin{gather*} \pi_1:X^2{\mathbb{Q}}[X^2] \to {\mathbb{Q}}[x_1,x_2],\\ p(X)\mapsto P_e(p(x_1-x_2)) \end{gather*} $$
$$ \begin{gather*} \pi_1:X^2{\mathbb{Q}}[X^2] \to {\mathbb{Q}}[x_1,x_2],\\ p(X)\mapsto P_e(p(x_1-x_2)) \end{gather*} $$
and
 $$ \begin{gather*} \pi_2:{\mathbb{Q}}[X^2,Y^2]_{>0}\to{\mathbb{Q}}[x_1,x_2,x_3],\\ p(X,Y)\mapsto P_e(p(x_1-x_2,x_2-x_3)), \end{gather*} $$
$$ \begin{gather*} \pi_2:{\mathbb{Q}}[X^2,Y^2]_{>0}\to{\mathbb{Q}}[x_1,x_2,x_3],\\ p(X,Y)\mapsto P_e(p(x_1-x_2,x_2-x_3)), \end{gather*} $$
where we write
![]() ${\mathbb {Q}}[X^2,Y^2]_{>0}$
for the subspace of polynomials of positive degree. We define a basis for the space of antisymmetric polynomials in
${\mathbb {Q}}[X^2,Y^2]_{>0}$
for the subspace of polynomials of positive degree. We define a basis for the space of antisymmetric polynomials in
![]() ${\mathbb {Q}}[X^2,Y^2]_{>0}$
given by
${\mathbb {Q}}[X^2,Y^2]_{>0}$
given by
The first map
![]() $\pi _1$
defines an isomorphism
$\pi _1$
defines an isomorphism
and it is not difficult to show that we have a commutative diagram

where the left vertical arrow is the map
and the right vertical arrow is the map induced by the Ihara bracket. By construction, the image of the right vertical arrow is contained in
![]() $\bigoplus _{n\geq 1}P_eV_n$
, and has kernel K. Note also that
$\bigoplus _{n\geq 1}P_eV_n$
, and has kernel K. Note also that
via the identification
again, by construction. Thus, we have a commutative diagram of short exact sequences

where we denote by
 $$\begin{align*}K_n:=\ker\left(\bigoplus_{k+l=n}{\mathbb{Q}} e_{2k+1}\wedge {\mathbb{Q}} e_{2\ell+1}\to P_eV_n\right).\end{align*}$$
$$\begin{align*}K_n:=\ker\left(\bigoplus_{k+l=n}{\mathbb{Q}} e_{2k+1}\wedge {\mathbb{Q}} e_{2\ell+1}\to P_eV_n\right).\end{align*}$$
A short diagram chase shows that F is an injection and is G a surjection. Thus, we must have
If
![]() $\dim K_n> \dim W_{2n}^+$
, then we must have
$\dim K_n> \dim W_{2n}^+$
, then we must have
But
by definition, and by the previous theorem
![]() $P_e{\mathfrak {rbg}}_{2,2n+2}=P_eV_n$
. Hence,
$P_e{\mathfrak {rbg}}_{2,2n+2}=P_eV_n$
. Hence,
![]() $\dim K_n = \dim W_{2n}^+$
for every
$\dim K_n = \dim W_{2n}^+$
for every
![]() $n>0$
.
$n>0$
.
This suggests that a possible approach to study depth graded motivic multiple zeta values and exploring Conjecture 1.1 is to consider the Lie algebra generated by the
![]() $\{e_{2k+1}\}_{k\geq 1}$
, or equivalently, the projection of
$\{e_{2k+1}\}_{k\geq 1}$
, or equivalently, the projection of
![]() ${\mathfrak {rbg}}$
onto
${\mathfrak {rbg}}$
onto
![]() $\bigoplus _{n\geq 2}{\mathbb {Q}}[x_1^2,x_2^2,\ldots ,x_n^2]$
. Indeed, the results of this section show that this is isomorphic to the depth graded motivic Lie algebra in depths 1 and 2, though this isomorphism cannot extend to depth 4 as the projection of
$\bigoplus _{n\geq 2}{\mathbb {Q}}[x_1^2,x_2^2,\ldots ,x_n^2]$
. Indeed, the results of this section show that this is isomorphic to the depth graded motivic Lie algebra in depths 1 and 2, though this isomorphism cannot extend to depth 4 as the projection of
![]() ${\mathfrak {rbg}}_4$
onto
${\mathfrak {rbg}}_4$
onto
![]() ${\mathbb {Q}}[x_1^2,x_2^2,x_3^2,x_4^2,x_5^2]$
is generated by the
${\mathbb {Q}}[x_1^2,x_2^2,x_3^2,x_4^2,x_5^2]$
is generated by the
![]() $\{e_{2k+1}\}_{k\geq 1}$
, and hence, we cannot find the ‘exceptional’ generators in depth 4 referred to in Remark 2.11 required to generate the full depth graded Lie algebra [Reference Brown9, Section 1.4]
$\{e_{2k+1}\}_{k\geq 1}$
, and hence, we cannot find the ‘exceptional’ generators in depth 4 referred to in Remark 2.11 required to generate the full depth graded Lie algebra [Reference Brown9, Section 1.4]
4. Proofs of the more technical results
We now explain the proofs of some of the more technical results used in the previous sections. It is worth noting that determining the statement of Lemma 4.1 required computing the full evaluation of
![]() $\zeta ^{\mathfrak {m}}(\{2\}^a,4,\{2\}^b)$
described in Appendices A and B. However, as we only use the evaluation of
$\zeta ^{\mathfrak {m}}(\{2\}^a,4,\{2\}^b)$
described in Appendices A and B. However, as we only use the evaluation of
![]() $\zeta ^{\mathfrak {l}}(\{2\}^a,4,\{2\}^b)$
in terms of double zetas modulo products, we have elected to give here a simpler direct proof using the motivic formalism.
$\zeta ^{\mathfrak {l}}(\{2\}^a,4,\{2\}^b)$
in terms of double zetas modulo products, we have elected to give here a simpler direct proof using the motivic formalism.
4.1. Evaluation of
 ${\zeta ^{\mathfrak {l}}}(\{2\}^a,4,\{2\}^b)$
${\zeta ^{\mathfrak {l}}}(\{2\}^a,4,\{2\}^b)$
Lemma 4.1. The following evaluation holds in the motivic coalgebra

Proof. For
![]() $Z $
a weight
$Z $
a weight
![]() $ w $
combination of motivic MZVs, it is sufficient to check, by Proposition 2.5, that
$ w $
combination of motivic MZVs, it is sufficient to check, by Proposition 2.5, that
for all
![]() $1<2r+1<w $
, as this would show that
$1<2r+1<w $
, as this would show that
![]() $Z=\alpha \zeta ^{\mathfrak {m}}(w) +\text {products} $
. If the weight of
$Z=\alpha \zeta ^{\mathfrak {m}}(w) +\text {products} $
. If the weight of
![]() $ Z $
is even, we have that
$ Z $
is even, we have that
![]() $\zeta ^{\mathfrak {l}}(w)=0 $
; this means checking that
$\zeta ^{\mathfrak {l}}(w)=0 $
; this means checking that
![]() $ \partial _{<w}Z=0 $
allows us to confirm that
$ \partial _{<w}Z=0 $
allows us to confirm that
![]() $\pi (Z)=0 $
on the nose, where
$\pi (Z)=0 $
on the nose, where
![]() $\pi \colon \mathcal {A}\to \mathcal {L}$
is the natural projection.
$\pi \colon \mathcal {A}\to \mathcal {L}$
is the natural projection.
Explicitly, it amounts to checking for
![]() $ 1<2r+1<w $
that
$ 1<2r+1<w $
that
where
![]() $ \tau (a\otimes b)= b\otimes a$
. For the case under consideration, we need to check for
$ \tau (a\otimes b)= b\otimes a$
. For the case under consideration, we need to check for
![]() $ 3 \leq 2r+1 \leq 2a + 2b + 1 $
$ 3 \leq 2r+1 \leq 2a + 2b + 1 $
It is a straightforward calculation, as explained in Section B.2, to show the following.
 $$ \begin{align*} (\operatorname{\mathrm{id}} \otimes \pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b) &= -\delta_{r \leq a} \zeta_1^{\mathfrak{l}}(\{2\}^r) \otimes {\zeta^{\mathfrak{l}}}(\{2\}^{a-r}, 3, \{2\}^b) \\ &\quad + \delta_{r \leq b} \zeta_1^{\mathfrak{l}}(\{2\}^r) \otimes {\zeta^{\mathfrak{l}}}(\{2\}^a, 3, \{2\}^{b-r}) . \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{id}} \otimes \pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b) &= -\delta_{r \leq a} \zeta_1^{\mathfrak{l}}(\{2\}^r) \otimes {\zeta^{\mathfrak{l}}}(\{2\}^{a-r}, 3, \{2\}^b) \\ &\quad + \delta_{r \leq b} \zeta_1^{\mathfrak{l}}(\{2\}^r) \otimes {\zeta^{\mathfrak{l}}}(\{2\}^a, 3, \{2\}^{b-r}) . \end{align*} $$
Recalling the motivic evaluations of
![]() $ \zeta ^{\mathfrak {m}}_1(\{2\}^r) $
and
$ \zeta ^{\mathfrak {m}}_1(\{2\}^r) $
and
![]() $ \zeta ^{\mathfrak {m}}(\{2\}^a, 3, \{2\}^b) $
from [Reference Brown5], we have that
$ \zeta ^{\mathfrak {m}}(\{2\}^a, 3, \{2\}^b) $
from [Reference Brown5], we have that
 $$ \begin{align*} {\zeta^{\mathfrak{l}}}_1(\{2\}^r) & {} = 2(-1)^r {\zeta^{\mathfrak{l}}}(2r+1), \\ {\zeta^{\mathfrak{l}}}(\{2\}^a, 3, \{2\}^b) & {}= 2 (-1)^{a + b + 1} \bigg( \binom{2a +2b + 2}{2a + 2} - (1 - 2^{-2a - 2b - 2}) \binom{2a + 2b + 2}{2b+1} \bigg) {\zeta^{\mathfrak{l}}}(2a + 2b + 3) . \end{align*} $$
$$ \begin{align*} {\zeta^{\mathfrak{l}}}_1(\{2\}^r) & {} = 2(-1)^r {\zeta^{\mathfrak{l}}}(2r+1), \\ {\zeta^{\mathfrak{l}}}(\{2\}^a, 3, \{2\}^b) & {}= 2 (-1)^{a + b + 1} \bigg( \binom{2a +2b + 2}{2a + 2} - (1 - 2^{-2a - 2b - 2}) \binom{2a + 2b + 2}{2b+1} \bigg) {\zeta^{\mathfrak{l}}}(2a + 2b + 3) . \end{align*} $$
Therefore
 $$ \begin{align*} & (\operatorname{\mathrm{id}} \otimes \pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b) \\ & \quad = \Bigg\{ 4\delta_{r \leq a} (-1)^{a+b} \bigg( \binom{2a + 2b + 2 - 2r}{2a - 2r + 2} - {} (1 - 2^{2r-2a-2b-2}) \binom{2a + 2b + 2 - 2r}{2b + 1} \bigg) \\ &\qquad - 4\delta_{r \leq b} (-1)^{a+b} \bigg( \binom{2a + 2b + 2 - 2r}{2a + 2} {} - (1 - 2^{2r-2a-2b-2}) \binom{2a + 2b + 2 - 2r}{2b -2r + 1} \bigg) \Bigg\} \\ & \qquad {} \cdot {\zeta^{\mathfrak{l}}}(2r+1) \otimes {\zeta^{\mathfrak{l}}}(2a + 2b + 3 - 2r). \end{align*} $$
$$ \begin{align*} & (\operatorname{\mathrm{id}} \otimes \pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b) \\ & \quad = \Bigg\{ 4\delta_{r \leq a} (-1)^{a+b} \bigg( \binom{2a + 2b + 2 - 2r}{2a - 2r + 2} - {} (1 - 2^{2r-2a-2b-2}) \binom{2a + 2b + 2 - 2r}{2b + 1} \bigg) \\ &\qquad - 4\delta_{r \leq b} (-1)^{a+b} \bigg( \binom{2a + 2b + 2 - 2r}{2a + 2} {} - (1 - 2^{2r-2a-2b-2}) \binom{2a + 2b + 2 - 2r}{2b -2r + 1} \bigg) \Bigg\} \\ & \qquad {} \cdot {\zeta^{\mathfrak{l}}}(2r+1) \otimes {\zeta^{\mathfrak{l}}}(2a + 2b + 3 - 2r). \end{align*} $$
Likewise from Section B.1
 $$ \begin{align*} (\operatorname{\mathrm{id}}\otimes\pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(p,q) & = \bigg( \delta_{2r+1 = p} + (-1)^p \binom{2r}{p-1} - (-1)^q \binom{2r}{q-1} \bigg) \\ & \quad {} \cdot {\zeta^{\mathfrak{l}}}(2r+1) \otimes {\zeta^{\mathfrak{l}}}(p+q - 2r - 1) . \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{id}}\otimes\pi) \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(p,q) & = \bigg( \delta_{2r+1 = p} + (-1)^p \binom{2r}{p-1} - (-1)^q \binom{2r}{q-1} \bigg) \\ & \quad {} \cdot {\zeta^{\mathfrak{l}}}(2r+1) \otimes {\zeta^{\mathfrak{l}}}(p+q - 2r - 1) . \end{align*} $$
So for the purpose of checking
where
![]() $ Z $
is the purported evaluation of
$ Z $
is the purported evaluation of
![]() $ {\zeta ^{\mathfrak {l}}}(\{2\}^a, 4, \{2\}^b) $
via double zeta values
$ {\zeta ^{\mathfrak {l}}}(\{2\}^a, 4, \{2\}^b) $
via double zeta values
![]() $ {\zeta ^{\mathfrak {l}}}(n_1, n_2) $
, we can project
$ {\zeta ^{\mathfrak {l}}}(n_1, n_2) $
, we can project
![]() $ {\zeta ^{\mathfrak {l}}}(2r+1) \otimes {\zeta ^{\mathfrak {l}}}(2a + 2b + 3 - 2r) \mapsto 1 $
, and reduce to an identity among binomial coefficients.
$ {\zeta ^{\mathfrak {l}}}(2r+1) \otimes {\zeta ^{\mathfrak {l}}}(2a + 2b + 3 - 2r) \mapsto 1 $
, and reduce to an identity among binomial coefficients.
After some straightforward simplification of the deltas and binomial coefficients in the expression for
for the range
![]() $ 3 \leq 2r+1 \leq 2a + 2b + 1 $
, and using that
$ 3 \leq 2r+1 \leq 2a + 2b + 1 $
, and using that
![]() $ i, j $
have the same parity in the sum, we find the claimed identity to be equivalent to the following purported identity
$ i, j $
have the same parity in the sum, we find the claimed identity to be equivalent to the following purported identity
 $$ \begin{align*} & \sum_{\substack{i + j = 2a + 2b \\ i,j \geq 0}} (-1)^i \bigg( 2^{-i} \binom{i+1}{2a+1} + 2^{-j} \binom{j+1}{2b+1} \bigg) \\ &\qquad {} \cdot \bigg( \binom{2r}{i+1} - \binom{2r}{j+1} - \binom{2a + 2b + 2 - 2r}{i+1} + \binom{2a + 2b + 2 - 2r}{j+1} \bigg) \\ &\quad \overset{?}{=} 2^{-(2a + 2b + 1 - 2r)} \binom{2a + 2b + 2 - 2r}{2b + 1} - 2^{-(2a + 2b + 1 - 2r)} \binom{2a + 2b + 2 - 2r}{2a + 1} \\ &\qquad - 2^{-(2r-1)} \binom{2r}{2b + 1} + 2^{-(2r - 1)} \binom{2r}{2a + 1} . \end{align*} $$
$$ \begin{align*} & \sum_{\substack{i + j = 2a + 2b \\ i,j \geq 0}} (-1)^i \bigg( 2^{-i} \binom{i+1}{2a+1} + 2^{-j} \binom{j+1}{2b+1} \bigg) \\ &\qquad {} \cdot \bigg( \binom{2r}{i+1} - \binom{2r}{j+1} - \binom{2a + 2b + 2 - 2r}{i+1} + \binom{2a + 2b + 2 - 2r}{j+1} \bigg) \\ &\quad \overset{?}{=} 2^{-(2a + 2b + 1 - 2r)} \binom{2a + 2b + 2 - 2r}{2b + 1} - 2^{-(2a + 2b + 1 - 2r)} \binom{2a + 2b + 2 - 2r}{2a + 1} \\ &\qquad - 2^{-(2r-1)} \binom{2r}{2b + 1} + 2^{-(2r - 1)} \binom{2r}{2a + 1} . \end{align*} $$
This is seen to be an exact identity using the results from Lemma 4.2 below.
Lemma 4.2. For
![]() $ 3 \leq 2r + 1 \leq 2k+2\ell -3 $
, the following identities hold
$ 3 \leq 2r + 1 \leq 2k+2\ell -3 $
, the following identities hold
 $$ \begin{align} & \sum_{i=0}^{2k-2} (-2)^{-i} \binom{i+2\ell-1}{2\ell-1} \binom{2r}{i + 2\ell-1} = 2^{-(2r + 1 - 2\ell)} \binom{2r}{2\ell-1} \end{align} $$
$$ \begin{align} & \sum_{i=0}^{2k-2} (-2)^{-i} \binom{i+2\ell-1}{2\ell-1} \binom{2r}{i + 2\ell-1} = 2^{-(2r + 1 - 2\ell)} \binom{2r}{2\ell-1} \end{align} $$
 $$ \begin{align} \sum_{i=0}^{2\ell-2} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} = \sum_{i=0}^{2k-2} (-2)^{-i-2\ell} \binom{i+2\ell-1}{2\ell-1} \binom{2r}{2k-i-1} , \end{align} $$
$$ \begin{align} \sum_{i=0}^{2\ell-2} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} = \sum_{i=0}^{2k-2} (-2)^{-i-2\ell} \binom{i+2\ell-1}{2\ell-1} \binom{2r}{2k-i-1} , \end{align} $$
that is, the left-hand side is symmetric in
![]() $ k \leftrightarrow \ell $
.
$ k \leftrightarrow \ell $
.
Proof. Given the restriction
![]() $ 2r + 1 \leq 2k + 2\ell - 3 $
, the sum in (i) can be truncated to
$ 2r + 1 \leq 2k + 2\ell - 3 $
, the sum in (i) can be truncated to
![]() $ i = 2r + 1 - 2\ell $
. It is then reduced to the binomial theorem after simplifying the summand.
$ i = 2r + 1 - 2\ell $
. It is then reduced to the binomial theorem after simplifying the summand.
For (ii), we show that the left-hand side is symmetric in
![]() $ k \leftrightarrow \ell $
, to obtain the equality. We remark, here, that the symmetry is not obvious, as even the number of nonzero therms differs between the two sides. To show the symmetry, note that
$ k \leftrightarrow \ell $
, to obtain the equality. We remark, here, that the symmetry is not obvious, as even the number of nonzero therms differs between the two sides. To show the symmetry, note that
 $$ \begin{align*} & \sum_{i=0}^{2\ell-2} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} \\ &\quad {} = {}\bigg. -(-2)^{-i-2k} \binom{i+2k-1}{2k-1} \underbrace{\binom{2r}{2\ell-i-1}}_{=1} \bigg\rvert_{i = 2\ell-1} + \sum_{i=0}^{\infty} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} , \end{align*} $$
$$ \begin{align*} & \sum_{i=0}^{2\ell-2} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} \\ &\quad {} = {}\bigg. -(-2)^{-i-2k} \binom{i+2k-1}{2k-1} \underbrace{\binom{2r}{2\ell-i-1}}_{=1} \bigg\rvert_{i = 2\ell-1} + \sum_{i=0}^{\infty} (-2)^{-i-2k} \binom{i+2k-1}{2k-1} \binom{2r}{2\ell-i-1} , \end{align*} $$
since the second binomial vanishes for
![]() $ i> 2\ell -1$
. The first term is equal to the coefficient of
$ i> 2\ell -1$
. The first term is equal to the coefficient of
![]() $ x^{2\ell -1} $
in
$ x^{2\ell -1} $
in
Likewise, the second term is the coefficient of
![]() $ x^{2\ell -1} $
in
$ x^{2\ell -1} $
in
Therefore, the left-hand side of (ii) is given by
 $$\begin{align*}[x^{2\ell-1}] \bigg( \frac{(1+x)^{2r} - 1}{(2+x)^{2k}} \bigg) = [x^{-1}] \bigg( \frac{(1+x)^{2r} - 1}{(2+x)^{2k} x^{2\ell}} \bigg) . \end{align*}$$
$$\begin{align*}[x^{2\ell-1}] \bigg( \frac{(1+x)^{2r} - 1}{(2+x)^{2k}} \bigg) = [x^{-1}] \bigg( \frac{(1+x)^{2r} - 1}{(2+x)^{2k} x^{2\ell}} \bigg) . \end{align*}$$
This is not obviously symmetric in
![]() $ k \leftrightarrow \ell $
; it is, however, equal to the following contour integral around 0 (along a sufficiently small circle
$ k \leftrightarrow \ell $
; it is, however, equal to the following contour integral around 0 (along a sufficiently small circle
![]() $ C_{\varepsilon }(0) $
) by the residue theorem
$ C_{\varepsilon }(0) $
) by the residue theorem
 $$\begin{align*}= \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z . \end{align*}$$
$$\begin{align*}= \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z . \end{align*}$$
The only poles of the integrand
 $$\begin{align*}f(z) = \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \end{align*}$$
$$\begin{align*}f(z) = \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \end{align*}$$
are at
![]() $ z = -2 $
, and at
$ z = -2 $
, and at
![]() $ z = 0 $
. Since
$ z = 0 $
. Since
![]() $ 2r + 1 \leq 2k + 2\ell - 3 $
, we see that
$ 2r + 1 \leq 2k + 2\ell - 3 $
, we see that
 $$\begin{align*}-\frac{1}{z^2}f\Big(\frac{1}{z}\Big) = \frac{z^{2r} - (1 + z)^{2r}}{(1 + 2z)^{2k}} \cdot z^{2k + 2l - 2 - 2r} \end{align*}$$
$$\begin{align*}-\frac{1}{z^2}f\Big(\frac{1}{z}\Big) = \frac{z^{2r} - (1 + z)^{2r}}{(1 + 2z)^{2k}} \cdot z^{2k + 2l - 2 - 2r} \end{align*}$$
has no pole at
![]() $ z = 0 $
, so that our original integrand
$ z = 0 $
, so that our original integrand
![]() $ f(z) $
has no pole (and hence no residue) at
$ f(z) $
has no pole (and hence no residue) at
![]() $ z = \infty $
. We therefore find that the residues at
$ z = \infty $
. We therefore find that the residues at
![]() $ z = 0 $
and at
$ z = 0 $
and at
![]() $ z = -2 $
must cancel, giving
$ z = -2 $
must cancel, giving
 $$ \begin{align} \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z + \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(-2)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z = 0 . \end{align} $$
$$ \begin{align} \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z + \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(-2)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z = 0 . \end{align} $$
Now put
![]() $ z \mapsto -2-w $
, with
$ z \mapsto -2-w $
, with
![]() $ \mathrm {d}z = -\mathrm {d}w $
, in the second integral, and we find
$ \mathrm {d}z = -\mathrm {d}w $
, in the second integral, and we find
 $$\begin{align*}\frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(-2)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z = \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(-1-w)^{2r} - 1}{(-w)^{2k} (-2-w)^{2\ell}} \mathrm{d}w . \end{align*}$$
$$\begin{align*}\frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(-2)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z = \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(-1-w)^{2r} - 1}{(-w)^{2k} (-2-w)^{2\ell}} \mathrm{d}w . \end{align*}$$
Putting this back into Equation (4.1) shows that
 $$\begin{align*}\frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z - \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+w)^{2r} - 1}{(w)^{2k} (2+w)^{2\ell}} \mathrm{d}w = 0 , \end{align*}$$
$$\begin{align*}\frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+z)^{2r} - 1}{(2+z)^{2k} z^{2\ell}} \mathrm{d}z - \frac{1}{2 \pi \mathrm{i}} \oint_{C_{\varepsilon}(0)} \frac{(1+w)^{2r} - 1}{(w)^{2k} (2+w)^{2\ell}} \mathrm{d}w = 0 , \end{align*}$$
and so establishes the symmetry in
![]() $ k \leftrightarrow \ell $
that we claimed.
$ k \leftrightarrow \ell $
that we claimed.
4.2. Computing the dimension of
 $\operatorname {\mathrm {im}} P_e$
$\operatorname {\mathrm {im}} P_e$
Proposition 3.2 [Reference Keilthy28].
Let
![]() $V_n$
be as above, and let
$V_n$
be as above, and let
![]() $P_e:V_n\to V_n$
denote the projection
$P_e:V_n\to V_n$
denote the projection
![]() $f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
. Then
$f(x_1,x_2,x_3)\mapsto f_e(x_1,x_2,x_3)$
. Then
 $$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &\leq\Big\lfloor\frac{n}{3}\Big\rfloor\, ,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2}\, , \end{align*} $$
$$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e &\leq\Big\lfloor\frac{n}{3}\Big\rfloor\, ,\\ \dim \ker P_e &=\Big\lfloor\frac{n-1}{2}\Big\rfloor = \dim {\mathfrak{g}^{\mathfrak{m}}}_{2,2n+2}\, , \end{align*} $$
where
![]() ${\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
denotes the vector space spanned by
${\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
denotes the vector space spanned by
![]() $\{\sigma _k,\sigma _\ell \}$
with
$\{\sigma _k,\sigma _\ell \}$
with
![]() $k+\ell =2n+2$
.
$k+\ell =2n+2$
.
Proof. Suppose
![]() $q(x_1,x_2,x_3)\in \ker P_e$
. Then Equation (Relation 3) implies
$q(x_1,x_2,x_3)\in \ker P_e$
. Then Equation (Relation 3) implies
 $$ \begin{align*} q(x_1,x_2,x_3) &=\sum_{i+j=2n} \alpha_{i,j} (x_1-x_2)^i(x_2-x_3)^j+\beta_{i,j}(x_1+x_2)^i(x_2-x_3)^j\\ &\quad + \gamma_{i,j}(x_1-x_2)^i(x_2+x_3)^j+\delta_{i,j}(x_1+x_2)^i(x_2+x_3)^j . \end{align*} $$
$$ \begin{align*} q(x_1,x_2,x_3) &=\sum_{i+j=2n} \alpha_{i,j} (x_1-x_2)^i(x_2-x_3)^j+\beta_{i,j}(x_1+x_2)^i(x_2-x_3)^j\\ &\quad + \gamma_{i,j}(x_1-x_2)^i(x_2+x_3)^j+\delta_{i,j}(x_1+x_2)^i(x_2+x_3)^j . \end{align*} $$
Define ![]() ; this is the part of q that is odd in
; this is the part of q that is odd in
![]() $x_1\text { and } x_3$
, and even in
$x_1\text { and } x_3$
, and even in
![]() $x_2$
. We can write
$x_2$
. We can write
 $$ \begin{align*} q_\star(x_1,x_2,x_3) &=\sum_{\substack{i+j=2n\\ i,j>0}} \rho_{i,j}\big( (x_1-x_2)^i(x_2-x_3)^j+(-1)^{i+1}(x_1+x_2)^i(x_2-x_3)^j \\ &\quad{} -(x_1-x_2)^i(x_2+x_3)^j+(-1)^i(x_1+x_2)^i(x_2+x_3)^j \big) ,\end{align*} $$
$$ \begin{align*} q_\star(x_1,x_2,x_3) &=\sum_{\substack{i+j=2n\\ i,j>0}} \rho_{i,j}\big( (x_1-x_2)^i(x_2-x_3)^j+(-1)^{i+1}(x_1+x_2)^i(x_2-x_3)^j \\ &\quad{} -(x_1-x_2)^i(x_2+x_3)^j+(-1)^i(x_1+x_2)^i(x_2+x_3)^j \big) ,\end{align*} $$
where ![]() . As
. As
![]() $q(x_1,x_2,x_3)=-q(x_3,x_2,x_1)$
, the same holds for
$q(x_1,x_2,x_3)=-q(x_3,x_2,x_1)$
, the same holds for
![]() $q_\star (x_1,x_2,x_3)$
, and thus
$q_\star (x_1,x_2,x_3)$
, and thus
![]() $\rho _{i,j}=-\rho _{j,i}$
.
$\rho _{i,j}=-\rho _{j,i}$
.
Then, as
![]() $q_e(x_1,x_2,x_3)=0$
, and
$q_e(x_1,x_2,x_3)=0$
, and
![]() $q(x_1,x_2,x_3)=q(x_2,x_3,x_1)$
, we must have
$q(x_1,x_2,x_3)=q(x_2,x_3,x_1)$
, we must have
Thus, q is uniquely determined by
![]() $q_\star $
. We currently have
$q_\star $
. We currently have
![]() $n-1$
free variables in
$n-1$
free variables in
![]() $q_\star $
, so in order for
$q_\star $
, so in order for
![]() $\dim \ker P_e$
to be equal to
$\dim \ker P_e$
to be equal to
![]() $\lfloor \frac {n-1}{2}\rfloor $
, we need (Relation 2) to impose
$\lfloor \frac {n-1}{2}\rfloor $
, we need (Relation 2) to impose
![]() $\lceil \frac {n-1}{2}\rceil $
independent constraints on the
$\lceil \frac {n-1}{2}\rceil $
independent constraints on the
![]() $\rho _{i,j}$
.
$\rho _{i,j}$
.
Writing (Relation 2) in terms of
![]() $q_\star (x_1,x_2,x_3)$
, we find that we must have
$q_\star (x_1,x_2,x_3)$
, we find that we must have
Evaluating the coefficient of
![]() $y^kz^l$
in this equation, we obtain
$y^kz^l$
in this equation, we obtain
 $$ \begin{align*}\rho_{l,k}=\sum_{\substack{0<j\leq k\\i+j=2n}}(-2)^j\binom{i}{l}\rho_{i,j} - \sum_{\substack{0<j\leq l\\i+j=2n}}(-2)^j\binom{i}{k}\rho_{i,j}\end{align*} $$
$$ \begin{align*}\rho_{l,k}=\sum_{\substack{0<j\leq k\\i+j=2n}}(-2)^j\binom{i}{l}\rho_{i,j} - \sum_{\substack{0<j\leq l\\i+j=2n}}(-2)^j\binom{i}{k}\rho_{i,j}\end{align*} $$
if k is odd, and
![]() $0=0$
if k is even, or if
$0=0$
if k is even, or if
![]() $k=l$
. As the coefficient of
$k=l$
. As the coefficient of
![]() $y^lz^k$
is just the negative of this, this gives us
$y^lz^k$
is just the negative of this, this gives us
![]() $\lceil \frac {n-1}{2}\rceil $
equations, so it suffices to show that they are independent. As we are solving for rational
$\lceil \frac {n-1}{2}\rceil $
equations, so it suffices to show that they are independent. As we are solving for rational
![]() $\rho _{i,j}$
, it is sufficient to show that these equations are independent modulo 2. But modulo 2, we obtain the system of equations
$\rho _{i,j}$
, it is sufficient to show that these equations are independent modulo 2. But modulo 2, we obtain the system of equations
which are clearly independent. Hence, we have
![]() $\lfloor \frac {n-1}{2}\rfloor $
free variables in
$\lfloor \frac {n-1}{2}\rfloor $
free variables in
![]() $q_\star $
and
$q_\star $
and
![]() $\dim \ker P_e=\lfloor \frac {n-1}{2}\rfloor $
.
$\dim \ker P_e=\lfloor \frac {n-1}{2}\rfloor $
.
Similarly, if
![]() $q(x_1,x_2,x_3)\in \operatorname {\mathrm {im}} P_e$
, then
$q(x_1,x_2,x_3)\in \operatorname {\mathrm {im}} P_e$
, then
 $$ \begin{align*} q(x_1,x_2,x_3) &=\sum_{\substack{i+j=2n\\ i,j\geq 0}} \eta_{i,j}\big( (x_1-x_2)^i(x_2-x_3)^j+(-1)^{i}(x_1+x_2)^i(x_2-x_3)^j \\ &\quad {} +(x_1-x_2)^i(x_2+x_3)^j+(-1)^i(x_1+x_2)^i(x_2+x_3)^j\big) . \end{align*} $$
$$ \begin{align*} q(x_1,x_2,x_3) &=\sum_{\substack{i+j=2n\\ i,j\geq 0}} \eta_{i,j}\big( (x_1-x_2)^i(x_2-x_3)^j+(-1)^{i}(x_1+x_2)^i(x_2-x_3)^j \\ &\quad {} +(x_1-x_2)^i(x_2+x_3)^j+(-1)^i(x_1+x_2)^i(x_2+x_3)^j\big) . \end{align*} $$
Indeed, the set

forms a basis for the space of totally even solutions of
 $$ \begin{align*}\frac{\partial^4{q}}{\partial x_1^4}+\frac{\partial^4{q}}{\partial x_2^4}+\frac{\partial^4{q}}{\partial x_3^4}-2\frac{\partial^4{q}}{\partial x_1^2\partial x_2^2}-2\frac{\partial^4{q}}{\partial x_2^2\partial x_3^2}-2\frac{\partial^4{q}}{\partial x_3^2\partial x_1^2}=0 .\end{align*} $$
$$ \begin{align*}\frac{\partial^4{q}}{\partial x_1^4}+\frac{\partial^4{q}}{\partial x_2^4}+\frac{\partial^4{q}}{\partial x_3^4}-2\frac{\partial^4{q}}{\partial x_1^2\partial x_2^2}-2\frac{\partial^4{q}}{\partial x_2^2\partial x_3^2}-2\frac{\partial^4{q}}{\partial x_3^2\partial x_1^2}=0 .\end{align*} $$
Then, as
![]() $\frac {1}{2}\left (q(0,y,z)-q(0,y,-z)\right )=q(-y,y,z)-q(y,-z,z)$
holds trivially for any totally even polynomial satisfying the symmetry conditions, it is sufficient to compute the dimension of the subspace of skew-symmetric polynomials spanned by
$\frac {1}{2}\left (q(0,y,z)-q(0,y,-z)\right )=q(-y,y,z)-q(y,-z,z)$
holds trivially for any totally even polynomial satisfying the symmetry conditions, it is sufficient to compute the dimension of the subspace of skew-symmetric polynomials spanned by
![]() $\mathcal {Q}$
. This is a simple representation theoretic argument: we consider
$\mathcal {Q}$
. This is a simple representation theoretic argument: we consider
![]() $\mathbf {Span}(\mathcal {Q})$
as a representation of the symmetric group
$\mathbf {Span}(\mathcal {Q})$
as a representation of the symmetric group
![]() $\mathcal {S}_3$
via the standard polynomial representation, and compute the dimension of the sign representation within this. In particular, representation theory says that
$\mathcal {S}_3$
via the standard polynomial representation, and compute the dimension of the sign representation within this. In particular, representation theory says that
 $$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e& {} =\frac{1}{6}\big[\operatorname{\mathrm{Tr}}(\operatorname{\mathrm{id}})-3\operatorname{\mathrm{Tr}}((1\,3))+2\operatorname{\mathrm{Tr}}((1\,2\,3))\big]\\ & {} =\frac{1}{6}\big[2n+1-3\operatorname{\mathrm{Tr}}((1\,3))+2\operatorname{\mathrm{Tr}}((1\,2\,3))\big]. \end{align*} $$
$$ \begin{align*} \dim \operatorname{\mathrm{im}} P_e& {} =\frac{1}{6}\big[\operatorname{\mathrm{Tr}}(\operatorname{\mathrm{id}})-3\operatorname{\mathrm{Tr}}((1\,3))+2\operatorname{\mathrm{Tr}}((1\,2\,3))\big]\\ & {} =\frac{1}{6}\big[2n+1-3\operatorname{\mathrm{Tr}}((1\,3))+2\operatorname{\mathrm{Tr}}((1\,2\,3))\big]. \end{align*} $$
Note that the vector space generated by
![]() $\{(x_1-x_2)^i(x_2-x_3)^j\}_{i+j=2n} $
is invariant under the action of
$\{(x_1-x_2)^i(x_2-x_3)^j\}_{i+j=2n} $
is invariant under the action of
![]() $\mathcal {S}_3$
, and there is a natural surjection onto
$\mathcal {S}_3$
, and there is a natural surjection onto
![]() $\mathcal {Q}$
, so it is sufficient to consider the trace of the action restricted to
$\mathcal {Q}$
, so it is sufficient to consider the trace of the action restricted to
![]() $\{(x_1-x_2)^i(x_2-x_3)^j\}_{i+j=2n}$
in order to get an upper bound.
$\{(x_1-x_2)^i(x_2-x_3)^j\}_{i+j=2n}$
in order to get an upper bound.
Clearly, the trace of
![]() $(1\,3)$
is
$(1\,3)$
is
![]() $1$
, as the only diagonal entry corresponds to
$1$
, as the only diagonal entry corresponds to
![]() $(x_1-x_2)^n(x_2-x_3)^n\mapsto (x_3-x_2)^n(x_2-x_1)^n$
. Now, computing the trace of
$(x_1-x_2)^n(x_2-x_3)^n\mapsto (x_3-x_2)^n(x_2-x_1)^n$
. Now, computing the trace of
![]() $(1\,2\,3)$
, we find that it is given by
$(1\,2\,3)$
, we find that it is given by
 $$ \begin{align*}\sum_{i=0}^{2n}(-1)^i\binom{2n-i}{i}.\end{align*} $$
$$ \begin{align*}\sum_{i=0}^{2n}(-1)^i\binom{2n-i}{i}.\end{align*} $$
To compute this, we consider the generating series
 $$ \begin{align*} \sum_{n\geq 0}\sum_{i=0}^{n}\binom{n-i}{i}x^iy^{n}&=\sum_{k\geq 0}\sum_{i\geq 0}\binom{k}{i}(xy)^iy^k\\ &=\sum_{k\geq 0}(1+xy)^ky^k\\ &=\frac{1}{1-y-xy^2}. \end{align*} $$
$$ \begin{align*} \sum_{n\geq 0}\sum_{i=0}^{n}\binom{n-i}{i}x^iy^{n}&=\sum_{k\geq 0}\sum_{i\geq 0}\binom{k}{i}(xy)^iy^k\\ &=\sum_{k\geq 0}(1+xy)^ky^k\\ &=\frac{1}{1-y-xy^2}. \end{align*} $$
Setting
![]() $x=-1$
, we obtain
$x=-1$
, we obtain
 $$ \begin{align*} \sum_{n\geq 0}\sum_{i=0}^n (-1)^i\binom{n-i}{i}(-y)^n&=\frac{1}{1+y+y^2}\\ &=\frac{1-y}{1-y^3}\\ &=\sum_{m\geq 0}y^{3m}-y^{3m+1}. \end{align*} $$
$$ \begin{align*} \sum_{n\geq 0}\sum_{i=0}^n (-1)^i\binom{n-i}{i}(-y)^n&=\frac{1}{1+y+y^2}\\ &=\frac{1-y}{1-y^3}\\ &=\sum_{m\geq 0}y^{3m}-y^{3m+1}. \end{align*} $$
Thus,
 $$\begin{align*}\sum_{i=0}^{2n}(-1)^i\binom{2n-i}{i} = \begin{cases} 1 &\text{if}\ 2n\equiv 0 \quad\pmod{6}\\ -1 &\text{if}\ 2n\equiv 4 \quad\pmod{6}\\ 0 &\text{if}\ 2n\equiv 2 \quad\pmod{6} \end{cases} .\end{align*}$$
$$\begin{align*}\sum_{i=0}^{2n}(-1)^i\binom{2n-i}{i} = \begin{cases} 1 &\text{if}\ 2n\equiv 0 \quad\pmod{6}\\ -1 &\text{if}\ 2n\equiv 4 \quad\pmod{6}\\ 0 &\text{if}\ 2n\equiv 2 \quad\pmod{6} \end{cases} .\end{align*}$$
Hence
where x is determined by
![]() $2n \quad\pmod {6}$
. A quick consideration of each case shows we obtain
$2n \quad\pmod {6}$
. A quick consideration of each case shows we obtain
![]() $\lfloor \frac {2n}{6}\rfloor =\lfloor \frac {n}{3}\rfloor $
.
$\lfloor \frac {2n}{6}\rfloor =\lfloor \frac {n}{3}\rfloor $
.
Remark 4.3. Recall that the weight
![]() $2n+2$
part of
$2n+2$
part of
![]() $\mathfrak {rbg}_2$
is a subspace of
$\mathfrak {rbg}_2$
is a subspace of
![]() $V_n$
of dimension
$V_n$
of dimension
![]() $\dim {\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
. In order to describe this subspace in terms of relations, we need to find nonzero linear maps
$\dim {\mathfrak {g}^{\mathfrak {m}}}_{2,2n+2}$
. In order to describe this subspace in terms of relations, we need to find nonzero linear maps
![]() $\{R_i:V_n\to W_i\}_{i\in I}$
, such that
$\{R_i:V_n\to W_i\}_{i\in I}$
, such that
![]() $\mathfrak {rbg}_{2,2n+2}\subset \cap _{i\in I} \ker R_i$
. However, the projection
$\mathfrak {rbg}_{2,2n+2}\subset \cap _{i\in I} \ker R_i$
. However, the projection
![]() $\mathfrak {rbg}_{2,2n+2}\to \ker P_e$
is an isomorphism, and, as a consequence of Proposition 3.5,
$\mathfrak {rbg}_{2,2n+2}\to \ker P_e$
is an isomorphism, and, as a consequence of Proposition 3.5,
![]() $P_e(\mathfrak {rbg}_{2,2n+2})=\operatorname {\mathrm {im}} P_e$
. As such, no such R can impose any additional relations that restrict nontrivially to either the totally even or not-totally-even parts. Equivalently, any such R must induce a map
$P_e(\mathfrak {rbg}_{2,2n+2})=\operatorname {\mathrm {im}} P_e$
. As such, no such R can impose any additional relations that restrict nontrivially to either the totally even or not-totally-even parts. Equivalently, any such R must induce a map
![]() $\ker P_e\to \operatorname {\mathrm {Gr}}(k_R,\operatorname {\mathrm {im}} P_e)$
to the space of
$\ker P_e\to \operatorname {\mathrm {Gr}}(k_R,\operatorname {\mathrm {im}} P_e)$
to the space of
![]() $k_R$
-dimensional subspaces of
$k_R$
-dimensional subspaces of
![]() $\operatorname {\mathrm {im}} P_e$
for some unique integer
$\operatorname {\mathrm {im}} P_e$
for some unique integer
![]() $k_R$
. From another perspective, if such a description of
$k_R$
. From another perspective, if such a description of
![]() $\mathfrak {rbg}_{2,2n+2}$
can be found, this would give an alternative proof of Conjecture 1.1 in depth 2.
$\mathfrak {rbg}_{2,2n+2}$
can be found, this would give an alternative proof of Conjecture 1.1 in depth 2.
5. Applications to multiple
 $ t $
values
$ t $
values
From [Reference Hoffman23], we recall the multiple t value
![]() $ t(n_1,\ldots ,n_d) $
is defined by restricting the denominators in the series defining an MZV to be odd. Namely
$ t(n_1,\ldots ,n_d) $
is defined by restricting the denominators in the series defining an MZV to be odd. Namely

By inserting the factor
![]() $ \frac {1}{2} (1 - (-1)^{i_j}) $
into the numerator, one may extend the sum to all denominators, and obtain the following expression [Reference Hoffman23, Corollary 4.1] for
$ \frac {1}{2} (1 - (-1)^{i_j}) $
into the numerator, one may extend the sum to all denominators, and obtain the following expression [Reference Hoffman23, Corollary 4.1] for
![]() $ t(n_1,\ldots ,n_d) $
in terms of alternating MZVs (with various signs) of the same set of indices
$ t(n_1,\ldots ,n_d) $
in terms of alternating MZVs (with various signs) of the same set of indices
 $$\begin{align*}t(k_1,\ldots,k_d) &= \frac{1}{2^d} \sum_{0 < n_1 < \cdots < n_d} \frac{(1 -(-1)^{n_1}) \cdots (1 - (-1)^{n_d})}{n_1^{k_1} \cdots n_d^{k_d}}\end{align*}$$
$$\begin{align*}t(k_1,\ldots,k_d) &= \frac{1}{2^d} \sum_{0 < n_1 < \cdots < n_d} \frac{(1 -(-1)^{n_1}) \cdots (1 - (-1)^{n_d})}{n_1^{k_1} \cdots n_d^{k_d}}\end{align*}$$
 $$ \begin{align} &= \frac{1}{2^d} \sum_{\varepsilon_1,\ldots,\varepsilon_d \in \{ \pm 1 \}} \varepsilon_1 \cdots \varepsilon_d \zeta(\varepsilon_1 \diamond k_1, \cdots \varepsilon_d \diamond k_d) . \end{align} $$
$$ \begin{align} &= \frac{1}{2^d} \sum_{\varepsilon_1,\ldots,\varepsilon_d \in \{ \pm 1 \}} \varepsilon_1 \cdots \varepsilon_d \zeta(\varepsilon_1 \diamond k_1, \cdots \varepsilon_d \diamond k_d) . \end{align} $$
Here, the operator
![]() $ \diamond $
is defined so that
$ \diamond $
is defined so that
![]() $ 1 \diamond x = x $
and
$ 1 \diamond x = x $
and
![]() $ -1 \diamond x = \overline {x} $
, where, as usual,
$ -1 \diamond x = \overline {x} $
, where, as usual,
![]() $ \overline {n_j} $
denotes the argument,
$ \overline {n_j} $
denotes the argument,
![]() $ n_j $
is accompanied with sign
$ n_j $
is accompanied with sign
![]() $ \varepsilon _i = -1 $
in the definition of an alternating MZV (giving character
$ \varepsilon _i = -1 $
in the definition of an alternating MZV (giving character
![]() $ (-1)^{n_j} $
in the numerator thereof).
$ (-1)^{n_j} $
in the numerator thereof).
From Murakami [Reference Murakami32, Theorem 1], we know that every multiple
![]() $ t $
value with all arguments
$ t $
value with all arguments
![]() $ \geq 2 $
– which would a priori be a combination of alternating MZVs – satisfies a Galois descent, and is expressible as a
$ \geq 2 $
– which would a priori be a combination of alternating MZVs – satisfies a Galois descent, and is expressible as a
![]() $ \mathbb {Q} $
-linear combination of classical multiple zeta values. Murakami’s theorem is actually a statement about motivic multiple
$ \mathbb {Q} $
-linear combination of classical multiple zeta values. Murakami’s theorem is actually a statement about motivic multiple
![]() $ t $
values but gives the same descent for classical MtVs after applying the period map. However, Murakami’s result is purely existential and does not give an explicit formula, nor does it put any limits on the depth of the resulting combination. Using the result of Proposition A.3 for alternating double zeta values, we will give explicit formulae in terms of depth 2 classical MZVs for any
$ t $
values but gives the same descent for classical MtVs after applying the period map. However, Murakami’s result is purely existential and does not give an explicit formula, nor does it put any limits on the depth of the resulting combination. Using the result of Proposition A.3 for alternating double zeta values, we will give explicit formulae in terms of depth 2 classical MZVs for any
![]() $ t(\mathrm {ev}, \mathrm {ev}) $
in Proposition 5.4.
$ t(\mathrm {ev}, \mathrm {ev}) $
in Proposition 5.4.
Remark 5.1 (Galois descent of
 $ t(\mathrm {od},\mathrm {ev}) $
and
$ t(\mathrm {od},\mathrm {ev}) $
and
 $ t(\mathrm {ev},\mathrm {od}) $
).
$ t(\mathrm {ev},\mathrm {od}) $
).
Observe that the depth-parity theorem in depth 2 for alternating MZVs [Reference Panzer33, Equation 3.5] implies that every multiple
![]() $ t(a,b) $
value of odd weight (with
$ t(a,b) $
value of odd weight (with
![]() $ a, b \neq 1 $
) is a polynomial in single zeta values. This already gives an explicit formula for the Galois descent of
$ a, b \neq 1 $
) is a polynomial in single zeta values. This already gives an explicit formula for the Galois descent of
![]() $ t(\text {od},\text {ev}) $
and
$ t(\text {od},\text {ev}) $
and
![]() $ t(\text {ev}, \text {od}) $
. Equivalent formulae were derived in [Reference Xu and Yan38, Theorems 4.1, and 4.2] using contour integral techniques (compare [Reference Flajolet and Salvy16] for classical MZVs handled in a similar way), namely
$ t(\text {ev}, \text {od}) $
. Equivalent formulae were derived in [Reference Xu and Yan38, Theorems 4.1, and 4.2] using contour integral techniques (compare [Reference Flajolet and Salvy16] for classical MZVs handled in a similar way), namely
 $$ \begin{align*} t(2a+1,2b) &= t(2a+1)t(2b) - \frac{1}{2} t(2a+2b+1) \\ &\quad - \sum_{s=1}^{a+b} \bigg\{ \binom{2a+2b-2s}{2a} + \binom{2a+2b-2s}{2b-1} \bigg\} \frac{\zeta(2a+2b+1-2s)}{2^{2a+2b+1-2s}} t(2s) , \\ t(2a,2b+1) & = - \frac{1}{2} t(2a+2b+1) \\ &\quad + \sum_{s=1}^{a+b} \bigg\{ \binom{2a+2b-2s}{2b} + \binom{2a+2b-2s}{2a-1} \bigg\} \frac{\zeta(2a+2b+1-2s)}{2^{2a+2b+1-2s}} t(2s) \, \end{align*} $$
$$ \begin{align*} t(2a+1,2b) &= t(2a+1)t(2b) - \frac{1}{2} t(2a+2b+1) \\ &\quad - \sum_{s=1}^{a+b} \bigg\{ \binom{2a+2b-2s}{2a} + \binom{2a+2b-2s}{2b-1} \bigg\} \frac{\zeta(2a+2b+1-2s)}{2^{2a+2b+1-2s}} t(2s) , \\ t(2a,2b+1) & = - \frac{1}{2} t(2a+2b+1) \\ &\quad + \sum_{s=1}^{a+b} \bigg\{ \binom{2a+2b-2s}{2b} + \binom{2a+2b-2s}{2a-1} \bigg\} \frac{\zeta(2a+2b+1-2s)}{2^{2a+2b+1-2s}} t(2s) \, \end{align*} $$
One has that
![]() $ t(a) = (1 - 2^{-a}) \zeta (a) $
, for
$ t(a) = (1 - 2^{-a}) \zeta (a) $
, for
![]() $ a> 1 $
, which can be applied to rewrite the above purely in terms of Riemann zeta values.
$ a> 1 $
, which can be applied to rewrite the above purely in terms of Riemann zeta values.
Remark 5.2 (Galois descent of
 $ t(\mathrm {od},\mathrm {od}) $
).
$ t(\mathrm {od},\mathrm {od}) $
).
On the other hand, the remaining case involving
![]() $ t(\mathrm {od},\mathrm {od}) $
is less tractable. Using the MZV Data Mine [Reference Blümlein, Broadhurst and Vermaseren1], one can check the following relation
$ t(\mathrm {od},\mathrm {od}) $
is less tractable. Using the MZV Data Mine [Reference Blümlein, Broadhurst and Vermaseren1], one can check the following relation
 $$ \begin{align*} t(3,9) &= \frac{9}{128} \zeta (1,1,4,6) +\frac{1305}{4096}\zeta (3,9) -\frac{27}{128} \zeta (2) \zeta (3,7) -\frac{27}{256} \zeta (4) \zeta (3,5) \\ &\quad +\frac{3131}{2048}\zeta (9) \zeta (3) -\frac{321}{1024} \zeta (5) \zeta(7) -\frac{3}{512} \zeta (3)^4 -\frac{45}{64} \zeta (2) \zeta (7) \zeta (3) -\frac{63}{256} \zeta (2) \zeta (5)^2 \\ &\quad +\frac{9}{256} \zeta (4) \zeta (5) \zeta (3) +\frac{81}{512} \zeta (6) \zeta (3)^2 +\frac{353139}{5660672}\zeta (12) . \end{align*} $$
$$ \begin{align*} t(3,9) &= \frac{9}{128} \zeta (1,1,4,6) +\frac{1305}{4096}\zeta (3,9) -\frac{27}{128} \zeta (2) \zeta (3,7) -\frac{27}{256} \zeta (4) \zeta (3,5) \\ &\quad +\frac{3131}{2048}\zeta (9) \zeta (3) -\frac{321}{1024} \zeta (5) \zeta(7) -\frac{3}{512} \zeta (3)^4 -\frac{45}{64} \zeta (2) \zeta (7) \zeta (3) -\frac{63}{256} \zeta (2) \zeta (5)^2 \\ &\quad +\frac{9}{256} \zeta (4) \zeta (5) \zeta (3) +\frac{81}{512} \zeta (6) \zeta (3)^2 +\frac{353139}{5660672}\zeta (12) . \end{align*} $$
In particular, the (conjecturally) irreducible depth 4 MZV
![]() $ \zeta (1,1,4,6) $
(or any equivalent choice) is necessary to obtain an expression for the Galois descent of
$ \zeta (1,1,4,6) $
(or any equivalent choice) is necessary to obtain an expression for the Galois descent of
![]() $ t(3,9) $
to classical MZVs. This already suggests describing the Galois descent explicitly (with the minimal necessary depth) would be challenging.
$ t(3,9) $
to classical MZVs. This already suggests describing the Galois descent explicitly (with the minimal necessary depth) would be challenging.
We can, conjecturally at least, say that depth 4 MZVs will be sufficient. Indeed, since we may write
![]() $t(a,b)$
as a sum of depth 2 alternating MZVs, the alternating analogue of Lemma 1.2 tells us that
$t(a,b)$
as a sum of depth 2 alternating MZVs, the alternating analogue of Lemma 1.2 tells us that
![]() $t(a,b)$
lies in coradical degree at most 2. Hence, if a Galois descent to classical MZVs exists, it must also lie in coradical degree at most 2. When depth 2 MZVs do not span this space in even weight, the homological version of the Broadhurst-Kreimer Conjecture [Reference Brown9, Conjecture 5] tells us that depth 2 MZVs along with irreducible depth 4 MZVs coming from cusp forms do.
$t(a,b)$
lies in coradical degree at most 2. Hence, if a Galois descent to classical MZVs exists, it must also lie in coradical degree at most 2. When depth 2 MZVs do not span this space in even weight, the homological version of the Broadhurst-Kreimer Conjecture [Reference Brown9, Conjecture 5] tells us that depth 2 MZVs along with irreducible depth 4 MZVs coming from cusp forms do.
More generally, if a depth d multiple t value has a Galois descent to classical MZVs, the same line of reasoning tells us that we should expect an expression in terms of MZVs of depth at most
![]() $2d$
.
$2d$
.
By combining the usual expression for
![]() $ t(a,b) $
in terms of alternating MZVs [Reference Hoffman23, Corollary 4.1], namely
$ t(a,b) $
in terms of alternating MZVs [Reference Hoffman23, Corollary 4.1], namely
with the distribution relation [Reference Goncharov20, Proposition 2.13]
we can write
More generally, see the alternative expression given by Hoffman, using a sum which inserts only an even number of bars into the argument string [Reference Hoffman23, Corollary 4.2].
Let us now note the following result from Section A.5, which gives an explicit form for the Galois descent of
![]() $ \zeta (\overline {2\ell }, \overline {2k}) $
in terms of classical double MZVs.
$ \zeta (\overline {2\ell }, \overline {2k}) $
in terms of classical double MZVs.
Proposition A.3 (Galois descent of
 $ \zeta (\overline {2\ell },\overline {2k}) $
).
$ \zeta (\overline {2\ell },\overline {2k}) $
).
The alternating double zeta value
![]() $ \zeta (\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 MZVs as follows
$ \zeta (\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 MZVs as follows
 $$ \begin{align} \nonumber \zeta(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ \nonumber & -\zeta(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
$$ \begin{align} \nonumber \zeta(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ \nonumber & -\zeta(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
Proof sketch.
We recall the notation
![]() $ \zeta _\ell (k_1,\ldots ,k_d) $
is defined by inserting
$ \zeta _\ell (k_1,\ldots ,k_d) $
is defined by inserting
![]() $ \ell $
leading 0’s at the start of the integral representation of
$ \ell $
leading 0’s at the start of the integral representation of
![]() $ \zeta (k_1,\ldots ,k_d) $
(c.f. Equations (2.1) or (A.1) for alternating MZVs). Now simultaneously solve the following equations: the dihedral symmetry Equation (A.8)
$ \zeta (k_1,\ldots ,k_d) $
(c.f. Equations (2.1) or (A.1) for alternating MZVs). Now simultaneously solve the following equations: the dihedral symmetry Equation (A.8)
 $$ \begin{align*} \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) &= \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) \\ &\quad - \sum_{\substack{r = 1}}^{2k+2\ell-2} \bigg( (-1)^r \binom{r-1}{2k-1} + \binom{r-1}{2\ell-1} \bigg) \zeta(\overline{r}) \zeta(2k+2\ell-r) , \end{align*} $$
$$ \begin{align*} \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) &= \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) \\ &\quad - \sum_{\substack{r = 1}}^{2k+2\ell-2} \bigg( (-1)^r \binom{r-1}{2k-1} + \binom{r-1}{2\ell-1} \bigg) \zeta(\overline{r}) \zeta(2k+2\ell-r) , \end{align*} $$
and the generalised doubling identity [Reference Blümlein, Broadhurst and Vermaseren1, Section 4], [Reference Zhao42, Section 14.2.5]
 $$ \begin{align*} & \zeta(\overline{s},\overline{t}) + (-1)^t \zeta_{t-1}(1,\overline{s}) \\ &\quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i, i) \\ &\qquad - \zeta(s,t) + (-1)^t \zeta_{t-1}(s,1) - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \zeta(\overline{s+t-i})\zeta(i) - \binom{s+t-1}{s} \zeta(s+t) \end{align*} $$
$$ \begin{align*} & \zeta(\overline{s},\overline{t}) + (-1)^t \zeta_{t-1}(1,\overline{s}) \\ &\quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i, i) \\ &\qquad - \zeta(s,t) + (-1)^t \zeta_{t-1}(s,1) - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \zeta(\overline{s+t-i})\zeta(i) - \binom{s+t-1}{s} \zeta(s+t) \end{align*} $$
(here slightly rewritten, see Section A.5) in the case
![]() $ t = 2k, s = 2\ell $
.
$ t = 2k, s = 2\ell $
.
Now substituting this Galois descent into Equation (5.2), we immediately have the following proposition.
Proposition 5.3. The multiple
![]() $ t $
value
$ t $
value
![]() $ t(2\ell ,2k) $
is expressed through classical double zeta values as follows
$ t(2\ell ,2k) $
is expressed through classical double zeta values as follows
 $$ \begin{align} \nonumber t(2\ell,2k) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i-1} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ \nonumber & -2^{-2k-2\ell} \zeta(2\ell,2k) - \sum_{r=2}^{2k+2\ell-2} (-2)^{-r-1} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ & - 2^{-2k-2\ell-1} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
$$ \begin{align} \nonumber t(2\ell,2k) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i-1} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ \nonumber & -2^{-2k-2\ell} \zeta(2\ell,2k) - \sum_{r=2}^{2k+2\ell-2} (-2)^{-r-1} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ & - 2^{-2k-2\ell-1} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
A Analytic evaluation of
 $ \zeta (\{2\}^a, 4, \{2\}^b) $
via double zeta values
$ \zeta (\{2\}^a, 4, \{2\}^b) $
via double zeta values
The goal of this section is to give an explicit evaluation for
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
in terms of double zeta values on the analytic (numerical) level. In Appendix B, we will then lift this to the corresponding identity among motivic MZVs.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
in terms of double zeta values on the analytic (numerical) level. In Appendix B, we will then lift this to the corresponding identity among motivic MZVs.
For the numerical evaluation, we need to assemble a number of ingredients. In particular, we need to use the stuffle antipode ([Reference Hoffman24], [Reference Li31] or [Reference Glanois18, Reference Glanois19]) to convert
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
to a corresponding multiple zeta star value. Then we can apply Zhao’s generalised 2-1 Theorem [Reference Zhao41] (in the block decomposition form [Reference Charlton12] for convenience) to rewrite the zeta star value as an alternating zeta-half value. By application of the parity theorem ([Reference Panzer33], or [Reference Goncharov21]), we reduce this to an explicit combination of depth 2 alternating MZVs. It becomes convenient to write these (combinations of) alternating double zeta values as certain shuffle-regularised alternating double zetas
$ \zeta (\{2\}^a, 4, \{2\}^b) $
to a corresponding multiple zeta star value. Then we can apply Zhao’s generalised 2-1 Theorem [Reference Zhao41] (in the block decomposition form [Reference Charlton12] for convenience) to rewrite the zeta star value as an alternating zeta-half value. By application of the parity theorem ([Reference Panzer33], or [Reference Goncharov21]), we reduce this to an explicit combination of depth 2 alternating MZVs. It becomes convenient to write these (combinations of) alternating double zeta values as certain shuffle-regularised alternating double zetas ![]() with a number of initial zeros; this presentation then manifests a dihedral symmetry modulo products and lower depth [Reference Glanois18],[Reference Glanois19], which we can describe explicitly. Finally (perhaps surprisingly), by combining this dihedral symmetry with a generalised doubling identity [Reference Blümlein, Broadhurst and Vermaseren1, Reference Zhao42], one can explicitly evaluate these alternating double zeta values in terms of classical double zeta values (as opposed to higher depth MZVs which would certainly suffice by the generalised 2-1 Theorem).
with a number of initial zeros; this presentation then manifests a dihedral symmetry modulo products and lower depth [Reference Glanois18],[Reference Glanois19], which we can describe explicitly. Finally (perhaps surprisingly), by combining this dihedral symmetry with a generalised doubling identity [Reference Blümlein, Broadhurst and Vermaseren1, Reference Zhao42], one can explicitly evaluate these alternating double zeta values in terms of classical double zeta values (as opposed to higher depth MZVs which would certainly suffice by the generalised 2-1 Theorem).
Alternating and interpolated MZVs:
Let us recall, again, the notions of alternating MZVs, and of multiple zeta star values and multiple zeta-half values, which will be useful imminently. Given a tuple
![]() $ (k_1,k_2,\ldots ,k_d) $
of positive integers, and a tuple
$ (k_1,k_2,\ldots ,k_d) $
of positive integers, and a tuple
![]() $ (\varepsilon _1,\varepsilon _2,\ldots ,\varepsilon _d) \in \{ \pm 1 \}^d $
, with
$ (\varepsilon _1,\varepsilon _2,\ldots ,\varepsilon _d) \in \{ \pm 1 \}^d $
, with
![]() $ (k_d,\varepsilon _d) \neq (1,1) $
, we define the alternating MZV (or Euler sum) with signs
$ (k_d,\varepsilon _d) \neq (1,1) $
, we define the alternating MZV (or Euler sum) with signs
![]() $ \varepsilon _1,\ldots ,\varepsilon _d $
as follows,
$ \varepsilon _1,\ldots ,\varepsilon _d $
as follows,

One then streamlines the notation by suppressing the
![]() $ \varepsilon _i $
’s and writing
$ \varepsilon _i $
’s and writing
![]() $ \overline {k_i} $
if
$ \overline {k_i} $
if
![]() $ \varepsilon _i = -1 $
, and just
$ \varepsilon _i = -1 $
, and just
![]() $ k_i $
if
$ k_i $
if
![]() $ \varepsilon _i = 1 $
otherwise. For example
$ \varepsilon _i = 1 $
otherwise. For example

An alternating MZV can be written as an iterated integral in the following way
 $$ \begin{align} \zeta\bigg(\begin{matrix} \varepsilon_1,\varepsilon_2,\ldots,\varepsilon_d \\ k_1,k_2,\ldots,k_d \end{matrix}\bigg) = (-1)^d I^{\mathfrak{m}}(0; \eta_1, \{0\}^{k_1-1}, \eta_2, \{0\}^{k_2-1}, \ldots, \eta_d, \{0\}^{k_d-1} ;1) , \end{align} $$
$$ \begin{align} \zeta\bigg(\begin{matrix} \varepsilon_1,\varepsilon_2,\ldots,\varepsilon_d \\ k_1,k_2,\ldots,k_d \end{matrix}\bigg) = (-1)^d I^{\mathfrak{m}}(0; \eta_1, \{0\}^{k_1-1}, \eta_2, \{0\}^{k_2-1}, \ldots, \eta_d, \{0\}^{k_d-1} ;1) , \end{align} $$
where
![]() $ \eta _i = \varepsilon _i \varepsilon _{i+1} \cdots \varepsilon _d $
.
$ \eta _i = \varepsilon _i \varepsilon _{i+1} \cdots \varepsilon _d $
.
Next, we have the interpolated multiple zeta values
![]() $ \zeta ^r(k_1,\ldots ,k_d) $
introduced by Yamamoto [Reference Yamamoto39],
$ \zeta ^r(k_1,\ldots ,k_d) $
introduced by Yamamoto [Reference Yamamoto39],
For example,
![]() $ \zeta ^r(a,b,c) = \zeta (a,b,c) + r \zeta (a+b,c) + r \zeta (a, b+c) + r^2 \zeta (a+b+c) $
. In the case
$ \zeta ^r(a,b,c) = \zeta (a,b,c) + r \zeta (a+b,c) + r \zeta (a, b+c) + r^2 \zeta (a+b+c) $
. In the case
![]() $ r = 0 $
, only the term with all
$ r = 0 $
, only the term with all
![]() $ \circ _i = \text{","} $
survives, and so
$ \circ _i = \text{","} $
survives, and so
![]() $ \zeta ^0(k_1,\ldots ,k_d) = \zeta (k_1,\ldots ,k_d) $
. When
$ \zeta ^0(k_1,\ldots ,k_d) = \zeta (k_1,\ldots ,k_d) $
. When
![]() $ r = 1 $
, then we have
$ r = 1 $
, then we have
![]() $ \zeta ^1(k_1,\ldots ,k_d) = \zeta ^\star (k_1,\ldots ,k_d) $
, where the multiple zeta star value (MZSV) is originally defined as
$ \zeta ^1(k_1,\ldots ,k_d) = \zeta ^\star (k_1,\ldots ,k_d) $
, where the multiple zeta star value (MZSV) is originally defined as

and arises by replacing the strict inequalities between
![]() $ n_i, n_{i+1} $
with a nonstrict inequality. For
$ n_i, n_{i+1} $
with a nonstrict inequality. For
![]() $ r = {{1 }/{2}} $
, we then obtain a new variant ‘mid-way’ between
$ r = {{1 }/{2}} $
, we then obtain a new variant ‘mid-way’ between
![]() $ \zeta $
and
$ \zeta $
and
![]() $ \zeta ^\star $
, called the multiple zeta-half value.
$ \zeta ^\star $
, called the multiple zeta-half value.
This formalism can be extended to allow for alternating interpolated MZVs, by replacing
![]() $ {`+}\text{'} $
, above with
$ {`+}\text{'} $
, above with
![]() $ {`}{\oplus} \text{'} $
, where
$ {`}{\oplus} \text{'} $
, where
![]() $ a \oplus b $
denotes addition of the absolute values and multiplication of the bars viewed as signs (i.e. if
$ a \oplus b $
denotes addition of the absolute values and multiplication of the bars viewed as signs (i.e. if
![]() $ k \in \mathbb {Z}_{>0} $
, we have
$ k \in \mathbb {Z}_{>0} $
, we have
![]() $ \left |k\right | = \left |\smash {\overline {k}}\right | = k $
with
$ \left |k\right | = \left |\smash {\overline {k}}\right | = k $
with
![]() $ \operatorname {\mathrm {sgn}}(\overline {k}) = -1 $
and
$ \operatorname {\mathrm {sgn}}(\overline {k}) = -1 $
and
![]() $ \operatorname {\mathrm {sgn}}(k) = 1 $
). In particular, for
$ \operatorname {\mathrm {sgn}}(k) = 1 $
). In particular, for
![]() $ \alpha ,\beta \in \mathbb {Z}_{>0} $
, we have
$ \alpha ,\beta \in \mathbb {Z}_{>0} $
, we have
![]() $ \alpha \oplus \beta = \alpha + \beta $
,
$ \alpha \oplus \beta = \alpha + \beta $
,
![]() $ \alpha \oplus \overline {\beta } = \overline {\alpha } \oplus \beta = \overline {\alpha + \beta } $
and
$ \alpha \oplus \overline {\beta } = \overline {\alpha } \oplus \beta = \overline {\alpha + \beta } $
and
![]() $ \overline {\alpha } \oplus \overline {\beta } = \alpha + \beta $
. Then, for example, we have the following interpolated alternating MZV
$ \overline {\alpha } \oplus \overline {\beta } = \alpha + \beta $
. Then, for example, we have the following interpolated alternating MZV
 $$ \begin{align*} \zeta^r(a, \overline{b},\overline{c}) & {} = \zeta(a,\overline{b},\overline{c}) + r \zeta(a\oplus \overline{b},\overline{c}) + r \zeta(a, \overline{b}\oplus\overline{c}) + r^2 \zeta(\overline{a}\oplus \overline{b} \oplus \overline{c}) \\ & {} = \zeta(a,\overline{b},\overline{c}) + r \zeta(\overline{a+b},\overline{c}) + r \zeta(a, b+c) + r^2 \zeta(\overline{a+b+c}) . \end{align*} $$
$$ \begin{align*} \zeta^r(a, \overline{b},\overline{c}) & {} = \zeta(a,\overline{b},\overline{c}) + r \zeta(a\oplus \overline{b},\overline{c}) + r \zeta(a, \overline{b}\oplus\overline{c}) + r^2 \zeta(\overline{a}\oplus \overline{b} \oplus \overline{c}) \\ & {} = \zeta(a,\overline{b},\overline{c}) + r \zeta(\overline{a+b},\overline{c}) + r \zeta(a, b+c) + r^2 \zeta(\overline{a+b+c}) . \end{align*} $$
The case
![]() $ r = {{1 }/{2}} $
of alternating interpolated MZVs is a convenient way of formulating Zhao’s [Reference Zhao41] generalised 2-1 Theorem, as we will see below.
$ r = {{1 }/{2}} $
of alternating interpolated MZVs is a convenient way of formulating Zhao’s [Reference Zhao41] generalised 2-1 Theorem, as we will see below.
A.1 Stuffle antipode
We define
![]() $ G^\star $
, the generating series of
$ G^\star $
, the generating series of
![]() $ \zeta ^\star (\{2\}^a, 4 ,\{2\}^b) $
,
$ \zeta ^\star (\{2\}^a, 4 ,\{2\}^b) $
,
![]() $ G $
, a related generating series for
$ G $
, a related generating series for
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
, and
$ \zeta (\{2\}^a, 4, \{2\}^b) $
, and
![]() $ S^\star $
the generating series of
$ S^\star $
the generating series of
![]() $ \zeta ^\star (\{2\}^n) $
as follows.
$ \zeta ^\star (\{2\}^n) $
as follows.

Then from [Reference Li31, Equation 2.4] (in the special case,
![]() $ a_2 = z_4 $
,
$ a_2 = z_4 $
,
![]() $ a_1 = a_3 = z_2 $
), we have that
$ a_1 = a_3 = z_2 $
), we have that
This is an identity in the stuffle algebra; in particular, it automatically lifts to a motivic identity since the stuffle product is known to be motivic (see [Reference Racinet34] or [Reference Soudères37]). Moreover, it is well-known (or readily verifiable by factoring the generating series as a product, see, for example [Reference Borwein, Bradley and Broadhurst2, Equation 36], and [Reference Zagier40, Equation 44]) that
 $$\begin{align*}\sum_{n=0}^\infty \zeta^\star(\{2\}^n) x^{2n} = \frac{\pi x}{\sin(\pi x)} , \text{ and } \sum_{n=0}^\infty \zeta(\{2\}^n) x^{2n} = \frac{\sin(\mathrm{i} \pi x)}{\mathrm{i} \pi x} . \end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty \zeta^\star(\{2\}^n) x^{2n} = \frac{\pi x}{\sin(\pi x)} , \text{ and } \sum_{n=0}^\infty \zeta(\{2\}^n) x^{2n} = \frac{\sin(\mathrm{i} \pi x)}{\mathrm{i} \pi x} . \end{align*}$$
By solving Equation (A.2) for
![]() $ G(y,x) $
, and extracting the coefficient of
$ G(y,x) $
, and extracting the coefficient of
![]() $ x^{2a} y^{2b} $
, we obtain the following explicit formula for
$ x^{2a} y^{2b} $
, we obtain the following explicit formula for
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
in terms of similar
$ \zeta (\{2\}^a, 4, \{2\}^b) $
in terms of similar
![]() $ \zeta ^\star $
values,
$ \zeta ^\star $
values,
 $$ \begin{align} \zeta(\{2\}^a,4,\{2\}^b) = \sum_{n=0}^a \sum_{m=0}^b (-1)^{m+n} \zeta^\star(\{2\}^m, 4, \{2\}^n) \zeta(\{2\}^{a-n}) \zeta(\{2\}^{b-m}) . \end{align} $$
$$ \begin{align} \zeta(\{2\}^a,4,\{2\}^b) = \sum_{n=0}^a \sum_{m=0}^b (-1)^{m+n} \zeta^\star(\{2\}^m, 4, \{2\}^n) \zeta(\{2\}^{a-n}) \zeta(\{2\}^{b-m}) . \end{align} $$
A similar identity holds for
![]() $ 4 $
replaced by any value
$ 4 $
replaced by any value
![]() $ k $
; these identities give the precise version of the stuffle antipode result
$ k $
; these identities give the precise version of the stuffle antipode result
considered in [Reference Glanois18, Lemma 4.2.2]. Moreover, since the stuffle algebra identity and the evaluations of
![]() $ \zeta (\{2\}^n) $
,
$ \zeta (\{2\}^n) $
,
![]() $ \zeta ^\star (\{2\}^n) $
are motivic ([Reference Brown5, Lemma 3.4], [Reference Glanois18, Lemma 4.4.3]), Equation (A.3) lifts automatically to a motivic version.
$ \zeta ^\star (\{2\}^n) $
are motivic ([Reference Brown5, Lemma 3.4], [Reference Glanois18, Lemma 4.4.3]), Equation (A.3) lifts automatically to a motivic version.
A.2 Generalised 2-1 Theorem
We now recall the generalised 2-1 Theorem, established by Zhao [Reference Zhao41], which evaluates each
![]() $ \zeta ^\star $
value in terms of a certain alternating
$ \zeta ^\star $
value in terms of a certain alternating
![]() $ \zeta ^{{1 }/{2}} $
value. It is more convenient – and indeed has a closer connection with the goal – to write the generalised 2-1 Theorem in the block decomposition form given in [Reference Charlton12, Lemma 3.1].
$ \zeta ^{{1 }/{2}} $
value. It is more convenient – and indeed has a closer connection with the goal – to write the generalised 2-1 Theorem in the block decomposition form given in [Reference Charlton12, Lemma 3.1].
Let
![]() $ \mathbf {\underline {s}} = (s_1,\ldots ,s_k) $
be a sequence of MZV arguments, and let
$ \mathbf {\underline {s}} = (s_1,\ldots ,s_k) $
be a sequence of MZV arguments, and let
![]() $ \mathbf {\underline {B}} = (\ell _1,\ldots ,\ell _n) $
be the corresponding block decomposition (see Section 2.3). Write
$ \mathbf {\underline {B}} = (\ell _1,\ldots ,\ell _n) $
be the corresponding block decomposition (see Section 2.3). Write
 $$\begin{align*}\widetilde{\,x\,} = \begin{cases} x & \text{if}\ x\ \text{odd}, \\ \overline{x} & \text{if}\ x\ \text{even} \end{cases} \end{align*}$$
$$\begin{align*}\widetilde{\,x\,} = \begin{cases} x & \text{if}\ x\ \text{odd}, \\ \overline{x} & \text{if}\ x\ \text{even} \end{cases} \end{align*}$$
Recall:
![]() $ \overline {x} $
denotes that the argument
$ \overline {x} $
denotes that the argument
![]() $ x $
in an alternating MZV has sign
$ x $
in an alternating MZV has sign
![]() $ -1 $
. Then
$ -1 $
. Then
where
![]() $ \varepsilon (\mathbf {\underline {s}}) = 1 $
if
$ \varepsilon (\mathbf {\underline {s}}) = 1 $
if
![]() $ s_1 = 1 $
and
$ s_1 = 1 $
and
![]() $ \varepsilon (\mathbf {\underline {s}}) = -1 $
if
$ \varepsilon (\mathbf {\underline {s}}) = -1 $
if
![]() $ s_1 \geq 2 $
, and if
$ s_1 \geq 2 $
, and if
![]() $ \ell _1-2 = 0 $
, one should neglect this argument. This follows by combining Zhao’s generalised 2-1 Theorem [Reference Zhao41], which involves a certain recursively constructed sequence of indices
$ \ell _1-2 = 0 $
, one should neglect this argument. This follows by combining Zhao’s generalised 2-1 Theorem [Reference Zhao41], which involves a certain recursively constructed sequence of indices
![]() $ \mathbf {\underline {s}}^{(i)} $
, with the description of the final such index string
$ \mathbf {\underline {s}}^{(i)} $
, with the description of the final such index string
![]() $ \mathbf {\underline {s}}^{(k)} $
, given in [Reference Charlton12, Lemma 3.1], in terms of the block decomposition. This final string supplies the
$ \mathbf {\underline {s}}^{(k)} $
, given in [Reference Charlton12, Lemma 3.1], in terms of the block decomposition. This final string supplies the
![]() $ \zeta ^{{1 }/{2}} $
arguments in Zhao’s formulation of the 2-1 Theorem.
$ \zeta ^{{1 }/{2}} $
arguments in Zhao’s formulation of the 2-1 Theorem.
In our case, we want to apply this to
![]() $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
. The block decomposition of
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
. The block decomposition of
![]() $ (\{2\}^a, 4, \{2\}^b) $
is given by
$ (\{2\}^a, 4, \{2\}^b) $
is given by
![]() $ (2a+3,1,2b+2) $
, and we therefore have
$ (2a+3,1,2b+2) $
, and we therefore have
Then expanding out, by definition of the interpolated
![]() $ \zeta ^{{1 }/{2}} $
, we have
$ \zeta ^{{1 }/{2}} $
, we have
 $$ \begin{align} \nonumber \zeta^\star(\{2\}^a, 4, \{2\}^b) = & -2 \zeta(\overline{2a + 2b + 4}) - 4 \zeta(2a+1, \overline{2b + 3}) \\ & - 4 \zeta(2a + 2, \overline{2b + 2}) - 8 \zeta(2a + 1, 1, \overline{2b+2}) . \end{align} $$
$$ \begin{align} \nonumber \zeta^\star(\{2\}^a, 4, \{2\}^b) = & -2 \zeta(\overline{2a + 2b + 4}) - 4 \zeta(2a+1, \overline{2b + 3}) \\ & - 4 \zeta(2a + 2, \overline{2b + 2}) - 8 \zeta(2a + 1, 1, \overline{2b+2}) . \end{align} $$
This reduces our task of evaluating
![]() $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
to understanding certain explicit depth 3 alternating MZVs.
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
to understanding certain explicit depth 3 alternating MZVs.
A.3 The parity theorem in depth 3
The parity theorem for MZVs states roughly that an MZV of weight
![]() $ w $
and depth
$ w $
and depth
![]() $ d $
can be reduced to a combination of lower depth MZVs and products, when
$ d $
can be reduced to a combination of lower depth MZVs and products, when
![]() $ w \not \equiv d \quad\pmod {2} $
. In particular, an MZV of depth 3 and even weight is reducible. This claim actually also holds for alternating MZVs, via the parity theorem for multiple polylogarithms [Reference Panzer33], as
$ w \not \equiv d \quad\pmod {2} $
. In particular, an MZV of depth 3 and even weight is reducible. This claim actually also holds for alternating MZVs, via the parity theorem for multiple polylogarithms [Reference Panzer33], as
![]() $ -1 $
is its own multiplicative inverse.
$ -1 $
is its own multiplicative inverse.
An explicit version of the depth 3 parity theorem is given for the multiple polylogarithm functions
![]() $ \operatorname {\mathrm {Li}}_{n_1,n_2,n_3}(z_1,z_2,z_3) $
in [Reference Panzer33, Equation 4.3]. By specialising to
$ \operatorname {\mathrm {Li}}_{n_1,n_2,n_3}(z_1,z_2,z_3) $
in [Reference Panzer33, Equation 4.3]. By specialising to
![]() $ z_i = \pm 1 $
, we recover the claimed reduction of depth 3 alternating MZVs, for any choice of signs
$ z_i = \pm 1 $
, we recover the claimed reduction of depth 3 alternating MZVs, for any choice of signs
![]() $ z_i $
(encoded with a ‘bar’ over the corresponding argument
$ z_i $
(encoded with a ‘bar’ over the corresponding argument
![]() $ \overline {n_i} $
, if
$ \overline {n_i} $
, if
![]() $ z_i = -1 $
), as follows. Namely, if
$ z_i = -1 $
), as follows. Namely, if
![]() $ \alpha + \beta + \gamma $
is even and
$ \alpha + \beta + \gamma $
is even and
![]() $ \gamma \neq 1 $
(although
$ \gamma \neq 1 $
(although
![]() $ \gamma = \bar {1} $
is okay), then with
$ \gamma = \bar {1} $
is okay), then with
![]() $\zeta (0) = \zeta (\overline {0}) = -\frac {1}{2}$
by convention, and stuffle-regularisation if necessary (see [Reference Ihara, Kaneko and Zagier25] for the notion of regularisation, and Remark A.1 below for the behaviour in this case) when
$\zeta (0) = \zeta (\overline {0}) = -\frac {1}{2}$
by convention, and stuffle-regularisation if necessary (see [Reference Ihara, Kaneko and Zagier25] for the notion of regularisation, and Remark A.1 below for the behaviour in this case) when
![]() $\zeta (1)$
appears, we have
$\zeta (1)$
appears, we have
 $$ \begin{align*} \zeta(\alpha,\beta,\gamma) &= \frac{1}{2} \zeta(\alpha) \big( \zeta(\beta,\gamma) - (-1)^{\left|\beta\right|+\left|\gamma\right|} \zeta(\beta,\gamma) \big) - \zeta(\beta,\alpha) \zeta(\gamma) \delta_{\left|\gamma\right| \text{even}} \\ &\quad - \frac{1}{2} \zeta(\alpha \oplus \beta, \gamma) + \frac{1}{2} \zeta(\beta \oplus \gamma, \alpha) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\alpha}\right| \\ s, \mu, \nu \geq 0}} (-1)^{\left|\beta\right| + \left|\gamma\right| + \mu+ \nu} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s)\binom{-\left|\beta\right|}{\mu} \binom{-\left|\gamma\right|}{\nu} \zeta(\beta\oplus \mu, \gamma \oplus \nu) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\beta}\right| \\ s, \mu, \nu \geq 0}} (-1)^{\gamma + \mu} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s)\binom{-\left|\gamma\right|}{\mu} \binom{-\left|\alpha\right|}{\nu} \zeta(\gamma \oplus \mu) \zeta( \alpha \oplus \nu) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\gamma}\right| \\ s, \mu,\nu \geq 0}} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s) \binom{-\left|\beta\right|}{\mu} \binom{-\left|\alpha\right|}{\nu} \zeta(\beta \oplus \mu, \alpha \oplus \nu) \, \end{align*} $$
$$ \begin{align*} \zeta(\alpha,\beta,\gamma) &= \frac{1}{2} \zeta(\alpha) \big( \zeta(\beta,\gamma) - (-1)^{\left|\beta\right|+\left|\gamma\right|} \zeta(\beta,\gamma) \big) - \zeta(\beta,\alpha) \zeta(\gamma) \delta_{\left|\gamma\right| \text{even}} \\ &\quad - \frac{1}{2} \zeta(\alpha \oplus \beta, \gamma) + \frac{1}{2} \zeta(\beta \oplus \gamma, \alpha) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\alpha}\right| \\ s, \mu, \nu \geq 0}} (-1)^{\left|\beta\right| + \left|\gamma\right| + \mu+ \nu} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s)\binom{-\left|\beta\right|}{\mu} \binom{-\left|\gamma\right|}{\nu} \zeta(\beta\oplus \mu, \gamma \oplus \nu) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\beta}\right| \\ s, \mu, \nu \geq 0}} (-1)^{\gamma + \mu} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s)\binom{-\left|\gamma\right|}{\mu} \binom{-\left|\alpha\right|}{\nu} \zeta(\gamma \oplus \mu) \zeta( \alpha \oplus \nu) \\ &\quad + \sum_{\substack{2s + \nu + \mu = \left|\smash{\gamma}\right| \\ s, \mu,\nu \geq 0}} \zeta(\operatorname{\mathrm{sgn}}(\alpha\beta\gamma) \diamond 2s) \binom{-\left|\beta\right|}{\mu} \binom{-\left|\alpha\right|}{\nu} \zeta(\beta \oplus \mu, \alpha \oplus \nu) \, \end{align*} $$
To avoid abuse of notation, we define ![]() , and
, and ![]() , to give the corresponding decoration for signed arguments.
, to give the corresponding decoration for signed arguments.
Now specialise to
![]() $ \alpha = 2a + 1, \beta = 1, \gamma = \overline {2b+2} $
. We can simplify various binomial coefficients and powers of
$ \alpha = 2a + 1, \beta = 1, \gamma = \overline {2b+2} $
. We can simplify various binomial coefficients and powers of
![]() $ -1 $
, using
$ -1 $
, using
![]() $ \binom {-k}{\ell } = (-1)^\ell \binom {\ell + k-1}{k-1} $
, and expand out the second summation into its two nontrivial terms
$ \binom {-k}{\ell } = (-1)^\ell \binom {\ell + k-1}{k-1} $
, and expand out the second summation into its two nontrivial terms
![]() $ (s,\mu ,\nu ) = (0, 1, 0), (0, 0, 1) $
. After doing so, and inserting the result into Equation (A.4), we note some simplifications. Firstly, the term
$ (s,\mu ,\nu ) = (0, 1, 0), (0, 0, 1) $
. After doing so, and inserting the result into Equation (A.4), we note some simplifications. Firstly, the term
![]() $ -4\zeta (2a+2,\overline {2b+2}) $
in the
$ -4\zeta (2a+2,\overline {2b+2}) $
in the
![]() $ \zeta ^{{1 }/{2}} $
cancels with one from the depth 3 reduction; secondly, the term
$ \zeta ^{{1 }/{2}} $
cancels with one from the depth 3 reduction; secondly, the term
![]() $ -4\zeta (2a+1,\overline {2b+3}) $
combines with one from the depth 3 reduction to produce
$ -4\zeta (2a+1,\overline {2b+3}) $
combines with one from the depth 3 reduction to produce
 $$ \begin{align*} & -4\zeta(2a+1,\overline{2b+3}) - 4\zeta(\overline{2b+3},2a+1) \\ &\quad = -4\zeta(2a+1)\zeta(\overline{2b+3}) + 4 \zeta(\overline{2a+2b+4}). \end{align*} $$
$$ \begin{align*} & -4\zeta(2a+1,\overline{2b+3}) - 4\zeta(\overline{2b+3},2a+1) \\ &\quad = -4\zeta(2a+1)\zeta(\overline{2b+3}) + 4 \zeta(\overline{2a+2b+4}). \end{align*} $$
Overall, this produces the following evaluation for
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
, as the first main stepping stone, with stuffle-regularisation applied where necessary
$ \zeta (\{2\}^a, 4, \{2\}^b) $
, as the first main stepping stone, with stuffle-regularisation applied where necessary
 $$ \begin{align} \nonumber \zeta^\star(\{2\}^a, 4, \{2\}^b) &= 2 \zeta(\overline{2a + 2b + 4}) + 8 \zeta(1, 2a+1) \zeta(\overline{2b+2}) - 8 \zeta(2a + 1)\zeta(1, \overline{2b + 2}) \\ \nonumber &\quad + 4 (2b + 1) \zeta(\overline{2b +3}) \zeta(2a + 1) - 4 (2a + 1) \zeta(\overline{2b + 2}) \zeta(2a + 2) \\ &\quad + 8 \sum_{\substack{2s + \nu + \mu = 2a+1 \\ s, \mu, \nu \geq 0}} \zeta(\overline{2s}) \binom{\nu+(2b+1)}{\nu} \zeta(1 + \mu, \overline{2b + 2 + \nu}) \\ \nonumber &\quad - 8 \sum_{\substack{2s + \nu + \mu = 2b+2 \\ s, \mu, \nu \geq 0}} \zeta(\overline{2s}) \binom{\nu + (2a)}{\nu} \zeta(1 + \mu, 2a + 1 + \nu) . \end{align} $$
$$ \begin{align} \nonumber \zeta^\star(\{2\}^a, 4, \{2\}^b) &= 2 \zeta(\overline{2a + 2b + 4}) + 8 \zeta(1, 2a+1) \zeta(\overline{2b+2}) - 8 \zeta(2a + 1)\zeta(1, \overline{2b + 2}) \\ \nonumber &\quad + 4 (2b + 1) \zeta(\overline{2b +3}) \zeta(2a + 1) - 4 (2a + 1) \zeta(\overline{2b + 2}) \zeta(2a + 2) \\ &\quad + 8 \sum_{\substack{2s + \nu + \mu = 2a+1 \\ s, \mu, \nu \geq 0}} \zeta(\overline{2s}) \binom{\nu+(2b+1)}{\nu} \zeta(1 + \mu, \overline{2b + 2 + \nu}) \\ \nonumber &\quad - 8 \sum_{\substack{2s + \nu + \mu = 2b+2 \\ s, \mu, \nu \geq 0}} \zeta(\overline{2s}) \binom{\nu + (2a)}{\nu} \zeta(1 + \mu, 2a + 1 + \nu) . \end{align} $$
Remark A.1 (Independence of regularisation).
Let us note here that the shuffle-regularised and stuffle-regularised versions of this formula agree (and, indeed, also for the depth 3 reduction, with
![]() $ c \neq 1 $
), and are independent of the regularisation parameter; we may therefore switch to the shuffle-regularisation at
$ c \neq 1 $
), and are independent of the regularisation parameter; we may therefore switch to the shuffle-regularisation at
![]() $ T = 0 $
for later convenience. This is expected since we are reducing a convergent triple zeta value.
$ T = 0 $
for later convenience. This is expected since we are reducing a convergent triple zeta value.
More precisely, this is because terms with a single trailing 1 are equal under either regularisation, and in the case
![]() $ a = 0 $
, the single term
$ a = 0 $
, the single term
![]() $ 8\zeta (\overline {2b+1})\zeta (1,1) $
with two trailing 1’s, which arises, arising from
$ 8\zeta (\overline {2b+1})\zeta (1,1) $
with two trailing 1’s, which arises, arising from
![]() $ (s,\nu ,\mu ) = (b+1, 0, 0) $
in the last sum, cancels with the corresponding term on the second line. Otherwise, when
$ (s,\nu ,\mu ) = (b+1, 0, 0) $
in the last sum, cancels with the corresponding term on the second line. Otherwise, when
![]() $ a = 1 $
, the regularisation parameter
$ a = 1 $
, the regularisation parameter
![]() $ T $
in terms arising from
$ T $
in terms arising from
![]() $ \nu = 0 $
in the last sum (with
$ \nu = 0 $
in the last sum (with
![]() $ \zeta ^{\ast ,T} $
explicitly denoting the stuffle-regularised version with
$ \zeta ^{\ast ,T} $
explicitly denoting the stuffle-regularised version with
![]() $ \zeta ^{\ast ,T} (1) = T $
),
$ \zeta ^{\ast ,T} (1) = T $
),
 $$\begin{align*}\sum_{\substack{2s + \mu = 2b + 2 \\ s \geq 0,\mu> 0}} \zeta(\overline{2s}) \zeta^{\ast,T}(1 + \mu, 1) = \sum_{\substack{2s + \mu = 2b + 2 \\ s \geq 0,\mu > 0}} \zeta(\overline{2s}) \big( T \zeta(1 + \mu) - \zeta(1, 1+\mu) - \zeta(2+\mu) \big) \end{align*}$$
$$\begin{align*}\sum_{\substack{2s + \mu = 2b + 2 \\ s \geq 0,\mu> 0}} \zeta(\overline{2s}) \zeta^{\ast,T}(1 + \mu, 1) = \sum_{\substack{2s + \mu = 2b + 2 \\ s \geq 0,\mu > 0}} \zeta(\overline{2s}) \big( T \zeta(1 + \mu) - \zeta(1, 1+\mu) - \zeta(2+\mu) \big) \end{align*}$$
can be seen to cancel with that arising from the terms
 $$ \begin{align*} & 8 \zeta^{\ast,T}(1) \zeta(1,\overline{2b+2}) + 4 (2b+1) \zeta(\overline{2b+3}) \zeta^{\ast,T}(1) \\ &\quad = 8 T \zeta(1, \overline{2b+2}) + 4 (2b+1) \zeta(\overline{2b+3}) T. \end{align*} $$
$$ \begin{align*} & 8 \zeta^{\ast,T}(1) \zeta(1,\overline{2b+2}) + 4 (2b+1) \zeta(\overline{2b+3}) \zeta^{\ast,T}(1) \\ &\quad = 8 T \zeta(1, \overline{2b+2}) + 4 (2b+1) \zeta(\overline{2b+3}) T. \end{align*} $$
In fact, this cancellation is equivalent to the following reduction which follows from the depth-parity theorem in depth 2 (see [Reference Panzer33, Equation 3.5]):
 $$ \begin{align} \zeta(1, \overline{2b+2}) = -\sum_{\substack{2s+k = 2b + 3 \\ s \geq 0, k \geq 2}} \zeta(\overline{2s}) \zeta(k) + \frac{2b+1}{2} \zeta(\overline{2b+3}) . \end{align} $$
$$ \begin{align} \zeta(1, \overline{2b+2}) = -\sum_{\substack{2s+k = 2b + 3 \\ s \geq 0, k \geq 2}} \zeta(\overline{2s}) \zeta(k) + \frac{2b+1}{2} \zeta(\overline{2b+3}) . \end{align} $$
A.4 Shuffle-regularisation and dihedral symmetries
Now let us take advantage of the shuffle-regularisation in earnest. Define
![]() $ \zeta _\ell (k_1,\ldots ,k_d) $
by inserting
$ \zeta _\ell (k_1,\ldots ,k_d) $
by inserting
![]() $ \ell $
leading 0’s at the start of the iterated integral representation of
$ \ell $
leading 0’s at the start of the iterated integral representation of
![]() $ \zeta (k_1,\ldots ,k_d) $
given in Equation (A.1) (see also Equations (2.1) and (B.1)), and write
$ \zeta (k_1,\ldots ,k_d) $
given in Equation (A.1) (see also Equations (2.1) and (B.1)), and write ![]() for the shuffle regularisation thereof (see Remark 2.2 above), with
for the shuffle regularisation thereof (see Remark 2.2 above), with ![]() . Then we have the regularisation formula (see, for example [Reference Brown10, Section 5.1 R2], and the obvious generalisation to alternating MZVs in [Reference Glanois18, Equation 2.28])
. Then we have the regularisation formula (see, for example [Reference Brown10, Section 5.1 R2], and the obvious generalisation to alternating MZVs in [Reference Glanois18, Equation 2.28])

In particular, using this, we can write

Substituting these and Equation (A.6) into Equation (A.5) gives us the following

Let us finally note that the term
![]() $ 8\zeta (1,2a+1) \zeta (\overline {2b+2}) $
cancels with the
$ 8\zeta (1,2a+1) \zeta (\overline {2b+2}) $
cancels with the
![]() $ s = b+1 $
term of the last sum. In particular, we obtain the second stepping stone in our quest to evaluate
$ s = b+1 $
term of the last sum. In particular, we obtain the second stepping stone in our quest to evaluate
![]() $ \zeta ^{\star }(\{2\}^a, 4, \{2\}^b) $
. Namely
$ \zeta ^{\star }(\{2\}^a, 4, \{2\}^b) $
. Namely

Henceforth, we shall always use the shuffle regularisation with ![]() , and will therefore drop the extraneous
, and will therefore drop the extraneous ![]() from our notation. This regularisation is consistent with the regularisation normally used in the motivic framework (c.f. Remark 2.2). Moreover, we will check in Section B.2 that this reduction is indeed motivic.
from our notation. This regularisation is consistent with the regularisation normally used in the motivic framework (c.f. Remark 2.2). Moreover, we will check in Section B.2 that this reduction is indeed motivic.
Now, we recall from [Reference Glanois18, Corollary 4.2.6] that depth
![]() $ p $
alternating zeta star values satisfy a dihedral symmetry of order
$ p $
alternating zeta star values satisfy a dihedral symmetry of order
![]() $ p + 1 $
, modulo products and lower depth. More precisely therein, this symmetry is phrased in terms of so-called multiple zeta star-star values, which incorporate the lower depth terms, making the symmetry hold already modulo products. In particular, in our case, we claim that
$ p + 1 $
, modulo products and lower depth. More precisely therein, this symmetry is phrased in terms of so-called multiple zeta star-star values, which incorporate the lower depth terms, making the symmetry hold already modulo products. In particular, in our case, we claim that
 $$ \begin{align*} \zeta_{2k-1}(1,\overline{2\ell}) &\equiv \zeta(\overline{2\ell},\overline{2k}) \quad\pmod{\text{products}} \\ \zeta_{2k}(1,2\ell+1) &\equiv \zeta(2\ell+1,2k+1) \quad\pmod{\text{products}} \, \end{align*} $$
$$ \begin{align*} \zeta_{2k-1}(1,\overline{2\ell}) &\equiv \zeta(\overline{2\ell},\overline{2k}) \quad\pmod{\text{products}} \\ \zeta_{2k}(1,2\ell+1) &\equiv \zeta(2\ell+1,2k+1) \quad\pmod{\text{products}} \, \end{align*} $$
The depth 1 terms in these cases are reducible, as the weight is even. We will not actually use the implicit form of the dihedral symmetry established by Glanois which immediately produces the above; instead, guided by the Glanois’s proof, we will establish an exact version in this depth 2 case. However, let us point out some technical issue which apparently occurs when considering the octagon relation, in an attempt to derive a so-called hybrid relation (Theorem 4.2.3 in [Reference Glanois18]), a key part of the proof of the dihedral symmetry.
Remark A.2 (Regularisation in the octagon relation).
The octagon relation for level
![]() $ N = 2 $
multiple zeta values (i.e. alternating MZVs) is obtained by integrating a word in
$ N = 2 $
multiple zeta values (i.e. alternating MZVs) is obtained by integrating a word in
![]() $ e_0, e_1, e_{-1} $
around the following closed loop.
$ e_0, e_1, e_{-1} $
around the following closed loop.

However, one must take into account the tangential base points, and how they are transformed under the Möbius transformation which cyclically maps the segments
![]() $ (0,1) \mapsto (-1,0) \mapsto (\infty ,-1) \mapsto (1,\infty ) $
. More precisely, the Möbius transformation
$ (0,1) \mapsto (-1,0) \mapsto (\infty ,-1) \mapsto (1,\infty ) $
. More precisely, the Möbius transformation
transforms the segments as indicated, and therefore the integral
![]() $ \int _{(-1,0)} $
is related to the integral
$ \int _{(-1,0)} $
is related to the integral
![]() $ \int _{(0,1)} $
via a suitable pullback. However, note that the straight line path
$ \int _{(0,1)} $
via a suitable pullback. However, note that the straight line path
with tangential base points
![]() $ \overrightarrow {0}_{1} $
and
$ \overrightarrow {0}_{1} $
and
![]() $ \overrightarrow {1}_{-1} $
is transformed into the path
$ \overrightarrow {1}_{-1} $
is transformed into the path
 $$ \begin{align*} (f^\ast \mathrm{dch})(t) \colon [0,1] &\to [-1,0] \\ t &\mapsto \frac{t-1}{t+1} \end{align*} $$
$$ \begin{align*} (f^\ast \mathrm{dch})(t) \colon [0,1] &\to [-1,0] \\ t &\mapsto \frac{t-1}{t+1} \end{align*} $$
with tangential base points
![]() $ \overrightarrow {-1}_{2} $
and
$ \overrightarrow {-1}_{2} $
and
![]() $ \overrightarrow {0}_{-\frac {1}{2}} $
. In particular, the semicircular integrals evaluate in the following way
$ \overrightarrow {0}_{-\frac {1}{2}} $
. In particular, the semicircular integrals evaluate in the following way
 $$\begin{align*}\int_{\overrightarrow{0}_{-\frac{1}{2}}}^{\overrightarrow{0}_1} \frac{\mathrm{d}t}{t} = \log(2) - \mathrm{i} \pi . \end{align*}$$
$$\begin{align*}\int_{\overrightarrow{0}_{-\frac{1}{2}}}^{\overrightarrow{0}_1} \frac{\mathrm{d}t}{t} = \log(2) - \mathrm{i} \pi . \end{align*}$$
So the octagon relation actually takes the form
 $$ \begin{align*} e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{-1}} & \Phi^{\mathfrak{m}}(e_0, e_{-1}, e_1) e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{0}} \Phi^{\mathfrak{m}}(e_0, e_{1}, e_{-1}) \\ & \cdot e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{1}} \Phi^{\mathfrak{m}}(e_\infty, e_{1}, e_{-1}) e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{\infty}} \Phi^{\mathfrak{m}}(e_\infty, e_{-1}, e_1) = 1 , \end{align*} $$
$$ \begin{align*} e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{-1}} & \Phi^{\mathfrak{m}}(e_0, e_{-1}, e_1) e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{0}} \Phi^{\mathfrak{m}}(e_0, e_{1}, e_{-1}) \\ & \cdot e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{1}} \Phi^{\mathfrak{m}}(e_\infty, e_{1}, e_{-1}) e^{\big(-\frac{\mathbb{L}^{\mathfrak{m}}}{2} + \log^{\mathfrak{m}}(2)\big) e_{\infty}} \Phi^{\mathfrak{m}}(e_\infty, e_{-1}, e_1) = 1 , \end{align*} $$
where
![]() $ e_\infty $
is defined, such that
$ e_\infty $
is defined, such that
![]() $ e_0 + e_1 + e_\infty + e_{-1} = 0 $
.
$ e_0 + e_1 + e_\infty + e_{-1} = 0 $
.
This change should not render Glanois’s hybrid identity invalid, as the derivation of the hybrid identity mainly requires the octagon relation modulo products, and these additional terms largely cancel out.
We now turn to the derivation of the exact identities which verify our earlier claim that
 $$ \begin{align*} \zeta_{2k-1}(1,\overline{2\ell}) &\equiv \zeta(\overline{2\ell},\overline{2k}) \quad\pmod{\text{products}} \\ \zeta_{2k}(1,2\ell+1) &\equiv \zeta(2\ell+1,2k+1) \quad\pmod{\text{products}} . \end{align*} $$
$$ \begin{align*} \zeta_{2k-1}(1,\overline{2\ell}) &\equiv \zeta(\overline{2\ell},\overline{2k}) \quad\pmod{\text{products}} \\ \zeta_{2k}(1,2\ell+1) &\equiv \zeta(2\ell+1,2k+1) \quad\pmod{\text{products}} . \end{align*} $$
We treat the first, as the second is exactly analogous; we will, nevertheless, give the full identity in each case. Firstly, apply shuffle regularisation to
to obtain
 $$\begin{align*}= (-1)^{z-1} \sum_{i+j = z-1} \binom{i+\alpha-1}{i} \binom{j+\beta-1}{j} \big\{ \zeta(\overline{i+\alpha}, j+\beta) + \zeta(j+\beta, \overline{i+\alpha}) \big\} \, \end{align*}$$
$$\begin{align*}= (-1)^{z-1} \sum_{i+j = z-1} \binom{i+\alpha-1}{i} \binom{j+\beta-1}{j} \big\{ \zeta(\overline{i+\alpha}, j+\beta) + \zeta(j+\beta, \overline{i+\alpha}) \big\} \, \end{align*}$$
Note, we have combined the two original sums by switching
![]() $ i \leftrightarrow j $
in the second sum. By the stuffle product (switching to stuffle regularisation is okay, as there is at most a single trailing 1), we have
$ i \leftrightarrow j $
in the second sum. By the stuffle product (switching to stuffle regularisation is okay, as there is at most a single trailing 1), we have
 $$\begin{align*}= (-1)^{z-1} \sum_{i+j = z-1} \binom{i+\alpha-1}{i} \binom{j+\beta-1}{j} \big\{ \zeta(j+\beta)\zeta(\overline{i+\alpha}) - \zeta(\overline{\alpha+\beta+z-1}) \big\} . \end{align*}$$
$$\begin{align*}= (-1)^{z-1} \sum_{i+j = z-1} \binom{i+\alpha-1}{i} \binom{j+\beta-1}{j} \big\{ \zeta(j+\beta)\zeta(\overline{i+\alpha}) - \zeta(\overline{\alpha+\beta+z-1}) \big\} . \end{align*}$$
On the other hand, apply the shuffle antipode [Reference Goncharov21, Equation 29]
 $$ \begin{align*} & (-1)^N I(a; x_N, \ldots, x_1; b) + I(a; x_1,\ldots,x_N; b) \\ &\quad + \sum_{i=1}^{N-1} (-1)^{N-i} I(a; x_1, \ldots, x_i; b) I(a; x_{N}, \ldots, x_{i+1}; b) = 0 \end{align*} $$
$$ \begin{align*} & (-1)^N I(a; x_N, \ldots, x_1; b) + I(a; x_1,\ldots,x_N; b) \\ &\quad + \sum_{i=1}^{N-1} (-1)^{N-i} I(a; x_1, \ldots, x_i; b) I(a; x_{N}, \ldots, x_{i+1}; b) = 0 \end{align*} $$
which effectively reverses the differential forms in an iterated integral
![]() $ I(a, x_1,\ldots ,x_N; b) $
, modulo explicit products terms, to
$ I(a, x_1,\ldots ,x_N; b) $
, modulo explicit products terms, to
and we find
 $$ \begin{align*} & \zeta_{z-1}(\overline{\alpha}, \beta) + (-1)^{z-1+\alpha+\beta} \zeta_{\beta-1}(\overline{\alpha}, \overline{z}) \\ &\quad =I(0; \{0\}^{z-1}, -1, \{0\}^{\alpha-1}, 1, \{0\}^{\beta-1}; 1) \\ & \qquad + (-1)^{z-1+\alpha+\beta} I(0; \{0\}^{\beta-1}, 1, \{0\}^{\alpha-1}, -1, \{0\}^{z-1}; 1) \\ &\quad = -\sum_{i=0}^{\alpha-1} (-1)^{z-1 + \alpha + i} \binom{z+i-1}{i} \binom{\alpha+\beta-2-i}{\beta-1} \zeta(\overline{z+i}) \zeta(\alpha+\beta-1-i) . \end{align*} $$
$$ \begin{align*} & \zeta_{z-1}(\overline{\alpha}, \beta) + (-1)^{z-1+\alpha+\beta} \zeta_{\beta-1}(\overline{\alpha}, \overline{z}) \\ &\quad =I(0; \{0\}^{z-1}, -1, \{0\}^{\alpha-1}, 1, \{0\}^{\beta-1}; 1) \\ & \qquad + (-1)^{z-1+\alpha+\beta} I(0; \{0\}^{\beta-1}, 1, \{0\}^{\alpha-1}, -1, \{0\}^{z-1}; 1) \\ &\quad = -\sum_{i=0}^{\alpha-1} (-1)^{z-1 + \alpha + i} \binom{z+i-1}{i} \binom{\alpha+\beta-2-i}{\beta-1} \zeta(\overline{z+i}) \zeta(\alpha+\beta-1-i) . \end{align*} $$
Finally, take the difference of these two identities, and set
![]() $ \alpha = 2\ell , \beta = 1, z = 2k $
, we then obtain the dihedral symmetry we claimed
$ \alpha = 2\ell , \beta = 1, z = 2k $
, we then obtain the dihedral symmetry we claimed
 $$ \begin{align*} \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) &= -\sum_{i=0}^{2k-1} \binom{i+2\ell-1}{i} \big\{ \zeta(\overline{i+2\ell}) \zeta(2k-i) - \zeta(\overline{2k+2\ell}) \big\} \\ &\quad - \sum_{i=0}^{2\ell-1} (-1)^i \binom{2k+i-1}{i} \zeta(\overline{2k+i}) \zeta(2\ell-i) .\end{align*} $$
$$ \begin{align*} \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) &= -\sum_{i=0}^{2k-1} \binom{i+2\ell-1}{i} \big\{ \zeta(\overline{i+2\ell}) \zeta(2k-i) - \zeta(\overline{2k+2\ell}) \big\} \\ &\quad - \sum_{i=0}^{2\ell-1} (-1)^i \binom{2k+i-1}{i} \zeta(\overline{2k+i}) \zeta(2\ell-i) .\end{align*} $$
A slightly more concise version of this is obtained by extending the sums to negative indices – where the binomial coefficients vanish – in order to combine them into one, and explicitly summing the coefficient of
![]() $ \zeta (\overline {2k+2\ell }) $
. This puts the identity in a form closer to that which one could directly check/derive with the motivic derivations, namely
$ \zeta (\overline {2k+2\ell }) $
. This puts the identity in a form closer to that which one could directly check/derive with the motivic derivations, namely
 $$ \begin{align} \nonumber \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) & = \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) \\ &\quad - \sum_{\substack{r = 1}}^{2k+2\ell-2} \bigg( (-1)^r \binom{r-1}{2k-1} + \binom{r-1}{2\ell-1} \bigg) \zeta(\overline{r}) \zeta(2k+2\ell-r) . \end{align} $$
$$ \begin{align} \nonumber \zeta_{2k-1}(1, \overline{2\ell}) - \zeta(\overline{2\ell}, \overline{2k}) & = \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) \\ &\quad - \sum_{\substack{r = 1}}^{2k+2\ell-2} \bigg( (-1)^r \binom{r-1}{2k-1} + \binom{r-1}{2\ell-1} \bigg) \zeta(\overline{r}) \zeta(2k+2\ell-r) . \end{align} $$
In an analogous way, we find the explicit form of the dihedral symmetry in the other case to be
 $$ \begin{align} \nonumber \zeta_{2k}(1, 2\ell+1) - {} & \zeta(2\ell+1,2k+1) = {} - \zeta(2) \delta_{k=\ell=0} - \binom{2k+2\ell+1}{2\ell+1} \zeta(2k+2\ell+2) \\ & + \sum_{\substack{r = 1}}^{2k+2\ell} \bigg( (-1)^r \binom{r-1}{2k} + \binom{r-1}{2\ell} \bigg) \zeta(r) \zeta(2k+2\ell+2-r) \, \end{align} $$
$$ \begin{align} \nonumber \zeta_{2k}(1, 2\ell+1) - {} & \zeta(2\ell+1,2k+1) = {} - \zeta(2) \delta_{k=\ell=0} - \binom{2k+2\ell+1}{2\ell+1} \zeta(2k+2\ell+2) \\ & + \sum_{\substack{r = 1}}^{2k+2\ell} \bigg( (-1)^r \binom{r-1}{2k} + \binom{r-1}{2\ell} \bigg) \zeta(r) \zeta(2k+2\ell+2-r) \, \end{align} $$
Here, the term
![]() $ \delta _{k=\ell =0} $
accounts for the difference in shuffle- and stuffle-regularisation in the case
$ \delta _{k=\ell =0} $
accounts for the difference in shuffle- and stuffle-regularisation in the case
![]() $ \zeta (1,1) $
.
$ \zeta (1,1) $
.
Both of these identities are easily verified to be motivic, either by direct calculation via
![]() $ \operatorname {\mathrm {D}}_{2r+1} $
, or by noting that the ingredients – namely, the shuffle and stuffle products, and the regularisation
$ \operatorname {\mathrm {D}}_{2r+1} $
, or by noting that the ingredients – namely, the shuffle and stuffle products, and the regularisation ![]() – are themselves motivic in nature.
– are themselves motivic in nature.
A.5 Generalised doubling identity
The final ingredient we require for our evaluation is one of the so-called generalised doubling identities, as described in [Reference Blümlein, Broadhurst and Vermaseren1, Section 4], and [Reference Zhao42, Section 14.2.5] (be aware these references use the opposite MZV convention).
In depth 2, the relevant relation is already given explicitly by Zhao, and states (with either shuffle or stuffle regularisation) that
 $$ \begin{align*} & \zeta(s,t) + \zeta(\overline{s},\overline{t}) \\ &\quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i,i) \\ &\qquad - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \big\{ \zeta(s+t-i,i) + \zeta(\overline{s+t-i},i) \big\} - \binom{s+t-1}{s} 2^{1-s-t} \zeta(s+t) .\end{align*} $$
$$ \begin{align*} & \zeta(s,t) + \zeta(\overline{s},\overline{t}) \\ &\quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i,i) \\ &\qquad - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \big\{ \zeta(s+t-i,i) + \zeta(\overline{s+t-i},i) \big\} - \binom{s+t-1}{s} 2^{1-s-t} \zeta(s+t) .\end{align*} $$
We then flip
![]() $ \zeta (\overline {a},b) $
to
$ \zeta (\overline {a},b) $
to
![]() $ \zeta (b,\overline {a}) $
using the stuffle product, rewrite the double zeta sums that lack powers of 2 using the shuffle regularisation as before, and simplify the resulting coefficient of
$ \zeta (b,\overline {a}) $
using the stuffle product, rewrite the double zeta sums that lack powers of 2 using the shuffle regularisation as before, and simplify the resulting coefficient of
![]() $ \zeta (s+t) $
(The power of 2 does indeed just disappear!) This gives the equivalent identity
$ \zeta (s+t) $
(The power of 2 does indeed just disappear!) This gives the equivalent identity
 $$ \begin{align*} & \zeta(\overline{s},\overline{t}) + (-1)^t \zeta_{t-1}(1,\overline{s}) \\ & \quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i, i) \\ &\qquad - \zeta(s,t) + (-1)^t \zeta_{t-1}(s,1) - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \zeta(\overline{s+t-i})\zeta(i) - \binom{s+t-1}{s} \zeta(s+t) . \end{align*} $$
$$ \begin{align*} & \zeta(\overline{s},\overline{t}) + (-1)^t \zeta_{t-1}(1,\overline{s}) \\ & \quad = \sum_{i=1}^s \binom{s+t-i-1}{t-1} 2^{1+i-s-t} \zeta(i, s+t-i) + \sum_{i=1}^t \binom{s+t-i-1}{s-1} 2^{1+i-s-t} \zeta(s+t-i, i) \\ &\qquad - \zeta(s,t) + (-1)^t \zeta_{t-1}(s,1) - \sum_{i=1}^t \binom{s+t-i-1}{s-1} \zeta(\overline{s+t-i})\zeta(i) - \binom{s+t-1}{s} \zeta(s+t) . \end{align*} $$
Finally, we note that upon substituting
![]() $ t = 2k, s = 2\ell $
, we can solve this identity simultaneously with Equation (A.8) to obtain expressions for both
$ t = 2k, s = 2\ell $
, we can solve this identity simultaneously with Equation (A.8) to obtain expressions for both
![]() $ \zeta (\overline {2\ell },\overline {2k}) $
and
$ \zeta (\overline {2\ell },\overline {2k}) $
and
![]() $ \zeta _{2k-1}(1,\overline {2\ell }) $
individually as combinations of classical depth 2 MZVs and products. In particular, we have established the following proposition (after substituting an expression for
$ \zeta _{2k-1}(1,\overline {2\ell }) $
individually as combinations of classical depth 2 MZVs and products. In particular, we have established the following proposition (after substituting an expression for
![]() $ (-1)^t \zeta _{t-1}(s,1) = \zeta _{2k-1}(2\ell ,1) \equiv \zeta (2k,2\ell ) \quad\pmod {\text {products}} $
using the shuffle antipode, or via a further dihedral symmetry, and simplifying).
$ (-1)^t \zeta _{t-1}(s,1) = \zeta _{2k-1}(2\ell ,1) \equiv \zeta (2k,2\ell ) \quad\pmod {\text {products}} $
using the shuffle antipode, or via a further dihedral symmetry, and simplifying).
Proposition A.3 (Galois descent of
 $ \zeta (\overline {2\ell },\overline {2k}) $
).
$ \zeta (\overline {2\ell },\overline {2k}) $
).
The alternating double zeta value
![]() $ \zeta (\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 MZVs as follows
$ \zeta (\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 MZVs as follows
 $$ \begin{align} \nonumber \zeta(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ & -\zeta(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ \nonumber & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
$$ \begin{align} \nonumber \zeta(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta(i,2k+2\ell-i) \bigg\} \\ & -\zeta(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta(r) \zeta(2k+2\ell-r) \\ \nonumber & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta(2k + 2\ell) . \end{align} $$
Moreover, by a direct calculation, since
![]() $ \operatorname {\mathrm {D}}_{2r+1} $
is a tensor product of single-zeta values in this case, we see Proposition A.3 (and the generalised doubling identity itself) lifts to the motivic level. This is checked in detail in Section B.1.
$ \operatorname {\mathrm {D}}_{2r+1} $
is a tensor product of single-zeta values in this case, we see Proposition A.3 (and the generalised doubling identity itself) lifts to the motivic level. This is checked in detail in Section B.1.
Remark A.4. It is clear from the generalised 2-1 Theorem that
![]() $ \zeta (\overline {2\ell },\overline {2k}) $
descends to a combination of classical MZVs; we can, in fact, easily give an explicit formula
$ \zeta (\overline {2\ell },\overline {2k}) $
descends to a combination of classical MZVs; we can, in fact, easily give an explicit formula
However, it is certainly not clear from this expression that depth 2 classical MZVs suffice, and so this would not help us in evaluating
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
in any useful manner. However, we do obtain an evaluation for
$ \zeta (\{2\}^a, 4, \{2\}^b) $
in any useful manner. However, we do obtain an evaluation for
![]() $ \zeta ^\star (1,\{2\}^{\ell -1}, 3, \{2\}^{k-1}) $
by substituting Proposition A.3 into the above.
$ \zeta ^\star (1,\{2\}^{\ell -1}, 3, \{2\}^{k-1}) $
by substituting Proposition A.3 into the above.
Moreover, since
![]() $ \zeta (1,1,4,6) $
is – according to the Data Mine [Reference Blümlein, Broadhurst and Vermaseren1] – a combination of depth 2 alternating MZVs and products
$ \zeta (1,1,4,6) $
is – according to the Data Mine [Reference Blümlein, Broadhurst and Vermaseren1] – a combination of depth 2 alternating MZVs and products
 $$ \begin{align*} \zeta (1,1,4,6) = & \frac{64}{9} \zeta (\overline{3},\overline{9}) +\frac{371}{144} \zeta (3,9) +3 \zeta (2) \zeta (3,7) +\frac{3}{2} \zeta (4) \zeta (3,5) -\frac{3131}{144} \zeta (9) \zeta (3) \\ &+\frac{107}{24} \zeta (5) \zeta (7) +10 \zeta (2) \zeta (7) \zeta (3) +\frac{7}{2} \zeta (2) \zeta (5)^2 -\frac{1}{2} \zeta (4) \zeta (5) \zeta (3) \\ &-\frac{9}{4} \zeta (6) \zeta (3)^2 +\frac{\zeta (3)^4}{12} -\frac{117713 }{132672}\zeta (12) , \end{align*} $$
$$ \begin{align*} \zeta (1,1,4,6) = & \frac{64}{9} \zeta (\overline{3},\overline{9}) +\frac{371}{144} \zeta (3,9) +3 \zeta (2) \zeta (3,7) +\frac{3}{2} \zeta (4) \zeta (3,5) -\frac{3131}{144} \zeta (9) \zeta (3) \\ &+\frac{107}{24} \zeta (5) \zeta (7) +10 \zeta (2) \zeta (7) \zeta (3) +\frac{7}{2} \zeta (2) \zeta (5)^2 -\frac{1}{2} \zeta (4) \zeta (5) \zeta (3) \\ &-\frac{9}{4} \zeta (6) \zeta (3)^2 +\frac{\zeta (3)^4}{12} -\frac{117713 }{132672}\zeta (12) , \end{align*} $$
but apparently irreducible as a classical MZV, one cannot, in general, expect the Galois descent to always respect the depth. However, as pointed out in Remark 5.2, one has – assuming the homological version of the Broadhurst-Kreimer Conjecture [Reference Broadhurst and Kreimer3] (see also Conjecture 1.1 above) – that the depth of an alternating MZV after Galois descent should be at most twice the original; here, the Galois descent of
![]() $ \zeta (\overline {3},\overline {9}) $
involving classical MZVs up to depth 4 corroborates this.
$ \zeta (\overline {3},\overline {9}) $
involving classical MZVs up to depth 4 corroborates this.
By substituting Proposition A.3 into Equation (A.8), and this result into Equation (A.7), we establish that
![]() $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
and (via Equation (A.3)) that
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
and (via Equation (A.3)) that
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
are both expressible in terms of only classical double zeta values.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
are both expressible in terms of only classical double zeta values.
Theorem A.5 (Nonexplicit form).
Both
![]() $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
and
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
and
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
are expressible in terms of classical double zeta values.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
are expressible in terms of classical double zeta values.
A.6 Generating series
In order to extract an explicit useable identity for
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
, we will convert everything to a generating series identity as a route to simplifying the resulting combinations.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
, we will convert everything to a generating series identity as a route to simplifying the resulting combinations.
Let us introduce the following generating series, whose names originate from Zagier’s evaluation of
![]() $ \zeta (\{2\}^a, 3, \{2\}^b) $
[Reference Zagier40], and some related generating series of even zeta values. The generating series of odd MZVs, and alternating odd MZVs, are given by
$ \zeta (\{2\}^a, 3, \{2\}^b) $
[Reference Zagier40], and some related generating series of even zeta values. The generating series of odd MZVs, and alternating odd MZVs, are given by
 $$ \begin{align*} A(z) &= \sum_{r=1}^\infty \zeta(2r+1) z^{2r} = \psi(1) - \frac{1}{2} \psi(1 - z) - \frac{1}{2} \psi(1+z), \\ B(z) &= \sum_{r=1}^\infty (-\zeta(\overline{2r+1})) z^{2r} = \sum_{r=1}^\infty (1 - 2^{-2r}) \zeta(2r+1) z^{2r} = A(z) - A(\tfrac{z}{2}) , \end{align*} $$
$$ \begin{align*} A(z) &= \sum_{r=1}^\infty \zeta(2r+1) z^{2r} = \psi(1) - \frac{1}{2} \psi(1 - z) - \frac{1}{2} \psi(1+z), \\ B(z) &= \sum_{r=1}^\infty (-\zeta(\overline{2r+1})) z^{2r} = \sum_{r=1}^\infty (1 - 2^{-2r}) \zeta(2r+1) z^{2r} = A(z) - A(\tfrac{z}{2}) , \end{align*} $$
where
![]() $ \psi (x) = \frac {\mathrm {d}}{\mathrm {d}x} \log \Gamma (x) $
is the digamma function, the logarithmic derivative of the Gamma function. We keep with the choice established by Zagier taking negatives in the series for alternating MZVs. The generating series for even versions, using the convention that
$ \psi (x) = \frac {\mathrm {d}}{\mathrm {d}x} \log \Gamma (x) $
is the digamma function, the logarithmic derivative of the Gamma function. We keep with the choice established by Zagier taking negatives in the series for alternating MZVs. The generating series for even versions, using the convention that
![]() $ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
, are given by
$ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
, are given by
 $$ \begin{align*} E(z) &= \sum_{r=0}^\infty \zeta(2r) z^{2r-1} = -\frac{\pi}{2} \cot(\pi z) , &\quad F(z) &= \sum_{r=0}^\infty (-\zeta(\overline{2r})) z^{2r-1} = \frac{\pi}{2} \csc(\pi z) . \\ \widetilde{E}(z) &= \sum_{r=1}^\infty \zeta(2r) z^{2r-1} = \frac{1}{2x}-\frac{\pi}{2} \cot(\pi z) , &\quad \widetilde{F}(z) &= \sum_{r=0}^\infty (-\zeta(\overline{2r})) z^{2r-1} = -\frac{1}{2x} + \frac{\pi}{2} \csc(\pi z) . \end{align*} $$
$$ \begin{align*} E(z) &= \sum_{r=0}^\infty \zeta(2r) z^{2r-1} = -\frac{\pi}{2} \cot(\pi z) , &\quad F(z) &= \sum_{r=0}^\infty (-\zeta(\overline{2r})) z^{2r-1} = \frac{\pi}{2} \csc(\pi z) . \\ \widetilde{E}(z) &= \sum_{r=1}^\infty \zeta(2r) z^{2r-1} = \frac{1}{2x}-\frac{\pi}{2} \cot(\pi z) , &\quad \widetilde{F}(z) &= \sum_{r=0}^\infty (-\zeta(\overline{2r})) z^{2r-1} = -\frac{1}{2x} + \frac{\pi}{2} \csc(\pi z) . \end{align*} $$
The
![]() $ \widetilde {\bullet } $
versions, which are missing the polar term, will be convenient later. Let us introduce the following double zeta generating series
$ \widetilde {\bullet } $
versions, which are missing the polar term, will be convenient later. Let us introduce the following double zeta generating series
 $$ \begin{align*} D_{\mathrm{ev}}(x,y) &= \sum_{a,b=1}^\infty \zeta(2a, 2b) x^{2a-1} y^{2b-1} , \quad D_{\mathrm{od}}(x,y) = \sum_{a,b=1}^\infty \zeta(2a + 1, 2b + 1) x^{2a} y^{2b} , \\ D(x,y) &= { \sum_{\substack{a,b=2 \\ a \equiv b \quad\pmod{2}}}^\infty \zeta(a,b) x^{a-1} y^{b-1} = D_{\mathrm{od}}(x,y) + D_{\mathrm{ev}}(x,y). } \end{align*} $$
$$ \begin{align*} D_{\mathrm{ev}}(x,y) &= \sum_{a,b=1}^\infty \zeta(2a, 2b) x^{2a-1} y^{2b-1} , \quad D_{\mathrm{od}}(x,y) = \sum_{a,b=1}^\infty \zeta(2a + 1, 2b + 1) x^{2a} y^{2b} , \\ D(x,y) &= { \sum_{\substack{a,b=2 \\ a \equiv b \quad\pmod{2}}}^\infty \zeta(a,b) x^{a-1} y^{b-1} = D_{\mathrm{od}}(x,y) + D_{\mathrm{ev}}(x,y). } \end{align*} $$
As an intermediate step, let us also introduce the following generating series to capture the shuffle-regularised zetas appearing in Equation (A.7), and in the dihedral symmetries in Equations (A.8) and (A.9), as well as the alternating zeta values as part of the Galois descent result
 $$ \begin{align*} K_{\mathrm{alt}}(x,y) &= \sum_{a,b=1}^\infty \zeta(\overline{2a},\overline{2b}) x^{2a-1} y^{2b-1} , & \quad & K_{\mathrm{ev}}(x,y) = \sum_{a,b=1}^\infty \zeta_{2b-1}(1,\overline{2a}) x^{2a-1} y^{2b-1} , \\ K_{\mathrm{od}}(x,y) &= \sum_{a,b=0}^\infty \zeta_{2b}(1,2a + 1) x^{2a} y^{2b}. \end{align*} $$
$$ \begin{align*} K_{\mathrm{alt}}(x,y) &= \sum_{a,b=1}^\infty \zeta(\overline{2a},\overline{2b}) x^{2a-1} y^{2b-1} , & \quad & K_{\mathrm{ev}}(x,y) = \sum_{a,b=1}^\infty \zeta_{2b-1}(1,\overline{2a}) x^{2a-1} y^{2b-1} , \\ K_{\mathrm{od}}(x,y) &= \sum_{a,b=0}^\infty \zeta_{2b}(1,2a + 1) x^{2a} y^{2b}. \end{align*} $$
Note that we sum from
![]() $ a,b = 0 $
in
$ a,b = 0 $
in
![]() $ K_{\mathrm {od}} $
but will restrict this to start from
$ K_{\mathrm {od}} $
but will restrict this to start from
![]() $ a,b = 1 $
in
$ a,b = 1 $
in
![]() $ D_{\mathrm {od}} $
, on account of the well-known reductions of
$ D_{\mathrm {od}} $
, on account of the well-known reductions of
![]() $ \zeta (1, 2b+1) $
, and
$ \zeta (1, 2b+1) $
, and
![]() $ \zeta (2a+1, 1) $
.
$ \zeta (2a+1, 1) $
.
Generating series for Equation (A.7).
To obtain the generating series
![]() $ G^\star (x,y) $
, we sum the left-hand side of Equation (A.7) weighted by
$ G^\star (x,y) $
, we sum the left-hand side of Equation (A.7) weighted by
![]() $ x^{2a} y^{2b} $
over all
$ x^{2a} y^{2b} $
over all
![]() $ a, b \geq 0 $
.
$ a, b \geq 0 $
.
We find then that the generating series of the first term on the right-hand side is
 $$ \begin{align*} \sum_{a,b=0}^\infty \zeta(\overline{2a+2b+4}) x^{2a} y^{2b} &= \sum_{r=0}^\infty \sum_{s=0}^r \zeta(\overline{2r+4}) x^{2r-2s} y^{2s} \\ &= \sum_{r=0}^\infty \zeta(\overline{2r+4}) \sum_{s=0}^r x^{2r-2s} y^{2s} \\ &= \sum_{r=0}^\infty \zeta(\overline{2r+4}) \cdot \frac{x^{2r+2} - y^{2r+2}}{x^2 - y^2} \\&= - \frac{y \widetilde{F}(x) - x \widetilde{F}(y)}{x y(x^2 - y^2)} . \end{align*} $$
$$ \begin{align*} \sum_{a,b=0}^\infty \zeta(\overline{2a+2b+4}) x^{2a} y^{2b} &= \sum_{r=0}^\infty \sum_{s=0}^r \zeta(\overline{2r+4}) x^{2r-2s} y^{2s} \\ &= \sum_{r=0}^\infty \zeta(\overline{2r+4}) \sum_{s=0}^r x^{2r-2s} y^{2s} \\ &= \sum_{r=0}^\infty \zeta(\overline{2r+4}) \cdot \frac{x^{2r+2} - y^{2r+2}}{x^2 - y^2} \\&= - \frac{y \widetilde{F}(x) - x \widetilde{F}(y)}{x y(x^2 - y^2)} . \end{align*} $$
Likewise, the second leads to
 $$ \begin{align*} \sum_{a,b=0}^\infty (2a+1) \zeta(2a+2) \zeta(\overline{2b+2}) x^{2a} y^{2b} &= \sum_{a=0}^\infty (2a+1) \zeta(2a+2) x^{2a} \cdot \sum_{b=0}^\infty \zeta(\overline{2b+2}) y^{2b} \\ &= \frac{1}{y} \frac{\mathrm{d} \widetilde{E}(x) }{\mathrm{d}x} \cdot \widetilde{F}(y). \end{align*} $$
$$ \begin{align*} \sum_{a,b=0}^\infty (2a+1) \zeta(2a+2) \zeta(\overline{2b+2}) x^{2a} y^{2b} &= \sum_{a=0}^\infty (2a+1) \zeta(2a+2) x^{2a} \cdot \sum_{b=0}^\infty \zeta(\overline{2b+2}) y^{2b} \\ &= \frac{1}{y} \frac{\mathrm{d} \widetilde{E}(x) }{\mathrm{d}x} \cdot \widetilde{F}(y). \end{align*} $$
The third and fourth terms are readily summed to give
 $$ \begin{align*} & \sum_{a,b=0}^\infty \zeta(2a+1) \cdot \sum_{k=1}^{b+1} \zeta(2k+1) \zeta(\overline{2b+2-2k}) x^{2a} y^{2b} = -\frac{1}{y} A(x) A(y) F(y) \\ & \sum_{a,b=0}^\infty \sum_{s=0}^a \zeta(\overline{2s}) \zeta_{2a+1-2s}(1, \overline{2b+2}) x^{2a} y^{2b} = - \frac{1}{y} F(x) K_{\mathrm{ev}}(y,x). \end{align*} $$
$$ \begin{align*} & \sum_{a,b=0}^\infty \zeta(2a+1) \cdot \sum_{k=1}^{b+1} \zeta(2k+1) \zeta(\overline{2b+2-2k}) x^{2a} y^{2b} = -\frac{1}{y} A(x) A(y) F(y) \\ & \sum_{a,b=0}^\infty \sum_{s=0}^a \zeta(\overline{2s}) \zeta_{2a+1-2s}(1, \overline{2b+2}) x^{2a} y^{2b} = - \frac{1}{y} F(x) K_{\mathrm{ev}}(y,x). \end{align*} $$
The last term requires a little care, as the summand
![]() $ \zeta _{0}(1,2a+1) $
does not appear, and so must be discounted via
$ \zeta _{0}(1,2a+1) $
does not appear, and so must be discounted via
![]() $ K_{\mathrm {od}}(x,0) $
, the constant-in-
$ K_{\mathrm {od}}(x,0) $
, the constant-in-
![]() $ y $
term of
$ y $
term of
![]() $ K_{\mathrm {od}}(x,y) $
. That is
$ K_{\mathrm {od}}(x,y) $
. That is
 $$ \begin{align*} & \sum_{a,b=0}^\infty \sum_{s=0}^b \zeta(\overline{2s}) \zeta_{2b+2-2s}(1, 2a+1) x^{2a} y^{2b} = -\frac{1}{y} F(y) ( K_{\mathrm{od}}(x,y) - K_{\mathrm{od}}(x,0) ) . \end{align*} $$
$$ \begin{align*} & \sum_{a,b=0}^\infty \sum_{s=0}^b \zeta(\overline{2s}) \zeta_{2b+2-2s}(1, 2a+1) x^{2a} y^{2b} = -\frac{1}{y} F(y) ( K_{\mathrm{od}}(x,y) - K_{\mathrm{od}}(x,0) ) . \end{align*} $$
This gives us
 $$ \begin{align*} G^\star(x,y) = & \frac{8}{y} A(x) A(y) F(y) + \frac{8}{y} F(x) K_{\mathrm{ev}}(y,x) + \frac{8}{y} F(y) (K_{\mathrm{od}}(x,y) - K_{\mathrm{od}}(x,0)) \\ & - 2 \cdot \frac{y \widetilde{F}(x) - x \widetilde{F}(y)}{x y(x^2 - y^2)} + \frac{4}{y} \frac{\mathrm{d} \widetilde{E}(x) }{\mathrm{d}x} \cdot \widetilde{F}(y). \end{align*} $$
$$ \begin{align*} G^\star(x,y) = & \frac{8}{y} A(x) A(y) F(y) + \frac{8}{y} F(x) K_{\mathrm{ev}}(y,x) + \frac{8}{y} F(y) (K_{\mathrm{od}}(x,y) - K_{\mathrm{od}}(x,0)) \\ & - 2 \cdot \frac{y \widetilde{F}(x) - x \widetilde{F}(y)}{x y(x^2 - y^2)} + \frac{4}{y} \frac{\mathrm{d} \widetilde{E}(x) }{\mathrm{d}x} \cdot \widetilde{F}(y). \end{align*} $$
Generating series for dihedral identities:
The generating series of the form given by summing
![]() $ \sum _{k,\ell =1}^\infty (\bullet ) y^{2k-1} x^{2\ell -1} $
(note the order of the variables), over the left-hand side of Equation (A.8) is simply just
$ \sum _{k,\ell =1}^\infty (\bullet ) y^{2k-1} x^{2\ell -1} $
(note the order of the variables), over the left-hand side of Equation (A.8) is simply just
![]() $ K_{\mathrm {ev}}(x,y) - K_{\mathrm {alt}}(x,y) $
. Then
$ K_{\mathrm {ev}}(x,y) - K_{\mathrm {alt}}(x,y) $
. Then
 $$ \begin{align*} \sum_{k,\ell=1}^\infty \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) y^{2k-1} x^{2\ell-1} &= \sum_{r=2}^\infty \zeta(\overline{2r}) \sum_{k=1}^{r-1} \binom{2r-1}{2k-1} y^{2k-1} x^{2r-2k-1} \\ &= \sum_{r=2}^\infty \zeta(\overline{2r}) \Big\{ {-}y^{2r} + \frac{y}{2} (y-x)^{2r-1} + \frac{y}{2} (y+x)^{2r-1} \Big\} \\ &= -\frac{1}{2x} \Big( \widetilde{F}(y-x) + \widetilde{F}(y+x) - 2 \widetilde{F}(y) \Big). \end{align*} $$
$$ \begin{align*} \sum_{k,\ell=1}^\infty \binom{2k+2\ell-1}{2k-1} \zeta(\overline{2k+2\ell}) y^{2k-1} x^{2\ell-1} &= \sum_{r=2}^\infty \zeta(\overline{2r}) \sum_{k=1}^{r-1} \binom{2r-1}{2k-1} y^{2k-1} x^{2r-2k-1} \\ &= \sum_{r=2}^\infty \zeta(\overline{2r}) \Big\{ {-}y^{2r} + \frac{y}{2} (y-x)^{2r-1} + \frac{y}{2} (y+x)^{2r-1} \Big\} \\ &= -\frac{1}{2x} \Big( \widetilde{F}(y-x) + \widetilde{F}(y+x) - 2 \widetilde{F}(y) \Big). \end{align*} $$
Similarly
 $$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{r=1}^{2k+2\ell-2} (-1)^r \binom{r-1}{2k-1} \zeta(\overline{r})\zeta(2k+2\ell-r) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \sum_{k,\ell=1}^\infty \bigg( {-}\sum_{r=0}^{k+\ell-2} \binom{2r}{2k-1} \zeta(\overline{2r+1}) \zeta(2k+2l-2r-1) \\ &\qquad + \sum_{r=1}^{k+\ell-1} \binom{2r+1}{2k-1} \zeta(\overline{2r}) \zeta(2k+2\ell-2r) \bigg) y^{2k-1} x^{2\ell-1} \\ & \quad = \sum_{r=0}^\infty \sum_{s=1}^\infty \sum_{k=1}^r \bigg( {-} \binom{2r}{2k-1} \zeta(\overline{2r+1}) \zeta(2s-1) + \binom{2r-1}{2k-1} \zeta(\overline{2r}) \zeta(2s) \bigg)y^{2k-1} x^{2s+2r-2k-1}. \end{align*} $$
$$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{r=1}^{2k+2\ell-2} (-1)^r \binom{r-1}{2k-1} \zeta(\overline{r})\zeta(2k+2\ell-r) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \sum_{k,\ell=1}^\infty \bigg( {-}\sum_{r=0}^{k+\ell-2} \binom{2r}{2k-1} \zeta(\overline{2r+1}) \zeta(2k+2l-2r-1) \\ &\qquad + \sum_{r=1}^{k+\ell-1} \binom{2r+1}{2k-1} \zeta(\overline{2r}) \zeta(2k+2\ell-2r) \bigg) y^{2k-1} x^{2\ell-1} \\ & \quad = \sum_{r=0}^\infty \sum_{s=1}^\infty \sum_{k=1}^r \bigg( {-} \binom{2r}{2k-1} \zeta(\overline{2r+1}) \zeta(2s-1) + \binom{2r-1}{2k-1} \zeta(\overline{2r}) \zeta(2s) \bigg)y^{2k-1} x^{2s+2r-2k-1}. \end{align*} $$
The sum over
![]() $ k $
can be evaluated explicitly, and (taking care with the
$ k $
can be evaluated explicitly, and (taking care with the
![]() $ r = 0 $
terms) one obtains
$ r = 0 $
terms) one obtains
 $$ \begin{align*} = \sum_{r,s=1}^\infty & \frac{1}{2} \big( (y-x)^{2r} - (y+x)^{2r} \big) \zeta(\overline{2r+1}) \zeta(2s-1) x^{2s-2} \\[-1ex] & + \sum_{r,s=1}^\infty \frac{1}{2} \big( (y-x)^{2r-1} + (y+x)^{2r-1} \big) \zeta(\overline{2r}) \zeta(2s) x^{2s-1} \\ = -\frac{1}{2} & \big( B(y-x) - B(y+x) \big) A(x) - \frac{1}{2} \big( \widetilde{F}(y-x) + \widetilde{F}(y+x) \big) \widetilde{E}(x) . \end{align*} $$
$$ \begin{align*} = \sum_{r,s=1}^\infty & \frac{1}{2} \big( (y-x)^{2r} - (y+x)^{2r} \big) \zeta(\overline{2r+1}) \zeta(2s-1) x^{2s-2} \\[-1ex] & + \sum_{r,s=1}^\infty \frac{1}{2} \big( (y-x)^{2r-1} + (y+x)^{2r-1} \big) \zeta(\overline{2r}) \zeta(2s) x^{2s-1} \\ = -\frac{1}{2} & \big( B(y-x) - B(y+x) \big) A(x) - \frac{1}{2} \big( \widetilde{F}(y-x) + \widetilde{F}(y+x) \big) \widetilde{E}(x) . \end{align*} $$
Likewise, one finds
 $$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{r=1}^{2k+2\ell-2} \binom{r-1}{2\ell-1} \zeta(\overline{r})\zeta(2k+2\ell-r) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \frac{1}{2} \big( B(y-x) - B(y+x) \big) A(y) + \frac{1}{2} \big( \widetilde{F}(y-x) - \widetilde{F}(y+x) \big) \widetilde{E}(y) , \end{align*} $$
$$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{r=1}^{2k+2\ell-2} \binom{r-1}{2\ell-1} \zeta(\overline{r})\zeta(2k+2\ell-r) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \frac{1}{2} \big( B(y-x) - B(y+x) \big) A(y) + \frac{1}{2} \big( \widetilde{F}(y-x) - \widetilde{F}(y+x) \big) \widetilde{E}(y) , \end{align*} $$
which essentially amounts to switching
![]() $ x \leftrightarrow y $
, and switching the sign between the two terms.
$ x \leftrightarrow y $
, and switching the sign between the two terms.
Overall, one obtains
 $$ \begin{align*} & K_{\mathrm{ev}}(x,y) - K_{\mathrm{alt}}(x,y)\\ &\quad = \frac{1}{2} (A(x) - A(y))(B(x-y) - B(x+y)) + \frac{1}{2} \widetilde{E}(y) (\widetilde{F}(x-y) + \widetilde{F}(x+y)) \\ &\qquad - \frac{1}{2} \widetilde{E}(x) (\widetilde{F}(x-y) - \widetilde{F}(x+y)) - \frac{\widetilde{F}(x+y) - \widetilde{F}(x-y) - 2 \widetilde{F}(y)}{2x}. \end{align*} $$
$$ \begin{align*} & K_{\mathrm{ev}}(x,y) - K_{\mathrm{alt}}(x,y)\\ &\quad = \frac{1}{2} (A(x) - A(y))(B(x-y) - B(x+y)) + \frac{1}{2} \widetilde{E}(y) (\widetilde{F}(x-y) + \widetilde{F}(x+y)) \\ &\qquad - \frac{1}{2} \widetilde{E}(x) (\widetilde{F}(x-y) - \widetilde{F}(x+y)) - \frac{\widetilde{F}(x+y) - \widetilde{F}(x-y) - 2 \widetilde{F}(y)}{2x}. \end{align*} $$
In exactly the same way, one finds for the second dihedral identity Equation (A.9) – taking care with the terms
![]() $ \zeta (1,2b+1) $
and
$ \zeta (1,2b+1) $
and
![]() $ \zeta (2a+1,1) $
missing from
$ \zeta (2a+1,1) $
missing from
![]() $ D_{\mathrm {od}}(x,y) $
– that
$ D_{\mathrm {od}}(x,y) $
– that
 $$ \begin{align*} & K_{\mathrm{od}}(x,y) - D_{\mathrm{od}}(x,y)\\ &\quad = 2\zeta(2) + \frac{1}{2} (A(x) - A(y))(A(x) - A(x-y) + A(y) - A(x+y)) \\ &\qquad + \frac{1}{2} ( \widetilde{E}(x) - \widetilde{E}(y) ) (\widetilde{E}(x) + \widetilde{E}(y) - \widetilde{E}(x-y)) + \frac{1}{2} \big( \widetilde{E}(x) + \widetilde{E}(y) \big) \widetilde{E}(x+y) \\ &\qquad - \frac{\widetilde{E}(x-y) + \widetilde{E}(x+y)}{2x} - \frac{\widetilde{E}(y)}{y}. \end{align*} $$
$$ \begin{align*} & K_{\mathrm{od}}(x,y) - D_{\mathrm{od}}(x,y)\\ &\quad = 2\zeta(2) + \frac{1}{2} (A(x) - A(y))(A(x) - A(x-y) + A(y) - A(x+y)) \\ &\qquad + \frac{1}{2} ( \widetilde{E}(x) - \widetilde{E}(y) ) (\widetilde{E}(x) + \widetilde{E}(y) - \widetilde{E}(x-y)) + \frac{1}{2} \big( \widetilde{E}(x) + \widetilde{E}(y) \big) \widetilde{E}(x+y) \\ &\qquad - \frac{\widetilde{E}(x-y) + \widetilde{E}(x+y)}{2x} - \frac{\widetilde{E}(y)}{y}. \end{align*} $$
One may observe from this, that
Generating series for Equation (A.10):
Now, we compute the generating series for the identity from Proposition A.3. Again, taking
![]() $ \sum _{k,\ell =1}^\infty (\bullet )y^{2k-1} x^{2\ell -1} $
, note the variable order, we find the left-hand side to be just
$ \sum _{k,\ell =1}^\infty (\bullet )y^{2k-1} x^{2\ell -1} $
, note the variable order, we find the left-hand side to be just
![]() $ K_{\mathrm {alt}}(x,y) $
. The binomial times double zeta terms can be summed as follows
$ K_{\mathrm {alt}}(x,y) $
. The binomial times double zeta terms can be summed as follows
 $$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \sum_{r,s=1}^\infty \Big\{ \zeta(2r,2s) \cdot 2^{-2s} \sum_{k=1}^s \binom{2s-1}{2k-1} x^{2r + 2s - 2k-1} y^{2k-1} \\ &\qquad + \zeta(2r + 1, 2s + 1) \cdot 2^{-2s-1} \sum_{k=1}^s \binom{2s}{2k-1} x^{2r + 2s + 1 - 2k} y^{2k-1} \Big\} \\ &\quad = \frac{1}{4} \sum_{r,s=1}^\infty \Big\{ \zeta(2r,2s) x^{2r-1} \Big\{ \Big( \frac{x+y}{2} \Big)^{2s-1} - \Big( \frac{x-y}{2} \Big)^{2s-1} \Big\} \\ &\qquad + \zeta(2r+1,2s+1) x^{2r} \Big\{ \Big( \frac{x+y}{2} \Big)^{2s} - \Big( \frac{x-y}{2} \Big)^{2s} \Big\} \Big\} \\ &\quad = \frac{1}{4} \Big( D\Big(x, \frac{x+y}{2}\Big) - D\Big(x, \frac{x-y}{2}\Big) \Big), \end{align*} $$
$$ \begin{align*} & \sum_{k,\ell=1}^\infty \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2k-1} \zeta(2k+2\ell-i,i) \cdot y^{2k-1} x^{2\ell-1} \\ &\quad = \sum_{r,s=1}^\infty \Big\{ \zeta(2r,2s) \cdot 2^{-2s} \sum_{k=1}^s \binom{2s-1}{2k-1} x^{2r + 2s - 2k-1} y^{2k-1} \\ &\qquad + \zeta(2r + 1, 2s + 1) \cdot 2^{-2s-1} \sum_{k=1}^s \binom{2s}{2k-1} x^{2r + 2s + 1 - 2k} y^{2k-1} \Big\} \\ &\quad = \frac{1}{4} \sum_{r,s=1}^\infty \Big\{ \zeta(2r,2s) x^{2r-1} \Big\{ \Big( \frac{x+y}{2} \Big)^{2s-1} - \Big( \frac{x-y}{2} \Big)^{2s-1} \Big\} \\ &\qquad + \zeta(2r+1,2s+1) x^{2r} \Big\{ \Big( \frac{x+y}{2} \Big)^{2s} - \Big( \frac{x-y}{2} \Big)^{2s} \Big\} \Big\} \\ &\quad = \frac{1}{4} \Big( D\Big(x, \frac{x+y}{2}\Big) - D\Big(x, \frac{x-y}{2}\Big) \Big), \end{align*} $$
The other terms may be handled similarly. Overall, we find the generating series identity
 $$ \begin{align*} K_{\mathrm{alt}}(x,y) = & \frac{1}{4} \Big( D\Big(x, \frac{x+y}{2}\Big) - D\Big(x, \frac{x-y}{2}\Big) + D\Big(\frac{x+y}{2},y\Big) - D\Big(-\frac{x-y}{2},y\Big) \Big) - D_{\mathrm{ev}}(x,y) \\ & + \frac{1}{4} \Big( \widetilde{E}\Big(\frac{x+y}{2}\Big) - \widetilde{E}\Big(\frac{x-y}{2}\Big) \Big) \widetilde{E}(x) - \frac{1}{4} A(x) \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) \\ & + \frac{3x - y}{4x(x-y)} \widetilde{E}\Big(\frac{x-y}{2}\Big) - \frac{3x + y}{4x(x+y)} \widetilde{E}\Big( \frac{x+y}{2} \Big) + \frac{1}{2x} \widetilde{E}\Big(\frac{y}{2} \Big). \end{align*} $$
$$ \begin{align*} K_{\mathrm{alt}}(x,y) = & \frac{1}{4} \Big( D\Big(x, \frac{x+y}{2}\Big) - D\Big(x, \frac{x-y}{2}\Big) + D\Big(\frac{x+y}{2},y\Big) - D\Big(-\frac{x-y}{2},y\Big) \Big) - D_{\mathrm{ev}}(x,y) \\ & + \frac{1}{4} \Big( \widetilde{E}\Big(\frac{x+y}{2}\Big) - \widetilde{E}\Big(\frac{x-y}{2}\Big) \Big) \widetilde{E}(x) - \frac{1}{4} A(x) \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) \\ & + \frac{3x - y}{4x(x-y)} \widetilde{E}\Big(\frac{x-y}{2}\Big) - \frac{3x + y}{4x(x+y)} \widetilde{E}\Big( \frac{x+y}{2} \Big) + \frac{1}{2x} \widetilde{E}\Big(\frac{y}{2} \Big). \end{align*} $$
A.7 Explicit evaluations for
 $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
After substituting the previous generating series into the expression for
![]() $ G^\star (x,y) $
given via Equation (A.7), performing a nontrivial amount of trigonometric manipulation, we find
$ G^\star (x,y) $
given via Equation (A.7), performing a nontrivial amount of trigonometric manipulation, we find
 $$ \begin{align*} G^\star(x,y) &= \frac{2 F(x)}{y} \Big( {-}D\Big(\frac{x-y}{2}, x\Big) - D\Big(y, -\frac{x-y}{2}\Big) + D\Big(y, \frac{x+y}{2}\Big) + D\Big(\frac{x+y}{2}, x\Big) \Big) \\ &\quad - \frac{8 F(x)}{y} D_{\mathrm{ev}}(y,x) + \frac{8 F(y)}{y} D_{\mathrm{od}}(x,y) \\ &\quad + \frac{2 F(x)}{y} \Big\{ - A(y) \cdot \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) + 2 \big( A(x) - A(y) \big) \cdot \big( B(x+y) - B(x-y) \big) \Big\} \\ &\quad + \frac{4 F(y)}{y} \Big\{ A(x) \cdot \big(A(x) - 2 A(y) \big) + \big(A(x) - A(y) \big) \cdot \big( A(x) + A(y) - A(x-y) - A(x+y) \big) \Big\} \\ &\quad - 3 \zeta(2) \cdot \frac{1 - y \widetilde{E}(y)}{y^2} \cdot \sec\Big(\frac{\pi(x-y)}{2} \Big) \sec\Big( \frac{\pi(x+y)}{2} \Big) - \frac{2 \big( x F(x) - y F(y) \big)}{y^2(x^2-y^2)} \\ &\quad + \frac{4 F(x)}{y} \bigg\{ \widetilde{E}(x) \Big( \frac{1}{y} + \widetilde{E}(x+y) - \widetilde{F}(x-y) \Big) - \frac{\widetilde{E}(\tfrac{1}{2} (x+y))}{x+y} + \frac{\widetilde{E}(\tfrac{1}{2} (x-y))}{x-y} \bigg\} \\ &\quad + \frac{4 F(y)}{y} \bigg\{ 2\zeta(2) + \widetilde{E}(y)^2 - \frac{2 \widetilde{E}(y)}{y} + \frac{x \widetilde{E}(x) - y \widetilde{E}(y)}{x^2 - y^2} \\ & \quad - \frac{(x+y) \widetilde{E}(x-y) - (x-y) \widetilde{E}(x+y)}{2 x y} \bigg\}. \end{align*} $$
$$ \begin{align*} G^\star(x,y) &= \frac{2 F(x)}{y} \Big( {-}D\Big(\frac{x-y}{2}, x\Big) - D\Big(y, -\frac{x-y}{2}\Big) + D\Big(y, \frac{x+y}{2}\Big) + D\Big(\frac{x+y}{2}, x\Big) \Big) \\ &\quad - \frac{8 F(x)}{y} D_{\mathrm{ev}}(y,x) + \frac{8 F(y)}{y} D_{\mathrm{od}}(x,y) \\ &\quad + \frac{2 F(x)}{y} \Big\{ - A(y) \cdot \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) + 2 \big( A(x) - A(y) \big) \cdot \big( B(x+y) - B(x-y) \big) \Big\} \\ &\quad + \frac{4 F(y)}{y} \Big\{ A(x) \cdot \big(A(x) - 2 A(y) \big) + \big(A(x) - A(y) \big) \cdot \big( A(x) + A(y) - A(x-y) - A(x+y) \big) \Big\} \\ &\quad - 3 \zeta(2) \cdot \frac{1 - y \widetilde{E}(y)}{y^2} \cdot \sec\Big(\frac{\pi(x-y)}{2} \Big) \sec\Big( \frac{\pi(x+y)}{2} \Big) - \frac{2 \big( x F(x) - y F(y) \big)}{y^2(x^2-y^2)} \\ &\quad + \frac{4 F(x)}{y} \bigg\{ \widetilde{E}(x) \Big( \frac{1}{y} + \widetilde{E}(x+y) - \widetilde{F}(x-y) \Big) - \frac{\widetilde{E}(\tfrac{1}{2} (x+y))}{x+y} + \frac{\widetilde{E}(\tfrac{1}{2} (x-y))}{x-y} \bigg\} \\ &\quad + \frac{4 F(y)}{y} \bigg\{ 2\zeta(2) + \widetilde{E}(y)^2 - \frac{2 \widetilde{E}(y)}{y} + \frac{x \widetilde{E}(x) - y \widetilde{E}(y)}{x^2 - y^2} \\ & \quad - \frac{(x+y) \widetilde{E}(x-y) - (x-y) \widetilde{E}(x+y)}{2 x y} \bigg\}. \end{align*} $$
If one so desires, the following explicit formula for the individual coefficient
![]() $\zeta ^\star (\{2\}^a, 4, \{2\}^b)$
can be extracted from the above.
$\zeta ^\star (\{2\}^a, 4, \{2\}^b)$
can be extracted from the above.
Theorem A.6 (Evaluation of
 $\zeta ^\star (\{2\}^a, 4, \{2\}^b)$
via double zeta valuesFootnote
2
).
$\zeta ^\star (\{2\}^a, 4, \{2\}^b)$
via double zeta valuesFootnote
2
).
Write as shorthand
![]() $ \zeta (\overline {n}) = -(1-2^{1-n})\zeta (n) $
, and employ the conventions that
$ \zeta (\overline {n}) = -(1-2^{1-n})\zeta (n) $
, and employ the conventions that
![]() $ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
and
$ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
and
![]() $ \zeta (1) = 0 $
. However, no further regularisation is necessary. Denote by
$ \zeta (1) = 0 $
. However, no further regularisation is necessary. Denote by
![]() $ E_n $
the
$ E_n $
the
![]() $ n $
-th Euler number, given as the coefficients of
$ n $
-th Euler number, given as the coefficients of
![]() $ \operatorname {sech}(t) = \sum _{n=0}^\infty \frac {E_n}{n!} t^n . $
Then for any
$ \operatorname {sech}(t) = \sum _{n=0}^\infty \frac {E_n}{n!} t^n . $
Then for any
![]() $ a, b \in \mathbb {Z}_{\geq 0} $
, the following evaluation holds, where we assume all summation variables start from
$ a, b \in \mathbb {Z}_{\geq 0} $
, the following evaluation holds, where we assume all summation variables start from
![]() $ 0 $
,
$ 0 $
,

A.8 Explicit evaluations for
 $ \zeta (\{2\}^a, 4, \{2\}^b) $
$ \zeta (\{2\}^a, 4, \{2\}^b) $
By substituting the expression for
![]() $ G^\star (x,y) $
into Equation (A.2), and finding
$ G^\star (x,y) $
into Equation (A.2), and finding
![]() $ G(x,y) $
via
$ G(x,y) $
via
 $$\begin{align*}G(x,y) = \sum_{a,b=0}^\infty (-1)^{a+b} \zeta(\{2\}^a, 4, \{2\}^b) x^{2a} y^{2b} = G^\star(y,x) \frac{\sin(\pi x)}{\pi x} \frac{\sin(\pi y)}{\pi y} , \end{align*}$$
$$\begin{align*}G(x,y) = \sum_{a,b=0}^\infty (-1)^{a+b} \zeta(\{2\}^a, 4, \{2\}^b) x^{2a} y^{2b} = G^\star(y,x) \frac{\sin(\pi x)}{\pi x} \frac{\sin(\pi y)}{\pi y} , \end{align*}$$
we obtain the following explicit expression for the generating series,
 $$ \begin{align*} G(x,y) &= \frac{\sin(\pi x)}{\pi x^2 y} \Big( {-}D\Big(-\frac{x-y}{2}, x\Big) - D\Big(x, \frac{x-y}{2}\Big) + D\Big(x, \frac{x+y}{2}\Big) + D\Big(\frac{x+y}{2}, y\Big) \Big) \\ &\quad - \frac{4\sin(\pi x)}{\pi x^2 y} D_{\mathrm{ev}}(x,y) + \frac{\sin(\pi y)}{\pi x^2 y} D_{\mathrm{od}}(y,x) \\ &\quad - \frac{\sin(\pi x)}{\pi x^2 y} \Big\{ A(x) \cdot \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) + 2 \big( A(x) - A(y) \big) \cdot \big( B(x+y) - B(x-y) \big) \Big\} \\ &\quad - \frac{\sin(\pi y)}{\pi x^2 y} \Big\{ A(y) \cdot \big(2A(x) - A(y) \big) + \big(A(x) - A(y) \big) \cdot \big( A(x) + A(y) - A(x-y) - A(x+y) \big) \Big\} \\ &\quad - 3 \zeta(2) \cdot \frac{1 - x \widetilde{E}(x)}{x^2} \cdot \sec\Big(\frac{\pi(x-y)}{2} \Big) \sec\Big( \frac{\pi(x+y)}{2} \Big) \frac{\sin(\pi x)}{\pi x}\frac{\sin(\pi y)}{\pi y} \\ & \quad - \frac{1}{x^2(x^2-y^2)} \Big( \frac{\sin(\pi x)}{\pi x} - \frac{\sin(\pi y)}{\pi y} \Big)\\ &\quad + \frac{2\sin(\pi x)}{\pi x^2 y} \bigg\{ \widetilde{E}(y) \Big( \frac{1}{x} + \widetilde{E}(x+y) + \widetilde{F}(x-y) \Big) - \frac{\widetilde{E}(\tfrac{1}{2} (x+y))}{x+y} + \frac{\widetilde{E}(\tfrac{1}{2} (x-y))}{x-y} \bigg\} \\ &\quad + \frac{2\sin(\pi y)}{\pi x^2 y} \bigg\{ 2\zeta(2) + \widetilde{E}(x)^2 - \frac{2 \widetilde{E}(x)}{x} + \frac{x \widetilde{E}(x) - y \widetilde{E}(y)}{x^2 - y^2} \\ & \quad + \frac{(x+y) \widetilde{E}(x-y) - (x-y) \widetilde{E}(x+y)}{2 x y} \bigg\} . \end{align*} $$
$$ \begin{align*} G(x,y) &= \frac{\sin(\pi x)}{\pi x^2 y} \Big( {-}D\Big(-\frac{x-y}{2}, x\Big) - D\Big(x, \frac{x-y}{2}\Big) + D\Big(x, \frac{x+y}{2}\Big) + D\Big(\frac{x+y}{2}, y\Big) \Big) \\ &\quad - \frac{4\sin(\pi x)}{\pi x^2 y} D_{\mathrm{ev}}(x,y) + \frac{\sin(\pi y)}{\pi x^2 y} D_{\mathrm{od}}(y,x) \\ &\quad - \frac{\sin(\pi x)}{\pi x^2 y} \Big\{ A(x) \cdot \Big( A\Big( \frac{x+y}{2} \Big) - A\Big( \frac{x-y}{2} \Big) \Big) + 2 \big( A(x) - A(y) \big) \cdot \big( B(x+y) - B(x-y) \big) \Big\} \\ &\quad - \frac{\sin(\pi y)}{\pi x^2 y} \Big\{ A(y) \cdot \big(2A(x) - A(y) \big) + \big(A(x) - A(y) \big) \cdot \big( A(x) + A(y) - A(x-y) - A(x+y) \big) \Big\} \\ &\quad - 3 \zeta(2) \cdot \frac{1 - x \widetilde{E}(x)}{x^2} \cdot \sec\Big(\frac{\pi(x-y)}{2} \Big) \sec\Big( \frac{\pi(x+y)}{2} \Big) \frac{\sin(\pi x)}{\pi x}\frac{\sin(\pi y)}{\pi y} \\ & \quad - \frac{1}{x^2(x^2-y^2)} \Big( \frac{\sin(\pi x)}{\pi x} - \frac{\sin(\pi y)}{\pi y} \Big)\\ &\quad + \frac{2\sin(\pi x)}{\pi x^2 y} \bigg\{ \widetilde{E}(y) \Big( \frac{1}{x} + \widetilde{E}(x+y) + \widetilde{F}(x-y) \Big) - \frac{\widetilde{E}(\tfrac{1}{2} (x+y))}{x+y} + \frac{\widetilde{E}(\tfrac{1}{2} (x-y))}{x-y} \bigg\} \\ &\quad + \frac{2\sin(\pi y)}{\pi x^2 y} \bigg\{ 2\zeta(2) + \widetilde{E}(x)^2 - \frac{2 \widetilde{E}(x)}{x} + \frac{x \widetilde{E}(x) - y \widetilde{E}(y)}{x^2 - y^2} \\ & \quad + \frac{(x+y) \widetilde{E}(x-y) - (x-y) \widetilde{E}(x+y)}{2 x y} \bigg\} . \end{align*} $$
If one desires, the following explicit formula for the individual coefficient
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
can be extracted from the above.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
can be extracted from the above.
Theorem A.7 (Evaluation of
 $\zeta (\{2\}^a, 4, \{2\}^b)$
via double zeta valuesFootnote
3
).
$\zeta (\{2\}^a, 4, \{2\}^b)$
via double zeta valuesFootnote
3
).
Write as shorthand
![]() $ \zeta (\overline {n}) = -(1-2^{1-n})\zeta (n) $
, and employ the conventions that
$ \zeta (\overline {n}) = -(1-2^{1-n})\zeta (n) $
, and employ the conventions that
![]() $ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
and
$ \zeta (0) = \zeta (\overline {0}) = -\frac {1}{2} $
and
![]() $ \zeta (1) = 0 $
. However, no further regularisation is necessary. Denote by
$ \zeta (1) = 0 $
. However, no further regularisation is necessary. Denote by
![]() $ E_n $
the
$ E_n $
the
![]() $ n $
-th Euler number, given as the coefficients of
$ n $
-th Euler number, given as the coefficients of
![]() $ \operatorname {sech}(t) = \sum _{n=0}^\infty \frac {E_n}{n!} t^n . $
Then for any
$ \operatorname {sech}(t) = \sum _{n=0}^\infty \frac {E_n}{n!} t^n . $
Then for any
![]() $ a, b \in \mathbb {Z}_{\geq 0} $
, the following evaluation holds, where we assume all summation variables start from
$ a, b \in \mathbb {Z}_{\geq 0} $
, the following evaluation holds, where we assume all summation variables start from
![]() $ 0 $
,
$ 0 $
,

In particular, we obtain the following corollary on the reduction of
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
modulo products. In essence, it extracts those double zeta terms above, which are not multiplied by a power of
$ \zeta (\{2\}^a, 4, \{2\}^b) $
modulo products. In essence, it extracts those double zeta terms above, which are not multiplied by a power of
![]() $ \pi $
.
$ \pi $
.
Corollary A.8. Modulo decomposables (i.e. products of MZVs), the following evaluation holds

B Motivic evaluation of
 $ \zeta ^{\mathfrak {m}}(\{2\}^a, 4, \{2\}^b) $
via motivic double zeta values
$ \zeta ^{\mathfrak {m}}(\{2\}^a, 4, \{2\}^b) $
via motivic double zeta values
In order to verify that the evaluation of
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
in Section A.8 (or at least, the evaluation in Corollary A.8) is motivic, we only need to show that the various ingredients used in Appendix A are motivic. More precisely, we need to show that Proposition A.3 and Equation (A.7) are motivic. All other identities used in the derivation of Corollary A.8 and Theorems A.6 and A.7 were obtained from the shuffle or stuffle product, and so are automatically motivic. The shuffle product is motivic by definition, for the stuffle-product, see [Reference Racinet34, Reference Soudères37].
$ \zeta (\{2\}^a, 4, \{2\}^b) $
in Section A.8 (or at least, the evaluation in Corollary A.8) is motivic, we only need to show that the various ingredients used in Appendix A are motivic. More precisely, we need to show that Proposition A.3 and Equation (A.7) are motivic. All other identities used in the derivation of Corollary A.8 and Theorems A.6 and A.7 were obtained from the shuffle or stuffle product, and so are automatically motivic. The shuffle product is motivic by definition, for the stuffle-product, see [Reference Racinet34, Reference Soudères37].
Framework of alternating motivic MZVs:
We note, here, that the motivic MZV framework of Section 2.1 generalises readily to the case of alternating motivic MZVs. For the technical details of this, we refer to [Reference Glanois18, Reference Glanois19]; the most important points are the comodule of alternating motivic MZVs
![]() $ \mathcal {H}^{(2)} $
is obtained by extending Definition 2.1 to allow
$ \mathcal {H}^{(2)} $
is obtained by extending Definition 2.1 to allow
![]() $ a_i \in \{0, \pm 1 \} $
(although functoriality in a useful form only applies when all
$ a_i \in \{0, \pm 1 \} $
(although functoriality in a useful form only applies when all
![]() $ a_i \in \{ 0, 1 \}$
). Then for a tuple
$ a_i \in \{ 0, 1 \}$
). Then for a tuple
![]() $ (k_1,\ldots ,k_d) $
of positive integers, and
$ (k_1,\ldots ,k_d) $
of positive integers, and
![]() $ (\varepsilon _1,\ldots ,\varepsilon _d) \in \{\pm 1\}^d $
of signs, and
$ (\varepsilon _1,\ldots ,\varepsilon _d) \in \{\pm 1\}^d $
of signs, and
![]() $ \ell \geq 0 $
, we define the motivic alternating MZV by
$ \ell \geq 0 $
, we define the motivic alternating MZV by

where
![]() $ \eta _i = \varepsilon _i \varepsilon _{i+1} \cdots \varepsilon _d $
, mimicking the integral representation of alternating MZVs in Equation (A.1). One can again streamline the notation by dropping the
$ \eta _i = \varepsilon _i \varepsilon _{i+1} \cdots \varepsilon _d $
, mimicking the integral representation of alternating MZVs in Equation (A.1). One can again streamline the notation by dropping the
![]() $ \varepsilon _i $
’s and writing
$ \varepsilon _i $
’s and writing
![]() $ \overline {k_i} $
if
$ \overline {k_i} $
if
![]() $ \varepsilon _i = -1 $
, and just
$ \varepsilon _i = -1 $
, and just
![]() $ k_i $
if
$ k_i $
if
![]() $ \varepsilon _i = 1 $
. Then
$ \varepsilon _i = 1 $
. Then ![]() and
and
![]() $ \mathcal {L}^{(2)} = \mathcal {A}^{(2)}_{>0} / \mathcal {A}^{(2)}_{>0}\mathcal {A}^{(2)}_{>0} $
define the obvious extensions of the Hopf algebra and the Lie coalgebra of irreducibles. The coaction
$ \mathcal {L}^{(2)} = \mathcal {A}^{(2)}_{>0} / \mathcal {A}^{(2)}_{>0}\mathcal {A}^{(2)}_{>0} $
define the obvious extensions of the Hopf algebra and the Lie coalgebra of irreducibles. The coaction
![]() $ \Delta \colon \mathcal {H}^{(2)} \to \mathcal {A}^{(2)} \otimes \mathcal {H}^{(2)} $
is defined by the same formula as in Equation (2.2), and the infinitesimal derivations
$ \Delta \colon \mathcal {H}^{(2)} \to \mathcal {A}^{(2)} \otimes \mathcal {H}^{(2)} $
is defined by the same formula as in Equation (2.2), and the infinitesimal derivations
![]() $ \operatorname {\mathrm {D}}_r \colon \mathcal {H}^{(2)} \to \mathcal {L}^{(2)}_r \otimes \mathcal {H}^{(2)} $
, with
$ \operatorname {\mathrm {D}}_r \colon \mathcal {H}^{(2)} \to \mathcal {L}^{(2)}_r \otimes \mathcal {H}^{(2)} $
, with
![]() $ \mathcal {L}^{(2)}_r $
the weight
$ \mathcal {L}^{(2)}_r $
the weight
![]() $ r $
component of
$ r $
component of
![]() $ \mathcal {L}^{(2)} $
, are given by the same formula as in Equation (2.3).
$ \mathcal {L}^{(2)} $
, are given by the same formula as in Equation (2.3).
For alternating motivic MZVs,
![]() $ \operatorname {\mathrm {D}}_1 $
plays a nontrivial role, as the weight 1 alternating MZV
$ \operatorname {\mathrm {D}}_1 $
plays a nontrivial role, as the weight 1 alternating MZV
![]() $ \zeta ^{\mathfrak {m}}(\overline {1}) = \log ^{\mathfrak {m}}(2) $
is nonzero. The analogue of Brown’s [Reference Brown5] characterisation of
$ \zeta ^{\mathfrak {m}}(\overline {1}) = \log ^{\mathfrak {m}}(2) $
is nonzero. The analogue of Brown’s [Reference Brown5] characterisation of
![]() $ \ker \operatorname {\mathrm {D}}_{<N} $
in the alternating case is given by Glanois as follows.
$ \ker \operatorname {\mathrm {D}}_{<N} $
in the alternating case is given by Glanois as follows.
Theorem B.1 (Glanois, Corollary 2.4.5 [Reference Glanois18]).
Let
![]() $ N \geq 1 $
, and denote by
$ N \geq 1 $
, and denote by
![]() $ \operatorname {\mathrm {D}}_{<N} = \bigoplus _{1 \leq 2r+1 < N} \operatorname {\mathrm {D}}_{2r+1} $
. Then in weight
$ \operatorname {\mathrm {D}}_{<N} = \bigoplus _{1 \leq 2r+1 < N} \operatorname {\mathrm {D}}_{2r+1} $
. Then in weight
![]() $ N $
, the kernel of
$ N $
, the kernel of
![]() $ D_{<N} $
on alternating motivic MZVs is one dimensional:
$ D_{<N} $
on alternating motivic MZVs is one dimensional:
 $$\begin{align*}\ker \operatorname{\mathrm{D}}_{<N} \cap \mathcal{H}^{(2)}_N = \begin{cases} \mathbb{Q} \zeta^{\mathfrak{m}}(\overline{1}) = \mathbb{Q} \log^{\mathfrak{m}}(2) & \text{if}\ N = 1 \\ \mathbb{Q} \zeta^{\mathfrak{m}}(N) & \text{if}\ N>1 . \end{cases} \end{align*}$$
$$\begin{align*}\ker \operatorname{\mathrm{D}}_{<N} \cap \mathcal{H}^{(2)}_N = \begin{cases} \mathbb{Q} \zeta^{\mathfrak{m}}(\overline{1}) = \mathbb{Q} \log^{\mathfrak{m}}(2) & \text{if}\ N = 1 \\ \mathbb{Q} \zeta^{\mathfrak{m}}(N) & \text{if}\ N>1 . \end{cases} \end{align*}$$
Since the identities we wish to lift involve alternating MZV terms in a nontrivial way, we necessarily have to use Glanois’s criterion to verify the motivic lift, even if, as it happens,
![]() $ \operatorname {\mathrm {D}}_1 = 0 $
in each case.
$ \operatorname {\mathrm {D}}_1 = 0 $
in each case.
B.1 Motivic version of Proposition A.3
We prove the following proposition which claims that Proposition A.3 lifts to a motivic version.
Proposition B.2 (Motivic Galois descent of
 $ \zeta ^{\mathfrak {m}}(\overline {2\ell },\overline {2k}) $
).
$ \zeta ^{\mathfrak {m}}(\overline {2\ell },\overline {2k}) $
).
The alternating motivic double zeta value
![]() $ \zeta ^{\mathfrak {m}}(\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 motivic MZVs as follows
$ \zeta ^{\mathfrak {m}}(\overline {2\ell },\overline {2k}) $
enjoys a Galois descent to classical depth 2 motivic MZVs as follows
 $$ \begin{align} \nonumber \zeta^{\mathfrak{m}}(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta^{\mathfrak{m}}(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta^{\mathfrak{m}}(i,2k+2\ell-i) \bigg\} \\ & -\zeta^{\mathfrak{m}}(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta^{\mathfrak{m}}(r) \zeta^{\mathfrak{m}}(2k+2\ell-r) \\ \nonumber & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta^{\mathfrak{m}}(2k + 2\ell) . \end{align} $$
$$ \begin{align} \nonumber \zeta^{\mathfrak{m}}(\overline{2\ell},\overline{2k}) = & \sum_{i=2}^{2k + 2\ell - 2} 2^{-i} \bigg\{ \binom{i-1}{2k-1} \zeta^{\mathfrak{m}}(2k+2\ell-i,i) + \binom{i-1}{2\ell-1} \zeta^{\mathfrak{m}}(i,2k+2\ell-i) \bigg\} \\ & -\zeta^{\mathfrak{m}}(2\ell,2k) + \sum_{r=2}^{2k+2\ell-2} (-2)^{-r} \binom{r-1}{2k-1} \zeta^{\mathfrak{m}}(r) \zeta^{\mathfrak{m}}(2k+2\ell-r) \\ \nonumber & - 2^{-2k-2\ell} \bigg\{ 2 \binom{2k+2\ell-2}{2k-1} + \binom{2k+2\ell-1}{2k-1} \bigg\} \zeta^{\mathfrak{m}}(2k + 2\ell) . \end{align} $$
Proof. We compute
![]() ${\operatorname {\mathrm {D}}}_{2r+1}$
of both sides, and verify they agree for
${\operatorname {\mathrm {D}}}_{2r+1}$
of both sides, and verify they agree for
![]() $1 \leq r \leq k+\ell -2$
. The case
$1 \leq r \leq k+\ell -2$
. The case
![]() $r = 0$
does not play a role, since
$r = 0$
does not play a role, since
![]() ${\operatorname {\mathrm {D}}}_1$
is known to be exactly zero by the Galois descent property established in [Reference Glanois18]; alternatively, one can directly compute it and see there is no contribution since the sequences
${\operatorname {\mathrm {D}}}_1$
is known to be exactly zero by the Galois descent property established in [Reference Glanois18]; alternatively, one can directly compute it and see there is no contribution since the sequences
![]() $(0, 1, -1), (0, -1, 1), (-1,1,0), (1,-1,0)$
which give rise to
$(0, 1, -1), (0, -1, 1), (-1,1,0), (1,-1,0)$
which give rise to
![]() $ \log ^{\mathfrak {l}}(2)$
are not present in the integral representation of any term. In the case,
$ \log ^{\mathfrak {l}}(2)$
are not present in the integral representation of any term. In the case,
![]() $r = k + \ell -1$
,
$r = k + \ell -1$
,
![]() ${\operatorname {\mathrm {D}}}_{2k+2\ell -1}$
is quickly checked to vanish, as only
${\operatorname {\mathrm {D}}}_{2k+2\ell -1}$
is quickly checked to vanish, as only
![]() $\zeta ^{\mathfrak {m}}(1) = 0$
appears in the right-hand tensor factor.
$\zeta ^{\mathfrak {m}}(1) = 0$
appears in the right-hand tensor factor.
Computation of
 $ {\operatorname {\mathrm {D}}}_{2r+1} \zeta ^{\mathfrak {m}}(\overline {2a},\overline {2b})$
and
$ {\operatorname {\mathrm {D}}}_{2r+1} \zeta ^{\mathfrak {m}}(\overline {2a},\overline {2b})$
and
 ${\operatorname {\mathrm {D}}}_{2r+1} \zeta ^{\mathfrak {m}}(2a, 2b)$
${\operatorname {\mathrm {D}}}_{2r+1} \zeta ^{\mathfrak {m}}(2a, 2b)$
We see that only the following subsequences can contribute to the motivic coaction. This is because any subsequence must start or end one of the three nonzero entries; one then checks whether the length
![]() $ 2r+1 $
subsequences which start/end at these points actually contribute
$ 2r+1 $
subsequences which start/end at these points actually contribute

We find
 $$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\overline{2a}, \overline{2b}) \\ &\quad = -\delta_{a \leq r} \zeta_{2r + 1 - 2a}^{\mathfrak{l}}(\overline{2a}) \otimes \zeta(2a + 2b - 2r - 1) + \delta_{b\leq r} \zeta_{2r + 1 - 2b}^{\mathfrak{l}}(\overline{2b}) \otimes \zeta^{\mathfrak{m}}(2a + 2b - 2r - 1) \\ &\quad = \bigg( \binom{2r}{2a-1} - \binom{2r}{2b-1} \bigg) \zeta^{\mathfrak{l}}(\overline{2r+1}) \otimes \zeta(2a + 2b - 2r - 1) \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\overline{2a}, \overline{2b}) \\ &\quad = -\delta_{a \leq r} \zeta_{2r + 1 - 2a}^{\mathfrak{l}}(\overline{2a}) \otimes \zeta(2a + 2b - 2r - 1) + \delta_{b\leq r} \zeta_{2r + 1 - 2b}^{\mathfrak{l}}(\overline{2b}) \otimes \zeta^{\mathfrak{m}}(2a + 2b - 2r - 1) \\ &\quad = \bigg( \binom{2r}{2a-1} - \binom{2r}{2b-1} \bigg) \zeta^{\mathfrak{l}}(\overline{2r+1}) \otimes \zeta(2a + 2b - 2r - 1) \end{align*} $$
The binomial factors should a prior retain the delta factors, but they can be removed as the binomials vanish already for the complementary condition. The corresponding result holds for
![]() $ \zeta ^{\mathfrak {m}}(2a, 2b) $
by removing all bars from the above result
$ \zeta ^{\mathfrak {m}}(2a, 2b) $
by removing all bars from the above result
 $$ \begin{align*} &\operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}({2a}, {2b}) = \bigg( \binom{2r}{2a-1} - \binom{2r}{2b-1} \bigg) \zeta^{\mathfrak{l}}({2r+1}) \otimes \zeta(2a + 2b - 2r - 1). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}({2a}, {2b}) = \bigg( \binom{2r}{2a-1} - \binom{2r}{2b-1} \bigg) \zeta^{\mathfrak{l}}({2r+1}) \otimes \zeta(2a + 2b - 2r - 1). \end{align*} $$
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(2a+1, 2b+1) $
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(2a+1, 2b+1) $
We see that only the following subsequences can contribute to the motivic coaction. This is because any subsequence must involve one of the three nonzero entries; one then checks whether the length
![]() $ 2r+1 $
subsequences which start/end at these points actually contribute
$ 2r+1 $
subsequences which start/end at these points actually contribute

We find
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}({2a+1}, {2b+1}) & = \delta_{a=r} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a + 2b + 1 - 2r) \\ &\quad + \Big( {-} \delta_{a\leq r} \zeta_{2r-2a}^{\mathfrak{l}}(2a+1) + \delta_{b \leq r} \zeta_{2r-2b}^{\mathfrak{l}}(2b+1) \Big) \otimes \zeta^{\mathfrak{m}}(2a+2b+1-2r) \\ & = \bigg( \delta_{a=r} - \binom{2r}{2a} + \binom{2r}{2b} \bigg) \zeta^{\mathfrak{l}}({2r+1}) \otimes \zeta(2a + 2b + 1 - 2r) . \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}({2a+1}, {2b+1}) & = \delta_{a=r} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a + 2b + 1 - 2r) \\ &\quad + \Big( {-} \delta_{a\leq r} \zeta_{2r-2a}^{\mathfrak{l}}(2a+1) + \delta_{b \leq r} \zeta_{2r-2b}^{\mathfrak{l}}(2b+1) \Big) \otimes \zeta^{\mathfrak{m}}(2a+2b+1-2r) \\ & = \bigg( \delta_{a=r} - \binom{2r}{2a} + \binom{2r}{2b} \bigg) \zeta^{\mathfrak{l}}({2r+1}) \otimes \zeta(2a + 2b + 1 - 2r) . \end{align*} $$
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(p, q) $
,
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(p, q) $
,
 $ p + q $
even
$ p + q $
even
We note that the two cases above can be combined to give the following, for
![]() $ p + q $
even
$ p + q $
even
 $$\begin{align*}\operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(p,q) = \bigg( \delta_{2r+1 = p} + (-1)^p \binom{2r}{p-1} - (-1)^q \binom{2r}{q-1} \bigg) \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta(p+q - 2r - 1) . \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(p,q) = \bigg( \delta_{2r+1 = p} + (-1)^p \binom{2r}{p-1} - (-1)^q \binom{2r}{q-1} \bigg) \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta(p+q - 2r - 1) . \end{align*}$$
Verification of Proposition B.2
The claim that
![]() $ \operatorname {\mathrm {D}}_{2r+1} $
of both sides agree is equivalent to the following putative identity among binomial coefficients, when
$ \operatorname {\mathrm {D}}_{2r+1} $
of both sides agree is equivalent to the following putative identity among binomial coefficients, when
![]() $ 1 \leq r \leq k+\ell -1 $
, which arises after projecting
$ 1 \leq r \leq k+\ell -1 $
, which arises after projecting
![]() $ \zeta ^{\mathfrak {l}}(2r+1) \otimes \zeta ^{\mathfrak {m}}(2k+2\ell -2r-1) \mapsto 1 $
.
$ \zeta ^{\mathfrak {l}}(2r+1) \otimes \zeta ^{\mathfrak {m}}(2k+2\ell -2r-1) \mapsto 1 $
.
 $$ \begin{align*} 0 &\overset{?}{=} (1-2^{-2r}) \bigg( \binom{2r}{2\ell-1} - \binom{2r}{2k-1} \bigg) \\ &\quad + \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2k-1} \bigg( \delta_{2k+2\ell-i = 2r+1} + (-1)^i \binom{2r}{2k+2\ell-i-1} - (-1)^{i} \binom{2r}{i-1} \bigg) \\ &\quad + \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2\ell-1} \bigg( \delta_{i = 2r+1} + (-1)^i \binom{2r}{i-1} - (-1)^{i} \binom{2r}{2k+2\ell-i-1} \bigg) \\ &\quad - \bigg( \binom{2r}{2l-1} - \binom{2r}{2k-1} \bigg) \\ &\quad + (-2)^{-(2r+1)} \binom{2r}{2k-1} + (-2)^{-(2k+2\ell-2r-1)} \binom{2k+2\ell-2r-2}{2k-1}. \end{align*} $$
$$ \begin{align*} 0 &\overset{?}{=} (1-2^{-2r}) \bigg( \binom{2r}{2\ell-1} - \binom{2r}{2k-1} \bigg) \\ &\quad + \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2k-1} \bigg( \delta_{2k+2\ell-i = 2r+1} + (-1)^i \binom{2r}{2k+2\ell-i-1} - (-1)^{i} \binom{2r}{i-1} \bigg) \\ &\quad + \sum_{i=2}^{2k+2\ell-2} 2^{-i} \binom{i-1}{2\ell-1} \bigg( \delta_{i = 2r+1} + (-1)^i \binom{2r}{i-1} - (-1)^{i} \binom{2r}{2k+2\ell-i-1} \bigg) \\ &\quad - \bigg( \binom{2r}{2l-1} - \binom{2r}{2k-1} \bigg) \\ &\quad + (-2)^{-(2r+1)} \binom{2r}{2k-1} + (-2)^{-(2k+2\ell-2r-1)} \binom{2k+2\ell-2r-2}{2k-1}. \end{align*} $$
After some simplification of the right-hand side, and reindexing the sums, we find that the claim is equivalent to the following
 $$ \begin{align*} 0 \overset{?}{=} & -2^{-2r-1} \bigg( \binom{2r}{2\ell-1} - \binom{2r}{2k-1} \bigg) \\ & + (-2)^{-2k} \sum_{i=0}^{2\ell-2} (-2)^{-i} \binom{i+2k-1}{2k-1} \bigg( \binom{2r}{2\ell-i-1} - \binom{2r}{2k+i-1} \bigg) \\ & + (-2)^{-2\ell} \sum_{i=0}^{2k-2} (-2)^{-i} \binom{i+2k-1}{2\ell-1} \bigg( \binom{2r}{2\ell+i-1} - \binom{2r}{2k-i-1} \bigg). \end{align*} $$
$$ \begin{align*} 0 \overset{?}{=} & -2^{-2r-1} \bigg( \binom{2r}{2\ell-1} - \binom{2r}{2k-1} \bigg) \\ & + (-2)^{-2k} \sum_{i=0}^{2\ell-2} (-2)^{-i} \binom{i+2k-1}{2k-1} \bigg( \binom{2r}{2\ell-i-1} - \binom{2r}{2k+i-1} \bigg) \\ & + (-2)^{-2\ell} \sum_{i=0}^{2k-2} (-2)^{-i} \binom{i+2k-1}{2\ell-1} \bigg( \binom{2r}{2\ell+i-1} - \binom{2r}{2k-i-1} \bigg). \end{align*} $$
This is verified to be exactly 0 from Lemma 4.2 of Section 4. With that, we have finished the proof of Proposition B.2.
B.2 Motivic version of Equation (A.7)
We prove the following proposition, which claims that Equation (A.7) lifts to a motivic version.
Proposition B.3. The following identity holds among motivic multiple zeta (star) values

Proof. We compute
![]() $ \operatorname {\mathrm {D}}_{2r+1} $
of both sides and will show that they agree. The analytic version of this identity, which is given in Equation (A.7) then fixes the remaining coefficient of
$ \operatorname {\mathrm {D}}_{2r+1} $
of both sides and will show that they agree. The analytic version of this identity, which is given in Equation (A.7) then fixes the remaining coefficient of
![]() $ \zeta ^{\mathfrak {m}}(2a+2b+4) $
(which, here, is expressed as a sum of two terms involving products of even zetas). Notice that the only place
$ \zeta ^{\mathfrak {m}}(2a+2b+4) $
(which, here, is expressed as a sum of two terms involving products of even zetas). Notice that the only place
![]() $ \operatorname {\mathrm {D}}_1 $
could contribute is from
$ \operatorname {\mathrm {D}}_1 $
could contribute is from
![]() $ \zeta ^{\mathfrak {m}}_{2a+1}(1, \overline {2b+2}) $
, but we will see momentarily that
$ \zeta ^{\mathfrak {m}}_{2a+1}(1, \overline {2b+2}) $
, but we will see momentarily that
![]() $ \operatorname {\mathrm {D}}_1 = 0 $
, hence, we can take
$ \operatorname {\mathrm {D}}_1 = 0 $
, hence, we can take
![]() $ r> 0 $
.
$ r> 0 $
.
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}_{2a+1}(1, \overline {2b+2}) $
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}_{2a+1}(1, \overline {2b+2}) $
We see that only the following subsequences can contribute to the motivic coaction. This is because any subsequence must start or end at one of the three nonzero entries; one then checks whether the length
![]() $ 2r+1 $
subsequences which start/end at these points actually contribute
$ 2r+1 $
subsequences which start/end at these points actually contribute

Hence, we have
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}_{2a+1}(1,\overline{2b+2}) & = \delta_{r\leq a} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2a+1-2r}(\overline{2b+2}) - \delta_{r \leq b} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2a+1}(\overline{2b+2-2r}) \\ & = \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq a} \binom{2a + 2b + 2 - 2r}{2b + 1} + \delta_{r \leq b} \binom{2a + 2b + 2 - 2r}{2a} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b+ 3 - 2r}) . \hspace{-3em} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}_{2a+1}(1,\overline{2b+2}) & = \delta_{r\leq a} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2a+1-2r}(\overline{2b+2}) - \delta_{r \leq b} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2a+1}(\overline{2b+2-2r}) \\ & = \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq a} \binom{2a + 2b + 2 - 2r}{2b + 1} + \delta_{r \leq b} \binom{2a + 2b + 2 - 2r}{2a} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b+ 3 - 2r}) . \hspace{-3em} \end{align*} $$
And, in particular,
![]() $ \operatorname {\mathrm {D}}_1 = 0 $
.
$ \operatorname {\mathrm {D}}_1 = 0 $
.
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}_{2b+2}(1, 2a+1) $
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}_{2b+2}(1, 2a+1) $
Similarly, only the following subsequences can contribute to the motivic coaction

Hence, we have
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}_{2b+2}(1,2a+1) & = \delta_{r\leq b+1} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2b+2-2r}(2a+1) - \delta_{r \leq a-1} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2b+2}(2a+1-2r) \\ & = \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq b+1} \binom{2a+2b+2-2r}{2a + 1} + \delta_{r \leq a-1} \binom{2a+2b+2 - 2r}{2b + 1} \bigg) \\ & \quad \cdot \zeta^{\mathfrak{m}}(2a + 2b+ 3 - 2r) .\hspace{-3em} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}_{2b+2}(1,2a+1) & = \delta_{r\leq b+1} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2b+2-2r}(2a+1) - \delta_{r \leq a-1} \zeta^{\mathfrak{l}}_{2r}(1) \otimes \zeta^{\mathfrak{m}}_{2b+2}(2a+1-2r) \\ & = \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq b+1} \binom{2a+2b+2-2r}{2a + 1} + \delta_{r \leq a-1} \binom{2a+2b+2 - 2r}{2b + 1} \bigg) \\ & \quad \cdot \zeta^{\mathfrak{m}}(2a + 2b+ 3 - 2r) .\hspace{-3em} \end{align*} $$
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} $
of right-hand side of Equation (B.3)
$ \operatorname {\mathrm {D}}_{2r+1} $
of right-hand side of Equation (B.3)
With the above two computations of the motivic coaction on the double zeta values in Equation (B.3), we can readily compute the rest of the coaction using the derivation property of
![]() $ \operatorname {\mathrm {D}}_{2r+1} $
, namely,
$ \operatorname {\mathrm {D}}_{2r+1} $
, namely,
![]() $ \operatorname {\mathrm {D}}_{2r+1} X Y = (1 \otimes Y) \operatorname {\mathrm {D}}_{2r+1}X + (1 \otimes X) \operatorname {\mathrm {D}}_{2r+1} Y $
, as well as the fact that
$ \operatorname {\mathrm {D}}_{2r+1} X Y = (1 \otimes Y) \operatorname {\mathrm {D}}_{2r+1}X + (1 \otimes X) \operatorname {\mathrm {D}}_{2r+1} Y $
, as well as the fact that
![]() $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(N) = \delta _{N=2r+1} \zeta ^{\mathfrak {l}}(N) \otimes 1 $
. Note also the first two terms on the right-hand side of Equation (B.3) are products of even zetas, and so do not contribute. So we find
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(N) = \delta _{N=2r+1} \zeta ^{\mathfrak {l}}(N) \otimes 1 $
. Note also the first two terms on the right-hand side of Equation (B.3) are products of even zetas, and so do not contribute. So we find
 $$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}}))\\ &\quad = 8 \delta_{r=a} \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{k=1}^{b+1} \zeta^{\mathfrak{m}}(2k+1) \zeta^{\mathfrak{m}}(\overline{2b+2-2k}) \\ &\qquad + 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\qquad - 8 \sum_{s = 0}^{a} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq a-s} \binom{2a + 2b + 2 - 2r - 2s}{2b+1} + \delta_{r \leq b} \binom{2a + 2b + 2 - 2r - 2s}{2b + 1 - 2r} \bigg) \\ &\qquad \cdot \zeta^{\mathfrak{m}}(\overline{2a - 2s + 2b + 3 - 2r}) \zeta^{\mathfrak{m}}(\overline{2s}) \\ &\qquad - 8 \sum_{s=0}^b \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \delta_{r\leq b-s+1} \binom{2a + 2b + 2 - 2r - 2s}{2a} - \delta_{r \leq a-1} \binom{2a + 2b + 2 - 2r - 2s}{2a - 2r} \bigg) \\ &\qquad \cdot \zeta^{\mathfrak{m}}(2a + 2b - 2s + 3 - 2r) \zeta^{\mathfrak{m}}(\overline{2s}). \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}}))\\ &\quad = 8 \delta_{r=a} \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{k=1}^{b+1} \zeta^{\mathfrak{m}}(2k+1) \zeta^{\mathfrak{m}}(\overline{2b+2-2k}) \\ &\qquad + 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\qquad - 8 \sum_{s = 0}^{a} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \delta_{r\leq a-s} \binom{2a + 2b + 2 - 2r - 2s}{2b+1} + \delta_{r \leq b} \binom{2a + 2b + 2 - 2r - 2s}{2b + 1 - 2r} \bigg) \\ &\qquad \cdot \zeta^{\mathfrak{m}}(\overline{2a - 2s + 2b + 3 - 2r}) \zeta^{\mathfrak{m}}(\overline{2s}) \\ &\qquad - 8 \sum_{s=0}^b \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \delta_{r\leq b-s+1} \binom{2a + 2b + 2 - 2r - 2s}{2a} - \delta_{r \leq a-1} \binom{2a + 2b + 2 - 2r - 2s}{2a - 2r} \bigg) \\ &\qquad \cdot \zeta^{\mathfrak{m}}(2a + 2b - 2s + 3 - 2r) \zeta^{\mathfrak{m}}(\overline{2s}). \end{align*} $$
Computation of
 $ \operatorname {\mathrm {D}}_{2r+1} $
of left-hand side of Equation (B.3)
$ \operatorname {\mathrm {D}}_{2r+1} $
of left-hand side of Equation (B.3)
We compute the derivation
![]() $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m},\star }(\{2\}^a, 4, \{2\}^b) $
by first applying the stuffle antipode to obtain an expression involving only
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m},\star }(\{2\}^a, 4, \{2\}^b) $
by first applying the stuffle antipode to obtain an expression involving only
![]() $ \zeta ^{\mathfrak {m}}(\{2\}^j, 4, \{2\}^i) $
, which has a simpler coaction.
$ \zeta ^{\mathfrak {m}}(\{2\}^j, 4, \{2\}^i) $
, which has a simpler coaction.
We see that only the following subsequences can contribute to the motivic coaction of
![]() $ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(\{2\}^a, 4, \{2\}^b) $
; all other subsequences will start and end at letters of the same parity
$ \operatorname {\mathrm {D}}_{2r+1} \zeta ^{\mathfrak {m}}(\{2\}^a, 4, \{2\}^b) $
; all other subsequences will start and end at letters of the same parity

Hence, we have
 $$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b)\\ &\quad = - \delta_{r \leq a} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \zeta^{\mathfrak{m}}(\{2\}^{a-r}, 3, \{2\}^b) + \delta_{r \leq b} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \zeta^{\mathfrak{m}}(\{2\}^a, 3, \{2\}^{b-r}) . \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^a, 4, \{2\}^b)\\ &\quad = - \delta_{r \leq a} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \zeta^{\mathfrak{m}}(\{2\}^{a-r}, 3, \{2\}^b) + \delta_{r \leq b} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \zeta^{\mathfrak{m}}(\{2\}^a, 3, \{2\}^{b-r}) . \end{align*} $$
Now, with the stuffle antipode formula extracted from Equation (A.2), we compute
 $$ \begin{align*} & D_{2r+1 }\zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) \\ &\quad = \sum_{i=0}^a \sum_{j=0}^b (-1)^{i+j} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^j, 4, \{2\}^i) \Big( 1 \otimes \zeta^{\mathfrak{m},\star}(\{2\}^{a-i}) \zeta^{\mathfrak{m},\star}(\{2\}^{b-j}) \Big) \\ &\quad = \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \sum_{i=0}^a \sum_{j=0}^b (-1)^{i+j} \big( - \delta_{r \leq j}\zeta^{\mathfrak{m}}(\{2\}^{j-r}, 3, \{2\}^i) + \delta_{r \leq i} \zeta^{\mathfrak{m}}(\{2\}^j, 3, \{2\}^{i-r}) \big) \\ & \qquad{} \cdot \zeta^{\mathfrak{m},\star}(\{2\}^{a-i}) \zeta^{\mathfrak{m},\star}(\{2\}^{b-j}). \end{align*} $$
$$ \begin{align*} & D_{2r+1 }\zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) \\ &\quad = \sum_{i=0}^a \sum_{j=0}^b (-1)^{i+j} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m}}(\{2\}^j, 4, \{2\}^i) \Big( 1 \otimes \zeta^{\mathfrak{m},\star}(\{2\}^{a-i}) \zeta^{\mathfrak{m},\star}(\{2\}^{b-j}) \Big) \\ &\quad = \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \sum_{i=0}^a \sum_{j=0}^b (-1)^{i+j} \big( - \delta_{r \leq j}\zeta^{\mathfrak{m}}(\{2\}^{j-r}, 3, \{2\}^i) + \delta_{r \leq i} \zeta^{\mathfrak{m}}(\{2\}^j, 3, \{2\}^{i-r}) \big) \\ & \qquad{} \cdot \zeta^{\mathfrak{m},\star}(\{2\}^{a-i}) \zeta^{\mathfrak{m},\star}(\{2\}^{b-j}). \end{align*} $$
Here, we can apply the motivic evaluation of
![]() $ \zeta ^{\mathfrak {m}}(\{2\}^\alpha , 3, \{2\}^\beta ) $
established by Brown [Reference Brown5]. Alternatively, we can apply the stuffle antipode again to rewrite the result instead of involving
$ \zeta ^{\mathfrak {m}}(\{2\}^\alpha , 3, \{2\}^\beta ) $
established by Brown [Reference Brown5]. Alternatively, we can apply the stuffle antipode again to rewrite the result instead of involving
![]() $ \zeta ^{\mathfrak {m},\star }(\{2\}^\alpha , 3, \{2\}^\beta ) $
and appeal to the motivic evaluation thereof, for a more direct formula (Glanois [Reference Glanois18] claims that the motivic evaluation of
$ \zeta ^{\mathfrak {m},\star }(\{2\}^\alpha , 3, \{2\}^\beta ) $
and appeal to the motivic evaluation thereof, for a more direct formula (Glanois [Reference Glanois18] claims that the motivic evaluation of
![]() $ \zeta ^{\mathfrak {m},\star }(\{2\}^\alpha , 3, \{2\}^\beta ) $
requires knowing exactly certain conjectural identities among so-called
$ \zeta ^{\mathfrak {m},\star }(\{2\}^\alpha , 3, \{2\}^\beta ) $
requires knowing exactly certain conjectural identities among so-called
![]() $ \zeta ^{\star \star } $
values, however, it seems that the stuffle antipode formula allows one to automatically transfer the
$ \zeta ^{\star \star } $
values, however, it seems that the stuffle antipode formula allows one to automatically transfer the
![]() $ \zeta ^{\mathfrak {m}}(\{2\}^\alpha , 3, \{2\}^\beta ) $
evaluation to a corresponding
$ \zeta ^{\mathfrak {m}}(\{2\}^\alpha , 3, \{2\}^\beta ) $
evaluation to a corresponding
![]() $ \zeta ^{\mathfrak {m},\star }(\{2\}^\beta , 3, \{2\}^\alpha ) $
evaluation).
$ \zeta ^{\mathfrak {m},\star }(\{2\}^\beta , 3, \{2\}^\alpha ) $
evaluation).
After (separately) shifting
![]() $ i $
and
$ i $
and
![]() $ j $
by
$ j $
by
![]() $ r $
, which gives the factor
$ r $
, which gives the factor
![]() $ (-1)^r $
below (and taking care with the signs; use the correspondence
$ (-1)^r $
below (and taking care with the signs; use the correspondence
![]() $ j \leftrightarrow b $
,
$ j \leftrightarrow b $
,
![]() $ i \rightarrow a $
), we find
$ i \rightarrow a $
), we find
 $$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1 }\zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) \\ &\quad = (-1)^{r} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \big( \delta_{r\leq a} \zeta^{\mathfrak{m},\star}(\{2\}^{a-r}, 3, \{2\}^{b}) - \delta_{r \leq b} \zeta^{\mathfrak{m},\star}(\{2\}^a, 3,\{2\}^{b-r}) \big) . \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{D}}_{2r+1 }\zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) \\ &\quad = (-1)^{r} \zeta^{\mathfrak{l}}_1(\{2\}^r) \otimes \big( \delta_{r\leq a} \zeta^{\mathfrak{m},\star}(\{2\}^{a-r}, 3, \{2\}^{b}) - \delta_{r \leq b} \zeta^{\mathfrak{m},\star}(\{2\}^a, 3,\{2\}^{b-r}) \big) . \end{align*} $$
We note that this is essentially the same expression as one obtains with Glanois’s setup involving the motivic coaction on
![]() $ \zeta ^{\star } $
values, after applying the dihedral symmetries to simplify terms in the coalgebra on the left-hand side. One only needs to apply the result that
$ \zeta ^{\star } $
values, after applying the dihedral symmetries to simplify terms in the coalgebra on the left-hand side. One only needs to apply the result that
![]() $ (-1)^r \zeta ^{\mathfrak {l}}_1(\{2\}^r) = 2 \zeta ^{\mathfrak {l}}(2r+1) = -\zeta ^{\mathfrak {l},\star }_1(\{2\}^r) $
to obtain exactly the same formula.
$ (-1)^r \zeta ^{\mathfrak {l}}_1(\{2\}^r) = 2 \zeta ^{\mathfrak {l}}(2r+1) = -\zeta ^{\mathfrak {l},\star }_1(\{2\}^r) $
to obtain exactly the same formula.
Now, apply the following motivic evaluations
 $$ \begin{align*} \zeta^{\mathfrak{l}}_1(\{2\}^r) & = 2 (-1)^r \zeta^{\mathfrak{l}}(2r+1) \\[3pt] \zeta^{\mathfrak{m},\star}(\{2\}^a, 3, \{2\}^b) & = - 2 \sum_{s=1}^{a+b+1} \bigg[ \binom{2s}{2a} {-} \delta_{s=a} - (1 - 2^{-2s}) \binom{2s}{2b+1} \bigg] \zeta^{\star,\mathfrak{m}}(\{2\}^{a+b+1-s}) \zeta^{\mathfrak{m}}(2s+1) \end{align*} $$
$$ \begin{align*} \zeta^{\mathfrak{l}}_1(\{2\}^r) & = 2 (-1)^r \zeta^{\mathfrak{l}}(2r+1) \\[3pt] \zeta^{\mathfrak{m},\star}(\{2\}^a, 3, \{2\}^b) & = - 2 \sum_{s=1}^{a+b+1} \bigg[ \binom{2s}{2a} {-} \delta_{s=a} - (1 - 2^{-2s}) \binom{2s}{2b+1} \bigg] \zeta^{\star,\mathfrak{m}}(\{2\}^{a+b+1-s}) \zeta^{\mathfrak{m}}(2s+1) \end{align*} $$
along with
![]() $ \zeta ^{\star ,\mathfrak {m}}(\{2\}^n) = -2 \zeta ^{\mathfrak {m}}(\overline {2n}) . $
We find
$ \zeta ^{\star ,\mathfrak {m}}(\{2\}^n) = -2 \zeta ^{\mathfrak {m}}(\overline {2n}) . $
We find
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) &= 8 \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{s=1}^{a+b+1-r} \bigg[ \binom{2s}{2a-2r} - \delta_{s=a-r} - (1-2^{-2s}) \binom{2s}{2b+1} \bigg] \\[3pt] & \quad\cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2s - 2r}) \zeta^{\mathfrak{m}}(2s+1) \\[3pt] &\quad - 8 \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{s=1}^{a+b+1-r} \bigg[ \binom{2s}{2a} - \delta_{s=a} - (1-2^{-2s}) \binom{2s}{2b-2r+1} \bigg] \\[3pt] &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2s - 2r}) \zeta^{\mathfrak{m}}(2s+1) . \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} \zeta^{\mathfrak{m},\star}(\{2\}^a, 4, \{2\}^b) &= 8 \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{s=1}^{a+b+1-r} \bigg[ \binom{2s}{2a-2r} - \delta_{s=a-r} - (1-2^{-2s}) \binom{2s}{2b+1} \bigg] \\[3pt] & \quad\cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2s - 2r}) \zeta^{\mathfrak{m}}(2s+1) \\[3pt] &\quad - 8 \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{s=1}^{a+b+1-r} \bigg[ \binom{2s}{2a} - \delta_{s=a} - (1-2^{-2s}) \binom{2s}{2b-2r+1} \bigg] \\[3pt] &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2s - 2r}) \zeta^{\mathfrak{m}}(2s+1) . \end{align*} $$
Comparison of left- and right-hand side of Equation (B.3)
Firstly, make the change of variables
![]() $ s \mapsto a + b + 1 - s - r $
in the sums for
$ s \mapsto a + b + 1 - s - r $
in the sums for
![]() $ \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
; after considering the cases in each resulting delta term – and dropping terms
$ \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
; after considering the cases in each resulting delta term – and dropping terms
![]() $ \zeta ^{\mathfrak {m}}(1) = 0 $
by regularisation– we find
$ \zeta ^{\mathfrak {m}}(1) = 0 $
by regularisation– we find
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}})) & = 8 \delta_{r=a} \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{k=1}^{b+1} \zeta^{\mathfrak{m}}(2k+1) \zeta^{\mathfrak{m}}(\overline{2b+2-2k}) \\ &\quad + 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\quad - 8 \sum_{s = \max(1, b-r+1)}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \binom{2s}{2b+1} + \binom{2s}{2b+1-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2s+1}) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) \\ &\quad - 8 \sum_{s=\max(1, a-r+1)}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \binom{2s}{2a} + \delta_{r=a} - \binom{2s}{2a-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(2s + 1) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) . \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}})) & = 8 \delta_{r=a} \zeta^{\mathfrak{l}}(2r+1) \otimes \sum_{k=1}^{b+1} \zeta^{\mathfrak{m}}(2k+1) \zeta^{\mathfrak{m}}(\overline{2b+2-2k}) \\ &\quad + 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\quad - 8 \sum_{s = \max(1, b-r+1)}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \binom{2s}{2b+1} + \binom{2s}{2b+1-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2s+1}) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) \\ &\quad - 8 \sum_{s=\max(1, a-r+1)}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \binom{2s}{2a} + \delta_{r=a} - \binom{2s}{2a-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(2s + 1) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) . \end{align*} $$
Note, here, that the two terms involving
![]() $ \delta _{r=a} $
cancel. Then the sums over
$ \delta _{r=a} $
cancel. Then the sums over
![]() $ s $
may be extended to start at
$ s $
may be extended to start at
![]() $ s = 1 $
. The first sum needs no correction term, as the numerators of each binomial are strictly greater than the denominators in this case, however, the term
$ s = 1 $
. The first sum needs no correction term, as the numerators of each binomial are strictly greater than the denominators in this case, however, the term
![]() $ \binom {2s}{2a-2r} $
in the second sum needs to be corrected when
$ \binom {2s}{2a-2r} $
in the second sum needs to be corrected when
![]() $ s = a-r $
for
$ s = a-r $
for
![]() $ a-r \geq 1 $
. We obtain
$ a-r \geq 1 $
. We obtain
 $$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}})) &= 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\quad - 8 \delta_{r \leq a-1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a + 1 - 2r) \zeta^{\mathfrak{m}}(\overline{2b+2}) \\ &\quad - 8 \sum_{s = 1}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \binom{2s}{2b+1} + \binom{2s}{2b+1-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2s+1}) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) \\ &\quad - 8 \sum_{s=1}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \binom{2s}{2a} - \binom{2s}{2a-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(2s + 1) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) .\end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{D}}_{2r+1} (\text{RHS Equation}~({\textrm{B.3}})) &= 8 \delta_{r \leq b+1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a+1) \zeta^{\mathfrak{m}}(\overline{2b + 2 - 2r}) \\ &\quad - 8 \delta_{r \leq a-1} \zeta^{\mathfrak{l}}(2r+1) \otimes \zeta^{\mathfrak{m}}(2a + 1 - 2r) \zeta^{\mathfrak{m}}(\overline{2b+2}) \\ &\quad - 8 \sum_{s = 1}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( {-} \binom{2s}{2b+1} + \binom{2s}{2b+1-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(\overline{2s+1}) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) \\ &\quad - 8 \sum_{s=1}^{a+b+1-r} \zeta^{\mathfrak{l}}(2r+1) \otimes \bigg( \binom{2s}{2a} - \binom{2s}{2a-2r} \bigg) \\ &\quad \cdot \zeta^{\mathfrak{m}}(2s + 1) \zeta^{\mathfrak{m}}(\overline{2a + 2b + 2 - 2r - 2s)}) .\end{align*} $$
Finally, write
![]() $ \zeta ^{\mathfrak {m}}(\overline {2s+1}) = -(1-2^{2s})\zeta ^{\mathfrak {m}}(2s+1) $
. It is now straightforward to check that
$ \zeta ^{\mathfrak {m}}(\overline {2s+1}) = -(1-2^{2s})\zeta ^{\mathfrak {m}}(2s+1) $
. It is now straightforward to check that
![]() $ \operatorname {\mathrm {D}}_{2r+1} ( \text {LHS Equation}~({\textrm{B.3}}) ) = \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
; the two terms outside the sum for
$ \operatorname {\mathrm {D}}_{2r+1} ( \text {LHS Equation}~({\textrm{B.3}}) ) = \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
; the two terms outside the sum for
![]() $ \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
above correspond to the deltas terms in the expression for
$ \operatorname {\mathrm {D}}_{2r+1} ( \text {RHS Equation}~({\textrm{B.3}}) ) $
above correspond to the deltas terms in the expression for
![]() $ \operatorname {\mathrm {D}}_{2r+1}( \text {LHS Equation}~({\textrm{B.3}}) ) $
.
$ \operatorname {\mathrm {D}}_{2r+1}( \text {LHS Equation}~({\textrm{B.3}}) ) $
.
This completes the proof of Proposition B.3, and shows the reduction of
![]() $ \zeta ^{\star }(\{2\}^a, 4, \{2\}^b) $
to depth 3 alternating MZVs is motivic.
$ \zeta ^{\star }(\{2\}^a, 4, \{2\}^b) $
to depth 3 alternating MZVs is motivic.
B.3 Motivic evaluation of
 $ \zeta ^{\mathfrak {l}}(\{2\}^a, 4, \{2\}^b) $
$ \zeta ^{\mathfrak {l}}(\{2\}^a, 4, \{2\}^b) $
Now that we have verified all of the ingredients for the evaluations of
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
and
$ \zeta (\{2\}^a, 4, \{2\}^b) $
and
![]() $ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
are motivic, we may conclude that the identities in Theorems A.6 and A.7 hold for
$ \zeta ^\star (\{2\}^a, 4, \{2\}^b) $
are motivic, we may conclude that the identities in Theorems A.6 and A.7 hold for
![]() $ \zeta ^{(\star )} $
replaced by their motivic counterparts, and
$ \zeta ^{(\star )} $
replaced by their motivic counterparts, and
![]() $ \mathrm {i}\pi $
replaced by
$ \mathrm {i}\pi $
replaced by
![]() $ \frac {1}{2} \mathbb {L}^{\mathfrak {m}} = (\mathrm {i}\pi )^{\mathfrak {m}} $
.
$ \frac {1}{2} \mathbb {L}^{\mathfrak {m}} = (\mathrm {i}\pi )^{\mathfrak {m}} $
.
More importantly, the evaluation of
![]() $ \zeta (\{2\}^a, 4, \{2\}^b) $
modulo products from Corollary A.8 is also motivic, and we obtain the result of Lemma 4.1 as an immediate corollary.
$ \zeta (\{2\}^a, 4, \{2\}^b) $
modulo products from Corollary A.8 is also motivic, and we obtain the result of Lemma 4.1 as an immediate corollary.
Corollary B.4. The following evaluation holds in the motivic coalgebra

Acknowledgments
The authors are grateful to the Max Planck Institute for Mathematics, Bonn, for the support and hospitality provided during their respective stays. The authors are very thankful to the referee for their insightful and considered comments. SC was supported by the Deutsche Forschungsgemeinschaft Eigene Stelle grant CH 2561/1-1, for Projektnummer 442093436, during the preparation of this work at Universität Hamburg, and by the Max Planck Institute for Mathematics, Bonn, during the revision process. AK was supported by the Max Planck Institute for Mathematics, Bonn, during the preparation of this work, and by the “Postdoctoral program in Mathematics for researchers from outside Sweden” (project KAW 2020.0254) at Chalmers Technical University during the revision process.
Competing interest
The authors have no competing interest to declare.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/fms.2024.16.