Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2025-01-01T19:04:04.516Z Has data issue: false hasContentIssue false
  • English
  • Français

EIGENVALUES AND LINEAR QUASIRANDOM HYPERGRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  14 January 2015

JOHN LENZ  and
DHRUV MUBAYI

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 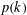$p(k)$ denote the partition function of 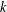$k$. For each 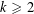$k\geqslant 2$, we describe a list of 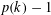$p(k)-1$ quasirandom properties that a 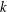$k$-uniform hypergraph can have. Our work connects previous notions on linear hypergraph quasirandomness by Kohayakawa, Rödl, and Skokan, and by Conlon, Hàn, Person, and Schacht, and the spectral approach of Friedman and Wigderson. For each of the quasirandom properties that is described, we define the largest and the second largest eigenvalues. We show that a hypergraph satisfies these quasirandom properties if and only if it has a large spectral gap. This answers a question of Conlon, Hàn, Person, and Schacht. Our work can be viewed as a partial extension to hypergraphs of the seminal spectral results of Chung, Graham, and Wilson for graphs.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.) 05C65: Hypergraphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e2
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Alon, N., ‘Eigenvalues and expanders’, Combinatorica 6(2) (1986), 83–96. Theory of computing (Singer Island, FL, 1984).Google Scholar
Alon, N. and Milman, V. D., ‘𝜆1, isoperimetric inequalities for graphs, and superconcentrators’, J. Combin. Theory Ser. B 38(1) (1985), 73–88.Google Scholar
Alon, N. and Pudlák, P., ‘Constructive lower bounds for off-diagonal Ramsey numbers’, Israel J. Math. 122 (2001), 243–251.CrossRefGoogle Scholar
Alon, N. and Rödl, V., ‘Sharp bounds for some multicolor Ramsey numbers’, Combinatorica 25(2) (2005), 125–141.Google Scholar
Alon, N. and Spencer, J. H., The Probabilistic Method, 3rd edn, Wiley-Interscience Series in Discrete Mathematics and Optimization, (John Wiley & Sons Inc., Hoboken, NJ, 2008), With an appendix on the life and work of Paul Erdős.Google Scholar
Austin, T. and Tao, T., ‘Testability and repair of hereditary hypergraph properties’, Random Structures Algorithms 36(4) (2010), 373–463.CrossRefGoogle Scholar
Bilu, Y. and Hoory, S., ‘On codes from hypergraphs’, European J. Combin. 25(3) (2004), 339–354.Google Scholar
Chung, F., ‘Quasi-random hypergraphs revisited’, Random Structures Algorithms 40(1) (2012), 39–48.Google Scholar
Chung, F. R. K., ‘Quasi-random classes of hypergraphs’, Random Structures Algorithms 1(4) (1990), 363–382.Google Scholar
Chung, F. R. K., ‘Regularity lemmas for hypergraphs and quasi-randomness’, Random Structures Algorithms 2(2) (1991), 241–252.Google Scholar
Chung, F. R. K., ‘The Laplacian of a hypergraph’, inExpanding Graphs (Princeton, NJ, 1992), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 10 (American Mathematical Society, Providence, RI, 1993), 21–36.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random hypergraphs’, Random Structures Algorithms 1(1) (1990), 105–124.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Quasi-random set systems’, J. Amer. Math. Soc. 4(1) (1991), 151–196.Google Scholar
Chung, F. R. K. and Graham, R. L., ‘Cohomological aspects of hypergraphs’, Trans. Amer. Math. Soc. 334(1) (1992), 365–388.Google Scholar
Chung, F. R. K., Graham, R. L. and Wilson, R. M., ‘Quasi-random graphs’, Combinatorica 9(4) (1989), 345–362.Google Scholar
Conlon, D., Hàn, H., Person, Y. and Schacht, M., ‘Weak quasi-randomness for uniform hypergraphs’, Random Structures Algorithms 40(1) (2012), 1–38.Google Scholar
Cooper, J. and Dutle, A., ‘Spectra of uniform hypergraphs’, Linear Algebra Appl. 436(9) (2012), 3268–3292.Google Scholar
Erdős, P. and Hajnal, A., ‘On Ramsey like theorems. Problems and results’, inCombinatorics (Proc. Conf. Combinatorial Math., Math. Inst., Oxford, 1972) (Inst. Math. Appl., Southend, 1972), 123–140.Google Scholar
Feng, K. and Li, W.-C. W., ‘Spectra of hypergraphs and applications’, J. Number Theory 60(1) (1996), 1–22.Google Scholar
Frankl, P. and Rödl, V., ‘The uniformity lemma for hypergraphs’, Graphs Combin. 8(4) (1992), 309–312.Google Scholar
Friedman, J., ‘Some graphs with small second eigenvalue’, Combinatorica 15(1) (1995), 31–42.Google Scholar
Friedman, J. and Wigderson, A., ‘On the second eigenvalue of hypergraphs’, Combinatorica 15(1) (1995), 43–65.Google Scholar
Gowers, W. T., ‘Quasirandomness, counting and regularity for 3-uniform hypergraphs’, Combin. Probab. Comput. 15(1–2) (2006), 143–184.Google Scholar
Gowers, W. T., ‘Hypergraph regularity and the multidimensional Szemerédi theorem’, Ann. of Math. (2) 166(3) (2007), 897–946.Google Scholar
Gowers, W. T., ‘Quasirandom groups’, Combin. Probab. Comput. 17(3) (2008), 363–387.Google Scholar
Hoory, S., Linial, N. and Wigderson, A., ‘Expander graphs and their applications’, Bull. Amer. Math. Soc. (N.S.) 43(4) (2006), 439–561. (electronic).Google Scholar
Keevash, P., ‘A hypergraph regularity method for generalized Turán problems’, Random Structures Algorithms 34(1) (2009), 123–164.Google Scholar
Kohayakawa, Y., Nagle, B., Rödl, V. and Schacht, M., ‘Weak hypergraph regularity and linear hypergraphs’, J. Combin. Theory Ser. B 100(2) (2010), 151–160.Google Scholar
Kohayakawa, Y., Rödl, V. and Skokan, J., ‘Hypergraphs, quasi-randomness, and conditions for regularity’, J. Combin. Theory Ser. A 97(2) (2002), 307–352.Google Scholar
Krivelevich, M. and Sudakov, B., ‘Pseudo-random graphs’, inMore Sets, Graphs and Numbers, Bolyai Society Mathematical Studies, 15 (Springer, Berlin, 2006), 199–262.Google Scholar
Lenz, J. and Mubayi, D., ‘Eigenvalues and linear quasirandom hypergraphs’, online at http://arxiv.org/abs/1208.4863.Google Scholar
Lenz, J. and Mubayi, D., ‘Eigenvalues of non-regular linear quasirandom hypergraphs’, online at http://www.math.uic.edu/ lenz/nonregular-art.pdf.Google Scholar
Lenz, J. and Mubayi, D., ‘Multicolor Ramsey numbers for complete bipartite versus complete graphs’, J. Graph Theory 77(1) (2014), 19–38.Google Scholar
Lenz, J. and Mubayi, D., ‘The poset of hypergraph quasirandomness’, Random Structures and Algorithms http://arxiv.org/abs/1208.5978 (accepted).Google Scholar
Lu, L. and Peng, X., ‘High-ordered random walks and generalized Laplacians on hypergraphs’, inAlgorithms and Models for the Web Graph, Lecture Notes in Computer Science, 6732 (Springer, Heidelberg, 2011), 14–25.Google Scholar
Lu, L. and Peng, X., ‘Loose Laplacian spectra of random hypergraphs’, Random Structures Algorithms 41(4) (2012), 521–545.CrossRefGoogle Scholar
Martínez, M. G., ‘The finite upper half space and related hypergraphs’, J. Number Theory 84(2) (2000), 342–360.Google Scholar
Martínez, M. G., Stark, H. M. and Terras, A. A., ‘Some Ramanujan hypergraphs associated to GL(n, Fq)’, Proc. Amer. Math. Soc. 129(6) (2001), 1623–1629. (electronic).Google Scholar
Steger, A., Die Kleitman–Rothschild Methode. PhD thesis, Forschungsinstitut für Diskrete Mathematik, Rheinische Friedrichs-Wilhelms-Universität Bonn, March 1990.Google Scholar
Storm, C. K., ‘The zeta function of a hypergraph’, Electron. J. Combin. 13(1) (2006), 26 Research Paper 84 (electronic).Google Scholar
Szabó, T., ‘On the spectrum of projective norm-graphs’, Inform. Process. Lett. 86(2) (2003), 71–74.Google Scholar
Tanner, R. M., ‘Explicit concentrators from generalized N-gons’, SIAM J. Algebra Discrete Meth. 5(3) (1984), 287–293.Google Scholar
Thomason, A., ‘Pseudorandom graphs’, inRandom graphs ’85 (Poznań, 1985), North-Holland Math. Stud., 144 (North-Holland, Amsterdam, 1987), 307–331.Google Scholar
Thomason, A., ‘Random graphs, strongly regular graphs and pseudorandom graphs’, inSurveys in Combinatorics 1987 (New Cross, 1987), London Mathematical Society Lecture Note Series, 123 (Cambridge University Press, Cambridge, 1987), 173–195.Google Scholar