Article contents
THE DIMENSION OF A SUBCATEGORY OF MODULES
Published online by Cambridge University Press: 09 October 2015
Abstract
Let 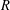 $R$ be a commutative noetherian local ring. As an analog of the notion of the dimension of a triangulated category defined by Rouquier, the notion of the dimension of a subcategory of finitely generated
$R$ be a commutative noetherian local ring. As an analog of the notion of the dimension of a triangulated category defined by Rouquier, the notion of the dimension of a subcategory of finitely generated 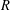 $R$-modules is introduced in this paper. We found evidence that certain categories over nice singularities have small dimensions. When
$R$-modules is introduced in this paper. We found evidence that certain categories over nice singularities have small dimensions. When 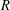 $R$ is Cohen–Macaulay, under a mild assumption it is proved that finiteness of the dimension of the full subcategory consisting of maximal Cohen–Macaulay modules which are locally free on the punctured spectrum is equivalent to saying that
$R$ is Cohen–Macaulay, under a mild assumption it is proved that finiteness of the dimension of the full subcategory consisting of maximal Cohen–Macaulay modules which are locally free on the punctured spectrum is equivalent to saying that 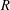 $R$ is an isolated singularity. As an application, the celebrated theorem of Auslander, Huneke, Leuschke, and Wiegand is not only recovered but also improved. The dimensions of stable categories of maximal Cohen–Macaulay modules as triangulated categories are also investigated in the case where
$R$ is an isolated singularity. As an application, the celebrated theorem of Auslander, Huneke, Leuschke, and Wiegand is not only recovered but also improved. The dimensions of stable categories of maximal Cohen–Macaulay modules as triangulated categories are also investigated in the case where 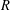 $R$ is Gorenstein, and special cases of the recent results of Aihara and Takahashi, and Oppermann and Št́ovíček are recovered and improved. Our key technique involves a careful study of annihilators and supports of
$R$ is Gorenstein, and special cases of the recent results of Aihara and Takahashi, and Oppermann and Št́ovíček are recovered and improved. Our key technique involves a careful study of annihilators and supports of 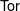 $\mathsf{Tor}$,
$\mathsf{Tor}$, 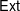 $\mathsf{Ext}$, and
$\mathsf{Ext}$, and 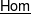 $\underline{\mathsf{Hom}}$ between two subcategories.
$\underline{\mathsf{Hom}}$ between two subcategories.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 12
- Cited by



