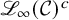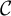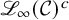Deformations of arcs and comparison of formal neighborhoods for a curve singularity

Abstract

Let $ {\mathcal C} $ be an algebraic curve and c be an analytically irreducible singular point of ${\mathcal C}$ . The set ${\mathscr {L}_{\infty }}({\mathcal C})^c$ of arcs with origin c is an irreducible closed subset of the space of arcs on ${\mathcal C}$ . We obtain a presentation of the formal neighborhood of the generic point of this set which can be interpreted in terms of deformations of the generic arc defined by this point. This allows us to deduce a strong connection between the aforementioned formal neighborhood and the formal neighborhood in the arc space of any primitive parametrization of the singularity c. This may be interpreted as the fact that analytically along ${\mathscr {L}_{\infty }}({\mathcal C})^c$ the arc space is a product of a finite dimensional singularity and an infinite dimensional affine space.

1 Introduction

1.1

Arc spaces are nowadays a prominent object of study in singularity theory. One of the main general guidelines is to understand the connection between the nature of the singularities of a variety and the geometric properties of its associated arc space, the first motivating question in this direction being the well-known Nash problem ([Nas95]). In particular, specific attention has been drawn by the local study of two important classes of arcs which we describe now.

The first one is the class of so-called stable arcs, which were introduced and studied by Reguera ([Reg06, Reg09]; subsequent works by Reguera and other authors include [Reg18, MR18, dFD20]). These are finite-codimensional points in the arc space (which is infinite-dimensional), whose formal neighborhood was shown by Reguera to be Noetherian, allowing her to establish a version of the curve selection lemma for arc spaces which was a crucial ingredient in subsequent works on the Nash problem ([FdBP12, dFD16, LJR12]).

The second one is the class of nondegenerate rational arcs. Here, nondegenerate means not entirely contained in the singular locus of the variety, and rational means that the arc is defined by formal power series with coefficients in the base field of the variety. Note that stable arcs are in some sense very far from being rational. Grinberg and Kazhdan ([GK00]) and Drinfeld ([Dri02]) showed that the formal neighborhood of a nondegenerate rational arc, though not Noetherian, may be written as the product of an infinite smooth factor and the formal neighborhood of a rational point of a scheme of finite type (a “finite formal model” of the arc under consideration). Their work was motivated by geometric representation theory and Langlands program; subsequent works in this direction include [BNS16, Bou20, Ngô17]. On the other hand, the first named author of the present paper and Julien Sebag suggested that there should be strong connections between the geometric properties of the finite formal models of a rational arc and the nature of the singularity at the origin of the arc, and gave some first evidences for that ([BS17a, BS17c, BS17b, BS19], see also [BS20] and [Bou21]).

1.2

Prompted, in particular, by the results of [BS19], Bourqui and Sebag pointed out that the study of the two classes of arcs, which until then had been led independently, should be intimately related, and suggested to compare the formal neighborhood of the generic (schematic) point of the maximal divisorial set associated with a divisorial valuation (which is a prototypical example of stable arc) and the formal neighborhood of a sufficiently generic k-rational arc of the same maximal divisorial set. Let us recall, here, the statement of [BS20, Questions 7.12 & 7.13].

Question 1.3. Let k be a field of characteristic zero and V be a k-variety. For any arc $\gamma $ on V, that is, any schematic point of ${\mathscr {L}_{\infty }}(V)$ , denote by $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}(V),\gamma }}$ the completion of the local ring at $\gamma $ .

Let $\nu $ be a divisorial valuation on V, ${\mathcal {N}}_{V}(\nu )$ be the associated maximal divisorial set in the arc space of V, and $\eta _{V,\nu }$ be the generic point of ${\mathcal {N}}_{V}(\nu )$ , with residue field denoted by $\kappa (\nu )$ .

1. 1. Does there exist a nonempty open subset U of ${\mathcal {N}}_{V}(\nu )$ , such that the isomorphism class of $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}$ is invariant when $\gamma $ runs over $U(k)$ ?

2. 2. Assume that the latter property holds. Let $\gamma \in U(k)$ . Choose a section of the quotient morphism $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}\to \kappa (\nu )$ . Are the topological local $\kappa (\nu )$ -algebras $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}{[[ {(t_i)_{i\in {\mathbf {N}}}} ]]}$ and $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}(V),\gamma }}\widehat {\otimes }_k \kappa (\nu )$ isomorphic?

Remark 1.4. Informally speaking, we are asking whether the formal neighborhood of the generic point of ${\mathcal {N}}_{V}(\nu )$ is a finite formal model of a sufficiently generic k-rational arc on V. More precisely, the following property clearly implies a positive answer to the second question: there exists a complete local Noetherian k-algebra ${\mathcal A}$ , such that $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}{\overset {\sim }{\to }} {\mathcal A}{[[ {(t_i)_{i\in {\mathbf {N}}}} ]]}$ (i.e., ${\mathcal A}$ is a finite formal model of $\gamma $ ) and the complete local $\kappa (\nu )$ -algebras $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}$ and ${\mathcal A}\widehat {\otimes }_k \kappa (\nu )$ are isomorphic. In fact, the latter property and the property considered in the second part of the above question turn out to be equivalent by Gabber’s cancellation theorem (see [BS17a, Theorem 7.2]).

Remark 1.5. Question 1.3 is challenging only when the center of the valuation $\nu $ (which is nothing but the center $\eta _{V,\nu }(0)$ of the arc $\eta _{V,\nu }$ ) is singular. In case it is smooth, the answer to Question 1.3 is positive, with ${\mathcal A}$ a k-algebra of formal power series over a finite number of variables. This easily follows from the compatibility of the formation of arc schemes with étale morphisms.

1.6

Question 1.3 has first been answered positively for normal toric varieties in case the valuation is toric. In this setting, the first part is easily answered by exploiting the torus action (see [BS19]). The second one, which is more involved, is addressed in [BMCS].

In the present article, we provide an affirmative answer to Question 1.3 for curve singularities and any divisorial valuation.

Again, the answer to the first part is easy, exploiting this time the reparametrization of the Puiseux series (one needs a slight generalization of [BS20, Corollary 7.4]). The answer to the second part is the main result of the paper:

Theorem 1.7. Let $ k $ be a field of characteristic zero. Let $ {\mathcal C} $ be a curve and $ c\in {\mathcal C}(k) $ , such that $ {\mathcal C} $ is analytically irreducible at $ c $ . Let $ \nu =\operatorname {\mathrm {ord}}_t\circ p$ be the valuation on $ {\mathcal C} $ induced by any primitive parametrization $p\colon \widehat {{\mathscr {O}}_{{\mathcal C},c}}\to k{[[ {t} ]]}$ of ${\mathcal C}$ at c, $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ the associated maximal divisorial set, $ \eta _{{\mathcal C},\nu } $ its generic point, and $ \kappa (\nu ) $ its residue field. Then there exists a nonempty open subset U of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(\nu )$ , a complete local Noetherian k-algebra ${\mathcal A}$ which is a finite formal model of any $\gamma \in U(k)$ , and a section $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},\nu }}}\to \kappa (\nu )$ of the quotient morphism, such that the complete local $\kappa (\nu )$ -algebras $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},\nu }}}}$ and ${\mathcal A}\widehat {\otimes }_k \kappa (\nu )$ are isomorphic. Moreover, the previous statement also holds when $\nu $ is replaced by a positive multiple $N\cdot \nu $ .

In fact, we prove a slightly more precise statement (see Theorem 7.2).

1.8

Let us say a few words about the proof of the above theorem. The key point consists in obtaining a presentation of the formal neighborhood of $ {\mathscr {L}_{\infty }}({\mathcal C}) $ at $ \eta _{{\mathcal C},N\cdot \nu } $ which may be naturally interpreted in terms of infinitesimal deformations of $ \eta _{{\mathcal C},N\cdot \nu } $ . Such an interpretation, which comes naturally at play when dealing with formal neighborhoods of k-rational arcs, is by no means evident in the case of $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}$ , which is not endowed with a canonical structure of $\kappa (N\cdot \nu )$ -algebra. Note that if Theorem 1.7 holds for one particular section of $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}\to \kappa (N\cdot \nu )$ , it will hold for any of them, that is, any choice of a coefficient field. But it turns out that in order to obtain our “deformation-theoretic” interpretation of $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}$ , one has first to show the existence of a coefficient field with specific properties. A similar strategy was used in [BMCS] for toric singularities, although in a rather implicit and indirect way; moreover, in the toric case, the existence of an adequate coefficient field was more directly obtained.

Let us point out that though the works of Reguera and Reguera-Mourtada ([Reg09, MR18, Reg18]) provide fairly general methods to obtain a presentation of the formal neighborhood of a stable arc, they do not provide the deformation-theoretic interpretation we need for our aim (one may compare [MR18, Example 2.2], dealing explicitly with the case of plane curves, with our approach).

Once the ad hoc interpretation of $\widehat {{\mathscr {O}}_{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}$ in terms of deformations is established, one can use the similar interpretation for the formal neighborhood of a sufficiently generic $\gamma \in {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )(k)$ (which, again, is natural in this context) to obtain the comparison theorem.

1.9

We now explain some consequences of our main result.

Corollary 1.10. Keep the notation of Theorem 1.7. Then the Noetherian complete local $\kappa (N\cdot \nu )$ -algebra $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}$ is algebraizable, that is, isomorphic to the quotient of a power series ring in finitely many variables over $ \kappa (N\cdot \nu ) $ by an ideal generated by polynomials.

Recall that it is well-known that there exist Noetherian complete algebras over a field which are not algebraizable (see, e.g., [CdFD22, Example 5.4]). A result similar to Corollary 1.10 also holds in case $\nu $ is a toric valuation on a normal toric variety, as a consequence of the comparison theorem in [BMCS]. But more generally, to the best of our knowledge, the following question is open (and would be answered affirmatively in case the answer to Question 1.3 is positive):

Question 1.11. Let $ V $ be a $ k $ -variety, $ \nu $ a divisorial valuation on $ V $ , and $ \eta _{V,\nu } $ the generic point of ${\mathcal {N}}_{V}(\nu )$ , with residue field $\kappa (\nu )$ . Choose a section of the quotient morphism $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}\to \kappa (\nu )$ . Is the Noetherian complete local $ \kappa (\nu ) $ -algebra $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}$ algebraizable?

1.12

We also have the following consequence on the structure of the formal neighborhood of the stable arc $\eta _{{\mathcal C},N\cdot \nu }$ (see Proposition 7.6).

Corollary 1.13. Keep the notation of Theorem 1.7. Then the Noetherian complete local $\kappa (N\cdot \nu )$ -algebra $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}$ is cancellable. That is, there exists a complete local $\kappa (N\cdot \nu )$ -algebra ${\mathcal A}$ , such that $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}$ is isomorphic to ${\mathcal A}{[[ {u} ]]}$ , where u is an indeterminate.

Previously, the result was only known for $\left (\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},N\cdot \nu }}}}\right )_{\operatorname {\mathrm {red}}}$ ([Reg09, Corollary 5.7]). Again, this cancellation phenomenon can also be observed in the case of toric singularities by the result of [BMCS].

1.14

In [BS17a, BS17b], the quantitative aspects of the nilpotency in the formal neighborhood of a k-rational arc on a curve is studied. To the best of our knowledge, so far, such a question has not been addressed in the literature for stable arcs. As a consequence of our main result and [BS17b, Theorem 1.6], one obtains the following. Recall that the nilpotency index of a ring is the supremum of the nilpotency indices of its nilpotent elements.

Corollary 1.15. Keep the notation of Theorem 1.7, and assume that $({\mathcal C},c)$ is a curve singularity of multiplicity two and degree $\delta ({\mathcal C},c)$ . Then the nilpotency index of $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\eta _{{\mathcal C},\nu }}}}$ equals $\delta ({\mathcal C},c)+1$ .

Remark 1.16. The equality is expected to hold for plane monomial curves, and can be efficiently checked numerically for a certain number of them, using the algorithm described in [BS17b] and Theorem 1.7. For example, it was checked using the aforementioned algorithm for the curve singularity $x^m=y^n$ for every pair of coprime integers $(n,m)$ with $n=3$ and $m\leq 100$ or $n=4$ and $m\leq 43$ or $n=5$ and $m\leq 21$ .

1.17

We now discuss some perspectives. In addition to shedding new light on the geometric properties of the maximal divisorial sets, the extension of the comparison results beyond the cases of curve and toric singularities would allow us to strengthen simultaneously our understanding of both classes of formal neighborhoods. For example (keeping the notation of Question 1.3), in case V is analytically irreducible at the center $\eta _{V,\nu }(0)$ of $\eta _V$ and ${\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}$ is a regular local ring, if the answer to Question 1.3 is positive, one may deduce from [BS17c, Theorem 1.6] that the center of $\eta _{V,\nu }$ is smooth, thus answering positively [Reg18, Question 2.10] with a detour by k-rational arcs.

Going the other way, one may hope that the formal neighborhoods of stable points may be helpful to understand some sufficiently simple finite formal models of a k-rational nondegenerate arc. The algorithmic description of the finite formal model of such an arc in [Dri02] allows Drinfeld to give a very clever and elegant proof of the Drinfeld-Grinberg-Kazhdan theorem alluded to before for any singularity but does not seem suited to apprehend the geometry of the finite formal models; moreover, its implementation is very poorly efficient, even for curves (see [BS17b]). In [BS17b] and [BS19], some useful alternative descriptions were described for monomial curves and toric varieties. One may hope that, in general, such useful alternative descriptions could come from an ad hoc description of the formal neighborhood of stable points. In the last section of the paper, we give some elements illustrating this line of thought in case $\nu $ is a valuation on a hypersurface V, such that the associated initial ideal is prime. We obtain a deformation-theoretic interpretation of the formal neighborhood of $\eta _{V,\nu }$ , which, as in the case of curves, is based on the construction of a coefficient field with specific properties. This allows us to give a conjectural simple description of a finite model of a sufficiently generic element of ${\mathcal {N}}_V(\nu )(k)$ . This conjectural description is equivalent to a weaker yet still meaningful form of Question 1.3, where the answer to its first part is not necessarily assumed to be positive (see Question 8.13). Although there are classes of varieties for which the first part of Question 1.3 is very likely to have a positive answer (e.g., beyond toric varieties, varieties equipped with a big action of a reductive group), we do not know whether it is sensible to hope for a positive answer in general (see Remark 8.14 for an example with a torus action whose generic orbits have codimension one).

1.18

The article is organized as follows: after introducing some notation and recalling some general facts about arc schemes and curves in Section 2, in Section 3, we focus on the properties of subsets of the arc schemes naturally defined by valuations and contact order conditions, paying particular attention to the case of curves. We obtain explicit equations (up to radical) of the generic point of the maximal divisorial set in the arc scheme of a curve associated with a valuation, and we recall the proof of the invariance of the formal neighborhoods at sufficiently generic rational arcs in that maximal divisorial set. We insist that Section 2 in its totality and most of Section 3 are nothing but a detailed account of definitions and results that have already appeared in the literature, for the comfort of the reader and for the sake of fixing notation. The results effectively proven in Section 3 are certainly well-known by the specialists, but we are not aware of convenient references for them. Sections 4, 5, and 6 are devoted to the computation of a presentation of the formal neighborhood of the generic point of a maximal divisorial set on a curve, which one may interpret in terms of deformations. In Section 4, we compute a coefficient field of the formal neighborhood with specific properties. Section 5 contains two useful technical results, in particular, a general existence theorem of “quasi-deformations” of a nondegenerate arc. In Section 6, combining, in particular, the results of the two previous sections, we obtain the sought-for presentation.

Section 7 contains the statement and the proof of Theorem 7.2 (a more precise version of the comparison Theorem 1.7). Finally, Section 8 contains the discussion of the case of hypersurfaces (as alluded to in the above introduction).

2 Notation and reminders

In this section, we recall several facts about the topology of local rings, arc spaces, and curve singularities, introducing along the way some notation to be used in the sequel.

In the whole paper, k designates an algebraically closed field of characteristic zero.

An algebraic variety over k, or k-variety, is an integral k-scheme of finite type over k. A curve over k is an algebraic variety over k of dimension $1$ .

Topology of local rings

A complete local ring is a local ring which is complete with respect to the adic topology defined by its maximal ideal, that is, a basis of neighborhoods of zero is given by the powers of the maximal ideal.

Note, in particular, that a formal power series ring over an infinite number of indeterminates, though it may be obtained by an adic completion of a local ring, is not a complete local ring in the previous sense (see Remark 2.2 below). Thus, we shall consider the category $\operatorname {\mathrm {\mathbf {TopLoc}}}$ (respectively, $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ , k a field), whose objects are the topological local rings (respectively, topological local k-algebras) which are isomorphic to the adic completion of a local ring (respectively of a local k-algebra with residue field k-isomorphic to k) and whose morphisms are continuous morphisms of rings (respectively of k-algebras). The complete local rings (respectively, the complete local k-algebras with residue field k-isomorphic to k) form a full subcategory $\operatorname {\mathrm {\mathbf {CplLoc}}}$ (respectively, $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ ) of $\operatorname {\mathrm {\mathbf {TopLoc}}}$ (respectively, $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ ). The following lemma will be useful (for the proof, see, e.g.,[BS17a, Section 2.1]).

Lemma 2.1. The functor ${\mathcal O}\mapsto (A\mapsto \operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {\mathbf {TopLoc}}}_k}({\mathcal O},A))$ from the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ to the category of precosheaves on the category $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ is fully faithful.

Remark 2.2. Let k be a field and $\{X_i\}_{i\in I}$ be a family of indeterminates indexed by a set I (finite or infinite). The topological k-algebra $k{[[ {(X_i)_{i\in I}} ]]}$ may be defined as the completion of the localization of $k[(X_i)_{i\in I}]$ at the maximal ideal ${\langle {X_i} \rangle }_{i\in I}$ . In case I is finite, it is a complete local ring. However, as soon as I is infinite, the local ring $k{[[ {(X_i)_{i\in I}} ]]}$ is by definition complete for the topology of the inverse limit, yet it is not a complete local ring in the above sense (see, e.g., [Hai20] or [Sta21, 05JA]).

In any case, from the point of view of the previous lemma, $k{[[ {(X_i)_{i\in I}} ]]}$ may be seen as the object of $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ representing the functor

$$\begin{align*}\begin{array}{rcl} {\operatorname{\mathrm{\mathbf{CplLoc}}}_k} & {\longrightarrow} & {\operatorname{\mathrm{Sets}}} \\ {(A,{\mathfrak{M}}_A)} & \longmapsto & {{\mathfrak{M}}_A^I} \end{array}. \end{align*}$$

We shall also consider the full subcategories $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k$ and $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k^{\text {alg}}$ of $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ consisting of those objects of $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ which are Noetherian (respectively, Noetherian and “algebraizable,” that is, isomorphic to the completion of a local algebra essentially of finite type over k).

Reminder on arc spaces

2.3 Arc spaces and the universal arc

Let V be an algebraic variety over k and ${\mathscr {L}_{\infty }}(V)$ be the associated arc space. For more details on arc spaces, see, for example, [CLNS18]. For the sake of simplicity, and since we are primarily interested in local properties of the arc space, we assume that V is affine. Recall, in particular, that ${\mathscr {L}_{\infty }}(V)$ is an affine k-scheme, such that, for any k-algebra A, one has a functorial bijection between the set of A-points of ${\mathscr {L}_{\infty }}(V)$ and the set of $A{[[ {t} ]]}$ -points of V.

We denote the k-algebra of regular functions on V (respectively, on ${\mathscr {L}_{\infty }}(V)$ ) by $\Gamma (V)$ (respectively, $\Gamma (V)_{\infty }$ ). The universal arc on V is the unique morphism of k-algebras $\Delta _{V}\colon \Gamma (V)\to \Gamma (V)_{\infty }{[[ {t} ]]},\,f\mapsto \sum _{j\ge 0}\Delta _{V,j}(f)\cdot t^j$ with the following property: for any k-algebra A and any A-point of ${\mathscr {L}_{\infty }}(V)$ , that is, any morphism of k-algebras $\theta \colon \Gamma (V)_{\infty }\to A$ , the corresponding $A{[[ {t} ]]}$ -point of V is obtained by composing $\Delta _V$ with the morphism $\Gamma (V)_{\infty }{[[ {t} ]]}\to A{[[ {t} ]]},\,\sum _{j\ge 0}f_j\cdot t^j\mapsto \sum _{j\ge 0}\theta (f_j)\cdot t^j$ . We will often write $\Delta =\Delta _V$ if the involved variety is clear from the context.

In case $V={\mathbf {A}}^n_k=\operatorname {\mathrm {Spec}}(k[X_1,\dots ,X_n])$ , we set $X_{i,j}:=\Delta _{{\mathbf {A}}^n_k,j}(X_i)$ . The $X_{i,j}$ ’s are algebraically independent over k and one has $\Gamma (V)_{\infty }=k[(X_{i,j})_{\substack {1\le i\le n\\j\in {\mathbf {N}}}}]$ . Moreover, for any $F\in k[X_1,\dots ,X_n]$ , one has

$$\begin{align*}\sum_{j\ge 0}\Delta_{{\mathbf{A}}^n_k,j}(F)\cdot t^j=F\left(\left(\sum_{j\ge 0}X_{i,j}\cdot t^j\right)_{1\le i\le n}\right). \end{align*}$$

In case $\Gamma (V)$ is presented as the quotient of $k[X_1,\dots ,X_n]$ by an ideal ${\mathfrak {i}}$ , then $\Gamma (V)_{\infty }$ is presented as the quotient of $k[(X_{i,j})_{\substack {1\le i\le n\\j\in {\mathbf {N}}}}]$ by the ideal ${\mathfrak {i}}_{\infty }$ generated by $\{\Delta _{{\mathbf {A}}^n,j}(F)\}_{\substack {F\in {\mathcal G}\\j\in {\mathbf {N}}}}$ , where ${\mathcal G}$ is any generating family of ${\mathfrak {i}}$ . Moreover, the following natural diagram is commutative:

2.4 Nondegenerate and constant arcs

Let $\gamma \in {\mathscr {L}_{\infty }}(V)$ , with residue field $\kappa (\gamma )$ . The image of the generic point (respectively of the closed point) of $\operatorname {\mathrm {Spec}}(\kappa (\gamma ){[[ {t} ]]})$ by the induced morphism $\operatorname {\mathrm {Spec}}(\kappa (\gamma ){[[ {t} ]]})\to V$ is called the generic point $\gamma (\eta )$ (respectively, the special point or the origin $\gamma (0)$ ) of $\gamma $ . Let $V^{\text {sing}}$ be the singular locus of V. The arc $\gamma $ is said to be nondegenerate if it does not belong to ${\mathscr {L}_{\infty }}(V^{\text {sing}})\subset {\mathscr {L}_{\infty }}(V)$ . In other words, $\gamma $ is nondegenerate if and only if its generic point does not belong to $V^{\text {sing}}$ . The arc $\gamma $ is said to be pseudo-constant if $\gamma (0)=\gamma (\eta )$ , and constant if the induced morphism $\Gamma (V)\to \kappa (\gamma ){[[ {t} ]]}$ has its image in $\kappa (\gamma )$ . Any constant arc is pseudoconstant; the arc $k[X_1]\to k(X_{1,j})_{j\in {\mathbf {N}}}{[[ {t} ]]}$ defined by $X_1\mapsto \sum _{j\in {\mathbf {N}}}X_{1,j}\cdot t^j$ is an example of a pseudoconstant yet not constant arc on ${\mathbf {A}}^1_k$ . Note, however, that if $\gamma $ is such that $\gamma (0)$ is a closed point of V, then $\gamma $ is constant if and only if $\gamma $ is pseudoconstant, since then the image of $\Gamma (V)\to \kappa (\gamma ){[[ {t} ]]}$ is algebraic over k, hence contained in $\kappa (\gamma )$ . In particular, in case V is a curve, any nonconstant arc on V is necessarily nondegenerate.

Definition 2.5. Let $\gamma \in {\mathscr {L}_{\infty }}(V)(k)$ be a nondegenerate arc. A finite formal model of $\gamma $ is an object ${\mathcal A}$ of $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k^{\text {alg}}$ , such that there is an isomorphism (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ ) between $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}$ and ${\mathcal A}{[[ {(u_i)} ]]}_{i\in {\mathbf {N}}}$ .

The Drinfeld-Grinberg-Kazhdan theorem ([GK00, Dri02]) states that in case $\dim (V)\ge 1$ , any nondegenerate k-rational arc $\gamma $ on V admits a finite formal model.

Moreover, any object ${\mathcal A}'$ of $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k$ , such that $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}$ is isomorphic to ${\mathcal A}'{[[ {(v_i)} ]]}_{i\in {\mathbf {N}}}$ in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ is in fact an object of $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k^{\text {alg}}$ : indeed, if ${\mathcal A}$ is a finite formal model of $ \gamma $ , by Gabber’s cancellation theorem (see [BS17a, Theorem 7.2]), there exist nonnegative integers n and m, such that ${\mathcal A}'{[[ {v_1,\dots ,v_n} ]]}$ and ${\mathcal A}{[[ {u_1,\dots ,u_m} ]]}$ are isomorphic. On the other hand, if ${\mathcal A}'\in \operatorname {\mathrm {\mathbf {NthCplLoc}}}_k$ is such that ${\mathcal A}'{[[ {u} ]]}\in \operatorname {\mathrm {\mathbf {NthCplLoc}}}_k^{\text {alg}}$ , then ${\mathcal A}'\in \operatorname {\mathrm {\mathbf {NthCplLoc}}}_k^{\text {alg}}$ ; this is a consequence of Zariski’s simplification lemma (see [BS18, Section 5.6]).

Some facts about curve singularities

2.6

Let us now consider a pointed k-curve $({\mathcal C},c)$ , that is, ${\mathcal C}$ is a k-curve and $c\in {\mathcal C}(k)$ . Since we are only interested in local properties, without restricting the generality of the arguments, we may in any circumstances replace ${\mathcal C}$ with a Zariski open set of ${\mathcal C}$ containing c. In particular, we may assume that ${\mathcal C}$ is affine and that c is the only singular point of ${\mathcal C}$ .

2.7 Primitive parametrizations and multiplicity of a germ of curve

We, hereafter, assume that the singularity at c is analytically irreducible, in other words, that the normalization of the local ring ${\mathscr {O}}_{{{\mathcal C},c}}$ is a domain.

In particular, any choice of an isomorphism $\theta $ between the normalization of $\widehat {{\mathscr {O}}_{{{\mathcal C},c}}}$ and $k{[[ {t} ]]}$ in turn induces an injective morphism $p_{\theta }\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}5}\to k{[[ {t} ]]}$ . Such a morphism will be called a primitive parametrization of the germ $({\mathcal C},c)$ . The integer $\min \big (\big \{\operatorname {\mathrm {ord}}_t(p_{\theta }(f))\;:\; f\in \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\big \}\setminus \{0\}\big )$ does not depend on $\theta $ and is called the multiplicity $\mu ({\mathcal C},c)$ of the germ. A morphism $p\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to k{[[ {t} ]]}$ is a primitive parametrization if and only if

$$\begin{align*}\min \left(\left\{\operatorname{\mathrm{ord}}_t(p(f))\;:\; f\in \widehat{{\mathscr{O}}_{{{\mathcal C},c}}}\right\}\setminus \{0\}\right)=\mu({\mathcal C},c). \end{align*}$$

More precisely, for any two primitive parametrizations $p_1$ , $p_2$ of the germ $({\mathcal C},c)$ , there exists an automorphism $\phi $ of $k{[[ {t} ]]}$ , such that $\phi \circ p_1=p_2$ .

2.8 Multiplicity of an arc centered at a singular point of a curve

Let $p\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to k{[[ {t} ]]}$ be a primitive parametrization of the germ $({\mathcal C},c)$ and $ \widehat {{\mathfrak {M}}_{{\mathcal C},c}} $ be the maximal ideal of $ \widehat {{\mathscr {O}}_{{{\mathcal C},c}}} $ . For any k-extension K and any morphism $\gamma ^{\ast }:\widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to K{[[ {t} ]]}$ , such that $\gamma ^{\ast }(\widehat {{\mathfrak {M}}_{{\mathcal C},c}})\neq \{0\}$ , there exists a unique positive integer N and a unique automorphism $\psi $ of $K{[[ {t} ]]}$ , such that $\gamma ^{\ast }$ coincides with the composition of $ \psi \circ p $ with the endomorphism of $K{[[ {t} ]]}$ induced by $t\mapsto t^N$ . The integer N is called the multiplicity of $\gamma ^{\ast }$ and denoted by $\mu (\gamma ^{\ast })$ . Note that the datum of a local morphism $\gamma ^{\ast }\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to K{[[ {t} ]]}$ , such that $\gamma ^{\ast }(\widehat {{\mathfrak {M}}_{{\mathcal C},c}})\neq \{0\}$ is equivalent with the datum of a K-arc on ${\mathcal C}$ , centered at c, and not entirely contained in c. This allows us to define the multiplicity $\mu (\gamma )$ of an arc $\gamma \in {\mathscr {L}_{\infty }}({\mathcal C})^{c,\circ }:={\mathscr {L}_{\infty }}({\mathcal C})^{c}\setminus \{c\}$ (here, $ {\mathscr {L}_{\infty }}({\mathcal C})^{c} $ denotes the set of arcs centered at $ c $ , and we still denote the constant arc at c by c) by considering the multiplicity of the $\kappa (\gamma )$ -arc induced by $\gamma $ .

For any positive integer N, we set

$$\begin{align*}\Theta_N:=\left\{\gamma\in {\mathscr{L}_{\infty}}({\mathcal C})^{c,\circ}\;:\;\mu(\gamma)=N\right\}. \end{align*}$$

Note that any two elements $\gamma _1,\gamma _2\in \Theta _N(K)$ are connected by an automorphism of $K{[[ {t} ]]}$ . Then, the arguments in the proof of [BS17b, Lemma 3.2] can be directly adapted to prove the following more general result.

Lemma 2.9. Keep the previous notation. Let $ N $ be a positive integer. Let $\gamma _1,\gamma _2\in \Theta _N(k)$ . Then $ \widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\gamma _1}}} $ and $ \widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\gamma _2}}} $ are isomorphic (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ , see Section 2).

2.10

Let us choose a presentation of the curve ${\mathcal C}\cong \operatorname {\mathrm {Spec}}\left (k[Y_0,Y_1,\dots ,Y_\ell ]/{\mathfrak {i}}\right )$ , that is, the ideal ${\mathfrak {i}}$ of $k[Y_0,Y_1\dots ,Y_\ell ]$ defines ${\mathcal C}$ as a closed subscheme of the affine space $\boldsymbol {A}_k^{\ell +1}$ . We may and shall assume that the singular point $ c $ is the origin ${\mathfrak {o}}$ of $\boldsymbol {A}_k^{\ell +1}$ , and that any element of the set $\{Y_0,Y_1,\dots ,Y_{\ell }\}$ induces a nonzero regular function on ${\mathcal C}$ .

The closed embedding of ${\mathcal C}$ into the affine space $\boldsymbol {A}_k^{\ell +1}$ induces a surjective morphism $\widehat {{\mathscr {O}}_{{\boldsymbol {A}_k^{\ell +1},{\mathfrak {o}}}}}=k{[[ {Y_0,Y_1,\dots ,Y_\ell } ]]}\to \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}$ with kernel generated by ${\mathfrak {i}}$ . Composing this morphism with a primitive parametrization $p\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to k{[[ {t} ]]}$ gives an $\ell +1$ -tuple of power series $(Y_{p,0}(t),Y_{p,1}(t),\dots ,Y_{p,\ell }(t))\in k{[[ {t} ]]}^{\ell +1}$ , such that $\min _{0\le i\le \ell } \{\operatorname {\mathrm {ord}}_t(Y_{p,i}(t))\}=\mu ({\mathcal C},c)$ and

$$\begin{align*}\forall F\in {\mathfrak{i}},\quad F(Y_{p,i}(t))_{0\le i\le \ell}=0. \end{align*}$$

Conversely, any $\ell +1$ -tuple $(Y_{0}(t),Y_{1}(t),\dots ,Y_{\ell }(t))\in k{[[ {t} ]]}^{\ell +1}$ , such that $\min _{0\le i\le \ell } \{\operatorname {\mathrm {ord}}_t(Y_{i}(t))\}=\mu ({\mathcal C},c)$ and

$$\begin{align*}\forall F\in {\mathfrak{i}},\quad F(Y_{i}(t))_{0\le i\le \ell}=0 \end{align*}$$

is induced by a primitive parametrization. More generally, one has the following result.

Proposition 2.11. Let $ k $ be a field, $\widehat {({\mathcal C},c)}$ a germ of curve, and $ N $ a positive integer. Let p be a primitive parametrization of $\widehat {({\mathcal C},c)}$ . Let K be an extension of k and $(Y_{0}(t),Y_{1}(t),\dots ,Y_{\ell }(t))\in K{[[ {t} ]]}^{\ell +1}$ , such that $\min _{0\le i\le \ell } \{\operatorname {\mathrm {ord}}_t(Y_{i}(t))\}=N\cdot \mu ({\mathcal C},c)$ and

$$\begin{align*}\forall F\in {\mathfrak{i}},\quad F(Y_{i}(t))_{0\le i\le \ell}=0. \end{align*}$$

Then there exists an automorphism $\psi $ of $K{[[ {t} ]]}$ , such that for $0\le i\le \ell $ , one has $Y_{i}(t)=\psi (Y_{p,i}(t^N))$ .

From now on, we denote by $ n:=\mu ({\mathcal C},c) $ the multiplicity of the germ. We set $ X:=Y_0 $ and, up to a permutation of the coordinates, we may assume that $ n=\operatorname {\mathrm {ord}}_t(X(t)) $ . We also denote $ m_i=\operatorname {\mathrm {ord}}_t(Y_{i}(t)) $ for $ 1\le i \le \ell $ . Let us note that, by a suitable choice of a primitive parametrization p, we may assume that the associated $ \ell +1 $ -tuple of power series $(X_{p}(t),Y_{p,1}(t),\dots ,Y_{p,\ell }(t))\in k{[[ {t} ]]}^{\ell +1}$ satisfies $X_{p}(t)=t^n$ .

With this notation, we observe that, for $ N\in {\mathbf {N}} $ , if the $ \ell +1 $ -tuple $(X(t),Y_{1}(t),\dots ,Y_{\ell }(t))$ is as in Proposition 2.11, then $ \operatorname {\mathrm {ord}}_t(X(t))=N\cdot n $ and $ \operatorname {\mathrm {ord}}_t(Y_{i}(t))=N\cdot m_i $ , for $ 1\le i \le \ell $ .

3 Arc schemes and valuations

In this section, we first recall some general definitions and facts about the subsets of the arc space of a variety associated with valuations or contact order conditions. Then we take a closer look at the particular case of curves. In particular, we will study the maximal divisorial sets of the arc scheme of a curve, and we will present two important facts for the sequel of this article: a presentation (up to radical) of the prime ideal defining a maximal divisorial set (Corollary 3.16) and the invariance of the formal neighborhood for rational arcs in a dense open subset of a maximal divisorial set (Corollary 3.19).

3.1 The semivaluation associated with an arc

Let $ V $ be an affine $ k $ -variety. In this paper, we adopt the following terminology regarding (semi)valuations.

Definition 3.2. A (k-)semivaluation on V is a map $\nu \colon \Gamma (V)\to {\mathbf {N}}\cup \{+\infty \}$ , such that

1. 1. $\nu (k)=\{0\}$

2. 2. $\forall f,g\in \Gamma (V),\quad \nu (fg)=\nu (f)+\nu (g)$

3. 3. $\forall f,g\in \Gamma (V),\quad \nu (f+g)\ge \inf (\nu (f),\nu (g))$

4. 4. $\nu (0)=+\infty $ .

It is a valuation if, moreover, $\nu ^{-1}(\{+\infty \})=\{0\}$ .

The center of a semivaluation $\nu $ is the prime ideal $\left \{f\in \Gamma (V)\;:\; \nu (f)>0\right \}$ (or the associated schematic point of V).

A valuation $\nu $ on V is divisorial if there exist a normal k-variety W birational to V, a prime divisor E on W, and a positive integer N, such that $\nu $ is the restriction on $\Gamma (V)$ of the valuation $N\cdot \operatorname {\mathrm {ord}}_E$ on $k(W)=k(V)$ .

Let $\gamma \in {\mathscr {L}_{\infty }}(V)$ be an arc, with residue field $\kappa (\gamma )$ . Then $\gamma $ induces a morphism of k-algebras $\gamma ^{\ast }\colon \Gamma (V)\to \kappa (\gamma ){[[ {t} ]]}$ . Composing with $\operatorname {\mathrm {ord}}_t$ , one defines, following [Ish05], a k-semivaluation $\operatorname {\mathrm {ord}}_{\gamma }$ on V. Note that $\operatorname {\mathrm {ord}}_{\gamma }$ is a valuation if and only if $\gamma ^{\ast }$ is injective, that is, if and only if the generic point of $\gamma $ is the generic point of V. Such arcs are called fat arcs in the literature. Note that any nonfat arc on a curve is necessarily a constant arc.

An elementary yet crucial fact is that the semivaluation associated with an arc “increases by specialization,” as expressed by the following proposition (see [Ish05, Proposition 2.7]).

Proposition 3.3. We keep the preceding notation. Let $\gamma _1,\gamma _2$ be elements of ${\mathscr {L}_{\infty }}(V)$ , such that $\gamma _2$ is a specialization of $\gamma _1$ , that is, it lies in the closure of $\gamma _1$ . Then

$$\begin{align*}\forall f\in \Gamma(V),\quad \operatorname{\mathrm{ord}}_{\gamma_1}(f)\le \operatorname{\mathrm{ord}}_{\gamma_2}(f). \end{align*}$$

3.4 Contact loci in arc spaces

Let $F\subset V$ be a closed subscheme of V, defined by the ideal ${\mathfrak {f}}\subset \Gamma (V)$ . Then the contact order $\operatorname {\mathrm {ord}}_F(\gamma )$ of $\gamma $ with F is the integer N, such that $t^N$ generates the ideal ${\langle {\gamma ^{\ast }({\mathfrak {f}})} \rangle }$ in $\kappa (\gamma ){[[ {t} ]]}$ , or $+\infty $ in case $\gamma ^{\ast }({\mathfrak {f}})=\{0\}$ , that is, in case $\gamma $ is entirely contained in F. Note that $\operatorname {\mathrm {ord}}_F(\gamma )=\operatorname {\mathrm {ord}}_{F^{\operatorname {\mathrm {red}}}}(\gamma )$ only depends on the underlying closed set supporting F and not on the schematic structure of F. One sets

$$\begin{align*}\operatorname{\mathrm{Cont}}^{N}(V,F):=\left\{\gamma\in {\mathscr{L}_{\infty}}(V)\;:\; \operatorname{\mathrm{ord}}_{F}(\gamma)=N\right\}; \end{align*}$$

$$\begin{align*}\operatorname{\mathrm{Cont}}^{\ge N}(V,F):=\left\{\gamma\in {\mathscr{L}_{\infty}}(V)\;:\; \operatorname{\mathrm{ord}}_{F}(\gamma)\ge N\right\}. \end{align*}$$

Note that $\operatorname {\mathrm {Cont}}^{\ge N}(V,F)$ is the closed subset of ${\mathscr {L}_{\infty }}(V)$ defined by the ideal

$$\begin{align*}{\langle {\Delta_i(f)} \rangle}_{\substack{0\le i\le N-1\\f\in {\mathfrak{f}}}}. \end{align*}$$

Also, $\operatorname {\mathrm {Cont}}^{N}(V,F)$ is the intersection of $\operatorname {\mathrm {Cont}}^{\ge N}(V,F)$ with the open set

$$\begin{align*}\bigcup_{f\in {\mathfrak{f}}}\{\Delta_N(f)\neq 0\} \end{align*}$$

and is thus locally closed.

The following fact, firstly observed in [ELM04], follows from a computation in local (étale) coordinates.

Lemma 3.5. Let V be a smooth $ k $ -variety, E be a prime divisor in V, and $ N $ be a positive integer. Then the set $\operatorname {\mathrm {Cont}}^{\ge N}(V,E)$ is irreducible. In particular, $\operatorname {\mathrm {Cont}}^{N}(V,E)$ is also irreducible and it is a dense open subset of $\operatorname {\mathrm {Cont}}^{\ge N}(V,E)$ .

Remark 3.6. Let ${\mathcal C}$ be a k-curve and $c\in {\mathcal C}(k)$ be an analytically irreducible point. Let $\bar {{\mathcal C}}$ be the normalization of ${\mathcal C}$ and $\bar {c}$ be the preimage of c in $\bar {{\mathcal C}}$ . Let N be a positive integer and $\gamma \in {\mathscr {L}_{\infty }}({\mathcal C})^c\setminus \{c\}$ be an element of $\Theta _N$ . Let $\bar {\gamma }\in {\mathscr {L}_{\infty }}(\bar {{\mathcal C}})$ be the unique lifting of $\gamma $ to ${\mathscr {L}_{\infty }}(\bar {{\mathcal C}})$ . It then follows from the definition of the multiplicity of a nonconstant arc centered at c that $\bar {\gamma }\in \operatorname {\mathrm {Cont}}^{N}(\bar {{\mathcal C}},\{\bar {c}\})$ . Note also that the constant arc $\{\bar {c}\}$ lies in $\operatorname {\mathrm {Cont}}^{\ge N}(\bar {{\mathcal C}},\{\bar {c}\})$ for any N.

3.7 Maximal divisorial sets in arc spaces

Let $ V $ be an affine $ k $ -variety. Being given $\nu $ a semivaluation on V trivial on k, one defines the closed set ${\mathcal {N}}_V(\nu )$ of ${\mathscr {L}_{\infty }}(V)$ as the Zariski closure of the set $\left \{\gamma \in {\mathscr {L}_{\infty }}(V)\;:\;\operatorname {\mathrm {ord}}_{\gamma }=\nu \right \}$ (which is nonempty by [Ish05, Proposition 2.11] in case $\nu $ is a divisorial valuation, and by [Mor09, Proposition 3.12] in general).

In case $\nu $ is a divisorial valuation, and following [Ish08], ${\mathcal {N}}_V(\nu )$ is called the maximal divisorial set associated with $\nu $ . By op.cit., it may be described as follows: take a resolution $\pi \colon W\to V$ of the singularities of V, such that the center of $\nu $ on W is a divisor E, and let N be the positive integer, such that $\nu =N\cdot \operatorname {\mathrm {ord}}_E$ . Then ${\mathcal {N}}_V(\nu )$ coincides with the closure of the image by ${\mathscr {L}_{\infty }}(\pi )$ of the set $ \operatorname {\mathrm {Cont}}^{N}(W,E) $ , and hence, also of the set $ \operatorname {\mathrm {Cont}}^{\ge N}(W,E) $ . In particular, ${\mathcal {N}}_V(\nu )$ is irreducible by Lemma 3.5. We denote by $\eta _{V,\nu }$ or $\eta _{\nu }$ its generic point. It follows from the definitions and Proposition 3.3 that $\operatorname {\mathrm {ord}}_{\eta _{\nu }}=\nu $ .

3.8

Let $ \nu $ be a semivaluation on V. Let us consider the subset $ {\mathcal D}_{V}(\nu ) $ of ${\mathscr {L}_{\infty }}(V)$ given by

$$\begin{align*}{\mathcal D}_{V}(\nu):=\left\{\gamma\in {\mathscr{L}_{\infty}}(V)\,:\, \forall f\in \Gamma(V),\,\operatorname{\mathrm{ord}}_{\gamma}(f)\ge \nu(f)\right\}. \end{align*}$$

The following lemma collects some basic properties connecting the different subsets of the arc scheme associated to valuations that we have defined.

Lemma 3.9. Let us keep the preceding notation. Then the following assertions hold true:

1. (i) Let $ \nu $ be a semivaluation on V. The set $ {\mathcal D}_{V}(\nu ) $ is the support of the closed subscheme of ${\mathscr {L}_{\infty }}(V)$ defined by the ideal

   $$\begin{align*}{\mathfrak{j}}_{V}(\nu):={\langle {\Delta_0(f),\dots,\Delta_{\nu(f)-1}(f)} \rangle}_{f\in \Gamma(V)}. \end{align*}$$

2. (ii) Let $ \nu $ be a divisorial valuation on V. Then the set $ {\mathcal {N}}_{V}(\nu ) $ is an irreducible component of $ {\mathcal D}_{V}(\nu ) $ . In particular, if $ {\mathfrak {p}}_{\nu } $ is the prime ideal of $ \Gamma (V)_{\infty } $ corresponding to the generic point of $ {\mathcal {N}}_{V}(\nu ) $ , then $\operatorname {\mathrm {rad}}({\mathfrak {j}}_{V}(\nu ))\subset {\mathfrak {p}}_{\nu }$ .

3. (iii) Let $ \nu $ be a divisorial valuation on V. Let $ f\in \Gamma (V) $ , such that $ f\ne 0 $ . Then $\Delta _{\nu (f)}(f)$ does not belong to the ideal ${\mathfrak {p}}_{\nu }$ of $ \Gamma (V)_{\infty } $ .

Proof. Part (i) directly follows from the definition of $\operatorname {\mathrm {ord}}_{\gamma }$ .

As for part (ii), by its very definition, ${\mathcal D}_{V}(\nu )$ contains $\left \{\gamma \in {\mathscr {L}_{\infty }}(V)\;:\;\operatorname {\mathrm {ord}}_{\gamma }=\nu \right \} $ , thus also its closure ${\mathcal {N}}_{V}(\nu )$ . Since $ \nu $ is a divisorial valuation, $ {\mathcal {N}}_{V}(\nu ) $ is irreducible. Let $\eta $ be the generic point of an irreducible component of ${\mathcal D}_{V}(\nu )$ containing ${\mathcal {N}}_{V}(\nu )$ . Let $\gamma $ be an arc with $\operatorname {\mathrm {ord}}_{\gamma }=\nu $ . Then $\gamma $ is a specialization of $\eta $ . Thus, by Proposition 3.3

$$\begin{align*}\forall f\in \Gamma(V),\quad \operatorname{\mathrm{ord}}_{\eta}(f)\le \nu(f). \end{align*}$$

Since $\eta \in {\mathcal D}_{V}(\nu )$ , and by the very definition of ${\mathcal D}_{V}(\nu )$ , one infers that $\operatorname {\mathrm {ord}}_{\eta }=\nu $ . Hence, $\eta \in {\mathcal {N}}_{V}(\nu )$ , thus, $\eta $ is the generic point of ${\mathcal {N}}_{V}(\nu )$ , which shows part (ii).

Let us prove part (iii). We argue by contradiction and assume that there exists $ f\in \Gamma (V) $ with $ f\ne 0 $ , such that $\Delta _{\nu (f)}(f)\in {\mathfrak {p}}_{\nu }$ . In particular, for any $\gamma \in {\mathcal {N}}_{V}(\nu )$ , the $t^{\nu (f)}$ -coefficient of $\gamma ^{\ast }(f)$ vanishes. Since $\gamma \in {\mathcal D}_{V}(\nu )$ , one infers that $\operatorname {\mathrm {ord}}_{\gamma }(f)>\nu (f)$ . Taking $\gamma =\eta _{\nu }$ gives a contradiction since $\operatorname {\mathrm {ord}}_{\eta _{\nu }}=\nu $ .

Remark 3.10. As a straightforward consequence of part (ii), we see that for any divisorial valuation $\nu $ on V, the following properties are equivalent:

1. 1. ${\mathcal {N}}_{V}(\nu )$ is a proper subset of ${\mathcal D}_{V}(\nu )$ .

2. 2. ${\mathcal D}_{V}(\nu )$ is not irreducible.

3. 3. There exists a semivaluation $\nu '$ on V, such that

   $$\begin{align*}\forall f\in \Gamma(V),\quad \nu(f)\le \nu'(f) \end{align*}$$
   yet ${\mathcal {N}}_{V}(\nu ')$ is not contained in ${\mathcal {N}}_{V}(\nu )$ .

See [Ish08, Theorem 4.3] for an example of such a divisorial valuation $\nu $ when V is the affine plane ${\mathbf {A}}^2$ . In case V is a curve, we shall see that for any divisorial valuation, one has ${\mathcal {N}}_{V}(\nu )={\mathcal D}_{V}(\nu )$ .

The case of curve singularities

3.11

Let us keep the assumptions and notation from Section 2.6; in particular, $ {\mathcal C} $ is an affine $ k $ -curve and $ c\in {\mathcal C}(k)$ is the only singular point of ${\mathcal C}$ , and is analytically irreducible. For any divisorial valuation $ \nu $ on $ {\mathcal C} $ centered at $ c $ , our aim in this article is to compare the formal neighborhood of the generic point of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ with the formal neighborhood of a generic element of the set of $ k $ -rational points of $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ .

Let p be a primitive parametrization of $\widehat {({\mathcal C},c)}$ . Then it induces a valuation

$$\begin{align*}\nu\colon f\in \Gamma({\mathcal C})\mapsto \operatorname{\mathrm{ord}}_t(p(f))\end{align*}$$

on $ {\mathcal C} $ , centered at $ c $ , which is a divisorial valuation. The following result is well-known.

Lemma 3.12. Let us keep the preceding notation. Let $ {\mathfrak {p}}_{c} $ be the maximal ideal of $ \Gamma ({\mathcal C}) $ corresponding to the singular point $ c $ of $ {\mathcal C} $ . Then any k-semivaluation $ \nu ' $ on $ {\mathcal C} $ centered at $ c $ is either the semivaluation $\nu _c$ which factorizes through $ \Gamma ({\mathcal C})/{\mathfrak {p}}_{c}\cong k $ or a divisorial valuation of the form $N\cdot \nu $ with N a positive integer.

Note that the constant arc $\{c\}$ is the only element $\gamma \in {\mathscr {L}_{\infty }}({\mathcal C})$ , such that $\operatorname {\mathrm {ord}}_{\gamma }=\nu _c$ .

Lemma 3.13. Let us keep the preceding notation. Let $ N $ be a positive integer.

1. (i) The set $ \Theta _N $ coincides with the set $ \left \{\gamma \in {\mathscr {L}_{\infty }}({\mathcal C})\,:\, \operatorname {\mathrm {ord}}_{\gamma }=N\cdot \nu \right \} $ .

2. (ii) One has:

   $$\begin{align*}{\mathcal D}_{{\mathcal C}}(N\cdot\nu)=\{c\}\cup_{N'\ge N}\Theta_{N'}. \end{align*}$$

3. (iii) For any arbitrary nonempty family $\{f_i\}_{i\in I}$ of nonzero elements $f_i\in \Gamma ({\mathcal C})$ , such that $\nu (f_i)>0$ , one has

   $$\begin{align*}{\mathcal D}_{{\mathcal C}}(N\cdot\nu)=\left\{\gamma\in {\mathscr{L}_{\infty}}({\mathcal C})^c\;:\; \forall i\in I, \operatorname{\mathrm{ord}}_{\gamma}(f_i)\ge N\cdot \nu(f_i)\right\}, \end{align*}$$
   $$\begin{align*}\Theta_N=\left\{\gamma\in {\mathscr{L}_{\infty}}({\mathcal C})^c\;:\;\forall i\in I, \operatorname{\mathrm{ord}}_{\gamma}(f_i)= N\cdot \nu(f_i)\right\}. \end{align*}$$

4. (iv) One has the equality ${\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )={\mathcal D}_{{\mathcal C}}(N\cdot \nu )$ .

Remark 3.14. In particular, one sees that $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ coincides with the set of arcs ${\mathscr {L}_{\infty }}({\mathcal C})^{c}$ centered at $ c $ , that is, centered at the singular locus of $ {\mathcal C} $ . In particular, the latter set is irreducible. This is the well know-fact that through an analytically irreducible curve singularity there is a unique maximal irreducible family of arcs (Such families are called Nash components in Ish08.).

Proof. As for part (i), let $ \gamma \in \Theta _N $ . Since $ \operatorname {\mathrm {ord}}_t $ is invariant by any automorphism of $ K{[[ {t} ]]} $ , by Section 2.8 and the definition of $\nu $ , we have $ \operatorname {\mathrm {ord}}_{\gamma }=N\cdot \nu $ . Conversely, if $\operatorname {\mathrm {ord}}_{\gamma }=N\cdot \nu $ , since $\operatorname {\mathrm {ord}}_{\gamma }$ is a valuation, $\gamma $ is nonconstant, and since $\operatorname {\mathrm {ord}}_{\gamma }$ is centered at c, $\gamma $ also is; by the previous argument, one has $\mu (\gamma )=N$ .

Part (ii) is a direct consequence of part (i) and Lemma 3.12.

Let us now prove part (iii). By part (ii), it is enough to prove the property for $ \Theta _N $ . One inclusion follows directly from part (i). Let us show the other inclusion. Let $ f\in \Gamma ({\mathcal C}) $ be a nonzero element, such that $ \nu (f)>0 $ and $ \gamma \in {\mathscr {L}_{\infty }}({\mathcal C})^c$ be an arc centered at c, such that $ \operatorname {\mathrm {ord}}_{\gamma }(f)=N\cdot \nu (f) $ . We have to show that $\gamma \in \Theta _N$ . Since $\gamma $ is centered at c, $\operatorname {\mathrm {ord}}_{\gamma }$ is also centered at c. Since $\operatorname {\mathrm {ord}}_{\gamma }(f)<+\infty $ , by Proposition 3.12, we deduce that $ \operatorname {\mathrm {ord}}_{\gamma }=N'\cdot \nu $ for some positive integer $ N'$ . From $ \operatorname {\mathrm {ord}}_{\gamma }(f)=N\cdot \nu (f)$ and $\nu (f)>0$ we deduce that $ N'=N $ .

Now for part (iv). By Lemma 3.9 part (ii), it suffices to prove that the set ${\mathcal D}_{{\mathcal C}}(N\cdot \nu )$ is contained in $ {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu ) $ . Let $ \gamma \in {\mathcal D}_{{\mathcal C}}(N\cdot \nu ) $ ; thus, for every $ f\in \Gamma ({\mathcal C}) $ , we have $ N\cdot \nu (f)\le \operatorname {\mathrm {ord}}_{\gamma }(f) $ . By Proposition 3.12, either $ \operatorname {\mathrm {ord}}_{\gamma } $ is the semivaluation which factorizes through $ \Gamma ({\mathcal C})/{\mathfrak {p}}_{c}\cong k $ or there exists a positive integer $ N' $ , such that $ \operatorname {\mathrm {ord}}_{\gamma }=N'\cdot \nu $ ; in the latter case, we deduce that $ N\le N' $ . By part (i), Remark 3.6, and Section 3.7, one deduces that $\gamma \in {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )$ .

3.15

The following corollary provides a presentation (up to radical) of the prime ideal $ {\mathfrak {p}}_{N\cdot \nu } $ of $ \Gamma ({\mathcal C})_{\infty } $ defining the generic point $ \eta _{N\cdot \nu } $ of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu ) $ .

Corollary 3.16. For any nonempty family $\{f_i\}_{i\in I}$ of nonzero elements $f_i\in \Gamma ({\mathcal C})$ , such that $\nu (f_i)>0$ , the prime ideal ${\mathfrak {p}}_{N\cdot \nu }$ of $\Gamma ({\mathcal C})_{\infty }$ corresponding to the generic point of ${\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )$ is the radical of the ideal

$$\begin{align*}{\langle {\Delta_0(f_i),\dots,\Delta_{N\cdot \nu(f_i)-1}(f_i)} \rangle}_{i\in I}. \end{align*}$$

Moreover, if $f\in \Gamma ({\mathcal C})$ is a nonzero element, such that $\nu (f)>0$ , then $\Delta _{N\cdot \nu (f)}(f)\notin {\mathfrak {p}}_{N\cdot \nu }$ .

Proof. The first assertion follows from Lemmas 3.9 part (i) and 3.13 parts (iii) and (iv), the second one from Lemma 3.9 part (iii).

Example 3.17. Let $ f $ be the polynomial $ f:=X^{5} + X^{4} + 3 X^{3} Y - Y^{3}$ of $ k[X,Y]$ and ${\mathcal C}=\operatorname {\mathrm {Spec}}(k[X,Y]/{\langle {f}\rangle })$ be the associated affine $ k $ -curve. It admits the primitive parametrization $\left (X_p(t)=t^3,Y_p(t)=t^4+t^5\right )$ . In particular, the multiplicity of the germ is $ n=\operatorname {\mathrm {ord}}_t(X_p(t))=3$ . The valuation $ \nu $ of $ {\mathcal C} $ induced by the primitive parametrization is given by $f\in \Gamma ({\mathcal C})\mapsto \operatorname {\mathrm {ord}}_t(f(X_p(t),Y_p(t)))$ . Then the prime ideal of $\Gamma ({\mathcal C})_{\infty }$ defining the generic point of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ is ${\mathfrak {p}}_{\nu }=\operatorname {\mathrm {rad}}({\langle {X_0,X_1,X_2,Y_0,Y_1,Y_2,Y_3} \rangle })=\operatorname {\mathrm {rad}}({\langle {X_0,X_1,X_2} \rangle })$ . Moreover, $ X_3 $ does not belong to $ {\mathfrak {p}}_{\nu } $ .

3.18

As a direct consequence of Lemmas 2.9 and 3.13, we can affirmatively answer the first part of Question 1.3.

Corollary 3.19. Let us keep the preceding notation. Let $ N $ be a positive integer. Then $\Theta _N$ is a dense open subset of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )$ . Moreover, for any $ \gamma _1,\gamma _2\in \Theta _N(k) $ , $ k $ -algebras $ \widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\gamma _1}}} $ and $ \widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}({\mathcal C}),\gamma _2}}} $ are isomorphic (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ , see Section 2).

Proof. In view of Lemma 2.9, the only thing remaining to show is that $\Theta _N$ is an open subset of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )$ . But by Lemma 3.13 part (ii), one has $\Theta _{N}={\mathcal D}_{{\mathcal C}}(N\cdot \nu )\setminus {\mathcal D}_{{\mathcal C}}((N+1)\cdot \nu )$ , thus, $\Theta _{N}$ is open in ${\mathcal D}_{{\mathcal C}}(N\cdot \nu )$ which allows us to conclude.

4 A suitable coefficient field of the formal neighborhood of the generic primitive arc on a curve singularity

Let $({\mathcal C},c)$ be an algebraic pointed k-curve. In this section, we provide an explicit presentation of a coefficient field of the formal neighborhood of the generic primitive arc in $ {\mathscr {L}_{\infty }}({\mathcal C})$ , with extra properties (see Proposition 4.8 for more details). This will allow us in Section 6 to obtain a description of this formal neighborhood which may be naturally interpreted in terms of (some of) the infinitesimal deformations of the arc, which is a key point in the proof of our comparison theorem.

4.1

We first introduce some generic notation and a definition. Let R be a k-algebra, ${\mathfrak {I}}$ be an ideal of R, and ${\mathfrak {P}}$ be a prime ideal of R containing ${\mathfrak {I}}$ . Let $(A,{\mathfrak {M}}_A)$ be the localization of $ R/{\mathfrak {I}}$ with respect to $ {\mathfrak {P}}$ , and let $(\widehat {A},{\mathfrak {M}}_{\widehat {A}}) $ be its completion, with residue field $\kappa _A=\kappa _{\widehat {A}}$ . Let $ \iota \colon R\to \widehat {A} $ be the composition of the natural morphism $ R\to A $ with the completion morphism $A\to \widehat {A} $ . Recall that a coefficient field in $ \widehat {A} $ is a subfield K of $\widehat {A}$ , such that the quotient morphism $p_{\widehat {A}}\colon \widehat {A} \to \kappa _{\widehat {A}}$ induces an isomorphism $K{\overset {\sim }{\to }} \kappa _{\widehat {A}}$ . Since R is a k-algebra, such a coefficient field exists by Cohen’s theorem (see, e.g., [Sta21, Tag 032A]).

Definition 4.2. With the above notation, an algebraic presentation of a coefficient field of $\widehat {A}$ is a k-algebra morphism $\rho \colon R\to \widehat {A}$ , such that $p_{\widehat {A}}\circ \rho =p_{\widehat {A}}\circ \iota $ and ${\mathfrak {P}}\subset \operatorname {\mathrm {Ker}}(\rho )$ .

Remark 4.3. If $\rho \colon R\to \widehat {A}$ is an algebraic presentation of a coefficient field of $\widehat {A}$ , then $\operatorname {\mathrm {Ker}}(\rho )={\mathfrak {P}}$ , $\rho (R)$ is a domain, $\rho (R)\cap {\mathfrak {M}}_{\widehat {A}}=\{0\}$ , and $\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ is a coefficient field of $\widehat {A}$ . In fact, it is easy to see that the datum of an algebraic presentation of a coefficient field of $\widehat {A}$ is equivalent to the datum of a coefficient field of $\widehat {A}$ . We adopt this definition because it is convenient for the characterization of a coefficient field suited to our aim.

Let $\pi \colon R\to \operatorname {\mathrm {Frac}}(R/{\mathfrak {P}}) $ be the composition of the quotient morphism $R\to R/{\mathfrak {P}}$ with the canonical injection $R/{\mathfrak {P}}\to \operatorname {\mathrm {Frac}}(R/{\mathfrak {P}})$ . Then $\pi $ factors through $R\to A\to \kappa _A$ , giving a natural isomorphism from $\kappa _A=\kappa _{\widehat {A}}$ with $ \operatorname {\mathrm {Frac}}(R/{\mathfrak {P}}) $ . The composition of the quotient morphism $p_{\widehat {A}}$ with the latter isomorphism is denoted by $\tau $ .

Remark 4.4. By construction, one has $\tau \circ \iota =\pi $ . Thus, a k-algebra morphism $\rho \colon R\to \widehat {A}$ , such that ${\mathfrak {P}}\subset \operatorname {\mathrm {Ker}}(\rho )$ is an algebraic presentation of a coefficient field if and only if $\tau \circ \rho =\pi $ .

In order to unpack the above definitions a little bit, note that, identifying $\rho $ with the induced morphism $R/{\mathfrak {P}}\to \widehat {A}$ , one has the following commutative diagram:

where the leftmost vertical arrow is the quotient morphism and the lower horizontal arrow is the natural inclusion. In our situation, we will have a rather explicit description of $\operatorname {\mathrm {Frac}}(R/{\mathfrak {P}})$ and the morphism $\tau $ is to be understood as a technical device to consider the reduction of an element of $\widehat {A}$ in an explicit field rather than in the a priori abstract residue field $\kappa _{\widehat {A}}$ . Let us now give a basic example: take $R=k[(X_i)_{i\in {\mathbf {N}}}]$ , ${\mathfrak {I}}=\{0\}$ and ${\mathfrak {P}}={\langle {X_0,\dots ,X_{N-1}} \rangle }$ . With the notation of the previous section, it corresponds to the generic point of ${\mathcal {N}}_{{\mathcal C}}(N\cdot \nu )$ , where $({\mathcal C},c)=({\mathbf {A}}^1_k,\text {origin})$ . Then for the most natural choice $\rho _0$ of $\rho $ , the above diagram reads as follows (all the injective arrows are the natural inclusions):

Of course, there are other possible “less natural” choices for $\rho $ , for example, choose any family $(Y_i)_{i\geq N}$ of elements of the maximal ideal of $k((X_i)_{i\geq N}){[[ {X_0,\dots ,X_{N-1}} ]]}$ and set $\rho (X_i)=X_i+Y_i$ for $i\geq N$ . Roughly speaking, in the case of a general curve singularity, our aim will be to construct an algebraic presentation of a coefficient field of the formal neighborhood of the generic primitive arc that is “as natural” as $\rho _0$ in the above situation.

4.5

We now come back to our algebraic pointed k-curve $({\mathcal C},c)$ . We work with the notation and under the hypotheses of Sections 2.6 and 2.10. We denote by $ p $ a primitive parametrization of $\widehat {({\mathcal C},c)}$ . Let $ \nu $ be the divisorial valuation induced by $ p $ as defined in Section 3.11. In particular, $ {\mathfrak {p}}_{\nu }$ is the prime ideal of the ring $ \Gamma ({\mathscr {L}_{\infty }}({\mathcal C}))\cong k[(X_j)_{j\in {\mathbf {N}}},(Y_{i,j})_{\substack {1\le i\le \ell \\ j\in {\mathbf {N}}}}]/{\mathfrak {i}}_{\infty }$ corresponding to the generic point $\eta _{{\mathcal C},\nu }$ of the maximal divisorial set $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ . In a slight abuse of notation, we also denote by $ {\mathfrak {p}}_{\nu }$ its unique preimage in $ k[(X_j)_{j\in {\mathbf {N}}},(Y_{i,j})_{\substack {1\le i\le \ell \\ j\in {\mathbf {N}}}}] $ containing $ {\mathfrak {i}}_{\infty } $ .

Remark 4.6. For the sake of simplicity, all the results and proofs in the present section and Sections 6 and 7 are written for the valuation $ \nu $ defined above. However, everything remains valid for a positive multiple $ N\cdot \nu $ of $\nu $ . Up to a few minor exceptions which will be duly indicated, it suffices to replace in the statements and the proofs each occurrence of $ \nu $ by $N\cdot \nu $ , each occurrence of ${n}$ by $ N\cdot {n} $ , each occurrence of ${m}_i$ by $N\cdot {m}_i$ ( $ 1\le i\le \ell $ ), and each occurrence of $Y_{p,i}$ ( $ 1\le i\le \ell $ ) by $Y^{(N)}_{p,i}$ , where $Y_{p,i}^{(N)}(t):=Y_{p,i}(t^N)$ .

Recall that $n = \operatorname {\mathrm {ord}}_t(X(t))$ is the multiplicity of the germ (see at the end of Section 2.10). We consider the $ k $ -algebras

$$\begin{align*}R:=k[(X_j)_{j\in {\mathbf{N}}},(Y_{i,j})_{\substack{1\le i\le \ell\\ j\in{\mathbf{N}}}},\frac{1}{X_{{n}}}] \end{align*}$$

$$\begin{align*}\text{and}\quad R^{\ge \nu}:=k[(X_j)_{j\ge {n}},(Y_{i,j})_{\substack{1\le i\le \ell\\ j\ge{m}_{i}}},\frac{1}{X_{{n}}}]. \end{align*}$$

For any $F\in k[X,Y_1,\dots ,Y_{\ell }]$ , let $ (F_{j})_{j\in {\mathbf {N}}} $ (respectively, $ (F^{\ge \nu }_{j})_{j\in {\mathbf {N}}} $ , respectively, $(F_{j}^{\ge \nu ,\circ })_{j\in {\mathbf {N}}}$ ) be the family of elements of R (respectively, $R^{\ge \nu }$ , respectively, $R^{\ge \nu }$ ) defined by the relation

(4.1) $$ \begin{align} \sum_{j\ge 0} F_{j}\cdot t^j:=F\left(\sum_{j\ge 0} X_j\cdot t^j,\left(\sum_{j\ge 0} Y_{i,j}\cdot t^j\right)_{1\le i\le \ell}\right), \end{align} $$

respectively

$$\begin{align*}\sum_{j\ge 0} F^{\ge\nu}_{j}\cdot t^j:=F\left(\sum_{j\ge {n}} X_j\cdot t^j,\left(\sum_{j\ge {m}_{i}} Y_{i,j}\cdot t^j\right)_{1\le i\le \ell}\right), \end{align*}$$

respectively

(4.2) $$ \begin{align} \sum_{j\ge 0} F_{j}^{\ge\nu,\circ}\cdot t^j:=F\left(X_{{n}}\cdot t^{{n}},\left(\sum_{j\ge {m}_{i}} Y_{i,j}\cdot t^j\right)_{1\le i\le \ell}\right). \end{align} $$

In particular, (the extension of) ${\mathfrak {i}}_{\infty }$ (in R) is the ideal of R generated by the elements $\left \{F_{j}; F\in {\mathfrak {i}}, j\in {\mathbf {N}}\right \}$ . We call $ {\mathfrak {i}}_{\infty }^{\ge \nu }$ the ideal of $R^{\ge \nu }$ generated by the elements $\left \{F^{\ge \nu }_{j}; F\in {\mathfrak {i}}, j\in {\mathbf {N}}\right \}$ , and $ {\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ the ideal of $R^{\ge \nu }$ generated by the elements $\left \{F^{\ge \nu ,\circ }_{j}; F\in {\mathfrak {i}}, j\in {\mathbf {N}}\right \}$ .

4.7

Let ${\mathfrak {q}}_{\nu }$ be the ideal of R given by ${\langle {(X_j)_{0\le j<{n}}, (Y_{i,j})_{\substack {1\le i\le \ell \\ 0\le j< {m}_i}}}\rangle }$ . By Corollary 3.16, $ {\mathfrak {p}}_{\nu } $ is a prime ideal of $ R/{\mathfrak {i}}_{\infty } $ and

(4.3) $$ \begin{align} {\mathfrak{p}}_{\nu}=\operatorname{\mathrm{rad}}({\mathfrak{q}}_{\nu}+{\mathfrak{i}}_{\infty})=\operatorname{\mathrm{rad}}({\mathfrak{q}}_{\nu}+{\mathfrak{i}}_{\infty}^{\ge \nu}). \end{align} $$

In order to study the formal neighborhood of $ \eta _{{\mathcal C},\nu } $ in $ {\mathscr {L}_{\infty }}({\mathcal C}) $ , we shall work on $R/{\mathfrak {i}}_{\infty } $ .

From now on, and until the end of the section, we use the notation of Section 4.1, with ${\mathfrak {I}}:={\mathfrak {i}}_{\infty }$ and ${\mathfrak {P}}:={\mathfrak {p}}_{\nu }$ . The following proposition is the main result in this section.

Proposition 4.8. With the preceding notation, there exists an algebraic presentation $ \rho \colon R\to \widehat {A} $ of a coefficient field of $\widehat {A}$ , such that for every $j\ge {n}$ , one has $\iota (X_{j})=\rho (X_j)$ .

Remark 4.9. The morphism $\rho $ will be explicitly constructed. However, for the application of the proposition in Section 6, only the properties of the statement (and their consequences, see, for example, Remark 4.10) are needed.

Remark 4.10. Assume that $\rho $ is a morphism as in the statement of Proposition 4.8. Then $\operatorname {\mathrm {Ker}}(\rho )={\mathfrak {p}}_{\nu }$ (Remark 4.3). In particular, $\operatorname {\mathrm {Ker}}(\rho )$ contains ${\mathfrak {q}}_{\nu }$ and $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }}$ , and for every $F\in {\mathfrak {i}}$ , one has by (4.1):

(4.4) $$ \begin{align} F\left(\sum_{j\ge {n}}\rho(X_{j})\cdot t^{j},\left(\sum_{j\ge {m}_{i}}\rho(Y_{i,j})\cdot t^j\right)_{1\le i\le \ell}\right)=0. \end{align} $$

4.11

In the rest of this section, we will state and prove some technical results leading to the proof of Proposition 4.8. First, observe that the k-algebras $ R/{\mathfrak {p}}_{\nu }$ and $ R^{\ge \nu }/\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }} $ are isomorphic. The next two results will provide a better understanding of the latter quotient ring.

Lemma 4.12. We keep the preceding notation. There exists an automorphism of the k-algebra $R^{\ge \nu }$ mapping ${\mathfrak {i}}_{\infty }^{\ge \nu }$ to ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ and fixing $ X_j $ for $ j\ge {n} $ .

Proof. There exist elements $\{H_j\}_{j\ge 1}$ in $k[(X_{j})_{j\ge {n}}][\frac {1}{X_{{n}}}]$ , such that

$$\begin{align*}\sum\limits_{j\ge {n}}X_{j}\cdot t^j = X_{{n}}\cdot t^{{n}}\cdot \left(1+\sum\limits_{j\ge 1}\frac{X_{{n}+j}}{X_{{n}}}\cdot t^j\right)=X_{{n}}\cdot t^{{n}}\cdot \left(1+\sum_{j\ge 1}H_j\cdot t^j\right)^{{n}}. \end{align*}$$

Let $u\theta (u)$ be the image of t by the inverse of the isomorphism $k[(X_{j})_{j\ge {n}}][\frac {1}{X_{{n}}}]{[[ {u} ]]}\to k[(X_{j})_{j\ge {n}}][\frac {1}{X_{{n}}}]{[[ {t} ]]}$ mapping u to $t\cdot \left (1+\sum _{j\ge 1}H_j\cdot t^j\right )$ .

Let $\{\widetilde {Y}_{i,j}\}_{\substack {1\le i\le \ell \\j\ge {m}_{i}}}$ be the family of elements of $R^{\ge \nu }$ defined, for $i\in \{1,\dots ,\ell \}$ , by the equality

$$\begin{align*}\sum_{j\ge {m}_{i}}\widetilde{Y}_{i,j}\cdot u^j=\sum_{j\ge {m}_{i}} Y_{i,j}\cdot (u\theta(u))^j. \end{align*}$$

The sought-for automorphism maps $X_{j}$ to $X_{j}$ for $j\ge {n}$ and $Y_{i,j}$ to $\widetilde {Y}_{i,j}$ for $1\le i\le \ell $ and $j\ge {m}_{i}$ .

For the next proposition, recall that the $Y_{p,i} (t)$ ’s are the explicit formal series induced by our choice of a primitive parametrization p and of an embedding of our germ (see Section 2.10 for our assumptions in that regard).

Proposition 4.13. We keep the previous notation. Let $\phi :k[X_{{n}},(Y_{i,j})_{\substack {1\le i\le \ell \\j\ge {m}_{i}}},\frac {1}{X_{{n}}}]\to k[u,u^{-1}]$ be the morphism of k-algebras mapping $X_{{n}}$ to $u^{{n}}$ and such that $\sum _{j\ge {m}_i}\phi (Y_{i,j})\cdot t^j=Y_{p,i}(ut)$ for $1\le i\le \ell $ .

Then $\phi $ induces an isomorphism between $ k[X_{{n}},(Y_{i,j})_{\substack {1\le i\le \ell \\j\ge {m}_{i}}},\frac {1}{X_{{n}}}]/\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}$ and a subring of $ k[u,u^{-1}] $ whose fraction field equals $ k(u) $ .

In the proof of the proposition, we will use the following well-known result, the proof of which, we include for the convenience of the reader.

Lemma 4.14. Let $\vartheta \colon C\to D$ be a morphism of k-algebras. Assume that C is reduced and that, for every algebraically closed k-extension K of k, the induced map $\vartheta _K\colon \operatorname {\mathrm {Hom}}_{k-\operatorname {\mathrm {Alg}}}(D,K)\to \operatorname {\mathrm {Hom}}_{k-\operatorname {\mathrm {Alg}}}(C,K)$ is onto. Then $\vartheta $ is injective.

Proof. Since C is reduced, it suffices to show that any prime ideal of C contains $\operatorname {\mathrm {Ker}}(\vartheta )$ . Let ${\mathfrak {c}}$ be a prime ideal of C and K be an algebraically closed extension of $\operatorname {\mathrm {Frac}}(C/{\mathfrak {c}})$ . Then the quotient morphism $C\to C/{\mathfrak {c}}$ induces an element $\eta \in \operatorname {\mathrm {Hom}}(C,K)$ with kernel ${\mathfrak {c}}$ . By assumption, $\eta $ factors through $\vartheta $ , thus $\operatorname {\mathrm {Ker}}(\vartheta )\subset {\mathfrak {c}}$ .

Proof of proposition 4.13

Since $ (t^{{n}},Y_{p,1}(t),\dots ,Y_{p,\ell }(t)) $ is a Puiseux parametrization of $({\mathcal C},c)$ , one has, for every $ F\in {\mathfrak {i}} $ ,

(4.5) $$ \begin{align} F\left(\phi(X_{{n}})\cdot t^{{n}},\left(\sum_{j\ge {m}_{i}}\phi(Y_{i,j})\cdot t^j\right)_{1\le i\le \ell}\right) =F((ut)^{{n}},Y_{p,1}(ut),\dots,Y_{p,\ell}(ut))=0. \end{align} $$

Thus, by the definition of the family $(F^{\ge \nu ,\circ }_{j})_{j\in {\mathbf {N}}}$ , one has $\sum _{j\ge 0}\phi (F^{\ge \nu ,\circ }_{j})\cdot t^j=0$ , and we deduce that the kernel of $\phi $ contains ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ , thus also $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}$ since $k[u,u^{-1}]$ is a domain. Therefore, $\phi $ factors through

$$\begin{align*}\psi:k[X_{{n}},(Y_{i,j})_{\substack{1\le i\le \ell\\j\ge {m}_{i}}},\frac{1}{X_{{n}}}]/\sqrt{{\mathfrak{i}}_{\infty}^{\ge\nu,\circ}}\to k[u,u^{-1}]. \end{align*}$$

We now show that $\psi $ is injective by applying Lemma 4.14.

Let K be an algebraically closed k-extension. A morphism

$$\begin{align*}k[X_{{n}},(Y_{i,j})_{\substack{1\le i\le \ell\\j\ge {m}_{i}}},\frac{1}{X_{{n}}}]/\sqrt{{\mathfrak{i}}_{\infty}^{\ge\nu,\circ}}\to K\end{align*}$$

is entirely and uniquely determined by a collection of elements $\beta _{{n}}\in K^{{\times }}$ , $(\beta _{i,j})_{\substack {0\le i\le \ell \\j\ge {m}_{i}}}\in K $ , such that one has

$$\begin{align*}\forall F\in {\mathfrak{i}},\quad F\left(\beta_{{n}}\cdot t^{{n}}, \left(\sum_{j\ge {m}_{i}}\beta_{i,j}\cdot t^j\right)_{1\le i\le \ell}\right)=0.\end{align*}$$

Let us fix such a collection. We have to prove that there exists $\omega \in K^{{\times }}$ , such that $ \beta _{{n}}=\omega ^{{n}} $ and $Y_{p,i}(\omega \cdot t)=\sum _{j\ge {m}_i}\beta _{i,j}\cdot t^j$ for $1\le i\le \ell $ .

Since K is algebraically closed, one may find $\mu \in K^{{\times }}$ , such that $\beta _{{n}}=\mu ^{{n}}$ . Thus, one has

(4.6) $$ \begin{align} \forall F\in {\mathfrak{i}},\quad F\left((\mu t)^{{n}},\left(\sum_{j\ge {m}_{i}}\beta_{i,j}\mu^{-j}\cdot (\mu t)^j\right)_{1\le i\le \ell}\right)=0. \end{align} $$

By Proposition 2.11, the $ \ell +1 $ -tuple $\left (t^{{n}},\left (\sum _{j\ge {m}_{i}}\beta _{i,j}\mu ^{-j}\cdot t^j\right )_{1\le i\le \ell }\right )$ can be obtained from $\left (t^{{n}},\left (Y_{p,i}(t)\right )_{1\le i\le \ell }\right )$ by composition with an automorphism of $K{[[ {t} ]]}$ . Since such an automorphism has to fix $t^{{n}} $ , it is of the form $t\mapsto \zeta t $ , with $ \zeta $ a ${n}$ -th root of unity. Hence, for any $1\le i\le \ell $ , we have

(4.7) $$ \begin{align} \sum_{j\ge {m}_i}\beta_{i,j}\cdot \mu^{-j}t^j=Y_p(\zeta\cdot t). \end{align} $$

Now we take $\omega =\zeta \cdot \mu $ .

It remains to show that the fraction field of $\operatorname {\mathrm {Im}}(\psi )$ is $k(u)$ . For $1\le i\le \ell $ , write $ Y_{p,i}(t)=\sum _{j\ge {m}_{i}}p_{i,j}\cdot t^j $ , where $p_{i,j}\in k$ and $p_{i,{m}_i}\neq 0$ .

Since $\left (t^{{n}},\left (\sum _{j\ge {m}_{i}}p_{i,j}\cdot t^j\right )_{1\le i\le \ell }\right )$ is a primitive Puiseux k-parametrization of $({\mathcal C},c)$ , one has

$$\begin{align*}\gcd({n},\{j\ge {m}_{i}: 1\le i\le \ell, p_{i,j}\neq 0\})=1.\end{align*}$$

Thus, one may find, for $1\le i \le \ell $ , integers $j_{i_1},\dots ,j_{i_r}\ge {m}_{i}$ with $p_{i,j_{i_q}}\neq 0$ for $ 1\le q\le r $ and $ a_0\in {\mathbf {Z}} $ , $a_{i_1}\dots ,a_{i_r},b_{i_1}\dots ,b_{i_r}\in {\mathbf {N}}$ , such that

(4.8) $$ \begin{align} a_0\cdot {n}+\sum_{q=1}^r a_{i_q}\cdot j_{i_{q}}=1+\sum_{q=1}^r b_{i_{q}}\cdot j_{i_q}. \end{align} $$

Thus, since $\phi (Y_{i,j} ) = u^j p_{i,j}$ , one has

$$\begin{align*}\phi\left(X_{{n}}^{a_0}\prod_{i=1}^{\ell}\prod_{q=1}^r Y_{i,j_{i_{q}}}^{a_{i_q}}\right)=\delta\cdot u\cdot \phi\left(\prod_{i=1}^{\ell}\prod_{q=1}^r Y_{i,j_{i_{q}}}^{b_{i_q}}\right)\end{align*}$$

with $\delta \in k^{{\times }}$ , and we conclude that $u\in \operatorname {\mathrm {Frac}}(\operatorname {\mathrm {Im}}(\phi ))$ , hence, also $u\in \operatorname {\mathrm {Frac}}(\operatorname {\mathrm {Im}}(\psi ))$ .

Remark 4.15. When considering the valuation $ N\cdot \nu $ instead of $\nu $ (see Remark 4.6), in addition to making the modifications described in the remark, each occurrence of $k(u)$ in the statement and the proof has to be replaced by $k(u^N)$ .

In the proof of the last statement, do not replace ${n}$ by $N\cdot {n}$ , and ${m}_i$ by $N\cdot {m}_i$ , and multiply (4.8) by N in order to conclude that $u^N\in \operatorname {\mathrm {Frac}}(\operatorname {\mathrm {Im}}(\phi ))$ .

Lemma 4.16. Let us keep the preceding notation (recall that we use, in particular, the notation of Section 4.1). Let $ \sigma $ be the inverse of the automorphism in Lemma 4.12 and $ \pi '\colon R^{\ge \nu }\to \operatorname {\mathrm {Frac}}(R/{\mathfrak {p}}_{\nu }) $ be the composition $\pi ':=\pi \circ (R^{\ge \nu }{\hookrightarrow } R)\circ \sigma $ . Then $ \ker (\pi ')=\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }} $ and $\operatorname {\mathrm {Im}}(\pi ')=R/{\mathfrak {p}}_{\nu }$ .

Proof. Observe that the ideals ${\mathfrak {p}}_{\nu } $ and $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }+{\mathfrak {q}}_{\nu }} $ of $ R $ coincide. Thus, $ \pi $ factors through the quotient morphism $ R\to R/{\mathfrak {q}}_{\nu }$ and the kernel of the factorization is $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }+{\mathfrak {q}}_{\nu }}/{\mathfrak {q}}_{\nu }$ . On the other hand, the composition of $ R^{\ge \nu }{\hookrightarrow } R $ with the quotient morphism $R/{\mathfrak {q}}_{\nu }$ is an isomorphism mapping $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }}$ to $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }+{\mathfrak {q}}_{\nu }}/{\mathfrak {q}}_{\nu }$ . Thus, the image of $\pi \circ (R^{\ge \nu }{\hookrightarrow } R)$ is $R/{\mathfrak {p}}_{\nu }$ , the kernel of $ \pi '=\pi \circ (R^{\ge \nu }\to R)\circ \sigma $ is $\sigma ^{-1}(\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }})=\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}$ , and the image of $ \pi ' $ is $R/{\mathfrak {p}}_{\nu }$ .

Proposition 4.17. We keep the preceding notation. Then there exists a morphism of $ k $ -algebras $ \rho '\colon R^{\ge \nu }\to \widehat {A} $ , such that

• • $ \tau \circ \rho ' = \pi ' $ ;

• • for every $ j\ge {n} $ , $ \rho '(X_{j})=\iota (X_{j}) $ ;

• • $\operatorname {\mathrm {Ker}}(\rho ')$ contains $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}$ .

Proof. The situation is described by the following diagram.

By Proposition 4.13, the morphism of k-algebras $ \phi \colon R^{\ge \nu }\to k[(X_j)_{j> {n}}, u, u^{-1}] $ sending $ X_j$ to $X_j $ for $ j>{n} $ , $ X_{{n}}$ to $u^{{n}} $ and such that $\sum _{j\ge {m}_i}\phi (Y_{i,j})\cdot t^j=Y_{p,i}(ut)$ for $ 1\le i\le \ell $ induces an isomorphism between $ R^{\ge \nu }/\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}$ and a subring of $ k[(X_j)_{j> {n}}, u, u^{-1}] $ , with fraction field $ k((X_j)_{j> {n}}, u)$ . By Lemma 4.16, the previous isomorphism induces an isomorphism $\theta $ of $ \operatorname {\mathrm {Frac}}\left (R/{\mathfrak {p}}_{\nu }\right )$ with $k((X_j)_{j> {n}}, u)$ which maps $ \pi '(X_j)$ to $X_j $ for $ j>{n} $ , $ \pi '(X_{{n}})$ to $u^{{n}} $ and such that $\sum _{j\ge {m}_i}\theta (\pi '(Y_{i,j}))\cdot t^j=Y_{p,i}(ut)$ for $ 1\le i\le \ell $ . Let $v\in \operatorname {\mathrm {Frac}}\left (R/{\mathfrak {p}}_{\nu }\right )$ be the preimage of u by $\theta $ . Since $v^{{n}}=\pi '(X_{{n}})=\tau (\iota (\sigma (X_{{n}})))$ and $\sigma (X_{{n}})=X_{{n}}$ (Lemma 4.12), by Hensel’s lemma, there exists a unique element $ {\mathcal U}\in \widehat {A} $ , such that ${\mathcal U}^{{n}}=\iota (X_{{n}})$ and $ \tau ({\mathcal U})=v $ . Now we define the morphism of $ k $ -algebras $\rho '\colon R^{\ge \nu }{\longrightarrow } \widehat {A}$ by setting

$$\begin{align*}\begin{array}{crcll} & \rho'(X_j) &=& \iota(\sigma(X_j))=\iota(X_j)&\text{ for } j\ge {n},\\ \text{and} &\sum_{j\ge {m}_i}\rho'(Y_{i,j})\cdot t^j&=&Y_{p,i}({\mathcal U}\cdot t)&\text{ for } 1\le i\le \ell. \end{array}\end{align*}$$

Since $\tau ({\mathcal U})=v$ , one has $ \tau \circ \rho '=\pi '$ (by the the above description of the isomorphism $\theta $ ), as well as $ \rho '(X_{j})=\iota (X_{j}) $ for every $ j\ge {n} $ .

Let us finally prove that $\sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }}\subset \ker (\rho ')$ . It suffices to show that $\rho '(R^{\ge \nu })$ is a domain and $\ker (\rho ')$ contains ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ .

Let us show that $\rho '(R^{\ge \nu })$ is a domain. By construction, it is clear that $\rho '(R^{\ge \nu })$ is a subring of $k[(\iota (X_j))_{j> {n}},{\mathcal U}]$ . If the elements $(\iota (X_j))_{j> {n}},{\mathcal U} $ were algebraically dependent over k, then their images $ (\tau \circ \iota (X_j)=\pi '(X_j))_{j> {n}},v $ by $\tau $ in $ \operatorname {\mathrm {Frac}}\left (R/{\mathfrak {p}}_{\nu }\right )$ would also be. By the above description of the isomorphism $\theta \colon \operatorname {\mathrm {Frac}}\left (R/{\mathfrak {p}}_{\nu }\right )\cong k((X_j)_{j> {n}},u)$ , this is not the case. Therefore, $\rho '(R^{\ge \nu })$ is a domain.

Let us show that $\ker (\rho ')$ contains ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ .

For every $F\in {\mathfrak {i}}$ , one has

$$ \begin{align*} \rho'\left(F\left(X_{{n}}\cdot t^{{n}},\left(\sum_{j\ge {m}_{i}}Y_{i,j}\cdot t^j\right)_{1\le i\le \ell}\right)\right) & =F\left(\rho'(X_{{n}})\cdot t^{{n}},\left(\sum_{j\ge {m}_{i}}\rho'(Y_{i,j})\cdot t^j\right)_{1\le i\le \ell}\right)\\ &=F\left( ({\mathcal U} t)^{{n}},\left(Y_{p,i}({\mathcal U}\cdot t)\right)_{1\le i\le \ell}\right)\\ &=0. \end{align*} $$

Thus, by the definition of $(F^{\ge \nu ,\circ }_{j})_{j\in {\mathbf {N}}}$ (see (4.2)), we have $\sum _{j\ge 0} \rho '(F^{\ge \nu ,\circ }_{j})\cdot t^{j}=0 $ , and we deduce that ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }\subset \ker (\rho ') $ .

Remark 4.18. When considering the valuation $ N\cdot \nu $ instead of $\nu $ (see Remark 4.6), in addition to making the modifications described in the remark, replace $k((X_j)_{j> {n}},u)$ by $k((X_j)_{j> N\cdot {n}},u^N)$ in the proof.

Proof of Proposition 4.8

For the ease of the reader, the diagram below shows the morphisms involved in the proof:

Let $\widetilde {\pi }:=\pi \circ (R^{\ge \nu }{\hookrightarrow } R)$ and $\widetilde {\rho }:=\rho '\circ \sigma ^{-1}$ . Since $\tau \circ \rho '=\pi '$ and $\widetilde {\pi }=\pi '\circ \sigma ^{-1}$ , one has $\tau \circ \widetilde {\rho }=\widetilde {\pi }$ . Moreover, since ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }\subset \operatorname {\mathrm {Ker}}(\rho ')$ and $\sigma ^{-1}$ maps ${\mathfrak {i}}_{\infty }^{\ge \nu ,\circ }$ to ${\mathfrak {i}}_{\infty }^{\ge \nu }$ , one has ${\mathfrak {i}}_{\infty }^{\ge \nu } \subset \operatorname {\mathrm {Ker}}(\widetilde {\rho })$ .

Let $\rho \colon R\to \widehat {A}$ be the morphism inducing $\widetilde {\rho }$ on $R^{\ge \nu }$ and such that $\rho (X_{j})=0$ for $j<{n}$ , $\rho (Y_{i,j})=0$ for $ 1\le i\le \ell $ and $j<{m}_i$ . Since $\tau \circ \widetilde {\rho }=\widetilde {\pi }$ , $\tau (X_{j})=0$ for $0\le j<{n}$ , $\tau (Y_{i,j})=0$ for $ 1\le i\le \ell $ , and $0\le j<{m}_i$ and the same holds for $\pi $ , one has $\tau \circ \rho =\pi $ . Moreover, by its very construction, $\operatorname {\mathrm {Ker}}(\rho )$ contains ${\mathfrak {q}}_{\nu }+{\mathfrak {i}}_{\infty }^{\ge \nu }$ and $\rho (R)=\widetilde {\rho }(R^{\ge \nu })=\rho '(R^{\ge \nu })$ is a domain, thus, $\operatorname {\mathrm {Ker}}(\rho )$ contains $\sqrt {{\mathfrak {q}}_{\nu }+{\mathfrak {i}}_{\infty }^{\ge \nu }}={\mathfrak {p}}_{\nu }$ .

The remaining assertion of Proposition 4.8 is a straightforward consequence of Proposition 4.17, recalling that, for any $j\ge {n}$ , one has $\sigma (X_j)=X_j$ .

5 Quasi-deformations of nondegenerate arcs and presentations of complete local rings

In this section, we will present two technical results which will be useful in order to obtain an explicit “deformation-theoretic” presentation of the formal neighborhood at the generic primitive arc of a curve. We will first state and prove them here, under a general form, and then in Section 6, we will show that they may be applied in our setting. In this section, we temporarily deviate from the preceding notation.

5.1

The first result may be interpreted as a statement about the existence and the uniqueness of some specific “infinitesimal quasi-deformations” of a nondegenerate arc. It is an application of a version of Hensel’s lemma for an arbitrary set of variables stated in [BMCS, Proposition 4.2], which we first recall.

Proposition 5.2. Let $({\mathcal A},{\mathfrak {M}}_{{\mathcal A}})$ be a complete local ring with residue field $\kappa $ . Let I be a set and ${\mathbf {Y}}=\{Y_{i}\}_{i\in I}$ be a collection of indeterminates. Let J be a set and $\{F_j;\,j\in J\}$ be a collection of elements in ${\mathcal A}[{\mathbf {Y}}]$ . For ${\boldsymbol {y}}\in {\mathcal A}^{I}$ , we denote by ${\mathbf {J}}_{{\boldsymbol {y}}}$ the ${\mathcal A}$ -linear map ${\mathcal A}^I\to {\mathcal A}^J$ induced by the Jacobian matrix $[\partial _{Y_i}F_j]|_{{\mathbf {Y}}={\boldsymbol {y}}}$ , and by ${\mathbf {F}}|_{{\mathbf {Y}}={\boldsymbol {y}}}\in {\mathcal A}^J$ , the J-tuple $(F_j|_{{\mathbf {Y}}={\boldsymbol {y}}};\,j\in J)$ .

We assume that there exists ${\boldsymbol {y}}^{(0)}\in {\mathcal A}^I$ , such that:

1. 1. One has ${\mathbf {F}}|_{{\mathbf {Y}}={\boldsymbol {y}}^{(0)}}=0 \pmod {{\mathfrak {M}}_{{\mathcal A}}}$ .

2. 2. The $\kappa $ -linear map $\kappa ^I\to \kappa ^J$ deduced from ${\mathbf {J}}_{{\boldsymbol {y}}^{(0)}}$ by reduction modulo ${\mathfrak {M}}_{{\mathcal A}}$ is invertible.

Then there exists a unique element $({\mathcal Y}_i)\in {\mathcal A}^I$ , such that:

1. 1. One has ${\mathbf {F}}|_{{\mathbf {Y}}=({\mathcal Y}_i)}=0$ .

2. 2. For every $i\in I$ , one has ${\mathcal Y}_i=y_i^{(0)}\pmod {{\mathfrak {M}}_{{\mathcal A}}}$ .

Proposition 5.3. Let K be a field, m and $\ell $ be positive integers, $F_1,\dots ,F_{\ell }$ be $\ell $ elements of $K[X_1,\dots ,X_m,Y_1,\dots ,Y_{\ell }]$ , and J be the Jacobian matrix $\left (\partial _{Y_i} F_r\right )_{\substack {1\le r\le \ell \\1\le i\le \ell }}$ . Let ${\boldsymbol {x}}(t)=(x_i(t))_{1\le i\le m}$ and ${\boldsymbol {y}}(t)=(y_i(t))_{1\le i\le \ell }$ be elements of $K{[[ {t} ]]}$ , such that:

$$\begin{align*}\forall 1\le r\le \ell,\quad F_r\left({\boldsymbol{x}}(t), {\boldsymbol{y}}(t)\right)=0\quad \text{and}\quad \det(J)\left({\boldsymbol{x}}(t), {\boldsymbol{y}}(t)\right)\ne 0. \end{align*}$$

Then there exist $\ell $ nonnegative integers $N_1,\dots ,N_{\ell }$ and $\ell $ elements $\widetilde {F_1},\dots ,\widetilde {F_{\ell }}$ of the ring $K{[[ {t} ]]}[X_1,\dots ,X_m,Y_1,\dots ,Y_{\ell }]$ , such that the following holds:

1. 1. For any K-algebra ${\mathcal A}$ and any elements $({\mathbf {X}}(t),{\mathbf {Y}}(t))\in ({\mathcal A}{[[ {t} ]]})^{m+\ell }$ , one has

   $$\begin{align*}\forall 1\le r\le \ell,\,F_r({\mathbf{X}}(t),{\mathbf{Y}}(t))=0 {\Longleftrightarrow} \forall 1\le r\le \ell,\,\widetilde{F_r}({\mathbf{X}}(t),{\mathbf{Y}}(t))=0. \end{align*}$$

2. 2. Let $(C,{\mathfrak {M}}_C)$ be a complete local K-algebra with residue field K, and let ${\mathbf {X}}(t)=(X_i(t))_{1\le i\le m}$ (respectively, ${\mathbf {Y}}(t)=(Y_i(t))_{1\le i\le \ell }$ ) be an m-tuple (respectively, an $\ell $ -tuple) of elements of $C{[[ {t} ]]}$ whose image in $(C/{\mathfrak {M}}_C){[[ {t} ]]}=K{[[ {t} ]]}$ is ${\boldsymbol {x}}(t)$ (respectively, ${\boldsymbol {y}}(t)$ ). Then there exists a unique family $({\mathcal Z}_{i,j})_{\substack {1\le i\le \ell \\j\ge \operatorname {\mathrm {ord}}_ty_i(t)}}$ of elements of $\;{\mathfrak {M}}_C $ , such that, setting , we have

   

Remark 5.4. The integers $N_r$ and the elements $\widetilde {F_r}$ will be explicitly constructed in the proof. In case $\ell =1$ , by a slight modification of the proof, one sees that one can take $\widetilde {F_1}=F_1$ and $N_1=\operatorname {\mathrm {ord}}_t(\partial _{Y_1}F_1({\boldsymbol {x}}(t),{\boldsymbol {y}}(t)))$ .

We also note that assertion (1) expresses the fact that the arc scheme associated to the K-scheme defined by the $F_i$ ’s on the one hand, and the arc scheme (or Greenberg scheme) associated to the $K{[[ {t} ]]}$ -scheme defined by the $\widetilde {F_i}$ ’s on the other hand (see [CLNS18, Chapter 4, Proposition 3.17 & (2.1.4)]), are isomorphic.

An infinitesimal deformation of the arc $({\boldsymbol {x}}(t),{\boldsymbol {y}}(t))$ in the aforementioned arc scheme with value in an object $(C,{\mathfrak {M}}_C)$ of $\operatorname {\mathrm {\mathbf {CplLoc}}}_K$ is the datum of two families $({\mathcal W}_{i,j})_{1\le i\le m}$ and $({\mathcal Z}_{i,j})_{1\le i\le \ell }$ of elements of ${\mathfrak {M}}_C $ , such that

(5.1)

Thus, assertion (2) may be interpreted as follows: starting from the datum of two families of elements of ${\mathfrak {M}}_C$ as above (not necessarily satisfying (5.1)) there is at most one way of perturbing the $({\mathcal Z}_{i,j})_{\substack {1\le i\le \ell \\j\ge \operatorname {\mathrm {ord}}_ty_i(t)}}$ in order to obtain a deformation of the arc $({\boldsymbol {x}}(t),{\boldsymbol {y}}(t))$ ; and, in general, it is only possible to obtain after this perturbation a “quasi-deformation”, that is, a deformation up to a finite number of terms, as expressed by the condition on the degrees in assertion (2). Note that this allows us to recover a weak form of the Drinfeld-Grinberg-Kazhdan theorem [GK00, Dri02], more precisely, the fact that the formal neighborhood of a rational nondegenerate arc is the quotient of a power series in countably many variables by a finitely generated ideal. This is due to the fact that the condition on the degrees of the $\widetilde {F_i}$ provide finitely many equations, that are a priori power series in the involved variables, and not necessarily polynomials (which would recover the full Drinfeld-Grinberg-Kazhdan theorem).

Proof. Consider the matrix

$$\begin{align*}M(t):=\left(t^{\operatorname{\mathrm{ord}}_t y_i(t)}\cdot \partial_{Y_i} F_r({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))\right)_{\substack{1\le r\le \ell\\1\le i\le \ell}}. \end{align*}$$

Since $\det (J)\left ({\boldsymbol {x}}(t), {\boldsymbol {y}}(t)\right )\neq 0$ , one also has $\det (M(t))\neq 0$ . Thus, there exist $\ell \times \ell $ matrices $A(t)$ and $B(t)$ with entries in $K{[[ {t} ]]}$ and determinant in $K{[[ {t} ]]}^{{\times }}$ , and nonnegative integers $N_1,\dots ,N_{\ell }$ , such that $A(t)\cdot M(t)\cdot B(t)^{-1}=\operatorname {\mathrm {Diag}}(t^{N_1},\dots ,t^{N_{\ell }})$ .

Let $[\widetilde {F_r}]_{1\le r\le \ell }$ be the $\ell $ -tuple of elements of $K{[[ {t} ]]}[X_1,\dots ,X_m,Y_1,\dots ,Y_{\ell }]$ defined by the relation $[\widetilde {F_r}]_{1\le r\le \ell }=A(t)\cdot [F_r]_{1\le r\le \ell }$ . It easily follows that assertion (1) holds.

Let us consider the set of variables $(Z_{i,j})_{\substack {1\le i\le \ell \\ j\ge \operatorname {\mathrm {ord}}_t(y_i(t))}}$ and

$$\begin{align*}{\mathbf{Z}}(t):=\left(\sum_{j\ge \operatorname{\mathrm{ord}}_t(y_i(t))}Z_{i,j}\cdot t^{j}\right)_{1\le i\le \ell}=:\left(Z_i(t)\right)_{1\le i\le \ell}. \end{align*}$$

For $1\le r\le \ell $ and $j\ge 0$ , let $\widetilde {F_{r,j}}\in C[(Z_{i,j})]$ be defined by the relation

$$\begin{align*}\sum_{j\ge 0} \widetilde{F_{r,j}}\cdot t^j=\widetilde{F_r}({\mathbf{X}}(t),{\mathbf{Y}}(t)+{\mathbf{Z}}(t)).\end{align*}$$

We also consider the following $\ell $ -tuple of elements of $C[(Z_{i,j})]{[[ {t} ]]}$ :

$$\begin{align*}\widetilde{{\mathbf{F}}}_{\ge \bullet}:= \left[ \sum\limits_{j\ge N_r} \widetilde{F_{r,j}}\cdot t^j \right]_{1\le r\le \ell}.\end{align*}$$

Thus, we aim to prove the existence of a unique solution with values in ${\mathfrak {M}}_C$ of the system of polynomial equations $\widetilde {{\mathbf {F}}}_{\ge \bullet }=0 $ with unknowns $Z_{i,j}$ (i.e., the equations obtained by requiring that all the t-coefficients of any component of the $\ell $ -tuple $\widetilde {{\mathbf {F}}}_{\ge \bullet }$ be zero). We seek to apply Proposition 5.2. By hypotheses and (1), for $1\le r\le \ell $ , one has $\widetilde {F_r}\left ({\boldsymbol {x}}(t), {\boldsymbol {y}}(t)\right )=0 $ . Thus, $ Z_{i,j}=0 $ for $ 1\le i\le \ell $ and $ j\ge \operatorname {\mathrm {ord}}_t(y_i) $ is a solution of the reduction modulo $ {\mathfrak {M}}_C $ of the system. Now we have to study the Jacobian matrix of the system at this solution. Let $ \widetilde {{\mathbf {F}}}_{\ge \bullet }^{\operatorname {\mathrm {red}}}=[\widetilde {F_r}({\boldsymbol {x}}(t),{\boldsymbol {y}}(t)+{\mathbf {Z}}(t))]_{1\le r\le \ell }= 0 $ be the reduction of the system $\widetilde {{\mathbf {F}}}_{\ge \bullet }=0 $ modulo $ {\mathfrak {M}}_{C}$ . By the Taylor formula, we have

(5.2) $$ \begin{align} \widetilde{{\mathbf{F}}}_{\ge \bullet}^{\operatorname{\mathrm{red}}}=\widetilde{J}({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))\cdot {\mathbf{Z}}(t)+H(t), \end{align} $$

where $\widetilde {J}:=\left (\partial \widetilde {F_r}/\partial Y_i\right )_{\substack {1\le r\le \ell \\1\le i\le \ell }}$ and the t-coefficients of the components of $H(t)$ contain only terms of degree at least 2 in the $Z_{i,j}$ ’s. By the definition of the $\widetilde {F_r}'s$ , one has

$$\begin{align*}\widetilde{J}({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))=A(t)\cdot J({\boldsymbol{x}}(t),{\boldsymbol{y}}(t)).\end{align*}$$

Now, setting ${\mathbf {Z}}^{\circ }(t):=\left (\sum _{j\ge 0}Z_{i,j-\operatorname {\mathrm {ord}}_t y_i(t)}\cdot t^{j}\right )_{1\le i\le \ell }$ , one has

$$\begin{align*}J({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))\cdot {\mathbf{Z}}(t)=M(t)\cdot {\mathbf{Z}}^{\circ}(t); \end{align*}$$

therefore

$$\begin{align*}\widetilde{J}({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))\cdot {\mathbf{Z}}(t)=\operatorname{\mathrm{Diag}}(t^{N_1},\dots,t^{N_{\ell}})\cdot B(t)\cdot {\mathbf{Z}}^{\circ}(t). \end{align*}$$

Since $\det (B(t))\in K{[[ {t} ]]}^{{\times }}$ , we deduce from the former relation that the K-linear map

$$\begin{align*}\prod_{i=1}^{\ell} K^{ {\mathbf{Z}}_{\ge \operatorname{\mathrm{ord}}_t(y_i(t))}}\to \prod_{i=1}^{\ell} K^{{\mathbf{Z}}_{\ge N_i}},\quad (z_{i,j})\mapsto \phi_{i,j}({\boldsymbol{z}}) \end{align*}$$

defined by

$$\begin{align*}[{\underset{{j\ge N_j}}{\sum}}\phi_{i,j}({\boldsymbol{z}})\cdot t^j]_{1\le i\le \ell} =\widetilde{J}({\boldsymbol{x}}(t),{\boldsymbol{y}}(t))\cdot [{\underset{{j\ge \operatorname{\mathrm{ord}}_ty_i(t)}}{\sum}}z_{i,j}\cdot t^j]_{1\le i\le \ell} \end{align*}$$

is invertible. Thus, Proposition 5.2 guarantees the existence and the uniqueness of a family $({\mathcal Z}_{i,j})_{\substack {1\le i\le \ell \\j\ge \operatorname {\mathrm {ord}}_t(y_i(t))}} $ of elements of $ {\mathfrak {M}}_C $ which is a solution of the system $ \widetilde {{\mathbf {F}}}_{\ge \bullet }=0 $ . This concludes the proof of (2).

5.5

We recall, here, the following known result about completions of local rings (see, e.g., [dFD20, Lemma 10.12] and [Hai21, Theorem A and Corollary 3.9]).

Lemma 5.6. Let $(A,{\mathfrak {M}}_A)$ be a local ring. We denote by $ \widehat {A} $ the completion of $ A $ and $ {\mathfrak {M}}_{\widehat {A}} $ its maximal ideal. Assume that $ {\mathfrak {M}}_A/{\mathfrak {M}}_A^2 $ is a finite dimensional vector space. Then $ \widehat {A} $ is Noetherian and a complete local ring, and the natural map $ {\mathfrak {M}}_A\to {\mathfrak {M}}_{\widehat {A}} $ induces an isomorphism $ {\mathfrak {M}}_A/{\mathfrak {M}}_A^2 {\overset {\sim }{\to }} {\mathfrak {M}}_{\widehat {A}}/{\mathfrak {M}}_{\widehat {A}}^2 $ .

The next technical proposition, whose output is a presentation of the involved completion $\widehat {A}$ , will be applied in the next section to obtain a presentation of the formal neighborhood of the generic primitive arc of a curve singularity that is suited to our needs.

Proposition 5.7. Let B be a ring, ${\mathbf {X}}=\{X_{\omega }\}_{\omega \in \Omega }$ be a finite set of indeterminates, and ${\mathfrak {j}}$ be an ideal of $B[{\mathbf {X}}]$ . We assume that:

1. (A) The radical ${\mathfrak {p}}$ of the ideal ${\langle {{\mathbf {X}}}\rangle }+{\mathfrak {j}}$ is prime.

Let A be the localization of $B[{\mathbf {X}}]/{\mathfrak {j}}$ with respect to the image of ${\mathfrak {p}}$ and $\widehat {A}$ be the completion of A. Let $p_{\widehat {A}}\colon \widehat {A}\to \kappa _{\widehat {A}}$ be the quotient morphism and $\iota \colon B[{\mathbf {X}}]\to \widehat {A}$ be the morphism obtained by composing the quotient morphism $B[{\mathbf {X}}]\to B[{\mathbf {X}}]/{\mathfrak {j}}$ , the localization morphism $B[{\mathbf {X}}]/{\mathfrak {j}}\to A$ , and the completion morphism $A\mapsto \widehat {A}$ . We also assume that:

1. (B) The set $\{\iota (X_{\omega })\}_{\omega \in \Omega }$ generates the cotangent space ${\mathfrak {M}}_{\widehat {A}}/{\mathfrak {M}}_{\widehat {A}}^2$ of $\widehat {A}$ .

2. (C) There exists a morphism $\rho \colon B\to \widehat {A}$ , such that $\rho (B)\cap {\mathfrak {M}}_{\widehat {A}}=\{0\}$ , the induced morphism $\operatorname {\mathrm {Frac}}(\rho (B)){\overset {{p_{\widehat {A}}}}{\to }} \kappa _{\widehat {A}}$ is an isomorphism and $p_{\widehat {A}}\circ \rho $ coincides with the morphism obtained by composing the natural morphism $B\to B[{\mathbf {X}}]$ with $B[{\mathbf {X}}]{\overset {{\iota }}{\to }} \widehat {A}{\overset {{p_{\widehat {A}}} }{\to }}\kappa _{\widehat {A}}$ .

3. (D) There exists a morphism $\varepsilon \colon B\to \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}$ , such that

   $$\begin{align*}\forall b\in B,\quad \varepsilon (b)-\rho(b)\in {\langle {{\mathbf{X}}} \rangle}. \end{align*}$$

4. (E) If $ \theta \colon \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}\to \widehat {A} $ is the morphism of complete local $\operatorname {\mathrm {Frac}}(\rho (B))$ -algebras mapping $X_{\omega }$ to $\iota (X_{\omega })$ , then $\varepsilon ({\mathfrak {j}})\subset \operatorname {\mathrm {Ker}}(\theta )$ .

Then $\operatorname {\mathrm {Ker}}(\theta )$ coincides with the ideal ${\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ of $\operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}$ generated by $\varepsilon ({\mathfrak {j}})$ , and $\theta $ is surjective.

Remark 5.8. In the statement, we still denote by $\varepsilon $ the unique extension of $\varepsilon $ to $B[{\mathbf {X}}]\to \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}$ mapping $X_{\omega }$ to $X_{\omega }$ and whose restriction to B equals $\varepsilon $ . Note that by (D), for any $P\in B[{\mathbf {X}}]$ , one has $\varepsilon (P)-\rho (P(0))\in {\langle {{\mathbf {X}}} \rangle }$ .

Also note that the extension of the morphism $\rho $ of the statement to $B[{\mathbf {X}}]$ given by $P\mapsto \rho (P(0))$ contains ${\mathfrak {p}}$ in its kernel (see the proof below) and is thus an algebraic presentation of a coefficient field of $\widehat {A}$ .

Proof. By assumption (E), $ \theta $ induces a morphism $ \widetilde {\theta }:\operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }\to \widehat {A} $ which is injective if and only if ${\langle {\varepsilon ({\mathfrak {j}})} \rangle }=\operatorname {\mathrm {Ker}}(\theta )$ . In order to conclude it suffices to construct a morphism $\phi \colon \widehat {A}\to \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ , such that $\widetilde {\theta }\circ \phi $ is an isomorphism and $\phi $ is onto, since this would prove that $\phi $ is an isomorphism, hence, $ \widetilde {\theta }$ also is.

First, note that for any $P\in B[{\mathbf {X}}]$ , one has $\rho (P(0))=0$ if and only if $P\in {\mathfrak {p}}$ . Indeed, by assumption (C), and since $\operatorname {\mathrm {Ker}}(p_{\widehat {A}}\circ \iota )={\mathfrak {p}}$ , one has $\rho (P(0))=0$ if and only if $P(0)\in {\mathfrak {p}}$ . But since ${\langle {{\mathbf {X}}} \rangle }\subset {\mathfrak {p}}$ , this is equivalent to $P\in {\mathfrak {p}}$ .

Second, we remark that $\varepsilon ({\mathfrak {j}})$ is contained in ${\langle {{\mathbf {X}}}\rangle }$ . Indeed, since ${\mathfrak {j}}\subset {\mathfrak {p}}$ , this is a consequence of Remark 5.8 and the previous fact.

We consider the morphism $ \widetilde {\varepsilon }\colon B[{\mathbf {X}}]\to \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ obtained by composing $ \varepsilon $ with the canonical quotient morphism. Clearly, $\widetilde {\varepsilon }$ factors through $B[{\mathbf {X}}]/{\mathfrak {j}}$ . Let us show that it also factors through the localization $(B[{\mathbf {X}}]/{\mathfrak {j}})_{{\mathfrak {p}}}$ . If $ P\in B[{\mathbf {X}}] $ is such that $ \widetilde {\varepsilon }(P)\in {\langle {{\mathbf {X}}} \rangle }$ , then $\varepsilon (P)\in {\langle {{\mathbf {X}}} \rangle } +{\langle {\varepsilon ({\mathfrak {j}})} \rangle } = {\langle {{\mathbf {X}}}\rangle }$ , thus $\rho (P(0))\in {\langle {{\mathbf {X}}} \rangle }$ , hence, $\rho (P(0))=0$ . By the above remark, one has $P\in {\mathfrak {p}}$ . Therefore, $\widetilde {\varepsilon }$ factors through $A=(B[{\mathbf {X}}]/{\mathfrak {j}})_{{\mathfrak {p}}}$ . Since $\operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ is a complete local ring, $\widetilde {\varepsilon }$ also factors through $ \widehat {A} $ . Let $\phi \colon \widehat {A}\to \operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ be the factorization. In order to prove that $\widetilde {\theta }\circ \phi $ is an isomorphism, we only have to show that it is surjective, since any surjective endomorphism of a Noetherian ring is an automorphism. Thus, all in all, it suffices to show that $\widetilde {\theta }$ and $\phi $ are surjective. Denote by $(C,{\mathfrak {M}}_C)$ the complete local ring $\operatorname {\mathrm {Frac}}(\rho (B)){[[ {{\mathbf {X}}} ]]}/{\langle {\varepsilon ({\mathfrak {j}})} \rangle }$ , and note that ${\mathfrak {M}}_C={\langle {{\mathbf {X}}} \rangle }$ . Since $ \widehat {A} $ and C are complete local rings, one only needs to prove that the morphisms ${\mathfrak {M}}_{\widehat {A}}/{\mathfrak {M}}_{\widehat {A}}^2\rightarrow {\mathfrak {M}}_{C}/{\mathfrak {M}}_{C}^2 $ and $\widehat {A}/{\mathfrak {M}}_{\widehat {A}}\to C/{\mathfrak {M}}_{C}$ induced by $\phi $ are surjective, and similarly for $\widetilde {\theta }$ . First, let us show that the local morphism $\phi $ induces a surjective morphism at the level of residue fields. For any $b\in B$ , by (D) and the very definition of $\widetilde {\varepsilon }$ , one has $\widetilde {\varepsilon }(b)\in \rho (b)+{\mathfrak {M}}_C$ . On the other hand, by the very definition of $\phi $ , one has $\widetilde {\varepsilon }(b)=\phi (\iota (b))$ , thus, $\phi (\iota (b)))\in \rho (b)+{\mathfrak {M}}_C$ . In case $\rho (b)\notin {\mathfrak {M}}_C$ , one has $\iota (b)\notin {\mathfrak {M}}_{\widehat {A}}$ since $\phi $ is local (by construction), and $\phi (\iota (b)^{-1})\in \rho (b)^{-1}+{\mathfrak {M}}_C$ . We conclude that the morphism $\widehat {A}/{\mathfrak {M}}_{\widehat {A}}\to C/{\mathfrak {M}}_{C}=\operatorname {\mathrm {Frac}}(\rho (B))$ induced by $\phi $ is onto. On the other hand, since $\widetilde {\theta }$ is a morphism of $\operatorname {\mathrm {Frac}}(\rho (B))$ -algebras and by (C), we see that the morphism $C/{\mathfrak {M}}_C\rightarrow \widehat {A}/{\mathfrak {M}}_{\widehat {A}}$ induced by $\widetilde {\theta }$ is surjective.

Finally, by the very definitions of $\phi $ and $\widetilde {\theta }$ , for any $\omega \in \Omega $ , one has $\phi (\iota (X_{\omega }))=X_{\omega }$ and $\widetilde {\theta }(X_{\omega })=\iota (X_{\omega })$ . By assumption (B), and the fact that the $X_{\omega }$ clearly generate ${\mathfrak {M}}_C/{\mathfrak {M}}_C^2$ , one concludes that the morphisms ${\mathfrak {M}}_{\widehat {A}}/{\mathfrak {M}}_{\widehat {A}}^2 \rightarrow {\mathfrak {M}}_C/{\mathfrak {M}}_C^2$ and ${\mathfrak {M}}_C/{\mathfrak {M}}_C^2\rightarrow {\mathfrak {M}}_{\widehat {A}}/{\mathfrak {M}}_{\widehat {A}}^2$ induced by $\widetilde {\theta }$ and $\phi $ are surjective. That concludes the proof.

6 A deformation-theoretic interpretation of the formal neighborhood of the generic primitive arc of a curve singularity

6.1

In this section, we recover the setting and notation from Section 4. As already explained, our aim is to provide a presentation of the formal neighborhood of $ {\mathscr {L}_{\infty }}({\mathcal C}) $ at its generic primitive arc $\eta _{{\mathcal C},\nu }$ which can be naturally interpreted in terms of infinitesimal deformations of the corresponding $\kappa (\eta _{{\mathcal C},\nu })$ -arc. This will be a consequence of the existence of a coefficient field with specific properties (Proposition 4.8) and of the technical results in Section 5, whose assumptions hold in our setting, as we will check. As in Section 4, all the results and arguments hold, with the corresponding modifications, if we consider a valuation $ N\cdot \nu $ of $ {\mathcal C} $ , for $ N\ge 1 $ (see Remark 4.6).

Let $\rho $ be a morphism as in the statement of Proposition 4.8. We set $K:=\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ which is a coefficient field of $\widehat {A}$ (Remark 4.3). For simplicity, we set

$$\begin{align*}x_{\rho}(t):=\sum_{j\ge {n}}\rho(X_j)\cdot t^j,\quad y_{\rho,i}(t):=\sum_{j\ge {m}_i}\rho(Y_{i,j})\cdot t^j\quad \text{and} \quad {\boldsymbol{y}}_{\rho}(t):=(y_{\rho,i}(t))_{1\le i\le \ell}. \end{align*}$$

Recall that, by Remark 4.10, one has

(6.1) $$ \begin{align} \forall F\in {\mathfrak{i}}, \quad F(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))=0. \end{align} $$

In other words, $(x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t))$ defines a K-arc on ${\mathcal C}$ , which is nondegenerate (see Section 2.4), since the image of this arc by $p_{\widehat {A}}$ is the nonconstant $\kappa _{\eta _{{\mathcal C},\nu }}$ -arc on ${\mathcal C}$ induced by $\eta _{{\mathcal C},\nu }$ .

For the sake of convenience, set $Y_0:=X$ . By a standard application of “Elkik’s trick” (see, e.g., [BS17a, Section 4.2]), there exist elements $F_1,\dots ,F_{\ell }\in {\mathfrak {i}}$ , an $\ell $ -minor $\Delta $ of the Jacobian matrix $[\partial _{Y_{i}}F_j]_{\substack {0\le i\le \ell \\1\le j\le \ell }}$ , and an element H of the quotient ideal ${\langle {F_1,\dots ,F_\ell } \rangle } :{\mathfrak {i}}$ , such that $H(x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t))\neq 0$ and $\Delta (x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t))\neq 0$ . In fact, by Lemma 6.7, one has

(6.2) $$ \begin{align} \det([\partial_{Y_j}{F_i}(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))]_{1\le i,j\le \ell}\neq 0. \end{align} $$

Remark 6.2. Let $({\mathcal A},{\mathfrak {M}}_{\mathcal A})$ be any object of $\operatorname {\mathrm {\mathbf {CplLoc}}}_K$ . Then for any $(x_A(t),{\boldsymbol {y}}_{A}(t))\in {\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]}^{\ell +1}$ , the conditions

$$\begin{align*}\forall F\in {\mathfrak{i}},\quad F(x_{A}(t) +x_{\rho}(t),{\boldsymbol{y}}_{A}(t)+{\boldsymbol{y}}_{\rho}(t))=0 \end{align*}$$

$$\begin{align*}\text{and}\quad \forall 1\le r\le \ell, \quad F_r(x_{A}(t) +x_{\rho}(t),{\boldsymbol{y}}_{A}(t)+{\boldsymbol{y}}_{\rho}(t))=0 \end{align*}$$

are equivalent. Indeed, $H(x_{A}(t)+x_{\rho }(t),{\boldsymbol {y}}_{A}(t)+{\boldsymbol {y}}_{\rho }(t))\in {\mathcal A}{[[ {t} ]]}$ is not a zero divisor, since it reduces modulo ${\mathfrak {M}}_{{\mathcal A}}$ to $H(x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t))\neq 0$ .

6.3

We will first prove that the complete ring $ \widehat {A} $ is Noetherian and obtain a suitable system of generators of its cotangent space (which is, in fact, a basis, though we do not need this fact for our present purposes; see Remark 6.15 below). The result is a particular case of Reguera and Reguera-Mourtada’s general study of stable points and their cotangent space (see, in particular, [MR18, Theorem 3.4] combined with [Reg09, Theorem 3.13]; see also [Reg18, Mou17]); as pointed out by the referee, this may also be seen as a consequence of [CdFD22, Theorem 8.1] by considering the projection associated to $k[X]\to k[X,Y_1,\dots ,Y_{\ell } ]$ . We provide a direct proof in our setting for the convenience of the reader, and since our viewpoint is more deformation-theoretic than in the above references and in some sense in the same vein as the arguments that are to be used later in the section.

Proposition 6.4. Recall that we retain the notation of Section 4. The $\kappa _A$ -vector space ${\mathfrak {M}}_{A}/{\mathfrak {M}}_{A}^2$ is generated by the images of the set $\{X_j\}_{0\le j<{n}}$ .

In particular, $\widehat {A}$ is Noetherian and the set $\{\iota (X_j)\}_{0\le j<{n}}$ generates the cotangent space of $\widehat {A}$ .

Proof. Recall that $ A $ is defined to be the localization of $ R/{\mathfrak {i}}_{\infty } $ with respect to $ {\mathfrak {p}}_{\nu } $ . By (4.3), $ {\mathfrak {M}}_{A} $ is generated by the image of ${\mathfrak {p}}_{\nu }:=\operatorname {\mathrm {rad}}\left ({\mathfrak {i}}_{\infty }+{\langle {(X_j)_{0\le j<{n}}, (Y_{i,j})_{\substack {1\le i\le \ell \\ 0\le j< {m}_i}}} \rangle }\right )\subset R$ in $ A $ .

Let $ {\mathfrak {h}} $ be the ideal of $\widehat {A}$ generated by the set

(6.3) $$ \begin{align} \{\iota(X_j)\}_{0\le j<{n}} \cup \{\iota(Y_{i,j})\}_{\substack{1\le i\le \ell\\ 0\le j< {m}_i}} \cup \{\iota(Y_{i,j})-\rho(Y_{i,j})\}_{\substack{1\le i\le \ell\\ j\ge {m}_i}}. \end{align} $$

We first show that the ideal generated by $\iota ({\mathfrak {p}}_{\nu })$ is contained in ${\mathfrak {h}}$ . Let $P\in {\mathfrak {p}}_{\nu }$ , seen as a polynomial in the indeterminates $(X_j)_{0\le j<{n}},(Y_{i,j})_{\substack {1\le i\le \ell \\ 0\le j< {m}_i}}$ with coefficients in $R^{\ge \nu }$ . Let us set $ Q:=P(0)\in R^{\ge \nu } $ , then it suffices to show that $ \iota (Q) $ lies in $ {\mathfrak {h}} $ . Since $P\in {\mathfrak {p}}_{\nu }$ , and by the definition of the latter ideal, we deduce that $Q\in \sqrt {{\mathfrak {i}}_{\infty }^{\ge \nu }}$ , in particular, $ \rho (Q)=0$ by Remark 4.10. Let us write $Q=\widetilde {Q}(Y_{i,j})$ , where $\widetilde {Q}$ is seen as a polynomial in the indeterminates $\{Y_{i,j}\}_{\substack {1\le i\le \ell \\ j\ge {m}_i}}$ with coefficients in $T:=k[(X_j)_{j\ge {n}}][\frac {1}{X_{{n}}}]$ . By Proposition 4.8, $\rho $ and $\iota $ coincide on T. Thus, the relation $\rho (Q)=0$ may be rewritten as $\iota (\widetilde {Q})(\rho (Y_{i,j}))=0$ , which shows that $\iota (\widetilde {Q})(Y_{i,j})$ lies in the ideal of $\iota (T)[(Y_{i,j})]$ generated by $Y_{i,j}-\rho (Y_{i,j})$ . Thus, $\iota (Q)=\iota (\widetilde {Q})(\iota (Y_{i,j}))$ lies in the ideal generated by the $\iota (Y_{i,j})-\rho (Y_{i,j})$ , in particular, $\iota (Q)$ lies in ${\mathfrak {h}}$ .

Since the image by the projection $\widehat {A}\to A/{\mathfrak {M}}_A^2$ of the ideal generated by $\iota ({\mathfrak {p}}_{\nu })$ is ${\mathfrak {M}}_A/{\mathfrak {M}}_A^2$ , we deduce that ${\mathfrak {M}}_A/{\mathfrak {M}}_A^2$ is generated by the image of the set (6.3). In the remainder of the proof, we still denote by $\rho $ and $\iota $ the composition of $\rho $ and $\iota $ with the projection morphism $\widehat {A}\to A/{\mathfrak {M}}_A^2$ . For every $1\le i\le \ell $ , we set $Z_{i,j}:=\iota (Y_{i,j})-\rho (Y_{i,j})\in {\mathfrak {M}}_{A}/{\mathfrak {M}}_A^2$ for $ j\ge {m}_i$ and $Z_{i,j}:=\iota (Y_{i,j})\in {\mathfrak {M}}_{A}/{\mathfrak {M}}_A^2$ for $0\le j <{m}_i $ .

For every $ 1\le r\le \ell $ , we have

$$\begin{align*}0=\iota(F_r)=F_r\left(\sum_{0\le j<{n}}\iota(X_j)\cdot t^{j} +x_{\rho}(t),\left(\sum_{j\ge 0}Z_{i,j}\cdot t^j+y_{\rho,i}(t) \right)_{1\le i\le \ell}\right).\end{align*}$$

Applying the Taylor expansion formula, we obtain, for $1\le r\le \ell $ , the relation

$$ \begin{align*} 0&=F_r(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))+\partial_{X} F_r(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))\cdot\sum_{0\le j<{n}}\iota(X_j)\cdot t^{j}\\ & \quad +\sum_{1\le i\le \ell}\partial_{Y_i}F_r(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))\cdot\sum_{j\ge 0}Z_{i,j}\cdot t^j. \end{align*} $$

For $0\le r \le \ell $ (and setting $Y_0:=X$ for the sake of convenience), set $J_{r}(t):=[\partial _{Y_i}{F_j}({\boldsymbol {y}}_{\rho }(t))]_{\substack {1\le j \le \ell \\ 0 \le i\neq r \le \ell }}$ . By (6.1), one obtains

$$\begin{align*}[\partial_{X} {\mathbf{F}}(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))]\cdot \sum_{0\le j<{n}}\iota(X_j)\cdot t^{j} = -J_0(t)\cdot \left[\sum_{j\ge 0}Z_{i,j}\cdot t^j\right]_{1\le i\le \ell}.\end{align*}$$

Multiplying this equality by the adjugate matrix of $ J_0(t) $ and using Lemma 6.8 below, we obtain

(6.4) $$ \begin{align} \left(\sum_{0\le j<{n}}\iota(X_j)\cdot t^{j} \right)[\det(J_{i}(t))]_{1\le i\le \ell} =-\det(J_0(t))\cdot \left[\sum_{j\ge 0}Z_{i,j}\cdot t^j\right]_{1\le i\le \ell}. \end{align} $$

By Lemma 6.7 below (recall that for any $1\le i\le \ell $ , one has $\operatorname {\mathrm {ord}}_t(y_0(t))\le \operatorname {\mathrm {ord}}_t(y_i(t))<+\infty $ , see Section 2.10), we know that

(6.5) $$ \begin{align} \operatorname{\mathrm{ord}}_t(\det(J_0(t))\le \operatorname{\mathrm{ord}}_t \det(J_i(t)),\; 1\le i\le \ell. \end{align} $$

Thus, we deduce from (6.4) that in ${\mathfrak {M}}_{A}/{\mathfrak {M}}_{A}^2 $ the elements $ Z_{i,j} $ lie in the $\kappa _{A}$ -vector space generated by the $\{\iota (X_j)\}_{0\le j<{n}}$ .

The last assertion of Proposition 6.4 is a consequence of Lemma 5.6.

Remark 6.5. Equation (6.4) and the fact that $\det (J_0(t))\neq 0$ (i.e., 6.2) are in fact sufficient to show the first assertion of the proposition. However, (6.5) allows to show that $\{\iota (X_j)\}_{0\le j<{n}}$ is in fact a basis of the cotangent space (see Remark 6.15 below).

6.6

We state and prove two elementary lemmas used before.

Lemma 6.7. Let k be a field, $\ell $ be an integer, $F_1,\dots ,F_{\ell }$ be $\ell $ elements of the polynomial ring $k[Y_0,Y_1,\dots ,Y_{\ell }]$ , K be an extension of k, and ${\boldsymbol {y}}(t)=(y_0(t),\dots ,y_\ell (t))$ be $\ell +1$ elements of $K{[[ {t} ]]}$ . For $0\le r \le \ell $ , set $J_{r}(t):=[\partial _{Y_i}{F_j}({\boldsymbol {y}}(t))]_{\substack {1\le j\le \ell \\ 0 \le i\ne r \le \ell }}$ . Assume that $F_r({\boldsymbol {y}}(t))=0,\,1\le r\le \ell $ , there exists $r_0\in \{0,\dots ,\ell \}$ , such that $\det (J_{r_0}(t))\neq 0$ and $\operatorname {\mathrm {ord}}_t(y_0(t))\ge 1$ . Then $\det (J_{0}(t))\neq 0$ .

Assume, moreover, that $\operatorname {\mathrm {ord}}_t(y_0(t))\le \operatorname {\mathrm {ord}}_t(y_i(t))<+\infty ,\,1\le i\le \ell $ . Then $\operatorname {\mathrm {ord}}_t(\det (J_{0}(t)))\le \operatorname {\mathrm {ord}}_t(\det (J_i(t))),\,1\le i\le \ell $ .

Proof. Differentiating the relations $F_r({\boldsymbol {y}}(t))=0,\,1\le r\le \ell $ , one obtains

$$\begin{align*}J_0(t)\cdot [y^{\prime}_i(t)]_{1\le i\le \ell}+y^{\prime}_0(t)\cdot [\partial_{Y_0}F_i({\boldsymbol{y}}(t))]_{1\le i\le \ell}=0. \end{align*}$$

Multiplying by the adjugate matrix of $J_0(t)$ and using Lemma 6.8 below, one finds the relation

(6.6) $$ \begin{align} \det(J_0(t))\cdot [y^{\prime}_i(t)]_{1\le i\le \ell}+y^{\prime}_0(t)\cdot [\det(J_i(t))]_{1\le i\le \ell}=0. \end{align} $$

If $r_0=0$ , there is nothing to do. Otherwise, one has $r_0\in \{1,\dots ,\ell \}$ , since $y^{\prime }_0(t)\neq 0$ and $k{[[ {t} ]]}$ is a domain, (6.6) for $i=r_0$ shows that $\det (J_0(t))\neq 0$ . The last assertion is also a straightforward consequence of (6.6).

Lemma 6.8. Let $[m_{i,j}]_{\substack {1\le i\le d\\0\le j\le d}}$ be a matrix with d rows and $d+1$ columns with coefficients in a ring B. For $0\le s\le d$ , let $M_s$ be the adjugate matrix of $[m_{i,j}]_{\substack {1 \le i \le d \\0\le j \neq s \le d}}$ . Then one has

$$\begin{align*}M_0\cdot [m_{i,0}]_{1\le i \le d}=\left[\det\left([m_{i,j}]_{\substack{1 \le i \le d \\0\le j \neq r \le d}}\right)\right]_{1\le r\le d}. \end{align*}$$

More generally

$$\begin{align*}M_{s}\cdot [m_{i,s}]_{1\le i \le d}=\left[\det\left([m_{i,j}]_{\substack{1 \le i \le d \\0\le j \neq \tau_s(r) \le d}}\right)\right]_{1\le r\le d}, \end{align*}$$

where $\tau _{s}$ is the unique increasing bijection from $\{1,\dots ,d\}$ to $\{0,\dots ,d+1\}\setminus \{s\}$ .

Proof. It is a direct application of the expansion of the determinant along a column.

6.9

From now on, we use the following notation:

$$\begin{align*}K{[[ {X^{<\bullet},{\mathbf{Y}}^{<\bullet}} ]]} :=K{[[ {(X_{j})_{0\le j<{n}}, (Y_{i,j})_{\substack{1\le i\le \ell\\ 0\le j< {m}_i}}} ]]},\quad \text{and} \quad K{[[ {X^{<\bullet},{\mathbf{Y}}} ]]} :=K{[[ {(X_{j})_{0\le j<{n}}, (Y_{i,j})_{\substack{1\le i\le \ell}}} ]]}. \end{align*}$$

The following result uses Proposition 5.3 (i.e., Hensel’s lemma for an arbitrary set of variables) in order to “eliminate” the $ Y_{i,j} $ for $ 1\le i\le \ell $ , $ j\ge {m}_{i} $ .

Proposition 6.10. Let us keep the preceding notation, in particular, $ K:=\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ is a coefficient field of the local ring $\widehat {A} $ . We denote by $ \Pi $ the morphism of complete local K-algebras $K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}\to \widehat {A}$ mapping $X_{j}$ to $\iota (X_j)$ for $0\le j<{n}$ and $Y_{i,j}$ to $\iota (Y_{i,j})$ for $1\le i\le \ell $ and $0\le j< {m}_i$ .

Then, there exist $\ell $ nonnegative integers $N_1,\dots ,N_{\ell }$ and $\ell $ elements $\widetilde {F_1},\dots ,\widetilde {F_{\ell }}$ of the ring $K{[[ {t} ]]}[X,Y_1,\dots ,Y_{\ell }]$ , such that the following holds:

1. 1. For any K-algebra ${\mathcal A}$ and any elements $(X(t),{\mathbf {Y}}(t))\in ({\mathcal A}{[[ {t} ]]})^{1+\ell }$ , one has

   $$\begin{align*}\forall 1\le r\le \ell,\,F_r(X(t),{\mathbf{Y}}(t))=0 {\Longleftrightarrow} \forall 1\le r\le \ell,\,\widetilde{F_r}(X(t),{\mathbf{Y}}(t))=0. \end{align*}$$

2. 2. There is a unique family $({\mathcal Y}_{i,j})_{\substack {1\le i\le \ell \\j\ge {m}_{i}}}$ of elements of the maximal ideal of $K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ , such that, for every $ 1\le r\le \ell $ , we have

   $$\begin{align*}\deg_t \widetilde{F_r}\left(\sum_{0\le j< {n}} X_j\cdot t^j + x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j+y_{\rho,i}(t) + \sum_{j\ge {m}_{i}} {\mathcal Y}_{i,j}\cdot t^j \right)\right)< N_r.\end{align*}$$

3. 3. For $ 1\le i\le \ell $ and $j\ge {m}_{i}$ , one has $\Pi ({\mathcal Y}_{i,j})=\iota (Y_{i,j})-\rho (Y_{i,j})$ .

Proof. Assertions (1) and (2) are a straightforward consequence of Proposition 5.3 with $m=1$ , the $F_r$ ’s are those introduced at the beginning of the section, and $C=K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ , taking

$$\begin{align*}X(t):=\sum_{0\le j< {n}}X_j\cdot t^j+\sum_{j\ge {n}}\rho(X_j)\cdot t^j\quad\text{and} \quad Y_i(t):=\sum_{0\le j< {m}_i}Y_j\cdot t^j+\sum_{j\ge {m}_i}\rho(Y_j)\cdot t^j,\quad 1\le i \le \ell.\end{align*}$$

Indeed, for $ 1\le r\le \ell $ , we have $F_r(x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t))=0 $ (by (6.1)) and

$$\begin{align*}\det([\partial_{Y_j}{F_i}(x_{\rho}(t), {\boldsymbol{y}}_{\rho}(t))]_{1\le i,j\le \ell})\neq 0 \quad \text{(by (6.2))}) .\end{align*}$$

Assertion (3) is also a consequence of Proposition 5.3, applied now to the complete local ring $ \widehat {A} $ , taking

$$\begin{align*}X(t):=\sum_{0\le j< {n}}\iota(X_j)\cdot t^j+x_{\rho}(t)\quad\text{and} \quad Y_i(t):=\sum_{0\le j< {m}_i}\iota(Y_j)\cdot t^j+y_{\rho,i}(t),\quad 1\le i \le \ell.\end{align*}$$

Indeed, on the one hand, since $ {\mathfrak {i}}_{\infty }\subset \ker (\iota )$ , and using assertion (1), one has, for $1\le r\le \ell $ ,

$$\begin{align*}\widetilde{F_r}\left(\sum_{j\ge 0} \iota(X_j)\cdot t^j,\left(\sum_{j \ge 0} \iota(Y_{i,j})\cdot t^j \right)_{1\le i\le \ell} \right)=0.\end{align*}$$

For $1\le i\le \ell $ and $j\ge {m}_i$ set ${\mathcal Z}_{i,j}:=\iota (Y_{i,j})-\rho (Y_{i,j})$ . Since $p_{\widehat {A}}\circ \iota =p_{\widehat {A}}\circ \rho $ (definition 4.2), ${\mathcal Z}_{i,j}\in {\mathfrak {M}}_{\widehat {A}}$ and, by Proposition 4.8, the above expression reads, for $1\le r\le \ell $ ,

$$\begin{align*}\widetilde{F_r}\left(\sum_{0\le j< {n}} \iota(X_j)\cdot t^j+x_{\rho}(t), \left( \sum_{0\le j< {m}_i}\iota(Y_{i,j})\cdot t^j +y_{\rho,i}(t)+\sum_{j\ge {m}_i}{\mathcal Z}_{i,j}\cdot t^j\right)_{1\le i\le \ell} \right)=0.\end{align*}$$

On the other hand, the second part of this proposition implies that, for $1\le r\le \ell $ , one has

$$ \begin{align*} \deg_t \Pi\left(\widetilde{F_r}\left(\sum_{0\le j< {n}} X_j\cdot t^j + x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j +y_{\rho,i}(t) + \sum_{j\ge {m}_{i}} {\mathcal Y}_{i,j}\cdot t^j \right)_{1\le i\le \ell} \right)\right) < N_r. \end{align*} $$

Thus, by the very definition of $ \Pi $ and Proposition 4.8, we have for $1\le r\le \ell $

$$\begin{align*}\deg_t\widetilde{F_r}\left( \sum_{0\le j< {n}} \iota(X_j)\cdot t^j + x_{\rho}(t), \sum_{0\le j< {m}_i}\iota(Y_j)\cdot t^j+ y_{\rho,i}(t) +\sum_{j\ge {m}_i}\Pi({\mathcal Y}_{i,j})\cdot t^j\right)<N_r. \end{align*}$$

Thus, for $ 1\le r\le \ell $ , the conditions

$$\begin{align*}\deg_t \widetilde{F_r}\left(\sum_{0\le j< {n}} \iota(X_j)\cdot t^j + x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} \iota(Y_{i,j})\cdot t^j+y_{\rho,i}(t)\cdot t^j + \sum_{j\ge {m}_{i}} z_{i,j}\cdot t^j \right)_{1\le i\le \ell} \right)<N_r \end{align*}$$

hold for both $z_{i,j}={\mathcal Z}_{i,j}=\iota (Y_{i,j})-\rho (Y_{i,j})$ and $z_{i,j}=\Pi ({\mathcal Y}_{i,j})$ . Then we may conclude by the uniqueness in Proposition 5.3.

6.11

We can finally obtain our “deformation-theoretic” presentation of the formal neighborhood of the primitive stable arc (see Remark 6.13).

Theorem 6.12. Let us keep the preceding notation, in particular, $ K:=\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ is a coefficient field of the local ring $\widehat {A} $ . Let $ \varepsilon \colon R\rightarrow K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ be the morphism of $ k $ -algebras, such that

• • for $j\ge {n}$ , $\varepsilon (X_j)=\rho (X_j)$ ;

• • for $ 1\le i\le \ell $ and $ j\ge {m}_i$ , $ \varepsilon (Y_{i,j})=\rho (Y_{i,j})+{\mathcal Y}_{i,j} $ , where $({\mathcal Y}_{i,j})_{\substack {1\le i\le \ell \\j\ge {m}_{i}}}$ is the family of elements of the maximal ideal of $K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ given by Proposition 6.10;

• • for $0\le j<{n}$ , $\varepsilon (X_{j})=X_j$ ;

• • for $1\le i\le \ell $ and $0\le j< {m}_i$ , $\varepsilon (Y_{i,j})=Y_{i,j}$ .

Then:

1. 1. The morphism $\Pi $ of Proposition 6.10 induces an isomorphism

   $$\begin{align*}K{[[ {X^{<\bullet},{\mathbf{Y}}^{<\bullet}} ]]}/{\langle {\varepsilon ({\mathfrak{i}}_{\infty})} \rangle}\cong \widehat{A}.\end{align*}$$

2. 2. Let $\phi \colon K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]} \to K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ be the morphism (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_K$ , see Section 2) mapping $X_j$ to $X_j$ for $0\le j<{n}$ , $Y_{i,j}$ to $Y_{i,j}$ for $1\le i\le \ell $ and $0\le j< {m}_i$ , and $Y_{i,j}$ to ${\mathcal Y}_{i,j}$ for $1\le i\le \ell $ and $j\ge {m}_i$ . Let ${\mathfrak {j}}$ by the ideal of $K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}$ generated by the t-coefficients of the formal power series

   $$\begin{align*}F\left(\sum_{0\le j< {n}} X_j\cdot t^j +x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j+y_{\rho,i}(t)+\sum_{j\ge{m}_{i}}Y_{i,j}\cdot t^j \right)\right),\quad F\in {\mathfrak{i}}. \end{align*}$$
   Then $\phi $ induces an isomorphism (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_K$ )
   $$\begin{align*}K{[[ {X^{<\bullet},{\mathbf{Y}}} ]]}/{\mathfrak{j}}\cong K{[[ {X^{<\bullet},{\mathbf{Y}}^{<\bullet}} ]]}/{\langle {\varepsilon ({\mathfrak{i}}_{\infty})} \rangle}. \end{align*}$$

Proof. We apply Proposition 5.7 with the following identifications: the ring $ B $ in Proposition 5.7 will be $ R^{\ge \nu }$ , the family $ {\mathbf {X}} $ will be $ \{X_{j}\}_{0\le j<{n}}\cup \{Y_{i,j}\}_{\substack {1\le i\le \ell \\ 0\le j< {m}_i}} $ (thus, $B[{\mathbf {X}}]=R$ ), the ideal $ {\mathfrak {j}} $ will be $ {\mathfrak {i}}_{\infty } $ , the morphism $ \theta $ will be $\Pi $ , and the other identifications are self-explanatory. Assumption (A) holds by (4.3), and also do assumption (B) (by Proposition 6.4) and assumption (C) (by Proposition 4.8). As for assumption (D), let us note that $ \varepsilon (X_j)=\rho (X_j) $ for $ j\ge {n} $ and $ \varepsilon (Y_{i,j})=\rho (Y_{i,j})+{\mathcal Y}_{i,j} $ for $ 1\le i\le \ell $ , $ j\ge {m}_i $ , and $ {\mathcal Y}_{i,j}\in {\langle {(X_{j})_{0\le j<{n}}, (Y_{i,j})_{\substack {1\le i\le \ell \\ 0\le j< {m}_i}}} \rangle }$ by definition (cf. Proposition 6.10). Let us prove that assumption (E) also holds. For every $ 1\le r\le \ell $ , we have that $ \Pi \circ \varepsilon (F_r(X(t),{\mathbf {Y}}(t))) $ equals

$$\begin{align*}\Pi\left(F_r\left(\sum_{0\le j< {n}} X_j\cdot t^j +x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j+\sum_{j\ge{m}_i}(\rho(Y_{i,j})+{\mathcal Y}_{i,j})\cdot t^j \right)_{1\le i\le \ell} \right)\right). \end{align*}$$

Now, by Propositions 4.8 and 6.10, this equals

$$\begin{align*}F_r\left(\sum_{0\le j< {n}} \iota(X_j)\cdot t^j +\sum_{j\ge{n}} \iota(X_j)\cdot t^{j}, \left(\sum_{0\le j < {m}_{i}} \iota(Y_{i,j})\cdot t^j+\sum_{j\ge{m}_i}\iota(Y_{i,j})\cdot t^j \right)_{1\le i\le \ell} \right)=0. \end{align*}$$

This shows that (E) holds.

Let us now show the second part of the theorem. Note that ${\langle {\varepsilon ({\mathfrak {i}}_{\infty })} \rangle }$ is the ideal of $K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}$ generated by the t-coefficients of the formal power series

$$\begin{align*}F\left(\sum_{0\le j< {n}} X_j\cdot t^j +x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j+ y_{\rho,i}(t)+\sum_{j\ge{m}_i}{\mathcal Y}_{i,j}\cdot t^j \right)\right),\quad (F\in {\mathfrak{i}}). \end{align*}$$

Thus, $\phi $ clearly induces a morphism $K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}/{\mathfrak {j}}\to K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}/{\langle {\varepsilon ({\mathfrak {i}}_{\infty })} \rangle }$ . In order to conclude, by Lemma 2.1, it suffices to show that, for any object $({\mathcal A},{\mathfrak {M}}_{\mathcal A})$ of $\operatorname {\mathrm {\mathbf {CplLoc}}}_K$ , the induced map $\varphi _{{\mathcal A}}\colon (K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}/{\mathfrak {j}})({\mathcal A})\to (K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}/{\langle {\varepsilon ({\mathfrak {i}}_{\infty })}\rangle })({\mathcal A})$ is a bijection.

The set $(K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}/{\mathfrak {j}})({\mathcal A})$ (respectively, $(K{[[ {X^{<\bullet },{\mathbf {Y}}^{<\bullet }} ]]}/{\langle {\varepsilon ({\mathfrak {i}}_{\infty })} \rangle })({\mathcal A})$ ) identifies with the set of elements $(x_{j})_{0\le j<{n}}, (y_{i,j})_{\substack {1\le i\le \ell \\ j\in {\mathbf {N}}}}$ (respectively, $(x_{j})_{0\le j<{n}}, (y_{i,j})_{\substack {1\le i\le \ell \\ 0\le j<{m}_i}}$ ) of ${\mathfrak {M}}_{{\mathcal A}}$ which satisfy the relations

(6.7) $$ \begin{align} F\left(\sum_{0\le j< {n}} x_j\cdot t^j +x_{\rho}(t), \left(\sum_{0\le j < {m}_{i}} y_{i,j}\cdot t^j+y_{\rho,i}(t) +\sum_{j\ge{m}_i}y_{i,j} \cdot t^j \right)\right)=0,\quad (F\in {\mathfrak{i}}); \end{align} $$

respectively

(6.8) $$ \begin{align} F\left( \sum_{0\le j< {n}} x_j\cdot t^j +x_{\rho}(t), \left(\sum_{0\le j < {m}_{i}} y_{i,j}\cdot t^j+y_{\rho,i}(t) +\sum_{j\ge{m}_i}{\mathcal Y}_{i,j}({\boldsymbol{x}},{\boldsymbol{y}})\cdot t^j\right) \right)=0,\quad (F\in {\mathfrak{i}}) \end{align} $$

and $\phi _{{\mathcal A}}$ maps an element $\left ((x_{j})_{0\le j<{n}},(y_{i,j})_{\substack {1\le i\le \ell \\j\in {\mathbf {N}}}}\right )$ to $\left ((x_{j})_{0\le j<{n}},(y_{i,j})_{\substack {1\le i\le \ell \\0\le j<{m}_i}}, ({\mathcal Y}_{i,j}({\boldsymbol {x}},{\boldsymbol {y}}))_{\substack {1\le i\le \ell \\ j\ge {m}_i}}\right )$ . But by Proposition 5.3, and arguing similarly as in the proof of part (3) in Proposition 6.10, from relations (6.7) and (6.8), we may deduce the relations $y_{i,j}={\mathcal Y}_{i,j}({\boldsymbol {x}},{\boldsymbol {y}})$ for $1\le i\le \ell $ and $j\ge {m}_i$ , which shows that $\phi _{{\mathcal A}}$ is bijective and concludes the proof.

Remark 6.13. For any object ${\mathcal A}$ of $\operatorname {\mathrm {\mathbf {CplLoc}}}_K$ , (6.7) gives us an explicit interpretation of the ${\mathcal A}$ -points of $\widehat {A}$ in terms of (a specific subset of the set of) deformations with values in ${\mathcal A}$ of the arc $(x_{\rho }(t),y_{\rho }(t))$ in the arc scheme ${\mathscr {L}_{\infty }}({\mathcal C})$ .

Remark 6.14. An explicit finite set of generators of the ideal ${\langle {\varepsilon ({\mathfrak {i}}_{\infty })} \rangle }$ is given by the union, for $1\le r\le \ell $ , of the $N_r \ t$ -coefficients of lowest degree of the power series

$$\begin{align*}\widetilde{F_r}\left(\sum_{0\le j< {n}} X_j\cdot t^j + x_{\rho}(t),\left(\sum_{0\le j < {m}_{i}} Y_{i,j}\cdot t^j+y_{\rho,i}(t) + \sum_{j\ge {m}_{i}} {\mathcal Y}_{i,j}\cdot t^j \right)\right).\end{align*}$$

Indeed, by Remark 6.2, relations (6.8) are equivalent to the same relations imposed only on the $F_r$ ’s. One concludes by assertions (1) and (2) of Proposition 6.10.

Remark 6.15. Using (6.7) in case ${\mathcal A}=K[u]/{\langle {u} \rangle }^2$ is the ring of dual numbers and only for $F_1,\dots ,F_{\ell }$ (see the previous remark), and arguing as in the proof of Proposition 6.4, one concludes that the classes of $X_0,\dots ,X_{n-1}$ are a basis of the cotangent space of $K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}/{\mathfrak {j}}{\overset {\sim }{\to }} \widehat {A}$ , thus recovering the main result of [MR18] in the case of curve singularities.

7 Proof of the comparison theorem

7.1

In this section, we prove Theorem 1.7, under the following more precise form.

Theorem 7.2. Let $ k $ be a field of characteristic zero. Let $ {\mathcal C} $ be a curve and $ c\in {\mathcal C}(k) $ , such that $ {\mathcal C} $ is analytically irreducible at $ c $ . Let $ \nu =\operatorname {\mathrm {ord}}_t\circ p$ be the valuation on $ {\mathcal C} $ induced by any primitive parametrization $p\colon \widehat {{\mathscr {O}}_{{{\mathcal C},c}}}\to k{[[ {t} ]]}$ of ${\mathcal C}$ at c. Let N be a positive integer, $ {\mathcal {N}}_{{\mathcal C}}(N\cdot \nu ) $ the maximal divisorial set associated with $N\cdot \nu $ , $ \eta _{{\mathcal C},N\cdot \nu } $ its generic point, and $ \kappa (N\cdot \nu ) $ its residue field. Let $\Theta _N$ be the nonempty open set of $ {\mathcal {N}}_{{\mathcal C}}(\nu ) $ defined in Section 2.8. Then there exists a Noetherian complete local $ k $ -algebra $ {{\mathcal M}}$ , such that:

1. (i) The complete local k-algebras $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}$ and $({{\mathcal M}}\widehat {\otimes }_k \kappa (\nu )){[[ {u} ]]}$ are isomorphic.

2. (ii) For every arc $ \gamma \in \Theta _N(k) $ , $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}$ and ${{\mathcal M}}{[[ {(u_i)_{i\in {\mathbf {N}}}} ]]}$ are isomorphic (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_k$ ), in other words, ${{\mathcal M}}$ is a finite formal model of $\gamma $ (see Section 2.4).

Remark 7.3. Until the statement and the proof of Proposition 7.6, we assume that $N=1$ (see Remark 4.6 for the modifications needed to make the arguments valid in the general case).

We retain all the previous notation. In particular, ${\mathcal C}\cong \operatorname {\mathrm {Spec}}\left (k[X,Y_1,\dots ,Y_\ell ]/{\mathfrak {i}}\right )$ , $ p $ is a primitive parametrization of $ {\mathcal C} $ , such that the associated $ \ell +1 $ -tuple of power series is $ \left (t^n,\left (Y_{p,i}(t)\right )_{1\le i\le \ell }\right ) $ , where $Y_{p,i}\in k{[[ {t} ]]}$ and $\operatorname {\mathrm {ord}}_t(Y_{p,i}(t))={m}_i$ . $\widehat {A}$ is a complete local ring isomorphic to $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\eta _{V,\nu }}}}$ (see Section 4.1), $ \rho \colon k[(X_j)_{j\in {\mathbf {N}}},(Y_{i,j})_{\substack {1\le i\le \ell \\ j\in {\mathbf {N}}}},\frac {1}{X_{{n}}}]\to \widehat {A} $ is an algebraic presentation of the coefficient field of $\widehat {A}$ as in Proposition 4.8, and $K:=\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ is a coefficient field of $\widehat {A}$ (see Remark 4.3).

For the sake of simplicity, we denote by $(C,{\mathfrak {M}}_C)$ the object of $\operatorname {\mathrm {\mathbf {TopLoc}}}_K$ given by $K{[[ {X^{<\bullet },{\mathbf {Y}}} ]]}$ .

Recall that, by Remark 4.10, one has

(7.1) $$ \begin{align} \forall F\in {\mathfrak{i}},\quad F(x_{\rho}(t),{\boldsymbol{y}}_{\rho}(t))=0. \end{align} $$

For any uniformizing parameter u of $K{[[ {t} ]]}$ , write $t=u\theta (u)$ , with $\theta (u)\in K{[[ {u} ]]}^{{\times }}$ and define the following elements of $C{[[ {u} ]]}$ :

$$\begin{align*}{\mathbf{X}}(u):=\sum_{0\le j< {n}}X_j\cdot (u\theta(u))^j+x_{\rho}(u\theta(u)) \end{align*}$$

and

$$\begin{align*}\text{and}\quad {\mathbf{Y}}_i(u):=\sum_{j\ge 0}Y_{i,j}\cdot (u\theta(u))^j+y_{\rho,i}(u\theta(u)). \end{align*}$$

Remark 7.4. Let ${\mathfrak {j}}_u$ be the ideal of C generated by the u-coefficients of the following elements of $C{[[ {u} ]]}$ :

(7.2) $$ \begin{align} F\left({\mathbf{X}}(u),({\mathbf{Y}}_i(u))_{1\le i\le \ell}\right),\quad (F\in {\mathfrak{i}}). \end{align} $$

Then ${\mathfrak {j}}_u$ coincides with the ideal ${\mathfrak {j}}$ of Theorem 6.12, and by the same theorem, $\widehat {A}$ is isomorphic to $C/{\mathfrak {j}}_u$ .

Recall that $\rho (X_{{n}})=\iota (X_{{n}})$ is a unit in $\widehat {A}$ and thus is a nonzero element of K. By Proposition 2.11 applied to $ (x_{\rho }(t),{\boldsymbol {y}}_{\rho }(t)) $ , there exists a uniformizing parameter u of $K{[[ {u} ]]}$ , such that

(7.3) $$ \begin{align} {\mathbf{X}}(u)=\sum_{0\le j< {n}}X_j\cdot (u\theta(u))^j+u^{{n}} \end{align} $$

(7.4) $$ \begin{align} \text{and}\quad \forall 1\le i\le \ell,\quad {\mathbf{Y}}_i(u):=\sum_{j\ge 0}Y_{i,j}\cdot (u\theta(u))^j+Y_p(u). \end{align} $$

From now on, we fix such a uniformizing parameter u.

Lemma 7.5. There exists a unique family $(v_r)_{r\ge 1}$ of elements of ${\mathfrak {M}}_C$ , such that, setting $v:=\sum _{r\ge 1}v_r\cdot u^r$ , one has

$$\begin{align*}\deg_u({\mathbf{X}}(u+v)-u^{{n}})\le {n}-1. \end{align*}$$

Moreover, let $(\tau ^X_j)_{0\le j\le {n}-1}$ and $(\tau ^Y_{i,j})_{\substack {1\le i\le \ell \\j\ge 0}}$ be the families of elements of ${\mathfrak {M}}_C$ defined by the relations

$$\begin{align*}{\mathbf{X}}(u+v)=u^{{n}}+\sum_{0\le j\le {n}-1}\tau^X_j\cdot u^j \end{align*}$$

$$\begin{align*}\text{and}\quad {\mathbf{Y}}_i(u+v)=\sum_{j\ge 0}\tau_{i,j}^Y\cdot u^j+Y_{p,i}(u),\quad 1 \le i\le \ell. \end{align*}$$

Then the endomorphism of C defined by

$$\begin{align*}X_j\mapsto \tau_j^X,\quad 0\le j\le {n}-1,\quad Y_{i,j}\mapsto \tau^Y_{i,j},\quad 1\le i\le \ell,\quad j\ge 0 \end{align*}$$

is an automorphism.

Proof. Define $(G_j)\in {\mathfrak {M}}_C^{{\mathbf {N}}}$ by

$$\begin{align*}{\mathbf{X}}(u)=u^{{n}}+\sum_{0\le j< {n}}X_j\cdot (u\theta(u))^j=u^{{n}}+\sum_{j\ge 0}G_j\cdot u^j.\end{align*}$$

Consider the homogeneous system of polynomial equations in the variables $(v_r)_{r\ge 0}$ given by the u-coefficients of degree $\ge {n}$ of the formal power series

$$\begin{align*}(u+\sum_{r\ge 1}v_r\cdot u^r)^{{n}}-u^{{n}}+\sum_{j\ge 0}G_j\cdot (u+\sum_{r\ge 1}v_r\cdot u^r)^{j}. \end{align*}$$

Then $v_r=0,\,r\ge 1$ is a solution modulo ${\mathfrak {M}}_C$ . Moreover, the linear terms of these polynomial equations are given by

$$\begin{align*}{n}\cdot v_{k-{n}+1}+\sum_{1\le j\le k} j\cdot G_j\cdot v_{k-j+1},\quad k\ge {n}. \end{align*}$$

Since $G_j\in {\mathfrak {M}}_C$ , Hensel’s lemma guarantees the existence and uniqueness of a family $(v_r)_{r\ge 1}$ of elements of ${\mathfrak {M}}_C$ as in the statement.

Now, from expressions (7.3) and (7.4), one sees that one may write

$$\begin{align*}{\mathbf{X}}(u+v)-u^{{n}}=\sum_{0\le j\le {n}-1}H^X_j\cdot u^j\quad \pmod{{\mathfrak{M}}_C^2{[[ {u} ]]}} \end{align*}$$

and, for $1\le i\le \ell $ ,

(7.5) $$ \begin{align} {\mathbf{Y}}_i(u+v) -Y_{p,i}(u) =\sum_{j\ge 0}H^Y_{i,j}\cdot u^j\quad \pmod{{\mathfrak{M}}_C^2{[[ {u} ]]}} ,\end{align} $$

where, for $0\le j\le {n}-1$ , $H_j^X-X_j$ is a linear form in $X_0,\dots ,X_{j-1}$ and, for $1\le i\le \ell $ and $j\ge 0$ , $H_{i,j}^Y-Y_{i,j}$ is a linear form in $Y_{i,0},\dots ,Y_{i,j-1}$ . This shows the second part of the statement.

Now let ${\mathfrak {j}}^{\prime }_u$ be the ideal of C generated by the u-coefficients of the following elements of $C{[[ {u} ]]}$ :

(7.6) $$ \begin{align} F\left(u^{{n}}+\sum_{0\le j\le {n}-1}X_i\cdot u^i, (Y_{p,i}(u)+\sum_{j\ge 0}Y_{i,j}\cdot u^j)_{1\le i\le \ell}\right),\quad (F\in {\mathfrak{i}}). \end{align} $$

Since $u\mapsto u+\sum _{r\ge 1}v_r\cdot u^r$ defines an automorphism of the C-algebra $C{[[ {u} ]]}$ , $C/{\mathfrak {j}}_u$ is isomorphic to the quotient of $ C $ by the ideal generated by the u-coefficients of the following elements of $C{[[ {u} ]]}$ :

(7.7) $$ \begin{align} F\left({\mathbf{X}}(u+v),({\mathbf{Y}}_i(u+v))_{1\le i\le \ell}\right),\quad (F\in {\mathfrak{i}}). \end{align} $$

By Lemma 7.5, the latter quotient is $ K $ -isomorphic to $C/{\mathfrak {j}}^{\prime }_u$ . Then Remark 7.4 shows that $\widehat {A}$ is isomorphic to $C/{\mathfrak {j}}^{\prime }_u$ .

Let $C_k:=k{[[ {(X_{j})_{0\le j<{n}}, (Y_{i,j})_{\substack {1\le i\le \ell \\ j\in {\mathbf {N}}}}} ]]}$ . Note that, since $Y_{p,i}(u)\in k{[[ {u} ]]}$ , the formal power series of (7.6) are elements of $C_k{[[ {u} ]]}$ . Denote by ${\mathfrak {j}}^{\prime }_{k}$ the ideal of $C_k$ generated by the coefficients of these formal power series. Then by the above result, $\widehat {A}$ is isomorphic to $(C_k/{\mathfrak {j}}^{\prime }_{k})\otimes _k K$ . Note that $C_k/{\mathfrak {j}}^{\prime }_{k}$ is an object of $\operatorname {\mathrm {\mathbf {NthCplLoc}}}_k$ .

The following proposition then concludes the proof of Theorem 7.2.

Proposition 7.6. Keep the above notation. Let $\gamma $ be the k-rational arc on ${\mathcal C}$ defined by $(t^{N\cdot {n}},(Y_{p,i}(t^N))_{1\le i\le \ell })$ . Then $C_k/{\mathfrak {j}}^{\prime }_{k}$ is a finite model of $\gamma $ and is cancellable.

Proof. We define functors ${\mathcal F}_1$ , ${\mathcal F}_2$ , and ${\mathcal F}_3$ on the category $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ : for any object $({\mathcal A},{\mathfrak {M}}_{{\mathcal A}})$ of this category, let $ {\mathcal F}_1({\mathcal A}) $ (respectively, ${\mathcal F}_2({\mathcal A})$ , respectively, ${\mathcal F}_3({\mathcal A})$ ) be the set of elements $(x_{{\mathcal A}}(t),(y_{i,{\mathcal A}}(t)))\in ({\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]})^{\ell +1}$ with $\deg _t(x_{{\mathcal A}}(t))\le N\cdot {n}-2$ (respectively, with $\deg _t(x_{{\mathcal A}}(t))\le N\cdot {n}-1$ , respectively, with no extra condition on $x_{{\mathcal A}}(t)$ ) and such that

$$\begin{align*}F(t^{N\cdot {n}}+x_{{\mathcal A}}(t),(Y_{p,i}(t^N)+y_{i,{\mathcal A}}(t)))=0,\quad (F\in {\mathfrak{i}}). \end{align*}$$

In particular, $C_k/{\mathfrak {j}}^{\prime }_{k}$ represents ${\mathcal F}_2$ and $\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}}$ prorepresents ${\mathcal F}_3$ , in the sense that for any object ${\mathcal A}\in \operatorname {\mathrm {\mathbf {CplLoc}}}_k$ , one has a functorial bijection between $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {\mathbf {TopLoc}}}_k}(\widehat {{\mathscr {O}}_{{{\mathscr {L}_{\infty }}(V),\gamma }}},{\mathcal A})$ and ${\mathcal F}_3(A)$ . Also, ${\mathcal F}_1$ is clearly representable by a quotient ${{\mathcal M}}$ of $C_k/{\mathfrak {j}}^{\prime }_{k}$ . Moreover, if $x_{{\mathcal A}}(t)\in {\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]}$ is such that $\deg _t(x_{\mathcal A}(t))\le N\cdot {n}-1$ , there is a unique element $a\in {\mathfrak {M}}_{{\mathcal A}}$ , such that $\deg _t((t+a)^{{n}}+x_{\mathcal A}(t+a)-t^{{n}})\le N\cdot {n}-2$ . This shows that the functors ${\mathcal F}_2$ and ${\mathcal A}\mapsto {\mathcal F}_1({\mathcal A})\times {\mathfrak {M}}_{{\mathcal A}}$ are isomorphic. Thus, $C_k/{\mathfrak {j}}^{\prime }_{k}\cong {{\mathcal M}}{[[ {u} ]]}$ is cancellable.

Now we claim the following (such a property is also used in [Bou21]): let $m\ge 2$ be an integer; for any $x_{{\mathcal A}}(t)\in {\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]}$ , there exists a unique element $f_{{\mathcal A}}\in {\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]}$ satisfying the following property: the image $t^{m}+\tilde {x}_{{\mathcal A}}(t)$ of $t^{m}+x_{{\mathcal A}}(t)$ by the automorphism ${\mathcal A}{[[ {t} ]]}{\overset {\sim }{\to }} {\mathcal A}{[[ {t} ]]}$ , $t\mapsto t+f_{{\mathcal A}}(t)$ is such that $\tilde {x}_{{\mathcal A}}(t)\in {\mathfrak {M}}_{{\mathcal A}}[t]$ and $\deg _t(\tilde {x}_{{\mathcal A}}(t))\le m-2$ . Indeed, one can check by successive approximations modulo ${\mathfrak {M}}_{{\mathcal A}}$ , ${\mathfrak {M}}_{{\mathcal A}}^2$ , etc., that the equation

$$\begin{align*}(t+f_{{\mathcal A}}(t))^m+\sum_{r=0}^{m-2}\alpha_{m-r}\cdot (t+f_{{\mathcal A}}(t))^r=t^m+x_{{\mathcal A}}(t), \end{align*}$$

with unknowns $f_{{\mathcal A}}(t)\in {\mathfrak {M}}_{{\mathcal A}}{[[ {t} ]]}$ , $\alpha _2,\dots ,\alpha _m\in {\mathfrak {M}}_{{\mathcal A}}$ , has a unique solution.

The above property (for $m=N\cdot {n}$ ) shows that the functors ${\mathcal F}_3$ and ${\mathcal A}\mapsto {\mathcal F}_1({\mathcal A})\times {\mathfrak {M}}_{{\mathcal A}}^{{\mathbf {N}}}$ are isomorphic, thus (Lemma 2.1) that ${{\mathcal M}}$ is a finite formal model of $\gamma $ (remember Definition 2.5 and the remark that follows it).

8 Deformations of arcs on hypersurfaces

In this section, we consider a divisorial valuation $ \nu $ on a hypersurface $ V $ (with additional assumptions, see Section 8.1), and we proceed similarly to the case of curves to obtain in Proposition 8.12 a presentation of the formal neighborhood of $ {\mathscr {L}_{\infty }}(V) $ at the generic point of the maximal divisorial set ${\mathcal {N}}_V(\nu )$ , which can also be interpreted in terms of infinitesimal deformations of this generic point. Finally, we state in Question 8.13 a conjectural connection between this formal neighborhood and that of a generic rational point of $ {\mathcal {N}}_V(\nu ) $ .

8.1 The setting

Let $V=\{F=0\}\subset {\mathbf {A}}^N_k=\operatorname {\mathrm {Spec}}(k[X_1,\dots ,X_N])$ be an affine hypersurface containing the origin, and equipped with a divisorial valuation $\nu $ , centered at the origin. As before, one denotes by ${\mathfrak {p}}_{\nu }$ the prime ideal of $\Gamma ({\mathscr {L}_{\infty }}(V))$ corresponding to the generic point $\eta _{V,\nu }$ of the maximal divisorial set ${\mathcal {N}}_V(\nu )$ .

For $1\le i\le N$ , set $\alpha _i:=\nu (X_i)$ . For any $G\in k[X_1,\dots ,X_N]$ and any $d\ge 0$ , let $G^{(d)}$ be the d-homogeneous part of G with respect to the weighted grading on $k[X_1,\dots ,X_N]$ defined by $(\alpha _1,\dots ,\alpha _N)$ . Write

$$\begin{align*}F=\sum_{d\ge a}F^{(d)}\quad\text{with}\quad F^{(a)}\neq 0. \end{align*}$$

We, hereafter, assume the following:

• • $F^{(a)}$ is irreducible.

• • The valuation $\nu $ is monomial with respect to the embedding $V\subset {\mathbf {A}}^N_k$ , by this we mean that, for any semivaluation $\nu '$ on V, one has:

  (8.1) $$ \begin{align} \forall 1\le i\le N,\quad \nu'(X_i)\ge \nu(X_i){\Rightarrow} \forall f\in \Gamma(X),\quad \nu'(f)\ge \nu(f). \end{align} $$

Example 8.2. Let $F:=X_1^2+X_2^3+X_3^5\in k[X_1,X_2,X_3]$ . The origin is the unique singular point of V and an $E_8$ -type singularity. One considers the action of ${\mathbf {G}}_m$ on V given by $\lambda \cdot (X_1,X_2,X_3):=(\lambda ^{15}\cdot X_1,\lambda ^{10}\cdot X_2,\lambda ^{6}\cdot X_3)$ , which corresponds to an ${\mathbf {N}}$ -grading $\Gamma (V)=\bigoplus _{n\in {\mathbf {N}}}\Gamma (V)_n$ on $\Gamma (V)$ . Let $\nu $ be the ${\mathbf {G}}_m$ -invariant valuation on V defined as follows: let $f=\sum _{n\in {\mathbf {N}}}f_n\in \Gamma (V)=\bigoplus _{n\in {\mathbf {N}}}\Gamma (V)_n$ ; then $\nu (f):=\operatorname {\mathrm {Inf}}\{n\in {\mathbf {N}},\,f_n\neq 0\}$ . Thus, $\nu $ is monomial with respect to the embedding $V\subset {\mathbf {A}}^3_k$ . Moreover, $a=30$ and $F=F^{(a)}$ .

8.3 Description of ${\mathfrak {p}}_{\nu }$

We denote the set of variables $\{X_{i,j}\}_{\substack {1\le i\le N\\j\ge 0}}$ (respectively, $\{X_{i,j}\}_{\substack {1\le i\le N\\0\le j <\alpha _i}}$ , respectively, $\{X_{i,j}\}_{\substack {1\le i\le N\\j\ge \alpha _i}}$ ) by ${\boldsymbol {X}}$ (respectively, ${\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}$ , respectively, ${\boldsymbol {X}}^{\ge {\boldsymbol {\alpha }}}$ ). Let $\{F_j\}_{j\in {\mathbf {N}}}$ be the family of elements of $k[{\boldsymbol {X}}]$ defined by the relation

$$\begin{align*}\sum_{j\ge 0} F_j\cdot t^j:=F\left(\sum_{j\ge 0} X_{i,j}\cdot t^j\right) \end{align*}$$

and ${\mathfrak {i}}_{\infty }$ be the ideal of $k[{\boldsymbol {X}}]$ generated by the $F_j$ ’s. Thus, ${\mathscr {L}_{\infty }}(V)$ is isomorphic to $\operatorname {\mathrm {Spec}}(k[{\boldsymbol {X}}]/{\mathfrak {i}}_{\infty })$ .

Let $\{F^{\ge {\boldsymbol {\alpha }}}_j\}_{j\in {\mathbf {N}}}$ be the family of elements of $k[{\boldsymbol {X}}^{\ge {\boldsymbol {\alpha }}}]$ defined by the relation

$$\begin{align*}\sum_{j\ge 0} F^{\ge {\boldsymbol{\alpha}}}_j\cdot t^j:=F\left(\sum_{j\ge \alpha_i} X_{i,j}\cdot t^j\right) \end{align*}$$

and ${\mathfrak {i}}_{\infty }^{\ge {\boldsymbol {\alpha }}}$ be the ideal of $k[{\boldsymbol {X}}^{\ge {\boldsymbol {\alpha }}}]$ generated by the $\{F^{\ge {\boldsymbol {\alpha }}}_j\}_{j\in {\mathbf {N}}}$ . In particular, the k-algebras $k[{\boldsymbol {X}}]/({\mathfrak {i}}_{\infty }+{\langle {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} \rangle })$ and $k[{\boldsymbol {X}}^{\ge {\boldsymbol {\alpha }}}]/{\mathfrak {i}}_{\infty }^{\ge {\boldsymbol {\alpha }}}$ are isomorphic. Set ${\mathscr {L}_{{\infty }}}^{\ge {\boldsymbol {\alpha }}}(V):=\operatorname {\mathrm {Spec}}(k[{\boldsymbol {X}}^{\ge {\boldsymbol {\alpha }}}]/{\mathfrak {i}}_{\infty }^{\ge {\boldsymbol {\alpha }}})$ . By (8.1) and the definition of ${\mathcal D}_V(\nu )$ , one has:

Lemma 8.4. The support of the closed subscheme ${\mathscr {L}_{{\infty }}}^{\ge {\boldsymbol {\alpha }}}(V)$ of ${\mathscr {L}_{\infty }}(V)$ is ${\mathcal D}_V(\nu )$ .

The following proposition is the analog in our new setting of Lemma 3.13 part (iv) and Corollary 3.16 in the case of curves, relating the maximal divisorial set ${\mathcal {N}}_{V}(\nu )$ with the set ${\mathcal D}_V(\nu )$ and thus providing an explicit description of the ideal $ {\mathfrak {p}}_{\nu } $ corresponding to its generic point $\eta _{V,\nu }$ .

Proposition 8.5. The scheme ${\mathscr {L}_{{\infty }}}^{\ge {\boldsymbol {\alpha }}}(V)$ is irreducible. In particular, its support is ${\mathcal {N}}_{V}(\nu )$ , and one has

$$\begin{align*}{\mathfrak{p}}_{\nu}=\operatorname{\mathrm{rad}}({\mathfrak{i}}_{\infty}+{\langle {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} \rangle})=\operatorname{\mathrm{rad}}({\mathfrak{i}}^{\ge {\boldsymbol{\alpha}}}_{\infty}+ {\langle {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} \rangle}). \end{align*}$$

Moreover, the natural morphism

$$\begin{align*}{\mathscr{L}_{{\infty}}}^{\ge {\boldsymbol{\alpha}}}(V)\to \operatorname{\mathrm{Spec}}(k[(X_{i,\alpha_i})]/{\langle {F^{(a)}((X_{i,\alpha_i}))} \rangle})\end{align*}$$

is dominant, and for any i, such that $X_i$ appears in $F^{(a)}$ , the preimage of the open set $\{\partial _{X_i}F^{(a)}((X_{i',\alpha _i'}))\neq 0\}$ in ${\mathscr {L}_{{\infty }}}^{\ge {\boldsymbol {\alpha }}}(V)$ is an integral scheme.

Remark 8.6. In particular, for any $1\le i\le N$ , such that $X_i$ appears in $F^{(a)}$ , one has $\partial _{X_i}F^{(a)}((X_{i',\alpha _{i'}}))\notin {\mathfrak {p}}_{\nu }$ and the extension of the ideal ${\mathfrak {p}}_{\nu }$ to the localization $k[{\mathbf {X}}]\left [\frac {1}{\partial _{X_i}F^{(a)}((X_{i',\alpha _{i'}})}\right ]$ coincides with the extension of the ideal ${\mathfrak {i}}_{\infty }+{\langle {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} \rangle }$ .

Proof. Write

(8.2) $$ \begin{align} F\left(\sum_{j\ge \alpha_i} X_{i,j}\cdot t^j\right)= \sum_{d\ge a}t^d\cdot F^{(d)}\left(\sum_{j\ge 0} X_{i,j+\alpha_i}\cdot t^{j}\right)=:t^a\left(\sum_{j\ge 0}G_j\cdot t^j\right), \end{align} $$

where $G_j$ is an element of $k[(X_{i,\ell })_{\substack {1\le i\le N\\\alpha _i\le \ell \le \alpha _i+j }}]$ . In particular, $G_0=F^{(a)}((X_{i,\alpha _i}))$ . Let $Y:=\operatorname {\mathrm {Spec}}(k[X_{i,\alpha _i}]/F^{(a)}((X_{i,\alpha _i})))$ , which is an integral $ k $ -scheme by assumption on $ F^{(a)} $ . For $n\in {\mathbf {N}}$ , set

$$\begin{align*}{\mathscr{L}_{{n}}}^{\ge {\boldsymbol{\alpha}}}(V):=\operatorname{\mathrm{Spec}}(k[(X_{i,j})_{\substack{1\le i\le N\\\alpha_i\le j\le\alpha_i+n }}]/{\langle {G_j} \rangle}_{0\le j\le n}). \end{align*}$$

Note that $ {\mathscr {L}_{{0}}}^{\ge {\boldsymbol {\alpha }}}(V)\cong Y $ and that, for $m\ge n$ , there are natural truncation morphisms $\pi _{m,n}\colon {\mathscr {L}_{{m}}}^{\ge {\boldsymbol {\alpha }}}(V)\to {\mathscr {L}_{{n}}}^{\ge {\boldsymbol {\alpha }}}(V)$ and ${\mathscr {L}_{{\infty }}}^{\ge {\boldsymbol {\alpha }}}(V)={\underset {{\longleftarrow }}{\lim }}\,\, {\mathscr {L}_{{n}}}^{\ge {\boldsymbol {\alpha }}}(V)$ by (8.2).

It suffices to address the case where $X_1$ appears in $F^{(a)}$ . Let $Y'$ be the dense open set $\{\partial _{X_1}F^{(a)}((X_{i,\alpha _i}))\neq 0\}$ of Y. Let $n\ge 0$ . The Taylor formula applied to $ G_{n+1} $ shows that there is an isomorphism of ${\mathscr {L}_{{n+1}}}^{\ge {\boldsymbol {\alpha }}}(V)$ with a closed subscheme $Z_n$ of ${\mathscr {L}_{{n}}}^{\ge {\boldsymbol {\alpha }}}(V)\times \operatorname {\mathrm {Spec}}(k[(X_{i,\alpha _{i}+n+1})_{1\le i\le N}])$ , such that $\pi _{n+1,n}$ corresponds to the first projection and $Z_n$ is defined by a relation of the shape

$$\begin{align*}\sum_{i=1}^{N}X_{i,\alpha_{i}+n+1}\cdot \partial_{X_i}F^{(a)}((X_{i',\alpha_{i'}})_{1\le i'\le N}) =H_n, \end{align*}$$

where $H_n$ is an element of $k[(X_{i,j})_{\substack {1\le i\le N\\\alpha _i\le j \le \alpha _i+n }}]$ . Thus, for any $n\ge 0$ , there is an isomorphism $\pi _{n+1,0}^{-1}(Y'){\overset {\sim }{\to }} \pi _{n,0}^{-1}(Y')\times {\mathbf {A}}^{N-1}_k$ , such that $\pi _{n+1,n}(Y')\colon \pi _{n+1,0}^{-1}(Y')\to \pi _{n,0}^{-1}(Y')$ corresponds to the first projection. In particular, $\pi _{\infty ,0}\colon {\mathscr {L}_{\infty }}^{\ge {\boldsymbol {\alpha }}}(V)\to Y$ is dominant. Moreover, let U be the open set of ${\mathscr {L}_{\infty }}(V)$ defined by $\partial _{X_1}F^{(a)}((X_{i,\alpha _i}))\neq 0$ . Thus, $U\cap {\mathscr {L}_{\infty }}^{\ge {\boldsymbol {\alpha }}}(V)=\pi _{n,0}^{-1}(Y')$ is an integral scheme. Now, by Kolchin’s irreducibility theorem [Kol73, Ch. IV/§17/Proposition 10], U is dense in ${\mathscr {L}_{\infty }}(V)$ . Thus, ${\mathscr {L}_{\infty }}^{\ge {\boldsymbol {\alpha }}}(V)$ is irreducible. Using Lemmas 3.9 and 8.4, one obtains the remaining assertions on ${\mathcal {N}}_V(\nu )$ and ${\mathfrak {p}}_{\nu }$ .

8.7 An algebraic presentation of a coefficient field

We use the generic notation of Section 4.1 with $R=k[{\mathbf {X}}]$ , ${\mathfrak {I}}={\mathfrak {i}}_{\infty }$ and

(8.3) $$ \begin{align} {\mathfrak{P}}:={\mathfrak{p}}_{\nu}=\operatorname{\mathrm{rad}}({\mathfrak{i}}_{\infty}+{\langle {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} \rangle})=\operatorname{\mathrm{rad}}({\mathfrak{i}}^{\ge {\boldsymbol{\alpha}}}_{\infty}+ {\langle {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} \rangle}). \end{align} $$

From now on, and without loss of generality, we assume that the indeterminate $X_1$ appears in $F^{(a)}$ .

Proposition 8.8. We keep the preceding notation. Then there exists an algebraic presentation $ \rho \colon R\to \widehat {A} $ of a coefficient field of $\widehat {A}$ , such that, for every $i\ge 2$ and $j\ge \alpha _i$ , one has $\iota (X_{i,j})=\rho (X_{i,j})$ .

Remark 8.9. Assume that $\rho $ is a morphism as in the statement of Proposition 8.8. We adopt the following notation: for $1\le i\le N$ , set $x_{\rho ,i}(t):=\sum _{j\ge \alpha _i}\rho (X_{i,j})\cdot t^j$ . In particular

(8.4) $$ \begin{align} F\left(\left(x_{\rho,i}(t)\right)_{1\le i\le N}\right)=0. \end{align} $$

Proof. (of Proposition 8.8) First, note that by the description (8.3) of ${\mathfrak {p}}_{\nu }$ , one has

(8.5) $$ \begin{align} \{\iota(X_{i,j})\}_{\substack{1\le i\le N \\ 0\le j\le \alpha_i-1}}\subset {\mathfrak{M}}_{\widehat{A}}. \end{align} $$

For $1\le i\le N$ and $0\le j\le \alpha _i-1$ , one sets $\rho (X_{i,j})=0$ . In particular, $\operatorname {\mathrm {Ker}}(\rho )$ will contain ${\langle {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} \rangle }$ . Moreover, for $2\le i\le N$ and $j\ge \alpha _i$ , one sets $\rho (X_{i,j}):=\iota (X_{i,j})$ .

Now one has to define $\rho (X_{1,j})$ for $j\ge \alpha _1$ . It suffices to show the following: there exists a family $({{\mathcal X}}_{1,j})_{j\ge \alpha _1}\in \widehat {A}$ , such that $p_{\widehat {A}}({{\mathcal X}}_{1,j})=p_{\widehat {A}}(\iota (X_{1,j}))$ for $j\ge \alpha _1$ and

$$\begin{align*}F\left(\sum_{j\ge \alpha_1} {{\mathcal X}}_{1,j}\cdot t^j,\left(\sum_{j\ge \alpha_i} \iota(X_{i,j})\cdot t^j\right)_{2\le i\le N}\right)=0. \end{align*}$$

Indeed, one may then set $\rho (X_{1,j})={{\mathcal X}}_{1,j}$ for $j\ge \alpha _1$ . Then, using, in particular, (8.5), the property $p_{\widehat {A}}\circ \rho =p_{\widehat {A}}\circ \iota $ is clear by construction. Moreover, by the definition of $\rho $ , one has

$$\begin{align*}F\left(\left(\sum_{j\ge \alpha_i} \rho(X_{i,j})\cdot t^j\right)_{1\le i\le N}\right)=0 .\end{align*}$$

Thus, $\operatorname {\mathrm {Ker}}(\rho )$ contains ${\mathfrak {i}}_{\infty }^{\ge {\boldsymbol {\alpha }}}$ , and, therefore, contains ${\mathfrak {i}}^{\ge {\boldsymbol {\alpha }}}_{\infty }+ {\langle {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} \rangle }$ by (8.5). On the other hand,

$$\begin{align*}(p_{\widehat{A}}\circ \rho)(\partial_{X_1}F^{(a)}((X_{i,\alpha_{i}}))) =p_{\widehat{A}}(\iota(\partial_{X_1}F^{(a)}((X_{i,\alpha_{i}})))) \end{align*}$$

and by Remark 8.6, $\iota (\partial _{X_1}F^{(a)}((X_{i,\alpha _{i}})))\in \widehat {A}^{{\times }}$ . Thus, also $\rho (\partial _{X_1}F^{(a)}((X_{i,\alpha _{i}})))\in \widehat {A}^{{\times }}$ . By Remark 8.6 and (8.3), one concludes that $\operatorname {\mathrm {Ker}}(\rho )$ contains ${\mathfrak {p}}_{\nu }$ .

Let us show the existence of the ${{\mathcal X}}_{1,j}$ ’s as above, using Hensel’s lemma for an arbitrary set of variables, that is, Proposition 5.3.

Let us consider (viewing now the $({{\mathcal X}}_{1,j})_{j\ge \alpha _1}$ as indeterminates) the infinite polynomial system defined by the vanishing of the t-coefficients of

$$\begin{align*}F\left(\sum_{j\ge \alpha_1} {{\mathcal X}}_{j}\cdot t^j,\left(\sum_{j\ge \alpha_i} \iota(X_{i,j})\cdot t^j\right)_{2\le i\le N}\right) \in t^{a}\cdot (\widehat{A}[({{\mathcal X}}_{1,j})_{j\ge \alpha_1}]{[[ {t} ]]}). \end{align*}$$

Note that, since ${\mathfrak {p}}_{\nu }$ contains ${\mathfrak {i}}_{\infty }^{\ge {\boldsymbol {\alpha }}}$ , then $ {{\mathcal X}}_{1,j}=p_{\widehat {A}}(\iota (X_{1,j})) $ , for $ j\ge \alpha _1 $ , is a solution of the reduction in $\kappa _{\widehat {A}}$ of this system. For $j'\ge \alpha _1$ , one may write

$$\begin{align*}\partial_{{{\mathcal X}}_{1,j'}} \left[ F\left(\sum_{j\ge \alpha_1} {{\mathcal X}}_{1,j}\cdot t^j,\left(\sum_{j\ge \alpha_i} \iota(X_{i,j})\cdot t^j\right)_{2\le i\le N}\right) \right] =t^{j'}\partial_{X_1}F\left(\sum_{j\ge \alpha_1} {{\mathcal X}}_{1,j}\cdot t^j,\left(\sum_{j\ge \alpha_i} \iota(X_{i,j})\cdot t^j\right)_{2\le i\le N}\right). \end{align*}$$

Using the weighted homogeneous decomposition $F=F^{(a)}+F^{(a+1)}+\cdots $ , this shows that the reduction in $\kappa _{\widehat {A}}$ of the Jacobian matrix of the polynomial system under consideration, evaluated at $(p_{\widehat {A}}(\iota (X_{1,j}))_{j\ge \alpha _1}$ , is upper triangular, and every coefficient on the diagonal equals $p_{\widehat {A}}(\partial _{X_1}F^{(a)}(\iota (X_{i,\alpha _i})))$ , which is nonzero by Remark 8.6. Thus, one may apply Proposition 5.3.

8.10 A presentation of the formal neighborhood and a conjectural comparison theorem

We fix a morphism $\rho $ , as in Proposition 8.8, and we set $K:=\operatorname {\mathrm {Frac}}(\rho (R))\subset \widehat {A}$ which is a coefficient field of $\widehat {A}$ . Arguing, as in the proof of Proposition 6.4, one shows the following. Again, the result may be seen as a particular case of Reguera and Reguera-Mourtada’s general study of the cotangent space of stable points [Reg09, Reg18, MR18], or of Chiu-Docampo-de Fernex’s result [CdFD22, Theorem 8.1].

Proposition 8.11. The $\kappa _A$ -vector space ${\mathfrak {M}}_{A}/{\mathfrak {M}}_{A}^2$ is generated by the images of the set $\{X_{i,j}\}_{\substack {2\le i\le N\\0\le j<\alpha _i}}$ . In particular, $\widehat {A}$ is Noetherian, and the set $\{\iota (X_{i,j})\}_{\substack {2\le i\le N\\0\le j<\alpha _i}}$ generates the cotangent space of $\widehat {A}$ .

We set

$$\begin{align*}K{[[{{\boldsymbol{X}}_1,({\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}_i)_{2\le i \le N}} ]]} :=K{[[ {(X_{1,j})_{j\ge 0},(X_{i,j})_{\substack{2\le i\le N\\j<\alpha_i}}} ]]}. \end{align*}$$

Now, arguing similarly as in Section 6, we obtain the following proposition, the last statement of which, as in the case of curve singularities, may be interpreted as a “deformation-theoretic” presentation of the formal neighborhood of the generic point of the maximal divisorial set ${\mathcal {N}}_V(\nu )$ .

Proposition 8.12. Let us keep the previous notation, and set $e:=\operatorname {\mathrm {ord}}_t(\partial _{X_1}F((x_{\rho ,i}(t))))$ .

1. 1. Let $(C,{\mathfrak {M}}_C)$ be an object of $\operatorname {\mathrm {\mathbf {CplLoc}}}_K$ . Let $(X_i(t))_{1\le i\le N}$ be an N-tuple of elements of $C{[[ {t} ]]}$ whose image in $(C/{\mathfrak {M}}_C){[[ {t} ]]}=K{[[ {t} ]]}$ is $(x_{\rho ,i}(t))_{1\le i\le N}$ .

   Then, there exists a unique family $({{\mathcal X}}_{1,j})_{j\ge \alpha _1}$ of elements of ${\mathfrak {M}}_C$ , such that:

   $$\begin{align*}\deg_t\left(F\left(X_1(t)+\sum_{j\ge \alpha_1}{{\mathcal X}}_{1,j}\cdot t^j,(X_{i}(t))_{2\le i\le N}\right)\right)< e. \end{align*}$$

2. 2. Let $\Pi \colon K{[[ {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} ]]} \to \widehat {A}$ be the morphism of complete local K-algebras mapping $X_{i,j}$ ( $1\le i\le N$ , $j<\alpha _i$ ) to $\iota (X_{i,j})$ . Let $({{\mathcal X}}_{1,j})_{j\ge \alpha _1}$ be the family of elements obtained by applying the first assertion to $C=K{[[ {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} ]]}$ and

   $$\begin{align*}X_i(t)=\sum_{0\le j\le \alpha_i}X_{i,j}\cdot t^j+\sum_{j\ge \alpha_i} \rho(X_{i,j})\cdot t^j .\end{align*}$$
   Then, for $j\ge \alpha _1$ , one has $\Pi ({{\mathcal X}}_{1,j})=\iota (X_{1,j})-\rho (X_{1,j})$ .

3. 3. Let $\varepsilon \colon k[{\boldsymbol {X}}]\to K{[[ {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} ]]}$ be the morphism of $ k $ -algebras, such that

   • • for $2\le i\le N$ and $j\ge \alpha _i$ , $\varepsilon (X_{i,j})=\rho (X_{i,j})$ ;

   • • for $j\ge \alpha _1$ , $\varepsilon (X_{1,j})=\rho (X_{1,j})+{{\mathcal X}}_{1,j}$ ;

   • • for $1\le i\le N$ and $j<\alpha _i$ , $\varepsilon (X_{i,j})=X_{i,j}$ .

   Then $\Pi $ induces an isomorphism

   $$\begin{align*}K{[[ {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} ]]}/{\langle {\varepsilon ({\mathfrak{i}}_{\infty})} \rangle}\cong \widehat{A}.\end{align*}$$

4. 4. Let $\phi \colon K{[[ {{\boldsymbol {X}}_1,({\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}_i)_{2\le i \le N}} ]]} \to K{[[ {{\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}} ]]}$ be the morphism (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_K$ ) mapping $X_{i,j}$ to $X_{i,j}$ for $1\le i\le N$ and $0\le j<\alpha _i$ , and $X_{1,j}$ to ${{\mathcal X}}_{1,j}$ for $j\ge \alpha _1$ . Let ${\mathfrak {j}}$ be the ideal of $K{[[ {{\boldsymbol {X}}_1,({\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}_i)_{2\le i \le N}} ]]}$ generated by the t-coefficients of the formal power series

   (8.6) $$ \begin{align} F\left(x_{\rho,1}(t) + \sum_{j\ge 0} X_{1,j}\cdot t^j, \left(x_{\rho,i}(t) + \sum_{0 \le j<\alpha_i} X_{i,j}\cdot t^j\right)_{2\le i\le N} \right). \end{align} $$
   Then $\phi $ induces an isomorphism (in the category $\operatorname {\mathrm {\mathbf {TopLoc}}}_K$ )
   $$\begin{align*}K{[[ {{\boldsymbol{X}}_1,({\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}_i)_{2\le i \le N}} ]]}/{\mathfrak{j}}\cong K{[[ {{\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}} ]]}/{\langle {\varepsilon ({\mathfrak{i}}_{\infty})} \rangle}. \end{align*}$$

Proposition 8.12 then provides a presentation of $\widehat {A}$ as a quotient of $K{[[ {{\boldsymbol {X}}_1,({\boldsymbol {X}}^{<{\boldsymbol {\alpha }}}_i)_{2\le i \le N}} ]]}$ whose relations are given by the t-coefficients of the formal power series (8.6). Recall that $\rho \colon k[{\boldsymbol {X}}]\to K\subset \widehat {A}$ has kernel ${\mathfrak {p}}_{\nu }$ , thus, it factors through $k[{\boldsymbol {X}}]/{\mathfrak {p}}_{\nu }$ . Therefore, setting

$$\begin{align*}D:=(k[{\boldsymbol{X}}]/{\mathfrak{p}}_{\nu}){[[ {{\boldsymbol{X}}_1,({\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}_i)_{2\le i \le N}} ]]} , \end{align*}$$

the power series (8.6) may be seen as an element of $D{[[ {t} ]]}$ , and the t-coefficients $(H_j)_{j\ge 0}$ of this element belong to the ideal of D generated by $\{(X_{1,j})_{j\ge 0},(X_{i,j})_{\substack {2\le i\le N\\j<\alpha _i}}\}$ . Informally speaking, the following question asks whether the formal neighborhood of $\eta _{V,\nu }$ specializes to a finite formal model of a sufficiently generic element of ${\mathcal {N}}_V(\nu )(k)$ . To the best of our knowledge, it is open, unless $\dim (V)=1$ or V is toric.

Question 8.13. Let us keep the preceding notation. Let $\gamma =(x_i(t))_{1\le i\le N}\in {\mathscr {L}_{\infty }}(V)(k)$ with $\operatorname {\mathrm {ord}}_t(x_i(t))=\alpha _i$ . In particular, $\gamma $ induces a morphism $\gamma ^{\ast }\colon k[{\boldsymbol {X}}]/{\mathfrak {p}}_{\nu }\to k$ . Is

$$\begin{align*}k{[[{{\boldsymbol{X}}_1,({\boldsymbol{X}}^{<{\boldsymbol{\alpha}}}_i)_{2\le i \le N}} ]]}/{\langle {\gamma^{\ast}(H_j)} \rangle}_{j\ge 0} \end{align*}$$

a finite formal model of $\gamma $ ?

Equivalently: consider the functor which associates with any object $({\mathcal A},{\mathfrak {M}}_{{\mathcal A}})$ of $\operatorname {\mathrm {\mathbf {CplLoc}}}_k$ the set of families $((x_{A,1,j})_{j\ge 0},(x_{A,i,j})_{\substack {2\le i\le N\\j<\alpha _i}})$ of elements of ${\mathfrak {M}}_{{\mathcal A}}$ , such that

$$\begin{align*}F\left(x_{1}(t)+\sum_{j\ge 0}x_{A,1,j}\cdot t^j,\left(x_{i}(t)+\sum_{0\le j< \alpha_i}x_{A,i,j}\cdot t^j\right)_{2\le i\le N}\right)=0. \end{align*}$$

Is this functor represented by a finite formal model of $\gamma $ ?

Remark 8.14. The fact that Question 8.13 admits a positive answer does not imply that the answer to the first part of Question 1.3 is also positive. Let us consider Example 8.2 again and the set of arcs

$$\begin{align*}{\mathcal{N}}_V(\nu)^{\circ}(k):=\{(x_i(t))_{1\le i\le 3}\in {\mathscr{L}_{\infty}}(V)(k), \quad \operatorname{\mathrm{ord}}_t(x_i(t))=\alpha_i\}, \end{align*}$$

which correspond to the set of k-rational points of a dense open subset of ${\mathcal {N}}_V(\nu )$ . Using the ${\mathscr {L}_{\infty }}({\mathbf {G}}_m)$ -action on ${\mathscr {L}_{\infty }}(V)$ induced by the ${\mathbf {G}}_m$ -action on V, one sees that, on the subset $\left \{\frac {x_1(t)^2}{x_3(t)^5}=\text {constant}\right \}$ of ${\mathcal {N}}_V(\nu )^{\circ }(k)$ , the isomorphism class of the formal neighborhood is constant. Now let $(x_1(t),x_2(t),x_3(t))$ and $(y_1(t),y_2(t),y_3(t))$ be two elements of ${\mathcal {N}}_V(\nu )^{\circ }(k)$ , such that $\frac {x_1(t)^2}{x_3(t)^5}\neq \frac {y_1(t)^2}{y_3(t)^5}$ . It would be interesting to decide whether or not the formal neighborhoods of these arcs are isomorphic.