Article contents
CUTTING A PART FROM MANY MEASURES
Published online by Cambridge University Press: 17 October 2019
Abstract
Holmsen, Kynčl and Valculescu recently conjectured that if a finite set 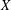 $X$ with
$X$ with 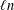 $\ell n$ points in
$\ell n$ points in 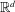 $\mathbb{R}^{d}$ that is colored by
$\mathbb{R}^{d}$ that is colored by 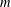 $m$ different colors can be partitioned into
$m$ different colors can be partitioned into  $n$ subsets of
$n$ subsets of 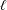 $\ell$ points each, such that each subset contains points of at least
$\ell$ points each, such that each subset contains points of at least 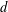 $d$ different colors, then there exists such a partition of
$d$ different colors, then there exists such a partition of 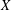 $X$ with the additional property that the convex hulls of the
$X$ with the additional property that the convex hulls of the  $n$ subsets are pairwise disjoint.
$n$ subsets are pairwise disjoint.
We prove a continuous analogue of this conjecture, generalized so that each subset contains points of at least  $c$ different colors, where we also allow
$c$ different colors, where we also allow  $c$ to be greater than
$c$ to be greater than 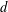 $d$. Furthermore, we give lower bounds on the fraction of the points each of the subsets contains from
$d$. Furthermore, we give lower bounds on the fraction of the points each of the subsets contains from  $c$ different colors. For example, when
$c$ different colors. For example, when 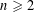 $n\geqslant 2$,
$n\geqslant 2$, 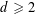 $d\geqslant 2$,
$d\geqslant 2$, 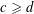 $c\geqslant d$ with
$c\geqslant d$ with 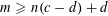 $m\geqslant n(c-d)+d$ are integers, and
$m\geqslant n(c-d)+d$ are integers, and 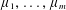 $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$ are
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$ are 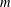 $m$ positive finite absolutely continuous measures on
$m$ positive finite absolutely continuous measures on 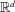 $\mathbb{R}^{d}$, we prove that there exists a partition of
$\mathbb{R}^{d}$, we prove that there exists a partition of 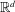 $\mathbb{R}^{d}$ into
$\mathbb{R}^{d}$ into  $n$ convex pieces which equiparts the measures
$n$ convex pieces which equiparts the measures 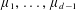 $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{d-1}$, and in addition every piece of the partition has positive measure with respect to at least
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{d-1}$, and in addition every piece of the partition has positive measure with respect to at least  $c$ of the measures
$c$ of the measures 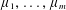 $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$.
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2019
References
- 3
- Cited by


