Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T01:48:22.019Z Has data issue: false hasContentIssue false
  • English
  • Français

COVER TIME FOR THE FROG MODEL ON TREES

Part of: Markov processes Special processes

Published online by Cambridge University Press:  08 November 2019

CHRISTOPHER HOFFMAN ,
TOBIAS JOHNSON Open the ORCID record for TOBIAS JOHNSON [Opens in a new window]  and
MATTHEW JUNGE
CHRISTOPHER HOFFMAN
Affiliation:
Department of Mathematics, University of Washington, USA; [email protected]
TOBIAS JOHNSON
Affiliation:
Department of Mathematics, College of Staten Island, USA; [email protected]
MATTHEW JUNGE
Affiliation:
Department of Mathematics, Duke University, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The frog model is a branching random walk on a graph in which particles branch only at unvisited sites. Consider an initial particle density of $\unicode[STIX]{x1D707}$ on the full 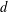$d$-ary tree of height $n$. If 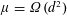$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FA}(d^{2})$, all of the vertices are visited in time 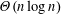$\unicode[STIX]{x1D6E9}(n\log n)$ with high probability. Conversely, if 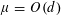$\unicode[STIX]{x1D707}=O(d)$ the cover time is 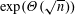$\exp (\unicode[STIX]{x1D6E9}(\sqrt{n}))$ with high probability.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e41
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Aldous, D. J., ‘Random walk covering of some special trees’, J. Math. Anal. Appl. 157(1) (1991), 271–283.Google Scholar
Alves, O. S. M., Machado, F. P., Popov, S. Yu. and Ravishankar, K., ‘The shape theorem for the frog model with random initial configuration’, Markov Process. Related Fields 7(4) (2001), 525–539.Google Scholar
Benjamini, I., Fontes, L. R., Hermon, J. and Machado, F. P., ‘On an epidemic model on finite graphs’, Preprint, 2018, arXiv:1610.04301.Google Scholar
Benjamini, I. and Hermon, J., ‘Rapid social connectivity’, Preprint, 2016, arXiv:1608.07621.Google Scholar
Dickman, R., Muñoz, M. A., Vespignani, A. and Zapperi, S., ‘Paths to self-organized criticality’, Braz. J. Phys. 30 (2000), 27–41. (en).Google Scholar
Hermon, J., ‘Frogs on trees?’, Electron. J. Probab. 23 (2018), Paper No. 17, 40.Google Scholar
Hermon, J., Morris, B., Qin, C. and Sly, A., ‘The social network model on infinite graphs’, Preprint, 2016, arXiv:1610.04293.Google Scholar
Hoffman, C., Johnson, T. and Junge, M., ‘From transience to recurrence with Poisson tree frogs’, Ann. Appl. Probab. 26(3) (2016), 1620–1635.Google Scholar
Hoffman, C., Johnson, T. and Junge, M., ‘Infection spread for the frog model on trees’, Electron. J. Probab. 24(112) (2019), 1–29.Google Scholar
Hoffman, C., Johnson, T. and Junge, M., ‘Recurrence and transience for the frog model on trees’, Ann. Probab. 45(5) (2017), 2826–2854.Google Scholar
Johnson, T. and Junge, M., ‘The critical density for the frog model is the degree of the tree’, Electron. Commun. Probab. 21 (2016), Paper No. 82, 12.Google Scholar
Johnson, T. and Junge, M., ‘Stochastic orders and the frog model’, Ann. Inst. Henri Poincaré Probab. Stat. 54(2) (2018), 1013–1030.Google Scholar
Kosygina, E. and Zerner, M. P. W., ‘A zero-one law for recurrence and transience of frog processes’, Probab. Theory Related Fields 168(1–2) (2017), 317–346.Google Scholar
Lyons, R. and Peres, Y., Probability on Trees and Networks, Cambridge Series in Statistical and Probabilistic Mathematics, 42 (Cambridge University Press, New York, 2016).Google Scholar
Rolla, L. T., Sidoravicius, V. and Zindy, O., ‘Critical density for activated random walks’, Preprint, 2017, arXiv:1707.06081.Google Scholar
Tetali, P., ‘Random walks and the effective resistance of networks’, J. Theoret. Probab. 4(1) (1991), 101–109.Google Scholar