Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T05:26:18.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous Maps from Spheres Converging to Boundaries of Convex Hulls

Part of: Polytopes and polyhedra Real functions: Miscellaneous topics

Published online by Cambridge University Press:  18 February 2021

Joseph Malkoun Open the ORCID record for Joseph Malkoun [Opens in a new window]  and
Peter J. Olver Open the ORCID record for Peter J. Olver [Opens in a new window]
Joseph Malkoun
Affiliation:
Department of Mathematics and Statistics, Faculty of Natural and Applied Sciences, Notre Dame University-Louaize, Zouk Mosbeh, P.O. Box 72, Zouk Mikael, Lebanon; E-mail: [email protected]
Peter J. Olver
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given n distinct points $\mathbf {x}_1, \ldots , \mathbf {x}_n$ in $\mathbb {R}^d$ , let K denote their convex hull, which we assume to be d-dimensional, and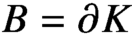 $B = \partial K $ its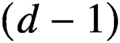 $(d-1)$ -dimensional boundary. 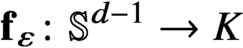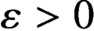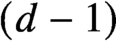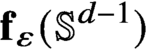We construct an explicit, easily computable one-parameter family of continuous maps $\mathbf {f}_{\varepsilon } \colon \mathbb {S}^{d-1} \to K$ which, for $\varepsilon> 0$ , are defined on the $(d-1)$ -dimensional sphere, and whose images $\mathbf {f}_{\varepsilon }({\mathbb {S}^{d-1}})$ are codimension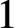 $1$ submanifolds contained in the interior of K. 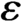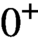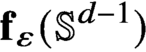Moreover, as the parameter $\varepsilon $ goes to $0^+$ , the images $\mathbf {f}_{\varepsilon } ({\mathbb {S}^{d-1}})$ converge, as sets, to the boundary B of the convex hull. We prove this theorem using techniques from convex geometry of (spherical) polytopes and set-valued homology. We further establish an interesting relationship with the Gauss map of the polytope B, appropriately defined. Several computer plots illustrating these results are included.

MSC classification

Primary: 52B55: Computational aspects related to convexity
Secondary: 26E25: Set-valued functions
Type
Discrete Mathematics
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e13
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - ND
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Arutyunov, A. V. and Obukhovskii, V., Convex and Set-Valued Analysis: Selected Topics (De Gruyter,Berlin, 2017).CrossRefGoogle Scholar
Aubin, J. P. and Frankowska, H., Set-Valued Analysis (Birkhäuser,Boston, 2009).CrossRefGoogle Scholar
Avis, D., Bremner, D. and Seidel, R., ‘How good are convex hull algorithms?’, Comput. Geom. 7 (1997), 265–301.CrossRefGoogle Scholar
Boyd, S. P. and Vandenberghe, L., Convex Optimization (Cambridge University Press,Cambridge, UK, 2004).CrossRefGoogle Scholar
Chen, H. and Padrol, A., ‘Scribability problems for polytopes’, European J. Combin. 64 (2017), 1–26.CrossRefGoogle Scholar
Firey, W. J., ‘Approximating convex bodies by algebraic ones’, Arch. Math. (Basel) 25 (1974), 424–425.CrossRefGoogle Scholar
Ghomi, M., ‘Optimal smoothing for convex polytopes’, Bull. Lond. Math. Soc. 36 (2004), 483–492.CrossRefGoogle Scholar
Gray, A., Abbena, E. and Salamon, S., Modern Differential Geometry of Curves and Surfaces with Mathematica, third edn (Chapman & Hall/CRC,Boca Raton, FL, 2006).Google Scholar
Grünbaum, B., Convex Polytopes, second edn, Graduate Texts in Mathematics, 227 (Springer-Verlag,New York, 2003).Google Scholar
Kuratowski, C., Topologie I (Monografje Matematyczne,Warszawa-Lwow, 1933).Google Scholar
Li, Y., ‘Set-valued homology’, Topology Appl. 83 (1998) 149–158.CrossRefGoogle Scholar
Maehara, H. and Martini, H., ‘Outer normal transforms of convex polytopes’, Results Math. 72 (2017), 87–103.CrossRefGoogle Scholar
McMullen, P. and Shephard, G. C., Convex Polytopes and the Upper Bound Conjecture, London Math. Soc. Lecture Note Series, 3 (Cambridge University Press,Cambridge, UK, 1971).Google Scholar
Minkowski, H. ‘Volumen und Oberfläche’, Math. Ann. 57 (1903), 447–495.CrossRefGoogle Scholar
Nishimura, T. and Sakemi, Y., ‘Topological aspect of Wulff shapes’, J. Math. Soc. Japan 66 (2014), 89–109.CrossRefGoogle Scholar
Padrol, A. and Ziegler, G. M., ‘Six topics on inscribable polytopes’, in Advances in Discrete Differential Geometry (Springer, New York, 2016), 407–419.CrossRefGoogle Scholar
Rockafellar, R. T., Convex Analysis (Princeton University Press,Princeton, NJ, 1970).CrossRefGoogle Scholar
Ziegler, G. M., Lectures on Polytopes, Graduate Texts in Mathematics, 152 (Springer,New York, 1995).CrossRefGoogle Scholar