Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T17:41:12.241Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONTACT INVARIANT IN SUTURED MONOPOLE HOMOLOGY

Part of: Symplectic geometry, contact geometry Differential topology

Published online by Cambridge University Press:  10 June 2016

JOHN A. BALDWIN  and
STEVEN SIVEK
JOHN A. BALDWIN
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA 02467-3806, USA; [email protected]
STEVEN SIVEK
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544-1000, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define an invariant of contact 3-manifolds with convex boundary using Kronheimer and Mrowka’s sutured monopole Floer homology theory ( 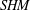$SHM$ ). Our invariant can be viewed as a generalization of Kronheimer and Mrowka’s contact invariant for closed contact 3-manifolds and as the monopole Floer analogue of Honda, Kazez, and Matić’s contact invariant in sutured Heegaard Floer homology ( 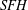$SFH$ ). In the process of defining our invariant, we construct maps on 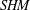$SHM$ associated to contact handle attachments, analogous to those defined by Honda, Kazez, and Matić in 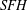$SFH$ . We use these maps to establish a bypass exact triangle in 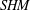$SHM$ analogous to Honda’s in 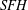$SFH$ . This paper also provides the topological basis for the construction of similar gluing maps in sutured instanton Floer homology, which are used in Baldwin and Sivek [Selecta Math. (N.S.), 22(2) (2016), 939–978] to define a contact invariant in the instanton Floer setting.

MSC classification

Primary: 53D10: Contact manifolds, general
Secondary: 53D40: Floer homology and cohomology, symplectic aspects 57R58: Floer homology
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e12
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Baldwin, J. A. and Sivek, S., ‘Naturality in sutured monopole and instanton homology’, J. Differential Geom. 100(3) (2015), 395–480.Google Scholar
Baldwin, J. A. and Sivek, S., ‘Instanton Floer homology and contact structures’, Selecta Math. (N.S.) 22(2) (2016), 939–978.CrossRefGoogle Scholar
Baldwin, J. A. and Sivek, S., ‘On the equivalence of contact invariants in sutured Floer homology theories’, 2016, arXiv:1601.04973.Google Scholar
Baldwin, J. A. and Sivek, S., ‘Invariants of Legendrian and transverse knots in monopole knot homology’, J. Symplectic Geom. to appear, arXiv:1405.3275.Google Scholar
Bloom, J. M., ‘The combinatorics of Morse theory with boundary’, inProceedings of the Gökova Geometry-Topology Conference 2012 (Int. Press, Somerville, MA, 2013), 43–88.Google Scholar
Colin, V., Ghiggini, P. and Honda, K., ‘The equivalence of Heegaard Floer homology and embedded contact homology III: from hat to plus’. math.SG/1208.1526, 2012.Google Scholar
Colin, V., Ghiggini, P. and Honda, K., ‘The equivalence of Heegaard Floer homology and embedded contact homology via open book decompositions I’. math.SG/1208.1074, 2012.Google Scholar
Colin, V., Ghiggini, P. and Honda, K., ‘The equivalence of Heegaard Floer homology and embedded contact homology via open book decompositions II’. math.SG/1208.1077, 2012.Google Scholar
Colin, V., Ghiggini, P., Honda, K. and Hutchings, M., ‘Sutures and contact homology I’, Geom. Topol. 15(3) (2011), 1749–1842.Google Scholar
Etgü, T. and Özbağcı, B., ‘Partial open book decompositions and the contact class in sutured Floer homology’, Turkish J. Math. 33(3) (2009), 295–312.Google Scholar
Etgü, T. and Ozbagci, B., ‘On the relative Giroux correspondence’, inLow-Dimensional and Symplectic Topology, Proc. Sympos. Pure Math. vol. 82 (American Mathematical Society, Providence, RI, 2011), 65–78.Google Scholar
Etnyre, J. B., Vela-Vick, D. S. and Zarev, R., ‘Sutured Floer homology and invariants of Legendrian and transverse knots’, 2014, arXiv:1408.5858.Google Scholar
Geiges, H., An introduction to contact topology, Cambridge Studies in Advanced Mathematics vol. 109 (Cambridge University Press, Cambridge, 2008).Google Scholar
Ghiggini, P., Honda, K. and Van Horn-Morris, J., ‘The vanishing of the contact invariant in the presence of torsion’, 2007, arXiv:0706.1602.Google Scholar
Giroux, E., ‘Convexité en topologie de contact’, Comment. Math. Helv. 66(4) (1991), 637–677.Google Scholar
Giroux, E., ‘Structures de contact en dimension trois et bifurcations des feuilletages de surfaces’, Invent. Math. 141(3) (2000), 615–689.CrossRefGoogle Scholar
Honda, K., ‘Contact structures, Heegaard Floer homology and triangulated categories’. In preparation.Google Scholar
Honda, K., ‘On the classification of tight contact structures. I’, Geom. Topol. 4 (2000), 309–368.Google Scholar
Honda, K., Kazez, William H. and Matić, G., ‘Contact structures, sutured Floer homology and TQFT’, 2008, arXiv:0807.2431.Google Scholar
Honda, K., Kazez, W. H. and Matić, G., ‘The contact invariant in sutured Floer homology’, Invent. Math. 176(3) (2009), 637–676.CrossRefGoogle Scholar
Hutchings, M. and Taubes, C. H., ‘Proof of the Arnold chord conjecture in three dimensions, II’, Geom. Topol. 17(5) (2013), 2601–2688.CrossRefGoogle Scholar
Juhász, András, ‘Cobordisms of sutured manifolds and the functoriality of link Floer homology’, 2015, arXiv:0910.4382v4.CrossRefGoogle Scholar
Juhász, A. and Thurston, D. P., ‘Naturality and mapping class groups in Heegaard Floer homology’, 2012, arXiv:1210.4996.Google Scholar
Kanda, Y., ‘On the Thurston–Bennequin invariant of Legendrian knots and nonexactness of Bennequin’s inequality’, Invent. Math. 133(2) (1998), 227–242.Google Scholar
Kronheimer, P., Mrowka, T., Ozsváth, P. and Szabó, Z., ‘Monopoles and lens space surgeries’, Ann. of Math. (2) 165(2) (2007), 457–546.CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., ‘Monopoles and contact structures’, Invent. Math. 130(2) (1997), 209–255.Google Scholar
Kronheimer, P. and Mrowka, T., Monopoles and Three-Manifolds, New Mathematical Monographs vol. 10 (Cambridge University Press, Cambridge, 2007).Google Scholar
Kronheimer, P. and Mrowka, T., ‘Knots, sutures, and excision’, J. Differential Geom. 84(2) (2010), 301–364.Google Scholar
Kutluhan, Ç., ‘Seiberg–Witten knot homology via holonomy filtration’. Preprint.Google Scholar
Kutluhan, Ç., Lee, Y.-J. and Taubes, C. H., ‘HF $=$ HM I: Heegaard Floer homology and Seiberg–Witten Floer homology’. math.SG/1007.1979, 2010.Google Scholar
Kutluhan, Ç., Lee, Y.-J. and Taubes, C. H., ‘HF $=$ HM II: Reeb orbits and holomorphic curves for the ech/Heegaard-Floer correspondence’. math.SG/1008.1595, 2010.Google Scholar
Kutluhan, Ç., Lee, Yi-Jen and Taubes, C. H., ‘HF $=$ HM III: Holomorphic curves and the differential for the ech/Heegaard-Floer correspondence’. math.SG/1010.3456, 2010.Google Scholar
Kutluhan, Ç., Lee, Yi-Jen and Taubes, C. H., ‘HF $=$ HM IV: The Seiberg–Witten Floer homology and ech correspondence’. math.GT/1107.2297, 2011.Google Scholar
Kutluhan, Ç., Lee, Y.-J. and Taubes, C. H., ‘HF $=$ HM V: Seiberg–Witten Floer homology and handle additions’. math.GT/1204.0115, 2012.Google Scholar
Lekili, Y., ‘Heegaard-Floer homology of broken fibrations over the circle’, Adv. Math. 244 (2013), 268–302.Google Scholar
Lipshitz, R., Ozsváth, P. and Thurston, D., ‘Bordered Heegaard Floer homology: invariance and pairing’. math.GT/0810.0687, 2008.Google Scholar
Lisca, P., Ozsváth, P., Stipsicz, A. I. and Szabó, Z., ‘Heegaard Floer invariants of Legendrian knots in contact three-manifolds’, J. Eur. Math. Soc. (JEMS) 11(6) (2009), 1307–1363.Google Scholar
Massot, P., ‘Topological methods in 3-dimensional contact geometry’, inContact and Symplectic Topology, Bolyai Soc. Math. Stud. vol. 26 (János Bolyai Math. Soc., Budapest, 2014), 27–83.Google Scholar
Niederkrüger, K. and Wendl, C., ‘Weak symplectic fillings and holomorphic curves’, Ann. Sci. Éc. Norm. Supér. (4) 44(5) (2011), 801–853.Google Scholar
Özbağcı, B., ‘Contact handle decompositions’, Topology Appl. 158(5) (2011), 718–727.Google Scholar
Ozsváth, P. and Szabó, Z., ‘Heegaard Floer homology and contact structures’, Duke Math. J. 129(1) (2005), 39–61.Google Scholar
Sivek, S., ‘Monopole Floer homology and Legendrian knots’, Geom. Topol. 16 (2012), 751–779.Google Scholar
Stipsicz, A. I. and Vértesi, V., ‘On invariants for Legendrian knots’, Pacific J. Math. 239(1) (2009), 157–177.Google Scholar
Taubes, C. H., ‘Embedded contact homology and Seiberg–Witten Floer cohomology I’, Geom. Topol. 14(5) (2010), 2497–2581.Google Scholar
Taubes, C. H., ‘Embedded contact homology and Seiberg–Witten Floer cohomology II’, Geom. Topol. 14(5) (2010), 2583–2720.Google Scholar
Taubes, C. H., ‘Embedded contact homology and Seiberg–Witten Floer cohomology III’, Geom. Topol. 14(5) (2010), 2721–2817.Google Scholar
Taubes., C. H., ‘Embedded contact homology and Seiberg–Witten Floer cohomology IV’, Geom. Topol. 14(5) (2010), 2819–2960.Google Scholar
Taubes., C. H., ‘Embedded contact homology and Seiberg–Witten Floer cohomology V’, Geom. Topol. 14(5) (2010), 2961–3000.Google Scholar
Tian, Y., ‘A categorification of $U_{q}(\mathfrak{s}\mathfrak{l}(1|1))$ as an algebra’. math.QA/1210.5680, 2012.Google Scholar
Tian, Y., ‘A categorification of U T (sl(1|1)) and its tensor product representations’, Geom. Topol. 18(3) (2014), 1635–1717.Google Scholar
Tian, Y., ‘A diagrammatic categorification of a Clifford algebra’, Int. Math. Res. Not. IMRN (21) (2015), 10872–10928.Google Scholar
Wendl, C., ‘A hierarchy of local symplectic filling obstructions for contact 3-manifolds’, Duke Math. J. 162(12) (2013), 2197–2283.Google Scholar
Zarev, R., ‘Joining and gluing sutured Floer homology’, 2010, arXiv:1010.3496.Google Scholar