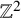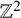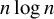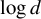1 Introduction
1.1 Harmonic activation and transport
Consider simple random walk
![]() $(S_j)_{j \geq 0}$
on
$(S_j)_{j \geq 0}$
on
![]() $\mathbb {Z}^2$
and with
$\mathbb {Z}^2$
and with
![]() $S_0 = x$
, the distribution of which we denote by
$S_0 = x$
, the distribution of which we denote by
![]() $\mathbb {P}_x$
. For a finite, nonempty subset
$\mathbb {P}_x$
. For a finite, nonempty subset
![]() $A \subset \mathbb {Z}^2$
, the hitting distribution of A from
$A \subset \mathbb {Z}^2$
, the hitting distribution of A from
![]() $x \in \mathbb {Z}^2$
is the function
$x \in \mathbb {Z}^2$
is the function
![]() ${\mathbb {H}}_A (x, \cdot ) : \mathbb {Z}^2 \to [0,1]$
defined as
${\mathbb {H}}_A (x, \cdot ) : \mathbb {Z}^2 \to [0,1]$
defined as
![]() ${\mathbb {H}}_A (x,y) = \mathbb {P}_x (S_{\tau _A} =y)$
, where
${\mathbb {H}}_A (x,y) = \mathbb {P}_x (S_{\tau _A} =y)$
, where
![]() $\tau _A = \inf \{j \geq 1 : S_j \in A\}$
is the return time to A. (We use the notation
$\tau _A = \inf \{j \geq 1 : S_j \in A\}$
is the return time to A. (We use the notation
![]() $\tau _A$
instead of the more common
$\tau _A$
instead of the more common
![]() $\tau _A^+$
for brevity.) The recurrence of random walk on
$\tau _A^+$
for brevity.) The recurrence of random walk on
![]() $\mathbb {Z}^2$
guarantees that
$\mathbb {Z}^2$
guarantees that
![]() $\tau _A$
is almost surely finite, and the existence of the limit
$\tau _A$
is almost surely finite, and the existence of the limit
![]() ${\mathbb {H}}_A (y) = \lim _{|x| \to \infty } {\mathbb {H}}_A (x,y)$
, called the harmonic measure of A, is well known [Reference LawlerLaw13]. Informally, the harmonic measure is the hitting distribution of a random walk ‘from infinity’.
${\mathbb {H}}_A (y) = \lim _{|x| \to \infty } {\mathbb {H}}_A (x,y)$
, called the harmonic measure of A, is well known [Reference LawlerLaw13]. Informally, the harmonic measure is the hitting distribution of a random walk ‘from infinity’.
In this paper, we introduce a Markov chain called harmonic activation and transport (HAT), wherein the elements of a subset of
![]() $\mathbb {Z}^2$
(respectively styled as ‘particles’ of a ‘configuration’) are iteratively selected according to harmonic measure and replaced according to the hitting distribution of a random walk started from the location of the selected element. We say that, with each step, a particle is ‘activated’ and then ‘transported’.
$\mathbb {Z}^2$
(respectively styled as ‘particles’ of a ‘configuration’) are iteratively selected according to harmonic measure and replaced according to the hitting distribution of a random walk started from the location of the selected element. We say that, with each step, a particle is ‘activated’ and then ‘transported’.
Definition 1.1 (Harmonic activation and transport).
Given a finite subset
![]() $U_0$
of
$U_0$
of
![]() $\mathbb {Z}^2$
with at least two elements, HAT is the discrete-time Markov chain
$\mathbb {Z}^2$
with at least two elements, HAT is the discrete-time Markov chain
![]() $(U_t)_{t \geq 0}$
on subsets of
$(U_t)_{t \geq 0}$
on subsets of
![]() $\mathbb {Z}^2$
, the dynamics of which consists of the following steps (Figure 1).
$\mathbb {Z}^2$
, the dynamics of which consists of the following steps (Figure 1).
-
Activation. At time t, remove a random element
 $X_t \sim {\mathbb {H}}_{U_t}$
from
$X_t \sim {\mathbb {H}}_{U_t}$
from
 $U_t$
, forming
$U_t$
, forming
 $V_t = U_t \setminus \{X_t\}$
.
$V_t = U_t \setminus \{X_t\}$
. -
Transport. Then, add a random element
 $Y_t \sim \mathbb {P}_{X_t} (S_{\tau _{V_t} - 1} \in \cdot \mid V_t)$
to
$Y_t \sim \mathbb {P}_{X_t} (S_{\tau _{V_t} - 1} \in \cdot \mid V_t)$
to
 $V_t$
, forming
$V_t$
, forming
 $U_{t+1} = V_t \cup \{Y_t\}$
.
$U_{t+1} = V_t \cup \{Y_t\}$
.
In other words,
![]() $(U_t)_{t \geq 0}$
has inhomogeneous transition probabilities given by
$(U_t)_{t \geq 0}$
has inhomogeneous transition probabilities given by
 $$ \begin{align*} \mathbf{P} \left(U_{t+1} = ( U_t{\setminus} \{x\}) \cup \{y\} \bigm\vert U_t \right) = \begin{cases} {\mathbb{H}}_{U_t} (x) \, \mathbb{P}_x \left( S_{\tau_{U_t{\setminus}\{x\}} - 1} = y \bigm\vert U_t\right) & x \neq y,\\ \sum_{z \in U_t} {\mathbb{H}}_{U_t} (z) \, \mathbb{P}_z \left( S_{\tau_{U_t{\setminus}\{z\}} - 1} = z \bigm\vert U_t\right) & x = y. \end{cases} \end{align*} $$
$$ \begin{align*} \mathbf{P} \left(U_{t+1} = ( U_t{\setminus} \{x\}) \cup \{y\} \bigm\vert U_t \right) = \begin{cases} {\mathbb{H}}_{U_t} (x) \, \mathbb{P}_x \left( S_{\tau_{U_t{\setminus}\{x\}} - 1} = y \bigm\vert U_t\right) & x \neq y,\\ \sum_{z \in U_t} {\mathbb{H}}_{U_t} (z) \, \mathbb{P}_z \left( S_{\tau_{U_t{\setminus}\{z\}} - 1} = z \bigm\vert U_t\right) & x = y. \end{cases} \end{align*} $$

Figure 1 The harmonic activation and transport dynamics. (A) A particle (indicated by a solid, red circle) in the configuration
![]() $U_t$
is activated according to harmonic measure. (B) The activated particle (following the solid, red path) hits another particle (indicated by a solid, blue circle); it is then fixed at the site visited during the previous step (indicated by a solid, red circle), giving
$U_t$
is activated according to harmonic measure. (B) The activated particle (following the solid, red path) hits another particle (indicated by a solid, blue circle); it is then fixed at the site visited during the previous step (indicated by a solid, red circle), giving
![]() $U_{t+1}$
. (C) A particle of U (indicated by a red circle) is activated and (D) if it tries to move into
$U_{t+1}$
. (C) A particle of U (indicated by a red circle) is activated and (D) if it tries to move into
![]() $U {\setminus } \{x\}$
, the particle will be placed at x. The notation
$U {\setminus } \{x\}$
, the particle will be placed at x. The notation
![]() $\partial U$
refers to the exterior vertex boundary of U.
$\partial U$
refers to the exterior vertex boundary of U.
To guide the presentation of our results, we highlight four features of HAT. Two of these reference the diameter of a configuration, defined as
![]() $\mathrm {diam} (U) = \sup _{x,y \in U} |x-y|$
, where
$\mathrm {diam} (U) = \sup _{x,y \in U} |x-y|$
, where
![]() $|\cdot |$
is the Euclidean norm.
$|\cdot |$
is the Euclidean norm.
-
• Conservation of mass. HAT conserves the number of particles in the initial configuration.
-
• Translation invariance. For any configurations
 $V, W$
and element
$V, W$
and element
 $x \in \mathbb {Z}^2$
, In words, the HAT dynamics is invariant under translation by elements of
$x \in \mathbb {Z}^2$
, In words, the HAT dynamics is invariant under translation by elements of $$\begin{align*}\mathbf{P} (U_{t+1} = V \bigm\vert U_t = W) = \mathbf{P} ( U_{t+1} = V + x \bigm\vert U_t = W + x). \end{align*}$$
$$\begin{align*}\mathbf{P} (U_{t+1} = V \bigm\vert U_t = W) = \mathbf{P} ( U_{t+1} = V + x \bigm\vert U_t = W + x). \end{align*}$$
 $\mathbb {Z}^2$
. Accordingly, to each configuration U, we can associate an equivalence class
$\mathbb {Z}^2$
. Accordingly, to each configuration U, we can associate an equivalence class  $$\begin{align*}\widehat U = \left\{ V \subseteq \mathbb{Z}^2: \exists x \in \mathbb{Z}^2: \, U = V + x\right\}.\end{align*}$$
$$\begin{align*}\widehat U = \left\{ V \subseteq \mathbb{Z}^2: \exists x \in \mathbb{Z}^2: \, U = V + x\right\}.\end{align*}$$
-
• Variable connectivity. The HAT dynamics does not preserve connectivity. Indeed, a configuration which is initially connected will eventually be disconnected by the HAT dynamics, and the resulting components may ‘treadmill’ away from one another, adopting configurations of arbitrarily large diameter.
-
• Asymmetric behavior of diameter. While the diameter of a configuration can increase by at most
 $1$
with each step, it can decrease abruptly. For example, if the configuration is a pair of particles separated by d, then the diameter will decrease by
$1$
with each step, it can decrease abruptly. For example, if the configuration is a pair of particles separated by d, then the diameter will decrease by
 $d-1$
in one step.
$d-1$
in one step.
We will shortly state the existence of the stationary distribution of HAT. By the translation invariance of the HAT dynamics, the stationary distribution will be supported on equivalence classes of configurations which, for brevity, we will simply refer to as configurations. In fact, the HAT dynamics cannot reach all such configurations. By an inductive argument, we will prove that the HAT dynamics is irreducible on the collection of configurations that have a nonisolated element with positive harmonic measure. Figure 2 depicts a configuration that HAT cannot reach because every element with positive harmonic measure has no neighbors in
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.

Figure 2 A configuration that HAT cannot reach.
Definition 1.2. Denote by
![]() $\mathrm {{Iso}}(n)$
the collection of n-element subsets U of
$\mathrm {{Iso}}(n)$
the collection of n-element subsets U of
![]() $\mathbb {Z}^2$
such that every x in U with
$\mathbb {Z}^2$
such that every x in U with
![]() ${\mathbb {H}}_U (x)> 0$
belongs to a singleton connected component. In other words, all exposed elements of U are isolated: They lack nearest neighbors in U. We will denote the collection of all other n-element subsets of
${\mathbb {H}}_U (x)> 0$
belongs to a singleton connected component. In other words, all exposed elements of U are isolated: They lack nearest neighbors in U. We will denote the collection of all other n-element subsets of
![]() $\mathbb {Z}^2$
by
$\mathbb {Z}^2$
by
![]() $\mathrm {NonIso} (n)$
and the corresponding equivalence class by
$\mathrm {NonIso} (n)$
and the corresponding equivalence class by
The variable connectivity of HAT configurations and concomitant opportunity for unchecked diameter growth seem to jeopardize the positive recurrence of the HAT dynamics on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. Indeed, if the diameter were to grow unabatedly, the HAT dynamics could not return to a configuration or equivalence class thereof and would therefore be doomed to transience. However, due to the asymmetric behavior of diameter under the HAT dynamics and the recurrence of random walk in
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. Indeed, if the diameter were to grow unabatedly, the HAT dynamics could not return to a configuration or equivalence class thereof and would therefore be doomed to transience. However, due to the asymmetric behavior of diameter under the HAT dynamics and the recurrence of random walk in
![]() $\mathbb {Z}^2$
, this will not be the case. For an arbitrary initial configuration of
$\mathbb {Z}^2$
, this will not be the case. For an arbitrary initial configuration of
![]() $n \geq 2$
particles, we will prove – up to a factor depending on n – sharp bounds on the ‘collapse’ time which, informally, is the first time the diameter is at most a certain function of n.
$n \geq 2$
particles, we will prove – up to a factor depending on n – sharp bounds on the ‘collapse’ time which, informally, is the first time the diameter is at most a certain function of n.
Definition 1.3. For a positive real number R, we define the level-R collapse time to be
![]() $\mathcal {T} (R) = \inf \{t \geq 0: \mathrm {diam} (U_t) \leq R\}$
.
$\mathcal {T} (R) = \inf \{t \geq 0: \mathrm {diam} (U_t) \leq R\}$
.
For a real number
![]() $r \geq 0$
, we define
$r \geq 0$
, we define
![]() $\theta _m = \theta _m (r)$
through
$\theta _m = \theta _m (r)$
through
In particular,
![]() $\theta _n (r)$
is approximately the n
th iterated exponential of r.
$\theta _n (r)$
is approximately the n
th iterated exponential of r.
Theorem 1. Let U be a finite subset of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 2$
elements and a diameter of d. There exists a universal positive constant c such that, if d exceeds
$n \geq 2$
elements and a diameter of d. There exists a universal positive constant c such that, if d exceeds
![]() $\theta = \theta _{4n} (cn)$
, then
$\theta = \theta _{4n} (cn)$
, then
For the sake of concreteness, this is true with
![]() $n^{-4}$
in the place of
$n^{-4}$
in the place of
![]() $o_n (1)$
.
$o_n (1)$
.
In words, for a given n, it typically takes
![]() $(\log d)^{1+o_n (1)}$
steps before the configuration of initial diameter d reaches a configuration with a diameter of no more than a large function of n. Here,
$(\log d)^{1+o_n (1)}$
steps before the configuration of initial diameter d reaches a configuration with a diameter of no more than a large function of n. Here,
![]() $o_n (1)$
denotes a nonnegative function of n that is at most
$o_n (1)$
denotes a nonnegative function of n that is at most
![]() $1$
and which tends to zero as n tends to
$1$
and which tends to zero as n tends to
![]() $\infty $
. The d dependence in Theorem 1 is essentially the best possible, aside from the
$\infty $
. The d dependence in Theorem 1 is essentially the best possible, aside from the
![]() $o_n (1)$
term, because two pairs of particles separated by a distance of d typically exchange particles over
$o_n (1)$
term, because two pairs of particles separated by a distance of d typically exchange particles over
![]() $\log d$
steps. We elaborate this point in Section 2.
$\log d$
steps. We elaborate this point in Section 2.
As a consequence of Theorem 1 and the preceding discussion, it will follow that the HAT dynamics constitutes an aperiodic, irreducible and positive recurrent Markov chain on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. In particular, this means that, from any configuration of
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. In particular, this means that, from any configuration of
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, the time it takes for the HAT dynamics to return to that configuration is finite in expectation. Aperiodicity, irreducibility and positive recurrence imply the existence and uniqueness of the stationary distribution
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, the time it takes for the HAT dynamics to return to that configuration is finite in expectation. Aperiodicity, irreducibility and positive recurrence imply the existence and uniqueness of the stationary distribution
![]() $\pi _n$
, to which HAT converges from any n-element configuration. Moreover – again, due to Theorem 1 – the stationary distribution is exponentially tight.
$\pi _n$
, to which HAT converges from any n-element configuration. Moreover – again, due to Theorem 1 – the stationary distribution is exponentially tight.
Theorem 2. For every
![]() $n \geq 2$
, from any n-element subset of
$n \geq 2$
, from any n-element subset of
![]() $\mathbb {Z}^2$
, HAT converges to a unique probability measure
$\mathbb {Z}^2$
, HAT converges to a unique probability measure
![]() $\pi _n$
supported on
$\pi _n$
supported on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. Moreover,
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
. Moreover,
![]() $\pi _n$
satisfies the following tightness estimate. There exists a universal positive constant c such that, for any
$\pi _n$
satisfies the following tightness estimate. There exists a universal positive constant c such that, for any
![]() $r \geq 2 \theta _{4n} (c n)$
,
$r \geq 2 \theta _{4n} (c n)$
,
 $$\begin{align*}\pi_{n}\big(\mathrm{{diam}}(\widehat U)\ge r\big)\le \exp \left( - \frac{r}{(\log r)^{1+o_n(1)}} \right).\end{align*}$$
$$\begin{align*}\pi_{n}\big(\mathrm{{diam}}(\widehat U)\ge r\big)\le \exp \left( - \frac{r}{(\log r)^{1+o_n(1)}} \right).\end{align*}$$
In particular, this is true with
![]() $6n^{-4}$
in the place of
$6n^{-4}$
in the place of
![]() $o_n (1)$
.
$o_n (1)$
.
The r dependence in the tail bound of Theorem 2 is likely suboptimal because its proof makes critical use of the fact that the diameter of a configuration increases by at most
![]() $1$
with each step. A sufficiently high probability, sublinear bound on the growth rate of diameter would improve the rate of exponential decay. We note that an analogue of Kesten’s sublinear bound on the diameter growth rate of diffusion-limited aggregation [Reference KestenKes87] would apply only to growth resulting from the exchange of particles between well separated ‘clusters’ of particles, not to growth from intracluster transport.
$1$
with each step. A sufficiently high probability, sublinear bound on the growth rate of diameter would improve the rate of exponential decay. We note that an analogue of Kesten’s sublinear bound on the diameter growth rate of diffusion-limited aggregation [Reference KestenKes87] would apply only to growth resulting from the exchange of particles between well separated ‘clusters’ of particles, not to growth from intracluster transport.
As a further consequence of Theorem 1, we will find that the HAT dynamics exhibits a renewal structure which underlies the diffusive behavior of the corresponding center of mass process.
Definition 1.4. For a sequence of configurations
![]() $(U_t)_{t \geq 0}$
with n particles, define the corresponding center of mass process
$(U_t)_{t \geq 0}$
with n particles, define the corresponding center of mass process
![]() $(\mathscr {M}_t)_{t \geq 0}$
by
$(\mathscr {M}_t)_{t \geq 0}$
by
![]() $\mathscr {M}_t = n^{-1} \sum _{x \in U_t} x$
.
$\mathscr {M}_t = n^{-1} \sum _{x \in U_t} x$
.
For the following statement, denote by
![]() $\mathscr {C} ([0,1])$
the continuous functions
$\mathscr {C} ([0,1])$
the continuous functions
![]() $f: [0,1] \to \mathbb {R}^2$
with
$f: [0,1] \to \mathbb {R}^2$
with
![]() $f(0)$
equal to the origin
$f(0)$
equal to the origin
![]() $o \in \mathbb {Z}^2$
, equipped with the topology induced by the supremum norm
$o \in \mathbb {Z}^2$
, equipped with the topology induced by the supremum norm
![]() $\sup _{0 \leq t \leq 1} | f(t) |$
.
$\sup _{0 \leq t \leq 1} | f(t) |$
.
Theorem 3. If
![]() $\mathscr {M}_t$
is linearly interpolated, then the law of the process
$\mathscr {M}_t$
is linearly interpolated, then the law of the process
![]() $\left (t^{-1/2} \mathscr {M}_{st}, \, s \in [0,1]\right )$
, viewed as a measure on
$\left (t^{-1/2} \mathscr {M}_{st}, \, s \in [0,1]\right )$
, viewed as a measure on
![]() $\mathscr {C} ( [0,1] )$
, converges weakly as
$\mathscr {C} ( [0,1] )$
, converges weakly as
![]() $t \to \infty $
to two-dimensional Brownian motion on
$t \to \infty $
to two-dimensional Brownian motion on
![]() $[0,1]$
with coordinate diffusivity
$[0,1]$
with coordinate diffusivity
![]() $\chi ^2 = \chi ^2 (n)$
. Moreover, for a universal positive constant c,
$\chi ^2 = \chi ^2 (n)$
. Moreover, for a universal positive constant c,
![]() $\chi ^2$
satisfies
$\chi ^2$
satisfies
The same argument allows us to extend the convergence to
![]() $[0,\infty )$
. The bounds on
$[0,\infty )$
. The bounds on
![]() $\chi ^2$
are not tight, and we have not attempted to optimize them; they primarily serve to show that
$\chi ^2$
are not tight, and we have not attempted to optimize them; they primarily serve to show that
![]() $\chi ^2$
is positive and finite.
$\chi ^2$
is positive and finite.
1.2 Extremal behavior of harmonic measure
As we elaborate in Section 2, the timescale of diameter collapse in Theorem 1 arises from novel estimates of harmonic measure and hitting probabilities, which control the activation and transport dynamics of HAT. Beyond their relevance to HAT, these results further the characterization of the extremal behavior of harmonic measure.
Estimates of harmonic measure often apply only to connected sets or depend on the diameter of the set. The discrete analogues of Beurling’s projection theorem [Reference KestenKes87] and Makarov’s theorem [Reference LawlerLaw93] are notable examples. Furthermore, estimates of hitting probabilities often approximate sets by Euclidean balls which contain them (for example, the estimates in Chapter 2 of [Reference LawlerLaw13]). Such approximations work well for connected sets but not for sets which are ‘sparse’ in the sense that they have large diameters relative to their cardinality; we elaborate this in Section 2.2. For the purpose of controlling the HAT dynamics, which adopts such sparse configurations, existing estimates of harmonic and hitting measures are inapplicable.
To highlight the difference in the behavior of harmonic measure for general (i.e., potentially sparse) and connected sets, consider a finite subset A of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 2$
elements. We ask: What is the greatest value of
$n \geq 2$
elements. We ask: What is the greatest value of
![]() ${\mathbb {H}}_A (x)$
? If we assume no more about A, then
${\mathbb {H}}_A (x)$
? If we assume no more about A, then
![]() ${\mathbb {H}}_A (x)$
can be as large as
${\mathbb {H}}_A (x)$
can be as large as
![]() $\frac 12$
(see Section 2.5 of [Reference LawlerLaw13] for an example). However, if A is connected, then the discrete analogue of Beurling’s projection theorem [Reference KestenKes87] provides a finite constant c such that
$\frac 12$
(see Section 2.5 of [Reference LawlerLaw13] for an example). However, if A is connected, then the discrete analogue of Beurling’s projection theorem [Reference KestenKes87] provides a finite constant c such that
This upper bound is realized (up to a constant factor) when A is a line segment and x is one of its endpoints.
Our next result provides lower bounds of harmonic measure to complement the preceding upper bounds, addressing the question: What is the least positive value of
![]() ${\mathbb {H}}_A (x)$
?
${\mathbb {H}}_A (x)$
?
Theorem 4. There exists a universal positive constant c such that, if A is a subset of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 1$
elements, then either
$n \geq 1$
elements, then either
![]() ${\mathbb {H}}_A (x) = 0$
or
${\mathbb {H}}_A (x) = 0$
or
It is much easier to prove that, if A is connected, then equation (1.2) can be replaced by
This lower bound is optimal in terms of its dependence on n, as we can choose A to be a narrow, rectangular ‘tunnel’ with a depth of order n and an element just above the ‘bottom’ of the tunnel, in which case the harmonic measure of this element is exponentially small in n; we will shortly discuss a related example in greater detail. We expect that the bound in equation (1.2) can be improved to an exponential decay with a rate of order n instead of
![]() $n \log n$
.
$n \log n$
.
We believe that the best possible lower bound would be realized by the harmonic measure of the innermost element of a square spiral (Figure 3). The virtue of the square spiral is that, essentially, with each additional element, the shortest path to the innermost element lengthens by two steps. This heuristic suggests that the least positive value of harmonic measure should decay no faster than
![]() $4^{-2n}$
, as
$4^{-2n}$
, as
![]() $n \to \infty $
. Indeed, Example 1.6 suggests an asymptotic decay rate of
$n \to \infty $
. Indeed, Example 1.6 suggests an asymptotic decay rate of
![]() $(2+\sqrt {3})^{-2n}$
. We formalize this observation as a conjecture. To state it, let
$(2+\sqrt {3})^{-2n}$
. We formalize this observation as a conjecture. To state it, let
![]() $\mathscr {H}_n$
be the collection of n-element subsets A of
$\mathscr {H}_n$
be the collection of n-element subsets A of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
![]() ${\mathbb {H}}_A (o)> 0$
.
${\mathbb {H}}_A (o)> 0$
.

Figure 3 A square spiral. The shortest path
![]() $\Gamma $
(red) from
$\Gamma $
(red) from
![]() $\Gamma _1$
to the origin, which first hits
$\Gamma _1$
to the origin, which first hits
![]() $A_n$
(black and gray dots) at the origin, has a length of approximately
$A_n$
(black and gray dots) at the origin, has a length of approximately
![]() $2n$
. Some elements (gray dots) of
$2n$
. Some elements (gray dots) of
![]() $A_n$
could be used to continue the spiral pattern (indicated by the black dots) but are presently placed to facilitate a calculation in Example 1.6.
$A_n$
could be used to continue the spiral pattern (indicated by the black dots) but are presently placed to facilitate a calculation in Example 1.6.
Conjecture 1.5. Asymptotically, the square spiral of Figure 3 realizes the least positive value of harmonic measure, in the sense that
Example 1.6. Figure 3 depicts the construction of an increasing sequence of sets
![]() $(A_1, A_2, \dots )$
such that, for all
$(A_1, A_2, \dots )$
such that, for all
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $A_n$
is an element of
$A_n$
is an element of
![]() $\mathscr {H}_n$
and the shortest path
$\mathscr {H}_n$
and the shortest path
![]() $\Gamma = (\Gamma _1, \Gamma _2, \dots , \Gamma _k)$
from the exterior boundary of
$\Gamma = (\Gamma _1, \Gamma _2, \dots , \Gamma _k)$
from the exterior boundary of
![]() $A_n \cup \partial A_n$
to
$A_n \cup \partial A_n$
to
![]() $\Gamma _k = o$
, which satisfies
$\Gamma _k = o$
, which satisfies
![]() $\Gamma _i \notin A_n$
for
$\Gamma _i \notin A_n$
for
![]() $1 \leq i \leq k - 1$
, has a length of
$1 \leq i \leq k - 1$
, has a length of
![]() $k = 2(1- o_n (1))n$
. Since
$k = 2(1- o_n (1))n$
. Since
![]() $\Gamma _1$
separates the origin from infinity in
$\Gamma _1$
separates the origin from infinity in
![]() $A_n^c$
, we have
$A_n^c$
, we have
Concerning the first factor of equation (1.3), one can show that there exist positive constants
![]() $b, c < \infty $
such that, for all sufficiently large n,
$b, c < \infty $
such that, for all sufficiently large n,
To address the second factor of equation (1.3), we sum over the last time
![]() $t < \tau _{A_n}$
that
$t < \tau _{A_n}$
that
![]() $S_t$
visits
$S_t$
visits
![]() $\Gamma _1$
:
$\Gamma _1$
:
 $$\begin{align*}\mathbb{P}_{\Gamma_1} \left( S_{\tau_{A_n}} = o \right) = \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n}; \{S_{t+1},\dots, S_{\tau_{A_n}}\} \subseteq \Gamma_{2:k} \right), \end{align*}$$
$$\begin{align*}\mathbb{P}_{\Gamma_1} \left( S_{\tau_{A_n}} = o \right) = \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n}; \{S_{t+1},\dots, S_{\tau_{A_n}}\} \subseteq \Gamma_{2:k} \right), \end{align*}$$
where
![]() $\Gamma _{2:k} = \{\Gamma _2,\dots ,\Gamma _k\}$
. The Markov property applied to t implies that
$\Gamma _{2:k} = \{\Gamma _2,\dots ,\Gamma _k\}$
. The Markov property applied to t implies that
Therefore,
 $$ \begin{align} \mathbb{P}_{\Gamma_1} \left( S_{\tau_{A_n}} = o \right) = \mathbb{P}_{\Gamma_2} \big( \tau_o < \tau_{\mathbb{Z}^2 \setminus \Gamma_{2:k}} \big) \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n} \right). \end{align} $$
$$ \begin{align} \mathbb{P}_{\Gamma_1} \left( S_{\tau_{A_n}} = o \right) = \mathbb{P}_{\Gamma_2} \big( \tau_o < \tau_{\mathbb{Z}^2 \setminus \Gamma_{2:k}} \big) \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n} \right). \end{align} $$
Denote the first hitting time of a set
![]() $B \subseteq \mathbb {Z}^2$
by
$B \subseteq \mathbb {Z}^2$
by
![]() $\sigma _B = \inf \{j \geq 0: S_j \in B\}$
, or
$\sigma _B = \inf \{j \geq 0: S_j \in B\}$
, or
![]() $\sigma _x$
if
$\sigma _x$
if
![]() $B = \{x\}$
for some
$B = \{x\}$
for some
![]() $x \in \mathbb {Z}^2$
. The first factor of equation (1.4) equals
$x \in \mathbb {Z}^2$
. The first factor of equation (1.4) equals
![]() $\mathbb {P}_{\Gamma _2} ( \sigma _o < \sigma _{\mathbb {Z}^2 \setminus \Gamma _{2:k}} )$
because
$\mathbb {P}_{\Gamma _2} ( \sigma _o < \sigma _{\mathbb {Z}^2 \setminus \Gamma _{2:k}} )$
because
![]() $\Gamma _2 \notin \{o\} \cup (\mathbb {Z}^2 \setminus \Gamma _{2:k})$
. We calculate it as
$\Gamma _2 \notin \{o\} \cup (\mathbb {Z}^2 \setminus \Gamma _{2:k})$
. We calculate it as
![]() $f(2)$
, where
$f(2)$
, where
![]() $f(i) = \mathbb {P}_{\Gamma _i} ( \sigma _o < \sigma _{\mathbb {Z}^2 \setminus \Gamma _{2:k}} )$
solves the system of difference equations
$f(i) = \mathbb {P}_{\Gamma _i} ( \sigma _o < \sigma _{\mathbb {Z}^2 \setminus \Gamma _{2:k}} )$
solves the system of difference equations
The solution of this system yields
 $$ \begin{align} \frac{1}{(2+\sqrt{3})^{k-1}} \leq f(2) = \frac{2\sqrt{3}}{(2+\sqrt{3})^{k-1} - (2-\sqrt{3})^{k-1}} \leq \frac{1}{(2+\sqrt{3})^{k-2}}. \end{align} $$
$$ \begin{align} \frac{1}{(2+\sqrt{3})^{k-1}} \leq f(2) = \frac{2\sqrt{3}}{(2+\sqrt{3})^{k-1} - (2-\sqrt{3})^{k-1}} \leq \frac{1}{(2+\sqrt{3})^{k-2}}. \end{align} $$
Lastly, note that the second factor of equation (1.4) is the expected number of visits that
![]() $S_t$
makes to
$S_t$
makes to
![]() $\Gamma _1$
before time
$\Gamma _1$
before time
![]() $\tau _A$
, which equals the reciprocal of
$\tau _A$
, which equals the reciprocal of
![]() $\mathbb {P}_{\Gamma _1} (\tau _{\Gamma _1} < \tau _{A_n})$
. Since
$\mathbb {P}_{\Gamma _1} (\tau _{\Gamma _1} < \tau _{A_n})$
. Since
![]() $\Gamma _1$
is adjacent to
$\Gamma _1$
is adjacent to
![]() $\tau _{A_n}$
, this probability is at least
$\tau _{A_n}$
, this probability is at least
![]() $\frac 14$
, hence
$\frac 14$
, hence
 $$\begin{align*}1 \leq \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n} \right) \leq 4. \end{align*}$$
$$\begin{align*}1 \leq \sum_{t=0}^\infty \mathbb{P}_{\Gamma_1} \left(S_t = \Gamma_1, t< \tau_{A_n} \right) \leq 4. \end{align*}$$
Combining the preceding bounds, we conclude that, for all sufficiently large n,
 $$ \begin{align*} \cfrac{c n^{-b}}{(2+\sqrt{3})^{k-1}} \leq {\mathbb{H}}_{A_n} (o) \leq \frac{4}{(2+\sqrt{3})^{k-2}}. \end{align*} $$
$$ \begin{align*} \cfrac{c n^{-b}}{(2+\sqrt{3})^{k-1}} \leq {\mathbb{H}}_{A_n} (o) \leq \frac{4}{(2+\sqrt{3})^{k-2}}. \end{align*} $$
Substituting
![]() $k = 2(1-o_n (1)) n$
and simplifying, we obtain
$k = 2(1-o_n (1)) n$
and simplifying, we obtain
which implies
We conclude the discussion of our main results by stating an estimate of hitting probabilities of the form
![]() $\mathbb {P}_x \left ( \tau _{\partial A_d} < \tau _A \right )$
, for
$\mathbb {P}_x \left ( \tau _{\partial A_d} < \tau _A \right )$
, for
![]() $x \in A$
and where
$x \in A$
and where
![]() $A_d$
is the set of all elements of
$A_d$
is the set of all elements of
![]() $\mathbb {Z}^2$
within distance d of A; we will call these escape probabilities from A. Among n-element subsets A of
$\mathbb {Z}^2$
within distance d of A; we will call these escape probabilities from A. Among n-element subsets A of
![]() $\mathbb {Z}^2$
, when d is sufficiently large relative to the diameter of A, the greatest escape probability to a distance d from A is at most the reciprocal of
$\mathbb {Z}^2$
, when d is sufficiently large relative to the diameter of A, the greatest escape probability to a distance d from A is at most the reciprocal of
![]() $\log d$
, up to a constant factor. We find that, in general, it is at least this much, up to an n-dependent factor.
$\log d$
, up to a constant factor. We find that, in general, it is at least this much, up to an n-dependent factor.
Theorem 5. There exists a universal positive constant c such that, if A is a finite subset of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 2$
elements and if
$n \geq 2$
elements and if
![]() $d \geq 2\, \mathrm {diam} (A)$
, then, for any
$d \geq 2\, \mathrm {diam} (A)$
, then, for any
![]() $x \in A$
,
$x \in A$
,
In particular,
In the context of the HAT dynamics, we will use equation (1.7) to control the transport step, ultimately producing the
![]() $\log d$
timescale appearing in Theorem 1. In the setting of its application, A and d will, respectively, represent a subset of a HAT configuration and the separation of A from the rest of the configuration. Reflecting the potential sparsity of HAT configurations, d may be arbitrarily large relative to n.
$\log d$
timescale appearing in Theorem 1. In the setting of its application, A and d will, respectively, represent a subset of a HAT configuration and the separation of A from the rest of the configuration. Reflecting the potential sparsity of HAT configurations, d may be arbitrarily large relative to n.
Organization
HAT motivates the development of new estimates of harmonic measure and escape probabilities. We attend to these estimates in Section 3, after we provide a conceptual overview of the proofs of Theorems 1 and 2 in Section 2. To analyze configurations of large diameter, we will decompose them into well separated ‘clusters’, using a construction introduced in Section 5 and used throughout Section 6. The estimates of Section 3 control the activation and transport steps of the dynamics and serve as the critical inputs to Section 6, in which we analyze the ‘collapse’ of HAT configurations. We then identify the class of configurations to which the HAT dynamics can return and prove the existence of a stationary distribution supported on this class; this is the primary focus of Section 7. The final section, Section 8, uses an exponential tail bound on the diameter of configurations under the stationary distribution – a result we obtain at the end of Section 7 – to show that the center of mass process, properly rescaled, converges in distribution to two-dimensional Brownian motion.
Forthcoming notation
We will denote expectation with respect to
![]() $\mathbf {P}_U$
, the law of HAT from the configuration U, by
$\mathbf {P}_U$
, the law of HAT from the configuration U, by
![]() $\mathbf {E}_U$
; the indicator of an event E by
$\mathbf {E}_U$
; the indicator of an event E by
![]() $\mathbf {1}_E$
or
$\mathbf {1}_E$
or
![]() $\mathbf {1} (E)$
; the Euclidean disk of radius r about x by
$\mathbf {1} (E)$
; the Euclidean disk of radius r about x by
![]() $D_x (r) = \{y \in \mathbb {Z}^2: | x - y | < r \}$
, or
$D_x (r) = \{y \in \mathbb {Z}^2: | x - y | < r \}$
, or
![]() $D(r)$
if
$D(r)$
if
![]() $x = o$
; its boundary by
$x = o$
; its boundary by
![]() $C_x (r) = \partial D_x (r)$
, or
$C_x (r) = \partial D_x (r)$
, or
![]() $C(r)$
if
$C(r)$
if
![]() $x = o$
; the radius of a finite set
$x = o$
; the radius of a finite set
![]() $A \subset \mathbb {Z}^2$
by
$A \subset \mathbb {Z}^2$
by
![]() $\mathrm {rad} (A) = \sup \{ |x|: x \in A\}$
; the R-fattening of A by
$\mathrm {rad} (A) = \sup \{ |x|: x \in A\}$
; the R-fattening of A by
![]() $A_R = \{x \in \mathbb {Z}^2: {\mathrm {dist}}(A,x) \leq R\}$
and the minimum of two random times
$A_R = \{x \in \mathbb {Z}^2: {\mathrm {dist}}(A,x) \leq R\}$
and the minimum of two random times
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
by
$\tau _2$
by
![]() $\tau _1 \wedge \tau _2$
.
$\tau _1 \wedge \tau _2$
.
When we refer to a (universal) constant, we will always mean a positive real number. When we cite standard results from [Reference LawlerLaw13] and [Reference PopovPop21], we will write
![]() $O(g)$
to denote a function f that uniformly satisfies
$O(g)$
to denote a function f that uniformly satisfies
![]() $|f| \leq c g$
for an implicit constant c. However, in all other instances, f will be nonnegative and we will simply mean the estimate
$|f| \leq c g$
for an implicit constant c. However, in all other instances, f will be nonnegative and we will simply mean the estimate
![]() $f \leq c g$
by
$f \leq c g$
by
![]() $O(g)$
. We will include a subscript to indicate the dependence of the implicit constant on a parameter, for example,
$O(g)$
. We will include a subscript to indicate the dependence of the implicit constant on a parameter, for example,
![]() $f = O_{\! n} (g)$
. We will use
$f = O_{\! n} (g)$
. We will use
![]() $\Omega (g)$
and
$\Omega (g)$
and
![]() $\Omega _n (g)$
for the reverse estimate. We will use
$\Omega _n (g)$
for the reverse estimate. We will use
![]() $o_n (1)$
to denote a nonnegative quantity that is at most
$o_n (1)$
to denote a nonnegative quantity that is at most
![]() $1$
and which tends to
$1$
and which tends to
![]() $0$
as
$0$
as
![]() $n \to \infty $
, for example,
$n \to \infty $
, for example,
![]() $n^{-1}$
for
$n^{-1}$
for
![]() $n \geq 1$
.
$n \geq 1$
.
2 Conceptual overview
2.1 Estimating the collapse time and proving the existence of the stationary distribution
Before providing precise details, we discuss some of the key steps in the proofs of Theorems 1 and 2. Since the initial configuration U of n particles is arbitrary, it will be advantageous to decompose any such configuration into clusters such that the separation between any two clusters is at least exponentially large relative to their diameters. As we will show later, we can always find such a clustering when the diameter of U is large enough in terms of n. For the purpose of illustration, let us start by assuming that U consists of just two clusters with separation d and hence the individual diameters of the clusters are no greater than
![]() $\log d$
(Figure 4).
$\log d$
(Figure 4).
The first step in our analysis is to show that in time comparable to
![]() $\log d,$
the diameter of U will shrink to
$\log d,$
the diameter of U will shrink to
![]() $\log d$
. This is the phenomenon we call collapse. Theorem 4 implies that every particle with positive harmonic measure has harmonic measure of at least
$\log d$
. This is the phenomenon we call collapse. Theorem 4 implies that every particle with positive harmonic measure has harmonic measure of at least
![]() $e^{-c n \log n}$
. In particular, the particle in each cluster with the greatest escape probability from that cluster has at least this harmonic measure. Our choice of clustering will ensure that each cluster has positive harmonic measure. Accordingly, we will treat each cluster as the entire configuration and Theorem 5 will imply that the greatest escape probability from each cluster will be at least
$e^{-c n \log n}$
. In particular, the particle in each cluster with the greatest escape probability from that cluster has at least this harmonic measure. Our choice of clustering will ensure that each cluster has positive harmonic measure. Accordingly, we will treat each cluster as the entire configuration and Theorem 5 will imply that the greatest escape probability from each cluster will be at least
![]() $(\log d)^{-1}$
, up to a factor depending upon n.
$(\log d)^{-1}$
, up to a factor depending upon n.
Together, these results will imply that, in
![]() $O_{\! n} (\log d)$
steps, with a probability depending only upon n, all the particles from one of the clusters in Figure 4 will move to the other cluster. Moreover, since the diameter of a cluster grows at most linearly in time, the final configuration will have diameter which is no greater than the diameter of the surviving cluster plus
$O_{\! n} (\log d)$
steps, with a probability depending only upon n, all the particles from one of the clusters in Figure 4 will move to the other cluster. Moreover, since the diameter of a cluster grows at most linearly in time, the final configuration will have diameter which is no greater than the diameter of the surviving cluster plus
![]() $O_{\! n} (\log d)$
. Essentially, we will iterate this estimate – by clustering anew the surviving cluster of Figure 4 – each time obtaining a cluster with a diameter which is the logarithm of the original diameter, until d becomes smaller than a deterministic function
$O_{\! n} (\log d)$
. Essentially, we will iterate this estimate – by clustering anew the surviving cluster of Figure 4 – each time obtaining a cluster with a diameter which is the logarithm of the original diameter, until d becomes smaller than a deterministic function
![]() $\theta _{4n}$
, which is approximately the
$\theta _{4n}$
, which is approximately the
![]() $4n$
th iterated exponential of
$4n$
th iterated exponential of
![]() $cn$
, for a constant c.
$cn$
, for a constant c.
Let us denote the corresponding stopping time by
![]() $\mathcal {T} (\text {below}\ \theta _{4n}).$
In the setting of the application, there may be multiple clusters and we collapse them one by one, reasoning as above. If any such collapse step fails, we abandon the experiment and repeat it. Of course, with each failure, the set we attempt to collapse may have a diameter which is additively larger by
$\mathcal {T} (\text {below}\ \theta _{4n}).$
In the setting of the application, there may be multiple clusters and we collapse them one by one, reasoning as above. If any such collapse step fails, we abandon the experiment and repeat it. Of course, with each failure, the set we attempt to collapse may have a diameter which is additively larger by
![]() $O_{\! n} (\log d)$
. Ultimately, our estimates allow us to conclude that the attempt to collapse is successful within the first
$O_{\! n} (\log d)$
. Ultimately, our estimates allow us to conclude that the attempt to collapse is successful within the first
![]() $(\log d)^{1+o_n (1)}$
tries with a high probability.
$(\log d)^{1+o_n (1)}$
tries with a high probability.
The preceding discussion roughly implies the following result, uniformly in the initial configuration U:
At this stage, we prove that, given any configuration
![]() $\widehat U$
and any configuration
$\widehat U$
and any configuration
![]() $\widehat V \in \widehat {\mathrm {N}} \mathrm {onIso} (n)$
, if K is sufficiently large in terms of n and the diameters of
$\widehat V \in \widehat {\mathrm {N}} \mathrm {onIso} (n)$
, if K is sufficiently large in terms of n and the diameters of
![]() $\widehat U$
and
$\widehat U$
and
![]() $\widehat V$
, then
$\widehat V$
, then
where
![]() $\mathcal {T} (\text {hits}\ \widehat V)$
is the first time the configuration is
$\mathcal {T} (\text {hits}\ \widehat V)$
is the first time the configuration is
![]() $\widehat V$
. To prove this estimate, we split it into two, simpler estimates. Specifically, we show that the particles of
$\widehat V$
. To prove this estimate, we split it into two, simpler estimates. Specifically, we show that the particles of
![]() $\widehat U$
form a line segment of length n in
$\widehat U$
form a line segment of length n in
![]() $K^4$
steps with high probability, and we prove by induction on n that any other nonisolated configuration
$K^4$
steps with high probability, and we prove by induction on n that any other nonisolated configuration
![]() $\widehat V$
is reachable from the line segment in
$\widehat V$
is reachable from the line segment in
![]() $K^5$
steps, with high probability. In addition to implying irreducibility of the HAT dynamics on
$K^5$
steps, with high probability. In addition to implying irreducibility of the HAT dynamics on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, we use this result to obtain a finite upper bound on the expected return time to any nonisolated configuration (i.e., it proves the positive recurrence of HAT on
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, we use this result to obtain a finite upper bound on the expected return time to any nonisolated configuration (i.e., it proves the positive recurrence of HAT on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
). Irreducibility and positive recurrence on
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
). Irreducibility and positive recurrence on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
imply the existence and uniqueness of the stationary distribution.
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
imply the existence and uniqueness of the stationary distribution.

Figure 4 Exponentially separated clusters.

Figure 5 Sparse sets like ones which appear in the proofs of Theorems 4 (left) and 5 (right). The elements of A are represented by dark green dots. On the left,
![]() $A {\setminus } \{o\}$
is a subset of
$A {\setminus } \{o\}$
is a subset of
![]() $D(R)^c$
. On the right, A is a subset of
$D(R)^c$
. On the right, A is a subset of
![]() $D(r)$
and
$D(r)$
and
![]() $A_R$
, the R-fattening of A (shaded green), is a subset of
$A_R$
, the R-fattening of A (shaded green), is a subset of
![]() $D(R+r)$
. The figure is not to scale, as
$D(R+r)$
. The figure is not to scale, as
![]() $R \geq e^n$
on the left, while
$R \geq e^n$
on the left, while
![]() $R \geq e^r$
on the right.
$R \geq e^r$
on the right.
2.2 Improved estimates of hitting probabilities for sparse sets
HAT configurations may include subsets with large diameters relative to the number of elements they contain, and in this sense they are sparse. Two such cases are depicted in Figure 5. A key component of the proofs of Theorems 4 and 5 is a method which improves two standard estimates of hitting probabilities when applied to sparse sets, as summarized by Table 1.
Table 1 Summary of improvements to standard estimates in sparse settings. The origin is denoted by o and
![]() $A_R$
denotes the set of all points in
$A_R$
denotes the set of all points in
![]() $\mathbb {Z}^d$
within a distance R of A.
$\mathbb {Z}^d$
within a distance R of A.

For the scenario depicted in Figure 5 (left), we estimate the probability that a random walk from
![]() $x \in C(\tfrac {R}{3})$
hits the origin before any element of
$x \in C(\tfrac {R}{3})$
hits the origin before any element of
![]() $A{\setminus } \{o\}$
. Since
$A{\setminus } \{o\}$
. Since
![]() $C(R)$
separates x from
$C(R)$
separates x from
![]() $A{\setminus }\{o\}$
, this probability is at least
$A{\setminus }\{o\}$
, this probability is at least
![]() $\mathbb {P}_x (\tau _o < \tau _{C(R)})$
. We can calculate this lower bound by combining the fact that the potential kernel (defined in Section 3) is harmonic away from the origin with the optional stopping theorem (e.g., Proposition 1.6.7 of [Reference LawlerLaw13]):
$\mathbb {P}_x (\tau _o < \tau _{C(R)})$
. We can calculate this lower bound by combining the fact that the potential kernel (defined in Section 3) is harmonic away from the origin with the optional stopping theorem (e.g., Proposition 1.6.7 of [Reference LawlerLaw13]):
 $$ \begin{align*} \mathbb{P}_x \left( \tau_{o} < \tau_{C(R)} \right) = \frac{\log R - \log |x| + O (R^{-1})}{\log R + O (R^{-1})}. \end{align*} $$
$$ \begin{align*} \mathbb{P}_x \left( \tau_{o} < \tau_{C(R)} \right) = \frac{\log R - \log |x| + O (R^{-1})}{\log R + O (R^{-1})}. \end{align*} $$
This implies
![]() $\mathbb {P}_x (\tau _{o} < \tau _{A \cap D(R)^c}) = \Omega (\tfrac {1}{\log R})$
since
$\mathbb {P}_x (\tau _{o} < \tau _{A \cap D(R)^c}) = \Omega (\tfrac {1}{\log R})$
since
![]() $x \in C(\tfrac {R}{3})$
.
$x \in C(\tfrac {R}{3})$
.
We can improve the lower bound to
![]() $\Omega (\tfrac {1}{n})$
by using the sparsity of A. We define the random variable
$\Omega (\tfrac {1}{n})$
by using the sparsity of A. We define the random variable
![]() $W = \sum _{y \in A{\setminus } \{o\}} \mathbf {1} \left ( \tau _y < \tau _{o} \right )$
and write
$W = \sum _{y \in A{\setminus } \{o\}} \mathbf {1} \left ( \tau _y < \tau _{o} \right )$
and write
 $$\begin{align*}\mathbb{P}_x \left (\tau_{o} < \tau_{A {\setminus} \{o\}} \right) = \mathbb{P}_x \left( W = 0 \right) = 1 - \frac{\mathbb{E}_x W}{\mathbb{E}_x [ W \bigm\vert W> 0 ]}.\end{align*}$$
$$\begin{align*}\mathbb{P}_x \left (\tau_{o} < \tau_{A {\setminus} \{o\}} \right) = \mathbb{P}_x \left( W = 0 \right) = 1 - \frac{\mathbb{E}_x W}{\mathbb{E}_x [ W \bigm\vert W> 0 ]}.\end{align*}$$
We will show that
![]() $\mathbb {E}_x [ W \bigm \vert W> 0 ] \geq \mathbb {E}_x W + \delta $
for some
$\mathbb {E}_x [ W \bigm \vert W> 0 ] \geq \mathbb {E}_x W + \delta $
for some
![]() $\delta $
which is uniformly positive in A and n. We will be able to find such a
$\delta $
which is uniformly positive in A and n. We will be able to find such a
![]() $\delta $
because random walk from x hits a given element of
$\delta $
because random walk from x hits a given element of
![]() $A{\setminus }\{o\}$
before o with a probability of at most
$A{\setminus }\{o\}$
before o with a probability of at most
![]() $1/2$
, so conditioning on
$1/2$
, so conditioning on
![]() $\{W>0\}$
effectively increases W by
$\{W>0\}$
effectively increases W by
![]() $1/2$
. Then
$1/2$
. Then
The second inequality follows from the monotonicity of
![]() $\tfrac {\mathbb {E}_x W}{\mathbb {E}_x W + \delta }$
in
$\tfrac {\mathbb {E}_x W}{\mathbb {E}_x W + \delta }$
in
![]() $\mathbb {E}_x W$
and the fact that
$\mathbb {E}_x W$
and the fact that
![]() $|A| \leq n$
, so
$|A| \leq n$
, so
![]() $\mathbb {E}_x W \leq n$
. This is a better lower bound than
$\mathbb {E}_x W \leq n$
. This is a better lower bound than
![]() $\Omega (\tfrac {1}{\log R})$
when R is at least
$\Omega (\tfrac {1}{\log R})$
when R is at least
![]() $e^n$
.
$e^n$
.
A variation of this method also improves a standard estimate for the scenario depicted in Figure 5 (right). In this case, we estimate the probability that a random walk from
![]() $x \in C(2r)$
hits
$x \in C(2r)$
hits
![]() $\partial A_R$
before A, where A is contained in
$\partial A_R$
before A, where A is contained in
![]() $D(r)$
and
$D(r)$
and
![]() $A_R$
consists of all elements of
$A_R$
consists of all elements of
![]() $\mathbb {Z}^2$
within a distance
$\mathbb {Z}^2$
within a distance
![]() $R \geq e^r$
of A. We can bound below this probability by using the fact that
$R \geq e^r$
of A. We can bound below this probability by using the fact that
A standard calculation with the potential kernel of random walk (e.g., Exercise 1.6.8 of [Reference LawlerLaw13]) shows that this lower bound is
![]() $\Omega _n (\tfrac {1}{\log R})$
since
$\Omega _n (\tfrac {1}{\log R})$
since
![]() $R \geq e^r$
and
$R \geq e^r$
and
![]() $r = \Omega (n^{1/2})$
.
$r = \Omega (n^{1/2})$
.
We can improve the lower bound to
![]() $\Omega _n (\tfrac {\log r}{\log R})$
by using the sparsity of A. We define
$\Omega _n (\tfrac {\log r}{\log R})$
by using the sparsity of A. We define
![]() $W' = \sum _{y \in A} \mathbf {1} \left ( \tau _y < \tau _{\partial A_R} \right )$
and write
$W' = \sum _{y \in A} \mathbf {1} \left ( \tau _y < \tau _{\partial A_R} \right )$
and write
 $$\begin{align*}\mathbb{P}_x \left( \tau_{\partial A_R} < \tau_A \right) = 1 - \frac{\mathbb{E}_x W'}{\mathbb{E}_x [W' \bigm\vert W'> 0 ]} \geq 1 - \frac{n\alpha}{1 + (n-1)\beta},\end{align*}$$
$$\begin{align*}\mathbb{P}_x \left( \tau_{\partial A_R} < \tau_A \right) = 1 - \frac{\mathbb{E}_x W'}{\mathbb{E}_x [W' \bigm\vert W'> 0 ]} \geq 1 - \frac{n\alpha}{1 + (n-1)\beta},\end{align*}$$
where
![]() $\alpha $
bounds above
$\alpha $
bounds above
![]() $\mathbb {P}_x \left ( \tau _y < \tau _{\partial A_R}\right )$
and
$\mathbb {P}_x \left ( \tau _y < \tau _{\partial A_R}\right )$
and
![]() $\beta $
bounds below
$\beta $
bounds below
![]() $\mathbb {P}_z \left ( \tau _y < \tau _{\partial A_R}\right )$
, uniformly for
$\mathbb {P}_z \left ( \tau _y < \tau _{\partial A_R}\right )$
, uniformly for
![]() $x \in C(2r)$
and distinct
$x \in C(2r)$
and distinct
![]() $y,z \in A$
. We will show that
$y,z \in A$
. We will show that
![]() $\alpha \leq \beta $
and
$\alpha \leq \beta $
and
![]() $\beta \leq 1 - \tfrac {\log (2r)}{\log R}$
. The former is plausible because
$\beta \leq 1 - \tfrac {\log (2r)}{\log R}$
. The former is plausible because
![]() $|x-y|$
is at least as great as
$|x-y|$
is at least as great as
![]() $|y-z|$
; the latter because
$|y-z|$
; the latter because
![]() ${\mathrm {dist}} (z,A) \geq R$
while
${\mathrm {dist}} (z,A) \geq R$
while
![]() $|y-z| \leq 2r$
, and because of equation (3.9). We apply these facts to the preceding display to conclude
$|y-z| \leq 2r$
, and because of equation (3.9). We apply these facts to the preceding display to conclude
This is a better lower bound than
![]() $\Omega _n (\tfrac {1}{\log R})$
because r can be as large as
$\Omega _n (\tfrac {1}{\log R})$
because r can be as large as
![]() $\log R$
.
$\log R$
.
In summary, by analyzing certain conditional expectations, we can better estimate hitting probabilities for sparse sets than we can by applying standard results. This approach may be useful in obtaining other sparse analogues of hitting probability estimates.
3 Harmonic measure estimates
The purpose of this section is to prove Theorem 4. We will describe the proof strategy in Section 3.1, before stating several estimates in Section 3.2 that streamline the presentation of the proof in Section 3.3.
Consider a subset A of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 2$
elements, which satisfies
$n \geq 2$
elements, which satisfies
![]() ${\mathbb {H}}_A (o)> 0$
(i.e.,
${\mathbb {H}}_A (o)> 0$
(i.e.,
![]() $A \in \mathscr {H}_n$
). We frame the proof of equation (1.2) in terms of advancing a random walk from infinity to the origin in three or four stages, while avoiding all other elements of A. We continue to use the phrase ‘random walk from infinity’ to refer to the limiting hitting probability of a fixed, finite subset of
$A \in \mathscr {H}_n$
). We frame the proof of equation (1.2) in terms of advancing a random walk from infinity to the origin in three or four stages, while avoiding all other elements of A. We continue to use the phrase ‘random walk from infinity’ to refer to the limiting hitting probability of a fixed, finite subset of
![]() $\mathbb {Z}^2$
by a random walk from
$\mathbb {Z}^2$
by a random walk from
![]() $x \in \mathbb {Z}^2$
as
$x \in \mathbb {Z}^2$
as
![]() $|x| \to \infty $
. We will write
$|x| \to \infty $
. We will write
![]() $\mathbb {P}_\infty $
as a shorthand for this limit.
$\mathbb {P}_\infty $
as a shorthand for this limit.
The stages of advancement are defined in terms of a sequence of annuli which partition
![]() $\mathbb {Z}^2$
. Denote by
$\mathbb {Z}^2$
. Denote by
![]() $\mathcal {A} (r,R) = D(R) {\setminus } D(r)$
the annulus with inner radius r and outer radius R. We will frequently need to reference the subset of A which lies within or beyond a disk. We denote
$\mathcal {A} (r,R) = D(R) {\setminus } D(r)$
the annulus with inner radius r and outer radius R. We will frequently need to reference the subset of A which lies within or beyond a disk. We denote
![]() $A_{< r} = A \cap D(r)$
and
$A_{< r} = A \cap D(r)$
and
![]() $A_{\geq r} = A \cap D(r)^c$
. Define radii
$A_{\geq r} = A \cap D(r)^c$
. Define radii
![]() $R_1, R_2, \dots $
and annuli
$R_1, R_2, \dots $
and annuli
![]() $\mathcal {A}_1, \mathcal {A}_2, \dots $
through
$\mathcal {A}_1, \mathcal {A}_2, \dots $
through
![]() $R_1 = 10^5$
, and
$R_1 = 10^5$
, and
![]() $R_\ell = R_1^\ell $
and
$R_\ell = R_1^\ell $
and
![]() $\mathcal {A}_\ell = \mathcal {A} (R_\ell , R_{\ell +1})$
for
$\mathcal {A}_\ell = \mathcal {A} (R_\ell , R_{\ell +1})$
for
![]() $\ell \geq 1$
. We fix
$\ell \geq 1$
. We fix
![]() $\delta = 10^{-2}$
for use in intermediate scales, like
$\delta = 10^{-2}$
for use in intermediate scales, like
![]() $C(\delta R_{\ell +1}) \subset \mathcal {A}_\ell $
. Additionally, we denote by
$C(\delta R_{\ell +1}) \subset \mathcal {A}_\ell $
. Additionally, we denote by
![]() $n_{0}$
,
$n_{0}$
,
![]() $n_\ell $
,
$n_\ell $
,
![]() $m_\ell $
, and
$m_\ell $
, and
![]() $n_{>J}$
the number of elements of A in
$n_{>J}$
the number of elements of A in
![]() $D(R_1)$
,
$D(R_1)$
,
![]() $\mathcal {A}_\ell $
,
$\mathcal {A}_\ell $
,
![]() $\mathcal {A}_\ell \cup \mathcal {A}_{\ell +1}$
, and
$\mathcal {A}_\ell \cup \mathcal {A}_{\ell +1}$
, and
![]() $D(R_{J+1})^c$
, respectively.
$D(R_{J+1})^c$
, respectively.
We will split the proof of equation (1.2) into an easy case when
![]() $n_0 = n$
and a difficult case when
$n_0 = n$
and a difficult case when
![]() $n_0 \neq n$
. If
$n_0 \neq n$
. If
![]() $n_0 \neq n$
, then
$n_0 \neq n$
, then
![]() $A_{\geq R_1}$
is nonempty and the following indices
$A_{\geq R_1}$
is nonempty and the following indices
![]() $I = I(A)$
and
$I = I(A)$
and
![]() $J =J(A)$
are well defined:
$J =J(A)$
are well defined:
 $$ \begin{align*} I &= \min \{\ell \geq 1:\ \mathcal{A}_\ell\text{ contains an element of}\ A {\setminus} \{o\} \}, \,\,\text{and}\\ J &= \min \{\ell> I: \ \mathcal{A}_\ell\ \text{contains no element of}\ A {\setminus} \{o\}\}. \end{align*} $$
$$ \begin{align*} I &= \min \{\ell \geq 1:\ \mathcal{A}_\ell\text{ contains an element of}\ A {\setminus} \{o\} \}, \,\,\text{and}\\ J &= \min \{\ell> I: \ \mathcal{A}_\ell\ \text{contains no element of}\ A {\setminus} \{o\}\}. \end{align*} $$
Figure 6 illustrates the definitions of I and J. We explain their roles in the following subsection.

Figure 6 The first annulus that intersects A (green dots) is
![]() $\mathcal {A}_I$
; the next empty annulus is
$\mathcal {A}_I$
; the next empty annulus is
![]() $\mathcal {A}_J$
.
$\mathcal {A}_J$
.
3.1 Strategy for the proof of Theorem 4
This section outlines a proof of equation (1.2) by induction on n. The induction step is easy when
![]() $n_0 = n$
because it implies that A is contained in
$n_0 = n$
because it implies that A is contained in
![]() $D(10^5)$
, hence
$D(10^5)$
, hence
![]() ${\mathbb {H}}_A (o)$
is at least a universal positive constant. The following strategy concerns the difficult case when
${\mathbb {H}}_A (o)$
is at least a universal positive constant. The following strategy concerns the difficult case when
![]() $n_0 \neq n$
.
$n_0 \neq n$
.
Stage 1: Advancing to
![]() $C(R_{J})$
. Assume
$C(R_{J})$
. Assume
![]() $n_0 \neq n$
and
$n_0 \neq n$
and
![]() $n \geq 3$
. By the induction hypothesis, there is a universal constant
$n \geq 3$
. By the induction hypothesis, there is a universal constant
![]() $c_1$
such that the harmonic measure at the origin is at least
$c_1$
such that the harmonic measure at the origin is at least
![]() $e^{-c_1 k \log k}$
, for any set in
$e^{-c_1 k \log k}$
, for any set in
![]() $\mathscr {H}_k$
,
$\mathscr {H}_k$
,
![]() $1 \leq k < n$
. Let
$1 \leq k < n$
. Let
![]() $k = n_{>J}+1$
. Because a random walk from
$k = n_{>J}+1$
. Because a random walk from
![]() $\infty $
which hits the origin before
$\infty $
which hits the origin before
![]() $A_{\geq R_{J}}$
also hits
$A_{\geq R_{J}}$
also hits
![]() $C(R_{J})$
before A, the induction hypothesis applied to
$C(R_{J})$
before A, the induction hypothesis applied to
![]() $A_{\geq R_{J}}\cup \{o\} \in \mathscr {H}_{k}$
implies that
$A_{\geq R_{J}}\cup \{o\} \in \mathscr {H}_{k}$
implies that
![]() $\mathbb {P}_\infty (\tau _{C(R_{J})} < \tau _A)$
is no smaller than exponential in
$\mathbb {P}_\infty (\tau _{C(R_{J})} < \tau _A)$
is no smaller than exponential in
![]() $k \log k$
. Note that
$k \log k$
. Note that
![]() $k < n$
because
$k < n$
because
![]() $A_{<R_{I+1}}$
has at least two elements by the definition of I.
$A_{<R_{I+1}}$
has at least two elements by the definition of I.
The reason we advance the random walk to
![]() $C(R_{J})$
instead of
$C(R_{J})$
instead of
![]() $C(R_{J-1})$
is that an adversarial choice of A could produce a ‘choke point’ which likely dooms the walk to be intercepted by
$C(R_{J-1})$
is that an adversarial choice of A could produce a ‘choke point’ which likely dooms the walk to be intercepted by
![]() $A{\setminus } \{o\}$
in the second stage of advancement (Figure 7). To avoid a choke point when advancing to the boundary of a disk D, it suffices for the conditional hitting distribution of
$A{\setminus } \{o\}$
in the second stage of advancement (Figure 7). To avoid a choke point when advancing to the boundary of a disk D, it suffices for the conditional hitting distribution of
![]() $\partial D$
given
$\partial D$
given
![]() $\{\tau _{\partial D} < \tau _A\}$
to be comparable to the uniform hitting distribution on
$\{\tau _{\partial D} < \tau _A\}$
to be comparable to the uniform hitting distribution on
![]() $\partial D$
. To prove this comparison, the annular region immediately beyond D and extending to a radius of, say, twice that of D, must be empty of A. This explains the need for exponentially growing radii and for
$\partial D$
. To prove this comparison, the annular region immediately beyond D and extending to a radius of, say, twice that of D, must be empty of A. This explains the need for exponentially growing radii and for
![]() $\mathcal {A}_J$
to be empty of A.
$\mathcal {A}_J$
to be empty of A.

Figure 7 An example of a choke point (left) and a strategy for avoiding it (right). The hitting distribution of a random walk conditioned to reach
![]() $\partial D$
before A (green dots) may favor the avoidance of
$\partial D$
before A (green dots) may favor the avoidance of
![]() $A \cap D^c$
in a way which localizes the walk (e.g., as indicated by the dark red arc of
$A \cap D^c$
in a way which localizes the walk (e.g., as indicated by the dark red arc of
![]() $\partial D$
) prohibitively close to
$\partial D$
) prohibitively close to
![]() $A \cap D$
. The hitting distribution on
$A \cap D$
. The hitting distribution on
![]() $C(R_{J})$
will be approximately uniform if the radii grow exponentially. The random walk can then avoid the choke point by ‘tunneling’ through it (e.g., by passing through the tan-shaded region).
$C(R_{J})$
will be approximately uniform if the radii grow exponentially. The random walk can then avoid the choke point by ‘tunneling’ through it (e.g., by passing through the tan-shaded region).
Stage 2: Advancing into
![]() $\mathcal {A}_{I-1}$
. For notational convenience, assume
$\mathcal {A}_{I-1}$
. For notational convenience, assume
![]() $I \geq 2$
so that
$I \geq 2$
so that
![]() $\mathcal {A}_{I-1}$
is defined; the argument is the same when
$\mathcal {A}_{I-1}$
is defined; the argument is the same when
![]() $I=1$
. Each annulus
$I=1$
. Each annulus
![]() $\mathcal {A}_\ell $
,
$\mathcal {A}_\ell $
,
![]() $\ell \in \{I,\dots ,J - 1\}$
, contains one or more elements of A, which the random walk must avoid on its journey to
$\ell \in \{I,\dots ,J - 1\}$
, contains one or more elements of A, which the random walk must avoid on its journey to
![]() $\mathcal {A}_{I-1}$
. Except in an easier subcase, which we address at the end of this subsection, we advance the walk into
$\mathcal {A}_{I-1}$
. Except in an easier subcase, which we address at the end of this subsection, we advance the walk into
![]() $\mathcal {A}_{I-1}$
by building an overlapping sequence of rectangular and annular tunnels, through and between each annulus, which are empty of A and through which the walk can enter
$\mathcal {A}_{I-1}$
by building an overlapping sequence of rectangular and annular tunnels, through and between each annulus, which are empty of A and through which the walk can enter
![]() $\mathcal {A}_{I-1}$
(Figure 8). Specifically, the walk reaches a particular subset
$\mathcal {A}_{I-1}$
(Figure 8). Specifically, the walk reaches a particular subset
![]() $\mathrm {Arc}_{I-1}$
in
$\mathrm {Arc}_{I-1}$
in
![]() $\mathcal {A}_{I-1}$
at the conclusion of the tunneling process. We will define
$\mathcal {A}_{I-1}$
at the conclusion of the tunneling process. We will define
![]() $\mathrm {Arc}_{I-1}$
in Lemma 3.3 as an arc of a circle in
$\mathrm {Arc}_{I-1}$
in Lemma 3.3 as an arc of a circle in
![]() $\mathcal {A}_{I-1}$
.
$\mathcal {A}_{I-1}$
.

Figure 8 Tunneling through nonempty annuli. We construct a contiguous series of sectors (tan) and annuli (blue) which contain no elements of A (green dots) and through which the random walk may advance from
![]() $C(R_{J - 1})$
to
$C(R_{J - 1})$
to
![]() $C(\delta R_{I - 1})$
(dashed).
$C(\delta R_{I - 1})$
(dashed).
By the pigeonhole principle applied to the angular coordinate, for each
![]() $\ell \geq I+1$
, there is a sector of aspect ratio
$\ell \geq I+1$
, there is a sector of aspect ratio
![]() $m_\ell = n_\ell + n_{\ell -1}$
, from the lower ‘
$m_\ell = n_\ell + n_{\ell -1}$
, from the lower ‘
![]() $\delta $
th’ of
$\delta $
th’ of
![]() $\mathcal {A}_{\ell }$
to that of
$\mathcal {A}_{\ell }$
to that of
![]() $\mathcal {A}_{\ell -1}$
, which contains no element of A (Figure 8). To reach the entrance of the analogous tunnel between
$\mathcal {A}_{\ell -1}$
, which contains no element of A (Figure 8). To reach the entrance of the analogous tunnel between
![]() $\mathcal {A}_{\ell -1}$
and
$\mathcal {A}_{\ell -1}$
and
![]() $\mathcal {A}_{\ell -2}$
, the random walk may need to circle the lower
$\mathcal {A}_{\ell -2}$
, the random walk may need to circle the lower
![]() $\delta $
th of
$\delta $
th of
![]() $\mathcal {A}_{\ell -1}$
. We apply the pigeonhole principle to the radial coordinate to conclude that there is an annular region contained in the lower
$\mathcal {A}_{\ell -1}$
. We apply the pigeonhole principle to the radial coordinate to conclude that there is an annular region contained in the lower
![]() $\delta $
th of
$\delta $
th of
![]() $\mathcal {A}_{\ell -1}$
, with an aspect ratio of
$\mathcal {A}_{\ell -1}$
, with an aspect ratio of
![]() $n_{\ell -1}$
, which contains no element of A.
$n_{\ell -1}$
, which contains no element of A.
The probability that the random walk reaches the annular tunnel before exiting the rectangular tunnel from
![]() $\mathcal {A}_{\ell }$
to
$\mathcal {A}_{\ell }$
to
![]() $\mathcal {A}_{\ell -1}$
is no smaller than exponential in
$\mathcal {A}_{\ell -1}$
is no smaller than exponential in
![]() $m_\ell $
. Similarly, the random walk reaches the rectangular tunnel from
$m_\ell $
. Similarly, the random walk reaches the rectangular tunnel from
![]() $\mathcal {A}_{\ell -1}$
to
$\mathcal {A}_{\ell -1}$
to
![]() $\mathcal {A}_{\ell -2}$
before exiting the annular tunnel in
$\mathcal {A}_{\ell -2}$
before exiting the annular tunnel in
![]() $\mathcal {A}_{\ell -1}$
with a probability no smaller than exponential in
$\mathcal {A}_{\ell -1}$
with a probability no smaller than exponential in
![]() $n_{\ell -1}$
. Overall, we conclude that the random walk reaches
$n_{\ell -1}$
. Overall, we conclude that the random walk reaches
![]() $\mathrm {Arc}_{I-1}$
without leaving the union of tunnels – and therefore without hitting an element of A – with a probability no smaller than exponential in
$\mathrm {Arc}_{I-1}$
without leaving the union of tunnels – and therefore without hitting an element of A – with a probability no smaller than exponential in
![]() $\sum _{\ell = I}^{J - 1} n_\ell $
.
$\sum _{\ell = I}^{J - 1} n_\ell $
.
Stage 3: Advancing to
![]() $C(R_1)$
. Figure 5 (left) essentially depicts the setting of the random walk upon reaching
$C(R_1)$
. Figure 5 (left) essentially depicts the setting of the random walk upon reaching
![]() $x \in \mathrm {Arc}_{I-1}$
, except with
$x \in \mathrm {Arc}_{I-1}$
, except with
![]() $C(R_I)$
in the place of
$C(R_I)$
in the place of
![]() $C(R)$
and the circle containing
$C(R)$
and the circle containing
![]() $\mathrm {Arc}_{I-1}$
in the place of
$\mathrm {Arc}_{I-1}$
in the place of
![]() $C(\frac {R}{3})$
and except for the possibility that
$C(\frac {R}{3})$
and except for the possibility that
![]() $D(R_1)$
contains other elements of A. Nevertheless, if the radius of
$D(R_1)$
contains other elements of A. Nevertheless, if the radius of
![]() $\mathrm {Arc}_{I-1}$
is at least
$\mathrm {Arc}_{I-1}$
is at least
![]() $e^n$
, then by pretending that
$e^n$
, then by pretending that
![]() $A_{<R_1} = \{o\}$
, the method highlighted in Section 2.2 will show that
$A_{<R_1} = \{o\}$
, the method highlighted in Section 2.2 will show that
![]() $\mathbb {P}_x (\tau _{C(R_1)} < \tau _{A}) = \Omega (\frac 1n)$
. A simple calculation will give the same lower bound (for a potentially smaller constant) in the case when the radius is less than
$\mathbb {P}_x (\tau _{C(R_1)} < \tau _{A}) = \Omega (\frac 1n)$
. A simple calculation will give the same lower bound (for a potentially smaller constant) in the case when the radius is less than
![]() $e^n$
.
$e^n$
.
Stage 4: Advancing to the origin. Once the random walk reaches
![]() $C(R_1)$
, we simply dictate a path for it to follow. There can be no more than
$C(R_1)$
, we simply dictate a path for it to follow. There can be no more than
![]() $O(R_1^2)$
elements of
$O(R_1^2)$
elements of
![]() $A_{<R_1}$
, so there is a path of length
$A_{<R_1}$
, so there is a path of length
![]() $O(R_1^2)$
to the origin which avoids all other elements of A, and a corresponding probability of at least a constant that the random walk follows it.
$O(R_1^2)$
to the origin which avoids all other elements of A, and a corresponding probability of at least a constant that the random walk follows it.
Conclusion of Stages 1–4. The lower bounds from the four stages imply that there are universal constants
![]() $c_1$
through
$c_1$
through
![]() $c_4$
such that
$c_4$
such that
It is easy to show that the second inequality holds if
![]() $c_1 \geq 8\max \{1, c_2, \log c_3,\log c_4\}$
, using the fact that
$c_1 \geq 8\max \{1, c_2, \log c_3,\log c_4\}$
, using the fact that
![]() $n - k = \sum _{\ell =I}^{J-1} n_\ell> 1$
and
$n - k = \sum _{\ell =I}^{J-1} n_\ell> 1$
and
![]() $\log n \geq 1$
. We are free to adjust
$\log n \geq 1$
. We are free to adjust
![]() $c_1$
to satisfy this bound because
$c_1$
to satisfy this bound because
![]() $c_2$
through
$c_2$
through
![]() $c_4$
do not depend on the induction hypothesis. This concludes the induction step.
$c_4$
do not depend on the induction hypothesis. This concludes the induction step.
A complication in Stage 2. If
![]() $R_{\ell }$
is not sufficiently large relative to
$R_{\ell }$
is not sufficiently large relative to
![]() $m_\ell $
, then we cannot tunnel the random walk through
$m_\ell $
, then we cannot tunnel the random walk through
![]() $\mathcal {A}_{\ell }$
into
$\mathcal {A}_{\ell }$
into
![]() $\mathcal {A}_{\ell -1}$
. We formalize this through the failure of the condition
$\mathcal {A}_{\ell -1}$
. We formalize this through the failure of the condition
The problem is that, if equation (3.1) fails, then there are too many elements of A in
![]() $\mathcal {A}_{\ell }$
and
$\mathcal {A}_{\ell }$
and
![]() $\mathcal {A}_{\ell -1}$
, and we cannot guarantee that there is a tunnel between the annuli which avoids A.
$\mathcal {A}_{\ell -1}$
, and we cannot guarantee that there is a tunnel between the annuli which avoids A.
Accordingly, we will stop Stage 2 tunneling once the random walk reaches a particular subset
![]() $\mathrm {Arc}_{K-1}$
of a circle in
$\mathrm {Arc}_{K-1}$
of a circle in
![]() $\mathcal {A}_{K-1}$
, where
$\mathcal {A}_{K-1}$
, where
![]() $\mathcal {A}_{K-1}$
is the outermost annulus which fails to satisfy equation (3.1). Specifically, we define K as:
$\mathcal {A}_{K-1}$
is the outermost annulus which fails to satisfy equation (3.1). Specifically, we define K as:
 $$ \begin{align} K = \begin{cases} I, & \text{if equation (3.1)}\\ & \quad \text{holds for}\ \ell \in \{I,\dots,J\};\\\min \{k \in \{I,\dots,J\}: \text{equation (3.1) holds for}\ \ell \in \{k,\dots,J\} \}, & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} K = \begin{cases} I, & \text{if equation (3.1)}\\ & \quad \text{holds for}\ \ell \in \{I,\dots,J\};\\\min \{k \in \{I,\dots,J\}: \text{equation (3.1) holds for}\ \ell \in \{k,\dots,J\} \}, & \text{otherwise.} \end{cases} \end{align} $$
Informally, when
![]() $K = I$
, the pigeonhole principle yields wide enough tunnels for the random walk to advance all the way to
$K = I$
, the pigeonhole principle yields wide enough tunnels for the random walk to advance all the way to
![]() $\mathcal {A}_{I-1}$
in Stage 2. When
$\mathcal {A}_{I-1}$
in Stage 2. When
![]() $K \neq I$
, the tunnels become too narrow, so we must halt tunneling before the random walk reaches
$K \neq I$
, the tunnels become too narrow, so we must halt tunneling before the random walk reaches
![]() $\mathcal {A}_{I-1}$
. However, this case is even simpler, as the failure of equation (3.1) for
$\mathcal {A}_{I-1}$
. However, this case is even simpler, as the failure of equation (3.1) for
![]() $\ell = K-1$
implies that there is a path of length
$\ell = K-1$
implies that there is a path of length
![]() $O(\sum _{\ell =I}^{K-1} n_\ell )$
from
$O(\sum _{\ell =I}^{K-1} n_\ell )$
from
![]() $\mathrm {Arc}_{K-1}$
to the origin which otherwise avoids A. In this case, instead of proceeding to Stages 3 and 4 as described above, the third and final stage consists of random walk from
$\mathrm {Arc}_{K-1}$
to the origin which otherwise avoids A. In this case, instead of proceeding to Stages 3 and 4 as described above, the third and final stage consists of random walk from
![]() $\mathrm {Arc}_{K-1}$
following this path to the origin with a probability no smaller than exponential in
$\mathrm {Arc}_{K-1}$
following this path to the origin with a probability no smaller than exponential in
![]() $\sum _{\ell =I}^{K-1} n_\ell $
.
$\sum _{\ell =I}^{K-1} n_\ell $
.
Overall, if
![]() $K \neq I$
, then Stages 2 and 3 contribute a rate of
$K \neq I$
, then Stages 2 and 3 contribute a rate of
![]() $\sum _{\ell =I}^{J-1} n_\ell $
. This rate is smaller than the one contributed by Stages 2–4 when
$\sum _{\ell =I}^{J-1} n_\ell $
. This rate is smaller than the one contributed by Stages 2–4 when
![]() $K = I$
, so the preceding conclusion holds.
$K = I$
, so the preceding conclusion holds.
3.2 Preparation for the proof of Theorem 4
3.2.1 Input to Stage 1
Let
![]() $A \in \mathscr {H}_n$
. Like in Section 3.1, we assume that
$A \in \mathscr {H}_n$
. Like in Section 3.1, we assume that
![]() $n_0 \neq n$
(i.e.,
$n_0 \neq n$
(i.e.,
![]() $A_{\geq R_1} \neq \emptyset $
) and defer the simpler complementary case to Section 3.3. Recall that the radii
$A_{\geq R_1} \neq \emptyset $
) and defer the simpler complementary case to Section 3.3. Recall that the radii
![]() $R_i$
must grow exponentially so that the conditional hitting distribution of
$R_i$
must grow exponentially so that the conditional hitting distribution of
![]() $C(R_J)$
is comparable to the uniform distribution, thus avoiding potential choke points (Figure 7). The next two results accomplish this comparison. We state them in terms of the uniform distribution on
$C(R_J)$
is comparable to the uniform distribution, thus avoiding potential choke points (Figure 7). The next two results accomplish this comparison. We state them in terms of the uniform distribution on
![]() $C(r)$
, which we denote by
$C(r)$
, which we denote by
![]() $\mu _{r}$
.
$\mu _{r}$
.
Lemma 3.1. Let
![]() $\varepsilon> 0$
, and denote
$\varepsilon> 0$
, and denote
![]() $\eta = \tau _{C(R)} \wedge \tau _{C (\varepsilon ^2 R)}$
. There is a constant c such that, if
$\eta = \tau _{C(R)} \wedge \tau _{C (\varepsilon ^2 R)}$
. There is a constant c such that, if
![]() $\varepsilon \leq \tfrac {1}{100}$
and
$\varepsilon \leq \tfrac {1}{100}$
and
![]() $R \geq 10\varepsilon ^{-2}$
and if
$R \geq 10\varepsilon ^{-2}$
and if
then, uniformly for
![]() $x \in C( \varepsilon R)$
and
$x \in C( \varepsilon R)$
and
![]() $y \in C (\varepsilon ^2 R)$
,
$y \in C (\varepsilon ^2 R)$
,
The proof, which is similar to that of Lemma 2.1 in [Reference Dembo, Peres, Rosen and ZeitouniDPRZ06], approximates the hitting distribution of
![]() $C(\varepsilon ^2 R)$
by the corresponding harmonic measure, which is comparable to the uniform distribution. The condition (3.3), and the assumptions on
$C(\varepsilon ^2 R)$
by the corresponding harmonic measure, which is comparable to the uniform distribution. The condition (3.3), and the assumptions on
![]() $\varepsilon $
and R, are used to control the error of this approximation. We defer the proof to Section A.3, along with the proof of the following application of Lemma 3.1.
$\varepsilon $
and R, are used to control the error of this approximation. We defer the proof to Section A.3, along with the proof of the following application of Lemma 3.1.
Lemma 3.2. There is a constant c such that, for every
![]() $z \in C(R_{J})$
,
$z \in C(R_{J})$
,
Under the conditioning in equation (3.4), the random walk reaches
![]() $C(\delta R_{J+1})$
before hitting A. A short calculation shows that it typically proceeds to hit
$C(\delta R_{J+1})$
before hitting A. A short calculation shows that it typically proceeds to hit
![]() $C(R_{J})$
before returning to
$C(R_{J})$
before returning to
![]() $C(R_{J+1})$
(i.e., it satisfies equation (3.3) with
$C(R_{J+1})$
(i.e., it satisfies equation (3.3) with
![]() $R_{J+1}$
in the place of R and
$R_{J+1}$
in the place of R and
![]() $\varepsilon ^2 = 10^{-5}$
). The inequality (3.4) then follows from Lemma 3.1.
$\varepsilon ^2 = 10^{-5}$
). The inequality (3.4) then follows from Lemma 3.1.
3.2.2 Inputs to Stage 2
We continue to assume that
![]() $n_0 \neq n$
so that I, J and K are well defined; the
$n_0 \neq n$
so that I, J and K are well defined; the
![]() $n_0 = n$
case is easy and we address it in Section 3.3. In this subsection, we will prove an estimate of the probability that a random walk passes through annuli
$n_0 = n$
case is easy and we address it in Section 3.3. In this subsection, we will prove an estimate of the probability that a random walk passes through annuli
![]() $\mathcal {A}_{J-1}$
to
$\mathcal {A}_{J-1}$
to
![]() $\mathcal {A}_K$
without hitting A. First, in Lemma 3.3, we will identify a sequence of ‘tunnels’ through the annuli, which are empty of A. Second, in Lemma 3.4 and Lemma 3.5, we will show that random walk traverses these tunnels through a series of rectangles, with a probability that is no smaller than exponential in the number of elements in
$\mathcal {A}_K$
without hitting A. First, in Lemma 3.3, we will identify a sequence of ‘tunnels’ through the annuli, which are empty of A. Second, in Lemma 3.4 and Lemma 3.5, we will show that random walk traverses these tunnels through a series of rectangles, with a probability that is no smaller than exponential in the number of elements in
![]() $\mathcal {A}_K, \dots , \mathcal {A}_{J-1}$
. We will combine these estimates in Lemma 3.6.
$\mathcal {A}_K, \dots , \mathcal {A}_{J-1}$
. We will combine these estimates in Lemma 3.6.
For each
![]() $\ell \in \mathbb {I} = \{K,\dots ,J\}$
, we define the annulus
$\ell \in \mathbb {I} = \{K,\dots ,J\}$
, we define the annulus
![]() $\mathcal {B}_\ell = \mathcal {A} (R_{\ell - 1}, \delta R_{\ell +1})$
. The radial and angular tunnels from
$\mathcal {B}_\ell = \mathcal {A} (R_{\ell - 1}, \delta R_{\ell +1})$
. The radial and angular tunnels from
![]() $\mathcal {A}_{\ell }$
into and around
$\mathcal {A}_{\ell }$
into and around
![]() $\mathcal {A}_{\ell -1}$
will be subsets of
$\mathcal {A}_{\ell -1}$
will be subsets of
![]() $\mathcal {B}_\ell $
. The inner radius of
$\mathcal {B}_\ell $
. The inner radius of
![]() $\mathcal {B}_\ell $
is at least
$\mathcal {B}_\ell $
is at least
![]() $R_1$
because
$R_1$
because
The first implication is due to equations (3.1) and (3.2); the second is due to the fact that
![]() $R_\ell = 10^{5\ell }$
.
$R_\ell = 10^{5\ell }$
.
The following lemma identifies subsets of
![]() $\mathcal {B}_\ell $
which are empty of A (Figure 9). Recall that
$\mathcal {B}_\ell $
which are empty of A (Figure 9). Recall that
![]() $m_\ell = n_\ell + n_{\ell -1}$
.
$m_\ell = n_\ell + n_{\ell -1}$
.

Figure 9 The regions identified in Lemma 3.3. The tan sectors and dark blue annuli are subsets of the overlapping annuli
![]() $\mathcal {B}_\ell $
and
$\mathcal {B}_\ell $
and
![]() $\mathcal {B}_{\ell -1}$
that are empty of A.
$\mathcal {B}_{\ell -1}$
that are empty of A.
Lemma 3.3. Let
![]() $\ell \in \mathbb {I}$
. Denote
$\ell \in \mathbb {I}$
. Denote
![]() $\varepsilon _\ell = (m_\ell +1)^{-1}$
and
$\varepsilon _\ell = (m_\ell +1)^{-1}$
and
![]() $\delta ' = \delta /10$
. For every
$\delta ' = \delta /10$
. For every
![]() $\ell \in \mathbb {I}$
, there is an angle
$\ell \in \mathbb {I}$
, there is an angle
![]() $\vartheta _\ell \in [0,2\pi )$
and a radius
$\vartheta _\ell \in [0,2\pi )$
and a radius
![]() $a_{\ell -1} \in [10 R_{\ell -1}, \delta ' R_{\ell })$
such that the following regions contain no element of A:
$a_{\ell -1} \in [10 R_{\ell -1}, \delta ' R_{\ell })$
such that the following regions contain no element of A:
-
• the sector of
 $\mathcal {B}_\ell $
subtending the angular interval
$\mathcal {B}_\ell $
subtending the angular interval
 $\left [\vartheta _\ell , \vartheta _\ell + 2\pi \varepsilon _\ell \right )$
, hence the ‘middle third’ subsector
$\left [\vartheta _\ell , \vartheta _\ell + 2\pi \varepsilon _\ell \right )$
, hence the ‘middle third’ subsector  $$\begin{align*}\mathrm{Sec}_\ell = \left[ R_{\ell}, \delta' R_{\ell+1} \right) \times \left[ \vartheta_\ell + \tfrac{2\pi}{3} \varepsilon_\ell, \, \vartheta_\ell + \tfrac{4\pi}{3} \varepsilon_\ell \right);\,\,\,\text{and}\end{align*}$$
$$\begin{align*}\mathrm{Sec}_\ell = \left[ R_{\ell}, \delta' R_{\ell+1} \right) \times \left[ \vartheta_\ell + \tfrac{2\pi}{3} \varepsilon_\ell, \, \vartheta_\ell + \tfrac{4\pi}{3} \varepsilon_\ell \right);\,\,\,\text{and}\end{align*}$$
-
• the subannulus
 $\mathrm {Ann}_{\ell -1} = \mathcal {A} (a_{\ell -1}, b_{\ell -1})$
of
$\mathrm {Ann}_{\ell -1} = \mathcal {A} (a_{\ell -1}, b_{\ell -1})$
of
 $\mathcal {B}_\ell $
, where we define and, in particular, the circle
$\mathcal {B}_\ell $
, where we define and, in particular, the circle $$ \begin{align*} b_{\ell-1} = a_{\ell-1} + \Delta_{\ell-1} \quad \text{for} \quad \Delta_{\ell-1} = \delta' \varepsilon_{\ell} R_{\ell} \end{align*} $$
$$ \begin{align*} b_{\ell-1} = a_{\ell-1} + \Delta_{\ell-1} \quad \text{for} \quad \Delta_{\ell-1} = \delta' \varepsilon_{\ell} R_{\ell} \end{align*} $$
 $\mathrm {Circ}_{\ell -1} = C\big ( \tfrac {a_{\ell -1} + b_{\ell -1}}{2} \big )$
and the ‘arc’
$\mathrm {Circ}_{\ell -1} = C\big ( \tfrac {a_{\ell -1} + b_{\ell -1}}{2} \big )$
and the ‘arc’  $$\begin{align*}\mathrm{Arc}_{\ell-1} = \mathrm{Circ}_{\ell-1} \cap \left\{x \in \mathbb{Z}^2: \arg x \in \left[\vartheta_\ell, \vartheta_\ell + 2\pi \varepsilon_\ell \right) \right\}.\end{align*}$$
$$\begin{align*}\mathrm{Arc}_{\ell-1} = \mathrm{Circ}_{\ell-1} \cap \left\{x \in \mathbb{Z}^2: \arg x \in \left[\vartheta_\ell, \vartheta_\ell + 2\pi \varepsilon_\ell \right) \right\}.\end{align*}$$
We take a moment to explain the parameters and regions. Aside from
![]() $\mathcal {B}_\ell $
, which overlaps
$\mathcal {B}_\ell $
, which overlaps
![]() $\mathcal {A}_\ell $
and
$\mathcal {A}_\ell $
and
![]() $\mathcal {A}_{\ell -1}$
, the subscripts of the regions indicate which annulus contains them (e.g.,
$\mathcal {A}_{\ell -1}$
, the subscripts of the regions indicate which annulus contains them (e.g.,
![]() $\mathrm {Sec}_\ell \subset \mathcal {A}_\ell $
and
$\mathrm {Sec}_\ell \subset \mathcal {A}_\ell $
and
![]() $\mathrm {Ann}_{\ell -1} \subset \mathcal {A}_{\ell -1}$
). The proof uses the pigeonhole principle to identify regions which contain none of the
$\mathrm {Ann}_{\ell -1} \subset \mathcal {A}_{\ell -1}$
). The proof uses the pigeonhole principle to identify regions which contain none of the
![]() $m_\ell $
elements of A in
$m_\ell $
elements of A in
![]() $\mathcal {B}_\ell $
and
$\mathcal {B}_\ell $
and
![]() $\mathrm {Ann}_{\ell -1}$
; this motivates our choice of
$\mathrm {Ann}_{\ell -1}$
; this motivates our choice of
![]() $\varepsilon _\ell $
. A key aspect of
$\varepsilon _\ell $
. A key aspect of
![]() $\mathrm {Sec}_\ell $
is that it is separated from
$\mathrm {Sec}_\ell $
is that it is separated from
![]() $\partial \mathcal {B}_\ell $
by a distance of at least
$\partial \mathcal {B}_\ell $
by a distance of at least
![]() $R_{\ell -1}$
, which will allow us to position one end of a rectangular tunnel of width
$R_{\ell -1}$
, which will allow us to position one end of a rectangular tunnel of width
![]() $R_{\ell -1}$
in
$R_{\ell -1}$
in
![]() $\mathrm {Sec}_\ell $
without the tunnel exiting
$\mathrm {Sec}_\ell $
without the tunnel exiting
![]() $\mathcal {B}_\ell $
. We also need the inner radius of
$\mathcal {B}_\ell $
. We also need the inner radius of
![]() $\mathrm {Ann}_{\ell -1}$
to be at least
$\mathrm {Ann}_{\ell -1}$
to be at least
![]() $R_{\ell -1}$
greater than that of
$R_{\ell -1}$
greater than that of
![]() $\mathcal {B}_\ell $
, hence the lower bound on
$\mathcal {B}_\ell $
, hence the lower bound on
![]() $a_{\ell -1}$
. The other key aspect of
$a_{\ell -1}$
. The other key aspect of
![]() $\mathrm {Ann}_{\ell -1}$
is its overlap with
$\mathrm {Ann}_{\ell -1}$
is its overlap with
![]() $\mathrm {Sec}_{\ell -1}$
. The specific constants (e.g.,
$\mathrm {Sec}_{\ell -1}$
. The specific constants (e.g.,
![]() $\tfrac {2\pi }{3}$
,
$\tfrac {2\pi }{3}$
,
![]() $10$
, and
$10$
, and
![]() $\delta '$
) are otherwise unimportant.
$\delta '$
) are otherwise unimportant.
Proof of Lemma 3.3.
Fix
![]() $\ell \in \mathbb {I}$
. For
$\ell \in \mathbb {I}$
. For
![]() $j \in \{0,\dots , m_\ell \}$
, form the intervals
$j \in \{0,\dots , m_\ell \}$
, form the intervals
![]() $\mathcal {B}_\ell $
contains at most
$\mathcal {B}_\ell $
contains at most
![]() $m_\ell $
elements of A, so the pigeonhole principle implies that there are
$m_\ell $
elements of A, so the pigeonhole principle implies that there are
![]() $j_1$
and
$j_1$
and
![]() $j_2$
in this range and such that, if
$j_2$
in this range and such that, if
![]() $\vartheta _\ell = j_1 2 \pi \varepsilon _\ell $
and if
$\vartheta _\ell = j_1 2 \pi \varepsilon _\ell $
and if
![]() $a_{\ell -1} = 10 R_{\ell -1} + j_2 \Delta _{\ell -1}$
, then
$a_{\ell -1} = 10 R_{\ell -1} + j_2 \Delta _{\ell -1}$
, then
Because
![]() $\mathcal {B}_\ell \supseteq \mathrm {Sec}_\ell $
and
$\mathcal {B}_\ell \supseteq \mathrm {Sec}_\ell $
and
![]() $\mathrm {Ann}_{\ell -1} \supseteq \mathrm {Arc}_{\ell -1} $
, for these choices of
$\mathrm {Ann}_{\ell -1} \supseteq \mathrm {Arc}_{\ell -1} $
, for these choices of
![]() $\vartheta _\ell $
and
$\vartheta _\ell $
and
![]() $a_{\ell -1}$
, we also have
$a_{\ell -1}$
, we also have
![]() $\mathrm {Sec}_\ell \cap A = \emptyset $
and
$\mathrm {Sec}_\ell \cap A = \emptyset $
and
![]() $\mathrm {Arc}_{\ell -1} \cap A = \emptyset $
.
$\mathrm {Arc}_{\ell -1} \cap A = \emptyset $
.
The next result bounds below the probability that the random walk tunnels ‘down’ from
![]() $\mathrm {Sec}_\ell $
to
$\mathrm {Sec}_\ell $
to
![]() $\mathrm {Arc}_{\ell -1}$
. We state it without proof, as it is a simple consequence of the known fact that a random walk from the ‘bulk’ of a rectangle exits its far, small side with a probability which is no smaller than exponential in the aspect ratio of the rectangle (Lemma A.4). In this case, the aspect ratio is
$\mathrm {Arc}_{\ell -1}$
. We state it without proof, as it is a simple consequence of the known fact that a random walk from the ‘bulk’ of a rectangle exits its far, small side with a probability which is no smaller than exponential in the aspect ratio of the rectangle (Lemma A.4). In this case, the aspect ratio is
![]() $O(m_\ell )$
.
$O(m_\ell )$
.
Lemma 3.4. There is a constant c such that, for any
![]() $\ell \in \mathbb {I}$
and every
$\ell \in \mathbb {I}$
and every
![]() $y \in \mathrm {Sec}_\ell $
,
$y \in \mathrm {Sec}_\ell $
,
The following lemma bounds below the probability that the random walk tunnels ‘around’
![]() $\mathrm {Ann}_{\ell -1}$
, from
$\mathrm {Ann}_{\ell -1}$
, from
![]() $\mathrm {Arc}_{\ell -1}$
to
$\mathrm {Arc}_{\ell -1}$
to
![]() $\mathrm {Sec}_{\ell -1}$
. (This result applies to
$\mathrm {Sec}_{\ell -1}$
. (This result applies to
![]() $\ell \in \mathbb {I} \setminus \{K\} = \{K+1, \dots , J\}$
because Lemma 3.3 defines
$\ell \in \mathbb {I} \setminus \{K\} = \{K+1, \dots , J\}$
because Lemma 3.3 defines
![]() $\mathrm {Sec}_\ell $
for
$\mathrm {Sec}_\ell $
for
![]() $\ell \in \mathbb {I}$
.) Like Lemma 3.4, we state it without proof because it is a simple consequence of Lemma A.4. Indeed, random walk from
$\ell \in \mathbb {I}$
.) Like Lemma 3.4, we state it without proof because it is a simple consequence of Lemma A.4. Indeed, random walk from
![]() $\mathrm {Arc}_{\ell -1}$
can reach
$\mathrm {Arc}_{\ell -1}$
can reach
![]() $\mathrm {Sec}_{\ell -1}$
without exiting
$\mathrm {Sec}_{\ell -1}$
without exiting
![]() $\mathrm {Ann}_{\ell -1}$
by appropriately exiting each rectangle in a sequence of
$\mathrm {Ann}_{\ell -1}$
by appropriately exiting each rectangle in a sequence of
![]() $O(m_\ell )$
rectangles of aspect ratio
$O(m_\ell )$
rectangles of aspect ratio
![]() $O(1)$
. Applying Lemma A.4 then implies equation (3.5).
$O(1)$
. Applying Lemma A.4 then implies equation (3.5).
Lemma 3.5. There is a constant c such that, for any
![]() $\ell \in \mathbb {I} \setminus \{K\}$
and every
$\ell \in \mathbb {I} \setminus \{K\}$
and every
![]() $z \in \mathrm {Arc}_{\ell -1}$
,
$z \in \mathrm {Arc}_{\ell -1}$
,
The next result combines Lemma 3.4 and Lemma 3.5 to tunnel from
![]() $\mathcal {A}_J$
into
$\mathcal {A}_J$
into
![]() $\mathcal {A}_{K-1}$
. Because the random walk tunnels from
$\mathcal {A}_{K-1}$
. Because the random walk tunnels from
![]() $\mathcal {A}_\ell $
to
$\mathcal {A}_\ell $
to
![]() $\mathcal {A}_{\ell -1}$
with a probability no smaller than exponential in
$\mathcal {A}_{\ell -1}$
with a probability no smaller than exponential in
![]() $m_\ell = n_\ell + n_{\ell -1}$
, the bound in equation (3.6) is no smaller than exponential in
$m_\ell = n_\ell + n_{\ell -1}$
, the bound in equation (3.6) is no smaller than exponential in
![]() $\sum _{\ell =K-1}^{J-1} n_\ell $
(recall that
$\sum _{\ell =K-1}^{J-1} n_\ell $
(recall that
![]() $n_J = 0$
).
$n_J = 0$
).
Lemma 3.6. There is a constant c such that
Proof. Denote by G the event
Lemma 3.4 and Lemma 3.5 imply that there is a constant
![]() $c_1$
such that
$c_1$
such that
The intersection of
![]() $\mathrm {Sec}_{J}$
and
$\mathrm {Sec}_{J}$
and
![]() $C(R_{J})$
subtends an angle of at least
$C(R_{J})$
subtends an angle of at least
![]() $n_{J-1}^{-1}$
, so there is a constant
$n_{J-1}^{-1}$
, so there is a constant
![]() $c_2$
such that
$c_2$
such that
The inequality (3.6) follows from
![]() $G \subseteq \{\tau _{\mathrm {Arc}_{K-1}} < \tau _A \}$
, and equations (3.7) and (3.8):
$G \subseteq \{\tau _{\mathrm {Arc}_{K-1}} < \tau _A \}$
, and equations (3.7) and (3.8):
For the third inequality, we take
![]() $c_3 = (c_1 c_2)^2$
.
$c_3 = (c_1 c_2)^2$
.
3.2.3 Inputs to Stage 3 when
 $K=I$
$K=I$
We continue to assume that
![]() $n_0 \neq n$
, as the alternative case is addressed in Section 3.3. Additionally, we assume
$n_0 \neq n$
, as the alternative case is addressed in Section 3.3. Additionally, we assume
![]() $K = I$
. We briefly recall some important context. When
$K = I$
. We briefly recall some important context. When
![]() $K=I$
, at the end of Stage 2, the random walk has reached
$K=I$
, at the end of Stage 2, the random walk has reached
![]() $\mathrm {Circ}_{I-1} \subseteq \mathcal {A}_{I-1}$
, where
$\mathrm {Circ}_{I-1} \subseteq \mathcal {A}_{I-1}$
, where
![]() $\mathrm {Circ}_{I-1}$
is a circle with a radius in
$\mathrm {Circ}_{I-1}$
is a circle with a radius in
![]() $[R_{I-1}, \delta ' R_I)$
. (Note that
$[R_{I-1}, \delta ' R_I)$
. (Note that
![]() $I>1$
when
$I>1$
when
![]() $K=I$
because I must then satisfy equation (3.1), so the radius of
$K=I$
because I must then satisfy equation (3.1), so the radius of
![]() $\mathrm {Circ}_{I-1}$
is at least
$\mathrm {Circ}_{I-1}$
is at least
![]() $R_1$
.) Since
$R_1$
.) Since
![]() $\mathcal {A}_I$
is the innermost annulus which contains an element of A, the random walk from
$\mathcal {A}_I$
is the innermost annulus which contains an element of A, the random walk from
![]() $\mathrm {Arc}_{I-1}$
must simply reach the origin before hitting
$\mathrm {Arc}_{I-1}$
must simply reach the origin before hitting
![]() $A_{> R_I}$
. In this subsection, we estimate this probability.
$A_{> R_I}$
. In this subsection, we estimate this probability.
We will use the potential kernel associated with random walk on
![]() $\mathbb {Z}^2$
. We denote it by
$\mathbb {Z}^2$
. We denote it by
![]() $\mathfrak {a}$
. It equals zero at the origin, is harmonic on
$\mathfrak {a}$
. It equals zero at the origin, is harmonic on
![]() $\mathbb {Z}^2 {\setminus } \{o\}$
and satisfies
$\mathbb {Z}^2 {\setminus } \{o\}$
and satisfies
 $$ \begin{align} \left| \mathfrak{a}(x) - \frac{2}{\pi}\log {|x|} - \kappa \right| \leq \lambda |x|^{-2}, \end{align} $$
$$ \begin{align} \left| \mathfrak{a}(x) - \frac{2}{\pi}\log {|x|} - \kappa \right| \leq \lambda |x|^{-2}, \end{align} $$
where
![]() $\kappa \in (1.02,1.03)$
is an explicit constant and
$\kappa \in (1.02,1.03)$
is an explicit constant and
![]() $\lambda $
is less than
$\lambda $
is less than
![]() $0.06882$
[Reference Kozma and SchreiberKS04]. In some instances, we will want to apply
$0.06882$
[Reference Kozma and SchreiberKS04]. In some instances, we will want to apply
![]() $\mathfrak {a}$
to an element which belongs to
$\mathfrak {a}$
to an element which belongs to
![]() $C(r)$
. It will be convenient to denote, for
$C(r)$
. It will be convenient to denote, for
![]() $r> 0$
,
$r> 0$
,
We will need the following standard hitting probability estimate (see, for example, Proposition 1.6.7 of [Reference LawlerLaw13]), which we state as a lemma because we will use it in other sections as well.
Lemma 3.7. Let
![]() $y \in D_x (r)$
for
$y \in D_x (r)$
for
![]() $r \geq 2 (|x| + 1)$
, and assume
$r \geq 2 (|x| + 1)$
, and assume
![]() $y \neq o$
. Then
$y \neq o$
. Then
 $$ \begin{align} \mathbb{P}_y \left( \tau_o < \tau_{C_x (r)} \right) = \frac{\mathfrak{a}' (r) - \mathfrak{a} (y) + O \left( \frac{| x | + 1}{r} \right)}{ \mathfrak{a}' (r) + O \left( \frac{|x| + 1}{r} \right)}.\end{align} $$
$$ \begin{align} \mathbb{P}_y \left( \tau_o < \tau_{C_x (r)} \right) = \frac{\mathfrak{a}' (r) - \mathfrak{a} (y) + O \left( \frac{| x | + 1}{r} \right)}{ \mathfrak{a}' (r) + O \left( \frac{|x| + 1}{r} \right)}.\end{align} $$
The implicit constants in the error terms are less than one.
If
![]() $R_{I} < e^{8n}$
, then no further machinery is needed to prove the Stage 3 estimate.
$R_{I} < e^{8n}$
, then no further machinery is needed to prove the Stage 3 estimate.
Lemma 3.8. There exists a constant c such that, if
![]() $R_{I} < e^{8n}$
, then
$R_{I} < e^{8n}$
, then
The bound holds because the random walk must exit
![]() $D(R_I)$
to hit
$D(R_I)$
to hit
![]() $A_{\geq R_I}$
. By a standard hitting estimate, the probability that the random walk hits the origin first is inversely proportional to
$A_{\geq R_I}$
. By a standard hitting estimate, the probability that the random walk hits the origin first is inversely proportional to
![]() $\log R_I$
which is
$\log R_I$
which is
![]() $O(n)$
when
$O(n)$
when
![]() $R_I < e^{8n}$
.
$R_I < e^{8n}$
.
Proof of Lemma 3.8.
Uniformly for
![]() $y \in \mathrm {Circ}_{I-1}$
, we have
$y \in \mathrm {Circ}_{I-1}$
, we have
 $$ \begin{align} \mathbb{P}_y \left( \tau_{C(R_1)} < \tau_A \right) \geq \mathbb{P}_y \left( \tau_{o} < \tau_{C(R_{I})} \right) \geq \frac{\mathfrak{a}' (R_{I}) - \mathfrak{a}' (\delta R_{I-1}) - \tfrac{1}{R_{I}} - \tfrac{1}{\delta R_{I}}}{\mathfrak{a}' (R_{I}) + \tfrac{1}{R_{I}}} \geq \frac{1}{\mathfrak{a}' (R_{I})}. \end{align} $$
$$ \begin{align} \mathbb{P}_y \left( \tau_{C(R_1)} < \tau_A \right) \geq \mathbb{P}_y \left( \tau_{o} < \tau_{C(R_{I})} \right) \geq \frac{\mathfrak{a}' (R_{I}) - \mathfrak{a}' (\delta R_{I-1}) - \tfrac{1}{R_{I}} - \tfrac{1}{\delta R_{I}}}{\mathfrak{a}' (R_{I}) + \tfrac{1}{R_{I}}} \geq \frac{1}{\mathfrak{a}' (R_{I})}. \end{align} $$
The first inequality follows from the observation that
![]() $C(R_1)$
and
$C(R_1)$
and
![]() $C(R_{I})$
separate y from o and A. The second inequality is due to Lemma 3.7, where we have replaced
$C(R_{I})$
separate y from o and A. The second inequality is due to Lemma 3.7, where we have replaced
![]() $\mathfrak {a} (y)$
by
$\mathfrak {a} (y)$
by
![]() $\mathfrak {a}' (\delta R_{I}) + \tfrac {1}{\delta R_{I}}$
using Lemma A.2 and the fact that
$\mathfrak {a}' (\delta R_{I}) + \tfrac {1}{\delta R_{I}}$
using Lemma A.2 and the fact that
![]() $|y| \leq \delta R_{I}$
. The third inequality follows from
$|y| \leq \delta R_{I}$
. The third inequality follows from
![]() $\delta R_{I} \geq 10^3$
. To conclude, we substitute
$\delta R_{I} \geq 10^3$
. To conclude, we substitute
![]() $\mathfrak {a}' (R_{I}) = \tfrac {2}{\pi } \log R_{I} + \kappa $
into equation (3.11) and use the assumption that
$\mathfrak {a}' (R_{I}) = \tfrac {2}{\pi } \log R_{I} + \kappa $
into equation (3.11) and use the assumption that
![]() $R_{I} < e^{8n}$
.
$R_{I} < e^{8n}$
.
We will use the rest of this subsection to prove the bound of Lemma 3.8, but under the complementary assumption
![]() $R_{I} \geq e^{8n}$
. This is one of the two estimates we highlighted in Section 2.2.
$R_{I} \geq e^{8n}$
. This is one of the two estimates we highlighted in Section 2.2.
Next is a standard result, which enables us to express certain hitting probabilities in terms of the potential kernel. We include a short proof for completeness.
Lemma 3.9. For any pair of points
![]() $x, y \in \mathbb {Z}^2$
, define
$x, y \in \mathbb {Z}^2$
, define
Then
![]() $M_{x,y} (z) = \mathbb {P}_z (\sigma _y < \sigma _x)$
.
$M_{x,y} (z) = \mathbb {P}_z (\sigma _y < \sigma _x)$
.
Proof. Fix
![]() $x, y \in \mathbb {Z}^2$
. Theorem 1.4.8 of [Reference LawlerLaw13] states that for any proper subset B of
$x, y \in \mathbb {Z}^2$
. Theorem 1.4.8 of [Reference LawlerLaw13] states that for any proper subset B of
![]() $\mathbb {Z}^2$
(including infinite B) and bounded function
$\mathbb {Z}^2$
(including infinite B) and bounded function
![]() $F: \partial B \to \mathbb {R}$
, the unique bounded function
$F: \partial B \to \mathbb {R}$
, the unique bounded function
![]() $f: B \cup \partial B \to \mathbb {R}$
which is harmonic in B and equals F on
$f: B \cup \partial B \to \mathbb {R}$
which is harmonic in B and equals F on
![]() $\partial B$
is
$\partial B$
is
![]() $f(z) = \mathbb {E}_z [ F (S_{\sigma _{\partial B}})] $
. Setting
$f(z) = \mathbb {E}_z [ F (S_{\sigma _{\partial B}})] $
. Setting
![]() $B = \mathbb {Z}^2 {\setminus } \{x,y\}$
and
$B = \mathbb {Z}^2 {\setminus } \{x,y\}$
and
![]() $F(z) = \mathbf {1} (z = y)$
, we have
$F(z) = \mathbf {1} (z = y)$
, we have
![]() $f(z) = \mathbb {P}_z (\sigma _y < \sigma _x)$
. Since
$f(z) = \mathbb {P}_z (\sigma _y < \sigma _x)$
. Since
![]() $M_{x,y}$
is bounded, harmonic on B and agrees with f on
$M_{x,y}$
is bounded, harmonic on B and agrees with f on
![]() $\partial B$
, the uniqueness of f implies
$\partial B$
, the uniqueness of f implies
![]() $M_{x,y} (z) = f(z)$
.
$M_{x,y} (z) = f(z)$
.
The next two results partly implement the first estimate that we discussed in Section 2.2.
Lemma 3.10. For any
![]() $z,z' \in \mathrm {Circ}_{I-1}$
and
$z,z' \in \mathrm {Circ}_{I-1}$
and
![]() $y \in D(R_{I})^c$
,
$y \in D(R_{I})^c$
,
The first inequality in equation (3.12) holds because z is appreciably closer to the origin than it is to y. The second inequality holds because a Taylor expansion of the numerator of
![]() $M_{o,y}(z) - M_{o,y} (z')$
shows that it is
$M_{o,y}(z) - M_{o,y} (z')$
shows that it is
![]() $O(1)$
, while the denominator of
$O(1)$
, while the denominator of
![]() $2\mathfrak {a} (y)$
is at least
$2\mathfrak {a} (y)$
is at least
![]() $\log R_{I}$
.
$\log R_{I}$
.
Proof of Lemma 3.10.
By Lemma 3.9,
The first inequality in equation (3.12) then follows from
![]() $\mathfrak {a} (y-z) \geq \mathfrak {a} (z)$
, which is due to (1) of Lemma A.1. This fact applies because
$\mathfrak {a} (y-z) \geq \mathfrak {a} (z)$
, which is due to (1) of Lemma A.1. This fact applies because
![]() $|y-z| \geq 2 |z| \geq 4$
. The first of these bounds holds because
$|y-z| \geq 2 |z| \geq 4$
. The first of these bounds holds because
![]() $|z| \leq \delta R_{I} + 1$
and
$|z| \leq \delta R_{I} + 1$
and
![]() $|y-z| \geq (1-\delta ) R_{I} -1$
since
$|y-z| \geq (1-\delta ) R_{I} -1$
since
![]() $\mathrm {Circ}_{I-1} \subseteq D(\delta R_{I})$
; the second holds because the radius of
$\mathrm {Circ}_{I-1} \subseteq D(\delta R_{I})$
; the second holds because the radius of
![]() $\mathrm {Circ}_{I-1}$
is at least
$\mathrm {Circ}_{I-1}$
is at least
![]() $R_1$
since
$R_1$
since
![]() $I>1$
when
$I>1$
when
![]() $K=I$
.
$K=I$
.
Using Lemma 3.9, the difference in equation (3.12) can be written as
By Lemma A.2, in terms of
![]() $r = \mathrm {rad} (\mathrm {Circ}_{I-1})$
,
$r = \mathrm {rad} (\mathrm {Circ}_{I-1})$
,
![]() $\mathfrak {a} (z)$
and
$\mathfrak {a} (z)$
and
![]() $\mathfrak {a} (z')$
differ from
$\mathfrak {a} (z')$
differ from
![]() $\mathfrak {a}' (r)$
by no more than
$\mathfrak {a}' (r)$
by no more than
![]() $r^{-1}$
. Since
$r^{-1}$
. Since
![]() $r \geq R_1$
, this implies
$r \geq R_1$
, this implies
![]() $| \mathfrak {a} (z) - \mathfrak {a} (z') | \leq 2R_1^{-1}$
. Concerning the denominator,
$| \mathfrak {a} (z) - \mathfrak {a} (z') | \leq 2R_1^{-1}$
. Concerning the denominator,
![]() $\mathfrak {a} (y)$
is at least
$\mathfrak {a} (y)$
is at least
![]() $\tfrac {2}{\pi } \log |y| \geq \tfrac {2}{\pi } \log R_{I}$
by (2) of Lemma A.1 because
$\tfrac {2}{\pi } \log |y| \geq \tfrac {2}{\pi } \log R_{I}$
by (2) of Lemma A.1 because
![]() $|y|$
is at least
$|y|$
is at least
![]() $1$
. We apply (3) of Lemma A.1 with
$1$
. We apply (3) of Lemma A.1 with
![]() $R = R_{I}$
and
$R = R_{I}$
and
![]() $r = \mathrm {rad} (\mathrm {Circ}_{I-1}) \leq \delta R_{I}$
to bound the numerator by
$r = \mathrm {rad} (\mathrm {Circ}_{I-1}) \leq \delta R_{I}$
to bound the numerator by
![]() $\tfrac {4}{\pi }$
. Substituting these bounds into equation (3.13) gives
$\tfrac {4}{\pi }$
. Substituting these bounds into equation (3.13) gives
 $$\begin{align*}\left| \mathbb{P}_z (\tau_{y}<\tau_{o})-\mathbb{P}_{z'}(\tau_{y}<\tau_{o}) \right| \leq \frac{1}{\frac{2}{\pi} R_1 \log R_I} + \frac{1}{\log R_I} \leq \frac{2}{\log R_I}. \end{align*}$$
$$\begin{align*}\left| \mathbb{P}_z (\tau_{y}<\tau_{o})-\mathbb{P}_{z'}(\tau_{y}<\tau_{o}) \right| \leq \frac{1}{\frac{2}{\pi} R_1 \log R_I} + \frac{1}{\log R_I} \leq \frac{2}{\log R_I}. \end{align*}$$
Label the k elements in
![]() $A_{\geq R_1}$
by
$A_{\geq R_1}$
by
![]() $x_i$
for
$x_i$
for
![]() $1 \leq i \leq k$
. Then let
$1 \leq i \leq k$
. Then let
![]() $Y_i = \mathbf {1} (\tau _{x_i} < \tau _o)$
and
$Y_i = \mathbf {1} (\tau _{x_i} < \tau _o)$
and
![]() $W = \sum _{i=1}^{k} Y_i$
. In words, W counts the number of elements of
$W = \sum _{i=1}^{k} Y_i$
. In words, W counts the number of elements of
![]() $A_{\geq R_1}$
which have been visited before the random walk returns to the origin.
$A_{\geq R_1}$
which have been visited before the random walk returns to the origin.
Lemma 3.11. If
![]() $R_{I} \geq e^{8n}$
, then, for all
$R_{I} \geq e^{8n}$
, then, for all
![]() $z \in \mathrm {Circ}_{I-1}$
,
$z \in \mathrm {Circ}_{I-1}$
,
The constant
![]() $\tfrac 14$
in equation (3.14) is unimportant, aside from being positive, independently of n. The inequality holds because random walk from
$\tfrac 14$
in equation (3.14) is unimportant, aside from being positive, independently of n. The inequality holds because random walk from
![]() $\mathrm {Circ}_{I-1}$
hits a given element of
$\mathrm {Circ}_{I-1}$
hits a given element of
![]() $A_{\geq R_1}$
before the origin with a probability of at most
$A_{\geq R_1}$
before the origin with a probability of at most
![]() $\frac 12$
. Consequently, given that some such element is hit, the conditional expectation of W is essentially larger than its unconditional one by a constant.
$\frac 12$
. Consequently, given that some such element is hit, the conditional expectation of W is essentially larger than its unconditional one by a constant.
Proof of Lemma 3.11.
Fix
![]() $z \in \mathrm {Circ}_{I-1}$
. When
$z \in \mathrm {Circ}_{I-1}$
. When
![]() $\{W>0\}$
occurs, some labeled element,
$\{W>0\}$
occurs, some labeled element,
![]() $x_f$
, is hit first. After
$x_f$
, is hit first. After
![]() $\tau _{x_f}$
, the random walk may proceed to hit other
$\tau _{x_f}$
, the random walk may proceed to hit other
![]() $x_i$
before returning to
$x_i$
before returning to
![]() $\mathrm {Circ}_{I-1}$
at a time
$\mathrm {Circ}_{I-1}$
at a time
![]() $\eta = \min \left \{ t \geq \tau _{x_f}: S_t \in \mathrm {Circ}_{I-1} \right \}.$
Let
$\eta = \min \left \{ t \geq \tau _{x_f}: S_t \in \mathrm {Circ}_{I-1} \right \}.$
Let
![]() $\mathcal {V}$
be the collection of labeled elements that the walk visits before time
$\mathcal {V}$
be the collection of labeled elements that the walk visits before time
![]() $\eta $
,
$\eta $
,
![]() $\{i: \tau _{x_i} < \eta \}$
. In terms of
$\{i: \tau _{x_i} < \eta \}$
. In terms of
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\eta $
, the conditional expectation of W is
$\eta $
, the conditional expectation of W is
 $$ \begin{align} \mathbb{E}_z [W\mid W>0]=\mathbb{E}_z \Big[ |\mathcal{V} | + \mathbb{E}_{S_\eta} \sum_{i\notin \mathcal{V}} Y_i \Bigm\vert W > 0\Big]. \end{align} $$
$$ \begin{align} \mathbb{E}_z [W\mid W>0]=\mathbb{E}_z \Big[ |\mathcal{V} | + \mathbb{E}_{S_\eta} \sum_{i\notin \mathcal{V}} Y_i \Bigm\vert W > 0\Big]. \end{align} $$
Let V be a nonempty subset of the labeled elements, and let
![]() $z' \in \mathrm {Circ}_{I-1}$
. We have
$z' \in \mathrm {Circ}_{I-1}$
. We have
 $$\begin{align*}\Big| \,\mathbb{E}_z \sum_{i \notin V} Y_i - \mathbb{E}_{z'} \sum_{i \notin V} Y_i \,\Big| \leq \frac{2n}{\log R_{I}} \leq \frac14.\end{align*}$$
$$\begin{align*}\Big| \,\mathbb{E}_z \sum_{i \notin V} Y_i - \mathbb{E}_{z'} \sum_{i \notin V} Y_i \,\Big| \leq \frac{2n}{\log R_{I}} \leq \frac14.\end{align*}$$
The first inequality is due to Lemma 3.10 and the fact that there are at most n labeled elements outside of V. The second inequality follows from the assumption that
![]() $R_{I} \geq e^{8n}$
.
$R_{I} \geq e^{8n}$
.
We use this bound to replace
![]() $S_\eta $
in equation (3.15) with z:
$S_\eta $
in equation (3.15) with z:
 $$ \begin{align} \mathbb{E}_z [W \bigm\vert W> 0] \geq \mathbb{E}_z \Big[ |\mathcal{V}| + \mathbb{E}_z \sum_{i\notin \mathcal{V}} Y_i \Bigm\vert W > 0 \Big] - \frac14. \end{align} $$
$$ \begin{align} \mathbb{E}_z [W \bigm\vert W> 0] \geq \mathbb{E}_z \Big[ |\mathcal{V}| + \mathbb{E}_z \sum_{i\notin \mathcal{V}} Y_i \Bigm\vert W > 0 \Big] - \frac14. \end{align} $$
By Lemma 3.10,
![]() $\mathbb {P}_z (\tau _{x_i} < \tau _{o}) \leq \tfrac 12$
. Accordingly, for a nonempty subset V of labeled elements,
$\mathbb {P}_z (\tau _{x_i} < \tau _{o}) \leq \tfrac 12$
. Accordingly, for a nonempty subset V of labeled elements,
 $$\begin{align*}\mathbb{E}_z \sum_{i \notin V} Y_i \geq \mathbb{E}_z W - \frac12 |V|.\end{align*}$$
$$\begin{align*}\mathbb{E}_z \sum_{i \notin V} Y_i \geq \mathbb{E}_z W - \frac12 |V|.\end{align*}$$
Substituting this into the inner expectation of equation (3.16), we find
 $$ \begin{align*} \mathbb{E}_z [W \bigm\vert W> 0] &\geq \mathbb{E}_z \Big[ |\mathcal{V}| + \mathbb{E}_z W - \frac12 |\mathcal{V}| \Bigm\vert W > 0 \Big] - \frac14\\ & \geq \mathbb{E}_z W + \mathbb{E}_z \left[ \frac12 |\mathcal{V}| \Bigm\vert W > 0 \right] - \frac14. \end{align*} $$
$$ \begin{align*} \mathbb{E}_z [W \bigm\vert W> 0] &\geq \mathbb{E}_z \Big[ |\mathcal{V}| + \mathbb{E}_z W - \frac12 |\mathcal{V}| \Bigm\vert W > 0 \Big] - \frac14\\ & \geq \mathbb{E}_z W + \mathbb{E}_z \left[ \frac12 |\mathcal{V}| \Bigm\vert W > 0 \right] - \frac14. \end{align*} $$
Since
![]() $\{W> 0\} = \{ |\mathcal {V}| \geq 1\}$
, this lower bound is at least
$\{W> 0\} = \{ |\mathcal {V}| \geq 1\}$
, this lower bound is at least
![]() $\mathbb {E}_z W + \frac 14$
.
$\mathbb {E}_z W + \frac 14$
.
We use the preceding lemma to prove the analogue of Lemma 3.8 when
![]() $R_{I} \geq e^{8n}$
. The proof uses the method highlighted in Section 2.2 and Figure 5 (left).
$R_{I} \geq e^{8n}$
. The proof uses the method highlighted in Section 2.2 and Figure 5 (left).
Lemma 3.12. There exists a constant c such that, if
![]() $R_{I} \geq e^{8n}$
, then
$R_{I} \geq e^{8n}$
, then
Proof. Conditionally on
![]() $\{\tau _{\mathrm {Circ}_{I-1}} < \tau _A\}$
, let the random walk hit
$\{\tau _{\mathrm {Circ}_{I-1}} < \tau _A\}$
, let the random walk hit
![]() $\mathrm {Circ}_{I-1}$
at z. Denote the positions of the
$\mathrm {Circ}_{I-1}$
at z. Denote the positions of the
![]() $k \leq n$
particles in
$k \leq n$
particles in
![]() $A_{\geq R_1}$
as
$A_{\geq R_1}$
as
![]() $x_i$
for
$x_i$
for
![]() $1 \leq i \leq k$
. Let
$1 \leq i \leq k$
. Let
![]() $Y_{i}=\mathbf {1} (\tau _{x_i} < \tau _{o})$
and
$Y_{i}=\mathbf {1} (\tau _{x_i} < \tau _{o})$
and
![]() $W=\sum _{i = 1}^{k} Y_i$
, just as we did for Lemma 3.11. The claimed bound (3.17) follows from
$W=\sum _{i = 1}^{k} Y_i$
, just as we did for Lemma 3.11. The claimed bound (3.17) follows from
The first inequality follows from the fact that
![]() $C(R_1)$
separates z from the origin. The second inequality is due to Lemma 3.11, which applies because
$C(R_1)$
separates z from the origin. The second inequality is due to Lemma 3.11, which applies because
![]() $R_{I} \geq e^{8n}$
. Since the resulting expression increases with
$R_{I} \geq e^{8n}$
. Since the resulting expression increases with
![]() $\mathbb {E}_z W$
, we obtain the third inequality by substituting n for
$\mathbb {E}_z W$
, we obtain the third inequality by substituting n for
![]() $\mathbb {E}_z W$
, as
$\mathbb {E}_z W$
, as
![]() $\mathbb {E}_z W \leq n$
. The fourth inequality follows from
$\mathbb {E}_z W \leq n$
. The fourth inequality follows from
![]() $n \geq 1$
.
$n \geq 1$
.
3.2.4 Inputs to Stage 4 when
 $K = I$
and Stage 3 when
$K = I$
and Stage 3 when
 $K\neq I$
$K\neq I$
The results in this subsection address the last stage of advancement in the two subcases of the case
![]() $n_0 \neq n$
:
$n_0 \neq n$
:
![]() $K = I$
and
$K = I$
and
![]() $K \neq I$
. In the former subcase, the random walk has reached
$K \neq I$
. In the former subcase, the random walk has reached
![]() $C(R_1)$
; in the latter subcase, it has reached
$C(R_1)$
; in the latter subcase, it has reached
![]() $\mathrm {Circ}_{K-1}$
. Both subcases will be addressed by corollaries of the following, known geometric fact, stated in a form convenient for our purposes.
$\mathrm {Circ}_{K-1}$
. Both subcases will be addressed by corollaries of the following, known geometric fact, stated in a form convenient for our purposes.
Let
![]() $\mathbb {Z}^{2\ast }$
be the graph with vertex set
$\mathbb {Z}^{2\ast }$
be the graph with vertex set
![]() $\mathbb {Z}^2$
and with an edge between distinct x and y in
$\mathbb {Z}^2$
and with an edge between distinct x and y in
![]() $\mathbb {Z}^2$
when x and y differ by at most
$\mathbb {Z}^2$
when x and y differ by at most
![]() $1$
in each coordinate. For
$1$
in each coordinate. For
![]() $B \subseteq \mathbb {Z}^2$
, we will define the
$B \subseteq \mathbb {Z}^2$
, we will define the
![]() $\ast $
-exterior boundary of B by
$\ast $
-exterior boundary of B by
 $$ \begin{align} \partial_{\mathrm{ext}}^\ast B = \{x \in \mathbb{Z}^2: & \,x\text{ is adjacent in}\ \mathbb{Z}^{2\ast}\text{ to some}\ y \in B, \nonumber\\ & \quad \qquad \text{and there is a path from}\ \infty\ \text{to}\ x\text{ disjoint from}\ B\}. \end{align} $$
$$ \begin{align} \partial_{\mathrm{ext}}^\ast B = \{x \in \mathbb{Z}^2: & \,x\text{ is adjacent in}\ \mathbb{Z}^{2\ast}\text{ to some}\ y \in B, \nonumber\\ & \quad \qquad \text{and there is a path from}\ \infty\ \text{to}\ x\text{ disjoint from}\ B\}. \end{align} $$
Lemma 3.13. Let
![]() $A \in \mathscr {H}_n$
and
$A \in \mathscr {H}_n$
and
![]() $r> 0$
. From any
$r> 0$
. From any
![]() $x \in C(r){\setminus }A$
, there is a path
$x \in C(r){\setminus }A$
, there is a path
![]() $\Gamma $
in
$\Gamma $
in
![]() $(A{\setminus }\{o\})^c$
from
$(A{\setminus }\{o\})^c$
from
![]() $\Gamma _1 = x$
to
$\Gamma _1 = x$
to
![]() $\Gamma _{|\Gamma |} = o$
with a length of at most
$\Gamma _{|\Gamma |} = o$
with a length of at most
![]() $10 \max \{r,n\}$
. Moreover, if
$10 \max \{r,n\}$
. Moreover, if
![]() $A \subseteq D(r)$
, then
$A \subseteq D(r)$
, then
![]() $\Gamma $
lies in
$\Gamma $
lies in
![]() $D(r+2)$
.
$D(r+2)$
.
We choose the constant factor of
![]() $10$
for convenience; it has no special significance. We use a radius of
$10$
for convenience; it has no special significance. We use a radius of
![]() $r+2$
in
$r+2$
in
![]() $D(r+2)$
to contain the boundary of
$D(r+2)$
to contain the boundary of
![]() $D(r)$
in
$D(r)$
in
![]() $\mathbb {Z}^{2\ast }$
.
$\mathbb {Z}^{2\ast }$
.
Proof of Lemma 3.13.
Let
![]() $\{B_\ell \}_\ell $
be the collection of
$\{B_\ell \}_\ell $
be the collection of
![]() $\ast $
-connected components of
$\ast $
-connected components of
![]() $A{\setminus }\{o\}$
. By Lemma 2.23 of [Reference KestenKes86] (alternatively, Theorem 4 of [Reference TimárTim13]), because
$A{\setminus }\{o\}$
. By Lemma 2.23 of [Reference KestenKes86] (alternatively, Theorem 4 of [Reference TimárTim13]), because
![]() $B_\ell $
is finite and
$B_\ell $
is finite and
![]() $\ast $
-connected,
$\ast $
-connected,
![]() $\partial _{\mathrm {ext}}^\ast B_\ell $
is connected.
$\partial _{\mathrm {ext}}^\ast B_\ell $
is connected.
Fix
![]() $r> 0$
and
$r> 0$
and
![]() $x \in C(r){\setminus }A$
. Let
$x \in C(r){\setminus }A$
. Let
![]() $\Gamma $
be the shortest path from x to the origin. If
$\Gamma $
be the shortest path from x to the origin. If
![]() $\Gamma $
is disjoint from
$\Gamma $
is disjoint from
![]() $A {\setminus } \{o\}$
, then we are done, as
$A {\setminus } \{o\}$
, then we are done, as
![]() $|\Gamma |$
is no greater than
$|\Gamma |$
is no greater than
![]() $2r$
. Otherwise, let
$2r$
. Otherwise, let
![]() $\ell _1$
be the label of the first
$\ell _1$
be the label of the first
![]() $\ast $
-connected component intersected by
$\ast $
-connected component intersected by
![]() $\Gamma $
. Let i and j be the first and last indices such that
$\Gamma $
. Let i and j be the first and last indices such that
![]() $\Gamma $
intersects
$\Gamma $
intersects
![]() $\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
, respectively. Because
$\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
, respectively. Because
![]() $\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
is connected, there is a path
$\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
is connected, there is a path
![]() $\Lambda $
in
$\Lambda $
in
![]() $\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
from
$\partial _{\mathrm {ext}}^\ast B_{\ell _1}$
from
![]() $\Gamma _i$
to
$\Gamma _i$
to
![]() $\Gamma _j$
. We then edit
$\Gamma _j$
. We then edit
![]() $\Gamma $
to form
$\Gamma $
to form
![]() $\Gamma '$
as
$\Gamma '$
as
If
![]() $\Gamma '$
is disjoint from
$\Gamma '$
is disjoint from
![]() $A {\setminus } \{o\}$
, then we are done, as
$A {\setminus } \{o\}$
, then we are done, as
![]() $\Gamma '$
is contained in the union of
$\Gamma '$
is contained in the union of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
. Since
$\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
. Since
![]() $\bigcup _\ell B_\ell $
has at most n elements,
$\bigcup _\ell B_\ell $
has at most n elements,
![]() $\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
has at most
$\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
has at most
![]() $8n$
elements. Accordingly, the length of
$8n$
elements. Accordingly, the length of
![]() $\Gamma '$
is at most
$\Gamma '$
is at most
![]() $2r + 8n \leq 10 \max \{r,n\}$
. Otherwise, if
$2r + 8n \leq 10 \max \{r,n\}$
. Otherwise, if
![]() $\Gamma '$
intersects another
$\Gamma '$
intersects another
![]() $\ast $
-connected component of
$\ast $
-connected component of
![]() $A {\setminus } \{o\}$
, we can simply relabel the preceding argument to continue inductively and obtain the same bound.
$A {\setminus } \{o\}$
, we can simply relabel the preceding argument to continue inductively and obtain the same bound.
Lastly, if
![]() $A \subseteq D(r)$
, then
$A \subseteq D(r)$
, then
![]() $\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
is contained in
$\bigcup _\ell \partial _{\mathrm {ext}}^\ast B_\ell $
is contained in
![]() $D(r+2)$
. Since
$D(r+2)$
. Since
![]() $\Gamma $
is also contained in
$\Gamma $
is also contained in
![]() $D(r+2)$
, this implies that
$D(r+2)$
, this implies that
![]() $\Gamma '$
is contained in
$\Gamma '$
is contained in
![]() $D(r+2)$
.
$D(r+2)$
.
Lemma 3.13 implies two other results. The first addresses Stage 4 when
![]() $K = I$
. By the definition of K (3.2), I must satisfy equation (3.1) when
$K = I$
. By the definition of K (3.2), I must satisfy equation (3.1) when
![]() $K = I$
, which implies that
$K = I$
, which implies that
![]() $I> 1$
, hence
$I> 1$
, hence
![]() $A_{\geq R_1} \subseteq D(R_1+2)^c$
. The next result follows from this observation and the fact that
$A_{\geq R_1} \subseteq D(R_1+2)^c$
. The next result follows from this observation and the fact that
![]() $|A_{<R_1}| = O(R_1^2)$
.
$|A_{<R_1}| = O(R_1^2)$
.
Lemma 3.14. There is a constant c such that
Lemma 3.13 also addresses Stage 3 when
![]() $K \neq I$
.
$K \neq I$
.
Lemma 3.15. Assume that
![]() $n_0 =1$
and
$n_0 =1$
and
![]() $K \neq I$
. There is a constant c such that
$K \neq I$
. There is a constant c such that
The bound (3.20) follows from Lemma 3.13 because
![]() $K \neq I$
implies that the radius r of
$K \neq I$
implies that the radius r of
![]() $\mathrm {Circ}_{K-1}$
is at most a constant factor times
$\mathrm {Circ}_{K-1}$
is at most a constant factor times
![]() $|A_{< r}|$
. Lemma 3.13 then implies that there is a path
$|A_{< r}|$
. Lemma 3.13 then implies that there is a path
![]() $\Gamma $
from
$\Gamma $
from
![]() $\mathrm {Circ}_{K-1}$
to the origin with a length of
$\mathrm {Circ}_{K-1}$
to the origin with a length of
![]() $O (|A_{<r}|)$
, which remains in
$O (|A_{<r}|)$
, which remains in
![]() $D(r+2)$
and otherwise avoids the elements of
$D(r+2)$
and otherwise avoids the elements of
![]() $A_{< r}$
. In fact, because
$A_{< r}$
. In fact, because
![]() $\mathrm {Circ}_{K-1}$
is a subset of
$\mathrm {Circ}_{K-1}$
is a subset of
![]() $\mathrm {Ann}_{K-1}$
, which contains no elements of A, by remaining in
$\mathrm {Ann}_{K-1}$
, which contains no elements of A, by remaining in
![]() $D(r+2)$
,
$D(r+2)$
,
![]() $\Gamma $
avoids
$\Gamma $
avoids
![]() $A_{\geq r}$
as well. This implies equation (3.20).
$A_{\geq r}$
as well. This implies equation (3.20).
3.3 Proof of Theorem 4
The proof is by induction on n. Since equation (1.2) clearly holds for
![]() $n=1$
and
$n=1$
and
![]() $n=2$
, we assume
$n=2$
, we assume
![]() $n \geq 3$
. Let
$n \geq 3$
. Let
![]() $A \in \mathscr {H}_n$
. There are three cases:
$A \in \mathscr {H}_n$
. There are three cases:
![]() $n_0 = n$
,
$n_0 = n$
,
![]() $n_0 \neq n$
and
$n_0 \neq n$
and
![]() $K = I$
, and
$K = I$
, and
![]() $n_0 \neq n$
and
$n_0 \neq n$
and
![]() $K \neq I$
. The first of these cases is easy: When
$K \neq I$
. The first of these cases is easy: When
![]() $n_0 = n$
, A is contained in
$n_0 = n$
, A is contained in
![]() $D(R_1)$
, so Lemma 3.14 implies that
$D(R_1)$
, so Lemma 3.14 implies that
![]() ${\mathbb {H}}_A (o)$
is at least a universal constant. Accordingly, in what follows, we assume that
${\mathbb {H}}_A (o)$
is at least a universal constant. Accordingly, in what follows, we assume that
![]() $n_0 \neq n$
and address the two subcases
$n_0 \neq n$
and address the two subcases
![]() $K=I$
and
$K=I$
and
![]() $K \neq I$
.
$K \neq I$
.
First subcase:
![]() $K = I$
. If
$K = I$
. If
![]() $K=I$
, then we write
$K=I$
, then we write
Because
![]() $C(R_{J})$
,
$C(R_{J})$
,
![]() $\mathrm {Circ}_{I-1}$
and
$\mathrm {Circ}_{I-1}$
and
![]() $C(R_1)$
, respectively, separate
$C(R_1)$
, respectively, separate
![]() $\mathrm {Circ}_{I-1}$
,
$\mathrm {Circ}_{I-1}$
,
![]() $C(R_1)$
, and the origin from
$C(R_1)$
, and the origin from
![]() $\infty $
, we can express the lower bound as the following product:
$\infty $
, we can express the lower bound as the following product:
 $$ \begin{align} {\mathbb{H}}_A (o) \geq \mathbb{P}_\infty (\tau_{C(R_{J})} < \tau_A) &\times \mathbb{P}_\infty \big(\tau_{\mathrm{Circ}_{I-1}} < \tau_A \bigm\vert \tau_{C(R_{J})} < \tau_A \big) \nonumber\\ &\times \mathbb{P}_\infty \big( \tau_{C(R_1)} < \tau_A \bigm\vert \tau_{\mathrm{Circ}_{I-1}} < \tau_A \big) \times \mathbb{P}_\infty \big( \tau_o \leq \tau_A \bigm\vert \tau_{C(R_1)} < \tau_A \big). \end{align} $$
$$ \begin{align} {\mathbb{H}}_A (o) \geq \mathbb{P}_\infty (\tau_{C(R_{J})} < \tau_A) &\times \mathbb{P}_\infty \big(\tau_{\mathrm{Circ}_{I-1}} < \tau_A \bigm\vert \tau_{C(R_{J})} < \tau_A \big) \nonumber\\ &\times \mathbb{P}_\infty \big( \tau_{C(R_1)} < \tau_A \bigm\vert \tau_{\mathrm{Circ}_{I-1}} < \tau_A \big) \times \mathbb{P}_\infty \big( \tau_o \leq \tau_A \bigm\vert \tau_{C(R_1)} < \tau_A \big). \end{align} $$
We address the four factors of equation (3.21) in turn. First, by the induction hypothesis, there is a constant
![]() $c_1$
such that
$c_1$
such that
where
![]() $k = n_{>J} + 1$
. Second, by the strong Markov property applied to
$k = n_{>J} + 1$
. Second, by the strong Markov property applied to
![]() $\tau _{C(R_{J})}$
and Lemma 3.2, and then by Lemma 3.6, there are constants
$\tau _{C(R_{J})}$
and Lemma 3.2, and then by Lemma 3.6, there are constants
![]() $c_2$
and
$c_2$
and
![]() $c_3$
such that
$c_3$
such that
Third and fourth, by Lemma 3.8 and Lemma 3.12, and by Lemma 3.14, there are constants
![]() $c_4$
and
$c_4$
and
![]() $c_5$
such that
$c_5$
such that
Substituting the preceding bounds into equation (3.21) completes the induction step for this subcase:
The second inequality follows from
![]() $n-k = \sum _{\ell =I}^{J-1} n_\ell> 1$
and
$n-k = \sum _{\ell =I}^{J-1} n_\ell> 1$
and
![]() $\log n \geq 1$
, and from potentially adjusting
$\log n \geq 1$
, and from potentially adjusting
![]() $c_1$
to satisfy
$c_1$
to satisfy
![]() $c_1 \geq 8 \max \{1,c_3,\log c_4, -\log c_5\}$
. We are free to adjust
$c_1 \geq 8 \max \{1,c_3,\log c_4, -\log c_5\}$
. We are free to adjust
![]() $c_1$
in this way since the other constants do not arise from the use of the induction hypothesis.
$c_1$
in this way since the other constants do not arise from the use of the induction hypothesis.
Second subcase:
![]() $K \neq I$
. If
$K \neq I$
. If
![]() $K \neq I$
, then we write
$K \neq I$
, then we write
![]() ${\mathbb {H}}_A (o) \geq \mathbb {P}_\infty (\tau _{C(R_{J})} < \tau _{\mathrm {Circ}_{K-1}} < \tau _o \leq \tau _A)$
. Because
${\mathbb {H}}_A (o) \geq \mathbb {P}_\infty (\tau _{C(R_{J})} < \tau _{\mathrm {Circ}_{K-1}} < \tau _o \leq \tau _A)$
. Because
![]() $C(R_{J})$
and
$C(R_{J})$
and
![]() $\mathrm {Circ}_{K-1}$
separate
$\mathrm {Circ}_{K-1}$
separate
![]() $\mathrm {Circ}_{K-1}$
and the origin from
$\mathrm {Circ}_{K-1}$
and the origin from
![]() $\infty $
, we can express the lower bound as
$\infty $
, we can express the lower bound as
As in the first subcase, the first factor is addressed by the induction hypothesis and the lower bound (3.22) applies to the second factor of equation (3.23) with K in the place of I. Concerning the third factor, Lemma 3.15 implies that there is a constant
![]() $c_6$
such that
$c_6$
such that
Substituting the three bounds into equation (3.23) concludes the induction step in this subcase:
The second inequality follows from potentially adjusting
![]() $c_1$
to satisfy
$c_1$
to satisfy
![]() $c_1 \geq 8 \max \{1,c_3,c_6\}$
. This completes the induction and establishes equation (1.2).
$c_1 \geq 8 \max \{1,c_3,c_6\}$
. This completes the induction and establishes equation (1.2).
4 Escape probability estimates
The purpose of this section is to prove Theorem 5. It suffices to prove the escape probability lower bound (1.6), as equation(1.7) follows from equation (1.6) by the pigeonhole principle. Let A be an n-element subset of
![]() $\mathbb {Z}^2$
with at least two elements. We assume w.l.o.g. that
$\mathbb {Z}^2$
with at least two elements. We assume w.l.o.g. that
![]() $o \in A$
. Denote
$o \in A$
. Denote
![]() $b = \mathrm {diam} (A)$
, and suppose
$b = \mathrm {diam} (A)$
, and suppose
![]() $d \geq 2b$
. We aim to show that there is a constant c such that, if
$d \geq 2b$
. We aim to show that there is a constant c such that, if
![]() $d \geq 2b$
, then, for every
$d \geq 2b$
, then, for every
![]() $x \in A$
,
$x \in A$
,
In fact, by adjusting c, we can reduce to the case when
![]() $d \geq kb$
for
$d \geq kb$
for
![]() $k = 200$
and when b is at least a large universal constant,
$k = 200$
and when b is at least a large universal constant,
![]() $b'$
. We proceed to prove equation (1.6) when
$b'$
. We proceed to prove equation (1.6) when
![]() $d \geq 200 b$
for sufficiently large b. Since
$d \geq 200 b$
for sufficiently large b. Since
![]() $C(kb)$
separates A from
$C(kb)$
separates A from
![]() $\partial A_d$
, we can write the escape probability as the product of two factors:
$\partial A_d$
, we can write the escape probability as the product of two factors:
Concerning the first factor of equation (4.1), we have the following lemma.
Lemma 4.1. Let
![]() $x \in A$
. Then
$x \in A$
. Then
The factor of
![]() $\log (kb)$
arises from evaluating the potential kernel at elements of
$\log (kb)$
arises from evaluating the potential kernel at elements of
![]() $C(kb)$
; the factor of
$C(kb)$
; the factor of
![]() $4$
is unimportant. The proof is an application of the optional stopping theorem to the martingale
$4$
is unimportant. The proof is an application of the optional stopping theorem to the martingale
![]() $\mathfrak {a} (S_{j \wedge \tau _o})$
.
$\mathfrak {a} (S_{j \wedge \tau _o})$
.
Proof of Lemma 4.1.
Let
![]() $x \in A$
. By conditioning on the first step, we have
$x \in A$
. By conditioning on the first step, we have
 $$ \begin{align} \mathbb{P}_x ( \tau_{C(kb)} < \tau_A ) = \frac14 \sum_{y \notin A, y \sim x} \mathbb{P}_y ( \tau_{C(kb)} < \tau_A ), \end{align} $$
$$ \begin{align} \mathbb{P}_x ( \tau_{C(kb)} < \tau_A ) = \frac14 \sum_{y \notin A, y \sim x} \mathbb{P}_y ( \tau_{C(kb)} < \tau_A ), \end{align} $$
where
![]() $y \sim x$
means
$y \sim x$
means
![]() $|x-y|=1$
. We apply the optional stopping theorem to the martingale
$|x-y|=1$
. We apply the optional stopping theorem to the martingale
![]() $\mathfrak {a} (S_{j \wedge \tau _o})$
with the stopping time
$\mathfrak {a} (S_{j \wedge \tau _o})$
with the stopping time
![]() $\tau _A \wedge \tau _{C(kb)}$
to find
$\tau _A \wedge \tau _{C(kb)}$
to find
 $$ \begin{align} \frac14 \sum_{y \notin A, y \sim x} \mathbb{P}_y ( \tau_{C(kb)} < \tau_A ) = \frac14 \sum_{y \notin A, y \sim x} \frac{\mathfrak{a} (y) - \mathbb{E}_y \mathfrak{a} (S_{\tau_A})}{\mathbb{E}_y \big[ \mathfrak{a} (S_{\tau_{C(kb)}}) - \mathfrak{a} (S_{\tau_A}) \bigm\vert \tau_{C(kb)} < \tau_A \big]}. \end{align} $$
$$ \begin{align} \frac14 \sum_{y \notin A, y \sim x} \mathbb{P}_y ( \tau_{C(kb)} < \tau_A ) = \frac14 \sum_{y \notin A, y \sim x} \frac{\mathfrak{a} (y) - \mathbb{E}_y \mathfrak{a} (S_{\tau_A})}{\mathbb{E}_y \big[ \mathfrak{a} (S_{\tau_{C(kb)}}) - \mathfrak{a} (S_{\tau_A}) \bigm\vert \tau_{C(kb)} < \tau_A \big]}. \end{align} $$
We need two facts. First,
![]() ${\mathbb {H}}_A (x)$
can be expressed as
${\mathbb {H}}_A (x)$
can be expressed as
![]() $\frac 14 \sum _{y \notin A, y \sim x} \big ( \mathfrak {a} (y) - \mathbb {E}_y \mathfrak {a} (S_{\tau _A}) \big )$
[Reference PopovPop21, Definition 3.15 and Theorem 3.16]. Second, for any
$\frac 14 \sum _{y \notin A, y \sim x} \big ( \mathfrak {a} (y) - \mathbb {E}_y \mathfrak {a} (S_{\tau _A}) \big )$
[Reference PopovPop21, Definition 3.15 and Theorem 3.16]. Second, for any
![]() $z \in C(kb)$
,
$z \in C(kb)$
,
![]() $\mathfrak {a} (z) \leq 4 \log (kb)$
by Lemma A.1. Applying these facts to equation (4.4) and the result to equation (4.3), we find
$\mathfrak {a} (z) \leq 4 \log (kb)$
by Lemma A.1. Applying these facts to equation (4.4) and the result to equation (4.3), we find
 $$\begin{align*}\mathbb{P}_x ( \tau_{C(kb)} < \tau_A ) \geq \frac{1}{4 \log (kb)} \cdot \frac14 \sum_{y \notin A, y \sim x} \big( \mathfrak{a} (y) - \mathbb{E}_y \mathfrak{a} (S_{\tau_A}) \big) = \frac{{\mathbb{H}}_A (x)}{4\log (kb)}. \end{align*}$$
$$\begin{align*}\mathbb{P}_x ( \tau_{C(kb)} < \tau_A ) \geq \frac{1}{4 \log (kb)} \cdot \frac14 \sum_{y \notin A, y \sim x} \big( \mathfrak{a} (y) - \mathbb{E}_y \mathfrak{a} (S_{\tau_A}) \big) = \frac{{\mathbb{H}}_A (x)}{4\log (kb)}. \end{align*}$$
Concerning the second factor of equation (4.1), given that
![]() $\{\tau _{C(kb)} < \tau _A\}$
occurs, we are essentially in the setting depicted on the right side of Figure 5, with
$\{\tau _{C(kb)} < \tau _A\}$
occurs, we are essentially in the setting depicted on the right side of Figure 5, with
![]() $x = S_{\tau _{C(kb)}}$
,
$x = S_{\tau _{C(kb)}}$
,
![]() $r = b$
,
$r = b$
,
![]() $kb$
in the place of
$kb$
in the place of
![]() $2r$
, and
$2r$
, and
![]() $R = d$
. The argument highlighted in Section 2.2 suggests that the second factor of equation (4.1) is at least proportional to
$R = d$
. The argument highlighted in Section 2.2 suggests that the second factor of equation (4.1) is at least proportional to
![]() $\frac {\log b}{n \log d}$
. We will prove this lower bound and combine it with equations (4.1) and (4.2) to obtain equation (1.6) of Theorem 5.
$\frac {\log b}{n \log d}$
. We will prove this lower bound and combine it with equations (4.1) and (4.2) to obtain equation (1.6) of Theorem 5.
Lemma 4.2. Let
![]() $y \in C(kb)$
. If
$y \in C(kb)$
. If
![]() $d \geq kb$
and if b is sufficiently large, then
$d \geq kb$
and if b is sufficiently large, then
Proof. Let
![]() $y \in C(kb)$
. We will follow the argument of Section 2.2. Label the points of A as
$y \in C(kb)$
. We will follow the argument of Section 2.2. Label the points of A as
![]() $x_1, x_2, \dots , x_n$
, and define
$x_1, x_2, \dots , x_n$
, and define
 $$\begin{align*}Y_{i} = \mathbf{1}\left(\tau_{x_i} < \tau_{\partial A_d}\right) \quad \text{and} \quad W =\sum_{i=1}^{n} Y_i. \end{align*}$$
$$\begin{align*}Y_{i} = \mathbf{1}\left(\tau_{x_i} < \tau_{\partial A_d}\right) \quad \text{and} \quad W =\sum_{i=1}^{n} Y_i. \end{align*}$$
From the definition of W, we see that
![]() $\{W = 0\} = \{\tau _{\partial A_d} < \tau _A \}$
. Thus, to obtain the lower bound in equation (4.5), it suffices to get a complementary upper bound on
$\{W = 0\} = \{\tau _{\partial A_d} < \tau _A \}$
. Thus, to obtain the lower bound in equation (4.5), it suffices to get a complementary upper bound on
 $$ \begin{align} \mathbb{P}_y (W>0)=\frac{\mathbb{E}_y W}{\mathbb{E}_y [W\mid W>0]}.\end{align} $$
$$ \begin{align} \mathbb{P}_y (W>0)=\frac{\mathbb{E}_y W}{\mathbb{E}_y [W\mid W>0]}.\end{align} $$
We will find
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that, uniformly for
$\beta $
such that, uniformly for
![]() $y \in C(kb)$
and
$y \in C(kb)$
and
![]() $x_i, x_j \in A$
,
$x_i, x_j \in A$
,
Moreover,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
will satisfy
$\beta $
will satisfy
The requirement that
![]() $\alpha \leq \beta $
prevents us from choosing
$\alpha \leq \beta $
prevents us from choosing
![]() $\beta = 0$
. Essentially, we will be able to satisfy equation (4.7) and the first condition of equation (4.8) because
$\beta = 0$
. Essentially, we will be able to satisfy equation (4.7) and the first condition of equation (4.8) because
![]() $|x_i - x_j|$
is smaller than
$|x_i - x_j|$
is smaller than
![]() $|y-x_i|$
. We will be able to satisfy the second condition because
$|y-x_i|$
. We will be able to satisfy the second condition because
![]() ${\mathrm {dist}}(x_i,\partial A_d) \geq d$
while
${\mathrm {dist}}(x_i,\partial A_d) \geq d$
while
![]() $|x_i-x_j| \leq b$
, which implies that
$|x_i-x_j| \leq b$
, which implies that
![]() $\mathbb {P}_{x_i} (\tau _{x_j} < \tau _{\partial A_d})$
is roughly
$\mathbb {P}_{x_i} (\tau _{x_j} < \tau _{\partial A_d})$
is roughly
![]() $1 - \frac {\log b}{\log d}$
.
$1 - \frac {\log b}{\log d}$
.
If
![]() $\alpha , \beta $
satisfy equation (4.7), then we can bound equation (4.6) as
$\alpha , \beta $
satisfy equation (4.7), then we can bound equation (4.6) as
Additionally, when
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
satisfy equations (4.8), (4.9) implies
$\beta $
satisfy equations (4.8), (4.9) implies
which gives the claimed bound (4.5).
Identifying
![]() $\alpha $
. We now find the
$\alpha $
. We now find the
![]() $\alpha $
promised in equation (4.7). Denote
$\alpha $
promised in equation (4.7). Denote
![]() $F_i = C_{x_i} (d + b)$
(Figure 10). Since
$F_i = C_{x_i} (d + b)$
(Figure 10). Since
![]() $\partial A_d$
separates y from
$\partial A_d$
separates y from
![]() $F_i$
, we have
$F_i$
, we have

Figure 10 Escape to
![]() $\partial A_d$
, for
$\partial A_d$
, for
![]() $n=3$
. Each
$n=3$
. Each
![]() $F_i$
is a circle centered on
$F_i$
is a circle centered on
![]() $x_i \in A$
, separating
$x_i \in A$
, separating
![]() $A_d$
from infinity. Lemma 3.7 bounds above the probability that the walk hits
$A_d$
from infinity. Lemma 3.7 bounds above the probability that the walk hits
![]() $x_i$
before
$x_i$
before
![]() $F_i$
, uniformly for
$F_i$
, uniformly for
![]() $y \in C(kb)$
.
$y \in C(kb)$
.
The hypotheses of Lemma 3.7 are met because
![]() $y - x_i \neq o$
and
$y - x_i \neq o$
and
![]() $y - x_i \in D(d+b)$
. Hence, equation (3.10) applies as
$y - x_i \in D(d+b)$
. Hence, equation (3.10) applies as
 $$ \begin{align} \mathbb{P}_{y-x_i} \left( \tau_{ o} < \tau_{C (d+b)} \right) = \frac{\mathfrak{a}' (d+b) - \mathfrak{a} (y-x_i) + O \left( |y-x_i|^{-1} \right)}{ \mathfrak{a}' (d+b) + O \left( |y-x_i|^{-1} \right)}. \end{align} $$
$$ \begin{align} \mathbb{P}_{y-x_i} \left( \tau_{ o} < \tau_{C (d+b)} \right) = \frac{\mathfrak{a}' (d+b) - \mathfrak{a} (y-x_i) + O \left( |y-x_i|^{-1} \right)}{ \mathfrak{a}' (d+b) + O \left( |y-x_i|^{-1} \right)}. \end{align} $$
Ignoring the error terms, the expression in equation (4.11) is at most
![]() $\frac {\log (d+b) - \log (kb)}{\log (d+b)}$
. A more careful calculation gives
$\frac {\log (d+b) - \log (kb)}{\log (d+b)}$
. A more careful calculation gives
where
![]() $\delta _1 = (\tfrac {\pi \kappa }{2} + O(b^{-1})) (\log d)^{-1}$
and
$\delta _1 = (\tfrac {\pi \kappa }{2} + O(b^{-1})) (\log d)^{-1}$
and
![]() $\varepsilon = \frac {b}{d \log d}$
. (Recall that
$\varepsilon = \frac {b}{d \log d}$
. (Recall that
![]() $\kappa \in (1.02,1.03)$
is a constant associated with the potential kernel (3.9).) The inequality results from applying the inequality
$\kappa \in (1.02,1.03)$
is a constant associated with the potential kernel (3.9).) The inequality results from applying the inequality
![]() $\log (1+x) \leq x$
, which holds for
$\log (1+x) \leq x$
, which holds for
![]() $x> -1$
, to the
$x> -1$
, to the
![]() $\log (d+b)$
term in the numerator, and reducing
$\log (d+b)$
term in the numerator, and reducing
![]() $\log (d+b)$
to
$\log (d+b)$
to
![]() $\log d$
in the denominator. By equation (4.10),
$\log d$
in the denominator. By equation (4.10),
![]() $\alpha $
satisfies equation (4.7).
$\alpha $
satisfies equation (4.7).
Identifying
![]() $\beta $
. We now find a suitable
$\beta $
. We now find a suitable
![]() $\beta $
. Since
$\beta $
. Since
![]() $C_{x_i} (d)$
separates A from
$C_{x_i} (d)$
separates A from
![]() $\partial A_d$
, we have
$\partial A_d$
, we have
The hypotheses of Lemma 3.7 are met because
![]() $x_i - x_j \neq o$
and
$x_i - x_j \neq o$
and
![]() $x_i - x_j \in D(d)$
. Hence, equation (3.10) applies as
$x_i - x_j \in D(d)$
. Hence, equation (3.10) applies as
 $$ \begin{align} \mathbb{P}_{x_i - x_j} \left( \tau_{o} < \tau_{C(d)} \right) = \frac{ \mathfrak{a}' (d) - \mathfrak{a} (x_i - x_j) + O (|x_i - x_j|^{-1})}{\mathfrak{a}' (d) + O(|x_i - x_j|^{-1})}. \end{align} $$
$$ \begin{align} \mathbb{P}_{x_i - x_j} \left( \tau_{o} < \tau_{C(d)} \right) = \frac{ \mathfrak{a}' (d) - \mathfrak{a} (x_i - x_j) + O (|x_i - x_j|^{-1})}{\mathfrak{a}' (d) + O(|x_i - x_j|^{-1})}. \end{align} $$
Ignoring the error terms, equation (4.13) is at least
![]() $\frac {\log d - \log b}{\log d + \kappa }$
. A more careful calculation gives
$\frac {\log d - \log b}{\log d + \kappa }$
. A more careful calculation gives
where
![]() $\delta _2 = (\tfrac {\pi \kappa }{2} + O(b^{-1}) ) (\log d)^{-1}$
. By equation (4.12),
$\delta _2 = (\tfrac {\pi \kappa }{2} + O(b^{-1}) ) (\log d)^{-1}$
. By equation (4.12),
![]() $\beta $
satisfies equation (4.7).
$\beta $
satisfies equation (4.7).
Verifying equation (4.8). To verify the first condition of equation (4.8), we calculate
The inequality is due to
![]() $k = 200$
,
$k = 200$
,
![]() $\tfrac {b}{d} \leq 0.5$
, and
$\tfrac {b}{d} \leq 0.5$
, and
![]() $\pi \kappa < 3.5$
. If b is sufficiently large, then
$\pi \kappa < 3.5$
. If b is sufficiently large, then
![]() $1+O(b^{-1})$
is nonnegative, which verifies equation (4.8).
$1+O(b^{-1})$
is nonnegative, which verifies equation (4.8).
Concerning the second condition of equation (4.8), if b is sufficiently large, then
We have identified
![]() $\alpha , \beta $
which satisfy equations (4.7) and (4.8) for sufficiently large b. By the preceding discussion, this proves equation (4.5).
$\alpha , \beta $
which satisfy equations (4.7) and (4.8) for sufficiently large b. By the preceding discussion, this proves equation (4.5).
Proof of Theorem 5.
By equation (4.1), Lemma 4.1 and Lemma 4.2, we have
whenever
![]() $x \in A$
and
$x \in A$
and
![]() $d \geq kb$
, for sufficiently large b. The second inequality is due to the fact that
$d \geq kb$
, for sufficiently large b. The second inequality is due to the fact that
![]() $\log (kb) \leq 2 \log b$
for sufficiently large b.
$\log (kb) \leq 2 \log b$
for sufficiently large b.
By the reductions discussed at the beginning of this section, equation (4.14) implies that there is a constant c such that equation (1.6) holds for
![]() $x \in A$
if A has at least two elements and if
$x \in A$
if A has at least two elements and if
![]() $d \geq 2\, \mathrm {diam} (A)$
. Equation (1.7) follows from equation (1.6) because, by the pigeonhole principle, some element of A has harmonic measure of at least
$d \geq 2\, \mathrm {diam} (A)$
. Equation (1.7) follows from equation (1.6) because, by the pigeonhole principle, some element of A has harmonic measure of at least
![]() $n^{-1}$
.
$n^{-1}$
.
5 Clustering sets of relatively large diameter
When a HAT configuration has a large diameter relative to the number of particles, we can decompose the configuration into clusters of particles, which are well separated in a sense. This is the content of Lemma 5.2, which will be a key input to the results in Section 6.
Definition 5.1 (Exponential clustering).
For a finite
![]() $A \subset \mathbb {Z}^2$
with
$A \subset \mathbb {Z}^2$
with
![]() $|A| = n$
, an exponential clustering of A with parameter
$|A| = n$
, an exponential clustering of A with parameter
![]() $r \geq 0$
, denoted
$r \geq 0$
, denoted
![]() $A \mapsto _r \{A^i, x_i, \theta ^{(i)}\}_{i=1}^k$
, is a partition of A into clusters
$A \mapsto _r \{A^i, x_i, \theta ^{(i)}\}_{i=1}^k$
, is a partition of A into clusters
![]() $A^1, A^2, \dots , A^k$
with
$A^1, A^2, \dots , A^k$
with
![]() $1 \leq k \leq n$
such that each cluster arises as
$1 \leq k \leq n$
such that each cluster arises as
![]() $A^i = A \cap D_{x_i} (\theta ^{(i)})$
for
$A^i = A \cap D_{x_i} (\theta ^{(i)})$
for
![]() $x_i \in \mathbb {Z}^2$
, with
$x_i \in \mathbb {Z}^2$
, with
![]() $\theta ^{(i)} \geq r$
, and
$\theta ^{(i)} \geq r$
, and
We will call
![]() $x_i$
the center of cluster i. In some instances, the values of r,
$x_i$
the center of cluster i. In some instances, the values of r,
![]() $x_i$
or
$x_i$
or
![]() $\theta ^{(i)}$
will be irrelevant and we will omit them from our notation. For example,
$\theta ^{(i)}$
will be irrelevant and we will omit them from our notation. For example,
![]() $A \mapsto \{A^i\}_{i=1}^k$
.
$A \mapsto \{A^i\}_{i=1}^k$
.
An exponential clustering of A with parameter r always exists because, if
![]() $A^1 = A$
,
$A^1 = A$
,
![]() $x_1 \in A$
, and
$x_1 \in A$
, and
![]() $\theta ^{(1)} \geq \max \{r,\mathrm {diam} (A)\}$
, then
$\theta ^{(1)} \geq \max \{r,\mathrm {diam} (A)\}$
, then
![]() $A \mapsto _r \{A^1,x_1,\theta ^{(1)}\}$
is such a clustering. However, to ensure that there is an exponential clustering of A (with parameter r) with more than one cluster, we require that the diameter of A exceeds
$A \mapsto _r \{A^1,x_1,\theta ^{(1)}\}$
is such a clustering. However, to ensure that there is an exponential clustering of A (with parameter r) with more than one cluster, we require that the diameter of A exceeds
![]() $2 \theta _{n-1} (r)$
. Recall that we defined
$2 \theta _{n-1} (r)$
. Recall that we defined
![]() $\theta _m (r)$
in equation (1.1) through
$\theta _m (r)$
in equation (1.1) through
![]() $\theta _0 (r) = r$
and
$\theta _0 (r) = r$
and
![]() $\theta _m (r) = \theta _{m-1} (r) + e^{\theta _{m-1} (r)}$
for
$\theta _m (r) = \theta _{m-1} (r) + e^{\theta _{m-1} (r)}$
for
![]() $m \geq 1$
.
$m \geq 1$
.
Lemma 5.2. Let
![]() $|A| = n$
. If
$|A| = n$
. If
![]() $\mathrm {diam} (A)> 2\theta _{n-1} (r)$
, then there exists an exponential clustering of A with parameter r into
$\mathrm {diam} (A)> 2\theta _{n-1} (r)$
, then there exists an exponential clustering of A with parameter r into
![]() $k> 1$
clusters.
$k> 1$
clusters.
To prove the lemma, we will identify disks with radii of at most
![]() $\theta _{n-1} (r)$
, which cover A. Although it is not required of an exponential clustering, the disks will be centered at elements of A. These disks will give rise to at least two clusters since
$\theta _{n-1} (r)$
, which cover A. Although it is not required of an exponential clustering, the disks will be centered at elements of A. These disks will give rise to at least two clusters since
![]() $\mathrm {diam} (A)$
exceeds
$\mathrm {diam} (A)$
exceeds
![]() $2\theta _{n-1} (r)$
. The disks will be surrounded by large annuli which are empty of A, which will imply that the clusters are exponentially separated.
$2\theta _{n-1} (r)$
. The disks will be surrounded by large annuli which are empty of A, which will imply that the clusters are exponentially separated.
Proof of Lemma 5.2.
For each
![]() $x \in A$
and
$x \in A$
and
![]() $m \geq 1$
, consider the annulus
$m \geq 1$
, consider the annulus
![]() $\mathcal {A}_x (\theta _m) = D_x (\theta _m) {\setminus } D_x (\theta _{m-1})$
. For each x, identify the smallest m such that
$\mathcal {A}_x (\theta _m) = D_x (\theta _m) {\setminus } D_x (\theta _{m-1})$
. For each x, identify the smallest m such that
![]() $\mathcal {A}_x (\theta _m) \cap A$
is empty and call it
$\mathcal {A}_x (\theta _m) \cap A$
is empty and call it
![]() $m_x$
. Note that, since
$m_x$
. Note that, since
![]() $|A|=n,\ m_{x}$
can be no more than n and hence
$|A|=n,\ m_{x}$
can be no more than n and hence
![]() $\theta _{m_x}\le \theta _n.$
Call the corresponding annulus
$\theta _{m_x}\le \theta _n.$
Call the corresponding annulus
![]() $\mathcal {A}^\ast _x$
, and denote
$\mathcal {A}^\ast _x$
, and denote
![]() $D_x^\ast = D_x (\theta _{m_x-1})$
. For convenience, we label the elements of A as
$D_x^\ast = D_x (\theta _{m_x-1})$
. For convenience, we label the elements of A as
![]() $x_1, x_2, \dots , x_n$
.
$x_1, x_2, \dots , x_n$
.
For
![]() $x_i \in A$
, we collect those disks
$x_i \in A$
, we collect those disks
![]() $D_{x_j}^\ast $
which contain it as
$D_{x_j}^\ast $
which contain it as
We observe that
![]() $\mathcal {E} (x_i)$
is always nonempty, as it contains
$\mathcal {E} (x_i)$
is always nonempty, as it contains
![]() $D_{x_i}^\ast $
. Now, observe that, for any two distinct
$D_{x_i}^\ast $
. Now, observe that, for any two distinct
![]() $D_{x_j}^\ast , D_{x_\ell }^\ast \in \mathcal {E}(x_i)$
, it must be that
$D_{x_j}^\ast , D_{x_\ell }^\ast \in \mathcal {E}(x_i)$
, it must be that
To see why, assume for the purpose of deriving a contradiction that each disk contains an element of A which the other does not. Without loss of generality, suppose
![]() $\theta _{m_{x_j}} \geq \theta _{m_{x_\ell }}$
and let
$\theta _{m_{x_j}} \geq \theta _{m_{x_\ell }}$
and let
![]() $y_\ell \in (D_{x_\ell }^\ast {\setminus } D_{x_j}^\ast ) \cap A$
. Because each disk must contain
$y_\ell \in (D_{x_\ell }^\ast {\setminus } D_{x_j}^\ast ) \cap A$
. Because each disk must contain
![]() $x_i$
, we have
$x_i$
, we have
![]() $|y_\ell - x_i | \leq 2\theta _{m_{x_\ell } - 1}$
and
$|y_\ell - x_i | \leq 2\theta _{m_{x_\ell } - 1}$
and
![]() $|x_i - x_j | \leq \theta _{m_{x_j} - 1}$
. The triangle inequality implies
$|x_i - x_j | \leq \theta _{m_{x_j} - 1}$
. The triangle inequality implies
By assumption,
![]() $y_\ell $
is not in
$y_\ell $
is not in
![]() $D_{x_j} (\theta _{m_{x_j} - 1}) \cap A$
, so
$D_{x_j} (\theta _{m_{x_j} - 1}) \cap A$
, so
![]() $y_\ell $
must be an element of
$y_\ell $
must be an element of
![]() $\mathcal {A}_{x_j} (\theta _{m_{x_j}}) \cap A$
, which contradicts the construction of
$\mathcal {A}_{x_j} (\theta _{m_{x_j}}) \cap A$
, which contradicts the construction of
![]() $m_{x_j}$
.
$m_{x_j}$
.
By equation (5.2), we may totally order the elements of
![]() $\mathcal {E} (x_i)$
by inclusion of intersection with A. For each
$\mathcal {E} (x_i)$
by inclusion of intersection with A. For each
![]() $x_i$
, we select the element of
$x_i$
, we select the element of
![]() $\mathcal {E} (x_i)$
which is greatest in this ordering. If we have not already established it as a cluster, we do so. After we have identified a cluster for each
$\mathcal {E} (x_i)$
which is greatest in this ordering. If we have not already established it as a cluster, we do so. After we have identified a cluster for each
![]() $x_i$
, we discard those
$x_i$
, we discard those
![]() $D_{x_j}^\ast $
which were not selected for any
$D_{x_j}^\ast $
which were not selected for any
![]() $x_i$
. For the remainder of the proof, we only refer to those
$x_i$
. For the remainder of the proof, we only refer to those
![]() $D_{x_j}^\ast $
which were established as clusters, and we relabel the
$D_{x_j}^\ast $
which were established as clusters, and we relabel the
![]() $x_i$
so that the clusters can be expressed as the collection
$x_i$
so that the clusters can be expressed as the collection
![]() $\big \{ D_{x_j}^\ast \big \}_{j=1}^k$
, for some
$\big \{ D_{x_j}^\ast \big \}_{j=1}^k$
, for some
![]() $1 \leq k \leq n$
. We will show that k is strictly greater than one.
$1 \leq k \leq n$
. We will show that k is strictly greater than one.
The collection of clusters contains all elements of A, and is associated to the collection of annuli
![]() $\big \{\mathcal {A}_{x_j}^\ast \big \}_{j=1}^k$
, which contain no elements of A. We observe that, for some distinct
$\big \{\mathcal {A}_{x_j}^\ast \big \}_{j=1}^k$
, which contain no elements of A. We observe that, for some distinct
![]() $x_j$
and
$x_j$
and
![]() $x_\ell $
, it may be that
$x_\ell $
, it may be that
![]() $\mathcal {A}_{x_j}^\ast \cap D_{x_\ell }^\ast \neq \emptyset $
. However, because the annuli contain no elements of A, it must be that
$\mathcal {A}_{x_j}^\ast \cap D_{x_\ell }^\ast \neq \emptyset $
. However, because the annuli contain no elements of A, it must be that
 $$ \begin{align*} {\mathrm{dist}}(D_{x_j}^\ast \cap A, D_{x_\ell}^\ast \cap A) &> \max \left\{ \theta_{m_{x_j}} - \theta_{m_{x_{j-1}}}, \theta_{m_{x_\ell}} - \theta_{m_{x_{\ell-1}}} \right\}\\ &= e^{\max \big\{ \theta_{m_{x_j} - 1}, \theta_{m_{x_\ell} - 1} \big\}}. \end{align*} $$
$$ \begin{align*} {\mathrm{dist}}(D_{x_j}^\ast \cap A, D_{x_\ell}^\ast \cap A) &> \max \left\{ \theta_{m_{x_j}} - \theta_{m_{x_{j-1}}}, \theta_{m_{x_\ell}} - \theta_{m_{x_{\ell-1}}} \right\}\\ &= e^{\max \big\{ \theta_{m_{x_j} - 1}, \theta_{m_{x_\ell} - 1} \big\}}. \end{align*} $$
As
![]() $D_{x_j}^\ast \cap A \subseteq D_{x_j}^\ast $
for any
$D_{x_j}^\ast \cap A \subseteq D_{x_j}^\ast $
for any
![]() $x_j$
in question, we conclude the desired separation of clusters by setting
$x_j$
in question, we conclude the desired separation of clusters by setting
![]() $A^i = D_{x_i}^\ast \cap A$
for each
$A^i = D_{x_i}^\ast \cap A$
for each
![]() $1 \leq i \leq k$
. Furthermore, since
$1 \leq i \leq k$
. Furthermore, since
![]() $m_{x_j} \leq n$
for all j,
$m_{x_j} \leq n$
for all j,
![]() $\theta _{m_{x_j} - 1} \le \theta _{n-1}$
for all j. Since A is contained in the union of the clusters, if
$\theta _{m_{x_j} - 1} \le \theta _{n-1}$
for all j. Since A is contained in the union of the clusters, if
![]() $\mathrm {diam} (A)> 2 \theta _{n-1}$
, then there must be at least two clusters. Lastly, as
$\mathrm {diam} (A)> 2 \theta _{n-1}$
, then there must be at least two clusters. Lastly, as
![]() $m_{x_j} \geq 1$
for all j,
$m_{x_j} \geq 1$
for all j,
![]() $\theta _{m_{x_j} - 1} \geq r$
for all j.
$\theta _{m_{x_j} - 1} \geq r$
for all j.
6 Estimates of the time of collapse
We proceed to prove the main collapse result, Theorem 1. As the proof requires several steps, we begin by discussing the organization of the section and introducing some key definitions. We avoid discussing the proof strategy in detail before making necessary definitions; an in-depth proof strategy is covered in Section 6.2.
Briefly, to estimate the time until the diameter of the configuration falls below a given function of n, we will perform exponential clustering and consider the more manageable task of (i) estimating the time until some cluster loses all of its particles to the other clusters. By iterating this estimate, we can (ii) control the time it takes for the clusters to consolidate into a single cluster. We will find that the surviving cluster has a diameter which is approximately the logarithm of the original diameter. Then, by repeatedly applying this estimate, we can (iii) control the time it takes for the diameter of the configuration to collapse.
The purpose of Section 6.1 is to wield (ii) in the form of Proposition 6.3 and prove Theorem 1, thus completing (iii). The remaining subsections are dedicated to proving the proposition. An overview of our strategy will be detailed in Section 6.2. In particular, we describe how the key harmonic measure estimate of Theorem 4 and the key escape probability estimate of Theorem 5 contribute to addressing (i). We then develop basic properties of cluster separation and explore the geometric consequences of timely cluster collapse in Section 6.3. Lastly, in Section 6.4, we prove a series of propositions which collectively control the timing of individual cluster collapse, culminating in the proof of Proposition 6.3.
Implicit in this discussion is a notion of ‘cluster’ which persists over multiple steps of the dynamics. Starting from an exponential clustering of
![]() $U_0$
, we define the clusters at later times by simply updating the original clusters to account for the movement of particles. Recall that an exponential clustering
$U_0$
, we define the clusters at later times by simply updating the original clusters to account for the movement of particles. Recall that an exponential clustering
![]() $U_0 \mapsto \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
of
$U_0 \mapsto \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
of
![]() $U_0$
is a partition of
$U_0$
is a partition of
![]() $U_0$
that arises from intersecting
$U_0$
that arises from intersecting
![]() $U_0$
with a collection of discs and which satisfies an exponential separation property (5.1).
$U_0$
with a collection of discs and which satisfies an exponential separation property (5.1).
Definition 6.1. Let
![]() $U_0$
have an exponential clustering
$U_0$
have an exponential clustering
![]() $U_0 \mapsto \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
. We define a sequence
$U_0 \mapsto \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
. We define a sequence
![]() $(\{U_t^i\}_{i=1}^k)_{t \geq 0}$
, starting with
$(\{U_t^i\}_{i=1}^k)_{t \geq 0}$
, starting with
![]() $\{U_0^i\}_{i=1}^k$
and such that
$\{U_0^i\}_{i=1}^k$
and such that
![]() $\{U_t^i\}_{i=1}^k$
is a partition of
$\{U_t^i\}_{i=1}^k$
is a partition of
![]() $U_t$
for each t in the following way. Given
$U_t$
for each t in the following way. Given
![]() $U_t$
,
$U_t$
,
![]() $X_t$
,
$X_t$
,
![]() $Y_t$
and the random walk
$Y_t$
and the random walk
![]() $S^t$
that accomplishes the transport step at time t, define
$S^t$
that accomplishes the transport step at time t, define
 $$ \begin{align} U_{t+1}^i = \begin{cases} \big( U_t^i \setminus \{X_t\} \big) \cup \{Y_t\} & S_{\tau_{U_t {\setminus}\{X_t\}}}^t \in U_t^i\\ U_t^i \setminus \{X_t\} & S_{\tau_{U_t {\setminus}\{X_t\}}}^t \notin U_t^i. \end{cases} \end{align} $$
$$ \begin{align} U_{t+1}^i = \begin{cases} \big( U_t^i \setminus \{X_t\} \big) \cup \{Y_t\} & S_{\tau_{U_t {\setminus}\{X_t\}}}^t \in U_t^i\\ U_t^i \setminus \{X_t\} & S_{\tau_{U_t {\setminus}\{X_t\}}}^t \notin U_t^i. \end{cases} \end{align} $$
We refer to the parts of
![]() $\{U_t^i\}_{i=1}^k$
as clusters.
$\{U_t^i\}_{i=1}^k$
as clusters.
Note that, since
![]() $\{U_t^i\}_{i=1}^k$
is a partition of
$\{U_t^i\}_{i=1}^k$
is a partition of
![]() $U_t$
, the removal of
$U_t$
, the removal of
![]() $X_t$
from each
$X_t$
from each
![]() $U_t^i$
in equation (6.1) only affects the cluster to which
$U_t^i$
in equation (6.1) only affects the cluster to which
![]() $X_t$
belongs. For example, if
$X_t$
belongs. For example, if
![]() $X_t$
belongs to
$X_t$
belongs to
![]() $U_t^i$
and the random walk
$U_t^i$
and the random walk
![]() $S^t$
first hits
$S^t$
first hits
![]() $U_t \setminus \{X_t\}$
at a different cluster
$U_t \setminus \{X_t\}$
at a different cluster
![]() $U_t^j$
, then the i
th cluster loses
$U_t^j$
, then the i
th cluster loses
![]() $X_t$
and the j
th cluster gains
$X_t$
and the j
th cluster gains
![]() $Y_t$
, while all other clusters remain the same.
$Y_t$
, while all other clusters remain the same.
Definition 6.2 (Cluster collapse times).
We define the
![]() $\ell $
-cluster collapse time inductively, according to
$\ell $
-cluster collapse time inductively, according to
![]() $\mathcal {T}_0 \equiv 0$
and
$\mathcal {T}_0 \equiv 0$
and
6.1 Proving Theorem 1
We now state the proposition to which most of the effort in this section is devoted and, assuming it, prove Theorem 1. We will denote by
-
• n, the number of elements of
 $U_0$
;
$U_0$
; -
•
 $\Phi (r)$
, the inverse function of
$\Phi (r)$
, the inverse function of
 $\theta _n (r)$
for all
$\theta _n (r)$
for all
 $r \geq 0$
(
$r \geq 0$
(
 $\theta _n (r)$
is an increasing function of
$\theta _n (r)$
is an increasing function of
 $r \geq 0$
for every n);
$r \geq 0$
for every n); -
•
 $\mathcal {F}_t$
, the sigma algebra generated by the initial configuration
$\mathcal {F}_t$
, the sigma algebra generated by the initial configuration
 $U_0$
, the first t activation sites
$U_0$
, the first t activation sites
 $X_0, X_1, \dots , X_{t-1}$
, and the first t random walks
$X_0, X_1, \dots , X_{t-1}$
, and the first t random walks
 $S^0, S^1, \dots , S^{t-1}$
, which accomplish the transport component of the dynamics.
$S^0, S^1, \dots , S^{t-1}$
, which accomplish the transport component of the dynamics.
We note that
![]() $\Phi $
is defined so that, if r equals
$\Phi $
is defined so that, if r equals
![]() $\Phi (\mathrm {diam} (U_0))$
, then the diameter of
$\Phi (\mathrm {diam} (U_0))$
, then the diameter of
![]() $U_0$
exceeds
$U_0$
exceeds
![]() $2 \theta _{n-1} (r)$
. Lemma 5.2 states that, in this case, an exponential clustering of
$2 \theta _{n-1} (r)$
. Lemma 5.2 states that, in this case, an exponential clustering of
![]() $U_0$
with parameter r has at least two clusters.
$U_0$
with parameter r has at least two clusters.
Proposition 6.3. There is a constant c such that, if the diameter d of
![]() $U_0$
exceeds
$U_0$
exceeds
![]() $\theta _{4n} (c n)$
, then for any number of clusters k resulting from an exponential clustering of
$\theta _{4n} (c n)$
, then for any number of clusters k resulting from an exponential clustering of
![]() $U_0$
with parameter
$U_0$
with parameter
![]() $r = \Phi (d)$
, we have
$r = \Phi (d)$
, we have
where
![]() $\delta = (2n)^{-4}$
.
$\delta = (2n)^{-4}$
.
In words, if
![]() $U_0$
has a diameter of d, it takes no more than
$U_0$
has a diameter of d, it takes no more than
![]() $(\log d)^{1+o_n (1)}$
steps to observe the collapse of all but one cluster, with high probability. Because no cluster begins with a diameter greater than
$(\log d)^{1+o_n (1)}$
steps to observe the collapse of all but one cluster, with high probability. Because no cluster begins with a diameter greater than
![]() $\log d$
(by exponential clustering) and, as the diameter of a cluster increases at most linearly in time, the remaining cluster at time
$\log d$
(by exponential clustering) and, as the diameter of a cluster increases at most linearly in time, the remaining cluster at time
![]() $\mathcal {T}_{k-1}$
has a diameter of no more than
$\mathcal {T}_{k-1}$
has a diameter of no more than
![]() $(\log d)^{1+o_n (1)}$
. We will obtain Theorem 1 by repeatedly applying Proposition 6.3. We prove the theorem here, assuming the proposition, and then prove the proposition in the following subsections.
$(\log d)^{1+o_n (1)}$
. We will obtain Theorem 1 by repeatedly applying Proposition 6.3. We prove the theorem here, assuming the proposition, and then prove the proposition in the following subsections.
Proof of Theorem 1.
We organize time into ‘rounds’ of collapse, which proceed in the following way. At the beginning of round
![]() $\ell \geq 1$
, regardless of the diameter
$\ell \geq 1$
, regardless of the diameter
![]() $d_\ell $
of the current configuration, we obtain an exponential clustering (with parameter
$d_\ell $
of the current configuration, we obtain an exponential clustering (with parameter
![]() $r_\ell = \Phi (d_\ell )$
) of this configuration, and we define clusters and their collapse times in analogy with Definitions 6.1 and 6.2. The round lasts until all but one of the clusters have collapsed or until
$r_\ell = \Phi (d_\ell )$
) of this configuration, and we define clusters and their collapse times in analogy with Definitions 6.1 and 6.2. The round lasts until all but one of the clusters have collapsed or until
![]() $(\log d_\ell )^{1+7\delta }$
steps have passed, at which time the next round begins.
$(\log d_\ell )^{1+7\delta }$
steps have passed, at which time the next round begins.
The idea of the proof is to use Proposition 6.3 to bound below the probability that the diameter drops from
![]() $d_\ell $
to at most
$d_\ell $
to at most
![]() $(\log d_\ell )^2$
, over each round
$(\log d_\ell )^2$
, over each round
![]() $\ell $
until the first round
$\ell $
until the first round
![]() $\eta $
that begins with a diameter of at most
$\eta $
that begins with a diameter of at most
![]() $\theta _{4n} (cn)$
(c is the constant from Proposition 6.3). When this event occurs, the rounds shorten rapidly enough that the cumulative time it takes to reach round
$\theta _{4n} (cn)$
(c is the constant from Proposition 6.3). When this event occurs, the rounds shorten rapidly enough that the cumulative time it takes to reach round
![]() $\eta $
is at most twice the maximum length
$\eta $
is at most twice the maximum length
![]() $(\log d)^{1+7\delta }$
of the first round.
$(\log d)^{1+7\delta }$
of the first round.
We define the rounds inductively. Set
![]() $\mathcal {R}_1 \equiv 0$
. Round
$\mathcal {R}_1 \equiv 0$
. Round
![]() $\ell \geq 1$
begins at time
$\ell \geq 1$
begins at time
![]() $\mathcal {R}_\ell $
, in configuration
$\mathcal {R}_\ell $
, in configuration
![]() $V_{\ell ,0} = U_{\mathcal {R}_{\ell }}$
. We further define
$V_{\ell ,0} = U_{\mathcal {R}_{\ell }}$
. We further define
![]() $V_{\ell ,t} = U_{\mathcal {R}_{\ell }+t}$
for
$V_{\ell ,t} = U_{\mathcal {R}_{\ell }+t}$
for
![]() $t \geq 0$
. To define when the round ends, let
$t \geq 0$
. To define when the round ends, let
![]() $d_{\ell } = \mathrm {diam} (V_{\ell ,0})$
and
$d_{\ell } = \mathrm {diam} (V_{\ell ,0})$
and
![]() $r_{\ell } = \Phi (d_{\ell })$
, and denote the exponential clustering of
$r_{\ell } = \Phi (d_{\ell })$
, and denote the exponential clustering of
![]() $V_{\ell ,0}$
with parameter
$V_{\ell ,0}$
with parameter
![]() $r_{\ell }$
by
$r_{\ell }$
by
![]() $\{V_{\ell ,0}^i\}_{i=1}^{k_{\ell }}$
. We define the clusters
$\{V_{\ell ,0}^i\}_{i=1}^{k_{\ell }}$
. We define the clusters
![]() $\{V_{\ell ,t}^i\}_{i=1}^{k_\ell }$
in analogy with Definition 6.1, and the corresponding cluster collapse times in analogy with Definition 6.2. Specifically, we define the latter according to
$\{V_{\ell ,t}^i\}_{i=1}^{k_\ell }$
in analogy with Definition 6.1, and the corresponding cluster collapse times in analogy with Definition 6.2. Specifically, we define the latter according to
![]() $\mathcal {T}_{\ell ,0} = \mathcal {R}_{\ell }$
and
$\mathcal {T}_{\ell ,0} = \mathcal {R}_{\ell }$
and
Round
![]() $\ell $
ends, and round
$\ell $
ends, and round
![]() $\ell +1$
begins, at time
$\ell +1$
begins, at time
The key event is the event that the diameter drops from
![]() $d_\ell $
to at most
$d_\ell $
to at most
![]() $(\log d_\ell )^2$
over each round, until round
$(\log d_\ell )^2$
over each round, until round
The round of the j th diameter drop is
where
![]() $\xi _0 \equiv 1$
. In these terms, the key event is
$\xi _0 \equiv 1$
. In these terms, the key event is
![]() $\mathcal {E}_{\eta -1}$
, where
$\mathcal {E}_{\eta -1}$
, where
If
![]() $\mathcal {E}_{\eta -1}$
occurs, then
$\mathcal {E}_{\eta -1}$
occurs, then
![]() $\xi _{j-1} = j$
for every
$\xi _{j-1} = j$
for every
![]() $j \leq \eta $
, and some algebra shows that
$j \leq \eta $
, and some algebra shows that
 $$ \begin{align} \frac{\log d_j}{\log d_1} = \frac{\log d_{\xi_{j-1}}}{\log d_1} \leq 2^{-(j-1)}, \quad 1 \leq j \leq \eta. \end{align} $$
$$ \begin{align} \frac{\log d_j}{\log d_1} = \frac{\log d_{\xi_{j-1}}}{\log d_1} \leq 2^{-(j-1)}, \quad 1 \leq j \leq \eta. \end{align} $$
We use equation (6.3) to bound the time
![]() $\mathcal {R}_\eta $
that it takes to reach round
$\mathcal {R}_\eta $
that it takes to reach round
![]() $\eta $
when
$\eta $
when
![]() $\mathcal {E}_{\eta -1}$
occurs:
$\mathcal {E}_{\eta -1}$
occurs:
 $$\begin{align*}\mathcal{R}_{\eta} \leq \sum_{j=1}^{\eta-1} (\log d_j)^{1+7\delta} \leq (\log d_1)^{1+7\delta} \sum_{j = 1}^{\eta-1} 2^{-(j-1)} \leq (\log d_1)^{1+8\delta}. \end{align*}$$
$$\begin{align*}\mathcal{R}_{\eta} \leq \sum_{j=1}^{\eta-1} (\log d_j)^{1+7\delta} \leq (\log d_1)^{1+7\delta} \sum_{j = 1}^{\eta-1} 2^{-(j-1)} \leq (\log d_1)^{1+8\delta}. \end{align*}$$
These inequalities are respectively justified by the fact that the
![]() $\ell $
th round lasts at most
$\ell $
th round lasts at most
![]() $(\log d_\ell )^{1+7\delta }$
steps by equation (6.3) and by the fact that
$(\log d_\ell )^{1+7\delta }$
steps by equation (6.3) and by the fact that
![]() $(\log d_1)^\delta $
is at least
$(\log d_1)^\delta $
is at least
![]() $2$
.
$2$
.
Since
![]() $\mathcal {R}_\eta $
is at least
$\mathcal {R}_\eta $
is at least
![]() $\mathcal {T} (\theta _{4n} (cn))$
, to complete the proof, it suffices to show that
$\mathcal {T} (\theta _{4n} (cn))$
, to complete the proof, it suffices to show that
![]() $\mathcal {E}_{\eta -1}^c$
occurs with a probability of at most
$\mathcal {E}_{\eta -1}^c$
occurs with a probability of at most
![]() $e^{-n}$
. We express the probability of
$e^{-n}$
. We express the probability of
![]() $\mathcal {E}_{\eta -1}^c$
in terms of
$\mathcal {E}_{\eta -1}^c$
in terms of
![]() $G_j = \mathcal {E}_{j-1} \cap \{\eta> \xi _{j-1}\}$
, as
$G_j = \mathcal {E}_{j-1} \cap \{\eta> \xi _{j-1}\}$
, as
 $$ \begin{align} \mathbf{P}_{U_0} (\mathcal{E}_{\eta-1}^c) = \mathbf{E}_{U_0} \sum_{j=1}^{\eta-1} \mathbf{1} (E_j^c \cap \mathcal{E}_{j-1}) = \mathbf{E}_{U_0} \sum_{j=1}^\infty \mathbf{1} (E_j^c \cap G_j) = \sum_{j=1}^\infty \mathbf{P}_{U_0} (E_j^c \cap G_j). \end{align} $$
$$ \begin{align} \mathbf{P}_{U_0} (\mathcal{E}_{\eta-1}^c) = \mathbf{E}_{U_0} \sum_{j=1}^{\eta-1} \mathbf{1} (E_j^c \cap \mathcal{E}_{j-1}) = \mathbf{E}_{U_0} \sum_{j=1}^\infty \mathbf{1} (E_j^c \cap G_j) = \sum_{j=1}^\infty \mathbf{P}_{U_0} (E_j^c \cap G_j). \end{align} $$
The three equalities hold by the disjointness of
![]() $\{E_j^c \cap \mathcal {E}_{j-1}\}_{j = 1}^\infty $
; the fact that
$\{E_j^c \cap \mathcal {E}_{j-1}\}_{j = 1}^\infty $
; the fact that
![]() $\xi _{j-1} = j$
when
$\xi _{j-1} = j$
when
![]() $\mathcal {E}_{j-1}$
occurs, hence
$\mathcal {E}_{j-1}$
occurs, hence
![]() $\{\eta> j\} = \{\eta > \xi _{j-1}\}$
; and Tonelli’s theorem, which applies because the summands are nonnegative.
$\{\eta> j\} = \{\eta > \xi _{j-1}\}$
; and Tonelli’s theorem, which applies because the summands are nonnegative.
For brevity, denote
![]() $\mathcal {R}_{\xi _{j-1}}$
by
$\mathcal {R}_{\xi _{j-1}}$
by
![]() $s_j$
. The summands on the right-hand side of equation (6.4) satisfy
$s_j$
. The summands on the right-hand side of equation (6.4) satisfy
The first equality holds by the tower rule and the fact that
![]() $G_j$
is measurable with respect to
$G_j$
is measurable with respect to
![]() $\mathcal {F}_{s_j}$
; the second equality follows from the strong Markov property applied to time
$\mathcal {F}_{s_j}$
; the second equality follows from the strong Markov property applied to time
![]() $s_j$
, which – when
$s_j$
, which – when
![]() $G_j$
occurs – is the time that the j
th round begins; the inequality is due to Proposition 6.3. Note that Proposition 6.3 applies because round j precedes round
$G_j$
occurs – is the time that the j
th round begins; the inequality is due to Proposition 6.3. Note that Proposition 6.3 applies because round j precedes round
![]() $\eta $
when
$\eta $
when
![]() $G_j$
occurs, hence the diameter of
$G_j$
occurs, hence the diameter of
![]() $V_{j,0}$
exceeds
$V_{j,0}$
exceeds
![]() $\theta _{4n} (cn)$
. We substitute equation (6.5) into equation (6.4) and use Tonelli’s theorem a second time to conclude that
$\theta _{4n} (cn)$
. We substitute equation (6.5) into equation (6.4) and use Tonelli’s theorem a second time to conclude that
 $$\begin{align*}\mathbf{P}_{U_0} (\mathcal{E}_{\eta-1}^c) \leq \mathbf{E}_{U_0} \left[ \sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \right]. \end{align*}$$
$$\begin{align*}\mathbf{P}_{U_0} (\mathcal{E}_{\eta-1}^c) \leq \mathbf{E}_{U_0} \left[ \sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \right]. \end{align*}$$
To finish the proof, it therefore suffices to establish the first inequality of
 $$ \begin{align} \sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \leq \sum_{j=1}^\infty e^{-2nj} \leq e^{-n}. \end{align} $$
$$ \begin{align} \sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \leq \sum_{j=1}^\infty e^{-2nj} \leq e^{-n}. \end{align} $$
Denote the number of drops before round
![]() $\eta $
by
$\eta $
by
![]() $N = \sup \{j \geq 0: \xi _j < \eta \}$
. When
$N = \sup \{j \geq 0: \xi _j < \eta \}$
. When
![]() $G_j$
occurs,
$G_j$
occurs,
![]() $r_j^\delta $
satisfies
$r_j^\delta $
satisfies
The first inequality follows from simple but cumbersome algebra, using the definitions of
![]() $r_\ell = \theta _n^{-1} (d_\ell )$
and
$r_\ell = \theta _n^{-1} (d_\ell )$
and
![]() $\xi _{j-1}$
and the fact that
$\xi _{j-1}$
and the fact that
![]() $d_\ell $
exceeds
$d_\ell $
exceeds
![]() $\theta _{4n} (cn)$
when
$\theta _{4n} (cn)$
when
![]() $\ell $
is at most
$\ell $
is at most
![]() $\xi _{N}$
. In particular, this fact implies that
$\xi _{N}$
. In particular, this fact implies that
![]() $r_{\xi _N}^\delta $
is at least
$r_{\xi _N}^\delta $
is at least
![]() $1$
, which justifies the second inequality. The first sum in equation (6.6) satisfies
$1$
, which justifies the second inequality. The first sum in equation (6.6) satisfies
 $$\begin{align*}\sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \leq \sum_{j=1}^{\eta - 1} e^{-2n (N + 2 - j)} \mathbf{1}_{G_j} \leq \sum_{j=1}^{N+1} e^{-2n (N + 2 - j)} \leq \sum_{j=1}^\infty e^{-2nj}. \end{align*}$$
$$\begin{align*}\sum_{j=1}^{\eta-1} e^{-2n r_{j}^\delta} \mathbf{1}_{G_j} \leq \sum_{j=1}^{\eta - 1} e^{-2n (N + 2 - j)} \mathbf{1}_{G_j} \leq \sum_{j=1}^{N+1} e^{-2n (N + 2 - j)} \leq \sum_{j=1}^\infty e^{-2nj}. \end{align*}$$
The first bound is due to the preceding lower bound on
![]() $r_j^\delta $
; the second holds because, by definition, N is at least
$r_j^\delta $
; the second holds because, by definition, N is at least
![]() $\eta -2$
; the third follows from reversing the order of the sum (
$\eta -2$
; the third follows from reversing the order of the sum (
![]() $N+2 - j \to j$
) and then replacing N with
$N+2 - j \to j$
) and then replacing N with
![]() $\infty $
in the resulting sum.
$\infty $
in the resulting sum.
For applications in Section 7, we extend Theorem 1 to a more general tail bound of
![]() $\mathcal {T} (\theta _{4n})$
.
$\mathcal {T} (\theta _{4n})$
.
Corollary 6.4 (Corollary of Theorem 1).
Let U be an n-element subset of
![]() $\mathbb {Z}^2$
with a diameter of d. There exists a universal positive constant c such that
$\mathbb {Z}^2$
with a diameter of d. There exists a universal positive constant c such that
for all
![]() $t \geq 1$
. For the sake of concreteness, this is true with
$t \geq 1$
. For the sake of concreteness, this is true with
![]() $2n^{-4}$
in the place of
$2n^{-4}$
in the place of
![]() $o_n (1)$
.
$o_n (1)$
.
In the proof of the corollary, it will be convenient to have notation for the timescale of collapse after j failed collapses, starting from a diameter of d. Because diameter increases at most linearly in time, if the initial configuration has a diameter of d and collapse does not occur in the next
![]() $(\log d)^{1+o_n(1)}$
steps, then the diameter after this period of time is at most
$(\log d)^{1+o_n(1)}$
steps, then the diameter after this period of time is at most
![]() $d + (\log d)^{1+o_n(1)}$
. In our next attempt to observe collapse, we would wait at most
$d + (\log d)^{1+o_n(1)}$
. In our next attempt to observe collapse, we would wait at most
![]() $\big ( \log ( d + (\log d)^{1+o_n(1)}) \big )^{1+o_n(1)}$
steps. This discussion motivates the definition of the functions
$\big ( \log ( d + (\log d)^{1+o_n(1)}) \big )^{1+o_n(1)}$
steps. This discussion motivates the definition of the functions
![]() $g_j = g_j (d,\varepsilon )$
by
$g_j = g_j (d,\varepsilon )$
by
 $$ \begin{align*} g_0 = (\log d)^{1+\varepsilon} \quad \text{and} \quad g_j = \Big(\log \big(d+\sum_{i=0}^{j-1} g_i\big) \Big)^{1+\varepsilon}, \quad j \geq 1. \end{align*} $$
$$ \begin{align*} g_0 = (\log d)^{1+\varepsilon} \quad \text{and} \quad g_j = \Big(\log \big(d+\sum_{i=0}^{j-1} g_i\big) \Big)^{1+\varepsilon}, \quad j \geq 1. \end{align*} $$
We will use
![]() $t_j = t_j (d,\varepsilon )$
to denote the cumulative time
$t_j = t_j (d,\varepsilon )$
to denote the cumulative time
![]() $\sum _{i=0}^j g_i$
.
$\sum _{i=0}^j g_i$
.
Proof of Corollary 6.4.
Let
![]() $\varepsilon = n^{-4}$
, and use this as the
$\varepsilon = n^{-4}$
, and use this as the
![]() $\varepsilon $
parameter for the collapse timescales
$\varepsilon $
parameter for the collapse timescales
![]() $g_j$
and cumulative times
$g_j$
and cumulative times
![]() $t_j$
. Additionally, denote
$t_j$
. Additionally, denote
![]() $\theta = \theta _{4n} (cn)$
for the constant c from Theorem 1 (this will also be the constant in the statement of the corollary). The bound (6.7) clearly holds when d is at most
$\theta = \theta _{4n} (cn)$
for the constant c from Theorem 1 (this will also be the constant in the statement of the corollary). The bound (6.7) clearly holds when d is at most
![]() $\theta $
, so we assume
$\theta $
, so we assume
![]() $d \geq \theta $
.
$d \geq \theta $
.
Because the diameter of U is d and as diameter grows at most linearly in time, conditionally on
![]() $F_j = \{\mathcal {T} (\theta )> t_j\}$
, the diameter of
$F_j = \{\mathcal {T} (\theta )> t_j\}$
, the diameter of
![]() $U_{t_j}$
is at most
$U_{t_j}$
is at most
![]() $d+t_j$
. Consequently, by the Markov property applied to time
$d+t_j$
. Consequently, by the Markov property applied to time
![]() $t_j$
, and by Theorem 1 (the diameter is at least
$t_j$
, and by Theorem 1 (the diameter is at least
![]() $\theta $
) and the fact that
$\theta $
) and the fact that
![]() $n \geq 1$
, the conditional probability
$n \geq 1$
, the conditional probability
![]() $\mathbf {P}_U (F_{j+1} | F_j)$
satisfies
$\mathbf {P}_U (F_{j+1} | F_j)$
satisfies
 $$ \begin{align} \mathbf{P}_U (F_{j+1} | F_j) = \mathbf{E}_U \left[ \mathbf{P}_{U_{t_j}} (\mathcal{T} (\theta)> g_{j+1}) \frac{\mathbf{1}_{F_j}}{\mathbf{P}_U (F_j)} \right] \leq e^{-1} \,\,\,\text{for any}\ j \geq 0. \end{align} $$
$$ \begin{align} \mathbf{P}_U (F_{j+1} | F_j) = \mathbf{E}_U \left[ \mathbf{P}_{U_{t_j}} (\mathcal{T} (\theta)> g_{j+1}) \frac{\mathbf{1}_{F_j}}{\mathbf{P}_U (F_j)} \right] \leq e^{-1} \,\,\,\text{for any}\ j \geq 0. \end{align} $$
In fact, Theorem 1 implies that the inequality holds with
![]() $e^{-n}$
in the place of
$e^{-n}$
in the place of
![]() $e^{-1}$
, but this will make no difference to us.
$e^{-1}$
, but this will make no difference to us.
Define J to be the greatest j such that
![]() $t_j \leq t$
. There are at least J consecutive collapse attempts which must fail in order for
$t_j \leq t$
. There are at least J consecutive collapse attempts which must fail in order for
![]() $\mathcal {T} (\theta _{4n})$
to exceed t. By equation (6.8),
$\mathcal {T} (\theta _{4n})$
to exceed t. By equation (6.8),
 $$ \begin{align} \mathbf{P}_U (\mathcal{T}(\theta)> t) \leq \prod_{i=0}^{J-1} \mathbf{P}_U (F_{i+1} | F_i) \leq e^{-J}. \end{align} $$
$$ \begin{align} \mathbf{P}_U (\mathcal{T}(\theta)> t) \leq \prod_{i=0}^{J-1} \mathbf{P}_U (F_{i+1} | F_i) \leq e^{-J}. \end{align} $$
To bound below J, note that
![]() $g_j$
increases with j, hence
$g_j$
increases with j, hence
![]() $t_j \leq (j+1) g_j$
and
$t_j \leq (j+1) g_j$
and
![]() $g_j \leq g_{j+1}$
, which implies that
$g_j \leq g_{j+1}$
, which implies that
By the definition of J, we have
![]() $t_J + g_{J+1} \geq t$
and
$t_J + g_{J+1} \geq t$
and
![]() $g_{J+1} \leq (\log (d+t))^{1+\varepsilon }$
. By combining the preceding display with these two facts, we find that
$g_{J+1} \leq (\log (d+t))^{1+\varepsilon }$
. By combining the preceding display with these two facts, we find that
 $$ \begin{align*} J \geq \frac{t_J - g_{J+1}}{g_{J+1}} \geq \frac{t - 2g_{J+1}}{g_{J+1}} \geq \frac{t - 2 \big( \log (d+t) \big)^{1+\varepsilon}}{\big( \log (d+t) \big)^{1+\varepsilon}}. \end{align*} $$
$$ \begin{align*} J \geq \frac{t_J - g_{J+1}}{g_{J+1}} \geq \frac{t - 2g_{J+1}}{g_{J+1}} \geq \frac{t - 2 \big( \log (d+t) \big)^{1+\varepsilon}}{\big( \log (d+t) \big)^{1+\varepsilon}}. \end{align*} $$
Returning to equation (6.9), we conclude that
We obtain equation (6.7) by replacing t with
![]() $t \big (\log \max \{t,d\} \big )^{1+2\varepsilon }$
in the preceding inequality and noting that, because
$t \big (\log \max \{t,d\} \big )^{1+2\varepsilon }$
in the preceding inequality and noting that, because
![]() $d \geq \theta $
and
$d \geq \theta $
and
![]() $\varepsilon < 1$
, the resulting bound is at most
$\varepsilon < 1$
, the resulting bound is at most
![]() $e^{-t}$
.
$e^{-t}$
.
6.2 Proof strategy for Proposition 6.3
We turn our attention to the proof of Proposition 6.3, which finds a high-probability bound on the time it takes for all but one cluster to collapse. Heuristically, if there are only two clusters, separated by a distance
![]() $\rho _1$
, then one of the clusters will lose all its particles to the other cluster in
$\rho _1$
, then one of the clusters will lose all its particles to the other cluster in
![]() $\log \rho _1$
steps (up to factors depending on n), due to the harmonic measure and escape probability lower bounds of Theorems 4 and 5. This heuristic suggests that, among k clusters, we should observe the collapse of some cluster on a timescale which depends on the smallest separation between any two of the k clusters. Similarly, at the time the
$\log \rho _1$
steps (up to factors depending on n), due to the harmonic measure and escape probability lower bounds of Theorems 4 and 5. This heuristic suggests that, among k clusters, we should observe the collapse of some cluster on a timescale which depends on the smallest separation between any two of the k clusters. Similarly, at the time the
![]() $\ell ^{\text {th}}$
cluster collapses, if the least separation among the remaining clusters is
$\ell ^{\text {th}}$
cluster collapses, if the least separation among the remaining clusters is
![]() $\rho _{\ell +1}$
, then we expect to wait
$\rho _{\ell +1}$
, then we expect to wait
![]() $\log \rho _{\ell +1}$
steps for the
$\log \rho _{\ell +1}$
steps for the
![]() $(\ell +1)^{\text {st}}$
collapse.
$(\ell +1)^{\text {st}}$
collapse.
If the timescale of collapse is small relative to the separation between clusters, then the pairwise separation and diameters of clusters cannot appreciably change while collapse occurs. In particular, the separation between any two clusters cannot significantly exceed the initial diameter d of the configuration, which suggests an overall bound of order
![]() $(\log d)^{1+o_n(1)}$
steps for all but one cluster to collapse, where the
$(\log d)^{1+o_n(1)}$
steps for all but one cluster to collapse, where the
![]() $o_n (1)$
factor accounts for various n-dependent factors. This is the upper bound that we establish.
$o_n (1)$
factor accounts for various n-dependent factors. This is the upper bound that we establish.
We now highlight some key aspects of the proof.
6.2.1 Expiry time
As described above, over the timescale typical of collapse, the diameters and separation of clusters will not change appreciably. Because these quantities determine the probability with which the least separated cluster loses a particle, we will be able to obtain estimates of this probability which hold uniformly from the time
![]() $\mathcal {T}_{\ell -1}$
of the
$\mathcal {T}_{\ell -1}$
of the
![]() $(\ell -1)^{\text {st}}$
cluster collapse and until the next time
$(\ell -1)^{\text {st}}$
cluster collapse and until the next time
![]() $\mathcal {T}_\ell $
that some cluster collapses, unless
$\mathcal {T}_\ell $
that some cluster collapses, unless
![]() $\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
is atypically large. Indeed, if
$\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
is atypically large. Indeed, if
![]() $\mathcal {T}_{\ell } - \mathcal {T}_{\ell -1}$
is as large as the separation
$\mathcal {T}_{\ell } - \mathcal {T}_{\ell -1}$
is as large as the separation
![]() $\rho _\ell $
of the least separated cluster at time
$\rho _\ell $
of the least separated cluster at time
![]() $\mathcal {T}_{\ell -1}$
, then two clusters may intersect or a cluster may no longer have an exposed element (e.g., due to a group of clusters surrounding it). We avoid this by defining a
$\mathcal {T}_{\ell -1}$
, then two clusters may intersect or a cluster may no longer have an exposed element (e.g., due to a group of clusters surrounding it). We avoid this by defining a
![]() $\mathcal {F}_{\mathcal {T}_{\ell -1}}$
-measurable expiry time
$\mathcal {F}_{\mathcal {T}_{\ell -1}}$
-measurable expiry time
![]() $\mathfrak {t}_\ell $
(which will effectively be
$\mathfrak {t}_\ell $
(which will effectively be
![]() $(\log \rho _\ell )^2$
) and restricting our estimates to the interval from
$(\log \rho _\ell )^2$
) and restricting our estimates to the interval from
![]() $\mathcal {T}_{\ell -1}$
to the minimum of
$\mathcal {T}_{\ell -1}$
to the minimum of
![]() $\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
and
$\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
and
![]() $\mathcal {T}_\ell $
. An expiry time of
$\mathcal {T}_\ell $
. An expiry time of
![]() $(\log \rho _\ell )^2$
is short enough that the relative separation of clusters will not change significantly before it, but long enough so that some cluster will collapse before it with overwhelming probability.
$(\log \rho _\ell )^2$
is short enough that the relative separation of clusters will not change significantly before it, but long enough so that some cluster will collapse before it with overwhelming probability.
6.2.2 Midway point
From time
![]() $\mathcal {T}_{\ell -1}$
to time
$\mathcal {T}_{\ell -1}$
to time
![]() $\mathcal {T}_\ell $
or until expiry, we will track activated particles which reach a circle of radius
$\mathcal {T}_\ell $
or until expiry, we will track activated particles which reach a circle of radius
![]() $\tfrac 12 \rho _\ell $
surrounding one of the least separated clusters, which we call the watched cluster. We will use this circle, called the midway point, to organize our argument with the following three estimates, which will hold uniformly over this interval of time (Figure 11).
$\tfrac 12 \rho _\ell $
surrounding one of the least separated clusters, which we call the watched cluster. We will use this circle, called the midway point, to organize our argument with the following three estimates, which will hold uniformly over this interval of time (Figure 11).
-
1. Activated particles which reach the midway point deposit at the watched cluster with a probability of at most
 $0.51$
.
$0.51$
. -
2. With a probability of at least
 $(\log \rho _\ell )^{-1-o_n(1)}$
, the activated particle reaches the midway point.
$(\log \rho _\ell )^{-1-o_n(1)}$
, the activated particle reaches the midway point. -
3. Conditionally on the activated particle reaching the midway point, the probability that it originated at the watched cluster is at least
 $(\log \log \rho _\ell )^{-1}$
.
$(\log \log \rho _\ell )^{-1}$
.

Figure 11 Setting of the proof of Proposition 6.3. Least separated clusters i and j (cluster i is the watched cluster), each with a diameter of approximately
![]() $\log \rho _\ell $
, are separated by a distance
$\log \rho _\ell $
, are separated by a distance
![]() $\rho _\ell $
at time
$\rho _\ell $
at time
![]() $\mathcal {T}_{\ell - 1}$
. The diameters of the clusters grow at most linearly in time, so over approximately
$\mathcal {T}_{\ell - 1}$
. The diameters of the clusters grow at most linearly in time, so over approximately
![]() $(\log \rho _\ell )^2$
steps, the clusters remain within the dotted circles. Crosses on the timeline indicate times before collapse and expiry at which an activated particle reaches the midway point (solid circle). At these times, the number of particles in the watched cluster may remain the same or increase or decrease by one (indicated by
$(\log \rho _\ell )^2$
steps, the clusters remain within the dotted circles. Crosses on the timeline indicate times before collapse and expiry at which an activated particle reaches the midway point (solid circle). At these times, the number of particles in the watched cluster may remain the same or increase or decrease by one (indicated by
![]() $0, \pm 1$
above the crosses). At time t, the watched cluster gains a particle from cluster j.
$0, \pm 1$
above the crosses). At time t, the watched cluster gains a particle from cluster j.
To explain the third estimate, we make two observations. First, consider a cluster j separated from the watched cluster by a distance of
![]() $\rho $
. In the relevant context, cluster j will essentially be exponentially separated, so its diameter will be at most
$\rho $
. In the relevant context, cluster j will essentially be exponentially separated, so its diameter will be at most
![]() $\log \rho $
. Consequently, a particle activated at cluster j reaches the midway point with a probability of at most
$\log \rho $
. Consequently, a particle activated at cluster j reaches the midway point with a probability of at most
![]() $\frac {\log \log \rho }{\log \rho }$
. (This follows from the fact that random walk starting at a distance of at most
$\frac {\log \log \rho }{\log \rho }$
. (This follows from the fact that random walk starting at a distance of at most
![]() $\log \rho $
from the origin escapes to a distance of
$\log \rho $
from the origin escapes to a distance of
![]() $\rho $
with a probability of at most
$\rho $
with a probability of at most
![]() $\frac {\log \log \rho }{\log \rho }$
, roughly.) Because this probability is decreasing in
$\frac {\log \log \rho }{\log \rho }$
, roughly.) Because this probability is decreasing in
![]() $\rho $
and because
$\rho $
and because
![]() $\rho \geq \rho _\ell $
,
$\rho \geq \rho _\ell $
,
![]() $\frac {\log \log \rho _\ell }{\log \rho _\ell }$
further bounds above it. Second, the probability that a particle activated at the watched cluster reaches the midway point is at least
$\frac {\log \log \rho _\ell }{\log \rho _\ell }$
further bounds above it. Second, the probability that a particle activated at the watched cluster reaches the midway point is at least
![]() $(\log \rho _\ell )^{-1}$
, up to a factor depending on n. Combining these two observations with Bayes’s rule, a particle which reaches the midway point was activated at the watched cluster with a probability of at least
$(\log \rho _\ell )^{-1}$
, up to a factor depending on n. Combining these two observations with Bayes’s rule, a particle which reaches the midway point was activated at the watched cluster with a probability of at least
![]() $( \log \log \rho _\ell )^{-1}$
, up to an n-dependent factor.
$( \log \log \rho _\ell )^{-1}$
, up to an n-dependent factor.
6.2.3 Coupling with random walk
Each time an activated particle reaches the midway point while the watched cluster persists, there is a chance of at least
![]() $(\log \log \rho _\ell )^{-1}$
up to an n-dependent factor that the particle originated at the watched cluster and will ultimately deposit at another cluster. When this occurs, the watched cluster loses a particle. Alternatively, the activated particle may return to its cluster of origin – in which case the watched cluster retains its particles – or it deposits at the watched cluster, having originated at a different one – in which case the watched cluster gains a particle (Figure 11).
$(\log \log \rho _\ell )^{-1}$
up to an n-dependent factor that the particle originated at the watched cluster and will ultimately deposit at another cluster. When this occurs, the watched cluster loses a particle. Alternatively, the activated particle may return to its cluster of origin – in which case the watched cluster retains its particles – or it deposits at the watched cluster, having originated at a different one – in which case the watched cluster gains a particle (Figure 11).
We will couple the number of elements in the watched cluster with a lazy, one-dimensional random walk, which will never exceed n and never hit zero before the size of the watched cluster does. It will take no more than
![]() $(\log \log \rho _\ell )^n$
instances of the activated particle reaching the midway point, for the random walk to make n consecutive down-steps. This is a coarse estimate; with more effort, we could improve the n-dependence of this term, but it would not qualitatively change the result. On a high probability event,
$(\log \log \rho _\ell )^n$
instances of the activated particle reaching the midway point, for the random walk to make n consecutive down-steps. This is a coarse estimate; with more effort, we could improve the n-dependence of this term, but it would not qualitatively change the result. On a high probability event,
![]() $\rho _\ell $
will be sufficiently large to ensure that
$\rho _\ell $
will be sufficiently large to ensure that
![]() $(\log \log \rho _\ell )^n \leq (\log \rho _\ell )^{o_n (1)}$
. Then, because it will typically take no more than
$(\log \log \rho _\ell )^n \leq (\log \rho _\ell )^{o_n (1)}$
. Then, because it will typically take no more than
![]() $(\log \rho _\ell )^{1+o_n(1)}$
steps to observe a visit to the midway point, we will wait a number of steps on the same order to observe the collapse of a cluster.
$(\log \rho _\ell )^{1+o_n(1)}$
steps to observe a visit to the midway point, we will wait a number of steps on the same order to observe the collapse of a cluster.
6.3 Basic properties of clusters and collapse times
We will work in the following setting.
-
• For brevity, if we write
 $\theta _m$
with no parenthetical argument, we will mean
$\theta _m$
with no parenthetical argument, we will mean
 $\theta _m (\gamma n)$
for the constant
$\theta _m (\gamma n)$
for the constant
 $\gamma $
given by (6.10)where
$\gamma $
given by (6.10)where $$ \begin{align} \gamma = 18 \max\{c_1,c_2^{-1}\} + 36, \end{align} $$
$$ \begin{align} \gamma = 18 \max\{c_1,c_2^{-1}\} + 36, \end{align} $$
 $c_1$
and
$c_1$
and
 $c_2$
are the constants in Theorems 4 and 5. Any constant larger than
$c_2$
are the constants in Theorems 4 and 5. Any constant larger than
 $\gamma $
would also work in its place.
$\gamma $
would also work in its place.
-
•
 $U_0$
has
$U_0$
has
 $n \geq 2$
elements and
$n \geq 2$
elements and
 $\mathrm {diam} (U_0)$
is at least
$\mathrm {diam} (U_0)$
is at least
 $\theta _{4n}$
.
$\theta _{4n}$
. -
• The clustering parameter r equals
 $\Phi (\mathrm {diam} (U_0))$
, where we continue to denote by
$\Phi (\mathrm {diam} (U_0))$
, where we continue to denote by
 $\Phi (\cdot )$
the inverse function of
$\Phi (\cdot )$
the inverse function of
 $\theta _n (\cdot )$
. In particular, r satisfies (6.11)
$\theta _n (\cdot )$
. In particular, r satisfies (6.11) $$ \begin{align} r \geq \Phi (\theta_{4n}) = \theta_{3n} \geq e^n. \end{align} $$
$$ \begin{align} r \geq \Phi (\theta_{4n}) = \theta_{3n} \geq e^n. \end{align} $$
-
• We will assume that the initial configuration is exponentially clustered with parameter r as
 $U_0 \mapsto _r \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
. In particular, we assume that clustering produces k clusters. We note that the choice of r guarantees
$U_0 \mapsto _r \{U_0^i, x_i, \theta ^{(i)}\}_{i=1}^k$
. In particular, we assume that clustering produces k clusters. We note that the choice of r guarantees
 $\mathrm {diam} (U_0)> 2 \theta _{n-1} (r)$
which, by Lemma 5.2, guarantees that
$\mathrm {diam} (U_0)> 2 \theta _{n-1} (r)$
which, by Lemma 5.2, guarantees that
 $k> 1$
.
$k> 1$
. -
• We denote a generic element of
 $\{1,2,\dots ,k-1\}$
by
$\{1,2,\dots ,k-1\}$
by
 $\ell $
.
$\ell $
.
6.3.1 Properties of cluster separation and diameter
We will use the following terms to describe the separation of clusters.
Definition 6.5. We define pairwise cluster separation and the least separation by
(By convention, the distance to an empty set is
![]() $\infty $
, so the separation of a cluster is
$\infty $
, so the separation of a cluster is
![]() $\infty $
at all times following its collapse.) If
$\infty $
at all times following its collapse.) If
![]() $U_t^i$
satisfies
$U_t^i$
satisfies
![]() $\mathrm {sep} (U_t^i) = \mathrm {sep} (U_t)$
, then we say that
$\mathrm {sep} (U_t^i) = \mathrm {sep} (U_t)$
, then we say that
![]() $U_t^i$
is least separated. Whenever there are at least two clusters, at least two clusters will be least separated. The least separation at a cluster collapse time will be an important quantity; we will denote it by
$U_t^i$
is least separated. Whenever there are at least two clusters, at least two clusters will be least separated. The least separation at a cluster collapse time will be an important quantity; we will denote it by
Next, we introduce the expiry time
![]() $\mathfrak {t}_\ell $
and the truncated collapse time
$\mathfrak {t}_\ell $
and the truncated collapse time
![]() ${\mathcal {T}_\ell }^-$
. As discussed in Section 6.2, if the least separation at time
${\mathcal {T}_\ell }^-$
. As discussed in Section 6.2, if the least separation at time
![]() $\mathcal {T}_{\ell -1}$
is
$\mathcal {T}_{\ell -1}$
is
![]() $\rho _\ell $
, then we will obtain a lower bound on the probability that a least separated cluster loses a particle, which holds uniformly from time
$\rho _\ell $
, then we will obtain a lower bound on the probability that a least separated cluster loses a particle, which holds uniformly from time
![]() $\mathcal {T}_{\ell -1}$
to the first of
$\mathcal {T}_{\ell -1}$
to the first of
![]() $\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
and
$\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
and
![]() $\mathcal {T}_\ell - 1$
(i.e., the time immediately preceding the
$\mathcal {T}_\ell - 1$
(i.e., the time immediately preceding the
![]() $\ell $
th collapse), which we call the truncated collapse time,
$\ell $
th collapse), which we call the truncated collapse time,
![]() ${\mathcal {T}_\ell }^-$
. Here,
${\mathcal {T}_\ell }^-$
. Here,
![]() $\mathfrak {t}_\ell $
is an
$\mathfrak {t}_\ell $
is an
![]() $\mathcal {F}_{\mathcal {T}_{\ell -1}}$
-measurable random variable which will effectively be
$\mathcal {F}_{\mathcal {T}_{\ell -1}}$
-measurable random variable which will effectively be
![]() $(\log \rho _\ell )^2$
. It will be rare for
$(\log \rho _\ell )^2$
. It will be rare for
![]() $\mathcal {T}_\ell $
to exceed
$\mathcal {T}_\ell $
to exceed
![]() $\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
, so
$\mathcal {T}_{\ell -1} + \mathfrak {t}_\ell $
, so
![]() ${\mathcal {T}_\ell }^-$
can be thought of as
${\mathcal {T}_\ell }^-$
can be thought of as
![]() $\mathcal {T}_\ell - 1$
.
$\mathcal {T}_\ell - 1$
.
Definition 6.6. Given the
![]() $\mathcal {F}_{\mathcal {T}_{\ell -1}}$
data (in particular
$\mathcal {F}_{\mathcal {T}_{\ell -1}}$
data (in particular
![]() $\rho _\ell $
and
$\rho _\ell $
and
![]() $\mathcal {T}_{\ell -1}$
), we define the expiry time
$\mathcal {T}_{\ell -1}$
), we define the expiry time
![]() $\mathfrak {t}_\ell $
to be the integer part of
$\mathfrak {t}_\ell $
to be the integer part of
We emphasize that
![]() $\mathfrak {t}_\ell $
should be thought of as
$\mathfrak {t}_\ell $
should be thought of as
![]() $(\log \rho _\ell )^2$
; the other terms will be much smaller and are included to simplify calculations which follow. Additionally, we define the
$(\log \rho _\ell )^2$
; the other terms will be much smaller and are included to simplify calculations which follow. Additionally, we define the
![]() $\ell $
th truncated cluster collapse time to be
$\ell $
th truncated cluster collapse time to be
Note that
![]() ${\mathcal {T}_\ell }^-$
is not a stopping time, but it will be useful to us anyway.
${\mathcal {T}_\ell }^-$
is not a stopping time, but it will be useful to us anyway.
Cluster diameter and separation have complementary behavior in the sense that diameter increases at most linearly in time but may decrease abruptly, while separation decreases at most linearly in time but may increase abruptly. We express these properties in the following lemma.
Lemma 6.7. Cluster diameter and separation obey the following properties.
-
1. Cluster diameter increases by at most
 $1$
each step: (6.12)
$1$
each step: (6.12) $$ \begin{align} \mathrm{diam} (U_t^i) \leq \mathrm{diam} (U_{t-1}^i) + 1. \end{align} $$
$$ \begin{align} \mathrm{diam} (U_t^i) \leq \mathrm{diam} (U_{t-1}^i) + 1. \end{align} $$
-
2. Cluster separation decreases by at most
 $1$
each step: (6.13)
$1$
each step: (6.13) $$ \begin{align} {\mathrm{dist}} (U_t^i, U_t^j) \geq {\mathrm{dist}} (U_{t-1}^i, U_{t-1}^j) - 1 \quad\text{and}\quad \mathrm{sep} (U_t^i) \geq \mathrm{sep} (U_{t-1}^i) - 1. \end{align} $$
$$ \begin{align} {\mathrm{dist}} (U_t^i, U_t^j) \geq {\mathrm{dist}} (U_{t-1}^i, U_{t-1}^j) - 1 \quad\text{and}\quad \mathrm{sep} (U_t^i) \geq \mathrm{sep} (U_{t-1}^i) - 1. \end{align} $$
-
3. For any two times s and t satisfying
 $\mathcal {T}_{\ell - 1} \leq s < t < \mathcal {T}_\ell $
and any two clusters i and j:
$\mathcal {T}_{\ell - 1} \leq s < t < \mathcal {T}_\ell $
and any two clusters i and j:  $$ \begin{align*} {\mathrm{dist}} (U_t^i,U_t^j) \leq {\mathrm{dist}} (U_s^i,U_s^j) + \mathrm{diam} (U_s^i) + \mathrm{diam} (U_s^j) + (t-s). \end{align*} $$
$$ \begin{align*} {\mathrm{dist}} (U_t^i,U_t^j) \leq {\mathrm{dist}} (U_s^i,U_s^j) + \mathrm{diam} (U_s^i) + \mathrm{diam} (U_s^j) + (t-s). \end{align*} $$
Proof. The first two properties are obvious; we prove the third. Let
![]() $i,j$
label two clusters which are nonempty at time
$i,j$
label two clusters which are nonempty at time
![]() $\mathcal {T}_{\ell -1}$
, and let
$\mathcal {T}_{\ell -1}$
, and let
![]() $s,t$
satisfy the hypotheses. If there are
$s,t$
satisfy the hypotheses. If there are
![]() $m_i$
activations at the i
th cluster from time s to time t, then for any
$m_i$
activations at the i
th cluster from time s to time t, then for any
![]() $x'$
in
$x'$
in
![]() $U_t^i$
, there is an x in
$U_t^i$
, there is an x in
![]() $U_s^i$
such that
$U_s^i$
such that
![]() $|x - x'| \leq m_i$
. The same is true of any
$|x - x'| \leq m_i$
. The same is true of any
![]() $y'$
in the j
th cluster with
$y'$
in the j
th cluster with
![]() $m_j$
in the place of
$m_j$
in the place of
![]() $m_i$
. Since the sum of
$m_i$
. Since the sum of
![]() $m_i$
and
$m_i$
and
![]() $m_j$
is at most
$m_j$
is at most
![]() $t-s$
, two uses of the triangle inequality give
$t-s$
, two uses of the triangle inequality give
This implies property (3) because, by two more uses of the triangle inequality,
6.3.2 Consequences of timely collapse
If clusters collapse before their expiry times – that is, if the event
occurs – then we will be able to control the separation (Lemma 6.8) and diameters (Lemma 6.10) of the clusters by combining the initial exponential separation of the clusters with the properties of Lemma 6.7. Moreover, we will be able to guarantee that every cluster that has not yet collapsed has an element with positive harmonic measure.
The next lemma states that, when cluster collapses are timely, cluster separation decreases little. To state it, we recall that
![]() $\mathrm {sep} (U_t^i)$
is the distance between
$\mathrm {sep} (U_t^i)$
is the distance between
![]() $U_t^i$
and the nearest other cluster and that
$U_t^i$
and the nearest other cluster and that
![]() $\rho _\ell $
is the least of these distances among all pairs of distinct clusters at time
$\rho _\ell $
is the least of these distances among all pairs of distinct clusters at time
![]() $\mathcal {T}_{\ell -1}$
. In particular,
$\mathcal {T}_{\ell -1}$
. In particular,
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
for each i.
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
for each i.
Lemma 6.8. For any cluster i, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
$\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
![]() ${\mathcal {T}_\ell }^-$
,
${\mathcal {T}_\ell }^-$
,
Additionally, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
The factor of
![]() $1-e^{-n}$
in equation (6.14) does not have special significance; other factors of
$1-e^{-n}$
in equation (6.14) does not have special significance; other factors of
![]() $1-o_n (1)$
would work, too. Equation (6.14) and the first inequality in equation (6.15) are consequences of the fact (6.13) that separation decreases at most linearly in time and, when
$1-o_n (1)$
would work, too. Equation (6.14) and the first inequality in equation (6.15) are consequences of the fact (6.13) that separation decreases at most linearly in time and, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
![]() $\mathcal {T}_{\ell -1}$
is small relative to the separation of the remaining clusters. The second inequality in equation (6.15) follows from our choice of r in equation (6.11).
$\mathcal {T}_{\ell -1}$
is small relative to the separation of the remaining clusters. The second inequality in equation (6.15) follows from our choice of r in equation (6.11).
Proof of Lemma 6.8.
We will prove equation (6.14) by induction, using the fact that separation decreases at most linearly in time (6.13) and that (by the definition of
![]() ${\mathcal {T}_\ell }^-$
) at most
${\mathcal {T}_\ell }^-$
) at most
![]() $\mathfrak {t}_\ell $
steps elapse between
$\mathfrak {t}_\ell $
steps elapse between
![]() $\mathcal {T}_{\ell -1}$
and
$\mathcal {T}_{\ell -1}$
and
![]() ${\mathcal {T}_\ell }^-$
.
${\mathcal {T}_\ell }^-$
.
For the base case, take
![]() $\ell = 1$
. Suppose cluster i is nonempty at time
$\ell = 1$
. Suppose cluster i is nonempty at time
![]() $\mathcal {T}_{\ell -1}$
. We must show that, when
$\mathcal {T}_{\ell -1}$
. We must show that, when
![]() $t \leq {\mathcal {T}_1}^-$
,
$t \leq {\mathcal {T}_1}^-$
,
Because separation decreases at most linearly in time (6.13) and because
![]() $t \leq {\mathcal {T}_1}^-$
,
$t \leq {\mathcal {T}_1}^-$
,
This implies equation (6.14) for
![]() $\ell =1$
because
$\ell =1$
because
The first inequality is a consequence of the definitions of
![]() ${\mathcal {T}_1}^-$
,
${\mathcal {T}_1}^-$
,
![]() $\mathfrak {t}_1$
, and
$\mathfrak {t}_1$
, and
![]() $\rho _1$
, which imply
$\rho _1$
, which imply
![]() ${\mathcal {T}_1}^- \leq \mathfrak {t}_1 \leq (\log \rho _1)^2$
and
${\mathcal {T}_1}^- \leq \mathfrak {t}_1 \leq (\log \rho _1)^2$
and
![]() $\mathrm {sep} (U_0^i) \geq \rho _1$
. Since the ratio of
$\mathrm {sep} (U_0^i) \geq \rho _1$
. Since the ratio of
![]() $(\log \rho _1)^2$
to
$(\log \rho _1)^2$
to
![]() $\rho _1$
decreases as
$\rho _1$
decreases as
![]() $\rho _1$
increases, the second inequality follows from the bound
$\rho _1$
increases, the second inequality follows from the bound
![]() $\rho _1 \geq e^{e^n}$
, which is implied by the fact that
$\rho _1 \geq e^{e^n}$
, which is implied by the fact that
![]() $U_0$
satisfies the exponential separation property (5.1) with parameter
$U_0$
satisfies the exponential separation property (5.1) with parameter
![]() $r \geq e^n$
(6.11).
$r \geq e^n$
(6.11).
The argument for
![]() $\ell> 1$
is similar. Assume equation (6.14) holds for
$\ell> 1$
is similar. Assume equation (6.14) holds for
![]() $\ell -1$
. We have
$\ell -1$
. We have
The first inequality is implied by equation (6.13). The second inequality follows from the definitions of
![]() ${\mathcal {T}_\ell }^-$
and
${\mathcal {T}_\ell }^-$
and
![]() $\mathfrak {t}_\ell $
, which imply
$\mathfrak {t}_\ell $
, which imply
![]() ${\mathcal {T}_\ell }^- - \mathcal {T}_{\ell -1} \leq \mathfrak {t}_\ell \leq (\log \rho _\ell )^2$
, and
${\mathcal {T}_\ell }^- - \mathcal {T}_{\ell -1} \leq \mathfrak {t}_\ell \leq (\log \rho _\ell )^2$
, and
![]() $t \leq {\mathcal {T}_\ell }^-$
. The third inequality is due to the same upper bound on
$t \leq {\mathcal {T}_\ell }^-$
. The third inequality is due to the same upper bound on
![]() $\mathfrak {t}_\ell $
and the fact that
$\mathfrak {t}_\ell $
and the fact that
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
by definition.
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
by definition.
We will bound below
![]() $\rho _\ell $
to complete the induction step with equation (6.16) because the ratio of
$\rho _\ell $
to complete the induction step with equation (6.16) because the ratio of
![]() $(\log \rho _\ell )^2$
to
$(\log \rho _\ell )^2$
to
![]() $\rho _\ell $
decreases as
$\rho _\ell $
decreases as
![]() $\rho _\ell $
increases. Specifically, we will prove equation (6.15). By definition, when
$\rho _\ell $
increases. Specifically, we will prove equation (6.15). By definition, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs so too does
$\mathsf {Timely}_{\ell -1}$
occurs so too does
![]() $\mathsf {Timely} (\ell -2)$
. Accordingly, the induction hypothesis applies and we apply it
$\mathsf {Timely} (\ell -2)$
. Accordingly, the induction hypothesis applies and we apply it
![]() $\ell -1$
times:
$\ell -1$
times:
The equalities follow from the definitions of
![]() $\rho _{\ell -1}$
and
$\rho _{\ell -1}$
and
![]() $\rho _1$
. We also have
$\rho _1$
. We also have
The first inequality is due to equation (6.13) and the fact that at most
![]() $\mathfrak {t}_{\ell -1}$
steps elapse between
$\mathfrak {t}_{\ell -1}$
steps elapse between
![]() $\mathcal {T}_{\ell -2}$
and
$\mathcal {T}_{\ell -2}$
and
![]() $\mathcal {T}_{\ell -1}$
when
$\mathcal {T}_{\ell -1}$
when
![]() $\mathsf {Timely}_{\ell -1}$
occurs. The second inequality is due to
$\mathsf {Timely}_{\ell -1}$
occurs. The second inequality is due to
![]() $\mathfrak {t}_{\ell -1} \leq (\log \rho _{\ell -1})^2$
, and the third is due to the fact that the ratio of
$\mathfrak {t}_{\ell -1} \leq (\log \rho _{\ell -1})^2$
, and the third is due to the fact that the ratio of
![]() $(\log \rho _{\ell -1})^2$
to
$(\log \rho _{\ell -1})^2$
to
![]() $\rho _{\ell -1}$
decreases as
$\rho _{\ell -1}$
decreases as
![]() $\rho _{\ell -1}$
increases.
$\rho _{\ell -1}$
increases.
Combining the two preceding displays and then using the fact that
![]() $\ell \leq n$
and
$\ell \leq n$
and
![]() $\rho _1 \geq e^{e^n}$
and the inequality
$\rho _1 \geq e^{e^n}$
and the inequality
![]() $(1+x)^r \geq 1 + rx$
, which holds for
$(1+x)^r \geq 1 + rx$
, which holds for
![]() $x> -1$
and
$x> -1$
and
![]() $r> 1$
, we find
$r> 1$
, we find
Because
![]() $ne^{-n} \leq \tfrac 12$
when
$ne^{-n} \leq \tfrac 12$
when
![]() $n \geq 2$
, this proves
$n \geq 2$
, this proves
![]() $\rho _\ell \geq \tfrac 12 \rho _1$
, which is the first inequality of equation (6.15). To prove the second inequality in equation (6.15), we note that
$\rho _\ell \geq \tfrac 12 \rho _1$
, which is the first inequality of equation (6.15). To prove the second inequality in equation (6.15), we note that
![]() $\rho _1$
is at least
$\rho _1$
is at least
![]() $\theta _{3n}$
by equation (6.11).
$\theta _{3n}$
by equation (6.11).
We now apply
![]() $\rho _\ell \geq \tfrac 12 \rho _1$
to the ratio in equation (6.16):
$\rho _\ell \geq \tfrac 12 \rho _1$
to the ratio in equation (6.16):
 $$\begin{align*}\frac{(\log \rho_\ell)^2}{\rho_\ell} \leq \frac{2(\log \rho_1)^2}{\rho_1} \leq e^{-n}.\end{align*}$$
$$\begin{align*}\frac{(\log \rho_\ell)^2}{\rho_\ell} \leq \frac{2(\log \rho_1)^2}{\rho_1} \leq e^{-n}.\end{align*}$$
The second inequality uses
![]() $\rho _1 \geq e^{e^n}$
. We complete the induction step, proving equation (6.14), by substituting this bound into equation (6.16).
$\rho _1 \geq e^{e^n}$
. We complete the induction step, proving equation (6.14), by substituting this bound into equation (6.16).
When cluster collapses are timely,
![]() ${\mathcal {T}_\ell }^-$
is at most
${\mathcal {T}_\ell }^-$
is at most
![]() $(\log \rho _\ell )^2$
, up to a factor depending on n.
$(\log \rho _\ell )^2$
, up to a factor depending on n.
Lemma 6.9. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
The factor of
![]() $2$
is for brevity; it could be replaced by
$2$
is for brevity; it could be replaced by
![]() $1+o_n (1)$
. The lower bound on the least separation
$1+o_n (1)$
. The lower bound on the least separation
![]() $\rho _\ell $
at time
$\rho _\ell $
at time
![]() $\mathcal {T}_{\ell -1}$
in equation (6.15) indicates that, while
$\mathcal {T}_{\ell -1}$
in equation (6.15) indicates that, while
![]() $\rho _\ell $
may be much larger than
$\rho _\ell $
may be much larger than
![]() $\rho _1$
, it is at least half of
$\rho _1$
, it is at least half of
![]() $\rho _1$
. Since the expiry time
$\rho _1$
. Since the expiry time
![]() $\mathfrak {t}_\ell $
is approximately
$\mathfrak {t}_\ell $
is approximately
![]() $(\log \rho _\ell )^2$
, the truncated collapse time
$(\log \rho _\ell )^2$
, the truncated collapse time
![]() ${\mathcal {T}_\ell }^-$
– which is at most the sum of the first
${\mathcal {T}_\ell }^-$
– which is at most the sum of the first
![]() $\ell $
expiry times – should be of the same order, up to a factor depending on
$\ell $
expiry times – should be of the same order, up to a factor depending on
![]() $\ell $
(which we will replace with n since
$\ell $
(which we will replace with n since
![]() $\ell \leq n$
).
$\ell \leq n$
).
Proof of Lemma 6.9.
We write
 $$\begin{align*}{\mathcal{T}_\ell}^- = {\mathcal{T}_\ell}^- - \mathcal{T}_{\ell -1} + \sum_{m=1}^{\ell-1} (\mathcal{T}_m - \mathcal{T}_{m-1}) \leq \sum_{m=1}^\ell \mathfrak{t}_m \leq \sum_{m=1}^{\ell} (\log \rho_m)^2.\end{align*}$$
$$\begin{align*}{\mathcal{T}_\ell}^- = {\mathcal{T}_\ell}^- - \mathcal{T}_{\ell -1} + \sum_{m=1}^{\ell-1} (\mathcal{T}_m - \mathcal{T}_{m-1}) \leq \sum_{m=1}^\ell \mathfrak{t}_m \leq \sum_{m=1}^{\ell} (\log \rho_m)^2.\end{align*}$$
The first inequality follows from the fact that, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
![]() $\mathcal {T}_m - \mathcal {T}_{m-1} \leq \mathfrak {t}_m$
for
$\mathcal {T}_m - \mathcal {T}_{m-1} \leq \mathfrak {t}_m$
for
![]() $m \leq \ell -1$
and
$m \leq \ell -1$
and
![]() ${\mathcal {T}_\ell }^- - \mathcal {T}_{\ell -1} \leq \mathfrak {t}_\ell $
. The second inequality holds because
${\mathcal {T}_\ell }^- - \mathcal {T}_{\ell -1} \leq \mathfrak {t}_\ell $
. The second inequality holds because
![]() $\mathfrak {t}_m \leq (\log \rho _m)^2$
by definition.
$\mathfrak {t}_m \leq (\log \rho _m)^2$
by definition.
Next, assume w.l.o.g. that cluster i is least separated at time
![]() $\mathcal {T}_{\ell -1}$
, meaning
$\mathcal {T}_{\ell -1}$
, meaning
![]() $\rho _\ell = \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
. Since
$\rho _\ell = \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
. Since
![]() $\mathsf {Timely}_{\ell -1}$
occurs, Lemma 6.8 applies and with its repeated use we establish equation (6.17):
$\mathsf {Timely}_{\ell -1}$
occurs, Lemma 6.8 applies and with its repeated use we establish equation (6.17):
 $$\begin{align*}\sum_{m=1}^{\ell} (\log \rho_m)^2 &\leq \sum_{m=1}^{\ell} \big( \log \mathrm{sep} (U_{\mathcal{T}_{m-1}}^i) \big)^2 \\ &\leq \sum_{m=1}^\ell \Big( \log \big( (1+\tfrac{e^{-n}}{1-e^{-n}})^{\ell-m} \rho_\ell \big) \Big)^2 \leq \ell (\log (2 \rho_\ell) )^2 \leq 2 n (\log \rho_\ell)^2.\end{align*}$$
$$\begin{align*}\sum_{m=1}^{\ell} (\log \rho_m)^2 &\leq \sum_{m=1}^{\ell} \big( \log \mathrm{sep} (U_{\mathcal{T}_{m-1}}^i) \big)^2 \\ &\leq \sum_{m=1}^\ell \Big( \log \big( (1+\tfrac{e^{-n}}{1-e^{-n}})^{\ell-m} \rho_\ell \big) \Big)^2 \leq \ell (\log (2 \rho_\ell) )^2 \leq 2 n (\log \rho_\ell)^2.\end{align*}$$
The first inequality is due to the definition of
![]() $\rho _m$
as the least separation at time
$\rho _m$
as the least separation at time
![]() $\mathcal {T}_{m-1}$
. This step is helpful because it replaces each summand with one concerning the i
th cluster. The second inequality holds because, by Lemma 6.8,
$\mathcal {T}_{m-1}$
. This step is helpful because it replaces each summand with one concerning the i
th cluster. The second inequality holds because, by Lemma 6.8,
The third inequality follows from
![]() $\ell \leq n$
and
$\ell \leq n$
and
![]() $(1+\tfrac {e^{-n}}{1-e^{-n}})^n \leq 2$
when
$(1+\tfrac {e^{-n}}{1-e^{-n}})^n \leq 2$
when
![]() $n \geq 2$
. The fourth inequality is due to
$n \geq 2$
. The fourth inequality is due to
![]() $\ell \leq n$
and
$\ell \leq n$
and
![]() $\rho _\ell \geq e^{\theta _{2n}}$
from equation (6.15). (The factor of
$\rho _\ell \geq e^{\theta _{2n}}$
from equation (6.15). (The factor of
![]() $2$
could be replaced by
$2$
could be replaced by
![]() $1+o_n (1)$
.) Combining the displays proves equation (6.17).
$1+o_n (1)$
.) Combining the displays proves equation (6.17).
When cluster collapse is timely, we can bound cluster diameter at time
![]() $t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
from above, in terms of its separation at time
$t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
from above, in terms of its separation at time
![]() $\mathcal {T}_{\ell -1}$
or at time t.
$\mathcal {T}_{\ell -1}$
or at time t.
Lemma 6.10. For any cluster i, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
$\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
![]() ${\mathcal {T}_\ell }^-$
,
${\mathcal {T}_\ell }^-$
,
Additionally, if
![]() $x_i$
is the center of the i
th cluster resulting from the exponential clustering of
$x_i$
is the center of the i
th cluster resulting from the exponential clustering of
![]() $U_0$
, then when t is at most
$U_0$
, then when t is at most
![]() ${\mathcal {T}_\ell }^-$
,
${\mathcal {T}_\ell }^-$
,
Lastly, if
![]() $i,j$
label any two clusters which are nonempty at time
$i,j$
label any two clusters which are nonempty at time
![]() $\mathcal {T}_{\ell -1}$
, then when t is at most
$\mathcal {T}_{\ell -1}$
, then when t is at most
![]() ${\mathcal {T}_\ell }^-$
,
${\mathcal {T}_\ell }^-$
,
 $$ \begin{align} \frac{\log \mathrm{diam} (U_t^i)}{\log {\mathrm{dist}}(U_t^i, U_t^j)} \leq \frac{2.1 \log \log \rho_\ell}{\log \rho_\ell}. \end{align} $$
$$ \begin{align} \frac{\log \mathrm{diam} (U_t^i)}{\log {\mathrm{dist}}(U_t^i, U_t^j)} \leq \frac{2.1 \log \log \rho_\ell}{\log \rho_\ell}. \end{align} $$
We use factors of
![]() $0.99$
and
$0.99$
and
![]() $2.1$
for concreteness; they could be replaced by
$2.1$
for concreteness; they could be replaced by
![]() $1-o_n(1)$
and
$1-o_n(1)$
and
![]() $2+o_n(1)$
. Lemma 6.10 implements the diameter and separation bounds we discussed in Section 6.2.2 (there, we used
$2+o_n(1)$
. Lemma 6.10 implements the diameter and separation bounds we discussed in Section 6.2.2 (there, we used
![]() $\rho $
in the place of
$\rho $
in the place of
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
). Before proving the lemma, we discuss some heuristics which explain equation (6.18) through (6.20).
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
). Before proving the lemma, we discuss some heuristics which explain equation (6.18) through (6.20).
If a cluster is initially separated by a distance
![]() $\rho $
, then it has a diameter of at most
$\rho $
, then it has a diameter of at most
![]() $2 \log \rho $
by equation (5.1), which is negligible relative to an expiry time of order
$2 \log \rho $
by equation (5.1), which is negligible relative to an expiry time of order
![]() $(\log \rho )^2$
. Diameter increases at most linearly in time by equation (6.12), so when cluster collapse is timely the diameter of
$(\log \rho )^2$
. Diameter increases at most linearly in time by equation (6.12), so when cluster collapse is timely the diameter of
![]() $U_t^i$
is at most
$U_t^i$
is at most
![]() $\big ( \log \mathrm {sep}(U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
. In fact, the definition of the expiry time subtracts the lower order terms, so the bound will be exactly this quantity. Moreover, since
$\big ( \log \mathrm {sep}(U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
. In fact, the definition of the expiry time subtracts the lower order terms, so the bound will be exactly this quantity. Moreover, since
![]() $(\log \rho )^2$
is negligible relative to the separation
$(\log \rho )^2$
is negligible relative to the separation
![]() $\rho $
, and as separation decreases at most linearly in time by equation (6.13), the separation of
$\rho $
, and as separation decreases at most linearly in time by equation (6.13), the separation of
![]() $U_t^i$
should be at least
$U_t^i$
should be at least
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
, up to a constant which is nearly one.
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
, up to a constant which is nearly one.
Combining these bounds on diameter and separation suggests that the ratio of the diameter of
![]() $U_t^i$
to its separation from another cluster
$U_t^i$
to its separation from another cluster
![]() $U_t^j$
should be roughly the ratio of
$U_t^j$
should be roughly the ratio of
![]() $\big (\log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
to
$\big (\log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
to
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
, up to a constant factor. Because this ratio is decreasing in the separation (for separation exceeding, say,
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
, up to a constant factor. Because this ratio is decreasing in the separation (for separation exceeding, say,
![]() $e^2$
) and because the separation at time
$e^2$
) and because the separation at time
![]() $\mathcal {T}_{\ell -1}$
is at least
$\mathcal {T}_{\ell -1}$
is at least
![]() $\rho _\ell $
, the ratio
$\rho _\ell $
, the ratio
![]() $\tfrac {(\log \rho _\ell )^2}{\rho _\ell }$
should provide a further upper bound, again up to a constant factor. These three observations correspond to equations (6.18) through (6.20).
$\tfrac {(\log \rho _\ell )^2}{\rho _\ell }$
should provide a further upper bound, again up to a constant factor. These three observations correspond to equations (6.18) through (6.20).
Proof of Lemma 6.10.
We first address equation (6.18) and use it to prove equation (6.19). We then combine the results to prove equation (6.20). We bound
![]() $\mathrm {diam} (U_t^i)$
from above in terms of
$\mathrm {diam} (U_t^i)$
from above in terms of
![]() $\mathrm {diam} (U_0^i)$
as
$\mathrm {diam} (U_0^i)$
as
The first inequality holds because diameter grows at most linearly in time (6.12) and because t is at most
![]() ${\mathcal {T}_\ell }^-$
. The second inequality is due to the definition of
${\mathcal {T}_\ell }^-$
. The second inequality is due to the definition of
![]() ${\mathcal {T}_\ell }^-$
. We then bound
${\mathcal {T}_\ell }^-$
. We then bound
![]() $\mathrm {diam} (U_0^i)$
from above in terms of
$\mathrm {diam} (U_0^i)$
from above in terms of
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
as
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
as
The exponential separation property (5.1) implies the first inequality, and equation (6.13) implies the second.
Combining the two preceding displays, we find
Substituting the definition of
![]() $\mathfrak {t}_\ell $
, the right-hand side becomes
$\mathfrak {t}_\ell $
, the right-hand side becomes
By definition,
![]() $\rho _\ell $
is the least separation at time
$\rho _\ell $
is the least separation at time
![]() $\mathcal {T}_{\ell -1}$
, so we can further bound
$\mathcal {T}_{\ell -1}$
, so we can further bound
![]() $\mathrm {diam} (U_t^i)$
from above by substituting
$\mathrm {diam} (U_t^i)$
from above by substituting
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
for
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
for
![]() $\rho _\ell $
:
$\rho _\ell $
:
Dropping the negative term gives equation (6.18).
We turn our attention to equation (6.19). To obtain the first inclusion of equation (6.19), we observe that
![]() $U_t^i$
is contained in the disk
$U_t^i$
is contained in the disk
![]() $D_{x_i} \big ( \mathrm {diam} (U_0^i) + \mathcal {T}_{\ell -1} + \mathfrak {t}_\ell \big )$
, the radius of which is the quantity in equation (6.21) that we ultimately bounded above by
$D_{x_i} \big ( \mathrm {diam} (U_0^i) + \mathcal {T}_{\ell -1} + \mathfrak {t}_\ell \big )$
, the radius of which is the quantity in equation (6.21) that we ultimately bounded above by
![]() $\big ( \log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
.
$\big ( \log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
.
Concerning the second inclusion of equation (6.19), we observe that for any y in
![]() $U_t {\setminus } U_t^i$
, there is some
$U_t {\setminus } U_t^i$
, there is some
![]() $y'$
in
$y'$
in
![]() $U_{\mathcal {T}_{\ell -1}} {\setminus } U_{\mathcal {T}_{\ell -1}}^i$
such that
$U_{\mathcal {T}_{\ell -1}} {\setminus } U_{\mathcal {T}_{\ell -1}}^i$
such that
![]() $|y-y'|$
is at most
$|y-y'|$
is at most
![]() $\mathfrak {t}_\ell $
because t is at most
$\mathfrak {t}_\ell $
because t is at most
![]() ${\mathcal {T}_\ell }^-$
. By the triangle inequality and the bound on
${\mathcal {T}_\ell }^-$
. By the triangle inequality and the bound on
![]() $|y-y'|$
,
$|y-y'|$
,
Next, we observe that the distance between
![]() $x_i$
and
$x_i$
and
![]() $y'$
is at least
$y'$
is at least
The two preceding displays and equation (6.22) imply
We continue (6.24) with
The first inequality follows from substituting the definition of
![]() $\mathfrak {t}_\ell $
into equation (6.24) and from
$\mathfrak {t}_\ell $
into equation (6.24) and from
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
. The second inequality holds because the ratio of
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
. The second inequality holds because the ratio of
![]() $\big ( \log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
to
$\big ( \log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
to
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
decreases as
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
decreases as
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
increases and because
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
increases and because
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
. The fact (6.15) that
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \geq \rho _\ell $
. The fact (6.15) that
![]() $\rho _\ell $
is at least
$\rho _\ell $
is at least
![]() $e^{\theta _{2n}} \geq e^{\theta _2 (\gamma )}$
when
$e^{\theta _{2n}} \geq e^{\theta _2 (\gamma )}$
when
![]() $\mathsf {Timely}_{\ell -1}$
occurs implies that the ratio in equation (6.25) is at most
$\mathsf {Timely}_{\ell -1}$
occurs implies that the ratio in equation (6.25) is at most
![]() $0.01$
because
$0.01$
because
![]() $\theta _{2}(\gamma )^2 \leq 0.01 e^{\theta _{2}(\gamma )}$
, which justifies the third inequality. Equation (6.25) proves the second inclusion of equation (6.19).
$\theta _{2}(\gamma )^2 \leq 0.01 e^{\theta _{2}(\gamma )}$
, which justifies the third inequality. Equation (6.25) proves the second inclusion of equation (6.19).
Lastly, to address equation (6.20), we observe that any element x in
![]() $U_t^i$
is within a distance
$U_t^i$
is within a distance
![]() $\big (\log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
of
$\big (\log \mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i) \big )^2$
of
![]() $x_i$
by equation (6.23). So, by equation (6.25) and simplifying with
$x_i$
by equation (6.23). So, by equation (6.25) and simplifying with
![]() $\rho _\ell \geq e^{\theta _{2n}}$
, the distance between
$\rho _\ell \geq e^{\theta _{2n}}$
, the distance between
![]() $U_t^i$
and
$U_t^i$
and
![]() $U_t^j$
is at least
$U_t^j$
is at least
Combining this with equation (6.18), and then using the fact that
![]() $\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
is at least
$\mathrm {sep} (U_{\mathcal {T}_{\ell -1}}^i)$
is at least
![]() $\rho _\ell $
, gives
$\rho _\ell $
, gives
 $$\begin{align*}\frac{\log \mathrm{diam} (U_t^i)}{\log {\mathrm{dist}}(U_t^i, U_t^j)} \leq \frac{2 \log \log \mathrm{sep} (U_{\mathcal{T}_{\ell-1}}^i)}{\log \big(0.99\, \mathrm{sep} (U_{\mathcal{T}_{\ell-1}}^i) \big)} \leq \frac{2.1\log \log \rho_\ell}{ \log \rho_\ell}.\end{align*}$$
$$\begin{align*}\frac{\log \mathrm{diam} (U_t^i)}{\log {\mathrm{dist}}(U_t^i, U_t^j)} \leq \frac{2 \log \log \mathrm{sep} (U_{\mathcal{T}_{\ell-1}}^i)}{\log \big(0.99\, \mathrm{sep} (U_{\mathcal{T}_{\ell-1}}^i) \big)} \leq \frac{2.1\log \log \rho_\ell}{ \log \rho_\ell}.\end{align*}$$
The next lemma concerns two properties of the midway point introduced in Section 6.2. We recall that the midway point (for the period beginning at time
![]() $\mathcal {T}_{\ell -1}$
and continuing until
$\mathcal {T}_{\ell -1}$
and continuing until
![]() ${\mathcal {T}_\ell }^-$
) is a circle of radius
${\mathcal {T}_\ell }^-$
) is a circle of radius
![]() $\tfrac 12 \rho _\ell $
, centered on the center
$\tfrac 12 \rho _\ell $
, centered on the center
![]() $x_i$
(given by the initial exponential clustering of
$x_i$
(given by the initial exponential clustering of
![]() $U_0$
) of a cluster i which is least separated at time
$U_0$
) of a cluster i which is least separated at time
![]() $\mathcal {T}_{\ell -1}$
. The first property is the simple fact that, when collapse is timely, the midway point separates
$\mathcal {T}_{\ell -1}$
. The first property is the simple fact that, when collapse is timely, the midway point separates
![]() $U_t^i$
from the rest of
$U_t^i$
from the rest of
![]() $U_t$
until time
$U_t$
until time
![]() ${\mathcal {T}_\ell }^-$
. This is clear because the midway point is a distance of
${\mathcal {T}_\ell }^-$
. This is clear because the midway point is a distance of
![]() $\tfrac 12 \rho _\ell $
from
$\tfrac 12 \rho _\ell $
from
![]() $U_{\mathcal {T}_{\ell -1}}$
and
$U_{\mathcal {T}_{\ell -1}}$
and
![]() ${\mathcal {T}_\ell }^-$
is no more than
${\mathcal {T}_\ell }^-$
is no more than
![]() $(\log \rho _\ell )^2$
steps away from
$(\log \rho _\ell )^2$
steps away from
![]() $\mathcal {T}_{\ell -1}$
when collapse is timely. The second property is the fact that a random walk from anywhere in the midway point hits
$\mathcal {T}_{\ell -1}$
when collapse is timely. The second property is the fact that a random walk from anywhere in the midway point hits
![]() $U_t^i$
before the rest of
$U_t^i$
before the rest of
![]() $U_t$
(excluding the site of the activated particle) with a probability of at most
$U_t$
(excluding the site of the activated particle) with a probability of at most
![]() $0.51$
, which is reasonable because the random walk begins effectively halfway between
$0.51$
, which is reasonable because the random walk begins effectively halfway between
![]() $U_t^i$
and the rest of
$U_t^i$
and the rest of
![]() $U_t$
. In terms of notation, when activation occurs at u, the bound applies to the probability of the event
$U_t$
. In terms of notation, when activation occurs at u, the bound applies to the probability of the event
We will stipulate that u belongs to a cluster in
![]() $U_t$
which is not a singleton as, otherwise, its activation at time t necessitates
$U_t$
which is not a singleton as, otherwise, its activation at time t necessitates
![]() $t = \mathcal {T}_\ell $
.
$t = \mathcal {T}_\ell $
.
Lemma 6.11. Suppose cluster i is least separated at time
![]() $\mathcal {T}_{\ell -1}$
and recall that
$\mathcal {T}_{\ell -1}$
and recall that
![]() $x_i$
denotes the center of the i
th cluster, determined by the exponential clustering of
$x_i$
denotes the center of the i
th cluster, determined by the exponential clustering of
![]() $U_0$
. When
$U_0$
. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
$\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
![]() ${\mathcal {T}_\ell }^-$
:
${\mathcal {T}_\ell }^-$
:
-
1. the midway point
 $C(i; \ell ) = C_{x_i} \left (\tfrac 12 \rho _\ell \right )$
separates
$C(i; \ell ) = C_{x_i} \left (\tfrac 12 \rho _\ell \right )$
separates
 $U_t^i$
from
$U_t^i$
from
 $U_t {\setminus } U_t^i$
, and
$U_t {\setminus } U_t^i$
, and -
2. for any u in
 $U_t$
which does not belong to a singleton cluster and any y in
$U_t$
which does not belong to a singleton cluster and any y in
 $C(i; \ell )$
, (6.26)
$C(i; \ell )$
, (6.26) $$ \begin{align} \mathbb{P}_y \left(\tau_{U_t^i {\setminus} \{u\}} < \tau_{U_t {\setminus} (U_t^i \,\cup\, \{u\})} \right) \leq 0.51. \end{align} $$
$$ \begin{align} \mathbb{P}_y \left(\tau_{U_t^i {\setminus} \{u\}} < \tau_{U_t {\setminus} (U_t^i \,\cup\, \{u\})} \right) \leq 0.51. \end{align} $$
Proof. Property (1) is an immediate consequence of equation (6.19) of Lemma 6.10 since
![]() $\tfrac 12 \rho _\ell $
is at least
$\tfrac 12 \rho _\ell $
is at least
![]() $(\log \rho _\ell )^2$
and less than
$(\log \rho _\ell )^2$
and less than
![]() $0.99 \rho _\ell $
.
$0.99 \rho _\ell $
.
Now, let u and y satisfy the hypotheses from #2, denote the center of the i
th cluster by
![]() $x_i$
, and denote
$x_i$
, and denote
![]() $C ((\log \rho _\ell )^2)$
by B. To prove property
$C ((\log \rho _\ell )^2)$
by B. To prove property
![]() $(2)$
, we will establish
$(2)$
, we will establish
for some
![]() $z \in U_t {\setminus } (U_t^i \, \cup \, \{u\})$
. This bound implies equation (6.26) because, equation by (6.19), B separates
$z \in U_t {\setminus } (U_t^i \, \cup \, \{u\})$
. This bound implies equation (6.26) because, equation by (6.19), B separates
![]() $U_t^i - x_i$
from the rest of
$U_t^i - x_i$
from the rest of
![]() $U_t - x_i$
.
$U_t - x_i$
.
We can express the probability in equation (6.27) in terms of hitting probabilities involving only three points:
 $$ \begin{align*} \mathbb{P}_{y-x_i} (\tau_{B} < \tau_{z-x_i}) & = \mathbb{P}_{y-x_i} (\tau_o < \tau_{z-x_i}) + \mathbb{E}_{y-x_i} \left[ \mathbb{P}_{S_{\tau_{B}}} ( \tau_{z-x_i} < \tau_o ) \mathbf{1} (\tau_{B} < \tau_{z-x_i}) \right] \nonumber\\ & \leq \mathbb{P}_{y-x_i} (\tau_o < \tau_{z-x_i}) + \max_{v \in B} \mathbb{P}_v (\tau_{z-x_i} < \tau_o) \, \mathbb{P}_{y-x_i} (\tau_{B} < \tau_{z-x_i}). \end{align*} $$
$$ \begin{align*} \mathbb{P}_{y-x_i} (\tau_{B} < \tau_{z-x_i}) & = \mathbb{P}_{y-x_i} (\tau_o < \tau_{z-x_i}) + \mathbb{E}_{y-x_i} \left[ \mathbb{P}_{S_{\tau_{B}}} ( \tau_{z-x_i} < \tau_o ) \mathbf{1} (\tau_{B} < \tau_{z-x_i}) \right] \nonumber\\ & \leq \mathbb{P}_{y-x_i} (\tau_o < \tau_{z-x_i}) + \max_{v \in B} \mathbb{P}_v (\tau_{z-x_i} < \tau_o) \, \mathbb{P}_{y-x_i} (\tau_{B} < \tau_{z-x_i}). \end{align*} $$
Rearranging, we find
We will choose z so that the points
![]() $y-x_i$
and
$y-x_i$
and
![]() $z-x_i$
will be at comparable distances from the origin and, consequently,
$z-x_i$
will be at comparable distances from the origin and, consequently,
![]() $\mathbb {P}_{y-x_i} (\tau _o < \tau _{z-x_i})$
will be nearly
$\mathbb {P}_{y-x_i} (\tau _o < \tau _{z-x_i})$
will be nearly
![]() $1/2$
. In contrast, every element of B will be far nearer to the origin than to
$1/2$
. In contrast, every element of B will be far nearer to the origin than to
![]() $z-x_i$
, so
$z-x_i$
, so
![]() $\mathbb {P}_v (\tau _{z-x_i} < \tau _o)$
will be nearly zero for every v in B. We will write these probabilities in terms of the potential kernel using Lemma 3.9. We will need bounds on the distances
$\mathbb {P}_v (\tau _{z-x_i} < \tau _o)$
will be nearly zero for every v in B. We will write these probabilities in terms of the potential kernel using Lemma 3.9. We will need bounds on the distances
![]() $|z-x_i|$
and
$|z-x_i|$
and
![]() $|z-y|$
to simplify the potential kernel terms; we take care of this now.
$|z-y|$
to simplify the potential kernel terms; we take care of this now.
Suppose cluster j was nearest to cluster i at time
![]() $\mathcal {T}_{\ell -1}$
. We then choose z to be the element of
$\mathcal {T}_{\ell -1}$
. We then choose z to be the element of
![]() $U_t^j$
nearest to
$U_t^j$
nearest to
![]() $U_t^i$
. Note that such an element exists because, when t is at most
$U_t^i$
. Note that such an element exists because, when t is at most
![]() ${\mathcal {T}_\ell }^-$
, every cluster surviving until time
${\mathcal {T}_\ell }^-$
, every cluster surviving until time
![]() $\mathcal {T}_{\ell -1}$
survives until time t. By equation (6.19) of Lemma 6.10,
$\mathcal {T}_{\ell -1}$
survives until time t. By equation (6.19) of Lemma 6.10,
Part (2) of Lemma A.1 then gives the lower bound
In the intercollapse period before
![]() ${\mathcal {T}_\ell }^-$
, the separation between z and y (initially
${\mathcal {T}_\ell }^-$
, the separation between z and y (initially
![]() $\tfrac 12 \rho _\ell $
) can grow by at most
$\tfrac 12 \rho _\ell $
) can grow by at most
![]() $\mathfrak {t}_\ell + \mathrm {diam} (U_{\mathcal {T}_{\ell -1}}^j)$
:
$\mathfrak {t}_\ell + \mathrm {diam} (U_{\mathcal {T}_{\ell -1}}^j)$
:
By equation (6.18), the diameter of cluster j at time
![]() $\mathcal {T}_{\ell -1}$
is at most
$\mathcal {T}_{\ell -1}$
is at most
![]() $(\log \rho _\ell )^2$
; this upper bound applies to
$(\log \rho _\ell )^2$
; this upper bound applies to
![]() $\mathfrak {t}_\ell $
as well, so
$\mathfrak {t}_\ell $
as well, so
We obtained the second inequality using the fact (6.15) that, when
![]() $\mathsf {Timely}(\ell -1)$
occurs,
$\mathsf {Timely}(\ell -1)$
occurs,
![]() $\rho _\ell $
is at least
$\rho _\ell $
is at least
![]() $e^{\theta _{2n}}$
. (In what follows, we will use this fact without restating it.)
$e^{\theta _{2n}}$
. (In what follows, we will use this fact without restating it.)
Accordingly, the difference between
![]() $\mathfrak {a} (z-y)$
and
$\mathfrak {a} (z-y)$
and
![]() $\mathfrak {a} (y-x_i)$
satisfies
$\mathfrak {a} (y-x_i)$
satisfies
By Lemma 3.9, the first term of equation (6.28) equals
Substituting equations (6.29) and (6.30) into equation (6.31), we find
We turn our attention to bounding above the maximum of
![]() $\mathbb {P}_v (\tau _{z-x_i} < \tau _o)$
over v in B. This quantity should be close to
$\mathbb {P}_v (\tau _{z-x_i} < \tau _o)$
over v in B. This quantity should be close to
![]() $0$
for every
$0$
for every
![]() $v \in B$
because the elements of B are only a distance of roughly
$v \in B$
because the elements of B are only a distance of roughly
![]() $(\log \rho _\ell )^2$
from the origin, but they are nearly
$(\log \rho _\ell )^2$
from the origin, but they are nearly
![]() $\rho _\ell $
from
$\rho _\ell $
from
![]() $z-x_i$
. For any such v, Lemma 3.9 gives
$z-x_i$
. For any such v, Lemma 3.9 gives
By Lemma A.2,
![]() $\mathfrak {a} (v)$
is at most
$\mathfrak {a} (v)$
is at most
![]() $\mathfrak {a}' ((\log \rho _\ell )^2) + 2 (\log \rho _\ell )^{-2}$
. Then, since
$\mathfrak {a}' ((\log \rho _\ell )^2) + 2 (\log \rho _\ell )^{-2}$
. Then, since
we have
Substituting equations (6.29) and (6.34) into equation (6.33), we find
This bound holds uniformly over v in B. Applying it and equation (6.32) to equation (6.28), we find
Combined with the separation lower bound (6.15) of Lemma 6.8, the inclusions (6.19) of Lemma 6.10 ensure that, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs, nonempty clusters at time
$\mathsf {Timely}_{\ell -1}$
occurs, nonempty clusters at time
![]() $t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
are contained in well-separated disks. A natural consequence is that, when
$t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
are contained in well-separated disks. A natural consequence is that, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs, every nonempty cluster has positive harmonic measure in
$\mathsf {Timely}_{\ell -1}$
occurs, every nonempty cluster has positive harmonic measure in
![]() $U_t$
. Later, we will use this fact in conjunction with Theorem 4 to control the activation step of the HAT dynamics.
$U_t$
. Later, we will use this fact in conjunction with Theorem 4 to control the activation step of the HAT dynamics.
Lemma 6.12. Let
![]() $I_\ell $
be the set of indices of nonempty clusters at time
$I_\ell $
be the set of indices of nonempty clusters at time
![]() $\mathcal {T}_{\ell -1}$
. When
$\mathcal {T}_{\ell -1}$
. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
$\mathsf {Timely}_{\ell -1}$
occurs and when t is at most
![]() ${\mathcal {T}_\ell }^-$
,
${\mathcal {T}_\ell }^-$
,
![]() ${\mathbb {H}}_{U_t} (U_t^i)> 0$
for every
${\mathbb {H}}_{U_t} (U_t^i)> 0$
for every
![]() $i \in I_\ell $
.
$i \in I_\ell $
.
The proof shares some ideas with the proof of Lemma 3.13. Recall the definition of the
![]() $\ast $
-exterior boundary (3.18) and define the disk
$\ast $
-exterior boundary (3.18) and define the disk
![]() $D^i$
to be the one from equation (6.19)
$D^i$
to be the one from equation (6.19)
For simplicity, assume
![]() $1 \in I_\ell $
. Most of the proof is devoted to showing that there is a path
$1 \in I_\ell $
. Most of the proof is devoted to showing that there is a path
![]() $\Gamma $
from
$\Gamma $
from
![]() $\partial _{\mathrm {ext}}^\ast D^1$
to a large circle C about
$\partial _{\mathrm {ext}}^\ast D^1$
to a large circle C about
![]() $U_t$
, which avoids
$U_t$
, which avoids
![]() $\cup _{i \in I_\ell } D^i$
and thus avoids
$\cup _{i \in I_\ell } D^i$
and thus avoids
![]() $U_t$
. To do so, we will specify a candidate path from
$U_t$
. To do so, we will specify a candidate path from
![]() $\partial _{\mathrm {ext}}^\ast D^1$
to C, and modify it as follows. If the path encounters a disk
$\partial _{\mathrm {ext}}^\ast D^1$
to C, and modify it as follows. If the path encounters a disk
![]() $D^i$
, then we will reroute the path around
$D^i$
, then we will reroute the path around
![]() $\partial _{\mathrm {ext}}^\ast D^i$
(which will be connected and will not intersect another disk). The fact that
$\partial _{\mathrm {ext}}^\ast D^i$
(which will be connected and will not intersect another disk). The fact that
![]() $\partial _{\mathrm {ext}}^\ast D^i$
will not intersect another disk is a consequence of the separation between clusters. The modified path encounters one fewer disk. We will iterate this argument until the path avoids every disk and therefore never returns to
$\partial _{\mathrm {ext}}^\ast D^i$
will not intersect another disk is a consequence of the separation between clusters. The modified path encounters one fewer disk. We will iterate this argument until the path avoids every disk and therefore never returns to
![]() $U_t$
.
$U_t$
.
Proof of Lemma 6.12.
Suppose
![]() $\mathsf {Timely}_{\ell -1}$
occurs and
$\mathsf {Timely}_{\ell -1}$
occurs and
![]() $t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
, and assume w.l.o.g. that
$t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
, and assume w.l.o.g. that
![]() $1 \in I_\ell $
. Let
$1 \in I_\ell $
. Let
![]() $y \in U_t^1$
satisfy
$y \in U_t^1$
satisfy
![]() ${\mathbb {H}}_{U_t^1} (y)> 0$
. (Note that there must be such a y because we are considering
${\mathbb {H}}_{U_t^1} (y)> 0$
. (Note that there must be such a y because we are considering
![]() $U_t^1$
, not
$U_t^1$
, not
![]() $U_t$
.) For each
$U_t$
.) For each
![]() $i \in I_\ell $
, let
$i \in I_\ell $
, let
![]() $D^i$
be the disk defined in equation (6.35). As
$D^i$
be the disk defined in equation (6.35). As
![]() ${\mathbb {H}}_{U_t^1} (y)$
is positive, there is a path from y to
${\mathbb {H}}_{U_t^1} (y)$
is positive, there is a path from y to
![]() $\partial _{\mathrm {ext}}^\ast D^1$
which does not return to
$\partial _{\mathrm {ext}}^\ast D^1$
which does not return to
![]() $U_t^1$
. In a moment, we will show that
$U_t^1$
. In a moment, we will show that
![]() $\partial _{\mathrm {ext}}^\ast D^1$
is connected, so it will suffice to prove that there is a subsequent path from
$\partial _{\mathrm {ext}}^\ast D^1$
is connected, so it will suffice to prove that there is a subsequent path from
![]() $\partial _{\mathrm {ext}}^\ast D^1$
to
$\partial _{\mathrm {ext}}^\ast D^1$
to
![]() $C = C_{x_1} (2 \, \mathrm {diam} (U_t))$
which does not return to
$C = C_{x_1} (2 \, \mathrm {diam} (U_t))$
which does not return to
![]() $E = \cup _{i \in I_\ell } D^i$
. This suffices when
$E = \cup _{i \in I_\ell } D^i$
. This suffices when
![]() $\mathsf {Timely}_{\ell -1}$
occurs because then, by Lemma 6.10,
$\mathsf {Timely}_{\ell -1}$
occurs because then, by Lemma 6.10,
![]() $U_t^i \subseteq D^i$
for each
$U_t^i \subseteq D^i$
for each
![]() $i \in I_\ell $
, so
$i \in I_\ell $
, so
![]() $U_t \subseteq E$
.
$U_t \subseteq E$
.
We make two observations. First, because each
![]() $D^i$
is finite and
$D^i$
is finite and
![]() $\ast $
-connected, Lemma 2.23 of [Reference KestenKes86] (alternatively, Theorem 4 of [Reference TimárTim13]) states that each
$\ast $
-connected, Lemma 2.23 of [Reference KestenKes86] (alternatively, Theorem 4 of [Reference TimárTim13]) states that each
![]() $\partial _{\mathrm {ext}}^\ast D^i$
is connected. Second,
$\partial _{\mathrm {ext}}^\ast D^i$
is connected. Second,
![]() $\partial _{\mathrm {ext}}^\ast D^i$
is disjoint from E when
$\partial _{\mathrm {ext}}^\ast D^i$
is disjoint from E when
![]() $\mathsf {Timely}_{\ell -1}$
occurs; this is an easy consequence of equation (6.19) and the separation lower bound (6.15).
$\mathsf {Timely}_{\ell -1}$
occurs; this is an easy consequence of equation (6.19) and the separation lower bound (6.15).
We now specify a candidate path from
![]() $\partial _{\mathrm {ext}}^\ast D^1$
to C and, if necessary, modify it to ensure that it does not return to E. Because
$\partial _{\mathrm {ext}}^\ast D^1$
to C and, if necessary, modify it to ensure that it does not return to E. Because
![]() ${\mathbb {H}}_{U_t^1} (y)$
is positive, there is a shortest path
${\mathbb {H}}_{U_t^1} (y)$
is positive, there is a shortest path
![]() $\Gamma $
from
$\Gamma $
from
![]() $\partial _{\mathrm {ext}}^\ast D^1$
to C, which does not return to
$\partial _{\mathrm {ext}}^\ast D^1$
to C, which does not return to
![]() $U_t^1$
. Let L be the set of labels of disks encountered by
$U_t^1$
. Let L be the set of labels of disks encountered by
![]() $\Gamma $
. If L is empty, then we are done. Otherwise, let i be the label of the first disk encountered by
$\Gamma $
. If L is empty, then we are done. Otherwise, let i be the label of the first disk encountered by
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $\Gamma _a$
and
$\Gamma _a$
and
![]() $\Gamma _b$
be the first and last elements of
$\Gamma _b$
be the first and last elements of
![]() $\Gamma $
which intersect
$\Gamma $
which intersect
![]() $\partial _{\mathrm {ext}}^\ast D^i$
. By our first observation,
$\partial _{\mathrm {ext}}^\ast D^i$
. By our first observation,
![]() $\partial _{\mathrm {ext}}^\ast D^i$
is connected, so there is a shortest path
$\partial _{\mathrm {ext}}^\ast D^i$
is connected, so there is a shortest path
![]() $\Lambda $
in
$\Lambda $
in
![]() $\partial _{\mathrm {ext}}^\ast D^i$
from
$\partial _{\mathrm {ext}}^\ast D^i$
from
![]() $\Gamma _a$
to
$\Gamma _a$
to
![]() $\Gamma _b$
. When edit
$\Gamma _b$
. When edit
![]() $\Gamma $
to form
$\Gamma $
to form
![]() $\Gamma '$
as
$\Gamma '$
as
Because
![]() $\Gamma _b$
was the last element of
$\Gamma _b$
was the last element of
![]() $\Gamma $
which intersected
$\Gamma $
which intersected
![]() $\partial _{\mathrm {ext}}^\ast D^i$
,
$\partial _{\mathrm {ext}}^\ast D^i$
,
![]() $\Gamma '$
avoids
$\Gamma '$
avoids
![]() $D^i$
. Additionally, by our second observation,
$D^i$
. Additionally, by our second observation,
![]() $\Lambda $
avoids E, so if
$\Lambda $
avoids E, so if
![]() $L'$
is the set of labels of disks encountered by
$L'$
is the set of labels of disks encountered by
![]() $\Gamma '$
, then
$\Gamma '$
, then
![]() $|L'| \leq |L|-1$
. If
$|L'| \leq |L|-1$
. If
![]() $L'$
is empty, then we are done. Otherwise, we can relabel
$L'$
is empty, then we are done. Otherwise, we can relabel
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma '$
and L to
$\Gamma '$
and L to
![]() $L'$
in the preceding argument to continue inductively, obtaining
$L'$
in the preceding argument to continue inductively, obtaining
![]() $\Gamma "$
and
$\Gamma "$
and
![]() $|L"| \leq |L| - 2$
, and so on. Because
$|L"| \leq |L| - 2$
, and so on. Because
![]() $|L| \leq n$
, we need to modify the path at most n times before the resulting path from y to C does not return to E.
$|L| \leq n$
, we need to modify the path at most n times before the resulting path from y to C does not return to E.
The last result of this section bounds above escape probabilities; we will shortly specialize it for our setting. Note that
![]() $\partial A_\rho $
denotes the exterior boundary of the
$\partial A_\rho $
denotes the exterior boundary of the
![]() $\rho $
-fattening of A, not the
$\rho $
-fattening of A, not the
![]() $\rho $
-fattening of
$\rho $
-fattening of
![]() $\partial A$
.
$\partial A$
.
Lemma 6.13. If A is a subset of
![]() $\mathbb {Z}^2$
with at least two elements and if
$\mathbb {Z}^2$
with at least two elements and if
![]() $\rho $
is at least twice the diameter of A, then, for x in A,
$\rho $
is at least twice the diameter of A, then, for x in A,
The added
![]() $2$
in equation (6.36) is unimportant. If
$2$
in equation (6.36) is unimportant. If
![]() $A \setminus \{x\} = \{o\}$
, then a standard result (e.g., [Reference LawlerLaw13, Proposition 1.6.7]) states that the probability in question is approximately
$A \setminus \{x\} = \{o\}$
, then a standard result (e.g., [Reference LawlerLaw13, Proposition 1.6.7]) states that the probability in question is approximately
![]() $\frac {\log |x|}{\log \rho } \leq \frac {\log \mathrm {diam} (A)}{\log \rho }$
. If A has more than two elements, then it can only be more difficult to escape
$\frac {\log |x|}{\log \rho } \leq \frac {\log \mathrm {diam} (A)}{\log \rho }$
. If A has more than two elements, then it can only be more difficult to escape
![]() $A \setminus \{x\}$
, hence this approximate bound continues to hold. However, it is more convenient for us to directly prove this bound with explicit constants.
$A \setminus \{x\}$
, hence this approximate bound continues to hold. However, it is more convenient for us to directly prove this bound with explicit constants.
Proof of Lemma 6.13.
We will replace the event in equation (6.36) with a more probable but simpler event and bound above its probability instead. By hypothesis, A has at least two elements, so for any x in A, there is some y in
![]() $A {\setminus } \{x\}$
nearest to x. To escape to
$A {\setminus } \{x\}$
nearest to x. To escape to
![]() $\partial (A{\setminus } \{x\})_\rho $
without hitting
$\partial (A{\setminus } \{x\})_\rho $
without hitting
![]() $A {\setminus } \{x\}$
it is necessary to escape to
$A {\setminus } \{x\}$
it is necessary to escape to
![]() $C_y (\rho )$
without hitting y. Accordingly, for a random walk from x, the following inclusion holds
$C_y (\rho )$
without hitting y. Accordingly, for a random walk from x, the following inclusion holds
To prove equation (6.36), it therefore suffices to obtain the same bound for the larger event.
The hypothesis
![]() $\rho \geq 2 \, \mathrm {diam} (A)$
ensures that
$\rho \geq 2 \, \mathrm {diam} (A)$
ensures that
![]() $x-y$
lies in
$x-y$
lies in
![]() $D(\rho )$
, so we can apply the optional stopping theorem to the martingale
$D(\rho )$
, so we can apply the optional stopping theorem to the martingale
![]() $\mathfrak {a} (S_{j \wedge \tau _{o}})$
at the stopping time
$\mathfrak {a} (S_{j \wedge \tau _{o}})$
at the stopping time
![]() $\tau _{C(\rho )}$
. Doing so, we find
$\tau _{C(\rho )}$
. Doing so, we find
 $$ \begin{align} \mathbb{P}_x (\tau_{C_y (\rho)} < \tau_y) = \mathbb{P}_{x-y} (\tau_{C(\rho)} < \tau_{o}) = \frac{\mathfrak{a} (x-y)}{\mathbb{E}_{x-y} [\mathfrak{a} (S_{\tau_{C(\rho)}}) \bigm\vert \tau_{C(\rho)} < \tau_{o}]}. \end{align} $$
$$ \begin{align} \mathbb{P}_x (\tau_{C_y (\rho)} < \tau_y) = \mathbb{P}_{x-y} (\tau_{C(\rho)} < \tau_{o}) = \frac{\mathfrak{a} (x-y)}{\mathbb{E}_{x-y} [\mathfrak{a} (S_{\tau_{C(\rho)}}) \bigm\vert \tau_{C(\rho)} < \tau_{o}]}. \end{align} $$
We apply Lemma A.2 with
![]() $r = \rho $
and
$r = \rho $
and
![]() $x = o$
to find
$x = o$
to find
By equation (3.9) and the facts that
![]() $1 \leq |x-y| \leq \mathrm {diam} (A)$
and
$1 \leq |x-y| \leq \mathrm {diam} (A)$
and
![]() $\kappa + \lambda \leq 1.1$
, the numerator of equation (6.38), is at most
$\kappa + \lambda \leq 1.1$
, the numerator of equation (6.38), is at most
Substituting equations (6.39) and (6.40) into equation (6.38), and simplifying with
![]() $\frac {1.1\pi }{2} \leq 2$
, we find
$\frac {1.1\pi }{2} \leq 2$
, we find
6.4 Proof of Proposition 6.3
Recall that, for
![]() $t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
, the midway point is a circle which surrounds one of the clusters which is least separated at time
$t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
, the midway point is a circle which surrounds one of the clusters which is least separated at time
![]() $\mathcal {T}_{\ell -1}$
. (We choose this cluster arbitrarily from the least separated clusters.) We call this cluster the watched cluster, to distinguish it from other clusters which are least separated at
$\mathcal {T}_{\ell -1}$
. (We choose this cluster arbitrarily from the least separated clusters.) We call this cluster the watched cluster, to distinguish it from other clusters which are least separated at
![]() $\mathcal {T}_{\ell -1}$
. The results of this section are phrased in these terms and through the following events.
$\mathcal {T}_{\ell -1}$
. The results of this section are phrased in these terms and through the following events.
Definition 6.14. For any
![]() $x \in \mathbb {Z}^2$
, time
$x \in \mathbb {Z}^2$
, time
![]() $t \geq 0$
and any
$t \geq 0$
and any
![]() $1 \leq i \leq k$
, define the activation events
$1 \leq i \leq k$
, define the activation events
 $$\begin{align*}\mathsf{Act} (x,t) = \left\{ x\ \text{is activated at time}\ t \right\} \quad \text{and} \quad \mathsf{Act} (i,t) = \bigcup_{x \in U_t^i} \mathsf{Act} (x,t).\end{align*}$$
$$\begin{align*}\mathsf{Act} (x,t) = \left\{ x\ \text{is activated at time}\ t \right\} \quad \text{and} \quad \mathsf{Act} (i,t) = \bigcup_{x \in U_t^i} \mathsf{Act} (x,t).\end{align*}$$
Additionally, define the deposition event
 $$\begin{align*}\mathsf{Dep} (i,t) = \bigcup_{x \in U_t} \mathsf{Act} (x,t) \cap \left\{ \tau_{U_t^i \, {\setminus} \, \{x\}} < \tau_{U_t \, {\setminus} \, (U_t^i \, \cup \, \{x\})} \right\}.\end{align*}$$
$$\begin{align*}\mathsf{Dep} (i,t) = \bigcup_{x \in U_t} \mathsf{Act} (x,t) \cap \left\{ \tau_{U_t^i \, {\setminus} \, \{x\}} < \tau_{U_t \, {\setminus} \, (U_t^i \, \cup \, \{x\})} \right\}.\end{align*}$$
In words, the deposition event requires that, at time t, the activated particle deposits at the i th cluster.
When
![]() $\mathsf {Timely}_{\ell -1}$
occurs, if the i
th cluster is the watched cluster at time
$\mathsf {Timely}_{\ell -1}$
occurs, if the i
th cluster is the watched cluster at time
![]() $\mathcal {T}_{\ell - 1}$
, then for any time
$\mathcal {T}_{\ell - 1}$
, then for any time
![]() $t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, define the ‘midway’ event as
$t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, define the ‘midway’ event as
In words, the midway event specifies that, at time t, the activated particle reaches
![]() $C(i; \ell )$
before deposition.
$C(i; \ell )$
before deposition.
We will now use the results of the preceding subsection to bound below the probability that activation occurs at the watched cluster and that the activated particle subsequently reaches the midway point. Essentially, Theorem 4 addresses the former probability and Theorem 5 addresses the latter. However, it is necessary to first ensure that the watched cluster has positive harmonic measure so that at least one of its particles can be activated and the lower bound (1.2) of Theorem 4 can apply. This is handled by Lemma 6.12, the hypotheses of which are satisfied whenever
![]() $\mathsf {Timely}_{\ell -1}$
occurs and
$\mathsf {Timely}_{\ell -1}$
occurs and
![]() $t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
. The hypotheses of Theorem 5 will be satisfied in this context so long as we estimate the probability of escape to a distance
$t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
. The hypotheses of Theorem 5 will be satisfied in this context so long as we estimate the probability of escape to a distance
![]() $\rho $
which is at least twice the cluster diameter. The distance from the watched cluster to the midway point is roughly
$\rho $
which is at least twice the cluster diameter. The distance from the watched cluster to the midway point is roughly
![]() $\rho _\ell $
, while the cluster diameter is at most
$\rho _\ell $
, while the cluster diameter is at most
![]() $(\log \rho _\ell )^2$
by equation (6.19) of Lemma 6.10, so this will be the case.
$(\log \rho _\ell )^2$
by equation (6.19) of Lemma 6.10, so this will be the case.
The lower bounds from Theorems 4 and 5 will imply that a particle with positive harmonic measure is activated and reaches the midway point with a probability of at least
for constants
![]() $c_1,c_2$
. By our choice of
$c_1,c_2$
. By our choice of
![]() $\gamma $
(6.10), the first factor in the preceding display is at least
$\gamma $
(6.10), the first factor in the preceding display is at least
![]() $\alpha _n^{-1}$
, where
$\alpha _n^{-1}$
, where
Proposition 6.15. Let cluster i be least separated at time
![]() $\mathcal {T}_{\ell - 1}$
. When
$\mathcal {T}_{\ell - 1}$
. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when
$\mathsf {Timely}_{\ell -1}$
occurs and when
![]() $t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, we have
$t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, we have
Proof. Fix
![]() $\ell $
, suppose the i
th cluster is least separated at time
$\ell $
, suppose the i
th cluster is least separated at time
![]() $\mathcal {T}_{\ell - 1}$
and
$\mathcal {T}_{\ell - 1}$
and
![]() $\mathsf {Timely}_{\ell -1}$
occurs, and let
$\mathsf {Timely}_{\ell -1}$
occurs, and let
![]() $t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
. For any
$t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
. For any
![]() $x \in U_t^i$
, we have
$x \in U_t^i$
, we have
Let B denote the set of all points within distance
![]() $\rho _\ell $
of
$\rho _\ell $
of
![]() $U_t^i$
. We have the following inclusion when
$U_t^i$
. We have the following inclusion when
![]() $\mathsf {Act} (x,t)$
occurs:
$\mathsf {Act} (x,t)$
occurs:
From equation (6.44), we have
Now, let x be an element of
![]() $U_t^i$
which is exposed and which maximizes the right-hand side of equation (6.45). Such an element must exist because, by Lemma 6.12, when
$U_t^i$
which is exposed and which maximizes the right-hand side of equation (6.45). Such an element must exist because, by Lemma 6.12, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when
$\mathsf {Timely}_{\ell -1}$
occurs and when
![]() $t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
,
$t \in [\mathcal {T}_{\ell -1},{\mathcal {T}_\ell }^-]$
,
![]() ${\mathbb {H}}_{U_t} (U_t^i)$
is positive. We aim to apply Theorem 5 to bound below the probability in equation (6.45). The hypotheses of Theorem 5 require
${\mathbb {H}}_{U_t} (U_t^i)$
is positive. We aim to apply Theorem 5 to bound below the probability in equation (6.45). The hypotheses of Theorem 5 require
![]() $|U_t^i| \geq 2$
and
$|U_t^i| \geq 2$
and
![]() $\rho _\ell \geq 2\, \mathrm {diam} (U_t^i)$
. First, the cluster
$\rho _\ell \geq 2\, \mathrm {diam} (U_t^i)$
. First, the cluster
![]() $U_t^i$
must contain at least two elements as, otherwise, activation at x would necessitate
$U_t^i$
must contain at least two elements as, otherwise, activation at x would necessitate
![]() $t = \mathcal {T}_\ell $
. Second,
$t = \mathcal {T}_\ell $
. Second,
![]() $\rho _\ell $
is indeed at least twice the diameter of
$\rho _\ell $
is indeed at least twice the diameter of
![]() $U_t^i$
because, when
$U_t^i$
because, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
![]() $U_t^i$
is contained in a disk of radius
$U_t^i$
is contained in a disk of radius
![]() $(\log \rho _\ell )^2$
by equation (6.19). Theorem 5 therefore applies to equation (6.45), giving
$(\log \rho _\ell )^2$
by equation (6.19). Theorem 5 therefore applies to equation (6.45), giving
The harmonic measure lower bound (1.2) of Theorem 4 applies because x has positive harmonic measure. According to equation (1.2), the harmonic measure of x is at least
Combining equations (6.46) and (6.47), we find
The second inequality is due to the definition of
![]() $\alpha _n$
(6.41).
$\alpha _n$
(6.41).
Next, we will bound below the conditional probability that activation occurs at the watched cluster, given that the activated particle reaches the midway point.
Proposition 6.16. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell - 1}$
. When
$\mathcal {T}_{\ell - 1}$
. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when
$\mathsf {Timely}_{\ell -1}$
occurs and when
![]() $t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, we have
$t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, we have
Proof. Suppose
![]() $t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
and
$t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
and
![]() $\mathsf {Timely}_{\ell -1}$
occurs. If we obtain a lower bound
$\mathsf {Timely}_{\ell -1}$
occurs. If we obtain a lower bound
![]() $p_1$
on
$p_1$
on
![]() $\mathbf {P} \left ( \mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (i,t) \bigm \vert \mathcal {F}_t \right )$
and an upper bound
$\mathbf {P} \left ( \mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (i,t) \bigm \vert \mathcal {F}_t \right )$
and an upper bound
![]() $p_2$
on
$p_2$
on
![]() $\mathbf {P} \left ( \bigcup _{j \neq i} \mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (j,t) \bigm \vert \mathcal {F}_t \right )$
, then
$\mathbf {P} \left ( \bigcup _{j \neq i} \mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (j,t) \bigm \vert \mathcal {F}_t \right )$
, then
First, the probability
![]() $\mathbf {P} \left (\mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (i,t) \bigm \vert \mathcal {F}_t \right )$
is precisely the one we used to establish (6.43) in the proof of Proposition 6.15;
$\mathbf {P} \left (\mathsf {Mid} (i,t; \ell ) \cap \mathsf {Act} (i,t) \bigm \vert \mathcal {F}_t \right )$
is precisely the one we used to establish (6.43) in the proof of Proposition 6.15;
![]() $p_1$
is therefore at least
$p_1$
is therefore at least
![]() $(\alpha _n \log \rho _\ell )^{-1}$
.
$(\alpha _n \log \rho _\ell )^{-1}$
.
Second, for any
![]() $j \neq i$
, we use the trivial upper bound
$j \neq i$
, we use the trivial upper bound
![]() $\mathbf {P} (\mathsf {Act} (j,t) \bigm \vert \mathcal {F}_t) \leq 1$
and address the midway component by writing
$\mathbf {P} (\mathsf {Act} (j,t) \bigm \vert \mathcal {F}_t) \leq 1$
and address the midway component by writing
Use
![]() $\rho $
to denote
$\rho $
to denote
![]() ${\mathrm {dist}} (U_{\mathcal {T}_{\ell -1}}^i, U_{\mathcal {T}_{\ell -1}}^j)$
and B to denote the set of all points within a distance
${\mathrm {dist}} (U_{\mathcal {T}_{\ell -1}}^i, U_{\mathcal {T}_{\ell -1}}^j)$
and B to denote the set of all points within a distance
![]() $\rho /3$
of
$\rho /3$
of
![]() $U_t^j{\setminus }\{X\}$
. We can use Lemma 6.13 to bound the probability in equation (6.50) because the following inclusion holds:
$U_t^j{\setminus }\{X\}$
. We can use Lemma 6.13 to bound the probability in equation (6.50) because the following inclusion holds:
If
![]() $\mathsf {Act} (j,t)$
occurs, then
$\mathsf {Act} (j,t)$
occurs, then
![]() $U_t^j$
must have least two elements as, otherwise, t would equal
$U_t^j$
must have least two elements as, otherwise, t would equal
![]() $\mathcal {T}_\ell $
. Then, because
$\mathcal {T}_\ell $
. Then, because
![]() $\rho /3$
is at least twice its diameter, an application of Lemma 6.13 with
$\rho /3$
is at least twice its diameter, an application of Lemma 6.13 with
![]() $A = U_t^j$
and
$A = U_t^j$
and
![]() $\rho $
yields
$\rho $
yields
 $$\begin{align*}\mathbb{P}_x \left( \tau_B < \tau_{U_t^j {\setminus} \{x\}}\right) \leq \frac{\log \mathrm{diam} (U_t^j) + 2}{\log \rho} \leq \frac{2.2 \log \log \rho_\ell}{ \log \rho_\ell},\end{align*}$$
$$\begin{align*}\mathbb{P}_x \left( \tau_B < \tau_{U_t^j {\setminus} \{x\}}\right) \leq \frac{\log \mathrm{diam} (U_t^j) + 2}{\log \rho} \leq \frac{2.2 \log \log \rho_\ell}{ \log \rho_\ell},\end{align*}$$
uniformly for x in
![]() $U_t^j$
. The second inequality follows from equation (6.20), which bounds the ratio of
$U_t^j$
. The second inequality follows from equation (6.20), which bounds the ratio of
![]() $\log \mathrm {diam} (U_t^j)$
to
$\log \mathrm {diam} (U_t^j)$
to
![]() $\log \rho $
by
$\log \rho $
by
![]() $\tfrac {2.1 \log \log \rho _\ell }{\log \rho _\ell }$
.
$\tfrac {2.1 \log \log \rho _\ell }{\log \rho _\ell }$
.
Applying the preceding bound to equation (6.50), we find
Then, substituting
![]() $p_1$
and
$p_1$
and
![]() $p_2$
in equation (6.49), we conclude
$p_2$
in equation (6.49), we conclude
We now use Lemma 6.11 to establish that an activated particle, upon reaching the midway point, deposits at the watched cluster with a probability of no more than
![]() $0.51$
.
$0.51$
.
Proposition 6.17. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
. When
$\mathcal {T}_{\ell -1}$
. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs and when
$\mathsf {Timely}_{\ell -1}$
occurs and when
![]() $t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, for x in
$t \in \left [ \mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^- \right ]$
, for x in
![]() $U_t$
, we have
$U_t$
, we have
Proof. Using the definitions of
![]() $\mathsf {Dep} (i,t)$
and
$\mathsf {Dep} (i,t)$
and
![]() $\mathsf {Mid}(i,t;\ell )$
, we write
$\mathsf {Mid}(i,t;\ell )$
, we write
 $$ \begin{align*} &\mathbf{P} \left( \mathsf{Dep} (i,t) \bigm\vert \mathsf{Mid} (i,t; \ell),\,\mathsf{Act} (x,t),\, \mathcal{F}_t\right)\\ & = \mathbf{P}\left( \bigcup_{y \in U_t} \mathsf{Act} (y,t) \cap \left\{ \tau_{U_t^i \, {\setminus} \, \{y\}} < \tau_{U_t \, {\setminus} \, (U_t^i \, \cup \, \{y\})} \right\} \Biggm\vert \bigcup_{y \in U_t} \mathsf{Act} (y,t) \cap \left\{ \tau_{C(i; \ell)} < \tau_{U_t {\setminus} \{y\}} \right\},\, \mathsf{Act} (x,t),\,\mathcal{F}_t\right). \end{align*} $$
$$ \begin{align*} &\mathbf{P} \left( \mathsf{Dep} (i,t) \bigm\vert \mathsf{Mid} (i,t; \ell),\,\mathsf{Act} (x,t),\, \mathcal{F}_t\right)\\ & = \mathbf{P}\left( \bigcup_{y \in U_t} \mathsf{Act} (y,t) \cap \left\{ \tau_{U_t^i \, {\setminus} \, \{y\}} < \tau_{U_t \, {\setminus} \, (U_t^i \, \cup \, \{y\})} \right\} \Biggm\vert \bigcup_{y \in U_t} \mathsf{Act} (y,t) \cap \left\{ \tau_{C(i; \ell)} < \tau_{U_t {\setminus} \{y\}} \right\},\, \mathsf{Act} (x,t),\,\mathcal{F}_t\right). \end{align*} $$
Because
![]() $\mathsf {Act} (y,t)$
only occurs for one particle y in
$\mathsf {Act} (y,t)$
only occurs for one particle y in
![]() $U_t^i$
at any given time t, the right-hand side simplifies to
$U_t^i$
at any given time t, the right-hand side simplifies to
We then apply the strong Markov property to
![]() $\tau _{C(i; \ell )}$
to find that the previous display equals
$\tau _{C(i; \ell )}$
to find that the previous display equals
where the inequality follows from the estimate (6.26).
The preceding three propositions realize the strategy of Section 6.2.2. We proceed to implement the strategy of Section 6.2.3. In brief, we will compare the number of particles in the watched cluster to a random walk and bound the collapse time using the hitting time of zero of the walk.
Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
, and denote by
$\mathcal {T}_{\ell -1}$
, and denote by
![]() $(\eta _{\ell ,m})_{m \geq 1}$
the consecutive times at which the midway event
$(\eta _{\ell ,m})_{m \geq 1}$
the consecutive times at which the midway event
![]() $\mathsf {Mid} (i,\cdot ;\ell )$
occurs. Set
$\mathsf {Mid} (i,\cdot ;\ell )$
occurs. Set
![]() $\eta _{\ell ,0} \equiv \mathcal {T}_{\ell -1}$
and for all
$\eta _{\ell ,0} \equiv \mathcal {T}_{\ell -1}$
and for all
![]() $m \geq 1$
define
$m \geq 1$
define
Additionally, we denote the number of midway event occurrences by time t as
 $$\begin{align*}N_\ell (t) = \sum_{m=1}^\infty \mathbf{1} (\eta_{\ell,m} \leq t).\end{align*}$$
$$\begin{align*}N_\ell (t) = \sum_{m=1}^\infty \mathbf{1} (\eta_{\ell,m} \leq t).\end{align*}$$
The number of elements in cluster i viewed at these times can be coupled to a lazy random walk
![]() $(W_m)_{m \geq 0}$
on
$(W_m)_{m \geq 0}$
on
![]() $\{0,\dots ,n\}$
from
$\{0,\dots ,n\}$
from
![]() $W_0 \equiv | U_{\eta _{\ell ,0}}^i |$
, which takes down-steps with probability
$W_0 \equiv | U_{\eta _{\ell ,0}}^i |$
, which takes down-steps with probability
![]() $q = (7 \alpha _n \log \log \rho _\ell )^{-1}$
and up-steps with probability
$q = (7 \alpha _n \log \log \rho _\ell )^{-1}$
and up-steps with probability
![]() $1-q$
, unless it attempts to take a down-step at
$1-q$
, unless it attempts to take a down-step at
![]() $W_m = 0$
or an up-step at
$W_m = 0$
or an up-step at
![]() $W_m = n$
, in which case it remains where it is.
$W_m = n$
, in which case it remains where it is.
When
![]() $\mathsf {Timely}_{\ell -1}$
occurs, at each time
$\mathsf {Timely}_{\ell -1}$
occurs, at each time
![]() $\eta _{\ell ,\cdot }$
, the watched cluster has a chance of losing a particle of at least
$\eta _{\ell ,\cdot }$
, the watched cluster has a chance of losing a particle of at least
![]() $0.49 (3 \alpha _n \log \log \rho _\ell )^{-1} \geq q$
(Propositions 6.15 and 6.16). The standard coupling of
$0.49 (3 \alpha _n \log \log \rho _\ell )^{-1} \geq q$
(Propositions 6.15 and 6.16). The standard coupling of
![]() $|U_{\eta _{\ell ,m}}^i|$
and
$|U_{\eta _{\ell ,m}}^i|$
and
![]() $W_m$
will then guarantee that
$W_m$
will then guarantee that
![]() $|U_{\eta _{\ell ,m}}^i| \leq W_m$
. However, this inequality will only hold when
$|U_{\eta _{\ell ,m}}^i| \leq W_m$
. However, this inequality will only hold when
![]() $N_\ell ({\mathcal {T}_\ell }^-) \geq m$
.
$N_\ell ({\mathcal {T}_\ell }^-) \geq m$
.
Lemma 6.18. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
. There is a coupling of
$\mathcal {T}_{\ell -1}$
. There is a coupling of
![]() $(|U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
$(|U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
![]() $(W_m)_{m \geq 0}$
such that, when
$(W_m)_{m \geq 0}$
such that, when
![]() $\mathsf {Timely}_{\ell -1}$
and
$\mathsf {Timely}_{\ell -1}$
and
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
![]() $| U_{\eta _{\ell ,m}}^i | \leq W_m$
for all
$| U_{\eta _{\ell ,m}}^i | \leq W_m$
for all
![]() $m \leq M$
.
$m \leq M$
.
Proof. Define
 $$\begin{align*}q_{\ell,m} = \mathbf{P} \Bigg( \mathsf{Act} (i,\eta_{\ell,m}) \cap \bigcup_{j \neq i} \mathsf{Dep} (j,\eta_{\ell,m}) \Biggm\vert \mathcal{F}_{\eta_{\ell,m}} \Bigg).\end{align*}$$
$$\begin{align*}q_{\ell,m} = \mathbf{P} \Bigg( \mathsf{Act} (i,\eta_{\ell,m}) \cap \bigcup_{j \neq i} \mathsf{Dep} (j,\eta_{\ell,m}) \Biggm\vert \mathcal{F}_{\eta_{\ell,m}} \Bigg).\end{align*}$$
In words, the event in the preceding display is the occurrence of
![]() $\mathsf {Mid} (i, \eta _{\ell ,m}; \ell )$
, preceded by activation at cluster i and followed by deposition at cluster
$\mathsf {Mid} (i, \eta _{\ell ,m}; \ell )$
, preceded by activation at cluster i and followed by deposition at cluster
![]() $j \neq i$
; the watched cluster loses a particle when this event occurs.
$j \neq i$
; the watched cluster loses a particle when this event occurs.
Couple
![]() $(| U_{\eta _{\ell ,m}}^i |)_{m\geq 0}$
and
$(| U_{\eta _{\ell ,m}}^i |)_{m\geq 0}$
and
![]() $(W_m)_{m \geq 0}$
using the standard monotone coupling. When
$(W_m)_{m \geq 0}$
using the standard monotone coupling. When
![]() $\mathsf {Timely}_{\ell -1}$
occurs, by Propositions 6.16 and 6.17, the estimates (6.48) and (6.51) hold for all
$\mathsf {Timely}_{\ell -1}$
occurs, by Propositions 6.16 and 6.17, the estimates (6.48) and (6.51) hold for all
![]() $t \in [\mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^-]$
. In particular, these estimates hold at time
$t \in [\mathcal {T}_{\ell - 1}, {\mathcal {T}_\ell }^-]$
. In particular, these estimates hold at time
![]() $\eta _{\ell ,m}$
for any
$\eta _{\ell ,m}$
for any
![]() $m \leq M$
when
$m \leq M$
when
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occurs. Accordingly, for any such m, we have
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occurs. Accordingly, for any such m, we have
![]() $q_{\ell ,m} \geq 0.49 (3 \alpha _n \log \log \rho _\ell )^{-1} \geq q$
.
$q_{\ell ,m} \geq 0.49 (3 \alpha _n \log \log \rho _\ell )^{-1} \geq q$
.
Denote by
![]() $\tau ^U_0$
and
$\tau ^U_0$
and
![]() $\tau ^W_0$
the first hitting times of zero for
$\tau ^W_0$
the first hitting times of zero for
![]() $( | U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
$( | U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
![]() $(W_m)_{m\geq 0}$
. Under the coupling,
$(W_m)_{m\geq 0}$
. Under the coupling,
![]() $\tau ^W_0$
cannot precede
$\tau ^W_0$
cannot precede
![]() $\tau _0^U$
. So an upper bound on
$\tau _0^U$
. So an upper bound on
![]() $\tau _0^W$
of m implies
$\tau _0^W$
of m implies
![]() $\tau _0^U \leq m$
and therefore it takes no more than m occurrences of the midway event after
$\tau _0^U \leq m$
and therefore it takes no more than m occurrences of the midway event after
![]() $\mathcal {T}_{\ell -1}$
for the collapse of the watched cluster to occur. In other words,
$\mathcal {T}_{\ell -1}$
for the collapse of the watched cluster to occur. In other words,
![]() $\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
is at most
$\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
is at most
![]() $\eta _{\ell ,m}$
.
$\eta _{\ell ,m}$
.
Lemma 6.19. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
. When
$\mathcal {T}_{\ell -1}$
. When
![]() $\mathsf {Timely}_{\ell -1}$
and
$\mathsf {Timely}_{\ell -1}$
and
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
Proof. From Lemma 6.18, there is a coupling of
![]() $( | U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
$( | U_{\eta _{\ell ,m}}^i |)_{m \geq 0}$
and
![]() $(W_m)_{m \geq 0}$
such that, when
$(W_m)_{m \geq 0}$
such that, when
![]() $\mathsf {Timely}_{\ell -1}$
and
$\mathsf {Timely}_{\ell -1}$
and
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur,
![]() $| U_{\eta _{\ell ,m}}^i | \leq W_m$
for all
$| U_{\eta _{\ell ,m}}^i | \leq W_m$
for all
![]() $m \leq M$
. In particular,
$m \leq M$
. In particular,
The inclusion (6.52) then follows from the fact that
![]() $\left \{\mathcal {T}_\ell - \mathcal {T}_{\ell -1}> \eta _{\ell ,M} \right \} \subseteq \left \{\tau _0^U > M\right \}$
.
$\left \{\mathcal {T}_\ell - \mathcal {T}_{\ell -1}> \eta _{\ell ,M} \right \} \subseteq \left \{\tau _0^U > M\right \}$
.
We now show that
![]() $\tau _0^W$
, the hitting time of zero for
$\tau _0^W$
, the hitting time of zero for
![]() $W_m$
, is at most
$W_m$
, is at most
![]() $(\log \log \rho _\ell )^n$
, up to a factor depending on n, with high probability. With more effort, we could prove a much better bound (in terms of its dependence on n), but this improvement would not affect the conclusion of Proposition 6.3. By Lemma 6.19, the bound on
$(\log \log \rho _\ell )^n$
, up to a factor depending on n, with high probability. With more effort, we could prove a much better bound (in terms of its dependence on n), but this improvement would not affect the conclusion of Proposition 6.3. By Lemma 6.19, the bound on
![]() $\tau _0^W$
will imply a bound on
$\tau _0^W$
will imply a bound on
![]() $\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
. For brevity, denote
$\mathcal {T}_\ell - \mathcal {T}_{\ell -1}$
. For brevity, denote
![]() $\beta _n = (8 \alpha _n)^n$
.
$\beta _n = (8 \alpha _n)^n$
.
Lemma 6.20. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
, and let
$\mathcal {T}_{\ell -1}$
, and let
![]() $K \geq 0$
be such that
$K \geq 0$
be such that
![]() $M = \lfloor K \beta _n (\log \log \rho _\ell )^n \rfloor $
satisfies
$M = \lfloor K \beta _n (\log \log \rho _\ell )^n \rfloor $
satisfies
![]() $\mathbf {P} (N_\ell ({\mathcal {T}_\ell }^-) \geq M \mid \mathcal {F}_{\mathcal {T}_{\ell -1}})> 0$
. Then
$\mathbf {P} (N_\ell ({\mathcal {T}_\ell }^-) \geq M \mid \mathcal {F}_{\mathcal {T}_{\ell -1}})> 0$
. Then
The factor
![]() $(\log \log \rho _\ell )^n$
appears because
$(\log \log \rho _\ell )^n$
appears because
![]() $(W_m)_{m \geq 0}$
takes down-steps with a probability which is the reciprocal of
$(W_m)_{m \geq 0}$
takes down-steps with a probability which is the reciprocal of
![]() $O_{\! n}(\log \log \rho _\ell )$
, and we will require it to take n consecutive down-steps. Note that
$O_{\! n}(\log \log \rho _\ell )$
, and we will require it to take n consecutive down-steps. Note that
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
cannot occur if K is large enough, because
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
cannot occur if K is large enough, because
![]() $N_\ell ({\mathcal {T}_\ell }^-)$
cannot exceed
$N_\ell ({\mathcal {T}_\ell }^-)$
cannot exceed
![]() $\mathfrak {t}_\ell \leq (\log \rho _\ell )^2$
(i.e., there can be no more occurrences of the midway event than there are HAT steps). The implicit bound on K is
$\mathfrak {t}_\ell \leq (\log \rho _\ell )^2$
(i.e., there can be no more occurrences of the midway event than there are HAT steps). The implicit bound on K is
![]() $(\log \rho _\ell )^{2-O_{n}(1)}$
. We will apply the lemma with a K of approximately
$(\log \rho _\ell )^{2-O_{n}(1)}$
. We will apply the lemma with a K of approximately
![]() $(\log \rho _\ell )^\delta $
for some
$(\log \rho _\ell )^\delta $
for some
![]() $\delta \in (0,1)$
.
$\delta \in (0,1)$
.
Proof of Lemma 6.20.
Denote the distribution of
![]() $(W_m)_{m \geq 0}$
by
$(W_m)_{m \geq 0}$
by
![]() $\mathbb {P}^W$
. If
$\mathbb {P}^W$
. If
![]() $\mathsf {Timely}_{\ell -1}$
and
$\mathsf {Timely}_{\ell -1}$
and
![]() $\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur, then by Lemma 6.19, we have the inclusion (6.52):
$\{N_\ell ({\mathcal {T}_\ell }^-) \geq M\}$
occur, then by Lemma 6.19, we have the inclusion (6.52):
Since
![]() $(W_m)_{m\geq 0}$
is never greater than n, it never takes more than n down-steps for
$(W_m)_{m\geq 0}$
is never greater than n, it never takes more than n down-steps for
![]() $W_m$
to hit zero. Since
$W_m$
to hit zero. Since
![]() $W_{m+1} = W_m - 1$
with a probability of
$W_{m+1} = W_m - 1$
with a probability of
![]() $q_W$
whenever
$q_W$
whenever
![]() $m \leq M-n$
, we have
$m \leq M-n$
, we have
Applying this fact
![]() $\lfloor M/n \rfloor $
times, we find that
$\lfloor M/n \rfloor $
times, we find that
For the second inequality, we used the fact that
![]() $\lfloor \beta _n (\log \log \rho _\ell )^n /n \rfloor $
is at least
$\lfloor \beta _n (\log \log \rho _\ell )^n /n \rfloor $
is at least
![]() $q_W^{-n}$
and therefore
$q_W^{-n}$
and therefore
![]() $\lfloor M/n \rfloor $
is at least
$\lfloor M/n \rfloor $
is at least
![]() $\lfloor K \rfloor \cdot q_W^{-n}$
. Combining this with equation (6.52) gives equation (6.53).
$\lfloor K \rfloor \cdot q_W^{-n}$
. Combining this with equation (6.52) gives equation (6.53).
For convenience, we will treat
![]() $(\log \rho _\ell )^{1+2\delta }$
as an integer, as the distinction will be unimportant. Define the time
$(\log \rho _\ell )^{1+2\delta }$
as an integer, as the distinction will be unimportant. Define the time
and the event that occurrences of the midway event are frequent:
When
![]() $\mathsf {Timely}_{\ell -1}$
occurs, the midway event occurs frequently, with high probability.
$\mathsf {Timely}_{\ell -1}$
occurs, the midway event occurs frequently, with high probability.
Proposition 6.21. Let cluster i be the watched cluster at time
![]() $\mathcal {T}_{\ell -1}$
and let
$\mathcal {T}_{\ell -1}$
and let
![]() $\delta = (2n)^{-4}$
. Then
$\delta = (2n)^{-4}$
. Then
Proof. Proposition 6.15 states that
when
![]() $\mathsf {Timely}_{\ell -1}$
and
$\mathsf {Timely}_{\ell -1}$
and
![]() $t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
occur. The probability that the time between consecutive midway events exceeds
$t \in [\mathcal {T}_{\ell -1}, {\mathcal {T}_\ell }^-]$
occur. The probability that the time between consecutive midway events exceeds
![]() $\mathfrak {s}_\ell (\delta )$
therefore satisfies
$\mathfrak {s}_\ell (\delta )$
therefore satisfies
 $$ \begin{align} \mathbf{P} \left( \eta_{\ell,N_\ell (t)} - \eta_{\ell,N_\ell (t)-1}> \mathfrak{s}_\ell (\delta) \bigm\vert \mathcal{F}_{\eta_{\ell,N_\ell (t)-1}}\right) \leq \left( 1 - \frac{1}{ \alpha_n \log \rho_\ell} \right)^{\mathfrak{s_\ell} (\delta)} \leq e^{-5 n (\log \rho_\ell)^{2\delta}}. \end{align} $$
$$ \begin{align} \mathbf{P} \left( \eta_{\ell,N_\ell (t)} - \eta_{\ell,N_\ell (t)-1}> \mathfrak{s}_\ell (\delta) \bigm\vert \mathcal{F}_{\eta_{\ell,N_\ell (t)-1}}\right) \leq \left( 1 - \frac{1}{ \alpha_n \log \rho_\ell} \right)^{\mathfrak{s_\ell} (\delta)} \leq e^{-5 n (\log \rho_\ell)^{2\delta}}. \end{align} $$
Since
![]() $\mathsf {FreqMid}_\ell (\delta )^c$
is a union of
$\mathsf {FreqMid}_\ell (\delta )^c$
is a union of
![]() $N_\ell ({\mathcal {T}_\ell }^-) \leq (\log \rho _\ell )^2$
such events, a union bound and equation (6.56) imply that
$N_\ell ({\mathcal {T}_\ell }^-) \leq (\log \rho _\ell )^2$
such events, a union bound and equation (6.56) imply that
The second inequality follows from the fact that
![]() $(\log \rho _\ell )^2 \leq e^{(\log \rho _\ell )^{2\delta }}$
since
$(\log \rho _\ell )^2 \leq e^{(\log \rho _\ell )^{2\delta }}$
since
![]() $\log \rho _\ell \geq (2\delta )^{-2}$
.
$\log \rho _\ell \geq (2\delta )^{-2}$
.
Proof of Proposition 6.3.
Let
![]() $\delta = (2n)^{-4}$
, and define the event that the
$\delta = (2n)^{-4}$
, and define the event that the
![]() $\ell $
th collapse is fast by
$\ell $
th collapse is fast by
We will use Lemma 6.20 and Proposition 6.21 to prove the bound
This implies the proposition because
![]() $\mathcal {T}_{k-1}$
is at most
$\mathcal {T}_{k-1}$
is at most
![]() $(\log d)^{1+7\delta }$
when every collapse is fast, that is, when
$(\log d)^{1+7\delta }$
when every collapse is fast, that is, when
![]() $\mathsf {FastCol} (\delta ) = \cap _{\ell =1}^{k-1} \mathsf {FastCol}_\ell (\delta )$
occurs, and because equation (6.57) implies
$\mathsf {FastCol} (\delta ) = \cap _{\ell =1}^{k-1} \mathsf {FastCol}_\ell (\delta )$
occurs, and because equation (6.57) implies
Note that this lower bound is at least the one in equation (6.2) because the clustering parameter r (6.11) satisfies
![]() $r \leq \log \rho _1$
.
$r \leq \log \rho _1$
.
Indeed,
![]() $\mathsf {FastCol} (\delta ) \subseteq \{\mathcal {T}_{k-1} \leq (\log d)^{1+7\delta }\}$
because, when
$\mathsf {FastCol} (\delta ) \subseteq \{\mathcal {T}_{k-1} \leq (\log d)^{1+7\delta }\}$
because, when
![]() $\mathsf {FastCol} (\delta )$
occurs, the collapse time satisfies
$\mathsf {FastCol} (\delta )$
occurs, the collapse time satisfies
 $$\begin{align*}\mathcal{T}_{k-1} = \sum_{\ell=1}^{k-1} (\mathcal{T}_\ell - \mathcal{T}_{\ell-1}) \leq \sum_{\ell=1}^{k-1} (\log \rho_\ell)^{1+6\delta} \leq 2n (\log d)^{1+6\delta} \leq (\log d)^{1+7\delta}. \end{align*}$$
$$\begin{align*}\mathcal{T}_{k-1} = \sum_{\ell=1}^{k-1} (\mathcal{T}_\ell - \mathcal{T}_{\ell-1}) \leq \sum_{\ell=1}^{k-1} (\log \rho_\ell)^{1+6\delta} \leq 2n (\log d)^{1+6\delta} \leq (\log d)^{1+7\delta}. \end{align*}$$
The second inequality holds because
![]() $\rho _\ell $
is never more than twice the diameter d of the initial configuration
$\rho _\ell $
is never more than twice the diameter d of the initial configuration
![]() $U_0$
when
$U_0$
when
![]() $\mathsf {FastCol} (\delta )$
occurs. The third follows from the fact that
$\mathsf {FastCol} (\delta )$
occurs. The third follows from the fact that
![]() $d \geq \theta _{4n}$
by assumption, so
$d \geq \theta _{4n}$
by assumption, so
![]() $\log d \geq (2n)^{\frac {1}{\delta }}$
in particular.
$\log d \geq (2n)^{\frac {1}{\delta }}$
in particular.
To see why equation (6.57) implies equation (6.58), note that
![]() $\cap _{i<j} \mathsf {FastCol}_i (\delta ) \subseteq \mathsf {Timely}_{j-1}$
for each
$\cap _{i<j} \mathsf {FastCol}_i (\delta ) \subseteq \mathsf {Timely}_{j-1}$
for each
![]() $j < k$
, so
$j < k$
, so
By equation (6.57), the right-hand side is at most
![]() $e^{-3n (\log \rho _1)^{2\delta }}$
. We use this bound and the fact that
$e^{-3n (\log \rho _1)^{2\delta }}$
. We use this bound and the fact that
![]() $k \leq n$
to conclude equation (6.58) as
$k \leq n$
to conclude equation (6.58) as
 $$ \begin{align*} \mathbf{P} \left( \mathsf{FastCol} (\delta)^c \bigm\vert \mathcal{F}_0 \right) & = \sum_{j=1}^{k-1} \mathbf{P} \left( \cap_{i < j} \mathsf{FastCol}_i (\delta) \cap \mathsf{FastCol}_j (\delta)^c \Bigm\vert \mathcal{F}_0 \right)\\ &\leq \sum_{j=1}^{k-1} e^{-3n (\log \rho_1)^{2\delta}} \leq e^{-2n (\log \rho_1)^{2\delta}}. \end{align*} $$
$$ \begin{align*} \mathbf{P} \left( \mathsf{FastCol} (\delta)^c \bigm\vert \mathcal{F}_0 \right) & = \sum_{j=1}^{k-1} \mathbf{P} \left( \cap_{i < j} \mathsf{FastCol}_i (\delta) \cap \mathsf{FastCol}_j (\delta)^c \Bigm\vert \mathcal{F}_0 \right)\\ &\leq \sum_{j=1}^{k-1} e^{-3n (\log \rho_1)^{2\delta}} \leq e^{-2n (\log \rho_1)^{2\delta}}. \end{align*} $$
It remains to prove equation (6.57). Consider the bound
Proposition 6.21 states that the second term on the right-hand side of equation (6.59) is at most
![]() $e^{- 4n (\log \rho _\ell )^{2\delta }}$
when
$e^{- 4n (\log \rho _\ell )^{2\delta }}$
when
![]() $\mathsf {Timely}_{\ell -1}$
occurs. We claim that the same is true of the first term. Note that when the
$\mathsf {Timely}_{\ell -1}$
occurs. We claim that the same is true of the first term. Note that when the
![]() $\ell $
th collapse is slow and when occurrences of the midway event are frequent, there must be many such occurrences. In other words,
$\ell $
th collapse is slow and when occurrences of the midway event are frequent, there must be many such occurrences. In other words,
![]() $\mathsf {FastCol}_\ell (\delta )^c \cap \mathsf {FreqMid}_\ell (\delta ) \subseteq \{N_\ell ({\mathcal {T}_\ell }^-) \geq M_\ell (\delta )\}$
, where
$\mathsf {FastCol}_\ell (\delta )^c \cap \mathsf {FreqMid}_\ell (\delta ) \subseteq \{N_\ell ({\mathcal {T}_\ell }^-) \geq M_\ell (\delta )\}$
, where
![]() $M_\ell (\delta ) = [\frac {(\log \rho _\ell )^{1+6\delta }}{\mathfrak {s}_\ell (\delta )}]> (\log \rho _\ell )^{3\delta }$
. Consequently, this term satisfies
$M_\ell (\delta ) = [\frac {(\log \rho _\ell )^{1+6\delta }}{\mathfrak {s}_\ell (\delta )}]> (\log \rho _\ell )^{3\delta }$
. Consequently, this term satisfies
It is easy to check that
![]() $M_\ell (\delta )$
is at least
$M_\ell (\delta )$
is at least
![]() $[K_\ell (\delta ) \beta _n (\log \log \rho _\ell )^n]$
for
$[K_\ell (\delta ) \beta _n (\log \log \rho _\ell )^n]$
for
![]() $K_\ell (\delta ) = 4n (\log \rho _\ell )^{2\delta }$
when
$K_\ell (\delta ) = 4n (\log \rho _\ell )^{2\delta }$
when
![]() $\mathsf {Timely}_{\ell -1}$
occurs because
$\mathsf {Timely}_{\ell -1}$
occurs because
![]() $\rho _\ell \geq e^{\theta _{2n}}$
by Lemma 6.8. Hence, by Lemma 6.20, the preceding bound is at most
$\rho _\ell \geq e^{\theta _{2n}}$
by Lemma 6.8. Hence, by Lemma 6.20, the preceding bound is at most
![]() $e^{- 4n (\log \rho _\ell )^{2\delta }}$
when
$e^{- 4n (\log \rho _\ell )^{2\delta }}$
when
![]() $\mathsf {Timely}_{\ell -1}$
occurs. We conclude that, when
$\mathsf {Timely}_{\ell -1}$
occurs. We conclude that, when
![]() $\mathsf {Timely}_{\ell -1}$
occurs,
$\mathsf {Timely}_{\ell -1}$
occurs,
The first inequality follows from the upper bound of
![]() $e^{-4n (\log \rho _\ell )^{2\delta }}$
on both of the terms on the right-hand side of equation (6.59); the second and third inequalities follow from Lemma 6.8.
$e^{-4n (\log \rho _\ell )^{2\delta }}$
on both of the terms on the right-hand side of equation (6.59); the second and third inequalities follow from Lemma 6.8.
7 Existence of the stationary distribution
In this section, we will prove Theorem 2, which has two parts. The first part states the existence of a unique stationary distribution,
![]() $\pi _n$
, supported on the equivalence classes of nonisolated configurations,
$\pi _n$
, supported on the equivalence classes of nonisolated configurations,
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, to which the HAT dynamics converges from any n-element configuration. The second part provides a tail bound on the diameter of configurations under
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, to which the HAT dynamics converges from any n-element configuration. The second part provides a tail bound on the diameter of configurations under
![]() $\pi _n$
. We will prove these parts separately, as the following two propositions.
$\pi _n$
. We will prove these parts separately, as the following two propositions.
Proposition 7.1. For all
![]() $n\geq 1$
, from any n-element subset U, HAT converges to a unique stationary distribution
$n\geq 1$
, from any n-element subset U, HAT converges to a unique stationary distribution
![]() $\pi _n$
on
$\pi _n$
on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, given by
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
, given by
 $$ \begin{align} \pi_n ( \widehat U) = \frac{1}{\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U}}, \,\,\, \text{for} \widehat U \in \widehat{\mathrm{N}} \mathrm{onIso} (n), \end{align} $$
$$ \begin{align} \pi_n ( \widehat U) = \frac{1}{\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U}}, \,\,\, \text{for} \widehat U \in \widehat{\mathrm{N}} \mathrm{onIso} (n), \end{align} $$
in terms of the return time
![]() $\mathcal {T}_{\widehat U} = \inf \{ t \geq 1: \widehat U_t = \widehat U\}$
.
$\mathcal {T}_{\widehat U} = \inf \{ t \geq 1: \widehat U_t = \widehat U\}$
.
Proposition 7.2. For any
![]() $d \geq 2\theta _{4n}$
,
$d \geq 2\theta _{4n}$
,
 $$ \begin{align} \pi_{n}\big( \mathrm{diam} (\widehat U) \ge d\big)\le \exp \left( - \frac{d}{(\log d)^{1+o_n(1)}} \right). \end{align} $$
$$ \begin{align} \pi_{n}\big( \mathrm{diam} (\widehat U) \ge d\big)\le \exp \left( - \frac{d}{(\log d)^{1+o_n(1)}} \right). \end{align} $$
For the sake of concreteness, this is true with
![]() $6n^{-4}$
in the place of
$6n^{-4}$
in the place of
![]() $o_n (1)$
.
$o_n (1)$
.
It will be relatively easy to establish Proposition 7.2 using the inputs to the proof of Proposition 7.1 and Corollary 6.4, so we focus on presenting the key components of the proof of Proposition 7.1.
By standard theory for countable state space Markov chains, to prove Proposition 7.1, we must prove that the HAT dynamics is positive recurrent, irreducible and aperiodic. We address each of these in turn.
Proposition 7.3 (Positive recurrent).
For any
![]() $U \in \mathrm {NonIso} (n)$
,
$U \in \mathrm {NonIso} (n)$
,
![]() $\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U} < \infty $
.
$\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U} < \infty $
.
To prove Proposition 7.3, we will estimate the return time to an arbitrary n-element configuration
![]() $\widehat U$
by separately estimating the time it takes to reach the line segment
$\widehat U$
by separately estimating the time it takes to reach the line segment
![]() $\widehat L_n$
from
$\widehat L_n$
from
![]() $\widehat U$
, where
$\widehat U$
, where
![]() $L_n = \left \{y \,e_2: y \in \{0, 1, \dots , n-1\} \right \}$
in terms of
$L_n = \left \{y \,e_2: y \in \{0, 1, \dots , n-1\} \right \}$
in terms of
![]() $e_2 = (0,1)$
, and the time it takes to hit
$e_2 = (0,1)$
, and the time it takes to hit
![]() $\widehat U$
from
$\widehat U$
from
![]() $\widehat L_n$
. The first estimate is the content of the following result.
$\widehat L_n$
. The first estimate is the content of the following result.
Proposition 7.4. There is a constant c such that, if U is a configuration in
![]() $\mathrm {NonIso} (n)$
with a diameter of R, then, for all
$\mathrm {NonIso} (n)$
with a diameter of R, then, for all
![]() $K \geq \max \{R,\theta _{5n} (cn)\}$
,
$K \geq \max \{R,\theta _{5n} (cn)\}$
,
The second estimate is provided by the next proposition.
Proposition 7.5. There is a constant c such that, if U is a configuration in
![]() $\mathrm {NonIso} (n)$
with a diameter of R, then, for all
$\mathrm {NonIso} (n)$
with a diameter of R, then, for all
![]() $K \geq \max \{e^{R^{2.1}},\theta _{5n} (cn)\}$
,
$K \geq \max \{e^{R^{2.1}},\theta _{5n} (cn)\}$
,
The proof of Proposition 7.3 applies equations (7.3) and (7.4) to the tail sum formula for
![]() $\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U}$
.
$\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U}$
.
Proof of Proposition 7.3.
Let
![]() $U \in \mathrm {NonIso} (n)$
. We have
$U \in \mathrm {NonIso} (n)$
. We have
 $$ \begin{align} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} = \sum_{t=0}^\infty \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat U}> t \big) \leq \sum_{t=0}^\infty \Big( \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat L_n} > \tfrac{t}{2} \big) + \mathbf{P}_{\widehat L_n} \big( \mathcal{T}_{\widehat U} > \tfrac{t}{2} \big) \Big). \end{align} $$
$$ \begin{align} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} = \sum_{t=0}^\infty \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat U}> t \big) \leq \sum_{t=0}^\infty \Big( \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat L_n} > \tfrac{t}{2} \big) + \mathbf{P}_{\widehat L_n} \big( \mathcal{T}_{\widehat U} > \tfrac{t}{2} \big) \Big). \end{align} $$
Suppose U has a diameter of at most R, and let
![]() $J = \max \{e^{R^{2.1}},\theta _{5n} (cn)\}$
, where c is the larger of the constants from Propositions 7.4 and 7.5. We group the sum (7.5) over t into blocks:
$J = \max \{e^{R^{2.1}},\theta _{5n} (cn)\}$
, where c is the larger of the constants from Propositions 7.4 and 7.5. We group the sum (7.5) over t into blocks:
 $$\begin{align*}\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \leq O(J^5) + \sum_{K=J}^\infty \sum_{t= 2K^5}^{2(K+1)^5} \Big( \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat L_n}> \tfrac{t}{2} \big) + \mathbf{P}_{\widehat L_n} \big( \mathcal{T}_{\widehat U} > \tfrac{t}{2} \big) \Big).\end{align*}$$
$$\begin{align*}\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \leq O(J^5) + \sum_{K=J}^\infty \sum_{t= 2K^5}^{2(K+1)^5} \Big( \mathbf{P}_{\widehat U} \big( \mathcal{T}_{\widehat L_n}> \tfrac{t}{2} \big) + \mathbf{P}_{\widehat L_n} \big( \mathcal{T}_{\widehat U} > \tfrac{t}{2} \big) \Big).\end{align*}$$
By equations (7.3) and (7.4) of Propositions 7.4 and 7.5, each of the
![]() $O(K^4)$
summands in the K
th block is at most
$O(K^4)$
summands in the K
th block is at most
Substituting equation (7.6) into equation (7.5), we find
 $$\begin{align*}\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \leq O(J^5) + O(1) \sum_{K=J}^\infty K^4 e^{-K} < \infty.\end{align*}$$
$$\begin{align*}\mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \leq O(J^5) + O(1) \sum_{K=J}^\infty K^4 e^{-K} < \infty.\end{align*}$$
Propositions 7.4 and 7.5 also imply irreducibility.
Proposition 7.6 (Irreducible).
For any
![]() $n \geq 1$
, HAT is irreducible on
$n \geq 1$
, HAT is irreducible on
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
.
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
.
Proof. Let
![]() $\widehat U, \widehat V \in \widehat {\mathrm {N}} \mathrm {onIso} (n)$
. It suffices to show that HAT reaches
$\widehat U, \widehat V \in \widehat {\mathrm {N}} \mathrm {onIso} (n)$
. It suffices to show that HAT reaches
![]() $\widehat V$
from
$\widehat V$
from
![]() $\widehat U$
in a finite number of steps with positive probability. By Propositions 7.4 and 7.5, there is a finite number of steps
$\widehat U$
in a finite number of steps with positive probability. By Propositions 7.4 and 7.5, there is a finite number of steps
![]() $K = K(U, V)$
such that
$K = K(U, V)$
such that
By the Markov property applied to
![]() $\mathcal {T}_{\widehat L_n}$
, the preceding bounds imply that
$\mathcal {T}_{\widehat L_n}$
, the preceding bounds imply that
![]() $\mathbf {P}_{\widehat U} (\mathcal {T}_{\widehat V} < 2K)> 0$
.
$\mathbf {P}_{\widehat U} (\mathcal {T}_{\widehat V} < 2K)> 0$
.
Lastly, because aperiodicity is a class property, it follows from irreducibility and the simple fact that
![]() $\widehat L_n$
is aperiodic.
$\widehat L_n$
is aperiodic.
Proposition 7.7 (Aperiodic).
![]() $\widehat L_n$
is aperiodic.
$\widehat L_n$
is aperiodic.
Proof. We claim that
![]() $\mathbf {P}_{L_n} (U_1 = L_n) \geq \frac 14$
, which implies that
$\mathbf {P}_{L_n} (U_1 = L_n) \geq \frac 14$
, which implies that
![]() $\mathbf {P}_{\widehat L_n} \big ( \widehat U_1 = \widehat L_n \big ) \geq \frac 14> 0$
. Indeed, every element of
$\mathbf {P}_{\widehat L_n} \big ( \widehat U_1 = \widehat L_n \big ) \geq \frac 14> 0$
. Indeed, every element of
![]() $L_n$
neighbors another, so, regardless of which one is activated, we can dictate one random walk step which results in transport to the site of activation and
$L_n$
neighbors another, so, regardless of which one is activated, we can dictate one random walk step which results in transport to the site of activation and
![]() $U_1 = L_n$
.
$U_1 = L_n$
.
The preceding results constitute a proof of Proposition 7.1.
The subsections are organized as follows. In Section 7.1, we prove some preliminary results, including a key lemma which states that it is possible to reach any configuration
![]() $U \in \mathrm {NonIso} (n)$
from
$U \in \mathrm {NonIso} (n)$
from
![]() $L_n$
, in a number of steps depending only on n and
$L_n$
, in a number of steps depending only on n and
![]() $\mathrm {diam} (U)$
. These results support the proofs of Propositions 7.4 and 7.5 in Section 7.2 and Section 7.3, respectively. In Section 7.4, we prove Proposition 7.2.
$\mathrm {diam} (U)$
. These results support the proofs of Propositions 7.4 and 7.5 in Section 7.2 and Section 7.3, respectively. In Section 7.4, we prove Proposition 7.2.
7.1 Preliminaries of hitting estimates for configurations
The purpose of this section is to prove that if HAT can reach
![]() $\widehat V$
from
$\widehat V$
from
![]() $\widehat L_n$
, then it does so in at most
$\widehat L_n$
, then it does so in at most
![]() $O_{\! n} (\mathrm {rad} (V) )$
steps with a probability of at least
$O_{\! n} (\mathrm {rad} (V) )$
steps with a probability of at least
![]() $e^{-O_{n} ( \mathrm {rad} (V)^2)}$
. (Recall that the radius of
$e^{-O_{n} ( \mathrm {rad} (V)^2)}$
. (Recall that the radius of
![]() $A \subseteq \mathbb {Z}^2$
is defined as
$A \subseteq \mathbb {Z}^2$
is defined as
![]() $\mathrm {rad} (A) = \sup \{|x|: x \in A\}$
.) We split the proof into two lemmas. The first states that if HAT can form
$\mathrm {rad} (A) = \sup \{|x|: x \in A\}$
.) We split the proof into two lemmas. The first states that if HAT can form
![]() $V_1$
from
$V_1$
from
![]() $V_0$
in one step, then it does so with a probability of at least
$V_0$
in one step, then it does so with a probability of at least
![]() $e^{-O_{n} (\mathrm {rad} (V_0))}$
.
$e^{-O_{n} (\mathrm {rad} (V_0))}$
.
Lemma 7.8. There is a constant c such that, if
![]() $V_0$
and
$V_0$
and
![]() $V_1$
are subsets of
$V_1$
are subsets of
![]() $\mathbb {Z}^2$
with
$\mathbb {Z}^2$
with
![]() $n \geq 2$
elements that satisfy
$n \geq 2$
elements that satisfy
![]() $\mathbf {P}_{V_0} (U_1 = V_1)> 0$
, then
$\mathbf {P}_{V_0} (U_1 = V_1)> 0$
, then
With more work, we could improve the lower bound in equation (7.7) to
![]() $\Omega _n ( \frac {1}{\log \mathrm {rad} (V_0)})$
, but this would make no difference in our application of the lemma.
$\Omega _n ( \frac {1}{\log \mathrm {rad} (V_0)})$
, but this would make no difference in our application of the lemma.
Proof of Lemma 7.8.
Since
![]() $\mathbf {P}_{V_0} (U_1 = V_1)$
is positive, the transition from
$\mathbf {P}_{V_0} (U_1 = V_1)$
is positive, the transition from
![]() $V_0$
to
$V_0$
to
![]() $V_1$
can be realized by activation at some x and transport to some y, where x is exposed in
$V_1$
can be realized by activation at some x and transport to some y, where x is exposed in
![]() $V_0$
and there is a path of length
$V_0$
and there is a path of length
![]() $O (n \mathrm {rad} (V_0))$
from x to y that lies outside of
$O (n \mathrm {rad} (V_0))$
from x to y that lies outside of
![]() $V_0 {\setminus } \{x\}$
(Lemma 3.13). The former implies that
$V_0 {\setminus } \{x\}$
(Lemma 3.13). The former implies that
![]() ${\mathbb {H}}_{V_0} (x) \geq e^{- O(n \log n)}$
(Theorem 4), while the latter implies that
${\mathbb {H}}_{V_0} (x) \geq e^{- O(n \log n)}$
(Theorem 4), while the latter implies that
![]() $\mathbb {P}_x ( S_{\tau _{V_0 {\setminus }\{x\}} - 1} = y) \geq 4^{-O (n \mathrm {rad} (V_0))}$
. The claimed bound (7.7) then follows from
$\mathbb {P}_x ( S_{\tau _{V_0 {\setminus }\{x\}} - 1} = y) \geq 4^{-O (n \mathrm {rad} (V_0))}$
. The claimed bound (7.7) then follows from
The second lemma proves that every
![]() $V \in \mathrm {NonIso} (n)$
can be reached from
$V \in \mathrm {NonIso} (n)$
can be reached from
![]() $L_n$
in
$L_n$
in
![]() $O_{\! n} (\mathrm {rad} (V))$
steps, through a sequence of configurations with diameters of
$O_{\! n} (\mathrm {rad} (V))$
steps, through a sequence of configurations with diameters of
![]() $O_{\! n} (\mathrm {rad} (V))$
.
$O_{\! n} (\mathrm {rad} (V))$
.
Lemma 7.9. For any number of elements
![]() $n \geq 2$
and configuration V in
$n \geq 2$
and configuration V in
![]() $\mathrm {NonIso} (n)$
, if the radius of V is at most an integer
$\mathrm {NonIso} (n)$
, if the radius of V is at most an integer
![]() $r \geq 10 n$
, then there is a sequence of
$r \geq 10 n$
, then there is a sequence of
![]() $k \leq 100 nr$
activation sites
$k \leq 100 nr$
activation sites
![]() $x_1, \dots , x_k$
and transport sites
$x_1, \dots , x_k$
and transport sites
![]() $y_1, \dots , y_k$
which can be ‘realized’ by HAT from
$y_1, \dots , y_k$
which can be ‘realized’ by HAT from
![]() $V_0 = L_n$
to
$V_0 = L_n$
to
![]() $V_k = V$
in the following sense: If we set
$V_k = V$
in the following sense: If we set
![]() $V_i = (V_{i-1} {\setminus } \{x_i\}) \cup \{y_i\}$
for each
$V_i = (V_{i-1} {\setminus } \{x_i\}) \cup \{y_i\}$
for each
![]() $i \in \{1,\dots ,k\}$
, then each transition probability
$i \in \{1,\dots ,k\}$
, then each transition probability
![]() $\mathbf {P}_{V_{i-1}} (U_i = V_i)$
is positive. Additionally, each
$\mathbf {P}_{V_{i-1}} (U_i = V_i)$
is positive. Additionally, each
![]() $V_i$
is contained in
$V_i$
is contained in
![]() $D(r+10n)$
.
$D(r+10n)$
.
The factors of
![]() $10$
and
$10$
and
![]() $100$
in the lemma statement are for convenience and have no further significance. We will prove Lemma 7.9 by induction on n. Informally, we will remove one element of
$100$
in the lemma statement are for convenience and have no further significance. We will prove Lemma 7.9 by induction on n. Informally, we will remove one element of
![]() $L_n$
to facilitate the use of the induction hypothesis, forming most of V before returning the removed element. There is a complication in this step, as we cannot allow the induction hypothesis to ‘interact’ with the removed element. We will resolve this problem by proving a slightly stronger claim than the lemma requires.
$L_n$
to facilitate the use of the induction hypothesis, forming most of V before returning the removed element. There is a complication in this step, as we cannot allow the induction hypothesis to ‘interact’ with the removed element. We will resolve this problem by proving a slightly stronger claim than the lemma requires.
The proof will overcome two main challenges. First, removing an element from a configuration V in
![]() $\mathrm {NonIso} (n)$
can produce a configuration in
$\mathrm {NonIso} (n)$
can produce a configuration in
![]() $\mathrm {Iso} (n-1)$
, in which case the induction hypothesis will not apply. Indeed, there are configurations of
$\mathrm {Iso} (n-1)$
, in which case the induction hypothesis will not apply. Indeed, there are configurations of
![]() $\mathrm {NonIso} (n)$
for which the removal of any exposed, nonisolated element produces a configuration of
$\mathrm {NonIso} (n)$
for which the removal of any exposed, nonisolated element produces a configuration of
![]() $\mathrm {Iso} (n-1)$
(such a V is depicted in Figure 12). Second, if an isolated element is removed alone, it cannot be returned to form V by a single step of the HAT dynamics. To see how these difficulties interact, suppose that
$\mathrm {Iso} (n-1)$
(such a V is depicted in Figure 12). Second, if an isolated element is removed alone, it cannot be returned to form V by a single step of the HAT dynamics. To see how these difficulties interact, suppose that
![]() $\partial _{\kern 0.05em \mathrm {exp}} V$
(defined as
$\partial _{\kern 0.05em \mathrm {exp}} V$
(defined as
![]() $\{x \in V: {\mathbb {H}}_V (x)> 0\}$
) contains only one nonisolated element (say, at v), which is part of a two-element connected component of V. We cannot remove it and still apply the induction hypothesis, as
$\{x \in V: {\mathbb {H}}_V (x)> 0\}$
) contains only one nonisolated element (say, at v), which is part of a two-element connected component of V. We cannot remove it and still apply the induction hypothesis, as
![]() $V{\setminus }\{v\}$
belongs to
$V{\setminus }\{v\}$
belongs to
![]() $\mathrm {Iso} (n-1)$
. We then have no choice but to remove an isolated element.
$\mathrm {Iso} (n-1)$
. We then have no choice but to remove an isolated element.

Figure 12 An instance of Case 2. If any nonisolated element of
![]() $\partial _{\kern 0.05em \mathrm {exp}} V$
is removed, the resulting set is isolated. We use the induction hypothesis to form
$\partial _{\kern 0.05em \mathrm {exp}} V$
is removed, the resulting set is isolated. We use the induction hypothesis to form
![]() $V' = (V{\setminus }\{v_{\mathsf {ne}},u\})\cup \{v_{\mathsf {sw}}-e_2\}$
. The subsequent steps to obtain V from
$V' = (V{\setminus }\{v_{\mathsf {ne}},u\})\cup \{v_{\mathsf {sw}}-e_2\}$
. The subsequent steps to obtain V from
![]() $V'$
are depicted in Figure 13.
$V'$
are depicted in Figure 13.
When we are forced to remove an isolated element, we will apply the induction hypothesis to form a configuration for which the removed element can be ‘treadmilled’ to its proper location, chaperoned by a element which is nonisolated in the final configuration and so can be returned once the removed element reaches its destination.
We briefly explain what we mean by treadmilling a pair of elements. Consider elements
![]() $v_1$
and
$v_1$
and
![]() $v_1 + e_2$
of a configuration V. If
$v_1 + e_2$
of a configuration V. If
![]() ${\mathbb {H}}_V (v_1)$
is positive and if there is a path from
${\mathbb {H}}_V (v_1)$
is positive and if there is a path from
![]() $v_1$
to
$v_1$
to
![]() $v_1+2e_2$
which lies outside of
$v_1+2e_2$
which lies outside of
![]() $V{\setminus }\{v_1\}$
, then we can activate at
$V{\setminus }\{v_1\}$
, then we can activate at
![]() $v_1$
and transport to
$v_1$
and transport to
![]() $v_1+2e_2$
. The result is that the pair
$v_1+2e_2$
. The result is that the pair
![]() $\{v_1,v_1+2e_2\}$
has shifted by
$\{v_1,v_1+2e_2\}$
has shifted by
![]() $e_2$
. Call the new configuration
$e_2$
. Call the new configuration
![]() $V'$
. If
$V'$
. If
![]() $v_1+e_2$
is exposed in
$v_1+e_2$
is exposed in
![]() $V'$
and if there is a path from
$V'$
and if there is a path from
![]() $v_1+e_2$
to
$v_1+e_2$
to
![]() $v_1+3e_2$
in
$v_1+3e_2$
in
![]() $V'{\setminus }\{v_1+e_2\}$
, we can analogously shift the pair
$V'{\setminus }\{v_1+e_2\}$
, we can analogously shift the pair
![]() $\{v_1+e_2,v_1+2e_2\}$
by another
$\{v_1+e_2,v_1+2e_2\}$
by another
![]() $e_2$
.
$e_2$
.
Proof of Lemma 7.9.
The proof is by induction on
![]() $n \geq 2$
. We will actually prove a stronger claim because it facilitates the induction step. To state the claim, we denote by
$n \geq 2$
. We will actually prove a stronger claim because it facilitates the induction step. To state the claim, we denote by
![]() $W_i = V_{i-1}{\setminus }\{x_i\}$
the HAT configuration ‘in between’
$W_i = V_{i-1}{\setminus }\{x_i\}$
the HAT configuration ‘in between’
![]() $V_{i-1}$
and
$V_{i-1}$
and
![]() $V_i$
and by
$V_i$
and by
![]() $E_i$
the event that, during the transition from
$E_i$
the event that, during the transition from
![]() $V_{i-1}$
to
$V_{i-1}$
to
![]() $V_i$
, the transport step takes place inside of
$V_i$
, the transport step takes place inside of
![]() $B_i = D(r+10n){\setminus } W_i$
:
$B_i = D(r+10n){\setminus } W_i$
:
We claim that Lemma 7.9 is true even if the conclusion
![]() $\mathbf {P}_{V_{i-1}} (U_i = V_i)> 0$
is replaced by
$\mathbf {P}_{V_{i-1}} (U_i = V_i)> 0$
is replaced by
![]() $\mathbf {P}_{V_{i-1}} (U_i = V_i, E_i)> 0$
.
$\mathbf {P}_{V_{i-1}} (U_i = V_i, E_i)> 0$
.
To prove this claim, we will show that, for any V satisfying the hypotheses, there are sequences of at most
![]() $100nr$
activation sites
$100nr$
activation sites
![]() $x_1, \dots , x_k$
, transport sites
$x_1, \dots , x_k$
, transport sites
![]() $y_1, \dots , y_k$
, and random walk paths
$y_1, \dots , y_k$
, and random walk paths
![]() $\Gamma ^1, \dots , \Gamma ^k$
such that the activation and transport sites can be realized by HAT from
$\Gamma ^1, \dots , \Gamma ^k$
such that the activation and transport sites can be realized by HAT from
![]() $V_0 = L_n$
to
$V_0 = L_n$
to
![]() $V_k = V$
, and such that each
$V_k = V$
, and such that each
![]() $\Gamma ^i$
is a finite random walk path from
$\Gamma ^i$
is a finite random walk path from
![]() $x_i$
to
$x_i$
to
![]() $y_i$
which lies in
$y_i$
which lies in
![]() $B_i$
. While it is possible to explicitly list these sequences of sites and paths in the proof which follows, the depictions in upcoming Figures 12 and 13 are easier to understand and so we omit some cumbersome details regarding them.
$B_i$
. While it is possible to explicitly list these sequences of sites and paths in the proof which follows, the depictions in upcoming Figures 12 and 13 are easier to understand and so we omit some cumbersome details regarding them.

Figure 13 An instance of Case 2 (continued). On the left, we depict the configuration which results from the use of the induction hypothesis. The element outside of the disk D (the boundary of which is the orange circle) is transported to
![]() $v_{\mathsf {sw}}-2e_2$
(unfilled circle). In the middle, we depict the treadmilling of the pair
$v_{\mathsf {sw}}-2e_2$
(unfilled circle). In the middle, we depict the treadmilling of the pair
![]() $\{v_{\mathsf {sw}}-e_2,v_{\mathsf {sw}}-2e_2\}$
through the quadrant
$\{v_{\mathsf {sw}}-e_2,v_{\mathsf {sw}}-2e_2\}$
through the quadrant
![]() $Q_{\mathsf {sw}}$
, around
$Q_{\mathsf {sw}}$
, around
![]() $D^c$
and through the quadrant
$D^c$
and through the quadrant
![]() $Q_{\mathsf {ne}}$
, until one of the treadmilled elements is at
$Q_{\mathsf {ne}}$
, until one of the treadmilled elements is at
![]() $v_{\mathsf {ne}}$
. The quadrants are depicted by dashed lines. On the right, the other element is returned to u (unfilled circle). The resulting configuration is V (see Figure 12).
$v_{\mathsf {ne}}$
. The quadrants are depicted by dashed lines. On the right, the other element is returned to u (unfilled circle). The resulting configuration is V (see Figure 12).
Concerning the base case of
![]() $n=2$
, note that
$n=2$
, note that
![]() $\mathrm {NonIso} (2)$
has the same elements as the equivalence class
$\mathrm {NonIso} (2)$
has the same elements as the equivalence class
![]() $\widehat L_2$
, so
$\widehat L_2$
, so
![]() $x_1 = e_2$
,
$x_1 = e_2$
,
![]() $y_1 = e_2$
,
$y_1 = e_2$
,
![]() $\Gamma ^1 = \emptyset $
works. Suppose the claim holds up to
$\Gamma ^1 = \emptyset $
works. Suppose the claim holds up to
![]() $n-1$
for
$n-1$
for
![]() $n \geq 3$
. There are two cases:
$n \geq 3$
. There are two cases:
-
1. There is a nonisolated v in
 $\partial _{\kern 0.05em \mathrm {exp}} V$
such that
$\partial _{\kern 0.05em \mathrm {exp}} V$
such that
 $V {\setminus } \{v\}$
belongs to
$V {\setminus } \{v\}$
belongs to
 $\mathrm {NonIso} (n-1)$
.
$\mathrm {NonIso} (n-1)$
. -
2. For every nonisolated v in
 $\partial _{\kern 0.05em \mathrm {exp}} V$
,
$\partial _{\kern 0.05em \mathrm {exp}} V$
,
 $V{\setminus } \{v\}$
belongs to
$V{\setminus } \{v\}$
belongs to
 $\mathrm {Iso} (n-1)$
.
$\mathrm {Iso} (n-1)$
.
It will be easy to form V using the induction hypothesis in Case 1. In Case 2, we will need to use the induction hypothesis to form a set related to V and subsequently form V from this related set. An instance of Case 2 is depicted in Figure 12.
Case 1. Let r be an integer exceeding
![]() $10n$
and the radius of V and denote
$10n$
and the radius of V and denote
![]() $R = r + 10(n-1)$
. Recall that
$R = r + 10(n-1)$
. Recall that
![]() $V_0 = L_n$
. Our strategy is to place one element of
$V_0 = L_n$
. Our strategy is to place one element of
![]() $L_n$
outside of
$L_n$
outside of
![]() $D(R)$
and then apply the induction hypothesis to
$D(R)$
and then apply the induction hypothesis to
![]() $L_{n-1}$
to form most of V. This explains the role of the event
$L_{n-1}$
to form most of V. This explains the role of the event
![]() $E_i$
– it ensures that the element outside of the disk does not interfere with our use of the induction hypothesis.
$E_i$
– it ensures that the element outside of the disk does not interfere with our use of the induction hypothesis.
To remove an element of
![]() $L_n$
to
$L_n$
to
![]() $D(R)^c$
, we treadmill (see the explanation following the lemma statement) the pair
$D(R)^c$
, we treadmill (see the explanation following the lemma statement) the pair
![]() $\{(n-2)e_2, (n-1)e_2\}$
to
$\{(n-2)e_2, (n-1)e_2\}$
to
![]() $\{Re_2,(R+1)e_2\}$
, after which we activate at
$\{Re_2,(R+1)e_2\}$
, after which we activate at
![]() $Re_2$
and transport to
$Re_2$
and transport to
![]() $(n-2)e_2$
. This process requires
$(n-2)e_2$
. This process requires
![]() $R-n+2$
steps. It is clear that every transport step can occur via a finite random walk path which lies in
$R-n+2$
steps. It is clear that every transport step can occur via a finite random walk path which lies in
![]() $D(r+10n)$
. Call
$D(r+10n)$
. Call
![]() $a = (R+1)e_2$
. The resulting configuration is
$a = (R+1)e_2$
. The resulting configuration is
![]() $L_{n-1} \cup \{a\}$
.
$L_{n-1} \cup \{a\}$
.
We will now apply induction hypothesis. Choose a nonisolated element v of
![]() $\partial _{\kern 0.05em \mathrm {exp}} V$
such that
$\partial _{\kern 0.05em \mathrm {exp}} V$
such that
![]() $V' = V {\setminus } \{v\}$
belongs to
$V' = V {\setminus } \{v\}$
belongs to
![]() $\mathrm {NonIso} (n-1)$
. Such a v exists because we are in Case 1. By the induction hypothesis and because the radius of
$\mathrm {NonIso} (n-1)$
. Such a v exists because we are in Case 1. By the induction hypothesis and because the radius of
![]() $V'$
is at most r, there are sequences of at most
$V'$
is at most r, there are sequences of at most
![]() $100 (n-1) r$
activation and transport sites, which can be realized by HAT from
$100 (n-1) r$
activation and transport sites, which can be realized by HAT from
![]() $L_{n-1} \cup \{a\}$
to
$L_{n-1} \cup \{a\}$
to
![]() $V' \cup \{a\}$
, and a corresponding sequence of finite random walk paths which lie in
$V' \cup \{a\}$
, and a corresponding sequence of finite random walk paths which lie in
![]() $D(R)$
.
$D(R)$
.
To complete this case, we activate at a and transport to v, which is possible because v was exposed and nonisolated in V. The existence of a random walk path from a to v which lies outside of
![]() $V'$
is a consequence of Lemma 3.13. Recall that Lemma 3.13 applies only to sets in
$V'$
is a consequence of Lemma 3.13. Recall that Lemma 3.13 applies only to sets in
![]() $\mathscr {H}_n$
(n-element sets which contain an exposed origin). If
$\mathscr {H}_n$
(n-element sets which contain an exposed origin). If
![]() $A = V \cup \{a\}$
, then
$A = V \cup \{a\}$
, then
![]() $A-v$
belongs to
$A-v$
belongs to
![]() $\mathscr {H}_n$
. By Lemma 3.13, there is a finite random walk path from a to v which does not hit
$\mathscr {H}_n$
. By Lemma 3.13, there is a finite random walk path from a to v which does not hit
![]() $V'$
and which is contained in
$V'$
and which is contained in
![]() $D(R+3) \subseteq D(r+10n)$
.
$D(R+3) \subseteq D(r+10n)$
.
In summary, there are sequences of at most
![]() $(R-n+2) + 100 (n-1) r + 1 \leq 100 n r$
(the inequality follows from the assumption that
$(R-n+2) + 100 (n-1) r + 1 \leq 100 n r$
(the inequality follows from the assumption that
![]() $r \geq 10n$
) activation and transport sites which can be realized by HAT from
$r \geq 10n$
) activation and transport sites which can be realized by HAT from
![]() $L_n$
to V, as well as corresponding finite random walk paths which remain within
$L_n$
to V, as well as corresponding finite random walk paths which remain within
![]() $D(r+10n)$
. This proves the claim in Case 1.
$D(r+10n)$
. This proves the claim in Case 1.
Case 2. In this case, the removal of any nonisolated element v of
![]() $\partial _{\kern 0.05em \mathrm {exp}} V$
results in an isolated set
$\partial _{\kern 0.05em \mathrm {exp}} V$
results in an isolated set
![]() $V {\setminus } \{v\}$
, hence we cannot form such a set using the induction hypothesis. Instead, we will form a related, nonisolated set.
$V {\setminus } \{v\}$
, hence we cannot form such a set using the induction hypothesis. Instead, we will form a related, nonisolated set.
The first
![]() $R-n+2$
steps, which produce
$R-n+2$
steps, which produce
![]() $L_{n-1} \cup \{a\}$
from
$L_{n-1} \cup \{a\}$
from
![]() $L_n$
, are identical to those of Case 1. We apply the induction hypothesis to form the set
$L_n$
, are identical to those of Case 1. We apply the induction hypothesis to form the set
which is depicted in Figure 12. Here,
![]() $v_{\textsf {ne}}$
is the easternmost of the northernmost elements of V,
$v_{\textsf {ne}}$
is the easternmost of the northernmost elements of V,
![]() $v_{\textsf {sw}}$
is the westernmost of the southernmost elements of V and u is any nonisolated element of
$v_{\textsf {sw}}$
is the westernmost of the southernmost elements of V and u is any nonisolated element of
![]() $\partial _{\kern 0.05em \mathrm {exp}} V$
(e.g.,
$\partial _{\kern 0.05em \mathrm {exp}} V$
(e.g.,
![]() $u = v_{\textsf {ne}}$
is allowed if
$u = v_{\textsf {ne}}$
is allowed if
![]() $v_{\textsf {ne}}$
is nonisolated).
$v_{\textsf {ne}}$
is nonisolated).
The remaining steps are depicted in Figure 13. By the induction hypothesis and because the radius of
![]() $V'$
is at most
$V'$
is at most
![]() $r+1$
, there are sequences of at most
$r+1$
, there are sequences of at most
![]() $100 (n-1) (r+1)$
activation and transport sites, which can be realized by HAT from
$100 (n-1) (r+1)$
activation and transport sites, which can be realized by HAT from
![]() $L_{n-1} \cup \{a\}$
to
$L_{n-1} \cup \{a\}$
to
![]() $V' \cup \{a\}$
, and a corresponding sequence of finite random walk paths which lie in
$V' \cup \{a\}$
, and a corresponding sequence of finite random walk paths which lie in
![]() $D(R+1)$
.
$D(R+1)$
.
Next, we activate at a and transport to
![]() $v_{\mathsf {sw}}-2e_2$
, which is possible because
$v_{\mathsf {sw}}-2e_2$
, which is possible because
![]() $v_{\mathsf {sw}}-2e_2$
is exposed and nonisolated in
$v_{\mathsf {sw}}-2e_2$
is exposed and nonisolated in
![]() $V'$
. Like in Case 1, the existence of a finite random walk path from a to
$V'$
. Like in Case 1, the existence of a finite random walk path from a to
![]() $v_{\mathsf {sw}}-2e_2$
which lies in
$v_{\mathsf {sw}}-2e_2$
which lies in
![]() $D(R+3){\setminus }V' \subseteq D(r+10n)$
is implied by Lemma 3.13. Denote the resulting configuration by
$D(R+3){\setminus }V' \subseteq D(r+10n)$
is implied by Lemma 3.13. Denote the resulting configuration by
![]() $V"$
.
$V"$
.
The choice of
![]() $v_{\mathsf {sw}}$
ensures that
$v_{\mathsf {sw}}$
ensures that
![]() $v_{\mathsf {sw}} - e_2$
and
$v_{\mathsf {sw}} - e_2$
and
![]() $v_{\mathsf {sw}} - 2e_2$
are the only elements of
$v_{\mathsf {sw}} - 2e_2$
are the only elements of
![]() $V"$
which lie in the quadrant defined by
$V"$
which lie in the quadrant defined by
Additionally, the quadrant defined by
contains no elements of
![]() $V"$
. As depicted in Figure 13, this enables us to treadmill the pair
$V"$
. As depicted in Figure 13, this enables us to treadmill the pair
![]() $\{v_{\mathsf {sw}} - e_2, v_{\mathsf {sw}} - 2e_2\}$
from
$\{v_{\mathsf {sw}} - e_2, v_{\mathsf {sw}} - 2e_2\}$
from
![]() $Q_{\mathsf {sw}}$
to
$Q_{\mathsf {sw}}$
to
![]() $D(R+3)^c$
and then to
$D(R+3)^c$
and then to
![]() $\{v_{\mathsf {ne}},v_{\mathsf {ne}}+e_2\}$
in
$\{v_{\mathsf {ne}},v_{\mathsf {ne}}+e_2\}$
in
![]() $Q_{\mathsf {ne}}$
, without the pair encountering the remaining elements of
$Q_{\mathsf {ne}}$
, without the pair encountering the remaining elements of
![]() $V"$
. It is clear that this can be accomplished by fewer than
$V"$
. It is clear that this can be accomplished by fewer than
![]() $10(R+3)$
activation and transport sites, with corresponding finite random walk paths which lie in
$10(R+3)$
activation and transport sites, with corresponding finite random walk paths which lie in
![]() $D(R+6)$
. The resulting configuration is
$D(R+6)$
. The resulting configuration is
![]() $V"' = V\cup \{v_{\mathsf {ne}}+e_2\}{\setminus }\{u\}$
.
$V"' = V\cup \{v_{\mathsf {ne}}+e_2\}{\setminus }\{u\}$
.
Lastly, we activate at
![]() $v_{\mathsf {ne}}+e_2$
and transport to u, which is possible because the former is exposed in
$v_{\mathsf {ne}}+e_2$
and transport to u, which is possible because the former is exposed in
![]() $V"'$
and the latter is exposed and nonisolated in V. As before, the fact that there is a finite random walk path in
$V"'$
and the latter is exposed and nonisolated in V. As before, the fact that there is a finite random walk path in
![]() $D(r+10n)$
which accomplishes the transport step is a consequence of Lemma 3.13. The resulting configuration is V.
$D(r+10n)$
which accomplishes the transport step is a consequence of Lemma 3.13. The resulting configuration is V.
In summary, there are sequences of fewer than
![]() $(R-n+2)+100(n-1)(r+1)+10(R+3)+2 \leq 100nr$
(the inequality follows from the assumption that
$(R-n+2)+100(n-1)(r+1)+10(R+3)+2 \leq 100nr$
(the inequality follows from the assumption that
![]() $r \geq 10n$
) activation and transport sites which can be realized by HAT from
$r \geq 10n$
) activation and transport sites which can be realized by HAT from
![]() $L_n$
to V, as well as corresponding finite random walk paths which remain in
$L_n$
to V, as well as corresponding finite random walk paths which remain in
![]() $D(r+10n)$
. This proves the claim in Case 2.
$D(r+10n)$
. This proves the claim in Case 2.
We can combine Lemma 7.8 and Lemma 7.9 to bound below the probability of forming a configuration from a line.
Lemma 7.10. There is a constant c such that, if V is a configuration in
![]() $\mathrm {NonIso} (n)$
with
$\mathrm {NonIso} (n)$
with
![]() $n \geq 2$
and a diameter of at most
$n \geq 2$
and a diameter of at most
![]() $R \geq 10n$
, then
$R \geq 10n$
, then
Proof. The hypotheses of Lemma 7.9 require an integer upper bound r on the radius of V of at least
![]() $10n$
. We are free to assume that V contains the origin, in which case a choice of
$10n$
. We are free to assume that V contains the origin, in which case a choice of
![]() $r = \lfloor R \rfloor + 1$
works, due to the assumption
$r = \lfloor R \rfloor + 1$
works, due to the assumption
![]() $R \geq 10n$
. We apply Lemma 7.9 with this r to obtain a sequence of configurations
$R \geq 10n$
. We apply Lemma 7.9 with this r to obtain a sequence of configurations
![]() $L_n = V_0, V_1, \dots , V_{k-1}, V_k = V$
such that
$L_n = V_0, V_1, \dots , V_{k-1}, V_k = V$
such that
![]() $k \leq 100 nr$
, and such that
$k \leq 100 nr$
, and such that
![]() $V_i \subseteq D(r+10n)$
and
$V_i \subseteq D(r+10n)$
and
![]() $\mathbf {P}_{V_{i-1}} (U_i = V_i)> 0$
for each i.
$\mathbf {P}_{V_{i-1}} (U_i = V_i)> 0$
for each i.
Because the transition probabilities are positive and because they concern sets
![]() $V_{i-1}$
in the disk of radius
$V_{i-1}$
in the disk of radius
![]() $r+10n \leq 3R$
, Lemma 7.8 implies that each transition probability is at least
$r+10n \leq 3R$
, Lemma 7.8 implies that each transition probability is at least
![]() $e^{-c_1 n^2 R}$
for a constant
$e^{-c_1 n^2 R}$
for a constant
![]() $c_1$
. We use this fact in the following string of inequalities:
$c_1$
. We use this fact in the following string of inequalities:
The first inequality holds because
![]() $k \leq 100nr \leq 200nR$
; the second because
$k \leq 100nr \leq 200nR$
; the second because
![]() $\{\widehat U_k = \widehat V\} \subseteq \{\mathcal {T}_{\widehat V} \leq k\}$
; the third follows from the Markov property,
$\{\widehat U_k = \widehat V\} \subseteq \{\mathcal {T}_{\widehat V} \leq k\}$
; the third follows from the Markov property,
![]() $k \leq 100nr$
, and the preceding bound from Lemma 7.8; the fourth from
$k \leq 100nr$
, and the preceding bound from Lemma 7.8; the fourth from
![]() $r \leq 2R$
.
$r \leq 2R$
.
7.2 Proof of Proposition 7.4
We now use Lemma 7.8 to obtain a tail bound on the time it takes for a given configuration to reach
![]() $ \widehat L_n$
. Our strategy is to repeatedly attempt to observe the formation of
$ \widehat L_n$
. Our strategy is to repeatedly attempt to observe the formation of
![]() $\widehat L_n$
in n consecutive steps. If the attempt fails then, because the diameter of the resulting set may be larger – worsening the estimate (7.7) – we will wait until the diameter becomes smaller before the next attempt.
$\widehat L_n$
in n consecutive steps. If the attempt fails then, because the diameter of the resulting set may be larger – worsening the estimate (7.7) – we will wait until the diameter becomes smaller before the next attempt.
Proof of Proposition 7.4.
To avoid confusion of U and
![]() $U_t$
, we will use
$U_t$
, we will use
![]() $V_0$
instead of U. We introduce a sequence of times, with consecutive times separated by at least n steps (which is enough time to attempt to form
$V_0$
instead of U. We introduce a sequence of times, with consecutive times separated by at least n steps (which is enough time to attempt to form
![]() $\widehat L_n$
) and at which the diameter of the configuration is at most
$\widehat L_n$
) and at which the diameter of the configuration is at most
![]() $\theta _1 = \theta _{4n} (c_1 n)$
(where
$\theta _1 = \theta _{4n} (c_1 n)$
(where
![]() $c_1$
is the constant in Corollary 6.4). These will be the times at which we attempt to observe the formation of
$c_1$
is the constant in Corollary 6.4). These will be the times at which we attempt to observe the formation of
![]() $\widehat L_n$
. Define
$\widehat L_n$
. Define
![]() $\eta _0 = \inf \{t \geq 0: \mathrm {diam} (U_t) \leq \theta _1\}$
and, for all
$\eta _0 = \inf \{t \geq 0: \mathrm {diam} (U_t) \leq \theta _1\}$
and, for all
![]() $i \geq 1$
, the times
$i \geq 1$
, the times
We use these times to define three events. Two of the events involve a parameter K which we assume is at least the maximum of R and
![]() $\theta _2$
, where
$\theta _2$
, where
![]() $\theta _2$
equals
$\theta _2$
equals
![]() $\theta _{5n} (c n)$
with
$\theta _{5n} (c n)$
with
![]() $c = c_1 + 2c_2$
and
$c = c_1 + 2c_2$
and
![]() $c_2$
is the constant guaranteed by Lemma 7.8. (The constant c is the one which appears in the statement of the proposition.) In particular, K is at least the maximum diameter
$c_2$
is the constant guaranteed by Lemma 7.8. (The constant c is the one which appears in the statement of the proposition.) In particular, K is at least the maximum diameter
![]() $\theta _1 + n$
of a configuration at time
$\theta _1 + n$
of a configuration at time
![]() $\eta _{i-1} + n$
.
$\eta _{i-1} + n$
.
According to Corollary 6.4, it takes no longer than
![]() $3K (\log (3K) )^{1+2n^{-4}} \leq K^2$
steps for the diameter to fall below
$3K (\log (3K) )^{1+2n^{-4}} \leq K^2$
steps for the diameter to fall below
![]() $\theta _1$
, except with a probability of at most
$\theta _1$
, except with a probability of at most
![]() $e^{-3K}$
. The first event is the event that it takes an unusually long time for the diameter to fall below
$e^{-3K}$
. The first event is the event that it takes an unusually long time for the diameter to fall below
![]() $\theta _1$
for the first time:
$\theta _1$
for the first time:
The second is the event that an unusually long time elapses between
![]() $\eta _{i-1} + n$
and
$\eta _{i-1} + n$
and
![]() $\eta _{i}$
for some
$\eta _{i}$
for some
![]() $1 \leq i \leq m$
:
$1 \leq i \leq m$
:
 $$\begin{align*}E_2 (m,K) = \bigcup_{i=1}^{m} \left\{ \eta_i - (\eta_{i-1}+n)> K^2 \right\}.\end{align*}$$
$$\begin{align*}E_2 (m,K) = \bigcup_{i=1}^{m} \left\{ \eta_i - (\eta_{i-1}+n)> K^2 \right\}.\end{align*}$$
The third is the event that we do not observe the formation of
![]() $\widehat L_n$
in
$\widehat L_n$
in
![]() $m \geq 1$
attempts:
$m \geq 1$
attempts:
 $$\begin{align*}E_3 (m) = \bigcap_{i=1}^{m} \left\{ \mathcal{T}_{\widehat L_n}> \eta_{i-1} + n\right\}.\end{align*}$$
$$\begin{align*}E_3 (m) = \bigcap_{i=1}^{m} \left\{ \mathcal{T}_{\widehat L_n}> \eta_{i-1} + n\right\}.\end{align*}$$
Call
![]() $E (m,K) = E_1 (K) \cup E_2(m,K) \cup E_3 (m)$
. When none of these events occur, we can bound
$E (m,K) = E_1 (K) \cup E_2(m,K) \cup E_3 (m)$
. When none of these events occur, we can bound
![]() $\mathcal {T}_{\widehat L_n}$
:
$\mathcal {T}_{\widehat L_n}$
:
 $$ \begin{align} \mathcal{T}_{\widehat L_n} \mathbf{1}_{E(m,K)^c} \leq \left(\eta_0 + \sum_{i=1}^m (\eta_i - (\eta_{i-1} + n))\right) \mathbf{1}_{E(m,K)^c} + (m+1)n \leq (m+1)(K^2 +n). \end{align} $$
$$ \begin{align} \mathcal{T}_{\widehat L_n} \mathbf{1}_{E(m,K)^c} \leq \left(\eta_0 + \sum_{i=1}^m (\eta_i - (\eta_{i-1} + n))\right) \mathbf{1}_{E(m,K)^c} + (m+1)n \leq (m+1)(K^2 +n). \end{align} $$
We will show that if
![]() $m = 3K \log \theta _2$
, then
$m = 3K \log \theta _2$
, then
![]() $\mathbf {P}_{V_0} (E (m,K))$
is at most
$\mathbf {P}_{V_0} (E (m,K))$
is at most
![]() $e^{-K}$
. Substituting this choice of m into (7.8) and simplifying with
$e^{-K}$
. Substituting this choice of m into (7.8) and simplifying with
![]() $K \geq \theta _2$
, we obtain a further upper bound of
$K \geq \theta _2$
, we obtain a further upper bound of
By equation (7.9), if we show that
![]() $\mathbf {P}_{V_0} (E(m,K)) \leq e^{-2K}$
, then we are done. We start with a bound on
$\mathbf {P}_{V_0} (E(m,K)) \leq e^{-2K}$
, then we are done. We start with a bound on
![]() $\mathbf {P}_{V_0} (E_1 (K))$
. Applying Corollary 6.4 with
$\mathbf {P}_{V_0} (E_1 (K))$
. Applying Corollary 6.4 with
![]() $3K$
in the place of t, r in the place of d, and
$3K$
in the place of t, r in the place of d, and
![]() $3K = \max \{3K,R\}$
in the place of
$3K = \max \{3K,R\}$
in the place of
![]() $\max \{t,d\}$
, gives
$\max \{t,d\}$
, gives
We will use Corollary 6.4 and a union bound to bound
![]() $\mathbf {P}_{V_0} (E_2(m,K))$
. Because diameter grows at most linearly in time, the diameter of
$\mathbf {P}_{V_0} (E_2(m,K))$
. Because diameter grows at most linearly in time, the diameter of
![]() $U_{\eta _{i-1} + n} \in \mathcal {F}_{\eta _{i-1}}$
is at most
$U_{\eta _{i-1} + n} \in \mathcal {F}_{\eta _{i-1}}$
is at most
![]() $\theta _1+n \leq 3K$
. Consequently, Corollary 6.4 implies
$\theta _1+n \leq 3K$
. Consequently, Corollary 6.4 implies
A union bound over the constituent events of
![]() $E_2 (m,K)$
and equation (7.11) give
$E_2 (m,K)$
and equation (7.11) give
To bound the probability of
![]() $E_3 (m)$
, we will use Lemma 7.8. First, we need to identify a suitable sequence of HAT transitions. For any
$E_3 (m)$
, we will use Lemma 7.8. First, we need to identify a suitable sequence of HAT transitions. For any
![]() $0 \leq j \leq m-1$
, given
$0 \leq j \leq m-1$
, given
![]() $\mathcal {F}_{\eta _j}$
, set
$\mathcal {F}_{\eta _j}$
, set
![]() $V_0' = U_{\eta _j} \in \mathcal {F}_{\eta _j}$
. There are pairs
$V_0' = U_{\eta _j} \in \mathcal {F}_{\eta _j}$
. There are pairs
![]() $\{(x_i, y_i):\,1 \leq i \leq n\}$
such that, setting
$\{(x_i, y_i):\,1 \leq i \leq n\}$
such that, setting
![]() $V_i' = (V_{i-1}' {\setminus } \{x_i\}) \cup \{y_i\}$
for
$V_i' = (V_{i-1}' {\setminus } \{x_i\}) \cup \{y_i\}$
for
![]() $1 \leq i \leq n$
, each transition probability
$1 \leq i \leq n$
, each transition probability
![]() $\mathbf {P}_{V_{i-1}'} (U_i = V_i')$
is positive and
$\mathbf {P}_{V_{i-1}'} (U_i = V_i')$
is positive and
![]() $V_n' \in \widehat L_n$
. The diameter of
$V_n' \in \widehat L_n$
. The diameter of
![]() $V_i'$
is at most
$V_i'$
is at most
![]() $\theta _1 +n \leq 2\theta _1$
for each i, so Lemma 7.8 implies that the transition probabilities satisfy
$\theta _1 +n \leq 2\theta _1$
for each i, so Lemma 7.8 implies that the transition probabilities satisfy
By the strong Markov property and equation (7.13),
Because
![]() $E_3 (j) \in \mathcal {F}_{\eta _j}$
, equation (7.14) implies
$E_3 (j) \in \mathcal {F}_{\eta _j}$
, equation (7.14) implies
Using equation (7.15) and observing that
![]() $\log \theta _2 \geq e^{2c_2 n^3 \theta _1}$
, hence
$\log \theta _2 \geq e^{2c_2 n^3 \theta _1}$
, hence
![]() $m \geq 3K e^{2c_2 n^3 \theta _1}$
, we calculate
$m \geq 3K e^{2c_2 n^3 \theta _1}$
, we calculate
 $$ \begin{align} \mathbf{P}_{V_0} (E_3 (m)) = \prod_{j=0}^{m-1} \mathbf{P}_{V_0} \left(\mathcal{T}_{\widehat L_n}> \eta_{j} + n \Bigm\vert E_3 (j) \right) \leq \left(1 - e^{-2 c_2 n^3 \theta_1} \right)^m \leq e^{-3K}. \end{align} $$
$$ \begin{align} \mathbf{P}_{V_0} (E_3 (m)) = \prod_{j=0}^{m-1} \mathbf{P}_{V_0} \left(\mathcal{T}_{\widehat L_n}> \eta_{j} + n \Bigm\vert E_3 (j) \right) \leq \left(1 - e^{-2 c_2 n^3 \theta_1} \right)^m \leq e^{-3K}. \end{align} $$
Combining equations (7.10), (7.12) and (7.16) and simplifying using the fact that
![]() $m \leq 3K^2$
, we find
$m \leq 3K^2$
, we find
7.3 Proof of Proposition 7.5
To prove this proposition, we will attempt to observe the formation of
![]() $\widehat U$
from
$\widehat U$
from
![]() $\widehat L_n$
and wait for the set to collapse if its diameter becomes too large, as we did in proving Proposition 7.4. Note that, at the time that the set collapses, it does not necessarily form
$\widehat L_n$
and wait for the set to collapse if its diameter becomes too large, as we did in proving Proposition 7.4. Note that, at the time that the set collapses, it does not necessarily form
![]() $\widehat L_n$
, so we will need to use Proposition 7.4 to return to
$\widehat L_n$
, so we will need to use Proposition 7.4 to return to
![]() $\widehat L_n$
before another attempt at forming
$\widehat L_n$
before another attempt at forming
![]() $\widehat U$
. For convenience, we package these steps together in the following lemma.
$\widehat U$
. For convenience, we package these steps together in the following lemma.
Lemma 7.11. There is a constant c such that, if
![]() $V_0$
is a configuration in
$V_0$
is a configuration in
![]() $\mathrm {NonIso} (n)$
with a diameter of R, then for any
$\mathrm {NonIso} (n)$
with a diameter of R, then for any
![]() $K \geq \max \{R, \theta _{5n} (cn)\}$
,
$K \geq \max \{R, \theta _{5n} (cn)\}$
,
Proof. Call
![]() $\theta = \theta _{5n} (c n)$
, where c is the constant guaranteed by Proposition 7.4. First, we wait until the diameter falls to
$\theta = \theta _{5n} (c n)$
, where c is the constant guaranteed by Proposition 7.4. First, we wait until the diameter falls to
![]() $\theta $
. Note that
$\theta $
. Note that
![]() $2K (\log (2K))^{1+2n^{-4}} \leq K^2$
, so Corollary 6.4 implies that
$2K (\log (2K))^{1+2n^{-4}} \leq K^2$
, so Corollary 6.4 implies that
Second, from
![]() $U_{\mathcal {T} (\theta )}$
, we wait until the configuration forms a line. By Proposition 7.4,
$U_{\mathcal {T} (\theta )}$
, we wait until the configuration forms a line. By Proposition 7.4,
Combining these bounds gives equation (7.17).
Proof of Proposition 7.5.
We will use V to denote the target configuration instead of U, to avoid confusion with
![]() $U_t$
. Recall that, for any configuration V in
$U_t$
. Recall that, for any configuration V in
![]() $\mathrm {NonIso} (n)$
with a diameter upper bound of
$\mathrm {NonIso} (n)$
with a diameter upper bound of
![]() $r \geq 10n$
, Lemma 7.10 gives a constant
$r \geq 10n$
, Lemma 7.10 gives a constant
![]() $c_1$
such that
$c_1$
such that
Since
![]() $10nR \geq 10n$
is a diameter upper bound on V, we can apply the preceding inequality with
$10nR \geq 10n$
is a diameter upper bound on V, we can apply the preceding inequality with
![]() $r = 10nR$
:
$r = 10nR$
:
With this result in mind, we denote
![]() $k = 2000n^2 R$
and define a sequence of times by
$k = 2000n^2 R$
and define a sequence of times by
Here, the buffer of k steps is the period during which we attempt to observe the formation of V. After each failed attempt, because the diameter increases by at most
![]() $1$
with each step, the diameter of
$1$
with each step, the diameter of
![]() $U_{\zeta _i + k}$
can be no larger than
$U_{\zeta _i + k}$
can be no larger than
![]() $k + n$
.
$k + n$
.
We define two rare events in terms of these times and a parameter K, which we assume to be at least
![]() $\max \{e^{R^{2.1}},\theta _{5n} (c_2n)\}$
, where
$\max \{e^{R^{2.1}},\theta _{5n} (c_2n)\}$
, where
![]() $c_2$
is the greater of
$c_2$
is the greater of
![]() $c_1$
and the constant from Lemma 7.11. In particular, under this assumption, K is greater than
$c_1$
and the constant from Lemma 7.11. In particular, under this assumption, K is greater than
![]() $e^{4c_1 n^5 R^2}$
and
$e^{4c_1 n^5 R^2}$
and
![]() $k+n$
– a fact we will use later.
$k+n$
– a fact we will use later.
The first rare event is the event that an unusually long time elapses between
![]() $\zeta _{i-1} + k$
and
$\zeta _{i-1} + k$
and
![]() $\zeta _i$
, for some
$\zeta _i$
, for some
![]() $i \leq m$
:
$i \leq m$
:
 $$\begin{align*}F_1 (m,K) = \bigcup_{i=1}^m \left\{ \zeta_i - (\zeta_{i-1} + k)> 72 K^3 \right\}.\end{align*}$$
$$\begin{align*}F_1 (m,K) = \bigcup_{i=1}^m \left\{ \zeta_i - (\zeta_{i-1} + k)> 72 K^3 \right\}.\end{align*}$$
The second is the event that we do not observe the formation of
![]() $\widehat V$
in
$\widehat V$
in
![]() $m \geq 1$
attempts:
$m \geq 1$
attempts:
 $$\begin{align*}F_2 (m) = \bigcap_{i=1}^m \left\{ \mathcal{T}_{\widehat V}> \zeta_{i-1} + k\right\}.\end{align*}$$
$$\begin{align*}F_2 (m) = \bigcap_{i=1}^m \left\{ \mathcal{T}_{\widehat V}> \zeta_{i-1} + k\right\}.\end{align*}$$
Call
![]() $F (m,K) = F_1 (m,K) \cup F_2 (m)$
. When
$F (m,K) = F_1 (m,K) \cup F_2 (m)$
. When
![]() $F (m,K)^c$
occurs, we can bound
$F (m,K)^c$
occurs, we can bound
![]() $\mathcal {T}_{\widehat V}$
as
$\mathcal {T}_{\widehat V}$
as
 $$ \begin{align} \mathcal{T}_{\widehat V} \mathbf{1}_{F(m,K)^c} &= \sum_{i=0}^{m-1} (\zeta_i - (\zeta_{i-1} + k)) \mathbf{1}_{E(m,K)^c} + mk \leq 72 m K^3 + mk. \end{align} $$
$$ \begin{align} \mathcal{T}_{\widehat V} \mathbf{1}_{F(m,K)^c} &= \sum_{i=0}^{m-1} (\zeta_i - (\zeta_{i-1} + k)) \mathbf{1}_{E(m,K)^c} + mk \leq 72 m K^3 + mk. \end{align} $$
We will show that if m is taken to be
![]() $2K e^{c_1 n^5 R^2}$
, then
$2K e^{c_1 n^5 R^2}$
, then
![]() $\mathbf {P}_{\widehat L_n} (F(m,K))$
is at most
$\mathbf {P}_{\widehat L_n} (F(m,K))$
is at most
![]() $e^{-K}$
. Substituting this value of m into equation (7.21) and simplifying with
$e^{-K}$
. Substituting this value of m into equation (7.21) and simplifying with
![]() $K \geq k$
and then
$K \geq k$
and then
![]() $K \geq e^{4c_1n^5 R^2}$
gives
$K \geq e^{4c_1n^5 R^2}$
gives
By equation (7.22), if we prove
![]() $\mathbf {P}_{\widehat L_n} (F(m,K)^c) \leq e^{-K}$
, then we are done. We start with a bound on
$\mathbf {P}_{\widehat L_n} (F(m,K)^c) \leq e^{-K}$
, then we are done. We start with a bound on
![]() $\mathbf {P}_{\widehat L_n} (F_1 (m,K))$
. By the strong Markov property applied to the stopping time
$\mathbf {P}_{\widehat L_n} (F_1 (m,K))$
. By the strong Markov property applied to the stopping time
![]() $\zeta _{i-1}+k$
,
$\zeta _{i-1}+k$
,
The inequality is due to Lemma 7.11, which applies to
![]() $U_{\zeta _{i-1}+k}$
and K because
$U_{\zeta _{i-1}+k}$
and K because
![]() $U_{\zeta _{i-1} + k}$
is a nonisolated configuration with a diameter of at most
$U_{\zeta _{i-1} + k}$
is a nonisolated configuration with a diameter of at most
![]() $k + n$
and because
$k + n$
and because
![]() $K \geq \max \{k+n,\theta _{5n} (c_2 n)\}$
. From a union bound over the events which comprise
$K \geq \max \{k+n,\theta _{5n} (c_2 n)\}$
. From a union bound over the events which comprise
![]() $F_1 (m,K)$
and equation (7.23), we find
$F_1 (m,K)$
and equation (7.23), we find
To bound
![]() $\mathbf {P}_{\widehat L_n} (F_2 (m))$
, we apply the strong Markov property to
$\mathbf {P}_{\widehat L_n} (F_2 (m))$
, we apply the strong Markov property to
![]() $\zeta _j$
and use equation (7.20):
$\zeta _j$
and use equation (7.20):
Then, because
![]() $F_2 (j) \in \mathcal {F}_{\zeta _j}$
and by equation (7.25),
$F_2 (j) \in \mathcal {F}_{\zeta _j}$
and by equation (7.25),
We use equation (7.26) to calculate
 $$ \begin{align} \mathbf{P}_{\widehat L_n} (F_2 (m)) = \prod_{j=0}^{m-1} \mathbf{P}_{\widehat L_n} \left( \mathcal{T}_{\widehat V}> \zeta_j + k \Bigm\vert F_2 (j) \right) \leq \prod_{j=0}^{m-1} (1 - e^{-c_1 n^5 R^2}) \leq e^{-2K}. \end{align} $$
$$ \begin{align} \mathbf{P}_{\widehat L_n} (F_2 (m)) = \prod_{j=0}^{m-1} \mathbf{P}_{\widehat L_n} \left( \mathcal{T}_{\widehat V}> \zeta_j + k \Bigm\vert F_2 (j) \right) \leq \prod_{j=0}^{m-1} (1 - e^{-c_1 n^5 R^2}) \leq e^{-2K}. \end{align} $$
The second inequality is due to the choice
![]() $m = 2K e^{c_1 n^5 R^2}$
.
$m = 2K e^{c_1 n^5 R^2}$
.
Recall that
![]() $F(m,K)$
is the union of
$F(m,K)$
is the union of
![]() $F_1 (m,K)$
and
$F_1 (m,K)$
and
![]() $F_2 (m)$
. We have
$F_2 (m)$
. We have
The first inequality is a union bound; the second is due to equations (7.24) and (7.27); the third holds because
![]() $m+1 \leq e^K$
.
$m+1 \leq e^K$
.
7.4 Proof of Proposition 7.2
We now prove a tightness estimate for the stationary distribution – that is, an upper bound on
![]() $\pi _n \big ( \mathrm {diam} (\widehat U) \geq d \big )$
. By Proposition 7.1, the stationary probability
$\pi _n \big ( \mathrm {diam} (\widehat U) \geq d \big )$
. By Proposition 7.1, the stationary probability
![]() $\pi _n (\widehat U)$
of any nonisolated, n-element configuration
$\pi _n (\widehat U)$
of any nonisolated, n-element configuration
![]() $\widehat U$
is the reciprocal of
$\widehat U$
is the reciprocal of
![]() $\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U}$
. When d is large (relative to
$\mathbf {E}_{\widehat U} \mathcal {T}_{\widehat U}$
. When d is large (relative to
![]() $\theta _{4n}$
), this expected return time will be at least exponentially large in
$\theta _{4n}$
), this expected return time will be at least exponentially large in
![]() $\tfrac {d}{(\log d)^{1+o_n (1)}}$
. This exponent arises from the consideration that, for a configuration with a diameter below
$\tfrac {d}{(\log d)^{1+o_n (1)}}$
. This exponent arises from the consideration that, for a configuration with a diameter below
![]() $\theta _{4n}$
to increase its diameter to d, it must avoid collapse over the timescale for which it is typical (i.e.,
$\theta _{4n}$
to increase its diameter to d, it must avoid collapse over the timescale for which it is typical (i.e.,
![]() $(\log d)^{1+o_n (1)}$
) approximately
$(\log d)^{1+o_n (1)}$
) approximately
![]() $\tfrac {d}{(\log d)^{1+o_n (1)}}$
times consecutively. Because the number of n-element configurations with a diameter of approximately d is negligible relative to their expected return times, the collective weight under
$\tfrac {d}{(\log d)^{1+o_n (1)}}$
times consecutively. Because the number of n-element configurations with a diameter of approximately d is negligible relative to their expected return times, the collective weight under
![]() $\pi _n$
of such configurations will be exponentially small in
$\pi _n$
of such configurations will be exponentially small in
![]() $\tfrac {d}{(\log d)^{1+o_n (1)}}$
.
$\tfrac {d}{(\log d)^{1+o_n (1)}}$
.
We note that, while there are abstract results which relate hitting times to the stationary distribution (e.g., [Reference Ganguly, Levine, Peres and ProppGLPP17, Lemma 4]), we cannot directly apply results that require bounds on hitting times which hold uniformly for any initial configuration. This is because hitting times from
![]() $\widehat V$
depend on its diameter. We could apply such results after partitioning
$\widehat V$
depend on its diameter. We could apply such results after partitioning
![]() $\widehat {\mathrm {N}} \mathrm {onIso} (n)$
by diameter, but we would then save little effort from their use.
$\widehat {\mathrm {N}} \mathrm {onIso} (n)$
by diameter, but we would then save little effort from their use.
Proof of Proposition 7.2.
Let d be at least
![]() $2\theta _{4n}$
, and take
$2\theta _{4n}$
, and take
![]() $\varepsilon = 2n^{-4}$
. We claim that, for any configuration
$\varepsilon = 2n^{-4}$
. We claim that, for any configuration
![]() $\widehat U$
with a diameter in
$\widehat U$
with a diameter in
![]() $[2^j d, 2^{j+1} d)$
for an integer
$[2^j d, 2^{j+1} d)$
for an integer
![]() $j \geq 0$
, the expected return time to
$j \geq 0$
, the expected return time to
![]() $\widehat U$
satisfies
$\widehat U$
satisfies
 $$ \begin{align} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \geq \exp \left( \frac{2^j d}{(\log (2^j d) )^{1+2\varepsilon}} \right). \end{align} $$
$$ \begin{align} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \geq \exp \left( \frac{2^j d}{(\log (2^j d) )^{1+2\varepsilon}} \right). \end{align} $$
We can use equation (7.28) to prove equation (7.2) in the following way. We write
![]() $\{ \mathrm {diam} (\widehat U) \geq d\}$
as a disjoint union of events of the form
$\{ \mathrm {diam} (\widehat U) \geq d\}$
as a disjoint union of events of the form
![]() $H_j = \{2^j \leq \mathrm {diam} (\widehat U) < 2^{j+1} d\}$
for
$H_j = \{2^j \leq \mathrm {diam} (\widehat U) < 2^{j+1} d\}$
for
![]() $j \geq 0$
. Because a disk with a diameter of at most
$j \geq 0$
. Because a disk with a diameter of at most
![]() $2^{j+1} d$
contains fewer than
$2^{j+1} d$
contains fewer than
![]() $\lfloor 4^{j+1} d^2 \rfloor $
elements of
$\lfloor 4^{j+1} d^2 \rfloor $
elements of
![]() $\mathbb {Z}^2$
, the number of nonisolated, n-element configurations with a diameter of at most
$\mathbb {Z}^2$
, the number of nonisolated, n-element configurations with a diameter of at most
![]() $2^{j+1} d$
satisfies
$2^{j+1} d$
satisfies
 $$ \begin{align} \big| \big\{\widehat U\ \text{in}\ \widehat{\mathrm{N}} \mathrm{onIso} (n)\ \text{with}\ 2^j d \leq \mathrm{diam} (\widehat U) < 2^{j+1} d\ \big\} \big| \leq \binom{\lfloor 4^{j+1} d^2 \rfloor}{n} \leq (4^{j+1} d^2)^n. \end{align} $$
$$ \begin{align} \big| \big\{\widehat U\ \text{in}\ \widehat{\mathrm{N}} \mathrm{onIso} (n)\ \text{with}\ 2^j d \leq \mathrm{diam} (\widehat U) < 2^{j+1} d\ \big\} \big| \leq \binom{\lfloor 4^{j+1} d^2 \rfloor}{n} \leq (4^{j+1} d^2)^n. \end{align} $$
We use equation (7.1) with equations (7.28) and (7.29) to estimate
 $$ \begin{align} \pi_n \big( \mathrm{diam} (\widehat U) \geq d \big) = \sum_{j = 0}^\infty \pi_n (H_j) = \sum_{j = 0}^\infty \sum_{\widehat U \in H_j} \pi_n (\widehat U) \leq \sum_{j = 0}^\infty (4^{j+1} d^2)^n e^{- \frac{2^j d}{(\log (2^j d))^{1+2\varepsilon}}}. \end{align} $$
$$ \begin{align} \pi_n \big( \mathrm{diam} (\widehat U) \geq d \big) = \sum_{j = 0}^\infty \pi_n (H_j) = \sum_{j = 0}^\infty \sum_{\widehat U \in H_j} \pi_n (\widehat U) \leq \sum_{j = 0}^\infty (4^{j+1} d^2)^n e^{- \frac{2^j d}{(\log (2^j d))^{1+2\varepsilon}}}. \end{align} $$
Using the fact that
![]() $d \geq 2\theta _{4n}$
, it is easy to check that the ratio of the
$d \geq 2\theta _{4n}$
, it is easy to check that the ratio of the
![]() $(j+1)$
st summand to the j
th summand in equation (7.30) is at most
$(j+1)$
st summand to the j
th summand in equation (7.30) is at most
![]() $e^{-j-1}$
, for all
$e^{-j-1}$
, for all
![]() $j \geq 0$
. Accordingly, we have
$j \geq 0$
. Accordingly, we have
 $$\begin{align*}\pi_n \big( \mathrm{diam} (\widehat U) \geq d \big) \leq (4d^2)^n e^{-\frac{d}{(\log d)^{1+2\varepsilon}}} \sum_{j=0}^\infty e^{-j} \leq e^{-\frac{d}{(\log d)^{1+3\varepsilon}}},\end{align*}$$
$$\begin{align*}\pi_n \big( \mathrm{diam} (\widehat U) \geq d \big) \leq (4d^2)^n e^{-\frac{d}{(\log d)^{1+2\varepsilon}}} \sum_{j=0}^\infty e^{-j} \leq e^{-\frac{d}{(\log d)^{1+3\varepsilon}}},\end{align*}$$
where the second inequality is justified by the fact that
![]() $d \geq 2 \theta _{4n}$
. This proves equation (7.2) when the claimed bound (7.28) holds.
$d \geq 2 \theta _{4n}$
. This proves equation (7.2) when the claimed bound (7.28) holds.
We will prove equation (7.28) by making a comparison with a geometric random variable on
![]() $\{0, 1, \dots \}$
with a ‘success’ probability of
$\{0, 1, \dots \}$
with a ‘success’ probability of
![]() $e^{-\frac {d}{(\log d)^{1+\varepsilon }}}$
(or with
$e^{-\frac {d}{(\log d)^{1+\varepsilon }}}$
(or with
![]() $2^j d$
in place of d). This geometric random variable will model the number of visits to configurations with diameters below
$2^j d$
in place of d). This geometric random variable will model the number of visits to configurations with diameters below
![]() $\theta _{4n}$
before reaching a diameter of d, and the success probability arises from the fact that, for a configuration to increase its diameter to d from
$\theta _{4n}$
before reaching a diameter of d, and the success probability arises from the fact that, for a configuration to increase its diameter to d from
![]() $\theta _{4n}$
, it must avoid collapse over
$\theta _{4n}$
, it must avoid collapse over
![]() $d-\theta _{4n}$
steps. By Corollary 6.4, this happens with a probability which is exponentially small in
$d-\theta _{4n}$
steps. By Corollary 6.4, this happens with a probability which is exponentially small in
![]() $\tfrac {d}{(\log d)^{1+\varepsilon }}$
.
$\tfrac {d}{(\log d)^{1+\varepsilon }}$
.
Let
![]() $\widehat U$
be a nonisolated, n-element configuration with a diameter in
$\widehat U$
be a nonisolated, n-element configuration with a diameter in
![]() $[2^j d,2^{j+1}d)$
, and let
$[2^j d,2^{j+1}d)$
, and let
![]() $\mathcal {\widehat W}$
be the set of configurations in
$\mathcal {\widehat W}$
be the set of configurations in
![]() $\mathrm {NonIso} (n)$
with a diameter of at most
$\mathrm {NonIso} (n)$
with a diameter of at most
![]() $\theta _{4n}$
. Define N to be the number of returns to
$\theta _{4n}$
. Define N to be the number of returns to
![]() $\mathcal {\widehat W}$
before time
$\mathcal {\widehat W}$
before time
![]() $\mathcal {T}_{\widehat U}$
, that is,
$\mathcal {T}_{\widehat U}$
, that is,
![]() $N = \sum _{t=1}^{\mathcal {T}_{\widehat U}} \mathbf {1} (\widehat U_t \in \mathcal {\widehat W})$
, and let
$N = \sum _{t=1}^{\mathcal {T}_{\widehat U}} \mathbf {1} (\widehat U_t \in \mathcal {\widehat W})$
, and let
![]() $\widehat V$
minimize
$\widehat V$
minimize
![]() $\mathbf {E}_{\widehat V} N$
among
$\mathbf {E}_{\widehat V} N$
among
![]() $\mathcal {\widehat W}$
. We claim that
$\mathcal {\widehat W}$
. We claim that
Indeed, the factor in front of
![]() $\mathbf {E}_{\widehat V} N$
comes from equation (7.13), which implies that
$\mathbf {E}_{\widehat V} N$
comes from equation (7.13), which implies that
This bound justifies the first of the following inequalities
The second inequality holds because the time it takes to reach
![]() $\widehat U$
is at least the number of returns to
$\widehat U$
is at least the number of returns to
![]() $\mathcal {\widehat W}$
before
$\mathcal {\widehat W}$
before
![]() $\mathcal {T}_{\widehat U}$
; the third is due to our choice of
$\mathcal {T}_{\widehat U}$
; the third is due to our choice of
![]() $\widehat V$
. Hence, equation (7.31) holds.
$\widehat V$
. Hence, equation (7.31) holds.
The virtue of the lower bound (7.31) is that we can bound below
![]() $\mathbf {E}_{\widehat V} N$
by
$\mathbf {E}_{\widehat V} N$
by
The inequality holds by the Markov property applied to
![]() $\mathcal {T}_{\mathcal {\widehat W}}$
and because
$\mathcal {T}_{\mathcal {\widehat W}}$
and because
![]() $\widehat V$
minimizes the expected number of returns to
$\widehat V$
minimizes the expected number of returns to
![]() $\mathcal {\widehat W}$
. This implies that
$\mathcal {\widehat W}$
. This implies that
![]() $\mathbf {E}_{\widehat V} N$
is at least the expected value of a geometric random variable on
$\mathbf {E}_{\widehat V} N$
is at least the expected value of a geometric random variable on
![]() $\{0,1,\dots \}$
with success parameter p of
$\{0,1,\dots \}$
with success parameter p of
![]() $\mathbf {P}_{\widehat V} (\mathcal {T}_{\widehat U} < \mathcal {T}_{\mathcal {\widehat W}})$
:
$\mathbf {P}_{\widehat V} (\mathcal {T}_{\widehat U} < \mathcal {T}_{\mathcal {\widehat W}})$
:
It remains to bound above p.
Because diameter increases at most linearly in time,
![]() $\mathcal {T}_{\widehat U}$
is at least
$\mathcal {T}_{\widehat U}$
is at least
![]() $2^j d - \theta _{4n}$
under
$2^j d - \theta _{4n}$
under
![]() $\mathbf {P}_{\widehat V}$
. Consequently,
$\mathbf {P}_{\widehat V}$
. Consequently,
We apply Corollary 6.4 with t equal to
![]() $\tfrac {2^j d-\theta _{4n}}{(\log (2^j d))^{1+\varepsilon }}$
, finding
$\tfrac {2^j d-\theta _{4n}}{(\log (2^j d))^{1+\varepsilon }}$
, finding
 $$ \begin{align*} \mathbf{P}_{\widehat V} (\mathcal{T} (\theta_{4n})> 2^j d - \theta_{4n}) \leq \exp \left( - \frac{2^j d-\theta_{4n}}{(\log (2^j d) )^{1+\varepsilon}} \right). \end{align*} $$
$$ \begin{align*} \mathbf{P}_{\widehat V} (\mathcal{T} (\theta_{4n})> 2^j d - \theta_{4n}) \leq \exp \left( - \frac{2^j d-\theta_{4n}}{(\log (2^j d) )^{1+\varepsilon}} \right). \end{align*} $$
By equation (7.33), this is also an upper bound on
![]() $p <\tfrac 12$
and so, by equation (7.32),
$p <\tfrac 12$
and so, by equation (7.32),
![]() $\mathbf {E}_{\widehat V} N$
is at least
$\mathbf {E}_{\widehat V} N$
is at least
![]() $(2p)^{-1}$
. Substituting these bounds into equation (7.31) and simplifying with the fact that
$(2p)^{-1}$
. Substituting these bounds into equation (7.31) and simplifying with the fact that
![]() $d \geq 2 \theta _{4n}$
, we find that the expected return time to
$d \geq 2 \theta _{4n}$
, we find that the expected return time to
![]() $\widehat U$
satisfies equation (7.28):
$\widehat U$
satisfies equation (7.28):
 $$ \begin{align*} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \geq \tfrac12 \big(\log (2^{j+1} d) \big)^{-2n} \exp \left( \frac{2^j d-\theta_{4n}}{\big(\log (2^j d)\big)^{1+\varepsilon}} \right) \geq \exp \left( \frac{2^j d}{\big(\log (2^j d) \big)^{1+2\varepsilon}} \right). \end{align*} $$
$$ \begin{align*} \mathbf{E}_{\widehat U} \mathcal{T}_{\widehat U} \geq \tfrac12 \big(\log (2^{j+1} d) \big)^{-2n} \exp \left( \frac{2^j d-\theta_{4n}}{\big(\log (2^j d)\big)^{1+\varepsilon}} \right) \geq \exp \left( \frac{2^j d}{\big(\log (2^j d) \big)^{1+2\varepsilon}} \right). \end{align*} $$
8 Motion of the center of mass
As a consequence of the results of Section 7 and standard renewal theory, the center of mass process
![]() $(\mathscr {M}_t)_{t\geq 0}$
, after linear interpolation and rescaling
$(\mathscr {M}_t)_{t\geq 0}$
, after linear interpolation and rescaling
![]() $(t^{-1/2}\mathscr {M}_{st})_{s \in [0,1]}$
and, when viewed as a measure on
$(t^{-1/2}\mathscr {M}_{st})_{s \in [0,1]}$
and, when viewed as a measure on
![]() $\mathscr {C} ([0,1])$
, converges weakly to two-dimensional Brownian motion as
$\mathscr {C} ([0,1])$
, converges weakly to two-dimensional Brownian motion as
![]() $t \to \infty $
. This is the content of Theorem 3.
$t \to \infty $
. This is the content of Theorem 3.
We will use the following lemma to bound the coordinate variances of the Brownian motion limit. To state it, we denote by
![]() $\tau _{i} = \inf \{t> \tau _{i-1} : \widehat U_t = \widehat L_n\}$
the i
th return time to
$\tau _{i} = \inf \{t> \tau _{i-1} : \widehat U_t = \widehat L_n\}$
the i
th return time to
![]() $\widehat L_n$
.
$\widehat L_n$
.
Lemma 8.1. Let c be the constant from Proposition 7.4 and abbreviate
![]() $\theta _{5n} (cn)$
by
$\theta _{5n} (cn)$
by
![]() $\theta $
. If, for some
$\theta $
. If, for some
![]() $i \geq 0$
, X is one of the random variables
$i \geq 0$
, X is one of the random variables
then the distribution of X satisfies the following tail bound
Consequently,
Proof. Because the diameter of
![]() $\widehat L_n$
is at most n, for any
$\widehat L_n$
is at most n, for any
![]() $K \geq \theta $
, Proposition 7.4 implies
$K \geq \theta $
, Proposition 7.4 implies
Applying the strong Markov property to
![]() $\tau _{i}$
, we find equation (8.1) for
$\tau _{i}$
, we find equation (8.1) for
![]() $X = \tau _{i+1} - \tau _i$
. Using equation (8.1) with the tail sum formulas for the first and second moments gives equation (8.2) for this X. The other cases of X then follow from
$X = \tau _{i+1} - \tau _i$
. Using equation (8.1) with the tail sum formulas for the first and second moments gives equation (8.2) for this X. The other cases of X then follow from
Proof of Theorem 3.
Standard arguments (e.g., Section 8 of [Reference BillingsleyBil99]) combined with the renewal theorem show that
![]() $\big (t^{-1/2} \mathscr {M}_{st}\big )_{t \geq 1}$
is a tight sequence of functions. We claim that the finite-dimensional distributions of the rescaled process converge as
$\big (t^{-1/2} \mathscr {M}_{st}\big )_{t \geq 1}$
is a tight sequence of functions. We claim that the finite-dimensional distributions of the rescaled process converge as
![]() $t \to \infty $
to those of two-dimensional Brownian motion.
$t \to \infty $
to those of two-dimensional Brownian motion.
For any
![]() $m \geq 1$
and times
$m \geq 1$
and times
![]() $0 =s_0 \leq s_1 < s_2 < \cdots < s_m \leq 1$
, form the random vector
$0 =s_0 \leq s_1 < s_2 < \cdots < s_m \leq 1$
, form the random vector
For s in
![]() $[0,1]$
, we denote by
$[0,1]$
, we denote by
![]() $I (s)$
the number of returns to
$I (s)$
the number of returns to
![]() $\widehat L_n$
by time
$\widehat L_n$
by time
![]() $st$
. Lemma 8.1 and Markov’s inequality imply that
$st$
. Lemma 8.1 and Markov’s inequality imply that
![]() $|\mathscr {M}_{s_i t} - \mathscr {M}_{\tau _{I (s_i)}}| \to 0$
in probability as
$|\mathscr {M}_{s_i t} - \mathscr {M}_{\tau _{I (s_i)}}| \to 0$
in probability as
![]() $t \to \infty $
, hence, by Slutsky’s theorem, the distributions of equation (8.3) and
$t \to \infty $
, hence, by Slutsky’s theorem, the distributions of equation (8.3) and
have the same
![]() $t \to \infty $
limit. By the renewal theorem,
$t \to \infty $
limit. By the renewal theorem,
![]() $I(s_1) < I (s_2) < \cdots < I (s_m)$
for all sufficiently large t, so the strong Markov property implies the independence of the entries in equation (8.4) for all such t.
$I(s_1) < I (s_2) < \cdots < I (s_m)$
for all sufficiently large t, so the strong Markov property implies the independence of the entries in equation (8.4) for all such t.
A generic entry in equation (8.4) is a sum of independent increments of the form
![]() $\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
. As noted in Section 1, the transition probabilities are unchanged when configurations are multiplied by elements of the symmetry group
$\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
. As noted in Section 1, the transition probabilities are unchanged when configurations are multiplied by elements of the symmetry group
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $\mathbb {Z}^2$
. This implies
$\mathbb {Z}^2$
. This implies
where
![]() $\Sigma $
is the variance-covariance matrix of
$\Sigma $
is the variance-covariance matrix of
![]() $\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
and
$\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
and
![]() $\nu $
is a constant which, by Lemma 8.1, is finite. The renewal theorem implies that the scaled variance
$\nu $
is a constant which, by Lemma 8.1, is finite. The renewal theorem implies that the scaled variance
![]() $t^{-1} \nu ^2 (I(s_i) - I(s_{i-1}))$
of the i
th entry converges almost surely to
$t^{-1} \nu ^2 (I(s_i) - I(s_{i-1}))$
of the i
th entry converges almost surely to
![]() $(s_i - s_{i-1}) \chi ^2$
where
$(s_i - s_{i-1}) \chi ^2$
where
![]() $\chi ^2 = \nu ^2 / \mathbf {E}_{\widehat L_n} [\tau _1]$
, hence, by Slutsky’s theorem, we can replace the scaled variance of each entry in equation (8.4) with this limit, without affecting the limiting distribution of the vector.
$\chi ^2 = \nu ^2 / \mathbf {E}_{\widehat L_n} [\tau _1]$
, hence, by Slutsky’s theorem, we can replace the scaled variance of each entry in equation (8.4) with this limit, without affecting the limiting distribution of the vector.
By the central limit theorem,
 $$\begin{align*}\frac{1}{\chi \sqrt{t}} \left( \mathscr{M}_{\tau_{I (s_i)}} - \mathscr{M}_{\tau_{I (s_{i-1})+1}} \right) \stackrel{\text{d}}{\longrightarrow} \mathcal{N} \left( o, (s_i - s_{i-1}) \mathbf{I} \right),\end{align*}$$
$$\begin{align*}\frac{1}{\chi \sqrt{t}} \left( \mathscr{M}_{\tau_{I (s_i)}} - \mathscr{M}_{\tau_{I (s_{i-1})+1}} \right) \stackrel{\text{d}}{\longrightarrow} \mathcal{N} \left( o, (s_i - s_{i-1}) \mathbf{I} \right),\end{align*}$$
which, by the independence of the entries in equation (8.4) for all sufficiently large t, implies
 $$ \begin{align} \frac{1}{\chi \sqrt{t}} ( \mathscr{M}_{s_1 t}, \, \mathscr{M}_{s_2 t} & - \mathscr{M}_{s_1 t}, \, \dots, \, \mathscr{M}_{s_m t} - \mathscr{M}_{s_{m-1} t} ) \nonumber\\ &\stackrel{\text{d}}{\longrightarrow} \left( \mathbf{B} (s_1), \mathbf{B} (s_2-s_1), \dots, \mathbf{B} (s_m - s_{m-1}) \right), \end{align} $$
$$ \begin{align} \frac{1}{\chi \sqrt{t}} ( \mathscr{M}_{s_1 t}, \, \mathscr{M}_{s_2 t} & - \mathscr{M}_{s_1 t}, \, \dots, \, \mathscr{M}_{s_m t} - \mathscr{M}_{s_{m-1} t} ) \nonumber\\ &\stackrel{\text{d}}{\longrightarrow} \left( \mathbf{B} (s_1), \mathbf{B} (s_2-s_1), \dots, \mathbf{B} (s_m - s_{m-1}) \right), \end{align} $$
as
![]() $t \to \infty $
. Because m and the
$t \to \infty $
. Because m and the
![]() $\{s_i\}_{i=1}^m$
were arbitrary, the continuous mapping theorem and equation (8.5) imply the convergence of the finite-dimensional distributions of
$\{s_i\}_{i=1}^m$
were arbitrary, the continuous mapping theorem and equation (8.5) imply the convergence of the finite-dimensional distributions of
![]() $\left (\frac {1}{\chi \sqrt {t}} \mathscr {M}_{st}, 0 \leq s \leq 1\right )$
to those of
$\left (\frac {1}{\chi \sqrt {t}} \mathscr {M}_{st}, 0 \leq s \leq 1\right )$
to those of
![]() $\left (\mathbf {B} (s), 0 \leq s \leq 1 \right )$
. This proves the weak convergence component of Theorem 3.
$\left (\mathbf {B} (s), 0 \leq s \leq 1 \right )$
. This proves the weak convergence component of Theorem 3.
It remains to bound
![]() $\chi ^2$
, which we do by estimating
$\chi ^2$
, which we do by estimating
![]() $\mathbf {E}_{\widehat L_n} [\tau _1]$
and
$\mathbf {E}_{\widehat L_n} [\tau _1]$
and
![]() $\nu ^2$
. The former is bounded above by
$\nu ^2$
. The former is bounded above by
![]() $2 \theta ^4$
, due to Lemma 8.1, and below by
$2 \theta ^4$
, due to Lemma 8.1, and below by
![]() $1$
. Here,
$1$
. Here,
![]() $\theta = \theta _{5n} (c_1n)$
and
$\theta = \theta _{5n} (c_1n)$
and
![]() $c_1$
is the constant from Proposition 7.4. To bound below
$c_1$
is the constant from Proposition 7.4. To bound below
![]() $\nu ^2$
, denote the
$\nu ^2$
, denote the
![]() $e_2$
component of
$e_2$
component of
![]() $\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
by X and observe that
$\mathscr {M}_{\tau _{i+1}} - \mathscr {M}_{\tau _i}$
by X and observe that
![]() $\mathbf {P}_{\widehat L_n} \left ( X = n^{-1} \right )$
is at least the probability that, from
$\mathbf {P}_{\widehat L_n} \left ( X = n^{-1} \right )$
is at least the probability that, from
![]() $L_n$
, the element at o is activated and subsequently deposited at
$L_n$
, the element at o is activated and subsequently deposited at
![]() $(0,n)$
(recall that
$(0,n)$
(recall that
![]() $L_n$
is the segment from o to
$L_n$
is the segment from o to
![]() $(0,n-1)$
), resulting in
$(0,n-1)$
), resulting in
![]() $\tau _1 = 1$
and
$\tau _1 = 1$
and
![]() $\mathscr {M}_{\tau _1} = \mathscr {M}_0 + n^{-1} e_2$
. This probability is at least
$\mathscr {M}_{\tau _1} = \mathscr {M}_0 + n^{-1} e_2$
. This probability is at least
![]() $e^{-c_2 n}$
for a constant
$e^{-c_2 n}$
for a constant
![]() $c_2$
. Markov’s inequality applied to
$c_2$
. Markov’s inequality applied to
![]() $X^2$
then gives
$X^2$
then gives
By Lemma 8.1,
![]() $\nu ^2$
is at most
$\nu ^2$
is at most
![]() $2 \theta ^{8}$
. In summary,
$2 \theta ^{8}$
. In summary,
which implies
with
![]() $c = \max \{c_1,c_3\}$
.
$c = \max \{c_1,c_3\}$
.
A Auxiliary lemmas
A.1 Potential kernel bounds
The following lemma collects several facts about the potential kernel which are used in Section 3. As each fact is a simple consequence of equation (3.9), we omit its proof.
Lemma A.1. In what follows,
![]() $x,y,z,z'$
are elements of
$x,y,z,z'$
are elements of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
-
1. For
 $\mathfrak {a} (y)$
to be at least
$\mathfrak {a} (y)$
to be at least
 $\mathfrak {a} (x)$
, it suffices to have
$\mathfrak {a} (x)$
, it suffices to have  $$\begin{align*}|y| \geq |x| (1 + \pi \lambda |x|^{-2} + (\pi \lambda)^2 |x|^{-4}).\end{align*}$$
$$\begin{align*}|y| \geq |x| (1 + \pi \lambda |x|^{-2} + (\pi \lambda)^2 |x|^{-4}).\end{align*}$$
In particular, if
 $|x| \geq 2$
, then
$|x| \geq 2$
, then
 $|y| \geq 1.06 |x|$
suffices.
$|y| \geq 1.06 |x|$
suffices. -
2. When
 $|x| \geq 1$
,
$|x| \geq 1$
,
 $\mathfrak {a} (x)$
is at least
$\mathfrak {a} (x)$
is at least
 $\tfrac {2}{\pi } \log |x|$
. When
$\tfrac {2}{\pi } \log |x|$
. When
 $|x| \geq 2$
,
$|x| \geq 2$
,
 $\mathfrak {a} (x)$
is at most
$\mathfrak {a} (x)$
is at most
 $4 \log |x|$
.
$4 \log |x|$
. -
3. If
 $z,z' \in C(r)$
and
$z,z' \in C(r)$
and
 $y \in D(R)^c$
for
$y \in D(R)^c$
for
 $r \leq \tfrac {1}{100} R$
and
$r \leq \tfrac {1}{100} R$
and
 $R \geq 100$
, then
$R \geq 100$
, then  $$\begin{align*}|\mathfrak{a} (y-z) - \mathfrak{a} (y-z') | \leq \tfrac{4}{\pi}.\end{align*}$$
$$\begin{align*}|\mathfrak{a} (y-z) - \mathfrak{a} (y-z') | \leq \tfrac{4}{\pi}.\end{align*}$$
-
4. If x and y satisfy
 $|x|, |y| \geq 1$
and
$|x|, |y| \geq 1$
and
 $K^{-1} \leq \tfrac {|y|}{|x|} \leq K$
for some
$K^{-1} \leq \tfrac {|y|}{|x|} \leq K$
for some
 $K \geq 2$
, then
$K \geq 2$
, then  $$\begin{align*}\mathfrak{a}(y) - \mathfrak{a} (x) \leq \log K.\end{align*}$$
$$\begin{align*}\mathfrak{a}(y) - \mathfrak{a} (x) \leq \log K.\end{align*}$$
-
5. If
 $|x| \geq 8 |y|$
and
$|x| \geq 8 |y|$
and
 $|y| \geq 10$
, then
$|y| \geq 10$
, then  $$\begin{align*}|\mathfrak{a} (x + y) - \mathfrak{a} (x)| \leq 0.7 \frac{|y|}{|x|}. \end{align*}$$
$$\begin{align*}|\mathfrak{a} (x + y) - \mathfrak{a} (x)| \leq 0.7 \frac{|y|}{|x|}. \end{align*}$$
-
6. Let
 $R \geq 10r$
and
$R \geq 10r$
and
 $r \geq 10$
. Then, uniformly for
$r \geq 10$
. Then, uniformly for
 $x \in C(R)$
and
$x \in C(R)$
and
 $y \in C(r)$
, we have
$y \in C(r)$
, we have  $$\begin{align*}0.56 \log (R/r) \leq \mathfrak{a} (x) - \mathfrak{a} (y) \leq \log (R/r).\end{align*}$$
$$\begin{align*}0.56 \log (R/r) \leq \mathfrak{a} (x) - \mathfrak{a} (y) \leq \log (R/r).\end{align*}$$
In the next section, we will need the following comparison of
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {a}'$
.
$\mathfrak {a}'$
.
Lemma A.2. Let
![]() $\mu $
be any probability measure on
$\mu $
be any probability measure on
![]() $C_x (r)$
. Suppose
$C_x (r)$
. Suppose
![]() $r \geq 2 (|x| + 1)$
. Then
$r \geq 2 (|x| + 1)$
. Then
 $$\begin{align*}\Big | \sum_{y \in C_x (r)} \mu (y) \mathfrak{a} (y) -\mathfrak{a}' (r) \Big| \leq \left(\frac{5}{2 \pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right).\end{align*}$$
$$\begin{align*}\Big | \sum_{y \in C_x (r)} \mu (y) \mathfrak{a} (y) -\mathfrak{a}' (r) \Big| \leq \left(\frac{5}{2 \pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right).\end{align*}$$
In particular, if
![]() $x = o$
, then
$x = o$
, then
![]() $|\mathfrak {a} (y) - \mathfrak {a}' (r) | \leq r^{-1}$
for every
$|\mathfrak {a} (y) - \mathfrak {a}' (r) | \leq r^{-1}$
for every
![]() $y \in C (r)$
.
$y \in C (r)$
.
Proof. We recall that, for any
![]() $x \in \mathbb {Z}^2$
, the potential kernel has the form specified in equation (3.9) where the error term conceals a constant of
$x \in \mathbb {Z}^2$
, the potential kernel has the form specified in equation (3.9) where the error term conceals a constant of
![]() $\lambda $
, which is no more than
$\lambda $
, which is no more than
![]() $0.07$
[Reference Kozma and SchreiberKS04]. That is,
$0.07$
[Reference Kozma and SchreiberKS04]. That is,
For
![]() $y \in C_x (r)$
, we have
$y \in C_x (r)$
, we have
![]() $r - |x| - 1 \leq |y| \leq r + |x| + 1$
. Accordingly,
$r - |x| - 1 \leq |y| \leq r + |x| + 1$
. Accordingly,
 $$ \begin{align*} \mathfrak{a} (y) & \leq \frac{2}{\pi} \log \left| r + |x| + 1 \right| + \kappa + O ( |r - |x| - 1|^{-2} )\\ & = \frac{2}{\pi} \log r + \kappa + \frac{2}{\pi} \log \left( 1 + \frac{|x| + 1}{r} \right) + O( |r - |x| - 1|^{-2}). \end{align*} $$
$$ \begin{align*} \mathfrak{a} (y) & \leq \frac{2}{\pi} \log \left| r + |x| + 1 \right| + \kappa + O ( |r - |x| - 1|^{-2} )\\ & = \frac{2}{\pi} \log r + \kappa + \frac{2}{\pi} \log \left( 1 + \frac{|x| + 1}{r} \right) + O( |r - |x| - 1|^{-2}). \end{align*} $$
Using the assumption
![]() $(|x|+1)/r \in (0,1/2)$
with Taylor’s remainder theorem gives
$(|x|+1)/r \in (0,1/2)$
with Taylor’s remainder theorem gives
 $$ \begin{align*} \mathfrak{a} (y) & \leq \mathfrak{a}' (r) + \frac{2}{\pi} \left( \frac{|x| + 1}{r} + \frac12 \left( \frac{|x| + 1}{r} \right)^2\right) + O( |r - |x| - 1|^{-2}). \end{align*} $$
$$ \begin{align*} \mathfrak{a} (y) & \leq \mathfrak{a}' (r) + \frac{2}{\pi} \left( \frac{|x| + 1}{r} + \frac12 \left( \frac{|x| + 1}{r} \right)^2\right) + O( |r - |x| - 1|^{-2}). \end{align*} $$
Simplifying with
![]() $r \geq 2(|x|+1)$
and
$r \geq 2(|x|+1)$
and
![]() $r \geq 2$
leads to
$r \geq 2$
leads to
 $$ \begin{align*} \mathfrak{a} (y) & \leq \mathfrak{a}' (r) + \frac{2}{\pi} \left(\frac54 + \pi \lambda \right) \left(\frac{|x| + 1}{r} \right) = \mathfrak{a}' (r) + \left( \frac{5}{2\pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right). \end{align*} $$
$$ \begin{align*} \mathfrak{a} (y) & \leq \mathfrak{a}' (r) + \frac{2}{\pi} \left(\frac54 + \pi \lambda \right) \left(\frac{|x| + 1}{r} \right) = \mathfrak{a}' (r) + \left( \frac{5}{2\pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right). \end{align*} $$
The lower bound is similar. Because this holds for any
![]() $y \in C_x (r)$
, for any probability measure
$y \in C_x (r)$
, for any probability measure
![]() $\mu $
on
$\mu $
on
![]() $C_x (r)$
, we have
$C_x (r)$
, we have
 $$\begin{align*}\Big| \sum_{y \in C_x (r)} \mu (y) \mathfrak{a} (y) - \mathfrak{a}' (r) \Big| \leq \left( \frac{5}{2\pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right).\end{align*}$$
$$\begin{align*}\Big| \sum_{y \in C_x (r)} \mu (y) \mathfrak{a} (y) - \mathfrak{a}' (r) \Big| \leq \left( \frac{5}{2\pi} + 2 \lambda \right) \left( \frac{|x| + 1}{r} \right).\end{align*}$$
A.2 Comparison between harmonic measure and hitting probabilities
To prove Lemma 3.2, we require a comparison (Lemma A.3) between certain values of harmonic measure and hitting probabilities. In fact, we need additional quantification of an error term which appears in standard versions of this result (e.g., [Reference LawlerLaw13, Theorem 2.1.3]). Effectively, this additional quantification comes from a bound on
![]() $\lambda $
, the implicit constant in equation (3.9). The proof is similar to that of Theorem 3.17 in [Reference PopovPop21].
$\lambda $
, the implicit constant in equation (3.9). The proof is similar to that of Theorem 3.17 in [Reference PopovPop21].
Lemma A.3. Let
![]() $x \in D(R)^c$
for
$x \in D(R)^c$
for
![]() $R \geq 100r$
and
$R \geq 100r$
and
![]() $r \geq 10$
. Then
$r \geq 10$
. Then
Proof. We have
 $$ \begin{align} {\mathbb{H}}_{C(r)} (x,y) - {\mathbb{H}}_{C(r)} (y) = - \mathfrak{a} (y-x) + \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z - x).\end{align} $$
$$ \begin{align} {\mathbb{H}}_{C(r)} (x,y) - {\mathbb{H}}_{C(r)} (y) = - \mathfrak{a} (y-x) + \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z - x).\end{align} $$
Since
![]() $C(10r)$
separates x from
$C(10r)$
separates x from
![]() $C(r)$
, the optional stopping theorem applied to
$C(r)$
, the optional stopping theorem applied to
![]() $\sigma _{C(10r)} \wedge \tau _{C(r)}$
and the martingale
$\sigma _{C(10r)} \wedge \tau _{C(r)}$
and the martingale
![]() $\mathfrak {a} \left (S_{t \wedge \tau _x} - x\right )$
gives
$\mathfrak {a} \left (S_{t \wedge \tau _x} - x\right )$
gives
 $$ \begin{align} &\mathfrak{a} (y-x) = \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z - x) \nonumber\\ & + \mathbb{E}_y \left[ \mathfrak{a} \left(S_{\sigma_{C(10r)}} - x \right) - \mathfrak{a} \left(S_{\tau_{C(r)}} - x \right) \Bigm\vert \sigma_{C(10r)} < \tau_{C(r)}\right] \mathbb{P}_y \left( \sigma_{C(10r)} < \tau_{C(r)} \right). \end{align} $$
$$ \begin{align} &\mathfrak{a} (y-x) = \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z - x) \nonumber\\ & + \mathbb{E}_y \left[ \mathfrak{a} \left(S_{\sigma_{C(10r)}} - x \right) - \mathfrak{a} \left(S_{\tau_{C(r)}} - x \right) \Bigm\vert \sigma_{C(10r)} < \tau_{C(r)}\right] \mathbb{P}_y \left( \sigma_{C(10r)} < \tau_{C(r)} \right). \end{align} $$
In the second term of equation (A.3), we analyze the difference in potentials by observing
Accordingly, letting
![]() $u = S_{\tau _{C(r)}} - x$
and
$u = S_{\tau _{C(r)}} - x$
and
![]() $v = S_{\sigma _{C(10r)}} - S_{\tau _{C(r)}}$
,
$v = S_{\sigma _{C(10r)}} - S_{\tau _{C(r)}}$
,
We observe that
![]() $|v| \leq 11r+2$
and
$|v| \leq 11r+2$
and
![]() $|u| \geq 99r-2$
, so
$|u| \geq 99r-2$
, so
![]() $|u| \geq 8 |v|$
. Since we also have
$|u| \geq 8 |v|$
. Since we also have
![]() $|v| \geq 9r-2 \geq 10$
, (5) of Lemma A.1 applies to give
$|v| \geq 9r-2 \geq 10$
, (5) of Lemma A.1 applies to give
We analyze the other factor of equation (A.3) as
 $$ \begin{align*} \mathbb{P}_y \left( \sigma_{C(10r)} < \tau_{C(r)} \right) & = \frac14 \sum_{z \notin C(r): z \sim y} \mathbb{P}_z \left( \sigma_{C(10r)} < \tau_{C(r)} \right)\\ &= \frac14 \sum_{z \notin C(r): z \sim y} \frac{\mathfrak{a} (z - z_0) - \mathbb{E}_z \mathfrak{a} \left( S_{\tau_{C(r)}} - z_0 \right)}{\mathbb{E}_z \left[ \mathfrak{a} \Big( S_{\sigma_{C(10r)}} \Big) - \mathfrak{a} \Big( S_{\tau_{C(r)}} \Big) \Bigm\vert \sigma_{C(10r)} < \sigma_{C(r)} \right]}, \end{align*} $$
$$ \begin{align*} \mathbb{P}_y \left( \sigma_{C(10r)} < \tau_{C(r)} \right) & = \frac14 \sum_{z \notin C(r): z \sim y} \mathbb{P}_z \left( \sigma_{C(10r)} < \tau_{C(r)} \right)\\ &= \frac14 \sum_{z \notin C(r): z \sim y} \frac{\mathfrak{a} (z - z_0) - \mathbb{E}_z \mathfrak{a} \left( S_{\tau_{C(r)}} - z_0 \right)}{\mathbb{E}_z \left[ \mathfrak{a} \Big( S_{\sigma_{C(10r)}} \Big) - \mathfrak{a} \Big( S_{\tau_{C(r)}} \Big) \Bigm\vert \sigma_{C(10r)} < \sigma_{C(r)} \right]}, \end{align*} $$
where
![]() $z_0 \in A$
. To obtain an upper bound on the potential difference in the denominator, we apply (6) of Lemma A.1, which gives
$z_0 \in A$
. To obtain an upper bound on the potential difference in the denominator, we apply (6) of Lemma A.1, which gives
Combining this with the other estimate for the second term of equation (A.3), we find
 $$\begin{align*}\mathfrak{a} (y-x) \leq \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z-x) + \underbrace{\frac{2}{25} \cdot \frac{1}{0.56 \log 10}}_{\leq 0.063} {\mathbb{H}}_{C(r)} (y).\end{align*}$$
$$\begin{align*}\mathfrak{a} (y-x) \leq \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z-x) + \underbrace{\frac{2}{25} \cdot \frac{1}{0.56 \log 10}}_{\leq 0.063} {\mathbb{H}}_{C(r)} (y).\end{align*}$$
Substituting this into equation (A.2), we have
We again apply (5) and (6) of Lemma A.1 to bound the factors in the second term of A.3 as
Substituting these into equation (A.3), we find
 $$\begin{align*}\mathfrak{a} (y-x) \geq \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z-x) - 0.0875 \cdot \frac{1}{\log 10} {\mathbb{H}}_{C(r)} (y).\end{align*}$$
$$\begin{align*}\mathfrak{a} (y-x) \geq \sum_{z \in C(r)} \mathbb{P}_y \left( S_{\tau_{C(r)}} = z \right) \mathfrak{a} (z-x) - 0.0875 \cdot \frac{1}{\log 10} {\mathbb{H}}_{C(r)} (y).\end{align*}$$
Consequently, equation (A.2) becomes
Rearranging, we find
A.3 Uniform lower bound on a conditional entrance measure
Recall that Lemma 3.1 bounds below the conditional hitting distribution of
![]() $C(\varepsilon ^2 R)$
from
$C(\varepsilon ^2 R)$
from
![]() $C(\varepsilon R)$
, given that
$C(\varepsilon R)$
, given that
![]() $C(\varepsilon ^2 R)$
is hit before
$C(\varepsilon ^2 R)$
is hit before
![]() $C(R)$
, in terms of the uniform distribution on
$C(R)$
, in terms of the uniform distribution on
![]() $C(\varepsilon ^2 R)$
. The idea of the proof is to use Lemma A.3 to approximate the hitting distribution of
$C(\varepsilon ^2 R)$
. The idea of the proof is to use Lemma A.3 to approximate the hitting distribution of
![]() $C(\varepsilon ^2 R)$
with the corresponding harmonic measure, which is comparable to the uniform distribution on
$C(\varepsilon ^2 R)$
with the corresponding harmonic measure, which is comparable to the uniform distribution on
![]() $C(\varepsilon ^2 R)$
. The proof is similar to that of Lemma 2.1 in [Reference Dembo, Peres, Rosen and ZeitouniDPRZ06].
$C(\varepsilon ^2 R)$
. The proof is similar to that of Lemma 2.1 in [Reference Dembo, Peres, Rosen and ZeitouniDPRZ06].
Proof of Lemma 3.1.
Fix
![]() $\varepsilon $
and R which satisfy the hypotheses. Let
$\varepsilon $
and R which satisfy the hypotheses. Let
![]() $x \in C(\varepsilon R)$
and
$x \in C(\varepsilon R)$
and
![]() $y \in C(\varepsilon ^2 R)$
. We have
$y \in C(\varepsilon ^2 R)$
. We have
By the strong Markov property applied to
![]() $\tau _{C(R)}$
,
$\tau _{C(R)}$
,
We use Lemma A.3 to uniformly bound the terms of the form
![]() ${\mathbb {H}}_{C(\varepsilon ^2 R)} (\cdot , y)$
appearing in equations (A.4) and (A.5). For any
${\mathbb {H}}_{C(\varepsilon ^2 R)} (\cdot , y)$
appearing in equations (A.4) and (A.5). For any
![]() $w \in C(R)$
, the hypotheses of Lemma A.3 are satisfied with
$w \in C(R)$
, the hypotheses of Lemma A.3 are satisfied with
![]() $\varepsilon ^2 R$
in the place of r, and R as presently defined because then
$\varepsilon ^2 R$
in the place of r, and R as presently defined because then
![]() $r \geq 10$
and
$r \geq 10$
and
![]() $R \geq 100 r$
. Therefore, by equation (A.1), uniformly for
$R \geq 100 r$
. Therefore, by equation (A.1), uniformly for
![]() $w \in C(R)$
,
$w \in C(R)$
,
Now, for any
![]() $x \in C(\varepsilon R)$
, the hypotheses of Lemma A.3 are again satisfied with the same r and with
$x \in C(\varepsilon R)$
, the hypotheses of Lemma A.3 are again satisfied with the same r and with
![]() $\varepsilon R$
in the place of R since
$\varepsilon R$
in the place of R since
![]() $\varepsilon R \geq 100 r = 100 \varepsilon ^2 R$
by the assumption
$\varepsilon R \geq 100 r = 100 \varepsilon ^2 R$
by the assumption
![]() $\varepsilon \leq \frac {1}{100}$
. We apply equation (A.1) to find
$\varepsilon \leq \frac {1}{100}$
. We apply equation (A.1) to find
Substituting equation (A.6) into equation (A.5), we find
Similarly, substituting equation (A.7) into equation (A.4) and using the previous display, we find
 $$ \begin{align*} &\mathbb{P}_x \left( S_{\tau_{C(\varepsilon^2 R)}} = y, \tau_{C(\varepsilon^2 R)} < \tau_{C(R)}\right) \geq 0.93 \, {\mathbb{H}}_{C(\varepsilon^2 R)} (y) \mathbb{P}_x \left( \tau_{C(\varepsilon^2 R)} < \tau_{C(R)} \right) \nonumber\\ &- \left( 1.04 - 0.93 \right) \, {\mathbb{H}}_{C(\varepsilon^2 R)} (y) \mathbb{P}_x \left( \tau_{C(\varepsilon^2 R)}> \tau_{C(R)} \right). \end{align*} $$
$$ \begin{align*} &\mathbb{P}_x \left( S_{\tau_{C(\varepsilon^2 R)}} = y, \tau_{C(\varepsilon^2 R)} < \tau_{C(R)}\right) \geq 0.93 \, {\mathbb{H}}_{C(\varepsilon^2 R)} (y) \mathbb{P}_x \left( \tau_{C(\varepsilon^2 R)} < \tau_{C(R)} \right) \nonumber\\ &- \left( 1.04 - 0.93 \right) \, {\mathbb{H}}_{C(\varepsilon^2 R)} (y) \mathbb{P}_x \left( \tau_{C(\varepsilon^2 R)}> \tau_{C(R)} \right). \end{align*} $$
Applying hypothesis (3.3), we find that the right-hand side is at least
for a positive constant
![]() $c_1$
. The result then follows the existence of a positive constant
$c_1$
. The result then follows the existence of a positive constant
![]() $c_2$
such that
$c_2$
such that
![]() ${\mathbb {H}}_{C(\varepsilon ^2 R)} (y) \geq c_2 \mu _{\varepsilon ^2 R} (y)$
for any
${\mathbb {H}}_{C(\varepsilon ^2 R)} (y) \geq c_2 \mu _{\varepsilon ^2 R} (y)$
for any
![]() $y \in C(\varepsilon ^2 R)$
.
$y \in C(\varepsilon ^2 R)$
.
The proof of Lemma 3.2 is a simple application of Lemma 3.1. A short calculation is needed to verify that the hypotheses of Lemma 3.1 are met.
Proof of Lemma 3.2.
Under the conditioning, the random walk must reach
![]() $C(\delta R_{J+1})$
before
$C(\delta R_{J+1})$
before
![]() $C(R_{J})$
. It therefore suffices to prove that there exists a positive constant
$C(R_{J})$
. It therefore suffices to prove that there exists a positive constant
![]() $c_1$
such that, uniformly for all
$c_1$
such that, uniformly for all
![]() $x \in C(\delta R_{J+1})$
and
$x \in C(\delta R_{J+1})$
and
![]() $z \in C(R_{J})$
,
$z \in C(R_{J})$
,
where
![]() $\eta = \tau _{C(R_{J})} \wedge \tau _A$
. Because
$\eta = \tau _{C(R_{J})} \wedge \tau _A$
. Because
![]() $\partial \mathcal {A}_{J}$
separates x from A, the conditional probability in equation (A.8) is at least
$\partial \mathcal {A}_{J}$
separates x from A, the conditional probability in equation (A.8) is at least
The first factor of equation (A.9) simplifies to
which we will bound below using Lemma 3.1.
We will verify the hypotheses of Lemma 3.1 with
![]() $\varepsilon = \delta $
and
$\varepsilon = \delta $
and
![]() $R = R_{J+1}$
. The first hypothesis is
$R = R_{J+1}$
. The first hypothesis is
![]() $R \geq 10\varepsilon ^{-2}$
, which is satisfied because
$R \geq 10\varepsilon ^{-2}$
, which is satisfied because
![]() $R_{J+1} \geq R_1 = 10\delta ^{-2}$
. The second hypothesis is equation (3.3) which, in our case, can be written as
$R_{J+1} \geq R_1 = 10\delta ^{-2}$
. The second hypothesis is equation (3.3) which, in our case, can be written as
Exercise 1.6.8 of [Reference LawlerLaw13] states that
 $$ \begin{align} \mathbb{P}_x \left( \tau_{C(R_{J+1})} < \tau_{C(R_{J})} \right) = \frac{\log (\tfrac{|x|}{R_{J}}) + O(R_{J}^{-1})}{\log (\tfrac{R_{J+1}}{R_{J}}) + O (R_{J}^{-1} + R_{J+1}^{-1})}, \end{align} $$
$$ \begin{align} \mathbb{P}_x \left( \tau_{C(R_{J+1})} < \tau_{C(R_{J})} \right) = \frac{\log (\tfrac{|x|}{R_{J}}) + O(R_{J}^{-1})}{\log (\tfrac{R_{J+1}}{R_{J}}) + O (R_{J}^{-1} + R_{J+1}^{-1})}, \end{align} $$
where the implicit constants are at most
![]() $2$
(i.e., the
$2$
(i.e., the
![]() $O(R_{J}^{-1})$
term is at most
$O(R_{J}^{-1})$
term is at most
![]() $2R_{J}^{-1}$
). For the moment, ignore the error terms and assume
$2R_{J}^{-1}$
). For the moment, ignore the error terms and assume
![]() $|x| = \delta R_{J+1}$
, in which case equation (A.12) evaluates to
$|x| = \delta R_{J+1}$
, in which case equation (A.12) evaluates to
![]() $\tfrac {5\log 10 - \log 25}{5\log 10} < 0.73$
. Because
$\tfrac {5\log 10 - \log 25}{5\log 10} < 0.73$
. Because
![]() $R_{J} \geq 10^5$
, even after allowing
$R_{J} \geq 10^5$
, even after allowing
![]() $|x|$
up to
$|x|$
up to
![]() $\delta R_{J+1} + 1$
and accounting for the error terms, equation (A.12) is less than
$\delta R_{J+1} + 1$
and accounting for the error terms, equation (A.12) is less than
![]() $\frac {9}{10}$
, which implies equation (A.11).
$\frac {9}{10}$
, which implies equation (A.11).
Applying Lemma 3.1 to equation (A.10), we obtain a constant
![]() $c_2$
such that
$c_2$
such that
By equation (A.11), the second factor of equation (A.9) is bounded below by
![]() $\frac {1}{10}$
. We conclude the claim of equation (A.8) by combining this bound and equation (A.13) with equation (A.9), and by setting
$\frac {1}{10}$
. We conclude the claim of equation (A.8) by combining this bound and equation (A.13) with equation (A.9), and by setting
![]() $c_1 = \frac {1}{10} c_2$
.
$c_1 = \frac {1}{10} c_2$
.
A.4 Estimate for the exit distribution of a rectangle
Informally, Lemma A.4 says that the probability a walk from one end of a rectangle (which may not be aligned with the coordinate axes) exits through the opposite end is bounded below by a quantity depending upon the aspect ratio of the rectangle. We believe this estimate is known but, as we are unable to find a reference for it, we provide one here. In brief, the proof uses an adaptive algorithm for constructing a sequence of squares which remain inside the rectangle and the sides of which are aligned with the axes. We then bound below the probability that the walk follows the path determined by the squares until exiting the opposite end of the rectangle.
Recall that
![]() $\mathrm {Rec} (\phi , w, \ell )$
denotes the rectangle of width w, centered along the line segment from
$\mathrm {Rec} (\phi , w, \ell )$
denotes the rectangle of width w, centered along the line segment from
![]() $-e^{\mathbf {i} \phi } w$
to
$-e^{\mathbf {i} \phi } w$
to
![]() $e^{\mathbf {i} \phi } \ell $
, intersected with
$e^{\mathbf {i} \phi } \ell $
, intersected with
![]() $\mathbb {Z}^2$
(see Figure 14).
$\mathbb {Z}^2$
(see Figure 14).

Figure 14 On the left, we depict the rectangles
![]() $\mathrm {Rec} = \mathrm {Rec} (\phi , w, l)$
(shaded blue) and
$\mathrm {Rec} = \mathrm {Rec} (\phi , w, l)$
(shaded blue) and
![]() $\mathrm {Rec}^+ = \mathrm {Rec} (\phi ,w,l + w)$
(union of blue- and red-shaded regions) for
$\mathrm {Rec}^+ = \mathrm {Rec} (\phi ,w,l + w)$
(union of blue- and red-shaded regions) for
![]() $\phi = \pi /4$
,
$\phi = \pi /4$
,
![]() $w = 4 \sqrt {2}$
, and
$w = 4 \sqrt {2}$
, and
![]() $\ell = 11\sqrt {2}$
.
$\ell = 11\sqrt {2}$
.
![]() $\mathcal {I}$
denotes
$\mathcal {I}$
denotes
![]() $\mathrm {Rec} \cap \partial (\mathrm {Rec}^+ {\setminus } \mathrm {Rec})$
.
$\mathrm {Rec} \cap \partial (\mathrm {Rec}^+ {\setminus } \mathrm {Rec})$
.
Lemma A.4. For any
![]() $24 \leq w \leq \ell $
and any
$24 \leq w \leq \ell $
and any
![]() $\phi $
, let
$\phi $
, let
![]() $\mathrm {Rec} = \mathrm {Rec} (\phi , w, \ell )$
and
$\mathrm {Rec} = \mathrm {Rec} (\phi , w, \ell )$
and
![]() $\mathrm {Rec}^+ = \mathrm {Rec} (\phi , w, \ell +w)$
. Then,
$\mathrm {Rec}^+ = \mathrm {Rec} (\phi , w, \ell +w)$
. Then,
for a universal positive constant
![]() $c < 1$
.
$c < 1$
.
We use the hypothesis
![]() $w \geq 24$
to deal with the effects of discreteness; the constant
$w \geq 24$
to deal with the effects of discreteness; the constant
![]() $24$
is otherwise unimportant, and many choices would work in its place.
$24$
is otherwise unimportant, and many choices would work in its place.
Proof of Lemma A.4.
We will first define a square, centered at the origin and with each corner in
![]() $\mathbb {Z}^2$
, which lies in
$\mathbb {Z}^2$
, which lies in
![]() $\mathrm {Rec}^+$
. We will then translate it to form a sequence of squares through which we will guide the walk to
$\mathrm {Rec}^+$
. We will then translate it to form a sequence of squares through which we will guide the walk to
![]() $\mathrm {Rec}^+ {\setminus } \mathrm {Rec}$
without leaving
$\mathrm {Rec}^+ {\setminus } \mathrm {Rec}$
without leaving
![]() $\mathrm {Rec}^+$
(see Figure 14). We split the proof into three steps: (1) constructing the squares; (2) proving that they lie in
$\mathrm {Rec}^+$
(see Figure 14). We split the proof into three steps: (1) constructing the squares; (2) proving that they lie in
![]() $\mathrm {Rec}^+$
; and (3) establishing a lower bound on the probability that the walk hits
$\mathrm {Rec}^+$
; and (3) establishing a lower bound on the probability that the walk hits
![]() $\partial \mathrm {Rec}$
before hitting the interior boundary of
$\partial \mathrm {Rec}$
before hitting the interior boundary of
![]() $\mathrm {Rec}^+$
.
$\mathrm {Rec}^+$
.
Step 1: Construction of the squares. Without loss of generality, assume
![]() $0 \leq \phi < \pi /2$
. For
$0 \leq \phi < \pi /2$
. For
![]() $x \in \mathbb {Z}^2$
, we will denote its first coordinate by
$x \in \mathbb {Z}^2$
, we will denote its first coordinate by
![]() $x^1$
and its second coordinate by
$x^1$
and its second coordinate by
![]() $x^2$
. We will use this convention only for this proof. Let
$x^2$
. We will use this convention only for this proof. Let
![]() $\mathfrak {l}$
be equal to
$\mathfrak {l}$
be equal to
![]() $\lfloor \tfrac {w}{8} \rfloor $
if it is even and equal to
$\lfloor \tfrac {w}{8} \rfloor $
if it is even and equal to
![]() $\lfloor \tfrac {w}{8} \rfloor - 1$
otherwise. With this choice, we define
$\lfloor \tfrac {w}{8} \rfloor - 1$
otherwise. With this choice, we define
Since
![]() $\mathfrak {l}$
is even, the translates of Q by integer multiples of
$\mathfrak {l}$
is even, the translates of Q by integer multiples of
![]() $\frac 12 \mathfrak {l}$
are also subsets of
$\frac 12 \mathfrak {l}$
are also subsets of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
We construct a sequence of squares
![]() $Q_i$
in the following way, where we make reference to the line
$Q_i$
in the following way, where we make reference to the line
![]() $L_\phi ^\infty = e^{\mathbf {i} \phi } \mathbb {R}$
. Let
$L_\phi ^\infty = e^{\mathbf {i} \phi } \mathbb {R}$
. Let
![]() $y_1 = o$
and
$y_1 = o$
and
![]() $Q_1 = y_1 + Q$
. For
$Q_1 = y_1 + Q$
. For
![]() $i \geq 1$
, let
$i \geq 1$
, let
 $$\begin{align*}y_{i+1} = \begin{cases} y_i + \tfrac12 \mathfrak{l} \, (0,1) & \text{if}\ y_i \text{lies on or below}\ L_\phi^\infty\\ y_i + \tfrac12 \mathfrak{l} \, (1,0) & \text{if}\ y_i\ \text{lies above}\ L_\phi^\infty\end{cases} \quad \text{and} \quad Q_{i+1} = y_{i+1} + Q .\end{align*}$$
$$\begin{align*}y_{i+1} = \begin{cases} y_i + \tfrac12 \mathfrak{l} \, (0,1) & \text{if}\ y_i \text{lies on or below}\ L_\phi^\infty\\ y_i + \tfrac12 \mathfrak{l} \, (1,0) & \text{if}\ y_i\ \text{lies above}\ L_\phi^\infty\end{cases} \quad \text{and} \quad Q_{i+1} = y_{i+1} + Q .\end{align*}$$
In words, if the center of the present square lies on or below the line
![]() $L_\phi ^\infty $
, then we translate the center north by
$L_\phi ^\infty $
, then we translate the center north by
![]() $\tfrac 12 \mathfrak {l}$
to obtain the next square. Otherwise, we translate the center to the east by
$\tfrac 12 \mathfrak {l}$
to obtain the next square. Otherwise, we translate the center to the east by
![]() $\tfrac 12 \mathfrak {l}$
.
$\tfrac 12 \mathfrak {l}$
.
We further define, for
![]() $i \geq 1$
,
$i \geq 1$
,
 $$ \begin{align*} M_i = \begin{cases} \left\{x \in Q_i : x^2 -y_i^2 = \tfrac12 \mathfrak{l} \,\,\,\text{and}\,\,\, | y_i^1 - x^1 | \leq \tfrac12 \mathfrak{l} - 1\right\} & \text{if}\ y_i\text{ lies on or below}\ L_\phi^\infty \\ \left\{x \in Q_i : x^1 - y_i^1 = \tfrac12 \mathfrak{l} \,\,\,\text{and}\,\,\, | y_i^2 - x^2 | \leq \tfrac12 \mathfrak{l} - 1\right\} & \text{if}\ y_i\ \text{lies above}\ L_\phi^\infty. \end{cases}\end{align*} $$
$$ \begin{align*} M_i = \begin{cases} \left\{x \in Q_i : x^2 -y_i^2 = \tfrac12 \mathfrak{l} \,\,\,\text{and}\,\,\, | y_i^1 - x^1 | \leq \tfrac12 \mathfrak{l} - 1\right\} & \text{if}\ y_i\text{ lies on or below}\ L_\phi^\infty \\ \left\{x \in Q_i : x^1 - y_i^1 = \tfrac12 \mathfrak{l} \,\,\,\text{and}\,\,\, | y_i^2 - x^2 | \leq \tfrac12 \mathfrak{l} - 1\right\} & \text{if}\ y_i\ \text{lies above}\ L_\phi^\infty. \end{cases}\end{align*} $$
In words, if
![]() $y_i$
lies on or below the line
$y_i$
lies on or below the line
![]() $L_\phi ^\infty $
, we choose
$L_\phi ^\infty $
, we choose
![]() $M_i$
to be the northernmost edge of
$M_i$
to be the northernmost edge of
![]() $Q_i$
, excluding the corners. Otherwise, we choose it to be the easternmost edge, excluding the corners (Figure 15). We exclude the corners to ensure that
$Q_i$
, excluding the corners. Otherwise, we choose it to be the easternmost edge, excluding the corners (Figure 15). We exclude the corners to ensure that
![]() $\mathbb {P}_\omega \left ( \tau _{M_{i+1}} \leq \tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}} \right )$
is harmonic for all
$\mathbb {P}_\omega \left ( \tau _{M_{i+1}} \leq \tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}} \right )$
is harmonic for all
![]() $\omega \in M_i$
; we will shortly need this to apply the Harnack inequality. Upcoming Figure 16 provides an illustration of
$\omega \in M_i$
; we will shortly need this to apply the Harnack inequality. Upcoming Figure 16 provides an illustration of
![]() $M_i$
in this context.
$M_i$
in this context.

Figure 15 Two steps in the construction of squares. Respectively on the left and right,
![]() $y_{i+1} \in M_i$
and
$y_{i+1} \in M_i$
and
![]() $y_{i+2} \in M_{i+1}$
(indicated by the
$y_{i+2} \in M_{i+1}$
(indicated by the
![]() $\times $
symbols) lie above
$\times $
symbols) lie above
![]() $L_\phi ^\infty $
, so
$L_\phi ^\infty $
, so
![]() $M_{i+1}$
and
$M_{i+1}$
and
![]() $M_{i+2}$
are situated on the eastern sides of
$M_{i+2}$
are situated on the eastern sides of
![]() $Q_{i+1}$
and
$Q_{i+1}$
and
![]() $Q_{i+2}$
. However, on the left, as
$Q_{i+2}$
. However, on the left, as
![]() $Q_i$
was translated north to form
$Q_i$
was translated north to form
![]() $Q_{i+1}$
, the relative orientation of
$Q_{i+1}$
, the relative orientation of
![]() $M_i$
and
$M_i$
and
![]() $M_{i+1}$
is perpendicular. In contrast, as
$M_{i+1}$
is perpendicular. In contrast, as
![]() $Q_{i+1}$
is translated east to form
$Q_{i+1}$
is translated east to form
![]() $Q_{i+2}$
, the right-hand side has parallel
$Q_{i+2}$
, the right-hand side has parallel
![]() $M_{i+1}$
and
$M_{i+1}$
and
![]() $M_{i+2}$
.
$M_{i+2}$
.

Figure 16 The two cases for lower-bounding
![]() $M_{i+1}$
hitting probabilities.
$M_{i+1}$
hitting probabilities.
We will guide the walk to
![]() $\partial \mathrm {Rec}$
without leaving
$\partial \mathrm {Rec}$
without leaving
![]() $\mathrm {Rec}^+$
by requiring that it exit each square
$\mathrm {Rec}^+$
by requiring that it exit each square
![]() $Q_i$
through
$Q_i$
through
![]() $M_i$
for
$M_i$
for
![]() $1 \leq i \leq J$
, where we define
$1 \leq i \leq J$
, where we define
That is, J is the first index for which
![]() $M_i$
is fully outside
$M_i$
is fully outside
![]() $\mathrm {Rec}$
. It is clear that J is finite.
$\mathrm {Rec}$
. It is clear that J is finite.
Step 2: Proof that
![]() $\cup _{i=1}^J Q_i$
is a subset of
$\cup _{i=1}^J Q_i$
is a subset of
![]() $\mathrm {Rec}^+$
. Let v be the northeastern endpoint of
$\mathrm {Rec}^+$
. Let v be the northeastern endpoint of
![]() $L_\phi $
, where
$L_\phi $
, where
![]() $L_\phi $
is the segment of
$L_\phi $
is the segment of
![]() $L_\phi ^\infty $
from o to
$L_\phi ^\infty $
from o to
![]() $e^{\mathbf {i} \phi } (\ell + w/2)$
and define k to be the first index for which
$e^{\mathbf {i} \phi } (\ell + w/2)$
and define k to be the first index for which
![]() $y_k$
satisfies
$y_k$
satisfies
It will also be convenient to denote by
![]() $\mathcal {I}$
the interface between
$\mathcal {I}$
the interface between
![]() $\mathrm {Rec}$
and
$\mathrm {Rec}$
and
![]() $\mathrm {Rec}^+ {\setminus } \mathrm {Rec}$
(the dashed line in Figure 14), given by
$\mathrm {Rec}^+ {\setminus } \mathrm {Rec}$
(the dashed line in Figure 14), given by
By construction, we have
![]() $|y_k - y_{k-1}| = \tfrac 12 \mathfrak {l}$
and
$|y_k - y_{k-1}| = \tfrac 12 \mathfrak {l}$
and
![]() $|y_k - v| \leq \tfrac 12 \mathfrak {l}$
. By the triangle inequality,
$|y_k - v| \leq \tfrac 12 \mathfrak {l}$
. By the triangle inequality,
![]() $|y_{k-1} - v| \leq \mathfrak {l}$
. As
$|y_{k-1} - v| \leq \mathfrak {l}$
. As
![]() $|v| = \ell + w/2$
and because
$|v| = \ell + w/2$
and because
![]() ${\mathrm {dist}}(o, \mathcal {I}) \leq \ell + 1$
, we must have – again by the triangle inequality – that
${\mathrm {dist}}(o, \mathcal {I}) \leq \ell + 1$
, we must have – again by the triangle inequality – that
![]() ${\mathrm {dist}}( v, \mathcal {I}) \geq w/2 - 1$
. From a third use of the triangle inequality and the hypothesized lower bound on w, we conclude
${\mathrm {dist}}( v, \mathcal {I}) \geq w/2 - 1$
. From a third use of the triangle inequality and the hypothesized lower bound on w, we conclude
To summarize in words,
![]() $y_{k-1}$
is not in
$y_{k-1}$
is not in
![]() $\mathrm {Rec}$
and it is separated from
$\mathrm {Rec}$
and it is separated from
![]() $\mathrm {Rec}$
by a distance strictly greater than
$\mathrm {Rec}$
by a distance strictly greater than
![]() $2\mathfrak {l}$
.
$2\mathfrak {l}$
.
Because the sides of
![]() $Q_{k-1}$
have length
$Q_{k-1}$
have length
![]() $\mathfrak {l}$
, equation (A.14) implies
$\mathfrak {l}$
, equation (A.14) implies
![]() $Q_{k-1} \subseteq \mathrm {Rec}^c$
. Since
$Q_{k-1} \subseteq \mathrm {Rec}^c$
. Since
![]() $M_{k-1}$
is a subset of
$M_{k-1}$
is a subset of
![]() $Q_{k-1}$
, we must also have
$Q_{k-1}$
, we must also have
![]() $M_{k-1} \subseteq \mathrm {Rec}^c$
, which implies
$M_{k-1} \subseteq \mathrm {Rec}^c$
, which implies
![]() $J \leq k-1$
. As k was the first index for which
$J \leq k-1$
. As k was the first index for which
![]() $y_k^1> v^1$
or
$y_k^1> v^1$
or
![]() $y_k^2> v^2$
,
$y_k^2> v^2$
,
![]() $y_J$
satisfies
$y_J$
satisfies
![]() $y_J^1 \leq v^1$
and
$y_J^1 \leq v^1$
and
![]() $y_J^2 \leq v^2$
. Then, by construction, for all
$y_J^2 \leq v^2$
. Then, by construction, for all
![]() $1 \leq i \leq J$
, the centers satisfy
$1 \leq i \leq J$
, the centers satisfy
From equation (A.15) and the fact that
![]() ${\mathrm {dist}} (y_i , L_\phi ^\infty ) \leq \tfrac 12 \mathfrak {l}$
, we have
${\mathrm {dist}} (y_i , L_\phi ^\infty ) \leq \tfrac 12 \mathfrak {l}$
, we have
As the diagonals of the
![]() $Q_i$
have length
$Q_i$
have length
![]() $\sqrt {2} \mathfrak {l}$
, equation (A.15) and the triangle inequality imply
$\sqrt {2} \mathfrak {l}$
, equation (A.15) and the triangle inequality imply
 $$\begin{align*}{\mathrm{dist}}(x, L_\phi) \leq {\mathrm{dist}}(y_i, L_\phi) + \frac12 \sqrt{2} \mathfrak{l} = \frac12 (1 + \sqrt{2}) \mathfrak{l} < \frac{w}{4} \quad \quad \forall \,\,x \in \bigcup_{i=1}^J Q_i.\end{align*}$$
$$\begin{align*}{\mathrm{dist}}(x, L_\phi) \leq {\mathrm{dist}}(y_i, L_\phi) + \frac12 \sqrt{2} \mathfrak{l} = \frac12 (1 + \sqrt{2}) \mathfrak{l} < \frac{w}{4} \quad \quad \forall \,\,x \in \bigcup_{i=1}^J Q_i.\end{align*}$$
To summarize, any element of
![]() $Q_i$
for some
$Q_i$
for some
![]() $1 \leq i \leq J$
is within a distance
$1 \leq i \leq J$
is within a distance
![]() $w/4$
of
$w/4$
of
![]() $L_\phi $
. As
$L_\phi $
. As
![]() $\mathrm {Rec}^+$
contains all points x within a distance
$\mathrm {Rec}^+$
contains all points x within a distance
![]() $\tfrac {w}{2}$
of
$\tfrac {w}{2}$
of
![]() $L_\phi $
, we conclude
$L_\phi $
, we conclude
 $$\begin{align*}\bigcup_{i=1}^J Q_i \subseteq \mathrm{Rec}^+.\end{align*}$$
$$\begin{align*}\bigcup_{i=1}^J Q_i \subseteq \mathrm{Rec}^+.\end{align*}$$
Step 3: Lower bound for
![]() $\mathbb {P}_{o} \left ( \tau _{\partial \mathrm {Rec}} < \tau _{\partial \mathrm {Rec}^+}\right )$
. From the previous step, to obtain a lower bound on the probability that the walk exits
$\mathbb {P}_{o} \left ( \tau _{\partial \mathrm {Rec}} < \tau _{\partial \mathrm {Rec}^+}\right )$
. From the previous step, to obtain a lower bound on the probability that the walk exits
![]() $\mathrm {Rec}$
before
$\mathrm {Rec}$
before
![]() $\mathrm {Rec}^+$
, it suffices to obtain an upper bound
$\mathrm {Rec}^+$
, it suffices to obtain an upper bound
![]() $J^\ast $
on J and a lower bound
$J^\ast $
on J and a lower bound
![]() $c < 1$
on
$c < 1$
on
uniformly for
![]() $\omega \in M_i$
, for
$\omega \in M_i$
, for
![]() $0 \leq i \leq J - 1$
. This way, if we denote
$0 \leq i \leq J - 1$
. This way, if we denote
![]() $Y_0 \equiv y$
and
$Y_0 \equiv y$
and
![]() $Y_i = S_{\tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_i}}$
for
$Y_i = S_{\tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_i}}$
for
![]() $1 \leq i \leq J-1$
, we can apply the strong Markov property to each
$1 \leq i \leq J-1$
, we can apply the strong Markov property to each
![]() $\tau _{M_i}$
and use the lower bound for each factor to obtain the lower bound
$\tau _{M_i}$
and use the lower bound for each factor to obtain the lower bound
To obtain an upper bound on J, we first recall that
![]() $L_\phi $
has a length of
$L_\phi $
has a length of
![]() $\ell + w/2$
, which satisfies
$\ell + w/2$
, which satisfies
 $$ \begin{align} \ell + w/2 = \frac{\mathfrak{l}}{2} \left( \frac{2 \ell}{\mathfrak{l}} + \frac{w}{\mathfrak{l}} \right) \leq \frac{\mathfrak{l}}{2} \left( \frac{2 \ell}{w/8 - 1} + \frac{w}{w /8- 1} \right) \leq \frac{\mathfrak{l}}{2} \left(48\frac{ \ell}{w} + 24\right),\end{align} $$
$$ \begin{align} \ell + w/2 = \frac{\mathfrak{l}}{2} \left( \frac{2 \ell}{\mathfrak{l}} + \frac{w}{\mathfrak{l}} \right) \leq \frac{\mathfrak{l}}{2} \left( \frac{2 \ell}{w/8 - 1} + \frac{w}{w /8- 1} \right) \leq \frac{\mathfrak{l}}{2} \left(48\frac{ \ell}{w} + 24\right),\end{align} $$
due to the fact that
![]() $\mathfrak {l} \geq \lfloor w/8 \rfloor - 1 \geq w/8 - 2$
and the hypothesis of
$\mathfrak {l} \geq \lfloor w/8 \rfloor - 1 \geq w/8 - 2$
and the hypothesis of
![]() $w \geq 24$
. The number of steps to reach J is no more than twice the ratio
$w \geq 24$
. The number of steps to reach J is no more than twice the ratio
![]() $(\ell + w/2)/(\mathfrak {l}/2)$
. Accordingly, using the bound in equation (A.17) and the hypothesis that
$(\ell + w/2)/(\mathfrak {l}/2)$
. Accordingly, using the bound in equation (A.17) and the hypothesis that
![]() $\ell /w \geq 1$
, we have
$\ell /w \geq 1$
, we have
 $$ \begin{align} J \leq 2 \left( 48 \frac{\ell}{w} + 24 \right) \leq 144 \frac{\ell}{w} =: J^\ast.\end{align} $$
$$ \begin{align} J \leq 2 \left( 48 \frac{\ell}{w} + 24 \right) \leq 144 \frac{\ell}{w} =: J^\ast.\end{align} $$
We now turn to the hitting probability lower bounds.
From the construction, there are only two possible orientations of
![]() $M_i$
relative to
$M_i$
relative to
![]() $M_{i+1}$
(Figure 16). Either
$M_{i+1}$
(Figure 16). Either
![]() $M_i$
and
$M_i$
and
![]() $M_{i+1}$
have parallel orientation or they do not. Consider the former case. The hitting probability
$M_{i+1}$
have parallel orientation or they do not. Consider the former case. The hitting probability
![]() $\mathbb {P}_\omega \left ( \tau _{M_{i+1}} \leq \tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}} \right )$
is a harmonic function of
$\mathbb {P}_\omega \left ( \tau _{M_{i+1}} \leq \tau _{\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}} \right )$
is a harmonic function of
![]() $\omega $
for all
$\omega $
for all
![]() $\omega $
in
$\omega $
in
![]() $Q_{i+1} {\setminus } \partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
and
$Q_{i+1} {\setminus } \partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
and
![]() $M_{i+1}$
in particular. Therefore, by the Harnack inequality [Reference LawlerLaw13, Theorem 1.7.6], there is a constant
$M_{i+1}$
in particular. Therefore, by the Harnack inequality [Reference LawlerLaw13, Theorem 1.7.6], there is a constant
![]() $a_1$
such that
$a_1$
such that
The same argument applies to the case when
![]() $M_i$
and
$M_i$
and
![]() $M_{i+1}$
do not have parallel orientation and we find there is a constant
$M_{i+1}$
do not have parallel orientation and we find there is a constant
![]() $a_2$
such that equation (A.19) holds with
$a_2$
such that equation (A.19) holds with
![]() $a_2$
in place of
$a_2$
in place of
![]() $a_1$
. Setting
$a_1$
. Setting
![]() $a = \min \{a_1, a_2\}$
, we conclude that, for all
$a = \min \{a_1, a_2\}$
, we conclude that, for all
![]() $0 \leq i \leq J - 1$
and any
$0 \leq i \leq J - 1$
and any
![]() $\omega \in M_i$
,
$\omega \in M_i$
,
We have reduced the lower bound for any
![]() $\omega \in M_i$
and either of the two relative orientations of
$\omega \in M_i$
and either of the two relative orientations of
![]() $M_i$
and
$M_i$
and
![]() $M_{i+1}$
to a lower bound on the hitting probability of one side of
$M_{i+1}$
to a lower bound on the hitting probability of one side of
![]() $Q_{i+1}$
from the center. By symmetry, the walk hits
$Q_{i+1}$
from the center. By symmetry, the walk hits
![]() $M_{i+1}$
first with a probability of exactly
$M_{i+1}$
first with a probability of exactly
![]() $1/4$
. We emphasize that the probability on the left-hand side of equation (A.20) is exactly
$1/4$
. We emphasize that the probability on the left-hand side of equation (A.20) is exactly
![]() $1/4$
as although
$1/4$
as although
![]() $M_{i+1}$
does not include the adjacent corners of
$M_{i+1}$
does not include the adjacent corners of
![]() $Q_{i+1}$
, which are elements of
$Q_{i+1}$
, which are elements of
![]() $\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
, the corners are separated from
$\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
, the corners are separated from
![]() $y_{i+1}$
by the other elements of
$y_{i+1}$
by the other elements of
![]() $\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
.
$\partial ^{\kern 0.05em \mathrm {int}} Q_{i+1}$
.
Calling
![]() $b = a/4$
and combining equations (A.18) and (A.20) with equation (A.16), we have
$b = a/4$
and combining equations (A.18) and (A.20) with equation (A.16), we have
for a positive constant
![]() $c < 1$
.
$c < 1$
.
Acknowledgements
We thank the anonymous referees for their valuable feedback, which improved this paper. J.C. thanks Joseph Slote for useful discussions concerning Conjecture 1.5 and Example 1.6. A.H. thanks Dmitry Belyaev for helpful discussions concerning the behavior of HAT configurations with well-separated clusters and for simulating HAT dynamics.
Competing interest
The authors have no competing interest to declare.
Financial support
J.C. was partially supported by NSF grant DMS-1512908. S.G. was partially supported by NSF grant DMS-1855688, NSF CAREER Award DMS-1945172 and a Sloan Fellowship. A.H. was partially supported by NSF grants DMS-1512908 and DMS-1855550 and a Miller Professorship from the Miller Institute for Basic Research in Science.