Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T18:06:54.681Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of continuous non-associative algebras arising from algebraic groups including 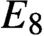$E_8$

Part of: Lie algebras and Lie superalgebras Other nonassociative rings and algebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  14 January 2021

Maurice Chayet  and
Skip Garibaldi Open the ORCID record for Skip Garibaldi [Opens in a new window]
Maurice Chayet
Affiliation:
ECAM-EPMI, 13 Boulevard de l'Hautil, 95092Cergy Pointoise Cedex, France; E-mail: [email protected]
Skip Garibaldi
Affiliation:
IDA Center for Communications Research-La Jolla, 4320 Westerra Ct, San Diego, CA92121, USA; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a construction that takes a simple linear algebraic group G over a field and produces a commutative, unital, and simple non-associative algebra A over that field. Two attractions of this construction are that (1) when G has type 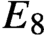$E_8$, the algebra A is obtained by adjoining a unit to the 3875-dimensional representation; and (2) it is effective, in that the product operation on A can be implemented on a computer. A description of the algebra in the 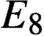$E_8$ case has been requested for some time, and interest has been increased by the recent proof that 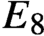$E_8$ is the full automorphism group of that algebra. The algebras obtained by our construction have an unusual Peirce spectrum.

MSC classification

Primary: 17B25: Exceptional (super)algebras
Secondary: 17D99: None of the above, but in this section 20G41: Exceptional groups
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e6
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Albert, A.A., On the power-associativity of rings, Summa Brasil. Math. 2 (1948), no. 2, 21–32.Google Scholar
Albert, A.A., A theory of power-associative commutative algebras, Trans. Amer. Math. Soc. 69 (1950), 503–527.CrossRefGoogle Scholar
Baez, J.C. and Huerta, J., ${\mathrm{G}}_2$ and the rolling ball, Trans. Amer. Math. Soc. 366 (2014), no. 10, 5257–5293.CrossRefGoogle Scholar
Borel, A. and Tits, J., Groupes réductifs, Publ. Math. IHES 27 (1965), 55–150.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system I: the user language, J. Symbolic Computation 9 (1990), 677–698.Google Scholar
Bourbaki, N., Lie groups and Lie algebras: Chapters 4–6, Springer-Verlag, Berlin, 2002.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras: Chapters 7–9, Springer-Verlag, Berlin, 2005.Google Scholar
Carini, L., Hentzel, I.R. and Piacentini Cattaneo, G.M., Degree four identities not implied by commutativity, Comm. Algebra 16 (1988), no. 2, 339–356.CrossRefGoogle Scholar
Cartan, E., Les groupes réels simples finis et continus, Ann. Sci. École Norm. Sup. (3) 31 (1914), 265–355.CrossRefGoogle Scholar
Cohen, A.M. and de Man, R., Computational evidence for Deligne's conjecture regarding exceptional Lie groups, C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), no. 5, 427–432.Google Scholar
De Medts, T. and Van Couwenberghe, M., Non-associative Frobenius algebras for simply laced Chevalley groups, arxiv:2005.02625, May 2020.Google Scholar
Deligne, P., La série exceptionnelle de groupes de Lie, C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), no. 4, 321–326.Google Scholar
Deligne, P. and Gross, B.H., On the exceptional series, and its descendants, C. R. Math. Acad. Sci. Paris 335 (2002), no. 11, 877–881.CrossRefGoogle Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes III: Structure des schemas en groupes reductifs, Société Mathématique de France, 2011, re-edition edited by Gille, P. and Polo, P..Google Scholar
Dynkin, E.B., Semisimple subalgebras of semisimple Lie algebras, Amer. Math. Soc. Transl. (2) 6 (1957), 111–244, [Russian original: Mat. Sbornik N.S. 30(72) (1952), 349–462].Google Scholar
Engel, F., Ein neues, dem linearen Komplexe analoges Gebilde, Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig. Mathematisch-Physische Klasse 52 (1900), 63–76, 220–239.Google Scholar
Fox, D.J.F., Commutative algebras with nondegenerate invariant trace form and trace-free multiplication endomorphisms, arxiv:2004.12343, April 2020.Google Scholar
Garibaldi, S., ${E}_8$, the most exceptional group, Bull. Amer. Math. Soc. (N.S.) 53 (2016), no. 4, 643–671.CrossRefGoogle Scholar
Garibaldi, S. and Guralnick, R.M., Simple groups stabilizing polynomials, Forum of Mathematics: Pi 3 (2015), e3 (41 pages).Google Scholar
Herz, C., Alternating $3$-forms and exceptional simple Lie groups of type ${G}_2$, Canad. J. Math. 35 (1983), no. 5, 776–806.CrossRefGoogle Scholar
Hiss, G., Die adjungierten Darstellungen der Chevalley-Gruppen, Arch. Math. (Basel) 42 (1984), 408–416.CrossRefGoogle Scholar
Jacobson, N., Structure and Representations of Jordan Algebras, Coll. Pub., vol. 39, Amer. Math. Soc., Providence, RI, 1968.CrossRefGoogle Scholar
Jantzen, J.C., Representations of Algebraic Groups, second edn, Math. Surveys and Monographs, vol. 107, Amer. Math. Soc., 2003.Google Scholar
Jenner, W.E., On non-associative algebras associated with bilinear forms, Pacific J. Math. 10 (1960), no. 2, 573–575.CrossRefGoogle Scholar
Killing, W., Die Zusammensetzung der stetigen endlichen Transformationsgruppen. Zweiter Theil, Math. Ann. 33 (1889), 1–48.CrossRefGoogle Scholar
Kokoris, L.A., New results on power-associative algebras, Trans. Amer. Math. Soc. 77 (1954), 363–373.CrossRefGoogle Scholar
Kokoris, L.A., Simple power-associative algebras of degree two, Ann. of Math. (2) 64 (1956), 544–550.CrossRefGoogle Scholar
Krasnov, Y. and Tkachev, V.G., Variety of idempotents in nonassociative algebras, Topics in Clifford Analysis: Special Volume in Honor of Wolfgang Sprößig (Bernstein, S., ed.), Springer International Publishing, 2019, pp. 405–436.CrossRefGoogle Scholar
Landsberg, J.M. and Manivel, L., Triality, exceptional Lie algebras, and Deligne dimension formulas, Adv. Math. 171 (2002), 59–85.CrossRefGoogle Scholar
Landsberg, J.M. and Manivel, L., A universal dimension formula for complex simple Lie algebras, Adv. Math. 201 (2006), no. 2, 379–407.CrossRefGoogle Scholar
Lübeck, F., Small degree representations of finite Chevalley groups in defining characteristic, LMS J. Comput. Math. 4 (2001), 135–169.CrossRefGoogle Scholar
McNinch, G.J., Dimensional criteria for semisimplicity of representations, Proc. London Math. Soc. (3) 76 (1998), 95–149.CrossRefGoogle Scholar
Meyberg, K., Okubo's quartic trace formula for exceptional Lie algebras, J. Algebra 84 (1983), 279–284.CrossRefGoogle Scholar
Okubo, S., Quartic trace identity for exceptional Lie algebras, J. Math. Phys. 20 (1979), 586–593.CrossRefGoogle Scholar
Orlik, P. and Solomon, L., Singularities II: automorphisms of forms, Math. Ann. 231 (1978), 229–240.CrossRefGoogle Scholar
Osborn, J.M., Identities of non-associative algebras, Canad. J. Math. 17 (1965), 78–92.CrossRefGoogle Scholar
Osborn, J.M., Commutative non-associative algebras and identities of degree four, Canadian J. Math. 20 (1968), 769–794.CrossRefGoogle Scholar
Popov, V.L., An Analogue of M. Artin's Conjecture on Invariants for Nonassociative Algebras, Lie groups and Lie algebras: E. B. Dynkin's Seminar, Amer. Math. Soc. Transl. Ser. 2, vol. 169, Amer. Math. Soc., Providence, RI, 1995, pp. 121–143.Google Scholar
Schafer, R., An Introduction to Nonassociative Algebras, Dover, 1994.Google Scholar
Serre, J-P., Galois Cohomology, Springer-Verlag, 2002, originally published as Cohomologie Galoisienne (1965).Google Scholar
Springer, T.A., Jordan Algebras and Algebraic Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 75, Springer-Verlag, 1973.Google Scholar
Springer, T.A., Linear Algebraic Groups, second edn, Birkhäuser, 1998.CrossRefGoogle Scholar
Springer, T.A. and Steinberg, R., Conjugacy Classes, Seminar on Algebraic Groups and Related Finite Groups (The Institute for Advanced Study, Princeton, N.J., 1968/69), Lecture Notes in Math., vol. 131, Springer, Berlin, 1970, [= Robert Steinberg: collected papers, pp. 293–394], pp. 167–266.Google Scholar
Steinberg, R., Lectures on Chevalley Groups, University Lecture Series, no. 66, American Math. Soc., Providence, RI, 2016.CrossRefGoogle Scholar
Suter, R., Coxeter and dual Coxeter numbers, Comm. Algebra 26 (1998), no. 1, 147–153.CrossRefGoogle Scholar
Tits, J., Représentations linéaires irréductibles d'un groupe réductif sur un corps quelconque, J. Reine Angew. Math. 247 (1971), 196–220.Google Scholar
Tkachev, V.G., The universality of one half in commutative nonassociative algebras with identities, J. Algebra 569 (2021), 466–510. CrossRefGoogle Scholar
Vogel, P., The universal Lie algebra, unpublished, June 1999.Google Scholar
Winter, P.W., On the modular representation theory of the two-dimensional special linear group over an algebraically closed field, J. London Math. Soc. (2) 16 (1977), no. 2, 237–252.CrossRefGoogle Scholar