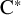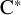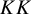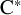1 Introduction
This article is an investigation of the tracial properties of endomorphisms of classifiable
![]() ${\mathrm {C}^*}$
-algebras. Here, ‘classifiable’ means specifically via the Elliott invariant
${\mathrm {C}^*}$
-algebras. Here, ‘classifiable’ means specifically via the Elliott invariant
whose components are K-theory
![]() $K_*(A)$
(together with its order structure
$K_*(A)$
(together with its order structure
![]() $K_0(A)_+$
and scale
$K_0(A)_+$
and scale
![]() $\Sigma (A)$
, which in the unital case is simply the
$\Sigma (A)$
, which in the unital case is simply the
![]() $K_0$
-class of the unit), the tracial state space
$K_0$
-class of the unit), the tracial state space
![]() $T(A)$
and the pairing
$T(A)$
and the pairing
![]() $\rho _A$
between the two. By [Reference Elliott, Gong, Lin and Niu40, Reference Gong, Lin and Niu50, Reference Gong, Lin and Niu51, Reference Elliott, Gong, Lin and Niu41, Reference Gong and Lin48, Reference Gong and Lin49] (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]), infinite-dimensional, simple, separable
$\rho _A$
between the two. By [Reference Elliott, Gong, Lin and Niu40, Reference Gong, Lin and Niu50, Reference Gong, Lin and Niu51, Reference Elliott, Gong, Lin and Niu41, Reference Gong and Lin48, Reference Gong and Lin49] (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]), infinite-dimensional, simple, separable
![]() ${\mathrm {C}^*}$
-algebras that have continuous scale, finite nuclear dimension (which by [Reference Castillejos and Evington17, Reference Castillejos, Evington, Tikuisis, White and Winter18, Reference Tikuisis87, Reference Winter92] is equivalent to tensorial absorption of the Jiang–Su algebra
${\mathrm {C}^*}$
-algebras that have continuous scale, finite nuclear dimension (which by [Reference Castillejos and Evington17, Reference Castillejos, Evington, Tikuisis, White and Winter18, Reference Tikuisis87, Reference Winter92] is equivalent to tensorial absorption of the Jiang–Su algebra
![]() ${\mathcal {Z}}$
) and satisfy the universal coefficient theorem (UCT), are classifiable. And by [Reference Toms89], a finer invariant than
${\mathcal {Z}}$
) and satisfy the universal coefficient theorem (UCT), are classifiable. And by [Reference Toms89], a finer invariant than
![]() $\operatorname {{\mathrm {Ell}}}$
is needed to extend classification beyond this class.
$\operatorname {{\mathrm {Ell}}}$
is needed to extend classification beyond this class.
In this paper, we consider both unital and nonunital classifiable
![]() ${\mathrm {C}^*}$
-algebras. ‘Continuous scale’ is a technical assumption that entails algebraic simplicity of A and compactness of
${\mathrm {C}^*}$
-algebras. ‘Continuous scale’ is a technical assumption that entails algebraic simplicity of A and compactness of
![]() $T(A)$
(see [Reference Elliott, Gong, Lin and Niu42, §5]). It is automatic for a separable, unital
$T(A)$
(see [Reference Elliott, Gong, Lin and Niu42, §5]). It is automatic for a separable, unital
![]() ${\mathrm {C}^*}$
-algebra and in the nonunital case it in particular ensures that the algebra does not support any unbounded lower semicontinuous traces. While the classification presented in [Reference Elliott, Gong, Lin and Niu41, Reference Gong and Lin48, Reference Gong and Lin49] goes beyond
${\mathrm {C}^*}$
-algebra and in the nonunital case it in particular ensures that the algebra does not support any unbounded lower semicontinuous traces. While the classification presented in [Reference Elliott, Gong, Lin and Niu41, Reference Gong and Lin48, Reference Gong and Lin49] goes beyond
![]() ${\mathrm {C}^*}$
-algebras with continuous scale, it is a necessary assumption for the analysis undertaken in the sequel.
${\mathrm {C}^*}$
-algebras with continuous scale, it is a necessary assumption for the analysis undertaken in the sequel.
An important problem in the study of group actions on simple, separable,
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() ${\mathrm {C}^*}$
-algebras is to determine when a given action
${\mathrm {C}^*}$
-algebras is to determine when a given action
![]() $\alpha \colon G\to \operatorname {{\mathrm {Aut}}}(A)$
is cocycle conjugate to its tensor product
$\alpha \colon G\to \operatorname {{\mathrm {Aut}}}(A)$
is cocycle conjugate to its tensor product
![]() $\alpha \otimes \operatorname {{\mathrm {id}}}_{{\mathcal {Z}}}$
with the trivial action on
$\alpha \otimes \operatorname {{\mathrm {id}}}_{{\mathcal {Z}}}$
with the trivial action on
![]() ${\mathcal {Z}}$
. (As discussed in the introduction of [Reference Wouters94], these are the actions one can expect to classify.) In [Reference Gardella, Hirshberg and Vaccaro46], the problem is solved for actions of discrete, countable, amenable groups G on unital
${\mathcal {Z}}$
. (As discussed in the introduction of [Reference Wouters94], these are the actions one can expect to classify.) In [Reference Gardella, Hirshberg and Vaccaro46], the problem is solved for actions of discrete, countable, amenable groups G on unital
![]() ${\mathrm {C}^*}$
-algebras A under the assumptions that the extreme boundary
${\mathrm {C}^*}$
-algebras A under the assumptions that the extreme boundary
![]() $\partial _e(T(A))$
of
$\partial _e(T(A))$
of
![]() $T(A)$
is compact and of finite covering dimension and that the action of G on
$T(A)$
is compact and of finite covering dimension and that the action of G on
![]() $\partial _e(T(A))$
has finite orbits of bounded size, with Hausdorff orbit space
$\partial _e(T(A))$
has finite orbits of bounded size, with Hausdorff orbit space
![]() $\partial _e(T(A))/G$
. This motivates us to pose the following.
$\partial _e(T(A))/G$
. This motivates us to pose the following.
Question A. What is the generic tracial behaviour of an automorphism of a stably finite classifiable
![]() ${\mathrm {C}^*}$
-algebra?
${\mathrm {C}^*}$
-algebra?
In our context, stable finiteness is equivalent to the trace space
![]() $T(A)$
being nonempty (see [Reference Rørdam and Størmer79, §1.1.3]). By ‘generic tracial behaviour’ we mean that we seek to identify properties of induced affine homeomorphisms
$T(A)$
being nonempty (see [Reference Rørdam and Størmer79, §1.1.3]). By ‘generic tracial behaviour’ we mean that we seek to identify properties of induced affine homeomorphisms
![]() $T(A)\to T(A)$
that hold residually, that is, for at least a dense
$T(A)\to T(A)$
that hold residually, that is, for at least a dense
![]() $G_{\delta }$
set of automorphisms
$G_{\delta }$
set of automorphisms
![]() $A\to A$
(in the topology of pointwise convergence). We will address Question A under the additional assumptions that:
$A\to A$
(in the topology of pointwise convergence). We will address Question A under the additional assumptions that:
-
• the extreme boundary
 $\partial _e(T(A))$
of
$\partial _e(T(A))$
of
 $T(A)$
is a finite-dimensional, compact, connected topological manifold;
$T(A)$
is a finite-dimensional, compact, connected topological manifold; -
• the automorphism
 $\alpha $
of A fixes an Oxtoby–Ulam (OU) trace (roughly, a noncommutative analogue of Lebesgue measure – see § 2.1 and § 3);
$\alpha $
of A fixes an Oxtoby–Ulam (OU) trace (roughly, a noncommutative analogue of Lebesgue measure – see § 2.1 and § 3); -
• the pairing
 $\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is trivial;
$\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is trivial; -
•
 $K_1(A)$
is torsion free.
$K_1(A)$
is torsion free.
With these hypotheses, we are able to use classification to lift known results about topological dynamical systems to the
![]() ${\mathrm {C}^*}$
-level. The strategy is simple (as long as we are willing to make free use of heavy classification machinery): Given an endomorphism
${\mathrm {C}^*}$
-level. The strategy is simple (as long as we are willing to make free use of heavy classification machinery): Given an endomorphism
![]() $\alpha $
, nudge its action on
$\alpha $
, nudge its action on
![]() $\partial _e(T(A))$
to be in a desired topological class, then lift the perturbed invariant to an endomorphism
$\partial _e(T(A))$
to be in a desired topological class, then lift the perturbed invariant to an endomorphism
![]() $\beta $
which, by virtue of the closeness of
$\beta $
which, by virtue of the closeness of
![]() $\operatorname {{\mathrm {Ell}}}(\beta )$
to
$\operatorname {{\mathrm {Ell}}}(\beta )$
to
![]() $\operatorname {{\mathrm {Ell}}}(\alpha )$
, is (up to conjugation by a unitary) within a given
$\operatorname {{\mathrm {Ell}}}(\alpha )$
, is (up to conjugation by a unitary) within a given
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $\alpha $
on a given finite set. Actually, the invariant we must use is not
$\alpha $
on a given finite set. Actually, the invariant we must use is not
![]() $\operatorname {{\mathrm {Ell}}}$
but one that also includes ‘total K-theory’ and ‘Hausdorffised algebraic
$\operatorname {{\mathrm {Ell}}}$
but one that also includes ‘total K-theory’ and ‘Hausdorffised algebraic
![]() $K_1$
’ (see the proof of Theorem 3.4 for a brief primer), together with suitable pairings. The above assumptions on K-theory ensure that the compatibility demanded by these pairings is automatically satisfied.
$K_1$
’ (see the proof of Theorem 3.4 for a brief primer), together with suitable pairings. The above assumptions on K-theory ensure that the compatibility demanded by these pairings is automatically satisfied.
In short, the following theorem indicates that, when there are infinitely many extremal traces, the typical situation can be very different to the one considered in [Reference Gardella, Hirshberg and Vaccaro46]. (Note, however, that it does not represent an obstruction to generalising [Reference Gardella, Hirshberg and Vaccaro46] for single automorphisms; in the breakthrough article [Reference Wouters94], it is shown how to treat the portion of
![]() $\partial _e(T(A))$
with unbounded orbits.)
$\partial _e(T(A))$
with unbounded orbits.)
Theorem A. For every OU trace
![]() $\tau $
on A, the generic
$\tau $
on A, the generic
![]() $\tau $
-preserving automorphism of A induces a homeomorphism of
$\tau $
-preserving automorphism of A induces a homeomorphism of
![]() $\partial _e(T(A))$
that is weakly mixing and is moreover Devaney-chaotic if
$\partial _e(T(A))$
that is weakly mixing and is moreover Devaney-chaotic if
![]() $\dim \partial _e(T(A)) \ge 2$
.
$\dim \partial _e(T(A)) \ge 2$
.
See § 2 for the definitions of chaos and mixing, which are properties that are satisfied by, for example, hyperbolic toral automorphisms like Arnold’s cat map. A particular consequence for the algebras covered by Theorem A is that, in contrast to the case of finitely many extremal traces, a typical tracial property of automorphisms is sensitive dependence on initial conditions: Arbitrarily close extremal traces eventually get moved far apart.
Whereas weak mixing is residual, in both the measure-theoretic [Reference Halmos53] and topological [Reference Katok and Stepin61, Reference Alpern2] settings, strong mixing is enjoyed by meagre sets of measure-preserving transformations [Reference Rohlin77]. On the other hand, many interesting dynamical systems, for example, those associated to Anosov diffeomorphisms [Reference Bowen and Chazottes12, §1E], are not just strongly mixing but have exponentially fast mixing rates. This chaotic behaviour is reflected in such statistical features as exponential decay of correlations (EDC) and the central limit theorem (CLT). Once again, classification will afford us
![]() ${\mathrm {C}^*}$
-interpretations of these phenomena.
${\mathrm {C}^*}$
-interpretations of these phenomena.
We will, however, need some additional structure in the ambient
![]() ${\mathrm {C}^*}$
-algebra to have satisfactory versions of the CLT and EDC, as these require not just continuous but Lipschitz (or at least Hölder continuous) observables. To that end, for a given compact, connected metric space
${\mathrm {C}^*}$
-algebra to have satisfactory versions of the CLT and EDC, as these require not just continuous but Lipschitz (or at least Hölder continuous) observables. To that end, for a given compact, connected metric space
![]() $(X,d)$
, we construct in Theorem 4.4 an approximately subhomogeneous
$(X,d)$
, we construct in Theorem 4.4 an approximately subhomogeneous
![]() ${\mathrm {C}^*}$
-algebra A with
${\mathrm {C}^*}$
-algebra A with
![]() $\partial _e(T(A))\cong X$
and for which
$\partial _e(T(A))\cong X$
and for which
![]() $\{a\mid \hat a \in \operatorname {{\mathrm {Lip}}}(X,d)\}$
is dense in the set
$\{a\mid \hat a \in \operatorname {{\mathrm {Lip}}}(X,d)\}$
is dense in the set
![]() $A_{sa}$
of self-adjoint elements of A (where
$A_{sa}$
of self-adjoint elements of A (where
![]() $\hat a\colon X\to \mathbb {R}$
, which we refer to as an observable of the tracial dynamics, denotes the evaluation map
$\hat a\colon X\to \mathbb {R}$
, which we refer to as an observable of the tracial dynamics, denotes the evaluation map
![]() $\tau \mapsto \tau (a)$
). Theorem 4.9 then provides the means of lifting a given dynamical system on X to the
$\tau \mapsto \tau (a)$
). Theorem 4.9 then provides the means of lifting a given dynamical system on X to the
![]() ${\mathrm {C}^*}$
-level. In the uniquely ergodic but not necessarily chaotic setting, following [Reference Benoist and Quint7] (see Proposition 4.3) this structure will allow for uniform estimates of large deviation, that is, finite-time estimates of the rate of the tracial convergence guaranteed by Birkhoff’s ergodic theorem.
${\mathrm {C}^*}$
-level. In the uniquely ergodic but not necessarily chaotic setting, following [Reference Benoist and Quint7] (see Proposition 4.3) this structure will allow for uniform estimates of large deviation, that is, finite-time estimates of the rate of the tracial convergence guaranteed by Birkhoff’s ergodic theorem.
The models of the previous paragraph will in general have complicated
![]() $K_1$
-groups. This is potentially vexing if one is interested in managing, via the Pimsner–Voiculescu sequence [Reference Pimsner and Voiculescu74], the K-theory of the crossed product of A by an automorphism
$K_1$
-groups. This is potentially vexing if one is interested in managing, via the Pimsner–Voiculescu sequence [Reference Pimsner and Voiculescu74], the K-theory of the crossed product of A by an automorphism
![]() $\alpha \colon A\to A$
constructed to witness a given topological dynamical system
$\alpha \colon A\to A$
constructed to witness a given topological dynamical system
![]() $h\colon X\to X$
. This issue can be addressed by lifting h not to an automorphism but to a
$h\colon X\to X$
. This issue can be addressed by lifting h not to an automorphism but to a
![]() $K_1$
-killing endomorphism, which, as in [Reference Stacey83], can be extended to an automorphism of a stably isomorphic
$K_1$
-killing endomorphism, which, as in [Reference Stacey83], can be extended to an automorphism of a stably isomorphic
![]() ${\mathrm {C}^*}$
-algebra. (Endomorphisms also allow for the inclusion of noninvertible tracial dynamics
${\mathrm {C}^*}$
-algebra. (Endomorphisms also allow for the inclusion of noninvertible tracial dynamics
![]() $h\colon X\to X$
, for example, the Pomeau–Manneville-type system described in [Reference Jacelon59, §5], and to appeal to and interpret existing results [Reference Bobok and Troubetzkoy9] about such systems.) In particular, if X is an odd sphere, then the extended action is on an inductive limit of prime dimension drop algebras; upon computing the Elliott invariant (see Example 4.10 and Remark 5.2), one learns via classification that these crossed products are just different descriptions of the ones considered in [Reference Deeley, Putnam and Strung31].
$h\colon X\to X$
, for example, the Pomeau–Manneville-type system described in [Reference Jacelon59, §5], and to appeal to and interpret existing results [Reference Bobok and Troubetzkoy9] about such systems.) In particular, if X is an odd sphere, then the extended action is on an inductive limit of prime dimension drop algebras; upon computing the Elliott invariant (see Example 4.10 and Remark 5.2), one learns via classification that these crossed products are just different descriptions of the ones considered in [Reference Deeley, Putnam and Strung31].
The above discussion of the range of the Elliott invariant of crossed products motivates our second question.
Question B. Which classifiable
![]() ${\mathrm {C}^*}$
-algebras can be described as crossed products of stably finite classifiable
${\mathrm {C}^*}$
-algebras can be described as crossed products of stably finite classifiable
![]() ${\mathrm {C}^*}$
-algebras by the integers?
${\mathrm {C}^*}$
-algebras by the integers?
Since Kirchberg algebras are already known to be included in the answer to Question B (see, for example, [Reference Rørdam and Størmer79, Proposition 4.3.3]), we focus our attention on stably finite targets. Combining work of Downarowicz [Reference Downarowicz37] and Szabó, Wu and Zacharias [Reference Szabó, Wu and Zacharias84], we show that every metrisable Choquet simplex is attainable as the tracial state space of a crossed product of a classifiable
![]() ${\mathrm {C}^*}$
-algebra A, for which
${\mathrm {C}^*}$
-algebra A, for which
![]() $\partial _e(T(A))$
is a Cantor space, by an automorphism with finite Rokhlin dimension. In the
$\partial _e(T(A))$
is a Cantor space, by an automorphism with finite Rokhlin dimension. In the
![]() $KK$
-contractible setting (or equivalently under the UCT, assuming that
$KK$
-contractible setting (or equivalently under the UCT, assuming that
![]() $K_*(A)=0$
), [Reference Elliott, Gong, Lin and Niu41] then shows that, up to stable isomorphism, the full class is exhausted.
$K_*(A)=0$
), [Reference Elliott, Gong, Lin and Niu41] then shows that, up to stable isomorphism, the full class is exhausted.
Theorem B. Let
![]() $\mathcal {K}$
be the class of infinite-dimensional, simple, separable,
$\mathcal {K}$
be the class of infinite-dimensional, simple, separable,
![]() $KK$
-contractible
$KK$
-contractible
![]() ${\mathrm {C}^*}$
-algebras that satisfy the UCT and have continuous scale, nonempty trace space and finite nuclear dimension. Then, for every
${\mathrm {C}^*}$
-algebras that satisfy the UCT and have continuous scale, nonempty trace space and finite nuclear dimension. Then, for every
![]() $B\in \mathcal {K}$
there exists
$B\in \mathcal {K}$
there exists
![]() $A\in \mathcal {K}$
and an automorphism
$A\in \mathcal {K}$
and an automorphism
![]() $\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
such that
$\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
such that
![]() $\partial _e(T(A))$
is compact and zero dimensional, and
$\partial _e(T(A))$
is compact and zero dimensional, and
![]() $A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
$A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
This article is organised as follows. In § 2, we collate relevant properties of measure-preserving topological dynamical systems. Then in § 3, we explain how to use classification to lift these properties to statements about
![]() ${\mathrm {C}^*}$
-dynamical systems. Examples of strongly chaotic dynamics, descriptions of associated statistical features like the CLT and EDC and the construction of models to suitably witness these phenomena are described in § 4. Finally, in § 5, we show how to obtain
${\mathrm {C}^*}$
-dynamical systems. Examples of strongly chaotic dynamics, descriptions of associated statistical features like the CLT and EDC and the construction of models to suitably witness these phenomena are described in § 4. Finally, in § 5, we show how to obtain
![]() $KK$
-contractible classifiable
$KK$
-contractible classifiable
![]() ${\mathrm {C}^*}$
-algebras as crossed products.
${\mathrm {C}^*}$
-algebras as crossed products.
2 Generic properties of topological dynamical systems
Chaos and mixing will be familiar notions to those working in dynamical systems but perhaps not to
![]() ${\mathrm {C}^*}$
-algebraists. We briefly introduce these concepts for the reader’s convenience.
${\mathrm {C}^*}$
-algebraists. We briefly introduce these concepts for the reader’s convenience.
2.1 Chaos
Definition 2.1. Let
![]() $(X,d)$
be an infinite metric space and
$(X,d)$
be an infinite metric space and
![]() $h\colon X\to X$
a continuous map. The dynamical system
$h\colon X\to X$
a continuous map. The dynamical system
![]() $(X,h)$
is said to be chaotic in the sense of Devaney [Reference Devaney33, Definition 8.5] if:
$(X,h)$
is said to be chaotic in the sense of Devaney [Reference Devaney33, Definition 8.5] if:
-
1. for every nonempty open sets
 $U,V\subseteq X$
, there exists
$U,V\subseteq X$
, there exists
 $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
 $h^n(U)\cap V\ne \emptyset $
(that is,
$h^n(U)\cap V\ne \emptyset $
(that is,
 $(X,h)$
is transitive or equivalently, irreducible);
$(X,h)$
is transitive or equivalently, irreducible); -
2. the periodic points of h are dense in X;
-
3. the system has sensitive dependence on initial conditions, that is, there exists
 $\delta>0$
such that, for every
$\delta>0$
such that, for every
 $x\in X$
and every
$x\in X$
and every
 $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
 $y\in X$
and
$y\in X$
and
 $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
 $d(x,y)<\varepsilon $
and
$d(x,y)<\varepsilon $
and
 $d(h^nx,h^ny)\ge \delta $
.
$d(h^nx,h^ny)\ge \delta $
.
As pointed out in [Reference Banks, Brooks, Cairns, Davis and Stacey6], (3) actually follows from (1) and (2) (and if X is compact, it is easy to see directly that (3) is preserved under topological conjugation). This means that this notion of chaos is genuinely topological. An equivalent characterisation is given in [Reference Touhey90]:
![]() $(X,h)$
is chaotic if and only if, for every nonempty open sets
$(X,h)$
is chaotic if and only if, for every nonempty open sets
![]() $U,V\subseteq X$
, there is a periodic point whose forward orbit intersects both U and V.
$U,V\subseteq X$
, there is a periodic point whose forward orbit intersects both U and V.
An important class of Devaney-chaotic dynamical systems is provided by the irreducible components of nonwandering Smale spaces. (See [Reference Bowen and Chazottes12, Theorem 3.5] and [Reference Bowen and Chazottes12, 3.8]. Note that these results, though stated for diffeomorphisms, apply just as well to the abstract setting of Smale spaces; see [Reference Ruelle80, Chapter 7].) We will see some more examples in § 4, but in fact, under certain circumstances that we now recall (Theorem 2.3 below), Devaney-chaotic maps are generic among measure-preserving homeomorphisms of topological manifolds.
The manifolds discussed in this paper will always be compact and will often be connected. Measures will typically be particularly tractable.
Definition 2.2 [Reference Alpern and Prasad4].
A Borel probability measure
![]() $\mu $
on a topological manifold X is called an Oxtoby–Ulam (OU) measure if it is faithful, nonatomic and zero on the boundary
$\mu $
on a topological manifold X is called an Oxtoby–Ulam (OU) measure if it is faithful, nonatomic and zero on the boundary
![]() $\partial X$
of X (if there is one).
$\partial X$
of X (if there is one).
When
![]() $X=[0,1]^n$
, OU measures are precisely those that are homeomorphic images of Lebesgue measure (see [Reference Oxtoby and Ulam72, Theorem 2]), and when X is boundaryless, OU measures are generic (see [Reference Fathi44, Proposition 1.4]).
$X=[0,1]^n$
, OU measures are precisely those that are homeomorphic images of Lebesgue measure (see [Reference Oxtoby and Ulam72, Theorem 2]), and when X is boundaryless, OU measures are generic (see [Reference Fathi44, Proposition 1.4]).
We equip the set
![]() $\mathcal {H}(X,\mu )$
(respectively,
$\mathcal {H}(X,\mu )$
(respectively,
![]() $\mathcal {C}(X,\mu )$
) of
$\mathcal {C}(X,\mu )$
) of
![]() $\mu $
-preserving homeomorphisms (respectively, continuous maps)
$\mu $
-preserving homeomorphisms (respectively, continuous maps)
![]() $X\to X$
with the compact open topology, which for compact metric spaces X means the topology of uniform convergence. A complete metric for the topology on
$X\to X$
with the compact open topology, which for compact metric spaces X means the topology of uniform convergence. A complete metric for the topology on
![]() $\mathcal {H}(X,\mu )$
is
$\mathcal {H}(X,\mu )$
is
Theorem 2.3 [Reference Aarts and Daalderop1, Reference Daalderop and Fokkink29].
Let X be a compact topological manifold of dimension
![]() $n\ge 2$
, and let
$n\ge 2$
, and let
![]() $\mu $
be an OU measure on X. Then, the set of Devaney-chaotic elements of
$\mu $
be an OU measure on X. Then, the set of Devaney-chaotic elements of
![]() $\mathcal {H}(X,\mu )$
is residual (that is, contains a dense
$\mathcal {H}(X,\mu )$
is residual (that is, contains a dense
![]() $G_{\delta }$
set).
$G_{\delta }$
set).
The density part of Theorem 2.3 is also a corollary of [Reference Alpern3, Lemma 2], which shows how to perturb a measure-preserving homeomorphism of the cube to one that cyclically permutes arbitrarily small dyadic cubes (and is therefore chaotic). As mentioned in [Reference Alpern3], this can be translated to the setting of compact, connected manifolds via a modification of a theorem of Brown (see [Reference Alpern and Prasad4, Theorem 9.6]). Moreover, Theorem 2.3 still holds if condition (3) is strengthened to a truly metric property called ‘maximal’ dependence on initial conditions (see [Reference Alpern and Prasad4, Theorem 4.8]).
2.2 Mixing
Definition 2.4. Let
![]() $(X,\Sigma ,\mu )$
be a probability space. A
$(X,\Sigma ,\mu )$
be a probability space. A
![]() $\mu $
-preserving measurable map
$\mu $
-preserving measurable map
![]() $h\colon X\to X$
is:
$h\colon X\to X$
is:
-
1. antiperiodic if the set of periodic points of h has measure zero;
-
2. ergodic if, for every
 $A,B\in \Sigma $
,
$A,B\in \Sigma $
,  $$\begin{align*}\lim_{n\to\infty}\frac{1}{n}\sum_{k=0}^{n-1}\mu(h^{-k}(A)\cap B) = \mu(A)\mu(B); \end{align*}$$
$$\begin{align*}\lim_{n\to\infty}\frac{1}{n}\sum_{k=0}^{n-1}\mu(h^{-k}(A)\cap B) = \mu(A)\mu(B); \end{align*}$$
-
3. weakly mixing if, for every
 $A,B\in \Sigma $
,
$A,B\in \Sigma $
,  $$\begin{align*}\lim_{n\to\infty}\frac{1}{n}\sum_{k=0}^{n-1}|\mu(h^{-k}(A)\cap B) - \mu(A)\mu(B)| = 0; \end{align*}$$
$$\begin{align*}\lim_{n\to\infty}\frac{1}{n}\sum_{k=0}^{n-1}|\mu(h^{-k}(A)\cap B) - \mu(A)\mu(B)| = 0; \end{align*}$$
-
4. strongly mixing if, for every
 $A,B\in \Sigma $
,
$A,B\in \Sigma $
,  $$\begin{align*}\lim_{n\to\infty}\mu(h^{-n}(A)\cap B) = \mu(A)\mu(B). \end{align*}$$
$$\begin{align*}\lim_{n\to\infty}\mu(h^{-n}(A)\cap B) = \mu(A)\mu(B). \end{align*}$$
Remark 2.5.
-
1. That this formulation of ergodicity is implied by the usual one (invariant sets having trivial measure) is an application of Birkhoff’s ergodic theorem (see [Reference Halmos54, ‘Consequences of ergodicity’]). The other direction is easily deduced upon taking
 $A=B^c$
.
$A=B^c$
. -
2. It is also immediate that strong mixing implies weak mixing, which implies ergodicity, which implies antiperiodicity. In fact (see [Reference Halmos54, ‘Mixing’]), an invertible transformation h is weakly mixing if and only if
 $h\times h$
is ergodic, which holds if and only if the only eigenvalue of the unitary operator
$h\times h$
is ergodic, which holds if and only if the only eigenvalue of the unitary operator
 $U_h\in \mathcal {B}(L^2(X,\Sigma ,\mu ))$
,
$U_h\in \mathcal {B}(L^2(X,\Sigma ,\mu ))$
,
 $f\mapsto f\circ h$
, is
$f\mapsto f\circ h$
, is
 $1$
with the constants as the only eigenfunctions.
$1$
with the constants as the only eigenfunctions. -
3. If X is a topological space and
 $\Sigma $
is its Borel
$\Sigma $
is its Borel
 $\sigma $
-algebra, then a strongly mixing continuous map h is topologically mixing on the support of
$\sigma $
-algebra, then a strongly mixing continuous map h is topologically mixing on the support of
 $\mu $
.
$\mu $
. -
4. If
 $(X,h)$
is a mixing axiom A diffeomorphism, then the ‘Bowen measure’ is strongly mixing (see, for example, [Reference Bowen and Chazottes12, Theorem 4.1, §1E]).
$(X,h)$
is a mixing axiom A diffeomorphism, then the ‘Bowen measure’ is strongly mixing (see, for example, [Reference Bowen and Chazottes12, Theorem 4.1, §1E]).
The measure algebra associated to
![]() $(X,\Sigma ,\mu )$
is the Boolean algebra
$(X,\Sigma ,\mu )$
is the Boolean algebra
![]() $\mathfrak {B}$
consisting of the equivalence classes of measurable sets (where equivalence of E and F means that their symmetric difference has measure zero) and equipped with the usual set operations (intersection, union, complementation). If
$\mathfrak {B}$
consisting of the equivalence classes of measurable sets (where equivalence of E and F means that their symmetric difference has measure zero) and equipped with the usual set operations (intersection, union, complementation). If
![]() $\mu $
is nonatomic and
$\mu $
is nonatomic and
![]() $\mathfrak {B}$
is separable (with respect to the metric
$\mathfrak {B}$
is separable (with respect to the metric
![]() $d(E,F)=E \triangle F$
), then
$d(E,F)=E \triangle F$
), then
![]() $\mathfrak {B}$
is isomorphic to the measure algebra of the unit interval I with Lebesgue measure
$\mathfrak {B}$
is isomorphic to the measure algebra of the unit interval I with Lebesgue measure
![]() $\lambda $
(see, for example, [Reference Bogachev10, Theorem 9.3.4]). In this setting, it was shown in [Reference Halmos53] (see also [Reference Halmos54, ‘Category’]) that, among invertible measure-preserving transformations of
$\lambda $
(see, for example, [Reference Bogachev10, Theorem 9.3.4]). In this setting, it was shown in [Reference Halmos53] (see also [Reference Halmos54, ‘Category’]) that, among invertible measure-preserving transformations of
![]() $(X,\Sigma ,\mu )$
, the weakly mixing ones are generic. This result was later adapted to topological dynamical systems.
$(X,\Sigma ,\mu )$
, the weakly mixing ones are generic. This result was later adapted to topological dynamical systems.
Theorem 2.6 [Reference Katok and Stepin61].
Let X be a compact, connected topological manifold, and let
![]() $\mu $
be an OU measure on X. Then, the weakly mixing elements of
$\mu $
be an OU measure on X. Then, the weakly mixing elements of
![]() $\mathcal {H}(X,\mu )$
form a dense
$\mathcal {H}(X,\mu )$
form a dense
![]() $G_{\delta }$
set.
$G_{\delta }$
set.
The conjugacy lemma of [Reference Alpern2] (see also [Reference Alpern and Prasad4, Theorem 10.1]), which is a strengthening of the prototypical result of Halmos, established a very general framework for transferring generic properties of measure-preserving systems to topological ones. Namely (see [Reference Alpern and Prasad4, Theorem 10.3]), if
![]() $\mathcal {V}$
is a
$\mathcal {V}$
is a
![]() $G_{\delta }$
subset of invertible measure-preserving transformations (with respect to the weak topology) that is invariant under conjugation and contains an antiperiodic transformation, then
$G_{\delta }$
subset of invertible measure-preserving transformations (with respect to the weak topology) that is invariant under conjugation and contains an antiperiodic transformation, then
![]() $\mathcal {V}\cap \mathcal {H}(X,\mu )$
is a dense
$\mathcal {V}\cap \mathcal {H}(X,\mu )$
is a dense
![]() $G_{\delta }$
subset of
$G_{\delta }$
subset of
![]() $\mathcal {H}(X,\mu )$
(with respect to the uniform topology). Theorem 2.6 is a special case of this observation. In § 3, we will use classification to lift from topological systems (viewed as actions on trace spaces) to
$\mathcal {H}(X,\mu )$
(with respect to the uniform topology). Theorem 2.6 is a special case of this observation. In § 3, we will use classification to lift from topological systems (viewed as actions on trace spaces) to
![]() ${\mathrm {C}^*}$
-algebras.
${\mathrm {C}^*}$
-algebras.
Various genericity results for noninvertible transformations of
![]() $([0,1],\mu )$
, where
$([0,1],\mu )$
, where
![]() $\mu $
is an OU measure on the interval
$\mu $
is an OU measure on the interval
![]() $[0,1]$
, are established in [Reference Bobok and Troubetzkoy9]. In particular, the following holds.
$[0,1]$
, are established in [Reference Bobok and Troubetzkoy9]. In particular, the following holds.
Theorem 2.7 [Reference Bobok and Troubetzkoy9].
In the set
![]() $\mathcal {C}([0,1],\mu )$
of
$\mathcal {C}([0,1],\mu )$
of
![]() $\mu $
-preserving continuous maps
$\mu $
-preserving continuous maps
![]() $[0,1]\to [0,1]$
, both the weakly mixing and (maximally) chaotic elements form dense
$[0,1]\to [0,1]$
, both the weakly mixing and (maximally) chaotic elements form dense
![]() $G_{\delta }$
sets. The strongly mixing elements are dense but meagre.
$G_{\delta }$
sets. The strongly mixing elements are dense but meagre.
Remark 2.8. Rather than the generic behaviour of
![]() $h\in \mathcal {H}(X,\mu )$
(or
$h\in \mathcal {H}(X,\mu )$
(or
![]() $h\in \mathcal {C}(X,\mu )$
) for a given
$h\in \mathcal {C}(X,\mu )$
) for a given
![]() $\mu $
, one might ask for the generic behaviour of
$\mu $
, one might ask for the generic behaviour of
![]() $\mu \in \mathcal {M}(X)^h$
, that is, of an h-invariant Borel probability measure
$\mu \in \mathcal {M}(X)^h$
, that is, of an h-invariant Borel probability measure
![]() $\mu $
, for a given homeomorphism (or continuous map) h. It is shown in [Reference Catsigeras and Troubetzkoy19] that, for a generic continuous h on a
$\mu $
, for a given homeomorphism (or continuous map) h. It is shown in [Reference Catsigeras and Troubetzkoy19] that, for a generic continuous h on a
![]() $C^1$
compact, connected manifold, ergodic measures are nowhere dense in
$C^1$
compact, connected manifold, ergodic measures are nowhere dense in
![]() $\mathcal {M}(X)^h$
. On the other hand, for an irreducible diffeomorphism on a compact manifold without boundary, ergodicity is generic [Reference Gelfert and Kwietniak47, Theorem 7.1]. For a mixing axiom A diffeomorphism, the generic invariant measure is OU [Reference Sigmund81] and weakly mixing [Reference Sigmund82], and the strongly mixing invariant measures are dense [Reference Sigmund82] but meagre [Reference Sigmund81].
$\mathcal {M}(X)^h$
. On the other hand, for an irreducible diffeomorphism on a compact manifold without boundary, ergodicity is generic [Reference Gelfert and Kwietniak47, Theorem 7.1]. For a mixing axiom A diffeomorphism, the generic invariant measure is OU [Reference Sigmund81] and weakly mixing [Reference Sigmund82], and the strongly mixing invariant measures are dense [Reference Sigmund82] but meagre [Reference Sigmund81].
3 Lifting via classification
The standing assumption in this section is that A is an infinite-dimensional, separable, algebraically simple
![]() ${\mathrm {C}^*}$
-algebra whose tracial state space
${\mathrm {C}^*}$
-algebra whose tracial state space
![]() $T(A)$
is nonempty and compact, with compact extreme boundary
$T(A)$
is nonempty and compact, with compact extreme boundary
![]() $\partial _e(T(A))$
. (In conjunction with
$\partial _e(T(A))$
. (In conjunction with
![]() $\mathcal {Z}$
-stability, these conditions in particular imply that A has ‘continuous scale’; see, for example, [Reference Elliott, Gong, Lin and Niu42, §5].) Throughout, the boundary
$\mathcal {Z}$
-stability, these conditions in particular imply that A has ‘continuous scale’; see, for example, [Reference Elliott, Gong, Lin and Niu42, §5].) Throughout, the boundary
![]() $\partial _e(T(A))$
is denoted by
$\partial _e(T(A))$
is denoted by
![]() $X_A$
(X for ‘extreme’). We equip
$X_A$
(X for ‘extreme’). We equip
![]() $T(A)$
with the
$T(A)$
with the
![]() $w^*$
-topology and fix a metric d on
$w^*$
-topology and fix a metric d on
![]() $X_A$
that induces the subspace topology. The set of continuous affine maps
$X_A$
that induces the subspace topology. The set of continuous affine maps
![]() $T(A)\to \mathbb {R}$
is denoted by
$T(A)\to \mathbb {R}$
is denoted by
![]() $\operatorname {{\mathrm {Aff}}}(T(A))$
.
$\operatorname {{\mathrm {Aff}}}(T(A))$
.
Endomorphism spaces
Let us write
![]() $\operatorname {{\mathrm {End}}}(A,X_A)$
for the set of what one might call ‘tracially nondegenerate’ endomorphisms of A, that is,
$\operatorname {{\mathrm {End}}}(A,X_A)$
for the set of what one might call ‘tracially nondegenerate’ endomorphisms of A, that is,
![]() $^*$
-homomorphisms
$^*$
-homomorphisms
![]() $\alpha \colon A\to A$
that induce continuous affine maps
$\alpha \colon A\to A$
that induce continuous affine maps
![]() $\alpha ^*=T(\alpha )\colon T(A)\to T(A)$
that preserve
$\alpha ^*=T(\alpha )\colon T(A)\to T(A)$
that preserve
![]() $X_A=\partial _e(T(A))$
. (Note, for example, that the shift endomorphisms of
$X_A=\partial _e(T(A))$
. (Note, for example, that the shift endomorphisms of
![]() $M_{n^{\infty }}$
discussed in § 4.4 are not covered by this definition.) For a given
$M_{n^{\infty }}$
discussed in § 4.4 are not covered by this definition.) For a given
![]() $\tau \in T(A)$
, let us write
$\tau \in T(A)$
, let us write
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
for those elements of
$\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
for those elements of
![]() $\operatorname {{\mathrm {End}}}(A,X_A)$
that fix
$\operatorname {{\mathrm {End}}}(A,X_A)$
that fix
![]() $\tau $
. Note that
$\tau $
. Note that
(that is, every automorphism preserves
![]() $X_A$
and fixes some
$X_A$
and fixes some
![]() $\tau $
). We write
$\tau $
). We write
![]() $\operatorname {{\mathrm {Aut}}}(A,\tau )$
for the set
$\operatorname {{\mathrm {Aut}}}(A,\tau )$
for the set
![]() $\operatorname {{\mathrm {Aut}}}(A)\cap \operatorname {{\mathrm {End}}}(A,X_A,\tau )$
.
$\operatorname {{\mathrm {Aut}}}(A)\cap \operatorname {{\mathrm {End}}}(A,X_A,\tau )$
.
Each of these spaces is equipped with a suitable topology of pointwise convergence. For
![]() $\operatorname {{\mathrm {End}}}(A,X_A)$
and
$\operatorname {{\mathrm {End}}}(A,X_A)$
and
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
, this means the topology induced by the family of pseudometrics
$\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
, this means the topology induced by the family of pseudometrics
To ensure that
![]() $\operatorname {{\mathrm {Aut}}}(A)$
and
$\operatorname {{\mathrm {Aut}}}(A)$
and
![]() $\operatorname {{\mathrm {Aut}}}(A,\tau )$
are Polish spaces, we should use the finer topology provided by
$\operatorname {{\mathrm {Aut}}}(A,\tau )$
are Polish spaces, we should use the finer topology provided by
where
![]() $d^{\prime }_F(\varphi ,\psi ) = \inf _{u}\max _{a\in F}\|u\varphi (a)u^*-\psi (a)\|$
, the infimum taken over all unitaries in (the minimal unitisation of) A. (Completeness follows from an approximate intertwining; see, for example, [Reference Rørdam and Størmer79, Corollary 2.3.3].) That said, we will not apply the Baire category theorem directly in
$d^{\prime }_F(\varphi ,\psi ) = \inf _{u}\max _{a\in F}\|u\varphi (a)u^*-\psi (a)\|$
, the infimum taken over all unitaries in (the minimal unitisation of) A. (Completeness follows from an approximate intertwining; see, for example, [Reference Rørdam and Størmer79, Corollary 2.3.3].) That said, we will not apply the Baire category theorem directly in
![]() $\operatorname {{\mathrm {Aut}}}(A)$
, instead lifting generic properties from the trace space to the
$\operatorname {{\mathrm {Aut}}}(A)$
, instead lifting generic properties from the trace space to the
![]() ${\mathrm {C}^*}$
-algebra via classification.
${\mathrm {C}^*}$
-algebra via classification.
Representing measures
Since
![]() $T(A)$
is a Choquet simplex, every
$T(A)$
is a Choquet simplex, every
![]() $\tau \in T(A)$
is represented by a unique Borel probability measure
$\tau \in T(A)$
is represented by a unique Borel probability measure
![]() $\mu =\mu _{\tau }$
supported on
$\mu =\mu _{\tau }$
supported on
![]() $X_A=\partial _e(T(A))$
; that is,
$X_A=\partial _e(T(A))$
; that is,
![]() $\mu $
is the unique measure on
$\mu $
is the unique measure on
![]() $X_A$
such that
$X_A$
such that
(The metric d on
![]() $X_A$
can then be extended to all of
$X_A$
can then be extended to all of
![]() $T(A)$
via a choice of Wasserstein metric between representing measures; see [Reference Jacelon59, §2]).
$T(A)$
via a choice of Wasserstein metric between representing measures; see [Reference Jacelon59, §2]).
In fact, every continuous affine functional
![]() $f\colon T(A)\to \mathbb {R}$
is of the form
$f\colon T(A)\to \mathbb {R}$
is of the form
![]() $f=\hat a$
for some self-adjoint element
$f=\hat a$
for some self-adjoint element
![]() $a\in A$
(see [Reference Lin66, Theorem 9.3], whose use of [Reference Cuntz and Pedersen28, §2] does not even require simplicity). The defining property (3.2) of the representing measure
$a\in A$
(see [Reference Lin66, Theorem 9.3], whose use of [Reference Cuntz and Pedersen28, §2] does not even require simplicity). The defining property (3.2) of the representing measure
![]() $\mu $
is therefore
$\mu $
is therefore
Conversely, every measure
![]() $\mu $
defines via equation (3.3) a trace
$\mu $
defines via equation (3.3) a trace
![]() $\tau =\tau _{\mu }\in T(A)$
. If
$\tau =\tau _{\mu }\in T(A)$
. If
![]() $\mu $
is an OU measure, we call
$\mu $
is an OU measure, we call
![]() $\tau _{\mu }$
an OU trace.
$\tau _{\mu }$
an OU trace.
We use representing measures to reduce the analysis of generic properties of the space
![]() $\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
of continuous
$\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
of continuous
![]() $X_A$
-preserving affine maps
$X_A$
-preserving affine maps
![]() $T(A)\to T(A)$
to those of
$T(A)\to T(A)$
to those of
![]() $C(X_A,X_A)$
. In particular, we can extend
$C(X_A,X_A)$
. In particular, we can extend
![]() $h\in C(X_A,X_A)$
to an element of
$h\in C(X_A,X_A)$
to an element of
![]() $\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
via the pushforward
$\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
via the pushforward
Lemma 3.1. The pushforward extension
![]() $h\mapsto h_*$
of equation (3.4) gives a homeomorphism between
$h\mapsto h_*$
of equation (3.4) gives a homeomorphism between
![]() $C(X_A,X_A)$
and
$C(X_A,X_A)$
and
![]() $\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
(with respect to the d-uniform topology).
$\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
(with respect to the d-uniform topology).
Proof. The map
![]() $h\mapsto h_*$
is continuous, and its continuous inverse is the restriction map
$h\mapsto h_*$
is continuous, and its continuous inverse is the restriction map
![]() $\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A)) \to C(X_A,X_A)$
.
$\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A)) \to C(X_A,X_A)$
.
The map
![]() $T(\cdot )\colon \operatorname {{\mathrm {End}}}(A,X_A)\to C(X_A,X_A)$
,
$T(\cdot )\colon \operatorname {{\mathrm {End}}}(A,X_A)\to C(X_A,X_A)$
,
![]() $\alpha \mapsto \alpha ^*|_{X_A}$
, is continuous. It sends
$\alpha \mapsto \alpha ^*|_{X_A}$
, is continuous. It sends
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
to the set
$\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
to the set
![]() $\mathcal {C}(X_A,\mu )$
of
$\mathcal {C}(X_A,\mu )$
of
![]() $\mu =\mu _{\tau }$
-preserving continuous maps
$\mu =\mu _{\tau }$
-preserving continuous maps
![]() $X_A\to X_A$
and
$X_A\to X_A$
and
![]() $\operatorname {{\mathrm {Aut}}}(A,\tau )$
to
$\operatorname {{\mathrm {Aut}}}(A,\tau )$
to
![]() $\mathcal {H}(X_A,\mu )$
(continuously with respect to equations (2.1) and (3.1)). The following is immediate.
$\mathcal {H}(X_A,\mu )$
(continuously with respect to equations (2.1) and (3.1)). The following is immediate.
Lemma 3.2. If
![]() $\mathcal {V}$
is an open (respectively,
$\mathcal {V}$
is an open (respectively,
![]() $G_{\delta }$
) subset of
$G_{\delta }$
) subset of
![]() $\mathcal {C}(X_A,\mu )$
, then
$\mathcal {C}(X_A,\mu )$
, then
![]() $T^{-1}\mathcal {V}$
is an open (respectively,
$T^{-1}\mathcal {V}$
is an open (respectively,
![]() $G_{\delta }$
) subset of
$G_{\delta }$
) subset of
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau _{\mu })$
that is invariant under approximate unitary equivalence. The same is true of
$\operatorname {{\mathrm {End}}}(A,X_A,\tau _{\mu })$
that is invariant under approximate unitary equivalence. The same is true of
![]() $T^{-1}\mathcal {V}\cap \operatorname {{\mathrm {Aut}}}(A)\subseteq \operatorname {{\mathrm {Aut}}}(A,\tau _{\mu })$
for
$T^{-1}\mathcal {V}\cap \operatorname {{\mathrm {Aut}}}(A)\subseteq \operatorname {{\mathrm {Aut}}}(A,\tau _{\mu })$
for
![]() $\mathcal {V}\subseteq \mathcal {H}(X_A,\mu )$
.
$\mathcal {V}\subseteq \mathcal {H}(X_A,\mu )$
.
If we further demand that A be classifiable by the Elliott invariant and impose suitable restrictions on K-theory and traces, we can also lift dense sets to dense sets.
First, we recall some notation. Every
![]() $\tau \in T(A)$
extends to a tracial state on the minimal unitisation
$\tau \in T(A)$
extends to a tracial state on the minimal unitisation
![]() $\tilde A$
of A via
$\tilde A$
of A via
![]() $a+\lambda 1 \mapsto \tau (a)+\lambda $
and also to a trace
$a+\lambda 1 \mapsto \tau (a)+\lambda $
and also to a trace
![]() $\tau \otimes \operatorname {{\mathrm {tr}}}_k$
on any matrix algebra
$\tau \otimes \operatorname {{\mathrm {tr}}}_k$
on any matrix algebra
![]() $A\otimes M_k \cong M_k(A)$
over A. We denote these extensions also by
$A\otimes M_k \cong M_k(A)$
over A. We denote these extensions also by
![]() $\tau $
. For a unital
$\tau $
. For a unital
![]() ${\mathrm {C}^*}$
-algebra A, the pairing map
${\mathrm {C}^*}$
-algebra A, the pairing map
![]() $\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is the homomorphism defined by
$\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is the homomorphism defined by
![]() $\rho _A([p])(\tau )=\tau (p)$
for
$\rho _A([p])(\tau )=\tau (p)$
for
![]() $p\in M_k(A)$
a projection.
$p\in M_k(A)$
a projection.
If A is nonunital, then
![]() $K_0(A)$
is the kernel of the map
$K_0(A)$
is the kernel of the map
![]() $K_0(\tilde A)\to K_0(\mathbb {C})$
induced by the quotient map
$K_0(\tilde A)\to K_0(\mathbb {C})$
induced by the quotient map
![]() $\Pi _A\colon \tilde A \to \mathbb {C}$
, and the pairing is defined by
$\Pi _A\colon \tilde A \to \mathbb {C}$
, and the pairing is defined by
![]() $\rho _A([p]-[q])(\tau )=\tau (p)-\tau (q)$
. Moreover,
$\rho _A([p]-[q])(\tau )=\tau (p)-\tau (q)$
. Moreover,
![]() $T(\tilde {A})$
is affinely homeomorphic to the convex hull of
$T(\tilde {A})$
is affinely homeomorphic to the convex hull of
![]() $T(A)$
and the trace
$T(A)$
and the trace
![]() $\tau _{\mathbb {C}}$
induced by
$\tau _{\mathbb {C}}$
induced by
![]() $\Pi _A$
; in particular, every continuous affine map from
$\Pi _A$
; in particular, every continuous affine map from
![]() $T(A)$
to itself extends uniquely to one from
$T(A)$
to itself extends uniquely to one from
![]() $T(\tilde {A})$
to itself that fixes
$T(\tilde {A})$
to itself that fixes
![]() $\tau _{\mathbb {C}}$
.
$\tau _{\mathbb {C}}$
.
Definition 3.3. A
![]() ${\mathrm {C}^*}$
-algebra A is said to have trivial tracial pairing if either
${\mathrm {C}^*}$
-algebra A is said to have trivial tracial pairing if either
-
1. A is unital and the image of
 $\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is contained in the constant functions, or
$\rho _A\colon K_0(A)\to \operatorname {{\mathrm {Aff}}}(T(A))$
is contained in the constant functions, or -
2. A is nonunital and
 $\ker \rho _A=K_0(A)$
.
$\ker \rho _A=K_0(A)$
.
Note that a simple
![]() ${\mathrm {C}^*}$
-algebra A must in fact be stably projectionless if
${\mathrm {C}^*}$
-algebra A must in fact be stably projectionless if
![]() $\ker \rho _A=K_0(A)$
. This condition holds, for example, for the
$\ker \rho _A=K_0(A)$
. This condition holds, for example, for the
![]() ${\mathrm {C}^*}$
-algebras classified in [Reference Gong and Lin48]. Examples of unital
${\mathrm {C}^*}$
-algebras classified in [Reference Gong and Lin48]. Examples of unital
![]() ${\mathrm {C}^*}$
-algebras with trivial tracial pairing are limits of subhomogeneous building blocks with connected spectra (in particular, the interval algebras
${\mathrm {C}^*}$
-algebras with trivial tracial pairing are limits of subhomogeneous building blocks with connected spectra (in particular, the interval algebras
![]() $C([0,1],M_n)$
considered in [Reference Thomsen85] and the prime dimension drop algebras considered in [Reference Jiang and Su60]).
$C([0,1],M_n)$
considered in [Reference Thomsen85] and the prime dimension drop algebras considered in [Reference Jiang and Su60]).
Theorem 3.4. Suppose that, in addition to the standing assumption of this section, A also satisfies the UCT and has finite nuclear dimension, trivial tracial pairing and torsion-free
![]() $K_1$
. Then, for every dense subset
$K_1$
. Then, for every dense subset
![]() $\mathcal {V}$
of
$\mathcal {V}$
of
![]() $\mathcal {C}(X_A,\mu )$
,
$\mathcal {C}(X_A,\mu )$
,
![]() $T^{-1}\mathcal {V}$
is a dense subset of
$T^{-1}\mathcal {V}$
is a dense subset of
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau _{\mu })$
. The same is true of
$\operatorname {{\mathrm {End}}}(A,X_A,\tau _{\mu })$
. The same is true of
![]() $T^{-1}\mathcal {V}\cap \operatorname {{\mathrm {Aut}}}(A)\subseteq \operatorname {{\mathrm {Aut}}}(A,\tau _{\mu })$
for
$T^{-1}\mathcal {V}\cap \operatorname {{\mathrm {Aut}}}(A)\subseteq \operatorname {{\mathrm {Aut}}}(A,\tau _{\mu })$
for
![]() $\mathcal {V}\subseteq \mathcal {H}(X_A,\mu )$
.
$\mathcal {V}\subseteq \mathcal {H}(X_A,\mu )$
.
Proof. We will prove the statement for automorphisms, noting that the same argument works for endomorphisms. Let
![]() $\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
with
$\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
with
![]() $T(\alpha )\in \mathcal {H}(X_A,\mu )$
(that is,
$T(\alpha )\in \mathcal {H}(X_A,\mu )$
(that is,
![]() $\tau _{\mu }\circ \alpha =\tau _{\mu }$
). Let
$\tau _{\mu }\circ \alpha =\tau _{\mu }$
). Let
![]() $F\subseteq A$
be finite, and let
$F\subseteq A$
be finite, and let
![]() $\varepsilon>0$
. We must show that there is an automorphism
$\varepsilon>0$
. We must show that there is an automorphism
![]() $\beta $
of A and a unitary w such that
$\beta $
of A and a unitary w such that
![]() $T(\beta )\in \mathcal {V}$
,
$T(\beta )\in \mathcal {V}$
,
and
To do this, we use the fact that under our hypotheses (see [Reference Gong, Lin and Niu52, 48, 16]) there is an invariant
![]() $\operatorname {{\mathrm {Inv}}}$
based on K-theory and traces that classifies morphisms (that is, tracially nondegenerate
$\operatorname {{\mathrm {Inv}}}$
based on K-theory and traces that classifies morphisms (that is, tracially nondegenerate
![]() $^*$
-homomorphisms)
$^*$
-homomorphisms)
![]() $A\to A$
, meaning:
$A\to A$
, meaning:
-
(existence) every morphism
 $\operatorname {{\mathrm {Inv}}}(A)\to \operatorname {{\mathrm {Inv}}}(A)$
can be lifted to a morphism
$\operatorname {{\mathrm {Inv}}}(A)\to \operatorname {{\mathrm {Inv}}}(A)$
can be lifted to a morphism
 $A\to A$
;
$A\to A$
; -
(uniqueness) for every morphism
 $\varphi \colon A\to A$
and F,
$\varphi \colon A\to A$
and F,
 $\varepsilon $
as above, there is
$\varepsilon $
as above, there is
 $\delta>0$
such that, if
$\delta>0$
such that, if
 $\psi \colon A\to A$
is a morphism for which
$\psi \colon A\to A$
is a morphism for which
 $\operatorname {{\mathrm {Inv}}}(\psi ) \ \delta $
-agrees with
$\operatorname {{\mathrm {Inv}}}(\psi ) \ \delta $
-agrees with
 $\operatorname {{\mathrm {Inv}}}(\varphi )$
(made precise below), then there is a unitary u in the minimal unitisation
$\operatorname {{\mathrm {Inv}}}(\varphi )$
(made precise below), then there is a unitary u in the minimal unitisation
 $\tilde {A}$
of A with
$\tilde {A}$
of A with
 $\max _{a\in F}\|u\psi (a)u^*-\varphi (a)\| < \varepsilon $
.
$\max _{a\in F}\|u\psi (a)u^*-\varphi (a)\| < \varepsilon $
.
Given such an invariant, the strategy is to:
-
1. perturb
 $\operatorname {{\mathrm {Inv}}}(\alpha )$
by keeping its K-theory part the same but replacing its tracial part
$\operatorname {{\mathrm {Inv}}}(\alpha )$
by keeping its K-theory part the same but replacing its tracial part
 $T(\alpha )$
by a nearby
$T(\alpha )$
by a nearby
 $h\in \mathcal {V}$
;
$h\in \mathcal {V}$
; -
2. use (existence) to lift this perturbed
 $\operatorname {{\mathrm {Inv}}}$
-morphism to a morphism
$\operatorname {{\mathrm {Inv}}}$
-morphism to a morphism
 $\alpha _h\colon A\to A$
;
$\alpha _h\colon A\to A$
; -
3. use (uniqueness) to deduce equations (3.5) and (3.6) for a unitary conjugate
 $\beta $
of
$\beta $
of
 $\alpha _h$
.
$\alpha _h$
.
For this to work, we must know that the perturbation in Step 1 still gives a valid
![]() $\operatorname {{\mathrm {Inv}}}$
-morphism. This is where assuming something like trivial tracial pairing becomes essential and where we must pay close attention to the actual structure of
$\operatorname {{\mathrm {Inv}}}$
-morphism. This is where assuming something like trivial tracial pairing becomes essential and where we must pay close attention to the actual structure of
![]() $\operatorname {{\mathrm {Inv}}}$
. Finally, then, here are its components:
$\operatorname {{\mathrm {Inv}}}$
. Finally, then, here are its components:
-
Traces. Like the Elliott invariant,
 $\operatorname {{\mathrm {Inv}}}$
includes the trace functor
$\operatorname {{\mathrm {Inv}}}$
includes the trace functor
 $T(\cdot )$
(or, dually,
$T(\cdot )$
(or, dually,
 $\operatorname {{\mathrm {Aff}}}(T(\cdot ))$
).
$\operatorname {{\mathrm {Aff}}}(T(\cdot ))$
). -
Total K-theory.
 $\operatorname {{\mathrm {Inv}}}$
includes not just the usual K-groups
$\operatorname {{\mathrm {Inv}}}$
includes not just the usual K-groups
 $K_*(A)$
, but K-theory with coefficients
$K_*(A)$
, but K-theory with coefficients
 $\underline {K}(A) = \bigoplus _{n=0}^{\infty } K_*(A;\mathbb {Z}/n)$
. By the universal multicoefficient theorem for separable
$\underline {K}(A) = \bigoplus _{n=0}^{\infty } K_*(A;\mathbb {Z}/n)$
. By the universal multicoefficient theorem for separable
 ${\mathrm {C}^*}$
-algebras satisfying the UCT (see [Reference Dadarlat and Loring30, §1.4]), the group of homomorphisms
${\mathrm {C}^*}$
-algebras satisfying the UCT (see [Reference Dadarlat and Loring30, §1.4]), the group of homomorphisms
 $\underline {K}(A) \to \underline {K}(A)$
that respect the ‘Bockstein operations’ is isomorphic to the group
$\underline {K}(A) \to \underline {K}(A)$
that respect the ‘Bockstein operations’ is isomorphic to the group
 $KL(A,A)$
(see [Reference Rørdam and Størmer79, 2.4.8]). For
$KL(A,A)$
(see [Reference Rørdam and Størmer79, 2.4.8]). For
 $\kappa \in KL(A,A)$
and
$\kappa \in KL(A,A)$
and
 $i=0,1$
, we write
$i=0,1$
, we write
 $\kappa _i$
for associated homomorphism
$\kappa _i$
for associated homomorphism
 $K_i(A)\to K_i(A)$
.
$K_i(A)\to K_i(A)$
. -
Hausdorffised algebraic
 $\boldsymbol{K}_\mathbf{1}$
. Let
$\boldsymbol{K}_\mathbf{1}$
. Let
 $CU(\tilde {A})$
denote the closure of the commutator subgroup of the unitary group
$CU(\tilde {A})$
denote the closure of the commutator subgroup of the unitary group
 $U(\tilde {A})$
of
$U(\tilde {A})$
of
 $\tilde {A}$
. Write
$\tilde {A}$
. Write
 $\overline {K_1}^{alg}(A):=U(\tilde {A})/CU(\tilde {A})$
. The
$\overline {K_1}^{alg}(A):=U(\tilde {A})/CU(\tilde {A})$
. The
 ${\mathrm {C}^*}$
-algebras we consider here are all of stable rank one (see [Reference Rørdam78, Theorem 6.7] and [Reference Fu, Li and Lin45, Corollary 6.8]), so we are justified in making this definition without passing to matrix algebras over A. Moreover, as in [Reference Nielsen and Thomsen71, Lemma 3.1] we have a short exact sequence (3.7)Here,
${\mathrm {C}^*}$
-algebras we consider here are all of stable rank one (see [Reference Rørdam78, Theorem 6.7] and [Reference Fu, Li and Lin45, Corollary 6.8]), so we are justified in making this definition without passing to matrix algebras over A. Moreover, as in [Reference Nielsen and Thomsen71, Lemma 3.1] we have a short exact sequence (3.7)Here,
 $\pi _A$
is the canonical surjection
$\pi _A$
is the canonical surjection
 $\pi _A([u]_{alg})=[u]_1$
. By divisibility of the group
$\pi _A([u]_{alg})=[u]_1$
. By divisibility of the group
 $\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
, the sequence (3.7) splits (unnaturally). We fix a splitting map
$\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
, the sequence (3.7) splits (unnaturally). We fix a splitting map
 $s_A\colon K_1(A)\to \overline {K_1}^{alg}(A)$
that is a right inverse of
$s_A\colon K_1(A)\to \overline {K_1}^{alg}(A)$
that is a right inverse of
 $\pi _A$
.
$\pi _A$
.
The inclusion
 $\lambda _A$
is the inverse of the map
$\lambda _A$
is the inverse of the map
 $U_0(\tilde {A})/CU(\tilde {A}) \to \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
induced by the de la Harpe–Skandalis determinant (see [Reference Thomsen86, §3], and note that stable rank one ensures that
$U_0(\tilde {A})/CU(\tilde {A}) \to \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
induced by the de la Harpe–Skandalis determinant (see [Reference Thomsen86, §3], and note that stable rank one ensures that
 $CU(\tilde {A})$
is contained in the connected component
$CU(\tilde {A})$
is contained in the connected component
 $U_0(\tilde {A})$
of
$U_0(\tilde {A})$
of
 $U(\tilde {A})$
). It is an isometry with respect to the quotient metric on
$U(\tilde {A})$
). It is an isometry with respect to the quotient metric on
 $U_0(\tilde {A})/CU(\tilde {A})$
and the metric
$U_0(\tilde {A})/CU(\tilde {A})$
and the metric
 $d_A$
on
$d_A$
on
 $\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
obtained by adjusting the quotient metric
$\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
obtained by adjusting the quotient metric
 $d^{\prime }_A$
to (3.8)
$d^{\prime }_A$
to (3.8) $$ \begin{align} d_A(f,g) = \begin{cases} \left|e^{2\pi i d^{\prime}_A(f,g)}-1\right| & \text{if } d^{\prime}_A(f,g) < \frac{1}{2}\\ 2 & \text{if } d^{\prime}_A(f,g) \ge \frac{1}{2}. \end{cases} \end{align} $$
$$ \begin{align} d_A(f,g) = \begin{cases} \left|e^{2\pi i d^{\prime}_A(f,g)}-1\right| & \text{if } d^{\prime}_A(f,g) < \frac{1}{2}\\ 2 & \text{if } d^{\prime}_A(f,g) \ge \frac{1}{2}. \end{cases} \end{align} $$
An
![]() $\operatorname {{\mathrm {Inv}}}$
-morphism consists of: an element
$\operatorname {{\mathrm {Inv}}}$
-morphism consists of: an element
![]() $\kappa \in KL(A,A)$
(which if A is unital is required to satisfy
$\kappa \in KL(A,A)$
(which if A is unital is required to satisfy
![]() $\kappa _0([1_A]_0)=[1_A]_0$
); a continuous affine map
$\kappa _0([1_A]_0)=[1_A]_0$
); a continuous affine map
![]() $\kappa _T\colon T(A)\to T(A)$
(inducing a positive unital linear map
$\kappa _T\colon T(A)\to T(A)$
(inducing a positive unital linear map
![]() $\kappa _T^*\colon \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))\to \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))$
) that is compatible with
$\kappa _T^*\colon \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))\to \operatorname {{\mathrm {Aff}}}(T(\tilde {A}))$
) that is compatible with
![]() $\kappa $
in the sense that
$\kappa $
in the sense that
![]() $\rho _A\circ \kappa _0 = \kappa _T^*\circ \rho _A$
(therefore inducing an endomorphism
$\rho _A\circ \kappa _0 = \kappa _T^*\circ \rho _A$
(therefore inducing an endomorphism
![]() $\overline {\kappa _T}$
of
$\overline {\kappa _T}$
of
![]() $\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
); and a homomorphism
$\operatorname {{\mathrm {Aff}}}(T(\tilde {A}))/\overline {\rho _A(K_0(\tilde {A}))}$
); and a homomorphism
![]() $\kappa _U\colon \overline {K_1}^{alg}(A) \to \overline {K_1}^{alg}(A)$
that is compatible with
$\kappa _U\colon \overline {K_1}^{alg}(A) \to \overline {K_1}^{alg}(A)$
that is compatible with
![]() $\overline {\kappa _T}$
in the sense that the diagram
$\overline {\kappa _T}$
in the sense that the diagram

commutes. (Importantly, the necessity of another family of commutative diagrams between
![]() $K_0$
with coefficients and
$K_0$
with coefficients and
![]() $\overline {K_1}^{alg}(A)$
is identified in [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]. There it is also shown that this additional compatibility is automatic if
$\overline {K_1}^{alg}(A)$
is identified in [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]. There it is also shown that this additional compatibility is automatic if
![]() $K_1(A)$
is torsion free.)
$K_1(A)$
is torsion free.)
That
![]() $\operatorname {{\mathrm {Inv}}}$
satisfies (existence) is provided by [Reference Gong, Lin and Niu52, Corollary 5.13] (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]), or in the stably projectionless case, [Reference Gong and Lin48, Theorem 12.8] (noting in this latter case that
$\operatorname {{\mathrm {Inv}}}$
satisfies (existence) is provided by [Reference Gong, Lin and Niu52, Corollary 5.13] (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16]), or in the stably projectionless case, [Reference Gong and Lin48, Theorem 12.8] (noting in this latter case that
![]() $A\in \mathcal {D}_0$
by [Reference Gong and Lin48, Theorem 15.2] and the proof of [Reference Gong and Lin48, Theorem 15.5] and that by [Reference Gong and Lin48, Theorem 13.1], the models
$A\in \mathcal {D}_0$
by [Reference Gong and Lin48, Theorem 15.2] and the proof of [Reference Gong and Lin48, Theorem 15.5] and that by [Reference Gong and Lin48, Theorem 13.1], the models
![]() $B_T$
constructed in [Reference Gong and Lin48, §7] cover the full class
$B_T$
constructed in [Reference Gong and Lin48, §7] cover the full class
![]() $\mathcal {D}_0$
; in other words, the hypotheses of [Reference Gong and Lin48, Theorem 12.8] hold for
$\mathcal {D}_0$
; in other words, the hypotheses of [Reference Gong and Lin48, Theorem 12.8] hold for
![]() $B_T=A$
).
$B_T=A$
).
We use (existence) as follows: For any
![]() $h\in C(X_A,X_A)$
(which we extend by Lemma 3.1 to
$h\in C(X_A,X_A)$
(which we extend by Lemma 3.1 to
![]() $\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
), there exists
$\operatorname {{\mathrm {Aff}}}_{X_A}(T(A),T(A))$
), there exists
![]() $\alpha _h\in \operatorname {{\mathrm {End}}}(A,X_A)$
(which by [Reference Gong, Lin and Niu51, Theorem 29.5], or in the stably projectionless case, [Reference Gong and Lin48, Theorem 13.1], is an automorphism if h is invertible) with
$\alpha _h\in \operatorname {{\mathrm {End}}}(A,X_A)$
(which by [Reference Gong, Lin and Niu51, Theorem 29.5], or in the stably projectionless case, [Reference Gong and Lin48, Theorem 13.1], is an automorphism if h is invertible) with
![]() $\kappa _T:=T(\alpha _h)=h$
,
$\kappa _T:=T(\alpha _h)=h$
,
![]() $\kappa :=KL(\alpha _h)=KL(\alpha )$
and
$\kappa :=KL(\alpha _h)=KL(\alpha )$
and
![]() $\kappa _U:=\overline {K_1}^{alg}(\alpha _h)$
defined by
$\kappa _U:=\overline {K_1}^{alg}(\alpha _h)$
defined by
![]() $\kappa _U\circ \lambda _A = \lambda _A\circ \kappa _T^*$
and
$\kappa _U\circ \lambda _A = \lambda _A\circ \kappa _T^*$
and
![]() $\kappa _U\circ s_A = \overline {K_1}^{alg}(\alpha )\circ s_A \colon K_1(A) \to \overline {K_1}^{alg}(A)$
. Note that these choices do provide a valid
$\kappa _U\circ s_A = \overline {K_1}^{alg}(\alpha )\circ s_A \colon K_1(A) \to \overline {K_1}^{alg}(A)$
. Note that these choices do provide a valid
![]() $\operatorname {{\mathrm {Inv}}}$
-morphism: The middle square of equation (3.9) commutes by construction, the right square commutes because it does for
$\operatorname {{\mathrm {Inv}}}$
-morphism: The middle square of equation (3.9) commutes by construction, the right square commutes because it does for
![]() $\operatorname {{\mathrm {Inv}}}(\alpha )$
and the left square commutes because A has trivial tracial pairing.
$\operatorname {{\mathrm {Inv}}}(\alpha )$
and the left square commutes because A has trivial tracial pairing.
For (uniqueness), we appeal to the approximate version of [Reference Gong, Lin and Niu52, Theorem 4.3] (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16], which includes a classification of
![]() $^*$
-homomorphisms into sequence algebras), or in the stably projectionless case, [Reference Gong and Lin48, Theorem 5.3] (again noting that our assumptions on A ensure that the hypotheses of this theorem are indeed satisfied for
$^*$
-homomorphisms into sequence algebras), or in the stably projectionless case, [Reference Gong and Lin48, Theorem 5.3] (again noting that our assumptions on A ensure that the hypotheses of this theorem are indeed satisfied for
![]() $B=A$
: by [Reference Gong and Lin48, Remark 3.11],
$B=A$
: by [Reference Gong and Lin48, Remark 3.11],
![]() $A\in \mathcal {D}_0\subseteq \mathcal {D}^d$
; the map
$A\in \mathcal {D}_0\subseteq \mathcal {D}^d$
; the map
![]() $\mathbf {T}\colon \mathbb {N}\times \mathbb {N}\to \mathbb {N}$
can be taken to be
$\mathbf {T}\colon \mathbb {N}\times \mathbb {N}\to \mathbb {N}$
can be taken to be
![]() $(n,k)\mapsto n$
(cf. [Reference Gong and Lin48, 5.2]); and the fullness condition can be dropped since we work only with tracially nondegenerate genuine
$(n,k)\mapsto n$
(cf. [Reference Gong and Lin48, 5.2]); and the fullness condition can be dropped since we work only with tracially nondegenerate genuine
![]() $^*$
-homomorphisms rather than more general approximately multiplicative maps (cf. [Reference Gong and Lin48, Remark 5.6])).
$^*$
-homomorphisms rather than more general approximately multiplicative maps (cf. [Reference Gong and Lin48, Remark 5.6])).
By commutativity of equation (3.9) and the fact that (the inverse of)
![]() $\lambda _A$
is an isometry (with respect to the quotient metric on
$\lambda _A$
is an isometry (with respect to the quotient metric on
![]() $\overline {K_1}^{alg}(A)$
and the metric
$\overline {K_1}^{alg}(A)$
and the metric
![]() $d_A$
of equation (3.8)), we can phrase (uniqueness) as follows: For our fixed finite set
$d_A$
of equation (3.8)), we can phrase (uniqueness) as follows: For our fixed finite set
![]() $F\subseteq A$
and tolerance
$F\subseteq A$
and tolerance
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $\delta>0$
such that, if
$\delta>0$
such that, if
then there is a unitary u such that equation (3.5) holds for
![]() $\beta :=u\alpha _h(\cdot )u^*$
, and if moreover
$\beta :=u\alpha _h(\cdot )u^*$
, and if moreover
then equation (3.6) also holds for some unitary w. By density of
![]() $\mathcal {V}$
, there exists
$\mathcal {V}$
, there exists
![]() $h\in \mathcal {V}$
such that equations (3.10) and (3.11) hold, so we are done.
$h\in \mathcal {V}$
such that equations (3.10) and (3.11) hold, so we are done.
Combining Lemma 3.2, Theorem 3.4, Theorem 2.3, Theorem 2.6 and Theorem 2.7, we immediately have the following.
Theorem 3.5. Let A be an infinite-dimensional, separable, algebraically simple
![]() ${\mathrm {C}^*}$
-algebra that satisfies the UCT, has finite nuclear dimension, trivial tracial pairing and torsion-free
${\mathrm {C}^*}$
-algebra that satisfies the UCT, has finite nuclear dimension, trivial tracial pairing and torsion-free
![]() $K_1$
and whose tracial state space
$K_1$
and whose tracial state space
![]() $T(A)$
is nonempty and compact, with compact extreme boundary
$T(A)$
is nonempty and compact, with compact extreme boundary
![]() $X_A=\partial _e(T(A))$
that has the structure of a topological manifold of dimension
$X_A=\partial _e(T(A))$
that has the structure of a topological manifold of dimension
![]() $n \ge 2$
. Let
$n \ge 2$
. Let
![]() $\mu $
be an OU measure on
$\mu $
be an OU measure on
![]() $X_A$
, and let
$X_A$
, and let
![]() $\tau =\tau _{\mu }$
be the corresponding element of
$\tau =\tau _{\mu }$
be the corresponding element of
![]() $T(A)$
. Then,
$T(A)$
. Then,
is a residual subset of
![]() $\operatorname {{\mathrm {Aut}}}(A,\tau )$
(that is, contains a dense
$\operatorname {{\mathrm {Aut}}}(A,\tau )$
(that is, contains a dense
![]() $G_{\delta }$
set). If
$G_{\delta }$
set). If
![]() $X_A=[0,1]$
, then
$X_A=[0,1]$
, then
is a residual subset of
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
, and
$\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
, and
is a dense but meagre subset of
![]() $\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
.
$\operatorname {{\mathrm {End}}}(A,X_A,\tau )$
.
Remark 3.6.
-
1. Torsion-free
 $K_1$
can be replaced by one of the other conditions in [Reference Gong, Lin and Niu52, Corollary 5.13] (for example, tracial rank
$K_1$
can be replaced by one of the other conditions in [Reference Gong, Lin and Niu52, Corollary 5.13] (for example, tracial rank
 $\le 1$
) and in fact by results of the forthcoming work [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16] can be removed as an assumption altogether. (Briefly, the map
$\le 1$
) and in fact by results of the forthcoming work [Reference Carrión, Gabe, Schafhauser, Tikuisis and White16] can be removed as an assumption altogether. (Briefly, the map
 $\overline {K_1}^{alg}(\alpha _h)$
constructed in the proof of Theorem 3.4 can be adjusted without changing
$\overline {K_1}^{alg}(\alpha _h)$
constructed in the proof of Theorem 3.4 can be adjusted without changing
 $T(\alpha _h)$
so that equation (3.9) still commutes, and so do the additional compatibility diagrams mentioned in the proof.) On the other hand, triviality of the tracial pairing is used rather crucially.
$T(\alpha _h)$
so that equation (3.9) still commutes, and so do the additional compatibility diagrams mentioned in the proof.) On the other hand, triviality of the tracial pairing is used rather crucially. -
2. Suppose that A is unital with
 $X_A=\partial _e(T(A))$
nonempty. Then,
$X_A=\partial _e(T(A))$
nonempty. Then,
 $\partial _e(T(\bigotimes _{n\in \mathbb {Z}}A)) \cong \prod _{n\in \mathbb {Z}}X_A$
(see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter11, Proposition 3.5]). The (right) shift automorphism of
$\partial _e(T(\bigotimes _{n\in \mathbb {Z}}A)) \cong \prod _{n\in \mathbb {Z}}X_A$
(see [Reference Bosa, Brown, Sato, Tikuisis, White and Winter11, Proposition 3.5]). The (right) shift automorphism of
 $\bigotimes _{n\in \mathbb {Z}}A$
induces the (left) shift on
$\bigotimes _{n\in \mathbb {Z}}A$
induces the (left) shift on
 $\prod _{n\in \mathbb {Z}}X_A$
, which is strongly mixing with respect to
$\prod _{n\in \mathbb {Z}}X_A$
, which is strongly mixing with respect to
 $\bigotimes _{n\in \mathbb {Z}}\mu $
, for any Borel probability measure
$\bigotimes _{n\in \mathbb {Z}}\mu $
, for any Borel probability measure
 $\mu $
on
$\mu $
on
 $X_A$
. This demonstrates the existence of automorphisms with strongly mixing actions on trace spaces for a collection of
$X_A$
. This demonstrates the existence of automorphisms with strongly mixing actions on trace spaces for a collection of
 ${\mathrm {C}^*}$
-algebras B with
${\mathrm {C}^*}$
-algebras B with
 $\partial _e(T(B))$
a Cantor space or Hilbert cube.
$\partial _e(T(B))$
a Cantor space or Hilbert cube. -
3. In [Reference Thomsen85, §4], Thomsen shows how to construct an approximately interval (AI) algebra that admits tracially chaotic endomorphisms. By Theorem 3.5, these endomorphisms are in fact typical for this algebra.
4 Strongly chaotic dynamics
In this section, we describe some well-known examples of ergodic topological dynamical systems
![]() $(X,\mu ,h)$
on compact metric spaces with striking statistical properties. We then construct model
$(X,\mu ,h)$
on compact metric spaces with striking statistical properties. We then construct model
![]() ${\mathrm {C}^*}$
-algebras admitting endomorphisms that exhibit these phenomena.
${\mathrm {C}^*}$
-algebras admitting endomorphisms that exhibit these phenomena.
4.1 Statistical features
It is straightforward to check that strong mixing is equivalent to
for every
![]() $f,g\in L^2(X,\mu )$
. It is sufficient to consider only observables that are continuous and in fact sufficient to verify equation (4.1) for observables
$f,g\in L^2(X,\mu )$
. It is sufficient to consider only observables that are continuous and in fact sufficient to verify equation (4.1) for observables
![]() $f=g$
.
$f=g$
.
We will write
![]() ${{\textrm{H\"{o}l}}}_{\eta }(X)$
for the set of Hölder continuous functions
${{\textrm{H\"{o}l}}}_{\eta }(X)$
for the set of Hölder continuous functions
![]() $f\colon X\to \mathbb {R}$
with exponent
$f\colon X\to \mathbb {R}$
with exponent
![]() $\eta>0$
, that is,
$\eta>0$
, that is,
Definition 4.1. The system
![]() $(X,\mu ,h)$
has exponential decay of correlations (EDC) (for Hölder continuous observables) if for every
$(X,\mu ,h)$
has exponential decay of correlations (EDC) (for Hölder continuous observables) if for every
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $\gamma \in (0,1)$
such that for every
$\gamma \in (0,1)$
such that for every
![]() $f,g\in {{\textrm{H\"{o}l}}}_{\eta }(X)$
there exists
$f,g\in {{\textrm{H\"{o}l}}}_{\eta }(X)$
there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$\begin{align*}\left|\int_X (f\circ h^n)g\;d\mu - \int_Xf\,d\mu \cdot \int_Xg\,d\mu\right| \le C\gamma^n. \end{align*}$$
$$\begin{align*}\left|\int_X (f\circ h^n)g\;d\mu - \int_Xf\,d\mu \cdot \int_Xg\,d\mu\right| \le C\gamma^n. \end{align*}$$
The central limit theorem (CLT) is closely related to exponential mixing. For instance, for the dispersing billiards described in § 4.2 below, the CLT can be deduced from correlation bounds (see [Reference Chernov24]). Given an observable
![]() $f\colon X\to \mathbb {R}$
, we write
$f\colon X\to \mathbb {R}$
, we write
![]() $S_nf$
for the ergodic sum
$S_nf$
for the ergodic sum
![]() $\sum _{k=0}^{n-1}f\circ h^k$
.
$\sum _{k=0}^{n-1}f\circ h^k$
.
Definition 4.2. The system
![]() $(X,\mu ,h)$
satisfies the CLT (for Hölder continuous observables) if for every
$(X,\mu ,h)$
satisfies the CLT (for Hölder continuous observables) if for every
![]() $\eta>0$
and every
$\eta>0$
and every
![]() $f\in {{\textrm{H\"{o}l}}}_{\eta }(X)$
that is not a coboundary and satisfies
$f\in {{\textrm{H\"{o}l}}}_{\eta }(X)$
that is not a coboundary and satisfies
![]() $\int _Xf\,d\mu =0$
, there exists
$\int _Xf\,d\mu =0$
, there exists
![]() $\sigma _f> 0$
such that the sequence of random variables
$\sigma _f> 0$
such that the sequence of random variables
![]() $\frac {1}{\sqrt {n}}S_nf$
converges in distribution as
$\frac {1}{\sqrt {n}}S_nf$
converges in distribution as
![]() $n\to \infty $
to the normal distribution
$n\to \infty $
to the normal distribution
![]() $\mathcal {N}(0,\sigma _f^2)$
. In other words, for every
$\mathcal {N}(0,\sigma _f^2)$
. In other words, for every
![]() $z\in \mathbb {R}$
,
$z\in \mathbb {R}$
,
 $$ \begin{align} \lim_{n\to\infty} \mu\left(\left\{x\in X \mid \frac{S_nf(x)}{\sqrt{n}} \le z \right\}\right) = \frac{1}{\sigma_f\sqrt{2\pi}}\int_{-\infty}^z\exp\left(-\frac{t^2}{2\sigma_f^2}\right)dt. \end{align} $$
$$ \begin{align} \lim_{n\to\infty} \mu\left(\left\{x\in X \mid \frac{S_nf(x)}{\sqrt{n}} \le z \right\}\right) = \frac{1}{\sigma_f\sqrt{2\pi}}\int_{-\infty}^z\exp\left(-\frac{t^2}{2\sigma_f^2}\right)dt. \end{align} $$
Here, the variance
![]() $\sigma _f^2$
can be computed as
$\sigma _f^2$
can be computed as
![]() $\sigma _f^2 = \lim _{n\to \infty } \frac {1}{n} \int _X (S_nf)^2d\mu $
. For coboundaries, that is, functions f for which
$\sigma _f^2 = \lim _{n\to \infty } \frac {1}{n} \int _X (S_nf)^2d\mu $
. For coboundaries, that is, functions f for which
![]() $f=g\circ h-g$
for some
$f=g\circ h-g$
for some
![]() $g\in L^2(X,\mu )$
, the variance is
$g\in L^2(X,\mu )$
, the variance is
![]() $0$
and equation (4.2) holds provided the right-hand side is interpreted as the Heaviside function (that is,
$0$
and equation (4.2) holds provided the right-hand side is interpreted as the Heaviside function (that is,
![]() $\frac {S_nf}{\sqrt {n}}$
converges almost surely to
$\frac {S_nf}{\sqrt {n}}$
converges almost surely to
![]() $0$
).
$0$
).
The CLT provides considerably more information than Birkhoff’s ergodic theorem, which for ergodic h says that, for every integrable f and almost every x,
![]() $\lim _{n\to \infty }\frac {1}{n}S_nf(x)=\int _X f\,d\mu $
. That said, in the compact, uniquely ergodic setting, the following finite-time estimate of large deviation from the mean is available even if the CLT is not.
$\lim _{n\to \infty }\frac {1}{n}S_nf(x)=\int _X f\,d\mu $
. That said, in the compact, uniquely ergodic setting, the following finite-time estimate of large deviation from the mean is available even if the CLT is not.
Proposition 4.3 [Reference Benoist and Quint7].
Suppose that X is a compact metric space and
![]() $(X,\mu ,h)$
is uniquely ergodic (that is,
$(X,\mu ,h)$
is uniquely ergodic (that is,
![]() $\mu $
is the unique invariant measure of h). Then, for every
$\mu $
is the unique invariant measure of h). Then, for every
![]() $\varepsilon>0$
and every
$\varepsilon>0$
and every
![]() $k\in \mathbb {N}$
, there exist constants
$k\in \mathbb {N}$
, there exist constants
![]() $c_1,c_2>0$
such that, for every k-Lipschitz
$c_1,c_2>0$
such that, for every k-Lipschitz
![]() $f\colon X\to \mathbb {R}$
and every
$f\colon X\to \mathbb {R}$
and every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$\begin{align*}\mu\left(\left\{x\in X \mid \left|\frac{1}{n}S_nf(x)-\int_X f\,d\mu\right|>\varepsilon\right\}\right) \le c_1e^{-c_2n\varepsilon^2}. \end{align*}$$
$$\begin{align*}\mu\left(\left\{x\in X \mid \left|\frac{1}{n}S_nf(x)-\int_X f\,d\mu\right|>\varepsilon\right\}\right) \le c_1e^{-c_2n\varepsilon^2}. \end{align*}$$
Actually, Proposition 4.3 holds for arbitrary continuous observables, not just Lipschitz ones, but in general the constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
will depend on f (see [Reference Benoist and Quint7, Proposition 3.1]). On the other hand, for systems like axiom A diffeomorphisms (see [Reference Chazottes20, §5]) and holomorphic endomorphisms of projective space (with
$c_2$
will depend on f (see [Reference Benoist and Quint7, Proposition 3.1]). On the other hand, for systems like axiom A diffeomorphisms (see [Reference Chazottes20, §5]) and holomorphic endomorphisms of projective space (with
![]() $n\varepsilon ^2$
replaced by
$n\varepsilon ^2$
replaced by
![]() $n(\log n)^{-2}p(\varepsilon )$
for a suitable function p; see [Reference Dinh, Nguyên and Sibony34]), the constants do not depend on
$n(\log n)^{-2}p(\varepsilon )$
for a suitable function p; see [Reference Dinh, Nguyên and Sibony34]), the constants do not depend on
![]() $\varepsilon $
.
$\varepsilon $
.
4.2 Examples
For the convenience of those not overly familiar with the statistics of dynamical systems, we present several well-known examples where the features described in § 4.1 can be observed. The reader should bear these examples in mind as candidate tracial dynamical systems to which Theorem 4.4 and Theorem 4.9 can be applied (provided that the space X is connected and the map
![]() $h\colon X\to X$
is continuous).
$h\colon X\to X$
is continuous).
Subshifts of finite type
Suppose that A is a
![]() $0$
-
$0$
-
![]() $1$
matrix which is mixing (that is, for some
$1$
matrix which is mixing (that is, for some
![]() $M\in \mathbb {N}$
, all of the entries of
$M\in \mathbb {N}$
, all of the entries of
![]() $A^M$
are nonzero),
$A^M$
are nonzero),
![]() $h\colon \Sigma _A\to \Sigma _A$
is the associated subshift of finite type and
$h\colon \Sigma _A\to \Sigma _A$
is the associated subshift of finite type and
![]() $\mu =\mu _{\varphi }$
is the Gibbs measure associated to some potential
$\mu =\mu _{\varphi }$
is the Gibbs measure associated to some potential
![]() $\varphi $
. Then, the CLT and EDC hold [Reference Bowen and Chazottes12, §1E]. Using Markov partitions [Reference Bowen and Chazottes12, §3C] to construct symbolic dynamics [Reference Bowen and Chazottes12, §3D], one sees that they also hold for mixing axiom A diffeomorphisms [Reference Bowen and Chazottes12, Theorem 4.1].
$\varphi $
. Then, the CLT and EDC hold [Reference Bowen and Chazottes12, §1E]. Using Markov partitions [Reference Bowen and Chazottes12, §3C] to construct symbolic dynamics [Reference Bowen and Chazottes12, §3D], one sees that they also hold for mixing axiom A diffeomorphisms [Reference Bowen and Chazottes12, Theorem 4.1].
Expanding circle maps
These types of dynamical systems are used to model the ‘intermittency’ of turbulent flows, which transition between periodic and chaotic behaviour (see [Reference Pomeau and Manneville75]). Here is one example (see [Reference Liverani, Saussol and Vaienti68] and [Reference Chazottes20, §3.5]). Let
![]() $\alpha \in \left (0,1/2\right )$
, and define
$\alpha \in \left (0,1/2\right )$
, and define
![]() $h\colon [0,1]\to [0,1]$
by
$h\colon [0,1]\to [0,1]$
by
 $$\begin{align*}h(t)= \begin{cases} t+2^{\alpha} t^{1+\alpha} & \text{ if }\ 0\le t < \frac{1}{2}\\ 2t-1 & \text{ if }\ \frac{1}{2} \le t\le 1. \end{cases}\\[-18pt] \end{align*}$$
$$\begin{align*}h(t)= \begin{cases} t+2^{\alpha} t^{1+\alpha} & \text{ if }\ 0\le t < \frac{1}{2}\\ 2t-1 & \text{ if }\ \frac{1}{2} \le t\le 1. \end{cases}\\[-18pt] \end{align*}$$
Identifying the boundary points of
![]() $[0,1]$
, we view this as a continuous map
$[0,1]$
, we view this as a continuous map
![]() $S^1\to S^1$
. There is a unique ergodic invariant probability measure
$S^1\to S^1$
. There is a unique ergodic invariant probability measure
![]() $\mu $
that is equivalent to Lebesgue measure. The dynamical system
$\mu $
that is equivalent to Lebesgue measure. The dynamical system
![]() $(S^1,\mu ,h)$
has polynomial (rather than exponential) mixing rates but still satisfies the CLT [Reference Young96, Theorem 6]. Moreover, the almost-sure CLT holds for any Lipschitz observable
$(S^1,\mu ,h)$
has polynomial (rather than exponential) mixing rates but still satisfies the CLT [Reference Young96, Theorem 6]. Moreover, the almost-sure CLT holds for any Lipschitz observable
![]() $f\colon S^1\to \mathbb {R}$
(see [Reference Chazottes20, Theorem 18]): If
$f\colon S^1\to \mathbb {R}$
(see [Reference Chazottes20, Theorem 18]): If
![]() $\int fd\mu =0$
and f is not a coboundary (so that the variance
$\int fd\mu =0$
and f is not a coboundary (so that the variance
![]() $\sigma _f^2$
of f is nonzero), then for
$\sigma _f^2$
of f is nonzero), then for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $t\in S^1$
, the sequence of weighted averages
$t\in S^1$
, the sequence of weighted averages
![]() $\frac {1}{D_n}\sum _{k=1}^n\frac {1}{k}\delta _{S_kf(t)/\sqrt {k}}$
, where
$\frac {1}{D_n}\sum _{k=1}^n\frac {1}{k}\delta _{S_kf(t)/\sqrt {k}}$
, where
![]() $\delta _x$
denotes the point mass at x and
$\delta _x$
denotes the point mass at x and
![]() $D_n=\sum _{k=1}^n\frac {1}{k}$
, is
$D_n=\sum _{k=1}^n\frac {1}{k}$
, is
![]() $w^*$
-convergent to
$w^*$
-convergent to
![]() $\mathcal {N}(0,\sigma _f^2)$
.
$\mathcal {N}(0,\sigma _f^2)$
.
For
![]() $\alpha =1/2$
, the normalising factor
$\alpha =1/2$
, the normalising factor
![]() $\sqrt {n}$
in equation (4.2) must be replaced by
$\sqrt {n}$
in equation (4.2) must be replaced by
![]() $\sqrt {n\log n}$
, and for parameters
$\sqrt {n\log n}$
, and for parameters
![]() $\alpha \in (1/2,1)$
, there is convergence to a suitable non-Gaussian ‘stable law’; see [Reference Chazottes20, Theorem 9].
$\alpha \in (1/2,1)$
, there is convergence to a suitable non-Gaussian ‘stable law’; see [Reference Chazottes20, Theorem 9].
Billiards
A billiard table is a closed connected domain Q in the plane
![]() $\mathbb {R}^2$
or the torus
$\mathbb {R}^2$
or the torus
![]() $\mathbb {T}^2$
whose boundary
$\mathbb {T}^2$
whose boundary
![]() $\partial Q$
consists of finitely many simple
$\partial Q$
consists of finitely many simple
![]() $C^3$
curves that meet each other only at their ends. The billiard on Q is the dynamical system in the unit tangent bundle M of the ambient manifold restricted to Q generated by the unit-speed motion of a tangent vector along a geodesic, whose interaction with
$C^3$
curves that meet each other only at their ends. The billiard on Q is the dynamical system in the unit tangent bundle M of the ambient manifold restricted to Q generated by the unit-speed motion of a tangent vector along a geodesic, whose interaction with
![]() $\partial Q$
is governed by the ‘angle of incidence equals angle of reflection’ rule. Billiards are analysed via the discrete dynamical system
$\partial Q$
is governed by the ‘angle of incidence equals angle of reflection’ rule. Billiards are analysed via the discrete dynamical system
![]() $(X,h,\mu )$
, where
$(X,h,\mu )$
, where
![]() $X=\partial Q\times [-\frac {\pi }{2},\frac {\pi }{2}]$
(parameterised by
$X=\partial Q\times [-\frac {\pi }{2},\frac {\pi }{2}]$
(parameterised by
![]() $(r,\varphi )$
, where r is arc length along
$(r,\varphi )$
, where r is arc length along
![]() $\partial Q$
and
$\partial Q$
and
![]() $\varphi $
is the angle of incidence relative to an inward-facing normal),
$\varphi $
is the angle of incidence relative to an inward-facing normal),
![]() $h\colon X\to X$
is the collision map and
$h\colon X\to X$
is the collision map and
![]() $\mu $
is normalised Liouville measure
$\mu $
is normalised Liouville measure
![]() $\mu =c\cos \varphi dr d\varphi $
. The behaviour of the system depends on the shape of the boundary. Dispersing billiards (for example, the periodic Lorentz gas), that is, those with convex boundary curves, admit the CLT and EDC (see [Reference Bunimovich, Sinaĭ and Chernov15, Reference Chernov23, Reference Chernov24]). Certain billiards called Bunimovich stadia [Reference Bunimovich14] whose boundaries consist only of focusing (concave) and neutral (rectilinear) components satisfy the CLT [Reference Bálint and Gouëzel5] (in some cases requiring
$\mu =c\cos \varphi dr d\varphi $
. The behaviour of the system depends on the shape of the boundary. Dispersing billiards (for example, the periodic Lorentz gas), that is, those with convex boundary curves, admit the CLT and EDC (see [Reference Bunimovich, Sinaĭ and Chernov15, Reference Chernov23, Reference Chernov24]). Certain billiards called Bunimovich stadia [Reference Bunimovich14] whose boundaries consist only of focusing (concave) and neutral (rectilinear) components satisfy the CLT [Reference Bálint and Gouëzel5] (in some cases requiring
![]() $\sqrt {n}$
to be replaced by
$\sqrt {n}$
to be replaced by
![]() $\sqrt {n\log n}$
) but have polynomial mixing rates [Reference Chernov and Zhang25]. In both cases, the almost-sure CLT is also observed to hold (see, for example, [Reference Chazottes, Collet and Schmitt21] or [Reference Leppänen and Stenlund64] for dispersing billiards and [Reference Chazottes and Gouëzel22] for stadia).
$\sqrt {n\log n}$
) but have polynomial mixing rates [Reference Chernov and Zhang25]. In both cases, the almost-sure CLT is also observed to hold (see, for example, [Reference Chazottes, Collet and Schmitt21] or [Reference Leppänen and Stenlund64] for dispersing billiards and [Reference Chazottes and Gouëzel22] for stadia).
Unfortunately, the map h will always have discontinuities (where boundary curves intersect nonsmoothly but also at instances of ‘grazing’ collisions), so it does not seem that billiards are immediately suitable for
![]() ${\mathrm {C}^*}$
-dynamics. However, they can be modelled via certain countable Markov partitions called ‘Young towers’ [Reference Young95], so while not covered by the constructions of § 4.3, they could be represented as actions on zero-dimensional spaces.
${\mathrm {C}^*}$
-dynamics. However, they can be modelled via certain countable Markov partitions called ‘Young towers’ [Reference Young95], so while not covered by the constructions of § 4.3, they could be represented as actions on zero-dimensional spaces.
Complex dynamics
The CLT and EDC are exhibited by many complex-geometric dynamical systems
![]() $(X,\mu ,h)$
, with
$(X,\mu ,h)$
, with
![]() $\mu $
the measure of maximal entropy, such as: holomorphic endomorphisms of projective space [Reference Dupont39, Reference Dinh, Nguyên and Sibony34], holomorphic automorphisms of positive entropy on compact Kähler surfaces [Reference Dinh and Sibony35] (at least EDC) and meromorphic automorphisms of the Riemann sphere [Reference Denker, Przytycki and Urbański32] (with X the Julia set of h; note that in some cases, the Julia set is known to be connected [Reference Inninger and Peherstorfer58, Reference Peherstorfer and Stroh73] or even the whole Riemann sphere [Reference Inninger and Peherstorfer57]).
$\mu $
the measure of maximal entropy, such as: holomorphic endomorphisms of projective space [Reference Dupont39, Reference Dinh, Nguyên and Sibony34], holomorphic automorphisms of positive entropy on compact Kähler surfaces [Reference Dinh and Sibony35] (at least EDC) and meromorphic automorphisms of the Riemann sphere [Reference Denker, Przytycki and Urbański32] (with X the Julia set of h; note that in some cases, the Julia set is known to be connected [Reference Inninger and Peherstorfer58, Reference Peherstorfer and Stroh73] or even the whole Riemann sphere [Reference Inninger and Peherstorfer57]).
4.3 Model building
Finally in this section, we show how to construct
![]() ${\mathrm {C}^*}$
-models that witness prescribed topological dynamical systems at the level of the trace space.
${\mathrm {C}^*}$
-models that witness prescribed topological dynamical systems at the level of the trace space.
Theorem 4.4. Let
![]() $(X,d)$
be a compact, connected Riemannian manifold. Then, there exists a separable, simple, unital, nuclear,
$(X,d)$
be a compact, connected Riemannian manifold. Then, there exists a separable, simple, unital, nuclear,
![]() ${\mathcal {Z}}$
-stable, projectionless
${\mathcal {Z}}$
-stable, projectionless
![]() ${\mathrm {C}^*}$
-algebra A that has trivial tracial pairing and satisfies the UCT such that
${\mathrm {C}^*}$
-algebra A that has trivial tracial pairing and satisfies the UCT such that
![]() $\partial _e(T(A))\cong X$
and
$\partial _e(T(A))\cong X$
and
![]() $\{a \mid \hat a \in \operatorname {{\mathrm {Lip}}}(X,d)\}$
is dense in
$\{a \mid \hat a \in \operatorname {{\mathrm {Lip}}}(X,d)\}$
is dense in
![]() $A_{sa}$
.
$A_{sa}$
.
Proof. The construction is based on that of [Reference Jacelon59, §4.4], with dimension drop algebras (over the interval) replaced by generalised dimension drop algebras (over X), in the sense of [Reference Toms88, Reference Lin67]. Specifically, fix
![]() $x_0,x_1\in X$
with
$x_0,x_1\in X$
with
![]() $d(x_0,x_1)=\operatorname {{\mathrm {diam}}} X$
and for coprime
$d(x_0,x_1)=\operatorname {{\mathrm {diam}}} X$
and for coprime
![]() $p,q\in \mathbb {N}$
define
$p,q\in \mathbb {N}$
define
The
![]() ${\mathrm {C}^*}$
-algebra
${\mathrm {C}^*}$
-algebra
![]() $X_{p,q}$
has the following properties. First, since p and q are coprime,
$X_{p,q}$
has the following properties. First, since p and q are coprime,
![]() $X_{p,q}$
has no nontrivial projections. Next, each trace on
$X_{p,q}$
has no nontrivial projections. Next, each trace on
![]() $X_{p,q}$
corresponds to some Borel probability measure on X, and
$X_{p,q}$
corresponds to some Borel probability measure on X, and
![]() $\partial _e(T(X_{p,q}))\cong X$
via point evaluations. Since X is connected, this means that
$\partial _e(T(X_{p,q}))\cong X$
via point evaluations. Since X is connected, this means that
![]() $\hat f\in \operatorname {{\mathrm {Aff}}}(T(X_{p,q}))$
is constant for any projection
$\hat f\in \operatorname {{\mathrm {Aff}}}(T(X_{p,q}))$
is constant for any projection
![]() $f\in X_{p,q}$
, which in turn means that
$f\in X_{p,q}$
, which in turn means that
![]() $X_{p,q}$
has trivial tracial pairing. Nuclearity and the UCT hold for
$X_{p,q}$
has trivial tracial pairing. Nuclearity and the UCT hold for
![]() $X_{p,q}$
since it is a type I
$X_{p,q}$
since it is a type I
![]() ${\mathrm {C}^*}$
-algebra (see [Reference Blackadar8, 15.8.2, 22.3.5]). Finally, by a suitable interpretation of Stone–Weierstrass (see, for example, [Reference Prolla76]), the Lipschitz elements
${\mathrm {C}^*}$
-algebra (see [Reference Blackadar8, 15.8.2, 22.3.5]). Finally, by a suitable interpretation of Stone–Weierstrass (see, for example, [Reference Prolla76]), the Lipschitz elements
![]() $\{f\in X_{p,q} \mid \exists K\:\forall x,y\in X\:(\|f(x)-f(y)\|\le Kd(x,y))\}$
are dense in
$\{f\in X_{p,q} \mid \exists K\:\forall x,y\in X\:(\|f(x)-f(y)\|\le Kd(x,y))\}$
are dense in
![]() $X_{p,q}$
.
$X_{p,q}$
.
Let
![]() $(y_m)_{m\in \mathbb {N}}$
be a dense sequence in X. We claim that, for each m, there exists a bi-Lipschitz path
$(y_m)_{m\in \mathbb {N}}$
be a dense sequence in X. We claim that, for each m, there exists a bi-Lipschitz path
![]() $\gamma _m\colon [0,1]\hookrightarrow X$
from
$\gamma _m\colon [0,1]\hookrightarrow X$
from
![]() $x_0$
to
$x_0$
to
![]() $x_1$
such that, for some
$x_1$
such that, for some
![]() $t_m\in [0,1]$
,
$t_m\in [0,1]$
,
![]() $z_m:=\gamma _m(t_m)$
satisfies
$z_m:=\gamma _m(t_m)$
satisfies
![]() $d(y_m,z_m)<\frac {1}{m}$
. To see this, first note that, by the Hopf–Rinow theorem (see [Reference do Carmo36, §5.3]), any two points in X can be joined by a length-minimising geodesic, which (when parameterised by arc length) is in the notation of [Reference Druţu, Mozes and Sapir38, §2] a ‘
$d(y_m,z_m)<\frac {1}{m}$
. To see this, first note that, by the Hopf–Rinow theorem (see [Reference do Carmo36, §5.3]), any two points in X can be joined by a length-minimising geodesic, which (when parameterised by arc length) is in the notation of [Reference Druţu, Mozes and Sapir38, §2] a ‘
![]() $(1,0)$
-quasi-geodesic’. Assume that
$(1,0)$
-quasi-geodesic’. Assume that
![]() $y_m\notin \{x_0,x_1\}$
, let
$y_m\notin \{x_0,x_1\}$
, let
![]() $\mathfrak {p}_0\colon I\to X$
be a geodesic from
$\mathfrak {p}_0\colon I\to X$
be a geodesic from
![]() $x_0$
to
$x_0$
to
![]() $y_m$
and
$y_m$
and
![]() $\mathfrak {p}_1\colon J\to X$
a geodesic from
$\mathfrak {p}_1\colon J\to X$
a geodesic from
![]() $y_m$
to
$y_m$
to
![]() $x_1$
. If necessary, the path
$x_1$
. If necessary, the path
![]() $\mathfrak {p}_1$
can be modified near to
$\mathfrak {p}_1$
can be modified near to
![]() $Y:=\mathfrak {p}_0(I)$
so that the concatenation
$Y:=\mathfrak {p}_0(I)$
so that the concatenation
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathfrak {p}_0$
and
$\mathfrak {p}_0$
and
![]() $\mathfrak {p}_1$
is simple and piecewise bi-Lipschitz. (In a small tubular neighbourhood of Y (which is diffeomorphic, hence locally Lipschitz equivalent, hence by compactness globally Lipschitz equivalent, to a convex neighbourhood of the normal bundle of Y in X) cut out any intermediate points of intersection of
$\mathfrak {p}_1$
is simple and piecewise bi-Lipschitz. (In a small tubular neighbourhood of Y (which is diffeomorphic, hence locally Lipschitz equivalent, hence by compactness globally Lipschitz equivalent, to a convex neighbourhood of the normal bundle of Y in X) cut out any intermediate points of intersection of
![]() $\mathfrak {p}_0$
and
$\mathfrak {p}_0$
and
![]() $\mathfrak {p}_1$
by going over or around Y via piecewise linear paths in the normal bundle. If
$\mathfrak {p}_1$
by going over or around Y via piecewise linear paths in the normal bundle. If
![]() $\dim X=1$
, then no modification is needed; if
$\dim X=1$
, then no modification is needed; if
![]() $\dim X\ge 3$
, there are sufficient dimensions to go up and over Y; if
$\dim X\ge 3$
, there are sufficient dimensions to go up and over Y; if
![]() $\dim X=2$
, we may assume that the geodesic
$\dim X=2$
, we may assume that the geodesic
![]() $\mathfrak {p}_0$
is defined on a larger interval
$\mathfrak {p}_0$
is defined on a larger interval
![]() $I'\supseteq I$
to give enough room to go around Y at its endpoints.) Applying [Reference Druţu, Mozes and Sapir38, Lemma 2.5] to
$I'\supseteq I$
to give enough room to go around Y at its endpoints.) Applying [Reference Druţu, Mozes and Sapir38, Lemma 2.5] to
![]() $\mathfrak {p}$
yields a simple bi-Lipschitz path
$\mathfrak {p}$
yields a simple bi-Lipschitz path
![]() $\mathfrak {p}'$
from
$\mathfrak {p}'$
from
![]() $x_0$
to
$x_0$
to
![]() $x_1$
at Hausdorff distance less than
$x_1$
at Hausdorff distance less than
![]() $\frac {1}{m}$
from
$\frac {1}{m}$
from
![]() $\mathfrak {p}$
(so, in particular, there is some point
$\mathfrak {p}$
(so, in particular, there is some point
![]() $z_m$
on the path with
$z_m$
on the path with
![]() $d(z_m,y_m)<\frac {1}{m}$
). We take this path
$d(z_m,y_m)<\frac {1}{m}$
). We take this path
![]() $\mathfrak {p}'$
as
$\mathfrak {p}'$
as
![]() $\gamma _m$
(suitably reparameterised so that its domain is
$\gamma _m$
(suitably reparameterised so that its domain is
![]() $[0,1]$
).
$[0,1]$
).
By [Reference Matoušková69, Theorem 2.4], for each m there exists
![]() $K_m>0$
and a
$K_m>0$
and a
![]() $K_m$
-Lipschitz map
$K_m$
-Lipschitz map
![]() $e_m\colon X\to \Gamma _m=\gamma _m([0,1])$
such that
$e_m\colon X\to \Gamma _m=\gamma _m([0,1])$
such that
![]() $e_m(x_0)=z_m$
and
$e_m(x_0)=z_m$
and
![]() $e_m(x_1)=x_1$
(that is, we extend the Lipschitz function
$e_m(x_1)=x_1$
(that is, we extend the Lipschitz function
![]() $\gamma _m\circ \max \{t_m,\operatorname {{\mathrm {id}}}\}\circ \gamma _m^{-1}\colon \Gamma _m\to \Gamma _m$
to X).
$\gamma _m\circ \max \{t_m,\operatorname {{\mathrm {id}}}\}\circ \gamma _m^{-1}\colon \Gamma _m\to \Gamma _m$
to X).
Now, we build an inductive limit
![]() $\varinjlim (X_{p_m,q_m},\varphi _m)$
, with each connecting map
$\varinjlim (X_{p_m,q_m},\varphi _m)$
, with each connecting map
![]() $\varphi _m$
of the form
$\varphi _m$
of the form
![]() $\varphi _m(f)=\operatorname {{\mathrm {Ad}}}_u\circ \operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})$
for some maps
$\varphi _m(f)=\operatorname {{\mathrm {Ad}}}_u\circ \operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})$
for some maps
![]() $\xi _i\colon X\to X$
, most of which are in fact the identity (to get the right trace space in the limit) and very few of which are not
$\xi _i\colon X\to X$
, most of which are in fact the identity (to get the right trace space in the limit) and very few of which are not
![]() $1$
-Lipschitz (so that Lipschitz elements in finite stages map to Lipschitz elements in the limit). To accomplish this, let
$1$
-Lipschitz (so that Lipschitz elements in finite stages map to Lipschitz elements in the limit). To accomplish this, let
![]() $(p_m,q_m)_{m\in \mathbb {N}}$
be the sequence of coprime positive integers constructed as in [Reference Jacelon59, §4.4], ensuring that the numbers
$(p_m,q_m)_{m\in \mathbb {N}}$
be the sequence of coprime positive integers constructed as in [Reference Jacelon59, §4.4], ensuring that the numbers
![]() $N_m=\frac {p_{m+1}q_{m+1}}{p_mq_m}$
satisfy
$N_m=\frac {p_{m+1}q_{m+1}}{p_mq_m}$
satisfy
![]() $\frac {q_{m+1}}{N_m} < \frac {1}{m^2}$
(for tracial control) and
$\frac {q_{m+1}}{N_m} < \frac {1}{m^2}$
(for tracial control) and
![]() $\frac {q_{m+1}}{N_m} < \frac {e^{\frac {1}{m^2}}-1}{K_m}$
(for Lipschitz control). We define the functions
$\frac {q_{m+1}}{N_m} < \frac {e^{\frac {1}{m^2}}-1}{K_m}$
(for Lipschitz control). We define the functions
![]() $\xi _i\colon X\to X$
,
$\xi _i\colon X\to X$
,
![]() $1\le i\le N_m$
, by
$1\le i\le N_m$
, by
 $$\begin{align*}\xi_i= \begin{cases} \operatorname{{\mathrm{id}}}_X & \text{ if }\ 1\le i\le N_m-q_{m+1}\\ z_m & \text{ if }\ N_m-q_{m+1}< i \le N_m-q_{m+1}+p_{m+1}\\ e_m & \text{ if }\ N_m-q_{m+1}+p_{m+1} < i\le N_m. \end{cases} \end{align*}$$
$$\begin{align*}\xi_i= \begin{cases} \operatorname{{\mathrm{id}}}_X & \text{ if }\ 1\le i\le N_m-q_{m+1}\\ z_m & \text{ if }\ N_m-q_{m+1}< i \le N_m-q_{m+1}+p_{m+1}\\ e_m & \text{ if }\ N_m-q_{m+1}+p_{m+1} < i\le N_m. \end{cases} \end{align*}$$
Then, there are unitaries
![]() $u_0,u_1\in M_{p_{m+1}}\otimes M_{q_{m+1}}$
(which can be connected via
$u_0,u_1\in M_{p_{m+1}}\otimes M_{q_{m+1}}$
(which can be connected via
![]() $u\colon X\to \Gamma _m\to [0,1]\to \mathcal {U}(M_{p_{m+1}}\otimes M_{q_{m+1}})$
similar to above) such that
$u\colon X\to \Gamma _m\to [0,1]\to \mathcal {U}(M_{p_{m+1}}\otimes M_{q_{m+1}})$
similar to above) such that
![]() $u_0\operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})u_0^*\in M_{p_{m+1}}\otimes 1_{q_{m+1}}$
and
$u_0\operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})u_0^*\in M_{p_{m+1}}\otimes 1_{q_{m+1}}$
and
![]() $u_1\operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})u_1^*\in 1_{p_{m+1}}\otimes M_{q_{m+1}}$
. This allows us to define the connecting map
$u_1\operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})u_1^*\in 1_{p_{m+1}}\otimes M_{q_{m+1}}$
. This allows us to define the connecting map
![]() $\varphi _m\colon X_{p_m,q_m}\to X_{p_{m+1},q_{m+1}}$
by
$\varphi _m\colon X_{p_m,q_m}\to X_{p_{m+1},q_{m+1}}$
by
![]() $\varphi _m(f)=\operatorname {{\mathrm {Ad}}}_u\circ \operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})$
.
$\varphi _m(f)=\operatorname {{\mathrm {Ad}}}_u\circ \operatorname {{\mathrm {diag}}}(f\circ \xi _1,\ldots ,f\circ \xi _{N_m})$
.
By construction,
![]() $A={\mathcal {Z}}\otimes \varinjlim (X_{p_m,q_m},\varphi _m)$
has the desired properties. (In fact, if X has finite covering dimension, then by [Reference Winter91, Theorem 1.6] and [Reference Winter92],
$A={\mathcal {Z}}\otimes \varinjlim (X_{p_m,q_m},\varphi _m)$
has the desired properties. (In fact, if X has finite covering dimension, then by [Reference Winter91, Theorem 1.6] and [Reference Winter92],
![]() ${\mathcal {Z}}$
-stability is automatic.) In particular, A is simple (by density of
${\mathcal {Z}}$
-stability is automatic.) In particular, A is simple (by density of
![]() $(z_m)_{m\in \mathbb {N}}\subseteq X$
),
$(z_m)_{m\in \mathbb {N}}\subseteq X$
),
![]() $\partial _e(T(A))\cong X$
(since at each stage, most, i.e. at least the fraction
$\partial _e(T(A))\cong X$
(since at each stage, most, i.e. at least the fraction
![]() $1-\frac {1}{m^2}$
, of the connecting maps are the identity), and
$1-\frac {1}{m^2}$
, of the connecting maps are the identity), and
![]() $\widehat {\varphi _{m,\infty }(f)}\in \operatorname {{\mathrm {Lip}}}(X,d)$
for every Lipschitz element
$\widehat {\varphi _{m,\infty }(f)}\in \operatorname {{\mathrm {Lip}}}(X,d)$
for every Lipschitz element
![]() $f\in X_{p_m,q_m}$
(its Lipschitz constant scaled by at most
$f\in X_{p_m,q_m}$
(its Lipschitz constant scaled by at most
![]() $\prod \limits _{m\in \mathbb {N}} e^{\frac {1}{m^2}}$
).
$\prod \limits _{m\in \mathbb {N}} e^{\frac {1}{m^2}}$
).
Remark 4.5.
-
1. The choice of the base points
 $x_0,x_1\in X$
in the proof of Theorem 4.4 is somewhat arbitrary, but if X happens to be a sphere (with d the geodesic metric), then requiring that
$x_0,x_1\in X$
in the proof of Theorem 4.4 is somewhat arbitrary, but if X happens to be a sphere (with d the geodesic metric), then requiring that
 $d(x_0,x_1)=\operatorname {{\mathrm {diam}}} X$
(that is, choosing antipodal base points) allows a choice of maps
$d(x_0,x_1)=\operatorname {{\mathrm {diam}}} X$
(that is, choosing antipodal base points) allows a choice of maps
 $e_m\colon X\to X$
that are
$e_m\colon X\to X$
that are
 $1$
-Lipschitz. Specifically, given
$1$
-Lipschitz. Specifically, given
 $y_m\in X$
, let
$y_m\in X$
, let
 $\gamma _m$
be a geodesic (which we view as the meridian of longitude
$\gamma _m$
be a geodesic (which we view as the meridian of longitude
 $0$
) from
$0$
) from
 $x_0$
to
$x_0$
to
 $x_1$
that passes through
$x_1$
that passes through
 $y_m$
, and define
$y_m$
, and define
 $e_m\colon X\to \Gamma _m=\gamma _m([0,1])$
by projection onto
$e_m\colon X\to \Gamma _m=\gamma _m([0,1])$
by projection onto
 $\Gamma _m$
. With this choice,
$\Gamma _m$
. With this choice,
 $\widehat {\varphi _m(f)}\in \operatorname {{\mathrm {Lip}}}^1(X,d)$
for every
$\widehat {\varphi _m(f)}\in \operatorname {{\mathrm {Lip}}}^1(X,d)$
for every
 $1$
-Lipschitz element
$1$
-Lipschitz element
 $f\in X_{p_m,q_m}$
. That said, while potentially important in the one-dimensional setting (see [Reference Jacelon59, §4]), in the present context this is largely an aesthetic observation.
$f\in X_{p_m,q_m}$
. That said, while potentially important in the one-dimensional setting (see [Reference Jacelon59, §4]), in the present context this is largely an aesthetic observation. -
2. The construction is much simpler if we drop the requirement that A be projectionless and is valid for any compact, connected metric space
 $(X,d)$
:
$(X,d)$
:
 $X_{p_m,q_m}$
can be replaced by
$X_{p_m,q_m}$
can be replaced by
 $A_m=C(X,M_{n_m})$
, with
$A_m=C(X,M_{n_m})$
, with
 $\varphi _m\colon A_m\to A_{m+1}$
defined just in terms of the identity map and point evaluations. In this case, we can arrange as in [Reference Thomsen85, Lemma 3.7] to have
$\varphi _m\colon A_m\to A_{m+1}$
defined just in terms of the identity map and point evaluations. In this case, we can arrange as in [Reference Thomsen85, Lemma 3.7] to have
 $\rho _A(K_0(A))=G\cdot 1\subseteq \operatorname {{\mathrm {Aff}}}(T(A))$
for any prescribed dense subgroup G of
$\rho _A(K_0(A))=G\cdot 1\subseteq \operatorname {{\mathrm {Aff}}}(T(A))$
for any prescribed dense subgroup G of
 $\mathbb {Q}$
. In the projectionless case, strict comparison of positive elements (see [Reference Rørdam78, Corollary 4.6]) implies that
$\mathbb {Q}$
. In the projectionless case, strict comparison of positive elements (see [Reference Rørdam78, Corollary 4.6]) implies that
 $\rho _A(K_0(A))=\mathbb {Z}\cdot 1$
.
$\rho _A(K_0(A))=\mathbb {Z}\cdot 1$
.
4.4 Finite Rokhlin dimension
Since the models constructed in Theorem 4.4 are classifiable by the Elliott invariant, we can lift endomorphisms of trace spaces to the
![]() ${\mathrm {C}^*}$
-level. By ensuring that the lifted action has finite Rokhlin dimension, a notion introduced in [Reference Hirshberg, Winter and Zacharias56] and extended in [Reference Hirshberg and Phillips55] to actions on not necessarily unital
${\mathrm {C}^*}$
-level. By ensuring that the lifted action has finite Rokhlin dimension, a notion introduced in [Reference Hirshberg, Winter and Zacharias56] and extended in [Reference Hirshberg and Phillips55] to actions on not necessarily unital
![]() ${\mathrm {C}^*}$
-algebras A and further in [Reference Szabó, Wu and Zacharias84] to (cocycle) actions of residually finite groups, we can arrange for the crossed product
${\mathrm {C}^*}$
-algebras A and further in [Reference Szabó, Wu and Zacharias84] to (cocycle) actions of residually finite groups, we can arrange for the crossed product
![]() $A\rtimes _{\alpha }\mathbb {N}$
to also be classifiable. This is not an essential requirement if our only interest is observing statistical features of the tracial dynamics, but this procedure will be used in § 5 to investigate the attainable range.
$A\rtimes _{\alpha }\mathbb {N}$
to also be classifiable. This is not an essential requirement if our only interest is observing statistical features of the tracial dynamics, but this procedure will be used in § 5 to investigate the attainable range.
Here,
![]() $A\rtimes _{\alpha }\mathbb {N}$
is the crossed product by an endomorphism in the sense of Cuntz [Reference Cuntz27, §6.1] (see also [Reference Stacey83]), namely,
$A\rtimes _{\alpha }\mathbb {N}$
is the crossed product by an endomorphism in the sense of Cuntz [Reference Cuntz27, §6.1] (see also [Reference Stacey83]), namely,
![]() $\alpha $
is extended to an automorphism
$\alpha $
is extended to an automorphism
![]() $\underset {\to }{\alpha }$
of
$\underset {\to }{\alpha }$
of
and
![]() $A\rtimes _{\alpha }\mathbb {N}$
is defined to be the corner
$A\rtimes _{\alpha }\mathbb {N}$
is defined to be the corner
![]() $p\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )p$
, where
$p\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )p$
, where
![]() $p\in M\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )$
is the image of
$p\in M\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )$
is the image of
![]() $1_{M(A)}$
in the inclusion
$1_{M(A)}$
in the inclusion
![]() $M(A) \to M\left (\underset {\to }{A}\right ) \to M\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )$
. In particular,
$M(A) \to M\left (\underset {\to }{A}\right ) \to M\left (\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}\right )$
. In particular,
![]() $A\rtimes _{\alpha }\mathbb {N}$
is stably isomorphic to
$A\rtimes _{\alpha }\mathbb {N}$
is stably isomorphic to
![]() $\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}$
, which means, for example, that finite nuclear dimension of one is equivalent to finite nuclear dimension of the other (see [Reference Winter and Zacharias93, Corollary 2.8]).
$\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}$
, which means, for example, that finite nuclear dimension of one is equivalent to finite nuclear dimension of the other (see [Reference Winter and Zacharias93, Corollary 2.8]).
For single endomorphisms
![]() $\alpha $
, Rokhlin dimension is defined in [Reference Hirshberg, Winter and Zacharias56, Reference Hirshberg and Phillips55, Reference Szabó, Wu and Zacharias84] only when
$\alpha $
, Rokhlin dimension is defined in [Reference Hirshberg, Winter and Zacharias56, Reference Hirshberg and Phillips55, Reference Szabó, Wu and Zacharias84] only when
![]() $\alpha $
is invertible, that is, for (cocycle) actions
$\alpha $
is invertible, that is, for (cocycle) actions
![]() $\mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
. However, just as in [Reference Brown and Hirshberg13, Definition 2.1], which covers the case of Rokhlin dimension
$\mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
. However, just as in [Reference Brown and Hirshberg13, Definition 2.1], which covers the case of Rokhlin dimension
![]() $0$
, the definition admits a natural extension to the noninvertible case. In [Reference Brown and Hirshberg13], the only tweak is that the finite set F that appears in the definition of Rokhlin dimension is taken to be an arbitrary subset not of A but of
$0$
, the definition admits a natural extension to the noninvertible case. In [Reference Brown and Hirshberg13], the only tweak is that the finite set F that appears in the definition of Rokhlin dimension is taken to be an arbitrary subset not of A but of
![]() $\alpha ^p(A)$
, where
$\alpha ^p(A)$
, where
![]() $p\in \mathbb {N}$
is the integer that specifies the height of the tower. As in [Reference Brown and Hirshberg13, Proposition 2.2], this is sufficient to guarantee that the automorphism
$p\in \mathbb {N}$
is the integer that specifies the height of the tower. As in [Reference Brown and Hirshberg13, Proposition 2.2], this is sufficient to guarantee that the automorphism
![]() $\underset {\to }{\alpha }$
has the usual Rokhlin property.
$\underset {\to }{\alpha }$
has the usual Rokhlin property.
But actually, the only reason for this restriction is to include degenerate (e.g., nonunital) examples, especially the shift
![]() $\alpha \colon \bigotimes _{\mathbb {N}} M_n = M_{n^{\infty }} \to M_{n^{\infty }}$
,
$\alpha \colon \bigotimes _{\mathbb {N}} M_n = M_{n^{\infty }} \to M_{n^{\infty }}$
,
![]() $a_1\otimes a_2\otimes a_3\otimes \cdots \mapsto e\otimes a_1\otimes a_2\otimes a_3\otimes \cdots $
(where
$a_1\otimes a_2\otimes a_3\otimes \cdots \mapsto e\otimes a_1\otimes a_2\otimes a_3\otimes \cdots $
(where
![]() $e\in M_n$
is a minimal projection), which yields
$e\in M_n$
is a minimal projection), which yields
![]() $M_{n^{\infty }}\rtimes _{\alpha }\mathbb {N}\cong \mathcal {O}_n$
(see [Reference Cuntz26, §2]). Since the unmodified version, that is, [Reference Hirshberg and Phillips55, Definition 1.21] with single noncommuting towers, can reasonably be expected to hold for nondegenerate (e.g., unital) endomorphisms, this is the definition we adopt. In other words, in [Reference Hirshberg and Phillips55, Definition 1.21] we drop condition (6) and insist that
$M_{n^{\infty }}\rtimes _{\alpha }\mathbb {N}\cong \mathcal {O}_n$
(see [Reference Cuntz26, §2]). Since the unmodified version, that is, [Reference Hirshberg and Phillips55, Definition 1.21] with single noncommuting towers, can reasonably be expected to hold for nondegenerate (e.g., unital) endomorphisms, this is the definition we adopt. In other words, in [Reference Hirshberg and Phillips55, Definition 1.21] we drop condition (6) and insist that
![]() $f^{(l)}_{1,j}=0$
for all
$f^{(l)}_{1,j}=0$
for all
![]() $0\le j\le p$
to arrive at the following.
$0\le j\le p$
to arrive at the following.
Definition 4.6. An endomorphism
![]() $\alpha $
of a
$\alpha $
of a
![]() ${\mathrm {C}^*}$
-algebra A is said to have Rokhlin dimension d if d is the least nonnegative integer with the following property. For any finite set
${\mathrm {C}^*}$
-algebra A is said to have Rokhlin dimension d if d is the least nonnegative integer with the following property. For any finite set
![]() $F\subseteq A$
, integer
$F\subseteq A$
, integer
![]() $p\ge 1$
and
$p\ge 1$
and
![]() $\varepsilon>0$
, there are positive contractions
$\varepsilon>0$
, there are positive contractions
![]() $f^{(l)}_{0},\dots ,f^{(l)}_{p-1}\in A$
,
$f^{(l)}_{0},\dots ,f^{(l)}_{p-1}\in A$
,
![]() $l\in \{0,1,\dots ,d\}$
, such that:
$l\in \{0,1,\dots ,d\}$
, such that:
-
1.
 $\|f^{(l)}_{k}f^{(l)}_{j}a\| < \varepsilon $
for every
$\|f^{(l)}_{k}f^{(l)}_{j}a\| < \varepsilon $
for every
 $a\in F$
,
$a\in F$
,
 $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
 $j\ne k\in \{0,1,\dots ,p-1\}$
;
$j\ne k\in \{0,1,\dots ,p-1\}$
; -
2.
 $\left \|\left (\sum _{l=0}^d\sum _{j=0}^{p-1}f^{(l)}_{j}\right )a-a\right \| < \varepsilon $
for every
$\left \|\left (\sum _{l=0}^d\sum _{j=0}^{p-1}f^{(l)}_{j}\right )a-a\right \| < \varepsilon $
for every
 $a\in F$
;
$a\in F$
; -
3.
 $\|[f^{(l)}_{j},a]\| < \varepsilon $
for every
$\|[f^{(l)}_{j},a]\| < \varepsilon $
for every
 $a\in F$
,
$a\in F$
,
 $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
 $j\in \{0,1,\dots ,p-1\}$
;
$j\in \{0,1,\dots ,p-1\}$
; -
4.
 $\left \|\left (\alpha (f^{(l)}_{j})-f^{(l)}_{j+1}\right )a\right \| < \varepsilon $
for every
$\left \|\left (\alpha (f^{(l)}_{j})-f^{(l)}_{j+1}\right )a\right \| < \varepsilon $
for every
 $a\in F$
,
$a\in F$
,
 $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
 $j\in \{0,1,\dots ,p-1\}$
, where
$j\in \{0,1,\dots ,p-1\}$
, where
 $f^{(l)}_{p}:=f^{(l)}_{0}$
.
$f^{(l)}_{p}:=f^{(l)}_{0}$
.
This is equivalent to the following more succinct version phrased in terms of Kirchberg’s central sequence algebra
![]() $F(A) = (A_{\mathcal {U}} \cap A')/\operatorname {{\mathrm {Ann}}}(A,A_{\mathcal {U}})$
associated to a free ultrafilter
$F(A) = (A_{\mathcal {U}} \cap A')/\operatorname {{\mathrm {Ann}}}(A,A_{\mathcal {U}})$
associated to a free ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\mathbb {N}$
(see [Reference Kirchberg62, §1] and [Reference Gardella, Hirshberg and Vaccaro46, Definition 2.6]). Namely,
$\mathbb {N}$
(see [Reference Kirchberg62, §1] and [Reference Gardella, Hirshberg and Vaccaro46, Definition 2.6]). Namely,
![]() $\alpha $
has Rokhlin dimension
$\alpha $
has Rokhlin dimension
![]() $\le d$
if and only if, for every p, there are positive contractions
$\le d$
if and only if, for every p, there are positive contractions
![]() $f^{(l)}_{\bar m}\in F(A)$
,
$f^{(l)}_{\bar m}\in F(A)$
,
![]() $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
![]() $\bar m\in \mathbb {Z}/p\mathbb {Z}$
, such that:
$\bar m\in \mathbb {Z}/p\mathbb {Z}$
, such that:
-
1.
 $f^{(l)}_{\bar m}f^{(l)}_{\bar n} = 0$
for every
$f^{(l)}_{\bar m}f^{(l)}_{\bar n} = 0$
for every
 $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
 $\bar m \ne \bar n\in \mathbb {Z}/p\mathbb {Z}$
;
$\bar m \ne \bar n\in \mathbb {Z}/p\mathbb {Z}$
; -
2.
 $\sum _{l=0}^d\sum _{\bar m \in \mathbb {Z}/p\mathbb {Z}} f^{(l)}_{\bar m} = 1$
;
$\sum _{l=0}^d\sum _{\bar m \in \mathbb {Z}/p\mathbb {Z}} f^{(l)}_{\bar m} = 1$
; -
3.
 $\bar \alpha (f^{(l)}_{\bar m}) = f^{(l)}_{\overline {m + 1}}$
for every
$\bar \alpha (f^{(l)}_{\bar m}) = f^{(l)}_{\overline {m + 1}}$
for every
 $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
 $\bar m\in \mathbb {Z}/p\mathbb {Z}$
, where
$\bar m\in \mathbb {Z}/p\mathbb {Z}$
, where
 $\bar \alpha $
is the action on
$\bar \alpha $
is the action on
 $F(A)$
induced by
$F(A)$
induced by
 $\alpha $
.
$\alpha $
.
Since the Elliott invariant is insensitive to (approximate) unitary equivalence, we obtain the following from [Reference Szabó, Wu and Zacharias84] (or in the unital setting, [Reference Hirshberg, Winter and Zacharias56, Theorem 3.4]). Note that we omit all cocycles and only consider the group
![]() $G=\mathbb {Z}$
.
$G=\mathbb {Z}$
.
Lemma 4.7. Let A be a separable,
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() ${\mathrm {C}^*}$
-algebra, and let
${\mathrm {C}^*}$
-algebra, and let
![]() $\beta \in \operatorname {{\mathrm {End}}}(A)$
be nondegenerate (that is,
$\beta \in \operatorname {{\mathrm {End}}}(A)$
be nondegenerate (that is,
![]() $\beta $
maps an(y) approximate unit of A to an approximate unit of A). Then, there is a nondegenerate
$\beta $
maps an(y) approximate unit of A to an approximate unit of A). Then, there is a nondegenerate
![]() $\alpha \in \operatorname {{\mathrm {End}}}(A)$
such that
$\alpha \in \operatorname {{\mathrm {End}}}(A)$
such that
![]() $\alpha $
has Rokhlin dimension
$\alpha $
has Rokhlin dimension
![]() $\le 1$
and
$\le 1$
and
![]() $\operatorname {{\mathrm {Ell}}}(\alpha )=\operatorname {{\mathrm {Ell}}}(\beta )$
.
$\operatorname {{\mathrm {Ell}}}(\alpha )=\operatorname {{\mathrm {Ell}}}(\beta )$
.
Proof. By [Reference Szabó, Wu and Zacharias84, Remark 11.13], there is an automorphism
![]() $\theta $
of
$\theta $
of
![]() ${\mathcal {Z}}$
(namely, a tensor product of shifts) that has Rokhlin dimension
${\mathcal {Z}}$
(namely, a tensor product of shifts) that has Rokhlin dimension
![]() $1$
. Note that
$1$
. Note that
![]() $\operatorname {{\mathrm {Ell}}}(\theta )$
is the identity. As in [Reference Szabó, Wu and Zacharias84, Theorem 11.5], since
$\operatorname {{\mathrm {Ell}}}(\theta )$
is the identity. As in [Reference Szabó, Wu and Zacharias84, Theorem 11.5], since
![]() ${\mathcal {Z}}$
is strongly self-absorbing there is an isomorphism
${\mathcal {Z}}$
is strongly self-absorbing there is an isomorphism
![]() $\varphi \colon A\to A\otimes {\mathcal {Z}}$
that is approximately unitarily equivalent to
$\varphi \colon A\to A\otimes {\mathcal {Z}}$
that is approximately unitarily equivalent to
![]() $\operatorname {{\mathrm {id}}}_A\otimes 1_{{\mathcal {Z}}}$
. By [Reference Szabó, Wu and Zacharias84, Proposition 11.7],
$\operatorname {{\mathrm {id}}}_A\otimes 1_{{\mathcal {Z}}}$
. By [Reference Szabó, Wu and Zacharias84, Proposition 11.7],
![]() $\beta \otimes \theta $
has Rokhlin dimension
$\beta \otimes \theta $
has Rokhlin dimension
![]() $\le 1$
, and hence so does
$\le 1$
, and hence so does
![]() $\alpha =\varphi ^{-1}\circ (\beta \otimes \theta )\circ \varphi $
.
$\alpha =\varphi ^{-1}\circ (\beta \otimes \theta )\circ \varphi $
.
Next, we observe that crossed products of classifiable
![]() ${\mathrm {C}^*}$
-algebras by endomorphisms with finite Rokhlin dimension are also classifiable.
${\mathrm {C}^*}$
-algebras by endomorphisms with finite Rokhlin dimension are also classifiable.
Lemma 4.8. Let A be a simple, separable
![]() ${\mathrm {C}^*}$
-algebra of finite nuclear dimension, and let
${\mathrm {C}^*}$
-algebra of finite nuclear dimension, and let
![]() $\alpha $
be a nondegenerate endomorphism of A with finite Rokhlin dimension. Then,
$\alpha $
be a nondegenerate endomorphism of A with finite Rokhlin dimension. Then,
![]() $A\rtimes _{\alpha }\mathbb {N}$
is simple and has finite nuclear dimension. Moreover,
$A\rtimes _{\alpha }\mathbb {N}$
is simple and has finite nuclear dimension. Moreover,
Proof. Extending to
![]() $\underset {\to }{A}$
, we may assume that
$\underset {\to }{A}$
, we may assume that
![]() $\alpha $
is an automorphism. Since
$\alpha $
is an automorphism. Since
![]() $\alpha $
has finite Rokhlin dimension,
$\alpha $
has finite Rokhlin dimension,
![]() $\alpha ^m$
is outer for every
$\alpha ^m$
is outer for every
![]() $m\in \mathbb {Z}\setminus \{0\}$
. In fact,
$m\in \mathbb {Z}\setminus \{0\}$
. In fact,
![]() $\alpha \colon \mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
is strongly outer, that is, for any
$\alpha \colon \mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
is strongly outer, that is, for any
![]() $m\ne 0$
and any
$m\ne 0$
and any
![]() $\alpha $
-invariant trace
$\alpha $
-invariant trace
![]() $\tau \in T(A)$
, the unique extension of
$\tau \in T(A)$
, the unique extension of
![]() $\alpha ^m$
to a trace-preserving automorphism
$\alpha ^m$
to a trace-preserving automorphism
![]() $\alpha ^m_{\tau }$
of
$\alpha ^m_{\tau }$
of
![]() $\mathcal {M}=\pi _{\tau }(A)"$
, the von Neumann closure of the Gelfand--Naimark--Segal (GNS) representation associated to
$\mathcal {M}=\pi _{\tau }(A)"$
, the von Neumann closure of the Gelfand--Naimark--Segal (GNS) representation associated to
![]() $\tau $
, is outer. To see this, one proceeds exactly as in the proof of [Reference Gardella, Hirshberg and Vaccaro46, Theorem 7.8
$\tau $
, is outer. To see this, one proceeds exactly as in the proof of [Reference Gardella, Hirshberg and Vaccaro46, Theorem 7.8
![]() $(3)\Rightarrow (1)$
], just replacing
$(3)\Rightarrow (1)$
], just replacing
![]() $A_{\mathcal {U}}\cap A'$
by
$A_{\mathcal {U}}\cap A'$
by
![]() $F(A)$
. We recall this argument here for convenience.
$F(A)$
. We recall this argument here for convenience.
By [Reference Nawata70, Propositions 2.2, 2.3], we have the required (unital, equivariant) quotient map
![]() $\kappa _{\tau }\colon F(A)\to \mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
. The key point is that, were
$\kappa _{\tau }\colon F(A)\to \mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
. The key point is that, were
![]() $\alpha ^m_{\tau }$
an inner automorphism of
$\alpha ^m_{\tau }$
an inner automorphism of
![]() $\mathcal {M}_{\tau }$
, say
$\mathcal {M}_{\tau }$
, say
![]() $\alpha ^m_{\tau }=\operatorname {{\mathrm {Ad}}}_u$
for some unitary
$\alpha ^m_{\tau }=\operatorname {{\mathrm {Ad}}}_u$
for some unitary
![]() $u\in \mathcal {M}_{\tau }$
, then every
$u\in \mathcal {M}_{\tau }$
, then every
![]() $x\in \mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
would commute with u and so the action
$x\in \mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
would commute with u and so the action
![]() $\overline {\alpha ^m_{\tau }}$
induced by
$\overline {\alpha ^m_{\tau }}$
induced by
![]() $\alpha ^m_{\tau }$
on
$\alpha ^m_{\tau }$
on
![]() $\mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
would be trivial. We now show that this is not the case. Choose p such that
$\mathcal {M}^{\mathcal {U}}_{\tau }\cap \mathcal {M}_{\tau }'$
would be trivial. We now show that this is not the case. Choose p such that
![]() $m\notin p\mathbb {Z}$
, and let
$m\notin p\mathbb {Z}$
, and let
![]() $f^{(l)}_{\bar k}\in F(A)$
,
$f^{(l)}_{\bar k}\in F(A)$
,
![]() $l\in \{0,1,\dots ,d\}$
,
$l\in \{0,1,\dots ,d\}$
,
![]() $\bar k\in \mathbb {Z}/p\mathbb {Z}$
be as in Definition 4.6 for this p. Since
$\bar k\in \mathbb {Z}/p\mathbb {Z}$
be as in Definition 4.6 for this p. Since
![]() $\kappa _{\tau }$
is unital, there is
$\kappa _{\tau }$
is unital, there is
![]() $l_0\in \{0,1,\dots ,d\}$
such that
$l_0\in \{0,1,\dots ,d\}$
such that
![]() $\kappa _{\tau }(f^{(l_0)}_{\bar k}) \ne 0$
for some (and hence, by equivariance, every)
$\kappa _{\tau }(f^{(l_0)}_{\bar k}) \ne 0$
for some (and hence, by equivariance, every)
![]() $\bar k \in \mathbb {Z}/p\mathbb {Z}$
. Then,
$\bar k \in \mathbb {Z}/p\mathbb {Z}$
. Then,
![]() $\left \{\kappa _{\tau }(f^{(l_0)}_{\bar k})\right \}_{\bar k \in \mathbb {Z}/p\mathbb {Z}}$
are pairwise orthogonal positive contractions with
$\left \{\kappa _{\tau }(f^{(l_0)}_{\bar k})\right \}_{\bar k \in \mathbb {Z}/p\mathbb {Z}}$
are pairwise orthogonal positive contractions with
![]() $\overline {\alpha ^m_{\tau }}(\kappa _{\tau }(f^{(l_0)}_{\bar k})) = \kappa _{\tau }(f^{(l_0)}_{\overline {m+k}})$
. Since
$\overline {\alpha ^m_{\tau }}(\kappa _{\tau }(f^{(l_0)}_{\bar k})) = \kappa _{\tau }(f^{(l_0)}_{\overline {m+k}})$
. Since
![]() $m\notin p\mathbb {Z}$
, there is
$m\notin p\mathbb {Z}$
, there is
![]() $\bar k$
such that
$\bar k$
such that
![]() $\overline {m+k}\ne \bar k$
in
$\overline {m+k}\ne \bar k$
in
![]() $\mathbb {Z}/p\mathbb {Z}$
, and so
$\mathbb {Z}/p\mathbb {Z}$
, and so
![]() $\overline {\alpha ^m_{\tau }}$
is indeed nontrivial.
$\overline {\alpha ^m_{\tau }}$
is indeed nontrivial.
By [Reference Kishimoto63, Theorem 3.1], outerness of
![]() $\alpha \colon \mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
implies that
$\alpha \colon \mathbb {Z}\to \operatorname {{\mathrm {Aut}}}(A)$
implies that
![]() $A\rtimes _{\alpha }\mathbb {Z}$
is simple. Finite nuclear dimension is guaranteed by [Reference Szabó, Wu and Zacharias84, Theorem 6.2]. The final statement follows from [Reference Liao65, Proposition 2.3], whose proof also works in the nonunital setting.
$A\rtimes _{\alpha }\mathbb {Z}$
is simple. Finite nuclear dimension is guaranteed by [Reference Szabó, Wu and Zacharias84, Theorem 6.2]. The final statement follows from [Reference Liao65, Proposition 2.3], whose proof also works in the nonunital setting.
Combining Lemma 4.7 and Lemma 4.8 yields the following.
Theorem 4.9. Let A be a simple, separable, unital,
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() ${\mathrm {C}^*}$
-algebra that has trivial tracial pairing and satisfies the UCT, and for which the extreme boundary
${\mathrm {C}^*}$
-algebra that has trivial tracial pairing and satisfies the UCT, and for which the extreme boundary
![]() $X_A$
of the trace space
$X_A$
of the trace space
![]() $T(A)$
is compact. Then, for every group homomorphism
$T(A)$
is compact. Then, for every group homomorphism
![]() $\kappa _1\colon K_1(A)\to K_1(A)$
and continuous map
$\kappa _1\colon K_1(A)\to K_1(A)$
and continuous map
![]() $h\colon X_A\to X_A$
, there exists a unital endomorphism
$h\colon X_A\to X_A$
, there exists a unital endomorphism
![]() $\alpha $
of A such that
$\alpha $
of A such that
![]() $K_1(\alpha )=\kappa _1$
,
$K_1(\alpha )=\kappa _1$
,
![]() $T(\alpha )|_{X_A}=h$
and the crossed product
$T(\alpha )|_{X_A}=h$
and the crossed product
![]() $A\rtimes _{\alpha }\mathbb {N}$
is classifiable.
$A\rtimes _{\alpha }\mathbb {N}$
is classifiable.
Proof. By Lemma 3.1, we can extend h to a continuous affine map
![]() $T(A)\to T(A)$
. Then, since A has trivial tracial pairing, h,
$T(A)\to T(A)$
. Then, since A has trivial tracial pairing, h,
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\operatorname {{\mathrm {id}}}\colon K_0(A)\to K_0(A)$
determine a homomorphism
$\operatorname {{\mathrm {id}}}\colon K_0(A)\to K_0(A)$
determine a homomorphism
![]() $\operatorname {{\mathrm {Ell}}}(A)\to \operatorname {{\mathrm {Ell}}}(A)$
. By [Reference Gong, Lin and Niu52, Theorem 5.12], there exists a unital endomorphism
$\operatorname {{\mathrm {Ell}}}(A)\to \operatorname {{\mathrm {Ell}}}(A)$
. By [Reference Gong, Lin and Niu52, Theorem 5.12], there exists a unital endomorphism
![]() $\beta \in \operatorname {{\mathrm {End}}}(A)$
such that
$\beta \in \operatorname {{\mathrm {End}}}(A)$
such that
![]() $T(\beta )=h$
and
$T(\beta )=h$
and
![]() $K_1(\beta )=\kappa _1$
. Finally, by Lemma 4.7, we can find
$K_1(\beta )=\kappa _1$
. Finally, by Lemma 4.7, we can find
![]() $\alpha \in \operatorname {{\mathrm {End}}}(A)$
with
$\alpha \in \operatorname {{\mathrm {End}}}(A)$
with
![]() $\operatorname {{\mathrm {Ell}}}(\alpha )=\operatorname {{\mathrm {Ell}}}(\beta )$
such that
$\operatorname {{\mathrm {Ell}}}(\alpha )=\operatorname {{\mathrm {Ell}}}(\beta )$
such that
![]() $\alpha $
has finite Rokhlin dimension, which by Lemma 4.8 implies that
$\alpha $
has finite Rokhlin dimension, which by Lemma 4.8 implies that
![]() $A\rtimes _{\alpha }\mathbb {N}$
is classifiable.
$A\rtimes _{\alpha }\mathbb {N}$
is classifiable.
Together, Theorems 4.4 and 4.9 provide the means of lifting a topological dynamical system
![]() $(X,h)$
on a compact metric space to a
$(X,h)$
on a compact metric space to a
![]() ${\mathrm {C}^*}$
-dynamical system
${\mathrm {C}^*}$
-dynamical system
![]() $(A,\alpha )$
on a model classifiable
$(A,\alpha )$
on a model classifiable
![]() ${\mathrm {C}^*}$
-algebra, such that the crossed product is also classifiable. Moreover, the statistical phenomena described in § 4.1 can be translated into tracial versions that are witnessed by the dense subset
${\mathrm {C}^*}$
-algebra, such that the crossed product is also classifiable. Moreover, the statistical phenomena described in § 4.1 can be translated into tracial versions that are witnessed by the dense subset
![]() $\operatorname {{\mathrm {Lip}}}(A) = \bigcup _{k\in \mathbb {N}}\operatorname {{\mathrm {Lip}}}^k(A)\subseteq A_{sa}$
, where
$\operatorname {{\mathrm {Lip}}}(A) = \bigcup _{k\in \mathbb {N}}\operatorname {{\mathrm {Lip}}}^k(A)\subseteq A_{sa}$
, where
Here are some illustrative examples.
Example 4.10 (Estimates of large tracial deviation).
Suppose that
![]() $h\colon X\to X$
is uniquely ergodic. Let
$h\colon X\to X$
is uniquely ergodic. Let
![]() $\mu $
be the measure fixed by h, and let
$\mu $
be the measure fixed by h, and let
![]() $\tau _{\mu }$
be the corresponding unique trace fixed by
$\tau _{\mu }$
be the corresponding unique trace fixed by
![]() $\alpha $
. Then, by Proposition 4.3, for every
$\alpha $
. Then, by Proposition 4.3, for every
![]() $\varepsilon>0$
and every
$\varepsilon>0$
and every
![]() $k\in \mathbb {N}$
, there exist constants
$k\in \mathbb {N}$
, there exist constants
![]() $c_1,c_2>0$
such that, for every
$c_1,c_2>0$
such that, for every
![]() $a\in \operatorname {{\mathrm {Lip}}}^k(A)$
and every
$a\in \operatorname {{\mathrm {Lip}}}^k(A)$
and every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$\begin{align*}\mu\left(\left\{\tau\in \partial_e(T(A)) \mid \left|\frac{1}{n}\sum_{i=0}^{n-1}\tau(\alpha^i(a))-\tau_{\mu}(a)\right|>\varepsilon\right\}\right) \le c_1e^{-c_2n\varepsilon^2}. \end{align*}$$
$$\begin{align*}\mu\left(\left\{\tau\in \partial_e(T(A)) \mid \left|\frac{1}{n}\sum_{i=0}^{n-1}\tau(\alpha^i(a))-\tau_{\mu}(a)\right|>\varepsilon\right\}\right) \le c_1e^{-c_2n\varepsilon^2}. \end{align*}$$
This in particular applies to minimal, uniquely ergodic homeomorphisms of odd spheres. In this case, one computes from the six-term exact sequence that
Taking
![]() $\kappa _1\colon K_1(A)\to K_1(A)$
in Theorem 4.9 to be the zero homomorphism, the extended algebra
$\kappa _1\colon K_1(A)\to K_1(A)$
in Theorem 4.9 to be the zero homomorphism, the extended algebra
![]() $\underset {\to }{A}$
has the same Elliott invariant as (and is therefore isomorphic to) a limit of prime dimension drop algebras. One computes from the Pimsner–Voiculescu sequence (see also [Reference Blackadar8, Theorem 10.10.4]) that
$\underset {\to }{A}$
has the same Elliott invariant as (and is therefore isomorphic to) a limit of prime dimension drop algebras. One computes from the Pimsner–Voiculescu sequence (see also [Reference Blackadar8, Theorem 10.10.4]) that
Therefore,
![]() $\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}$
is isomorphic (hence,
$\underset {\to }{A}\rtimes _{\underset {\to }{\alpha }}\mathbb {Z}$
is isomorphic (hence,
![]() $A\rtimes _{\alpha }\mathbb {N}$
is at least stably isomorphic) to the
$A\rtimes _{\alpha }\mathbb {N}$
is at least stably isomorphic) to the
![]() ${\mathrm {C}^*}$
-algebra
${\mathrm {C}^*}$
-algebra
![]() $C(Z)\rtimes _{\zeta }\mathbb {Z}$
of [Reference Deeley, Putnam and Strung31, Proposition 2.8], which contains
$C(Z)\rtimes _{\zeta }\mathbb {Z}$
of [Reference Deeley, Putnam and Strung31, Proposition 2.8], which contains
![]() ${\mathcal {Z}}$
as a large subalgebra.
${\mathcal {Z}}$
as a large subalgebra.
Example 4.11 (Exponentially fast tracial mixing).
Suppose that
![]() $(X,\mu ,h)$
has EDC (see Definition 4.1). Then, there exists
$(X,\mu ,h)$
has EDC (see Definition 4.1). Then, there exists
![]() $\gamma \in (0,1)$
such that for every
$\gamma \in (0,1)$
such that for every
![]() $a,b\in \operatorname {{\mathrm {Lip}}}(A)$
there exists
$a,b\in \operatorname {{\mathrm {Lip}}}(A)$
there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $n\in \mathbb {N}$
$n\in \mathbb {N}$
 $$\begin{align*}\left|\int_{\partial_e(T(A))} \widehat{\alpha^n(a)}\hat b\;d\mu - \tau_{\mu}(a) \cdot \tau_{\mu}(b)\right| \le C\gamma^n. \end{align*}$$
$$\begin{align*}\left|\int_{\partial_e(T(A))} \widehat{\alpha^n(a)}\hat b\;d\mu - \tau_{\mu}(a) \cdot \tau_{\mu}(b)\right| \le C\gamma^n. \end{align*}$$
This holds, for example, when the tracial dynamical system is given by a holomorphic automorphism h of positive entropy on a compact Kähler surface X (see § 4.2).
Example 4.12 (The tracial CLT).
Suppose that
![]() $(X,\mu ,h)$
satisfies the CLT (see Definition 4.2). Then, for every
$(X,\mu ,h)$
satisfies the CLT (see Definition 4.2). Then, for every
![]() $a\in \operatorname {{\mathrm {Lip}}}(A)$
with
$a\in \operatorname {{\mathrm {Lip}}}(A)$
with
![]() $\sigma =\sigma _{\hat {a}|_X}> 0$
(which is the typical case) translated so that
$\sigma =\sigma _{\hat {a}|_X}> 0$
(which is the typical case) translated so that
![]() $\tau _{\mu }(a)=0$
,
$\tau _{\mu }(a)=0$
,
 $$\begin{align*}\lim_{n\to\infty} \mu\left(\left\{\tau\in \partial_e(T(A)) \mid \frac{1}{\sqrt{n}}\sum_{i=0}^{n-1}\tau(\alpha^i(a)) \le z \right\}\right) = \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^z\exp\left(-\frac{t^2}{2\sigma^2}\right)dt \end{align*}$$
$$\begin{align*}\lim_{n\to\infty} \mu\left(\left\{\tau\in \partial_e(T(A)) \mid \frac{1}{\sqrt{n}}\sum_{i=0}^{n-1}\tau(\alpha^i(a)) \le z \right\}\right) = \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^z\exp\left(-\frac{t^2}{2\sigma^2}\right)dt \end{align*}$$
for every
![]() $z\in \mathbb {R}$
. This holds, for example, for tracial dynamical systems given by mixing axiom A diffeomorphisms like hyperbolic toral automorphisms, various systems arising from complex geometry, and certain expanding circle maps (see § 4.2).
$z\in \mathbb {R}$
. This holds, for example, for tracial dynamical systems given by mixing axiom A diffeomorphisms like hyperbolic toral automorphisms, various systems arising from complex geometry, and certain expanding circle maps (see § 4.2).
5 The range of the invariant
Theorem 5.1. Let
![]() $\mathcal {K}$
be the class of infinite-dimensional, simple, separable,
$\mathcal {K}$
be the class of infinite-dimensional, simple, separable,
![]() $KK$
-contractible
$KK$
-contractible
![]() ${\mathrm {C}^*}$
-algebras that satisfy the UCT and have continuous scale, nonempty trace space and finite nuclear dimension. Then, for every
${\mathrm {C}^*}$
-algebras that satisfy the UCT and have continuous scale, nonempty trace space and finite nuclear dimension. Then, for every
![]() $B\in \mathcal {K}$
there exists
$B\in \mathcal {K}$
there exists
![]() $A\in \mathcal {K}$
and an automorphism
$A\in \mathcal {K}$
and an automorphism
![]() $\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
such that
$\alpha \in \operatorname {{\mathrm {Aut}}}(A)$
such that
![]() $\partial _e(T(A))$
is compact and zero dimensional, and
$\partial _e(T(A))$
is compact and zero dimensional, and
![]() $A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
$A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
Proof. By [Reference Downarowicz37, Theorem 3], there is a subshift X of the full shift
![]() $(\{0,1\}^{\mathbb {Z}},h)$
such that the simplex
$(\{0,1\}^{\mathbb {Z}},h)$
such that the simplex
![]() $\mathcal {M}(X)^h$
of h-invariant Borel probability measures on X is affinely homeomorphic to
$\mathcal {M}(X)^h$
of h-invariant Borel probability measures on X is affinely homeomorphic to
![]() $T(B)$
. Let K be a Bauer simplex with
$T(B)$
. Let K be a Bauer simplex with
![]() $\partial _e(K)\cong X$
(namely, the simplex of Borel probability measures on X), and let A be the unique object in
$\partial _e(K)\cong X$
(namely, the simplex of Borel probability measures on X), and let A be the unique object in
![]() $\mathcal {K}$
(up to isomorphism) with
$\mathcal {K}$
(up to isomorphism) with
![]() $T(A)\cong K$
. As in the proof of Theorem 4.9, but appealing to [Reference Elliott, Gong, Lin and Niu41, Theorem 7.5] instead of [Reference Gong, Lin and Niu52, Theorem 5.12], we can extend h to an affine homeomorphism
$T(A)\cong K$
. As in the proof of Theorem 4.9, but appealing to [Reference Elliott, Gong, Lin and Niu41, Theorem 7.5] instead of [Reference Gong, Lin and Niu52, Theorem 5.12], we can extend h to an affine homeomorphism
![]() $T(A)\to T(A)$
and lift it to an automorphism
$T(A)\to T(A)$
and lift it to an automorphism
![]() $\alpha \colon A\to A$
with finite Rokhlin dimension. By Lemma 4.8,
$\alpha \colon A\to A$
with finite Rokhlin dimension. By Lemma 4.8,
![]() $A\rtimes _{\alpha }\mathbb {Z}$
is simple and
$A\rtimes _{\alpha }\mathbb {Z}$
is simple and
![]() ${\mathcal {Z}}$
-stable (since it has finite nuclear dimension – see [Reference Tikuisis87]), and
${\mathcal {Z}}$
-stable (since it has finite nuclear dimension – see [Reference Tikuisis87]), and
The Pimsner–Voiculescu sequence shows that
![]() $A\rtimes _{\alpha }\mathbb {Z}$
is
$A\rtimes _{\alpha }\mathbb {Z}$
is
![]() $KK$
-contractible. The UCT for A passes to the crossed product
$KK$
-contractible. The UCT for A passes to the crossed product
![]() $A\rtimes _{\alpha }\mathbb {Z}$
(see [Reference Blackadar8, 22.3.5]). Finally,
$A\rtimes _{\alpha }\mathbb {Z}$
(see [Reference Blackadar8, 22.3.5]). Finally,
![]() $A\rtimes _{\alpha }\mathbb {Z}$
also satisfies the definition [Reference Elliott, Gong, Lin and Niu42, Definition 5.1] of continuous scale: Fix an increasing approximate unit
$A\rtimes _{\alpha }\mathbb {Z}$
also satisfies the definition [Reference Elliott, Gong, Lin and Niu42, Definition 5.1] of continuous scale: Fix an increasing approximate unit
![]() $(e_n)_{n\in \mathbb {N}}$
for A that satisfies
$(e_n)_{n\in \mathbb {N}}$
for A that satisfies
and such that, for any nonzero positive element
![]() $a\in A$
, there exists
$a\in A$
, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
(where
![]() $\lesssim $
denotes Cuntz subequivalence). Note that
$\lesssim $
denotes Cuntz subequivalence). Note that
![]() $(e_n)_{n\in \mathbb {N}}$
passes to an approximate unit for
$(e_n)_{n\in \mathbb {N}}$
passes to an approximate unit for
![]() $A\rtimes _{\alpha }\mathbb {Z}$
. Since
$A\rtimes _{\alpha }\mathbb {Z}$
. Since
![]() $\|\tau \|=\lim _{n\to \infty }\tau (e_n)$
for any trace
$\|\tau \|=\lim _{n\to \infty }\tau (e_n)$
for any trace
![]() $\tau $
, it follows that all traces on
$\tau $
, it follows that all traces on
![]() $A\rtimes _{\alpha }\mathbb {Z}$
are bounded. Since
$A\rtimes _{\alpha }\mathbb {Z}$
are bounded. Since
![]() $A\rtimes _{\alpha }\mathbb {Z}$
is simple and
$A\rtimes _{\alpha }\mathbb {Z}$
is simple and
![]() ${\mathcal {Z}}$
-stable, it has strict comparison of positive elements (see [Reference Elliott, Robert and Santiago43, Theorem 4.4, Theorem 6.6], and note that there are no compact elements of
${\mathcal {Z}}$
-stable, it has strict comparison of positive elements (see [Reference Elliott, Robert and Santiago43, Theorem 4.4, Theorem 6.6], and note that there are no compact elements of
![]() $\operatorname {{\mathrm {Cu}}}(A\rtimes _{\alpha }\mathbb {Z})$
since
$\operatorname {{\mathrm {Cu}}}(A\rtimes _{\alpha }\mathbb {Z})$
since
![]() $A\rtimes _{\alpha }\mathbb {Z}$
is stably projectionless). In other words, to demonstrate equation (5.1) for some fixed nonzero positive element
$A\rtimes _{\alpha }\mathbb {Z}$
is stably projectionless). In other words, to demonstrate equation (5.1) for some fixed nonzero positive element
![]() $b\in A\rtimes _{\alpha }\mathbb {Z}$
on the right-hand side, it suffices to show that
$b\in A\rtimes _{\alpha }\mathbb {Z}$
on the right-hand side, it suffices to show that
Here,
![]() $d_{\tau }\colon x\mapsto \lim _{n\to \infty }\tau (x^{\frac {1}{n}})$
is the rank function associated to the trace
$d_{\tau }\colon x\mapsto \lim _{n\to \infty }\tau (x^{\frac {1}{n}})$
is the rank function associated to the trace
![]() $\tau $
. For this fixed
$\tau $
. For this fixed
![]() $b\in A\rtimes _{\alpha }\mathbb {Z}$
, the function
$b\in A\rtimes _{\alpha }\mathbb {Z}$
, the function
![]() $T(A)^{\alpha } \to (0,\infty )$
,
$T(A)^{\alpha } \to (0,\infty )$
,
![]() $\tau \mapsto d_{\tau }(b)$
(first extending
$\tau \mapsto d_{\tau }(b)$
(first extending
![]() $\tau \in T(A)^{\alpha }$
uniquely to
$\tau \in T(A)^{\alpha }$
uniquely to
![]() $T(A\rtimes _{\alpha }\mathbb {Z})$
) is lower semicontinuous, hence attains its nonzero minimum
$T(A\rtimes _{\alpha }\mathbb {Z})$
) is lower semicontinuous, hence attains its nonzero minimum
![]() $\varepsilon $
on the compact set
$\varepsilon $
on the compact set
![]() $T(A)^{\alpha }$
. By [Reference Elliott, Robert and Santiago43, Theorem 6.6], there exists a positive element
$T(A)^{\alpha }$
. By [Reference Elliott, Robert and Santiago43, Theorem 6.6], there exists a positive element
![]() $a\in A$
whose Cuntz class corresponds to the constant function
$a\in A$
whose Cuntz class corresponds to the constant function
![]() $\frac {\varepsilon }{2}$
on
$\frac {\varepsilon }{2}$
on
![]() $T(A)$
, that is, for which
$T(A)$
, that is, for which
![]() $d_{\tau }(a)=\frac {\varepsilon }{2}$
for every
$d_{\tau }(a)=\frac {\varepsilon }{2}$
for every
![]() $\tau \in T(A)$
. (We may assume that a is in A, rather than its stabilisation, by replacing
$\tau \in T(A)$
. (We may assume that a is in A, rather than its stabilisation, by replacing
![]() $\varepsilon $
by
$\varepsilon $
by
![]() $\min \{\varepsilon ,1\}$
. Since for any strictly positive element
$\min \{\varepsilon ,1\}$
. Since for any strictly positive element
![]() $h\in A$
, the function
$h\in A$
, the function
![]() $\tau \mapsto d_{\tau }(h)=\|\tau \|$
is constantly
$\tau \mapsto d_{\tau }(h)=\|\tau \|$
is constantly
![]() $1$
on
$1$
on
![]() $T(A)$
, this implies that
$T(A)$
, this implies that
![]() $a\lesssim h$
. By [Reference Elliott, Gong, Lin and Niu42, Theorem 11.5] or [Reference Fu, Li and Lin45, Corollary 6.8], A has stable rank one, so it follows that a is Cuntz equivalent, in fact Murray–von Neumann equivalent, to an element of the hereditary subalgebra generated by h, which is A.) By equation (5.1), there exists
$a\lesssim h$
. By [Reference Elliott, Gong, Lin and Niu42, Theorem 11.5] or [Reference Fu, Li and Lin45, Corollary 6.8], A has stable rank one, so it follows that a is Cuntz equivalent, in fact Murray–von Neumann equivalent, to an element of the hereditary subalgebra generated by h, which is A.) By equation (5.1), there exists
![]() $N\in \mathbb {N}$
such that, for every
$N\in \mathbb {N}$
such that, for every
![]() $m>n\ge N$
and every
$m>n\ge N$
and every
![]() $\tau \in T(A)^{\alpha }$
,
$\tau \in T(A)^{\alpha }$
,
![]() $d_{\tau }(e_m-e_n) \le d_{\tau }(a) < d_{\tau }(b)$
, that is, such that equation (5.2) holds.
$d_{\tau }(e_m-e_n) \le d_{\tau }(a) < d_{\tau }(b)$
, that is, such that equation (5.2) holds.
We have now verified that
![]() $A\rtimes _{\alpha }\mathbb {Z}\in \mathcal {K}$
, and so by the classification obtained in [Reference Elliott, Gong, Lin and Niu41],
$A\rtimes _{\alpha }\mathbb {Z}\in \mathcal {K}$
, and so by the classification obtained in [Reference Elliott, Gong, Lin and Niu41],
![]() $A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
$A\rtimes _{\alpha }\mathbb {Z}\cong B$
.
Remark 5.2.
-
1. Dropping the assumption of continuous scale, the crossed products of Theorem 5.1 cover, up to stable isomorphism, the full class of infinite-dimensional, simple, separable, stably projectionless,
 $KK$
-contractible
$KK$
-contractible
 ${\mathrm {C}^*}$
-algebras that have finite nuclear dimension and satisfy the UCT.
${\mathrm {C}^*}$
-algebras that have finite nuclear dimension and satisfy the UCT. -
2. Suppose that instead of a
 $KK$
-contractible
$KK$
-contractible
 ${\mathrm {C}^*}$
-algebra, A is taken to be a limit of prime dimension drop algebras. Then,
${\mathrm {C}^*}$
-algebra, A is taken to be a limit of prime dimension drop algebras. Then,
 $B=A\rtimes _{\alpha }\mathbb {Z}$
has K-theory
$B=A\rtimes _{\alpha }\mathbb {Z}$
has K-theory  $$\begin{align*}(K_0(B),(K_0(B))_+,[1],K_1(B)) \cong (\mathbb{Z},\mathbb{N},1,\mathbb{Z}). \end{align*}$$
$$\begin{align*}(K_0(B),(K_0(B))_+,[1],K_1(B)) \cong (\mathbb{Z},\mathbb{N},1,\mathbb{Z}). \end{align*}$$
Therefore, the
 ${\mathrm {C}^*}$
-algebras constructed in this way include (up to isomorphism) the algebras
${\mathrm {C}^*}$
-algebras constructed in this way include (up to isomorphism) the algebras
 $C(Z_{\varphi })\rtimes _{\zeta }\mathbb {Z}$
of [Reference Deeley, Putnam and Strung31, §3].
$C(Z_{\varphi })\rtimes _{\zeta }\mathbb {Z}$
of [Reference Deeley, Putnam and Strung31, §3].
Acknowledgements
I am grateful to Ali Asadi–Vasfi, Karen Strung, Andrea Vaccaro, Stuart White and Huaxin Lin for many helpful discussions and to Cape Breton University for giving me the opportunity to teach its statistics courses. I would also like to thank the anonymous referee whose suggestions helped improve the clarity of the article.
Competing interest
The authors have no competing interest to declare.
Financial support
This research was supported by the GAČR project 20-17488Y and RVO: 67985840.