Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T03:50:33.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for twisted symmetric square L-functions via half-integral weight periods

Part of: Partial differential equations on manifolds; differential operators Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  09 November 2020

Paul D. Nelson
Paul D. Nelson*
Affiliation:
ETH Zürich, Department of Mathematics, Rämistrasse 101, CH-8092, Zürich, Switzerland; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish the first moment bound

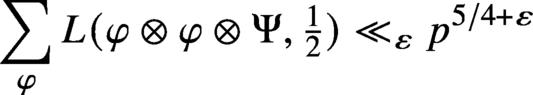
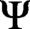$$\begin{align*}\sum_{\varphi} L(\varphi \otimes \varphi \otimes \Psi, \tfrac{1}{2}) \ll_\varepsilon p^{5/4+\varepsilon} \end{align*}$$
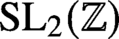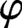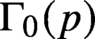for triple product L-functions, where $\Psi $ is a fixed Hecke–Maass form on $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$ and $\varphi $ runs over the Hecke–Maass newforms on $\Gamma _0(p)$ of bounded eigenvalue. The proof is via the theta correspondence and analysis of periods of half-integral weight modular forms. This estimate is not expected to be optimal, but the exponent 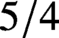$5/4$ is the strongest obtained to date for a moment problem of this shape. We show that the expected upper bound follows if one assumes the Ramanujan conjecture in both the integral and half-integral weight cases.

Under the triple product formula, our result may be understood as a strong level aspect form of quantum ergodicity: for a large prime p, all but very few Hecke–Maass newforms on 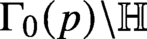$\Gamma _0(p) \backslash \mathbb {H}$ of bounded eigenvalue have very uniformly distributed mass after pushforward to 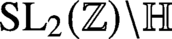$\operatorname {\mathrm {SL}}_2(\mathbb {Z}) \backslash \mathbb {H}$ .

Our main result turns out to be closely related to estimates such as

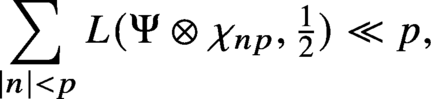
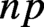$$\begin{align*}\sum_{|n| < p} L(\Psi \otimes \chi_{n p},\tfrac{1}{2}) \ll p, \end{align*}$$
where the sum is over those n for which $n p$ is a fundamental discriminant and 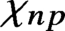$\chi _{n p}$ denotes the corresponding quadratic character. Such estimates improve upon bounds of Duke–Iwaniec.

Keywords

L-functionsfor each term replaceand give space andmodular formshalf-integral weightquadratic twists

MSC classification

Primary: 11F27: Theta series; Weil representation; theta correspondences
Secondary: 11F37: Forms of half-integer weight; nonholomorphic modular forms 58J51: Relations between spectral theory and ergodic theory, e.g. quantum unique ergodicity
Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e44
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Bernstein, Joseph and Reznikov, Andre, ‘Subconvexity bounds for triple $L$ -functions and representation theory’, Ann. of Math. (2) 172(3):1679–1718, 2010.CrossRefGoogle Scholar
Biró, András, ‘A relation between triple products of weight 0 and weight $\frac{1}{2}$ cusp forms’, Israel J. Math. 182:61–101, 2011.CrossRefGoogle Scholar
Blomer, Valentin, ‘Period integrals and Rankin-Selberg $L$ -functions on $\mathrm{GL}(n)$ ’, Geom. Funct. Anal. 22(3):608–620, 2012.CrossRefGoogle Scholar
Colin de Verdière, Y., ‘Ergodicité et fonctions propres du laplacien’, In Bony-Sjöstrand-Meyer seminar, 1984–1985, pages Exp. No. 13, 8 (École Polytech., Palaiseau, 1985).Google Scholar
Conrey, J. B. and Iwaniec, H., ‘The cubic moment of central values of automorphic $L$ -functions’, Ann. of Math. (2) 151(3):1175–1216, 2000.CrossRefGoogle Scholar
NIST Digital Library of Mathematical Functions , http://dlmf.nist.gov/, Release 1.0.26 of 2020-03-15, Olver, F. W. J., Lozier, A. B. Olde Daalhuis D. W., Schneider, B. I., Boisvert, R. F., Clark, C. W., Miller, B. R., Saunders, B. V., Cohl, H. S., and McClain, M. A., eds.Google Scholar
Duke, W., Imamoḡlu, Ö., and Tóth, Á., ‘Geometric invariants for real quadratic fields’, Ann. of Math. (2) 184(3):949–990, 2016.CrossRefGoogle Scholar
Duke, W. and Iwaniec, H., ‘Bilinear forms in the Fourier coefficients of half-integral weight cusp forms and sums over primes’, Math. Ann. 286(4):783–802, 1990.CrossRefGoogle Scholar
Feigon, Brooke and Whitehouse, David, ‘Exact averages of central values of triple product $L$ -functions’, Int. J. Number Theory 6(7):1609–1624, 2010.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘A mean value estimate for real character sums’, Acta Arith. 72(3):235–275, 1995.CrossRefGoogle Scholar
Hoffstein, Jeffrey and Lockhart, Paul, ‘Coefficients of Maass forms and the Siegel zero’, Ann. of Math. (2) 140(1):161–181, 1994, with an appendix by Dorian Goldfeld, Jeffrey Hoffstein, and Daniel Lieman.CrossRefGoogle Scholar
Ichino, Atsushi, ‘Pullbacks of Saito-Kurokawa lifts’, Invent. Math. 162(3):551–647, 2005.CrossRefGoogle Scholar
Iwaniec, H. and Michel, P., ‘The second moment of the symmetric square $L$ -functions’, Ann. Acad. Sci. Fenn. Math. 26(2):465–482, 2001.Google Scholar
Iwaniec, Henryk, Topics in classical automorphic forms , volume 17 of Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 1997).Google Scholar
Iwaniec, Henryk, Spectral methods of automorphic forms , volume 53 of Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 2e, 2002).Google Scholar
Iwaniec, Henryk and Kowalski, Emmanuel. Analytic number theory , volume 53 of American Mathematical Society Colloquium Publications (American Mathematical Society, Providence, RI, 2004).Google Scholar
Jung, Junehyuk, ‘Quantitative quantum ergodicity and the nodal domains of Hecke-Maass cusp forms’, Comm. Math. Phys. 348(2):603–653, 2016.CrossRefGoogle Scholar
Katok, Svetlana and Sarnak, Peter, ‘Heegner points, cycles and Maass forms’, Israel J. Math. 84(1-2):193–227, 1993.CrossRefGoogle Scholar
Le Masson, Etienne and Sahlsten, Tuomas, ‘Quantum ergodicity and Benjamini-Schramm convergence of hyperbolic surfaces’, Duke Math. J. 166(18):3425–3460, 2017.CrossRefGoogle Scholar
Lester, S. and Radziwiłł, M., ‘Quantum Unique Ergodicity for Half-Integral Weight Forms, ArXiv e-prints, June 2016.Google Scholar
Luo, Wenzhi and Sarnak, Peter, ‘Quantum ergodicity of eigenfunctions on ${\mathrm{PSL}}_2(Z)\backslash{H}^2$ ’, Inst. Hautes Études Sci. Publ. Math. (81):207–237, 1995.CrossRefGoogle Scholar
Luo, Wenzhi and Sarnak, Peter, ‘Mass equidistribution for Hecke eigenforms’, Comm. Pure Appl. Math. 56(7):874–891, 2003, dedicated to the memory of Jürgen K. Moser.CrossRefGoogle Scholar
Luo, Wenzhi and Sarnak, Peter, ‘Quantum variance for Hecke eigenforms’, Ann. Sci. École Norm. Sup. (4) 37(5):769–799, 2004.CrossRefGoogle Scholar
Michel, Philippe and Venkatesh, Akshay, ‘The subconvexity problem for ${\mathrm{GL}}_2$ ’, Publ. Math. Inst. Hautes Études Sci. (111):171–271, 2010.CrossRefGoogle Scholar
Nelson, Paul D., ‘Equidistribution of cusp forms in the level aspect’, Duke Math. J. 160(3):467–501, 2011.CrossRefGoogle Scholar
Nelson, Paul D., ‘Evaluating modular forms on Shimura curves’, Math. Comp. 84(295):2471–2503, 2015.CrossRefGoogle Scholar
Nelson, Paul D., ‘Quantum variance on quaternion algebras, I’, preprint, 2016.Google Scholar
Nelson, Paul D., ‘The spectral decomposition of ${\left|\theta \right|}^2$ ’, preprint, 2016.Google Scholar
Nelson, Paul D., ‘Quantum variance on quaternion algebras, II’, preprint, 2017.Google Scholar
Nelson, Paul D., ‘Quantum variance on quaternion algebras, III’, preprint, 2019.Google Scholar
Nelson, Paul D., ‘Subconvex equidistribution of cusp forms: Reduction to Eisenstein observables’, Duke Math. J. 168(9):1665–1722, 2019.CrossRefGoogle Scholar
Qiu, Yannan, ‘Periods of Saito-Kurokawa representations’, Int. Math. Res. Not. IMRN (24):6698–6755, 2014.CrossRefGoogle Scholar
Raimbault, Jean, ‘On the convergence of arithmetic orbifolds’, Ann. Inst. Fourier (Grenoble) 67(6):2547–2596, 2017.CrossRefGoogle Scholar
Sarnak, Peter, ‘Fourth moments of Grössencharakteren zeta functions’, Comm. Pure Appl. Math. 38(2):167–178, 1985.CrossRefGoogle Scholar
Schnirelman, A. I., ‘Ergodic properties of eigenfunctions’, Uspehi Mat. Nauk 29(6(180)):181–182, 1974.Google Scholar
Shimura, Goro, Introduction to the arithmetic theory of automorphic functions . Publications of the Mathematical Society of Japan , No. 11 (Iwanami Shoten, Publishers, Tokyo, 1971), Kanô Memorial Lectures, No. 1.Google Scholar
Shimura, Goro, ‘On modular forms of half integral weight’, Ann. of Math. ( 2 ) 97:440–481, 1973.CrossRefGoogle Scholar
Shintani, Takuro, ‘On construction of holomorphic cusp forms of half integral weight’, Nagoya Math. J. 58:83–126, 1975.CrossRefGoogle Scholar
Soundararajan, K. and Young, Matthew P., ‘The second moment of quadratic twists of modular $L$ -functions’, J. Eur. Math. Soc. (JEMS) 12(5):1097–1116, 2010.CrossRefGoogle Scholar
Steiner, Raphael S., ‘Sup-norm of Hecke-Laplace Eigenforms on ${S}^3$ ’, arXiv e-prints page arXiv:1811.03949, Nov 2018.Google Scholar
Templier, Nicolas and Tsimerman, Jacob, ‘Non-split sums of coefficients of $\mathrm{GL}(2)$ -automorphic forms’, Israel J. Math. 195(2):677–723, 2013.CrossRefGoogle Scholar
Venkatesh, Akshay, ‘Sparse equidistribution problems, period bounds and subconvexity’, Ann. of Math. (2) 172(2):989–1094, 2010.CrossRefGoogle Scholar
Watson, Thomas C., ‘Rankin triple products and quantum chaos’, arXiv.org:0810.0425, 2008.Google Scholar
Zelditch, Steven, ‘Uniform distribution of eigenfunctions on compact hyperbolic surfaces’, Duke Math. J. 55(4):919–941, 1987.CrossRefGoogle Scholar
Zhao, Peng, ‘Quantum variance of Maass-Hecke cusp forms’, Comm. Math. Phys. 297(2):475–514, 2010.CrossRefGoogle Scholar