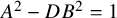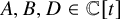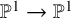1 Introduction
In the last few years Betti maps associated to sections of abelian schemes have been extensively studied and applied to problems of diophantine nature. In this article, we present an apparently new approach, already sketched by the third author in [Reference Zannier34], to study Betti maps in a special case, which is strictly related to the polynomial Pell equation. In particular, we explain how some properties of certain ramified covers of the projective line with prescribed ramification and arising from such equations can be used to prove a special case of a result by André, Corvaja and the third named author [Reference André, Corvaja and Zannier2] on the distribution of the rational values of the Betti map given by a particular section of the family of Jacobians of hyperelliptic curves. In this special case, our approach actually gives something more precise than the result in [Reference André, Corvaja and Zannier2] and allows in principle to obtain a description of the preimage of the set of rational points with fixed denominator; see Corollary 1.6 and the subsequent discussion.
Given an abelian scheme
![]() $\mathcal {A}\rightarrow S$
of relative dimension
$\mathcal {A}\rightarrow S$
of relative dimension
![]() $g\geq 1$
over a smooth complex algebraic variety S and a section
$g\geq 1$
over a smooth complex algebraic variety S and a section
![]() $\sigma :S\rightarrow \mathcal {A}$
, a Betti map for
$\sigma :S\rightarrow \mathcal {A}$
, a Betti map for
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\sigma $
is a real analytic map
$\sigma $
is a real analytic map
![]() $\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2g}$
, where
$\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2g}$
, where
![]() $\tilde {S}$
is the universal covering of
$\tilde {S}$
is the universal covering of
![]() $S(\mathbb {C})$
. This map is of particular relevance in many different contexts; for example, rational points in the image of
$S(\mathbb {C})$
. This map is of particular relevance in many different contexts; for example, rational points in the image of
![]() $\tilde {\beta } $
correspond to torsion values for the section, thus linking the Betti map to other diophantine problems. For an account about the use and the study of Betti maps, see [Reference André, Corvaja and Zannier2, Section 1].
$\tilde {\beta } $
correspond to torsion values for the section, thus linking the Betti map to other diophantine problems. For an account about the use and the study of Betti maps, see [Reference André, Corvaja and Zannier2, Section 1].
The rank
![]() $\operatorname {{\mathrm {rk}}} \tilde {\beta }$
of the Betti map, namely the maximal value of the rank of the derivative
$\operatorname {{\mathrm {rk}}} \tilde {\beta }$
of the Betti map, namely the maximal value of the rank of the derivative
![]() $d\tilde {\beta }(\tilde {s})$
when
$d\tilde {\beta }(\tilde {s})$
when
![]() $\tilde {s}$
runs through
$\tilde {s}$
runs through
![]() $\tilde {S}$
, is of particular interest. Indeed, if
$\tilde {S}$
, is of particular interest. Indeed, if
![]() $\dim S\geq g$
, its maximality is equivalent to the fact that the image of the map contains a dense open subset of
$\dim S\geq g$
, its maximality is equivalent to the fact that the image of the map contains a dense open subset of
![]() $\mathbb {R}^{2g}$
and implies that the preimage of the set of torsion points of
$\mathbb {R}^{2g}$
and implies that the preimage of the set of torsion points of
![]() $\mathcal {A}$
via
$\mathcal {A}$
via
![]() $\sigma $
is dense in
$\sigma $
is dense in
![]() $S(\mathbb {C})$
; see [Reference André, Corvaja and Zannier2, 2.1.1 Proposition].
$S(\mathbb {C})$
; see [Reference André, Corvaja and Zannier2, 2.1.1 Proposition].
In [Reference Corvaja, Masser and Zannier11], the authors studied the rank of Betti maps associated to abelian surface schemes in the context of a relative Manin–Mumford problem. This work initiated more general investigations that led to [Reference André, Corvaja and Zannier2], in which the authors conjectured a sufficient condition for the maximality of
![]() $\operatorname {{\mathrm {rk}}}\tilde {\beta }$
, proving it under some quite general and natural hypotheses (see also [Reference Gao16] for further results on this topic).
$\operatorname {{\mathrm {rk}}}\tilde {\beta }$
, proving it under some quite general and natural hypotheses (see also [Reference Gao16] for further results on this topic).
In particular, in [Reference André, Corvaja and Zannier2], the authors handled the case of a specific nontorsion section of the Jacobian of the universal hyperelliptic curve of genus
![]() $g>0$
. This case is relevant by itself, but it is also linked to an issue raised by Serre [Reference Serre30], who noticed a gap in an article by Robinson [Reference Robinson27], in which the family of hyperelliptic curves over the real numbers appears in connection with the Pell equation in polynomials. In [Reference André, Corvaja and Zannier2, Section 9], the authors give an argument fixing this gap using Betti maps; see also [Reference Bogatyrev7, Reference Peherstorfer25, Reference Totik31, Reference Lawrence18] for independent proofs of the same result.
$g>0$
. This case is relevant by itself, but it is also linked to an issue raised by Serre [Reference Serre30], who noticed a gap in an article by Robinson [Reference Robinson27], in which the family of hyperelliptic curves over the real numbers appears in connection with the Pell equation in polynomials. In [Reference André, Corvaja and Zannier2, Section 9], the authors give an argument fixing this gap using Betti maps; see also [Reference Bogatyrev7, Reference Peherstorfer25, Reference Totik31, Reference Lawrence18] for independent proofs of the same result.
In the first part of this paper, we give an alternative proof of this result in the complex case for a particular but significant section. We obtain this as a consequence of the characterization of the dimension of particular subvarieties arising from solvable Pell equations in the ‘moduli space’ of polynomials of even degree
![]() $\geq 4$
.
$\geq 4$
.
Let
![]() $\mathcal {B}_{2d}$
be the Zariski-open subset of
$\mathcal {B}_{2d}$
be the Zariski-open subset of
![]() $\mathbb {A}^{2d}_{\mathbb {C}}$
defined by
$\mathbb {A}^{2d}_{\mathbb {C}}$
defined by
Given a point
![]() $\overline {s}=(s_1,\dots , s_{2d} ) \in \mathcal {B}_{2d}$
, we consider the affine hyperelliptic curve defined by
$\overline {s}=(s_1,\dots , s_{2d} ) \in \mathcal {B}_{2d}$
, we consider the affine hyperelliptic curve defined by
![]() $y^2=t^{2d}+s_{1}t^{2d-1}+\dots +s_{2d} $
. If we homogenize this equation, we obtain a projective curve which is singular at infinity. There exists, however, a nonsingular model
$y^2=t^{2d}+s_{1}t^{2d-1}+\dots +s_{2d} $
. If we homogenize this equation, we obtain a projective curve which is singular at infinity. There exists, however, a nonsingular model
![]() $H_{\overline {s}}$
with two points at infinity which we denote by
$H_{\overline {s}}$
with two points at infinity which we denote by
![]() $\infty ^+$
and
$\infty ^+$
and
![]() $\infty ^-$
. We fix them by stipulating that the function
$\infty ^-$
. We fix them by stipulating that the function
![]() $t^d\pm y$
has a zero at
$t^d\pm y$
has a zero at
![]() $\infty ^{\pm }$
. The curve
$\infty ^{\pm }$
. The curve
![]() $H_{\overline {s}}$
is then a hyperelliptic curve of genus
$H_{\overline {s}}$
is then a hyperelliptic curve of genus
![]() $d-1$
.
$d-1$
.
We denote by
![]() $\mathcal {J}_{\overline {s}}$
the Jacobian variety of
$\mathcal {J}_{\overline {s}}$
the Jacobian variety of
![]() $H_{\overline {s}}$
; then, letting
$H_{\overline {s}}$
; then, letting
![]() $\overline {s}$
vary in
$\overline {s}$
vary in
![]() $\mathcal {B}_{2d}$
, we have an abelian scheme
$\mathcal {B}_{2d}$
, we have an abelian scheme
![]() $\mathcal {J}\rightarrow S:=\mathcal {B}_{2d}$
of relative dimension
$\mathcal {J}\rightarrow S:=\mathcal {B}_{2d}$
of relative dimension
![]() $g:=d-1$
. We call
$g:=d-1$
. We call
![]() $\sigma :S\rightarrow \mathcal {J}$
the section corresponding to the point
$\sigma :S\rightarrow \mathcal {J}$
the section corresponding to the point
![]() $[\infty ^+-\infty ^-]$
.
$[\infty ^+-\infty ^-]$
.
Let us give an informal definition of the Betti map associated to
![]() $\sigma $
; for a precise definition we refer to [Reference André, Corvaja and Zannier2, Section 3].
$\sigma $
; for a precise definition we refer to [Reference André, Corvaja and Zannier2, Section 3].
In the constant case (that is, when
![]() $\mathcal {J}$
is a complex abelian variety), an abelian logarithm of a point of
$\mathcal {J}$
is a complex abelian variety), an abelian logarithm of a point of
![]() $\mathcal {J}(\mathbb {C})$
can be expressed as an
$\mathcal {J}(\mathbb {C})$
can be expressed as an
![]() $\mathbb {R}$
-linear combination of the elements of a basis of the period lattice. These real coordinates are called Betti coordinates. Note that they depend on the choice of the abelian logarithm and of the basis of the period lattice.
$\mathbb {R}$
-linear combination of the elements of a basis of the period lattice. These real coordinates are called Betti coordinates. Note that they depend on the choice of the abelian logarithm and of the basis of the period lattice.
In the relative setting, the Betti map describes the variation of the Betti coordinates; locally (in the complex topology) on
![]() $S(\mathbb {C})$
, the Lie algebra
$S(\mathbb {C})$
, the Lie algebra
![]() $\text {Lie}(\mathcal {J})$
is the trivial vector bundle of rank g. Moreover, the kernel of the exponential map is a locally constant sheaf on
$\text {Lie}(\mathcal {J})$
is the trivial vector bundle of rank g. Moreover, the kernel of the exponential map is a locally constant sheaf on
![]() $S(\mathbb {C})$
. One can then locally define a real analytic function that associates a point
$S(\mathbb {C})$
. One can then locally define a real analytic function that associates a point
![]() $\overline {s}$
of
$\overline {s}$
of
![]() $S(\mathbb {C})$
to the Betti coordinates of
$S(\mathbb {C})$
to the Betti coordinates of
![]() $\sigma (\overline {s})$
.
$\sigma (\overline {s})$
.
Betti maps are defined for general abelian schemes, and one of the easiest cases which has been deeply studied in literature is that of the Legendre scheme
![]() $\mathcal {L}$
. In this case, the base S is the curve
$\mathcal {L}$
. In this case, the base S is the curve
![]() $\mathbb {P}^1 \setminus \{0,1,\infty \}$
and
$\mathbb {P}^1 \setminus \{0,1,\infty \}$
and
![]() $\mathcal {L}\rightarrow \mathbb {P}^1$
is the abelian scheme having fibers in
$\mathcal {L}\rightarrow \mathbb {P}^1$
is the abelian scheme having fibers in
![]() $\mathbb {P}^2$
defined by
$\mathbb {P}^2$
defined by
for every
![]() $\lambda \in \mathbb {P}^1 \setminus \{0,1,\infty \}$
. Consequently,
$\lambda \in \mathbb {P}^1 \setminus \{0,1,\infty \}$
. Consequently,
![]() $\mathcal {L}$
is embedded in
$\mathcal {L}$
is embedded in
![]() $\mathbb {P}^1\setminus \{0,1,\infty \}\times \mathbb {P}^2$
. Locally, one can define a basis of periods using the hypergeometric functions. Indeed, for example, for
$\mathbb {P}^1\setminus \{0,1,\infty \}\times \mathbb {P}^2$
. Locally, one can define a basis of periods using the hypergeometric functions. Indeed, for example, for
![]() $\lambda $
in the region
$\lambda $
in the region
![]() $D=\{|\lambda |<1 \mbox { and } |1-\lambda |<1\}\subseteq S$
, a suitable basis of periods is given by
$D=\{|\lambda |<1 \mbox { and } |1-\lambda |<1\}\subseteq S$
, a suitable basis of periods is given by
![]() $f(\lambda ):=\pi F(\lambda )$
and
$f(\lambda ):=\pi F(\lambda )$
and
![]() $g(\lambda ):=\pi iF(1-\lambda )$
, where
$g(\lambda ):=\pi iF(1-\lambda )$
, where
![]() $F(\lambda )=\sum _{m=0}^{\infty } \frac {(m!)^2}{2^{4m}(m!)^4}\lambda ^m$
. Given a section
$F(\lambda )=\sum _{m=0}^{\infty } \frac {(m!)^2}{2^{4m}(m!)^4}\lambda ^m$
. Given a section
![]() $\sigma : S \rightarrow \mathcal L$
, locally over D one can take its elliptic logarithm z and write it as
$\sigma : S \rightarrow \mathcal L$
, locally over D one can take its elliptic logarithm z and write it as
![]() $z=u_1f+u_2g$
, where the functions
$z=u_1f+u_2g$
, where the functions
![]() $u_i$
are real analytic functions. Hence, the Betti map
$u_i$
are real analytic functions. Hence, the Betti map
![]() $\beta : D \rightarrow \mathbb {R}^2$
associated to
$\beta : D \rightarrow \mathbb {R}^2$
associated to
![]() $\sigma $
is given by
$\sigma $
is given by
![]() $\beta (\lambda )=(u_1(\lambda ), u_2(\lambda ))$
.
$\beta (\lambda )=(u_1(\lambda ), u_2(\lambda ))$
.
In general, this map cannot be extended to the whole of
![]() $S(\mathbb {C})$
because of monodromy, but we can pass to the universal covering
$S(\mathbb {C})$
because of monodromy, but we can pass to the universal covering
![]() $\tilde {S}$
of
$\tilde {S}$
of
![]() $S(\mathbb {C})$
and define a Betti map
$S(\mathbb {C})$
and define a Betti map
![]() $\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
, which is not unique and depends on several choices. The following is our first result.
$\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
, which is not unique and depends on several choices. The following is our first result.
Theorem 1.1. Let d be an integer
![]() $\geq 2$
, and let
$\geq 2$
, and let
![]() $\mathcal {J}\rightarrow S$
and
$\mathcal {J}\rightarrow S$
and
![]() $\sigma :S\rightarrow \mathcal {J}$
be the abelian scheme and the section defined above. Then the corresponding Betti map
$\sigma :S\rightarrow \mathcal {J}$
be the abelian scheme and the section defined above. Then the corresponding Betti map
![]() $\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
satisfies
$\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
satisfies
![]() $\operatorname {{\mathrm {rk}}} \tilde {\beta }\geq 2(d-1)$
; equivalently,
$\operatorname {{\mathrm {rk}}} \tilde {\beta }\geq 2(d-1)$
; equivalently,
![]() $\tilde {\beta }$
is submersive on a dense open subset of
$\tilde {\beta }$
is submersive on a dense open subset of
![]() $\tilde {S}$
. In particular, the set of
$\tilde {S}$
. In particular, the set of
![]() $\overline {s}\in S(\mathbb {C})$
such that
$\overline {s}\in S(\mathbb {C})$
such that
![]() $\sigma (\overline {s})$
is torsion on
$\sigma (\overline {s})$
is torsion on
![]() $\mathcal {J}_{\overline {s}}$
is dense in
$\mathcal {J}_{\overline {s}}$
is dense in
![]() $S(\mathbb {C})$
in the complex topology.
$S(\mathbb {C})$
in the complex topology.
The above theorem is a special case of [Reference André, Corvaja and Zannier2, 2.3.3 Theorem]; however, we are going to give a different proof of it in Section 3. Our proof makes use of the connection between the torsion values of the section
![]() $\sigma : S \rightarrow \mathcal {J}$
corresponding to the point
$\sigma : S \rightarrow \mathcal {J}$
corresponding to the point
![]() $[\infty ^+ - \infty ^-]$
and the polynomial Pell equation.
$[\infty ^+ - \infty ^-]$
and the polynomial Pell equation.
We recall that the classical Pell equation is an equation of the form
![]() $A^2-DB^2=1$
where D is a positive integer to be solved in integers A and B with
$A^2-DB^2=1$
where D is a positive integer to be solved in integers A and B with
![]() $B\neq 0$
. A theorem of Lagrange says that such an equation is nontrivially solvable if and only if D is not a perfect square.
$B\neq 0$
. A theorem of Lagrange says that such an equation is nontrivially solvable if and only if D is not a perfect square.
We consider the polynomial analogue of this problem, replacing
![]() $\mathbb {Z}$
by a polynomial ring over a field. This variant is old as well and can be dated back to studies by Abel [Reference Abel1] especially in the context of integration in finite terms of certain algebraic differentials. Lately, these studies have been carried out by several authors (see [Reference Bogatyrev8, Reference Serre30, Reference Masser and Zannier23] for more details). Apart from their link with points of finite order in Jacobians of hyperelliptic curves, the polynomial Pell equation, which from now on we will call a Pell–Abel equation as suggested by Serre in [Reference Serre30], has several connections with other mathematical problems, like polynomial continued fractions [Reference Zannier35] and elliptical billiards [Reference Dragović and Radnovic13, Reference Corvaja and Zannier12] but also problems in mathematical physics [Reference Burskii and Zhedanov9] and dynamical systems [Reference McMullen20].
$\mathbb {Z}$
by a polynomial ring over a field. This variant is old as well and can be dated back to studies by Abel [Reference Abel1] especially in the context of integration in finite terms of certain algebraic differentials. Lately, these studies have been carried out by several authors (see [Reference Bogatyrev8, Reference Serre30, Reference Masser and Zannier23] for more details). Apart from their link with points of finite order in Jacobians of hyperelliptic curves, the polynomial Pell equation, which from now on we will call a Pell–Abel equation as suggested by Serre in [Reference Serre30], has several connections with other mathematical problems, like polynomial continued fractions [Reference Zannier35] and elliptical billiards [Reference Dragović and Radnovic13, Reference Corvaja and Zannier12] but also problems in mathematical physics [Reference Burskii and Zhedanov9] and dynamical systems [Reference McMullen20].
Let K be a field of characteristic 0. For a nonconstant polynomial
![]() $D(t)\in K[t]$
, we look for solutions of
$D(t)\in K[t]$
, we look for solutions of
where
![]() $A(t),B(t)\in K[t]$
and
$A(t),B(t)\in K[t]$
and
![]() $B\neq 0$
; if such a solution exists, we call the polynomial D Pellian. Clearly, necessary conditions for a polynomial D to be Pellian are that D has even degree and it is not a square in
$B\neq 0$
; if such a solution exists, we call the polynomial D Pellian. Clearly, necessary conditions for a polynomial D to be Pellian are that D has even degree and it is not a square in
![]() $K[t]$
, but the leading coefficient is a square in K. Unlike the integer case, these conditions are not sufficient to guarantee the existence of a nontrivial solution, and there are examples of non-Pellian polynomials satisfying these conditions (see, for example, [Reference Zannier34]).
$K[t]$
, but the leading coefficient is a square in K. Unlike the integer case, these conditions are not sufficient to guarantee the existence of a nontrivial solution, and there are examples of non-Pellian polynomials satisfying these conditions (see, for example, [Reference Zannier34]).
If K is algebraically closed (in particular
![]() $K=\mathbb {C}$
) there is a criterion, attributed to Chebyshev in [Reference Berry4], that links the solvability of a Pell–Abel equation to the order of the point
$K=\mathbb {C}$
) there is a criterion, attributed to Chebyshev in [Reference Berry4], that links the solvability of a Pell–Abel equation to the order of the point
![]() $[\infty ^+-\infty ^-]$
in the Jacobian of the hyperelliptic curve defined by the equation
$[\infty ^+-\infty ^-]$
in the Jacobian of the hyperelliptic curve defined by the equation
![]() $y^2=D(t)$
.
$y^2=D(t)$
.
Proposition 1.2 (see [Reference Zannier34, Proposition 12.1]).
Let
![]() $D\in K[t]$
be a squarefree polynomial of degree
$D\in K[t]$
be a squarefree polynomial of degree
![]() $2d\geq 4$
. Then the Pell–Abel equation
$2d\geq 4$
. Then the Pell–Abel equation
![]() $A^2-DB^2=1$
has a nontrivial solution
$A^2-DB^2=1$
has a nontrivial solution
![]() $A,B \in \overline {K}[t]$
with
$A,B \in \overline {K}[t]$
with
![]() $B \neq 0$
if and only if the point
$B \neq 0$
if and only if the point
![]() $[\infty ^+-\infty ^-]$
has finite order in the Jacobian of the smooth projective model of the affine hyperelliptic curve of equation
$[\infty ^+-\infty ^-]$
has finite order in the Jacobian of the smooth projective model of the affine hyperelliptic curve of equation
![]() $y^2=D(t)$
. Moreover, the order of
$y^2=D(t)$
. Moreover, the order of
![]() $[\infty ^+-\infty ^-]$
is the minimal degree of the polynomial A of a nontrivial solution.
$[\infty ^+-\infty ^-]$
is the minimal degree of the polynomial A of a nontrivial solution.
We point out that a similar criterion holds as well in the case of nonsquarefree D, by using generalized Jacobians (for more on this, see [Reference Zannier35]).
As in the integer case, if
![]() $D(t)$
is Pellian, then the associated Pell–Abel equation has infinitely many solutions in
$D(t)$
is Pellian, then the associated Pell–Abel equation has infinitely many solutions in
![]() $\overline {K}[t]$
. Indeed, a possible nontrivial solution
$\overline {K}[t]$
. Indeed, a possible nontrivial solution
![]() $(A,B)$
generates infinitely many ones by taking powers
$(A,B)$
generates infinitely many ones by taking powers
![]() $A_m+\sqrt {D}B_m:=\pm \left (A\pm \sqrt {D}B\right )^m$
. Moreover, solutions to the Pell–Abel equation correspond to the units of the ring
$A_m+\sqrt {D}B_m:=\pm \left (A\pm \sqrt {D}B\right )^m$
. Moreover, solutions to the Pell–Abel equation correspond to the units of the ring
![]() $\overline {K}[\sqrt {D}]$
which form a group isomorphic to
$\overline {K}[\sqrt {D}]$
which form a group isomorphic to
![]() $\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
.
$\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
.
We will call a solution primitive if it has minimal degree among all the nontrivial ones. On the other hand, we say that a solution
![]() $(A_m,B_m)$
is an m-th power when it can be obtained from another one as explained above. Notice that every solution of the Pell–Abel equation will then be a power of a primitive one.
$(A_m,B_m)$
is an m-th power when it can be obtained from another one as explained above. Notice that every solution of the Pell–Abel equation will then be a power of a primitive one.
We call degree of a solution
![]() $(A,B)$
the degree of A. Thus, the order of
$(A,B)$
the degree of A. Thus, the order of
![]() $[\infty ^+-\infty ^-]$
, if finite, is the degree of a primitive solution of the corresponding Pell–Abel equation.
$[\infty ^+-\infty ^-]$
, if finite, is the degree of a primitive solution of the corresponding Pell–Abel equation.
If we consider the abelian scheme
![]() $\mathcal {J} \rightarrow S=\mathcal {B}_{2d}$
as above and the section
$\mathcal {J} \rightarrow S=\mathcal {B}_{2d}$
as above and the section
![]() $\sigma : S\rightarrow \mathcal {J}$
corresponding to the point
$\sigma : S\rightarrow \mathcal {J}$
corresponding to the point
![]() $[\infty ^+-\infty ^-]$
, we have that the polynomial
$[\infty ^+-\infty ^-]$
, we have that the polynomial
![]() $D_{\overline {s}}=t^{2d}+s_{1}t^{2d-1}+\dots +s_{2d}$
is Pellian with primitive solution of degree n if and only if
$D_{\overline {s}}=t^{2d}+s_{1}t^{2d-1}+\dots +s_{2d}$
is Pellian with primitive solution of degree n if and only if
![]() $\sigma (\overline {s})$
is a torsion point of order n.
$\sigma (\overline {s})$
is a torsion point of order n.
We define the Pellian locus
![]() $\mathcal {P}_{2d}$
in
$\mathcal {P}_{2d}$
in
![]() $\mathcal {B}_{2d}$
to be
$\mathcal {B}_{2d}$
to be
We have the following result.
Theorem 1.3. For
![]() $d\geq 2$
, the set
$d\geq 2$
, the set
![]() $\mathcal {P}_{2d}(\mathbb {C})$
of Pellian complex polynomials is dense in
$\mathcal {P}_{2d}(\mathbb {C})$
of Pellian complex polynomials is dense in
![]() $\mathcal {B}_{2d}(\mathbb {C})$
with respect to the complex topology.
$\mathcal {B}_{2d}(\mathbb {C})$
with respect to the complex topology.
We point out here that the distribution of Pellian polynomials in families, and its connection to problems of unlikely intersections has been investigated (often using Betti maps) in recent years, mainly in the case of curves in
![]() $\mathcal {B}_{2d}$
where the behaviour is completely opposite to what happens in the setting of the above theorem (for a general account on the problems of unlikely intersections, see [Reference Zannier33]). Indeed, for instance, in [Reference Masser and Zannier22] and [Reference Masser and Zannier23], the authors show that a generic curve in
$\mathcal {B}_{2d}$
where the behaviour is completely opposite to what happens in the setting of the above theorem (for a general account on the problems of unlikely intersections, see [Reference Zannier33]). Indeed, for instance, in [Reference Masser and Zannier22] and [Reference Masser and Zannier23], the authors show that a generic curve in
![]() $\mathcal {B}_{2d}$
, where
$\mathcal {B}_{2d}$
, where
![]() $d\geq 3$
, contains at most finitely many complex points that correspond to Pellian polynomials. One can see also [Reference Bertrand, Masser, Pillay and Zannier6] and [Reference Schmidt29] for the nonsquarefree case and [Reference Barroero and Capuano3] for similar results for the generalized Pell–Abel equation.
$d\geq 3$
, contains at most finitely many complex points that correspond to Pellian polynomials. One can see also [Reference Bertrand, Masser, Pillay and Zannier6] and [Reference Schmidt29] for the nonsquarefree case and [Reference Barroero and Capuano3] for similar results for the generalized Pell–Abel equation.
Clearly, Theorem 1.3 is a consequence of Proposition 1.2 and Theorem 1.1 (and thus of [Reference André, Corvaja and Zannier2]); however, in this paper we present a different proof of these two results with the principal aim of showing the link between the Betti maps and some properties of certain ramified covers of the projective line with fixed ramification. Moreover, we are able to study more deeply the Pellian locus
![]() $\mathcal {P}_{2d} \subseteq \mathcal {B}_{2d}$
and to show that it consists of a denumerable union of algebraic subvarieties of
$\mathcal {P}_{2d} \subseteq \mathcal {B}_{2d}$
and to show that it consists of a denumerable union of algebraic subvarieties of
![]() $\mathcal {B}_{2d}$
of dimension at most
$\mathcal {B}_{2d}$
of dimension at most
![]() $d+1$
(see Proposition 3.1), each one coming from the preimage of a rational point of a Betti map
$d+1$
(see Proposition 3.1), each one coming from the preimage of a rational point of a Betti map
![]() $\tilde {\beta } $
. If
$\tilde {\beta } $
. If
![]() $\tilde {\beta }$
did not have maximal rank, then these preimages would have dimension strictly larger than
$\tilde {\beta }$
did not have maximal rank, then these preimages would have dimension strictly larger than
![]() $d+1$
.
$d+1$
.
To study the Pellian locus
![]() $\mathcal {P}_{2d}$
, we associate to a degree n solution
$\mathcal {P}_{2d}$
, we associate to a degree n solution
![]() $(A,B)$
of a Pell–Abel equation the ramified cover of degree
$(A,B)$
of a Pell–Abel equation the ramified cover of degree
![]() $2n$
given by
$2n$
given by
![]() $A^2:\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
. Because of the Pell–Abel equation, the latter has to be ramified above 0, 1 and
$A^2:\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
. Because of the Pell–Abel equation, the latter has to be ramified above 0, 1 and
![]() $\infty $
and, by the Riemann–Hurwitz formula, at most
$\infty $
and, by the Riemann–Hurwitz formula, at most
![]() $d-1$
additional points, independently of n. For this reason, we call these maps, following the third author in [Reference Zannier34], almost-Belyi maps.
$d-1$
additional points, independently of n. For this reason, we call these maps, following the third author in [Reference Zannier34], almost-Belyi maps.
The Riemann existence theorem gives a link between such covers and permutation representations. To be more precise, if our cover of degree
![]() $2n$
has h branch points, an h-tuple
$2n$
has h branch points, an h-tuple
![]() $\Sigma $
of elements of
$\Sigma $
of elements of
![]() $S_{2n}$
can be associated to it. These permutations satisfy certain properties, for example, they have very strong constrains on their cycle structure. On the other hand, fixing the branch points and a tuple of permutations satisfying these properties determines the map up to automorphisms of the domain.
$S_{2n}$
can be associated to it. These permutations satisfy certain properties, for example, they have very strong constrains on their cycle structure. On the other hand, fixing the branch points and a tuple of permutations satisfying these properties determines the map up to automorphisms of the domain.
It turns out that one can determine whether a solution associated to a certain representation is primitive or a power of another one by looking at the partitions of
![]() $\{1, \dots , 2n\}$
preserved by the subgroup of
$\{1, \dots , 2n\}$
preserved by the subgroup of
![]() $S_{2n}$
generated by the same representation, that is, the monodromy group of the cover.
$S_{2n}$
generated by the same representation, that is, the monodromy group of the cover.
Theorem 1.4 (Theorem 6.2).
Let
![]() $(A,B)$
be a solution of degree n of a Pell–Abel equation
$(A,B)$
be a solution of degree n of a Pell–Abel equation
![]() $A^2-DB^2=1$
with
$A^2-DB^2=1$
with
![]() $\deg D=2d$
, and let
$\deg D=2d$
, and let
![]() $G_A$
be the monodromy group of
$G_A$
be the monodromy group of
![]() $A^2$
. Then, for every integer
$A^2$
. Then, for every integer
![]() $m\mid n$
with
$m\mid n$
with
![]() $\frac {n}{m} \ge d$
,
$\frac {n}{m} \ge d$
,
![]() $(A,B)$
is the m-th power of another solution if and only if
$(A,B)$
is the m-th power of another solution if and only if
![]() $G_A$
preserves a partition of the set
$G_A$
preserves a partition of the set
![]() $\{1,\dots , 2n\}$
in
$\{1,\dots , 2n\}$
in
![]() $2m$
subsets, each of cardinality
$2m$
subsets, each of cardinality
![]() $\frac {n}{m}$
.
$\frac {n}{m}$
.
In [Reference Zannier34], the third author gives an example of a permutation representation associated to a Pell–Abel equation of arbitrary degree; see Example 2.4 below. Using the above criterion it is easy to see that the corresponding solution of the Pell–Abel equation is primitive, and this implies that, after fixing their degree, there are Pellian polynomials with primitive solutions of any possible degree.
Corollary 1.5. Let
![]() $d,n$
be positive integers with
$d,n$
be positive integers with
![]() $n\geq d\geq 2$
. Then there exists a squarefree Pellian
$n\geq d\geq 2$
. Then there exists a squarefree Pellian
![]() $D\in \mathbb {C}[t]$
of degree
$D\in \mathbb {C}[t]$
of degree
![]() $2d$
such that a primitive solution of the corresponding Pell–Abel equation (1.2) has degree n.
$2d$
such that a primitive solution of the corresponding Pell–Abel equation (1.2) has degree n.
Going back to our Betti map
![]() $\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
associated to the abelian scheme
$\tilde {\beta }: \tilde {S}\rightarrow \mathbb {R}^{2(d-1)}$
associated to the abelian scheme
![]() $\mathcal {J} \rightarrow S$
, we can deduce some properties of the rational points in the image
$\mathcal {J} \rightarrow S$
, we can deduce some properties of the rational points in the image
![]() $\tilde {\beta }(\tilde {S})$
. We call the denominator of a rational point of
$\tilde {\beta }(\tilde {S})$
. We call the denominator of a rational point of
![]() $\mathbb {R}^{2(d-1)}$
the positive least common denominator of the coordinates of the point.
$\mathbb {R}^{2(d-1)}$
the positive least common denominator of the coordinates of the point.
It is easy to see that there are no nonzero points of denominator
![]() $< d$
, since a nontrivial solution of the Pell–Abel equation has degree at least d. From [Reference André, Corvaja and Zannier2], one can easily deduce that
$< d$
, since a nontrivial solution of the Pell–Abel equation has degree at least d. From [Reference André, Corvaja and Zannier2], one can easily deduce that
![]() $\tilde {\beta }(\tilde {S})$
contains rational points of every denominator
$\tilde {\beta }(\tilde {S})$
contains rational points of every denominator
![]() $\geq n_0$
for some large enough natural number
$\geq n_0$
for some large enough natural number
![]() $n_0$
. Our Corollary 1.5 implies the following result.
$n_0$
. Our Corollary 1.5 implies the following result.
Corollary 1.6. The image
![]() $\tilde {\beta }(\tilde {S})$
of the Betti map contains a point of denominator n for all
$\tilde {\beta }(\tilde {S})$
of the Betti map contains a point of denominator n for all
![]() $n\geq d$
.
$n\geq d$
.
In a recent work [Reference Corvaja, Demeio, Masser and Zannier10], the authors consider the distribution of points of the base of an elliptic scheme where a section takes torsion values. Those are exactly the points of the base where the corresponding Betti map takes rational values. More specifically, they prove that the number of points where the Betti map takes a rational value with denominator (dividing) n is, for large n, essentially
![]() $n^2$
times the area of the base with respect to the measure obtained locally by pulling back the Lebesgue measure on
$n^2$
times the area of the base with respect to the measure obtained locally by pulling back the Lebesgue measure on
![]() $\mathbb {R}^2$
by the Betti map. Moreover, they show that the constant of the main term is equal to
$\mathbb {R}^2$
by the Betti map. Moreover, they show that the constant of the main term is equal to
![]() $\hat {h}(\sigma )$
, where
$\hat {h}(\sigma )$
, where
![]() $\hat h$
is the canonical height associated to twice the divisor at infinity on the elliptic scheme.
$\hat h$
is the canonical height associated to twice the divisor at infinity on the elliptic scheme.
The corresponding result for our family of Jacobians
![]() $\mathcal {J} \rightarrow S$
and our section would probably give an asymptotic formula for the number of equivalence classes of polynomials D of fixed degree
$\mathcal {J} \rightarrow S$
and our section would probably give an asymptotic formula for the number of equivalence classes of polynomials D of fixed degree
![]() $2d\geq 4$
satisfying a Pell–Abel equation
$2d\geq 4$
satisfying a Pell–Abel equation
![]() $A^2-DB^2=1$
with A of degree n, for n tending to infinity.
$A^2-DB^2=1$
with A of degree n, for n tending to infinity.
On the other hand, using the correspondence given by the Riemann existence theorem explained above, one is able to determine the exact number of equivalence classes of Pell–Abel equations of fixed degree n. In Section 8, we compute this number in the case
![]() $d=2$
. We point out that, as d grows, the combinatorics behind the problem becomes more complicated, but this approach would still work in principle.
$d=2$
. We point out that, as d grows, the combinatorics behind the problem becomes more complicated, but this approach would still work in principle.
In turn, this complete classification should allow to compute the number of components of
![]() $\mathcal {P}_{2d}\subseteq \mathcal {B}_{2d}$
that map via the Betti map to rational points of fixed denominator rather than just an asymptotic formula analogous to the one in [Reference Corvaja, Demeio, Masser and Zannier10].
$\mathcal {P}_{2d}\subseteq \mathcal {B}_{2d}$
that map via the Betti map to rational points of fixed denominator rather than just an asymptotic formula analogous to the one in [Reference Corvaja, Demeio, Masser and Zannier10].
Right before this article was published, Fedor Pakovich pointed out his paper [Reference Pakovitch24] to the authors. It contains several remarks about the Pell–Abel equation, points of finite order on Jacobians and Belyi maps which are deeply related to our work.
2 Almost-Belyi maps
Given a (squarefree) Pellian polynomial
![]() $D(t)$
of degree
$D(t)$
of degree
![]() $2d$
and a solution
$2d$
and a solution
![]() $(A, B)$
of degree n of the corresponding Pell–Abel equation
$(A, B)$
of degree n of the corresponding Pell–Abel equation
![]() $A^2-D(t)B^2=1$
, we consider the map
$A^2-D(t)B^2=1$
, we consider the map
![]() $\phi _A:=A^2 : \mathbb {P}^1(\mathbb {C}) \rightarrow \mathbb {P}^1(\mathbb {C})$
of degree
$\phi _A:=A^2 : \mathbb {P}^1(\mathbb {C}) \rightarrow \mathbb {P}^1(\mathbb {C})$
of degree
![]() $2n$
.
$2n$
.
It is easy to see that the Pell–Abel equation forces the branching of the map
![]() $\phi _A$
to be ‘concentrated’ in
$\phi _A$
to be ‘concentrated’ in
![]() $ 0,\ 1$
and
$ 0,\ 1$
and
![]() $\infty $
. First, since
$\infty $
. First, since
![]() $\phi _A$
is a polynomial, there is total ramification above
$\phi _A$
is a polynomial, there is total ramification above
![]() $\infty $
. Moreover, as
$\infty $
. Moreover, as
![]() $\phi _{A}$
is a square and
$\phi _{A}$
is a square and
![]() $\phi _A-1=DB^2$
, we have that the ramification indices above
$\phi _A-1=DB^2$
, we have that the ramification indices above
![]() $0$
are all even, while the ones above
$0$
are all even, while the ones above
![]() $1$
are all even with the exception of
$1$
are all even with the exception of
![]() $2d$
points (the simple roots of
$2d$
points (the simple roots of
![]() $D(t)$
). Hence, counting the branching of
$D(t)$
). Hence, counting the branching of
![]() $\phi _A$
as the sum of
$\phi _A$
as the sum of
![]() $e-1$
over the ramification indices e, we have that above
$e-1$
over the ramification indices e, we have that above
![]() $0$
the branching is at least n, above
$0$
the branching is at least n, above
![]() $1$
at least
$1$
at least
![]() $n-d$
and above
$n-d$
and above
![]() $\infty $
it is exactly
$\infty $
it is exactly
![]() $2n-1$
. On the other hand, by the Riemann–Hurwitz formula (see [Reference Hindry and Silverman17, Theorem A.4.2.5., p. 72]), the total branching is equal to
$2n-1$
. On the other hand, by the Riemann–Hurwitz formula (see [Reference Hindry and Silverman17, Theorem A.4.2.5., p. 72]), the total branching is equal to
![]() $4n-2$
. This means that the branching outside
$4n-2$
. This means that the branching outside
![]() $0,1,\infty $
is at most
$0,1,\infty $
is at most
![]() $d-1$
, and thus there cannot be more than
$d-1$
, and thus there cannot be more than
![]() $d-1$
further branch points. Following the third author [Reference Zannier34], we call
$d-1$
further branch points. Following the third author [Reference Zannier34], we call
![]() $\phi _A$
an almost-Belyi map as its branching is ‘concentrated’ above
$\phi _A$
an almost-Belyi map as its branching is ‘concentrated’ above
![]() $0,1, \infty $
(in the sense that the number of branch points outside this set does not depend on the degree n of
$0,1, \infty $
(in the sense that the number of branch points outside this set does not depend on the degree n of
![]() $\phi _A$
but only on the degree of D which is fixed)Footnote
1
.
$\phi _A$
but only on the degree of D which is fixed)Footnote
1
.
To each such map, we can associate a monodromy permutation representation in the following way (for references see [Reference Fried15], [Reference Miranda21] or [Reference Völklein32]).
Let us call
![]() $\mathcal {B}=\{b_1, \ldots , b_{h}\}$
the set of the branch points of
$\mathcal {B}=\{b_1, \ldots , b_{h}\}$
the set of the branch points of
![]() $\phi _A$
(where
$\phi _A$
(where
![]() $h\le d+2$
), and let us choose a base point q different from the
$h\le d+2$
), and let us choose a base point q different from the
![]() $b_i$
. Let us moreover call
$b_i$
. Let us moreover call
![]() $V:=\mathbb {P}^1(\mathbb {C})\setminus \mathcal {B}$
. The fundamental group
$V:=\mathbb {P}^1(\mathbb {C})\setminus \mathcal {B}$
. The fundamental group
![]() $\pi _1(V,q)$
of V is a free group on h generators
$\pi _1(V,q)$
of V is a free group on h generators
![]() $[\gamma _1],\ldots ,[\gamma _{h}]$
modulo the relation
$[\gamma _1],\ldots ,[\gamma _{h}]$
modulo the relation
where each
![]() $\gamma _i:[0,1]\rightarrow V$
is a closed path which winds once around
$\gamma _i:[0,1]\rightarrow V$
is a closed path which winds once around
![]() $b_i$
. Now, consider the fiber
$b_i$
. Now, consider the fiber
![]() $\phi _A^{-1}(q)$
above q, and denote by
$\phi _A^{-1}(q)$
above q, and denote by
![]() $q_1, \ldots , q_{2n}$
the
$q_1, \ldots , q_{2n}$
the
![]() $2n$
distinct points in this fiber. Every loop
$2n$
distinct points in this fiber. Every loop
![]() $\gamma \subseteq V$
based at q and not passing through the
$\gamma \subseteq V$
based at q and not passing through the
![]() $b_i$
can be lifted to
$b_i$
can be lifted to
![]() $2n$
paths
$2n$
paths
![]() $\tilde {\gamma }_1, \ldots , \tilde {\gamma }_{2n}$
, where
$\tilde {\gamma }_1, \ldots , \tilde {\gamma }_{2n}$
, where
![]() $\tilde {\gamma }_j$
is the unique lift of
$\tilde {\gamma }_j$
is the unique lift of
![]() $\gamma $
starting at
$\gamma $
starting at
![]() $q_j$
. Hence,
$q_j$
. Hence,
![]() $\tilde {\gamma }_j(0)=q_j$
for every j. Now, consider the endpoints
$\tilde {\gamma }_j(0)=q_j$
for every j. Now, consider the endpoints
![]() $\tilde {\gamma }_j(1)$
; these also lie in the fiber
$\tilde {\gamma }_j(1)$
; these also lie in the fiber
![]() $\phi _A^{-1}(q)$
and indeed form the entire preimage set
$\phi _A^{-1}(q)$
and indeed form the entire preimage set
![]() $\{q_1, \ldots , q_{2n}\}$
. We call
$\{q_1, \ldots , q_{2n}\}$
. We call
![]() $\sigma (j)$
the index in
$\sigma (j)$
the index in
![]() $\{1, \ldots , 2n\}$
such that
$\{1, \ldots , 2n\}$
such that
![]() $\tilde {\gamma }_j(1)=q_{\sigma (j)}$
. The function
$\tilde {\gamma }_j(1)=q_{\sigma (j)}$
. The function
![]() $\sigma $
is then a permutation of the set
$\sigma $
is then a permutation of the set
![]() $\{1, \ldots , 2n\}$
which depends only on the homotopy class of
$\{1, \ldots , 2n\}$
which depends only on the homotopy class of
![]() $\gamma $
; therefore, we have a group homomorphism
$\gamma $
; therefore, we have a group homomorphism
![]() $\rho :\pi _1(V,q) \longrightarrow S_{2n}$
called the monodromy representation of the covering map
$\rho :\pi _1(V,q) \longrightarrow S_{2n}$
called the monodromy representation of the covering map
![]() $\phi _A$
. This is clearly determined by the images
$\phi _A$
. This is clearly determined by the images
![]() $\sigma _i=\rho ([\gamma _i])$
of the generators of
$\sigma _i=\rho ([\gamma _i])$
of the generators of
![]() $\pi _1(V,q)$
, and the image of
$\pi _1(V,q)$
, and the image of
![]() $\rho $
must be a transitive subgroup of
$\rho $
must be a transitive subgroup of
![]() $S_{2n}$
, as V is connected.
$S_{2n}$
, as V is connected.
Note that these permutations must have a precise cycle structure depending on the branch points of the map. Following the notation of [Reference Bilu5], we say that a branch point c of a rational map f is of type
![]() $(m_1, \ldots , m_k)$
if, for
$(m_1, \ldots , m_k)$
if, for
![]() $ f^{-1}(c)=\{c_1, \dots , c_k\}$
, the point
$ f^{-1}(c)=\{c_1, \dots , c_k\}$
, the point
![]() $c_j$
has ramification index
$c_j$
has ramification index
![]() $m_j$
for every
$m_j$
for every
![]() $j=1, \ldots , k$
. The type of a branch point corresponds to the cycle structure of the corresponding permutation, meaning that, going back to
$j=1, \ldots , k$
. The type of a branch point corresponds to the cycle structure of the corresponding permutation, meaning that, going back to
![]() $\phi _A$
, if
$\phi _A$
, if
![]() $b_i$
is of type
$b_i$
is of type
![]() $(m_1, \ldots , m_k)$
, then
$(m_1, \ldots , m_k)$
, then
![]() $\sigma _i$
is the product of k disjoint cycles
$\sigma _i$
is the product of k disjoint cycles
![]() $\tau _1,\dots , \tau _k$
with
$\tau _1,\dots , \tau _k$
with
![]() $\tau _j$
of length
$\tau _j$
of length
![]() $m_j$
.
$m_j$
.
We just showed how to associate to a covering a certain tuple of permutations satisfying some specific decomposition properties; the Riemann existence theorem tells us that we can do the opposite, that is, to any tuple of permutations satisfying certain properties we can associate a covering. One can actually say more: There exists a 1-1 correspondence between these two sets if one mods out by the following equivalence relations on both sides.
Definition 2.1. Two rational maps
![]() $F_1,F_2:\mathbb {P}^1(\mathbb {C}) \longrightarrow \mathbb {P}^1(\mathbb {C})$
are called equivalent if there is an automorphism
$F_1,F_2:\mathbb {P}^1(\mathbb {C}) \longrightarrow \mathbb {P}^1(\mathbb {C})$
are called equivalent if there is an automorphism
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {P}^1(\mathbb {C})$
such that
$\mathbb {P}^1(\mathbb {C})$
such that
![]() $F_1=F_2\circ \varphi $
.
$F_1=F_2\circ \varphi $
.
Definition 2.2. If
![]() $\Sigma =(\sigma _1, \sigma _2, \cdots ,\sigma _{h})$
and
$\Sigma =(\sigma _1, \sigma _2, \cdots ,\sigma _{h})$
and
![]() $\Sigma '=(\sigma ^{\prime }_1, \sigma ^{\prime }_2, \cdots , \sigma ^{\prime }_{h})$
are two h-tuples of permutations of
$\Sigma '=(\sigma ^{\prime }_1, \sigma ^{\prime }_2, \cdots , \sigma ^{\prime }_{h})$
are two h-tuples of permutations of
![]() $S_{2n}$
, we say that they are conjugated if there exists a
$S_{2n}$
, we say that they are conjugated if there exists a
![]() $\tau \in S_{2n}$
such that
$\tau \in S_{2n}$
such that
![]() $\tau ^{-1}\sigma _i\tau =\sigma _i'$
for every
$\tau ^{-1}\sigma _i\tau =\sigma _i'$
for every
![]() $i=1, \ldots , h$
. If this holds, we use the notation
$i=1, \ldots , h$
. If this holds, we use the notation
![]() $\tau ^{-1}\Sigma \tau =\Sigma '$
.
$\tau ^{-1}\Sigma \tau =\Sigma '$
.
We can finally state this consequence of the Riemann existence theorem.
Theorem 2.3 ([Reference Miranda21], Corollary 4.10).
Fix a finite set
![]() $\mathcal B=\{b_1, \ldots , b_h\}\subseteq \mathbb {P}^1(\mathbb {C})$
. Then there is a 1-1 correspondence between
$\mathcal B=\{b_1, \ldots , b_h\}\subseteq \mathbb {P}^1(\mathbb {C})$
. Then there is a 1-1 correspondence between
 $$\begin{align*}\begin{Bmatrix} \text{equivalence classes}\\ \text{ of rational maps} \\ F:\mathbb{P}^1(\mathbb{C}) \longrightarrow \mathbb{P}^1(\mathbb{C}) \\ \text{of degree }2n \\ \text{whose branch points lie in }\mathcal{B} \end{Bmatrix} \text{ and } \begin{Bmatrix} \text{conjugacy classes } (\sigma_1, \ldots, \sigma_{h})\in S_{2n}^h \\ \text{such that }\sigma_1\cdots \sigma_{h}=\mathrm{id},\\ \text{the subgroup generated by the } \sigma_i \\ \text{is transitive and } \sum_{i,j}(m_{ij}-1)=4n-2, \\ \text{where } (m_{i1},\dots, m_{ik_i}) \text{ is the cycle structure of } \sigma_i \end{Bmatrix}. \end{align*}$$
$$\begin{align*}\begin{Bmatrix} \text{equivalence classes}\\ \text{ of rational maps} \\ F:\mathbb{P}^1(\mathbb{C}) \longrightarrow \mathbb{P}^1(\mathbb{C}) \\ \text{of degree }2n \\ \text{whose branch points lie in }\mathcal{B} \end{Bmatrix} \text{ and } \begin{Bmatrix} \text{conjugacy classes } (\sigma_1, \ldots, \sigma_{h})\in S_{2n}^h \\ \text{such that }\sigma_1\cdots \sigma_{h}=\mathrm{id},\\ \text{the subgroup generated by the } \sigma_i \\ \text{is transitive and } \sum_{i,j}(m_{ij}-1)=4n-2, \\ \text{where } (m_{i1},\dots, m_{ik_i}) \text{ is the cycle structure of } \sigma_i \end{Bmatrix}. \end{align*}$$
Moreover, given the tuple of permutations
![]() $(\sigma _1, \ldots , \sigma _{h})$
, for each
$(\sigma _1, \ldots , \sigma _{h})$
, for each
![]() $i=1,\dots , h$
there are
$i=1,\dots , h$
there are
![]() $k_i$
preimages
$k_i$
preimages
![]() $b_{i1}, \ldots , b_{ik_i}$
of
$b_{i1}, \ldots , b_{ik_i}$
of
![]() $b_i$
for the corresponding cover
$b_i$
for the corresponding cover
![]() $F: \mathbb {P}^1(\mathbb {C}) \longrightarrow \mathbb {P}^1(\mathbb {C}) $
, with
$F: \mathbb {P}^1(\mathbb {C}) \longrightarrow \mathbb {P}^1(\mathbb {C}) $
, with
![]() $e_{F}(b_{ij})=m_{ij}$
.
$e_{F}(b_{ij})=m_{ij}$
.
As seen before, given a Pell–Abel equation (1.2) with A of degree n and D of degree
![]() $2d$
, we get the map
$2d$
, we get the map
![]() $\phi _A$
that is branched in
$\phi _A$
that is branched in
![]() $\{0,1,\infty \}$
and in further
$\{0,1,\infty \}$
and in further
![]() $k $
points, where
$k $
points, where
![]() $0\leq k \le d-1$
. Call
$0\leq k \le d-1$
. Call
![]() $\mathcal {B}:=\{0,1,\infty ,b_1, \ldots , b_{k}\}$
and
$\mathcal {B}:=\{0,1,\infty ,b_1, \ldots , b_{k}\}$
and
![]() $V:=\mathbb {P}^1(\mathbb {C})\setminus \mathcal {B}$
. We fix a
$V:=\mathbb {P}^1(\mathbb {C})\setminus \mathcal {B}$
. We fix a
![]() $q\in V$
, and we let
$q\in V$
, and we let
![]() $\rho :\pi _1(V,q) \longrightarrow S_{2n}$
be the associated monodromy representation (as explained above). We now let
$\rho :\pi _1(V,q) \longrightarrow S_{2n}$
be the associated monodromy representation (as explained above). We now let
![]() $\gamma _0,\gamma _{\infty },\gamma _{1}$
be closed paths winding once around
$\gamma _0,\gamma _{\infty },\gamma _{1}$
be closed paths winding once around
![]() $0,\infty ,1$
, respectively, and
$0,\infty ,1$
, respectively, and
![]() $\delta _i$
be a closed path winding once around
$\delta _i$
be a closed path winding once around
![]() $b_i$
for all
$b_i$
for all
![]() $i=1, \ldots , k$
. Then
$i=1, \ldots , k$
. Then
![]() $[\gamma _0] [\gamma _{\infty }] [\gamma _{1}] [\delta _1] \cdots [\delta _{k}]=1$
and all these classes generate
$[\gamma _0] [\gamma _{\infty }] [\gamma _{1}] [\delta _1] \cdots [\delta _{k}]=1$
and all these classes generate
![]() $\pi _1(V,q)$
.
$\pi _1(V,q)$
.
We let
![]() $\sigma _0=\rho (\gamma _0)$
,
$\sigma _0=\rho (\gamma _0)$
,
![]() $\sigma _{\infty }=\rho (\gamma _{\infty })$
,
$\sigma _{\infty }=\rho (\gamma _{\infty })$
,
![]() $\sigma _1=\rho (\gamma _1)$
and
$\sigma _1=\rho (\gamma _1)$
and
![]() $\tau _i=\rho (\delta _i)$
for
$\tau _i=\rho (\delta _i)$
for
![]() $i=1, \ldots , k$
. Then we have that
$i=1, \ldots , k$
. Then we have that
-
1 -
 $\sigma _0\sigma _{\infty }\sigma _1\tau _1\cdots \tau _{k}=\mathrm {id}$
;
$\sigma _0\sigma _{\infty }\sigma _1\tau _1\cdots \tau _{k}=\mathrm {id}$
; -
2 - the subgroup of
 $S_{2n}$
generated by these permutations is transitive;
$S_{2n}$
generated by these permutations is transitive; -
3 -
 $\sigma _0$
and
$\sigma _0$
and
 $\sigma _{\infty }$
do not fix any index;
$\sigma _{\infty }$
do not fix any index; -
4 -
 $\sigma _1$
fixes exactly
$\sigma _1$
fixes exactly
 $2d$
indexes.
$2d$
indexes.
Moreover, concerning the decomposition of these permutations in disjoint cycles we have that
-
5 - all nontrivial cycles in
 $\sigma _0$
and
$\sigma _0$
and
 $\sigma _1$
have even length;
$\sigma _1$
have even length; -
6 -
 $\sigma _{\infty }$
must be a
$\sigma _{\infty }$
must be a
 $2n$
-cycle;
$2n$
-cycle; -
7 - the sum over all cycles of
 $\sigma _0, \dots , \tau _k$
of their lengths minus 1 must give
$\sigma _0, \dots , \tau _k$
of their lengths minus 1 must give
 $4n-2$
.
$4n-2$
.
The permutations
![]() $\sigma _0, \dots , \tau _k$
depend on the chosen labelling of the preimages of q, so a Pell–Abel equation gives exactly one conjugacy class of
$\sigma _0, \dots , \tau _k$
depend on the chosen labelling of the preimages of q, so a Pell–Abel equation gives exactly one conjugacy class of
![]() $(k+3)$
-tuples and a
$(k+3)$
-tuples and a
![]() $\mathcal {B}$
for some
$\mathcal {B}$
for some
![]() $k\in \{0,\dots , d-1\}$
.
$k\in \{0,\dots , d-1\}$
.
On the other hand, fixing
![]() $k\in \{0,\dots , d-1\}$
and
$k\in \{0,\dots , d-1\}$
and
![]() $\mathcal {B}$
, a conjugacy class of
$\mathcal {B}$
, a conjugacy class of
![]() $(k+3)$
-tuples satisfying the above conditions gives a cover
$(k+3)$
-tuples satisfying the above conditions gives a cover
![]() $\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
that is a polynomial branched exactly in
$\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
that is a polynomial branched exactly in
![]() $\mathcal {B}$
. Moreover, the cycle structures of
$\mathcal {B}$
. Moreover, the cycle structures of
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
make this polynomial satisfy a Pell–Abel equation.
$\sigma _1$
make this polynomial satisfy a Pell–Abel equation.
We see an example.
Example 2.4. Let us consider the case in which the branching outside
![]() $0,1, \infty $
is maximal, that is,
$0,1, \infty $
is maximal, that is,
![]() $k=d-1$
. In this case,
$k=d-1$
. In this case,
![]() $\sigma _1$
is the product of
$\sigma _1$
is the product of
![]() $n-d$
transpositions,
$n-d$
transpositions,
![]() $\sigma _0$
is the product of n transpositions and each
$\sigma _0$
is the product of n transpositions and each
![]() $\tau _i$
consists of a single transposition.
$\tau _i$
consists of a single transposition.
A possible choice given by the third author in [Reference Zannier34] and leading to a Pell–Abel equation (1.2), is
![]() $\sigma _{\infty }=(2n, \ldots , 1)$
,
$\sigma _{\infty }=(2n, \ldots , 1)$
,
![]() $\sigma _0=(1,2n)(2,2n-1)\cdots (n,n+1)$
,
$\sigma _0=(1,2n)(2,2n-1)\cdots (n,n+1)$
,
![]() $\sigma _1=(1,2n-1)(2,2n-2)\cdots (n-d,n+d)$
and
$\sigma _1=(1,2n-1)(2,2n-2)\cdots (n-d,n+d)$
and
![]() $\tau _i=(n-i,n+i)$
,
$\tau _i=(n-i,n+i)$
,
![]() $i=1, \ldots , d-1$
. We will prove in the next sections that this example corresponds to a primitive solution of a Pell–Abel equation.
$i=1, \ldots , d-1$
. We will prove in the next sections that this example corresponds to a primitive solution of a Pell–Abel equation.
3 Proof of Theorem 1.1
This section is devoted to proving Theorem 1.1. For the reader’s convenience, we recall the notations and the statement of the theorem. Given a point
![]() $\overline {s}=(s_1, \ldots , s_{2d})\in \mathcal {B}_{2d}$
, we denote by
$\overline {s}=(s_1, \ldots , s_{2d})\in \mathcal {B}_{2d}$
, we denote by
![]() $H_{\overline s}$
a nonsingular model of the hyperelliptic curve defined by
$H_{\overline s}$
a nonsingular model of the hyperelliptic curve defined by
![]() $y^2=t^{2d}+ \cdots +s_{2d}$
with two points at infinity that we call
$y^2=t^{2d}+ \cdots +s_{2d}$
with two points at infinity that we call
![]() $\infty ^+$
and
$\infty ^+$
and
![]() $\infty ^-$
, and by
$\infty ^-$
, and by
![]() $\mathcal {J}_{\overline s}$
its Jacobian variety. We denote by
$\mathcal {J}_{\overline s}$
its Jacobian variety. We denote by
![]() $\mathcal {J} \rightarrow S=\mathcal {B}_{2d}$
the abelian scheme of relative dimension
$\mathcal {J} \rightarrow S=\mathcal {B}_{2d}$
the abelian scheme of relative dimension
![]() $d-1$
whose fibers are the
$d-1$
whose fibers are the
![]() $\mathcal {J}_{s}$
and by
$\mathcal {J}_{s}$
and by
![]() $\sigma :S \rightarrow \mathcal {J}$
the section corresponding to the point
$\sigma :S \rightarrow \mathcal {J}$
the section corresponding to the point
![]() $[\infty ^+-\infty ^-]$
. We recall moreover that
$[\infty ^+-\infty ^-]$
. We recall moreover that
![]() $\tilde {S}$
is the universal covering of
$\tilde {S}$
is the universal covering of
![]() $S(\mathbb {C})$
.
$S(\mathbb {C})$
.
Theorem. Let
![]() $\tilde {\beta }: \tilde {S} \rightarrow \mathbb {R}^{2(d-1)}$
be the Betti map associated to the section
$\tilde {\beta }: \tilde {S} \rightarrow \mathbb {R}^{2(d-1)}$
be the Betti map associated to the section
![]() $\sigma $
; then
$\sigma $
; then
![]() $\operatorname {{\mathrm {rk}}} \tilde {\beta }\ge 2(d-1)$
and, equivalently,
$\operatorname {{\mathrm {rk}}} \tilde {\beta }\ge 2(d-1)$
and, equivalently,
![]() $\tilde {\beta }$
is submersive on a dense open subset of
$\tilde {\beta }$
is submersive on a dense open subset of
![]() $\tilde S$
. In particular, the set of
$\tilde S$
. In particular, the set of
![]() $\overline {s}\in S(\mathbb {C})$
such that
$\overline {s}\in S(\mathbb {C})$
such that
![]() $\sigma (\overline s)$
is torsion on
$\sigma (\overline s)$
is torsion on
![]() $\mathcal {J}_{\overline s}$
is dense in
$\mathcal {J}_{\overline s}$
is dense in
![]() $S(\mathbb {C})$
with respect to the complex topology.
$S(\mathbb {C})$
with respect to the complex topology.
Proof. The rank of
![]() $\tilde {\beta }$
is trivially bounded from above by
$\tilde {\beta }$
is trivially bounded from above by
![]() $2(d-1)$
, so it is enough to show that there exists a point
$2(d-1)$
, so it is enough to show that there exists a point
![]() $\tilde {s}\in \tilde {S}$
where the rank is
$\tilde {s}\in \tilde {S}$
where the rank is
![]() $\geq 2(d-1)$
.
$\geq 2(d-1)$
.
Recall that S has dimension
![]() $2d$
. Suppose by contradiction that the maximal rank is
$2d$
. Suppose by contradiction that the maximal rank is
![]() $ r< 2(d-1)$
; then the nonempty fibers of
$ r< 2(d-1)$
; then the nonempty fibers of
![]() $\tilde {\beta }$
are complex analytic varieties of dimension
$\tilde {\beta }$
are complex analytic varieties of dimension
![]() $\ge 2d-r/2>d+1$
; see [Reference Corvaja, Masser and Zannier11, Propositions 2.1 and 2.2].
$\ge 2d-r/2>d+1$
; see [Reference Corvaja, Masser and Zannier11, Propositions 2.1 and 2.2].
Now, by applying Example 2.4 and Theorem 2.3, we have that the set of Pellian polynomials of degree
![]() $2d$
is not empty, and this gives the existence of a rational point, with denominator say n, in the image of
$2d$
is not empty, and this gives the existence of a rational point, with denominator say n, in the image of
![]() $\tilde {\beta }$
. We call
$\tilde {\beta }$
. We call
![]() $\tilde {V}$
an irreducible component of the preimage of that point; we may assume it has dimension
$\tilde {V}$
an irreducible component of the preimage of that point; we may assume it has dimension
![]() $>d+1$
. Moreover, we let V be its image in
$>d+1$
. Moreover, we let V be its image in
![]() $S(\mathbb {C})$
; this must again have dimension
$S(\mathbb {C})$
; this must again have dimension
![]() $>d+1$
and we have that each point of
$>d+1$
and we have that each point of
![]() $\sigma (V)$
is a torsion point of order n in the respective fiber.
$\sigma (V)$
is a torsion point of order n in the respective fiber.
Then we have
![]() $V\subseteq \mathcal {P}_{2d}(\mathbb {C})$
, where
$V\subseteq \mathcal {P}_{2d}(\mathbb {C})$
, where
![]() $\mathcal {P}_{2d}$
is the Pellian locus defined in equation (1.3) as, by Proposition 1.2, points of V correspond to some Pellian polynomials with a solution of degree n.
$\mathcal {P}_{2d}$
is the Pellian locus defined in equation (1.3) as, by Proposition 1.2, points of V correspond to some Pellian polynomials with a solution of degree n.
The following Proposition 3.1 concludes the proof of Theorem 1.1 since it contradicts the lower bound
![]() $\dim V>d+1$
.
$\dim V>d+1$
.
Proposition 3.1. The Pellian locus
![]() $\mathcal {P}_{2d}$
consists of denumerably many algebraic subvarieties of
$\mathcal {P}_{2d}$
consists of denumerably many algebraic subvarieties of
![]() $\mathcal {B}_{2d}$
of dimension at most
$\mathcal {B}_{2d}$
of dimension at most
![]() $d+1$
.
$d+1$
.
Proof. As the irreducible components of
![]() $\mathcal {P}_{2d}$
correspond to rational values of the Betti map, we clearly have that the number of components of
$\mathcal {P}_{2d}$
correspond to rational values of the Betti map, we clearly have that the number of components of
![]() $\mathcal {P}_{2d}$
is countable. Moreover, they are components of projections on
$\mathcal {P}_{2d}$
is countable. Moreover, they are components of projections on
![]() $\mathcal {B}_{2d}$
of intersections of torsion subgroup schemes of
$\mathcal {B}_{2d}$
of intersections of torsion subgroup schemes of
![]() $\mathcal {J}$
with the image of the section
$\mathcal {J}$
with the image of the section
![]() $\sigma $
. Therefore, they are algebraic subvarieties of
$\sigma $
. Therefore, they are algebraic subvarieties of
![]() $\mathcal {B}_{2d}$
.
$\mathcal {B}_{2d}$
.
Fix now a component U of
![]() $\mathcal {P}_{2d}$
of dimension
$\mathcal {P}_{2d}$
of dimension
![]() $>d+1$
mapping to a rational point of denominator n. Then every point of U corresponds to a Pellian polynomial with a solution of degree n. We let W be the closure of
$>d+1$
mapping to a rational point of denominator n. Then every point of U corresponds to a Pellian polynomial with a solution of degree n. We let W be the closure of
 $$ \begin{align*} \{(a_0,\dots ,a_{2n})\in \mathbb{A}_{\mathbb{C}}^{2n+1}: a_{0}t^{2n}+a_{1}t^{2n-1}+\dots+ a_{2n} &=A^2 \mbox{ is a square} \\ &\qquad\text{and } A^2-D_{\overline{s}}B^2=1 \mbox{ for some }\overline{s}\in U \} \end{align*} $$
$$ \begin{align*} \{(a_0,\dots ,a_{2n})\in \mathbb{A}_{\mathbb{C}}^{2n+1}: a_{0}t^{2n}+a_{1}t^{2n-1}+\dots+ a_{2n} &=A^2 \mbox{ is a square} \\ &\qquad\text{and } A^2-D_{\overline{s}}B^2=1 \mbox{ for some }\overline{s}\in U \} \end{align*} $$
in
Note that W is the closure of the projection on
![]() $\mathcal {A}_{2n}$
of
$\mathcal {A}_{2n}$
of
 $$ \begin{align*} \{ (a_0,\dots ,a_{2n},&b_0,\dots, b_{2n-2d},\overline{s})\in \mathcal{A}_{2n}\times \mathbb{A}_{\mathbb{C}}^{2n-2d+1}\times U: \\ &a_{0}t^{2n}+\dots+ a_{2n} =A^2 \text{ and } b_{0}t^{2n-2d}+\dots+ b_{2n-2d} =B^2 \mbox{ are squares} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\text{and } A^2-D_{\overline{s}}B^2=1 \}. \end{align*} $$
$$ \begin{align*} \{ (a_0,\dots ,a_{2n},&b_0,\dots, b_{2n-2d},\overline{s})\in \mathcal{A}_{2n}\times \mathbb{A}_{\mathbb{C}}^{2n-2d+1}\times U: \\ &a_{0}t^{2n}+\dots+ a_{2n} =A^2 \text{ and } b_{0}t^{2n-2d}+\dots+ b_{2n-2d} =B^2 \mbox{ are squares} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\text{and } A^2-D_{\overline{s}}B^2=1 \}. \end{align*} $$
Such projection has finite fibers, therefore W has dimension
![]() $>d+1$
.
$>d+1$
.
Note that it is possible to compose any degree
![]() $2n$
complex polynomial f with a linear polynomial and obtain a monic polynomial with no term of degree
$2n$
complex polynomial f with a linear polynomial and obtain a monic polynomial with no term of degree
![]() $2n-1$
. Moreover, there are at most
$2n-1$
. Moreover, there are at most
![]() $2n$
possible polynomials of this special form that can be obtained in this way from a given f. We let
$2n$
possible polynomials of this special form that can be obtained in this way from a given f. We let
and define the morphism
![]() $\varphi :\mathcal {C}_{2n}\times \mathcal {L}\rightarrow \mathcal {A}_{2n}$
,
$\varphi :\mathcal {C}_{2n}\times \mathcal {L}\rightarrow \mathcal {A}_{2n}$
,
 $$ \begin{align*} \varphi((c_2,\dots ,c_{2n}),(a,b)) &=(a_0,\dots ,a_{2n}) \iff \\ & a_0t^{2n}+\dots +a_{2n}=(at+b)^{2n}+c_{2}(at+b)^{2n-2}+\cdots+ c_{2n-1}(at+b)+ c_{2n}. \end{align*} $$
$$ \begin{align*} \varphi((c_2,\dots ,c_{2n}),(a,b)) &=(a_0,\dots ,a_{2n}) \iff \\ & a_0t^{2n}+\dots +a_{2n}=(at+b)^{2n}+c_{2}(at+b)^{2n-2}+\cdots+ c_{2n-1}(at+b)+ c_{2n}. \end{align*} $$
By the above considerations,
![]() $\varphi $
is surjective and the fibers are finite of cardinality at most
$\varphi $
is surjective and the fibers are finite of cardinality at most
![]() $2n$
.
$2n$
.
If we let
![]() $\pi $
be the projection
$\pi $
be the projection
![]() $ \mathcal {C}_{2n}\times \mathcal {L}\to \mathcal {C}_{2n}$
and
$ \mathcal {C}_{2n}\times \mathcal {L}\to \mathcal {C}_{2n}$
and
![]() $Z=\pi (\varphi ^{-1}(W))$
, as the fibers of
$Z=\pi (\varphi ^{-1}(W))$
, as the fibers of
![]() $\pi $
have dimension 2, Z must have dimension
$\pi $
have dimension 2, Z must have dimension
![]() $>d-1$
.
$>d-1$
.
Now, for
![]() $\overline {c}=(c_2,\dots ,c_{2n})\in Z$
, the corresponding polynomial
$\overline {c}=(c_2,\dots ,c_{2n})\in Z$
, the corresponding polynomial
![]() $f_{\overline {c}}(t)=t^{2n}+c_{2}t^{2n-2}+\cdots + c_{2n}$
is a square and we have
$f_{\overline {c}}(t)=t^{2n}+c_{2}t^{2n-2}+\cdots + c_{2n}$
is a square and we have
![]() $f_{\overline {c}}(t)-D(t)B(t)^2=1$
for some polynomials
$f_{\overline {c}}(t)-D(t)B(t)^2=1$
for some polynomials
![]() $D(t),B(t)$
with D of degree
$D(t),B(t)$
with D of degree
![]() $2d$
. We let
$2d$
. We let
 $$ \begin{align*} \tilde{Z}&= \{ (\overline{c},c^{\prime}_{2},\dots, c^{\prime}_{2n-1},r_1,\dots, r_{2n-1})\in Z \times \mathbb{A}_{\mathbb{C}}^{2n-2}\times \mathbb{A}_{\mathbb{C}}^{2n-1} : f^{\prime}_{\overline{c}}= 2n t^{2n-1}+ c^{\prime}_{2} t^{2n-3}+\dots+ c^{\prime}_{2n-1} \\ &\qquad\qquad\qquad\qquad\text{and } f^{\prime}_{\overline{c}} = 2n(t^{2n-1}+ \sigma_2(r_1,\dots, r_{2n-1})t^{2n-3}+\dots+ \sigma_{2n-1}(r_1,\dots, r_{2n-1})) \}, \end{align*} $$
$$ \begin{align*} \tilde{Z}&= \{ (\overline{c},c^{\prime}_{2},\dots, c^{\prime}_{2n-1},r_1,\dots, r_{2n-1})\in Z \times \mathbb{A}_{\mathbb{C}}^{2n-2}\times \mathbb{A}_{\mathbb{C}}^{2n-1} : f^{\prime}_{\overline{c}}= 2n t^{2n-1}+ c^{\prime}_{2} t^{2n-3}+\dots+ c^{\prime}_{2n-1} \\ &\qquad\qquad\qquad\qquad\text{and } f^{\prime}_{\overline{c}} = 2n(t^{2n-1}+ \sigma_2(r_1,\dots, r_{2n-1})t^{2n-3}+\dots+ \sigma_{2n-1}(r_1,\dots, r_{2n-1})) \}, \end{align*} $$
where
![]() $\sigma _i(X_1,\dots , X_{2n-1})$
is the i-th elementary symmetric polynomial in
$\sigma _i(X_1,\dots , X_{2n-1})$
is the i-th elementary symmetric polynomial in
![]() $2n-1$
variables and
$2n-1$
variables and
![]() $f^{\prime }_{\overline {c}}$
is the derivative of
$f^{\prime }_{\overline {c}}$
is the derivative of
![]() $f_{\overline {c}}$
. In other words, given
$f_{\overline {c}}$
. In other words, given
![]() $\overline c \in Z$
,
$\overline c \in Z$
,
![]() $c_2',\ldots , c_{2n-1}'$
are the coefficients of the derivative of the polynomial
$c_2',\ldots , c_{2n-1}'$
are the coefficients of the derivative of the polynomial
![]() $f_{\overline c}(t)$
and
$f_{\overline c}(t)$
and
![]() $r_1,\ldots , r_{2n-1}$
are the ramification points of the same polynomial (not necessarily distinct). Clearly,
$r_1,\ldots , r_{2n-1}$
are the ramification points of the same polynomial (not necessarily distinct). Clearly,
![]() $\tilde {Z}$
must have dimension
$\tilde {Z}$
must have dimension
![]() $>d-1$
.
$>d-1$
.
Finally, if we consider the morphism
![]() $\psi :\tilde {Z} \to \mathbb {A}_{\mathbb {C}}^{2n-1} $
defined by
$\psi :\tilde {Z} \to \mathbb {A}_{\mathbb {C}}^{2n-1} $
defined by
then
![]() $f_{\overline {c}}(r_1), \dots , f_{\overline {c}}( r_{2n-1})$
are the (not necessarily distinct) branch points of
$f_{\overline {c}}(r_1), \dots , f_{\overline {c}}( r_{2n-1})$
are the (not necessarily distinct) branch points of
![]() $f_{\overline {c}}$
. By the Riemann existence theorem and the above considerations, the fibers of
$f_{\overline {c}}$
. By the Riemann existence theorem and the above considerations, the fibers of
![]() $\psi $
are finite and have cardinality at most
$\psi $
are finite and have cardinality at most
![]() $2n$
, and therefore
$2n$
, and therefore
![]() $\psi (\tilde {Z})$
has dimension
$\psi (\tilde {Z})$
has dimension
![]() $>d-1$
.
$>d-1$
.
This gives a contradiction because the considerations of the previous section imply that the polynomial
![]() $f_{\overline {c}}$
, since it fits in a Pell–Abel equation, may have not more than
$f_{\overline {c}}$
, since it fits in a Pell–Abel equation, may have not more than
![]() $d+1$
finite branch points, two of which are 0 and 1. Therefore, not more than
$d+1$
finite branch points, two of which are 0 and 1. Therefore, not more than
![]() $d-1$
branch points are allowed to vary and
$d-1$
branch points are allowed to vary and
![]() $\psi (\tilde {Z})$
must have dimension
$\psi (\tilde {Z})$
must have dimension
![]() $\leq d-1$
, as wanted.
$\leq d-1$
, as wanted.
4 Chebychev polynomials and powers of solutions of the Pell–Abel equation
This section is devoted to describing the group of solutions of a Pell–Abel equation. As seen in the introduction, if a Pell–Abel equation
![]() $A^2-DB^2=1$
has a nontrivial solution, then it has infinitely many ones, obtained by taking powers
$A^2-DB^2=1$
has a nontrivial solution, then it has infinitely many ones, obtained by taking powers
![]() $A_m+\sqrt D B_m=(A+\sqrt D B)^m$
. Our goal for this section is to prove that
$A_m+\sqrt D B_m=(A+\sqrt D B)^m$
. Our goal for this section is to prove that
![]() $A_m^2=f_m(A^2)$
, for some polynomial
$A_m^2=f_m(A^2)$
, for some polynomial
![]() $f_m$
related to the m-th Chebychev polynomial.
$f_m$
related to the m-th Chebychev polynomial.
We recall that Chebychev polynomials of the first kind are defined recursively as
 $$ \begin{align*} \begin{cases} T_0(t)=1, \\ T_1(t)=t, \\ T_{n+1}(t)=2tT_n(t)-T_{n-1}(t), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} T_0(t)=1, \\ T_1(t)=t, \\ T_{n+1}(t)=2tT_n(t)-T_{n-1}(t), \end{cases} \end{align*} $$
so
![]() $T_n$
is a polynomial of degree n, and, for every
$T_n$
is a polynomial of degree n, and, for every
![]() $n>1$
, the two terms of highest degree of
$n>1$
, the two terms of highest degree of
![]() $T_n$
are
$T_n$
are
![]() $2^{n-1}t^n$
and
$2^{n-1}t^n$
and
![]() $-n2^{n-3}t^{n-2}$
. This polynomial satisfies many important properties; for example, for every
$-n2^{n-3}t^{n-2}$
. This polynomial satisfies many important properties; for example, for every
![]() $n\ge 0$
, we have that
$n\ge 0$
, we have that
![]() $T_n(t+t^{-1})=t^n+t^{-n}$
. Explicitly, we have that
$T_n(t+t^{-1})=t^n+t^{-n}$
. Explicitly, we have that
 $$ \begin{align} T_{n}(t):=\sum _{h=0}^{[n/2]}\binom{n}{2h}t^{n-2h}(t^{2}-1)^{h}, \end{align} $$
$$ \begin{align} T_{n}(t):=\sum _{h=0}^{[n/2]}\binom{n}{2h}t^{n-2h}(t^{2}-1)^{h}, \end{align} $$
where
![]() $[\cdot ]$
denotes the floor function. For a survey on these topics, see [Reference Lidl, Mullen and Turnwald19].
$[\cdot ]$
denotes the floor function. For a survey on these topics, see [Reference Lidl, Mullen and Turnwald19].
Suppose now that
![]() $(A,B)$
is a solution of the Pell equation
$(A,B)$
is a solution of the Pell equation
![]() $A^2-DB^2=1$
. Then
$A^2-DB^2=1$
. Then
![]() $(A_m,B_m)$
defined by
$(A_m,B_m)$
defined by
![]() $A_m+\sqrt D B_m=(A+\sqrt D B)^m$
is another solution of the same Pell–Abel equation, and
$A_m+\sqrt D B_m=(A+\sqrt D B)^m$
is another solution of the same Pell–Abel equation, and
![]() $A_m=\sum _{j=0}^{[m/2]} \binom {m}{2j} (DB^2)^j A^{m-2j}$
. Using that
$A_m=\sum _{j=0}^{[m/2]} \binom {m}{2j} (DB^2)^j A^{m-2j}$
. Using that
![]() $DB^2=A^2-1$
, we have
$DB^2=A^2-1$
, we have
 $$ \begin{align} A_m=\sum_{j=0}^{[m/2]} \binom{m}{2j} (A^2-1)^j A^{m-2j}=T_m(A). \end{align} $$
$$ \begin{align} A_m=\sum_{j=0}^{[m/2]} \binom{m}{2j} (A^2-1)^j A^{m-2j}=T_m(A). \end{align} $$
For the rest of the paper, we will denote by
![]() $\phi $
the square function
$\phi $
the square function
![]() $\phi (t)=t^2$
and by
$\phi (t)=t^2$
and by
![]() $\phi _g$
the composition
$\phi _g$
the composition
![]() $\phi \circ g=g^2$
.
$\phi \circ g=g^2$
.
For our purposes, it will be useful to express
![]() $\phi _{A_m}$
as a function of
$\phi _{A_m}$
as a function of
![]() $\phi _A$
. By equation (4.2), one can see that
$\phi _A$
. By equation (4.2), one can see that
![]() $\phi _{A_m}=f_m(\phi _A)$
, where
$\phi _{A_m}=f_m(\phi _A)$
, where
 $$ \begin{align} f_{2k}(w):=\left ( \sum_{j=0}^{k} \binom{2k}{2j} (w-1)^j w^{k-j} \right )^2, \end{align} $$
$$ \begin{align} f_{2k}(w):=\left ( \sum_{j=0}^{k} \binom{2k}{2j} (w-1)^j w^{k-j} \right )^2, \end{align} $$
and
 $$ \begin{align} f_{2k+1}(w):=w\left ( \sum_{j=0}^{k} \binom{2k+1}{2j} (w-1)^j w^{k-j} \right )^2. \end{align} $$
$$ \begin{align} f_{2k+1}(w):=w\left ( \sum_{j=0}^{k} \binom{2k+1}{2j} (w-1)^j w^{k-j} \right )^2. \end{align} $$
For every
![]() $m\ge 1$
we call
$m\ge 1$
we call
![]() $f_m$
the m-th power polynomial. Notice that
$f_m$
the m-th power polynomial. Notice that
![]() $f_m \circ \phi =\phi \circ T_m$
.
$f_m \circ \phi =\phi \circ T_m$
.
For our purposes we will also need a description of the branch locus of the
![]() $f_m$
; this can be easily done by looking at the branch locus of the Chebychev polynomials which is well-known in the literature. We recall that, given a polynomial f, we say that a branch point b of f is of type
$f_m$
; this can be easily done by looking at the branch locus of the Chebychev polynomials which is well-known in the literature. We recall that, given a polynomial f, we say that a branch point b of f is of type
![]() $(\mu _1, \ldots , \mu _k)$
if the
$(\mu _1, \ldots , \mu _k)$
if the
![]() $\mu _i$
are the ramification indexes of the points in the preimage of b. This is also equal to the array of the multiplicities of the roots of
$\mu _i$
are the ramification indexes of the points in the preimage of b. This is also equal to the array of the multiplicities of the roots of
![]() $f(t)-b$
.
$f(t)-b$
.
Proposition 4.1. The polynomials
![]() $f_m$
are branched only at
$f_m$
are branched only at
![]() $0$
,
$0$
,
![]() $1$
and
$1$
and
![]() $\infty $
. Moreover,
$\infty $
. Moreover,
-
• if m is even, then
 $0$
is of type
$0$
is of type
 $(2,2, \ldots , 2)$
and
$(2,2, \ldots , 2)$
and
 $1$
is of type
$1$
is of type
 $(1,1,2, \ldots ,2)$
; furthermore, the two unramified points above
$(1,1,2, \ldots ,2)$
; furthermore, the two unramified points above
 $1$
are
$1$
are
 $0$
and
$0$
and
 $1$
;
$1$
; -
• if m is odd, then
 $0$
is of type
$0$
is of type
 $(1,2, \ldots , 2)$
, and
$(1,2, \ldots , 2)$
, and
 $0$
is the only unramified point above
$0$
is the only unramified point above
 $0$
; furthermore,
$0$
; furthermore,
 $1$
is of type
$1$
is of type
 $(1,2, \ldots , 2)$
, and
$(1,2, \ldots , 2)$
, and
 $1$
is the only unramified point above
$1$
is the only unramified point above
 $1$
.
$1$
.
Proof. For
![]() $m=2$
we have that
$m=2$
we have that
![]() $f_m(t)=(2t-1)^2$
, and the proposition holds trivially. We will then assume that
$f_m(t)=(2t-1)^2$
, and the proposition holds trivially. We will then assume that
![]() $m\ge 3$
.
$m\ge 3$
.
The Chebychev polynomials are strictly related to Dickson polynomials
![]() $D_m(x,a)$
(for a definition of these polynomials and their properties, see [Reference Bilu5, Section 3]). Indeed, we have that
$D_m(x,a)$
(for a definition of these polynomials and their properties, see [Reference Bilu5, Section 3]). Indeed, we have that
![]() $T_m(t)=\frac {1}{2}D_m(2t,1)$
. Using this relation and [Reference Bilu5, Proposition 3.3, (b)] we have that, if
$T_m(t)=\frac {1}{2}D_m(2t,1)$
. Using this relation and [Reference Bilu5, Proposition 3.3, (b)] we have that, if
![]() $m\ge 3$
, the finite branching of
$m\ge 3$
, the finite branching of
![]() $T_m$
happens only in
$T_m$
happens only in
![]() $\pm 1$
. If m is odd, both
$\pm 1$
. If m is odd, both
![]() $\pm 1$
are of type
$\pm 1$
are of type
![]() $(1,2, \ldots , 2)$
, while if m is even we have that
$(1,2, \ldots , 2)$
, while if m is even we have that
![]() $1$
is of type
$1$
is of type
![]() $(1,1,2, \ldots , 2)$
and
$(1,1,2, \ldots , 2)$
and
![]() $-1$
is of type
$-1$
is of type
![]() $(2,\ldots ,2)$
. Using that
$(2,\ldots ,2)$
. Using that
![]() $\phi \circ T_m= f_m \circ \phi $
, the finite branch points of
$\phi \circ T_m= f_m \circ \phi $
, the finite branch points of
![]() $f_m$
are exactly the ones of
$f_m$
are exactly the ones of
![]() $\phi \circ T_m$
,that is,
$\phi \circ T_m$
,that is,
![]() $0$
and
$0$
and
![]() $1$
. Moreover, since
$1$
. Moreover, since
![]() $0$
is not a branch point for
$0$
is not a branch point for
![]() $T_m$
, then the ramification points of
$T_m$
, then the ramification points of
![]() $f_m\circ \phi $
have ramification index
$f_m\circ \phi $
have ramification index
![]() $2$
.
$2$
.
Assume first that m is even. By equation (4.3), since
![]() $f_m$
is a square, then
$f_m$
is a square, then
![]() $0$
is a branch point for
$0$
is a branch point for
![]() $f_m$
. As
$f_m$
. As
![]() $0$
is not contained
$0$
is not contained
![]() $f_m^{-1}(0)$
, then it is of type
$f_m^{-1}(0)$
, then it is of type
![]() $(2,2, \ldots , 2)$
. Let us now consider the branch point
$(2,2, \ldots , 2)$
. Let us now consider the branch point
![]() $1$
; notice that
$1$
; notice that
![]() $\{0,1\}\subseteq f_m^{-1}(1)$
. Since
$\{0,1\}\subseteq f_m^{-1}(1)$
. Since
![]() $\phi $
is ramified in
$\phi $
is ramified in
![]() $0$
, we have that
$0$
, we have that
![]() $f_m$
is unramified in
$f_m$
is unramified in
![]() $0$
. Using that
$0$
. Using that
![]() $f_m \circ (1-t)=f_m$
, this implies that
$f_m \circ (1-t)=f_m$
, this implies that
![]() $f_m$
is unramified also in
$f_m$
is unramified also in
![]() $1$
. By comparing the other ramification indexes, it follows that
$1$
. By comparing the other ramification indexes, it follows that
![]() $1$
is of type
$1$
is of type
![]() $(1,1,2, \ldots , 2)$
as wanted.
$(1,1,2, \ldots , 2)$
as wanted.
Assume now m odd. By equation (4.4), we have
![]() $f_m$
is unramified in
$f_m$
is unramified in
![]() $0$
, and all the other points in the preimage of
$0$
, and all the other points in the preimage of
![]() $0$
have ramification index
$0$
have ramification index
![]() $2$
, so
$2$
, so
![]() $0$
is of type
$0$
is of type
![]() $(1,2, \ldots , 2)$
. Using the relation
$(1,2, \ldots , 2)$
. Using the relation
we have that the type of
![]() $0$
and the type of
$0$
and the type of
![]() $1$
are the same, and
$1$
are the same, and
![]() $1$
is the unramified point over
$1$
is the unramified point over
![]() $1$
, concluding the proof.
$1$
, concluding the proof.
5 Monodromy groups and polynomial decompositions
The problem of finding (functional) decompositions of polynomials is very classical and was studied first by Ritt in [Reference Ritt26] and then by several authors (see, for instance, [Reference Fried14]). In this section, we recall some basic facts that will be used in the paper.
Let f be a nonconstant polynomial in
![]() $\mathbb {C}[t]$
, let u be transcendental over
$\mathbb {C}[t]$
, let u be transcendental over
![]() $\mathbb {C}$
and L be the splitting field of
$\mathbb {C}$
and L be the splitting field of
![]() $f(t)-u$
over
$f(t)-u$
over
![]() $\mathbb {C}(u)$
. The monodromy group
$\mathbb {C}(u)$
. The monodromy group
![]() $\text {Mon}(f)$
of f is the Galois group of L over
$\text {Mon}(f)$
of f is the Galois group of L over
![]() $\mathbb {C}(u)$
, viewed as a group of permutations of the roots of
$\mathbb {C}(u)$
, viewed as a group of permutations of the roots of
![]() $f(t)-u$
. By Gauss’ lemma, it follows that
$f(t)-u$
. By Gauss’ lemma, it follows that
![]() $f(t) - u$
is irreducible over
$f(t) - u$
is irreducible over
![]() $\mathbb {C}(u)$
, so
$\mathbb {C}(u)$
, so
![]() $\text {Mon}(f)$
is a transitive permutation group. If x is a root of
$\text {Mon}(f)$
is a transitive permutation group. If x is a root of
![]() $f(t)-u$
in L, then
$f(t)-u$
in L, then
![]() $u=f(x)$
and
$u=f(x)$
and
![]() $\text {Mon}(f)=\text {Gal}(L/\mathbb {C}(f(x)))$
. We denote moreover by H the stabilizer of x, that is,
$\text {Mon}(f)=\text {Gal}(L/\mathbb {C}(f(x)))$
. We denote moreover by H the stabilizer of x, that is,
![]() $H=\text {Gal}(L/\mathbb {C}(x))$
. Note that, by Theorem 2.3, the polynomial f of degree n seen as a map
$H=\text {Gal}(L/\mathbb {C}(x))$
. Note that, by Theorem 2.3, the polynomial f of degree n seen as a map
![]() $\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
corresponds to a conjugacy class of h-tuples of permutations in
$\mathbb {P}^1(\mathbb {C})\rightarrow \mathbb {P}^1(\mathbb {C})$
corresponds to a conjugacy class of h-tuples of permutations in
![]() $S_n$
, where h is the cardinality of the branch locus of f. Then, once we fix a labelling of the roots of
$S_n$
, where h is the cardinality of the branch locus of f. Then, once we fix a labelling of the roots of
![]() $f(t)-u$
(which corresponds to fixing a representative
$f(t)-u$
(which corresponds to fixing a representative
![]() $(\sigma _1, \ldots , \sigma _h)$
in the conjugacy class), the monodromy group of f is isomorphic to the subgroup of
$(\sigma _1, \ldots , \sigma _h)$
in the conjugacy class), the monodromy group of f is isomorphic to the subgroup of
![]() $S_n$
generated by
$S_n$
generated by
![]() $\sigma _1, \ldots , \sigma _h$
. Applying Lüroth’s theorem [Reference Schinzel28, Theorem 2] and [Reference Schinzel28, Theorem 4], we have the following proposition.
$\sigma _1, \ldots , \sigma _h$
. Applying Lüroth’s theorem [Reference Schinzel28, Theorem 2] and [Reference Schinzel28, Theorem 4], we have the following proposition.
Proposition 5.1. Given a polynomial
![]() $f\in \mathbb {C}[x]$
, there is a correspondence between polynomial decompositions of f and subfields of
$f\in \mathbb {C}[x]$
, there is a correspondence between polynomial decompositions of f and subfields of
![]() $\mathbb {C}(x)$
containing
$\mathbb {C}(x)$
containing
![]() $\mathbb {C}(f(x))$
. Moreover, if
$\mathbb {C}(f(x))$
. Moreover, if
![]() $\mathbb {C}(f(x)) \subseteq K \subseteq \mathbb {C}(x)$
, then
$\mathbb {C}(f(x)) \subseteq K \subseteq \mathbb {C}(x)$
, then
![]() $f=g \circ h$
with
$f=g \circ h$
with
![]() $g,h$
polynomials and
$g,h$
polynomials and
![]() $\deg h=[\mathbb {C}(x): K]$
.
$\deg h=[\mathbb {C}(x): K]$
.
Using the Galois correspondence, this shows that the study of the polynomial decompositions of f reduces to the study of subgroups of the monodromy group of f containing H.
We give the following definition.
Definition 5.2. We say that two polynomials
![]() $f,g\in \mathbb {C}[t]$
are linearly equivalent if there exists two linear polynomials
$f,g\in \mathbb {C}[t]$
are linearly equivalent if there exists two linear polynomials
![]() $\ell _1, \ell _2\in \mathbb {C}[t]$
such that
$\ell _1, \ell _2\in \mathbb {C}[t]$
such that
![]() $f= \ell _1 \circ g \circ \ell _2$
.
$f= \ell _1 \circ g \circ \ell _2$
.
Notice that, if
![]() $f=g\circ h$
, we can always change the decomposition up to composing with linear polynomials, so it makes sense to study the polynomial decompositions up to linear equivalence. Moreover, notice that two linearly equivalent polynomials have the same monodromy group.
$f=g\circ h$
, we can always change the decomposition up to composing with linear polynomials, so it makes sense to study the polynomial decompositions up to linear equivalence. Moreover, notice that two linearly equivalent polynomials have the same monodromy group.
We are now interested in computing the monodromy group of the polynomials
![]() $f_m$
defined in the previous section.
$f_m$
defined in the previous section.
Proposition 5.3. For every
![]() $m\ge 2$
, the monodromy group of
$m\ge 2$
, the monodromy group of
![]() $f_m$
is exactly
$f_m$
is exactly
![]() $D_{2m}$
, where
$D_{2m}$
, where
![]() $D_{2m}$
denotes the dihedral group of order
$D_{2m}$
denotes the dihedral group of order
![]() $2m$
.
$2m$
.
Proof. By Proposition 4.1, the polynomials
![]() $f_m$
are branched only in
$f_m$
are branched only in
![]() $0$
and
$0$
and
![]() $1$
, both of type
$1$
, both of type
![]() $(1,2 \ldots , 2)$
if m is odd or of type
$(1,2 \ldots , 2)$
if m is odd or of type
![]() $(2,\ldots , 2)$
and
$(2,\ldots , 2)$
and
![]() $(1,1,2\ldots , 2)$
, respectively, if m is even. Applying [Reference Bilu5, Theorem 3.4], this implies that
$(1,1,2\ldots , 2)$
, respectively, if m is even. Applying [Reference Bilu5, Theorem 3.4], this implies that
![]() $f_m$
is linearly equivalent to the Dickson polynomial
$f_m$
is linearly equivalent to the Dickson polynomial
![]() $D_m(x,a)$
with
$D_m(x,a)$
with
![]() $a \neq 0$
. By [Reference Bilu5, Theorem 3.6], the monodromy group of
$a \neq 0$
. By [Reference Bilu5, Theorem 3.6], the monodromy group of
![]() $D_m(x,a)$
with
$D_m(x,a)$
with
![]() $a \neq 0$
is the dihedral group
$a \neq 0$
is the dihedral group
![]() $D_{2m}$
, which gives that
$D_{2m}$
, which gives that
![]() $\text {Mon} (f_m)=D_{2m}$
as wanted.
$\text {Mon} (f_m)=D_{2m}$
as wanted.
6 Characterization of primitivity
In this section, we want to give a criterion to detect the primitivity of a solution of the Pell–Abel equation in terms of the associated conjugacy class of permutations. We start with a definition.
Definition 6.1. For positive integers
![]() $n,\ell $
with
$n,\ell $
with
![]() $\ell \mid 2 n$
, we call a partition
$\ell \mid 2 n$
, we call a partition
![]() $\mathcal {F}=\{F_1,\ldots , F_{\ell }\}$
of
$\mathcal {F}=\{F_1,\ldots , F_{\ell }\}$
of
![]() $\{1,\dots , 2n \}$
an
$\{1,\dots , 2n \}$
an
![]() $\ell $
-partition if
$\ell $
-partition if
![]() $\mathcal {F}$
consists of
$\mathcal {F}$
consists of
![]() $\ell $
subsets each of cardinality
$\ell $
subsets each of cardinality
![]() $\frac {2n}{\ell }$
. A subgroup
$\frac {2n}{\ell }$
. A subgroup
![]() $G < S_{2n}$
is said to be
$G < S_{2n}$
is said to be
![]() $\ell $
-imprimitive if there exists an
$\ell $
-imprimitive if there exists an
![]() $\ell $
-partition
$\ell $
-partition
![]() $\mathcal {F}=\{F_1,\ldots , F_{\ell }\}$
which is preserved by the action of G, that is, for every
$\mathcal {F}=\{F_1,\ldots , F_{\ell }\}$
which is preserved by the action of G, that is, for every
![]() $\sigma \in G$
and every
$\sigma \in G$
and every
![]() $a\in \{1, \ldots , \ell \}$
, there exists
$a\in \{1, \ldots , \ell \}$
, there exists
![]() $b\in \{1, \ldots , \ell \}$
such that
$b\in \{1, \ldots , \ell \}$
such that
![]() $\sigma (F_a)=F_b$
.
$\sigma (F_a)=F_b$
.
It is well-known (see [Reference Ritt26]) that, if
![]() $f= g \circ h$
is a polynomial of degree r which is the composition of two polynomials g and h, where
$f= g \circ h$
is a polynomial of degree r which is the composition of two polynomials g and h, where
![]() $\deg h=s$
and
$\deg h=s$
and
![]() $\deg g=r$
, then
$\deg g=r$
, then
![]() $\text {Mon}(f)$
is r-imprimitive. Indeed, if q is not a branch point for f, then the set of its preimages via f is partitioned in subsets whose elements map via h to the same preimage of q via g.
$\text {Mon}(f)$
is r-imprimitive. Indeed, if q is not a branch point for f, then the set of its preimages via f is partitioned in subsets whose elements map via h to the same preimage of q via g.
We now give a criterion for determining whether a solution
![]() $(A,B)$
of a Pell–Abel equation is primitive or an m-th power for some
$(A,B)$
of a Pell–Abel equation is primitive or an m-th power for some
![]() $m\geq 2$
, and this behavior is completely determined by the monodromy group
$m\geq 2$
, and this behavior is completely determined by the monodromy group
![]() $G_A$
of
$G_A$
of
![]() $\phi _A$
. Note that
$\phi _A$
. Note that
![]() $G_A$
is always
$G_A$
is always
![]() $2$
-imprimitive since
$2$
-imprimitive since
![]() $\phi _A$
is the square of a polynomial.
$\phi _A$
is the square of a polynomial.
Theorem 6.2. Let
![]() $(A,B)$
be a solution of degree n of a Pell–Abel equation
$(A,B)$
be a solution of degree n of a Pell–Abel equation
![]() $A^2-DB^2=1$
with
$A^2-DB^2=1$
with
![]() $\deg D=2d$
, and let
$\deg D=2d$
, and let
![]() $G_A$
be the monodromy group of
$G_A$
be the monodromy group of
![]() $\phi _A$
. Then, for every integer
$\phi _A$
. Then, for every integer
![]() $m\mid n$
with
$m\mid n$
with
![]() $\frac {n}{m} \ge d$
,
$\frac {n}{m} \ge d$
,
![]() $(A,B)$
is the m-th power of another solution if and only if
$(A,B)$
is the m-th power of another solution if and only if
![]() $G_A$
is
$G_A$
is
![]() $2m$
-imprimitive.
$2m$
-imprimitive.
We will prove the above theorem in the next section. Before this, we show how Corollary 1.5 can be deduced from Theorem 6.2.
Proof of Corollary 1.5.
We prove that a solution
![]() $(A,B)$
associated to the conjugacy class of the tuple
$(A,B)$
associated to the conjugacy class of the tuple
![]() $(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{d-1})$
given in Example 2.4 is primitive for every
$(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{d-1})$
given in Example 2.4 is primitive for every
![]() $n\ge d \ge 2$
.
$n\ge d \ge 2$
.
We recall that
![]() $\sigma _{\infty }=(2n, \ldots , 1)$
,
$\sigma _{\infty }=(2n, \ldots , 1)$
,
![]() $\sigma _0=(1,2n) (2,2n-1)\cdots (n,n+1)$
,
$\sigma _0=(1,2n) (2,2n-1)\cdots (n,n+1)$
,
![]() $\sigma _1=(1,2n-1) (2,2n-2)\cdots (n-d,n+d)$
and
$\sigma _1=(1,2n-1) (2,2n-2)\cdots (n-d,n+d)$
and
![]() $\tau _i=(n-i,n+i)$
, for
$\tau _i=(n-i,n+i)$
, for
![]() $i=1, \ldots , d-1$
.
$i=1, \ldots , d-1$
.
Suppose by contradiction that
![]() $(A,B)$
is the m-th power of another solution
$(A,B)$
is the m-th power of another solution
![]() $(A',B')$
for some
$(A',B')$
for some
![]() $m \mid n$
,
$m \mid n$
,
![]() $1<m<n$
. By Theorem 6.2,
$1<m<n$
. By Theorem 6.2,
![]() $G_A$
has to preserve a
$G_A$
has to preserve a
![]() $2m$
-partition of
$2m$
-partition of
![]() $\{1, \ldots , 2n\}$
. We see that the only
$\{1, \ldots , 2n\}$
. We see that the only
![]() $2m$
-partition preserved by
$2m$
-partition preserved by
![]() $\sigma _{\infty }$
is
$\sigma _{\infty }$
is
![]() $\mathcal F_{2m}:=\{F_1,\ldots , F_{2m}\}$
, where for every
$\mathcal F_{2m}:=\{F_1,\ldots , F_{2m}\}$
, where for every
![]() $1\le h\le 2m$
, we set
$1\le h\le 2m$
, we set
On the other hand,
![]() $\tau _{1}=(n-1, n+1)$
and
$\tau _{1}=(n-1, n+1)$
and
![]() $n-1,\ n+1$
are not in the same congruence class modulo
$n-1,\ n+1$
are not in the same congruence class modulo
![]() $2m$
if
$2m$
if
![]() $m\ge 2$
, so
$m\ge 2$
, so
![]() $\mathcal F_{2m}$
is not preserved by
$\mathcal F_{2m}$
is not preserved by
![]() $G_A$
. This implies that
$G_A$
. This implies that
![]() $G_A$
does not preserve any
$G_A$
does not preserve any
![]() $2m$
-partition, hence proving the theorem.
$2m$
-partition, hence proving the theorem.
7 Proof of Theorem 6.2
In view of what we explained in the previous section, one direction is quite easy. Indeed, let
![]() $(A,B)$
be a solution of a Pell–Abel equation that is the m-th power of another solution
$(A,B)$
be a solution of a Pell–Abel equation that is the m-th power of another solution
![]() $(A', B')$
. In Section 4, we showed that
$(A', B')$
. In Section 4, we showed that
![]() $\phi _{A}=f_m(\phi _{A'})=f_m \circ \phi \circ A'$
, where
$\phi _{A}=f_m(\phi _{A'})=f_m \circ \phi \circ A'$
, where
![]() $\phi (t)=t^2$
. As
$\phi (t)=t^2$
. As
![]() $f_m$
is a polynomial of degree m, it follows immediately that
$f_m$
is a polynomial of degree m, it follows immediately that
![]() $G_{A}$
is
$G_{A}$
is
![]() $2m$
-imprimitive.
$2m$
-imprimitive.
The proof of the converse is much more involved.
Let us consider a solution
![]() $(A,B)$
with A of degree n and the associated almost-Belyi map
$(A,B)$
with A of degree n and the associated almost-Belyi map
![]() $\phi _A$
. By Theorem 2.3, the map
$\phi _A$
. By Theorem 2.3, the map
![]() $\phi _A$
corresponds to the conjugacy class of a
$\phi _A$
corresponds to the conjugacy class of a
![]() $(k+3)$
-tuple of permutations in
$(k+3)$
-tuple of permutations in
![]() $S_{2n}$
given by
$S_{2n}$
given by
![]() $\Sigma _A:=(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k})$
with
$\Sigma _A:=(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k})$
with
![]() $k \le d-1$
, where we recall that
$k \le d-1$
, where we recall that
![]() $\sigma _{\infty }$
is a
$\sigma _{\infty }$
is a
![]() $2n$
-cycle,
$2n$
-cycle,
![]() $\sigma _0$
is the product of disjoint cycles of even length,
$\sigma _0$
is the product of disjoint cycles of even length,
![]() $\sigma _1$
fixes exactly
$\sigma _1$
fixes exactly
![]() $2d$
indexes and is the product of disjoint cycles of even length; see properties 1 to 7 after Theorem 2.3. We call
$2d$
indexes and is the product of disjoint cycles of even length; see properties 1 to 7 after Theorem 2.3. We call
![]() $b_1, \ldots , b_k$
the further k branch points different from
$b_1, \ldots , b_k$
the further k branch points different from
![]() $0,1, \infty $
.
$0,1, \infty $
.
Conjugating by a suitable permutation, we can and will always assume that
![]() $\sigma _{\infty }=(2n,2n-1,\ldots , 1)$
.
$\sigma _{\infty }=(2n,2n-1,\ldots , 1)$
.
We recall that the sum over all cycles of
![]() $\sigma _0, \dots , \tau _k$
of their lengths minus 1 must give
$\sigma _0, \dots , \tau _k$
of their lengths minus 1 must give
![]() $4n-2$
. Looking at the cycle structure of
$4n-2$
. Looking at the cycle structure of
![]() $\sigma _0$
,
$\sigma _0$
,
![]() $\sigma _\infty $
and
$\sigma _\infty $
and
![]() $\sigma _1$
we have that
$\sigma _1$
we have that
![]() $\sigma _1$
fixes
$\sigma _1$
fixes
![]() $2d$
indexes and
$2d$
indexes and
![]() $\sum _{i,j}(m_{ij}-1)\leq d-1$
, where
$\sum _{i,j}(m_{ij}-1)\leq d-1$
, where
![]() $(m_{i1},\dots , m_{ih_i})$
is the cycle structure of
$(m_{i1},\dots , m_{ih_i})$
is the cycle structure of
![]() $\tau _i$
. Therefore, there are at least two indexes which are fixed by
$\tau _i$
. Therefore, there are at least two indexes which are fixed by
![]() $\sigma _1$
and, at the same time, by every
$\sigma _1$
and, at the same time, by every
![]() $\tau _i$
. Without loss of generality, we are going to assume that one of them is
$\tau _i$
. Without loss of generality, we are going to assume that one of them is
![]() $2n$
. Moreover, each
$2n$
. Moreover, each
![]() $\tau _i$
must fix at least
$\tau _i$
must fix at least
![]() $2n-2(d-1)$
indexes.
$2n-2(d-1)$
indexes.
The monodromy group
![]() $G_A$
of
$G_A$
of
![]() $\phi _A$
is the subgroup of
$\phi _A$
is the subgroup of
![]() $S_{2n}$
generated by
$S_{2n}$
generated by
![]() $\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k}$
; by assumption,
$\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k}$
; by assumption,
![]() $G_A$
preserves a
$G_A$
preserves a
![]() $2m$
-partition of
$2m$
-partition of
![]() $\{1, \ldots ,2n\}$
. As mentioned before, the only
$\{1, \ldots ,2n\}$
. As mentioned before, the only
![]() $2m$
-partition preserved by
$2m$
-partition preserved by
![]() $\sigma _{\infty }$
is
$\sigma _{\infty }$
is
![]() $\mathcal F_{2m}=\{F_1,\ldots , F_{2m}\}$
, where, for every
$\mathcal F_{2m}=\{F_1,\ldots , F_{2m}\}$
, where, for every
![]() $h=1,\ldots , 2m$
, we defined
$h=1,\ldots , 2m$
, we defined
![]() $F_h=\{j\in \{1, \ldots , 2n\} : j\equiv h\ \ \mod 2m\}$
; we can then assume that
$F_h=\{j\in \{1, \ldots , 2n\} : j\equiv h\ \ \mod 2m\}$
; we can then assume that
![]() $G_A$
preserves this specific partition.
$G_A$
preserves this specific partition.
For
![]() $h=1, \ldots , m$
we let
$h=1, \ldots , m$
we let
![]() $E_h=\{ j\in \{1, \ldots , 2n\} : j\equiv h\ \ \mod m \}$
. Then
$E_h=\{ j\in \{1, \ldots , 2n\} : j\equiv h\ \ \mod m \}$
. Then
![]() $\mathcal E_m=\{E_1, \ldots , E_m\}$
gives another partition of
$\mathcal E_m=\{E_1, \ldots , E_m\}$
gives another partition of
![]() $\{1,\ldots , 2n\}$
and we have that
$\{1,\ldots , 2n\}$
and we have that
![]() $E_h=F_h \cup F_{m+h}$
. We start by proving the following lemma.
$E_h=F_h \cup F_{m+h}$
. We start by proving the following lemma.
Lemma 7.1. Suppose
![]() $G_A$
preserves the
$G_A$
preserves the
![]() $2m$
-partition
$2m$
-partition
![]() $\mathcal F_{2m}$
, then
$\mathcal F_{2m}$
, then
![]() $G_A$
preserves the m-partition
$G_A$
preserves the m-partition
![]() $\mathcal E_m$
. More precisely, the action of
$\mathcal E_m$
. More precisely, the action of
![]() $\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k}$
on
$\sigma _0,\sigma _{\infty },\sigma _1,\tau _1, \ldots ,\tau _{k}$
on
![]() $\mathcal F_{2m}$
and
$\mathcal F_{2m}$
and
![]() $\mathcal E_m$
is the following:
$\mathcal E_m$
is the following:
 $$ \begin{align} \begin{cases} \sigma_{\infty}(F_1)=F_{2m} \mbox{ and } \sigma_{\infty}(F_i)= F_{i-1} \ \forall{i=2,\ldots, 2m};\\ \sigma_1(F_{2m})=F_{2m} \mbox{ and } \sigma_1(F_i)=F_{2m-i}\ \forall i=1, \ldots, 2m-1; \\ \sigma_0(F_i)=F_{2m-i+1} \quad \forall i=1,\ldots, 2m; \\ \tau_j(F_i)=F_i \ \forall i=1, \ldots, 2m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \sigma_{\infty}(F_1)=F_{2m} \mbox{ and } \sigma_{\infty}(F_i)= F_{i-1} \ \forall{i=2,\ldots, 2m};\\ \sigma_1(F_{2m})=F_{2m} \mbox{ and } \sigma_1(F_i)=F_{2m-i}\ \forall i=1, \ldots, 2m-1; \\ \sigma_0(F_i)=F_{2m-i+1} \quad \forall i=1,\ldots, 2m; \\ \tau_j(F_i)=F_i \ \forall i=1, \ldots, 2m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align} $$
and:
 $$ \begin{align*} \begin{cases} \sigma_{\infty}(E_1)=E_{m} \mbox{ and } \sigma_{\infty}(E_i)= E_{i-1} \ \forall{i=2,\ldots, m};\\ \sigma_1(E_m)=E_{m} \mbox{ and } \sigma_1(E_i)=E_{m-i}\ \forall i=1, \ldots, m-1; \\ \sigma_0(E_i)=E_{m-i+1}\quad \forall i=1,\ldots, m; \\ \tau_j(E_i)=E_i \ \forall i=1, \ldots, m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma_{\infty}(E_1)=E_{m} \mbox{ and } \sigma_{\infty}(E_i)= E_{i-1} \ \forall{i=2,\ldots, m};\\ \sigma_1(E_m)=E_{m} \mbox{ and } \sigma_1(E_i)=E_{m-i}\ \forall i=1, \ldots, m-1; \\ \sigma_0(E_i)=E_{m-i+1}\quad \forall i=1,\ldots, m; \\ \tau_j(E_i)=E_i \ \forall i=1, \ldots, m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align*} $$
In particular, by equation (7.1),
![]() $\mathrm {Fix}(\sigma _1):=\{a\in \{1,\ldots , 2n\}\ |\ \sigma _1(a)=a\}\subseteq E_m$
.
$\mathrm {Fix}(\sigma _1):=\{a\in \{1,\ldots , 2n\}\ |\ \sigma _1(a)=a\}\subseteq E_m$
.
Proof. By construction
![]() $\sigma _1(2n)=2n$
, thus we have
$\sigma _1(2n)=2n$
, thus we have
![]() $\sigma _1(F_{2m})=F_{2m}$
. Moreover, we have that
$\sigma _1(F_{2m})=F_{2m}$
. Moreover, we have that
![]() $|F_h|=\frac {n}{m} \ge d$
for all h, and for all i at most
$|F_h|=\frac {n}{m} \ge d$
for all h, and for all i at most
![]() $2d-2$
indexes are not fixed by
$2d-2$
indexes are not fixed by
![]() $\tau _i$
. This implies that
$\tau _i$
. This implies that
![]() $\tau _i(F_h)=F_h$
for every
$\tau _i(F_h)=F_h$
for every
![]() $i=1, \ldots , k$
and
$i=1, \ldots , k$
and
![]() $h=1, \ldots , 2m$
.
$h=1, \ldots , 2m$
.
In what follows the indexes of the
![]() $F_h$
are considered modulo
$F_h$
are considered modulo
![]() $2m$
. Using
$2m$
. Using
![]() $\sigma _0\sigma _{\infty }\sigma _1\prod _{i=1}^{k}\tau _i=\mathrm {id}$
, we deduce that
$\sigma _0\sigma _{\infty }\sigma _1\prod _{i=1}^{k}\tau _i=\mathrm {id}$
, we deduce that
![]() $\sigma _0\sigma _{\infty }\sigma _1(F_h)=F_h$
for every
$\sigma _0\sigma _{\infty }\sigma _1(F_h)=F_h$
for every
![]() $h=1, \ldots , 2m$
. As we know that
$h=1, \ldots , 2m$
. As we know that
![]() $\sigma _{\infty }( F_{h})=F_{h-1}$
, this gives that
$\sigma _{\infty }( F_{h})=F_{h-1}$
, this gives that
 $$ \begin{align} \begin{cases} \sigma_0(F_{i_1})=F_{i_2} \ \Rightarrow\ \sigma_1(F_{i_2-1})=F_{i_1}; \\ \sigma_1(F_{j_1})=F_{j_2} \ \Rightarrow\ \sigma_0(F_{j_2})=F_{j_1+1}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \sigma_0(F_{i_1})=F_{i_2} \ \Rightarrow\ \sigma_1(F_{i_2-1})=F_{i_1}; \\ \sigma_1(F_{j_1})=F_{j_2} \ \Rightarrow\ \sigma_0(F_{j_2})=F_{j_1+1}. \end{cases} \end{align} $$
Moreover, we claim that, if
![]() $\sigma _1(F_{k_1})=F_{k_2}$
for some indexes
$\sigma _1(F_{k_1})=F_{k_2}$
for some indexes
![]() $k_1$
and
$k_1$
and
![]() $k_2$
, we must have that
$k_2$
, we must have that
![]() $\sigma _1(F_{k_2})=F_{k_1}$
. Indeed, suppose by contradiction that this is not the case; since the nontrivial cycles appearing in
$\sigma _1(F_{k_2})=F_{k_1}$
. Indeed, suppose by contradiction that this is not the case; since the nontrivial cycles appearing in
![]() $\sigma _1$
have even length, there exist pairwise distinct
$\sigma _1$
have even length, there exist pairwise distinct
![]() $k_1, k_2,k_3, k_4\in \{1,\dots , 2m\}$
such that
$k_1, k_2,k_3, k_4\in \{1,\dots , 2m\}$
such that
![]() $\sigma _1(F_{k_1})=F_{k_2}$
,
$\sigma _1(F_{k_1})=F_{k_2}$
,
![]() $\sigma _1(F_{k_2})=F_{k_3}$
and
$\sigma _1(F_{k_2})=F_{k_3}$
and
![]() $\sigma _1(F_{k_3})=F_{k_4}$
. Now, each of the
$\sigma _1(F_{k_3})=F_{k_4}$
. Now, each of the
![]() $n/m$
elements of
$n/m$
elements of
![]() $F_{k_1}$
gives a contribution of at least
$F_{k_1}$
gives a contribution of at least
![]() $3$
to the branching above 1, where we recall that we count the branching of
$3$
to the branching above 1, where we recall that we count the branching of
![]() $\phi _A$
above a point p as the sum of
$\phi _A$
above a point p as the sum of
![]() $e-1$
over the ramification indices e of the preimages of p.
$e-1$
over the ramification indices e of the preimages of p.
Using moreover that
![]() $\sigma _1$
fixes
$\sigma _1$
fixes
![]() $2d$
points, we have that the branching above
$2d$
points, we have that the branching above
![]() $1$
must be at least
$1$
must be at least
![]() $3\frac {n}{m}+(n-2\frac {n}{m}-d)\ge n$
since
$3\frac {n}{m}+(n-2\frac {n}{m}-d)\ge n$
since
![]() $\frac {n}{m}\ge d$
, and this is impossible as the branching above
$\frac {n}{m}\ge d$
, and this is impossible as the branching above
![]() $1$
can be at most
$1$
can be at most
![]() $n-1$
(recall properties 1–7 after Theorem 2.3).
$n-1$
(recall properties 1–7 after Theorem 2.3).
Therefore, we can rewrite equation (7.2) as
 $$ \begin{align} \begin{cases} \sigma_0(F_{i_1})=F_{i_2} \ \Rightarrow\ \sigma_1(F_{i_1})=F_{{i_2}-1}; \\ \sigma_1(F_{j_1})=F_{j_2} \ \Rightarrow\ \sigma_0(F_{j_2})=F_{j_1+1}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \sigma_0(F_{i_1})=F_{i_2} \ \Rightarrow\ \sigma_1(F_{i_1})=F_{{i_2}-1}; \\ \sigma_1(F_{j_1})=F_{j_2} \ \Rightarrow\ \sigma_0(F_{j_2})=F_{j_1+1}. \end{cases} \end{align} $$
Now, since
![]() $\sigma _1(F_{2m})=F_{2m}$
, using equation (7.3) we have that
$\sigma _1(F_{2m})=F_{2m}$
, using equation (7.3) we have that
and
Now, for every
![]() $h=1,\ldots , m$
, the set
$h=1,\ldots , m$
, the set
![]() $E_h$
is equal to
$E_h$
is equal to
![]() $F_h \cup F_{m+h}$
. Using the previous relations, we have that
$F_h \cup F_{m+h}$
. Using the previous relations, we have that
![]() $\sigma _1(E_h)=F_{2m-h}\cup F_{m-h}=E_{m-h}$
;
$\sigma _1(E_h)=F_{2m-h}\cup F_{m-h}=E_{m-h}$
;
![]() $\sigma _0(E_h)=F_{2m-h+1}\cup F_{m-h+1}=E_{m-h+1}$
,
$\sigma _0(E_h)=F_{2m-h+1}\cup F_{m-h+1}=E_{m-h+1}$
,
![]() $\tau _i$
stabilizes
$\tau _i$
stabilizes
![]() $\{E_1, \ldots , E_m\}$
for every
$\{E_1, \ldots , E_m\}$
for every
![]() $i=1, \ldots , d-1$
and
$i=1, \ldots , d-1$
and
![]() $\sigma _{\infty }(E_h)=F_{h-1}\cup F_{m+h-1}=E_{h-1}$
, which concludes the proof.
$\sigma _{\infty }(E_h)=F_{h-1}\cup F_{m+h-1}=E_{h-1}$
, which concludes the proof.
For
![]() $G < S_{2n}$
and
$G < S_{2n}$
and
![]() $C_1,\ldots , C_{\ell }\subseteq \{1, \ldots , 2n\}$
, we define
$C_1,\ldots , C_{\ell }\subseteq \{1, \ldots , 2n\}$
, we define
 $$ \begin{align*}\mathrm{Stab}_G(C_1, \ldots, C_{\ell}):=\bigcap_{i=1}^{\ell} \mathrm{Stab}_G(C_i),\end{align*} $$
$$ \begin{align*}\mathrm{Stab}_G(C_1, \ldots, C_{\ell}):=\bigcap_{i=1}^{\ell} \mathrm{Stab}_G(C_i),\end{align*} $$
where, for every
![]() $i=1, \ldots , \ell $
,
$i=1, \ldots , \ell $
,
First, we prove this preliminary lemma.
Lemma 7.2. Let us assume that
![]() $G_A$
preserves
$G_A$
preserves
![]() $\mathcal F_{2m}$
, and set
$\mathcal F_{2m}$
, and set
![]() $S:=\mathrm {Stab}_{G_A}(\{2n\})$
. Then there exist
$S:=\mathrm {Stab}_{G_A}(\{2n\})$
. Then there exist
![]() $H_1, H_2$
subgroups of
$H_1, H_2$
subgroups of
![]() $G_A$
satisfying
$G_A$
satisfying
![]() $S \subseteq H_1< H_2 < G_A$
with
$S \subseteq H_1< H_2 < G_A$
with
![]() $[G_A:H_2]=m$
and
$[G_A:H_2]=m$
and
![]() $[H_2:H_1]=2$
. Moreover, if
$[H_2:H_1]=2$
. Moreover, if
![]() $m>2$
, then there exists a normal subgroup K of
$m>2$
, then there exists a normal subgroup K of
![]() $G_A$
containing S and contained in
$G_A$
containing S and contained in
![]() $H_2$
such that
$H_2$
such that
![]() $G_A/K \cong D_{2m}$
.
$G_A/K \cong D_{2m}$
.
Proof. As by assumption
![]() $G_A$
preserves
$G_A$
preserves
![]() $\mathcal {F}_{2m}$
, by Lemma 7.1 it preserves also
$\mathcal {F}_{2m}$
, by Lemma 7.1 it preserves also
![]() $\mathcal {E}_m$
, hence it induces an action on
$\mathcal {E}_m$
, hence it induces an action on
![]() $\{F_1, \ldots , F_{2m}\}$
and on
$\{F_1, \ldots , F_{2m}\}$
and on
![]() $\{E_1, \ldots , E_m\}$
.
$\{E_1, \ldots , E_m\}$
.
Let us define
![]() $H_1:=\mathrm {Stab}_{G_A}(F_{2m})$
and
$H_1:=\mathrm {Stab}_{G_A}(F_{2m})$
and
![]() $H_2:=\mathrm {Stab}_{G_A}(E_m)$
. As
$H_2:=\mathrm {Stab}_{G_A}(E_m)$
. As
![]() $2n \in F_{2m} \subseteq E_m$
, by Lemma 7.1 it follows that
$2n \in F_{2m} \subseteq E_m$
, by Lemma 7.1 it follows that
![]() $S\subseteq H_1 \subseteq H_2$
.
$S\subseteq H_1 \subseteq H_2$
.
The group
![]() $G_A$
acts transitively on
$G_A$
acts transitively on
![]() $\{1,\ldots , 2n\}$
; therefore, the action on
$\{1,\ldots , 2n\}$
; therefore, the action on
![]() $\{F_1, \ldots , F_{2m}\}$
and on
$\{F_1, \ldots , F_{2m}\}$
and on
![]() $\{E_1, \ldots , E_m\}$
is transitive as well, so the orbits of
$\{E_1, \ldots , E_m\}$
is transitive as well, so the orbits of
![]() $F_i$
and
$F_i$
and
![]() $E_j$
have cardinality
$E_j$
have cardinality
![]() $2m$
and m, respectively. This implies that
$2m$
and m, respectively. This implies that
![]() $|G_A|/|H_2|=|G_A\cdot E_m|=m$
and
$|G_A|/|H_2|=|G_A\cdot E_m|=m$
and
![]() $|G_A|/|H_1|=|G_A\cdot F_{2m}|=2m$
, where
$|G_A|/|H_1|=|G_A\cdot F_{2m}|=2m$
, where
![]() $G_A \cdot C$
denotes the orbit of C with respect to the action of
$G_A \cdot C$
denotes the orbit of C with respect to the action of
![]() $G_A$
. This proves that
$G_A$
. This proves that
![]() $[G_A:H_2]=m$
and
$[G_A:H_2]=m$
and
![]() $[H_2:H_1]=2$
as wanted.
$[H_2:H_1]=2$
as wanted.
We now prove the second part of the statement.
For
![]() $m>2$
let us define
$m>2$
let us define
![]() $K:= \mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
. Note that
$K:= \mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
. Note that
![]() $K \subseteq H_2$
and, if
$K \subseteq H_2$
and, if
![]() $m>2$
, then
$m>2$
, then
![]() $K\neq H_2$
(as
$K\neq H_2$
(as
![]() $\sigma _1 \in H_2$
and
$\sigma _1 \in H_2$
and
![]() $\sigma _1 \not \in K$
). To conclude the proof, we have to show that K is a normal subgroup of
$\sigma _1 \not \in K$
). To conclude the proof, we have to show that K is a normal subgroup of
![]() $G_A$
and
$G_A$
and
![]() $G_A/K\cong D_{2m}$
.
$G_A/K\cong D_{2m}$
.
First, let us prove that
![]() $K\lhd G_A$
. Take
$K\lhd G_A$
. Take
![]() $h\in K$
and
$h\in K$
and
![]() $g\in G_A$
, then, if
$g\in G_A$
, then, if
![]() $g(E_i)=E_{j_i}$
for some
$g(E_i)=E_{j_i}$
for some
![]() $j_i$
, we have that
$j_i$
, we have that
so
![]() $g^{-1}hg \in K$
as wanted.
$g^{-1}hg \in K$
as wanted.
Finally, we show that
![]() $G_A/K\cong D_{2m}$
. As
$G_A/K\cong D_{2m}$
. As
![]() $G_A$
induces an action on
$G_A$
induces an action on
![]() $\{E_1,\ldots , E_m\}$
, we can define a homomorphism
$\{E_1,\ldots , E_m\}$
, we can define a homomorphism
![]() $\varphi : G_A \rightarrow S_m$
given by
$\varphi : G_A \rightarrow S_m$
given by
![]() $\varphi (\alpha )=\beta $
where
$\varphi (\alpha )=\beta $
where
![]() $\beta \in S_m$
is defined by
$\beta \in S_m$
is defined by
![]() $\beta (i)=j$
if
$\beta (i)=j$
if
![]() $\alpha (E_i)=E_j$
. Since
$\alpha (E_i)=E_j$
. Since
![]() $K=\mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
, then
$K=\mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
, then
![]() $\varphi $
induces an injective homomorphism
$\varphi $
induces an injective homomorphism
![]() $\tilde \varphi : G_A/K \rightarrow S_m$
. We want now to prove that
$\tilde \varphi : G_A/K \rightarrow S_m$
. We want now to prove that
![]() $\tilde \varphi (G_A/K)\cong D_{2m}$
. By Lemma 7.1,
$\tilde \varphi (G_A/K)\cong D_{2m}$
. By Lemma 7.1,
![]() $\tilde \varphi (\tau _i)=\mathrm {id}$
for every
$\tilde \varphi (\tau _i)=\mathrm {id}$
for every
![]() $i=1, \ldots , k$
, so
$i=1, \ldots , k$
, so
![]() $\tilde \varphi (G_A/K)$
is generated by the images of
$\tilde \varphi (G_A/K)$
is generated by the images of
![]() $\sigma _{\infty }$
and
$\sigma _{\infty }$
and
![]() $\sigma _1$
, which we denote by r and s, respectively. We have to prove that
$\sigma _1$
, which we denote by r and s, respectively. We have to prove that
![]() $r^m=\mathrm {id}$
,
$r^m=\mathrm {id}$
,
![]() $s^2=\mathrm {id}$
and
$s^2=\mathrm {id}$
and
![]() $srsr=\mathrm {id}$
. Notice that, if
$srsr=\mathrm {id}$
. Notice that, if
![]() $\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
, then
$\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
, then
![]() $r=(m,m-1, \ldots , 1)$
, so
$r=(m,m-1, \ldots , 1)$
, so
![]() $r^m=\mathrm {id}$
. Moreover, by Lemma 7.1, s is a product of transpositions, so it has order
$r^m=\mathrm {id}$
. Moreover, by Lemma 7.1, s is a product of transpositions, so it has order
![]() $2$
as wanted. Let us finally prove that
$2$
as wanted. Let us finally prove that
![]() $srsr=\mathrm {id}$
. By Lemma 7.1 we have that
$srsr=\mathrm {id}$
. By Lemma 7.1 we have that
![]() $\sigma _1(E_m)=E_m$
,
$\sigma _1(E_m)=E_m$
,
![]() $\sigma _1(E_i)=E_{m-i}$
for all
$\sigma _1(E_i)=E_{m-i}$
for all
![]() $i=1,\dots , m-1$
and
$i=1,\dots , m-1$
and
![]() $\sigma _{\infty }(E_1)=E_{m}$
and
$\sigma _{\infty }(E_1)=E_{m}$
and
![]() $\sigma _{\infty }(E_j)=E_{j-1}$
for all
$\sigma _{\infty }(E_j)=E_{j-1}$
for all
![]() $j=2, \ldots , m$
. So, for every
$j=2, \ldots , m$
. So, for every
![]() $i=1,\ldots , m$
,
$i=1,\ldots , m$
,
This shows that
![]() $G_A/K\cong D_{2m}$
, concluding the proof.
$G_A/K\cong D_{2m}$
, concluding the proof.
Using the previous lemma, we can finally prove the following result about the polynomial decomposition of
![]() $\phi _A$
, which concludes the proof of Theorem 6.2.
$\phi _A$
, which concludes the proof of Theorem 6.2.
Proposition 7.3. Suppose
![]() $G_A$
preserves
$G_A$
preserves
![]() $\mathcal {F}_{2m}$
with
$\mathcal {F}_{2m}$
with
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $n/m \ge d$
. Then
$n/m \ge d$
. Then
![]() $\phi _A=f_m(\phi _{A'})$
, where
$\phi _A=f_m(\phi _{A'})$
, where
![]() $A'$
is another solution of the same Pell–Abel equation.
$A'$
is another solution of the same Pell–Abel equation.
Proof. By Lemma 7.2, there exists a chain of groups
where
![]() $[G_A:H_2]=m$
and
$[G_A:H_2]=m$
and
![]() $[H_2:H_1]=2$
, where we recall that
$[H_2:H_1]=2$
, where we recall that
![]() $H_1=\mathrm {Stab}_{G_A}(F_{2m})$
and
$H_1=\mathrm {Stab}_{G_A}(F_{2m})$
and
![]() $H_2=\mathrm {Stab}_{G_A}(E_m)$
. By Galois theory, this implies that there exists a tower of subfields of
$H_2=\mathrm {Stab}_{G_A}(E_m)$
. By Galois theory, this implies that there exists a tower of subfields of
![]() $\mathbb {C}(t)$
$\mathbb {C}(t)$
with
![]() $[L_2:\mathbb {C}(\phi _A)]=m$
and
$[L_2:\mathbb {C}(\phi _A)]=m$
and
![]() $[L_1:L_2]=2$
. Together with Proposition 5.1, this implies that
$[L_1:L_2]=2$
. Together with Proposition 5.1, this implies that
where
![]() $h_1,h_2$
and z are polynomials with
$h_1,h_2$
and z are polynomials with
![]() $\deg h_1=2$
and
$\deg h_1=2$
and
![]() $\deg h_2=m$
.
$\deg h_2=m$
.
Let us first prove that
![]() $h_2$
is linearly equivalent to
$h_2$
is linearly equivalent to
![]() $f_m$
. If
$f_m$
. If
![]() $m=2$
, this is trivial since polynomials of degree
$m=2$
, this is trivial since polynomials of degree
![]() $2$
are linearly equivalent to each other, so let us assume that
$2$
are linearly equivalent to each other, so let us assume that
![]() $m>2$
. By Lemma 7.2, the subgroup
$m>2$
. By Lemma 7.2, the subgroup
![]() $K=\mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
is a normal subgroup of
$K=\mathrm {Stab}_{G_A}(E_1, \ldots , E_m)$
is a normal subgroup of
![]() $G_A$
contained in
$G_A$
contained in
![]() $H_2$
and such that
$H_2$
and such that
![]() $G_A/K\cong D_{2m}$
. Then K corresponds to a field
$G_A/K\cong D_{2m}$
. Then K corresponds to a field
![]() $F\subseteq \mathbb {C}(t)$
containing
$F\subseteq \mathbb {C}(t)$
containing
![]() $L_2$
and such that
$L_2$
and such that
![]() $F/T$
is a normal extension. We want to show that
$F/T$
is a normal extension. We want to show that
![]() $F/T$
is the Galois closure of
$F/T$
is the Galois closure of
![]() $L_2/T$
.
$L_2/T$
.
As the action of
![]() $G_A$
on
$G_A$
on
![]() $\{E_1, \ldots , E_m\}$
is transitive, the subgroups
$\{E_1, \ldots , E_m\}$
is transitive, the subgroups
![]() $\mathrm {Stab}_{G_A}(E_1), \ldots , \mathrm {Stab}_{G_A}(E_m)$
are exactly all the conjugates of
$\mathrm {Stab}_{G_A}(E_1), \ldots , \mathrm {Stab}_{G_A}(E_m)$
are exactly all the conjugates of
![]() $\mathrm {Stab}_{G_A}(E_m)=\text {Gal}(\mathbb {C}(t)/L_2)$
in
$\mathrm {Stab}_{G_A}(E_m)=\text {Gal}(\mathbb {C}(t)/L_2)$
in
![]() $G_A$
. Therefore, the Galois closure of
$G_A$
. Therefore, the Galois closure of
![]() $L_2/T$
will be equal to the subfield of
$L_2/T$
will be equal to the subfield of
![]() $\mathbb {C}(t)$
corresponding to
$\mathbb {C}(t)$
corresponding to
![]() $\mathrm {Stab}_{G_A}(E_1)\cap \ldots \cap \mathrm {Stab}_{G_A}(E_m)=K$
that is F as wanted.
$\mathrm {Stab}_{G_A}(E_1)\cap \ldots \cap \mathrm {Stab}_{G_A}(E_m)=K$
that is F as wanted.
As by construction
![]() $\text {Gal}(F/K)=\text {Mon}(h_2)\cong D_{2m}$
, by Proposition 5.3 we have that the polynomial
$\text {Gal}(F/K)=\text {Mon}(h_2)\cong D_{2m}$
, by Proposition 5.3 we have that the polynomial
![]() $h_2$
is linearly equivalent to the Chebychev polynomial
$h_2$
is linearly equivalent to the Chebychev polynomial
![]() $T_m$
, and so to
$T_m$
, and so to
![]() $f_m$
as proved in Section 5. This gives that there exist linear polynomials
$f_m$
as proved in Section 5. This gives that there exist linear polynomials
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
such that
$\alpha _2$
such that
where
![]() $h_3=\alpha _2 \circ h_1$
is a polynomial of degree
$h_3=\alpha _2 \circ h_1$
is a polynomial of degree
![]() $2$
.
$2$
.
We want to prove that
![]() $\phi _A= f_m \circ \phi \circ A'$
where
$\phi _A= f_m \circ \phi \circ A'$
where
![]() $ A'$
fits in the same Pell–Abel equation of A.
$ A'$
fits in the same Pell–Abel equation of A.
For the rest of the proof, as we are dealing with polynomials, we only consider branching at finite points.
By Section 4,
![]() $f_m$
has two branch points, namely
$f_m$
has two branch points, namely
![]() $0$
and
$0$
and
![]() $1$
. As
$1$
. As
![]() $\alpha _1$
is a linear map,
$\alpha _1$
is a linear map,
![]() $\alpha _1\circ f_m$
will be branched only at
$\alpha _1\circ f_m$
will be branched only at
![]() $\xi _0=\alpha _1(0)$
and
$\xi _0=\alpha _1(0)$
and
![]() $\xi _1=\alpha _1(1)$
with the same ramification indexes. As the branch points of
$\xi _1=\alpha _1(1)$
with the same ramification indexes. As the branch points of
![]() $\alpha _1\circ f_m$
lie among the ones of
$\alpha _1\circ f_m$
lie among the ones of
![]() $\phi _A$
, this means that
$\phi _A$
, this means that
![]() $\xi _0, \xi _1 \in \{0,1,b_1, \ldots , b_{k}\}$
. We now consider two cases and write
$\xi _0, \xi _1 \in \{0,1,b_1, \ldots , b_{k}\}$
. We now consider two cases and write
![]() $\alpha _1(t)=pt+q$
. We recall that in Proposition 4.1 we gave a characterization of the ramification behavior of
$\alpha _1(t)=pt+q$
. We recall that in Proposition 4.1 we gave a characterization of the ramification behavior of
![]() $f_m$
, and we are going to use this for the rest of the proof.
$f_m$
, and we are going to use this for the rest of the proof.
If m is even, as 0 is the only point with no simple preimage via
![]() $\phi _{A}$
, we necessarily have
$\phi _{A}$
, we necessarily have
![]() $\xi _0=0$
and thus
$\xi _0=0$
and thus
![]() $q=0$
. If
$q=0$
. If
![]() $m>2$
, we have that the branching above
$m>2$
, we have that the branching above
![]() $\xi _1$
is at least
$\xi _1$
is at least
![]() $(m-2)/2 \cdot (n/m)\geq (m/2-1)d>d-1$
while above any of
$(m-2)/2 \cdot (n/m)\geq (m/2-1)d>d-1$
while above any of
![]() $b_1,\dots , b_k$
is at most
$b_1,\dots , b_k$
is at most
![]() $d-1$
. This forces
$d-1$
. This forces
![]() $\xi _1=1$
and
$\xi _1=1$
and
![]() $p=1$
. If
$p=1$
. If
![]() $m=2$
, we have
$m=2$
, we have
![]() $\alpha _1\circ f_2=p (2t-1)^2=(2(\sqrt {p} t +(1-\sqrt {p})/2)-1)^2=f_2\circ (\sqrt {p} t +(1-\sqrt {p})/2)$
. In any case, we have or we may suppose that
$\alpha _1\circ f_2=p (2t-1)^2=(2(\sqrt {p} t +(1-\sqrt {p})/2)-1)^2=f_2\circ (\sqrt {p} t +(1-\sqrt {p})/2)$
. In any case, we have or we may suppose that
![]() $\alpha _1=t$
.
$\alpha _1=t$
.
Assume now m is odd; then the branching above
![]() $\xi _0$
is at least
$\xi _0$
is at least
![]() $(m-1)/2 \cdot (n/m)\geq d>d-1$
and the same for
$(m-1)/2 \cdot (n/m)\geq d>d-1$
and the same for
![]() $\xi _1$
. As before, above
$\xi _1$
. As before, above
![]() $b_1,\dots , b_k$
the branching is at most
$b_1,\dots , b_k$
the branching is at most
![]() $d-1$
. This implies that
$d-1$
. This implies that
![]() $\{\xi _0,\xi _1\} = \{0,1\}$
. In particular, if
$\{\xi _0,\xi _1\} = \{0,1\}$
. In particular, if
![]() $\xi _0=0$
and
$\xi _0=0$
and
![]() $\xi _1=1$
, then
$\xi _1=1$
, then
![]() $\alpha _1=t$
while if
$\alpha _1=t$
while if
![]() $\xi _0=1$
and
$\xi _0=1$
and
![]() $\xi _1=0$
we have
$\xi _1=0$
we have
![]() $\alpha _1=1-t$
. We can reduce to the first case by noticing that
$\alpha _1=1-t$
. We can reduce to the first case by noticing that
![]() $(1-t) \circ f_m = f_m \circ (1-t)$
.
$(1-t) \circ f_m = f_m \circ (1-t)$
.
Finally, we have
where
![]() $h_3$
is a polynomial of degree
$h_3$
is a polynomial of degree
![]() $2$
.
$2$
.
We write
![]() $w=h_3 \circ z$
and let r be the unique finite branch point of
$w=h_3 \circ z$
and let r be the unique finite branch point of
![]() $h_3$
. We claim that
$h_3$
. We claim that
![]() $r\in \{0,1\}$
. Suppose not; the fact that
$r\in \{0,1\}$
. Suppose not; the fact that
![]() $f_m(\{0,1\})\subseteq \{0,1\}$
and that
$f_m(\{0,1\})\subseteq \{0,1\}$
and that
![]() $\phi _A$
fits in a Pell–Abel equation implies that
$\phi _A$
fits in a Pell–Abel equation implies that
![]() $w^{-1}(\{0,1\}) $
contains exactly
$w^{-1}(\{0,1\}) $
contains exactly
![]() $2d$
simple preimages, and thus the sum of the branching above 0 and 1 of w is at least
$2d$
simple preimages, and thus the sum of the branching above 0 and 1 of w is at least
![]() $2(n/m)-d$
. On the other hand, the branching of w above r is at least
$2(n/m)-d$
. On the other hand, the branching of w above r is at least
![]() $n/m$
making the whole branching to be at least
$n/m$
making the whole branching to be at least
![]() $3(n/m)-d\geq 2(n/m)=\deg w$
. This contradicts the Riemann–Hurwitz formula, and we have
$3(n/m)-d\geq 2(n/m)=\deg w$
. This contradicts the Riemann–Hurwitz formula, and we have
![]() $r\in \{0,1\}$
.
$r\in \{0,1\}$
.
If m is odd, then we must have
![]() $r=0$
because
$r=0$
because
![]() $1$
, being the only simple preimage of 1 via
$1$
, being the only simple preimage of 1 via
![]() $f_m$
must have simple preimages via w.
$f_m$
must have simple preimages via w.
If m is even and
![]() $r=1$
, we observe that
$r=1$
, we observe that
![]() $f_m=f_m\circ (1-t) $
. We then can simply replace
$f_m=f_m\circ (1-t) $
. We then can simply replace
![]() $h_3$
by
$h_3$
by
![]() $(1-t)\circ h_3$
, and thus we may assume
$(1-t)\circ h_3$
, and thus we may assume
![]() $r=0$
.
$r=0$
.
In any case, we have
![]() $h_3=st^2=(\sqrt {s}t)^2$
and then, possibly composing with a suitable linear polynomial on the right, we can assume that
$h_3=st^2=(\sqrt {s}t)^2$
and then, possibly composing with a suitable linear polynomial on the right, we can assume that
![]() $h_3$
is exactly the square function
$h_3$
is exactly the square function
![]() $\phi $
, so
$\phi $
, so
We are left with proving that
![]() $A'$
is another solution of the same Pell–Abel equation, that is, that
$A'$
is another solution of the same Pell–Abel equation, that is, that
![]() $\phi _{A'}-1=D B^{\prime 2}$
for some polynomial
$\phi _{A'}-1=D B^{\prime 2}$
for some polynomial
![]() $B'$
. Notice that, since A is a solution of the Pell–Abel equation,
$B'$
. Notice that, since A is a solution of the Pell–Abel equation,
![]() $\phi _A^{-1}(1)$
contains exactly
$\phi _A^{-1}(1)$
contains exactly
![]() $2d$
simple points
$2d$
simple points
![]() $\{r_1, \ldots , r_{2d}\}$
(the zeros of D); as
$\{r_1, \ldots , r_{2d}\}$
(the zeros of D); as
![]() $1$
(and
$1$
(and
![]() $0$
if m is even) is the only point in
$0$
if m is even) is the only point in
![]() $f_m^{-1}(1)$
with ramification index
$f_m^{-1}(1)$
with ramification index
![]() $1$
and
$1$
and
![]() $\phi _{A'}=\phi \circ A'$
is a square, then
$\phi _{A'}=\phi \circ A'$
is a square, then
![]() $\{r_1, \ldots r_{2d}\} \subset \phi _{A'}^{-1}(1)$
. This shows that
$\{r_1, \ldots r_{2d}\} \subset \phi _{A'}^{-1}(1)$
. This shows that
![]() $(\phi _{A'}-1)/D={B'}^2$
for some polynomial
$(\phi _{A'}-1)/D={B'}^2$
for some polynomial
![]() $B'$
as wanted.
$B'$
as wanted.
Corollary 7.4. Let m be a positive integer. Let
![]() $(A,B)$
be a solution of degree n of the Pell–Abel equation
$(A,B)$
be a solution of degree n of the Pell–Abel equation
![]() $A^2-DB^2=1$
, and, for
$A^2-DB^2=1$
, and, for
![]() $i=1, \ldots , 2m$
, let
$i=1, \ldots , 2m$
, let
![]() $F_i=\{j\in \{1, \ldots , 2n\}\ |\ j\equiv i\ \ \mod 2m\}$
, and, after conjugating, assume that
$F_i=\{j\in \{1, \ldots , 2n\}\ |\ j\equiv i\ \ \mod 2m\}$
, and, after conjugating, assume that
![]() $\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and that one of the points which are fixed by
$\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and that one of the points which are fixed by
![]() $\sigma _1$
and by all the
$\sigma _1$
and by all the
![]() $\tau _i$
is
$\tau _i$
is
![]() $2n$
. Then
$2n$
. Then
![]() $(A,B)$
is the
$(A,B)$
is the
![]() $m^{th}$
-power of a solution
$m^{th}$
-power of a solution
![]() $(A', B')$
of the same Pell–Abel equation if and only if the permutations
$(A', B')$
of the same Pell–Abel equation if and only if the permutations
![]() $\sigma _{\infty }, \sigma _0, \sigma _1, \tau _1, \ldots , \tau _{k}$
associated to A satisfy the following conditions:
$\sigma _{\infty }, \sigma _0, \sigma _1, \tau _1, \ldots , \tau _{k}$
associated to A satisfy the following conditions:
 $$ \begin{align} \begin{cases} \sigma_{\infty}(F_1)=F_{2m} \mbox{ and } \sigma_{\infty}(F_h)= F_{h-1} \quad \forall{h=2,\ldots, 2m};\\ \sigma_1(F_{2m})=F_{2m} \mbox{ and } \sigma_1(F_h)=F_{2m-h}\quad \forall h=1, \ldots, 2m-1; \\ \sigma_0(F_i)=F_{2m-i+1} \quad \forall i=1,\ldots, 2m; \\ \tau_j(F_i)=F_i \quad \forall i=1, \ldots, 2m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \sigma_{\infty}(F_1)=F_{2m} \mbox{ and } \sigma_{\infty}(F_h)= F_{h-1} \quad \forall{h=2,\ldots, 2m};\\ \sigma_1(F_{2m})=F_{2m} \mbox{ and } \sigma_1(F_h)=F_{2m-h}\quad \forall h=1, \ldots, 2m-1; \\ \sigma_0(F_i)=F_{2m-i+1} \quad \forall i=1,\ldots, 2m; \\ \tau_j(F_i)=F_i \quad \forall i=1, \ldots, 2m \mbox{ and } j=1,\ldots, k. \end{cases} \end{align} $$
Example 7.5. Let us see an example with
![]() $n=6$
and
$n=6$
and
![]() $d=2$
, so the permutations are in
$d=2$
, so the permutations are in
![]() $S_{12}$
. In this case, we have that the solution of the Pell–Abel equation can be either primitive or a square of a solution of degree 3 or the cube of a solution of degree 2.
$S_{12}$
. In this case, we have that the solution of the Pell–Abel equation can be either primitive or a square of a solution of degree 3 or the cube of a solution of degree 2.
Consider
![]() $\sigma _{\infty }=(12, 11, \ldots , 1)$
and
$\sigma _{\infty }=(12, 11, \ldots , 1)$
and
![]() $\sigma _0=(1, 12)(2,11)(3,10)(4,9)(5,8) (6,7)$
. As
$\sigma _0=(1, 12)(2,11)(3,10)(4,9)(5,8) (6,7)$
. As
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau _1=1$
, we have that
$\sigma _0\sigma _{\infty }\sigma _1\tau _1=1$
, we have that
![]() $\sigma _1\tau _1=(1,11)(2,10)(3,9)(4,8)(5,7)$
. So the solution will depend on the choice of
$\sigma _1\tau _1=(1,11)(2,10)(3,9)(4,8)(5,7)$
. So the solution will depend on the choice of
![]() $\tau _1$
among these transpositions. In particular, if we choose
$\tau _1$
among these transpositions. In particular, if we choose
![]() $\tau _1=(1,11)$
or
$\tau _1=(1,11)$
or
![]() $\tau _1=(5,7)$
, the associated solution is primitive. In fact, by equation (7.4), we have that the solution associated to these permutations is neither a square nor a cube (otherwise,
$\tau _1=(5,7)$
, the associated solution is primitive. In fact, by equation (7.4), we have that the solution associated to these permutations is neither a square nor a cube (otherwise,
![]() $1, 11$
or
$1, 11$
or
![]() $5,7$
would lie in the same congruence class modulo
$5,7$
would lie in the same congruence class modulo
![]() $4$
in the case of a square or modulo
$4$
in the case of a square or modulo
![]() $6$
in the case of a cube). Moreover, if
$6$
in the case of a cube). Moreover, if
![]() $\tau _1=(2,10)$
or
$\tau _1=(2,10)$
or
![]() $\tau _1=(4,8)$
, the solutions are squares. In fact, in this case it is easy to see that
$\tau _1=(4,8)$
, the solutions are squares. In fact, in this case it is easy to see that
![]() $(\sigma _{\infty },\sigma _0,\sigma _1,\tau _1)$
satisfies equation (7.4) for
$(\sigma _{\infty },\sigma _0,\sigma _1,\tau _1)$
satisfies equation (7.4) for
![]() $m=2$
, while, if
$m=2$
, while, if
![]() $\tau _1=(3,9)$
, the solution is a cube. Note, however, that the two 4-tuples with
$\tau _1=(3,9)$
, the solution is a cube. Note, however, that the two 4-tuples with
![]() $\tau _1=(2,10)$
and
$\tau _1=(2,10)$
and
![]() $\tau _1=(4,8)$
are actually conjugated by
$\tau _1=(4,8)$
are actually conjugated by
![]() $\sigma _{\infty }^6$
.
$\sigma _{\infty }^6$
.
8 Counting the conjugacy classes of permutations
In this section, we want to show how to apply Theorem 2.3 and use combinatorial arguments to count equivalence classes of Pellian polynomials with a solution of degree n.
As discussed in the introduction, the advantage of the combinatorial argument is that it allows to compute the precise number instead of only an asymptotic formula, and this can be done algorithmically given n and d. On the other hand, the combinatorics becomes more difficult as soon as d grows due to the number of different configurations that the permutations can have. For this reason, in this section we are going to stick to the case
![]() $d=2$
and to maximal branching, that is when the map
$d=2$
and to maximal branching, that is when the map
![]() $\phi _A$
is branched over
$\phi _A$
is branched over
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $\infty $
and over another point which we will denote by b. In this case, using the arguments of Section 2 and the Riemann–Hurwitz formula, if we count the branching of
$\infty $
and over another point which we will denote by b. In this case, using the arguments of Section 2 and the Riemann–Hurwitz formula, if we count the branching of
![]() $\phi _A$
as the sum of
$\phi _A$
as the sum of
![]() $e-1$
over the ramification indices e, we have that, above
$e-1$
over the ramification indices e, we have that, above
![]() $0$
the branching is exactly n, above
$0$
the branching is exactly n, above
![]() $1$
is
$1$
is
![]() $n-1$
, above
$n-1$
, above
![]() $\infty $
it is
$\infty $
it is
![]() $2n-1$
and above b is
$2n-1$
and above b is
![]() $1$
. This implies that the cycle decomposition of
$1$
. This implies that the cycle decomposition of
![]() $\sigma _0, \sigma _{\infty }, \sigma _1$
and
$\sigma _0, \sigma _{\infty }, \sigma _1$
and
![]() $\tau _1=:\tau $
is fixed, and we have that:
$\tau _1=:\tau $
is fixed, and we have that:
-
1 -
 $\sigma _0$
is the product of n disjoint transpositions;
$\sigma _0$
is the product of n disjoint transpositions; -
2 -
 $\sigma _{\infty }$
is a
$\sigma _{\infty }$
is a
 $2n$
-cycle;
$2n$
-cycle; -
3 -
 $\sigma _1$
is the product of
$\sigma _1$
is the product of
 $n-1$
disjoint transpositions;
$n-1$
disjoint transpositions; -
4 -
 $\tau $
is a transposition.
$\tau $
is a transposition.
Moreover, we know that
![]() $\sigma _0, \sigma _{\infty }, \sigma _1$
and
$\sigma _0, \sigma _{\infty }, \sigma _1$
and
![]() $\tau $
satisfy
$\tau $
satisfy
![]() $\sigma _0 \sigma _{\infty }\sigma _1\tau =$
id.
$\sigma _0 \sigma _{\infty }\sigma _1\tau =$
id.
As said before each conjugacy class of
![]() $4$
-tuples
$4$
-tuples
![]() $(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
has at least one representative with
$(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
has at least one representative with
![]() $\sigma _{\infty }=(2n,2n-1, \ldots , 1)$
since
$\sigma _{\infty }=(2n,2n-1, \ldots , 1)$
since
![]() $\sigma _{\infty }$
is a
$\sigma _{\infty }$
is a
![]() $2n$
-cycle and one can relabel the element using a suitable conjugation. Moreover, there are at least two indexes that are fixed by
$2n$
-cycle and one can relabel the element using a suitable conjugation. Moreover, there are at least two indexes that are fixed by
![]() $\sigma _1$
and by
$\sigma _1$
and by
![]() $\tau $
; without loss of generality we will always assume that one of the two indexes is
$\tau $
; without loss of generality we will always assume that one of the two indexes is
![]() $2n$
. We will call such a representative special.
$2n$
. We will call such a representative special.
Now, since
![]() $\sigma _1$
is the product of
$\sigma _1$
is the product of
![]() $n-1$
disjoint transpositions and
$n-1$
disjoint transpositions and
![]() $\tau $
is a transposition, we have three different cases:
$\tau $
is a transposition, we have three different cases:
-
•
 $\sigma _1$
and
$\sigma _1$
and
 $\tau $
are disjoint permutations;
$\tau $
are disjoint permutations; -
•
 $\sigma _1\tau $
is the product of
$\sigma _1\tau $
is the product of
 $n-2$
transpositions and a
$n-2$
transpositions and a
 $3$
-cycle;
$3$
-cycle; -
•
 $\sigma _1\tau $
is the product of
$\sigma _1\tau $
is the product of
 $n-3$
transpositions and a
$n-3$
transpositions and a
 $4$
-cycle.
$4$
-cycle.
In what follows, we are going to study the special
![]() $4$
-tuples, analysing in particular how many special
$4$
-tuples, analysing in particular how many special
![]() $4$
-tuples we have in each conjugacy class. As the conjugation preserves the cycle decomposition, we have to analyse these three cases separately.
$4$
-tuples we have in each conjugacy class. As the conjugation preserves the cycle decomposition, we have to analyse these three cases separately.
8.1 The disjoint case
Let
![]() $\Sigma $
be a special
$\Sigma $
be a special
![]() $4$
-tuple, that is,
$4$
-tuple, that is,
![]() $\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
$\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
both fix
$\tau $
both fix
![]() $2n$
. Suppose moreover that
$2n$
. Suppose moreover that
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
are disjoint permutations.
$\tau $
are disjoint permutations.
Since
![]() $2n$
is fixed by both
$2n$
is fixed by both
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
and
$\tau $
and
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =$
id, then
$\sigma _0\sigma _{\infty }\sigma _1\tau =$
id, then
![]() $2n$
is fixed by
$2n$
is fixed by
![]() $\sigma _0\sigma _{\infty }$
; moreover, as
$\sigma _0\sigma _{\infty }$
; moreover, as
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =$
id, we must have that
$\sigma _0\sigma _{\infty }\sigma _1\tau =$
id, we must have that
![]() $\sigma _0(2n)=1$
. Since
$\sigma _0(2n)=1$
. Since
![]() $\sigma _0$
is composed only by transpositions, we have also that
$\sigma _0$
is composed only by transpositions, we have also that
![]() $\sigma _0(1)=2n$
, hence
$\sigma _0(1)=2n$
, hence
![]() $\sigma _1\tau (2n-1)=1$
. Now as
$\sigma _1\tau (2n-1)=1$
. Now as
![]() $\sigma _1\tau $
is composed only by transpositions, we have that
$\sigma _1\tau $
is composed only by transpositions, we have that
![]() $\sigma _1\tau (1)=2n-1$
, so
$\sigma _1\tau (1)=2n-1$
, so
![]() $\sigma _0(2n-1)=2$
and so on. Going on with this argument, we have that
$\sigma _0(2n-1)=2$
and so on. Going on with this argument, we have that
![]() $\sigma _0$
must have the form
$\sigma _0$
must have the form
![]() $(1,2n)(2,2n-1) \cdots (n,n+1)$
and
$(1,2n)(2,2n-1) \cdots (n,n+1)$
and
![]() $\sigma _0\sigma _{\infty }$
fixes also n. In this case,
$\sigma _0\sigma _{\infty }$
fixes also n. In this case,
![]() $\sigma _1 \tau =(1,2n-1)(2,2n-2) \cdots (n-1, n+1)$
and we may choose as
$\sigma _1 \tau =(1,2n-1)(2,2n-2) \cdots (n-1, n+1)$
and we may choose as
![]() $\tau $
any of the
$\tau $
any of the
![]() $n-1$
transpositions
$n-1$
transpositions
![]() $(1,2n-1),(2,2n-2), \cdots , (n-1, n+1)$
.
$(1,2n-1),(2,2n-2), \cdots , (n-1, n+1)$
.
Now, assume that
![]() $\Sigma '=(\sigma _0',\sigma _{\infty },\sigma _1',\tau ')$
is another special
$\Sigma '=(\sigma _0',\sigma _{\infty },\sigma _1',\tau ')$
is another special
![]() $4$
-tuple lying in the same conjugacy class of
$4$
-tuple lying in the same conjugacy class of
![]() $\Sigma $
, that is,
$\Sigma $
, that is,
![]() $\Sigma '=\gamma ^{-1}\Sigma \gamma $
for some
$\Sigma '=\gamma ^{-1}\Sigma \gamma $
for some
![]() $\gamma \in S_{2n}$
; then, since by assumption
$\gamma \in S_{2n}$
; then, since by assumption
![]() $\sigma _{\infty }$
has to be fixed by the conjugation, we have that
$\sigma _{\infty }$
has to be fixed by the conjugation, we have that
![]() $\gamma $
will be a power of
$\gamma $
will be a power of
![]() $\sigma _{\infty }$
. Furthermore, since we want
$\sigma _{\infty }$
. Furthermore, since we want
![]() $\sigma _1'$
and
$\sigma _1'$
and
![]() $\tau '$
both to fix
$\tau '$
both to fix
![]() $2n$
, then the conjugation has to permute
$2n$
, then the conjugation has to permute
![]() $2n$
with n (which is the only other point fixed by
$2n$
with n (which is the only other point fixed by
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
); consequently,
$\tau $
); consequently,
![]() $\gamma =\sigma _{\infty }^n$
. Notice finally that, given a special
$\gamma =\sigma _{\infty }^n$
. Notice finally that, given a special
![]() $4$
-tuple
$4$
-tuple
![]() $\Sigma $
, we have
$\Sigma $
, we have
![]() $\sigma _{\infty }^{-n}\Sigma \sigma _{\infty }^n= \Sigma $
if and only if n is even and
$\sigma _{\infty }^{-n}\Sigma \sigma _{\infty }^n= \Sigma $
if and only if n is even and
![]() $\tau =\left ( \frac {n}{2}, 2n-\frac {n}{2} \right )$
.
$\tau =\left ( \frac {n}{2}, 2n-\frac {n}{2} \right )$
.
This implies that:
-
• if n is odd, then we have
 $\frac {1}{2}(n-1)$
conjugacy classes, because every conjugacy class contains two special
$\frac {1}{2}(n-1)$
conjugacy classes, because every conjugacy class contains two special
 $4$
-tuples;
$4$
-tuples; -
• if n is even, then we have
 $\frac {1}{2}n$
conjugacy classes because every conjugacy class contains exactly two special
$\frac {1}{2}n$
conjugacy classes because every conjugacy class contains exactly two special
 $4$
-tuples, except for the conjugacy class of the
$4$
-tuples, except for the conjugacy class of the
 $4$
-tuple with
$4$
-tuple with
 $\tau =\left (\frac {n}{2}, 2n-\frac {n}{2}\right )$
which contains only one special
$\tau =\left (\frac {n}{2}, 2n-\frac {n}{2}\right )$
which contains only one special
 $4$
-tuple.
$4$
-tuple.
In general we have
We point out that, in the disjoint case, Corollary 7.4 gives an easier way to detect whether the solution
![]() $(A,B)$
is primitive by looking only at the corresponding
$(A,B)$
is primitive by looking only at the corresponding
![]() $\tau $
of a special representative.
$\tau $
of a special representative.
Proposition 8.1. Consider the
![]() $4$
-tuple
$4$
-tuple
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
with
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
with
![]() $\sigma _{\infty }=(2n,2n-1,\ldots ,1)$
and
$\sigma _{\infty }=(2n,2n-1,\ldots ,1)$
and
![]() $\sigma _0=(1,2n)(2,2n-1)\ldots (n,n+1)$
associated to a solution
$\sigma _0=(1,2n)(2,2n-1)\ldots (n,n+1)$
associated to a solution
![]() $(A,B)$
of a Pell–Abel equation. Then
$(A,B)$
of a Pell–Abel equation. Then
![]() $(A,B)$
is the m-th power of another solution if and only if
$(A,B)$
is the m-th power of another solution if and only if
![]() $\tau =(h,2n-h)$
with
$\tau =(h,2n-h)$
with
![]() $m\mid h$
.
$m\mid h$
.
In particular, there are exactly
![]() $\varphi (n)/2$
equivalence classes corresponding to primitive solutions.
$\varphi (n)/2$
equivalence classes corresponding to primitive solutions.
Proof. By Corollary 7.4,
![]() $\Sigma $
corresponds to an m-th power if and only if equation (7.4) holds. The conditions on
$\Sigma $
corresponds to an m-th power if and only if equation (7.4) holds. The conditions on
![]() $\sigma _0$
,
$\sigma _0$
,
![]() $\sigma _\infty $
are always satisfied. The condition on
$\sigma _\infty $
are always satisfied. The condition on
![]() $\tau $
is satisfied if and only if
$\tau $
is satisfied if and only if
![]() $\tau =(h,2n-h)$
with
$\tau =(h,2n-h)$
with
![]() $h \equiv 2n-h\equiv -h\ \ \mod {2m}$
, that is,
$h \equiv 2n-h\equiv -h\ \ \mod {2m}$
, that is,
![]() $m\mid h$
. Finally, if
$m\mid h$
. Finally, if
![]() $m\mid h$
, also
$m\mid h$
, also
![]() $\sigma _1$
satisfies the conditions of equation (7.4), proving the claim.
$\sigma _1$
satisfies the conditions of equation (7.4), proving the claim.
8.2 The 3-cycle case
Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
![]() $4$
-tuple, that is, with
$4$
-tuple, that is, with
![]() $\sigma _{\infty }=(2n, \ldots , 1)$
and such that
$\sigma _{\infty }=(2n, \ldots , 1)$
and such that
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
fix both
$\tau $
fix both
![]() $2n$
, and assume that
$2n$
, and assume that
![]() $\sigma _1\tau $
decomposes as a product of
$\sigma _1\tau $
decomposes as a product of
![]() $n-3$
transpositions and a 3-cycle.
$n-3$
transpositions and a 3-cycle.
First, we are going to prove the following result that describes the possible shapes of
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1\tau $
of such a
$\sigma _1\tau $
of such a
![]() $4$
-tuple.
$4$
-tuple.
Proposition 8.2. Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
be a special
![]() $4$
-tuple such that
$4$
-tuple such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $3$
-cycle. Then there exist
$3$
-cycle. Then there exist
![]() $h,k$
with
$h,k$
with
![]() $1\le h\leq n-2$
,
$1\le h\leq n-2$
,
![]() $h< k <2n-h$
and
$h< k <2n-h$
and
![]() $h\equiv k\ \ \mod 2$
such that
$h\equiv k\ \ \mod 2$
such that
 $$ \begin{align} \sigma_0 &=\prod_{i=1}^h(i,2n+1-i) \prod_{j=1}^{\frac{k-h}{2}}(h+j, k+1-j) \prod_{t=1}^{\frac{2n-h-k}{2}}(k+t, 2n-h+1-t);\\ \sigma_1\tau & =\prod_{i=1}^{h-1}(i,2n-i)\prod_{j=1}^{\frac{k-h}{2}-1} (h+j, k-j) \prod_{t=1}^{\frac{2n-h-k}{2}}(k+t,2n-h-t)\ (2n-h, h, k). \nonumber \end{align} $$
$$ \begin{align} \sigma_0 &=\prod_{i=1}^h(i,2n+1-i) \prod_{j=1}^{\frac{k-h}{2}}(h+j, k+1-j) \prod_{t=1}^{\frac{2n-h-k}{2}}(k+t, 2n-h+1-t);\\ \sigma_1\tau & =\prod_{i=1}^{h-1}(i,2n-i)\prod_{j=1}^{\frac{k-h}{2}-1} (h+j, k-j) \prod_{t=1}^{\frac{2n-h-k}{2}}(k+t,2n-h-t)\ (2n-h, h, k). \nonumber \end{align} $$
In particular,
![]() $\sigma _1\tau $
fixes 3 indexes:
$\sigma _1\tau $
fixes 3 indexes:
![]() $2n, \frac {k+h}{2}$
and
$2n, \frac {k+h}{2}$
and
![]() $\frac {2n-h+k}{2}.$
Moreover, there are three different
$\frac {2n-h+k}{2}.$
Moreover, there are three different
![]() $\Sigma $
satisfying equation (8.2) corresponding to different choices of
$\Sigma $
satisfying equation (8.2) corresponding to different choices of
![]() $\tau $
, that is,
$\tau $
, that is,
![]() $\tau \in \{(h,k), (h, 2n-h), (k, 2n-h)\}$
.
$\tau \in \{(h,k), (h, 2n-h), (k, 2n-h)\}$
.
Proof. Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
![]() $4$
-tuple and assume that
$4$
-tuple and assume that
![]() $\sigma _1\tau $
is a product of
$\sigma _1\tau $
is a product of
![]() $n-3$
disjoint transpositions and a disjoint 3-cycle. In this case,
$n-3$
disjoint transpositions and a disjoint 3-cycle. In this case,
![]() $\sigma _1\tau $
fixes
$\sigma _1\tau $
fixes
![]() $3$
indexes, and one of them is
$3$
indexes, and one of them is
![]() $2n$
. Then, since
$2n$
. Then, since
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we must have that
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we must have that
![]() $\sigma _0(2n)=1$
. As
$\sigma _0(2n)=1$
. As
![]() $\sigma _0$
is the product of n disjoint transpositions, we have also that
$\sigma _0$
is the product of n disjoint transpositions, we have also that
![]() $\sigma _0(1)=2n$
, hence
$\sigma _0(1)=2n$
, hence
![]() $\sigma _1\tau (2n-1)=1$
. Now, we have two choices: Either
$\sigma _1\tau (2n-1)=1$
. Now, we have two choices: Either
![]() $\sigma _1\tau (1)=2n-1$
(so
$\sigma _1\tau (1)=2n-1$
(so
![]() $(2n-1,1)$
is one of the disjoint transpositions in the decomposition of
$(2n-1,1)$
is one of the disjoint transpositions in the decomposition of
![]() $\sigma _1\tau $
), or
$\sigma _1\tau $
), or
![]() $\sigma _1\tau (1)=k\neq 2n-1$
(giving rise to the 3-cycle in the product). We can go on as in the disjoint case described in the previous section until we reach the situation in which there exist
$\sigma _1\tau (1)=k\neq 2n-1$
(giving rise to the 3-cycle in the product). We can go on as in the disjoint case described in the previous section until we reach the situation in which there exist
![]() $1\le h\le n-2$
and
$1\le h\le n-2$
and
![]() $h+1\le k\le 2n-h-1$
such that
$h+1\le k\le 2n-h-1$
such that
![]() $\sigma _0$
contains the disjoint transpositions
$\sigma _0$
contains the disjoint transpositions
![]() $(1, 2n),(2,2n-1)\cdots (h,2n-h+1)$
and
$(1, 2n),(2,2n-1)\cdots (h,2n-h+1)$
and
![]() $\sigma _1\tau $
contains the disjoint transpositions
$\sigma _1\tau $
contains the disjoint transpositions
![]() $(1,2n-1)\ldots , (2n-h+1,h-1)$
and the 3-cycle
$(1,2n-1)\ldots , (2n-h+1,h-1)$
and the 3-cycle
![]() $(2n-h,h,k)$
.
$(2n-h,h,k)$
.
Notice that
![]() $k\neq h+1, 2n-h-1$
, otherwise
$k\neq h+1, 2n-h-1$
, otherwise
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
would imply that
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
would imply that
![]() $\sigma _0$
fixes
$\sigma _0$
fixes
![]() $h+1$
(or in the second case
$h+1$
(or in the second case
![]() $2n-h-1$
), which is impossible because
$2n-h-1$
), which is impossible because
![]() $\sigma _0$
has no fixed points. So,
$\sigma _0$
has no fixed points. So,
![]() $h+1 <k< 2n-h-1$
. Now, if
$h+1 <k< 2n-h-1$
. Now, if
![]() $\sigma _1\tau (h)=k$
, as
$\sigma _1\tau (h)=k$
, as
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
![]() $\sigma _0(k)=h+1$
and so
$\sigma _0(k)=h+1$
and so
![]() $\sigma _0(h+1)=k$
. This means that
$\sigma _0(h+1)=k$
. This means that
![]() $\sigma _1\tau (h+1)=k-1$
and
$\sigma _1\tau (h+1)=k-1$
and
![]() $\sigma _1\tau (k-1)=h+1$
and so on. This process ends when one reaches the conditions
$\sigma _1\tau (k-1)=h+1$
and so on. This process ends when one reaches the conditions
![]() $\sigma _0 \left( \frac {k+h}{2} \right)=\frac {k+h}{2}+1$
and vice versa,
$\sigma _0 \left( \frac {k+h}{2} \right)=\frac {k+h}{2}+1$
and vice versa,
![]() $\sigma _1\tau \left(\frac {k+h}{2}-1 \right)=\frac {k+h}{2}+1$
and vice versa and
$\sigma _1\tau \left(\frac {k+h}{2}-1 \right)=\frac {k+h}{2}+1$
and vice versa and
![]() $\frac {k+h}{2}$
is fixed by
$\frac {k+h}{2}$
is fixed by
![]() $\sigma _1\tau $
. Notice that this gives the additional condition that
$\sigma _1\tau $
. Notice that this gives the additional condition that
![]() $h\equiv k\ \ \mod 2$
.
$h\equiv k\ \ \mod 2$
.
On the other hand, if
![]() $\sigma _1\tau $
contains the 3-cycle
$\sigma _1\tau $
contains the 3-cycle
![]() $(2n-h,h,k)$
, we also have that
$(2n-h,h,k)$
, we also have that
![]() $\sigma _1\tau (k)=2n-h$
, giving other conditions to satisfy. In fact,
$\sigma _1\tau (k)=2n-h$
, giving other conditions to satisfy. In fact,
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
implies
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
implies
![]() $\sigma _0(2n-h)=k+1$
and
$\sigma _0(2n-h)=k+1$
and
![]() $\sigma _0(k+1)=2n-h$
. This means, as before, that
$\sigma _0(k+1)=2n-h$
. This means, as before, that
![]() $\sigma _1\tau (2n-h-1)=k+1$
and vice versa, and so on. This process ends when one reaches the conditions
$\sigma _1\tau (2n-h-1)=k+1$
and vice versa, and so on. This process ends when one reaches the conditions
![]() $\sigma _0 \left( \frac {2n-h+k}{2}\right)=\frac {2n-h+k}{2}+1$
and viceversa,
$\sigma _0 \left( \frac {2n-h+k}{2}\right)=\frac {2n-h+k}{2}+1$
and viceversa,
![]() $\sigma _1 \tau \left( \frac {2n-h+k}{2}-1\right)=\frac {2n-h+k}{2}+1$
and
$\sigma _1 \tau \left( \frac {2n-h+k}{2}-1\right)=\frac {2n-h+k}{2}+1$
and
![]() $\frac {2n-h+k}{2}$
is fixed by
$\frac {2n-h+k}{2}$
is fixed by
![]() $\sigma _1\tau $
, proving the first part of the assertion.
$\sigma _1\tau $
, proving the first part of the assertion.
Finally, let us denote by
that is, the product of the
![]() $n-2$
disjoint transpositions that appear in the decomposition of
$n-2$
disjoint transpositions that appear in the decomposition of
![]() $\sigma _1\tau $
.
$\sigma _1\tau $
.
Notice that, if
![]() $\sigma _1\tau $
contains the
$\sigma _1\tau $
contains the
![]() $3$
-cycle
$3$
-cycle
![]() $(2n-h, h, k)$
, then we have three choices for
$(2n-h, h, k)$
, then we have three choices for
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
, namely
$\tau $
, namely
![]() $\sigma _1=\alpha _{hk} (2n-h, h)$
and
$\sigma _1=\alpha _{hk} (2n-h, h)$
and
![]() $\tau =(2n-h,k)$
or
$\tau =(2n-h,k)$
or
![]() $\sigma _1=\alpha _{hk} (h,k)$
and
$\sigma _1=\alpha _{hk} (h,k)$
and
![]() $\tau =(h, 2n-h)$
or
$\tau =(h, 2n-h)$
or
![]() $\sigma _1=\alpha _{hk}(k, 2n-h)$
and
$\sigma _1=\alpha _{hk}(k, 2n-h)$
and
![]() $\tau =(k,h)$
, giving three different special
$\tau =(k,h)$
, giving three different special
![]() $4$
-tuples as wanted.
$4$
-tuples as wanted.
We now want to count how many special
![]() $4$
-tuples are contained in each conjugacy class. First of all, notice that if we have two special
$4$
-tuples are contained in each conjugacy class. First of all, notice that if we have two special
![]() $4$
-tuples
$4$
-tuples
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
and
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
and
![]() $\Sigma '=(\sigma _0',\sigma _{\infty }',\sigma _1',\tau ')$
with
$\Sigma '=(\sigma _0',\sigma _{\infty }',\sigma _1',\tau ')$
with
![]() $\sigma _{\infty }=\sigma _{\infty }'=(2n, 2n-1, \ldots , 1)$
and such that
$\sigma _{\infty }=\sigma _{\infty }'=(2n, 2n-1, \ldots , 1)$
and such that
![]() $\Sigma '=\gamma ^{-1} \Sigma \gamma $
for some
$\Sigma '=\gamma ^{-1} \Sigma \gamma $
for some
![]() $\gamma \in S_{2n}$
, then
$\gamma \in S_{2n}$
, then
![]() $\gamma $
must be equal to a power of
$\gamma $
must be equal to a power of
![]() $\sigma _{\infty }$
. We will consider this conjugation from a geometric point of view; namely, if we consider the regular
$\sigma _{\infty }$
. We will consider this conjugation from a geometric point of view; namely, if we consider the regular
![]() $2n$
-gon with vertices labelled by
$2n$
-gon with vertices labelled by
![]() $1,2,\ldots , 2n$
, then conjugating by a permutation of the form
$1,2,\ldots , 2n$
, then conjugating by a permutation of the form
![]() $\sigma _{\infty }^\ell $
with
$\sigma _{\infty }^\ell $
with
![]() $\ell \in \{1,\ldots ,2n\}$
corresponds to a rotation of angle
$\ell \in \{1,\ldots ,2n\}$
corresponds to a rotation of angle
![]() $\frac {\pi }{n} \ell $
.
$\frac {\pi }{n} \ell $
.
Let us denote by
![]() $p:=\frac {k+h}{2}$
and
$p:=\frac {k+h}{2}$
and
![]() $q:=\frac {2n-h+k}{2}$
the two points different from
$q:=\frac {2n-h+k}{2}$
the two points different from
![]() $2n$
fixed by
$2n$
fixed by
![]() $\sigma _1\tau $
. Then, if we conjugate the set
$\sigma _1\tau $
. Then, if we conjugate the set
![]() $\{2n, q, p\}$
by a power of
$\{2n, q, p\}$
by a power of
![]() $\sigma _{\infty }$
, it corresponds to a rotation of the triangle of vertices
$\sigma _{\infty }$
, it corresponds to a rotation of the triangle of vertices
![]() $\{2n, q, p\}$
. As we want
$\{2n, q, p\}$
. As we want
![]() $\Sigma '$
to be special, then
$\Sigma '$
to be special, then
![]() $\sigma _1'\tau $
has to fix
$\sigma _1'\tau $
has to fix
![]() $2n$
, hence we are interested in the rotations which send one of the vertices to
$2n$
, hence we are interested in the rotations which send one of the vertices to
![]() $2n$
. This means that we can conjugate only by
$2n$
. This means that we can conjugate only by
![]() $\sigma _{\infty }^{2n-p}$
or by
$\sigma _{\infty }^{2n-p}$
or by
![]() $\sigma _{\infty }^{2n-q}$
. In the first case, the set of fixed points
$\sigma _{\infty }^{2n-q}$
. In the first case, the set of fixed points
![]() $\{2n, p, q\}$
is sent to
$\{2n, p, q\}$
is sent to
![]() $\{2n, 2n-p, q-p\}$
, while, in the second case, it is sent to
$\{2n, 2n-p, q-p\}$
, while, in the second case, it is sent to
![]() $\{2n, 2n-(q-p), 2n-q\}$
.
$\{2n, 2n-(q-p), 2n-q\}$
.
We have the following result:
Proposition 8.3. Let
![]() $\Sigma $
be a special
$\Sigma $
be a special
![]() $4$
-tuple
$4$
-tuple
![]() $(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
such that
$(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
such that
![]() $\sigma _1\tau $
contains the
$\sigma _1\tau $
contains the
![]() $3$
-cycle
$3$
-cycle
![]() $(2n-h,h,k)$
. Then the conjugacy class of
$(2n-h,h,k)$
. Then the conjugacy class of
![]() $\Sigma $
contains exactly three special
$\Sigma $
contains exactly three special
![]() $4$
-tuples.
$4$
-tuples.
Proof. Since the
![]() $4$
-tuple
$4$
-tuple
![]() $\Sigma =(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
is special, we have that
$\Sigma =(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
is special, we have that
![]() $\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
$\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
![]() $\sigma _1\tau $
fixes
$\sigma _1\tau $
fixes
![]() $2n$
; moreover, by assumption it contains the
$2n$
; moreover, by assumption it contains the
![]() $3$
-cycle
$3$
-cycle
![]() $(2n-h,h,k)$
. Then, as proved before,
$(2n-h,h,k)$
. Then, as proved before,
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1\tau $
will have the shape (8.2). As discussed before, if
$\sigma _1\tau $
will have the shape (8.2). As discussed before, if
![]() $\Sigma '\neq \Sigma $
is a special
$\Sigma '\neq \Sigma $
is a special
![]() $4$
-tuple conjugated to
$4$
-tuple conjugated to
![]() $\Sigma $
, then
$\Sigma $
, then
![]() $\Sigma '=\gamma ^{-1}\Sigma \gamma $
with
$\Sigma '=\gamma ^{-1}\Sigma \gamma $
with
 $\gamma \in \left \{ \sigma _{\infty }^{2n-\frac {k+h}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k}{2}} \right\}$
. To prove the assertion, we have to show that no
$\gamma \in \left \{ \sigma _{\infty }^{2n-\frac {k+h}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k}{2}} \right\}$
. To prove the assertion, we have to show that no
![]() $4$
-tuple is fixed by such a conjugation. To do this, we consider two cases.
$4$
-tuple is fixed by such a conjugation. To do this, we consider two cases.
Assume first that
![]() $3 \mid n$
and that the
$3 \mid n$
and that the
![]() $3$
-cycle contained in
$3$
-cycle contained in
![]() $\sigma _1\tau $
is
$\sigma _1\tau $
is
![]() $ \left(\frac {n}{3}, \frac {5}{3}n, n \right)$
, that is,
$ \left(\frac {n}{3}, \frac {5}{3}n, n \right)$
, that is,
![]() $(h,k)= (\frac {n}{3}, n)$
. By the description above,
$(h,k)= (\frac {n}{3}, n)$
. By the description above,
![]() $\tau \in \left\{ \left(\frac {n}{3}, n \right), \left(n, \frac {5}{3}n \right), \left(\frac {n}{3}, \frac {5}{3} n \right) \right\}$
and
$\tau \in \left\{ \left(\frac {n}{3}, n \right), \left(n, \frac {5}{3}n \right), \left(\frac {n}{3}, \frac {5}{3} n \right) \right\}$
and
![]() $\sigma _1\tau $
fixes
$\sigma _1\tau $
fixes
![]() $ \left\{\frac {2n}{3}, \frac {4n}{3},2n \right\}$
(which are the vertices of an equilateral triangle). Let us assume without loss of generality that
$ \left\{\frac {2n}{3}, \frac {4n}{3},2n \right\}$
(which are the vertices of an equilateral triangle). Let us assume without loss of generality that
![]() $\tau = \left(\frac {n}{3}, n \right)$
. If we conjugate
$\tau = \left(\frac {n}{3}, n \right)$
. If we conjugate
![]() $\Sigma $
by
$\Sigma $
by
 $\gamma \in \left\{\sigma _{\infty }^{\frac {2n}{3}},\sigma _{\infty }^{\frac {4n}{3}} \right\}$
, then
$\gamma \in \left\{\sigma _{\infty }^{\frac {2n}{3}},\sigma _{\infty }^{\frac {4n}{3}} \right\}$
, then
![]() $\gamma ^{-1}\sigma _0 \gamma =\sigma _0$
and
$\gamma ^{-1}\sigma _0 \gamma =\sigma _0$
and
![]() $\gamma ^{-1}(\sigma _1\tau ) \gamma =\sigma _1\tau $
; hence,
$\gamma ^{-1}(\sigma _1\tau ) \gamma =\sigma _1\tau $
; hence,
![]() $\Sigma $
will be conjugated to
$\Sigma $
will be conjugated to
![]() $\Sigma '= \left(\sigma _\infty , \sigma _0, \sigma _1', \left(\frac {5}{3}n, n \right) \right)$
and
$\Sigma '= \left(\sigma _\infty , \sigma _0, \sigma _1', \left(\frac {5}{3}n, n \right) \right)$
and
![]() $\Sigma "= \left(\sigma _\infty , \sigma _0, \sigma _1", \left(\frac {n}{3}, \frac {5}{3} n \right)\right)$
.
$\Sigma "= \left(\sigma _\infty , \sigma _0, \sigma _1", \left(\frac {n}{3}, \frac {5}{3} n \right)\right)$
.
Assume now
![]() $(h,k)\neq (\frac {n}{3}, n)$
. As the conjugation preserves the disjoint cycle structure,
$(h,k)\neq (\frac {n}{3}, n)$
. As the conjugation preserves the disjoint cycle structure,
![]() $\sigma _1\tau $
will contain a
$\sigma _1\tau $
will contain a
![]() $3$
-cycle and by construction one of the indexes fixed by
$3$
-cycle and by construction one of the indexes fixed by
![]() $\sigma _1\tau $
is
$\sigma _1\tau $
is
![]() $2n$
, so the conjugated
$2n$
, so the conjugated
![]() $4$
-tuples will have the shape (8.2). We have only to compute the images of the
$4$
-tuples will have the shape (8.2). We have only to compute the images of the
![]() $3$
-cycles. A direct computation shows that, if we conjugate by
$3$
-cycles. A direct computation shows that, if we conjugate by
![]() $\sigma _{\infty }^{2n-\frac {k+h}{2}}$
we have
$\sigma _{\infty }^{2n-\frac {k+h}{2}}$
we have
![]() $\Sigma '$
with
$\Sigma '$
with
![]() $(h',k')= \left( \frac {k-h}{2}, 2n- \frac {3h+k}{2}\right)$
while if we conjugate by
$(h',k')= \left( \frac {k-h}{2}, 2n- \frac {3h+k}{2}\right)$
while if we conjugate by
![]() $\sigma _{\infty }^{2n-\frac {2n-h-k}{2}}$
we have
$\sigma _{\infty }^{2n-\frac {2n-h-k}{2}}$
we have
![]() $\Sigma '$
with
$\Sigma '$
with
![]() $(h',k')= \left( n- \frac {h+k}{2}, n+\frac {3h-k}{2}\right)$
, as wanted.
$(h',k')= \left( n- \frac {h+k}{2}, n+\frac {3h-k}{2}\right)$
, as wanted.
Using these two propositions we can count the different conjugacy classes of
![]() $4$
-tuples such that
$4$
-tuples such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $3$
-cycle.
$3$
-cycle.
Let us consider a special
![]() $4$
-tuple
$4$
-tuple
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1)$
such that
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1)$
such that
![]() $\sigma _1\tau _1$
contains the
$\sigma _1\tau _1$
contains the
![]() $3$
-cycle
$3$
-cycle
![]() $(2n-h,h,k)$
. By equation (8.2), we have
$(2n-h,h,k)$
. By equation (8.2), we have
![]() $h\equiv k\ \ \mod 2$
; moreover, every choice of the couple
$h\equiv k\ \ \mod 2$
; moreover, every choice of the couple
![]() $(h,k)$
gives rise to three different choices of the couple
$(h,k)$
gives rise to three different choices of the couple
![]() $(\sigma _1,\tau )$
, and by the previous proposition, each conjugacy class contains exactly three special
$(\sigma _1,\tau )$
, and by the previous proposition, each conjugacy class contains exactly three special
![]() $4$
-tuples. Consequently, the number of conjugacy classes is equal to the number of different choices of the couple
$4$
-tuples. Consequently, the number of conjugacy classes is equal to the number of different choices of the couple
![]() $(h,k)$
, that is, to the number of couples
$(h,k)$
, that is, to the number of couples
![]() $\{h,k\}$
such that
$\{h,k\}$
such that
![]() $1\le h\le n-2$
,
$1\le h\le n-2$
,
![]() $h+1<k<2n-h-1$
and
$h+1<k<2n-h-1$
and
![]() $h\equiv k$
(mod
$h\equiv k$
(mod
![]() $2$
), hence
$2$
), hence
 $$\begin{align*}\# \textrm{ conjugacy classes}= \sum_{h=1}^{n-2} \frac{2n-2(h+1)}{2}=\sum_{h=1}^{n-2} (n-h-1)= \sum_{j=1}^{n-2} j= \frac{(n-1)(n-2)}{2}. \end{align*}$$
$$\begin{align*}\# \textrm{ conjugacy classes}= \sum_{h=1}^{n-2} \frac{2n-2(h+1)}{2}=\sum_{h=1}^{n-2} (n-h-1)= \sum_{j=1}^{n-2} j= \frac{(n-1)(n-2)}{2}. \end{align*}$$
8.3 The 4-cycle case
Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
![]() $4$
-tuple, that is, with
$4$
-tuple, that is, with
![]() $\sigma _{\infty }=(2n, \ldots , 1)$
and such that
$\sigma _{\infty }=(2n, \ldots , 1)$
and such that
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\tau $
fix both
$\tau $
fix both
![]() $2n$
, and assume that
$2n$
, and assume that
![]() $\sigma _1\tau $
is a product of
$\sigma _1\tau $
is a product of
![]() $n-4$
disjoint transpositions and a disjoint
$n-4$
disjoint transpositions and a disjoint
![]() $4$
-cycle.
$4$
-cycle.
As in the previous section, our first result describes the shape of a special
![]() $4$
-tuple of this kind.
$4$
-tuple of this kind.
Proposition 8.4. Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty }, \sigma _1, \tau )$
be a special
![]() $4$
-tuple such that
$4$
-tuple such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $4$
-cycle. Then there exist
$4$
-cycle. Then there exist
![]() $1\le h< k_1 <k_2<2n-h$
with
$1\le h< k_1 <k_2<2n-h$
with
![]() $h\equiv k_1\equiv k_2\ \ \mod 2$
such that
$h\equiv k_1\equiv k_2\ \ \mod 2$
such that
 $$ \begin{align} \sigma_0 &=\prod_{i=1}^h(i,2n+1-i) \prod_{j=1}^{\frac{k_1-h}{2}}(h+j, k_1+1-j) \prod_{t=1}^{\frac{k_2-k_1}{2}} (k_1+t, k_2+1-t) \nonumber \\[-2pt] &\prod_{v=1}^{\frac{2n-h-k_2}{2}}(k_2+v, 2n-h+1-v); \\[-2pt] \sigma_1\tau &=\prod_{i=1}^{h-1}(i,2n-i)\prod_{j=1}^{\frac{k_1-h}{2}-1} (h+j, k_1-j) \prod_{t=1}^{\frac{k_2-k_1}{2}-1} (k_1+t, k_2-t) \nonumber \\[-2pt] &\prod_{v=1}^{\frac{2n-h-k_2}{2}-1}(k_2+v,2n-h-v)\ (2n-h, h, k_1, k_2). \nonumber \end{align} $$
$$ \begin{align} \sigma_0 &=\prod_{i=1}^h(i,2n+1-i) \prod_{j=1}^{\frac{k_1-h}{2}}(h+j, k_1+1-j) \prod_{t=1}^{\frac{k_2-k_1}{2}} (k_1+t, k_2+1-t) \nonumber \\[-2pt] &\prod_{v=1}^{\frac{2n-h-k_2}{2}}(k_2+v, 2n-h+1-v); \\[-2pt] \sigma_1\tau &=\prod_{i=1}^{h-1}(i,2n-i)\prod_{j=1}^{\frac{k_1-h}{2}-1} (h+j, k_1-j) \prod_{t=1}^{\frac{k_2-k_1}{2}-1} (k_1+t, k_2-t) \nonumber \\[-2pt] &\prod_{v=1}^{\frac{2n-h-k_2}{2}-1}(k_2+v,2n-h-v)\ (2n-h, h, k_1, k_2). \nonumber \end{align} $$
In particular
![]() $\sigma _1\tau $
fixes four indexes:
$\sigma _1\tau $
fixes four indexes:
![]() $2n, \frac {k_1+h}{2}$
,
$2n, \frac {k_1+h}{2}$
,
![]() $\frac {k_1+k_2}{2}$
and
$\frac {k_1+k_2}{2}$
and
![]() $\frac {2n-h+k_2}{2}$
. Moreover, there are two different
$\frac {2n-h+k_2}{2}$
. Moreover, there are two different
![]() $\Sigma $
satisfying equation (8.3) corresponding to different choices of
$\Sigma $
satisfying equation (8.3) corresponding to different choices of
![]() $\tau $
, that is,
$\tau $
, that is,
![]() $\tau \in \{(h,k_2), (k_1, 2n-h)\}$
.
$\tau \in \{(h,k_2), (k_1, 2n-h)\}$
.
Proof. Let
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau )$
be a special
![]() $4$
-tuple, and assume that
$4$
-tuple, and assume that
![]() $\sigma _1\tau $
is a product of
$\sigma _1\tau $
is a product of
![]() $n-4$
disjoint transpositions and a disjoint
$n-4$
disjoint transpositions and a disjoint
![]() $4$
-cycle. In this case,
$4$
-cycle. In this case,
![]() $\sigma _1\tau $
fixes
$\sigma _1\tau $
fixes
![]() $4$
indexes, and one of them is
$4$
indexes, and one of them is
![]() $2n$
. Then, as
$2n$
. Then, as
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have that
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have that
![]() $\sigma _0(2n)=1$
. As
$\sigma _0(2n)=1$
. As
![]() $\sigma _0$
is composed only by transpositions, we have also that
$\sigma _0$
is composed only by transpositions, we have also that
![]() $\sigma _0(1)=2n$
, hence
$\sigma _0(1)=2n$
, hence
![]() $\sigma _1\tau (2n-1)=1$
. Now, we have two choices: Either
$\sigma _1\tau (2n-1)=1$
. Now, we have two choices: Either
![]() $\sigma _1\tau (1)=2n-1$
(so
$\sigma _1\tau (1)=2n-1$
(so
![]() $(2n-1,1)$
is one of the disjoint transpositions in the decomposition of
$(2n-1,1)$
is one of the disjoint transpositions in the decomposition of
![]() $\sigma _1\tau $
), or
$\sigma _1\tau $
), or
![]() $\sigma _1\tau (1)=k\neq 2n-1$
(giving rise to the
$\sigma _1\tau (1)=k\neq 2n-1$
(giving rise to the
![]() $4$
-cycle in the product). We go on as in the disjoint case described in Subsection 8.1 until we reach the situation in which there exist
$4$
-cycle in the product). We go on as in the disjoint case described in Subsection 8.1 until we reach the situation in which there exist
![]() $1\le h\le n-2$
,
$1\le h\le n-2$
,
![]() $h+1\le k_1\le 2n-h-3$
,
$h+1\le k_1\le 2n-h-3$
,
![]() $k_1+1\le k_2\le 2n-h-1$
such that
$k_1+1\le k_2\le 2n-h-1$
such that
![]() $\sigma _0$
contains the disjoint transpositions
$\sigma _0$
contains the disjoint transpositions
![]() $(1, 2n),(2,2n-1)\cdots (h,2n-h+1)$
and
$(1, 2n),(2,2n-1)\cdots (h,2n-h+1)$
and
![]() $\sigma _1\tau $
contains the disjoint transpositions
$\sigma _1\tau $
contains the disjoint transpositions
![]() $(1,2n-1),\ldots , (2n-h+1,h-1)$
and the 4-cycle
$(1,2n-1),\ldots , (2n-h+1,h-1)$
and the 4-cycle
![]() $(2n-h,h,k_1, k_2)$
. It is easy to see that
$(2n-h,h,k_1, k_2)$
. It is easy to see that
![]() $k_1\neq h+1, 2n-h-3$
and
$k_1\neq h+1, 2n-h-3$
and
![]() $k_2\neq k_1+1, 2n-h-1$
. For example, let us assume by contradiction that
$k_2\neq k_1+1, 2n-h-1$
. For example, let us assume by contradiction that
![]() $k_1=h+1$
; then, as we have that
$k_1=h+1$
; then, as we have that
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau _1=\mathrm {id}$
, we would have that
$\sigma _0\sigma _{\infty }\sigma _1\tau _1=\mathrm {id}$
, we would have that
![]() $\sigma _0$
fixes
$\sigma _0$
fixes
![]() $h+1$
, which is impossible because
$h+1$
, which is impossible because
![]() $\sigma _0$
has no fixed points. For the other cases we can argue similarly. So,
$\sigma _0$
has no fixed points. For the other cases we can argue similarly. So,
![]() $h+2 \le k_1 \le 2n-h-4$
and
$h+2 \le k_1 \le 2n-h-4$
and
![]() $k_1+2\le k_2\le 2n-h-2$
, which implies that
$k_1+2\le k_2\le 2n-h-2$
, which implies that
![]() $1\le h\le n-3$
.
$1\le h\le n-3$
.
Now, if
![]() $\sigma _1\tau (h)=k_1$
, then by
$\sigma _1\tau (h)=k_1$
, then by
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
we have
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
we have
![]() $\sigma _0(k_1)=h+1$
and so
$\sigma _0(k_1)=h+1$
and so
![]() $\sigma _0(h+1)=k_1$
. This means that
$\sigma _0(h+1)=k_1$
. This means that
![]() $\sigma _1\tau (h+1)=k_1-1$
and
$\sigma _1\tau (h+1)=k_1-1$
and
![]() $\sigma _1\tau (k_1-1)=h+1$
and so on. This process ends when one reaches the conditions
$\sigma _1\tau (k_1-1)=h+1$
and so on. This process ends when one reaches the conditions
![]() $\sigma _0 \left( \frac {k_1+h}{2}\right)=\frac {k_1+h}{2}+1$
and vice versa,
$\sigma _0 \left( \frac {k_1+h}{2}\right)=\frac {k_1+h}{2}+1$
and vice versa,
![]() $\sigma _1\tau \left(\frac {k_1+h}{2}-1 \right)=\frac {k_1+h}{2}+1$
and vice versa and
$\sigma _1\tau \left(\frac {k_1+h}{2}-1 \right)=\frac {k_1+h}{2}+1$
and vice versa and
![]() $\frac {k_1+h}{2}$
is fixed by
$\frac {k_1+h}{2}$
is fixed by
![]() $\sigma _1\tau $
. Notice that also in this case this gives the additional condition that
$\sigma _1\tau $
. Notice that also in this case this gives the additional condition that
![]() $h\equiv k_1\ \ \mod 2$
. Here we also see that
$h\equiv k_1\ \ \mod 2$
. Here we also see that
![]() $k_2$
cannot lie between h and
$k_2$
cannot lie between h and
![]() $k_1$
.
$k_1$
.
On the other hand, if
![]() $\sigma _1\tau $
contains the 4-cycle
$\sigma _1\tau $
contains the 4-cycle
![]() $(2n-h,h,k_1,k_2)$
, we also have that
$(2n-h,h,k_1,k_2)$
, we also have that
![]() $\sigma _1\tau (k_1)=k_2$
and
$\sigma _1\tau (k_1)=k_2$
and
![]() $\sigma _1\tau (k_2)=2n-h$
, giving other conditions to satisfy. Indeed, by
$\sigma _1\tau (k_2)=2n-h$
, giving other conditions to satisfy. Indeed, by
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
![]() $\sigma _0(2n-h)=k_2+1$
and
$\sigma _0(2n-h)=k_2+1$
and
![]() $\sigma _0(k_2+1)=2n-h$
. This implies that
$\sigma _0(k_2+1)=2n-h$
. This implies that
![]() $\sigma _1\tau (2n-h-1)=k_2+1$
and vice versa, and so on. This process ends when one reaches the conditions
$\sigma _1\tau (2n-h-1)=k_2+1$
and vice versa, and so on. This process ends when one reaches the conditions
![]() $\sigma _0 \left(\frac {2n-h+k_2}{2}\right)=\frac {2n-h+k_2}{2}+1$
and vice versa,
$\sigma _0 \left(\frac {2n-h+k_2}{2}\right)=\frac {2n-h+k_2}{2}+1$
and vice versa,
![]() $\sigma _1 \tau \left( \frac {2n-h+k_2}{2}-1\right)=\frac {2n-h+k_2}{2}+1$
and
$\sigma _1 \tau \left( \frac {2n-h+k_2}{2}-1\right)=\frac {2n-h+k_2}{2}+1$
and
![]() $\frac {2n-h+k_2}{2}$
is fixed by
$\frac {2n-h+k_2}{2}$
is fixed by
![]() $\sigma _1\tau $
. With the same argument, as
$\sigma _1\tau $
. With the same argument, as
![]() $\sigma _1\tau (k_1)=k_2$
, by
$\sigma _1\tau (k_1)=k_2$
, by
![]() $\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
$\sigma _0\sigma _{\infty }\sigma _1\tau =\mathrm {id}$
, we have
![]() $\sigma _0(k_1+1)=k_2$
and
$\sigma _0(k_1+1)=k_2$
and
![]() $\sigma _0(k_2)=k_1+1$
. This means that
$\sigma _0(k_2)=k_1+1$
. This means that
![]() $\sigma _1\tau (k_1+1)=k_2-1$
and vice versa, and so on. This process ends when one reaches the conditions
$\sigma _1\tau (k_1+1)=k_2-1$
and vice versa, and so on. This process ends when one reaches the conditions
![]() $\sigma _0 \left( \frac {k_1+k_2}{2} \right)=\frac {k_2+k_2}{2}+1$
and vice versa,
$\sigma _0 \left( \frac {k_1+k_2}{2} \right)=\frac {k_2+k_2}{2}+1$
and vice versa,
![]() $\sigma _1 \tau \left( \frac {k_1+k_2}{2}-1\right)=\frac {k_1+k_2}{2}+1$
and
$\sigma _1 \tau \left( \frac {k_1+k_2}{2}-1\right)=\frac {k_1+k_2}{2}+1$
and
![]() $\frac {k_1+k_2}{2}$
is fixed by
$\frac {k_1+k_2}{2}$
is fixed by
![]() $\sigma _1\tau $
. This gives, as before, the additional condition that
$\sigma _1\tau $
. This gives, as before, the additional condition that
![]() $k_1\equiv k_2\ \ \mod 2$
. This proves that
$k_1\equiv k_2\ \ \mod 2$
. This proves that
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1\tau $
have the shape (8.3), proving the first part of the proposition.
$\sigma _1\tau $
have the shape (8.3), proving the first part of the proposition.
In particular
![]() $\sigma _1\tau $
fixes 4 indexes, that is,
$\sigma _1\tau $
fixes 4 indexes, that is,
![]() $\frac {k_1+h}{2}$
,
$\frac {k_1+h}{2}$
,
![]() $\frac {k_1+k_2}{2}$
and
$\frac {k_1+k_2}{2}$
and
![]() $\frac {2n-h+k_2}{2}$
and
$\frac {2n-h+k_2}{2}$
and
![]() $2n$
. Let us denote by
$2n$
. Let us denote by
that is, the product of the disjoint transpositions appearing in the decomposition of
![]() $\sigma _1\tau $
. Then we have two different choices for the couple
$\sigma _1\tau $
. Then we have two different choices for the couple
![]() $(\sigma _1,\tau )$
giving the same product, namely
$(\sigma _1,\tau )$
giving the same product, namely
![]() $\sigma _1=\beta _{hk_1k_2} (2n-h, h)(k_1,k_2)$
and
$\sigma _1=\beta _{hk_1k_2} (2n-h, h)(k_1,k_2)$
and
![]() $\tau =(2n-h,k_1)$
or
$\tau =(2n-h,k_1)$
or
![]() $\sigma _1=\beta _{hk_1k_2} (h,k_1)(2n-h, k_2)$
and
$\sigma _1=\beta _{hk_1k_2} (h,k_1)(2n-h, k_2)$
and
![]() $\tau =(h, k_2)$
. This concludes the proof.
$\tau =(h, k_2)$
. This concludes the proof.
As in the previous section, we want to count the number of special
![]() $4$
-tuples such that
$4$
-tuples such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $4$
-cycle in a given conjugacy class.
$4$
-cycle in a given conjugacy class.
Notice that, if we have two special
![]() $4$
-tuples
$4$
-tuples
![]() $\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1)$
and
$\Sigma =(\sigma _0,\sigma _{\infty },\sigma _1,\tau _1)$
and
![]() $\Sigma '=(\sigma _0',\sigma _{\infty }',\sigma _1',\tau _1')$
with
$\Sigma '=(\sigma _0',\sigma _{\infty }',\sigma _1',\tau _1')$
with
![]() $\sigma _{\infty }\kern1.5pt{=}\kern1.5pt\sigma _{\infty }'\kern1.5pt{=}\kern1.5pt(2n, 2n-1, \ldots , 1)$
and such that
$\sigma _{\infty }\kern1.5pt{=}\kern1.5pt\sigma _{\infty }'\kern1.5pt{=}\kern1.5pt(2n, 2n-1, \ldots , 1)$
and such that
![]() $\Sigma '\kern1.5pt{=}\kern1.5pt\gamma ^{-1} \Sigma \gamma $
for some
$\Sigma '\kern1.5pt{=}\kern1.5pt\gamma ^{-1} \Sigma \gamma $
for some
![]() $\gamma \kern1.5pt{\in}\kern1.5pt S_{2n}$
, then
$\gamma \kern1.5pt{\in}\kern1.5pt S_{2n}$
, then
![]() $\gamma $
must be a power of
$\gamma $
must be a power of
![]() $\sigma _{\infty }$
.
$\sigma _{\infty }$
.
Let us call
![]() $p:= \frac {k_1+h}{2},q:=\frac {k_1+k_2}{2}$
and
$p:= \frac {k_1+h}{2},q:=\frac {k_1+k_2}{2}$
and
![]() $r:=\frac {2n-h+k_2}{2}$
the three indexes other than
$r:=\frac {2n-h+k_2}{2}$
the three indexes other than
![]() $2n$
fixed by
$2n$
fixed by
![]() $\sigma _1\tau $
. Since we are interested in conjugations by permutations of the form
$\sigma _1\tau $
. Since we are interested in conjugations by permutations of the form
![]() $\sigma _{\infty }^\ell $
that send the set
$\sigma _{\infty }^\ell $
that send the set
![]() $\{p,q,r,2n\}$
into a set containing
$\{p,q,r,2n\}$
into a set containing
![]() $\{2n\}$
, the only admissible
$\{2n\}$
, the only admissible
![]() $\gamma $
will be
$\gamma $
will be
![]() $\sigma _{\infty }^{2n-p}$
,
$\sigma _{\infty }^{2n-p}$
,
![]() $\sigma _{\infty }^{2n-q}$
or
$\sigma _{\infty }^{2n-q}$
or
![]() $\sigma _{\infty }^{2n-r}$
. In particular, in the first case the set
$\sigma _{\infty }^{2n-r}$
. In particular, in the first case the set
![]() $\{2n, p, q, r\}$
is sent to
$\{2n, p, q, r\}$
is sent to
![]() $\{2n, 2n-p, q-p, r-p\}$
; in the second case to
$\{2n, 2n-p, q-p, r-p\}$
; in the second case to
![]() $\{2n, 2n-(q-p), r-q, 2n-q\}$
and, in the last case, to
$\{2n, 2n-(q-p), r-q, 2n-q\}$
and, in the last case, to
![]() $\{2n-r, 2n-(r-p), 2n-(r-q), 2n\}$
.
$\{2n-r, 2n-(r-p), 2n-(r-q), 2n\}$
.
The following proposition describes how many special
![]() $4$
-tuples we have in every conjugacy class of a
$4$
-tuples we have in every conjugacy class of a
![]() $4$
-tuple; in this case, this depends on the configuration of
$4$
-tuple; in this case, this depends on the configuration of
![]() $\{p,q,r,2n\}$
.
$\{p,q,r,2n\}$
.
Proposition 8.5. Let
![]() $\Sigma =(\sigma _0, \sigma _{\infty },\sigma _1,\tau _1)$
be a special
$\Sigma =(\sigma _0, \sigma _{\infty },\sigma _1,\tau _1)$
be a special
![]() $4$
-tuple such that
$4$
-tuple such that
![]() $\sigma _1\tau $
contains the
$\sigma _1\tau $
contains the
![]() $4$
-cycle
$4$
-cycle
![]() $(h,k_1,k_2,2n-h)$
, then we have two possibilities.
$(h,k_1,k_2,2n-h)$
, then we have two possibilities.
-
• If n is even and the
 $4$
-cycle is of the form
$4$
-cycle is of the form
 $(h,n-h,n+h,2n-h)$
, then the conjugacy class of
$(h,n-h,n+h,2n-h)$
, then the conjugacy class of
 $\Sigma $
contains only two special
$\Sigma $
contains only two special
 $4$
-tuples;
$4$
-tuples; -
• If not, then the conjugacy class of
 $\Sigma $
contains exactly four special
$\Sigma $
contains exactly four special
 $4$
-tuples.
$4$
-tuples.
We point out that, looking at the symmetry of the problem, the number of special
![]() $4$
-tuples contained in the conjugacy class of
$4$
-tuples contained in the conjugacy class of
![]() $\Sigma $
depends on the configuration of the points fixed by
$\Sigma $
depends on the configuration of the points fixed by
![]() $\sigma _1\tau $
. Indeed, in the first case, the set of fixed points is exactly
$\sigma _1\tau $
. Indeed, in the first case, the set of fixed points is exactly
![]() $ \left\{\frac {n}{2}, n, \frac {3}{2}n, 2n \right\}$
, which are the vertices of a square.
$ \left\{\frac {n}{2}, n, \frac {3}{2}n, 2n \right\}$
, which are the vertices of a square.
Proof. Since
![]() $4$
-tuple
$4$
-tuple
![]() $\Sigma =(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
is special, we have that
$\Sigma =(\sigma _{\infty }, \sigma _0,\sigma _1,\tau )$
is special, we have that
![]() $\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
$\sigma _{\infty }=(2n, 2n-1, \ldots , 1)$
and
![]() $\sigma _1\tau $
fixes
$\sigma _1\tau $
fixes
![]() $2n$
; moreover, by assumption it contains the
$2n$
; moreover, by assumption it contains the
![]() $4$
-cycle
$4$
-cycle
![]() $(h,k_1,k_2,2n-h)$
. Then, as proved before,
$(h,k_1,k_2,2n-h)$
. Then, as proved before,
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1\tau $
will have the shape (8.3). As discussed before, if
$\sigma _1\tau $
will have the shape (8.3). As discussed before, if
![]() $\Sigma '\neq \Sigma $
is a special
$\Sigma '\neq \Sigma $
is a special
![]() $4$
-tuple conjugated to
$4$
-tuple conjugated to
![]() $\Sigma $
then
$\Sigma $
then
![]() $\Sigma '=\gamma ^{-1}\Sigma \gamma $
with
$\Sigma '=\gamma ^{-1}\Sigma \gamma $
with
 $\gamma \in \left\{ \sigma _{\infty }^{2n-\frac {h+k_1}{2}}, \sigma _{\infty }^{2n-\frac {k_1+k_2}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k_2}{2}} \right\}$
. We distinguish two cases.
$\gamma \in \left\{ \sigma _{\infty }^{2n-\frac {h+k_1}{2}}, \sigma _{\infty }^{2n-\frac {k_1+k_2}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k_2}{2}} \right\}$
. We distinguish two cases.
Suppose that n is even and the
![]() $4$
-cycle is of the form
$4$
-cycle is of the form
![]() $(h,n-h,n+h,2n-h)$
Footnote
2
; then the points fixed by
$(h,n-h,n+h,2n-h)$
Footnote
2
; then the points fixed by
![]() $\sigma _1\tau $
are exactly
$\sigma _1\tau $
are exactly
![]() $ \left\{\frac {n}{2}, n, \frac {3}{2}n, 2n \right\}$
. As discussed before, the other special
$ \left\{\frac {n}{2}, n, \frac {3}{2}n, 2n \right\}$
. As discussed before, the other special
![]() $4$
-tuples contained in the conjugacy class of
$4$
-tuples contained in the conjugacy class of
![]() $\Sigma $
will be of the form
$\Sigma $
will be of the form
![]() $\gamma ^{-1}\Sigma \gamma $
, with
$\gamma ^{-1}\Sigma \gamma $
, with
 $\gamma \in \left\{ \sigma _{\infty }^{\frac {n}{2}}, \sigma _{\infty }^ {n}, \sigma _{\infty }^{\frac {3}{2}n}\right\}$
. But for this special configuration, a direct computation shows that
$\gamma \in \left\{ \sigma _{\infty }^{\frac {n}{2}}, \sigma _{\infty }^ {n}, \sigma _{\infty }^{\frac {3}{2}n}\right\}$
. But for this special configuration, a direct computation shows that
![]() $\sigma _{\infty }^{-n}\Sigma \sigma _{\infty }^n=\Sigma $
, and
$\sigma _{\infty }^{-n}\Sigma \sigma _{\infty }^n=\Sigma $
, and
![]() $\sigma _{\infty }^{-n/2}\Sigma \sigma _{\infty }^{n/2}=\sigma _{\infty }^{n/2}\Sigma \sigma _{\infty }^{-n/2}\neq \Sigma $
, hence there are only two special
$\sigma _{\infty }^{-n/2}\Sigma \sigma _{\infty }^{n/2}=\sigma _{\infty }^{n/2}\Sigma \sigma _{\infty }^{-n/2}\neq \Sigma $
, hence there are only two special
![]() $4$
-tuples contained in the conjugacy class of
$4$
-tuples contained in the conjugacy class of
![]() $\Sigma $
.
$\Sigma $
.
Suppose now that the
![]() $4$
-cycle contained in
$4$
-cycle contained in
![]() $\sigma _1\tau $
is not of the previous shape; we have that either
$\sigma _1\tau $
is not of the previous shape; we have that either
![]() $k_1\neq n-h$
or
$k_1\neq n-h$
or
![]() $k_2\neq n+h$
. In this case, a direct computation shows that if we conjugate
$k_2\neq n+h$
. In this case, a direct computation shows that if we conjugate
![]() $\Sigma $
by some
$\Sigma $
by some
 $\gamma \in \left\{ \sigma _{\infty }^{2n-\frac {h+k_1}{2}}, \sigma _{\infty }^{2n-\frac {k_1+k_2}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k_2}{2}} \right\}$
, then
$\gamma \in \left\{ \sigma _{\infty }^{2n-\frac {h+k_1}{2}}, \sigma _{\infty }^{2n-\frac {k_1+k_2}{2}}, \sigma _{\infty }^{2n-\frac {2n-h+k_2}{2}} \right\}$
, then
![]() $\sigma _0$
is not fixed, hence every conjugation gives rise to a special
$\sigma _0$
is not fixed, hence every conjugation gives rise to a special
![]() $4$
-tuple in the conjugacy class of
$4$
-tuple in the conjugacy class of
![]() $\Sigma $
, which concludes the proof.
$\Sigma $
, which concludes the proof.
Using the proposition, we can count the number of different conjugacy classes such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $4$
-cycle; in this case, we have to distinguish the case n odd and n even.
$4$
-cycle; in this case, we have to distinguish the case n odd and n even.
Suppose first n odd; in this case, by Proposition 8.5, every conjugacy class contains exactly four special
![]() $4$
-tuples. Moreover, a special
$4$
-tuples. Moreover, a special
![]() $4$
-tuple containing a
$4$
-tuple containing a
![]() $4$
-cycle
$4$
-cycle
![]() $(h,k_1,k_2, 2n-h)$
with
$(h,k_1,k_2, 2n-h)$
with
![]() $h<k_1<k_2$
will have the shape (8.3), and there are two different choices of the couple
$h<k_1<k_2$
will have the shape (8.3), and there are two different choices of the couple
![]() $(\sigma _1, \tau )$
which gives the same permutation
$(\sigma _1, \tau )$
which gives the same permutation
![]() $\sigma _1\tau $
.
$\sigma _1\tau $
.
Putting all together, we have to count the number of ordered
![]() $3$
-tuples
$3$
-tuples
![]() $h<k_1<k_2$
with
$h<k_1<k_2$
with
![]() $h\equiv k_1 \equiv k_2\ \ \mod 2$
and such that
$h\equiv k_1 \equiv k_2\ \ \mod 2$
and such that
![]() $1\le h\le n-3$
,
$1\le h\le n-3$
,
![]() $h+2\le k_1\le 2n-4-h$
and
$h+2\le k_1\le 2n-4-h$
and
![]() $k_1+2\le k_2\le 2n-2-h$
, which are equal to
$k_1+2\le k_2\le 2n-2-h$
, which are equal to
 $$\begin{align*}C_1= \sum_{h=1}^{n-3} \left [ \sum_{\substack{ k=h+2 \\ k \equiv h\ \ \mod 2 }}^{2n-4-h} \left ( n-1 -\frac{k+h}{2} \right ) \right ]. \end{align*}$$
$$\begin{align*}C_1= \sum_{h=1}^{n-3} \left [ \sum_{\substack{ k=h+2 \\ k \equiv h\ \ \mod 2 }}^{2n-4-h} \left ( n-1 -\frac{k+h}{2} \right ) \right ]. \end{align*}$$
Then we have that, if n is odd, the number of conjugacy classes of a
![]() $4$
-tuple such that
$4$
-tuple such that
![]() $\sigma _1\tau $
contains a
$\sigma _1\tau $
contains a
![]() $4$
-cycle is
$4$
-cycle is
Suppose now n even; in this case, we have to distinguish the cases in which the
![]() $4$
-cycle is of the special form
$4$
-cycle is of the special form
![]() $(h,n-h,n+h,2n)$
, which are
$(h,n-h,n+h,2n)$
, which are
![]() $C_2=\frac {n}{2}-1$
. Recall that, for every configuration of the
$C_2=\frac {n}{2}-1$
. Recall that, for every configuration of the
![]() $4$
-cycle, we have two choices of the couple
$4$
-cycle, we have two choices of the couple
![]() $(\sigma _1, \tau )$
giving rise to the same product. For this special configuration of the
$(\sigma _1, \tau )$
giving rise to the same product. For this special configuration of the
![]() $4$
-cycle, the conjugacy class contains indeed only two special
$4$
-cycle, the conjugacy class contains indeed only two special
![]() $4$
-tuples. The number of conjugacy classes in this case is given by
$4$
-tuples. The number of conjugacy classes in this case is given by
Acknowledgements
The authors would like to thank the anonymous referee for several valuable comments and suggestions.
They also thank Fedor Pakovich for pointing out his work and for useful discussions.
The three authors started this work in Pisa, where they were funded by the European Research Council, grant number 267273. The first author was also founded by the Engineering and Physical Sciences Research Council [EP/N007956/1] and by the Swiss National Science Foundation [165525]. The second author was also founded by Istituto Nazionale di Alta Matematica [Borsa Ing. G. Schirillo], and by the Engineering and Physical Sciences Research Council [EP/N008359/1].
Conflict of Interests
None.