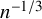1. Introduction
The length
![]() $L_n(\sigma )$
of longest increasing subsequencesFootnote
1
of permutations
$L_n(\sigma )$
of longest increasing subsequencesFootnote
1
of permutations
![]() $\sigma $
on
$\sigma $
on
![]() $\{1,2,\ldots ,n\}$
becomes a discrete random variable when the permutations are drawn randomly with uniform distribution. This way, the problem of enumerating all permutations
$\{1,2,\ldots ,n\}$
becomes a discrete random variable when the permutations are drawn randomly with uniform distribution. This way, the problem of enumerating all permutations
![]() $\sigma $
that satisfy
$\sigma $
that satisfy
![]() $L_n(\sigma )\leqslant l$
gets encoded in the discrete probability distribution
$L_n(\sigma )\leqslant l$
gets encoded in the discrete probability distribution
![]() ${\mathbb P}(L_n \leqslant l)$
. The present paper studies an asymptotic expansion of this distribution when n grows large. As there are relations to KPZ growth models (directly so for the PNG model with droplet initial condition, see [Reference Ferrari and Frings36, Reference Prähofer and Spohn68, Reference Prähofer and Spohn69] and [Reference Forrester43, Chap. 10]), we expect our findings to have a bearing there, too.
${\mathbb P}(L_n \leqslant l)$
. The present paper studies an asymptotic expansion of this distribution when n grows large. As there are relations to KPZ growth models (directly so for the PNG model with droplet initial condition, see [Reference Ferrari and Frings36, Reference Prähofer and Spohn68, Reference Prähofer and Spohn69] and [Reference Forrester43, Chap. 10]), we expect our findings to have a bearing there, too.
1.1. Prior work
We start by recalling some fundamental results and notions. More details and references can be found in the outstanding surveys and monographs [Reference Aldous and Diaconis3, Reference Baik, Deift and Suidan10, Reference Romik71, Reference Stanley75].
1.1.1. Ulam’s problem
The study of the behavior as n grows large dates back to Ulam [Reference Ulam80] in 1961, who mentioned that Monte-Carlo computations of E. Neighbor would indicate
![]() ${\mathbb E}(L_n)\approx 1.7\sqrt {n}$
. Ulam continued by stating, ‘Another question of interest would be to find the distribution of the length of the maximum monotone subsequence around this average’.
${\mathbb E}(L_n)\approx 1.7\sqrt {n}$
. Ulam continued by stating, ‘Another question of interest would be to find the distribution of the length of the maximum monotone subsequence around this average’.
Refined numerical experiments by Baer and Brock [Reference Baer and Brock5] in 1968 suggested that
![]() ${\mathbb E}(L_n) \sim 2\sqrt {n}$
might be the precise leading order. In a 1970 lecture, Hammersley [Reference Hammersley50] presented a proof, based on subadditive ergodic theory, that the limit
${\mathbb E}(L_n) \sim 2\sqrt {n}$
might be the precise leading order. In a 1970 lecture, Hammersley [Reference Hammersley50] presented a proof, based on subadditive ergodic theory, that the limit
![]() $c = \lim _{n\to \infty } {\mathbb E}(L_n)/\sqrt {n}$
exists. Finally, in 1977, Vershik and Kerov [Reference Veršik and Kerov82] as well as Logan and Shepp [Reference Logan and Shepp59] succeeded in proving
$c = \lim _{n\to \infty } {\mathbb E}(L_n)/\sqrt {n}$
exists. Finally, in 1977, Vershik and Kerov [Reference Veršik and Kerov82] as well as Logan and Shepp [Reference Logan and Shepp59] succeeded in proving
![]() $c=2$
.
$c=2$
.
1.1.2. Poissonization
A major tool used by Hammersley was a random process that is, basically, equivalent to the following Poissonization of the random variable
![]() $L_n$
: by drawing from the different permutation groups independently and by taking
$L_n$
: by drawing from the different permutation groups independently and by taking
![]() $N_r \in \{0,1,2,\ldots \}$
to be a further independent random variable with a Poisson distribution of intensity
$N_r \in \{0,1,2,\ldots \}$
to be a further independent random variable with a Poisson distribution of intensity
![]() $r>0$
, the combined random variable
$r>0$
, the combined random variable
![]() $L_{N_r}$
is distributed according to
$L_{N_r}$
is distributed according to
 $$\begin{align*}{\mathbb P}(L_{N_r} \leqslant l) = e^{-r} \sum_{n=0}^{\infty} {\mathbb P}(L_n\leqslant l)\frac{r^n}{n!} =: P(r;l). \end{align*}$$
$$\begin{align*}{\mathbb P}(L_{N_r} \leqslant l) = e^{-r} \sum_{n=0}^{\infty} {\mathbb P}(L_n\leqslant l)\frac{r^n}{n!} =: P(r;l). \end{align*}$$
The entire functionFootnote
2
![]() $P(z;l)$
is the Poisson generating function of the sequence
$P(z;l)$
is the Poisson generating function of the sequence
![]() ${\mathbb P}(L_n \leqslant l)$
(
${\mathbb P}(L_n \leqslant l)$
(
![]() $n=0,1,\ldots $
), and
$n=0,1,\ldots $
), and
![]() $f(z;l):=e^{z}P(z;l)$
is the corresponding exponential generating function. As it turns out, it is much simpler to analyze the Poissonized distribution of
$f(z;l):=e^{z}P(z;l)$
is the corresponding exponential generating function. As it turns out, it is much simpler to analyze the Poissonized distribution of
![]() $L_{N_r}$
as the intensity r grows large than the original distribution of
$L_{N_r}$
as the intensity r grows large than the original distribution of
![]() $L_n$
as n grows large.
$L_n$
as n grows large.
There is, however, also a way back from
![]() $L_{N_r}$
to
$L_{N_r}$
to
![]() $L_n$
– namely, the expected value of the Poisson distribution being
$L_n$
– namely, the expected value of the Poisson distribution being
![]() ${\mathbb E}(N_r) = r$
, combined with some level of concentration, suggests
${\mathbb E}(N_r) = r$
, combined with some level of concentration, suggests
when
![]() $n\to \infty $
while l is kept near the mode of the distribution. Being a Tauberian result, such a de-Poissonization is subject to additional conditions, which we will discuss in a moment.
$n\to \infty $
while l is kept near the mode of the distribution. Being a Tauberian result, such a de-Poissonization is subject to additional conditions, which we will discuss in a moment.
Starting in the early 1990s, the Poisson generating function
![]() $P(z;l)$
(or the exponential one to the same end) has been represented in terms of one of the following interrelated forms:
$P(z;l)$
(or the exponential one to the same end) has been represented in terms of one of the following interrelated forms:
-
• a Toeplitz determinant in terms of modified Bessel functions [Reference Gessel47],
-
• Fredholm determinants of various (discrete) integral operators [Reference Baik, Deift and Johansson8, Reference Baik, Deift and Rains9, Reference Borodin and Forrester21, Reference Borodin, Okounkov and Olshanski22, Reference Johansson56],
-
• a unitary group integral [Reference Rains70].
A particular case of those representations plays a central role in our study – namely,Footnote 3
whereFootnote
4
![]() $E_2^{\text {hard}}(s;\nu )$
denotes the probability that, in the hard-edge scaling limit, the scaled smallest eigenvalue of the Laguerre unitary ensemble (LUE) with real parameter
$E_2^{\text {hard}}(s;\nu )$
denotes the probability that, in the hard-edge scaling limit, the scaled smallest eigenvalue of the Laguerre unitary ensemble (LUE) with real parameter
![]() $\nu> 0$
is bounded from below by
$\nu> 0$
is bounded from below by
![]() $s\geqslant 0$
. This probability is known to be given in terms of a Fredholm determinant (see [Reference Forrester42]):
$s\geqslant 0$
. This probability is known to be given in terms of a Fredholm determinant (see [Reference Forrester42]):
where
![]() $K_\nu $
denotes the Bessel kernel in
$K_\nu $
denotes the Bessel kernel in
![]() $x,y \geqslant 0$
(for the integral formula see [Reference Tracy and Widom79, Eq. (2.2)]):
$x,y \geqslant 0$
(for the integral formula see [Reference Tracy and Widom79, Eq. (2.2)]):
 $$ \begin{align} K_\nu^{\text{Bessel}}(x,y) := \frac{J_\nu(\sqrt{x}) \sqrt{y}J_\nu^{\prime}(\sqrt{y})-J_\nu(\sqrt{y}) \sqrt{x}J_\nu^{\prime}(\sqrt{x})}{2(x-y)} = \frac{1}{4}\int_0^1 J_\nu(\sqrt{\sigma x})J_\nu(\sqrt{\sigma y})\,d\sigma. \end{align} $$
$$ \begin{align} K_\nu^{\text{Bessel}}(x,y) := \frac{J_\nu(\sqrt{x}) \sqrt{y}J_\nu^{\prime}(\sqrt{y})-J_\nu(\sqrt{y}) \sqrt{x}J_\nu^{\prime}(\sqrt{x})}{2(x-y)} = \frac{1}{4}\int_0^1 J_\nu(\sqrt{\sigma x})J_\nu(\sqrt{\sigma y})\,d\sigma. \end{align} $$
Obviously, the singularities at the diagonal
![]() $x=y$
are removable.
$x=y$
are removable.
The work of Tracy and Widom [Reference Tracy and Widom79] establishes that the Fredholm determinant (1.2) can be expressed in terms of Painlevé III. Recently, based on Okamoto’s Hamiltonian
![]() $\sigma $
-PIII
$\sigma $
-PIII
![]() $'$
framework, Forrester and Mays [Reference Forrester and Mays45] used that connection to compile a table of the exact rational values of
$'$
framework, Forrester and Mays [Reference Forrester and Mays45] used that connection to compile a table of the exact rational values of
![]() ${\mathbb P}(L_n \leqslant l)$
for up to
${\mathbb P}(L_n \leqslant l)$
for up to
![]() $n=700$
,Footnote
5
whereas in our work [Reference Bornemann19], based on an equivalent representation in terms of a Chazy I equation, we have compiled such a tableFootnote
6
for up to
$n=700$
,Footnote
5
whereas in our work [Reference Bornemann19], based on an equivalent representation in terms of a Chazy I equation, we have compiled such a tableFootnote
6
for up to
![]() $n=1000$
.
$n=1000$
.
In their seminal 1999 work [Reference Baik, Deift and Johansson7], by relating the representation of
![]() $P(z;l)$
in terms of the Toeplitz determinant to the machinery of Riemann–Hilbert problems and studying the underlying double-scaling limit by the Deift–Zhou method of steepest descent, Baik, Deift and Johansson answered Ulam’s question and proved that, for t being any fixed real number,
$P(z;l)$
in terms of the Toeplitz determinant to the machinery of Riemann–Hilbert problems and studying the underlying double-scaling limit by the Deift–Zhou method of steepest descent, Baik, Deift and Johansson answered Ulam’s question and proved that, for t being any fixed real number,
 $$ \begin{align} \lim_{r\to\infty}{\mathbb P}\left(\frac{L_{N_r}-2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F(t), \end{align} $$
$$ \begin{align} \lim_{r\to\infty}{\mathbb P}\left(\frac{L_{N_r}-2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F(t), \end{align} $$
where F is the GUE Tracy–Widom distribution – that is, the distribution which expresses, among many other limit laws, the probability that in the soft-edge scaling limit of the Gaussian unitary ensemble (GUE), the scaled largest eigenvalue is bounded from above by t. As for the Poissonized length distribution itself, the Tracy–Widom distribution can be represented in terms of a Fredholm determinant (see [Reference Forrester42]) – namely,
where
![]() $K_0$
denotes the Airy kernel in
$K_0$
denotes the Airy kernel in
![]() $x,y\in {\mathbb R}$
(for the integral formula see [Reference Tracy and Widom78, Eq. (4.5)]):
$x,y\in {\mathbb R}$
(for the integral formula see [Reference Tracy and Widom78, Eq. (4.5)]):
Obviously, also in this case, the singularities at the diagonal
![]() $x=y$
are removable. Since the limit distribution in (1.4) is continuous, by a standard Tauberian follow-up [Reference van der Vaart81, Lemma 2.1] of the Portmanteau theorem, the limit law holds uniformly in t.
$x=y$
are removable. Since the limit distribution in (1.4) is continuous, by a standard Tauberian follow-up [Reference van der Vaart81, Lemma 2.1] of the Portmanteau theorem, the limit law holds uniformly in t.
In 2003, Borodin and Forrester gave an alternative proof of (1.4) which is based on studying the hard-to-soft edge transition of LUE for
![]() $\nu \to \infty $
in form of the limit law [Reference Borodin and Forrester21, Thm. 1]
$\nu \to \infty $
in form of the limit law [Reference Borodin and Forrester21, Thm. 1]
(see also [Reference Forrester43, §10.8.4]), which will be the starting point of our study. Still, there are other proofs of (1.4) based on representations in terms of Fredholm determinants of further (discrete) integral operators; for expositions and references, see the monographs [Reference Baik, Deift and Suidan10, Reference Romik71].
1.1.3. De-Poissonization
In the literature, the de-Poissonization of the limit law (1.4) has so far been based exclusively on variants of the following lemma (cf. [Reference Baik, Deift and Suidan10, Cor. 2.5], originally stated as [Reference Johansson55, Lemma 2.5]), which uses monotonicity as the underlying Tauberian condition.
Lemma 1.1 (Johansson’s de-Poissonization lemma [Reference Johansson55]).
Suppose the sequence
![]() $a_n$
of probabilities
$a_n$
of probabilities
![]() $0\leqslant a_n \leqslant 1$
satisfies the monotonicity condition
$0\leqslant a_n \leqslant 1$
satisfies the monotonicity condition
![]() $a_{n+1} \leqslant a_n$
for all
$a_{n+1} \leqslant a_n$
for all
![]() $n=0,1,2,\ldots $
and denote its Poisson generating function by
$n=0,1,2,\ldots $
and denote its Poisson generating function by
 $$ \begin{align} P(z) = e^{-z} \sum_{n=0}^\infty a_n \frac{z^n}{n!}. \end{align} $$
$$ \begin{align} P(z) = e^{-z} \sum_{n=0}^\infty a_n \frac{z^n}{n!}. \end{align} $$
Then, for
![]() $s\geqslant 1$
and
$s\geqslant 1$
and
![]() $n\geqslant 2\,$
,Footnote
7
$n\geqslant 2\,$
,Footnote
7
![]() $P\big (n + 2\sqrt {s n \log n} \big ) - n^{-s} \leqslant a_n \leqslant P \big (n - 2\sqrt {s n \log n} \big ) + n^{-s}$
.
$P\big (n + 2\sqrt {s n \log n} \big ) - n^{-s} \leqslant a_n \leqslant P \big (n - 2\sqrt {s n \log n} \big ) + n^{-s}$
.
After establishing the Tauberian condition of monotonicity and applying a variant of Lemma 1.1 to (1.4), Baik, Deift and Johansson [Reference Baik, Deift and Johansson7, Thm. 1.1] got
 $$ \begin{align} \lim_{n\to\infty}{\mathbb P}\left(\frac{L_{n}-2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F(t), \end{align} $$
$$ \begin{align} \lim_{n\to\infty}{\mathbb P}\left(\frac{L_{n}-2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F(t), \end{align} $$
which holds uniformly in t for the same reasons as given above. (The simple calculations based on Lemma 1.1 are given in [Reference Baik, Deift and Suidan10, p. 239]; note that the uniformity of the limit law (1.4) is used there without explicitly saying so.) Adding tail estimates to the picture, those authors were also able to lift the limit law to the moments and got, expanding on Ulam’s problem, that the expected value satisfies [Reference Baik, Deift and Johansson7, Thm. 1.2]
1.1.4. Expansions
To our knowledge, only for the Poissonized limit law (1.4) a finite-size correction term has been rigorously established prior to the present paperFootnote
8
– namely, as a by-product along the way of their study of the limiting distribution of maximal crossings and nestings of Poissonized random matchings, Baik and Jenkins [Reference Baik and Jenkins11, Thm. 1.3] obtained (using the machinery of Riemann–Hilbert problems and Painlevé representations of the Tracy–Widom distribution), as
![]() $r\to \infty $
with t being any fixed real number,
$r\to \infty $
with t being any fixed real number,
 $$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) - \frac{1}{10}\Big(F"(t) + \frac{t^2}{6} F'(t)\Big)r^{-1/3} + O(r^{-1/2}), \end{align} $$
$$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) - \frac{1}{10}\Big(F"(t) + \frac{t^2}{6} F'(t)\Big)r^{-1/3} + O(r^{-1/2}), \end{align} $$
where (with
![]() $\lfloor \cdot \rfloor $
denoting the Gauss bracket)
$\lfloor \cdot \rfloor $
denoting the Gauss bracket)
However, even if there is enough uniformity in this result and the option to Taylor expand the Poisson generating function
![]() $P(r)$
at n with a uniform bound while l is kept near the mode of the distributions (see Section 5.1 for details on this option), the sandwiching in Johansson’s de-Poissonization Lemma 1.1 does not allow us to obtain a result better than (cf. [Reference Baik and Jenkins11, §9])
$P(r)$
at n with a uniform bound while l is kept near the mode of the distributions (see Section 5.1 for details on this option), the sandwiching in Johansson’s de-Poissonization Lemma 1.1 does not allow us to obtain a result better than (cf. [Reference Baik and Jenkins11, §9])
 $$ \begin{align} {\mathbb P}\left(\frac{L_n - 2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F\big(t^{(n)}\big) + O\big(n^{-1/6} \sqrt{\log n}\,\big). \end{align} $$
$$ \begin{align} {\mathbb P}\left(\frac{L_n - 2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F\big(t^{(n)}\big) + O\big(n^{-1/6} \sqrt{\log n}\,\big). \end{align} $$
In their recent study of finite-size effects, Forrester and Mays [Reference Forrester and Mays45, Prop. 1.1] gave a different proof of (1.11) based on the Bessel kernel determinant (1.2). Moreover, suggested by exact data for
![]() $n=700$
and a Monte-Carlo simulation for
$n=700$
and a Monte-Carlo simulation for
![]() $n=20\,000$
, they were led to conjecture [Reference Forrester and Mays45, Conj. 4.2]
$n=20\,000$
, they were led to conjecture [Reference Forrester and Mays45, Conj. 4.2]
 $$ \begin{align} {\mathbb P}\left(\frac{L_n - 2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F\big(t^{(n)}\big) + F^D_1(t)n^{-1/3} + \cdots \end{align} $$
$$ \begin{align} {\mathbb P}\left(\frac{L_n - 2\sqrt{n}}{n^{1/6}}\leqslant t\right) = F\big(t^{(n)}\big) + F^D_1(t)n^{-1/3} + \cdots \end{align} $$
with the approximate graphical form of
![]() $F^D_1(t)$
displayed in [Reference Forrester and Mays45, Fig. 7].
$F^D_1(t)$
displayed in [Reference Forrester and Mays45, Fig. 7].
The presence of the Gauss bracket in
![]() $t^{(r)}$
and
$t^{(r)}$
and
![]() $t^{(n)}$
, while keeping t at other places of the expansions (1.11) and (1.13), causes undesirable effects in the error terms (see Remark 4.2 below for a detailed discussion). Therefore, in our work [Reference Bornemann19] on a Stirling-type formula approximating the distribution
$t^{(n)}$
, while keeping t at other places of the expansions (1.11) and (1.13), causes undesirable effects in the error terms (see Remark 4.2 below for a detailed discussion). Therefore, in our work [Reference Bornemann19] on a Stirling-type formula approximating the distribution
![]() ${\mathbb P}(L_n \leqslant l)$
, we suggested to use the integer l in the continuous expansion terms instead of introducing the continuous variable t into the discrete distribution in the first place, with the latter variant turning the discrete distribution into a piecewise constant function of t. By introducing the scaling
${\mathbb P}(L_n \leqslant l)$
, we suggested to use the integer l in the continuous expansion terms instead of introducing the continuous variable t into the discrete distribution in the first place, with the latter variant turning the discrete distribution into a piecewise constant function of t. By introducing the scaling
we were led (based on numerical experiments using the Stirling-type approximation for n getting as large as
![]() $10^{10}$
) to conjecture the expansion
$10^{10}$
) to conjecture the expansion
displaying the graphical form of the functions
![]() $F^D_1(t)$
,
$F^D_1(t)$
,
![]() $F^D_2(t)$
in the left panels of [Reference Bornemann19, Figs. 4/6]. Moreover, as a note added in proof (see [Reference Bornemann19, Eq. (11)]), we announced that inserting the Baik–Jenkins expansion (1.11) into the Stirling-type formula and using its (numerically observed) apparent order
$F^D_2(t)$
in the left panels of [Reference Bornemann19, Figs. 4/6]. Moreover, as a note added in proof (see [Reference Bornemann19, Eq. (11)]), we announced that inserting the Baik–Jenkins expansion (1.11) into the Stirling-type formula and using its (numerically observed) apparent order
![]() $O(n^{-2/3})$
of approximation would yield the functional form of
$O(n^{-2/3})$
of approximation would yield the functional form of
![]() $F_1^D$
to be
$F_1^D$
to be
 $$ \begin{align} F_1^D(t) = -\frac{1}{10}\left(6 F"(t) + \frac{t^2}{6} F'(t) \right). \end{align} $$
$$ \begin{align} F_1^D(t) = -\frac{1}{10}\left(6 F"(t) + \frac{t^2}{6} F'(t) \right). \end{align} $$
The quest for a proof, and for a similar expression for
![]() $F_2^D$
, motivated our present work.
$F_2^D$
, motivated our present work.
1.2. The new findings of the paper
In the analysis of algorithms in theoretical computer science, or the enumeration of combinatorial structures to the same end, the original enumeration problem is often represented in form of recurrences or functional/differential equations. For instance, this situation arises in a large class of algorithms involving a splitting process, trees or hashing. Embedding such processes into a Poisson processFootnote
9
often leads to more tractable equations, so that sharp tools for a subsequent de-Poissonization were developed in the 1990s; for references and details, see [Reference Jacquet and Szpankowski53, Reference Jacquet and Szpankowski54, Reference Szpankowski77] and Appendix A.1. In particular, if the Poisson generating function
![]() $P(z)$
of a sequence of real
$P(z)$
of a sequence of real
![]() $a_n>0$
, as defined in (1.8), is an entire function, an application of the saddle point method to the Cauchy integral
$a_n>0$
, as defined in (1.8), is an entire function, an application of the saddle point method to the Cauchy integral
yields, under suitable growth conditions on
![]() $P(z)$
as
$P(z)$
as
![]() $z\to \infty $
in the complex plane, the JaszFootnote
10
expansion
$z\to \infty $
in the complex plane, the JaszFootnote
10
expansion
 $$\begin{align*}a_n \sim P(n) + \sum_{j=2}^\infty b_j(n) P^{(j)}(n), \end{align*}$$
$$\begin{align*}a_n \sim P(n) + \sum_{j=2}^\infty b_j(n) P^{(j)}(n), \end{align*}$$
where the polynomial coefficients
![]() $b_j(n)$
are the diagonal Poisson–Charlier polynomials (that is, with intensity
$b_j(n)$
are the diagonal Poisson–Charlier polynomials (that is, with intensity
![]() $r=n$
). In Appendix A.1, we give a heuristic derivation of that expansion and recall, in the detailed form of Theorem A.2, a specific analytic de-Poissonization result from the comprehensive memoir [Reference Jacquet and Szpankowski53] of Jacquet and Szpankowski – a result which applies to a family of Poisson generating functions at once, providing uniform error bounds.
$r=n$
). In Appendix A.1, we give a heuristic derivation of that expansion and recall, in the detailed form of Theorem A.2, a specific analytic de-Poissonization result from the comprehensive memoir [Reference Jacquet and Szpankowski53] of Jacquet and Szpankowski – a result which applies to a family of Poisson generating functions at once, providing uniform error bounds.
Now, the difficult part of applying Theorem A.2 is checking the Tauberian growth conditions in the complex plane, which are required to hold uniformly for the family of Poisson generating functions (recall that, in the case of the longest increasing subsequence problem,
![]() $P(z)=P(z;l)$
depends on the integer l near the mode of the length distribution). After observing a striking similarity of those growth conditions with the notion of H-admissibility for the corresponding exponential generating function (as introduced by Hayman in his memoir [Reference Hayman51] on the generalization of Stirling’s formula), a closer look at the proof of Hayman’s [Reference Hayman51, Thm. XI] revealed the following result (see Theorem A.5 for a precise quantitative statement):
$P(z)=P(z;l)$
depends on the integer l near the mode of the length distribution). After observing a striking similarity of those growth conditions with the notion of H-admissibility for the corresponding exponential generating function (as introduced by Hayman in his memoir [Reference Hayman51] on the generalization of Stirling’s formula), a closer look at the proof of Hayman’s [Reference Hayman51, Thm. XI] revealed the following result (see Theorem A.5 for a precise quantitative statement):
The family of all entire functions of genus zero which have, for some
![]() $\epsilon>0,$
no zeros in the sector
$\epsilon>0,$
no zeros in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
satisfies a universal bound that implies Tauberian growth conditions suitable for analytic de-Poissonization.
$|\!\arg z| \leqslant \pi /2+ \epsilon $
satisfies a universal bound that implies Tauberian growth conditions suitable for analytic de-Poissonization.
However, in our work [Reference Bornemann19, Thm. 2.2] on Stirling-type formulae for the problem of longest increasing subsequences, when proving the H-admissibility of the exponential generating functions
![]() $f(z;l)=e^z P(z;l)$
(for each l), we had established, based on the representation [Reference Rains70] of
$f(z;l)=e^z P(z;l)$
(for each l), we had established, based on the representation [Reference Rains70] of
![]() $P(z;l)$
as a group integral, the following:
$P(z;l)$
as a group integral, the following:
For any integer
![]() $l\geqslant 0$
and any
$l\geqslant 0$
and any
![]() $\delta>0$
, the exponential generating function
$\delta>0$
, the exponential generating function
![]() $f(z;l)$
is an entire function of genus zero having at most finitely many zeros in the sector
$f(z;l)$
is an entire function of genus zero having at most finitely many zeros in the sector
![]() $|\!\arg z| \leqslant \pi - \delta $
, none of them being real.
$|\!\arg z| \leqslant \pi - \delta $
, none of them being real.
Under the reasonable assumption (supported by numerical experiments) that those finitely many complex zeros do not come too close to the real axis and do not grow too fast as
![]() $n\to \infty $
while l stays near the mode of the length distribution, the uniformity of the Tauberian growth conditions can be preserved (see Corollary A.7 for the technical details). We call this assumption the tameness hypothesis
Footnote
11
concerning the zeros of the family of
$n\to \infty $
while l stays near the mode of the length distribution, the uniformity of the Tauberian growth conditions can be preserved (see Corollary A.7 for the technical details). We call this assumption the tameness hypothesis
Footnote
11
concerning the zeros of the family of
![]() $P(z;l)$
.
$P(z;l)$
.
Subject to the tameness hypothesis, the main result of the present paper, Theorem 5.1, gives the asymptotic expansion
 $$\begin{align*}{\mathbb P}(L_n \leqslant l) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O\big(n^{-(m+1)/3}\big)\,\bigg|_{t=t_l(n)}, \end{align*}$$
$$\begin{align*}{\mathbb P}(L_n \leqslant l) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O\big(n^{-(m+1)/3}\big)\,\bigg|_{t=t_l(n)}, \end{align*}$$
which is uniformly valid when
![]() $n,l \to \infty $
while
$n,l \to \infty $
while
![]() $t_l(n)$
stays boundedFootnote
12
and the
$t_l(n)$
stays boundedFootnote
12
and the
![]() $F_j^D$
are certain smooth functions.
$F_j^D$
are certain smooth functions.
Finally, now without any detour via the Stirling-type formula, Theorem 5.1 confirms that the expansion term
![]() $F_1^D$
is given by (1.14), indeed, and yields the striking formula
$F_1^D$
is given by (1.14), indeed, and yields the striking formula
see (3.4) for a display of a similarly structured expression for
![]() $F_3^D(t)$
.
$F_3^D(t)$
.
Put to the extreme, with the help of a CAS such as Mathematica, the methods of the present paper can be used to calculate the concrete functional form of the expansion terms for up to
![]() $m=10$
and larger.Footnote
13
In all cases inspected, we observe that the expansion terms take the form of a linear combination of higher order derivatives of the limit law (that is, the Tracy–Widom distribution F) with certain rational polynomials as coefficients; we conjecture that this is generally true for the problem at hand.
$m=10$
and larger.Footnote
13
In all cases inspected, we observe that the expansion terms take the form of a linear combination of higher order derivatives of the limit law (that is, the Tracy–Widom distribution F) with certain rational polynomials as coefficients; we conjecture that this is generally true for the problem at hand.
1.3. Generalization: involutions, orthogonal and symplectic ensembles
In our subsequent work [Reference Bornemann18], we present a similar structure for the expansion terms relating to longest monotone subsequences in (fixed-point free) random involutions, F then being one of the Tracy–Widom distributions for
![]() $\beta =1$
or
$\beta =1$
or
![]() $\beta =4$
. The limit laws were first obtained by Baik and Rains [Reference Baik and Rains12], using the machinery of Riemann–Hilbert problems, and later reclaimed by Borodin and Forrester [Reference Borodin and Forrester21] through establishing hard-to-soft edge transition laws for LOE and LSE similar to (1.7). In [Reference Bornemann18], we derive the asymptotic expansions by using determinantal formulae [Reference Desrosiers and Forrester29, Reference Ferrari and Spohn37] of the hard and soft edge limits for
$\beta =4$
. The limit laws were first obtained by Baik and Rains [Reference Baik and Rains12], using the machinery of Riemann–Hilbert problems, and later reclaimed by Borodin and Forrester [Reference Borodin and Forrester21] through establishing hard-to-soft edge transition laws for LOE and LSE similar to (1.7). In [Reference Bornemann18], we derive the asymptotic expansions by using determinantal formulae [Reference Desrosiers and Forrester29, Reference Ferrari and Spohn37] of the hard and soft edge limits for
![]() $\beta =1,4$
while taking advantage of their algebraic interrelations with the
$\beta =1,4$
while taking advantage of their algebraic interrelations with the
![]() $\beta =2$
case studied in the present paper (basically, the expansions of the hard-to-soft edge limit laws for
$\beta =2$
case studied in the present paper (basically, the expansions of the hard-to-soft edge limit laws for
![]() $\beta =1,4$
turn out to correspond to a certain factorization of the
$\beta =1,4$
turn out to correspond to a certain factorization of the
![]() $\beta =2$
case). This is then followed by applying analytic de-Poissonization, once again subject to a tameness hypothesis.
$\beta =2$
case). This is then followed by applying analytic de-Poissonization, once again subject to a tameness hypothesis.
1.4. Organization of the paper
The paper splits into two parts: a first one, where all results and proofs are unconditional, addressing asymptotic expansions of Fredholm determinants, of the hard-to-soft edge transition law and the Poissonized length distribution; and a second one, where we restrict ourselves to assuming the tameness hypothesis when addressing analytic de-Poissonization and its various consequences.
Part I: Unconditional results. In Section 2, we start with a careful discussion of expansions of perturbed Airy kernel determinants. We stress the importance of such kernel expansions to be differentiable (i.e., one can differentiate into the error term) to easily lift the error bounds to trace norms. The subtle, but fundamental difficulty of such a lift seems to have been missed, more often than not, in the existing literature on convergence rates and expansions of limit laws in random matrix theory (notable exceptions are, for example, [Reference El Karoui33, Reference Johnstone57, Reference Johnstone and Ma58]).
In the rather lengthy Section 3, we study the asymptotic expansion of the Borodin–Forrester hard-to-soft edge transition law (1.7). It is based on a uniform version of Olver’s asymptotic expansion of Bessel functions of large order in the transition region, which we discuss in Appendix A.3. In Section 3, we lay the foundational work for the concrete functional form of all subsequent finite-size correction terms. We reduce the complexity of computing these terms by using a coordinate transform on the level of kernels to simplify the kernel expansion – a coordinate transform which gets subsequently reversed on the level of the distributions.Footnote 14 As yet another application of that technique, we simplify in Section 3.4 the finite-size correction terms of Choup [Reference Choup24] to the soft-edge limit law of GUE and LUE.
In Section 4, we expand the Poissonized length distribution, thereby generalizing the result (1.12) of Baik and Jenkins. In Section 4, we also discuss the potentially detrimental effect of using Gauss brackets, as in (1.12), alongside with the continuous variable t in the expansion terms.
Part II: Results based on the tameness hypothesis. In Section 5, we state and prove the main result of the paper: the expansion of the Baik–Deift–Johansson limit law (1.9) of the length distribution. Here we use the Jasz expansion of analytic de-Poissonization (as detailed in Appendix A.1). The universal bounds for entire functions of genus zero, which are used to prove the Tauberian growth conditions in the complex plane, and their relation to the theory of H-admissibility are prepared for in Appendix A.2. Additionally, in Section 5, we discuss the modifications that apply to the discrete density
![]() ${\mathbb P}(L_n=l)$
(that is, to the PDF of the length distribution).
${\mathbb P}(L_n=l)$
(that is, to the PDF of the length distribution).
In Section 6, we apply our findings to the asymptotic expansion of the Stirling-type formula which we introduced in [Reference Bornemann19] as an accurate tool for the numerical approximation of the length distribution. Subject to the tameness hypothesis, we prove the observation [Reference Bornemann19, Eq. (8b)] about a leading
![]() $O(n^{-2/3})$
error of that formula.
$O(n^{-2/3})$
error of that formula.
Finally, in Section 7, we study the asymptotic expansion of the expected value and variance. Based on a reasonable hypothesis about some uniformity in the tail bounds, we add several more concrete expansion terms to the Baik–Deift–Johansson solution (1.10) of Ulam’s problem.
Part I: Unconditional results
2. Expansions of perturbed Airy kernel determinants
In Section 3, we will get, with m being some non-negative integer and
![]() $t_0$
some real number, kernel expansions of the form
$t_0$
some real number, kernel expansions of the form
 $$ \begin{align} K_{(h)}(x,y) = K_0(x,y) + \sum_{j=1}^m h^j K_j(x,y) + h^{m+1} O\big(e^{-(x+y)}\big), \end{align} $$
$$ \begin{align} K_{(h)}(x,y) = K_0(x,y) + \sum_{j=1}^m h^j K_j(x,y) + h^{m+1} O\big(e^{-(x+y)}\big), \end{align} $$
which are
-
• uniformly valid for
 $t_0 \leqslant x,y < c h^{-1}$
as
$t_0 \leqslant x,y < c h^{-1}$
as
 $h\to 0^+$
, where
$h\to 0^+$
, where
 $c>0$
is some constant;
$c>0$
is some constant; -
• repeatedly differentiable w.r.t. x, y as uniform expansions under the same conditions.
Here,
![]() $K_{(h)}$
is a family of smooth kernels,
$K_{(h)}$
is a family of smooth kernels,
![]() $K_0$
denotes the Airy kernel (1.6) and the
$K_0$
denotes the Airy kernel (1.6) and the
![]() $K_j(x,y)$
are finite sums of rank one kernels
$K_j(x,y)$
are finite sums of rank one kernels
![]() $u(x)v(y)$
, with factors
$u(x)v(y)$
, with factors
![]() $u(\xi )$
,
$u(\xi )$
,
![]() $v(\xi )$
of the functional form
$v(\xi )$
of the functional form
where
![]() $p(\xi )$
is a polynomial in
$p(\xi )$
is a polynomial in
![]() $\xi $
. Since the existing literature tends to neglect the issue of estimating trace norms in terms of kernel bounds, this section aims at establishing a relatively easy framework for lifting such an expansion to one of the Fredholm determinant.
$\xi $
. Since the existing literature tends to neglect the issue of estimating trace norms in terms of kernel bounds, this section aims at establishing a relatively easy framework for lifting such an expansion to one of the Fredholm determinant.
2.1. Bounds on the kernels and induced trace norms
Bounds on the kernels
![]() $K_j$
, and on the trace norms of the induced integral operators, can be deduced from the estimates,Footnote
15
with p being any polynomial,
$K_j$
, and on the trace norms of the induced integral operators, can be deduced from the estimates,Footnote
15
with p being any polynomial,
where the constant
![]() $a_p$
does only depend on p (note that we can take
$a_p$
does only depend on p (note that we can take
![]() $a_p=1$
when
$a_p=1$
when
![]() $p(\xi )\equiv 1$
). This way, we get from (1.6)
$p(\xi )\equiv 1$
). This way, we get from (1.6)
and, for
![]() $1\leqslant j\leqslant m$
, constants
$1\leqslant j\leqslant m$
, constants
![]() $c_j$
such that
$c_j$
such that
For a given continuous kernel
![]() $K(x,y)$
, we denote the induced integral operator on
$K(x,y)$
, we denote the induced integral operator on
![]() $L^2(t,c h^{-1})$
by
$L^2(t,c h^{-1})$
by
![]() $\bar {\mathbf K}$
and the one on
$\bar {\mathbf K}$
and the one on
![]() $L^2(t,\infty )$
, if defined, by
$L^2(t,\infty )$
, if defined, by
![]() ${\mathbf K}$
(suppressing the dependence on t in both cases). The spaces of trace class and Hilbert–Schmidt operators acting on
${\mathbf K}$
(suppressing the dependence on t in both cases). The spaces of trace class and Hilbert–Schmidt operators acting on
![]() $L^2(t,s)$
are written as
$L^2(t,s)$
are written as
![]() ${\mathcal J}^p(t,s)$
with
${\mathcal J}^p(t,s)$
with
![]() $p=1$
and
$p=1$
and
![]() $p=2$
. By using the orthogonal projection of
$p=2$
. By using the orthogonal projection of
![]() $L^2(t,\infty )$
onto the subspace
$L^2(t,\infty )$
onto the subspace
![]() $L^2(t,ch^{-1})$
, we see that
$L^2(t,ch^{-1})$
, we see that
The Airy operator
![]() ${\mathbf K}_0$
(being by (1.6) the square of the Hilbert–Schmidt operator
${\mathbf K}_0$
(being by (1.6) the square of the Hilbert–Schmidt operator
![]() ${\mathbf A}_t$
with kernel
${\mathbf A}_t$
with kernel
![]() $\operatorname {Ai}(x+y-t)$
) and the expansion operators
$\operatorname {Ai}(x+y-t)$
) and the expansion operators
![]() ${\mathbf K}_j$
(
${\mathbf K}_j$
(
![]() $j\geqslant 1$
) (being finite rank operators) are trace class on the space
$j\geqslant 1$
) (being finite rank operators) are trace class on the space
![]() $L^2(t,\infty )$
. Their trace norms are bounded by
$L^2(t,\infty )$
. Their trace norms are bounded by
 $$ \begin{align*} \|{\mathbf K}_0\|_{{\mathcal J}^1(t,\infty)} &\leqslant \|{\mathbf A}_t\|_{{\mathcal J}^2(t,\infty)}^2 = \int_t^\infty \int_t^\infty |\operatorname{Ai}(x+y-t)|^2 \,dx\,dy \\ &= \int_0^\infty \int_0^\infty |\operatorname{Ai}(x+y+t)|^2 \,dx\,dy \leqslant e^{-2t} \int_0^\infty\int_0^\infty e^{-2(x+y)}\,dx\,dy = \tfrac{1}{4} e^{-2t} \quad (t\in{\mathbb R}), \end{align*} $$
$$ \begin{align*} \|{\mathbf K}_0\|_{{\mathcal J}^1(t,\infty)} &\leqslant \|{\mathbf A}_t\|_{{\mathcal J}^2(t,\infty)}^2 = \int_t^\infty \int_t^\infty |\operatorname{Ai}(x+y-t)|^2 \,dx\,dy \\ &= \int_0^\infty \int_0^\infty |\operatorname{Ai}(x+y+t)|^2 \,dx\,dy \leqslant e^{-2t} \int_0^\infty\int_0^\infty e^{-2(x+y)}\,dx\,dy = \tfrac{1}{4} e^{-2t} \quad (t\in{\mathbb R}), \end{align*} $$
and, likewise with some constants
![]() $c_j^*$
, by
$c_j^*$
, by
Here, we have used
for factors
![]() $u(\xi )$
,
$u(\xi )$
,
![]() $v(\xi )$
of the form (2.2) with some polynomials p and q.
$v(\xi )$
of the form (2.2) with some polynomials p and q.
However, there is in general no direct relation between kernel bounds and bounds of the trace norm of induced integral operators (see [Reference Simon74, p. 25]). Writing the kernel of the error term in (2.1), and its bound, in the form
does therefore not offer, as it stands, any direct method of lifting the bound to trace norm.Footnote 16
By taking, however, the explicitly assumed differentiability of the kernel expansion into account, there is a constant
![]() $c_\sharp $
such that
$c_\sharp $
such that
holds true for all
![]() $t_0 \leqslant x,y < c h^{-1}$
and
$t_0 \leqslant x,y < c h^{-1}$
and
![]() $0<h\leqslant h_0$
(
$0<h\leqslant h_0$
(
![]() $h_0$
chosen sufficiently small). If we denote an indicator function by
$h_0$
chosen sufficiently small). If we denote an indicator function by
![]() $\chi $
and choose some
$\chi $
and choose some
![]() $c_* < c$
close to c, integration gives
$c_* < c$
close to c, integration gives
 $$\begin{align*}R_{m+1,h}(x,y) = R_{m+1}(x,c_*h^{-1}) -\int_t^{c_* h^{-1}} S_{m+1,h}(x,\sigma)e^{\sigma/2} \cdot e^{-\sigma/2} \chi_{[t,\sigma]}(y)\,d\sigma \end{align*}$$
$$\begin{align*}R_{m+1,h}(x,y) = R_{m+1}(x,c_*h^{-1}) -\int_t^{c_* h^{-1}} S_{m+1,h}(x,\sigma)e^{\sigma/2} \cdot e^{-\sigma/2} \chi_{[t,\sigma]}(y)\,d\sigma \end{align*}$$
if
![]() $t_0 \leqslant x,y \leqslant c_* h^{-1}$
. This shows that the induced integral operator on
$t_0 \leqslant x,y \leqslant c_* h^{-1}$
. This shows that the induced integral operator on
![]() $L^2(t,c_* h^{-1})$
, briefly written accordingly as
$L^2(t,c_* h^{-1})$
, briefly written accordingly as
is trace class since it is the sum of a rank-one operator and a product of two Hilbert–Schmidt operators. In fact, for
![]() $t_0 \leqslant t \leqslant c_* h^{-1}$
, the trace norms of those terms are bounded by (denoting the implied constant in (2.4) by
$t_0 \leqslant t \leqslant c_* h^{-1}$
, the trace norms of those terms are bounded by (denoting the implied constant in (2.4) by
![]() $c_\flat $
)
$c_\flat $
)
 $$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}^{\flat}\|_{{\mathcal J}^1(t,c_* h^{-1})}^2 &\leqslant \|1\|_{L^2(t,c_*h^{-1})}^2 \cdot \|R_{m+1,h}(\,\cdot\,,c_*h^{-1})\|_{L^2(t,c_*h^{-1})}^2 \\ &\leqslant (ch^{-1} - t_0) \cdot c_{\flat}^2 e^{-2c_*h^{-1}} \int_t^\infty e^{-2x}\,dx = h^{-1}e^{-2c_*h^{-1}} O(e^{-2t}) \end{align*} $$
$$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}^{\flat}\|_{{\mathcal J}^1(t,c_* h^{-1})}^2 &\leqslant \|1\|_{L^2(t,c_*h^{-1})}^2 \cdot \|R_{m+1,h}(\,\cdot\,,c_*h^{-1})\|_{L^2(t,c_*h^{-1})}^2 \\ &\leqslant (ch^{-1} - t_0) \cdot c_{\flat}^2 e^{-2c_*h^{-1}} \int_t^\infty e^{-2x}\,dx = h^{-1}e^{-2c_*h^{-1}} O(e^{-2t}) \end{align*} $$
and
 $$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}^{\sharp}\|_{{\mathcal J}^1(t,c_* h^{-1})}^2 &\leqslant \left(\int_t^{c_*h^{-1}}\int_t^{c_*h^{-1}} S_{m+1,h}(x,y)^2e^{y}\,dx\,dy\right)\cdot \left(\int_t^{c_*h^{-1}}\int_t^x e^{-x}\,dx\,dy\right)\\ &\leqslant c_\sharp^2 \left(\int_t^\infty\int_t^\infty e^{-2x-y}\,dx\,dy\right)\cdot \left(\int_t^\infty\int_t^x e^{-x}\,dx\,dy\right) = O(e^{-4t}). \end{align*} $$
$$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}^{\sharp}\|_{{\mathcal J}^1(t,c_* h^{-1})}^2 &\leqslant \left(\int_t^{c_*h^{-1}}\int_t^{c_*h^{-1}} S_{m+1,h}(x,y)^2e^{y}\,dx\,dy\right)\cdot \left(\int_t^{c_*h^{-1}}\int_t^x e^{-x}\,dx\,dy\right)\\ &\leqslant c_\sharp^2 \left(\int_t^\infty\int_t^\infty e^{-2x-y}\,dx\,dy\right)\cdot \left(\int_t^\infty\int_t^x e^{-x}\,dx\,dy\right) = O(e^{-4t}). \end{align*} $$
Here, the implied constants are independent of the particular choice of
![]() $c_*$
. By noting that the orthogonal projection of
$c_*$
. By noting that the orthogonal projection of
![]() $L^2(t,ch^{-1})$
onto
$L^2(t,ch^{-1})$
onto
![]() $L^2(t,c_*h^{-1})$
converges, as
$L^2(t,c_*h^{-1})$
converges, as
![]() $c_* \to c$
, to the identity in the strong operator topology, we obtain by a continuity theoremFootnote
17
of Grümm [Reference Grümm49, Thm. 1]
$c_* \to c$
, to the identity in the strong operator topology, we obtain by a continuity theoremFootnote
17
of Grümm [Reference Grümm49, Thm. 1]
 $$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}\|_{{\mathcal J}^1(t,c h^{-1})} & = \lim_{c_*\to c} \| \bar{\mathbf R}_{m+1,h}\|_{{\mathcal J}^1(t,c_* h^{-1})} \\ &\leq \limsup_{c_*\to c}\| \bar{\mathbf R}_{m+1,h}^{\flat}\|_{{\mathcal J}^1(t,c_* h^{-1})} + \limsup_{c_*\to c}\| \bar{\mathbf R}_{m+1,h}^{\sharp}\|_{{\mathcal J}^1(t,c_* h^{-1})}\\ &= h^{-1/2} e^{-c h^{-1}} O(e^{-t}) + O(e^{-2t}). \end{align*} $$
$$ \begin{align*} \| \bar{\mathbf R}_{m+1,h}\|_{{\mathcal J}^1(t,c h^{-1})} & = \lim_{c_*\to c} \| \bar{\mathbf R}_{m+1,h}\|_{{\mathcal J}^1(t,c_* h^{-1})} \\ &\leq \limsup_{c_*\to c}\| \bar{\mathbf R}_{m+1,h}^{\flat}\|_{{\mathcal J}^1(t,c_* h^{-1})} + \limsup_{c_*\to c}\| \bar{\mathbf R}_{m+1,h}^{\sharp}\|_{{\mathcal J}^1(t,c_* h^{-1})}\\ &= h^{-1/2} e^{-c h^{-1}} O(e^{-t}) + O(e^{-2t}). \end{align*} $$
We have thus lifted the kernel expansion (2.1) to an operator expansion in
![]() ${\mathcal J}^1(t,ch^{-1})$
– namely,
${\mathcal J}^1(t,ch^{-1})$
– namely,
 $$ \begin{align} \bar{\mathbf K}_{(h)} = \bar{\mathbf K}_0 + \sum_{j=1}^m h^j \bar{\mathbf K}_j + h^{m+1} \bar{\mathbf R}_{m+1,h}, \end{align} $$
$$ \begin{align} \bar{\mathbf K}_{(h)} = \bar{\mathbf K}_0 + \sum_{j=1}^m h^j \bar{\mathbf K}_j + h^{m+1} \bar{\mathbf R}_{m+1,h}, \end{align} $$
with the bounds (recall (2.3) and observe that we can absorb
![]() $h^{m+1/2} e^{-c h^{-1}}$
into
$h^{m+1/2} e^{-c h^{-1}}$
into
![]() $O(e^{-c h^{-1}})$
)
$O(e^{-c h^{-1}})$
)
uniformly valid for
![]() $t_0 \leqslant t < c h^{-1}$
as
$t_0 \leqslant t < c h^{-1}$
as
![]() $h\to 0^+$
.
$h\to 0^+$
.
2.2. Fredholm determinants
Given a continuous kernel
![]() $K(x,y)$
on the bounded rectangle
$K(x,y)$
on the bounded rectangle
![]() $t_0 \leqslant x,y \leqslant t_1$
, the Fredholm determinant (cf. [Reference Anderson, Guionnet and Zeitouni4, §3.4])
$t_0 \leqslant x,y \leqslant t_1$
, the Fredholm determinant (cf. [Reference Anderson, Guionnet and Zeitouni4, §3.4])
 $$ \begin{align} \det(I - K)|_{L^2(t,s)} := \sum_{m=0}^\infty \frac{(-1)^m}{m!} \int_t^s \cdots\int_t^s \det_{j,k=1}^m K(x_j,x_k) \,dx_1\cdots\, dx_m \end{align} $$
$$ \begin{align} \det(I - K)|_{L^2(t,s)} := \sum_{m=0}^\infty \frac{(-1)^m}{m!} \int_t^s \cdots\int_t^s \det_{j,k=1}^m K(x_j,x_k) \,dx_1\cdots\, dx_m \end{align} $$
is well-defined for
![]() $t_0\leqslant t < s \leqslant t_1$
. If, as is the case for the kernels
$t_0\leqslant t < s \leqslant t_1$
. If, as is the case for the kernels
![]() $K_j$
(see Section 2.1), the kernel is also continuous for all
$K_j$
(see Section 2.1), the kernel is also continuous for all
![]() $x,y\geqslant t_0$
and there is a weighted uniform bound of the form
$x,y\geqslant t_0$
and there is a weighted uniform bound of the form
the Fredholm determinant (2.6) is well-defined even if we choose
![]() $s=\infty $
(this can be seen by writing the integrals in terms of the weighted measure
$s=\infty $
(this can be seen by writing the integrals in terms of the weighted measure
![]() $e^{-x}\,dx$
; cf. [Reference Anderson, Guionnet and Zeitouni4, §3.4]).
$e^{-x}\,dx$
; cf. [Reference Anderson, Guionnet and Zeitouni4, §3.4]).
Now, if the induced integral operator
![]() ${\mathbf K}|_{L^2(t,s)}$
on
${\mathbf K}|_{L^2(t,s)}$
on
![]() $L^2(t,s)$
is trace class, the Fredholm determinant can be expressed in terms of the operator determinant (cf. [Reference Simon74, Chap. 3]):
$L^2(t,s)$
is trace class, the Fredholm determinant can be expressed in terms of the operator determinant (cf. [Reference Simon74, Chap. 3]):
Using the orthogonal decomposition
and writing the operator expansion (2.5) in the form
 $$\begin{align*}\bar{\mathbf K}_{(h)} = \bar{\mathbf K}_{m,h} + h^{m+1} \bar{\mathbf R}_{m+1,h}, \qquad \bar{\mathbf K}_{m,h}:=\bar{\mathbf K}_0 + \sum_{j=1}^m h^j \bar{\mathbf K}_j, \end{align*}$$
$$\begin{align*}\bar{\mathbf K}_{(h)} = \bar{\mathbf K}_{m,h} + h^{m+1} \bar{\mathbf R}_{m+1,h}, \qquad \bar{\mathbf K}_{m,h}:=\bar{\mathbf K}_0 + \sum_{j=1}^m h^j \bar{\mathbf K}_j, \end{align*}$$
we get from the error estimate in (2.5c), by the local Lipschitz continuity of operator determinants w.r.t. trace norm (cf. [Reference Simon74, Thm. 3.4]), that
 $$ \begin{align*} \det\big(I - K_{(h)}\big)|_{L^2(t,ch^{-1})} &= \det({\mathbf I}- \bar{\mathbf K}_{(h)}) = \det\big({\mathbf I}- \bar{\mathbf K}_{m,h}\big) + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}) \\ &= \det\big({\mathbf I}- {\mathbf K}_{m,h}\big) + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}), \end{align*} $$
$$ \begin{align*} \det\big(I - K_{(h)}\big)|_{L^2(t,ch^{-1})} &= \det({\mathbf I}- \bar{\mathbf K}_{(h)}) = \det\big({\mathbf I}- \bar{\mathbf K}_{m,h}\big) + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}) \\ &= \det\big({\mathbf I}- {\mathbf K}_{m,h}\big) + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}), \end{align*} $$
uniformly for
![]() $t_0 \leqslant t < ch^{-1}$
as
$t_0 \leqslant t < ch^{-1}$
as
![]() $h\to 0^+$
. Here, the last estimate comes from a block decomposition of
$h\to 0^+$
. Here, the last estimate comes from a block decomposition of
![]() $\bar {\mathbf K}_{(h)}$
according to (2.8) and applying the trace norm bounds of
$\bar {\mathbf K}_{(h)}$
according to (2.8) and applying the trace norm bounds of
![]() ${\mathbf K}_j$
in Section 2.1 to the boundary case
${\mathbf K}_j$
in Section 2.1 to the boundary case
![]() $t=ch^{-1}$
, which yields
$t=ch^{-1}$
, which yields
note that the error term of order
![]() $O(e^{-2ch^{-1}})$
can be absorbed into
$O(e^{-2ch^{-1}})$
can be absorbed into
![]() $e ^{-c h^{-1}} O(e^{-t})$
if
$e ^{-c h^{-1}} O(e^{-t})$
if
![]() $t < c h^{-1}$
.
$t < c h^{-1}$
.
2.3. Expansions of operator determinants
Plemelj’s formula gives, for trace class perturbations
![]() $\mathbf E$
of the identity on
$\mathbf E$
of the identity on
![]() $L^2(t,\infty )$
bounded by
$L^2(t,\infty )$
bounded by
![]() $\|{\mathbf E}\|_{{\mathcal J}^1(t,\infty )} < 1$
, the convergent series expansion (cf. [Reference Simon74, Eq. (5.12)])
$\|{\mathbf E}\|_{{\mathcal J}^1(t,\infty )} < 1$
, the convergent series expansion (cf. [Reference Simon74, Eq. (5.12)])
 $$ \begin{align} \det({\mathbf I} - {\mathbf E}) &= \exp\left(-\sum_{n=1}^\infty n^{-1} \operatorname{tr}({\mathbf E}^n)\right) \\ = 1- \operatorname{tr} {\mathbf E} + \frac{1}{2}\left((\operatorname{tr} {\mathbf E})^2-\operatorname{tr}({\mathbf E}^2)\right) + \frac{1}{6}&\left(-(\operatorname{tr} {\mathbf E})^3 + 3 \operatorname{tr}{\mathbf E}\operatorname{tr} {\mathbf E}^2 - 2 \operatorname{tr} {\mathbf E}^3 \right)+ O\Big(\|{\mathbf E}\|_{{\mathcal J}^1(t,\infty)}^4\Big).\notag \end{align} $$
$$ \begin{align} \det({\mathbf I} - {\mathbf E}) &= \exp\left(-\sum_{n=1}^\infty n^{-1} \operatorname{tr}({\mathbf E}^n)\right) \\ = 1- \operatorname{tr} {\mathbf E} + \frac{1}{2}\left((\operatorname{tr} {\mathbf E})^2-\operatorname{tr}({\mathbf E}^2)\right) + \frac{1}{6}&\left(-(\operatorname{tr} {\mathbf E})^3 + 3 \operatorname{tr}{\mathbf E}\operatorname{tr} {\mathbf E}^2 - 2 \operatorname{tr} {\mathbf E}^3 \right)+ O\Big(\|{\mathbf E}\|_{{\mathcal J}^1(t,\infty)}^4\Big).\notag \end{align} $$
Thus, since
![]() ${\mathbf I}-{\mathbf K_0}$
is invertible with a uniformly bounded inverse as
${\mathbf I}-{\mathbf K_0}$
is invertible with a uniformly bounded inverse as
![]() $t\geqslant t_0$
,Footnote
18
we have
$t\geqslant t_0$
,Footnote
18
we have
 $$\begin{align*}\det\big({\mathbf I}-{\mathbf K}_{m,h}\big) = \det({\mathbf I}-{\mathbf K_0}) \det\big({\mathbf I}-{\mathbf E}_{m,h} \big), \qquad {\mathbf E}_{m,h} := \sum_{j=1}^m h^j ({\mathbf I}-{\mathbf K_0})^{-1}{\mathbf K_j}, \end{align*}$$
$$\begin{align*}\det\big({\mathbf I}-{\mathbf K}_{m,h}\big) = \det({\mathbf I}-{\mathbf K_0}) \det\big({\mathbf I}-{\mathbf E}_{m,h} \big), \qquad {\mathbf E}_{m,h} := \sum_{j=1}^m h^j ({\mathbf I}-{\mathbf K_0})^{-1}{\mathbf K_j}, \end{align*}$$
with the trace norm of
![]() ${\mathbf E}_{m,h} $
being bounded as follows (using the results of Section 2.1 and observing that the trace class forms an ideal within the algebra of bounded operators):
${\mathbf E}_{m,h} $
being bounded as follows (using the results of Section 2.1 and observing that the trace class forms an ideal within the algebra of bounded operators):
uniformly for
![]() $t\geqslant t_0$
as
$t\geqslant t_0$
as
![]() $h\to 0^+$
. By (2.9), this implies, uniformly under the same conditions,
$h\to 0^+$
. By (2.9), this implies, uniformly under the same conditions,
 $$\begin{align*}\det\big({\mathbf I}-{\mathbf E}_{m,h} \big) = 1 + \sum_{j=1}^m{d_j(t) h^j} + h^{m+1}\cdot O(e^{-2t}). \end{align*}$$
$$\begin{align*}\det\big({\mathbf I}-{\mathbf E}_{m,h} \big) = 1 + \sum_{j=1}^m{d_j(t) h^j} + h^{m+1}\cdot O(e^{-2t}). \end{align*}$$
Here,
![]() $d_j(t)$
depends smoothly on t and satisfies the (right) tail bound
$d_j(t)$
depends smoothly on t and satisfies the (right) tail bound
![]() $d_j(t) = O(e^{-2t})$
. If we write briefly
$d_j(t) = O(e^{-2t})$
. If we write briefly
the first few cases are given by the expressions (because the traces are taken for trace class operators acting on
![]() $L^2(t,\infty )$
they depend on t)
$L^2(t,\infty )$
they depend on t)
Since the
![]() ${\mathbf K}_{j}$
are trace class, those trace expressions can be recast in terms of resolvent kernels and integral traces (cf. [Reference Simon74, Thm. (3.9)]).
${\mathbf K}_{j}$
are trace class, those trace expressions can be recast in terms of resolvent kernels and integral traces (cf. [Reference Simon74, Thm. (3.9)]).
Taking the bound
![]() $0\leqslant F(t)\leqslant 1$
of the Tracy–Widom distribution (being a probability distribution) into account, the results of Section 2 can be summarized in form of the following:
$0\leqslant F(t)\leqslant 1$
of the Tracy–Widom distribution (being a probability distribution) into account, the results of Section 2 can be summarized in form of the following:
Theorem 2.1. Let
![]() $K_{(h)}(x,y)$
be a continuous kernel,
$K_{(h)}(x,y)$
be a continuous kernel,
![]() $K_0$
the Airy kernel (1.6), and let the
$K_0$
the Airy kernel (1.6), and let the
![]() $K_j(x,y)$
be finite sums of rank one kernels with factors of the form (2.2). If, for some fixed non-negative integer m and some real number
$K_j(x,y)$
be finite sums of rank one kernels with factors of the form (2.2). If, for some fixed non-negative integer m and some real number
![]() $t_0$
, there is a kernel expansion of the form
$t_0$
, there is a kernel expansion of the form
 $$\begin{align*}K_{(h)}(x,y) = K_0(x,y) + \sum_{j=1}^m h^j K_j(x,y) + h^{m+1} \cdot O\big(e^{-(x+y)}\big), \end{align*}$$
$$\begin{align*}K_{(h)}(x,y) = K_0(x,y) + \sum_{j=1}^m h^j K_j(x,y) + h^{m+1} \cdot O\big(e^{-(x+y)}\big), \end{align*}$$
which, for some constant
![]() $c>0$
, holds uniformly in
$c>0$
, holds uniformly in
![]() $t_0\leqslant x,y < ch^{-1}$
as
$t_0\leqslant x,y < ch^{-1}$
as
![]() $h\to 0^+$
and which can be repeatedly differentiated w.r.t. x and y as uniform expansions, then the Fredholm determinant of
$h\to 0^+$
and which can be repeatedly differentiated w.r.t. x and y as uniform expansions, then the Fredholm determinant of
![]() $K_{(h)}$
on
$K_{(h)}$
on
![]() $(t,ch^{-1})$
satisfies
$(t,ch^{-1})$
satisfies
 $$ \begin{align} \det\big(I-K_{(h)}\big)|_{L^2(t,ch^{-1})} = F(t) + \sum_{j=1}^m G_j(t) h^j + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}), \end{align} $$
$$ \begin{align} \det\big(I-K_{(h)}\big)|_{L^2(t,ch^{-1})} = F(t) + \sum_{j=1}^m G_j(t) h^j + h^{m+1} O(e^{-2t}) + e ^{-c h^{-1}} O(e^{-t}), \end{align} $$
uniformly for
![]() $t_0\leqslant t < ch^{-1}$
as
$t_0\leqslant t < ch^{-1}$
as
![]() $h\to 0^+$
. Here, F denotes the Tracy–Widom distribution (1.5) and the
$h\to 0^+$
. Here, F denotes the Tracy–Widom distribution (1.5) and the
![]() $G_j(t)$
are smooth functions depending on the kernels
$G_j(t)$
are smooth functions depending on the kernels
![]() $K_1,\ldots ,K_j$
, satisfying the (right) tail bounds
$K_1,\ldots ,K_j$
, satisfying the (right) tail bounds
![]() $G_j(t) = O(e^{-2t})$
. The first two are
$G_j(t) = O(e^{-2t})$
. The first two are
 $$ \begin{align*} G_1(t) &= - F(t) \cdot \left.\operatorname{tr}\big((I-K_0)^{-1}K_1\big)\right|{}_{L^2(t,\infty)}, \\ G_2(t) &= F(t)\cdot \bigg(\frac{1}{2} \Big(\!\left.\operatorname{tr}\big((I-K_0)^{-1}K_1\big)\right|{}_{L^2(t,\infty)}\Big)^2\\ &\qquad- \frac{1}{2}\left.\operatorname{tr}\big(((I-{K_0})^{-1}{K_1})^2\big)\right|{}_{L^2(t,\infty)} - \left.\operatorname{tr}\big(({I}-{K_0})^{-1}{K_2}\big)\right|{}_{L^2(t,\infty)}\bigg), \end{align*} $$
$$ \begin{align*} G_1(t) &= - F(t) \cdot \left.\operatorname{tr}\big((I-K_0)^{-1}K_1\big)\right|{}_{L^2(t,\infty)}, \\ G_2(t) &= F(t)\cdot \bigg(\frac{1}{2} \Big(\!\left.\operatorname{tr}\big((I-K_0)^{-1}K_1\big)\right|{}_{L^2(t,\infty)}\Big)^2\\ &\qquad- \frac{1}{2}\left.\operatorname{tr}\big(((I-{K_0})^{-1}{K_1})^2\big)\right|{}_{L^2(t,\infty)} - \left.\operatorname{tr}\big(({I}-{K_0})^{-1}{K_2}\big)\right|{}_{L^2(t,\infty)}\bigg), \end{align*} $$
where
![]() $(I-K_0)^{-1}$
is understood as a resolvent kernel and the traces as integrals. The determinantal expansion (2.11) can repeatedly be differentiated w.r.t. t, preserving uniformity.
$(I-K_0)^{-1}$
is understood as a resolvent kernel and the traces as integrals. The determinantal expansion (2.11) can repeatedly be differentiated w.r.t. t, preserving uniformity.
3. Expansion of the hard-to-soft edge transition
In this section, we prove an expansion for the hard-to-soft edge transition limit (1.7). To avoid notational clutter, we use the quantity
and study expansions in powers of
![]() $h_\nu $
as
$h_\nu $
as
![]() $h_\nu \to 0^+$
. The transform
$h_\nu \to 0^+$
. The transform
![]() $s=\phi _\nu (t)$
used in the transition limit can briefly be written as
$s=\phi _\nu (t)$
used in the transition limit can briefly be written as
Theorem 3.1. There holds the hard-to-soft edge transition expansion
 $$ \begin{align} E_2^{\text{hard}}(\phi_\nu(t);\nu) = F(t) + \sum_{j=1}^m F_{j}(t) h_\nu^j + h_\nu^{m+1}\cdot O(e^{-3t/2}), \end{align} $$
$$ \begin{align} E_2^{\text{hard}}(\phi_\nu(t);\nu) = F(t) + \sum_{j=1}^m F_{j}(t) h_\nu^j + h_\nu^{m+1}\cdot O(e^{-3t/2}), \end{align} $$
which is uniformly valid when
![]() $t_0\leqslant t < h_\nu ^{-1}$
as
$t_0\leqslant t < h_\nu ^{-1}$
as
![]() $h_\nu \to 0^+$
, m being any fixed non-negative integer and
$h_\nu \to 0^+$
, m being any fixed non-negative integer and
![]() $t_0$
any fixed real number. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable t. Here, the
$t_0$
any fixed real number. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable t. Here, the
![]() $F_{j}$
are certain smooth functions starting with
$F_{j}$
are certain smooth functions starting with
 $$\begin{align*} &\qquad +\Big(-\frac{122}{7875} -\frac{8 t^3}{125} + \frac{9 t^6}{2000}\Big) F"'(t) +\Big(\frac{16t}{875} -\frac{9 t^4}{1000} \Big)F^{(4)}(t)\notag\\ &\qquad +\frac{3 t^2 }{500}F^{(5)}(t) -\frac{1}{750} F^{(6)}(t).\end{align*}$$
$$\begin{align*} &\qquad +\Big(-\frac{122}{7875} -\frac{8 t^3}{125} + \frac{9 t^6}{2000}\Big) F"'(t) +\Big(\frac{16t}{875} -\frac{9 t^4}{1000} \Big)F^{(4)}(t)\notag\\ &\qquad +\frac{3 t^2 }{500}F^{(5)}(t) -\frac{1}{750} F^{(6)}(t).\end{align*}$$
It is rewarding to validate intriguing formulae such as (3.4a–c) by numerical methods: Figure 1 plots the functions
![]() $F_{1}(t)$
,
$F_{1}(t)$
,
![]() $F_{2}(t)$
,
$F_{2}(t)$
,
![]() $F_3(t)$
next to the approximation
$F_3(t)$
next to the approximation
for
![]() $\nu =100$
and
$\nu =100$
and
![]() $\nu =800$
: the close matching with
$\nu =800$
: the close matching with
![]() $F_3(t)$
as displayed by the latter is a very strong testament of the correctness of (3.4a–c) (in fact, some slips in preliminary calculations have been caught looking at plots which exhibited mismatches).
$F_3(t)$
as displayed by the latter is a very strong testament of the correctness of (3.4a–c) (in fact, some slips in preliminary calculations have been caught looking at plots which exhibited mismatches).

Figure 1 Plots of
![]() $F_{1}(t)$
(left panel) and
$F_{1}(t)$
(left panel) and
![]() $F_{2}(t)$
(middle panel) as in (3.4a/b). The right panel shows
$F_{2}(t)$
(middle panel) as in (3.4a/b). The right panel shows
![]() $F_{3}(t)$
as in (3.4c) (black solid line) with the approximations (3.5) for
$F_{3}(t)$
as in (3.4c) (black solid line) with the approximations (3.5) for
![]() $\nu =100$
(red dotted line) and
$\nu =100$
(red dotted line) and
![]() $\nu =800$
(green dashed line): the close agreement validates the functional forms displayed in (3.4). Details about the numerical method can be found in [Reference Bornemann14, Reference Bornemann15, Reference Bornemann19, Reference Bornemann, Forrester and Mays20].
$\nu =800$
(green dashed line): the close agreement validates the functional forms displayed in (3.4). Details about the numerical method can be found in [Reference Bornemann14, Reference Bornemann15, Reference Bornemann19, Reference Bornemann, Forrester and Mays20].
The proof of Theorem 3.1 is split into several steps and will be concluded in Sections 3.2 and 3.3.
3.1. Kernel expansions
We start with an auxiliary result.
Lemma 3.2. Define for
![]() $h>0$
and
$h>0$
and
![]() $x,y<h^{-1}$
the function
$x,y<h^{-1}$
the function
 $$ \begin{align} \Phi(x,y;h):=\frac{\sqrt{(1- hx)(1-hy)}} {1-h(x+y)/2}. \end{align} $$
$$ \begin{align} \Phi(x,y;h):=\frac{\sqrt{(1- hx)(1-hy)}} {1-h(x+y)/2}. \end{align} $$
This function
![]() $\Phi $
satisfies the bound
$\Phi $
satisfies the bound
and has the convergent power series expansion
 $$ \begin{align} \Phi(x,y;h) = 1 - (x-y)^2 \sum_{k=2}^\infty r_k(x,y) h^k, \end{align} $$
$$ \begin{align} \Phi(x,y;h) = 1 - (x-y)^2 \sum_{k=2}^\infty r_k(x,y) h^k, \end{align} $$
where the
![]() $r_k(x,y)$
are certain homogeneous symmetric rationalFootnote
19
polynomials of degree
$r_k(x,y)$
are certain homogeneous symmetric rationalFootnote
19
polynomials of degree
![]() $k-2$
, the first few of them being
$k-2$
, the first few of them being
The series converges uniformly for
![]() $x,y<(1-\delta )h^{-1}$
,
$x,y<(1-\delta )h^{-1}$
,
![]() $\delta $
being any fixed real positive number.
$\delta $
being any fixed real positive number.
Proof. The bound (3.7) is the inequality of arithmetic and geometric means for the two positive real quantities
![]() $1-hx$
and
$1-hx$
and
![]() $1-hy$
. By using
$1-hy$
. By using
 $$\begin{align*}\lim_{y\to x} \frac{1}{(x-y)^2}\Big(\Phi(x,y;h) -1\Big) = -\frac{1}{8}\left(\frac{h}{1-hx}\right)^2, \end{align*}$$
$$\begin{align*}\lim_{y\to x} \frac{1}{(x-y)^2}\Big(\Phi(x,y;h) -1\Big) = -\frac{1}{8}\left(\frac{h}{1-hx}\right)^2, \end{align*}$$
the analyticity of
![]() $\Phi (x,y;h)$
w.r.t. h, and the scaling law
$\Phi (x,y;h)$
w.r.t. h, and the scaling law
we deduce the claims about the form and uniformity of the power series expansion (3.8).
Because of the representation (1.2) of
![]() $E_2^{\text {hard}}(s;\nu )$
in terms of a Fredholm determinant of the Bessel kernel (1.3), we have to expand the induced transformation of that kernel.
$E_2^{\text {hard}}(s;\nu )$
in terms of a Fredholm determinant of the Bessel kernel (1.3), we have to expand the induced transformation of that kernel.
Lemma 3.3. The change of variables
![]() $s=\phi _\nu (t)$
, mapping
$s=\phi _\nu (t)$
, mapping
![]() $t< h_\nu ^{-1}$
monotonically decreasing to
$t< h_\nu ^{-1}$
monotonically decreasing to
![]() $s> 0$
, induces the symmetrically transformed Bessel kernel
$s> 0$
, induces the symmetrically transformed Bessel kernel
There holds the kernel expansion
 $$ \begin{align} \hat K_\nu^{\mathrm{Bessel}}(x,y) &= K_0(x,y) + \sum_{j=1}^m K_j(x,y) h_\nu^j + h_\nu^{m+1}\cdot O\big(e^{-(x+y)}\big), \end{align} $$
$$ \begin{align} \hat K_\nu^{\mathrm{Bessel}}(x,y) &= K_0(x,y) + \sum_{j=1}^m K_j(x,y) h_\nu^j + h_\nu^{m+1}\cdot O\big(e^{-(x+y)}\big), \end{align} $$
which is uniformly valid when
![]() $t_0 \leqslant x,y < h_\nu ^{-1}$
as
$t_0 \leqslant x,y < h_\nu ^{-1}$
as
![]() $h_\nu \to 0^+$
, m being any fixed non-negative integer and
$h_\nu \to 0^+$
, m being any fixed non-negative integer and
![]() $t_0$
any fixed real number. Here, the
$t_0$
any fixed real number. Here, the
![]() $K_j$
are certain finite rank kernels of the form
$K_j$
are certain finite rank kernels of the form
where
![]() $p_{j,\kappa \lambda }(x,y)$
are rational polynomials; the first two kernels are
$p_{j,\kappa \lambda }(x,y)$
are rational polynomials; the first two kernels are
 $$ \begin{align} K_1(x,y) &= \frac{1}{10} \Big( -3\big(x^2+xy+y^2\big)\operatorname{Ai}(x)\operatorname{Ai}(y)\\&\qquad + 2 \big(\!\operatorname{Ai}(x)\operatorname{Ai}'(y) + \operatorname{Ai}'(x)\operatorname{Ai}(y)\big)+ 3(x+y)\operatorname{Ai}'(x)\operatorname{Ai}'(y) \Big),\notag \end{align} $$
$$ \begin{align} K_1(x,y) &= \frac{1}{10} \Big( -3\big(x^2+xy+y^2\big)\operatorname{Ai}(x)\operatorname{Ai}(y)\\&\qquad + 2 \big(\!\operatorname{Ai}(x)\operatorname{Ai}'(y) + \operatorname{Ai}'(x)\operatorname{Ai}(y)\big)+ 3(x+y)\operatorname{Ai}'(x)\operatorname{Ai}'(y) \Big),\notag \end{align} $$
 $$ \begin{align}K_2(x,y) &= \frac{1}{1400}\Big(\big(-235 \left(x^3+y^3\right)-319 x y (x+y)+56\big) \operatorname{Ai}(x)\operatorname{Ai}(y)\\&\qquad +\big(63(x^4+x^3 y-x^2 y^2-x y^3-y^4)-55 x+239 y\big) \operatorname{Ai}(x)\operatorname{Ai}'(y) \notag\\ &\qquad\quad +\big(63(-x^4-x^3 y-x^2 y^2+x y^3+y^4)+239 x-55 y\big) \operatorname{Ai}'(x)\operatorname{Ai}(y) \notag\\ &\qquad\qquad +\big(340(x^2+y^2)+256 x y\big) \operatorname{Ai}'(x)\operatorname{Ai}'(y)\Big). \notag \end{align} $$
$$ \begin{align}K_2(x,y) &= \frac{1}{1400}\Big(\big(-235 \left(x^3+y^3\right)-319 x y (x+y)+56\big) \operatorname{Ai}(x)\operatorname{Ai}(y)\\&\qquad +\big(63(x^4+x^3 y-x^2 y^2-x y^3-y^4)-55 x+239 y\big) \operatorname{Ai}(x)\operatorname{Ai}'(y) \notag\\ &\qquad\quad +\big(63(-x^4-x^3 y-x^2 y^2+x y^3+y^4)+239 x-55 y\big) \operatorname{Ai}'(x)\operatorname{Ai}(y) \notag\\ &\qquad\qquad +\big(340(x^2+y^2)+256 x y\big) \operatorname{Ai}'(x)\operatorname{Ai}'(y)\Big). \notag \end{align} $$
Preserving uniformity, the kernel expansion (3.9) can repeatedly be differentiated w.r.t. x, y.
Proof. We have to prove, analytically, the claim about the domain of uniformity of the error of the expansion and, algebraically, the finite-rank structure of the expansion kernels
![]() $K_j$
. In our original proof,Footnote
20
presented below, we use Olver’s expansion of Bessel functions of large order in the transition region (see Appendix A.3), and the finite-rank structure is obtained by explicitly inspecting (with Mathematica) a certain algebraic condition (see (3.14)) for the first instances
$K_j$
. In our original proof,Footnote
20
presented below, we use Olver’s expansion of Bessel functions of large order in the transition region (see Appendix A.3), and the finite-rank structure is obtained by explicitly inspecting (with Mathematica) a certain algebraic condition (see (3.14)) for the first instances
![]() $j=1,\ldots ,m_*$
– we choose to stop at
$j=1,\ldots ,m_*$
– we choose to stop at
![]() $m_*=100$
. However, using the machinery of Riemann–Hilbert problem, this restriction was recently removed by Yao and Zhang [Reference Yao and Zhang85] (their proof extends over 18 pages); we will comment on their work at the end.
$m_*=100$
. However, using the machinery of Riemann–Hilbert problem, this restriction was recently removed by Yao and Zhang [Reference Yao and Zhang85] (their proof extends over 18 pages); we will comment on their work at the end.
The original proof, requiring
![]() $m\leqslant m_*$
. By using
$m\leqslant m_*$
. By using
![]() $\Phi (x,y;h)$
as defined in (3.6) and writing
$\Phi (x,y;h)$
as defined in (3.6) and writing
 $$\begin{align*}\begin{aligned} \phi_\nu(t) = \omega_\nu(t)^2,\quad \omega_\nu(t)=\nu(1-h_\nu t),\\ a_\nu(x,y)= (1-h_\nu y) \cdot \frac{1}{\sqrt{2h_\nu}}J_\nu\big(\omega_\nu(x)\big)\cdot \frac{d}{dy} \frac{1}{\sqrt{2h_\nu}}J_\nu\big(\omega_\nu(y)\big), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \phi_\nu(t) = \omega_\nu(t)^2,\quad \omega_\nu(t)=\nu(1-h_\nu t),\\ a_\nu(x,y)= (1-h_\nu y) \cdot \frac{1}{\sqrt{2h_\nu}}J_\nu\big(\omega_\nu(x)\big)\cdot \frac{d}{dy} \frac{1}{\sqrt{2h_\nu}}J_\nu\big(\omega_\nu(y)\big), \end{aligned} \end{align*}$$
we can factor the transformed Bessel kernel in the simple form
noting, by symmetry, the removability of the singularities at
![]() $x=y$
of the second factor.
$x=y$
of the second factor.
First, if x or y is between
![]() $\tfrac 34 \cdot h_\nu ^{-1}$
and
$\tfrac 34 \cdot h_\nu ^{-1}$
and
![]() $h_\nu ^{-1}$
, using the bound
$h_\nu ^{-1}$
, using the bound
![]() $0<\Phi \leqslant 1$
(see (3.7)), one can argue as in the proof of Lemma A.9: since at least one of the Bessel factors is of the form
$0<\Phi \leqslant 1$
(see (3.7)), one can argue as in the proof of Lemma A.9: since at least one of the Bessel factors is of the form
![]() $J_\nu ^{(\kappa )}(z)$
with
$J_\nu ^{(\kappa )}(z)$
with
![]() $0\leqslant z \leqslant 1/4$
, which plainly falls into the superexponentially decaying region as
$0\leqslant z \leqslant 1/4$
, which plainly falls into the superexponentially decaying region as
![]() $\nu \to \infty $
, and since at least one of the Airy factors of each term of the expansion is also superexponentially decaying as
$\nu \to \infty $
, and since at least one of the Airy factors of each term of the expansion is also superexponentially decaying as
![]() $\nu \to \infty $
, the transformed Bessel kernel and the expansion terms in (3.9) get completely absorbed into the error term (bounding the other factors as in Section 2.1)
$\nu \to \infty $
, the transformed Bessel kernel and the expansion terms in (3.9) get completely absorbed into the error term (bounding the other factors as in Section 2.1)
Here, the removable singularities at
![]() $x=y$
are dealt with by using the differentiability of the corresponding bounds (or by extending to the complex domain and using Cauchy’s integral formula as in the proof of [Reference Borodin and Forrester21, Prop. 8]).
$x=y$
are dealt with by using the differentiability of the corresponding bounds (or by extending to the complex domain and using Cauchy’s integral formula as in the proof of [Reference Borodin and Forrester21, Prop. 8]).
Therefore, we may suppose from now on that
![]() $t_0 \leqslant x,y \leqslant \tfrac 34 \cdot h_\nu ^{-1}$
. By Lemma 3.2, in this range of x and y, the power series expansion
$t_0 \leqslant x,y \leqslant \tfrac 34 \cdot h_\nu ^{-1}$
. By Lemma 3.2, in this range of x and y, the power series expansion
 $$ \begin{align} \Phi(x,y;h_\nu) = 1 - (x-y)^2 \sum_{k=2}^\infty r_k(x,y) h_\nu^k \end{align} $$
$$ \begin{align} \Phi(x,y;h_\nu) = 1 - (x-y)^2 \sum_{k=2}^\infty r_k(x,y) h_\nu^k \end{align} $$
converges uniformly. Here, the
![]() $r_k(x,y)$
are certain homogeneous symmetric rational polynomials of degree
$r_k(x,y)$
are certain homogeneous symmetric rational polynomials of degree
![]() $k-2$
, the first of them being
$k-2$
, the first of them being
![]() $r_2(x,y)=1/8$
.
$r_2(x,y)=1/8$
.
Next, we rewrite the uniform version of the large order expansion of Bessel functions in the transition region, as given in Lemma A.9, in the form
where the estimate of the remainder is uniform for
![]() $t_0 \leqslant t < h_\nu ^{-1}$
as
$t_0 \leqslant t < h_\nu ^{-1}$
as
![]() $h_\nu \to 0^+$
and
$h_\nu \to 0^+$
and
 $$\begin{align*}p_m(t;h) = 2^{1/3}\sum_{k=0}^{m-1} A_{k+1}(-t/2^{1/3}) \,(2^{1/3}h)^{k}, \quad q_m(t;h) = 2^{2/3}\sum_{k=0}^{m-1} B_{k+1}(-t/2^{1/3}) \,(2^{1/3}h)^{k}, \end{align*}$$
$$\begin{align*}p_m(t;h) = 2^{1/3}\sum_{k=0}^{m-1} A_{k+1}(-t/2^{1/3}) \,(2^{1/3}h)^{k}, \quad q_m(t;h) = 2^{2/3}\sum_{k=0}^{m-1} B_{k+1}(-t/2^{1/3}) \,(2^{1/3}h)^{k}, \end{align*}$$
with the polynomials
![]() $A_k(\tau )$
and
$A_k(\tau )$
and
![]() $B_k(\tau )$
from (A.16). It follows from Remark A.8 that
$B_k(\tau )$
from (A.16). It follows from Remark A.8 that
![]() $p_m(t;h)$
and
$p_m(t;h)$
and
![]() $q_m(t;h)$
are rational polynomials in t and h, starting with
$q_m(t;h)$
are rational polynomials in t and h, starting with
Also given in Lemma A.9, under the same conditions, the expansion (3.12) can be repeatedly differentiated w.r.t t while preserving uniformity. From this, we obtain, using the Airy differential equation
![]() $\operatorname {Ai}"(\xi ) = \xi \operatorname {Ai}(\xi )$
, that uniformly (given the range x and y)Footnote
21
$\operatorname {Ai}"(\xi ) = \xi \operatorname {Ai}(\xi )$
, that uniformly (given the range x and y)Footnote
21
where
 $$ \begin{align*} p^m_{00}(x,y;h) &= h(1- hy)(1 + hp_m(x;h))\big(yq_m(y;h)+\partial_y p_m(y;h)\big), \\ p^m_{01}(x,y;h) &= (1- hy)(1 + hp_m(x;h))\big(1+h(p_m(y;h)+\partial_y q_m(y;h))\big),\\ p^m_{10}(x,y;h) &= h^2(1- hy)q_m(x;h)\big(y q_m(y;h)+\partial_y p_m(y;h)\big),\\ p^m_{11}(x,y;h) &= h(1- hy)q_m(x;h)\big(1+h(p_m(y;h)+\partial_y q_m(y;h))\big) \end{align*} $$
$$ \begin{align*} p^m_{00}(x,y;h) &= h(1- hy)(1 + hp_m(x;h))\big(yq_m(y;h)+\partial_y p_m(y;h)\big), \\ p^m_{01}(x,y;h) &= (1- hy)(1 + hp_m(x;h))\big(1+h(p_m(y;h)+\partial_y q_m(y;h))\big),\\ p^m_{10}(x,y;h) &= h^2(1- hy)q_m(x;h)\big(y q_m(y;h)+\partial_y p_m(y;h)\big),\\ p^m_{11}(x,y;h) &= h(1- hy)q_m(x;h)\big(1+h(p_m(y;h)+\partial_y q_m(y;h))\big) \end{align*} $$
are rational polynomials in x, y and h. In particular, those factorizations show
 $$\begin{align*}\begin{aligned} p^m_{00}(x,y;h) = O(h), \qquad p^m_{11}(x,y;h) = O(h),\\ p^m_{01}(x,y;h) = 1 + O(h), \qquad p^m_{10}(x,y;h) = O(h^2). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} p^m_{00}(x,y;h) = O(h), \qquad p^m_{11}(x,y;h) = O(h),\\ p^m_{01}(x,y;h) = 1 + O(h), \qquad p^m_{10}(x,y;h) = O(h^2). \end{aligned} \end{align*}$$
If we denote by
![]() $\hat p^m_{\kappa \lambda }(x,y;h)$
the polynomials obtained from
$\hat p^m_{\kappa \lambda }(x,y;h)$
the polynomials obtained from
![]() $p^m_{\kappa \lambda }(x,y;h)$
after dropping all powers of h that have an exponent larger than m (thus contributing terms to the expansion that get absorbed in the error term), we obtain
$p^m_{\kappa \lambda }(x,y;h)$
after dropping all powers of h that have an exponent larger than m (thus contributing terms to the expansion that get absorbed in the error term), we obtain
with a polynomial expansion
 $$\begin{align*}\hat p^m_{\kappa\lambda}(x,y;h) = \sum_{j=1}^m \hat p_{j,\kappa\lambda}(x,y) h^j, \end{align*}$$
$$\begin{align*}\hat p^m_{\kappa\lambda}(x,y;h) = \sum_{j=1}^m \hat p_{j,\kappa\lambda}(x,y) h^j, \end{align*}$$
whose coefficient polynomials
![]() $\hat p_{j,\kappa \lambda }(x,y)$
, being the unique expansion coefficients as
$\hat p_{j,\kappa \lambda }(x,y)$
, being the unique expansion coefficients as
![]() $h_\nu \to 0^+$
, are now independent of m. Hence, the anti-symmetrization of
$h_\nu \to 0^+$
, are now independent of m. Hence, the anti-symmetrization of
![]() $a_\nu (x,y)$
satisfies the uniform expansion (given the range of x and y)
$a_\nu (x,y)$
satisfies the uniform expansion (given the range of x and y)
 $$ \begin{align} a_\nu(x,y)-a_\nu(y,x) = \operatorname{Ai}(x)\operatorname{Ai}'&(y)- \operatorname{Ai}'(x)\operatorname{Ai}(y) \notag \\ &+ \sum_{\kappa,\lambda\in\{0,1\}} \hat q^m_{\kappa\lambda}(x,y;h_\nu) \operatorname{Ai}^{(\kappa)}(x)\operatorname{Ai}^{(\lambda)}(y) + h_\nu^{m+1} O(e^{-(x+y)}) \end{align} $$
$$ \begin{align} a_\nu(x,y)-a_\nu(y,x) = \operatorname{Ai}(x)\operatorname{Ai}'&(y)- \operatorname{Ai}'(x)\operatorname{Ai}(y) \notag \\ &+ \sum_{\kappa,\lambda\in\{0,1\}} \hat q^m_{\kappa\lambda}(x,y;h_\nu) \operatorname{Ai}^{(\kappa)}(x)\operatorname{Ai}^{(\lambda)}(y) + h_\nu^{m+1} O(e^{-(x+y)}) \end{align} $$
with the polynomial expansion
 $$\begin{align*}\begin{aligned} \hat q^m_{\kappa\lambda}(x,y;h) &= \sum_{j=1}^m \hat q_{j,\kappa\lambda}(x,y) h^j,\\ \hat q_{j,00}(x,y) = \hat p_{j,00}(x,y) - \hat p_{j,00}(y,x),&\qquad \hat q_{j,11}(x,y) = \hat p_{j,11}(x,y) - \hat p_{j,11}(y,x)\\ \hat q_{j,01}(x,y) = \hat p_{j,01}(x,y) - \hat p_{j,10}(y,x),&\qquad \hat q_{j,10}(x,y) = - \hat q_{j,01}(y,x). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \hat q^m_{\kappa\lambda}(x,y;h) &= \sum_{j=1}^m \hat q_{j,\kappa\lambda}(x,y) h^j,\\ \hat q_{j,00}(x,y) = \hat p_{j,00}(x,y) - \hat p_{j,00}(y,x),&\qquad \hat q_{j,11}(x,y) = \hat p_{j,11}(x,y) - \hat p_{j,11}(y,x)\\ \hat q_{j,01}(x,y) = \hat p_{j,01}(x,y) - \hat p_{j,10}(y,x),&\qquad \hat q_{j,10}(x,y) = - \hat q_{j,01}(y,x). \end{aligned} \end{align*}$$
Since the rational polynomials
![]() $\hat q_{j,00}(x,y)$
and
$\hat q_{j,00}(x,y)$
and
![]() $\hat q_{j,11}(x,y)$
are anti-symmetric in x, y, they factor in the form
$\hat q_{j,11}(x,y)$
are anti-symmetric in x, y, they factor in the form
the first few cases are
 $$ \begin{align*} \hat q_{1,00}(x,y) &= -\frac{3}{10}(x-y)(x^2+xy+y^2),\\ \hat q_{1,11}(x,y) &= \frac{3}{10}(x-y)(x+y),\\ \hat q_{2,00}(x,y) &= \frac{1}{1400} (x-y)\Big(-235\big(x^3+y^3\big)-319xy(x+y)+56\Big),\\ \hat q_{2,11}(x,y) &= \frac{1}{1400} (x-y)\Big(340\big(x^2+y^2\big)+256xy\Big). \end{align*} $$
$$ \begin{align*} \hat q_{1,00}(x,y) &= -\frac{3}{10}(x-y)(x^2+xy+y^2),\\ \hat q_{1,11}(x,y) &= \frac{3}{10}(x-y)(x+y),\\ \hat q_{2,00}(x,y) &= \frac{1}{1400} (x-y)\Big(-235\big(x^3+y^3\big)-319xy(x+y)+56\Big),\\ \hat q_{2,11}(x,y) &= \frac{1}{1400} (x-y)\Big(340\big(x^2+y^2\big)+256xy\Big). \end{align*} $$
Even though there is no straightforward structural reason for the rational polynomials
![]() $\hat q_{j,01}$
(and thus
$\hat q_{j,01}$
(and thus
![]() $\hat q_{j,10}$
) to be divisible by
$\hat q_{j,10}$
) to be divisible by
![]() $x-y$
as well, an inspectionFootnote
22
of the first cases reveals this to be true for at least
$x-y$
as well, an inspectionFootnote
22
of the first cases reveals this to be true for at least
![]() $j=1,\ldots ,m_*$
, the first two of them being
$j=1,\ldots ,m_*$
, the first two of them being
 $$ \begin{align*} \hat q_{1,01}(x,y) &= \frac{2}{10}(x-y),\\ \hat q_{2,01}(x,y) &= \frac{1}{1400}(x-y) \Big(63\big(x^4+x^3 y-x^2 y^2-x y^3-y^4\big) +120 x + 64y\Big). \end{align*} $$
$$ \begin{align*} \hat q_{1,01}(x,y) &= \frac{2}{10}(x-y),\\ \hat q_{2,01}(x,y) &= \frac{1}{1400}(x-y) \Big(63\big(x^4+x^3 y-x^2 y^2-x y^3-y^4\big) +120 x + 64y\Big). \end{align*} $$
Now, by restricting ourselves to the explicitly checked cases
![]() $m\leqslant m_*$
, we denote by
$m\leqslant m_*$
, we denote by
![]() $q^m_{\kappa \lambda }(x,y;h)$
the polynomials obtained from
$q^m_{\kappa \lambda }(x,y;h)$
the polynomials obtained from
![]() $\hat q^m_{\kappa \lambda }(x,y;h)$
after division by the factor
$\hat q^m_{\kappa \lambda }(x,y;h)$
after division by the factor
![]() $x-y$
. Since (3.13) is an expansion of an anti-symmetric function with anti-symmetric remainder which can repeatedly be differentiated, division by
$x-y$
. Since (3.13) is an expansion of an anti-symmetric function with anti-symmetric remainder which can repeatedly be differentiated, division by
![]() $x-y$
yields removable singularities at
$x-y$
yields removable singularities at
![]() $x=y$
and does not change the character of the expansion (see also the argument given in the proof of [Reference Borodin and Forrester21, Prop. 8]):
$x=y$
and does not change the character of the expansion (see also the argument given in the proof of [Reference Borodin and Forrester21, Prop. 8]):
 $$\begin{align*}\frac{a_\nu(x,y)-a_\nu(y,x)}{x-y} = K_0(x,y)+ \sum_{\kappa,\lambda\in\{0,1\}} q^m_{\kappa\lambda}(x,y;h_\nu) \operatorname{Ai}^{(\kappa)}(x)\operatorname{Ai}^{(\lambda)}(y) + h_\nu^{m+1} O\big(e^{-(x+y)}\big). \end{align*}$$
$$\begin{align*}\frac{a_\nu(x,y)-a_\nu(y,x)}{x-y} = K_0(x,y)+ \sum_{\kappa,\lambda\in\{0,1\}} q^m_{\kappa\lambda}(x,y;h_\nu) \operatorname{Ai}^{(\kappa)}(x)\operatorname{Ai}^{(\lambda)}(y) + h_\nu^{m+1} O\big(e^{-(x+y)}\big). \end{align*}$$
The lemma now follows by multiplying this expansion with (3.11), noting that the terms
also take the form asserted for the terms in the kernels
![]() $K_j$
(
$K_j$
(
![]() $j\geqslant 1$
).
$j\geqslant 1$
).
Finally, since all the expansions can repeatedly be differentiated under the same conditions while preserving their uniformity, the same holds for the resulting expansion of the kernel.
Comments on the unconditional proof of Yao and Zhang [Reference Yao and Zhang85]. Instead of using expansions of the Bessel functions of large order in the transition region, Yao and Zhang address expanding the integrable kernel
directly by the machinery of Riemann–Hilbert problems (see [Reference Deift27] for a general discussion of kernels of that form and their induced integral operators). The advantage of such a direct approach is a better understanding of the polynomial coefficients in (3.13), and the divisibility by
![]() $x-y$
follows from an interesting algebraic structure of the Airy functions; namely, by the Airy differential equation, there are rational polynomials
$x-y$
follows from an interesting algebraic structure of the Airy functions; namely, by the Airy differential equation, there are rational polynomials
![]() $\alpha _k, \beta _k \in {\mathbb Q}[\xi ]$
such that
$\alpha _k, \beta _k \in {\mathbb Q}[\xi ]$
such that
and the divisibility (3.14) turns out to be equivalent [Reference Yao and Zhang85, pp. 18–20] to the relation [Reference Yao and Zhang85, Lemma 4.1]
 $$\begin{align*}\sum_{j=0}^m \binom{m}{j} \begin{vmatrix} \alpha_j & \alpha_{m+1-j} \\ \beta_j & \beta_{m+1-j} \end{vmatrix} = 0 \qquad (m\geqslant 1), \end{align*}$$
$$\begin{align*}\sum_{j=0}^m \binom{m}{j} \begin{vmatrix} \alpha_j & \alpha_{m+1-j} \\ \beta_j & \beta_{m+1-j} \end{vmatrix} = 0 \qquad (m\geqslant 1), \end{align*}$$
which can be proved by induction.
Remark 3.4. The case
![]() $m=0$
of Lemma 3.3,
$m=0$
of Lemma 3.3,
is the
![]() $\beta =2$
case of [Reference Borodin and Forrester21, Eq. (4.8)] in the work of Borodin and Forrester. There, in [Reference Borodin and Forrester21, Prop. 8], it is stated that this expansion would be uniformly valid for
$\beta =2$
case of [Reference Borodin and Forrester21, Eq. (4.8)] in the work of Borodin and Forrester. There, in [Reference Borodin and Forrester21, Prop. 8], it is stated that this expansion would be uniformly valid for
![]() $x,y \geqslant t_0$
. However, stated in such a generality, it is not correct (see Footnote A.10) and, in fact, similar to our proof given above, their proof is restricted to the range
$x,y \geqslant t_0$
. However, stated in such a generality, it is not correct (see Footnote A.10) and, in fact, similar to our proof given above, their proof is restricted to the range
![]() $t_0\leqslant x,y < h_\nu ^{-1}$
, which completely suffices to address the hard-to-soft edge transition. (See Remark A.10 for yet another issue with [Reference Borodin and Forrester21, Prop. 8].)
$t_0\leqslant x,y < h_\nu ^{-1}$
, which completely suffices to address the hard-to-soft edge transition. (See Remark A.10 for yet another issue with [Reference Borodin and Forrester21, Prop. 8].)
To reduce the complexity of calculating the functional form of the first three finite-size correction terms in the hard-to-soft edge transition (3.3), we consider a second kernel transform.
Lemma 3.5. For
![]() $h>0$
, the Airy kernel
$h>0$
, the Airy kernel
![]() $K_0$
and the first expansion kernels
$K_0$
and the first expansion kernels
![]() $K_1$
,
$K_1$
,
![]() $K_2$
,
$K_2$
,
![]() $K_3$
from Lemma 3.3 we consider
$K_3$
from Lemma 3.3 we consider
and the transformation,Footnote
23
where
![]() $\zeta (z)$
is defined as in Section A.3,
$\zeta (z)$
is defined as in Section A.3,
Then
![]() $t=\psi _h(s)$
maps
$t=\psi _h(s)$
maps
![]() $s \in {\mathbb R}$
monotonically increasing to
$s \in {\mathbb R}$
monotonically increasing to
![]() $-\infty < t < h^{-1}$
, with
$-\infty < t < h^{-1}$
, with
![]() $t\leqslant \mu h^{-1}$
,
$t\leqslant \mu h^{-1}$
,
![]() $\mu = 0.94884\cdots $
, when
$\mu = 0.94884\cdots $
, when
![]() $s\leqslant 2h^{-1}$
, and induces the symmetrically transformed kernel
$s\leqslant 2h^{-1}$
, and induces the symmetrically transformed kernel
which expands as
uniformly in
![]() $s_0 \leqslant x,y \leqslant 2h^{-1}$
as
$s_0 \leqslant x,y \leqslant 2h^{-1}$
as
![]() $h\to 0^+$
,
$h\to 0^+$
,
![]() $s_0$
being a fixed real number. The three kernels are
$s_0$
being a fixed real number. The three kernels are
Preserving uniformity, the kernel expansion can repeatedly be differentiated w.r.t. x, y.
Proof. Reversing the power series (A.19) gives
which is uniformly convergent for
![]() $s_0 \leqslant s \leqslant 2h^{-1}$
since
$s_0 \leqslant s \leqslant 2h^{-1}$
since
![]() $|ht| \leqslant \mu < 1$
. Taking the expressions for
$|ht| \leqslant \mu < 1$
. Taking the expressions for
![]() $K_1$
,
$K_1$
,
![]() $K_2$
given in (3.10), and for
$K_2$
given in (3.10), and for
![]() $K_3$
from the supplementary Mathematica notebook referred to in Footnote 13, a routine calculation with truncated power series gives formula (3.16c) for
$K_3$
from the supplementary Mathematica notebook referred to in Footnote 13, a routine calculation with truncated power series gives formula (3.16c) for
![]() $\tilde K_1$
and
$\tilde K_1$
and
 $$\begin{align*}\begin{aligned} \tilde K_2(x,y) = \frac{1}{350} \Big(14\operatorname{Ai}(x)\operatorname{Ai}(y) + (-51 x + 55 y)\operatorname{Ai}(x)\operatorname{Ai}'(y) + (55x -51 y) \operatorname{Ai}'(x)\operatorname{Ai}(y) \Big),\\ \tilde K_3(x,y) = \frac{1}{15750}\Big(266(x+y)\operatorname{Ai}(x)\operatorname{Ai}(y) + (-1749 x^2+910 x y+455 y^2) \operatorname{Ai}(x)\operatorname{Ai}'(y)\\ \qquad + (455 x^2+910 x y-1749 y^2) \operatorname{Ai}'(x)\operatorname{Ai}(y) + 460 \operatorname{Ai}'(x)\operatorname{Ai}'(y)\Big). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \tilde K_2(x,y) = \frac{1}{350} \Big(14\operatorname{Ai}(x)\operatorname{Ai}(y) + (-51 x + 55 y)\operatorname{Ai}(x)\operatorname{Ai}'(y) + (55x -51 y) \operatorname{Ai}'(x)\operatorname{Ai}(y) \Big),\\ \tilde K_3(x,y) = \frac{1}{15750}\Big(266(x+y)\operatorname{Ai}(x)\operatorname{Ai}(y) + (-1749 x^2+910 x y+455 y^2) \operatorname{Ai}(x)\operatorname{Ai}'(y)\\ \qquad + (455 x^2+910 x y-1749 y^2) \operatorname{Ai}'(x)\operatorname{Ai}(y) + 460 \operatorname{Ai}'(x)\operatorname{Ai}'(y)\Big). \end{aligned} \end{align*}$$
The Airy differential equation
![]() $\xi \operatorname {Ai}(\xi ) = \operatorname {Ai}"(\xi )$
implies the replacement rule
$\xi \operatorname {Ai}(\xi ) = \operatorname {Ai}"(\xi )$
implies the replacement rule
which, if repeatedly applied to a kernel of the given structure, allows us to absorb any powers of x and y into higher order derivatives of
![]() $\operatorname {Ai}$
. This process yields the asserted form of
$\operatorname {Ai}$
. This process yields the asserted form of
![]() $\tilde K_2$
and
$\tilde K_2$
and
![]() $\tilde K_3$
, which will be the preferred form in course of the calculations in Section 3.3.
$\tilde K_3$
, which will be the preferred form in course of the calculations in Section 3.3.
Since we stay within the range of uniformity of the power series expansions and calculations with truncated powers series are amenable to repeated differentiation, the result now follows from the bounds given in Section 2.1.
3.2. Proof of the general form of the expansion
By Lemma 3.3 and Theorem 2.1, we get (the Fredholm determinants are seen to be equal by transforming the integrals)
 $$ \begin{align*} E_2^{\text{hard}}(\phi_\nu(t);\nu) = \det(I - K_\nu^{\text{Bessel}})|_{L^2(0,\phi_\nu(t))} &= \det(I - \hat K_\nu^{\text{Bessel}})|_{L^2(t,h_\nu^{-1})} \\ &= F(t) + \sum_{j=1}^m F_{j}(t) h_\nu^j + h_\nu^{m+1} O(e^{-2t}) + e^{-h_\nu^{-1}} O(e^{-t}), \end{align*} $$
$$ \begin{align*} E_2^{\text{hard}}(\phi_\nu(t);\nu) = \det(I - K_\nu^{\text{Bessel}})|_{L^2(0,\phi_\nu(t))} &= \det(I - \hat K_\nu^{\text{Bessel}})|_{L^2(t,h_\nu^{-1})} \\ &= F(t) + \sum_{j=1}^m F_{j}(t) h_\nu^j + h_\nu^{m+1} O(e^{-2t}) + e^{-h_\nu^{-1}} O(e^{-t}), \end{align*} $$
uniformly for
![]() $t_0\leqslant t < h_\nu ^{-1}$
as
$t_0\leqslant t < h_\nu ^{-1}$
as
![]() $h_\nu \to 0^+$
; preserving uniformity, this expansion can be repeatedly differentiated w.r.t. the variable t. By Theorem 2.1, the
$h_\nu \to 0^+$
; preserving uniformity, this expansion can be repeatedly differentiated w.r.t. the variable t. By Theorem 2.1, the
![]() $F_{j}(t)$
are certain smooth functions that can be expressed in terms of traces of integral operators of the form given in Theorem 2.1. Observing
$F_{j}(t)$
are certain smooth functions that can be expressed in terms of traces of integral operators of the form given in Theorem 2.1. Observing
we can combine the two error terms as
![]() $h_\nu ^{m+1} O(e^{-3t/2})$
. This finishes the proof of (3.3).
$h_\nu ^{m+1} O(e^{-3t/2})$
. This finishes the proof of (3.3).
3.3. Functional form of
 $F_{1}(t)$
,
$F_{1}(t)$
,
 $F_{2}(t)$
and
$F_{2}(t)$
and
 $F_3(t)$
$F_3(t)$
Instead of calculating
![]() $F_{1}$
,
$F_{1}$
,
![]() $F_{2}$
,
$F_{2}$
,
![]() $F_3$
directly from the formulae in Theorem 2.1 applied to the kernels
$F_3$
directly from the formulae in Theorem 2.1 applied to the kernels
![]() $K_1$
,
$K_1$
,
![]() $K_2$
in (3.10) (and to the unwieldy expression for
$K_2$
in (3.10) (and to the unwieldy expression for
![]() $K_3$
obtained in the supplementary Mathematica notebook referred to in Footnote 13), we will reduce them to the corresponding functions
$K_3$
obtained in the supplementary Mathematica notebook referred to in Footnote 13), we will reduce them to the corresponding functions
![]() $\tilde F_1, \tilde F_2, \tilde F_3$
induced by the much simpler kernels
$\tilde F_1, \tilde F_2, \tilde F_3$
induced by the much simpler kernels
![]() $\tilde K_1$
,
$\tilde K_1$
,
![]() $\tilde K_2$
,
$\tilde K_2$
,
![]() $\tilde K_3$
in (3.16).
$\tilde K_3$
in (3.16).
3.3.1. Functional form of
 $\tilde F_{1}(t)$
and
$\tilde F_{1}(t)$
and
 $\tilde F_{2}(t)$
$\tilde F_{2}(t)$
Upon writing
and observing (the symmetry of the resolvent kernel implies the symmetry
![]() $u_{jk}(t)= u_{kj}(t)$
)
$u_{jk}(t)= u_{kj}(t)$
)
 $$ \begin{align*} \operatorname{tr}\big((I-K_0)^{-1} \tilde K_1\big)\big|_{L^2(t,\infty)} &= \frac{2}{5} u_{10}(t),\\ \operatorname{tr}\big(((I-K_0)^{-1} \tilde K_1)^2\big)\big|_{L^2(t,\infty)} &= \frac{2}{25} \big(u_{00}(t)u_{11}(t) + u_{10}(t)^2\big),\\ \operatorname{tr}\big((I-K_0)^{-1} \tilde K_2\big)\big|_{L^2(t,\infty)} &= \frac{1}{175}\big(-48u_{00}(t)-51u_{21}(t) +55u_{30}(t)\big), \end{align*} $$
$$ \begin{align*} \operatorname{tr}\big((I-K_0)^{-1} \tilde K_1\big)\big|_{L^2(t,\infty)} &= \frac{2}{5} u_{10}(t),\\ \operatorname{tr}\big(((I-K_0)^{-1} \tilde K_1)^2\big)\big|_{L^2(t,\infty)} &= \frac{2}{25} \big(u_{00}(t)u_{11}(t) + u_{10}(t)^2\big),\\ \operatorname{tr}\big((I-K_0)^{-1} \tilde K_2\big)\big|_{L^2(t,\infty)} &= \frac{1}{175}\big(-48u_{00}(t)-51u_{21}(t) +55u_{30}(t)\big), \end{align*} $$
the formulae of Theorem 2.1 applied to
![]() $\tilde K_1$
and
$\tilde K_1$
and
![]() $\tilde K_2$
give
$\tilde K_2$
give
 $$ \begin{align} \tilde F_{2}(t) &= F(t)\left(\frac{48}{175} u_{00}(t) - \frac{1}{25} \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix} +\frac{51}{175} u_{21}(t) - \frac{11}{35} u_{30}(t) \right). \end{align} $$
$$ \begin{align} \tilde F_{2}(t) &= F(t)\left(\frac{48}{175} u_{00}(t) - \frac{1}{25} \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix} +\frac{51}{175} u_{21}(t) - \frac{11}{35} u_{30}(t) \right). \end{align} $$
We recall from [Reference Bornemann19, Remark 3.1] that the simple recursion
yields similar formulae for the first few derivatives of the distribution
![]() $F(t)$
:
$F(t)$
:
 $$ \begin{align} \begin{aligned} F'(t) = F(t)\cdot &u_{00}(t),\quad F"(t) = 2F(t)\cdot u_{10}(t),\quad F"'(t) = 2F(t)\cdot \big(u_{11}(t)+u_{20}(t)\big),\\ &F^{(4)}(t) = 2F(t)\cdot\left( \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix} + 3u_{21}(t) + u_{30}(t) \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} F'(t) = F(t)\cdot &u_{00}(t),\quad F"(t) = 2F(t)\cdot u_{10}(t),\quad F"'(t) = 2F(t)\cdot \big(u_{11}(t)+u_{20}(t)\big),\\ &F^{(4)}(t) = 2F(t)\cdot\left( \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix} + 3u_{21}(t) + u_{30}(t) \right). \end{aligned} \end{align} $$
By a linear elimination of the terms
 $$\begin{align*}u_{00}(t), \quad u_{10}(t),\quad \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix}, \end{align*}$$
$$\begin{align*}u_{00}(t), \quad u_{10}(t),\quad \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{10}(t) & u_{11}(t) \end{vmatrix}, \end{align*}$$
we obtain, as an intermediate step,
To simplify even further, we have to refer to the full power of the general Tracy–Widom theory (i.e., representing F in terms of Painlevé II): by advancing its set of formulae, Shinault and Tracy [Reference Shinault and Tracy73, p. 68] showed, through an explicit inspection of each single case, that the functions
![]() $F(t)\cdot u_{jk}(t)$
in the range
$F(t)\cdot u_{jk}(t)$
in the range
![]() $0 \leqslant j+k\leqslant 8$
are linear combinations of the form
$0 \leqslant j+k\leqslant 8$
are linear combinations of the form
with rational polynomials
![]() $p_\kappa (t)$
(depending, of course, on j, k). They conjectured this structure to be true for all j, k. In particular, their table [Reference Shinault and Tracy73, p. 68] has the entries
$p_\kappa (t)$
(depending, of course, on j, k). They conjectured this structure to be true for all j, k. In particular, their table [Reference Shinault and Tracy73, p. 68] has the entries
This way, we get, rather unexpectedly, the simple and short formFootnote 24
3.3.2. Functional form of
 $\tilde F_{3}(t)$
$\tilde F_{3}(t)$
For the
![]() $\tilde F_j(t)$
with
$\tilde F_j(t)$
with
![]() $j\geqslant 3$
, calculating such functional forms requires a more systematic, algorithmic approach. By ‘reverse engineering’ the remarks of Shinault and Tracy about validating their table [Reference Shinault and Tracy73, p. 68], we have actually found an algorithm to compile such a table; see Appendix B. This algorithm can also be applied to nonlinear rational polynomials of the terms
$j\geqslant 3$
, calculating such functional forms requires a more systematic, algorithmic approach. By ‘reverse engineering’ the remarks of Shinault and Tracy about validating their table [Reference Shinault and Tracy73, p. 68], we have actually found an algorithm to compile such a table; see Appendix B. This algorithm can also be applied to nonlinear rational polynomials of the terms
![]() $u_{jk}$
, resulting either in an expression of the desired form (3.20b) (with
$u_{jk}$
, resulting either in an expression of the desired form (3.20b) (with
![]() $j+k+1$
replaced by some n), or a message that such a form does not exist (for the given n).
$j+k+1$
replaced by some n), or a message that such a form does not exist (for the given n).
Now, if we evaluate the expansion function
![]() $G_3(t)=F(t)d_3(t)$
of Theorem 2.1 by using (2.10c) and rewrite the traces in terms of the
$G_3(t)=F(t)d_3(t)$
of Theorem 2.1 by using (2.10c) and rewrite the traces in terms of the
![]() $u_{jk}$
, we obtain
$u_{jk}$
, we obtain
 $$ \begin{align} \tilde F_3(t) &= F(t) \left(-\frac{3728 }{7875}u_{11}(t) +\frac{352 }{1125}u_{20}(t) -\frac{51}{875} \begin{vmatrix} u_{10}(t) & u_{11}(t) \\ u_{20}(t) & u_{21}(t) \end{vmatrix} \right. \end{align} $$
$$ \begin{align} \tilde F_3(t) &= F(t) \left(-\frac{3728 }{7875}u_{11}(t) +\frac{352 }{1125}u_{20}(t) -\frac{51}{875} \begin{vmatrix} u_{10}(t) & u_{11}(t) \\ u_{20}(t) & u_{21}(t) \end{vmatrix} \right. \end{align} $$
 $$\begin{align*} &\hspace{50pt} \left. -\frac{11}{175} \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{30}(t) & u_{31}(t) \end{vmatrix}-\frac{26}{225} u_{32}(t)+\frac{583 }{2625}u_{41}(t)-\frac{13}{225} u_{50}(t)\right)\notag, \end{align*}$$
$$\begin{align*} &\hspace{50pt} \left. -\frac{11}{175} \begin{vmatrix} u_{00}(t) & u_{01}(t) \\ u_{30}(t) & u_{31}(t) \end{vmatrix}-\frac{26}{225} u_{32}(t)+\frac{583 }{2625}u_{41}(t)-\frac{13}{225} u_{50}(t)\right)\notag, \end{align*}$$
which evaluates by the algorithm of Appendix B further to
Alternatively, we arrive here by combining the tabulated expressions for
![]() $u_{11}$
,
$u_{11}$
,
![]() $u_{20}$
,
$u_{20}$
,
![]() $u_{32}$
,
$u_{32}$
,
![]() $u_{41}$
,
$u_{41}$
,
![]() $u_{50}$
as displayed in [Reference Shinault and Tracy73, p. 68] with those for both of the
$u_{50}$
as displayed in [Reference Shinault and Tracy73, p. 68] with those for both of the
![]() $2\times 2$
determinants in (B.8).
$2\times 2$
determinants in (B.8).
3.3.3. Lifting to the functional form of
 $F_{1}(t)$
,
$F_{1}(t)$
,
 $F_{2}(t)$
,
$F_{2}(t)$
,
 $F_{3}(t)$
$F_{3}(t)$
The relation between
![]() $F_{1}(t)$
,
$F_{1}(t)$
,
![]() $F_{2}(t)$
,
$F_{2}(t)$
,
![]() $F_3(t)$
and their counterparts with a tilde is established by Lemma 3.5. By using the notation introduced there, with t being any fixed real number, the expansion parameter h sufficiently small and
$F_3(t)$
and their counterparts with a tilde is established by Lemma 3.5. By using the notation introduced there, with t being any fixed real number, the expansion parameter h sufficiently small and
![]() $s=\psi _{h}^{-1}(t)$
, Theorem 2.1 yields (the Fredholm determinants are seen to be equal by transforming the integrals)
$s=\psi _{h}^{-1}(t)$
, Theorem 2.1 yields (the Fredholm determinants are seen to be equal by transforming the integrals)
 $$ \begin{align} \begin{aligned} & \det\big(I-K_{(h)}\big)|_{L^2(t, \,\mu h^{-1})} = F(t) + F_{1}(t) h + F_{2}(t)h^2 + F_{3}(t)h^3 + O(h^4) \\ = &\det\big(I-\tilde K_{(h)}\big)|_{L^2(s, \, 2 h^{-1})} = F(s) + \tilde F_{1}(s) h + \tilde F_{2}(s)h^2 + \tilde F_{3}(s)h^3 + O(h^4), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \det\big(I-K_{(h)}\big)|_{L^2(t, \,\mu h^{-1})} = F(t) + F_{1}(t) h + F_{2}(t)h^2 + F_{3}(t)h^3 + O(h^4) \\ = &\det\big(I-\tilde K_{(h)}\big)|_{L^2(s, \, 2 h^{-1})} = F(s) + \tilde F_{1}(s) h + \tilde F_{2}(s)h^2 + \tilde F_{3}(s)h^3 + O(h^4), \end{aligned} \end{align} $$
where we have absorbed the exponentially small contributions
![]() $e^{-\mu h^{-1}} O(e^{-t})$
and
$e^{-\mu h^{-1}} O(e^{-t})$
and
![]() $e^{-2h^{-1}} O(e^{-s})$
into the
$e^{-2h^{-1}} O(e^{-s})$
into the
![]() $O(h^4)$
error term. Using the power series (A.19),
$O(h^4)$
error term. Using the power series (A.19),
we get by Taylor expansion, for any smooth function
![]() $G(s)$
,
$G(s)$
,
 $$ \begin{align*} G(s) &= G(t) + \frac{3t^2}{10} G'(t) h + \left(\frac{32t^3}{175} G'(t) + \frac{9t^4}{200} G"(t) \right) h^2 \\ &\qquad +\left(\frac{1037 t^4}{7875} G'(t)+\frac{48t^5}{875} G"(t)+ \frac{9 t^6 }{2000}G"'(t)\right)h^3 + O(h^4). \end{align*} $$
$$ \begin{align*} G(s) &= G(t) + \frac{3t^2}{10} G'(t) h + \left(\frac{32t^3}{175} G'(t) + \frac{9t^4}{200} G"(t) \right) h^2 \\ &\qquad +\left(\frac{1037 t^4}{7875} G'(t)+\frac{48t^5}{875} G"(t)+ \frac{9 t^6 }{2000}G"'(t)\right)h^3 + O(h^4). \end{align*} $$
By plugging this into (3.22) and comparing coefficients, we obtain
 $$ \begin{align*} F_{1}(t) &= \tilde F_{1}(t) + \frac{3t^2}{10} F'(t),\\ F_{2}(t) &=\tilde F_{2}(t) + \frac{3t^2}{10} \tilde F_{1}^{\prime}(t) + \frac{32t^3}{175} F'(t) + \frac{9t^4}{200} F"(t),\\ F_{3}(t) &= \tilde F_3(t) + \frac{32t^3}{175} \tilde F_1^{\prime}(t)+\frac{9t^4}{200} \tilde F_1^{\prime\prime}(t)+\frac{3t^2}{10} \tilde F_2^{\prime}(t) +\frac{1037 t^4 }{7875}F'(t)+\frac{48t^5 }{875} F"(t)+ \frac{9 t^6 F"'(t)}{2000}. \end{align*} $$
$$ \begin{align*} F_{1}(t) &= \tilde F_{1}(t) + \frac{3t^2}{10} F'(t),\\ F_{2}(t) &=\tilde F_{2}(t) + \frac{3t^2}{10} \tilde F_{1}^{\prime}(t) + \frac{32t^3}{175} F'(t) + \frac{9t^4}{200} F"(t),\\ F_{3}(t) &= \tilde F_3(t) + \frac{32t^3}{175} \tilde F_1^{\prime}(t)+\frac{9t^4}{200} \tilde F_1^{\prime\prime}(t)+\frac{3t^2}{10} \tilde F_2^{\prime}(t) +\frac{1037 t^4 }{7875}F'(t)+\frac{48t^5 }{875} F"(t)+ \frac{9 t^6 F"'(t)}{2000}. \end{align*} $$
3.4. Simplifying the form of Choup’s Edgeworth expansions
When, instead of the detour via
![]() $\tilde K_1$
, Theorem 2.1 is directly applied to the kernel
$\tilde K_1$
, Theorem 2.1 is directly applied to the kernel
![]() $K_1$
in (3.10a), we get
$K_1$
in (3.10a), we get
where
Now, a comparison with (3.4a) proves the useful formulaFootnote 25
As an application to the existing literature, this formula helps us to simplify the results obtained by Choup for the soft-edge limit expansions of GUE and LUE – that is, when studying the distribution of the largest eigenvalue distribution function in
![]() $\text {GUE}_n$
and
$\text {GUE}_n$
and
![]() $\text {LUE}_{n,\nu }$
(dimension n, parameter
$\text {LUE}_{n,\nu }$
(dimension n, parameter
![]() $\nu $
) as
$\nu $
) as
![]() $n\to \infty $
. In fact, since the kernel L appears in the first finite-size correction term of a corresponding kernel expansion [Reference Choup24, Thm. 1.2/1.3], lifting that expansion to the Fredholm determinant by Theorem 2.1 allows us to recast [Reference Choup24, Thm. 1.4] in a simplified form; namely, denoting the maximum eigenvalues by
$n\to \infty $
. In fact, since the kernel L appears in the first finite-size correction term of a corresponding kernel expansion [Reference Choup24, Thm. 1.2/1.3], lifting that expansion to the Fredholm determinant by Theorem 2.1 allows us to recast [Reference Choup24, Thm. 1.4] in a simplified form; namely, denoting the maximum eigenvalues by
![]() $\lambda _{n}^{\text {G}}$
and
$\lambda _{n}^{\text {G}}$
and
![]() $\lambda _{n,\nu }^{\text {L}}$
, we obtain, locally uniform in t as
$\lambda _{n,\nu }^{\text {L}}$
, we obtain, locally uniform in t as
![]() $n\to \infty $
,
$n\to \infty $
,
a result, which answers a question suggested by Baik and Jenkins [Reference Baik and Jenkins11, p. 4367].
4. Expansion of the Poissonized length distribution
The Poissonization of the length distribution requires the hard-to-soft edge transition of Theorem 3.1 to be applied to the probability distribution
![]() $E_2^{\text {hard}}(4r;\nu )$
(for integer
$E_2^{\text {hard}}(4r;\nu )$
(for integer
![]() $\nu =l$
, but we consider the case of general
$\nu =l$
, but we consider the case of general
![]() $\nu>0$
first). For large intensities r, the mode of this distribution is located in the range of those parameters
$\nu>0$
first). For large intensities r, the mode of this distribution is located in the range of those parameters
![]() $\nu $
for which the scaled variable
$\nu $
for which the scaled variable
stays bounded. It is convenient to note that
![]() $t_\nu (r)$
satisfies the differential equation
$t_\nu (r)$
satisfies the differential equation
In these terms, we get the following theorem.
Theorem 4.1. There holds the expansion
 $$ \begin{align} E_2^{\text{hard}}(4r;\nu) = F(t) + \sum_{j=1}^m F_{j}^P(t)\, r^{-j/3} + r^{-(m+1)/3} \cdot O\big(e^{-t}\big)\bigg|_{t=t_\nu(r)}, \end{align} $$
$$ \begin{align} E_2^{\text{hard}}(4r;\nu) = F(t) + \sum_{j=1}^m F_{j}^P(t)\, r^{-j/3} + r^{-(m+1)/3} \cdot O\big(e^{-t}\big)\bigg|_{t=t_\nu(r)}, \end{align} $$
which is uniformly valid when
![]() $r,\nu \to \infty $
subject to
$r,\nu \to \infty $
subject to
with m being any fixed non-negative integer and
![]() $t_0$
any fixed real number. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r. Here, the
$t_0$
any fixed real number. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r. Here, the
![]() $F_{j}^P$
are certain smooth functions; the first three areFootnote
26
$F_{j}^P$
are certain smooth functions; the first three areFootnote
26
 $$\begin{align*} &\qquad-\Big(\frac{61}{31500}+\frac{19 t^3}{63000}+\frac{t^6}{1296000} \Big) F"'(t) -\Big(\frac{11 t}{10500} + \frac{t^4}{72000}\Big) F^{(4)}(t) \notag \\ &\qquad -\frac{t^2}{12000}F^{(5)}(t) -\frac{1}{6000}F^{(6)}(t). \notag \end{align*}$$
$$\begin{align*} &\qquad-\Big(\frac{61}{31500}+\frac{19 t^3}{63000}+\frac{t^6}{1296000} \Big) F"'(t) -\Big(\frac{11 t}{10500} + \frac{t^4}{72000}\Big) F^{(4)}(t) \notag \\ &\qquad -\frac{t^2}{12000}F^{(5)}(t) -\frac{1}{6000}F^{(6)}(t). \notag \end{align*}$$

Figure 2 Plots of
![]() $F_{1}^P(t)$
(left panel) and
$F_{1}^P(t)$
(left panel) and
![]() $F_{2}^P(t)$
(middle panel) as in (4.4a/b). The right panel shows
$F_{2}^P(t)$
(middle panel) as in (4.4a/b). The right panel shows
![]() $F_3^P(t)$
as in (4.4c) (black solid line) with the approximations (4.3) for
$F_3^P(t)$
as in (4.4c) (black solid line) with the approximations (4.3) for
![]() $r=250$
(red dotted line) and
$r=250$
(red dotted line) and
![]() $r=2000$
(green dashed line); the parameter
$r=2000$
(green dashed line); the parameter
![]() $\nu $
has been varied such that
$\nu $
has been varied such that
![]() $t_\nu (r)$
covers the range of t on display. Note that the functions
$t_\nu (r)$
covers the range of t on display. Note that the functions
![]() $F_{j}^P(t)$
(
$F_{j}^P(t)$
(
![]() $j=1,2,3$
) are about two orders of magnitude smaller in scale than their counterparts in Figure 1.
$j=1,2,3$
) are about two orders of magnitude smaller in scale than their counterparts in Figure 1.
Proof. For
![]() $r, \nu> 0$
(i.e., equivalently,
$r, \nu> 0$
(i.e., equivalently,
![]() $t>-2r^{1/3}$
and
$t>-2r^{1/3}$
and
![]() $s < h_\nu ^{-1}$
), the transformations
$s < h_\nu ^{-1}$
), the transformations
are inverted by the expressions
 $$ \begin{align} s = \frac{t}{\big(1+\tfrac{t}2 r^{-1/3}\big)^{1/3}},\quad h_\nu = \frac{r^{-1/3}}{2\big(1+\tfrac{t}2 r^{-1/3}\big)^{2/3}}. \end{align} $$
$$ \begin{align} s = \frac{t}{\big(1+\tfrac{t}2 r^{-1/3}\big)^{1/3}},\quad h_\nu = \frac{r^{-1/3}}{2\big(1+\tfrac{t}2 r^{-1/3}\big)^{2/3}}. \end{align} $$
For
![]() $t_0\leqslant t \leqslant r^{1/3}$
, we get
$t_0\leqslant t \leqslant r^{1/3}$
, we get
and observe that in this range of t the expressions in (4.5) expand as uniformly convergent power series in powers of
![]() $r^{-1/3}$
, starting with
$r^{-1/3}$
, starting with
If we plug these uniformly convergent power series into the uniform expansion of Theorem 3.1,
 $$\begin{align*}E_2^{\text{hard}}(4r;\nu) = E_2^{\text{hard}}(\phi_\nu(s);\nu) = F(s) + \sum_{j=1}^m F_{1}(s) h_\nu^j + h_\nu^{m+1} O(e^{-3s/2}), \end{align*}$$
$$\begin{align*}E_2^{\text{hard}}(4r;\nu) = E_2^{\text{hard}}(\phi_\nu(s);\nu) = F(s) + \sum_{j=1}^m F_{1}(s) h_\nu^j + h_\nu^{m+1} O(e^{-3s/2}), \end{align*}$$
we obtain the asserted form of the expansion (4.2) (as well as the claim about the repeated differentiability), simplifying the exponential error term by observing that
![]() $(3/2)^{2/3}> 1$
. In particular, the first three correction terms in (4.2) are thus
$(3/2)^{2/3}> 1$
. In particular, the first three correction terms in (4.2) are thus
 $$ \begin{align*} F_{1}^P(t) &= \frac{1}{2} F_{1}(t) - \frac{t^2}{6} F'(t),\\ F_{2}^P(t) &= \frac{1}{4} F_{2}(t) - \frac{t}{6} F_{1}(t) - \frac{t^2}{12} F_{1}^{\prime}(t) + \frac{t^3}{18} F'(t) + \frac{t^4}{72}F"(t),\\ F_{3}^P(t) &= \frac{1}{8}F_3(t) -\frac{t}{6} F_2(t)-\frac{t^2}{24} F_2^{\prime}(t)+\frac{5t^2}{72} F_1(t)+\frac{ t^3}{18} F_1^{\prime}(t)+\frac{t^4}{144} F_1^{\prime\prime}(t)\\ &\qquad -\frac{7t^4}{324} F'(t) -\frac{t^5}{108} F"(t)-\frac{t^6 }{1296}F"'(t). \end{align*} $$
$$ \begin{align*} F_{1}^P(t) &= \frac{1}{2} F_{1}(t) - \frac{t^2}{6} F'(t),\\ F_{2}^P(t) &= \frac{1}{4} F_{2}(t) - \frac{t}{6} F_{1}(t) - \frac{t^2}{12} F_{1}^{\prime}(t) + \frac{t^3}{18} F'(t) + \frac{t^4}{72}F"(t),\\ F_{3}^P(t) &= \frac{1}{8}F_3(t) -\frac{t}{6} F_2(t)-\frac{t^2}{24} F_2^{\prime}(t)+\frac{5t^2}{72} F_1(t)+\frac{ t^3}{18} F_1^{\prime}(t)+\frac{t^4}{144} F_1^{\prime\prime}(t)\\ &\qquad -\frac{7t^4}{324} F'(t) -\frac{t^5}{108} F"(t)-\frac{t^6 }{1296}F"'(t). \end{align*} $$
Together with the expressions given in (3.4), this yields the functional form asserted in (4.4).
By (1.1), specializing Theorem 4.1 to the case of integer parameter
![]() $\nu = l$
yields the expansion
$\nu = l$
yields the expansion
 $$ \begin{align} {\mathbb P}\big(L_{N_r} \leqslant l\big) = F(t) + \sum_{j=1}^m F_{j}^P(t)\, r^{-j/3} + r^{-(m+1)/3} \cdot O\big(e^{-t}\big) \bigg|_{t=t_l(r)}, \end{align} $$
$$ \begin{align} {\mathbb P}\big(L_{N_r} \leqslant l\big) = F(t) + \sum_{j=1}^m F_{j}^P(t)\, r^{-j/3} + r^{-(m+1)/3} \cdot O\big(e^{-t}\big) \bigg|_{t=t_l(r)}, \end{align} $$
which is uniformly valid under the conditions stated there.
Remark 4.2. In the literature, scalings are often applied to the probability distribution rather than to the expansion terms. Since
![]() $L_{N_r}$
is a an integer-valued random variable, one has to exercise some care with the scaled distribution function being piecewise constant. Namely, for
$L_{N_r}$
is a an integer-valued random variable, one has to exercise some care with the scaled distribution function being piecewise constant. Namely, for
![]() $t\in {\mathbb R}$
being any fixed number, one has
$t\in {\mathbb R}$
being any fixed number, one has
 $$\begin{align*}{\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = {\mathbb P}\big(L_{N_r} \leqslant l\big),\qquad l = \big\lfloor2\sqrt{r} + tr^{1/6}\big\rfloor, \end{align*}$$
$$\begin{align*}{\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = {\mathbb P}\big(L_{N_r} \leqslant l\big),\qquad l = \big\lfloor2\sqrt{r} + tr^{1/6}\big\rfloor, \end{align*}$$
where
![]() $\lfloor \cdot \rfloor $
denotes the Gauss bracket. Thus, by defining
$\lfloor \cdot \rfloor $
denotes the Gauss bracket. Thus, by defining
 $$\begin{align*}t^{(r)} = \frac{\big\lfloor2\sqrt{r} + tr^{1/6}\big\rfloor - 2\sqrt{r}}{r^{1/6}} \end{align*}$$
$$\begin{align*}t^{(r)} = \frac{\big\lfloor2\sqrt{r} + tr^{1/6}\big\rfloor - 2\sqrt{r}}{r^{1/6}} \end{align*}$$
and noting that
![]() $t^{(r)}$
stays bounded when
$t^{(r)}$
stays bounded when
![]() $r\to \infty $
while t is fixed, (4.6) takes the form
$r\to \infty $
while t is fixed, (4.6) takes the form
 $$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) + \sum_{j=1}^m F_{j}^P\big(t^{(r)}\big)\, r^{-j/3} + O\big(r^{-(m+1)/3}\big)\qquad (r\to\infty). \end{align} $$
$$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) + \sum_{j=1}^m F_{j}^P\big(t^{(r)}\big)\, r^{-j/3} + O\big(r^{-(m+1)/3}\big)\qquad (r\to\infty). \end{align} $$
If one chooses to re-introduce the continuous variable t in (parts of) the expansion terms, one has to take into account that
where the exponent
![]() $-1/6$
in the error term is sharp. For example, this gives (as previously obtained by Baik and Jenkins [Reference Baik and Jenkins11, Thm. 1.3] using the technology of Riemann–Hilbert problems to prove the expansion and Painlevé representations to put
$-1/6$
in the error term is sharp. For example, this gives (as previously obtained by Baik and Jenkins [Reference Baik and Jenkins11, Thm. 1.3] using the technology of Riemann–Hilbert problems to prove the expansion and Painlevé representations to put
![]() $F_{1}^P$
into the simple functional form (4.4a))
$F_{1}^P$
into the simple functional form (4.4a))
 $$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) + F_{1}^P(t)\, r^{-1/3} + O(r^{-1/2})\qquad (r\to\infty), \end{align} $$
$$ \begin{align} {\mathbb P}\left(\frac{L_{N_r} - 2\sqrt{r}}{r^{1/6}}\leqslant t\right) = F\big(t^{(r)}\big) + F_{1}^P(t)\, r^{-1/3} + O(r^{-1/2})\qquad (r\to\infty), \end{align} $$
where the
![]() $O(r^{-1/2})$
error term is governed by the Gauss bracket in (4.8) and cannot be improved upon – completely dominating the order
$O(r^{-1/2})$
error term is governed by the Gauss bracket in (4.8) and cannot be improved upon – completely dominating the order
![]() $O(r^{-2/3})$
correction term in (4.7). Therefore, claiming an
$O(r^{-2/3})$
correction term in (4.7). Therefore, claiming an
![]() $O(r^{-2/3})$
error term to hold in (4.9) as stated in [Reference Forrester and Mays45, Prop. 1.1] neglects the effect of the Gauss bracket.Footnote
27
$O(r^{-2/3})$
error term to hold in (4.9) as stated in [Reference Forrester and Mays45, Prop. 1.1] neglects the effect of the Gauss bracket.Footnote
27
Part II: Results based on the tameness hypothesis
5. De-Poissonization and the expansion of the length distribution
5.1. Expansion of the CDF
In this section, we prove (subject to a tameness hypothesis on the zeros of the generating functions in a sector of the complex plane) an expansion of the CDF
![]() ${\mathbb P}(L_n \leqslant l)$
of the length distribution near its mode. The general form of such an expansion was conjectured in the recent papers [Reference Bornemann19, Reference Forrester and Mays45] where approximations of the graphical form of the first few terms were provided (see [Reference Bornemann19, Figs. 4/6] and [Reference Forrester and Mays45, Fig. 7]). Here, for the first time, we give the functional form of these terms. The underlying tool is analytic de-Poissonization, a technique that was developed in the 1990s in theoretical computer science and analytic combinatorics.
${\mathbb P}(L_n \leqslant l)$
of the length distribution near its mode. The general form of such an expansion was conjectured in the recent papers [Reference Bornemann19, Reference Forrester and Mays45] where approximations of the graphical form of the first few terms were provided (see [Reference Bornemann19, Figs. 4/6] and [Reference Forrester and Mays45, Fig. 7]). Here, for the first time, we give the functional form of these terms. The underlying tool is analytic de-Poissonization, a technique that was developed in the 1990s in theoretical computer science and analytic combinatorics.
To prepare for the application of analytic de-Poissonization in the form of the Jacquet–Szpankowski Theorem A.2, we consider any fixed compact interval
![]() $[t_0,t_1]$
and a sequence of integers
$[t_0,t_1]$
and a sequence of integers
![]() $l_n \to \infty $
such that
$l_n \to \infty $
such that
When
![]() $n-n^{3/5} \leqslant r \leqslant n+n^{3/5}$
and
$n-n^{3/5} \leqslant r \leqslant n+n^{3/5}$
and
![]() $n\geqslant n_0$
with
$n\geqslant n_0$
with
![]() $n_0$
large enough (depending only on
$n_0$
large enough (depending only on
![]() $t_0, t_1$
), we thus get the uniform boundsFootnote
28
$t_0, t_1$
), we thus get the uniform boundsFootnote
28
We write the induced Poisson generating function, and exponential generating function, of the length distribution as
 $$ \begin{align} P_k(z) := P(z; l_k) = e^{-z} \sum_{n=0}^\infty {\mathbb P}(L_n \leqslant l_k) \frac{z^n}{n!},\qquad f_k(z):= e^z P_k(z). \end{align} $$
$$ \begin{align} P_k(z) := P(z; l_k) = e^{-z} \sum_{n=0}^\infty {\mathbb P}(L_n \leqslant l_k) \frac{z^n}{n!},\qquad f_k(z):= e^z P_k(z). \end{align} $$
By (1.1), we have
![]() $P_n(r) = E_2^{\text {hard}}(4r;l_n)$
for real
$P_n(r) = E_2^{\text {hard}}(4r;l_n)$
for real
![]() $r>0$
, so that Theorem 4.1 (see also (4.6)) gives the expansion
$r>0$
, so that Theorem 4.1 (see also (4.6)) gives the expansion
 $$ \begin{align} P_n(r) = F(t) + \sum_{j=1}^m F_{j}^P(t) \, r^{-j/3} + O(r^{-(m+1)/3})\,\bigg|_{t=t_{l_n}(r)}, \end{align} $$
$$ \begin{align} P_n(r) = F(t) + \sum_{j=1}^m F_{j}^P(t) \, r^{-j/3} + O(r^{-(m+1)/3})\,\bigg|_{t=t_{l_n}(r)}, \end{align} $$
uniformly valid when
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
![]() $n\to \infty $
, m being any fixed non-negative integer. Here, the implied constant in the error term depends only on
$n\to \infty $
, m being any fixed non-negative integer. Here, the implied constant in the error term depends only on
![]() $t_0, t_1$
, but not on the specific sequence
$t_0, t_1$
, but not on the specific sequence
![]() $l_n$
. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r. In particular, using the differential equation (4.1b), we get that
$l_n$
. Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r. In particular, using the differential equation (4.1b), we get that
![]() $P_n^{(j)}(n)$
expands in powers of
$P_n^{(j)}(n)$
expands in powers of
![]() $n^{-1/3}$
, starting with a leading order term of the form
$n^{-1/3}$
, starting with a leading order term of the form
the specific cases to be used below are (see (6.7) for
![]() $P_n^{\prime }(n)$
)
$P_n^{\prime }(n)$
)
 $$ \begin{align} P_n(n) &= F(t) + F_{1}^P(t) n^{-1/3} + F_{2}^P(t) n^{-2/3} + F_{3}^P(t) n^{-1} + O(n^{-4/3})\,\bigg|_{t=t_n^*},\end{align} $$
$$ \begin{align} P_n(n) &= F(t) + F_{1}^P(t) n^{-1/3} + F_{2}^P(t) n^{-2/3} + F_{3}^P(t) n^{-1} + O(n^{-4/3})\,\bigg|_{t=t_n^*},\end{align} $$
 $$ \begin{align} P_n^{\prime\prime}(n) &= F"(t) n^{-4/3} + \left(F_{1}^{P}\!\!\phantom{|}"(t) + \frac{5}{6} F'(t) + \frac{t}{3} F"(t) \right) n^{-5/3} \end{align} $$
$$ \begin{align} P_n^{\prime\prime}(n) &= F"(t) n^{-4/3} + \left(F_{1}^{P}\!\!\phantom{|}"(t) + \frac{5}{6} F'(t) + \frac{t}{3} F"(t) \right) n^{-5/3} \end{align} $$
 $$ \begin{align} &+ \left(\frac{3}{2}F_{1}^{P}\!\!\phantom{|}'(t) + \frac{t}{3} F_{1}^{P}\!\!\phantom{|}"(t) + F_{2}^{P}\!\!\phantom{|}"(t)+ \frac{7 t}{36} F'(t)+\frac{t^2}{36} F"(t) \right) n^{-2}+ O(n^{-7/3})\,\bigg|_{t=t_n^*},\notag\\ P_n^{\prime\prime\prime}(n) &= -F"'(t) n^{-2} + O(n^{-7/3}) \,\bigg|_{t=t_n^*}, \end{align} $$
$$ \begin{align} &+ \left(\frac{3}{2}F_{1}^{P}\!\!\phantom{|}'(t) + \frac{t}{3} F_{1}^{P}\!\!\phantom{|}"(t) + F_{2}^{P}\!\!\phantom{|}"(t)+ \frac{7 t}{36} F'(t)+\frac{t^2}{36} F"(t) \right) n^{-2}+ O(n^{-7/3})\,\bigg|_{t=t_n^*},\notag\\ P_n^{\prime\prime\prime}(n) &= -F"'(t) n^{-2} + O(n^{-7/3}) \,\bigg|_{t=t_n^*}, \end{align} $$
 $$ \begin{align} P_n^{(4)}(n) &= F^{(4)}(t) n^{-8/3} + \left(F_{1}^{P}\!\!\phantom{|}^{(4)}(t)+5 F"'(t)+ \frac{2 t}{3} F^{(4)}(t)\right) n^{-3} + O(n^{-10/3})\,\bigg|_{t=t_n^*}, \end{align} $$
$$ \begin{align} P_n^{(4)}(n) &= F^{(4)}(t) n^{-8/3} + \left(F_{1}^{P}\!\!\phantom{|}^{(4)}(t)+5 F"'(t)+ \frac{2 t}{3} F^{(4)}(t)\right) n^{-3} + O(n^{-10/3})\,\bigg|_{t=t_n^*}, \end{align} $$
 $$ \begin{align} P_n^{(6)}(n) &= F^{(6)}(t) n^{-4} + O(n^{-13/3})\,\bigg|_{t=t_n^*}, \end{align} $$
$$ \begin{align} P_n^{(6)}(n) &= F^{(6)}(t) n^{-4} + O(n^{-13/3})\,\bigg|_{t=t_n^*}, \end{align} $$
where the implied constants in the error terms depend only on
![]() $t_0, t_1$
.
$t_0, t_1$
.
We recall from the results of [Reference Bornemann19, Sect. 2] (note the slight differences in notation), and the proofs given there, that the exponential generating functions
![]() $f_n(z)$
are entire functions of genus zero having, for each
$f_n(z)$
are entire functions of genus zero having, for each
![]() $0<\epsilon <\pi /2$
, only finitely many zerosFootnote
29
in the sector
$0<\epsilon <\pi /2$
, only finitely many zerosFootnote
29
in the sector
![]() $|\!\arg z| \leqslant \pi /2 + \epsilon $
. If we denote the real auxiliary functions (cf. Definition A.1) of
$|\!\arg z| \leqslant \pi /2 + \epsilon $
. If we denote the real auxiliary functions (cf. Definition A.1) of
![]() $f_n(r) = e^r P_n(r)$
by
$f_n(r) = e^r P_n(r)$
by
![]() $a_n(r)$
and
$a_n(r)$
and
![]() $b_n(r)$
, the expansion (5.3), and its derivatives based on (4.1b), give (cf. also (6.8))
$b_n(r)$
, the expansion (5.3), and its derivatives based on (4.1b), give (cf. also (6.8))
uniformly valid when
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
![]() $n\to \infty $
; the implied constants in the error terms depend only on
$n\to \infty $
; the implied constants in the error terms depend only on
![]() $t_0, t_1$
.
$t_0, t_1$
.
Analytically, we lack the tools to study the asymptotic distribution of the finitely many zeros of
![]() $f_n(z)$
in the sector
$f_n(z)$
in the sector
![]() $|\!\arg z| \leqslant \pi /2 + \epsilon $
as
$|\!\arg z| \leqslant \pi /2 + \epsilon $
as
![]() $n\to \infty $
. Numerically, we proceed as follows. The meromorphic logarithmic derivative of
$n\to \infty $
. Numerically, we proceed as follows. The meromorphic logarithmic derivative of
![]() $f_n(z)$
takes the form [Reference Bornemann19, §3.1]
$f_n(z)$
takes the form [Reference Bornemann19, §3.1]
 $$\begin{align*}\frac{f_n^{\prime}(z)}{f_n(z)} = 1 - \frac{v_{l_n}(z)}{z}, \end{align*}$$
$$\begin{align*}\frac{f_n^{\prime}(z)}{f_n(z)} = 1 - \frac{v_{l_n}(z)}{z}, \end{align*}$$
where
![]() $v_l$
satisfies a Jimbo–Miwa–Okamoto
$v_l$
satisfies a Jimbo–Miwa–Okamoto
![]() $\sigma $
-form of the Painlevé III equation [Reference Bornemann19, Eq. (31)], or alternatively, a certain Chazy I equation [Reference Bornemann19, Eq. (34)]. Because of
$\sigma $
-form of the Painlevé III equation [Reference Bornemann19, Eq. (31)], or alternatively, a certain Chazy I equation [Reference Bornemann19, Eq. (34)]. Because of
![]() $f_n(0)=1$
, the zeros of
$f_n(0)=1$
, the zeros of
![]() $f_n$
are in a one-to-one correspondence to the pole field of the meromorphic function
$f_n$
are in a one-to-one correspondence to the pole field of the meromorphic function
![]() $v_{l_n}$
. Fornberg and Weideman [Reference Fornberg and Weideman39] developed a numerical method, the pole field solver, specifically for the task of numerically studying the pole fields of equations of the Painlevé class. They documented results for Painlevé I [Reference Fornberg and Weideman39], Painlevé II [Reference Fornberg and Weideman40], its imaginary variant [Reference Fornberg and Weideman41] and, together with Fasondini, for (multivalued) variants of the Painlevé III, V and VI equations [Reference Fasondini, Fornberg and Weideman34, Reference Fasondini, Fornberg and Weideman35].
$v_{l_n}$
. Fornberg and Weideman [Reference Fornberg and Weideman39] developed a numerical method, the pole field solver, specifically for the task of numerically studying the pole fields of equations of the Painlevé class. They documented results for Painlevé I [Reference Fornberg and Weideman39], Painlevé II [Reference Fornberg and Weideman40], its imaginary variant [Reference Fornberg and Weideman41] and, together with Fasondini, for (multivalued) variants of the Painlevé III, V and VI equations [Reference Fasondini, Fornberg and Weideman34, Reference Fasondini, Fornberg and Weideman35].
Now, extensive numerical experiments with the pole field solver applied to
![]() $v_{l_n}$
(which will be documented in a separate publication) strongly hint at the property that the zeros of the exponential generating functions
$v_{l_n}$
(which will be documented in a separate publication) strongly hint at the property that the zeros of the exponential generating functions
![]() $f_n(z)$
in the sectors
$f_n(z)$
in the sectors
![]() $|\!\arg z| \leqslant \pi /2 + \epsilon $
satisfy a uniform tameness condition as in Definition A.2 (see also Remark A.6): the zeros are neither coming too close to the positive real axis nor are they getting too large. Given this state of affairs, the results on the expansions of the length distribution will be subject to the following:
$|\!\arg z| \leqslant \pi /2 + \epsilon $
satisfy a uniform tameness condition as in Definition A.2 (see also Remark A.6): the zeros are neither coming too close to the positive real axis nor are they getting too large. Given this state of affairs, the results on the expansions of the length distribution will be subject to the following:

Figure 3 Plots of
![]() $F_{1}^D(t)$
(left panel),
$F_{1}^D(t)$
(left panel),
![]() $F_{2}^D(t)$
(middle panel) as in (5.8); both agree with the numerical prediction of their graphical form given in the left panels of [Reference Bornemann19, Figs. 4/6]. The right panel shows
$F_{2}^D(t)$
(middle panel) as in (5.8); both agree with the numerical prediction of their graphical form given in the left panels of [Reference Bornemann19, Figs. 4/6]. The right panel shows
![]() $F_3^D(t)$
as in (5.8) (black solid line) with the approximations (5.7) for
$F_3^D(t)$
as in (5.8) (black solid line) with the approximations (5.7) for
![]() $n=250$
(red
$n=250$
(red
![]() $+$
),
$+$
),
![]() $n=500$
(green
$n=500$
(green
![]() $\circ $
) and
$\circ $
) and
![]() $n=1000$
(blue
$n=1000$
(blue
![]() $\bullet $
); the integer l has been varied such that
$\bullet $
); the integer l has been varied such that
![]() $t_l(n)$
spreads over the range of t displayed here. Evaluation of (5.7) uses the table of exact values of
$t_l(n)$
spreads over the range of t displayed here. Evaluation of (5.7) uses the table of exact values of
![]() ${\mathbb P}(L_n\leqslant l)$
up to
${\mathbb P}(L_n\leqslant l)$
up to
![]() $n=1000$
that was compiled in [Reference Bornemann19].
$n=1000$
that was compiled in [Reference Bornemann19].
Tameness hypothesis. For any real
![]() $t_0<t_1$
and sequence of integers
$t_0<t_1$
and sequence of integers
![]() $l_n\to \infty $
satisfying (5.1), the zeros of the induced family
$l_n\to \infty $
satisfying (5.1), the zeros of the induced family
![]() $f_n(z)$
of exponential generating functions (5.2) are uniformly tame (see Definition A.2), with parameters and implied constants only depending on
$f_n(z)$
of exponential generating functions (5.2) are uniformly tame (see Definition A.2), with parameters and implied constants only depending on
![]() $t_0$
and
$t_0$
and
![]() $t_1$
.
$t_1$
.
Theorem 5.1. Let
![]() $t_0<t_1$
be any real numbers and assume the tameness hypothesis. Then there holds the expansion
$t_0<t_1$
be any real numbers and assume the tameness hypothesis. Then there holds the expansion
 $$ \begin{align} {\mathbb P}(L_n \leqslant l) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_l(n)}, \end{align} $$
$$ \begin{align} {\mathbb P}(L_n \leqslant l) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_l(n)}, \end{align} $$
which is uniformly valid when
![]() $n,l \to \infty $
subject to
$n,l \to \infty $
subject to
![]() $t_0 \leqslant t_l(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
$t_0 \leqslant t_l(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
![]() $F_{j}^D$
are certain smooth functions; the first three areFootnote
30
$F_{j}^D$
are certain smooth functions; the first three areFootnote
30
 $$ \begin{align}F_3^D(t) &= -\Big(\frac{562 t }{7875} +\frac{41t^4}{283500}\Big) F'(t) +\Big(\frac{t^2}{300}-\frac{t^5}{47250}\Big) F"(t)\\&\qquad+\Big(\frac{5137}{15750}+\frac{9 t^3}{7000}-\frac{t^6}{1296000}\Big) F"'(t) +\Big(\frac{129 t}{1750}-\frac{t^4}{12000}\Big) F^{(4)}(t)\notag\\ &\qquad-\frac{3 t^2}{1000}F^{(5)}(t) -\frac{9}{250}F^{(6)}(t).\notag \end{align} $$
$$ \begin{align}F_3^D(t) &= -\Big(\frac{562 t }{7875} +\frac{41t^4}{283500}\Big) F'(t) +\Big(\frac{t^2}{300}-\frac{t^5}{47250}\Big) F"(t)\\&\qquad+\Big(\frac{5137}{15750}+\frac{9 t^3}{7000}-\frac{t^6}{1296000}\Big) F"'(t) +\Big(\frac{129 t}{1750}-\frac{t^4}{12000}\Big) F^{(4)}(t)\notag\\ &\qquad-\frac{3 t^2}{1000}F^{(5)}(t) -\frac{9}{250}F^{(6)}(t).\notag \end{align} $$
Proof. Following up the preparations preceding the formulation of the theorem, the tameness hypothesis allows us to apply Corollary A.7, bounding
![]() $f_n(z)=e^z P_n(z)$
by
$f_n(z)=e^z P_n(z)$
by
 $$ \begin{align} \big| f_n(re^{i\theta}) \big| \leqslant \begin{cases} 2f_n(r) e^{-\frac{1}{2}\theta^2 r}, &\qquad 0\leqslant |\theta| \leqslant r^{-2/5},\\ 2f_n(r) e^{-\frac{1}{2}r^{1/5}}, &\qquad r^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
$$ \begin{align} \big| f_n(re^{i\theta}) \big| \leqslant \begin{cases} 2f_n(r) e^{-\frac{1}{2}\theta^2 r}, &\qquad 0\leqslant |\theta| \leqslant r^{-2/5},\\ 2f_n(r) e^{-\frac{1}{2}r^{1/5}}, &\qquad r^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
for
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
![]() $n\geqslant n_0$
when
$n\geqslant n_0$
when
![]() $n_0$
is sufficiently large (depending on
$n_0$
is sufficiently large (depending on
![]() $t_0$
,
$t_0$
,
![]() $t_1$
). Using the trivial bounds (for
$t_1$
). Using the trivial bounds (for
![]() $r>0$
and
$r>0$
and
![]() $|\theta |\leqslant \pi $
)
$|\theta |\leqslant \pi $
)
the first case in (5.9) can be recast in form of the bound
which proves condition (I) of Theorem A.2 with
![]() $B=2$
,
$B=2$
,
![]() $D=1$
,
$D=1$
,
![]() $\beta =0$
and
$\beta =0$
and
![]() $\delta =2/5$
, whereas the second case implies
$\delta =2/5$
, whereas the second case implies
which proves condition (O) of Theorem A.2 with
![]() $A=1/2$
,
$A=1/2$
,
![]() $C=0$
,
$C=0$
,
![]() $\alpha =1/5$
and
$\alpha =1/5$
and
![]() $\gamma =0$
. Hence, there holds the Jasz expansion (A.7) – namely,
$\gamma =0$
. Hence, there holds the Jasz expansion (A.7) – namely,
 $$\begin{align*}{\mathbb P}(L_n \leqslant l_n) = P_n(n) + \sum_{j=2}^M b_j(n) P_n^{(j)}(n) + O(n^{-(M+1)/5}) \end{align*}$$
$$\begin{align*}{\mathbb P}(L_n \leqslant l_n) = P_n(n) + \sum_{j=2}^M b_j(n) P_n^{(j)}(n) + O(n^{-(M+1)/5}) \end{align*}$$
for any
![]() $M=0,1,2,\ldots $
as
$M=0,1,2,\ldots $
as
![]() $n\geqslant n_1$
; here,
$n\geqslant n_1$
; here,
![]() $n_1$
and the implied constant depend on
$n_1$
and the implied constant depend on
![]() $t_0$
,
$t_0$
,
![]() $t_1$
. By noting that the diagonal Poisson–Charlier polynomials
$t_1$
. By noting that the diagonal Poisson–Charlier polynomials
![]() $b_j$
have degree
$b_j$
have degree
![]() $\leqslant \lfloor j/2\rfloor $
and by choosing M large enough, the expansions (5.4) of
$\leqslant \lfloor j/2\rfloor $
and by choosing M large enough, the expansions (5.4) of
![]() $P_n^{(j)}(n)$
in terms of powers of
$P_n^{(j)}(n)$
in terms of powers of
![]() $n^{-1/3}$
yield that there are smooth functions
$n^{-1/3}$
yield that there are smooth functions
![]() $F_{j}^D$
such that
$F_{j}^D$
such that
 $$\begin{align*}{\mathbb P}(L_n \leqslant l_n) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_n^*} \end{align*}$$
$$\begin{align*}{\mathbb P}(L_n \leqslant l_n) = F(t) + \sum_{j=1}^m F_{j}^D(t)\, n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_n^*} \end{align*}$$
as
![]() $n\to \infty $
, with m being any fixed non-negative integer. Given the uniformity of the bound for fixed
$n\to \infty $
, with m being any fixed non-negative integer. Given the uniformity of the bound for fixed
![]() $t_0$
and
$t_0$
and
![]() $t_1$
, we can replace
$t_1$
, we can replace
![]() $l_n$
by l and
$l_n$
by l and
![]() $t_n^*$
by
$t_n^*$
by
![]() $t_l(n)$
as long as we respect
$t_l(n)$
as long as we respect
![]() $t_0 \leqslant t_l(n) \leqslant t_1$
. This finishes the proof of (5.6).
$t_0 \leqslant t_l(n) \leqslant t_1$
. This finishes the proof of (5.6).
The first three functions
![]() $F_{1}^D$
,
$F_{1}^D$
,
![]() $F_{2}^D(t)$
,
$F_{2}^D(t)$
,
![]() $F_{3}^D(t)$
can be determined using the particular case (A.8) of the Jasz expansion from Example A.3 (which applies here because of (5.4a)) – namely,
$F_{3}^D(t)$
can be determined using the particular case (A.8) of the Jasz expansion from Example A.3 (which applies here because of (5.4a)) – namely,
Inserting the formulae displayed in (5.4), we thus obtain
Together with the expressions given in (4.4), this yields the functional form asserted in (5.8).
5.2. Expansion of the PDF
Subject to its assumptions, Theorem 5.1 implies for the PDF of the length distribution that
 $$ \begin{align*} {\mathbb P}(L_n=l) &= {\mathbb P}(L_n \leqslant l) - {\mathbb P}(L_n \leqslant l-1) \\ &\qquad = \big(F(t_l(n)) - F(t_{l-1}(n))\big) + \sum_{j=1}^m \big(F_{j}^D(t_l(n))-F_{j}^D(t_{l-1}(n))\big)\, n^{-j/3} + O(n^{-(m+1)/3}). \end{align*} $$
$$ \begin{align*} {\mathbb P}(L_n=l) &= {\mathbb P}(L_n \leqslant l) - {\mathbb P}(L_n \leqslant l-1) \\ &\qquad = \big(F(t_l(n)) - F(t_{l-1}(n))\big) + \sum_{j=1}^m \big(F_{j}^D(t_l(n))-F_{j}^D(t_{l-1}(n))\big)\, n^{-j/3} + O(n^{-(m+1)/3}). \end{align*} $$
Applying the central differencing formula (which is, basically, just a Taylor expansion for smooth G centered at the midpoint)
with increment
![]() $h=n^{-1/6}$
, we immediately get the following corollary of Theorem 5.1.
$h=n^{-1/6}$
, we immediately get the following corollary of Theorem 5.1.
Corollary 5.2. Let
![]() $t_0<t_1$
be any real numbers, and assume the tameness hypothesis. Then there holds the expansion
$t_0<t_1$
be any real numbers, and assume the tameness hypothesis. Then there holds the expansion
 $$ \begin{align} n^{1/6}\, {\mathbb P}(L_n=l) = F' (t) + \sum_{j=1}^m F_{j}^*(t) n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_{l-1/2}(n)}, \end{align} $$
$$ \begin{align} n^{1/6}\, {\mathbb P}(L_n=l) = F' (t) + \sum_{j=1}^m F_{j}^*(t) n^{-j/3} + O(n^{-(m+1)/3})\,\bigg|_{t=t_{l-1/2}(n)}, \end{align} $$
which is uniformly valid when
![]() $n,l \to \infty $
subject to the constraint
$n,l \to \infty $
subject to the constraint
![]() $t_0 \leqslant t_{l-1/2}(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
$t_0 \leqslant t_{l-1/2}(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
![]() $F_{j}^*$
are certain smooth functions; in particular,Footnote
31
$F_{j}^*$
are certain smooth functions; in particular,Footnote
31
 $$ \begin{align}F_3^*(t) &= -\Big(\frac{373}{5250} + \frac{41 t^3}{70875} \Big) F'(t) -\Big(\frac{1781 t}{28000} + \frac{71 t^4 }{283500}\Big) F"(t)\\&\qquad+\Big(\frac{63 t^2}{8000}-\frac{13 t^5}{504000}\Big) F"'(t) +\Big(\frac{41473 }{112000}+\frac{13 t^3}{12096} -\frac{t^6}{1296000} \Big) F^{(4)}(t)\notag\\ &\qquad+\Big(\frac{131057 t}{2016000} - \frac{67 t^4}{864000}\Big) F^{(5)}(t) -\frac{1493 t^2}{576000} F^{(6)}(t) -\frac{232319}{8064000}F^{(7)}(t).\notag \end{align} $$
$$ \begin{align}F_3^*(t) &= -\Big(\frac{373}{5250} + \frac{41 t^3}{70875} \Big) F'(t) -\Big(\frac{1781 t}{28000} + \frac{71 t^4 }{283500}\Big) F"(t)\\&\qquad+\Big(\frac{63 t^2}{8000}-\frac{13 t^5}{504000}\Big) F"'(t) +\Big(\frac{41473 }{112000}+\frac{13 t^3}{12096} -\frac{t^6}{1296000} \Big) F^{(4)}(t)\notag\\ &\qquad+\Big(\frac{131057 t}{2016000} - \frac{67 t^4}{864000}\Big) F^{(5)}(t) -\frac{1493 t^2}{576000} F^{(6)}(t) -\frac{232319}{8064000}F^{(7)}(t).\notag \end{align} $$
Remark 5.3. The case
![]() $m=0$
of Corollary 5.2 gives
$m=0$
of Corollary 5.2 gives
where the exponent in the error term cannot be improved. By noting
we understand that, for fixed large n, visualizing the discrete length distribution near its mode by plotting the points
next to the graph
![]() $(t,F'(t))$
introduces a perceivable bias; namely, all points are shifted by an amount of
$(t,F'(t))$
introduces a perceivable bias; namely, all points are shifted by an amount of
![]() $n^{-1/6}/2$
to the right of the graph. Exactly such a bias can be observed in the first ever published plot of the PDF vs. the density of the Tracy–Widom distribution by Odlyzko and Rains in [Reference Odlyzko and Rains62, Fig. 1]: the Monte-Carlo data for
$n^{-1/6}/2$
to the right of the graph. Exactly such a bias can be observed in the first ever published plot of the PDF vs. the density of the Tracy–Widom distribution by Odlyzko and Rains in [Reference Odlyzko and Rains62, Fig. 1]: the Monte-Carlo data for
![]() $n=10^6$
display a consistent shift by
$n=10^6$
display a consistent shift by
![]() $0.05$
.
$0.05$
.
A bias free plot is shown in Figure 5, which, in addition, displays an improvement of the error of the limit law by a factor of
![]() $O(n^{-2/3})$
that is obtained by adding the first two finite-size correction terms.
$O(n^{-2/3})$
that is obtained by adding the first two finite-size correction terms.

Figure 4 Plots of
![]() $F_{1}^*(t)$
(left panel) and
$F_{1}^*(t)$
(left panel) and
![]() $F_{2}^*(t)$
(middle panel) as in (5.13a/b); both agree with the numerical prediction of their graphical form given in the right panels of [Reference Bornemann19, Figs. 4/6]. The right panel shows
$F_{2}^*(t)$
(middle panel) as in (5.13a/b); both agree with the numerical prediction of their graphical form given in the right panels of [Reference Bornemann19, Figs. 4/6]. The right panel shows
![]() $F_3^*$
as in (5.13c) (black solid line) with the approximations (5.12) for
$F_3^*$
as in (5.13c) (black solid line) with the approximations (5.12) for
![]() $n=250$
(red
$n=250$
(red
![]() $+$
),
$+$
),
![]() $n=500$
(green
$n=500$
(green
![]() $\circ $
) and
$\circ $
) and
![]() $n=1000$
(blue
$n=1000$
(blue
![]() $\bullet $
); the integer l has been varied such that
$\bullet $
); the integer l has been varied such that
![]() $t_{l-1/2}(n)$
spreads over the range of t displayed here. Evaluation of (5.12) uses the table of exact values of
$t_{l-1/2}(n)$
spreads over the range of t displayed here. Evaluation of (5.12) uses the table of exact values of
![]() ${\mathbb P}(L_n= l)$
up to
${\mathbb P}(L_n= l)$
up to
![]() $n=1000$
that was compiled in [Reference Bornemann19].
$n=1000$
that was compiled in [Reference Bornemann19].

Figure 5 The exact discrete length distribution
![]() ${\mathbb P}(L_{n}=l)$
(blue bars centered at the integers l) vs. the asymptotic expansion (5.11) for
${\mathbb P}(L_{n}=l)$
(blue bars centered at the integers l) vs. the asymptotic expansion (5.11) for
![]() $m=0$
(the Baik–Deift–Johansson limit, dotted line) and for
$m=0$
(the Baik–Deift–Johansson limit, dotted line) and for
![]() $m=2$
(the limit with the first two finite-size correction terms added, solid line). Left:
$m=2$
(the limit with the first two finite-size correction terms added, solid line). Left:
![]() $n=100$
; right:
$n=100$
; right:
![]() $n=1000$
. The expansions are displayed as functions of the continuous variable
$n=1000$
. The expansions are displayed as functions of the continuous variable
![]() $\nu $
, evaluating the right-hand side of (5.11) in
$\nu $
, evaluating the right-hand side of (5.11) in
![]() $t=t_{\nu -1/2}(n)$
. The exact values are from the table compiled in [Reference Bornemann19]. Note that a graphically accurate continuous approximation of the discrete distribution must intersect the bars right in the middle of their top sides: this is, indeed, the case for
$t=t_{\nu -1/2}(n)$
. The exact values are from the table compiled in [Reference Bornemann19]. Note that a graphically accurate continuous approximation of the discrete distribution must intersect the bars right in the middle of their top sides: this is, indeed, the case for
![]() $m=2$
(except at the left tail for
$m=2$
(except at the left tail for
![]() $n=100$
). In contrast, the uncorrected limit law (
$n=100$
). In contrast, the uncorrected limit law (
![]() $m=0$
) is noticeable inaccurate for this range of n.
$m=0$
) is noticeable inaccurate for this range of n.
6. Expansions of Stirling-type formulae
In our work [Reference Bornemann19], we advocated the use of a Stirling-type formula to approximate the length distribution for larger n (because of being much more efficient and accurate than Monte-Carlo simulations). To recall some of our findings there, let us denote the exponential generating function and its Poisson counterpart simply by
 $$\begin{align*}f(z) = \sum_{n=0}^\infty {\mathbb P}(L_n\leqslant l) \frac{z^n}{n!},\qquad P(z) = e^{-z} f(z), \end{align*}$$
$$\begin{align*}f(z) = \sum_{n=0}^\infty {\mathbb P}(L_n\leqslant l) \frac{z^n}{n!},\qquad P(z) = e^{-z} f(z), \end{align*}$$
suppressing the dependence on the integer parameter l from the notation for the sake of brevity. It was shown in [Reference Bornemann19, Thm. 2.2] that the entire function f is H-admissible so that there is the normal approximation (see Definition A.1 and Theorem A.4)
 $$ \begin{align} {\mathbb P}(L_n\leqslant l) = \frac{n! f(r)}{r^n \sqrt{2\pi b(r)}} \left(\exp\left(-\frac{(n-a(r))^2}{2b(r)}\right)+ o(1)\right) \qquad (r\to \infty) \end{align} $$
$$ \begin{align} {\mathbb P}(L_n\leqslant l) = \frac{n! f(r)}{r^n \sqrt{2\pi b(r)}} \left(\exp\left(-\frac{(n-a(r))^2}{2b(r)}\right)+ o(1)\right) \qquad (r\to \infty) \end{align} $$
uniformly in
![]() $n=0,1,2,\ldots $
while l is any fixed integer. Here,
$n=0,1,2,\ldots $
while l is any fixed integer. Here,
![]() $a(r)$
and
$a(r)$
and
![]() $b(r)$
are the real auxiliary functions
$b(r)$
are the real auxiliary functions
We consider the two cases
![]() $r=r_n$
,
$r=r_n$
,
![]() $a(r_n)=n$
and
$a(r_n)=n$
and
![]() $r=n$
. After dividing (6.1) by the classical Stirling factor (which does not change anything of substance; see Remark 6.2)
$r=n$
. After dividing (6.1) by the classical Stirling factor (which does not change anything of substance; see Remark 6.2)
 $$ \begin{align} \tau_n := \frac{n!}{\sqrt{2\pi n}} \left(\frac{e}{n}\right)^n \sim 1+\frac{n^{-1}}{12} + \frac{n^{-2}}{288} + \cdots, \end{align} $$
$$ \begin{align} \tau_n := \frac{n!}{\sqrt{2\pi n}} \left(\frac{e}{n}\right)^n \sim 1+\frac{n^{-1}}{12} + \frac{n^{-2}}{288} + \cdots, \end{align} $$
we get after some rearranging of terms the Stirling-type formula
![]() $S_{n,l}$
(
$S_{n,l}$
(
![]() $r=r_n$
) and the simplified Stirling-type formula
$r=r_n$
) and the simplified Stirling-type formula
![]() $\tilde S_{n,l}$
(
$\tilde S_{n,l}$
(
![]() $r=n$
):
$r=n$
):
 $$ \begin{align} S_{n,l} &:= \frac{P(r_n)}{\sqrt{b(r_n)/n}} \exp\left(n\,\Lambda\left(\frac{r_n-n}n\right)\right),\quad \Lambda(h) = h - \log(1+h), \end{align} $$
$$ \begin{align} S_{n,l} &:= \frac{P(r_n)}{\sqrt{b(r_n)/n}} \exp\left(n\,\Lambda\left(\frac{r_n-n}n\right)\right),\quad \Lambda(h) = h - \log(1+h), \end{align} $$
 $$ \begin{align} \tilde S_{n,l} &:= \frac{P(n)}{\sqrt{b(n)/n}} \exp\left(-\frac{(n-a(n))^2}{2b(n)}\right). \end{align} $$
$$ \begin{align} \tilde S_{n,l} &:= \frac{P(n)}{\sqrt{b(n)/n}} \exp\left(-\frac{(n-a(n))^2}{2b(n)}\right). \end{align} $$
As shown in [Reference Bornemann19], both approximations are amenable for a straightforward numerical evaluation using the tools developed in [Reference Bornemann14, Reference Bornemann15, Reference Bornemann, Forrester and Mays20]. For fixed l, the normal approximation (6.1) implies
but numerical experiments reported in [Reference Bornemann19, Fig. 3, Eq. (8b)] suggest that there holds
uniformly when
![]() $n,l\to \infty $
while
$n,l\to \infty $
while
![]() $t_l(n)$
stays bounded. Subject to the tameness hypothesis of Theorem 5.1, we prove this observation as well as its counterpart for the simplified Stirling-type formula, thereby unveiling the functional form of the error term
$t_l(n)$
stays bounded. Subject to the tameness hypothesis of Theorem 5.1, we prove this observation as well as its counterpart for the simplified Stirling-type formula, thereby unveiling the functional form of the error term
![]() $O(n^{-2/3})$
:Footnote
32
$O(n^{-2/3})$
:Footnote
32
Theorem 6.1. Let
![]() $t_0<t_1$
be any real numbers, and assume the tameness hypothesis. Then, for the Stirling-type formula
$t_0<t_1$
be any real numbers, and assume the tameness hypothesis. Then, for the Stirling-type formula
![]() $S_{n,l}$
and its simplification
$S_{n,l}$
and its simplification
![]() $\tilde S_{n,l}$
, there hold the expansions (note that both are starting at
$\tilde S_{n,l}$
, there hold the expansions (note that both are starting at
![]() $j=2$
)
$j=2$
)
 $$ \begin{align} {\mathbb P}(L_n \leqslant l) &= S_{n,l} + \sum_{j=2}^m F_{j}^S\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align} $$
$$ \begin{align} {\mathbb P}(L_n \leqslant l) &= S_{n,l} + \sum_{j=2}^m F_{j}^S\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align} $$
 $$ \begin{align} {\mathbb P}(L_n \leqslant l) &= \tilde S_{n,l} + \sum_{j=2}^m \tilde F_{j}^S\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align} $$
$$ \begin{align} {\mathbb P}(L_n \leqslant l) &= \tilde S_{n,l} + \sum_{j=2}^m \tilde F_{j}^S\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align} $$
which are uniformly valid when
![]() $n,l \to \infty $
subject to
$n,l \to \infty $
subject to
![]() $t_0 \leqslant t_l(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
$t_0 \leqslant t_l(n) \leqslant t_1$
with m being any fixed non-negative integer. Here, the
![]() $F_{j}^S$
and
$F_{j}^S$
and
![]() $\tilde F_{j}^S$
are certain smooth functions – the first beingFootnote
33
$\tilde F_{j}^S$
are certain smooth functions – the first beingFootnote
33
 $$ \begin{align} F_{2}^S(t) &= -\frac{3}{4}\frac{F'(t)^4}{F(t)^3} + \frac{3}{2}\frac{F'(t)^2F"(t)}{F(t)^2}- \frac{3}{8}\frac{F"(t)^2}{F(t)} - \frac{1}{2}\frac{F'(t) F"'(t)}{F(t)} + \frac{1}{8} F^{(4)}_2(t) , \end{align} $$
$$ \begin{align} F_{2}^S(t) &= -\frac{3}{4}\frac{F'(t)^4}{F(t)^3} + \frac{3}{2}\frac{F'(t)^2F"(t)}{F(t)^2}- \frac{3}{8}\frac{F"(t)^2}{F(t)} - \frac{1}{2}\frac{F'(t) F"'(t)}{F(t)} + \frac{1}{8} F^{(4)}_2(t) , \end{align} $$
 $$ \begin{align} \tilde F_{2}^S(t) &= -\frac{1}{2}F'(t) + \frac{1}{4}\frac{F'(t)^4}{F(t)^3}- \frac{3}{8}\frac{F"(t)^2}{F(t)} + \frac{1}{8} F^{(4)}_2(t). \end{align} $$
$$ \begin{align} \tilde F_{2}^S(t) &= -\frac{1}{2}F'(t) + \frac{1}{4}\frac{F'(t)^4}{F(t)^3}- \frac{3}{8}\frac{F"(t)^2}{F(t)} + \frac{1}{8} F^{(4)}_2(t). \end{align} $$
The solution
![]() $r_n$
of the equation
$r_n$
of the equation
![]() $a(r_n)=n$
, required to evaluate
$a(r_n)=n$
, required to evaluate
![]() $S_{n,l}$
, satisfies the expansionFootnote
34
$S_{n,l}$
, satisfies the expansionFootnote
34
 $$\begin{align*}r_n = n + \frac{F'\big(t_l(n) \big)}{F \big(t_l(n) \big)} n^{1/3} + O(1), \end{align*}$$
$$\begin{align*}r_n = n + \frac{F'\big(t_l(n) \big)}{F \big(t_l(n) \big)} n^{1/3} + O(1), \end{align*}$$
which is uniformly valid under the same conditions.
Proof. We restrict ourselves to the case
![]() $m=2$
, focusing on the concrete functional form of the expansion terms; nevertheless, the general form of the expansions (6.4) should become clear along the way.
$m=2$
, focusing on the concrete functional form of the expansion terms; nevertheless, the general form of the expansions (6.4) should become clear along the way.
Preparatory steps. Because of
![]() $P(r) = E_2^{\text {hard}}(4r;l)$
(using the notation preceding Theorem 6.1), Theorem 4.1 gives that
$P(r) = E_2^{\text {hard}}(4r;l)$
(using the notation preceding Theorem 6.1), Theorem 4.1 gives that
which is uniformly valid when
![]() $r,l \to \infty $
subject to the constraint
$r,l \to \infty $
subject to the constraint
![]() $t_0 \leqslant t_l(r) \leqslant t_1$
(the same constraint applies to the expansions to follow). Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r, which yields by using the differential equation (4.1b) satisfied by
$t_0 \leqslant t_l(r) \leqslant t_1$
(the same constraint applies to the expansions to follow). Preserving uniformity, the expansion can be repeatedly differentiated w.r.t. the variable r, which yields by using the differential equation (4.1b) satisfied by
![]() $t_l(r)$
(cf. also (5.4a))
$t_l(r)$
(cf. also (5.4a))
Recalling
![]() $f(r) = e^r P(r)$
, we thus get
$f(r) = e^r P(r)$
, we thus get
with the coefficient functions
 $$ \begin{align} a_1(t) = -\frac{F'(t)}{F(t)},\qquad a_2(t) = -\frac{1}{F(t)}\Big(F_{1}^P\!\!\phantom{|}'(t) + \frac{t}{6} F'(t) \Big) + \frac{F_{1}^P(t)F'(t)}{F(t)^2}; \end{align} $$
$$ \begin{align} a_1(t) = -\frac{F'(t)}{F(t)},\qquad a_2(t) = -\frac{1}{F(t)}\Big(F_{1}^P\!\!\phantom{|}'(t) + \frac{t}{6} F'(t) \Big) + \frac{F_{1}^P(t)F'(t)}{F(t)^2}; \end{align} $$
a further differentiation yields
 $$ \begin{align} b(r) = r a'(r) = {\left. r- a_1'(t) r^{2/3} + \Big(\frac{1}{3} a_1(t) - \frac{t}{6}a_1^{\prime}(t) - a_2^{\prime}(t) \Big) r^{1/3} + O(1)\, \right|}_{t=t_l(r)}. \end{align} $$
$$ \begin{align} b(r) = r a'(r) = {\left. r- a_1'(t) r^{2/3} + \Big(\frac{1}{3} a_1(t) - \frac{t}{6}a_1^{\prime}(t) - a_2^{\prime}(t) \Big) r^{1/3} + O(1)\, \right|}_{t=t_l(r)}. \end{align} $$
The simplified Stirling-type formula. Here, we have
![]() $r=n$
, and we write
$r=n$
, and we write
![]() $t_* := t_l(n)$
to be brief. By inserting the expansions (6.6) and (6.8) into the expression (6.3b), we obtain after a routine calculation with truncated power series and collecting terms as in (5.10) that
$t_* := t_l(n)$
to be brief. By inserting the expansions (6.6) and (6.8) into the expression (6.3b), we obtain after a routine calculation with truncated power series and collecting terms as in (5.10) that
where the remaining
![]() $\tilde F_{2}^S(t)$
is given by (6.5b); a subtraction from (5.6) yields (6.4b).
$\tilde F_{2}^S(t)$
is given by (6.5b); a subtraction from (5.6) yields (6.4b).
The Stirling-type formula. Here, we have
![]() $r=r_n$
, and we have to distinguish between
$r=r_n$
, and we have to distinguish between
![]() $t_*$
and
$t_*$
and
By inserting the expansion
into
![]() $t_n(r_n)$
and
$t_n(r_n)$
and
![]() $a(r_n)$
, we obtain
$a(r_n)$
, we obtain
Thus, the solution of
![]() $a(r_n) = n$
, which by Theorem A.4 is unique, leads to the relations
$a(r_n) = n$
, which by Theorem A.4 is unique, leads to the relations
By inserting, first, the expansions (6.10) into the expansions (6.6) and (6.8) for the particular choice
![]() $r=r_n$
and, next, the thus obtained results into the expression (6.3a), we obtain after a routine calculation with truncated power series and collecting terms as in (5.10) that
$r=r_n$
and, next, the thus obtained results into the expression (6.3a), we obtain after a routine calculation with truncated power series and collecting terms as in (5.10) that
where the remaining
![]() $F_{2}^S(t)$
is given by (6.5a); a subtraction from (5.6) yields (6.4a).
$F_{2}^S(t)$
is given by (6.5a); a subtraction from (5.6) yields (6.4a).
To validate the expansions (6.4) and the formulae (6.5a/b), Figure 6 plots the approximations

Figure 6 Left panel: plots of
![]() $\tilde F_{2}^S(t)$
(solid line) and
$\tilde F_{2}^S(t)$
(solid line) and
![]() $\tilde F_{2}^S(t)$
(dash-dotted line) as in (6.5). The middle and right panel show the approximations of
$\tilde F_{2}^S(t)$
(dash-dotted line) as in (6.5). The middle and right panel show the approximations of
![]() $F_{3}^S(t)$
and
$F_{3}^S(t)$
and
![]() $\tilde F_{3}^S(t)$
in (6.12) for
$\tilde F_{3}^S(t)$
in (6.12) for
![]() $n=250$
(red
$n=250$
(red
![]() $+$
),
$+$
),
![]() $n=500$
(green
$n=500$
(green
![]() $\circ $
) and
$\circ $
) and
![]() $n=1000$
(blue
$n=1000$
(blue
![]() $\bullet $
); the integer l has been varied such that
$\bullet $
); the integer l has been varied such that
![]() $t_l(n)$
spreads over the range of the variable t displayed here; the dotted line displays a polynomial fit to the data points of degree
$t_l(n)$
spreads over the range of the variable t displayed here; the dotted line displays a polynomial fit to the data points of degree
![]() $30$
to help visualizing their joint graphical form. Evaluation of (6.12) uses the table of exact values of
$30$
to help visualizing their joint graphical form. Evaluation of (6.12) uses the table of exact values of
![]() ${\mathbb P}(L_n\leqslant l)$
up to
${\mathbb P}(L_n\leqslant l)$
up to
![]() $n=1000$
that was compiled in [Reference Bornemann19].
$n=1000$
that was compiled in [Reference Bornemann19].
for
![]() $n=250$
,
$n=250$
,
![]() $n=500$
and
$n=500$
and
![]() $n=1000$
, varying the integer l in such a way that
$n=1000$
, varying the integer l in such a way that
![]() $t=t_l(n)$
spreads over
$t=t_l(n)$
spreads over
![]() $[-6,3]$
. The plot suggests the following observations:
$[-6,3]$
. The plot suggests the following observations:
-
• Apparently there holds
 $\tilde F_{2}^S(t) < F_{2}^S(t) < 0$
for
$\tilde F_{2}^S(t) < F_{2}^S(t) < 0$
for
 $t\in [-6,3]$
, which if generally true would imply for n being sufficiently large and l near the mode of the distribution. This one-sided approximation of the length distribution by the Stirling formula
$t\in [-6,3]$
, which if generally true would imply for n being sufficiently large and l near the mode of the distribution. This one-sided approximation of the length distribution by the Stirling formula $$\begin{align*}{\mathbb P}(L_n \leqslant l) < S_{n,l} < \tilde S_{n,l} \end{align*}$$
$$\begin{align*}{\mathbb P}(L_n \leqslant l) < S_{n,l} < \tilde S_{n,l} \end{align*}$$
 $S_{n,l}$
from above is also clearly visible in [Reference Bornemann19, Tables 1/2].
$S_{n,l}$
from above is also clearly visible in [Reference Bornemann19, Tables 1/2].
-
• Comparing
 $F_{2}^S(t)$
in Figure 6 to
$F_{2}^S(t)$
in Figure 6 to
 $F_{2}^D(t)$
in Figure 3 shows that the maximum error of approximating the length distribution by the first finite-size correction in Theorem 5.1 is about an order of magnitude larger than the maximum error of the Stirling-type formula,
$F_{2}^D(t)$
in Figure 3 shows that the maximum error of approximating the length distribution by the first finite-size correction in Theorem 5.1 is about an order of magnitude larger than the maximum error of the Stirling-type formula, $$\begin{align*}\qquad\quad \max_{l=1,\ldots,n} \left| {\mathbb P}(L_n \leqslant l) - \big(F(t) + F_{1}^D(t) n^{-1/3}\big)\big|_{t=t_l(n)}\right| \approx n^{-2/3} \|F_{2}^D\|_\infty \approx 0.25n^{-2/3} \end{align*}$$
This property of the Stirling-type formula was already observed in [Reference Bornemann19, Fig. 3] and was used there to approximate the graphical form of
$$\begin{align*}\qquad\quad \max_{l=1,\ldots,n} \left| {\mathbb P}(L_n \leqslant l) - \big(F(t) + F_{1}^D(t) n^{-1/3}\big)\big|_{t=t_l(n)}\right| \approx n^{-2/3} \|F_{2}^D\|_\infty \approx 0.25n^{-2/3} \end{align*}$$
This property of the Stirling-type formula was already observed in [Reference Bornemann19, Fig. 3] and was used there to approximate the graphical form of $$\begin{align*}\max_{l=1,\ldots,n} \left| {\mathbb P}(L_n \leqslant l) - S_{n,l}\right| \approx n^{-2/3} \|F_{2}^S\|_\infty \approx 0.031n^{-2/3}. \end{align*}$$
$$\begin{align*}\max_{l=1,\ldots,n} \left| {\mathbb P}(L_n \leqslant l) - S_{n,l}\right| \approx n^{-2/3} \|F_{2}^S\|_\infty \approx 0.031n^{-2/3}. \end{align*}$$
 $F_{2}^D(t)$
(see [Reference Bornemann19, Fig. 6]).
$F_{2}^D(t)$
(see [Reference Bornemann19, Fig. 6]).
Remark 6.2. If one includes the classical Stirling factor (6.2) into the Stirling-type formula by replacing (6.3a) with the unmodified normal approximation (6.1), that is, with
 $$\begin{align*}S_{n,l}^* := \tau_n\frac{P(r_n)}{\sqrt{b(r_n)/n}} \exp\left(n\,\Lambda\left(\frac{r_n-n}n\right)\right) = \tau_n S_{n,l}, \end{align*}$$
$$\begin{align*}S_{n,l}^* := \tau_n\frac{P(r_n)}{\sqrt{b(r_n)/n}} \exp\left(n\,\Lambda\left(\frac{r_n-n}n\right)\right) = \tau_n S_{n,l}, \end{align*}$$
Theorem 6.1 would remain valid: in fact, multiplication of (6.4a) by the expansion (6.2) of
![]() $\tau _n$
in powers of
$\tau _n$
in powers of
![]() $n^{-1}$
gives, by taking (5.6) into account,
$n^{-1}$
gives, by taking (5.6) into account,
 $$\begin{align*}{\mathbb P}(L_n \leqslant l) = S^*_{n,l} + \sum_{j=2}^m F_{j}^{S^*}\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align*}$$
$$\begin{align*}{\mathbb P}(L_n \leqslant l) = S^*_{n,l} + \sum_{j=2}^m F_{j}^{S^*}\big(t_l(n)\big)\, n^{-j/3} + O(n^{-(m+1)/3}), \end{align*}$$
where the first two coefficient functions are
Because of
![]() $\lim _{t\to +\infty }F(t) = 1$
, we would loose the decay of
$\lim _{t\to +\infty }F(t) = 1$
, we would loose the decay of
![]() $F_{3}^S(t)$
for large t, leaving us with a nonzero residual value coming from the classical Stirling factor. For this reason, we recommend dropping the factor
$F_{3}^S(t)$
for large t, leaving us with a nonzero residual value coming from the classical Stirling factor. For this reason, we recommend dropping the factor
![]() $\tau _n$
, thereby resolving an ambiguity expressed in [Reference Bornemann19, Fn. 28].
$\tau _n$
, thereby resolving an ambiguity expressed in [Reference Bornemann19, Fn. 28].
7. Expansions of expected value and variance
Lifting the expansion (5.11) of the PDF of the length distribution to one of the expected value and variance requires a control of the tails (of the distribution itself and of the expansion terms) which, at least right now, we can only conjecture to hold true.
To get to a reasonable conjecture, we recall the tail estimates for the discrete distribution (see [Reference Baik, Deift and Johansson7, Eqn. (9.6/9.12)]),
 $$ \begin{align*} {\mathbb P}(L_n= l) &\leqslant C e^{- c |t_l(n)|^3} & (t_l(n) \leqslant t_0 < 0),\\ {\mathbb P}(L_n= l) &\leqslant C e^{-c |t_l(n)|^{3/5}} & ( 0< t_1 \leqslant t_l(n)), \end{align*} $$
$$ \begin{align*} {\mathbb P}(L_n= l) &\leqslant C e^{- c |t_l(n)|^3} & (t_l(n) \leqslant t_0 < 0),\\ {\mathbb P}(L_n= l) &\leqslant C e^{-c |t_l(n)|^{3/5}} & ( 0< t_1 \leqslant t_l(n)), \end{align*} $$
when n is large enough with
![]() $c>0$
being some absolute constant and
$c>0$
being some absolute constant and
![]() $C>0$
a constant that depends on
$C>0$
a constant that depends on
![]() $t_0, t_1$
.
$t_0, t_1$
.
However, from Theorem 5.1 and its proof we see that the
![]() $F_{j}^*(t)$
take the form
$F_{j}^*(t)$
take the form
where the kernels K are finite sums of rank one kernels with factors of the form (2.2). The results of Section 2.3 thus show that the
![]() $F_{j}^*(t)$
are exponentially decaying when
$F_{j}^*(t)$
are exponentially decaying when
![]() $t\to \infty $
. Now, looking at the left tail, the (heuristic) estimate of the largest eigenvalue of the Airy operator
$t\to \infty $
. Now, looking at the left tail, the (heuristic) estimate of the largest eigenvalue of the Airy operator
![]() ${\mathbf K_0}$
on
${\mathbf K_0}$
on
![]() $L^2(t,\infty )$
as given in the work of Tracy and Widom [Reference Tracy and Widom78, Eq. (1.23)] shows a superexponential growth bound of the operator norm
$L^2(t,\infty )$
as given in the work of Tracy and Widom [Reference Tracy and Widom78, Eq. (1.23)] shows a superexponential growth bound of the operator norm
This, together with the superexponential decay (see [Reference Baik, Buckingham and DiFranco6, Cor. 1.3] and [Reference Deift, Its and Krasovsky28, Thm. 1] for the specific constants)
of the Tracy–Widom distribution itself, and with an at most polynomial growth of the trace norms
![]() $\|{\mathbf K}\|_{{\mathcal J}^1(t,\infty )}$
as
$\|{\mathbf K}\|_{{\mathcal J}^1(t,\infty )}$
as
![]() $t\to -\infty $
, shows that the bounds for the discrete distribution find a counterpart for the expansion terms
$t\to -\infty $
, shows that the bounds for the discrete distribution find a counterpart for the expansion terms
![]() $F_{j}^*(t)$
:
$F_{j}^*(t)$
:
 $$ \begin{align} \begin{aligned} |F_{j}^*(t)| &\leqslant C e^{- c |t|^3} &\quad (t\leqslant t_0 < 0),\\ |F_{j}^*(t)| &\leqslant C e^{-c |t|} &\quad ( 0< t_1 \leqslant t). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |F_{j}^*(t)| &\leqslant C e^{- c |t|^3} &\quad (t\leqslant t_0 < 0),\\ |F_{j}^*(t)| &\leqslant C e^{-c |t|} &\quad ( 0< t_1 \leqslant t). \end{aligned} \end{align} $$
Thus, assuming an additional amount of uniformity that would allow us to absorb the exponentially small tails in the error term of Corollary 5.2, we conjecture the following:
Uniform Tails Hypothesis. The expansion (5.11) can be sharpened to include the tails in the form
 $$ \begin{align} n^{1/6}\,{\mathbb P}(L_n=l) = F' (t) + \sum_{j=1}^m F_{j}^*(t) n^{-j/3} + n^{-(m+1)/3} \cdot O\Big( e^{-c |t|^{3/5}}\Big)\,\bigg|_{t=t_{l-1/2}(n)}, \end{align} $$
$$ \begin{align} n^{1/6}\,{\mathbb P}(L_n=l) = F' (t) + \sum_{j=1}^m F_{j}^*(t) n^{-j/3} + n^{-(m+1)/3} \cdot O\Big( e^{-c |t|^{3/5}}\Big)\,\bigg|_{t=t_{l-1/2}(n)}, \end{align} $$
uniformly valid in
![]() $l=1,\ldots ,n$
as
$l=1,\ldots ,n$
as
![]() $n\to \infty $
.
$n\to \infty $
.
We now follow the ideas sketched in our work [Reference Bornemann19, §4.3] on the Stirling-type formula. By shift and rescale, the expected value of
![]() $L_n$
can be written in the form
$L_n$
can be written in the form
 $$\begin{align*}{\mathbb E}(L_n) = \sum_{l=1}^n l\cdot {\mathbb P}(L_n=l) = 2\sqrt{n} +\frac{1}{2} + \sum_{l=1}^n t_{l-1/2}(n)\cdot n^{1/6}\, {\mathbb P}(L_n=l). \end{align*}$$
$$\begin{align*}{\mathbb E}(L_n) = \sum_{l=1}^n l\cdot {\mathbb P}(L_n=l) = 2\sqrt{n} +\frac{1}{2} + \sum_{l=1}^n t_{l-1/2}(n)\cdot n^{1/6}\, {\mathbb P}(L_n=l). \end{align*}$$
Inserting the expansion (7.3) of the uniform tail hypothesis gives, since its error term is uniformly summable,
 $$ \begin{align} {\mathbb E}(L_n) = 2\sqrt{n} +\frac{1}{2} + \sum_{j=0}^m \mu_j^{(n)} n^{1/6 - j/3} + O(n^{-1/6-m/3}), \end{align} $$
$$ \begin{align} {\mathbb E}(L_n) = 2\sqrt{n} +\frac{1}{2} + \sum_{j=0}^m \mu_j^{(n)} n^{1/6 - j/3} + O(n^{-1/6-m/3}), \end{align} $$
with coefficients (still depending on n, though), writing
![]() $F_0^* := F'$
,
$F_0^* := F'$
,
 $$\begin{align*}\mu^{(n)}_j := n^{-1/6} \sum_{l=1}^n t_{l-1/2}(n) F_j^*\big(t_{l-1/2}(n)\big). \end{align*}$$
$$\begin{align*}\mu^{(n)}_j := n^{-1/6} \sum_{l=1}^n t_{l-1/2}(n) F_j^*\big(t_{l-1/2}(n)\big). \end{align*}$$
By the tail estimates (7.2), we have, writing
![]() $a :=- n^{-1/6}(2\sqrt {n} + \tfrac 12)$
and
$a :=- n^{-1/6}(2\sqrt {n} + \tfrac 12)$
and
![]() $h:=n^{-1/6}$
,
$h:=n^{-1/6}$
,
 $$\begin{align*}\mu^{(n)}_j = h \sum_{l=-\infty}^\infty (a+lh) F_j^*(a+l h) + O(e^{-c n^{1/3}}). \end{align*}$$
$$\begin{align*}\mu^{(n)}_j = h \sum_{l=-\infty}^\infty (a+lh) F_j^*(a+l h) + O(e^{-c n^{1/3}}). \end{align*}$$
Now, based on a precise description of its pole field in [Reference Huang, Xu and Zhang52], it is known that the Hastings–McLeod solution of Painlevé II and a fortiori, by the Tracy–Widom theory [Reference Tracy and Widom78], also F and its derivatives can be continued analytically to the strip
![]() $|\Im z| < 2.9$
. Therefore, we assume the following:
$|\Im z| < 2.9$
. Therefore, we assume the following:
Uniform strip hypothesis. The
![]() $F_j^*$
(
$F_j^*$
(
![]() $j=1,\ldots ,m$
) extend analytically to a strip
$j=1,\ldots ,m$
) extend analytically to a strip
![]() $|\Im z| \leqslant s$
of the complex z-plane, uniformly converging to
$|\Im z| \leqslant s$
of the complex z-plane, uniformly converging to
![]() $0$
as
$0$
as
![]() $z\to \infty $
in that strip.
$z\to \infty $
in that strip.
Under that hypothesis, a classical result about the rectangular rule in quadrature theory (see, for example, [Reference Davis and Rabinowitz26, Eq. (3.4.14)]) gives
 $$\begin{align*}h \sum_{l=-\infty}^\infty (a+lh) F_j^*(a+l h) = \int_{-\infty}^\infty F_j^*(t)\,dt + O(e^{-\pi s /h}). \end{align*}$$
$$\begin{align*}h \sum_{l=-\infty}^\infty (a+lh) F_j^*(a+l h) = \int_{-\infty}^\infty F_j^*(t)\,dt + O(e^{-\pi s /h}). \end{align*}$$
Thus, the
![]() $\mu _j^{(n)}$
and their limit quantities
$\mu _j^{(n)}$
and their limit quantities
differ only by an exponential small error of at most
![]() $O(e^{-c n^{1/6}})$
, which can be absorbed in the error term of (7.4); an illustration of such a rapid convergence is given in [Reference Bornemann19, Table 3] for the case
$O(e^{-c n^{1/6}})$
, which can be absorbed in the error term of (7.4); an illustration of such a rapid convergence is given in [Reference Bornemann19, Table 3] for the case
![]() $j=0$
.
$j=0$
.
The functional form of
![]() $F_0^* = F'$
,
$F_0^* = F'$
,
![]() $F_1^*$
,
$F_1^*$
,
![]() $F_2^*$
and
$F_2^*$
and
![]() $F_3^*$
– namely, being a linear combination of higher order derivatives of F with polynomial coefficients (see (5.13)) – allows us to express
$F_3^*$
– namely, being a linear combination of higher order derivatives of F with polynomial coefficients (see (5.13)) – allows us to express
![]() $\mu _0,\mu _1,\mu _2, \mu _3$
in terms of the moments
$\mu _0,\mu _1,\mu _2, \mu _3$
in terms of the moments
of the Tracy–Widom distribution F. In fact, repeated integration by parts yields the simplifying rule (where
![]() $k\geqslant 1$
)
$k\geqslant 1$
)
 $$\begin{align*}\int_{-\infty}^\infty t^j\, F^{(k)}(t) \,dt = \begin{cases} \displaystyle\frac{(-1)^{k-1} j!}{(j-k+1)!} M_{j-k+1} &\quad k\leqslant j+1,\\ 0 &\quad\text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\int_{-\infty}^\infty t^j\, F^{(k)}(t) \,dt = \begin{cases} \displaystyle\frac{(-1)^{k-1} j!}{(j-k+1)!} M_{j-k+1} &\quad k\leqslant j+1,\\ 0 &\quad\text{otherwise}. \end{cases} \end{align*}$$
Repeated application of that rule proves, in summary, the following contribution to Ulam’s problem about the expected value when n grows large.
Theorem 7.1. Let m be any fixed non-negative integer. Then, subject to the tameness, the uniform tails and the uniform strip hypotheses there holds, as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$ \begin{align} {\mathbb E}(L_n) = 2\sqrt{n} +\frac{1}{2} + \sum_{j=0}^m \mu_j n^{1/6 - j/3} + O(n^{-1/6-m/3}), \end{align} $$
$$ \begin{align} {\mathbb E}(L_n) = 2\sqrt{n} +\frac{1}{2} + \sum_{j=0}^m \mu_j n^{1/6 - j/3} + O(n^{-1/6-m/3}), \end{align} $$
where the constants
![]() $\mu _j$
are given by
$\mu _j$
are given by
The first few cases can be expressed in terms of the moments of the Tracy–Widom distribution:
highly accurate numerical values are listed in Table 1.
Table 1 Highly accurate values of
![]() $\mu _0,\ldots ,\mu _3$
and
$\mu _0,\ldots ,\mu _3$
and
![]() $\nu _0,\ldots ,\nu _3$
as computed from (7.6), (7.8) based on values for
$\nu _0,\ldots ,\nu _3$
as computed from (7.6), (7.8) based on values for
![]() $M_j$
obtained as in [Reference Bornemann19, Table 3] (cf. Prähofer’s values for
$M_j$
obtained as in [Reference Bornemann19, Table 3] (cf. Prähofer’s values for
![]() $M_1,\ldots ,M_4$
, published in [Reference Shinault and Tracy73, p. 70]). For the values of
$M_1,\ldots ,M_4$
, published in [Reference Shinault and Tracy73, p. 70]). For the values of
![]() $\mu _4,\mu _5$
and
$\mu _4,\mu _5$
and
![]() $\nu _4,\nu _5$
, see the supplementary material mentioned in Footnote 13
$\nu _4,\nu _5$
, see the supplementary material mentioned in Footnote 13

Likewise, by shift and rescale, the variance of
![]() $L_n$
can be written in the form
$L_n$
can be written in the form
 $$\begin{align*}\begin{aligned} {\mathrm Var}(L_n) &= \sum_{l=1}^n l^2\cdot {\mathbb P}(L_n=l) - {\mathbb E}(L_n)^2\\ & = n^{1/3} \sum_{l=1}^n t_{l-1/2}(n)^2 \cdot {\mathbb P}(L_n=l) - \Big( {\mathbb E}(L_n) - 2\sqrt{n} - \frac{1}{2}\Big)^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} {\mathrm Var}(L_n) &= \sum_{l=1}^n l^2\cdot {\mathbb P}(L_n=l) - {\mathbb E}(L_n)^2\\ & = n^{1/3} \sum_{l=1}^n t_{l-1/2}(n)^2 \cdot {\mathbb P}(L_n=l) - \Big( {\mathbb E}(L_n) - 2\sqrt{n} - \frac{1}{2}\Big)^2. \end{aligned} \end{align*}$$
By inserting the expansions (7.3), (7.5) and arguing as for Theorem 7.1 we get the following:
Corollary 7.2. Let m be any fixed non-negative integer. Then, subject to the tameness, the uniform tails and the uniform strip hypotheses there holds, as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$ \begin{align} {\mathrm Var}(L_n) = \sum_{j=0}^m \nu_j n^{1/3 - j/3} + O(n^{-m/3}), \end{align} $$
$$ \begin{align} {\mathrm Var}(L_n) = \sum_{j=0}^m \nu_j n^{1/3 - j/3} + O(n^{-m/3}), \end{align} $$
with certain constants
![]() $\nu _j$
. The first few cases can be expressed in terms of the moments of the Tracy–Widom distribution
$\nu _j$
. The first few cases can be expressed in terms of the moments of the Tracy–Widom distribution
 $$ \begin{align} \begin{aligned} \nu_0 &= -M_1^2 + M_2, \quad \nu_1 = -\frac{67}{60} + \frac{1}{30} \big(-M_1 M_2 + M_3\big),\\ \nu_2 &= -\frac{57}{175} M_1 + \frac{1}{700} M_1 M_3 - \frac{1}{3600}M_2^2 - \frac{29}{25200}M_4,\\ \nu_3 &= -\frac{1076}{7875}M_1^2 -\frac{281}{2268000}M_1M_4 +\frac{893}{7875}M_2 +\frac{1}{42000}M_2M_3 + \frac{227}{2268000} M_5; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \nu_0 &= -M_1^2 + M_2, \quad \nu_1 = -\frac{67}{60} + \frac{1}{30} \big(-M_1 M_2 + M_3\big),\\ \nu_2 &= -\frac{57}{175} M_1 + \frac{1}{700} M_1 M_3 - \frac{1}{3600}M_2^2 - \frac{29}{25200}M_4,\\ \nu_3 &= -\frac{1076}{7875}M_1^2 -\frac{281}{2268000}M_1M_4 +\frac{893}{7875}M_2 +\frac{1}{42000}M_2M_3 + \frac{227}{2268000} M_5; \end{aligned} \end{align} $$
highly accurate numerical values are listed in Table 1.
The expansions of expected value and variance can be cross-validated by looking at the numerical values for the coefficients
![]() $\mu _1,\mu _2,\mu _3$
and
$\mu _1,\mu _2,\mu _3$
and
![]() $\nu _1,\nu _2,\nu _3$
that we predicted in [Reference Bornemann19, §4.3]: those values were computed by fitting, in high precision arithmetic, expansions (back then only conjectured) of the form (7.5) with
$\nu _1,\nu _2,\nu _3$
that we predicted in [Reference Bornemann19, §4.3]: those values were computed by fitting, in high precision arithmetic, expansions (back then only conjectured) of the form (7.5) with
![]() $m=9$
and (7.7) with
$m=9$
and (7.7) with
![]() $m=8$
to the exact tabulated data for
$m=8$
to the exact tabulated data for
![]() $n=500,\ldots ,1000$
. A decision about which digits were to be considered correct was made by comparing the result against a similar computation for
$n=500,\ldots ,1000$
. A decision about which digits were to be considered correct was made by comparing the result against a similar computation for
![]() $n=600,\ldots ,1000$
. As it turns out, the predictions of [Reference Bornemann19, §4.3] agree to all the decimal places shown there (that is, to
$n=600,\ldots ,1000$
. As it turns out, the predictions of [Reference Bornemann19, §4.3] agree to all the decimal places shown there (that is, to
![]() $7$
,
$7$
,
![]() $7$
,
$7$
,
![]() $6$
and
$6$
and
![]() $9$
,
$9$
,
![]() $6$
,
$6$
,
![]() $4$
places) with the theory-based, highly accurate values given in Table 1.
$4$
places) with the theory-based, highly accurate values given in Table 1.
Appendices
A Variations on the saddle point method
A.1 Analytic de-Poissonization and the Jasz expansion
In their comprehensive 1998 memoir [Reference Jacquet and Szpankowski53], Jacquet and Szpankowski gave a detailed study of what they termed analytic de-Poissonization (in form of a useful repackaging of the saddle point method), proving a selection of asymptotic expansions and applying them to various asymptotic problems in analytic algorithmics and combinatorics (with generating functions given in terms of functional equations amenable for checking the Tauberian growth conditions in the complex plane). Expositions with a selection of further applications can be found in [Reference Jacquet and Szpankowski54, Sect. 7.2] and [Reference Szpankowski77, Chap. 10].
A.1.1 Formal derivation of the Jasz expansion
Following the ideas of [Reference Jacquet and Szpankowski53, Remark 3], let us start with a purely formal derivation to motivate the algebraic form of the expansion. Suppose that the Poisson generating function
 $$\begin{align*}P(z) = e^{-z}\sum_{n=0}^\infty a_n \frac{z^n}{n!} \end{align*}$$
$$\begin{align*}P(z) = e^{-z}\sum_{n=0}^\infty a_n \frac{z^n}{n!} \end{align*}$$
of a sequence
![]() $a_n$
is an entire function and consider some
$a_n$
is an entire function and consider some
![]() $r>0$
. If we write the power series expansion of
$r>0$
. If we write the power series expansion of
![]() $P(z)$
, centered at
$P(z)$
, centered at
![]() $z=r$
, in the operator form
$z=r$
, in the operator form
where D denotes differentiation w.r.t. the variable r, we get by Cauchy’s formula (with a contour encircling
![]() $z=0$
counter-clockwise with index one)
$z=0$
counter-clockwise with index one)
 $$ \begin{align} a_n = \frac{n!}{2\pi i} \oint P(z) e^z \frac{dz}{z^{n+1}} = e^{-rD} \left(\frac{n!}{2\pi i} \oint e^{z(D+1)} \frac{dz}{z^{n+1}}\right) P(r) = e^{-rD} (D+1)^n P(r). \end{align} $$
$$ \begin{align} a_n = \frac{n!}{2\pi i} \oint P(z) e^z \frac{dz}{z^{n+1}} = e^{-rD} \left(\frac{n!}{2\pi i} \oint e^{z(D+1)} \frac{dz}{z^{n+1}}\right) P(r) = e^{-rD} (D+1)^n P(r). \end{align} $$
By the Cauchy product of power series
 $$ \begin{align} e^{-r x} (x+1)^n = \sum_{j=0}^\infty c_j(n;r) x^j,\quad c_j(n;r):= \sum_{k=0}^j \binom{n}{k}\frac{(-r)^{j-k}}{(j-k)!}, \end{align} $$
$$ \begin{align} e^{-r x} (x+1)^n = \sum_{j=0}^\infty c_j(n;r) x^j,\quad c_j(n;r):= \sum_{k=0}^j \binom{n}{k}\frac{(-r)^{j-k}}{(j-k)!}, \end{align} $$
we get from (A.1) the formal expansion
 $$ \begin{align} a_n \sim \sum_{j=0}^\infty c_j(n;r) P^{(j)}(r). \end{align} $$
$$ \begin{align} a_n \sim \sum_{j=0}^\infty c_j(n;r) P^{(j)}(r). \end{align} $$
Note that the coefficients
![]() $c_j(n;r)$
are polynomials of degree j in n and r. From (A.2), one easily verifies that they satisfy the three-term recurrence
$c_j(n;r)$
are polynomials of degree j in n and r. From (A.2), one easily verifies that they satisfy the three-term recurrence
with initial data
![]() $c_0(n;r) =1$
and
$c_0(n;r) =1$
and
![]() $c_1(n;r) = n-r$
.
$c_1(n;r) = n-r$
.
Remark A.1. From (A.2) and [Reference Szegő76, §2.81], one immediately gets that the
![]() $c_j(n;r)$
are, up to normalization, the Poisson–Charlier polynomials:
$c_j(n;r)$
are, up to normalization, the Poisson–Charlier polynomials:
 $$\begin{align*}\sum_{n=0}^\infty c_j(n;r) c_k(n;r) \frac{e^{-r}r^n}{n!} = \delta_{jk} \frac{r^j}{j!}\qquad (j,k = 0,1,2,\ldots), \end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty c_j(n;r) c_k(n;r) \frac{e^{-r}r^n}{n!} = \delta_{jk} \frac{r^j}{j!}\qquad (j,k = 0,1,2,\ldots), \end{align*}$$
so that they are orthogonal w.r.t. the Poisson distribution of intensity
![]() $r>0$
. In particular, [Reference Szegő76, Eq. (2.81.6)] gives (with
$r>0$
. In particular, [Reference Szegő76, Eq. (2.81.6)] gives (with
![]() $L^{(\nu )}_k(x)$
the Laguerre polynomials) the representation
$L^{(\nu )}_k(x)$
the Laguerre polynomials) the representation
Things simplify for the particular choice
![]() $r=n$
which is suggested by the expected value of the Poisson distribution (cf. Lemma 1.1). The corresponding polynomials
$r=n$
which is suggested by the expected value of the Poisson distribution (cf. Lemma 1.1). The corresponding polynomials
![]() $b_j(n):=c_j(n;n)$
, which we call the diagonal Poisson–Charlier polynomials, satisfy the three-term recurrence
$b_j(n):=c_j(n;n)$
, which we call the diagonal Poisson–Charlier polynomials, satisfy the three-term recurrence
 $$ \begin{align} \begin{aligned} b_0(n)=1,\quad &b_1(n)=0,\\ (j+1) b_{j+1}(n) + j b_j(n) &+ n b_{j-1}(n) = 0\quad (j=0,1,2,\ldots). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} b_0(n)=1,\quad &b_1(n)=0,\\ (j+1) b_{j+1}(n) + j b_j(n) &+ n b_{j-1}(n) = 0\quad (j=0,1,2,\ldots). \end{aligned} \end{align} $$
From this, we infer inductively that
Now the formal expansion (A.1) becomes what is dubbed the Jasz expansion in [Reference Flajolet and Sedgewick38, §VIII.18]:
 $$ \begin{align} \begin{aligned} a_n &\sim P(n) + \sum_{j=2}^\infty b_j(n) P^{(j)}(n) \\ &= P(n) - \frac{n}{2} P"(n) + \frac{n}{3}P"'(n) + \left(\frac{n^2}{8} - \frac{n}{4}\right) P^{(4)}(n) \\ & \quad\qquad + \left(-\frac{n^2}{6} + \frac{n}{5}\right) P^{(5)}(n) + \left(-\frac{n^3}{48} + \frac{13n^2}{72}- \frac{n}{6}\right) P^{(6)}(n)+ \cdots. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} a_n &\sim P(n) + \sum_{j=2}^\infty b_j(n) P^{(j)}(n) \\ &= P(n) - \frac{n}{2} P"(n) + \frac{n}{3}P"'(n) + \left(\frac{n^2}{8} - \frac{n}{4}\right) P^{(4)}(n) \\ & \quad\qquad + \left(-\frac{n^2}{6} + \frac{n}{5}\right) P^{(5)}(n) + \left(-\frac{n^3}{48} + \frac{13n^2}{72}- \frac{n}{6}\right) P^{(6)}(n)+ \cdots. \end{aligned} \end{align} $$
A.1.2 Diagonal analytic de-Poissonization
Jacquet and Szpankowski were able to prove that the expansion (A.5) can be made rigorous if the Poisson generating function satisfies a Tauberian condition in form of a growth condition at the essential singularity at
![]() $z=\infty $
in the complex plane. In fact, this can be cast to accomodate the needs of double scaling limits in a uniform fashion: for a two-parameter family of coefficients
$z=\infty $
in the complex plane. In fact, this can be cast to accomodate the needs of double scaling limits in a uniform fashion: for a two-parameter family of coefficients
![]() $a_{n,k}$
, one expands the diagonal term
$a_{n,k}$
, one expands the diagonal term
![]() $a_{n,n}$
by, first, applying the Jasz expansion w.r.t. to n for k fixed and, then, selecting
$a_{n,n}$
by, first, applying the Jasz expansion w.r.t. to n for k fixed and, then, selecting
![]() $k=n$
only afterwards (a process that is called diagonal de-Poissonization in [Reference Jacquet and Szpankowski53]).
$k=n$
only afterwards (a process that is called diagonal de-Poissonization in [Reference Jacquet and Szpankowski53]).
The following theorem is a particular case of [Reference Jacquet and Szpankowski53, Thm. 4] (with
![]() $\Psi =1$
and the modifications discussed preceding [Reference Jacquet and Szpankowski53, Eq. (27)]). It repackages the saddle point method (cf. [Reference de Bruijn23, Chap. 5] and [Reference Wasow83, Chap. VI]) for the asymptotic evaluation of the Cauchy integral
$\Psi =1$
and the modifications discussed preceding [Reference Jacquet and Szpankowski53, Eq. (27)]). It repackages the saddle point method (cf. [Reference de Bruijn23, Chap. 5] and [Reference Wasow83, Chap. VI]) for the asymptotic evaluation of the Cauchy integral
in a far more directly applicable fashion. Concerning the asserted uniform bounds of the implied constants, see the beginning of [Reference Jacquet and Szpankowski53, §5.2].
Theorem A.2 (Jacquet–Szpankowski 1998).
Let a family of entire Poisson generating functions of the form
 $$\begin{align*}P_k(z) = e^{-z} \sum_{n=0}^\infty a_{n,k} \frac{z^n}{n!} \qquad (k=0,1,2,\ldots) \end{align*}$$
$$\begin{align*}P_k(z) = e^{-z} \sum_{n=0}^\infty a_{n,k} \frac{z^n}{n!} \qquad (k=0,1,2,\ldots) \end{align*}$$
satisfy the following two conditionsFootnote
35
for
![]() $n\geqslant n_0$
where
$n\geqslant n_0$
where
![]() $A, B,C, D$
,
$A, B,C, D$
,
![]() $\alpha ,\beta ,\gamma ,\delta $
are some constants with
$\alpha ,\beta ,\gamma ,\delta $
are some constants with
![]() $A, \alpha>0$
and
$A, \alpha>0$
and
![]() $0\leqslant \delta < 1/2$
:
$0\leqslant \delta < 1/2$
:
-
(I) If
 $|r - n| \leqslant D n^{1-\delta }$
and
$|r - n| \leqslant D n^{1-\delta }$
and
 $|\theta | \leqslant Dr^{-\delta }$
, then
$|\theta | \leqslant Dr^{-\delta }$
, then
 $|P_n(r e^{i\theta })| \leqslant B n^\beta $
.
$|P_n(r e^{i\theta })| \leqslant B n^\beta $
. -
(O) If
 $|\theta |>Dn^{-\delta }$
, then
$|\theta |>Dn^{-\delta }$
, then
 $|P_n(n e^{i\theta }) \exp (n e^{i\theta })| \leqslant C n^\gamma \exp (n - An^\alpha )$
.
$|P_n(n e^{i\theta }) \exp (n e^{i\theta })| \leqslant C n^\gamma \exp (n - An^\alpha )$
.
Then, for any
![]() $m = 0,1,2,\ldots $
there holds, when
$m = 0,1,2,\ldots $
there holds, when
![]() $n\geqslant n_1$
with
$n\geqslant n_1$
with
![]() $n_1$
large enough,
$n_1$
large enough,
 $$ \begin{align} a_{n,n} = P_n(n) + \sum_{j=2}^m b_j(n) P_n^{(j)}(n) + O\big(n^{\beta - (m+1)(1-2\delta)}\big), \end{align} $$
$$ \begin{align} a_{n,n} = P_n(n) + \sum_{j=2}^m b_j(n) P_n^{(j)}(n) + O\big(n^{\beta - (m+1)(1-2\delta)}\big), \end{align} $$
where the
![]() $b_j(n)$
are the diagonal Poisson–Charlier polynomials (A.4) which have degree
$b_j(n)$
are the diagonal Poisson–Charlier polynomials (A.4) which have degree
![]() $\leqslant \lfloor j/2\rfloor $
and satisfy
$\leqslant \lfloor j/2\rfloor $
and satisfy
![]() $b_j(0)=0\; (j\geqslant 1)$
. The implied constant in (A.7) and the constant
$b_j(0)=0\; (j\geqslant 1)$
. The implied constant in (A.7) and the constant
![]() $n_1$
depend only on
$n_1$
depend only on
![]() $n_0$
and the constants entering the conditions (I) and (O).
$n_0$
and the constants entering the conditions (I) and (O).
Example A.3. In the proof of Theorem 5.1, we use Theorem A.2 in the particular case
![]() $\beta = 0$
,
$\beta = 0$
,
![]() $\delta =2/5$
for a family of Poisson generating functions with (cf. (5.4a))
$\delta =2/5$
for a family of Poisson generating functions with (cf. (5.4a))
For
![]() $m=6$
the expansion (A.7) is then given by the terms shown in (A.5) up to an error of order
$m=6$
the expansion (A.7) is then given by the terms shown in (A.5) up to an error of order
![]() $O(n^{-7/5})$
– that is,
$O(n^{-7/5})$
– that is,
 $$ \begin{align*} a_{n,n} = P_n(n) - \frac{n}{2} P_n^{\prime\prime}(n) + \frac{n}{3}P_n^{\prime\prime\prime} &(n) + \left(\frac{n^2}{8} - \frac{n}{4}\right) P_n^{(4)}(n) \\ &\ \ + \left(-\frac{n^2}{6} + \frac{n}{5}\right) P_n^{(5)}(n) + \left(-\frac{n^3}{48} + \frac{13n^2}{72}- \frac{n}{6}\right) P_n^{(6)}(n)+ O(n^{-7/5}). \end{align*} $$
$$ \begin{align*} a_{n,n} = P_n(n) - \frac{n}{2} P_n^{\prime\prime}(n) + \frac{n}{3}P_n^{\prime\prime\prime} &(n) + \left(\frac{n^2}{8} - \frac{n}{4}\right) P_n^{(4)}(n) \\ &\ \ + \left(-\frac{n^2}{6} + \frac{n}{5}\right) P_n^{(5)}(n) + \left(-\frac{n^3}{48} + \frac{13n^2}{72}- \frac{n}{6}\right) P_n^{(6)}(n)+ O(n^{-7/5}). \end{align*} $$
Upon relaxing the error to
![]() $O(n^{-4/3})$
and keeping only those terms which do not get absorbed in the error term, the Jasz expansion then simplifies to
$O(n^{-4/3})$
and keeping only those terms which do not get absorbed in the error term, the Jasz expansion then simplifies to
A.2 H-admissibility and Hayman’s Theorem XI
In his 1956 memoir [Reference Hayman51] on a generalization of Stirling’s formula, Hayman gave a related but different repackaging of the saddle point method for the asymptotic evaluation of the Cauchy integral (A.6) by introducing the notion of H-admissible functions. We collect estimates given in course of the proofs of some of Hayman’s theorems that will help us to establish the conditions (I) and (O) required for applying analytic de-Poissonization in form of Theorem A.2.
Definition A.1 (Hayman [Reference Hayman51, p. 68]).
An entire function
![]() $f(z)$
is said to be H-admissible if the following four conditions are satisfied:
$f(z)$
is said to be H-admissible if the following four conditions are satisfied:
-
– [positivity] for sufficiently large
 $r>0$
, there holds
$r>0$
, there holds
 $f(r)>0$
; inducing there the real functions (which we call the auxiliary functions associated with f) by Hadamard’s convexity theorem
$f(r)>0$
; inducing there the real functions (which we call the auxiliary functions associated with f) by Hadamard’s convexity theorem $$\begin{align*}a(r) = r \frac{f'(r)}{f(r)},\qquad b(r) = r a'(r), \end{align*}$$
$$\begin{align*}a(r) = r \frac{f'(r)}{f(r)},\qquad b(r) = r a'(r), \end{align*}$$
 $a(r)$
is monotonely increasing and
$a(r)$
is monotonely increasing and
 $b(r)$
is positive.
$b(r)$
is positive.
-
– [capture]
 $b(r) \to \infty $
as
$b(r) \to \infty $
as
 $r\to \infty $
;
$r\to \infty $
; -
– [locality] for some function
 $0<\theta _0(r)<\pi $
there holdsFootnote
36
$0<\theta _0(r)<\pi $
there holdsFootnote
36
 $$\begin{align*}f(r e^{i\theta}) = f(r) e^{i\theta a(r) - \theta^2 b(r)/2}\, (1+ o(1)) \qquad (r\to\infty,\; |\theta|\leqslant \theta_0(r)); \end{align*}$$
$$\begin{align*}f(r e^{i\theta}) = f(r) e^{i\theta a(r) - \theta^2 b(r)/2}\, (1+ o(1)) \qquad (r\to\infty,\; |\theta|\leqslant \theta_0(r)); \end{align*}$$
-
– [decay] for the angles in the complement there holds
 $$\begin{align*}f(r e^{i\theta}) = \frac{o(f(r))}{\sqrt{b(r)}}\qquad (r\to\infty,\; \theta_0(r) \leqslant |\theta| \leqslant \pi). \end{align*}$$
$$\begin{align*}f(r e^{i\theta}) = \frac{o(f(r))}{\sqrt{b(r)}}\qquad (r\to\infty,\; \theta_0(r) \leqslant |\theta| \leqslant \pi). \end{align*}$$
Instead of providing an asymptotic expansion (with an additive error term) as in Theorem A.2, H-admissibility gives just a versatile leading order term of
![]() $a_n$
in form of a normal approximation. However, the error term is multiplicative then.
$a_n$
in form of a normal approximation. However, the error term is multiplicative then.
Theorem A.4 (Hayman [Reference Hayman51, Thm. I, Cor. II]).
Let f be an entire H-admissible function with Maclaurin series
 $$\begin{align*}f(z) = \sum_{n=0}^\infty a_nz^n\qquad (z\in {\mathbb C}). \end{align*}$$
$$\begin{align*}f(z) = \sum_{n=0}^\infty a_nz^n\qquad (z\in {\mathbb C}). \end{align*}$$
Then,
-
I. [normal approximation] there holds, uniformly in
 $n \in {\mathbb N}_0=\{0,1,2,\ldots \}$
, that (A.9)
$n \in {\mathbb N}_0=\{0,1,2,\ldots \}$
, that (A.9) $$ \begin{align} \frac{a_n r^n}{f(r)} = \frac{1}{\sqrt{2\pi b(r)}}\left(\exp\left(-\frac{(n-a(r))^2}{2b(r)}\right)+ o(1)\right) \qquad (r\to\infty); \end{align} $$
$$ \begin{align} \frac{a_n r^n}{f(r)} = \frac{1}{\sqrt{2\pi b(r)}}\left(\exp\left(-\frac{(n-a(r))^2}{2b(r)}\right)+ o(1)\right) \qquad (r\to\infty); \end{align} $$
-
II. [Stirling-type formula] for n sufficiently large, it follows from the positivity and capture conditions of H-admissibility that
 $a(r_n) = n$
has a unique solution
$a(r_n) = n$
has a unique solution
 $r_n$
such that
$r_n$
such that
 $r_n\to \infty $
as
$r_n\to \infty $
as
 $n\to \infty $
and therefore, by the normal approximation (A.9), there holds (A.10)
$n\to \infty $
and therefore, by the normal approximation (A.9), there holds (A.10) $$ \begin{align} a_n = \frac{f(r_n)}{r_n^n \sqrt{2\pi b(r_n)}} (1+ o(1)) \qquad (n\to\infty). \end{align} $$
$$ \begin{align} a_n = \frac{f(r_n)}{r_n^n \sqrt{2\pi b(r_n)}} (1+ o(1)) \qquad (n\to\infty). \end{align} $$
For the probabilistic content of the normal approximation (A.9), see, for example, [Reference Duchon, Flajolet, Louchard and Schaeffer30] and [Reference Bornemann19, Remark 2.1].
We observe the similarity of the locality and decay conditions to the conditions (I) and (O) in the Jacquet–Szpankowski Theorem A.2. In fact, in establishing the H-admissibility of certain families of functions, Hayman proved estimates that allow us to infer the validity of conditions (I) and (O). A striking example is given by the following theorem, which gives uniform bounds for a class of functions that is of particular interest to our study.
Theorem A.5 (Hayman [Reference Hayman51, Thm. XI]).
Let f be an entire function of genus zero, having for some
![]() $\epsilon>0$
no zeros in the sector
$\epsilon>0$
no zeros in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
. If f satisfies the positivity condition of Definition A.1, then there is the universal bound
$|\!\arg z| \leqslant \pi /2+ \epsilon $
. If f satisfies the positivity condition of Definition A.1, then there is the universal bound
 $$ \begin{align} \big| f(re^{i\theta}) \big| \leqslant \begin{cases} 2f(r) e^{-\frac{1}{2}\theta^2 b(r)}, &\qquad 0\leqslant |\theta| \leqslant b(r)^{-2/5},\\ 2f(r) e^{-\frac{1}{2}b(r)^{1/5}}, &\qquad b(r)^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
$$ \begin{align} \big| f(re^{i\theta}) \big| \leqslant \begin{cases} 2f(r) e^{-\frac{1}{2}\theta^2 b(r)}, &\qquad 0\leqslant |\theta| \leqslant b(r)^{-2/5},\\ 2f(r) e^{-\frac{1}{2}b(r)^{1/5}}, &\qquad b(r)^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
which is valid when
![]() $b(r)$
is large enough to ensure
$b(r)$
is large enough to ensure
![]() $8b(r)^{-1/5} \csc ^2(\epsilon /2)\csc (\epsilon ) \leqslant \log 2$
. Hence, if f also satisfies the capture condition of Definition A.1, then it is H-admissible.
$8b(r)^{-1/5} \csc ^2(\epsilon /2)\csc (\epsilon ) \leqslant \log 2$
. Hence, if f also satisfies the capture condition of Definition A.1, then it is H-admissible.
Proof. Since the bound (A.11) is hidden in the two-page long proof of [Reference Hayman51, Thm. XI] (only the H-admissibility is stated explicitly there), we collect the details here. First, [Reference Hayman51, Eq. (15.6)] states that, if
![]() $|\theta | \leqslant 1/4$
, then
$|\theta | \leqslant 1/4$
, then
where the error term is bounded by
Now, for
![]() $b(r)$
large enough to ensure
$b(r)$
large enough to ensure
we thus get with
![]() $0 < \theta _0(r) := b(r)^{-2/5} \leqslant \min \big (2\epsilon ,1/4\big )$
and
$0 < \theta _0(r) := b(r)^{-2/5} \leqslant \min \big (2\epsilon ,1/4\big )$
and
![]() $0\leqslant |\theta | \leqslant \theta _0(r)$
that
$0\leqslant |\theta | \leqslant \theta _0(r)$
that
Exponentiation gives, for
![]() $0\leqslant |\theta | \leqslant \theta _0(r)$
,
$0\leqslant |\theta | \leqslant \theta _0(r)$
,
Next, if we combine this estimate with [Reference Hayman51, Lemma 8], we get, since
![]() $\theta _0(r)\leqslant 2\epsilon $
, that
$\theta _0(r)\leqslant 2\epsilon $
, that
which finishes the proof of the universal bound (A.11).
If, instead of having no zeros in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
at all, the entire function f has a finite number of them, Theorem A.5 remains valid, but the lower bound on
$|\!\arg z| \leqslant \pi /2+ \epsilon $
at all, the entire function f has a finite number of them, Theorem A.5 remains valid, but the lower bound on
![]() $b(r)$
will now depend on these finitely many zeros. To restore uniformity, we consider families of such functions whose zeros satisfy the following tameness condition.
$b(r)$
will now depend on these finitely many zeros. To restore uniformity, we consider families of such functions whose zeros satisfy the following tameness condition.
Definition A.2. Let
![]() $f_n$
be a family of entire functions such that, for some fixed
$f_n$
be a family of entire functions such that, for some fixed
![]() $\epsilon>0$
, each of them has finitely many zeros (listed according to their multiplicities)
$\epsilon>0$
, each of them has finitely many zeros (listed according to their multiplicities)
in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
, none of them being a positive real number. We call these zeros uniformly tame (w.r.t. the positive real axis and w.r.t. infinity) if there are some constants
$|\!\arg z| \leqslant \pi /2+ \epsilon $
, none of them being a positive real number. We call these zeros uniformly tame (w.r.t. the positive real axis and w.r.t. infinity) if there are some constants
![]() $1/5 < \mu \leqslant 1/3$
and
$1/5 < \mu \leqslant 1/3$
and
![]() $\nu>0$
such that the family of polynomials
$\nu>0$
such that the family of polynomials
satisfies
 $$ \begin{align} \Big(r \frac{d}{dr}\Big)^2 \log p_n(r) = -\sum_{j=1}^{m_n} \frac{r z_{n,j}}{(r -z_{n,j})^2} = O(r^{1 -\mu}), \quad \quad |p_n(r e^{i\theta})| = p_n(r)(1+O(r^{-\nu})), \end{align} $$
$$ \begin{align} \Big(r \frac{d}{dr}\Big)^2 \log p_n(r) = -\sum_{j=1}^{m_n} \frac{r z_{n,j}}{(r -z_{n,j})^2} = O(r^{1 -\mu}), \quad \quad |p_n(r e^{i\theta})| = p_n(r)(1+O(r^{-\nu})), \end{align} $$
uniformly in
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Remark A.6. Note that a single function f would satisfy condition (A.13) with error terms of the form
![]() $O(r^{-1})$
in both places. Therefore, the tameness condition allows us to accommodate a significant growth of the implied constants in these
$O(r^{-1})$
in both places. Therefore, the tameness condition allows us to accommodate a significant growth of the implied constants in these
![]() $O(r^{-1})$
terms as
$O(r^{-1})$
terms as
![]() $n\to \infty $
– in the first case because of zeros of
$n\to \infty $
– in the first case because of zeros of
![]() $f_n$
getting close to the positive real axis and in the second case because of them getting large.
$f_n$
getting close to the positive real axis and in the second case because of them getting large.
Corollary A.7. Let
![]() $f_n$
be a family of entire functions of genus zero with positive Maclaurin coefficients such that, for some fixed
$f_n$
be a family of entire functions of genus zero with positive Maclaurin coefficients such that, for some fixed
![]() $\epsilon>0$
, each of them has a most finitely many zeros in the sector
$\epsilon>0$
, each of them has a most finitely many zeros in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
. If these zeros are uniformly tame in the sense of Definition A.2 and if the auxiliary functions belonging to
$|\!\arg z| \leqslant \pi /2+ \epsilon $
. If these zeros are uniformly tame in the sense of Definition A.2 and if the auxiliary functions belonging to
![]() $f_n$
satisfy
$f_n$
satisfy
uniformly in
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
![]() $n\to \infty $
, then there holds the bound
$n\to \infty $
, then there holds the bound
 $$ \begin{align} \big| f_n(re^{i\theta}) \big| \leqslant \begin{cases} 2f_n(r) e^{-\frac{1}{2}\theta^2 r}, &\qquad 0\leqslant |\theta| \leqslant r^{-2/5},\\ 2f_n(r) e^{-\frac{1}{2}r^{1/5}}, &\qquad r^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
$$ \begin{align} \big| f_n(re^{i\theta}) \big| \leqslant \begin{cases} 2f_n(r) e^{-\frac{1}{2}\theta^2 r}, &\qquad 0\leqslant |\theta| \leqslant r^{-2/5},\\ 2f_n(r) e^{-\frac{1}{2}r^{1/5}}, &\qquad r^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align} $$
for all
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
![]() $n\geqslant n_0$
,
$n\geqslant n_0$
,
![]() $n_0$
being sufficiently large. Here,
$n_0$
being sufficiently large. Here,
![]() $n_0$
depends only on the parameters of the tameness condition and the implied constants in (A.13) and (A.14).
$n_0$
depends only on the parameters of the tameness condition and the implied constants in (A.13) and (A.14).
Proof. Factoring out the finitely many zeros of
![]() $f_n$
in the sector
$f_n$
in the sector
![]() $|\!\arg z| \leqslant \pi /2+ \epsilon $
by using the polynomials (A.12), we have
$|\!\arg z| \leqslant \pi /2+ \epsilon $
by using the polynomials (A.12), we have
where
![]() $f_n^*$
is an entire function of genus zero that has no zeros in that sector. Since
$f_n^*$
is an entire function of genus zero that has no zeros in that sector. Since
![]() $f_n(r)>0$
for
$f_n(r)>0$
for
![]() $r>0$
and the leading coefficient of the polynomial
$r>0$
and the leading coefficient of the polynomial
![]() $p_n(z)$
is one,
$p_n(z)$
is one,
![]() $f_n^*$
satisfies the positivity condition of Definition A.1. Denoting the auxiliary functions of
$f_n^*$
satisfies the positivity condition of Definition A.1. Denoting the auxiliary functions of
![]() $f_n^*$
by
$f_n^*$
by
![]() $a_n^*$
and
$a_n^*$
and
![]() $b_n^*$
, the tameness condition (A.13) yields
$b_n^*$
, the tameness condition (A.13) yields
uniformly in
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
as
![]() $n\to \infty $
.
$n\to \infty $
.
By (A.14), this gives
![]() $b_n^*(r) = r(1 + O(r^{-\mu }))$
, so that by Theorem A.5 (its proof shows that we can take a factor
$b_n^*(r) = r(1 + O(r^{-\mu }))$
, so that by Theorem A.5 (its proof shows that we can take a factor
![]() $3/2$
instead of
$3/2$
instead of
![]() $2$
if
$2$
if
![]() $\log 2$
is replaced by
$\log 2$
is replaced by
![]() $\log (3/2)$
in the lower bound on
$\log (3/2)$
in the lower bound on
![]() $b(r)$
),
$b(r)$
),
 $$\begin{align*}\big| f_n^*(re^{i\theta}) \big| \leqslant \begin{cases} \tfrac{3}{2}f_n^*(r) e^{-\frac{1}{2}\theta^2 b_n^*(r)}, &\qquad 0\leqslant |\theta| \leqslant b_n^*(r)^{-2/5},\\ \tfrac{3}{2}f_n^*(r) e^{-\frac{1}{2}b_n^*(r)^{1/5}}, &\qquad b_n^*(r)^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align*}$$
$$\begin{align*}\big| f_n^*(re^{i\theta}) \big| \leqslant \begin{cases} \tfrac{3}{2}f_n^*(r) e^{-\frac{1}{2}\theta^2 b_n^*(r)}, &\qquad 0\leqslant |\theta| \leqslant b_n^*(r)^{-2/5},\\ \tfrac{3}{2}f_n^*(r) e^{-\frac{1}{2}b_n^*(r)^{1/5}}, &\qquad b_n^*(r)^{-2/5}\leqslant |\theta| \leqslant \pi, \end{cases} \end{align*}$$
for n large enough to ensure
![]() $8b_n^*(r)^{-1/5} \csc ^2(\epsilon /2)\csc (\epsilon ) \leqslant \log (3/2)$
. We write this briefly as
$8b_n^*(r)^{-1/5} \csc ^2(\epsilon /2)\csc (\epsilon ) \leqslant \log (3/2)$
. We write this briefly as
for
![]() $n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
$n - n^{3/5} \leqslant r \leqslant n + n^{3/5}$
and
![]() $n\geqslant n_0$
where
$n\geqslant n_0$
where
![]() $n_0$
is large enough (just depending on the parameters and the implied constants in the tameness condition). If we multiply this bound by
$n_0$
is large enough (just depending on the parameters and the implied constants in the tameness condition). If we multiply this bound by
and use
![]() $b_n^*(r) = r(1 + O(r^{-\mu }))$
to infer
$b_n^*(r) = r(1 + O(r^{-\mu }))$
to infer
we obtain the asserted estimate in the compact form
for
![]() $n-n^{3/5}\leqslant r \leqslant n + n^{3/5}$
and
$n-n^{3/5}\leqslant r \leqslant n + n^{3/5}$
and
![]() $n\geqslant n_0$
, where
$n\geqslant n_0$
, where
![]() $n_0$
is large enough.
$n_0$
is large enough.
A.3 Bessel functions of large order in the transition region
In the 1950s, F. Olver started a systematic and exhaustive study of asymptotic expansions of the Bessel functions
![]() $J_\nu (z)$
for large order
$J_\nu (z)$
for large order
![]() $\nu $
and argument z. For the transition regionFootnote
37
$\nu $
and argument z. For the transition regionFootnote
37
![]() $z= \nu +\tau \nu ^{1/3}$
, he obtained from applying the saddle point method to integral representations of Sommerfeld’s type the asymptotic expansion [Reference Olver63, Eq. (3.1)] (cf. also [Reference Olver, Lozier, Boisvert and Clark66, §10.19 (iii)])
$z= \nu +\tau \nu ^{1/3}$
, he obtained from applying the saddle point method to integral representations of Sommerfeld’s type the asymptotic expansion [Reference Olver63, Eq. (3.1)] (cf. also [Reference Olver, Lozier, Boisvert and Clark66, §10.19 (iii)])
 $$ \begin{align} J_\nu(\nu+\tau \nu^{1/3}) \sim \frac{2^{1/3}}{\nu^{1/3}} \operatorname{Ai}(-2^{1/3}\tau)\sum_{k=0}^\infty \frac{A_k(\tau)}{\nu^{2k/3}} + \frac{2^{2/3}}{\nu^{1/3}} \operatorname{Ai}'(-2^{1/3}\tau) \sum_{k=1}^\infty \frac{B_k(\tau)}{\nu^{2k/3}} \end{align} $$
$$ \begin{align} J_\nu(\nu+\tau \nu^{1/3}) \sim \frac{2^{1/3}}{\nu^{1/3}} \operatorname{Ai}(-2^{1/3}\tau)\sum_{k=0}^\infty \frac{A_k(\tau)}{\nu^{2k/3}} + \frac{2^{2/3}}{\nu^{1/3}} \operatorname{Ai}'(-2^{1/3}\tau) \sum_{k=1}^\infty \frac{B_k(\tau)}{\nu^{2k/3}} \end{align} $$
valid when
![]() $|\!\arg \nu | \leqslant \pi /2 - \delta < \pi $
with
$|\!\arg \nu | \leqslant \pi /2 - \delta < \pi $
with
![]() $\tau $
being any fixed complex number. Here,
$\tau $
being any fixed complex number. Here,
![]() $A_k(\tau )$
and
$A_k(\tau )$
and
![]() $B_k(\tau )$
are certain rational polynomials of increasing degree; the first few are [Reference Olver63, Eq. (2.42)]Footnote
38
$B_k(\tau )$
are certain rational polynomials of increasing degree; the first few are [Reference Olver63, Eq. (2.42)]Footnote
38
Remark A.8. The sequence [Reference Olver63, Eqs. (2.10), (2.14), (2.18), (2.38), (2.40)] of formulae in Olver’s 1952 paper gives an actual methodFootnote
39
to calculate
![]() $A_k(\tau )$
and
$A_k(\tau )$
and
![]() $B_k(\tau )$
(combining reversion and nesting of power series with recursive formulae). The degrees of
$B_k(\tau )$
(combining reversion and nesting of power series with recursive formulae). The degrees of
![]() $A_k$
are the positive integers congruent to
$A_k$
are the positive integers congruent to
![]() $0,1$
mod
$0,1$
mod
![]() $5$
(starting with
$5$
(starting with
![]() $\deg A_1=1$
) and the degrees of
$\deg A_1=1$
) and the degrees of
![]() $B_k$
are the positive integers congruent to
$B_k$
are the positive integers congruent to
![]() $2,3$
mod
$2,3$
mod
![]() $5$
(starting with
$5$
(starting with
![]() $\deg B_1=2$
). In both families of polynomials, the coefficients of
$\deg B_1=2$
). In both families of polynomials, the coefficients of
![]() $\tau ^m$
are zero when m is not congruent mod
$\tau ^m$
are zero when m is not congruent mod
![]() $3$
to the degree.
$3$
to the degree.
As stated in [Reference Olver63, p. 422], the expansion (A.16) can be repeatedly differentiated with respect to
![]() $\tau $
, valid under the same conditions. For a modern account of differentiability w.r.t.
$\tau $
, valid under the same conditions. For a modern account of differentiability w.r.t.
![]() $\tau $
and
$\tau $
and
![]() $\nu $
, adding uniformity for
$\nu $
, adding uniformity for
![]() $\tau $
from any compact real set, see the recent work of Sher [Reference Sher72, Prop. 2.8] which is based on the (microlocal) theory of so-called polyhomogeneous conormal joint asymptotic expansions.
$\tau $
from any compact real set, see the recent work of Sher [Reference Sher72, Prop. 2.8] which is based on the (microlocal) theory of so-called polyhomogeneous conormal joint asymptotic expansions.
The purposes of Section 3 require to identify a larger region of real
![]() $\tau $
where the expansion (A.16) is uniform as
$\tau $
where the expansion (A.16) is uniform as
![]() $\nu \to \infty $
through positive real values. To this end, we use the uniform asymptotic expansions of Bessel functions for large order
$\nu \to \infty $
through positive real values. To this end, we use the uniform asymptotic expansions of Bessel functions for large order
![]() $\nu $
, pioneered by Olver [Reference Olver64] in 1954 by analyzing turning points of the Bessel differential equation (cf. [Reference Olver65, Chap. 11], [Reference Wasow83, Chap. VIII] and, for exponential representations of the asymptotic series, also [Reference Dunster, Gil and Segura31, §4]),
$\nu $
, pioneered by Olver [Reference Olver64] in 1954 by analyzing turning points of the Bessel differential equation (cf. [Reference Olver65, Chap. 11], [Reference Wasow83, Chap. VIII] and, for exponential representations of the asymptotic series, also [Reference Dunster, Gil and Segura31, §4]),
 $$ \begin{align} J_\nu(\nu z) \sim \left(\frac{4\zeta}{1-z^2}\right)^{1/4} \left(\frac{\operatorname{Ai}(\nu^{2/3}\zeta)}{\nu^{1/3}} \sum_{k=0}^\infty \frac{A_k^*(\zeta)}{\nu^{2k}}+ \frac{\operatorname{Ai}'(\nu^{2/3}\zeta)}{\nu^{5/3}} \sum_{k=0}^\infty \frac{B_k^*(\zeta)}{\nu^{2k}}\right), \end{align} $$
$$ \begin{align} J_\nu(\nu z) \sim \left(\frac{4\zeta}{1-z^2}\right)^{1/4} \left(\frac{\operatorname{Ai}(\nu^{2/3}\zeta)}{\nu^{1/3}} \sum_{k=0}^\infty \frac{A_k^*(\zeta)}{\nu^{2k}}+ \frac{\operatorname{Ai}'(\nu^{2/3}\zeta)}{\nu^{5/3}} \sum_{k=0}^\infty \frac{B_k^*(\zeta)}{\nu^{2k}}\right), \end{align} $$
uniformly for
![]() $z\in (0,\infty )$
as
$z\in (0,\infty )$
as
![]() $\nu \to \infty $
. Here, the parameters and coefficients are, for
$\nu \to \infty $
. Here, the parameters and coefficients are, for
![]() $0<z<1$
,
$0<z<1$
,
 $$ \begin{align} \frac{2}{3} \zeta^{3/2} = \log\left(\frac{1+\sqrt{1-z^2}}{z}\right) - \sqrt{1-z^2}, \end{align} $$
$$ \begin{align} \frac{2}{3} \zeta^{3/2} = \log\left(\frac{1+\sqrt{1-z^2}}{z}\right) - \sqrt{1-z^2}, \end{align} $$
and
 $$ \begin{align} A_k^*(\zeta) &= \sum_{j=0}^{2k} \left(\frac{3}{2}\right)^j v_j \zeta^{-3j/2} U_{2k-j}\big((1-z^2)^{-1/2}\big), \end{align} $$
$$ \begin{align} A_k^*(\zeta) &= \sum_{j=0}^{2k} \left(\frac{3}{2}\right)^j v_j \zeta^{-3j/2} U_{2k-j}\big((1-z^2)^{-1/2}\big), \end{align} $$
 $$ \begin{align} B_k^*(\zeta) &= -\zeta^{-1/2}\sum_{j=0}^{2k+1} \left(\frac{3}{2}\right)^j u_j \zeta^{-3j/2} U_{2k-j+1}\big((1-z^2)^{-1/2}\big), \end{align} $$
$$ \begin{align} B_k^*(\zeta) &= -\zeta^{-1/2}\sum_{j=0}^{2k+1} \left(\frac{3}{2}\right)^j u_j \zeta^{-3j/2} U_{2k-j+1}\big((1-z^2)^{-1/2}\big), \end{align} $$
where the
![]() $U_k(x)$
are recursively defined rational polynomials of degree
$U_k(x)$
are recursively defined rational polynomials of degree
![]() $3k$
(cf. [Reference Olver64, Eq. (2.19)]) and
$3k$
(cf. [Reference Olver64, Eq. (2.19)]) and
![]() $u_k, v_k$
(
$u_k, v_k$
(
![]() $u_0=v_0=1$
) are the rational coefficients of the asymptotic expansions of the Airy function and its derivative in a sector containing the positive real axis,
$u_0=v_0=1$
) are the rational coefficients of the asymptotic expansions of the Airy function and its derivative in a sector containing the positive real axis,
 $$ \begin{align} \operatorname{Ai}(z) \sim \frac{e^{-\xi}}{2\sqrt{\pi}z^{1/4}} \sum_{k=0}^\infty (-1)^k \frac{u_k}{\xi^k}, \quad \operatorname{Ai}'(z) \sim -\frac{z^{1/4}e^{-\xi}}{2\sqrt{\pi}} \sum_{k=0}^\infty (-1)^k \frac{v_k}{\xi^k},\quad \xi = \frac{2}{3}z^{3/2}, \end{align} $$
$$ \begin{align} \operatorname{Ai}(z) \sim \frac{e^{-\xi}}{2\sqrt{\pi}z^{1/4}} \sum_{k=0}^\infty (-1)^k \frac{u_k}{\xi^k}, \quad \operatorname{Ai}'(z) \sim -\frac{z^{1/4}e^{-\xi}}{2\sqrt{\pi}} \sum_{k=0}^\infty (-1)^k \frac{v_k}{\xi^k},\quad \xi = \frac{2}{3}z^{3/2}, \end{align} $$
as
![]() $z \to \infty $
within
$z \to \infty $
within
![]() $|\!\arg z| \leqslant \pi - \delta $
. Note that
$|\!\arg z| \leqslant \pi - \delta $
. Note that
![]() $\zeta =\zeta (z)$
can be continued analytically to the z-plane cut along the negative real axis;Footnote
40
$\zeta =\zeta (z)$
can be continued analytically to the z-plane cut along the negative real axis;Footnote
40
![]() $A_k^*(\zeta )$
and
$A_k^*(\zeta )$
and
![]() $B_k^*(\zeta )$
can be continued accordingly. As stated in [Reference Olver64, p. 342], valid under the same conditions while preserving uniformity, the expansion can be repeatedly differentiated with respect to z.
$B_k^*(\zeta )$
can be continued accordingly. As stated in [Reference Olver64, p. 342], valid under the same conditions while preserving uniformity, the expansion can be repeatedly differentiated with respect to z.
In particular, with
![]() $0<\delta <1$
fixed, the power series expansion
$0<\delta <1$
fixed, the power series expansion
converges uniformly for
![]() $|1-z| \leqslant 1- \delta $
(because of the logarithmic singularity at
$|1-z| \leqslant 1- \delta $
(because of the logarithmic singularity at
![]() $z=0$
the radius of convergence of this series is exactly
$z=0$
the radius of convergence of this series is exactly
![]() $1$
, so that this range of uniformity cannot be extended). If we put
$1$
, so that this range of uniformity cannot be extended). If we put
plugging the uniformly convergent series
![]() $\zeta (z)$
into the uniform large
$\zeta (z)$
into the uniform large
![]() $\nu $
expansion (A.17) recovers the form of the transition region expansion (A.16) and proves that it holds uniformly for
$\nu $
expansion (A.17) recovers the form of the transition region expansion (A.16) and proves that it holds uniformly for
as
![]() $\nu \to \infty $
through positive real values.
$\nu \to \infty $
through positive real values.
At the expense of considerably larger error terms, this result can be extended as follows:
Lemma A.9. For any non-negative integer m and any real
![]() $\tau _0$
, there holds, as
$\tau _0$
, there holds, as
![]() $\nu \to \infty $
through positive real values,
$\nu \to \infty $
through positive real values,
 $$ \begin{align} J_\nu(\nu+\tau \nu^{1/3}) = 2^{1/3} \operatorname{Ai}(-2^{1/3}\tau)\sum_{k=0}^m \frac{A_k(\tau)}{\nu^{(2k+1)/3}} + 2^{2/3}\operatorname{Ai}'&(-2^{1/3}\tau) \sum_{k=1}^{m} \frac{B_{k}(\tau)}{\nu^{(2k+1)/3}}\notag \\ &\qquad\quad + \nu^{-1-2m/3} \cdot O\big(\exp(2^{1/3}\tau)\big), \end{align} $$
$$ \begin{align} J_\nu(\nu+\tau \nu^{1/3}) = 2^{1/3} \operatorname{Ai}(-2^{1/3}\tau)\sum_{k=0}^m \frac{A_k(\tau)}{\nu^{(2k+1)/3}} + 2^{2/3}\operatorname{Ai}'&(-2^{1/3}\tau) \sum_{k=1}^{m} \frac{B_{k}(\tau)}{\nu^{(2k+1)/3}}\notag \\ &\qquad\quad + \nu^{-1-2m/3} \cdot O\big(\exp(2^{1/3}\tau)\big), \end{align} $$
uniformly for
![]() $-\nu ^{2/3}< \tau \leqslant \tau _0$
. Here,
$-\nu ^{2/3}< \tau \leqslant \tau _0$
. Here,
![]() $A_k(\tau )$
and
$A_k(\tau )$
and
![]() $B_k(\tau )$
are the rational polynomials in (A.16). Preserving uniformity, the expansion (A.20) can be repeatedly differentiated w.r.t.
$B_k(\tau )$
are the rational polynomials in (A.16). Preserving uniformity, the expansion (A.20) can be repeatedly differentiated w.r.t.
![]() $\tau $
.
$\tau $
.
Proof. Let us write
where
![]() $E_m$
denotes the sum of the expansion terms in (A.20) and
$E_m$
denotes the sum of the expansion terms in (A.20) and
![]() $R_m$
is the remainder. We split the range of
$R_m$
is the remainder. We split the range of
![]() $\tau $
into the two parts
$\tau $
into the two parts
In part (I), as argued above for
![]() $\delta =1/4$
, the expansion (A.16) is uniformly valid – that is,
$\delta =1/4$
, the expansion (A.16) is uniformly valid – that is,
uniformly for these
![]() $\tau $
. Now, the superexponential decay of the Airy function
$\tau $
. Now, the superexponential decay of the Airy function
![]() $\operatorname {Ai}(x)$
and its derivative as
$\operatorname {Ai}(x)$
and its derivative as
![]() $x\to \infty $
through positive values, as displayed in the expansions (A.18), imply the asserted uniform bound
$x\to \infty $
through positive values, as displayed in the expansions (A.18), imply the asserted uniform bound
in part (I) of the range of
![]() $\tau $
.
$\tau $
.
However, in part (II) of the range of
![]() $\tau $
, we infer from (A.18) that, for
$\tau $
, we infer from (A.18) that, for
![]() $0<\epsilon < 1/2$
,
$0<\epsilon < 1/2$
,
We now show that also
uniformly in part (II) of the range of
![]() $\tau $
, so that all terms in (A.20) are absorbed in the asserted error term. Here, we observe
$\tau $
, so that all terms in (A.20) are absorbed in the asserted error term. Here, we observe
so that the leading order terms in (A.17) and (A.18) yield the bound
 $$\begin{align*}J_\nu(\nu z) \sim \nu^{-1/2} \left(\frac{4}{1-z^2}\right)^{1/4} (\nu^{2/3} \zeta)^{1/4}\operatorname{Ai}(\nu^{2/3}\zeta) = \nu^{-1/2} \cdot O\big(\exp(- \tfrac{2}{3}\zeta^{3/2}\nu)\big), \end{align*}$$
$$\begin{align*}J_\nu(\nu z) \sim \nu^{-1/2} \left(\frac{4}{1-z^2}\right)^{1/4} (\nu^{2/3} \zeta)^{1/4}\operatorname{Ai}(\nu^{2/3}\zeta) = \nu^{-1/2} \cdot O\big(\exp(- \tfrac{2}{3}\zeta^{3/2}\nu)\big), \end{align*}$$
uniformly for the
![]() $\tau $
in (II). Because of
$\tau $
in (II). Because of
![]() $\frac {2}{3}\zeta ^{3/2} \geqslant 1.095$
and
$\frac {2}{3}\zeta ^{3/2} \geqslant 1.095$
and
![]() $-\nu \leqslant -2^{1/3}\nu ^{2/3} < 2^{1/3}\tau $
for
$-\nu \leqslant -2^{1/3}\nu ^{2/3} < 2^{1/3}\tau $
for
![]() $\nu \geqslant 2$
, this bound can be relaxed, as required, to
$\nu \geqslant 2$
, this bound can be relaxed, as required, to
Finally, the claim about the derivatives follows from the repeated differentiability of the uniform expansion (A.17) and the differential equation of the Airy function,
![]() $\operatorname {Ai}"(x) = x \operatorname {Ai}(x)$
(so that the general form of the expansions underlying the proof does not change).
$\operatorname {Ai}"(x) = x \operatorname {Ai}(x)$
(so that the general form of the expansions underlying the proof does not change).
Remark A.10. The cases
![]() $m=0$
and
$m=0$
and
![]() $m=1$
of Lemma A.9 have previously been stated as [Reference Borodin and Forrester21, Eq. (4.11)] and [Reference Forrester and Mays45, Eq. (2.10)]. However, the proofs given there are incomplete: in [Reference Borodin and Forrester21, p. 2978], the power series (A.19) is used up to the boundary of its circle of convergence, so that uniformity becomes an issue, whereas in [Reference Forrester and Mays45, p. 9], it is claimed that Olver’s transition expansion (A.16) would be uniform w.r.t.
$m=1$
of Lemma A.9 have previously been stated as [Reference Borodin and Forrester21, Eq. (4.11)] and [Reference Forrester and Mays45, Eq. (2.10)]. However, the proofs given there are incomplete: in [Reference Borodin and Forrester21, p. 2978], the power series (A.19) is used up to the boundary of its circle of convergence, so that uniformity becomes an issue, whereas in [Reference Forrester and Mays45, p. 9], it is claimed that Olver’s transition expansion (A.16) would be uniform w.r.t.
![]() $\tau \in (-\infty ,\tau _0]$
, which is not the case.Footnote
41
$\tau \in (-\infty ,\tau _0]$
, which is not the case.Footnote
41
B Compilation of the Shinault–Tracy table and a general conjecture
B.1 The Shinault–Tracy table
Shinault and Tracy [Reference Shinault and Tracy73, p. 68] tabulated, for
![]() $0 \leqslant j+k\leqslant 8$
, explicit representations of the terms
$0 \leqslant j+k\leqslant 8$
, explicit representations of the terms
as linear combinations of the form (called a linear F-form of order n here)
 $$ \begin{align} T_n(s) = p_1(s) \frac{F'(s)}{F(s)} + p_2(s) \frac{F"(s)}{F(s)} + \cdots + p_{n}(s) \frac{F^{(n)}(s)}{F(s)}, \end{align} $$
$$ \begin{align} T_n(s) = p_1(s) \frac{F'(s)}{F(s)} + p_2(s) \frac{F"(s)}{F(s)} + \cdots + p_{n}(s) \frac{F^{(n)}(s)}{F(s)}, \end{align} $$
where
![]() $p_1,\ldots ,p_n$
are certain rational polynomials (depending on j, k) and
$p_1,\ldots ,p_n$
are certain rational polynomials (depending on j, k) and
![]() $n=j+k+1$
. Though they sketched a method to validate each entry of their table, Shinault and Tracy did not describe how they had found those entries in the first place. However, by ‘reverse engineering’ their validation method, we can give an algorithm to compile such a table.
$n=j+k+1$
. Though they sketched a method to validate each entry of their table, Shinault and Tracy did not describe how they had found those entries in the first place. However, by ‘reverse engineering’ their validation method, we can give an algorithm to compile such a table.
Starting point is the Tracy–Widom theory [Reference Tracy and Widom78] of representing F in terms of the Hastings–McLeod solution
![]() $q(s)$
of Painlevé II,
$q(s)$
of Painlevé II,
From these formulae, we get immediately that
where
![]() ${\mathbb Q}[s] [q,q']$
denotes the space of polynomials in q and
${\mathbb Q}[s] [q,q']$
denotes the space of polynomials in q and
![]() $q'$
with coefficients being rational polynomials. Because q satisfies Painlevé II,
$q'$
with coefficients being rational polynomials. Because q satisfies Painlevé II,
![]() ${\mathbb Q}[s] [q,q']$
is closed under differentiation. For a term
${\mathbb Q}[s] [q,q']$
is closed under differentiation. For a term
![]() $T \in {\mathbb Q}[s] [q,q']$
, we define the q-degree
$T \in {\mathbb Q}[s] [q,q']$
, we define the q-degree
![]() $\deg _q T$
to be the largest
$\deg _q T$
to be the largest
![]() $\alpha +\beta $
of a q-monomial
$\alpha +\beta $
of a q-monomial
that appears in expanding T. Inductively, the general linear F-form
![]() $T_n(s)$
of order n satisfies
$T_n(s)$
of order n satisfies
 $$ \begin{align*} \deg_q T_n = \deg_q T_n^{\prime} &= 4n,\\ \#(q\text{-monomials with nonzero coefficient in } T_n) &= 2(n^2 - n + 2) \quad (n\geqslant 2), \\ \#(q\text{-monomials with nonzero coefficient in } T_n^{\prime}) &= 2n^2+1. \end{align*} $$
$$ \begin{align*} \deg_q T_n = \deg_q T_n^{\prime} &= 4n,\\ \#(q\text{-monomials with nonzero coefficient in } T_n) &= 2(n^2 - n + 2) \quad (n\geqslant 2), \\ \#(q\text{-monomials with nonzero coefficient in } T_n^{\prime}) &= 2n^2+1. \end{align*} $$
By advancing the set of formulae of [Reference Tracy and Widom78], Shinault and Tracy [Reference Shinault and Tracy73, pp. 64–66] obtained
where
![]() $n=2,3,\ldots $
(ignoring the term
$n=2,3,\ldots $
(ignoring the term
![]() $(n-2) q_{n-3}(s)$
if
$(n-2) q_{n-3}(s)$
if
![]() $n=2$
). It follows that
$n=2$
). It follows that
This suggests the following algorithm to recursively compute the linear F-form of order n representing
![]() $u_{jk}$
(if such a form exists in the first place).Suppose such forms have already been found for all smaller
$u_{jk}$
(if such a form exists in the first place).Suppose such forms have already been found for all smaller
![]() $j+k$
; we have to find polynomials
$j+k$
; we have to find polynomials
![]() $p_1,\ldots ,p_n \in {\mathbb Q}[s]$
such that
$p_1,\ldots ,p_n \in {\mathbb Q}[s]$
such that
By differentiating and then comparing the coefficients of all q-monomials, we get an overdetermined linear system of equations in
![]() ${\mathbb Q}[s]$
of size
${\mathbb Q}[s]$
of size
![]() $(2n^2+1)\times 2n$
that is to be satisfied by the polynomials
$(2n^2+1)\times 2n$
that is to be satisfied by the polynomials
![]() $p_1,\ldots ,p_n, p_1^{\prime },\ldots , p_n^{\prime }$
.
$p_1,\ldots ,p_n, p_1^{\prime },\ldots , p_n^{\prime }$
.
For instance, the term
![]() $u_{30}$
(as used in Section 3.3) can be calculated from the previously established linear F-forms (cf. (3.19) and [Reference Shinault and Tracy73, p. 68])
$u_{30}$
(as used in Section 3.3) can be calculated from the previously established linear F-forms (cf. (3.19) and [Reference Shinault and Tracy73, p. 68])
by setting up the
![]() $33\times 8$
linear system displayed in Table 2
$33\times 8$
linear system displayed in Table 2
Table 2 The
![]() $33\times 8$
linear system for constructing the entry
$33\times 8$
linear system for constructing the entry
![]() $u_{30}(s)$
in the table [Reference Shinault and Tracy73, p. 68].
$u_{30}(s)$
in the table [Reference Shinault and Tracy73, p. 68].

which, as a linear system in
![]() $8$
unknown polynomials, is uniquely solved by
$8$
unknown polynomials, is uniquely solved by
Since the last four entries are the derivatives of the first four, this solution is consistent with the form of solution we are interested in. Generally, we first solve the linear system for
and then check for consistency
![]() $p_m^{\prime } =r_m$
,
$p_m^{\prime } =r_m$
,
![]() $m=1,\ldots ,n$
. If consistent, such a solution also satisfies (B.4) by integrating its differentiated form: the constant of integration vanishes because both sides decay (rapidly) to zero as
$m=1,\ldots ,n$
. If consistent, such a solution also satisfies (B.4) by integrating its differentiated form: the constant of integration vanishes because both sides decay (rapidly) to zero as
![]() $s\to \infty $
. In the example, we have thus obtained
$s\to \infty $
. In the example, we have thus obtained
 $$\begin{align*}u_{30}(s) = \frac{7F'(s)}{12F(s)} +\frac{s F"(s)}{3F(s)} + \frac{F^{(4)}(s)}{24F(s)}. \end{align*}$$
$$\begin{align*}u_{30}(s) = \frac{7F'(s)}{12F(s)} +\frac{s F"(s)}{3F(s)} + \frac{F^{(4)}(s)}{24F(s)}. \end{align*}$$
So, two effects of integrability must happen for this recursive algorithm to work properly:
-
• the overdetermined
 $(2n^2+1)\times 2n$
linear system has actually a solution in
$(2n^2+1)\times 2n$
linear system has actually a solution in
 ${\mathbb Q}[s]^{2n}$
,
${\mathbb Q}[s]^{2n}$
, -
• the solution is consistent (the last n entries being the derivatives of the first n ones).
Because of the algebraic independence of the solution
![]() $q,q'$
of Painlevé II over
$q,q'$
of Painlevé II over
![]() ${\mathbb Q}[s]$
(cf. [Reference Gromak, Laine and Shimomura48, Thm. 21.1]), the converse is also true: if there is a representation as a linear F-form at all, the algorithm succeeds by finding its unique coefficient polynomials.
${\mathbb Q}[s]$
(cf. [Reference Gromak, Laine and Shimomura48, Thm. 21.1]), the converse is also true: if there is a representation as a linear F-form at all, the algorithm succeeds by finding its unique coefficient polynomials.
Based on a CAS implementation of the algorithm, we can report that the
![]() $u_{jk}$
are represented as linear F-forms of degree
$u_{jk}$
are represented as linear F-forms of degree
![]() $j+k+1$
for
$j+k+1$
for
![]() $0\leqslant j+k\leqslant 50$
,Footnote
42
adding further evidence to the conjecture of Shinault and Tracy; a general proof, however, would require theoretical insight into the underlying integrability of (B.3). If true, an induction shows that
$0\leqslant j+k\leqslant 50$
,Footnote
42
adding further evidence to the conjecture of Shinault and Tracy; a general proof, however, would require theoretical insight into the underlying integrability of (B.3). If true, an induction shows that
B.2 A general conjecture
As a matter of fact, even certain nonlinear rational polynomials of the terms
![]() $u_{jk}$
, such as those representing
$u_{jk}$
, such as those representing
![]() $\tilde F_j/F$
in (3.18b) and (3.21a), can be represented as linear F-forms.
$\tilde F_j/F$
in (3.18b) and (3.21a), can be represented as linear F-forms.
Namely, Theorem 2.1, Section 3.3 and the perturbation theory of finite-dimensional determinants imply that
![]() $\tilde F_j/F$
can be written as a rational linear combination of the minors of
$\tilde F_j/F$
can be written as a rational linear combination of the minors of
![]() $(u_{jk})_{j,k=0}^\infty $
– that is, of determinants of the form
$(u_{jk})_{j,k=0}^\infty $
– that is, of determinants of the form
 $$ \begin{align} \begin{vmatrix} u_{j_1 k_1} & \cdots & u_{j_1 k_m} \\ \vdots & & \vdots \\ u_{j_m k_1} & \cdots & u_{j_m k_m} \end{vmatrix}. \end{align} $$
$$ \begin{align} \begin{vmatrix} u_{j_1 k_1} & \cdots & u_{j_1 k_m} \\ \vdots & & \vdots \\ u_{j_m k_1} & \cdots & u_{j_m k_m} \end{vmatrix}. \end{align} $$
We are thus led to the following conjecture (checked computationally up to order
![]() $n=50$
):
$n=50$
):
Conjecture. Each minor of the form (B.5) can be represented as linear F-forms of order
(Here, the case
![]() $m=1$
corresponds to the conjecture of Shinault and Tracy.) Aside from those terms which can be recast as linear combinations of minors with coefficients in
$m=1$
corresponds to the conjecture of Shinault and Tracy.) Aside from those terms which can be recast as linear combinations of minors with coefficients in
![]() ${\mathbb Q}[s]$
, there are no other polynomial expressions of the
${\mathbb Q}[s]$
, there are no other polynomial expressions of the
![]() $u_{jk}$
with coefficients in
$u_{jk}$
with coefficients in
![]() ${\mathbb Q}[s]$
that can be represented as linear F-forms.
${\mathbb Q}[s]$
that can be represented as linear F-forms.
There are abundant examples of nonlinear rational polynomials of the terms
![]() $u_{jk}$
which cannot be represented as linear F-forms. For instance, as we have checked computationally, none of the terms (which are subterms of the minors shown below)
$u_{jk}$
which cannot be represented as linear F-forms. For instance, as we have checked computationally, none of the terms (which are subterms of the minors shown below)
can be represented as linear F-forms of an order up to
![]() $n=50$
.
$n=50$
.
Algorithmically, based on the already tabulated
![]() $u_{jk}$
, the linear F-form of order n for a given term T such as (B.5) can be found, if existent, as follows: by expanding the equation
$u_{jk}$
, the linear F-form of order n for a given term T such as (B.5) can be found, if existent, as follows: by expanding the equation
in
![]() ${\mathbb Q}[s][q,q']$
and comparing coefficients of the q-monomials, we get an overdetermined linear system of size
${\mathbb Q}[s][q,q']$
and comparing coefficients of the q-monomials, we get an overdetermined linear system of size
![]() $2(n^2-n+2)\times n$
for the coefficient polynomials
$2(n^2-n+2)\times n$
for the coefficient polynomials
![]() $p_1,\ldots ,p_n \in {\mathbb Q}[s]$
. If there is a solution, we have found the linear F-form. If not, there is no such form of order n.
$p_1,\ldots ,p_n \in {\mathbb Q}[s]$
. If there is a solution, we have found the linear F-form. If not, there is no such form of order n.
For instance, the nonlinear part in (3.18b) is
 $$\begin{align*}u_{00}(s) u_{11}(s) - u_{10}(s)^2 = \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{10}(s) & u_{11}(s) \end{vmatrix}, \end{align*}$$
$$\begin{align*}u_{00}(s) u_{11}(s) - u_{10}(s)^2 = \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{10}(s) & u_{11}(s) \end{vmatrix}, \end{align*}$$
which yields, for the order
![]() $n=4$
taken from (B.6), the
$n=4$
taken from (B.6), the
![]() $28\times 4$
linear system in
$28\times 4$
linear system in
![]() ${\mathbb Q}[s]$
displayed in Table 3.
${\mathbb Q}[s]$
displayed in Table 3.
Table 3 The
![]() $28\times 4$
linear system for representing
$28\times 4$
linear system for representing
![]() $u_{00}(s) u_{11}(s) - u_{10}(s)^2$
as in (B.7).
$u_{00}(s) u_{11}(s) - u_{10}(s)^2$
as in (B.7).

Its unique solution is
so that we obtain the linear F-form
 $$ \begin{align} \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{10}(s) & u_{11}(s) \end{vmatrix} = \frac{F'(s)}{6F(s)} -\frac{sF"(s)}{3F(s)} + \frac{F^{(4)}(s)}{12F(s)}. \end{align} $$
$$ \begin{align} \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{10}(s) & u_{11}(s) \end{vmatrix} = \frac{F'(s)}{6F(s)} -\frac{sF"(s)}{3F(s)} + \frac{F^{(4)}(s)}{12F(s)}. \end{align} $$
Likewise, we see that the integrability displayed in the evaluation of (3.21) is based on the fact that the two minors which appear as subexpressions can be represented as linear F-forms; indeed, in both cases, (B.6) yields the order
![]() $n=6$
, and by solving the corresponding
$n=6$
, and by solving the corresponding
![]() $64\times 6$
linear systems, we getFootnote
43
$64\times 6$
linear systems, we getFootnote
43
 $$ \begin{align} \begin{vmatrix} u_{10}(s) & u_{11}(s) \\ u_{20}(s) & u_{21}(s) \end{vmatrix} &= -\frac{sF'(s)}{18F(s)} + \frac{s^2F"(s)}{9F(s)} -\frac{F"'(s)}{24F(s)} -\frac{sF^{(4)}(s)}{18F(s)} + \frac{F^{(6)}(s)}{144F(s)}, \end{align} $$
$$ \begin{align} \begin{vmatrix} u_{10}(s) & u_{11}(s) \\ u_{20}(s) & u_{21}(s) \end{vmatrix} &= -\frac{sF'(s)}{18F(s)} + \frac{s^2F"(s)}{9F(s)} -\frac{F"'(s)}{24F(s)} -\frac{sF^{(4)}(s)}{18F(s)} + \frac{F^{(6)}(s)}{144F(s)}, \end{align} $$
 $$ \begin{align} \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{30}(s) & u_{31}(s) \end{vmatrix} &= \frac{sF'(s)}{10F(s)} -\frac{s^2F"(s)}{5F(s)} -\frac{3F"'(s)}{40F(s)} + \frac{F^{(6)}(s)}{80F(s)}. \end{align} $$
$$ \begin{align} \begin{vmatrix} u_{00}(s) & u_{01}(s) \\ u_{30}(s) & u_{31}(s) \end{vmatrix} &= \frac{sF'(s)}{10F(s)} -\frac{s^2F"(s)}{5F(s)} -\frac{3F"'(s)}{40F(s)} + \frac{F^{(6)}(s)}{80F(s)}. \end{align} $$
Remark B.1. Other applications of the technique discussed here can be found in [Reference Bornemann18, §3.3].
Acknowledgements
I am grateful to the anonymous reviewers for suggesting helpful corrections and clarifications to the text. I would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge (UK), for support and hospitality during the 2022 program ‘Applicable resurgent asymptotics: towards a universal theory (ARA2)’ where work on the present paper was undertaken. This work was supported by EPSRC Grant No EP/R014604/1.
Competing interest
The author has no competing interest to declare.
Data availability statement
Supporting and supplementary Mathematica code comes with the source files at arxiv:2301.02022.