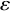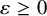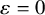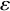1 Introduction
1.1 Context and problem statement
The notion of fiber bundle is fundamental in mathematics and physics [Reference Husemöller, Joachim, Jurčo, Schottenloher, Echterhoff, Fredenhagen and Krötz33, Reference Luke and Mishchenko43, Reference Balachandran, Marmo, Skagerstam and Stern3, Reference Bott6]. Informally, a fiber bundle with fiber F consists of a continuous function
![]() $p: Y \to X$
from the total space Y to the base space X, that, locally, looks like a projection
$p: Y \to X$
from the total space Y to the base space X, that, locally, looks like a projection
![]() $U \times F \to U$
, in the following sense: X can be covered by open sets
$U \times F \to U$
, in the following sense: X can be covered by open sets
![]() $U \subseteq X$
, each equipped with a homeomorphism
$U \subseteq X$
, each equipped with a homeomorphism
![]() $i : U \times F \to p^{-1}(U)$
such that
$i : U \times F \to p^{-1}(U)$
such that
![]() $(p\circ i)(x,f) = x$
for every
$(p\circ i)(x,f) = x$
for every
![]() $(x,f) \in U\times F$
. In particular,
$(x,f) \in U\times F$
. In particular,
![]() $p^{-1}(x)$
is homeomorphic to F for every
$p^{-1}(x)$
is homeomorphic to F for every
![]() $x \in X$
. Vector bundles are fiber bundles for which F is a vector space, and a key example is the tangent bundle
$x \in X$
. Vector bundles are fiber bundles for which F is a vector space, and a key example is the tangent bundle
![]() $T\mathcal {M} \to \mathcal {M}$
of a d-dimensional differentiable manifold
$T\mathcal {M} \to \mathcal {M}$
of a d-dimensional differentiable manifold
![]() $\mathcal {M}$
. The fiber of this bundle is
$\mathcal {M}$
. The fiber of this bundle is
![]() $\mathbb {R}^d$
, as the tangent space at each point of
$\mathbb {R}^d$
, as the tangent space at each point of
![]() $\mathcal {M}$
is d-dimensional. The Möbius band
$\mathcal {M}$
is d-dimensional. The Möbius band
![]() $\mathsf {Mob} \to S^1$
is another example of a vector bundle, interpreted as a collection of one-dimensional real vector spaces that change orientation as one goes around the equatorial circle
$\mathsf {Mob} \to S^1$
is another example of a vector bundle, interpreted as a collection of one-dimensional real vector spaces that change orientation as one goes around the equatorial circle
![]() $S^1$
. Of particular interest are fiber bundles for which the fiber F is only allowed to ‘twist’ according to a certain group G of automorphisms of F; these correspond to principal G-bundles. Vector bundles can be identified with principal G-bundles with G the general linear group, while Euclidean vector bundles arise when G is the orthogonal group.
$S^1$
. Of particular interest are fiber bundles for which the fiber F is only allowed to ‘twist’ according to a certain group G of automorphisms of F; these correspond to principal G-bundles. Vector bundles can be identified with principal G-bundles with G the general linear group, while Euclidean vector bundles arise when G is the orthogonal group.
Many problems in mathematics and physics can be reduced to finding sections of a fiber bundle (that is, maps
![]() $s : X\to Y$
for which
$s : X\to Y$
for which
![]() $p \circ s = \mathsf {id}_X$
) satisfying certain properties. For this reason, one is interested in finding computable obstructions to the existence of certain sections and, more generally, in defining computable invariants of fiber bundles that can aid in their classification up to isomorphism.
$p \circ s = \mathsf {id}_X$
) satisfying certain properties. For this reason, one is interested in finding computable obstructions to the existence of certain sections and, more generally, in defining computable invariants of fiber bundles that can aid in their classification up to isomorphism.
Characteristic classes are examples of such invariants [Reference Milnor and Stasheff47]. Indeed, any principal bundle determines a collection of elements in the cohomology of its base space, called the characteristic classes of the bundle. This is done in such a way that isomorphic bundles have the same characteristic classes. The Stiefel–Whitney classes of a vector bundle are a particular type of characteristic class, which provide obstructions to solving several geometric problems. For instance, the first Stiefel–Whitney class determines whether or not the vector bundle is orientable, while, for a differentiable manifold
![]() $\mathcal {M}$
, the Stiefel–Whitney classes of its tangent bundle provide obstructions to embedding
$\mathcal {M}$
, the Stiefel–Whitney classes of its tangent bundle provide obstructions to embedding
![]() $\mathcal {M}$
in
$\mathcal {M}$
in
![]() $\mathbb {R}^n$
for small n. Similarly, the Euler class of an oriented vector bundle is yet another characteristic class, which provides an obstruction to the existence of a nowhere vanishing section.
$\mathbb {R}^n$
for small n. Similarly, the Euler class of an oriented vector bundle is yet another characteristic class, which provides an obstruction to the existence of a nowhere vanishing section.
Part of the ubiquity of principal bundles stems from the fact that they can be defined in several, a posteriori, equivalent ways. Of particular interest to us are: (1) the definition of principal G-bundles by means of G-valued Čech cocycles, which, roughly speaking, consist of local data on the base space specifying how the fibers must be glued to reconstruct the total space, and (2) the definition of principal G-bundles by means of classifying maps, which are continuous functions from the base space to a certain classifying space
![]() $\mathcal {B} G$
.
$\mathcal {B} G$
.
Principal bundles and their characteristic classes appear also in practical applications. Many synchronization problems, in which independent, local measurements need to be assembled into a global quantity, can be interpreted as the problem of trivializing a Čech cochain of pairwise alignments. Dimensionality reduction problems, where a high-dimensional point cloud concentrated around a low-dimensional manifold needs to be represented with low distortion in a low-dimensional space, can be interpreted as an embedding problem for which estimates of the tangential characteristic classes can provide obstructions. Although it is informally clear that vector bundles are relevant for these kinds of problems, the discrete and noisy nature of the input data makes it unclear whether the data actually determine a true vector bundle and whether topological information of this bundle can be extracted from the noisy and incomplete input.
We identify two main difficulties for working with vector bundles in a practical setting. One comes from a discrete aspect: Mathematically, vector bundles are continuous entities specified, for instance, by (continuous) cocycles or by classifying maps. How can one specify arbitrary vector bundles on, say, the geometric realization of a finite simplicial complex using a finite amount of data? The other difficulty comes from the fact that, in practical applications, nothing is exact (e.g., cocycle conditions from noisy pairwise alignments), so one needs a notion of vector bundle that is robust to some degree of noise. Although the results in this paper are mainly theoretical, they are motivated by problems in applied topology. In the rest of this introduction, we describe some of these problems in more detail.
1.1.1 Synchronization and cocycles
Consider a synchronization problem with input a set V of local measurements that are pairwise aligned by elements
![]() $\{g_{ij}\}_{i,j \in V}$
of a group G. One instance of this problem arises in cryogenic electron microscopy (cryo-EM), where, broadly speaking, one seeks to reconstruct the three-dimensional (3D) shape of a molecule from several two-dimensional (2D) projections taken from unknown viewing directions [Reference Frank18, Reference van Heel, Gowen, Matadeen, Orlova, Finn, Pape, Cohen, Stark, Schmidt, Schatz and Patwardhan28]. Here, the measurements are the 2D pictures, which are pairwise aligned by elements of the rotation group
$\{g_{ij}\}_{i,j \in V}$
of a group G. One instance of this problem arises in cryogenic electron microscopy (cryo-EM), where, broadly speaking, one seeks to reconstruct the three-dimensional (3D) shape of a molecule from several two-dimensional (2D) projections taken from unknown viewing directions [Reference Frank18, Reference van Heel, Gowen, Matadeen, Orlova, Finn, Pape, Cohen, Stark, Schmidt, Schatz and Patwardhan28]. Here, the measurements are the 2D pictures, which are pairwise aligned by elements of the rotation group
![]() $SO(2)$
. Figure 1 shows examples of the input data for this kind of problem.
$SO(2)$
. Figure 1 shows examples of the input data for this kind of problem.

Figure 1 2D projections of an unknown 3D shape.
Letting K be the graph with vertex set V and an edge
![]() $(ij)$
if
$(ij)$
if
![]() $g_{ij}$
aligns i and j sufficiently well, one expects the family of elements
$g_{ij}$
aligns i and j sufficiently well, one expects the family of elements
![]() $\{g_{ij}\}_{(ij) \in K}$
to satisfy an approximate cocycle condition. This means that if
$\{g_{ij}\}_{(ij) \in K}$
to satisfy an approximate cocycle condition. This means that if
![]() $(ij)$
,
$(ij)$
,
![]() $(jk)$
and
$(jk)$
and
![]() $(ik)$
are edges of V, then
$(ik)$
are edges of V, then
![]() $\|g_{ij} g_{jk} - g_{ik}\| < \varepsilon $
for some sufficiently small
$\|g_{ij} g_{jk} - g_{ik}\| < \varepsilon $
for some sufficiently small
![]() $\varepsilon> 0$
. This condition indicates that the measurements can be approximately locally synchronized: In the case of cryo-EM, this implies that sets of 2D projections with very similar viewing directions can be aligned simultaneously; this is key for averaging and thus denoising images with similar viewing directions. Global synchronization is a different matter: In the case of cryo-EM, we do not expect to be able to align all 2D projections simultaneously. This is justified in [Reference Singer, Zhao, Shkolnisky and Hadani58] by observing that the pairwise alignments
$\varepsilon> 0$
. This condition indicates that the measurements can be approximately locally synchronized: In the case of cryo-EM, this implies that sets of 2D projections with very similar viewing directions can be aligned simultaneously; this is key for averaging and thus denoising images with similar viewing directions. Global synchronization is a different matter: In the case of cryo-EM, we do not expect to be able to align all 2D projections simultaneously. This is justified in [Reference Singer, Zhao, Shkolnisky and Hadani58] by observing that the pairwise alignments
![]() $\{g_{ij}\}$
approximate an
$\{g_{ij}\}$
approximate an
![]() $SO(2)$
-cocycle representing the tangent bundle of the
$SO(2)$
-cocycle representing the tangent bundle of the
![]() $2$
-sphere, which is nontrivial. We will demonstrate in Section 7.4 how a data-derived estimate of the associated Euler class yields a nontrivial obstruction to globally aligning the data from Figure 1.
$2$
-sphere, which is nontrivial. We will demonstrate in Section 7.4 how a data-derived estimate of the associated Euler class yields a nontrivial obstruction to globally aligning the data from Figure 1.
In the general case, if the approximate cocycle
![]() $\{g_{ij}\}$
does indeed determine a true principal G-bundle, then global synchronization corresponds to the bundle being trivial. This view of synchronization is studied in-depth in [Reference Gao, Brodzki and Mukherjee19] for the case of flat principal G-bundles (i.e., bundles determined by a group morphism from
$\{g_{ij}\}$
does indeed determine a true principal G-bundle, then global synchronization corresponds to the bundle being trivial. This view of synchronization is studied in-depth in [Reference Gao, Brodzki and Mukherjee19] for the case of flat principal G-bundles (i.e., bundles determined by a group morphism from
![]() $\pi _1$
of the base to G). However, as it is observed in [Reference Ye and Lim69], the bundles underlying the cryo-EM problem are not flat.
$\pi _1$
of the base to G). However, as it is observed in [Reference Ye and Lim69], the bundles underlying the cryo-EM problem are not flat.
To our knowledge, the problem of determining when an arbitrary approximate
![]() $O(d)$
-valued cocycle defines a true vector bundle has not yet been addressed in the literature. This is one of the goals of this paper. Possible applications of a general theory of approximate
$O(d)$
-valued cocycle defines a true vector bundle has not yet been addressed in the literature. This is one of the goals of this paper. Possible applications of a general theory of approximate
![]() $O(d)$
-cocycles are the usage of characteristic classes of the underlying true vector bundle for model validation, detecting nonsynchronizability in data and for guiding local synchronization and averaging algorithms.
$O(d)$
-cocycles are the usage of characteristic classes of the underlying true vector bundle for model validation, detecting nonsynchronizability in data and for guiding local synchronization and averaging algorithms.
1.1.2 Local trivializations and dimensionality reduction
Consider a point cloud
![]() $X \subseteq \mathbb {R}^D$
concentrated around a d-dimensional embedded manifold
$X \subseteq \mathbb {R}^D$
concentrated around a d-dimensional embedded manifold
![]() $\mathcal {M}$
and the ensuing problem of extracting information about the tangent bundle
$\mathcal {M}$
and the ensuing problem of extracting information about the tangent bundle
![]() $T \mathcal {M} \to \mathcal {M}$
from the sample X. Possible applications of this include using the tangential characteristic classes as computable obstructions for local-to-global dimensionality reduction on X.
$T \mathcal {M} \to \mathcal {M}$
from the sample X. Possible applications of this include using the tangential characteristic classes as computable obstructions for local-to-global dimensionality reduction on X.
Here is an example of such an approach. Fix
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
![]() $N_x$
denote the set of the k closest neighbors of x in X. The application of principal component analysis (PCA) to each
$N_x$
denote the set of the k closest neighbors of x in X. The application of principal component analysis (PCA) to each
![]() $N_x$
with target dimension d yields an ordered orthonormal basis
$N_x$
with target dimension d yields an ordered orthonormal basis
![]() $\Phi (x)$
of the d-dimensional linear subspace that best approximates
$\Phi (x)$
of the d-dimensional linear subspace that best approximates
![]() $N_x$
. This method, or variations thereof, is sometimes known as local PCA [Reference Singer59] and can be used, for instance, to estimate the local dimension of the data [Reference Little, Lee, Jung and Maggioni41].
$N_x$
. This method, or variations thereof, is sometimes known as local PCA [Reference Singer59] and can be used, for instance, to estimate the local dimension of the data [Reference Little, Lee, Jung and Maggioni41].
The aforementioned process defines a function
![]() $\Phi : X \to \mathsf {V}(d,D)$
from the data to the Stiefel manifold of orthonormal d-frames in
$\Phi : X \to \mathsf {V}(d,D)$
from the data to the Stiefel manifold of orthonormal d-frames in
![]() $\mathbb {R}^D$
, which can be interpreted as an approximate vector bundle given by local trivializations. One expects this construction to approximate the tangent bundle of the manifold
$\mathbb {R}^D$
, which can be interpreted as an approximate vector bundle given by local trivializations. One expects this construction to approximate the tangent bundle of the manifold
![]() $\mathcal {M}$
. Our goal here is to formalize this intuition and, in particular, to quantify the extent to which an approximate local trivialization induces a true vector bundle and whether topological information of the bundle can be extracted from the approximation.
$\mathcal {M}$
. Our goal here is to formalize this intuition and, in particular, to quantify the extent to which an approximate local trivialization induces a true vector bundle and whether topological information of the bundle can be extracted from the approximation.
We apply these ideas in Section 7.2 to the problem of distinguishing nonhomeomorphic but homotopy equivalent attractors in the double-gyre dynamical system. Indeed, we do so by combining local trivializations and data-driven estimates of the first tangential Stiefel–Whitney class. Moreover, we also demonstrate in Section 7.3 how the first two Stiefel–Whitney classes can be estimated from data to yield nontrivial obstructions to dimensionality reduction and parallelization.
1.2 Contributions
In this paper, we introduce relaxations and discretizations of the notion of vector bundle, we determine the extent to which these approximate representations determine true vector bundles and we give algorithms for the effective computation of low-dimensional characteristic classes of the true vector bundle directly from approximate and discrete representations. We run these algorithms on examples to illustrate their usage.
The notions of vector bundle we focus on correspond to Euclidean vector bundles, that is, to vector bundles endowed with a compatible, fiberwise inner product, or, equivalently, vector bundles whose structure group is an orthogonal group. To avoid cumbersome nomenclature, we drop the modifier ‘Euclidean’ in our main definitions.
Approximate notions of vector bundle
Let
![]() $\varepsilon \geq 0$
. For a topological space B with an open cover
$\varepsilon \geq 0$
. For a topological space B with an open cover
![]() $\mathcal {U}$
, we define the set of
$\mathcal {U}$
, we define the set of
![]() $\varepsilon $
-approximate
$\varepsilon $
-approximate
![]() $O(d)$
-valued
$O(d)$
-valued
![]() $1$
-cocycles
$1$
-cocycles
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
(Definition 3.3), which we use to define the
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
(Definition 3.3), which we use to define the
![]() $\varepsilon $
-approximate cohomology set
$\varepsilon $
-approximate cohomology set
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
(Definition 3.5). We also introduce the set of
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
(Definition 3.5). We also introduce the set of
![]() $\varepsilon $
-approximate classifying maps
$\varepsilon $
-approximate classifying maps
![]() $\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
(Definition 3.9), which consists of continuous maps with codomain a thickened Grassmannian (Section 2.1.3), and the set of
$\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
(Definition 3.9), which consists of continuous maps with codomain a thickened Grassmannian (Section 2.1.3), and the set of
![]() $\varepsilon $
-approximate classifying maps up to homotopy
$\varepsilon $
-approximate classifying maps up to homotopy
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. In order to relate these notions, we define the set of
$\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. In order to relate these notions, we define the set of
![]() $\varepsilon $
-approximate local trivializations
$\varepsilon $
-approximate local trivializations
![]() $\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
(Definition 3.8). We introduce metrics on these sets, the most relevant of which being the metric
$\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
(Definition 3.8). We introduce metrics on these sets, the most relevant of which being the metric
![]() $\mathsf {d}_{\check {\mathsf {H}}}$
on
$\mathsf {d}_{\check {\mathsf {H}}}$
on
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, which we use to state stability results, below.
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, which we use to state stability results, below.
When B is a paracompact topological space and
![]() $\mathcal {U}$
is a countable open cover, we define maps between the sets, as follows:
$\mathcal {U}$
is a countable open cover, we define maps between the sets, as follows:

Here, a sub- or superscript with a constant c at an arrow tip indicates that the map sends one kind of
![]() $\varepsilon $
-approximate vector bundle to another kind of
$\varepsilon $
-approximate vector bundle to another kind of
![]() $c\varepsilon $
-approximate vector bundle. The maps
$c\varepsilon $
-approximate vector bundle. The maps
![]() $\mathsf {triv}$
and
$\mathsf {triv}$
and
![]() $\mathsf {w}$
are defined in Section 4.1, the map
$\mathsf {w}$
are defined in Section 4.1, the map
![]() $\mathsf {av}$
is defined in Construction 4.15 and the map
$\mathsf {av}$
is defined in Construction 4.15 and the map
![]() $\mathsf {cl}$
is defined in Theorem 4.21, which, in particular, also implies that the diagram above commutes when going from top left to bottom right. In Section 4.11, we describe a way in which
$\mathsf {cl}$
is defined in Theorem 4.21, which, in particular, also implies that the diagram above commutes when going from top left to bottom right. In Section 4.11, we describe a way in which
![]() $\mathsf {triv}$
and
$\mathsf {triv}$
and
![]() $\mathsf {w}$
are approximate inverses of each other.
$\mathsf {w}$
are approximate inverses of each other.
By a result of Tinarrage [Reference Tinarrage63, Lemma 2.1], there is a bijection
![]() $\pi _* : \left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon }} \right \rbrack \to \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
whenever
$\pi _* : \left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon }} \right \rbrack \to \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
whenever
![]() $\varepsilon \leq \sqrt {2}/2$
. In particular, when
$\varepsilon \leq \sqrt {2}/2$
. In particular, when
![]() $\varepsilon \leq 1/2$
, the composite
$\varepsilon \leq 1/2$
, the composite
assigns a true (classical) vector bundle to every
![]() $\varepsilon $
-approximate cohomology class. In this sense, an
$\varepsilon $
-approximate cohomology class. In this sense, an
![]() $\varepsilon $
-approximate cocycle determines a true vector bundle, as long as
$\varepsilon $
-approximate cocycle determines a true vector bundle, as long as
![]() $\varepsilon $
is sufficiently small.
$\varepsilon $
is sufficiently small.
The following result, which appears as Theorem 4.21 and Theorem 4.27, says in particular that the map
![]() $\mathsf {cl}$
is stable.
$\mathsf {cl}$
is stable.
Theorem A. For any
![]() $\varepsilon \geq 0$
, the map
$\varepsilon \geq 0$
, the map
![]() $\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
is independent of arbitrary choices, such as a choice of a partition of unity subordinate to
$\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
is independent of arbitrary choices, such as a choice of a partition of unity subordinate to
![]() $\mathcal {U}$
or a choice of enumeration of the opens of
$\mathcal {U}$
or a choice of enumeration of the opens of
![]() $\mathcal {U}$
, and is such that, if
$\mathcal {U}$
, and is such that, if
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < \delta $
in
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < \delta $
in
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, then
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, then
![]() $\mathsf {cl}(\Omega )$
and
$\mathsf {cl}(\Omega )$
and
![]() $\mathsf {cl}(\Lambda )$
become equal in
$\mathsf {cl}(\Lambda )$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \delta )}} \right \rbrack $
. Moreover, if
$\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \delta )}} \right \rbrack $
. Moreover, if
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
and
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
and
![]() $\varepsilon \leq \sqrt {2}/4$
, then there exists
$\varepsilon \leq \sqrt {2}/4$
, then there exists
![]() $\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
$\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
![]() $\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda ) \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
and
$\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda ) \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
and
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) \leq 9\varepsilon $
.
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) \leq 9\varepsilon $
.
Theorem 4.21 also addresses refinements of covers and their action on approximate cohomology classes; see also Remark 4.22 for a notion of approximate Čech cohomology independent of a cover.
Discrete approximate notions of vector bundle
For a simplicial complex K, we introduce discrete analogues of approximate cocycles, approximate cohomology and approximate local trivializations. Most importantly, we introduce the discrete approximate cohomology set
![]() $\mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right )$
and the set of discrete approximate local trivializations
$\mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right )$
and the set of discrete approximate local trivializations
![]() $\mathsf {DT}_{\varepsilon }\left ( K; d \right )$
. These are useful in practice, as specifying elements of these sets requires a finite amount of data when K is finite. To highlight their simplicity, we give here the notion of discrete approximate cocycle over a simplicial complex K:
$\mathsf {DT}_{\varepsilon }\left ( K; d \right )$
. These are useful in practice, as specifying elements of these sets requires a finite amount of data when K is finite. To highlight their simplicity, we give here the notion of discrete approximate cocycle over a simplicial complex K:
so that a discrete approximate cocycle consists of a set of orthogonal matrices indexed by the ordered
![]() $1$
-simplices of K, which satisfies an approximate cocycle condition. The definition of discrete approximate local trivialization is equally simple.
$1$
-simplices of K, which satisfies an approximate cocycle condition. The definition of discrete approximate local trivialization is equally simple.
We motivate the introduction of these constructions by showing that, when
![]() $\varepsilon \leq 1/2$
, any discrete
$\varepsilon \leq 1/2$
, any discrete
![]() $\varepsilon $
-approximate cocycle and any discrete
$\varepsilon $
-approximate cocycle and any discrete
![]() $\varepsilon $
-approximate local trivialization represent a true vector bundle on the geometric realization of K. Moreover, we prove a completeness result (Proposition 5.7), which says that any vector bundle over a compact triangulable space can be represented by a discrete approximate cocycle on a sufficiently fine triangulation of the space.
$\varepsilon $
-approximate local trivialization represent a true vector bundle on the geometric realization of K. Moreover, we prove a completeness result (Proposition 5.7), which says that any vector bundle over a compact triangulable space can be represented by a discrete approximate cocycle on a sufficiently fine triangulation of the space.
We remark here that the map
![]() $\mathsf {w}$
restricts to an algorithmic map from discrete approximate local trivializations to discrete approximate cocycles (Remark 5.6).
$\mathsf {w}$
restricts to an algorithmic map from discrete approximate local trivializations to discrete approximate cocycles (Remark 5.6).
Reconstruction from finite samples
Building on a result of Niyogi, Smale and Weinberger [Reference Partha Niyogi49], we prove a reconstruction result for vector bundles on compact, embedded manifolds. For readability, we give here a version of the result using big-
![]() $\mathcal {O}$
notation and an informal notion of
$\mathcal {O}$
notation and an informal notion of
![]() $(\varepsilon ,\delta )$
-closeness; a formal statement with precise bounds is given in Theorem 5.15. In the statement,
$(\varepsilon ,\delta )$
-closeness; a formal statement with precise bounds is given in Theorem 5.15. In the statement,
![]() $\mathsf {Gr}(d,n)$
is the Grassmannian of d-planes in
$\mathsf {Gr}(d,n)$
is the Grassmannian of d-planes in
![]() $\mathbb {R}^n$
, which we metrize using the Frobenius distance (Section 2.1.1).
$\mathbb {R}^n$
, which we metrize using the Frobenius distance (Section 2.1.1).
Theorem B. Let
![]() $\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold with reach
$\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold with reach
![]() $\tau> 0$
, and let
$\tau> 0$
, and let
![]() $f : \mathcal {M} \to \mathsf {Gr}(d,n)$
be
$f : \mathcal {M} \to \mathsf {Gr}(d,n)$
be
![]() $\ell $
-Lipschitz. Let
$\ell $
-Lipschitz. Let
![]() $P \subseteq \mathbb {R}^N$
be a finite set, and let
$P \subseteq \mathbb {R}^N$
be a finite set, and let
![]() $g : P \to \mathsf {Gr}(d,n)$
be a function such that
$g : P \to \mathsf {Gr}(d,n)$
be a function such that
![]() $(P,g)$
is
$(P,g)$
is
![]() $(\varepsilon ,\delta )$
-close to
$(\varepsilon ,\delta )$
-close to
![]() $(\mathcal {M},f)$
. If
$(\mathcal {M},f)$
. If
![]() $\alpha \in \left (\mathcal {O}(\varepsilon ), \tau - \mathcal {O}(\varepsilon )\right ) \cap \left (0,\sqrt {2}/4 \ell ^{-1} - 2\delta \ell ^{-1} - \varepsilon \right )$
, then there exists a homotopy commutative diagram as follows, in which the vertical maps are homotopy equivalences:
$\alpha \in \left (\mathcal {O}(\varepsilon ), \tau - \mathcal {O}(\varepsilon )\right ) \cap \left (0,\sqrt {2}/4 \ell ^{-1} - 2\delta \ell ^{-1} - \varepsilon \right )$
, then there exists a homotopy commutative diagram as follows, in which the vertical maps are homotopy equivalences:

Moreover, the map
![]() $\check{\mathsf{C}}(g)$
can be represented by a discrete local trivialization
$\check{\mathsf{C}}(g)$
can be represented by a discrete local trivialization
![]() $\Phi \in \mathsf {DT}_{2\ell \varepsilon + \delta }\left ( \check{\mathsf{C}}(P)(\varepsilon ); d \right )$
, in the sense that
$\Phi \in \mathsf {DT}_{2\ell \varepsilon + \delta }\left ( \check{\mathsf{C}}(P)(\varepsilon ); d \right )$
, in the sense that
![]() $\check{\mathsf{C}}(g) = \mathsf {av}(\Phi )$
.
$\check{\mathsf{C}}(g) = \mathsf {av}(\Phi )$
.
Applying
![]() $\mathsf {w}$
to the discrete local trivialization of Theorem B, we get an approximate cocycle that can be used to compute low-dimensional characteristic classes of the true vector bundle using the algorithms of Section 6, which we describe next. The extent to which the approximate cocycle
$\mathsf {w}$
to the discrete local trivialization of Theorem B, we get an approximate cocycle that can be used to compute low-dimensional characteristic classes of the true vector bundle using the algorithms of Section 6, which we describe next. The extent to which the approximate cocycle
![]() $\mathsf {w}(\Phi )$
recovers the true vector bundle f is made precise in Lemma 5.10; see also Remark 5.17.
$\mathsf {w}(\Phi )$
recovers the true vector bundle f is made precise in Lemma 5.10; see also Remark 5.17.
Effective computation of characteristic classes
Our last main contribution is the definition of algorithms for the stable and consistent computation of the one- and two-dimensional characteristic classes of a vector bundle given by an approximate
![]() $O(d)$
-cocycle.
$O(d)$
-cocycle.
The algorithms are based on well-known results which say that the characteristic classes we consider are obstructions to lifting the structure group of the cocycle from an orthogonal group to certain other Lie groups. In this sense, the algorithms are classical and most of our work goes into adapting them to the approximate setting and into giving precise bounds for their stability and consistency. The following theorem is a summary of the results in Section 6. In the theorem,
![]() $\check {\mathsf {H}}$
denotes Čech cohomology.
$\check {\mathsf {H}}$
denotes Čech cohomology.
Theorem C. Let
![]() $\mathcal {U}$
be a cover of a topological space B with the property that nonempty binary intersections are locally path connected and simply connected. There are maps
$\mathcal {U}$
be a cover of a topological space B with the property that nonempty binary intersections are locally path connected and simply connected. There are maps
 $$ \begin{align*} \mathsf{sw}_1 &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; O(d) \right) \to \check{\mathsf{H}}^{1}_{}\left( \mathcal{U}; \mathbb{Z}/2 \right) \text{ for }\varepsilon \leq 2;\\ \mathsf{sw}_2 &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; O(d) \right) \to \check{\mathsf{H}}^{2}_{}\left( \mathcal{U}; \mathbb{Z}/2 \right) \text{ for }\varepsilon \leq 1;\\ \mathsf{eu} &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; SO(2) \right) \to \check{\mathsf{H}}^{2}_{}\left( \mathcal{U}; \mathbb{Z} \right) \text{ for }\varepsilon \leq 1. \end{align*} $$
$$ \begin{align*} \mathsf{sw}_1 &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; O(d) \right) \to \check{\mathsf{H}}^{1}_{}\left( \mathcal{U}; \mathbb{Z}/2 \right) \text{ for }\varepsilon \leq 2;\\ \mathsf{sw}_2 &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; O(d) \right) \to \check{\mathsf{H}}^{2}_{}\left( \mathcal{U}; \mathbb{Z}/2 \right) \text{ for }\varepsilon \leq 1;\\ \mathsf{eu} &: \check{\mathsf{H}}^{1}_{\varepsilon}\left( \mathcal{U}; SO(2) \right) \to \check{\mathsf{H}}^{2}_{}\left( \mathcal{U}; \mathbb{Z} \right) \text{ for }\varepsilon \leq 1. \end{align*} $$
The map
![]() $\mathsf {sw}_1$
is
$\mathsf {sw}_1$
is
![]() $2$
-stable, in the sense that, if
$2$
-stable, in the sense that, if
![]() $\Omega , \Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
with
$\Omega , \Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
with
![]() $\varepsilon \leq 2$
, and
$\varepsilon \leq 2$
, and
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < 2$
, then
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < 2$
, then
![]() $\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. In this same sense, the maps
$\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. In this same sense, the maps
![]() $\mathsf {sw}_2$
and
$\mathsf {sw}_2$
and
![]() $\mathsf {eu}$
are
$\mathsf {eu}$
are
![]() $1$
-stable.
$1$
-stable.
Assume that
![]() $\mathcal {U}$
is countable and that B is paracompact and locally contractible. The map
$\mathcal {U}$
is countable and that B is paracompact and locally contractible. The map
![]() $\mathsf {sw}_1$
is
$\mathsf {sw}_1$
is
![]() $2/9$
-consistent, in the sense that, if
$2/9$
-consistent, in the sense that, if
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
with
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
with
![]() $\varepsilon < 2/9$
, then
$\varepsilon < 2/9$
, then
![]() $\mathsf {sw}_1(\Omega )$
is the first Stiefel–Whitney class of the vector bundle classified by
$\mathsf {sw}_1(\Omega )$
is the first Stiefel–Whitney class of the vector bundle classified by
![]() $\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
. In this same sense, the map
$\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
. In this same sense, the map
![]() $\mathsf {sw}_2$
is
$\mathsf {sw}_2$
is
![]() $1/9$
-consistent and computes the second Stiefel–Whitney class, and the map
$1/9$
-consistent and computes the second Stiefel–Whitney class, and the map
![]() $\mathsf {eu}$
is
$\mathsf {eu}$
is
![]() $1/9$
-consistent and computes the Euler class of an oriented vector bundle of rank
$1/9$
-consistent and computes the Euler class of an oriented vector bundle of rank
![]() $2$
.
$2$
.
We show that the maps of Theorem C are algorithmic when the input approximate cocycles are discrete approximate cocycles on a finite simplicial complex (see Tables 1-3). The time and space complexity of the algorithms is polynomial in the number of vertices of the simplicial complex. For
![]() $\mathsf {sw}_1$
, the complexity is also polynomial in d, while, for
$\mathsf {sw}_1$
, the complexity is also polynomial in d, while, for
![]() $\mathsf {sw}_2$
, the complexity is exponential in d and depends on calculating geodesic distances on the Spin group. In Section 6.4, we explain how to perform these calculations for small values of d.
$\mathsf {sw}_2$
, the complexity is exponential in d and depends on calculating geodesic distances on the Spin group. In Section 6.4, we explain how to perform these calculations for small values of d.
Table 1 Pseudocode for the algorithm
![]() $\mathsf {sw}_1$
.
$\mathsf {sw}_1$
.

Table 2 Pseudocode for the algorithm
![]() $\mathsf {eu}$
.
$\mathsf {eu}$
.

Table 3 Pseudocode for the algorithm
![]() $\mathsf {sw}_2$
.
$\mathsf {sw}_2$
.

Computational examples
We demonstrate our algorithms on data and show how they can be combined with persistent cohomology computations to obtain cohomological as well as bundle-theoretical information of the data; this is done in Section 7. A proof-of-concept implementation of our algorithms, together with code to replicate the examples, can be found at [Reference Scoccola and Perea56].
1.3 Related work
Cohomology of synchronization problems
Cohomological aspects of synchronization problems are discussed in [Reference Ye and Lim69, Reference Gao, Brodzki and Mukherjee19, Reference Hansen and Ghrist25].
In [Reference Gao, Brodzki and Mukherjee19], Gao, Brodzki and Mukherjee describe a general framework for studying cohomological obstructions to synchronization problems using principal G-bundles. Although useful in many practical applications, the approach is limited by the fact that it only encompasses so-called flat principal G-bundles, namely, bundles over a space B classified by group homomorphisms
![]() $\pi _1(B) \to G$
. To see that this is indeed a limitation, note that no nontrivial vector bundle over
$\pi _1(B) \to G$
. To see that this is indeed a limitation, note that no nontrivial vector bundle over
![]() $S^2$
can be represented by a group homomorphism
$S^2$
can be represented by a group homomorphism
![]() $\pi _1(S^2) \to O(d)$
since
$\pi _1(S^2) \to O(d)$
since
![]() $\pi _1(S^2) = 0$
. As mentioned previously, vector bundles over
$\pi _1(S^2) = 0$
. As mentioned previously, vector bundles over
![]() $S^2$
are central in the cryo-EM synchronization problem.
$S^2$
are central in the cryo-EM synchronization problem.
The fact that the cryo-EM bundles cannot be represented by discrete and exact
![]() $SO(2)$
-cocycles on a triangulation of
$SO(2)$
-cocycles on a triangulation of
![]() $S^2$
is observed by Ye and Lim in [Reference Ye and Lim69], where a solution to this problem is proposed in the special case of
$S^2$
is observed by Ye and Lim in [Reference Ye and Lim69], where a solution to this problem is proposed in the special case of
![]() $SO(2)$
-cocycles over a two-dimensional simplicial complex.
$SO(2)$
-cocycles over a two-dimensional simplicial complex.
Vector bundles over simplicial complexes
In [Reference Knöppel, Pinkall and Bobenko37], Knöppel and Pinkall give a method for describing arbitrary complex line bundles over finite simplicial complexes using a finite amount of data. They also describe applications to physics and computer graphics. Their theory relies on the fact that, up to isomorphism, a complex line bundle over a simplicial complex can be described exactly using a finite amount of data consisting of an angle
![]() $\eta _{ij} \in S^1$
(encoded as a complex number of absolute value
$\eta _{ij} \in S^1$
(encoded as a complex number of absolute value
![]() $1$
) for each edge
$1$
) for each edge
![]() $(ij)$
of the simplicial complex as well as a real number
$(ij)$
of the simplicial complex as well as a real number
![]() $\Omega _{ijk} \in \mathbb {R}$
for each
$\Omega _{ijk} \in \mathbb {R}$
for each
![]() $2$
-simplex
$2$
-simplex
![]() $(ijk)$
of the simplicial complex, which satisfy
$(ijk)$
of the simplicial complex, which satisfy
![]() $\eta _{ki} \eta _{jk} \eta _{ij} = e^{\iota \Omega _{ijk}}$
for every
$\eta _{ki} \eta _{jk} \eta _{ij} = e^{\iota \Omega _{ijk}}$
for every
![]() $2$
-simplex
$2$
-simplex
![]() $(ijk)$
, where
$(ijk)$
, where
![]() $\iota $
denotes the imaginary unit. This fact does not seem to generalize in a direct way to vector bundles of higher rank.
$\iota $
denotes the imaginary unit. This fact does not seem to generalize in a direct way to vector bundles of higher rank.
In [Reference Hansen and Ghrist25], Hansen and Ghrist discuss synchronization on networks and describe a framework based on cellular sheaves. The framework specializes to encompass flat vector bundles over a simplicial complex. This application of their theory has the same limitation as [Reference Gao, Brodzki and Mukherjee19]: By having the vector bundles be described by a family of matrices
![]() $\{\Omega _{ij}\}$
indexed by the edges of the simplicial complex, subject to the restriction that
$\{\Omega _{ij}\}$
indexed by the edges of the simplicial complex, subject to the restriction that
![]() $\Omega _{jk} \Omega _{ij} = \Omega _{ik}$
for every 2-simplex
$\Omega _{jk} \Omega _{ij} = \Omega _{ik}$
for every 2-simplex
![]() $(ijk)$
of the simplicial complex, only flat vector bundles can be described.
$(ijk)$
of the simplicial complex, only flat vector bundles can be described.
These two approaches require a certain equality to hold for each
![]() $2$
-simplex of the simplicial complex. The main difference between these approaches and the approach described in this paper is that we do not require an equality to hold for each
$2$
-simplex of the simplicial complex. The main difference between these approaches and the approach described in this paper is that we do not require an equality to hold for each
![]() $2$
-simplex; instead, we keep track of how much a certain equality does not hold.
$2$
-simplex; instead, we keep track of how much a certain equality does not hold.
Computation of characteristic classes
In [Reference Singer59], Singer and Wu describe an algorithm for the consistent estimation of the orientability of an embedded manifold. This can be interpreted as estimating whether
![]() $\mathsf {sw}_1(\Omega )$
is zero or not, where
$\mathsf {sw}_1(\Omega )$
is zero or not, where
![]() $\Omega $
is the approximate cocycle given by the transition functions of the approximate local trivialization defined using a local PCA computation, as sketched in Section 1.1.2. Their approach is robust to outliers, a property not enjoyed by the approach presented in this paper. But the algorithm does not provide the user with an actual cocycle and thus, in the case
$\Omega $
is the approximate cocycle given by the transition functions of the approximate local trivialization defined using a local PCA computation, as sketched in Section 1.1.2. Their approach is robust to outliers, a property not enjoyed by the approach presented in this paper. But the algorithm does not provide the user with an actual cocycle and thus, in the case
![]() $\mathsf {sw}_1(\Omega )$
is deemed to be nonzero by the algorithm, it is not clear how one can write it in a basis of the cohomology of a simplicial complex built from the data.
$\mathsf {sw}_1(\Omega )$
is deemed to be nonzero by the algorithm, it is not clear how one can write it in a basis of the cohomology of a simplicial complex built from the data.
In [Reference Tinarrage63], Tinarrage presents a framework for the consistent estimation of characteristic classes of vector bundles over embedded compact manifolds. The input data of the framework consist of the value of a sufficiently tame classifying map on a sufficiently dense sample of the manifold. Theoretical algorithms are given for the stable and consistent computation of arbitrary characteristic classes. The characteristic classes are computed in a geometric way, as the algorithm uses explicit triangulations of the Grassmannians and pulls back the universal characteristic classes to a simplicial complex built from the sample. The practicality of the algorithms is limited by the fact that the number of simplices required to triangulate a Grassmannian
![]() $\mathsf {Gr}(d,n)$
is exponential in both d and n [Reference Govc, Marzantowicz and Pavešić21] and the fact that the algorithm often requires iterated subdivisions of the simplicial complex built from the data.
$\mathsf {Gr}(d,n)$
is exponential in both d and n [Reference Govc, Marzantowicz and Pavešić21] and the fact that the algorithm often requires iterated subdivisions of the simplicial complex built from the data.
Vector bundles from finite samples
As mentioned above, in [Reference Tinarrage63] Tinarrage presents a framework for the consistent estimation of characteristic classes of a vector bundle, given a sample.
In [Reference Rieffel53], Rieffel addresses the problem of giving a precise correspondence between vector bundles on metric spaces X and Y that are at small Gromov–Hausdorff distance. In particular, one can use Rieffel’s framework to extend a vector bundle on a sample of a manifold to the entire manifold.
1.4 Structure of the paper
In Section 2, we give basic background. In Section 3, we present our three notions of approximate vector bundle, and in Section 4, we relate them to each other and to classical vector bundles. In particular, we prove Theorem 4.21 and Theorem 4.27. In Section 5, we introduce our notions of discrete approximate vector bundles and show that they can be used to represent vector bundles over triangulable spaces and to reconstruct vector bundles from finite samples. In Section 6, we give algorithms for the stable and consistent computation of low-dimensional characteristic classes starting from a discrete and approximate cocycle. In Section 7, we run our algorithms on examples. In Section 8, we discuss open questions.
2 Background
In this section, we introduce the basic background needed to state and prove the results in this paper. Some more technical definitions and results are in Appendix A. In Section 2.1, we introduce orthogonal groups, Grassmannians and Stiefel manifolds and fix notation. In Section 2.2, we recall some of the basics of the theory of principal bundles and vector bundles. We assume familiarity with the very basics of algebraic topology, including cohomology.
2.1 Orthogonal groups, Grassmannians and Stiefel manifolds
2.1.1 Main definitions
We start by recalling the definition of the Frobenius norm. Let
![]() $l,m \in \mathbb {N}_{\geq 1}$
, and let
$l,m \in \mathbb {N}_{\geq 1}$
, and let
![]() $\mathbb {R}^{l \times m}$
denote the set of
$\mathbb {R}^{l \times m}$
denote the set of
![]() $l \times m$
matrices with real coefficients. Let
$l \times m$
matrices with real coefficients. Let
![]() $A \in \mathbb {R}^{l \times m}$
. The Frobenius norm of A is defined by
$A \in \mathbb {R}^{l \times m}$
. The Frobenius norm of A is defined by
 $$\begin{align*}\| A\| = \sqrt{\operatorname{\mathrm{tr}}(A^t A)} = \sqrt{\sum_{ 1 \leq i \leq l, 1 \leq j \leq m} A_{ij}^2}, \end{align*}$$
$$\begin{align*}\| A\| = \sqrt{\operatorname{\mathrm{tr}}(A^t A)} = \sqrt{\sum_{ 1 \leq i \leq l, 1 \leq j \leq m} A_{ij}^2}, \end{align*}$$
where
![]() $A^t \in \mathbb {R}^{m \times l}$
denotes the transpose of A. The Frobenius norm, as any norm, induces a distance on
$A^t \in \mathbb {R}^{m \times l}$
denotes the transpose of A. The Frobenius norm, as any norm, induces a distance on
![]() $\mathbb {R}^{l \times m}$
defined by
$\mathbb {R}^{l \times m}$
defined by
![]() $\mathsf {d}_{\mathsf {Fr}}\left ( A, B \right ) = \|A - B\|$
. We refer to this distance as the Frobenius distance.
$\mathsf {d}_{\mathsf {Fr}}\left ( A, B \right ) = \|A - B\|$
. We refer to this distance as the Frobenius distance.
We now introduce the spaces of matrices we are most interested in. Let
![]() $n\geq d \geq 1 \in \mathbb {N}$
.
$n\geq d \geq 1 \in \mathbb {N}$
.
The Grassmannian
![]() $\mathsf {Gr}(d,n)$
has as elements the
$\mathsf {Gr}(d,n)$
has as elements the
![]() $n \times n$
real matrices A that satisfy
$n \times n$
real matrices A that satisfy
![]() $A = A^t = A^2$
and have rank equal to d and is thus a subset of
$A = A^t = A^2$
and have rank equal to d and is thus a subset of
![]() $\mathbb {R}^{n \times n}$
. We metrize and topologize
$\mathbb {R}^{n \times n}$
. We metrize and topologize
![]() $\mathsf {Gr}(d,n)$
using the Frobenius distance. Note that the elements of
$\mathsf {Gr}(d,n)$
using the Frobenius distance. Note that the elements of
![]() $\mathsf {Gr}(d,n)$
are canonically identified with the orthogonal projection operators
$\mathsf {Gr}(d,n)$
are canonically identified with the orthogonal projection operators
![]() $\mathbb {R}^n \to \mathbb {R}^n$
of rank d. Since these orthogonal projections are completely determined by the subspace of
$\mathbb {R}^n \to \mathbb {R}^n$
of rank d. Since these orthogonal projections are completely determined by the subspace of
![]() $\mathbb {R}^n$
which they span, it follows that the elements of
$\mathbb {R}^n$
which they span, it follows that the elements of
![]() $\mathsf {Gr}(d,n)$
correspond precisely to the d-dimensional subspaces of
$\mathsf {Gr}(d,n)$
correspond precisely to the d-dimensional subspaces of
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
The (compact) Stiefel manifold
![]() $\mathsf {V}(d,n)$
has as elements the set of
$\mathsf {V}(d,n)$
has as elements the set of
![]() $n \times d$
real matrices with orthonormal columns. We metrize
$n \times d$
real matrices with orthonormal columns. We metrize
![]() $\mathsf {V}(d,n)$
with the Frobenius distance. Note that the elements of
$\mathsf {V}(d,n)$
with the Frobenius distance. Note that the elements of
![]() $\mathsf {V}(d,n)$
can be identified with the d-dimensional subspaces of
$\mathsf {V}(d,n)$
can be identified with the d-dimensional subspaces of
![]() $\mathbb {R}^n$
equipped with an ordered orthonormal basis. The elements of a Stiefel manifold are sometimes referred to as frames.
$\mathbb {R}^n$
equipped with an ordered orthonormal basis. The elements of a Stiefel manifold are sometimes referred to as frames.
When
![]() $d = n$
, the Stiefel manifold
$d = n$
, the Stiefel manifold
![]() $\mathsf {V}(d,n)$
coincides with the orthogonal group
$\mathsf {V}(d,n)$
coincides with the orthogonal group
![]() $O(d)$
, which consists of real
$O(d)$
, which consists of real
![]() $d \times d$
matrices
$d \times d$
matrices
![]() $\Omega $
such that
$\Omega $
such that
![]() $\Omega \Omega ^t = \mathsf {id}$
. We metrize
$\Omega \Omega ^t = \mathsf {id}$
. We metrize
![]() $O(d)$
using the Frobenius distance. With this definition,
$O(d)$
using the Frobenius distance. With this definition,
![]() $O(d)$
is a topological group, as matrix multiplication and inversion are continuous.
$O(d)$
is a topological group, as matrix multiplication and inversion are continuous.
We remark here that, although we shall encounter other metrics for
![]() $O(d)$
and
$O(d)$
and
![]() $\mathsf {Gr}(d,n)$
, our main results are stated using the Frobenius distance. The relevant results about other metrics on the orthogonal group can be found in Appendix A.4, and the ones about other metrics on the Grassmannian are in Appendix A.4.
$\mathsf {Gr}(d,n)$
, our main results are stated using the Frobenius distance. The relevant results about other metrics on the orthogonal group can be found in Appendix A.4, and the ones about other metrics on the Grassmannian are in Appendix A.4.
2.1.2 Infinite-dimensional Grassmannians and Stiefel manifolds
Let
![]() $n\geq d \geq 1 \in \mathbb {N}$
. There is an inclusion
$n\geq d \geq 1 \in \mathbb {N}$
. There is an inclusion
![]() $\mathsf {Gr}(d,n) \subseteq \mathsf {Gr}(d,n+1)$
given by adding a row and a column of zeros at the bottom and right, respectively. This inclusion is norm-preserving and thus metric-preserving. We define the infinite-dimensional Grassmannian as
$\mathsf {Gr}(d,n) \subseteq \mathsf {Gr}(d,n+1)$
given by adding a row and a column of zeros at the bottom and right, respectively. This inclusion is norm-preserving and thus metric-preserving. We define the infinite-dimensional Grassmannian as
![]() $\mathsf {Gr}(d) = \bigcup _{n \in \mathbb {N}} \mathsf {Gr}(d,n)$
. We topologize
$\mathsf {Gr}(d) = \bigcup _{n \in \mathbb {N}} \mathsf {Gr}(d,n)$
. We topologize
![]() $\mathsf {Gr}(d)$
using the direct limit topology; recall that the direct limit topology on a union
$\mathsf {Gr}(d)$
using the direct limit topology; recall that the direct limit topology on a union
![]() $X = \bigcup _{n \in \mathbb {N}} X_n$
of topological spaces
$X = \bigcup _{n \in \mathbb {N}} X_n$
of topological spaces
![]() $\{X_n\}_{n \in \mathbb {N}}$
, where
$\{X_n\}_{n \in \mathbb {N}}$
, where
![]() $X_n$
is a subspace of
$X_n$
is a subspace of
![]() $X_{n+1}$
for all
$X_{n+1}$
for all
![]() $n \in \mathbb {N}$
, is the topology where
$n \in \mathbb {N}$
, is the topology where
![]() $A \subseteq X$
is open if and only if
$A \subseteq X$
is open if and only if
![]() $A \cap X_n$
is open in
$A \cap X_n$
is open in
![]() $X_n$
for all
$X_n$
for all
![]() $n \in \mathbb {N}$
. Note that this topology is finer (i.e., has more opens) than the topology induced by the metric inherited by
$n \in \mathbb {N}$
. Note that this topology is finer (i.e., has more opens) than the topology induced by the metric inherited by
![]() $\mathsf {Gr}(d)$
by virtue of it being an increasing union of metric spaces.
$\mathsf {Gr}(d)$
by virtue of it being an increasing union of metric spaces.
Similarly, we have an inclusion
![]() $\mathsf {V}(d,n) \subseteq \mathsf {V}(d,n+1)$
given by taking the matrix representation of a d-frame in
$\mathsf {V}(d,n) \subseteq \mathsf {V}(d,n+1)$
given by taking the matrix representation of a d-frame in
![]() $\mathbb {R}^n$
and adding a row of zeros at the bottom of the matrix. Again, these inclusions are metric preserving, and we define
$\mathbb {R}^n$
and adding a row of zeros at the bottom of the matrix. Again, these inclusions are metric preserving, and we define
![]() $\mathsf {V}(d) = \bigcup _{n \in \mathbb {N}} \mathsf {V}(d,n)$
, with the direct limit topology induced by the inclusions
$\mathsf {V}(d) = \bigcup _{n \in \mathbb {N}} \mathsf {V}(d,n)$
, with the direct limit topology induced by the inclusions
![]() $\mathsf {V}(d,n) \to \mathsf {V}(d)$
.
$\mathsf {V}(d,n) \to \mathsf {V}(d)$
.
There is a principal
![]() $O(d)$
-bundle
$O(d)$
-bundle
![]() $\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
, defined by mapping a d-frame M to the matrix
$\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
, defined by mapping a d-frame M to the matrix
![]() $MM^t$
(see Section 2.2.2 for the notion of principal bundle). Note that the maps
$MM^t$
(see Section 2.2.2 for the notion of principal bundle). Note that the maps
![]() $\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
for each
$\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
for each
![]() $n \geq 1$
assemble into a map
$n \geq 1$
assemble into a map
It is clear that
![]() $\mathsf {Proj}$
is continuous, as it restricts to a continuous map
$\mathsf {Proj}$
is continuous, as it restricts to a continuous map
![]() $\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
for each
$\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
for each
![]() $n \geq d$
.
$n \geq d$
.
2.1.3 Thickenings of Grassmannians
For the general notion of thickening and some basic properties, we refer the reader to Appendix A.1; here, we briefly introduce the thickenings of Grassmannians, as they play an important role in our results.
We will be interested in thickenings of Grassmannians, and for that we need to include Grassmannians into a larger metric space. A natural candidate is to let
![]() $\mathsf {Gr}(d,n) \subseteq \mathbb {R}^{n\times n}$
, which is metric preserving if we metrize
$\mathsf {Gr}(d,n) \subseteq \mathbb {R}^{n\times n}$
, which is metric preserving if we metrize
![]() $\mathbb {R}^{n\times n}$
using the Frobenius distance. Similarly, we have
$\mathbb {R}^{n\times n}$
using the Frobenius distance. Similarly, we have
![]() $\mathsf {V}(d,n) \subseteq \mathbb {R}^{n \times d}$
. Analogously to what we did for Grassmannians and Stiefel manifolds, we define
$\mathsf {V}(d,n) \subseteq \mathbb {R}^{n \times d}$
. Analogously to what we did for Grassmannians and Stiefel manifolds, we define
![]() $\mathbb {R}^{\infty \times \infty } := \bigcup _{n \in \mathbb {N}} \mathbb {R}^{n\times n}$
and
$\mathbb {R}^{\infty \times \infty } := \bigcup _{n \in \mathbb {N}} \mathbb {R}^{n\times n}$
and
![]() $\mathbb {R}^{\infty \times d} := \bigcup _{n \in \mathbb {N}} \mathbb {R}^{n \times d}$
.
$\mathbb {R}^{\infty \times d} := \bigcup _{n \in \mathbb {N}} \mathbb {R}^{n \times d}$
.
The elements of
![]() $\mathbb {R}^{\infty \times \infty }$
thus consist of infinite matrices with rows and columns indexed by the positive natural numbers, which have finite support, meaning that they have only finitely many nonzero entries. Similarly, the elements of
$\mathbb {R}^{\infty \times \infty }$
thus consist of infinite matrices with rows and columns indexed by the positive natural numbers, which have finite support, meaning that they have only finitely many nonzero entries. Similarly, the elements of
![]() $\mathbb {R}^{\infty \times d}$
are matrices with finite support, with d columns and rows indexed by the positive natural numbers. Again, although
$\mathbb {R}^{\infty \times d}$
are matrices with finite support, with d columns and rows indexed by the positive natural numbers. Again, although
![]() $\mathbb {R}^{\infty \times \infty }$
and
$\mathbb {R}^{\infty \times \infty }$
and
![]() $\mathbb {R}^{\infty \times d}$
inherit natural metrics, we use instead the direct limit topologies induced by inclusions
$\mathbb {R}^{\infty \times d}$
inherit natural metrics, we use instead the direct limit topologies induced by inclusions
![]() $\mathbb {R}^{n \times n} \to \mathbb {R}^{\infty \times \infty }$
and
$\mathbb {R}^{n \times n} \to \mathbb {R}^{\infty \times \infty }$
and
![]() $\mathbb {R}^{n \times d} \to \mathbb {R}^{\infty \times d}$
, respectively.
$\mathbb {R}^{n \times d} \to \mathbb {R}^{\infty \times d}$
, respectively.
Let
![]() $\varepsilon> 0$
. The
$\varepsilon> 0$
. The
![]() $\boldsymbol {\varepsilon }$
-thickening of
$\boldsymbol {\varepsilon }$
-thickening of
![]() $\mathsf {Gr}(d,n)$
, denoted
$\mathsf {Gr}(d,n)$
, denoted
![]() $\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathbb {R}^{n \times n}$
, consists of all matrices in
$\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathbb {R}^{n \times n}$
, consists of all matrices in
![]() $\mathbb {R}^{n \times n}$
at Frobenius distance strictly less than
$\mathbb {R}^{n \times n}$
at Frobenius distance strictly less than
![]() $\varepsilon $
from a matrix in
$\varepsilon $
from a matrix in
![]() $\mathsf {Gr}(d,n)$
. Similarly, we define
$\mathsf {Gr}(d,n)$
. Similarly, we define
![]() $\mathsf {Gr}(d)^\varepsilon \subseteq \mathbb {R}^{\infty \times \infty }$
. Clearly, we have
$\mathsf {Gr}(d)^\varepsilon \subseteq \mathbb {R}^{\infty \times \infty }$
. Clearly, we have
![]() $\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathsf {Gr}(d,n+1)^\varepsilon \subseteq \mathsf {Gr}(d)^\varepsilon $
. The
$\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathsf {Gr}(d,n+1)^\varepsilon \subseteq \mathsf {Gr}(d)^\varepsilon $
. The
![]() $\varepsilon $
-thickenings
$\varepsilon $
-thickenings
![]() $\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathbb {R}^{n\times n}$
and
$\mathsf {Gr}(d,n)^\varepsilon \subseteq \mathbb {R}^{n\times n}$
and
![]() $\mathsf {Gr}(d)^\varepsilon \subseteq \mathbb {R}^{\infty \times \infty }$
are open subsets. If
$\mathsf {Gr}(d)^\varepsilon \subseteq \mathbb {R}^{\infty \times \infty }$
are open subsets. If
![]() $\varepsilon = 0$
, it is convenient to define
$\varepsilon = 0$
, it is convenient to define
![]() $\mathsf {Gr}(d,n)^\varepsilon = \mathsf {Gr}(d,n)$
and
$\mathsf {Gr}(d,n)^\varepsilon = \mathsf {Gr}(d,n)$
and
![]() $\mathsf {Gr}(d)^\varepsilon = \mathsf {Gr}(d)$
.
$\mathsf {Gr}(d)^\varepsilon = \mathsf {Gr}(d)$
.
The main result about thickenings of Grassmannians we will need is Proposition A.12. The result follows directly from a result of Tinarrage (Lemma A.11) and says that, if
![]() $\varepsilon \leq \sqrt {2}/2$
, then
$\varepsilon \leq \sqrt {2}/2$
, then
![]() $\mathsf {Gr}(d,n)^\varepsilon $
deformation-retracts onto
$\mathsf {Gr}(d,n)^\varepsilon $
deformation-retracts onto
![]() $\mathsf {Gr}(d,n)$
.
$\mathsf {Gr}(d,n)$
.
2.2 Principal bundles and vector bundles
We recall the main notions and results that are relevant to this article. For a thorough exposition, we refer the reader to, for example, [38, Appendices A and B], [Reference Steenrod61], [Reference Husemöller34] and [Reference Husemöller, Joachim, Jurčo, Schottenloher, Echterhoff, Fredenhagen and Krötz33]. The classic book [Reference Milnor and Stasheff47] contains all of the standard results on vector bundles we need; see also [Reference Hatcher27] for a modern exposition.
2.2.1 Covers and nerve
A cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
of a topological space B consists of an indexing set I together with, for every
$\mathcal {U} = \{U_i\}_{i \in I}$
of a topological space B consists of an indexing set I together with, for every
![]() $i \in I$
, an open subset
$i \in I$
, an open subset
![]() $U_i \subseteq B$
such that
$U_i \subseteq B$
such that
![]() $B = \cup _{i \in I} U_i$
. The nerve of
$B = \cup _{i \in I} U_i$
. The nerve of
![]() $\mathcal {U}$
, denoted
$\mathcal {U}$
, denoted
![]() $N(\mathcal {U})$
, is the simplicial complex with underlying set I and simplices consisting of finite, nonempty subsets
$N(\mathcal {U})$
, is the simplicial complex with underlying set I and simplices consisting of finite, nonempty subsets
![]() $J \subseteq I$
such that
$J \subseteq I$
such that
![]() $\cap _{j \in J} U_j \neq \emptyset $
. An ordered simplex of
$\cap _{j \in J} U_j \neq \emptyset $
. An ordered simplex of
![]() $N(\mathcal {U})$
consists of a list
$N(\mathcal {U})$
consists of a list
![]() $(i_0 i_1 \dots i_n)$
such that
$(i_0 i_1 \dots i_n)$
such that
![]() $U_{i_n} \cap U_{i_{n-1}} \cap \dots \cap U_{i_0} \neq \emptyset $
. When quantifying over ordered
$U_{i_n} \cap U_{i_{n-1}} \cap \dots \cap U_{i_0} \neq \emptyset $
. When quantifying over ordered
![]() $1$
-simplices of
$1$
-simplices of
![]() $N(\mathcal {U})$
, we will write
$N(\mathcal {U})$
, we will write
![]() $(ij) \in N(\mathcal {U})$
, and, similarly, when quantifying over ordered
$(ij) \in N(\mathcal {U})$
, and, similarly, when quantifying over ordered
![]() $2$
-simplices of
$2$
-simplices of
![]() $N(\mathcal {U})$
we will write
$N(\mathcal {U})$
we will write
![]() $(ijk) \in N(\mathcal {U})$
.
$(ijk) \in N(\mathcal {U})$
.
2.2.2 Principal bundles
Let B and F be topological spaces. A fiber bundle over B with fiber F consists of a continuous map
![]() $p : E \to B$
such that, for every
$p : E \to B$
such that, for every
![]() $y \in B$
, there exists an open neighborhood
$y \in B$
, there exists an open neighborhood
![]() $U \subseteq B$
of y and a homeomorphism
$U \subseteq B$
of y and a homeomorphism
![]() $\rho _U : U \times F \to p^{-1}(U)$
such that
$\rho _U : U \times F \to p^{-1}(U)$
such that
![]() $p \circ \rho _U = \pi _1 : U \times F \to U$
, where
$p \circ \rho _U = \pi _1 : U \times F \to U$
, where
![]() $\pi _1$
denotes projection onto the first factor. Let
$\pi _1$
denotes projection onto the first factor. Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B. A collection of maps
$\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B. A collection of maps
![]() $\{\rho _i : U_i \times F \to p^{-1}(U_i)\}_{i \in I}$
with the property above is referred to as a local trivialization of p. By definition, any fiber bundle admits some local trivialization.
$\{\rho _i : U_i \times F \to p^{-1}(U_i)\}_{i \in I}$
with the property above is referred to as a local trivialization of p. By definition, any fiber bundle admits some local trivialization.
Let G be a topological group. A principal
![]() $\boldsymbol {G}$
-bundle over B consists of a fiber bundle
$\boldsymbol {G}$
-bundle over B consists of a fiber bundle
![]() $p : E \to B$
with fiber G together with a continuous, fiberwise right action
$p : E \to B$
with fiber G together with a continuous, fiberwise right action
![]() $- \cdot - : E \times G \to E$
such that there exists a cover
$- \cdot - : E \times G \to E$
such that there exists a cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
and a local trivialization
$\mathcal {U} = \{U_i\}_{i \in I}$
and a local trivialization
![]() $\{\rho _i : U_i \times G \to p^{-1}(U_i)\}_{i \in I}$
that is equivariant, meaning that, for every
$\{\rho _i : U_i \times G \to p^{-1}(U_i)\}_{i \in I}$
that is equivariant, meaning that, for every
![]() $g,h \in G$
and
$g,h \in G$
and
![]() $y \in U_i$
, we have
$y \in U_i$
, we have
![]() $\rho _i(y,g h) = \rho _i(y,g) \cdot h \in E$
.
$\rho _i(y,g h) = \rho _i(y,g) \cdot h \in E$
.
Two principal G-bundles
![]() $p : E \to B$
and
$p : E \to B$
and
![]() $p' : E' \to B$
are isomorphic if there exists a G-equivariant map
$p' : E' \to B$
are isomorphic if there exists a G-equivariant map
![]() $m : E \to E'$
such that
$m : E \to E'$
such that
![]() $p' \circ m = p$
. Denote by
$p' \circ m = p$
. Denote by
![]() $\mathsf {Prin}_G(B)$
the set of isomorphisms classes of principal G-bundles over B (this is a set and not a proper class).
$\mathsf {Prin}_G(B)$
the set of isomorphisms classes of principal G-bundles over B (this is a set and not a proper class).
We remark that the definitions we have given are sometimes referred to as locally trivial fiber bundle and locally trivial principal bundle.
2.2.3 Čech cocycles
Let B be a topological space, G a topological group and
![]() $\mathcal {U}$
a cover of B. A Čech
$\mathcal {U}$
a cover of B. A Čech
![]() $1$
-cocycle subordinate to
$1$
-cocycle subordinate to
![]() $\mathcal {U}$
with coefficients in G consists of a family of continuous maps
$\mathcal {U}$
with coefficients in G consists of a family of continuous maps
![]() $\{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
indexed by the ordered
$\{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
indexed by the ordered
![]() $1$
-simplices of
$1$
-simplices of
![]() $N(\mathcal {U})$
, which satisfies the cocycle condition, meaning that for every
$N(\mathcal {U})$
, which satisfies the cocycle condition, meaning that for every
![]() $(ijk) \in N(\mathcal {U})$
and
$(ijk) \in N(\mathcal {U})$
and
![]() $y \in U_k \cap U_j \cap U_i$
, we have
$y \in U_k \cap U_j \cap U_i$
, we have
We remark that we are using a convention for defining
![]() $\rho _{ij}$
so that
$\rho _{ij}$
so that
![]() $\rho _{ij}$
and
$\rho _{ij}$
and
![]() $\rho _{jk}$
can be composed from left to right. The opposite convention is also common. The set of
$\rho _{jk}$
can be composed from left to right. The opposite convention is also common. The set of
![]() $1$
-cocycles subordinate to
$1$
-cocycles subordinate to
![]() $\mathcal {U}$
with coefficients in G is denoted by
$\mathcal {U}$
with coefficients in G is denoted by
![]() $Z^1(\mathcal {U};G)$
.
$Z^1(\mathcal {U};G)$
.
The following construction associates a cocycle to any principal G-bundle and motivates the notion of cocycle. Given a principal G-bundle over B, there exists, by definition, a cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
and a family of G-equivariant local trivializations
$\mathcal {U} = \{U_i\}_{i \in I}$
and a family of G-equivariant local trivializations
![]() $\{\rho _i : U_i \times G \to p^{-1}(U_i)\}_{i \in I}$
. Note that, whenever
$\{\rho _i : U_i \times G \to p^{-1}(U_i)\}_{i \in I}$
. Note that, whenever
![]() $i,j \in I$
are such that
$i,j \in I$
are such that
![]() $U_j \cap U_i \neq \emptyset $
, the map
$U_j \cap U_i \neq \emptyset $
, the map
![]() $\rho _j^{-1} \circ \rho _i : (U_j \cap U_i) \times G \to (U_j \cap U_i) \times G$
is G-equivariant. It follows that
$\rho _j^{-1} \circ \rho _i : (U_j \cap U_i) \times G \to (U_j \cap U_i) \times G$
is G-equivariant. It follows that
![]() $\rho _j^{-1} \circ \rho _i$
induces a continuous map
$\rho _j^{-1} \circ \rho _i$
induces a continuous map
![]() $\rho _{ij} : U_j \cap U_i \to G$
satisfying
$\rho _{ij} : U_j \cap U_i \to G$
satisfying
![]() $(\rho _j^{-1}\circ \rho _i)(y,g) = (y, g \cdot \rho _{ij}(y))$
for all
$(\rho _j^{-1}\circ \rho _i)(y,g) = (y, g \cdot \rho _{ij}(y))$
for all
![]() $(y,g) \in (U_j \cap U_i) \times G$
, and that the family
$(y,g) \in (U_j \cap U_i) \times G$
, and that the family
![]() $\{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
satisfies the cocycle condition.
$\{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
satisfies the cocycle condition.
2.2.4 Čech cohomology
Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B. A Čech
$\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B. A Čech
![]() $\boldsymbol {0}$
-cochain subordinate to
$\boldsymbol {0}$
-cochain subordinate to
![]() $\mathcal {U}$
with values in G consists of a family of continuous maps
$\mathcal {U}$
with values in G consists of a family of continuous maps
![]() $\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
. Let
$\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
. Let
![]() $C^0(\mathcal {U};G)$
denote the set of
$C^0(\mathcal {U};G)$
denote the set of
![]() $0$
-cochains subordinate to
$0$
-cochains subordinate to
![]() $\mathcal {U}$
with values in G. There is an action
$\mathcal {U}$
with values in G. There is an action
![]() $C^0(\mathcal {U};G) \curvearrowright Z^1(\mathcal {U};G)$
with
$C^0(\mathcal {U};G) \curvearrowright Z^1(\mathcal {U};G)$
with
![]() $\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
acting on a cocycle
$\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
acting on a cocycle
![]() $\rho = \{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
by
$\rho = \{\rho _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
by
![]() $\Theta \cdot \rho = \{\Theta _i \rho _{ij} \Theta _j^{-1} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
. The quotient of
$\Theta \cdot \rho = \{\Theta _i \rho _{ij} \Theta _j^{-1} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
. The quotient of
![]() $Z^1(\mathcal {U};G)$
by the action of
$Z^1(\mathcal {U};G)$
by the action of
![]() $C^0(\mathcal {U};G)$
is denoted by
$C^0(\mathcal {U};G)$
is denoted by
![]() $\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right )$
.
$\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right )$
.
Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
and
$\mathcal {U} = \{U_i\}_{i \in I}$
and
![]() $\mathcal {V} = \{V_j\}_{j \in J}$
be two covers of a common topological space B. A refinement
$\mathcal {V} = \{V_j\}_{j \in J}$
be two covers of a common topological space B. A refinement
![]() $\nu : \mathcal {U} \to \mathcal {V}$
consists of a function
$\nu : \mathcal {U} \to \mathcal {V}$
consists of a function
![]() $\nu : I \to J$
such that for every
$\nu : I \to J$
such that for every
![]() $i \in I$
we have
$i \in I$
we have
![]() $U_i \subseteq V_{\nu (i)}$
. Given a refinement
$U_i \subseteq V_{\nu (i)}$
. Given a refinement
![]() $\nu : \mathcal {U} \to \mathcal {V}$
and
$\nu : \mathcal {U} \to \mathcal {V}$
and
![]() $\rho \in Z^1(\mathcal {V};G)$
, define a cocycle
$\rho \in Z^1(\mathcal {V};G)$
, define a cocycle
![]() $\nu (\rho ) \in Z^1(\mathcal {U};G)$
by
$\nu (\rho ) \in Z^1(\mathcal {U};G)$
by
![]() $\nu (\rho )_{ij} = \rho _{\nu (i)\nu (j)}$
. It is not hard to check that any two refinements
$\nu (\rho )_{ij} = \rho _{\nu (i)\nu (j)}$
. It is not hard to check that any two refinements
![]() $\nu , \nu ' : \mathcal {U} \to \mathcal {V}$
induce the same map
$\nu , \nu ' : \mathcal {U} \to \mathcal {V}$
induce the same map
![]() $\check {\mathsf {H}}^{1}_{}\left ( \mathcal {V}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right )$
. One then defines the Čech cohomology of B with coefficients in G as
$\check {\mathsf {H}}^{1}_{}\left ( \mathcal {V}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right )$
. One then defines the Čech cohomology of B with coefficients in G as
where the colimit is indexed by the poset whose objects are covers of B and where
![]() $\mathcal {V} \preceq \mathcal {U}$
if there exists a refinement
$\mathcal {V} \preceq \mathcal {U}$
if there exists a refinement
![]() $\mathcal {U} \to \mathcal {V}$
.
$\mathcal {U} \to \mathcal {V}$
.
As we saw previously, any principal G-bundle over B can be trivialized over some cover of B and induces a cocycle over that cover. It is well known, and easy to see, that this construction induces a bijection
For a description of principal G-bundles from this point of view, see [Reference Lawson and Michelsohn38, Appendix A].
2.2.5 Vector bundles
Let
![]() $d \in \mathbb {N}_{\geq 1}$
. A vector bundle of rank d over B consists of a fiber bundle
$d \in \mathbb {N}_{\geq 1}$
. A vector bundle of rank d over B consists of a fiber bundle
![]() $p : E \to B$
with fiber
$p : E \to B$
with fiber
![]() $\mathbb {R}^d$
, where each fiber comes with the structure of a real vector space of dimension d and such that p admits a local trivialization that is linear on each fiber.
$\mathbb {R}^d$
, where each fiber comes with the structure of a real vector space of dimension d and such that p admits a local trivialization that is linear on each fiber.
It follows that
![]() $\rho _j^{-1} \circ \rho _i$
induces a well-defined continuous map
$\rho _j^{-1} \circ \rho _i$
induces a well-defined continuous map
![]() $\rho _{ij} : U_j \cap U_i \to GL(d)$
satisfying
$\rho _{ij} : U_j \cap U_i \to GL(d)$
satisfying
![]() $(\rho _j^{-1}\circ \rho _i)(y,g) = (y, g \cdot \rho _{ij}(y))$
for all
$(\rho _j^{-1}\circ \rho _i)(y,g) = (y, g \cdot \rho _{ij}(y))$
for all
![]() $(y,g) \in (U_j \cap U_i) \times \mathbb {R}^d$
. So every vector bundle of rank d over B that trivializes over a cover
$(y,g) \in (U_j \cap U_i) \times \mathbb {R}^d$
. So every vector bundle of rank d over B that trivializes over a cover
![]() $\mathcal {U}$
gives a cocycle in
$\mathcal {U}$
gives a cocycle in
![]() $Z^1(\mathcal {U};GL(d))$
.
$Z^1(\mathcal {U};GL(d))$
.
An isomorphism between vector bundles
![]() $p : E \to B$
and
$p : E \to B$
and
![]() $p' : E' \to B$
consists of a fiberwise map
$p' : E' \to B$
consists of a fiberwise map
![]() $m : E \to E'$
that is a linear isomorphism on each fiber. The family of isomorphism classes of rank-d vector bundles over B is denoted by
$m : E \to E'$
that is a linear isomorphism on each fiber. The family of isomorphism classes of rank-d vector bundles over B is denoted by
![]() $\mathsf {Vect}_d(B)$
.
$\mathsf {Vect}_d(B)$
.
A partition of unity argument shows that, if B is paracompact (in the sense of [Reference Milnor and Stasheff47, Section 5.8]), the trivialization of a vector bundle on B can be taken so that the associated cocycle takes values in the orthogonal group. When B is paracompact, this gives a bijection
In particular,
![]() $\mathsf {Vect}_d(B) \cong \check {\mathsf {H}}^{1}_{}\left ( B; O(d) \right ) \cong \mathsf {Prin}_{O(d)}(B)$
.
$\mathsf {Vect}_d(B) \cong \check {\mathsf {H}}^{1}_{}\left ( B; O(d) \right ) \cong \mathsf {Prin}_{O(d)}(B)$
.
2.2.6 Classifying maps
For details about the claims in this section, see [Reference Milnor45, Theorem 3.1] for the existence of classifying spaces of topological groups and [Reference Lawson and Michelsohn38, Appendix B] for an account of classifying spaces of Lie groups.
For every topological group G, there exists a classifying space
![]() $\mathcal {B} G$
, which consists of a topological space with the property that, for every paracompact topological space B, there is a natural bijection
$\mathcal {B} G$
, which consists of a topological space with the property that, for every paracompact topological space B, there is a natural bijection
The classifying space of the orthogonal group
![]() $O(d)$
is the Grassmannian
$O(d)$
is the Grassmannian
![]() $\mathsf {Gr}(d)$
, and thus
$\mathsf {Gr}(d)$
, and thus
The map
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack \to \mathsf {Prin}_{O(d)}(B)$
is constructed as follows. Given
$\left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack \to \mathsf {Prin}_{O(d)}(B)$
is constructed as follows. Given
![]() $[f] \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
, let
$[f] \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
, let
![]() $f : B \to \mathsf {Gr}(d)$
be a representative. Then, the pullback of
$f : B \to \mathsf {Gr}(d)$
be a representative. Then, the pullback of
![]() $\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
along f is a principal
$\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
along f is a principal
![]() $O(d)$
-bundle over B, whose isomorphism type is independent of the choice of representative for
$O(d)$
-bundle over B, whose isomorphism type is independent of the choice of representative for
![]() $[f]$
.
$[f]$
.
2.2.7 Characteristic classes
Let G be a topological group, B a paracompact topological space and p be a principal G-bundle over B. Fix an abelian group A, and let
![]() $n \in \mathbb {N}$
. The bundle p can be represented by a continuous map
$n \in \mathbb {N}$
. The bundle p can be represented by a continuous map
![]() $f : B \to \mathcal {B} G$
, which can then be used to pull back any cohomology class
$f : B \to \mathcal {B} G$
, which can then be used to pull back any cohomology class
![]() $x \in H^n(\mathcal {B} G; A)$
to a class
$x \in H^n(\mathcal {B} G; A)$
to a class
![]() $f^*(x) \in H^n(B; A)$
. The cohomology classes
$f^*(x) \in H^n(B; A)$
. The cohomology classes
![]() $f^*(x)$
obtained in this way are the characteristic classes of the principal G-bundle p, and they are invariant under isomorphism of principal G-bundles. For a presentation of characteristic classes from this point of view, see [Reference Lawson and Michelsohn38, Appendix B].
$f^*(x)$
obtained in this way are the characteristic classes of the principal G-bundle p, and they are invariant under isomorphism of principal G-bundles. For a presentation of characteristic classes from this point of view, see [Reference Lawson and Michelsohn38, Appendix B].
The cohomology ring
![]() $H^\bullet (\mathsf {Gr}(d); \mathbb {Z}/2)$
is isomorphic to a polynomial ring
$H^\bullet (\mathsf {Gr}(d); \mathbb {Z}/2)$
is isomorphic to a polynomial ring
![]() $(\mathbb {Z}/2)[\sigma _1, \dots , \sigma _d]$
with
$(\mathbb {Z}/2)[\sigma _1, \dots , \sigma _d]$
with
![]() $\sigma _i \in H^i(\mathsf {Gr}(d); \mathbb {Z}/2)$
[Reference Milnor and Stasheff47, Section 7]. For
$\sigma _i \in H^i(\mathsf {Gr}(d); \mathbb {Z}/2)$
[Reference Milnor and Stasheff47, Section 7]. For
![]() $p : E \to B$
a rank-d vector bundle over a paracompact topological space B, one defines the ith Stiefel–Whitney class of p as the characteristic class corresponding to
$p : E \to B$
a rank-d vector bundle over a paracompact topological space B, one defines the ith Stiefel–Whitney class of p as the characteristic class corresponding to
![]() $\sigma _i \in H^i(\mathsf {Gr}(d); \mathbb {Z}/2)$
.
$\sigma _i \in H^i(\mathsf {Gr}(d); \mathbb {Z}/2)$
.
For any even
![]() $d \geq 1$
, there is a distinguished element
$d \geq 1$
, there is a distinguished element
![]() $e_d \in H^d(\mathcal {B} SO(d); \mathbb {Z})$
, the universal Euler class [Reference Milnor and Stasheff47, Section 9],[Reference Feshbach17, Theorem 1]. For
$e_d \in H^d(\mathcal {B} SO(d); \mathbb {Z})$
, the universal Euler class [Reference Milnor and Stasheff47, Section 9],[Reference Feshbach17, Theorem 1]. For
![]() $p : E \to B$
an oriented, rank-d vector bundle over a paracompact topological space B, which corresponds, up to isomorphism, to an principal
$p : E \to B$
an oriented, rank-d vector bundle over a paracompact topological space B, which corresponds, up to isomorphism, to an principal
![]() $SO(d)$
-bundle, one defines the Euler class of p as the characteristic class corresponding to
$SO(d)$
-bundle, one defines the Euler class of p as the characteristic class corresponding to
![]() $e_d \in H^d(\mathcal {B} SO(d); \mathbb {Z})$
. We remark that the Euler class can be defined for odd d too, but in this case it is often less useful as, for odd d, we have
$e_d \in H^d(\mathcal {B} SO(d); \mathbb {Z})$
. We remark that the Euler class can be defined for odd d too, but in this case it is often less useful as, for odd d, we have
![]() $2 e_d = 0$
[Reference Milnor and Stasheff47, Property 9.4].
$2 e_d = 0$
[Reference Milnor and Stasheff47, Property 9.4].
3 Three notions of approximate vector bundle
In this section, we introduce relaxations of three standard definitions of vector bundle. The base space of our bundles will be denoted by B and a typical element will usually be denoted by
![]() $y \in B$
.
$y \in B$
.
The classical notions of vector bundle that we consider are those of a vector bundle given by an
![]() $O(d)$
-valued Čech cocycle, a vector bundle given by a family of compatible maps from opens of a cover of B to the Stiefel manifold
$O(d)$
-valued Čech cocycle, a vector bundle given by a family of compatible maps from opens of a cover of B to the Stiefel manifold
![]() $\mathsf {V}(d)$
, which we interpret as a local trivialization; and a vector bundle given by a continuous map from B to the Grassmannian
$\mathsf {V}(d)$
, which we interpret as a local trivialization; and a vector bundle given by a continuous map from B to the Grassmannian
![]() $\mathsf {Gr}(d)$
.
$\mathsf {Gr}(d)$
.
The reader may be more familiar with the notion of vector bundle given by a
![]() $GL(d)$
-valued cocycle. Being able to lift the structure group from
$GL(d)$
-valued cocycle. Being able to lift the structure group from
![]() $GL(d)$
to
$GL(d)$
to
![]() $O(d)$
corresponds to endowing the vector bundle with a compatible, fiberwise inner product. Vector bundles endowed with this extra structure are sometimes referred to as Euclidean vector bundles. Any vector bundle over a paracompact space can be endowed with an inner product in an essentially unique way [Reference Milnor and Stasheff47, Problems 2-C and 2-E], and thus is isomorphic to the underlying vector bundle of a Euclidean vector bundle. The main reason for working with Euclidean vector bundles is that, for many choices of distance on the orthogonal group
$O(d)$
corresponds to endowing the vector bundle with a compatible, fiberwise inner product. Vector bundles endowed with this extra structure are sometimes referred to as Euclidean vector bundles. Any vector bundle over a paracompact space can be endowed with an inner product in an essentially unique way [Reference Milnor and Stasheff47, Problems 2-C and 2-E], and thus is isomorphic to the underlying vector bundle of a Euclidean vector bundle. The main reason for working with Euclidean vector bundles is that, for many choices of distance on the orthogonal group
![]() $O(d)$
, the group acts on itself by isometries. This is not the case for
$O(d)$
, the group acts on itself by isometries. This is not the case for
![]() $GL(d)$
.
$GL(d)$
.
3.1 Approximate cocycles
The notion of approximate cocycle makes sense for any metric group, which we define next. This extra generality makes some arguments clearer and will be of use in Section 6.1.
Definition 3.1. A metric group consists of a group G endowed with the structure of a metric space such that left and right multiplication by any fixed element
![]() $g \in G$
, and taking inverse are all isometries
$g \in G$
, and taking inverse are all isometries
![]() $G \to G$
.
$G \to G$
.
The main example of metric group to keep in mind is that of the orthogonal group
![]() $O(d)$
endowed with the Frobenius distance. Other relevant examples include all connected Lie groups endowed with the geodesic distance induced by a bi-invariant Riemannian metric; recall that all compact Lie groups, such as the orthogonal groups, the unitary groups and the compact symplectic groups, admit a bi-invariant Riemannian metric (see, e.g., [Reference Milnor46, Corollary 1.4]). It is also relevant to note that the Frobenius distance on
$O(d)$
endowed with the Frobenius distance. Other relevant examples include all connected Lie groups endowed with the geodesic distance induced by a bi-invariant Riemannian metric; recall that all compact Lie groups, such as the orthogonal groups, the unitary groups and the compact symplectic groups, admit a bi-invariant Riemannian metric (see, e.g., [Reference Milnor46, Corollary 1.4]). It is also relevant to note that the Frobenius distance on
![]() $O(d)$
does not arise as the geodesic distance induced by a Riemannian metric; Section A.4 deals with some of the relationships between the Frobenius distance and the (usual) geodesic distance on
$O(d)$
does not arise as the geodesic distance induced by a Riemannian metric; Section A.4 deals with some of the relationships between the Frobenius distance and the (usual) geodesic distance on
![]() $O(d)$
.
$O(d)$
.
Let G be a metric group and let us denote its distance by
![]() $d_G : G \times G \to \mathbb {R}$
. Let B be a topological space and let
$d_G : G \times G \to \mathbb {R}$
. Let B be a topological space and let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B.
$\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of B.
Definition 3.2. A
![]() $\boldsymbol {1}$
-cochain on B subordinate to
$\boldsymbol {1}$
-cochain on B subordinate to
![]() $\mathcal {U}$
with values in G consists of a family of continuous maps
$\mathcal {U}$
with values in G consists of a family of continuous maps
![]() $\Omega = \{\Omega _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
indexed by the ordered
$\Omega = \{\Omega _{ij} : U_j \cap U_i \to G\}_{(ij) \in N(\mathcal {U})}$
indexed by the ordered
![]() $1$
-simplices of
$1$
-simplices of
![]() $N(\mathcal {U})$
that is symmetric, that is, such that for all
$N(\mathcal {U})$
that is symmetric, that is, such that for all
![]() $(ij) \in N(\mathcal {U})$
and
$(ij) \in N(\mathcal {U})$
and
![]() $y \in U_j \cap U_i$
we have
$y \in U_j \cap U_i$
we have
![]() $\Omega _{ij}(y) = \Omega _{ji}(y)^{-1}$
.
$\Omega _{ij}(y) = \Omega _{ji}(y)^{-1}$
.
We denote the set of all
![]() $1$
-cochains on B subordinate to
$1$
-cochains on B subordinate to
![]() $\mathcal {U}$
with values in G by
$\mathcal {U}$
with values in G by
![]() $C^1(\mathcal {U};G)$
. If there is no risk of confusion, we may refer to an element of
$C^1(\mathcal {U};G)$
. If there is no risk of confusion, we may refer to an element of
![]() $C^1(\mathcal {U};G)$
simply as a cochain subordinate to
$C^1(\mathcal {U};G)$
simply as a cochain subordinate to
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Definition 3.3. Let
![]() $\varepsilon \in (0,\infty ]$
. A cochain
$\varepsilon \in (0,\infty ]$
. A cochain
![]() $\Omega $
subordinate to
$\Omega $
subordinate to
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\boldsymbol {\varepsilon }$
-approximate cocycle if for every
$\boldsymbol {\varepsilon }$
-approximate cocycle if for every
![]() $(ijk) \in N(\mathcal {U})$
and every
$(ijk) \in N(\mathcal {U})$
and every
![]() $y \in U_k \cap U_j \cap U_i$
we have
$y \in U_k \cap U_j \cap U_i$
we have
![]() $d_G\left (\Omega _{ij}(y) \Omega _{jk}(y), \Omega _{ik}(y)\right ) < \varepsilon $
, and an exact cocycle if we have
$d_G\left (\Omega _{ij}(y) \Omega _{jk}(y), \Omega _{ik}(y)\right ) < \varepsilon $
, and an exact cocycle if we have
![]() $\Omega _{ij}(y) \Omega _{jk}(y) = \Omega _{ik}(y)$
.
$\Omega _{ij}(y) \Omega _{jk}(y) = \Omega _{ik}(y)$
.
We denote the set of
![]() $\varepsilon $
-approximate cocycles by
$\varepsilon $
-approximate cocycles by
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \subseteq C^1(\mathcal {U};G)$
, and the set of exact cocycles by either
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \subseteq C^1(\mathcal {U};G)$
, and the set of exact cocycles by either
![]() $\mathsf {Z}^{1}_{0}\left ( \mathcal {U}; G \right )$
or simply
$\mathsf {Z}^{1}_{0}\left ( \mathcal {U}; G \right )$
or simply
![]() $\mathsf {Z}^{1}_{}\left ( \mathcal {U}; G \right )$
. Of course, when
$\mathsf {Z}^{1}_{}\left ( \mathcal {U}; G \right )$
. Of course, when
![]() $\varepsilon = \infty $
,
$\varepsilon = \infty $
,
![]() $\varepsilon $
-approximate cocycles are merely cochains, so to keep notation uniform, we denote
$\varepsilon $
-approximate cocycles are merely cochains, so to keep notation uniform, we denote
![]() $C^1(\mathcal {U};G)$
by
$C^1(\mathcal {U};G)$
by
![]() $\mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
. We endow the set
$\mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
. We endow the set
![]() $\mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
with the metric given by
$\mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
with the metric given by
for
![]() $\Omega ,\Lambda \in \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
. This induces a metric on all spaces of approximate and exact cocycles. In particular, for
$\Omega ,\Lambda \in \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
. This induces a metric on all spaces of approximate and exact cocycles. In particular, for
![]() $\varepsilon \leq \varepsilon '$
, we have metric embeddings
$\varepsilon \leq \varepsilon '$
, we have metric embeddings
Definition 3.4. A
![]() $\boldsymbol {0}$
-cochain subordinate to
$\boldsymbol {0}$
-cochain subordinate to
![]() $\mathcal {U}$
with values in G consists of a family of continuous maps
$\mathcal {U}$
with values in G consists of a family of continuous maps
![]() $\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
.
$\Theta = \{\Theta _i : U_i \to G\}_{i \in I}$
.
We denote the set of all
![]() $0$
-cochains by
$0$
-cochains by
![]() $C^0(\mathcal {U};G)$
. The set
$C^0(\mathcal {U};G)$
. The set
![]() $C^0(\mathcal {U};G)$
forms a group, by pointwise multiplication. There is an action
$C^0(\mathcal {U};G)$
forms a group, by pointwise multiplication. There is an action
![]() $C^0(\mathcal {U};G) \curvearrowright \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
with
$C^0(\mathcal {U};G) \curvearrowright \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
with
![]() $\Theta $
acting on
$\Theta $
acting on
![]() $\Omega $
by
$\Omega $
by
for every
![]() $y \in U_j \cap U_i$
. Since G acts on itself by isometries, the above action restricts to an action on
$y \in U_j \cap U_i$
. Since G acts on itself by isometries, the above action restricts to an action on
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
for every
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
for every
![]() $\varepsilon \geq 0$
.
$\varepsilon \geq 0$
.
Definition 3.5. Let
![]() $\varepsilon \in [0,\infty ]$
. Define the
$\varepsilon \in [0,\infty ]$
. Define the
![]() $\boldsymbol {\varepsilon }$
-approximate cohomology set
$\boldsymbol {\varepsilon }$
-approximate cohomology set
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
as the quotient of
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
as the quotient of
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
by the action of
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
by the action of
![]() $C^0(\mathcal {U};G)$
.
$C^0(\mathcal {U};G)$
.
Notation 3.6. We denote a typical element of
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
by
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
by
![]() $\Omega $
, or by
$\Omega $
, or by
![]() $[\Omega ]$
if we want to refer to the equivalence class of an approximate cocycle
$[\Omega ]$
if we want to refer to the equivalence class of an approximate cocycle
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
. In the latter case, we say that the approximate cocycle
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
. In the latter case, we say that the approximate cocycle
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
is a representative of the approximate cohomology class
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
is a representative of the approximate cohomology class
![]() $[\Omega ] \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
.
$[\Omega ] \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
.
Since the action
![]() $C^0(\mathcal {U};G) \curvearrowright \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
is by isometries, the set
$C^0(\mathcal {U};G) \curvearrowright \mathsf {Z}^{1}_{\infty }\left ( \mathcal {U}; G \right )$
is by isometries, the set
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
inherits a metric
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
inherits a metric
![]() $\mathsf {d}_{\check {\mathsf {H}}}$
from
$\mathsf {d}_{\check {\mathsf {H}}}$
from
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, given as follows. For
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, given as follows. For
![]() $\Omega ,\Lambda \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, we have
$\Omega ,\Lambda \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, we have
where
![]() $\overline {\Omega }$
and
$\overline {\Omega }$
and
![]() $\overline {\Lambda }$
range over all representatives of
$\overline {\Lambda }$
range over all representatives of
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
, respectively.
$\Lambda $
, respectively.
Remark 3.7. Although we will not use this in what follows, we remark that, for
![]() $\mathcal {U}$
a cover of a topological space and G a metric group, we have constructed a filtered (or persistent) metric space
$\mathcal {U}$
a cover of a topological space and G a metric group, we have constructed a filtered (or persistent) metric space
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, parametrized by
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, parametrized by
![]() $\varepsilon \in [0,\infty ]$
, which one can interpret as a functor
$\varepsilon \in [0,\infty ]$
, which one can interpret as a functor
![]() $\check {\mathsf {H}}^{1}_{-}\left ( \mathcal {U}; G \right ) : ([0,\infty ], \leq ) \to \mathbf {Met}$
.
$\check {\mathsf {H}}^{1}_{-}\left ( \mathcal {U}; G \right ) : ([0,\infty ], \leq ) \to \mathbf {Met}$
.
3.2 Approximate local trivializations
We start with some considerations about the notion of local trivialization of a vector bundle (Section 2.2.5), which motivate our notion of approximate local trivialization. Any rank-d Euclidean vector bundle
![]() $p : E \to B$
admits an isometric local trivialization, that is, a local trivialization over an open cover
$p : E \to B$
admits an isometric local trivialization, that is, a local trivialization over an open cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
of B given by a family of homeomorphisms
$\mathcal {U} = \{U_i\}_{i \in I}$
of B given by a family of homeomorphisms
![]() $\{U_i \times \mathbb {R}^d \to p^{-1}(U_i) \}_{i \in I}$
with the property that, given
$\{U_i \times \mathbb {R}^d \to p^{-1}(U_i) \}_{i \in I}$
with the property that, given
![]() $y \in U_i$
, we obtain an orthonormal basis of the vector space
$y \in U_i$
, we obtain an orthonormal basis of the vector space
![]() $p^{-1}(y)$
by evaluating the map
$p^{-1}(y)$
by evaluating the map
![]() $U_i \times \mathbb {R}^d \to p^{-1}(U_i)$
on
$U_i \times \mathbb {R}^d \to p^{-1}(U_i)$
on
![]() $(y,e_j)$
for
$(y,e_j)$
for
![]() $1 \leq j \leq d$
, where
$1 \leq j \leq d$
, where
![]() $e_j$
is the jth canonical basis vector of
$e_j$
is the jth canonical basis vector of
![]() $\mathbb {R}^d$
. Recall that any vector bundle over a paracompact base B is classified by some continuous map
$\mathbb {R}^d$
. Recall that any vector bundle over a paracompact base B is classified by some continuous map
![]() $B \to \mathsf {Gr}(d)$
(Section 2.2.6). This implies, in particular, that, up to isomorphism of vector bundles, any vector bundle
$B \to \mathsf {Gr}(d)$
(Section 2.2.6). This implies, in particular, that, up to isomorphism of vector bundles, any vector bundle
![]() $p : E \to B$
over a paracompact base is a Euclidean vector bundle whose fibers
$p : E \to B$
over a paracompact base is a Euclidean vector bundle whose fibers
![]() $p^{-1}(y)$
that are not just abstract vector spaces, but d-dimensional subspaces of
$p^{-1}(y)$
that are not just abstract vector spaces, but d-dimensional subspaces of
![]() $\mathbb {R}^\infty $
.
$\mathbb {R}^\infty $
.
With the above in mind, any isometric local trivialization of a Euclidean vector bundle over a paracompact base B gives us maps
![]() $\{\Phi _i : U_i \to \mathsf {V}(d)\}$
, where, as in Section 2.1.1, the space
$\{\Phi _i : U_i \to \mathsf {V}(d)\}$
, where, as in Section 2.1.1, the space
![]() $\mathsf {V}(d)$
stands for the Stiefel manifold of d-frames in
$\mathsf {V}(d)$
stands for the Stiefel manifold of d-frames in
![]() $\mathbb {R}^\infty $
. One can check that a family of maps
$\mathbb {R}^\infty $
. One can check that a family of maps
![]() $\{\Phi _i : U_i \to \mathsf {V}(d)\}_{i \in I}$
comes from a vector bundle over B precisely when, for every intersection
$\{\Phi _i : U_i \to \mathsf {V}(d)\}_{i \in I}$
comes from a vector bundle over B precisely when, for every intersection
![]() $U_j \cap U_i \neq \emptyset $
and every
$U_j \cap U_i \neq \emptyset $
and every
![]() $y \in U_j \cap U_i$
, we have that
$y \in U_j \cap U_i$
, we have that
![]() $\Phi _i(y)$
and
$\Phi _i(y)$
and
![]() $\Phi _j(y)$
span the same subspace of
$\Phi _j(y)$
span the same subspace of
![]() $\mathbb {R}^\infty $
and thus, equivalently, when there exist continuous maps
$\mathbb {R}^\infty $
and thus, equivalently, when there exist continuous maps
![]() $\{\Omega _{ij} : U_j \cap U_i \to O(d)\}_{(ij) \in N(\mathcal {U})}$
such that
$\{\Omega _{ij} : U_j \cap U_i \to O(d)\}_{(ij) \in N(\mathcal {U})}$
such that
![]() $\Phi _i(y) \Omega _{ij}(y) = \Phi _j(y)$
for all
$\Phi _i(y) \Omega _{ij}(y) = \Phi _j(y)$
for all
![]() $y \in U_j \cap U_i$
. Our notion of approximate local trivialization is based on this last equivalent characterization of local trivializations and, specifically, on relaxing this last equality.
$y \in U_j \cap U_i$
. Our notion of approximate local trivialization is based on this last equivalent characterization of local trivializations and, specifically, on relaxing this last equality.
Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of a topological space B.
$\mathcal {U} = \{U_i\}_{i \in I}$
be a cover of a topological space B.
Definition 3.8. Let
![]() $\varepsilon \in (0,\infty ]$
. An
$\varepsilon \in (0,\infty ]$
. An
![]() $\boldsymbol {\varepsilon }$
-approximate local trivialization subordinate to
$\boldsymbol {\varepsilon }$
-approximate local trivialization subordinate to
![]() $\mathcal {U}$
consists of a family of continuous maps
$\mathcal {U}$
consists of a family of continuous maps
![]() $\Phi = \{\Phi _i : U_i \to \mathsf {V}(d)\}_{i \in I}$
such that, for every
$\Phi = \{\Phi _i : U_i \to \mathsf {V}(d)\}_{i \in I}$
such that, for every
![]() $(ij) \in N(\mathcal {U})$
, there exists a continuous map
$(ij) \in N(\mathcal {U})$
, there exists a continuous map
![]() $\Omega _{ij} : U_j \cap U_i \to O(d)$
such that, for every
$\Omega _{ij} : U_j \cap U_i \to O(d)$
such that, for every
![]() $y \in U_j \cap U_i$
, we have
$y \in U_j \cap U_i$
, we have
![]() $\| \Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| < \varepsilon $
. An exact local trivialization is an approximate local trivialization for which
$\| \Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| < \varepsilon $
. An exact local trivialization is an approximate local trivialization for which
![]() $\Phi _i(y) \Omega _{ij}(y) = \Phi _j(y)$
.
$\Phi _i(y) \Omega _{ij}(y) = \Phi _j(y)$
.
We say that the family
![]() $\Omega = \{\Omega _{ij}\}_{(ij) \in N(\mathcal {U})}$
in Definition 3.8 is a witness of the fact that
$\Omega = \{\Omega _{ij}\}_{(ij) \in N(\mathcal {U})}$
in Definition 3.8 is a witness of the fact that
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate (or exact) local trivialization. We remark that this witness is not part of the data of an
$\varepsilon $
-approximate (or exact) local trivialization. We remark that this witness is not part of the data of an
![]() $\varepsilon $
-approximate local trivialization and that we merely require that a witness exists.
$\varepsilon $
-approximate local trivialization and that we merely require that a witness exists.
An approximate local trivialization consists of an
![]() $\varepsilon $
-approximate local trivialization for some
$\varepsilon $
-approximate local trivialization for some
![]() $\varepsilon \in [0,\infty ]$
. We denote the set of
$\varepsilon \in [0,\infty ]$
. We denote the set of
![]() $\varepsilon $
-approximate local trivializations subordinate to
$\varepsilon $
-approximate local trivializations subordinate to
![]() $\mathcal {U}$
by
$\mathcal {U}$
by
![]() $\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
. We define a metric on
$\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
. We define a metric on
![]() $\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
by
$\mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
by
An approximate local trivialization
![]() $\{\Phi _i\}_{i \in I}$
is nondegenerate if, for every
$\{\Phi _i\}_{i \in I}$
is nondegenerate if, for every
![]() $(ij) \in N(\mathcal {U})$
and every
$(ij) \in N(\mathcal {U})$
and every
![]() $y \in U_j \cap U_i$
, the
$y \in U_j \cap U_i$
, the
![]() $d\times d$
matrix
$d\times d$
matrix
![]() $\Phi _i(y)^t \Phi _j(y)$
has full rank.
$\Phi _i(y)^t \Phi _j(y)$
has full rank.
3.3 Approximate classifying maps
Recall from Section 2.1.3 the definition of the thickened Grassmannians, and recall, in particular, that the topology of
![]() $\mathsf {Gr}(d)^\varepsilon $
is the direct limit topology and not the one induced by the Frobenius metric. Let B be a topological space.
$\mathsf {Gr}(d)^\varepsilon $
is the direct limit topology and not the one induced by the Frobenius metric. Let B be a topological space.
Definition 3.9. An
![]() $\boldsymbol {\varepsilon }$
-approximate classifying map consists of a continuous map
$\boldsymbol {\varepsilon }$
-approximate classifying map consists of a continuous map
![]() $B \to \mathsf {Gr}(d)^\varepsilon $
.
$B \to \mathsf {Gr}(d)^\varepsilon $
.
The set of
![]() $\varepsilon $
-approximate classifying maps is denoted by
$\varepsilon $
-approximate classifying maps is denoted by
![]() $\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
. We define a metric on this set by
$\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
. We define a metric on this set by
We are also interested in the set of classifying maps up to homotopy, which we denote by
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. Although we will not make use of this fact, we mention that one can interpret this as a persistent set
$\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. Although we will not make use of this fact, we mention that one can interpret this as a persistent set
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{-}} \right \rbrack : ([0,\infty ], \leq ) \to \mathbf {Set}$
, in the sense of [Reference Curry15, Definition 2.2]. The following result is easily proven using a linear homotopy.
$\left \lbrack {B}, {\mathsf {Gr}(d)^{-}} \right \rbrack : ([0,\infty ], \leq ) \to \mathbf {Set}$
, in the sense of [Reference Curry15, Definition 2.2]. The following result is easily proven using a linear homotopy.
Lemma 3.10. Let
![]() $f,g \in \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
, and let
$f,g \in \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right )$
, and let
![]() $[f]$
and
$[f]$
and
![]() $[g]$
denote their images in
$[g]$
denote their images in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. Let
$\left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
. Let
![]() $\delta> 0$
. If
$\delta> 0$
. If
![]() $\|f(y) - g(y)\| < \delta $
for all
$\|f(y) - g(y)\| < \delta $
for all
![]() $y \in B$
, then
$y \in B$
, then
![]() $[f]$
and
$[f]$
and
![]() $[g]$
become equal in
$[g]$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon + \delta }} \right \rbrack $
. In particular, if
$\left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon + \delta }} \right \rbrack $
. In particular, if
![]() $\mathsf {d}_{\mathsf {C}}\left ( f, g \right ) < \delta $
, then
$\mathsf {d}_{\mathsf {C}}\left ( f, g \right ) < \delta $
, then
![]() $[f]$
and
$[f]$
and
![]() $[g]$
become equal in
$[g]$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon + \delta }} \right \rbrack $
.
$\left \lbrack {B}, {\mathsf {Gr}(d)^{\varepsilon + \delta }} \right \rbrack $
.
4 Relationships between the notions
We now consider the problem of going back and forth between the different notions of approximate vector bundle. As a consequence of this study, we relate approximate vector bundles to true (exact) vector bundles. In particular, this lets us extract a true vector bundle from an
![]() $\varepsilon $
-approximate vector bundle when
$\varepsilon $
-approximate vector bundle when
![]() $\varepsilon $
is sufficiently small.
$\varepsilon $
is sufficiently small.
There are two main results in this section. Theorem 4.21 associates an approximate classifying map to any approximate cocycle and lets us, in particular, assign a true vector bundle to any
![]() $\varepsilon $
-approximate cocycle as long as
$\varepsilon $
-approximate cocycle as long as
![]() $\varepsilon \leq 1/2$
. This is done in a way that is stable and independent of arbitrary choices. Theorem 4.27 gives an upper bound for the distance from an
$\varepsilon \leq 1/2$
. This is done in a way that is stable and independent of arbitrary choices. Theorem 4.27 gives an upper bound for the distance from an
![]() $\varepsilon $
-approximate cocycle to an exact cocycle representing the same true vector bundle when
$\varepsilon $
-approximate cocycle to an exact cocycle representing the same true vector bundle when
![]() $\varepsilon \leq \sqrt {2}/4$
. This is used in Section 6 to prove the consistency of algorithms to compute characteristic classes.
$\varepsilon \leq \sqrt {2}/4$
. This is used in Section 6 to prove the consistency of algorithms to compute characteristic classes.
Many proofs in this section rely on various results stated and proven in Appendix A.
4.1 Cocycles and local trivializations
In this section, we relate approximate cocycles and approximate local trivializations. We give constructions (Construction 4.2 and Construction 4.8) to go back and forth between the notions, and we show that, in a sense, these constructions are approximate inverses of each other (Remark 4.11). The construction to go from approximate local trivializations to approximate cocycles is in general not canonical; we conclude the section by showing that, when
![]() $\varepsilon \leq 1$
, the construction can be made canonical.
$\varepsilon \leq 1$
, the construction can be made canonical.
To motivate the assumptions made in the following construction, recall that a set I is countable if there exists an injection
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
. Recall also that any vector bundle on a paracompact topological space can be trivialized on a countable open cover [Reference Milnor and Stasheff47, Lemma 5.9], and that every open cover of a paracompact topological space admits a subordinate partition of unity.
$\iota : I \to \mathbb {N}_{\geq 1}$
. Recall also that any vector bundle on a paracompact topological space can be trivialized on a countable open cover [Reference Milnor and Stasheff47, Lemma 5.9], and that every open cover of a paracompact topological space admits a subordinate partition of unity.
We start with a simplification. Given
![]() $\mathcal {V} = \{V_i\}_{i \in I}$
a countable open cover of a topological space B and an injection
$\mathcal {V} = \{V_i\}_{i \in I}$
a countable open cover of a topological space B and an injection
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
, consider a new open cover
$\iota : I \to \mathbb {N}_{\geq 1}$
, consider a new open cover
![]() $\mathcal {U} = \iota _*(\mathcal {V})$
of B indexed by
$\mathcal {U} = \iota _*(\mathcal {V})$
of B indexed by
![]() $\mathbb {N}_{\geq 1}$
with
$\mathbb {N}_{\geq 1}$
with
![]() $U_n = V_i$
if
$U_n = V_i$
if
![]() $\iota (i) = n$
or
$\iota (i) = n$
or
![]() $U_n = \emptyset $
if there is no
$U_n = \emptyset $
if there is no
![]() $i \in I$
such that
$i \in I$
such that
![]() $\iota (i) = n$
.
$\iota (i) = n$
.
Remark 4.1. Note that, using
![]() $\iota $
, one can construct a canonical bijection between the set of partitions of unity subordinate to
$\iota $
, one can construct a canonical bijection between the set of partitions of unity subordinate to
![]() $\mathcal {V}$
and the set of partitions of unity subordinate to
$\mathcal {V}$
and the set of partitions of unity subordinate to
![]() $\mathcal {U}$
. The same is true for the sets of approximate cocycles subordinate to
$\mathcal {U}$
. The same is true for the sets of approximate cocycles subordinate to
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\mathcal {U}$
and for the sets of approximate local trivializations subordinate to
$\mathcal {U}$
and for the sets of approximate local trivializations subordinate to
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
We give the main constructions of this section for covers indexed by
![]() $\mathbb {N}_{\geq 1}$
, and we will later generalize them to arbitrary countable covers, as this simplifies exposition.
$\mathbb {N}_{\geq 1}$
, and we will later generalize them to arbitrary countable covers, as this simplifies exposition.
Construction 4.2. Let B be a paracompact topological space and let
![]() $\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
be a cover of B. Let
$\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
be a cover of B. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {V}$
. Given a cochain
$\mathcal {V}$
. Given a cochain
![]() $\Omega $
subordinate to
$\Omega $
subordinate to
![]() $\mathcal {V}$
define, for each
$\mathcal {V}$
define, for each
![]() $i \in \mathbb {N}_{\geq 1}$
, a map
$i \in \mathbb {N}_{\geq 1}$
, a map
![]() $\Phi _i : V_i \to \mathsf {V}(d)$
, where the rows of
$\Phi _i : V_i \to \mathsf {V}(d)$
, where the rows of
![]() $\Phi _i(y)$
from
$\Phi _i(y)$
from
![]() $d\times j$
to
$d\times j$
to
![]() $d \times (j+1)-1$
are given by
$d \times (j+1)-1$
are given by
![]() $\vartriangleleft $
$\vartriangleleft $
Note that the maps
![]() $\Phi _i$
of Construction 4.2 are continuous and are well defined since, if
$\Phi _i$
of Construction 4.2 are continuous and are well defined since, if
![]() $y \not \in V_j$
, then
$y \not \in V_j$
, then
![]() $\varphi _j(y) = 0$
.
$\varphi _j(y) = 0$
.
Lemma 4.3. Let
![]() $\varepsilon \in [0,\infty ]$
and let
$\varepsilon \in [0,\infty ]$
and let
![]() $\Omega $
be an
$\Omega $
be an
![]() $\varepsilon $
-approximate cocycle subordinate to an open cover
$\varepsilon $
-approximate cocycle subordinate to an open cover
![]() $\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
of a paracompact topological space. The maps
$\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
of a paracompact topological space. The maps
![]() $\Phi _i$
of Construction 4.2 form an
$\Phi _i$
of Construction 4.2 form an
![]() $\varepsilon $
-approximate local trivialization.
$\varepsilon $
-approximate local trivialization.
Proof. We give the proof for
![]() $\varepsilon \in (0,\infty ]$
, the case
$\varepsilon \in (0,\infty ]$
, the case
![]() $\varepsilon = 0$
being similar. Let
$\varepsilon = 0$
being similar. Let
![]() $(ij) \in N(\mathcal {V})$
. We claim that the original
$(ij) \in N(\mathcal {V})$
. We claim that the original
![]() $\varepsilon $
-approximate cocycle
$\varepsilon $
-approximate cocycle
![]() $\Omega $
is a witness that the family
$\Omega $
is a witness that the family
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate local trivialization. To prove this, we must show that, for all
$\varepsilon $
-approximate local trivialization. To prove this, we must show that, for all
![]() $y \in V_j \cap V_i$
, the Frobenius distance between
$y \in V_j \cap V_i$
, the Frobenius distance between
![]() $\Phi _i(y) \Omega _{ij}(y)$
and
$\Phi _i(y) \Omega _{ij}(y)$
and
![]() $\Phi _j(y)$
is less than
$\Phi _j(y)$
is less than
![]() $\varepsilon $
. Carrying out the product
$\varepsilon $
. Carrying out the product
![]() $\Phi _i(y) \Omega _{ij}(y)$
, we get an element of
$\Phi _i(y) \Omega _{ij}(y)$
, we get an element of
![]() $\mathsf {V}(d)$
with rows from
$\mathsf {V}(d)$
with rows from
![]() $d\times k$
to
$d\times k$
to
![]() $d \times (k+1)-1$
given by
$d \times (k+1)-1$
given by
So
![]() $\|\Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| = \left (\sum _{k \geq 1} \| \sqrt {\varphi _k(y)} \left (\Omega _{ik}(y)^t \Omega _{ij}(y) - \Omega _{kj}(y)\right )\| ^2\right )^{1/2} < \varepsilon $
, as required.
$\|\Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| = \left (\sum _{k \geq 1} \| \sqrt {\varphi _k(y)} \left (\Omega _{ik}(y)^t \Omega _{ij}(y) - \Omega _{kj}(y)\right )\| ^2\right )^{1/2} < \varepsilon $
, as required.
We have thus constructed a map
for any cover
![]() $\mathcal {V}$
of a paracompact topological space B that is indexed by
$\mathcal {V}$
of a paracompact topological space B that is indexed by
![]() $\mathbb {N}_{\geq 1}$
. It is important to note that this map depends on the choice of partition of unity
$\mathbb {N}_{\geq 1}$
. It is important to note that this map depends on the choice of partition of unity
![]() $\varphi $
. Nevertheless, using two different partitions of unity gives homotopic local trivializations, in the following sense.
$\varphi $
. Nevertheless, using two different partitions of unity gives homotopic local trivializations, in the following sense.
Lemma 4.4. Let
![]() $\Omega $
be an
$\Omega $
be an
![]() $\varepsilon $
-approximate cocycle subordinate to
$\varepsilon $
-approximate cocycle subordinate to
![]() $\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
. If
$\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
. If
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are two partitions of unity subordinate to
$\varphi '$
are two partitions of unity subordinate to
![]() $\mathcal {V}$
, then
$\mathcal {V}$
, then
![]() $\mathsf {triv}^\varphi (\Omega )$
and
$\mathsf {triv}^\varphi (\Omega )$
and
![]() $\mathsf {triv}^{\varphi '}(\Omega )$
are homotopic through a family of
$\mathsf {triv}^{\varphi '}(\Omega )$
are homotopic through a family of
![]() $\varepsilon $
-approximate local trivializations that admit
$\varepsilon $
-approximate local trivializations that admit
![]() $\Omega $
as a witness.
$\Omega $
as a witness.
Proof. For any
![]() $\alpha \in [0,1]$
, the formula
$\alpha \in [0,1]$
, the formula
![]() $\varphi _i^\alpha = \alpha \varphi _i + (1-\alpha ) \varphi ^{\prime }_i$
gives a partition of unity. Now observe that the family of
$\varphi _i^\alpha = \alpha \varphi _i + (1-\alpha ) \varphi ^{\prime }_i$
gives a partition of unity. Now observe that the family of
![]() $\varepsilon $
-approximate local trivializations
$\varepsilon $
-approximate local trivializations
![]() $\mathsf {triv}^{\varphi ^\alpha }(\Omega )$
admit
$\mathsf {triv}^{\varphi ^\alpha }(\Omega )$
admit
![]() $\Omega $
as a witness.
$\Omega $
as a witness.
Next, we show that the construction assigning an approximate local trivialization to an approximate cocycle is stable.
Lemma 4.5. Let
![]() $\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
be a cover of a paracompact topological space B, and let
$\mathcal {V} = \{V_i\}_{i \in \mathbb {N}_{\geq 1}}$
be a cover of a paracompact topological space B, and let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {V}$
. For
$\mathcal {V}$
. For
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda\ \varepsilon $
-approximate cocycles subordinate to
$\Lambda\ \varepsilon $
-approximate cocycles subordinate to
![]() $\mathcal {V}$
,
$\mathcal {V}$
,
Proof. Let
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) = \delta $
,
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) = \delta $
,
![]() $\Phi := \mathsf {triv}^\varphi (\Omega )$
, and
$\Phi := \mathsf {triv}^\varphi (\Omega )$
, and
![]() $\Psi := \mathsf {triv}^\varphi (\Lambda )$
. For
$\Psi := \mathsf {triv}^\varphi (\Lambda )$
. For
![]() $y \in V_i$
, we have
$y \in V_i$
, we have
which proves the claim.
Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a countable open cover of a paracompact topological space B, and let
$\mathcal {U} = \{U_i\}_{i \in I}$
be a countable open cover of a paracompact topological space B, and let
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Using Remark 4.1, we can generalize Construction 4.2, Lemma 4.3, Lemma 4.4 and Lemma 4.5 to
$\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Using Remark 4.1, we can generalize Construction 4.2, Lemma 4.3, Lemma 4.4 and Lemma 4.5 to
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
In particular, we have a map
![]() $\mathsf {triv}^{\varphi ,\iota } : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
that now also depends on the choice of injection
$\mathsf {triv}^{\varphi ,\iota } : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right )$
that now also depends on the choice of injection
![]() $\iota $
. We now prove that, up to homotopy,
$\iota $
. We now prove that, up to homotopy,
![]() $\mathsf {triv}$
is independent of the choice of
$\mathsf {triv}$
is independent of the choice of
![]() $\iota $
. In order to show this, we prove a more general lemma that will be of use later.
$\iota $
. In order to show this, we prove a more general lemma that will be of use later.
Lemma 4.6. Given an injection
![]() $\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
define
$\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
define
![]() $\chi ^\iota : \mathsf {V}(d) \to \mathsf {V}(d)$
by mapping a frame
$\chi ^\iota : \mathsf {V}(d) \to \mathsf {V}(d)$
by mapping a frame
![]() $\Phi \in \mathsf {V}(d)$
to the frame whose
$\Phi \in \mathsf {V}(d)$
to the frame whose
![]() $\iota (k)$
th row is the kth row of
$\iota (k)$
th row is the kth row of
![]() $\Phi $
and whose other rows are identically
$\Phi $
and whose other rows are identically
![]() $0$
. If
$0$
. If
![]() $\iota , \iota ' : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
are injections, then
$\iota , \iota ' : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
are injections, then
![]() $\chi ^\iota $
and
$\chi ^\iota $
and
![]() $\chi ^{\iota '} : \mathsf {V}(d) \to \mathsf {V}(d)$
are homotopic.
$\chi ^{\iota '} : \mathsf {V}(d) \to \mathsf {V}(d)$
are homotopic.
The proof of the lemma is standard, but we give it here for completeness.
Proof. Assume that
![]() $\iota $
and
$\iota $
and
![]() $\iota '$
have disjoint images. Then, there is a homotopy between
$\iota '$
have disjoint images. Then, there is a homotopy between
![]() $\chi ^\iota $
and
$\chi ^\iota $
and
![]() $\chi ^{\iota '}$
given by
$\chi ^{\iota '}$
given by
![]() $\sqrt {\alpha } \chi ^{\iota } + \sqrt {1-\alpha } \chi ^{\iota '}$
for
$\sqrt {\alpha } \chi ^{\iota } + \sqrt {1-\alpha } \chi ^{\iota '}$
for
![]() $\alpha \in [0,1]$
. Let
$\alpha \in [0,1]$
. Let
![]() $2\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
be given by
$2\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
be given by
![]() $2\iota (k) = 2 \times \iota (k)$
and define
$2\iota (k) = 2 \times \iota (k)$
and define
![]() $2\iota ' + 1$
in an analogous way. Since
$2\iota ' + 1$
in an analogous way. Since
![]() $2\iota $
and
$2\iota $
and
![]() $2\iota '+1$
have disjoint images, our previous reasoning reduces the problem to showing that
$2\iota '+1$
have disjoint images, our previous reasoning reduces the problem to showing that
![]() $\chi ^{\iota }$
and
$\chi ^{\iota }$
and
![]() $\chi ^{2\iota }$
are homotopic and that
$\chi ^{2\iota }$
are homotopic and that
![]() $\chi ^{\iota '}$
and
$\chi ^{\iota '}$
and
![]() $\chi ^{2\iota ' - 1}$
are homotopic. Since the two proofs are entirely analogous, we give the details only for the case of
$\chi ^{2\iota ' - 1}$
are homotopic. Since the two proofs are entirely analogous, we give the details only for the case of
![]() $\iota $
. Moreover, since
$\iota $
. Moreover, since
![]() $2\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
is the composite of
$2\iota : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
is the composite of
![]() $\iota $
with multiplication by
$\iota $
with multiplication by
![]() $2$
, it is enough to give the proof for
$2$
, it is enough to give the proof for
![]() $\iota = \mathsf {id}$
, which we now do.
$\iota = \mathsf {id}$
, which we now do.
We must show that the identity
![]() $\mathsf {V}(d) \to \mathsf {V}(d)$
is homotopic to
$\mathsf {V}(d) \to \mathsf {V}(d)$
is homotopic to
![]() $\chi ^2 : \mathsf {V}(d) \to \mathsf {V}(d)$
. Informally, the proof works by moving each row of
$\chi ^2 : \mathsf {V}(d) \to \mathsf {V}(d)$
. Informally, the proof works by moving each row of
![]() $\Phi $
at a time. To simplify exposition, in the rest of this proof, the notation
$\Phi $
at a time. To simplify exposition, in the rest of this proof, the notation
![]() $\Phi _m$
will be used to refer to the mth row of a frame
$\Phi _m$
will be used to refer to the mth row of a frame
![]() $\Phi \in \mathsf {V}(d)$
. Consider the family of functions
$\Phi \in \mathsf {V}(d)$
. Consider the family of functions
![]() $f^\alpha : \mathsf {V}(d) \to \mathsf {V}(d)$
indexed by
$f^\alpha : \mathsf {V}(d) \to \mathsf {V}(d)$
indexed by
![]() $\alpha \in [0,1]$
defined as follows. For
$\alpha \in [0,1]$
defined as follows. For
![]() $\alpha = 0$
, let
$\alpha = 0$
, let
![]() $f^\alpha = \mathsf {id}$
. For
$f^\alpha = \mathsf {id}$
. For
![]() $n \in \mathbb {N}_{\geq 1}$
,
$n \in \mathbb {N}_{\geq 1}$
,
![]() $\alpha \in [1/(n+1), 1/n]$
, and
$\alpha \in [1/(n+1), 1/n]$
, and
![]() $m \in \mathbb {N}_{\geq 1}$
, define
$m \in \mathbb {N}_{\geq 1}$
, define
 $$\begin{align*}\left(f^{\alpha}(\Phi)\right)_m = \begin{cases} \Phi_m, & m < n\\ \sqrt{\beta}\,\, \Phi_m, & m = n\\ 0, & n < m < 2n\\ \sqrt{1-\beta}\,\, \Phi_m, & m = 2n\\ \Phi_{m/2}, & m> 2n\text{ and }m\text{ even}\\ 0, & m > 2n\text{ and }m\text{ odd,} \end{cases} \end{align*}$$
$$\begin{align*}\left(f^{\alpha}(\Phi)\right)_m = \begin{cases} \Phi_m, & m < n\\ \sqrt{\beta}\,\, \Phi_m, & m = n\\ 0, & n < m < 2n\\ \sqrt{1-\beta}\,\, \Phi_m, & m = 2n\\ \Phi_{m/2}, & m> 2n\text{ and }m\text{ even}\\ 0, & m > 2n\text{ and }m\text{ odd,} \end{cases} \end{align*}$$
where
![]() $\beta = (1/n - \alpha ) \times (1/n - 1/(n+1))$
. By inspection, we see that
$\beta = (1/n - \alpha ) \times (1/n - 1/(n+1))$
. By inspection, we see that
![]() $f^\alpha $
gives a homotopy between the identity and
$f^\alpha $
gives a homotopy between the identity and
![]() $\chi ^2$
, using that
$\chi ^2$
, using that
![]() $\mathsf {V}(d)$
has the direct limit topology.
$\mathsf {V}(d)$
has the direct limit topology.
Lemma 4.7. Let
![]() $\Omega $
be an
$\Omega $
be an
![]() $\varepsilon $
-approximate cocycle subordinate to a countable open cover
$\varepsilon $
-approximate cocycle subordinate to a countable open cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
and let
$\mathcal {U} = \{U_i\}_{i \in I}$
and let
![]() $\iota ,\iota ' : I \to \mathbb {N}_{\geq 1}$
be injections. Let
$\iota ,\iota ' : I \to \mathbb {N}_{\geq 1}$
be injections. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $\mathsf {triv}^{\varphi ,\iota }(\Omega )$
and
$\mathsf {triv}^{\varphi ,\iota }(\Omega )$
and
![]() $\mathsf {triv}^{\varphi ,\iota '}(\Omega )$
are homotopic through a family of
$\mathsf {triv}^{\varphi ,\iota '}(\Omega )$
are homotopic through a family of
![]() $\varepsilon $
-approximate local trivializations that admit
$\varepsilon $
-approximate local trivializations that admit
![]() $\Omega $
as a witness.
$\Omega $
as a witness.
Proof. The result follows at once from Lemma 4.6 by noticing that, for any two injections
![]() $\iota ,\iota ' : I \to \mathbb {N}_{\geq 1}$
, there exists a bijection b of
$\iota ,\iota ' : I \to \mathbb {N}_{\geq 1}$
, there exists a bijection b of
![]() $\mathbb {N}_{\geq 1}$
such that
$\mathbb {N}_{\geq 1}$
such that
![]() $\iota ' = b \circ \iota $
.
$\iota ' = b \circ \iota $
.
We now consider the problem of assigning an approximate cocycle to an approximate local trivialization.
Construction 4.8. Let
![]() $\Phi {\kern-1pt}={\kern-1pt} \{\Phi _i\}_{i \in I}$
be an
$\Phi {\kern-1pt}={\kern-1pt} \{\Phi _i\}_{i \in I}$
be an
![]() $\varepsilon $
-approximate local trivialization subordinate to
$\varepsilon $
-approximate local trivialization subordinate to
![]() $\mathcal {U} {\kern-1pt}={\kern-1pt} \{U_i\}_{i \in I}$
. By definition, there exists a witness that
$\mathcal {U} {\kern-1pt}={\kern-1pt} \{U_i\}_{i \in I}$
. By definition, there exists a witness that
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate local trivialization. Choose, arbitrarily, such a witness
$\varepsilon $
-approximate local trivialization. Choose, arbitrarily, such a witness
![]() $\Omega $
. Without loss of generality, we may assume that
$\Omega $
. Without loss of generality, we may assume that
![]() $\Omega $
is symmetric and thus that it is a cochain.
$\Omega $
is symmetric and thus that it is a cochain.
Lemma 4.9. Let
![]() $\varepsilon \in [0,\infty ]$
. Let
$\varepsilon \in [0,\infty ]$
. Let
![]() $\Phi $
be an
$\Phi $
be an
![]() $\varepsilon $
-approximate local trivialization. Then, the cochain described in Construction 4.8 is a
$\varepsilon $
-approximate local trivialization. Then, the cochain described in Construction 4.8 is a
![]() $3 \varepsilon $
-approximate cocycle. Thus, Construction 4.8 gives a map
$3 \varepsilon $
-approximate cocycle. Thus, Construction 4.8 gives a map
![]() $\mathsf {w} : \mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right ) \to \mathsf {Z}^{1}_{3\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
$\mathsf {w} : \mathsf {T}_{\varepsilon }\left ( \mathcal {U}; d \right ) \to \mathsf {Z}^{1}_{3\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
Proof. We address the case
![]() $\varepsilon \in (0,\infty ]$
, the case
$\varepsilon \in (0,\infty ]$
, the case
![]() $\varepsilon = 0$
being similar. Let
$\varepsilon = 0$
being similar. Let
![]() $(ijk) \in N(\mathcal {U})$
and let
$(ijk) \in N(\mathcal {U})$
and let
![]() $y \in U_k \cap U_j \cap U_i$
. Since
$y \in U_k \cap U_j \cap U_i$
. Since
![]() $\| \Phi _i(y) \Omega _{ik}(y) - \Phi _k(y)\| < \varepsilon $
, we have that
$\| \Phi _i(y) \Omega _{ik}(y) - \Phi _k(y)\| < \varepsilon $
, we have that
![]() $\| \Phi _k(y)^t \Phi _i(y) \Omega _{ik}(y) - \mathsf {id}\| < \varepsilon $
, by Lemma A.5. This implies that
$\| \Phi _k(y)^t \Phi _i(y) \Omega _{ik}(y) - \mathsf {id}\| < \varepsilon $
, by Lemma A.5. This implies that
![]() $\| \Phi _i(y)^t \Phi _k(y) - \Omega _{ik}(y)\| < \varepsilon $
.
$\| \Phi _i(y)^t \Phi _k(y) - \Omega _{ik}(y)\| < \varepsilon $
.
A similar computation shows that
![]() $\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Phi _i(y)^t \Phi _k(y)\| < \varepsilon $
. Using the triangle inequality and the first bound in the proof, we get that
$\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Phi _i(y)^t \Phi _k(y)\| < \varepsilon $
. Using the triangle inequality and the first bound in the proof, we get that
![]() $\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Omega _{ik}(y) \| < 2\varepsilon $
. By Lemma A.5 and the first bound in this proof but for i and j, we have that
$\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Omega _{ik}(y) \| < 2\varepsilon $
. By Lemma A.5 and the first bound in this proof but for i and j, we have that
![]() $\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Omega _{ij}(y) \Omega _{jk}(y)\| < \varepsilon $
. The triangle inequality then finishes the proof.
$\| \Phi _i(y)^t \Phi _j(y) \Omega _{jk}(y) - \Omega _{ij}(y) \Omega _{jk}(y)\| < \varepsilon $
. The triangle inequality then finishes the proof.
Although we can associate a
![]() $3\varepsilon $
-approximate cocycle to every
$3\varepsilon $
-approximate cocycle to every
![]() $\varepsilon $
-approximate local trivialization, this choice is not canonical, as an approximate local trivialization can have many distinct witnesses. Nonetheless, the following result says that any two witnesses cannot be too far apart.
$\varepsilon $
-approximate local trivialization, this choice is not canonical, as an approximate local trivialization can have many distinct witnesses. Nonetheless, the following result says that any two witnesses cannot be too far apart.
Lemma 4.10. Let
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
be witnesses that
$\Lambda $
be witnesses that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are, respectively,
$\Psi $
are, respectively,
![]() $\varepsilon $
- and
$\varepsilon $
- and
![]() $\delta $
-approximate local trivializations. Then
$\delta $
-approximate local trivializations. Then
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq \varepsilon + \delta + \sqrt {2} \mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right )$
.
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq \varepsilon + \delta + \sqrt {2} \mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right )$
.
Proof. We address the case in which
![]() $\varepsilon ,\delta>0$
, the case in which any of them is
$\varepsilon ,\delta>0$
, the case in which any of them is
![]() $0$
being similar. Let
$0$
being similar. Let
![]() $(ij) \in N(\mathcal {U})$
and
$(ij) \in N(\mathcal {U})$
and
![]() $y \in U_j \cap U_i$
. We have
$y \in U_j \cap U_i$
. We have
![]() $\| \Omega _{ij}(y) - \Phi _i(y)^t \Phi _j(y)\| < \varepsilon $
and
$\| \Omega _{ij}(y) - \Phi _i(y)^t \Phi _j(y)\| < \varepsilon $
and
![]() $\| \Lambda _{ij}(y) - \Psi _i(y)^t \Psi _j(y)\| < \delta $
, so it suffices to show that
$\| \Lambda _{ij}(y) - \Psi _i(y)^t \Psi _j(y)\| < \delta $
, so it suffices to show that
![]() $\| \Phi _i(y)^t \Phi _j(y) - \Psi _i(y)^t \Psi _j(y)\| \leq \sqrt {2} \| \Phi _i(y) - \Psi _i(y)\| $
, which follows from Lemma A.6.
$\| \Phi _i(y)^t \Phi _j(y) - \Psi _i(y)^t \Psi _j(y)\| \leq \sqrt {2} \| \Phi _i(y) - \Psi _i(y)\| $
, which follows from Lemma A.6.
Remark 4.11. From Lemma 4.10, it follows that, if
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
are witnesses that
$\Lambda $
are witnesses that
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate local trivialization, then
$\varepsilon $
-approximate local trivialization, then
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq 2\varepsilon $
, and thus
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq 2\varepsilon $
, and thus
![]() $\mathsf {w}$
is, approximately, a left inverse of
$\mathsf {w}$
is, approximately, a left inverse of
![]() $\mathsf {triv}^\varphi $
, in the sense that
$\mathsf {triv}^\varphi $
, in the sense that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \mathsf {w}(\mathsf {triv}^\varphi (\Omega )) \right ) \leq 2\varepsilon $
for every
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \mathsf {w}(\mathsf {triv}^\varphi (\Omega )) \right ) \leq 2\varepsilon $
for every
![]() $\varepsilon $
-approximate cocycle
$\varepsilon $
-approximate cocycle
![]() $\Omega $
. The following result can be interpreted as saying that
$\Omega $
. The following result can be interpreted as saying that
![]() $\mathsf {w}$
is also a right inverse of
$\mathsf {w}$
is also a right inverse of
![]() $\mathsf {triv}^\varphi $
since it implies, in particular, that
$\mathsf {triv}^\varphi $
since it implies, in particular, that
![]() $\mathsf {triv}^\varphi (\mathsf {w}(\Phi ))$
is homotopic to
$\mathsf {triv}^\varphi (\mathsf {w}(\Phi ))$
is homotopic to
![]() $\Phi $
through
$\Phi $
through
![]() $3\varepsilon $
-approximate local trivializations, whenever
$3\varepsilon $
-approximate local trivializations, whenever
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate local trivialization.
$\varepsilon $
-approximate local trivialization.
Lemma 4.12. Let
![]() $\varepsilon \geq 0$
. Let
$\varepsilon \geq 0$
. Let
![]() $\Omega $
be a witness that
$\Omega $
be a witness that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are
$\Psi $
are
![]() $\varepsilon $
-approximate cocycles. Then
$\varepsilon $
-approximate cocycles. Then
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are homotopic through
$\Psi $
are homotopic through
![]() $\varepsilon $
-approximate local trivializations subordinate to
$\varepsilon $
-approximate local trivializations subordinate to
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
that admit
$\mathcal {U} = \{U_i\}_{i \in I}$
that admit
![]() $\Omega $
as a witness.
$\Omega $
as a witness.
Proof. We use the language of Lemma 4.6. Consider the maps
![]() $\iota , \iota ' : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
given by
$\iota , \iota ' : \mathbb {N}_{\geq 1} \to \mathbb {N}_{\geq 1}$
given by
![]() $\iota (k) = 2k$
and
$\iota (k) = 2k$
and
![]() $\iota '(k) = 2k - 1$
. It is clear that
$\iota '(k) = 2k - 1$
. It is clear that
![]() $\Omega $
is a witness that
$\Omega $
is a witness that
![]() $\{\chi ^\iota \circ \Phi _i\}_{i \in I}$
is an
$\{\chi ^\iota \circ \Phi _i\}_{i \in I}$
is an
![]() $\varepsilon $
-local trivialization, and Lemma 4.6 implies that
$\varepsilon $
-local trivialization, and Lemma 4.6 implies that
![]() $\Phi $
is homotopic to
$\Phi $
is homotopic to
![]() $\{\chi ^\iota \circ \Phi _i\}_{i \in I}$
through
$\{\chi ^\iota \circ \Phi _i\}_{i \in I}$
through
![]() $\varepsilon $
-approximate local trivializations that admit
$\varepsilon $
-approximate local trivializations that admit
![]() $\Omega $
as a witness. Similarly, we deduce that
$\Omega $
as a witness. Similarly, we deduce that
![]() $\Psi $
is homotopic to
$\Psi $
is homotopic to
![]() $\{\chi ^{\iota '} \circ \Psi _i\}_{i \in I}$
through
$\{\chi ^{\iota '} \circ \Psi _i\}_{i \in I}$
through
![]() $\varepsilon $
-approximate local trivializations that admit
$\varepsilon $
-approximate local trivializations that admit
![]() $\Omega $
as a witness.
$\Omega $
as a witness.
Consider, for
![]() $\alpha \in [0,1]$
, the family
$\alpha \in [0,1]$
, the family
![]() $\{\sqrt {\alpha }(\chi ^\iota \circ \Phi _i) + \sqrt {1-\alpha } (\chi ^{\iota '} \circ \Psi _i)\}_{i \in I}$
. Since the images of
$\{\sqrt {\alpha }(\chi ^\iota \circ \Phi _i) + \sqrt {1-\alpha } (\chi ^{\iota '} \circ \Psi _i)\}_{i \in I}$
. Since the images of
![]() $\iota $
and
$\iota $
and
![]() $\iota '$
are disjoint, this constitutes an
$\iota '$
are disjoint, this constitutes an
![]() $\varepsilon $
-approximate local trivialization that admits
$\varepsilon $
-approximate local trivialization that admits
![]() $\Omega $
as a witness that varies continuously with
$\Omega $
as a witness that varies continuously with
![]() $\alpha $
. The result follows.
$\alpha $
. The result follows.
The following result gives conditions under which there is a canonical approximate cocycle associated to an approximate local trivialization.
Lemma 4.13. Let
![]() $\Phi $
be a nondegenerate
$\Phi $
be a nondegenerate
![]() $\varepsilon $
-approximate local trivialization. For
$\varepsilon $
-approximate local trivialization. For
![]() $(ij) \in N(\mathcal {U})$
and
$(ij) \in N(\mathcal {U})$
and
![]() $y \in U_j \cap U_i$
, let
$y \in U_j \cap U_i$
, let
![]() $\Omega _{ij}(y) \in O(d)$
minimize
$\Omega _{ij}(y) \in O(d)$
minimize
![]() $\| \Phi _i(y) \Omega - \Phi _j(y)\| $
, where
$\| \Phi _i(y) \Omega - \Phi _j(y)\| $
, where
![]() $\Omega $
ranges over
$\Omega $
ranges over
![]() $O(d)$
. Then, the matrices
$O(d)$
. Then, the matrices
![]() $\Omega _{ij}(y)$
assemble into a
$\Omega _{ij}(y)$
assemble into a
![]() $3\varepsilon $
-approximate cocycle.
$3\varepsilon $
-approximate cocycle.
Proof. To see that the mappings
![]() $\Omega _{ij} : U_j \cap U_i \to O(d)$
are continuous, use Corollary A.4. To see that
$\Omega _{ij} : U_j \cap U_i \to O(d)$
are continuous, use Corollary A.4. To see that
![]() $\Omega _{ij} = \Omega _{ji}^t$
use that the minimizers are unique. Then, Lemma 4.9 directly implies that
$\Omega _{ij} = \Omega _{ji}^t$
use that the minimizers are unique. Then, Lemma 4.9 directly implies that
![]() $\Omega $
satisfies the
$\Omega $
satisfies the
![]() $3\varepsilon $
-approximate cocycle condition, as required.
$3\varepsilon $
-approximate cocycle condition, as required.
We now give sufficient conditions for an approximate local trivialization to be nondegenerate.
Lemma 4.14. If
![]() $\varepsilon \leq 1$
, then any
$\varepsilon \leq 1$
, then any
![]() $\varepsilon $
-approximate local trivialization is nondegenerate.
$\varepsilon $
-approximate local trivialization is nondegenerate.
Proof. This is a consequence Lemma A.15, which says that a matrix that is at Frobenius distance less than
![]() $1$
from an orthogonal matrix is invertible.
$1$
from an orthogonal matrix is invertible.
We conclude by remarking that Lemma 4.14 implies that, if
![]() $\varepsilon \leq 1$
, we have a canonical map (that is independent of any arbitrary choices)
$\varepsilon \leq 1$
, we have a canonical map (that is independent of any arbitrary choices)
given by taking the best witness, as in Lemma 4.13.
4.2 Local trivializations and classifying maps
In this section, we give a construction that, given an approximate local trivialization, returns an approximate classifying map. We also observe that this construction behaves well with respect to homotopies between approximate local trivializations.
Recall from Section 2.1.2 the definition of the map
![]() $\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
.
$\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
.
Construction 4.15. Let
![]() $\mathcal {U}$
be a countable open cover of a paracompact topological space B and let
$\mathcal {U}$
be a countable open cover of a paracompact topological space B and let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
. Let
$\mathcal {U}$
. Let
![]() $\Phi $
be an approximate local trivialization subordinate to
$\Phi $
be an approximate local trivialization subordinate to
![]() $\mathcal {U}$
. Define a map
$\mathcal {U}$
. Define a map
![]() $\mathsf {av}^\varphi (\Phi ) : B \to \mathbb {R}^{\infty \times \infty }$
by
$\mathsf {av}^\varphi (\Phi ) : B \to \mathbb {R}^{\infty \times \infty }$
by
![]() $\vartriangleleft $
$\vartriangleleft $
Note that the map
![]() $\mathsf {av}^\varphi (\Phi )$
is continuous.
$\mathsf {av}^\varphi (\Phi )$
is continuous.
Lemma 4.16. Let
![]() $\varepsilon \in [0,\infty ]$
. Under the hypotheses of Construction 4.15, if
$\varepsilon \in [0,\infty ]$
. Under the hypotheses of Construction 4.15, if
![]() $\Phi $
is an
$\Phi $
is an
![]() $\varepsilon $
-approximate local trivialization, then
$\varepsilon $
-approximate local trivialization, then
![]() $\mathsf {av}^\varphi (\Phi )$
is a
$\mathsf {av}^\varphi (\Phi )$
is a
![]() $\sqrt {2}\varepsilon $
-approximate classifying map.
$\sqrt {2}\varepsilon $
-approximate classifying map.
Proof. We address the case
![]() $\varepsilon \in (0,\infty ]$
, the case
$\varepsilon \in (0,\infty ]$
, the case
![]() $\varepsilon = 0$
being similar. By definition, there exist, for each
$\varepsilon = 0$
being similar. By definition, there exist, for each
![]() $(ij) \in N(\mathcal {U})$
, a continuous map
$(ij) \in N(\mathcal {U})$
, a continuous map
![]() $\Omega _{ij} : U_j \cap U_i \to O(d)$
such that
$\Omega _{ij} : U_j \cap U_i \to O(d)$
such that
![]() $\| \Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| < \varepsilon $
for every
$\| \Phi _i(y) \Omega _{ij}(y) - \Phi _j(y)\| < \varepsilon $
for every
![]() $y \in U_j \cap U_i$
. Since
$y \in U_j \cap U_i$
. Since
![]() $\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
is
$\mathsf {Proj} : \mathsf {V}(d) \to \mathsf {Gr}(d)$
is
![]() $O(d)$
-invariant and
$O(d)$
-invariant and
![]() $\sqrt {2}$
-Lipschitz (Lemma A.6), it follows that
$\sqrt {2}$
-Lipschitz (Lemma A.6), it follows that
![]() $\| \mathsf {Proj}(\Phi _i(y)) - \mathsf {Proj}(\Phi _j(y))\| < \sqrt {2}\varepsilon $
. The result then follows from Lemma A.2.
$\| \mathsf {Proj}(\Phi _i(y)) - \mathsf {Proj}(\Phi _j(y))\| < \sqrt {2}\varepsilon $
. The result then follows from Lemma A.2.
The following is clear.
Lemma 4.17. Let
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
be approximate local trivializations subordinate to
$\Psi $
be approximate local trivializations subordinate to
![]() $\mathcal {U}$
, a countable open cover of a paracompact topological space B. Let
$\mathcal {U}$
, a countable open cover of a paracompact topological space B. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
-
1. We have that
 $\mathsf {d}_{\mathsf {C}}\left ( \mathsf {av}^\varphi (\Phi ), \mathsf {av}^\varphi (\Psi ) \right ) \leq \sqrt {2} \mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right )$
.
$\mathsf {d}_{\mathsf {C}}\left ( \mathsf {av}^\varphi (\Phi ), \mathsf {av}^\varphi (\Psi ) \right ) \leq \sqrt {2} \mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right )$
. -
2. If
 $\Phi $
and
$\Phi $
and
 $\Psi $
are homotopic through
$\Psi $
are homotopic through
 $\varepsilon $
-approximate local trivializations subordinate to
$\varepsilon $
-approximate local trivializations subordinate to
 $\mathcal {U}$
, then
$\mathcal {U}$
, then
 $\mathsf {av}^\varphi (\Phi )$
and
$\mathsf {av}^\varphi (\Phi )$
and
 $\mathsf {av}^\varphi (\Psi )$
are homotopic as maps
$\mathsf {av}^\varphi (\Psi )$
are homotopic as maps
 $B \to \mathsf {Gr}(d)^{\sqrt {2}\varepsilon }$
.
$B \to \mathsf {Gr}(d)^{\sqrt {2}\varepsilon }$
.
4.3 Cocycles and classifying maps
In this section, we relate approximate cocycles to approximate classifying maps in a way that is independent of any partition of unity and of any enumeration of the sets in the open cover the cocycle is subordinate to (Theorem 4.21). We also study the action of refinements on approximate cohomology.
Let B be a paracompact topological space and let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be a countable open cover. Let
$\mathcal {U} = \{U_i\}_{i \in I}$
be a countable open cover. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
and let
$\mathcal {U}$
and let
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Using Lemma 4.3 and Lemma 4.16, we get a map
$\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Using Lemma 4.3 and Lemma 4.16, we get a map
![]() $\mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right )$
which we compose with the quotient map
$\mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right )$
which we compose with the quotient map
![]() $\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
to obtain a map
$\mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
to obtain a map
Together, Lemma 4.4, Lemma 4.17, and Lemma 4.7 imply that this map is independent of the choice of partition of unity
![]() $\varphi $
and of injection
$\varphi $
and of injection
![]() $\iota $
. The following result says that two approximate cocycles that differ in a
$\iota $
. The following result says that two approximate cocycles that differ in a
![]() $0$
-cochain are sent to the same approximate classifying map by
$0$
-cochain are sent to the same approximate classifying map by
![]() $\mathsf {cl}'$
.
$\mathsf {cl}'$
.
Lemma 4.18. Let B be a paracompact topological space and let
![]() $\mathcal {U}$
be a countable open cover. The map
$\mathcal {U}$
be a countable open cover. The map
![]() $\mathsf {cl}' : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
factors through
$\mathsf {cl}' : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
factors through
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
Proof. By construction, we may assume that
![]() $\mathcal {U}$
is indexed by
$\mathcal {U}$
is indexed by
![]() $I = \mathbb {N}$
. Consider the following open cover
$I = \mathbb {N}$
. Consider the following open cover
![]() $\mathcal {V} = \{V_j\}_{j \in J}$
indexed by
$\mathcal {V} = \{V_j\}_{j \in J}$
indexed by
![]() $J = \mathbb {N}$
. Let
$J = \mathbb {N}$
. Let
![]() $V_j = U_i$
whenever
$V_j = U_i$
whenever
![]() $j = 2i + z$
with
$j = 2i + z$
with
![]() $z = 0$
or
$z = 0$
or
![]() $z = 1$
. So the open cover
$z = 1$
. So the open cover
![]() $\mathcal {V}$
consists of two copies of each open set of
$\mathcal {V}$
consists of two copies of each open set of
![]() $\mathcal {U}$
, where each open
$\mathcal {U}$
, where each open
![]() $U_i$
appears with an even index as
$U_i$
appears with an even index as
![]() $V_{2i}$
and with an odd index as
$V_{2i}$
and with an odd index as
![]() $V_{2i+1}$
.
$V_{2i+1}$
.
Suppose that
![]() $\Omega $
and
$\Omega $
and
![]() $\Omega '$
are equal in
$\Omega '$
are equal in
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
so that there is a
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
so that there is a
![]() $0$
-cochain
$0$
-cochain
![]() $\Theta $
such that
$\Theta $
such that
![]() $\Theta \cdot \Omega = \Omega '$
. Let
$\Theta \cdot \Omega = \Omega '$
. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
. This induces two partitions of unity
$\mathcal {U}$
. This induces two partitions of unity
![]() $\varphi ^0$
and
$\varphi ^0$
and
![]() $\varphi ^1$
subordinate to
$\varphi ^1$
subordinate to
![]() $\mathcal {V}$
, where
$\mathcal {V}$
, where
![]() $\varphi ^0_j$
is equal to
$\varphi ^0_j$
is equal to
![]() $\varphi _{j/2}$
if j is even and is identically
$\varphi _{j/2}$
if j is even and is identically
![]() $0$
if j is odd. Similarly,
$0$
if j is odd. Similarly,
![]() $\varphi ^1_j$
is equal to
$\varphi ^1_j$
is equal to
![]() $\varphi _{(j-1)/2}$
if j is odd and identically
$\varphi _{(j-1)/2}$
if j is odd and identically
![]() $0$
if j is even.
$0$
if j is even.
Consider the following cochain
![]() $\Lambda $
subordinate to
$\Lambda $
subordinate to
![]() $\mathcal {V}$
. For
$\mathcal {V}$
. For
![]() $(jk) \in N(\mathcal {V})$
, define
$(jk) \in N(\mathcal {V})$
, define
![]() $\Lambda _{jk} = \Omega _{j/2\,k/2}$
if j and k are even,
$\Lambda _{jk} = \Omega _{j/2\,k/2}$
if j and k are even,
![]() $\Lambda _{jk} = \Theta _{(j-1)/2}^t \Omega _{(j-1)/2\, (k-1)/2} \Theta _{(k-1)/2}$
if j and k are odd,
$\Lambda _{jk} = \Theta _{(j-1)/2}^t \Omega _{(j-1)/2\, (k-1)/2} \Theta _{(k-1)/2}$
if j and k are odd,
![]() $\Lambda _{jk} = \Theta _{(j-1)/2}^t \Omega _{(j-1)/2\,k/2}$
if j is odd and k is even, and
$\Lambda _{jk} = \Theta _{(j-1)/2}^t \Omega _{(j-1)/2\,k/2}$
if j is odd and k is even, and
![]() $\Lambda _{jk} = \Omega _{j/2\,(k-1)/2} \Theta _{(k-1)/2}$
if j is even and k is odd. It is clear that
$\Lambda _{jk} = \Omega _{j/2\,(k-1)/2} \Theta _{(k-1)/2}$
if j is even and k is odd. It is clear that
![]() $\Lambda $
is an
$\Lambda $
is an
![]() $\varepsilon $
-approximate cocycle subordinate to
$\varepsilon $
-approximate cocycle subordinate to
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
Finally, using Lemma 4.7, if we use the partition of unity
![]() $\varphi ^0$
, we see that
$\varphi ^0$
, we see that
![]() $\mathsf {cl}'(\Lambda ) = \mathsf {cl}'(\Omega )$
, and if we use the partition of unity
$\mathsf {cl}'(\Lambda ) = \mathsf {cl}'(\Omega )$
, and if we use the partition of unity
![]() $\varphi ^1$
, we see that
$\varphi ^1$
, we see that
![]() $\mathsf {cl}'(\Lambda ) = \mathsf {cl}'(\Omega ')$
. The result follows.
$\mathsf {cl}'(\Lambda ) = \mathsf {cl}'(\Omega ')$
. The result follows.
Recall from Section 2.2.4 the notion of refinement of a cover.
Construction 4.19. Let
![]() $\nu : \mathcal {U} \to \mathcal {V}$
be a refinement of covers of a topological space B and let
$\nu : \mathcal {U} \to \mathcal {V}$
be a refinement of covers of a topological space B and let
![]() $\varepsilon \in [0,\infty ]$
. Let
$\varepsilon \in [0,\infty ]$
. Let
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right )$
. Define
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right )$
. Define
![]() $\nu (\Omega ) \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
by letting
$\nu (\Omega ) \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
by letting
![]() $\nu (\Omega )_{jk} = \Omega _{\nu (j)\nu (k)}$
for all
$\nu (\Omega )_{jk} = \Omega _{\nu (j)\nu (k)}$
for all
![]() $(jk) \in N(\mathcal {U})$
.
$(jk) \in N(\mathcal {U})$
.
Construction 4.19 gives a map
![]() $\nu : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
that descends to a map
$\nu : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
that descends to a map
It is clear that both these maps are
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $\mathsf {d}_{\mathsf {Z}}$
and with respect to
$\mathsf {d}_{\mathsf {Z}}$
and with respect to
![]() $\mathsf {d}_{\check {\mathsf {H}}}$
.
$\mathsf {d}_{\check {\mathsf {H}}}$
.
Lemma 4.20. Let
![]() $\varepsilon \in [0,\infty ]$
, let
$\varepsilon \in [0,\infty ]$
, let
![]() $\mu ,\nu : \mathcal {U} \to \mathcal {V}$
and let
$\mu ,\nu : \mathcal {U} \to \mathcal {V}$
and let
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right )$
. Then, for all
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {V}; O(d) \right )$
. Then, for all
![]() $(jk) \in N(\mathcal {U})$
and
$(jk) \in N(\mathcal {U})$
and
![]() $y \in U_k \cap U_j$
, we have
$y \in U_k \cap U_j$
, we have
![]() $\|\mu (\Omega )_{jk}(y) - \nu (\Omega )_{jk}(y)\|< 2\varepsilon $
, and thus
$\|\mu (\Omega )_{jk}(y) - \nu (\Omega )_{jk}(y)\|< 2\varepsilon $
, and thus
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \mu (\Omega ), \nu (\Omega ) \right ) \leq 2\varepsilon $
.
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \mu (\Omega ), \nu (\Omega ) \right ) \leq 2\varepsilon $
.
Proof. We address the case
![]() $\varepsilon \in (0,\infty ]$
, the case
$\varepsilon \in (0,\infty ]$
, the case
![]() $\varepsilon = 0$
being similar. We start by defining a
$\varepsilon = 0$
being similar. We start by defining a
![]() $0$
-cochain
$0$
-cochain
![]() $\Theta $
subordinate to
$\Theta $
subordinate to
![]() $\mathcal {U}$
. Given
$\mathcal {U}$
. Given
![]() $j \in N(\mathcal {U})$
, let
$j \in N(\mathcal {U})$
, let
![]() $\Theta _j = \Omega _{\mu (j)\nu (j)}$
if
$\Theta _j = \Omega _{\mu (j)\nu (j)}$
if
![]() $\mu (j) \neq \nu (j)$
and the identity if
$\mu (j) \neq \nu (j)$
and the identity if
![]() $\mu (j) = \nu (j)$
. Let
$\mu (j) = \nu (j)$
. Let
![]() $(jk) \in N(\mathcal {U})$
, and let
$(jk) \in N(\mathcal {U})$
, and let
![]() $y \in U_k \cap U_j$
. To simplify notation in the rest of this proof, let us denote
$y \in U_k \cap U_j$
. To simplify notation in the rest of this proof, let us denote
![]() $\Omega _{ab}(y)$
by
$\Omega _{ab}(y)$
by
![]() $\Omega _{ab}$
. We have
$\Omega _{ab}$
. We have
 $$ \begin{align*} \|\mu(\Omega)_{jk}(y) - (\Theta \cdot \nu(\Omega))_{jk}(y)\| &= \|\Omega_{\mu(j)\mu(k)} - \Omega_{\mu(j)\nu(j)}\Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\| \\ &= \|\Omega_{\nu(j)\mu(j)}\Omega_{\mu(j)\mu(k)} - \Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\|\\ &\leq \|\Omega_{\nu(j)\mu(j)}\Omega_{\mu(j)\mu(k)} - \Omega_{\nu(j)\mu(k)}\|\\ &\;\;\;\;\;\;+ \|\Omega_{\nu(j)\mu(k)} - \Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\|\\ &< 2 \varepsilon, \end{align*} $$
$$ \begin{align*} \|\mu(\Omega)_{jk}(y) - (\Theta \cdot \nu(\Omega))_{jk}(y)\| &= \|\Omega_{\mu(j)\mu(k)} - \Omega_{\mu(j)\nu(j)}\Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\| \\ &= \|\Omega_{\nu(j)\mu(j)}\Omega_{\mu(j)\mu(k)} - \Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\|\\ &\leq \|\Omega_{\nu(j)\mu(j)}\Omega_{\mu(j)\mu(k)} - \Omega_{\nu(j)\mu(k)}\|\\ &\;\;\;\;\;\;+ \|\Omega_{\nu(j)\mu(k)} - \Omega_{\nu(j)\nu(k)}\Omega_{\nu(k)\mu(k)}\|\\ &< 2 \varepsilon, \end{align*} $$
where for the second equality we used the fact that
![]() $\Omega _{\nu (j)\mu (j)} = \Omega _{\mu (j)\nu (j)}^{-1}$
combined with the fact that the Frobenius norm is invariant under multiplication by an orthogonal matrix, and for the inequalities we used the triangle inequality and the approximate cocycle condition.
$\Omega _{\nu (j)\mu (j)} = \Omega _{\mu (j)\nu (j)}^{-1}$
combined with the fact that the Frobenius norm is invariant under multiplication by an orthogonal matrix, and for the inequalities we used the triangle inequality and the approximate cocycle condition.
We are now ready to state and prove the main result of this section.
Theorem 4.21. Let B be a paracompact topological space, and let
![]() $\mathcal {U}$
be a countable cover of B. Let
$\mathcal {U}$
be a countable cover of B. Let
![]() $\varepsilon \in [0,\infty ]$
. The map
$\varepsilon \in [0,\infty ]$
. The map
![]() $\mathsf {cl}'$
induces a map
$\mathsf {cl}'$
induces a map
such that, if
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < \delta $
in
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < \delta $
in
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, then
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
, then
![]() $\mathsf {cl}(\Omega )$
and
$\mathsf {cl}(\Omega )$
and
![]() $\mathsf {cl}(\Lambda )$
become equal in
$\mathsf {cl}(\Lambda )$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \delta )}} \right \rbrack $
. Moreover, if
$\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \delta )}} \right \rbrack $
. Moreover, if
![]() $\mu ,\nu : \mathcal {V} \to \mathcal {U}$
are refinements and
$\mu ,\nu : \mathcal {V} \to \mathcal {U}$
are refinements and
![]() $\mathcal {V}$
is a countable cover of B, then
$\mathcal {V}$
is a countable cover of B, then
![]() $\mathsf {cl}(\mu (\Omega ))$
and
$\mathsf {cl}(\mu (\Omega ))$
and
![]() $\mathsf {cl}(\nu (\Omega ))$
become equal in
$\mathsf {cl}(\nu (\Omega ))$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{2\sqrt {2}\varepsilon }} \right \rbrack $
.
$\left \lbrack {B}, {\mathsf {Gr}(d)^{2\sqrt {2}\varepsilon }} \right \rbrack $
.
Proof. The map
![]() $\mathsf {cl}$
is well defined thanks to Lemma 4.18. For the stability of
$\mathsf {cl}$
is well defined thanks to Lemma 4.18. For the stability of
![]() $\mathsf {cl}$
, note that, using Lemma 4.17, we see that if
$\mathsf {cl}$
, note that, using Lemma 4.17, we see that if
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
are
$\Lambda $
are
![]() $\varepsilon $
-approximate cocycles subordinate to a countable cover
$\varepsilon $
-approximate cocycles subordinate to a countable cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
,
$\mathcal {U} = \{U_i\}_{i \in I}$
,
![]() $\varphi $
is a partition of unity subordinate to
$\varphi $
is a partition of unity subordinate to
![]() $\mathcal {U}$
, and
$\mathcal {U}$
, and
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
is an injection, then
$\iota : I \to \mathbb {N}_{\geq 1}$
is an injection, then
The stability then follows from Lemma 3.10. Finally, the claim about refinements follows directly from Lemma 4.20.
Note that the map
![]() $\mathsf {cl}$
is independent of any choice of partition of unity or enumeration of the cover
$\mathsf {cl}$
is independent of any choice of partition of unity or enumeration of the cover
![]() $\mathcal {U}$
. We conclude with an interesting remark that is not used in the rest of the paper.
$\mathcal {U}$
. We conclude with an interesting remark that is not used in the rest of the paper.
Remark 4.22. Let
![]() $\mathsf {cov}(B)$
be the category whose objects are the countable covers of a paracompact topological space B and whose morphisms are the refinements. Let
$\mathsf {cov}(B)$
be the category whose objects are the countable covers of a paracompact topological space B and whose morphisms are the refinements. Let
![]() $\varepsilon \in [0,\infty ]$
. Construction 4.19 gives a functor
$\varepsilon \in [0,\infty ]$
. Construction 4.19 gives a functor
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( -; O(d) \right ) : \mathsf {cov}(B)^{\mathsf {op}} \to \mathbf {Met}$
. We can then define
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( -; O(d) \right ) : \mathsf {cov}(B)^{\mathsf {op}} \to \mathbf {Met}$
. We can then define
with the caveat that
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( B; O(d) \right )$
may be a pseudo metric space. Theorem 4.21 implies that there is a well-defined map
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( B; O(d) \right )$
may be a pseudo metric space. Theorem 4.21 implies that there is a well-defined map
![]() $\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( B; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{2\sqrt {2}\varepsilon }} \right \rbrack $
, natural in
$\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( B; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{2\sqrt {2}\varepsilon }} \right \rbrack $
, natural in
![]() $\varepsilon \in [0,\infty ]$
.
$\varepsilon \in [0,\infty ]$
.
4.4 Relationship to classical vector bundles
We now relate approximate vector bundles to exact vector bundles, following the intuition that
![]() $\varepsilon $
-approximate vector bundles should correspond to true vector bundles as long as
$\varepsilon $
-approximate vector bundles should correspond to true vector bundles as long as
![]() $\varepsilon $
is sufficiently small. For this, we use Theorem 4.21. In the case where an approximate cocycle represents a true vector bundle, we study the problem of constructing an exact cocycle that represents the same vector bundle. We also give upper and lower bounds for the distance from an approximate cocycle to an exact cocycle representing the same vector bundle (Theorem 4.27 and Lemma 4.30).
$\varepsilon $
is sufficiently small. For this, we use Theorem 4.21. In the case where an approximate cocycle represents a true vector bundle, we study the problem of constructing an exact cocycle that represents the same vector bundle. We also give upper and lower bounds for the distance from an approximate cocycle to an exact cocycle representing the same vector bundle (Theorem 4.27 and Lemma 4.30).
We start by recalling that small thickenings of the Grassmannian embedded in
![]() $\mathbb {R}^{\infty \times \infty }$
retract to the Grassmannian. More precisely, if
$\mathbb {R}^{\infty \times \infty }$
retract to the Grassmannian. More precisely, if
![]() $\varepsilon \leq \sqrt {2}/2$
, there is a map
$\varepsilon \leq \sqrt {2}/2$
, there is a map
![]() $\pi : \mathsf {Gr}(d)^\varepsilon \to \mathsf {Gr}(d)$
which is a homotopy inverse of the inclusion
$\pi : \mathsf {Gr}(d)^\varepsilon \to \mathsf {Gr}(d)$
which is a homotopy inverse of the inclusion
![]() $\mathsf {Gr}(d) \subseteq \mathsf {Gr}(d)^\varepsilon $
, by Proposition A.12. Let B be a topological space. By postcomposing with
$\mathsf {Gr}(d) \subseteq \mathsf {Gr}(d)^\varepsilon $
, by Proposition A.12. Let B be a topological space. By postcomposing with
![]() $\pi $
, we get an inverse for the natural map
$\pi $
, we get an inverse for the natural map
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack \to \left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
which we denote by
$\left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack \to \left \lbrack {B}, {\mathsf {Gr}(d)^\varepsilon } \right \rbrack $
which we denote by
By an abuse of notation, we also let
![]() $\pi _* : \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right ) \to \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)} \right )$
.
$\pi _* : \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)^\varepsilon } \right ) \to \mathsf {Maps}\left ( {B}, {\mathsf {Gr}(d)} \right )$
.
Recall that we constructed a map
![]() $\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
, so, if
$\mathsf {cl} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}\varepsilon }} \right \rbrack $
, so, if
![]() $\varepsilon \leq 1/2$
, then any
$\varepsilon \leq 1/2$
, then any
![]() $\varepsilon $
-approximate cocycle
$\varepsilon $
-approximate cocycle
![]() $\Omega $
represents a true vector bundle, namely
$\Omega $
represents a true vector bundle, namely
![]() $\pi _*(\mathsf {cl}(\Omega )) \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
. To summarize, if
$\pi _*(\mathsf {cl}(\Omega )) \in \left \lbrack {B}, {\mathsf {Gr}(d)} \right \rbrack $
. To summarize, if
![]() $\varepsilon \leq 1/2$
, we have defined a map
$\varepsilon \leq 1/2$
, we have defined a map
Upper bound
For the rest of this section, we let
![]() $\Phi $
be an
$\Phi $
be an
![]() $\varepsilon $
-approximate local trivialization subordinate to a countable cover
$\varepsilon $
-approximate local trivialization subordinate to a countable cover
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
of a paracompact topological space B, with
$\mathcal {U} = \{U_i\}_{i \in I}$
of a paracompact topological space B, with
![]() $\varepsilon \in [0,\infty ]$
; we let
$\varepsilon \in [0,\infty ]$
; we let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
and let
$\mathcal {U}$
and let
![]() $\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Recall from Lemma 4.16 that
$\iota : I \to \mathbb {N}_{\geq 1}$
be an injection. Recall from Lemma 4.16 that
defines a
![]() $\sqrt {2}\varepsilon $
-approximate classifying map
$\sqrt {2}\varepsilon $
-approximate classifying map
![]() $B \to \mathsf {Gr}(d)^{\sqrt {2}\varepsilon }$
. We will make use of results in Appendix A.2.
$B \to \mathsf {Gr}(d)^{\sqrt {2}\varepsilon }$
. We will make use of results in Appendix A.2.
Lemma 4.23. If
![]() $\varepsilon \in (0,\infty ]$
, then for,
$\varepsilon \in (0,\infty ]$
, then for,
![]() $i \in I$
and
$i \in I$
and
![]() $y \in U_i$
, we have
$y \in U_i$
, we have
If
![]() $\varepsilon = 0$
, then
$\varepsilon = 0$
, then
![]() $\Phi _i(y)\Phi _i(y)^t = \pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )$
and
$\Phi _i(y)\Phi _i(y)^t = \pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )$
and
![]() $\Phi _i(y) = \pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )\Phi _i(y)$
.
$\Phi _i(y) = \pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )\Phi _i(y)$
.
Proof. We address the case
![]() $\varepsilon \in (0,\infty ]$
, the case
$\varepsilon \in (0,\infty ]$
, the case
![]() $\varepsilon = 0$
being similar. The second inequality is a consequence of the first one and Lemma A.5. For the first inequality, use Lemma A.2 together with Lemma A.6.
$\varepsilon = 0$
being similar. The second inequality is a consequence of the first one and Lemma A.5. For the first inequality, use Lemma A.2 together with Lemma A.6.
Lemma 4.24. Assume that
![]() $\varepsilon \leq \sqrt {2}/4$
. For every
$\varepsilon \leq \sqrt {2}/4$
. For every
![]() $i \in I$
and
$i \in I$
and
![]() $y \in U_i$
, the matrix
$y \in U_i$
, the matrix
![]() $\pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )\Phi _i(y)$
has rank d.
$\pi _*\left (\mathsf {av}^\varphi (\Phi )(y)\right )\Phi _i(y)$
has rank d.
Proof. To simplify notation, let us omit from the formulas the evaluations on
![]() $y \in U_i$
. It is enough to show that
$y \in U_i$
. It is enough to show that
![]() $\left (\pi _*(\mathsf {av}^\varphi (\Phi ))\Phi _i\right )^t\pi _*(\mathsf {av}^\varphi (\Phi ))\Phi _i$
has full rank. Note that
$\left (\pi _*(\mathsf {av}^\varphi (\Phi ))\Phi _i\right )^t\pi _*(\mathsf {av}^\varphi (\Phi ))\Phi _i$
has full rank. Note that
Using Lemma 4.23 and Lemma A.5, we conclude that
The result then follows from Lemma A.15, as
![]() $2\sqrt {2}\varepsilon \leq 1$
by assumption.
$2\sqrt {2}\varepsilon \leq 1$
by assumption.
Given an
![]() $\varepsilon $
-approximate local trivialization
$\varepsilon $
-approximate local trivialization
![]() $\Phi $
with
$\Phi $
with
![]() $\varepsilon \leq \sqrt {2}/4$
, we now define an exact local trivialization
$\varepsilon \leq \sqrt {2}/4$
, we now define an exact local trivialization
![]() $\Psi $
that represents the same vector bundle. Given
$\Psi $
that represents the same vector bundle. Given
![]() $i \in I$
and
$i \in I$
and
![]() $y \in U_i$
, we let
$y \in U_i$
, we let
where the map Q is the one of Corollary A.4. By Lemma 4.24 and Corollary A.4, the maps
![]() $\Psi _i$
are well defined and continuous. To see that it is an exact local trivialization it suffices to check that, if
$\Psi _i$
are well defined and continuous. To see that it is an exact local trivialization it suffices to check that, if
![]() $y \in U_j \cap U_i$
, then the columns of
$y \in U_j \cap U_i$
, then the columns of
![]() $\Psi _i(y)$
and
$\Psi _i(y)$
and
![]() $\Psi _j(y)$
span the same subspace of
$\Psi _j(y)$
span the same subspace of
![]() $\mathbb {R}^\infty $
. This is a consequence of the fact that the columns of
$\mathbb {R}^\infty $
. This is a consequence of the fact that the columns of
![]() $\Psi _i(y)$
span the image of
$\Psi _i(y)$
span the image of
![]() $\pi _*(\mathsf {av}^\varphi (\Phi )(y)$
. We also deduce the following.
$\pi _*(\mathsf {av}^\varphi (\Phi )(y)$
. We also deduce the following.
Lemma 4.25. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $\mathsf {av}^\varphi (\Psi ) = \pi _*(\mathsf {av}^\varphi (\Phi ))$
.
$\mathsf {av}^\varphi (\Psi ) = \pi _*(\mathsf {av}^\varphi (\Phi ))$
.
We now bound the distance between
![]() $\Psi $
and
$\Psi $
and
![]() $\Phi $
.
$\Phi $
.
Lemma 4.26. Assume that
![]() $\varepsilon \leq \sqrt {2}/4$
, then
$\varepsilon \leq \sqrt {2}/4$
, then
![]() $\mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right ) \leq 4 \sqrt {2}\varepsilon $
.
$\mathsf {d}_{\mathsf {T}}\left ( \Phi , \Psi \right ) \leq 4 \sqrt {2}\varepsilon $
.
Proof. To simplify notation, let us omit from the formulas the evaluations on
![]() $y \in U_i$
. For every
$y \in U_i$
. For every
![]() $i \in I$
and
$i \in I$
and
![]() $y \in U_i$
, we have
$y \in U_i$
, we have
 $$ \begin{align*} \left\| \Phi_i - Q\left(\pi_*\left(\mathsf{av}^\varphi(\Phi)\right)\Phi_i\right)\right\| \leq &\,\,\, \| \Phi_i - \pi_*(\mathsf{av}^\varphi(\Phi))\Phi_i\| + \left\| \pi_*(\mathsf{av}^\varphi(\Phi))\Phi_i - Q\left(\pi_*\left(\mathsf{av}^\varphi(\Phi)\right)\Phi_i\right)\right\| \\ < &\,\,\, 2\sqrt{2}\varepsilon + 2\sqrt{2}\varepsilon = 4\sqrt{2} \varepsilon, \end{align*} $$
$$ \begin{align*} \left\| \Phi_i - Q\left(\pi_*\left(\mathsf{av}^\varphi(\Phi)\right)\Phi_i\right)\right\| \leq &\,\,\, \| \Phi_i - \pi_*(\mathsf{av}^\varphi(\Phi))\Phi_i\| + \left\| \pi_*(\mathsf{av}^\varphi(\Phi))\Phi_i - Q\left(\pi_*\left(\mathsf{av}^\varphi(\Phi)\right)\Phi_i\right)\right\| \\ < &\,\,\, 2\sqrt{2}\varepsilon + 2\sqrt{2}\varepsilon = 4\sqrt{2} \varepsilon, \end{align*} $$
where we bounded the first summand using Lemma 4.23 and the second summand using Lemma A.8. In order to satisfy the hypotheses of Lemma A.8, we use the same argument as in Lemma 4.24.
Theorem 4.27. Let
![]() $\varepsilon \leq \sqrt {2}/4$
and let
$\varepsilon \leq \sqrt {2}/4$
and let
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. There exists
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. There exists
![]() $\Lambda \in \mathsf {Z}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
$\Lambda \in \mathsf {Z}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
![]() $\mathsf {cl}(\Lambda ) = \pi _*(\mathsf {cl}(\Omega ))$
and such that
$\mathsf {cl}(\Lambda ) = \pi _*(\mathsf {cl}(\Omega ))$
and such that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq 9\varepsilon $
.
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq 9\varepsilon $
.
Proof. Let
![]() $\varphi $
be a partition of unity subordinate to
$\varphi $
be a partition of unity subordinate to
![]() $\mathcal {U}$
. Since
$\mathcal {U}$
. Since
![]() $\varepsilon \leq \sqrt {2}/4 \leq 1/2$
, it follows that
$\varepsilon \leq \sqrt {2}/4 \leq 1/2$
, it follows that
![]() $\pi _*(\mathsf {cl}(\Omega ))$
is well defined. By construction,
$\pi _*(\mathsf {cl}(\Omega ))$
is well defined. By construction,
![]() $\pi _*(\mathsf {cl}(\Omega ))$
is the homotopy class of
$\pi _*(\mathsf {cl}(\Omega ))$
is the homotopy class of
![]() $\pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota }(\Omega )$
. By Lemma 4.26, there is an exact local trivialization
$\pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota }(\Omega )$
. By Lemma 4.26, there is an exact local trivialization
![]() $\Psi $
such that
$\Psi $
such that
![]() $\mathsf {d}_{\mathsf {T}}\left ( \mathsf {triv}^{\varphi ,\iota }(\Omega ), \Psi \right ) \leq 4\sqrt {2} \varepsilon $
and such that
$\mathsf {d}_{\mathsf {T}}\left ( \mathsf {triv}^{\varphi ,\iota }(\Omega ), \Psi \right ) \leq 4\sqrt {2} \varepsilon $
and such that
![]() $\mathsf {av}^\varphi (\Psi ) = \pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota }(\Omega ) $
. Let
$\mathsf {av}^\varphi (\Psi ) = \pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota }(\Omega ) $
. Let
![]() $\Lambda = \mathsf {w}(\Psi )$
. Then
$\Lambda = \mathsf {w}(\Psi )$
. Then
![]() $\Lambda $
is a witness that
$\Lambda $
is a witness that
![]() $\Psi $
is an exact cocycle, so, by Lemma 4.10, we have that
$\Psi $
is an exact cocycle, so, by Lemma 4.10, we have that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq \varepsilon + \sqrt {2} \times 4\sqrt {2} \varepsilon = 9 \varepsilon $
. To conclude, note that
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right ) \leq \varepsilon + \sqrt {2} \times 4\sqrt {2} \varepsilon = 9 \varepsilon $
. To conclude, note that
![]() $\mathsf {cl}(\Lambda ) = [\mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } \circ \mathsf {w}(\Psi )] = [\mathsf {av}^\varphi (\Psi )] = [\pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } (\Omega )] = \pi _*(\mathsf {cl}(\Omega ))$
, where in the second equality we used Lemma 4.12 to conclude that
$\mathsf {cl}(\Lambda ) = [\mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } \circ \mathsf {w}(\Psi )] = [\mathsf {av}^\varphi (\Psi )] = [\pi _* \circ \mathsf {av}^\varphi \circ \mathsf {triv}^{\varphi ,\iota } (\Omega )] = \pi _*(\mathsf {cl}(\Omega ))$
, where in the second equality we used Lemma 4.12 to conclude that
![]() $\mathsf {triv}^{\varphi ,\iota }(\mathsf {w}(\Psi ))$
and
$\mathsf {triv}^{\varphi ,\iota }(\mathsf {w}(\Psi ))$
and
![]() $\Psi $
are homotopic through
$\Psi $
are homotopic through
![]() $0$
-approximate local trivializations.
$0$
-approximate local trivializations.
Lower bound
The following definition and result are inspired by Robinson’s notion of consistency radius [Reference Robinson55, Reference Robinson54]. The idea of this short section is to give a lower bound for the distance from an approximate cocycle to an exact cocycle.
Definition 4.28. Let
![]() $\Omega $
be a cochain subordinate to
$\Omega $
be a cochain subordinate to
![]() $\mathcal {U}$
. The consistency radius of
$\mathcal {U}$
. The consistency radius of
![]() $\Omega $
, denoted by
$\Omega $
, denoted by
![]() $r(\Omega )$
, is the infimum over all
$r(\Omega )$
, is the infimum over all
![]() $\varepsilon $
such that
$\varepsilon $
such that
![]() $\Omega $
belongs to
$\Omega $
belongs to
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
.
A similar argument to the one in Lemma 4.9 proves the following.
Lemma 4.29. Let
![]() $\Lambda \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
and
$\Lambda \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
and
![]() $\Omega \in C^1(\mathcal {U}; O(d))$
. Let
$\Omega \in C^1(\mathcal {U}; O(d))$
. Let
![]() $\delta> 0$
. If
$\delta> 0$
. If
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Lambda , \Omega \right ) < \delta $
, then
$\mathsf {d}_{\mathsf {Z}}\left ( \Lambda , \Omega \right ) < \delta $
, then
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon + 3\delta }\left ( \mathcal {U}; O(d) \right )$
.
$\Omega \in \mathsf {Z}^{1}_{\varepsilon + 3\delta }\left ( \mathcal {U}; O(d) \right )$
.
Lemma 4.30. Let
![]() $\Omega $
be a cochain, and let
$\Omega $
be a cochain, and let
![]() $\varepsilon> r(\Omega )$
. Then, the distance from
$\varepsilon> r(\Omega )$
. Then, the distance from
![]() $\Omega $
to
$\Omega $
to
![]() $\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
is bounded below by
$\check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
is bounded below by
![]() $\frac {r(\Omega ) - \varepsilon }{3}$
. In particular, if
$\frac {r(\Omega ) - \varepsilon }{3}$
. In particular, if
![]() $\Lambda $
is an exact cocycle, then
$\Lambda $
is an exact cocycle, then
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) \geq r(\Omega )/3$
.
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) \geq r(\Omega )/3$
.
Proof. Let
![]() $\Lambda $
be an exact cocycle, and let
$\Lambda $
be an exact cocycle, and let
![]() $\delta> \mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right )$
. It is enough to show that
$\delta> \mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda \right )$
. It is enough to show that
![]() $\delta \geq r(\Omega )/3$
. Equivalently, it is enough to show that, for every
$\delta \geq r(\Omega )/3$
. Equivalently, it is enough to show that, for every
![]() $(ijk) \in N(\mathcal {U})$
and
$(ijk) \in N(\mathcal {U})$
and
![]() $y \in U_k \cap U_j \cap U_i$
, we have
$y \in U_k \cap U_j \cap U_i$
, we have
![]() $\| \Omega _{ij}(y) \Omega _{jk}(y) - \Omega _{ik}(y)\| < 3\delta $
. This follows from Lemma 4.29.
$\| \Omega _{ij}(y) \Omega _{jk}(y) - \Omega _{ik}(y)\| < 3\delta $
. This follows from Lemma 4.29.
5 Discrete approximate vector bundles
In this section, we specialize the notions of approximate cocycle and approximate local trivialization to a certain open cover associated to any simplicial complex. This gives us the notions of discrete approximate cocycle and of discrete approximate local trivializations.
We show in Proposition 5.7 that any vector bundle over a compact triangulable space can be represented by a discrete approximate cocycle over a sufficiently fine triangulation of the space. In Section 5.2, we study the problem of reconstructing a vector bundle from finite samples as a discrete approximate local trivialization and as a discrete approximate cocycle. We prove in Theorem 5.15 that this is possible provided the classifying map of the vector bundle we wish to reconstruct is sufficiently regular and that we are given a sufficiently dense sample.
5.1 Discrete approximate vector bundles over simplicial complexes
We introduce two notions of discrete approximate vector bundle over a simplicial complex. These notions of discrete approximate vector bundle induce approximate vector bundles over the geometric realization of the simplicial complex.
Since this will be relevant in Section 6, we define discrete approximate cocycles with values in an arbitrary metric group G. Fix a simplicial complex K.
Definition 5.1. A discrete
![]() $\boldsymbol {\varepsilon }$
-approximate cocycle on K with values in G consists of, for every ordered
$\boldsymbol {\varepsilon }$
-approximate cocycle on K with values in G consists of, for every ordered
![]() $1$
-simplex
$1$
-simplex
![]() $(ij) \in K$
, an element
$(ij) \in K$
, an element
![]() $\Omega _{ij} \in G$
such that, for every ordered
$\Omega _{ij} \in G$
such that, for every ordered
![]() $2$
-simplex
$2$
-simplex
![]() $(ijk) \in K$
, we have
$(ijk) \in K$
, we have
![]() $d_G\left (\Omega _{ij} \Omega _{jk}, \Omega _{ik}\right ) < \varepsilon $
, and such that
$d_G\left (\Omega _{ij} \Omega _{jk}, \Omega _{ik}\right ) < \varepsilon $
, and such that
![]() $\Omega = \{\Omega _{ij}\}_{(ij) \in K}$
is symmetric, that is, we have
$\Omega = \{\Omega _{ij}\}_{(ij) \in K}$
is symmetric, that is, we have
![]() $\Omega _{ij} = \Omega _{ji}^t$
. A discrete exact cocycle consists of the same data but subject to
$\Omega _{ij} = \Omega _{ji}^t$
. A discrete exact cocycle consists of the same data but subject to
![]() $\Omega _{ij} \Omega _{jk} = \Omega _{ik}$
.
$\Omega _{ij} \Omega _{jk} = \Omega _{ik}$
.
We denote the set of discrete
![]() $\varepsilon $
-approximate cocycles on a simplicial complex K with values in G by
$\varepsilon $
-approximate cocycles on a simplicial complex K with values in G by
![]() $\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right )$
.
$\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right )$
.
Definition 5.2. Let
![]() $i \in K$
be a vertex. Let
$i \in K$
be a vertex. Let
![]() $\mathsf {st}(i)$
be the geometric realization of the open star of i seen as a vertex of the geometric realization
$\mathsf {st}(i)$
be the geometric realization of the open star of i seen as a vertex of the geometric realization
![]() $|K|$
. The star cover of
$|K|$
. The star cover of
![]() $|K|$
consists of the family of open sets
$|K|$
consists of the family of open sets
![]() $\{\mathsf {st}(i)\}_{(i) \in K}$
. Denote the star cover of
$\{\mathsf {st}(i)\}_{(i) \in K}$
. Denote the star cover of
![]() $|K|$
by
$|K|$
by
![]() $\mathsf {st}_K$
.
$\mathsf {st}_K$
.
Note that there is a canonical isomorphism of simplicial complexes
![]() $N(\mathsf {st}_K) \cong K$
that maps a vertex
$N(\mathsf {st}_K) \cong K$
that maps a vertex
![]() $i \in K$
to itself.
$i \in K$
to itself.
Construction 5.3. Let
![]() $\Omega $
be a discrete
$\Omega $
be a discrete
![]() $\varepsilon $
-approximate cocycle on a simplicial complex K with values in G. Define, for each
$\varepsilon $
-approximate cocycle on a simplicial complex K with values in G. Define, for each
![]() $(ij) \in K$
, a continuous map
$(ij) \in K$
, a continuous map
![]() $\mathsf {st}(j) \cap \mathsf {st}(i) \to G$
that is constantly
$\mathsf {st}(j) \cap \mathsf {st}(i) \to G$
that is constantly
![]() $\Omega _{ij}$
. This defines a natural map
$\Omega _{ij}$
. This defines a natural map
![]() $\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
.
$\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
.
Note that the map
![]() $\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
is injective. With this in mind, we endow
$\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
is injective. With this in mind, we endow
![]() $\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right )$
with the metric
$\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right )$
with the metric
![]() $\mathsf {d}_{\mathsf {Z}}$
, and interpret the map
$\mathsf {d}_{\mathsf {Z}}$
, and interpret the map
![]() $\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
as an embedding of metric spaces.
$\mathsf {DZ}^{1}_{\varepsilon }\left ( K; G \right ) \to \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_K; G \right )$
as an embedding of metric spaces.
Definition 5.4. A discrete
![]() $\boldsymbol {\varepsilon }$
-approximate local trivialization on a simplicial complex K consists of a frame
$\boldsymbol {\varepsilon }$
-approximate local trivialization on a simplicial complex K consists of a frame
![]() $\Phi _i \in \mathsf {V}(d)$
for every
$\Phi _i \in \mathsf {V}(d)$
for every
![]() $(i) \in K$
such that, for every
$(i) \in K$
such that, for every
![]() $(ij) \in K$
, there exists
$(ij) \in K$
, there exists
![]() $\Omega _{ij} \in O(d)$
such that
$\Omega _{ij} \in O(d)$
such that
![]() $\| \Phi _i \Omega _{ij} - \Phi _j\| < \varepsilon $
. A discrete exact local trivialization consists of the same data but subject to
$\| \Phi _i \Omega _{ij} - \Phi _j\| < \varepsilon $
. A discrete exact local trivialization consists of the same data but subject to
![]() $\Phi _i \Omega _{ij} = \Phi _j$
.
$\Phi _i \Omega _{ij} = \Phi _j$
.
Denote the set of discrete
![]() $\varepsilon $
-approximate local trivializations on a simplicial complex K by
$\varepsilon $
-approximate local trivializations on a simplicial complex K by
![]() $\mathsf {DT}_{\varepsilon }\left ( K; d \right )$
. In this discrete case too, the witness
$\mathsf {DT}_{\varepsilon }\left ( K; d \right )$
. In this discrete case too, the witness
![]() $\Omega $
that
$\Omega $
that
![]() $\Phi $
is a discrete
$\Phi $
is a discrete
![]() $\varepsilon $
-approximate local trivialization is not part of the data of the approximate local trivialization.
$\varepsilon $
-approximate local trivialization is not part of the data of the approximate local trivialization.
Construction 5.5. Let
![]() $\Phi $
be a discrete
$\Phi $
be a discrete
![]() $\varepsilon $
-approximate local trivialization on K. Define, for each
$\varepsilon $
-approximate local trivialization on K. Define, for each
![]() $(i) \in K$
, a map
$(i) \in K$
, a map
![]() $\mathsf {st}(i) \to \mathsf {V}(d)$
that is constantly
$\mathsf {st}(i) \to \mathsf {V}(d)$
that is constantly
![]() $\Phi _i$
. This defines a natural map
$\Phi _i$
. This defines a natural map
![]() $\mathsf {DT}_{\varepsilon }\left ( K; d \right ) \to \mathsf {T}_{\varepsilon }\left ( \mathsf {st}_K; d \right )$
.
$\mathsf {DT}_{\varepsilon }\left ( K; d \right ) \to \mathsf {T}_{\varepsilon }\left ( \mathsf {st}_K; d \right )$
.
Remark 5.6. Using Construction 4.8 we obtain a map
![]() $\mathsf {DT}_{\varepsilon }\left ( K; d \right ) \to \mathsf {DZ}^{1}_{3\varepsilon }\left ( K; O(d) \right )$
. If K is finite, this map is algorithmic since the minimization problem
$\mathsf {DT}_{\varepsilon }\left ( K; d \right ) \to \mathsf {DZ}^{1}_{3\varepsilon }\left ( K; O(d) \right )$
. If K is finite, this map is algorithmic since the minimization problem
can be solved by using the polar decomposition (Appendix A.2).
The next result guarantees that any vector bundle on a compact triangulable space can be encoded as a discrete approximate cocycle on a sufficiently fine triangulation of the space.
Proposition 5.7. Let
![]() $E \to B$
be a vector bundle over a compact triangulable space B, and let
$E \to B$
be a vector bundle over a compact triangulable space B, and let
![]() $\varepsilon \leq 3/8$
. There exists a triangulation K of B and a discrete
$\varepsilon \leq 3/8$
. There exists a triangulation K of B and a discrete
![]() $\varepsilon $
-approximate cocycle
$\varepsilon $
-approximate cocycle
![]() $\Omega \in \mathsf {DZ}^{1}_{\varepsilon }\left ( K; O(d) \right )$
such that
$\Omega \in \mathsf {DZ}^{1}_{\varepsilon }\left ( K; O(d) \right )$
such that
![]() $\pi _*(\mathsf {cl}(\Omega ))$
represents the vector bundle
$\pi _*(\mathsf {cl}(\Omega ))$
represents the vector bundle
![]() $E \to B$
.
$E \to B$
.
Proof. Let S be a finite simplicial complex such that
![]() $|S| \cong B$
. Without loss of generality, we assume
$|S| \cong B$
. Without loss of generality, we assume
![]() $|S| = B$
. Since the star cover of S consists of contractible sets, the vector bundle
$|S| = B$
. Since the star cover of S consists of contractible sets, the vector bundle
![]() $E \to |S|$
trivializes over
$E \to |S|$
trivializes over
![]() $\mathsf {st}_{S}$
and thus is represented by an exact cocycle
$\mathsf {st}_{S}$
and thus is represented by an exact cocycle
![]() $\Lambda \in \mathsf {Z}^{1}_{}\left ( \mathsf {st}_{S}; O(d) \right )$
. Moreover, since the closed stars
$\Lambda \in \mathsf {Z}^{1}_{}\left ( \mathsf {st}_{S}; O(d) \right )$
. Moreover, since the closed stars
![]() $\overline {\mathsf {st}(i)}$
are also contractible, for each
$\overline {\mathsf {st}(i)}$
are also contractible, for each
![]() $(ij) \in S$
, the continuous map
$(ij) \in S$
, the continuous map
![]() $\Lambda _{ij} : \mathsf {st}(j) \cap \mathsf {st}(i) \to O(d)$
can be taken such that it extends to
$\Lambda _{ij} : \mathsf {st}(j) \cap \mathsf {st}(i) \to O(d)$
can be taken such that it extends to
![]() $\overline {\mathsf {st}(j)} \cap \overline {\mathsf {st}(i)}$
, which is a closed set. Pick a metric that metrizes
$\overline {\mathsf {st}(j)} \cap \overline {\mathsf {st}(i)}$
, which is a closed set. Pick a metric that metrizes
![]() $|S|$
, which must exists since S is a finite simplicial complex. It follows that the maps
$|S|$
, which must exists since S is a finite simplicial complex. It follows that the maps
![]() $\Lambda _{ij}$
are uniformly continuous, and thus there exists
$\Lambda _{ij}$
are uniformly continuous, and thus there exists
![]() $\delta> 0$
such that for every
$\delta> 0$
such that for every
![]() $(ij) \in S$
and every
$(ij) \in S$
and every
![]() $T \subseteq \mathsf {st}(j) \cap \mathsf {st}(i)$
of diameter less than
$T \subseteq \mathsf {st}(j) \cap \mathsf {st}(i)$
of diameter less than
![]() $\delta $
, the diameter of
$\delta $
, the diameter of
![]() $\Lambda _{ij}(T) \subseteq O(d)$
is less than
$\Lambda _{ij}(T) \subseteq O(d)$
is less than
![]() $\varepsilon /3$
.
$\varepsilon /3$
.
For
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $S^{(n)}$
denote the nth barycentric subdivision of S. Note that, for every
$S^{(n)}$
denote the nth barycentric subdivision of S. Note that, for every
![]() $n \in \mathbb {N}$
, the star cover
$n \in \mathbb {N}$
, the star cover
![]() $\mathsf {st}_{S^{(n+1)}}$
refines the star cover
$\mathsf {st}_{S^{(n+1)}}$
refines the star cover
![]() $\mathsf {st}_{S^{(n)}}$
. Choose a refinement map
$\mathsf {st}_{S^{(n)}}$
. Choose a refinement map
![]() $r^n : \mathsf {st}_{S^{(n+1)}} \to \mathsf {st}_{S^{(n)}}$
for each n, and let
$r^n : \mathsf {st}_{S^{(n+1)}} \to \mathsf {st}_{S^{(n)}}$
for each n, and let
![]() $\Lambda ^n \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_{S^{(n)}}; O(d) \right )$
denote the restriction of
$\Lambda ^n \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathsf {st}_{S^{(n)}}; O(d) \right )$
denote the restriction of
![]() $\Lambda $
along these refinements, obtained by using Construction 4.19. Note that, by Lemma 4.20,
$\Lambda $
along these refinements, obtained by using Construction 4.19. Note that, by Lemma 4.20,
![]() $\Lambda $
still represents the original vector bundle
$\Lambda $
still represents the original vector bundle
![]() $E \to |S|$
.
$E \to |S|$
.
As n goes to
![]() $\infty $
, the maximum of the diameters
$\infty $
, the maximum of the diameters
![]() $\max _{i \in S^{(n)}}\mathsf {diam}(\mathsf {st}_i)$
goes to
$\max _{i \in S^{(n)}}\mathsf {diam}(\mathsf {st}_i)$
goes to
![]() $0$
, since the diameter of simplices goes to
$0$
, since the diameter of simplices goes to
![]() $0$
uniformly, as S has finitely many simplices. In particular, there exists
$0$
uniformly, as S has finitely many simplices. In particular, there exists
![]() $n_0$
such that the diameter of the image of
$n_0$
such that the diameter of the image of
![]() $\Lambda ^{n_0}_{ij}$
is less than
$\Lambda ^{n_0}_{ij}$
is less than
![]() $\varepsilon /3$
for every
$\varepsilon /3$
for every
![]() $(ij) \in S^{(n_0)}$
since the original
$(ij) \in S^{(n_0)}$
since the original
![]() $\Lambda $
consists of uniformly continuous maps. Let
$\Lambda $
consists of uniformly continuous maps. Let
![]() $K = S^{n_0}$
.
$K = S^{n_0}$
.
For every
![]() $(ij) \in K$
, pick a matrix
$(ij) \in K$
, pick a matrix
![]() $\Omega _{ij}$
in the image of
$\Omega _{ij}$
in the image of
![]() $\Lambda ^{n_0}_{ij}$
in such a way that
$\Lambda ^{n_0}_{ij}$
in such a way that
![]() $\Omega _{ij} = \Omega _{ji}^t$
. The matrices
$\Omega _{ij} = \Omega _{ji}^t$
. The matrices
![]() $\Omega _{ij}$
assemble into a cochain
$\Omega _{ij}$
assemble into a cochain
![]() $\Omega \in C^1(\mathsf {st}_{K}; O(d))$
such that
$\Omega \in C^1(\mathsf {st}_{K}; O(d))$
such that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda ^{n_0} \right ) < \varepsilon /3$
. It follows from Lemma 4.29 that
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Lambda ^{n_0} \right ) < \varepsilon /3$
. It follows from Lemma 4.29 that
![]() $\Omega $
is a
$\Omega $
is a
![]() $\varepsilon $
-approximate cocycle, and since it is constant on each intersection, we have
$\varepsilon $
-approximate cocycle, and since it is constant on each intersection, we have
![]() $\Omega \in \mathsf {DZ}^{1}_{\varepsilon }\left ( K; O(d) \right )$
.
$\Omega \in \mathsf {DZ}^{1}_{\varepsilon }\left ( K; O(d) \right )$
.
To conclude, note that, by Theorem 4.21, we have that
![]() $\mathsf {cl}(\Omega )$
and
$\mathsf {cl}(\Omega )$
and
![]() $\mathsf {cl}(\Lambda ^{n_0}) = \mathsf {cl}(\Lambda )$
become equal in
$\mathsf {cl}(\Lambda ^{n_0}) = \mathsf {cl}(\Lambda )$
become equal in
![]() $\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \varepsilon /3)}} \right \rbrack $
. Since
$\left \lbrack {B}, {\mathsf {Gr}(d)^{\sqrt {2}(\varepsilon + \varepsilon /3)}} \right \rbrack $
. Since
![]() $\sqrt {2}(\varepsilon + \varepsilon /3) \leq \sqrt {2}/2$
, by assumption, we have that
$\sqrt {2}(\varepsilon + \varepsilon /3) \leq \sqrt {2}/2$
, by assumption, we have that
![]() $\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
, as required.
$\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
, as required.
5.2 Reconstruction of vector bundles from finite samples
Let
![]() $\delta \geq 0$
and
$\delta \geq 0$
and
![]() $\ell> 0$
. A function
$\ell> 0$
. A function
![]() $f : X \to Y$
between metric spaces is a
$f : X \to Y$
between metric spaces is a
![]() $\boldsymbol {\delta }$
-approximate
$\boldsymbol {\delta }$
-approximate
![]() $\boldsymbol {\ell }$
-Lipschitz map if, for every
$\boldsymbol {\ell }$
-Lipschitz map if, for every
![]() $x,x' \in X$
, we have
$x,x' \in X$
, we have
![]() $\ell d_X(x,x') + \delta \geq d_Y(f(x), f(x'))$
.
$\ell d_X(x,x') + \delta \geq d_Y(f(x), f(x'))$
.
Definition 5.8. Let
![]() $X \subseteq \mathbb {R}^N$
. The Čech complex of X at distance scale
$X \subseteq \mathbb {R}^N$
. The Čech complex of X at distance scale
![]() $\varepsilon> 0$
, denoted
$\varepsilon> 0$
, denoted
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
, consists of the simplicial complex given by the nerve of the cover
$\check{\mathsf{C}}(X)(\varepsilon )$
, consists of the simplicial complex given by the nerve of the cover
![]() $\{ B(x, \varepsilon ) \}_{x \in X}$
of
$\{ B(x, \varepsilon ) \}_{x \in X}$
of
![]() $X^\varepsilon $
.
$X^\varepsilon $
.
Note that the cover
![]() $\{ B(x, \varepsilon )\}_{x \in X}$
is indexed by the elements of X, so the
$\{ B(x, \varepsilon )\}_{x \in X}$
is indexed by the elements of X, so the
![]() $0$
-simplices of
$0$
-simplices of
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
consist of the elements of X. As a set,
$\check{\mathsf{C}}(X)(\varepsilon )$
consist of the elements of X. As a set,
![]() $|\check{\mathsf{C}}(X)(\varepsilon )|$
consists of formal linear combinations
$|\check{\mathsf{C}}(X)(\varepsilon )|$
consists of formal linear combinations
such that
![]() $S_p = \{x \in X : c_x> 0\}$
is a finite set with the property that the intersection
$S_p = \{x \in X : c_x> 0\}$
is a finite set with the property that the intersection
![]() $\cap _{x \in S_p} B(x,\varepsilon ) \subseteq \mathbb {R}^N$
is nonempty. We will often write
$\cap _{x \in S_p} B(x,\varepsilon ) \subseteq \mathbb {R}^N$
is nonempty. We will often write
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
for the geometric realization
$\check{\mathsf{C}}(X)(\varepsilon )$
for the geometric realization
![]() $|\check{\mathsf{C}}(X)(\varepsilon )|$
.
$|\check{\mathsf{C}}(X)(\varepsilon )|$
.
Construction 5.9. Let
![]() $X \subseteq \mathbb {R}^N$
and let
$X \subseteq \mathbb {R}^N$
and let
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $\delta \geq 0$
and
$\delta \geq 0$
and
![]() $\ell> 0$
. Assume that X is finite. Let
$\ell> 0$
. Assume that X is finite. Let
![]() $Y \subseteq \mathbb {R}^M$
, and let
$Y \subseteq \mathbb {R}^M$
, and let
![]() $f : X \to Y$
be a
$f : X \to Y$
be a
![]() $\delta $
-approximate
$\delta $
-approximate
![]() $\ell $
-Lipschitz map with respect to the distances induced by the Euclidean norm
$\ell $
-Lipschitz map with respect to the distances induced by the Euclidean norm
![]() $\|-\|_2$
. Define a continuous map
$\|-\|_2$
. Define a continuous map
 $$ \begin{align*} \check{\mathsf{C}}(f)(\varepsilon) : \check{\mathsf{C}}(X)(\varepsilon) &\to Y^{2\ell \varepsilon + \delta} \subseteq \mathbb{R}^M\\ \sum_{x \in X} c_x [x] &\mapsto \sum_{x \in X}c_x f(x).\\[-46pt] \end{align*} $$
$$ \begin{align*} \check{\mathsf{C}}(f)(\varepsilon) : \check{\mathsf{C}}(X)(\varepsilon) &\to Y^{2\ell \varepsilon + \delta} \subseteq \mathbb{R}^M\\ \sum_{x \in X} c_x [x] &\mapsto \sum_{x \in X}c_x f(x).\\[-46pt] \end{align*} $$
![]() $\vartriangleleft $
$\vartriangleleft $
The map
![]() $\check{\mathsf{C}}(f)$
is well defined since, if
$\check{\mathsf{C}}(f)$
is well defined since, if
![]() $p = \sum _{x \in X} c_x [x]$
is such that
$p = \sum _{x \in X} c_x [x]$
is such that
![]() $c_{x_0}> 0$
, then
$c_{x_0}> 0$
, then
![]() $\|f(z) - f(x_0)\|_2 < \ell 2\varepsilon + \delta $
for every
$\|f(z) - f(x_0)\|_2 < \ell 2\varepsilon + \delta $
for every
![]() $z \in X$
such that
$z \in X$
such that
![]() $c_z> 0$
, since, in that case,
$c_z> 0$
, since, in that case,
![]() $\|x_0 - z\| < 2\varepsilon $
, as the balls
$\|x_0 - z\| < 2\varepsilon $
, as the balls
![]() $B(x_0, \varepsilon )$
and
$B(x_0, \varepsilon )$
and
![]() $B(z,\varepsilon )$
must intersect.
$B(z,\varepsilon )$
must intersect.
Lemma 5.10. Let
![]() $X \subseteq \mathbb {R}^N$
and let
$X \subseteq \mathbb {R}^N$
and let
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $\delta \geq 0$
and
$\delta \geq 0$
and
![]() $\ell> 0$
. Assume that X is finite. Let
$\ell> 0$
. Assume that X is finite. Let
![]() $f : X \to \mathsf {Gr}(n,d) \subseteq \mathbb {R}^{n \times n}$
be a
$f : X \to \mathsf {Gr}(n,d) \subseteq \mathbb {R}^{n \times n}$
be a
![]() $\delta $
-approximate
$\delta $
-approximate
![]() $\ell $
-Lipschitz map with respect to the Euclidean norm and the Frobenius norm. The
$\ell $
-Lipschitz map with respect to the Euclidean norm and the Frobenius norm. The
![]() $(2\ell \varepsilon + \delta )$
-approximate classifying map
$(2\ell \varepsilon + \delta )$
-approximate classifying map
![]() $\check{\mathsf{C}}(f)(\varepsilon ) : \check{\mathsf{C}}(X)(\varepsilon ) \to \mathsf {Gr}(d,n)^{2\ell \varepsilon + \delta }$
of Construction 5.9 can be represented by a discrete approximate local trivialization, in the sense that there exists a partition of unity
$\check{\mathsf{C}}(f)(\varepsilon ) : \check{\mathsf{C}}(X)(\varepsilon ) \to \mathsf {Gr}(d,n)^{2\ell \varepsilon + \delta }$
of Construction 5.9 can be represented by a discrete approximate local trivialization, in the sense that there exists a partition of unity
![]() $\varphi $
of the star cover of
$\varphi $
of the star cover of
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
and
$\check{\mathsf{C}}(X)(\varepsilon )$
and
![]() $\Phi \in \mathsf {DT}_{2\ell \varepsilon + \delta }\left ( \check{\mathsf{C}}(X)(\varepsilon ); d \right )$
such that
$\Phi \in \mathsf {DT}_{2\ell \varepsilon + \delta }\left ( \check{\mathsf{C}}(X)(\varepsilon ); d \right )$
such that
![]() $\mathsf {av}^\varphi (\Phi ) = \check{\mathsf{C}}(f)(\varepsilon )$
.
$\mathsf {av}^\varphi (\Phi ) = \check{\mathsf{C}}(f)(\varepsilon )$
.
Moreover, there is a discrete
![]() $(3(2\ell \varepsilon + \delta ))$
-approximate cocycle
$(3(2\ell \varepsilon + \delta ))$
-approximate cocycle
![]() $\mathsf {w}(\Phi )$
such that
$\mathsf {w}(\Phi )$
such that
![]() $\mathsf {cl}(\Omega )$
is equal to
$\mathsf {cl}(\Omega )$
is equal to
![]() $\check{\mathsf{C}}(f)(\varepsilon )$
in
$\check{\mathsf{C}}(f)(\varepsilon )$
in
![]() $\left \lbrack {\check{\mathsf{C}}(X)(\varepsilon )}, {\mathsf {Gr}(d,n)^{3\sqrt {2}(2\ell \varepsilon +\delta )}} \right \rbrack $
.
$\left \lbrack {\check{\mathsf{C}}(X)(\varepsilon )}, {\mathsf {Gr}(d,n)^{3\sqrt {2}(2\ell \varepsilon +\delta )}} \right \rbrack $
.
Proof. The second claim is a consequence of the first one and Lemma 4.12, where
![]() $\mathsf {w}$
is the map defined in Lemma 4.9.
$\mathsf {w}$
is the map defined in Lemma 4.9.
For the first claim, for each
![]() $x \in X$
, let
$x \in X$
, let
![]() $\Phi _x \in \mathsf {V}(d,n)$
be an orthonormal basis of the subspace of
$\Phi _x \in \mathsf {V}(d,n)$
be an orthonormal basis of the subspace of
![]() $\mathbb {R}^n$
spanned by
$\mathbb {R}^n$
spanned by
![]() $f(x) \in \mathsf {Gr}(d,n)$
. Since f is a
$f(x) \in \mathsf {Gr}(d,n)$
. Since f is a
![]() $\delta $
-approximate
$\delta $
-approximate
![]() $\ell $
-Lipschitz map, the family
$\ell $
-Lipschitz map, the family
![]() $\{\Phi _x\}_{x \in X}$
constitutes a discrete
$\{\Phi _x\}_{x \in X}$
constitutes a discrete
![]() $(2\ell \varepsilon +\delta )$
-approximate local trivialization on the simplicial complex
$(2\ell \varepsilon +\delta )$
-approximate local trivialization on the simplicial complex
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
, by Lemma A.9. By taking the partition of unity
$\check{\mathsf{C}}(X)(\varepsilon )$
, by Lemma A.9. By taking the partition of unity
![]() $\varphi $
subordinate to the star cover of
$\varphi $
subordinate to the star cover of
![]() $\check{\mathsf{C}}(X)(\varepsilon )$
given by
$\check{\mathsf{C}}(X)(\varepsilon )$
given by
![]() $\varphi _x(\sum _{x \in X} c_x [x]) = c_x$
, we see that
$\varphi _x(\sum _{x \in X} c_x [x]) = c_x$
, we see that
![]() $\mathsf {av}^\varphi (\Phi ) = \check{\mathsf{C}}(f)(\varepsilon )$
.
$\mathsf {av}^\varphi (\Phi ) = \check{\mathsf{C}}(f)(\varepsilon )$
.
The following result is well known; see, for example, [Reference Hatcher26, Corollary 4G.3].
Lemma 5.11 (Nerve lemma).
Let
![]() $\mathcal {U} = \{U_i\}_{i \in I}$
be an open cover of a paracompact topological space B, and let
$\mathcal {U} = \{U_i\}_{i \in I}$
be an open cover of a paracompact topological space B, and let
![]() $\varphi $
be a partition of unity subordinate to B. If
$\varphi $
be a partition of unity subordinate to B. If
![]() $\mathcal {U}$
has the property that any finite intersection of its elements is either contractible or empty, then the map
$\mathcal {U}$
has the property that any finite intersection of its elements is either contractible or empty, then the map
![]() $B \to |N(\mathcal {U})|$
that sends y to
$B \to |N(\mathcal {U})|$
that sends y to
![]() $\sum _{i \in I} \varphi _i(y) [i]$
is well defined, continuous and a homotopy equivalence.
$\sum _{i \in I} \varphi _i(y) [i]$
is well defined, continuous and a homotopy equivalence.
Corollary 5.12. Let
![]() $X \subseteq \mathbb {R}^N$
be a finite subset, let
$X \subseteq \mathbb {R}^N$
be a finite subset, let
![]() $\varepsilon> 0$
and let
$\varepsilon> 0$
and let
![]() $\varphi = \{\varphi _x\}_{x\in X}$
be a partition of unity subordinate to
$\varphi = \{\varphi _x\}_{x\in X}$
be a partition of unity subordinate to
![]() $\{ B(x,\varepsilon ) \}_{x \in X}$
. Then, the following map is a homotopy equivalence:
$\{ B(x,\varepsilon ) \}_{x \in X}$
. Then, the following map is a homotopy equivalence:
 $$ \begin{align*} R^\varphi : X^\varepsilon &\to \check{\mathsf{C}}(X)(\varepsilon) \\ z &\mapsto \sum_{x \in X} \varphi_x(z) [x].\\[-46pt] \end{align*} $$
$$ \begin{align*} R^\varphi : X^\varepsilon &\to \check{\mathsf{C}}(X)(\varepsilon) \\ z &\mapsto \sum_{x \in X} \varphi_x(z) [x].\\[-46pt] \end{align*} $$
□
Our reconstruction theorem for vector bundles builds on the following result by Niyogi, Smale and Weinberger, which allows one to recover the homotopy type of a compact manifold smoothly embedded into
![]() $\mathbb {R}^N$
from a sufficiently close and dense sample. In the result,
$\mathbb {R}^N$
from a sufficiently close and dense sample. In the result,
![]() $d_H$
denotes the Hausdorff distance.
$d_H$
denotes the Hausdorff distance.
Proposition 5.13 [Reference Partha Niyogi49, Proposition 7.1].
Let
![]() $\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold with
$\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold with
![]() $\tau = \operatorname {\mathrm {reach}}(M)> 0$
. Let
$\tau = \operatorname {\mathrm {reach}}(M)> 0$
. Let
![]() $P\subseteq \mathbb {R}^N$
such that
$P\subseteq \mathbb {R}^N$
such that
![]() $d_H(P,\mathcal {M}) < \varepsilon < (3 - \sqrt {8}) \tau $
and let
$d_H(P,\mathcal {M}) < \varepsilon < (3 - \sqrt {8}) \tau $
and let
 $$\begin{align*}\alpha \in \left( \frac{( \varepsilon + \tau) - \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2}, \frac{( \varepsilon + \tau) + \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2} \right), \end{align*}$$
$$\begin{align*}\alpha \in \left( \frac{( \varepsilon + \tau) - \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2}, \frac{( \varepsilon + \tau) + \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2} \right), \end{align*}$$
which is a nonempty open interval. Then
![]() $\mathcal {M} \subseteq P^\alpha $
and the inclusion
$\mathcal {M} \subseteq P^\alpha $
and the inclusion
![]() $\mathcal {M} \to P^\alpha $
is a homotopy equivalence.
$\mathcal {M} \to P^\alpha $
is a homotopy equivalence.
We are now ready to prove the reconstruction theorem for vector bundles. Before doing so, we give a short remark about representing vector bundles by Lipschitz maps.
Remark 5.14. In [Reference Rieffel53, Proposition 3.1] it is shown that any rank-d vector bundle on a compact metric space X can be represented by a Lipschitz map
![]() $X \to \mathsf {Gr}(d,n)$
for some n, where
$X \to \mathsf {Gr}(d,n)$
for some n, where
![]() $\mathsf {Gr}(d,n)$
is seen as a subspace of the space of square matrices
$\mathsf {Gr}(d,n)$
is seen as a subspace of the space of square matrices
![]() $\mathbb {R}^{n \times n}$
with the operator norm. It follows that a vector bundle on X can also be represented by a Lipschitz map
$\mathbb {R}^{n \times n}$
with the operator norm. It follows that a vector bundle on X can also be represented by a Lipschitz map
![]() $X \to \mathsf {Gr}(d,n)$
where now we use the Frobenius distance on
$X \to \mathsf {Gr}(d,n)$
where now we use the Frobenius distance on
![]() $\mathsf {Gr}(d,n)$
, as we do in this paper. This motivates the assumptions made in the following result.
$\mathsf {Gr}(d,n)$
, as we do in this paper. This motivates the assumptions made in the following result.
Theorem 5.15. Let
![]() $\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold and let
$\mathcal {M} \subseteq \mathbb {R}^N$
be a smoothly embedded compact manifold and let
![]() $f : \mathcal {M} \to \mathsf {Gr}(d,n)$
be an
$f : \mathcal {M} \to \mathsf {Gr}(d,n)$
be an
![]() $\ell $
-Lipschitz map with respect to the Euclidean distance on
$\ell $
-Lipschitz map with respect to the Euclidean distance on
![]() $\mathcal {M}$
and the Frobenius distance on
$\mathcal {M}$
and the Frobenius distance on
![]() $\mathsf {Gr}(d,n)$
. Assume that
$\mathsf {Gr}(d,n)$
. Assume that
![]() $\operatorname {\mathrm {reach}}(\mathcal {M}) = \tau> 0$
. Let
$\operatorname {\mathrm {reach}}(\mathcal {M}) = \tau> 0$
. Let
![]() $P \subseteq \mathbb {R}^N$
be a finite set and let
$P \subseteq \mathbb {R}^N$
be a finite set and let
![]() $g : P \to \mathsf {Gr}(d,n)$
be a function. Let
$g : P \to \mathsf {Gr}(d,n)$
be a function. Let
![]() $\varepsilon , \delta> 0$
be such that
$\varepsilon , \delta> 0$
be such that
-
• for every
 $x \in \mathcal {M}$
there exists
$x \in \mathcal {M}$
there exists
 $p \in P$
such that
$p \in P$
such that
 $\|p - x\|_2 < \varepsilon $
;
$\|p - x\|_2 < \varepsilon $
; -
• for every
 $p \in P$
there exists
$p \in P$
there exists
 $x \in \mathcal {M}$
such that
$x \in \mathcal {M}$
such that
 $\|p - x\|_2 < \varepsilon $
and
$\|p - x\|_2 < \varepsilon $
and
 $\|g(p) - f(x)\| < \delta $
$\|g(p) - f(x)\| < \delta $
so that g is a
![]() $2(\delta + \ell \varepsilon )$
-approximate
$2(\delta + \ell \varepsilon )$
-approximate
![]() $\ell $
-Lipschitz map. If
$\ell $
-Lipschitz map. If
![]() $\varepsilon < (3 - \sqrt {8}) \tau $
, then, for every
$\varepsilon < (3 - \sqrt {8}) \tau $
, then, for every
 $$\begin{align*}\alpha \in \left( \frac{( \varepsilon + \tau) - \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2}, \frac{( \varepsilon + \tau) + \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2} \right) \cap \left(0, \frac{\sqrt{2}/2-2\delta - 2\ell \varepsilon}{2\ell}\right), \end{align*}$$
$$\begin{align*}\alpha \in \left( \frac{( \varepsilon + \tau) - \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2}, \frac{( \varepsilon + \tau) + \sqrt{ \varepsilon^2 + \tau^2 - 6\tau \varepsilon}}{2} \right) \cap \left(0, \frac{\sqrt{2}/2-2\delta - 2\ell \varepsilon}{2\ell}\right), \end{align*}$$
there is a homotopy commutative diagram as follows, in which the vertical maps are homotopy equivalences:

Note that the interval to which
![]() $\alpha $
must belong to is nonempty as long as
$\alpha $
must belong to is nonempty as long as
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\delta $
are sufficiently small, a condition that depends only on
$\delta $
are sufficiently small, a condition that depends only on
![]() $\tau $
and
$\tau $
and
![]() $\ell $
.
$\ell $
.
Proof. We start by showing that g is indeed a
![]() $2(\delta + \ell \varepsilon )$
-approximate
$2(\delta + \ell \varepsilon )$
-approximate
![]() $\ell $
-Lipschitz map so that the bottom map of the diagram in the statement is well defined. To do this, note that, if
$\ell $
-Lipschitz map so that the bottom map of the diagram in the statement is well defined. To do this, note that, if
![]() $p,q \in P$
, then there exist
$p,q \in P$
, then there exist
![]() $x,y \in \mathcal {M}$
with
$x,y \in \mathcal {M}$
with
![]() $\|p - x\|_2, \|q - y\|_2 < \varepsilon $
and
$\|p - x\|_2, \|q - y\|_2 < \varepsilon $
and
![]() $\|g(p) - f(x)\|, \|g(q) - f(y)\| < \delta $
. Since f is
$\|g(p) - f(x)\|, \|g(q) - f(y)\| < \delta $
. Since f is
![]() $\ell $
-Lipschitz, we have
$\ell $
-Lipschitz, we have
![]() $\|g(p) - g(q)\| \leq 2\delta + \ell \|x - y\| \leq 2\delta + \ell 2\varepsilon + \ell \|p - q\|$
, as required.
$\|g(p) - g(q)\| \leq 2\delta + \ell \|x - y\| \leq 2\delta + \ell 2\varepsilon + \ell \|p - q\|$
, as required.
The homotopy equivalence
![]() $\mathcal {M} \to \check{\mathsf{C}}(P)(\alpha )$
is given by composing the inclusion
$\mathcal {M} \to \check{\mathsf{C}}(P)(\alpha )$
is given by composing the inclusion
![]() $\mathcal {M} \subseteq P^\alpha $
with the map
$\mathcal {M} \subseteq P^\alpha $
with the map
![]() $R^\varphi : P^\alpha \to \check{\mathsf{C}}(P)(\alpha )$
for a choice of partition of unity
$R^\varphi : P^\alpha \to \check{\mathsf{C}}(P)(\alpha )$
for a choice of partition of unity
![]() $\varphi $
subordinate to
$\varphi $
subordinate to
![]() $\{B(p,\alpha )\}_{p\in P}$
. The map
$\{B(p,\alpha )\}_{p\in P}$
. The map
![]() $R^\varphi $
is a homotopy equivalence by Corollary 5.12. The fact that the inclusion
$R^\varphi $
is a homotopy equivalence by Corollary 5.12. The fact that the inclusion
![]() $\mathcal {M} \to P^\alpha $
is well defined and a homotopy equivalence is the content of Proposition 5.13, whose hypotheses are satisfied since our conditions imply that
$\mathcal {M} \to P^\alpha $
is well defined and a homotopy equivalence is the content of Proposition 5.13, whose hypotheses are satisfied since our conditions imply that
![]() $d_H(P,\mathcal {M}) < \varepsilon $
.
$d_H(P,\mathcal {M}) < \varepsilon $
.
The map
![]() $\mathsf {Gr}(n,d) \to \mathsf {Gr}(n,d)^{2(\ell \alpha + \ell \varepsilon + \delta )}$
is simply the inclusion and it is a homotopy equivalence by Proposition A.12 since
$\mathsf {Gr}(n,d) \to \mathsf {Gr}(n,d)^{2(\ell \alpha + \ell \varepsilon + \delta )}$
is simply the inclusion and it is a homotopy equivalence by Proposition A.12 since
![]() $\alpha < (\sqrt {2}/2-2\delta - 2\ell \varepsilon )/(2\ell )$
.
$\alpha < (\sqrt {2}/2-2\delta - 2\ell \varepsilon )/(2\ell )$
.
To conclude the proof, we must show that the diagram in the statement commutes up to homotopy. For this, let
![]() $z \in \mathcal {M}$
. We have
$z \in \mathcal {M}$
. We have
![]() $\check{\mathsf{C}}(g)(R^\varphi (z)) = \check{\mathsf{C}}(g)\left ( \sum _{p \in P} \varphi _p(z) [p] \right ) = \sum _{p \in P} \varphi _p(z) g(x)$
. Consider the linear path
$\check{\mathsf{C}}(g)(R^\varphi (z)) = \check{\mathsf{C}}(g)\left ( \sum _{p \in P} \varphi _p(z) [p] \right ) = \sum _{p \in P} \varphi _p(z) g(x)$
. Consider the linear path
![]() $\beta f(z) + (1-\beta ) \sum _{p \in P} \varphi _p(z) g(p)$
for
$\beta f(z) + (1-\beta ) \sum _{p \in P} \varphi _p(z) g(p)$
for
![]() $\beta \in [0,1]$
. It suffices to show that it is included in
$\beta \in [0,1]$
. It suffices to show that it is included in
![]() $\mathsf {Gr}(n,d)^{2\ell \alpha + 2\ell \varepsilon + 2\delta }$
for all
$\mathsf {Gr}(n,d)^{2\ell \alpha + 2\ell \varepsilon + 2\delta }$
for all
![]() $\beta \in [0,1]$
, and we will show that it is at distance less than
$\beta \in [0,1]$
, and we will show that it is at distance less than
![]() $\ell \alpha + \ell \varepsilon + \delta $
from
$\ell \alpha + \ell \varepsilon + \delta $
from
![]() $f(z)$
. We compute
$f(z)$
. We compute
 $$ \begin{align*} &\;\left\| f(z) - \left(\beta f(z) + (1-\beta) \sum_{p \in P} \varphi_p(z) g(x)\right)\right\|_2\\ =&\; \left\|\beta f(z) + (1-\beta) f(x) - \left(\beta f(z) + (1-\beta) \sum_{p \in P} \varphi_p(z) g(p)\right)\right\|_2\\ \leq&\; (1-\beta) \sum_{p\in P} \varphi_p(z) \,\, \| f(z) - g(p) \|_2\\ <&\; (1-\beta) \sum_{x\in X} \varphi_x(z) \,\,(\ell \alpha + \ell \varepsilon + \delta) \leq \ell \alpha + \ell \varepsilon + \delta, \end{align*} $$
$$ \begin{align*} &\;\left\| f(z) - \left(\beta f(z) + (1-\beta) \sum_{p \in P} \varphi_p(z) g(x)\right)\right\|_2\\ =&\; \left\|\beta f(z) + (1-\beta) f(x) - \left(\beta f(z) + (1-\beta) \sum_{p \in P} \varphi_p(z) g(p)\right)\right\|_2\\ \leq&\; (1-\beta) \sum_{p\in P} \varphi_p(z) \,\, \| f(z) - g(p) \|_2\\ <&\; (1-\beta) \sum_{x\in X} \varphi_x(z) \,\,(\ell \alpha + \ell \varepsilon + \delta) \leq \ell \alpha + \ell \varepsilon + \delta, \end{align*} $$
where the strict inequality comes from the fact that, if
![]() $\varphi _p(z)$
is nonzero, then
$\varphi _p(z)$
is nonzero, then
![]() $z \in B(p,\alpha )$
, and thus there exists
$z \in B(p,\alpha )$
, and thus there exists
![]() $x \in \mathcal {M}$
such that
$x \in \mathcal {M}$
such that
![]() $\|f(z) - g(p)\|_2 \leq \|f(z) - f(x) \| +\|f(x) - g(p)\| < \ell \|z-x\|_2 + \delta \leq \ell (\|z - p\|_2 + \|p - x\|_2) + \delta < \ell \alpha + \ell \varepsilon + \delta $
.
$\|f(z) - g(p)\|_2 \leq \|f(z) - f(x) \| +\|f(x) - g(p)\| < \ell \|z-x\|_2 + \delta \leq \ell (\|z - p\|_2 + \|p - x\|_2) + \delta < \ell \alpha + \ell \varepsilon + \delta $
.
We conclude this section with a few remarks.
Remark 5.16. For simplicity, we have proven Theorem 5.15 using the Čech complex. A similar result can be obtained for the Vietoris–Rips complex, using, for instance, the results of [Reference Attali, Lieutier and Salinas2].
Remark 5.17. As proven in Lemma 5.10, the map reconstructed in Theorem 5.15 has a combinatorial description using a discrete approximate local trivialization that in turn induces a discrete approximate cocycle. This discrete approximate cocycle can be used to compute characteristic classes combinatorially, which is the subject of the next section.
6 Effective computation of characteristic classes
In this section, we present three algorithms to compute, respectively, the first two Stiefel–Whitney classes of an approximate vector bundle given by an approximate
![]() $O(d)$
-cocycle and the Euler class of an oriented approximate vector bundle of rank
$O(d)$
-cocycle and the Euler class of an oriented approximate vector bundle of rank
![]() $2$
given by an approximate
$2$
given by an approximate
![]() $SO(2)$
-cocycle. The algorithms are based on well-known results which say that the characteristic classes we consider are obstructions to lifting the structure group of the cocycle to certain other Lie groups. The difficulty is in showing that these algorithms can be extended in a stable and consistent way to
$SO(2)$
-cocycle. The algorithms are based on well-known results which say that the characteristic classes we consider are obstructions to lifting the structure group of the cocycle to certain other Lie groups. The difficulty is in showing that these algorithms can be extended in a stable and consistent way to
![]() $\varepsilon $
-approximate cocycles, provided
$\varepsilon $
-approximate cocycles, provided
![]() $\varepsilon $
is sufficiently small. Throughout the section, we will make use of basic Riemannian geometry; a reference for this topic is [Reference Lee39].
$\varepsilon $
is sufficiently small. Throughout the section, we will make use of basic Riemannian geometry; a reference for this topic is [Reference Lee39].
In Section 6.1, we recall two standard constructions used to change the coefficient group of a Čech cocycle and we extend them to approximate cocycles. In Section 6.2, we give the algorithm for the first Stiefel–Whitney class, in Section 6.3 we give the algorithm for the Euler class and in Section 6.4 we give the algorithm for the second Stiefel–Whitney class.
6.1 Change of coefficients
In this section, we will make use of basic Čech cohomology with coefficients in a sheaf of abelian groups. We recall the essential components now; for an introduction to the subject, see, for example, [Reference Warner66, Chapter 5].
Let
![]() $\mathcal {U}$
be a cover of a topological space B. For A an abelian group and
$\mathcal {U}$
be a cover of a topological space B. For A an abelian group and
![]() $n \in \mathbb {N}$
, we let
$n \in \mathbb {N}$
, we let
![]() $\check {\mathsf {H}}^{n}_{}\left ( \mathcal {U}; A \right )$
denote the nth Čech cohomology group of
$\check {\mathsf {H}}^{n}_{}\left ( \mathcal {U}; A \right )$
denote the nth Čech cohomology group of
![]() $(B,\mathcal {U})$
with coefficients in the sheaf of locally constant functions with values in A [Reference Warner66, p. 201]. This cohomology group is a quotient of the subgroup of cocycles of
$(B,\mathcal {U})$
with coefficients in the sheaf of locally constant functions with values in A [Reference Warner66, p. 201]. This cohomology group is a quotient of the subgroup of cocycles of
![]() $C^n(\mathcal {U};A)$
, which is the abelian group of locally constant functions defined on all
$C^n(\mathcal {U};A)$
, which is the abelian group of locally constant functions defined on all
![]() $(n+1)$
-fold intersections
$(n+1)$
-fold intersections
![]() $U_{i_n} \cap \cdots \cap U_{i_0} \to A$
. As usual, the Čech cohomology of B with values in A is defined as
$U_{i_n} \cap \cdots \cap U_{i_0} \to A$
. As usual, the Čech cohomology of B with values in A is defined as
![]() $\check {\mathsf {H}}^{n}_{}\left ( B; A \right ) = \operatorname *{\mathrm {colim}}_{\mathcal {U} \text { cover}} \check {\mathsf {H}}^{n}_{}\left ( \mathcal {U}; A \right )$
. It is well known that, when B is paracompact and locally contractible, there is a natural isomorphism
$\check {\mathsf {H}}^{n}_{}\left ( B; A \right ) = \operatorname *{\mathrm {colim}}_{\mathcal {U} \text { cover}} \check {\mathsf {H}}^{n}_{}\left ( \mathcal {U}; A \right )$
. It is well known that, when B is paracompact and locally contractible, there is a natural isomorphism
![]() $\check {\mathsf {H}}^{n}_{}\left ( B; A \right ) \cong H^n(B;A)$
, where the right-hand side denotes singular cohomology with coefficients in A.
$\check {\mathsf {H}}^{n}_{}\left ( B; A \right ) \cong H^n(B;A)$
, where the right-hand side denotes singular cohomology with coefficients in A.
Since we use these constructions only for
![]() $n = 1,2$
, we elaborate on these two cases. For
$n = 1,2$
, we elaborate on these two cases. For
![]() $n=1$
, the Čech cohomology is precisely the one we introduced in Section 2.2.4, where the group A is endowed with the discrete topology. For
$n=1$
, the Čech cohomology is precisely the one we introduced in Section 2.2.4, where the group A is endowed with the discrete topology. For
![]() $n=2$
, the
$n=2$
, the
![]() $2$
-cocycles
$2$
-cocycles
![]() $\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
consist of families of locally constant functions
$\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
consist of families of locally constant functions
![]() $\{\Gamma _{ijk} : U_k \cap U_j \cap U_i \to A\}_{(ijk) \in N(\mathcal {U})}$
such that, for every
$\{\Gamma _{ijk} : U_k \cap U_j \cap U_i \to A\}_{(ijk) \in N(\mathcal {U})}$
such that, for every
![]() $(ijkl) \in N(\mathcal {U})$
and every
$(ijkl) \in N(\mathcal {U})$
and every
![]() $y \in U_l \cap U_k \cap U_j \cap U_i$
, we have
$y \in U_l \cap U_k \cap U_j \cap U_i$
, we have
where we are writing the operations of the abelian group A multiplicatively. The operation on
![]() $\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
is pointwise multiplication. The cohomology group
$\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
is pointwise multiplication. The cohomology group
![]() $\check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; A \right )$
is the quotient of
$\check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; A \right )$
is the quotient of
![]() $\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
by the subgroup of
$\mathsf {Z}^{2}_{}\left ( \mathcal {U}; A \right )$
by the subgroup of
![]() $2$
-cocycles of the form
$2$
-cocycles of the form
![]() $y \mapsto \Omega _{ij}(y) \Omega _{jk}(y) \Omega _{ki}(y)$
, for
$y \mapsto \Omega _{ij}(y) \Omega _{jk}(y) \Omega _{ki}(y)$
, for
![]() $\Omega \in C^1(\mathcal {U};A)$
.
$\Omega \in C^1(\mathcal {U};A)$
.
Let G and H be topological groups, and let
![]() $\zeta : G \to H$
be a continuous group morphism. The map
$\zeta : G \to H$
be a continuous group morphism. The map
![]() $\zeta $
induces a map
$\zeta $
induces a map
![]() $\mathsf {Z}^{1}_{}\left ( \mathcal {U}; G \right ) \to \mathsf {Z}^{1}_{}\left ( \mathcal {U}; H \right )$
, simply by applying
$\mathsf {Z}^{1}_{}\left ( \mathcal {U}; G \right ) \to \mathsf {Z}^{1}_{}\left ( \mathcal {U}; H \right )$
, simply by applying
![]() $\zeta $
pointwise to a cocycle. This map induces a well-defined map
$\zeta $
pointwise to a cocycle. This map induces a well-defined map
![]() $\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
. A bit more interestingly, given a central extension of groups
$\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
. A bit more interestingly, given a central extension of groups
![]() $1 \to F \to G \to H \to 1$
, there is a well-defined so-called connecting morphism
$1 \to F \to G \to H \to 1$
, there is a well-defined so-called connecting morphism
![]() $\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
. For a short introduction to these concepts, see [Reference Lawson and Michelsohn38, Appendix A].
$\check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
. For a short introduction to these concepts, see [Reference Lawson and Michelsohn38, Appendix A].
In this section, we generalize these two constructions to the case of approximate cocycles when F, G and H are well-behaved metric groups. We start by generalizing the first construction.
Construction 6.1. Let
![]() $\zeta : G \to H$
be a continuous group morphism between topological groups. Given
$\zeta : G \to H$
be a continuous group morphism between topological groups. Given
![]() $\Omega \in C^1(\mathcal {U}; G)$
, define a cochain
$\Omega \in C^1(\mathcal {U}; G)$
, define a cochain
![]() $\zeta (\Omega )$
with values in H by
$\zeta (\Omega )$
with values in H by
![]() $\zeta (\Omega )_{(ij)}(y) = \zeta (\Omega _{(ij)}(y))$
for every
$\zeta (\Omega )_{(ij)}(y) = \zeta (\Omega _{(ij)}(y))$
for every
![]() $(ij) \in N(\mathcal {U})$
and
$(ij) \in N(\mathcal {U})$
and
![]() $y \in U_j \cap U_i$
.
$y \in U_j \cap U_i$
.
Lemma 6.2. Let G and H be metric groups and let
![]() $\zeta : G \to H$
be an
$\zeta : G \to H$
be an
![]() $\ell $
-Lipschitz group morphism. Let
$\ell $
-Lipschitz group morphism. Let
![]() $\varepsilon \in [0,\infty ]$
. Construction 6.1 induces maps
$\varepsilon \in [0,\infty ]$
. Construction 6.1 induces maps
![]() $\zeta : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \mathsf {Z}^{1}_{\ell \varepsilon }\left ( \mathcal {U}; H \right )$
and
$\zeta : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \mathsf {Z}^{1}_{\ell \varepsilon }\left ( \mathcal {U}; H \right )$
and
![]() $\zeta : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{\ell \varepsilon }\left ( \mathcal {U}; H \right )$
and these maps are
$\zeta : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{\ell \varepsilon }\left ( \mathcal {U}; H \right )$
and these maps are
![]() $\ell $
-Lipschitz with respect to the distances
$\ell $
-Lipschitz with respect to the distances
![]() $\mathsf {d}_{\mathsf {Z}}$
and
$\mathsf {d}_{\mathsf {Z}}$
and
![]() $\mathsf {d}_{\check {\mathsf {H}}}$
, respectively.
$\mathsf {d}_{\check {\mathsf {H}}}$
, respectively.
In particular, if the infimum over all distances between distinct elements of H is bounded below by
![]() $\delta $
and
$\delta $
and
![]() $\ell \varepsilon \leq \delta $
, then
$\ell \varepsilon \leq \delta $
, then
![]() $\zeta $
induces a map
$\zeta $
induces a map
![]() $\zeta : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
, such that, if
$\zeta : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
, such that, if
![]() $\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
satisfy
$\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
satisfy
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < \delta /\ell $
, then
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < \delta /\ell $
, then
![]() $\zeta (\Omega ) = \zeta (\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
.
$\zeta (\Omega ) = \zeta (\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; H \right )$
.
Proof. We start by checking that, if
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, then
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
, then
![]() $\zeta (\Omega )$
is an
$\zeta (\Omega )$
is an
![]() $\ell \varepsilon $
-approximate cocycle. For this, let
$\ell \varepsilon $
-approximate cocycle. For this, let
![]() $(ijk) \in N(\mathcal {U})$
and let
$(ijk) \in N(\mathcal {U})$
and let
![]() $y \in U_k \cap U_j \cap U_i$
. We have
$y \in U_k \cap U_j \cap U_i$
. We have
![]() $d_H\left (\zeta (\Omega )_{ij}(y) \zeta (\Omega )_{jk}(y), \zeta (\Omega )_{ik}(y)\right ) = d_H\left (\zeta ( \Omega _{ij}(y) \Omega _{jk}(y) ), \zeta (\Omega _{ik}(y) )\right ) \leq \ell d_G\left (\Omega _{ij}(y) \Omega _{jk}(y), \Omega _{ik}(y)\right ) < \ell \varepsilon $
, using the fact that
$d_H\left (\zeta (\Omega )_{ij}(y) \zeta (\Omega )_{jk}(y), \zeta (\Omega )_{ik}(y)\right ) = d_H\left (\zeta ( \Omega _{ij}(y) \Omega _{jk}(y) ), \zeta (\Omega _{ik}(y) )\right ) \leq \ell d_G\left (\Omega _{ij}(y) \Omega _{jk}(y), \Omega _{ik}(y)\right ) < \ell \varepsilon $
, using the fact that
![]() $\zeta $
is an
$\zeta $
is an
![]() $\ell $
-Lipschitz group morphism. The fact that the maps are
$\ell $
-Lipschitz group morphism. The fact that the maps are
![]() $\ell $
-Lipschitz is clear.
$\ell $
-Lipschitz is clear.
To see that
![]() $\zeta $
descends to approximate cohomology, note that, if
$\zeta $
descends to approximate cohomology, note that, if
![]() $\Theta \in C^0(\mathcal {U}; G)$
, then we can define
$\Theta \in C^0(\mathcal {U}; G)$
, then we can define
![]() $\zeta (\Theta ) \in C^0(\mathcal {U}; H)$
by
$\zeta (\Theta ) \in C^0(\mathcal {U}; H)$
by
![]() $\zeta (\Theta )_i(y) = \zeta (\Theta _i(y))$
for all
$\zeta (\Theta )_i(y) = \zeta (\Theta _i(y))$
for all
![]() $i \in N(\mathcal {U})$
and
$i \in N(\mathcal {U})$
and
![]() $y \in U_i$
and that, with this definition, we have
$y \in U_i$
and that, with this definition, we have
![]() $\zeta (\Theta ) \cdot \zeta (\Omega ) = \zeta (\Theta \cdot \Omega )$
, for every
$\zeta (\Theta ) \cdot \zeta (\Omega ) = \zeta (\Theta \cdot \Omega )$
, for every
![]() $\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
.
$\Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; G \right )$
.
The second claim is a consequence of the first one.
We now generalize the connecting morphism construction.
Construction 6.3. Let
![]() $\zeta : G \to H$
be a continuous and surjective group morphism between metric groups and let
$\zeta : G \to H$
be a continuous and surjective group morphism between metric groups and let
![]() $\varepsilon \geq 0$
. Let F be the kernel of
$\varepsilon \geq 0$
. Let F be the kernel of
![]() $\zeta $
and assume that F is locally compact and discrete in G so that, in particular,
$\zeta $
and assume that F is locally compact and discrete in G so that, in particular,
![]() $G \to H$
is a covering map. Suppose that
$G \to H$
is a covering map. Suppose that
![]() $\mathcal {U}$
is a cover of a topological space with the property that nonempty binary intersections of elements of
$\mathcal {U}$
is a cover of a topological space with the property that nonempty binary intersections of elements of
![]() $\mathcal {U}$
are locally path connected and simply connected. Let
$\mathcal {U}$
are locally path connected and simply connected. Let
![]() $\Omega \in C^1(\mathcal {U}; H)$
. Given
$\Omega \in C^1(\mathcal {U}; H)$
. Given
![]() $(ij) \in N(\mathcal {U})$
, choose a continuous lift
$(ij) \in N(\mathcal {U})$
, choose a continuous lift
![]() $\Lambda _{ij} : U_j \cap U_i \to G$
of
$\Lambda _{ij} : U_j \cap U_i \to G$
of
![]() $\Omega _{ij} : U_j \cap U_i \to H$
such that
$\Omega _{ij} : U_j \cap U_i \to H$
such that
![]() $\Lambda _{ij} = (\Lambda _{ji})^{-1}$
. Finally, for
$\Lambda _{ij} = (\Lambda _{ji})^{-1}$
. Finally, for
![]() $(ijk) \in N(\mathcal {U})$
and
$(ijk) \in N(\mathcal {U})$
and
![]() $y \in U_k \cap U_j \cap U_i$
, let
$y \in U_k \cap U_j \cap U_i$
, let
![]() $\Gamma _{ijk}(y) \in F$
be a closest point of F to
$\Gamma _{ijk}(y) \in F$
be a closest point of F to
![]() $\Lambda _{ij}(y)\Lambda _{jk}(y)\Lambda _{ki}(y)$
.
$\Lambda _{ij}(y)\Lambda _{jk}(y)\Lambda _{ki}(y)$
.
A priori, the maps
![]() $\Gamma _{ijk}$
of Construction 6.3 do not necessarily assemble into a
$\Gamma _{ijk}$
of Construction 6.3 do not necessarily assemble into a
![]() $2$
-cocycle with values in F since the maps may not even be continuous. We now give conditions under which the maps
$2$
-cocycle with values in F since the maps may not even be continuous. We now give conditions under which the maps
![]() $\Gamma _{ijk}$
constitute a
$\Gamma _{ijk}$
constitute a
![]() $2$
-cocycle. In order to do this, we need to introduce some definitions.
$2$
-cocycle. In order to do this, we need to introduce some definitions.
Definition 6.4. Let M be a metric space. The systole of M, denoted
![]() $\mathsf {sys}(M)$
, is the infimum of the lengths of all nonnullhomotopic loops of M.
$\mathsf {sys}(M)$
, is the infimum of the lengths of all nonnullhomotopic loops of M.
Recall from, for example, [Reference Lee39, Chapter 2], that any connected Riemannian manifold M can be endowed with the geodesic distance where the distance between two points is taken to be the infimum of the lengths of all piecewise regular (i.e., with nonzero velocity) paths between the two points. If the manifold is not connected, then the same construction gives an extended distance, meaning a distance that can also take the value
![]() $\infty $
. Whenever we endow a Riemannian manifold with the geodesic distance, we are referring to this extended distance. Finally, recall that, if the manifold is complete (as are all the examples we consider here), then the geodesic distance between two points can be calculated as the infimum of the length of all geodesics between the two points [Reference Lee39, Corollary 6.21].
$\infty $
. Whenever we endow a Riemannian manifold with the geodesic distance, we are referring to this extended distance. Finally, recall that, if the manifold is complete (as are all the examples we consider here), then the geodesic distance between two points can be calculated as the infimum of the length of all geodesics between the two points [Reference Lee39, Corollary 6.21].
Before being able to give conditions under which the connecting morphism is well behaved, we need to prove the following technical lemma.
Lemma 6.5. Let
![]() $F \subseteq G$
be an isometric inclusion of a discrete subgroup into a metric group. Let
$F \subseteq G$
be an isometric inclusion of a discrete subgroup into a metric group. Let
![]() $2r$
be the infimum of the distances between distinct elements of F. Let
$2r$
be the infimum of the distances between distinct elements of F. Let
![]() $\langle - \rangle : F^r \to F$
denote the projection to the closest element of F, which is well-defined and continuous.
$\langle - \rangle : F^r \to F$
denote the projection to the closest element of F, which is well-defined and continuous.
-
1. If
 $a \in F^s$
,
$a \in F^s$
,
 $b \in F^t$
,
$b \in F^t$
,
 $c \in F^u$
with
$c \in F^u$
with
 $s + t + u \leq r$
then
$s + t + u \leq r$
then
 $\langle a \rangle \langle b \rangle \langle c \rangle = \langle a b c \rangle $
.
$\langle a \rangle \langle b \rangle \langle c \rangle = \langle a b c \rangle $
. -
2. If
 $a \in F^r$
and
$a \in F^r$
and
 $b \in F$
, then
$b \in F$
, then
 $\langle a b\rangle = \langle a \rangle b$
.
$\langle a b\rangle = \langle a \rangle b$
. -
3. If
 $a,c \in G$
,
$a,c \in G$
,
 $b \in F^{s}$
, and
$b \in F^{s}$
, and
 $a \langle b \rangle c \in F^{t}$
with
$a \langle b \rangle c \in F^{t}$
with
 $s + t \leq r$
, then
$s + t \leq r$
, then
 $\langle a \langle b \rangle c\rangle = \langle a b c \rangle $
.
$\langle a \langle b \rangle c\rangle = \langle a b c \rangle $
.
Proof. As we will use this for each claim, start by noting that, if
![]() $g \in G$
,
$g \in G$
,
![]() $h \in F$
and
$h \in F$
and
![]() $d_G(g,h) < r$
, then
$d_G(g,h) < r$
, then
![]() $\langle g \rangle = h$
. Since multiplication is an isometry, we have
$\langle g \rangle = h$
. Since multiplication is an isometry, we have
![]() $d_G(abc,\langle a \rangle b c) < s$
. Using this idea two more times and the triangle inequality, we deduce
$d_G(abc,\langle a \rangle b c) < s$
. Using this idea two more times and the triangle inequality, we deduce
![]() $d_G(abc, \langle a \rangle \langle b \rangle \langle c \rangle ) < s + t + u \leq r$
and the first claim follows. For the second claim, note that
$d_G(abc, \langle a \rangle \langle b \rangle \langle c \rangle ) < s + t + u \leq r$
and the first claim follows. For the second claim, note that
![]() $d_G(a b, \langle a \rangle b) < r$
. Since
$d_G(a b, \langle a \rangle b) < r$
. Since
![]() $\langle a \rangle b \in F$
, the second claim follows. Finally,
$\langle a \rangle b \in F$
, the second claim follows. Finally,
![]() $d_G(\langle a \langle b \rangle c \rangle , a \langle b \rangle c) < s$
and
$d_G(\langle a \langle b \rangle c \rangle , a \langle b \rangle c) < s$
and
![]() $d_G(a \langle b \rangle c, a b c) < t$
, so
$d_G(a \langle b \rangle c, a b c) < t$
, so
![]() $d_G(\langle a \langle b \rangle c \rangle , abc) < s + t \leq r$
and the third claim follows.
$d_G(\langle a \langle b \rangle c \rangle , abc) < s + t \leq r$
and the third claim follows.
Theorem 6.6. Let
![]() $1 \to F \to G \to H \to 1$
be a central extension of Lie groups with H compact and F discrete. Fix a bi-invariant Riemannian metric on H and use it to metrize H and G with the geodesic distance and F with the distance inherited from G. Let
$1 \to F \to G \to H \to 1$
be a central extension of Lie groups with H compact and F discrete. Fix a bi-invariant Riemannian metric on H and use it to metrize H and G with the geodesic distance and F with the distance inherited from G. Let
![]() $\mathcal {U}$
be a cover of a topological space B such that each set and each nonempty binary intersection is locally path connected and simply connected. Let
$\mathcal {U}$
be a cover of a topological space B such that each set and each nonempty binary intersection is locally path connected and simply connected. Let
![]() $\varepsilon \leq \mathsf {sys}(H)/8$
. Then, Construction 6.3 induces maps
$\varepsilon \leq \mathsf {sys}(H)/8$
. Then, Construction 6.3 induces maps
![]() $\partial : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \mathsf {Z}^{2}_{}\left ( \mathcal {U}; F \right )$
and
$\partial : \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \mathsf {Z}^{2}_{}\left ( \mathcal {U}; F \right )$
and
![]() $\partial : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
.
$\partial : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
.
The second map is independent of any choice of lift and is stable in the sense that if
![]() $\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
are such that
$\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
are such that
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < \mathsf {sys}(H)/8$
, then
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < \mathsf {sys}(H)/8$
, then
![]() $\partial (\Omega ) = \partial (\Omega ') \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
.
$\partial (\Omega ) = \partial (\Omega ') \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
.
Proof. Let
![]() $2r$
denote the infimum over the distances between distinct elements of F. By Lemma A.19, we have
$2r$
denote the infimum over the distances between distinct elements of F. By Lemma A.19, we have
![]() $\mathsf {sys}(H)/2 \leq r$
and thus
$\mathsf {sys}(H)/2 \leq r$
and thus
![]() $\varepsilon \leq r/4$
. For
$\varepsilon \leq r/4$
. For
![]() $x \in F^r$
, let
$x \in F^r$
, let
![]() $\langle x \rangle \in F$
denote its closest point in F, which is well defined and continuous.
$\langle x \rangle \in F$
denote its closest point in F, which is well defined and continuous.
We start by showing that, for
![]() $(ijk) \in N(\mathcal {U})$
, the map
$(ijk) \in N(\mathcal {U})$
, the map
![]() $\Gamma _{ijk} : U_k \cap U_j \cap U_i \to F$
is continuous. It suffices to show that
$\Gamma _{ijk} : U_k \cap U_j \cap U_i \to F$
is continuous. It suffices to show that
![]() $\Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y) \in F^r$
, as
$\Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y) \in F^r$
, as
![]() $\Gamma _{ijk}(y) = \langle \Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y) \rangle $
. By definition of the metrics on G and H, the distance from
$\Gamma _{ijk}(y) = \langle \Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y) \rangle $
. By definition of the metrics on G and H, the distance from
![]() $\Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y)$
to F is equal to the distance from
$\Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y)$
to F is equal to the distance from
![]() $\Omega _{ij}(y) \Omega _{jk}(y) \Omega _{ki}(y)$
to the identity of H, which is less than
$\Omega _{ij}(y) \Omega _{jk}(y) \Omega _{ki}(y)$
to the identity of H, which is less than
![]() $\varepsilon \leq r/4$
, by assumption.
$\varepsilon \leq r/4$
, by assumption.
We now show that
![]() $\Gamma $
is an H-valued
$\Gamma $
is an H-valued
![]() $2$
-cocycle. Fix
$2$
-cocycle. Fix
![]() $y \in U_l \cap U_k \cap U_j \cap U_i$
and let us write
$y \in U_l \cap U_k \cap U_j \cap U_i$
and let us write
![]() $(ij)$
for
$(ij)$
for
![]() $\Lambda _{ij}(y)$
and likewise for the other elements of G. We must show that
$\Lambda _{ij}(y)$
and likewise for the other elements of G. We must show that
Note that, although F is abelian, we are using multiplicative notation to be consistent with the fact that G need not be abelian. We now compute:

We now prove that the composite
![]() $\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \mathsf {Z}^{2}_{}\left ( \mathcal {U}; F \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
is independent of the choice of lifts
$\mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \mathsf {Z}^{2}_{}\left ( \mathcal {U}; F \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
is independent of the choice of lifts
![]() $\Lambda $
. In order to see this note that, if
$\Lambda $
. In order to see this note that, if
![]() $\Lambda _{ij}, \Lambda ^{\prime }_{ij} : U_j \cap U_i \to G$
are two lifts of
$\Lambda _{ij}, \Lambda ^{\prime }_{ij} : U_j \cap U_i \to G$
are two lifts of
![]() $\Omega _{ij} : U_j \cap U_i \to H$
, then they differ by a function
$\Omega _{ij} : U_j \cap U_i \to H$
, then they differ by a function
![]() $f_{ij} : U_j \cap U_i \to F$
. Since F is central, it follows that
$f_{ij} : U_j \cap U_i \to F$
. Since F is central, it follows that
![]() $\Gamma _{ijk}$
and
$\Gamma _{ijk}$
and
![]() $\Gamma ^{\prime }_{ijk}$
differ by
$\Gamma ^{\prime }_{ijk}$
differ by
![]() $f_{ij} f_{jk} f_{ki}$
, using Lemma 6.5(2).
$f_{ij} f_{jk} f_{ki}$
, using Lemma 6.5(2).
Now, let
![]() $\Theta \in C^0(\mathcal {U}; H)$
and let
$\Theta \in C^0(\mathcal {U}; H)$
and let
![]() $\Pi \in C^0(\mathcal {U}; G)$
be a lift of it, which exists since the elements of
$\Pi \in C^0(\mathcal {U}; G)$
be a lift of it, which exists since the elements of
![]() $\mathcal {U}$
are simply connected. Let us write
$\mathcal {U}$
are simply connected. Let us write
![]() $(i)$
for
$(i)$
for
![]() $\Pi _i(y)$
. A lift for
$\Pi _i(y)$
. A lift for
![]() $\Theta \cdot \Omega $
is given by
$\Theta \cdot \Omega $
is given by
![]() $\Pi \cdot \Lambda $
and the
$\Pi \cdot \Lambda $
and the
![]() $2$
-cochain in this case is
$2$
-cochain in this case is
 $$ \begin{align*} \langle (i) (ij) (j)^{-1} (j) (jk) (k)^{-1} (k) (ki) (i)^{-1} \rangle &= \langle (i) (ij) (jk) (ki) (i)^{-1} \rangle = \left\langle (i)\; \langle (ij) (jk) (ki) \rangle \; (i)^{-1} \right\rangle\\ &= \left\langle\; (i) (i)^{-1} \; \langle (ij) (jk) (ki) \rangle \; \right\rangle = \Gamma_{ijk}(y), \end{align*} $$
$$ \begin{align*} \langle (i) (ij) (j)^{-1} (j) (jk) (k)^{-1} (k) (ki) (i)^{-1} \rangle &= \langle (i) (ij) (jk) (ki) (i)^{-1} \rangle = \left\langle (i)\; \langle (ij) (jk) (ki) \rangle \; (i)^{-1} \right\rangle\\ &= \left\langle\; (i) (i)^{-1} \; \langle (ij) (jk) (ki) \rangle \; \right\rangle = \Gamma_{ijk}(y), \end{align*} $$
where in the second equality we used Lemma 6.5(3) and in the third one we used that F is central. This shows that the map
![]() $\partial : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
is well defined.
$\partial : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; F \right )$
is well defined.
We conclude the proof by proving the stability claim. Let
![]() $[\Omega ],[\Omega '] \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
be such that
$[\Omega ],[\Omega '] \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
be such that
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( [\Omega ], [\Omega '] \right ) < \mathsf {sys}(H)/8$
and choose representatives
$\mathsf {d}_{\check {\mathsf {H}}}\left ( [\Omega ], [\Omega '] \right ) < \mathsf {sys}(H)/8$
and choose representatives
![]() $\Omega ,\Omega ' \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
such that
$\Omega ,\Omega ' \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; H \right )$
such that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < \mathsf {sys}(H)/8$
. By Lemma A.20(2), we can pick lifts
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < \mathsf {sys}(H)/8$
. By Lemma A.20(2), we can pick lifts
![]() $\Lambda , \Lambda ' \in C^1(\mathcal {U}; G)$
of
$\Lambda , \Lambda ' \in C^1(\mathcal {U}; G)$
of
![]() $\Omega $
and
$\Omega $
and
![]() $\Omega '$
, respectively, such that
$\Omega '$
, respectively, such that
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Lambda , \Lambda ' \right ) < \mathsf {sys}(H)/8$
. Now, let
$\mathsf {d}_{\mathsf {Z}}\left ( \Lambda , \Lambda ' \right ) < \mathsf {sys}(H)/8$
. Now, let
![]() $y \in U_k \cap U_j \cap U_i$
, and let us write
$y \in U_k \cap U_j \cap U_i$
, and let us write
![]() $(ij)'$
for
$(ij)'$
for
![]() $\Lambda _{ij}'(y)$
. We have
$\Lambda _{ij}'(y)$
. We have
 $$ \begin{align*} d_G\left((ij)' (jk)' (ki)', \langle (ij) (jk) (ki)\rangle\right) &\leq d_G\left((ij)' (jk)' (ki)', (ij) (jk) (ki)\right)\\ & \;\;\;\;\;+ d_G\left((ij) (jk) (ki), \langle (ij) (jk) (ki)\rangle \right)\\ &< 3\, \mathsf{sys}(H)/8 + \varepsilon = \mathsf{sys}(H)/2, \end{align*} $$
$$ \begin{align*} d_G\left((ij)' (jk)' (ki)', \langle (ij) (jk) (ki)\rangle\right) &\leq d_G\left((ij)' (jk)' (ki)', (ij) (jk) (ki)\right)\\ & \;\;\;\;\;+ d_G\left((ij) (jk) (ki), \langle (ij) (jk) (ki)\rangle \right)\\ &< 3\, \mathsf{sys}(H)/8 + \varepsilon = \mathsf{sys}(H)/2, \end{align*} $$
so
![]() $\langle \Lambda ^{\prime }_{ij}(y) \Lambda ^{\prime }_{jk}(y) \Lambda ^{\prime }_{ki}(y) \rangle = \langle \Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y)\rangle $
, and the result follows.
$\langle \Lambda ^{\prime }_{ij}(y) \Lambda ^{\prime }_{jk}(y) \Lambda ^{\prime }_{ki}(y) \rangle = \langle \Lambda _{ij}(y) \Lambda _{jk}(y) \Lambda _{ki}(y)\rangle $
, and the result follows.
6.2 First Stiefel–Whitney class
Consider the map
![]() $\det : O(d) \to \{\pm 1\} \cong \mathbb {Z}/2$
, and metrize
$\det : O(d) \to \{\pm 1\} \cong \mathbb {Z}/2$
, and metrize
![]() $O(d)$
using the Frobenius distance and
$O(d)$
using the Frobenius distance and
![]() $\{\pm 1\}$
by
$\{\pm 1\}$
by
![]() $d(1,-1) = 2$
. It follows from Lemma A.13 that
$d(1,-1) = 2$
. It follows from Lemma A.13 that
![]() $\det $
is
$\det $
is
![]() $1$
-Lipschitz.
$1$
-Lipschitz.
Algorithm
Let
![]() $\mathcal {U}$
be a cover of a topological space. Let
$\mathcal {U}$
be a cover of a topological space. Let
![]() $\varepsilon \leq 2$
. By applying
$\varepsilon \leq 2$
. By applying
![]() $\det $
to a representative cocycle, we get a map
$\det $
to a representative cocycle, we get a map
![]() $\mathsf {sw}_1 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
such that, if
$\mathsf {sw}_1 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
such that, if
![]() $\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
satisfy
$\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
satisfy
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 2$
, then
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 2$
, then
![]() $\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. This follows directly from Lemma 6.2.
$\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. This follows directly from Lemma 6.2.
In particular, if K is a simplicial complex, we get an algorithm
![]() $\mathsf {sw}_1 : \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right ) \to H^1(K;\mathbb {Z}/2)$
that is polynomial in the number of vertices of K; see Table 1 for the pseudocode of this algorithm. From Lemma 6.2, it follows that the algorithm is stable, in the sense that if
$\mathsf {sw}_1 : \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right ) \to H^1(K;\mathbb {Z}/2)$
that is polynomial in the number of vertices of K; see Table 1 for the pseudocode of this algorithm. From Lemma 6.2, it follows that the algorithm is stable, in the sense that if
![]() $\Omega ,\Omega ' \in \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right )$
satisfy
$\Omega ,\Omega ' \in \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right )$
satisfy
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 2$
, then
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 2$
, then
![]() $\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in H^1(K;\mathbb {Z}/2)$
.
$\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Omega ') \in H^1(K;\mathbb {Z}/2)$
.
Oriented approximate vector bundles
The following observation is relevant for the computation of Euler classes in the next section. Let
![]() $\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. If
$\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. If
![]() $\varepsilon \leq 2$
and
$\varepsilon \leq 2$
and
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
is such that
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
is such that
![]() $\mathsf {sw}_1(\Omega ) = 0$
, then
$\mathsf {sw}_1(\Omega ) = 0$
, then
![]() $\Omega = [\Lambda ]$
for some
$\Omega = [\Lambda ]$
for some
![]() $\Lambda \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(d) \right )$
. To prove this, let
$\Lambda \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(d) \right )$
. To prove this, let
![]() $[\Gamma ] = \mathsf {sw}_1(\Omega )$
, let
$[\Gamma ] = \mathsf {sw}_1(\Omega )$
, let
![]() $\Theta \in C^0(\mathcal {U};\mathbb {Z}/2)$
be such that
$\Theta \in C^0(\mathcal {U};\mathbb {Z}/2)$
be such that
![]() $\Theta \cdot \Gamma = \mathsf {id}$
and lift
$\Theta \cdot \Gamma = \mathsf {id}$
and lift
![]() $\Theta $
to
$\Theta $
to
![]() $\Pi \in C^0(\mathcal {U};O(d))$
. Then
$\Pi \in C^0(\mathcal {U};O(d))$
. Then
![]() $\Pi \cdot \Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(d) \right )$
.
$\Pi \cdot \Omega \in \mathsf {Z}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(d) \right )$
.
Consistency of the algorithm
The following well-known result can be found in, for example, [Reference Lawson and Michelsohn38, Example A.3].
Lemma 6.7. Let
![]() $\mathcal {U}$
be a cover of a locally contractible topological space. If
$\mathcal {U}$
be a cover of a locally contractible topological space. If
![]() $\varepsilon = 0$
, the construction
$\varepsilon = 0$
, the construction
![]() $\mathsf {sw}_1 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
computes the first Stiefel–Whitney class of the vector bundle represented by the cocycle.
$\mathsf {sw}_1 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
computes the first Stiefel–Whitney class of the vector bundle represented by the cocycle.
Proposition 6.8. Let
![]() $\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B. Let
$\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B. Let
![]() $\varepsilon < 2/9$
, and let
$\varepsilon < 2/9$
, and let
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
![]() $\mathsf {sw}_1(\Omega ) \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
coincides with the first Stiefel–Whitney class of the vector bundle classified by
$\mathsf {sw}_1(\Omega ) \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
coincides with the first Stiefel–Whitney class of the vector bundle classified by
![]() $\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
.
$\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
.
Proof. Since
![]() $2/9 \leq \sqrt {2}/4$
, there exists, by Theorem 4.27, an exact cocycle
$2/9 \leq \sqrt {2}/4$
, there exists, by Theorem 4.27, an exact cocycle
![]() $\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
$\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < 2/9 \times 9 = 2$
and such that
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < 2/9 \times 9 = 2$
and such that
![]() $\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
. From the stability of
$\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
. From the stability of
![]() $\mathsf {sw}_1$
, it follows that
$\mathsf {sw}_1$
, it follows that
![]() $\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Lambda )$
. Finally, by Lemma 6.7,
$\mathsf {sw}_1(\Omega ) = \mathsf {sw}_1(\Lambda )$
. Finally, by Lemma 6.7,
![]() $\mathsf {sw}_1(\Lambda )$
is the first Stiefel–Whitney class of the vector bundle classified by
$\mathsf {sw}_1(\Lambda )$
is the first Stiefel–Whitney class of the vector bundle classified by
![]() $\mathsf {cl}(\Lambda )$
, so the result follows.
$\mathsf {cl}(\Lambda )$
, so the result follows.
6.3 Euler class of oriented, rank-
 $2$
vector bundles
$2$
vector bundles
Consider the group
![]() $SO(2)$
of orthogonal
$SO(2)$
of orthogonal
![]() $2$
-by-
$2$
-by-
![]() $2$
matrices with positive determinant. There is a short exact sequence of Lie groups
$2$
matrices with positive determinant. There is a short exact sequence of Lie groups
![]() $1 \to \mathbb {Z} \to \mathbb {R} \to SO(2) \to 1$
given by mapping a real number r to the rotation matrix
$1 \to \mathbb {Z} \to \mathbb {R} \to SO(2) \to 1$
given by mapping a real number r to the rotation matrix
 $$\begin{align*}\begin{pmatrix} \cos(2\pi r) & -\sin(2\pi r) \\ \sin(2\pi r) & \cos(2\pi r) \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} \cos(2\pi r) & -\sin(2\pi r) \\ \sin(2\pi r) & \cos(2\pi r) \end{pmatrix}. \end{align*}$$
Algorithm
Let
![]() $\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. As usual, we endow
$\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. As usual, we endow
![]() $SO(2)$
with the Frobenius distance, and we let
$SO(2)$
with the Frobenius distance, and we let
![]() $SO(2)_g$
denote the same group but endowed with the geodesic distance, with Riemannian structure inherited from the inclusion
$SO(2)_g$
denote the same group but endowed with the geodesic distance, with Riemannian structure inherited from the inclusion
![]() $SO(2) \subseteq \mathbb {R}^{2 \times 2} = \mathbb {R}^4$
.
$SO(2) \subseteq \mathbb {R}^{2 \times 2} = \mathbb {R}^4$
.
By Lemma A.18, we have
![]() $\mathsf {sys}(SO(2)) = 2\sqrt {2} \pi $
, so, applying Theorem 6.6 to the extension
$\mathsf {sys}(SO(2)) = 2\sqrt {2} \pi $
, so, applying Theorem 6.6 to the extension
![]() $1 \to \mathbb {Z} \to \mathbb {R} \to SO(2)_g \to 1$
, we see that Construction 6.3 gives a map
$1 \to \mathbb {Z} \to \mathbb {R} \to SO(2)_g \to 1$
, we see that Construction 6.3 gives a map
![]() $\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2)_g \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
, as long as
$\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2)_g \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
, as long as
![]() $\varepsilon \leq \sqrt {2}\pi /4$
. In order to give an algorithm using Frobenius distances, we note that, if
$\varepsilon \leq \sqrt {2}\pi /4$
. In order to give an algorithm using Frobenius distances, we note that, if
![]() $\varepsilon \leq 1$
, then, by Corollary A.17, any
$\varepsilon \leq 1$
, then, by Corollary A.17, any
![]() $\varepsilon $
-approximate
$\varepsilon $
-approximate
![]() $SO(2)$
-cocycle is a
$SO(2)$
-cocycle is a
![]() $(\sqrt {2}\pi /4)$
-approximate
$(\sqrt {2}\pi /4)$
-approximate
![]() $SO(2)_g$
-cocycle. So Construction 6.3 gives a map
$SO(2)_g$
-cocycle. So Construction 6.3 gives a map
![]() $\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
, as long as
$\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
, as long as
![]() $\varepsilon \leq 1$
. By the stability statement of Theorem 6.6, we see that, if
$\varepsilon \leq 1$
. By the stability statement of Theorem 6.6, we see that, if
![]() $\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right )$
are such that
$\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right )$
are such that
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < 1$
, then
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Omega ' \right ) < 1$
, then
![]() $\mathsf {eu}(\Omega ) = \mathsf {eu}(\Omega ')$
.
$\mathsf {eu}(\Omega ) = \mathsf {eu}(\Omega ')$
.
In particular, if K is a simplicial complex, we get a
![]() $1$
-stable algorithm
$1$
-stable algorithm
![]() $\mathsf {eu} : \mathsf {DH}^{1}_{\varepsilon }\left ( K; SO(2) \right ) \to H^2(K;\mathbb {Z})$
; see Table 2 for the pseudocode of this algorithm.
$\mathsf {eu} : \mathsf {DH}^{1}_{\varepsilon }\left ( K; SO(2) \right ) \to H^2(K;\mathbb {Z})$
; see Table 2 for the pseudocode of this algorithm.
Consistency of the algorithm
We need the following well known result.
Lemma 6.9. Let
![]() $\mathcal {U}$
be a cover of locally contractible space with the property that nonempty binary intersections are locally path connected and simply connected. If
$\mathcal {U}$
be a cover of locally contractible space with the property that nonempty binary intersections are locally path connected and simply connected. If
![]() $\varepsilon = 0$
, the construction
$\varepsilon = 0$
, the construction
![]() $\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
computes the Euler class of the vector bundle represented by the cocycle.
$\mathsf {eu} : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; SO(2) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
computes the Euler class of the vector bundle represented by the cocycle.
Proof. In this proof, we freely use the language of complex vector bundles. The Lie group
![]() $SO(2)$
is isomorphic to the group of unit complex numbers
$SO(2)$
is isomorphic to the group of unit complex numbers
![]() $U(1)$
and thus, up to isomorphism, real, oriented, rank-
$U(1)$
and thus, up to isomorphism, real, oriented, rank-
![]() $2$
vector bundles are exactly the same as complex rank-
$2$
vector bundles are exactly the same as complex rank-
![]() $1$
vector bundles. By [Reference Bott and Tu7, (20.10.6)], the top Chern class of a complex vector bundle coincides with the Euler class of the bundle, seen as an oriented real vector bundle in view of the inclusions
$1$
vector bundles. By [Reference Bott and Tu7, (20.10.6)], the top Chern class of a complex vector bundle coincides with the Euler class of the bundle, seen as an oriented real vector bundle in view of the inclusions
![]() $U(n) \subseteq SO(2n)$
. Finally, when
$U(n) \subseteq SO(2n)$
. Finally, when
![]() $\varepsilon = 0$
, the construction
$\varepsilon = 0$
, the construction
![]() $\mathsf {eu}$
computes the first Chern class [Reference Lawson and Michelsohn38, Example A.5].
$\mathsf {eu}$
computes the first Chern class [Reference Lawson and Michelsohn38, Example A.5].
Proposition 6.10. Let
![]() $\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B, with the property that nonempty binary intersections are locally path connected and simply connected. Let
$\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B, with the property that nonempty binary intersections are locally path connected and simply connected. Let
![]() $\varepsilon < 1/9$
and let
$\varepsilon < 1/9$
and let
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
![]() $\mathsf {eu}(\Omega ) \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
coincides with the Euler class of the vector bundle classified by
$\mathsf {eu}(\Omega ) \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z} \right )$
coincides with the Euler class of the vector bundle classified by
![]() $\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
.
$\pi _*(\mathsf {cl}(\Omega )) : B \to \mathsf {Gr}(d)$
.
Proof. Since
![]() $1/9 \leq \sqrt {2}/4$
, there exists, by Theorem 4.27, an exact cocycle
$1/9 \leq \sqrt {2}/4$
, there exists, by Theorem 4.27, an exact cocycle
![]() $\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
$\Lambda \in \check {\mathsf {H}}^{1}_{}\left ( \mathcal {U}; O(d) \right )$
such that
![]() $\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < 1$
and such that
$\mathsf {d}_{\check {\mathsf {H}}}\left ( \Omega , \Lambda \right ) < 1$
and such that
![]() $\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
. From the stability of
$\pi _*(\mathsf {cl}(\Omega )) = \mathsf {cl}(\Lambda )$
. From the stability of
![]() $\mathsf {eu}$
, it follows that
$\mathsf {eu}$
, it follows that
![]() $\mathsf {eu}(\Omega ) = \mathsf {eu}(\Lambda )$
. Finally, by Lemma 6.9,
$\mathsf {eu}(\Omega ) = \mathsf {eu}(\Lambda )$
. Finally, by Lemma 6.9,
![]() $\mathsf {eu}(\Lambda )$
is the Euler class of the vector bundle classified by
$\mathsf {eu}(\Lambda )$
is the Euler class of the vector bundle classified by
![]() $\mathsf {cl}(\Lambda )$
.
$\mathsf {cl}(\Lambda )$
.
6.4 Second Stiefel–Whitney class
In order to compute the second Stiefel–Whitney class, we will use a certain short exact sequence
![]() $1 \to \mathbb {Z}/2 \to \mathsf {Pin}(d) \to O(d) \to 1$
. To describe this sequence, we introduce the Clifford algebra associated to the standard inner product of
$1 \to \mathbb {Z}/2 \to \mathsf {Pin}(d) \to O(d) \to 1$
. To describe this sequence, we introduce the Clifford algebra associated to the standard inner product of
![]() $\mathbb {R}^d$
. We state some well-known results whose proofs can be found in [Reference Kirby and Taylor36], [Reference Lawson and Michelsohn38, Chapter 1] and [Reference Bröcker and Dieck8, Chapter 1, Section 6].
$\mathbb {R}^d$
. We state some well-known results whose proofs can be found in [Reference Kirby and Taylor36], [Reference Lawson and Michelsohn38, Chapter 1] and [Reference Bröcker and Dieck8, Chapter 1, Section 6].
The group
 $\mathsf {Pin}$
.
$\mathsf {Pin}$
.
Fix
![]() $d \in \mathbb {N}_{\geq 1}$
. The Clifford algebra corresponding to the inner product space
$d \in \mathbb {N}_{\geq 1}$
. The Clifford algebra corresponding to the inner product space
![]() $\left (\mathbb {R}^d, \langle -, -\rangle \right )$
, which we denote by
$\left (\mathbb {R}^d, \langle -, -\rangle \right )$
, which we denote by
![]() $\mathsf {Cl}(d)$
, is the quotient of the tensor algebra
$\mathsf {Cl}(d)$
, is the quotient of the tensor algebra
![]() $\mathsf {T}(\mathbb {R}^d)$
by the two-sided ideal generated by elements of the form
$\mathsf {T}(\mathbb {R}^d)$
by the two-sided ideal generated by elements of the form
![]() $v \otimes w + w \otimes v - 2\langle v, w\rangle \, \mathbf {1}$
, for
$v \otimes w + w \otimes v - 2\langle v, w\rangle \, \mathbf {1}$
, for
![]() $v,w \in \mathbb {R}^d$
, where
$v,w \in \mathbb {R}^d$
, where
![]() $\mathbf {1}$
is the unit of
$\mathbf {1}$
is the unit of
![]() $\mathsf {T}(\mathbb {R}^d)$
. We denote the product of two elements
$\mathsf {T}(\mathbb {R}^d)$
. We denote the product of two elements
![]() $x,y \in \mathsf {Cl}(d)$
by
$x,y \in \mathsf {Cl}(d)$
by
![]() $x \cdot y \in \mathsf {Cl}(d)$
.
$x \cdot y \in \mathsf {Cl}(d)$
.
Here, we are using the ‘positive convention’ for Clifford algebras, as we want the
![]() $\mathsf {Pin}$
group to be the group
$\mathsf {Pin}$
group to be the group
![]() $\mathsf {Pin}^+$
discussed in, for example, [Reference Kirby and Taylor36]. We refer the interested reader to [Reference Kirby and Taylor36, Section 1] for further details about this choice.
$\mathsf {Pin}^+$
discussed in, for example, [Reference Kirby and Taylor36]. We refer the interested reader to [Reference Kirby and Taylor36, Section 1] for further details about this choice.
Remark 6.11. A more concrete description of
![]() $\mathsf {Cl}(d)$
is given by the free noncommutative
$\mathsf {Cl}(d)$
is given by the free noncommutative
![]() $\mathbb {R}$
-algebra generated by elements
$\mathbb {R}$
-algebra generated by elements
![]() $\{e_1, \dots , e_d\}$
subject to the relations
$\{e_1, \dots , e_d\}$
subject to the relations
![]() $e_i \cdot e_j = - e_j \cdot e_i$
if
$e_i \cdot e_j = - e_j \cdot e_i$
if
![]() $i> j$
, and
$i> j$
, and
![]() $e_i^2 = \mathbf {1}$
. This description makes it evident that
$e_i^2 = \mathbf {1}$
. This description makes it evident that
![]() $\dim (\mathsf {Cl}(d)) = 2^d$
since the elements of the form
$\dim (\mathsf {Cl}(d)) = 2^d$
since the elements of the form
![]() $e_{i_1}\cdots e_{i_k}$
for
$e_{i_1}\cdots e_{i_k}$
for
![]() $i_1 < \dots < i_k$
form a basis of
$i_1 < \dots < i_k$
form a basis of
![]() $\mathsf {Cl}(d)$
[Reference Bröcker and Dieck8, Chapter 1, Corollary 6.7].
$\mathsf {Cl}(d)$
[Reference Bröcker and Dieck8, Chapter 1, Corollary 6.7].
If
![]() $v \in \mathbb {R}^d$
is of unit length, then it is invertible when seen as an element of
$v \in \mathbb {R}^d$
is of unit length, then it is invertible when seen as an element of
![]() $\mathsf {Cl}(d)$
since
$\mathsf {Cl}(d)$
since
![]() $v \cdot v = \mathbf {1}$
. Let
$v \cdot v = \mathbf {1}$
. Let
![]() $\mathsf {Pin}(d) \subseteq \mathsf {Cl}(d)^\times $
be the subgroup of the group of units of
$\mathsf {Pin}(d) \subseteq \mathsf {Cl}(d)^\times $
be the subgroup of the group of units of
![]() $\mathsf {Cl}(d)$
generated by elements
$\mathsf {Cl}(d)$
generated by elements
![]() $v \in \mathbb {R}^d$
of unit length. There is a group morphism
$v \in \mathbb {R}^d$
of unit length. There is a group morphism
![]() $\rho : \mathsf {Pin}(d) \to O(d)$
that is defined on generators by mapping
$\rho : \mathsf {Pin}(d) \to O(d)$
that is defined on generators by mapping
![]() $v \in \mathbb {R}^d$
with
$v \in \mathbb {R}^d$
with
![]() $\|v \| = 1$
to the orthogonal transformation given by reflection about the hyperplane orthogonal to v. This morphism is surjective and its kernel consists of
$\|v \| = 1$
to the orthogonal transformation given by reflection about the hyperplane orthogonal to v. This morphism is surjective and its kernel consists of
![]() $\{\pm \mathbf {1}\}$
[Reference Kirby and Taylor36, Section 1]. This gives a central sequence of Lie groups
$\{\pm \mathbf {1}\}$
[Reference Kirby and Taylor36, Section 1]. This gives a central sequence of Lie groups
![]() $\mathbb {Z}/2 \cong \{\pm \mathbf {1}\} \to \mathsf {Pin}(d) \to O(d)$
.
$\mathbb {Z}/2 \cong \{\pm \mathbf {1}\} \to \mathsf {Pin}(d) \to O(d)$
.
Algorithm
Let
![]() $\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. Let
$\mathcal {U}$
be a cover of a topological space with the property that nonempty binary intersections are locally path connected and simply connected. Let
![]() $\varepsilon \leq 1$
. An analogous analysis to the one made for the Euler class shows that, applying Theorem 6.6 to the extension
$\varepsilon \leq 1$
. An analogous analysis to the one made for the Euler class shows that, applying Theorem 6.6 to the extension
![]() $1 \to \mathbb {Z}/2 \to \mathsf {Pin}(d) \to O(d) \to 1$
, we get a map
$1 \to \mathbb {Z}/2 \to \mathsf {Pin}(d) \to O(d) \to 1$
, we get a map
![]() $\mathsf {sw}_2 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. And that
$\mathsf {sw}_2 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
. And that
![]() $\mathsf {sw}_2$
is such that, if
$\mathsf {sw}_2$
is such that, if
![]() $\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
satisfy
$\Omega ,\Omega ' \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
satisfy
![]() $\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 1$
, then
$\mathsf {d}_{\mathsf {Z}}\left ( \Omega , \Omega ' \right ) < 1$
, then
![]() $\mathsf {sw}_2(\Omega ) = \mathsf {sw}_2(\Omega ') \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
.
$\mathsf {sw}_2(\Omega ) = \mathsf {sw}_2(\Omega ') \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
.
In particular, if K is a simplicial complex, we get a
![]() $1$
-stable algorithm
$1$
-stable algorithm
![]() $\mathsf {sw}_2 : \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right ) \to H^2(K;\mathbb {Z}/2)$
; see Table 3 for the pseudocode of this algorithm.
$\mathsf {sw}_2 : \mathsf {DH}^{1}_{\varepsilon }\left ( K; O(d) \right ) \to H^2(K;\mathbb {Z}/2)$
; see Table 3 for the pseudocode of this algorithm.
Technicalities about the algorithm
In order to see that
![]() $\mathsf {sw}_2$
is really an algorithm, we must explain how to lift elements from
$\mathsf {sw}_2$
is really an algorithm, we must explain how to lift elements from
![]() $O(d)$
to
$O(d)$
to
![]() $\mathsf {Pin}(d)$
, how to multiply elements in
$\mathsf {Pin}(d)$
, how to multiply elements in
![]() $\mathsf {Pin}(d)$
and how to decide, given an element
$\mathsf {Pin}(d)$
and how to decide, given an element
![]() $x \in \mathsf {Pin}(d)$
, which one of
$x \in \mathsf {Pin}(d)$
, which one of
![]() $\mathbf {1}$
or
$\mathbf {1}$
or
![]() $-\mathbf {1}$
is closest to it in the geodesic distance.
$-\mathbf {1}$
is closest to it in the geodesic distance.
We see
![]() $\mathsf {Pin}(d)$
as a subset of the Clifford algebra, which we represent as in Remark 6.11. By definition of the map
$\mathsf {Pin}(d)$
as a subset of the Clifford algebra, which we represent as in Remark 6.11. By definition of the map
![]() $\rho : \mathsf {Pin}(d) \to O(d)$
, to lift a matrix
$\rho : \mathsf {Pin}(d) \to O(d)$
, to lift a matrix
![]() $M \in O(d)$
to an element of
$M \in O(d)$
to an element of
![]() $\mathsf {Pin}(d)$
, we must write M as a product of reflection matrices, which is exactly what the QR factorization of an orthogonal matrix by means of Householder reflections does [Reference Horn and Johnson31, Theorem 2.1.14].
$\mathsf {Pin}(d)$
, we must write M as a product of reflection matrices, which is exactly what the QR factorization of an orthogonal matrix by means of Householder reflections does [Reference Horn and Johnson31, Theorem 2.1.14].
In order to multiply elements of
![]() $\mathsf {Pin}(d)$
, we again use the representation of Remark 6.11. We can thus multiply elements of
$\mathsf {Pin}(d)$
, we again use the representation of Remark 6.11. We can thus multiply elements of
![]() $\mathsf {Pin}(d)$
in
$\mathsf {Pin}(d)$
in
![]() $\mathcal {O}(4^d)$
time.
$\mathcal {O}(4^d)$
time.
The problem of deciding which of
![]() $\mathbf {1}$
or
$\mathbf {1}$
or
![]() $-\mathbf {1}$
is closest to an arbitrary element of
$-\mathbf {1}$
is closest to an arbitrary element of
![]() $\mathsf {Pin}(d)$
in the geodesic distance is more involved, as it depends on the geometry of
$\mathsf {Pin}(d)$
in the geodesic distance is more involved, as it depends on the geometry of
![]() $\mathsf {Pin}(d)$
. We explain how this can be done explicitly for the cases
$\mathsf {Pin}(d)$
. We explain how this can be done explicitly for the cases
![]() $d = 2,3,4$
using extraordinary isomorphisms. The same idea works for
$d = 2,3,4$
using extraordinary isomorphisms. The same idea works for
![]() $d = 5, 6$
but one must be able to compute geodesic distances in
$d = 5, 6$
but one must be able to compute geodesic distances in
![]() $Sp(4)$
and
$Sp(4)$
and
![]() $SU(4)$
.
$SU(4)$
.
We first remark that, since
![]() $O(d)$
has two connected components, so must
$O(d)$
has two connected components, so must
![]() $\mathsf {Pin}(d)$
, and that
$\mathsf {Pin}(d)$
, and that
![]() $+\mathbf {1}$
and
$+\mathbf {1}$
and
![]() $-\mathbf {1}$
belong to the same connected component of
$-\mathbf {1}$
belong to the same connected component of
![]() $\mathsf {Pin}(d)$
, as they are both preimages of the identity matrix under the covering map
$\mathsf {Pin}(d)$
, as they are both preimages of the identity matrix under the covering map
![]() $\mathsf {Pin}(d) \to O(d)$
. Let the spin group
$\mathsf {Pin}(d) \to O(d)$
. Let the spin group
![]() $\mathsf {Spin}(d) \subseteq \mathsf {Pin}(d)$
be the connected component of
$\mathsf {Spin}(d) \subseteq \mathsf {Pin}(d)$
be the connected component of
![]() $+\mathbf {1}$
. Checking if
$+\mathbf {1}$
. Checking if
![]() $x \in \mathsf {Pin}(d)$
belongs to
$x \in \mathsf {Pin}(d)$
belongs to
![]() $\mathsf {Spin}(d)$
is easy since it amounts to checking if its image in
$\mathsf {Spin}(d)$
is easy since it amounts to checking if its image in
![]() $O(d)$
has positive determinant.
$O(d)$
has positive determinant.
If
![]() $x \in \mathsf {Pin}(d)$
does not belong to
$x \in \mathsf {Pin}(d)$
does not belong to
![]() $\mathsf {Spin}(d)$
, then its distance to
$\mathsf {Spin}(d)$
, then its distance to
![]() $+\mathbf {1}$
is the same as the distance to
$+\mathbf {1}$
is the same as the distance to
![]() $-\mathbf {1}$
, namely infinity. With this in mind, we may assume that
$-\mathbf {1}$
, namely infinity. With this in mind, we may assume that
![]() $x \in \mathsf {Spin}(d)$
and that we want to know if x is closest to
$x \in \mathsf {Spin}(d)$
and that we want to know if x is closest to
![]() $+\mathbf {1}$
or to
$+\mathbf {1}$
or to
![]() $-\mathbf {1}$
in the geodesic distance of
$-\mathbf {1}$
in the geodesic distance of
![]() $\mathsf {Spin}(d)$
.
$\mathsf {Spin}(d)$
.
For explicit formulas for the extraordinary isomorphisms mentioned below, see the example after Lemma 1.8.3 in [Reference Jost35] or [Reference Lounesto42]. One should keep in mind that [Reference Jost35] is working with the ‘negative convention’ for the Clifford algebra, and thus the isomorphisms are given for
![]() $\mathsf {Spin}(d) \subseteq \mathsf {Cl}^-(d)$
, but it is not hard to modify their formulas to get the isomorphisms when
$\mathsf {Spin}(d) \subseteq \mathsf {Cl}^-(d)$
, but it is not hard to modify their formulas to get the isomorphisms when
![]() $\mathsf {Spin}(d) \subseteq \mathsf {Cl}(d)$
.
$\mathsf {Spin}(d) \subseteq \mathsf {Cl}(d)$
.
-
(d = 2) In this case,
 $\mathsf {Spin}(d)$
is isomorphic to the circle as Lie groups, so the geodesic distance on
$\mathsf {Spin}(d)$
is isomorphic to the circle as Lie groups, so the geodesic distance on
 $\mathsf {Spin}(2)$
can be computed, up to a multiplicative constant, using arclengths on the circle. Note that the multiplicative constant is inconsequential for the purposes of determining if an element is closer to
$\mathsf {Spin}(2)$
can be computed, up to a multiplicative constant, using arclengths on the circle. Note that the multiplicative constant is inconsequential for the purposes of determining if an element is closer to
 $+\mathbf {1}$
or to
$+\mathbf {1}$
or to
 $-\mathbf {1}$
.
$-\mathbf {1}$
. -
(d = 3) In this case,
 $\mathsf {Spin}(d)$
is isomorphic to
$\mathsf {Spin}(d)$
is isomorphic to
 $SU(2)$
, which in turn is diffeomorphic to the
$SU(2)$
, which in turn is diffeomorphic to the
 $3$
-sphere
$3$
-sphere
 $S^3$
. The geodesic distance is again computed, up to a multiplicative constant, using arcs.
$S^3$
. The geodesic distance is again computed, up to a multiplicative constant, using arcs. -
(d = 4) In this case,
 $\mathsf {Spin}(d)$
is isomorphic to
$\mathsf {Spin}(d)$
is isomorphic to
 $SU(2) \times SU(2)$
, which in turn is diffeomorphic to
$SU(2) \times SU(2)$
, which in turn is diffeomorphic to
 $S^3 \times S^3$
. Moreover, the Riemannian metric on
$S^3 \times S^3$
. Moreover, the Riemannian metric on
 $\mathsf {Spin}(4)$
induced by the double cover
$\mathsf {Spin}(4)$
induced by the double cover
 $\mathsf {Spin}(4) \to SO(4)$
coincides, up to a multiplicative constant, with the product metric on
$\mathsf {Spin}(4) \to SO(4)$
coincides, up to a multiplicative constant, with the product metric on
 $S^3 \times S^3$
, where the two copies of
$S^3 \times S^3$
, where the two copies of
 $S^3$
are endowed with the Riemannian metric inherited from the inclusion
$S^3$
are endowed with the Riemannian metric inherited from the inclusion
 $S^3 \subseteq \mathbb {R}^4$
. To compute the geodesic distance on
$S^3 \subseteq \mathbb {R}^4$
. To compute the geodesic distance on
 $S^3 \times S^3$
, recall that a geodesic in a product Riemannian manifold corresponds to a pair of geodesics, one on each factor [Reference Lee39, Problem 5-7]. This implies that, in a product of complete Riemannian manifolds
$S^3 \times S^3$
, recall that a geodesic in a product Riemannian manifold corresponds to a pair of geodesics, one on each factor [Reference Lee39, Problem 5-7]. This implies that, in a product of complete Riemannian manifolds
 $X\times Y$
, the geodesic distance satisfies the Pythagorean theorem, meaning that the geodesic distance from
$X\times Y$
, the geodesic distance satisfies the Pythagorean theorem, meaning that the geodesic distance from
 $(x,y)$
to
$(x,y)$
to
 $(x',y')$
is equal to the square root of the sum of the squares of the geodesic distances from x to
$(x',y')$
is equal to the square root of the sum of the squares of the geodesic distances from x to
 $x'$
and from y to
$x'$
and from y to
 $y'$
.
$y'$
.
So, when
![]() $d = 2,3,4$
, this results in a numerical algorithm
$d = 2,3,4$
, this results in a numerical algorithm
![]() $\mathsf {sw}_2$
that is polynomial in the number of vertices of K.
$\mathsf {sw}_2$
that is polynomial in the number of vertices of K.
Consistency of the algorithm
We need a well-known result; see, for example, [Reference Kirby and Taylor36, Lemma 1.3].
Lemma 6.12. Let
![]() $\mathcal {U}$
be a cover of a locally contractible space with the property that nonempty binary intersections are locally path connected and simply connected. If
$\mathcal {U}$
be a cover of a locally contractible space with the property that nonempty binary intersections are locally path connected and simply connected. If
![]() $\varepsilon = 0$
, the construction
$\varepsilon = 0$
, the construction
![]() $\mathsf {sw}_2 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
computes the second Stiefel–Whitney class of the vector bundle represented by the cocycle.
$\mathsf {sw}_2 : \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right ) \to \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
computes the second Stiefel–Whitney class of the vector bundle represented by the cocycle.
Note that, also by [Reference Kirby and Taylor36, Lemma 1.3], if we would have used the negative convention for the Clifford algebra, the algorithm would be computing
![]() $\mathsf {sw}_1^2 + \mathsf {sw}_2$
instead of
$\mathsf {sw}_1^2 + \mathsf {sw}_2$
instead of
![]() $\mathsf {sw}_2$
.
$\mathsf {sw}_2$
.
The proof of the following proposition is analogous to the proof of Proposition 6.10 but uses Lemma 6.12 instead of Lemma 6.9.
Proposition 6.13. Let
![]() $\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B, with the property that nonempty binary intersections are locally path connected and simply connected. Let
$\mathcal {U}$
be a countable cover of a locally contractible, paracompact space B, with the property that nonempty binary intersections are locally path connected and simply connected. Let
![]() $\varepsilon < 1/9$
and let
$\varepsilon < 1/9$
and let
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
$\Omega \in \check {\mathsf {H}}^{1}_{\varepsilon }\left ( \mathcal {U}; O(d) \right )$
. Then
![]() $\mathsf {sw}_2(\Omega ) \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
is the second Stiefel–Whitney class of
$\mathsf {sw}_2(\Omega ) \in \check {\mathsf {H}}^{2}_{}\left ( \mathcal {U}; \mathbb {Z}/2 \right )$
is the second Stiefel–Whitney class of
![]() $\pi _*(\mathsf {cl}(\Omega ))$
.
$\pi _*(\mathsf {cl}(\Omega ))$
.
7 Computational examples
In this section, we run the algorithms of Section 6 on data. We describe the basic pipeline used in the examples in Lemma 7.1.
In Section 7.2, we use
![]() $\mathsf {sw}_1$
to study the topology and, in particular, the orientability of attractors in the time-variant double-gyre dynamical system. This illustrates how characteristic classes can be used to classify such attractors. The trajectory of particles in the dynamical system was computed numerically using the code in [Reference Fernández16].
$\mathsf {sw}_1$
to study the topology and, in particular, the orientability of attractors in the time-variant double-gyre dynamical system. This illustrates how characteristic classes can be used to classify such attractors. The trajectory of particles in the dynamical system was computed numerically using the code in [Reference Fernández16].
In Section 7.3, we use
![]() $\mathsf {sw}_1$
and
$\mathsf {sw}_1$
and
![]() $\mathsf {sw}_2$
to provide experimental evidence that confirms that a certain dataset of lines in
$\mathsf {sw}_2$
to provide experimental evidence that confirms that a certain dataset of lines in
![]() $\mathbb {R}^2$
can be parametrized by a projective plane. The theoretical explanation of this phenomenon appears in [Reference Perea and Carlsson52, Section 2.4]. The code used to generate the dataset is from [Reference Tralie, Mease and Perea64].
$\mathbb {R}^2$
can be parametrized by a projective plane. The theoretical explanation of this phenomenon appears in [Reference Perea and Carlsson52, Section 2.4]. The code used to generate the dataset is from [Reference Tralie, Mease and Perea64].
In Section 7.4, we show how
![]() $\mathsf {eu}$
can be used to detect nonsynchronizability of data. The example is a version of the cryo-EM problem mentioned in Section 1.1.1.
$\mathsf {eu}$
can be used to detect nonsynchronizability of data. The example is a version of the cryo-EM problem mentioned in Section 1.1.1.
In Table 4, we summarize the runtime of our algorithms. Code to replicate these examples can be found at [Reference Scoccola and Perea56].
Table 4 Runtime of the algorithms on laptop with a 2.20 GHz Intel Core i7 and 16GB of RAM.

7.1 Pipeline
We make free use of basic tools from persistence theory such as Vietoris–Rips complexes, persistent cohomology and persistence diagrams; see, for example, [Reference Ghrist20, Reference Oudot50]. The persistent cohomology computations are done using the Python interface [Reference Tralie, Saul and Bar-On65] for Ripser [Reference Bauer4].
Let
![]() $\{K_r\}_{r \in \mathbb {R}_{\geq 0}}$
be a filtration of a finite simplicial complex K by subcomplexes so that we have
$\{K_r\}_{r \in \mathbb {R}_{\geq 0}}$
be a filtration of a finite simplicial complex K by subcomplexes so that we have
![]() $K_s \subseteq K_r \subseteq K$
for
$K_s \subseteq K_r \subseteq K$
for
![]() $s \leq r \in \mathbb {R}$
. For
$s \leq r \in \mathbb {R}$
. For
![]() $\Omega \in \check {\mathsf {H}}^{1}_{\infty }\left ( K; O(d) \right )$
and
$\Omega \in \check {\mathsf {H}}^{1}_{\infty }\left ( K; O(d) \right )$
and
![]() $\varepsilon \geq 0$
, define the
$\varepsilon \geq 0$
, define the
![]() $\boldsymbol {\varepsilon }$
-death of
$\boldsymbol {\varepsilon }$
-death of
![]() $\Omega $
as
$\Omega $
as
The
![]() $\boldsymbol {\varepsilon }$
-span of
$\boldsymbol {\varepsilon }$
-span of
![]() $\Omega $
is the subset of the persistence diagram of K of classes whose (homological) birth is at most
$\Omega $
is the subset of the persistence diagram of K of classes whose (homological) birth is at most
![]() $\delta $
and whose (homological) death is at least
$\delta $
and whose (homological) death is at least
![]() $\delta $
.
$\delta $
.
Fix a basis for the persistent cohomology of K, that is, cocycles
![]() $B = \{\Lambda _1, \dots , \Lambda _n\}$
representing each point of the persistence diagram of the
$B = \{\Lambda _1, \dots , \Lambda _n\}$
representing each point of the persistence diagram of the
![]() $\mathbb {Z}/2$
-cohomology of K. Let
$\mathbb {Z}/2$
-cohomology of K. Let
![]() $\varepsilon = 2$
. For any
$\varepsilon = 2$
. For any
![]() $r < \delta $
, we can write
$r < \delta $
, we can write
![]() $\mathsf {sw}_1(\Omega )$
in the basis B. To represent
$\mathsf {sw}_1(\Omega )$
in the basis B. To represent
![]() $\mathsf {sw}_1(\Omega )$
in the persistence diagram of K, we decorate the diagram by circling the classes of B that appear with a nonzero coefficient. Note that any such class must live inside the
$\mathsf {sw}_1(\Omega )$
in the persistence diagram of K, we decorate the diagram by circling the classes of B that appear with a nonzero coefficient. Note that any such class must live inside the
![]() $2$
-span of
$2$
-span of
![]() $\Omega $
. An analogous analysis, replacing
$\Omega $
. An analogous analysis, replacing
![]() $2$
with
$2$
with
![]() $1$
, applies for
$1$
, applies for
![]() $\mathsf {sw}_2$
. For
$\mathsf {sw}_2$
. For
![]() $\mathsf {eu}$
, we use
$\mathsf {eu}$
, we use
![]() $\mathbb {Z}/3$
-cohomology and the mod
$\mathbb {Z}/3$
-cohomology and the mod
![]() $3$
reduction of the Euler class.
$3$
reduction of the Euler class.
7.2 Orientability of attractors
The double-gyre is the dynamical system characterized by the differential equations
![]() $\dot {x} = \partial \psi /\partial y$
and
$\dot {x} = \partial \psi /\partial y$
and
![]() $\dot {y} = - \partial \psi /\partial x$
, where
$\dot {y} = - \partial \psi /\partial x$
, where
and A,
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\omega $
are positive parameters. The system is defined over the domain
$\omega $
are positive parameters. The system is defined over the domain
![]() $(x,y) \in [0,2] \times [0,1]$
with
$(x,y) \in [0,2] \times [0,1]$
with
![]() $t \in \mathbb {R}$
representing time. It was introduced in [Reference Shadden, Lekien and Marsden57] as a simplified model of the double-gyre pattern observed in geophysical flows. Geometrically, the double-gyre system consists of a pair of vortices oscillating back and forth, horizontally, in time; see, for example, [Reference Shadden, Lekien and Marsden57, Figure 5].
$t \in \mathbb {R}$
representing time. It was introduced in [Reference Shadden, Lekien and Marsden57] as a simplified model of the double-gyre pattern observed in geophysical flows. Geometrically, the double-gyre system consists of a pair of vortices oscillating back and forth, horizontally, in time; see, for example, [Reference Shadden, Lekien and Marsden57, Figure 5].
Since the vector field characterizing the system varies periodically with time, the flow line of a particle initially at
![]() $(x_0,y_0)$
depends on the time
$(x_0,y_0)$
depends on the time
![]() $t_0$
at which the particle is at that spot. Because of this, the phase space of the system (the space parametrizing the possible states of a particle) is
$t_0$
at which the particle is at that spot. Because of this, the phase space of the system (the space parametrizing the possible states of a particle) is
![]() $[0,2] \times [0,1] \times S^1$
, where the last coordinate represents time
$[0,2] \times [0,1] \times S^1$
, where the last coordinate represents time
![]() $\mathbb {R}$
modulo the period
$\mathbb {R}$
modulo the period
![]() $\pi /\omega $
.
$\pi /\omega $
.
Dynamical systems can be analyzed by studying the topology of their attractors [Reference Takens62, Reference Abarbanel1, Reference Perea51]. Informally, an attractor
![]() $\mathcal {M}$
of a dynamical system consists of a subset of the phase space that is invariant under the action of the system and such that any point sufficiently close to the attractor gets arbitrarily close to it as the system evolves. We refer the interested reader to [Reference Smale60, Reference Williams67, Reference Takens62] for formal notions of attractor.
$\mathcal {M}$
of a dynamical system consists of a subset of the phase space that is invariant under the action of the system and such that any point sufficiently close to the attractor gets arbitrarily close to it as the system evolves. We refer the interested reader to [Reference Smale60, Reference Williams67, Reference Takens62] for formal notions of attractor.
Usually, one only has access to partial information about the trajectory of a particle, which one wants to use to study the topology of the attractor
![]() $\mathcal {M}$
the particle is converging to. For example, one may be given a real-valued time series
$\mathcal {M}$
the particle is converging to. For example, one may be given a real-valued time series
![]() $\{x_n\}_{n=1,\dots ,N}$
, which comes from applying a differentiable map F defined on the phase space to a finite sample of the trajectory of the particle. If the attractor
$\{x_n\}_{n=1,\dots ,N}$
, which comes from applying a differentiable map F defined on the phase space to a finite sample of the trajectory of the particle. If the attractor
![]() $\mathcal {M}$
is a smooth manifold and certain other technical conditions are satisfied, a theorem of Takens [Reference Takens62] implies that the delay embedding of the time series
$\mathcal {M}$
is a smooth manifold and certain other technical conditions are satisfied, a theorem of Takens [Reference Takens62] implies that the delay embedding of the time series
is concentrated around a diffeomorphic copy of
![]() $\mathcal {M}$
, and is sufficiently dense in
$\mathcal {M}$
, and is sufficiently dense in
![]() $\mathcal {M}$
so that the Vietoris–Rips complex of X can be used to estimate the homology of
$\mathcal {M}$
so that the Vietoris–Rips complex of X can be used to estimate the homology of
![]() $\mathcal {M}$
, and local PCA can be used to estimate the tangent bundle of
$\mathcal {M}$
, and local PCA can be used to estimate the tangent bundle of
![]() $\mathcal {M}$
. Here, d is the target dimension and
$\mathcal {M}$
. Here, d is the target dimension and
![]() $\tau $
is the delay. We refer the reader to [Reference Takens62, Reference Abarbanel1, Reference Perea51, Reference Xu, Tralie, Antia, Lin and Perea68] for more information about recovering the geometry of attractors from a delay embedding.
$\tau $
is the delay. We refer the reader to [Reference Takens62, Reference Abarbanel1, Reference Perea51, Reference Xu, Tralie, Antia, Lin and Perea68] for more information about recovering the geometry of attractors from a delay embedding.
In [Reference Charó, Artana and Sciamarella13, Section 4.1], four attractors of the double-gyre dynamical system are studied. The four attractors can be distinguished using their homology, except for two of them which, topologically, look like a cylinder and a Möbius strip, respectively, and thus have the same homology groups. In order to deal with such examples, the authors of [Reference Charó, Artana and Sciamarella13] develop an algorithm for detecting orientability of this kind of data. Here, we show that our general purpose algorithms readily apply to this kind of data and confirm, using
![]() $\mathsf {sw}_1$
, that [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 4] is parametrized by a Möbius band and [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 1] by a cylinder.
$\mathsf {sw}_1$
, that [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 4] is parametrized by a Möbius band and [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 1] by a cylinder.
Fixing the initial condition
![]() $(x_0,y_0,t_0) = (0.55,0.5,0) \in [0,2] \times [0,1] \times S^1$
, for a double-gyre with
$(x_0,y_0,t_0) = (0.55,0.5,0) \in [0,2] \times [0,1] \times S^1$
, for a double-gyre with
![]() $A=0.1$
,
$A=0.1$
,
![]() $\varepsilon = 0.1$
, and
$\varepsilon = 0.1$
, and
![]() $\omega =\pi /5$
, as in [Reference Charó, Artana and Sciamarella13], we sample the trajectory of the particle at
$\omega =\pi /5$
, as in [Reference Charó, Artana and Sciamarella13], we sample the trajectory of the particle at
![]() $2000$
equally spaced times from
$2000$
equally spaced times from
![]() $t=0$
to
$t=0$
to
![]() $t=1000$
, obtaining a time series of positions
$t=1000$
, obtaining a time series of positions
![]() $\{(x_n,y_n)\}_{n=1,\dots ,2000} \subseteq [0,2] \times [0,1]$
. We take the function F to be projection onto the x-coordinate, as in [Reference Charó, Artana and Sciamarella13], the delay
$\{(x_n,y_n)\}_{n=1,\dots ,2000} \subseteq [0,2] \times [0,1]$
. We take the function F to be projection onto the x-coordinate, as in [Reference Charó, Artana and Sciamarella13], the delay
![]() $\tau =5$
and the target dimension
$\tau =5$
and the target dimension
![]() $d=5$
. A 2D projection of X is depicted in Figure 2a. The dataset ATTR1 consists of a subsample of
$d=5$
. A 2D projection of X is depicted in Figure 2a. The dataset ATTR1 consists of a subsample of
![]() $1000$
points of X.
$1000$
points of X.

Figure 2 2D projections of samples approximating two attractors of the double-gyre dynamical system. Consecutive samples are joined by an edge.
We approximate the tangent bundle of
![]() $\mathcal {M}$
using local PCA as sketched in Section 1.1.2. This give us a discrete approximate local trivialization
$\mathcal {M}$
using local PCA as sketched in Section 1.1.2. This give us a discrete approximate local trivialization
![]() $\Phi $
, which we use to compute an approximate cocycle
$\Phi $
, which we use to compute an approximate cocycle
![]() $\Omega = \mathsf {w}(\Phi )$
over the Vietoris–Rips complex of X. We choose
$\Omega = \mathsf {w}(\Phi )$
over the Vietoris–Rips complex of X. We choose
![]() $k = 58$
for the local PCA computations as this value maximizes the
$k = 58$
for the local PCA computations as this value maximizes the
![]() $2$
-death of
$2$
-death of
![]() $\Omega $
.
$\Omega $
.
Finally, we apply the algorithm
![]() $\mathsf {sw}_1$
to
$\mathsf {sw}_1$
to
![]() $\Omega $
and write the cohomology class thus obtained in the basis of the persistent cohomology provided by Ripser. The classes circled in red in Figure 3a are the classes that sum to
$\Omega $
and write the cohomology class thus obtained in the basis of the persistent cohomology provided by Ripser. The classes circled in red in Figure 3a are the classes that sum to
![]() $\mathsf {sw}_1(\Omega )$
. The fact that the most persistent class of the persistent diagram is colored in red tells us that, as one goes around the one-dimensional hole this class represents, the approximate vector bundle given by local PCA is changing orientation. This, coupled with the fact that the dataset is locally two-dimensional, suggests that the dataset is parametrized by a Möbius band.
$\mathsf {sw}_1(\Omega )$
. The fact that the most persistent class of the persistent diagram is colored in red tells us that, as one goes around the one-dimensional hole this class represents, the approximate vector bundle given by local PCA is changing orientation. This, coupled with the fact that the dataset is locally two-dimensional, suggests that the dataset is parametrized by a Möbius band.

Figure 3 Persistence diagrams of the Vietoris–Rips cohomology of finite samples approximating two attractors of the double-gyre dynamical system, with Stiefel–Whitney classes highlighted.
We run the same pipeline but with initial condition
![]() $(x_0,y_0,t_0) = (0.25, 0.125, 0)$
, as in [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 1]; we refer to this second dataset as ATTR2. In this case, regardless of the parameters chosen for local PCA, the first Stiefel–Whitney class of the approximate cocycle it gives is zero, as we see in Figure 3b.
$(x_0,y_0,t_0) = (0.25, 0.125, 0)$
, as in [Reference Charó, Artana and Sciamarella13, Section 4.1, Example 1]; we refer to this second dataset as ATTR2. In this case, regardless of the parameters chosen for local PCA, the first Stiefel–Whitney class of the approximate cocycle it gives is zero, as we see in Figure 3b.
7.3 Projective space of lines
Datasets of simple geometrical shapes, such as lines in
![]() $\mathbb {R}^2$
with different orientations, appear, for instance, as datasets of weights learned by autoencoders and other neural networks [Reference Hinton and Salakhutdinov29, Figure 2.A], [Reference Hinton, Krizhevsky and Wang30, Figures 2 and 3] and as datasets of local patches of natural images [Reference Carlsson, Ishkhanov, de Silva and Zomorodian12]. It has been shown that topology can be used to understand these datasets by giving insight into the functions learned by the hidden layers of neural networks [Reference Gabrielsson and Carlsson10, Reference Naitzat, Zhitnikov and Lim48], and by finding convenient parametrizations of spaces of image patches [Reference Perea and Carlsson52].
$\mathbb {R}^2$
with different orientations, appear, for instance, as datasets of weights learned by autoencoders and other neural networks [Reference Hinton and Salakhutdinov29, Figure 2.A], [Reference Hinton, Krizhevsky and Wang30, Figures 2 and 3] and as datasets of local patches of natural images [Reference Carlsson, Ishkhanov, de Silva and Zomorodian12]. It has been shown that topology can be used to understand these datasets by giving insight into the functions learned by the hidden layers of neural networks [Reference Gabrielsson and Carlsson10, Reference Naitzat, Zhitnikov and Lim48], and by finding convenient parametrizations of spaces of image patches [Reference Perea and Carlsson52].
Here, we show how characteristic classes can be used to understand the topology of a set of lines in
![]() $\mathbb {R}^2$
. The dataset LINES consists of
$\mathbb {R}^2$
. The dataset LINES consists of
![]() $160$
grayscale images represented by a
$160$
grayscale images represented by a
![]() $10 \times 10$
real matrix. Each image represents a fuzzy line in
$10 \times 10$
real matrix. Each image represents a fuzzy line in
![]() $\mathbb {R}^2$
with a certain slope and offset. A sample of
$\mathbb {R}^2$
with a certain slope and offset. A sample of
![]() $56$
elements of LINES is displayed in Figure 4a. We interpret this dataset as a point cloud
$56$
elements of LINES is displayed in Figure 4a. We interpret this dataset as a point cloud
![]() $X \subseteq \mathbb {R}^{10 \times 10}$
.
$X \subseteq \mathbb {R}^{10 \times 10}$
.

Figure 4 Samples of a dataset parametrized by the real projective plane and the persistence diagram of its Vietoris–Rips cohomology, with Stiefel–Whitney classes highlighted.
We proceed with the same pipeline as in Section 7.2. We compute the persistence diagram of
![]() $\mathsf {VR}(X)$
with coefficients in
$\mathsf {VR}(X)$
with coefficients in
![]() $\mathbb {Z}/2$
and observe that there are two significant classes, one in
$\mathbb {Z}/2$
and observe that there are two significant classes, one in
![]() $H^1$
and the other in
$H^1$
and the other in
![]() $H^2$
(Figure 4b). By applying local PCA with a range of values k, we see that the dataset seems to have an intrinsic dimension of
$H^2$
(Figure 4b). By applying local PCA with a range of values k, we see that the dataset seems to have an intrinsic dimension of
![]() $2$
. This may lead one to suspect that the dataset is parametrized by the real projective plane. One way to confirm this suspicion is by computing persistent cohomology with coefficients in
$2$
. This may lead one to suspect that the dataset is parametrized by the real projective plane. One way to confirm this suspicion is by computing persistent cohomology with coefficients in
![]() $\mathbb {Z}/3$
and seeing that the most persistent classes in
$\mathbb {Z}/3$
and seeing that the most persistent classes in
![]() $H^1$
and
$H^1$
and
![]() $H^2$
disappear.
$H^2$
disappear.
Another method to corroborate the hypothesis is the following. Local PCA gives a discrete approximate local trivialization
![]() $\Phi $
over
$\Phi $
over
![]() $\mathsf {VR}(X)$
, and the
$\mathsf {VR}(X)$
, and the
![]() $1$
-death of
$1$
-death of
![]() $\Omega = \mathsf {w}(\Phi )$
is maximized using
$\Omega = \mathsf {w}(\Phi )$
is maximized using
![]() $k = 18$
. We apply the algorithms
$k = 18$
. We apply the algorithms
![]() $\mathsf {sw}_1$
and
$\mathsf {sw}_1$
and
![]() $\mathsf {sw}_2$
to
$\mathsf {sw}_2$
to
![]() $\Omega $
and see that the cohomology classes thus obtained coincide with the most persistent
$\Omega $
and see that the cohomology classes thus obtained coincide with the most persistent
![]() $H^1$
and
$H^1$
and
![]() $H^2$
classes of Figure 4b, respectively. This confirms the hypothesis that the dataset is parametrized by a projective plane, as we know that
$H^2$
classes of Figure 4b, respectively. This confirms the hypothesis that the dataset is parametrized by a projective plane, as we know that
![]() $H^1(\mathbb {R} P^2; \mathbb {Z}/2) \cong H^2(\mathbb {R} P^2; \mathbb {Z}/2) \cong \mathbb {Z}/2$
and that the Stiefel–Whitney classes of the tangent bundle of
$H^1(\mathbb {R} P^2; \mathbb {Z}/2) \cong H^2(\mathbb {R} P^2; \mathbb {Z}/2) \cong \mathbb {Z}/2$
and that the Stiefel–Whitney classes of the tangent bundle of
![]() $\mathbb {R} P^2$
are nonzero.
$\mathbb {R} P^2$
are nonzero.
7.4 Lack of global synchronization in cryo-EM
We give an example of how characteristic classes provide an obstruction to synchronization. In order to do this, we simulate an instance of the main problem of cryo-EM [Reference Frank18, Reference van Heel, Gowen, Matadeen, Orlova, Finn, Pape, Cohen, Stark, Schmidt, Schatz and Patwardhan28]. In this problem, one is given a set of 2D projections of an unknown 3D shape and is asked to reconstruct the shape. One possible formalism is to assume that the shape is given by a density
![]() $S : \mathbb {R}^3 \to \mathbb {R}$
. We think of the projection process as first acting on the molecule by an unknown element
$S : \mathbb {R}^3 \to \mathbb {R}$
. We think of the projection process as first acting on the molecule by an unknown element
![]() $v \in SO(3)$
, which we call projection angle, giving
$v \in SO(3)$
, which we call projection angle, giving
![]() $S \circ v : \mathbb {R}^3 \to \mathbb {R}$
, and then integrating
$S \circ v : \mathbb {R}^3 \to \mathbb {R}$
, and then integrating
![]() $S\circ v$
along the z-axis, yielding a map
$S\circ v$
along the z-axis, yielding a map
![]() $S_v : \mathbb {R}^2 \to \mathbb {R}$
.
$S_v : \mathbb {R}^2 \to \mathbb {R}$
.
One of the main difficulties is that one is only given a set of projected images and is not given the projection angle v corresponding to each image. Much attention has thus been given to the problem of recovering the projection matrices corresponding to each image, up to a global rigid automorphism of
![]() $S^2$
, that is, an element of
$S^2$
, that is, an element of
![]() $SO(3)$
.
$SO(3)$
.
Let X be a set of 2D projections of an unknown 3D shape. A successful approach [Reference Hadani and Singer23, Reference Hadani and Singer24, Reference Ye and Lim69] to recovering the projection angles starts by computing rotations
![]() $g_{ij} \in SO(2)$
that best align
$g_{ij} \in SO(2)$
that best align
![]() $x_i,x_j \in X$
. Formally, one chooses a distance d between maps
$x_i,x_j \in X$
. Formally, one chooses a distance d between maps
![]() $\mathbb {R}^2 \to \mathbb {R}$
and finds
$\mathbb {R}^2 \to \mathbb {R}$
and finds
![]() $g_{ij} \in SO(2)$
that minimizes the distance between
$g_{ij} \in SO(2)$
that minimizes the distance between
![]() $x_i : \mathbb {R}^2 \to \mathbb {R}$
and
$x_i : \mathbb {R}^2 \to \mathbb {R}$
and
![]() $g_{ij} \circ x_j : \mathbb {R}^2 \to \mathbb {R}$
. One then fixes a threshold
$g_{ij} \circ x_j : \mathbb {R}^2 \to \mathbb {R}$
. One then fixes a threshold
![]() $\delta $
and constructs a two-dimensional simplicial complex K with
$\delta $
and constructs a two-dimensional simplicial complex K with
![]() $0$
-simplices given by the elements of X,
$0$
-simplices given by the elements of X,
![]() $1$
-simplices given by pairs
$1$
-simplices given by pairs
![]() $(ij)$
such that
$(ij)$
such that
![]() $d(x_i, g_{ij}x_j) < \delta $
and having a
$d(x_i, g_{ij}x_j) < \delta $
and having a
![]() $2$
-simplex
$2$
-simplex
![]() $(ijk)$
anytime
$(ijk)$
anytime
![]() $(ij)$
,
$(ij)$
,
![]() $(jk)$
and
$(jk)$
and
![]() $(ik)$
are
$(ik)$
are
![]() $1$
-simplices of K. This construction can be interpreted as giving an approximate
$1$
-simplices of K. This construction can be interpreted as giving an approximate
![]() $SO(2)$
-cocycle over K. This cocycle approximates the tangent bundle of
$SO(2)$
-cocycle over K. This cocycle approximates the tangent bundle of
![]() $S^2 \subseteq \mathbb {R}^3$
and can be used to recover the projection angles.
$S^2 \subseteq \mathbb {R}^3$
and can be used to recover the projection angles.
We are interested in simulating an instance of this problem and in computing the Euler class of the approximate cocycle. As we expect this class to be nonzero, this shows that characteristic classes of approximate vector bundles can be used for model validation and to detect nonsynchronizability of data. This also confirms the theoretical analysis of [Reference Singer, Zhao, Shkolnisky and Hadani58], which shows that global synchronization is not possible.
In order to construct an instance of the problem, we define
![]() $S : \mathbb {R}^3 \to \mathbb {R}$
to be the characteristic function of a union of four balls of different radii, centered at different points of
$S : \mathbb {R}^3 \to \mathbb {R}$
to be the characteristic function of a union of four balls of different radii, centered at different points of
![]() $\mathbb {R}^3$
. We then compute
$\mathbb {R}^3$
. We then compute
![]() $400$
projections
$400$
projections
![]() $\{S_{v_i} : \mathbb {R}^2 \to \mathbb {R}\}_{i = 1, \dots , 400}$
for
$\{S_{v_i} : \mathbb {R}^2 \to \mathbb {R}\}_{i = 1, \dots , 400}$
for
![]() $\{v_i \in SO(3)\}$
a well-distributed random sample of
$\{v_i \in SO(3)\}$
a well-distributed random sample of
![]() $SO(3)$
. We save these projections as
$SO(3)$
. We save these projections as
![]() $100 \times 100$
grayscale images, which constitute the dataset PROJS. A sample of
$100 \times 100$
grayscale images, which constitute the dataset PROJS. A sample of
![]() $9$
elements of PROJS is displayed in Figure 5a.
$9$
elements of PROJS is displayed in Figure 5a.

Figure 5 A sample of a synchronization problem parametrized by a bundle over the sphere and the persistence diagram of the base of the bundle with the Stiefel–Whitney classes highlighted.
Since aligning images optimally is a difficult problem in itself, we simplify our computations by using our knowledge of the projection angles
![]() $v_i$
and
$v_i$
and
![]() $v_j$
to align the images
$v_j$
to align the images
![]() $x_i$
and
$x_i$
and
![]() $x_i$
. More specifically, given
$x_i$
. More specifically, given
![]() $v \in SO(3)$
, let
$v \in SO(3)$
, let
![]() $v^3 \in S^2$
denote its third column. We compose
$v^3 \in S^2$
denote its third column. We compose
![]() $v_i$
with the rotation
$v_i$
with the rotation
![]() $r_{ij} \in SO(3)$
along a minimizing geodesic between
$r_{ij} \in SO(3)$
along a minimizing geodesic between
![]() $v_i^3$
and
$v_i^3$
and
![]() $v_j^3$
and define
$v_j^3$
and define
![]() $\Omega _{ij} \in SO(2)$
such that
$\Omega _{ij} \in SO(2)$
such that
 $$\begin{align*}r_{ij} v_i = \begin{pmatrix} \Omega_{ij} & 0 \\ 0 & 1 \end{pmatrix} v_j. \end{align*}$$
$$\begin{align*}r_{ij} v_i = \begin{pmatrix} \Omega_{ij} & 0 \\ 0 & 1 \end{pmatrix} v_j. \end{align*}$$
We let X be a sample of
![]() $300$
elements of PROJS and compute the Vietoris–Rips complex of X, where the dissimilarity function
$300$
elements of PROJS and compute the Vietoris–Rips complex of X, where the dissimilarity function
![]() $d(i,j)$
is given by the distance between the image
$d(i,j)$
is given by the distance between the image
![]() $x_i$
and the rotated image
$x_i$
and the rotated image
![]() $\Omega _{ij}x_j$
.
$\Omega _{ij}x_j$
.
Finally, we compute the persistence diagram of
![]() $\mathsf {VR}(X)$
with coefficients in
$\mathsf {VR}(X)$
with coefficients in
![]() $\mathbb {Z}/3$
, compute the Euler class of
$\mathbb {Z}/3$
, compute the Euler class of
![]() $\Omega $
at its
$\Omega $
at its
![]() $1$
-death, reduce it mod
$1$
-death, reduce it mod
![]() $3$
and write it in the basis provided by the persistent cohomology computations. We see that the persistent class representing the reduction mod
$3$
and write it in the basis provided by the persistent cohomology computations. We see that the persistent class representing the reduction mod
![]() $3$
of the Euler class, which appears circled in red in Figure 5b, is the most persistent class of
$3$
of the Euler class, which appears circled in red in Figure 5b, is the most persistent class of
![]() $\mathsf {VR}(X)$
.
$\mathsf {VR}(X)$
.
8 Future work
Robustness and applications
The notions of vector bundle we have presented can tolerate a certain amount of noise but are not robust to outliers. What this means is that an
![]() $\varepsilon $
-approximate cocycle on a simplicial complex can satisfy the
$\varepsilon $
-approximate cocycle on a simplicial complex can satisfy the
![]() $\delta $
-approximate cocycle condition for a very small
$\delta $
-approximate cocycle condition for a very small
![]() $\delta $
on almost all
$\delta $
on almost all
![]() $2$
-simplices, except on very few, and this can still make
$2$
-simplices, except on very few, and this can still make
![]() $\varepsilon $
very large. This problem is similar to the robustness problem of persistent homology, where the addition of a few outliers to the dataset can completely alter the inferred persistent homology.
$\varepsilon $
very large. This problem is similar to the robustness problem of persistent homology, where the addition of a few outliers to the dataset can completely alter the inferred persistent homology.
We are interested in studying extensions of our framework that lead to algorithms for the inference of topological information of approximate vector bundles even in the presence of outliers. The work in [Reference Singer59] is an example of such an algorithm, as it can be interpreted as a robust algorithm for inferring whether the first Stiefel–Whitney class of the tangent space of an embedded manifold is
![]() $0$
or not.
$0$
or not.
Invariants of approximate cocycles
A related problem is that of defining invariants of
![]() $\varepsilon $
-approximate cocycles that do not require
$\varepsilon $
-approximate cocycles that do not require
![]() $\varepsilon $
to be sufficiently small. A possible avenue is to consider the persistent cohomology of the thickened Grassmannians and use
$\varepsilon $
to be sufficiently small. A possible avenue is to consider the persistent cohomology of the thickened Grassmannians and use
![]() $\varepsilon $
-approximate classifying maps to pull back the cohomology classes of these Grassmannians. The question of how long the universal Stiefel–Whintey classes persist in the thickened Grassmannians is related to the filling radius introduced by Gromov [Reference Gromov22] and to the generalization considered by Lim, Mémoli and Okutan in [Reference Lim, Memoli and Okutan40]. A related question is whether better bounds for our results can be obtained by using the Vietoris–Rips complex of the Grassmannians, instead of the thickening.
$\varepsilon $
-approximate classifying maps to pull back the cohomology classes of these Grassmannians. The question of how long the universal Stiefel–Whintey classes persist in the thickened Grassmannians is related to the filling radius introduced by Gromov [Reference Gromov22] and to the generalization considered by Lim, Mémoli and Okutan in [Reference Lim, Memoli and Okutan40]. A related question is whether better bounds for our results can be obtained by using the Vietoris–Rips complex of the Grassmannians, instead of the thickening.
Approximate sections
In applications, one is interested in finding sections of approximate vector bundles. In order to do this in practice and to prove consistency theorems for this kind of computation, a notion of approximate section needs to be introduced and studied.
Approximate vector bundles with connection
Discrete approximate cocycles over simplicial complexes, as in Definition 5.1, appear in the physics literature (e.g., [Reference Christiansen and Halvorsen14]), where they have a different interpretation: The value
![]() $\Omega _{ij} \in O(d)$
of the (discrete) cocycle
$\Omega _{ij} \in O(d)$
of the (discrete) cocycle
![]() $\Omega $
on the
$\Omega $
on the
![]() $1$
-simplex
$1$
-simplex
![]() $(ij)$
represents parallel transport from the fiber of the vertex i to the fiber of the vertex j. It would be interesting to relate this intepretation to the results in this paper and to study to what extent a discrete approximate cocycle can be used to reconstruct a vector bundle together with a connection.
$(ij)$
represents parallel transport from the fiber of the vertex i to the fiber of the vertex j. It would be interesting to relate this intepretation to the results in this paper and to study to what extent a discrete approximate cocycle can be used to reconstruct a vector bundle together with a connection.
Algorithms for higher characteristic classes
Finding algorithms for the effective computation of higher characteristic classes, at least in the exact case, has been the subject of much research in the past. For instance, [Reference Brylinski and McLaughlin9] and [Reference McLaughlin44] give cocycles representing Chern, Pontryajin, Stiefel–Whitney and Euler classes of vector bundles over compact manifolds. One should note that many of the formulas are not entirely algorithmic, as they require to determine, for example, whether certain singular cycles are
![]() $0$
in homology or not.
$0$
in homology or not.
Other structure groups
Some synchronization problems are most naturally described using a structure group different from the orthogonal group
![]() $O(d)$
. We hope our theory can be extended to bundles having other structure groups, such as
$O(d)$
. We hope our theory can be extended to bundles having other structure groups, such as
![]() $U(d)$
,
$U(d)$
,
![]() $PO(d)$
, and
$PO(d)$
, and
![]() $(\mathbb {R}^n, +)$
.
$(\mathbb {R}^n, +)$
.
A Technical details
A.1 Reach and thickenings
Let
![]() $\emptyset \neq X \subseteq \mathbb {R}^N$
be closed. For
$\emptyset \neq X \subseteq \mathbb {R}^N$
be closed. For
![]() $\varepsilon \in [0,\infty ]$
, define the
$\varepsilon \in [0,\infty ]$
, define the
![]() $\boldsymbol {\varepsilon }$
-thickening of X by
$\boldsymbol {\varepsilon }$
-thickening of X by
![]() $X^\varepsilon = X$
if
$X^\varepsilon = X$
if
![]() $\varepsilon = 0$
, and otherwise by
$\varepsilon = 0$
, and otherwise by
A closest point of
![]() $y \in \mathbb {R}^N$
in X is a point
$y \in \mathbb {R}^N$
in X is a point
![]() $x \in X$
that minimizes
$x \in X$
that minimizes
![]() $\| x - y\| _2$
. The medial axis of X, denoted
$\| x - y\| _2$
. The medial axis of X, denoted
![]() $\operatorname {\mathrm {med}}(X)$
, consists of all points
$\operatorname {\mathrm {med}}(X)$
, consists of all points
![]() $y \in \mathbb {R}^N$
that admit more than one closest point in X. The reach of X is the supremum of
$y \in \mathbb {R}^N$
that admit more than one closest point in X. The reach of X is the supremum of
![]() $\varepsilon \geq 0$
such that
$\varepsilon \geq 0$
such that
![]() $X^\varepsilon $
does not intersect
$X^\varepsilon $
does not intersect
![]() $\operatorname {\mathrm {med}}(X)$
. Define a function
$\operatorname {\mathrm {med}}(X)$
. Define a function
![]() $\pi : \mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X) \to X$
by mapping a point y to its closest point of X.
$\pi : \mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X) \to X$
by mapping a point y to its closest point of X.
Lemma A.1. If
![]() $\emptyset \neq X \subseteq \mathbb {R}^N$
is closed, then the map
$\emptyset \neq X \subseteq \mathbb {R}^N$
is closed, then the map
![]() $\pi : \mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X) \to X$
is continuous. In particular, if X has strictly positive reach and
$\pi : \mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X) \to X$
is continuous. In particular, if X has strictly positive reach and
![]() $\varepsilon \leq \operatorname {\mathrm {reach}}(X)$
, then
$\varepsilon \leq \operatorname {\mathrm {reach}}(X)$
, then
![]() $\pi : X^\varepsilon \to X$
is well defined and continuous. It follows that the map
$\pi : X^\varepsilon \to X$
is well defined and continuous. It follows that the map
![]() $\pi : X^\varepsilon \to X$
is a homotopy equivalence, with inverse the inclusion
$\pi : X^\varepsilon \to X$
is a homotopy equivalence, with inverse the inclusion
![]() $X \to X^\varepsilon $
.
$X \to X^\varepsilon $
.
Proof. We start by proving the first claim. For this, we show that
![]() $\pi $
maps convergent sequences to convergent sequences. Let
$\pi $
maps convergent sequences to convergent sequences. Let
![]() $y_n \to y$
be a convergent sequence in
$y_n \to y$
be a convergent sequence in
![]() $\mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X)$
. By the triangle inequality, we have
$\mathbb {R}^N \setminus \operatorname {\mathrm {med}}(X)$
. By the triangle inequality, we have
Thus, for n sufficiently large, we have that
![]() $y_n$
is inside the closed ball of radius
$y_n$
is inside the closed ball of radius
![]() $2d(y,X) + 1$
around
$2d(y,X) + 1$
around
![]() $\pi (y)$
, which is a compact set. Combining this with the fact that X is closed, we can assume, without loss of generality, that
$\pi (y)$
, which is a compact set. Combining this with the fact that X is closed, we can assume, without loss of generality, that
![]() $\pi (y_n)$
converges to some point
$\pi (y_n)$
converges to some point
![]() $x \in X$
. We must show that
$x \in X$
. We must show that
![]() $x = \pi (y)$
, and to prove this it is enough to show that
$x = \pi (y)$
, and to prove this it is enough to show that
![]() $\| y - x\| _2 = d(y,X)$
, by uniqueness of minimizers. By definition,
$\| y - x\| _2 = d(y,X)$
, by uniqueness of minimizers. By definition,
![]() $\| y_n - \pi (y_n)\| _2 = d(y_n, X)$
and
$\| y_n - \pi (y_n)\| _2 = d(y_n, X)$
and
![]() $d(-,X)$
is a continuous function, so, taking a limit, we see that
$d(-,X)$
is a continuous function, so, taking a limit, we see that
![]() $\| y - x\|_2 = d(y, X)$
.
$\| y - x\|_2 = d(y, X)$
.
For the second claim, it suffices to show that
![]() $X^{\operatorname {\mathrm {reach}}(X)}$
does not intersect
$X^{\operatorname {\mathrm {reach}}(X)}$
does not intersect
![]() $\operatorname {\mathrm {med}}(X)$
, which is clear since any point of
$\operatorname {\mathrm {med}}(X)$
, which is clear since any point of
![]() $X^{\operatorname {\mathrm {reach}}(X)}$
belongs to
$X^{\operatorname {\mathrm {reach}}(X)}$
belongs to
![]() $X^\delta $
for some
$X^\delta $
for some
![]() $\delta < \operatorname {\mathrm {reach}}(X)$
.
$\delta < \operatorname {\mathrm {reach}}(X)$
.
Finally, to see that
![]() $\pi $
is a homotopy equivalence, note that the inclusion followed by the projection is certainly the identity of X and the projection followed by the inclusion is homotopic to the identity of
$\pi $
is a homotopy equivalence, note that the inclusion followed by the projection is certainly the identity of X and the projection followed by the inclusion is homotopic to the identity of
![]() $X^\varepsilon $
by means of a linear homotopy.
$X^\varepsilon $
by means of a linear homotopy.
Lemma A.2. Let
![]() $X \subseteq \mathbb {R}^N$
be closed with strictly positive reach r. Let z be a convex combination of
$X \subseteq \mathbb {R}^N$
be closed with strictly positive reach r. Let z be a convex combination of
![]() $x_1,\dots ,x_n \in X$
such that
$x_1,\dots ,x_n \in X$
such that
![]() $\| x_i - x_j\| < r$
for all
$\| x_i - x_j\| < r$
for all
![]() $1 \leq i,j \leq n$
. Then
$1 \leq i,j \leq n$
. Then
![]() $\| z - x_j\| < r$
and
$\| z - x_j\| < r$
and
![]() $\| \pi (z) - x_j\| < 2 r$
for all
$\| \pi (z) - x_j\| < 2 r$
for all
![]() $1 \leq j \leq n$
.
$1 \leq j \leq n$
.
Proof. Fix
![]() $1 \leq j \leq n$
. The points
$1 \leq j \leq n$
. The points
![]() $x_1, \dots , x_n$
are all contained in the open ball of radius r around
$x_1, \dots , x_n$
are all contained in the open ball of radius r around
![]() $x_j$
. It follows that z is also contained in this ball by the convexity of open balls. In particular,
$x_j$
. It follows that z is also contained in this ball by the convexity of open balls. In particular,
![]() $z \in X^r$
and
$z \in X^r$
and
![]() $\|\pi (z) - z\| < r$
. By the triangle inequality, we have
$\|\pi (z) - z\| < r$
. By the triangle inequality, we have
![]() $\|\pi(x) - x_j\| < 2r$
, as required.
$\|\pi(x) - x_j\| < 2r$
, as required.
A.2 Polar decomposition and orthogonal Procrustes problem
In this section, we collect a few standard facts about the orthogonal Procrustes problem; a standard reference is [Reference Horn and Johnson31].
Let
![]() $n \geq m \geq 1 \in \mathbb {N}$
. Let
$n \geq m \geq 1 \in \mathbb {N}$
. Let
![]() $N \in \mathbb {R}^{n \times m}$
. A polar decomposition of N consists of matrices
$N \in \mathbb {R}^{n \times m}$
. A polar decomposition of N consists of matrices
![]() $U \in \mathbb {R}^{n \times m}$
and
$U \in \mathbb {R}^{n \times m}$
and
![]() $P \in \mathbb {R}^{m\times m}$
such that
$P \in \mathbb {R}^{m\times m}$
such that
![]() $N = U P$
, the matrix U has orthonormal columns and the matrix P is positive semidefinite. We will need the following well known fact about polar decompositions; for a reference, see [Reference Horn and Johnson31, Theorem 7.3.1]. In the statement, for A a symmetric positive semidefinite matrix,
$N = U P$
, the matrix U has orthonormal columns and the matrix P is positive semidefinite. We will need the following well known fact about polar decompositions; for a reference, see [Reference Horn and Johnson31, Theorem 7.3.1]. In the statement, for A a symmetric positive semidefinite matrix,
![]() $A^{1/2}$
denotes the unique positive semidefinite square root [Reference Horn and Johnson31, Theorem 7.2.6], also called the principal square root of A.
$A^{1/2}$
denotes the unique positive semidefinite square root [Reference Horn and Johnson31, Theorem 7.2.6], also called the principal square root of A.
Lemma A.3. Any matrix admits a polar decomposition. The factor P is uniquely determined and satisfies
![]() $P = (N^t N)^{1/2}$
. The factor U is uniquely determined if N has full rank.
$P = (N^t N)^{1/2}$
. The factor U is uniquely determined if N has full rank.
Let
![]() $\mathsf {V}(m,n) \subseteq \mathbb {R}^{n \times m}$
denote the subset of matrices with orthonormal columns. Consider the map
$\mathsf {V}(m,n) \subseteq \mathbb {R}^{n \times m}$
denote the subset of matrices with orthonormal columns. Consider the map
![]() $Q : \mathbb {R}^{n \times m} \to \mathsf {V}(m,n)$
that assigns to a matrix N a matrix U that is part of a polar decomposition
$Q : \mathbb {R}^{n \times m} \to \mathsf {V}(m,n)$
that assigns to a matrix N a matrix U that is part of a polar decomposition
![]() $N = UP$
. Note that, for general matrices, this map depends on a choice of polar decomposition.
$N = UP$
. Note that, for general matrices, this map depends on a choice of polar decomposition.
Corollary A.4. The map
![]() $Q : \mathbb {R}^{n \times m} \to \mathsf {V}(m,n)$
is uniquely determined and continuous if we restrict its domain to matrices with full rank.
$Q : \mathbb {R}^{n \times m} \to \mathsf {V}(m,n)$
is uniquely determined and continuous if we restrict its domain to matrices with full rank.
Proof. By Lemma A.3, if N has full rank, we have
![]() $U = N P^{-1} = N \left ((N^t N)^{1/2}\right )^{-1}$
. The map
$U = N P^{-1} = N \left ((N^t N)^{1/2}\right )^{-1}$
. The map
![]() $A \mapsto A^{1/2}$
that takes a symmetric positive definite matrix to its principal square root is continuous [Reference Horn and Johnson32, Chapter 6.2, Problem 26] and so is the map that takes an invertible matrix to its inverse. The result follows.
$A \mapsto A^{1/2}$
that takes a symmetric positive definite matrix to its principal square root is continuous [Reference Horn and Johnson32, Chapter 6.2, Problem 26] and so is the map that takes an invertible matrix to its inverse. The result follows.
For
![]() $M,N \in \mathbb {R}^{n\times d}$
, the orthogonal Procrustes problem is the following optimization problem:
$M,N \in \mathbb {R}^{n\times d}$
, the orthogonal Procrustes problem is the following optimization problem:
It is well known (see, e.g., [Reference Horn and Johnson31, Section 7.4.5]) that the solutions to the above orthogonal Procrustes problem are precisely the orthogonal matrices U that are part of a polar decomposition
![]() $M^t N = U P$
. In particular, if
$M^t N = U P$
. In particular, if
![]() $M^t N$
has full rank, then the above problem admits exactly one solution. Moreover, this solution varies continuously in
$M^t N$
has full rank, then the above problem admits exactly one solution. Moreover, this solution varies continuously in
![]() $M^t$
and N, as long as we restrict ourselves to problems for which
$M^t$
and N, as long as we restrict ourselves to problems for which
![]() $M^t N$
has full rank.
$M^t N$
has full rank.
A.3 Metrics on Grassmannians
In this section, we compare two metrics on the Grassmannians and we recall the computation of the reach of the Grassmannians due to Tinarrage [Reference Tinarrage63].
Recall that
![]() $\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
is
$\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
is
![]() $O(d)$
-invariant, with
$O(d)$
-invariant, with
![]() $O(d)$
acting by matrix multiplication on the right. This means that we have
$O(d)$
acting by matrix multiplication on the right. This means that we have
![]() $\mathsf {Proj}(M) = \mathsf {Proj}(M \Omega )$
for every
$\mathsf {Proj}(M) = \mathsf {Proj}(M \Omega )$
for every
![]() $\Omega \in O(d)$
. In fact, it is easy to see that, for
$\Omega \in O(d)$
. In fact, it is easy to see that, for
![]() $N,M \in \mathsf {V}(d,n)$
, one has
$N,M \in \mathsf {V}(d,n)$
, one has
![]() $\mathsf {Proj}(N) = \mathsf {Proj}(M)$
if and only if
$\mathsf {Proj}(N) = \mathsf {Proj}(M)$
if and only if
![]() $N \Omega = M$
for some
$N \Omega = M$
for some
![]() $\Omega \in O(d)$
. This shows that, as a set,
$\Omega \in O(d)$
. This shows that, as a set,
![]() $\mathsf {Gr}(d,n)$
is the quotient of
$\mathsf {Gr}(d,n)$
is the quotient of
![]() $\mathsf {V}(d,n)$
by the action of
$\mathsf {V}(d,n)$
by the action of
![]() $O(d)$
by matrix multiplication on the right. Since
$O(d)$
by matrix multiplication on the right. Since
![]() $O(d)$
acts by isometries, this induces a metric
$O(d)$
acts by isometries, this induces a metric
![]() $\mathsf {d}_{\mathsf {q}}$
on
$\mathsf {d}_{\mathsf {q}}$
on
![]() $\mathsf {Gr}(d,n)$
, given by
$\mathsf {Gr}(d,n)$
, given by
We now prove some useful comparisons between the metric and the Frobenius distance.
Lemma A.5. Let
![]() $M \in \mathsf {V}(d,n)$
,
$M \in \mathsf {V}(d,n)$
,
![]() $A \in \mathbb {R}^{d \times m}$
, and
$A \in \mathbb {R}^{d \times m}$
, and
![]() $B \in \mathbb {R}^{n \times m}$
. Then
$B \in \mathbb {R}^{n \times m}$
. Then
![]() $\| MA\| = \| A\| $
and
$\| MA\| = \| A\| $
and
![]() $\| M^t B\| \leq \| B\| $
.
$\| M^t B\| \leq \| B\| $
.
Proof. For the first claim, we compute
For the second, note that
![]() $\| M^tB\| ^2 = \operatorname {\mathrm {tr}}(M M^t B B^t)$
. Since
$\| M^tB\| ^2 = \operatorname {\mathrm {tr}}(M M^t B B^t)$
. Since
![]() $M M^t$
is an orthogonal projection to a subspace, there is an orthogonal change of basis such that
$M M^t$
is an orthogonal projection to a subspace, there is an orthogonal change of basis such that
![]() $M M^t$
is diagonal, with diagonal entries
$M M^t$
is diagonal, with diagonal entries
![]() $1$
repeated d times and
$1$
repeated d times and
![]() $0$
repeated
$0$
repeated
![]() $n-d$
times. The result follows by computing
$n-d$
times. The result follows by computing
![]() $\operatorname {\mathrm {tr}}(M M^t B B^t)$
in that basis.
$\operatorname {\mathrm {tr}}(M M^t B B^t)$
in that basis.
Let
![]() $\mathsf {d}_{\mathsf {Fr}}$
denote the metric on Grassmannians induced by the Frobenius norm.
$\mathsf {d}_{\mathsf {Fr}}$
denote the metric on Grassmannians induced by the Frobenius norm.
Lemma A.6. The map
![]() $\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
given by
$\mathsf {Proj} : \mathsf {V}(d,n) \to \mathsf {Gr}(d,n)$
given by
![]() $\mathsf {Proj}(M) = M M^t$
is
$\mathsf {Proj}(M) = M M^t$
is
![]() $\sqrt {2}$
-Lipschitz. In particular, we have
$\sqrt {2}$
-Lipschitz. In particular, we have
![]() $\mathsf {d}_{\mathsf {Fr}} \leq \sqrt {2} \mathsf {d}_{\mathsf {q}}$
.
$\mathsf {d}_{\mathsf {Fr}} \leq \sqrt {2} \mathsf {d}_{\mathsf {q}}$
.
Simple examples with
![]() $d = 1$
and
$d = 1$
and
![]() $n=2$
show that this bound is tight.
$n=2$
show that this bound is tight.
Proof. The second claim is a consequence the first one. For the first claim, we start by recalling that, for any matrix A, one has
![]() $\| A^t A\| = \| A A^t\| $
. In particular, if A is square,
$\| A^t A\| = \| A A^t\| $
. In particular, if A is square,
![]() $\| AA^t - \mathsf {id}\| ^2 = \| AA^t\| ^2 + \| \mathsf {id}\| ^2 - 2\operatorname {\mathrm {tr}}(AA^t) = \| A^t A\| ^2 + \| \mathsf {id}\| ^2 - 2\operatorname {\mathrm {tr}}(A^t A) = \| A^t A - \mathsf {id}\| ^2$
.
$\| AA^t - \mathsf {id}\| ^2 = \| AA^t\| ^2 + \| \mathsf {id}\| ^2 - 2\operatorname {\mathrm {tr}}(AA^t) = \| A^t A\| ^2 + \| \mathsf {id}\| ^2 - 2\operatorname {\mathrm {tr}}(A^t A) = \| A^t A - \mathsf {id}\| ^2$
.
Now, let
![]() $M,N \in \mathsf {V}(d,n)$
. Since multiplication by an orthogonal matrix preserves the Frobenius norm, we may assume that M and N are matrices given by blocks:
$M,N \in \mathsf {V}(d,n)$
. Since multiplication by an orthogonal matrix preserves the Frobenius norm, we may assume that M and N are matrices given by blocks:
 $$\begin{align*}M = \begin{bmatrix} A \\ B \end{bmatrix},\;\; N = \begin{bmatrix} \mathsf{id} \\ 0 \end{bmatrix}, \end{align*}$$
$$\begin{align*}M = \begin{bmatrix} A \\ B \end{bmatrix},\;\; N = \begin{bmatrix} \mathsf{id} \\ 0 \end{bmatrix}, \end{align*}$$
where the top block is
![]() $d \times d$
and the bottom one is
$d \times d$
and the bottom one is
![]() $(n-d) \times d$
. Note that, by assumption, we have
$(n-d) \times d$
. Note that, by assumption, we have
![]() $A^t A + B^t B = \mathsf {id}$
. We now bound as follows:
$A^t A + B^t B = \mathsf {id}$
. We now bound as follows:
 $$ \begin{align*} \| MM^t - \mathsf{id}\| ^2 &= \| A A^t - \mathsf{id}\| ^2 + \| A B^t\| ^2 + \| BA^t\| ^2 + \| B B^t\| ^2\\ &= \| A^tA - \mathsf{id}\| ^2 + 2\| BA^t\| ^2 + \| B B^t\| ^2\\ &= 2\left(\| BA^t\| ^2 + \| B B^t\| ^2\right) = 2 \| B M^t\| ^2 = 2 \| B\| ^2\\ &\leq 2 \left(\| A-\mathsf{id}\| ^2 + \| B^t\| ^2\right) = 2\| M - \mathsf{id}\| ^2, \end{align*} $$
$$ \begin{align*} \| MM^t - \mathsf{id}\| ^2 &= \| A A^t - \mathsf{id}\| ^2 + \| A B^t\| ^2 + \| BA^t\| ^2 + \| B B^t\| ^2\\ &= \| A^tA - \mathsf{id}\| ^2 + 2\| BA^t\| ^2 + \| B B^t\| ^2\\ &= 2\left(\| BA^t\| ^2 + \| B B^t\| ^2\right) = 2 \| B M^t\| ^2 = 2 \| B\| ^2\\ &\leq 2 \left(\| A-\mathsf{id}\| ^2 + \| B^t\| ^2\right) = 2\| M - \mathsf{id}\| ^2, \end{align*} $$
where we used the previous observations in the second and third equality and Lemma A.5 in the fifth equality.
To prove a partial converse, we need the following lemma.
Lemma A.7. If P is a symmetric and positive semidefinite
![]() $d\times d$
matrix, then
$d\times d$
matrix, then
![]() $\| P^{1/2} - \mathsf {id}\| \leq \| P - \mathsf {id}\|$
.
$\| P^{1/2} - \mathsf {id}\| \leq \| P - \mathsf {id}\|$
.
Proof. Diagonalizing P in an orthonormal basis, we can assume that P is diagonal with nonnegative entries. Since then the square root of P corresponds to taking the square root of each diagonal entry, it is enough to prove that, for any nonnegative real number a one has
![]() $|\sqrt {a} - 1| \leq |a - 1|$
, which is clear.
$|\sqrt {a} - 1| \leq |a - 1|$
, which is clear.
The next lemma is not needed in what follows, but, since it is a direct consequence of the previous result, we give it here.
Lemma A.8. Let
![]() $M \in \mathbb {R}^{n \times d}$
and
$M \in \mathbb {R}^{n \times d}$
and
![]() $M = UP$
be a polar decomposition. Then
$M = UP$
be a polar decomposition. Then
![]() $\| M - U\| \leq \| M^t M - \mathsf {id}\| $
.
$\| M - U\| \leq \| M^t M - \mathsf {id}\| $
.
Proof. By definition,
![]() $P^2 = M^t M$
. So the result follows from Lemma A.7.
$P^2 = M^t M$
. So the result follows from Lemma A.7.
We are ready to prove the converse.
Lemma A.9. Let
![]() $M,N \in \mathsf {V}(d,n)$
. Then there exists
$M,N \in \mathsf {V}(d,n)$
. Then there exists
![]() $\Omega \in O(d)$
such that
$\Omega \in O(d)$
such that
![]() $\| M \Omega - N\| \leq \| MM^t - NN^t\|$
. In particular,
$\| M \Omega - N\| \leq \| MM^t - NN^t\|$
. In particular,
![]() $\mathsf {d}_{\mathsf {q}} \leq \mathsf {d}_{\mathsf {Fr}}$
.
$\mathsf {d}_{\mathsf {q}} \leq \mathsf {d}_{\mathsf {Fr}}$
.
Proof. The second claim is a consequence of the first one. For the first claim, let
![]() $\Omega \in O(d)$
minimize
$\Omega \in O(d)$
minimize
![]() $\| M \Omega - N\| $
. From Appendix A.2, we know that
$\| M \Omega - N\| $
. From Appendix A.2, we know that
![]() $\Omega $
is part of a polar decomposition
$\Omega $
is part of a polar decomposition
![]() $M^t N = \Omega (N^t M M^t N)^{1/2}$
. Now,
$M^t N = \Omega (N^t M M^t N)^{1/2}$
. Now,
![]() $\|M \Omega - N\| \leq \|\Omega - M^t N\| = \|\Omega - \Omega (N^t M M^t N)^{1/2}\| = \|(N^t M M^t N)^{1/2} - \mathsf {id}\| \leq \|(N^t M M^t N)^{1/2} - \mathsf {id}\|$
, by Lemma A.7.
$\|M \Omega - N\| \leq \|\Omega - M^t N\| = \|\Omega - \Omega (N^t M M^t N)^{1/2}\| = \|(N^t M M^t N)^{1/2} - \mathsf {id}\| \leq \|(N^t M M^t N)^{1/2} - \mathsf {id}\|$
, by Lemma A.7.
We now recall the computation of the reach of the Grassmannians due to Tinarrage [Reference Tinarrage63].
Construction A.10. Let
![]() $A \in \mathbb {R}^{n \times n}$
. Define
$A \in \mathbb {R}^{n \times n}$
. Define
![]() $A^s = (A + A^t)/2$
and let
$A^s = (A + A^t)/2$
and let
![]() $A^s = \Omega D \Omega ^t$
be a diagonalization of
$A^s = \Omega D \Omega ^t$
be a diagonalization of
![]() $A^s$
by an ordered orthonormal basis
$A^s$
by an ordered orthonormal basis
![]() $\Omega \in O(n)$
, where the diagonal entries of D contain the eigenvalues of
$\Omega \in O(n)$
, where the diagonal entries of D contain the eigenvalues of
![]() $A^s$
in decreasing order. Let
$A^s$
in decreasing order. Let
![]() $J_d$
be the diagonal
$J_d$
be the diagonal
![]() $n\times n$
matrix with the first d diagonal entries equal to
$n\times n$
matrix with the first d diagonal entries equal to
![]() $1$
and the rest equal to
$1$
and the rest equal to
![]() $0$
. Let
$0$
. Let
![]() $\pi (A) = \Omega J_d \Omega ^t$
.
$\pi (A) = \Omega J_d \Omega ^t$
.
Lemma A.11 [Reference Tinarrage63, Lemma 2.1].
If
![]() $\mathsf {d}_{\mathsf {Fr}}\left ( A, \mathsf {Gr}(d,n) \right ) < \sqrt {2}/2$
, then
$\mathsf {d}_{\mathsf {Fr}}\left ( A, \mathsf {Gr}(d,n) \right ) < \sqrt {2}/2$
, then
![]() $\pi (A)$
is the unique minimizer of
$\pi (A)$
is the unique minimizer of
Moreover, we have
![]() $\operatorname {\mathrm {reach}}(\mathsf {Gr}(d,n)) = \sqrt {2}/2$
.
$\operatorname {\mathrm {reach}}(\mathsf {Gr}(d,n)) = \sqrt {2}/2$
.
In particular, if
![]() $A \in \mathsf {Gr}(d,n)^\varepsilon $
for
$A \in \mathsf {Gr}(d,n)^\varepsilon $
for
![]() $\varepsilon \leq \sqrt {2}/2$
, then
$\varepsilon \leq \sqrt {2}/2$
, then
![]() $\pi (A)$
is independent of the choice of orthonormal basis
$\pi (A)$
is independent of the choice of orthonormal basis
![]() $\Omega $
. We deduce the following.
$\Omega $
. We deduce the following.
Proposition A.12. Let
![]() $\varepsilon \leq \sqrt {2}/2$
. The inclusion
$\varepsilon \leq \sqrt {2}/2$
. The inclusion
![]() $\mathsf {Gr}(d,n) \subseteq \mathsf {Gr}(d,n)^\varepsilon $
is a homotopy equivalence, with inverse given by the projection
$\mathsf {Gr}(d,n) \subseteq \mathsf {Gr}(d,n)^\varepsilon $
is a homotopy equivalence, with inverse given by the projection
![]() $\pi $
. This is natural in both n and
$\pi $
. This is natural in both n and
![]() $\varepsilon $
. Moreover, the projections assemble into a homotopy inverse of the inclusion
$\varepsilon $
. Moreover, the projections assemble into a homotopy inverse of the inclusion
![]() $\mathsf {Gr}(d) \subseteq \mathsf {Gr}(d)^\varepsilon $
.
$\mathsf {Gr}(d) \subseteq \mathsf {Gr}(d)^\varepsilon $
.
Proof. The first claim follows from Lemma A.1 and Lemma A.11. In the second claim, naturality means that the inclusion maps
![]() $i : \mathsf {Gr}(d,n) \to \mathsf {Gr}(d,n)^\varepsilon $
commute with the inclusions into
$i : \mathsf {Gr}(d,n) \to \mathsf {Gr}(d,n)^\varepsilon $
commute with the inclusions into
![]() $\mathsf {Gr}(d,n+1)$
and
$\mathsf {Gr}(d,n+1)$
and
![]() $\mathsf {Gr}(d,n+1)^\varepsilon $
, which is clear, and that the projections do as well. The fact that projections commute with the inclusion i follows from Construction A.10. The third claim follows at once from naturality.
$\mathsf {Gr}(d,n+1)^\varepsilon $
, which is clear, and that the projections do as well. The fact that projections commute with the inclusion i follows from Construction A.10. The third claim follows at once from naturality.
A.4 Metrics on orthogonal groups
In this section, we will make use of basic Riemannian geometry; see, for instance, [Reference Lee39]. Our main goals are to calculate the reach (Appendix A.1) of the orthogonal groups, seen as a subspace of the metric space of square matrices, with metric given by the Frobenius distance; to compare the Frobenius distance to the geodesic distance; and to calculate the systole (Definition 6.4) of the orthogonal groups using the geodesic distance.
The geodesic distance we consider on the orthogonal groups is the one that comes from the bi-invariant metric given by the smooth inclusion
![]() $O(d) \subseteq \mathbb {R}^{d\times d}$
, where the inner product on
$O(d) \subseteq \mathbb {R}^{d\times d}$
, where the inner product on
![]() $\mathbb {R}^{d \times d}$
is the one associated to the Frobenius norm [Reference Lee39, Example 3.16(e)].
$\mathbb {R}^{d \times d}$
is the one associated to the Frobenius norm [Reference Lee39, Example 3.16(e)].
Lemma A.13. Let
![]() $M,N \in O(d)$
such that
$M,N \in O(d)$
such that
![]() $\det (M) = 1 = - \det (N)$
. Then
$\det (M) = 1 = - \det (N)$
. Then
![]() $\| M-N\| \geq 2$
.
$\| M-N\| \geq 2$
.
Proof. Since
![]() $O(d)$
acts on itself by isometries, it suffices to show that
$O(d)$
acts on itself by isometries, it suffices to show that
![]() $\| N - \mathsf {id}\| \geq 2$
whenever
$\| N - \mathsf {id}\| \geq 2$
whenever
![]() $\det (N) = -1$
. Since N is orthogonal, there is an orthogonal change of basis that takes it to be diagonal by blocks, where blocks are
$\det (N) = -1$
. Since N is orthogonal, there is an orthogonal change of basis that takes it to be diagonal by blocks, where blocks are
![]() $1 \times 1$
and equal
$1 \times 1$
and equal
![]() $1$
or
$1$
or
![]() $-1$
, or
$-1$
, or
![]() $2 \times 2$
and rotation matrices. We can thus assume that N is diagonal by blocks of the form above. If any of the blocks is a
$2 \times 2$
and rotation matrices. We can thus assume that N is diagonal by blocks of the form above. If any of the blocks is a
![]() $1\times 1$
block of the form
$1\times 1$
block of the form
![]() $-1$
we are done. Otherwise, there must be a block that consists of a rotation with negative determinant. In this case,
$-1$
we are done. Otherwise, there must be a block that consists of a rotation with negative determinant. In this case,
The following lemma appears in [Reference Boissonnat, Lieutier and Wintraecken5] and is a key result that lets us compare the geodesic distance of the orthogonal groups to the Frobenius distance. Before giving the result, we recall that any metric space has an induced geodesic distance (also known as a path-length distance), where the distance between any two points is taken to be the infimum of the lengths of the continuous paths between them [Reference Boissonnat, Lieutier and Wintraecken5, Section 2], [Reference Burago, Burago and Ivanov11, Section 2.3.3]. If the metric space is not connected, this is an extended distance. Finally, if the metric space consists of a manifold smoothly embedded in Euclidean space, then this geodesic distance coincides with the geodesic distance associated to the Riemannian metric induced by the embedding into Euclidean space [Reference Burago, Burago and Ivanov11, Exercise 5.1.8].
Lemma A.14 [Reference Boissonnat, Lieutier and Wintraecken5, Lemma 3].
Let
![]() $S \subseteq \mathbb {R}^N$
be a closed set such that
$S \subseteq \mathbb {R}^N$
be a closed set such that
![]() $R = \operatorname {\mathrm {reach}}(S)> 0$
. Let
$R = \operatorname {\mathrm {reach}}(S)> 0$
. Let
![]() $d_S$
denote the geodesic distance on S induced by the restriction of the Euclidean distance. If
$d_S$
denote the geodesic distance on S induced by the restriction of the Euclidean distance. If
![]() $x,y \in S$
are such that
$x,y \in S$
are such that
![]() $\|x - y\|_2 < 2R$
, then
$\|x - y\|_2 < 2R$
, then
![]() $d_{S}(x,y) \leq 2\, R\, \arcsin \left (\frac {\|x - y\|}{2R}\right )$
.
$d_{S}(x,y) \leq 2\, R\, \arcsin \left (\frac {\|x - y\|}{2R}\right )$
.
Lemma A.15. Let
![]() $A \in \mathbb {R}^{d \times d}$
and
$A \in \mathbb {R}^{d \times d}$
and
![]() $\Omega \in O(d)$
such that
$\Omega \in O(d)$
such that
![]() $\| A - \Omega \| < 1$
, then A has full rank.
$\| A - \Omega \| < 1$
, then A has full rank.
Proof. It is enough to show that
![]() $\Omega ^t A$
has full rank, so, since the Frobenius norm is
$\Omega ^t A$
has full rank, so, since the Frobenius norm is
![]() $O(d)$
-invariant, it is sufficient to prove it for the case
$O(d)$
-invariant, it is sufficient to prove it for the case
![]() $\Omega = \mathsf {id}$
. Let
$\Omega = \mathsf {id}$
. Let
![]() $B = \mathsf {id} - A$
. Since
$B = \mathsf {id} - A$
. Since
![]() $\|B\| < 1$
, and the Frobenius norm is submultiplicative, the matrix
$\|B\| < 1$
, and the Frobenius norm is submultiplicative, the matrix
![]() $\sum _{n \geq 0} B^n$
is well defined. Finally, we have
$\sum _{n \geq 0} B^n$
is well defined. Finally, we have
![]() $(\mathsf {id} - B) \left (\sum _{n \geq 0} B^n\right ) = \mathsf {id}$
, so
$(\mathsf {id} - B) \left (\sum _{n \geq 0} B^n\right ) = \mathsf {id}$
, so
![]() $\mathsf {id} - B = A$
is invertible, as required.
$\mathsf {id} - B = A$
is invertible, as required.
Lemma A.16. Consider
![]() $O(d) \subseteq \mathbb {R}^{d \times d}$
with the Frobenius distance. Then
$O(d) \subseteq \mathbb {R}^{d \times d}$
with the Frobenius distance. Then
![]() $\operatorname {\mathrm {reach}}(O(d)) = 1$
.
$\operatorname {\mathrm {reach}}(O(d)) = 1$
.
Proof. Let
![]() $M_x$
denote the
$M_x$
denote the
![]() $d\times d$
diagonal matrix with
$d\times d$
diagonal matrix with
![]() $1$
in all diagonal entries except the first one, which is x. Since a polar decomposition of
$1$
in all diagonal entries except the first one, which is x. Since a polar decomposition of
![]() $M_0$
is given by
$M_0$
is given by
![]() $M_0 = \mathsf {id} M_0$
, we have that the identity is a closest orthogonal matrix to
$M_0 = \mathsf {id} M_0$
, we have that the identity is a closest orthogonal matrix to
![]() $M_0$
, by Appendix A.2. Now, note that
$M_0$
, by Appendix A.2. Now, note that
![]() $\|M_0 - \mathsf {id}\| = 1 = \|M_0 - M_{-1}\|$
, so
$\|M_0 - \mathsf {id}\| = 1 = \|M_0 - M_{-1}\|$
, so
![]() $M_{-1}$
is a closest orthogonal matrix to
$M_{-1}$
is a closest orthogonal matrix to
![]() $M_0$
too, and thus
$M_0$
too, and thus
![]() $\operatorname {\mathrm {reach}}(O(d)) \leq 1$
.
$\operatorname {\mathrm {reach}}(O(d)) \leq 1$
.
To conclude, we must show that, if
![]() $\|M - \mathsf {id}\| < 1$
, then M has a unique closest orthogonal matrix. This is a consequence of Lemma A.15 and Lemma A.3.
$\|M - \mathsf {id}\| < 1$
, then M has a unique closest orthogonal matrix. This is a consequence of Lemma A.15 and Lemma A.3.
Combined, Lemma A.14 and Lemma A.16 give us upper bounds for the geodesic distance of
![]() $O(d)$
in terms of the Frobenius distance. We will need the following specific bound.
$O(d)$
in terms of the Frobenius distance. We will need the following specific bound.
Corollary A.17. Let
![]() $d_G$
be the geodesic distance on
$d_G$
be the geodesic distance on
![]() $O(d)$
induced by the embedding
$O(d)$
induced by the embedding
![]() $O(d) \subseteq \mathbb {R}^{d \times d}$
. For
$O(d) \subseteq \mathbb {R}^{d \times d}$
. For
![]() $M,N \in O(d)$
, if
$M,N \in O(d)$
, if
![]() $\|M - N\| < 1$
, then
$\|M - N\| < 1$
, then
![]() $d_G(M,N) < \sqrt {2} \pi / 4$
.
$d_G(M,N) < \sqrt {2} \pi / 4$
.
Proof. By inspection,
![]() $2 \arcsin (1/2) < \sqrt {2} \pi /4$
. Note that a slightly tighter bound is possible, but we prefer this one for readability.
$2 \arcsin (1/2) < \sqrt {2} \pi /4$
. Note that a slightly tighter bound is possible, but we prefer this one for readability.
Lemma A.18. Using the geodesic distance
![]() $d_G$
, we have
$d_G$
, we have
![]() $\mathsf {sys}(O(d)) = 2 \sqrt {2} \pi $
.
$\mathsf {sys}(O(d)) = 2 \sqrt {2} \pi $
.
Proof. Since
![]() $O(d)$
is a group acting on itself by isometries, to compute
$O(d)$
is a group acting on itself by isometries, to compute
![]() $\mathsf {sys}(O(d))$
, it suffices to consider loops on the identity matrix
$\mathsf {sys}(O(d))$
, it suffices to consider loops on the identity matrix
![]() $\mathsf {id} \in O(d)$
. We observe that the constant speed, locally length-minimizing curves from the identity to itself are in bijection with the logarithms
$\mathsf {id} \in O(d)$
. We observe that the constant speed, locally length-minimizing curves from the identity to itself are in bijection with the logarithms
![]() $L \in \mathfrak {so}(d)$
of the identity. More specifically, any such curve can be written as
$L \in \mathfrak {so}(d)$
of the identity. More specifically, any such curve can be written as
![]() $t \mapsto \exp (t L)$
with
$t \mapsto \exp (t L)$
with
![]() $L \in \mathfrak {so}(d)$
[Reference Lee39, Proposition 5.19]. We also observe that the speed of such a curve is
$L \in \mathfrak {so}(d)$
[Reference Lee39, Proposition 5.19]. We also observe that the speed of such a curve is
![]() $\|L\|$
, the Frobenius norm of L.
$\|L\|$
, the Frobenius norm of L.
So let
![]() $L \in \mathfrak {so}(d)$
be a skew-symmetric matrix such that
$L \in \mathfrak {so}(d)$
be a skew-symmetric matrix such that
![]() $\exp (L) = \mathsf {id}$
. Since L is skew-symmetric, there exists an orthogonal change of basis such that L is a block-diagonal matrix with either
$\exp (L) = \mathsf {id}$
. Since L is skew-symmetric, there exists an orthogonal change of basis such that L is a block-diagonal matrix with either
![]() $1 \times 1$
blocks containing a
$1 \times 1$
blocks containing a
![]() $0$
or
$0$
or
![]() $2\times 2$
blocks with
$2\times 2$
blocks with
![]() $0$
in the diagonal and
$0$
in the diagonal and
![]() $\lambda , -\lambda \in \mathbb {R}$
in the antidiagonal. Since L is a logarithm of the identity, the number
$\lambda , -\lambda \in \mathbb {R}$
in the antidiagonal. Since L is a logarithm of the identity, the number
![]() $\lambda $
in any of these blocks must be an integer multiple of
$\lambda $
in any of these blocks must be an integer multiple of
![]() $2\pi $
. It follows that
$2\pi $
. It follows that
![]() $\|L\| = \sqrt { 2 \sum (2 \pi n_i)^2} = 2\pi \sqrt {2} \sqrt { \sum n_i^2 }$
. Since we are considering nonnullhomotopic loops, at least one of the integers
$\|L\| = \sqrt { 2 \sum (2 \pi n_i)^2} = 2\pi \sqrt {2} \sqrt { \sum n_i^2 }$
. Since we are considering nonnullhomotopic loops, at least one of the integers
![]() $n_i$
must be nonzero, and thus the smallest value of
$n_i$
must be nonzero, and thus the smallest value of
![]() $\|L\|$
is attained when one of the
$\|L\|$
is attained when one of the
![]() $n_i$
is
$n_i$
is
![]() $1$
and the rest are zero, and in such case we have
$1$
and the rest are zero, and in such case we have
![]() $\|L\| = 2 \sqrt {2}\pi $
, concluding the proof.
$\|L\| = 2 \sqrt {2}\pi $
, concluding the proof.
A.5 Riemannian manifolds and covering spaces
In this section, we use the systole to give a lower bound for the distance between two distinct elements in the fiber of a covering map between Riemannian manifolds and we prove a metrically controlled lifting property for covering maps between Riemannian manifolds.
Lemma A.19. Let
![]() $G \to H$
be a covering map between Riemannian manifolds. Fix
$G \to H$
be a covering map between Riemannian manifolds. Fix
![]() $h \in H$
, and let
$h \in H$
, and let
![]() $F \subseteq G$
be the fiber of h. Then, the infimum of the distances between distinct elements of F is bounded below by
$F \subseteq G$
be the fiber of h. Then, the infimum of the distances between distinct elements of F is bounded below by
![]() $\mathsf {sys}(H)$
.
$\mathsf {sys}(H)$
.
Proof. Let
![]() $a \neq b \in F$
and consider a geodesic between them. The length of this path is equal to the length of the path mapped to H since
$a \neq b \in F$
and consider a geodesic between them. The length of this path is equal to the length of the path mapped to H since
![]() $G \to H$
is a local isometry. The path mapped to H cannot be nullhomotopic since a and b are distinct points of the fiber, so its length is bounded below by the systole of H.
$G \to H$
is a local isometry. The path mapped to H cannot be nullhomotopic since a and b are distinct points of the fiber, so its length is bounded below by the systole of H.
Lemma A.20. Let
![]() $\zeta : G \to H$
be a covering map between Riemannian manifolds, with H compact.
$\zeta : G \to H$
be a covering map between Riemannian manifolds, with H compact.
-
1. Let
 $h,h' \in H$
be such that
$h,h' \in H$
be such that
 $d_H(h,h') < \mathsf {sys}(H)/2$
and let
$d_H(h,h') < \mathsf {sys}(H)/2$
and let
 $g \in G$
be a preimage of h. Then, there exists a unique preimage
$g \in G$
be a preimage of h. Then, there exists a unique preimage
 $g'$
of
$g'$
of
 $h'$
such that
$h'$
such that
 $d_G(g, g') < \mathsf {sys}(H)/2$
and
$d_G(g, g') < \mathsf {sys}(H)/2$
and
 $g'$
has the property that
$g'$
has the property that
 $d_G(g,g') = d_H(h,h')$
.
$d_G(g,g') = d_H(h,h')$
. -
2. Let U be locally path connected and simply connected and let
 $v,w : U \to H$
continuous such that, for all
$v,w : U \to H$
continuous such that, for all
 $z \in U$
,
$z \in U$
,
 $d_H(v(z),w(z)) < \mathsf {sys}(H)/2$
. Then, there exist lifts
$d_H(v(z),w(z)) < \mathsf {sys}(H)/2$
. Then, there exist lifts
 $\overline {v},\overline {w} : U \to G$
of v and w, respectively, such that, for all
$\overline {v},\overline {w} : U \to G$
of v and w, respectively, such that, for all
 $z \in U$
,
$z \in U$
,
 $d_G(\overline {v}(z), \overline {w}(z)) = d_H(v(z), w(z))$
.
$d_G(\overline {v}(z), \overline {w}(z)) = d_H(v(z), w(z))$
.
Proof. We start with the first claim. To prove existence, consider a shortest geodesic from h to
![]() $h'$
, whose length must be strictly less than
$h'$
, whose length must be strictly less than
![]() $\mathsf {sys}(H)/2$
. By lifting this path, we get a preimage
$\mathsf {sys}(H)/2$
. By lifting this path, we get a preimage
![]() $g'$
of
$g'$
of
![]() $h'$
such that
$h'$
such that
![]() $d_G(g,g') \leq d_H(h,h')$
. To prove uniqueness, suppose that
$d_G(g,g') \leq d_H(h,h')$
. To prove uniqueness, suppose that
![]() $g" \neq g'$
is a preimage of
$g" \neq g'$
is a preimage of
![]() $h'$
. By Lemma A.19, we have
$h'$
. By Lemma A.19, we have
![]() $d_G(g",g') \geq \mathsf {sys}(H)$
, so
$d_G(g",g') \geq \mathsf {sys}(H)$
, so
![]() $d_G(g,g") \geq \mathsf {sys}(H)/2$
. Finally, since
$d_G(g,g") \geq \mathsf {sys}(H)/2$
. Finally, since
![]() $G \to H$
is
$G \to H$
is
![]() $1$
-Lipschitz, we have
$1$
-Lipschitz, we have
![]() $d_H(h,h') \leq d_G(g,g')$
, and thus
$d_H(h,h') \leq d_G(g,g')$
, and thus
![]() $d_G(g,g') = d_H(h,h')$
.
$d_G(g,g') = d_H(h,h')$
.
For the second claim, let
![]() $y \in U$
and use the first claim to choose lifts
$y \in U$
and use the first claim to choose lifts
![]() $g,g' \in G$
of
$g,g' \in G$
of
![]() $v(y)$
and
$v(y)$
and
![]() $w(y)$
, respectively, such that
$w(y)$
, respectively, such that
![]() $d_G(g,g') = d_H(v(y),w(y))$
. Since U is locally path connected and simply connected, there exist unique lifts
$d_G(g,g') = d_H(v(y),w(y))$
. Since U is locally path connected and simply connected, there exist unique lifts
![]() $\overline {v}$
and
$\overline {v}$
and
![]() $\overline {w}$
of v and w, respectively, such that
$\overline {w}$
of v and w, respectively, such that
![]() $\overline {v}(y) = g$
and
$\overline {v}(y) = g$
and
![]() $\overline {w}(y) = g'$
. Consider the subset
$\overline {w}(y) = g'$
. Consider the subset
![]() $U' = \{z \in U : d_G(\overline {v}(z),\overline {w}(z)) = d_H(v(z), w(z))\} \subseteq U$
. This subset is closed and nonempty, so it suffices to show that it is open, since U is connected. We conclude the proof by proving this fact.
$U' = \{z \in U : d_G(\overline {v}(z),\overline {w}(z)) = d_H(v(z), w(z))\} \subseteq U$
. This subset is closed and nonempty, so it suffices to show that it is open, since U is connected. We conclude the proof by proving this fact.
Let
![]() $z \in U'$
, and let
$z \in U'$
, and let
![]() $\varepsilon = \mathsf {sys}(H)/2 - d_H(v(z),w(z))> 0$
. Let N be an open neighborhood of z such that
$\varepsilon = \mathsf {sys}(H)/2 - d_H(v(z),w(z))> 0$
. Let N be an open neighborhood of z such that
![]() $\overline {v}(N)$
is contained in the open ball of radius
$\overline {v}(N)$
is contained in the open ball of radius
![]() $\varepsilon /2$
around
$\varepsilon /2$
around
![]() $\overline {v}(z)$
, and
$\overline {v}(z)$
, and
![]() $\overline {w}(N)$
is contained in the open ball of radius
$\overline {w}(N)$
is contained in the open ball of radius
![]() $\varepsilon /2$
around
$\varepsilon /2$
around
![]() $\overline {w}(z)$
. If
$\overline {w}(z)$
. If
![]() $z' \in N$
, then
$z' \in N$
, then
 $$ \begin{align*} d_G(\overline{v}(z'),\overline{w}(z')) &\leq d_G(\overline{v}(z'),\overline{v}(z)) + d_G(\overline{v}(z), \overline{w}(z)) + d_G(\overline{w}(z),\overline{w}(z'))\\ &= d_G(\overline{v}(z'),\overline{v}(z)) + d_H(v(z), w(z)) + d_G(\overline{w}(z),\overline{w}(z'))\\ &< d_H(v(z), w(z)) + 2 \varepsilon/2 = \mathsf{sys}(H)/2. \end{align*} $$
$$ \begin{align*} d_G(\overline{v}(z'),\overline{w}(z')) &\leq d_G(\overline{v}(z'),\overline{v}(z)) + d_G(\overline{v}(z), \overline{w}(z)) + d_G(\overline{w}(z),\overline{w}(z'))\\ &= d_G(\overline{v}(z'),\overline{v}(z)) + d_H(v(z), w(z)) + d_G(\overline{w}(z),\overline{w}(z'))\\ &< d_H(v(z), w(z)) + 2 \varepsilon/2 = \mathsf{sys}(H)/2. \end{align*} $$
From the first claim, it follows that
![]() $d_G(\overline {v}(z'), \overline {w}(z')) = d_H(v(z'), w(z'))$
, so
$d_G(\overline {v}(z'), \overline {w}(z')) = d_H(v(z'), w(z'))$
, so
![]() $N \subseteq U'$
, and thus
$N \subseteq U'$
, and thus
![]() $U'$
is open, concluding the proof.
$U'$
is open, concluding the proof.
Acknowledgements
We thank Dan Christensen, Peter Landweber, Fernando Martin and Raphäel Tinarrage for helpful conversations and comments, and Ximena Fernández for discussions and suggesting the example in Section 7.2. We also thank Peter Landweber for suggesting improvements to the proofs in Appendix A.1. Finally, we thank the anonymous reviewers for helpful feedback, which has improved this paper.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
This work was partially supported by the National Science Foundation through grants CCF-2006661 and CAREER award DMS-1943758.