Article contents
Annihilator varieties of distinguished modules of reductive Lie algebras
Published online by Cambridge University Press: 26 July 2021
Abstract
We provide a microlocal necessary condition for distinction of admissible representations of real reductive groups in the context of spherical pairs.
Let
 ${\mathbf {G}}$
be a complex algebraic reductive group and
${\mathbf {G}}$
be a complex algebraic reductive group and
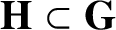 ${\mathbf {H}}\subset {\mathbf {G}}$
be a spherical algebraic subgroup. Let
${\mathbf {H}}\subset {\mathbf {G}}$
be a spherical algebraic subgroup. Let
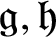 ${\mathfrak {g}},{\mathfrak {h}}$
denote the Lie algebras of
${\mathfrak {g}},{\mathfrak {h}}$
denote the Lie algebras of
 ${\mathbf {G}}$
and
${\mathbf {G}}$
and
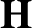 ${\mathbf {H}}$
, and let
${\mathbf {H}}$
, and let
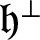 ${\mathfrak {h}}^{\bot }$
denote the orthogonal complement to
${\mathfrak {h}}^{\bot }$
denote the orthogonal complement to
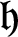 ${\mathfrak {h}}$
in
${\mathfrak {h}}$
in
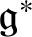 ${\mathfrak {g}}^*$
. A
${\mathfrak {g}}^*$
. A
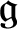 ${\mathfrak {g}}$
-module is called
${\mathfrak {g}}$
-module is called
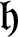 ${\mathfrak {h}}$
-distinguished if it admits a nonzero
${\mathfrak {h}}$
-distinguished if it admits a nonzero
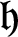 ${\mathfrak {h}}$
-invariant functional. We show that the maximal
${\mathfrak {h}}$
-invariant functional. We show that the maximal
 ${\mathbf {G}}$
-orbit in the annihilator variety of any irreducible
${\mathbf {G}}$
-orbit in the annihilator variety of any irreducible
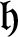 ${\mathfrak {h}}$
-distinguished
${\mathfrak {h}}$
-distinguished
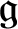 ${\mathfrak {g}}$
-module intersects
${\mathfrak {g}}$
-module intersects
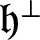 ${\mathfrak {h}}^{\bot }$
. This generalises a result of Vogan [Vog91].
${\mathfrak {h}}^{\bot }$
. This generalises a result of Vogan [Vog91].
We apply this to Casselman–Wallach representations of real reductive groups to obtain information on branching problems, translation functors and Jacquet modules. Further, we prove in many cases that – as suggested by [Pra19, Question 1] – when H is a symmetric subgroup of a real reductive group G, the existence of a tempered H-distinguished representation of G implies the existence of a generic H-distinguished representation of G.
Many of the models studied in the theory of automorphic forms involve an additive character on the unipotent radical of the subgroup
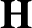 $\bf H$
, and we have devised a twisted version of our theorem that yields necessary conditions for the existence of those mixed models. Our method of proof here is inspired by the theory of modules over W-algebras. As an application of our theorem we derive necessary conditions for the existence of Rankin–Selberg, Bessel, Klyachko and Shalika models. Our results are compatible with the recent Gan–Gross–Prasad conjectures for nongeneric representations [GGP20].
$\bf H$
, and we have devised a twisted version of our theorem that yields necessary conditions for the existence of those mixed models. Our method of proof here is inspired by the theory of modules over W-algebras. As an application of our theorem we derive necessary conditions for the existence of Rankin–Selberg, Bessel, Klyachko and Shalika models. Our results are compatible with the recent Gan–Gross–Prasad conjectures for nongeneric representations [GGP20].
Finally, we provide more general results that ease the sphericity assumption on the subgroups, and apply them to local theta correspondence in type II and to degenerate Whittaker models.
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 3
- Cited by



