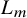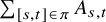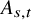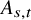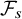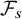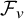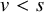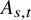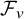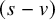1. Introduction and the main theorem
In analysis and probability theory, we often consider the convergence of sums
Here,
![]() $\pi $
is a partition of an interval
$\pi $
is a partition of an interval
![]() $[0, T]$
, and we consider the limit of
$[0, T]$
, and we consider the limit of
For instance, if ![]() , then we consider a Riemann sum approximation of
, then we consider a Riemann sum approximation of
![]() $\int _0^T f(s) \, \mathrm {d} s$
, and if
$\int _0^T f(s) \, \mathrm {d} s$
, and if ![]() , where W is a Brownian motion and X is an adapted process, then we consider the Itô approximation of the stochastic integral
, where W is a Brownian motion and X is an adapted process, then we consider the Itô approximation of the stochastic integral
![]() $\int _0^T X_r \, \mathrm {d} W_r$
.
$\int _0^T X_r \, \mathrm {d} W_r$
.
Gubinelli [Reference Gubinelli17], inspired by Lyons’ results on almost multiplicative functionals in the theory of rough paths [Reference Lyons30], showed that if
satisfies
![]() $ \lvert {\delta A_{s, u, t}}\rvert \lesssim \lvert {t - s} \rvert ^{1 + \epsilon }$
for some
$ \lvert {\delta A_{s, u, t}}\rvert \lesssim \lvert {t - s} \rvert ^{1 + \epsilon }$
for some
![]() $\epsilon> 0$
, then the sums (1.1) converge. This result is now called the sewing lemma, named so in the work of Feyel and de La Pradelle [Reference Feyel and de La Pradelle13]. This lemma is so powerful that many applications and many extensions are known. For instance, it can be used to define rough integrals (see [Reference Gubinelli17] and the monograph [Reference Friz and Hairer14] of Friz and Hairer).
$\epsilon> 0$
, then the sums (1.1) converge. This result is now called the sewing lemma, named so in the work of Feyel and de La Pradelle [Reference Feyel and de La Pradelle13]. This lemma is so powerful that many applications and many extensions are known. For instance, it can be used to define rough integrals (see [Reference Gubinelli17] and the monograph [Reference Friz and Hairer14] of Friz and Hairer).
When
![]() $(A_{s, t})_{s \leq t}$
is random, and when we want to prove the convergence of the sums (1.1), the above sewing lemma is often not sufficient. For instance, if
$(A_{s, t})_{s \leq t}$
is random, and when we want to prove the convergence of the sums (1.1), the above sewing lemma is often not sufficient. For instance, if ![]() , the sums converge to the quadratic variation of the Brownian motion. However, we only have
, the sums converge to the quadratic variation of the Brownian motion. However, we only have
almost surely for every
![]() $\epsilon> 0$
, and hence, we cannot apply the sewing lemma.
$\epsilon> 0$
, and hence, we cannot apply the sewing lemma.
Lê [Reference Lê24] proved a stochastic version of the sewing lemma (stochastic sewing lemma): if a filtration
![]() $(\mathcal {F}_t)_{t \in [0, T]}$
is given, such that
$(\mathcal {F}_t)_{t \in [0, T]}$
is given, such that
-
•
 $A_{s, t}$
is
$A_{s, t}$
is
 $\mathcal {F}_t$
-measurable and
$\mathcal {F}_t$
-measurable and -
• for some
 $\epsilon _1, \epsilon _2> 0$
and
$\epsilon _1, \epsilon _2> 0$
and
 $m \in [2, \infty )$
, we have for every
$m \in [2, \infty )$
, we have for every
 $s < u < t$
, (1.3)
$s < u < t$
, (1.3) $$ \begin{align} \lVert {\mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_s]} \rVert _{L_m(\mathbb{P})} \lesssim \lvert {t - s} \rvert ^{1 + \epsilon_2}, \end{align} $$
(1.4)
$$ \begin{align} \lVert {\mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_s]} \rVert _{L_m(\mathbb{P})} \lesssim \lvert {t - s} \rvert ^{1 + \epsilon_2}, \end{align} $$
(1.4) $$ \begin{align} \lVert {\delta A_{s, u, t}} \rVert _{L_m(\mathbb{P})} \lesssim \lvert {t - s} \rvert ^{\frac{1}{2} + \epsilon_1}, \end{align} $$
$$ \begin{align} \lVert {\delta A_{s, u, t}} \rVert _{L_m(\mathbb{P})} \lesssim \lvert {t - s} \rvert ^{\frac{1}{2} + \epsilon_1}, \end{align} $$
then the sums (1.1) converge in
![]() $L_m(\mathbb {P})$
. As usual, the Banach space
$L_m(\mathbb {P})$
. As usual, the Banach space
![]() $L_m(\mathbb {P})$
is equipped with the norm
$L_m(\mathbb {P})$
is equipped with the norm

If ![]() , then we have
, then we have
![]() $\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_s] = 0$
and (1.4) is satisfied with
$\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_s] = 0$
and (1.4) is satisfied with
![]() $\epsilon _1 = \frac {1}{2}$
. Therefore, we can prove the convergence of (1.1) in
$\epsilon _1 = \frac {1}{2}$
. Therefore, we can prove the convergence of (1.1) in
![]() $L_m(\mathbb {P})$
. The stochastic sewing lemma has been already shown to be very powerful in the original work [Reference Lê24] of Lê, and an increasing number of papers are appearing that take advantage of the lemma.
$L_m(\mathbb {P})$
. The stochastic sewing lemma has been already shown to be very powerful in the original work [Reference Lê24] of Lê, and an increasing number of papers are appearing that take advantage of the lemma.
However, there are situations where Lê’s stochastic sewing lemma seems insufficient. For instance, consider
where B is a fractional Brownian motion with Hurst parameter
![]() $H \in (0, 1)$
. It is well-known that the sums (1.1) converge to
$H \in (0, 1)$
. It is well-known that the sums (1.1) converge to
![]() $c_H T$
in
$c_H T$
in
![]() $L_m(\mathbb {P})$
. Although we have the estimate (1.4), we fail to obtain the estimate (1.3) unless
$L_m(\mathbb {P})$
. Although we have the estimate (1.4), we fail to obtain the estimate (1.3) unless
![]() $H = \frac {1}{2}$
.
$H = \frac {1}{2}$
.
To get an idea on how Lê’s stochastic sewing lemma should be modified for this problem, observe the following trivial fact:
This suggests that we consider estimates that interpolate
![]() $\mathbb {E}[\delta A_{s, u, t}]$
and
$\mathbb {E}[\delta A_{s, u, t}]$
and
![]() $\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_s]$
. In fact, we can obtain the following estimates:
$\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_s]$
. In fact, we can obtain the following estimates:
We can prove (1.6), for instance, by applying Picard’s result [Reference Picard37, Lemma A.1] on the asymptotic independence of fractional Brownian increments, or more directly by doing a similar calculation as in Section 4. This discussion motivates the following main theorem of our paper.
Theorem 1.1. Suppose that we have a filtration
![]() $(\mathcal {F}_t)_{t \in [0, T]}$
and a family of
$(\mathcal {F}_t)_{t \in [0, T]}$
and a family of
![]() $\mathbb {R}^d$
-valued random variables
$\mathbb {R}^d$
-valued random variables
![]() $(A_{s, t})_{0 \leq s \leq t \leq T}$
, such that
$(A_{s, t})_{0 \leq s \leq t \leq T}$
, such that
![]() $A_{s, s} = 0$
for every
$A_{s, s} = 0$
for every
![]() $s \in [0, T]$
and such that
$s \in [0, T]$
and such that
![]() $A_{s, t}$
is
$A_{s, t}$
is
![]() $\mathcal {F}_t$
-measurable. We define
$\mathcal {F}_t$
-measurable. We define
![]() $\delta A_{s, u, t}$
by (1.2). Furthermore, suppose that there exist constants
$\delta A_{s, u, t}$
by (1.2). Furthermore, suppose that there exist constants
such that the following conditions are satisfied.
-
• For every
 $0 \leq t_0 < t_1 < t_2 < t_3 \leq T$
, we have (1.7)
$0 \leq t_0 < t_1 < t_2 < t_3 \leq T$
, we have (1.7) $$ \begin{align} \lVert {\mathbb{E}[\delta A_{t_1, t_2, t_3} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_1 (t_1 - t_0)^{-\alpha} (t_3 - t_1)^{\beta_1}, \quad \text{if } M(t_3 - t_1) \leq t_1 - t_0, \end{align} $$
(1.8)
$$ \begin{align} \lVert {\mathbb{E}[\delta A_{t_1, t_2, t_3} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_1 (t_1 - t_0)^{-\alpha} (t_3 - t_1)^{\beta_1}, \quad \text{if } M(t_3 - t_1) \leq t_1 - t_0, \end{align} $$
(1.8) $$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_2 (t_2 - t_0)^{\beta_2}. \end{align} $$
$$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_2 (t_2 - t_0)^{\beta_2}. \end{align} $$
-
• We have
(1.9) $$ \begin{align} \beta_1> 1, \quad \beta_2 > \frac{1}{2}, \quad \beta_1 - \alpha > \frac{1}{2}. \end{align} $$
$$ \begin{align} \beta_1> 1, \quad \beta_2 > \frac{1}{2}, \quad \beta_1 - \alpha > \frac{1}{2}. \end{align} $$
Then, there exists a unique, up to modifications,
![]() $\mathbb {R}^d$
-valued stochastic process
$\mathbb {R}^d$
-valued stochastic process
![]() $(\mathcal {A}_t)_{t \in [0, T]}$
with the following properties.
$(\mathcal {A}_t)_{t \in [0, T]}$
with the following properties.
-
•
 $\mathcal {A}_0 = 0$
,
$\mathcal {A}_0 = 0$
,
 $\mathcal {A}_t$
is
$\mathcal {A}_t$
is
 $\mathcal {F}_t$
-measurable, and
$\mathcal {F}_t$
-measurable, and
 $\mathcal {A}_t$
belongs to
$\mathcal {A}_t$
belongs to
 $L_m(\mathbb {P})$
.
$L_m(\mathbb {P})$
. -
• There exist nonnegative constants
 $C_1$
,
$C_1$
,
 $C_2$
, and
$C_2$
, and
 $C_3$
, such that (1.10)
$C_3$
, such that (1.10) $$ \begin{align} \lVert {\mathbb{E}[\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} \leq C_1 \lvert {t_1 - t_0} \rvert ^{-\alpha} \lvert {t_2 - t_1} \rvert ^{\beta_1} , \end{align} $$
(1.11)where
$$ \begin{align} \lVert {\mathbb{E}[\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} \leq C_1 \lvert {t_1 - t_0} \rvert ^{-\alpha} \lvert {t_2 - t_1} \rvert ^{\beta_1} , \end{align} $$
(1.11)where $$ \begin{align} \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_2 \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha} + C_3 \lvert {t_2 - t_1} \rvert ^{\beta_2}, \end{align} $$
$$ \begin{align} \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_2 \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha} + C_3 \lvert {t_2 - t_1} \rvert ^{\beta_2}, \end{align} $$
 $t_2 - t_1 \leq M^{-1}(t_1 - t_0)$
is assumed for the inequality (1.10).
$t_2 - t_1 \leq M^{-1}(t_1 - t_0)$
is assumed for the inequality (1.10).
In fact, we can choose
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and
$C_2$
, and
![]() $C_3$
so that
$C_3$
so that
where
![]() $\kappa _{m,d}$
is the constant of the Burkholder-Davis-Gundy inequality (see (1.14)). Furthermore, for
$\kappa _{m,d}$
is the constant of the Burkholder-Davis-Gundy inequality (see (1.14)). Furthermore, for
![]() $\tau \in [0, T]$
, if we set
$\tau \in [0, T]$
, if we set
then the family
![]() $(A^{\pi }_{\tau })_{\pi }$
converges to
$(A^{\pi }_{\tau })_{\pi }$
converges to
![]() $\mathcal {A}_{\tau }$
in
$\mathcal {A}_{\tau }$
in
![]() $L_m(\mathbb {P})$
as
$L_m(\mathbb {P})$
as
![]() $ \lvert {\pi } \rvert $
tends to
$ \lvert {\pi } \rvert $
tends to
![]() $0$
.
$0$
.
Remark 1.2. We discuss the optimality of the condition (1.9). By considering a deterministic
![]() $(A_{s,t})$
, we see that the condition
$(A_{s,t})$
, we see that the condition
![]() $\beta _1> 1$
is necessary. To see that the conditions
$\beta _1> 1$
is necessary. To see that the conditions
![]() $\beta _2> \frac {1}{2}$
and
$\beta _2> \frac {1}{2}$
and
![]() $\beta _1 - \alpha> \frac {1}{2}$
are necessary, let
$\beta _1 - \alpha> \frac {1}{2}$
are necessary, let
![]() $B^1$
and
$B^1$
and
![]() $B^2$
be two independent one-dimensional fractional Brownian motions with Hurst parameter
$B^2$
be two independent one-dimensional fractional Brownian motions with Hurst parameter
![]() $\frac {1}{4}$
(see Definition 3.1), and we set
$\frac {1}{4}$
(see Definition 3.1), and we set ![]() . It is well-known since the work [Reference Coutin and Qian10] of Coutin and Qian that the iterated integral
. It is well-known since the work [Reference Coutin and Qian10] of Coutin and Qian that the iterated integral
![]() $\int B^1 \mathrm {d} B^2$
does not exist, and, therefore, the Riemann sum with respect to
$\int B^1 \mathrm {d} B^2$
does not exist, and, therefore, the Riemann sum with respect to
![]() $(A_{s, t})$
should not converge. In fact, the family
$(A_{s, t})$
should not converge. In fact, the family
![]() $(A_{s, t})$
, with filtration
$(A_{s, t})$
, with filtration
![]() $(\mathcal {F}_t)$
generated by
$(\mathcal {F}_t)$
generated by
![]() $(B^1, B^2)$
, satisfies (1.7) and (1.8) with
$(B^1, B^2)$
, satisfies (1.7) and (1.8) with
To see this, we observe
![]() $\delta A_{t_1, t_2, t_3} = - B^1_{t_1, t_2} B^2_{t_2, t_3}$
, and
$\delta A_{t_1, t_2, t_3} = - B^1_{t_1, t_2} B^2_{t_2, t_3}$
, and
To compute the conditional expectation, we observe
and by the estimate (3.4), we have
Remark 1.3. The proof shows that if
then we have
![]() $C_2 \lesssim _{\alpha , \beta _1, \beta _2, M} \Gamma _1$
, and we can omit the factor
$C_2 \lesssim _{\alpha , \beta _1, \beta _2, M} \Gamma _1$
, and we can omit the factor
![]() $\kappa _{m,d}$
. This is similar to [Reference Lê24], where
$\kappa _{m,d}$
. This is similar to [Reference Lê24], where
![]() $C_2$
also does not depend on
$C_2$
also does not depend on
![]() $\kappa _{m,d}$
. If
$\kappa _{m,d}$
. If
![]() $\alpha = 0$
and
$\alpha = 0$
and
![]() $M = 0$
, Theorem 1.1 recovers Lê’s stochastic sewing lemma [Reference Lê24, Theorem 2.1]. If
$M = 0$
, Theorem 1.1 recovers Lê’s stochastic sewing lemma [Reference Lê24, Theorem 2.1]. If
![]() $\alpha = 0$
and
$\alpha = 0$
and
![]() $M>0 $
, it recovers a lemma [Reference Gerencsér16, Lemma 2.2] by Gerencsér.
$M>0 $
, it recovers a lemma [Reference Gerencsér16, Lemma 2.2] by Gerencsér.
Recently, Gerencsér’s stochastic sewing lemma is called shifted stochastic sewing lemma. In the follow-up works, we continue to refer to Theorem 1.1 by the same name.
Remark 1.4. The proof shows that there exists
![]() $\epsilon = \epsilon (\alpha , \beta _1, \beta _2)> 0$
, such that
$\epsilon = \epsilon (\alpha , \beta _1, \beta _2)> 0$
, such that
for every
![]() $\tau \in [0, T]$
and every partition
$\tau \in [0, T]$
and every partition
![]() $\pi $
of
$\pi $
of
![]() $[0, \tau ]$
. A similar remark holds in the setting of Corollary 2.7.
$[0, \tau ]$
. A similar remark holds in the setting of Corollary 2.7.
Remark 1.5. As in another work [Reference Lê26] of Lê, it should be possible to extend Theorem 1.1 so that the stochastic process
![]() $(A_{s,t})_{s,t \in [0, T]}$
takes values in a certain Banach space.
$(A_{s,t})_{s,t \in [0, T]}$
takes values in a certain Banach space.
Remark 1.6. A multidimensional version of the sewing lemma is the reconstruction theorem [Reference Hairer18, Theorem 3.10] of Hairer. A stochastic version of the reconstruction theorem was obtained by Kern [Reference Kern21]. It could be possible to extend Theorem 1.1 in the multidimensional setting, but we will not pursue it in this paper.
The proof of Theorem 1.1 is given in Section 2. If
![]() $A_{s, t}$
is given by (1.5), then we can apply Theorem 1.1 with
$A_{s, t}$
is given by (1.5), then we can apply Theorem 1.1 with
However, the application of Theorem 1.1 goes beyond this simple problem of
![]() $\frac {1}{H}$
-variation of the fractional Brownian motion. Indeed, in Section 3, we prove the convergence of Itô and Stratonovich approximations to the stochastic integrals
$\frac {1}{H}$
-variation of the fractional Brownian motion. Indeed, in Section 3, we prove the convergence of Itô and Stratonovich approximations to the stochastic integrals
 $$ \begin{align*} \int_0^T f(B_s) \, \mathrm{d} B_s \quad \text{and } \quad \int_0^T f(B_s) \circ \, \mathrm{d} B_s \end{align*} $$
$$ \begin{align*} \int_0^T f(B_s) \, \mathrm{d} B_s \quad \text{and } \quad \int_0^T f(B_s) \circ \, \mathrm{d} B_s \end{align*} $$
with
![]() $H> \frac {1}{2}$
in Itô’s case and with
$H> \frac {1}{2}$
in Itô’s case and with
![]() $H> \frac {1}{6}$
in Stratonovich’s case, under rather general assumptions on the regularity of f, in fact,
$H> \frac {1}{6}$
in Stratonovich’s case, under rather general assumptions on the regularity of f, in fact,
![]() $f \in C^2_b(\mathbb {R}^d, \mathbb {R}^d)$
works for all
$f \in C^2_b(\mathbb {R}^d, \mathbb {R}^d)$
works for all
![]() $H> \frac 16$
. In Section 4, we obtain new representations of local times of fractional Brownian motions via discretization.
$H> \frac 16$
. In Section 4, we obtain new representations of local times of fractional Brownian motions via discretization.
Finally, we remark that one of the most interesting applications of Lê’s stochastic sewing lemma lies in the phenomenon of regularization by noise (see, e.g. [Reference Lê24], Athreya et al. [Reference Athreya, Butkovsky, Lê and Mytnik2], [Reference Gerencsér16], and Anzeletti et al. [Reference Anzeletti, Richard and Tanré1]). In these works, they consider the stochastic differential equation (SDE)
with an additive noise Y, which is often a fractional Brownian motion. It is interesting that, although in absence of noise the coefficient b needs to belong to
![]() $C^1$
for well-posedness, the presence of noise enables us to prove the certain well-posedness of (1.13) under much weaker assumption, in fact, b can be even a distribution; hence the name regularization by noise. In Section 5 of our paper, we are interested in a related but different problem. Indeed, we are interested in improving the regularity of the diffusion coefficient rather than the drift coefficient. We consider the Young SDE
$C^1$
for well-posedness, the presence of noise enables us to prove the certain well-posedness of (1.13) under much weaker assumption, in fact, b can be even a distribution; hence the name regularization by noise. In Section 5 of our paper, we are interested in a related but different problem. Indeed, we are interested in improving the regularity of the diffusion coefficient rather than the drift coefficient. We consider the Young SDE
driven by a fractional Brownian motion B with Hurst parameter
![]() $H \in (\frac {1}{2}, 1)$
. The pathwise theory of Young’s differential equation requires that the regularity of
$H \in (\frac {1}{2}, 1)$
. The pathwise theory of Young’s differential equation requires that the regularity of
![]() $\sigma $
is better than
$\sigma $
is better than
![]() $1/H$
for uniqueness, and this condition is sharp for general drivers B of the same regularity as the fractional Brownian motion. We will improve this regularity assumption for pathwise uniqueness and strong existence. Again, a stochastic sewing lemma (Lemma 5.5), which is a variant of Theorem 1.1, will play a key role.
$1/H$
for uniqueness, and this condition is sharp for general drivers B of the same regularity as the fractional Brownian motion. We will improve this regularity assumption for pathwise uniqueness and strong existence. Again, a stochastic sewing lemma (Lemma 5.5), which is a variant of Theorem 1.1, will play a key role.
Notation
We write ![]() and
and ![]() . Given a function
. Given a function
![]() $f:[S, T] \to \mathbb {R}^d$
, we write
$f:[S, T] \to \mathbb {R}^d$
, we write ![]() . We denote by
. We denote by
![]() $\kappa _{m, d}$
the best constant of the discrete Burkholder-Davis-Gundy (BDG) inequality for
$\kappa _{m, d}$
the best constant of the discrete Burkholder-Davis-Gundy (BDG) inequality for
![]() $\mathbb {R}^d$
-valued martingale differences [Reference Burkholder, Davis and Gundy6]. Namely, if we are given a filtration
$\mathbb {R}^d$
-valued martingale differences [Reference Burkholder, Davis and Gundy6]. Namely, if we are given a filtration
![]() $(\mathcal {F}_n)_{n=1}^{\infty }$
and a sequence
$(\mathcal {F}_n)_{n=1}^{\infty }$
and a sequence
![]() $(X_n)_{n=1}^{\infty }$
of
$(X_n)_{n=1}^{\infty }$
of
![]() $\mathbb {R}^d$
-valued random variables, such that
$\mathbb {R}^d$
-valued random variables, such that
![]() $X_n$
is
$X_n$
is
![]() $\mathcal {F}_{n}$
-measurable for every
$\mathcal {F}_{n}$
-measurable for every
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $\mathbb {E}[X_n \vert \mathcal {F}_{n-1}] = 0$
for every
$\mathbb {E}[X_n \vert \mathcal {F}_{n-1}] = 0$
for every
![]() $n \geq 2$
, then
$n \geq 2$
, then
 $$ \begin{align} \lVert {\sum_{n=1}^{\infty} X_n} \rVert _{L_m(\mathbb{P})} \leq \kappa_{m, d} \lVert {\sum_{n=1}^{\infty} X_n^2}\rVert _{L_{\frac{m}{2}}(\mathbb{P})}^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \lVert {\sum_{n=1}^{\infty} X_n} \rVert _{L_m(\mathbb{P})} \leq \kappa_{m, d} \lVert {\sum_{n=1}^{\infty} X_n^2}\rVert _{L_{\frac{m}{2}}(\mathbb{P})}^{\frac{1}{2}}. \end{align} $$
Rather than (1.14), we mostly use the inequality
 $$ \begin{align} \lVert {\sum_{n=1}^{\infty} X_n} \rVert _{L_m(\mathbb{P})} \leq \kappa_{m, d} \Big(\sum_{n=1}^{\infty} \lVert {X_n} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \end{align} $$
$$ \begin{align} \lVert {\sum_{n=1}^{\infty} X_n} \rVert _{L_m(\mathbb{P})} \leq \kappa_{m, d} \Big(\sum_{n=1}^{\infty} \lVert {X_n} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \end{align} $$
for
![]() $m \geq 2$
, which follows from (1.14) by Minkowski’s inequality. We write
$m \geq 2$
, which follows from (1.14) by Minkowski’s inequality. We write
![]() $A \lesssim B$
or
$A \lesssim B$
or
![]() $A = O(B)$
if there exists a nonnegative constant C, such that
$A = O(B)$
if there exists a nonnegative constant C, such that
![]() $A \leq C B$
. To emphasize the dependence of C on some parameters
$A \leq C B$
. To emphasize the dependence of C on some parameters
![]() $a, b, \ldots $
, we write
$a, b, \ldots $
, we write
![]() $A \lesssim _{a, b, \ldots } B$
.
$A \lesssim _{a, b, \ldots } B$
.
2. Proof of the main theorem
The overall strategy of the proof is the same as that of the original work [Reference Lê24] of Lê. Namely, we combine the argument of the deterministic sewing lemma ([Reference Gubinelli17], [Reference Feyel and de La Pradelle13], and Yaskov [Reference Yaskov40]) with the discrete BDG inequality [Reference Burkholder, Davis and Gundy6]. However, the proof of Theorem 1.1 requires more labor at a technical level. Some proofs will be postponed to Appendix A.
As in [Reference Lê24], the following lemma, which originates from [Reference Yaskov40], will be needed. It allows us to replace general partitions by dyadic partitions.
Lemma 2.1 [Reference Lê24, Lemma 2.14].
Under the setting of Theorem 1.1, let
Then, we have
 $$ \begin{align} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i, \end{align} $$
$$ \begin{align} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i, \end{align} $$
where
and
and where
![]() $R^n_i = 0$
for all sufficiently large n.
$R^n_i = 0$
for all sufficiently large n.
The next two lemmas (Lemmas 2.2 and 2.3) correspond to the estimates [Reference Lê24, (2.50) and (2.51)], respectively.
Lemma 2.2. Under the setting of Theorem 1.1, let
Then,
 $$ \begin{align*} \lVert {\mathbb{E}[A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})} \lesssim_{\beta_1} \Gamma_1 \lvert {t_0 - s} \rvert ^{-\alpha} \lvert {t_N - t_0} \rvert ^{\beta_1}. \end{align*} $$
$$ \begin{align*} \lVert {\mathbb{E}[A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})} \lesssim_{\beta_1} \Gamma_1 \lvert {t_0 - s} \rvert ^{-\alpha} \lvert {t_N - t_0} \rvert ^{\beta_1}. \end{align*} $$
Proof. In view of the decomposition (2.1), the triangle inequality gives
 $$ \begin{align*} \lVert {\mathbb{E}[A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})} \leq \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} \lVert {\mathbb{E}[R_i^n \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
$$ \begin{align*} \lVert {\mathbb{E}[A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})} \leq \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} \lVert {\mathbb{E}[R_i^n \vert \mathcal{F}_{s}]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
Therefore, recalling
![]() $\beta _1> 1$
from (1.9), the claim follows.
$\beta _1> 1$
from (1.9), the claim follows.
The following lemma is the most important technical ingredient for the proof of Theorem 1.1.
Lemma 2.3. Under the setting of Theorem 1.1, let
Then,
 $$ \begin{align*} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} } \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
$$ \begin{align*} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} } \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
Under (1.12), we can replace
![]() $\kappa _{m, d} \Gamma _1$
by
$\kappa _{m, d} \Gamma _1$
by
![]() $\Gamma _1$
.
$\Gamma _1$
.
Proof under (1.12).
To simplify the proof, here, we assume (1.12), that is, that the additional technical condition
![]() $1+\alpha -\beta _1 < 2\alpha \beta _2 - \alpha $
holds. The proof in the general setting will be given in Appendix A.
$1+\alpha -\beta _1 < 2\alpha \beta _2 - \alpha $
holds. The proof in the general setting will be given in Appendix A.
We, again, use the representation (2.1). We fix a large
![]() $n \in \mathbb {N}$
and set
$n \in \mathbb {N}$
and set ![]() . Fix an integer
. Fix an integer
![]() $L = L_n \in [M + 1, 2^n]$
, which will be chosen later. We have
$L = L_n \in [M + 1, 2^n]$
, which will be chosen later. We have

We estimate the first term of (2.3). By the BDG inequality together with Minkowski’s inequality (see (1.15)), we have

Using (1.8) and (2.2) and noting that we include more terms in the sum by requiring
![]() $j \le 2^n/L$
only instead of
$j \le 2^n/L$
only instead of
![]() $Lj+l \le 2^n - 1$
, we get
$Lj+l \le 2^n - 1$
, we get
 $$ \begin{align*} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \lVert { R^n_{Lj + l} } \rVert _{L_m(\mathbb{P})}^2 \leq 4 \Gamma_2^2 2^{-n (2\beta_2 - 1)} L^{-1} \lvert {t_N - t_0} \rvert ^{2 \beta_2}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \lVert { R^n_{Lj + l} } \rVert _{L_m(\mathbb{P})}^2 \leq 4 \Gamma_2^2 2^{-n (2\beta_2 - 1)} L^{-1} \lvert {t_N - t_0} \rvert ^{2 \beta_2}. \end{align*} $$
Therefore,

We next estimate the second term of (2.3). The triangle inequality yields
 $$ \begin{align*} \lVert {\sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \leq \sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \lVert {\mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
$$ \begin{align*} \lVert {\sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \leq \sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \lVert {\mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
By (1.7),
Therefore,
 $$ \begin{align*} \lVert {\sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha}. \end{align*} $$
$$ \begin{align*} \lVert {\sum_{l = 0}^{L - 1} \sum_{\substack{j \ge 0:\\ L j + l < 2^n}} \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha}. \end{align*} $$
In conclusion,
 $$ \begin{align} \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align} $$
$$ \begin{align} \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align} $$
We wish to choose
![]() $L = L_n$
so that (2.4) is summable with respect to n. We therefore set
$L = L_n$
so that (2.4) is summable with respect to n. We therefore set ![]() , where
, where
Such a
![]() $\delta $
exists exactly under the additional technical assumption (1.12), namely, if
$\delta $
exists exactly under the additional technical assumption (1.12), namely, if
![]() $1 + \alpha - \beta _1 < 2 \alpha \beta _2 - \alpha $
. Then, (2.4) yields
$1 + \alpha - \beta _1 < 2 \alpha \beta _2 - \alpha $
. Then, (2.4) yields
 $$ \begin{align*} \lVert { \sum_{n: 2^{n \delta} \geq M + 2}\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
$$ \begin{align*} \lVert { \sum_{n: 2^{n \delta} \geq M + 2}\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
To estimate the contribution coming from the small n with
![]() $2^{n\delta } < M+2$
, we apply (1.8) which yields
$2^{n\delta } < M+2$
, we apply (1.8) which yields
 $$ \begin{align*} \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \leq 2 \Gamma_2 \sum_{i=0}^{2^n - 1} 2^{-n \beta_2} \lvert {t_N - t_0} \rvert ^{\beta_2} = \Gamma_2 2^{1 + n (1 - \beta_2)} \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
$$ \begin{align*} \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \leq 2 \Gamma_2 \sum_{i=0}^{2^n - 1} 2^{-n \beta_2} \lvert {t_N - t_0} \rvert ^{\beta_2} = \Gamma_2 2^{1 + n (1 - \beta_2)} \lvert {t_N - t_0} \rvert ^{\beta_2}. \end{align*} $$
Thus, we conclude
 $$ \begin{align*} \lVert { \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}, \end{align*} $$
$$ \begin{align*} \lVert { \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2}, \end{align*} $$
where the fact
![]() $\kappa _{m, d} \geq 1$
is used.
$\kappa _{m, d} \geq 1$
is used.
Lemma 2.4. Under the setting of Theorem 1.1, let
![]() $\pi , \pi '$
be partitions of
$\pi , \pi '$
be partitions of
![]() $[0, T]$
, such that
$[0, T]$
, such that
![]() $\pi $
refines
$\pi $
refines
![]() $\pi '$
. Suppose that we have
$\pi '$
. Suppose that we have
Then, there exists
![]() $\epsilon \in (0, 1)$
, such that
$\epsilon \in (0, 1)$
, such that
Sketch of the proof.
Here, we give a sketch of the proof under (1.12). The complete proof is given in Appendix A. The argument is similar to Lemma 2.3.
Write
and
We set ![]() , where
, where
![]() $\delta $
satisfies (2.5). We set
$\delta $
satisfies (2.5). We set

As in Lemma 2.3, we consider the decomposition
![]() $A^{\pi '}_T - A^{\pi }_T = A + B$
, where
$A^{\pi '}_T - A^{\pi }_T = A + B$
, where

We estimate A by using the BDG inequality, Lemma 2.3, and (2.6), to obtain
We estimate B by using the triangle inequality, Lemma 2.2, and (2.6), to obtain
As in Lemma 2.3, we choose ![]() with
with
![]() $\delta $
satisfying (2.5). We then obtain the claimed estimate.
$\delta $
satisfying (2.5). We then obtain the claimed estimate.
Remark 2.5. In the setting of Lemma 2.4, assume that the adapted process
![]() $(\mathcal A_t)_{t \in [0,T]}$
satisfies (1.10) and (1.11). Then we obtain for some
$(\mathcal A_t)_{t \in [0,T]}$
satisfies (1.10) and (1.11). Then we obtain for some
![]() $\varepsilon> 0$
:
$\varepsilon> 0$
:
Indeed, it suffices to replace
![]() $A_{t_{jL + l}, t_{jL + l +1}}$
by
$A_{t_{jL + l}, t_{jL + l +1}}$
by
![]() $\mathcal A_{t_{jL + l}, t_{jL + l +1}}$
in the previous proof.
$\mathcal A_{t_{jL + l}, t_{jL + l +1}}$
in the previous proof.
Lemma 2.6. Let
![]() $\pi $
be a partition of
$\pi $
be a partition of
![]() $[0, T]$
. Then, there exists a partition
$[0, T]$
. Then, there exists a partition
![]() $\pi '$
of
$\pi '$
of
![]() $[0, T]$
, such that
$[0, T]$
, such that
![]() $\pi $
refines
$\pi $
refines
![]() $\pi '$
,
$\pi '$
,
![]() $ \lvert {\pi '} \rvert \leq 3 \lvert {\pi } \rvert $
and
$ \lvert {\pi '} \rvert \leq 3 \lvert {\pi } \rvert $
and
Proof. We write
![]() $\pi = \{0=t_0 < t_1 < \cdots <t_{N-1} < t_N = T\}$
. We set
$\pi = \{0=t_0 < t_1 < \cdots <t_{N-1} < t_N = T\}$
. We set ![]() , and for
, and for
![]() $l\in \mathbb {N}$
, we inductively set
$l\in \mathbb {N}$
, we inductively set
Set ![]() . Then, we define
. Then, we define

By construction,
![]() $\pi '= \{s_j\}_{j=1}^L$
satisfies the claimed properties:
$\pi '= \{s_j\}_{j=1}^L$
satisfies the claimed properties:
![]() $s_{j+1} - s_j \le 2|\pi |$
if
$s_{j+1} - s_j \le 2|\pi |$
if
![]() $j<L-2$
, and
$j<L-2$
, and
![]() $s_L - s_{L-1} \le 3 |\pi |$
, so
$s_L - s_{L-1} \le 3 |\pi |$
, so
![]() $|\pi '| \le 3 |\pi |$
; moreover,
$|\pi '| \le 3 |\pi |$
; moreover,
![]() $\min _{[s,t] \in \pi '}|t-s| \ge |\pi | \ge 3^{-1} |\pi '|$
.
$\min _{[s,t] \in \pi '}|t-s| \ge |\pi | \ge 3^{-1} |\pi '|$
.
Proof of Theorem 1.1.
We will not write down dependence on
![]() $\alpha , \beta _1, \beta _2, M, m, d, T$
. We first prove the convergence of
$\alpha , \beta _1, \beta _2, M, m, d, T$
. We first prove the convergence of
![]() $(A^{\pi }_{\tau })_{\pi }$
. Without loss of generality, we assume
$(A^{\pi }_{\tau })_{\pi }$
. Without loss of generality, we assume
![]() $\tau = T$
. Let
$\tau = T$
. Let
![]() $\pi _1, \pi _2$
be partitions of
$\pi _1, \pi _2$
be partitions of
![]() $[0, T]$
. By Lemma 2.6, there exist partitions
$[0, T]$
. By Lemma 2.6, there exist partitions
![]() $\pi _1'$
,
$\pi _1'$
,
![]() $\pi _2'$
, such that for
$\pi _2'$
, such that for
![]() $j \in \{1, 2\}$
, the partition
$j \in \{1, 2\}$
, the partition
![]() $\pi _j$
refines
$\pi _j$
refines
![]() $\pi _j'$
,
$\pi _j'$
,
![]() $ \lvert {\pi ^{\prime }_j} \rvert \leq 3 \lvert {\pi _j} \rvert $
and
$ \lvert {\pi ^{\prime }_j} \rvert \leq 3 \lvert {\pi _j} \rvert $
and
Lemma 2.4 shows that for some
![]() $\epsilon> 0$
, we have
$\epsilon> 0$
, we have
Therefore, by the triangle inequality,
Let
![]() $\pi $
refine both
$\pi $
refine both
![]() $\pi _1'$
and
$\pi _1'$
and
![]() $\pi _2'$
. Lemma 2.4 implies that
$\pi _2'$
. Lemma 2.4 implies that
The estimates (2.7) and (2.8) show
Thus,
![]() $\{A^{\pi }_T\}_{\pi }$
forms a Cauchy net in
$\{A^{\pi }_T\}_{\pi }$
forms a Cauchy net in
![]() $L_m(\mathbb {P})$
. We denote the limit by
$L_m(\mathbb {P})$
. We denote the limit by
![]() $\mathscr {S}_T$
. We next prove that
$\mathscr {S}_T$
. We next prove that
![]() $(\mathscr {S}_t)_{t \in [0, T]}$
satisfies (1.10) and (1.11). Let
$(\mathscr {S}_t)_{t \in [0, T]}$
satisfies (1.10) and (1.11). Let
![]() $t_0 < t_1 < t_2$
be such that
$t_0 < t_1 < t_2$
be such that
![]() $M(t_2 - t_1) \leq t_1 - t_0$
. Let
$M(t_2 - t_1) \leq t_1 - t_0$
. Let
![]() $\pi _n = \{ t_1 + k 2^{-n}(t_2-t_1): k=0,\dots , 2^n\}$
be the nth dyadic partition of
$\pi _n = \{ t_1 + k 2^{-n}(t_2-t_1): k=0,\dots , 2^n\}$
be the nth dyadic partition of
![]() $[t_1, t_2]$
, and we write
$[t_1, t_2]$
, and we write
We have
By Lemma 2.2,
In this estimate, we can replace
![]() $A^n_{t_1, t_2}$
by
$A^n_{t_1, t_2}$
by
![]() $\mathscr {S}_{t_1, t_2}$
in view of (2.9). Similarly, by Lemma 2.3, we obtain
$\mathscr {S}_{t_1, t_2}$
in view of (2.9). Similarly, by Lemma 2.3, we obtain
Under (1.12), we can replace
![]() $ \kappa _{m, d} \Gamma _1$
by
$ \kappa _{m, d} \Gamma _1$
by
![]() $\Gamma _1$
.
$\Gamma _1$
.
Finally, let us prove the uniqueness of
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $(\tilde {\mathcal {A}}_t)_{t \in [0, T]}$
be another adapted process satisfying
$(\tilde {\mathcal {A}}_t)_{t \in [0, T]}$
be another adapted process satisfying
![]() $\tilde {\mathcal {A}}_0 = 0$
, (1.10) and (1.11). It suffices to show
$\tilde {\mathcal {A}}_0 = 0$
, (1.10) and (1.11). It suffices to show
![]() $\mathcal {A}_T = \tilde {\mathcal {A}}_T$
almost surely. Let
$\mathcal {A}_T = \tilde {\mathcal {A}}_T$
almost surely. Let
![]() $\pi _n$
be the nth dyadic partition of
$\pi _n$
be the nth dyadic partition of
![]() $[0, T]$
. By Remark 2.5, we have
$[0, T]$
. By Remark 2.5, we have
Since
![]() $n \in \mathbb {N}$
is arbitrary, we must have
$n \in \mathbb {N}$
is arbitrary, we must have
![]() $\mathcal {A}_T = \tilde {\mathcal {A}}_T$
almost surely.
$\mathcal {A}_T = \tilde {\mathcal {A}}_T$
almost surely.
As in [Reference Athreya, Butkovsky, Lê and Mytnik2, Theorem 4.1] of Athreya et al., we will give an extension of Theorem 1.1 that allows singularity at
![]() $t = 0$
, which will be needed in Section 4.
$t = 0$
, which will be needed in Section 4.
Corollary 2.7. Suppose that we have a filtration
![]() $(\mathcal {F}_t)_{t \in [0, T]}$
and a family of
$(\mathcal {F}_t)_{t \in [0, T]}$
and a family of
![]() $\mathbb {R}^d$
-valued random variables
$\mathbb {R}^d$
-valued random variables
![]() $(A_{s, t})_{0 \leq s \leq t \leq T}$
, such that
$(A_{s, t})_{0 \leq s \leq t \leq T}$
, such that
![]() $A_{s, s} = 0$
for every
$A_{s, s} = 0$
for every
![]() $s \in [0, T]$
and such that
$s \in [0, T]$
and such that
![]() $A_{s, t}$
is
$A_{s, t}$
is
![]() $\mathcal {F}_t$
-measurable. Furthermore, suppose that there exist constants
$\mathcal {F}_t$
-measurable. Furthermore, suppose that there exist constants
such that the following conditions are satisfied.
-
• For every
 $0 \leq t_0 < t_1 < t_2 < t_3 \leq T$
, we have (2.10)
$0 \leq t_0 < t_1 < t_2 < t_3 \leq T$
, we have (2.10) $$ \begin{align} \lVert {\mathbb{E}[\delta A_{t_1, t_2, t_3} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_1 t_1^{-\gamma_1} (t_1 - t_0)^{-\alpha} (t_3 - t_1)^{\beta_1}, \end{align} $$
(2.11)
$$ \begin{align} \lVert {\mathbb{E}[\delta A_{t_1, t_2, t_3} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_1 t_1^{-\gamma_1} (t_1 - t_0)^{-\alpha} (t_3 - t_1)^{\beta_1}, \end{align} $$
(2.11) $$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_2 t_0^{-\gamma_2} (t_2 - t_0)^{\beta_2}, \end{align} $$
(2.12)where
$$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_2 t_0^{-\gamma_2} (t_2 - t_0)^{\beta_2}, \end{align} $$
(2.12)where $$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_3 (t_2 - t_0)^{\beta_3}, \end{align} $$
$$ \begin{align} \lVert {\delta A_{t_0, t_1, t_2}} \rVert _{L_m(\mathbb{P})} &\leq \Gamma_3 (t_2 - t_0)^{\beta_3}, \end{align} $$
 $M(t_3 - t_1) \leq t_1 - t_0$
is assumed for (2.10) and
$M(t_3 - t_1) \leq t_1 - t_0$
is assumed for (2.10) and
 $t_0> 0$
is assumed for (2.11).
$t_0> 0$
is assumed for (2.11).
-
• We have
(2.13) $$ \begin{align} \beta_1> 1, \quad \beta_2 > \frac{1}{2}, \quad \beta_1 - \alpha > \frac{1}{2}, \quad \gamma_1, \gamma_2 < \frac{1}{2}, \quad \beta_3> 0. \end{align} $$
$$ \begin{align} \beta_1> 1, \quad \beta_2 > \frac{1}{2}, \quad \beta_1 - \alpha > \frac{1}{2}, \quad \gamma_1, \gamma_2 < \frac{1}{2}, \quad \beta_3> 0. \end{align} $$
Then, there exists a unique, up to modifications,
![]() $\mathbb {R}^d$
-valued stochastic process
$\mathbb {R}^d$
-valued stochastic process
![]() $(\mathcal {A}_t)_{t \in [0, T]}$
with the following properties.
$(\mathcal {A}_t)_{t \in [0, T]}$
with the following properties.
-
•
 $\mathcal {A}_0 = 0$
,
$\mathcal {A}_0 = 0$
,
 $\mathcal {A}_t$
is
$\mathcal {A}_t$
is
 $\mathcal {F}_t$
-measurable and
$\mathcal {F}_t$
-measurable and
 $\mathcal {A}_t$
belongs to
$\mathcal {A}_t$
belongs to
 $L_m(\mathbb {P})$
.
$L_m(\mathbb {P})$
. -
• There exist nonnegative constants
 $C_1, \ldots , C_6$
, such that (2.14)
$C_1, \ldots , C_6$
, such that (2.14) $$ \begin{align} & \lVert {\mathbb{E}[\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} \leq C_1 t_1^{-\gamma_1} \lvert {t_1 - t_0} \rvert ^{-\alpha} \lvert {t_2 - t_1} \rvert ^{\beta_1},\end{align} $$
(2.15)
$$ \begin{align} & \lVert {\mathbb{E}[\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} \vert \mathcal{F}_{t_0}]} \rVert _{L_m(\mathbb{P})} \leq C_1 t_1^{-\gamma_1} \lvert {t_1 - t_0} \rvert ^{-\alpha} \lvert {t_2 - t_1} \rvert ^{\beta_1},\end{align} $$
(2.15) $$ \begin{align} & \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_2 t_1^{-\gamma_1} \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha} + C_3 t_1^{-\gamma_2} \lvert {t_2 - t_1} \rvert ^{\beta_2}, \end{align} $$
(2.16)where
$$ \begin{align} & \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_2 t_1^{-\gamma_1} \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha} + C_3 t_1^{-\gamma_2} \lvert {t_2 - t_1} \rvert ^{\beta_2}, \end{align} $$
(2.16)where $$ \begin{align} & \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_4 \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha_1 -\gamma_1} + C_5 \lvert {t_2 - t_1} \rvert ^{\beta_2 - \gamma_2} + C_6 \lvert {t_2 - t_1} \rvert ^{\beta_3}, \end{align} $$
$$ \begin{align} & \lVert {\mathcal{A}_{t_2} - \mathcal{A}_{t_1} - A_{t_1, t_2} } \rVert _{L_m(\mathbb{P})} \leq C_4 \lvert {t_2 - t_1} \rvert ^{\beta_1 - \alpha_1 -\gamma_1} + C_5 \lvert {t_2 - t_1} \rvert ^{\beta_2 - \gamma_2} + C_6 \lvert {t_2 - t_1} \rvert ^{\beta_3}, \end{align} $$
 $t_2 - t_1 \leq M^{-1}(t_1 - t_0)$
is assumed for the inequality (2.14) and
$t_2 - t_1 \leq M^{-1}(t_1 - t_0)$
is assumed for the inequality (2.14) and
 $t_1> 0$
is assumed for the inequality (2.15).
$t_1> 0$
is assumed for the inequality (2.15).
In fact, we can choose
![]() $C_1, \ldots , C_6$
so that
$C_1, \ldots , C_6$
so that
 $$ \begin{align*} &C_1 \lesssim_{\beta_1} \Gamma_1, \quad C_2 \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1, \quad C_3 \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_2, \\ &C_4 \lesssim_{\alpha, \beta_1, \gamma_1, M} \kappa_{m, d} \Gamma_1, \quad C_5 \lesssim_{\beta_2, \gamma_2, M} \kappa_{m, d} \Gamma_2, \quad C_6 \lesssim_{\beta_3, M} \kappa_{m, d} \Gamma_3. \end{align*} $$
$$ \begin{align*} &C_1 \lesssim_{\beta_1} \Gamma_1, \quad C_2 \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1, \quad C_3 \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_2, \\ &C_4 \lesssim_{\alpha, \beta_1, \gamma_1, M} \kappa_{m, d} \Gamma_1, \quad C_5 \lesssim_{\beta_2, \gamma_2, M} \kappa_{m, d} \Gamma_2, \quad C_6 \lesssim_{\beta_3, M} \kappa_{m, d} \Gamma_3. \end{align*} $$
Furthermore, for
![]() $\tau \in [0, T]$
, if we set
$\tau \in [0, T]$
, if we set
then the family
![]() $(A^{\pi }_{\tau })_{\pi }$
converges to
$(A^{\pi }_{\tau })_{\pi }$
converges to
![]() $\mathcal {A}_{\tau }$
in
$\mathcal {A}_{\tau }$
in
![]() $L_m(\mathbb {P})$
as
$L_m(\mathbb {P})$
as
![]() $ \lvert {\pi } \rvert \to 0$
.
$ \lvert {\pi } \rvert \to 0$
.
The proof is given in Appendix A.
3. Integration along fractional Brownian motions
The goal of this section is to prove the convergence of Itô and Stratonovich approximations of
 $$ \begin{align*} \int_0^t f(B_s) \, \mathrm{d} B_s \quad \text{and} \quad \int_0^t f(B_s) \circ \, \mathrm{d} B_s \end{align*} $$
$$ \begin{align*} \int_0^t f(B_s) \, \mathrm{d} B_s \quad \text{and} \quad \int_0^t f(B_s) \circ \, \mathrm{d} B_s \end{align*} $$
along a multidimensional fractional Brownian motion B with Hurst parameter H, using Theorem 1.1. For Itô’s case, we let
![]() $H \in (\frac {1}{2}, 1)$
, and for Stratonovich’s case, we let
$H \in (\frac {1}{2}, 1)$
, and for Stratonovich’s case, we let
![]() $H \in (\frac {1}{6}, \frac {1}{2})$
.
$H \in (\frac {1}{6}, \frac {1}{2})$
.
Definition 3.1. Let
![]() $(\mathcal {F})_{t \in \mathbb {R}}$
be a filtration. We say that a process B is an
$(\mathcal {F})_{t \in \mathbb {R}}$
be a filtration. We say that a process B is an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
$(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
![]() $H \in (0, 1)$
if
$H \in (0, 1)$
if
-
• a two-sided d-dimensional
 $(\mathcal {F}_t)$
-Brownian motion
$(\mathcal {F}_t)$
-Brownian motion
 $(W_t)_{t \in \mathbb {R}}$
is given;
$(W_t)_{t \in \mathbb {R}}$
is given; -
• a random variable
 $B(0)$
is a (not necessarily centered)
$B(0)$
is a (not necessarily centered)
 $\mathcal {F}_0$
-measurable
$\mathcal {F}_0$
-measurable
 $\mathbb {R}^d$
-valued Gaussian random variable and is independent of
$\mathbb {R}^d$
-valued Gaussian random variable and is independent of
 $(W_t)_{t \in \mathbb {R}}$
;
$(W_t)_{t \in \mathbb {R}}$
; -
• we set
then we have the Mandelbrot–Van Ness representation ([Reference Mandelbrot and Van Ness31]) (3.1)
(3.1) $$ \begin{align} B_t = B(0) + \int_{\mathbb{R}} K_H(t, s) \, \mathrm{d} W_s. \end{align} $$
$$ \begin{align} B_t = B(0) + \int_{\mathbb{R}} K_H(t, s) \, \mathrm{d} W_s. \end{align} $$
If B has the representation (3.1), then
where we write
![]() $B = (B^i)_{i=1}^d$
in components and
$B = (B^i)_{i=1}^d$
in components and
![]() $\mathcal {B}$
is the Beta function
$\mathcal {B}$
is the Beta function

Regarding the expression of the constant
![]() $c_H$
, see [Reference Picard, Donati-Martin, Lejay and Rouault38, Appendix B]. In particular, we have
$c_H$
, see [Reference Picard, Donati-Martin, Lejay and Rouault38, Appendix B]. In particular, we have
In this section, we always write B for an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion. An advantage of the representation (3.1) is that given
$(\mathcal {F}_t)$
-fractional Brownian motion. An advantage of the representation (3.1) is that given
![]() $v < s$
, we have the decomposition
$v < s$
, we have the decomposition
where the second term
![]() $\int _v^s K(s, r) \, \mathrm {d} W_r$
is independent of
$\int _v^s K(s, r) \, \mathrm {d} W_r$
is independent of
![]() $\mathcal {F}_v$
. Later, we will need to estimate the correlation of
$\mathcal {F}_v$
. Later, we will need to estimate the correlation of
We note that for
![]() $s \leq t$
$s \leq t$
 $$ \begin{align*} \mathbb{E}[\int_v^s K(s, r) \, \mathrm{d} W_r^i \int_v^t K(t, r) \, \mathrm{d} W_r^j ] = \delta_{ij} \int_v^s K(s, r) K(t, r) \, \mathrm{d} r. \end{align*} $$
$$ \begin{align*} \mathbb{E}[\int_v^s K(s, r) \, \mathrm{d} W_r^i \int_v^t K(t, r) \, \mathrm{d} W_r^j ] = \delta_{ij} \int_v^s K(s, r) K(t, r) \, \mathrm{d} r. \end{align*} $$
Lemma 3.2. Let
![]() $H \neq \frac {1}{2}$
. Let
$H \neq \frac {1}{2}$
. Let
![]() $0 \leq v < s \leq t$
be such that
$0 \leq v < s \leq t$
be such that
![]() $t-s \leq s - v$
. Then,
$t-s \leq s - v$
. Then,
where we have
uniformly over such
![]() $v, s, t$
.
$v, s, t$
.
Proof. See Appendix A.
We apply Theorem 1.1 to construct a stochastic integral
 $$ \begin{align*} \int_0^T f(B_s) \, \mathrm{d} B_s, \quad H \in (1/2, 1) \end{align*} $$
$$ \begin{align*} \int_0^T f(B_s) \, \mathrm{d} B_s, \quad H \in (1/2, 1) \end{align*} $$
as the limit of Riemann type approximations. An advantage of the stochastic sewing lemma is that we do not need any regularity of f. We denote by
![]() $L_{\infty }(\mathbb {R}^d,\mathbb {R}^d)$
the space of bounded measurable maps from
$L_{\infty }(\mathbb {R}^d,\mathbb {R}^d)$
the space of bounded measurable maps from
![]() $\mathbb {R}^d$
to
$\mathbb {R}^d$
to
![]() $\mathbb {R}^d$
. We write
$\mathbb {R}^d$
. We write

for the inner product of
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Proposition 3.3. Let
![]() $H \in (1/2, 1)$
and
$H \in (1/2, 1)$
and
![]() $f \in L_{\infty }(\mathbb {R}^d, \mathbb {R}^d)$
. Then, for any
$f \in L_{\infty }(\mathbb {R}^d, \mathbb {R}^d)$
. Then, for any
![]() $\tau \in [0, T]$
and
$\tau \in [0, T]$
and
![]() $m \in [2, \infty )$
, the sequence
$m \in [2, \infty )$
, the sequence
converges in
![]() $L_m(\mathbb {P})$
for every
$L_m(\mathbb {P})$
for every
![]() $m < \infty $
as
$m < \infty $
as
![]() $ \lvert {\pi } \rvert \to 0$
. Furthermore, if we denote the limit by
$ \lvert {\pi } \rvert \to 0$
. Furthermore, if we denote the limit by
![]() $\int _0^{\tau } f(B_r) \, \mathrm {d} B_r$
and if we write
$\int _0^{\tau } f(B_r) \, \mathrm {d} B_r$
and if we write

then for every
![]() $0 \leq s < t \leq T$
,
$0 \leq s < t \leq T$
,
 $$ \begin{align*} \lVert {\int_s^t f(B_r) \, \mathrm{d} B_r} \rVert _{L_m(\mathbb{P})} \lesssim_{d, H, m} \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} \lvert {t-s} \rvert ^H. \end{align*} $$
$$ \begin{align*} \lVert {\int_s^t f(B_r) \, \mathrm{d} B_r} \rVert _{L_m(\mathbb{P})} \lesssim_{d, H, m} \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} \lvert {t-s} \rvert ^H. \end{align*} $$
Remark 3.4. We can replace
![]() $f(B_s)$
by
$f(B_s)$
by
![]() $f(B_u)$
for any
$f(B_u)$
for any
![]() $u \in [s, t]$
. It is well-known that the sums converge to the Young integral if
$u \in [s, t]$
. It is well-known that the sums converge to the Young integral if
![]() $f \in C^{\gamma } (\mathbb {R})$
with
$f \in C^{\gamma } (\mathbb {R})$
with
![]() $\gamma> H^{-1} (1 - H)$
. Yaskov [Reference Yaskov40, Theorem 3.7] proves that the sums converge in some
$\gamma> H^{-1} (1 - H)$
. Yaskov [Reference Yaskov40, Theorem 3.7] proves that the sums converge in some
![]() $L_p(\mathbb {P})$
-space if f is of bounded variation.
$L_p(\mathbb {P})$
-space if f is of bounded variation.
Proof. We will not write down dependence on d, H, and m. The filtration
![]() $(\mathcal {F}_t)_{t \in \mathbb {R}}$
is generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1). We will apply Theorem 1.1 with
$(\mathcal {F}_t)_{t \in \mathbb {R}}$
is generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1). We will apply Theorem 1.1 with ![]() . Let
. Let
![]() $m \geq 2$
. We have
$m \geq 2$
. We have
To estimate conditional expectations, let
![]() $0 \leq v < s < t$
be such that
$0 \leq v < s < t$
be such that
![]() $t-s \leq s-v$
and set
$t-s \leq s-v$
and set
We write ![]() , if conditioned under
, if conditioned under
![]() $\mathcal {F}_v$
. Namely, we write, for instance
$\mathcal {F}_v$
. Namely, we write, for instance
We are going to compute
![]() $\mathbb {E}[A_{s, t} \vert \mathcal {F}_v]$
. Conditionally on
$\mathbb {E}[A_{s, t} \vert \mathcal {F}_v]$
. Conditionally on
![]() $\mathcal {F}_v$
, we have the Wiener chaos expansion [Reference Nualart34, Theorem 1.1.1]
$\mathcal {F}_v$
, we have the Wiener chaos expansion [Reference Nualart34, Theorem 1.1.1]
 $$ \begin{align*} f(B_s) = f(y_s + \tilde{B}_s) = a_0(s) + \sum_{i=1}^d a_i(s) \tilde{B}^i_s + \tilde{B}^{\perp}_s, \end{align*} $$
$$ \begin{align*} f(B_s) = f(y_s + \tilde{B}_s) = a_0(s) + \sum_{i=1}^d a_i(s) \tilde{B}^i_s + \tilde{B}^{\perp}_s, \end{align*} $$
where
![]() $\tilde {B}^{\perp }_s$
is orthogonal in
$\tilde {B}^{\perp }_s$
is orthogonal in
![]() $L_2(\mathbb {P})$
to the subspace spanned by the constant
$L_2(\mathbb {P})$
to the subspace spanned by the constant
![]() $1$
and
$1$
and
Note that
 $$ \begin{align*} a_0(s) &= \mathbb{E}[f(y_s + \tilde{B}_s)], \\ a_i(s) &= \mathbb{E}[(\tilde{B}_s^i)^2]^{-1} \mathbb{E}[f(y_s + \tilde{B}_s) \tilde{B}_s^i] \overset{\text{Lem. } {{3.2}}}{=} 2H (s-v)^{-2H} \mathbb{E}[f(y_s + \tilde{B}_s) \tilde{B}_s^i]. \end{align*} $$
$$ \begin{align*} a_0(s) &= \mathbb{E}[f(y_s + \tilde{B}_s)], \\ a_i(s) &= \mathbb{E}[(\tilde{B}_s^i)^2]^{-1} \mathbb{E}[f(y_s + \tilde{B}_s) \tilde{B}_s^i] \overset{\text{Lem. } {{3.2}}}{=} 2H (s-v)^{-2H} \mathbb{E}[f(y_s + \tilde{B}_s) \tilde{B}_s^i]. \end{align*} $$
Then, by the orthogonality of the Wiener chaos decomposition,
 $$ \begin{align*} \mathbb{E}[A_{s, t} \vert \mathcal{F}_v] = a_0(s) \cdot Y_{s,t} + \sum_{i=1}^d a_i(s) \cdot \mathbb{E}[\tilde{B_s^i} \tilde{B}_{s, t}]. \end{align*} $$
$$ \begin{align*} \mathbb{E}[A_{s, t} \vert \mathcal{F}_v] = a_0(s) \cdot Y_{s,t} + \sum_{i=1}^d a_i(s) \cdot \mathbb{E}[\tilde{B_s^i} \tilde{B}_{s, t}]. \end{align*} $$
Hence, for
![]() $u \in (s, t)$
,
$u \in (s, t)$
,
 $$ \begin{align*} \mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v] = A^0_{s, u, t} + \sum_{i=1}^d A^i_{s, u, t}, \end{align*} $$
$$ \begin{align*} \mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v] = A^0_{s, u, t} + \sum_{i=1}^d A^i_{s, u, t}, \end{align*} $$
where

Here,
![]() $\boldsymbol {e}_i$
is the ith unit vector of
$\boldsymbol {e}_i$
is the ith unit vector of
![]() $\mathbb {R}^d$
. We first estimate
$\mathbb {R}^d$
. We first estimate
![]() $A^0_{s, u, t}$
, for which we begin with estimating
$A^0_{s, u, t}$
, for which we begin with estimating
![]() $a_0(s) - a_0(u)$
. We set
$a_0(s) - a_0(u)$
. We set
where X has the standard normal distribution in
![]() $\mathbb {R}^d$
. Note that
$\mathbb {R}^d$
. Note that
and similarly for
![]() $a_0(u)$
, we have
$a_0(u)$
, we have
 $$ \begin{align*} \partial_{m^i} F(m, \sigma) &= \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} f(x + m) \, \mathrm{d} x, \\ \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} f(m + x) e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x + \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 f(m + x) e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
$$ \begin{align*} \partial_{m^i} F(m, \sigma) &= \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} f(x + m) \, \mathrm{d} x, \\ \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} f(m + x) e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x + \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 f(m + x) e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
Therefore,
This yields
 $$ \begin{align*} \lvert {a_0(s) - a_0(u)} \rvert &\leq \lvert {F(Y_s, (2H)^{-\frac{1}{2}}(s - v)^H) - F(Y_u, (2H)^{-\frac{1}{2}}(s - v)^H)} \rvert \\ &\phantom{\leq}+ \lvert {F(Y_u, (2H)^{-\frac{1}{2}}(s - v)^H) - F(Y_u, (2H)^{-\frac{1}{2}}(u - v)^H)} \rvert \\ &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-H} \lvert {Y_{s, u}} \rvert + \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-H} ( \lvert {u-v} \rvert ^H - \lvert {s - v} \rvert ^H) \\ &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-H} \lvert {Y_{s, u}} \rvert + \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-1}(t - s). \end{align*} $$
$$ \begin{align*} \lvert {a_0(s) - a_0(u)} \rvert &\leq \lvert {F(Y_s, (2H)^{-\frac{1}{2}}(s - v)^H) - F(Y_u, (2H)^{-\frac{1}{2}}(s - v)^H)} \rvert \\ &\phantom{\leq}+ \lvert {F(Y_u, (2H)^{-\frac{1}{2}}(s - v)^H) - F(Y_u, (2H)^{-\frac{1}{2}}(u - v)^H)} \rvert \\ &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-H} \lvert {Y_{s, u}} \rvert + \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-H} ( \lvert {u-v} \rvert ^H - \lvert {s - v} \rvert ^H) \\ &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-H} \lvert {Y_{s, u}} \rvert + \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)}(s-v)^{-1}(t - s). \end{align*} $$
Therefore,
The random variable
![]() $Y_{s, u}$
is Gaussian and
$Y_{s, u}$
is Gaussian and
 $$ \begin{align} \mathbb{E}[ \lvert {Y_{s, u}} \rvert ^2] &= d\int_{-\infty}^v (K(s, r) - K(u, r))^2 \, \mathrm{d} r = d \int_{s - v}^{\infty} ((u - s + r)^{H- \frac{1}{2}} - r^{H-\frac{1}{2}})^2 \, \mathrm{d} r \notag \\ &\lesssim (u - s)^2 \int_{s - v}^{\infty} r^{2H - 3} \, \mathrm{d} r \lesssim (s - v)^{2H - 2} (u - s)^2. \end{align} $$
$$ \begin{align} \mathbb{E}[ \lvert {Y_{s, u}} \rvert ^2] &= d\int_{-\infty}^v (K(s, r) - K(u, r))^2 \, \mathrm{d} r = d \int_{s - v}^{\infty} ((u - s + r)^{H- \frac{1}{2}} - r^{H-\frac{1}{2}})^2 \, \mathrm{d} r \notag \\ &\lesssim (u - s)^2 \int_{s - v}^{\infty} r^{2H - 3} \, \mathrm{d} r \lesssim (s - v)^{2H - 2} (u - s)^2. \end{align} $$
We have a similar estimate for
![]() $Y_{u, t}$
. Therefore,
$Y_{u, t}$
. Therefore,
Now we move to estimate
![]() $A^i_{s, u, t}$
. By Lemma 3.2, we have
$A^i_{s, u, t}$
. By Lemma 3.2, we have
Therefore, if we write ![]() ,
,
If we set
then
![]() $a_i^i(s) = G_i(Y_s, (2H)^{-\frac {1}{2}} (s - v)^H)$
and similarly for
$a_i^i(s) = G_i(Y_s, (2H)^{-\frac {1}{2}} (s - v)^H)$
and similarly for
![]() $a_i^i(u)$
. Since
$a_i^i(u)$
. Since
we have
 $$ \begin{align*} (2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{m^j} G_i(m, \sigma) &= \int_{\mathbb{R}^d} f^i(m + \sigma x) [- \delta_{ij} + x^i x^j] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x\\(2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{\sigma} G_i(m, \sigma) &= \int_{\mathbb{R}^d} f^i(m + \sigma x) x^i [- (d+2) + \lvert {x} \rvert ^2] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x. \end{align*} $$
$$ \begin{align*} (2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{m^j} G_i(m, \sigma) &= \int_{\mathbb{R}^d} f^i(m + \sigma x) [- \delta_{ij} + x^i x^j] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x\\(2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{\sigma} G_i(m, \sigma) &= \int_{\mathbb{R}^d} f^i(m + \sigma x) x^i [- (d+2) + \lvert {x} \rvert ^2] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x. \end{align*} $$
Therefore,
and thus
 $$ \begin{align*} \lvert {a^i_i(s)} \rvert &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-H},\\\lvert {a^i_i(s) - a^i_i(u)} \rvert &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-2H} \big( \lvert {Y_{s,u}} \rvert + (u-v)^H - (s-v)^H \big) \\&\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-2H} \big( \lvert {Y_{s,u}} \rvert + (s-v)^{H-1} (u-s) \big). \end{align*} $$
$$ \begin{align*} \lvert {a^i_i(s)} \rvert &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-H},\\\lvert {a^i_i(s) - a^i_i(u)} \rvert &\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-2H} \big( \lvert {Y_{s,u}} \rvert + (u-v)^H - (s-v)^H \big) \\&\lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} (s-v)^{-2H} \big( \lvert {Y_{s,u}} \rvert + (s-v)^{H-1} (u-s) \big). \end{align*} $$
This yields
 $$ \begin{align*} & \lvert {A^i_{s, u, t}} \rvert \lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} \big[ (s -v)^{-1} (t-s) \lvert {y_{s, u}} \rvert + (s-v)^{H-2}(t-s)^{2} \\& \quad + (s-v)^{H-2}(t-s)^{2} + (s - v)^{-H}(t - s)^{2H} \big] \end{align*} $$
$$ \begin{align*} & \lvert {A^i_{s, u, t}} \rvert \lesssim \lVert {f} \rVert _{L_{\infty}(\mathbb{R}^d)} \big[ (s -v)^{-1} (t-s) \lvert {y_{s, u}} \rvert + (s-v)^{H-2}(t-s)^{2} \\& \quad + (s-v)^{H-2}(t-s)^{2} + (s - v)^{-H}(t - s)^{2H} \big] \end{align*} $$
and
if
![]() $t-s \leq s - v$
.
$t-s \leq s - v$
.
Therefore, by (3.3) and (3.5),
if
![]() $t-s \leq s - v$
. Hence,
$t-s \leq s - v$
. Hence,
![]() $(A_{s, t})$
satisfies the assumption of Theorem 1.1 with
$(A_{s, t})$
satisfies the assumption of Theorem 1.1 with
Next, we consider the case
![]() $H \in (\frac {1}{6}, \frac {1}{2})$
. The following result reproduces [Reference Nourdin35, Theorem 3.5], with a more elementary proof and with improvement of the regularity of f. More precisely, the cited result requires
$H \in (\frac {1}{6}, \frac {1}{2})$
. The following result reproduces [Reference Nourdin35, Theorem 3.5], with a more elementary proof and with improvement of the regularity of f. More precisely, the cited result requires
![]() $f \in C^6$
while here
$f \in C^6$
while here
![]() $f \in C^\gamma $
with
$f \in C^\gamma $
with
![]() $\gamma> \frac {1}{2H}-1$
is sufficient and thus, in particular,
$\gamma> \frac {1}{2H}-1$
is sufficient and thus, in particular,
![]() $f \in C^2$
works for all
$f \in C^2$
works for all
![]() $H \in (\frac {1}{6}, \frac {1}{2})$
. We denote by
$H \in (\frac {1}{6}, \frac {1}{2})$
. We denote by
![]() $C^{\gamma } (\mathbb {R}^d,\mathbb {R}^d)$
the space of
$C^{\gamma } (\mathbb {R}^d,\mathbb {R}^d)$
the space of
![]() $\gamma $
-Hölder maps from
$\gamma $
-Hölder maps from
![]() $\mathbb {R}^d$
to
$\mathbb {R}^d$
to
![]() $\mathbb {R}^d$
, with the norm
$\mathbb {R}^d$
, with the norm

if
![]() $\gamma \in (0, 1)$
and
$\gamma \in (0, 1)$
and

if
![]() $\gamma \in (1, 2)$
.
$\gamma \in (1, 2)$
.
Proposition 3.5. Let
![]() $H \in (\frac {1}{6}, \frac {1}{2})$
,
$H \in (\frac {1}{6}, \frac {1}{2})$
,
![]() $\gamma> \frac {1}{2H} - 1$
and
$\gamma> \frac {1}{2H} - 1$
and
![]() $f \in C^{\gamma }(\mathbb {R}^d, \mathbb {R}^d)$
. If
$f \in C^{\gamma }(\mathbb {R}^d, \mathbb {R}^d)$
. If
![]() $H \leq \frac {1}{4}$
and
$H \leq \frac {1}{4}$
and
![]() $d> 1$
, assume furthermore that
$d> 1$
, assume furthermore that
Then, for every
![]() $m \in [2, \infty )$
and
$m \in [2, \infty )$
and
![]() $\tau \in [0, T]$
, the family of Stratonovich approximations
$\tau \in [0, T]$
, the family of Stratonovich approximations
 $$ \begin{align*} \sum_{[s, t] \in \pi} \frac{f(B_s) + f(B_t)}{2} \cdot B_{s, t}, \quad \text{where }\pi\text{ is a partition of }[0, \tau], \end{align*} $$
$$ \begin{align*} \sum_{[s, t] \in \pi} \frac{f(B_s) + f(B_t)}{2} \cdot B_{s, t}, \quad \text{where }\pi\text{ is a partition of }[0, \tau], \end{align*} $$
converges in
![]() $L_m(\mathbb {P})$
as
$L_m(\mathbb {P})$
as
![]() $ \lvert {\pi } \rvert \to 0$
. Moreover, if we denote the limit by
$ \lvert {\pi } \rvert \to 0$
. Moreover, if we denote the limit by
![]() $\int _0^{\tau } f(B_r) \circ \, \mathrm {d} B_r$
and if we write
$\int _0^{\tau } f(B_r) \circ \, \mathrm {d} B_r$
and if we write

then for every
![]() $0 \leq s < t \leq T$
, we have
$0 \leq s < t \leq T$
, we have
 $$ \begin{align*} \Big\lVert \int_s^t f(B_r) \circ \, \mathrm{d} B_r - \frac{f(B_s) + f(B_t)}{2} \cdot B_{s, t}\Big\rVert_{L_m(\mathbb{P})} \lesssim_{d, H, m, \gamma} \lVert {f} \rVert _{C^{\gamma}} \lvert {t-s} \rvert ^{(\gamma+1)H}. \end{align*} $$
$$ \begin{align*} \Big\lVert \int_s^t f(B_r) \circ \, \mathrm{d} B_r - \frac{f(B_s) + f(B_t)}{2} \cdot B_{s, t}\Big\rVert_{L_m(\mathbb{P})} \lesssim_{d, H, m, \gamma} \lVert {f} \rVert _{C^{\gamma}} \lvert {t-s} \rvert ^{(\gamma+1)H}. \end{align*} $$
Proof. We will not write down dependence on d, H, m, and
![]() $\gamma $
. The filtration
$\gamma $
. The filtration
![]() $(\mathcal {F}_t)_{t \in \mathbb {R}}$
is generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1). We can assume
$(\mathcal {F}_t)_{t \in \mathbb {R}}$
is generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1). We can assume
We will apply Theorem 1.1 with
We first claim
Observe
If
![]() $H> \frac {1}{4}$
, the claim (3.7) follows from the estimates
$H> \frac {1}{4}$
, the claim (3.7) follows from the estimates
If
![]() $H \leq \frac {1}{4}$
, then
$H \leq \frac {1}{4}$
, then
![]() $\gamma> 1$
, and we have
$\gamma> 1$
, and we have
 $$ \begin{align*} \delta A_{s, u, t} = \Big(f(B)_{u, t} - \sum_{j=1}^d \partial_j f(B_u) B_{u, t}^j\Big) \cdot B_{s, u} + \Big(f(B)_{u, s} - \sum_{j=1}^d \partial_j f(B_u) B_{u, s}^j \Big) \cdot B_{u, t}, \end{align*} $$
$$ \begin{align*} \delta A_{s, u, t} = \Big(f(B)_{u, t} - \sum_{j=1}^d \partial_j f(B_u) B_{u, t}^j\Big) \cdot B_{s, u} + \Big(f(B)_{u, s} - \sum_{j=1}^d \partial_j f(B_u) B_{u, s}^j \Big) \cdot B_{u, t}, \end{align*} $$
where (3.6) is used. Then, the claim (3.7) follows, again, from the Hölder estimate of f. Note that the condition
![]() $\gamma> \frac {1}{2H} - 1$
is equivalent to
$\gamma> \frac {1}{2H} - 1$
is equivalent to
![]() $(\gamma + 1) H> \frac {1}{2}$
.
$(\gamma + 1) H> \frac {1}{2}$
.
The rest of the proof consists of estimating the conditional expectation
![]() $\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_v]$
. Let
$\mathbb {E}[\delta A_{s, u, t} \vert \mathcal {F}_v]$
. Let
![]() $t -s \leq s - v$
. We will use the same notation as in the proof of Proposition 3.3. We have
$t -s \leq s - v$
. We will use the same notation as in the proof of Proposition 3.3. We have
 $$ \begin{align*} \mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v] = D^0_{s, u, t} + \sum_{i=1}^d D^i_{s, u, t}, \end{align*} $$
$$ \begin{align*} \mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v] = D^0_{s, u, t} + \sum_{i=1}^d D^i_{s, u, t}, \end{align*} $$
where

and

We first estimate
![]() $D^0_{s, u, t}$
. Suppose that
$D^0_{s, u, t}$
. Suppose that
![]() $H> \frac {1}{4}$
. Recall
$H> \frac {1}{4}$
. Recall
 $$ \begin{align*} \partial_{m^i} F(m, \sigma) &= \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} [f(x + m) - f(m)] \, \mathrm{d} x, \\ \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} [f(m + x) - f(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x \\ &\hspace{2cm}+ \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 [f(m + x) - f(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
$$ \begin{align*} \partial_{m^i} F(m, \sigma) &= \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} [f(x + m) - f(m)] \, \mathrm{d} x, \\ \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} [f(m + x) - f(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x \\ &\hspace{2cm}+ \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 [f(m + x) - f(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
Therefore,
This yields
Therefore, by (3.4),
Now suppose that
![]() $H \leq \frac {1}{4}$
. To simplify notation, we write
$H \leq \frac {1}{4}$
. To simplify notation, we write ![]() . Since (3.6) gives
. Since (3.6) gives
![]() $\partial _{m^i} I^j = \partial _{m^j} I^i$
for every
$\partial _{m^i} I^j = \partial _{m^j} I^i$
for every
![]() $i, j$
, we have
$i, j$
, we have
 $$ \begin{align*} D^0_{s, u, t} &= [I(Y_s, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, s}^i] \cdot Y_{u, t} \\ &\phantom{=}+ [I(Y_t, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, t}^i] \cdot Y_{s, u} \\ &\phantom{=}+ [I(Y_s, (s-v)^H) - I(Y_s, (u - v)^H)] \cdot Y_{u, t} + [I(Y_t, (t-v)^H) - I(Y_t, (u - v)^H)] \cdot Y_{s, u}. \end{align*} $$
$$ \begin{align*} D^0_{s, u, t} &= [I(Y_s, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, s}^i] \cdot Y_{u, t} \\ &\phantom{=}+ [I(Y_t, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, t}^i] \cdot Y_{s, u} \\ &\phantom{=}+ [I(Y_s, (s-v)^H) - I(Y_s, (u - v)^H)] \cdot Y_{u, t} + [I(Y_t, (t-v)^H) - I(Y_t, (u - v)^H)] \cdot Y_{s, u}. \end{align*} $$
Since
 $$ \begin{align*} \partial_{m^i} \partial_{m^j} F(m, \sigma) = \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} [\partial_jf(x + m) - \partial_jf(m)] \, \mathrm{d} x, \end{align*} $$
$$ \begin{align*} \partial_{m^i} \partial_{m^j} F(m, \sigma) = \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+2}} \int_{\mathbb{R}^d} x^i e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} [\partial_jf(x + m) - \partial_jf(m)] \, \mathrm{d} x, \end{align*} $$
we have
 $$ \begin{align*} \lvert {I(Y_s, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, s}^i} \rvert \lesssim \lVert {f} \rVert _{C^{\gamma} } (s - v)^{(\gamma - 2)H} \lvert {Y_{s, u}} \rvert ^2. \end{align*} $$
$$ \begin{align*} \lvert {I(Y_s, (u - v)^H) - I(Y_u, (u - v)^H) - \sum_{i=1}^d \partial_{m^i} I(Y_u, (u-v)^H) Y_{u, s}^i} \rvert \lesssim \lVert {f} \rVert _{C^{\gamma} } (s - v)^{(\gamma - 2)H} \lvert {Y_{s, u}} \rvert ^2. \end{align*} $$
Notice
 $$ \begin{align*} \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} [f(m + x) - f(m) - \sum_{i=1}^d \partial_i f(m) x^i] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x \\ &+ \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 [f(m + x) - f(m) - \sum_{i=1}^d \partial_i f(m) x^i] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
$$ \begin{align*} \partial_{\sigma} F(m, \sigma) &= \frac{-d}{(2 \pi)^{\frac{d}{2}} \sigma^{d+1}} \int_{\mathbb{R}^d} [f(m + x) - f(m) - \sum_{i=1}^d \partial_i f(m) x^i] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x \\ &+ \frac{1}{(2 \pi)^{\frac{d}{2}} \sigma^{d+3}} \int_{\mathbb{R}^d} \lvert {x} \rvert ^2 [f(m + x) - f(m) - \sum_{i=1}^d \partial_i f(m) x^i] e^{-\frac{ \lvert {x} \rvert ^2}{2 \sigma^2}} \, \mathrm{d} x. \end{align*} $$
Therefore,
This yields
Hence, we obtain the estimate (3.10) when
![]() $H \leq \frac {1}{4}$
.
$H \leq \frac {1}{4}$
.
We move to estimate
![]() $D^i_{s, u, t}$
. By using the identity,
$D^i_{s, u, t}$
. By using the identity,
we obtain
 $$ \begin{align} &D^i_{s, u, t} = (a_i^i(t) - a_i^i(u)) \mathbb{E}[\tilde{B}_t^i \tilde{B}_{s, t}^i] + (a_i^i(s) - a_i^i(u)) \mathbb{E}[\tilde{B}_s^i \tilde{B}_{s, t}^i] \nonumber\\ &-(a_i^i(s) - a_i^i(u)) \mathbb{E}[\tilde{B}_s^i \tilde{B}_{s, u}^i] -(a_i^i(t) - a_i^i(u)) \mathbb{E}[\tilde{B}_t^i \tilde{B}_{u, t}^i]. \end{align} $$
$$ \begin{align} &D^i_{s, u, t} = (a_i^i(t) - a_i^i(u)) \mathbb{E}[\tilde{B}_t^i \tilde{B}_{s, t}^i] + (a_i^i(s) - a_i^i(u)) \mathbb{E}[\tilde{B}_s^i \tilde{B}_{s, t}^i] \nonumber\\ &-(a_i^i(s) - a_i^i(u)) \mathbb{E}[\tilde{B}_s^i \tilde{B}_{s, u}^i] -(a_i^i(t) - a_i^i(u)) \mathbb{E}[\tilde{B}_t^i \tilde{B}_{u, t}^i]. \end{align} $$
Since the other terms can be estimated similarly, we only estimate
![]() $(a_i^i(t) - a_i^i(u)) \mathbb {E}[\tilde {B}_t^i \tilde {B}_{s, t}^i]$
. By Lemma 3.2,
$(a_i^i(t) - a_i^i(u)) \mathbb {E}[\tilde {B}_t^i \tilde {B}_{s, t}^i]$
. By Lemma 3.2,
Now we estimate
![]() $ \lvert {a_i^i(t) - a_i^i(u)} \rvert $
. Recall
$ \lvert {a_i^i(t) - a_i^i(u)} \rvert $
. Recall
![]() $a_i^i(s) = G_i(Y_s, (2H)^{-\frac {1}{2}} (s - v)^H)$
,
$a_i^i(s) = G_i(Y_s, (2H)^{-\frac {1}{2}} (s - v)^H)$
,
 $$ \begin{align*} (2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{m^j} G_i(m, \sigma) &= - \delta_{ij} \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x \\& \quad + \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i x^j e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x, \\(2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{\sigma} G(m, \sigma) &= -(d+2) \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x \\& \quad + \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i \lvert {x} \rvert ^2 e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x. \end{align*} $$
$$ \begin{align*} (2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{m^j} G_i(m, \sigma) &= - \delta_{ij} \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x \\& \quad + \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i x^j e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x, \\(2 \pi)^{\frac{d}{2}} \sigma^2 \partial_{\sigma} G(m, \sigma) &= -(d+2) \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x \\& \quad + \int_{\mathbb{R}^d} [f^i(m + \sigma x) - f^i(m)] x^i \lvert {x} \rvert ^2 e^{-\frac{ \lvert {x} \rvert ^2}{2}} \, \mathrm{d} x. \end{align*} $$
If
![]() $H \leq \frac {1}{4}$
, we can replace
$H \leq \frac {1}{4}$
, we can replace
![]() $f^i(m + \sigma x) - f^i(m)$
by
$f^i(m + \sigma x) - f^i(m)$
by
 $$ \begin{align*} f^i(m + \sigma x) - f^i(m) - \sum_{k=1}^d \partial_k f^i(m) \sigma x^k. \end{align*} $$
$$ \begin{align*} f^i(m + \sigma x) - f^i(m) - \sum_{k=1}^d \partial_k f^i(m) \sigma x^k. \end{align*} $$
Therefore,
This yields
and hence
Therefore, we obtain
By (3.10) and (3.12), we conclude
 $$ \begin{align*} \lVert {\mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v]} \rVert _{L_m(\mathbb{P})} &\lesssim \lVert {f} \rVert _{C^{\gamma} } [(s - v)^{(1 + \gamma) H - 2} (t - s)^2 + (s - v)^{(\gamma - 1) H - 1} (t - s)^{1 + 2H}] \\ &\lesssim \lVert {f} \rVert _{C^{\gamma} } (s - v)^{(\gamma - 1) H - 1} (t - s)^{1 + 2H} \end{align*} $$
$$ \begin{align*} \lVert {\mathbb{E}[\delta A_{s, u, t} \vert \mathcal{F}_v]} \rVert _{L_m(\mathbb{P})} &\lesssim \lVert {f} \rVert _{C^{\gamma} } [(s - v)^{(1 + \gamma) H - 2} (t - s)^2 + (s - v)^{(\gamma - 1) H - 1} (t - s)^{1 + 2H}] \\ &\lesssim \lVert {f} \rVert _{C^{\gamma} } (s - v)^{(\gamma - 1) H - 1} (t - s)^{1 + 2H} \end{align*} $$
if
![]() $t-s \leq s- v$
. Therefore, we can apply Theorem 1.1 with
$t-s \leq s- v$
. Therefore, we can apply Theorem 1.1 with
4. Local times of fractional Brownian motions
In this section, we set
![]() $d = 1$
, and we are interested in local times of fractional Brownian motions. In case of a Brownian motion W, or, more generally, semimartingales as discussed in Łochowski et al. [Reference Łochowski, Obłój, Prömel and Siorpaes28], there are three major methods to construct its local time.
$d = 1$
, and we are interested in local times of fractional Brownian motions. In case of a Brownian motion W, or, more generally, semimartingales as discussed in Łochowski et al. [Reference Łochowski, Obłój, Prömel and Siorpaes28], there are three major methods to construct its local time.
-
1. Via occupation measure. The local time
 $L_T^W(\cdot )$
of W is defined as the density with respect to the Lebesgue measure of Heuristically,
$L_T^W(\cdot )$
of W is defined as the density with respect to the Lebesgue measure of Heuristically, where
where $$ \begin{align*} L_T^W(a) = \int_0^T \delta(W_s - a) \, \mathrm{d} s, \end{align*} $$
$$ \begin{align*} L_T^W(a) = \int_0^T \delta(W_s - a) \, \mathrm{d} s, \end{align*} $$
 $\delta $
is Dirac’s delta function concentrated at
$\delta $
is Dirac’s delta function concentrated at
 $0$
.
$0$
.
-
2. Via discretization. The local time
 $L_T^W(a)$
is defined by where
$L_T^W(a)$
is defined by where
 $\pi $
is a partition of
$\pi $
is a partition of
 $[0, T]$
and the convergence is in probability. This representation of the local time is often used in the pathwise stochastic calculus (see Wuermli [Reference Wuermli and Föllmer39], Perkowski and Prömel [Reference Perkowski and Prömel36], Davis et al. [Reference Davis, Obłój and Siorpaes12], Cont and Perkowski [Reference Cont and Perkowski9], and Kim [Reference Kim23]).
$[0, T]$
and the convergence is in probability. This representation of the local time is often used in the pathwise stochastic calculus (see Wuermli [Reference Wuermli and Föllmer39], Perkowski and Prömel [Reference Perkowski and Prömel36], Davis et al. [Reference Davis, Obłój and Siorpaes12], Cont and Perkowski [Reference Cont and Perkowski9], and Kim [Reference Kim23]).
-
3. Via numbers of interval crossing. For
 $n \in \mathbb {N}$
, we set
$n \in \mathbb {N}$
, we set  and inductively Then, the local time
and inductively Then, the local time
 $L_T^W(a)$
is defined by where the convergence holds almost surely. See the monograph [Reference Mörters and Peres32] for the Brownian motion. For general semimartingales, see El Karoui [Reference El Karoui22], Lemieux [Reference Lemieux27], and [Reference Łochowski, Obłój, Prömel and Siorpaes28].
$L_T^W(a)$
is defined by where the convergence holds almost surely. See the monograph [Reference Mörters and Peres32] for the Brownian motion. For general semimartingales, see El Karoui [Reference El Karoui22], Lemieux [Reference Lemieux27], and [Reference Łochowski, Obłój, Prömel and Siorpaes28].
In case of a fractional Brownian motion, the construction of its local time via the method 1 is well-known, see the survey [Reference Geman and Horowitz15] and the monograph [Reference Biagini, Hu, Øksendal and Zhang5]. In contrast, there are few results in the literature in which the local time of a fractional Brownian motion is constructed via the method 2 or 3. Because of this, the construction of the local time via the method 3 was stated as a conjecture in [Reference Cont and Perkowski9]. We are aware of only two results in this direction. One is the work [Reference Azaïs4] of Azaïs, who proves Corollary 4.8 below. The other is the work [Reference Mukeru33] of Mukeru, who proves that the local time
![]() $L_T(a)$
of a fractional Brownian motion with Hurst parameter less than
$L_T(a)$
of a fractional Brownian motion with Hurst parameter less than
![]() $\frac {1}{2}$
is represented as
$\frac {1}{2}$
is represented as
Our goal in this section is to give new representations of the local times of fractional Brownian motions in the spirit of the method (b) along deterministic partitions. The representation in Corollary 4.9 is compatible with [Reference Cont and Perkowski9, Definition 3.1].
Theorem 4.1. Let B be an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
$(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
![]() $H \neq \frac {1}{2}$
, in the sense of Definition 3.1. Let
$H \neq \frac {1}{2}$
, in the sense of Definition 3.1. Let
![]() $m \in [2, \infty )$
,
$m \in [2, \infty )$
,
![]() $\gamma \in [0, \infty )$
, and
$\gamma \in [0, \infty )$
, and
![]() $a \in \mathbb {R}$
. If
$a \in \mathbb {R}$
. If
![]() $H> \frac {1}{2}$
, assume that m satisfies
$H> \frac {1}{2}$
, assume that m satisfies
Then, as
![]() $ \lvert {\pi } \rvert \to 0$
, where
$ \lvert {\pi } \rvert \to 0$
, where
![]() $\pi $
is a partition of
$\pi $
is a partition of
![]() $[0, T]$
, the family of
$[0, T]$
, the family of
 $$ \begin{align*} \sum_{[s, t] \in \pi, B_s < a < B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} \end{align*} $$
$$ \begin{align*} \sum_{[s, t] \in \pi, B_s < a < B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} \end{align*} $$
converges in
![]() $L_m(\mathbb {P})$
to
$L_m(\mathbb {P})$
to
![]() $\mathfrak {c}_{H, \gamma } L_T(a)$
, where
$\mathfrak {c}_{H, \gamma } L_T(a)$
, where
![]() $L_T(a)$
is the local time of B at level a and
$L_T(a)$
is the local time of B at level a and

Furthermore, we have
 $$ \begin{align} \lim_{ \lvert {\pi} \rvert \to 0} \mathbb{E}\Big[\int_{\mathbb{R}} \Big\lvert\mathfrak{c}_{H, \gamma} L_T(x) - \sum_{[s, t] \in \pi, B_s < x < B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma}\Big\rvert^m \, \mathrm{d} x \Big]= 0. \end{align} $$
$$ \begin{align} \lim_{ \lvert {\pi} \rvert \to 0} \mathbb{E}\Big[\int_{\mathbb{R}} \Big\lvert\mathfrak{c}_{H, \gamma} L_T(x) - \sum_{[s, t] \in \pi, B_s < x < B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma}\Big\rvert^m \, \mathrm{d} x \Big]= 0. \end{align} $$
Remark 4.2. A similar result holds for a Brownian motion (
![]() $H = \frac {1}{2}$
). However, we omit a proof since it is easier but requires a special treatment.
$H = \frac {1}{2}$
). However, we omit a proof since it is easier but requires a special treatment.
Remark 4.3. We can similarly prove
 $$ \begin{align*} \lim_{ \lvert {\pi} \rvert \to 0} \sum_{[s, t] \in \pi, B_s> a > B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} = \mathfrak{c}_{H, \gamma} L_T(a). \end{align*} $$
$$ \begin{align*} \lim_{ \lvert {\pi} \rvert \to 0} \sum_{[s, t] \in \pi, B_s> a > B_t} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} = \mathfrak{c}_{H, \gamma} L_T(a). \end{align*} $$
Consequently,
 $$ \begin{align*} \lim_{ \lvert {\pi} \rvert \to 0} \sum_{[s, t] \in \pi, \min\{B_s, B_t\} < a < \max\{B_s, B_t\}} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} = 2 \mathfrak{c}_{H, \gamma} L_T(a), \end{align*} $$
$$ \begin{align*} \lim_{ \lvert {\pi} \rvert \to 0} \sum_{[s, t] \in \pi, \min\{B_s, B_t\} < a < \max\{B_s, B_t\}} (t-s)^{1 - (1 + \gamma)H} \lvert {B_t - B_s} \rvert ^{\gamma} = 2 \mathfrak{c}_{H, \gamma} L_T(a), \end{align*} $$
where the convergence is in
![]() $L_m(\mathbb {P})$
.
$L_m(\mathbb {P})$
.
Proof. We will not write down dependence on H,
![]() $\gamma $
, and m. Without loss of generality, we can assume
$\gamma $
, and m. Without loss of generality, we can assume
![]() $\mathbb {E}[B(0)] = 0$
. To apply Theorem 1.1 (for
$\mathbb {E}[B(0)] = 0$
. To apply Theorem 1.1 (for
![]() $H < \frac {1}{2}$
) or Corollary 2.7 (for
$H < \frac {1}{2}$
) or Corollary 2.7 (for
![]() $H> \frac {1}{2}$
), respectively, we set
$H> \frac {1}{2}$
), respectively, we set
If we set ![]() , it suffices to show that the estimates (1.10) and (1.11) are satisfied for
, it suffices to show that the estimates (1.10) and (1.11) are satisfied for
![]() $H < \frac {1}{2}$
, and that the estimates (2.14), (2.15), and (2.16) are satisfied for
$H < \frac {1}{2}$
, and that the estimates (2.14), (2.15), and (2.16) are satisfied for
![]() $H> \frac {1}{2}$
. Since the proof is rather long, we split the main arguments into three lemmas.
$H> \frac {1}{2}$
. Since the proof is rather long, we split the main arguments into three lemmas.
Lemma 4.4. We have
 $$ \begin{align*} \lVert {A_{s, t}} \rVert _{L_m(\mathbb{P})} \lesssim_T \begin{cases} \lvert {t-s} \rvert ^{1 - H} f_H(a), & \text{for all } H \in (0, 1), \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}} f_H(a), & \text{if } H> \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} \lVert {A_{s, t}} \rVert _{L_m(\mathbb{P})} \lesssim_T \begin{cases} \lvert {t-s} \rvert ^{1 - H} f_H(a), & \text{for all } H \in (0, 1), \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}} f_H(a), & \text{if } H> \frac{1}{2}, \end{cases} \end{align*} $$
where in either case there exists a constant
![]() $c = c(H)> 0$
, such that
$c = c(H)> 0$
, such that
 $$ \begin{align} \lvert {f_H(a)} \rvert \leq \exp\Big(-\frac{c a^2}{m (\mathbb{E}[B(0)^2] + T^{2H})} \Big), \quad \forall a \in \mathbb{R}. \end{align} $$
$$ \begin{align} \lvert {f_H(a)} \rvert \leq \exp\Big(-\frac{c a^2}{m (\mathbb{E}[B(0)^2] + T^{2H})} \Big), \quad \forall a \in \mathbb{R}. \end{align} $$
Remark 4.5. Due to (4.1), the exponent
![]() $1 + \frac {H}{m} - H$
is greater than
$1 + \frac {H}{m} - H$
is greater than
![]() $\frac {1}{2}$
.
$\frac {1}{2}$
.
Proof. We have
 $$ \begin{align*} \lVert {A_{s,t}} \rVert _{L_m(\mathbb{P})} &\leq (t-s)^{1 - (1 + \gamma)H} \lVert { \lvert {B_t - B_s} \rvert ^{2\gamma}} \rVert _{L_m(\mathbb{P})}^{\frac{1}{2}} \mathbb{P}(B_s < a < B_t)^{\frac{1}{2m}} \\ &\lesssim \lvert {t-s} \rvert ^{1-H} e^{- \frac{a^2}{4 m c_H (\mathbb{E}[B(0)^2] + T^{2H})}}. \end{align*} $$
$$ \begin{align*} \lVert {A_{s,t}} \rVert _{L_m(\mathbb{P})} &\leq (t-s)^{1 - (1 + \gamma)H} \lVert { \lvert {B_t - B_s} \rvert ^{2\gamma}} \rVert _{L_m(\mathbb{P})}^{\frac{1}{2}} \mathbb{P}(B_s < a < B_t)^{\frac{1}{2m}} \\ &\lesssim \lvert {t-s} \rvert ^{1-H} e^{- \frac{a^2}{4 m c_H (\mathbb{E}[B(0)^2] + T^{2H})}}. \end{align*} $$
Now we consider the case
![]() $H> \frac {1}{2}$
.
$H> \frac {1}{2}$
.
Set
Since
![]() $H> \frac {1}{2}$
,
$H> \frac {1}{2}$
,
![]() $\chi _1 \geq 0$
, and
$\chi _1 \geq 0$
, and
Then, if X and Y are two independent standard normal distributions on
![]() $\mathbb {R}$
, we have
$\mathbb {R}$
, we have
Therefore, if we set
We first estimate ![]() . Using the estimate
. Using the estimate
we have
Then,

where in the third line we applied
And,

Therefore,

We now estimate ![]() . Similarly to (4.5), we have
. Similarly to (4.5), we have
and similarly

Therefore, we conclude
 $$ \begin{align*} \lVert {\hat{A}_{s, t}} \rVert _{L_m(\mathbb{P})} \lesssim \Big(\frac{\chi_1 + \chi_2}{\chi_0} \Big)^{\frac{1}{m}} (\chi_1^{\gamma} + \chi_2^{\gamma}) e^{-\frac{a^2}{4 m (\chi_0^2 + \chi_2^2) }} \lesssim_T \chi_0^{-\frac{1}{m}} \lvert {t-s} \rvert ^{(\gamma + \frac{1}{m})H} e^{-\frac{a^2}{4 m (\mathbb{E}[B(0)^2] + T^{2H}) }}, \end{align*} $$
$$ \begin{align*} \lVert {\hat{A}_{s, t}} \rVert _{L_m(\mathbb{P})} \lesssim \Big(\frac{\chi_1 + \chi_2}{\chi_0} \Big)^{\frac{1}{m}} (\chi_1^{\gamma} + \chi_2^{\gamma}) e^{-\frac{a^2}{4 m (\chi_0^2 + \chi_2^2) }} \lesssim_T \chi_0^{-\frac{1}{m}} \lvert {t-s} \rvert ^{(\gamma + \frac{1}{m})H} e^{-\frac{a^2}{4 m (\mathbb{E}[B(0)^2] + T^{2H}) }}, \end{align*} $$
which completes the proof of the lemma.
Recall the Mandelbrot–Van Ness representation (3.1), and recall that W is an
![]() $(\mathcal {F}_t)_{t \in \mathbb {R}}$
-Brownian motion.
$(\mathcal {F}_t)_{t \in \mathbb {R}}$
-Brownian motion.
Lemma 4.6. Let
![]() $v < s < t$
, and set
$v < s < t$
, and set
If
![]() $\frac {t-s}{s-v}$
is sufficiently small, then
$\frac {t-s}{s-v}$
is sufficiently small, then
 $$ \begin{align*} \mathbb{E}[A_{s, t} \vert \mathcal{F}_v] = \mathfrak{c}_{H, \gamma} \frac{e^{-\frac{(Y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s}(t-s) + R, \end{align*} $$
$$ \begin{align*} \mathbb{E}[A_{s, t} \vert \mathcal{F}_v] = \mathfrak{c}_{H, \gamma} \frac{e^{-\frac{(Y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s}(t-s) + R, \end{align*} $$
where for some
![]() $c = c(H, m)> 0$
,
$c = c(H, m)> 0$
,
Proof. As in the proof of Proposition 3.3, for
![]() $s> v$
, we set
$s> v$
, we set
and we write ![]() under the conditioning of
under the conditioning of
![]() $\mathcal {F}_v$
. Then, recalling
$\mathcal {F}_v$
. Then, recalling
![]() $\hat {A}_{s,t}$
from (4.4), we have
$\hat {A}_{s,t}$
from (4.4), we have
To compute, we set
By Lemma 3.2,
and
We have the decomposition
where the second term is independent of
![]() $\tilde {B}_{s}$
. If we set
$\tilde {B}_{s}$
. If we set
and if we write X and Y for two independent standard normal distributions, then the quantity (4.6) equals to

where

For a while, assume
![]() $\gamma> 0$
. Using the estimate
$\gamma> 0$
. Using the estimate
we have

We set

We have for
![]() $y> 0$
$y> 0$
 $$ \begin{align*} I_{\gamma}'(y) = - \lvert {y} \rvert ^{\gamma} \frac{e^{-\frac{y^2}{2}}}{\sqrt{2 \pi}}, \end{align*} $$
$$ \begin{align*} I_{\gamma}'(y) = - \lvert {y} \rvert ^{\gamma} \frac{e^{-\frac{y^2}{2}}}{\sqrt{2 \pi}}, \end{align*} $$
and if
![]() $q \geq 2 \lvert {p} \rvert $
and
$q \geq 2 \lvert {p} \rvert $
and
![]() $y \in [q - \lvert {p} \rvert , q + \lvert {p} \rvert ]$
, then
$y \in [q - \lvert {p} \rvert , q + \lvert {p} \rvert ]$
, then
Therefore, if
![]() $q \geq 2 \lvert {p} \rvert $
, we have
$q \geq 2 \lvert {p} \rvert $
, we have
Therefore,

When
![]() $\gamma = 0$
, we have
$\gamma = 0$
, we have
and thus (4.9) holds for
![]() $\gamma = 0$
. We estimate the expectation (with respect to Y) of each term.
$\gamma = 0$
. We estimate the expectation (with respect to Y) of each term.
We have

By using the estimate
we obtain

Next, we estimate the second term of (4.9). We have for
![]() $n \in \{0, 1\}$
,
$n \in \{0, 1\}$
,
 $$ \begin{align*} \mathbb{E}[ \lvert {Y} \rvert ^n e^{-\frac{q(Y)^2}{16}}] &= \frac{\kappa_{s, t}}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \int_{\mathbb{R}} \left\lvert {\frac{\kappa_{s,t} z + a - y_{s,t} - y_s}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} } \right\rvert ^n e^{-\frac{z^2}{16}} \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} \Big(\frac{\kappa_{s,t} z + a - y_{s,t} - y_s}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \Big)^2} \, \mathrm{d} z \\&\lesssim \frac{\kappa_{s, t}}{\sigma_s + \sigma_s^{-1} \rho_{s, t}} \Big(\frac{\kappa_{s,t} + \lvert {a - y_t} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \Big)^n \\& \quad \times \Big[ e^{-\frac{(y_t - a)^2}{2 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}} + e^{-\frac{(y_t - a)^2}{16 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}} \frac{\kappa_{s,t}}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} + e^{-\frac{(y_t - a)^2}{32 \kappa_{s,t}^2}} \Big], \end{align*} $$
$$ \begin{align*} \mathbb{E}[ \lvert {Y} \rvert ^n e^{-\frac{q(Y)^2}{16}}] &= \frac{\kappa_{s, t}}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \int_{\mathbb{R}} \left\lvert {\frac{\kappa_{s,t} z + a - y_{s,t} - y_s}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} } \right\rvert ^n e^{-\frac{z^2}{16}} \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} \Big(\frac{\kappa_{s,t} z + a - y_{s,t} - y_s}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \Big)^2} \, \mathrm{d} z \\&\lesssim \frac{\kappa_{s, t}}{\sigma_s + \sigma_s^{-1} \rho_{s, t}} \Big(\frac{\kappa_{s,t} + \lvert {a - y_t} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s,t}} \Big)^n \\& \quad \times \Big[ e^{-\frac{(y_t - a)^2}{2 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}} + e^{-\frac{(y_t - a)^2}{16 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}} \frac{\kappa_{s,t}}{\sigma_s + \sigma_s^{-1} \rho_{s,t}} + e^{-\frac{(y_t - a)^2}{32 \kappa_{s,t}^2}} \Big], \end{align*} $$
where we applied (4.10) to get the last inequality. Therefore, we obtain
 $$ \begin{align*} \mathbb{E}[ \lvert {p(Y)} \rvert e^{-\frac{q(Y)^2}{16}}] \lesssim \Big(\frac{ \lvert {y_{s, t}} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s, t}} + \sigma_s^{-1} \lvert {\rho_{s, t}} \rvert \frac{\kappa_{s,t} + \lvert {y_t - a} \rvert }{(\sigma_s + \sigma_s^{-1} \rho_{s,t})^2} \Big) e^{-\frac{(y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}. \end{align*} $$
$$ \begin{align*} \mathbb{E}[ \lvert {p(Y)} \rvert e^{-\frac{q(Y)^2}{16}}] \lesssim \Big(\frac{ \lvert {y_{s, t}} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s, t}} + \sigma_s^{-1} \lvert {\rho_{s, t}} \rvert \frac{\kappa_{s,t} + \lvert {y_t - a} \rvert }{(\sigma_s + \sigma_s^{-1} \rho_{s,t})^2} \Big) e^{-\frac{(y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}. \end{align*} $$
Finally, we estimate the third term of (4.9). Suppose that
![]() $\frac {t-s}{s-v}$
is so small that
$\frac {t-s}{s-v}$
is so small that
![]() $ \lvert {\sigma _s^{-2} \rho _{s, t}} \rvert \leq \frac {1}{24}$
, and then we have
$ \lvert {\sigma _s^{-2} \rho _{s, t}} \rvert \leq \frac {1}{24}$
, and then we have

Hence,

and
This gives the estimate of the third term.
In summary, recalling that
![]() $\mathbb {E}[\hat {A}_{s,t} \vert \mathcal {F}_v]$
equals to (4.8), we obtain
$\mathbb {E}[\hat {A}_{s,t} \vert \mathcal {F}_v]$
equals to (4.8), we obtain
 $$ \begin{align*} \mathbb{E}[\hat{A}_{s, t} \vert \mathcal{F}_v] = \frac{\kappa_{s,t}^{\gamma+1} e^{-\frac{(Y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s} \int_0^{\infty} \lvert {x} \rvert ^{\gamma+1} \frac{e^{-\frac{x^2}{2}}}{\sqrt{2 \pi}} \, \mathrm{d} x + R_1, \end{align*} $$
$$ \begin{align*} \mathbb{E}[\hat{A}_{s, t} \vert \mathcal{F}_v] = \frac{\kappa_{s,t}^{\gamma+1} e^{-\frac{(Y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s} \int_0^{\infty} \lvert {x} \rvert ^{\gamma+1} \frac{e^{-\frac{x^2}{2}}}{\sqrt{2 \pi}} \, \mathrm{d} x + R_1, \end{align*} $$
where

Let us estimate
![]() $ \lVert {R_1} \rVert _{L_m(\mathbb {P})}$
. Recall that
$ \lVert {R_1} \rVert _{L_m(\mathbb {P})}$
. Recall that
and
 $$ \begin{align*} \lvert {\rho_{s, t}} \rvert \lesssim \begin{cases} \lvert {s - v} \rvert ^{2H -1} \lvert {t-s} \rvert , \quad &H> \frac{1}{2}, \\ \lvert {t-s} \rvert ^{2H}, \quad &H < \frac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} \lvert {\rho_{s, t}} \rvert \lesssim \begin{cases} \lvert {s - v} \rvert ^{2H -1} \lvert {t-s} \rvert , \quad &H> \frac{1}{2}, \\ \lvert {t-s} \rvert ^{2H}, \quad &H < \frac{1}{2}. \end{cases} \end{align*} $$
We have the estimate (3.4) of
![]() $Y_{s, t}$
. Since
$Y_{s, t}$
. Since
there is a constant
![]() $c = c(H)> 0$
, such that
$c = c(H)> 0$
, such that
Therefore, for some constant
![]() $c_1 = c(H, m)>0$
,
$c_1 = c(H, m)>0$
,
 $$ \begin{align*} &\lVert {\kappa_{s,t}^{\gamma} \frac{ \lvert {Y_{s, t}} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s, t}} e^{-\frac{(Y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} \kappa_{s,t}^{\gamma} \sigma_s^{-1 + \frac{1}{m}} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert e^{-\frac{c_1 a^2}{\chi_s^2}} \lesssim \chi_s^{-\frac{1}{m}} \lvert {s-v} \rvert ^{\frac{H}{m} - 1} \lvert {t-s} \rvert ^{\gamma H + 1}e^{-\frac{c_1 a^2}{\chi_s^2}}, \end{align*} $$
$$ \begin{align*} &\lVert {\kappa_{s,t}^{\gamma} \frac{ \lvert {Y_{s, t}} \rvert }{\sigma_s + \sigma_s^{-1} \rho_{s, t}} e^{-\frac{(Y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} \kappa_{s,t}^{\gamma} \sigma_s^{-1 + \frac{1}{m}} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert e^{-\frac{c_1 a^2}{\chi_s^2}} \lesssim \chi_s^{-\frac{1}{m}} \lvert {s-v} \rvert ^{\frac{H}{m} - 1} \lvert {t-s} \rvert ^{\gamma H + 1}e^{-\frac{c_1 a^2}{\chi_s^2}}, \end{align*} $$
 $$ \begin{align*} & \lVert { \kappa_{s,t}^{\gamma} \sigma_s^{-1} \lvert {\rho_{s, t}} \rvert \frac{\kappa_{s,t} + \lvert {Y_t - a} \rvert }{(\sigma_s + \sigma_s^{-1} \rho_{s,t})^2} e^{-\frac{(Y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}} \rVert _{L_m(\mathbb{P})} \lesssim \chi_s^{-\frac{1}{m}} \kappa_{s, t}^{\gamma} \sigma_s^{-2 + \frac{1}{m}} \lvert {\rho_{s,t}} \rvert e^{-\frac{c_1 a^2}{\chi_s^2}} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{-1 + \frac{H}{m}} \lvert {t-s} \rvert ^{\gamma H + 1}, \quad &H> \frac{1}{2}, \\\lvert {s-v} \rvert ^{-2H + \frac{H}{m} } \lvert {t-s} \rvert ^{(\gamma+2)H}, & H < \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} & \lVert { \kappa_{s,t}^{\gamma} \sigma_s^{-1} \lvert {\rho_{s, t}} \rvert \frac{\kappa_{s,t} + \lvert {Y_t - a} \rvert }{(\sigma_s + \sigma_s^{-1} \rho_{s,t})^2} e^{-\frac{(Y_t - a)^2}{32 (\sigma_s + \sigma_s^{-1} \rho_{s,t})^2}}} \rVert _{L_m(\mathbb{P})} \lesssim \chi_s^{-\frac{1}{m}} \kappa_{s, t}^{\gamma} \sigma_s^{-2 + \frac{1}{m}} \lvert {\rho_{s,t}} \rvert e^{-\frac{c_1 a^2}{\chi_s^2}} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{-1 + \frac{H}{m}} \lvert {t-s} \rvert ^{\gamma H + 1}, \quad &H> \frac{1}{2}, \\\lvert {s-v} \rvert ^{-2H + \frac{H}{m} } \lvert {t-s} \rvert ^{(\gamma+2)H}, & H < \frac{1}{2}, \end{cases} \end{align*} $$
 $$ \begin{align*} &\lVert { \kappa_{s,t}^{\gamma} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s - a} \rvert ) } \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-1} \kappa_{s,t}^{\gamma}(\sigma_s^{\frac{1}{m} - 1} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert + \sigma_s^{-2+\frac{1}{m}} \lvert {\rho_{s,t}} \rvert ) e^{-\frac{c_1 a^2}{\chi_s^2}}\\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{\frac{H}{m} - 1} \lvert {t-s} \rvert ^{2-H}, &H> \frac{1}{2}, \\ ( \lvert {s-v} \rvert ^{\frac{H}{m} -1} \lvert {t-s} \rvert ^{2-H} + \lvert {s-v} \rvert ^{(-2+\frac{1}{m})H} \lvert {t-s} \rvert ^{1+H}), &H < \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} &\lVert { \kappa_{s,t}^{\gamma} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s - a} \rvert ) } \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-1} \kappa_{s,t}^{\gamma}(\sigma_s^{\frac{1}{m} - 1} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert + \sigma_s^{-2+\frac{1}{m}} \lvert {\rho_{s,t}} \rvert ) e^{-\frac{c_1 a^2}{\chi_s^2}}\\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{\frac{H}{m} - 1} \lvert {t-s} \rvert ^{2-H}, &H> \frac{1}{2}, \\ ( \lvert {s-v} \rvert ^{\frac{H}{m} -1} \lvert {t-s} \rvert ^{2-H} + \lvert {s-v} \rvert ^{(-2+\frac{1}{m})H} \lvert {t-s} \rvert ^{1+H}), &H < \frac{1}{2}, \end{cases} \end{align*} $$
 $$ \begin{align*} &\lVert { \lvert {Y_{s,t}} \rvert ^{\gamma} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s - a} \rvert ) } \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \sigma_s^{-1} \lVert { \lvert {Y_{s,t}} \rvert ^{\gamma + 1} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}}} \rVert _{L_m(\mathbb{P})} + \sigma_s^{-2} \rho_{s, t} \lVert { \lvert {Y_{s,t}} \rvert ^{\gamma} e^{-\frac{(Y_s - a)^2}{6 \sigma_s^2}}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \big[ \sigma_s^{\frac{1}{m} - 1} \lvert {s-v} \rvert ^{(\gamma +1)(H - 1)} \lvert {t-s} \rvert ^{(\gamma + 1) } \\& \qquad\quad\qquad\qquad + \sigma_s^{-2+\frac{1}{m}} \lvert {\rho_{s,t}} \rvert \lvert {v-s} \rvert ^{\gamma(H-1)} \lvert {t-s} \rvert ^{\gamma} \big]\\& \quad \lesssim_{H, m} \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \\& \qquad \times \begin{cases} \lvert {s-v} \rvert ^{(\gamma+\frac{1}{m})H - (\gamma+1)} \lvert {t-s} \rvert ^{\gamma+1}, &H> \frac{1}{2}, \\ ( \lvert {s-v} \rvert ^{(\gamma+\frac{1}{m})H - (\gamma+1)} \lvert {t-s} \rvert ^{\gamma+1} + \lvert {s-v} \rvert ^{(-2 + \frac{1}{m} + \gamma)H - \gamma} \lvert {t-s} \rvert ^{\gamma+ 2H}), &H< \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} &\lVert { \lvert {Y_{s,t}} \rvert ^{\gamma} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s - a} \rvert ) } \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \sigma_s^{-1} \lVert { \lvert {Y_{s,t}} \rvert ^{\gamma + 1} e^{-\frac{(Y_s - a)^2}{5 \sigma_s^2}}} \rVert _{L_m(\mathbb{P})} + \sigma_s^{-2} \rho_{s, t} \lVert { \lvert {Y_{s,t}} \rvert ^{\gamma} e^{-\frac{(Y_s - a)^2}{6 \sigma_s^2}}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \big[ \sigma_s^{\frac{1}{m} - 1} \lvert {s-v} \rvert ^{(\gamma +1)(H - 1)} \lvert {t-s} \rvert ^{(\gamma + 1) } \\& \qquad\quad\qquad\qquad + \sigma_s^{-2+\frac{1}{m}} \lvert {\rho_{s,t}} \rvert \lvert {v-s} \rvert ^{\gamma(H-1)} \lvert {t-s} \rvert ^{\gamma} \big]\\& \quad \lesssim_{H, m} \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \\& \qquad \times \begin{cases} \lvert {s-v} \rvert ^{(\gamma+\frac{1}{m})H - (\gamma+1)} \lvert {t-s} \rvert ^{\gamma+1}, &H> \frac{1}{2}, \\ ( \lvert {s-v} \rvert ^{(\gamma+\frac{1}{m})H - (\gamma+1)} \lvert {t-s} \rvert ^{\gamma+1} + \lvert {s-v} \rvert ^{(-2 + \frac{1}{m} + \gamma)H - \gamma} \lvert {t-s} \rvert ^{\gamma+ 2H}), &H< \frac{1}{2}, \end{cases} \end{align*} $$
 $$ \begin{align*} &\lVert { (\sigma_s^{-1} \rho_{s,t})^{\gamma} e^{-\frac{Y_s^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s} \rvert ) } \rVert _{L_m(\mathbb{P})} \\&\quad\lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \big[ \sigma_s^{\frac{1}{m} - 1 - \gamma} \lvert {\rho_{s,t}} \rvert ^{\gamma} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert + \sigma_s^{-2 + \frac{1}{m} - \gamma} \lvert {\rho_{s,t}} \rvert ^{\gamma+ 1} \big] \\&\quad\lesssim \chi_{s}^{-\frac{1}{m}}e^{-\frac{c_1 a^2}{\chi_s^2}} \\&\qquad\times \begin{cases} \lvert {s-v} \rvert ^{(\gamma + \frac{1}{m})H - (\gamma + 1)} \lvert {t-s} \rvert ^{\gamma + 1}, & H> \frac{1}{2}, \\ \lvert {s-v} \rvert ^{(\frac{1}{m} - \gamma)H - 1} \lvert {t-s} \rvert ^{1+ 2 H \gamma} + \lvert {s-v} \rvert ^{(-2 + \frac{1}{m} - \gamma)H} \lvert {t-s} \rvert ^{2H(\gamma+1)}, & H < \frac{1}{2}, \\ \end{cases} \end{align*} $$
$$ \begin{align*} &\lVert { (\sigma_s^{-1} \rho_{s,t})^{\gamma} e^{-\frac{Y_s^2}{5 \sigma_s^2}} (\sigma_s^{-1} \lvert {Y_{s,t}} \rvert + \sigma_s^{-3} \lvert {\rho_{s,t}} \rvert \lvert {Y_s} \rvert ) } \rVert _{L_m(\mathbb{P})} \\&\quad\lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \big[ \sigma_s^{\frac{1}{m} - 1 - \gamma} \lvert {\rho_{s,t}} \rvert ^{\gamma} \lvert {s-v} \rvert ^{H-1} \lvert {t-s} \rvert + \sigma_s^{-2 + \frac{1}{m} - \gamma} \lvert {\rho_{s,t}} \rvert ^{\gamma+ 1} \big] \\&\quad\lesssim \chi_{s}^{-\frac{1}{m}}e^{-\frac{c_1 a^2}{\chi_s^2}} \\&\qquad\times \begin{cases} \lvert {s-v} \rvert ^{(\gamma + \frac{1}{m})H - (\gamma + 1)} \lvert {t-s} \rvert ^{\gamma + 1}, & H> \frac{1}{2}, \\ \lvert {s-v} \rvert ^{(\frac{1}{m} - \gamma)H - 1} \lvert {t-s} \rvert ^{1+ 2 H \gamma} + \lvert {s-v} \rvert ^{(-2 + \frac{1}{m} - \gamma)H} \lvert {t-s} \rvert ^{2H(\gamma+1)}, & H < \frac{1}{2}, \\ \end{cases} \end{align*} $$
and finally

After this long calculation, we conclude
 $$ \begin{align} \lVert {R_1} \rVert _{L_m(\mathbb{P})} \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \Big(\frac{t-s}{s-v} \Big)^{\min\{1, 2H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{(\gamma + \frac{1}{m}) H} \end{align} $$
$$ \begin{align} \lVert {R_1} \rVert _{L_m(\mathbb{P})} \lesssim \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \Big(\frac{t-s}{s-v} \Big)^{\min\{1, 2H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{(\gamma + \frac{1}{m}) H} \end{align} $$
if
![]() $\frac {t-s}{s-v}$
is sufficiently small.
$\frac {t-s}{s-v}$
is sufficiently small.
By (4.7), we have
 $$ \begin{align*} \frac{\kappa_{s,t}^{\gamma+1} e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s} \int_0^{\infty} \lvert {x} \rvert ^{\gamma+1} \frac{e^{-\frac{x^2}{2}}}{\sqrt{2 \pi}} \, \mathrm{d} x = \mathfrak{c}_{H, \gamma} \frac{e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}} \lvert {t-s} \rvert ^{(\gamma+1)H}}{ \sqrt{2 \pi} \sigma_s} + R_2, \end{align*} $$
$$ \begin{align*} \frac{\kappa_{s,t}^{\gamma+1} e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}}}{ \sqrt{2 \pi} \sigma_s} \int_0^{\infty} \lvert {x} \rvert ^{\gamma+1} \frac{e^{-\frac{x^2}{2}}}{\sqrt{2 \pi}} \, \mathrm{d} x = \mathfrak{c}_{H, \gamma} \frac{e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}} \lvert {t-s} \rvert ^{(\gamma+1)H}}{ \sqrt{2 \pi} \sigma_s} + R_2, \end{align*} $$
where
 $$ \begin{align} \lvert {R_2} \rvert \lesssim_H \frac{e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}} }{ \sigma_s} \Big(\frac{t-s}{s-v} \Big)^{2 \min\{H, 1-H\}} \lvert {t-s} \rvert ^{(\gamma+1)H}. \end{align} $$
$$ \begin{align} \lvert {R_2} \rvert \lesssim_H \frac{e^{-\frac{(y_s - a)^2}{2 \sigma_s^2}} }{ \sigma_s} \Big(\frac{t-s}{s-v} \Big)^{2 \min\{H, 1-H\}} \lvert {t-s} \rvert ^{(\gamma+1)H}. \end{align} $$
Therefore,
 $$ \begin{align*} \lVert {R_2} \rVert _{L_m(\mathbb{P})} \lesssim_{H} \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{(\frac{1}{m} + 1)H - 2} \lvert {t-s} \rvert ^{2 + (\gamma - 1) H}, &H> \frac{1}{2},\\ \lvert {s-v} \rvert ^{(\frac{1}{m} - 3)H} \lvert {t-s} \rvert ^{(\gamma + 3) H}, &H < \frac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} \lVert {R_2} \rVert _{L_m(\mathbb{P})} \lesssim_{H} \chi_s^{-\frac{1}{m}} e^{-\frac{c_1 a^2}{\chi_s^2}} \begin{cases} \lvert {s-v} \rvert ^{(\frac{1}{m} + 1)H - 2} \lvert {t-s} \rvert ^{2 + (\gamma - 1) H}, &H> \frac{1}{2},\\ \lvert {s-v} \rvert ^{(\frac{1}{m} - 3)H} \lvert {t-s} \rvert ^{(\gamma + 3) H}, &H < \frac{1}{2}. \end{cases} \end{align*} $$
This completes the proof of the lemma.
Lemma 4.7. We have
 $$ \begin{align} \lVert {L_t(a) - L_s(a)} \rVert _{L_m(\mathbb{P})} \lesssim_T \begin{cases} \lvert {t-s} \rvert ^{1 - H} f_H(a), & \hspace{-2cm}\text{for all } H \in (0, 1), \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}} f_H(a), & \text{if } H> \frac{1}{2}, \end{cases} \end{align} $$
$$ \begin{align} \lVert {L_t(a) - L_s(a)} \rVert _{L_m(\mathbb{P})} \lesssim_T \begin{cases} \lvert {t-s} \rvert ^{1 - H} f_H(a), & \hspace{-2cm}\text{for all } H \in (0, 1), \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}} f_H(a), & \text{if } H> \frac{1}{2}, \end{cases} \end{align} $$
where
![]() $f_H(a)$
satisfies the estimate (4.3). Moreover, if
$f_H(a)$
satisfies the estimate (4.3). Moreover, if
![]() $\frac {t-s}{s-v}$
is sufficiently small, then
$\frac {t-s}{s-v}$
is sufficiently small, then
 $$ \begin{align*} \mathbb{E}[L_t(a) - L_s(a) \vert \mathcal{F}_v] = \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sqrt{2 \pi} \sigma_s} (t-s) + \tilde{R}, \end{align*} $$
$$ \begin{align*} \mathbb{E}[L_t(a) - L_s(a) \vert \mathcal{F}_v] = \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sqrt{2 \pi} \sigma_s} (t-s) + \tilde{R}, \end{align*} $$
where for some
![]() $c = c(H, m)> 0$
,
$c = c(H, m)> 0$
,
Proof. The estimate in (4.15) follows from [Reference Ayache, Wu and Xiao3, (3.38)]. However, since this is not entirely obvious, we sketch here an alternative derivation, which is motivated by [Reference Butkovsky, Lê and Mytnik7]. In view of the formal expression
![]() $L_t(a) = \int _0^t \delta _a(B_r) \, \mathrm {d} r$
, we set
$L_t(a) = \int _0^t \delta _a(B_r) \, \mathrm {d} r$
, we set

We note
![]() $\mathbb {E}[\delta \bar {A}_{s,u,t}(a) \vert \mathcal {F}_s] =0$
. By Lê’s stochastic sewing lemma [Reference Lê24], to prove (4.15), it suffices to show
$\mathbb {E}[\delta \bar {A}_{s,u,t}(a) \vert \mathcal {F}_s] =0$
. By Lê’s stochastic sewing lemma [Reference Lê24], to prove (4.15), it suffices to show
-
• the estimate
 $$ \begin{align*} \lVert {e^{-\frac{ H(Y_s - a)^2}{c_H (r-s)^{2H}}}} \rVert _{L_m(\mathbb{P})} \lesssim_{T} \begin{cases} f_H(a), & H < \frac{1}{2}, \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {r-s} \rvert ^{\frac{H}{m}} f_H(a), & H> \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} \lVert {e^{-\frac{ H(Y_s - a)^2}{c_H (r-s)^{2H}}}} \rVert _{L_m(\mathbb{P})} \lesssim_{T} \begin{cases} f_H(a), & H < \frac{1}{2}, \\ (\mathbb{E}[B(0)^2] + s^{2H})^{-\frac{1}{2m}} \lvert {r-s} \rvert ^{\frac{H}{m}} f_H(a), & H> \frac{1}{2}, \end{cases} \end{align*} $$
-
• and the identity
 $L_t(a) = \lim _{ \lvert {\pi } \rvert \to 0} \sum _{[u,v] \in \pi } \bar {A}_{u, v}(a)$
, where
$L_t(a) = \lim _{ \lvert {\pi } \rvert \to 0} \sum _{[u,v] \in \pi } \bar {A}_{u, v}(a)$
, where
 $\pi $
is a partition of
$\pi $
is a partition of
 $[0, t]$
.
$[0, t]$
.
The first point is essentially given in Lemma 4.4. The second point follows from the identity
 $$ \begin{align*} \int_{\mathbb{R}} \Big(\sum_{[u,v] \in \pi} \bar{A}_{u,v}(a) \Big) f(a) \, \mathrm{d} a = \sum_{[u,v] \in \pi} \int_u^v \mathbb{E}[f(B_r) \vert \mathcal{F}_u] \, \mathrm{d} r. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}} \Big(\sum_{[u,v] \in \pi} \bar{A}_{u,v}(a) \Big) f(a) \, \mathrm{d} a = \sum_{[u,v] \in \pi} \int_u^v \mathbb{E}[f(B_r) \vert \mathcal{F}_u] \, \mathrm{d} r. \end{align*} $$
Thus, we now focus on the estimate (4.16). We have the identity
 $$ \begin{align*} \mathbb{E}[L_t - L_s \vert \mathcal{F}_v] = \int_s^t \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sqrt{2 \pi} \sigma_r} \, \mathrm{d} r. \end{align*} $$
$$ \begin{align*} \mathbb{E}[L_t - L_s \vert \mathcal{F}_v] = \int_s^t \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sqrt{2 \pi} \sigma_r} \, \mathrm{d} r. \end{align*} $$
Indeed, we can convince ourselves of the validity of the identity from the formal expression
 $$ \begin{align*} L_t - L_s = \int_s^t \delta(B_r - a) \, \mathrm{d} r. \end{align*} $$
$$ \begin{align*} L_t - L_s = \int_s^t \delta(B_r - a) \, \mathrm{d} r. \end{align*} $$
We have the decomposition
 $$ \begin{align*} &\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_r} - \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} = \Big[\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_r} - \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_s} \Big] \\& \quad + \Big[ \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_s} - \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} \Big] + \Big[\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} - \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} \Big] =: R_3 + R_4 + R_5. \end{align*} $$
$$ \begin{align*} &\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_r} - \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} = \Big[\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_r} - \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_s} \Big] \\& \quad + \Big[ \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_r^2}}}{\sigma_s} - \frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} \Big] + \Big[\frac{e^{-\frac{ \lvert {Y_r - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} - \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sigma_s} \Big] =: R_3 + R_4 + R_5. \end{align*} $$
By (4.11), we obtain
We have
Hence, by (4.11),
To estimate
![]() $R_5$
, observe
$R_5$
, observe
By (4.12),
To estimate
![]() $\mathbb {P}( \lvert {Y_s - a} \rvert \leq 2 \lvert {Y_{s,r}} \rvert )$
, consider the decomposition
$\mathbb {P}( \lvert {Y_s - a} \rvert \leq 2 \lvert {Y_{s,r}} \rvert )$
, consider the decomposition
If
![]() $\frac {t-s}{s-v}$
is sufficiently small, then
$\frac {t-s}{s-v}$
is sufficiently small, then
![]() $ \lvert {\mathbb {E}[Y_s^2]^{-1} \mathbb {E}[Y_s Y_{s,r}]} \rvert \leq \frac {1}{4}$
. Therefore,
$ \lvert {\mathbb {E}[Y_s^2]^{-1} \mathbb {E}[Y_s Y_{s,r}]} \rvert \leq \frac {1}{4}$
. Therefore,
This gives an estimate of
![]() $R_5$
. Thus, we conclude
$R_5$
. Thus, we conclude
 $$ \begin{align*} \mathbb{E}[L_t - L_s \vert \mathcal{F}_v] = \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sqrt{2 \pi} \sigma_s} \lvert {t-s} \rvert + R_6, \end{align*} $$
$$ \begin{align*} \mathbb{E}[L_t - L_s \vert \mathcal{F}_v] = \frac{e^{-\frac{ \lvert {Y_s - a} \rvert ^2}{2 \sigma_s^2}}}{\sqrt{2 \pi} \sigma_s} \lvert {t-s} \rvert + R_6, \end{align*} $$
where
This completes the proof of the lemma.
Now we can complete the proof of Theorem 4.1. The above lemmas show
 $$ \begin{align*} \lVert {\mathfrak{c}_{H, \gamma}(L_t(a) - L_t(a)) - A_{s, t}(a)} \rVert _{L_m(\mathbb{P})} \begin{cases} \lesssim_T \lvert {t-s} \rvert ^{1 - H}, & \text{for all } H \in (0, 1), \\ \lesssim_{T} s^{-\frac{H}{m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}}, & \text{if } H> \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} \lVert {\mathfrak{c}_{H, \gamma}(L_t(a) - L_t(a)) - A_{s, t}(a)} \rVert _{L_m(\mathbb{P})} \begin{cases} \lesssim_T \lvert {t-s} \rvert ^{1 - H}, & \text{for all } H \in (0, 1), \\ \lesssim_{T} s^{-\frac{H}{m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}}, & \text{if } H> \frac{1}{2}, \end{cases} \end{align*} $$
and if
![]() $\frac {t-s}{s-v}$
is sufficiently small, then
$\frac {t-s}{s-v}$
is sufficiently small, then
 $$ \begin{align*} & \lVert {\mathbb{E}[\mathfrak{c}_{H, \gamma}(L_t(a) - L_s(a)) - A_{s, t}(a) \vert \mathcal{F}_v]} \rVert _{L_m(\mathbb{P})} \\ & \quad \begin{cases} \lesssim_T e^{- c (\mathbb{E}[B(0)^2] + T^{2H})^{-1} a^2} \Big(\frac{t-s}{s-v} \Big)^{\min\{2H, \frac{1}{m} + H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{1 - H}, & H < \frac{1}{2}, \\ \lesssim_{T} s^{-\frac{H}{m}} e^{- c (\mathbb{E}[B(0)^2] + T^{2H})^{-1} a^2} \Big(\frac{t-s}{s-v} \Big)^{\min\{1, \frac{1}{m} + H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}}, & H> \frac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} & \lVert {\mathbb{E}[\mathfrak{c}_{H, \gamma}(L_t(a) - L_s(a)) - A_{s, t}(a) \vert \mathcal{F}_v]} \rVert _{L_m(\mathbb{P})} \\ & \quad \begin{cases} \lesssim_T e^{- c (\mathbb{E}[B(0)^2] + T^{2H})^{-1} a^2} \Big(\frac{t-s}{s-v} \Big)^{\min\{2H, \frac{1}{m} + H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{1 - H}, & H < \frac{1}{2}, \\ \lesssim_{T} s^{-\frac{H}{m}} e^{- c (\mathbb{E}[B(0)^2] + T^{2H})^{-1} a^2} \Big(\frac{t-s}{s-v} \Big)^{\min\{1, \frac{1}{m} + H\} - \frac{H}{m}} \lvert {t-s} \rvert ^{1 - H + \frac{H}{m}}, & H> \frac{1}{2}. \end{cases} \end{align*} $$
Noting that the exponents satisfy the assumption of Theorem 1.1 or Corollary 2.7, Remark 1.4 implies
Hence, we complete the proof of Theorem 4.1.
Corollary 4.8. We have
 $$ \begin{align*} \lim_{n \to \infty} \Big(\frac{T}{n} \Big)^{1-H} \# \{k \in \{1, \ldots, n\} \mid B_{\frac{(k-1)T}{n}} < a < B_{\frac{kT}{n}}\} = \sqrt{\frac{c_H}{2 \pi}} L_T(a), \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \Big(\frac{T}{n} \Big)^{1-H} \# \{k \in \{1, \ldots, n\} \mid B_{\frac{(k-1)T}{n}} < a < B_{\frac{kT}{n}}\} = \sqrt{\frac{c_H}{2 \pi}} L_T(a), \end{align*} $$
where the convergence is in
![]() $L_m(\mathbb {P})$
with m satisfying (4.1).
$L_m(\mathbb {P})$
with m satisfying (4.1).
Proof. The claim is a special case of Theorem 4.1 with
![]() $\gamma = 0$
. When
$\gamma = 0$
. When
![]() $m = 2$
, it is proved in [Reference Azaïs4, Theorem 5].
$m = 2$
, it is proved in [Reference Azaïs4, Theorem 5].
For applications to pathwise stochastic calculus, a representation of the local time as in (b) above is more useful. In [Reference Cont and Perkowski9, Theorem 3.2], a pathwise Itô-Tanaka formula is derived under the assumption that

converges weakly in
![]() $L_m(\mathbb {R})$
for some
$L_m(\mathbb {R})$
for some
![]() $m> 1$
. But as already suggested by [Reference Cont and Perkowski9, Lemma 3.5], this weak convergence in
$m> 1$
. But as already suggested by [Reference Cont and Perkowski9, Lemma 3.5], this weak convergence in
![]() $L_m(\mathbb {R})$
follows from our convergence result in Theorem 4.1:
$L_m(\mathbb {R})$
follows from our convergence result in Theorem 4.1:
Corollary 4.9. Let
![]() $B \in C([0,T], \mathbb {R})$
, and for any partition
$B \in C([0,T], \mathbb {R})$
, and for any partition
![]() $\pi $
of
$\pi $
of
![]() $[0,T]$
, let
$[0,T]$
, let
![]() $\tilde {L}^{\pi }_T(a)$
be defined as in (4.18). Assume that
$\tilde {L}^{\pi }_T(a)$
be defined as in (4.18). Assume that
![]() $m> 1$
and that
$m> 1$
and that
![]() $(\pi _n)$
is a sequence of partitions of
$(\pi _n)$
is a sequence of partitions of
![]() $[0,T]$
, such that
$[0,T]$
, such that
![]() $\lim _{n \to \infty } \sup _{[s,t] \in \pi _n} |B_t - B_s| = 0$
and for a limit
$\lim _{n \to \infty } \sup _{[s,t] \in \pi _n} |B_t - B_s| = 0$
and for a limit
![]() $L_T \in L_m(\mathbb {R})$
:
$L_T \in L_m(\mathbb {R})$
:

Then
Remark 4.10. If B is a sample path of the fractional Brownian motion with Hurst index
![]() $H \in (0,1)$
, then by Theorem 4.1, the convergence (4.19) holds in probability for any sequence of partitions
$H \in (0,1)$
, then by Theorem 4.1, the convergence (4.19) holds in probability for any sequence of partitions
![]() $(\pi _n)_{n \in \mathbb {N}}$
, provided that m satisfies (4.1). Therefore, we can find a subsequence so that the convergence along the subsequence holds almost surely. In fact, by (4.17), we even control the convergence rate in terms of the mesh size of the partition, and this easily gives us specific sequences of partitions along which the convergence holds almost surely and not only in probability. For example, if
$(\pi _n)_{n \in \mathbb {N}}$
, provided that m satisfies (4.1). Therefore, we can find a subsequence so that the convergence along the subsequence holds almost surely. In fact, by (4.17), we even control the convergence rate in terms of the mesh size of the partition, and this easily gives us specific sequences of partitions along which the convergence holds almost surely and not only in probability. For example, if
![]() $\pi _n$
is the nth dyadic partition of
$\pi _n$
is the nth dyadic partition of
![]() $[0, T]$
, the estimate (4.17) gives
$[0, T]$
, the estimate (4.17) gives
Since the right-hand side is summable with respect to n, the Borel–Cantelli lemma implies the almost sure convergence. Along any such sequence of partitions, we therefore obtain the almost sure weak convergence of
![]() $\tilde L^{\pi _n}_T$
in
$\tilde L^{\pi _n}_T$
in
![]() $L_m(\mathbb {R})$
.
$L_m(\mathbb {R})$
.
Proof. Set
It suffices to show that
![]() $\sum _{[s,t] \in \pi _n} \tilde {A}_{s, t}(\cdot )$
converge weakly to
$\sum _{[s,t] \in \pi _n} \tilde {A}_{s, t}(\cdot )$
converge weakly to
![]() $0$
in
$0$
in
![]() $L_m(\mathbb {R})$
. Since
$L_m(\mathbb {R})$
. Since
and since ![]() is bounded in
is bounded in
![]() $L_m(\mathbb {P})$
by assumption, it suffices to show that
$L_m(\mathbb {P})$
by assumption, it suffices to show that
 $$ \begin{align*} \lim_{n \to \infty} \int_{\mathbb{R}} \Big( \sum_{[s,t] \in \pi_n} \tilde{A}_{s, t}(a) \Big) g(a) \, \mathrm{d} a = 0 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \int_{\mathbb{R}} \Big( \sum_{[s,t] \in \pi_n} \tilde{A}_{s, t}(a) \Big) g(a) \, \mathrm{d} a = 0 \end{align*} $$
for every compactly supported continuous function g. Since for
![]() $B_s < B_t$
we have
$B_s < B_t$
we have
 $$ \begin{align*} B_{s,t}^{-1}\int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} \, \mathrm{d} a = H \lvert {B_{s, t}} \rvert ^{\frac{1}{H} - 1}, \end{align*} $$
$$ \begin{align*} B_{s,t}^{-1}\int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} \, \mathrm{d} a = H \lvert {B_{s, t}} \rvert ^{\frac{1}{H} - 1}, \end{align*} $$
we obtain
 $$ \begin{align*} \int_{B_s}^{B_t} \tilde{A}_{s, t}(a) g(a) \, \mathrm{d} a = \int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} (g(a) - B_{s,t}^{-1} \int_{B_s}^{B_t} g(x) \, \mathrm{d} x) \, \mathrm{d} a. \end{align*} $$
$$ \begin{align*} \int_{B_s}^{B_t} \tilde{A}_{s, t}(a) g(a) \, \mathrm{d} a = \int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} (g(a) - B_{s,t}^{-1} \int_{B_s}^{B_t} g(x) \, \mathrm{d} x) \, \mathrm{d} a. \end{align*} $$
Therefore,
 $$ \begin{align*} \int_{\mathbb{R}} \Big( \sum_{[s,t] \in \pi_n} \tilde{A}_{s, t}(a) \Big) g(a) \, \mathrm{d} a &= \sum_{[s, t] \in \pi_n} \int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} (g(a) - B_{s,t}^{-1} \int_{B_s}^{B_t} g(x) \, \mathrm{d} x) \, \mathrm{d} a \\ &\leq \int_{\mathbb{R}} \tilde{L}^{\pi_n}_T(a) \, \mathrm{d} a \times \sup_{ \lvert {x-y} \rvert \leq \sup_{[s,t] \in \pi} \lvert {B_t - B_s} \rvert } \lvert {g(x) - g(y)} \rvert \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}} \Big( \sum_{[s,t] \in \pi_n} \tilde{A}_{s, t}(a) \Big) g(a) \, \mathrm{d} a &= \sum_{[s, t] \in \pi_n} \int_{B_s}^{B_t} \lvert {B_t - a} \rvert ^{\frac{1}{H} - 1} (g(a) - B_{s,t}^{-1} \int_{B_s}^{B_t} g(x) \, \mathrm{d} x) \, \mathrm{d} a \\ &\leq \int_{\mathbb{R}} \tilde{L}^{\pi_n}_T(a) \, \mathrm{d} a \times \sup_{ \lvert {x-y} \rvert \leq \sup_{[s,t] \in \pi} \lvert {B_t - B_s} \rvert } \lvert {g(x) - g(y)} \rvert \end{align*} $$
which converges to
![]() $0$
.
$0$
.
Remark 4.11. As noted in [Reference Mukeru33], we can use Theorem 4.1 to simulate the local time of a fractional Brownian motion (see Figures 1 (
![]() $H = 0.1$
) and 2 (
$H = 0.1$
) and 2 (
![]() $H=0.6$
)).Footnote
1
$H=0.6$
)).Footnote
1

Figure 1 Left: a fractional Brownian motion with
![]() $H=0.1$
, right: its local time at
$H=0.1$
, right: its local time at
![]() $0$
.
$0$
.

Figure 2 Left: a fractional Brownian motion with
![]() $H=0.6$
, right: its local time at
$H=0.6$
, right: its local time at
![]() $0$
.
$0$
.
5. Regularization by noise for diffusion coefficients
Let
![]() $y \in C^{\alpha } ([0, T] , \mathbb {R}^d)$
with
$y \in C^{\alpha } ([0, T] , \mathbb {R}^d)$
with
![]() $\alpha \in ( \frac {1}{2}, 1 )$
. We consider a Young differential equation
$\alpha \in ( \frac {1}{2}, 1 )$
. We consider a Young differential equation
We suppose that the drift coefficient b belongs to
![]() $C^1_b (\mathbb {R}^d , \mathbb {R}^d)$
, where
$C^1_b (\mathbb {R}^d , \mathbb {R}^d)$
, where
![]() $C^1_b(\mathbb {R}^d , \mathbb {R}^d)$
is the space of continuously differentiable bounded functions between
$C^1_b(\mathbb {R}^d , \mathbb {R}^d)$
is the space of continuously differentiable bounded functions between
![]() $\mathbb {R}^d$
with bounded derivatives. If the diffusion coefficient
$\mathbb {R}^d$
with bounded derivatives. If the diffusion coefficient
![]() $\sigma $
belongs to
$\sigma $
belongs to
![]() $C^1_b (\mathbb {R}^d , \mathcal {M}_d)$
, where
$C^1_b (\mathbb {R}^d , \mathcal {M}_d)$
, where
![]() $\mathcal {M}_d$
is the space of
$\mathcal {M}_d$
is the space of
![]() $d\times d$
matrices, then we can prove the existence of a solution to (5.1). However, to prove the uniqueness of solutions, the coefficient
$d\times d$
matrices, then we can prove the existence of a solution to (5.1). However, to prove the uniqueness of solutions, the coefficient
![]() $\sigma $
needs to be more regular. The following result is well-known (e.g. [Reference Lyons29]), but we give a proof for the sake of later discussion.
$\sigma $
needs to be more regular. The following result is well-known (e.g. [Reference Lyons29]), but we give a proof for the sake of later discussion.
Proposition 5.1. Let
![]() $b \in C^1_b(\mathbb {R}^d, \mathbb {R}^d)$
and
$b \in C^1_b(\mathbb {R}^d, \mathbb {R}^d)$
and
![]() $\sigma \in C^{1 + \delta }(\mathbb {R}^d, \mathcal {M}_d)$
with
$\sigma \in C^{1 + \delta }(\mathbb {R}^d, \mathcal {M}_d)$
with
![]() $\delta> \frac {1-\alpha }{\alpha }$
. Then the Young differential equation (5.1) has a unique solution.
$\delta> \frac {1-\alpha }{\alpha }$
. Then the Young differential equation (5.1) has a unique solution.
Proof. The argument is very similar to that of [Reference Lê24, Theorem 6.2]. Let
![]() $x^{(i)}$
(
$x^{(i)}$
(
![]() $i = 1, 2$
) be two solutions to (5.1). Then,
$i = 1, 2$
) be two solutions to (5.1). Then,
 $$ \begin{align*} x^{(1)}_t - x^{(2)}_t = \int_0^t \{ b (x^{(1)}_s) - b (x^{(2)}_s) \} \, \mathrm{d} s + \int_0^t \{ \sigma (x^{(1)}_s) - \sigma (x^{(2)}_s) \} \, \mathrm{d} y_s = \int_0^t \{ x^{(1)}_s - x^{(2)}_s \} \, \mathrm{d} v_s, \end{align*} $$
$$ \begin{align*} x^{(1)}_t - x^{(2)}_t = \int_0^t \{ b (x^{(1)}_s) - b (x^{(2)}_s) \} \, \mathrm{d} s + \int_0^t \{ \sigma (x^{(1)}_s) - \sigma (x^{(2)}_s) \} \, \mathrm{d} y_s = \int_0^t \{ x^{(1)}_s - x^{(2)}_s \} \, \mathrm{d} v_s, \end{align*} $$
where

Note that the second term is well-defined as a Young integral since
is
![]() $\delta \alpha $
-Hölder continuous and
$\delta \alpha $
-Hölder continuous and
![]() $\delta \alpha + \alpha> 1$
by our assumption of
$\delta \alpha + \alpha> 1$
by our assumption of
![]() $\delta $
. Therefore,
$\delta $
. Therefore,
![]() $x^{(1)} - x^{(2)}$
is a solution of the Young differential equation
$x^{(1)} - x^{(2)}$
is a solution of the Young differential equation
The uniqueness of this linear Young differential equation is known. Hence,
![]() $x^{(1)} - x^{(2)} = 0.$
$x^{(1)} - x^{(2)} = 0.$
Proposition 5.1 is sharp in the sense that for any
![]() $\alpha \in (1,2)$
and any
$\alpha \in (1,2)$
and any
![]() $\delta \in (0, \frac {1-\alpha }{\alpha })$
, we can find
$\delta \in (0, \frac {1-\alpha }{\alpha })$
, we can find
![]() $\sigma \in C^{\gamma }(\mathbb {R}^2,\mathcal {M}_2)$
and
$\sigma \in C^{\gamma }(\mathbb {R}^2,\mathcal {M}_2)$
and
![]() $y \in C^{\alpha }([0,T],\mathbb {R}^2)$
, such that the Young differential equation
$y \in C^{\alpha }([0,T],\mathbb {R}^2)$
, such that the Young differential equation
has more than one solution (see Davie [Reference Davie11, Section 5]). However, if the driver y is random, we could hope to obtain the uniqueness of solutions in a probabilistic sense even when the regularity of
![]() $\sigma $
does not satisfy the assumption of Proposition 5.1. For instance, if the driver y is a Brownian motion and the integral is understood in Itô’s sense, the condition
$\sigma $
does not satisfy the assumption of Proposition 5.1. For instance, if the driver y is a Brownian motion and the integral is understood in Itô’s sense, the condition
![]() $\sigma \in C^1_b$
is sufficient to prove pathwise uniqueness.
$\sigma \in C^1_b$
is sufficient to prove pathwise uniqueness.
The goal of this section is to prove the following.
Theorem 5.2. Suppose that B is an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
$(\mathcal {F}_t)$
-fractional Brownian motion with Hurst parameter
![]() $H \in (\frac {1}{2}, 1)$
in the sense of Definition 3.1. Let
$H \in (\frac {1}{2}, 1)$
in the sense of Definition 3.1. Let
![]() $b \in C^1_b (\mathbb {R}^d , \mathbb {R}^d)$
and
$b \in C^1_b (\mathbb {R}^d , \mathbb {R}^d)$
and
![]() $\sigma \in C^{1}_b (\mathbb {R}^d , \mathcal {M}_d)$
. Assume one of the following.
$\sigma \in C^{1}_b (\mathbb {R}^d , \mathcal {M}_d)$
. Assume one of the following.
-
1. We have
 $b \equiv 0$
and
$b \equiv 0$
and
 $\sigma \in C^{1+\delta } (\mathbb {R}^d , \mathcal {M}_d)$
with (5.2)
$\sigma \in C^{1+\delta } (\mathbb {R}^d , \mathcal {M}_d)$
with (5.2) $$ \begin{align} \delta> \frac{(1 - H) (2 - H)}{H (3 - H)}. \end{align} $$
$$ \begin{align} \delta> \frac{(1 - H) (2 - H)}{H (3 - H)}. \end{align} $$
-
2. For all
 $x \in \mathbb {R}^d$
, the matrix
$x \in \mathbb {R}^d$
, the matrix
 $\sigma (x)$
is symmetric and satisfies and
$\sigma (x)$
is symmetric and satisfies and $$ \begin{align*} y \cdot \sigma(x) y> 0, \quad \forall y \in \mathbb{R}^d, \end{align*} $$
$$ \begin{align*} y \cdot \sigma(x) y> 0, \quad \forall y \in \mathbb{R}^d, \end{align*} $$
 $\sigma \in C^{1+\delta }(\mathbb {R}^d , \mathcal {M}_d)$
with
$\sigma \in C^{1+\delta }(\mathbb {R}^d , \mathcal {M}_d)$
with
 $\delta $
satisfying (5.2).
$\delta $
satisfying (5.2).
-
3. We have
 $\sigma \in C^{1+\delta }(\mathbb {R}^d; \mathcal {M}_d)$
with (5.3)
$\sigma \in C^{1+\delta }(\mathbb {R}^d; \mathcal {M}_d)$
with (5.3) $$ \begin{align} \delta> \frac{(1-H)(2-H)}{1+H-H^2}. \end{align} $$
$$ \begin{align} \delta> \frac{(1-H)(2-H)}{1+H-H^2}. \end{align} $$
The graphs of (5.2) and (5.3) can be found in Figure 3.
Then, for every
![]() $x \in \mathbb {R}^d$
, there exists a unique, up to modifications, process
$x \in \mathbb {R}^d$
, there exists a unique, up to modifications, process
![]() $(X_t)_{t \in [0, \infty )}$
with the following properties.
$(X_t)_{t \in [0, \infty )}$
with the following properties.
-
• The process
 $(X_t)$
is
$(X_t)$
is
 $(\mathcal {F}_t)$
-adapted and is
$(\mathcal {F}_t)$
-adapted and is
 $\alpha $
-Hölder continuous for every
$\alpha $
-Hölder continuous for every
 $\alpha < H$
.
$\alpha < H$
. -
• The process
 $(X_t)$
solves the Young differential equation (5.4)
$(X_t)$
solves the Young differential equation (5.4) $$ \begin{align} \, \mathrm{d} X_t = b (X_t) \, \mathrm{d} t + \sigma (X_t) \, \mathrm{d} B_t, \quad X_0 = x. \end{align} $$
$$ \begin{align} \, \mathrm{d} X_t = b (X_t) \, \mathrm{d} t + \sigma (X_t) \, \mathrm{d} B_t, \quad X_0 = x. \end{align} $$
Furthermore, in that case the process
![]() $(X_t)_{t \in [0, \infty )}$
is a strong solution, that is, it is adapted to the natural filtration generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1).
$(X_t)_{t \in [0, \infty )}$
is a strong solution, that is, it is adapted to the natural filtration generated by the Brownian motion W appearing in the Mandelbrot–Van Ness representation (3.1).

Figure 3 Some graphs of H from Theorem 5.2.
Remark 5.3. In the case 2, we assume the positive-definiteness of
![]() $\sigma $
to ensure that for every
$\sigma $
to ensure that for every
![]() $x, y \in \mathbb {R}^d$
and
$x, y \in \mathbb {R}^d$
and
![]() $\theta \in [0,1]$
, the matrix
$\theta \in [0,1]$
, the matrix
![]() $\theta \sigma (x) + (1 - \theta ) \sigma (y)$
is invertible.
$\theta \sigma (x) + (1 - \theta ) \sigma (y)$
is invertible.
Remark 5.4. Since the seminal work [Reference Catellier and Gubinelli8] of Catellier and Gubinelli, many works have appeared to establish weak or strong existence or uniqueness to the SDE
for an irregular drift b and a fractional Brownian motion B. In contrast, there are much fewer works that attempt to optimize the regularity of the diffusion coefficient
![]() $\sigma $
. The work [Reference Hinz, Tölle and Viitasaari20] by Hinz et al., where
$\sigma $
. The work [Reference Hinz, Tölle and Viitasaari20] by Hinz et al., where
![]() $b \equiv 0$
, considers certain existence and uniqueness for
$b \equiv 0$
, considers certain existence and uniqueness for
![]() $\sigma $
that is merely of bounded variation, at the cost of additional restrictive assumptions (variability and [Reference Hinz, Tölle and Viitasaari20, Assumption 3.15]). It seems that Theorem 5.2 is the first result to improve the regularity of
$\sigma $
that is merely of bounded variation, at the cost of additional restrictive assumptions (variability and [Reference Hinz, Tölle and Viitasaari20, Assumption 3.15]). It seems that Theorem 5.2 is the first result to improve the regularity of
![]() $\sigma $
without any additional assumption (except
$\sigma $
without any additional assumption (except
![]() $\sigma $
being invertible for the case 2). However, we believe that our assumption of
$\sigma $
being invertible for the case 2). However, we believe that our assumption of
![]() $\delta $
is not optimal (see Remark 5.9).
$\delta $
is not optimal (see Remark 5.9).
The proof of Proposition 5.1 suggests that the pathwise uniqueness holds if, for any two
![]() $(\mathcal {F}_t)$
-adapted solutions
$(\mathcal {F}_t)$
-adapted solutions
![]() $X^{(1)}$
and
$X^{(1)}$
and
![]() $X^{(2)}$
to (5.4), we can construct the integral
$X^{(2)}$
to (5.4), we can construct the integral
 $$ \begin{align} \int_0^t \int_0^1 \nabla \sigma (\theta X^{(1)}_s + (1 - \theta) X^{(2)}_s) \, \mathrm{d} \theta \, \mathrm{d} B_s. \end{align} $$
$$ \begin{align} \int_0^t \int_0^1 \nabla \sigma (\theta X^{(1)}_s + (1 - \theta) X^{(2)}_s) \, \mathrm{d} \theta \, \mathrm{d} B_s. \end{align} $$
If
![]() $\theta X^{(1)}_s + (1 - \theta ) X^{(2)}_s$
is replaced by
$\theta X^{(1)}_s + (1 - \theta ) X^{(2)}_s$
is replaced by
![]() $B_s$
, then the integral is constructed in Proposition 3.3. The difficulty here is that
$B_s$
, then the integral is constructed in Proposition 3.3. The difficulty here is that
![]() $X^{(i)}$
is not Gaussian and the Wiener chaos decomposition crucially used in the proof of Proposition 3.3 cannot be applied. Yet, the process
$X^{(i)}$
is not Gaussian and the Wiener chaos decomposition crucially used in the proof of Proposition 3.3 cannot be applied. Yet, the process
![]() $X^{(i)}$
is locally controlled by the Gaussian process B (whose precise meaning will be clarified later), and by taking advantage of this fact, we can still make sense of the integral (5.5).
$X^{(i)}$
is locally controlled by the Gaussian process B (whose precise meaning will be clarified later), and by taking advantage of this fact, we can still make sense of the integral (5.5).
As a technical ingredient, we need a variant of Theorem 1.1.
Lemma 5.5. Let
![]() $(A_{s, t})_{0 \leq s < t \leq T}$
be a family of two-parameter random variables, and let
$(A_{s, t})_{0 \leq s < t \leq T}$
be a family of two-parameter random variables, and let
![]() $(\mathcal {F}_t)_{t \in [0, T]}$
be a filtration, such that
$(\mathcal {F}_t)_{t \in [0, T]}$
be a filtration, such that
![]() $A_{s, t}$
is
$A_{s, t}$
is
![]() $\mathcal {F}_t$
-measurable for every
$\mathcal {F}_t$
-measurable for every
![]() $0 \leq s \leq t \leq T$
. Suppose that for some
$0 \leq s \leq t \leq T$
. Suppose that for some
![]() $m \geq 2$
,
$m \geq 2$
,
![]() $\Gamma _1, \Gamma _{2,} \Gamma _3 \in [0, \infty )$
and
$\Gamma _1, \Gamma _{2,} \Gamma _3 \in [0, \infty )$
and
![]() $\alpha , \gamma , \beta _1, \beta _2, \beta _3 \in [0, \infty )$
, we have for every
$\alpha , \gamma , \beta _1, \beta _2, \beta _3 \in [0, \infty )$
, we have for every
![]() $0 \leq v < s < u < t \leq T$
$0 \leq v < s < u < t \leq T$
 $$ \begin{align*} \| \mathbb{E} [\delta A_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} &\leq \Gamma_1 | s - v |^{- \alpha} | t - s |^{\beta_1} + \Gamma_2 | t - v |^{\gamma} | t - s |^{\beta_2}, \quad \text{if } t-s \leq s - v, \\ \| \delta_{} A_{s, u, t} \|_{L_m (\mathbb{P})} &\leq \Gamma_3 | t - s |^{\beta_3}. \end{align*} $$
$$ \begin{align*} \| \mathbb{E} [\delta A_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} &\leq \Gamma_1 | s - v |^{- \alpha} | t - s |^{\beta_1} + \Gamma_2 | t - v |^{\gamma} | t - s |^{\beta_2}, \quad \text{if } t-s \leq s - v, \\ \| \delta_{} A_{s, u, t} \|_{L_m (\mathbb{P})} &\leq \Gamma_3 | t - s |^{\beta_3}. \end{align*} $$
Suppose that
Finally, suppose that there exists a stochastic process
![]() $(\mathcal {A}_t)_{t \in [0,T]}$
, such that
$(\mathcal {A}_t)_{t \in [0,T]}$
, such that
where the convergence is in
![]() $L_m(\mathbb {P})$
. Then, we have
$L_m(\mathbb {P})$
. Then, we have
Remark 5.6. It should be possible to formulate Lemma 5.5 at the generality of Theorem 1.1. However, such generality is irrelevant to prove Theorem 5.2, and we do not pursue the generality to simplify the presentation.
Proof. Here, we consider dyadic partitions. Fix
![]() $s < t$
, and set
$s < t$
, and set

Since
![]() $\mathcal {A}_{s,t} = \lim _{n \to \infty } A^n_{s, t}$
, it suffices to show
$\mathcal {A}_{s,t} = \lim _{n \to \infty } A^n_{s, t}$
, it suffices to show
for some
![]() $\delta> 0$
and all sufficiently large n. As in the proof of Theorem 1.1, we decompose
$\delta> 0$
and all sufficiently large n. As in the proof of Theorem 1.1, we decompose
 $$ \begin{align*} A^n_{s, t} - A^{n + 1}_{s, t} = \!\sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1}^{}\! \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} + \!\sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \!\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n]. \end{align*} $$
$$ \begin{align*} A^n_{s, t} - A^{n + 1}_{s, t} = \!\sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1}^{}\! \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} + \!\sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \!\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n]. \end{align*} $$
By the BDG inequality,
 $$ \begin{align*} &\Big\| \sum_{j : l + j L \leq 2^n - 1}^{} \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} \Big\|_{L_m (\mathbb{P})} \\& \quad \lesssim \kappa_{m, d} \Big( \sum_{j : l + j L \leq 2^n - 1} \| \delta A^n_{l + j L} \|^2_{L_m (\mathbb{P})} \Big)^{\frac{1}{2}} \leq \kappa_{m, d} \Gamma_3 \Big( \sum_{j : l + j L \leq 2^n - 1} (2^{- n} | t - s |)^{2 \beta_3} \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} &\Big\| \sum_{j : l + j L \leq 2^n - 1}^{} \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} \Big\|_{L_m (\mathbb{P})} \\& \quad \lesssim \kappa_{m, d} \Big( \sum_{j : l + j L \leq 2^n - 1} \| \delta A^n_{l + j L} \|^2_{L_m (\mathbb{P})} \Big)^{\frac{1}{2}} \leq \kappa_{m, d} \Gamma_3 \Big( \sum_{j : l + j L \leq 2^n - 1} (2^{- n} | t - s |)^{2 \beta_3} \Big)^{\frac{1}{2}}. \end{align*} $$
Thus,
 $$\begin{align*}\Big\| \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1}^{} \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} \Big\|_{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \Gamma_3 L^{\frac{1}{2}} 2^{- n ( \beta_3 - \frac{1}{2} )} | t - s |^{\beta_3}. \end{align*}$$
$$\begin{align*}\Big\| \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1}^{} \{ \delta A^n_{l + j L} -\mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \} \Big\|_{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \Gamma_3 L^{\frac{1}{2}} 2^{- n ( \beta_3 - \frac{1}{2} )} | t - s |^{\beta_3}. \end{align*}$$
Furthermore,
 $$ \begin{align*} & \Big\| \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \Big\|_{L_m (\mathbb{P})} \\& \quad \leq \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \| \mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \|_{L_m (\mathbb{P})}\\& \quad \leq \Gamma_1 \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \Big( \frac{L - 1}{2^n} | t - s | \Big)^{- \alpha} (2^{- n} | t - s |)^{\beta_1} \\& \qquad \phantom{\leq} + \Gamma_2 \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \Big( \frac{L }{2^n} | t - s | \Big)^{\gamma} (2^{- n} | t - s |)^{\beta_2}\\& \quad \lesssim \Gamma_1 2^{- n (\beta_1 - \alpha - 1)} L^{- \alpha} | t - s |^{\beta_1 - \alpha} + \Gamma_2 2^{- n (\gamma + \beta_2 - 1)} L^{\gamma} | t - s |^{\gamma + \beta_2}. \end{align*} $$
$$ \begin{align*} & \Big\| \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \Big\|_{L_m (\mathbb{P})} \\& \quad \leq \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \| \mathbb{E} [\delta A^n_{l + j L} | \mathcal{F}_{l + (j - 1) L + 1}^n] \|_{L_m (\mathbb{P})}\\& \quad \leq \Gamma_1 \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \Big( \frac{L - 1}{2^n} | t - s | \Big)^{- \alpha} (2^{- n} | t - s |)^{\beta_1} \\& \qquad \phantom{\leq} + \Gamma_2 \sum_{l = 0}^L \sum_{j : l + j L \leq 2^n - 1} \Big( \frac{L }{2^n} | t - s | \Big)^{\gamma} (2^{- n} | t - s |)^{\beta_2}\\& \quad \lesssim \Gamma_1 2^{- n (\beta_1 - \alpha - 1)} L^{- \alpha} | t - s |^{\beta_1 - \alpha} + \Gamma_2 2^{- n (\gamma + \beta_2 - 1)} L^{\gamma} | t - s |^{\gamma + \beta_2}. \end{align*} $$
Therefore,
 $$ \begin{align*} &\| A^n_{s, t} - A^{n + 1}_{s, t} \|_{L_m (\mathbb{P})} \lesssim \Gamma_1 2^{- n (\beta_1 - \alpha - 1)} L^{- \alpha} | t - s |^{\beta_1 - \alpha} \\& \quad + \Gamma_2 2^{- n (\gamma + \beta_2 - 1)} L^{\gamma} | t - s |^{\gamma + \beta_2} + \kappa_{m, d} \Gamma_3 L^{\frac{1}{2}} 2^{- n ( \beta_3 - \frac{1}{2} )} | t - s |^{\beta_3}. \end{align*} $$
$$ \begin{align*} &\| A^n_{s, t} - A^{n + 1}_{s, t} \|_{L_m (\mathbb{P})} \lesssim \Gamma_1 2^{- n (\beta_1 - \alpha - 1)} L^{- \alpha} | t - s |^{\beta_1 - \alpha} \\& \quad + \Gamma_2 2^{- n (\gamma + \beta_2 - 1)} L^{\gamma} | t - s |^{\gamma + \beta_2} + \kappa_{m, d} \Gamma_3 L^{\frac{1}{2}} 2^{- n ( \beta_3 - \frac{1}{2} )} | t - s |^{\beta_3}. \end{align*} $$
We choose
![]() $L = \lfloor 2^{n \varepsilon } \rfloor $
with
$L = \lfloor 2^{n \varepsilon } \rfloor $
with
![]() $\varepsilon \in (0, 1)$
so that
$\varepsilon \in (0, 1)$
so that
Namely,
Such an
![]() $\epsilon $
exists exactly under our assumption (5.6).
$\epsilon $
exists exactly under our assumption (5.6).
We mentioned that a solution to (5.4) is controlled by B. Here comes a more precise statement. We fix
![]() $\alpha \in ( \frac {1}{2}, H )$
and let X be a solution to (5.4). We have the estimates
$\alpha \in ( \frac {1}{2}, H )$
and let X be a solution to (5.4). We have the estimates
 $$\begin{align*}\Big| \int_s^t b (X_r) \, \mathrm{d} r - b (X_s) (t - s) \Big| \leq \| b \|_{C^1_b} \| X \|_{C^{\alpha} }^{} (t - s)^{1 + \alpha}, \end{align*}$$
$$\begin{align*}\Big| \int_s^t b (X_r) \, \mathrm{d} r - b (X_s) (t - s) \Big| \leq \| b \|_{C^1_b} \| X \|_{C^{\alpha} }^{} (t - s)^{1 + \alpha}, \end{align*}$$
 $$ \begin{align} \Big| \int_s^t \sigma (X_r) \, \mathrm{d} B_r - \sigma (X_s) B_{s, t} \Big| \lesssim_{\alpha} \| \sigma \|_{C^1_b} \| X \|_{C^{\alpha} } \| B \|_{C^{\alpha} } | t - s |^{2 \alpha}. \end{align} $$
$$ \begin{align} \Big| \int_s^t \sigma (X_r) \, \mathrm{d} B_r - \sigma (X_s) B_{s, t} \Big| \lesssim_{\alpha} \| \sigma \|_{C^1_b} \| X \|_{C^{\alpha} } \| B \|_{C^{\alpha} } | t - s |^{2 \alpha}. \end{align} $$
Furthermore, the a priori estimate of the Young differential equation ([Reference Friz and Hairer14, Proposition 8.1]) gives
Therefore, we have
where
This motivates the following definition. Recall that B is an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion in the sense of Definition 3.1.
$(\mathcal {F}_t)$
-fractional Brownian motion in the sense of Definition 3.1.
Definition 5.7. Let Z be a random path in
![]() $C^{\alpha } ([0, T] , \mathbb {R}^d)$
. For
$C^{\alpha } ([0, T] , \mathbb {R}^d)$
. For
![]() $\beta \in (\alpha , \infty )$
, we write
$\beta \in (\alpha , \infty )$
, we write
![]() $Z \in \mathcal {D} (\alpha , \beta )$
, if for every
$Z \in \mathcal {D} (\alpha , \beta )$
, if for every
![]() $s < t$
, we have
$s < t$
, we have
where
-
• the random variables
 $z^{(1)}(s), z^{(3)}(s) \in \mathbb {R}^d$
, and
$z^{(1)}(s), z^{(3)}(s) \in \mathbb {R}^d$
, and
 $z^{(2)}(s) \in \mathcal {M}_d$
are
$z^{(2)}(s) \in \mathcal {M}_d$
are
 $\mathcal {F}_s$
-measurable and
$\mathcal {F}_s$
-measurable and -
• there exists a (random) constant
 $C \in [0, \infty )$
, such that for all
$C \in [0, \infty )$
, such that for all
 $s < t$
$s < t$
 $$\begin{align*}| R_{s, t} | \leq C | t - s |^{\beta}. \end{align*}$$
$$\begin{align*}| R_{s, t} | \leq C | t - s |^{\beta}. \end{align*}$$
We set
Furthermore, we set

and ![]() .
.
Proposition 5.8. Let
![]() $f \in C^1_b (\mathbb {R}^d; \mathbb {R}^d)$
and
$f \in C^1_b (\mathbb {R}^d; \mathbb {R}^d)$
and
![]() $Z \in \mathcal {D}_1(\alpha , \beta )$
. If
$Z \in \mathcal {D}_1(\alpha , \beta )$
. If
 $$ \begin{align} \max \Big\{ \frac{1 - H}{\beta}, \frac{2 - 3 H + H^2}{\beta + H - H^2}, \frac{3 - \sqrt{3}}{2 H} - 1 \Big\} < \delta < 1, \end{align} $$
$$ \begin{align} \max \Big\{ \frac{1 - H}{\beta}, \frac{2 - 3 H + H^2}{\beta + H - H^2}, \frac{3 - \sqrt{3}}{2 H} - 1 \Big\} < \delta < 1, \end{align} $$
and if
![]() $\alpha $
is sufficiently close to H, then for every
$\alpha $
is sufficiently close to H, then for every
![]() $m \in [2, \infty )$
,
$m \in [2, \infty )$
,
 $$ \begin{align*} &\Big\| \int_s^t f (Z_r) \, \mathrm{d} B_r - \frac{f (Z_s) + f (Z_t)}{2} \cdot B_{s, t} \Big\|_{L_m (\mathbb{P})} \\ & \quad \lesssim_{T, \alpha, \delta, m} \lVert {f} \rVert _{C^{\delta}} \lVert {\lVert{Z}\rVert_{\mathcal{D}_1(\alpha,\beta)}^{\delta}} \rVert _{L_{3m}(\mathbb{P})} (1 + \lVert {\lVert{Z}\rVert_{\mathcal{D}_1(\alpha,\beta)}} \rVert _{L_{3m}(\mathbb{P})}) \lvert {t-s} \rvert ^{H + \alpha \delta}. \end{align*} $$
$$ \begin{align*} &\Big\| \int_s^t f (Z_r) \, \mathrm{d} B_r - \frac{f (Z_s) + f (Z_t)}{2} \cdot B_{s, t} \Big\|_{L_m (\mathbb{P})} \\ & \quad \lesssim_{T, \alpha, \delta, m} \lVert {f} \rVert _{C^{\delta}} \lVert {\lVert{Z}\rVert_{\mathcal{D}_1(\alpha,\beta)}^{\delta}} \rVert _{L_{3m}(\mathbb{P})} (1 + \lVert {\lVert{Z}\rVert_{\mathcal{D}_1(\alpha,\beta)}} \rVert _{L_{3m}(\mathbb{P})}) \lvert {t-s} \rvert ^{H + \alpha \delta}. \end{align*} $$
If
![]() $Z \in \mathcal {D}_0(\alpha , \beta )$
, a similar estimate holds with
$Z \in \mathcal {D}_0(\alpha , \beta )$
, a similar estimate holds with
![]() $ \lVert {Z} \rVert _{\mathcal {D}_1(\alpha ,\beta )}$
replaced by
$ \lVert {Z} \rVert _{\mathcal {D}_1(\alpha ,\beta )}$
replaced by
![]() $ \lVert {Z} \rVert _{\mathcal {D}(\alpha ,\beta )}$
.
$ \lVert {Z} \rVert _{\mathcal {D}(\alpha ,\beta )}$
.
Proof. Our tool is Lemma 5.5. Since arguments are similar, we only prove the claim for
![]() $Z \in \mathcal {D}_1(\alpha , \beta )$
. We set
$Z \in \mathcal {D}_1(\alpha , \beta )$
. We set
We have
Hence
Let
![]() $v < s$
with
$v < s$
with
![]() $t-s \leq s- v$
. As
$t-s \leq s- v$
. As
![]() $Z \in \mathcal {D}_1 (\alpha , \beta )$
, we write
$Z \in \mathcal {D}_1 (\alpha , \beta )$
, we write
Then, if we write ![]() ,
,
Hence, if we write ![]() , then
, then
Next, we will estimate
![]() $ \lVert {\mathbb {E} [\delta \hat {A}_{s, u, t} \vert \mathcal {F}_v]} \rVert _{L_m(\mathbb {P})}$
. The rest of the calculation resembles the proof of Proposition 3.5. We write
$ \lVert {\mathbb {E} [\delta \hat {A}_{s, u, t} \vert \mathcal {F}_v]} \rVert _{L_m(\mathbb {P})}$
. The rest of the calculation resembles the proof of Proposition 3.5. We write ![]() and
and ![]() as before. We can decompose
as before. We can decompose
where
![]() $\hat {Y}_r$
is
$\hat {Y}_r$
is
![]() $\mathcal {F}_v$
-measurable and
$\mathcal {F}_v$
-measurable and
![]() $\tilde {B}_r$
is independent of
$\tilde {B}_r$
is independent of
![]() $\mathcal {F}_v$
. We set
$\mathcal {F}_v$
. We set

Then, as in the proof of Proposition 3.5, we have the decomposition
 $$\begin{align*}\mathbb{E} [\delta \hat{A}_{s, u, t} | \mathcal{F}_v] = \hat{D}^0_{s, u, t} + \sum_{i = 1}^d \hat{D}_{s, u, t}^i, \end{align*}$$
$$\begin{align*}\mathbb{E} [\delta \hat{A}_{s, u, t} | \mathcal{F}_v] = \hat{D}^0_{s, u, t} + \sum_{i = 1}^d \hat{D}_{s, u, t}^i, \end{align*}$$
where, as in (3.8) and (3.11),

The map
![]() $\mathbb {R}^d \ni x \mapsto f (z^{(2)} (v)^{} x) \in \mathbb {R}^d$
belongs to
$\mathbb {R}^d \ni x \mapsto f (z^{(2)} (v)^{} x) \in \mathbb {R}^d$
belongs to
![]() $C^{\delta } (\mathbb {R}^d)$
with its norm bounded by
$C^{\delta } (\mathbb {R}^d)$
with its norm bounded by
Therefore, by repeating the argument used to obtain (3.9), we obtain
 $$ \begin{align*} &| \hat{D}^0_{s, u, t} | \leq | z^{(2)} (v) |^{\delta} \| f \|_{C^{\delta} (\mathbb{R}^d)} \Big\{ (s - v)^{\delta H - 1} (t - s) (| Y_{s, u} | + | Y_{u, t} |) \\ & \quad + (s - v)^{(\delta - 1) H} \Big( | (z^{(2)} (v))^{- 1} \hat{Y}_{s, u} | | Y_{u, t} | + | z^{(2)} (v)^{- 1} \hat{Y}_{u, t} | | Y_{s, u} | \Big) \Big\}. \end{align*} $$
$$ \begin{align*} &| \hat{D}^0_{s, u, t} | \leq | z^{(2)} (v) |^{\delta} \| f \|_{C^{\delta} (\mathbb{R}^d)} \Big\{ (s - v)^{\delta H - 1} (t - s) (| Y_{s, u} | + | Y_{u, t} |) \\ & \quad + (s - v)^{(\delta - 1) H} \Big( | (z^{(2)} (v))^{- 1} \hat{Y}_{s, u} | | Y_{u, t} | + | z^{(2)} (v)^{- 1} \hat{Y}_{u, t} | | Y_{s, u} | \Big) \Big\}. \end{align*} $$
Referring to (3.4), we have
Therefore,
 $$ \begin{align*} &\| \hat{D}^0_{s, u, t} \|_{L_m (\mathbb{P})} \lesssim \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\ & \quad \times \{ (s - v)^{(\delta + 1) H - 2} (t - s)^2 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})} (s - v)^{\delta H - 1} (t - s)^2 \}. \end{align*} $$
$$ \begin{align*} &\| \hat{D}^0_{s, u, t} \|_{L_m (\mathbb{P})} \lesssim \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\ & \quad \times \{ (s - v)^{(\delta + 1) H - 2} (t - s)^2 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})} (s - v)^{\delta H - 1} (t - s)^2 \}. \end{align*} $$
Similarly as before, we have
As
![]() $H> \frac {1}{2}$
, by Lemma 3.2, we have
$H> \frac {1}{2}$
, by Lemma 3.2, we have
Therefore,
 $$ \begin{align*} &\| \hat{D}^i_{s, u, t} \|_{L_m (\mathbb{P})} \lesssim \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\ &\quad \times \{ (s - v)^{(\delta + 1) H - 2} (t - s)^2 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})} (s - v)^{\delta H - 1} (t - s)^2 \}. \end{align*} $$
$$ \begin{align*} &\| \hat{D}^i_{s, u, t} \|_{L_m (\mathbb{P})} \lesssim \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\ &\quad \times \{ (s - v)^{(\delta + 1) H - 2} (t - s)^2 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})} (s - v)^{\delta H - 1} (t - s)^2 \}. \end{align*} $$
Combining our estimates, we have
 $$ \begin{align} &\| \mathbb{E} [\delta \hat{A}_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} \lesssim_T \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \nonumber\\ & \quad \times (1 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})}) (s - v)^{(\delta + 1) H - 2} (t - s)^2. \end{align} $$
$$ \begin{align} &\| \mathbb{E} [\delta \hat{A}_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} \lesssim_T \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \nonumber\\ & \quad \times (1 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})}) (s - v)^{(\delta + 1) H - 2} (t - s)^2. \end{align} $$
Hence, combining (5.11), (5.12), and (5.13)
and
 $$ \begin{align*} &\| \mathbb{E} [\delta A_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} \lesssim_{\alpha, \delta, T} \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\& \quad \times (1 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})}) (s - v)^{(\delta + 1) H - 2} (t - s)^2 \\& \quad +\| f \|_{C^{\delta}} \lVert {\lVert{Z}\rVert_{\mathcal{D}(\alpha,\beta)}^{\delta}} \rVert _{L_{2m}(\mathbb{P})} | t - v |^{\delta \beta} | t - s |^H. \end{align*} $$
$$ \begin{align*} &\| \mathbb{E} [\delta A_{s, u, t} | \mathcal{F}_v] \|_{L_m (\mathbb{P})} \lesssim_{\alpha, \delta, T} \| f \|_{C^{\delta}} \| | z^{(2)} (v) |^{\delta} \|_{L_{3 m} (\mathbb{P})} \\& \quad \times (1 + \| z^{(2)}(v)^{-1} z^{(3)} (v) \|_{L_{3 m} (\mathbb{P})}) (s - v)^{(\delta + 1) H - 2} (t - s)^2 \\& \quad +\| f \|_{C^{\delta}} \lVert {\lVert{Z}\rVert_{\mathcal{D}(\alpha,\beta)}^{\delta}} \rVert _{L_{2m}(\mathbb{P})} | t - v |^{\delta \beta} | t - s |^H. \end{align*} $$
To apply Lemma 5.5, we need
which, if
![]() $\alpha $
is sufficiently close to H, are fulfilled under (5.10).
$\alpha $
is sufficiently close to H, are fulfilled under (5.10).
Proof of Theorem 5.2.
We first prove the pathwise uniqueness. We suppose that the assumption in the case 2 mentioned in Theorem 5.2 holds, and the other cases will be discussed later. Let
![]() $X^{(1)}$
and
$X^{(1)}$
and
![]() $X^{(2)}$
be
$X^{(2)}$
be
![]() $(\mathcal {F}_t)$
-adapted solutions. Our strategy is similar to Proposition 5.1, but, here, we must construct the integral (5.5) stochastically. For each
$(\mathcal {F}_t)$
-adapted solutions. Our strategy is similar to Proposition 5.1, but, here, we must construct the integral (5.5) stochastically. For each
![]() $k \in \mathbb {N}$
, we set
$k \in \mathbb {N}$
, we set
we let
![]() $\sigma ^{k} \in C^{1 + \delta }(\mathbb {R}^d; \mathcal {M}_d)$
be such that
$\sigma ^{k} \in C^{1 + \delta }(\mathbb {R}^d; \mathcal {M}_d)$
be such that
![]() $\sigma ^k = \sigma $
in
$\sigma ^k = \sigma $
in
![]() $\{x \mid \lvert {x} \rvert \leq k\}$
and
$\{x \mid \lvert {x} \rvert \leq k\}$
and
and we set

If we write
then in the event
![]() $\Omega _k$
, we have
$\Omega _k$
, we have
![]() $X^{(i)}_t = X^{(i), k}_t$
,
$X^{(i)}_t = X^{(i), k}_t$
,
![]() $t \in [0, T]$
.
$t \in [0, T]$
.
Let
![]() $\{\sigma ^{k, n}\}_{n=1}^{\infty }$
be a smooth approximation of
$\{\sigma ^{k, n}\}_{n=1}^{\infty }$
be a smooth approximation of
![]() $\sigma ^k$
. In general, we can only guarantee the convergence in
$\sigma ^k$
. In general, we can only guarantee the convergence in
![]() $C^{1+\delta '}(\mathbb {R}^d, \mathcal {M}_d)$
for any
$C^{1+\delta '}(\mathbb {R}^d, \mathcal {M}_d)$
for any
![]() $\delta '<\delta $
, which is still sufficient to make the following argument work. To simplify the notation, we assume that we can take
$\delta '<\delta $
, which is still sufficient to make the following argument work. To simplify the notation, we assume that we can take
![]() $\delta '=\delta $
.
$\delta '=\delta $
.
We have
 $$ \begin{align*} \int_{0}^t \sigma^k(X^{(i)}_r) \, \mathrm{d} B_r = \lim_{n \to \infty} \int_{0}^t \sigma^{k, n}(X^{(i)}_r) \, \mathrm{d} B_r \end{align*} $$
$$ \begin{align*} \int_{0}^t \sigma^k(X^{(i)}_r) \, \mathrm{d} B_r = \lim_{n \to \infty} \int_{0}^t \sigma^{k, n}(X^{(i)}_r) \, \mathrm{d} B_r \end{align*} $$
and in
![]() $\Omega _k$
$\Omega _k$
 $$ \begin{align*} \int_{0}^t \{ \sigma^{k, n}(X^{(1)}_r) - \sigma^{k, n}(X^{(2)}_r)\} \, \mathrm{d} B_r = \int_0^t \{X^{(1), k}_r - X^{(2), k}_r \} \, \mathrm{d} V^{k, n}_r, \end{align*} $$
$$ \begin{align*} \int_{0}^t \{ \sigma^{k, n}(X^{(1)}_r) - \sigma^{k, n}(X^{(2)}_r)\} \, \mathrm{d} B_r = \int_0^t \{X^{(1), k}_r - X^{(2), k}_r \} \, \mathrm{d} V^{k, n}_r, \end{align*} $$
where

For a fixed
![]() $\theta \in (0, 1)$
, we set
$\theta \in (0, 1)$
, we set
By the a priori estimate (5.9), for
![]() $\alpha \in (\frac {1}{2}, H)$
, we have
$\alpha \in (\frac {1}{2}, H)$
, we have
 $$ \begin{align*} Z_t^{\theta, k} - Z_s^{\theta, k} &= \{\theta \sigma^k(X_s^{(1), k}) + (1 - \theta) \sigma^k(X_s^{(1), k})\} B_{s,t} \\ & \quad + \{\theta b(X_s^{(1), k}) + (1 - \theta) b (X_s^{(1), k})\}(t-s) + R_{s, t} \end{align*} $$
$$ \begin{align*} Z_t^{\theta, k} - Z_s^{\theta, k} &= \{\theta \sigma^k(X_s^{(1), k}) + (1 - \theta) \sigma^k(X_s^{(1), k})\} B_{s,t} \\ & \quad + \{\theta b(X_s^{(1), k}) + (1 - \theta) b (X_s^{(1), k})\}(t-s) + R_{s, t} \end{align*} $$
with
Note that we have
and hence
Therefore, we have
![]() $Z^{\theta , k} \in \mathcal {D}_1(\alpha , 2 \alpha )$
with
$Z^{\theta , k} \in \mathcal {D}_1(\alpha , 2 \alpha )$
with
Since
 $$ \begin{align*} \max \Big\{ \frac{1 - H}{2 \alpha}, \frac{2 - 3 H + H^2}{2 \alpha + H - H^2}, \frac{3 - \sqrt{3}}{2 H} - 1 \Big\} = \frac{2 - 3 H + H^2}{2 \alpha + H - H^2}< \delta \end{align*} $$
$$ \begin{align*} \max \Big\{ \frac{1 - H}{2 \alpha}, \frac{2 - 3 H + H^2}{2 \alpha + H - H^2}, \frac{3 - \sqrt{3}}{2 H} - 1 \Big\} = \frac{2 - 3 H + H^2}{2 \alpha + H - H^2}< \delta \end{align*} $$
if
![]() $\alpha $
is sufficiently close to H, by Proposition 5.8,
$\alpha $
is sufficiently close to H, by Proposition 5.8,
By Kolmogorov’s continuity theorem, the sequence
![]() $(V^{k, n})_{n \in \mathbb {N}}$
converges to some
$(V^{k, n})_{n \in \mathbb {N}}$
converges to some
![]() $V^k$
in
$V^k$
in
![]() $C^{\alpha }([0, T], \mathbb {R}^d)$
.
$C^{\alpha }([0, T], \mathbb {R}^d)$
.
Therefore, we conclude that almost surely in
![]() $\Omega _k$
, the path
$\Omega _k$
, the path
![]() $z = X^{(1)} - X^{(2)}$
solves the linear Young equation
$z = X^{(1)} - X^{(2)}$
solves the linear Young equation

and hence
![]() $X^{(1)} = X^{(2)}$
. Since
$X^{(1)} = X^{(2)}$
. Since
![]() $\mathbb {P}(\Omega _k) \to 1$
, we conclude
$\mathbb {P}(\Omega _k) \to 1$
, we conclude
![]() $X^{(1)} = X^{(2)}$
almost surely. Thus, we completed the proof of the uniqueness under the case 2. The other cases can be handled similarly. Indeed, under the case 1, we have
$X^{(1)} = X^{(2)}$
almost surely. Thus, we completed the proof of the uniqueness under the case 2. The other cases can be handled similarly. Indeed, under the case 1, we have
![]() $X^{(i)} \in \mathcal {D}_0(\alpha , 2 \alpha )$
, and under the case 3, we have
$X^{(i)} \in \mathcal {D}_0(\alpha , 2 \alpha )$
, and under the case 3, we have
![]() $X^{(i)} \in \mathcal {D}_0(\alpha , 1)$
.
$X^{(i)} \in \mathcal {D}_0(\alpha , 1)$
.
Now, it remains to prove the existence of a strong solution. However, in view of the Yamada-Watanabe theorem (Proposition B.2), it suffices to show the existence of a weak solution, which will be proved in Lemma B.3 based on a standard compactness argument.
Remark 5.9. We believe that our assumption in Theorem 5.2 is not optimal. One possible approach to relax the assumption is to consider a higher order approximation in (5.7). Yet, we believe that this will not lead to an optimal assumption, as long as we apply Lemma 5.5. Thus, finding an optimal regularity of
![]() $\sigma $
for the pathwise uniqueness and the strong existence remains an interesting open question that is likely to require a new idea.
$\sigma $
for the pathwise uniqueness and the strong existence remains an interesting open question that is likely to require a new idea.
A. Proofs of technical results
Proofs of Lemmas 2.3 and 2.4
Proof of Lemma 2.3 without (1.12).
Let us first recall our previous strategy under (1.12). We used Lemma 2.1 to write
 $$ \begin{align} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i. \end{align} $$
$$ \begin{align} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n \in \mathbb{N}_0} \sum_{i=0}^{2^n - 1} R^n_i. \end{align} $$
Then, we decomposed

where ![]() . We estimated the first term of (A.2) by the BDG inequality and (1.8):
. We estimated the first term of (A.2) by the BDG inequality and (1.8):

In the proof under (1.12), we estimated the second term of (A.2) by the triangle inequality and (1.7):
 $$ \begin{align} \lVert {\sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha}. \end{align} $$
$$ \begin{align} \lVert {\sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n]} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha} \Gamma_1 L^{-\alpha} 2^{-(\beta_1 - \alpha - 1) n} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha}. \end{align} $$
Then, we chose L so that both (A.3) and (A.4) are summable with respect to n, for which to be possible, we had to assume (1.12).
In order to remove the assumption (1.12), let us think again why we did the decomposition (A.2). This is because we do not want to apply the simplest estimate, namely, the triangle inequality, since the condition (1.7) implies that
![]() $(A_{s,t})_{[s,t] \in \pi }$
are not so correlated. This point of view teaches us that, to estimate
$(A_{s,t})_{[s,t] \in \pi }$
are not so correlated. This point of view teaches us that, to estimate
 $$ \begin{align*} \sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n], \end{align*} $$
$$ \begin{align*} \sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n], \end{align*} $$
we should not simply apply the triangle inequality. That is, we should again apply the decomposition as in (A.2).
To carry out our new strategy, set
For this new strategy, we can set ![]() . In particular, L does not depend on n. We use the convention
. In particular, L does not depend on n. We use the convention
![]() $\mathbb {E}[X \vert \mathcal {G}^{(1), l}_j] = 0$
for
$\mathbb {E}[X \vert \mathcal {G}^{(1), l}_j] = 0$
for
![]() $j \leq 0$
. Then,
$j \leq 0$
. Then,
 $$ \begin{align} \sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n] = \sum_{l=0}^{L-1} \sum_{j=1}^{L^{-1} 2^n} \mathbb{E}[S^{(1), l}_j \vert \mathcal{G}^{(1), l}_j] = \sum_{l_1=0}^{L-1} \sum_{l_2=0}^{L-1} \sum_{j=0}^{L^{-2} 2^n} \mathbb{E}[S^{(1), l_1}_{jL + l_2} \vert \mathcal{G}^{(1), l_1}_{jL + l_2 }]. \end{align} $$
$$ \begin{align} \sum_{l = 0}^{L - 1} \sum_{j=1}^{2^n/L } \mathbb{E}[R^n_{L j + l} \vert \mathcal{F}_{L (j-1) + l + 1}^n] = \sum_{l=0}^{L-1} \sum_{j=1}^{L^{-1} 2^n} \mathbb{E}[S^{(1), l}_j \vert \mathcal{G}^{(1), l}_j] = \sum_{l_1=0}^{L-1} \sum_{l_2=0}^{L-1} \sum_{j=0}^{L^{-2} 2^n} \mathbb{E}[S^{(1), l_1}_{jL + l_2} \vert \mathcal{G}^{(1), l_1}_{jL + l_2 }]. \end{align} $$
By setting
the quantity (A.5) equals to
 $$ \begin{align*} \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=0}^{L^{-2} 2^n} \big(\mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j+1}] - \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j}] \big) + \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=0}^{L^{-2} 2^n} \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j }]. \end{align*} $$
$$ \begin{align*} \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=0}^{L^{-2} 2^n} \big(\mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j+1}] - \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j}] \big) + \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=0}^{L^{-2} 2^n} \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j }]. \end{align*} $$
The
![]() $L_m(\mathbb {P})$
-norm of the first term can be estimated by the BDG inequality: it is bounded by
$L_m(\mathbb {P})$
-norm of the first term can be estimated by the BDG inequality: it is bounded by
 $$ \begin{align} 2 \kappa_{m, d} \sum_{l_1, l_2 \leq L} \Big( \sum_{j \leq L^{-2} 2^n} \lVert {\mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j+1}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} 2 \kappa_{m, d} \sum_{l_1, l_2 \leq L} \Big( \sum_{j \leq L^{-2} 2^n} \lVert {\mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j+1}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align} $$
By (1.7), we have
Therefore, the quantity (A.6) is bounded by
As the reader may realize, we will repeat the same argument for
 $$ \begin{align*} \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=1}^{L^{-2} 2^n} \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j - 1}] \end{align*} $$
$$ \begin{align*} \sum_{l_1=0}^{L} \sum_{l_2=0}^L \sum_{j=1}^{L^{-2} 2^n} \mathbb{E}[S^{(2), l_1, l_2}_j \vert \mathcal{G}^{(2), l_1, l_2}_{j - 1}] \end{align*} $$
and continue. To state more precisely, set inductively,
We claim that, if
![]() $L^k \leq 2^n$
, we have
$L^k \leq 2^n$
, we have
 $$ \begin{align*} &\lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \leq 2 \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2} \\& \quad +2 \kappa_{m, d} \Gamma_1 \Big(\sum_{j=1}^{k-1} L^{\frac{j}{2} - (j-1) \alpha} \Big) L^{\frac{1}{2}} 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} \\& \quad + \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
$$ \begin{align*} &\lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \leq 2 \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2} \\& \quad +2 \kappa_{m, d} \Gamma_1 \Big(\sum_{j=1}^{k-1} L^{\frac{j}{2} - (j-1) \alpha} \Big) L^{\frac{1}{2}} 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} \\& \quad + \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
The proof of the claim is based on induction. The case
![]() $k=1$
and
$k=1$
and
![]() $k=2$
is obtained. Suppose that the claim is correct for
$k=2$
is obtained. Suppose that the claim is correct for
![]() $k \geq 2$
, and consider the case
$k \geq 2$
, and consider the case
![]() $k+1$
. Again, decompose
$k+1$
. Again, decompose
 $$ \begin{align*} &\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }] \\& \quad = \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \sum_{j \leq L^{-(k+1)} 2^n} \big(\mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1} }_{j+1}] - \mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1}}_{j}] \big) \\& \qquad + \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \sum_{j \leq L^{-(k+1)} 2^n} \mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1}}_{j}]. \end{align*} $$
$$ \begin{align*} &\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }] \\& \quad = \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \sum_{j \leq L^{-(k+1)} 2^n} \big(\mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1} }_{j+1}] - \mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1}}_{j}] \big) \\& \qquad + \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \sum_{j \leq L^{-(k+1)} 2^n} \mathbb{E}[S^{(k+1), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1}}_{j}]. \end{align*} $$
To prove the claim, it suffices to estimate the first sum in the right-hand side. By the BDG inequality, its
![]() $L_m(\mathbb {P})$
-norm is bounded by
$L_m(\mathbb {P})$
-norm is bounded by
 $$ \begin{align} 2 \kappa_{m, d} \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \Big(\sum_{j \leq L^{-(k+1)} 2^n} \lVert {\mathbb{E}[S^{(k+1), l_1, \ldots, l_k, l_{k+1}}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1} }_{j+1}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{1/2}. \end{align} $$
$$ \begin{align} 2 \kappa_{m, d} \sum_{l_1, \ldots, l_k, l_{k+1} \leq L} \Big(\sum_{j \leq L^{-(k+1)} 2^n} \lVert {\mathbb{E}[S^{(k+1), l_1, \ldots, l_k, l_{k+1}}_j \vert \mathcal{G}^{(k+1), l_1, \ldots, l_k, l_{k+1} }_{j+1}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{1/2}. \end{align} $$
By (1.7),
Therefore, the quantity (A.8) is bounded by
and the claim follows.
Now let us estimate
 $$ \begin{align} \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})} \end{align} $$
$$ \begin{align} \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})} \end{align} $$
by the triangle inequality:
 $$ \begin{align*} & \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})} \\ & \quad\leq \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \lVert {\mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
$$ \begin{align*} & \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})} \\ & \quad\leq \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq L^{-k} 2^{n}} \lVert {\mathbb{E}[S^{(k), l_1, \ldots, l_k}_j \vert \mathcal{G}^{(k), l_1, \ldots, l_k}_{j }]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
By (1.7) (or essentially the estimate (A.9)),
and hence, the quantity (A.10) is bounded by
In conclusion, we obtained for
![]() $L^k \leq 2^n$
,
$L^k \leq 2^n$
,
 $$ \begin{align} & \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2} \nonumber\\ & \quad + \kappa_{m, d} \Gamma_1 f_k 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \Gamma_1 L^{-\alpha k} 2^{-n(\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha }, \end{align} $$
$$ \begin{align} & \lVert {\sum_{i=0}^{2^n - 1} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \Gamma_2 L^{\frac{1}{2}} 2^{-n(\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2} \nonumber\\ & \quad + \kappa_{m, d} \Gamma_1 f_k 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \Gamma_1 L^{-\alpha k} 2^{-n(\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha }, \end{align} $$
where

We recall that
![]() $L = \max \{2, \lceil M \rceil \}$
. To respect
$L = \max \{2, \lceil M \rceil \}$
. To respect
![]() $L^k \leq 2^n$
, we set
$L^k \leq 2^n$
, we set ![]() . We then have
. We then have
 $$ \begin{align*} f_k 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lesssim_{M} \begin{cases} 2^{-n (\beta_1 - 1)}, &\text{if } \alpha < \frac{1}{2}, \\ n 2^{-n(\beta_1 - \alpha - \frac{1}{2})}, &\text{if } \alpha \geq \frac{1}{2}, \end{cases} \end{align*} $$
$$ \begin{align*} f_k 2^{-n(\beta_1 - \alpha - \frac{1}{2})} \lesssim_{M} \begin{cases} 2^{-n (\beta_1 - 1)}, &\text{if } \alpha < \frac{1}{2}, \\ n 2^{-n(\beta_1 - \alpha - \frac{1}{2})}, &\text{if } \alpha \geq \frac{1}{2}, \end{cases} \end{align*} $$
and
Therefore, we note that the right-hand side of (A.11) is summable with respect to n and
 $$ \begin{align*} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} } \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2} + \kappa_{m, d} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1}.\\[-45pt] \end{align*} $$
$$ \begin{align*} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} } \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2} + \kappa_{m, d} \Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1}.\\[-45pt] \end{align*} $$
Proof of Lemma 2.4.
The proof is similar to Lemma 2.3. Write
and
By (2.6), we have
![]() $N \leq 3 \lvert {\pi '} \rvert ^{-1} T$
. We fix a parameter L, which will be chosen later, and set
$N \leq 3 \lvert {\pi '} \rvert ^{-1} T$
. We fix a parameter L, which will be chosen later, and set

Inductively, we set
As in Lemma 2.3, for each
![]() $k \in \mathbb {N}$
, we consider the decomposition
$k \in \mathbb {N}$
, we consider the decomposition
where

For this decomposition, we must have
![]() $L^k \leq N$
. By the BDG inequality and the Cauchy-Schwarz inequality,
$L^k \leq N$
. By the BDG inequality and the Cauchy-Schwarz inequality,
 $$ \begin{align*} \lVert {A} \rVert _{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \sum_{p=1}^k L^{\frac{p}{2}} \Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq N L^{-p}} \lVert {\mathbb{E}[Z^{(p), l_1, \ldots, l_p}_j \vert \mathcal{H}_{j+1}^{(p), l_1, \ldots, l_p}] } \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \lVert {A} \rVert _{L_m(\mathbb{P})} \lesssim \kappa_{m, d} \sum_{p=1}^k L^{\frac{p}{2}} \Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq N L^{-p}} \lVert {\mathbb{E}[Z^{(p), l_1, \ldots, l_p}_j \vert \mathcal{H}_{j+1}^{(p), l_1, \ldots, l_p}] } \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
By Lemma 2.3,
For
![]() $p \geq 2$
, by Lemma 2.2 and (2.6),
$p \geq 2$
, by Lemma 2.2 and (2.6),
Therefore, we obtain
where
![]() $f_k$
is defined by (A.12).
$f_k$
is defined by (A.12).
We move to estimate B. By Lemma 2.2 and (2.6),
Therefore,
Combining (A.13) and (A.14), we obtain
 $$ \begin{align*} & \lVert {A^{\pi'}_T - A^{\pi}_T} \rVert _{L_m(\mathbb{P})} \\ & \quad \lesssim_{\alpha, \beta_1, \beta_2, m, d, T} L^{\frac{1}{2}}(\Gamma_1 \lvert {\pi'} \rvert ^{\beta_1 - \alpha - \frac{1}{2}} + \Gamma_2 \lvert {\pi'} \rvert ^{\beta_2 - \frac{1}{2}}) + \Gamma_1 f_{k} \lvert {\pi'} \rvert ^{\beta_1 - \alpha - \frac{1}{2}} + \Gamma_1 L^{-\alpha k} \lvert {\pi'} \rvert ^{\beta_1 - \alpha - 1}. \end{align*} $$
$$ \begin{align*} & \lVert {A^{\pi'}_T - A^{\pi}_T} \rVert _{L_m(\mathbb{P})} \\ & \quad \lesssim_{\alpha, \beta_1, \beta_2, m, d, T} L^{\frac{1}{2}}(\Gamma_1 \lvert {\pi'} \rvert ^{\beta_1 - \alpha - \frac{1}{2}} + \Gamma_2 \lvert {\pi'} \rvert ^{\beta_2 - \frac{1}{2}}) + \Gamma_1 f_{k} \lvert {\pi'} \rvert ^{\beta_1 - \alpha - \frac{1}{2}} + \Gamma_1 L^{-\alpha k} \lvert {\pi'} \rvert ^{\beta_1 - \alpha - 1}. \end{align*} $$
As in the proof of Lemma 2.3, we set ![]() and
and ![]() . We then obtain the claimed estimate.
. We then obtain the claimed estimate.
Proof of Corollary 2.7
The argument is similar to that of Theorem 1.1. Therefore, we only prove an analogue of Lemma 2.3.
Analogue of Lemma 2.3.
Given a partition
we have
 $$ \begin{align} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i}} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1 t_0^{-\gamma_1} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 t_0^{-\gamma_2} \lvert {t_N - t_0} \rvert ^{\beta_2}, \end{align} $$
$$ \begin{align} \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i}} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, M} \kappa_{m, d} \Gamma_1 t_0^{-\gamma_1} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha} + \kappa_{m, d} \Gamma_2 t_0^{-\gamma_2} \lvert {t_N - t_0} \rvert ^{\beta_2}, \end{align} $$
 $$ \begin{align} & \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i}} \rVert _{L_m(\mathbb{P})} \nonumber\\ & \quad \lesssim_{\alpha, \beta_1, \beta_2, \beta_3, \gamma_1, \gamma_2, M} \kappa_{m,d} (\Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1 - \gamma_1} + \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} + \Gamma_3 \lvert {t_N - t_0} \rvert ^{\beta_3}), \end{align} $$
$$ \begin{align} & \lVert {A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i}} \rVert _{L_m(\mathbb{P})} \nonumber\\ & \quad \lesssim_{\alpha, \beta_1, \beta_2, \beta_3, \gamma_1, \gamma_2, M} \kappa_{m,d} (\Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1 - \gamma_1} + \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} + \Gamma_3 \lvert {t_N - t_0} \rvert ^{\beta_3}), \end{align} $$
where
![]() $t_0> 0$
is assumed for (A.15). In fact, the proof of (A.15) is the same as that of Lemma 2.3, since we can simply replace
$t_0> 0$
is assumed for (A.15). In fact, the proof of (A.15) is the same as that of Lemma 2.3, since we can simply replace
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
by
$\Gamma _2$
by
![]() $t_0^{-\gamma _1} \Gamma _1$
and
$t_0^{-\gamma _1} \Gamma _1$
and
![]() $t_0^{-\gamma _2} \Gamma _2$
. Therefore, we focus on proving (A.16).
$t_0^{-\gamma _2} \Gamma _2$
. Therefore, we focus on proving (A.16).
Yet, the proof of (A.16) is similar to that of Lemma 2.3. Recalling the notation therein, namely, (A.1) and (A.7), we have
 $$ \begin{align*} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n=0}^{\infty} \sum_{i=0}^{2^n} R^n_i, \end{align*} $$
$$ \begin{align*} A_{t_0, t_N} - \sum_{i=1}^N A_{t_{i-1}, t_i} = \sum_{n=0}^{\infty} \sum_{i=0}^{2^n} R^n_i, \end{align*} $$
 $$ \begin{align} &\sum_{i=0}^{2^n} R^n_i = \sum_{p=1}^k \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \Big\{ \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}] - \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j}^{(p), l_1, \ldots, l_p}] \Big\} \nonumber\\& \quad + \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]. \end{align} $$
$$ \begin{align} &\sum_{i=0}^{2^n} R^n_i = \sum_{p=1}^k \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \Big\{ \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}] - \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j}^{(p), l_1, \ldots, l_p}] \Big\} \nonumber\\& \quad + \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]. \end{align} $$
We fix a large n. To estimate the first term of (A.17), we apply the BDG inequality to obtain
 $$ \begin{align*} & \lVert {\sum_{j \leq 2^n L^{-p}} \Big\{ \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}] - \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j}^{(p), l_1, \ldots, l_p}] \Big\}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \kappa_{m, d} \Big( \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} & \lVert {\sum_{j \leq 2^n L^{-p}} \Big\{ \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}] - \mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j}^{(p), l_1, \ldots, l_p}] \Big\}} \rVert _{L_m(\mathbb{P})} \\& \quad \lesssim \kappa_{m, d} \Big( \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
For
![]() $p=1$
, since
$p=1$
, since
![]() $S^{(1), l_1}_j = R^n_{j L + l_1}$
, by the Cauchy-Schwarz inequality,
$S^{(1), l_1}_j = R^n_{j L + l_1}$
, by the Cauchy-Schwarz inequality,
 $$ \begin{align*} \sum_{l_1 \leq L} \Big( \sum_{j \leq 2^n L^{-1}} \lVert {S_j^{(1), l_1}} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \leq L^{\frac{1}{2}} \Big( \sum_{i=0}^{2^n} \lVert {R^n_i} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \sum_{l_1 \leq L} \Big( \sum_{j \leq 2^n L^{-1}} \lVert {S_j^{(1), l_1}} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \leq L^{\frac{1}{2}} \Big( \sum_{i=0}^{2^n} \lVert {R^n_i} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
For
![]() $i \geq 1$
, by (2.11), we have
$i \geq 1$
, by (2.11), we have
and by (2.12)
Therefore,
 $$ \begin{align*} \Big(\sum_{i=0}^{2^n} \lVert {R^n_i} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \lesssim \Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n \beta_2} \lvert {t_N - t_0} \rvert ^{\beta_2} \Big( \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{-2 \gamma_2} \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \Big(\sum_{i=0}^{2^n} \lVert {R^n_i} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \lesssim \Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n \beta_2} \lvert {t_N - t_0} \rvert ^{\beta_2} \Big( \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{-2 \gamma_2} \Big)^{\frac{1}{2}}. \end{align*} $$
We observe
 $$ \begin{align} \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{-2 \gamma_2} \leq 2^n \lvert {t_N - t_0} \rvert ^{-1} \int_0^{ \lvert {t_N - t_0} \rvert } s^{-2 \gamma_2} \, \mathrm{d} s = \frac{2^n \lvert {t_N - t_0} \rvert ^{- 2 \gamma_2}}{1 - 2 \gamma_2}, \end{align} $$
$$ \begin{align} \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{-2 \gamma_2} \leq 2^n \lvert {t_N - t_0} \rvert ^{-1} \int_0^{ \lvert {t_N - t_0} \rvert } s^{-2 \gamma_2} \, \mathrm{d} s = \frac{2^n \lvert {t_N - t_0} \rvert ^{- 2 \gamma_2}}{1 - 2 \gamma_2}, \end{align} $$
where the condition
![]() $\gamma _2 < \frac {1}{2}$
is used. We conclude
$\gamma _2 < \frac {1}{2}$
is used. We conclude
 $$ \begin{align*} \sum_{l_1 \leq L} \Big( \sum_{j \leq 2^n L^{-1}} \lVert {S_j^{(1), l_1}} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \lesssim_{\gamma_2} L^{\frac{1}{2}} (\Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n (\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} ). \end{align*} $$
$$ \begin{align*} \sum_{l_1 \leq L} \Big( \sum_{j \leq 2^n L^{-1}} \lVert {S_j^{(1), l_1}} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \lesssim_{\gamma_2} L^{\frac{1}{2}} (\Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n (\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} ). \end{align*} $$
For
![]() $2 \leq p \leq k$
, the argument is similar but now we use (2.10). By the Cauchy-Schwarz inequality,
$2 \leq p \leq k$
, the argument is similar but now we use (2.10). By the Cauchy-Schwarz inequality,
 $$ \begin{align*} &\sum_{l_1, \ldots, l_p \leq L} \Big( \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \\ & \quad \leq L^{\frac{p}{2}} \Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} &\sum_{l_1, \ldots, l_p \leq L} \Big( \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \\ & \quad \leq L^{\frac{p}{2}} \Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}}. \end{align*} $$
We note that for each index
![]() $l_1, \ldots , l_p$
and j in the sum, there exists a unique
$l_1, \ldots , l_p$
and j in the sum, there exists a unique
![]() $i = i(l_1, \ldots , l_p; j)$
, such that
$i = i(l_1, \ldots , l_p; j)$
, such that
As
![]() $p \geq 2$
, we know
$p \geq 2$
, we know
![]() $i \geq L$
. By (2.10) (as in the estimate (A.9)),
$i \geq L$
. By (2.10) (as in the estimate (A.9)),
 $$ \begin{align*} & \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})} \\ & \quad \leq 2 \Gamma_1 (L^{p-1} 2^{-n} \lvert {t_N - t_0} \rvert )^{-\alpha} (t_0 + 2^{-n} i(l_1, \ldots, l_p;j) \lvert {t_N - t_0} \rvert )^{- \gamma_1} (2^{-n } \lvert {t_N - t_0} \rvert )^{\beta_1}. \end{align*} $$
$$ \begin{align*} & \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})} \\ & \quad \leq 2 \Gamma_1 (L^{p-1} 2^{-n} \lvert {t_N - t_0} \rvert )^{-\alpha} (t_0 + 2^{-n} i(l_1, \ldots, l_p;j) \lvert {t_N - t_0} \rvert )^{- \gamma_1} (2^{-n } \lvert {t_N - t_0} \rvert )^{\beta_1}. \end{align*} $$
Therefore,
 $$ \begin{align*} &\Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \\ & \quad \lesssim \Gamma_1 (L^{p-1} 2^{-n} \lvert {t_N - t_0} \rvert )^{-\alpha} (2^{-n } \lvert {t_N - t_0} \rvert )^{\beta_1} \Big( \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{- 2\gamma_1} \Big)^{\frac{1}{2}} \\ & \quad \lesssim_{\gamma_1} \Gamma_1 L^{-\alpha(p-1)} 2^{- n (\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }, \end{align*} $$
$$ \begin{align*} &\Big( \sum_{l_1, \ldots, l_p \leq L} \sum_{j \leq 2^n L^{-p}} \lVert {\mathbb{E}[S_j^{(p), l_1, \ldots, l_p} \vert \mathcal{G}_{j+1}^{(p), l_1, \ldots, l_p}]} \rVert _{L_m(\mathbb{P})}^2 \Big)^{\frac{1}{2}} \\ & \quad \lesssim \Gamma_1 (L^{p-1} 2^{-n} \lvert {t_N - t_0} \rvert )^{-\alpha} (2^{-n } \lvert {t_N - t_0} \rvert )^{\beta_1} \Big( \sum_{i=1}^{2^n} (t_0 + 2^{-n} i \lvert {t_N - t_0} \rvert )^{- 2\gamma_1} \Big)^{\frac{1}{2}} \\ & \quad \lesssim_{\gamma_1} \Gamma_1 L^{-\alpha(p-1)} 2^{- n (\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }, \end{align*} $$
where to obtain the second inequality, we applied the estimate (A.18).
Now we consider the estimate of the second term of (A.17). By the triangle inequality,
 $$ \begin{align*} & \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})} \\ & \quad \leq \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \lVert {\mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
$$ \begin{align*} & \lVert {\sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})} \\ & \quad \leq \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \lVert {\mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})}. \end{align*} $$
But the estimate of the right-hand side was just discussed. In fact, we have
 $$ \begin{align*} \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \lVert {\mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})} \lesssim_{\gamma_1} \Gamma_1 L^{-\alpha k} 2^{- n (\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }. \end{align*} $$
$$ \begin{align*} \sum_{l_1, \ldots, l_k \leq L} \sum_{j \leq 2^n L^{-k}} \lVert {\mathbb{E}[S_j^{(k), l_1, \ldots, l_k} \vert \mathcal{G}_{j}^{(k), l_1, \ldots, l_k}]} \rVert _{L_m(\mathbb{P})} \lesssim_{\gamma_1} \Gamma_1 L^{-\alpha k} 2^{- n (\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }. \end{align*} $$
Hence, we obtain the estimate
 $$ \begin{align*} & \lVert {\sum_{i=0}^{2^n} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\gamma_1, \gamma_2} \kappa_{m, d} L^{\frac{1}{2}} (\Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n (\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} ) \\ & \quad + \kappa_{m, d} \Gamma_1 \sum_{p=2}^k L^{\frac{p}{2} -\alpha(p-1)} 2^{- n (\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 } \\ &\quad + \Gamma_1 L^{-\alpha k} 2^{- n (\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }. \end{align*} $$
$$ \begin{align*} & \lVert {\sum_{i=0}^{2^n} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\gamma_1, \gamma_2} \kappa_{m, d} L^{\frac{1}{2}} (\Gamma_3 2^{-n \beta_3} \lvert {t_N - t_0} \rvert ^{\beta_3} + \Gamma_2 2^{-n (\beta_2 - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} ) \\ & \quad + \kappa_{m, d} \Gamma_1 \sum_{p=2}^k L^{\frac{p}{2} -\alpha(p-1)} 2^{- n (\beta_1 - \alpha - \frac{1}{2})} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 } \\ &\quad + \Gamma_1 L^{-\alpha k} 2^{- n (\beta_1 - \alpha - 1)} \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha - \gamma_1 }. \end{align*} $$
By choosing L and k exactly as in the proof of Lemma 2.3, we conclude that there exists an
![]() $\epsilon = \epsilon (\alpha , \beta _1, \beta _2, \beta _3)> 0$
, such that for all large n
$\epsilon = \epsilon (\alpha , \beta _1, \beta _2, \beta _3)> 0$
, such that for all large n
 $$ \begin{align*} \lVert {\sum_{i=0}^{2^n} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, \beta_3, \gamma_1, \gamma_2} \kappa_{m,d} 2^{-n \epsilon} (\Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1 - \gamma_1} + \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} + \Gamma_3 \lvert {t_N - t_0} \rvert ^{\beta_3}), \end{align*} $$
$$ \begin{align*} \lVert {\sum_{i=0}^{2^n} R^n_i} \rVert _{L_m(\mathbb{P})} \lesssim_{\alpha, \beta_1, \beta_2, \beta_3, \gamma_1, \gamma_2} \kappa_{m,d} 2^{-n \epsilon} (\Gamma_1 \lvert {t_N - t_0} \rvert ^{\beta_1 - \alpha_1 - \gamma_1} + \Gamma_2 \lvert {t_N - t_0} \rvert ^{\beta_2 - \gamma_2} + \Gamma_3 \lvert {t_N - t_0} \rvert ^{\beta_3}), \end{align*} $$
from which we obtain (A.16).
Proof of Lemma 3.2
Let
![]() $d = 1$
. For
$d = 1$
. For
![]() $u> v$
, we set
$u> v$
, we set
so that
![]() $B_u - B(0) = B^{(1)}_u + B^{(2)}_u$
and
$B_u - B(0) = B^{(1)}_u + B^{(2)}_u$
and
![]() $B^{(1)}$
and
$B^{(1)}$
and
![]() $B^{(2)}$
are independent. Then, we have
$B^{(2)}$
are independent. Then, we have
and by (3.2), we have
and thus, we will estimate
![]() $\mathbb {E}[B^{(1)}_s B^{(1)}_t]$
. We have
$\mathbb {E}[B^{(1)}_s B^{(1)}_t]$
. We have
 $$ \begin{align} \mathbb{E}[B^{(1)}_s B^{(1)}_t] &= \int_0^{\infty} \big[(s+r)^{H-1/2} - r^{H-1/2} \big] \big[(t+r)^{H-1/2} - r^{H-1/2} \big] \, \mathrm{d} r \nonumber\\ & \quad + \int_0^v (s-r)^{H-1/2} (t-r)^{H-1/2} \, \mathrm{d} r. \end{align} $$
$$ \begin{align} \mathbb{E}[B^{(1)}_s B^{(1)}_t] &= \int_0^{\infty} \big[(s+r)^{H-1/2} - r^{H-1/2} \big] \big[(t+r)^{H-1/2} - r^{H-1/2} \big] \, \mathrm{d} r \nonumber\\ & \quad + \int_0^v (s-r)^{H-1/2} (t-r)^{H-1/2} \, \mathrm{d} r. \end{align} $$
By [Reference Picard, Donati-Martin, Lejay and Rouault38, Theorem 33], the first term of (A.19) equals to
Since
the second term of (A.20) equals to
By [Reference Picard, Donati-Martin, Lejay and Rouault38, Theorem 33],
Similarly, the second term of (A.19) equals to
Therefore,
![]() $\mathbb {E}[B^{(1)}_s B^{(1)}_t]$
equals to
$\mathbb {E}[B^{(1)}_s B^{(1)}_t]$
equals to
Since
 $$ \begin{align*} &\frac{c_H}{2} (s^{2H} + t^{2H} - \lvert {t-s} \rvert ^{2H}) - c_H s^{2H} + H c_H s^{2H-1} (t-s) -\frac{1}{2H} (v-s)^{2H} \\ & \quad = - \frac{c_H}{2} (t-s)^{2H} + O((s-v)^{2H-2} (t-s)^2), \end{align*} $$
$$ \begin{align*} &\frac{c_H}{2} (s^{2H} + t^{2H} - \lvert {t-s} \rvert ^{2H}) - c_H s^{2H} + H c_H s^{2H-1} (t-s) -\frac{1}{2H} (v-s)^{2H} \\ & \quad = - \frac{c_H}{2} (t-s)^{2H} + O((s-v)^{2H-2} (t-s)^2), \end{align*} $$
the proof is complete.
B. Yamada-Watanabe theorem for fractional SDEs
We consider a Young differential equation
where
![]() $b \in L_{\infty }(\mathbb {R}^d,\mathbb {R}^d)$
and B is an
$b \in L_{\infty }(\mathbb {R}^d,\mathbb {R}^d)$
and B is an
![]() $(\mathcal {F}_t)_{t \in \mathbb {R}}$
fractional Brownian motion with Hurst parameter
$(\mathcal {F}_t)_{t \in \mathbb {R}}$
fractional Brownian motion with Hurst parameter
![]() $H \in (\frac {1}{2}, 1)$
. We fix
$H \in (\frac {1}{2}, 1)$
. We fix
![]() $\alpha \in (\frac {1}{2}, H)$
, and we assume that
$\alpha \in (\frac {1}{2}, H)$
, and we assume that
![]() $\sigma \in C^{\frac {1-\alpha }{\alpha }}(\mathbb {R}^d; \mathcal {M}_d)$
so that the integral
$\sigma \in C^{\frac {1-\alpha }{\alpha }}(\mathbb {R}^d; \mathcal {M}_d)$
so that the integral
 $$ \begin{align*} \int_s^t \sigma(X_r) \, \mathrm{d} B_r \end{align*} $$
$$ \begin{align*} \int_s^t \sigma(X_r) \, \mathrm{d} B_r \end{align*} $$
is interpreted as a Young integral.
Definition B.1. We say that a quintuple
![]() $(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P}, B, X)$
is a weak solution to (B.1) if
$(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P}, B, X)$
is a weak solution to (B.1) if
![]() $(B, X)$
are random variables defined on the filtered probability space
$(B, X)$
are random variables defined on the filtered probability space
![]() $(\Omega , (\mathcal {F}_t), \mathbb {R})$
, if B is an
$(\Omega , (\mathcal {F}_t), \mathbb {R})$
, if B is an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion, if
$(\mathcal {F}_t)$
-fractional Brownian motion, if
![]() $X \in C^{\alpha }([0, T])$
is adapted to
$X \in C^{\alpha }([0, T])$
is adapted to
![]() $(\mathcal {F}_t)$
, and if X solves the Young differential equation (B.1). Given a filtered probability space
$(\mathcal {F}_t)$
, and if X solves the Young differential equation (B.1). Given a filtered probability space
![]() $(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P})$
and an
$(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P})$
and an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion B, we say that a
$(\mathcal {F}_t)$
-fractional Brownian motion B, we say that a
![]() $C^{\alpha }([0,T])$
-valued random variable X defined on
$C^{\alpha }([0,T])$
-valued random variable X defined on
![]() $(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P})$
is a strong solution if it solves (B.1) and if it is adapted to the natural filtration generated by B. We say that the pathwise uniqueness holds for (B.1) if, for any two adapted
$(\Omega , (\mathcal {F}_t)_{t \in \mathbb {R}}, \mathbb {P})$
is a strong solution if it solves (B.1) and if it is adapted to the natural filtration generated by B. We say that the pathwise uniqueness holds for (B.1) if, for any two adapted
![]() $C^{\alpha }([0, T])$
-valued random process X and Y defined on a common filtered probability space that solve (B.1) driven by a common
$C^{\alpha }([0, T])$
-valued random process X and Y defined on a common filtered probability space that solve (B.1) driven by a common
![]() $(\mathcal {F}_t)$
-Brownian motion, we have
$(\mathcal {F}_t)$
-Brownian motion, we have
![]() $X = Y$
almost surely.
$X = Y$
almost surely.
We will prove a Yamada-Watanabe type theorem for (B.1) based on Kurtz [Reference Kurtz25]. To this end, we recall that an
![]() $(\mathcal {F}_t)$
-fractional Brownian motion has the representation (3.1), and we view (B.1) as an equation of X and the Brownian motion W.
$(\mathcal {F}_t)$
-fractional Brownian motion has the representation (3.1), and we view (B.1) as an equation of X and the Brownian motion W.
Proposition B.2. Suppose that a weak solution to (B.1) exists and that the pathwise uniqueness holds for (B.1). Then, there exists a strong solution to (B.1).
Proof. We would like to apply [Reference Kurtz25, Theorem 3.14]. For this purpose, we need a setup. We follow the notation in [Reference Kurtz25]. We fix
![]() $\beta> 0$
that is less than but sufficiently close to
$\beta> 0$
that is less than but sufficiently close to
![]() $\frac {1}{2}$
. As before, we set
$\frac {1}{2}$
. As before, we set ![]() , and we set
, and we set ![]() and define
and define
![]() $S_2$
as a subspace of
$S_2$
as a subspace of
 $$ \begin{align*} \{w \in C^{\beta}(\mathbb{R}) \mid \lim_{r \to -\infty} \lvert {w_r} \rvert (-r)^{H - \frac{3}{2}} = 0, \,\, \int_{-\infty}^{-1} \lvert {w(r)} \rvert (-r)^{H - \frac{3}{2}} \, \mathrm{d} r < \infty\} \end{align*} $$
$$ \begin{align*} \{w \in C^{\beta}(\mathbb{R}) \mid \lim_{r \to -\infty} \lvert {w_r} \rvert (-r)^{H - \frac{3}{2}} = 0, \,\, \int_{-\infty}^{-1} \lvert {w(r)} \rvert (-r)^{H - \frac{3}{2}} \, \mathrm{d} r < \infty\} \end{align*} $$
that is Polish and the Brownian motion lives in
![]() $S_2$
. We note that for
$S_2$
. We note that for
![]() $w \in S_2$
, the improper integral
$w \in S_2$
, the improper integral
 $$ \begin{align*} \int_{-\infty}^t K_H(t, r) \, \mathrm{d} w_r = \lim_{M \to \infty} \int_{-M}^t K_H(t, r) \, \mathrm{d} w_r \end{align*} $$
$$ \begin{align*} \int_{-\infty}^t K_H(t, r) \, \mathrm{d} w_r = \lim_{M \to \infty} \int_{-M}^t K_H(t, r) \, \mathrm{d} w_r \end{align*} $$
is well-defined. For
![]() $t \in [0, T]$
, we denote by
$t \in [0, T]$
, we denote by
![]() $(\mathcal {B}^{S_1}_t)_{t \in [0, T]}$
and
$(\mathcal {B}^{S_1}_t)_{t \in [0, T]}$
and
![]() $(\mathcal {B}^{S_2}_t)_{t \in [0, T]}$
the filtration generated by the coordinate maps in
$(\mathcal {B}^{S_2}_t)_{t \in [0, T]}$
the filtration generated by the coordinate maps in
![]() $S_1$
and
$S_1$
and
![]() $S_2$
, respectively. We set
$S_2$
, respectively. We set
as our compatibility structure in the sense of [Reference Kurtz25, Definition 3.4]. We denote by
![]() $\mathcal {S}_{\Gamma , \mathcal {C}, W}$
the set of probability measures
$\mathcal {S}_{\Gamma , \mathcal {C}, W}$
the set of probability measures
![]() $\mu $
on
$\mu $
on
![]() $S_1 \times S_2$
, such that
$S_1 \times S_2$
, such that
-
• we have
where $$ \begin{align*} \mu(\{(x,y) \in S_1 \times S_2 \mid x_t = x + \int_0^t b(x_r) \, \mathrm{d} r + \int_0^t \sigma(x_r) \, \mathrm{d} Iy_r\,\, \text{for all }t \in [0,T]\} ) = 1, \end{align*} $$
$$ \begin{align*} \mu(\{(x,y) \in S_1 \times S_2 \mid x_t = x + \int_0^t b(x_r) \, \mathrm{d} r + \int_0^t \sigma(x_r) \, \mathrm{d} Iy_r\,\, \text{for all }t \in [0,T]\} ) = 1, \end{align*} $$
 ;
;
-
•
 $\mu $
is
$\mu $
is
 $\mathcal {C}$
-compatible in the sense of [Reference Kurtz25, Definition 3.6];
$\mathcal {C}$
-compatible in the sense of [Reference Kurtz25, Definition 3.6]; -
•
 $\mu (S_1 \times \cdot )$
has the law of the Brownian motion.
$\mu (S_1 \times \cdot )$
has the law of the Brownian motion.
By [Reference Kurtz25, Lemma 3.8],
![]() $\mathcal {S}_{\Gamma , \mathcal {C}, W}$
is convex. In view of [Reference Kurtz25, Lemma 3.2], the existence of weak solutions implies
$\mathcal {S}_{\Gamma , \mathcal {C}, W}$
is convex. In view of [Reference Kurtz25, Lemma 3.2], the existence of weak solutions implies
![]() $\mathcal {S}_{\Gamma , \mathcal {C}, W} \neq \varnothing $
.
$\mathcal {S}_{\Gamma , \mathcal {C}, W} \neq \varnothing $
.
Therefore, to apply [Reference Kurtz25, Theorem 3.14], it remains to prove the pointwise uniqueness in the sense of [Reference Kurtz25, Definition 3.12]. Suppose that
![]() $(X_1, X_2, W)$
are defined on a common probability space, that the laws of
$(X_1, X_2, W)$
are defined on a common probability space, that the laws of
![]() $(X_1, Y)$
and
$(X_1, Y)$
and
![]() $(X_2, Y)$
belong to
$(X_2, Y)$
belong to
![]() $\mathcal {S}_{\Gamma , \mathcal {C}, W}$
, and that
$\mathcal {S}_{\Gamma , \mathcal {C}, W}$
, and that
![]() $(X_1, X_2)$
are jointly compatible with W in the sense of [Reference Kurtz25, Definition 3.12]. But then, if we denote by
$(X_1, X_2)$
are jointly compatible with W in the sense of [Reference Kurtz25, Definition 3.12]. But then, if we denote by
![]() $(\mathcal {F}_t)$
the filtration generated by
$(\mathcal {F}_t)$
the filtration generated by
![]() $(X_1, X_2, W)$
, by [Reference Kurtz25, Lemma 3.2], the joint compatibility implies that W is an
$(X_1, X_2, W)$
, by [Reference Kurtz25, Lemma 3.2], the joint compatibility implies that W is an
![]() $(\mathcal {F}_t)$
-Brownian motion, and therefore the pathwise uniqueness implies
$(\mathcal {F}_t)$
-Brownian motion, and therefore the pathwise uniqueness implies
![]() $X_1 = X_2$
almost surely.
$X_1 = X_2$
almost surely.
Hence, by [Reference Kurtz25, Theorem 3.14], there exists a measurable map
![]() $F: S_2 \to S_1$
, such that for a Brownian motion W, the law of
$F: S_2 \to S_1$
, such that for a Brownian motion W, the law of
![]() $(F(W), W)$
belongs to
$(F(W), W)$
belongs to
![]() $\mathcal {S}_{\Gamma , \mathcal {C}, W}$
. Then, [Reference Kurtz25, Lemma 3.11] implies that
$\mathcal {S}_{\Gamma , \mathcal {C}, W}$
. Then, [Reference Kurtz25, Lemma 3.11] implies that
![]() $F(W)$
is a strong solution.
$F(W)$
is a strong solution.
Lemma B.3. Let
![]() $b \in C_b^1(\mathbb {R}^d)$
and
$b \in C_b^1(\mathbb {R}^d)$
and
![]() $\sigma \in C^1_b(\mathbb {R}^d)$
. Then, there exists a weak solution to (B.1).
$\sigma \in C^1_b(\mathbb {R}^d)$
. Then, there exists a weak solution to (B.1).
Proof. Let
![]() $(\sigma ^n)_{n \in \mathbb {N}}$
be a smooth approximation to
$(\sigma ^n)_{n \in \mathbb {N}}$
be a smooth approximation to
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $X^n$
be the solution to
$X^n$
be the solution to
 $$ \begin{align*} X^n_t = x + \int_0^t b(X^n_r) \, \mathrm{d} r + \int_0^t \sigma^n(X^n_r) \, \mathrm{d} B_r. \end{align*} $$
$$ \begin{align*} X^n_t = x + \int_0^t b(X^n_r) \, \mathrm{d} r + \int_0^t \sigma^n(X^n_r) \, \mathrm{d} B_r. \end{align*} $$
Let W be the Brownian motion, such that
![]() $B_t = \int _{-\infty }^t K_H(t, r) \, \mathrm {d} W_r$
. Let
$B_t = \int _{-\infty }^t K_H(t, r) \, \mathrm {d} W_r$
. Let
![]() $\epsilon $
be greater than but sufficiently close to
$\epsilon $
be greater than but sufficiently close to
![]() $0$
, and let S be a subspace of
$0$
, and let S be a subspace of
 $$ \begin{align*} \{w \in C^{\frac{1}{2} - \epsilon}(\mathbb{R}) \mid \lim_{r \to -\infty} \lvert {w_r} \rvert (-r)^{H - \frac{3}{2}} = 0, \,\, \int_{-\infty}^{-1} \lvert {w(r)} \rvert (-r)^{H - \frac{3}{2}} \, \mathrm{d} r < \infty\} \end{align*} $$
$$ \begin{align*} \{w \in C^{\frac{1}{2} - \epsilon}(\mathbb{R}) \mid \lim_{r \to -\infty} \lvert {w_r} \rvert (-r)^{H - \frac{3}{2}} = 0, \,\, \int_{-\infty}^{-1} \lvert {w(r)} \rvert (-r)^{H - \frac{3}{2}} \, \mathrm{d} r < \infty\} \end{align*} $$
that is Polish and where the Brownian motion lives. By the a priori estimate (5.8), we see that a sequence of the laws of
![]() $(X^n, W)$
is tight in
$(X^n, W)$
is tight in
![]() $C^{H - \epsilon }([0, T]) \times S$
. Thus, replacing it with a subsequence, we suppose that the sequence
$C^{H - \epsilon }([0, T]) \times S$
. Thus, replacing it with a subsequence, we suppose that the sequence
![]() $(X^n, W)$
converges to some limit
$(X^n, W)$
converges to some limit
![]() $(\tilde {X}, \tilde {W})$
in law.
$(\tilde {X}, \tilde {W})$
in law.
To see that
![]() $(\tilde {X}, \tilde {W})$
solves (5.4), we write
$(\tilde {X}, \tilde {W})$
solves (5.4), we write ![]() , and for
, and for
![]() $\delta>0$
, we set
$\delta>0$
, we set

Then, we have
 $$ \begin{align*} \mathbb{P}((\tilde{X}, \tilde{W}) \in A_{\delta}) &\leq \liminf_{n \to \infty} \mathbb{P}((X^n, W) \in A_{\delta}) \\ &\leq \liminf_{n \to \infty} \mathbb{P}(\sup_{t \in [0, T]} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert> \delta). \end{align*} $$
$$ \begin{align*} \mathbb{P}((\tilde{X}, \tilde{W}) \in A_{\delta}) &\leq \liminf_{n \to \infty} \mathbb{P}((X^n, W) \in A_{\delta}) \\ &\leq \liminf_{n \to \infty} \mathbb{P}(\sup_{t \in [0, T]} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert> \delta). \end{align*} $$
However, by the estimate of Young’s integral,
 $$ \begin{align*} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert \lesssim_{H, \epsilon} \lVert {\sigma - \sigma^n} \rVert _{C^1_b} \lVert {X^n} \rVert _{C^1_b} \lVert {B} \rVert _{C^1_b}. \end{align*} $$
$$ \begin{align*} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert \lesssim_{H, \epsilon} \lVert {\sigma - \sigma^n} \rVert _{C^1_b} \lVert {X^n} \rVert _{C^1_b} \lVert {B} \rVert _{C^1_b}. \end{align*} $$
Thus, combined with the a priori estimate (5.8), we observe
 $$ \begin{align*} \liminf_{n \to \infty} \mathbb{P}(\sup_{t \in [0, T]} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert > \delta) = 0, \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \mathbb{P}(\sup_{t \in [0, T]} \lvert {\int_0^t \{\sigma - \sigma^n\} (X^n_r) \, \mathrm{d} B_r} \rvert > \delta) = 0, \end{align*} $$
and hence,
![]() $\mathbb {P}((\tilde {X}, \tilde {W}) \in A_{\delta }) = 0$
. Since
$\mathbb {P}((\tilde {X}, \tilde {W}) \in A_{\delta }) = 0$
. Since
![]() $\delta $
is arbitrary, this implies
$\delta $
is arbitrary, this implies
 $$ \begin{align*} \mathbb{P}(\tilde{X}_t = x + \int_0^t b(\tilde{X}_r) \, \mathrm{d} r + \int_0^t \sigma(\tilde{X}_r) \, \mathrm{d} (I \tilde{W})_r \,\, \forall t \in [0, T]) = 1. \end{align*} $$
$$ \begin{align*} \mathbb{P}(\tilde{X}_t = x + \int_0^t b(\tilde{X}_r) \, \mathrm{d} r + \int_0^t \sigma(\tilde{X}_r) \, \mathrm{d} (I \tilde{W})_r \,\, \forall t \in [0, T]) = 1. \end{align*} $$
Finally, since
![]() $W_t - W_s$
is independent of the
$W_t - W_s$
is independent of the
![]() $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
![]() $(X^n_r)_{r \leq s}$
and
$(X^n_r)_{r \leq s}$
and
![]() $(W_r)_{r \leq s}$
, we know that
$(W_r)_{r \leq s}$
, we know that
![]() $\tilde {W}_t - \tilde {W}_s$
is independent of
$\tilde {W}_t - \tilde {W}_s$
is independent of
or equivalently,
![]() $\tilde {W}$
is an
$\tilde {W}$
is an
![]() $(\tilde {\mathcal {F}}_t)$
-Brownian motion.
$(\tilde {\mathcal {F}}_t)$
-Brownian motion.
Acknowledgements
We thank Khoa Lê for suggesting a simpler proof of Lemma 2.3 in Appendix A than the original one. TM thanks Henri Altman, Hannes Kern, and Helena Kremp for the discussions related to this paper. The main part of the work was done while TM was a Ph.D. student at Freie Universität Berlin under the financial support of the German Science Foundation (DFG) via the IRTG 2544. NP gratefully acknowledges funding by DFG through the Heinz Maier-Leibnitz Prize.
Competing interest
The author has no competing interest to declare.