Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-04T09:36:24.693Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXTENSION OF ROHRLICH’S THEOREM TO THE 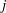$j$-FUNCTION

Published online by Cambridge University Press:  15 January 2020

KATHRIN BRINGMANN  and
BEN KANE Open the ORCID record for BEN KANE [Opens in a new window]
KATHRIN BRINGMANN
Affiliation:
Mathematical Institute, University of Cologne, Weyertal 86-90, D–50931 Cologne, Germany; [email protected]
BEN KANE
Affiliation:
Department of Mathematics, University of Hong Kong, Pokfulam, Hong Kong; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We start by recalling the following theorem of Rohrlich [17]. To state it, let 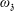$\unicode[STIX]{x1D714}_{\mathfrak{z}}$ denote half of the size of the stabilizer 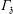$\unicode[STIX]{x1D6E4}_{\mathfrak{z}}$ of 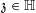$\mathfrak{z}\in \mathbb{H}$ in 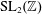$\text{SL}_{2}(\mathbb{Z})$ and for a meromorphic function 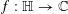$f:\mathbb{H}\rightarrow \mathbb{C}$ let 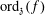$\text{ord}_{\mathfrak{z}}(f)$ be the order of vanishing of 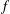$f$ at $\mathfrak{z}$. Moreover, define 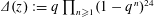$\unicode[STIX]{x1D6E5}(z):=q\prod _{n\geqslant 1}(1-q^{n})^{24}$, where 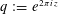$q:=e^{2\unicode[STIX]{x1D70B}iz}$, and set 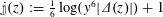$\unicode[STIX]{x1D55B}(z):=\frac{1}{6}\log (y^{6}|\unicode[STIX]{x1D6E5}(z)|)+1$, where 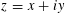$z=x+iy$. Rohrlich’s theorem may be stated in terms of the Petersson inner product, denoted by 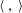$\langle ~,\,\rangle$.

Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e3
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Asai, T., Kaneko, M. and Ninomiya, H., ‘Zeros of certain modular functions and an application’, Comment. Math. Univ. St. Pauli 46 (1997), 93–101.Google Scholar
Borcherds, R., ‘Automorphic forms with singularities on Grassmannians’, Invent. Math. 132 (1998), 491–562.CrossRefGoogle Scholar
Bringmann, K., Diamantis, N. and Ehlen, S., ‘Regularized inner products and errors of modularity’, Int. Math. Res. Not. IMRN 2017 (2017), 7420–7458.Google Scholar
Bringmann, K., Ehlen, S. and Schwagenscheidt, M., ‘On the modular completion of certain generating functions’, Int. Math. Res. Not. IMRN (2019), to appear.CrossRefGoogle Scholar
Bruinier, J. and Funke, J., ‘Traces of CM values of modular functions’, J. Reine Angew. Math. 594 (2006), 1–33.CrossRefGoogle Scholar
Bruinier, J., Kohnen, W. and Ono, K., ‘The arithmetic of the values of modular functions and the divisors of modular forms’, Compos. Math. 130 (2004), 552–566.CrossRefGoogle Scholar
Digital Library of Mathematical Functions, National Institute of Standards and Technology, website http://dlmf.nist.gov/.Google Scholar
Gross, B. and Zagier, D., ‘On singular moduli’, J. Reine Angew. Math. 355 (1985), 191–220.Google Scholar
Gross, B. and Zagier, D., ‘Heegner points and derivatives of L-series’, Invent. Math. 84 (1986), 225–320.CrossRefGoogle Scholar
Harvey, J. and Moore, G., ‘Algebras, BPS states, and strings’, Nuclear Phys. B 463 (1996), 315–368.CrossRefGoogle Scholar
Hejhal, D., The Selberg Trace Formula for SL2(ℝ), Vol. 2, Lecture Notes in Mathematics, 1001 (Springer, Berlin, 1983).CrossRefGoogle Scholar
Herrero, S., Imamoḡlu, Ö., von Pippich, A. and Tóth, Á., ‘A Jensen–Rohrlich type formula for the hyperbolic 3-space’, Trans. Amer. Math. Soc. 371 (2019), 6421–6446.CrossRefGoogle Scholar
Lagarias, J. and Rhoades, R., ‘Polyharmonic Maass forms for PSL(2, ℤ)’, Ramanujan J. 41 (2016), 191–232.CrossRefGoogle Scholar
Niebur, D., ‘A class of nonanalytic automorphic functions’, Nagoya Math. J. 52 (1973), 133–145.CrossRefGoogle Scholar
Petersson, H., ‘Automorphe Formen als metrische Invarianten I’, Math. Nachr. 1 (1948), 158–212.CrossRefGoogle Scholar
Petersson, H., ‘Über automorphe Orthogonalfunktionen und die Konstruktion der automorphen Formen von positiver reeller Dimension’, Math. Ann. 127 (1954), 33–81.CrossRefGoogle Scholar
Rohrlich, D., ‘A modular version of Jensen’s formula’, Math. Proc. Cambridge Philos. Soc. 95 (1984), 15–20.CrossRefGoogle Scholar
Zagier, D., ‘Traces of singular moduli’, inMotives, Polylogarithms and Hodge Theory, (eds. Bogomolov, F. and Katzarkov, L.) International Press Lecture Note Series, 3 (International Press of Boston, Inc., Boston, 2002), 209–244.Google Scholar