Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T06:38:52.476Z Has data issue: false hasContentIssue false
  • English
  • Français

An approach to Quillen’s conjecture via centralisers of simple groups

Part of: Representation theory of groups Ordered sets Connections with homological algebra and category theory Algebraic combinatorics

Published online by Cambridge University Press:  07 June 2021

Kevin Iván Piterman Open the ORCID record for Kevin Iván Piterman [Opens in a new window]
Kevin Iván Piterman*
Affiliation:
Departamento de Matemática, IMAS-CONICET, FCEyN, Universidad de Buenos Aires, Buenos Aires, Argentina; E-mail: [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any given subgroup H of a finite group G, the Quillen poset 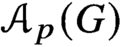${\mathcal {A}}_p(G)$ of nontrivial elementary abelian p-subgroups is obtained from 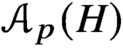${\mathcal {A}}_p(H)$ by attaching elements via their centralisers in H. We exploit this idea to study Quillen’s conjecture, which asserts that if 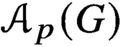${\mathcal {A}}_p(G)$ is contractible then G has a nontrivial normal p-subgroup. We prove that the original conjecture is equivalent to the ${{\mathbb {Z}}}$-acyclic version of the conjecture (obtained by replacing ‘contractible’ by ‘${{\mathbb {Z}}}$-acyclic’). We also work with the 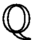${\mathbb {Q}}$-acyclic (strong) version of the conjecture, reducing its study to extensions of direct products of simple groups of p-rank at least 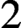$2$. This allows us to extend results of Aschbacher and Smith and to establish the strong conjecture for groups of p-rank at most 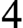$4$.

MSC classification

Primary: 06A11: Algebraic aspects of posets 20D30: Series and lattices of subgroups 20J05: Homological methods in group theory
Secondary: 05E18: Group actions on combinatorial structures 20D05: Finite simple groups and their classification 20D25: Special subgroups (Frattini, Fitting, etc.)
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e48
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Alperin, J. L., ‘A Lie approach to finite groups’, in Groups—Canberra 1989, Lecture Notes in Mathematics, vol.~1456 (Springer, Berlin, 1990), 1–9.Google Scholar
Aschbacher, M., ‘Simple connectivity of $p$-group complexes’, Israel J. Math. 82(1-3) (1993), 1–43.CrossRefGoogle Scholar
Aschbacher, M., Finite Group Theory, second edn, Cambridge Studies in Advanced Mathematics, vol. 10 (Cambridge University Press, Cambridge, UK, 2000).CrossRefGoogle Scholar
Aschbacher, M. and Kleidman, P.B., ‘On a conjecture of Quillen and a lemma of Robinson’, Arch. Math. (Basel) 55(3) (1990), 209–217.CrossRefGoogle Scholar
Aschbacher, M. and Smith, S. D., ‘On Quillen’s conjecture for the $p$-groups complex’, Ann. of Math. (2) 137(3) (1993), 473–529.CrossRefGoogle Scholar
Brown, K. S., ‘Euler characteristics of groups: the $p$-fractional part’, Invent. Math. 29(1) (1975), 1–5.CrossRefGoogle Scholar
Díaz Ramos, A., ‘On Quillen’s conjecture for $p$-solvable groups’, J. Algebra 513 (2018), 246–264.CrossRefGoogle Scholar
Gorenstein, D. and Lyons, R., ‘The local structure of finite groups of characteristic $2$ type’, Mem. Amer. Math. Soc. 42(276) (1983).Google Scholar
Grodal, J., ‘Higher limits via subgroup complexes’, Ann. of Math. (2) 155(2) (2002), 405–457.CrossRefGoogle Scholar
Jacobsen, M. W. and Møller, J. M., ‘Euler characteristics and Möbius algebras of $p$-subgroup categories’, J. Pure Appl. Algebra 216(12) (2012), 2665–2696.CrossRefGoogle Scholar
Minian, E. G. and Piterman, K. I., ‘The homotopy types of the posets of $p$-subgroups of a finite group’, Adv. Math. 328 (2018), 1217–1233.CrossRefGoogle Scholar
Minian, E. G. and Piterman, K. I., ‘The fundamental group of the $p$-subgroup complex’, J. Lond. Math. Soc. (2) 103 (2021), 449–469.CrossRefGoogle Scholar
Piterman, K. I., ‘A stronger reformulation of Webb’s conjecture in terms of finite topological spaces’, J. Algebra 527 (2019), 280–305.CrossRefGoogle Scholar
Piterman, K. I., Sadofschi Costa, I. and Viruel, A., ‘Acyclic $2$-dimensional complexes and Quillen’s conjecture’, Publ. Mat. 65 (2021), 129–140.CrossRefGoogle Scholar
Pulkus, J. and Welker, V., ‘On the homotopy type of the $p$-subgroup complex for finite solvable groups’, J. Aust. Math. Soc. Ser. A 69(2) (2000), 212–228.CrossRefGoogle Scholar
Quillen, D., ‘Homotopy properties of the poset of nontrivial $p$-subgroups of a group’, Adv. Math. 28(2) (1978), 101–128.CrossRefGoogle Scholar
Robinson, G. R., ‘Some remarks on permutation modules’, J. Algebra 118 (1988), 46–62.CrossRefGoogle Scholar
Segev, Y., ‘Quillen’s conjecture and the kernel on components’, Comm. Algebra 24(3) (1996), 955–962.CrossRefGoogle Scholar
Segev, Y. and Webb, P., ‘Extensions of $G$-posets and Quillen’s complex’, J. Aust. Math. Soc. Ser. A 57(1) (1994), 60–75.CrossRefGoogle Scholar
Smith, S.D., Subgroup Complexes, Mathematical Surveys and Monographs, vol. 179 (American Mathematical Society, Providence, RI, 2011).Google Scholar