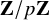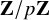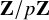1 Introduction
In this paper, we prove several results on cyclic base change in the Langlands correspondence over function fields. To set the context for our results, let us recall some history. Global cyclic base change functoriality for reductive groups over number fields, established over many years in increasing generality by work of Saito [Reference SaitoSai77], Shintani [Reference ShintaniShi79], Langlands [Reference LanglandsLan80], Arthur-Clozel [Reference Arthur and ClozelAC89], Labesse [Reference LabesseLab99], Harris-Labesse [Reference Harris and LabesseHL04] and others for cuspidal automorphic representations with characteristic zero coefficients (under some technical assumptions for general groups), is one of the major triumphs of Langlands’ program thus far. In addition to its initial applications towards Artin’s Conjecture, it plays a crucial role in much subsequent work, such as in automorphy lifting arguments following in the tradition of Wiles, Taylor, etc.
Our main progress in the present paper is on understanding cyclic base change in the Local Langlands correspondence, which was constructed (in a semisimplified form) for all reductive groups over local function fields by Genestier-Lafforgue [Reference Genestier and LafforgueGL]. The proof (over number fields) of global cyclic base change is founded upon the twisted trace formula, a tool which does not seem to apply to our (local and mod p) context, and is in any case currently unavailable over function fields due to nontrivial analytic difficulties. We introduce a new strategy, which we use to prove the first general existence results for local base change of all irreducible representations of arbitrary reductive groups over local function fields. Furthermore, we establish descent theorems for cyclic base change that were conjectured by Treumann-Venkatesh; these are new even for specific groups such as
![]() $\operatorname {\mathrm {GL}}_n$
, where the full Local Langlands correspondence (hence, in particular, the existence of local base change) is already known. These advances involve the construction of a base change homomorphism for Bernstein centers, as has been envisaged by Haines in the case of characteristic zero coefficients. En route to the local results, we establish new global results as well: we prove the first general existence theorem for cyclic base change of mod p automorphic forms on arbitrary reductive groups over global function fields, again without any trace formula arguments. A major novelty of these results is their applicability to completely general groups and representations.
$\operatorname {\mathrm {GL}}_n$
, where the full Local Langlands correspondence (hence, in particular, the existence of local base change) is already known. These advances involve the construction of a base change homomorphism for Bernstein centers, as has been envisaged by Haines in the case of characteristic zero coefficients. En route to the local results, we establish new global results as well: we prove the first general existence theorem for cyclic base change of mod p automorphic forms on arbitrary reductive groups over global function fields, again without any trace formula arguments. A major novelty of these results is their applicability to completely general groups and representations.
The proofs assemble a diverse selection of tools ranging from topology (particularly equivariant localization and Tate cohomology) to arithmetic geometry (of moduli stacks of shtukas) to p-adic groups (exploiting new constructions with Hecke algebras and Bernstein centers) to modular representation theory (using crucially the recent inventions of parity sheaves and Treumann-Smith theory).
We now proceed to give more precise descriptions of our results.
1.1 Local results
Genestier-Lafforgue have constructed a semi-simplified form of the Local Langlands correspondence over function fields [Reference Genestier and LafforgueGL]. More precisely, let
![]() $F_v$
be a local field of positive characteristic not equal to p and
$F_v$
be a local field of positive characteristic not equal to p and
![]() $W_v$
the Weil group of
$W_v$
the Weil group of
![]() $F_v$
. Let k be an algebraic closure of
$F_v$
. Let k be an algebraic closure of
![]() $\mathbf {F}_p$
.Footnote
1
For any reductive group G over
$\mathbf {F}_p$
.Footnote
1
For any reductive group G over
![]() $F_v$
, [Reference Genestier and LafforgueGL] constructs a map
$F_v$
, [Reference Genestier and LafforgueGL] constructs a map
 $$ \begin{align} \left\{ \begin{array}{@{}c@{}} \text{irreducible admissible representations} \\ \pi\text{ of }G(F_v)\text{ over }k\end{array} \right\}/\sim & \longrightarrow \left\{ \begin{array}{@{}c@{}} \text{semi-simple } L\text{-parameters} \\ \rho_{\pi} \colon W_v \rightarrow {}^L G(k) \end{array} \right\}/\sim. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{@{}c@{}} \text{irreducible admissible representations} \\ \pi\text{ of }G(F_v)\text{ over }k\end{array} \right\}/\sim & \longrightarrow \left\{ \begin{array}{@{}c@{}} \text{semi-simple } L\text{-parameters} \\ \rho_{\pi} \colon W_v \rightarrow {}^L G(k) \end{array} \right\}/\sim. \end{align} $$
Here,
![]() ${}^L G$
is Langlands’ L-group, regarded over k.
${}^L G$
is Langlands’ L-group, regarded over k.
Langlands’ principle of functoriality predicts that given two reductive groups H and G over
![]() $F_v$
, and a map of L-groups
$F_v$
, and a map of L-groups
![]() $\phi \colon {}^L H \rightarrow {}^L G$
, every L-packet of irreducible representations of
$\phi \colon {}^L H \rightarrow {}^L G$
, every L-packet of irreducible representations of
![]() $H(F_v)$
should admit a ‘transfer’ to
$H(F_v)$
should admit a ‘transfer’ to
![]() $G(F_v)$
compatible with
$G(F_v)$
compatible with
![]() $\phi $
. In this paper, we are concerned with a specific type of functoriality: base change functoriality, arising from the case where H is any reductive group over
$\phi $
. In this paper, we are concerned with a specific type of functoriality: base change functoriality, arising from the case where H is any reductive group over
![]() $F_v$
and
$F_v$
and
![]() $G = \operatorname {\mathrm {Res}}_{E_v/F_v} (H_{E_v})$
for a cyclic p-extension
$G = \operatorname {\mathrm {Res}}_{E_v/F_v} (H_{E_v})$
for a cyclic p-extension
![]() $E_v/F_v$
. The relevant map
$E_v/F_v$
. The relevant map
![]() $ \phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
is characterized by the property that it is admissible and induces the diagonal embedding on their underlying identity connected components (i.e., the respective Langlands dual groups). We emphasize that it is crucial for our results that the degree of the extension coincides with the characteristic of our representations. In this situation, let us say that an irreducible representation
$ \phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
is characterized by the property that it is admissible and induces the diagonal embedding on their underlying identity connected components (i.e., the respective Langlands dual groups). We emphasize that it is crucial for our results that the degree of the extension coincides with the characteristic of our representations. In this situation, let us say that an irreducible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G(F_v)$
is a base change of an irreducible representation
$G(F_v)$
is a base change of an irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $H(F_v)$
if
$H(F_v)$
if
![]() $\phi _{\mathsf {BC}} \circ \rho _{\pi } \cong \rho _{\Pi }$
.
$\phi _{\mathsf {BC}} \circ \rho _{\pi } \cong \rho _{\Pi }$
.
Theorem 1.1 (Existence of local base change).
Let
![]() $\pi $
be any irreducible representation of
$\pi $
be any irreducible representation of
![]() $H(F_v)$
over k. Then a base change of
$H(F_v)$
over k. Then a base change of
![]() $\pi $
to
$\pi $
to
![]() $G(F_v)$
exists.
$G(F_v)$
exists.
For
![]() $H = \operatorname {\mathrm {GL}}_n$
, a full Local Langlands correspondence has been established by Vignéras [Reference VignérasVig01], giving a much more precise result than Theorem 1.1. It seems reasonable to expect that Vignéras’ methods could (eventually) be extended to some classical groups, after the stabilization of the twisted trace formula for automorphic forms over function fields is achieved. The novelty of Theorem 1.1 is that it applies uniformly to all reductive groups and all irreducible representations. A motivation for Theorem 1.1 is a program of the author to compute explicitly the Genestier-Lafforgue parameters of explicit supercuspidal representations, such as those arising in [Reference Chan and OiCO]; this depends on the residue field being ‘large enough’, so is convenient to be able to make an unramified base change.
$H = \operatorname {\mathrm {GL}}_n$
, a full Local Langlands correspondence has been established by Vignéras [Reference VignérasVig01], giving a much more precise result than Theorem 1.1. It seems reasonable to expect that Vignéras’ methods could (eventually) be extended to some classical groups, after the stabilization of the twisted trace formula for automorphic forms over function fields is achieved. The novelty of Theorem 1.1 is that it applies uniformly to all reductive groups and all irreducible representations. A motivation for Theorem 1.1 is a program of the author to compute explicitly the Genestier-Lafforgue parameters of explicit supercuspidal representations, such as those arising in [Reference Chan and OiCO]; this depends on the residue field being ‘large enough’, so is convenient to be able to make an unramified base change.
We also prove a descent result for the above base change situation which was conjectured by Treumann-Venkatesh and is new even for
![]() $H = \operatorname {\mathrm {GL}}_n$
whenever
$H = \operatorname {\mathrm {GL}}_n$
whenever
![]() $n> 1$
. Let
$n> 1$
. Let
![]() $\sigma $
be a generatorFootnote
2
of
$\sigma $
be a generatorFootnote
2
of
![]() $\operatorname {Gal}(E_v/F_v)$
; it acts on G, and its induced action on
$\operatorname {Gal}(E_v/F_v)$
; it acts on G, and its induced action on
![]() $G(F_v) = H(E_v)$
is the Galois action. It is expected that if the isomorphism class of a k-representation
$G(F_v) = H(E_v)$
is the Galois action. It is expected that if the isomorphism class of a k-representation
![]() $\Pi $
of
$\Pi $
of
![]() $G(F_v)$
is preserved by
$G(F_v)$
is preserved by
![]() $\sigma $
, then it should come from base change. For any irreducible admissible representation
$\sigma $
, then it should come from base change. For any irreducible admissible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G(F_v)$
whose isomorphism class is fixed by
$G(F_v)$
whose isomorphism class is fixed by
![]() $\sigma $
, there is a unique
$\sigma $
, there is a unique
![]() $\sigma $
-action on
$\sigma $
-action on
![]() $\Pi $
compatible with the
$\Pi $
compatible with the
![]() $G(F_v)$
-action (Lemma 6.16). Hence, we can form the Tate cohomology groups
$G(F_v)$
-action (Lemma 6.16). Hence, we can form the Tate cohomology groups
![]() $T^0(\Pi )$
,
$T^0(\Pi )$
,
![]() $T^1(\Pi )$
with respect to the
$T^1(\Pi )$
with respect to the
![]() $\sigma $
-action (cf. §3.4), which retain actions of
$\sigma $
-action (cf. §3.4), which retain actions of
![]() $H(F_v) = G(F_v)^{\sigma }$
and are conjecturally admissible
$H(F_v) = G(F_v)^{\sigma }$
and are conjecturally admissible
![]() $H(F_v)$
-representations. We prove the following:
$H(F_v)$
-representations. We prove the following:
Theorem 1.2 (Tate cohomology realizes cyclic base change).
Assume p is an odd good primeFootnote
3
for
![]() $\widehat {G}$
. Let
$\widehat {G}$
. Let
![]() $\Pi $
be an irreducible representation of
$\Pi $
be an irreducible representation of
![]() $G(F_v)$
whose isomorphism class is fixed by
$G(F_v)$
whose isomorphism class is fixed by
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\Pi ^{(p)}: = \Pi \otimes _{k, \operatorname {\mathrm {Frob}}} k$
be the Frobenius twist of
$\Pi ^{(p)}: = \Pi \otimes _{k, \operatorname {\mathrm {Frob}}} k$
be the Frobenius twist of
![]() $\Pi $
. Let
$\Pi $
. Let
![]() $\pi $
be any irreducible admissible subquotient of
$\pi $
be any irreducible admissible subquotient of
![]() $T^0(\Pi )$
or
$T^0(\Pi )$
or
![]() $T^1(\Pi )$
as an
$T^1(\Pi )$
as an
![]() $H(F_v)$
-representation and
$H(F_v)$
-representation and
![]() $\rho _{\pi } \colon W_v \rightarrow {}^L H(k)$
be the corresponding L-parameter constructed by Genestier-Lafforgue. Then
$\rho _{\pi } \colon W_v \rightarrow {}^L H(k)$
be the corresponding L-parameter constructed by Genestier-Lafforgue. Then
![]() $\phi _{\mathsf {BC}} \circ \rho _{\pi } \cong \rho _{\Pi ^{(p)}}$
.
$\phi _{\mathsf {BC}} \circ \rho _{\pi } \cong \rho _{\Pi ^{(p)}}$
.
This verifies, for the Genestier-Lafforgue construction of the semi-simplified Local Langlands correspondence, a Conjecture of Treumann-Venkatesh [Reference Treumann and VenkateshTV16, Conjecture 6.3] that ‘Tate cohomology realizes functoriality’. It had previously been proved for certain depth-zero supercuspidal representations of
![]() $\operatorname {\mathrm {GL}}_n(F_v)$
by Ronchetti [Reference RonchettiRon16], by direct calculation of the Tate cohomology and comparison to Vignéras’ work. The difficulty of the calculations, even in those special cases, made them inaccessible to generalization. By contrast, our proof applies uniformly for all groups and all representations under only a very mild condition on p and is completely conceptual; in particular, it avoids any computations with specific models of representations – for example, as compact inductions of Deligne-Lusztig representations.
$\operatorname {\mathrm {GL}}_n(F_v)$
by Ronchetti [Reference RonchettiRon16], by direct calculation of the Tate cohomology and comparison to Vignéras’ work. The difficulty of the calculations, even in those special cases, made them inaccessible to generalization. By contrast, our proof applies uniformly for all groups and all representations under only a very mild condition on p and is completely conceptual; in particular, it avoids any computations with specific models of representations – for example, as compact inductions of Deligne-Lusztig representations.
Remark 1.3. In [Reference Böckle, Feng, Harris, Khare and ThorneBFH+ ], we will compute Tate cohomology for an interesting class of supercuspidal representations (of arbitrary depth) studied by Chan-Oi [Reference Chan and OiCO], which provides many examples where Theorem 1.2 can be made very concrete.
We now proceed to describe our third main local result. Recall that the Bernstein center (with coefficients in k) of
![]() $G(F_v)$
, denoted
$G(F_v)$
, denoted
![]() $\mathfrak {Z}(G)$
, is the ring of endomorphisms of the identity functor on the category of smooth
$\mathfrak {Z}(G)$
, is the ring of endomorphisms of the identity functor on the category of smooth
![]() $G(F_v)$
-representations (on k-vector spaces). Informally speaking, an element of
$G(F_v)$
-representations (on k-vector spaces). Informally speaking, an element of
![]() $\mathfrak {Z}(G)$
is represented by a system of compatible endomorphisms of all smooth
$\mathfrak {Z}(G)$
is represented by a system of compatible endomorphisms of all smooth
![]() $G(F_v)$
-representations (commuting with the
$G(F_v)$
-representations (commuting with the
![]() $G(F_v)$
-action). In particular,
$G(F_v)$
-action). In particular,
![]() $\mathfrak {Z}(G)$
acts on any irreducible smooth
$\mathfrak {Z}(G)$
acts on any irreducible smooth
![]() $G(F_v)$
-representation
$G(F_v)$
-representation
![]() $\Pi $
through a character
$\Pi $
through a character
![]() $\chi _{\Pi } \colon \mathfrak {Z}(G) \rightarrow k$
. Furthermore, the correspondence (1.1) turns out to assign isomorphic L-parameters to irreducible representations inducing the same character of
$\chi _{\Pi } \colon \mathfrak {Z}(G) \rightarrow k$
. Furthermore, the correspondence (1.1) turns out to assign isomorphic L-parameters to irreducible representations inducing the same character of
![]() $\mathfrak {Z}(G)$
. The ideas used to establish the preceding theorems also allow us to construct a base change homomorphism between the Bernstein centers of
$\mathfrak {Z}(G)$
. The ideas used to establish the preceding theorems also allow us to construct a base change homomorphism between the Bernstein centers of
![]() $G(F_v)$
and
$G(F_v)$
and
![]() $H(F_v)$
with the property detailed in the following Theorem.
$H(F_v)$
with the property detailed in the following Theorem.
Theorem 1.4 (Base change homomorphism for Bernstein centers).
Assume p is an odd good prime for
![]() $\widehat {G}$
. Then there is a homomorphism
$\widehat {G}$
. Then there is a homomorphism
such that for each irreducible
![]() $H(F_v)$
-representation
$H(F_v)$
-representation
![]() $\pi $
, the character
$\pi $
, the character
![]() $\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}} \colon \mathfrak {Z}(G) \xrightarrow {\mathfrak {Z}_{\operatorname {\mathrm {TV}}}} \mathfrak {Z}(H) \xrightarrow {\chi _{\pi }} k$
has the property that for any irreducible
$\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}} \colon \mathfrak {Z}(G) \xrightarrow {\mathfrak {Z}_{\operatorname {\mathrm {TV}}}} \mathfrak {Z}(H) \xrightarrow {\chi _{\pi }} k$
has the property that for any irreducible
![]() $G(F_v)$
-representation
$G(F_v)$
-representation
![]() $\Pi $
on which
$\Pi $
on which
![]() $\mathfrak {Z}(G)$
acts through
$\mathfrak {Z}(G)$
acts through
![]() $\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
, there is an isomorphism of semi-simple L-parameters
$\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
, there is an isomorphism of semi-simple L-parameters
![]() $\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
$\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
A base change homomorphism for Bernstein centers, with characteristic zero coefficients, has been sought by Haines [Reference HainesHai14] and was constructed in some low-depth cases [Reference HainesHai09, Reference HainesHai12] (cf. also [Reference FengFen20] for the function field case). Haines also constructed a base change homomorphism for the stable Bernstein center of general groups, which in the case of
![]() $\operatorname {\mathrm {GL}}_n$
coincides with the Bernstein center; since the stable Bernstein center is defined directly in terms of Galois representations, this is rather more direct. Our Theorem 1.4 is somewhat different since it concerns characteristic p, but it is the first such construction that applies to general groups and depth. Its generality and provable connection to the Local Langlands correspondence make it rather new and compelling evidence for Haines’ vision.
$\operatorname {\mathrm {GL}}_n$
coincides with the Bernstein center; since the stable Bernstein center is defined directly in terms of Galois representations, this is rather more direct. Our Theorem 1.4 is somewhat different since it concerns characteristic p, but it is the first such construction that applies to general groups and depth. Its generality and provable connection to the Local Langlands correspondence make it rather new and compelling evidence for Haines’ vision.
Remark 1.5. The construction of the map
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
applies equally well for local fields of characteristic
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
applies equally well for local fields of characteristic
![]() $0$
having residue characteristic distinct from p. However, our argument for proving that it has the ‘correct’ effect in terms of the Local Langlands correspondence only works for function fields. The future work [Reference FengFen] aims to prove analogous results with respect to Fargues-Scholze’s construction [Reference Fargues and ScholzeFS] of the (semisimplified) local Langlands correspondence for arbitrary local fields.
$0$
having residue characteristic distinct from p. However, our argument for proving that it has the ‘correct’ effect in terms of the Local Langlands correspondence only works for function fields. The future work [Reference FengFen] aims to prove analogous results with respect to Fargues-Scholze’s construction [Reference Fargues and ScholzeFS] of the (semisimplified) local Langlands correspondence for arbitrary local fields.
1.2 Global results
Although our most striking progress is on the local Langlands correspondence, we also obtain new results in the global Langlands correspondence. In fact, the local results mentioned above are themselves deduced from analysis of Lafforgue’s machine for constructing the global Langlands correspondence.
Now let G be a reductive group over a global function field F, of characteristic not equal to p. Vincent Lafforgue has constructed in [Reference LafforgueLaf18, §13] a global ‘mod p’ Langlands correspondence, decomposing the space of cuspidal automorphic functions
![]() $C_{\operatorname {\mathrm {cusp}}}^{\infty }(G(F) \backslash G(\mathbf {A}_F), k)$
into summands indexed by semi-simple L-parameters, which are certain
$C_{\operatorname {\mathrm {cusp}}}^{\infty }(G(F) \backslash G(\mathbf {A}_F), k)$
into summands indexed by semi-simple L-parameters, which are certain
![]() $\widehat {G}(k)$
-conjugacy classes of continuous homomorphisms
$\widehat {G}(k)$
-conjugacy classes of continuous homomorphisms
![]() $\rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L G(k)$
. Work of Cong Xue [Reference XueXue20, Reference XueXuea, Reference XueXueb] extends Lafforgue’s theory to the space of all compactly supported automorphic functions,
$\rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L G(k)$
. Work of Cong Xue [Reference XueXue20, Reference XueXuea, Reference XueXueb] extends Lafforgue’s theory to the space of all compactly supported automorphic functions,
![]() $C_c^{\infty }(G(F) \backslash G(\mathbf {A}_F), k)$
. See §5.2.4 for a more precise discussion. Let us call an L-parameter
$C_c^{\infty }(G(F) \backslash G(\mathbf {A}_F), k)$
. See §5.2.4 for a more precise discussion. Let us call an L-parameter
![]() $\rho $
automorphic if it arises from Lafforgue(-Xue)’s construction.
$\rho $
automorphic if it arises from Lafforgue(-Xue)’s construction.
Let H be a reductive group over F, and
![]() $G = \operatorname {\mathrm {Res}}_{E/F} (H_E)$
for a cyclic p-extension
$G = \operatorname {\mathrm {Res}}_{E/F} (H_E)$
for a cyclic p-extension
![]() $E/F$
. The relevant map
$E/F$
. The relevant map
![]() $\phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
is the diagonal on the identity connected components.
$\phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
is the diagonal on the identity connected components.
Theorem 1.6 (Existence of global base change).
Assume p is an odd good prime for
![]() $\widehat {G}$
. If
$\widehat {G}$
. If
![]() $\rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L H(k)$
is automorphic, then
$\rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L H(k)$
is automorphic, then
![]() $\phi _{\mathsf {BC}} \circ \rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L G(k)$
is automorphic.
$\phi _{\mathsf {BC}} \circ \rho \colon \operatorname {Gal}(F^s/F) \rightarrow {}^L G(k)$
is automorphic.
We comment on the relation of Theorem 1.6 to other base change theorems known in global contexts. To appreciate this, it is important to highlight the distinction between ‘weak base change’, which is determined Hecke eigensystems at almost all places of the global function, and ‘strong base change’ as provided by Theorem 1.6, which concerns the entire L-parameter. These notions are equivalent for
![]() $H = \operatorname {\mathrm {GL}}_n$
, but for general groups, ‘strong base change’ is a strictly stronger notion. Indeed, Lafforgue’s correspondence can assign different Langlands parameters to Hecke eigenfunctions with the same unramified eigensystem; in fact, it can even assign different parameters to different automorphic forms generating isomorphic automorphic representations,Footnote
4
with examples occurring already for
$H = \operatorname {\mathrm {GL}}_n$
, but for general groups, ‘strong base change’ is a strictly stronger notion. Indeed, Lafforgue’s correspondence can assign different Langlands parameters to Hecke eigenfunctions with the same unramified eigensystem; in fact, it can even assign different parameters to different automorphic forms generating isomorphic automorphic representations,Footnote
4
with examples occurring already for
![]() $\operatorname {\mathrm {SL}}_n$
when
$\operatorname {\mathrm {SL}}_n$
when
![]() $n \geq 3$
[Reference BlasiusBla94, Reference LapidLap99]. The reason for this is the failure of local conjugacy to imply global conjugacy; see [Reference LafforgueLaf18, §0.7] for more discussion of this phenomenon.
$n \geq 3$
[Reference BlasiusBla94, Reference LapidLap99]. The reason for this is the failure of local conjugacy to imply global conjugacy; see [Reference LafforgueLaf18, §0.7] for more discussion of this phenomenon.
Remark 1.7. The distinction between weak and strong base change can be quite important in applications. For example, recent work of Sawin-Templier [Reference Sawin and TemplierST21] shows that the Ramanujan Conjecture for cuspidal automorphic forms satisfying appropriate local conditions is implied by a strong form of cyclic base change, but weak base change does not suffice for their argument.
Our proof of Theorem 1.6 is inspired by work of Treumann-Venkatesh [Reference Treumann and VenkateshTV16], which establishes existence of ‘weak base change’ for the cohomology of locally symmetric spaces. The analogue of [Reference Treumann and VenkateshTV16] in the function field context would guarantee the existence of a ‘weak base change’ for mod p automorphic forms. The work of Treumann-Venkatesh is about Hecke operators, but in the function field, context it is possible to go beyond Hecke operators to Lafforgue’s excursion operators, and this is necessary to obtain ‘strong base change’; it is also what provides our handhold on the Local Langlands correspondence.
Over number fields, weak base change results with characteristic zero coefficients are known using the twisted trace formula, for all cuspidal automorphic representations of
![]() $\operatorname {\mathrm {GL}}_n$
[Reference Arthur and ClozelAC89] or, on more general groups, cuspidal automorphic representations satisfying certain local conditions [Reference LabesseLab99]. Over function fields, the analogous results are known for
$\operatorname {\mathrm {GL}}_n$
[Reference Arthur and ClozelAC89] or, on more general groups, cuspidal automorphic representations satisfying certain local conditions [Reference LabesseLab99]. Over function fields, the analogous results are known for
![]() $H=\operatorname {\mathrm {GL}}_n$
because the full global Langlands correspondence is already known in that case, again using the trace formula. But there are analytic difficulties in the theory of the twisted trace formula over function fields, which prevent parallel results from being known more generally. Instead, forthcoming work [Reference Böckle, Feng, Harris, Khare and ThorneBFH+
] will combine Theorem 1.6 with automorphy lifting theorems, generalizing those of [Reference Böckle, Harris, Khare and ThorneBHKT19], in order to obtain existence of cyclic order p base change for automorphic forms on split semisimple groups with characteristic
$H=\operatorname {\mathrm {GL}}_n$
because the full global Langlands correspondence is already known in that case, again using the trace formula. But there are analytic difficulties in the theory of the twisted trace formula over function fields, which prevent parallel results from being known more generally. Instead, forthcoming work [Reference Böckle, Feng, Harris, Khare and ThorneBFH+
] will combine Theorem 1.6 with automorphy lifting theorems, generalizing those of [Reference Böckle, Harris, Khare and ThorneBHKT19], in order to obtain existence of cyclic order p base change for automorphic forms on split semisimple groups with characteristic
![]() $0$
coefficients, for sufficiently large p and under a ‘large image’ assumption (the latter is needed to make the notions of weak and strong base change coincide).
$0$
coefficients, for sufficiently large p and under a ‘large image’ assumption (the latter is needed to make the notions of weak and strong base change coincide).
1.3 Remarks on the proofs
We emphasize at the outset that our arguments make no use of the traditional tool for analyzing cyclic base change – namely, the twisted trace formula (which is in any case unavailable in our situation). Any serious discussion of the proofs of our main results would require an explanation of the construction of Lafforgue’s and Genestier-Lafforgue’s correspondences, in addition to a number of other ideas and definitions. To prevent this introduction from becoming overly technical, we confine ourselves to vague hints here.
The Genestier-Lafforgue correspondence is characterized by local-global compatibility, so the main input to the local results comes from an analysis of the global situation. The Global Langlands parametrization is extracted from the cohomology of moduli stacks of shtukas. This idea goes back to Drinfeld [Reference Drinfel’dDri87], who introduced it to establish the global Langlands correspondence for
![]() $\operatorname {\mathrm {GL}}_2$
over function fields, later extended to
$\operatorname {\mathrm {GL}}_2$
over function fields, later extended to
![]() $\operatorname {\mathrm {GL}}_n$
by Laurent Lafforgue [Reference LafforgueLaf02]. For general groups, the role that Langlands’ L-group
$\operatorname {\mathrm {GL}}_n$
by Laurent Lafforgue [Reference LafforgueLaf02]. For general groups, the role that Langlands’ L-group
![]() ${}^L G$
should play presented a puzzle that was definitively resolved by Vincent Lafforgue: via the Geometric Satake equivalence, the category
${}^L G$
should play presented a puzzle that was definitively resolved by Vincent Lafforgue: via the Geometric Satake equivalence, the category
![]() $\operatorname {\mathrm {Rep}}({}^L G)$
naturally indexes perverse sheaves that lives on the moduli stacks of G-shtukas, called
$\operatorname {\mathrm {Rep}}({}^L G)$
naturally indexes perverse sheaves that lives on the moduli stacks of G-shtukas, called
![]() $\operatorname {\mathrm {Sht}}_G$
.
$\operatorname {\mathrm {Sht}}_G$
.
Summarizing roughly, the global Langlands correspondence involves two major inputs:
-
1. A ‘topological’ input, wherein the p-adic cohomology of spaces
 $\operatorname {\mathrm {Sht}}_G$
supplies interesting
$\operatorname {\mathrm {Sht}}_G$
supplies interesting
 $\operatorname {Gal}(F^s/F)$
-representations.
$\operatorname {Gal}(F^s/F)$
-representations. -
2. A representation-theoretic input, wherein L-parameters into
 ${}^L G$
are extracted using that the coefficient sheaves for these cohomology groups are indexed functorially by
${}^L G$
are extracted using that the coefficient sheaves for these cohomology groups are indexed functorially by
 $\operatorname {\mathrm {Rep}}({}^L G)$
.
$\operatorname {\mathrm {Rep}}({}^L G)$
.
This will be explained more in §5. For now, it is enough to appreciate that in order to produce a functorial transfer from H to G, we then need to address both of these aspects of Lafforgue’s construction. More precisely, we need to
-
1. Show that cohomology classes on
 $\operatorname {\mathrm {Sht}}_H$
can be ‘transferred’ to cohomology classes on
$\operatorname {\mathrm {Sht}}_H$
can be ‘transferred’ to cohomology classes on
 $\operatorname {\mathrm {Sht}}_G$
.
$\operatorname {\mathrm {Sht}}_G$
. -
2. Give a geometric interpretation of the restriction functor
 $\operatorname {\mathrm {Rep}}({}^L G) \rightarrow \operatorname {\mathrm {Rep}}({}^L H)$
at the level of perverse sheaves.
$\operatorname {\mathrm {Rep}}({}^L G) \rightarrow \operatorname {\mathrm {Rep}}({}^L H)$
at the level of perverse sheaves.
The immediate difficulty of (1) is that, in general, there is not so much as a nontrivial map relating
![]() $\operatorname {\mathrm {Sht}}_H$
and
$\operatorname {\mathrm {Sht}}_H$
and
![]() $\operatorname {\mathrm {Sht}}_G$
. In the base change situation, there is a natural map, but it is not even Hecke-equivariant, nor is it clear a priori that the map is not too destructive to cohomology groups. Ultimately, we solve (1) in our situation by looking at Tate cohomology instead of cohomology and using a form of equivariant localization that relates the Tate cohomology of a space and its fixed points under a
$\operatorname {\mathrm {Sht}}_G$
. In the base change situation, there is a natural map, but it is not even Hecke-equivariant, nor is it clear a priori that the map is not too destructive to cohomology groups. Ultimately, we solve (1) in our situation by looking at Tate cohomology instead of cohomology and using a form of equivariant localization that relates the Tate cohomology of a space and its fixed points under a
![]() $\mathbf {Z}/p\mathbf {Z}$
-action. Here, we were inspired by work of Treumann-Venkatesh [Reference Treumann and VenkateshTV16], where it was shown that such equivariant localization for locally symmetric spaces realized functoriality in that context.
$\mathbf {Z}/p\mathbf {Z}$
-action. Here, we were inspired by work of Treumann-Venkatesh [Reference Treumann and VenkateshTV16], where it was shown that such equivariant localization for locally symmetric spaces realized functoriality in that context.
For (2), the obvious difficulty, in general, is again that we are seeking to transport sheaves between two spaces that are not connected by any visible nontrivial geometric maps. In the base change situation, there is a map, but the obvious functors it induces on sheaves do not come close to having the desired effect. In some sense, the problem is a categorified and local version of the problem in the previous paragraph. Our solution to this problem passes through certain ‘exotic’ localizations of categories of sheaves called Tate categories, which can be seen as a categorification of Tate cohomology. The point is, vaguely speaking, that the desired relations of functoriality are satisfied in the relevant Tate categories. However, this does not interface well with Lafforgue’s construction because localization to the Tate category does not interact well with the theory of perverse sheaves; our second main idea here is that this can be fixed by reworking the theory in terms of parity sheaves invented by Juteau-Mautner-Williamson [Reference Juteau, Mautner and WilliamsonJMW14]. Here, we were inspired by work of Leslie-Lonergan [Reference Leslie and LonerganLL21], which used these tools to give a geometric interpretation of the Frobenius contraction functor in modular representation theory. (The key idea that parity sheaves play well with localization to the Tate category is also at the heart of recent work of Riche-Williamson [Reference Riche and WilliamsonRW22].) Ultimately, we are able to construct a ‘base change functor’ that categorifies the base change homomorphism for spherical Hecke algebras, and which is suitable for input into the global setup. The construction is completed in the joint appendix with Gus Lonergan.
To complete the proofs of the local results, we also need to exploit some new constructions with local Hecke algebras – in particular, the base change homomorphism
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
for Bernstein centers. A key insight in [Reference Treumann and VenkateshTV16] is that the base change homomorphism for spherical Hecke algebras admits a more ‘geometric’ description when the field extension is cyclic of order p and the coefficients also have characteristic p. We generalize this observation to the centers of higher depth Hecke algebras, and then to the Bernstein center, by an analysis of Hecke algebras with respect to the subgroups coming from the Moy-Prasad filtration at a special vertex of the Bruhat-Tits building of G.
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
for Bernstein centers. A key insight in [Reference Treumann and VenkateshTV16] is that the base change homomorphism for spherical Hecke algebras admits a more ‘geometric’ description when the field extension is cyclic of order p and the coefficients also have characteristic p. We generalize this observation to the centers of higher depth Hecke algebras, and then to the Bernstein center, by an analysis of Hecke algebras with respect to the subgroups coming from the Moy-Prasad filtration at a special vertex of the Bruhat-Tits building of G.
1.4 Organization of the paper
The outline of this paper is as follows.
In §2, we define excursion algebras and recall their relation to Langlands parameters. We explain functoriality from the perspective of excursion algebras.
In §3, we generalize the basic framework of sheaf-theoretic Smith theory from [Reference TreumannTre19, Reference Riche and WilliamsonRW22], which worked for topological spaces and finite type schemes respectively, to locally finite type schemes. This is needed because our spaces of interest are not of finite type. More specifically, we introduce the notion of Tate categories, the Smith functor
![]() $\operatorname {\mathrm {Psm}}$
and its properties and Tate cohomology, and we explain the relation to classical equivariant localization theorems for
$\operatorname {\mathrm {Psm}}$
and its properties and Tate cohomology, and we explain the relation to classical equivariant localization theorems for
![]() $\mathbf {Z}/p\mathbf {Z}$
-actions.
$\mathbf {Z}/p\mathbf {Z}$
-actions.
In §4, we recall the fundamentals of parity sheaves due to Juteau-Mautner-Williamson and the analogous notion of ‘Tate-parity sheaves’ due to Leslie-Lonergan. We explain how to combine these with the functor
![]() $\operatorname {\mathrm {Psm}}$
to construct a base change functor for parity objects in the Satake category. This functor plays the categorified role of the base change homomorphism for Hecke algebras.
$\operatorname {\mathrm {Psm}}$
to construct a base change functor for parity objects in the Satake category. This functor plays the categorified role of the base change homomorphism for Hecke algebras.
In §5, we prove a collection of global results, including Theorem 1.6. First, we recall background on moduli spaces of shtukas and Lafforgue’s global Langlands correspondence in terms of actions of the excursion algebra on the cohomology of shtukas. Then we establish certain equivariant localization isomorphisms for the Tate cohomology of shtukas in the setting of
![]() $\mathbf {Z}/p\mathbf {Z}$
-base change, which gives relations between excursion operators in the context of functoriality. These are used later in the local applications, and Theorem 1.6 is also deduced as an application.
$\mathbf {Z}/p\mathbf {Z}$
-base change, which gives relations between excursion operators in the context of functoriality. These are used later in the local applications, and Theorem 1.6 is also deduced as an application.
In §6, we prove our local results. We review the relevant aspects of the Genestier-Lafforgue correspondence. After analyzing the Brauer homomorphism for Hecke algebras with respect to subgroups arising from the Moy-Prasad filtration, we are able to construct the map
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
from Theorem 1.4, which we then establish using the global theory and local-global compatibility. Finally, we deduce Theorem 1.1 and Theorem 1.2.
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
from Theorem 1.4, which we then establish using the global theory and local-global compatibility. Finally, we deduce Theorem 1.1 and Theorem 1.2.
1.5 Notation
-
• (Coefficients) We let k be an algebraic closure of
 $\mathbf {F}_p$
(considered with the discrete topology). In general, we will consider geometric objects over fields of characteristic
$\mathbf {F}_p$
(considered with the discrete topology). In general, we will consider geometric objects over fields of characteristic
 $\neq p$
and étale sheaves over p-adically complete coefficients.
$\neq p$
and étale sheaves over p-adically complete coefficients. -
• (
 $\sigma $
-actions) Throughout the paper,
$\sigma $
-actions) Throughout the paper,
 $\sigma $
denotes a generator of a group isomorphic to
$\sigma $
denotes a generator of a group isomorphic to
 $\mathbf {Z}/p\mathbf {Z}$
. When we say that a widget has a ‘
$\mathbf {Z}/p\mathbf {Z}$
. When we say that a widget has a ‘
 $\sigma $
-action’, what we mean is that the widget has an action of a cyclic group of order p with chosen generator
$\sigma $
-action’, what we mean is that the widget has an action of a cyclic group of order p with chosen generator
 $\sigma $
.
$\sigma $
.Let
 $N := 1 + \sigma + \ldots + \sigma ^{p-1} \in \mathbf {Z}[\sigma ]$
. We will also denote by N the induced operation on any
$N := 1 + \sigma + \ldots + \sigma ^{p-1} \in \mathbf {Z}[\sigma ]$
. We will also denote by N the induced operation on any
 $\mathbf {Z}[\sigma ]$
-module.Footnote
5
$\mathbf {Z}[\sigma ]$
-module.Footnote
5
If A is a ring or module for
 $\mathbf {Z}[\sigma ]$
, then
$\mathbf {Z}[\sigma ]$
, then
 $A^{\sigma }$
denotes the
$A^{\sigma }$
denotes the
 $\sigma $
-invariants in A.
$\sigma $
-invariants in A. -
• (Reductive groups) For us, reductive groups are connected by definition. The Langlands dual group
 $\widehat {G}$
is considered as a split reductive group over k. For our conventions on the L-group, see §2.1.For any group,
$\widehat {G}$
is considered as a split reductive group over k. For our conventions on the L-group, see §2.1.For any group,  denotes the trivial representation (with the group made clear by context).
denotes the trivial representation (with the group made clear by context). -
• (Derived categories of sheaves) If Y is a locally finite type stack and
 $\Lambda $
is a coefficient ring in which the characteristic of Y is invertible, we let
$\Lambda $
is a coefficient ring in which the characteristic of Y is invertible, we let
 $D^b_c(Y;\Lambda )$
denote the bounded constructible derived category of étale sheaves over
$D^b_c(Y;\Lambda )$
denote the bounded constructible derived category of étale sheaves over
 $\Lambda $
; by this, we mean complexes whose restriction to any quasi-compact open substack
$\Lambda $
; by this, we mean complexes whose restriction to any quasi-compact open substack
 $U \subset Y$
lies in
$U \subset Y$
lies in
 $D^b_c(U; \Lambda )$
.
$D^b_c(U; \Lambda )$
.We shall also have occasion to consider larger categories of sheaves, where the constructibility condition is weakened. We let
 $D^b(Y; \Lambda )$
denote the bounded derived category of étale sheaves over
$D^b(Y; \Lambda )$
denote the bounded derived category of étale sheaves over
 $\Lambda $
that are ind-constructible. In other words, it is the full subcategory of the (co-complete) category
$\Lambda $
that are ind-constructible. In other words, it is the full subcategory of the (co-complete) category
 $D(Y; \Lambda )$
, of ind-constructible étale sheaves over
$D(Y; \Lambda )$
, of ind-constructible étale sheaves over
 $\Lambda $
, spanned by the bounded objects.
$\Lambda $
, spanned by the bounded objects.If
 $S = \{Y_\lambda \}$
is a stratification of Y, then we denote by
$S = \{Y_\lambda \}$
is a stratification of Y, then we denote by
 $D_S^b(Y; \Lambda )$
the full subcategory of
$D_S^b(Y; \Lambda )$
the full subcategory of
 $D^b(Y; \Lambda )$
consisting of complexes constructible with respect to the stratification S.
$D^b(Y; \Lambda )$
consisting of complexes constructible with respect to the stratification S. -
• (Equivariant derived categories) If a (pro-)algebraic group
 $\Sigma $
acts on Y, then we denote by
$\Sigma $
acts on Y, then we denote by
 $D_{c,\Sigma }^b(Y; \Lambda )$
or
$D_{c,\Sigma }^b(Y; \Lambda )$
or
 $D^b_c(X;\Lambda )^{B\Sigma }$
the
$D^b_c(X;\Lambda )^{B\Sigma }$
the
 $\Sigma $
-equivariant bounded derived category of constructible sheaves with coefficients in
$\Sigma $
-equivariant bounded derived category of constructible sheaves with coefficients in
 $\Lambda $
. We denote by
$\Lambda $
. We denote by
 $D_{\Sigma }^b(Y; \Lambda )$
or
$D_{\Sigma }^b(Y; \Lambda )$
or
 $D^b(X;\Lambda )^{B\Sigma }$
the analogous categories with the constructibility condition replaced by ind-constructibility, as above.
$D^b(X;\Lambda )^{B\Sigma }$
the analogous categories with the constructibility condition replaced by ind-constructibility, as above.When
 $\Lambda = k$
, we may suppress it from the notation, writing instead
$\Lambda = k$
, we may suppress it from the notation, writing instead
 $D^b_c(Y ) := D^b_c(Y; k)$
, etc.
$D^b_c(Y ) := D^b_c(Y; k)$
, etc. -
• Functors between derived categories (e.g.,
 $f_!, f_*, f^!, f^*$
) will always denote the derived functors.
$f_!, f_*, f^!, f^*$
) will always denote the derived functors.
2 Functoriality and the excursion algebra
In this section, we formalize the abstract excursion algebra
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, a device used to decompose a space into pieces indexed by Langlands parameters. This notion appears implicitly in [Reference LafforgueLaf18], but there it is the imageFootnote
6
of the abstract excursion algebra in a certain endomorphism algebra which is emphasized.
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, a device used to decompose a space into pieces indexed by Langlands parameters. This notion appears implicitly in [Reference LafforgueLaf18], but there it is the imageFootnote
6
of the abstract excursion algebra in a certain endomorphism algebra which is emphasized.
Since we work with non-split groups, we first clarify in §2.1 our conventions regarding L-groups. This is a bit subtle, as one finds (at least) two natural versions of the L-group in the literature: the ‘algebraic L-group’
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
, following Langlands, and the ‘geometric L-group’
${}^L G^{\operatorname {\mathrm {alg}}}$
, following Langlands, and the ‘geometric L-group’
![]() ${}^L G^{\operatorname {\mathrm {geom}}}$
, derived from the Geometric Satake equivalence. The difference between them is parallel to the difference between L-algebraicity and C-algebraicity emphasized in [Reference Buzzard and GeeBG14].
${}^L G^{\operatorname {\mathrm {geom}}}$
, derived from the Geometric Satake equivalence. The difference between them is parallel to the difference between L-algebraicity and C-algebraicity emphasized in [Reference Buzzard and GeeBG14].
We emphasize that the unadorned notation
![]() ${}^L G$
denotes the algebraic L-group, to be consistent with [Reference LafforgueLaf18], although the geometric L-group is really what appears more naturally in our arguments.
${}^L G$
denotes the algebraic L-group, to be consistent with [Reference LafforgueLaf18], although the geometric L-group is really what appears more naturally in our arguments.
We introduce two explicit presentations for the excursion algebra in §2.2 and §2.4. The first presentation is more natural for making the connection to Langlands parameters, which we recall in 2.3. The second presentation is more amenable to constructing actions of the excursion algebra, which makes it more convenient for our purposes, and it is the only one that will be used in the sequel.
Finally, in §2.5, we explain how functoriality is interpreted in terms of excursion algebras.
2.1 Conventions on L-groups and Langlands parameters
For a reductive group G over a field
![]() $\mathbf {F}$
with separable closure
$\mathbf {F}$
with separable closure
![]() $\mathbf {F}^s$
, we regard its Langlands dual group
$\mathbf {F}^s$
, we regard its Langlands dual group
![]() $\widehat {G}$
as a split reductive group over k. The L-group is a certain semi-direct product
$\widehat {G}$
as a split reductive group over k. The L-group is a certain semi-direct product
![]() ${}^L G = \widehat {G} \rtimes \operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
. Actually, in the case where
${}^L G = \widehat {G} \rtimes \operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
. Actually, in the case where
![]() $\mathbf {F}$
is a local field, we shall instead work with the ‘Weil form’
$\mathbf {F}$
is a local field, we shall instead work with the ‘Weil form’
![]() $\widehat {G} \rtimes \operatorname {\mathrm {Weil}}(\mathbf {F}^s/\mathbf {F})$
. (This is just for consistency with [Reference Genestier and LafforgueGL]; because we consider representations over k, in our case, it would make no difference to work with the Galois form.)
$\widehat {G} \rtimes \operatorname {\mathrm {Weil}}(\mathbf {F}^s/\mathbf {F})$
. (This is just for consistency with [Reference Genestier and LafforgueGL]; because we consider representations over k, in our case, it would make no difference to work with the Galois form.)
2.1.1 Algebraic L-group
In fact, there are at least two conventions for the definition of the L-group. The one which is more traditionally used in the literature is what we shall call the algebraic L-group, denoted
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
, defined as in [Reference Treumann and VenkateshTV16, §2.5]. The root datum
${}^L G^{\operatorname {\mathrm {alg}}}$
, defined as in [Reference Treumann and VenkateshTV16, §2.5]. The root datum
![]() $\Psi (G)$
of
$\Psi (G)$
of
![]() $G_{\mathbf {F}^s}$
determines a pinning for
$G_{\mathbf {F}^s}$
determines a pinning for
![]() $\widehat {G}$
, which, in turn, gives a splitting
$\widehat {G}$
, which, in turn, gives a splitting
![]() $\mathrm {Out}(\widehat {G}) \rightarrow \operatorname {\mathrm {Aut}}(\widehat {G})$
and an identification
$\mathrm {Out}(\widehat {G}) \rightarrow \operatorname {\mathrm {Aut}}(\widehat {G})$
and an identification
![]() $\operatorname {\mathrm {Aut}}(\Psi (G)) \cong \mathrm {Out}(\widehat {G})$
. The
$\operatorname {\mathrm {Aut}}(\Psi (G)) \cong \mathrm {Out}(\widehat {G})$
. The
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
-action on
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
-action on
![]() $\Psi (G)$
transports to an action
$\Psi (G)$
transports to an action
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}$
of
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}$
of
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
![]() $\widehat {G}$
, and we define
$\widehat {G}$
, and we define
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
to be the semidirect product
${}^L G^{\operatorname {\mathrm {alg}}}$
to be the semidirect product
Since the action
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}$
factors through a finite quotient, we may regard
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}$
factors through a finite quotient, we may regard
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
as a pro-algebraic group over k.
${}^L G^{\operatorname {\mathrm {alg}}}$
as a pro-algebraic group over k.
2.1.2 Geometric L-group
We now make a different construction of the L-group, using the Tannakian theory, following [Reference Richarz and ZhuRZ15, Appendix A] and [Reference ZhuZhu17, §5.5]. We begin with the Geometric Satake equivalence,
The Galois group
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
acts on
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
acts on
![]() $\operatorname {\mathrm {Gr}}_{G,\mathbf {F}^s}$
, inducing an action on the neutralized Tannakian category
$\operatorname {\mathrm {Gr}}_{G,\mathbf {F}^s}$
, inducing an action on the neutralized Tannakian category
 $(\operatorname {\mathrm {P}}_{L^+G_{\mathbf {F}^s}}(\operatorname {\mathrm {Gr}}_{G,\mathbf {F}^s};k), \underbrace {H^*(-)}_{\text {fiber functor}})$
. By [Reference Richarz and ZhuRZ15, Lemma A.1], this, in turn, induces an action
$(\operatorname {\mathrm {P}}_{L^+G_{\mathbf {F}^s}}(\operatorname {\mathrm {Gr}}_{G,\mathbf {F}^s};k), \underbrace {H^*(-)}_{\text {fiber functor}})$
. By [Reference Richarz and ZhuRZ15, Lemma A.1], this, in turn, induces an action
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
of
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
of
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
![]() $\widehat {G}_k$
. We define
$\widehat {G}_k$
. We define
In the case at hand, we shall see that
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
also factors through a finite quotient of
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
also factors through a finite quotient of
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
, so we may also regard
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
, so we may also regard
![]() ${}^L G^{\operatorname {\mathrm {geom}}}$
as a pro-algebraic group.
${}^L G^{\operatorname {\mathrm {geom}}}$
as a pro-algebraic group.
2.1.3 Relation between the two L-groups
The relation between these two actions is as follows. We let
![]() $\rho $
be the half sum of positive coroots of
$\rho $
be the half sum of positive coroots of
![]() $\widehat {G}$
, and we denote by
$\widehat {G}$
, and we denote by
![]() $\rho \colon \mathbf {G}_m \rightarrow \widehat {G}_{\operatorname {\mathrm {ad}}}$
the corresponding cocharacter. With
$\rho \colon \mathbf {G}_m \rightarrow \widehat {G}_{\operatorname {\mathrm {ad}}}$
the corresponding cocharacter. With
![]() $\mathrm {cyc}_p \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \mathbf {F}_p^{\times } $
denoting the mod p cyclotomic character, let
$\mathrm {cyc}_p \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \mathbf {F}_p^{\times } $
denoting the mod p cyclotomic character, let
![]() $\chi $
denote the composite
$\chi $
denote the composite
This induces a homomorphism
![]() $\operatorname {\mathrm {Ad}}_{\chi } \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \operatorname {\mathrm {Aut}}(\widehat {G})$
.
$\operatorname {\mathrm {Ad}}_{\chi } \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \operatorname {\mathrm {Aut}}(\widehat {G})$
.
Proposition 2.1. We have
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}} = \operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}} \circ \operatorname {\mathrm {Ad}}_{\chi }$
.
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}} = \operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}} \circ \operatorname {\mathrm {Ad}}_{\chi }$
.
Proof. When
![]() $\widehat {G}$
is over
$\widehat {G}$
is over
![]() $\mathbf {Q}_{p}$
, this is [Reference Richarz and ZhuRZ15, Proposition 1.6]. More generally, it is established in [Reference Fargues and ScholzeFS, §VI.11] over any p-adic ring.
$\mathbf {Q}_{p}$
, this is [Reference Richarz and ZhuRZ15, Proposition 1.6]. More generally, it is established in [Reference Fargues and ScholzeFS, §VI.11] over any p-adic ring.
Given a choice of lift
![]() $\widetilde {\chi } \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \widehat {G}(k)$
of
$\widetilde {\chi } \colon \operatorname {Gal}(\mathbf {F}^s/\mathbf {F}) \rightarrow \widehat {G}(k)$
of
![]() $\chi $
, which could, for example, come from a square root of the mod p cyclotomic character, we get an isomorphism
$\chi $
, which could, for example, come from a square root of the mod p cyclotomic character, we get an isomorphism
![]() ${}^L G^{\operatorname {\mathrm {alg}}} \xrightarrow {\sim } {}^L G^{\operatorname {\mathrm {geom}}}$
by
${}^L G^{\operatorname {\mathrm {alg}}} \xrightarrow {\sim } {}^L G^{\operatorname {\mathrm {geom}}}$
by
By [Reference ZhuZhu17, Remark 5.5.8], a square root of the cyclotomic character exists whenever
![]() $\mathrm {char}(\mathbf {F})>0$
. (However, in general, it can happen that
$\mathrm {char}(\mathbf {F})>0$
. (However, in general, it can happen that
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
and
${}^L G^{\operatorname {\mathrm {alg}}}$
and
![]() ${}^L G^{\operatorname {\mathrm {geom}}} $
are not isomorphic; for an example, see [Reference ZhuZhu17, Example 5.5.9].)
${}^L G^{\operatorname {\mathrm {geom}}} $
are not isomorphic; for an example, see [Reference ZhuZhu17, Example 5.5.9].)
At different points, we will want to consider both versions of L-groups. If we write
![]() ${}^L G$
without a superscript, then by default we mean the algebraic L-group
${}^L G$
without a superscript, then by default we mean the algebraic L-group
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
.
${}^L G^{\operatorname {\mathrm {alg}}}$
.
2.1.4 Representation categories
For any Galois extension
![]() $\mathbf {F}'/\mathbf {F}$
such that
$\mathbf {F}'/\mathbf {F}$
such that
![]() $G_{\mathbf {F}'}$
is split, the analogous construction to §2.1.1 gives a ‘finite form’ algebraic L-group
$G_{\mathbf {F}'}$
is split, the analogous construction to §2.1.1 gives a ‘finite form’ algebraic L-group
![]() $\widehat {G} \rtimes _{\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}} \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
. We define the category of (k-linear) algebraic representations of
$\widehat {G} \rtimes _{\operatorname {\mathrm {act}}^{\operatorname {\mathrm {alg}}}} \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
. We define the category of (k-linear) algebraic representations of
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
to be
${}^L G^{\operatorname {\mathrm {alg}}}$
to be
Let
![]() $ \operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {geom}}}) := \operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
denote the category of continuously
$ \operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {geom}}}) := \operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
denote the category of continuously
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
-equivariant objects in
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
-equivariant objects in
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
with respect to the geometric action. The Geometric Satake equivalence induces by descent an equivalence
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
with respect to the geometric action. The Geometric Satake equivalence induces by descent an equivalence
where the action of
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
on
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
on the RHS is via
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
on the RHS is via
![]() $\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
, and on the LHS,
$\operatorname {\mathrm {act}}^{\operatorname {\mathrm {geom}}}$
, and on the LHS,
![]() $\operatorname {\mathrm {Gr}}_G$
is considered over
$\operatorname {\mathrm {Gr}}_G$
is considered over
![]() $\mathbf {F}$
. By definition, on the right side we take are taking objects on which
$\mathbf {F}$
. By definition, on the right side we take are taking objects on which
![]() $\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
acts continuously with its Krull topology. Since k is algebraic over
$\operatorname {Gal}(\mathbf {F}^s/\mathbf {F})$
acts continuously with its Krull topology. Since k is algebraic over
![]() $\mathbf {F}_p$
, in this case,
$\mathbf {F}_p$
, in this case,
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
can be identified with
$\operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
can be identified with
![]() $\varinjlim _{\mathbf {F}'/\mathbf {F}} \operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}'/\mathbf {F}), \operatorname {\mathrm {geom}}}$
, where the limit runs over finite Galois extensions
$\varinjlim _{\mathbf {F}'/\mathbf {F}} \operatorname {\mathrm {Rep}}_k(\widehat {G})^{B\operatorname {Gal}(\mathbf {F}'/\mathbf {F}), \operatorname {\mathrm {geom}}}$
, where the limit runs over finite Galois extensions
![]() $\mathbf {F}'/\mathbf {F}$
over which the geometric action factors.
$\mathbf {F}'/\mathbf {F}$
over which the geometric action factors.
An isomorphism (2.1) gives an embedding
![]() $\operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {alg}}}) \hookrightarrow \operatorname {\mathrm {Rep}}_k(\widehat {G})^{\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
, which, as just remarked, is an equivalence for our choice of k. See [Reference Richarz and ZhuRZ15, Proposition A.10] for a description of the essential image in general.
$\operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {alg}}}) \hookrightarrow \operatorname {\mathrm {Rep}}_k(\widehat {G})^{\operatorname {Gal}(\mathbf {F}^s/\mathbf {F}), \operatorname {\mathrm {geom}}}$
, which, as just remarked, is an equivalence for our choice of k. See [Reference Richarz and ZhuRZ15, Proposition A.10] for a description of the essential image in general.
2.1.5 L-parameters
Definition 2.2. Let
![]() $\Gamma $
be a topological group and
$\Gamma $
be a topological group and
![]() $\overline {\Gamma }$
be a quotient of
$\overline {\Gamma }$
be a quotient of
![]() $\Gamma $
acting on
$\Gamma $
acting on
![]() $\widehat {G}$
. An L-parameter from
$\widehat {G}$
. An L-parameter from
![]() $\Gamma $
to
$\Gamma $
to
![]() $\widehat {G}(k) \rtimes \overline {\Gamma }$
is a
$\widehat {G}(k) \rtimes \overline {\Gamma }$
is a
![]() $\widehat {G}(k)$
-conjugacy class of continuous homomorphisms
$\widehat {G}(k)$
-conjugacy class of continuous homomorphisms
![]() $\rho \colon \Gamma \rightarrow \widehat {G}(k) \rtimes \overline {\Gamma }$
, which has the property that the composite map
$\rho \colon \Gamma \rightarrow \widehat {G}(k) \rtimes \overline {\Gamma }$
, which has the property that the composite map
![]() $\Gamma \rightarrow \widehat {G} \rtimes \Gamma \rightarrow \overline {\Gamma }$
is the given quotient
$\Gamma \rightarrow \widehat {G} \rtimes \Gamma \rightarrow \overline {\Gamma }$
is the given quotient
![]() $\Gamma \twoheadrightarrow \overline {\Gamma }$
.
$\Gamma \twoheadrightarrow \overline {\Gamma }$
.
Equivalently, we may view
![]() $\rho $
as an element of the continuous cohomology group
$\rho $
as an element of the continuous cohomology group
![]() $H^1_{\operatorname {\mathrm {cts}}}(\Gamma , \widehat {G}(k))$
, where the action of
$H^1_{\operatorname {\mathrm {cts}}}(\Gamma , \widehat {G}(k))$
, where the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\widehat {G}(k)$
is the given one (via
$\widehat {G}(k)$
is the given one (via
![]() $\Gamma \rightarrow \overline {\Gamma }$
) in the semi-direct product.
$\Gamma \rightarrow \overline {\Gamma }$
) in the semi-direct product.
We will consider L-parameters with
![]() $\widehat {G}(k) \rtimes \Gamma $
being either
$\widehat {G}(k) \rtimes \Gamma $
being either
![]() ${}^L \widehat {G}^{\operatorname {\mathrm {alg}}}(k)$
or
${}^L \widehat {G}^{\operatorname {\mathrm {alg}}}(k)$
or
![]() ${}^L \widehat {G}^{\operatorname {\mathrm {geom}}}(k)$
, and
${}^L \widehat {G}^{\operatorname {\mathrm {geom}}}(k)$
, and
![]() $\Gamma $
being either
$\Gamma $
being either
![]() $\operatorname {Gal}(F^s/F)$
for a global field F or
$\operatorname {Gal}(F^s/F)$
for a global field F or
![]() $\operatorname {\mathrm {Weil}}(F_v^s/F_v)$
for a local field
$\operatorname {\mathrm {Weil}}(F_v^s/F_v)$
for a local field
![]() $F_v$
.
$F_v$
.
Note that the algebraic
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\widehat {G}(k)$
factors through a finite quotient
$\widehat {G}(k)$
factors through a finite quotient
![]() $\Gamma \twoheadrightarrow \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
. It is clear that L-parameters into
$\Gamma \twoheadrightarrow \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
. It is clear that L-parameters into
![]() ${}^L G^{\operatorname {\mathrm {alg}}}(k)$
are in bijection (under restriction) with L-parameters into
${}^L G^{\operatorname {\mathrm {alg}}}(k)$
are in bijection (under restriction) with L-parameters into
![]() $\widehat {G}(k) \rtimes \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
for any such
$\widehat {G}(k) \rtimes \operatorname {Gal}(\mathbf {F}'/\mathbf {F})$
for any such
![]() $\mathbf {F}'$
; indeed, the set of all such L-parameters is identified with
$\mathbf {F}'$
; indeed, the set of all such L-parameters is identified with
![]() $H^1_{\mathrm {cts}}(\Gamma , \widehat {G}(k))$
.
$H^1_{\mathrm {cts}}(\Gamma , \widehat {G}(k))$
.
We say that a homomorphism
![]() $\rho \colon \Gamma \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}(k)$
is semisimple
Footnote
7
if whenever it factors though a parabolic
$\rho \colon \Gamma \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}(k)$
is semisimple
Footnote
7
if whenever it factors though a parabolic
![]() ${}^L P^{\operatorname {\mathrm {alg}}}(k) \subset {}^L G^{\operatorname {\mathrm {alg}}}(k)$
, it also factors through a Levi
${}^L P^{\operatorname {\mathrm {alg}}}(k) \subset {}^L G^{\operatorname {\mathrm {alg}}}(k)$
, it also factors through a Levi
![]() ${}^L M^{\operatorname {\mathrm {alg}}}(k) \subset {}^L P^{\operatorname {\mathrm {alg}}}(k)$
(see [Reference BorelBor79, §3] for the notion of parabolic and Levi subgroups of an L-group).
${}^L M^{\operatorname {\mathrm {alg}}}(k) \subset {}^L P^{\operatorname {\mathrm {alg}}}(k)$
(see [Reference BorelBor79, §3] for the notion of parabolic and Levi subgroups of an L-group).
2.2 Presentation of the excursion algebra
Let
![]() $\Gamma $
be a group, which is either
$\Gamma $
be a group, which is either
![]() $\operatorname {Gal}(F^s/F)$
for a global field F or
$\operatorname {Gal}(F^s/F)$
for a global field F or
![]() $\operatorname {\mathrm {Weil}}(F^s/F)$
for a local field F. Let G be a reductive group over F and
$\operatorname {\mathrm {Weil}}(F^s/F)$
for a local field F. Let G be a reductive group over F and
![]() ${}^L G^{\operatorname {\mathrm {alg}}}$
the algebraic L-group as defined in §2.1.1.
${}^L G^{\operatorname {\mathrm {alg}}}$
the algebraic L-group as defined in §2.1.1.
We will define the excursion algebra
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
to be the commutative algebra over k presented by explicit generators and relations given below. (The topology on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
to be the commutative algebra over k presented by explicit generators and relations given below. (The topology on
![]() $\Gamma $
will not be relevant for the definition of
$\Gamma $
will not be relevant for the definition of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.) For a more conceptual perspective, see [Reference ZhuZhu, §2], wherein the excursion algebra is denoted
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.) For a more conceptual perspective, see [Reference ZhuZhu, §2], wherein the excursion algebra is denoted
![]() $k[\mathcal {R}_{\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}//\widehat {G}}]$
.
$k[\mathcal {R}_{\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}//\widehat {G}}]$
.
2.2.1 Generators
We define
![]() $\mathcal {O}({}^L G_k^{\operatorname {\mathrm {alg}}}) := \varinjlim _{F'/F} \mathcal {O}(\widehat {G}_k \rtimes \operatorname {Gal}(F'/F))$
, where the limit runs over finite extensions
$\mathcal {O}({}^L G_k^{\operatorname {\mathrm {alg}}}) := \varinjlim _{F'/F} \mathcal {O}(\widehat {G}_k \rtimes \operatorname {Gal}(F'/F))$
, where the limit runs over finite extensions
![]() $F'/F$
over which the
$F'/F$
over which the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\widehat {G}_k$
factors.
$\widehat {G}_k$
factors.
Generators of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
will be denoted
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
will be denoted
![]() $S_{I, f, (\gamma _i)_{i \in I}}$
, where the indexing set
$S_{I, f, (\gamma _i)_{i \in I}}$
, where the indexing set
![]() $(I, f, (\gamma _i)_{i \in I})$
consists of
$(I, f, (\gamma _i)_{i \in I})$
consists of
-
(i) I is a finite (possibly empty) set,
-
(ii)
 $f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k) := \mathcal {O}(({}^L G_k^{\operatorname {\mathrm {alg}}})^I )^{\widehat {G}_k \times \widehat {G}_k }$
, where the quotient is for the actions of
$f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k) := \mathcal {O}(({}^L G_k^{\operatorname {\mathrm {alg}}})^I )^{\widehat {G}_k \times \widehat {G}_k }$
, where the quotient is for the actions of
 $\widehat {G}_k$
by diagonal left and right translation, respectively, and
$\widehat {G}_k$
by diagonal left and right translation, respectively, and -
(iii)
 $\gamma _i \in \Gamma $
for each
$\gamma _i \in \Gamma $
for each
 $i \in I$
.
$i \in I$
.
2.2.2 Relations
Next, we describe the relations. (Compare [Reference LafforgueLaf18, §10].)
-
(i)
 $S_{\emptyset , f, *} = f(1_G)$
, an element of
$S_{\emptyset , f, *} = f(1_G)$
, an element of
 $k \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
$k \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
. -
(ii) The map
 $f \mapsto S_{I, f, (\gamma _i)_{i \in I}}$
is a k-algebra homomorphism in f; that is, and
$f \mapsto S_{I, f, (\gamma _i)_{i \in I}}$
is a k-algebra homomorphism in f; that is, and $$ \begin{align*} S_{I, f+f', (\gamma_i)_{i \in I}} &= S_{I, f, (\gamma_i)_{i \in I}} + S_{I, f', (\gamma_i)_{i \in I}}, \\ S_{I, ff', (\gamma_i)_{i \in I}} &= S_{I, f, (\gamma_i)_{i \in I}} \cdot S_{I, f', (\gamma_i)_{i \in I}}, \end{align*} $$
$$ \begin{align*} S_{I, f+f', (\gamma_i)_{i \in I}} &= S_{I, f, (\gamma_i)_{i \in I}} + S_{I, f', (\gamma_i)_{i \in I}}, \\ S_{I, ff', (\gamma_i)_{i \in I}} &= S_{I, f, (\gamma_i)_{i \in I}} \cdot S_{I, f', (\gamma_i)_{i \in I}}, \end{align*} $$
 $$\begin{align*}S_{I, \lambda f, (\gamma_i)_{i \in I}} = \lambda S_{I, f, (\gamma_i)_{i \in I}} \text{ for all }\lambda \in k. \end{align*}$$
$$\begin{align*}S_{I, \lambda f, (\gamma_i)_{i \in I}} = \lambda S_{I, f, (\gamma_i)_{i \in I}} \text{ for all }\lambda \in k. \end{align*}$$
-
(iii) For all maps of finite sets
 $\zeta \colon I \rightarrow J$
, all
$\zeta \colon I \rightarrow J$
, all
 $f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k)$
, and all
$f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k)$
, and all
 $(\gamma _j)_{j \in J} \in \Gamma ^J$
, we have where
$(\gamma _j)_{j \in J} \in \Gamma ^J$
, we have where $$\begin{align*}S_{J, f^{\zeta}, (\gamma_j)_{j \in J}} = S_{I, f, (\gamma_{\zeta(i)})_{i \in I}}, \end{align*}$$
$$\begin{align*}S_{J, f^{\zeta}, (\gamma_j)_{j \in J}} = S_{I, f, (\gamma_{\zeta(i)})_{i \in I}}, \end{align*}$$
 $f^{\zeta } \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^J / \widehat {G}_k)$
is defined by
$f^{\zeta } \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^J / \widehat {G}_k)$
is defined by
 $f^{\zeta } ((g_j)_{j \in J}) := f((g_{\zeta (i)})_{i \in I})$
.
$f^{\zeta } ((g_j)_{j \in J}) := f((g_{\zeta (i)})_{i \in I})$
.
-
(iv) For all
 $f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k)$
and
$f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^I / \widehat {G}_k)$
and
 $(\gamma _i)_{i \in I}, (\gamma _i')_{i \in I}, (\gamma _i")_{i \in I} \in \Gamma ^I$
, we have where
$(\gamma _i)_{i \in I}, (\gamma _i')_{i \in I}, (\gamma _i")_{i \in I} \in \Gamma ^I$
, we have where $$\begin{align*}S_{I \sqcup I \sqcup I, \widetilde{f}, (\gamma_i)_{i \in I} \times (\gamma_i')_{i \in I} \times (\gamma_i")_{i \in I} } = S_{I, f, (\gamma_i (\gamma_i')^{-1} \gamma_i")_{i \in I} }, \end{align*}$$
$$\begin{align*}S_{I \sqcup I \sqcup I, \widetilde{f}, (\gamma_i)_{i \in I} \times (\gamma_i')_{i \in I} \times (\gamma_i")_{i \in I} } = S_{I, f, (\gamma_i (\gamma_i')^{-1} \gamma_i")_{i \in I} }, \end{align*}$$
 $\widetilde {f} \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^{I \sqcup I \sqcup I}/ \widehat {G}_k)$
is defined by
$\widetilde {f} \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^{I \sqcup I \sqcup I}/ \widehat {G}_k)$
is defined by  $$\begin{align*}\widetilde{f}((g_i)_{i \in I} \times (g_i')_{i \in I} \times (g_i")_{i \in I}) = f((g_i (g_i')^{-1} g_i")_{i \in I}). \end{align*}$$
$$\begin{align*}\widetilde{f}((g_i)_{i \in I} \times (g_i')_{i \in I} \times (g_i")_{i \in I}) = f((g_i (g_i')^{-1} g_i")_{i \in I}). \end{align*}$$
-
(v) If f is inflated from a function on
 $\Gamma ^I$
, then
$\Gamma ^I$
, then
 $S_{I , f, (\gamma _i)_{i \in I}}$
equals the scalar
$S_{I , f, (\gamma _i)_{i \in I}}$
equals the scalar
 $f((\gamma _i)_{i \in I})$
. More generally, if J is a subset of I and f is inflated from a function on
$f((\gamma _i)_{i \in I})$
. More generally, if J is a subset of I and f is inflated from a function on
 $(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^J / \widehat {G}_k) \times \Gamma ^{I \setminus J}$
, then we have where
$(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^J / \widehat {G}_k) \times \Gamma ^{I \setminus J}$
, then we have where $$\begin{align*}S_{I, f, (\gamma_i)_{i \in I}} = S_{J, \check{f}, (\gamma_j)_{j \in J}}, \end{align*}$$
$$\begin{align*}S_{I, f, (\gamma_i)_{i \in I}} = S_{J, \check{f}, (\gamma_j)_{j \in J}}, \end{align*}$$
 $\check {f}((g_j)_{j \in J}) := f((g_j)_{j \in J}, (\gamma _i)_{i \in I \setminus J})$
. (Compare [Reference LafforgueLaf18, p. 164].)
$\check {f}((g_j)_{j \in J}) := f((g_j)_{j \in J}, (\gamma _i)_{i \in I \setminus J})$
. (Compare [Reference LafforgueLaf18, p. 164].)
Definition 2.3. The excursion algebra
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
is the k-algebra with generators and relations specified as above.
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
is the k-algebra with generators and relations specified as above.
2.3 Constructing Galois representations
The following result of Lafforgue (generalized to modular coefficients by Böckle-Harris-Khare-Thorne) explains how to obtain Langlands parameters from characters of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
Proposition 2.4 [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 4.5], [Reference LafforgueLaf18, §13].
For any character
![]() $\nu \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow k$
, there is a semisimple L-parameter
$\nu \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow k$
, there is a semisimple L-parameter
![]() $\rho _{\nu } \colon \Gamma \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}(k)$
(for the discrete topology on
$\rho _{\nu } \colon \Gamma \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}(k)$
(for the discrete topology on
![]() $\Gamma $
), unique up to conjugation by
$\Gamma $
), unique up to conjugation by
![]() $\widehat {G}(k)$
, which is characterized by the following condition:
$\widehat {G}(k)$
, which is characterized by the following condition:
For all
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
![]() $f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^{n+1}/ \widehat {G}_k)$
, and
$f \in \mathcal {O}(\widehat {G}_k \backslash ({}^L G_k^{\operatorname {\mathrm {alg}}})^{n+1}/ \widehat {G}_k)$
, and
![]() $(\gamma _0, \ldots , \gamma _n)\in \Gamma ^{n+1}$
, we have
$(\gamma _0, \ldots , \gamma _n)\in \Gamma ^{n+1}$
, we have
Remark 2.5. See also [Reference Fargues and ScholzeFS, Corollary VIII.4.3] for more perspectives on, and generalizations of, this statement.
Remark 2.6. In Proposition 2.4, the datum of
![]() $\rho _{\nu }$
up to conjugation is equivalent to that of a cohomology class
$\rho _{\nu }$
up to conjugation is equivalent to that of a cohomology class
![]() $[\rho _{\nu }] \in H^1(\Gamma , \widehat {G}(k))$
, where
$[\rho _{\nu }] \in H^1(\Gamma , \widehat {G}(k))$
, where
![]() $\Gamma $
is given the discrete topology.
$\Gamma $
is given the discrete topology.
2.4 Another presentation for the excursion algebra
We will now describe a second presentation of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
, following [Reference LafforgueLaf18, Lemma 0.31], which is more useful for constructing actions of
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
, following [Reference LafforgueLaf18, Lemma 0.31], which is more useful for constructing actions of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
in practice.
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
in practice.
2.4.1 Generators
We take a set of generators indexed by tuples of data of the form
![]() $(I, W, x, \xi , (\gamma _i)_{i \in I})$
, where
$(I, W, x, \xi , (\gamma _i)_{i \in I})$
, where
-
(i) I is a finite set,
-
(ii)
 $W \in \operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I)$
(cf. §2.1.4),
$W \in \operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I)$
(cf. §2.1.4), -
(iii)
 $x \in W$
is a vector invariant under the diagonal
$x \in W$
is a vector invariant under the diagonal
 $\widehat {G}_k$
-action,
$\widehat {G}_k$
-action, -
(iv)
 $\xi \in W^*$
is a functional invariant under the diagonal
$\xi \in W^*$
is a functional invariant under the diagonal
 $\widehat {G}_k$
-action,
$\widehat {G}_k$
-action, -
(v)
 $\gamma _i \in \Gamma $
for each i.
$\gamma _i \in \Gamma $
for each i.
The corresponding generator of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
will be denoted by
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
will be denoted by
![]() $S_{I, W, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
$S_{I, W, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
2.4.2 Relations
Next, we describe the relations.
-
(i)
 $S_{\emptyset , x, \xi , \emptyset } = \langle x, \xi \rangle $
, an element of
$S_{\emptyset , x, \xi , \emptyset } = \langle x, \xi \rangle $
, an element of
 $k \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
.
$k \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
. -
(ii) For any morphism of
 $({}^L G_k^{\operatorname {\mathrm {alg}}})^I$
-representations
$({}^L G_k^{\operatorname {\mathrm {alg}}})^I$
-representations
 $u \colon W \rightarrow W'$
and functional
$u \colon W \rightarrow W'$
and functional
 $\xi ' \in (W')^*$
invariant under the diagonal
$\xi ' \in (W')^*$
invariant under the diagonal
 $\widehat {G}_k$
-action, we have (2.4)where
$\widehat {G}_k$
-action, we have (2.4)where $$ \begin{align} S_{I, W, x, u^* (\xi'), (\gamma_i)_{i \in I} } = S_{I, W', u(x), \xi', (\gamma_i)_{i \in I}}, \end{align} $$
$$ \begin{align} S_{I, W, x, u^* (\xi'), (\gamma_i)_{i \in I} } = S_{I, W', u(x), \xi', (\gamma_i)_{i \in I}}, \end{align} $$
 $u^* \colon (W')^* \rightarrow W^*$
denotes the dual to u.
$u^* \colon (W')^* \rightarrow W^*$
denotes the dual to u.
-
(iii) For two tuples
 $(I_1, W_1, x_1, \xi _1, (\gamma _i^1)_{i \in I_1})$
and
$(I_1, W_1, x_1, \xi _1, (\gamma _i^1)_{i \in I_1})$
and
 $(I_2, W_2, x_2, \xi _2, (\gamma _i^2)_{i \in I_2})$
as in §2.4.1, we have (2.5)Also,
$(I_2, W_2, x_2, \xi _2, (\gamma _i^2)_{i \in I_2})$
as in §2.4.1, we have (2.5)Also, $$ \begin{align} S_{I_1 \sqcup I_2, W_1 \boxtimes W_2, x_1 \boxtimes x_2, \xi_1 \boxtimes \xi_2, (\gamma_i^1)_{i \in I_1} \times (\gamma_i^2)_{i \in I_2}} = S_{I_1, W_1, x_1, \xi_1, (\gamma_i^1)_{i \in I_1}} \circ S_{I_2, W_2, x_2, \xi_2, (\gamma_i^2)_{i \in I_2}}. \end{align} $$
(2.6)Furthermore, the assignment
$$ \begin{align} S_{I_1 \sqcup I_2, W_1 \boxtimes W_2, x_1 \boxtimes x_2, \xi_1 \boxtimes \xi_2, (\gamma_i^1)_{i \in I_1} \times (\gamma_i^2)_{i \in I_2}} = S_{I_1, W_1, x_1, \xi_1, (\gamma_i^1)_{i \in I_1}} \circ S_{I_2, W_2, x_2, \xi_2, (\gamma_i^2)_{i \in I_2}}. \end{align} $$
(2.6)Furthermore, the assignment $$ \begin{align} S_{I_1 \sqcup I_2, W_1 \oplus W_2, (x_1, x_2) , \xi_1 \oplus \xi_2, (\gamma_i^1)_{i \in I_1} \times (\gamma_i^2)_{i \in I_2}} = S_{I_1, W_1, x_1, \xi_1, (\gamma_i^1)_{i \in I_1}} + S_{I_2, W_2, x_2, \xi_2, (\gamma_i^2)_{i \in I_2}}. \end{align} $$
$$ \begin{align} S_{I_1 \sqcup I_2, W_1 \oplus W_2, (x_1, x_2) , \xi_1 \oplus \xi_2, (\gamma_i^1)_{i \in I_1} \times (\gamma_i^2)_{i \in I_2}} = S_{I_1, W_1, x_1, \xi_1, (\gamma_i^1)_{i \in I_1}} + S_{I_2, W_2, x_2, \xi_2, (\gamma_i^2)_{i \in I_2}}. \end{align} $$
 $(I,W, x, \xi , (\gamma _i)_{i \in I}) \mapsto S_{I, W, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
is k-linear in x and
$(I,W, x, \xi , (\gamma _i)_{i \in I}) \mapsto S_{I, W, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
is k-linear in x and
 $\xi $
.
$\xi $
.
-
(iv) Let
 $\zeta \colon I \rightarrow J$
be a map of finite sets. Suppose
$\zeta \colon I \rightarrow J$
be a map of finite sets. Suppose
 $W \in \operatorname {\mathrm {Rep}}(({}^L G)^I)$
,
$W \in \operatorname {\mathrm {Rep}}(({}^L G)^I)$
,
 $x \in W^{\Delta (\widehat {G})}$
,
$x \in W^{\Delta (\widehat {G})}$
,
 $\xi \colon (W^*)^{\Delta (\widehat {G})}$
, and
$\xi \colon (W^*)^{\Delta (\widehat {G})}$
, and
 $(\gamma _j)_{j \in J} \in \Gamma ^J$
. Letting
$(\gamma _j)_{j \in J} \in \Gamma ^J$
. Letting
 $W^{\zeta }$
be the restriction of W under the functor
$W^{\zeta }$
be the restriction of W under the functor
 $\operatorname {\mathrm {Rep}}(({}^L G)^I) \rightarrow \operatorname {\mathrm {Rep}}(({}^L G)^J)$
induced by
$\operatorname {\mathrm {Rep}}(({}^L G)^I) \rightarrow \operatorname {\mathrm {Rep}}(({}^L G)^J)$
induced by
 $\zeta $
, we have (2.7)
$\zeta $
, we have (2.7) $$ \begin{align} S_{J, W^{\zeta}, x, \xi, (\gamma_j)_{j \in J}}= S_{I, W, x, \xi, (\gamma_{\zeta(i)})_{i \in I}}. \end{align} $$
$$ \begin{align} S_{J, W^{\zeta}, x, \xi, (\gamma_j)_{j \in J}}= S_{I, W, x, \xi, (\gamma_{\zeta(i)})_{i \in I}}. \end{align} $$
-
(v) Let
 and
and  be the natural counit and unit. Conflating x with a
be the natural counit and unit. Conflating x with a
 $\widehat {G}$
-invariant map
$\widehat {G}$
-invariant map  and similarly for
and similarly for
 $\xi $
, we have (2.8)
$\xi $
, we have (2.8) $$ \begin{align} S_{I, W, x, \xi, (\gamma_i (\gamma^{\prime}_i)^{-1} \gamma_i")_{i \in I}} = S_{I \sqcup I \sqcup I, W \boxtimes W^* \boxtimes W, \delta_W \boxtimes x, \xi \boxtimes \operatorname{\mathrm{ev}}_W, (\gamma_i)_{i \in I} \times (\gamma_i')_{i \in I} \times (\gamma_i")_{i \in I}}. \end{align} $$
$$ \begin{align} S_{I, W, x, \xi, (\gamma_i (\gamma^{\prime}_i)^{-1} \gamma_i")_{i \in I}} = S_{I \sqcup I \sqcup I, W \boxtimes W^* \boxtimes W, \delta_W \boxtimes x, \xi \boxtimes \operatorname{\mathrm{ev}}_W, (\gamma_i)_{i \in I} \times (\gamma_i')_{i \in I} \times (\gamma_i")_{i \in I}}. \end{align} $$
-
(vi) For
 $J \subset I$
, if W is inflated from a representation of
$J \subset I$
, if W is inflated from a representation of
 $({}^L G^{\operatorname {\mathrm {alg}}})^J \times \Gamma ^{I \setminus J}$
, then we have
$({}^L G^{\operatorname {\mathrm {alg}}})^J \times \Gamma ^{I \setminus J}$
, then we have  $$\begin{align*}S_{I, W, x, \xi, (\gamma_i)_{i \in I}} = S_{J, W|_{({}^L G^{\operatorname{\mathrm{alg}}})^J }, ((1_j)_{j \in J}, (\gamma_i)_{i \in I \setminus J}) \cdot x , \xi, (\gamma_j)_{j \in J}}. \end{align*}$$
$$\begin{align*}S_{I, W, x, \xi, (\gamma_i)_{i \in I}} = S_{J, W|_{({}^L G^{\operatorname{\mathrm{alg}}})^J }, ((1_j)_{j \in J}, (\gamma_i)_{i \in I \setminus J}) \cdot x , \xi, (\gamma_j)_{j \in J}}. \end{align*}$$
2.4.3 Relation between the presentations
The two presentations in §2.2 and §2.4 are related as follows. The generator
![]() $S_{I, W, x, \xi , (\gamma _i)_{i \in I}}$
corresponds to
$S_{I, W, x, \xi , (\gamma _i)_{i \in I}}$
corresponds to
![]() $S_{I, f_{x, \xi }, (\gamma _i)_{i \in I}}$
, where
$S_{I, f_{x, \xi }, (\gamma _i)_{i \in I}}$
, where
![]() $f_{x, \xi }$
is the function on
$f_{x, \xi }$
is the function on
![]() $({}^L G_k)^I$
given by
$({}^L G_k)^I$
given by
![]() $(g_i)_{i \in I} \mapsto \langle \xi , (g_i)_{i \in I} \cdot x \rangle $
. The assumptions on
$(g_i)_{i \in I} \mapsto \langle \xi , (g_i)_{i \in I} \cdot x \rangle $
. The assumptions on
![]() $\xi $
and x imply that
$\xi $
and x imply that
![]() $f_{x, \xi }$
is invariant under the left and right diagonal
$f_{x, \xi }$
is invariant under the left and right diagonal
![]() $\widehat {G}_k$
-actions. The relations in §2.4.2 imply that
$\widehat {G}_k$
-actions. The relations in §2.4.2 imply that
![]() $S_{I, W, x, \xi , (\gamma _i)_{i\in I}}$
depends only on
$S_{I, W, x, \xi , (\gamma _i)_{i\in I}}$
depends only on
![]() $f_{x, \xi }$
(and not on the choice of
$f_{x, \xi }$
(and not on the choice of
![]() $x, \xi $
) by [Reference LafforgueLaf18, Lemme 10.6].
$x, \xi $
) by [Reference LafforgueLaf18, Lemme 10.6].
2.5 Functoriality for excursion algebras
A homomorphism of L-groups
![]() $\phi \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
is admissible if it lies over the identity map on
$\phi \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
is admissible if it lies over the identity map on
![]() $\Gamma $
(i.e., the diagram below commutes).
$\Gamma $
(i.e., the diagram below commutes).

Lemma 2.7. Let
![]() $\phi \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
be an admissible homomorphism. Then there is a homomorphism
$\phi \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
be an admissible homomorphism. Then there is a homomorphism
![]() $\phi ^* \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L H^{\operatorname {\mathrm {alg}}})$
, which, in terms of the description of k-points of their corresponding spectra given in Proposition 2.4, sends
$\phi ^* \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L H^{\operatorname {\mathrm {alg}}})$
, which, in terms of the description of k-points of their corresponding spectra given in Proposition 2.4, sends
![]() $\rho \in H^1(\Gamma , \widehat {H}(k))$
to
$\rho \in H^1(\Gamma , \widehat {H}(k))$
to
![]() $\phi \circ \rho \in H^1(\Gamma , \widehat {G}(k))$
.
$\phi \circ \rho \in H^1(\Gamma , \widehat {G}(k))$
.
Proof. The map
![]() $\phi $
induces
$\phi $
induces
![]() $\operatorname {\mathrm {Res}}_{\phi } \colon \operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow \operatorname {\mathrm {Rep}}_k({}^L H^{\operatorname {\mathrm {alg}}})$
. At the level of generators, the map
$\operatorname {\mathrm {Res}}_{\phi } \colon \operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {alg}}}) \rightarrow \operatorname {\mathrm {Rep}}_k({}^L H^{\operatorname {\mathrm {alg}}})$
. At the level of generators, the map
![]() $\phi ^*$
sends
$\phi ^*$
sends
We verify by inspection that this map sends relations to relations. To see that this indeed induces composition with
![]() $\phi $
at the level of Langlands parameters, use (2.3).
$\phi $
at the level of Langlands parameters, use (2.3).
Definition 2.8 (Base change).
In the base change situation, where H is a reductive group over F and
![]() $G = \operatorname {\mathrm {Res}}_{E/F} (H_E)$
, the relevant morphism of L-groups
$G = \operatorname {\mathrm {Res}}_{E/F} (H_E)$
, the relevant morphism of L-groups
![]() $\phi _{\mathsf {BC}} \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
is defined by the formula
$\phi _{\mathsf {BC}} \colon {}^L H^{\operatorname {\mathrm {alg}}} \rightarrow {}^L G^{\operatorname {\mathrm {alg}}}$
is defined by the formula
![]() $(h, \gamma ) \mapsto (\Delta (h), \gamma )$
. In fact, this same formula also defines the corrresponding map of geometric L-groups
$(h, \gamma ) \mapsto (\Delta (h), \gamma )$
. In fact, this same formula also defines the corrresponding map of geometric L-groups
![]() $\phi _{\mathsf {BC}}^{\operatorname {\mathrm {geom}}} \colon {}^L H^{\operatorname {\mathrm {geom}}} \rightarrow {}^L G^{\operatorname {\mathrm {geom}}}$
, so
$\phi _{\mathsf {BC}}^{\operatorname {\mathrm {geom}}} \colon {}^L H^{\operatorname {\mathrm {geom}}} \rightarrow {}^L G^{\operatorname {\mathrm {geom}}}$
, so
![]() $\phi _{\mathsf {BC}}^{\operatorname {\mathrm {geom}}}$
and
$\phi _{\mathsf {BC}}^{\operatorname {\mathrm {geom}}}$
and
![]() $\phi _{\mathsf {BC}}$
are compatible with (2.1) if we use the same choice of square root of the cyclotomic character in the latter to define isomorphisms
$\phi _{\mathsf {BC}}$
are compatible with (2.1) if we use the same choice of square root of the cyclotomic character in the latter to define isomorphisms
![]() ${}^L H^{\operatorname {\mathrm {alg}}} \simeq {}^L H^{\operatorname {\mathrm {geom}}}$
and
${}^L H^{\operatorname {\mathrm {alg}}} \simeq {}^L H^{\operatorname {\mathrm {geom}}}$
and
![]() ${}^L G^{\operatorname {\mathrm {alg}}} \simeq {}^L G^{\operatorname {\mathrm {geom}}}$
. We denote
${}^L G^{\operatorname {\mathrm {alg}}} \simeq {}^L G^{\operatorname {\mathrm {geom}}}$
. We denote
the induced map of excursion algebras.
3 Smith theory in locally finite type
Classical Smith theory concerns a type of equivariant localization that relates the mod p cohomology of a topological space with the mod p cohomology of its fixed points under a
![]() $\mathbf {Z}/p\mathbf {Z}$
-action. Treumann proposed in [Reference TreumannTre19] that this could be understood in terms of a ‘sheaf-theoretic Smith theory’ formalism, which he developed at least in the context of complex algebraic varieties in the analytic topology. An algebraic version of this theory was built in [Reference Riche and WilliamsonRW22] for p-adic étale sheaves on finite type schemes (over fields where p is invertible). We will need generalizations of this theory from finite type to locally finite type. This is because we will want to apply the theory to the moduli spaces of shtukas, which are not of finite type, but are locally of finite type.
$\mathbf {Z}/p\mathbf {Z}$
-action. Treumann proposed in [Reference TreumannTre19] that this could be understood in terms of a ‘sheaf-theoretic Smith theory’ formalism, which he developed at least in the context of complex algebraic varieties in the analytic topology. An algebraic version of this theory was built in [Reference Riche and WilliamsonRW22] for p-adic étale sheaves on finite type schemes (over fields where p is invertible). We will need generalizations of this theory from finite type to locally finite type. This is because we will want to apply the theory to the moduli spaces of shtukas, which are not of finite type, but are locally of finite type.
Let us comment on some of the technical issues that arise in doing so. Because the cohomology of locally finite type schemes is not necessarily finite-dimensional, already the basic formalism of constructible sheaves and perfect complexes from [Reference TreumannTre19, Reference Riche and WilliamsonRW22] does not apply. For example, we will have to enlarge the notion of ‘Tate category’ to encompass the objects of interest.
We do not strive for the maximum possible generality, but our theory at least encompass all examples of interest that will show up in this paper. In particular, we will use tricks to avoid discussing Smith theory for stacks, which presents an interesting problem that could potentially refine our applications. For steps that are very similar to the case of finite type schemes as treated already in [Reference Riche and WilliamsonRW22], we will only sketch the proofs.
3.1 The Tate category
Let
![]() $\Lambda $
be a p-adic coefficient ring; we will be interested in the cases where
$\Lambda $
be a p-adic coefficient ring; we will be interested in the cases where
![]() $\Lambda = k$
or
$\Lambda = k$
or
![]() $W(k)$
. We will denote by
$W(k)$
. We will denote by
![]() $\Lambda [\sigma ]$
the group ring of
$\Lambda [\sigma ]$
the group ring of
![]() $\langle \sigma \rangle $
with coefficients in
$\langle \sigma \rangle $
with coefficients in
![]() $\Lambda $
. Our geometric objects will be over a field of characteristic
$\Lambda $
. Our geometric objects will be over a field of characteristic
![]() $\neq p$
, and we will consider
$\neq p$
, and we will consider
![]() $\Lambda $
-adic sheaves.
$\Lambda $
-adic sheaves.
Let Y be a separated, locally finite type scheme over a field. We let
![]() $\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ]) \subset D^b_c(Y; \Lambda [\sigma ])$
be the full subcategory consisting of complexes whose stalks at all geometric points of Y are perfect over
$\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ]) \subset D^b_c(Y; \Lambda [\sigma ])$
be the full subcategory consisting of complexes whose stalks at all geometric points of Y are perfect over
![]() $\Lambda [\sigma ]$
.
$\Lambda [\sigma ]$
.
Definition 3.1. We define
![]() $\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ]) \subset D^b(Y; \Lambda [\sigma ])$
to be the full subcategory consisting of bounded complexes whose stalks at all geometric points of Y are represented by bounded complexes of flat (but not necessarily finite)
$\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ]) \subset D^b(Y; \Lambda [\sigma ])$
to be the full subcategory consisting of bounded complexes whose stalks at all geometric points of Y are represented by bounded complexes of flat (but not necessarily finite)
![]() $\Lambda [\sigma ]$
-modules.
$\Lambda [\sigma ]$
-modules.
The following Lemma will not be used essentially in the rest of the paper, but it may help to clarify the nature of
![]() $\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) $
. We thank Jesper Grodal for pointing out a gap in the original argument and also for suggesting its fix.
$\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) $
. We thank Jesper Grodal for pointing out a gap in the original argument and also for suggesting its fix.
Lemma 3.2. The subcategory
![]() $\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) \subset D^b(Y; k[\sigma ])$
coincides with the full subcategory of objects which locally have finite tor-amplitude over
$\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) \subset D^b(Y; k[\sigma ])$
coincides with the full subcategory of objects which locally have finite tor-amplitude over
![]() $k[\sigma ]$
.
$k[\sigma ]$
.
Proof. For any commutative ring A, a complex of A-modules has finite tor-amplitude if and only if it is represented by a bounded complex of flat A-modules [Sta20, Tag 08G1]. This shows that any object of
![]() $D^b(Y; k[\sigma ])$
with locally finite tor-amplitude over
$D^b(Y; k[\sigma ])$
with locally finite tor-amplitude over
![]() $k[\sigma ]$
lies in
$k[\sigma ]$
lies in
![]() $\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) $
.
$\operatorname {\mathrm {Flat}}^b(Y; k[\sigma ]) $
.
For the converse direction, note that a complex has tor-amplitude in
![]() $[a,b]$
if and only if all its stalks at geometric points have tor-amplitude in
$[a,b]$
if and only if all its stalks at geometric points have tor-amplitude in
![]() $[a,b]$
by [Sta20, Tag 0DJJ]. Hence, it suffices to show that if
$[a,b]$
by [Sta20, Tag 0DJJ]. Hence, it suffices to show that if
![]() $\mathcal {K} \in D^b(Y; k[\sigma ])$
has finite tor-amplitude at all stalks, then its tor-amplitude is uniformly bounded. The key observation is as follows: if
$\mathcal {K} \in D^b(Y; k[\sigma ])$
has finite tor-amplitude at all stalks, then its tor-amplitude is uniformly bounded. The key observation is as follows: if
![]() $\mathcal {K} \in D^b(Y; k[\sigma ])$
is represented by a global complex concentrated in degrees
$\mathcal {K} \in D^b(Y; k[\sigma ])$
is represented by a global complex concentrated in degrees
![]() $[a,b]$
and all its stalks at geometric points have finite tor-amplitude, then, in fact, all of its stalks at geometric points have tor-amplitude in
$[a,b]$
and all its stalks at geometric points have finite tor-amplitude, then, in fact, all of its stalks at geometric points have tor-amplitude in
![]() $[a,b]$
. Given this observation, we may conclude by using [Sta20, Tag 0DJJ].
$[a,b]$
. Given this observation, we may conclude by using [Sta20, Tag 0DJJ].
Next, we prove the observation. It suffices to show that if
![]() $\mathcal {K}$
is a complex over
$\mathcal {K}$
is a complex over
![]() $k[\sigma ]$
supported in degrees
$k[\sigma ]$
supported in degrees
![]() $[a,b]$
which has finite tor-amplitude, then
$[a,b]$
which has finite tor-amplitude, then
![]() $\mathcal {K}$
has tor-amplitude
$\mathcal {K}$
has tor-amplitude
![]() $[a,b]$
. Since k is Artinian,
$[a,b]$
. Since k is Artinian,
![]() $k[\sigma ]$
is also Artinian. For a module over an Artinian local ring, the properties of being flat and projective coincide [Sta20, Tag 051E]. Therefore,
$k[\sigma ]$
is also Artinian. For a module over an Artinian local ring, the properties of being flat and projective coincide [Sta20, Tag 051E]. Therefore,
![]() $\mathcal {K}$
also has finite projective dimension [Sta20, Tag 0A5M]. Furthermore, since
$\mathcal {K}$
also has finite projective dimension [Sta20, Tag 0A5M]. Furthermore, since
![]() $k[\sigma ]$
has finitistic dimension zero, the projective amplitude of
$k[\sigma ]$
has finitistic dimension zero, the projective amplitude of
![]() $\mathcal {K}$
lies in
$\mathcal {K}$
lies in
![]() $[a,b]$
. Hence,
$[a,b]$
. Hence,
![]() $\mathcal {K}$
is represented by a complex of projective
$\mathcal {K}$
is represented by a complex of projective
![]() $k[\sigma ]$
-modules supported in degrees
$k[\sigma ]$
-modules supported in degrees
![]() $[a,b]$
and therefore has tor-amplitude in
$[a,b]$
and therefore has tor-amplitude in
![]() $[a,b]$
.
$[a,b]$
.
Definition 3.3. The (constructible) Tate category of Y (with respect to
![]() $\Lambda $
) is the Verdier quotient category
$\Lambda $
) is the Verdier quotient category
![]() $D^b_c(Y; \Lambda [\sigma ]) / \operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
.
$D^b_c(Y; \Lambda [\sigma ]) / \operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
.
This is the construction considered under the name ‘Tate category’ in [Reference TreumannTre19], at least when Y is a complex-analytic variety. According to [Reference TreumannTre19, Remark 4.1], the category
![]() $D^b_c(Y; \Lambda [\sigma ]) / \operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
can be regarded as a derived category of perfect complexes over a certain ‘
$D^b_c(Y; \Lambda [\sigma ]) / \operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
can be regarded as a derived category of perfect complexes over a certain ‘
![]() $E_{\infty }$
-ring spectrum’
$E_{\infty }$
-ring spectrum’
![]() $\mathcal {T}_{\Lambda }$
. So we will denote the corresponding Tate categories by
$\mathcal {T}_{\Lambda }$
. So we will denote the corresponding Tate categories by
![]() $\operatorname {\mathrm {Perf}}(Y; \mathcal {T}_\Lambda )$
. For our purposes,
$\operatorname {\mathrm {Perf}}(Y; \mathcal {T}_\Lambda )$
. For our purposes,
![]() $\mathcal {T}_{\Lambda }$
can be thought of as just a notational device.
$\mathcal {T}_{\Lambda }$
can be thought of as just a notational device.
We will require the following enlargement of the constructible Tate category. We define the (bounded ind-constructible) Tate category of Y (with respect to
![]() $\Lambda $
) to be the Verdier quotient category
$\Lambda $
) to be the Verdier quotient category
We denote the tautological projection maps from
![]() $D^b_c(Y; \Lambda [\sigma ])$
to
$D^b_c(Y; \Lambda [\sigma ])$
to
![]() $\operatorname {\mathrm {Perf}}(Y; \mathcal {T}_\Lambda )$
and from
$\operatorname {\mathrm {Perf}}(Y; \mathcal {T}_\Lambda )$
and from
![]() $D^b(Y; \Lambda [\sigma ])$
to
$D^b(Y; \Lambda [\sigma ])$
to
![]() $\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_{\Lambda })$
by
$\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_{\Lambda })$
by
Note that the fully faithful embedding
![]() $D^b_c(Y; \Lambda [\sigma ]) \rightarrow D^b(Y; \Lambda [\sigma ])$
carries
$D^b_c(Y; \Lambda [\sigma ]) \rightarrow D^b(Y; \Lambda [\sigma ])$
carries
![]() $\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
into
$\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ])$
into
![]() $\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
and so induces a functor
$\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
and so induces a functor
which is conservative (e.g., because
![]() $\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ]) \subset D^b_c(Y; \Lambda [\sigma ])$
can also be characterized as the full subcategory of objects locally having finite tor-amplitude over
$\operatorname {\mathrm {Perf}}(Y; \Lambda [\sigma ]) \subset D^b_c(Y; \Lambda [\sigma ])$
can also be characterized as the full subcategory of objects locally having finite tor-amplitude over
![]() $\Lambda [\sigma ]$
, according to Lemma 3.2).
$\Lambda [\sigma ]$
, according to Lemma 3.2).
Example 3.4 [Reference TreumannTre19, Proposition 4.2].
The (bounded ind-constructible) Tate category over a point (meaning the spectrum of a separably closed field) is
![]() $D^b(\Lambda [\sigma ])/\operatorname {\mathrm {Flat}}^b(\Lambda [\sigma ])$
. In this category, the shift-by-2 functor is isomorphic to the identity functor, as one sees by considering the nullhomotopic complex
$D^b(\Lambda [\sigma ])/\operatorname {\mathrm {Flat}}^b(\Lambda [\sigma ])$
. In this category, the shift-by-2 functor is isomorphic to the identity functor, as one sees by considering the nullhomotopic complex
whose middle two terms project to
![]() $0$
in the Tate category.
$0$
in the Tate category.
3.2 The Smith operation
Let Y be a separated, locally finite type scheme with a
![]() $\sigma $
-action that is admissible in the sense of [SGA1, Exposé 5, Définition 1.7]. By [Reference Riche and WilliamsonRW22, Remark 2.2], this is automatic if Y is exhausted by quasi-projective schemes over a field.
$\sigma $
-action that is admissible in the sense of [SGA1, Exposé 5, Définition 1.7]. By [Reference Riche and WilliamsonRW22, Remark 2.2], this is automatic if Y is exhausted by quasi-projective schemes over a field.
There is an equivariant bounded derived category
![]() $D_\sigma ^b(Y; \Lambda )$
. We distinguish this from the equivariant bounded constructible derived category
$D_\sigma ^b(Y; \Lambda )$
. We distinguish this from the equivariant bounded constructible derived category
![]() $D_{c, \sigma }^b(Y; \Lambda ) $
, a full subcategory of
$D_{c, \sigma }^b(Y; \Lambda ) $
, a full subcategory of
![]() $D_\sigma ^b(Y; \Lambda )$
that will also be of interest to us. Note that since
$D_\sigma ^b(Y; \Lambda )$
that will also be of interest to us. Note that since
![]() $\sigma $
acts trivially on the
$\sigma $
acts trivially on the
![]() $\sigma $
-fixed subscheme
$\sigma $
-fixed subscheme
![]() $Y^\sigma \subset Y$
, we have an equivalence of derived categories
$Y^\sigma \subset Y$
, we have an equivalence of derived categories
Then the ‘Smith operation’ (cf. [Reference TreumannTre19, Definition 4.2]) is the functor
defined as the composition of
![]() $i^* \colon D_{c,\sigma }^b(Y; \Lambda ) \rightarrow D_{c,\sigma }^b(Y^{\sigma }; \Lambda ) \stackrel {(3.2)}\cong D^b_c(Y^{\sigma }; \Lambda [\sigma ])$
with the projection
$i^* \colon D_{c,\sigma }^b(Y; \Lambda ) \rightarrow D_{c,\sigma }^b(Y^{\sigma }; \Lambda ) \stackrel {(3.2)}\cong D^b_c(Y^{\sigma }; \Lambda [\sigma ])$
with the projection
![]() $\mathbb {T}^*$
to
$\mathbb {T}^*$
to
![]() $\operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
.
$\operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
.
We extend this definition to bounded ind-constructible Tate categories in the analogous manner, defining
Remark 3.5. For
![]() $\mathcal {F} \in D_{c,\sigma }^b(Y; \Lambda )$
, there is potential confusion about whether ‘
$\mathcal {F} \in D_{c,\sigma }^b(Y; \Lambda )$
, there is potential confusion about whether ‘
![]() $\operatorname {\mathrm {Psm}}(\mathcal {F})$
’ denotes the result of applying (3.3) or (3.4). But there is a natural isomorphism between the functors
$\operatorname {\mathrm {Psm}}(\mathcal {F})$
’ denotes the result of applying (3.3) or (3.4). But there is a natural isomorphism between the functors
and
so the meaning is unambiguous once the ambient category is specified. When the distinction is important, we will take care to specify the ambient category.
The following properties are used to prove that our extended version of
![]() $\operatorname {\mathrm {Psm}}$
retains the good behavior enjoyed by the constructible version.
$\operatorname {\mathrm {Psm}}$
retains the good behavior enjoyed by the constructible version.
Lemma 3.6. Retain the notation and assumptions above. Assume that the
![]() $\sigma $
-action on Y is free. Let
$\sigma $
-action on Y is free. Let
![]() $q \colon Y \rightarrow Y / \sigma $
denote the quotient (which exists as a map of schemes by admissibility of the
$q \colon Y \rightarrow Y / \sigma $
denote the quotient (which exists as a map of schemes by admissibility of the
![]() $\sigma $
-action on Y). Then for any
$\sigma $
-action on Y). Then for any
![]() $\mathcal {F} \in D^b(Y; \Lambda [\sigma ])$
, we have
$\mathcal {F} \in D^b(Y; \Lambda [\sigma ])$
, we have
![]() $q_* \mathcal {F} \in \operatorname {\mathrm {Flat}}^b(Y/\sigma; \Lambda [\sigma ]) \subset D^b(Y/\sigma; \Lambda [\sigma ])$
.
$q_* \mathcal {F} \in \operatorname {\mathrm {Flat}}^b(Y/\sigma; \Lambda [\sigma ]) \subset D^b(Y/\sigma; \Lambda [\sigma ])$
.
Proof. The same argument as [Reference Riche and WilliamsonRW22, Lemma 2.3] works here. To summarize, for any geometric point
![]() $\overline {y} \rightarrow Y/\sigma $
, and
$\overline {y} \rightarrow Y/\sigma $
, and
![]() $\overline {x} \rightarrow Y$
lifting it, we have
$\overline {x} \rightarrow Y$
lifting it, we have
which is visibly in
![]() $\operatorname {\mathrm {Flat}}^b(\overline {y}; \Lambda [\sigma ])$
.
$\operatorname {\mathrm {Flat}}^b(\overline {y}; \Lambda [\sigma ])$
.
Lemma 3.7. Retain the notation and assumptions above. Let
![]() $U := Y \setminus Y^{\sigma }$
be the open complement of the
$U := Y \setminus Y^{\sigma }$
be the open complement of the
![]() $\sigma $
-fixed locus of Y, and
$\sigma $
-fixed locus of Y, and
![]() $j \colon U \hookrightarrow Y$
be its inclusion into Y. Then for any
$j \colon U \hookrightarrow Y$
be its inclusion into Y. Then for any
![]() $\mathcal {F} \in D^b(U; \Lambda [\sigma ])$
and any geometric point
$\mathcal {F} \in D^b(U; \Lambda [\sigma ])$
and any geometric point
![]() $\overline {y}$
of
$\overline {y}$
of
![]() $Y^{\sigma }$
, the stalk
$Y^{\sigma }$
, the stalk
![]() $(Rj_* \mathcal {F})_{\overline {y}}$
lies in
$(Rj_* \mathcal {F})_{\overline {y}}$
lies in
![]() $\operatorname {\mathrm {Flat}}^b(\overline {y}; \Lambda [\sigma ]) \subset D^b(\overline {y}; \Lambda [\sigma ])$
.
$\operatorname {\mathrm {Flat}}^b(\overline {y}; \Lambda [\sigma ]) \subset D^b(\overline {y}; \Lambda [\sigma ])$
.
Proof. A similar argument as in [Reference Riche and WilliamsonRW22, Proposition 2.5] works here. Since the map
![]() $q \colon Y \rightarrow Y/\sigma $
is totally ramified at
$q \colon Y \rightarrow Y/\sigma $
is totally ramified at
![]() $\overline {y}$
, we have a
$\overline {y}$
, we have a
![]() $\sigma $
-equivariant identification
$\sigma $
-equivariant identification
![]() $(Rj_* \mathcal {F})_{\overline {y}} \cong (q_* Rj_* \mathcal {F})_{q(\overline {y})}$
. Then by the commutativity of the diagram
$(Rj_* \mathcal {F})_{\overline {y}} \cong (q_* Rj_* \mathcal {F})_{q(\overline {y})}$
. Then by the commutativity of the diagram

we have
![]() $(q_* Rj_* \mathcal {F})_{q(\overline {y})} \cong (R\overline {j}_* q_{U*} \mathcal {F})_{q(\overline {y})}$
. Now Lemma 3.6 implies that
$(q_* Rj_* \mathcal {F})_{q(\overline {y})} \cong (R\overline {j}_* q_{U*} \mathcal {F})_{q(\overline {y})}$
. Now Lemma 3.6 implies that
![]() $q_{U*} \mathcal {F}$
has finite tor-amplitude, and combining [Sta20, Tag 0F10] with [SGA4-3, Exposé XVII, Théorème 5.2.11] implies that
$q_{U*} \mathcal {F}$
has finite tor-amplitude, and combining [Sta20, Tag 0F10] with [SGA4-3, Exposé XVII, Théorème 5.2.11] implies that
![]() $R\overline {j}_*$
preserves finiteness of tor-amplitude, so their composition has locally finite tor-amplitude.
$R\overline {j}_*$
preserves finiteness of tor-amplitude, so their composition has locally finite tor-amplitude.
The good properties of
![]() $\operatorname {\mathrm {Psm}}$
come from the following Lemma, which was proved for finite type schemes in [Reference Riche and WilliamsonRW22, Lemma 3.5] (following [Reference TreumannTre19, Theorem 4.7] in the topological situation).
$\operatorname {\mathrm {Psm}}$
come from the following Lemma, which was proved for finite type schemes in [Reference Riche and WilliamsonRW22, Lemma 3.5] (following [Reference TreumannTre19, Theorem 4.7] in the topological situation).
Lemma 3.8. Retain the notation and assumptions above. Let
![]() $i \colon Y^\sigma \hookrightarrow Y$
. Then for any
$i \colon Y^\sigma \hookrightarrow Y$
. Then for any
![]() $\mathcal {F} \in D^b_{\sigma }(Y; \Lambda )$
, the cone of
$\mathcal {F} \in D^b_{\sigma }(Y; \Lambda )$
, the cone of
![]() $i^! \mathcal {F} \rightarrow i^* \mathcal {F}$
belongs to
$i^! \mathcal {F} \rightarrow i^* \mathcal {F}$
belongs to
![]() $\operatorname {\mathrm {Flat}}^b(Y^\sigma; \Lambda [\sigma ])$
.
$\operatorname {\mathrm {Flat}}^b(Y^\sigma; \Lambda [\sigma ])$
.
Proof. Let
![]() $j \colon Y \setminus Y^\sigma \hookrightarrow Y$
. Consider the exact triangle
$j \colon Y \setminus Y^\sigma \hookrightarrow Y$
. Consider the exact triangle
![]() $i_* i^! \mathcal {F} \rightarrow \mathcal {F} \rightarrow j_* j^* \mathcal {F}$
on Y. Applying
$i_* i^! \mathcal {F} \rightarrow \mathcal {F} \rightarrow j_* j^* \mathcal {F}$
on Y. Applying
![]() $i^*$
to it yields the exact triangle in
$i^*$
to it yields the exact triangle in
![]() $D^b(Y^{\sigma }; \Lambda [\sigma ])$
:
$D^b(Y^{\sigma }; \Lambda [\sigma ])$
:
By Lemma 3.7,
![]() $i^* Rj_* j^* \mathcal {F} \in \operatorname {\mathrm {Flat}}^b(Y^{\sigma }; \Lambda [\sigma ])$
.
$i^* Rj_* j^* \mathcal {F} \in \operatorname {\mathrm {Flat}}^b(Y^{\sigma }; \Lambda [\sigma ])$
.
Lemma 3.9. Suppose
![]() $f \colon Y \rightarrow S$
is a locally finite type and separated
$f \colon Y \rightarrow S$
is a locally finite type and separated
![]() $\sigma $
-equivariant morphism between locally finite type schemes, of bounded dimension. Then
$\sigma $
-equivariant morphism between locally finite type schemes, of bounded dimension. Then
![]() $Rf_! \colon D^b(Y; \Lambda [\sigma ]) \rightarrow D^b(S; \Lambda [\sigma ])$
carries
$Rf_! \colon D^b(Y; \Lambda [\sigma ]) \rightarrow D^b(S; \Lambda [\sigma ])$
carries
![]() $\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
to
$\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
to
![]() $\operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
.
$\operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
.
Proof. We may write Y as a filtered colimit of open subschemes
![]() $Y_{\alpha }$
of finite type. Then for
$Y_{\alpha }$
of finite type. Then for
![]() $\mathcal {F} \in D^b(Y; \Lambda [\sigma ])$
, we have an identification of
$\mathcal {F} \in D^b(Y; \Lambda [\sigma ])$
, we have an identification of
![]() $Rf_! \mathcal {F}$
with the colimit over
$Rf_! \mathcal {F}$
with the colimit over
![]() $Rf_! (\mathcal {F}|_{Y_{\alpha }})$
. Since filtered colimits preserve flatness, we are reduced to the same statement in the finite type situation (where one can also replace ‘
$Rf_! (\mathcal {F}|_{Y_{\alpha }})$
. Since filtered colimits preserve flatness, we are reduced to the same statement in the finite type situation (where one can also replace ‘
![]() $\operatorname {\mathrm {Flat}}^b$
’ by
$\operatorname {\mathrm {Flat}}^b$
’ by
![]() $\operatorname {\mathrm {Perf}}$
), which is obtained by combining [Sta20, Tag 0F10] and [SGA4-3, Exposé XVII, Théorème 5.2.10].
$\operatorname {\mathrm {Perf}}$
), which is obtained by combining [Sta20, Tag 0F10] and [SGA4-3, Exposé XVII, Théorème 5.2.10].
Remark 3.10. Note that Lemma 3.9 would not have been true with ‘
![]() $\operatorname {\mathrm {Flat}}^b$
’ replaced by ‘
$\operatorname {\mathrm {Flat}}^b$
’ replaced by ‘
![]() $\operatorname {\mathrm {Perf}}$
’. This is why we need to consider ind-constructible sheaves when not in a finite type situation.
$\operatorname {\mathrm {Perf}}$
’. This is why we need to consider ind-constructible sheaves when not in a finite type situation.
Corollary 3.11. Suppose
![]() $f \colon Y \rightarrow S$
is a locally finite type and separated morphism between locally finite type schemes, of bounded dimension. Suppose
$f \colon Y \rightarrow S$
is a locally finite type and separated morphism between locally finite type schemes, of bounded dimension. Suppose
![]() $\sigma $
acts trivially on S and freely on Y, and f is
$\sigma $
acts trivially on S and freely on Y, and f is
![]() $\sigma $
-equivariant. Then
$\sigma $
-equivariant. Then
![]() $Rf_! \colon D^b(Y; \Lambda [\sigma ]) \rightarrow D^b(S; \Lambda [\sigma ])$
lands in
$Rf_! \colon D^b(Y; \Lambda [\sigma ]) \rightarrow D^b(S; \Lambda [\sigma ])$
lands in
![]() $\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
.
$\operatorname {\mathrm {Flat}}^b(Y; \Lambda [\sigma ])$
.
3.3 Functors on Tate categories
Throughout this subsection, we let
![]() $f \colon Y \rightarrow S$
denote a
$f \colon Y \rightarrow S$
denote a
![]() $\sigma $
-equivariant locally finite type morphism of locally finite type schemes with admissible
$\sigma $
-equivariant locally finite type morphism of locally finite type schemes with admissible
![]() $\sigma $
-action, of bounded dimension.
$\sigma $
-action, of bounded dimension.
3.3.1 Pullback
Since
![]() $f^* \colon D^b_{\sigma }(S^{\sigma }; k) \rightarrow D^b_{\sigma }(Y^{\sigma }; k)$
preserves stalks, it preserves flat and perfect complexes and so descends to the Tate category to induce
$f^* \colon D^b_{\sigma }(S^{\sigma }; k) \rightarrow D^b_{\sigma }(Y^{\sigma }; k)$
preserves stalks, it preserves flat and perfect complexes and so descends to the Tate category to induce
![]() $f^* \colon \operatorname {\mathrm {Shv}}(S^{\sigma }; \mathcal {T}_{\Lambda }) \rightarrow \operatorname {\mathrm {Shv}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
and
$f^* \colon \operatorname {\mathrm {Shv}}(S^{\sigma }; \mathcal {T}_{\Lambda }) \rightarrow \operatorname {\mathrm {Shv}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
and
![]() $f^* \colon \operatorname {\mathrm {Perf}}(S^{\sigma }; \mathcal {T}_{\Lambda }) \rightarrow \operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
.
$f^* \colon \operatorname {\mathrm {Perf}}(S^{\sigma }; \mathcal {T}_{\Lambda }) \rightarrow \operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\Lambda })$
.
3.3.2 Proper pushforward
By Lemma 3.9,
![]() $Rf_!\colon D^b(Y^{\sigma }; \Lambda [\sigma ]) \rightarrow D^b(S^{\sigma }; \Lambda [\sigma ])$
descends to
$Rf_!\colon D^b(Y^{\sigma }; \Lambda [\sigma ]) \rightarrow D^b(S^{\sigma }; \Lambda [\sigma ])$
descends to
Proposition 3.12. The following diagram commutes:

Proof. We may as well replace S by
![]() $S^{\sigma }$
and thus assume that the
$S^{\sigma }$
and thus assume that the
![]() $\sigma $
-action on S is trivial. Let
$\sigma $
-action on S is trivial. Let
![]() $\mathcal {F} \in D_\sigma ^b(Y;\Lambda )$
. Denoting
$\mathcal {F} \in D_\sigma ^b(Y;\Lambda )$
. Denoting
![]() $i \colon Y^{\sigma } \hookrightarrow Y$
and j the inclusion of the open complement, we have a distinguished triangle in
$i \colon Y^{\sigma } \hookrightarrow Y$
and j the inclusion of the open complement, we have a distinguished triangle in
![]() $D^b_{\sigma }(Y; \Lambda )$
:
$D^b_{\sigma }(Y; \Lambda )$
:
Abbreviate
![]() $f^{\sigma } := f \circ i \colon Y^{\sigma } \rightarrow S$
. By definition,
$f^{\sigma } := f \circ i \colon Y^{\sigma } \rightarrow S$
. By definition,
![]() $\sigma $
acts freely on U, which implies that
$\sigma $
acts freely on U, which implies that
![]() $Rf_! \circ (j_! j^* \mathcal {F}) \in \operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
by Corollary 3.11. Hence, the cone of
$Rf_! \circ (j_! j^* \mathcal {F}) \in \operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
by Corollary 3.11. Hence, the cone of
![]() $Rf_! \mathcal {F} \rightarrow Rf^{\sigma }_! (i^* \mathcal {F})$
lies in
$Rf_! \mathcal {F} \rightarrow Rf^{\sigma }_! (i^* \mathcal {F})$
lies in
![]() $\operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
and therefore becomes
$\operatorname {\mathrm {Flat}}^b(S; \Lambda [\sigma ])$
and therefore becomes
![]() $0$
in
$0$
in
![]() $\operatorname {\mathrm {Shv}}(S; \mathcal {T}_{\Lambda })$
. Hence, we have
$\operatorname {\mathrm {Shv}}(S; \mathcal {T}_{\Lambda })$
. Hence, we have
which exactly expresses the desired commutativity.
3.4 Tate cohomology
For a
![]() $\Lambda [\sigma ]$
-module M, its Tate cohomology groups are
$\Lambda [\sigma ]$
-module M, its Tate cohomology groups are
(Recall that
![]() $N := 1 + \sigma + \ldots + \sigma ^{p-1}$
.) We will generalize this to complexes and then sheaves.
$N := 1 + \sigma + \ldots + \sigma ^{p-1}$
.) We will generalize this to complexes and then sheaves.
3.4.1 Tate cohomology of complexes
The exact sequence of
![]() $\Lambda [\sigma ]$
-modules
$\Lambda [\sigma ]$
-modules
induces a morphism
Given a bounded-below complex of
![]() $\Lambda [\sigma ]$
-modules
$\Lambda [\sigma ]$
-modules
![]() $C^{\bullet }$
, we define its Tate cohomology as
$C^{\bullet }$
, we define its Tate cohomology as
where the transition maps are those induced by (3.5).
Evidently,
![]() $T^i(C^{\bullet })$
is 2-periodic in i. It is clear that this construction descends to the derived category, so we can view Tate cohomology as a collection of functors
$T^i(C^{\bullet })$
is 2-periodic in i. It is clear that this construction descends to the derived category, so we can view Tate cohomology as a collection of functors
Now we specialize to the case where
![]() $\Lambda = k $
. Note that by [Sta20, Tag 051E], a module over
$\Lambda = k $
. Note that by [Sta20, Tag 051E], a module over
![]() $k[\sigma ]$
is flat if and only if it is free. Since Tate cohomology of free
$k[\sigma ]$
is flat if and only if it is free. Since Tate cohomology of free
![]() $k[\sigma ]$
-complexes vanishes (by inspection), this construction further factors through the Tate category, inducing
$k[\sigma ]$
-complexes vanishes (by inspection), this construction further factors through the Tate category, inducing
Remark 3.13. If
![]() $C^{\bullet }$
is a bounded
$C^{\bullet }$
is a bounded
![]() $k[\sigma ]$
-module, which will always be the case for us in practice, then we may regard
$k[\sigma ]$
-module, which will always be the case for us in practice, then we may regard
![]() $C^{\bullet } \in D(\operatorname {\mathrm {pt}}; k[\sigma ])$
and the argument of [Reference Leslie and LonerganLL21, Proposition 4.5.1] gives a natural isomorphism
$C^{\bullet } \in D(\operatorname {\mathrm {pt}}; k[\sigma ])$
and the argument of [Reference Leslie and LonerganLL21, Proposition 4.5.1] gives a natural isomorphism
The following is obvious from the definition but important enough to record.
Lemma 3.14. Suppose
![]() $C^{\bullet } \in D^b(k[\sigma ])$
is inflated from
$C^{\bullet } \in D^b(k[\sigma ])$
is inflated from
![]() $D^b(k)$
(i.e.,
$D^b(k)$
(i.e.,
![]() $\sigma $
acts trivially on
$\sigma $
acts trivially on
![]() $C^\bullet $
). Then
$C^\bullet $
). Then
![]() $T^* C^\bullet \cong H^*(C^{\bullet }) \otimes T^*(k)$
, where k is equipped with the trivial
$T^* C^\bullet \cong H^*(C^{\bullet }) \otimes T^*(k)$
, where k is equipped with the trivial
![]() $\sigma $
-action in the formation of
$\sigma $
-action in the formation of
![]() $T^*(k)$
.
$T^*(k)$
.
3.4.2 Tate cohomology sheaves
If S has the trivial
![]() $\sigma $
-action, then
$\sigma $
-action, then
![]() $\operatorname {\mathrm {Shv}}(S; \mathcal {T}_\Lambda )$
is defined. Given
$\operatorname {\mathrm {Shv}}(S; \mathcal {T}_\Lambda )$
is defined. Given
![]() $\mathcal {F} \in D^b(S; \Lambda [\sigma ])$
, we define Tate cohomology sheaves
$\mathcal {F} \in D^b(S; \Lambda [\sigma ])$
, we define Tate cohomology sheaves
where the transition maps are induced by the map
![]() $\Lambda \rightarrow \Lambda [2] \in D(S; \Lambda [\sigma ])$
pulled back from (3.5). The
$\Lambda \rightarrow \Lambda [2] \in D(S; \Lambda [\sigma ])$
pulled back from (3.5). The
![]() $T^i\mathcal {F}$
are étale sheaves of
$T^i\mathcal {F}$
are étale sheaves of
![]() $T^0\Lambda $
-modules, where
$T^0\Lambda $
-modules, where
![]() $T^0\Lambda $
is the 0th Tate cohomology of
$T^0\Lambda $
is the 0th Tate cohomology of
![]() $\Lambda $
viewed as a trivial
$\Lambda $
viewed as a trivial
![]() $\sigma $
-module.
$\sigma $
-module.
For
![]() $\Lambda = k$
, we also have the description
$\Lambda = k$
, we also have the description
on S, which is an étale sheaf of
![]() $T^0(k) = k$
-modules.
$T^0(k) = k$
-modules.
3.4.3 Tate cohomology for a morphism
For
![]() $\mathcal {F} \in D^b_{\sigma }(Y; k)$
, we have
$\mathcal {F} \in D^b_{\sigma }(Y; k)$
, we have
![]() $Rf_! \mathcal {F} \in D^b_{\sigma }(S; k)$
. If S has the trivial
$Rf_! \mathcal {F} \in D^b_{\sigma }(S; k)$
. If S has the trivial
![]() $\sigma $
-action, then we can form
$\sigma $
-action, then we can form
![]() $T^i Rf_! \mathcal {F}$
, which we call the ‘relative Tate cohomology of
$T^i Rf_! \mathcal {F}$
, which we call the ‘relative Tate cohomology of
![]() $\mathcal {F}$
’.
$\mathcal {F}$
’.
If S is the spectrum of a separably closed field equipped with the trivial
![]() $\sigma $
-action, then we will abbreviate
$\sigma $
-action, then we will abbreviate
![]() $T^i(Y;\mathcal {F}) := T^i (Rf_! \mathcal {F})$
and call it the ‘Tate cohomology of Y with coefficients in
$T^i(Y;\mathcal {F}) := T^i (Rf_! \mathcal {F})$
and call it the ‘Tate cohomology of Y with coefficients in
![]() $\mathcal {F}$
’.
$\mathcal {F}$
’.
Remark 3.15. Note that if
![]() $\sigma $
acts trivially on Y and on S, then the construction
$\sigma $
acts trivially on Y and on S, then the construction
![]() $\mathcal {F} \mapsto Rf_! \mathcal {F}$
factors over
$\mathcal {F} \mapsto Rf_! \mathcal {F}$
factors over
![]() $\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_k)$
by Lemma 3.9. In this situation, we will also regard
$\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_k)$
by Lemma 3.9. In this situation, we will also regard
![]() $T^i Rf_!$
as a functor on
$T^i Rf_!$
as a functor on
![]() $\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_k)$
.
$\operatorname {\mathrm {Shv}}(Y; \mathcal {T}_k)$
.
3.4.4 The long exact sequence for Tate cohomology
Given a distinguished triangle
![]() $\mathcal {F}' \rightarrow \mathcal {F} \rightarrow \mathcal {F}" \in D^b_\sigma (Y;k)$
, we have a long exact sequence
$\mathcal {F}' \rightarrow \mathcal {F} \rightarrow \mathcal {F}" \in D^b_\sigma (Y;k)$
, we have a long exact sequence

3.4.5 Equivariant localization
We explain that Proposition 3.12 encompasses the classical equivariant localization theorems of ‘Smith theory’ (e.g., [Reference QuillenQui71, Theorem 4.2]). Proposition 3.12 says that for
![]() $\mathcal {F} \in D_{\sigma }^b(Y; k)$
, we have
$\mathcal {F} \in D_{\sigma }^b(Y; k)$
, we have
In particular, if L is the spectrum of a separably closed with the trivial action of
![]() $\sigma $
, we get
$\sigma $
, we get
4 Parity sheaves and the base change functor
We begin by indicating where this section is headed.
The Geometric Satake equivalence
![]() $\operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G;k) \cong \operatorname {\mathrm {Rep}}_k(\widehat {G})$
provides the link between G and its Langlands dual group. In the situation of functoriality, we have a map
$\operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G;k) \cong \operatorname {\mathrm {Rep}}_k(\widehat {G})$
provides the link between G and its Langlands dual group. In the situation of functoriality, we have a map
![]() $\widehat {H} \rightarrow \widehat {G}$
, and we would like to describe the induced restriction operation
$\widehat {H} \rightarrow \widehat {G}$
, and we would like to describe the induced restriction operation
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G}) \rightarrow \operatorname {\mathrm {Rep}}_k(\widehat {H})$
on the other side of the Geometric Satake equivalence, as a geometric operation on perverse sheaves.
$\operatorname {\mathrm {Rep}}_k(\widehat {G}) \rightarrow \operatorname {\mathrm {Rep}}_k(\widehat {H})$
on the other side of the Geometric Satake equivalence, as a geometric operation on perverse sheaves.
In the context of base change, it is even the case that there is an embedding
![]() $\operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_G$
, and when seeking to describe functoriality, it is natural to look to the Smith operation. (One motivation is that the papers [Reference TreumannTre19, Reference Treumann and VenkateshTV16] verify that the function-theoretic Smith operation is indeed related to functoriality for Hecke algebras.) However, the Smith operation lands in a Tate category, and in Example 3.4 we saw that in the Tate category, the shift-by-
$\operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_G$
, and when seeking to describe functoriality, it is natural to look to the Smith operation. (One motivation is that the papers [Reference TreumannTre19, Reference Treumann and VenkateshTV16] verify that the function-theoretic Smith operation is indeed related to functoriality for Hecke algebras.) However, the Smith operation lands in a Tate category, and in Example 3.4 we saw that in the Tate category, the shift-by-
![]() $2$
functor is isomorphic to the identity functor. This makes it seem unlikely that one can capture the notion of ‘perverse sheaf’ in the Tate category.
$2$
functor is isomorphic to the identity functor. This makes it seem unlikely that one can capture the notion of ‘perverse sheaf’ in the Tate category.
Juteau-Mautner-Williamson invented the theory of parity sheaves, which have seen significance in modular representation theory. Parity sheaves are cut out in the derived category by constraints on the parity of cohomological degrees and can therefore make sense in a context where cohomological degrees are only defined modulo
![]() $2$
. The notion of Tate-parity sheaves was introduced in [Reference Leslie and LonerganLL21] as an analog of parity sheaves for the Tate category and was found to enjoy analogous properties.
$2$
. The notion of Tate-parity sheaves was introduced in [Reference Leslie and LonerganLL21] as an analog of parity sheaves for the Tate category and was found to enjoy analogous properties.
After briefly reviewing the notions of parity and Tate-parity sheaves in §4.1 and §4.2, we will establish that the Smith operation respects the parity property, at least under certain conditions satisfied in our application of interest. Using ‘coefficient lifting’ properties of parity sheaves, this will allow us to ultimately define a functor
![]() $\mathsf {BC}$
from parity sheaves on
$\mathsf {BC}$
from parity sheaves on
![]() $\operatorname {\mathrm {Gr}}_G$
to parity sheaves on
$\operatorname {\mathrm {Gr}}_G$
to parity sheaves on
![]() $\operatorname {\mathrm {Gr}}_H$
, which realizes base change functoriality on the geometric side. We note that in this section, we will only need the ‘constructible’ version of Smith theory for schemes and not the generalizations developed in §3.
$\operatorname {\mathrm {Gr}}_H$
, which realizes base change functoriality on the geometric side. We note that in this section, we will only need the ‘constructible’ version of Smith theory for schemes and not the generalizations developed in §3.
4.1 Parity sheaves
We begin with a quick review of the theory of parity sheaves. We will take coefficients in a ring
![]() $\Lambda $
which is a complete local PID (i.e., a field or complete DVR) – in our applications of interest will be either k or
$\Lambda $
which is a complete local PID (i.e., a field or complete DVR) – in our applications of interest will be either k or
![]() $\mathbb {O} := W(k)$
.
$\mathbb {O} := W(k)$
.
Let Y be a stratified variety over a separably closed field of characteristic
![]() $\neq p$
, with stratification
$\neq p$
, with stratification
![]() $S = \{Y_{\lambda }\}$
. For the theory of parity sheaves to work, we need to assume that the (induced) stratification on Y is JMW, meaning
$S = \{Y_{\lambda }\}$
. For the theory of parity sheaves to work, we need to assume that the (induced) stratification on Y is JMW, meaning
-
• for any two finite
 $\Lambda $
-free local systems
$\Lambda $
-free local systems
 $\mathcal {L}, \mathcal {L}'$
on a stratum
$\mathcal {L}, \mathcal {L}'$
on a stratum
 $Y_{\lambda }$
, we have
$Y_{\lambda }$
, we have
 $\operatorname {\mathrm {Ext}}^i(\mathcal {L}, \mathcal {L}')$
is free over
$\operatorname {\mathrm {Ext}}^i(\mathcal {L}, \mathcal {L}')$
is free over
 $\Lambda $
for all i and vanishes when i is odd.
$\Lambda $
for all i and vanishes when i is odd.
This holds for Kac-Moody flag varieties over separably closed fields and, in particular, for affine flag varieties over separably closed fields [Reference Juteau, Mautner and WilliamsonJMW14, §4.1].
Fix a pariversity
![]() $\dagger \colon S \rightarrow \mathbf {Z}/2\mathbf {Z}$
. In this paper, we will always take the dimension pariversity
$\dagger \colon S \rightarrow \mathbf {Z}/2\mathbf {Z}$
. In this paper, we will always take the dimension pariversity
![]() $\dagger (Y_\lambda ) := \dim Y_{\lambda }\ \mod {2}$
, so we will sometimes omit the pariversity from the discussion. Recall that [Reference Juteau, Mautner and WilliamsonJMW14] define even complexes (with respect to the pariversity
$\dagger (Y_\lambda ) := \dim Y_{\lambda }\ \mod {2}$
, so we will sometimes omit the pariversity from the discussion. Recall that [Reference Juteau, Mautner and WilliamsonJMW14] define even complexes (with respect to the pariversity
![]() $\dagger $
) to be those
$\dagger $
) to be those
![]() $\mathcal {F} \in D_S^b(Y; \Lambda )$
such that for all
$\mathcal {F} \in D_S^b(Y; \Lambda )$
such that for all
![]() $i_{\lambda } \colon Y_{\lambda } \hookrightarrow Y$
, for
$i_{\lambda } \colon Y_{\lambda } \hookrightarrow Y$
, for
![]() $Y_\lambda \in S$
,
$Y_\lambda \in S$
,
![]() $i_{\lambda }^* \mathcal {F}$
and
$i_{\lambda }^* \mathcal {F}$
and
![]() $i_{\lambda }^!\mathcal {F}$
have cohomology sheaves which are
$i_{\lambda }^!\mathcal {F}$
have cohomology sheaves which are
![]() $\Lambda $
-free and supported in degrees congruent to
$\Lambda $
-free and supported in degrees congruent to
![]() $\dagger (Y_\lambda )$
modulo
$\dagger (Y_\lambda )$
modulo
![]() $2$
, and odd complexes analogously. They define parity complexes to be direct sums of even and odd complexes. The full subcategory of (S-constructible) parity complexes (with coefficients in
$2$
, and odd complexes analogously. They define parity complexes to be direct sums of even and odd complexes. The full subcategory of (S-constructible) parity complexes (with coefficients in
![]() $\Lambda $
) is denoted
$\Lambda $
) is denoted
![]() $\operatorname {\mathrm {Parity}}_S(Y; \Lambda )$
.
$\operatorname {\mathrm {Parity}}_S(Y; \Lambda )$
.
Theorem 4.1 [Reference Juteau, Mautner and WilliamsonJMW14, Theorem 2.12].
Let
![]() $\mathcal {F}$
be an indecomposable parity complex. Then
$\mathcal {F}$
be an indecomposable parity complex. Then
-
•
 $\mathcal {F}$
has irreducible support, which is therefore of the form
$\mathcal {F}$
has irreducible support, which is therefore of the form
 $\overline {Y}_{\lambda }$
for some
$\overline {Y}_{\lambda }$
for some
 $Y_\lambda \in S$
,
$Y_\lambda \in S$
, -
•
 $i_{\lambda }^* \mathcal {F}$
is a shifted
$i_{\lambda }^* \mathcal {F}$
is a shifted
 $\Lambda $
-free local system
$\Lambda $
-free local system
 $\mathcal {L}[m]$
and
$\mathcal {L}[m]$
and -
• Any indecomposable parity complex supported on
 $\overline {Y}_{\lambda }$
and extending
$\overline {Y}_{\lambda }$
and extending
 $\mathcal {L}[m]$
is isomorphic to
$\mathcal {L}[m]$
is isomorphic to
 $\mathcal {F}$
.
$\mathcal {F}$
.
A parity sheaf (with respect to
![]() $\dagger $
) is an indecomposable parity complex (with respect to
$\dagger $
) is an indecomposable parity complex (with respect to
![]() $\dagger $
), with
$\dagger $
), with
![]() $Y_{\lambda }$
the dense stratum in its support and extending
$Y_{\lambda }$
the dense stratum in its support and extending
![]() $\mathcal {L}[\dim Y_{\lambda }]$
. Given
$\mathcal {L}[\dim Y_{\lambda }]$
. Given
![]() $\mathcal {L}[\dim Y_{\lambda }]$
, it is not clear, in general, that a parity sheaf extending it exists. If it does exist, then Theorem 4.1 guarantees its uniqueness, and we denote it by
$\mathcal {L}[\dim Y_{\lambda }]$
, it is not clear, in general, that a parity sheaf extending it exists. If it does exist, then Theorem 4.1 guarantees its uniqueness, and we denote it by
![]() $\mathcal {E}(\lambda , \mathcal {L})$
. The existence is guaranteed for
$\mathcal {E}(\lambda , \mathcal {L})$
. The existence is guaranteed for
![]() $\operatorname {\mathrm {Gr}}_G$
with the usual stratification by
$\operatorname {\mathrm {Gr}}_G$
with the usual stratification by
![]() $L^+G$
-orbits;
$L^+G$
-orbits;
![]() $\mathcal {E}(\lambda , \mathcal {L})$
can moreover be promoted to a
$\mathcal {E}(\lambda , \mathcal {L})$
can moreover be promoted to a
![]() $L^+G$
-equivariant complex if p is not a torsion prime for G [Reference Juteau, Mautner and WilliamsonJMW16, Theorem 1.4]. If
$L^+G$
-equivariant complex if p is not a torsion prime for G [Reference Juteau, Mautner and WilliamsonJMW16, Theorem 1.4]. If
![]() $\mathcal {E}(\lambda , \mathcal {L})$
exists for all
$\mathcal {E}(\lambda , \mathcal {L})$
exists for all
![]() $\lambda $
and
$\lambda $
and
![]() $\mathcal {L}$
, we will say that ‘all parity sheaves exist’.
$\mathcal {L}$
, we will say that ‘all parity sheaves exist’.
4.2 Tate-parity sheaves
As we have seen, the cohomological grading in the Tate category is only well defined modulo
![]() $2$
, so it does not seem to make sense to talk about perverse sheaves in the Tate category. However, elements of the Tate category have Tate cohomology sheaves (§3.4.2), which are indexed by
$2$
, so it does not seem to make sense to talk about perverse sheaves in the Tate category. However, elements of the Tate category have Tate cohomology sheaves (§3.4.2), which are indexed by
![]() $\mathbf {Z}/2\mathbf {Z}$
, so it could make sense to talk about an analog of parity sheaves in the Tate category. As Leslie-Lonergan [Reference Leslie and LonerganLL21] observed, for this to work, we must take coefficients in the integral version of the Tate category, meaning
$\mathbf {Z}/2\mathbf {Z}$
, so it could make sense to talk about an analog of parity sheaves in the Tate category. As Leslie-Lonergan [Reference Leslie and LonerganLL21] observed, for this to work, we must take coefficients in the integral version of the Tate category, meaning
![]() $\Lambda = \mathbb {O} = W(k)$
, because then we have that (say by [Reference Leslie and LonerganLL21, Proposition 4.6.1])
$\Lambda = \mathbb {O} = W(k)$
, because then we have that (say by [Reference Leslie and LonerganLL21, Proposition 4.6.1])
is supported in even degrees. This is necessary for the assumption of nonvanishing odd Exts in the definition of the JMW stratification.
For a stratification S on Y, we define
![]() $\operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}}) \subset \operatorname {\mathrm {Perf}}(Y; \mathcal {T}_{\mathbb {O}})$
to be the full subcategory generated by images of objects in
$\operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}}) \subset \operatorname {\mathrm {Perf}}(Y; \mathcal {T}_{\mathbb {O}})$
to be the full subcategory generated by images of objects in
![]() $D^b_S(Y; \mathbb {O}[\sigma ])$
. Letting
$D^b_S(Y; \mathbb {O}[\sigma ])$
. Letting
![]() $\operatorname {\mathrm {Perf}}_S(Y; \mathbb {O}[\sigma ]) \subset \operatorname {\mathrm {Perf}}(Y; \mathbb {O}[\sigma ])$
be the full thick subcategory of S-constructible objects, we have by [Reference Leslie and LonerganLL21, Corollary 4.5.2] that
$\operatorname {\mathrm {Perf}}_S(Y; \mathbb {O}[\sigma ]) \subset \operatorname {\mathrm {Perf}}(Y; \mathbb {O}[\sigma ])$
be the full thick subcategory of S-constructible objects, we have by [Reference Leslie and LonerganLL21, Corollary 4.5.2] that
Definition 4.2 [Reference Leslie and LonerganLL21, Definition 5.3.1].
Let
![]() $\mathcal {F} \in \operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
. Fix a pariversity
$\mathcal {F} \in \operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
. Fix a pariversity
![]() $\dagger \colon S \rightarrow \mathbf {Z}/2\mathbf {Z}$
.
$\dagger \colon S \rightarrow \mathbf {Z}/2\mathbf {Z}$
.
-
1. For
 $? \in \{*,!\}$
, we say
$? \in \{*,!\}$
, we say
 $\mathcal {F}$
is
$\mathcal {F}$
is
 $?$
-Tate-even (with respect to
$?$
-Tate-even (with respect to
 $\dagger $
) if for each
$\dagger $
) if for each
 $Y_\lambda \in S$
, we have
$Y_\lambda \in S$
, we have  $$\begin{align*}T^{\dagger(Y_\lambda)+1}(i_{\lambda}^?\mathcal{F}) = 0. \end{align*}$$
$$\begin{align*}T^{\dagger(Y_\lambda)+1}(i_{\lambda}^?\mathcal{F}) = 0. \end{align*}$$
-
2. For
 $? \in \{*,!\}$
, we say
$? \in \{*,!\}$
, we say
 $\mathcal {F}$
is
$\mathcal {F}$
is
 $?$
-Tate-odd (with respect to
$?$
-Tate-odd (with respect to
 $\dagger $
) if
$\dagger $
) if
 $\mathcal {F}[1]$
is ?-Tate-even.
$\mathcal {F}[1]$
is ?-Tate-even. -
3. We say
 $\mathcal {F}$
is Tate-even (resp. Tate-odd) if
$\mathcal {F}$
is Tate-even (resp. Tate-odd) if
 $\mathcal {F}$
is both
$\mathcal {F}$
is both
 $*$
-Tate even (resp. odd) and
$*$
-Tate even (resp. odd) and
 $!$
-Tate even (resp. odd).
$!$
-Tate even (resp. odd). -
4. We say
 $\mathcal {F}$
is Tate-parity complex (with respect to
$\mathcal {F}$
is Tate-parity complex (with respect to
 $\dagger $
) if it is isomorphic within
$\dagger $
) if it is isomorphic within
 $\operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
to the direct sum of a Tate-even complex and a Tate-odd complex.Footnote
8
$\operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
to the direct sum of a Tate-even complex and a Tate-odd complex.Footnote
8
The full subcategory of (S-constructible) Tate-parity complexes (with coefficients in
![]() $\mathcal {T}_{\mathbb {O}}$
) is denoted
$\mathcal {T}_{\mathbb {O}}$
) is denoted
![]() $\operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
. If S arises from the orbits of a group G, then the corresponding stratification is denoted with a subscript
$\operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
. If S arises from the orbits of a group G, then the corresponding stratification is denoted with a subscript
![]() $(G)$
.
$(G)$
.
Parallel to Theorem 4.1, we have the following result in this context:
Proposition 4.3 [Reference Leslie and LonerganLL21, Theorem 5.5.6].
Let
![]() $\mathcal {F}$
be an indecomposable Tate-parity complex.
$\mathcal {F}$
be an indecomposable Tate-parity complex.
-
1. The support of
 $\mathcal {F}$
is of the form
$\mathcal {F}$
is of the form
 $\overline {Y}_{\lambda }$
for a unique stratum
$\overline {Y}_{\lambda }$
for a unique stratum
 $Y_{\lambda }$
.
$Y_{\lambda }$
. -
2. Suppose
 $\mathcal {G}$
and
$\mathcal {G}$
and
 $\mathcal {F}$
are two indecomposable Tate-parity complexes such that
$\mathcal {F}$
are two indecomposable Tate-parity complexes such that
 $\mathrm {supp}(\mathcal {G}) = \mathrm {supp}(\mathcal {F})$
. Letting
$\mathrm {supp}(\mathcal {G}) = \mathrm {supp}(\mathcal {F})$
. Letting
 $j_{\lambda } \colon Y_{\lambda } \hookrightarrow Y$
be the inclusion of the unique stratum open in this support, if
$j_{\lambda } \colon Y_{\lambda } \hookrightarrow Y$
be the inclusion of the unique stratum open in this support, if
 $j_{\lambda }^* \mathcal {G} \cong j_{\lambda }^* \mathcal {F}$
, then
$j_{\lambda }^* \mathcal {G} \cong j_{\lambda }^* \mathcal {F}$
, then
 $\mathcal {G} \cong \mathcal {F}$
.
$\mathcal {G} \cong \mathcal {F}$
.
Proof. The same argument as in [Reference Juteau, Mautner and WilliamsonJMW14, Theorem 2.12] works.
We define
![]() $\epsilon ^* \colon D_c^b(Y;\mathbb {O}) \rightarrow D_c^b(Y;\mathbb {O}[\sigma ])$
for the inflation through the augmentation
$\epsilon ^* \colon D_c^b(Y;\mathbb {O}) \rightarrow D_c^b(Y;\mathbb {O}[\sigma ])$
for the inflation through the augmentation
![]() $\epsilon \colon \mathbb {O}[\sigma ] \twoheadrightarrow \mathbb {O}$
. Recall that
$\epsilon \colon \mathbb {O}[\sigma ] \twoheadrightarrow \mathbb {O}$
. Recall that
![]() $\mathbb {T}^* \colon D_c^b(Y;\mathbb {O}[\sigma ]) \rightarrow \operatorname {\mathrm {Perf}}(Y; \mathcal {T}_{\mathbb {O}})$
denotes projection to the Tate category. We are interested in Tate complexes that come from the composite functor
$\mathbb {T}^* \colon D_c^b(Y;\mathbb {O}[\sigma ]) \rightarrow \operatorname {\mathrm {Perf}}(Y; \mathcal {T}_{\mathbb {O}})$
denotes projection to the Tate category. We are interested in Tate complexes that come from the composite functor
Definition 4.4. A Tate-parity sheaf
![]() $\mathcal {F} \in \operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
is an indecomposable Tate-parity complex with the property that its restriction to the unique stratum
$\mathcal {F} \in \operatorname {\mathrm {Perf}}_S(Y; \mathcal {T}_{\mathbb {O}})$
is an indecomposable Tate-parity complex with the property that its restriction to the unique stratum
![]() $Y_{\lambda }$
which is dense in its support is of the form
$Y_{\lambda }$
which is dense in its support is of the form
![]() $\mathbb {T}^* \epsilon ^* \mathcal {L}[\dim Y_{\lambda }]$
for an indecomposable
$\mathbb {T}^* \epsilon ^* \mathcal {L}[\dim Y_{\lambda }]$
for an indecomposable
![]() $\mathbb {O}$
-free local system
$\mathbb {O}$
-free local system
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $Y_{\lambda }$
. If such an
$Y_{\lambda }$
. If such an
![]() $\mathcal {F}$
exists, then it is unique, and we denote it by
$\mathcal {F}$
exists, then it is unique, and we denote it by
![]() $\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
.
$\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
.
If
![]() $\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
exists for all
$\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
exists for all
![]() $Y_\lambda \in S$
and all
$Y_\lambda \in S$
and all
![]() $\mathcal {L}$
, we will say that ‘all Tate-parity sheaves exist’ (for
$\mathcal {L}$
, we will say that ‘all Tate-parity sheaves exist’ (for
![]() $Y,S$
).
$Y,S$
).
4.3 Modular reduction
We now explain that the functor
![]() $\mathbb {T}^*$
has good properties that one would expect from ‘base change of coefficients’ functors for categories of sheaves in classical rings. We will suppress mention of the pariversity
$\mathbb {T}^*$
has good properties that one would expect from ‘base change of coefficients’ functors for categories of sheaves in classical rings. We will suppress mention of the pariversity
![]() $\dagger $
.
$\dagger $
.
Proposition 4.5 [Reference Leslie and LonerganLL21, Proposition 5.6.3, Theorem 5.6.4].
(1) If
![]() $\mathcal {F} \in D_S^b(X; \mathbb {O})$
is even/odd, then
$\mathcal {F} \in D_S^b(X; \mathbb {O})$
is even/odd, then
![]() $\mathbb {T}^* \epsilon ^* \mathcal {F} \in \operatorname {\mathrm {Perf}}_S(X; \mathcal {T}_{\mathbb {O}})$
is Tate-even/odd.
$\mathbb {T}^* \epsilon ^* \mathcal {F} \in \operatorname {\mathrm {Perf}}_S(X; \mathcal {T}_{\mathbb {O}})$
is Tate-even/odd.
(2) If the parity sheaf
![]() $\mathcal {E} = \mathcal {E}(\lambda , \mathcal {L})$
exists and satisfies
$\mathcal {E} = \mathcal {E}(\lambda , \mathcal {L})$
exists and satisfies
![]() $\operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}, \mathcal {E}[n]) = 0$
for all
$\operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}, \mathcal {E}[n]) = 0$
for all
![]() $n<0$
(this holds for example if
$n<0$
(this holds for example if
![]() $\mathcal {E}$
is perverseFootnote
9
), then
$\mathcal {E}$
is perverseFootnote
9
), then
![]() $\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
exists, and we have
$\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
exists, and we have
Remark 4.6. The Proposition (and its proof) are analogous to the following results of parity sheaves [Reference Juteau, Mautner and WilliamsonJMW14, §2.5]. Let
![]() $\mathbb {F}$
denote the base change functor
$\mathbb {F}$
denote the base change functor
The functor
![]() $\mathbb {F}$
enjoys the following properties.
$\mathbb {F}$
enjoys the following properties.
-
1.
 $\mathcal {F} \in D^b_S(X; \mathbb {O})$
is a parity sheaf if and only if
$\mathcal {F} \in D^b_S(X; \mathbb {O})$
is a parity sheaf if and only if
 $\mathbb {F}(\mathcal {E}) \in D^b_S(X; k)$
is a parity sheaf.
$\mathbb {F}(\mathcal {E}) \in D^b_S(X; k)$
is a parity sheaf. -
2. If
 $\mathcal {E}(\lambda , \mathcal {L}) $
exists, then
$\mathcal {E}(\lambda , \mathcal {L}) $
exists, then
 $\mathcal {E}(\lambda , \mathbb {F} \mathcal {L})$
exists, and we have
$\mathcal {E}(\lambda , \mathbb {F} \mathcal {L})$
exists, and we have  $$\begin{align*}\mathbb{F}\mathcal{E}(\lambda, \mathcal{L}) \cong \mathcal{E}(\lambda, \mathbb{F} \mathcal{L}). \end{align*}$$
$$\begin{align*}\mathbb{F}\mathcal{E}(\lambda, \mathcal{L}) \cong \mathcal{E}(\lambda, \mathbb{F} \mathcal{L}). \end{align*}$$
Proof of Proposition 4.5.
We reproduce the proof from [Reference Leslie and LonerganLL21] because it brings up certain ideas that will be needed later. The operation
![]() $\mathbb {T}^* \epsilon ^* $
is compatible with formation of
$\mathbb {T}^* \epsilon ^* $
is compatible with formation of
![]() $i_{\lambda }^*$
or
$i_{\lambda }^*$
or
![]() $i_{\lambda }^!$
. Hence, to prove (1), we reduce to examining
$i_{\lambda }^!$
. Hence, to prove (1), we reduce to examining
![]() $T^i \epsilon ^* \mathcal {L}$
for a local system
$T^i \epsilon ^* \mathcal {L}$
for a local system
![]() $\mathcal {L}$
of free
$\mathcal {L}$
of free
![]() $\mathbb {O}$
-modules, with the trivial
$\mathbb {O}$
-modules, with the trivial
![]() $\sigma $
-action. This reduces to the fact that the Tate cohomology of
$\sigma $
-action. This reduces to the fact that the Tate cohomology of
![]() $\mathbb {O}$
is supported in even degrees, which is (4.1).
$\mathbb {O}$
is supported in even degrees, which is (4.1).
For (2), we just need to check that
![]() $\mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L})$
is indecomposable. Since
$\mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L})$
is indecomposable. Since
![]() $\operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
is Krull-Remak-Schmidt by [Reference Leslie and LonerganLL21, Proposition 5.5.2], it suffices to check that the endomorphism ring of
$\operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
is Krull-Remak-Schmidt by [Reference Leslie and LonerganLL21, Proposition 5.5.2], it suffices to check that the endomorphism ring of
![]() $\mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L})$
is local. According to [Reference Leslie and LonerganLL21, Proposition 4.6.1], for
$\mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L})$
is local. According to [Reference Leslie and LonerganLL21, Proposition 4.6.1], for
![]() $\mathcal {F}, \mathcal {G} \in D^b_S(Y; \mathbb {O})$
, we have
$\mathcal {F}, \mathcal {G} \in D^b_S(Y; \mathbb {O})$
, we have
We apply this to
![]() $\mathcal {F} = \mathcal {G} = \mathcal {E}(\lambda , \mathcal {L})$
. Since
$\mathcal {F} = \mathcal {G} = \mathcal {E}(\lambda , \mathcal {L})$
. Since
![]() $\mathcal {E}(\lambda , \mathcal {L})$
is parity, [Reference Juteau, Mautner and WilliamsonJMW14, (2.13)] applies to show that
$\mathcal {E}(\lambda , \mathcal {L})$
is parity, [Reference Juteau, Mautner and WilliamsonJMW14, (2.13)] applies to show that
By indecomposability of
![]() $\mathcal {E}(\lambda , \mathcal {L})$
, the ring
$\mathcal {E}(\lambda , \mathcal {L})$
, the ring
![]() $\operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}(\lambda , \mathcal {L}), \mathcal {E}(\lambda , \mathcal {L}))$
is local, so
$\operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}(\lambda , \mathcal {L}), \mathcal {E}(\lambda , \mathcal {L}))$
is local, so
![]() $ \mathbb {F} \otimes \operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}(\lambda , \mathcal {L}), \mathcal {E}(\lambda , \mathcal {L}))$
is also local. This shows that the subalgebra on the RHS of (4.2) indexed by
$ \mathbb {F} \otimes \operatorname {\mathrm {Hom}}_{D^b_S(Y; \mathbb {O})} (\mathcal {E}(\lambda , \mathcal {L}), \mathcal {E}(\lambda , \mathcal {L}))$
is also local. This shows that the subalgebra on the RHS of (4.2) indexed by
![]() $i=0$
is local, and the assumption implies that the summands of (4.2) indexed by negative i vanish. This implies the desired locality of the graded algebra (4.2).
$i=0$
is local, and the assumption implies that the summands of (4.2) indexed by negative i vanish. This implies the desired locality of the graded algebra (4.2).
What we have seen can be summarized by the following slogan:
If all parity sheaves exist and have vanishing negative self-Exts, then all Tate-parity sheaves exist, and
![]() $\mathbb {T}^* \circ \epsilon ^*$
induces a bijection between parity sheaves and Tate-parity sheaves.
$\mathbb {T}^* \circ \epsilon ^*$
induces a bijection between parity sheaves and Tate-parity sheaves.
4.4 The lifting functor
We will now define a functor lifting Tate-parity sheaves to parity sheaves. In fact, the preceding slogan already tells us what to do about objects, so we just need to specify what happens on morphisms.
Definition 4.7. A normalized (Tate-)parity complex is a direct sum of (Tate-)parity sheaves with no shifts. Hence, under our assumptions, an indecomposable (Tate)-parity complex is normalized if and only if its restriction to the dense open stratum in its support
![]() $Y_{\lambda }$
is isomorphic to
$Y_{\lambda }$
is isomorphic to
![]() $\mathcal {L}[\dim Y_{\lambda }]$
(resp.
$\mathcal {L}[\dim Y_{\lambda }]$
(resp.
![]() $\mathbb {T}^* \epsilon ^* \mathcal {L}[\dim Y_{\lambda }]$
) for an indecomposable local system
$\mathbb {T}^* \epsilon ^* \mathcal {L}[\dim Y_{\lambda }]$
) for an indecomposable local system
![]() $\mathcal {L}$
. We denote the full subcategory of normalized (Tate)-parity complexes by
$\mathcal {L}$
. We denote the full subcategory of normalized (Tate)-parity complexes by
![]() $\operatorname {\mathrm {Parity}}^0_S(Y; \mathbb {O}) \subset \operatorname {\mathrm {Parity}}_S(Y; \mathbb {O})$
(resp.
$\operatorname {\mathrm {Parity}}^0_S(Y; \mathbb {O}) \subset \operatorname {\mathrm {Parity}}_S(Y; \mathbb {O})$
(resp.
![]() $\operatorname {\mathrm {Parity}}^0_S(Y; \mathcal {T}_{\mathbb {O}}) \subset \operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
) and call them the categories of normalized (Tate)-parity sheaves.
$\operatorname {\mathrm {Parity}}^0_S(Y; \mathcal {T}_{\mathbb {O}}) \subset \operatorname {\mathrm {Parity}}_S(Y; \mathcal {T}_{\mathbb {O}})$
) and call them the categories of normalized (Tate)-parity sheaves.
Under the assumption that all parity sheaves exist and have vanishing negative self-Exts, Proposition 4.5 implies that
![]() $\mathcal {E}(\lambda , \mathcal {L}) \mapsto \mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L}) \cong \mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
induces a bijection between normalized parity sheaves and normalized Tate-parity sheaves. We then have a ‘lifting functor’ [Reference Leslie and LonerganLL21, Theorem 5.6.6]
$\mathcal {E}(\lambda , \mathcal {L}) \mapsto \mathbb {T}^* \epsilon ^* \mathcal {E}(\lambda , \mathcal {L}) \cong \mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
induces a bijection between normalized parity sheaves and normalized Tate-parity sheaves. We then have a ‘lifting functor’ [Reference Leslie and LonerganLL21, Theorem 5.6.6]
sending
![]() $\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
to
$\mathcal {E}_{\mathcal {T}}(\lambda , \mathcal {L})$
to
![]() $\mathcal {E}(\lambda , \mathcal {L} \otimes _{\mathbb {O}} k)$
on objects and on morphisms inducing projection to the summand indexed by
$\mathcal {E}(\lambda , \mathcal {L} \otimes _{\mathbb {O}} k)$
on objects and on morphisms inducing projection to the summand indexed by
![]() $i=0$
under identification (4.2). It can be thought of as an ‘intermediate’ reduction between
$i=0$
under identification (4.2). It can be thought of as an ‘intermediate’ reduction between
![]() $\mathbb {O}$
and k in the sense that the following diagram commutes:
$\mathbb {O}$
and k in the sense that the following diagram commutes:

4.5 Parity sheaves on the affine Grassmannian and tilting modules
We now consider the preceding theory in the context of the affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_G$
over a separably closed field
$\operatorname {\mathrm {Gr}}_G$
over a separably closed field
![]() $\mathbf {F}$
, with the stratification by
$\mathbf {F}$
, with the stratification by
![]() $L^+G$
-orbits. Since this is a special case of a Kac-Moody flag variety, the stratification is JMW by [Reference Juteau, Mautner and WilliamsonJMW14, §4.1].
$L^+G$
-orbits. Since this is a special case of a Kac-Moody flag variety, the stratification is JMW by [Reference Juteau, Mautner and WilliamsonJMW14, §4.1].
If p is a good prime for
![]() $\widehat {G}$
, [Reference Mautner and RicheMR18, Corollary 1.6] implies that all parity sheaves exist and that all normalized parity sheaves are perverse. Therefore, the category of normalized parity sheaves corresponds under the Geometric Satake equivalence to some subcategory of
$\widehat {G}$
, [Reference Mautner and RicheMR18, Corollary 1.6] implies that all parity sheaves exist and that all normalized parity sheaves are perverse. Therefore, the category of normalized parity sheaves corresponds under the Geometric Satake equivalence to some subcategory of
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, and it is natural to ask what this is. The answer is given in terms of tilting modules for
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, and it is natural to ask what this is. The answer is given in terms of tilting modules for
![]() $\widehat {G}$
(recall that these are the objects of
$\widehat {G}$
(recall that these are the objects of
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
having both a filtration by standard objects and a filtration by costandard objects). The tilting property is preserved by direct sum and tensor products (the latter assertion is a nontrivial theorem). Let
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
having both a filtration by standard objects and a filtration by costandard objects). The tilting property is preserved by direct sum and tensor products (the latter assertion is a nontrivial theorem). Let
![]() $\operatorname {\mathrm {Tilt}}_k(\widehat {G}) \subset \operatorname {\mathrm {Rep}}_k(\widehat {G})$
denote the full subcategory of tilting modules.
$\operatorname {\mathrm {Tilt}}_k(\widehat {G}) \subset \operatorname {\mathrm {Rep}}_k(\widehat {G})$
denote the full subcategory of tilting modules.
Theorem 4.8 [Reference Mautner and RicheMR18, Corollary 1.6].
If p is good for G, then the Geometric Satake equivalence restricts to an equivalenceFootnote 10
Proof. The proof in [Reference Mautner and RicheMR18] is written for the affine Grassmannian over the complex numbers but adapts to our situation with some small modifications. First, one takes
![]() $\operatorname {\mathrm {Gr}}_G$
over
$\operatorname {\mathrm {Gr}}_G$
over
![]() $\mathbf {F}$
instead of over
$\mathbf {F}$
instead of over
![]() $\mathbf {C}$
as in [Reference Mautner and RicheMR18]. The proof of Theorem 4.8 follows formally as in [Reference Mautner and RicheMR18, §6.5] from an equivalence of categories between the category of Iwahori-equivariant parity sheaves with coefficients in k on
$\mathbf {C}$
as in [Reference Mautner and RicheMR18]. The proof of Theorem 4.8 follows formally as in [Reference Mautner and RicheMR18, §6.5] from an equivalence of categories between the category of Iwahori-equivariant parity sheaves with coefficients in k on
![]() $\operatorname {\mathrm {Gr}}_G$
and the category of tilting objects in the heart of Bezrukavnikov’s exotic t-structure on
$\operatorname {\mathrm {Gr}}_G$
and the category of tilting objects in the heart of Bezrukavnikov’s exotic t-structure on
![]() $\check {G} \times \mathbf {G}_m$
-equivariant tilting objects on the Springer resolution
$\check {G} \times \mathbf {G}_m$
-equivariant tilting objects on the Springer resolution
![]() $\widetilde {\mathcal {N}}$
. This equivalence is, in turn, proved by a Soergel bimodule argument. The analysis of the ‘coherent side’ in [Reference Mautner and RicheMR18, §4,5] is literally the same as in our situation. The analysis of the ‘constructible side’ in [Reference Mautner and RicheMR18, §3] applies verbatim to
$\widetilde {\mathcal {N}}$
. This equivalence is, in turn, proved by a Soergel bimodule argument. The analysis of the ‘coherent side’ in [Reference Mautner and RicheMR18, §4,5] is literally the same as in our situation. The analysis of the ‘constructible side’ in [Reference Mautner and RicheMR18, §3] applies verbatim to
![]() $\operatorname {\mathrm {Gr}}_G$
over
$\operatorname {\mathrm {Gr}}_G$
over
![]() $\mathbf {F}$
except at one point: in [Reference Mautner and RicheMR18, Proof of Lemma 3.6, p.22], the property that ‘the map
$\mathbf {F}$
except at one point: in [Reference Mautner and RicheMR18, Proof of Lemma 3.6, p.22], the property that ‘the map
![]() $\mathcal {O}(\mathfrak {t}^*/W \times \mathfrak {t}^*/W) \rightarrow H^*_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathfrak {R})$
factors through
$\mathcal {O}(\mathfrak {t}^*/W \times \mathfrak {t}^*/W) \rightarrow H^*_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathfrak {R})$
factors through
![]() $\mathcal {O}(\Delta )$
’ is proved using the ‘loop group presentation’ of the complex affine Grassmannian; an alternate argument for this fact that works in arbitrary characteristic is provided in [Reference ZhuZhu17, Lemma 5.2.4].
$\mathcal {O}(\Delta )$
’ is proved using the ‘loop group presentation’ of the complex affine Grassmannian; an alternate argument for this fact that works in arbitrary characteristic is provided in [Reference ZhuZhu17, Lemma 5.2.4].
Remark 4.9. A much shorter argument for Theorem 4.8, but with a slightly worse bound on p, is given in [Reference Juteau, Mautner and WilliamsonJMW16, Theorem 1.8].
We need a few facts about the representation theory of tilting modules. For our arithmetic applications, the key point is that there are ‘enough’ tilting modules to generate the derived category of
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, as articulated by the statement below (which, in fact, applies to general highest weight categories).
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, as articulated by the statement below (which, in fact, applies to general highest weight categories).
Proposition 4.10 [Reference RicheRic, Proposition 7.17].
The natural projection from the bounded homotopy category
![]() $K^b(\operatorname {\mathrm {Tilt}}_k(\widehat {G}))$
to
$K^b(\operatorname {\mathrm {Tilt}}_k(\widehat {G}))$
to
![]() $D^b(\operatorname {\mathrm {Rep}}_k(\widehat {G}))$
is an equivalence.
$D^b(\operatorname {\mathrm {Rep}}_k(\widehat {G}))$
is an equivalence.
4.6 Base change functoriality for the Satake category
We now consider a specific geometric situation relevant to Langlands functoriality for p-cyclic base change. Let
![]() $\mathbf {F}$
be a field of characteristic
$\mathbf {F}$
be a field of characteristic
![]() $\neq p$
. We will consider reductive groups and their affine Grassmannians over
$\neq p$
. We will consider reductive groups and their affine Grassmannians over
![]() $\mathbf {F}$
.
$\mathbf {F}$
.
4.6.1 The base change setup
We now specialize the situation a bit further: H is any reductive group over
![]() $\mathbf {F}$
and
$\mathbf {F}$
and
![]() $G = H^p$
. We let
$G = H^p$
. We let
![]() $\sigma $
act on G by cyclic rotation, sending the ith factor to the
$\sigma $
act on G by cyclic rotation, sending the ith factor to the
![]() $(i+1)$
st (mod p) factor. Then it is clear that the stratification on
$(i+1)$
st (mod p) factor. Then it is clear that the stratification on
![]() $\operatorname {\mathrm {Gr}}_G$
by
$\operatorname {\mathrm {Gr}}_G$
by
![]() $L^+G$
-orbits induces by restriction the stratification on
$L^+G$
-orbits induces by restriction the stratification on
![]() $\operatorname {\mathrm {Gr}}_H$
by
$\operatorname {\mathrm {Gr}}_H$
by
![]() $L^+H$
-orbits.
$L^+H$
-orbits.
Evidently the ‘diagonal’ embedding
![]() $H \hookrightarrow G$
realizes H as the fixed points of G under the automorphism
$H \hookrightarrow G$
realizes H as the fixed points of G under the automorphism
![]() $\sigma $
. This map
$\sigma $
. This map
![]() $H \hookrightarrow G$
also induces a diagonal map
$H \hookrightarrow G$
also induces a diagonal map
![]() $\operatorname {\mathrm {Gr}}_H \rightarrow \operatorname {\mathrm {Gr}}_G$
.
$\operatorname {\mathrm {Gr}}_H \rightarrow \operatorname {\mathrm {Gr}}_G$
.
Lemma 4.11. The diagonal map induces an isomorphism
![]() $\operatorname {\mathrm {Gr}}_H \cong \operatorname {\mathrm {Gr}}_G^{\sigma }$
as subfunctors of
$\operatorname {\mathrm {Gr}}_H \cong \operatorname {\mathrm {Gr}}_G^{\sigma }$
as subfunctors of
![]() $\operatorname {\mathrm {Gr}}_G$
.
$\operatorname {\mathrm {Gr}}_G$
.
Proof. We have
![]() $\operatorname {\mathrm {Gr}}_G \cong (\operatorname {\mathrm {Gr}}_H)^p$
, with
$\operatorname {\mathrm {Gr}}_G \cong (\operatorname {\mathrm {Gr}}_H)^p$
, with
![]() $\sigma $
acting by cyclic rotation of the factors, from which the claim is clear.
$\sigma $
acting by cyclic rotation of the factors, from which the claim is clear.
Henceforth, we assume that p is odd and good for
![]() $\widehat {G}$
so that the results of §4.5 apply.
$\widehat {G}$
so that the results of §4.5 apply.
We aim to give a ‘geometric’ description of the corresponding functor under the Geometric Satake equivalence,
![]() $\operatorname {\mathrm {Parity}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \rightarrow \operatorname {\mathrm {Parity}}_{L^+H}(\operatorname {\mathrm {Gr}}_H;k)$
, in terms of Smith theory. (Of course, one could give an ‘ad hoc’ description using that
$\operatorname {\mathrm {Parity}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \rightarrow \operatorname {\mathrm {Parity}}_{L^+H}(\operatorname {\mathrm {Gr}}_H;k)$
, in terms of Smith theory. (Of course, one could give an ‘ad hoc’ description using that
![]() $G = H^p$
. The point is to define a functor that does not make reference to this, which will then generalize well, using descent, to the situation where
$G = H^p$
. The point is to define a functor that does not make reference to this, which will then generalize well, using descent, to the situation where
![]() $G = \operatorname {\mathrm {Res}}_{\mathbf {E}/\mathbf {F}}(H)$
for a nontrivial field extension
$G = \operatorname {\mathrm {Res}}_{\mathbf {E}/\mathbf {F}}(H)$
for a nontrivial field extension
![]() $\mathbf {E}/\mathbf {F}$
.)
$\mathbf {E}/\mathbf {F}$
.)
Definition 4.12. Given
![]() $\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \Lambda )$
, we define
$\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \Lambda )$
, we define
equipped with the
![]() $\sigma $
-equivariant structure coming from the commutativity constraint for
$\sigma $
-equivariant structure coming from the commutativity constraint for
![]() $(\operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda ), \star )$
:
$(\operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda ), \star )$
:
Using the realization functor
![]() $\operatorname {\mathrm {P}}_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \Lambda ) \rightarrow D_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \Lambda )$
, we view
$\operatorname {\mathrm {P}}_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \Lambda ) \rightarrow D_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \Lambda )$
, we view
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F}) \in D_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G;\Lambda )$
(so that we may apply the Smith functor, for example). Equipping a general object of
$\operatorname {\mathrm {Nm}}(\mathcal {F}) \in D_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G;\Lambda )$
(so that we may apply the Smith functor, for example). Equipping a general object of
![]() $D_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda )$
with a
$D_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda )$
with a
![]() $\sigma $
-equivariant structure is much more involved than just specifying isomorphisms (4.4) (satisfying cocycle conditions), so we emphasize that we construct
$\sigma $
-equivariant structure is much more involved than just specifying isomorphisms (4.4) (satisfying cocycle conditions), so we emphasize that we construct
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F})$
first as a
$\operatorname {\mathrm {Nm}}(\mathcal {F})$
first as a
![]() $\sigma $
-equivariant perverse sheaf and then apply the realization functor to get a
$\sigma $
-equivariant perverse sheaf and then apply the realization functor to get a
![]() $\sigma $
-equivariant object of
$\sigma $
-equivariant object of
![]() $D_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda )$
.
$D_{L^+G}(\operatorname {\mathrm {Gr}}_G;\Lambda )$
.
Remark 4.13. In our applications, we will assume that p is large enough so that all parity sheaves are perverse. The properties of being
![]() $L^+G$
-constructible and
$L^+G$
-constructible and
![]() $L^+G$
-equivariant are equivalent for perverse sheaves on
$L^+G$
-equivariant are equivalent for perverse sheaves on
![]() $\operatorname {\mathrm {Gr}}_G$
. Therefore, we will not need to worry about any extra complications coming from the equivariance.
$\operatorname {\mathrm {Gr}}_G$
. Therefore, we will not need to worry about any extra complications coming from the equivariance.
Lemma 4.14. Let
![]() $i \colon \operatorname {\mathrm {Gr}}_H \cong \operatorname {\mathrm {Gr}}_G^{\sigma } \hookrightarrow \operatorname {\mathrm {Gr}}_G$
. For
$i \colon \operatorname {\mathrm {Gr}}_H \cong \operatorname {\mathrm {Gr}}_G^{\sigma } \hookrightarrow \operatorname {\mathrm {Gr}}_G$
. For
![]() $\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
, regard
$\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
, regard
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F}) \in \operatorname {\mathrm {P}}_{L^+G \rtimes \sigma }^b(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
as in Definition 4.12 above. Suppose that all the cohomology sheaves of
$\operatorname {\mathrm {Nm}}(\mathcal {F}) \in \operatorname {\mathrm {P}}_{L^+G \rtimes \sigma }^b(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
as in Definition 4.12 above. Suppose that all the cohomology sheaves of
![]() $\mathcal {F}$
have
$\mathcal {F}$
have
![]() $\mathbb {O}$
-free stalks and costalks.
$\mathbb {O}$
-free stalks and costalks.
-
(i) The stalks of the cohomology sheaves of
 $i^* \operatorname {\mathrm {Nm}}(\mathcal {F})$
have an
$i^* \operatorname {\mathrm {Nm}}(\mathcal {F})$
have an
 $\mathbb {O}[\sigma ]$
-stable filtration with associated graded a direct sum of either trivial or free
$\mathbb {O}[\sigma ]$
-stable filtration with associated graded a direct sum of either trivial or free
 $\mathbb {O}[\sigma ]$
-modules.
$\mathbb {O}[\sigma ]$
-modules. -
(ii) The costalks of the cohomology sheaves of
 $i^! \operatorname {\mathrm {Nm}}(\mathcal {F})$
have an
$i^! \operatorname {\mathrm {Nm}}(\mathcal {F})$
have an
 $\mathbb {O}[\sigma ]$
-stable filtration with associated graded a direct sum of either trivial or free
$\mathbb {O}[\sigma ]$
-stable filtration with associated graded a direct sum of either trivial or free
 $\mathbb {O}[\sigma ]$
-modules.
$\mathbb {O}[\sigma ]$
-modules.
Proof. If
![]() $\mathcal {F}$
has a finite
$\mathcal {F}$
has a finite
![]() $L^+G$
-equivariant filtration whose associated graded satisfies the hypotheses of the Lemma, then the statement of Lemma for
$L^+G$
-equivariant filtration whose associated graded satisfies the hypotheses of the Lemma, then the statement of Lemma for
![]() $\mathcal {F}$
can be checked on the associated graded. Since
$\mathcal {F}$
can be checked on the associated graded. Since
![]() $\operatorname {\mathrm {Gr}}_G^{\underline {\lambda }}$
is a product of homogeneous spaces for (a finite type quotient of)
$\operatorname {\mathrm {Gr}}_G^{\underline {\lambda }}$
is a product of homogeneous spaces for (a finite type quotient of)
![]() $L^+ H$
, there is a finite
$L^+ H$
, there is a finite
![]() $L^+G$
-equivariant filtration of
$L^+G$
-equivariant filtration of
![]() $\mathcal {F}$
with associated graded of being a direct sum of sheaves of the form
$\mathcal {F}$
with associated graded of being a direct sum of sheaves of the form
![]() $\mathcal {F}_1 \boxtimes \ldots \boxtimes \mathcal {F}_p$
, where each
$\mathcal {F}_1 \boxtimes \ldots \boxtimes \mathcal {F}_p$
, where each
![]() $\mathcal {F}_i \in \operatorname {\mathrm {P}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathbb {O})$
. Hence, we reduce to the case where
$\mathcal {F}_i \in \operatorname {\mathrm {P}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathbb {O})$
. Hence, we reduce to the case where
![]() $\mathcal {F}$
is itself of this form. Then
$\mathcal {F}$
is itself of this form. Then
with
![]() $\sigma $
acting by rotating the tensor factors and the
$\sigma $
acting by rotating the tensor factors and the
![]() $\sigma $
-equivariant structure coming from the commutativity constraint.
$\sigma $
-equivariant structure coming from the commutativity constraint.
Write
![]() $\mathcal {F}' := \mathcal {F}_1 \star \mathcal {F}_2 \star \ldots \star \mathcal {F}_p \in \operatorname {\mathrm {P}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathbb {O})$
. Since i may be identified with the diagonal embedding
$\mathcal {F}' := \mathcal {F}_1 \star \mathcal {F}_2 \star \ldots \star \mathcal {F}_p \in \operatorname {\mathrm {P}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathbb {O})$
. Since i may be identified with the diagonal embedding
![]() $\operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_H^p$
, we have
$\operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_H^p$
, we have
![]() $i^*(\operatorname {\mathrm {Nm}} \mathcal {F}) \approx (\mathcal {F}')^{\otimes p}$
, with
$i^*(\operatorname {\mathrm {Nm}} \mathcal {F}) \approx (\mathcal {F}')^{\otimes p}$
, with
![]() $\sigma $
-equivariant structure given by cyclic rotation of the tensor factors. In particular, the stalk of
$\sigma $
-equivariant structure given by cyclic rotation of the tensor factors. In particular, the stalk of
![]() $i^* (\operatorname {\mathrm {Nm}} \mathcal {F})$
at
$i^* (\operatorname {\mathrm {Nm}} \mathcal {F})$
at
![]() $x \in \operatorname {\mathrm {Gr}}_H$
is the tensor-induction of the stalk of
$x \in \operatorname {\mathrm {Gr}}_H$
is the tensor-induction of the stalk of
![]() $\mathcal {F}^{\prime }_x$
from
$\mathcal {F}^{\prime }_x$
from
![]() $\mathbb {O}$
to
$\mathbb {O}$
to
![]() $\mathbb {O}[\sigma ]$
. Hence, it suffices to prove that any cohomology sheaf of such a tensor induction has an
$\mathbb {O}[\sigma ]$
. Hence, it suffices to prove that any cohomology sheaf of such a tensor induction has an
![]() $\mathbb {O}[\sigma ]$
-equivariant filtration by either trivial or free
$\mathbb {O}[\sigma ]$
-equivariant filtration by either trivial or free
![]() $\mathbb {O}[\sigma ]$
-modules. This is verified by explicit inspection: choosing a basis for
$\mathbb {O}[\sigma ]$
-modules. This is verified by explicit inspection: choosing a basis for
![]() $\mathcal {H}^j(\mathcal {F}^{\prime }_x)$
, the induced basis of
$\mathcal {H}^j(\mathcal {F}^{\prime }_x)$
, the induced basis of
![]() $\mathcal {H}^j(\mathcal {F}^{\prime }_x)^{\otimes p}$
is grouped into either trivial or free orbits under the
$\mathcal {H}^j(\mathcal {F}^{\prime }_x)^{\otimes p}$
is grouped into either trivial or free orbits under the
![]() $\sigma $
-action.
$\sigma $
-action.
The argument for (ii) is completely analogous (alternatively, we could deduce it simply by applying Verdier duality to (i)).
4.6.2 Smith theory for parity sheaves
We return momentarily to the general setup for Smith theory: Y is a variety over
![]() $\mathbf {F}$
with an admissible
$\mathbf {F}$
with an admissible
![]() $\sigma $
-action and
$\sigma $
-action and
![]() $Z = Y^{\sigma }$
. We assume that
$Z = Y^{\sigma }$
. We assume that
![]() $\mathbf {F}$
is separably closed and the stratification S on Y satisfies the JMW condition.
$\mathbf {F}$
is separably closed and the stratification S on Y satisfies the JMW condition.
Proposition 4.15 (Variant of [Reference Leslie and LonerganLL21, Theorem 6.1.1]).
Assume that each stratum
![]() $Y_\lambda $
is smooth. Suppose
$Y_\lambda $
is smooth. Suppose
![]() $\mathcal {E} \in D^b_{S, \sigma }(Y; \mathbb {O})$
is a parity complex satisfying the following condition:
$\mathcal {E} \in D^b_{S, \sigma }(Y; \mathbb {O})$
is a parity complex satisfying the following condition:
-
• all
 $*$
and
$*$
and
 $!$
-stalks of cohomology sheaves of
$!$
-stalks of cohomology sheaves of
 $\mathcal {E}$
at fixed points
$\mathcal {E}$
at fixed points
 $y \in Y$
have an
$y \in Y$
have an
 $\mathbb {O}[\sigma ]$
-stable filtration with associated graded being a direct sum of trivial or free
$\mathbb {O}[\sigma ]$
-stable filtration with associated graded being a direct sum of trivial or free
 $\mathbb {O}[\sigma ]$
-modules.
$\mathbb {O}[\sigma ]$
-modules.
Then
![]() $\operatorname {\mathrm {Psm}}(\mathcal {E}) \in \operatorname {\mathrm {Perf}}_S(Z; \mathcal {T}_{\mathbb {O}})$
is Tate-parity with respect to the induced stratification
$\operatorname {\mathrm {Psm}}(\mathcal {E}) \in \operatorname {\mathrm {Perf}}_S(Z; \mathcal {T}_{\mathbb {O}})$
is Tate-parity with respect to the induced stratification
![]() $Z_{\lambda } = Y_{\lambda } \cap Z$
and the induced pariversity
$Z_{\lambda } = Y_{\lambda } \cap Z$
and the induced pariversity
![]() $\dagger _{Z}(\lambda ) := \dagger _Y(\lambda )$
.
$\dagger _{Z}(\lambda ) := \dagger _Y(\lambda )$
.
Proof. This theorem is closely related to [Reference Leslie and LonerganLL21, Theorem 6.1.1], but loc. cit. imposes the stronger condition that the
![]() $\sigma $
-action on all stalks is trivial. This is satisfied in their application (to the loop-rotation action), but not in ours, so we need to redo the argument in the requisite generality.
$\sigma $
-action on all stalks is trivial. This is satisfied in their application (to the loop-rotation action), but not in ours, so we need to redo the argument in the requisite generality.
Let
![]() $Z = Y^{\sigma }$
and take the induced stratification on Z. Let
$Z = Y^{\sigma }$
and take the induced stratification on Z. Let
![]() $i \colon Z \rightarrow Y$
,
$i \colon Z \rightarrow Y$
,
![]() $i_{\lambda }^Y \colon Y_{\lambda } \hookrightarrow Y$
,
$i_{\lambda }^Y \colon Y_{\lambda } \hookrightarrow Y$
,
![]() $i_{\lambda }^Z \colon Z_{\lambda } \hookrightarrow Z$
,
$i_{\lambda }^Z \colon Z_{\lambda } \hookrightarrow Z$
,
![]() $i^{\lambda } \colon Z_{\lambda } \hookrightarrow Y_{\lambda }$
. Without loss of generality, suppose
$i^{\lambda } \colon Z_{\lambda } \hookrightarrow Y_{\lambda }$
. Without loss of generality, suppose
![]() $\mathcal {E}$
is an even complex on Y. We are given that
$\mathcal {E}$
is an even complex on Y. We are given that
![]() $(i_{\lambda }^Y)^{?} \mathcal {E}$
has
$(i_{\lambda }^Y)^{?} \mathcal {E}$
has
![]() $\mathbb {O}$
-free cohomology sheaves supported in degrees congruent to
$\mathbb {O}$
-free cohomology sheaves supported in degrees congruent to
![]() $\dagger _Y(\lambda )$
mod
$\dagger _Y(\lambda )$
mod
![]() $2$
, where
$2$
, where
![]() $? \in \{*, !\}$
; we want to show that
$? \in \{*, !\}$
; we want to show that
![]() $(i_{\lambda }^Z)^? \operatorname {\mathrm {Psm}}(\mathcal {E})$
has Tate-cohomology sheaves supported in degrees congruent to
$(i_{\lambda }^Z)^? \operatorname {\mathrm {Psm}}(\mathcal {E})$
has Tate-cohomology sheaves supported in degrees congruent to
![]() $\dagger _Z(\lambda )$
mod
$\dagger _Z(\lambda )$
mod
![]() $2$
. Unraveling the definitions, we have
$2$
. Unraveling the definitions, we have
Similarly, using Lemma 3.8, we have
By hypothesis,
![]() $(i_{\lambda }^Y)^* \mathcal {E}$
has its cohomology sheaves supported in degrees congruent to
$(i_{\lambda }^Y)^* \mathcal {E}$
has its cohomology sheaves supported in degrees congruent to
![]() $\dagger _Y(\lambda ) \pmod {2}$
. So the stalks of
$\dagger _Y(\lambda ) \pmod {2}$
. So the stalks of
![]() $(i^{\lambda })^* (i_{\lambda }^Y)^* \mathcal {E}$
are supported in degrees congruent to
$(i^{\lambda })^* (i_{\lambda }^Y)^* \mathcal {E}$
are supported in degrees congruent to
![]() $\dagger _Y(\lambda ) \pmod {2}$
, and we must verify that their Tate cohomology groups are also supported in degrees of a single parity.
$\dagger _Y(\lambda ) \pmod {2}$
, and we must verify that their Tate cohomology groups are also supported in degrees of a single parity.
By assumption (*), all the stalks have an
![]() $\mathbb {O}[\sigma ]$
-stable filtration with associated graded being a direct sum of trivial or free
$\mathbb {O}[\sigma ]$
-stable filtration with associated graded being a direct sum of trivial or free
![]() $\mathbb {O}[\sigma ]$
-modules. For trivial
$\mathbb {O}[\sigma ]$
-modules. For trivial
![]() $\mathbb {O}[\sigma ]$
-modules, the odd Tate cohomology groups vanish by (4.1), while for free
$\mathbb {O}[\sigma ]$
-modules, the odd Tate cohomology groups vanish by (4.1), while for free
![]() $\mathbb {O}[\sigma ]$
-modules, all the Tate cohomology groups vanish. Hence, all odd Tate cohomology groups vanish by the long exact sequence for Tate cohomology (§3.4.4). This shows that the Tate cohomology sheaves of
$\mathbb {O}[\sigma ]$
-modules, all the Tate cohomology groups vanish. Hence, all odd Tate cohomology groups vanish by the long exact sequence for Tate cohomology (§3.4.4). This shows that the Tate cohomology sheaves of
![]() $(i^{\lambda })^* (i_{\lambda }^Y)^* \mathcal {E}$
are supported in degrees congruent to
$(i^{\lambda })^* (i_{\lambda }^Y)^* \mathcal {E}$
are supported in degrees congruent to
![]() $\dagger _Y(Y_\lambda ) \pmod {2}$
.
$\dagger _Y(Y_\lambda ) \pmod {2}$
.
To show that
![]() $(i^{\lambda })^! (i_{\lambda }^Y)^! \mathcal {E}$
also has Tate cohomology sheaves supported in degrees congruent to
$(i^{\lambda })^! (i_{\lambda }^Y)^! \mathcal {E}$
also has Tate cohomology sheaves supported in degrees congruent to
![]() $\dagger _Y(\lambda ) \pmod {2}$
, we make a similar analogous argument using (4.5) instead. This shows that
$\dagger _Y(\lambda ) \pmod {2}$
, we make a similar analogous argument using (4.5) instead. This shows that
![]() $ \mathbb {T}^* (i^{\lambda })^* (i_{\lambda }^Y)^! \mathcal {E}$
lies in degrees congruent to
$ \mathbb {T}^* (i^{\lambda })^* (i_{\lambda }^Y)^! \mathcal {E}$
lies in degrees congruent to
![]() $\dagger _Y(Y_\lambda )\ \pmod {2}$
, and then we conclude by observing that
$\dagger _Y(Y_\lambda )\ \pmod {2}$
, and then we conclude by observing that
![]() $(i^{\lambda })^* (i_{\lambda }^Y)^! \mathcal {E}$
differs from
$(i^{\lambda })^* (i_{\lambda }^Y)^! \mathcal {E}$
differs from
![]() $(i^{\lambda })^! (i_{\lambda }^Y)^! \mathcal {E}$
by an even shift (and twist) by the Gysin isomorphism, which applies because the strata are assumed to be smooth (noting that the smoothness of
$(i^{\lambda })^! (i_{\lambda }^Y)^! \mathcal {E}$
by an even shift (and twist) by the Gysin isomorphism, which applies because the strata are assumed to be smooth (noting that the smoothness of
![]() $Z_\lambda $
follows from the smoothness of
$Z_\lambda $
follows from the smoothness of
![]() $Y_\lambda $
by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.8.11], so
$Y_\lambda $
by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.8.11], so
![]() $Z_\lambda \hookrightarrow Y_\lambda $
is a regular embedding).
$Z_\lambda \hookrightarrow Y_\lambda $
is a regular embedding).
For an
![]() $\mathbb {O}$
-linear abelian category
$\mathbb {O}$
-linear abelian category
![]() $\mathsf {C}$
, with all Hom-spaces being free
$\mathsf {C}$
, with all Hom-spaces being free
![]() $\mathbb {O}$
-modules, we abbreviate
$\mathbb {O}$
-modules, we abbreviate
Lemma 4.16. Suppose that all the strata
![]() $Y_{\lambda }$
are simply connected and all parity sheaves
$Y_{\lambda }$
are simply connected and all parity sheaves
![]() $\mathcal {E}(\lambda , \mathcal {L})$
exist for all
$\mathcal {E}(\lambda , \mathcal {L})$
exist for all
![]() $Y_\lambda \in S$
. Then we have that
$Y_\lambda \in S$
. Then we have that
Proof. To see that the functor is well defined, we note the following:
-
• The Hom-spaces of
 $\mathrm {Parity}^0_{S, \sigma }(Y; \mathbb {O}) $
are all free
$\mathrm {Parity}^0_{S, \sigma }(Y; \mathbb {O}) $
are all free
 $\mathbb {O}$
-modules by [Reference Juteau, Mautner and WilliamsonJMW14, Remark 2.7], so that the domain is well defined.
$\mathbb {O}$
-modules by [Reference Juteau, Mautner and WilliamsonJMW14, Remark 2.7], so that the domain is well defined. -
• The functor lands in parity sheaves since the modular reduction of a
 $\mathbb {O}$
-parity sheaf is a k-parity sheaf by Remark 4.6.
$\mathbb {O}$
-parity sheaf is a k-parity sheaf by Remark 4.6.
It is essentially surjective because every k-parity sheaf lifts to a
![]() $\mathbb {O}$
-parity sheaf under our assumption that all parity sheaves exist and all strata are simply connected (which implies that all k-local systems on strata lift to
$\mathbb {O}$
-parity sheaf under our assumption that all parity sheaves exist and all strata are simply connected (which implies that all k-local systems on strata lift to
![]() $\mathbb {O}$
since they are trivial). The fact that the functor is fully faithful follows from [Reference Juteau, Mautner and WilliamsonJMW14, (2.39)].
$\mathbb {O}$
since they are trivial). The fact that the functor is fully faithful follows from [Reference Juteau, Mautner and WilliamsonJMW14, (2.39)].
4.6.3 The base change functor
We return now to the base change setup of §4.6.1, with
![]() $\mathbf {F}$
separably closed. Let
$\mathbf {F}$
separably closed. Let
![]() $\mathcal {F} \in \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
. Then
$\mathcal {F} \in \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
. Then
![]() $\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
is perverse since p is good for
$\mathcal {F} \in \operatorname {\mathrm {P}}_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
is perverse since p is good for
![]() $\widehat {G}$
(this is a part of Theorem 4.8), and
$\widehat {G}$
(this is a part of Theorem 4.8), and
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F}) \in \operatorname {\mathrm {Parity}}^0_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
is a parity sheaf by [Reference Juteau, Mautner and WilliamsonJMW16, Theorem 1.5]. Furthermore, the
$\operatorname {\mathrm {Nm}}(\mathcal {F}) \in \operatorname {\mathrm {Parity}}^0_{L^+G \rtimes \sigma }(\operatorname {\mathrm {Gr}}_G; \mathbb {O})$
is a parity sheaf by [Reference Juteau, Mautner and WilliamsonJMW16, Theorem 1.5]. Furthermore, the
![]() $\sigma $
-equivariant structure on
$\sigma $
-equivariant structure on
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F})$
satisfies the assumption (*) of Proposition 4.15 by Lemma 4.14.
$\operatorname {\mathrm {Nm}}(\mathcal {F})$
satisfies the assumption (*) of Proposition 4.15 by Lemma 4.14.
The Schubert cells of
![]() $\operatorname {\mathrm {Gr}}_G$
are indexed by tuples
$\operatorname {\mathrm {Gr}}_G$
are indexed by tuples
![]() $\lambda := (\lambda _1, \ldots , \lambda _p) \in X_*(G)^+$
, with each
$\lambda := (\lambda _1, \ldots , \lambda _p) \in X_*(G)^+$
, with each
![]() $\lambda _i \in X_*(H)^+$
, and we have
$\lambda _i \in X_*(H)^+$
, and we have
 $$\begin{align*}\begin{cases} \operatorname{\mathrm{Gr}}_G^{\lambda} \cap \operatorname{\mathrm{Gr}}_H = \operatorname{\mathrm{Gr}}_H^{\lambda_1} & \lambda = (\lambda_1, \ldots, \lambda_1), \\ \operatorname{\mathrm{Gr}}_G^{\lambda} \cap \operatorname{\mathrm{Gr}}_H = \emptyset & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} \operatorname{\mathrm{Gr}}_G^{\lambda} \cap \operatorname{\mathrm{Gr}}_H = \operatorname{\mathrm{Gr}}_H^{\lambda_1} & \lambda = (\lambda_1, \ldots, \lambda_1), \\ \operatorname{\mathrm{Gr}}_G^{\lambda} \cap \operatorname{\mathrm{Gr}}_H = \emptyset & \text{otherwise.} \end{cases} \end{align*}$$
We claim that as long as
![]() $p>2$
, the induced pariversity coincides with the dimension pariversity on
$p>2$
, the induced pariversity coincides with the dimension pariversity on
![]() $\operatorname {\mathrm {Gr}}_H$
– that is, for
$\operatorname {\mathrm {Gr}}_H$
– that is, for
![]() $\lambda = (\lambda _1, \ldots , \lambda _p) \in X_*(G)^+$
, we have
$\lambda = (\lambda _1, \ldots , \lambda _p) \in X_*(G)^+$
, we have
This will imply the following:
-
1. We may apply Proposition 4.15 to deduce that
 $\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F})) \in \operatorname {\mathrm {Parity}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}})$
is Tate-parity with respect to the dimension pariversity on
$\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F})) \in \operatorname {\mathrm {Parity}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}})$
is Tate-parity with respect to the dimension pariversity on
 $\operatorname {\mathrm {Gr}}_H$
.
$\operatorname {\mathrm {Gr}}_H$
. -
2.
 $\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F})) \in \operatorname {\mathrm {Parity}}^0_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}})$
(i.e., is normalized).
$\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F})) \in \operatorname {\mathrm {Parity}}^0_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}})$
(i.e., is normalized).
To prove the claim, we may focus on the case where
![]() $\lambda _1 = \ldots = \lambda _p$
or else the statement is vacuous. By [Reference ZhuZhu17, Proposition 2.1.5], we have
$\lambda _1 = \ldots = \lambda _p$
or else the statement is vacuous. By [Reference ZhuZhu17, Proposition 2.1.5], we have
![]() $\dim \operatorname {\mathrm {Gr}}_G^{\lambda } = \langle 2\rho _G, \lambda \rangle $
. So we just have to verify that
$\dim \operatorname {\mathrm {Gr}}_G^{\lambda } = \langle 2\rho _G, \lambda \rangle $
. So we just have to verify that
![]() $\langle 2 \rho _G , (\lambda _1, \ldots , \lambda _1) \rangle \equiv \langle 2\rho _H, \lambda _1 \rangle\ \pmod {2}$
. Indeed,
$\langle 2 \rho _G , (\lambda _1, \ldots , \lambda _1) \rangle \equiv \langle 2\rho _H, \lambda _1 \rangle\ \pmod {2}$
. Indeed,
![]() $\rho _G = (\rho _H, \ldots , \rho _H)$
, so
$\rho _G = (\rho _H, \ldots , \rho _H)$
, so
![]() $\langle 2 \rho _G , (\lambda _1, \ldots , \lambda _1) \rangle = p \langle 2 \rho _H, \lambda _1 \rangle $
, and p is odd.
$\langle 2 \rho _G , (\lambda _1, \ldots , \lambda _1) \rangle = p \langle 2 \rho _H, \lambda _1 \rangle $
, and p is odd.
Thanks to points (1) and (2) above, we can apply the lifting functor L to
![]() $\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F}))$
. By Lemma 4.16, the composite functor
$\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\mathcal {F}))$
. By Lemma 4.16, the composite functor
![]() $L \circ \operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
factors uniquely through a functor
$L \circ \operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
factors uniquely through a functor
![]() $\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G;k) \rightarrow \mathrm {Parity}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; k)$
.
$\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G;k) \rightarrow \mathrm {Parity}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; k)$
.
Construction 4.17 (Frobenius twist of categories).
Let
![]() $\operatorname {\mathrm {Frob}}$
be the absolute Frobenius of k. Given a k-linear category
$\operatorname {\mathrm {Frob}}$
be the absolute Frobenius of k. Given a k-linear category
![]() $\mathsf {C}$
, there is another k-linear category
$\mathsf {C}$
, there is another k-linear category
![]() $\mathsf {C}^{(p)} := \mathsf {C} \otimes _{k, \operatorname {\mathrm {Frob}}} k$
. Concretely, it is equivalent to the category which has the same objects as
$\mathsf {C}^{(p)} := \mathsf {C} \otimes _{k, \operatorname {\mathrm {Frob}}} k$
. Concretely, it is equivalent to the category which has the same objects as
![]() $\mathsf {C}$
, and morphisms
$\mathsf {C}$
, and morphisms
The tautological map
![]() $\operatorname {\mathrm {Hom}}_{\mathsf {C}}(x,y) \rightarrow \operatorname {\mathrm {Hom}}_{\mathsf {C}}(x,y)^{(p)}$
is
$\operatorname {\mathrm {Hom}}_{\mathsf {C}}(x,y) \rightarrow \operatorname {\mathrm {Hom}}_{\mathsf {C}}(x,y)^{(p)}$
is
![]() $\operatorname {\mathrm {Frob}}$
-semilinear over k and induces an equivalence
$\operatorname {\mathrm {Frob}}$
-semilinear over k and induces an equivalence
![]() $\operatorname {\mathrm {Frob}}_{\mathsf {C}} \colon \mathsf {C} \xrightarrow {\sim } \mathsf {C}^{(p)}$
, which is
$\operatorname {\mathrm {Frob}}_{\mathsf {C}} \colon \mathsf {C} \xrightarrow {\sim } \mathsf {C}^{(p)}$
, which is
![]() $\operatorname {\mathrm {Frob}}$
-semilinear. The functor
$\operatorname {\mathrm {Frob}}$
-semilinear. The functor
![]() $\operatorname {\mathrm {Frob}}_{\mathsf {C}} \colon \mathsf {C} \rightarrow \mathsf {C}^{(p)}$
is characterized by the universal property that any
$\operatorname {\mathrm {Frob}}_{\mathsf {C}} \colon \mathsf {C} \rightarrow \mathsf {C}^{(p)}$
is characterized by the universal property that any
![]() $\operatorname {\mathrm {Frob}}$
-semilinear functor
$\operatorname {\mathrm {Frob}}$
-semilinear functor
![]() $F \colon \mathsf {C} \rightarrow \mathsf {D}$
(meaning a functor between k-linear categories that is
$F \colon \mathsf {C} \rightarrow \mathsf {D}$
(meaning a functor between k-linear categories that is
![]() $\operatorname {\mathrm {Frob}}$
-semilinear over k on morphisms) factors uniquely through a k-linear functor
$\operatorname {\mathrm {Frob}}$
-semilinear over k on morphisms) factors uniquely through a k-linear functor
![]() $\mathsf {C}^{(p)} \rightarrow \mathsf {D}$
.
$\mathsf {C}^{(p)} \rightarrow \mathsf {D}$
.

Now, given a presentation
for some
![]() $\mathbf {F}_p$
-linear category
$\mathbf {F}_p$
-linear category
![]() $\mathsf {C}_0$
, then there is another k-linear equivalence
$\mathsf {C}_0$
, then there is another k-linear equivalence
![]() $ \mathsf {C} \xrightarrow {\sim } \mathsf {C}^{(p)}$
, which with reference to (4.6) is the tensor product of
$ \mathsf {C} \xrightarrow {\sim } \mathsf {C}^{(p)}$
, which with reference to (4.6) is the tensor product of
![]() $\operatorname {\mathrm {Id}}_{\mathsf {C}_0}$
with the k-linear equivalence
$\operatorname {\mathrm {Id}}_{\mathsf {C}_0}$
with the k-linear equivalence
![]() $\operatorname {\mathrm {Vect}}_{/k}^{(p)} \cong \operatorname {\mathrm {Vect}}_{/k}$
induced by the k-linear isomorphism
$\operatorname {\mathrm {Vect}}_{/k}^{(p)} \cong \operatorname {\mathrm {Vect}}_{/k}$
induced by the k-linear isomorphism
![]() $k \otimes _{\operatorname {\mathrm {Frob}}, k} k \cong k$
. Therefore, (4.6) induces a
$k \otimes _{\operatorname {\mathrm {Frob}}, k} k \cong k$
. Therefore, (4.6) induces a
![]() $\operatorname {\mathrm {Frob}}$
-semilinear equivalence
$\operatorname {\mathrm {Frob}}$
-semilinear equivalence
![]() $\operatorname {\mathrm {Frob}}_{F_0} \colon \mathsf {C} \xrightarrow {\sim } \mathsf {C}$
.
$\operatorname {\mathrm {Frob}}_{F_0} \colon \mathsf {C} \xrightarrow {\sim } \mathsf {C}$
.
Definition 4.18. We define
to be the functor unique filling in the commutative diagram

One more step is required to define what we call the base change functor
![]() $\mathsf {BC}$
. Note that
$\mathsf {BC}$
. Note that
![]() $\mathsf {BC}^{(p)}$
is
$\mathsf {BC}^{(p)}$
is
![]() $\operatorname {\mathrm {Frob}}$
-semilinear over k; we wish to linearize it. It is evident from the definitions that the equivalence
$\operatorname {\mathrm {Frob}}$
-semilinear over k; we wish to linearize it. It is evident from the definitions that the equivalence
![]() $D(\operatorname {\mathrm {Gr}}_G; k) \cong D(\operatorname {\mathrm {Gr}}_G; \mathbf {F}_p) \otimes _{\mathbf {F}_p} k$
induces
$D(\operatorname {\mathrm {Gr}}_G; k) \cong D(\operatorname {\mathrm {Gr}}_G; \mathbf {F}_p) \otimes _{\mathbf {F}_p} k$
induces
Let
![]() $\operatorname {\mathrm {Frob}}_p := \operatorname {\mathrm {Frob}}_{F_0} \colon \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \xrightarrow {\sim } \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k)$
be the k-semilinear equivalence induced by
$\operatorname {\mathrm {Frob}}_p := \operatorname {\mathrm {Frob}}_{F_0} \colon \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \xrightarrow {\sim } \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k)$
be the k-semilinear equivalence induced by
![]() $F_0$
, as explained in Construction 4.17. We define
$F_0$
, as explained in Construction 4.17. We define
Remark 4.19. The construction of
![]() $\mathsf {BC}$
was motivated by a similar functor ‘
$\mathsf {BC}$
was motivated by a similar functor ‘
![]() $LL$
’ appearing in [Reference Leslie and LonerganLL21, §6.2], which gives a partial geometric description of the Frobenius contraction functor on
$LL$
’ appearing in [Reference Leslie and LonerganLL21, §6.2], which gives a partial geometric description of the Frobenius contraction functor on
![]() $\widehat {G}$
. Another motivation was the ‘normalized Brauer homomorphism’ of [Reference Treumann and VenkateshTV16, §4.3], which our construction categorifies.
$\widehat {G}$
. Another motivation was the ‘normalized Brauer homomorphism’ of [Reference Treumann and VenkateshTV16, §4.3], which our construction categorifies.
Theorem 4.20. Let
![]() $\operatorname {\mathrm {Res}}_{\mathsf {BC}} \colon \operatorname {\mathrm {Rep}}_k(\widehat {G}) \rightarrow \operatorname {\mathrm {Rep}}_k(\widehat {H})$
be a restriction along the diagonal embedding. We also denote by
$\operatorname {\mathrm {Res}}_{\mathsf {BC}} \colon \operatorname {\mathrm {Rep}}_k(\widehat {G}) \rightarrow \operatorname {\mathrm {Rep}}_k(\widehat {H})$
be a restriction along the diagonal embedding. We also denote by
![]() $\operatorname {\mathrm {Res}}_{\mathsf {BC}}$
the same functor restricted to the subcategories of tilting modules.
Footnote
11
The following diagram commutes:
$\operatorname {\mathrm {Res}}_{\mathsf {BC}}$
the same functor restricted to the subcategories of tilting modules.
Footnote
11
The following diagram commutes:

The proof is given in Appendix A.
The triangulated structure on
![]() $D_{L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
equips
$D_{L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
equips
![]() $\operatorname {\mathrm {Perf}}_{L^+H}(\operatorname {\mathrm {Gr}}_G; \mathcal {T}_k)$
with the notion of cone (namely, the image of a cone in
$\operatorname {\mathrm {Perf}}_{L^+H}(\operatorname {\mathrm {Gr}}_G; \mathcal {T}_k)$
with the notion of cone (namely, the image of a cone in
![]() $D_{L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
). We say that a sequence
$D_{L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
). We say that a sequence
![]() $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {C}$
in
$\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {C}$
in
![]() $D_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
is exact if the induced map
$D_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
is exact if the induced map
![]() $\mathrm {Cone}(\mathcal {A} \rightarrow \mathcal {B}) \rightarrow \mathcal {C} $
in
$\mathrm {Cone}(\mathcal {A} \rightarrow \mathcal {B}) \rightarrow \mathcal {C} $
in
![]() $\operatorname {\mathrm {Perf}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
is an isomorphism.
$\operatorname {\mathrm {Perf}}_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
is an isomorphism.
Lemma 4.21. The composite functor
is exact (i.e., sends exact sequences to exact sequences in the above sense).
The proof requires some notions from Appendix A and will be postponed to §A.6.
4.6.4 Equivariantization and Galois descent
Assuming Theorem 4.20, let us give a few variants related to descent to a ground field which is not separably closed. Suppose H base changed from some subfield
![]() $\mathbf {F}_0 \subset \mathbf {F}$
, and
$\mathbf {F}_0 \subset \mathbf {F}$
, and
![]() $G = \operatorname {\mathrm {Res}}_{\mathbf {E}_0/\mathbf {F}_0} (H_{\mathbf {E}_0})$
for some Galois extension
$G = \operatorname {\mathrm {Res}}_{\mathbf {E}_0/\mathbf {F}_0} (H_{\mathbf {E}_0})$
for some Galois extension
![]() $\mathbf {E}_0/\mathbf {F}_0$
with Galois group
$\mathbf {E}_0/\mathbf {F}_0$
with Galois group
![]() $\mathbf {Z}/p\mathbf {Z}$
. Then
$\mathbf {Z}/p\mathbf {Z}$
. Then
![]() $G_{\mathbf {F}} \approx (H_{\mathbf {F}})^p$
and
$G_{\mathbf {F}} \approx (H_{\mathbf {F}})^p$
and
![]() $\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
acts on
$\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
acts on
![]() $H_{\mathbf {F}},G_{\mathbf {F}}$
and therefore also on
$H_{\mathbf {F}},G_{\mathbf {F}}$
and therefore also on
![]() $\operatorname {\mathrm {Gr}}_{H, {\mathbf {F}}}, \operatorname {\mathrm {Gr}}_{G, {\mathbf {F}}}$
.
$\operatorname {\mathrm {Gr}}_{H, {\mathbf {F}}}, \operatorname {\mathrm {Gr}}_{G, {\mathbf {F}}}$
.
Lemma 4.22 (Galois equivariance).
In the situation above, the functor
is equivariant with respect to the action of
![]() $\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
.
$\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
.
Proof. The constituent functors
![]() $\operatorname {\mathrm {Nm}}$
,
$\operatorname {\mathrm {Nm}}$
,
![]() $i^*$
,
$i^*$
,
![]() $\mathbb {T}^*$
and L are all
$\mathbb {T}^*$
and L are all
![]() $\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariant, as is
$\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariant, as is
![]() $\operatorname {\mathrm {Frob}}_p^{-1}$
. It remains only to see that the dashed arrow in (4.7) is
$\operatorname {\mathrm {Frob}}_p^{-1}$
. It remains only to see that the dashed arrow in (4.7) is
![]() $\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariant. This follows because
$\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariant. This follows because
![]() $L \circ \operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
and
$L \circ \operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
and
![]() $\mathbb {F}$
both have this property, and
$\mathbb {F}$
both have this property, and
![]() $\mathbb {F}$
is essentially surjective and full.
$\mathbb {F}$
is essentially surjective and full.
We refer to [Reference Drinfeld, Gelaki, Nikshych and OstrikDGNO10] for the theory of ‘equivariantization’ and ‘de-equivariantization’ of categories. Given a group
![]() $\Gamma $
acting on categories
$\Gamma $
acting on categories
![]() $\mathsf {C}, \mathsf {D}$
and a
$\mathsf {C}, \mathsf {D}$
and a
![]() $\Gamma $
-equivariant functor
$\Gamma $
-equivariant functor
![]() $F \colon \mathsf {C} \rightarrow \mathsf {D}$
, the
$F \colon \mathsf {C} \rightarrow \mathsf {D}$
, the
![]() $\Gamma $
-equivariantization of F is the functor
$\Gamma $
-equivariantization of F is the functor
![]() $F^{B \Gamma } \colon \mathsf {C}^{B \Gamma } \rightarrow \mathsf {D}^{B \Gamma }$
. If
$F^{B \Gamma } \colon \mathsf {C}^{B \Gamma } \rightarrow \mathsf {D}^{B \Gamma }$
. If
![]() $\mathsf {C}$
and
$\mathsf {C}$
and
![]() $\mathsf {D}$
are derived categories of sheaves and F is induced by geometric operations that are
$\mathsf {D}$
are derived categories of sheaves and F is induced by geometric operations that are
![]() $\Gamma $
-equivariant, then the equivariantization construction exists for equivariant derived categories. (We make this remark because if the
$\Gamma $
-equivariant, then the equivariantization construction exists for equivariant derived categories. (We make this remark because if the
![]() $\Gamma $
-equivariantization of a derived category is not the same as the
$\Gamma $
-equivariantization of a derived category is not the same as the
![]() $\Gamma $
-equivariant derived category; it is the latter that we want to consider.)
$\Gamma $
-equivariant derived category; it is the latter that we want to consider.)
Thanks to Lemma 4.22, the equivariantization of
![]() $\mathsf {BC}$
induces
$\mathsf {BC}$
induces
We define
![]() $\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_{G, \mathbf {F}_0};k) := \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_{G, \mathbf {F}}; k)^{B\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)} $
and similarly for H (note that in §4.1, parity sheaves were only defined for varieties over separably closed fields since the axioms of a JMW stratification would not otherwise be satisfied). We define
$\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_{G, \mathbf {F}_0};k) := \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_{G, \mathbf {F}}; k)^{B\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)} $
and similarly for H (note that in §4.1, parity sheaves were only defined for varieties over separably closed fields since the axioms of a JMW stratification would not otherwise be satisfied). We define
![]() $\operatorname {\mathrm {Tilt}}_k({}^L G)$
to be the subcategory of
$\operatorname {\mathrm {Tilt}}_k({}^L G)$
to be the subcategory of
![]() $\operatorname {\mathrm {Rep}}_k({}^L G)$
consisting of representations whose restriction to
$\operatorname {\mathrm {Rep}}_k({}^L G)$
consisting of representations whose restriction to
![]() $\widehat {G}$
is tilting and
$\widehat {G}$
is tilting and
![]() $\mathrm {Tilt}_k({}^L G^{\operatorname {\mathrm {geom}}})$
to be the full subcategory of
$\mathrm {Tilt}_k({}^L G^{\operatorname {\mathrm {geom}}})$
to be the full subcategory of
![]() $\operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {geom}}})$
consisting of representations whose restriction to
$\operatorname {\mathrm {Rep}}_k({}^L G^{\operatorname {\mathrm {geom}}})$
consisting of representations whose restriction to
![]() $\widehat {G}$
is tilting; then
$\widehat {G}$
is tilting; then
![]() $\mathrm {Tilt}_k({}^L G^{\operatorname {\mathrm {geom}}}) \cong \operatorname {\mathrm {Tilt}}_k(\widehat {G})^{\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0), \operatorname {\mathrm {geom}}}$
, and similarly for
$\mathrm {Tilt}_k({}^L G^{\operatorname {\mathrm {geom}}}) \cong \operatorname {\mathrm {Tilt}}_k(\widehat {G})^{\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0), \operatorname {\mathrm {geom}}}$
, and similarly for
![]() ${}^L H$
.
${}^L H$
.
Then applying
![]() $\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariantization to Theorem 4.20 yields:
$\operatorname {\mathrm {Aut}}(\mathbf {F}/\mathbf {F}_0)$
-equivariantization to Theorem 4.20 yields:
Corollary 4.23. The following diagram is commutative.

4.6.5
Let
![]() $H/\mathbf {F}_0$
and
$H/\mathbf {F}_0$
and
![]() $G/\mathbf {F}_0$
be as before. The following compatibility statement will be needed later.
$G/\mathbf {F}_0$
be as before. The following compatibility statement will be needed later.
Lemma 4.24. The cube

commutes, where L is lifting functor
![]() $L \colon \operatorname {\mathrm {Parity}}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}}) \rightarrow \operatorname {\mathrm {Parity}}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; k)$
from §4.4, and the unlabeled arrow is defined as the one that makes the top face commute. (It exists by the universal property of the categorical tensor product.)
$L \colon \operatorname {\mathrm {Parity}}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_{\mathbb {O}}) \rightarrow \operatorname {\mathrm {Parity}}^0_{L^+H}(\operatorname {\mathrm {Gr}}_H; k)$
from §4.4, and the unlabeled arrow is defined as the one that makes the top face commute. (It exists by the universal property of the categorical tensor product.)
Proof. The left face commutes by definition of
![]() $\mathbb {F}$
. It is obvious from the definition that the front face commutes. The bottom face commutes by compatibility of
$\mathbb {F}$
. It is obvious from the definition that the front face commutes. The bottom face commutes by compatibility of
![]() $\operatorname {\mathrm {Psm}}$
with tensoring coefficients. The top face commutes by definition.
$\operatorname {\mathrm {Psm}}$
with tensoring coefficients. The top face commutes by definition.
To see that the right face commutes, consider the diagram

The right square of (4.9) is the right square of the cube (4.8), which we want to show commutes. Since the middle column is a Verdier quotient of the left column, it suffices to show that the outer square of (4.9) commutes. Next, note that the composite of the upper horizontal arrows in (4.9) is the modular reduction functor
![]() $\mathbb {F}$
by definition (4.3), so we can factor the outer square of (4.9) as the outer quadrilateral in the diagram below.
$\mathbb {F}$
by definition (4.3), so we can factor the outer square of (4.9) as the outer quadrilateral in the diagram below.

Obviously the commutativity of the outer quadilateral follows from the commutativity of the inner rectangle, which is then immediate from the definition of
![]() $\mathbb {F}$
.
$\mathbb {F}$
.
It remains to show that the back face commutes. Consider juxtaposing the top and back faces of cube (4.8) to get

We want to show that the lower square commutes. The composite vertical arrows on left and right columns are both the modular reduction functor
![]() $\mathbb {F}$
from
$\mathbb {F}$
from
![]() $\mathbb {O}$
-coefficients to k coefficients, so the outer square commutes. The dashed arrow is defined as the k-linearization of
$\mathbb {O}$
-coefficients to k coefficients, so the outer square commutes. The dashed arrow is defined as the k-linearization of
![]() $L \circ \operatorname {\mathrm {Psm}}$
, noting that
$L \circ \operatorname {\mathrm {Psm}}$
, noting that
![]() $\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \cong \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O}) \otimes _{\mathbb {O}} k$
. Therefore, the right-then-down (resp. down-then-right) composite functor in the lower square is the k-linearization of the right-then-down (resp. down-then-right) composite functor in the upper square, so the commutativity of the lower square follows from that of the upper square, completing the proof.
$\operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; k) \cong \operatorname {\mathrm {Parity}}^0_{L^+G}(\operatorname {\mathrm {Gr}}_G; \mathbb {O}) \otimes _{\mathbb {O}} k$
. Therefore, the right-then-down (resp. down-then-right) composite functor in the lower square is the k-linearization of the right-then-down (resp. down-then-right) composite functor in the upper square, so the commutativity of the lower square follows from that of the upper square, completing the proof.
Remark 4.25. Let us try to make some vague remarks about the utility of Lemma 4.24. The unlabeled arrow in the top face is a priori somewhat mysterious, but the Lemma says that after projecting to the Tate category, it has a simple description in terms of
![]() $\operatorname {\mathrm {Psm}}$
. Later, we will take Tate cohomology with coefficients indexed by the type of parity sheaves constructed in this section. Note that Tate cohomology factors through the projection of these sheaves to the Tate category. Therefore, the computation of Tate cohomology is not so sensitive to the subtleties in the constructions of this section; the purpose of this section has more to do with the indexing of coefficient sheaves, in terms of the discussion of §1.3.
$\operatorname {\mathrm {Psm}}$
. Later, we will take Tate cohomology with coefficients indexed by the type of parity sheaves constructed in this section. Note that Tate cohomology factors through the projection of these sheaves to the Tate category. Therefore, the computation of Tate cohomology is not so sensitive to the subtleties in the constructions of this section; the purpose of this section has more to do with the indexing of coefficient sheaves, in terms of the discussion of §1.3.
5 On global base change
In this section, we will apply the preceding theory to moduli stacks of shtukas in the context of Lafforgue’s construction of the global Langlands parametrization for function fields. In particular, we will prove Theorem 1.6, among other results.
We briefly review the relevant parts of Lafforgue’s construction in §5.1 and §5.2. Then in §5.3, we use a variant of Lafforgue’s ideas to construct and analyze an action of the excursion action on Tate cohomology of moduli spaces of shtukas. In the situation of base change, equivariant localization mediates between the Tate cohomology of shtukas for G and for H, allowing us to relate certain excursion operators for the two groups. This is then used in §5.6 to establish the existence of base change for mod p automorphic forms; this relation will also be the crucial input for our local results in the next section.
5.1 Moduli of shtukas
We will use the theory of moduli stacks of shtukas, due to Drinfeld and generalized by Varshavsky. Here, we very briefly recall the relevant definitions in order to set notation. More comprehensive references include [Reference VarshavskyVar04] and [Reference LafforgueLaf18].
5.1.1 Shtukas
Fix a smooth projective curve X over a finite field
![]() $\mathbf {F}_{\ell }$
of characteristic
$\mathbf {F}_{\ell }$
of characteristic
![]() $\neq p$
. Let G be a smooth algebraic group scheme over X. We assume that G is generically reductive. Let
$\neq p$
. Let G be a smooth algebraic group scheme over X. We assume that G is generically reductive. Let
![]() $\stackrel {\circ }X \hookrightarrow X$
be the locus where G is reductive. For each finite set I, the stack
$\stackrel {\circ }X \hookrightarrow X$
be the locus where G is reductive. For each finite set I, the stack
![]() $\operatorname {\mathrm {Sht}}_{G,I}$
has the following functor of points on
$\operatorname {\mathrm {Sht}}_{G,I}$
has the following functor of points on
![]() $\mathbf {F}_{\ell }$
-schemes S:
$\mathbf {F}_{\ell }$
-schemes S:
 $$\begin{align*}\operatorname{\mathrm{Sht}}_{G,I} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in X^I(S) \\ \mathcal{E} = \acute{\text{e}}\text{tale }G\text{-torsor over }X \times S \\ \varphi \colon \mathcal{E}|_{X \times S - \bigcup_{i \in I} \Gamma_{x_i}} \xrightarrow{\sim} {}^{\tau} \mathcal{E}|_{X \times S - \bigcup_{i \in I} \Gamma_{x_i}} \end{array} \right\}, \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Sht}}_{G,I} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in X^I(S) \\ \mathcal{E} = \acute{\text{e}}\text{tale }G\text{-torsor over }X \times S \\ \varphi \colon \mathcal{E}|_{X \times S - \bigcup_{i \in I} \Gamma_{x_i}} \xrightarrow{\sim} {}^{\tau} \mathcal{E}|_{X \times S - \bigcup_{i \in I} \Gamma_{x_i}} \end{array} \right\}, \end{align*}$$
where
![]() $\tau $
is the Frobenius
$\tau $
is the Frobenius
![]() $\operatorname {\mathrm {Frob}}_{\ell }$
on the S factor in
$\operatorname {\mathrm {Frob}}_{\ell }$
on the S factor in
![]() $X \times S$
, and
$X \times S$
, and
![]() ${}^{\tau } \mathcal {E}$
is the pullback of
${}^{\tau } \mathcal {E}$
is the pullback of
![]() $\mathcal {E}$
under the map
$\mathcal {E}$
under the map
![]() $1 \times \tau \colon X \times S \rightarrow X \times S$
.
$1 \times \tau \colon X \times S \rightarrow X \times S$
.
Geometrically,
![]() $\operatorname {\mathrm {Sht}}_{G,I}$
has a Schubert stratification whose strata are Deligne-Mumford stacks locally of finite type. We regard it as an ind-(locally finite type) Deligne-Mumford stack.
$\operatorname {\mathrm {Sht}}_{G,I}$
has a Schubert stratification whose strata are Deligne-Mumford stacks locally of finite type. We regard it as an ind-(locally finite type) Deligne-Mumford stack.
There is a map
projecting a tuple
![]() $(\{x_i\}_{i \in I}, \mathcal {E}, \varphi _i)$
to
$(\{x_i\}_{i \in I}, \mathcal {E}, \varphi _i)$
to
![]() $\{x_i\}_{i \in I}$
. Let
$\{x_i\}_{i \in I}$
. Let
![]() $\stackrel {\circ } {\mathrm {Sht}}_{G,I} := {\mathrm {Sht}}_{G,I} \times _{X^I} (\stackrel {\circ }{X})^I$
.
$\stackrel {\circ } {\mathrm {Sht}}_{G,I} := {\mathrm {Sht}}_{G,I} \times _{X^I} (\stackrel {\circ }{X})^I$
.
5.1.2 Hecke stack
The Hecke stack
![]() $\operatorname {\mathrm {Hk}}_{G,I}$
classifies
$\operatorname {\mathrm {Hk}}_{G,I}$
classifies
 $$\begin{align*}\operatorname{\mathrm{Hk}}_{G,I} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in X^I(S) \ \\ \mathcal{E} , \mathcal{E}' = \acute{\text{e}}\text{tale }G\text{-torsors over }X \times S \\ \varphi \colon \mathcal{E}|_{X \times S - \bigcup \Gamma_{x_i}} \xrightarrow{\sim} \mathcal{E}'|_{X \times S - \bigcup \Gamma_{x_i}} \end{array} \right\}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hk}}_{G,I} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in X^I(S) \ \\ \mathcal{E} , \mathcal{E}' = \acute{\text{e}}\text{tale }G\text{-torsors over }X \times S \\ \varphi \colon \mathcal{E}|_{X \times S - \bigcup \Gamma_{x_i}} \xrightarrow{\sim} \mathcal{E}'|_{X \times S - \bigcup \Gamma_{x_i}} \end{array} \right\}. \end{align*}$$
Recall that
![]() $G \rightarrow X$
is reductive over
$G \rightarrow X$
is reductive over
![]() $\stackrel {\circ }X$
. Let
$\stackrel {\circ }X$
. Let
![]() $\stackrel {\circ }{\mathrm {Hk}}_{G,I} := {\mathrm {Hk}}_{G,I} \times _{X^I} (\stackrel {\circ }{X})^I$
. The Geometric Satake equivalence provides a functor
$\stackrel {\circ }{\mathrm {Hk}}_{G,I} := {\mathrm {Hk}}_{G,I} \times _{X^I} (\stackrel {\circ }{X})^I$
. The Geometric Satake equivalence provides a functor
![]() $\operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow D(\stackrel {\circ }{\mathrm {Hk}}_{G,I};k)$
, which we normalize as in [Reference LafforgueLaf18, Theorem 0.9].
$\operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow D(\stackrel {\circ }{\mathrm {Hk}}_{G,I};k)$
, which we normalize as in [Reference LafforgueLaf18, Theorem 0.9].
5.1.3 Satake sheaves
There is a map
![]() $\operatorname {\mathrm {Sht}}_{G,I} \rightarrow \operatorname {\mathrm {Hk}}_{G,I}$
sending
$\operatorname {\mathrm {Sht}}_{G,I} \rightarrow \operatorname {\mathrm {Hk}}_{G,I}$
sending
![]() $(\{x_i\}_{i \in I}, \mathcal {E}, \varphi )$
to
$(\{x_i\}_{i \in I}, \mathcal {E}, \varphi )$
to
![]() $(\{x_i\}_{i \in I}, \mathcal {E}, {}^{\tau } \mathcal {E}, \varphi )$
. Composing with the
$(\{x_i\}_{i \in I}, \mathcal {E}, {}^{\tau } \mathcal {E}, \varphi )$
. Composing with the
![]() $*$
-pullback through
$*$
-pullback through
![]() $\operatorname {\mathrm {Sht}}_{G,I} \rightarrow \operatorname {\mathrm {Hk}}_{G,I}$
induces a functor
$\operatorname {\mathrm {Sht}}_{G,I} \rightarrow \operatorname {\mathrm {Hk}}_{G,I}$
induces a functor
Finally, we may identify
![]() $\operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I) \xrightarrow {\sim } \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)^{B\operatorname {Gal}(F^s/F), \operatorname {\mathrm {geom}}}$
as in §2.1.4, giving a functor (cf. [Reference LafforgueLaf18, Theorem 0.11])
$\operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I) \xrightarrow {\sim } \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)^{B\operatorname {Gal}(F^s/F), \operatorname {\mathrm {geom}}}$
as in §2.1.4, giving a functor (cf. [Reference LafforgueLaf18, Theorem 0.11])
The Schubert stratification is defined by the support of the sheaves in the image of
![]() $\operatorname {\mathrm {Sat}}$
, with the closure relations corresponding to the Bruhat order. (In particular,
$\operatorname {\mathrm {Sat}}$
, with the closure relations corresponding to the Bruhat order. (In particular,
![]() $\operatorname {\mathrm {Sat}}$
lands in the derived category of sheaves constructible with respect to the Schubert stratification on
$\operatorname {\mathrm {Sat}}$
lands in the derived category of sheaves constructible with respect to the Schubert stratification on
![]() $\stackrel {\circ }{\mathrm {Sht}}_{G,I}$
.)
$\stackrel {\circ }{\mathrm {Sht}}_{G,I}$
.)
5.1.4 Level structures
For
![]() $D \subset X$
a closed finite subscheme, there are level covers
$D \subset X$
a closed finite subscheme, there are level covers
![]() $\operatorname {\mathrm {Sht}}_{G,D,I} \rightarrow \operatorname {\mathrm {Sht}}_{G,I}|_{(X \setminus D)^I}$
which parametrize the additional datum of a trivialization of
$\operatorname {\mathrm {Sht}}_{G,D,I} \rightarrow \operatorname {\mathrm {Sht}}_{G,I}|_{(X \setminus D)^I}$
which parametrize the additional datum of a trivialization of
![]() $\mathcal {E}$
over
$\mathcal {E}$
over
![]() $S \times D$
compatible with
$S \times D$
compatible with
![]() $\tau $
and
$\tau $
and
![]() $\varphi $
. Note that by definition, the ‘legs’
$\varphi $
. Note that by definition, the ‘legs’
![]() $\{x_i\}_{i \in I} \in (X \setminus D)(S)^I$
avoid D.
$\{x_i\}_{i \in I} \in (X \setminus D)(S)^I$
avoid D.
5.1.5 Iterated shtukas
Let
![]() $I_1, \ldots , I_r$
be a partition of I. We define
$I_1, \ldots , I_r$
be a partition of I. We define
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)}$
(sometimes called a moduli stack of iterated shtukas) to be the stack
$\operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)}$
(sometimes called a moduli stack of iterated shtukas) to be the stack
 $$\begin{align*}\operatorname{\mathrm{Sht}}_{G,D,I}^{(I_1, \ldots, I_r)} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in (X - D)^I(S) \\ \mathcal{E}_0,\ldots, \mathcal{E}_r = \acute{\text{e}}\text{tale }G\text{-torsors over }X \times S \\ \varphi_j \colon \mathcal{E}_{j-1}|_{X \times S - \bigcup_{i \in I_j} \Gamma_{x_i}} \xrightarrow{\sim} \mathcal{E}_{j}|_{X \times S - \bigcup_{i \in I_j} \Gamma_{x_i}} \quad j = 1, \ldots, r \\ \varphi \colon \mathcal{E}_r \xrightarrow{\sim} {}^{\tau} \mathcal{E}_0 \\ \upsilon = \text{level structure over }D \times S \end{array} \right\}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Sht}}_{G,D,I}^{(I_1, \ldots, I_r)} \colon S \mapsto \left\{ \begin{array}{@{}c@{}} (x_i)_{i \in I} \in (X - D)^I(S) \\ \mathcal{E}_0,\ldots, \mathcal{E}_r = \acute{\text{e}}\text{tale }G\text{-torsors over }X \times S \\ \varphi_j \colon \mathcal{E}_{j-1}|_{X \times S - \bigcup_{i \in I_j} \Gamma_{x_i}} \xrightarrow{\sim} \mathcal{E}_{j}|_{X \times S - \bigcup_{i \in I_j} \Gamma_{x_i}} \quad j = 1, \ldots, r \\ \varphi \colon \mathcal{E}_r \xrightarrow{\sim} {}^{\tau} \mathcal{E}_0 \\ \upsilon = \text{level structure over }D \times S \end{array} \right\}. \end{align*}$$
Here, by ‘level structure’ we mean a trivialization of the restriction of each
![]() $\mathcal {E}_i$
over
$\mathcal {E}_i$
over
![]() $D \times S$
, compatible with the
$D \times S$
, compatible with the
![]() $\varphi _j$
and
$\varphi _j$
and
![]() $\varphi $
. There is a map
$\varphi $
. There is a map
![]() $\nu \colon \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)} \rightarrow \operatorname {\mathrm {Sht}}_{G,D,I}$
. A key property of this morphism is that it is stratified small (with respect to the Schubert stratification), which is a consequence of the same property of the convolution morphism for Beilinson-Drinfeld Grassmannians.
$\nu \colon \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)} \rightarrow \operatorname {\mathrm {Sht}}_{G,D,I}$
. A key property of this morphism is that it is stratified small (with respect to the Schubert stratification), which is a consequence of the same property of the convolution morphism for Beilinson-Drinfeld Grassmannians.
Define
and
5.1.6 Partial Frobenius
There is a partial Frobenius
![]() $F_{I_1} \colon \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, I_2, \ldots , I_r)} \rightarrow \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_2, \ldots , I_r, I_1)} $
sending
$F_{I_1} \colon \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, I_2, \ldots , I_r)} \rightarrow \operatorname {\mathrm {Sht}}_{G,D,I}^{(I_2, \ldots , I_r, I_1)} $
sending
 $$ \begin{align*} x_i & \mapsto \begin{cases} {}^{\tau} x_i & i \in I_1\\ x_i &\text{otherwise}\end{cases} \\ (\mathcal{E}_0, \ldots, \mathcal{E}_r) & \mapsto (\mathcal{E}_1, \ldots, \mathcal{E}_r, {}^{\tau} \mathcal{E}_0) \\ (\varphi_1, \ldots, \varphi_r) &\mapsto (\varphi_2, \ldots, \varphi_r, {}^{\tau} \varphi_1). \end{align*} $$
$$ \begin{align*} x_i & \mapsto \begin{cases} {}^{\tau} x_i & i \in I_1\\ x_i &\text{otherwise}\end{cases} \\ (\mathcal{E}_0, \ldots, \mathcal{E}_r) & \mapsto (\mathcal{E}_1, \ldots, \mathcal{E}_r, {}^{\tau} \mathcal{E}_0) \\ (\varphi_1, \ldots, \varphi_r) &\mapsto (\varphi_2, \ldots, \varphi_r, {}^{\tau} \varphi_1). \end{align*} $$
It lies over the partial Frobenius
![]() $\operatorname {\mathrm {Frob}}_{I_1}$
on
$\operatorname {\mathrm {Frob}}_{I_1}$
on
![]() $X^I$
(applying
$X^I$
(applying
![]() $\operatorname {\mathrm {Frob}}_\ell $
to the coordinates indexed by
$\operatorname {\mathrm {Frob}}_\ell $
to the coordinates indexed by
![]() $i \in I_1$
), so that the diagram below is commutative (and cartesian up to radiciel maps):
$i \in I_1$
), so that the diagram below is commutative (and cartesian up to radiciel maps):

5.1.7 Base change setup
We now consider the following ‘base change setup’. Let F be the function field of X and
![]() $H_F$
a reductive group over F. We choose a parahoric extension of
$H_F$
a reductive group over F. We choose a parahoric extension of
![]() $H_F$
to a smooth affine group scheme H over X.
$H_F$
to a smooth affine group scheme H over X.
Let
![]() $E/F$
be a cyclic extension of F having degree p, so E corresponds to the function field of a smooth projective curve
$E/F$
be a cyclic extension of F having degree p, so E corresponds to the function field of a smooth projective curve
![]() $X'$
. Define
$X'$
. Define
![]() $G := \operatorname {\mathrm {Res}}_{X'/X} (H_{X'})$
, which is an algebraic group scheme over X with generic fiber
$G := \operatorname {\mathrm {Res}}_{X'/X} (H_{X'})$
, which is an algebraic group scheme over X with generic fiber
![]() $G_F \cong \operatorname {\mathrm {Res}}_{E/F}(H_E)$
. The group scheme
$G_F \cong \operatorname {\mathrm {Res}}_{E/F}(H_E)$
. The group scheme
![]() $G \rightarrow X$
comes with an induced action of
$G \rightarrow X$
comes with an induced action of
![]() $\langle \sigma \rangle = \operatorname {\mathrm {Aut}}(X'/X)$
.
$\langle \sigma \rangle = \operatorname {\mathrm {Aut}}(X'/X)$
.
5.2 Review of V. Lafforgue’s global Langlands correspondence
Write
![]() $\Gamma := \operatorname {\mathrm {Weil}}(F, \overline {F}) = \operatorname {\mathrm {Weil}}(F^s/F)$
. In [Reference LafforgueLaf18, §13], Lafforgue constructs an action of
$\Gamma := \operatorname {\mathrm {Weil}}(F, \overline {F}) = \operatorname {\mathrm {Weil}}(F^s/F)$
. In [Reference LafforgueLaf18, §13], Lafforgue constructs an action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
on the space of cusp forms for G with coefficients in k. This has been improved by Cong Xue, who extended the action to all compactly supported functions ([Reference XueXuea, §7] for split G and [Reference XueXueb, §6] for all G).
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
on the space of cusp forms for G with coefficients in k. This has been improved by Cong Xue, who extended the action to all compactly supported functions ([Reference XueXuea, §7] for split G and [Reference XueXueb, §6] for all G).
We summarize the construction of the excursion action, as we shall make use of some of its internal aspects, and we also need to explain why it can be used to construct some excursion actions on Tate cohomology.
5.2.1 Constructing actions of the excursion algebra
We will explain an abstract setup that gives rise to actions of the excursion algebra.
Definition 5.1. Let A be a (not necessarily commutative) ring. A family of functors
![]() $H_I \colon \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_A(\Gamma ^I)$
, where I runs over (possibly empty) finite sets, is admissible if it satisfies the two conditions below.
$H_I \colon \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_A(\Gamma ^I)$
, where I runs over (possibly empty) finite sets, is admissible if it satisfies the two conditions below.
-
1. (Compatibility with fusion) For all
 $\zeta \colon I \rightarrow J$
, there is a natural isomorphism
$\zeta \colon I \rightarrow J$
, there is a natural isomorphism
 $\chi _{\zeta }$
between the functors
$\chi _{\zeta }$
between the functors
 $H_I \circ \operatorname {\mathrm {Res}}_{\zeta }$
and
$H_I \circ \operatorname {\mathrm {Res}}_{\zeta }$
and
 $\operatorname {\mathrm {Res}}_{\zeta } \circ H_J$
in the diagram (5.2)
$\operatorname {\mathrm {Res}}_{\zeta } \circ H_J$
in the diagram (5.2)
-
2. (Compatibility with composition) For
 $I' \xrightarrow {\zeta '} I \xrightarrow {\zeta } J $
, we have
$I' \xrightarrow {\zeta '} I \xrightarrow {\zeta } J $
, we have
 $\chi _{\zeta \circ \zeta '} = \chi _{\zeta } \circ \chi _{\zeta '}$
.
$\chi _{\zeta \circ \zeta '} = \chi _{\zeta } \circ \chi _{\zeta '}$
.
Construction 5.2. Let ![]() denote the trivial representation of
denote the trivial representation of
![]() ${}^L {G}$
. Given an admissible family of functors
${}^L {G}$
. Given an admissible family of functors
![]() $H_I \colon \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_A(\Gamma ^I)$
, we get an A-linear action of
$H_I \colon \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_A(\Gamma ^I)$
, we get an A-linear action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L{G})$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L{G})$
on ![]() as follows.
as follows.
For a tuple
![]() $(I, W, x, \xi , (\gamma _i)_{i \in I})$
, we define an endomorphism, which gives the image of
$(I, W, x, \xi , (\gamma _i)_{i \in I})$
, we define an endomorphism, which gives the image of
![]() $S_{I, W, x, \xi , (\gamma _i)_{i \in I}}$
in
$S_{I, W, x, \xi , (\gamma _i)_{i \in I}}$
in ![]() , by the following composition:
, by the following composition:
(Here, we again conflate the vector
![]() $x \in W^{\Delta (\widehat {G})}$
with a
$x \in W^{\Delta (\widehat {G})}$
with a
![]() $\widehat {G}$
-equivariant map
$\widehat {G}$
-equivariant map ![]() .) From the assumptions of admissibility, it is straightforward to check the relations in §2.4.2.
.) From the assumptions of admissibility, it is straightforward to check the relations in §2.4.2.
Remark 5.3. Note that it follows from admissibility that the A-module underlying ![]() for any I is identified with
for any I is identified with ![]() by
by
![]() $\chi _{\emptyset \rightarrow I}$
. Proposition 2.4 then attaches a Galois representation to each generalized eigenvector for the
$\chi _{\emptyset \rightarrow I}$
. Proposition 2.4 then attaches a Galois representation to each generalized eigenvector for the
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on ![]() . (Of course, such an eigenvector is not guaranteed to exist a priori.)
. (Of course, such an eigenvector is not guaranteed to exist a priori.)
5.2.2 Excursion action on the cohomology of shtukas
Let
![]() $\mathcal {H}_G$
be the Hecke algebra acting on
$\mathcal {H}_G$
be the Hecke algebra acting on
![]() $\operatorname {\mathrm {Sht}}_{G, D,I}$
; it is the tensor product of local Hecke algebras with the level structure dictated by D. For any finite set I, we have a map
$\operatorname {\mathrm {Sht}}_{G, D,I}$
; it is the tensor product of local Hecke algebras with the level structure dictated by D. For any finite set I, we have a map
remembering the points of the curve indexed by I (which avoid D by definition). Let
![]() $\eta ^I$
denote the generic point of
$\eta ^I$
denote the generic point of
![]() $X^I$
and
$X^I$
and
![]() $\overline {\eta ^I}$
the spectrum of an algebraic closure, viewed as a geometric generic point of
$\overline {\eta ^I}$
the spectrum of an algebraic closure, viewed as a geometric generic point of
![]() $X^I$
. When I is a singleton, we will just abbreviate these by
$X^I$
. When I is a singleton, we will just abbreviate these by
![]() $\eta $
and
$\eta $
and
![]() $\overline {\eta }$
.
$\overline {\eta }$
.
We will define a family of functors indexed by finite sets I:
sending
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I)$
to
$V \in \operatorname {\mathrm {Rep}}_k(({}^L G^{\operatorname {\mathrm {alg}}})^I)$
to
Note that a priori
![]() $H_I^j(V)$
has an action of
$H_I^j(V)$
has an action of
![]() $\pi _1(\eta ^{I}, \overline {\eta ^{I}})$
, which mapsFootnote
12
to
$\pi _1(\eta ^{I}, \overline {\eta ^{I}})$
, which mapsFootnote
12
to
![]() $\Gamma ^{I}$
but neither injectively nor surjectively.
$\Gamma ^{I}$
but neither injectively nor surjectively.
5.2.3
We explain why the action of
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
extends canonically to an action of
$\pi _1(\eta ^I, \overline {\eta ^I})$
extends canonically to an action of
![]() $\Gamma ^I$
. Assume I is nonempty, since otherwise there is nothing to prove. The Satake functor of §5.1.3 generalizes to a functor
$\Gamma ^I$
. Assume I is nonempty, since otherwise there is nothing to prove. The Satake functor of §5.1.3 generalizes to a functor
such that the map
has the property that
![]() $R\nu _! \operatorname {\mathrm {Sat}}^{(I_1, \ldots , I_r)}(V) \cong \operatorname {\mathrm {Sat}}(V)$
. Furthermore, there are natural isomorphisms
$R\nu _! \operatorname {\mathrm {Sat}}^{(I_1, \ldots , I_r)}(V) \cong \operatorname {\mathrm {Sat}}(V)$
. Furthermore, there are natural isomorphisms
where
![]() $F_{I_1}$
is the partial Frobenius from §5.1.6.
$F_{I_1}$
is the partial Frobenius from §5.1.6.
Write
![]() $I = \{1, \ldots , n\}$
. Thanks to the above properties and (5.1), the partial Frobenius maps on
$I = \{1, \ldots , n\}$
. Thanks to the above properties and (5.1), the partial Frobenius maps on
![]() $\operatorname {\mathrm {Sht}}_{G,D, I}^{(\{1\}, \ldots , \{n\})}$
then induce maps
$\operatorname {\mathrm {Sht}}_{G,D, I}^{(\{1\}, \ldots , \{n\})}$
then induce maps
That equips
![]() $H_I^j(V)$
with the action of the larger group
$H_I^j(V)$
with the action of the larger group
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) $
that we now recall, summarizing [Reference LafforgueLaf18, Remarque 8.18]. Let
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) $
that we now recall, summarizing [Reference LafforgueLaf18, Remarque 8.18]. Let
![]() $F^I$
denote the function field of
$F^I$
denote the function field of
![]() $X^I$
, so
$X^I$
, so
![]() $\eta ^I = \operatorname {\mbox {Spec }} F^I$
, and
$\eta ^I = \operatorname {\mbox {Spec }} F^I$
, and
![]() $\overline {F^I}$
an algebraic closure, so we may take
$\overline {F^I}$
an algebraic closure, so we may take
![]() $\overline {\eta ^I} = \operatorname {\mbox {Spec }} \overline {F^I}$
. Write
$\overline {\eta ^I} = \operatorname {\mbox {Spec }} \overline {F^I}$
. Write
![]() $(F^I)^{\operatorname {\mathrm {perf}}}$
for the perfect closure of
$(F^I)^{\operatorname {\mathrm {perf}}}$
for the perfect closure of
![]() $F^I$
and
$F^I$
and
![]() $\operatorname {\mathrm {Frob}}_{\{i\}}$
for the ‘partial Frobenius’ automorphism of
$\operatorname {\mathrm {Frob}}_{\{i\}}$
for the ‘partial Frobenius’ automorphism of
![]() $(F^I)^{\operatorname {\mathrm {perf}}}$
induced by
$(F^I)^{\operatorname {\mathrm {perf}}}$
induced by
![]() $\operatorname {\mathrm {Frob}}_\ell $
on the ith factor. We define
$\operatorname {\mathrm {Frob}}_\ell $
on the ith factor. We define
Writing
![]() $\pi _1^{\operatorname {\mathrm {geom}}}(\eta ^I, \overline {\eta ^I}) := \ker (\pi _1(\eta ^I, \overline {\eta ^I}) \xrightarrow {\deg } \widehat {\mathbf {Z}})$
, this fits into an extension
$\pi _1^{\operatorname {\mathrm {geom}}}(\eta ^I, \overline {\eta ^I}) := \ker (\pi _1(\eta ^I, \overline {\eta ^I}) \xrightarrow {\deg } \widehat {\mathbf {Z}})$
, this fits into an extension
Fixing a specialization morphism
![]() $\overline {\eta ^I} \rightsquigarrow \Delta (\eta ^{\{1\}})$
induces a surjection
$\overline {\eta ^I} \rightsquigarrow \Delta (\eta ^{\{1\}})$
induces a surjection
A form of Drinfeld’s Lemma [Reference XueXuea, Lemma 7.4.2] is used to show that the action of
![]() $\operatorname {\mathrm {FWeil}} (\eta ^I, \overline {\eta ^I})$
on
$\operatorname {\mathrm {FWeil}} (\eta ^I, \overline {\eta ^I})$
on
![]() $H_I^j(V)$
factors through
$H_I^j(V)$
factors through
![]() $\operatorname {\mathrm {Weil}}(F^s/F)^I$
.
$\operatorname {\mathrm {Weil}}(F^s/F)^I$
.
Example 5.4. Let us unravel
By Remark 5.3, the underlying Hecke module of ![]() is isomorphic to
is isomorphic to ![]() . According to [Reference LafforgueLaf18, Remarque 12.2], this is the space of compactly supported k-valued functions on the discrete groupoid
. According to [Reference LafforgueLaf18, Remarque 12.2], this is the space of compactly supported k-valued functions on the discrete groupoid
 $$ \begin{align} \operatorname{\mathrm{Bun}}_{G,D}(\mathbf{F}_\ell) = \coprod_{\alpha \in \ker^1(F,G)} \left( G_{\alpha}(F) \backslash G_{\alpha}(\mathbf{A}_F) / \prod_v K_v \right), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Bun}}_{G,D}(\mathbf{F}_\ell) = \coprod_{\alpha \in \ker^1(F,G)} \left( G_{\alpha}(F) \backslash G_{\alpha}(\mathbf{A}_F) / \prod_v K_v \right), \end{align} $$
where
![]() $G_{\alpha }$
is the pure inner form of G corresponding to
$G_{\alpha }$
is the pure inner form of G corresponding to
![]() $\alpha $
,
$\alpha $
,
![]() $K_v = G(\mathcal {O}_v)$
for
$K_v = G(\mathcal {O}_v)$
for
![]() $v \notin D$
, and
$v \notin D$
, and
![]() $K_v = \ker (G(\mathcal {O}_v) \rightarrow G_D)$
.
$K_v = \ker (G(\mathcal {O}_v) \rightarrow G_D)$
.
The excursion action preserves the decomposition (5.6) and so gives an action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on each
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on each ![]() .
.
The family of functors
![]() $H_I^j$
is admissible; this is an immediate consequence of the fact that
$H_I^j$
is admissible; this is an immediate consequence of the fact that
![]() $\operatorname {\mathrm {Sat}}$
is already compatible with composition and fusion. Hence, Construction 5.2 applies to define an action of
$\operatorname {\mathrm {Sat}}$
is already compatible with composition and fusion. Hence, Construction 5.2 applies to define an action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. Elements of the image of
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. Elements of the image of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
in
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
in
![]() $\operatorname {\mathrm {End}}(C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k))$
are called ‘excursion operators’.
$\operatorname {\mathrm {End}}(C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k))$
are called ‘excursion operators’.
5.2.4 Xue’s generalization
Lafforgue defined an
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on the finite-dimensional subspace of cuspidal functions
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on the finite-dimensional subspace of cuspidal functions
![]() $C_{\mathrm {cusp}}^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k) \subset C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. This decomposes
$C_{\mathrm {cusp}}^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k) \subset C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. This decomposes
![]() $C_{\mathrm {cusp}}^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
into a direct sum of generalized eigenspaces under the action of
$C_{\mathrm {cusp}}^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
into a direct sum of generalized eigenspaces under the action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Using Proposition 2.4, this decomposition corresponds to a parametrization by Langlands parameters.
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Using Proposition 2.4, this decomposition corresponds to a parametrization by Langlands parameters.
Thanks to Xue’s extension of the action to
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G) \curvearrowright C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
, it is meaningful to speak of Langlands parameters arising from
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G) \curvearrowright C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
, it is meaningful to speak of Langlands parameters arising from
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. However, since the excursion action does not stabilize any finite-dimensional subspaces of
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
. However, since the excursion action does not stabilize any finite-dimensional subspaces of
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
unless they are contained in the space of cusp forms, we must broaden what it means to have an L-parameter ‘come from’ an automorphic function.
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
unless they are contained in the space of cusp forms, we must broaden what it means to have an L-parameter ‘come from’ an automorphic function.
Definition 5.5. We say that an L-parameter
![]() $\rho \in H^1(\operatorname {Gal}(F^s/F), \widehat {G}(k))$
arises from
$\rho \in H^1(\operatorname {Gal}(F^s/F), \widehat {G}(k))$
arises from
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
if it arises via Proposition 2.4 from the
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
if it arises via Proposition 2.4 from the
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on some irreducible Hecke-subquotient of
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-action on some irreducible Hecke-subquotient of
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
– equivalently, if the corresponding maximal ideal
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
– equivalently, if the corresponding maximal ideal
![]() $\mathfrak {m}_{\rho } \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
is in the support of
$\mathfrak {m}_{\rho } \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
is in the support of
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
as an
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
as an
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-module. We say will be called automorphic if it arises via Proposition 2.4 from
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
-module. We say will be called automorphic if it arises via Proposition 2.4 from
![]() $C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
for some D – equivalently if the corresponding maximal ideal
$C_c^{\infty }(\operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_\ell ); k)$
for some D – equivalently if the corresponding maximal ideal
![]() $\mathfrak {m}_{\rho } \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
is in the support of
$\mathfrak {m}_{\rho } \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
is in the support of
![]() $C_c^{\infty }(G_{\alpha }(F) \backslash G_{\alpha }(\mathbf {A}_F);k)$
for some
$C_c^{\infty }(G_{\alpha }(F) \backslash G_{\alpha }(\mathbf {A}_F);k)$
for some
![]() $\alpha $
.
$\alpha $
.
5.3 Excursion action on the Tate cohomology of shtukas
For a category
![]() $\mathsf {C}$
with
$\mathsf {C}$
with
![]() $\sigma $
-action, recall that we let
$\sigma $
-action, recall that we let
![]() $\mathsf {C}^{B \sigma }$
denote the category of
$\mathsf {C}^{B \sigma }$
denote the category of
![]() $\sigma $
-equivariant objects in
$\sigma $
-equivariant objects in
![]() $\mathsf {C}$
. This comes equipped with a forgetful functor to
$\mathsf {C}$
. This comes equipped with a forgetful functor to
![]() $\mathsf {C}$
.
$\mathsf {C}$
.
5.3.1 Tate cohomology of moduli of shtukas
If
![]() $\sigma $
acts on G, it induces an action
$\sigma $
acts on G, it induces an action
![]() $V \mapsto {}^{\sigma }V$
on
$V \mapsto {}^{\sigma }V$
on
![]() $\operatorname {\mathrm {Rep}}({}^L G)$
.
$\operatorname {\mathrm {Rep}}({}^L G)$
.
Given a
![]() $\sigma $
-equivariant representation
$\sigma $
-equivariant representation
![]() $V \in \operatorname {\mathrm {Rep}}_k( ({}^L G^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma }$
, we can form
$V \in \operatorname {\mathrm {Rep}}_k( ({}^L G^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma }$
, we can form
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
as above. The
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
as above. The
![]() $\sigma $
-equivariant structure on V equips this with a
$\sigma $
-equivariant structure on V equips this with a
![]() $\sigma $
-equivariant structure; more formally, because
$\sigma $
-equivariant structure; more formally, because
![]() $\operatorname {\mathrm {Sat}}$
and
$\operatorname {\mathrm {Sat}}$
and
![]() $\pi _I \colon \operatorname {\mathrm {Sht}}_{G,D,I} \rightarrow (X \setminus D)^I$
are
$\pi _I \colon \operatorname {\mathrm {Sht}}_{G,D,I} \rightarrow (X \setminus D)^I$
are
![]() $\sigma $
-equivariant,
$\sigma $
-equivariant,
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(-))$
lifts to a functor
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(-))$
lifts to a functor
![]() $ \operatorname {\mathrm {Rep}}_k( ({}^L G^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma } \rightarrow D^b((X \setminus D)^I; k)^{B\sigma }$
. Hence, we can form
$ \operatorname {\mathrm {Rep}}_k( ({}^L G^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma } \rightarrow D^b((X \setminus D)^I; k)^{B\sigma }$
. Hence, we can form
![]() $T^j(R\Gamma _c (\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)))$
, the Tate cohomology (§3.4) of
$T^j(R\Gamma _c (\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)))$
, the Tate cohomology (§3.4) of
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
. To ease notation, we will abbreviate
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
. To ease notation, we will abbreviate
Let us explain in what category we regard (5.7). Since
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
has commuting actions of
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
has commuting actions of
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
and the Hecke algebra
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
and the Hecke algebra
![]() $\mathcal {H}_G$
(the former commuting with the
$\mathcal {H}_G$
(the former commuting with the
![]() $\sigma $
-action), its Tate cohomology has commuting actions of
$\sigma $
-action), its Tate cohomology has commuting actions of
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
and of
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
and of
![]() $T^0(\mathcal {H}_G)$
, where Tate cohomology is formed with respect to the
$T^0(\mathcal {H}_G)$
, where Tate cohomology is formed with respect to the
![]() $\sigma $
-action. A priori we regard (5.7) as a
$\sigma $
-action. A priori we regard (5.7) as a
![]() $T^0( \mathcal {H}_G)[\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})]$
-module. However, in Appendix B, we will prove the following:
$T^0( \mathcal {H}_G)[\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})]$
-module. However, in Appendix B, we will prove the following:
Proposition 5.6. For any
![]() $G,D,I,V$
, the
$G,D,I,V$
, the
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-action on
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-action on
![]() $T^j (\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
factors through
$T^j (\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
factors through
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
.
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
.
It will then be natural to regard (5.7) as a
![]() $T^0 (\mathcal {H}_G)[\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I]$
-module.
$T^0 (\mathcal {H}_G)[\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I]$
-module.
Using Lemma 3.14, we deduce the following simple but important identity: if
![]() $\sigma $
acts trivially on
$\sigma $
acts trivially on
![]() $\operatorname {\mathrm {Sht}}_H$
and
$\operatorname {\mathrm {Sht}}_H$
and
![]() $\mathcal {F}$
, then
$\mathcal {F}$
, then
5.3.2 Excursion action
Since
![]() $\sigma $
acts on G, it acts on
$\sigma $
acts on G, it acts on
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
by transport of structure. Concretely, we have
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G^{\operatorname {\mathrm {alg}}})$
by transport of structure. Concretely, we have
In general, given a
![]() $k[\sigma ]$
-algebra A and an A-module M, there is a natural
$k[\sigma ]$
-algebra A and an A-module M, there is a natural
![]() $T^0(A) = A^\sigma /(N \cdot A)$
-module structure on
$T^0(A) = A^\sigma /(N \cdot A)$
-module structure on
![]() $T^*(M)$
. This equips
$T^*(M)$
. This equips ![]() with a natural
with a natural
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
-action. If all the data
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
-action. If all the data
![]() $(V, x, \xi )$
are
$(V, x, \xi )$
are
![]() $\sigma $
-equivariant, then the action of
$\sigma $
-equivariant, then the action of
![]() $S_{V, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
can be described more concretely as follows: it is given by composition
$S_{V, x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
can be described more concretely as follows: it is given by composition
Here, we used Proposition 5.6 to define the middle arrow.
5.4 Preparations for equivariant localization
5.4.1 Analysis of fixed points
We study the
![]() $\sigma $
-fixed points of
$\sigma $
-fixed points of
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}$
in anticipation of applying the theory of §3 to it.
$\operatorname {\mathrm {Sht}}_{G,D,I}$
in anticipation of applying the theory of §3 to it.
According to [Reference VarshavskyVar04, Proposition 2.16] (stated there for split G, but valid for all G by the same argument),
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}$
is exhausted by quasi-compact open substacks
$\operatorname {\mathrm {Sht}}_{G,D,I}$
is exhausted by quasi-compact open substacks
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
as
$\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
as
![]() $\mu $
runs over dominant coweights and the Harder-Narasimhan truncation
$\mu $
runs over dominant coweights and the Harder-Narasimhan truncation
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
is defined as in [Reference LafforgueLaf18, (1.3)]. The open substack is determined by the Cartesian square
$\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
is defined as in [Reference LafforgueLaf18, (1.3)]. The open substack is determined by the Cartesian square

Furthermore, for fixed
![]() $\mu $
, the Deligne-Mumford stack
$\mu $
, the Deligne-Mumford stack
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
can be presented as a quotient of a quasi-projective scheme by a finite group; for any closed point
$\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }$
can be presented as a quotient of a quasi-projective scheme by a finite group; for any closed point
![]() $x_0 \in X$
, the quasi-projective scheme can be taken to be
$x_0 \in X$
, the quasi-projective scheme can be taken to be
![]() $\operatorname {\mathrm {Sht}}_{G, D + n x_0, I}^{\leq \mu }$
for sufficiently large n relative to
$\operatorname {\mathrm {Sht}}_{G, D + n x_0, I}^{\leq \mu }$
for sufficiently large n relative to
![]() $\mu $
, and the group is then the automorphisms of the level structure. The same applies for the variants
$\mu $
, and the group is then the automorphisms of the level structure. The same applies for the variants
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)}$
.
$\operatorname {\mathrm {Sht}}_{G,D,I}^{(I_1, \ldots , I_r)}$
.
We fix the following notation below. Let
![]() $\mu $
be a coweight of H and let
$\mu $
be a coweight of H and let
![]() $\widetilde {\mu }$
be the induced coweight of G. Then we have a Cartesian square
$\widetilde {\mu }$
be the induced coweight of G. Then we have a Cartesian square

which induces the Cartesian square

Lemma 5.7. If n is sufficiently large so that
![]() $\operatorname {\mathrm {Sht}}_{H,D + nx_0,I}^{(I_1, \ldots , I_r), \leq \mu }$
and
$\operatorname {\mathrm {Sht}}_{H,D + nx_0,I}^{(I_1, \ldots , I_r), \leq \mu }$
and
![]() $\operatorname {\mathrm {Sht}}_{G,D + nx_0,I}^{(I_1, \ldots , I_r), \leq \widetilde {\mu }}$
are representable by schemes, then the diagonal map
$\operatorname {\mathrm {Sht}}_{G,D + nx_0,I}^{(I_1, \ldots , I_r), \leq \widetilde {\mu }}$
are representable by schemes, then the diagonal map
![]() $H \rightarrow G$
induces an isomorphism
$H \rightarrow G$
induces an isomorphism
Proof. For notational convenience, we just treat the case of non-iterated shtukas,
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}$
; the general case is essentially the same but with cumbersome extra notation.
$\operatorname {\mathrm {Sht}}_{G,D,I}$
; the general case is essentially the same but with cumbersome extra notation.
There is an obvious map in one direction,
![]() $\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{ \leq \mu } \rightarrow (\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }})^{\sigma }$
. We will construct the inverse.
$\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{ \leq \mu } \rightarrow (\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }})^{\sigma }$
. We will construct the inverse.
Notate the S-points of
![]() $\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }}$
as the set
$\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }}$
as the set
![]() $\{(\{x_i\}_{i \in I}, \mathcal {E}, \varphi , \upsilon )\}$
. For any S, there is an equivalence of categories between
$\{(\{x_i\}_{i \in I}, \mathcal {E}, \varphi , \upsilon )\}$
. For any S, there is an equivalence of categories between
![]() $\operatorname {\mathrm {Res}}_{X'/X}(H)$
-torsors on
$\operatorname {\mathrm {Res}}_{X'/X}(H)$
-torsors on
![]() $X_S$
and H-torsors on
$X_S$
and H-torsors on
![]() $X^{\prime }_S$
, which we denote
$X^{\prime }_S$
, which we denote
![]() $\mathcal {E} \mapsto \mathcal {E}'$
. The datum of a
$\mathcal {E} \mapsto \mathcal {E}'$
. The datum of a
![]() $\sigma $
-fixed point of
$\sigma $
-fixed point of
![]() $\operatorname {\mathrm {Bun}}_{G,D}$
translates under the above equivalence to the datum of an H-torsor
$\operatorname {\mathrm {Bun}}_{G,D}$
translates under the above equivalence to the datum of an H-torsor
![]() $\mathcal {E}'$
on
$\mathcal {E}'$
on
![]() $X^{\prime }_S$
together with an isomorphism
$X^{\prime }_S$
together with an isomorphism
![]() $h \colon \mathcal {E}' \xrightarrow {\sim } \sigma ^* \mathcal {E}'$
. We claim that, since the point
$h \colon \mathcal {E}' \xrightarrow {\sim } \sigma ^* \mathcal {E}'$
. We claim that, since the point
![]() $(\{x_i\}_{i \in I}, \mathcal {E}, \varphi , \upsilon )$
has no nontrivial automorphisms, such an isomorphism automatically satisfies the cocycle condition and hence is equivalent to a descent datum from
$(\{x_i\}_{i \in I}, \mathcal {E}, \varphi , \upsilon )$
has no nontrivial automorphisms, such an isomorphism automatically satisfies the cocycle condition and hence is equivalent to a descent datum from
![]() $\mathcal {E}'$
to an H-torsor over
$\mathcal {E}'$
to an H-torsor over
![]() $X_S$
. Furthermore, the map
$X_S$
. Furthermore, the map
![]() $\varphi $
and level structure
$\varphi $
and level structure
![]() $\upsilon $
will similarly descend uniquely.
$\upsilon $
will similarly descend uniquely.
Let
![]() $\operatorname {\mathrm {Nm}}(h) := (\sigma ^{p-1}h) \circ \ldots \circ (\sigma h) \circ h \colon \mathcal {E}' \xrightarrow {\sim } \mathcal {E}'$
. The claim amounts to checking that
$\operatorname {\mathrm {Nm}}(h) := (\sigma ^{p-1}h) \circ \ldots \circ (\sigma h) \circ h \colon \mathcal {E}' \xrightarrow {\sim } \mathcal {E}'$
. The claim amounts to checking that
![]() $\operatorname {\mathrm {Nm}}(h)$
is the identity automorphism of
$\operatorname {\mathrm {Nm}}(h)$
is the identity automorphism of
![]() $\mathcal {E}'$
. By definition, it corresponds to some automorphism of
$\mathcal {E}'$
. By definition, it corresponds to some automorphism of
![]() $\mathcal {E}$
compatible with
$\mathcal {E}$
compatible with
![]() $\varphi $
and the level structure
$\varphi $
and the level structure
![]() $\upsilon $
. But by assumption, this datum had no nontrivial automorphisms, so
$\upsilon $
. But by assumption, this datum had no nontrivial automorphisms, so
![]() $\operatorname {\mathrm {Nm}}(h)$
can only be the identity automorphism.
$\operatorname {\mathrm {Nm}}(h)$
can only be the identity automorphism.
This constructs a map
![]() $\operatorname {\mathrm {Sht}}_{H,D+nx_0,I} \leftarrow (\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }})^{\sigma }$
which is manifestly a one-sided inverse; we conclude by using (5.11) to see that it lands in
$\operatorname {\mathrm {Sht}}_{H,D+nx_0,I} \leftarrow (\operatorname {\mathrm {Sht}}_{G,D+nx_0,I}^{\leq \widetilde {\mu }})^{\sigma }$
which is manifestly a one-sided inverse; we conclude by using (5.11) to see that it lands in
![]() $\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
.
$\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
.
5.4.2 Cohomology at infinite level
We will use Lemma 5.7 to apply Smith theory. However, the excursion action does not stabilize the piece of cohomology coming from bounding the HN polygon, so we need to let
![]() $\mu $
and n both go ‘off to infinity’.
$\mu $
and n both go ‘off to infinity’.
Definition 5.8. Fix a closed point
![]() $x_0 \in X$
and consider the system of Deligne-Mumford stacks
$x_0 \in X$
and consider the system of Deligne-Mumford stacks
![]() $\{\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }\}$
as n and
$\{\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }\}$
as n and
![]() $\mu $
vary. For
$\mu $
vary. For
![]() $V \in \operatorname {\mathrm {Rep}}(({}^L H^{\operatorname {\mathrm {alg}}})^I)$
, we define
$V \in \operatorname {\mathrm {Rep}}(({}^L H^{\operatorname {\mathrm {alg}}})^I)$
, we define
where the maps in the
![]() $\mu $
variable are the covariant maps induced by open embeddings, while the maps in the n variable are the contravariant maps induced by pullback. Note that the colimit is filtered because both indexing posets are filtered.
$\mu $
variable are the covariant maps induced by open embeddings, while the maps in the n variable are the contravariant maps induced by pullback. Note that the colimit is filtered because both indexing posets are filtered.
Remark 5.9. As explained above, for any fixed
![]() $\mu $
, and all sufficiently large n depending on
$\mu $
, and all sufficiently large n depending on
![]() $\mu $
,
$\mu $
,
![]() $\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }$
is representable by a scheme. Hence, the subposet of indices
$\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }$
is representable by a scheme. Hence, the subposet of indices
![]() $(n, \mu )$
for which
$(n, \mu )$
for which
![]() $\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }$
is representable by a scheme is cofinal, so
$\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }$
is representable by a scheme is cofinal, so
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
is naturally isomorphic to the colimit taken along this subposet.
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
is naturally isomorphic to the colimit taken along this subposet.
Definition 5.10. Fix a closed point
![]() $x_0 \in X$
and
$x_0 \in X$
and
![]() $V \in \operatorname {\mathrm {Rep}}_k( ({}^L H^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma }$
. We define
$V \in \operatorname {\mathrm {Rep}}_k( ({}^L H^{\operatorname {\mathrm {alg}}}) ^I)^{B\sigma }$
. We define
We note that
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)) $
is bounded, since the dimension of the support of
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)) $
is bounded, since the dimension of the support of
![]() $\operatorname {\mathrm {Sat}}(V)$
on each
$\operatorname {\mathrm {Sat}}(V)$
on each
![]() $\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }|_{\overline {\eta ^I}}$
is uniformly bounded for all
$\operatorname {\mathrm {Sht}}_{H, D + n x_0, I}^{\leq \mu }|_{\overline {\eta ^I}}$
is uniformly bounded for all
![]() $n,\mu $
.
$n,\mu $
.
Furthermore, note that for any cofinal subposet of HN polygons
![]() $\mu $
for H, the induced HN polygons
$\mu $
for H, the induced HN polygons
![]() $\widetilde {\mu }$
form a cofinal poset for G. We make the analogous definitions
$\widetilde {\mu }$
form a cofinal poset for G. We make the analogous definitions
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
and
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G, D + \infty x_0, I}|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V))$
and
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D + \infty x_0,I};V)$
for G.
$T^j(\operatorname {\mathrm {Sht}}_{G,D + \infty x_0,I};V)$
for G.
5.5 Equivariant localization for excursion operators
We define
![]() $\operatorname {\mathrm {Nm}} \colon \operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)^{B\sigma }$
to be the functor taking a representation V to
$\operatorname {\mathrm {Nm}} \colon \operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)^{B\sigma }$
to be the functor taking a representation V to
![]() $V \otimes _k {}^{\sigma } V \otimes _k \ldots \otimes _k {}^{\sigma ^{p-1}}V$
, with the
$V \otimes _k {}^{\sigma } V \otimes _k \ldots \otimes _k {}^{\sigma ^{p-1}}V$
, with the
![]() $\sigma $
-equivariant structure
$\sigma $
-equivariant structure
given by the commutativity constraint for tensor products. It corresponds under Geometric Satake to Definition 4.12. Given
![]() $h \colon V \rightarrow V' \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we set
$h \colon V \rightarrow V' \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we set
Note that
![]() $\operatorname {\mathrm {Nm}}$
is not an additive functor, nor is it even k-linear. We linearize it by defining
$\operatorname {\mathrm {Nm}}$
is not an additive functor, nor is it even k-linear. We linearize it by defining
![]() $\operatorname {\mathrm {Nm}}^{(p^{-1})} := \operatorname {\mathrm {Nm}} \circ \operatorname {\mathrm {Frob}}_p^{-1}$
, where (as in §4.6.3)
$\operatorname {\mathrm {Nm}}^{(p^{-1})} := \operatorname {\mathrm {Nm}} \circ \operatorname {\mathrm {Frob}}_p^{-1}$
, where (as in §4.6.3)
![]() $ \operatorname {\mathrm {Frob}}_p^{-1}$
is the identity on objects, and on morphisms, it is
$ \operatorname {\mathrm {Frob}}_p^{-1}$
is the identity on objects, and on morphisms, it is
![]() $(-) \otimes _{k, \operatorname {\mathrm {Frob}}_p^{-1}} k$
. Then
$(-) \otimes _{k, \operatorname {\mathrm {Frob}}_p^{-1}} k$
. Then
![]() $\operatorname {\mathrm {Nm}}^{(p^{-1})} \colon \operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)^{B\sigma }$
is k-linear, although still not additive.
$\operatorname {\mathrm {Nm}}^{(p^{-1})} \colon \operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)^{B\sigma }$
is k-linear, although still not additive.
For
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we denote by
$V \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we denote by
![]() $N \cdot V$
the
$N \cdot V$
the
![]() $\sigma $
-equivariant representation
$\sigma $
-equivariant representation
![]() $V \oplus {}^{\sigma } V \oplus \ldots \oplus {}^{\sigma ^{p-1}}V$
, with
$V \oplus {}^{\sigma } V \oplus \ldots \oplus {}^{\sigma ^{p-1}}V$
, with
![]() $\sigma $
-equivariant structure
$\sigma $
-equivariant structure
given by the commutativity constraint for direct sums. For
![]() $h \colon V \rightarrow V' \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we denote by
$h \colon V \rightarrow V' \in \operatorname {\mathrm {Rep}}_k(({}^L{G})^I)$
, we denote by
![]() $N \cdot h \colon N \cdot V \rightarrow N \cdot V'$
the
$N \cdot h \colon N \cdot V \rightarrow N \cdot V'$
the
![]() $\sigma $
-equivariant map
$\sigma $
-equivariant map
![]() $h \oplus {}^{\sigma } h \oplus \ldots \oplus {}^{\sigma ^{p-1}} h$
. Let
$h \oplus {}^{\sigma } h \oplus \ldots \oplus {}^{\sigma ^{p-1}} h$
. Let ![]() denote the diagonal map and
denote the diagonal map and ![]() denote the sum map.
denote the sum map.
Our goal in this subsection is to prove the theorem below.
Theorem 5.11. Fixed a closed point
![]() $x_0$
on X and let D be any closed finite subscheme of X.
$x_0$
on X and let D be any closed finite subscheme of X.
(i) For each
![]() $j \in \{0,1\}$
, with respect to the isomorphism
$j \in \{0,1\}$
, with respect to the isomorphism
induced by Lemma 5.7, the action of
![]() $S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
on
$S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
on ![]() is identified with the action of
is identified with the action of
![]() $S_{I, \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V), x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
on
$S_{I, \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V), x, \xi , (\gamma _i)_{i \in I}} \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
on ![]() .
.
(ii) For each
![]() $j \in \{0,1\}$
, the action of
$j \in \{0,1\}$
, the action of
![]() $S_{I, N \cdot V, (N \cdot x) \circ \Delta _p, \nabla _p \circ (N \cdot \xi ), (\gamma _i)_{i \in I}}\in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
on
$S_{I, N \cdot V, (N \cdot x) \circ \Delta _p, \nabla _p \circ (N \cdot \xi ), (\gamma _i)_{i \in I}}\in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
on ![]() is
is
![]() $0$
.
$0$
.
This will be established in several steps. The heart of the matter is the following equivariant localization isomorphism.
Proposition 5.12. Fixed a closed point
![]() $x_0$
on X and let D be any closed finite subscheme of X. Let G be a reductive group over F. We equip
$x_0$
on X and let D be any closed finite subscheme of X. Let G be a reductive group over F. We equip
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G}^I) $
with the
$\operatorname {\mathrm {Rep}}_k(\widehat {G}^I) $
with the
![]() $\pi _1(\eta , \overline {\eta })^I$
-action coming from the geometric action of
$\pi _1(\eta , \overline {\eta })^I$
-action coming from the geometric action of
![]() $\pi _1(\eta , \overline {\eta })$
on
$\pi _1(\eta , \overline {\eta })$
on
![]() $\widehat {G}$
(§2.1.2).
$\widehat {G}$
(§2.1.2).
(i) For each
![]() $j \in \{0,1\}$
, there is a natural isomorphism of
$j \in \{0,1\}$
, there is a natural isomorphism of
![]() $\pi _1(\eta ^I, \overline {\eta }^I)$
-equivariant functors
$\pi _1(\eta ^I, \overline {\eta }^I)$
-equivariant functors
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G}^I) \rightarrow \mathrm {Vect}_{/k}$
,
$\operatorname {\mathrm {Rep}}_k(\widehat {G}^I) \rightarrow \mathrm {Vect}_{/k}$
,
(ii) For each
![]() $j \in \{0,1\}$
, there is a natural isomorphism of functors
$j \in \{0,1\}$
, there is a natural isomorphism of functors
![]() $\operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I)$
,
$\operatorname {\mathrm {Rep}}_k(({}^L{G})^I) \rightarrow \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I)$
,
which is compatible with fusion and composition.
Proof. (i) We will first construct a natural isomorphism of
![]() $\pi _1(\eta ^I, \overline {\eta }^I)$
-equivariant functors
$\pi _1(\eta ^I, \overline {\eta }^I)$
-equivariant functors
![]() $\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I) \rightarrow \operatorname {\mathrm {Shv}}(\overline {\eta }^I; \mathcal {T}_k)$
,
$\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I) \rightarrow \operatorname {\mathrm {Shv}}(\overline {\eta }^I; \mathcal {T}_k)$
,
By Lemma 4.24 (specifically, the commutativity of the back face), the diagram

commutes. The composite functor that follows along the left and then bottom is
![]() $\operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}} \circ \operatorname {\mathrm {Sat}} $
, while Theorem 4.20 identifies the composite functor that follows along the top and right with
$\operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}} \circ \operatorname {\mathrm {Sat}} $
, while Theorem 4.20 identifies the composite functor that follows along the top and right with
![]() $\mathbb {T}^* \epsilon ^* \operatorname {\mathrm {Res}}_{\mathsf {BC}^{(p)}}$
. We therefore have a
$\mathbb {T}^* \epsilon ^* \operatorname {\mathrm {Res}}_{\mathsf {BC}^{(p)}}$
. We therefore have a
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphism between these two composite functors. (The only non-tautological aspect of the equivariance is handled in Lemma 4.22.) Linearizing this natural isomorphism, we get a
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphism between these two composite functors. (The only non-tautological aspect of the equivariance is handled in Lemma 4.22.) Linearizing this natural isomorphism, we get a
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphism of functors
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphism of functors
![]() $\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I) \rightarrow \operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k) $
,
$\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I) \rightarrow \operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k) $
,
For any coweight
![]() $\mu $
for H, inducing the coweight
$\mu $
for H, inducing the coweight
![]() $\widetilde {\mu }$
for G, and n sufficiently large so that
$\widetilde {\mu }$
for G, and n sufficiently large so that
![]() $\operatorname {\mathrm {Sht}}_{G, D+nx_0,I}^{\leq \widetilde {\mu }}$
and
$\operatorname {\mathrm {Sht}}_{G, D+nx_0,I}^{\leq \widetilde {\mu }}$
and
![]() $\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
are schemes, Lemma 5.7 identifies the
$\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
are schemes, Lemma 5.7 identifies the
![]() $\sigma $
-fixed points of
$\sigma $
-fixed points of
![]() $\operatorname {\mathrm {Sht}}_{G, D+\infty x_0, I}$
with
$\operatorname {\mathrm {Sht}}_{G, D+\infty x_0, I}$
with
![]() $\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}$
. Therefore, we may apply (3.6) to obtain an isomorphism in
$\operatorname {\mathrm {Sht}}_{H, D + \infty x_0, I}$
. Therefore, we may apply (3.6) to obtain an isomorphism in
![]() $\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
$\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
 $$ \begin{align} \mathbb{T}^* R\Gamma_c (\operatorname{\mathrm{Sht}}_{G, D+nx_0,I}^{\leq \widetilde{\mu}}; \operatorname{\mathrm{Nm}}^{(p^{-1})}(V)) & := \mathbb{T}^* R\Gamma_c (\operatorname{\mathrm{Sht}}_{G,D+nx_0,I}^{\leq \widetilde{\mu}}; \operatorname{\mathrm{Sat}}(\operatorname{\mathrm{Nm}}^{(p^{-1})}(V))) \nonumber \\ & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}}( \operatorname{\mathrm{Nm}}(\operatorname{\mathrm{Sat}}( \operatorname{\mathrm{Frob}}_p^{-1} V)))), \end{align} $$
$$ \begin{align} \mathbb{T}^* R\Gamma_c (\operatorname{\mathrm{Sht}}_{G, D+nx_0,I}^{\leq \widetilde{\mu}}; \operatorname{\mathrm{Nm}}^{(p^{-1})}(V)) & := \mathbb{T}^* R\Gamma_c (\operatorname{\mathrm{Sht}}_{G,D+nx_0,I}^{\leq \widetilde{\mu}}; \operatorname{\mathrm{Sat}}(\operatorname{\mathrm{Nm}}^{(p^{-1})}(V))) \nonumber \\ & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}}( \operatorname{\mathrm{Nm}}(\operatorname{\mathrm{Sat}}( \operatorname{\mathrm{Frob}}_p^{-1} V)))), \end{align} $$
which is natural in
![]() $V \in \operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
and
$V \in \operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
and
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant. The commutative diagram
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant. The commutative diagram

induces a natural isomorphism between the two restriction functors
![]() $D^b_c(\operatorname {\mathrm {Hk}}_{G,I}|_{\overline {\eta ^I}};k) \rightarrow D^b_c(\operatorname {\mathrm {Sht}}_{H,I}|_{\overline {\eta ^I}};k)$
, one by
$D^b_c(\operatorname {\mathrm {Hk}}_{G,I}|_{\overline {\eta ^I}};k) \rightarrow D^b_c(\operatorname {\mathrm {Sht}}_{H,I}|_{\overline {\eta ^I}};k)$
, one by
![]() $*$
-pullback through the right then top maps and the other by
$*$
-pullback through the right then top maps and the other by
![]() $*$
-pullback through the bottom then left maps. Furthermore, the pullbacks are
$*$
-pullback through the bottom then left maps. Furthermore, the pullbacks are
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant, as is the natural isomorphism between them. The same discussion applies with any level structure and HN truncation. Therefore, there is no risk of confusion in the expression
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant, as is the natural isomorphism between them. The same discussion applies with any level structure and HN truncation. Therefore, there is no risk of confusion in the expression
![]() $\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\operatorname {\mathrm {Sat}}(V))$
whether we first regard
$\operatorname {\mathrm {Psm}}(\operatorname {\mathrm {Nm}}(\operatorname {\mathrm {Sat}}(V))$
whether we first regard
![]() $\operatorname {\mathrm {Nm}}(\operatorname {\mathrm {Sat}}(V))$
as a sheaf on
$\operatorname {\mathrm {Nm}}(\operatorname {\mathrm {Sat}}(V))$
as a sheaf on
![]() $\operatorname {\mathrm {Sht}}_{G, D+nx_0,I}^{\leq \widetilde {\mu }}$
and then apply
$\operatorname {\mathrm {Sht}}_{G, D+nx_0,I}^{\leq \widetilde {\mu }}$
and then apply
![]() $\operatorname {\mathrm {Psm}}$
or first apply
$\operatorname {\mathrm {Psm}}$
or first apply
![]() $\operatorname {\mathrm {Psm}}$
and then pull back to
$\operatorname {\mathrm {Psm}}$
and then pull back to
![]() $\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
; the two are naturally identified. Now, (5.15) induces an isomorphism in
$\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }$
; the two are naturally identified. Now, (5.15) induces an isomorphism in
![]() $\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
$\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
which is natural in
![]() $V \in \operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
and
$V \in \operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
and
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant.
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant.
We conclude (5.14) by taking the colimit of these isomorphisms (5.16) and (5.17) along such n and
![]() $\mu $
, using that they form a cofinal poset by Remark 5.9.
$\mu $
, using that they form a cofinal poset by Remark 5.9.
Next we bootstrap from
![]() $\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
to
$\operatorname {\mathrm {Tilt}}_k(\widehat {G}^I)$
to
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
. For this, we use Proposition 4.10, which allows for any
$\operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
. For this, we use Proposition 4.10, which allows for any
![]() $V \in \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
to produce a resolution of V by a complex
$V \in \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
to produce a resolution of V by a complex
![]() $V^{\bullet } = (\ldots \rightarrow V^{-1} \rightarrow V^0 \rightarrow \ldots )$
of tilting modules which is well defined up to homotopy. Then Lemma 4.21 gives a natural isomorphism in
$V^{\bullet } = (\ldots \rightarrow V^{-1} \rightarrow V^0 \rightarrow \ldots )$
of tilting modules which is well defined up to homotopy. Then Lemma 4.21 gives a natural isomorphism in
![]() $\operatorname {\mathrm {Perf}}(\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }; \mathcal {T}_k)$
,
$\operatorname {\mathrm {Perf}}(\operatorname {\mathrm {Sht}}_{H,D+nx_0,I}^{\leq \mu }; \mathcal {T}_k)$
,
So using the earlier observations and (3.6), we have
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphisms in
$\pi _1(\eta ^I, \overline {\eta ^I})$
-equivariant natural isomorphisms in
![]() $\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
$\operatorname {\mathrm {Shv}}(\overline {\eta ^I}; \mathcal {T}_k)$
,
 $$ \begin{align*} \mathbb{T}^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{G,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Nm}}^{(p^{-1})} V) & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V)) \\ & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V^{\bullet})). \end{align*} $$
$$ \begin{align*} \mathbb{T}^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{G,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Nm}}^{(p^{-1})} V) & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V)) \\ & \cong R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V^{\bullet})). \end{align*} $$
Then using (5.14), we have
 $$ \begin{align*} R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V^{\bullet})) & \cong \mathbb{T}^* \epsilon^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V^{\bullet})) \\ & \cong \mathbb{T}^* \epsilon^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V)). \end{align*} $$
$$ \begin{align*} R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Psm}} \operatorname{\mathrm{Nm}}^{(p^{-1})} (V^{\bullet})) & \cong \mathbb{T}^* \epsilon^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V^{\bullet})) \\ & \cong \mathbb{T}^* \epsilon^* R\Gamma_c(\operatorname{\mathrm{Sht}}_{H,D+nx_0,I}^{\leq \mu}; \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V)). \end{align*} $$
Now take the jth Tate cohomology group to obtain (5.12).
(ii) Since
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, it suffices to show a natural isomorphism as
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, it suffices to show a natural isomorphism as
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }^I)$
-modules. Then, since the
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }^I)$
-modules. Then, since the
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-actions on
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-actions on
![]() $T^*(\operatorname {\mathrm {Sht}}_{G,D+ \infty x_0, I}; \operatorname {\mathrm {Nm}}^{(p^{-1})}(V)) $
and on
$T^*(\operatorname {\mathrm {Sht}}_{G,D+ \infty x_0, I}; \operatorname {\mathrm {Nm}}^{(p^{-1})}(V)) $
and on
![]() $T^*(\operatorname {\mathrm {Sht}}_{H, D+ \infty x_0, I}; \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V)) $
are determined by their respective
$T^*(\operatorname {\mathrm {Sht}}_{H, D+ \infty x_0, I}; \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V)) $
are determined by their respective
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-actions plus partial Frobenius morphisms, we can and will focus on these two equivariance structures separately.
$\pi _1(\eta ^I, \overline {\eta ^I})$
-actions plus partial Frobenius morphisms, we can and will focus on these two equivariance structures separately.
Applying
![]() $(-)^{B \pi _1(\eta ^I, \overline {\eta ^I})}$
(see the references on equivariantization in §4.6.4) to the natural isomorphism in (i) gives a natural isomorphism
$(-)^{B \pi _1(\eta ^I, \overline {\eta ^I})}$
(see the references on equivariantization in §4.6.4) to the natural isomorphism in (i) gives a natural isomorphism
of functors
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_k(\pi _1(\eta ^I, \overline {\eta ^I}))$
.
$V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I) \rightarrow \operatorname {\mathrm {Mod}}_k(\pi _1(\eta ^I, \overline {\eta ^I}))$
.
Finally, we check the compatibility with partial Frobenius. We want to show that the diagram

commutes, where the vertical isomorphisms (as
![]() $\pi _1(\eta ^I, \overline {\eta ^I})$
-modules) have just been established. By Lemma 5.7, there is a cofinal system of
$\pi _1(\eta ^I, \overline {\eta ^I})$
-modules) have just been established. By Lemma 5.7, there is a cofinal system of
![]() $n,\mu ,\mu '$
such that applying
$n,\mu ,\mu '$
such that applying
![]() $\sigma $
-fixed points to the diagram
$\sigma $
-fixed points to the diagram
yields the diagram
(The need for
![]() $\mu '$
arises because
$\mu '$
arises because
![]() $F_{\{1\}}$
does not preserve HN polygons.) This implies that the natural isomorphims (5.16) and (5.17) are compatible with the maps
$F_{\{1\}}$
does not preserve HN polygons.) This implies that the natural isomorphims (5.16) and (5.17) are compatible with the maps
![]() $F_{\{1\}}^*$
. Taking the (filtered) colimit along such
$F_{\{1\}}^*$
. Taking the (filtered) colimit along such
![]() $n,\mu ,\mu '$
completes the proof.
$n,\mu ,\mu '$
completes the proof.
Proof of Theorem 5.11.
(i) Proposition 5.12(ii) gives a chain of compatible identifications:

The operator
![]() $S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}}$
on
$S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}}$
on ![]() is obtained by tracing along the upper row, while the operator
is obtained by tracing along the upper row, while the operator
![]() $S_{I, \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V), x, \xi , (\gamma _i)_{i \in I}}$
on
$S_{I, \operatorname {\mathrm {Res}}_{\mathsf {BC}}(V), x, \xi , (\gamma _i)_{i \in I}}$
on ![]() is obtained by tracing along the lower row. Hence, they coincide under the vertical identifications.
is obtained by tracing along the lower row. Hence, they coincide under the vertical identifications.
(ii) By Lemma 5.7 and (3.6), we have a chain of compatible identifications:

The operator
![]() $S_{I, N \cdot V, (N \cdot x) \circ \Delta _p, \nabla _p \circ (N \cdot \xi ), (\gamma _i)_{i \in I}}$
on
$S_{I, N \cdot V, (N \cdot x) \circ \Delta _p, \nabla _p \circ (N \cdot \xi ), (\gamma _i)_{i \in I}}$
on ![]() is obtained by tracing along the upper row. But the stalks and costalks of
is obtained by tracing along the upper row. But the stalks and costalks of
![]() $N \cdot \operatorname {\mathrm {Sat}}(V)|_{\operatorname {\mathrm {Gr}}_H}$
are all complexes of induced
$N \cdot \operatorname {\mathrm {Sat}}(V)|_{\operatorname {\mathrm {Gr}}_H}$
are all complexes of induced
![]() $k[\sigma ]$
-modules, and, in fact, they are perfect complexes over
$k[\sigma ]$
-modules, and, in fact, they are perfect complexes over
![]() $k[\sigma ]$
. Hence,
$k[\sigma ]$
. Hence,
![]() $\operatorname {\mathrm {Psm}}( N \cdot V)$
is equivalent to
$\operatorname {\mathrm {Psm}}( N \cdot V)$
is equivalent to
![]() $0$
in the Tate category of
$0$
in the Tate category of
![]() $\operatorname {\mathrm {Sht}}_{H,D,I}$
for all D, so
$\operatorname {\mathrm {Sht}}_{H,D,I}$
for all D, so
![]() $T^j(\operatorname {\mathrm {Sht}}_{H,D + \infty x_0,I}; \operatorname {\mathrm {Psm}}( N \cdot V) ) = 0$
. Therefore, the endomorphism in question factors through the zero map and hence is itself zero.
$T^j(\operatorname {\mathrm {Sht}}_{H,D + \infty x_0,I}; \operatorname {\mathrm {Psm}}( N \cdot V) ) = 0$
. Therefore, the endomorphism in question factors through the zero map and hence is itself zero.
5.6 Applications to base change for automorphic forms
In §5.2, we described Lafforgue’s action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on ![]() . By (5.6), we have
. By (5.6), we have

Here,
![]() $\ker ^1(F,G) := \ker (H^1(F,G) \rightarrow \prod _v H^1(F_v, G)) $
is the isomorphism class of the generic fiber of the G-torsor. More generally, this defines a decomposition
$\ker ^1(F,G) := \ker (H^1(F,G) \rightarrow \prod _v H^1(F_v, G)) $
is the isomorphism class of the generic fiber of the G-torsor. More generally, this defines a decomposition
 $$ \begin{align} \operatorname{\mathrm{Sht}}_{G,D,I} = \coprod_{\alpha \in \ker^1(F,G)} (\operatorname{\mathrm{Sht}}_{G,D,I})_{\alpha} \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Sht}}_{G,D,I} = \coprod_{\alpha \in \ker^1(F,G)} (\operatorname{\mathrm{Sht}}_{G,D,I})_{\alpha} \end{align} $$
according to the isomorphism class of the generic fiber of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
In the base change situation, the ‘diagonal embedding’ map
![]() $\phi \colon H \rightarrow G$
induces a map
$\phi \colon H \rightarrow G$
induces a map
![]() $\phi _* \colon \ker ^1(F, H) \rightarrow \ker ^1(F, G)$
compatible with the map
$\phi _* \colon \ker ^1(F, H) \rightarrow \ker ^1(F, G)$
compatible with the map
![]() $\operatorname {\mathrm {Bun}}_{H,D}(\mathbf {F}_{\ell }) \rightarrow \operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_{\ell })$
. Theorem 1.6 is evidently implied by the theorem below, whose proof occupies this subsection.
$\operatorname {\mathrm {Bun}}_{H,D}(\mathbf {F}_{\ell }) \rightarrow \operatorname {\mathrm {Bun}}_{G,D}(\mathbf {F}_{\ell })$
. Theorem 1.6 is evidently implied by the theorem below, whose proof occupies this subsection.
Theorem 5.13. Fix any closed point
![]() $x_0 \in X$
and any closed finite subscheme on X. Let
$x_0 \in X$
and any closed finite subscheme on X. Let
![]() $[\rho ] \in H^1(\Gamma , \widehat {H}(k))$
be an L-parameter arising from the action of
$[\rho ] \in H^1(\Gamma , \widehat {H}(k))$
be an L-parameter arising from the action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L{H})$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L{H})$
on ![]() in the sense of §5.2.4. Then the image of
in the sense of §5.2.4. Then the image of
![]() $[\rho ]$
in
$[\rho ]$
in
![]() $H^1(\Gamma , \widehat {G}(k))$
arises in the action of
$H^1(\Gamma , \widehat {G}(k))$
arises in the action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
on ![]() in the sense of §5.2.4.
in the sense of §5.2.4.
We establish some preliminaries in preparation for the proof.
Definition 5.14 (The Tate diagonal).
For a commutative algebra A in characteristic p with
![]() $\sigma $
-action, we denote by
$\sigma $
-action, we denote by
![]() $N \cdot A$
the subset consisting of elements of the form
$N \cdot A$
the subset consisting of elements of the form
![]() $(1+\sigma + \ldots + \sigma ^{p-1}) a$
for
$(1+\sigma + \ldots + \sigma ^{p-1}) a$
for
![]() $a \in A$
. One easily checks that
$a \in A$
. One easily checks that
![]() $N \cdot A$
is an ideal in
$N \cdot A$
is an ideal in
![]() $A^{\sigma }$
.
$A^{\sigma }$
.
We denote by
![]() $\operatorname {\mathrm {Nm}} \colon A \rightarrow A^{\sigma }$
the set map sending
$\operatorname {\mathrm {Nm}} \colon A \rightarrow A^{\sigma }$
the set map sending
![]() $a \mapsto a \cdot \sigma (a) \cdot \ldots \cdot \sigma ^{p-1}(a)$
. It is multiplicative but not additive. It is an exercise to verify that the composition of
$a \mapsto a \cdot \sigma (a) \cdot \ldots \cdot \sigma ^{p-1}(a)$
. It is multiplicative but not additive. It is an exercise to verify that the composition of
![]() $\operatorname {\mathrm {Nm}}$
with the quotient
$\operatorname {\mathrm {Nm}}$
with the quotient
![]() $A^{\sigma } \twoheadrightarrow A^{\sigma }/N \cdot A$
is an algebra homomorphism, which we call the Tate diagonal homomorphism
$A^{\sigma } \twoheadrightarrow A^{\sigma }/N \cdot A$
is an algebra homomorphism, which we call the Tate diagonal homomorphism
![]() $\Delta ^p \colon A \rightarrow T^0(A)$
.
$\Delta ^p \colon A \rightarrow T^0(A)$
.
Lemma 5.15. Let A be a commutative ring over
![]() $\mathbf {F}_p$
with a
$\mathbf {F}_p$
with a
![]() $\sigma $
-action. Let
$\sigma $
-action. Let
![]() $\kappa $
be any perfect field over
$\kappa $
be any perfect field over
![]() $\mathbf {F}_p$
. Let
$\mathbf {F}_p$
. Let
![]() $A' \subset A^{\sigma }$
be a subring containing
$A' \subset A^{\sigma }$
be a subring containing
![]() $\operatorname {\mathrm {Nm}} (A)$
and
$\operatorname {\mathrm {Nm}} (A)$
and
![]() $N \cdot A$
. (Since
$N \cdot A$
. (Since
![]() $N \cdot A$
is an ideal in
$N \cdot A$
is an ideal in
![]() $A^{\sigma }$
, it is also an ideal in any such
$A^{\sigma }$
, it is also an ideal in any such
![]() $A'$
.) Any character
$A'$
.) Any character
![]() $\chi \colon A' \rightarrow \kappa $
factoring through
$\chi \colon A' \rightarrow \kappa $
factoring through
![]() $A'/N\cdot A$
extends uniquely to a character
$A'/N\cdot A$
extends uniquely to a character
![]() $\widetilde {\chi } \colon A \rightarrow \kappa $
, which is explicitly given by
$\widetilde {\chi } \colon A \rightarrow \kappa $
, which is explicitly given by
Proof. The same proof as that of [Reference Treumann and VenkateshTV16, §3.4] works, but since our situation is a little more general, we reproduce it. One easily checks that the given formula (5.20) defines a valid extension (it is a ring homomorphism since
![]() $\kappa $
is in characteristic p, and it clearly extends
$\kappa $
is in characteristic p, and it clearly extends
![]() $\chi $
).
$\chi $
).
Next, we check that it is the unique extension. Note that
![]() $\sigma $
acts on characters
$\sigma $
acts on characters
![]() $A \rightarrow \kappa $
by pre-composition; we denote this action by
$A \rightarrow \kappa $
by pre-composition; we denote this action by
![]() $\widetilde {\chi } \mapsto \sigma \cdot \widetilde {\chi } := \widetilde {\chi } \circ \sigma ^{-1}$
. Clearly, (5.20) is the unique
$\widetilde {\chi } \mapsto \sigma \cdot \widetilde {\chi } := \widetilde {\chi } \circ \sigma ^{-1}$
. Clearly, (5.20) is the unique
![]() $\sigma $
-fixed extension, so we will show that any extension
$\sigma $
-fixed extension, so we will show that any extension
![]() $\widetilde {\chi }'$
must be
$\widetilde {\chi }'$
must be
![]() $\sigma $
-fixed. Indeed, since any extension
$\sigma $
-fixed. Indeed, since any extension
![]() $\widetilde {\chi }'$
is trivial on
$\widetilde {\chi }'$
is trivial on
![]() $N \cdot A$
by the assumption that
$N \cdot A$
by the assumption that
![]() $\chi $
factors through
$\chi $
factors through
![]() $A'/N \cdot A$
, we have
$A'/N \cdot A$
, we have
 $$\begin{align*}\sum_{i=0}^{p-1} \sigma^i \cdot \widetilde{\chi}' = 0. \end{align*}$$
$$\begin{align*}\sum_{i=0}^{p-1} \sigma^i \cdot \widetilde{\chi}' = 0. \end{align*}$$
By linear independence of characters [Sta20, Tag 0CKK], we must have
![]() $\sigma ^i \cdot \widetilde {\chi }' = \widetilde {\chi }'$
for all i (i.e.,
$\sigma ^i \cdot \widetilde {\chi }' = \widetilde {\chi }'$
for all i (i.e.,
![]() $\widetilde {\chi }'$
is
$\widetilde {\chi }'$
is
![]() $\sigma $
-fixed).
$\sigma $
-fixed).
Lemma 5.16. Inside
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, we have
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, we have
and
Proof. The first equality follows from repeated application of the relations (2.7), (2.5) and the explicit description of the
![]() $\sigma $
-action in (5.9). The second equality follows from repeated application of relations (2.7), (2.6) and the explicit description of the
$\sigma $
-action in (5.9). The second equality follows from repeated application of relations (2.7), (2.6) and the explicit description of the
![]() $\sigma $
-action in (5.9).
$\sigma $
-action in (5.9).
Construction 5.17 (Frobenius twist of algebras).
This discussion is parallel to Construction 4.17. Let
![]() $\operatorname {\mathrm {Frob}}$
be the absolute Frobenius of k. Given a k-algebra A, we denote by
$\operatorname {\mathrm {Frob}}$
be the absolute Frobenius of k. Given a k-algebra A, we denote by
![]() $A^{(p)} := A \otimes _{k, \operatorname {\mathrm {Frob}}} k$
its Frobenius twist. The map
$A^{(p)} := A \otimes _{k, \operatorname {\mathrm {Frob}}} k$
its Frobenius twist. The map
![]() $A \rightarrow A^{(p)}$
sending
$A \rightarrow A^{(p)}$
sending
![]() $a \mapsto a \otimes 1$
is a k-semilinear isomorphism. It is characterized by the universal property that any
$a \mapsto a \otimes 1$
is a k-semilinear isomorphism. It is characterized by the universal property that any
![]() $\operatorname {\mathrm {Frob}}$
-semilinear homomorphism
$\operatorname {\mathrm {Frob}}$
-semilinear homomorphism
![]() $f \colon A \rightarrow B$
(i.e.,
$f \colon A \rightarrow B$
(i.e.,
![]() $f(\lambda a) = \lambda ^p f(a)$
for
$f(\lambda a) = \lambda ^p f(a)$
for
![]() $\lambda \in k$
) factors uniquely through a k-linear homomorphism
$\lambda \in k$
) factors uniquely through a k-linear homomorphism

If A is equipped with an
![]() $\mathbf {F}_p$
-structure
$\mathbf {F}_p$
-structure
![]() $\varphi _0 \colon A \cong A_0 \mathop{\otimes _{\mathbf {F}_p}} k$
, then there is a k-linear isomorphism
$\varphi _0 \colon A \cong A_0 \mathop{\otimes _{\mathbf {F}_p}} k$
, then there is a k-linear isomorphism
![]() $A \cong A^{(p)}$
characterized by the property that it sends
$A \cong A^{(p)}$
characterized by the property that it sends
![]() $A_0$
to
$A_0$
to
![]() $A_0 \otimes 1$
via
$A_0 \otimes 1$
via
![]() $\operatorname {\mathrm {Id}} \otimes 1$
. We denote by
$\operatorname {\mathrm {Id}} \otimes 1$
. We denote by
![]() $\operatorname {\mathrm {Frob}}_{\varphi _0} \colon A \xrightarrow {\sim } A$
the
$\operatorname {\mathrm {Frob}}_{\varphi _0} \colon A \xrightarrow {\sim } A$
the
![]() $\operatorname {\mathrm {Frob}}$
-semilinear isomorphism which is the identity on
$\operatorname {\mathrm {Frob}}$
-semilinear isomorphism which is the identity on
![]() $A_0$
; it is the composition of the k-linear isomorphism
$A_0$
; it is the composition of the k-linear isomorphism
![]() $ A^{(p)} \cong A$
above and the
$ A^{(p)} \cong A$
above and the
![]() $\operatorname {\mathrm {Frob}}$
-semilinear isomorphism
$\operatorname {\mathrm {Frob}}$
-semilinear isomorphism
![]() $A \xrightarrow {\sim } A^{(p)}$
above. The k-linear homomorphism
$A \xrightarrow {\sim } A^{(p)}$
above. The k-linear homomorphism
![]() $A \rightarrow B$
obtained by precomposing f with the inverse of
$A \rightarrow B$
obtained by precomposing f with the inverse of
![]() $\operatorname {\mathrm {Frob}}_{\varphi _0}$
will be called the linearization of f (with respect to
$\operatorname {\mathrm {Frob}}_{\varphi _0}$
will be called the linearization of f (with respect to
![]() $\varphi _0$
).
$\varphi _0$
).
Example 5.18. Note that
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
has an
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
has an
![]() $\mathbf {F}_p$
-structure coming from the fact that
$\mathbf {F}_p$
-structure coming from the fact that
![]() ${}^L G$
is defined over
${}^L G$
is defined over
![]() $\mathbf {F}_p$
.
$\mathbf {F}_p$
.
Definition 5.19. Let
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
be the k-subalgebra generated by
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
be the k-subalgebra generated by
![]() $N \cdot \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
and all elements of the form
$N \cdot \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
and all elements of the form
![]() $\operatorname {\mathrm {Nm}} (S_{I, V, x, \xi , (\gamma _i)_{i \in I}}) = S_{I, \operatorname {\mathrm {Nm}} (V), \operatorname {\mathrm {Nm}}(x), \operatorname {\mathrm {Nm}}(\xi ), (\gamma _i)_{i \in I}} $
(the equality by Lemma 5.16).
$\operatorname {\mathrm {Nm}} (S_{I, V, x, \xi , (\gamma _i)_{i \in I}}) = S_{I, \operatorname {\mathrm {Nm}} (V), \operatorname {\mathrm {Nm}}(x), \operatorname {\mathrm {Nm}}(\xi ), (\gamma _i)_{i \in I}} $
(the equality by Lemma 5.16).
Proof of Theorem 5.13.
A trivial case of Proposition 5.12 gives an isomorphism
The right side has an action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
through the quotient map
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
through the quotient map
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L H) \twoheadrightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
, and the left side has an action of
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L H) \twoheadrightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L H)$
, and the left side has an action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
through the map
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
through the map
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma } \rightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Theorem 5.11 says that the isomorphism (5.21) is equivariant for the action of the subalgebra
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma } \rightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Theorem 5.11 says that the isomorphism (5.21) is equivariant for the action of the subalgebra
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
, which acts on the right side via the map
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)^{\sigma }$
, which acts on the right side via the map
The L-parameter
![]() $[\rho ] \in H^1(\Gamma , \widehat {H}(k))$
corresponds to a character
$[\rho ] \in H^1(\Gamma , \widehat {H}(k))$
corresponds to a character
![]() $\chi _{\rho } \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L H) \rightarrow k$
under Proposition 2.4. Therefore,
$\chi _{\rho } \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L H) \rightarrow k$
under Proposition 2.4. Therefore,
![]() $\chi _{\rho }$
induces a character
$\chi _{\rho }$
induces a character
![]() $\chi _{\rho }' \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \rightarrow k$
sending
$\chi _{\rho }' \colon \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \rightarrow k$
sending
 $$ \begin{align*} S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} & \mapsto \chi_{\rho}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}), \\ N \cdot S & \mapsto 0 \text{ for any }S \in \operatorname{\mathrm{Exc}}(\Gamma, {}^L G). \end{align*} $$
$$ \begin{align*} S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} & \mapsto \chi_{\rho}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}), \\ N \cdot S & \mapsto 0 \text{ for any }S \in \operatorname{\mathrm{Exc}}(\Gamma, {}^L G). \end{align*} $$
Let
![]() $\mathfrak {m}_{\rho }' = \ker (\chi _{\rho }') \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
be the corresponding maximal ideal. The assumption that
$\mathfrak {m}_{\rho }' = \ker (\chi _{\rho }') \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
be the corresponding maximal ideal. The assumption that
![]() $\chi _{\rho }'$
arises in the action of
$\chi _{\rho }'$
arises in the action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
on ![]() means that
means that ![]() is supported at
is supported at
![]() $\mathfrak {m}_{\rho }'$
. For any
$\mathfrak {m}_{\rho }'$
. For any
![]() $\mathbf {F}_p$
-module
$\mathbf {F}_p$
-module
![]() $M_0$
, there is semilinear action of
$M_0$
, there is semilinear action of
![]() $\operatorname {\mathrm {Aut}}(k)$
on
$\operatorname {\mathrm {Aut}}(k)$
on
![]() $M := M_0 \otimes _{\mathbf {F}_p} k$
through the second factor. This applies, in particular, to
$M := M_0 \otimes _{\mathbf {F}_p} k$
through the second factor. This applies, in particular, to
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
and
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
and ![]() since they are defined over
since they are defined over
![]() $\mathbf {F}_p \subset k$
. Since the action of
$\mathbf {F}_p \subset k$
. Since the action of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
on
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
on ![]() is also defined over
is also defined over
![]() $\mathbf {F}_p$
, the image of
$\mathbf {F}_p$
, the image of
![]() $\mathfrak {m}_{\rho }'$
under the automorphism of
$\mathfrak {m}_{\rho }'$
under the automorphism of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
induced by
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
induced by
![]() $\operatorname {\mathrm {Frob}}_p \in \operatorname {\mathrm {Aut}}(k)$
also appears in the support of
$\operatorname {\mathrm {Frob}}_p \in \operatorname {\mathrm {Aut}}(k)$
also appears in the support of ![]() . We denote this maximal ideal by
. We denote this maximal ideal by
![]() $\mathfrak {n}_{\rho }'$
; its associated character
$\mathfrak {n}_{\rho }'$
; its associated character
![]() $\eta _\rho $
is characterized by the property that
$\eta _\rho $
is characterized by the property that
![]() $\eta _\rho $
kills
$\eta _\rho $
kills
![]() $N \cdot S$
for any
$N \cdot S$
for any
![]() $S \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, and for
$S \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, and for
![]() $(V, x, \xi )$
defined over
$(V, x, \xi )$
defined over
![]() $\mathbf {F}_p$
it sends
$\mathbf {F}_p$
it sends
(we omitted Frobenius twists because they have no effect on maps defined over
![]() $\mathbf {F}_p$
).
$\mathbf {F}_p$
).
At the start of the proof, we identified ![]() with
with ![]() as modules over
as modules over
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
. The latter is a subquotient of
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
. The latter is a subquotient of ![]() viewed as a
viewed as a
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
-module via the composition
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
-module via the composition
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \hookrightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Since
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)' \hookrightarrow \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. Since ![]() is supported at
is supported at
![]() $\mathfrak {n}_\rho ' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
, it is also supported at some maximal ideal
$\mathfrak {n}_\rho ' \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)'$
, it is also supported at some maximal ideal
![]() $\mathfrak {n}_{\rho }$
of
$\mathfrak {n}_{\rho }$
of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
lying over
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
lying over
![]() $\mathfrak {n}_\rho '$
. Lemma 5.15 implies that there is a unique maximal ideal of
$\mathfrak {n}_\rho '$
. Lemma 5.15 implies that there is a unique maximal ideal of
![]() $\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
lying over
$\operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
lying over
![]() $\mathfrak {n}_\rho '$
, which by Lemma 5.16 corresponds to the character sending
$\mathfrak {n}_\rho '$
, which by Lemma 5.16 corresponds to the character sending
This is precisely
![]() $\chi _{\rho } \circ \phi _{\mathsf {BC}}^*$
, so its kernel is
$\chi _{\rho } \circ \phi _{\mathsf {BC}}^*$
, so its kernel is
![]() $\mathfrak {n}_{\rho }$
. We conclude that
$\mathfrak {n}_{\rho }$
. We conclude that ![]() must be supported at
must be supported at
![]() $\ker (\chi _{\rho } \circ \phi _{\mathsf {BC}}^*) \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, as desired.
$\ker (\chi _{\rho } \circ \phi _{\mathsf {BC}}^*) \subset \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
, as desired.
6 On local base change
In this section, we will prove the main local results mentioned in the introduction. We begin by reviewing the relevant aspects of the Genestier-Lafforgue correspondence in §6.1. Its key property is local-global compatibility, which will allow us to leverage the global results proved in the preceding section.
After that, we embark on the construction of the map
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
from Theorem 1.4. Its definition does not require any geometry and works equally well over local fields of characteristic zero (and residue characteristic different from p), but requires some technical preliminaries on Hecke algebras, which we establish in §6.2. Then we review the Brauer homomorphism in §6.3, which is needed to finally construct
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
from Theorem 1.4. Its definition does not require any geometry and works equally well over local fields of characteristic zero (and residue characteristic different from p), but requires some technical preliminaries on Hecke algebras, which we establish in §6.2. Then we review the Brauer homomorphism in §6.3, which is needed to finally construct
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
and prove Theorem 1.4. We then use it (and intermediate results established along the way) to prove Theorem 1.2 in §6.5 and Theorem 1.1 in §6.6.
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}}$
and prove Theorem 1.4. We then use it (and intermediate results established along the way) to prove Theorem 1.2 in §6.5 and Theorem 1.1 in §6.6.
6.1 Review of the Genestier-Lafforgue correspondence
Let
![]() $F_v$
be a local function field with ring of integers
$F_v$
be a local function field with ring of integers
![]() $\mathcal {O}_v$
and residue characteristic
$\mathcal {O}_v$
and residue characteristic
![]() $\ell \neq p$
. Let
$\ell \neq p$
. Let
![]() $W_v$
be the Weil group of
$W_v$
be the Weil group of
![]() $F_v$
. Let G be a reductive group over
$F_v$
. Let G be a reductive group over
![]() $F_v$
and denote
$F_v$
and denote
![]() $G_v := G(F_v)$
. In [Reference Genestier and LafforgueGL, Théorèm 8.1], Genestier-Lafforgue construct a map
$G_v := G(F_v)$
. In [Reference Genestier and LafforgueGL, Théorèm 8.1], Genestier-Lafforgue construct a map
 $$ \begin{align*} \left\{ \begin{array}{@{}c@{}} \text{irreducible admissible representations} \\ \pi\text{ of }G_v\text{ over }k\end{array} \right\}/\sim & \longrightarrow \left\{ \begin{array}{@{}c@{}} \text{semi-simple }L\text{-parameters} \\ \rho_{\pi} \colon W_v \rightarrow {}^L G(k) \end{array} \right\}/\sim, \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{@{}c@{}} \text{irreducible admissible representations} \\ \pi\text{ of }G_v\text{ over }k\end{array} \right\}/\sim & \longrightarrow \left\{ \begin{array}{@{}c@{}} \text{semi-simple }L\text{-parameters} \\ \rho_{\pi} \colon W_v \rightarrow {}^L G(k) \end{array} \right\}/\sim, \end{align*} $$
which is characterized by local-global compatibility with Lafforgue’s Global Langlands correspondence.
We briefly summarize the aspects of the Genestier-Lafforgue correspondence that we will need.
6.1.1 The Bernstein center
We begin by recalling the formalism of the Bernstein center [Reference Bernstein and DeligneBer84]. Let
![]() $K \subset G_v$
be an open compact subgroup with prime-to-p order. The Hecke algebra of G with respect to K with coefficients in
$K \subset G_v$
be an open compact subgroup with prime-to-p order. The Hecke algebra of G with respect to K with coefficients in
![]() $\Lambda $
is
$\Lambda $
is
the compactly supported functions on
![]() $K \backslash G_v / K$
valued in
$K \backslash G_v / K$
valued in
![]() $\Lambda $
. This forms an algebra under convolution, normalized so that the indicator function
$\Lambda $
. This forms an algebra under convolution, normalized so that the indicator function ![]() is the unit. We let
is the unit. We let
![]() $\mathfrak {Z}(G,K; \Lambda ) := Z(\mathcal {H}(G,K; \Lambda ))$
be the center of
$\mathfrak {Z}(G,K; \Lambda ) := Z(\mathcal {H}(G,K; \Lambda ))$
be the center of
![]() $\mathcal {H}(G,K; \Lambda )$
.
$\mathcal {H}(G,K; \Lambda )$
.
If
![]() $K \subset K'$
have prime-to-p pro-order (e.g., this will be true as long as they are sufficiently small), then convolution with
$K \subset K'$
have prime-to-p pro-order (e.g., this will be true as long as they are sufficiently small), then convolution with ![]() gives a homomorphism
gives a homomorphism
![]() $\mathfrak {Z}(G,K; \Lambda ) \rightarrow \mathfrak {Z}(G,K'; \Lambda )$
. The Bernstein center of G (with coefficients in
$\mathfrak {Z}(G,K; \Lambda ) \rightarrow \mathfrak {Z}(G,K'; \Lambda )$
. The Bernstein center of G (with coefficients in
![]() $\Lambda $
) is
$\Lambda $
) is
where the transition maps to
![]() $\mathfrak {Z}(G,K; \Lambda )$
are as above, and the inverse limit is taken over K with prime-to-p pro-order.
$\mathfrak {Z}(G,K; \Lambda )$
are as above, and the inverse limit is taken over K with prime-to-p pro-order.
If
![]() $\Lambda = k$
, we abbreviate
$\Lambda = k$
, we abbreviate
![]() $\mathcal {H}(G,K) := \mathcal {H}(G,K; k)$
,
$\mathcal {H}(G,K) := \mathcal {H}(G,K; k)$
,
![]() $\mathfrak {Z}(G,K) := \mathfrak {Z}(G,K; k)$
, and
$\mathfrak {Z}(G,K) := \mathfrak {Z}(G,K; k)$
, and
![]() $\mathfrak {Z}(G) := \mathfrak {Z}(G; k)$
.
$\mathfrak {Z}(G) := \mathfrak {Z}(G; k)$
.
The ring
![]() $\mathfrak {Z}(G)$
has another interpretation as the ring of endomorphisms of the identity functor of the category of smooth k-representations of
$\mathfrak {Z}(G)$
has another interpretation as the ring of endomorphisms of the identity functor of the category of smooth k-representations of
![]() $G_v$
. Explicitly, smoothness of
$G_v$
. Explicitly, smoothness of
![]() $\Pi $
implies that
$\Pi $
implies that
![]() $\Pi = \bigcup _{\text {open compact }K \subset G_v} \Pi ^{K}$
, and
$\Pi = \bigcup _{\text {open compact }K \subset G_v} \Pi ^{K}$
, and
![]() $\mathfrak {Z}(G,K)$
acts on
$\mathfrak {Z}(G,K)$
acts on
![]() $\Pi ^{K}$
as an
$\Pi ^{K}$
as an
![]() $\mathcal {H}(G,K)$
-module; this assembles into action of
$\mathcal {H}(G,K)$
-module; this assembles into action of
![]() $\mathfrak {Z}(G)$
on
$\mathfrak {Z}(G)$
on
![]() $\Pi $
. In particular, any irreducible admissible representation
$\Pi $
. In particular, any irreducible admissible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_v$
over k induces a character of
$G_v$
over k induces a character of
![]() $\mathfrak {Z}(G)$
.
$\mathfrak {Z}(G)$
.
6.1.2 Action of the excursion algebra
The main result of [Reference Genestier and LafforgueGL] is the construction of a homomorphism
Let
![]() $x \in \mathcal {B}(G/F_v)$
be a point of the Bruhat-Tits building of G and use it to extend G to a parahoric group scheme over
$x \in \mathcal {B}(G/F_v)$
be a point of the Bruhat-Tits building of G and use it to extend G to a parahoric group scheme over
![]() $\mathcal {O}_v$
. (Some reminders on Bruhat-Tits theory will appear in §6.2.2.) For
$\mathcal {O}_v$
. (Some reminders on Bruhat-Tits theory will appear in §6.2.2.) For
![]() $r \geq 0$
, let
$r \geq 0$
, let
![]() $K_{r} := G(F_v)_{x,r}$
; this is an open compact subgroup of
$K_{r} := G(F_v)_{x,r}$
; this is an open compact subgroup of
![]() $F_v$
. We write
$F_v$
. We write
![]() $Z_{G,r} \colon \operatorname {\mathrm {Exc}}(W_v, {}^L {G}) \rightarrow \mathfrak {Z}(G, K_{r})$
for the composition of
$Z_{G,r} \colon \operatorname {\mathrm {Exc}}(W_v, {}^L {G}) \rightarrow \mathfrak {Z}(G, K_{r})$
for the composition of
![]() $Z_G$
with the tautological projection to
$Z_G$
with the tautological projection to
![]() $\mathcal {H}(G, K_{r})$
.
$\mathcal {H}(G, K_{r})$
.
We will shortly give a characterization of (6.1). First, let us indicate how (6.1) defines the correspondence
![]() $\Pi \mapsto \rho _{\Pi }$
. An irreducible admissible
$\Pi \mapsto \rho _{\Pi }$
. An irreducible admissible
![]() $\Pi $
induces a character of
$\Pi $
induces a character of
![]() $\mathfrak {Z}(G)$
, as discussed above. Composing with
$\mathfrak {Z}(G)$
, as discussed above. Composing with
![]() $Z_G$
then gives a character of
$Z_G$
then gives a character of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L {G}) $
, which by Proposition 2.4 gives a semisimple Langlands parameter
$\operatorname {\mathrm {Exc}}(W_v, {}^L {G}) $
, which by Proposition 2.4 gives a semisimple Langlands parameter
![]() $\rho _{\Pi } \in H^1(W_v, \widehat {G}(k))$
.
$\rho _{\Pi } \in H^1(W_v, \widehat {G}(k))$
.
6.1.3 Local-global compatibility
Choose a smooth projective curve X over
![]() $\mathbf {F}_{\ell }$
and a point
$\mathbf {F}_{\ell }$
and a point
![]() $v \in X$
so that
$v \in X$
so that
![]() $X_v = \operatorname {\mbox {Spec }} \mathcal {O}_v$
, and G extends to a reductive group over the generic point of X. Then choose a further extension of G to a parahoric group scheme over all of X, such that
$X_v = \operatorname {\mbox {Spec }} \mathcal {O}_v$
, and G extends to a reductive group over the generic point of X. Then choose a further extension of G to a parahoric group scheme over all of X, such that
![]() $G/\mathcal {O}_v$
is the parahoric group scheme corresponding to the chosen point
$G/\mathcal {O}_v$
is the parahoric group scheme corresponding to the chosen point
![]() $x \in \mathcal {B}(G/F_v)$
.
$x \in \mathcal {B}(G/F_v)$
.
Choose an embedding of the local Weil group
![]() $W_v$
into the global Weil group of X, which we denote
$W_v$
into the global Weil group of X, which we denote
![]() $\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })$
. The map (6.1) is characterized by local-global compatibility with the global excursion action. The idea is that for
$\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })$
. The map (6.1) is characterized by local-global compatibility with the global excursion action. The idea is that for
![]() $(\gamma _i)_{i \in I} \subset W_v^I \subset \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, the action of the the excursion operator
$(\gamma _i)_{i \in I} \subset W_v^I \subset \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, the action of the the excursion operator
![]() $S_{I, f, (\gamma _i)_{i \in I}}$
on
$S_{I, f, (\gamma _i)_{i \in I}}$
on ![]() is local at v (i.e., it acts through a Hecke operator for
is local at v (i.e., it acts through a Hecke operator for
![]() $G_v$
). Moreover, it commutes with other Hecke operators because all excursion operators commute with all Hecke operators; hence, it must actually be in the center of the relevant Hecke algebra. This idea is affirmed by the Proposition below.
$G_v$
). Moreover, it commutes with other Hecke operators because all excursion operators commute with all Hecke operators; hence, it must actually be in the center of the relevant Hecke algebra. This idea is affirmed by the Proposition below.
Proposition 6.1 (Genestier-Lafforgue Proposition 1.3).
Let
![]() $r \geq 0$
be an integer and
$r \geq 0$
be an integer and
![]() $D := rv + D^v$
a closed finite subscheme of X, with
$D := rv + D^v$
a closed finite subscheme of X, with
![]() $D^v$
supported away from v. For
$D^v$
supported away from v. For
![]() $(\gamma _i)_{i \in I} \subset W_v^I$
, the operator
$(\gamma _i)_{i \in I} \subset W_v^I$
, the operator
![]() $S_{I, f, (\gamma _i)_{i \in I}}$
acts on
$S_{I, f, (\gamma _i)_{i \in I}}$
acts on ![]() as convolution by
as convolution by
![]() $Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}}) \in \mathfrak {Z}(G, K_{r})$
.
$Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}}) \in \mathfrak {Z}(G, K_{r})$
.
Remark 6.2. By [Reference Genestier and LafforgueGL, Lemme 1.4], for large enough (depending on r)
![]() $D^v$
the action of
$D^v$
the action of
![]() $Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}})$
on
$Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}})$
on ![]() is faithful. Therefore, Proposition 6.1 certainly characterizes the map (6.1). What is not clear is that the resulting
is faithful. Therefore, Proposition 6.1 certainly characterizes the map (6.1). What is not clear is that the resulting
![]() $Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}})$
is independent of choices (of the global curve, or the integral model of the affine group scheme). In [Reference Genestier and LafforgueGL], this is established by giving a purely local construction of (6.1) in terms of ‘restricted shtukas’, but for our purposes, it will be enough to accept Proposition 6.1 as a black box.
$Z_{G,r}(S_{I, f, (\gamma _i)_{i \in I}})$
is independent of choices (of the global curve, or the integral model of the affine group scheme). In [Reference Genestier and LafforgueGL], this is established by giving a purely local construction of (6.1) in terms of ‘restricted shtukas’, but for our purposes, it will be enough to accept Proposition 6.1 as a black box.
6.2 Preliminary results on Hecke algebras
We next establish some technical lemmas which aid to study the properties of the Brauer homomorphism. The only result that will be needed in later subsections is Corollary 6.4.
6.2.1 Assumptions
In this subsection, we allow
![]() $F_v$
to be any local field (including one of characteristic zero) of residue characteristic
$F_v$
to be any local field (including one of characteristic zero) of residue characteristic
![]() $\ell \neq p$
. Let
$\ell \neq p$
. Let
![]() $E_v/F_v$
be a finite Galois assumption such that
$E_v/F_v$
be a finite Galois assumption such that
![]() $\operatorname {Gal}(E_v/F_v)$
has order coprime to
$\operatorname {Gal}(E_v/F_v)$
has order coprime to
![]() $\ell $
. We let H be any (connected) reductive group over
$\ell $
. We let H be any (connected) reductive group over
![]() $F_v$
and
$F_v$
and
![]() $G := \operatorname {\mathrm {Res}}_{E_v/F_v}(H_{E_v})$
. We abbreviate
$G := \operatorname {\mathrm {Res}}_{E_v/F_v}(H_{E_v})$
. We abbreviate
![]() $H_v = H(F_v)$
and
$H_v = H(F_v)$
and
![]() $G_v = G(F_v) = H(E_v)$
.
$G_v = G(F_v) = H(E_v)$
.
6.2.2 Reminders on Bruhat-Tits theory
First, we recall some relevant facts from Bruhat-Tits theory, originally developed in [Reference Bruhat and TitsBT72] but explained in the form used below in [Reference Kaletha and PrasadKP23].
Let
![]() $\mathcal {B}(H/F_v)$
be the Bruhat-Tits building of
$\mathcal {B}(H/F_v)$
be the Bruhat-Tits building of
![]() $H/F_v$
and
$H/F_v$
and
![]() $x \in \mathcal {B}(H/F_v)$
. Associated to x, there is the parahoric group
$x \in \mathcal {B}(H/F_v)$
. Associated to x, there is the parahoric group
![]() $H(F_v)_x^0 := H(F_v)_{x,0}$
, along with its decreasing filtration
$H(F_v)_x^0 := H(F_v)_{x,0}$
, along with its decreasing filtration
![]() $H(F_v)_{x,r}$
for
$H(F_v)_{x,r}$
for
![]() $r \geq 0$
. The subgroup
$r \geq 0$
. The subgroup
![]() $H(F_v)_{x,0+} := \bigcup _{s> 0} H(F_v)_{x,s}$
is pro-
$H(F_v)_{x,0+} := \bigcup _{s> 0} H(F_v)_{x,s}$
is pro-
![]() $\ell $
.
$\ell $
.
We record some descent properties: if
![]() $E_v/F_v$
is unramified, then
$E_v/F_v$
is unramified, then
![]() $H(E_v)_{x,r}^{\operatorname {Gal}(E_v/F_v)} = H(F_v)_{x,r}$
, and if
$H(E_v)_{x,r}^{\operatorname {Gal}(E_v/F_v)} = H(F_v)_{x,r}$
, and if
![]() $E_v/F_v$
is tamely ramified, then
$E_v/F_v$
is tamely ramified, then
![]() $H(E_v)_{x,r}^{\operatorname {Gal}(E_v/F_v)} \supset H(F_v)_{x,r}$
as explained in [Reference Kaletha and PrasadKP23, §12].
$H(E_v)_{x,r}^{\operatorname {Gal}(E_v/F_v)} \supset H(F_v)_{x,r}$
as explained in [Reference Kaletha and PrasadKP23, §12].
We shall make use of the Cartan decomposition. We follow the description in [Reference Kaletha and PrasadKP23, §5.2]. Let S be a maximal
![]() $F_v$
-split torus of H, and
$F_v$
-split torus of H, and
![]() $Z = Z_H(S)$
. Referring to [Reference Kaletha and PrasadKP23, (5.2.1)] for undefined notation, we have a subset
$Z = Z_H(S)$
. Referring to [Reference Kaletha and PrasadKP23, (5.2.1)] for undefined notation, we have a subset
According to [Reference Kaletha and PrasadKP23, Theorem 5.2.1], for a special vertex x in the apartment of S, we have
-
1.
 $H(F_v) = H(F_v)_{x,0} \cdot \mathcal {Z} \cdot H(F_v)_{x,0}$
, and
$H(F_v) = H(F_v)_{x,0} \cdot \mathcal {Z} \cdot H(F_v)_{x,0}$
, and -
2. for
 $z, z' \in \mathcal {Z}$
,
$z, z' \in \mathcal {Z}$
,
 $H(F_v)_{x,0} \, z \, H(F_v)_{x,0} = H(F_v)_x^0 \, z' \, H(F_v)_x^0$
if and only if
$H(F_v)_{x,0} \, z \, H(F_v)_{x,0} = H(F_v)_x^0 \, z' \, H(F_v)_x^0$
if and only if
 $z'(z^{-1}) \in Z(F_v)^0$
,
$z'(z^{-1}) \in Z(F_v)^0$
,
where for a Levi subgroup
![]() $M \subset G$
, the subgroup
$M \subset G$
, the subgroup
![]() $M(F_v)^0 \subset M(F_v)$
is the kernel of the Kottwitz homomorphism
$M(F_v)^0 \subset M(F_v)$
is the kernel of the Kottwitz homomorphism
![]() $\kappa _M \colon M(F_v) \rightarrow \pi _1(M)_I^{\operatorname {Gal}(\breve {F}_v/F_v)}$
; it may be defined alternatively as in [Reference Kaletha and PrasadKP23, Definition 2.6.23]. We have
$\kappa _M \colon M(F_v) \rightarrow \pi _1(M)_I^{\operatorname {Gal}(\breve {F}_v/F_v)}$
; it may be defined alternatively as in [Reference Kaletha and PrasadKP23, Definition 2.6.23]. We have
![]() $Z(F_v)^0 \subset H(F_v)_{x,0}$
.
$Z(F_v)^0 \subset H(F_v)_{x,0}$
.
6.2.3 Maps of double coset spaces
Following the notation of §6.2.1, let
![]() $S_G$
be a maximal
$S_G$
be a maximal
![]() $F_v$
-split torus of G and define
$F_v$
-split torus of G and define
![]() $Z_E := Z_G(S_G)$
, and
$Z_E := Z_G(S_G)$
, and
![]() $\mathcal {Z}_E \subset Z_E(F_v)$
as in (6.2). Let
$\mathcal {Z}_E \subset Z_E(F_v)$
as in (6.2). Let
![]() $S_F$
be a maximal
$S_F$
be a maximal
![]() $F_v$
-split torus of H contained in
$F_v$
-split torus of H contained in
![]() $S_G$
,
$S_G$
,
![]() $Z_F = Z_H(S_H)$
, and
$Z_F = Z_H(S_H)$
, and
![]() $\mathcal {Z}_F \subset Z_F(F_v)$
as in (6.2). Let
$\mathcal {Z}_F \subset Z_F(F_v)$
as in (6.2). Let
![]() $x \in \mathcal {B}(G/F_v)$
be a special vertex in the apartment of
$x \in \mathcal {B}(G/F_v)$
be a special vertex in the apartment of
![]() $S_G$
. We will abbreviate
$S_G$
. We will abbreviate
![]() $K_r := G(F_v)_{x,r}$
and
$K_r := G(F_v)_{x,r}$
and
![]() $U_r = K_r^{\operatorname {Gal}(E_v/F_v)} \supset H(F_v)_{x,r}$
. The goal of this subsection is to prove the following.
$U_r = K_r^{\operatorname {Gal}(E_v/F_v)} \supset H(F_v)_{x,r}$
. The goal of this subsection is to prove the following.
Proposition 6.3. If
![]() $r \geq 0$
, then the map
$r \geq 0$
, then the map
![]() $U_r \backslash H_v / U_r \rightarrow K_r \backslash G_v / K_r$
is injective.
$U_r \backslash H_v / U_r \rightarrow K_r \backslash G_v / K_r$
is injective.
Proof. We first handle the case
![]() $r=0$
, which will seen to be a consequence of Cartan decomposition. Since
$r=0$
, which will seen to be a consequence of Cartan decomposition. Since
![]() $U_0 \supset H(F_v)_{x,0}$
, the Cartan decomposition implies that double cosets
$U_0 \supset H(F_v)_{x,0}$
, the Cartan decomposition implies that double cosets
![]() $U_0 \backslash G_v / U_0$
are represented by
$U_0 \backslash G_v / U_0$
are represented by
![]() $z \in \mathcal {Z}_F$
. If
$z \in \mathcal {Z}_F$
. If
![]() $z_1, z_2 \in \mathcal {Z}_F$
are such that
$z_1, z_2 \in \mathcal {Z}_F$
are such that
![]() $K_0 z_1 K_0 = K_0 z_2 K_0$
, then
$K_0 z_1 K_0 = K_0 z_2 K_0$
, then
![]() $z_2z_1^{-1} \in Z_E(F_v)^0 \subset K_0$
. At the same time, clearly
$z_2z_1^{-1} \in Z_E(F_v)^0 \subset K_0$
. At the same time, clearly
![]() $z_2z_1^{-1} \in H(F_v)$
, so we conclude that
$z_2z_1^{-1} \in H(F_v)$
, so we conclude that
![]() $z_2z_1^{-1} \in K_0 \cap H_v = U_0$
. Therefore,
$z_2z_1^{-1} \in K_0 \cap H_v = U_0$
. Therefore,
![]() $U_0 z_1 U_0 = U_0 z_2 U_0$
, and the case
$U_0 z_1 U_0 = U_0 z_2 U_0$
, and the case
![]() $r=0$
is concluded.
$r=0$
is concluded.
Now suppose
![]() $r>0$
. Let
$r>0$
. Let
![]() $a,b \in U_r \backslash H_v$
be two elements whose images in
$a,b \in U_r \backslash H_v$
be two elements whose images in
![]() $K_r \backslash G_v$
lie in the same orbit for the right translation of
$K_r \backslash G_v$
lie in the same orbit for the right translation of
![]() $K_r$
. In other words,
$K_r$
. In other words,
![]() $a = bk$
for some
$a = bk$
for some
![]() $k \in K_r$
. Since
$k \in K_r$
. Since
![]() $a,b$
are fixed by
$a,b$
are fixed by
![]() $\sigma $
, this implies that
$\sigma $
, this implies that
and therefore,
![]() $\sigma (k) k^{-1} \in \operatorname {\mathrm {Stab}}_{K_r}(b) =: K^b_r$
. Note that
$\sigma (k) k^{-1} \in \operatorname {\mathrm {Stab}}_{K_r}(b) =: K^b_r$
. Note that
![]() $\operatorname {Gal}(E_r/F_r)$
is of order prime-to-
$\operatorname {Gal}(E_r/F_r)$
is of order prime-to-
![]() $\ell $
, while
$\ell $
, while
![]() $K_r$
is pro-
$K_r$
is pro-
![]() $\ell $
thanks to the assumption
$\ell $
thanks to the assumption
![]() $r>0$
, so then
$r>0$
, so then
![]() $H^1(\operatorname {Gal}(E_r/F_r); K^b_r) = 0$
. This means that there exists
$H^1(\operatorname {Gal}(E_r/F_r); K^b_r) = 0$
. This means that there exists
![]() $y \in K^b_r$
such that
$y \in K^b_r$
such that
![]() $\sigma (k) k^{-1} = \sigma (y) y^{-1}$
. Then
$\sigma (k) k^{-1} = \sigma (y) y^{-1}$
. Then
![]() $y^{-1} k$
is fixed by
$y^{-1} k$
is fixed by
![]() $\sigma $
, so
$\sigma $
, so
![]() $y^{-1} k \in H_v \cap K_r = U_r$
. But then
$y^{-1} k \in H_v \cap K_r = U_r$
. But then
which shows that a and b lie in the same orbit for the right translation of
![]() $U_r$
on
$U_r$
on
![]() $U_r \backslash H_v$
.
$U_r \backslash H_v$
.
In the following Corollary, we let
![]() $\operatorname {Gal}(E_v/F_v)$
act on
$\operatorname {Gal}(E_v/F_v)$
act on
![]() $G_v = H(E_v)$
by the natural Galois action, which induces an action on
$G_v = H(E_v)$
by the natural Galois action, which induces an action on
![]() $\mathcal {H}(G, K_r; \Lambda )$
.
$\mathcal {H}(G, K_r; \Lambda )$
.
Corollary 6.4. Suppose
![]() $r\geq 0$
. Then the restriction map
$r\geq 0$
. Then the restriction map
![]() $\mathcal {H}(G, K_r; \Lambda )^{\operatorname {Gal}(E_v/F_v)} \rightarrow \mathcal {H}(H, U_r; \Lambda )$
is surjective.
$\mathcal {H}(G, K_r; \Lambda )^{\operatorname {Gal}(E_v/F_v)} \rightarrow \mathcal {H}(H, U_r; \Lambda )$
is surjective.
6.3 The Brauer homomorphism
We introduce the notion of the Brauer homomorphism from [Reference Treumann and VenkateshTV16], whose utility for our purpose is to capture the relationship between
![]() $\Pi $
and its Tate cohomology from the perspective of Hecke algebras.
$\Pi $
and its Tate cohomology from the perspective of Hecke algebras.
6.3.1 Assumptions
In this subsection, we allow
![]() $F_v$
to be any local field (including one of characteristic zero) of residue characteristic
$F_v$
to be any local field (including one of characteristic zero) of residue characteristic
![]() $\ell \neq p$
. We assume that
$\ell \neq p$
. We assume that
![]() $\operatorname {Gal}(E_v/F_v)$
is cyclic of order p, and we let
$\operatorname {Gal}(E_v/F_v)$
is cyclic of order p, and we let
![]() $\sigma \in \operatorname {Gal}(E_v/F_v)$
be a generator. We let H be any (connected) reductive group over
$\sigma \in \operatorname {Gal}(E_v/F_v)$
be a generator. We let H be any (connected) reductive group over
![]() $F_v$
and
$F_v$
and
![]() $G := \operatorname {\mathrm {Res}}_{E_v/F_v}(H_{E_v})$
. Subgroups
$G := \operatorname {\mathrm {Res}}_{E_v/F_v}(H_{E_v})$
. Subgroups
![]() $K_r \subset G_v$
,
$K_r \subset G_v$
,
![]() $U_r \subset H_v$
are defined as in §6.2.3.
$U_r \subset H_v$
are defined as in §6.2.3.
6.3.2 The (un-normalized) Brauer homomorphism
Let
![]() $K \subset G_v$
be an open compact subgroup and let
$K \subset G_v$
be an open compact subgroup and let
![]() $U := K^{\sigma } \subset H_v$
. We say that
$U := K^{\sigma } \subset H_v$
. We say that
![]() $K \subset G_v$
is a plain subgroup if
$K \subset G_v$
is a plain subgroup if
![]() $(G_v/K)^{\sigma } = H_v/U$
.
$(G_v/K)^{\sigma } = H_v/U$
.
We can view
![]() $\mathcal {H}(G, K)$
as the ring of
$\mathcal {H}(G, K)$
as the ring of
![]() $G_v$
-invariant (for the diagonal action) functions on
$G_v$
-invariant (for the diagonal action) functions on
![]() $(G_v / K) \times (G_v / K)$
under convolution.
$(G_v / K) \times (G_v / K)$
under convolution.
Lemma 6.5. If
![]() $K \subset G_v$
is a plain subgroup, then the restriction map
$K \subset G_v$
is a plain subgroup, then the restriction map
 $$ \begin{align} \mathcal{H}(G, K)^{\sigma} &= \mathrm{Fun}_{G_v,c}((G_v / K) \times (G_v / K), k)^{\sigma} \\ & \xrightarrow{\text{restrict}} \mathrm{Fun}_{H_v,c}((H_v/U) \times (H_v/U), k) = \mathcal{H}(H_v, U) \nonumber \end{align} $$
$$ \begin{align} \mathcal{H}(G, K)^{\sigma} &= \mathrm{Fun}_{G_v,c}((G_v / K) \times (G_v / K), k)^{\sigma} \\ & \xrightarrow{\text{restrict}} \mathrm{Fun}_{H_v,c}((H_v/U) \times (H_v/U), k) = \mathcal{H}(H_v, U) \nonumber \end{align} $$
is an algebra homomorphism.
Proof. What we must verify is that for
![]() $x,z \in H_v/U$
and
$x,z \in H_v/U$
and
![]() $f,g \in \mathcal {H}(G, K)^{\sigma }$
we have
$f,g \in \mathcal {H}(G, K)^{\sigma }$
we have
 $$ \begin{align} \sum_{y \in G_v/K} f(x, y) g(y,z) = \sum_{y \in H_v/U} f(x,y) g(y,z). \end{align} $$
$$ \begin{align} \sum_{y \in G_v/K} f(x, y) g(y,z) = \sum_{y \in H_v/U} f(x,y) g(y,z). \end{align} $$
Since f and g are
![]() $\sigma $
-invariant, we have
$\sigma $
-invariant, we have
If
![]() $y \notin H_v/U$
, then the plain-ness assumption implies that y is not fixed by
$y \notin H_v/U$
, then the plain-ness assumption implies that y is not fixed by
![]() $\sigma $
. Therefore, the contribution from the orbit of
$\sigma $
. Therefore, the contribution from the orbit of
![]() $\sigma $
on y to (6.4) is a multiple of p, which is
$\sigma $
on y to (6.4) is a multiple of p, which is
![]() $0$
in k.
$0$
in k.
The map of Lemma 6.5 was introduced in [Reference Treumann and VenkateshTV16, §4] and called the (un-normalized) Brauer homomorphism. We denote it
Lemma 6.6. If
![]() $K \subset G(F_v)_{x,0+}$
for any
$K \subset G(F_v)_{x,0+}$
for any
![]() $x \in \mathcal {B}(G/F_v)$
, then K is plain.
$x \in \mathcal {B}(G/F_v)$
, then K is plain.
Proof. By the long exact sequence for group cohomology, the plain-ness of
![]() $K \subset G_v$
is equivalent to condition that the map on non-abelian cohomology
$K \subset G_v$
is equivalent to condition that the map on non-abelian cohomology
![]() $H^1( \langle \sigma \rangle; K) \rightarrow H^1(\langle \sigma \rangle; G_v)$
has trivial fiber over the trivial class. But since
$H^1( \langle \sigma \rangle; K) \rightarrow H^1(\langle \sigma \rangle; G_v)$
has trivial fiber over the trivial class. But since
![]() $G(F_v)_{x,0+}$
is pro-
$G(F_v)_{x,0+}$
is pro-
![]() $\ell $
, all its subgroups are acyclic for
$\ell $
, all its subgroups are acyclic for
![]() $H^1( \langle \sigma \rangle , -)$
as
$H^1( \langle \sigma \rangle , -)$
as
![]() $\sigma $
has order p. Therefore,
$\sigma $
has order p. Therefore,
![]() $H^1( \langle \sigma \rangle , K)$
vanishes for all such
$H^1( \langle \sigma \rangle , K)$
vanishes for all such
![]() $K \subset G(F_v)_{x,0+}$
.
$K \subset G(F_v)_{x,0+}$
.
Lemma 6.7 (Relation to the Brauer homomorphism).
Assume
![]() $K \subset G_v$
is plain. Suppose
$K \subset G_v$
is plain. Suppose
![]() $\Pi $
is a
$\Pi $
is a
![]() $\sigma $
-fixed representation of
$\sigma $
-fixed representation of
![]() $G_v$
. Then the map of Tate cohomology groups
$G_v$
. Then the map of Tate cohomology groups
![]() $T^*(\Pi ^{K}) \rightarrow T^*(\Pi )$
lands in the U-invariants, and for any
$T^*(\Pi ^{K}) \rightarrow T^*(\Pi )$
lands in the U-invariants, and for any
![]() $h \in \mathcal {H}(G, K)^{\sigma }$
, we have the commutative diagram below.
$h \in \mathcal {H}(G, K)^{\sigma }$
, we have the commutative diagram below.

(Here,
![]() $T^0 h$
is the element of
$T^0 h$
is the element of
![]() $T^0 (\mathcal {H}(G, K))$
represented by h.)
$T^0 (\mathcal {H}(G, K))$
represented by h.)
Proof. This is [Reference Treumann and VenkateshTV16, §6.2]; it follows from a direct computation similar to the proof of Lemma 6.5.
6.3.3 Treumann-Venkatesh homomorphism
If we take
![]() $K = K_r$
as in Corollary 6.4, then the Brauer homomorphism
$K = K_r$
as in Corollary 6.4, then the Brauer homomorphism
![]() $ \operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r)$
is a surjective algebra homomorphism and hence induces a map on centers
$ \operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r)$
is a surjective algebra homomorphism and hence induces a map on centers
It is evident from the definition that
![]() $Z(\operatorname {\mathrm {Br}})$
through the quotient
$Z(\operatorname {\mathrm {Br}})$
through the quotient
![]() $Z(\mathcal {H}(G, K_r)^{\sigma }) / N \cdot \mathfrak {Z}(G, K_r)$
.
$Z(\mathcal {H}(G, K_r)^{\sigma }) / N \cdot \mathfrak {Z}(G, K_r)$
.
Since
![]() $\mathfrak {Z}(G, K_r)$
is commutative, it has a Tate diagonal homomorphism (Definition 5.14)
$\mathfrak {Z}(G, K_r)$
is commutative, it has a Tate diagonal homomorphism (Definition 5.14)
![]() $\mathfrak {Z}(G, K_r) \xrightarrow {\Delta ^p} T^0(\mathfrak {Z}(G,K_r))$
. Since
$\mathfrak {Z}(G, K_r) \xrightarrow {\Delta ^p} T^0(\mathfrak {Z}(G,K_r))$
. Since
![]() $Z(\mathcal {H}(G, K_r))^{\sigma } \subset Z(\mathcal {H}(G, K_r)^{\sigma }) $
, we may compose with
$Z(\mathcal {H}(G, K_r))^{\sigma } \subset Z(\mathcal {H}(G, K_r)^{\sigma }) $
, we may compose with
![]() $Z(\operatorname {\mathrm {Br}})$
to obtain a map
$Z(\operatorname {\mathrm {Br}})$
to obtain a map
Note, however, that it is not k-linear since
![]() $\Delta ^p$
is
$\Delta ^p$
is
![]() $\operatorname {\mathrm {Frob}}$
-semilinear over k. Then there is a (unique) homomorphism
$\operatorname {\mathrm {Frob}}$
-semilinear over k. Then there is a (unique) homomorphism
![]() $Z'$
fitting into the commutative diagram
$Z'$
fitting into the commutative diagram

We have
![]() $\mathfrak {Z}(G, K_r) \cong \mathfrak {Z}(G, K_r; \mathbf {F}_p) \otimes _{\mathbf {F}_p} k$
, which as explained in Construction 5.17 induces a k-linear isomorphism
$\mathfrak {Z}(G, K_r) \cong \mathfrak {Z}(G, K_r; \mathbf {F}_p) \otimes _{\mathbf {F}_p} k$
, which as explained in Construction 5.17 induces a k-linear isomorphism
Definition 6.8. We define Treumann-Venkatesh homomorphism
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}},r}$
to be the homomorphism
$\mathfrak {Z}_{\operatorname {\mathrm {TV}},r}$
to be the homomorphism
![]() $ \mathfrak {Z}(G, K_r) \rightarrow \mathfrak {Z}(H, U_r)$
obtained by linearization of
$ \mathfrak {Z}(G, K_r) \rightarrow \mathfrak {Z}(H, U_r)$
obtained by linearization of
![]() $Z'$
in the sense of Construction 5.17 with respect to the
$Z'$
in the sense of Construction 5.17 with respect to the
![]() $\mathbf {F}_p$
structure (6.8).
$\mathbf {F}_p$
structure (6.8).
Remark 6.9. Definition 6.8 is not considered in [Reference Treumann and VenkateshTV16], but it is inspired by the definition of the normalized Brauer homomorphism in [Reference Treumann and VenkateshTV16, §4.3].
6.4 The base change homomorphism for Bernstein centers
For now, assumptions are as in §6.3.1. Suppose
![]() $K_r$
has prime-to-p pro-order. For
$K_r$
has prime-to-p pro-order. For
![]() $s>r$
, so that
$s>r$
, so that
![]() $K_s \subset K_r$
, we have a map
$K_s \subset K_r$
, we have a map
![]() $e_G^{s \rightarrow r} \colon \mathfrak {Z}(G, K_s) \rightarrow \mathfrak {Z}(G, K_r)$
given by convolution with
$e_G^{s \rightarrow r} \colon \mathfrak {Z}(G, K_s) \rightarrow \mathfrak {Z}(G, K_r)$
given by convolution with ![]() . (Technically,
. (Technically,
![]() $e_G^{s \rightarrow r}$
also depends on the point
$e_G^{s \rightarrow r}$
also depends on the point
![]() $x \in \mathcal {B}(G/F_v)$
used to define the
$x \in \mathcal {B}(G/F_v)$
used to define the
![]() $K_r$
, but we suppress this from our notation.) Similarly, we have
$K_r$
, but we suppress this from our notation.) Similarly, we have
![]() $e_H^{s \rightarrow r} \colon \mathfrak {Z}(H, U_s) \rightarrow \mathfrak {Z}(H, U_r)$
given by convolution with
$e_H^{s \rightarrow r} \colon \mathfrak {Z}(H, U_s) \rightarrow \mathfrak {Z}(H, U_r)$
given by convolution with ![]() .
.
Lemma 6.10. The diagram

commutes.
Definition 6.11 (Base change homomorphism for Bernstein centers).
We define the map
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}} \colon \mathfrak {Z}(G) \rightarrow \mathfrak {Z}(H)$
as
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}} \colon \mathfrak {Z}(G) \rightarrow \mathfrak {Z}(H)$
as
Definition 6.11 is well defined over local fields of any residue characteristic
![]() $\ell \neq p$
, but in this paper we will only prove properties of it for local function fields. Hence, for the rest of the paper, we assume that
$\ell \neq p$
, but in this paper we will only prove properties of it for local function fields. Hence, for the rest of the paper, we assume that
![]() $F_v$
is a local field of positive characteristic. The rest of this subsection shall be devoted to the proof of Theorem 1.4.
$F_v$
is a local field of positive characteristic. The rest of this subsection shall be devoted to the proof of Theorem 1.4.
6.4.1
The maps
induce upon applying Tate cohomology,
Fix a closed point
![]() $x_0 $
on X distinct from v. For each integer r, we will impose level structure along
$x_0 $
on X distinct from v. For each integer r, we will impose level structure along
![]() $D := r v + \infty x_0$
, interpreted as in §5.4.2. By Remark 6.2, the map
$D := r v + \infty x_0$
, interpreted as in §5.4.2. By Remark 6.2, the map ![]() is injective.
is injective.
6.4.3
For any set S, we let
![]() $k[S]$
denote the k-vector space of k-valued functions on S.
$k[S]$
denote the k-vector space of k-valued functions on S.
Now suppose
![]() $\widetilde {S}$
is a set with an action of
$\widetilde {S}$
is a set with an action of
![]() $G_v \rtimes \langle \sigma \rangle $
, on which an open compact subgroup
$G_v \rtimes \langle \sigma \rangle $
, on which an open compact subgroup
![]() $K \subset G_v$
acts freely. Then for
$K \subset G_v$
acts freely. Then for
![]() $S := \widetilde {S}/K$
, there is a natural action of
$S := \widetilde {S}/K$
, there is a natural action of
![]() $\mathcal {H}(G,K)$
on
$\mathcal {H}(G,K)$
on
![]() $k[S]$
since we may view
$k[S]$
since we may view
![]() $\mathcal {H}(G, K) = \operatorname {\mathrm {Hom}}_{G_v}(k[G_v/K], k[G_v/K])$
and
$\mathcal {H}(G, K) = \operatorname {\mathrm {Hom}}_{G_v}(k[G_v/K], k[G_v/K])$
and
![]() $k[S] = \operatorname {\mathrm {Hom}}_{G_v}(k[G_v/K], k[\widetilde {S}])$
. This induces an action of
$k[S] = \operatorname {\mathrm {Hom}}_{G_v}(k[G_v/K], k[\widetilde {S}])$
. This induces an action of
![]() $T^0 (\mathcal {H}(G, K))$
on
$T^0 (\mathcal {H}(G, K))$
on
![]() $T^0(k[S]) \cong k[S^{\sigma }]$
and then by inflation an action of
$T^0(k[S]) \cong k[S^{\sigma }]$
and then by inflation an action of
![]() $\mathcal {H}(G,K)^{\sigma }$
on
$\mathcal {H}(G,K)^{\sigma }$
on
![]() $k[S^{\sigma }]$
.
$k[S^{\sigma }]$
.
By the same mechanism, for
![]() $U := K^\sigma $
, there is an induced action of
$U := K^\sigma $
, there is an induced action of
![]() $\mathcal {H}(H, U)$
on
$\mathcal {H}(H, U)$
on
![]() $k[\widetilde {S}^{\sigma }/K^{\sigma }] = k[\widetilde {S}^{\sigma }/U]$
. We define
$k[\widetilde {S}^{\sigma }/K^{\sigma }] = k[\widetilde {S}^{\sigma }/U]$
. We define
![]() $Z_{H,r} \colon \operatorname {\mathrm {Exc}}(W_v, {}^L {H}) \rightarrow \mathfrak {Z}(H, U_{r})$
similarly to
$Z_{H,r} \colon \operatorname {\mathrm {Exc}}(W_v, {}^L {H}) \rightarrow \mathfrak {Z}(H, U_{r})$
similarly to
![]() $Z_{G,r}$
.
$Z_{G,r}$
.
Lemma 6.12. Assume
![]() $K \subset G_v$
is a plain subgroup. Then
$K \subset G_v$
is a plain subgroup. Then
![]() $k[\widetilde {S}^{\sigma }/U]$
is a
$k[\widetilde {S}^{\sigma }/U]$
is a
![]() $\mathcal {H}(G,K)^{\sigma }$
-direct summand of
$\mathcal {H}(G,K)^{\sigma }$
-direct summand of
![]() $k[S^{\sigma }]$
, and for all
$k[S^{\sigma }]$
, and for all
![]() $h \in \mathcal {H}(G,K)^{\sigma }$
, we have
$h \in \mathcal {H}(G,K)^{\sigma }$
, we have
Proof. See [Reference Treumann and VenkateshTV16, equation (4.2.2)].
From §6.4.1, we have the diagram

Here, the right vertical map is the identity map on endomorphisms with respect to the identification ![]() . Note that the surjectivity statement of Corollary 6.4, plus Lemma 6.5 and Lemma 6.7 giving compatibility of the respective actions with the Brauer homomorphism, are what guarantees that an endomorphism commuting with the
. Note that the surjectivity statement of Corollary 6.4, plus Lemma 6.5 and Lemma 6.7 giving compatibility of the respective actions with the Brauer homomorphism, are what guarantees that an endomorphism commuting with the
![]() $T^0(\mathcal {H}_G)$
-action also commutes with the
$T^0(\mathcal {H}_G)$
-action also commutes with the
![]() $\mathcal {H}_H$
-action.
$\mathcal {H}_H$
-action.
Corollary 6.13. For all
![]() $r \geq 1$
, the action of
$r \geq 1$
, the action of
![]() $z \in T^0\mathfrak {Z}(G, K_{r}) $
on
$z \in T^0\mathfrak {Z}(G, K_{r}) $
on ![]() in (6.9) agrees with the action of
in (6.9) agrees with the action of
![]() $Z(\operatorname {\mathrm {Br}})(z)$
on
$Z(\operatorname {\mathrm {Br}})(z)$
on ![]() in (6.9) under the identification
in (6.9) under the identification ![]() from §3.4.5. In other words, the square in diagram (6.9) commutes.
from §3.4.5. In other words, the square in diagram (6.9) commutes.
Proof. Apply Lemma 6.12 with
![]() $S := \operatorname {\mathrm {Sht}}_{G, D, \emptyset }$
and
$S := \operatorname {\mathrm {Sht}}_{G, D, \emptyset }$
and
![]() $\widetilde {S} := \operatorname {\mathrm {Sht}}_{G, \infty v + \infty x_0, \emptyset } := \varprojlim _{j \geq 0} \operatorname {\mathrm {Sht}}_{G, (r+j) v + j x_0, \emptyset }$
. Then
$\widetilde {S} := \operatorname {\mathrm {Sht}}_{G, \infty v + \infty x_0, \emptyset } := \varprojlim _{j \geq 0} \operatorname {\mathrm {Sht}}_{G, (r+j) v + j x_0, \emptyset }$
. Then
![]() $k[S]$
is identified with the functions on
$k[S]$
is identified with the functions on
![]() $\operatorname {\mathrm {Sht}}_{G, rv+ \infty x_0, \emptyset }$
, and Lemma 5.7 plus §3.4.5 identify
$\operatorname {\mathrm {Sht}}_{G, rv+ \infty x_0, \emptyset }$
, and Lemma 5.7 plus §3.4.5 identify
![]() $k[\widetilde {S}^{\sigma }/K^{\sigma } ]$
with the functions on
$k[\widetilde {S}^{\sigma }/K^{\sigma } ]$
with the functions on
![]() $\operatorname {\mathrm {Sht}}_{H, rv+\infty x_0, \emptyset }$
.
$\operatorname {\mathrm {Sht}}_{H, rv+\infty x_0, \emptyset }$
.
As compactly supported functions are dual to functions, the assertions for compactly supported functions then follow by duality.
Corollary 6.14. For all
![]() $r \geq 1$
, for all
$r \geq 1$
, for all
![]() $\{V, x, \xi , (\gamma _i)_{i \in I}\}$
as in §2.4,
$\{V, x, \xi , (\gamma _i)_{i \in I}\}$
as in §2.4,
![]() $\operatorname {\mathrm {Br}}$
sends
$\operatorname {\mathrm {Br}}$
sends
 $$ \begin{align*} Z_{G,r}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) & \in \mathfrak{Z}(G, K_{r}) \subset \mathcal{H}(G, K_{r}) \\ \hspace{1cm} \xrightarrow{\operatorname{\mathrm{Br}}} Z_{H,r}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) & \in \mathfrak{Z}(H,U_{r}) \subset \mathcal{H}(H, U_{r}). \end{align*} $$
$$ \begin{align*} Z_{G,r}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) & \in \mathfrak{Z}(G, K_{r}) \subset \mathcal{H}(G, K_{r}) \\ \hspace{1cm} \xrightarrow{\operatorname{\mathrm{Br}}} Z_{H,r}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) & \in \mathfrak{Z}(H,U_{r}) \subset \mathcal{H}(H, U_{r}). \end{align*} $$
Proof. The equality from §6.4.2 shows that

At the same time, Corollary 6.13 shows that the left-hand side of (6.10) agrees with the image of
![]() $\operatorname {\mathrm {Br}}(Z_{G,r}(S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}}))$
via (6.9) for all
$\operatorname {\mathrm {Br}}(Z_{G,r}(S_{I, \operatorname {\mathrm {Nm}}^{(p^{-1})}(V), \operatorname {\mathrm {Nm}}^{(p^{-1})}(x), \operatorname {\mathrm {Nm}}^{(p^{-1})}(\xi ), (\gamma _i)_{i \in I}}))$
via (6.9) for all
![]() $r \geq 1$
. We conclude using that the map
$r \geq 1$
. We conclude using that the map ![]() in (6.9) is injective, which follows from Remark 6.2.
in (6.9) is injective, which follows from Remark 6.2.
6.4.4
Recall that in Definition 2.8 we have defined a map
![]() $\phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
over k.
$\phi _{\mathsf {BC}} \colon {}^L H \rightarrow {}^L G$
over k.
Corollary 6.15. The following diagram commutes:

Proof. The commutativity of the diagram

implies that
![]() $Z(\operatorname {\mathrm {Br}}) \circ \Delta ^p \circ Z_G = Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p $
. By definition,
$Z(\operatorname {\mathrm {Br}}) \circ \Delta ^p \circ Z_G = Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p $
. By definition,
![]() $\mathfrak {Z}_{\operatorname {\mathrm {TV}}} \circ Z_G$
is the linearization of
$\mathfrak {Z}_{\operatorname {\mathrm {TV}}} \circ Z_G$
is the linearization of
![]() $Z(\operatorname {\mathrm {Br}}) \circ \Delta ^p \circ Z_G$
, so it is also the linearization of
$Z(\operatorname {\mathrm {Br}}) \circ \Delta ^p \circ Z_G$
, so it is also the linearization of
![]() $Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p$
.
$Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p$
.
By Lemma 5.16, the Tate diagonal
![]() $\Delta ^p \colon \operatorname {\mathrm {Exc}}(W_v, {}^L G) \rightarrow T^0(\operatorname {\mathrm {Exc}}(W_v, {}^L G))$
sends
$\Delta ^p \colon \operatorname {\mathrm {Exc}}(W_v, {}^L G) \rightarrow T^0(\operatorname {\mathrm {Exc}}(W_v, {}^L G))$
sends
Its linearization therefore sends
since this is a k-algebra homomorphism that agrees with (6.12) when
![]() $(V, x, \xi )$
are defined over
$(V, x, \xi )$
are defined over
![]() $\mathbf {F}_p$
. Applying Corollary 6.14 with
$\mathbf {F}_p$
. Applying Corollary 6.14 with
![]() $r \rightarrow \infty $
, we have
$r \rightarrow \infty $
, we have
 $$ \begin{align*} Z(\operatorname{\mathrm{Br}}) \circ Z_{G}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) &= Z_H(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \\ & = Z_H( \phi_{\mathsf{BC}}^* (S_{I, V, x, \xi , (\gamma_i)_{i \in I}})). \end{align*} $$
$$ \begin{align*} Z(\operatorname{\mathrm{Br}}) \circ Z_{G}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) &= Z_H(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \\ & = Z_H( \phi_{\mathsf{BC}}^* (S_{I, V, x, \xi , (\gamma_i)_{i \in I}})). \end{align*} $$
Therefore, the linearization of
![]() $Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p$
agrees with
$Z(\operatorname {\mathrm {Br}}) \circ T^0(Z_G) \circ \Delta ^p$
agrees with
![]() $Z_H \circ \phi _{\mathsf {BC}}^*$
.
$Z_H \circ \phi _{\mathsf {BC}}^*$
.
Completion of the proof of Theorem 1.4.
Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $H_v$
and
$H_v$
and
![]() $\chi _{\pi } \colon \mathfrak {Z}(H) \rightarrow k$
the induced character. By the definition of the Genestier-Lafforgue parametrization,
$\chi _{\pi } \colon \mathfrak {Z}(H) \rightarrow k$
the induced character. By the definition of the Genestier-Lafforgue parametrization,
![]() $\rho _{\pi }$
corresponds to
$\rho _{\pi }$
corresponds to
![]() $\chi _{\pi } \circ Z_H$
via Proposition 2.4. Then (6.11) implies that
$\chi _{\pi } \circ Z_H$
via Proposition 2.4. Then (6.11) implies that
![]() $\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}} \circ Z_G = \chi _{\pi } \circ Z_H \circ \phi _{\mathsf {BC}}^*$
is associated to the L-parameter
$\chi _{\pi } \circ \mathfrak {Z}_{\operatorname {\mathrm {TV}}} \circ Z_G = \chi _{\pi } \circ Z_H \circ \phi _{\mathsf {BC}}^*$
is associated to the L-parameter
![]() $\phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
$\phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
6.5 The Treumann-Venkatesh Conjecture
In this subsection, we will prove Theorem 1.2. We begin by formulating the Treumann-Venkatesh Conjecture precisely in this setting. (The original phrasing of [Reference Treumann and VenkateshTV16] is in terms of a hypothetical Local Langlands correspondence which was not defined at the time for general groups.)
6.5.1 Assumptions
In this subsection, the assumptions are as in §6.3, and we furthermore assume
![]() $F_v$
is a local function field. We note, however, that the formulation of all the statements in §6.11 makes sense for any local field
$F_v$
is a local function field. We note, however, that the formulation of all the statements in §6.11 makes sense for any local field
![]() $F_v$
of residue field
$F_v$
of residue field
![]() $\ell \neq p$
, with a suitable replacement for the Genestier-Lafforgue correspondence and that all our arguments in this subsection apply if those statements are true for
$\ell \neq p$
, with a suitable replacement for the Genestier-Lafforgue correspondence and that all our arguments in this subsection apply if those statements are true for
![]() $F_v$
.
$F_v$
.
6.5.2 Formulation of the Conjecture
Let
![]() $\Pi $
be an irreducible admissible representation of
$\Pi $
be an irreducible admissible representation of
![]() $G_v$
over k. Let
$G_v$
over k. Let
![]() $\Pi ^{\sigma }$
be the representation of
$\Pi ^{\sigma }$
be the representation of
![]() $G_v$
obtained by composing
$G_v$
obtained by composing
![]() $\Pi $
with
$\Pi $
with
![]() $\sigma \colon G_v \rightarrow G_v$
. We say that
$\sigma \colon G_v \rightarrow G_v$
. We say that
![]() $\Pi $
is
$\Pi $
is
![]() $\sigma $
-fixed if
$\sigma $
-fixed if
![]() $\Pi \approx \Pi ^{\sigma }$
as
$\Pi \approx \Pi ^{\sigma }$
as
![]() $G_v$
-representations.
$G_v$
-representations.
Lemma 6.16 [Reference Treumann and VenkateshTV16, Proposition 6.1].
If
![]() $\Pi $
is
$\Pi $
is
![]() $\sigma $
-fixed, then the
$\sigma $
-fixed, then the
![]() $G_v$
-action on
$G_v$
-action on
![]() $\Pi $
extends uniquely to an action of
$\Pi $
extends uniquely to an action of
![]() $G_v \rtimes \langle \sigma \rangle $
.
$G_v \rtimes \langle \sigma \rangle $
.
Using Lemma 6.16, we can form the Tate cohomology groups
![]() $T^0(\Pi )$
and
$T^0(\Pi )$
and
![]() $T^1(\Pi )$
with respect to the
$T^1(\Pi )$
with respect to the
![]() $\sigma $
-action, which are then representations of
$\sigma $
-action, which are then representations of
![]() $H_v$
. Treumann-Venkatesh conjecture that they are, in fact, admissible representations of
$H_v$
. Treumann-Venkatesh conjecture that they are, in fact, admissible representations of
![]() $H_v$
, but we do not prove or use this.
$H_v$
, but we do not prove or use this.
Definition 6.17 (Linkage).
An irreducible admissible representation
![]() $\pi $
of
$\pi $
of
![]() $H_v$
is linked with an irreducible admissible representation
$H_v$
is linked with an irreducible admissible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_v$
if
$G_v$
if
![]() $\pi ^{(p)}$
appears in
$\pi ^{(p)}$
appears in
![]() $T^0(\Pi )$
or
$T^0(\Pi )$
or
![]() $T^1(\Pi )$
, where
$T^1(\Pi )$
, where
![]() $\pi ^{(p)}$
is the Frobenius twist
$\pi ^{(p)}$
is the Frobenius twist
Conjecture 6.18 [Reference Treumann and VenkateshTV16, Conjecture 6.3].
If
![]() $\pi $
is linked to
$\pi $
is linked to
![]() $\Pi $
, then
$\Pi $
, then
![]() $\pi $
base changes to
$\pi $
base changes to
![]() $\Pi $
.
$\Pi $
.
Example 6.19. The need for the Frobenius twist can be seen in a simple example. Suppose
![]() $G = H^p$
and
$G = H^p$
and
![]() $\sigma $
acts by cyclic permutation. Then
$\sigma $
acts by cyclic permutation. Then
![]() $G^\sigma $
is the diagonal copy of H. In this case, a representation
$G^\sigma $
is the diagonal copy of H. In this case, a representation
![]() $\pi $
of
$\pi $
of
![]() $H_v$
should transfer to
$H_v$
should transfer to
![]() $\pi ^{\boxtimes p}$
of
$\pi ^{\boxtimes p}$
of
![]() $G_v$
. And indeed,
$G_v$
. And indeed,
Remark 6.20. Conjecture 6.18 is highly nontrivial even for groups such as
![]() $\operatorname {\mathrm {GL}}_n$
where the full Local Langlands correspondence – hence, in particular, the existence of cyclic base change – is already known. In fact, the main result of [Reference RonchettiRon16] is a special case of the conjecture for depth-zero supercuspidal representations of
$\operatorname {\mathrm {GL}}_n$
where the full Local Langlands correspondence – hence, in particular, the existence of cyclic base change – is already known. In fact, the main result of [Reference RonchettiRon16] is a special case of the conjecture for depth-zero supercuspidal representations of
![]() $\operatorname {\mathrm {GL}}_n$
compactly induced from cuspidal Deligne-Lusztig representations. Despite the very explicit nature of the Local Langlands Correspondence for such representations, the proof in loc. cit. involves rather hefty calculations, which were not amenable to generalization.
$\operatorname {\mathrm {GL}}_n$
compactly induced from cuspidal Deligne-Lusztig representations. Despite the very explicit nature of the Local Langlands Correspondence for such representations, the proof in loc. cit. involves rather hefty calculations, which were not amenable to generalization.
Our proof of Conjecture 6.18 (when p is odd and good for
![]() $\widehat {G}$
) is conceptual and applies to all representations without using any explicit models such as models for supercuspidal representations as compact inductions. Furthermore, the unramified and tamely ramified base change are handled completely differently in [Reference RonchettiRon16], whereas our proof will be completely uniform in the field extension, the reductive group and the irreducible representation.
$\widehat {G}$
) is conceptual and applies to all representations without using any explicit models such as models for supercuspidal representations as compact inductions. Furthermore, the unramified and tamely ramified base change are handled completely differently in [Reference RonchettiRon16], whereas our proof will be completely uniform in the field extension, the reductive group and the irreducible representation.
Theorem 6.21. Assume p is an odd good prime for
![]() $\widehat {G}$
. Let
$\widehat {G}$
. Let
![]() $\Pi $
be an irreducible admissible representation of
$\Pi $
be an irreducible admissible representation of
![]() $G_v$
and let
$G_v$
and let
be the associated character of
![]() $\Pi ^{(p)}$
. Form
$\Pi ^{(p)}$
. Form
![]() $T^*(\Pi ) := T^*(\langle \sigma \rangle , \Pi )$
, viewed as a smooth
$T^*(\Pi ) := T^*(\langle \sigma \rangle , \Pi )$
, viewed as a smooth
![]() $H_v$
-representation. Then for any irreducible character
$H_v$
-representation. Then for any irreducible character
![]() $\chi \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow k$
appearing in the action on
$\chi \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow k$
appearing in the action on
![]() $T^*(\Pi )$
via
$T^*(\Pi )$
via
![]() $Z_H \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow \mathfrak {Z}(H)$
, the composite character
$Z_H \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow \mathfrak {Z}(H)$
, the composite character
agrees with
![]() $\chi _{\Pi ^{(p)}}$
.
$\chi _{\Pi ^{(p)}}$
.
It is clear that Theorem 6.21 implies Theorem 1.2.
Proof. Let
![]() $\Pi $
be a representation of
$\Pi $
be a representation of
![]() $G_v$
. Then
$G_v$
. Then
![]() $\mathfrak {Z}(G)$
acts
$\mathfrak {Z}(G)$
acts
![]() $G_v$
-equivariantly on
$G_v$
-equivariantly on
![]() $\Pi $
, inducing an
$\Pi $
, inducing an
![]() $H_v$
-equivariant action of
$H_v$
-equivariant action of
![]() $\mathfrak {Z}(G)^{\sigma }$
on
$\mathfrak {Z}(G)^{\sigma }$
on
![]() $T^*(\Pi )$
. In particular, as
$T^*(\Pi )$
. In particular, as
![]() $Z_G$
maps
$Z_G$
maps
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)^\sigma \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
into
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)^\sigma \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
into
![]() $\mathfrak {Z}(G)^{\sigma }$
, we get an
$\mathfrak {Z}(G)^{\sigma }$
, we get an
![]() $H_v$
-equivariant action of
$H_v$
-equivariant action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)^{\sigma }$
on
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)^{\sigma }$
on
![]() $T^*(\Pi )$
.
$T^*(\Pi )$
.
By Lemma 6.6,
![]() $K_{r}$
is plain as soon as
$K_{r}$
is plain as soon as
![]() $r \geq 1$
. Taking the (filtered) colimit over r in Lemma 6.7 with
$r \geq 1$
. Taking the (filtered) colimit over r in Lemma 6.7 with
![]() $K = K_r$
, we find that for all
$K = K_r$
, we find that for all
![]() $S \in \operatorname {\mathrm {Exc}}(W_v, {}^L G)^{\sigma }$
, we have
$S \in \operatorname {\mathrm {Exc}}(W_v, {}^L G)^{\sigma }$
, we have
 $$\begin{align*}\left(\begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of} \\ Z_{G}(S) \end{array} \right) = \left( \begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of}\\ \operatorname{\mathrm{Br}}(Z_{G}(S)) \end{array}\right). \end{align*}$$
$$\begin{align*}\left(\begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of} \\ Z_{G}(S) \end{array} \right) = \left( \begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of}\\ \operatorname{\mathrm{Br}}(Z_{G}(S)) \end{array}\right). \end{align*}$$
In other words, the diagram below commutes:

At the same time, taking the inverse limit over r in Corollary 6.14 yields that
for all
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
.
$V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
.
Combining (6.13) and (6.14) shows that
 $$ \begin{align} \left(\begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of} \\ Z_{G}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) \end{array} \right) = \left( \begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of}\\ Z_{H}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \end{array}\right) \end{align} $$
$$ \begin{align} \left(\begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of} \\ Z_{G}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}}) \end{array} \right) = \left( \begin{array}{@{}c@{}} \text{the action on }T^*(\Pi)\text{ of}\\ Z_{H}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \end{array}\right) \end{align} $$
for all
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
.
$V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
.
From now on, assume
![]() $\Pi $
is an irreducible (smooth) representation of
$\Pi $
is an irreducible (smooth) representation of
![]() $G_v$
. Then
$G_v$
. Then
![]() $\operatorname {\mathrm {End}}_{G_v} (\Pi ) \cong k$
(by Schur’s Lemma applied to the Hecke action on the invariants of
$\operatorname {\mathrm {End}}_{G_v} (\Pi ) \cong k$
(by Schur’s Lemma applied to the Hecke action on the invariants of
![]() $\Pi $
for every compact open subgroup of
$\Pi $
for every compact open subgroup of
![]() $G_v$
). The L-parameter attached to
$G_v$
). The L-parameter attached to
![]() $\Pi $
corresponds under Proposition 2.4 to the character
$\Pi $
corresponds under Proposition 2.4 to the character
This induces
The action of
![]() $T^0 \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
on
$T^0 \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
on
![]() $T^*(\Pi )$
is through
$T^*(\Pi )$
is through
![]() $T^0 \chi _{\Pi }$
composed with the natural map
$T^0 \chi _{\Pi }$
composed with the natural map
![]() $\iota \colon T^0 \operatorname {\mathrm {End}}_{G_v}(\Pi ) \rightarrow \operatorname {\mathrm {End}}_{H_v}(T^* \Pi )$
.
$\iota \colon T^0 \operatorname {\mathrm {End}}_{G_v}(\Pi ) \rightarrow \operatorname {\mathrm {End}}_{H_v}(T^* \Pi )$
.
We also consider the homomorphism
Then (6.15) implies that for all
![]() $V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
, we have
$V \in \operatorname {\mathrm {Rep}}_k(({}^L G)^I)$
, we have
Note that the fact that the right-hand side of (6.16) lies in k is already non-obvious. In particular, (6.16) implies that for any irreducible subquotient
![]() $\pi $
of
$\pi $
of
![]() $T^* \Pi $
, we have
$T^* \Pi $
, we have
 $$ \begin{align} \chi_{\pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) &= \chi_{T^* \Pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}} ) \nonumber \\ & = (T^0 \chi_{\Pi}) (S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} ) \nonumber\\ & = \chi_{\Pi}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} ). \end{align} $$
$$ \begin{align} \chi_{\pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) &= \chi_{T^* \Pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}} ) \nonumber \\ & = (T^0 \chi_{\Pi}) (S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} ) \nonumber\\ & = \chi_{\Pi}(S_{I, \operatorname{\mathrm{Nm}}^{(p^{-1})}(V), \operatorname{\mathrm{Nm}}^{(p^{-1})}(x), \operatorname{\mathrm{Nm}}^{(p^{-1})}(\xi), (\gamma_i)_{i \in I}} ). \end{align} $$
The character
![]() $\chi _{\Pi ^{(p)}}$
giving the k-linearized action of
$\chi _{\Pi ^{(p)}}$
giving the k-linearized action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
on
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
on
![]() $\Pi ^{(p)} := \Pi \otimes _{k, \operatorname {\mathrm {Frob}}_p} k$
satisfies
$\Pi ^{(p)} := \Pi \otimes _{k, \operatorname {\mathrm {Frob}}_p} k$
satisfies
Definition 6.22. Similarly to Definition 5.19, let
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
be the k-subalgebra generated by
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
be the k-subalgebra generated by
![]() $N \cdot \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
and all elements of the form
$N \cdot \operatorname {\mathrm {Exc}}(W_v, {}^L G)$
and all elements of the form
![]() $\operatorname {\mathrm {Nm}} (S_{I, V, x, \xi , (\gamma _i)_{i \in I}}) = S_{I, \operatorname {\mathrm {Nm}} (V), \operatorname {\mathrm {Nm}}(x), \operatorname {\mathrm {Nm}}(\xi ), (\gamma _i)_{i \in I}}$
.
$\operatorname {\mathrm {Nm}} (S_{I, V, x, \xi , (\gamma _i)_{i \in I}}) = S_{I, \operatorname {\mathrm {Nm}} (V), \operatorname {\mathrm {Nm}}(x), \operatorname {\mathrm {Nm}}(\xi ), (\gamma _i)_{i \in I}}$
.
Then the combination of (6.17) and (6.18) tells us that the action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)'$
on
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)'$
on
![]() $\Pi ^{(p)}$
via
$\Pi ^{(p)}$
via
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \rightarrow \operatorname {\mathrm {Exc}}(W_v, {}^L G) \xrightarrow {Z_G} \mathfrak {Z}(G)$
is given by the character
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \rightarrow \operatorname {\mathrm {Exc}}(W_v, {}^L G) \xrightarrow {Z_G} \mathfrak {Z}(G)$
is given by the character
![]() $\chi ^{\prime }_{\Pi ^{(p)}}$
that sends
$\chi ^{\prime }_{\Pi ^{(p)}}$
that sends
and (using Theorem 5.11(ii))
![]() $N \cdot S \mapsto 0$
for any
$N \cdot S \mapsto 0$
for any
![]() $S \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. By Lemma 5.15, the unique extension of this character to
$S \in \operatorname {\mathrm {Exc}}(\Gamma , {}^L G)$
. By Lemma 5.15, the unique extension of this character to
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is (using Lemma 5.16)
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is (using Lemma 5.16)
 $$ \begin{align*} S_{I, V, x, \xi, (\gamma_i)_{i \in I}} & \mapsto \chi_{\Pi^{(p)}}'(S_{I, \operatorname{\mathrm{Nm}}(V), \operatorname{\mathrm{Nm}}(x), \operatorname{\mathrm{Nm}}(\xi), (\gamma_i)_{i \in I}})^{1/p} \\ [(6.19) \implies] &= \chi_{\pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \\ &= \chi_{\pi} \circ \phi_{\mathsf{BC}}^* (S_{I, V, x, \xi, (\gamma_i)_{i \in I}}). \end{align*} $$
$$ \begin{align*} S_{I, V, x, \xi, (\gamma_i)_{i \in I}} & \mapsto \chi_{\Pi^{(p)}}'(S_{I, \operatorname{\mathrm{Nm}}(V), \operatorname{\mathrm{Nm}}(x), \operatorname{\mathrm{Nm}}(\xi), (\gamma_i)_{i \in I}})^{1/p} \\ [(6.19) \implies] &= \chi_{\pi}(S_{I, \operatorname{\mathrm{Res}}_{\mathsf{BC}}(V), x, \xi, (\gamma_i)_{i \in I}}) \\ &= \chi_{\pi} \circ \phi_{\mathsf{BC}}^* (S_{I, V, x, \xi, (\gamma_i)_{i \in I}}). \end{align*} $$
At the same time, since
![]() $\chi _{\Pi ^{(p)}}$
is tautologically an extension of
$\chi _{\Pi ^{(p)}}$
is tautologically an extension of
![]() $\chi _{\Pi ^{(p)}}'$
to
$\chi _{\Pi ^{(p)}}'$
to
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
, it must be the case that
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
, it must be the case that
![]() $\chi _{\Pi ^{(p)}} = \chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
as characters of
$\chi _{\Pi ^{(p)}} = \chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
as characters of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
for any irreducible subquotient
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
for any irreducible subquotient
![]() $\pi $
of
$\pi $
of
![]() $T^*(\Pi )$
.
$T^*(\Pi )$
.
6.6 Local mod p cyclic base change
In this subsection, we will prove Theorem 1.1. Assumptions are as in §6.5. We note, however, that the formulation of all the statements in §6.11 makes sense for any local field
![]() $F_v$
of residue field
$F_v$
of residue field
![]() $\ell \neq p$
, with a suitable replacement for the Genestier-Lafforgue correspondence, and that all our arguments in this subsection apply if those statements are true for
$\ell \neq p$
, with a suitable replacement for the Genestier-Lafforgue correspondence, and that all our arguments in this subsection apply if those statements are true for
![]() $F_v$
.
$F_v$
.
6.6.1 Formulation of local base change
We begin by formulating a precise notion of local base change.
Definition 6.23. Let
![]() $\pi $
be an irreducible admissible representation of
$\pi $
be an irreducible admissible representation of
![]() $H_v$
over k, and
$H_v$
over k, and
![]() $\Pi $
be an irreducible admissible representation of
$\Pi $
be an irreducible admissible representation of
![]() $G_v$
over k. We say that
$G_v$
over k. We say that
![]() $\pi $
base changes to
$\pi $
base changes to
![]() $\Pi $
if
$\Pi $
if
![]() $\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi } \in H^1(W_v, \widehat {G}(k))$
.
$\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi } \in H^1(W_v, \widehat {G}(k))$
.
This definition is an approximation to the notion of base change for L-packets. An L-packet for
![]() $H_v$
should be said to base change to an L-packet for
$H_v$
should be said to base change to an L-packet for
![]() $G_v$
if the corresponding L-parameters are related by
$G_v$
if the corresponding L-parameters are related by
![]() $\phi _{\mathsf {BC}}$
. A more refined version of Definition 6.23 would declare
$\phi _{\mathsf {BC}}$
. A more refined version of Definition 6.23 would declare
![]() $\pi $
to base change to
$\pi $
to base change to
![]() $\Pi $
if the L-packet of
$\Pi $
if the L-packet of
![]() $\pi $
base changes to the L-packet of
$\pi $
base changes to the L-packet of
![]() $\Pi $
, but we lack a definition of L-packets for general groups and representations; therefore, we use the fibers of the Genestier-Lafforgue correspondence as a substitute for L-packets.
$\Pi $
, but we lack a definition of L-packets for general groups and representations; therefore, we use the fibers of the Genestier-Lafforgue correspondence as a substitute for L-packets.
6.6.2 Finiteness conditions on Hecke algebras
We will use the following recent result of Dat-Helm-Kurinczuk-Moss. We are keeping the running assumption that p differs from the residue characteristic of
![]() $F_v$
.
$F_v$
.
Theorem 6.24 [Reference Dat, Helm, Kurinczuk and MossDHKM].
For every
![]() $x \in \mathcal {B}(G/F_v)$
and every
$x \in \mathcal {B}(G/F_v)$
and every
![]() $r \geq 0$
, and
$r \geq 0$
, and
![]() $K_r := G(F_v)_{x,r}$
, the Hecke algebra
$K_r := G(F_v)_{x,r}$
, the Hecke algebra
![]() $\mathcal {H}(G, K_r)$
is finite over its center
$\mathcal {H}(G, K_r)$
is finite over its center
![]() $\mathfrak {Z}(G, K_r)$
, which is itself a finitely generated algebra over k.
$\mathfrak {Z}(G, K_r)$
, which is itself a finitely generated algebra over k.
Remark 6.25. The paper [Reference Dat, Helm, Kurinczuk and MossDHKM] proves a much stronger result, where coefficients are allowed to be an arbitrary
![]() $\mathbf {Z}_p$
-algebra. The analogous result with coefficients in a characteristic zero field is an old result of Bernstein. The case where p is banal for G was known to experts to follow in a similar manner from work of Vignéras, although it is not explicitly written down in the literature.
$\mathbf {Z}_p$
-algebra. The analogous result with coefficients in a characteristic zero field is an old result of Bernstein. The case where p is banal for G was known to experts to follow in a similar manner from work of Vignéras, although it is not explicitly written down in the literature.
6.6.3 Existence of local base change
Fix
![]() $x \in \mathcal {B}(H/F_v)$
and let
$x \in \mathcal {B}(H/F_v)$
and let
![]() $K_r := G(F_v)_{x,r}$
and
$K_r := G(F_v)_{x,r}$
and
![]() $U_r := K_r^{\sigma }$
. We prove the following theorem, which, in particular, implies Theorem 1.1.
$U_r := K_r^{\sigma }$
. We prove the following theorem, which, in particular, implies Theorem 1.1.
Theorem 6.26. Suppose p is an odd good prime for
![]() $\widehat {G}$
. Let
$\widehat {G}$
. Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $H_v$
over k, having nonzero
$H_v$
over k, having nonzero
![]() $U_r$
-fixed vectors, with L-parameter
$U_r$
-fixed vectors, with L-parameter
![]() $\rho _{\pi } \in H^1(W_v, \widehat {H}(k))$
. Then there is an irreducible representation
$\rho _{\pi } \in H^1(W_v, \widehat {H}(k))$
. Then there is an irreducible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_v$
over k, having nonzero
$G_v$
over k, having nonzero
![]() $K_r$
-fixed vectors, such that
$K_r$
-fixed vectors, such that
![]() $\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
$\rho _{\Pi } \cong \phi _{\mathsf {BC}} \circ \rho _{\pi }$
.
Proof. If
![]() $r = 0$
, then the result is classical, so we assume
$r = 0$
, then the result is classical, so we assume
![]() $r>0$
. Then
$r>0$
. Then
![]() $U_r, K_r$
have prime-to-p pro-order, so the theory of the Bernstein center applies. Recall that the functor
$U_r, K_r$
have prime-to-p pro-order, so the theory of the Bernstein center applies. Recall that the functor
![]() $\Pi \mapsto \Pi ^{K_r}$
induces a bijection between irreducible admissible
$\Pi \mapsto \Pi ^{K_r}$
induces a bijection between irreducible admissible
![]() $G_v$
-representations with nonzero
$G_v$
-representations with nonzero
![]() $K_r$
-invariants and irreducible
$K_r$
-invariants and irreducible
![]() $\mathcal {H}(G_v, K_r)$
-modules. It therefore suffices to construct an irreducible representation of
$\mathcal {H}(G_v, K_r)$
-modules. It therefore suffices to construct an irreducible representation of
![]() $\mathcal {H}(G_v, K_r)$
whose induced character of
$\mathcal {H}(G_v, K_r)$
whose induced character of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is
![]() $\chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
, where
$\chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
, where
![]() $\chi _{\pi } \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow k$
is the character of
$\chi _{\pi } \colon \operatorname {\mathrm {Exc}}(W_v, {}^L H) \rightarrow k$
is the character of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L H)$
corresponding to
$\operatorname {\mathrm {Exc}}(W_v, {}^L H)$
corresponding to
![]() $\pi $
.
$\pi $
.
By hypothesis, we have a nonzero algebra homomorphism
![]() $\mathcal {H}(H, U_r) \rightarrow \operatorname {\mathrm {End}}(\pi ^{U_r})$
, which has the property that the composite homomorphism
$\mathcal {H}(H, U_r) \rightarrow \operatorname {\mathrm {End}}(\pi ^{U_r})$
, which has the property that the composite homomorphism
has kernel the maximal ideal
![]() $\mathfrak {m}_{\pi } = \ker ( \chi _{\pi }) \subset \operatorname {\mathrm {Exc}}(W_v, {}^L H)$
. The Brauer homomorphism
$\mathfrak {m}_{\pi } = \ker ( \chi _{\pi }) \subset \operatorname {\mathrm {Exc}}(W_v, {}^L H)$
. The Brauer homomorphism
![]() $\operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r)$
fits into a commutative diagramFootnote
13
$\operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r)$
fits into a commutative diagramFootnote
13

where
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)^\sigma $
is as in Definition 6.22. Let
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)^\sigma $
is as in Definition 6.22. Let
![]() $\mathfrak {m}_{\pi }' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L{G})' $
be the kernel of the map
$\mathfrak {m}_{\pi }' \subset \operatorname {\mathrm {Exc}}(W_v, {}^L{G})' $
be the kernel of the map
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L {G})' \rightarrow \operatorname {\mathrm {End}}_k(\pi ^{U_r}) $
obtained by tracing through the diagram above. We claim that
$\operatorname {\mathrm {Exc}}(W_v, {}^L {G})' \rightarrow \operatorname {\mathrm {End}}_k(\pi ^{U_r}) $
obtained by tracing through the diagram above. We claim that
![]() $\mathfrak {m}_{\pi }'$
is a maximal ideal. First of all, we observe that the map
$\mathfrak {m}_{\pi }'$
is a maximal ideal. First of all, we observe that the map
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \rightarrow \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
lands in the subring of scalars
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' \rightarrow \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
lands in the subring of scalars
![]() $k \subset \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
, since by Corollary 6.14 the action of
$k \subset \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
, since by Corollary 6.14 the action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L {G})'$
on
$\operatorname {\mathrm {Exc}}(W_v, {}^L {G})'$
on
![]() $\operatorname {\mathrm {End}}_k(\pi ^{U_r})$
factors through the action of
$\operatorname {\mathrm {End}}_k(\pi ^{U_r})$
factors through the action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L H)$
, which is through
$\operatorname {\mathrm {Exc}}(W_v, {}^L H)$
, which is through
![]() $\chi _{\pi }$
. On the other hand, since all maps in the diagram are maps of k-algebras,
$\chi _{\pi }$
. On the other hand, since all maps in the diagram are maps of k-algebras,
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
must surject onto the full ring of scalars
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
must surject onto the full ring of scalars
![]() $ k \subset \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
.
$ k \subset \operatorname {\mathrm {End}}_k(\pi ^{U_r})$
.
Note that
![]() $\operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r) $
vanishes on
$\operatorname {\mathrm {Br}} \colon \mathcal {H}(G, K_r)^{\sigma } \rightarrow \mathcal {H}(H, U_r) $
vanishes on
![]() $N \cdot \mathcal {H}( G, K_r) \subset \mathcal {H}(G, K_r)^{\sigma } $
. By the commutativity of the bottom part of the diagram, the composition from
$N \cdot \mathcal {H}( G, K_r) \subset \mathcal {H}(G, K_r)^{\sigma } $
. By the commutativity of the bottom part of the diagram, the composition from
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
to
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
to
![]() $\mathcal {H}(H, U_r)$
therefore vanishes on
$\mathcal {H}(H, U_r)$
therefore vanishes on
![]() $N \cdot \operatorname {\mathrm {Exc}}(W_v, {}^L G) \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
. Therefore, we may apply Lemma 5.15 to see that the homomorphism
$N \cdot \operatorname {\mathrm {Exc}}(W_v, {}^L G) \subset \operatorname {\mathrm {Exc}}(W_v, {}^L G)' $
. Therefore, we may apply Lemma 5.15 to see that the homomorphism
![]() $\chi _{\pi }' \colon \operatorname {\mathrm {Exc}}(W_v, {}^L{G} )' \rightarrow k$
corresponding to
$\chi _{\pi }' \colon \operatorname {\mathrm {Exc}}(W_v, {}^L{G} )' \rightarrow k$
corresponding to
![]() $\mathfrak {m}_{\pi }'$
has a unique extension to a character
$\mathfrak {m}_{\pi }'$
has a unique extension to a character
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L{G}) \rightarrow k$
. Since Corollary 6.14 shows that
$\operatorname {\mathrm {Exc}}(W_v, {}^L{G}) \rightarrow k$
. Since Corollary 6.14 shows that
![]() $\chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
is such an extension, its kernel must be the unique maximal ideal of
$\chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
is such an extension, its kernel must be the unique maximal ideal of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
lying over
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
lying over
![]() $\mathfrak {m}_{\pi }'$
.
$\mathfrak {m}_{\pi }'$
.
The preceding paragraph implies that the localization of
![]() $\mathcal {H}(G,K_r)^{\sigma }$
at
$\mathcal {H}(G,K_r)^{\sigma }$
at
![]() $\mathfrak {m}_{\pi }'$
is nonzero since the character
$\mathfrak {m}_{\pi }'$
is nonzero since the character
![]() $\chi _\pi '$
factors through this localization. Since the action of
$\chi _\pi '$
factors through this localization. Since the action of
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)'$
on
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)'$
on
![]() $\mathcal {H}(G, K_r)^\sigma $
factors through the action of
$\mathcal {H}(G, K_r)^\sigma $
factors through the action of
![]() $\mathfrak {Z}(G, K_r)^\sigma $
, there exists a maximal ideal
$\mathfrak {Z}(G, K_r)^\sigma $
, there exists a maximal ideal
![]() $\mathfrak {n}_{\pi }$
of
$\mathfrak {n}_{\pi }$
of
![]() $\mathfrak {Z}(G, K_r)$
lying over
$\mathfrak {Z}(G, K_r)$
lying over
![]() $\mathfrak {m}_{\pi }' $
at which
$\mathfrak {m}_{\pi }' $
at which
![]() $\mathcal {H}(G, K_r)$
is supported. Since the pullback of
$\mathcal {H}(G, K_r)$
is supported. Since the pullback of
![]() $\mathfrak {n}_{\pi }$
to
$\mathfrak {n}_{\pi }$
to
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L{G})$
contains
$\operatorname {\mathrm {Exc}}(W_v, {}^L{G})$
contains
![]() $\mathfrak {m}_{\pi }'$
, it must equal
$\mathfrak {m}_{\pi }'$
, it must equal
![]() $\ker (\chi _{\pi } \circ \phi _{\mathsf {BC}}^*)$
by the preceding paragraph.
$\ker (\chi _{\pi } \circ \phi _{\mathsf {BC}}^*)$
by the preceding paragraph.
By Theorem 6.24 and the Artin-Tate Lemma,
![]() $\mathfrak {Z}(G, K_r)$
is finite over
$\mathfrak {Z}(G, K_r)$
is finite over
![]() $\mathfrak {Z}(G, K_r)^{\sigma }$
, and then
$\mathfrak {Z}(G, K_r)^{\sigma }$
, and then
![]() $\mathcal {H}(G, K_r)$
is finite over
$\mathcal {H}(G, K_r)$
is finite over
![]() $\mathfrak {Z}(G, K_r)^{\sigma }$
. So Nakayama’s Lemma implies that the left
$\mathfrak {Z}(G, K_r)^{\sigma }$
. So Nakayama’s Lemma implies that the left
![]() $\mathcal {H}(G, K_r)$
-module quotient
$\mathcal {H}(G, K_r)$
-module quotient
![]() $\mathcal {H}(G, K_r) /\mathcal {H}(G, K_r) \mathfrak {n}_{\pi }$
is finite-dimensional and nonzero. By design, the only maximal ideal in its support over
$\mathcal {H}(G, K_r) /\mathcal {H}(G, K_r) \mathfrak {n}_{\pi }$
is finite-dimensional and nonzero. By design, the only maximal ideal in its support over
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
is
![]() $\ker (\chi _{\pi } \circ \phi _{\mathsf {BC}}^*)$
, so there is an irreducible
$\ker (\chi _{\pi } \circ \phi _{\mathsf {BC}}^*)$
, so there is an irreducible
![]() $\mathcal {H}(G, K_r)$
-subquotient
$\mathcal {H}(G, K_r)$
-subquotient
![]() $\Xi $
of
$\Xi $
of
![]() $\mathcal {H}(G, K_r) / \mathcal {H}(G, K_r) \mathfrak {n}_{\pi }$
on which
$\mathcal {H}(G, K_r) / \mathcal {H}(G, K_r) \mathfrak {n}_{\pi }$
on which
![]() $\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
acts through
$\operatorname {\mathrm {Exc}}(W_v, {}^L G)$
acts through
![]() $ \chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
, as was to be showed.
$ \chi _{\pi } \circ \phi _{\mathsf {BC}}^*$
, as was to be showed.
Remark 6.27 (Depth estimates).
For applications, it is useful to have control of the depth of the base change. The proof of Theorem 6.26 implies an estimate on the depth, which we now spell out. Recall from [Reference Moy and PrasadMP96] that the depth of an irreducible representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_v$
is the minimal r such that for some
$G_v$
is the minimal r such that for some
![]() $x \in \mathcal {B}(G/F_v)$
,
$x \in \mathcal {B}(G/F_v)$
,
![]() $\Pi ^{G(F_v)_{x, r+}} \neq 0$
. Let us emphasize that the definition of the Moy-Prasad filtration
$\Pi ^{G(F_v)_{x, r+}} \neq 0$
. Let us emphasize that the definition of the Moy-Prasad filtration
![]() $\{G(F_v)_{x, r}\}$
is normalized so that
$\{G(F_v)_{x, r}\}$
is normalized so that
![]() $F_v^{\times }$
has value group
$F_v^{\times }$
has value group
![]() $\mathbf {Z}$
.
$\mathbf {Z}$
.
Let
![]() $\pi $
be an irreducible representation of H of depth r and let
$\pi $
be an irreducible representation of H of depth r and let
![]() $x \in \mathcal {B}(H/F_v)$
such that
$x \in \mathcal {B}(H/F_v)$
such that
![]() $\pi ^{H(F_v)_{x,r+}} \neq 0$
. First, assume that
$\pi ^{H(F_v)_{x,r+}} \neq 0$
. First, assume that
![]() $E_v/F_v$
is unramified. Then
$E_v/F_v$
is unramified. Then
![]() $\mathcal {B}(H/F_v) = \mathcal {B}(G/F_v)^{\operatorname {Gal}(E_v/F_v)}$
, and we have
$\mathcal {B}(H/F_v) = \mathcal {B}(G/F_v)^{\operatorname {Gal}(E_v/F_v)}$
, and we have
![]() $H(F_v)_{x,r+} = G(F_v)_{x,r+}^{\operatorname {Gal}(E_v/F_v)}$
[Reference Kaletha and PrasadKP23, §9]. The proof of Theorem 6.26 shows that there exists a local base change
$H(F_v)_{x,r+} = G(F_v)_{x,r+}^{\operatorname {Gal}(E_v/F_v)}$
[Reference Kaletha and PrasadKP23, §9]. The proof of Theorem 6.26 shows that there exists a local base change
![]() $\Pi $
of
$\Pi $
of
![]() $\pi $
such that
$\pi $
such that
![]() $\Pi ^{G(F_v)_{x,r+}} \neq 0$
, so that
$\Pi ^{G(F_v)_{x,r+}} \neq 0$
, so that
![]() $\operatorname {\mathrm {depth}}(\Pi )\leq \operatorname {\mathrm {depth}}(\pi )$
. (The proof does not use Corollary 6.4 or the Treumann-Venkatesh homomorphism.)
$\operatorname {\mathrm {depth}}(\Pi )\leq \operatorname {\mathrm {depth}}(\pi )$
. (The proof does not use Corollary 6.4 or the Treumann-Venkatesh homomorphism.)
Next, suppose
![]() $E_v/F_v$
is tamely ramified. By [Reference PrasadPra20], we still have
$E_v/F_v$
is tamely ramified. By [Reference PrasadPra20], we still have
![]() $\mathcal {B}(H/F_v) = \mathcal {B}(G/F_v)^{\operatorname {Gal}(E_v/F_v)}$
, and by [Reference Kaletha and PrasadKP23, Proposition 12.9.2], we have
$\mathcal {B}(H/F_v) = \mathcal {B}(G/F_v)^{\operatorname {Gal}(E_v/F_v)}$
, and by [Reference Kaletha and PrasadKP23, Proposition 12.9.2], we have
![]() $(G(F_v)_{x, r^+})^{\operatorname {Gal}(E_v/F_v)} = H(F_v)_{x, r^+}$
for all
$(G(F_v)_{x, r^+})^{\operatorname {Gal}(E_v/F_v)} = H(F_v)_{x, r^+}$
for all
![]() $r \geq 0$
. Hence, in this case, the proof of Theorem 6.26 shows that there exists a local base change
$r \geq 0$
. Hence, in this case, the proof of Theorem 6.26 shows that there exists a local base change
![]() $\Pi $
of
$\Pi $
of
![]() $\pi $
such that
$\pi $
such that
![]() $\Pi ^{G(F_v)_{x,r+}} \neq 0$
, so that
$\Pi ^{G(F_v)_{x,r+}} \neq 0$
, so that
![]() $\operatorname {\mathrm {depth}}(\Pi )\leq \operatorname {\mathrm {depth}}(\pi )$
. Let us caution, however, that if we regard
$\operatorname {\mathrm {depth}}(\Pi )\leq \operatorname {\mathrm {depth}}(\pi )$
. Let us caution, however, that if we regard
![]() $x \in \mathcal {B}(H/E_v)$
instead of
$x \in \mathcal {B}(H/E_v)$
instead of
![]() $\mathcal {B}(G/F_v)$
and
$\mathcal {B}(G/F_v)$
and
![]() $\Pi $
as a representation of
$\Pi $
as a representation of
![]() $H(E_v)$
instead of
$H(E_v)$
instead of
![]() $G(F_v)$
, then it is natural to define the Moy-Prasad filtration
$G(F_v)$
, then it is natural to define the Moy-Prasad filtration
![]() $H(E_v)_{x,r}$
so that
$H(E_v)_{x,r}$
so that
![]() $E_v^{\times }$
has value group
$E_v^{\times }$
has value group
![]() $\mathbf {Z}$
, for which
$\mathbf {Z}$
, for which
![]() $H(E_v)_{x,pr}= G(F_v)_{x, r}$
. Hence, in this normalization, our estimate would instead be ‘
$H(E_v)_{x,pr}= G(F_v)_{x, r}$
. Hence, in this normalization, our estimate would instead be ‘
![]() $\operatorname {\mathrm {depth}}(\Pi ) \leq p \cdot \operatorname {\mathrm {depth}}(\pi )$
’.
$\operatorname {\mathrm {depth}}(\Pi ) \leq p \cdot \operatorname {\mathrm {depth}}(\pi )$
’.
In both cases, the inequalities we obtain are expected to be optimal [Reference Adler and LanskyAL10].
A The base change functor realizes Langlands functoriality by Tony Feng and Gus Lonergan
In this section, we prove Theorem 4.20.
First, we recall some general properties of Smith theory for schemes.
A.1 Recollections on Smith theory for schemes
The Tate category for schemes enjoys a robust 6-functor formalism (observed in the topological case in [Reference TreumannTre19, §4.3] and proved for schemes in [Reference Riche and WilliamsonRW22, §2,3]). Let us recall the statements for later use. Let
![]() $f \colon Y \rightarrow S$
be a
$f \colon Y \rightarrow S$
be a
![]() $\sigma $
-equivariant morphism of varieties with admissible
$\sigma $
-equivariant morphism of varieties with admissible
![]() $\sigma $
-action over a field of characteristic
$\sigma $
-action over a field of characteristic
![]() $\ell \neq p$
. Let
$\ell \neq p$
. Let
![]() $\Lambda $
be a p-adic ring of coefficients; we are most interested in
$\Lambda $
be a p-adic ring of coefficients; we are most interested in
![]() $\Lambda \in \{ W(k), k\}$
.
$\Lambda \in \{ W(k), k\}$
.
-
• The pullback functor
 $f^* \colon D^b_{c}(S^{\sigma };\Lambda [\sigma ]) \rightarrow D^b_{c}(Y^{\sigma }; \Lambda [\sigma ])$
descends to The proper pushforward
$f^* \colon D^b_{c}(S^{\sigma };\Lambda [\sigma ]) \rightarrow D^b_{c}(Y^{\sigma }; \Lambda [\sigma ])$
descends to The proper pushforward $$\begin{align*}f^* \colon \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
$$\begin{align*}f^* \colon \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
 $Rf_! \colon D^b_{c}(Y^{\sigma }; \Lambda [\sigma ]) \rightarrow D^b_{c}(S^{\sigma };\Lambda [\sigma ])$
descends to
$Rf_! \colon D^b_{c}(Y^{\sigma }; \Lambda [\sigma ]) \rightarrow D^b_{c}(S^{\sigma };\Lambda [\sigma ])$
descends to  $$\begin{align*}Rf_! \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
$$\begin{align*}Rf_! \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
-
• As Verdier duality
 $\mathbb {D} \colon D^b_{c,\sigma }(Y^{\sigma }; \Lambda ) \rightarrow D^b_{c,\sigma }(Y^{\sigma }; \Lambda )$
preserves
$\mathbb {D} \colon D^b_{c,\sigma }(Y^{\sigma }; \Lambda ) \rightarrow D^b_{c,\sigma }(Y^{\sigma }; \Lambda )$
preserves
 $\operatorname {\mathrm {Perf}}(Y^{\sigma }; \Lambda [\sigma ])$
, it descends to the Tate category to define Using this, we may define the operations
$\operatorname {\mathrm {Perf}}(Y^{\sigma }; \Lambda [\sigma ])$
, it descends to the Tate category to define Using this, we may define the operations $$\begin{align*}\mathbb{D} \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
and
$$\begin{align*}\mathbb{D} \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
and $$\begin{align*}f^! := \mathbb{D} \circ f^* \circ \mathbb{D} \colon \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \end{align*}$$
$$\begin{align*}f^! := \mathbb{D} \circ f^* \circ \mathbb{D} \colon \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \end{align*}$$
 $$\begin{align*}Rf_* := \mathbb{D} \circ f_! \circ \mathbb{D} \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
$$\begin{align*}Rf_* := \mathbb{D} \circ f_! \circ \mathbb{D} \colon \operatorname{\mathrm{Perf}}(Y^{\sigma}; \mathcal{T}_{\Lambda}) \rightarrow \operatorname{\mathrm{Perf}}(S^{\sigma}; \mathcal{T}_{\Lambda}). \end{align*}$$
We now list some properties which could be remembered under the slogan, ‘the Smith operation commutes with all operations’ (cf. [Reference TreumannTre19, §4.4]).
A.1.1 Compatibility with pullback
If f satisfies the assumptions above, then the following diagrams commute:

The proof for the first square is formal; for the second, it follows immediately from the first plus [Reference Riche and WilliamsonRW22, Lemma 3.5], whose proof is the same as that for Lemma 3.8.
A.2 Setup for the proof of Theorem 4.20
We keep the setup of §4.6.1: H is any reductive group over a separably closed field
![]() $\mathbf {F}$
of characteristic
$\mathbf {F}$
of characteristic
![]() $\neq p$
, and
$\neq p$
, and
![]() $G = H^p$
. We let
$G = H^p$
. We let
![]() $\sigma $
act on G by cyclic rotation, sending the ith factor to the
$\sigma $
act on G by cyclic rotation, sending the ith factor to the
![]() $(i+1)$
st (mod p) factor.
$(i+1)$
st (mod p) factor.
A.3 Proof of additivity
We first prove that
![]() $\mathsf {BC}$
is additive (i.e., we exhibit a natural isomorphism
$\mathsf {BC}$
is additive (i.e., we exhibit a natural isomorphism
![]() $\mathsf {BC}(\mathcal {F} \oplus \mathcal {F}') \cong \mathsf {BC}(\mathcal {F}) \oplus \mathsf {BC}(\mathcal {F}')$
). We have
$\mathsf {BC}(\mathcal {F} \oplus \mathcal {F}') \cong \mathsf {BC}(\mathcal {F}) \oplus \mathsf {BC}(\mathcal {F}')$
). We have
 $$ \begin{align*} \operatorname{\mathrm{Nm}}(\mathcal{F} \oplus \mathcal{F}') &= (\mathcal{F} \oplus \mathcal{F}') * ({}^{\sigma}\mathcal{F} \oplus {}^{\sigma}\mathcal{F}') * \ldots * ({}^{\sigma^{p-1}}\mathcal{F} \oplus {}^{\sigma^{p-1}}\mathcal{F}') \\ &\cong \operatorname{\mathrm{Nm}}(\mathcal{F}) \oplus \operatorname{\mathrm{Nm}}(\mathcal{F}') \oplus (\text{direct sum of free }\sigma\text{-orbits}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Nm}}(\mathcal{F} \oplus \mathcal{F}') &= (\mathcal{F} \oplus \mathcal{F}') * ({}^{\sigma}\mathcal{F} \oplus {}^{\sigma}\mathcal{F}') * \ldots * ({}^{\sigma^{p-1}}\mathcal{F} \oplus {}^{\sigma^{p-1}}\mathcal{F}') \\ &\cong \operatorname{\mathrm{Nm}}(\mathcal{F}) \oplus \operatorname{\mathrm{Nm}}(\mathcal{F}') \oplus (\text{direct sum of free }\sigma\text{-orbits}). \end{align*} $$
Therefore, the restrictions of
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F} \oplus \mathcal {F}') $
and
$\operatorname {\mathrm {Nm}}(\mathcal {F} \oplus \mathcal {F}') $
and
![]() $ \operatorname {\mathrm {Nm}}(\mathcal {F}) \oplus \operatorname {\mathrm {Nm}}(\mathcal {F}')$
to
$ \operatorname {\mathrm {Nm}}(\mathcal {F}) \oplus \operatorname {\mathrm {Nm}}(\mathcal {F}')$
to
![]() $Y^{\sigma }$
differ by a perfect complex of
$Y^{\sigma }$
differ by a perfect complex of
![]() $\mathbb {O}[\sigma ]$
-modules and hence project to isomorphic objects in the Tate category
$\mathbb {O}[\sigma ]$
-modules and hence project to isomorphic objects in the Tate category
![]() $\operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\mathbb {O}})$
. This shows that
$\operatorname {\mathrm {Perf}}(Y^{\sigma }; \mathcal {T}_{\mathbb {O}})$
. This shows that
![]() $\operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
is additive. Since the lifting functor L is also additive, diagram (4.7) shows that
$\operatorname {\mathrm {Psm}} \circ \operatorname {\mathrm {Nm}}$
is additive. Since the lifting functor L is also additive, diagram (4.7) shows that
![]() $\mathsf {BC}^{(p)} \circ \mathbb {F}$
is additive. Since
$\mathsf {BC}^{(p)} \circ \mathbb {F}$
is additive. Since
![]() $\mathbb {F}$
is essentially surjective as our assumptions imply that all parity sheaves exist,
$\mathbb {F}$
is essentially surjective as our assumptions imply that all parity sheaves exist,
![]() $\mathsf {BC}^{(p)}$
is additive. Finally,
$\mathsf {BC}^{(p)}$
is additive. Finally,
![]() $\operatorname {\mathrm {Frob}}_p^{-1}$
is an equivalence so also additive, so
$\operatorname {\mathrm {Frob}}_p^{-1}$
is an equivalence so also additive, so
![]() $\mathsf {BC}$
is additive.
$\mathsf {BC}$
is additive.
A.4 Reduction to the case of a torus
Fix a regular
![]() $\sigma $
-equivariant cocharacter
$\sigma $
-equivariant cocharacter
![]() $\kappa \colon \mathbf {G}_m \rightarrow H$
. Its centralizer in G is a maximal torus
$\kappa \colon \mathbf {G}_m \rightarrow H$
. Its centralizer in G is a maximal torus
![]() $T \subset G$
, such that
$T \subset G$
, such that
![]() $T_H := T \cap H$
is a maximal torus of H. We recall the following statements relating the restriction functor
$T_H := T \cap H$
is a maximal torus of H. We recall the following statements relating the restriction functor
![]() $\operatorname {\mathrm {Rep}}(\widehat {H}) \rightarrow \operatorname {\mathrm {Rep}}(\widehat {T}_H)$
with the hyperbolic localization functor under the Geometric Satake equivalence.
$\operatorname {\mathrm {Rep}}(\widehat {H}) \rightarrow \operatorname {\mathrm {Rep}}(\widehat {T}_H)$
with the hyperbolic localization functor under the Geometric Satake equivalence.
The fixed points of
![]() $\mathbf {G}_m$
acting by left translation on
$\mathbf {G}_m$
acting by left translation on
![]() $\operatorname {\mathrm {Gr}}_G$
via
$\operatorname {\mathrm {Gr}}_G$
via
![]() $\kappa $
are the
$\kappa $
are the
![]() $t^{\nu }$
for
$t^{\nu }$
for
![]() $\nu \in X_*(T)$
. The attracting locus to
$\nu \in X_*(T)$
. The attracting locus to
![]() $t^{\nu }$
is the semi-infinite orbit
$t^{\nu }$
is the semi-infinite orbit
![]() $S_{\nu }$
. These semi-infinite orbits form a stratification of
$S_{\nu }$
. These semi-infinite orbits form a stratification of
![]() $\operatorname {\mathrm {Gr}}_G$
. Let
$\operatorname {\mathrm {Gr}}_G$
. Let
![]() $i_{\nu } \colon S_{\nu } \rightarrow \operatorname {\mathrm {Gr}}_G$
be the inclusion (a locally closed embedding of ind-schemes) and
$i_{\nu } \colon S_{\nu } \rightarrow \operatorname {\mathrm {Gr}}_G$
be the inclusion (a locally closed embedding of ind-schemes) and
![]() $p_{\nu } \colon S_{\nu } \rightarrow t^\nu $
, viewed as a point of
$p_{\nu } \colon S_{\nu } \rightarrow t^\nu $
, viewed as a point of
![]() $\operatorname {\mathrm {Gr}}_T$
. The hyperbolic localization functor (for G) is the functor
$\operatorname {\mathrm {Gr}}_T$
. The hyperbolic localization functor (for G) is the functor
where the superscript
![]() $\mathbf {G}_m\mathrm {-mon}$
means monodromic for the
$\mathbf {G}_m\mathrm {-mon}$
means monodromic for the
![]() $\mathbf {G}_m$
-action via
$\mathbf {G}_m$
-action via
![]() $\kappa $
(i.e., the full subcategory spanned by objects pulled back from the
$\kappa $
(i.e., the full subcategory spanned by objects pulled back from the
![]() $\mathbf {G}_m$
-equivariant derived category).
$\mathbf {G}_m$
-equivariant derived category).
Denote by
![]() $[\deg _G]$
the function
$[\deg _G]$
the function
![]() $X_*(T) \xrightarrow {\langle 2 \rho _G, - \rangle } \mathbf {Z}$
, and similarly for H. Set
$X_*(T) \xrightarrow {\langle 2 \rho _G, - \rangle } \mathbf {Z}$
, and similarly for H. Set
and
![]() $\operatorname {\mathrm {CT}}_H[\deg _H]$
similarly. Then
$\operatorname {\mathrm {CT}}_H[\deg _H]$
similarly. Then
![]() $\operatorname {\mathrm {CT}}_G[\deg _G]$
and
$\operatorname {\mathrm {CT}}_G[\deg _G]$
and
![]() $\operatorname {\mathrm {CT}}_H[\deg _H]$
are t-exact and under the Geometric Satake equivalence; they are intertwined with restriction along
$\operatorname {\mathrm {CT}}_H[\deg _H]$
are t-exact and under the Geometric Satake equivalence; they are intertwined with restriction along
![]() $\widehat {T} \rightarrow \widehat {G}$
and
$\widehat {T} \rightarrow \widehat {G}$
and
![]() $\widehat {T}_H \rightarrow \widehat {H}$
, respectively:
$\widehat {T}_H \rightarrow \widehat {H}$
, respectively:

(Here,
![]() $\operatorname {\mathrm {CT}}$
is defined because equivariance implies monodromicity.)
$\operatorname {\mathrm {CT}}$
is defined because equivariance implies monodromicity.)
Remark A.1. In the stated generality – with the scheme-theoretic
![]() $\operatorname {\mathrm {Gr}}_G$
in equal characteristic and the coefficients being modular étale sheaves – the commutative diagram (A.1) is perhaps not completely documented in the literature. It does appear for general coefficients on the complex affine Grassmannian [Reference Baumann and RicheBR18, p.66] and the
$\operatorname {\mathrm {Gr}}_G$
in equal characteristic and the coefficients being modular étale sheaves – the commutative diagram (A.1) is perhaps not completely documented in the literature. It does appear for general coefficients on the complex affine Grassmannian [Reference Baumann and RicheBR18, p.66] and the
![]() $B_{\mathrm {dR}}^+$
-affine Grassmannian (in arbitrary characteristic) [Reference Fargues and ScholzeFS, p.233]. The proofs in either case are essentially the same – the commutativity of the diagram is baked into the step of identifying the Tannakian group
$B_{\mathrm {dR}}^+$
-affine Grassmannian (in arbitrary characteristic) [Reference Fargues and ScholzeFS, p.233]. The proofs in either case are essentially the same – the commutativity of the diagram is baked into the step of identifying the Tannakian group
![]() $\widehat {G}$
– and they carry over essentially verbatim to our setting.
$\widehat {G}$
– and they carry over essentially verbatim to our setting.
The functor
![]() $\operatorname {\mathrm {CT}}_H[\deg _H]$
induces
$\operatorname {\mathrm {CT}}_H[\deg _H]$
induces
Since
![]() $*/!$
-restriction and
$*/!$
-restriction and
![]() $*/!$
-pushforward all commute with
$*/!$
-pushforward all commute with
![]() $\operatorname {\mathrm {Psm}}$
by §A.1, the Constant Term functor commutes with
$\operatorname {\mathrm {Psm}}$
by §A.1, the Constant Term functor commutes with
![]() $\operatorname {\mathrm {Psm}}$
in the sense of the following commutative diagram:
$\operatorname {\mathrm {Psm}}$
in the sense of the following commutative diagram:

and the same holds with the shifts by
![]() $\deg _H$
and
$\deg _H$
and
![]() $\deg _G$
, thanks to the parity calculations in §4.6.3.
$\deg _G$
, thanks to the parity calculations in §4.6.3.
Lemma A.2. Consider the cube

where all diagonal arrows are the Geometric Satake equivalence (using Theorem 4.8). The back, front, left and right faces commute.
Proof. The back face obviously commutes. The left and right faces commute by (A.1). It remains to analyze the front square.
Consider the diagram

The left square commutes because
![]() $\operatorname {\mathrm {CT}}_G[\deg G]$
is symmetric monoidal. The middle square commutes because
$\operatorname {\mathrm {CT}}_G[\deg G]$
is symmetric monoidal. The middle square commutes because
![]() $\operatorname {\mathrm {Psm}}$
is compatible with
$\operatorname {\mathrm {Psm}}$
is compatible with
![]() $*$
-pullback and
$*$
-pullback and
![]() $!$
-pushforward, as explained in §A.1. We claim that the right square commutes. To see this, we consider the diagram
$!$
-pushforward, as explained in §A.1. We claim that the right square commutes. To see this, we consider the diagram

The upper and lower caps commute by (4.3). Then it is immediate from the definition of the modular reduction functor
![]() $\mathbb {F}$
that the outer square commutes. In the left square, the vertical arrows are essentially surjective since all (Tate-)parity sheaves exist for all strata. The maps on morphisms are given by (4.2). Hence, the outer commutative diagram induces the right one.
$\mathbb {F}$
that the outer square commutes. In the left square, the vertical arrows are essentially surjective since all (Tate-)parity sheaves exist for all strata. The maps on morphisms are given by (4.2). Hence, the outer commutative diagram induces the right one.
We have now established that the outer rectangle in (A.4) commutes. Therefore, by (4.7), the diagram

commutes. Finally, applying the Frobenius linearization process of Definition 4.18 completes the proof for commutativity of the front face of (A.3).
Theorem 4.20 is the statement that the top face commutes. The bottom face is the special case of Theorem 4.20 for a torus, which we will check directly. We may reduce the general case to the torus case as follows. The restriction functor
![]() $\operatorname {\mathrm {Rep}}(\widehat {H}) \rightarrow \operatorname {\mathrm {Rep}}(T_{\widehat {H}})$
is faithful and injective on tilting objects (i.e. ‘tilting modules are determined by their characters’) by [Reference DonkinDon93, p. 46]. Hence, by Lemma A.2, to check that the top face commutes, it suffices to check that the bottom face commutes (i.e., to prove Theorem 4.20 in the special case where H is a torus).
$\operatorname {\mathrm {Rep}}(\widehat {H}) \rightarrow \operatorname {\mathrm {Rep}}(T_{\widehat {H}})$
is faithful and injective on tilting objects (i.e. ‘tilting modules are determined by their characters’) by [Reference DonkinDon93, p. 46]. Hence, by Lemma A.2, to check that the top face commutes, it suffices to check that the bottom face commutes (i.e., to prove Theorem 4.20 in the special case where H is a torus).
A.5 Proof in the case of a torus
Finally, we examine the case when H is a torus. Since the theorem is compatible with products, we can even reduce to the case
![]() $H = \mathbf {G}_m$
. For
$H = \mathbf {G}_m$
. For
![]() $H = \mathbf {G}_m$
, the underlying reduced scheme of
$H = \mathbf {G}_m$
, the underlying reduced scheme of
![]() $\operatorname {\mathrm {Gr}}_H$
is a disjoint union of points labeled by the integers.
$\operatorname {\mathrm {Gr}}_H$
is a disjoint union of points labeled by the integers.
The irreducible algebraic representations of
![]() $\widehat {H}$
are indexed by
$\widehat {H}$
are indexed by
![]() $n \in \mathbf {Z}$
, with
$n \in \mathbf {Z}$
, with
![]() $V_n \in \operatorname {\mathrm {Rep}}(\widehat {H})$
corresponding to the constant sheaf supported on the component
$V_n \in \operatorname {\mathrm {Rep}}(\widehat {H})$
corresponding to the constant sheaf supported on the component
![]() $\operatorname {\mathrm {Gr}}_{H}^n$
labeled by n. The irreducible algebraic representations of
$\operatorname {\mathrm {Gr}}_{H}^n$
labeled by n. The irreducible algebraic representations of
![]() $\widehat {G}$
are then labeled by p-tuples of integers
$\widehat {G}$
are then labeled by p-tuples of integers
![]() $(n_1, \ldots , n_p) \in \mathbf {Z}^p$
. By the additivity of
$(n_1, \ldots , n_p) \in \mathbf {Z}^p$
. By the additivity of
![]() $\mathsf {BC}$
established in §A.3 and the complete reducibility of algebraic representations of tori, we may assume that
$\mathsf {BC}$
established in §A.3 and the complete reducibility of algebraic representations of tori, we may assume that
![]() $\mathcal {F}$
is irreducible, say
$\mathcal {F}$
is irreducible, say
![]() $\mathcal {F} = \mathcal {F}(n_1, \ldots , n_p)$
is the constant sheaf supported on
$\mathcal {F} = \mathcal {F}(n_1, \ldots , n_p)$
is the constant sheaf supported on
![]() $\operatorname {\mathrm {Gr}}_{G}^{(n_1, \ldots , n_p)}$
. Then the
$\operatorname {\mathrm {Gr}}_{G}^{(n_1, \ldots , n_p)}$
. Then the
![]() $\sigma $
-equivariant sheaf
$\sigma $
-equivariant sheaf
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F})$
is the constant sheaf
$\operatorname {\mathrm {Nm}}(\mathcal {F})$
is the constant sheaf
![]() $\underline {k}$
supported on the component
$\underline {k}$
supported on the component
![]() $\operatorname {\mathrm {Gr}}_{G}^{ (n_1 + \ldots + n_p, \ldots , n_1 + \ldots + n_p)}$
. Its restriction to the diagonal copy of
$\operatorname {\mathrm {Gr}}_{G}^{ (n_1 + \ldots + n_p, \ldots , n_1 + \ldots + n_p)}$
. Its restriction to the diagonal copy of
![]() $\operatorname {\mathrm {Gr}}_H$
is the constant sheaf with value k supported on
$\operatorname {\mathrm {Gr}}_H$
is the constant sheaf with value k supported on
![]() $\operatorname {\mathrm {Gr}}_H^{n_1+\ldots +n_p}$
. This is already an indecomposable k-parity sheaf, which tautologically lifts its own image in the Tate category. Hence, we have shown that
$\operatorname {\mathrm {Gr}}_H^{n_1+\ldots +n_p}$
. This is already an indecomposable k-parity sheaf, which tautologically lifts its own image in the Tate category. Hence, we have shown that
And indeed, this is precisely the sheaf which corresponds under geometric Satake to
![]() $\operatorname {\mathrm {Res}}_{\mathsf {BC}}(V_{n_1} \boxtimes V_{n_2} \boxtimes \ldots \boxtimes V_{n_p}) \cong V_{n_1 + n_2 + \ldots + n_p} \in \operatorname {\mathrm {Rep}}(\widehat {H})$
. This confirms the commutativity of the diagram
$\operatorname {\mathrm {Res}}_{\mathsf {BC}}(V_{n_1} \boxtimes V_{n_2} \boxtimes \ldots \boxtimes V_{n_p}) \cong V_{n_1 + n_2 + \ldots + n_p} \in \operatorname {\mathrm {Rep}}(\widehat {H})$
. This confirms the commutativity of the diagram

at the level of objects. Our final step is to verify the commutativity on morphisms. Since (as H is a torus) the categories involved are all semi-simple, the commutativity at the level of morphisms reduces to examining a scalar endomorphism of the simple object
![]() $\mathcal {F}$
above, which corresponds to the simple representation
$\mathcal {F}$
above, which corresponds to the simple representation
![]() $V_{n_1, \ldots , n_p}$
. The restriction functor
$V_{n_1, \ldots , n_p}$
. The restriction functor
![]() $\operatorname {\mathrm {Res}}_{\mathsf {BC}}$
is k-linear, so what we have to check is that
$\operatorname {\mathrm {Res}}_{\mathsf {BC}}$
is k-linear, so what we have to check is that
![]() $\mathsf {BC}$
sends multiplication by
$\mathsf {BC}$
sends multiplication by
![]() $\lambda $
on
$\lambda $
on
![]() $\mathcal {F}$
to multiplication by
$\mathcal {F}$
to multiplication by
![]() $\lambda $
on
$\lambda $
on
![]() $\mathsf {BC}(\mathcal {F})$
. Now, multiplication by
$\mathsf {BC}(\mathcal {F})$
. Now, multiplication by
![]() $\lambda $
on
$\lambda $
on
![]() $\mathcal {F}$
is sent under
$\mathcal {F}$
is sent under
![]() $\operatorname {\mathrm {Nm}}$
to multiplication by
$\operatorname {\mathrm {Nm}}$
to multiplication by
![]() $\lambda ^p$
on
$\lambda ^p$
on
![]() $\operatorname {\mathrm {Nm}}(\mathcal {F})$
, which restricts to multiplication by
$\operatorname {\mathrm {Nm}}(\mathcal {F})$
, which restricts to multiplication by
![]() $\lambda ^p$
on
$\lambda ^p$
on
![]() $\mathsf {BC}^{(p)}(\mathcal {F})$
. Then the inverse Frobenius twist
$\mathsf {BC}^{(p)}(\mathcal {F})$
. Then the inverse Frobenius twist
![]() $\operatorname {\mathrm {Frob}}_p^{-1}$
sends it to multiplication by
$\operatorname {\mathrm {Frob}}_p^{-1}$
sends it to multiplication by
![]() $\lambda $
, so
$\lambda $
, so
![]() $\mathsf {BC} := \operatorname {\mathrm {Frob}}_p^{-1} \circ \mathsf {BC}^{(p)}$
behaves as desired.
$\mathsf {BC} := \operatorname {\mathrm {Frob}}_p^{-1} \circ \mathsf {BC}^{(p)}$
behaves as desired.
A.6 Proof of Lemma 4.21
In this subsection, we prove Lemma 4.21. We keep the notations from §A.4.
Lemma A.3. The functor
![]() $\operatorname {\mathrm {CT}} \colon \operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k) \rightarrow \operatorname {\mathrm {Perf}}_{(L^+T_H)}(\operatorname {\mathrm {Gr}}_{T_H}; \mathcal {T}_k)$
is conservative.
$\operatorname {\mathrm {CT}} \colon \operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k) \rightarrow \operatorname {\mathrm {Perf}}_{(L^+T_H)}(\operatorname {\mathrm {Gr}}_{T_H}; \mathcal {T}_k)$
is conservative.
Proof. Suppose
![]() $\operatorname {\mathrm {CT}}(\mathcal {K}) = 0$
for some nonzero
$\operatorname {\mathrm {CT}}(\mathcal {K}) = 0$
for some nonzero
![]() $\mathcal {K} \in \operatorname {\mathrm {Shv}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
. Let
$\mathcal {K} \in \operatorname {\mathrm {Shv}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
. Let
![]() $\operatorname {\mathrm {Gr}}_H^\lambda = L^+H t^\lambda \subset \operatorname {\mathrm {Gr}}_H$
be the maximal stratum (for the closure order) on which
$\operatorname {\mathrm {Gr}}_H^\lambda = L^+H t^\lambda \subset \operatorname {\mathrm {Gr}}_H$
be the maximal stratum (for the closure order) on which
![]() $\mathcal {K}$
is supported. Then for
$\mathcal {K}$
is supported. Then for
![]() $w_0$
, the longest Weyl element, the semi-infinite orbit
$w_0$
, the longest Weyl element, the semi-infinite orbit
![]() $S_{w_0(\lambda )}$
intersects
$S_{w_0(\lambda )}$
intersects
![]() $\operatorname {\mathrm {Gr}}_H^\lambda $
in a single point
$\operatorname {\mathrm {Gr}}_H^\lambda $
in a single point
![]() $t^{w_0(\lambda )}$
[Reference Baumann and RicheBR18, Theorem 5.2]. Hence, the stalk at
$t^{w_0(\lambda )}$
[Reference Baumann and RicheBR18, Theorem 5.2]. Hence, the stalk at
![]() $t^{w_0(\lambda )}$
vanishes, which shows (by the assumed constructibility for
$t^{w_0(\lambda )}$
vanishes, which shows (by the assumed constructibility for
![]() $L^+H$
-orbits) that
$L^+H$
-orbits) that
![]() $\mathcal {K}$
vanishes on
$\mathcal {K}$
vanishes on
![]() $\operatorname {\mathrm {Gr}}_\lambda $
, which contradicts the assumption on the support of
$\operatorname {\mathrm {Gr}}_\lambda $
, which contradicts the assumption on the support of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Let
![]() $i \colon \operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_G$
. Since apply
$i \colon \operatorname {\mathrm {Gr}}_H \hookrightarrow \operatorname {\mathrm {Gr}}_G$
. Since apply
![]() $\operatorname {\mathrm {Frob}}_p^{-1}$
preserves exact sequences, Lemma 4.21 is equivalent to the following: if
$\operatorname {\mathrm {Frob}}_p^{-1}$
preserves exact sequences, Lemma 4.21 is equivalent to the following: if
![]() $A \rightarrow B \rightarrow C$
is an exact sequence in
$A \rightarrow B \rightarrow C$
is an exact sequence in
![]() $\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, then the map in
$\operatorname {\mathrm {Rep}}_k(\widehat {G})$
, then the map in
![]() $D^b_{c,L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
,
$D^b_{c,L^+H}(\operatorname {\mathrm {Gr}}_H; k[\sigma ])$
,
projects to an isomorphism in
![]() $\operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
. By Lemma A.3, this can be checked after applying
$\operatorname {\mathrm {Perf}}_{(L^+H)}(\operatorname {\mathrm {Gr}}_H; \mathcal {T}_k)$
. By Lemma A.3, this can be checked after applying
![]() $\operatorname {\mathrm {CT}}[\deg _G]$
. Using the commutative diagram analogous to (A.2) but with k-coefficients, and that
$\operatorname {\mathrm {CT}}[\deg _G]$
. Using the commutative diagram analogous to (A.2) but with k-coefficients, and that
![]() $\operatorname {\mathrm {CT}}[\deg _G]$
is intertwined with restriction from
$\operatorname {\mathrm {CT}}[\deg _G]$
is intertwined with restriction from
![]() $\widehat {G}$
to
$\widehat {G}$
to
![]() $\widehat {T}$
under Geometric Satake, we have a commutative diagram
$\widehat {T}$
under Geometric Satake, we have a commutative diagram

The question of whether the composition of functors along the top then right is an isomorphism is equivalent to the question of whether the composition of functors along the left then bottom is an isomorphism. This reduces us to the case where
![]() $\widehat {G} = \widehat {T}$
is a torus. In this case, since all maps in
$\widehat {G} = \widehat {T}$
is a torus. In this case, since all maps in
![]() $\operatorname {\mathrm {Rep}}(\widehat {T})$
have splittings, the exactness statement reduces to the additivity, which was verified in §A.3.
$\operatorname {\mathrm {Rep}}(\widehat {T})$
have splittings, the exactness statement reduces to the additivity, which was verified in §A.3.
B Applying Drinfeld’s Lemma to Tate cohomology
Here, we prove Proposition 5.6, that the action of
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }_I)$
on
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }_I)$
on
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
factors through the quotient
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
factors through the quotient
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
. This statement is analogous to results in [Reference LafforgueLaf18] and [Reference XueXueb] for ordinary cohomology, the latter of which incorporates simplifications by [Reference Xiao and ZhuXZ], and our argument will follow the same broad lines. Here is an outline of the strategy:
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I}) \twoheadrightarrow \operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
. This statement is analogous to results in [Reference LafforgueLaf18] and [Reference XueXueb] for ordinary cohomology, the latter of which incorporates simplifications by [Reference Xiao and ZhuXZ], and our argument will follow the same broad lines. Here is an outline of the strategy:
-
1. Prove an Eichler-Shimura relation, relating the action of partial Frobenii and Hecke operators.
-
2. Using (1), express
 $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
as the filtered colimit of submodules stable under the partial Frobenii, with each module being finite type over some finitely generated k-algebra (depending on the submodule; it will be taken to a suitable tensor product of local Hecke algebras).
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
as the filtered colimit of submodules stable under the partial Frobenii, with each module being finite type over some finitely generated k-algebra (depending on the submodule; it will be taken to a suitable tensor product of local Hecke algebras). -
3. Apply Drinfeld’s Lemma, which says roughly that any continuous A-linear
 $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }_I)$
-action on a finite-type A-module automatically factors over
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta }_I)$
-action on a finite-type A-module automatically factors over
 $\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, to each of the submodules produced in (1).
$\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
, to each of the submodules produced in (1).
B.1 The Eichler-Shimura relation
Regarding the first step, Xue proves the following:
Proposition B.1 [Reference XueXueb, Proposition 7.2.6].
Let
![]() $v \in \stackrel {\circ }X$
be a closed point with degree
$v \in \stackrel {\circ }X$
be a closed point with degree
![]() $\deg v$
. For any finite set
$\deg v$
. For any finite set
![]() $I = \widetilde {I} \sqcup \{0\}$
and any
$I = \widetilde {I} \sqcup \{0\}$
and any
![]() $V \in \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
, there exists
$V \in \operatorname {\mathrm {Rep}}_k(\widehat {G}^I)$
, there exists
![]() $W \in \operatorname {\mathrm {Rep}}_k(\widehat {G})$
such that
$W \in \operatorname {\mathrm {Rep}}_k(\widehat {G})$
such that
 $$\begin{align*}\sum_{\alpha = 0}^{\dim W} (-1)^\alpha S_{\wedge^{\dim W - \alpha} W, v}(F_{\{0\}}^{\deg v})^\alpha = 0 \in \operatorname{\mathrm{End}}_{D^c((\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v; k)}(R^j \pi_{I!} (\stackrel{\circ}{\mathrm{Sht}}_{G,D,I}|_{(\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v}; \operatorname{\mathrm{Sat}}(V))). \end{align*}$$
$$\begin{align*}\sum_{\alpha = 0}^{\dim W} (-1)^\alpha S_{\wedge^{\dim W - \alpha} W, v}(F_{\{0\}}^{\deg v})^\alpha = 0 \in \operatorname{\mathrm{End}}_{D^c((\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v; k)}(R^j \pi_{I!} (\stackrel{\circ}{\mathrm{Sht}}_{G,D,I}|_{(\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v}; \operatorname{\mathrm{Sat}}(V))). \end{align*}$$
Here, for a representation W of
![]() $\widehat {G}$
, the operator
$\widehat {G}$
, the operator
![]() $S_{W,v}$
is defined in [Reference LafforgueLaf18, §6] by a process similar to one defining excursion operators. The only thing we need to know about
$S_{W,v}$
is defined in [Reference LafforgueLaf18, §6] by a process similar to one defining excursion operators. The only thing we need to know about
![]() $S_{W,v}$
is the following.
$S_{W,v}$
is the following.
Theorem B.2 (“S=T Theorem”).
![]() $S_{W,v}$
agrees with the Hecke operator
$S_{W,v}$
agrees with the Hecke operator
![]() $T_{W,v}$
after restricting to
$T_{W,v}$
after restricting to
![]() ${(X \setminus (D \cup v))^I}$
.
${(X \setminus (D \cup v))^I}$
.
This fact is proved in [Reference LafforgueLaf18, §6] in characteristic zero; a simpler proof is a consequence [Reference Xiao and ZhuXZ, Theorem 6.0.1(2)], which already shows the equality at the level of cohomological correspondences on local shtukas. The argument of Xiao-Zhu is written with integral coefficients in [Reference YuYu22, Theorem 5.1 and Corollary 5.5]. Since it holds at the level of cohomological correspondences, it holds in particular for Tate cohomology.
Xue’s proof of Proposition B.1 (which is a small generalization of an argument appearing in [Reference Xiao and ZhuXZ, §6]) works essentially verbatim for Tate cohomology, replacing her
![]() $\mathcal {H}^{j, \mathcal {O}_E}_{G, N, I, W}$
by
$\mathcal {H}^{j, \mathcal {O}_E}_{G, N, I, W}$
by
![]() $T^j \pi _{I!} (\operatorname {\mathrm {Sht}}_{G,D,I}|_{(\stackrel {\circ }X \setminus D)^{\widetilde {I}} \times v}; \operatorname {\mathrm {Sat}}(V)))$
. It yields the following:
$T^j \pi _{I!} (\operatorname {\mathrm {Sht}}_{G,D,I}|_{(\stackrel {\circ }X \setminus D)^{\widetilde {I}} \times v}; \operatorname {\mathrm {Sat}}(V)))$
. It yields the following:
Lemma B.3. Let
![]() $v \in X$
be a closed point with degree
$v \in X$
be a closed point with degree
![]() $\deg v$
. For any finite set
$\deg v$
. For any finite set
![]() $I = \widetilde {I} \sqcup \{0\}$
and any
$I = \widetilde {I} \sqcup \{0\}$
and any
![]() $V \in \operatorname {\mathrm {Rep}}_{k}(\widehat {G}^I)$
, there exists
$V \in \operatorname {\mathrm {Rep}}_{k}(\widehat {G}^I)$
, there exists
![]() $W \in \operatorname {\mathrm {Rep}}_k(\widehat {G})$
such that
$W \in \operatorname {\mathrm {Rep}}_k(\widehat {G})$
such that
 $$\begin{align*}\sum_{\alpha = 0}^{\dim W} (-1)^\alpha S_{\wedge^{\dim W - \alpha} W, v}(F_{\{0\}}^{\deg v})^\alpha = 0 \in \operatorname{\mathrm{End}}_{D((\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v; k)}(T^j R\pi_{I!} (\operatorname{\mathrm{Sht}}_{G,D,I}|_{(\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v}; \operatorname{\mathrm{Sat}}(V))). \end{align*}$$
$$\begin{align*}\sum_{\alpha = 0}^{\dim W} (-1)^\alpha S_{\wedge^{\dim W - \alpha} W, v}(F_{\{0\}}^{\deg v})^\alpha = 0 \in \operatorname{\mathrm{End}}_{D((\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v; k)}(T^j R\pi_{I!} (\operatorname{\mathrm{Sht}}_{G,D,I}|_{(\stackrel{\circ}X \setminus D)^{\widetilde{I}} \times v}; \operatorname{\mathrm{Sat}}(V))). \end{align*}$$
B.2 The filtration
We carry out Step (2) of the outline, following [Reference XueXueb, §1].
Harder-Narasimhan truncation presents
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}$
as a filtered colimit
$\operatorname {\mathrm {Sht}}_{G,D,I}$
as a filtered colimit
where
![]() $\mu $
runs over dominant coweights of G.
$\mu $
runs over dominant coweights of G.
Since the support of
![]() $\operatorname {\mathrm {Sat}}(V)$
on
$\operatorname {\mathrm {Sat}}(V)$
on
![]() $\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }|_{\overline {\eta ^I}}$
is of finite type over
$\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }|_{\overline {\eta ^I}}$
is of finite type over
![]() $\overline {\eta }^I$
,
$\overline {\eta }^I$
,
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu };V) := T^j(R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)))$
is finite-dimensional over k. We have a filtered colimit
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu };V) := T^j(R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,D,I}^{\leq \mu }|_{\overline {\eta ^I}}; \operatorname {\mathrm {Sat}}(V)))$
is finite-dimensional over k. We have a filtered colimit
We will express
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
as an increasing union of submodules
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
as an increasing union of submodules
![]() $\mathfrak {M}^{\mu }$
which are stable under
$\mathfrak {M}^{\mu }$
which are stable under
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
, and such that for each
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
, and such that for each
![]() $\mathfrak {M}^{\mu }$
, there is a finite set of points
$\mathfrak {M}^{\mu }$
, there is a finite set of points
![]() $v_i$
(depending on
$v_i$
(depending on
![]() $\mathfrak {M}^{\mu }$
) so that
$\mathfrak {M}^{\mu }$
) so that
![]() $\mathfrak {M}^{\mu }$
is stable under the partial Frobenii and finite type over
$\mathfrak {M}^{\mu }$
is stable under the partial Frobenii and finite type over
![]() $\otimes _{i \in I} \mathcal {H}_{G, v_i}$
.
$\otimes _{i \in I} \mathcal {H}_{G, v_i}$
.
Write
and
Note that proper base change gives an isomorphism
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V) \cong \mathfrak {T}|_{\overline {\eta ^I}}$
. Since
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V) \cong \mathfrak {T}|_{\overline {\eta ^I}}$
. Since
![]() $ \mathfrak {T}^{\mu }$
is constructible, there is an open dense subscheme
$ \mathfrak {T}^{\mu }$
is constructible, there is an open dense subscheme
![]() $\Omega \subset (\stackrel {\circ }X \setminus D)^I$
such that
$\Omega \subset (\stackrel {\circ }X \setminus D)^I$
such that
![]() $ \mathfrak {T}^\mu $
is a local system over
$ \mathfrak {T}^\mu $
is a local system over
![]() $\Omega $
. Choose a closed point
$\Omega $
. Choose a closed point
![]() $v \in \Omega $
and let
$v \in \Omega $
and let
![]() $v_i = \operatorname {\mathrm {pr}}_i(v)$
for
$v_i = \operatorname {\mathrm {pr}}_i(v)$
for
![]() $i \in I$
. Then
$i \in I$
. Then
![]() $\times _{i \in I} v_i \in (\stackrel {\circ }X \setminus D)^I$
is a finite union of closed points containing v. Let
$\times _{i \in I} v_i \in (\stackrel {\circ }X \setminus D)^I$
is a finite union of closed points containing v. Let
![]() $\mathfrak {M}^{\mu }$
be the subspace of
$\mathfrak {M}^{\mu }$
be the subspace of
![]() $T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
given by
$T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
given by
 $$ \begin{align} \mathfrak{M}^\mu := \sum_{n_i \in {\mathbb{N}}^I} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) \prod_{i \in I} F_{\{i\}}^{n_i} \left( \prod_{i \in I} (\operatorname{\mathrm{Frob}}_{\{i\}}^{n_i})^* \operatorname{\mbox{Im }}\left(\mathfrak{T}^{\mu}|_{\overline{\eta^I}} \rightarrow \mathfrak{T}|_{\overline{\eta^I}} \right) \right). \end{align} $$
$$ \begin{align} \mathfrak{M}^\mu := \sum_{n_i \in {\mathbb{N}}^I} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) \prod_{i \in I} F_{\{i\}}^{n_i} \left( \prod_{i \in I} (\operatorname{\mathrm{Frob}}_{\{i\}}^{n_i})^* \operatorname{\mbox{Im }}\left(\mathfrak{T}^{\mu}|_{\overline{\eta^I}} \rightarrow \mathfrak{T}|_{\overline{\eta^I}} \right) \right). \end{align} $$
Then it is clear that
![]() $ T^j(\operatorname {\mathrm {Sht}}_{G,D,I};V) = \bigcup _{\mu } \mathfrak {M}^{\mu }$
.
$ T^j(\operatorname {\mathrm {Sht}}_{G,D,I};V) = \bigcup _{\mu } \mathfrak {M}^{\mu }$
.
We regard
![]() $\mathfrak {M}^{\mu }$
as a module over the finite type k-algebra
$\mathfrak {M}^{\mu }$
as a module over the finite type k-algebra
![]() $A^{\mu } := \otimes _{i \in I} \mathcal {H}_{i,v_i}$
. The following Lemma and its proof are variants of [Reference XueXueb, Lemma 1.3.11].
$A^{\mu } := \otimes _{i \in I} \mathcal {H}_{i,v_i}$
. The following Lemma and its proof are variants of [Reference XueXueb, Lemma 1.3.11].
Lemma B.4. The submodule
![]() $\mathfrak {M}^{\mu } \subset \mathfrak {T}|_{\overline {\eta ^I}} \cong T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
is stable under the partial Frobenii
$\mathfrak {M}^{\mu } \subset \mathfrak {T}|_{\overline {\eta ^I}} \cong T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
is stable under the partial Frobenii
![]() $F_{\{i\}}$
and of finite type over
$F_{\{i\}}$
and of finite type over
![]() $A^\mu $
.
$A^\mu $
.
Proof. The stability under partial Frobenii is clear by construction. Let
![]() $\overline {v}$
be a geometric point over v. We have a specialization map
$\overline {v}$
be a geometric point over v. We have a specialization map
![]() $\mathfrak {sp} \colon \overline {\eta ^I} \rightsquigarrow \overline {v}$
. For any
$\mathfrak {sp} \colon \overline {\eta ^I} \rightsquigarrow \overline {v}$
. For any
![]() $n_i$
, we have the partial Frobenius
$n_i$
, we have the partial Frobenius
Altough partial Frobenius does not preserve the HN truncation, there exists
![]() $\kappa $
fitting into a commutative diagram
$\kappa $
fitting into a commutative diagram

We have
![]() $\operatorname {\mathrm {Frob}}_{\{i\}}^{n_i \deg (v_i) }(v) = v \in \Omega $
. Then using Proposition B.3, we may eliminate all powers of partial Frobenius with exponent
$\operatorname {\mathrm {Frob}}_{\{i\}}^{n_i \deg (v_i) }(v) = v \in \Omega $
. Then using Proposition B.3, we may eliminate all powers of partial Frobenius with exponent
![]() $\geq \dim W$
in (B.1) in terms of S-operators because for
$\geq \dim W$
in (B.1) in terms of S-operators because for
![]() $d \geq \dim W$
, we have
$d \geq \dim W$
, we have
 $$\begin{align*}F_{\{i\}}^{d \deg v_i} (\operatorname{\mathrm{Frob}}_{\{i\}}^{d \deg(v_i)})^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{v}} \rightarrow \mathfrak{T}|_{\overline{v}} ) \subset \sum_{\alpha=0}^{\dim W-w} S_? F_{\{i\}}^{\alpha \deg(v_i) } (\operatorname{\mathrm{Frob}}_{\{i\}}^{\alpha \deg(v_i) })^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{v}} \rightarrow \mathfrak{T} |_{\overline{v}}). \end{align*}$$
$$\begin{align*}F_{\{i\}}^{d \deg v_i} (\operatorname{\mathrm{Frob}}_{\{i\}}^{d \deg(v_i)})^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{v}} \rightarrow \mathfrak{T}|_{\overline{v}} ) \subset \sum_{\alpha=0}^{\dim W-w} S_? F_{\{i\}}^{\alpha \deg(v_i) } (\operatorname{\mathrm{Frob}}_{\{i\}}^{\alpha \deg(v_i) })^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{v}} \rightarrow \mathfrak{T} |_{\overline{v}}). \end{align*}$$
Since the S-operators and the
![]() $F_{\{i\}}$
are morphisms of sheaves, they commute with the specialization map
$F_{\{i\}}$
are morphisms of sheaves, they commute with the specialization map
![]() $\mathfrak {sp}^*$
. The upper arrow in (B.2) an isomorphism because
$\mathfrak {sp}^*$
. The upper arrow in (B.2) an isomorphism because
![]() $\overline {v} \in \Omega $
lies in the lisse locus of
$\overline {v} \in \Omega $
lies in the lisse locus of
![]() $\mathfrak {T}^\mu $
by construction. Therefore, the Eichler-Shimura relation from Proposition B.3 is also satisfied in the right column. Now over
$\mathfrak {T}^\mu $
by construction. Therefore, the Eichler-Shimura relation from Proposition B.3 is also satisfied in the right column. Now over
![]() $\overline {\eta ^I}$
we can apply the same elimination argument and use Theorem B.2 to replace S-operators by Hecke operators, thus deducing that for
$\overline {\eta ^I}$
we can apply the same elimination argument and use Theorem B.2 to replace S-operators by Hecke operators, thus deducing that for
![]() $d \geq \dim W$
, we have
$d \geq \dim W$
, we have
 $$\begin{align*}F_{\{i\}}^{d \deg v_i} (\operatorname{\mathrm{Frob}}_{\{i\}}^{d \deg(v_i)})^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{\eta^I}} \rightarrow \mathfrak{T}|_{\overline{\eta^I}} ) \subset \sum_{\alpha=0}^{\dim W-1} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) F_{\{i\}}^{\alpha \deg(v_i) } (\operatorname{\mathrm{Frob}}_{\{i\}}^{\alpha \deg(v_i) })^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{\eta^I}} \rightarrow \mathfrak{T} |_{\overline{\eta^I}}). \end{align*}$$
$$\begin{align*}F_{\{i\}}^{d \deg v_i} (\operatorname{\mathrm{Frob}}_{\{i\}}^{d \deg(v_i)})^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{\eta^I}} \rightarrow \mathfrak{T}|_{\overline{\eta^I}} ) \subset \sum_{\alpha=0}^{\dim W-1} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) F_{\{i\}}^{\alpha \deg(v_i) } (\operatorname{\mathrm{Frob}}_{\{i\}}^{\alpha \deg(v_i) })^* \operatorname{\mbox{Im }}(\mathfrak{T}^\mu|_{\overline{\eta^I}} \rightarrow \mathfrak{T} |_{\overline{\eta^I}}). \end{align*}$$
Therefore, we actually have
 $$\begin{align*}\mathfrak{M}^\mu = \sum_{0 \leq n_i < \dim W \deg v_i} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) \prod_{i \in I} F_{\{i\}}^{n_i} \left( \prod_{i \in I} (\operatorname{\mathrm{Frob}}_{\{i\}}^{n_i})^* \operatorname{\mbox{Im }}\left(\mathfrak{T}^{\mu} |_{\overline{\eta^I}}\rightarrow \mathfrak{T}|_{\overline{\eta^I}}) \right) \right). \end{align*}$$
$$\begin{align*}\mathfrak{M}^\mu = \sum_{0 \leq n_i < \dim W \deg v_i} \left( \otimes_{i \in I} \mathcal{H}_{i,v_i} \right) \prod_{i \in I} F_{\{i\}}^{n_i} \left( \prod_{i \in I} (\operatorname{\mathrm{Frob}}_{\{i\}}^{n_i})^* \operatorname{\mbox{Im }}\left(\mathfrak{T}^{\mu} |_{\overline{\eta^I}}\rightarrow \mathfrak{T}|_{\overline{\eta^I}}) \right) \right). \end{align*}$$
Since
![]() $\mathfrak {T}^{\mu }|_{\overline {\eta ^I}}$
is finite-dimensional over k,
$\mathfrak {T}^{\mu }|_{\overline {\eta ^I}}$
is finite-dimensional over k,
![]() $\mathfrak {M}^{\mu }$
is finite-type over
$\mathfrak {M}^{\mu }$
is finite-type over
![]() $A^{\mu }$
.
$A^{\mu }$
.
B.3 Drinfeld’s Lemma
The following result of Xue is a generalization of the so-called ‘Drinfeld’s Lemma’.
Lemma B.5 [Reference XueXuea, Lemma 7.4.2].
Let A be a finitely generated k-algebra. Let M be an A-module of finite type. Then any continuous
![]() $A[\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})]$
-action on M factors through
$A[\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})]$
-action on M factors through
![]() $\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
.
$\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
.
Proof of Proposition 5.6.
Applying Lemma B.5 to each
![]() $\mathfrak {M}^\mu $
, we deduce that the
$\mathfrak {M}^\mu $
, we deduce that the
![]() $\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-action on
$\operatorname {\mathrm {FWeil}}(\eta ^I, \overline {\eta ^I})$
-action on
![]() $\mathfrak {M}^\mu $
factors through
$\mathfrak {M}^\mu $
factors through
![]() $\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
. Then the same holds for
$\operatorname {\mathrm {Weil}}(\eta , \overline {\eta })^I$
. Then the same holds for
![]() $\varinjlim _{\mu } \mathfrak {M}^\mu = T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
.
$\varinjlim _{\mu } \mathfrak {M}^\mu = T^j(\operatorname {\mathrm {Sht}}_{G,D,I}; V)$
.
Acknowledgements
We thank Jean-François Dat, David Helm, Gus Lonergan, Simon Riche, Gordan Savin, David Treumann, Marie-France Vignéras, Geordie Williamson, Zhiwei Yun and Xinwen Zhu for helpful correspondence related to this work. We thank Laurent Clozel, Jesper Grodal, Tom Haines and Michael Harris for comments on a draft. We especially thank Michael Harris for many stimulating questions, which led us to discover several new results and applications after the initial version of this paper. The paper benefited immensely from many comments and corrections by the incisive referee, who, in particular, suggested a big simplification of the proof of Proposition 6.3.
Competing interest
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
During the writing of this paper, the author was supported by the Friends of the Institute for Advanced Study, an NSF Postdoctoral Fellowship (DMS #1902927), an NSF Standard Grant (DMS #2302520), and a Viterbi Postdoctoral Fellowship at the Simons-Laufer Mathematical Sciences Institute.