Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-12T19:42:18.019Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIMES REPRESENTED BY INCOMPLETE NORM FORMS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  06 February 2020

JAMES MAYNARD Open the ORCID record for JAMES MAYNARD [Opens in a new window]
JAMES MAYNARD*
Affiliation:
Magdalen College, Oxford, EnglandOX1 4AU, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

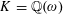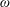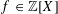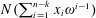Let $K=\mathbb{Q}(\unicode[STIX]{x1D714})$ with $\unicode[STIX]{x1D714}$ the root of a degree $n$ monic irreducible polynomial $f\in \mathbb{Z}[X]$. We show that the degree $n$ polynomial $N(\sum _{i=1}^{n-k}x_{i}\unicode[STIX]{x1D714}^{i-1})$ in 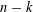$n-k$ variables takes the expected asymptotic number of prime values if $n\geqslant 4k$. In the special case 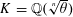$K=\mathbb{Q}(\sqrt[n]{\unicode[STIX]{x1D703}})$, we show that 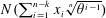$N(\sum _{i=1}^{n-k}x_{i}\sqrt[n]{\unicode[STIX]{x1D703}^{i-1}})$ takes infinitely many prime values, provided 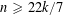$n\geqslant 22k/7$.

Our proof relies on using suitable ‘Type I’ and ‘Type II’ estimates in Harman’s sieve, which are established in a similar overall manner to the previous work of Friedlander and Iwaniec on prime values of 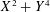$X^{2}+Y^{4}$ and of Heath-Brown on 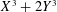$X^{3}+2Y^{3}$. Our proof ultimately relies on employing explicit elementary estimates from the geometry of numbers and algebraic geometry to control the number of highly skewed lattices appearing in our final estimates.

MSC classification

Primary: 11N05: Distribution of primes
Secondary: 11N35: Sieves 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Type
Number Theory
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2020

References

Bateman, P. T. and Horn, R. A., ‘A heuristic asymptotic formula concerning the distribution of prime numbers’, Math. Comp. 16 (1962), 363–367.CrossRefGoogle Scholar
Birch, B. J., ‘Forms in many variables’, Proc. R. Soc. Ser. A 265 (1961/1962), 245–263.Google Scholar
Cassels, J. W. S., An Introduction to the Geometry of Numbers, Classics in Mathematics (Springer, Berlin, 1997), Corrected reprint of the 1971 edition.Google Scholar
Coleman, M. D., ‘A zero-free region for the Hecke L-functions’, Mathematika 37(2) (1990), 287–304.CrossRefGoogle Scholar
Davenport, H., ‘On a principle of Lipschitz’, J. Lond. Math. Soc. (2) 26 (1951), 179–183.CrossRefGoogle Scholar
Davenport, H., ‘Indefinite quadratic forms in many variables. II’, Proc. Lond. Math. Soc. (3) 8 (1958), 109–126.CrossRefGoogle Scholar
Duke, W., ‘Some problems in multidimensional analytic number theory’, Acta Arith. 52(3) (1989), 203–228.CrossRefGoogle Scholar
Friedlander, J. and Iwaniec, H., ‘The polynomial X 2 + Y 4 captures its primes’, Ann. of Math. (2) 148(3) (1998), 945–1040.CrossRefGoogle Scholar
Halberstam, H. and Richert, H.E., Sieve Methods, L.M.S. monographs (Academic Press, 1974).Google Scholar
Harman, G., ‘On the distribution of 𝛼p modulo one. II’, Proc. Lond. Math. Soc. (3) 72(2) (1996), 241–260.CrossRefGoogle Scholar
Harman, G., Prime-detecting Sieves, London Mathematical Society Monographs Series, 33 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Heath-Brown, D. R., ‘Diophantine approximation with square-free numbers’, Math. Z. 187(3) (1984), 335–344.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Primes represented by x 3 + 2y 3’, Acta Math. 186(1) (2001), 1–84.CrossRefGoogle Scholar
Heath-Brown, D. R. and Li, X., ‘Prime values of a 2 + p 4’, Invent. Math. 208(2) (2017), 441–499.CrossRefGoogle Scholar
Heath-Brown, D. R. and Moroz, B. Z., ‘Primes represented by binary cubic forms’, Proc. Lond. Math. Soc. (3) 84(2) (2002), 257–288.CrossRefGoogle Scholar
Heath-Brown, D. R. and Moroz, B. Z., ‘On the representation of primes by cubic polynomials in two variables’, Proc. Lond. Math. Soc. (3) 88(2) (2004), 289–312.CrossRefGoogle Scholar
Iwaniec, H., ‘Primes represented by quadratic polynomials in two variables’, Acta Arith. 24 (1973/74), 435–459. Collection of articles dedicated to Carl Ludwig Siegel on the occasion of his seventy-fifth birthday, V.CrossRefGoogle Scholar
Lang, S., Diophantine Geometry, Interscience Tracts in Pure and Applied Mathematics, 11 (Interscience Publishers (a division of John Wiley & Sons), New York–London, 1962).Google Scholar
Neukirch, J., Algebraic Number Theory, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 322 (Springer, Berlin, 1999), Translated from the 1992 German original and with a note by Norbert Schappacher, with a foreword by G. Harder.CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, 2nd edn (The Clarendon Press, Oxford University Press, New York, 1986), edited and with a preface by D. R. Heath-Brown.Google Scholar
Weiss, A., ‘The least prime ideal’, J. Reine Angew. Math. 338 (1983), 56–94.CrossRefGoogle Scholar