Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T17:24:12.338Z Has data issue: false hasContentIssue false
  • English
  • Français

A PATCHWORK QUILT SEWN FROM BROWNIAN FABRIC: REGULARITY OF POLYMER WEIGHT PROFILES IN BROWNIAN LAST PASSAGE PERCOLATION

Part of: Stochastic analysis Time-dependent statistical mechanics (dynamic and nonequilibrium) Equilibrium statistical mechanics Applications to specific types of physical systems

Published online by Cambridge University Press:  16 July 2019

ALAN HAMMOND
ALAN HAMMOND*
Affiliation:
Departments of Mathematics and Statistics, U.C. Berkeley, Evans Hall, Berkeley, CA 94720-3840, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In last passage percolation models lying in the Kardar–Parisi–Zhang (KPZ) universality class, the energy of long energy-maximizing paths may be studied as a function of the paths’ pair of endpoint locations. Scaled coordinates may be introduced, so that these maximizing paths, or polymers, now cross unit distances with unit-order fluctuations, and have scaled energy, or weight, of unit order. In this article, we consider Brownian last passage percolation in these scaled coordinates. In the narrow wedge case, when one endpoint of such polymers is fixed, say at 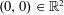$(0,0)\in \mathbb{R}^{2}$, and the other is varied horizontally, over 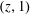$(z,1)$, 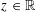$z\in \mathbb{R}$, the polymer weight profile as a function of 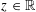$z\in \mathbb{R}$ is locally Brownian; indeed, by Hammond [‘Brownian regularity for the Airy line ensemble, and multi-polymer watermelons in Brownian last passage percolation’, Preprint (2016), arXiv:1609.02971, Theorem 2.11 and Proposition 2.5], the law of the profile is known to enjoy a very strong comparison to Brownian bridge on a given compact interval, with a Radon–Nikodym derivative in every 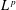$L^{p}$ space for 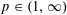$p\in (1,\infty )$, uniformly in the scaling parameter, provided that an affine adjustment is made to the weight profile before the comparison is made. In this article, we generalize this narrow wedge case and study polymer weight profiles begun from a very general initial condition. We prove that the profiles on a compact interval resemble Brownian bridge in a uniform sense: splitting the compact interval into a random but controlled number of patches, the profile in each patch after affine adjustment has a Radon–Nikodym derivative that lies in every 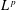$L^{p}$ space for $p\in (1,3)$. This result is proved by harnessing an understanding of the uniform coalescence structure in the field of polymers developed in Hammond [‘Exponents governing the rarity of disjoint polymers in Brownian last passage percolation’, Preprint (2017a), arXiv:1709.04110] using techniques from Hammond (2016) and [‘Modulus of continuity of polymer weight profiles in Brownian last passage percolation’, Preprint (2017b), arXiv:1709.04115].

MSC classification

Primary: 82D30: Random media, disordered materials (including liquid crystals and spin glasses)
Secondary: 82C22: Interacting particle systems 82B23: Exactly solvable models; Bethe ansatz 60H15: Stochastic partial differential equations
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 7 , 2019 , e2
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits noncommercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author 2019

References

Baik, J., Deift, P. and Johansson, K., ‘On the distribution of the length of the longest increasing subsequence of random permutations’, J. Amer. Math. Soc. 12(4) (1999), 1119–1178.Google Scholar
Baryshnikov, Y., ‘GUEs and queues’, Probab. Theory Related Fields 119(2) (2001), 256–274.Google Scholar
Basu, R., Sarkar, S. and Sly, A., ‘Invariant measures for TASEP with a slow bond’, Preprint (2017), arXiv:1704.07799.Google Scholar
Basu, R., Sidoravicius, V. and Sly, A., ‘Last passage percolation with a defect line and the solution of the slow bond problem’, Preprint (2016), arXiv:1408.3464.Google Scholar
Borodin, A., Ferrari, P. L., Prähofer, M. and Sasamoto, T., ‘Fluctuation properties of the TASEP with periodic initial configuration’, J. Stat. Phys. 129(5–6) (2007), 1055–1080.Google Scholar
Cator, E. and Pimentel, L. P. R., ‘On the local fluctuations of last-passage percolation models’, Stoch. Process. Appl. 125(2) (2015), 538–551.Google Scholar
Corwin, I., ‘The Kardar–Parisi–Zhang equation and universality class’, Random Matrices Theory Appl. 1(1) (2012), 1130001, 76.Google Scholar
Corwin, I. and Hammond, A., ‘Brownian Gibbs property for Airy line ensembles’, Invent. Math. 195(2) (2014), 441–508.Google Scholar
Corwin, I., Quastel, J. and Remenik, D., ‘Renormalization fixed point of the KPZ universality class’, J. Stat. Phys. 160(4) (2015), 815–834.Google Scholar
Dauvergne, D., Ortmann, J. and Virág, B., ‘The directed landscape’, Preprint (2018), arXiv:1812.00309.Google Scholar
Dauvergne, D. and Virág, B., ‘Basic properties of the Airy line ensemble’, Preprint (2018), arXiv:1812.00311.Google Scholar
Eden, M., ‘A two-dimensional growth process’, inProc. 4th Berkeley Sympos. Math. Statist. and Prob., Vol. IV (University of California Press, Berkeley, CA, 1961), 223–239.Google Scholar
Glynn, P. W. and Whitt, W., ‘Departures from many queues in series’, Ann. Appl. Probab. 1(4) (1991), 546–572.Google Scholar
Gravner, J., Tracy, C. A. and Widom, H., ‘Limit theorems for height fluctuations in a class of discrete space and time growth models’, J. Stat. Phys. 102(5–6) (2001), 1085–1132.Google Scholar
Hägg, J., ‘Local Gaussian fluctuations in the Airy and discrete PNG processes’, Ann. Probab. 36(3) (2008), 1059–1092.Google Scholar
Hammond, A., ‘Brownian regularity for the Airy line ensemble, and multi-polymer watermelons in Brownian last passage percolation’, Mem. Amer. Math. Soc., to appear. Preprint (2016), arXiv:1609.02971.Google Scholar
Hammond, A., ‘Exponents governing the rarity of disjoint polymers in Brownian last passage percolation’, Proc. Lond. Math. Soc., to appear. Preprint (2017),arXiv:1709.04110.Google Scholar
Hammond, A., ‘Modulus of continuity of polymer weight profiles in Brownian last passage percolation’, Ann. Probab., to appear. Preprint (2017), arXiv:1709.04115.Google Scholar
Johansson, K., ‘Transversal fluctuations for increasing subsequences on the plane’, Probab. Theory Related Fields 116(4) (2000), 445–456.Google Scholar
Johansson, K., ‘Discrete polynuclear growth and determinantal processes’, Comm. Math. Phys. 242(1–2) (2003), 277–329.Google Scholar
Matetski, K., Quastel, J. and Remenik, D., ‘The KPZ fixed point’, Preprint (2017), arXiv:1701.00018.Google Scholar
Moreno Flores, G., Quastel, J. and Remenik, D., ‘Endpoint distribution of directed polymers in 1 + 1 dimensions’, Comm. Math. Phys. 317(2) (2013), 363–380.Google Scholar
O’Connell, N. and Yor, M., ‘A representation for non-colliding random walks’, Electron. Comm. Probab. 7(1–12) (2002) (electronic).Google Scholar
Pimentel, L. P. R., ‘On the location of the maximum of a continuous stochastic process’, J. Appl. Probab. 51(1) (2014), 152–161.Google Scholar
Pimentel, L., ‘Local behavior of Airy processes’, Preprint (2017), arXiv:1704.01903.Google Scholar
Prähofer, M. and Spohn, H., ‘Scale invariance of the PNG droplet and the Airy process’, J. Stat. Phys. 108(5–6) (2002), 1071–1106. Dedicated to David Ruelle and Yasha Sinai on the occasion of their 65th birthdays.Google Scholar
Quastel, J. and Remenik, D., ‘Local behavior and hitting probabilities of the Airy1 process’, Probab. Theory Related Fields 157(3–4) (2013), 605–634.Google Scholar
Sasamoto, T., ‘Spatial correlations of the 1D KPZ surface on a flat substrate’, J. Phys. A 38(33) (2005), L549–L556.Google Scholar