Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-12T19:43:24.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Modules over algebraic cobordism

Part of: (Co)homology theory Families, fibrations

Published online by Cambridge University Press:  17 December 2020

Elden Elmanto ,
Marc Hoyois ,
Adeel A. Khan ,
Vladimir Sosnilo  and
Maria Yakerson
Elden Elmanto
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford St., Cambridge, MA02138, USA; E-mail: [email protected]
Marc Hoyois
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford St., Cambridge, MA02138, USA; E-mail: [email protected] Fakultät für Mathematik, Universität Regensburg, Universitätsstr. 31, 93040Regensburg, Germany; E-mail: [email protected]
Adeel A. Khan
Affiliation:
IHES, 35 route de Chartres, 91440Bures-sur-Yvette, France; E-mail: [email protected]
Vladimir Sosnilo
Affiliation:
Laboratory “Modern Algebra and Applications”, St. Petersburg State University, 14th line, 29B, 199178Saint Petersburg, Russia; E-mail: [email protected]
Maria Yakerson
Affiliation:
Institute for Mathematical Research (FIM), ETH Zürich, Rämistr. 101, 8092Zürich, Switzerland; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the 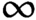$\infty $-category of 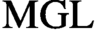$\mathrm{MGL} $-modules over any scheme is equivalent to the 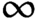$\infty $-category of motivic spectra with finite syntomic transfers. Using the recognition principle for infinite 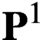$\mathbf{P} ^1$-loop spaces, we deduce that very effective 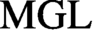$\mathrm{MGL} $-modules over a perfect field are equivalent to grouplike motivic spaces with finite syntomic transfers.

Along the way, we describe any motivic Thom spectrum built from virtual vector bundles of nonnegative rank in terms of the moduli stack of finite quasi-smooth derived schemes with the corresponding tangential structure. In particular, over a regular equicharacteristic base, we show that 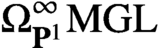$\Omega ^\infty _{\mathbf{P} ^1}\mathrm{MGL} $ is the 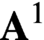$\mathbf{A} ^1$-homotopy type of the moduli stack of virtual finite flat local complete intersections, and that for 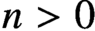$n>0$, 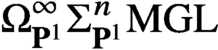$\Omega ^\infty _{\mathbf{P} ^1} \Sigma ^n_{\mathbf{P} ^1} \mathrm{MGL} $ is the 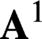$\mathbf{A} ^1$-homotopy type of the moduli stack of finite quasi-smooth derived schemes of virtual dimensio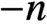n $-n$.

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory
Secondary: 14D23: Stacks and moduli problems
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e14
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Ananyevskiy, A., Garkusha, G. and Panin, I., ‘Cancellation theorem for framed motives of algebraic varieties’, Preprint, 2018, arXiv:1601.06642v2.Google Scholar
Barwick, C., ‘On the algebraic $K$-theory of higher categories’, J. Topol. 9(1) (2016), 245–347.CrossRefGoogle Scholar
Bachmann, T., Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., ‘On the infinite loop spaces of algebraic cobordism and the motivic sphere’, Preprint, 2020, arXiv:1911.02262v3.Google Scholar
Bachmann, T. and Fasel, J., ‘On the effectivity of spectra representing motivic cohomology theories’, Preprint, 2018, arXiv:1710.00594v3.Google Scholar
Bachmann, T. and Hoyois, M., ‘Norms in motivic homotopy theory’, to appear in Astérisque (2020). Preprint at arXiv:1711.03061.Google Scholar
Bhatt, B. and Halpern-Leistner, D., ‘Tannaka duality revisited’, Adv. Math. 316 (2017), 576–612.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., ‘Integral mixed motives in equal characteristic’, Doc. Math., extra volume: Alexander S. Merkurjev’s Sixtieth Birthday (2015), 145–194.Google Scholar
Clausen, D., Mathew, A., Naumann, N. and Noel, J., ‘Descent in algebraic $K$-theory and a conjecture of Ausoni–Rognes’, J. Eur. Math. Soc. (JEMS) 22(4) (2020), 1149–1200.CrossRefGoogle Scholar
Déglise, F., ‘Orientation theory in arithmetic geometry’, in $K$-theory, Tata Institute of Fundamental Research Publications, 19 (Hindustan Book Agency, New Delhi, 2018), 241–350. Available at https://protect-eu.mimecast.com/s/8MGZCz6z6tnOn35uKRwK1?domain=bookstore.ams.org.Google Scholar
Déglise, F., Jin, F. and Khan, A. A., ‘Fundamental classes in motivic homotopy theory’, to appear in J. Eur. Math. Soc. (JEMS) (2020). Preprint at arXiv:1805.05920.Google Scholar
Druzhinin, A., ‘Framed motives of smooth affine pairs’, Preprint, 2020, arXiv:1803.11388v8.Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., ‘Motivic infinite loop spaces’, Preprint, 2019, arXiv:1711.05248v5.Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., ‘Framed transfers and motivic fundamental classes’, J. Topol. 13(2) (2020), 460–500.CrossRefGoogle Scholar
Elmanto, E. and Kolderup, H., ‘On modules over motivic ring spectra’, Ann. K-Theory 5(2) (2020), 327–355.CrossRefGoogle Scholar
Galatius, S., Madsen, I., Tillmann, U. and Weiss, M., ‘The homotopy type of the cobordism category’, Acta Math. 202(2) (2009), 195–239.CrossRefGoogle Scholar
Garkusha, G. and Neshitov, A., ‘Fibrant resolutions for motivic Thom spectra’, Preprint, 2018, arXiv:1804.07621v1.Google Scholar
Garkusha, G., Neshitov, A. and Panin, I., ‘Framed motives of relative motivic spheres’, Preprint, 2018, arXiv:1604.02732v3.Google Scholar
Garkusha, G. and Panin, I., ‘Framed motives of algebraic varieties (after V. Voevodsky)’, to appear in J. Amer. Math. Soc. (2020). Preprint at arXiv:1409.4372.Google Scholar
Garkusha, G. and Panin, I., ‘Homotopy invariant presheaves with framed transfers’, Camb. J. Math. 8(1) (2020), 1–94.CrossRefGoogle Scholar
Grothendieck, A., Éléments de Géométrie Algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième partie, Publ. Math. I.H.É.S. 32 (1967). Available at https://protect-eu.mimecast.com/s/W7FNCA6l6tVGVgkiQpapc?domain=numdam.org.Google Scholar
Gruson, L., Une propriété des couples henséliens, Colloque d’algèbre commutative, exp. no 10, Publications des séminaires de mathématiques et informatique de Rennes, 1972. Available at https://protect-eu.mimecast.com/s/FgLkCBrmrSAzA1YU1oJRb?domain=numdam.org.Google Scholar
Haugseng, R., ‘Iterated spans and classical topological field theories’, Math. Z. 289(3) (2018), 1427–1488.CrossRefGoogle Scholar
Hoyois, M., ‘The localization theorem for framed motivic spaces’, to appear in Compos. Math. (2020). Preprint at arXiv:1807.04253.Google Scholar
Khan, A. A., ‘Motivic homotopy theory in derived algebraic geometry’, Ph.D. thesis, Universität Duisburg-Essen, 2016. Available at https://www.preschema.com/thesis/thesis.pdf.Google Scholar
Khan, A. A. and Rydh, D., ‘Virtual Cartier divisors and blow-ups’, Preprint, 2019, arXiv:1802.05702v2.Google Scholar
Levine, M. and Morel, F., Algebraic Cobordism (Springer, Location, 2007).Google Scholar
Lowrey, P. and Schürg, T., ‘Derived algebraic cobordism’, J. Inst. Math. Jussieu 15 (2016), 407–443.CrossRefGoogle Scholar
Lurie, J., ‘Derived Algebraic Geometry’, Ph.D. thesis, Massachusetts Institute of Technology, 2004. Available at https://www.math.ias.edu/~lurie/papers/DAG.pdf.Google Scholar
Lurie, J., ‘$\left(\infty, 2\right)$ -categories and the Goodwillie calculus I’, unpublished paper (2009). URL: https://www.math.ias.edu/~lurie/papers/GoodwillieI.pdf.Google Scholar
Lurie, J., ‘Higher algebra’, unpublished paper (2017). URL: https://www.math.ias.edu/~lurie/papers/HA.pdf.Google Scholar
Lurie, J., ‘Higher topos theory’, unpublished paper (2017). URL: https://www.math.ias.edu/~lurie/papers/HTT.pdf.Google Scholar
Lurie, J., ‘Spectral algebraic geometry’, unpublished paper (2018). URL: https://www.math.ias.edu/~lurie/papers/SAG-rootfile.pdf.Google Scholar
Navarro, A., ‘Riemann–Roch for homotopy invariant $K$-theory and Gysin morphisms’, Preprint, 2016, arXiv:1605.00980v1.Google Scholar
Nikolaus, T., ‘The group completion theorem via localizations of ring spectra’, unpublished paper (2017). URL: https://www.uni-muenster.de/IVV5WS/WebHop/user/nikolaus/papers.html.Google Scholar
Panin, I., ‘Oriented cohomology theories of algebraic varieties II’, Homology Homotopy Appl. 11(1) (2009), 349–405.CrossRefGoogle Scholar
Quillen, D., ‘Elementary proofs of some results of cobordism theory using Steenrod operations’, Adv. Math. 7(1) (1971), 29–56.CrossRefGoogle Scholar
Raptis, G., ‘Some characterizations of acyclic maps’, J. Homotopy Relat. Struct. 14 (2019), 773–785.CrossRefGoogle Scholar
Röndigs, O. and Østvær, P. A., ‘Modules over motivic cohomology’, Adv. Math. 219(2) (2008), 689–727.CrossRefGoogle Scholar
Randal-Williams, O., ‘“Group-completion”, local coefficient systems and perfection’, Q. J. Math. 64(3) (2013), 795–803.CrossRefGoogle Scholar
Rydh, D., ‘Noetherian approximation of algebraic spaces and stacks’, J. Algebra 422 (2015), 105–147.CrossRefGoogle Scholar
Spitzweck, M., ‘A commutative $\mathbf{P} ^1$-spectrum representing motivic cohomology over Dedekind domains’, Mém. Soc. Math. Fr. 157 (2018).Google Scholar
The Stacks Project Authors, ‘The Stacks Project’, URL: http://stacks.math.columbia.edu.Google Scholar
Toën, B. and Vezzosi, G., ‘Homotopical Algebraic Geometry. II: Geometric stacks and applications’, Mem. Amer. Math. Soc. 193(902) (2008).Google Scholar
Voevodsky, V., ‘Notes on framed correspondences’, unpublished paper (2001). URL: http://www.math.ias.edu/vladimir/files/framed.pdf.Google Scholar
Yakerson, M., ‘Motivic stable homotopy groups via framed correspondences’, Ph.D. thesis, University of Duisburg-Essen, 2019. Available at https://duepublico2.uni-due.de/receive/duepublico_mods_00070044?q=iakerson.Google Scholar