Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T00:41:44.914Z Has data issue: false hasContentIssue false
  • English
  • Français

THE KATZ–KLEMM–VAFA CONJECTURE FOR $K3$ SURFACES

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  06 June 2016

R. PANDHARIPANDE  and
R. P. THOMAS
R. PANDHARIPANDE
Affiliation:
Departement Mathematik, ETH Zürich, Switzerland; [email protected]
R. P. THOMAS
Affiliation:
Department of Mathematics, Imperial College, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

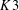We prove the KKV conjecture expressing Gromov–Witten invariants of $K3$ surfaces in terms of modular forms. Our results apply in every genus and for every curve class. The proof uses the Gromov–Witten/Pairs correspondence for $K3$ -fibered hypersurfaces of dimension 3 to reduce the KKV conjecture to statements about stable pairs on (thickenings of) 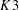$K3$ surfaces. Using degeneration arguments and new multiple cover results for stable pairs, we reduce the KKV conjecture further to the known primitive cases. Our results yield a new proof of the full Yau–Zaslow formula, establish new Gromov–Witten multiple cover formulas, and express the fiberwise Gromov–Witten partition functions of $K3$ -fibered 3-folds in terms of explicit modular forms.

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Altman, A., Iarrobino, A. and Kleiman, S., ‘Irreducibility of the compactified Jacobian’, inReal and Complex Singularities (Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976) (1977), 1–12.Google Scholar
Behrend, K., ‘Gromov–Witten invariants in algebraic geometry’, Invent. Math. 127 (1997), 601–617.Google Scholar
Behrend, K. and Fantechi, B., ‘The intrinsic normal cone’, Invent. Math. 128 (1997), 45–88.Google Scholar
Beauville, A., ‘Counting rational curves on K3 surfaces’, Duke Math. J. 97 (1999), 99–108.Google Scholar
Borcherds, R., ‘The Gross–Kohnen–Zagier theorem in higher dimensions’, Duke Math. J. 97 (1999), 219–233.Google Scholar
Bridgeland, T., ‘Hall algebras and curve-counting invariants’, J. Amer. Math. Soc. 24 (2011), 969–998.Google Scholar
Bryan, J., Katz, S. and Leung, C., ‘Multiple covers and the integrality conjecture for rational curves in Calabi–Yau threefolds’, J. Algebraic Geom. 10 (2001), 549–568.Google Scholar
Bryan, J. and Leung, C., ‘The enumerative geometry of K3 surfaces and modular forms’, J. Amer. Math. Soc. 13 (2000), 371–410.CrossRefGoogle Scholar
Buchweitz, R.-O. and Flenner, H., ‘A semiregularity map for modules and applications to deformations’, Compos. Math. 137 (2003), 135–210.CrossRefGoogle Scholar
Candelas, P., de la Ossa, X., Green, P. and Parkes, L., ‘A pair of Calabi–Yau manifolds as an exactly soluble superconformal field theory’, Nuclear Phys. B 359 (1991), 21–74.Google Scholar
Chen, X., ‘Rational curves on K3 surfaces’, J. Algebraic Geom. 8 (1999), 245–278.Google Scholar
Dolgachev, I. and Kondo, S., ‘Moduli of $K3$ surfaces and complex ball quotients, Lectures in Istambul’, Preprint, 2005, arXiv:math.AG/0511051.Google Scholar
Faber, C. and Pandharipande, R., ‘Hodge integrals and Gromov–Witten theory’, Invent. Math. 139 (2000), 173–199.Google Scholar
Fantechi, B., Göttsche, L. and van Straten, D., ‘Euler number of the compactified Jacobian and multiplicity of rational curves’, J. Algebraic Geom. 8 (1999), 115–133.Google Scholar
Fulton, W., Intersection Theory (Springer, Berlin, 1998).Google Scholar
Gopakumar, R. and Vafa, C., ‘ $M$ -theory and topological strings I’, Preprint, 1998, arXiv:hep-th/9809187.Google Scholar
Gopakumar, R. and Vafa, C., ‘ $M$ -theory and topological strings II’, Preprint, 1998, arXiv:hep-th/9812127.Google Scholar
Graber, T. and Pandharipande, R., ‘Localization of virtual classes’, Invent. Math. 135 (1999), 487–518.Google Scholar
Huybrechts, D., Lectures on K3 Surfaces (Cambridge University Press, Cambridge, 2016).Google Scholar
Huybrechts, D. and Thomas, R. P., ‘Deformation-obstruction theory for complexes via Atiyah and Kodaira–Spencer classes’, Math. Ann. 346 (2010), 545–569.Google Scholar
Illusie, L., Complexe cotangent et déformations I, Lecture Notes in Mathematics, 239 (Springer, Berlin, 1971).Google Scholar
Joyce, D. and Song, Y., A Theory of Generalized Donaldson–Thomas Invariants, Memoirs of the American Mathematical Society, 217 (American Mathematical Society, 2012), iv+199 pp.Google Scholar
Katz, S., Klemm, A. and Pandharipande, R., ‘On the motivic stable pairs invariants of K3 surfaces, with an appendix by R. Thomas’, inK3 Surfaces and their Moduli (eds. Faber, C., Farkas, G. and van der Geer, G.) Birkhauser Progress in Mathematics, 315 (Birkhäuser, Basel, 2016), 111–146.Google Scholar
Katz, S., Klemm, A. and Vafa, C., ‘ M-theory, topological strings, and spinning black holes’, Adv. Theor. Math. Phys. 3 (1999), 1445–1537.Google Scholar
Kawai, T. and Yoshioka, K., ‘String partition functions and infinite products’, Adv. Theor. Math. Phys. 4 (2000), 397–485.Google Scholar
Kiem, Y. H. and Li, J., ‘Localized virtual cycles by cosections’, J. Amer. Math. Soc. 26 (2013), 1025–1050.Google Scholar
Klemm, A., Kreuzer, M., Riegler, E. and Scheidegger, E., ‘Topological string amplitudes, complete intersections Calabi–Yau spaces, and threshold corrections’, J. High Energy Phys. 05 023 (2005).Google Scholar
Klemm, A., Maulik, D., Pandharipande, R. and Scheidegger, E., ‘Noether–Lefschetz theory and the Yau–Zaslow conjecture’, J. Amer. Math. Soc. 23 (2010), 1013–1040.Google Scholar
Kool, M. and Thomas, R. P., ‘Reduced classes and curve counting on surfaces I: theory’, Algebr. Geom. 1 (2014), 334–383.CrossRefGoogle Scholar
Kool, M. and Thomas, R. P., ‘Reduced classes and curve counting on surfaces II: calculations’, Algebr. Geom. 1 (2014), 384–399.CrossRefGoogle Scholar
Kudla, S. and Millson, J., ‘Intersection numbers of cycles on locally symmetric spaces and Fourier coefficients of holomorphic modular forms in several complex variables’, Pub. IHES 71 (1990), 121–172.CrossRefGoogle Scholar
Lee, J. and Leung, C., ‘Yau–Zaslow formula for non-primitive classes in K3 surfaces’, Geom. Topol. 9 (2005), 1977–2012.CrossRefGoogle Scholar
Li, J., ‘Stable morphisms to singular schemes and relative stable morphisms’, J. Differential Geom. 57 (2001), 509–578.Google Scholar
Li, J., ‘A degeneration formula for Gromov–Witten invariants’, J. Differential Geom. 60 (2002), 199–293.Google Scholar
Li, J. and Wu, B., ‘Good degeneration of Quot-schemes and coherent systems’, Preprint, 2011, arXiv:1110.0390.Google Scholar
Maulik, D. and Pandharipande, R., ‘Gromov–Witten theory and Noether–Lefschetz theory’, inA Celebration of Algebraic Geometry, Clay Mathematics Proceedings, 18 (AMS, Providence, RI, 2010), 469–507.Google Scholar
Maulik, D., Pandharipande, R. and Thomas, R., ‘Curves on K3 surfaces and modular forms’, J. Topol. 3 (2010), 937–996.Google Scholar
Oberdieck, G. and Pandharipande, R., ‘Curve counting on K3 × E, the Igusa cusp form 𝜒10 , and descendent integration’, in K3 Surfaces and their Moduli (eds. Faber, C., Farkas, G. and van der Geer, G.) Birkhauser Progress in Mathematics, 315 (Birkhäuser, Basel, 2016), 245–278.Google Scholar
Pandharipande, R. and Pixton, A., ‘Gromov–Witten/Pairs correspondence for the quintic 3-fold’, J. Amer. Math. Soc. (2016), doi:10.1090/jams/858.Google Scholar
Pandharipande, R. and Thomas, R. P., ‘Curve counting via stable pairs in the derived category’, Invent. Math. 178 (2009), 407–447.Google Scholar
Pandharipande, R. and Thomas, R. P., ‘Stable pairs and BPS invariants’, J. Amer. Math. Soc. 23 (2010), 267–297.Google Scholar
Pridham, J., ‘Semiregularity as a consequence of Goodwillie’s theorem’, Preprint, 2012, arXiv:1208.3111.Google Scholar
Schürg, T., Toën, B. and Vezzosi, G., ‘Derived algebraic geometry, determinants of perfect complexes, and applications to obstruction theories for maps and complexes’, Preprint, 2011, arXiv:1102.1150.Google Scholar
Siebert, B., ‘An update on (small) quantum cohomology’, inMirror Symmetry, III (Montreal, PQ, 1995), AMS/IP Studies in Advanced Mathematics, 10 (American Mathematical Society, Providence, RI, 1999), 279–312.Google Scholar
Toda, Y., ‘Curve counting theories via stable objects I. DT/PT correspondence’, J. Amer. Math. Soc. 23 (2010), 1119–1157.Google Scholar
Toda, Y., ‘Stable pairs on local K3 surfaces’, J. Differential Geom. 92 (2012), 285–370.Google Scholar
Wall, C. T. C., ‘On the orthogonal groups of unimodular quadratic forms’, Math. Ann. 147 (1962), 328–338.Google Scholar
Yau, S.-T. and Zaslow, E., ‘BPS states, string duality, and nodal curves on K3’, Nuclear Phys. B 457 (1995), 484–512.Google Scholar