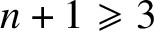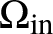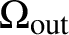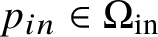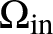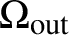1 Introduction
Let
![]() $(M,g)$
be a smooth Lorentzian manifold of dimension
$(M,g)$
be a smooth Lorentzian manifold of dimension
![]() $1+n$
with
$1+n$
with
![]() $n\geqslant 2$
and signature
$n\geqslant 2$
and signature
![]() $(-,+,\ldots ,+)$
. Using the standard notations, for
$(-,+,\ldots ,+)$
. Using the standard notations, for
![]() $p,q\in M$
we write
$p,q\in M$
we write
![]() $p \le q$
if there is a causal path on M from p to q or
$p \le q$
if there is a causal path on M from p to q or
![]() $p=q$
. Also, we write
$p=q$
. Also, we write
![]() $p\ll q$
if there is a time-like path on M from p to q. Using these relations, we define the causal future past and future of a point
$p\ll q$
if there is a time-like path on M from p to q. Using these relations, we define the causal future past and future of a point
![]() $p\in M$
through
$p\in M$
through
The chronological future and past of p are defined analogously with the causal relation replaced by the chronological relation,
We will make the standing assumption that
![]() $(M,g)$
is globally hyperbolic. Here, by global hyperbolicity we mean that
$(M,g)$
is globally hyperbolic. Here, by global hyperbolicity we mean that
![]() $(M,g)$
is causal (i.e., no closed causal curve exists) and, additionally, if
$(M,g)$
is causal (i.e., no closed causal curve exists) and, additionally, if
![]() $p,q \in M$
with
$p,q \in M$
with
![]() $p\le q$
, then
$p\le q$
, then
![]() $J^+(p)\cap J^-(q)$
is compact [Reference Alinhac1
Reference Ambartsoumian, Felea, Nolan and Quinto3]. Global hyperbolicity implies that the relation
$J^+(p)\cap J^-(q)$
is compact [Reference Alinhac1
Reference Ambartsoumian, Felea, Nolan and Quinto3]. Global hyperbolicity implies that the relation
![]() $\le $
is closed while
$\le $
is closed while
![]() $\ll $
is open and consequently that
$\ll $
is open and consequently that
![]() $J^{\pm }$
is closed while
$J^{\pm }$
is closed while
![]() $I^{\pm }$
is open. It also implies that there exists a global splitting in ‘time’ and ‘space’ in the sense that
$I^{\pm }$
is open. It also implies that there exists a global splitting in ‘time’ and ‘space’ in the sense that
![]() $(M,g)$
is isometric to
$(M,g)$
is isometric to
![]() $\mathbb R\times M_0$
with the metric taking the form
$\mathbb R\times M_0$
with the metric taking the form
 $$ \begin{align} g=c(x^0,x')\left(-dx^0\otimes\,dx^0+g_0(x^0,x')\right), \quad \forall x^0 \in \mathbb R,\ x' \in M_0, \end{align} $$
$$ \begin{align} g=c(x^0,x')\left(-dx^0\otimes\,dx^0+g_0(x^0,x')\right), \quad \forall x^0 \in \mathbb R,\ x' \in M_0, \end{align} $$
where c is a smooth positive function and
![]() $g_0$
is a Riemannian metric on the n-dimensional manifold
$g_0$
is a Riemannian metric on the n-dimensional manifold
![]() $M_0$
smoothly depending on the parameter
$M_0$
smoothly depending on the parameter
![]() $x^0$
. Moreover, each set
$x^0$
. Moreover, each set
![]() $\{x^0\}\times M_0$
is a Cauchy hypersurface in M; that is, any inextendible causal curve intersects it exactly once. For the sake of brevity, we will sometimes identify points, functions and tensors over the manifold
$\{x^0\}\times M_0$
is a Cauchy hypersurface in M; that is, any inextendible causal curve intersects it exactly once. For the sake of brevity, we will sometimes identify points, functions and tensors over the manifold
![]() $(M,g)$
with their preimage in
$(M,g)$
with their preimage in
![]() $\mathbb R\times M_0$
without explicitly writing the diffeomorphism.
$\mathbb R\times M_0$
without explicitly writing the diffeomorphism.
In this article, we consider the inverse problems with partial data for semi-linear and quasi-linear wave equations, where the set
![]() $\Omega _{\mathrm{in}}$
, where the sources are supported, and the set
$\Omega _{\mathrm{in}}$
, where the sources are supported, and the set
![]() ${\Omega _{\mathrm{out}}}$
, where the observations are made, may be separated. Motivated by applications, such problems can be called remote sensing problems. Similar problems with separated sources and measurements are encountered in radar imaging problems [Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Ambartsoumian, Felea, Quinto and Nolan4, Reference Cheney and Borden18, Reference Felea, Gaburro, Greenleaf and Nolan30] and seismic imaging [Reference Ambartsoumian, Felea, Nolan and Quinto3
Reference Alinhac1, Reference Felea, Greenleaf and Pramanik32, Reference Felea, Krishnan, Nolan and Quinto33, Reference Stolk and de Hoop88]. Recently, uniqueness results for inverse problems with separated sources and receivers have been obtained for the fractional powers of elliptic differential operators; see, for example, results in [Reference Ghosh, Rüland, Salo and Uhlmann34, Reference Ghosh, Salo and Uhlmann35] for the fractional Schrödinger operators and [Reference Babich and Ulin6
Reference Babich and Ulin6] for the nonlinear fractional Schrödinger equations. The study of the semi-linear model is carried out throughout the article as a simpler analytical model that clarifies the main methodology. A quasi-linear model is also considered to show the robustness of the method to various kinds of nonlinearities.
${\Omega _{\mathrm{out}}}$
, where the observations are made, may be separated. Motivated by applications, such problems can be called remote sensing problems. Similar problems with separated sources and measurements are encountered in radar imaging problems [Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Ambartsoumian, Felea, Quinto and Nolan4, Reference Cheney and Borden18, Reference Felea, Gaburro, Greenleaf and Nolan30] and seismic imaging [Reference Ambartsoumian, Felea, Nolan and Quinto3
Reference Alinhac1, Reference Felea, Greenleaf and Pramanik32, Reference Felea, Krishnan, Nolan and Quinto33, Reference Stolk and de Hoop88]. Recently, uniqueness results for inverse problems with separated sources and receivers have been obtained for the fractional powers of elliptic differential operators; see, for example, results in [Reference Ghosh, Rüland, Salo and Uhlmann34, Reference Ghosh, Salo and Uhlmann35] for the fractional Schrödinger operators and [Reference Babich and Ulin6
Reference Babich and Ulin6] for the nonlinear fractional Schrödinger equations. The study of the semi-linear model is carried out throughout the article as a simpler analytical model that clarifies the main methodology. A quasi-linear model is also considered to show the robustness of the method to various kinds of nonlinearities.
The main novelties of the article are that we develop a framework for inverse problems for nonlinear equations, where one uses interaction of only three waves. To this end, we formulate the concept of three-to-one scattering relation that is applicable for a wide class of nonlinear equations (see Theorem 1.3). This approach makes it possible to study the inverse problem in all dimensions
![]() $n+1\geqslant 3$
and the partial data problems with separated sources and observations.
$n+1\geqslant 3$
and the partial data problems with separated sources and observations.
1.1 The semi-linear model
Our main aim is to study quasi-linear equations, but to describe how the method works, we start our considerations with semi-linear equations. We consider the model setup
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g}u+u^m=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{g}u+u^m=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$
Here,
![]() $m\geqslant 3$
is an integer and
$m\geqslant 3$
is an integer and
![]() $T>0$
is a parameter to be fixed later and the source f is real-valued and compactly supported in the set
$T>0$
is a parameter to be fixed later and the source f is real-valued and compactly supported in the set
![]() $(-T,T)\times M_0$
. The wave operator,
$(-T,T)\times M_0$
. The wave operator,
![]() $\Box _g$
, is defined in local coordinates
$\Box _g$
, is defined in local coordinates
![]() $(x^0,\ldots ,x^n)$
by the expression
$(x^0,\ldots ,x^n)$
by the expression
 $$ \begin{align*}\Box_{g} u = -\sum_{j,k=0}^n\left|\det g\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j}( \left|\det g\right|{}^{\frac{1}{2}}g^{jk} \frac{\partial u}{\partial x^k}),\end{align*} $$
$$ \begin{align*}\Box_{g} u = -\sum_{j,k=0}^n\left|\det g\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j}( \left|\det g\right|{}^{\frac{1}{2}}g^{jk} \frac{\partial u}{\partial x^k}),\end{align*} $$
where
![]() $g^{jk}$
stands for the elements of the inverse of g. Note that we are using the
$g^{jk}$
stands for the elements of the inverse of g. Note that we are using the
![]() $(x^0,x')$
-coordinate system on M that is given by (1.1).
$(x^0,x')$
-coordinate system on M that is given by (1.1).
1.2 The quasi-linear model
For the quasi-linear wave equation, we first consider a family of smooth real-valued symmetric tensors
 $G_z(x)=G(x,z){=(G_{jk}(x,z))_{j,k=0}^n}$
with
$G_z(x)=G(x,z){=(G_{jk}(x,z))_{j,k=0}^n}$
with
![]() $x \in M$
and
$x \in M$
and
![]() $z \in \mathbb R$
satisfying
$z \in \mathbb R$
satisfying
-
(i)
 $G(x,0)=g(x)$
and
$G(x,0)=g(x)$
and
 $\partial _z G(x,0)=0$
for all
$\partial _z G(x,0)=0$
for all
 $x \in M$
.
$x \in M$
. -
(ii) The tensor
 $h(x)=\frac {1}{2}\partial ^2_z G(x,0)$
satisfies
$h(x)=\frac {1}{2}\partial ^2_z G(x,0)$
satisfies
 $\langle v,v\rangle _h\neq 0$
for all nonzero
$\langle v,v\rangle _h\neq 0$
for all nonzero
 $v\in LM$
.
$v\in LM$
.
Here,
![]() $LM$
denotes the bundle of light-like vectors on M with respect to the metric g. We subsequently consider the equation
$LM$
denotes the bundle of light-like vectors on M with respect to the metric g. We subsequently consider the equation
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{G_u}u=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{G_u}u=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$
Here, the quasi-linear wave operator
![]() $\Box _{G_u}$
is defined in local coordinates
$\Box _{G_u}$
is defined in local coordinates
![]() $(x^0,\ldots ,x^n)$
through
$(x^0,\ldots ,x^n)$
through
 $$ \begin{align*}\Box_{G_u}u = -\sum_{j,k=0}^n\left|\det G(x,{ u(x)})\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j} \bigg( \left|\det G(x,{ u(x)})\right|{}^{\frac{1}{2}}G^{jk}(x,{ u(x)}) \frac{\partial u}{\partial x^k}{ (x)}\bigg),\end{align*} $$
$$ \begin{align*}\Box_{G_u}u = -\sum_{j,k=0}^n\left|\det G(x,{ u(x)})\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j} \bigg( \left|\det G(x,{ u(x)})\right|{}^{\frac{1}{2}}G^{jk}(x,{ u(x)}) \frac{\partial u}{\partial x^k}{ (x)}\bigg),\end{align*} $$
where
![]() $G^{jk}$
stands for elements of the inverse of G. We will assume that the source f in (1.3) is real-valued and compactly supported in
$G^{jk}$
stands for elements of the inverse of G. We will assume that the source f in (1.3) is real-valued and compactly supported in
![]() $(-T,T)\times M_0$
.
$(-T,T)\times M_0$
.
Remark 1. The need to work with real-valued sources f in our quasi-linear model is physically motivated due to the fact that the solution u to equation (1.3) appears in the real-valued tensor
![]() $G(x,z)$
. This imposition is not necessary in the semi-linear model.
$G(x,z)$
. This imposition is not necessary in the semi-linear model.
In Subsection 2.1 we show that each of the Cauchy problems (1.2)–(1.3) above admits a unique solution
where given any relatively compact open set
![]() $\mathcal O \subset (-T,T)\times M_0$
, we define
$\mathcal O \subset (-T,T)\times M_0$
, we define
 $$ \begin{align} \mathscr C_{\mathcal O}=\{h \in H^{n+1}(\mathbb R\times M_0;\mathbb R)\,:\,\operatorname{\mathrm{supp}} h \subset \mathcal O,\quad \|h\|_{H^{n+1}(\mathbb R\times M_0)}\leqslant r_{\mathcal O}\}\end{align} $$
$$ \begin{align} \mathscr C_{\mathcal O}=\{h \in H^{n+1}(\mathbb R\times M_0;\mathbb R)\,:\,\operatorname{\mathrm{supp}} h \subset \mathcal O,\quad \|h\|_{H^{n+1}(\mathbb R\times M_0)}\leqslant r_{\mathcal O}\}\end{align} $$
and
![]() $r_{\mathcal O}$
is a sufficiently small constant depending on
$r_{\mathcal O}$
is a sufficiently small constant depending on
![]() $(M,g)$
,
$(M,g)$
,
![]() $\mathcal O$
and T.
$\mathcal O$
and T.
1.3 Source-to-solution map and the remote sensing inverse problem
Our primary interest lies in the setting that the sources can be actively placed near a world line
![]() $\mu _{\mathrm{in}}$
and the corresponding unique small solution u will be be measured near another disjoint world line
$\mu _{\mathrm{in}}$
and the corresponding unique small solution u will be be measured near another disjoint world line
![]() $\mu _{\mathrm{out}}$
corresponding to some observer. The main question is whether such experiments corresponding to the separated source and observation regions determine the structure of the background unperturbed media; that is,
$\mu _{\mathrm{out}}$
corresponding to some observer. The main question is whether such experiments corresponding to the separated source and observation regions determine the structure of the background unperturbed media; that is,
![]() $(M,g)$
.
$(M,g)$
.
To state the inverse problem precisely, let us consider two disjoint time-like future-pointing smooth paths
and impose the conditions that
Next, let us consider the source and observation regions
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
as small neighbourhoods of
$\Omega _{\mathrm{out}}$
as small neighbourhoods of
![]() $\mu _{\mathrm{in}}([t_0^-,t_0^+])$
and
$\mu _{\mathrm{in}}([t_0^-,t_0^+])$
and
![]() $\mu _{\mathrm{out}}([s_0^-,s_0^+])$
in M, respectively. These two open neighbourhoods will be precisely defined in Subsection 1.4. We will also make the standing assumption that
$\mu _{\mathrm{out}}([s_0^-,s_0^+])$
in M, respectively. These two open neighbourhoods will be precisely defined in Subsection 1.4. We will also make the standing assumption that
are a priori known as Lorentzian manifolds; that is, we are given local coordinates, the transition functions between the local charts and the metric tensors on these coordinate charts.
The partial data inverse problem with separated sources and observations (or the remote sensing problem) can now be formulated as follows. Is it possible to uniquely determine the unperturbed manifold
![]() $(M,g)$
(recall that
$(M,g)$
(recall that
![]() $G(x,0)=g(x)$
) by observing solutions to the nonlinear wave equations (1.2) or (1.3) in
$G(x,0)=g(x)$
) by observing solutions to the nonlinear wave equations (1.2) or (1.3) in
![]() $\Omega _{\mathrm{out}}$
that arise from small sources placed in
$\Omega _{\mathrm{out}}$
that arise from small sources placed in
![]() $\Omega _{\mathrm{in}}$
? The inverse problems with partial data are widely encountered in applications. The partial data problems where the sources and observations are made only on a part of boundary have been a focus of research for inverse problems for linear elliptic equations [Reference Dos Santos Ferreira, Kenig, Salo and Uhlmann22, Reference Alinhac and Baouendi2
Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Guillarmou and Tzou37, Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Barreto, Uhlmann and Wang7, Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Belishev8, Reference Imanuvilov, Uhlmann and Yamamoto49, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Alinhac1, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Babich and Ulin6, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Barreto, Uhlmann and Wang7, Reference Krupchyk and Uhlmann59, Reference Krupchyk and Uhlmann60, Reference Babich and Ulin6
Reference Alinhac and Baouendi2, Reference Lassas, Liimatainen, Lin and Salo68, Reference Barreto, Uhlmann and Wang7
Reference Alinhac and Baouendi2]. However, in most of these results it is assumed that the sets where the sources are supported and where the solutions are observed do intersect, with the notable exceptions in [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Belishev8, Reference Imanuvilov, Uhlmann and Yamamoto49, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Babich and Ulin6]. In particular, in inverse problems for hyperbolic equations it is essential that the sources, which are physically implemented by acoustic transducers, or by air guns or explosives in seismic imaging, are located far away from the sensors that observe the wave fields with a high precision. This is why the partial data problems are essential in applications. The partial data problems with separated sources and observations have been studied for linear hyperbolic equations, but the present results require convexity or other geometrical restrictions that guarantee the exact controllability of the system [Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Belishev8, Reference Lassas and Saksala70]. Let us remark that we can also apply the results in this article in the case when
$\Omega _{\mathrm{in}}$
? The inverse problems with partial data are widely encountered in applications. The partial data problems where the sources and observations are made only on a part of boundary have been a focus of research for inverse problems for linear elliptic equations [Reference Dos Santos Ferreira, Kenig, Salo and Uhlmann22, Reference Alinhac and Baouendi2
Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Guillarmou and Tzou37, Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Barreto, Uhlmann and Wang7, Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Belishev8, Reference Imanuvilov, Uhlmann and Yamamoto49, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Alinhac1, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Babich and Ulin6, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Barreto, Uhlmann and Wang7, Reference Krupchyk and Uhlmann59, Reference Krupchyk and Uhlmann60, Reference Babich and Ulin6
Reference Alinhac and Baouendi2, Reference Lassas, Liimatainen, Lin and Salo68, Reference Barreto, Uhlmann and Wang7
Reference Alinhac and Baouendi2]. However, in most of these results it is assumed that the sets where the sources are supported and where the solutions are observed do intersect, with the notable exceptions in [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Belishev8, Reference Imanuvilov, Uhlmann and Yamamoto49, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Babich and Ulin6]. In particular, in inverse problems for hyperbolic equations it is essential that the sources, which are physically implemented by acoustic transducers, or by air guns or explosives in seismic imaging, are located far away from the sensors that observe the wave fields with a high precision. This is why the partial data problems are essential in applications. The partial data problems with separated sources and observations have been studied for linear hyperbolic equations, but the present results require convexity or other geometrical restrictions that guarantee the exact controllability of the system [Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5
Reference Belishev8, Reference Lassas and Saksala70]. Let us remark that we can also apply the results in this article in the case when
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
intersect.
$\Omega _{\mathrm{out}}$
intersect.
To formulate the inverse problem precisely, we define the source-to-solution map
![]() $\mathscr L$
associated to the semi-linear Cauchy equation (1.2) through the expression
$\mathscr L$
associated to the semi-linear Cauchy equation (1.2) through the expression
where u is the unique small solution to (1.2) subject to the source f and the set
![]() $\mathscr C_{\Omega _{\mathrm{in}}}$
is as defined by (1.4). Analogously, we define the source-to-solution map
$\mathscr C_{\Omega _{\mathrm{in}}}$
is as defined by (1.4). Analogously, we define the source-to-solution map
![]() $\mathscr N$
for the quasi-linear Cauchy equation (1.3) through the expression
$\mathscr N$
for the quasi-linear Cauchy equation (1.3) through the expression
where u is the unique small solution to (1.3) subject to the source f.
Our inverse problem can now be restated as whether the manifold
![]() $(M,g)$
can be uniquely recovered given the source-to-solution map
$(M,g)$
can be uniquely recovered given the source-to-solution map
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
. Recall that
$\mathscr N$
. Recall that
![]() $g(x)=G(x,0)$
in the quasi-linear model.
$g(x)=G(x,0)$
in the quasi-linear model.
Due to finite speed of propagation for the wave equation, the optimal region where one can recover the geometry is the causal diamond generated by the source region
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
that is defined through
$\Omega _{\mathrm{out}}$
that is defined through
 $$ \begin{align} \mathbb D_e=\left(\bigcup_{q \in \Omega_{\text{in}}} I^{+}(q)\right) \cap \left(\bigcup_{q \in \Omega_{\text{out}}} {I}^{-}(q)\right),\end{align} $$
$$ \begin{align} \mathbb D_e=\left(\bigcup_{q \in \Omega_{\text{in}}} I^{+}(q)\right) \cap \left(\bigcup_{q \in \Omega_{\text{out}}} {I}^{-}(q)\right),\end{align} $$
given the knowledge of the source-to-solution map
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
. As we will see, we are able to recover the geometry in the slightly smaller set; that is, a causal diamond determined by the points
$\mathscr N$
. As we will see, we are able to recover the geometry in the slightly smaller set; that is, a causal diamond determined by the points
![]() $\mu _{\mathrm{in}}(t_0^-)$
and
$\mu _{\mathrm{in}}(t_0^-)$
and
![]() $\mu _{\mathrm{out}}(s_0^+)$
,
$\mu _{\mathrm{out}}(s_0^+)$
,
1.4 Main results
Before stating the main results, let us define, in detail, the source and observation neighbourhoods of the two future-pointing time-like curves
satisfying (1.5). We begin by extending the time-like paths to slightly larger intervals
and proceed to define the source and observation regions as a foliation of time-like future-pointing paths near the paths
![]() $\mu _{\mathrm{in}}((t_1^-,t_1^+))$
and
$\mu _{\mathrm{in}}((t_1^-,t_1^+))$
and
![]() $\mu _{\mathrm{out}}((s_1^-,s_1^+))$
. To make this precise, we use Fermi coordinates near these paths.
$\mu _{\mathrm{out}}((s_1^-,s_1^+))$
. To make this precise, we use Fermi coordinates near these paths.
Let
![]() $\{\alpha _{i}\}_{i=1}^n$
be an orthonormal basis for
$\{\alpha _{i}\}_{i=1}^n$
be an orthonormal basis for
![]() $\dot {\mu }_{\mathrm{in}}(t_1^-)^\perp $
and subsequently consider
$\dot {\mu }_{\mathrm{in}}(t_1^-)^\perp $
and subsequently consider
![]() $\{e_{i}(t)\}_{i=1}^{n}$
to denote the parallel transport of
$\{e_{i}(t)\}_{i=1}^{n}$
to denote the parallel transport of
![]() $\{\alpha _i\}_{i=1}^n$
along
$\{\alpha _i\}_{i=1}^n$
along
![]() $\mu _{\mathrm{in}}$
to the point
$\mu _{\mathrm{in}}$
to the point
![]() $\mu _{\mathrm{in}}(t)$
. Let
$\mu _{\mathrm{in}}(t)$
. Let
be defined through
 $$ \begin{align*}F_{\text{in}}(t,y) = \exp_{\mu_{\text{in}}(t)}(\sum_{i=1}^n y^i e_{i}(t)).\end{align*} $$
$$ \begin{align*}F_{\text{in}}(t,y) = \exp_{\mu_{\text{in}}(t)}(\sum_{i=1}^n y^i e_{i}(t)).\end{align*} $$
Here,
![]() $B(0,\delta )$
is the ball of radius
$B(0,\delta )$
is the ball of radius
![]() $\delta $
in
$\delta $
in
![]() $\mathbb R^n$
. For
$\mathbb R^n$
. For
![]() $\delta $
sufficiently small, the map
$\delta $
sufficiently small, the map
![]() $F_{\mathrm{in}}$
is a smooth diffeomorphism and the paths
$F_{\mathrm{in}}$
is a smooth diffeomorphism and the paths
are smooth time-like paths. We define
![]() $F_{\mathrm{out}}: (s_1^-,s_1^+)\times B(0,\delta )\to M$
analogously as above with
$F_{\mathrm{out}}: (s_1^-,s_1^+)\times B(0,\delta )\to M$
analogously as above with
![]() $\mu _{\mathrm{in}}$
replaced by
$\mu _{\mathrm{in}}$
replaced by
![]() $\mu _{\mathrm{out}}$
. Finally, we define the source and observation regions through the expression
$\mu _{\mathrm{out}}$
. Finally, we define the source and observation regions through the expression
 $$ \begin{align} \begin{aligned} \Omega_{\text{in}}&= \{ F_{\text{in}}(t,y)\,:\, t \in (t_1^-,t_1^+),\quad y\in B(0,\delta)\}\\ \Omega_{\text{out}}&= \{ F_{\text{out}}(t,y)\,:\, t \in (s_1^-,s_1^+),\quad y \in B(0,\delta)\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Omega_{\text{in}}&= \{ F_{\text{in}}(t,y)\,:\, t \in (t_1^-,t_1^+),\quad y\in B(0,\delta)\}\\ \Omega_{\text{out}}&= \{ F_{\text{out}}(t,y)\,:\, t \in (s_1^-,s_1^+),\quad y \in B(0,\delta)\}. \end{aligned} \end{align} $$
We will impose that
![]() $\delta $
is small enough so that the following condition is satisfied. This can always be guaranteed in view of (1.5).
$\delta $
is small enough so that the following condition is satisfied. This can always be guaranteed in view of (1.5).
 $$ \begin{align} \Omega_{\text{in}} \cap J^{-}(F_{\text{out}}(\{s_1^-\}\times B(0,\delta))=\emptyset \quad \text{and}\quad \overline{\Omega_{\text{out}}}\cap J^+(\mu_{\text{in}}(t_1^+))=\emptyset. \end{align} $$
$$ \begin{align} \Omega_{\text{in}} \cap J^{-}(F_{\text{out}}(\{s_1^-\}\times B(0,\delta))=\emptyset \quad \text{and}\quad \overline{\Omega_{\text{out}}}\cap J^+(\mu_{\text{in}}(t_1^+))=\emptyset. \end{align} $$
Our main result regarding the inverse problems for the semi-linear and quasi-linear models above can be stated as follows.
Theorem 1.1. Let
![]() $m \geqslant 3$
be an integer and
$m \geqslant 3$
be an integer and
![]() $(M^{(1)},g^{(1)})$
,
$(M^{(1)},g^{(1)})$
,
![]() $(M^{(2)},g^{(2)})$
be smooth globally hyperbolic Lorentzian manifolds of dimension
$(M^{(2)},g^{(2)})$
be smooth globally hyperbolic Lorentzian manifolds of dimension
![]() $1+n\geqslant 3$
. Let
$1+n\geqslant 3$
. Let
 $G^{(j)}_z$
,
$G^{(j)}_z$
,
![]() $j=1,2$
, be a symmetric tensor on
$j=1,2$
, be a symmetric tensor on
![]() $M^{(j)}$
that satisfies conditions (i)–(ii) and recall that
$M^{(j)}$
that satisfies conditions (i)–(ii) and recall that
![]() $g^{(j)}(x)=G^{(j)}(x,0)$
for all
$g^{(j)}(x)=G^{(j)}(x,0)$
for all
![]() $x \in M^{(j)}$
. Let
$x \in M^{(j)}$
. Let
 $\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$
and
$\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$
and
 $\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$
be smooth time-like paths satisfying (1.5). For
$\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$
be smooth time-like paths satisfying (1.5). For
![]() $j=1,2$
, let the source region
$j=1,2$
, let the source region
 $\Omega _{\mathrm{in}}^{(j)}$
and the observation region
$\Omega _{\mathrm{in}}^{(j)}$
and the observation region
 $\Omega ^{(j)}_{\mathrm{out}}$
be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Let
$\Omega ^{(j)}_{\mathrm{out}}$
be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Let
![]() $T>0$
be sufficiently large so that
$T>0$
be sufficiently large so that
 $$ \begin{align*}\mathbb D_e^{(j)}\subset (-T,T)\times M^{(j)}_0\quad \text{for}\ j=1,2,\end{align*} $$
$$ \begin{align*}\mathbb D_e^{(j)}\subset (-T,T)\times M^{(j)}_0\quad \text{for}\ j=1,2,\end{align*} $$
and also that there exists isometric diffeomorphisms
 $$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{\textit{in},{\textit{out}}\}.\end{align*} $$
$$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{\textit{in},{\textit{out}}\}.\end{align*} $$
Next, and for
![]() $j=1,2$
, we consider the source-to-solution maps
$j=1,2$
, we consider the source-to-solution maps
![]() $\mathscr L^{(j)}$
and
$\mathscr L^{(j)}$
and
![]() $\mathscr N^{(j)}$
associated to (1.2)–(1.3) respectively and assume that one of the following statements hold:
$\mathscr N^{(j)}$
associated to (1.2)–(1.3) respectively and assume that one of the following statements hold:
-
(i)
 $\Psi ^{\text {in}}\circ (\mathscr L^{(1)}(f))= \mathscr L^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$
for all sources
$\Psi ^{\text {in}}\circ (\mathscr L^{(1)}(f))= \mathscr L^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$
for all sources
 $f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$
,
$f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$
,
or
-
(ii)
 $\Psi ^{\text {in}}\circ (\mathscr N^{(1)}(f))= \mathscr N^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$
for all sources
$\Psi ^{\text {in}}\circ (\mathscr N^{(1)}(f))= \mathscr N^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$
for all sources
 $f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$
,
$f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$
,
where the set
 $\mathscr C^{(1)}_{\Omega ^{(1)}_{\mathrm{in}}}$
is defined by (1.4) associated to
$\mathscr C^{(1)}_{\Omega ^{(1)}_{\mathrm{in}}}$
is defined by (1.4) associated to
![]() $T>0$
and the manifold
$T>0$
and the manifold
![]() $(M^{(1)},g^{(1)})$
.
$(M^{(1)},g^{(1)})$
.
Then, under the hypotheses above, there exists a smooth diffeomorphism
![]() $\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$
that is equal to
$\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$
that is equal to
![]() $\Psi ^{\text {in}}$
on the set
$\Psi ^{\text {in}}$
on the set
 $\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$
and equals
$\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$
and equals
![]() $\Psi ^{\text {out}}$
on the set
$\Psi ^{\text {out}}$
on the set
 $\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$
and such that
$\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$
and such that
for some smooth real-valued function
![]() $c=c(x)$
,
$c=c(x)$
,
![]() $c:\mathbb D^{(1)}\to \mathbb R_+$
.
$c:\mathbb D^{(1)}\to \mathbb R_+$
.
Moreover, in the case that statement (i) holds and if
![]() $(n,m)\neq (3,3)$
, we have
$(n,m)\neq (3,3)$
, we have
![]() $c\equiv 1$
on the causal diamond
$c\equiv 1$
on the causal diamond
![]() $\mathbb D^{(1)}$
.
$\mathbb D^{(1)}$
.
Remark 2. Note that if
![]() $\mu _{\mathrm{out}}(s_1^+) \notin I^+(\mu _{\mathrm{in}}(t_1^-))$
, then
$\mu _{\mathrm{out}}(s_1^+) \notin I^+(\mu _{\mathrm{in}}(t_1^-))$
, then
![]() $\mathbb D$
is the empty set and the content of the previous theorem is empty. Therefore, it is implicitly assumed in this article in addition to (1.5) that
$\mathbb D$
is the empty set and the content of the previous theorem is empty. Therefore, it is implicitly assumed in this article in addition to (1.5) that
![]() $\mu _{\mathrm{out}}(s_1^+) \in I^+(\mu _{\mathrm{in}}(t_1^-))$
. We also remark that the recovery of the conformal factor in the exceptional case
$\mu _{\mathrm{out}}(s_1^+) \in I^+(\mu _{\mathrm{in}}(t_1^-))$
. We also remark that the recovery of the conformal factor in the exceptional case
![]() $(n,m)=(3,3)$
is briefly addressed in the last section of the article.
$(n,m)=(3,3)$
is briefly addressed in the last section of the article.
Remark 3. Let us make a brief remark about the restriction
![]() $m\geqslant 3$
in our semi-linear model (1.2). Our methodology to prove Theorem 1.1 is based on the nonlinear interaction of three waves to reduce the inverse problem to a purely geometric problem, namely, the study of the three-to-one scattering relation that we will formulate in the next section. To analyse the interaction of the three waves, we use Gaussian beams. In the case
$m\geqslant 3$
in our semi-linear model (1.2). Our methodology to prove Theorem 1.1 is based on the nonlinear interaction of three waves to reduce the inverse problem to a purely geometric problem, namely, the study of the three-to-one scattering relation that we will formulate in the next section. To analyse the interaction of the three waves, we use Gaussian beams. In the case
![]() $m\geqslant 3$
this interaction together with an application of Green’s identity leads, at a principal level, to the study of product of four Gaussian beams that is sufficient to obtain the three-to-one scattering relation. For this reason, the case
$m\geqslant 3$
this interaction together with an application of Green’s identity leads, at a principal level, to the study of product of four Gaussian beams that is sufficient to obtain the three-to-one scattering relation. For this reason, the case
![]() $m=2$
lies outside the scope of the current article. In our quasi-linear model (1.3), the assumptions on the first and second derivatives of
$m=2$
lies outside the scope of the current article. In our quasi-linear model (1.3), the assumptions on the first and second derivatives of
![]() $G(x,z)$
at
$G(x,z)$
at
![]() $z=0$
are also based on a similar observation.
$z=0$
are also based on a similar observation.
1.5 Recovery of geometry from the three-to-one scattering relation
The proof of Theorem 1.1 will be divided into an analytical and a geometrical part, with Sections 2–5 covering the analytical part and Sections 6–7 covering the geometric part of the analysis. In the analysis part, we use the idea of multiple-fold linearisation of the wave equation first used in [Reference Kurylev, Lassas and Uhlmann64] together with the principle of propagation of singularities for the wave equation, resulting in a geometrical data on the set
![]() $\mathbb D$
, the three-to-one scattering relation, that we will next define.
$\mathbb D$
, the three-to-one scattering relation, that we will next define.
Before formulation of the definition, we set some notations. We say that geodesics
![]() $\gamma _{v_{1}}$
and
$\gamma _{v_{1}}$
and
![]() $\gamma _{v_2}$
are distinct if the maximal geodesics that are extensions of
$\gamma _{v_2}$
are distinct if the maximal geodesics that are extensions of
![]() $\gamma _{v_{1}}$
and
$\gamma _{v_{1}}$
and
![]() $\gamma _{v_{2}}$
do not coincide as subsets of M. Also, for
$\gamma _{v_{2}}$
do not coincide as subsets of M. Also, for
![]() $v=(x,\eta )\in L^+M$
, let
$v=(x,\eta )\in L^+M$
, let
![]() $s(v)=\sup \{s>0:\ \gamma _{v}([0,s))\subset M\}$
and
$s(v)=\sup \{s>0:\ \gamma _{v}([0,s))\subset M\}$
and
![]() $\rho (v)=\sup \{s\in [0,s(v)]:\ \gamma _{v}(s)\not \in I^+(x)\}$
. As discussed in Subsection 6.3,
$\rho (v)=\sup \{s\in [0,s(v)]:\ \gamma _{v}(s)\not \in I^+(x)\}$
. As discussed in Subsection 6.3,
![]() $\gamma _v(\rho (v))$
is called the first cut point of
$\gamma _v(\rho (v))$
is called the first cut point of
![]() $\gamma _v$
.
$\gamma _v$
.
For
![]() $v=(x,\eta )\in L^+M$
, let
$v=(x,\eta )\in L^+M$
, let
 $\overrightarrow {\;\gamma _{v}}=\gamma _{x,\eta }([0,s(x,\eta )))$
be the light-like geodesics that are maximally extended in M to the future from v. Also, let
$\overrightarrow {\;\gamma _{v}}=\gamma _{x,\eta }([0,s(x,\eta )))$
be the light-like geodesics that are maximally extended in M to the future from v. Also, let
 $\overleftarrow {\;\gamma _{v}}=\gamma _{x,-\eta }([0,s(x,-\eta )))$
be the geodesic that emanates from v to the past.
$\overleftarrow {\;\gamma _{v}}=\gamma _{x,-\eta }([0,s(x,-\eta )))$
be the geodesic that emanates from v to the past.
Next we consider a set
![]() $\operatorname {\mathrm {R}}\subset (L^+M)^4$
of 4-tuples of vectors
$\operatorname {\mathrm {R}}\subset (L^+M)^4$
of 4-tuples of vectors
![]() $(v_0,v_1, v_2,v_3)$
and say that these vectors satisfy relation
$(v_0,v_1, v_2,v_3)$
and say that these vectors satisfy relation
![]() $\operatorname {\mathrm {R}}$
if
$\operatorname {\mathrm {R}}$
if
![]() $(v_0,v_1, v_2,v_3)\in \operatorname {\mathrm {R}}$
.
$(v_0,v_1, v_2,v_3)\in \operatorname {\mathrm {R}}$
.
Definition 1.2. Let
![]() $\Omega _{\mathrm{in}}, \Omega _{\mathrm{out}} \subset M$
be open. We say that a relation
$\Omega _{\mathrm{in}}, \Omega _{\mathrm{out}} \subset M$
be open. We say that a relation
![]() $\operatorname {\mathrm {R}} \subset L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$
is a three-to-one scattering relation if it has the following two properties:
$\operatorname {\mathrm {R}} \subset L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$
is a three-to-one scattering relation if it has the following two properties:
-
(R1) If
 $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then there exists an intersection point
$(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then there exists an intersection point
 $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
$y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. -
(R2) Let
 $(v_0,v_1,v_2,v_3)\in (L^+M)^4$
. Assume that
$(v_0,v_1,v_2,v_3)\in (L^+M)^4$
. Assume that
 $\gamma _{v_{j}}$
,
$\gamma _{v_{j}}$
,
 $j=0,1,2,3$
, are distinct and there exists
$j=0,1,2,3$
, are distinct and there exists
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
 $y=\gamma _{v_{0}}(s_0)$
with
$y=\gamma _{v_{0}}(s_0)$
with
 $s_0\in (-\rho (v_0),0]$
and
$s_0\in (-\rho (v_0),0]$
and
 $y=\gamma _{v_{j}}(s_j)$
for all
$y=\gamma _{v_{j}}(s_j)$
for all
 $j=1,2,3$
, with
$j=1,2,3$
, with
 $s_j\in [0,\rho (v_j))$
. Denote
$s_j\in [0,\rho (v_j))$
. Denote
 $\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
$\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
 $j=0,1,2,3$
and assume that
$j=0,1,2,3$
and assume that
 $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, it holds that
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, it holds that
 $(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$
.
$(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$
.
In other words, (R1) means that if
![]() $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then it is necessary that the future-pointing geodesics
$(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then it is necessary that the future-pointing geodesics
![]() $\gamma _{v_1},\gamma _{v_2}$
and
$\gamma _{v_1},\gamma _{v_2}$
and
![]() $\gamma _{v_3}$
must intersect at some point y and some future-pointing geodesic emanating from y arrives to
$\gamma _{v_3}$
must intersect at some point y and some future-pointing geodesic emanating from y arrives to
![]() $v_0$
. The condition (R2) means for
$v_0$
. The condition (R2) means for
![]() $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
it is sufficient that the future-pointing geodesics
$(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
it is sufficient that the future-pointing geodesics
![]() $\gamma _{v_1},\gamma _{v_2}$
and
$\gamma _{v_1},\gamma _{v_2}$
and
![]() $\gamma _{v_3}$
intersect at some point y before their first cut points and that the past-pointing null geodesic
$\gamma _{v_3}$
intersect at some point y before their first cut points and that the past-pointing null geodesic
![]() $\gamma _{v_0}$
arrives to the point y in the direction
$\gamma _{v_0}$
arrives to the point y in the direction
![]() $\xi _0$
that is in the span of the velocity vectors of
$\xi _0$
that is in the span of the velocity vectors of
![]() $\gamma _{v_1},\gamma _{v_2}$
and
$\gamma _{v_1},\gamma _{v_2}$
and
![]() $\gamma _{v_3}$
at the point y and, finally, that the geodesic
$\gamma _{v_3}$
at the point y and, finally, that the geodesic
![]() $\gamma _{v_0}([s_0,0])$
has no cut points. The relation
$\gamma _{v_0}([s_0,0])$
has no cut points. The relation
![]() $\operatorname {\mathrm {R}}$
is visualised in Figure 3.
$\operatorname {\mathrm {R}}$
is visualised in Figure 3.

Figure 1 Nonlinear interaction of three waves when
![]() $m=3$
and g is the Minkowski metric. The four figures are snapshots of the waves in the space
$m=3$
and g is the Minkowski metric. The four figures are snapshots of the waves in the space
![]() $\mathbb R^3$
at different times, with time progressing from top to bottom. First figure from the top: Plane waves before interactions. Second figure: The 2-wave interactions (black line segments) appear but do not cause singularities that propagate in new directions. Third figure: The 3-wave interactions generate a new wave (blue cone). Fourth figure: The new wave propagates near the
$\mathbb R^3$
at different times, with time progressing from top to bottom. First figure from the top: Plane waves before interactions. Second figure: The 2-wave interactions (black line segments) appear but do not cause singularities that propagate in new directions. Third figure: The 3-wave interactions generate a new wave (blue cone). Fourth figure: The new wave propagates near the
![]() $x^1, x^2$
plane. By varying the directions of the incoming plane waves, a wave propagating near any plane can be generated. Note that, for general g, the picture may be more complicated due to caustics.
$x^1, x^2$
plane. By varying the directions of the incoming plane waves, a wave propagating near any plane can be generated. Note that, for general g, the picture may be more complicated due to caustics.

Figure 2 Schematic of the geometric setting. The time-like paths
![]() $\mu _{\mathrm{in}}$
and
$\mu _{\mathrm{in}}$
and
![]() $\mu _{\mathrm{out}}$
are in green and their neighbourhoods
$\mu _{\mathrm{out}}$
are in green and their neighbourhoods
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{\rm out}}$
are in orange. The set
$\Omega _{\mathrm{\rm out}}$
are in orange. The set
![]() $\mathbb D$
is enclosed by the black rectangle. The set
$\mathbb D$
is enclosed by the black rectangle. The set
![]() $I^+({ \mu _{\mathrm{\rm in}}(t_1^+)})$
is in light blue, and the set
$I^+({ \mu _{\mathrm{\rm in}}(t_1^+)})$
is in light blue, and the set
![]() $J^-({ \mu _{\mathrm{out}}(s_1^+)})$
is in light red; cf. (1.5).
$J^-({ \mu _{\mathrm{out}}(s_1^+)})$
is in light red; cf. (1.5).

Figure 3 Three-to-one scattering relation
![]() $\operatorname {\mathrm {R}}$
in the
$\operatorname {\mathrm {R}}$
in the
![]() $1+2$
-dimensional Minkowski space. The red vectors
$1+2$
-dimensional Minkowski space. The red vectors
![]() $v_1$
,
$v_1$
,
![]() $v_2$
and
$v_2$
and
![]() $v_3$
and the green vector
$v_3$
and the green vector
![]() $v_0$
satisfy
$v_0$
satisfy
![]() $(v_0,v_1,v_2,v_3) \in \operatorname {\mathrm {R}}$
. The vector
$(v_0,v_1,v_2,v_3) \in \operatorname {\mathrm {R}}$
. The vector
![]() $\xi _0$
in Definition 1.2 is in blue and the vectors
$\xi _0$
in Definition 1.2 is in blue and the vectors
![]() $\xi _1$
,
$\xi _1$
,
![]() $\xi _2$
and
$\xi _2$
and
![]() $\xi _3$
are in black. The latter three have the same base point with
$\xi _3$
are in black. The latter three have the same base point with
![]() $\xi _0$
and are not labelled.
$\xi _0$
and are not labelled.
We emphasise that in Definition 1.2 there are no requirements for the 4-tuples
![]() $(v_0,v_1, v_2,v_3)$
for which the conditions in (R1) or (R2) are not valid. This has the important consequence that to verify that the source-to-solution map
$(v_0,v_1, v_2,v_3)$
for which the conditions in (R1) or (R2) are not valid. This has the important consequence that to verify that the source-to-solution map
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
determines a three-to-one scattering relation, we need to consider only those 4-tuples
$\mathscr N$
determines a three-to-one scattering relation, we need to consider only those 4-tuples
![]() $(v_0,v_1, v_2,v_3)$
for which the geodesics
$(v_0,v_1, v_2,v_3)$
for which the geodesics
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=0,1,2,3$
do not intersect at the conjugate points and the structure of the multiple pairwise intersections of the geodesics is simple. This makes it possible to avoid technical geometrical difficulties encountered in several studies on inverse problems for linear and nonlinear differential equations; see, for example, [Reference Dos Santos Ferreira, Kurylev, Lassas, Liimatainen and Salo23, Reference Dos Santos Ferreira, Kurylev, Lassas and Salo24, Reference Hintz, Uhlmann and Zhai40, Reference Kurylev, Lassas and Uhlmann64].
$j=0,1,2,3$
do not intersect at the conjugate points and the structure of the multiple pairwise intersections of the geodesics is simple. This makes it possible to avoid technical geometrical difficulties encountered in several studies on inverse problems for linear and nonlinear differential equations; see, for example, [Reference Dos Santos Ferreira, Kurylev, Lassas, Liimatainen and Salo23, Reference Dos Santos Ferreira, Kurylev, Lassas and Salo24, Reference Hintz, Uhlmann and Zhai40, Reference Kurylev, Lassas and Uhlmann64].
The following theorem states that the three-to-one scattering relation determines uniquely the topological, differential and conformal structure of the set
![]() $\mathbb D$
.
$\mathbb D$
.
Theorem 1.3. Let
![]() $(M^{(1)},g^{(1)})$
,
$(M^{(1)},g^{(1)})$
,
![]() $(M^{(2)},g^{(2)})$
be smooth globally hyperbolic Lorentzian manifolds of dimension
$(M^{(2)},g^{(2)})$
be smooth globally hyperbolic Lorentzian manifolds of dimension
![]() $1+n\geqslant 3$
. Let
$1+n\geqslant 3$
. Let
 $\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$
and
$\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$
and
 $\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$
be smooth time-like paths satisfying (1.5). For
$\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$
be smooth time-like paths satisfying (1.5). For
![]() $j=1,2$
, let the source region
$j=1,2$
, let the source region
 $\Omega _{\mathrm{in}}^{(j)}$
and the observation region
$\Omega _{\mathrm{in}}^{(j)}$
and the observation region
 $\Omega ^{(j)}_{\mathrm{out}}$
be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Moreover, we assume that there are isometric diffeomorphisms
$\Omega ^{(j)}_{\mathrm{out}}$
be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Moreover, we assume that there are isometric diffeomorphisms
 $$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{{\textit{in}},{\textit{out}}\}.\end{align*} $$
$$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{{\textit{in}},{\textit{out}}\}.\end{align*} $$
Suppose next that there are relations
 $\operatorname {\mathrm {R}}^{(j)}\subset L^+\Omega _{out}^{(j)}\times (L^+\Omega _{in}^{(j)})^3$
,
$\operatorname {\mathrm {R}}^{(j)}\subset L^+\Omega _{out}^{(j)}\times (L^+\Omega _{in}^{(j)})^3$
,
![]() $j=1,2$
, that satisfy conditions (R1) and (R2) in Definition 1.2 for manifolds
$j=1,2$
, that satisfy conditions (R1) and (R2) in Definition 1.2 for manifolds
![]() $(M^{(j)},g^{(j)})$
and that
$(M^{(j)},g^{(j)})$
and that
 $$ \begin{align} \operatorname{\mathrm{R}}^{(2)}=\bigg\{(\Psi^{in}_*v_0,\Psi^{out}_*v_1,\Psi^{out}_*v_2,\Psi^{out}_*v_3)\ \bigg|\ (v_0,v_1,v_2,v_3)\in \operatorname{\mathrm{R}}^{(1)}\bigg\}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{R}}^{(2)}=\bigg\{(\Psi^{in}_*v_0,\Psi^{out}_*v_1,\Psi^{out}_*v_2,\Psi^{out}_*v_3)\ \bigg|\ (v_0,v_1,v_2,v_3)\in \operatorname{\mathrm{R}}^{(1)}\bigg\}. \end{align} $$
Then there exists a smooth diffeomorphism
![]() $\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$
that is equal to
$\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$
that is equal to
![]() $\Psi ^{\text {in}}$
on the set
$\Psi ^{\text {in}}$
on the set
 $\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$
and equals
$\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$
and equals
![]() $\Psi ^{\text {out}}$
on the set
$\Psi ^{\text {out}}$
on the set
 $\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$
and such that
$\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$
and such that
for some smooth real-valued function
![]() $c=c(x)$
,
$c=c(x)$
,
![]() $c:\mathbb D^{(1)}\to \mathbb R_+$
.
$c:\mathbb D^{(1)}\to \mathbb R_+$
.
The motivation of Definition 1.2 and Theorem 1.3 is to provide a general framework that allows the results of this article to be applicable for other nonlinear hyperbolic equations similar to those studied in this article. Indeed, to consider some different kind of nonlinear hyperbolic equation (for example, such as
 $\square _g u+\|\nabla u\|_g^3=f$
in
$\square _g u+\|\nabla u\|_g^3=f$
in
![]() $\mathbb R^{1+n}$
; see [Reference Wang and Zhou92] for the case
$\mathbb R^{1+n}$
; see [Reference Wang and Zhou92] for the case
![]() $n=3$
) one can define that
$n=3$
) one can define that
![]() $(v_0,v_1, v_2,v_3)$
satisfies the relation
$(v_0,v_1, v_2,v_3)$
satisfies the relation
![]() $\operatorname {\mathrm {R}}_{sim}$
if three singular waves sent to directions
$\operatorname {\mathrm {R}}_{sim}$
if three singular waves sent to directions
![]() $v_1,v_2$
and
$v_1,v_2$
and
![]() $v_3$
interact so that the interaction produces a wave whose wave front contains the covector corresponding to
$v_3$
interact so that the interaction produces a wave whose wave front contains the covector corresponding to
![]() $v_0$
. Then to apply Theorem 1.3 one has to show that
$v_0$
. Then to apply Theorem 1.3 one has to show that
![]() $\operatorname {\mathrm {R}}_{sim}$
satisfies conditions (R1) and (R2). We note that condition (R1) is natural as the second-order interaction of waves does not produce singularities that propagate to new directions; see [Reference Greenleaf and Uhlmann36, Reference Kurylev, Lassas and Uhlmann64]. Condition (R2) is motivated by the general results for the interaction of three waves; see [Reference Barreto, Uhlmann and Wang7, Reference Barreto, Uhlmann and Wang7
Reference Barreto, Uhlmann and Wang7, Reference Sa Barreto and Wang83] and references therein. We emphasise that to verify condition (R2) one has to consider only geodesics that have no conjugate points and thus this condition can be verified without analysing interaction of waves near caustics.
$\operatorname {\mathrm {R}}_{sim}$
satisfies conditions (R1) and (R2). We note that condition (R1) is natural as the second-order interaction of waves does not produce singularities that propagate to new directions; see [Reference Greenleaf and Uhlmann36, Reference Kurylev, Lassas and Uhlmann64]. Condition (R2) is motivated by the general results for the interaction of three waves; see [Reference Barreto, Uhlmann and Wang7, Reference Barreto, Uhlmann and Wang7
Reference Barreto, Uhlmann and Wang7, Reference Sa Barreto and Wang83] and references therein. We emphasise that to verify condition (R2) one has to consider only geodesics that have no conjugate points and thus this condition can be verified without analysing interaction of waves near caustics.
1.6 Previous literature
The study of nonlinear wave equations is a fascinating topic in analysis with a rich literature. In contrast with the study of linear wave equations, there are numerous challenges in studying the existence, uniqueness and stability of solutions to such equations. These equations physically arise in the study of general relativity, such as the Einstein field equations. They also appear in the study of vibrating systems or the detection of perturbations arising in electronics, such as the telegraph equation or the study of semi-conductors; see, for instance, [Reference Cazenave and Haraux15]. We mention in particular that the quasi-linear model (1.3) studied in this article is a model for studying Einstein’s equations in wave coordinates [Reference Barreto, Uhlmann and Wang7 Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5].
This article uses extensively the nonlinear interaction of three waves to solve the inverse problems. To analyse this, we use Gaussian beams. An alternative way to consider the nonlinear interaction is to use microlocal analysis and conormal singularities; see [Reference Greenleaf and Uhlmann36, Reference Guillemin and Uhlmann38, Reference Barreto, Uhlmann and Wang7 Reference Belishev8]. There are many results on such nonlinear interaction, starting with the studies of Bony [Reference Alinhac1 Reference Ambartsoumian, Felea, Quinto and Nolan4], Melrose and Ritter [Reference Melrose and Ritter77] and Rauch and Reed [Reference Belishev8 Reference Alinhac and Baouendi2]. However, these studies concern the direct problem and differ from the setting of this article in that they assumed that the geometrical setting of the interacting singularities and, in particular, the locations and types of caustics, is known a priori. In inverse problems we need to study waves on an unknown manifold, so we do not know the underlying geometry and, therefore, the location of the singularities of the waves. For example, the waves can have caustics that may even be of an unstable type.
Earlier, inverse problems for nonlinear hyperbolic equations with unknown metric have been studied using interaction of waves only in the (1+3)-dimensional case using interaction of four or more waves. Inverse problems for nonlinear scalar wave equations with a quadratic nonlinearity were studied in [Reference Kurylev, Lassas and Uhlmann64] using multiple-fold linearisation. Together with the phenomenon of propagation of singularities for the wave equation, the authors reduced the inverse problem for the wave equation to the study of light observation sets. This approach was extended in [Reference de Hoop, Uhlmann and Wang19, Reference Hintz and Uhlmann39, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5 Reference Alinhac and Baouendi2, Reference Barreto, Uhlmann and Wang7 Reference Alinhac1]. In [Reference Kurylev, Lassas, Oksanen and Uhlmann63], the coupled Einstein and scalar field equations were studied. The result has been more recently strengthened in [Reference Barreto, Uhlmann and Wang7 Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Uhlmann and Wang91] for the Einstein scalar field equations with general sources and for the Einstein–Maxwell equations. In particular, a technique to determine the conformal factor using the microlocal symbols of the observed waves was developed in [Reference Uhlmann and Wang91].
Aside from the works mentioned above, the majority of works have been on inverse problems for semi-linear wave equations, with quadratic nonlinearities studied in [Reference Kurylev, Lassas and Uhlmann64], a general semi-linear term studied in [Reference Hintz, Uhlmann and Zhai40, Reference Barreto, Uhlmann and Wang7
Reference Ambartsoumian, Felea, Nolan and Quinto3] and quadratic derivatives studied in [Reference Wang and Zhou92]; see also [Reference Babich and Ulin6
Reference Barreto, Uhlmann and Wang7] and references therein. All these works concern the
![]() $(1+3)$
-dimensional case. In recent works [Reference Chen, Lassas, Oksanen and Paternain16, Reference Chen, Lassas, Oksanen and Paternain17, Reference Feizmohammadi and Oksanen29], the authors have also studied problems of recovering zeroth- and first-order terms for semi-linear wave equations with Minkowski metric. We note that three wave interactions were used in [Reference Chen, Lassas, Oksanen and Paternain16, Reference Chen, Lassas, Oksanen and Paternain17] to determine the lower order terms in the equations and in modelling nonlinear elastic scattering from discontinuities [Reference de Hoop, Uhlmann and Wang20, Reference Alinhac and Baouendi2
Reference Alinhac1]. In [Reference Feizmohammadi and Oksanen28, Reference Babich and Ulin6
Reference Belishev and Katchalov9] similar multiple-fold linearisation methods were introduced to study inverse problems for elliptic nonlinear equations; see also [Reference Krupchyk and Uhlmann61].
$(1+3)$
-dimensional case. In recent works [Reference Chen, Lassas, Oksanen and Paternain16, Reference Chen, Lassas, Oksanen and Paternain17, Reference Feizmohammadi and Oksanen29], the authors have also studied problems of recovering zeroth- and first-order terms for semi-linear wave equations with Minkowski metric. We note that three wave interactions were used in [Reference Chen, Lassas, Oksanen and Paternain16, Reference Chen, Lassas, Oksanen and Paternain17] to determine the lower order terms in the equations and in modelling nonlinear elastic scattering from discontinuities [Reference de Hoop, Uhlmann and Wang20, Reference Alinhac and Baouendi2
Reference Alinhac1]. In [Reference Feizmohammadi and Oksanen28, Reference Babich and Ulin6
Reference Belishev and Katchalov9] similar multiple-fold linearisation methods were introduced to study inverse problems for elliptic nonlinear equations; see also [Reference Krupchyk and Uhlmann61].
All of the aforementioned works consider inverse problems for various types of nonlinear wave equations subject to small sources. The presence of a nonlinear term in the partial differential equation (PDE) is a strong tool in obtaining the uniqueness results. To discuss this feature in some detail, we note that the analogous inverse problem for the linear wave equation (see (2.1)) is still a major open problem. For this problem, much is known in the special setting that the coefficients of the metric are time-independent. We refer the reader to the work of Belishev and Kurylev in [Reference Alinhac1 Reference Alinhac and Baouendi2] that uses the boundary control method introduced in [Reference Belishev and Kurylev10] to solve this problem and to [Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5, Reference Isozaki and Kurylev50, Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5 Reference Ambartsoumian, Felea, Nolan and Quinto3, Reference Babich and Ulin6 Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5] for a state-of-the-art result in the application of the boundary control method and finally to [Reference Hörmander41] for the related scattering control method. The boundary control method is known to fail in the case of general time-dependent coefficients, since it uses the unique continuation principle of Tataru [Reference Tataru89]. This principle is known to be false in the cases that the time dependence of coefficients is not real-analytic [Reference Alinhac1, Reference Alinhac and Baouendi2]. We refer the reader to [Reference Eskin25] for recovery of coefficients of a general linear wave equation under an analyticity assumption with respect to the time coordinate.
In the more challenging framework of general time-dependent coefficients and by using the alternative technique of studying the propagation of singularities for the wave equation, the inverse problem for the linear wave equation (see (2.1)) is reduced to the injectivity of the scattering relation on M; see the definition (5.1). The injectivity of the scattering relation is open unless the geometry of the manifold is static and an additional convex foliation codition is satisfied [Reference Stefanov, Uhlmann and Vasy86] on the spatial part of the manifold. In the studies of recovery of sub-principal coefficients for the linear wave equation, we refer the reader to the recent works [Reference Feizmohammadi, Ilmavirta, Kian and Oksanen26, Reference Feizmohammadi, Ilmavirta and Oksanen27, Reference Stefanov85] for recovery of zeroth- and first-order coefficients and to [Reference Stefanov and Yang87] for a reduction from the boundary data for the inverse problem associated to (2.1) to the study of geometrical transforms on M. This latter approach has been recently extended to general real principal type differential operators [Reference Ralston80].
The main underlying principle in the presence of a nonlinearity is that linearisation of the equation near the trivial solution results in a nonlinear interaction of solutions to the linear wave equation producing much richer dynamics for propagation of singularities. Owing to this richer dynamics, and somewhat paradoxically, inverse problems for nonlinear wave equations have been solved in much more general geometrical contexts than their counterparts for the linear wave equations.
Let us now discuss some of the main novelties of the present work. Firstly, we consider threefold linearisation of the nonlinear equations (1.2)–(1.3) and can therefore analyse inverse problems using interaction of three waves instead of earlier works relying on interaction of four waves. This makes it possible to consider more general equations with simpler techniques. Due to the new techniques, we can consider inverse problems on Lorenzian manifolds with any dimension
![]() $n+1\ge 3$
. As a second novelty, we introduce a new concept, the three-to-one scattering relation that can be applied for many kinds of nonlinear equations and which we hope to be useful for other researchers in the field of inverse problems. Also, this makes it possible to consider inverse problems in the remote sensing setting that includes both forward- and back-scattering problems. Finally, we mention our quite general quasi-linear model problem (1.3) with an unknown nonlinearity in the leading order term. We successfully study this complicated model with the use of Gaussian beams and show that the source-to-solution map determines the three-to-one scattering relation.
$n+1\ge 3$
. As a second novelty, we introduce a new concept, the three-to-one scattering relation that can be applied for many kinds of nonlinear equations and which we hope to be useful for other researchers in the field of inverse problems. Also, this makes it possible to consider inverse problems in the remote sensing setting that includes both forward- and back-scattering problems. Finally, we mention our quite general quasi-linear model problem (1.3) with an unknown nonlinearity in the leading order term. We successfully study this complicated model with the use of Gaussian beams and show that the source-to-solution map determines the three-to-one scattering relation.
1.7 Outline of the article
We begin with some preliminaries in Section 2, starting with Proposition 2.1 that shows that the forward problems (1.2)–(1.3) are well-posed. We also recall the technique of multiple-fold linearisation and apply it to the semi-linear and quasi-linear equations separately. This will relate the source-to-solution maps,
![]() $\mathscr L$
and
$\mathscr L$
and
![]() $\mathscr N$
, to the study of products of solutions to the linear wave equation; see (2.6) and (2.10). In Section 3, we briefly recall the construction of the classical Gaussian beams for the linear wave equation. We also show that it is possible to explicitly construct real-valued sources supported in the source and observation regions that generate exact solutions to the linear wave equations that are close in a suitable sense to the real parts of Gaussian beams. In Section 5 we prove the main analytical theorems, showing that the source-to-solution maps lead to a three-to-one scattering relation; see Theorem 5.1–5.2. Combined with Theorem 1.3, this proves the first half of Theorem 1.1 on the recovery of the topological, differential and conformal structure of the casual diamond
$\mathscr N$
, to the study of products of solutions to the linear wave equation; see (2.6) and (2.10). In Section 3, we briefly recall the construction of the classical Gaussian beams for the linear wave equation. We also show that it is possible to explicitly construct real-valued sources supported in the source and observation regions that generate exact solutions to the linear wave equations that are close in a suitable sense to the real parts of Gaussian beams. In Section 5 we prove the main analytical theorems, showing that the source-to-solution maps lead to a three-to-one scattering relation; see Theorem 5.1–5.2. Combined with Theorem 1.3, this proves the first half of Theorem 1.1 on the recovery of the topological, differential and conformal structure of the casual diamond
![]() $\mathbb D$
.
$\mathbb D$
.
The geometrical sections of the article are concerned with the study of a general three-to-one scattering relation
![]() $\operatorname {\mathrm {R}}$
on M and the proof of Theorem 1.3. In Section 6, we recall some technical lemmas on globally hyperbolic Lorentzian geometries. In Section 7, we prove Theorem 7.10, showing that it is possible to use the three-to-one scattering relation to construct the earliest arrivals on
$\operatorname {\mathrm {R}}$
on M and the proof of Theorem 1.3. In Section 6, we recall some technical lemmas on globally hyperbolic Lorentzian geometries. In Section 7, we prove Theorem 7.10, showing that it is possible to use the three-to-one scattering relation to construct the earliest arrivals on
![]() $\mathbb D$
. Combining this with the results of [Reference Kurylev, Lassas and Uhlmann64] leads to unique recovery of the topological, differential and conformal structure of
$\mathbb D$
. Combining this with the results of [Reference Kurylev, Lassas and Uhlmann64] leads to unique recovery of the topological, differential and conformal structure of
![]() $(\mathbb D, g|_{\mathbb D})$
that completes the proof of Theorem 1.3.
$(\mathbb D, g|_{\mathbb D})$
that completes the proof of Theorem 1.3.
Finally, Section 8 is concerned with the proof of Theorem 1.1. The first half of the proof – that is, the recovery of the topological, differential and conformal structure of the manifold – follows immediately from combining Theorems 5.1–5.2 together with Theorem 1.3. The remainder of this section deals with the recovery of the conformal factor c on
![]() $\mathbb D$
.
$\mathbb D$
.
2 Preliminaries
2.1 Forward problem
In this section, we record the following proposition about existence and uniqueness of solutions to (1.2)–(1.3) subject to suitable sources f. The local existence of solutions to semi-linear and quasi-linear wave equations is well-studied in the literature; see, for example, [Reference Ambartsoumian, Felea, Quinto and Nolan4 Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5, Reference Sogge84, Reference Taylor90, Reference Wang93].
Proposition 2.1. Given any open and bounded set
![]() $O \subset (-T,T)\times M_0$
, there exists a sufficiently small
$O \subset (-T,T)\times M_0$
, there exists a sufficiently small
![]() $r_O>0$
such that given any
$r_O>0$
such that given any
![]() $f \in \mathscr C_O$
(with
$f \in \mathscr C_O$
(with
![]() $\mathscr C_O$
as defined by (1.4)), each of the equations (1.2) or (1.3) admits a unique real-valued solution u in the energy space
$\mathscr C_O$
as defined by (1.4)), each of the equations (1.2) or (1.3) admits a unique real-valued solution u in the energy space
Moreover, the dependence of u to the source f is continuous.
The proof of this proposition in the semi-linear case (1.2) follows by minor modifications to [Reference Kenig and Salo55]. In the quasi-linear case, the proof follows with minor modifications to the proof of [Reference Wang93, Theorem 6].
2.2 Multiple-fold linearisation
We will discuss the technique of multiple-fold linearisation of nonlinear equations that was first used in [Reference Kurylev, Lassas and Uhlmann64]. Before presenting the approach in our semi-linear and quasi-linear settings, we consider the linear wave equation on M,
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^+(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^+(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$
with real-valued sources
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. We also need to consider the wave equation with reversed causality; that is,
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. We also need to consider the wave equation with reversed causality; that is,
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$
with real-valued sources
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{out}})$
.
$f \in C^{\infty }_c(\Omega _{\mathrm{out}})$
.
2.2.1 m-Fold linearisation of the semi-linear equation (1.2)
Let
![]() $m\geqslant 3$
. We consider real-valued sources
$m\geqslant 3$
. We consider real-valued sources
![]() $f_0 \in C^{\infty }_c(\Omega _{\mathrm{out}})$
and
$f_0 \in C^{\infty }_c(\Omega _{\mathrm{out}})$
and
![]() $f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
$f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
![]() $j=1,\ldots ,m$
. We denote by
$j=1,\ldots ,m$
. We denote by
![]() $u_j$
,
$u_j$
,
![]() $j=1,\ldots ,m$
the unique solution to (2.1) subject to source
$j=1,\ldots ,m$
the unique solution to (2.1) subject to source
![]() $f_j$
and denote by
$f_j$
and denote by
![]() $u_0$
the unique solution to (2.2) subject to source
$u_0$
the unique solution to (2.2) subject to source
![]() $f_0$
. Let
$f_0$
. Let
![]() $\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _m) \in \mathbb R^m$
be a small vector and define the source
$\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _m) \in \mathbb R^m$
be a small vector and define the source
 $$ \begin{align*}f_\varepsilon{(x)}= \sum_{j=1}^m\varepsilon_j f_{j}{(x),\quad x\in M}.\end{align*} $$
$$ \begin{align*}f_\varepsilon{(x)}= \sum_{j=1}^m\varepsilon_j f_{j}{(x),\quad x\in M}.\end{align*} $$
Given
![]() $\varepsilon $
sufficiently close to the origin in
$\varepsilon $
sufficiently close to the origin in
![]() $\mathbb R^m$
, we have
$\mathbb R^m$
, we have
![]() $f_\epsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
. Let us define
$f_\epsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
. Let us define
 $$ \begin{align} w{(x)} = \frac{\partial^m}{\partial\varepsilon_1 \partial\varepsilon_2\ldots\partial\varepsilon_m}\,u_\varepsilon{(x)}\bigg |_{\varepsilon=0},\end{align} $$
$$ \begin{align} w{(x)} = \frac{\partial^m}{\partial\varepsilon_1 \partial\varepsilon_2\ldots\partial\varepsilon_m}\,u_\varepsilon{(x)}\bigg |_{\varepsilon=0},\end{align} $$
where
![]() $u_\varepsilon $
is the unique small solution to (1.2) subject to the source
$u_\varepsilon $
is the unique small solution to (1.2) subject to the source
![]() $f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
.
$f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
.
It is straightforward to see that the function w defined by (2.3) solves
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} w =-m! \,u_1\,u_2\,u_3\ldots u_m, &\text{on}\ M, \\ w=0, &\text{on}\ M\setminus J^+(\bigcup_{j=1}^m\operatorname{\mathrm{supp}} f_m). \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} w =-m! \,u_1\,u_2\,u_3\ldots u_m, &\text{on}\ M, \\ w=0, &\text{on}\ M\setminus J^+(\bigcup_{j=1}^m\operatorname{\mathrm{supp}} f_m). \end{cases} \end{aligned} \end{align} $$
Multiplying the latter equation with
![]() $u_0$
and using the Green’s identity,
$u_0$
and using the Green’s identity,
 $$ \begin{align} \int_M w\,\Box_g u_0\,dV_g=\int_M u_0\,\Box_g w \,dV_g, \end{align} $$
$$ \begin{align} \int_M w\,\Box_g u_0\,dV_g=\int_M u_0\,\Box_g w \,dV_g, \end{align} $$
we deduce that
 $$ \begin{align} \int_{\Omega_{\text{out}}} f_0 \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} \mathscr L f_\varepsilon \bigg|_{\varepsilon=0}\,dV_g = -m!\,\int_M u_0\,u_1\ldots u_m\,dV_g. \end{align} $$
$$ \begin{align} \int_{\Omega_{\text{out}}} f_0 \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} \mathscr L f_\varepsilon \bigg|_{\varepsilon=0}\,dV_g = -m!\,\int_M u_0\,u_1\ldots u_m\,dV_g. \end{align} $$
We emphasise that by global hyperbolicity, the integrand on the right-hand side is supported on the compact set
 $$ \begin{align} J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align} $$
$$ \begin{align} J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align} $$
which makes the integral well-defined (see (1.8)). Note that the latter inclusion is due to the hypothesis of Theorem 1.1 on the size of T. We deduce from (2.6) that the source-to-solution map
![]() $\mathscr L$
for the semi-linear equation (1.2) determines the knowledge of integrals of products of m solutions to the linear wave equation (2.1) and a solution to (2.2).
$\mathscr L$
for the semi-linear equation (1.2) determines the knowledge of integrals of products of m solutions to the linear wave equation (2.1) and a solution to (2.2).
2.2.2 Three-fold linearisation of the quasi-linear equation (1.3)
We consider sources
![]() $f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
$f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
![]() $j=0,1,2,3$
and for each small vector
$j=0,1,2,3$
and for each small vector
![]() $\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3)\in \mathbb R^3$
consider the three-parameter family of sources
$\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3)\in \mathbb R^3$
consider the three-parameter family of sources
Let
![]() $u_\varepsilon $
be the unique small solution to (1.3) subject to the source
$u_\varepsilon $
be the unique small solution to (1.3) subject to the source
![]() $f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
. Recall that, by definition,
$f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$
. Recall that, by definition,
![]() $G(x,0)=g(x)$
,
$G(x,0)=g(x)$
,
![]() $\partial _z G(x,0)=0$
and
$\partial _z G(x,0)=0$
and
 $h(x)=\frac {1}{2} \frac {\partial ^2}{\partial z^2} G(x,0)$
. First, we note that the following identities hold in a neighbourhood of
$h(x)=\frac {1}{2} \frac {\partial ^2}{\partial z^2} G(x,0)$
. First, we note that the following identities hold in a neighbourhood of
![]() $z=0$
:
$z=0$
:
 $$ \begin{align*}G_z^{jk}=g^{jk}-S^{jk}\,z^2+\mathcal O(|z|^3),\end{align*} $$
$$ \begin{align*}G_z^{jk}=g^{jk}-S^{jk}\,z^2+\mathcal O(|z|^3),\end{align*} $$
where
 $S^{jk}=\sum _{j',k'=0}^n g^{jj'}\,h_{j'k'}\,g^{k'k}.$
Using these identities in the expression for
$S^{jk}=\sum _{j',k'=0}^n g^{jj'}\,h_{j'k'}\,g^{k'k}.$
Using these identities in the expression for
![]() $\Box _{G_z}$
with z replaced with
$\Box _{G_z}$
with z replaced with
![]() $u_\varepsilon $
, it follows that the function
$u_\varepsilon $
, it follows that the function
 $$ \begin{align} w = \frac{\partial^3}{\partial\varepsilon_1 \partial\varepsilon_2\partial\varepsilon_3}\,u_\varepsilon \bigg |_{\varepsilon=0} \end{align} $$
$$ \begin{align} w = \frac{\partial^3}{\partial\varepsilon_1 \partial\varepsilon_2\partial\varepsilon_3}\,u_\varepsilon \bigg |_{\varepsilon=0} \end{align} $$
solves the following equation on M:
 $$ \begin{align} &\Box_g w - \operatorname{\mathrm{Tr}}(hg^{-1}) u_1u_2f_3- \operatorname{\mathrm{Tr}}(hg^{-1}) u_2u_3f_1- \operatorname{\mathrm{Tr}}(hg^{-1}) u_3u_1f_2\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})=0, \end{align} $$
$$ \begin{align} &\Box_g w - \operatorname{\mathrm{Tr}}(hg^{-1}) u_1u_2f_3- \operatorname{\mathrm{Tr}}(hg^{-1}) u_2u_3f_1- \operatorname{\mathrm{Tr}}(hg^{-1}) u_3u_1f_2\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})=0, \end{align} $$
subject to the initial conditions
![]() $w=0$
on
$w=0$
on
 $M\setminus J^+(\bigcup _{j=1}^3\operatorname {\mathrm {supp}} f_j)$
. Note that the knowledge of the source-to-solution map
$M\setminus J^+(\bigcup _{j=1}^3\operatorname {\mathrm {supp}} f_j)$
. Note that the knowledge of the source-to-solution map
![]() $\mathscr N$
determines
$\mathscr N$
determines
![]() $w|_{\Omega _{\mathrm{out}}}$
. Also,
$w|_{\Omega _{\mathrm{out}}}$
. Also,
 $$ \begin{align*}\nabla^g u = \sum_{j,k=0}^ng^{jk}\frac{\partial u}{\partial x^j} \frac{\partial}{\partial x^k}\quad \forall\, u \in \mathcal C^{\infty}(M),\end{align*} $$
$$ \begin{align*}\nabla^g u = \sum_{j,k=0}^ng^{jk}\frac{\partial u}{\partial x^j} \frac{\partial}{\partial x^k}\quad \forall\, u \in \mathcal C^{\infty}(M),\end{align*} $$
which implies that
 $$ \begin{align*}\sum_{j,k=0}^n g^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_g\end{align*} $$
$$ \begin{align*}\sum_{j,k=0}^n g^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_g\end{align*} $$
and
 $$ \begin{align*}\sum_{j,k=0}^nS^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_h,\end{align*} $$
$$ \begin{align*}\sum_{j,k=0}^nS^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_h,\end{align*} $$
for all
![]() $u, v \in \mathcal C^{\infty }(M)$
. Therefore, recalling that
$u, v \in \mathcal C^{\infty }(M)$
. Therefore, recalling that
 $$ \begin{align*}dV_g = \left|\det g\right|{}^{\frac{1}{2}}\, dx^0\wedge dx^1\wedge \ldots \wedge dx^n\end{align*} $$
$$ \begin{align*}dV_g = \left|\det g\right|{}^{\frac{1}{2}}\, dx^0\wedge dx^1\wedge \ldots \wedge dx^n\end{align*} $$
and multiplying equation (2.9) with
![]() $u_0$
that solves (2.2) subject to a source
$u_0$
that solves (2.2) subject to a source
![]() $f_0\in \mathcal C^{\infty }_c(\Omega _{\mathrm{out}})$
followed by integrating by parts (analogously to (2.5)), we deduce that
$f_0\in \mathcal C^{\infty }_c(\Omega _{\mathrm{out}})$
followed by integrating by parts (analogously to (2.5)), we deduce that
 $$ \begin{align} &\int_{\Omega_{\text{out}}} f_0 \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} \mathscr N f_\varepsilon \bigg |_{\varepsilon=0}\,dV_g \nonumber\\ &\quad = 2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\nonumber\\ &\qquad-\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g\nonumber\\ &\qquad+\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g. \end{align} $$
$$ \begin{align} &\int_{\Omega_{\text{out}}} f_0 \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} \mathscr N f_\varepsilon \bigg |_{\varepsilon=0}\,dV_g \nonumber\\ &\quad = 2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\nonumber\\ &\qquad-\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g\nonumber\\ &\qquad+\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g. \end{align} $$
Analogous to (2.6), the integrands on the right-hand side expression are all supported on the compact set
 $$ \begin{align*}J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align*} $$
$$ \begin{align*}J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align*} $$
for T sufficiently large as stated in the hypothesis of Theorem 1.1.
3 Gaussian beams
Gaussian beams are approximate solutions to the linear wave equation
that concentrate on a finite piece of a null geodesic
![]() $\gamma : [a,b] \to (-T,T)\times M_0$
, exhibiting a Gaussian profile of decay away from the segment of the geodesic. Here, we are considering an affine parametrisation of the null geodesic
$\gamma : [a,b] \to (-T,T)\times M_0$
, exhibiting a Gaussian profile of decay away from the segment of the geodesic. Here, we are considering an affine parametrisation of the null geodesic
![]() $\gamma $
; that is,
$\gamma $
; that is,
 $$ \begin{align} \nabla^g_{\dot{\gamma}(s)}\dot{\gamma}(s)=0,\quad \langle \dot{\gamma}(s),\dot{\gamma}(s)\rangle_g=0\quad \forall\, s \in [a,b]. \end{align} $$
$$ \begin{align} \nabla^g_{\dot{\gamma}(s)}\dot{\gamma}(s)=0,\quad \langle \dot{\gamma}(s),\dot{\gamma}(s)\rangle_g=0\quad \forall\, s \in [a,b]. \end{align} $$
We will make the standing assumption that the end points
![]() $\gamma (a)$
and
$\gamma (a)$
and
![]() $\gamma (b)$
lie outside
$\gamma (b)$
lie outside
![]() $(-T,T)\times M_0$
. Gaussian beams are a classical construction and go back to [Reference Babich and Ulin6, Reference Belishev8
Reference Alinhac1]. They have been used in the context of inverse problems in many works; see, for example, [Reference Beem, Ehrlich and Easley11, Reference Feizmohammadi, Ilmavirta, Kian and Oksanen26, Reference Feizmohammadi and Oksanen29, Reference Katchalov, Kurylev and Lassas54]. In order to recall the expression of Gaussian beams in local coordinates, we first briefly recall the well-known Fermi coordinates near a null geodesic.
$(-T,T)\times M_0$
. Gaussian beams are a classical construction and go back to [Reference Babich and Ulin6, Reference Belishev8
Reference Alinhac1]. They have been used in the context of inverse problems in many works; see, for example, [Reference Beem, Ehrlich and Easley11, Reference Feizmohammadi, Ilmavirta, Kian and Oksanen26, Reference Feizmohammadi and Oksanen29, Reference Katchalov, Kurylev and Lassas54]. In order to recall the expression of Gaussian beams in local coordinates, we first briefly recall the well-known Fermi coordinates near a null geodesic.
Lemma 3.1 Fermi coordinates
Let
![]() $\hat \delta> 0$
,
$\hat \delta> 0$
,
![]() $a < b$
and let
$a < b$
and let
![]() $\gamma : (a-\hat {\delta },b+\hat {\delta }) \to M$
be a null geodesic on M parametrised as given by (3.1) and whose end points lie outside
$\gamma : (a-\hat {\delta },b+\hat {\delta }) \to M$
be a null geodesic on M parametrised as given by (3.1) and whose end points lie outside
![]() $(-T,T)\,\times\, M_0$
. There exists a coordinate neighbourhood
$(-T,T)\,\times\, M_0$
. There exists a coordinate neighbourhood
![]() $(U,\psi )$
of
$(U,\psi )$
of
![]() $\gamma ([a,b])$
, with the coordinates denoted by
$\gamma ([a,b])$
, with the coordinates denoted by
![]() $(y^0:=s,y^1,\ldots ,y^n)=(s,y')$
, such that
$(y^0:=s,y^1,\ldots ,y^n)=(s,y')$
, such that
-
(i)
 $\psi (U)=(a-\delta ',b+\delta ') \times B(0,\delta ')$
where
$\psi (U)=(a-\delta ',b+\delta ') \times B(0,\delta ')$
where
 $B(0,\delta ')$
is the ball in
$B(0,\delta ')$
is the ball in
 $\mathbb {R}^{n}$
centred at the origin with radius
$\mathbb {R}^{n}$
centred at the origin with radius
 $\delta '> 0$
.
$\delta '> 0$
. -
(ii)
 $\psi (\gamma (s))=(s,\underbrace {0,\ldots ,0}_{n \hspace {1mm}\text {times}})$
.
$\psi (\gamma (s))=(s,\underbrace {0,\ldots ,0}_{n \hspace {1mm}\text {times}})$
.
Moreover, the metric tensor g satisfies in this coordinate system
 $$ \begin{align} g|_\gamma = 2ds\otimes dy^1+ \sum_{\alpha=2}^n \,dy^\alpha\otimes \,dy^\alpha \end{align} $$
$$ \begin{align} g|_\gamma = 2ds\otimes dy^1+ \sum_{\alpha=2}^n \,dy^\alpha\otimes \,dy^\alpha \end{align} $$
and
 $\frac {\partial }{\partial y^i} g_{jk}|_\gamma = 0$
for
$\frac {\partial }{\partial y^i} g_{jk}|_\gamma = 0$
for
![]() $i,j,k=0,\ldots ,n$
. Here,
$i,j,k=0,\ldots ,n$
. Here,
![]() $|_\gamma $
denotes the restriction on the curve
$|_\gamma $
denotes the restriction on the curve
![]() $\gamma $
.
$\gamma $
.
We refer the reader to [Reference Feizmohammadi and Oksanen29, Section 4.1, Lemma 1] for a proof of this lemma. Using the Fermi coordinates discussed above, Gaussian beams can be written through the expressions
and
 $$ \begin{align} \mathcal U_\lambda(y) = e^{-i\lambda\bar{\phi}(y)}\bar{A}_\lambda(y) \quad \text{for}\quad\lambda<0.\end{align} $$
$$ \begin{align} \mathcal U_\lambda(y) = e^{-i\lambda\bar{\phi}(y)}\bar{A}_\lambda(y) \quad \text{for}\quad\lambda<0.\end{align} $$
Here,
![]() $\bar {\cdot }$
stands for the complex conjugation and the phase function
$\bar {\cdot }$
stands for the complex conjugation and the phase function
![]() $\phi $
and the amplitude function
$\phi $
and the amplitude function
![]() $A_\lambda $
are given by the expressions
$A_\lambda $
are given by the expressions
 $$ \begin{align} \begin{aligned} \phi(s,y') = \sum_{j=0}^{N} \phi_j(s,y')& \quad \text{and} \quad A_\lambda(s,y')= \chi(\frac{|y'|}{\delta'}) \sum_{j=0}^{N} \lambda^{-j}a_{j}(s,y'),\\ &a_j(s,y')=\sum_{k=0}^{N} a_{j,k}(s,y'), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \phi(s,y') = \sum_{j=0}^{N} \phi_j(s,y')& \quad \text{and} \quad A_\lambda(s,y')= \chi(\frac{|y'|}{\delta'}) \sum_{j=0}^{N} \lambda^{-j}a_{j}(s,y'),\\ &a_j(s,y')=\sum_{k=0}^{N} a_{j,k}(s,y'), \end{aligned} \end{align} $$
where for each
![]() $j,k=0,\ldots ,N$
,
$j,k=0,\ldots ,N$
,
![]() $\phi _j$
is a complex-valued homogeneous polynomial of degree j in the variables
$\phi _j$
is a complex-valued homogeneous polynomial of degree j in the variables
![]() $y^{1},\ldots , y^n$
and
$y^{1},\ldots , y^n$
and
![]() $a_{j,k}$
is a complex-valued homogeneous polynomial of degree k with respect to the variables
$a_{j,k}$
is a complex-valued homogeneous polynomial of degree k with respect to the variables
![]() $y^1,\ldots ,y^n$
and, finally,
$y^1,\ldots ,y^n$
and, finally,
![]() $\chi :\mathbb R\to \mathbb R$
is a nonnegative smooth function of compact support such that
$\chi :\mathbb R\to \mathbb R$
is a nonnegative smooth function of compact support such that
![]() $\chi (t)=1$
for
$\chi (t)=1$
for
 $|t| \leqslant \frac {1}{4}$
and
$|t| \leqslant \frac {1}{4}$
and
![]() $\chi (t)=0$
for
$\chi (t)=0$
for
 $|t|\geqslant \frac {1}{2}$
.
$|t|\geqslant \frac {1}{2}$
.
The determination of the phase terms
![]() $\phi _j$
and amplitudes
$\phi _j$
and amplitudes
![]() $a_j$
with
$a_j$
with
![]() $j=0,1,2,\ldots ,N$
is carried out by following the method of Wentzel–Kramers–Brillouin (WKB in short) in the semi-classical parameter
$j=0,1,2,\ldots ,N$
is carried out by following the method of Wentzel–Kramers–Brillouin (WKB in short) in the semi-classical parameter
![]() $\lambda $
, based on the requirement that
$\lambda $
, based on the requirement that
 $$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\langle d\phi,d\phi\rangle_g=0 \quad \text{on}\ (a,b)\times\{y'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\left( 2\langle d\phi,da_j \rangle_g- (\Box_g\phi)a_j + i \Box_ga_{j-1}\right)=0\quad \text{on}\ (a,b)\times\{y'=0\}, \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\langle d\phi,d\phi\rangle_g=0 \quad \text{on}\ (a,b)\times\{y'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\left( 2\langle d\phi,da_j \rangle_g- (\Box_g\phi)a_j + i \Box_ga_{j-1}\right)=0\quad \text{on}\ (a,b)\times\{y'=0\}, \end{aligned}\end{align} $$
for all
![]() $j=0,1,\ldots ,N$
and all multi-indices
$j=0,1,\ldots ,N$
and all multi-indices
![]() $\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$
with
$\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$
with
![]() $|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$
.
$|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$
.
We do not proceed to solve these equations here as this can be found in all the works mentioned above but instead summarise the main properties of Gaussian beams as follows:
-
(1)
 $\phi (s,0)=0$
.
$\phi (s,0)=0$
. -
(2)
 $\Im (\phi )(s,y') \geqslant C |y'|^2$
for all points
$\Im (\phi )(s,y') \geqslant C |y'|^2$
for all points
 $y \in (a,b)\times B(0,\delta ')$
.
$y \in (a,b)\times B(0,\delta ')$
. -
(3)
 $\| \Box _{g} \mathcal U_\lambda \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda |^{-K},$
where
$\| \Box _{g} \mathcal U_\lambda \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda |^{-K},$
where
 $K=\frac {N+1}{2}+\frac {n}{4}-k-2$
.
$K=\frac {N+1}{2}+\frac {n}{4}-k-2$
.
Here,
![]() $\Im $
stands for the imaginary part of a complex number and by the notation
$\Im $
stands for the imaginary part of a complex number and by the notation
![]() $A\lesssim B$
we mean that there exists a constant C independent of the parameter
$A\lesssim B$
we mean that there exists a constant C independent of the parameter
![]() $\lambda $
such that
$\lambda $
such that
![]() $A \leqslant C B$
.
$A \leqslant C B$
.
For the purposes of our analysis, we also need to recall the Fermi coordinate expressions for
![]() $\phi _1$
,
$\phi _1$
,
![]() $\phi _2$
and
$\phi _2$
and
![]() $a_{0,0}$
; see (3.5). We recall from [Reference Feizmohammadi and Oksanen29] that
$a_{0,0}$
; see (3.5). We recall from [Reference Feizmohammadi and Oksanen29] that
 $$ \begin{align} \begin{aligned} \phi_0(s,y')=0,\quad \phi_1(s,y')&= y_1,\quad \phi_2(s,y')=\sum_{j,k=1}^n H_{jk}(s)y^jy^k,\\ \quad a_{0,0}(s)&=(\det Y(s))^{-\frac{1}{2}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \phi_0(s,y')=0,\quad \phi_1(s,y')&= y_1,\quad \phi_2(s,y')=\sum_{j,k=1}^n H_{jk}(s)y^jy^k,\\ \quad a_{0,0}(s)&=(\det Y(s))^{-\frac{1}{2}}. \end{aligned} \end{align} $$
The matrices H and Y are described as follows. The symmetric complex-valued matrix H solves the Riccati equation
 $$ \begin{align} \frac{d}{ds} H + HCH + D=0, \quad \forall s \in (a,b), \quad H(\hat{s}_0)=H_0,\quad \Im H_0>0, \end{align} $$
$$ \begin{align} \frac{d}{ds} H + HCH + D=0, \quad \forall s \in (a,b), \quad H(\hat{s}_0)=H_0,\quad \Im H_0>0, \end{align} $$
where C and D are the matrices defined through
 $$ \begin{align} \begin{cases} C_{11}= 0&\\ C_{jj}=2& \quad j=2,\ldots,n, \\ C_{jk}=0& \quad \text{otherwise,} \end{cases} \qquad \text{where}\ D_{jk}= \frac{1}{4} \frac{\partial^2 g^{11}}{\partial y^j \partial y^k}. \end{align} $$
$$ \begin{align} \begin{cases} C_{11}= 0&\\ C_{jj}=2& \quad j=2,\ldots,n, \\ C_{jk}=0& \quad \text{otherwise,} \end{cases} \qquad \text{where}\ D_{jk}= \frac{1}{4} \frac{\partial^2 g^{11}}{\partial y^j \partial y^k}. \end{align} $$
We recall the following result from [Reference Anderson, Katsuda, Kurylev, Lassas and Taylor5 Reference Ambartsoumian, Felea, Nolan and Quinto3, Section 8] regarding solvability of the Riccati equation.
Lemma 3.2. Let
![]() $\hat {s}_0 \in (a,b)$
and let
$\hat {s}_0 \in (a,b)$
and let
 $H_0=Z_0Y_0^{-1}$
be a symmetric matrix with
$H_0=Z_0Y_0^{-1}$
be a symmetric matrix with
![]() $\Im H_0> 0$
. The Riccati equation (3.8), together with the initial condition
$\Im H_0> 0$
. The Riccati equation (3.8), together with the initial condition
![]() $H(\hat {s}_0) = H_0$
, has a unique solution
$H(\hat {s}_0) = H_0$
, has a unique solution
![]() $H(s)$
for all
$H(s)$
for all
![]() $s \in (a,b)$
. We have
$s \in (a,b)$
. We have
![]() $\Im H>0$
and
$\Im H>0$
and
![]() $H(s)=Z(s)Y^{-1}(s)$
, where the matrix-valued functions
$H(s)=Z(s)Y^{-1}(s)$
, where the matrix-valued functions
![]() $Z(s),Y(s)$
solve the first-order linear system
$Z(s),Y(s)$
solve the first-order linear system
 $$ \begin{align*}\frac{d}{ds} Y = CZ\quad \text{and}\quad \frac{d}{ds} Z = -DY, \quad \text{subject to} \quad Y(\hat{s}_0)=Y_0,\quad Z(\hat{s}_0)=H_0.\end{align*} $$
$$ \begin{align*}\frac{d}{ds} Y = CZ\quad \text{and}\quad \frac{d}{ds} Z = -DY, \quad \text{subject to} \quad Y(\hat{s}_0)=Y_0,\quad Z(\hat{s}_0)=H_0.\end{align*} $$
Moreover, the matrix
![]() $Y(s)$
is nondegenerate on
$Y(s)$
is nondegenerate on
![]() $(a,b)$
and there holds
$(a,b)$
and there holds
As for the remainder of the terms
![]() $\phi _j$
with
$\phi _j$
with
![]() $j\geqslant 3$
and the rest of the amplitude terms
$j\geqslant 3$
and the rest of the amplitude terms
![]() $a_{j,k}$
with
$a_{j,k}$
with
![]() $j,k$
not both simultaneously zero, we recall from [Reference Feizmohammadi and Oksanen29] that they solve first-order ordinary differential equations (ODEs) along the null geodesic
$j,k$
not both simultaneously zero, we recall from [Reference Feizmohammadi and Oksanen29] that they solve first-order ordinary differential equations (ODEs) along the null geodesic
![]() $\gamma $
and can be determined uniquely by fixing their values at some fixed point
$\gamma $
and can be determined uniquely by fixing their values at some fixed point
![]() $\hat {s}_0 \in (a,b)$
.
$\hat {s}_0 \in (a,b)$
.
4 Source terms that generate real parts of Gaussian beams
Let
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
or
$v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
or
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
, where
$v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
, where
![]() $L^+\Omega _{\mathrm{in}}$
and
$L^+\Omega _{\mathrm{in}}$
and
![]() $L^+\Omega _{\mathrm{out}}$
denote the bundle of future-pointing light-like vectors in
$L^+\Omega _{\mathrm{out}}$
denote the bundle of future-pointing light-like vectors in
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
, respectively. We consider a Gaussian beam solution
$\Omega _{\mathrm{out}}$
, respectively. We consider a Gaussian beam solution
![]() $\mathcal U_\lambda $
of order
$\mathcal U_\lambda $
of order
 $N=\lceil \frac {3n}{2}\rceil +8$
as in the previous section, concentrating on a future-pointing null geodesic
$N=\lceil \frac {3n}{2}\rceil +8$
as in the previous section, concentrating on a future-pointing null geodesic
![]() $\gamma _{q,\xi }:[a,b]\to M$
passing through q in the direction
$\gamma _{q,\xi }:[a,b]\to M$
passing through q in the direction
![]() $\xi $
. Here
$\xi $
. Here
![]() $\gamma _{q,\xi }$
is parametrised as in (3.1) subject to
$\gamma _{q,\xi }$
is parametrised as in (3.1) subject to
As before, we assume that the end points of the null geodesic lie outside the set
![]() $(-T,T)\times M_0$
.
$(-T,T)\times M_0$
.
In this section, we would like to give a canonical way of constructing Gaussian beams followed by a canonical method of constructing real-valued sources that generate the real parts of these Gaussian beams. Recall that the construction of a Gaussian beam
![]() $\mathcal U_\lambda $
that concentrates on
$\mathcal U_\lambda $
that concentrates on
![]() $\gamma _{q,\xi }$
has a large degree of freedom associated with the various initial data for the governing ODEs of the phase and amplitude terms in (3.5). The support of a Gaussian beam around a geodesic that is given by the parameter
$\gamma _{q,\xi }$
has a large degree of freedom associated with the various initial data for the governing ODEs of the phase and amplitude terms in (3.5). The support of a Gaussian beam around a geodesic that is given by the parameter
![]() $\delta '$
is also another degree of freedom in the construction.
$\delta '$
is also another degree of freedom in the construction.
We start with fixing the choice of the phase terms
![]() $\phi _j$
with
$\phi _j$
with
![]() $j\geqslant 3$
and the amplitude terms
$j\geqslant 3$
and the amplitude terms
![]() $a_{j,k}$
with
$a_{j,k}$
with
![]() $j,k=0,1,\ldots ,N$
(and both indices not simultaneously zero), by assigning zero initial value for their respective ODEs along the null geodesic
$j,k=0,1,\ldots ,N$
(and both indices not simultaneously zero), by assigning zero initial value for their respective ODEs along the null geodesic
![]() $\gamma _{q,\xi }$
at the point
$\gamma _{q,\xi }$
at the point
![]() $q=\gamma _{q,\xi }(0)$
. Therefore, to complete the construction of the Gaussian beam
$q=\gamma _{q,\xi }(0)$
. Therefore, to complete the construction of the Gaussian beam
![]() $\mathcal U_\lambda $
, it suffices to fix a small parameter
$\mathcal U_\lambda $
, it suffices to fix a small parameter
![]() $\delta '>0$
and also to choose
$\delta '>0$
and also to choose
![]() $Y(0)$
and
$Y(0)$
and
![]() $Z(0)$
in Lemma 3.2. This will then fix the remaining functions
$Z(0)$
in Lemma 3.2. This will then fix the remaining functions
![]() $\phi _2$
and
$\phi _2$
and
![]() $a_{0,0}$
in the Gaussian beam construction. To account for the latter two degrees of freedom in the construction, we introduce the notation
$a_{0,0}$
in the Gaussian beam construction. To account for the latter two degrees of freedom in the construction, we introduce the notation
![]() $\iota =(Y(0),Z(0))\in \mathcal T$
where
$\iota =(Y(0),Z(0))\in \mathcal T$
where
 $$ \begin{align} \begin{aligned} \mathcal T = \{ (Y_0,Z_0)\in \mathbb C^{(1+n)^2}\times \mathbb C^{(1+n)^2}\,:\,& Z_0Y_0^{-1}\ \text{is symmetric} \\ &\text{and}\ \Im( Z_0Y_0^{-1})>0\}.\end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} \mathcal T = \{ (Y_0,Z_0)\in \mathbb C^{(1+n)^2}\times \mathbb C^{(1+n)^2}\,:\,& Z_0Y_0^{-1}\ \text{is symmetric} \\ &\text{and}\ \Im( Z_0Y_0^{-1})>0\}.\end{aligned}\end{align} $$
Using the notations above, we can explicitly determine (or identify) Gaussian beam functions
subject to each
![]() $\lambda \in \mathbb R$
that denotes the asymptotic parameter in the construction, a vector
$\lambda \in \mathbb R$
that denotes the asymptotic parameter in the construction, a vector
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
or
$v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
or
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
that fixes the geodesic
$v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
that fixes the geodesic
![]() $\gamma _{v}$
, a small
$\gamma _{v}$
, a small
![]() $\delta '>0$
that fixes the support around the geodesic and the choice of
$\delta '>0$
that fixes the support around the geodesic and the choice of
![]() $\iota \in \mathcal T$
that fixes the initial values for the ODEs governing
$\iota \in \mathcal T$
that fixes the initial values for the ODEs governing
![]() $\phi _2$
and
$\phi _2$
and
![]() $a_{0,0}$
. As discussed above, the rest of the terms in the Gaussian beam are fixed by setting the initial values for their ODEs to be zero at the point q. For the sake of brevity and where there is no confusion, we will hide these parameters in the notation
$a_{0,0}$
. As discussed above, the rest of the terms in the Gaussian beam are fixed by setting the initial values for their ODEs to be zero at the point q. For the sake of brevity and where there is no confusion, we will hide these parameters in the notation
![]() $\mathcal U_\lambda $
.
$\mathcal U_\lambda $
.
Our aim in the remainder of this section is to construct a source
![]() $f\in \mathcal C^{\infty }_c(\Omega _{\mathrm{in}})$
such that the solution to the linear wave equation (2.1) with this source term is close to the real part of the complex-valued Gaussian beam
$f\in \mathcal C^{\infty }_c(\Omega _{\mathrm{in}})$
such that the solution to the linear wave equation (2.1) with this source term is close to the real part of the complex-valued Gaussian beam
![]() $\mathcal U_\lambda $
, in a sense that will be made precise below. We then give an analogous construction of sources for
$\mathcal U_\lambda $
, in a sense that will be made precise below. We then give an analogous construction of sources for
![]() $\Omega _{\mathrm{out}}$
.
$\Omega _{\mathrm{out}}$
.
Remark 4. Let us emphasise that the need to work with real-valued sources is due to the fact that in the case of the quasi-linear wave equation (1.3), the solution to the wave equation appears in the tensor
![]() $G(x,u)$
. Therefore, for the sake of physical motivations of our inverse problem, it is crucial to work with real-valued solutions to the wave equations (1.2)–(1.3).
$G(x,u)$
. Therefore, for the sake of physical motivations of our inverse problem, it is crucial to work with real-valued solutions to the wave equations (1.2)–(1.3).
To simplify the notations, we use the embedding of M into
![]() $\mathbb R \times M_0$
to define the
$\mathbb R \times M_0$
to define the
![]() $(x^0,x')$
-coordinates on M described in the introduction. Next, we write
$(x^0,x')$
-coordinates on M described in the introduction. Next, we write
![]() $q=(q_0,q')$
and define two function
$q=(q_0,q')$
and define two function
![]() $\zeta _{\pm ,v,\delta '} \in \mathcal C^\infty (\mathbb R)$
such that
$\zeta _{\pm ,v,\delta '} \in \mathcal C^\infty (\mathbb R)$
such that
 $$ \begin{align} \zeta_{-,v,\delta'}(x^0)= \begin{cases} 0 & \text{if}\,\, x^0\leqslant q_0-\delta',\\ 1 & \text{if}\,\,x^0\geqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$
$$ \begin{align} \zeta_{-,v,\delta'}(x^0)= \begin{cases} 0 & \text{if}\,\, x^0\leqslant q_0-\delta',\\ 1 & \text{if}\,\,x^0\geqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$
and
 $$ \begin{align} \zeta_{+,v,\delta'}(x^0) = \begin{cases} 0 & \text{if}\,\, x^0\geqslant q_0,\\ 1 & \text{if}\,\,x^0 \leqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$
$$ \begin{align} \zeta_{+,v,\delta'}(x^0) = \begin{cases} 0 & \text{if}\,\, x^0\geqslant q_0,\\ 1 & \text{if}\,\,x^0 \leqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$
We are now ready to define the source. Emphasising the dependence on
![]() $\lambda $
,
$\lambda $
,
![]() $v=(q,\xi )$
,
$v=(q,\xi )$
,
![]() $\delta '$
and the initial values for ODEs of
$\delta '$
and the initial values for ODEs of
![]() $Y(s)$
and
$Y(s)$
and
![]() $Z(s)$
at the point
$Z(s)$
at the point
![]() $s=0$
(see (4.1)) that is governed by
$s=0$
(see (4.1)) that is governed by
![]() $\iota \in \mathcal T$
, we write
$\iota \in \mathcal T$
, we write
 $$ \begin{align} f^{+}_{\lambda,v,\iota,\delta'} = \zeta_{+,v,\delta'} \Box_{g} (\zeta_{-,v,\delta'} \Re \,\mathcal U_\lambda) \in \mathcal C^{\infty}_c(\Omega_{\text{in}}), \end{align} $$
$$ \begin{align} f^{+}_{\lambda,v,\iota,\delta'} = \zeta_{+,v,\delta'} \Box_{g} (\zeta_{-,v,\delta'} \Re \,\mathcal U_\lambda) \in \mathcal C^{\infty}_c(\Omega_{\text{in}}), \end{align} $$
where
![]() $\Re $
denotes the real part of a complex number. We require the parameter
$\Re $
denotes the real part of a complex number. We require the parameter
![]() $\delta '$
to be sufficiently small so that
$\delta '$
to be sufficiently small so that
 $$ \begin{align*}\operatorname{\mathrm{supp}} f^{+}_{\lambda,v,\iota,\delta'} \subset \Omega_{\text{in}}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{supp}} f^{+}_{\lambda,v,\iota,\delta'} \subset \Omega_{\text{in}}.\end{align*} $$
Note that since
![]() $(\Omega _{\mathrm{in}},g|_{\Omega _{\mathrm{in}}})$
is assumed to be known (see the hypothesis of Theorem 1.1),
$(\Omega _{\mathrm{in}},g|_{\Omega _{\mathrm{in}}})$
is assumed to be known (see the hypothesis of Theorem 1.1),
 $f_{\lambda ,v,\iota ,\delta '}^+$
will also be known. As
$f_{\lambda ,v,\iota ,\delta '}^+$
will also be known. As
![]() $\zeta _{-,v,\delta '} = 1$
on the support of
$\zeta _{-,v,\delta '} = 1$
on the support of
![]() $1-\zeta _{+,v,\delta '}$
, it holds that
$1-\zeta _{+,v,\delta '}$
, it holds that
 $$ \begin{align*}\Box_{g} (\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} = (1-\zeta_{+,v,\delta'})\Box_{g} \Re \mathcal U_\lambda. \end{align*} $$
$$ \begin{align*}\Box_{g} (\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} = (1-\zeta_{+,v,\delta'})\Box_{g} \Re \mathcal U_\lambda. \end{align*} $$
Now applying the property (3) of Gaussian beams in Section 3 with
![]() $k=\frac {n}{2}+2$
and the fact that
$k=\frac {n}{2}+2$
and the fact that
 $N=\lceil \frac {3n}{2}\rceil +8$
implies the bound
$N=\lceil \frac {3n}{2}\rceil +8$
implies the bound
 $$ \begin{align*}\|\Box_{g}(\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align*} $$
$$ \begin{align*}\|\Box_{g}(\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align*} $$
We write
 $u^+_{\lambda ,v,\iota ,\delta '} = u$
where u is the solution of the linear wave equation (2.1) with the source
$u^+_{\lambda ,v,\iota ,\delta '} = u$
where u is the solution of the linear wave equation (2.1) with the source
 $f = f^+_{\lambda ,v,\iota ,\delta '}$
. By combining the above estimate with the usual energy estimate for the wave equation and the Sobolev embedding of
$f = f^+_{\lambda ,v,\iota ,\delta '}$
. By combining the above estimate with the usual energy estimate for the wave equation and the Sobolev embedding of
![]() $\mathcal C^1((-T,T)\times M_0)$
in
$\mathcal C^1((-T,T)\times M_0)$
in
![]() $H^{k}((-T,T)\times M_0)$
with
$H^{k}((-T,T)\times M_0)$
with
![]() $k=\frac {n}{2}+2$
, we obtain
$k=\frac {n}{2}+2$
, we obtain
 $$ \begin{align} \|\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda - u^+_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align} $$
$$ \begin{align} \|\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda - u^+_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align} $$
Observe that while the Gaussian beam
![]() $\mathcal U_\lambda $
is supported near the geodesic
$\mathcal U_\lambda $
is supported near the geodesic
![]() $\gamma $
, the function
$\gamma $
, the function
 $u^+_{\lambda ,v,\iota ,\delta '}$
is not supported near this geodesic anymore but nevertheless, as can be seen from the latter estimate, it is rather small away from the geodesic.
$u^+_{\lambda ,v,\iota ,\delta '}$
is not supported near this geodesic anymore but nevertheless, as can be seen from the latter estimate, it is rather small away from the geodesic.
We will also need a test function corresponding to
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
whose construction differs from that of
$v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$
whose construction differs from that of
 $f^+_{\lambda ,v,\iota ,\delta '}$
above only to the extent that the roles of
$f^+_{\lambda ,v,\iota ,\delta '}$
above only to the extent that the roles of
![]() $\zeta _{+,v,\delta '}$
and
$\zeta _{+,v,\delta '}$
and
![]() $\zeta _{-,v,\delta '}$
are reversed in (4.6). That is, we define
$\zeta _{-,v,\delta '}$
are reversed in (4.6). That is, we define
Since
![]() $(\Omega _{\mathrm{out}},g|_{\Omega _{\mathrm{out}}})$
is assumed to be known,
$(\Omega _{\mathrm{out}},g|_{\Omega _{\mathrm{out}}})$
is assumed to be known,
![]() $f_{\lambda ,v,\delta '}^-$
will also be known, and the analogue of (4.7) reads
$f_{\lambda ,v,\delta '}^-$
will also be known, and the analogue of (4.7) reads
 $$ \begin{align} \|\zeta_{+,v,\delta'} \Re\, \mathcal U_\lambda - u^-_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}, \end{align} $$
$$ \begin{align} \|\zeta_{+,v,\delta'} \Re\, \mathcal U_\lambda - u^-_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}, \end{align} $$
where
![]() $u^-_{\lambda ,v,\iota ,\delta '}=u$
is now defined as the solution to the linear wave equation with reversed causality
$u^-_{\lambda ,v,\iota ,\delta '}=u$
is now defined as the solution to the linear wave equation with reversed causality
 $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u = f, &\text{on}\ M, \\ u=0& \text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f), \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u = f, &\text{on}\ M, \\ u=0& \text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f), \end{cases} \end{aligned} \end{align} $$
with the source
![]() $f=f_{\lambda ,v,\iota ,\delta '}^-$
.
$f=f_{\lambda ,v,\iota ,\delta '}^-$
.
Finally, and before closing the section, we record the following estimate for the compactly supported sources
 $f^{\pm }_{\lambda ,v,\iota ,\delta '}$
that follows from the definitions (4.6), (4.8) and property (3) of Gaussian beams in Section 3:
$f^{\pm }_{\lambda ,v,\iota ,\delta '}$
that follows from the definitions (4.6), (4.8) and property (3) of Gaussian beams in Section 3:
 $$ \begin{align} \|f^{\pm}_{\lambda,v,\iota,\delta'}\|_{L^2(M)} \lesssim |\lambda|^{1-\frac{n}{2}}. \end{align} $$
$$ \begin{align} \|f^{\pm}_{\lambda,v,\iota,\delta'}\|_{L^2(M)} \lesssim |\lambda|^{1-\frac{n}{2}}. \end{align} $$
5 Reduction from the source-to-solution map to the three-to-one scattering relation
We begin by considering
and require that the null geodesics
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=0,1,$
are distinct. Here,
$j=0,1,$
are distinct. Here,
![]() $L^{\pm }\Omega _{\mathrm{out}}$
and
$L^{\pm }\Omega _{\mathrm{out}}$
and
![]() $L^{\pm }\Omega _{\mathrm{in}}$
denote the bundle of future- and past-pointing light-like vectors on
$L^{\pm }\Omega _{\mathrm{in}}$
denote the bundle of future- and past-pointing light-like vectors on
![]() $\Omega _{\mathrm{out}}$
and
$\Omega _{\mathrm{out}}$
and
![]() $\Omega _{\mathrm{in}}$
, respectively.
$\Omega _{\mathrm{in}}$
, respectively.
As mentioned above, we impose that
![]() $\gamma _{v_0}$
and
$\gamma _{v_0}$
and
![]() $\gamma _{v_1}$
are not reparametrisations of the same curve. This condition can always be checked via the map
$\gamma _{v_1}$
are not reparametrisations of the same curve. This condition can always be checked via the map
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
. To sketch this argument, we note that based on a simple first-order linearisation of the source-to-solution map – that is
$\mathscr N$
. To sketch this argument, we note that based on a simple first-order linearisation of the source-to-solution map – that is
![]() $\partial _{\varepsilon } \mathscr N(\varepsilon f)|_{\varepsilon =0}$
or
$\partial _{\varepsilon } \mathscr N(\varepsilon f)|_{\varepsilon =0}$
or
![]() $\partial _{\varepsilon } \mathscr L(\varepsilon f)|_{\varepsilon =0}$
– we can obtain the source-to-solution map
$\partial _{\varepsilon } \mathscr L(\varepsilon f)|_{\varepsilon =0}$
– we can obtain the source-to-solution map
 $L^{\mathrm{lin}}_g$
associated to the linearised operator
$L^{\mathrm{lin}}_g$
associated to the linearised operator
![]() $\Box _{g}$
with sources in
$\Box _{g}$
with sources in
![]() $\Omega _{\mathrm{in}}$
and receivers in
$\Omega _{\mathrm{in}}$
and receivers in
![]() $\Omega _{\mathrm{out}}$
. To be precise,
$\Omega _{\mathrm{out}}$
. To be precise,
 $L^{\mathrm{lin}}_g: L^2(\Omega _{\mathrm{in}}) \to H^1(\Omega _{\mathrm{out}})$
is defined through the mapping
$L^{\mathrm{lin}}_g: L^2(\Omega _{\mathrm{in}}) \to H^1(\Omega _{\mathrm{out}})$
is defined through the mapping
 $$ \begin{align*}L^{\mathrm{lin}}_g f = u|_{\Omega_{\text{out}}}\quad \forall\, f \in L^2(\Omega_{\text{in}}),\end{align*} $$
$$ \begin{align*}L^{\mathrm{lin}}_g f = u|_{\Omega_{\text{out}}}\quad \forall\, f \in L^2(\Omega_{\text{in}}),\end{align*} $$
where u is the unique solution to (2.1) subject to the source f.
Then, for example, based on the main result of [Reference Stefanov and Yang87], we can determine the scattering relation,
![]() $\Lambda _g$
for sources in
$\Lambda _g$
for sources in
![]() $\Omega _{\mathrm{in}}$
and receivers in
$\Omega _{\mathrm{in}}$
and receivers in
![]() $\Omega _{\mathrm{out}}$
; that is, the source-to-solution map
$\Omega _{\mathrm{out}}$
; that is, the source-to-solution map
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
uniquely determines
$\mathscr N$
uniquely determines
Using this scattering map, it is possible to determine if the two null geodesics
![]() $\gamma _{v_0}$
and
$\gamma _{v_0}$
and
![]() $\gamma _{v_1}$
above are distinct or not. Indeed, to remove the possibility of identical null geodesics, we must have
$\gamma _{v_1}$
above are distinct or not. Indeed, to remove the possibility of identical null geodesics, we must have
Having fixed
![]() $v_0\in L^+\Omega _{\mathrm{out}}$
,
$v_0\in L^+\Omega _{\mathrm{out}}$
,
![]() $v_1\in L^+\Omega _{\mathrm{in}}$
subject to the requirement (5.2), we proceed to define the test set
$v_1\in L^+\Omega _{\mathrm{in}}$
subject to the requirement (5.2), we proceed to define the test set
![]() $\Sigma _{v_0,v_1}$
as the set of all tuplets given by
$\Sigma _{v_0,v_1}$
as the set of all tuplets given by
 $$ \begin{align} \begin{aligned} \Sigma_{v_0,v_1}=\{(v_0,\kappa_0,\iota_{0},\ldots, v_3,\kappa_3, \iota_{3})\,:\, &v_2, v_3 \in L^+\Omega_{\text{in}}, \quad \kappa_j \in \mathbb R\setminus \{0\},\\ & \iota_j \in \mathcal T,\quad j=0,1,2,3,\} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Sigma_{v_0,v_1}=\{(v_0,\kappa_0,\iota_{0},\ldots, v_3,\kappa_3, \iota_{3})\,:\, &v_2, v_3 \in L^+\Omega_{\text{in}}, \quad \kappa_j \in \mathbb R\setminus \{0\},\\ & \iota_j \in \mathcal T,\quad j=0,1,2,3,\} \end{aligned} \end{align} $$
where we recall that
![]() $\mathcal T$
is defined by (4.2). Note that
$\mathcal T$
is defined by (4.2). Note that
![]() $v_0$
and
$v_0$
and
![]() $v_1$
are a priori fixed and their inclusion in the tuplets
$v_1$
are a priori fixed and their inclusion in the tuplets
![]() $\sigma \in \Sigma _{v_0,v_1}$
is purely for aesthetic reasons.
$\sigma \in \Sigma _{v_0,v_1}$
is purely for aesthetic reasons.
Given any small
![]() $\delta '>0$
and
$\delta '>0$
and
![]() $\sigma =(v_0,\kappa _0,\iota _{0},\ldots , v_3,\kappa _3, \iota _{3}) \in \Sigma _{v_0,v_1}$
, we consider the null geodesics
$\sigma =(v_0,\kappa _0,\iota _{0},\ldots , v_3,\kappa _3, \iota _{3}) \in \Sigma _{v_0,v_1}$
, we consider the null geodesics
![]() $\gamma _{v_{j}}$
,
$\gamma _{v_{j}}$
,
![]() $j=0,1,2,3$
, passing through
$j=0,1,2,3$
, passing through
![]() $q_{j}$
in the directions
$q_{j}$
in the directions
![]() $\xi _{j}$
and parametrisation as in (3.1). Recall that we are writing
$\xi _{j}$
and parametrisation as in (3.1). Recall that we are writing
![]() $v_j=(q_j,\xi _j)$
for
$v_j=(q_j,\xi _j)$
for
![]() $j=0,1,2,3$
. We also denote by
$j=0,1,2,3$
. We also denote by
![]() $y^{(j)}$
the Fermi coordinates near
$y^{(j)}$
the Fermi coordinates near
![]() $\gamma _{v_j}$
given by Lemma 3.1 and subsequently, following the notation (4.3), we construct for each
$\gamma _{v_j}$
given by Lemma 3.1 and subsequently, following the notation (4.3), we construct for each
![]() $\lambda>0$
the Gaussian beams
$\lambda>0$
the Gaussian beams
 $\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
of order
$\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
of order
 $$ \begin{align} N=\lceil\frac{3n}{2}\rceil+8 \end{align} $$
$$ \begin{align} N=\lceil\frac{3n}{2}\rceil+8 \end{align} $$
and the form
 $$ \begin{align} \mathcal U^{(j)}_{\kappa_j\lambda}(x)= \begin{cases} e^{i\kappa_j\lambda\phi^{(j)}(x)}A^{(j)}_{\kappa_j\lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ e^{i\kappa_j\lambda\bar{\phi}^{(j)}(x)}\bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
$$ \begin{align} \mathcal U^{(j)}_{\kappa_j\lambda}(x)= \begin{cases} e^{i\kappa_j\lambda\phi^{(j)}(x)}A^{(j)}_{\kappa_j\lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ e^{i\kappa_j\lambda\bar{\phi}^{(j)}(x)}\bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
We recall that the functions
 $\phi ^{(j)}, A^{(j)}_{\kappa _j\lambda }$
are exactly as in Section 3 with a support
$\phi ^{(j)}, A^{(j)}_{\kappa _j\lambda }$
are exactly as in Section 3 with a support
![]() $\delta '$
around the null geodesic
$\delta '$
around the null geodesic
![]() $\gamma _{v_j}$
(see (3.5)) and the initial conditions for all ODEs assigned at the points
$\gamma _{v_j}$
(see (3.5)) and the initial conditions for all ODEs assigned at the points
![]() $q^{(j)}$
. As discussed in Section 4, we set the initial values for the phase terms
$q^{(j)}$
. As discussed in Section 4, we set the initial values for the phase terms
 $\phi ^{(j)}_k$
with
$\phi ^{(j)}_k$
with
![]() $k=3,\ldots ,N$
and all
$k=3,\ldots ,N$
and all
 $a^{(j)}_{k,l}$
with
$a^{(j)}_{k,l}$
with
![]() $k,l=0,1,\ldots ,N$
(and not both simultaneously zero) to be zero at the point
$k,l=0,1,\ldots ,N$
(and not both simultaneously zero) to be zero at the point
![]() $q_{j}$
. Finally, and to complete the construction of the Gaussian beams, we set
$q_{j}$
. Finally, and to complete the construction of the Gaussian beams, we set
 $$ \begin{align*}(Y^{(j)}(0),Z^{(j)}(0)) = \iota_j \in \mathcal T.\end{align*} $$
$$ \begin{align*}(Y^{(j)}(0),Z^{(j)}(0)) = \iota_j \in \mathcal T.\end{align*} $$
5.1 Reduction from the source-to-solution map
 $\mathscr L$
to the three-to-one scattering relation
$\mathscr L$
to the three-to-one scattering relation
Let
![]() $v_0 \in L^+\Omega _{\mathrm{out}}$
and
$v_0 \in L^+\Omega _{\mathrm{out}}$
and
![]() $v_1\in L^+\Omega _{\mathrm{in}}$
subject to (5.2). We begin by considering an arbitrary element
$v_1\in L^+\Omega _{\mathrm{in}}$
subject to (5.2). We begin by considering an arbitrary element
![]() $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3) \in \Sigma _{v_0,v_1}$
and also an arbitrary function
$\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3) \in \Sigma _{v_0,v_1}$
and also an arbitrary function
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. Let the source terms
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. Let the source terms
 $f^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
for
$f^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
for
![]() $j=1,2,3$
and the test source
$j=1,2,3$
and the test source
![]() $f_{\kappa _0\lambda ,v_0,\iota _0,\delta '}^-$
be defined as in Section 4 and define for each small vector
$f_{\kappa _0\lambda ,v_0,\iota _0,\delta '}^-$
be defined as in Section 4 and define for each small vector
![]() $\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _m) \in \mathbb R^m$
the source
$\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _m) \in \mathbb R^m$
the source
 $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
given by the equation
$F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
given by the equation
 $$ \begin{align} F^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f}= \begin{cases} \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'} & \text{if}\,\, m=3,\\ \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}+\sum_{j=4}^m \varepsilon_j\,f, & \text{if}\,\, m\geqslant 4.\\ \end{cases} \end{align} $$
$$ \begin{align} F^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f}= \begin{cases} \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'} & \text{if}\,\, m=3,\\ \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}+\sum_{j=4}^m \varepsilon_j\,f, & \text{if}\,\, m\geqslant 4.\\ \end{cases} \end{align} $$
For a fixed
![]() $\lambda>0$
and small enough
$\lambda>0$
and small enough
![]() $\varepsilon _j$
,
$\varepsilon _j$
,
![]() $j=1,2,3,\ldots ,m$
, it holds that
$j=1,2,3,\ldots ,m$
, it holds that
 $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f} \in \mathscr C_{\Omega _{\mathrm{in}}}$
. We let
$F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f} \in \mathscr C_{\Omega _{\mathrm{in}}}$
. We let
 $u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
denote the unique small solution to (1.2) subject to this source term. Note that, in particular, there holds
$u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
denote the unique small solution to (1.2) subject to this source term. Note that, in particular, there holds
 $$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=\begin{cases} u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'} & \text{if}\,\, j=1,2,3,\\ u_f & \text{if }\ m \geqslant 4\ \text{and}\ j=4,\ldots,m, \end{cases} \end{align*} $$
$$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=\begin{cases} u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'} & \text{if}\,\, j=1,2,3,\\ u_f & \text{if }\ m \geqslant 4\ \text{and}\ j=4,\ldots,m, \end{cases} \end{align*} $$
where
![]() $u_f$
is the unique solution to (2.1) subject to the source f and, as discussed in Section 4,
$u_f$
is the unique solution to (2.1) subject to the source f and, as discussed in Section 4,
 $u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
is the unique solution to equation (2.1) subject to the source
$u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
is the unique solution to equation (2.1) subject to the source
 $f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$
and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a
$f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$
and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a
![]() $\delta '$
-neighbourhood of the light ray
$\delta '$
-neighbourhood of the light ray
![]() $\gamma _{v_j}$
with
$\gamma _{v_j}$
with
![]() $j=1,2,3$
.
$j=1,2,3$
.
Finally, we define for each small
![]() $\delta '>0$
,
$\delta '>0$
,
![]() $\sigma \in \Sigma _{v_0,v_1}$
and
$\sigma \in \Sigma _{v_0,v_1}$
and
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
the analytical data
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
the analytical data
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
corresponding to the semi-linear equation (1.2) by the expression
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
corresponding to the semi-linear equation (1.2) by the expression
 $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n+1}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n+1}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$
where we recall that
 $u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
is the unique solution to (1.2) subject to the source
$u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
is the unique solution to (1.2) subject to the source
 $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
given by (5.6). Let us emphasise that the knowledge of the source-to-solution map,
$F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$
given by (5.6). Let us emphasise that the knowledge of the source-to-solution map,
![]() $\mathscr L$
, determines the analytical data
$\mathscr L$
, determines the analytical data
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. We have the following theorem.
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. We have the following theorem.
Theorem 5.1. Let
![]() $v_0\in L^+\Omega _{\mathrm{out}}$
and
$v_0\in L^+\Omega _{\mathrm{out}}$
and
![]() $v_1\in L^+\Omega _{\mathrm{in}}$
be such that (5.2) holds. The following statements hold:
$v_1\in L^+\Omega _{\mathrm{in}}$
be such that (5.2) holds. The following statements hold:
-
(i) If
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ^{\prime }_j,f} \neq 0$
for some
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ^{\prime }_j,f} \neq 0$
for some
 $\sigma \in \Sigma _{v_0,v_1}$
and
$\sigma \in \Sigma _{v_0,v_1}$
and
 $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and a sequence
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and a sequence
 $\{\delta ^{\prime }_j\}_{j=1}^{\infty }$
converging to zero, then there exists an intersection point
$\{\delta ^{\prime }_j\}_{j=1}^{\infty }$
converging to zero, then there exists an intersection point
 $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
$y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. -
(ii) Let
 $v_2,v_3 \in L^+\Omega _{\mathrm{in}}$
. Assume that
$v_2,v_3 \in L^+\Omega _{\mathrm{in}}$
. Assume that
 $\gamma _{v_{j}}$
,
$\gamma _{v_{j}}$
,
 $j=0,1,2,3$
, are distinct and there exists a point
$j=0,1,2,3$
, are distinct and there exists a point
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
 $y=\gamma _{v_{0}}(s_0)$
with
$y=\gamma _{v_{0}}(s_0)$
with
 $s_0\in (-\rho (v_0),0]$
and
$s_0\in (-\rho (v_0),0]$
and
 $y=\gamma _{v_{j}}(s_j)$
for all
$y=\gamma _{v_{j}}(s_j)$
for all
 $j=1,2,3$
, with
$j=1,2,3$
, with
 $s_j\in [0,\rho (v_j))$
. Denote
$s_j\in [0,\rho (v_j))$
. Denote
 $\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
$\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
 $j=0,1,2,3$
and assume that
$j=0,1,2,3$
and assume that
 $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, there exists
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, there exists
 $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
,
 $\kappa _j \in \mathbb R\setminus \{0\}$
and
$\kappa _j \in \mathbb R\setminus \{0\}$
and
 $\iota _j \in \mathcal T$
,
$\iota _j \in \mathcal T$
,
 $j=0,1,2,3$
such that
$j=0,1,2,3$
such that
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}\neq 0$
for all
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}\neq 0$
for all
 $\delta '$
sufficiently small.
$\delta '$
sufficiently small.
We will prove Theorem 5.1 in Subsection 5.3. Observe that as an immediate corollary of Theorem 5.1 it follows that the relation
 $$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$
is a three-to-one scattering relation; that is, it satisfies (R1) and (R2) in Definition 1.2. Therefore, since the source-to-solution map
![]() $\mathscr L$
determines
$\mathscr L$
determines
![]() $\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$
, the first part of Theorem 1.1 – that is, the recovery of the topological, differential and conformal structure of
$\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$
, the first part of Theorem 1.1 – that is, the recovery of the topological, differential and conformal structure of
![]() $\mathbb D$
from the source-to-solution map
$\mathbb D$
from the source-to-solution map
![]() $\mathscr L$
– follows immediately from combining Theorem 5.1 and Theorem 1.3.
$\mathscr L$
– follows immediately from combining Theorem 5.1 and Theorem 1.3.
5.2 Reduction from the source-to-solution map
 $\mathscr N$
to the three-to-one scattering relation
$\mathscr N$
to the three-to-one scattering relation
Analogous to the previous section, we begin by considering an arbitrary element
![]() $\sigma \in \Sigma _{v_0,v_1}$
. Next, we define the three-parameter family of sources
$\sigma \in \Sigma _{v_0,v_1}$
. Next, we define the three-parameter family of sources
 $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
with
$F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
with
![]() $\varepsilon = (\varepsilon _1, \varepsilon _2, \varepsilon _3)$
given by the equation
$\varepsilon = (\varepsilon _1, \varepsilon _2, \varepsilon _3)$
given by the equation
 $$ \begin{align} F^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}= \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}. \end{align} $$
$$ \begin{align} F^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}= \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}. \end{align} $$
For a fixed
![]() $\lambda>0$
and small enough
$\lambda>0$
and small enough
![]() $\varepsilon _j$
,
$\varepsilon _j$
,
![]() $j=1,2,3$
, it holds that
$j=1,2,3$
, it holds that
 $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '} \in \mathscr C_{\Omega _{\mathrm{in}}}$
. We let
$F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '} \in \mathscr C_{\Omega _{\mathrm{in}}}$
. We let
 $u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
denote the unique small solution to (1.3) subject to this source term. Note that
$u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
denote the unique small solution to (1.3) subject to this source term. Note that
 $$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'}\quad \text{for}\ j=1,2,3,\end{align*} $$
$$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'}\quad \text{for}\ j=1,2,3,\end{align*} $$
where we recall from Section 4 that
 $u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
is the unique solution to equation (2.1) subject to the source
$u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$
is the unique solution to equation (2.1) subject to the source
 $f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$
and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a
$f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$
and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a
![]() $\delta '$
-neighbourhood of the light ray
$\delta '$
-neighbourhood of the light ray
![]() $\gamma _{v_j}$
with
$\gamma _{v_j}$
with
![]() $j=1,2,3$
.
$j=1,2,3$
.
Finally, we define for each small
![]() $\delta '>0$
and
$\delta '>0$
and
![]() $\sigma \in \Sigma _{v_0,v_1}$
the analytical data
$\sigma \in \Sigma _{v_0,v_1}$
the analytical data
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
by the expression
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
by the expression
 $$ \begin{align} \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n-3}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n-3}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$
where we recall that
 $u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
is the unique solution to (1.3) subject to the source
$u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$
is the unique solution to (1.3) subject to the source
 $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,v,\delta '}$
given by (5.8). Let us emphasise that the knowledge of the source-to-solution map,
$F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,v,\delta '}$
given by (5.8). Let us emphasise that the knowledge of the source-to-solution map,
![]() $\mathscr N$
, determines the analytical data
$\mathscr N$
, determines the analytical data
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
. Note also that the scaling in (5.9) differs from that of (5.7) as the asymptotic behavior of the corresponding integrands varies in the semi-linear and quasi-linear models. We have the following theorem.
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
. Note also that the scaling in (5.9) differs from that of (5.7) as the asymptotic behavior of the corresponding integrands varies in the semi-linear and quasi-linear models. We have the following theorem.
Theorem 5.2. Let
![]() $v_0\in L^+\Omega _{\mathrm{out}}$
and
$v_0\in L^+\Omega _{\mathrm{out}}$
and
![]() $v_1\in L^+\Omega _{\mathrm{in}}$
be such that (5.2) holds. The following statements hold:
$v_1\in L^+\Omega _{\mathrm{in}}$
be such that (5.2) holds. The following statements hold:
-
(i) If
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta ^{\prime }_j} \neq 0$
for some
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta ^{\prime }_j} \neq 0$
for some
 $\sigma \in \Sigma _{v_0,v_1}$
and a sequence
$\sigma \in \Sigma _{v_0,v_1}$
and a sequence
 $\{\delta ^{\prime }_j\}_{j=1}^{\infty }$
converging to zero, then there exists an intersection point
$\{\delta ^{\prime }_j\}_{j=1}^{\infty }$
converging to zero, then there exists an intersection point
 $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
$y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. -
(ii) Let
 $v_2,v_3 \in L^+\Omega _{\mathrm{in}}$
. Assume that
$v_2,v_3 \in L^+\Omega _{\mathrm{in}}$
. Assume that
 $\gamma _{v_{j}}$
,
$\gamma _{v_{j}}$
,
 $j=0,1,2,3$
, are distinct and there exists a point
$j=0,1,2,3$
, are distinct and there exists a point
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
 $y=\gamma _{v_{0}}(s_0)$
with
$y=\gamma _{v_{0}}(s_0)$
with
 $s_0\in (-\rho (v_0),0]$
and
$s_0\in (-\rho (v_0),0]$
and
 $y=\gamma _{v_{j}}(s_j)$
for all
$y=\gamma _{v_{j}}(s_j)$
for all
 $j=1,2,3$
, with
$j=1,2,3$
, with
 $s_j\in [0,\rho (v_j))$
. Denote
$s_j\in [0,\rho (v_j))$
. Denote
 $\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
$\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
 $j=0,1,2,3$
and assume that
$j=0,1,2,3$
and assume that
 $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, there exists
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, there exists
 $\kappa _j \in \mathbb R\setminus \{0\}$
and
$\kappa _j \in \mathbb R\setminus \{0\}$
and
 $\iota _j \in \mathcal T$
,
$\iota _j \in \mathcal T$
,
 $j=0,1,2,3$
such that
$j=0,1,2,3$
such that
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
for all
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
for all
 $\delta '$
sufficiently small.
$\delta '$
sufficiently small.
We prove Theorem 5.2 in Subsection 5.4. Observe that as an immediate corollary of Theorem 5.2 it follows that the relation
 $$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$
is a three-to-one scattering relation; that is, it satisfies (R1) and (R2) in Definition 1.2. Therefore, since the source-to-solution map
![]() $\mathscr N$
determines
$\mathscr N$
determines
![]() $\operatorname {\mathrm {R}}_{\mathrm{quasi}}$
, the first part of Theorem 1.1 – that is, the recovery of the topological, differential and differential structure of
$\operatorname {\mathrm {R}}_{\mathrm{quasi}}$
, the first part of Theorem 1.1 – that is, the recovery of the topological, differential and differential structure of
![]() $\mathbb D$
from the source-to-solution map
$\mathbb D$
from the source-to-solution map
![]() $\mathscr N$
– follows immediately from combining Theorem 5.2 and Theorem 1.3.
$\mathscr N$
– follows immediately from combining Theorem 5.2 and Theorem 1.3.
5.3 Proof of Theorem 5.1
Note that by expression (2.6) in Subsection 2.2, the source-to-solution map
![]() $\mathscr L$
determines the knowledge of the expression
$\mathscr L$
determines the knowledge of the expression
 $$ \begin{align*}\mathcal I_{\lambda,\sigma,\delta',f}=\int_M u^{-}_{\kappa_0\lambda,v_0,\iota_0,\delta'} u^{+}_{\kappa_1\lambda,v_1,\iota_1,\delta'}u^{+}_{\kappa_2\lambda,v_2,\iota_2,\delta'} u^{+}_{\kappa_3\lambda,v_3,\iota_3,\delta'}\,u_f^{m-3}dV_g,\end{align*} $$
$$ \begin{align*}\mathcal I_{\lambda,\sigma,\delta',f}=\int_M u^{-}_{\kappa_0\lambda,v_0,\iota_0,\delta'} u^{+}_{\kappa_1\lambda,v_1,\iota_1,\delta'}u^{+}_{\kappa_2\lambda,v_2,\iota_2,\delta'} u^{+}_{\kappa_3\lambda,v_3,\iota_3,\delta'}\,u_f^{m-3}dV_g,\end{align*} $$
where we recall that the notations
 $u^{\pm }_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
are as defined in Section 5. Recall also that the function
$u^{\pm }_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
are as defined in Section 5. Recall also that the function
 $u^{+}_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
,
$u^{+}_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
,
![]() $j=1,2,3$
(respectively
$j=1,2,3$
(respectively
![]() $u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
) is close in the sense of (4.7) (respectively (4.9)) to the Gaussian beams
$u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
) is close in the sense of (4.7) (respectively (4.9)) to the Gaussian beams
 $\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
(respectively
$\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
(respectively
 $\mathcal U_{\kappa _0\lambda }^{(0)}=\mathcal U_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
). Finally, the function
$\mathcal U_{\kappa _0\lambda }^{(0)}=\mathcal U_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
). Finally, the function
![]() $u_f$
is the unique solution to (2.1) subject to the source
$u_f$
is the unique solution to (2.1) subject to the source
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. Note also that by (2.6), there holds
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. Note also that by (2.6), there holds
 $$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} = -m! \lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \mathcal I_{\lambda,\sigma,\delta',f}.\end{align*} $$
$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} = -m! \lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \mathcal I_{\lambda,\sigma,\delta',f}.\end{align*} $$
Next, we observe from the definitions (3.5) that the Gaussian beams
 $\mathcal U^{(j)}_{\kappa _j\lambda }$
,
$\mathcal U^{(j)}_{\kappa _j\lambda }$
,
![]() $j=0,1,2,3$
satisfy the uniform bounds
$j=0,1,2,3$
satisfy the uniform bounds
 $$ \begin{align} \|\mathcal U_{\kappa_j\lambda}^{(j)}\|_{L^{\infty}((-T,T)\times M_0)}\leqslant C_j,\end{align} $$
$$ \begin{align} \|\mathcal U_{\kappa_j\lambda}^{(j)}\|_{L^{\infty}((-T,T)\times M_0)}\leqslant C_j,\end{align} $$
for some constants
![]() $C_j$
independent of
$C_j$
independent of
![]() $\lambda $
. Together with the estimates (4.7)–(4.9), it follows that
$\lambda $
. Together with the estimates (4.7)–(4.9), it follows that
 $$ \begin{align*}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}+\mathcal O(\lambda^{-1}),\end{align*} $$
$$ \begin{align*}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}+\mathcal O(\lambda^{-1}),\end{align*} $$
which implies that
 $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}. \end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}. \end{align} $$
Note that given
![]() $\delta '>0$
sufficiently small, the latter integrand is supported on a compact subset of
$\delta '>0$
sufficiently small, the latter integrand is supported on a compact subset of
![]() $\mathbb D_e$
(see (1.8)).
$\mathbb D_e$
(see (1.8)).
Before proving Theorem 5.1, we state the following lemma.
Lemma 5.3. Given any point p in M that lies on a null geodesic
![]() $\overrightarrow {\gamma _v}$
with
$\overrightarrow {\gamma _v}$
with
![]() $v \in L^+\Omega _{\mathrm{in}}$
, there exists a real-valued source
$v \in L^+\Omega _{\mathrm{in}}$
, there exists a real-valued source
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
such that the solution
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
such that the solution
![]() $u_f$
to (2.1) with source f satisfies
$u_f$
to (2.1) with source f satisfies
Proof. Let
![]() $p=\gamma _v(s)$
for some
$p=\gamma _v(s)$
for some
![]() $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
and some
$v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$
and some
![]() $s\geqslant 0$
. Let
$s\geqslant 0$
. Let
![]() $y=(y^0,y^1,\ldots ,y^n)$
denote the Fermi coordinate system in a tubular neighbourhood of
$y=(y^0,y^1,\ldots ,y^n)$
denote the Fermi coordinate system in a tubular neighbourhood of
![]() $\gamma $
and note that
$\gamma $
and note that
![]() $p=(s,0)$
. We consider for each
$p=(s,0)$
. We consider for each
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $\iota \in \mathcal T$
and
$\iota \in \mathcal T$
and
![]() $\delta '$
small the Gaussian beam
$\delta '$
small the Gaussian beam
![]() $\mathcal U_\lambda $
of order
$\mathcal U_\lambda $
of order
 $N=\lceil \frac {3n}{2}\rceil +8$
, near the geodesic
$N=\lceil \frac {3n}{2}\rceil +8$
, near the geodesic
![]() $\gamma $
that is fixed by the choices
$\gamma $
that is fixed by the choices
![]() $\lambda $
,
$\lambda $
,
![]() $\delta '$
and
$\delta '$
and
![]() $\iota $
(see Section 4). Next, consider the source
$\iota $
(see Section 4). Next, consider the source
 $f=f^+_{\lambda ,v,\iota ,\delta '}$
and recall that the solution
$f=f^+_{\lambda ,v,\iota ,\delta '}$
and recall that the solution
 $u=u^+_{\lambda ,v,\iota ,\delta '}$
to equation (2.1) with source term f is asymptotically close to
$u=u^+_{\lambda ,v,\iota ,\delta '}$
to equation (2.1) with source term f is asymptotically close to
![]() $\mathcal U_{\lambda }$
in the sense of (4.7). Together with the explicit expressions (3.5), we deduce that
$\mathcal U_{\lambda }$
in the sense of (4.7). Together with the explicit expressions (3.5), we deduce that
 $$ \begin{align*}u(p)=u(s,0)= a_{0,0}(s)+\mathcal O(\lambda^{-1}).\end{align*} $$
$$ \begin{align*}u(p)=u(s,0)= a_{0,0}(s)+\mathcal O(\lambda^{-1}).\end{align*} $$
Recalling the expression for the principal amplitude term
![]() $a_{0,0}$
(see (3.7)), we deduce that there exists
$a_{0,0}$
(see (3.7)), we deduce that there exists
![]() $\iota \in \mathcal T$
such that
$\iota \in \mathcal T$
such that
![]() $a_{0,0}(s)=1$
. The claim follows trivially with this choice of
$a_{0,0}(s)=1$
. The claim follows trivially with this choice of
![]() $\iota $
and
$\iota $
and
![]() $\lambda $
sufficiently large.
$\lambda $
sufficiently large.
5.3.1 Proof of statement (i) in Theorem 5.1
We assume that
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for some
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for some
![]() $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)\in \Sigma _{v_0,v_1}$
and
$\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)\in \Sigma _{v_0,v_1}$
and
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and a family of
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and a family of
![]() $\delta '$
s converging to zero. First, observe that the corresponding null geodesics
$\delta '$
s converging to zero. First, observe that the corresponding null geodesics
![]() $\gamma _{v_j}$
with
$\gamma _{v_j}$
with
![]() $j=0,1,2,3$
must simultaneously intersect at least once on
$j=0,1,2,3$
must simultaneously intersect at least once on
![]() $\mathbb D_e$
, since otherwise the support of the amplitude functions
$\mathbb D_e$
, since otherwise the support of the amplitude functions
 $A^{(j)}_{\kappa _j\lambda }$
in the expression (5.11) become disjoint sets for all sufficiently small
$A^{(j)}_{\kappa _j\lambda }$
in the expression (5.11) become disjoint sets for all sufficiently small
![]() $\delta '$
. Subsequently, the integrand in (5.11) vanishes independent of the parameter
$\delta '$
. Subsequently, the integrand in (5.11) vanishes independent of the parameter
![]() $\lambda $
, implying that
$\lambda $
, implying that
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}=0$
for all
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}=0$
for all
![]() $\delta '$
small. Let
$\delta '$
small. Let
![]() $\mathcal A=\{y_1,\ldots ,y_N\}$
denote the set of intersection points of the four null geodesics
$\mathcal A=\{y_1,\ldots ,y_N\}$
denote the set of intersection points of the four null geodesics
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=0,1,2,3$
on
$j=0,1,2,3$
on
![]() $\mathbb D_e$
. In terms of the set
$\mathbb D_e$
. In terms of the set
![]() $\mathcal A$
, we observe that given
$\mathcal A$
, we observe that given
![]() $\delta '$
sufficiently small, the expression (5.11) reduces as follows:
$\delta '$
sufficiently small, the expression (5.11) reduces as follows:
 $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\sum_{\ell=1}^N\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)u_f\,dV_{g},\end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\sum_{\ell=1}^N\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)u_f\,dV_{g},\end{align} $$
where
![]() $U_\ell $
,
$U_\ell $
,
![]() $\ell =1,\ldots ,N,$
is a small open neighbourhood of the point
$\ell =1,\ldots ,N,$
is a small open neighbourhood of the point
![]() $y_\ell $
in
$y_\ell $
in
![]() $\mathbb D_e$
that depends on
$\mathbb D_e$
that depends on
![]() $\delta '$
.
$\delta '$
.
To complete the proof of statement (i), we need to show that there is a point
![]() $y \in \mathcal A$
that satisfies the more restrictive casual condition
$y \in \mathcal A$
that satisfies the more restrictive casual condition
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. It is straightforward to see that if
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. It is straightforward to see that if
 $y_\ell \notin \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
for some
$y_\ell \notin \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
for some
![]() $\ell =1,\ldots ,N$
, then
$\ell =1,\ldots ,N$
, then
 $$ \begin{align*}\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)dV_{g}=0,\end{align*} $$
$$ \begin{align*}\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)dV_{g}=0,\end{align*} $$
for all
![]() $\delta '$
sufficiently small. Indeed, this follows from the definitions of the cutoff functions
$\delta '$
sufficiently small. Indeed, this follows from the definitions of the cutoff functions
![]() $\zeta _{+,v_0,\delta '}$
and
$\zeta _{+,v_0,\delta '}$
and
![]() $\zeta _{-,v_j,\delta '}$
,
$\zeta _{-,v_j,\delta '}$
,
![]() $j=1,2,3$
; see (4.4)–(4.5). Since
$j=1,2,3$
; see (4.4)–(4.5). Since
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for a sequence
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for a sequence
![]() $\{\delta ^{\prime }_k\}_{k=1}^{\infty }$
converging to zero by the hypothesis (i) of the theorem, it follows that there must exist a point
$\{\delta ^{\prime }_k\}_{k=1}^{\infty }$
converging to zero by the hypothesis (i) of the theorem, it follows that there must exist a point
![]() $y \in \mathcal A$
such that
$y \in \mathcal A$
such that
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
5.3.2 Proof of statement (ii) in Theorem 5.1
We are assuming here that
satisfies the hypothesis of statement (ii) and want to prove that there exists a real-valued function
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
and
![]() $\kappa_j \in \mathbb R\setminus \{0\} \mbox{ and } \iota_j \in \mathcal T $
with
$\kappa_j \in \mathbb R\setminus \{0\} \mbox{ and } \iota_j \in \mathcal T $
with
![]() $j=0,1,2,3$
such that given
$j=0,1,2,3$
such that given
and all
![]() $\delta '>0$
sufficiently small, there holds
$\delta '>0$
sufficiently small, there holds
 $$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \neq 0.\end{align*} $$
$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \neq 0.\end{align*} $$
Let us first emphasise that given the hypothesis of statement (ii), there is a unique point
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. To show this, we give a proof by contradiction and suppose that there is another distinct point
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. To show this, we give a proof by contradiction and suppose that there is another distinct point
 $\tilde {y} \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. If
$\tilde {y} \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. If
![]() $\tilde y \le y$
, then there exists a broken path consisting of null geodesics that connects one of the points
$\tilde y \le y$
, then there exists a broken path consisting of null geodesics that connects one of the points
![]() $\pi (v_j)$
,
$\pi (v_j)$
,
![]() $j=1,2,3,$
to the point y. Together with [Reference O’Neill79, Proposition 10.46] we obtain that
$j=1,2,3,$
to the point y. Together with [Reference O’Neill79, Proposition 10.46] we obtain that
![]() $\tau (\pi (v_j),y)>0$
, yielding a contradiction since
$\tau (\pi (v_j),y)>0$
, yielding a contradiction since
![]() $y=\gamma _{v_j}(s_j)$
with
$y=\gamma _{v_j}(s_j)$
with
![]() $s_j \in [0,\rho (v_j))$
. In the alternative case that
$s_j \in [0,\rho (v_j))$
. In the alternative case that
![]() $y \le \tilde {y}$
, there exists a broken path consisting of null geodesics that connects the point y to the point
$y \le \tilde {y}$
, there exists a broken path consisting of null geodesics that connects the point y to the point
![]() $\pi (v_0)$
. Together with [Reference O’Neill79, Proposition 10.46] we obtain that
$\pi (v_0)$
. Together with [Reference O’Neill79, Proposition 10.46] we obtain that
![]() $\tau (y,\pi (v_0))>0$
, yielding a contradiction since
$\tau (y,\pi (v_0))>0$
, yielding a contradiction since
![]() $y=\gamma _{v_0}(s_0)$
with
$y=\gamma _{v_0}(s_0)$
with
![]() $s_0 \in (-\rho (v_0),0]$
.
$s_0 \in (-\rho (v_0),0]$
.
Next, we observe that given
![]() $\delta '$
sufficiently small together with the fact that
$\delta '$
sufficiently small together with the fact that
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
, the expression (5.11) reduces as follows:
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
, the expression (5.11) reduces as follows:
 $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\left(\prod_{j=0}^3\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)\,u_f^{m-3}\,dV_{g}. \end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\left(\prod_{j=0}^3\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)\,u_f^{m-3}\,dV_{g}. \end{align} $$
We will use the method of stationary phase to analyse the product of the four Gaussian beams in (5.13). Let us begin by considering the unique point
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. We choose the real-valued function
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. We choose the real-valued function
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
such that
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
such that
![]() $u_f(y) \neq 0$
. This is possible thanks to Lemma 5.3. Next, we choose the nonzero constants
$u_f(y) \neq 0$
. This is possible thanks to Lemma 5.3. Next, we choose the nonzero constants
![]() $\kappa _0,\ldots ,\kappa _3$
, so that
$\kappa _0,\ldots ,\kappa _3$
, so that
 $$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0,\end{align} $$
$$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0,\end{align} $$
where
![]() $\gamma _{v_j}(s_j)=y$
. Recall that these constants exist by our assumption that the tangents to
$\gamma _{v_j}(s_j)=y$
. Recall that these constants exist by our assumption that the tangents to
![]() $\gamma _{v_j}$
are linearly dependent at y. The constants
$\gamma _{v_j}$
are linearly dependent at y. The constants
![]() $\kappa _j$
,
$\kappa _j$
,
![]() $j=0,1,2,3$
can be chosen to be all nonzero, since any three pair-wise linearly independent null vectors are linearly independent (see Lemma 6.21 for the proof).
$j=0,1,2,3$
can be chosen to be all nonzero, since any three pair-wise linearly independent null vectors are linearly independent (see Lemma 6.21 for the proof).
We consider the four families of Gaussian beams along the geodesics
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=0,1,2,3$
, as in (5.5). We choose the initial datum
$j=0,1,2,3$
, as in (5.5). We choose the initial datum
![]() $\iota _j \in \mathcal T$
for the initial values
$\iota _j \in \mathcal T$
for the initial values
![]() $(Y^{(j)}(0),Z^{(j)}(0))$
governing ODEs of the matrices
$(Y^{(j)}(0),Z^{(j)}(0))$
governing ODEs of the matrices
![]() $Y^{(j)}(s)$
and
$Y^{(j)}(s)$
and
![]() $Z^{(j)}(s)$
, so that
$Z^{(j)}(s)$
, so that
 $$ \begin{align} Y^{(j)}(s_j)=I \quad \text{and}\quad Z^{(j)}(s_j) = i\, I,\end{align} $$
$$ \begin{align} Y^{(j)}(s_j)=I \quad \text{and}\quad Z^{(j)}(s_j) = i\, I,\end{align} $$
where we recall that
![]() $\gamma _{v_j}(s_j)=y$
. Note in particular that given this choice of
$\gamma _{v_j}(s_j)=y$
. Note in particular that given this choice of
![]() $\iota _j \in \mathcal T$
,
$\iota _j \in \mathcal T$
,
![]() $j=0,1,2,3$
, there holds
$j=0,1,2,3$
, there holds
 $$ \begin{align} a_{0,0}^{(j)}(y)= 1\quad \text{for}\ j=0,1,2,3.\end{align} $$
$$ \begin{align} a_{0,0}^{(j)}(y)= 1\quad \text{for}\ j=0,1,2,3.\end{align} $$
In the remainder of the proof, we show that given the function f and the tuplet
![]() $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$
constructed as above and all
$\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$
constructed as above and all
![]() $\delta '>0$
sufficiently small, there holds
$\delta '>0$
sufficiently small, there holds
 $ \mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0.$
$ \mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0.$
It can be easily verified from the choice of the parametrisation (3.1), Lemma 3.1 and the expression for the phase function given by (3.7) that
 $$ \begin{align} \dot{\gamma}_{v_j}(s)=\nabla^g\phi^{(j)}|_{\gamma_{v_j}(s)}=\nabla^g\bar{\phi}^{(j)}|_{\gamma_{v_j}(s)}\quad \text{for}\ j=0,1,2,3. \end{align} $$
$$ \begin{align} \dot{\gamma}_{v_j}(s)=\nabla^g\phi^{(j)}|_{\gamma_{v_j}(s)}=\nabla^g\bar{\phi}^{(j)}|_{\gamma_{v_j}(s)}\quad \text{for}\ j=0,1,2,3. \end{align} $$
Let us define
where
 $$ \begin{align} \Phi^{(j)}(x) = \begin{cases} \kappa_j\phi^{(j)}(x) &\quad\text{if}\quad \kappa_j>0,\\ \kappa_j\bar{\phi}^{(j)}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
$$ \begin{align} \Phi^{(j)}(x) = \begin{cases} \kappa_j\phi^{(j)}(x) &\quad\text{if}\quad \kappa_j>0,\\ \kappa_j\bar{\phi}^{(j)}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
We have the following lemma.
Lemma 5.4. Suppose that
 $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
and that (5.14) holds. Let S be defined by (5.18) and denote by d an auxiliary Riemannian distance function on M. There holds
$y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
and that (5.14) holds. Let S be defined by (5.18) and denote by d an auxiliary Riemannian distance function on M. There holds
-
(i)
 $S(y)=0$
.
$S(y)=0$
. -
(ii)
 $\nabla ^{g}S(y)=0$
.
$\nabla ^{g}S(y)=0$
. -
(iii)
 $\Im S(\tilde {y}) \geqslant a\, d(\tilde {y},y)^2$
for all points
$\Im S(\tilde {y}) \geqslant a\, d(\tilde {y},y)^2$
for all points
 $\tilde {y}$
in a neighbourhood of y. Here
$\tilde {y}$
in a neighbourhood of y. Here
 $a>0$
is a constant.
$a>0$
is a constant.
We refer the reader to [Reference Feizmohammadi and Oksanen29, Lemma 5] for the proof of this lemma.
Lemma 5.5. Suppose that
 $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
and that (5.14) holds. Let S be defined by (5.18) and let
$y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
and that (5.14) holds. Let S be defined by (5.18) and let
![]() $F \in \mathcal C^1(M)$
be compactly supported in a sufficiently small neighbourhood of the point y. There holds
$F \in \mathcal C^1(M)$
be compactly supported in a sufficiently small neighbourhood of the point y. There holds
 $$ \begin{align*}\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g = C_0\,F(y),\end{align*} $$
$$ \begin{align*}\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g = C_0\,F(y),\end{align*} $$
where
![]() $C_0 \in \mathbb C$
only depends on
$C_0 \in \mathbb C$
only depends on
![]() $(M,g)$
and
$(M,g)$
and
![]() $c_0=\Re \, C_0 \neq 0$
.
$c_0=\Re \, C_0 \neq 0$
.
Proof. We fix a coordinate system
![]() $(x^0,\ldots ,x^n)$
in a small neighbourhood about the point y, so that
$(x^0,\ldots ,x^n)$
in a small neighbourhood about the point y, so that
![]() $y=(0,\ldots ,0)$
. By Lemma 5.4, there holds
$y=(0,\ldots ,0)$
. By Lemma 5.4, there holds
 $$ \begin{align*}S(x) = \sum_{j,k=0}^n Q_{jk}x^jx^k + R(x),\end{align*} $$
$$ \begin{align*}S(x) = \sum_{j,k=0}^n Q_{jk}x^jx^k + R(x),\end{align*} $$
where
![]() $|R(x)|=\mathcal O(|x|^3)$
and the matrix
$|R(x)|=\mathcal O(|x|^3)$
and the matrix
 $Q=(Q_{jk})_{j,k=0}^n$
has a positive definite imaginary part. We assume that F is supported in a sufficiently small neighbourhood U of the point y, so that
$Q=(Q_{jk})_{j,k=0}^n$
has a positive definite imaginary part. We assume that F is supported in a sufficiently small neighbourhood U of the point y, so that
 $$ \begin{align*}\Im S(x) \geqslant \frac{1}{2}(\sum_{j,k=0}^n \Im Q_{jk}x^jx^k)\geqslant C|x|^2\quad \text{on}\ U,\end{align*} $$
$$ \begin{align*}\Im S(x) \geqslant \frac{1}{2}(\sum_{j,k=0}^n \Im Q_{jk}x^jx^k)\geqslant C|x|^2\quad \text{on}\ U,\end{align*} $$
for some
![]() $C>0$
that depends on
$C>0$
that depends on
![]() $(M,g)$
. Next, we note that
$(M,g)$
. Next, we note that
 $$ \begin{align*} \left|\int_{U} (F(x)-F(0)) e^{i\lambda S(x)}\,dV_g\right| &\leqslant \int_{U} |F(x)-F(0)| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\\ &\leqslant \|F\|_{\mathcal C^1(M)} \int_U |x| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\lesssim \lambda^{-\frac{n+1}{2}}\lambda^{-\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \left|\int_{U} (F(x)-F(0)) e^{i\lambda S(x)}\,dV_g\right| &\leqslant \int_{U} |F(x)-F(0)| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\\ &\leqslant \|F\|_{\mathcal C^1(M)} \int_U |x| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\lesssim \lambda^{-\frac{n+1}{2}}\lambda^{-\frac{1}{2}}. \end{align*} $$
Therefore,
 $$ \begin{align*} &\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g= F(0)\left|\det g(0)\right|{}^{\frac{1}{2}}\lim_{\lambda\to\infty} \lambda^{\frac{n+1}{2}} \int_Ue^{i\lambda\sum_{j,k=0}^nQ_{jk}x^jx^k}\,dx\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= C_0 F(y), \end{align*} $$
$$ \begin{align*} &\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g= F(0)\left|\det g(0)\right|{}^{\frac{1}{2}}\lim_{\lambda\to\infty} \lambda^{\frac{n+1}{2}} \int_Ue^{i\lambda\sum_{j,k=0}^nQ_{jk}x^jx^k}\,dx\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= C_0 F(y), \end{align*} $$
where we applied the method of stationary phase in the last step; see, for example, Theorem 7.7.5 in [Reference Hörmander42].
Let us now return to the expression (5.13) and note that it reduces as follows:
 $$ \begin{align} &\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_{M}u_f^{m-3}\Re \,\mathcal U_{\kappa_0\lambda}^{(0)}\,\Re\, \mathcal U_{\kappa_1\lambda}^{(1)}\, \Re\, \mathcal U_{\kappa_2\lambda}^{(2)}\,\Re \,\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\nonumber\\ &= \lim_{\lambda\to\infty}2^{-4}\lambda^{\frac{n+1}{2}}\sum_{\ell_0,\ell_1,\ell_2,\ell_3 =1,2}\int_{M}u_f^{m-3}\vartheta_{\ell_0}(\mathcal U_{\kappa_0\lambda}^{(0)})\vartheta_{\ell_1}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_2}(\mathcal U_{\kappa_2\lambda}^{(2)})\vartheta_{\ell_3}(\mathcal U_{\kappa_3\lambda}^{(3)})\,dV_{g}, \end{align} $$
$$ \begin{align} &\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_{M}u_f^{m-3}\Re \,\mathcal U_{\kappa_0\lambda}^{(0)}\,\Re\, \mathcal U_{\kappa_1\lambda}^{(1)}\, \Re\, \mathcal U_{\kappa_2\lambda}^{(2)}\,\Re \,\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\nonumber\\ &= \lim_{\lambda\to\infty}2^{-4}\lambda^{\frac{n+1}{2}}\sum_{\ell_0,\ell_1,\ell_2,\ell_3 =1,2}\int_{M}u_f^{m-3}\vartheta_{\ell_0}(\mathcal U_{\kappa_0\lambda}^{(0)})\vartheta_{\ell_1}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_2}(\mathcal U_{\kappa_2\lambda}^{(2)})\vartheta_{\ell_3}(\mathcal U_{\kappa_3\lambda}^{(3)})\,dV_{g}, \end{align} $$
where
Lemma 5.6. Given
![]() $\sigma \in \Sigma _{v_0,v_1}$
, with
$\sigma \in \Sigma _{v_0,v_1}$
, with
 $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
, the choice of
$y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
, the choice of
![]() $\kappa _0,\ldots ,\kappa _3$
satisfying (5.14) and the initial data
$\kappa _0,\ldots ,\kappa _3$
satisfying (5.14) and the initial data
![]() $\iota _0,\ldots \iota _3\in \mathcal T$
satisfying (5.15), there holds
$\iota _0,\ldots \iota _3\in \mathcal T$
satisfying (5.15), there holds
 $$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=\lim_{\lambda\to \infty}2^{-3}\lambda^{\frac{n+1}{2}} \Re\left(\int_{M}u_f^{m-3}\,\mathcal U_{\kappa_0\lambda}^{(0)}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\right).\end{align*} $$
$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=\lim_{\lambda\to \infty}2^{-3}\lambda^{\frac{n+1}{2}} \Re\left(\int_{M}u_f^{m-3}\,\mathcal U_{\kappa_0\lambda}^{(0)}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\right).\end{align*} $$
Proof. Observe that the summation in expression (5.20) contains 16 terms and we are claiming that only two terms here contribute in the limit as
![]() $\lambda $
approaches infinity, when
$\lambda $
approaches infinity, when
![]() $(\ell _0,\ell _1,\ell _2,\ell _3)\in \{(1,1,1,1),(2,2,2,2)\}$
. To see that the other terms do not contribute, we note that
$(\ell _0,\ell _1,\ell _2,\ell _3)\in \{(1,1,1,1),(2,2,2,2)\}$
. To see that the other terms do not contribute, we note that
 $$ \begin{align} \int_{M}u_f^{m-3}\prod_{j=0}^3\vartheta_{\ell_j}(\mathcal U_{\kappa_j\lambda}^{(j)})\,dV_{g}= \int_M u_f^{m-3}\,e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))\,dV_g,\end{align} $$
$$ \begin{align} \int_{M}u_f^{m-3}\prod_{j=0}^3\vartheta_{\ell_j}(\mathcal U_{\kappa_j\lambda}^{(j)})\,dV_{g}= \int_M u_f^{m-3}\,e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))\,dV_g,\end{align} $$
where
 $S_{\ell _0,\ell _1,\ell _2,\ell _3}(x)= \sum _{j=0}^3\vartheta _{\ell _j}(\Phi ^{(j)}(x))$
and
$S_{\ell _0,\ell _1,\ell _2,\ell _3}(x)= \sum _{j=0}^3\vartheta _{\ell _j}(\Phi ^{(j)}(x))$
and
 $$ \begin{align} B^{(j)}_{\kappa_j\lambda}(x) = \begin{cases} A^{(j)}_{\kappa_j \lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ \bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
$$ \begin{align} B^{(j)}_{\kappa_j\lambda}(x) = \begin{cases} A^{(j)}_{\kappa_j \lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ \bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$
We observe that since y is the only point of the intersection between the four null geodesics
![]() $\gamma _{v_j}$
in
$\gamma _{v_j}$
in
![]() $\mathbb D_e \subset (-T,T)\times M_0$
, the integral above is supported in a small neighbourhood of the point y. It is easy to verify that
$\mathbb D_e \subset (-T,T)\times M_0$
, the integral above is supported in a small neighbourhood of the point y. It is easy to verify that
where S is as defined in (5.18). Thus, by Lemma 5.4, there holds
Moreover, using the identity (5.17) together with the fact that
![]() $\kappa _j$
,
$\kappa _j$
,
![]() $j=0,1,2,3$
are all nonzero, we conclude that
$j=0,1,2,3$
are all nonzero, we conclude that
This implies that for all
![]() $(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$
, the phase function
$(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$
, the phase function
![]() $S_{\ell _0,\ell _1,\ell _2,\ell _3}$
appearing in (5.21) does not have a critical point near y. Thus, we can repeatedly use integration by parts to conclude that
$S_{\ell _0,\ell _1,\ell _2,\ell _3}$
appearing in (5.21) does not have a critical point near y. Thus, we can repeatedly use integration by parts to conclude that
 $$ \begin{align*}\lim_{\lambda\to \infty}\int_M e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))u_f^{m-3}\,dV_g= \mathcal O(\lambda^{-\infty}),\end{align*} $$
$$ \begin{align*}\lim_{\lambda\to \infty}\int_M e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))u_f^{m-3}\,dV_g= \mathcal O(\lambda^{-\infty}),\end{align*} $$
whenever
![]() $(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$
. By combining the above arguments, we obtain
$(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$
. By combining the above arguments, we obtain
 $$ \begin{align*} &\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= 2^{-4}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\left(\int_{M}u_f^{m-3}\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\,dV_{g}+\int_{M}u_f^{m-3}\prod_{j=0}^3\overline{\mathcal U_{\kappa_j\lambda}^{(j)}}\,dV_{g}\right)\\ &\qquad\qquad\qquad\qquad\qquad\qquad=2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re \int_{M}\left(\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}.\end{align*} $$
$$ \begin{align*} &\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= 2^{-4}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\left(\int_{M}u_f^{m-3}\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\,dV_{g}+\int_{M}u_f^{m-3}\prod_{j=0}^3\overline{\mathcal U_{\kappa_j\lambda}^{(j)}}\,dV_{g}\right)\\ &\qquad\qquad\qquad\qquad\qquad\qquad=2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re \int_{M}\left(\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}.\end{align*} $$
Using Lemma 5.6, we conclude that the expression for
![]() $\mathscr D_{\sigma ,\delta '}$
reduces to
$\mathscr D_{\sigma ,\delta '}$
reduces to
 $$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=2^{-3}\Re\left(\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_M e^{i\lambda S(x)} u_f^{m-3}(x)\,B_{\kappa_0\lambda}^{(0)}(x)B_{\kappa_1\lambda}^{(1)}(x)B_{\kappa_2\lambda}^{(2)}(x)B_{\kappa_3\lambda}^{(3)}(x)\,dV_g\right).\end{align*} $$
$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=2^{-3}\Re\left(\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_M e^{i\lambda S(x)} u_f^{m-3}(x)\,B_{\kappa_0\lambda}^{(0)}(x)B_{\kappa_1\lambda}^{(1)}(x)B_{\kappa_2\lambda}^{(2)}(x)B_{\kappa_3\lambda}^{(3)}(x)\,dV_g\right).\end{align*} $$
Note that thanks to (5.16), there holds
 $$ \begin{align} B^{(j)}_{\kappa_j\lambda}(y)=1,\quad \text{for}\ j=0,1,2,3.\end{align} $$
$$ \begin{align} B^{(j)}_{\kappa_j\lambda}(y)=1,\quad \text{for}\ j=0,1,2,3.\end{align} $$
We expand the amplitudes
 $a_{\kappa _j\lambda }^{(j)}$
in the expressions for
$a_{\kappa _j\lambda }^{(j)}$
in the expressions for
 $B^{(j)}_{\kappa _j \lambda }$
in terms of the functions
$B^{(j)}_{\kappa _j \lambda }$
in terms of the functions
 $a_k^{(j)}$
as in (3.5) and apply Lemma 5.4 together with the method of stationary phase (see, e.g., Theorem 7.7.5 in [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Alinhac and Baouendi2]) to (5.13), term-wise after this expansion. Using the key hypothesis (5.23) together with Lemma 5.5, we conclude that
$a_k^{(j)}$
as in (3.5) and apply Lemma 5.4 together with the method of stationary phase (see, e.g., Theorem 7.7.5 in [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Alinhac and Baouendi2]) to (5.13), term-wise after this expansion. Using the key hypothesis (5.23) together with Lemma 5.5, we conclude that
 $$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= c_{0}u_f(y), \end{align*} $$
$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= c_{0}u_f(y), \end{align*} $$
where
![]() $c_0$
is a nonzero real constant as given by Lemma 5.5 and y is the unique intersection point given in hypothesis (ii) of the Theorem. Note that the application of Lemma 5.5 is justified here since the product of the four amplitude functions is supported in a small neighbourhood of y that depends on the parameter
$c_0$
is a nonzero real constant as given by Lemma 5.5 and y is the unique intersection point given in hypothesis (ii) of the Theorem. Note that the application of Lemma 5.5 is justified here since the product of the four amplitude functions is supported in a small neighbourhood of y that depends on the parameter
![]() $\delta '$
and so the hypothesis of Lemma 5.5 is satisfied for
$\delta '$
and so the hypothesis of Lemma 5.5 is satisfied for
![]() $\delta '$
sufficiently small. Finally, since
$\delta '$
sufficiently small. Finally, since
![]() $u_f(y) \neq 0$
, it follows that
$u_f(y) \neq 0$
, it follows that
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
, thus completing the proof of Theorem 5.1.
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
, thus completing the proof of Theorem 5.1.
5.4 Proof of Theorem 5.2
Applying the linearisation argument in Subsection 2.2, we deduce that the source-to-solution map
![]() $\mathscr N$
determines the knowledge of the expression
$\mathscr N$
determines the knowledge of the expression
 $$ \begin{align*} \tilde{\mathcal I}_{\lambda,\sigma,\delta'}&=\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g\\ &\quad+2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\\ &\quad -\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g, \end{align*} $$
$$ \begin{align*} \tilde{\mathcal I}_{\lambda,\sigma,\delta'}&=\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g\\ &\quad+2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\\ &\quad -\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g, \end{align*} $$
where
 $u_j= u^+_{\kappa _j\lambda ,v_j,\delta '}$
for
$u_j= u^+_{\kappa _j\lambda ,v_j,\delta '}$
for
![]() $j=1,2,3$
and
$j=1,2,3$
and
![]() $u_0=u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
. Also,
$u_0=u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
. Also,
![]() $f_0=f^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
and
$f_0=f^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$
and
 $f_j=f^+_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
for
$f_j=f^+_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$
for
![]() $j=1,2,3$
. Note also that
$j=1,2,3$
. Note also that
 $$ \begin{align*}\mathscr D_{\sigma,\delta'}= \lim_{\lambda\to\infty}\lambda^{\frac{n-3}{2}}\tilde{\mathcal I}_{\lambda,\sigma,\delta'}.\end{align*} $$
$$ \begin{align*}\mathscr D_{\sigma,\delta'}= \lim_{\lambda\to\infty}\lambda^{\frac{n-3}{2}}\tilde{\mathcal I}_{\lambda,\sigma,\delta'}.\end{align*} $$
The proof of (i) in Theorem 5.2 is exactly as the proof of (i) in Theorem 5.1. To show (ii), we proceed as before by showing that if there is a point
 $y\in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
that satisfies the hypothesis of statement (ii), then there exists
$y\in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
that satisfies the hypothesis of statement (ii), then there exists
![]() $\kappa _j \in \mathbb R\setminus \{0\}$
and
$\kappa _j \in \mathbb R\setminus \{0\}$
and
![]() $\iota _j \in \mathcal T$
, such that
$\iota _j \in \mathcal T$
, such that
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
, for all
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
, for all
![]() $\delta '$
sufficiently small and
$\delta '$
sufficiently small and
![]() $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$
.
$\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$
.
Observe that using the same argument as in the preceding section, we can show that there is a unique point in
 $\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. Again, analogous to the previous section, we observe that since the tangent vectors to
$\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. Again, analogous to the previous section, we observe that since the tangent vectors to
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=1,2,3,$
are linearly dependent at the point y, there exist nonzero constants
$j=1,2,3,$
are linearly dependent at the point y, there exist nonzero constants
![]() $\kappa _0,\kappa _1,\kappa _2,\kappa _3$
such that the linear dependence equation (5.14) holds at the point y. We also choose
$\kappa _0,\kappa _1,\kappa _2,\kappa _3$
such that the linear dependence equation (5.14) holds at the point y. We also choose
![]() $\iota _j \in \mathcal T$
such that (5.15) holds at the point y and subsequently define the Gaussian beams along the geodesics
$\iota _j \in \mathcal T$
such that (5.15) holds at the point y and subsequently define the Gaussian beams along the geodesics
![]() $\gamma _{v_j}$
,
$\gamma _{v_j}$
,
![]() $j=0,1,2,3$
, as in (5.5). Recall that due to the choice of initial conditions given by (5.15), the amplitude functions satisfy (5.16).
$j=0,1,2,3$
, as in (5.5). Recall that due to the choice of initial conditions given by (5.15), the amplitude functions satisfy (5.16).
We proceed to show that given this choice of
![]() $\sigma $
, there holds
$\sigma $
, there holds
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
for all
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$
for all
![]() $\delta '$
small. This will be achieved by proving the following three estimates:
$\delta '$
small. This will be achieved by proving the following three estimates:
 $$ \begin{align} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g=0,\end{align} $$
$$ \begin{align} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g=0,\end{align} $$
and
 $$ \begin{align} \begin{aligned} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g&+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g=0 \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g&+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g=0 \end{aligned} \end{align} $$
and, finally, that
 $$ \begin{align} &\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_{M} (u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h)\,dV_g=c_0\,\kappa_0^2\,h(\dot{\gamma}^{(0)}(s_0),\dot{\gamma}^{(0)}(s_0)), \end{align} $$
$$ \begin{align} &\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_{M} (u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h)\,dV_g=c_0\,\kappa_0^2\,h(\dot{\gamma}^{(0)}(s_0),\dot{\gamma}^{(0)}(s_0)), \end{align} $$
where
![]() $c_0$
is a nonzero constant depending on the geometry
$c_0$
is a nonzero constant depending on the geometry
![]() $(M,g)$
. Note that by assumption (ii) on the family of metrics
$(M,g)$
. Note that by assumption (ii) on the family of metrics
![]() $G_z$
, h is nondegenerate on null vectors and therefore the right-hand side of the above expression is nonzero. Thus, it follows from the above three estimates that
$G_z$
, h is nondegenerate on null vectors and therefore the right-hand side of the above expression is nonzero. Thus, it follows from the above three estimates that
 $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
is nonzero.
$\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$
is nonzero.
Let us begin by showing that (5.24) holds. Using the estimates (4.7)–(4.9) together with the uniform boundedness of Gaussian beams in
![]() $\lambda $
(see (5.10)) and the estimate (4.11), it follows that
$\lambda $
(see (5.10)) and the estimate (4.11), it follows that
 $$ \begin{align*} &\left| \int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g \right| \\ &\qquad\qquad\lesssim \|u_0\|_{\mathcal C(V)}(\|u_1\|_{\mathcal C(V)} \|u_2\|_{\mathcal C(V)}\|f_3\|_{\mathcal C(V)}+ \|u_2\|_{\mathcal C(V)} \|u_3\|_{\mathcal C(V)}\|f_1\|_{\mathcal C(V)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\|u_3\|_{\mathcal C(V)} \|u_1\|_{\mathcal C(V)}\|f_2\|_{\mathcal C(V)}) \lesssim \lambda^{1-\frac{n}{2}}, \end{align*} $$
$$ \begin{align*} &\left| \int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g \right| \\ &\qquad\qquad\lesssim \|u_0\|_{\mathcal C(V)}(\|u_1\|_{\mathcal C(V)} \|u_2\|_{\mathcal C(V)}\|f_3\|_{\mathcal C(V)}+ \|u_2\|_{\mathcal C(V)} \|u_3\|_{\mathcal C(V)}\|f_1\|_{\mathcal C(V)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\|u_3\|_{\mathcal C(V)} \|u_1\|_{\mathcal C(V)}\|f_2\|_{\mathcal C(V)}) \lesssim \lambda^{1-\frac{n}{2}}, \end{align*} $$
where
 $V=J^-(\operatorname {\mathrm {supp}} f_0) \cap \bigcup _{j=1}^3 J^+(\operatorname {\mathrm {supp}} f_j)$
is compact and lies inside
$V=J^-(\operatorname {\mathrm {supp}} f_0) \cap \bigcup _{j=1}^3 J^+(\operatorname {\mathrm {supp}} f_j)$
is compact and lies inside
![]() $(-T,T)\times M_0$
by the hypothesis of Theorem 1.1.
$(-T,T)\times M_0$
by the hypothesis of Theorem 1.1.
Next, we show that (5.25) holds. We use again the estimates (4.7)–(4.9) together with the uniform boundedness of Gaussian beams in
![]() $\lambda $
(see (5.10)) to write
$\lambda $
(see (5.10)) to write
 $$ \begin{align*} &\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle du_3,du_0 \rangle_g\,dV_g\\ &\quad =2^{-4}\sum_{\ell_0,\ldots,\ell_3=1,2}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\vartheta_{\ell_j}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_j}(\mathcal U_{\kappa_2\lambda}^{(2)})\langle \vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_3\lambda}^{(3)}),\vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}) \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\mathcal O(\lambda^{-1}\lambda^{-\frac{n-3}{2}}). \end{align*} $$
$$ \begin{align*} &\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle du_3,du_0 \rangle_g\,dV_g\\ &\quad =2^{-4}\sum_{\ell_0,\ldots,\ell_3=1,2}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\vartheta_{\ell_j}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_j}(\mathcal U_{\kappa_2\lambda}^{(2)})\langle \vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_3\lambda}^{(3)}),\vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}) \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\mathcal O(\lambda^{-1}\lambda^{-\frac{n-3}{2}}). \end{align*} $$
Here, recalling (5.17) and applying property (ii) in Lemma 5.4 together with a similar argument as in the proof of Lemma 5.6, we can show that as
![]() $\lambda $
approaches infinity, only two terms in the above sum contribute so that
$\lambda $
approaches infinity, only two terms in the above sum contribute so that
 $$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(g^{-1}h) \mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g\,dV_g\right). \end{align*} $$
$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(g^{-1}h) \mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g\,dV_g\right). \end{align*} $$
Here, using the defining expressions (5.5) and (5.18) together with the uniform boundedness of Gaussian beams in the parameter
![]() $\lambda $
(see (5.10)), we write
$\lambda $
(see (5.10)), we write
 $$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_g\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$
$$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_g\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$
where
 $B^{(j)}_{\kappa _j\lambda }$
are defined as in (5.22). Using this identity, together with (5.16) and Lemma 5.5, we obtain that
$B^{(j)}_{\kappa _j\lambda }$
are defined as in (5.22). Using this identity, together with (5.16) and Lemma 5.5, we obtain that
 $$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad= -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{g(y)}, \end{align*} $$
$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad= -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{g(y)}, \end{align*} $$
where we recall that
![]() $c_0\neq 0$
is as given by Lemma 5.5. Thus, adding the contributions from the other two terms in (5.25), we deduce that
$c_0\neq 0$
is as given by Lemma 5.5. Thus, adding the contributions from the other two terms in (5.25), we deduce that
 $$ \begin{align*} & \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g\\ &\qquad\qquad =-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\left(\sum_{j=1}^3 \langle \nabla^g\Phi^{(j)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}\right)\\ &\qquad\qquad=-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\,\langle \underbrace{\sum_{j=1}^3 \nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{g(y)} \\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}=0, \end{align*} $$
$$ \begin{align*} & \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g\\ &\qquad\qquad =-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\left(\sum_{j=1}^3 \langle \nabla^g\Phi^{(j)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}\right)\\ &\qquad\qquad=-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\,\langle \underbrace{\sum_{j=1}^3 \nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{g(y)} \\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}=0, \end{align*} $$
where we used property (ii) in Lemma 5.4 to get the last step and there we applied (5.17) and the fact that
![]() $\gamma _{v_0}$
is a null geodesic.
$\gamma _{v_0}$
is a null geodesic.
Finally, we proceed to prove the remaining estimate (5.26). Note that analogous to the proof of (5.25), there holds
 $$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_h\,dV_g\right). \end{align*} $$
$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_h\,dV_g\right). \end{align*} $$
Now, using the expression
 $$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_h\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$
$$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_h\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$
together with Lemma 5.5 and the key identity (5.16), we obtain
 $$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad = -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{h(y)}, \end{align*} $$
$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad = -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{h(y)}, \end{align*} $$
where we recall that
![]() $c_0\neq 0$
is as given by Lemma 5.5. Finally, adding the analogous contributions from the remaining two terms in (5.26), we obtain
$c_0\neq 0$
is as given by Lemma 5.5. Finally, adding the analogous contributions from the remaining two terms in (5.26), we obtain
 $$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_h\\ &\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_h)\,dV_g=-2^{-3}c_0\,\langle \sum_{j=1}^3\underbrace{\nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =2^{-3}c_0\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\neq 0, \end{align*} $$
$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_h\\ &\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_h)\,dV_g=-2^{-3}c_0\,\langle \sum_{j=1}^3\underbrace{\nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =2^{-3}c_0\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\neq 0, \end{align*} $$
where we used property (ii) in the definition of the tensor
![]() $G(x,z)$
in the last step. This concludes the proof of the Theorem 5.2.
$G(x,z)$
in the last step. This concludes the proof of the Theorem 5.2.
6 On globally hyperbolic manifolds
We start the geometric part of our analysis. In this section, we give some geometric notations and results that will be used to prove Theorem 1.3. As before, we assume
![]() $(M,g)$
to be a globally hyperbolic Lorentzian manifold of dimension
$(M,g)$
to be a globally hyperbolic Lorentzian manifold of dimension
![]() $1+n$
with
$1+n$
with
![]() $n \geqslant 2$
. We write
$n \geqslant 2$
. We write
![]() $\le $
and
$\le $
and
![]() $\ll $
for the causal and chronological relations on M and recall that the length L of a causal curve
$\ll $
for the causal and chronological relations on M and recall that the length L of a causal curve
![]() $\alpha :I\to M$
is given by
$\alpha :I\to M$
is given by
 $$ \begin{align*}L(\alpha)=\int_I \sqrt{-g(\dot{\alpha}(s),\dot{\alpha}(s))}\,ds.\end{align*} $$
$$ \begin{align*}L(\alpha)=\int_I \sqrt{-g(\dot{\alpha}(s),\dot{\alpha}(s))}\,ds.\end{align*} $$
We write
![]() $\tau $
for the time separation function on
$\tau $
for the time separation function on
![]() $M \times M$
that is defined for each
$M \times M$
that is defined for each
![]() $p \le q$
via
$p \le q$
via
We define
![]() $\tau (p,q)=0$
if
$\tau (p,q)=0$
if
![]() $p\le q$
does not hold. Recall that
$p\le q$
does not hold. Recall that
![]() $\le $
is closed,
$\le $
is closed,
![]() $\ll $
is open and that
$\ll $
is open and that
![]() $\tau $
is continuous; see, for example, [Reference O’Neill79, Lemmas 3 (p. 403), 21–22 (p. 412)]. Occasionally we will consider causal relations on a subset
$\tau $
is continuous; see, for example, [Reference O’Neill79, Lemmas 3 (p. 403), 21–22 (p. 412)]. Occasionally we will consider causal relations on a subset
![]() $\Omega \subset M$
, and we say that
$\Omega \subset M$
, and we say that
![]() $x \le y$
in
$x \le y$
in
![]() $\Omega $
if there is a causal future-pointing path from x to y, staying in
$\Omega $
if there is a causal future-pointing path from x to y, staying in
![]() $\Omega $
, or if
$\Omega $
, or if
![]() $x = y$
. Analogously,
$x = y$
. Analogously,
![]() $x \ll y$
in
$x \ll y$
in
![]() $\Omega $
if there is a time-like future-pointing path from x to y, staying in
$\Omega $
if there is a time-like future-pointing path from x to y, staying in
![]() $\Omega $
.
$\Omega $
.
The next shortcut argument (see [Reference O’Neill79, Prop. 46 (p. 294)]) will be very useful in what follows.
Lemma 6.1. If there is a future-pointing causal path from x to y on M that is not a null pregeodesic, then
![]() $x \ll y$
.
$x \ll y$
.
The above lemma implies that
![]() $x \ll y$
is equivalent with
$x \ll y$
is equivalent with
![]() $\tau (x,y)> 0$
. On the other hand, if
$\tau (x,y)> 0$
. On the other hand, if
![]() $x \le y$
and
$x \le y$
and
![]() $\tau (x,y) = 0$
, then there is a null geodesic joining x and y and all causal paths joining x and y are null geodesics, up to reparametrisation. While
$\tau (x,y) = 0$
, then there is a null geodesic joining x and y and all causal paths joining x and y are null geodesics, up to reparametrisation. While
![]() $L(\gamma )$
vanishes for all null geodesics
$L(\gamma )$
vanishes for all null geodesics
![]() $\gamma $
, it may happen that
$\gamma $
, it may happen that
![]() $\tau (x,y)> 0$
for some points x and y joined by a null geodesic
$\tau (x,y)> 0$
for some points x and y joined by a null geodesic
![]() $\gamma $
. In this case we say that
$\gamma $
. In this case we say that
![]() $\gamma $
is not optimising. In Subsection 6.2 we will recall the notion of cut function that tells when a null geodesic stops being optimising. Optimising null geodesics are discussed further in Subsection 6.3.
$\gamma $
is not optimising. In Subsection 6.2 we will recall the notion of cut function that tells when a null geodesic stops being optimising. Optimising null geodesics are discussed further in Subsection 6.3.
It should be emphasised that all technical complications in the geometric proof in the next section are related to cases where not all null geodesics are optimising. In fact, if all null geodesics are optimising, then Theorem 1.3 follows immediately from Lemma 7.3 and [Reference Kurylev, Lassas and Uhlmann64, Theorem 1.2] and many tools discussed in the present section are not needed.
To simplify the notations we often lift functions and relations from M to
![]() $TM$
by using the natural projection
$TM$
by using the natural projection
![]() $\pi : TM \to M$
. For example, we write
$\pi : TM \to M$
. For example, we write
![]() $v \le w$
if
$v \le w$
if
![]() $\pi (v) \le \pi (w)$
and
$\pi (v) \le \pi (w)$
and
![]() $\tau (v,w) =\tau (\pi (v), \pi (w))$
, for
$\tau (v,w) =\tau (\pi (v), \pi (w))$
, for
![]() $v,w \in TM$
. The bundle of light-like vectors is denoted by
$v,w \in TM$
. The bundle of light-like vectors is denoted by
![]() $LM$
, and
$LM$
, and
![]() $L^+ M$
and
$L^+ M$
and
![]() $L^-M$
are the future and past-pointing subbundles. We define the causal bundle (with boundary)
$L^-M$
are the future and past-pointing subbundles. We define the causal bundle (with boundary)
and write again
![]() $C^+ M$
and
$C^+ M$
and
![]() $C^- M$
for the future- and past-pointing subbundles. When
$C^- M$
for the future- and past-pointing subbundles. When
![]() $K \subset M$
, we write
$K \subset M$
, we write
![]() $LK = \{(x,\xi ) \in LM : x \in K\}$
and use the analogous notation for other bundles as well.
$LK = \{(x,\xi ) \in LM : x \in K\}$
and use the analogous notation for other bundles as well.
We denote by
![]() $\gamma _{v} : (a,b) \to M$
the inextendible geodesic on M with the initial data
$\gamma _{v} : (a,b) \to M$
the inextendible geodesic on M with the initial data
![]() $v \in CM$
and write
$v \in CM$
and write
Then
![]() $\beta _v(0) = v$
and
$\beta _v(0) = v$
and
![]() $a < 0 < b$
.
$a < 0 < b$
.
6.1 Compactness results
For
![]() $p, q \in M$
the causal future and past of p and q, respectively, are
$p, q \in M$
the causal future and past of p and q, respectively, are
The causal diamonds
are compact. More generally, we write
![]() $J^\pm (S) = \bigcup _{x \in S} J^\pm (x)$
for a set
$J^\pm (S) = \bigcup _{x \in S} J^\pm (x)$
for a set
![]() $S \subset M$
. If
$S \subset M$
. If
![]() $K_1, K_2 \subset M$
are compact, then
$K_1, K_2 \subset M$
are compact, then
![]() $J^+(K_1) \cap J^-(K_2)$
is also compact. Indeed, writing
$J^+(K_1) \cap J^-(K_2)$
is also compact. Indeed, writing
![]() $K = K_1 \cup K_2$
, this follows from
$K = K_1 \cup K_2$
, this follows from
![]() $J^+(K) \cap J^-(K)$
being compact and both
$J^+(K) \cap J^-(K)$
being compact and both
![]() $J^+(K_1)$
and
$J^+(K_1)$
and
![]() $J^-(K_2)$
being closed; see [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Babich and Ulin6, Th. 2.1 and Prop. 2.3].
$J^-(K_2)$
being closed; see [Reference Ambartsoumian, Felea, Quinto and Nolan4
Reference Babich and Ulin6, Th. 2.1 and Prop. 2.3].
The fact that
![]() $(M,g)$
is not assumed to be geodesically complete causes some technical difficulties. We will typically handle these issues by working in a compact subset. We have the following variation of [Reference Belishev and Katchalov9, Lem. 9.34].
$(M,g)$
is not assumed to be geodesically complete causes some technical difficulties. We will typically handle these issues by working in a compact subset. We have the following variation of [Reference Belishev and Katchalov9, Lem. 9.34].
Lemma 6.2. Let
![]() $K \subset M$
be compact and suppose that
$K \subset M$
be compact and suppose that
![]() $v_j \to v$
in
$v_j \to v$
in
![]() $C^+ K$
,
$C^+ K$
,
![]() $s_j \to s \geqslant 0$
in
$s_j \to s \geqslant 0$
in
![]() $\mathbb R$
and that
$\mathbb R$
and that
![]() $\gamma _{v_j}(s_j) \in K$
. Then the inextendible geodesic
$\gamma _{v_j}(s_j) \in K$
. Then the inextendible geodesic
![]() $\gamma _v : (a,b) \to M$
satisfies
$\gamma _v : (a,b) \to M$
satisfies
![]() $b> s$
.
$b> s$
.
Proof. As K is compact, by passing to a subsequence, still denoted by
![]() $(v_j, s_j)$
, we may assume that
$(v_j, s_j)$
, we may assume that
![]() $\gamma _{v_j}(s_j) \to x$
in K. Let
$\gamma _{v_j}(s_j) \to x$
in K. Let
![]() $\tilde x \in M$
satisfy
$\tilde x \in M$
satisfy
![]() $x \ll \tilde x$
. To get a contradiction, suppose that
$x \ll \tilde x$
. To get a contradiction, suppose that
![]() $b \le s$
. Let
$b \le s$
. Let
![]() $0 < t < b$
. Then
$0 < t < b$
. Then
![]() $\gamma _v(t) = \lim _{j \to \infty } \gamma _{v_j}(t)$
and for large j it holds that
$\gamma _v(t) = \lim _{j \to \infty } \gamma _{v_j}(t)$
and for large j it holds that
![]() $\gamma _{v_j}(t) \le \gamma _{v_j}(s_j) \ll \tilde x$
. As the relation
$\gamma _{v_j}(t) \le \gamma _{v_j}(s_j) \ll \tilde x$
. As the relation
![]() $\le $
is closed, it follows that
$\le $
is closed, it follows that
![]() $\gamma _v(t) \le \tilde x$
for
$\gamma _v(t) \le \tilde x$
for
![]() $0 < t < b$
. Now the future inextendible causal curve
$0 < t < b$
. Now the future inextendible causal curve
![]() $\gamma _v(t)$
,
$\gamma _v(t)$
,
![]() $0 < t < b$
, never leaves the compact set
$0 < t < b$
, never leaves the compact set
![]() $J^+(p) \cap J^-(q)$
where
$J^+(p) \cap J^-(q)$
where
![]() $p = \pi (v)$
and
$p = \pi (v)$
and
![]() $q = \tilde x$
. This is a contradiction with [Reference O’Neill79, Lem. 13, p. 408].
$q = \tilde x$
. This is a contradiction with [Reference O’Neill79, Lem. 13, p. 408].
Lemma 6.3. Let
![]() $K \subset M$
be compact. The exit function
$K \subset M$
be compact. The exit function
is finite and upper semi-continuous.
Proof. Finiteness follows from [Reference O’Neill79, Lem. 13 (p. 408)]. Suppose that
![]() $v_j \to v$
in
$v_j \to v$
in
![]() $C^+ K$
and that
$C^+ K$
and that
![]() $t_j := R(v_j) \to t$
for some
$t_j := R(v_j) \to t$
for some
![]() $t \geqslant 0$
. The upper semi-continuity
$t \geqslant 0$
. The upper semi-continuity
![]() $t \le R(v)$
follows from the convergence
$t \le R(v)$
follows from the convergence
![]() $\gamma _{v_{j}}(t_{j}) \to \gamma _v(t)$
in K, which again follows from Lemma 6.2.
$\gamma _{v_{j}}(t_{j}) \to \gamma _v(t)$
in K, which again follows from Lemma 6.2.
Lemma 6.4. Suppose that
![]() $v_j \to v$
in
$v_j \to v$
in
![]() $C^+M$
. If a sequence
$C^+M$
. If a sequence
![]() $s_j \geqslant 0$
,
$s_j \geqslant 0$
,
![]() $j \in \mathbb N$
, satisfies
$j \in \mathbb N$
, satisfies
![]() $\gamma _{v_j}(s_j) \to y$
for some
$\gamma _{v_j}(s_j) \to y$
for some
![]() $y \in M$
, then
$y \in M$
, then
![]() $s_j$
converges.
$s_j$
converges.
Proof. We write
![]() $\pi (v) = x$
,
$\pi (v) = x$
,
![]() $\pi (v_j) = x_j$
and
$\pi (v_j) = x_j$
and
![]() $\gamma _{v_j}(s_j) = y_j$
. Let X and Y be bounded neighbourhoods of x and y, respectively, and write
$\gamma _{v_j}(s_j) = y_j$
. Let X and Y be bounded neighbourhoods of x and y, respectively, and write
![]() $K= J^+(\overline X) \cap J^-(\overline Y)$
. Then we have
$K= J^+(\overline X) \cap J^-(\overline Y)$
. Then we have
![]() $x_j, y_j \in K$
for large j. Now Lemma 6.3 implies that
$x_j, y_j \in K$
for large j. Now Lemma 6.3 implies that
![]() $s_j < R(v_j) \le R(v) + 1$
for large j, where R is the exit function of K. Write
$s_j < R(v_j) \le R(v) + 1$
for large j, where R is the exit function of K. Write
![]() $t^+ = \limsup _{j \to \infty } s_j$
and
$t^+ = \limsup _{j \to \infty } s_j$
and
![]() $t^- = \liminf _{j \to \infty } s_j$
. These are both finite. There are subsequences
$t^- = \liminf _{j \to \infty } s_j$
. These are both finite. There are subsequences
![]() $s_{j_k}^\pm $
converging to
$s_{j_k}^\pm $
converging to
![]() $t^\pm $
and
$t^\pm $
and
 $\gamma _{v_{j_k}}(s_{j_k}^\pm ) \to \gamma _v(t^\pm ) = y$
. Now
$\gamma _{v_{j_k}}(s_{j_k}^\pm ) \to \gamma _v(t^\pm ) = y$
. Now
![]() $t^- = t^+$
by global hyperbolicity.
$t^- = t^+$
by global hyperbolicity.
The analogues of Lemmas 6.2–6.4 hold also for past-pointing vectors.
6.2 Cut function
The cut function is defined by
We define
![]() $\rho (v)$
also for
$\rho (v)$
also for
![]() $v \in L^- M$
by the above expression but with respect to the opposite time orientation. It follows from the definition of
$v \in L^- M$
by the above expression but with respect to the opposite time orientation. It follows from the definition of
![]() $\rho $
and Lemma 6.1 that if
$\rho $
and Lemma 6.1 that if
![]() $\gamma _v(s)$
is well-defined for some
$\gamma _v(s)$
is well-defined for some
![]() $s> \rho (v)$
, then there is a time-like path from
$s> \rho (v)$
, then there is a time-like path from
![]() $\gamma _v(0)$
to
$\gamma _v(0)$
to
![]() $\gamma _v(s)$
. On the other hand, [Reference Belishev and Katchalov9, Lem. 9.13] implies the following.
$\gamma _v(s)$
. On the other hand, [Reference Belishev and Katchalov9, Lem. 9.13] implies the following.
Lemma 6.5. Let
![]() $v \in L^+M$
and
$v \in L^+M$
and
![]() $s < \rho (v)$
. Then the geodesic segment along
$s < \rho (v)$
. Then the geodesic segment along
![]() $\gamma _v$
is the only causal path from
$\gamma _v$
is the only causal path from
![]() $\gamma _v(0)$
to
$\gamma _v(0)$
to
![]() $\gamma _v(s)$
up to a reparametrisation.
$\gamma _v(s)$
up to a reparametrisation.
The following lemma is a variant of [Reference Belishev and Katchalov9, Prop. 9.7].
Lemma 6.6. The cut function
![]() $\rho : L^+ M \to [0,\infty ]$
is lower semi-continuous.
$\rho : L^+ M \to [0,\infty ]$
is lower semi-continuous.
Proof. Suppose that
![]() $v_j \to v$
in
$v_j \to v$
in
![]() $L^+M$
and write
$L^+M$
and write
![]() $t_j = \rho (v_j)$
. We need to show that if
$t_j = \rho (v_j)$
. We need to show that if
![]() $t_j \to t$
for some
$t_j \to t$
for some
![]() $t \geqslant 0$
then
$t \geqslant 0$
then
![]() $t \geqslant \rho (v)$
. To get a contradiction, suppose that the opposite holds. Then there is
$t \geqslant \rho (v)$
. To get a contradiction, suppose that the opposite holds. Then there is
![]() $\delta> 0$
such that
$\delta> 0$
such that
![]() $t + \delta < \rho (v)$
. In particular,
$t + \delta < \rho (v)$
. In particular,
![]() $\gamma _v(t+\delta )$
is well-defined, and this implies that
$\gamma _v(t+\delta )$
is well-defined, and this implies that
![]() $\gamma _{v_j}(t_j + \delta )$
is also well-defined for large j. Writing
$\gamma _{v_j}(t_j + \delta )$
is also well-defined for large j. Writing
![]() $x_j = \pi (v_j)$
and
$x_j = \pi (v_j)$
and
![]() $y_j = \gamma _{v_j}(t_j + \delta )$
, there holds
$y_j = \gamma _{v_j}(t_j + \delta )$
, there holds
![]() $\tau (x_j, y_j)> 0$
since
$\tau (x_j, y_j)> 0$
since
![]() $t_j + \delta> \rho (v_j)$
. We also write
$t_j + \delta> \rho (v_j)$
. We also write
![]() $(x,\xi ) = v$
and
$(x,\xi ) = v$
and
![]() $y = \gamma _v(t + \delta )$
. Then
$y = \gamma _v(t + \delta )$
. Then
![]() $x_j \to x$
and
$x_j \to x$
and
![]() $y_j \to y$
. Let X be a bounded neighbourhood of x and define
$y_j \to y$
. Let X be a bounded neighbourhood of x and define
![]() $K= \overline X$
.
$K= \overline X$
.
Let us choose an auxiliary Riemannian metric on M and denote by
![]() $SM$
the unit sphere bundle with respect to that metric. By [Reference O’Neill79, Prop. 19, p. 411] there is a time-like geodesic from
$SM$
the unit sphere bundle with respect to that metric. By [Reference O’Neill79, Prop. 19, p. 411] there is a time-like geodesic from
![]() $x_j$
to
$x_j$
to
![]() $y_j$
. We may reparametrise this geodesic to obtain time-like
$y_j$
. We may reparametrise this geodesic to obtain time-like
![]() $\xi _j$
in
$\xi _j$
in
 $C^+_{x_j} K \cap S_{x_j} M$
and
$C^+_{x_j} K \cap S_{x_j} M$
and
![]() $s_j> 0$
satisfying
$s_j> 0$
satisfying
![]() $\gamma _{x_j,\xi _j}(s_j) = y_j$
. As
$\gamma _{x_j,\xi _j}(s_j) = y_j$
. As
![]() $C^+ K \cap SM$
is compact, by passing to a subsequence, we may assume that
$C^+ K \cap SM$
is compact, by passing to a subsequence, we may assume that
![]() $\xi _j \to \tilde \xi $
for some
$\xi _j \to \tilde \xi $
for some
![]() $\tilde \xi \in C^+_{x} K \cap S_x M$
. Lemma 6.4 implies that
$\tilde \xi \in C^+_{x} K \cap S_x M$
. Lemma 6.4 implies that
![]() $s_j \to s$
for some
$s_j \to s$
for some
![]() $s \geqslant 0$
.
$s \geqslant 0$
.
If there is no
![]() $c \in \mathbb R$
such that
$c \in \mathbb R$
such that
![]() $\tilde \xi = c \xi $
, then there are two distinct causal geodesics from x to y. This is a contradiction in view of Lemma 6.5 since
$\tilde \xi = c \xi $
, then there are two distinct causal geodesics from x to y. This is a contradiction in view of Lemma 6.5 since
![]() $x = \pi (v)$
,
$x = \pi (v)$
,
![]() $y = \gamma _v(t+\delta )$
and
$y = \gamma _v(t+\delta )$
and
![]() $t + \delta < \rho (v)$
. Hence, there is
$t + \delta < \rho (v)$
. Hence, there is
![]() $c \in \mathbb R$
such that
$c \in \mathbb R$
such that
![]() $\tilde \xi = c \xi $
, and, in fact,
$\tilde \xi = c \xi $
, and, in fact,
![]() $c> 0$
since
$c> 0$
since
![]() $\xi , \tilde \xi \in C^+_{x} K$
and
$\xi , \tilde \xi \in C^+_{x} K$
and
![]() $\tilde \xi \in S_x M.$
Now
$\tilde \xi \in S_x M.$
Now
![]() $(x_j,c^{-1}\xi _j) \to v$
and
$(x_j,c^{-1}\xi _j) \to v$
and
![]() $cs_j \to t + \delta $
. None of the points
$cs_j \to t + \delta $
. None of the points
![]() $\gamma _v(r)$
,
$\gamma _v(r)$
,
![]() $0 \le r \le t + \delta $
, is conjugate to x along
$0 \le r \le t + \delta $
, is conjugate to x along
![]() $\gamma _v$
by [Reference Belishev and Katchalov9, Th. 10.72], and the map
$\gamma _v$
by [Reference Belishev and Katchalov9, Th. 10.72], and the map
![]() $s \mapsto \gamma _v(s)$
is injective due to global hyperbolicity. Hence, there is a neighbourhood U of
$s \mapsto \gamma _v(s)$
is injective due to global hyperbolicity. Hence, there is a neighbourhood U of
![]() $[0, t+\delta ] v$
such that
$[0, t+\delta ] v$
such that
![]() $\pi \times \exp $
is injective on U. But
$\pi \times \exp $
is injective on U. But
![]() $t_j v_j, (x_j, s_j \xi _j) \in U$
for large j and both are mapped to
$t_j v_j, (x_j, s_j \xi _j) \in U$
for large j and both are mapped to
![]() $(x_j, y_j)$
. This is a contradiction since the former is light-like and the latter is time-like.
$(x_j, y_j)$
. This is a contradiction since the former is light-like and the latter is time-like.
The following lemma is a variant of [Reference Belishev and Katchalov9, Prop. 9.5].
Lemma 6.7. Let
![]() $v_j \to v$
in
$v_j \to v$
in
![]() $L^+M$
and
$L^+M$
and
![]() $\rho (v_j) \to t$
in
$\rho (v_j) \to t$
in
![]() $\mathbb R$
. Suppose that
$\mathbb R$
. Suppose that
![]() $\gamma _v(t)$
is well-defined. Then
$\gamma _v(t)$
is well-defined. Then
![]() $\rho (v) = t$
.
$\rho (v) = t$
.
Proof. Lower semi-continuity of
![]() $\rho $
implies that
$\rho $
implies that
![]() $\rho (v) \le t$
. To get a contradiction, suppose there is
$\rho (v) \le t$
. To get a contradiction, suppose there is
![]() $\delta> 0$
such that
$\delta> 0$
such that
![]() $\rho (v) + \delta < t$
. Then
$\rho (v) + \delta < t$
. Then
![]() $\rho (v) + \delta < \rho (v_j)$
for large j. We are led to the contradiction
$\rho (v) + \delta < \rho (v_j)$
for large j. We are led to the contradiction
 $$ \begin{align*} \tau(v, \beta_{v}(\rho(v) + \delta)) = \lim_{j \to \infty} \tau(v_j, \beta_{v_j}(\rho(v) + \delta)) = 0. \end{align*} $$
$$ \begin{align*} \tau(v, \beta_{v}(\rho(v) + \delta)) = \lim_{j \to \infty} \tau(v_j, \beta_{v_j}(\rho(v) + \delta)) = 0. \end{align*} $$
The analogues of Lemmas 6.5–6.7 hold also for past-pointing vectors. Moreover, the cut function has the following symmetry.
Lemma 6.8. Let
![]() $v \in L^+M$
and suppose that
$v \in L^+M$
and suppose that
![]() $\gamma _v(\rho (v))$
is well-defined. Then
$\gamma _v(\rho (v))$
is well-defined. Then
Proof. Write
![]() $w = -\beta _v(\rho (v))$
. To get a contradiction, suppose that
$w = -\beta _v(\rho (v))$
. To get a contradiction, suppose that
![]() $\rho (w) < s < \rho (v)$
. Then there is a past-pointing time-like path from
$\rho (w) < s < \rho (v)$
. Then there is a past-pointing time-like path from
![]() $\gamma _w(0)$
to
$\gamma _w(0)$
to
![]() $\gamma _w(s)$
, a contradiction with
$\gamma _w(s)$
, a contradiction with
![]() $\tau (v,w) = 0$
. To get a contradiction, suppose that
$\tau (v,w) = 0$
. To get a contradiction, suppose that
![]() $\rho (v) < \rho (w)$
. For small
$\rho (v) < \rho (w)$
. For small
![]() $\epsilon> 0$
the vector
$\epsilon> 0$
the vector
![]() $\tilde w = -\beta _v(\rho (v) + \epsilon )$
is well-defined. Moreover, lower semi-continuity of
$\tilde w = -\beta _v(\rho (v) + \epsilon )$
is well-defined. Moreover, lower semi-continuity of
![]() $\rho $
implies that
$\rho $
implies that
![]() $\rho (v) + \epsilon < \rho (\tilde w)$
for small enough
$\rho (v) + \epsilon < \rho (\tilde w)$
for small enough
![]() $\epsilon> 0$
. Lemma 6.5 implies then that
$\epsilon> 0$
. Lemma 6.5 implies then that
![]() $\gamma _{\tilde w}$
is the only causal path from
$\gamma _{\tilde w}$
is the only causal path from
![]() $\gamma _{\tilde w}(0)$
to
$\gamma _{\tilde w}(0)$
to
![]() $\gamma _{\tilde w}(\rho (v) + \epsilon ) = \pi (v)$
. Therefore,
$\gamma _{\tilde w}(\rho (v) + \epsilon ) = \pi (v)$
. Therefore,
![]() $\tau (v, \tilde w) = 0$
, a contradiction with the definition of
$\tau (v, \tilde w) = 0$
, a contradiction with the definition of
![]() $\tilde w$
.
$\tilde w$
.
The above lemma implies that if
![]() $\gamma _v(s)$
, with
$\gamma _v(s)$
, with
![]() $s < 0$
, and
$s < 0$
, and
![]() $\gamma _v(\rho (v))$
are both well-defined, then there is a time-like path from
$\gamma _v(\rho (v))$
are both well-defined, then there is a time-like path from
![]() $\gamma _v(s)$
to
$\gamma _v(s)$
to
![]() $\gamma _v(\rho (v))$
.
$\gamma _v(\rho (v))$
.
6.3 Optimising geodesics and earliest observation functions
Recall that a null geodesic
![]() $\gamma $
from x to y on M is not optimising if
$\gamma $
from x to y on M is not optimising if
![]() $\tau (x,y)> 0$
. In other words, if
$\tau (x,y)> 0$
. In other words, if
![]() $\gamma = \gamma _v$
for some
$\gamma = \gamma _v$
for some
![]() $v \in L^+M$
, then it is optimising from
$v \in L^+M$
, then it is optimising from
![]() $x = \gamma _v(0)$
to
$x = \gamma _v(0)$
to
![]() $y = \gamma _v(s)$
if and only if
$y = \gamma _v(s)$
if and only if
![]() $s \leqslant \rho (v)$
. In the case
$s \leqslant \rho (v)$
. In the case
![]() $s = \rho (v)$
there may be other optimising null geodesics from x to y, corresponding to different initial directions at x. One more simple, but nonetheless useful, observation is that if there is an optimising null geodesic from x to y, then all causal paths from x to y are optimising null geodesics. This follows from Lemma 6.1.
$s = \rho (v)$
there may be other optimising null geodesics from x to y, corresponding to different initial directions at x. One more simple, but nonetheless useful, observation is that if there is an optimising null geodesic from x to y, then all causal paths from x to y are optimising null geodesics. This follows from Lemma 6.1.
The results below will be applied to one of the paths
![]() $\mu _{\mathrm{in}}:[t_1^-,t_1^+]\to M$
and
$\mu _{\mathrm{in}}:[t_1^-,t_1^+]\to M$
and
![]() $\mu _{\mathrm{out}}:[s_1^-,s_1^+]\to M$
. However, to simplify the notations, we consider here a time-like future-pointing path
$\mu _{\mathrm{out}}:[s_1^-,s_1^+]\to M$
. However, to simplify the notations, we consider here a time-like future-pointing path
![]() $\mu : [-1,1] \to M$
. The paths
$\mu : [-1,1] \to M$
. The paths
![]() $\mu _{\mathrm{in}}$
and
$\mu _{\mathrm{in}}$
and
![]() $\mu _{\mathrm{out}}$
can be reparametrised so that they are of this form.
$\mu _{\mathrm{out}}$
can be reparametrised so that they are of this form.
We define the earliest observation functions
 $$ \begin{align*} f_\mu^+(x) &=\inf\{s\in(-1,1] : \tau(x,\mu(s))>0\ \text{or}\ s = 1 \}, \quad &x \in M,\\ f_\mu^-(x) &=\sup\{s\in[-1,1) : \tau(\mu(s),x)>0\ \text{or}\ s = -1 \}, \quad &x \in M. \end{align*} $$
$$ \begin{align*} f_\mu^+(x) &=\inf\{s\in(-1,1] : \tau(x,\mu(s))>0\ \text{or}\ s = 1 \}, \quad &x \in M,\\ f_\mu^-(x) &=\sup\{s\in[-1,1) : \tau(\mu(s),x)>0\ \text{or}\ s = -1 \}, \quad &x \in M. \end{align*} $$
We could also work with an alternative definition of
![]() $f_\mu ^+(x)$
omitting ‘or
$f_\mu ^+(x)$
omitting ‘or
![]() $s=1$
’ above, with the understanding that the infimum of the empty set is
$s=1$
’ above, with the understanding that the infimum of the empty set is
![]() $\infty $
. However, we prefer to follow [Reference Kurylev, Lassas and Uhlmann64] where the above choice was used. A convenient consequence of the choice is that both
$\infty $
. However, we prefer to follow [Reference Kurylev, Lassas and Uhlmann64] where the above choice was used. A convenient consequence of the choice is that both
![]() $f_\mu ^+$
and
$f_\mu ^+$
and
![]() $f_\mu ^-$
are continuous on the whole M; see [Reference Kurylev, Lassas and Uhlmann64, Lemma 2.3 (iv)].
$f_\mu ^-$
are continuous on the whole M; see [Reference Kurylev, Lassas and Uhlmann64, Lemma 2.3 (iv)].
Lemma 6.9. Let
![]() $\mu : [-1,1] \to M$
be a time-like future-pointing path. Suppose that a point
$\mu : [-1,1] \to M$
be a time-like future-pointing path. Suppose that a point
![]() $x \le \mu (1)$
satisfies
$x \le \mu (1)$
satisfies
![]() $x \not \le \mu (-1)$
; in other words,
$x \not \le \mu (-1)$
; in other words,
![]() $x \notin J^-(\mu (-1))$
. Then there is
$x \notin J^-(\mu (-1))$
. Then there is
![]() $s \in (-1, 1]$
such that either there is an optimising null geodesic from x to
$s \in (-1, 1]$
such that either there is an optimising null geodesic from x to
![]() $\mu (s)$
or
$\mu (s)$
or
![]() $x = \mu (s)$
. In both cases
$x = \mu (s)$
. In both cases
![]() $s = f_\mu ^+(x)$
.
$s = f_\mu ^+(x)$
.
Proof. We set
![]() $s = f_\mu ^+(x)$
and
$s = f_\mu ^+(x)$
and
![]() $y = \mu (s)$
. If
$y = \mu (s)$
. If
![]() $s = 1$
, then
$s = 1$
, then
![]() $x \le y$
by the assumption
$x \le y$
by the assumption
![]() $x \le \mu (1)$
. On the other hand, if
$x \le \mu (1)$
. On the other hand, if
![]() $s < 1$
, then
$s < 1$
, then
![]() $x \le y$
also since the causal relation
$x \le y$
also since the causal relation
![]() $\le $
is closed. Hence, there is a causal path from x to y or
$\le $
is closed. Hence, there is a causal path from x to y or
![]() $x=y$
. It remains to show that in the former case there holds
$x=y$
. It remains to show that in the former case there holds
![]() $\tau (x,y) = 0$
, since the path from x to y is then a null geodesic up to a reparametrisation by Lemma 6.1. There holds
$\tau (x,y) = 0$
, since the path from x to y is then a null geodesic up to a reparametrisation by Lemma 6.1. There holds
![]() $s> -1$
since
$s> -1$
since
![]() $x \not \le \mu (-1)$
. This again implies that
$x \not \le \mu (-1)$
. This again implies that
![]() $\tau (x,y) = 0$
.
$\tau (x,y) = 0$
.
A variation of the above proof gives the following.
Lemma 6.10. Let
![]() $\mu : [-1,1] \to M$
be a time-like future-pointing path. Suppose that
$\mu : [-1,1] \to M$
be a time-like future-pointing path. Suppose that
![]() $\mu (-1) \le x$
and
$\mu (-1) \le x$
and
![]() $\mu (1) \not \le x$
. Then there is
$\mu (1) \not \le x$
. Then there is
![]() $s \in [-1, 1)$
such that there is an optimising null geodesic from
$s \in [-1, 1)$
such that there is an optimising null geodesic from
![]() $\mu (s)$
to x or
$\mu (s)$
to x or
![]() $x = \mu (s)$
. In both cases
$x = \mu (s)$
. In both cases
![]() $s = f_\mu ^-(x)$
.
$s = f_\mu ^-(x)$
.
Lemma 6.11. Let
![]() $\mu : [-1,1] \to M$
be a time-like future-pointing path, let
$\mu : [-1,1] \to M$
be a time-like future-pointing path, let
![]() $v \in L^+M$
and write
$v \in L^+M$
and write
![]() $f(s) = f_\mu ^+(\gamma _v(s))$
. Suppose that
$f(s) = f_\mu ^+(\gamma _v(s))$
. Suppose that
![]() $\mu $
and
$\mu $
and
![]() $\gamma _{v}$
do not intersect. Then
$\gamma _{v}$
do not intersect. Then
-
(1) f is increasing;
-
(2) if
 $-1 < f(s_0) < 1$
for some
$-1 < f(s_0) < 1$
for some
 $s_0$
, then f is strictly increasing near
$s_0$
, then f is strictly increasing near
 $s_0$
;
$s_0$
; -
(3) if
 $f(s_0) = 1$
and
$f(s_0) = 1$
and
 $\gamma _v(s_0) < \mu (1)$
for some
$\gamma _v(s_0) < \mu (1)$
for some
 $s_0$
, then f is strictly increasing for
$s_0$
, then f is strictly increasing for
 $s < s_0$
near
$s < s_0$
near
 $s_0$
.
$s_0$
.
Proof. If there is
![]() $s> s_0$
such that
$s> s_0$
such that
![]() $f(s) \leqslant f(s_0)$
and
$f(s) \leqslant f(s_0)$
and
![]() $f(s) < 1$
, then there is a causal path from
$f(s) < 1$
, then there is a causal path from
![]() $\gamma _v(s_0)$
to
$\gamma _v(s_0)$
to
![]() $\mu (f(s_0))$
via
$\mu (f(s_0))$
via
![]() $\gamma _v(s)$
that is not a null pregeodesic and therefore
$\gamma _v(s)$
that is not a null pregeodesic and therefore
![]() $\tau (\gamma _v(s_0), \mu (f(s_0)))> 0$
by Lemma 6.1. If also
$\tau (\gamma _v(s_0), \mu (f(s_0)))> 0$
by Lemma 6.1. If also
![]() $-1 < f(s_0)$
then there holds
$-1 < f(s_0)$
then there holds
![]() $\tau (\gamma _v(s_0), \mu (f(s_0))) = 0$
, a contradiction. This shows (2) and also that if
$\tau (\gamma _v(s_0), \mu (f(s_0))) = 0$
, a contradiction. This shows (2) and also that if
![]() $f(s_0) = 1$
then
$f(s_0) = 1$
then
![]() $f(s) = 1$
for
$f(s) = 1$
for
![]() $s> s_0$
.
$s> s_0$
.
If
![]() $f(s_0) = -1$
, then
$f(s_0) = -1$
, then
![]() $f(s) = -1$
for
$f(s) = -1$
for
![]() $s < s_0$
. Indeed, there is a causal path from
$s < s_0$
. Indeed, there is a causal path from
![]() $\gamma _v(s)$
to
$\gamma _v(s)$
to
![]() $\mu (-1)$
via
$\mu (-1)$
via
![]() $\gamma _v(s_0)$
that is not a null pregeodesic. We have shown (1).
$\gamma _v(s_0)$
that is not a null pregeodesic. We have shown (1).
Let us now suppose that
![]() $f(s_0) = 1$
and there is a causal path from
$f(s_0) = 1$
and there is a causal path from
![]() $\gamma _v(s_0)$
to
$\gamma _v(s_0)$
to
![]() $\mu (1)$
. Let
$\mu (1)$
. Let
![]() $s < s_0$
be near
$s < s_0$
be near
![]() $s_0$
. There is a causal path from
$s_0$
. There is a causal path from
![]() $\gamma _v(s)$
to
$\gamma _v(s)$
to
![]() $\mu (1)$
via
$\mu (1)$
via
![]() $\gamma _v(s_0)$
that is not a null pregeodesic and therefore
$\gamma _v(s_0)$
that is not a null pregeodesic and therefore
![]() $\tau (\gamma _v(s_0), \mu (1))> 0$
. But then also
$\tau (\gamma _v(s_0), \mu (1))> 0$
. But then also
![]() $\tau (\gamma _v(s_0), \mu (t))> 0$
for t close to 1 by continuity. This implies that
$\tau (\gamma _v(s_0), \mu (t))> 0$
for t close to 1 by continuity. This implies that
![]() $f(s) < 1$
and as also
$f(s) < 1$
and as also
![]() $-1 < f(s)$
by continuity, we see that (3) follows from (2).
$-1 < f(s)$
by continuity, we see that (3) follows from (2).
We have the following variant of [Reference Kurylev, Lassas and Uhlmann64, Lemma 2.3(iv)].
Lemma 6.12. Let
![]() $\mu _a : [-1,1] \to M$
be a family of time-like future-pointing paths and suppose that
$\mu _a : [-1,1] \to M$
be a family of time-like future-pointing paths and suppose that
![]() $\mu _a(s) = (s, a)$
,
$\mu _a(s) = (s, a)$
,
![]() $a \in U \subset \mathbb R^n$
, in some local coordinates. Suppose that
$a \in U \subset \mathbb R^n$
, in some local coordinates. Suppose that
![]() $x_j \to x$
in M and
$x_j \to x$
in M and
![]() $a_j \to a$
in U. Then
$a_j \to a$
in U. Then
 $f_{\mu _{a_j}}^+(x_j) \to f_{\mu _a}^+(x)$
.
$f_{\mu _{a_j}}^+(x_j) \to f_{\mu _a}^+(x)$
.
Proof. Let us consider first the case that
![]() $s:=f_{\mu _a}^+(x) < 1$
. Then
$s:=f_{\mu _a}^+(x) < 1$
. Then
![]() $\tau (x, (s + \epsilon , a))> 0$
for any small
$\tau (x, (s + \epsilon , a))> 0$
for any small
![]() $\epsilon> 0$
. Continuity of
$\epsilon> 0$
. Continuity of
![]() $\tau $
implies that
$\tau $
implies that
![]() $\tau (x_j, (s + \epsilon , a_j))> 0$
for large j. Hence,
$\tau (x_j, (s + \epsilon , a_j))> 0$
for large j. Hence,
 $\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s + \epsilon \to s$
as
$\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s + \epsilon \to s$
as
![]() $\epsilon \to 0$
. Clearly, also
$\epsilon \to 0$
. Clearly, also
 $\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s$
in the case
$\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s$
in the case
![]() $s = 1$
.
$s = 1$
.
To get a contradiction, suppose that
 $\tilde s := \liminf _{j\to \infty }f_{\mu _{a_j}}^+(x_j) < s$
. By passing to a subsequence, we may replace
$\tilde s := \liminf _{j\to \infty }f_{\mu _{a_j}}^+(x_j) < s$
. By passing to a subsequence, we may replace
![]() $\liminf $
by
$\liminf $
by
![]() $\lim $
above. Moreover,
$\lim $
above. Moreover,
and letting
![]() $j \to \infty $
, we obtain
$j \to \infty $
, we obtain
This is in contradiction with
![]() $s=f_{\mu _a}^+(x)$
since
$s=f_{\mu _a}^+(x)$
since
![]() $s> \tilde s \geqslant -1$
.
$s> \tilde s \geqslant -1$
.
6.4 Three shortcut arguments
We denote the image of a path
![]() $\mu : I \to M$
, with I an interval in
$\mu : I \to M$
, with I an interval in
![]() $\mathbb R$
, by
$\mathbb R$
, by
and use also the shorthand notations
We say that two geodesics
![]() $\gamma _v$
and
$\gamma _v$
and
![]() $\gamma _w$
are distinct if
$\gamma _w$
are distinct if
![]() $\overline {\gamma _v} \ne \overline {\gamma _w}$
.
$\overline {\gamma _v} \ne \overline {\gamma _w}$
.
Lemma 6.13. Let
![]() $x_1, x_2, y \in M$
and
$x_1, x_2, y \in M$
and
![]() $v_1, v_2, w \in L^+ M$
. Suppose that
$v_1, v_2, w \in L^+ M$
. Suppose that
![]() $\gamma _{v_j}$
is optimising from
$\gamma _{v_j}$
is optimising from
![]() $x_j$
to y for
$x_j$
to y for
![]() $j=1,2$
and that
$j=1,2$
and that
![]() $\gamma _{v_1}$
,
$\gamma _{v_1}$
,
![]() $\gamma _{v_2}$
and
$\gamma _{v_2}$
and
![]() $\gamma _{w}$
are all distinct. Suppose, furthermore, that
$\gamma _{w}$
are all distinct. Suppose, furthermore, that
![]() $y_j \in \overline {\gamma _{v_j}} \cap \overline {\gamma _{w}}$
satisfy
$y_j \in \overline {\gamma _{v_j}} \cap \overline {\gamma _{w}}$
satisfy
![]() $x_j < y_j$
for both
$x_j < y_j$
for both
![]() $j=1,2$
. Then either
$j=1,2$
. Then either
![]() $y=y_1=y_2$
or at least one of
$y=y_1=y_2$
or at least one of
![]() $y_1$
,
$y_1$
,
![]() $y_2$
satisfies
$y_2$
satisfies
![]() $y < y_j$
.
$y < y_j$
.
Proof. As
![]() $y_j, y \in \overline {\gamma _{v_j}}$
, there holds either
$y_j, y \in \overline {\gamma _{v_j}}$
, there holds either
![]() $y < y_j$
or
$y < y_j$
or
![]() $y_j \le y$
. We suppose that
$y_j \le y$
. We suppose that
![]() $y_j \le y$
for both
$y_j \le y$
for both
![]() $j=1,2$
and show that
$j=1,2$
and show that
![]() $y=y_1=y_2$
.
$y=y_1=y_2$
.
To get a contradiction, suppose that
![]() $y_1 < y_2$
. The path from
$y_1 < y_2$
. The path from
![]() $x_1$
to y obtained by first following
$x_1$
to y obtained by first following
![]() $\gamma _{v_1}$
from
$\gamma _{v_1}$
from
![]() $x_1$
to
$x_1$
to
![]() $y_1$
, then
$y_1$
, then
![]() $\gamma _{w}$
from
$\gamma _{w}$
from
![]() $y_1$
to
$y_1$
to
![]() $y_2$
and finally
$y_2$
and finally
![]() $\gamma _{v_2}$
from
$\gamma _{v_2}$
from
![]() $y_2$
to y is not a null pregeodesic since
$y_2$
to y is not a null pregeodesic since
![]() $\gamma _{v_1}$
and
$\gamma _{v_1}$
and
![]() $\gamma _w$
are distinct and
$\gamma _w$
are distinct and
![]() $x_1 < y_1 < y_2$
. But Lemma 6.1 implies that
$x_1 < y_1 < y_2$
. But Lemma 6.1 implies that
![]() $x_1 \ll y$
, a contradiction with
$x_1 \ll y$
, a contradiction with
![]() $\gamma _{v_1}$
being optimising from
$\gamma _{v_1}$
being optimising from
![]() $x_1$
to y. By symmetry,
$x_1$
to y. By symmetry,
![]() $y_2 < y_1$
also leads to a contradiction.
$y_2 < y_1$
also leads to a contradiction.
We have shown that
![]() $y_1 = y_2$
. To get a contradiction, suppose that
$y_1 = y_2$
. To get a contradiction, suppose that
![]() $y_1 < y$
. The path obtained by first following
$y_1 < y$
. The path obtained by first following
![]() $\gamma _{v_1}$
from
$\gamma _{v_1}$
from
![]() $x_1$
to
$x_1$
to
![]() $y_1$
and then
$y_1$
and then
![]() $\gamma _{v_2}$
from
$\gamma _{v_2}$
from
![]() $y_1$
to y is not a null pregeodesic, leading again to the contradiction
$y_1$
to y is not a null pregeodesic, leading again to the contradiction
![]() $x_1 \ll y$
.
$x_1 \ll y$
.
Lemma 6.14. Let
![]() $v \in L^+ M$
, let
$v \in L^+ M$
, let
![]() $K \subset M$
be compact and let
$K \subset M$
be compact and let
![]() $x \in \overline {\gamma _v}$
satisfy
$x \in \overline {\gamma _v}$
satisfy
![]() $x < \pi (v)$
. Then there is a neighbourhood
$x < \pi (v)$
. Then there is a neighbourhood
![]() $\mathcal U \subset L^+ M$
of v such that for all
$\mathcal U \subset L^+ M$
of v such that for all
![]() $w \in \mathcal U$
it holds that if there are
$w \in \mathcal U$
it holds that if there are
![]() $y \in \overrightarrow {\gamma _{w}} \cap K$
and
$y \in \overrightarrow {\gamma _{w}} \cap K$
and
![]() $z \in \overrightarrow {\gamma _{v}} \cap K$
satisfying
$z \in \overrightarrow {\gamma _{v}} \cap K$
satisfying
![]() $y < z$
and two distinct geodesics from y to z, then
$y < z$
and two distinct geodesics from y to z, then
![]() $\gamma _v$
is not optimising from x to z.
$\gamma _v$
is not optimising from x to z.
Proof. Suppose that there are
 $\{w_j\}_{j=1}^{\infty }\subset L^+M$
with
$\{w_j\}_{j=1}^{\infty }\subset L^+M$
with
![]() $\lim _{j\to \infty }w_j=v$
and
$\lim _{j\to \infty }w_j=v$
and
 $$ \begin{align*} y_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad z_j \in \overrightarrow{\gamma_{v}} \cap K, \end{align*} $$
$$ \begin{align*} y_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad z_j \in \overrightarrow{\gamma_{v}} \cap K, \end{align*} $$
satisfying
![]() $y_j < z_j$
and two distinct geodesics from
$y_j < z_j$
and two distinct geodesics from
![]() $y_j$
to
$y_j$
to
![]() $z_j$
. Due to compactness, we may pass to a subsequence and assume without loss of generality that
$z_j$
. Due to compactness, we may pass to a subsequence and assume without loss of generality that
![]() $y_j \to y$
and
$y_j \to y$
and
![]() $z_j \to z$
for some
$z_j \to z$
for some
![]() $y, z \in K$
. Now
$y, z \in K$
. Now
![]() $w_j \to v$
and
$w_j \to v$
and
![]() $y_j \to y$
imply that
$y_j \to y$
imply that
![]() $y \in \overrightarrow {\gamma _{v}}$
.
$y \in \overrightarrow {\gamma _{v}}$
.
We show first that the points y and z must be distinct. To get a contradiction, suppose that
![]() $y=z$
. As M is globally hyperbolic, y has an arbitrarily small neighbourhood U such that no causal path that leaves U ever returns to U. Thus, for large j the two distinct causal geodesics from
$y=z$
. As M is globally hyperbolic, y has an arbitrarily small neighbourhood U such that no causal path that leaves U ever returns to U. Thus, for large j the two distinct causal geodesics from
![]() $y_j$
to
$y_j$
to
![]() $z_j$
are contained in U. But when U is small, it is contained in a convex neighbourhood of y; see, for example, [Reference O’Neill79, Prop. 7 (p. 130)], a contradiction.
$z_j$
are contained in U. But when U is small, it is contained in a convex neighbourhood of y; see, for example, [Reference O’Neill79, Prop. 7 (p. 130)], a contradiction.
As
![]() $y_j < z_j$
, the relation
$y_j < z_j$
, the relation
![]() $\le $
is closed and
$\le $
is closed and
![]() $y \ne z$
, we have
$y \ne z$
, we have
![]() $y < z$
. Denote by
$y < z$
. Denote by
![]() $\eta _j$
the direction of a geodesic from
$\eta _j$
the direction of a geodesic from
![]() $y_j$
to
$y_j$
to
![]() $z_j$
, normalised with respect to some auxiliary Riemannian metric. Due to compactness, we may pass to a subsequence and assume without loss of generality that
$z_j$
, normalised with respect to some auxiliary Riemannian metric. Due to compactness, we may pass to a subsequence and assume without loss of generality that
![]() $\eta _j \to \eta $
.
$\eta _j \to \eta $
.
If
![]() $\eta $
is not tangent to
$\eta $
is not tangent to
![]() $\gamma _v$
at y, then the causal path given by
$\gamma _v$
at y, then the causal path given by
![]() $\gamma _v$
from
$\gamma _v$
from
![]() $x < \pi (v) \le y$
to y and by
$x < \pi (v) \le y$
to y and by
![]() $\gamma _{y,\eta }$
from
$\gamma _{y,\eta }$
from
![]() $y < z$
to z is not a null pregeodesic. Hence,
$y < z$
to z is not a null pregeodesic. Hence,
![]() $\gamma _v$
is not optimising from x to z as required.
$\gamma _v$
is not optimising from x to z as required.
Let us now suppose that
![]() $\eta $
is tangent to
$\eta $
is tangent to
![]() $\gamma _v$
at y. We write
$\gamma _v$
at y. We write
![]() $z_j = \gamma _{y, \eta _j}(s_j)$
. Lemma 6.4 implies that
$z_j = \gamma _{y, \eta _j}(s_j)$
. Lemma 6.4 implies that
![]() $s_j \to s$
for some
$s_j \to s$
for some
![]() $s \geqslant 0$
and therefore
$s \geqslant 0$
and therefore
![]() $z = \gamma _{y, \eta }(s)$
. Moreover,
$z = \gamma _{y, \eta }(s)$
. Moreover,
![]() $\rho (y,\eta _j) \leqslant s_j$
by Lemma 6.5, and by passing once again to a subsequence we may assume that
$\rho (y,\eta _j) \leqslant s_j$
by Lemma 6.5, and by passing once again to a subsequence we may assume that
![]() $\rho (y,\eta _j) \to t$
for some
$\rho (y,\eta _j) \to t$
for some
![]() $t \leqslant s$
. Now
$t \leqslant s$
. Now
![]() $\gamma _{y,\eta }(t)$
is well-defined and Lemma 6.7 implies that
$\gamma _{y,\eta }(t)$
is well-defined and Lemma 6.7 implies that
![]() $\rho (y,\eta ) = t$
. Finally, Lemma 6.8 implies that
$\rho (y,\eta ) = t$
. Finally, Lemma 6.8 implies that
![]() $\gamma _v$
is not optimising from x to
$\gamma _v$
is not optimising from x to
![]() $z = \gamma _{y, \eta }(s)$
.
$z = \gamma _{y, \eta }(s)$
.
Lemma 6.15. Let
![]() $v \in L^+ M$
, let
$v \in L^+ M$
, let
![]() $K \subset M$
be compact and let
$K \subset M$
be compact and let
![]() $x \in \overline {\gamma _v}$
satisfy
$x \in \overline {\gamma _v}$
satisfy
![]() $x < \pi (v)$
. Let
$x < \pi (v)$
. Let
![]() $\mu _a : [-1,1] \to M$
be a family of time-like and future-pointing paths and suppose that
$\mu _a : [-1,1] \to M$
be a family of time-like and future-pointing paths and suppose that
![]() $\mu _a(s) = (s, a)$
,
$\mu _a(s) = (s, a)$
,
![]() $a \in U \subset \mathbb R^n$
, in some local coordinates. Suppose, furthermore, that
$a \in U \subset \mathbb R^n$
, in some local coordinates. Suppose, furthermore, that
![]() $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
and
$\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
and
![]() $f_{\mu _0}^+(x)> -1$
. Then there are neighbourhoods
$f_{\mu _0}^+(x)> -1$
. Then there are neighbourhoods
![]() $\mathcal U \subset L^+ M$
of v and
$\mathcal U \subset L^+ M$
of v and
![]() $U' \subset U$
of the origin in
$U' \subset U$
of the origin in
![]() $\mathbb R^n$
such that for all
$\mathbb R^n$
such that for all
![]() $w \in \mathcal U$
and all
$w \in \mathcal U$
and all
![]() $a \in U'$
it holds that if there are
$a \in U'$
it holds that if there are
![]() $y \in \overrightarrow {\gamma _{v}} \cap K$
and
$y \in \overrightarrow {\gamma _{v}} \cap K$
and
![]() $z \in \overrightarrow {\gamma _{w}} \cap K$
satisfying
$z \in \overrightarrow {\gamma _{w}} \cap K$
satisfying
![]() $y < z$
and two distinct geodesics from y to z, then
$y < z$
and two distinct geodesics from y to z, then
![]() $f_{\mu _a}^+(z) \geqslant f_{\mu _a}^+(\gamma _v(t))$
whenever
$f_{\mu _a}^+(z) \geqslant f_{\mu _a}^+(\gamma _v(t))$
whenever
![]() $\gamma _v$
is optimising from x to
$\gamma _v$
is optimising from x to
![]() $\gamma _v(t)$
.
$\gamma _v(t)$
.
Proof. Let
![]() $\xi \in L_x^+ M$
satisfy
$\xi \in L_x^+ M$
satisfy
![]() $\overline {\gamma _{x,\xi }} = \overline {\gamma _v}$
. To get a contradiction, suppose that there are
$\overline {\gamma _{x,\xi }} = \overline {\gamma _v}$
. To get a contradiction, suppose that there are
 $$ \begin{align*} w_j \in L^+ M,\quad a_j \in U,\quad y_j \in \overrightarrow{\gamma_{v}} \cap K, \quad z_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad t_j \in (0, \rho(x,\xi)], \end{align*} $$
$$ \begin{align*} w_j \in L^+ M,\quad a_j \in U,\quad y_j \in \overrightarrow{\gamma_{v}} \cap K, \quad z_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad t_j \in (0, \rho(x,\xi)], \end{align*} $$
and two distinct geodesics from
![]() $y_j$
to
$y_j$
to
![]() $z_j$
, satisfying
$z_j$
, satisfying
![]() $w_j \to v$
,
$w_j \to v$
,
![]() $a_j \to 0$
,
$a_j \to 0$
,
![]() $y_j < z_j$
and
$y_j < z_j$
and
 $$ \begin{align} f_{\mu_{a_j}}^+(z_j) < f_{\mu_{a_j}}^+(\gamma_v(t_j)). \end{align} $$
$$ \begin{align} f_{\mu_{a_j}}^+(z_j) < f_{\mu_{a_j}}^+(\gamma_v(t_j)). \end{align} $$
Due to compactness, we may pass to a subsequence and assume without loss of generality that
![]() $y_j \to y$
and
$y_j \to y$
and
![]() $z_j \to z$
for some
$z_j \to z$
for some
![]() $y, z \in K$
. Now
$y, z \in K$
. Now
![]() $w_j \to v$
and
$w_j \to v$
and
![]() $z_j \to z$
imply that
$z_j \to z$
imply that
![]() $z \in \overrightarrow {\gamma _{v}}$
. As in the proof of Lemma 6.14, we see that
$z \in \overrightarrow {\gamma _{v}}$
. As in the proof of Lemma 6.14, we see that
![]() $\gamma _v$
is not optimising from
$\gamma _v$
is not optimising from
![]() $x < y$
to z. In particular,
$x < y$
to z. In particular,
![]() $z = \gamma _{x,\xi }(s)$
for some
$z = \gamma _{x,\xi }(s)$
for some
![]() $s> \rho (x,\xi )$
.
$s> \rho (x,\xi )$
.
It follows from (6.2) that
 $f_{\mu _{a_j}}^+(z_j) < 1$
and therefore
$f_{\mu _{a_j}}^+(z_j) < 1$
and therefore
![]() $z_j < \mu _{a_j}(1)$
. As the relation
$z_j < \mu _{a_j}(1)$
. As the relation
![]() $\le $
is closed, we have
$\le $
is closed, we have
![]() $z \le \mu _0(1)$
and, in fact,
$z \le \mu _0(1)$
and, in fact,
![]() $z < \mu _0(1)$
as
$z < \mu _0(1)$
as
![]() $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
. Using the assumptions
$\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
. Using the assumptions
![]() $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
and
$\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $
and
![]() $f_{\mu _0}^+(x)> -1$
, Lemma 6.11 implies that the function
$f_{\mu _0}^+(x)> -1$
, Lemma 6.11 implies that the function
![]() $t \mapsto f_{\mu _0}^+(\gamma _{x,\xi }(t))$
is strictly increasing for
$t \mapsto f_{\mu _0}^+(\gamma _{x,\xi }(t))$
is strictly increasing for
![]() $t < s$
near s. Hence,
$t < s$
near s. Hence,
 $$ \begin{align*} f_{\mu_0}^+(\gamma_{x,\xi}(\rho(x,\xi))) < f_{\mu_0}^+(\gamma_{x,\xi}(s)) = f^+_{\mu_0}(z). \end{align*} $$
$$ \begin{align*} f_{\mu_0}^+(\gamma_{x,\xi}(\rho(x,\xi))) < f_{\mu_0}^+(\gamma_{x,\xi}(s)) = f^+_{\mu_0}(z). \end{align*} $$
Moreover,
 $$ \begin{align*} f_{\mu_{a_j}}^+(z_j) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(t_j)) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(\rho(x,\xi))), \end{align*} $$
$$ \begin{align*} f_{\mu_{a_j}}^+(z_j) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(t_j)) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(\rho(x,\xi))), \end{align*} $$
and letting
![]() $j \to \infty $
leads to the contradiction
$j \to \infty $
leads to the contradiction
![]() $f_{\mu _0}^+(z)<f_{\mu _0}^+(z)$
.
$f_{\mu _0}^+(z)<f_{\mu _0}^+(z)$
.
6.5 Flowout from a point
Consider the following set given by the flowout along null rays from a point
![]() $x \in M$
$x \in M$
It is easy to see that
![]() $C(x)$
is a smooth submanifold of dimension n in
$C(x)$
is a smooth submanifold of dimension n in
![]() $TM$
.
$TM$
.
Lemma 6.16. Let
![]() $\mathcal F \subset M$
be finite and nonempty, write
$\mathcal F \subset M$
be finite and nonempty, write
![]() $C = \bigcup _{x \in \mathcal F} \overline {C(x)}$
and let
$C = \bigcup _{x \in \mathcal F} \overline {C(x)}$
and let
![]() $v \in C$
. Then there is a neighbourhood
$v \in C$
. Then there is a neighbourhood
![]() $V \subset L^+M$
of v such that any
$V \subset L^+M$
of v such that any
![]() $w \in C \cap V$
satisfies
$w \in C \cap V$
satisfies
![]() $\overleftarrow {\;\gamma _v} \cap \overleftarrow {\;\gamma _w} \cap \mathcal F \ne \emptyset $
.
$\overleftarrow {\;\gamma _v} \cap \overleftarrow {\;\gamma _w} \cap \mathcal F \ne \emptyset $
.
Proof. Write
![]() $K=J^+(\mathcal F) \cap J^-(\mathcal F)$
and let R be the corresponding exit function. There are a neighbourhood
$K=J^+(\mathcal F) \cap J^-(\mathcal F)$
and let R be the corresponding exit function. There are a neighbourhood
![]() $W_0 \subset L^+M$
of v and
$W_0 \subset L^+M$
of v and
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
![]() $\gamma _w(s)$
is well-defined for
$\gamma _w(s)$
is well-defined for
![]() $w \in W_0$
and
$w \in W_0$
and
![]() $s \in I$
where
$s \in I$
where
![]() $I = [-R(-v)-\epsilon , 0]$
. As R is upper semi-continuous, there is a neighbourhood
$I = [-R(-v)-\epsilon , 0]$
. As R is upper semi-continuous, there is a neighbourhood
![]() $W_1 \subset W_0$
of v such that
$W_1 \subset W_0$
of v such that
![]() $R(-w) \leqslant R(-v) + \epsilon $
for all
$R(-w) \leqslant R(-v) + \epsilon $
for all
![]() $w \in \overline W_1$
. We may assume that
$w \in \overline W_1$
. We may assume that
![]() $W_1$
is bounded. Choose an auxiliary Riemannian metric on M and denote by d the distance function with respect to this metric. Define the function
$W_1$
is bounded. Choose an auxiliary Riemannian metric on M and denote by d the distance function with respect to this metric. Define the function
Then h is uniformly continuous and there is
![]() $c> 0$
such that
$c> 0$
such that
![]() $h(v,s)> c$
for all
$h(v,s)> c$
for all
![]() $s \in I$
. Hence, there is a neighbourhood
$s \in I$
. Hence, there is a neighbourhood
![]() $W_2 \subset W_1$
of v such that
$W_2 \subset W_1$
of v such that
![]() $h(w,s)> 0$
for all
$h(w,s)> 0$
for all
![]() $w \in W_2$
and
$w \in W_2$
and
![]() $s \in I$
. Now
$s \in I$
. Now
![]() $w \in C \cap W_2$
satisfies
$w \in C \cap W_2$
satisfies
![]() $\overleftarrow {\;\gamma _w} \cap (\mathcal F \setminus \overleftarrow {\;\gamma _v}) = \emptyset $
. Therefore,
$\overleftarrow {\;\gamma _w} \cap (\mathcal F \setminus \overleftarrow {\;\gamma _v}) = \emptyset $
. Therefore,
![]() $w \in C$
implies that
$w \in C$
implies that
![]() $\overleftarrow {\;\gamma _w} \cap (\mathcal F \cap \overleftarrow {\;\gamma _v}) \ne \emptyset $
.
$\overleftarrow {\;\gamma _w} \cap (\mathcal F \cap \overleftarrow {\;\gamma _v}) \ne \emptyset $
.
6.6 Earliest observation sets
We define the set of earliest observations
![]() $E(x)$
of null rays from
$E(x)$
of null rays from
![]() $x \in M$
to
$x \in M$
to
![]() $\Omega \subset M$
by
$\Omega \subset M$
by
The sets
![]() $E(x)$
and
$E(x)$
and
![]() $C(x)$
are illustrated in Figure 4. We will assume that
$C(x)$
are illustrated in Figure 4. We will assume that
![]() $\Omega $
has the following form in some local coordinates
$\Omega $
has the following form in some local coordinates
![]() $F:U\subset \mathbb R^{1+n}\to M$
,
$F:U\subset \mathbb R^{1+n}\to M$
,
-
(F)
 $\Omega = F((-1,1) \times B(0,\delta ))$
for a small
$\Omega = F((-1,1) \times B(0,\delta ))$
for a small
 $\delta>0$
and that the paths
$\delta>0$
and that the paths
 $s\mapsto (s,a)$
are time-like and future-pointing for all
$s\mapsto (s,a)$
are time-like and future-pointing for all
 $s\in (-1,1)$
and
$s\in (-1,1)$
and
 $a \in B(0,\delta )$
.
$a \in B(0,\delta )$
.
Note that the abstract condition (F) is satisfied, for example, for the set
![]() $\Omega =\Omega _{\mathrm{out}}$
and
$\Omega =\Omega _{\mathrm{out}}$
and
![]() $\Omega =\Omega _{\mathrm{in}}$
given by (1.10).
$\Omega =\Omega _{\mathrm{in}}$
given by (1.10).

Figure 4 Geometric setting of Lemma 7.3 in the
![]() $1+2$
-dimensional Minkowski space. The time axis is vertical. Set
$1+2$
-dimensional Minkowski space. The time axis is vertical. Set
![]() $\Omega _{\mathrm{out}}$
is the orange solid cylinder, projection
$\Omega _{\mathrm{out}}$
is the orange solid cylinder, projection
![]() $\pi (C(y))$
is the light blue cone, and
$\pi (C(y))$
is the light blue cone, and
![]() $\pi (E(y))$
is drawn in dark blue. Point y is in blue, points
$\pi (E(y))$
is drawn in dark blue. Point y is in blue, points
![]() $x_1, x_2$
are in black and vectors
$x_1, x_2$
are in black and vectors
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
are in red. Geodesics
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
are in red. Geodesics
![]() $\gamma _{v_1}$
and
$\gamma _{v_1}$
and
![]() $\gamma _{v_2}$
are the black lines.
$\gamma _{v_2}$
are the black lines.
Lemma 6.17. Let an open set
![]() $\Omega \subset M$
satisfy (F) and let a point
$\Omega \subset M$
satisfy (F) and let a point
![]() $x \in M$
satisfy
$x \in M$
satisfy
![]() $x \notin J^-(F(\{-1\}\times B(0,\delta )))$
. Then
$x \notin J^-(F(\{-1\}\times B(0,\delta )))$
. Then
Proof. Denote by
![]() $E_0$
the right-hand side of (6.5), let
$E_0$
the right-hand side of (6.5), let
![]() $v \in E_0$
and write
$v \in E_0$
and write
![]() $y=\pi (v)$
. If
$y=\pi (v)$
. If
![]() $x=y$
, then clearly
$x=y$
, then clearly
![]() $v \in E(x)$
. Let us now consider the case that there are
$v \in E(x)$
. Let us now consider the case that there are
![]() $\xi \in L_x^+ M$
and
$\xi \in L_x^+ M$
and
![]() $0 < s\leqslant \rho (x,\xi )$
such that
$0 < s\leqslant \rho (x,\xi )$
such that
![]() $v=\beta _{x,\xi }(s)$
. Clearly,
$v=\beta _{x,\xi }(s)$
. Clearly,
![]() $v\in C(x)$
and
$v\in C(x)$
and
![]() $\gamma _{x,\xi }$
is optimising from x to y. To get a contradiction, suppose that
$\gamma _{x,\xi }$
is optimising from x to y. To get a contradiction, suppose that
![]() $v\notin E(x)$
. Then there exists
$v\notin E(x)$
. Then there exists
![]() $\tilde v\in C(x)$
such that
$\tilde v\in C(x)$
such that
![]() $\tilde v \ll v$
, and writing
$\tilde v \ll v$
, and writing
![]() $\tilde y = \pi (\tilde v)$
we are led to the contradiction
$\tilde y = \pi (\tilde v)$
we are led to the contradiction
![]() $x \le \tilde y \ll y$
with
$x \le \tilde y \ll y$
with
![]() $\gamma _{x,\xi }$
being optimising from x to y. This shows that
$\gamma _{x,\xi }$
being optimising from x to y. This shows that
![]() $v \in E(x)$
.
$v \in E(x)$
.
On the other hand, let
![]() $v\in E(x)$
and
$v\in E(x)$
and
![]() $y=\pi (v)$
. If
$y=\pi (v)$
. If
![]() $x=y$
, then clearly
$x=y$
, then clearly
![]() $v \in E_0$
. Let us now consider the case that there are are
$v \in E_0$
. Let us now consider the case that there are are
![]() $\xi \in L_x^+ M$
and
$\xi \in L_x^+ M$
and
![]() $r> 0$
such that
$r> 0$
such that
![]() $v=\beta _{x,\xi }(r)$
. Working in the local coordinates (F), there is
$v=\beta _{x,\xi }(r)$
. Working in the local coordinates (F), there is
![]() $(s_0,a) \in (-1,1) \times B(0,\delta )$
such that
$(s_0,a) \in (-1,1) \times B(0,\delta )$
such that
![]() $y = F(s_0,a)$
. We define
$y = F(s_0,a)$
. We define
![]() $\mu _a : [-1,1] \to M$
by
$\mu _a : [-1,1] \to M$
by
![]() $\mu _a(s) = F(s,a)$
. Now
$\mu _a(s) = F(s,a)$
. Now
![]() $x < y \le \mu _a(1)$
and we assumed also
$x < y \le \mu _a(1)$
and we assumed also
![]() $x \not \le \mu _a(-1)$
. Lemma 6.9 implies then that
$x \not \le \mu _a(-1)$
. Lemma 6.9 implies then that
![]() $x \in \overline {\mu _a}$
or there is an optimising geodesic from x to
$x \in \overline {\mu _a}$
or there is an optimising geodesic from x to
![]() $\mu _a(s_1)$
for some
$\mu _a(s_1)$
for some
![]() $s_1 \in (-1,1]$
. The former case is not possible, since
$s_1 \in (-1,1]$
. The former case is not possible, since
![]() $x < y$
and
$x < y$
and
![]() $x,y \in \overline {\mu _a}$
imply
$x,y \in \overline {\mu _a}$
imply
![]() $x \ll y$
, and this is a contradiction with
$x \ll y$
, and this is a contradiction with
![]() $v \in E(x)$
. Hence, there is an optimising geodesic
$v \in E(x)$
. Hence, there is an optimising geodesic
![]() $\tilde \gamma $
from x to
$\tilde \gamma $
from x to
![]() $\mu _a(s_1)$
for some
$\mu _a(s_1)$
for some
![]() $s_1 \in (-1,1]$
. We have
$s_1 \in (-1,1]$
. We have
![]() $s_0 = s_1$
since
$s_0 = s_1$
since
![]() $s_0 < s_1$
is a contradiction with
$s_0 < s_1$
is a contradiction with
![]() $\tilde \gamma $
being optimising, and
$\tilde \gamma $
being optimising, and
![]() $s_0> s_1$
is a contradiction with
$s_0> s_1$
is a contradiction with
![]() $v \in E(x)$
. Hence,
$v \in E(x)$
. Hence,
![]() $\tilde \gamma $
is optimising from x to y, and so is
$\tilde \gamma $
is optimising from x to y, and so is
![]() $\gamma _{x,\xi }$
. Moreover,
$\gamma _{x,\xi }$
. Moreover,
![]() $\gamma _{x,\xi }$
being optimising from x to
$\gamma _{x,\xi }$
being optimising from x to
![]() $y = \pi (v)$
implies that
$y = \pi (v)$
implies that
![]() $v \in E_0$
.
$v \in E_0$
.
Lemma 6.18. Let
![]() $\Omega \subset M$
and
$\Omega \subset M$
and
![]() $x \in M$
be as in Lemma 6.17. Then
$x \in M$
be as in Lemma 6.17. Then
 $$ \begin{align} E(x) = \{(y,\eta) \in L^+ \Omega :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{y,\eta}(s) \in \pi(E(x))& \\\notag\text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align} $$
$$ \begin{align} E(x) = \{(y,\eta) \in L^+ \Omega :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{y,\eta}(s) \in \pi(E(x))& \\\notag\text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align} $$
Proof. Denote by
![]() $E_0$
the right-hand side of (6.6) and let
$E_0$
the right-hand side of (6.6) and let
![]() $(y,\eta ) \in E(x)$
. If
$(y,\eta ) \in E(x)$
. If
![]() $x = y$
, then
$x = y$
, then
![]() $\gamma _{y,\eta }(s) \in \pi (E(x))$
for
$\gamma _{y,\eta }(s) \in \pi (E(x))$
for
![]() $s \geqslant 0$
close to zero, since
$s \geqslant 0$
close to zero, since
![]() $\Omega $
is open and (6.5) holds. Analogously, if
$\Omega $
is open and (6.5) holds. Analogously, if
![]() $x \ne y$
, then
$x \ne y$
, then
![]() $\gamma _{y,\eta }(s) \in \pi (E(x))$
for
$\gamma _{y,\eta }(s) \in \pi (E(x))$
for
![]() $s \leqslant 0$
close to zero. Hence,
$s \leqslant 0$
close to zero. Hence,
![]() $E(x) \subset E_0$
.
$E(x) \subset E_0$
.
We show that
![]() $(y,\eta ) \in E_0$
implies
$(y,\eta ) \in E_0$
implies
![]() $(y,\eta ) \in E(x)$
only in the case that there is
$(y,\eta ) \in E(x)$
only in the case that there is
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
![]() $\gamma _{y,\eta }(s) \in \pi (E(x))$
for all
$\gamma _{y,\eta }(s) \in \pi (E(x))$
for all
![]() $s \in [-\epsilon ,0]$
. The other case is analogous. We write
$s \in [-\epsilon ,0]$
. The other case is analogous. We write
![]() $\tilde y = \gamma _{y,\eta }(-\epsilon )$
. Then (6.5) implies that
$\tilde y = \gamma _{y,\eta }(-\epsilon )$
. Then (6.5) implies that
![]() $\tau (x,y) = 0$
and that there is
$\tau (x,y) = 0$
and that there is
![]() $\xi \in L^+_x M$
such that
$\xi \in L^+_x M$
such that
![]() $\tilde y = \gamma _{x,\xi }(s)$
for some
$\tilde y = \gamma _{x,\xi }(s)$
for some
![]() $s \in (0,\rho (x,\xi )]$
. The path from x to y along
$s \in (0,\rho (x,\xi )]$
. The path from x to y along
![]() $\gamma _{x,\xi }$
from x to
$\gamma _{x,\xi }$
from x to
![]() $\tilde y$
and along
$\tilde y$
and along
![]() $\gamma _{y,\eta }$
from
$\gamma _{y,\eta }$
from
![]() $\tilde y$
to y is a null pregeodesic since
$\tilde y$
to y is a null pregeodesic since
![]() $\tau (x,y) = 0$
. Therefore,
$\tau (x,y) = 0$
. Therefore,
![]() $(y,\eta ) = \beta _{x,\xi }(r)$
for some
$(y,\eta ) = \beta _{x,\xi }(r)$
for some
![]() $r \in (0,\rho (x,\xi )]$
and
$r \in (0,\rho (x,\xi )]$
and
![]() $(y,\eta ) \in E(x)$
.
$(y,\eta ) \in E(x)$
.
Lemma 6.19. Let
![]() $\Omega \subset M$
and
$\Omega \subset M$
and
![]() $x \in M$
be as in Lemma 6.17. Suppose that a set
$x \in M$
be as in Lemma 6.17. Suppose that a set
![]() $C \subset \Omega $
satisfies
$C \subset \Omega $
satisfies
![]() $\pi (E(x)) \subset C \subset J^+(x)$
. Then
$\pi (E(x)) \subset C \subset J^+(x)$
. Then
Proof. Denote by
![]() $E_0$
the right-hand side of (6.7) and let
$E_0$
the right-hand side of (6.7) and let
![]() $y \in \pi (E(x))$
. If
$y \in \pi (E(x))$
. If
![]() $x = y$
, then there is no
$x = y$
, then there is no
![]() $\tilde y \in C$
such that
$\tilde y \in C$
such that
![]() $\tilde y \ll y$
since
$\tilde y \ll y$
since
![]() $x \le \tilde y$
by the assumption
$x \le \tilde y$
by the assumption
![]() $C \subset J^+(x)$
. Hence,
$C \subset J^+(x)$
. Hence,
![]() $y \in E_0$
. Suppose now that
$y \in E_0$
. Suppose now that
![]() $y \ne x$
. By Lemma 6.17 there are
$y \ne x$
. By Lemma 6.17 there are
![]() $\xi \in L_x^+ M$
and
$\xi \in L_x^+ M$
and
![]() $0 < s\leqslant \rho (x,\xi )$
such that
$0 < s\leqslant \rho (x,\xi )$
such that
![]() $y=\gamma _{x,\xi }(s)$
. Moreover,
$y=\gamma _{x,\xi }(s)$
. Moreover,
![]() $y \in C$
and
$y \in C$
and
![]() $\gamma _{x,\xi }$
is optimising from x to y. To get a contradiction, suppose that there exists
$\gamma _{x,\xi }$
is optimising from x to y. To get a contradiction, suppose that there exists
![]() $\tilde y\in C$
such that
$\tilde y\in C$
such that
![]() $\tilde y \ll y$
. As
$\tilde y \ll y$
. As
![]() $C \subset J^+(x)$
, we are led to the contradiction
$C \subset J^+(x)$
, we are led to the contradiction
![]() $x \le \tilde y \ll y$
with
$x \le \tilde y \ll y$
with
![]() $\gamma _{x,\xi }$
being optimising from x to y. This shows that
$\gamma _{x,\xi }$
being optimising from x to y. This shows that
![]() $y \in E_0$
.
$y \in E_0$
.
Let
![]() $y \in E_0$
. If
$y \in E_0$
. If
![]() $x = y$
, then
$x = y$
, then
![]() $y \in \pi (E(x))$
. Let us now assume that
$y \in \pi (E(x))$
. Let us now assume that
![]() $x \ne y$
. In the local coordinates (F) we may write
$x \ne y$
. In the local coordinates (F) we may write
![]() $y = F(s_0,a)$
for some
$y = F(s_0,a)$
for some
![]() $(s_0,a) \in (-1,1) \times B(0,\delta )$
and define the path
$(s_0,a) \in (-1,1) \times B(0,\delta )$
and define the path
![]() $\mu _a(s) = F(s,a)$
. There holds
$\mu _a(s) = F(s,a)$
. There holds
![]() $x < y \le \mu _a(1)$
since
$x < y \le \mu _a(1)$
since
![]() $C \subset J^+(x)$
. As in the proof of Lemma 6.17, there is an optimising geodesic
$C \subset J^+(x)$
. As in the proof of Lemma 6.17, there is an optimising geodesic
![]() $\tilde \gamma $
from x to
$\tilde \gamma $
from x to
![]() $\tilde y := F(s_1, a)$
for some
$\tilde y := F(s_1, a)$
for some
![]() $s_1 \in (-1,1]$
. Lemma 6.17 implies that
$s_1 \in (-1,1]$
. Lemma 6.17 implies that
![]() $\tilde y \in \pi (E(x))$
. Now
$\tilde y \in \pi (E(x))$
. Now
![]() $s_0 < s_1$
is a contradiction with
$s_0 < s_1$
is a contradiction with
![]() $\tilde \gamma $
being optimising since
$\tilde \gamma $
being optimising since
![]() $x \le y \ll \tilde y$
in this case, and
$x \le y \ll \tilde y$
in this case, and
![]() $s_0> s_1$
is a contradiction with
$s_0> s_1$
is a contradiction with
![]() $y \in E_0$
since
$y \in E_0$
since
![]() $\tilde y \in \pi (E(x)) \subset C$
and
$\tilde y \in \pi (E(x)) \subset C$
and
![]() $\tilde y \ll y$
in this case. Therefore,
$\tilde y \ll y$
in this case. Therefore,
![]() $s_0 = s_1$
and
$s_0 = s_1$
and
![]() $y = \tilde y \in \pi (E(x))$
.
$y = \tilde y \in \pi (E(x))$
.
Lemma 6.20. Let
![]() $\Omega \subset M$
,
$\Omega \subset M$
,
![]() $x \in M$
and
$x \in M$
and
![]() $C \subset \Omega $
be as in Lemma 6.19. Then the path
$C \subset \Omega $
be as in Lemma 6.19. Then the path
![]() $\mu _a : [-1,1] \to M$
, defined by
$\mu _a : [-1,1] \to M$
, defined by
![]() $\mu _a(s) = F(s,a)$
with
$\mu _a(s) = F(s,a)$
with
![]() $a \in B(0,\delta )$
in the local coordinates (F), satisfies
$a \in B(0,\delta )$
in the local coordinates (F), satisfies
 $$ \begin{align} f_{\mu_a}^+(x) &= \inf \{s \in [-1,1] : F(s,a) \in C\ \text{or}\ s=1\}. \end{align} $$
$$ \begin{align} f_{\mu_a}^+(x) &= \inf \{s \in [-1,1] : F(s,a) \in C\ \text{or}\ s=1\}. \end{align} $$
Proof. Suppose for the moment that
![]() $x \le F(1,a)$
. We write
$x \le F(1,a)$
. We write
![]() $s_0$
and
$s_0$
and
![]() $s_1$
for the left- and right-hand sides of (6.8), respectively. Lemma 6.9 implies that
$s_1$
for the left- and right-hand sides of (6.8), respectively. Lemma 6.9 implies that
![]() $s_0> -1$
and that either
$s_0> -1$
and that either
![]() $x = F(s_0, a)$
or there is an optimising geodesic from x to
$x = F(s_0, a)$
or there is an optimising geodesic from x to
![]() $F(s_0, a)$
.
$F(s_0, a)$
.
Case
![]() $x = F(s_0, a)$
and
$x = F(s_0, a)$
and
![]() $s_0 < 1$
. Then
$s_0 < 1$
. Then
![]() $x \in \Omega $
and
$x \in \Omega $
and
![]() $x \in \pi (E(x)) \subset C$
. Now
$x \in \pi (E(x)) \subset C$
. Now
![]() $s_1 \leqslant s_0$
and
$s_1 \leqslant s_0$
and
![]() $s_1 < s_0$
is a contradiction with
$s_1 < s_0$
is a contradiction with
![]() $C \subset J^+(x)$
. Hence,
$C \subset J^+(x)$
. Hence,
![]() $s_0 = s_1$
in this case.
$s_0 = s_1$
in this case.
Case
![]() $x = F(s_0, a)$
and
$x = F(s_0, a)$
and
![]() $s_0 = 1$
. Then
$s_0 = 1$
. Then
![]() $J^+(x) \cap \Omega = \emptyset $
and also
$J^+(x) \cap \Omega = \emptyset $
and also
![]() $s_1 = 1$
.
$s_1 = 1$
.
Case that
![]() $s_0 < 1$
and there is an optimising geodesic
$s_0 < 1$
and there is an optimising geodesic
![]() $\gamma $
from x to
$\gamma $
from x to
![]() $y_0 := F(s_0, a)$
. As
$y_0 := F(s_0, a)$
. As
![]() $\gamma $
is optimising from x to
$\gamma $
is optimising from x to
![]() $y_0$
, Lemma 6.17 implies that
$y_0$
, Lemma 6.17 implies that
![]() $y_0 \in \pi (E(x)) \subset C$
. Hence,
$y_0 \in \pi (E(x)) \subset C$
. Hence,
![]() $s_1 \leqslant s_0$
. Moreover,
$s_1 \leqslant s_0$
. Moreover,
![]() $y_1 := F(s_1, a) \in \overline C$
and
$y_1 := F(s_1, a) \in \overline C$
and
![]() $x \le y_1$
since
$x \le y_1$
since
![]() $C \subset J^+(x)$
and the causal relation
$C \subset J^+(x)$
and the causal relation
![]() $\le $
is closed. Finally,
$\le $
is closed. Finally,
![]() $s_1 < s_0$
leads to the contradiction
$s_1 < s_0$
leads to the contradiction
![]() $x \le y_1 \ll y_0$
with
$x \le y_1 \ll y_0$
with
![]() $\gamma $
being optimising from x to
$\gamma $
being optimising from x to
![]() $y_0$
.
$y_0$
.
Case that there is an optimising geodesic
![]() $\gamma $
from x to
$\gamma $
from x to
![]() $F(1, a)$
or
$F(1, a)$
or
![]() $x \not \le F(1,a)$
. Then
$x \not \le F(1,a)$
. Then
![]() $x \not \le F(s,a)$
for all
$x \not \le F(s,a)$
for all
![]() $-1 < s < 1$
. In other words,
$-1 < s < 1$
. In other words,
![]() $F(s, a) \notin J^+(x)$
for all
$F(s, a) \notin J^+(x)$
for all
![]() $-1 < s < 1$
, and
$-1 < s < 1$
, and
![]() $s_0 = s_1 = 1$
.
$s_0 = s_1 = 1$
.
6.7 On the span of three light-like vectors
We start with a simple lemma about the linear span of two light-like vectors on Lorentzian manifolds.
Lemma 6.21. Let y be a point on a Lorentzian manifold
![]() $(M,g)$
of dimension
$(M,g)$
of dimension
![]() $1+n$
with
$1+n$
with
![]() $n \geqslant 2$
. Let
$n \geqslant 2$
. Let
![]() $\xi _1,\xi _2,\xi _3 \in T_y M\setminus 0$
be light-like vectors such that they are not all multiples of each other. Then,
$\xi _1,\xi _2,\xi _3 \in T_y M\setminus 0$
be light-like vectors such that they are not all multiples of each other. Then,
Proof. It suffices to work in the normal coordinate system at the point y where the metric evaluated at the point y is the Minkowski metric. After scaling and without loss of generality, we can write
 $\xi _j= (1,\xi ^{\prime }_j)$
,
$\xi _j= (1,\xi ^{\prime }_j)$
,
![]() $j=1,2,3$
for vectors
$j=1,2,3$
for vectors
 $\xi ^{\prime }_j \in \mathbb R^{n}$
that satisfy
$\xi ^{\prime }_j \in \mathbb R^{n}$
that satisfy
 $|\xi ^{\prime }_j|=1$
. Thus, it follows that
$|\xi ^{\prime }_j|=1$
. Thus, it follows that
Two of the numbers
![]() $c_1,c_2,c_3$
must be nonpositive or nonnegative. Without loss of generality, we assume
$c_1,c_2,c_3$
must be nonpositive or nonnegative. Without loss of generality, we assume
![]() $c_1$
and
$c_1$
and
![]() $c_2$
have this property, namely,
$c_2$
have this property, namely,
![]() $c_1,c_2 \geqslant 0$
or
$c_1,c_2 \geqslant 0$
or
![]() $c_1,c_2 \leqslant 0$
. Then, the previous identity implies that
$c_1,c_2 \leqslant 0$
. Then, the previous identity implies that
Since the vectors
![]() $\xi ^{\prime }_1$
,
$\xi ^{\prime }_1$
,
![]() $\xi ^{\prime }_2$
are not multiples of each other, it follows that
$\xi ^{\prime }_2$
are not multiples of each other, it follows that
![]() $c_1=c_2=0$
and, subsequently, that
$c_1=c_2=0$
and, subsequently, that
![]() $c_3=0$
.
$c_3=0$
.
Next, we consider the linear span of three light-like vectors. The following lemma is taken from [Reference Chen, Lassas, Oksanen and Paternain16, Lemma 1].
Lemma 6.22. Let y be a point on a Lorentzian manifold
![]() $(M,g)$
of dimension
$(M,g)$
of dimension
![]() $1+n$
with
$1+n$
with
![]() $n \geqslant 2$
. Let
$n \geqslant 2$
. Let
![]() $\xi _1, \eta \in T_y M \setminus 0$
be light-like. In any neighbourhood of
$\xi _1, \eta \in T_y M \setminus 0$
be light-like. In any neighbourhood of
![]() $\xi _1$
in
$\xi _1$
in
![]() $T_y M$
, there exist two light-like vectors
$T_y M$
, there exist two light-like vectors
![]() $\xi _2, \xi _3$
such that
$\xi _2, \xi _3$
such that
![]() $\eta $
is in
$\eta $
is in
![]() $\operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
.
$\operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
.
We will also need a variation of the above lemma as follows.
Lemma 6.23. Let
![]() $x \in M$
,
$x \in M$
,
![]() $\xi _0, \xi _1 \in L^+_x M$
and let
$\xi _0, \xi _1 \in L^+_x M$
and let
![]() $U \subset L^+_x M$
be a neighbourhood of
$U \subset L^+_x M$
be a neighbourhood of
![]() $\xi _1$
. Suppose that
$\xi _1$
. Suppose that
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$
. There is a neighbourhood
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$
. There is a neighbourhood
![]() $V \subset T_x M$
of
$V \subset T_x M$
of
![]() $\xi _0$
and
$\xi _0$
and
![]() $\xi _2 \in U$
such that for any
$\xi _2 \in U$
such that for any
![]() $\eta \in V$
there is
$\eta \in V$
there is
![]() $\xi _3 \in U$
such that
$\xi _3 \in U$
such that
![]() $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
$\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
![]() $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
$\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
![]() $j=1,2,3$
.
$j=1,2,3$
.
Proof. We choose normal coordinates centred at y. Then g is the Minkowski metric on the fibre
![]() $T_y M = \mathbb R^{1+n}$
. The statement is invariant with respect to nonvanishing rescaling of
$T_y M = \mathbb R^{1+n}$
. The statement is invariant with respect to nonvanishing rescaling of
![]() $\xi _0$
and
$\xi _0$
and
![]() $\xi _1$
, and we assume without loss of generality that
$\xi _1$
, and we assume without loss of generality that
 $\xi _j = (1,\xi _j')$
with
$\xi _j = (1,\xi _j')$
with
![]() $\xi _j'$
a unit vector in
$\xi _j'$
a unit vector in
![]() $\mathbb R^n$
,
$\mathbb R^n$
,
![]() $j=0,1$
. We choose an orthonormal basis
$j=0,1$
. We choose an orthonormal basis
![]() $e_1,\dots ,e_n$
of
$e_1,\dots ,e_n$
of
![]() $\mathbb R^n$
such that
$\mathbb R^n$
such that
![]() $e_1 = \xi _1'$
and
$e_1 = \xi _1'$
and
![]() $\xi _0' \in \operatorname {\mathrm {span}}(e_1,e_2)$
. Then in this basis it holds for some
$\xi _0' \in \operatorname {\mathrm {span}}(e_1,e_2)$
. Then in this basis it holds for some
![]() $a,b \in \mathbb R$
that
$a,b \in \mathbb R$
that
 $$ \begin{align} \xi_1 = (1,1,0,\underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_0 = (1, a, b, \underbrace{0,\dots,0}_{n-2\ \text{times}}). \end{align} $$
$$ \begin{align} \xi_1 = (1,1,0,\underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_0 = (1, a, b, \underbrace{0,\dots,0}_{n-2\ \text{times}}). \end{align} $$
Choose a small enough
![]() $r> 0$
so that both vectors
$r> 0$
so that both vectors
 $$ \begin{align*} \xi_+ = (1, \sqrt{1-r^2}, r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_- = (1, \sqrt{1-r^2}, -r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \end{align*} $$
$$ \begin{align*} \xi_+ = (1, \sqrt{1-r^2}, r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_- = (1, \sqrt{1-r^2}, -r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \end{align*} $$
are in U and
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _\pm )$
. We set
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _\pm )$
. We set
![]() $\xi _2 = \xi _+$
.
$\xi _2 = \xi _+$
.
Let
![]() $\delta = (\delta _0, \delta _1, \delta _2) \in \mathbb R^3$
and
$\delta = (\delta _0, \delta _1, \delta _2) \in \mathbb R^3$
and
![]() $\epsilon \in \mathbb R^{n-2}$
be close to the respective origins. Consider the following perturbation of
$\epsilon \in \mathbb R^{n-2}$
be close to the respective origins. Consider the following perturbation of
![]() $\xi _0$
:
$\xi _0$
:
and
![]() $\xi _3$
of the form
$\xi _3$
of the form
 $$ \begin{align*} \xi_3 = (1, \sqrt{1-r^2 - c^2 |\epsilon|^2}, -r, c\epsilon), \end{align*} $$
$$ \begin{align*} \xi_3 = (1, \sqrt{1-r^2 - c^2 |\epsilon|^2}, -r, c\epsilon), \end{align*} $$
where
![]() $c \in \mathbb R$
. The system
$c \in \mathbb R$
. The system
![]() $c_1 \xi _1 + c_2 \xi _2 + c_3 \xi _3 = \eta $
for
$c_1 \xi _1 + c_2 \xi _2 + c_3 \xi _3 = \eta $
for
![]() $c_1, c_2, c_3 \in \mathbb R$
reads in matrix form
$c_1, c_2, c_3 \in \mathbb R$
reads in matrix form
 $$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 1 & \sqrt{1-r^2} & \sqrt{1-r^2 - c^2 |\epsilon|^2} & a + \delta_1 \\ 0 & r & -r & b + \delta_2 \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 1 & \sqrt{1-r^2} & \sqrt{1-r^2 - c^2 |\epsilon|^2} & a + \delta_1 \\ 0 & r & -r & b + \delta_2 \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$
and two steps of the Gaussian elimination algorithm reduces this to
 $$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 0 & 1 & w & z \\ 0 & 0 & x & y \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 0 & 1 & w & z \\ 0 & 0 & x & y \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$
where the specific form of
![]() $y = y(\delta ,\epsilon )$
,
$y = y(\delta ,\epsilon )$
,
![]() $z = z(\delta ,\epsilon )$
and
$z = z(\delta ,\epsilon )$
and
![]() $w=w(c,\epsilon )$
is not important to us, and
$w=w(c,\epsilon )$
is not important to us, and
 $$ \begin{align*} x = x(c,\epsilon) = \frac{r}{\sqrt{1-r^2}-1} \left(2-\sqrt{1-r^2}-\sqrt{1-r^2-c^2|\epsilon|^2}\right). \end{align*} $$
$$ \begin{align*} x = x(c,\epsilon) = \frac{r}{\sqrt{1-r^2}-1} \left(2-\sqrt{1-r^2}-\sqrt{1-r^2-c^2|\epsilon|^2}\right). \end{align*} $$
As
![]() $x \ne 0$
, the above system has a solution if and only if
$x \ne 0$
, the above system has a solution if and only if
To get a contradiction, suppose that
![]() $y(0,0) = 0$
. Then
$y(0,0) = 0$
. Then
![]() $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2)$
, and as
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2)$
, and as
![]() $\xi _0, \xi _1$
and
$\xi _0, \xi _1$
and
![]() $\xi _2$
are all light-like, Lemma 6.21 applies to show that
$\xi _2$
are all light-like, Lemma 6.21 applies to show that
![]() $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1)$
or
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1)$
or
![]() $\xi _0 \in \operatorname {\mathrm {span}}(\xi _2)$
. But
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _2)$
. But
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$
for both
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$
for both
![]() $j=1,2$
, a contradiction.
$j=1,2$
, a contradiction.
We write
![]() $F(c,\delta ,\epsilon )$
for the left-hand side of (6.10) and
$F(c,\delta ,\epsilon )$
for the left-hand side of (6.10) and
![]() $y_0 = y(0,0)$
and
$y_0 = y(0,0)$
and
![]() $x_0 = x(c,0)$
, the latter being independent from c. Setting
$x_0 = x(c,0)$
, the latter being independent from c. Setting
![]() $c_0 = x_0 / y_0$
, we see that
$c_0 = x_0 / y_0$
, we see that
![]() $F(c_0, 0, 0) = 0$
and
$F(c_0, 0, 0) = 0$
and
![]() $\partial _c F(c_0, 0, 0) = -y_0 \ne 0$
. By the implicit function theorem there is a neighbourhood
$\partial _c F(c_0, 0, 0) = -y_0 \ne 0$
. By the implicit function theorem there is a neighbourhood
![]() $V_0 \subset \mathbb R^{3+(n-2)}$
of the origin and a smooth map
$V_0 \subset \mathbb R^{3+(n-2)}$
of the origin and a smooth map
![]() $h : V_0 \to \mathbb R$
such that
$h : V_0 \to \mathbb R$
such that
![]() $h(0,0) = c_0$
and
$h(0,0) = c_0$
and
![]() $F(h(\delta , \epsilon ), \delta , \epsilon ) = 0$
for all
$F(h(\delta , \epsilon ), \delta , \epsilon ) = 0$
for all
![]() $(\delta , \epsilon ) \in V_0$
. As
$(\delta , \epsilon ) \in V_0$
. As
![]() $\xi _3 = \xi _-$
when
$\xi _3 = \xi _-$
when
![]() $\epsilon = 0$
, by making
$\epsilon = 0$
, by making
![]() $V_0$
smaller if necessary, we have that
$V_0$
smaller if necessary, we have that
![]() $\xi _3$
, with
$\xi _3$
, with
![]() $c=h(\delta , \epsilon )$
, is in U for all
$c=h(\delta , \epsilon )$
, is in U for all
![]() $(\delta , \epsilon ) \in V_0$
.
$(\delta , \epsilon ) \in V_0$
.
By making
![]() $V_0$
smaller if necessary, we can also guarantee that
$V_0$
smaller if necessary, we can also guarantee that
![]() $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
for
$\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
for
![]() $j=1,2,3$
, since
$j=1,2,3$
, since
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$
,
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$
,
![]() $j=1,2$
and
$j=1,2$
and
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _-)$
.
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _-)$
.
7 Recovery of earliest observation sets and proof of Theorem 1.3
The aim of this section is to prove Theorem 1.3. As in the hypothesis of the theorem, we consider time-like paths
![]() $\mu _{\mathrm{in}}:[t_0^-,t_0^+]\to M$
and
$\mu _{\mathrm{in}}:[t_0^-,t_0^+]\to M$
and
![]() $\mu _{\mathrm{out}}:[s_0^-,s_0^+]\to M$
and define the source and observe regions
$\mu _{\mathrm{out}}:[s_0^-,s_0^+]\to M$
and define the source and observe regions
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
by (1.10). Recall that the extensions
$\Omega _{\mathrm{out}}$
by (1.10). Recall that the extensions
![]() $\mu _{\mathrm{in}} : (t_1^-,t_1^+)\to M$
and
$\mu _{\mathrm{in}} : (t_1^-,t_1^+)\to M$
and
![]() $\mu _{\mathrm{out}}:(s_1^-,s_1^+)\to M$
are contained in
$\mu _{\mathrm{out}}:(s_1^-,s_1^+)\to M$
are contained in
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
, respectively. We will assume as in the hypothesis of the theorem that
$\Omega _{\mathrm{out}}$
, respectively. We will assume as in the hypothesis of the theorem that
![]() $\delta $
is sufficiently small so that (1.11) holds.
$\delta $
is sufficiently small so that (1.11) holds.
Remark 5. Throughout the remainder of the article and without loss of generality, we will assume that
![]() $s_1^\pm = \pm 1$
and that
$s_1^\pm = \pm 1$
and that
![]() $t_1^\pm =\pm 1$
. With this convenient choice of notation, we have
$t_1^\pm =\pm 1$
. With this convenient choice of notation, we have
and therefore the abstract foliation condition (F), which was studied in the previous section, holds for these sets.
We recall from Definition 1.2 that
![]() $\operatorname {\mathrm {R}} \in L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$
is a three-to-one scattering relation if it has the following two properties:
$\operatorname {\mathrm {R}} \in L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$
is a three-to-one scattering relation if it has the following two properties:
-
(R1) If
 $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then there is
$(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$
, then there is
 $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
.
$y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$
. -
(R2) Assume that
 $\gamma _{v_{j}}$
,
$\gamma _{v_{j}}$
,
 $j=0,1,2,3$
, are distinct and there exists
$j=0,1,2,3$
, are distinct and there exists
 $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
$y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$
Moreover, assume that
 $y=\gamma _{v_{0}}(s_0)$
with
$y=\gamma _{v_{0}}(s_0)$
with
 $s_0\in (-\rho (v_0),0]$
and
$s_0\in (-\rho (v_0),0]$
and
 $y=\gamma _{v_{j}}(s_j)$
for all
$y=\gamma _{v_{j}}(s_j)$
for all
 $j=1,2,3$
, with
$j=1,2,3$
, with
 $s_j\in [0,\rho (v_j))$
. Denote
$s_j\in [0,\rho (v_j))$
. Denote
 $\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
$\xi _j=\dot \gamma _{v_{j}}(s_j)$
for
 $j=0,1,2,3$
and assume that
$j=0,1,2,3$
and assume that
 $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, it holds that
$\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$
. Then, it holds that
 $(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$
.
$(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$
.
7.1 Lower and upper bounds for conical pieces
We define a conical piece associated to a three-to-one scattering relation
![]() $\operatorname {\mathrm {R}}$
and
$\operatorname {\mathrm {R}}$
and
![]() $v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$
by
$v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$
by
Lemma 7.1. Let
![]() $v_{1} \in L^+ \Omega _{\mathrm{in}}$
,
$v_{1} \in L^+ \Omega _{\mathrm{in}}$
,
![]() $v_{0} \in L^+ \Omega _{\mathrm{out}}$
and write
$v_{0} \in L^+ \Omega _{\mathrm{out}}$
and write
![]() $\pi (v_{1}) = x$
and
$\pi (v_{1}) = x$
and
![]() $\pi (v_{0}) = z$
. Suppose that
$\pi (v_{0}) = z$
. Suppose that
![]() $\gamma _{v_{1}}$
is optimising from x to a point y in M and that
$\gamma _{v_{1}}$
is optimising from x to a point y in M and that
![]() $\gamma _{v_{0}}$
is optimising from y to z. Suppose furthermore that
$\gamma _{v_{0}}$
is optimising from y to z. Suppose furthermore that
![]() $\gamma _{v_{1}}$
and
$\gamma _{v_{1}}$
and
![]() $\gamma _{v_{0}}$
do not intersect at x or at z. Then there is a vector
$\gamma _{v_{0}}$
do not intersect at x or at z. Then there is a vector
![]() $v_{2} \in L^+ \Omega _{\mathrm{in}}$
, arbitrarily close to
$v_{2} \in L^+ \Omega _{\mathrm{in}}$
, arbitrarily close to
![]() $v_{1}$
and a set
$v_{1}$
and a set
![]() $C \subset \operatorname {\mathrm {CP}}(v_{1}, v_{2})$
such that C is a neighbourhood of
$C \subset \operatorname {\mathrm {CP}}(v_{1}, v_{2})$
such that C is a neighbourhood of
![]() $v_{0}$
in
$v_{0}$
in
![]() $C(y)$
.
$C(y)$
.
Proof. Let
![]() $s_{j} \in \mathbb R$
satisfy
$s_{j} \in \mathbb R$
satisfy
![]() $\gamma _{v_{j}}(-s_j) = y$
,
$\gamma _{v_{j}}(-s_j) = y$
,
![]() $j=0,1$
and write
$j=0,1$
and write
![]() $\xi _j = \dot \gamma _{v_{j}}(-s_j)$
. As
$\xi _j = \dot \gamma _{v_{j}}(-s_j)$
. As
![]() $\gamma _{v_{1}}$
is optimising from x to y and
$\gamma _{v_{1}}$
is optimising from x to y and
![]() $\gamma _{v_{0}}$
is optimising from y to z, these two geodesics do not intersect at any point
$\gamma _{v_{0}}$
is optimising from y to z, these two geodesics do not intersect at any point
![]() $\tilde y \ne y$
satisfying
$\tilde y \ne y$
satisfying
![]() $x < \tilde y < z$
. We have also assumed that they do not intersect at x or z. Hence, there is such a neighbourhood
$x < \tilde y < z$
. We have also assumed that they do not intersect at x or z. Hence, there is such a neighbourhood
![]() $V_0 \subset L_y^+ M$
of
$V_0 \subset L_y^+ M$
of
![]() $\xi _0$
that y is the unique point satisfying
$\xi _0$
that y is the unique point satisfying
![]() $y \in \overleftarrow {\;\gamma _{\tilde v_{0}}} \cap \overrightarrow {\gamma _{v_{1}}}$
where
$y \in \overleftarrow {\;\gamma _{\tilde v_{0}}} \cap \overrightarrow {\gamma _{v_{1}}}$
where
![]() $\tilde v_{0} = \beta _{y,\eta }(s_0)$
and
$\tilde v_{0} = \beta _{y,\eta }(s_0)$
and
![]() $\eta \in V_0$
.
$\eta \in V_0$
.
Observe that
![]() $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$
since
$\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$
since
![]() $\gamma _{v_{1}}$
and
$\gamma _{v_{1}}$
and
![]() $\gamma _{v_{0}}$
do not intersect at x. Let
$\gamma _{v_{0}}$
do not intersect at x. Let
![]() $U \subset L_y^+ M$
be a neighbourhood of
$U \subset L_y^+ M$
be a neighbourhood of
![]() $\xi _1$
such that
$\xi _1$
such that
![]() $\gamma _{y,\xi }(s_1) \in \Omega _{\mathrm{in}}$
for all
$\gamma _{y,\xi }(s_1) \in \Omega _{\mathrm{in}}$
for all
![]() $\xi \in U$
. By Lemma 6.23 there is a neighbourhood
$\xi \in U$
. By Lemma 6.23 there is a neighbourhood
![]() $V \subset V_0$
of
$V \subset V_0$
of
![]() $\xi _0$
and
$\xi _0$
and
![]() $\xi _2 \in U$
such that for any
$\xi _2 \in U$
such that for any
![]() $\eta \in V$
there is
$\eta \in V$
there is
![]() $\xi _3 \in U$
such that
$\xi _3 \in U$
such that
![]() $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
$\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
![]() $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
$\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
![]() $j=1,2,3$
. Writing
$j=1,2,3$
. Writing
![]() $v_{j} = \beta _{y,\xi _j}(s_j)$
,
$v_{j} = \beta _{y,\xi _j}(s_j)$
,
![]() $j=2,3$
, we have
$j=2,3$
, we have
![]() $(\tilde v_{0}, v_{1}, v_{2}, v_{3}) \in \operatorname {\mathrm {R}}$
for
$(\tilde v_{0}, v_{1}, v_{2}, v_{3}) \in \operatorname {\mathrm {R}}$
for
![]() $\eta \in V$
, due to (R2). To conclude, we use the fact that the image of V under the map
$\eta \in V$
, due to (R2). To conclude, we use the fact that the image of V under the map
![]() $\eta \mapsto \beta _{y, \eta }(s_0)$
is a smooth submanifold of dimension n in
$\eta \mapsto \beta _{y, \eta }(s_0)$
is a smooth submanifold of dimension n in
![]() $T M$
.
$T M$
.
Lemma 7.2. Let
![]() $v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$
satisfy
$v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$
satisfy
![]() $\overline {\gamma _{v_{1}}} \ne \overline {\gamma _{v_{2}}}$
. We write
$\overline {\gamma _{v_{1}}} \ne \overline {\gamma _{v_{2}}}$
. We write
Then the set
![]() $\mathcal F = \overrightarrow {\gamma _{v_{1}}} \cap \overrightarrow {\gamma _{v_{2}}} \cap K$
is finite and
$\mathcal F = \overrightarrow {\gamma _{v_{1}}} \cap \overrightarrow {\gamma _{v_{2}}} \cap K$
is finite and
 $$ \begin{align*} \operatorname{\mathrm{CP}}(v_{1}, v_{2}) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{CP}}(v_{1}, v_{2}) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$
Proof. Observe that K is compact since both
![]() $\Omega _{\mathrm{in}}$
and
$\Omega _{\mathrm{in}}$
and
![]() $\Omega _{\mathrm{out}}$
are bounded. If
$\Omega _{\mathrm{out}}$
are bounded. If
![]() $\mathcal F$
is not finite, then it has an accumulation point, and using Lemma 6.4 we obtain the contradiction
$\mathcal F$
is not finite, then it has an accumulation point, and using Lemma 6.4 we obtain the contradiction
![]() $\overline {\gamma _{v_{1}}} = \overline {\gamma _{v_{2}}}$
. The second claim follows immediately from (R1).
$\overline {\gamma _{v_{1}}} = \overline {\gamma _{v_{2}}}$
. The second claim follows immediately from (R1).
7.2 Relating earliest observation sets to a three-to-one scattering relation
Recall that the observation set
![]() $\Omega _{\mathrm{out}}$
satisfies (F) and take
$\Omega _{\mathrm{out}}$
satisfies (F) and take
![]() $\Omega = \Omega _{\mathrm{out}}$
and
$\Omega = \Omega _{\mathrm{out}}$
and
![]() $F = F_{\mathrm{out}}$
in the definition (6.4) of the earliest observation sets
$F = F_{\mathrm{out}}$
in the definition (6.4) of the earliest observation sets
![]() $E(y)$
,
$E(y)$
,
![]() $y \in M$
. We will next relate
$y \in M$
. We will next relate
![]() $E(y)$
to a set constructed from
$E(y)$
to a set constructed from
![]() $\operatorname {\mathrm {R}}$
. To this end, define the set
$\operatorname {\mathrm {R}}$
. To this end, define the set
![]() $E(v,w)$
for
$E(v,w)$
for
![]() $v,w \in L^+\Omega _{\mathrm{in}}$
as follows: let
$v,w \in L^+\Omega _{\mathrm{in}}$
as follows: let
![]() $C(v,w)$
be the closure in
$C(v,w)$
be the closure in
![]() $T \Omega _{\mathrm{out}}$
of the union
$T \Omega _{\mathrm{out}}$
of the union
![]() $\bigcup _{C \in \mathcal C(v,w)} C$
where
$\bigcup _{C \in \mathcal C(v,w)} C$
where
 $$ \begin{align*} \mathcal C(v,w) = \{ C : & C \subset T\Omega_{\text{out}}\ \text{is a smooth manifold of dimension}\ n\ \text{s.t.} \\& C \subset \operatorname{\mathrm{CP}}(v,\tilde v) \cap \operatorname{\mathrm{CP}}(w,\tilde w)\ \text{for some}\ \tilde v, \tilde w \in L^+\Omega_{\text{in}} \\&\text{ satisfying}\ \overline{\gamma_v} \ne \overline{\gamma_{\tilde v}}\ \text{and}\ \overline{\gamma_w} \ne \overline{\gamma_{\tilde w}} \}, \end{align*} $$
$$ \begin{align*} \mathcal C(v,w) = \{ C : & C \subset T\Omega_{\text{out}}\ \text{is a smooth manifold of dimension}\ n\ \text{s.t.} \\& C \subset \operatorname{\mathrm{CP}}(v,\tilde v) \cap \operatorname{\mathrm{CP}}(w,\tilde w)\ \text{for some}\ \tilde v, \tilde w \in L^+\Omega_{\text{in}} \\&\text{ satisfying}\ \overline{\gamma_v} \ne \overline{\gamma_{\tilde v}}\ \text{and}\ \overline{\gamma_w} \ne \overline{\gamma_{\tilde w}} \}, \end{align*} $$
then we set
and
 $$ \begin{align*} E(v,w) = \{(z,\zeta) :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{z,\zeta}(s) \in \pi(\tilde E(v,w))& \\ \text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align*} $$
$$ \begin{align*} E(v,w) = \{(z,\zeta) :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{z,\zeta}(s) \in \pi(\tilde E(v,w))& \\ \text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align*} $$
The following lemma describes the basic idea that we will use to construct earliest observation sets given a three-to-one scattering relation
![]() $\operatorname {\mathrm {R}}$
. The geometric setting of the lemma is shown in Figure 4.
$\operatorname {\mathrm {R}}$
. The geometric setting of the lemma is shown in Figure 4.
Lemma 7.3. Let
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and suppose that there are
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and suppose that there are
![]() $x_j < \pi (v_j)$
such that
$x_j < \pi (v_j)$
such that
![]() $\gamma _{v_j}$
is optimising from
$\gamma _{v_j}$
is optimising from
![]() $x_j$
to a point
$x_j$
to a point
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
for
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
for
![]() $j=1,2$
. Suppose furthermore that
$j=1,2$
. Suppose furthermore that
![]() $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
and that
$\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
and that
![]() $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
. Then
$y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
. Then
![]() $E(y) \subset C(v_1,v_2)$
,
$E(y) \subset C(v_1,v_2)$
,
![]() $\pi (C(v_1, v_2)) \subset J^+(y)$
and
$\pi (C(v_1, v_2)) \subset J^+(y)$
and
![]() $E(y) = E(v_1, v_2)$
.
$E(y) = E(v_1, v_2)$
.
Proof. Let
![]() $u \in E(y)$
. We will show that
$u \in E(y)$
. We will show that
![]() $u \in C(v_1,v_2)$
. Note that
$u \in C(v_1,v_2)$
. Note that
![]() $\gamma _{u}$
is optimising from y to
$\gamma _{u}$
is optimising from y to
![]() $z := \pi (u)$
by Lemma 6.17. Suppose for the moment that neither
$z := \pi (u)$
by Lemma 6.17. Suppose for the moment that neither
![]() $\gamma _{v_1}$
nor
$\gamma _{v_1}$
nor
![]() $\gamma _{v_2}$
intersects
$\gamma _{v_2}$
intersects
![]() $\gamma _u$
at z. As
$\gamma _u$
at z. As
![]() $\gamma _{v_j}$
is optimising from
$\gamma _{v_j}$
is optimising from
![]() $x_j$
to y, the geodesics
$x_j$
to y, the geodesics
![]() $\gamma _u$
and
$\gamma _u$
and
![]() $\gamma _{v_j}$
cannot intersect at
$\gamma _{v_j}$
cannot intersect at
![]() $\pi (v_j)$
, and Lemma 7.1 implies that there are
$\pi (v_j)$
, and Lemma 7.1 implies that there are
![]() $\tilde v_j \in L^+ \Omega _{\mathrm{in}}$
and
$\tilde v_j \in L^+ \Omega _{\mathrm{in}}$
and
![]() $C_j \subset \operatorname {\mathrm {CP}}(v_j, \tilde v_j)$
such that
$C_j \subset \operatorname {\mathrm {CP}}(v_j, \tilde v_j)$
such that
![]() $C_j$
is a neighbourhood of u in
$C_j$
is a neighbourhood of u in
![]() $C(y)$
. As
$C(y)$
. As
![]() $C(y)$
is a smooth manifold of dimension n, the intersection
$C(y)$
is a smooth manifold of dimension n, the intersection
![]() $C_1 \cap C_2$
is a smooth manifold of dimension n containing u. Hence,
$C_1 \cap C_2$
is a smooth manifold of dimension n containing u. Hence,
![]() $u \in C(v_1,v_2)$
.
$u \in C(v_1,v_2)$
.
Let us now consider the case that
![]() $\gamma _{v_1}$
or
$\gamma _{v_1}$
or
![]() $\gamma _{v_2}$
intersects
$\gamma _{v_2}$
intersects
![]() $\gamma _u$
at z. Choose
$\gamma _u$
at z. Choose
![]() $\eta \in L_y^+ M$
and
$\eta \in L_y^+ M$
and
![]() $t> 0$
so that
$t> 0$
so that
![]() $\overline {\gamma _{y,\eta }} = \overline {\gamma _u}$
and
$\overline {\gamma _{y,\eta }} = \overline {\gamma _u}$
and
![]() $\gamma _{y,\eta }(t) = z$
. We have
$\gamma _{y,\eta }(t) = z$
. We have
![]() $t \leqslant \rho (y,\eta )$
and there are
$t \leqslant \rho (y,\eta )$
and there are
![]() $\eta _k \in L_y^+ M$
and
$\eta _k \in L_y^+ M$
and
![]() $0 < t_k < \rho (y,\eta _k)$
such that writing
$0 < t_k < \rho (y,\eta _k)$
such that writing
![]() $u_k = \beta _{y,\eta _k}(t_k)$
and
$u_k = \beta _{y,\eta _k}(t_k)$
and
![]() $z_k = \pi (u_k)$
there holds
$z_k = \pi (u_k)$
there holds
![]() $u_k \to u$
and neither
$u_k \to u$
and neither
![]() $\gamma _{v_1}$
nor
$\gamma _{v_1}$
nor
![]() $\gamma _{v_2}$
intersects
$\gamma _{v_2}$
intersects
![]() $\gamma _{u_k}$
at
$\gamma _{u_k}$
at
![]() $z_k$
. The argument above implies that
$z_k$
. The argument above implies that
![]() $u_k \in C(v_1,v_2)$
. As
$u_k \in C(v_1,v_2)$
. As
![]() $C(v_1,v_2)$
is closed, also
$C(v_1,v_2)$
is closed, also
![]() $u \in C(v_1,v_2)$
.
$u \in C(v_1,v_2)$
.
Let
![]() $u \in C(v_1, v_2)$
. We will show that
$u \in C(v_1, v_2)$
. We will show that
![]() $\pi (u) \in J^+(y)$
. Consider first the case that
$\pi (u) \in J^+(y)$
. Consider first the case that
![]() $u \in C$
for some
$u \in C$
for some
![]() $C \in \mathcal C(v_1,v_2)$
and
$C \in \mathcal C(v_1,v_2)$
and
![]() $\overline {\gamma _{v_j}} \ne \overline {\gamma _{u}}$
for
$\overline {\gamma _{v_j}} \ne \overline {\gamma _{u}}$
for
![]() $j=1,2$
. Then there are
$j=1,2$
. Then there are
 $y_j \in \overleftarrow {\;\gamma _{u}} \cap \overrightarrow {\gamma _{v_j}}$
. As
$y_j \in \overleftarrow {\;\gamma _{u}} \cap \overrightarrow {\gamma _{v_j}}$
. As
![]() $x_j < \pi (v_j) \le y_j$
, Lemma 6.13 implies that either
$x_j < \pi (v_j) \le y_j$
, Lemma 6.13 implies that either
![]() $y=y_1=y_2$
or at least one of
$y=y_1=y_2$
or at least one of
![]() $y_1$
and
$y_1$
and
![]() $y_2$
satisfies
$y_2$
satisfies
![]() $y < y_j$
. In both cases
$y < y_j$
. In both cases
![]() $y \le \pi (u)$
; that is,
$y \le \pi (u)$
; that is,
![]() $\pi (u) \in J^+(y)$
. Consider now the case that there is sequence
$\pi (u) \in J^+(y)$
. Consider now the case that there is sequence
![]() $u_k$
,
$u_k$
,
![]() $k \in \mathbb N$
, such that
$k \in \mathbb N$
, such that
![]() $u_k \in C_k$
for some
$u_k \in C_k$
for some
![]() $C_k \in \mathcal C(v_1,v_2)$
and
$C_k \in \mathcal C(v_1,v_2)$
and
![]() $u_k \to u$
. The sequence
$u_k \to u$
. The sequence
![]() $u_k$
can be chosen so that
$u_k$
can be chosen so that
![]() $\overline {\gamma _{v_j}} \ne \overline {\gamma _{u_k}}$
also for
$\overline {\gamma _{v_j}} \ne \overline {\gamma _{u_k}}$
also for
![]() $j=1,2$
and
$j=1,2$
and
![]() $k=1,2,\dots $
. We obtain
$k=1,2,\dots $
. We obtain
![]() $y \le \pi (u)$
also in this case since the relation
$y \le \pi (u)$
also in this case since the relation
![]() $\le $
is closed.
$\le $
is closed.
We have shown, in particular, that
![]() $\pi (E(y)) \subset \pi (C(v_1,v_2)) \subset J^+(y)$
. Lemma 6.19 implies now that
$\pi (E(y)) \subset \pi (C(v_1,v_2)) \subset J^+(y)$
. Lemma 6.19 implies now that
![]() $\pi (\tilde E(v_1,v_2)) = \pi (E(y))$
. Finally,
$\pi (\tilde E(v_1,v_2)) = \pi (E(y))$
. Finally,
![]() $E(y) = E(v_1, v_2)$
follows immediately from Lemma 6.18.
$E(y) = E(v_1, v_2)$
follows immediately from Lemma 6.18.
7.3 Local test for optimality before intersection
In Lemma 7.3 the geodesic
![]() $\gamma _{v_1}$
needs to be optimising from
$\gamma _{v_1}$
needs to be optimising from
![]() $x_1$
to y. We will give a construction that allows us to distinguis the optimising and nonoptimising but close to optimising cases, given
$x_1$
to y. We will give a construction that allows us to distinguis the optimising and nonoptimising but close to optimising cases, given
![]() $\operatorname {\mathrm {R}}$
. We begin with an auxiliary lemma.
$\operatorname {\mathrm {R}}$
. We begin with an auxiliary lemma.
Lemma 7.4. Let
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and let
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and let
![]() $u_1 \in C \in \mathcal C(v_1, v_2)$
. Then there is
$u_1 \in C \in \mathcal C(v_1, v_2)$
. Then there is
![]() $u_2 \in C$
such that
$u_2 \in C$
such that
![]() $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
and
$\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
and
 $\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_j}} \ne \emptyset $
for both
$\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_j}} \ne \emptyset $
for both
![]() $j=1,2$
.
$j=1,2$
.
Proof. As C is a smooth manifold of dimension n there is
![]() $u_2$
satisfying
$u_2$
satisfying
![]() $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
in any neighbourhood of
$\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
in any neighbourhood of
![]() $u_1$
in C. Lemma 7.2 implies that for some
$u_1$
in C. Lemma 7.2 implies that for some
![]() $\tilde v_1 \in L^+ \Omega _{\mathrm{in}}$
and finite
$\tilde v_1 \in L^+ \Omega _{\mathrm{in}}$
and finite
![]() $\mathcal F \subset \overrightarrow {\gamma _{v_1}}$
there holds
$\mathcal F \subset \overrightarrow {\gamma _{v_1}}$
there holds
 $$ \begin{align*} C \subset \operatorname{\mathrm{CP}}(v_1, \tilde v_1) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$
$$ \begin{align*} C \subset \operatorname{\mathrm{CP}}(v_1, \tilde v_1) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$
Then Lemma 6.16 implies that
![]() $\mathcal F \cap \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}}\ne \emptyset $
when
$\mathcal F \cap \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}}\ne \emptyset $
when
![]() $u_2 \in C$
is close enough to
$u_2 \in C$
is close enough to
![]() $u_1$
. The proof that
$u_1$
. The proof that
![]() $\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_2}} \ne \emptyset $
is analogous.
$\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_2}} \ne \emptyset $
is analogous.
Lemma 7.5. Let
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
![]() $x_1 \in M$
be as in Lemma 7.3. Then there do not exist
$x_1 \in M$
be as in Lemma 7.3. Then there do not exist
![]() $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
$\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
![]() $C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
$C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
![]() $C \subset E(v_1, v_2)$
and
$C \subset E(v_1, v_2)$
and
![]() $x_1 \ll \tilde x_1$
for some
$x_1 \ll \tilde x_1$
for some
![]() $\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$
.
$\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$
.
Proof. To get a contradiction, we suppose that there are
![]() $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
$\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
![]() $C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
$C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
![]() $C \subset E(v_1, v_2)$
and
$C \subset E(v_1, v_2)$
and
![]() $x_1 \ll \tilde x_1$
for some
$x_1 \ll \tilde x_1$
for some
![]() $\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$
. By Lemma 7.4 there are
$\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$
. By Lemma 7.4 there are
![]() $u_1, u_2 \in C$
and
$u_1, u_2 \in C$
and
![]() $\tilde y \in M$
such that
$\tilde y \in M$
such that
![]() $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
and
$\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
and
![]() $\tilde y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{\tilde v_1}}$
. Lemma 7.3 gives
$\tilde y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{\tilde v_1}}$
. Lemma 7.3 gives
![]() $E(v_1, v_2) = E(y)$
, and as
$E(v_1, v_2) = E(y)$
, and as
![]() $C \subset E(v_1, v_2)$
, there holds
$C \subset E(v_1, v_2)$
, there holds
![]() $y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_1}}$
. As
$y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_1}}$
. As
![]() $y, \tilde y \in \overline {\gamma _{u_1}}$
, we have
$y, \tilde y \in \overline {\gamma _{u_1}}$
, we have
![]() $\tilde y \le y$
or
$\tilde y \le y$
or
![]() $y < \tilde y$
.
$y < \tilde y$
.
Case
![]() $y < \tilde y$
. The causal path from y to
$y < \tilde y$
. The causal path from y to
![]() $\pi (u_1)$
, given by
$\pi (u_1)$
, given by
![]() $\gamma _{u_2}$
from y to
$\gamma _{u_2}$
from y to
![]() $\tilde y$
and
$\tilde y$
and
![]() $\gamma _{u_1}$
from
$\gamma _{u_1}$
from
![]() $\tilde y$
to
$\tilde y$
to
![]() $\pi (u_1)$
, is not a null pregeodesic. This is a contradiction with
$\pi (u_1)$
, is not a null pregeodesic. This is a contradiction with
![]() $u_1 \in E(y)$
.
$u_1 \in E(y)$
.
Case
![]() $\tilde y \le y$
. There is a causal path from
$\tilde y \le y$
. There is a causal path from
![]() $x_1$
to
$x_1$
to
![]() $\tilde x_1$
, and there is a causal path from
$\tilde x_1$
, and there is a causal path from
![]() $\tilde x_1$
to y given by
$\tilde x_1$
to y given by
![]() $\gamma _{\tilde v_1}$
from
$\gamma _{\tilde v_1}$
from
![]() $\tilde x_1$
to
$\tilde x_1$
to
![]() $\tilde y$
and by
$\tilde y$
and by
![]() $\gamma _{u_1}$
from
$\gamma _{u_1}$
from
![]() $\tilde y$
to y. Therefore, there is a causal path from
$\tilde y$
to y. Therefore, there is a causal path from
![]() $x_1$
to y via
$x_1$
to y via
![]() $\tilde x_1$
and
$\tilde x_1$
and
![]() $x_1 \ll \tilde x_1$
, a contradiction with
$x_1 \ll \tilde x_1$
, a contradiction with
![]() $\gamma _v$
being optimising from
$\gamma _v$
being optimising from
![]() $x_1$
to y.
$x_1$
to y.
Lemma 7.6. Let
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
![]() $x_1, y \in M$
be as in Lemma 7.3, and let
$x_1, y \in M$
be as in Lemma 7.3, and let
be a time-like and future-pointing path. Suppose that
![]() $\mu _{\mathrm{in}}(s) \in \overline {\gamma _{v_1}}$
for some
$\mu _{\mathrm{in}}(s) \in \overline {\gamma _{v_1}}$
for some
![]() $s \in [-1,1)$
and
$s \in [-1,1)$
and
![]() $\mu _{\mathrm{in}}(s) \ll y$
. Suppose furthermore that
$\mu _{\mathrm{in}}(s) \ll y$
. Suppose furthermore that
![]() $\mu _{\mathrm{in}}(1) \not \le y$
and
$\mu _{\mathrm{in}}(1) \not \le y$
and
![]() $E(v_1, v_2) \ne \emptyset $
. Then there are
$E(v_1, v_2) \ne \emptyset $
. Then there are
![]() $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
$\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and nonempty
![]() $C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
$C \in \mathcal C(\tilde v_1, \tilde v_2)$
such that
![]() $C \subset E(v_1, v_2)$
and
$C \subset E(v_1, v_2)$
and
![]() $\mu _{\mathrm{in}}(\tilde s) \in \overleftarrow {\;\gamma _{\tilde v_1}}$
for some
$\mu _{\mathrm{in}}(\tilde s) \in \overleftarrow {\;\gamma _{\tilde v_1}}$
for some
![]() $\tilde s> s$
.
$\tilde s> s$
.
Proof. By Lemma 7.3 we have
![]() $E(v_1, v_2) = E(y)$
. As
$E(v_1, v_2) = E(y)$
. As
![]() $E(y)$
is a nonempty manifold with (nonsmooth) boundary, there is
$E(y)$
is a nonempty manifold with (nonsmooth) boundary, there is
![]() $u \in E(y)$
such that
$u \in E(y)$
such that
![]() $E(y)$
is a smooth manifold near u. Then
$E(y)$
is a smooth manifold near u. Then
![]() $\gamma _u$
is optimising from y to
$\gamma _u$
is optimising from y to
![]() $z:=\pi (u)$
and also slightly past z.
$z:=\pi (u)$
and also slightly past z.
By Lemma 6.10 there is
![]() $\tilde s \in (s,1)$
such that either there is an optimising geodesic from
$\tilde s \in (s,1)$
such that either there is an optimising geodesic from
![]() $\mu _{\mathrm{in}}(\tilde s)$
to y or
$\mu _{\mathrm{in}}(\tilde s)$
to y or
![]() $y = \mu _{\mathrm{in}}(\tilde s)$
.
$y = \mu _{\mathrm{in}}(\tilde s)$
.
Let us consider the former case first. Choose
![]() $\tilde v_1$
in the tangent bundle of that geodesic so that
$\tilde v_1$
in the tangent bundle of that geodesic so that
![]() $\tilde x:=\pi (\tilde v_1) \in \Omega _{\mathrm{in}}$
and
$\tilde x:=\pi (\tilde v_1) \in \Omega _{\mathrm{in}}$
and
![]() $\mu _{\mathrm{in}}(\tilde s) < \tilde x < y$
. By Lemma 7.1 there are
$\mu _{\mathrm{in}}(\tilde s) < \tilde x < y$
. By Lemma 7.1 there are
![]() $\tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and
$\tilde v_2 \in L^+ \Omega _{\mathrm{in}}$
and
![]() $C \subset \operatorname {\mathrm {CP}}(\tilde v_{1}, \tilde v_{2})$
such that C is a neighbourhood of u in
$C \subset \operatorname {\mathrm {CP}}(\tilde v_{1}, \tilde v_{2})$
such that C is a neighbourhood of u in
![]() $C(y)$
. But
$C(y)$
. But
![]() $C(y) \subset E(y)$
near u.
$C(y) \subset E(y)$
near u.
Let us now suppose that
![]() $y = \mu _{\mathrm{in}}(\tilde s)$
. Choose
$y = \mu _{\mathrm{in}}(\tilde s)$
. Choose
![]() $\xi _0, \xi _1 \in L^+_y M$
such that
$\xi _0, \xi _1 \in L^+_y M$
such that
![]() $\overline {\gamma _{y,\xi _0}} = \overline {\gamma _{u}}$
and
$\overline {\gamma _{y,\xi _0}} = \overline {\gamma _{u}}$
and
![]() $\overline {\gamma _{y,\xi _1}} \ne \overline {\gamma _{u}}$
. By Lemma 6.23 there is a neighbourhood
$\overline {\gamma _{y,\xi _1}} \ne \overline {\gamma _{u}}$
. By Lemma 6.23 there is a neighbourhood
![]() $V \subset L_y^+ M$
of
$V \subset L_y^+ M$
of
![]() $\xi _0$
and
$\xi _0$
and
![]() $\xi _2 \in L_y^+ M$
such that for any
$\xi _2 \in L_y^+ M$
such that for any
![]() $\eta \in V$
there is
$\eta \in V$
there is
![]() $\xi _3 \in L_y^+ M$
such that
$\xi _3 \in L_y^+ M$
such that
![]() $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
$\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$
and
![]() $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
$\eta \notin \operatorname {\mathrm {span}}(\xi _j)$
,
![]() $j=1,2,3$
. We write
$j=1,2,3$
. We write
![]() $\tilde v_j = (y, \xi _j)$
,
$\tilde v_j = (y, \xi _j)$
,
![]() $j=1,2$
. Observe that y is the only point in
$j=1,2$
. Observe that y is the only point in
![]() $\overleftarrow {\;\gamma _{\tilde u}} \cap \overrightarrow {\gamma _{\tilde v_1}}$
for
$\overleftarrow {\;\gamma _{\tilde u}} \cap \overrightarrow {\gamma _{\tilde v_1}}$
for
![]() $\tilde u$
close to u since
$\tilde u$
close to u since
![]() $\gamma _u$
is optimising from y to a point past
$\gamma _u$
is optimising from y to a point past
![]() $\pi (u)$
. As in the proof of Lemma 7.1, we see that there is
$\pi (u)$
. As in the proof of Lemma 7.1, we see that there is
![]() $C \subset \operatorname {\mathrm {CP}}(\tilde v_1, \tilde v_2)$
such that C is a neighbourhood of u in
$C \subset \operatorname {\mathrm {CP}}(\tilde v_1, \tilde v_2)$
such that C is a neighbourhood of u in
![]() $C(y)$
.
$C(y)$
.
7.4 Global recovery
Let
![]() $\mu _a$
be as in Lemma 6.20, with
$\mu _a$
be as in Lemma 6.20, with
![]() $\Omega =\Omega _{\mathrm{out}}$
, and define for
$\Omega =\Omega _{\mathrm{out}}$
, and define for
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
,
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
,
Figure 5 illustrates the function
![]() $f_a(v_1, v_2)$
.
$f_a(v_1, v_2)$
.

Figure 5 Function
![]() $f_0(v_1, v_2)$
in the
$f_0(v_1, v_2)$
in the
![]() $1+2$
-dimensional Minkowski space. Left. The time-like path
$1+2$
-dimensional Minkowski space. Left. The time-like path
![]() $\mu _0 = \mu _{\mathrm{out}}$
is the green line segment, and the point
$\mu _0 = \mu _{\mathrm{out}}$
is the green line segment, and the point
![]() $z=\mu _0(f_0(v_1,v_2))$
is also green. The thick blue line segment is the optimising geodesic from y to z. It is contained in the cone
$z=\mu _0(f_0(v_1,v_2))$
is also green. The thick blue line segment is the optimising geodesic from y to z. It is contained in the cone
![]() $\pi (C(y))$
. The time axis is vertical, and the sets
$\pi (C(y))$
. The time axis is vertical, and the sets
![]() $\Omega _{\mathrm{out}}$
,
$\Omega _{\mathrm{out}}$
,
![]() $\pi (C(y))$
,
$\pi (C(y))$
,
![]() $\pi (E(y))$
, as well as the points
$\pi (E(y))$
, as well as the points
![]() $y, x_1, x_2$
, vectors
$y, x_1, x_2$
, vectors
![]() $v_1, v_2$
and geodesics
$v_1, v_2$
and geodesics
![]() $\gamma _{v_1}, \gamma _{v_2}$
, are as in Figure 4. Right. Inequality
$\gamma _{v_1}, \gamma _{v_2}$
, are as in Figure 4. Right. Inequality
![]() $f_0(v_1,v_2) \le f_0(v_1, w_2)$
as in Lemma 7.8. The vector
$f_0(v_1,v_2) \le f_0(v_1, w_2)$
as in Lemma 7.8. The vector
![]() $w_2$
is dashed red and the points
$w_2$
is dashed red and the points
![]() $z=\mu _0(f_0(v_1,v_2))$
and
$z=\mu _0(f_0(v_1,v_2))$
and
![]() $\tilde z=\mu _0(f_0(v_1,w_2))$
are green. The points
$\tilde z=\mu _0(f_0(v_1,w_2))$
are green. The points
![]() $y, x_1, x_2$
, vectors
$y, x_1, x_2$
, vectors
![]() $v_1, v_2$
, geodesics
$v_1, v_2$
, geodesics
![]() $\gamma _{v_1}, \gamma _{v_2}$
and path
$\gamma _{v_1}, \gamma _{v_2}$
and path
![]() $\mu _0$
are as on the left.
$\mu _0$
are as on the left.
Lemma 7.7. Let
![]() $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
$v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$
and
![]() $y \in M$
be as in Lemma 7.3. Then
$y \in M$
be as in Lemma 7.3. Then
 $$ \begin{align*}f_a(v_1,v_2) = f_{\mu_a}^+(y).\end{align*} $$
$$ \begin{align*}f_a(v_1,v_2) = f_{\mu_a}^+(y).\end{align*} $$
Lemma 7.8. Let
![]() $v_1 \in L^+ \Omega _{\mathrm{in}}$
and let
$v_1 \in L^+ \Omega _{\mathrm{in}}$
and let
![]() $x_1 \in \overline {\gamma _{v_1}}$
satisfy
$x_1 \in \overline {\gamma _{v_1}}$
satisfy
![]() $x_1 < \pi (v_1)$
. Suppose that
$x_1 < \pi (v_1)$
. Suppose that
![]() $\overline {\gamma _{v_1}} \cap \overline {\mu _0} = \emptyset $
and
$\overline {\gamma _{v_1}} \cap \overline {\mu _0} = \emptyset $
and
![]() $f_{\mu _0}^+(x_1)> -1$
. Then there is a neighbourhood
$f_{\mu _0}^+(x_1)> -1$
. Then there is a neighbourhood
![]() $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
$\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
![]() $v_1$
such that all
$v_1$
such that all
![]() $v_2 \in L^+ \Omega _{\mathrm{in}}$
and
$v_2 \in L^+ \Omega _{\mathrm{in}}$
and
![]() $w_2 \in \mathcal U$
satisfy the following. If there is
$w_2 \in \mathcal U$
satisfy the following. If there is
![]() $x_2 < \pi (v_2)$
such that
$x_2 < \pi (v_2)$
such that
![]() $\gamma _{v_j}$
is optimising from
$\gamma _{v_j}$
is optimising from
![]() $x_j$
to a point
$x_j$
to a point
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
for
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
for
![]() $j=1,2$
,
$j=1,2$
,
![]() $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
,
$\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
,
![]() $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
and
$y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
and
![]() $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
, then
$\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
, then
![]() $f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$
.
$f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$
.
Proof. Let
![]() $\mathcal U$
be small enough so that it is contained in the two neighbourhoods given by Lemmas 6.14 and 6.15. When applying Lemmas 6.14 and 6.15 we take
$\mathcal U$
be small enough so that it is contained in the two neighbourhoods given by Lemmas 6.14 and 6.15. When applying Lemmas 6.14 and 6.15 we take
![]() $v = v_1$
,
$v = v_1$
,
![]() $x = x_1$
and
$x = x_1$
and
![]() $K = J^+(\overline {\Omega _{\mathrm{in}}}) \cap J^-(\overline {\Omega _{\mathrm{out}}})$
. Moreover, let
$K = J^+(\overline {\Omega _{\mathrm{in}}}) \cap J^-(\overline {\Omega _{\mathrm{out}}})$
. Moreover, let
![]() $U'$
be as in Lemma 6.15.
$U'$
be as in Lemma 6.15.
Let
![]() $w_2 \in \mathcal U$
,
$w_2 \in \mathcal U$
,
![]() $C \in \mathcal C(v_1,w_2)$
and let
$C \in \mathcal C(v_1,w_2)$
and let
![]() $u_1 \in C$
satisfy
$u_1 \in C$
satisfy
![]() $\pi (u) \in \overline {\mu _a}$
for
$\pi (u) \in \overline {\mu _a}$
for
![]() $a \in U'$
. We write
$a \in U'$
. We write
![]() $\pi (u_1) = F_{\mathrm{out}}(s, a)$
for some
$\pi (u_1) = F_{\mathrm{out}}(s, a)$
for some
![]() $s \in [-1,1]$
and begin by showing that
$s \in [-1,1]$
and begin by showing that
By Lemma 7.4 there are
![]() $u_2 \in C$
, satisfying
$u_2 \in C$
, satisfying
![]() $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
, and
$\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$
, and
Case
![]() $y_1 = y_2$
. Now
$y_1 = y_2$
. Now
![]() $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
implies
$\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
implies
![]() $y < y_1$
. Hence, by Lemma 7.7
$y < y_1$
. Hence, by Lemma 7.7
 $$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_1) \leqslant s. \end{align*} $$
$$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_1) \leqslant s. \end{align*} $$
Case
![]() $y_2 < y_1$
. It follows from Lemma 6.14 that the geodesic
$y_2 < y_1$
. It follows from Lemma 6.14 that the geodesic
![]() $\gamma _{v_1}$
is not optimising from
$\gamma _{v_1}$
is not optimising from
![]() $x_1$
to
$x_1$
to
![]() $y_1$
. Therefore,
$y_1$
. Therefore,
![]() $y < y_1$
. As above, this implies
$y < y_1$
. As above, this implies
![]() $f_a(v_1,v_2) \leqslant s$
.
$f_a(v_1,v_2) \leqslant s$
.
Case
![]() $y_1 < y_2$
. Lemma 6.15 implies
$y_1 < y_2$
. Lemma 6.15 implies
 $$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_2) \leqslant s. \end{align*} $$
$$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_2) \leqslant s. \end{align*} $$
We have shown (7.2).
Let
![]() $u \in C(v_1,w_2)$
satisfy
$u \in C(v_1,w_2)$
satisfy
![]() $\pi (u) = F_{\mathrm{out}}(s,0)$
for some
$\pi (u) = F_{\mathrm{out}}(s,0)$
for some
![]() $s \in [-1,1]$
. Then there are
$s \in [-1,1]$
. Then there are
![]() $C_j \in \mathcal C(v_1,w_2)$
,
$C_j \in \mathcal C(v_1,w_2)$
,
![]() $u_j \in C_j$
,
$u_j \in C_j$
,
![]() $s_j \in (-1,1)$
and
$s_j \in (-1,1)$
and
![]() $a_j \in U'$
such that
$a_j \in U'$
such that
![]() $\pi (u_j) = F(s_j, a_j)$
and
$\pi (u_j) = F(s_j, a_j)$
and
![]() $u_j \to u$
. Now (7.2) implies
$u_j \to u$
. Now (7.2) implies
![]() $f_{a_j}(v_1, v_2) \leqslant s_j$
, and letting
$f_{a_j}(v_1, v_2) \leqslant s_j$
, and letting
![]() $j \to \infty $
, we obtain
$j \to \infty $
, we obtain
![]() $f_0(v_1, v_2) \leqslant s$
.
$f_0(v_1, v_2) \leqslant s$
.
Lemma 7.9. Let
![]() $v_1 \in L^+ \Omega _{\mathrm{in}}$
and let
$v_1 \in L^+ \Omega _{\mathrm{in}}$
and let
![]() $x_1 \in \overline {\gamma _{v_1}}$
satisfy
$x_1 \in \overline {\gamma _{v_1}}$
satisfy
![]() $x_1 < \pi (v_1)$
. Suppose that
$x_1 < \pi (v_1)$
. Suppose that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $x_1$
to a point y. Then there is a neighbourhood
$x_1$
to a point y. Then there is a neighbourhood
![]() $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
$\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
![]() $v_1$
such that all
$v_1$
such that all
![]() $v_2 \in \mathcal U$
satisfy the following. If there is
$v_2 \in \mathcal U$
satisfy the following. If there is
![]() $\tilde y \in \overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y)$
, then there is
$\tilde y \in \overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y)$
, then there is
![]() $x_2 < \pi (v_2)$
such that
$x_2 < \pi (v_2)$
such that
![]() $\gamma _{v_2}$
is optimising from
$\gamma _{v_2}$
is optimising from
![]() $x_2$
to
$x_2$
to
![]() $\tilde y$
.
$\tilde y$
.
Proof. To get a contradiction, suppose that there are sequences
![]() $L^+M\ni v_j \to v_1$
and
$L^+M\ni v_j \to v_1$
and
 $$ \begin{align*} \tilde y_j \in \overrightarrow{\gamma_{v_j}} \cap \overrightarrow{\gamma_{v_1}} \cap J^-(y) \end{align*} $$
$$ \begin{align*} \tilde y_j \in \overrightarrow{\gamma_{v_j}} \cap \overrightarrow{\gamma_{v_1}} \cap J^-(y) \end{align*} $$
such that for all
![]() $x \in \overline {\gamma _{v_j}}$
there holds: if
$x \in \overline {\gamma _{v_j}}$
there holds: if
![]() $x < \pi (v_j)$
then
$x < \pi (v_j)$
then
![]() $x \ll \tilde y_j$
. Due to compactness of
$x \ll \tilde y_j$
. Due to compactness of
![]() $J^+(\pi (v_1)) \cap J^-(y)$
, we may assume that
$J^+(\pi (v_1)) \cap J^-(y)$
, we may assume that
![]() $\tilde y_j \to \tilde y$
for some
$\tilde y_j \to \tilde y$
for some
![]() $\tilde y \in M$
. Then
$\tilde y \in M$
. Then
![]() $\tilde y \in \overrightarrow {\gamma _{v_1}}$
and
$\tilde y \in \overrightarrow {\gamma _{v_1}}$
and
![]() $\tilde y \le y$
. We choose
$\tilde y \le y$
. We choose
 $\eta _j \in L_{\tilde y_j}^- M$
and
$\eta _j \in L_{\tilde y_j}^- M$
and
![]() $r_j \geqslant 0$
so that
$r_j \geqslant 0$
so that
![]() $\overline {\gamma _{\tilde y_j, \eta _j}} = \overline {\gamma _{v_j}}$
,
$\overline {\gamma _{\tilde y_j, \eta _j}} = \overline {\gamma _{v_j}}$
,
![]() $\gamma _{\tilde y_j, \eta _j}(r_j) = \pi (v_j)$
and so that
$\gamma _{\tilde y_j, \eta _j}(r_j) = \pi (v_j)$
and so that
![]() $\eta _j \to \eta $
and
$\eta _j \to \eta $
and
![]() $r_j \to r$
for some
$r_j \to r$
for some
![]() $\eta \in L_y^- M$
and
$\eta \in L_y^- M$
and
![]() $r \geqslant 0$
. Then
$r \geqslant 0$
. Then
![]() $\rho (\tilde y_j, \eta _j) \leqslant r_j$
and
$\rho (\tilde y_j, \eta _j) \leqslant r_j$
and
![]() $\gamma _{\tilde y,\eta }(r) = \pi (v_1)$
. Lemma 6.7 implies that
$\gamma _{\tilde y,\eta }(r) = \pi (v_1)$
. Lemma 6.7 implies that
![]() $\rho (\tilde y,\eta ) \leqslant r$
. But this is a contradiction with
$\rho (\tilde y,\eta ) \leqslant r$
. But this is a contradiction with
![]() $\gamma _{v_1}$
being optimising from
$\gamma _{v_1}$
being optimising from
![]() $x_1 < \pi (v_1)$
to y since
$x_1 < \pi (v_1)$
to y since
![]() $\tilde y \le y$
.
$\tilde y \le y$
.
We are now ready to prove the main theorem in this section, which shows that the earliest arrivals can be reconstructed from the relation
![]() $\operatorname {\mathrm {R}}$
. Figure 6 outlines the geometric setting of the theorem.
$\operatorname {\mathrm {R}}$
. Figure 6 outlines the geometric setting of the theorem.

Figure 6 Schematic of the geometric setting of Theorem 7.10. The time-like paths
![]() $\mu _{\mathrm{in}}$
and
$\mu _{\mathrm{in}}$
and
![]() $\mu _0$
in green. Vectors
$\mu _0$
in green. Vectors
![]() $v_1$
,
$v_1$
,
![]() $\tilde v_1$
and
$\tilde v_1$
and
![]() $v_2$
are in red. Points
$v_2$
are in red. Points
![]() $x = \mu _{\mathrm{in}}(s)$
and
$x = \mu _{\mathrm{in}}(s)$
and
![]() $\tilde x = \mu _{\mathrm{in}}(\tilde s)$
are in black and point
$\tilde x = \mu _{\mathrm{in}}(\tilde s)$
are in black and point
![]() $z = \mu _0(f_0(v_1,v_2))$
is in green. Here
$z = \mu _0(f_0(v_1,v_2))$
is in green. Here
![]() $f_0(v_1, v_2) \ge f_{\mathrm{crit}}(v_1)$
. Observe that this case cannot arise in the Minkowski space.
$f_0(v_1, v_2) \ge f_{\mathrm{crit}}(v_1)$
. Observe that this case cannot arise in the Minkowski space.
Theorem 7.10. Let
![]() $s \in [-1,1)$
and let
$s \in [-1,1)$
and let
![]() $v_1 \in L^+ \Omega _{\mathrm{in}}$
satisfy
$v_1 \in L^+ \Omega _{\mathrm{in}}$
satisfy
Suppose also that
![]() $\mu _{\mathrm{in}}(s)$
and
$\mu _{\mathrm{in}}(s)$
and
![]() $\pi (v_1)$
are close enough so that
$\pi (v_1)$
are close enough so that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $\mu _{\mathrm{in}}(s)$
to a point beyond
$\mu _{\mathrm{in}}(s)$
to a point beyond
![]() $\pi (v_1)$
. Then there is a neighbourhood
$\pi (v_1)$
. Then there is a neighbourhood
![]() $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
$\mathcal U \subset L^+ \Omega _{\mathrm{in}}$
of
![]() $v_1$
such that for all neighbourhoods
$v_1$
such that for all neighbourhoods
![]() $\mathcal U' \subset \mathcal U$
of
$\mathcal U' \subset \mathcal U$
of
![]() $v_1$
there holds
$v_1$
there holds
 $$ \begin{align} &\{E(v_1, v_2) : v_2 \in \mathcal U', f_0(v_1,v_2) \leqslant f_{\text{crit}}\ \text{and}\ f_0(v_1, v_2) < 1\} \\\notag&\qquad= \{E(y) : y=\gamma_{v_1}(r), 0\leqslant r \leqslant \rho(v_1)\ \text{and}\ f_{\mu_0}^+(y) < 1\}, \end{align} $$
$$ \begin{align} &\{E(v_1, v_2) : v_2 \in \mathcal U', f_0(v_1,v_2) \leqslant f_{\text{crit}}\ \text{and}\ f_0(v_1, v_2) < 1\} \\\notag&\qquad= \{E(y) : y=\gamma_{v_1}(r), 0\leqslant r \leqslant \rho(v_1)\ \text{and}\ f_{\mu_0}^+(y) < 1\}, \end{align} $$
where
![]() $f_{\mathrm{crit}} = \inf \{ f_0(v_1, v_2) : v_2 \in \mathcal W \}$
and
$f_{\mathrm{crit}} = \inf \{ f_0(v_1, v_2) : v_2 \in \mathcal W \}$
and
 $$ \begin{align*} \mathcal W=\{ v_2 \in \mathcal U' : \ &\overline{\gamma_{v_1}} \ne \overline{\gamma_{v_2}}\ \text{and there are}\ \tilde v_1, \tilde v_2 \in L^+ \Omega_{\text{in}} \\& \text{and nonempty}\ C \in \mathcal C(\tilde v_1, \tilde v_2)\ \text{such that} \\& C \subset E(v_1, v_2)\ \text{and}\ \mu_{\text{in}}(\tilde s) \in \overleftarrow{\;\gamma_{\tilde v_1}}\ \text{for some}\ \tilde s> s\}. \end{align*} $$
$$ \begin{align*} \mathcal W=\{ v_2 \in \mathcal U' : \ &\overline{\gamma_{v_1}} \ne \overline{\gamma_{v_2}}\ \text{and there are}\ \tilde v_1, \tilde v_2 \in L^+ \Omega_{\text{in}} \\& \text{and nonempty}\ C \in \mathcal C(\tilde v_1, \tilde v_2)\ \text{such that} \\& C \subset E(v_1, v_2)\ \text{and}\ \mu_{\text{in}}(\tilde s) \in \overleftarrow{\;\gamma_{\tilde v_1}}\ \text{for some}\ \tilde s> s\}. \end{align*} $$
Proof. Write
![]() $x_1 = \mu _{\mathrm{in}}(s)$
and observe that
$x_1 = \mu _{\mathrm{in}}(s)$
and observe that
![]() $f^+_{\mu _0}(x_1)> -1$
since
$f^+_{\mu _0}(x_1)> -1$
since
Let
![]() $\mathcal U$
be small enough so that it is contained in the two neighbourhoods given by Lemmas 7.8 and 7.9.
$\mathcal U$
be small enough so that it is contained in the two neighbourhoods given by Lemmas 7.8 and 7.9.
Denote the left-hand side of (7.3) by
![]() $\mathcal E$
. Let
$\mathcal E$
. Let
![]() $y \in \overrightarrow {\gamma _{v_1}}$
and suppose that
$y \in \overrightarrow {\gamma _{v_1}}$
and suppose that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $x_1$
to a point beyond y and that
$x_1$
to a point beyond y and that
![]() $f_{\mu _0}^+(y) < 1$
. We will show that
$f_{\mu _0}^+(y) < 1$
. We will show that
![]() $E(y) \in \mathcal E$
. Lower semi-continuity of
$E(y) \in \mathcal E$
. Lower semi-continuity of
![]() $\rho $
implies that there is
$\rho $
implies that there is
![]() $v_2 \in \mathcal U'$
and
$v_2 \in \mathcal U'$
and
![]() $x_2 < \pi (v_2)$
such that
$x_2 < \pi (v_2)$
such that
![]() $\gamma _{v_2}$
is optimising from
$\gamma _{v_2}$
is optimising from
![]() $x_2$
to y and
$x_2$
to y and
![]() $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
. Moreover, (7.4) implies that
$\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$
. Moreover, (7.4) implies that
![]() $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
. Now Lemmas 7.3 and 7.7 give
$y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$
. Now Lemmas 7.3 and 7.7 give
![]() $E(v_1, v_2) = E(y)$
and
$E(v_1, v_2) = E(y)$
and
![]() $f_0(v_1, v_2) = f_{\mu _0}^+(y)$
. Hence,
$f_0(v_1, v_2) = f_{\mu _0}^+(y)$
. Hence,
![]() $E(y) \in \mathcal E$
follows after we show that
$E(y) \in \mathcal E$
follows after we show that
![]() $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
.
$f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
.
Let
![]() $w_2 \in \mathcal U'$
satisfy
$w_2 \in \mathcal U'$
satisfy
![]() $\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$
. If
$\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$
. If
![]() $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
, then
$\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $
, then
![]() $f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$
by Lemma 7.8. On the other hand, if
$f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$
by Lemma 7.8. On the other hand, if
![]() $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) \ne \emptyset $
, then Lemmas 7.9 and 7.5 imply that
$\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) \ne \emptyset $
, then Lemmas 7.9 and 7.5 imply that
![]() $w_2 \notin \mathcal W$
. Hence,
$w_2 \notin \mathcal W$
. Hence,
![]() $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
.
$f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
.
We turn to the opposite inclusion and suppose that
![]() $v_2 \in \mathcal U'$
,
$v_2 \in \mathcal U'$
,
![]() $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
and
$f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$
and
![]() $f_0(v_1, v_2) < 1$
. To get a contradiction, suppose that there does not exist
$f_0(v_1, v_2) < 1$
. To get a contradiction, suppose that there does not exist
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $x_1$
to y. This implies that there is also
$x_1$
to y. This implies that there is also
![]() $\tilde x_1 \in \overline {\gamma _{v_1}}$
such that
$\tilde x_1 \in \overline {\gamma _{v_1}}$
such that
![]() $x_1 < \tilde x_1 < \pi (v_1)$
and there does not exist
$x_1 < \tilde x_1 < \pi (v_1)$
and there does not exist
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $\tilde x_1$
to y. Consider a point
$\tilde x_1$
to y. Consider a point
![]() $\tilde y \in \overline {\gamma _{v_1}}$
such that
$\tilde y \in \overline {\gamma _{v_1}}$
such that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $\tilde x_1$
to
$\tilde x_1$
to
![]() $\tilde y$
and
$\tilde y$
and
![]() $\pi (v_1) < \tilde y$
. Then there are
$\pi (v_1) < \tilde y$
. Then there are
![]() $w_2 \in \mathcal U'$
and
$w_2 \in \mathcal U'$
and
![]() $\tilde x_2 < \pi (w_2)$
such that
$\tilde x_2 < \pi (w_2)$
such that
![]() $\gamma _{w_2}$
is optimising from
$\gamma _{w_2}$
is optimising from
![]() $\tilde x_2$
to
$\tilde x_2$
to
![]() $\tilde y$
and
$\tilde y$
and
![]() $\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$
. Note that
$\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$
. Note that
![]() $\overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(\tilde y) = \emptyset $
as there does not exist
$\overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(\tilde y) = \emptyset $
as there does not exist
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $\tilde x_1$
to y. Lemmas 7.7 and 7.8 imply that
$\tilde x_1$
to y. Lemmas 7.7 and 7.8 imply that
 $$ \begin{align} f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align} $$
$$ \begin{align} f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align} $$
We will now consider two cases.
Case that there is
![]() $y \in \overline {\gamma _{v_1}}$
such that
$y \in \overline {\gamma _{v_1}}$
such that
![]() $x_1 \ll y$
and
$x_1 \ll y$
and
![]() $y \in J^-(\overline {\Omega _{\mathrm{out}}})$
. Then the point
$y \in J^-(\overline {\Omega _{\mathrm{out}}})$
. Then the point
![]() $\tilde y$
can be chosen so that
$\tilde y$
can be chosen so that
![]() $x_1 \ll \tilde y$
. Observe that
$x_1 \ll \tilde y$
. Observe that
![]() $f_0(v_1, v_2) < 1$
implies
$f_0(v_1, v_2) < 1$
implies
![]() $E(v_1, v_2) \ne \emptyset $
. Moreover,
$E(v_1, v_2) \ne \emptyset $
. Moreover,
![]() $\overline {\Omega _{\mathrm{out}}} \cap J^+(\mu _{\mathrm{in}}(1)) = \emptyset $
implies that
$\overline {\Omega _{\mathrm{out}}} \cap J^+(\mu _{\mathrm{in}}(1)) = \emptyset $
implies that
![]() $\mu _{\mathrm{in}}(1) \not \le y$
. Lemma 7.6 gives
$\mu _{\mathrm{in}}(1) \not \le y$
. Lemma 7.6 gives
![]() $w_2 \in \mathcal W$
. Therefore,
$w_2 \in \mathcal W$
. Therefore,
 $$ \begin{align*} f_0(v_1,v_2) \leqslant f_{\text{crit}} \leqslant f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align*} $$
$$ \begin{align*} f_0(v_1,v_2) \leqslant f_{\text{crit}} \leqslant f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align*} $$
But here
![]() $\tilde y \in \overline {\gamma _{v_1}}$
can be any point satisfying
$\tilde y \in \overline {\gamma _{v_1}}$
can be any point satisfying
![]() $\pi (v_1) < \tilde y$
,
$\pi (v_1) < \tilde y$
,
![]() $\tau (\tilde x_1, \tilde y) = 0$
and
$\tau (\tilde x_1, \tilde y) = 0$
and
![]() $\tau (x_1, \tilde y)> 0$
. In particular, there is an open interval of numbers
$\tau (x_1, \tilde y)> 0$
. In particular, there is an open interval of numbers
![]() $r> 0$
such that
$r> 0$
such that
 $$ \begin{align*} f_{\mu_0}^+(\gamma_{v_1}(r)) = f_0(v_1,v_2). \end{align*} $$
$$ \begin{align*} f_{\mu_0}^+(\gamma_{v_1}(r)) = f_0(v_1,v_2). \end{align*} $$
Taking into account the assumption that
![]() $f_0(v_1,v_2) < 1$
, Lemma 6.11 implies that
$f_0(v_1,v_2) < 1$
, Lemma 6.11 implies that
![]() $f_0(v_1,v_2) = -1$
. But
$f_0(v_1,v_2) = -1$
. But
![]() $f^+_{\mu _0}(x_1)> -1$
and
$f^+_{\mu _0}(x_1)> -1$
and
![]() $f^+_{\mu _0}$
is increasing along
$f^+_{\mu _0}$
is increasing along
![]() $\gamma _{v_1}$
, a contradiction.
$\gamma _{v_1}$
, a contradiction.
Case that there does not exist
![]() $y \in \overline {\gamma _{v_1}}$
such that
$y \in \overline {\gamma _{v_1}}$
such that
![]() $x_1 \ll y$
and
$x_1 \ll y$
and
![]() $y \in J^-(\overline {\Omega _{\mathrm{out}}})$
. By Lemma 6.3 the point
$y \in J^-(\overline {\Omega _{\mathrm{out}}})$
. By Lemma 6.3 the point
![]() $\tilde y \in \overline {\gamma _{v_1}}$
can be chosen so that
$\tilde y \in \overline {\gamma _{v_1}}$
can be chosen so that
![]() $\tilde y$
is not in the interior of the set K in (7.1). Then
$\tilde y$
is not in the interior of the set K in (7.1). Then
![]() $f_{\mu _0}^+(\tilde y) = 1$
and (7.5) gives a contradiction with
$f_{\mu _0}^+(\tilde y) = 1$
and (7.5) gives a contradiction with
![]() $f_0(v_1, v_2) < 1$
.
$f_0(v_1, v_2) < 1$
.
There is
![]() $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
$y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$
such that
![]() $\gamma _{v_1}$
is optimising from
$\gamma _{v_1}$
is optimising from
![]() $x_1$
to y. Lemma 7.9 implies that there is
$x_1$
to y. Lemma 7.9 implies that there is
![]() $x_2 < \pi (v_2)$
such that
$x_2 < \pi (v_2)$
such that
![]() $\gamma _{v_2}$
is optimising from
$\gamma _{v_2}$
is optimising from
![]() $x_2$
to y. Now Lemmas 7.3 and 7.7 give
$x_2$
to y. Now Lemmas 7.3 and 7.7 give
![]() $E(v_1, v_2) = E(y)$
and
$E(v_1, v_2) = E(y)$
and
![]() $f_0(v_1, v_2) = f_{\mu _0}^+(y)$
, and
$f_0(v_1, v_2) = f_{\mu _0}^+(y)$
, and
![]() $E(v_1, v_2)$
is in the set on the right-hand side of (7.3).
$E(v_1, v_2)$
is in the set on the right-hand side of (7.3).
We are now ready to complete the proof of Theorem 1.3. Recall that
![]() $\pi :TM\to M$
is the map to the base point of the vector. Writing
$\pi :TM\to M$
is the map to the base point of the vector. Writing
![]() $U=\Omega _{\mathrm{out}}$
, we have
$U=\Omega _{\mathrm{out}}$
, we have
where the notation
![]() $\mathcal E_U(y)$
stands for the earliest light observation set of a point y with respect to the observation set U; see [Reference Kurylev, Lassas and Uhlmann64]. Roughly speaking, the set
$\mathcal E_U(y)$
stands for the earliest light observation set of a point y with respect to the observation set U; see [Reference Kurylev, Lassas and Uhlmann64]. Roughly speaking, the set
![]() $\mathcal E_U(y)$
corresponds to the first observations made in the set U when there is a point source at y that sends light to all directions. Letting
$\mathcal E_U(y)$
corresponds to the first observations made in the set U when there is a point source at y that sends light to all directions. Letting
![]() $v_1 \in L^+ \Omega _{\mathrm{in}}$
in Theorem 7.10 converge to a vector
$v_1 \in L^+ \Omega _{\mathrm{in}}$
in Theorem 7.10 converge to a vector
![]() $v \in L_x^+ M$
, with
$v \in L_x^+ M$
, with
![]() $x=\mu _{\mathrm{in}}(s)$
for some
$x=\mu _{\mathrm{in}}(s)$
for some
![]() $s\in (-1,1)$
, we see that the relation
$s\in (-1,1)$
, we see that the relation
![]() $\operatorname {\mathrm {R}}$
determines the set
$\operatorname {\mathrm {R}}$
determines the set
for all such v. Here
![]() $E(y)\cap \mu _0([-1,1)) \ne \emptyset $
is equivalent with
$E(y)\cap \mu _0([-1,1)) \ne \emptyset $
is equivalent with
![]() $f_{\mu _0}^+(y) < 1$
.
$f_{\mu _0}^+(y) < 1$
.
Recalling the normalisation in Remark 5, we define
Then the causal diamond
![]() $\mathbb D$
defined by (1.9) is contained in this larger diamond
$\mathbb D$
defined by (1.9) is contained in this larger diamond
![]() $\tilde {\mathbb D}$
. We see that the relation
$\tilde {\mathbb D}$
. We see that the relation
![]() $\operatorname {\mathrm {R}}$
uniquely determines the set
$\operatorname {\mathrm {R}}$
uniquely determines the set
 $$ \begin{align*} E(\tilde{\mathbb D})= \{E(y)\subset T\Omega_{\text{out}}: &y=\gamma_{v}(r),\ v \in L^+_{\mu_{\text{in}}(s)} M,\ s\in (-1,1),\ r\in [0,\rho(v)],\ \\ &E(y)\cap \mu_0([-1,1)) \ne \emptyset \}. \end{align*} $$
$$ \begin{align*} E(\tilde{\mathbb D})= \{E(y)\subset T\Omega_{\text{out}}: &y=\gamma_{v}(r),\ v \in L^+_{\mu_{\text{in}}(s)} M,\ s\in (-1,1),\ r\in [0,\rho(v)],\ \\ &E(y)\cap \mu_0([-1,1)) \ne \emptyset \}. \end{align*} $$
Here
![]() $\mu _0 = \mu _{\mathrm{out}}$
. Thus, R determines
$\mu _0 = \mu _{\mathrm{out}}$
. Thus, R determines
This reduces the proof of Theorem 1.3 to the inverse problem with passive measurements studied in [Reference Kurylev, Lassas and Uhlmann64]. By [Reference Kurylev, Lassas and Uhlmann64, Theorem 1.2], the set
![]() $\mathcal E_U(\tilde {\mathbb D})$
determines the topological, differential and conformal structures of the smaller diamond
$\mathcal E_U(\tilde {\mathbb D})$
determines the topological, differential and conformal structures of the smaller diamond
![]() $\mathbb D$
. This proves Theorem 1.3.
$\mathbb D$
. This proves Theorem 1.3.
![]() $\square $
$\square $
8 Proof of Theorem 1.1
This section is concerned with the proof of Theorem 1.1. The first claim in the theorem, namely, determining the conformal, topological and differential structure of the manifold
![]() $(M,g)$
from either of the source-to-solution maps
$(M,g)$
from either of the source-to-solution maps
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
, follows from Theorems 5.1–5.2 and Theorem 1.3. To see this, we begin by defining the relations
$\mathscr N$
, follows from Theorems 5.1–5.2 and Theorem 1.3. To see this, we begin by defining the relations
 $$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \} \end{align*} $$
and
 $$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}. \end{align*} $$
It follows as a consequence of Theorems 5.1–5.2 that the source-to-solution map
![]() $\mathscr L$
(respectively
$\mathscr L$
(respectively
![]() $\mathscr N$
) determines
$\mathscr N$
) determines
![]() $\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$
(respectively
$\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$
(respectively
![]() $\operatorname {\mathrm {R}}_{\mathrm{quasi-lin}}$
) and that the latter relations are both examples of three-to-one scattering relations; that is, they both satisfy conditions (R1) and (R2). We can therefore apply Theorem 1.3 to uniquely determine the topological, differential and conformal structure of the manifold
$\operatorname {\mathrm {R}}_{\mathrm{quasi-lin}}$
) and that the latter relations are both examples of three-to-one scattering relations; that is, they both satisfy conditions (R1) and (R2). We can therefore apply Theorem 1.3 to uniquely determine the topological, differential and conformal structure of the manifold
![]() $(M,g)$
on
$(M,g)$
on
![]() $\mathbb D$
from either of the source-to-solution maps
$\mathbb D$
from either of the source-to-solution maps
![]() $\mathscr L$
or
$\mathscr L$
or
![]() $\mathscr N$
.
$\mathscr N$
.
In the remainder of this section, we complete the proof of Theorem 1.1 by showing that in the case of the semi-linear equation (1.2) and if
![]() $(n,m)\neq 3$
, the conformal factor can also be determined uniquely. We will follow the ideas set out in [Reference Uhlmann and Wang91]. Here, there will be some modifications as we are using Gaussian beams. The exceptional case
$(n,m)\neq 3$
, the conformal factor can also be determined uniquely. We will follow the ideas set out in [Reference Uhlmann and Wang91]. Here, there will be some modifications as we are using Gaussian beams. The exceptional case
![]() $(n,m)=(3,3)$
will require an alternative approach that will be briefly discussed at the end of this section.
$(n,m)=(3,3)$
will require an alternative approach that will be briefly discussed at the end of this section.
To set the idea in motion, we write
![]() $g=c\hat {g}$
for the metric on
$g=c\hat {g}$
for the metric on
![]() $\mathbb D$
, where
$\mathbb D$
, where
![]() $\hat {g}$
is known and
$\hat {g}$
is known and
![]() $c>0$
is a smooth unknown function. Naturally, we will think of the metrics g and
$c>0$
is a smooth unknown function. Naturally, we will think of the metrics g and
![]() $\hat {g}$
as metrics on the manifold M that are conformal to each other only on the set
$\hat {g}$
as metrics on the manifold M that are conformal to each other only on the set
![]() $\mathbb D$
. Let us consider the Gaussian beams
$\mathbb D$
. Let us consider the Gaussian beams
![]() $\mathcal U_\lambda $
described in Section 3. Our aim here is to show that the values of the phase function
$\mathcal U_\lambda $
described in Section 3. Our aim here is to show that the values of the phase function
![]() $\phi $
restricted to the set
$\phi $
restricted to the set
![]() $\mathbb D$
are independent of the conformal factor, while the principal part of the amplitude function,
$\mathbb D$
are independent of the conformal factor, while the principal part of the amplitude function,
![]() $a_{0,0}$
, restricted to the set
$a_{0,0}$
, restricted to the set
![]() $\mathbb D$
is given by
$\mathbb D$
is given by
 $$ \begin{align} a_{0,0}=c^{-\frac{n-1}{4}}\hat{a}_{0,0}, \end{align} $$
$$ \begin{align} a_{0,0}=c^{-\frac{n-1}{4}}\hat{a}_{0,0}, \end{align} $$
where
![]() $\hat {a}_{0,0}$
is independent of the conformal factor. Showing that
$\hat {a}_{0,0}$
is independent of the conformal factor. Showing that
![]() $\phi $
is independent of the conformal factor is trivial since the equation (3.6) for the phase function is conformally invariant.
$\phi $
is independent of the conformal factor is trivial since the equation (3.6) for the phase function is conformally invariant.
To show (8.1), we start by recalling that the wave operator changes under conformal scalings of the metric according to the expression
 $$ \begin{align} \Box_{c\hat g} u = c^{-\frac{n+3}{4}} (\Box_{\hat{g}} + q_c) (c^{\frac{n-1}{4}}u)\quad \text{on}\ \mathbb D, \end{align} $$
$$ \begin{align} \Box_{c\hat g} u = c^{-\frac{n+3}{4}} (\Box_{\hat{g}} + q_c) (c^{\frac{n-1}{4}}u)\quad \text{on}\ \mathbb D, \end{align} $$
where
 $q_c= -c^{\frac {1-n}{4}}\Box _{\hat {g}}(c^{\frac {n-1}{4}})$
.
$q_c= -c^{\frac {1-n}{4}}\Box _{\hat {g}}(c^{\frac {n-1}{4}})$
.
We now return to the construction of Gaussian beams associated to the operator
![]() $\Box _g$
on M and note that due to the scaling property above on the set
$\Box _g$
on M and note that due to the scaling property above on the set
![]() $\mathbb D$
, there is a one-to-one correspondence between Gaussian beams for
$\mathbb D$
, there is a one-to-one correspondence between Gaussian beams for
![]() $\Box _g$
and
$\Box _g$
and
![]() $\Box _{\hat {g}}+q_c$
. Here, by a Gaussian beam for
$\Box _{\hat {g}}+q_c$
. Here, by a Gaussian beam for
![]() $\Box _{\hat g} +q_c$
, we mean an ansatz
$\Box _{\hat g} +q_c$
, we mean an ansatz
 $$ \begin{align*}\hat{\mathcal U}_\lambda = e^{i\lambda \hat{\phi}} \hat{A}_{\lambda} \quad \text{for}\ \lambda>0\end{align*} $$
$$ \begin{align*}\hat{\mathcal U}_\lambda = e^{i\lambda \hat{\phi}} \hat{A}_{\lambda} \quad \text{for}\ \lambda>0\end{align*} $$
and
 $$ \begin{align*}\hat{\mathcal U}_\lambda = \overline{e^{i\lambda \hat{\phi}}\hat{A}_{\lambda}} \quad \text{for}\ \lambda<0,\end{align*} $$
$$ \begin{align*}\hat{\mathcal U}_\lambda = \overline{e^{i\lambda \hat{\phi}}\hat{A}_{\lambda}} \quad \text{for}\ \lambda<0,\end{align*} $$
where we are using Fermi coordinates
![]() $(\hat {s},\hat {y}')$
near
$(\hat {s},\hat {y}')$
near
![]() $\gamma $
with respect to the metric
$\gamma $
with respect to the metric
![]() $\hat {g}$
and define the phase,
$\hat {g}$
and define the phase,
![]() $\hat {\phi }$
, and amplitude,
$\hat {\phi }$
, and amplitude,
![]() $\hat {A}_{\lambda }$
, analogously to (3.5). Here, because of the presence of the zeroth-order term
$\hat {A}_{\lambda }$
, analogously to (3.5). Here, because of the presence of the zeroth-order term
![]() $q_c$
, the governing equations for construction of the phase and amplitude terms read as follows:
$q_c$
, the governing equations for construction of the phase and amplitude terms read as follows:
 $$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\langle d\hat{\phi},d\hat{\phi}\rangle_{\hat g}=0 \quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\left( 2\langle d\hat{\phi},d\hat{a}_j \rangle_{\hat g}- (\Box_{\hat g}\hat{\phi})\hat{a}_j + i (\Box_{\hat g}+q_c)\hat{a}_{j-1}\right)=0\quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\}, \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\langle d\hat{\phi},d\hat{\phi}\rangle_{\hat g}=0 \quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\left( 2\langle d\hat{\phi},d\hat{a}_j \rangle_{\hat g}- (\Box_{\hat g}\hat{\phi})\hat{a}_j + i (\Box_{\hat g}+q_c)\hat{a}_{j-1}\right)=0\quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\}, \end{aligned}\end{align} $$
for all
![]() $j=0,1,\ldots ,N$
and all multi-indices
$j=0,1,\ldots ,N$
and all multi-indices
![]() $\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$
with
$\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$
with
![]() $|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$
. Thus, by setting
$|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$
. Thus, by setting
![]() $j=0$
in (8.3), it follows that at each point
$j=0$
in (8.3), it follows that at each point
![]() $y \in \mathbb D$
,
$y \in \mathbb D$
,
![]() $\hat {a}_{0,0}(y)$
is independent of the conformal factor c. To summarise, the principal part of the amplitude
$\hat {a}_{0,0}(y)$
is independent of the conformal factor c. To summarise, the principal part of the amplitude
![]() $a_{0,0}$
for the Gaussian beams
$a_{0,0}$
for the Gaussian beams
![]() $\mathcal U_\lambda $
on the set
$\mathcal U_\lambda $
on the set
![]() $\mathbb D$
must be given by (8.1) for some
$\mathbb D$
must be given by (8.1) for some
![]() $\hat {a}_{0,0}$
that arises from solving (8.3) and is only dependent on the conformal class of the metric on
$\hat {a}_{0,0}$
that arises from solving (8.3) and is only dependent on the conformal class of the metric on
![]() $\mathbb D$
.
$\mathbb D$
.
We now return to the task of showing that the conformal factor c can be uniquely determined at every point
![]() $y \in \mathbb D$
. Applying arguments similar to the proof of [Reference Feizmohammadi and Oksanen29, Lemma 4], we can show that there exists a null geodesic
$y \in \mathbb D$
. Applying arguments similar to the proof of [Reference Feizmohammadi and Oksanen29, Lemma 4], we can show that there exists a null geodesic
![]() $\gamma _{v_0}$
for some
$\gamma _{v_0}$
for some
![]() $v_0 \in L^{-}\Omega _{\mathrm{out}}$
passing through y and a null geodesic
$v_0 \in L^{-}\Omega _{\mathrm{out}}$
passing through y and a null geodesic
![]() $\gamma _{v_1}$
with
$\gamma _{v_1}$
with
![]() $v_1 \in L^+\Omega _{\mathrm{in}}$
passing through y, such that
$v_1 \in L^+\Omega _{\mathrm{in}}$
passing through y, such that
![]() $\gamma _{v_0}$
and
$\gamma _{v_0}$
and
![]() $\gamma _{v_1}$
have a single intersection point on the set
$\gamma _{v_1}$
have a single intersection point on the set
![]() $\mathbb D$
. Note that this property can be checked via the knowledge of the topological, differential and conformal structure of the manifold since null vectors are conformally invariant.
$\mathbb D$
. Note that this property can be checked via the knowledge of the topological, differential and conformal structure of the manifold since null vectors are conformally invariant.
We now consider two null geodesics
![]() $\gamma _{v_2}$
and
$\gamma _{v_2}$
and
![]() $\gamma _{v_3}$
in a small neighbourhood of
$\gamma _{v_3}$
in a small neighbourhood of
![]() $\gamma _{v_1}$
passing through y and such that
$\gamma _{v_1}$
passing through y and such that
forms a linearly dependent set. Here,
![]() $\gamma _{v_j}(s_j)=y$
for
$\gamma _{v_j}(s_j)=y$
for
![]() $j=0,1,2,3$
. We emphasise that the existence of such null geodesics is guaranteed by Lemma 6.22. Now given any choice
$j=0,1,2,3$
. We emphasise that the existence of such null geodesics is guaranteed by Lemma 6.22. Now given any choice
![]() $v_0,\ldots ,v_3$
as above, we pick
$v_0,\ldots ,v_3$
as above, we pick
![]() $\iota _j \in \mathcal T_{v_j}$
such that the amplitude term
$\iota _j \in \mathcal T_{v_j}$
such that the amplitude term
 $a_{0,0}^{(j)}$
is real-valued and nonzero at the point y. We note from (8.1) that this condition can also be checked via just the conformal structure of
$a_{0,0}^{(j)}$
is real-valued and nonzero at the point y. We note from (8.1) that this condition can also be checked via just the conformal structure of
![]() $\mathbb D$
. Finally, we set
$\mathbb D$
. Finally, we set
![]() $\kappa _0=1$
and let
$\kappa _0=1$
and let
![]() $\kappa _1,\kappa _2,\kappa _3\in \mathbb R\setminus \{0\}$
be arbitrary. We then consider
$\kappa _1,\kappa _2,\kappa _3\in \mathbb R\setminus \{0\}$
be arbitrary. We then consider
![]() $\sigma \in \Sigma _{v_0,v_1}$
given by
$\sigma \in \Sigma _{v_0,v_1}$
given by
![]() $v_j$
,
$v_j$
,
![]() $\iota _j$
and
$\iota _j$
and
![]() $\kappa _j$
with
$\kappa _j$
with
![]() $j=0,1,2,3$
constructed as above. As discussed, the choice
$j=0,1,2,3$
constructed as above. As discussed, the choice
![]() $\sigma $
can be determined by just knowning the topological, differential and conformal structure of
$\sigma $
can be determined by just knowning the topological, differential and conformal structure of
![]() $\mathbb D$
.
$\mathbb D$
.
Note that although
![]() $\kappa _0=1$
is fixed and
$\kappa _0=1$
is fixed and
![]() $v_j$
,
$v_j$
,
![]() $\iota _j$
are also fixed for
$\iota _j$
are also fixed for
![]() $j=0,1,2,3$
, we are free to vary
$j=0,1,2,3$
, we are free to vary
![]() $\kappa _1$
,
$\kappa _1$
,
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $\kappa _3$
and also an arbitrary real-valued source term
$\kappa _3$
and also an arbitrary real-valued source term
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. For each choice of f and each nonzero
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
. For each choice of f and each nonzero
![]() $\kappa _1,\kappa _2,\kappa _3$
, we proceed to compute
$\kappa _1,\kappa _2,\kappa _3$
, we proceed to compute
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. Following the steps of the proof in Theorem 5.1 and in view of the linear dependence of
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. Following the steps of the proof in Theorem 5.1 and in view of the linear dependence of
 $\{\dot {\gamma }_{v_j}(s_j)\}_{j=0}^3$
and the fact that
$\{\dot {\gamma }_{v_j}(s_j)\}_{j=0}^3$
and the fact that
 $a^{(j)}_{0,0}(y)$
are all real-valued, we conclude that if
$a^{(j)}_{0,0}(y)$
are all real-valued, we conclude that if
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for some choice of
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$
for some choice of
![]() $\kappa _1$
,
$\kappa _1$
,
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $\kappa _3$
and some function
$\kappa _3$
and some function
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
, then there holds
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
, then there holds
 $$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0.\end{align} $$
$$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0.\end{align} $$
We fix
![]() $\sigma $
corresponding to such a choice of
$\sigma $
corresponding to such a choice of
![]() $\kappa _1$
,
$\kappa _1$
,
![]() $\kappa _2$
and
$\kappa _2$
and
![]() $\kappa _3$
and proceed to explicitly find the value of
$\kappa _3$
and proceed to explicitly find the value of
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta '}$
showing that it determines c. Indeed, by retracing the proof of Theorem 5.1, using the fact that
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta '}$
showing that it determines c. Indeed, by retracing the proof of Theorem 5.1, using the fact that
 $dV_{g}=c^{\frac {n+1}{2}}dV_{\hat g}$
, together with fact that the values of the phase functions
$dV_{g}=c^{\frac {n+1}{2}}dV_{\hat g}$
, together with fact that the values of the phase functions
![]() $\phi ^{(j)}$
,
$\phi ^{(j)}$
,
![]() $j=0,1,2,3$
are independent of the conformal factor and that
$j=0,1,2,3$
are independent of the conformal factor and that
 $a_{0,0}^{(j)}$
is real-valued at y and (8.1) holds, we obtain
$a_{0,0}^{(j)}$
is real-valued at y and (8.1) holds, we obtain
 $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= C \,c(y)^{\frac{n+1}{2}} \,(c(y)^{-\frac{n-1}{4}})^4u_f(y)^{m-3}= C c(y)^{-\frac{n-3}{2}}u_f^{m-3}(y),\end{align} $$
$$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= C \,c(y)^{\frac{n+1}{2}} \,(c(y)^{-\frac{n-1}{4}})^4u_f(y)^{m-3}= C c(y)^{-\frac{n-3}{2}}u_f^{m-3}(y),\end{align} $$
where C is a constant that only depends on the conformal class in a neighbourhood of y.
The preceding analysis shows that given each
![]() $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
, we can recover the value of
$f \in C^{\infty }_c(\Omega _{\mathrm{in}})$
, we can recover the value of
 $c(y)^{-\frac {n-3}{2}}u_f^{m-3}(y)$
at each point
$c(y)^{-\frac {n-3}{2}}u_f^{m-3}(y)$
at each point
![]() $y \in \mathbb D$
. This can be simplified further by using sources f that generate real parts of Gaussian beams and such that they have (asymptotically) prescribed values at each point
$y \in \mathbb D$
. This can be simplified further by using sources f that generate real parts of Gaussian beams and such that they have (asymptotically) prescribed values at each point
![]() $y \in \mathbb D$
as in Lemma 5.3. Indeed, owing to equations (8.2)–(8.3), we can repeat the argument in the proof of Lemma 5.3 to construct explicit sources
$y \in \mathbb D$
as in Lemma 5.3. Indeed, owing to equations (8.2)–(8.3), we can repeat the argument in the proof of Lemma 5.3 to construct explicit sources
![]() $f_\lambda \in C^{\infty }_c(\Omega _{\mathrm{in}})$
only depending on the conformal class
$f_\lambda \in C^{\infty }_c(\Omega _{\mathrm{in}})$
only depending on the conformal class
![]() $\hat {g}$
on
$\hat {g}$
on
![]() $\mathbb D$
such that
$\mathbb D$
such that
 $$ \begin{align*}u_{f_\lambda}(y)= c(y)^{-\frac{n-1}{4}}+\mathcal O(\lambda^{-1}),\end{align*} $$
$$ \begin{align*}u_{f_\lambda}(y)= c(y)^{-\frac{n-1}{4}}+\mathcal O(\lambda^{-1}),\end{align*} $$
where
![]() $\lambda>0$
is a large parameter. Combining this with (8.5) and taking a limit as
$\lambda>0$
is a large parameter. Combining this with (8.5) and taking a limit as
![]() $\lambda \to \infty $
, we conclude that the knowledge of the source-to-solution map
$\lambda \to \infty $
, we conclude that the knowledge of the source-to-solution map
![]() $\mathscr L$
determines uniquely the values
$\mathscr L$
determines uniquely the values
 $$ \begin{align*}c(y)^{-\frac{n-3}{2}} \,c(y)^{-\frac{(n-1)(m-3)}{4}},\end{align*} $$
$$ \begin{align*}c(y)^{-\frac{n-3}{2}} \,c(y)^{-\frac{(n-1)(m-3)}{4}},\end{align*} $$
at each point
![]() $y \in \mathbb D$
. Thus, it follows that c can be determined uniquely on the set
$y \in \mathbb D$
. Thus, it follows that c can be determined uniquely on the set
![]() $\mathbb D$
, unless
$\mathbb D$
, unless
![]() $(n,m)=(3,3)$
.
$(n,m)=(3,3)$
.
We remark that in the case
![]() $(n,m)=(3,3)$
this simple approach does not yield any information. To treat this case, one needs to look further in the asymptotic expansion of
$(n,m)=(3,3)$
this simple approach does not yield any information. To treat this case, one needs to look further in the asymptotic expansion of
![]() $\mathcal I_{\lambda ,\sigma ,\delta ',f}$
(see Subsection 5.3) with respect to the parameter
$\mathcal I_{\lambda ,\sigma ,\delta ',f}$
(see Subsection 5.3) with respect to the parameter
![]() $\lambda $
than just the principal behavior that is captured by
$\lambda $
than just the principal behavior that is captured by
 $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. This will also require explicitly evaluating the subprincipal term
$\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$
. This will also require explicitly evaluating the subprincipal term
![]() $a_{1,0}$
in the expression for the Gaussian beams (see (3.5)). As one of the main novelties of this article is the generalisation to arbitrary dimensions and also for the sake of brevity, we omit this analysis in this article. Note also that the paper [Reference Uhlmann and Wang91] already deals with the particular case
$a_{1,0}$
in the expression for the Gaussian beams (see (3.5)). As one of the main novelties of this article is the generalisation to arbitrary dimensions and also for the sake of brevity, we omit this analysis in this article. Note also that the paper [Reference Uhlmann and Wang91] already deals with the particular case
![]() $n=3$
, although there the authors use a four-wave interaction.
$n=3$
, although there the authors use a four-wave interaction.
Before closing the section, we also remark that in the case of the quasi-linear source-to-solution map
![]() $\mathscr N$
, this approach entangles information about the tensors h and the conformal factor c at the point y and additional efforts may be needed to uniquely reconstruct the conformal factor.
$\mathscr N$
, this approach entangles information about the tensors h and the conformal factor c at the point y and additional efforts may be needed to uniquely reconstruct the conformal factor.
Acknowledgements
M.L. was partially supported by the Academy of Finland (Grants 284715, 312110) and the Finnish Centre of Excellence of Inverse Modelling and Imaging. A.F. gratefully acknowledges support from the Fields institute for research in mathematical sciences.
Conflict of Interest
None.