Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-18T21:20:15.492Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic anomaly equation for 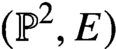$({\mathbb P}^2,E)$ and the Nekrasov-Shatashvili limit of local 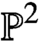${\mathbb P}^2$

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  03 May 2021

Pierrick Bousseau ,
Honglu Fan ,
Shuai Guo  and
Longting Wu
Pierrick Bousseau
Affiliation:
Laboratoire de mathématiques d’Orsay, Université Paris-Saclay, CNRS, 91405, Orsay, France; E-mail: [email protected].
Honglu Fan
Affiliation:
Department of Mathematics, University of Geneva, 24, rue du Général Dufour, Case postale 64, 1211Geneva 4, Switzerland; E-mail: [email protected].
Shuai Guo
Affiliation:
School of Mathematical Sciences, Peking University, No.5 Yiheyuan Road Haidian District, 100871, Beijing, China; E-mail: [email protected].
Longting Wu
Affiliation:
Department of Mathematics, ETH Zurich, Rämistrasse 101, 8092Zurich, Switzerland; E-mail: [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a higher genus version of the genus 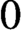$0$ local-relative correspondence of van Garrel-Graber-Ruddat: for 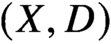$(X,D)$ a pair with X a smooth projective variety and D a nef smooth divisor, maximal contact Gromov-Witten theory of 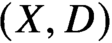$(X,D)$ with 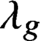$\lambda _g$-insertion is related to Gromov-Witten theory of the total space of 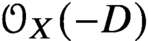${\mathcal O}_X(-D)$ and local Gromov-Witten theory of D.

Specializing to 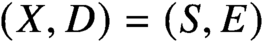$(X,D)=(S,E)$ for S a del Pezzo surface or a rational elliptic surface and E a smooth anticanonical divisor, we show that maximal contact Gromov-Witten theory of 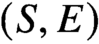$(S,E)$ is determined by the Gromov-Witten theory of the Calabi-Yau 3-fold 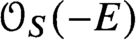${\mathcal O}_S(-E)$ and the stationary Gromov-Witten theory of the elliptic curve E.

Specializing further to 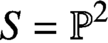$S={\mathbb P}^2$, we prove that higher genus generating series of maximal contact Gromov-Witten invariants of 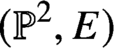$({\mathbb P}^2,E)$ are quasimodular and satisfy a holomorphic anomaly equation. The proof combines the quasimodularity results and the holomorphic anomaly equations previously known for local 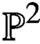${\mathbb P}^2$ and the elliptic curve.

Furthermore, using the connection between maximal contact Gromov-Witten invariants of 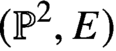$({\mathbb P}^2,E)$ and Betti numbers of moduli spaces of semistable one-dimensional sheaves on 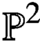${\mathbb P}^2$, we obtain a proof of the quasimodularity and holomorphic anomaly equation predicted in the physics literature for the refined topological string free energy of local 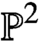${\mathbb P}^2$ in the Nekrasov-Shatashvili limit.

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Type
Mathematical Physics
Information
Forum of Mathematics, Pi , Volume 9 , 2021 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Abramovich, D., Marcus, S., and Wise, J., ‘Comparison theorems for Gromov-Witten invariants of smooth pairs and of degenerations’, Ann. Inst. Fourier (Grenoble) 64 (2014), no. 4, 1611–1667.CrossRefGoogle Scholar
Aganagic, M., Bouchard, V., and Klemm, A., ‘Topological strings and (almost) modular forms’, Comm. Math. Phys. 277 (2008), no. 3, 771–819.CrossRefGoogle Scholar
Alim, M., Länge, J. D., and Mayr, P., ‘Global properties of topological string amplitudes and orbifold invariants’, J. High Energy Phys. 3 (2010), 113, 30.Google Scholar
Alim, M., Scheidegger, E., Yau, S.-T., and Zhou, J., ‘Special polynomial rings, quasi modular forms and duality of topological strings’, Adv. Theor. Math. Phys. 18 (2014), no. 2, 401–467.CrossRefGoogle Scholar
Bershadsky, M., Cecotti, S., Ooguri, H., and Vafa, C., ‘Holomorphic anomalies in topological field theories’, Nuclear Phys. B 405 (1993), no. 2-3, 279–304.CrossRefGoogle Scholar
Bershadsky, M., Cecotti, S., Ooguri, H., and Vafa, C., ‘Kodaira-Spencer theory of gravity and exact results for quantum string amplitudes’, Comm. Math. Phys. 165 (1994), no. 2, 311–427.CrossRefGoogle Scholar
Bloch, S. and Okounkov, A., ‘The character of the infinite wedge representation’, Adv. Math. 149 (2000), no. 1, 1–60.CrossRefGoogle Scholar
Bousseau, P., A proof of N. Takahashi’s conjecture for $\left({\mathbb{P}}^2,E\right)$ and a refined sheaves/Gromov–Witten correspondence, Preprint, 2019, arXiv:1909.02992.Google Scholar
Bousseau, P., Scattering diagrams, stability conditions and coherent sheaves on ${\mathbb{P}}^2$, Preprint, 2019, arXiv:1909.02985.Google Scholar
Bousseau, P., ‘Tropical refined curve counting from higher genera and lambda classes’., Invent. Math. 215 (2019), no. 1, 1–79.CrossRefGoogle Scholar
Bousseau, P., ‘The quantum tropical vertex’, Geom. Topol. 24 (2020), no. 3, 1297–1379.CrossRefGoogle Scholar
Cao, Y., Maulik, D., and Toda, Y., ‘Genus zero Gopakumar-Vafa type invariants for Calabi-Yau 4-folds’, Adv. Math. 338 (2018), 41–92.CrossRefGoogle Scholar
Chang, H.-L., Guo, S., and Li, J., BCOV’s Feynman rule of quintic 3-folds, Preprint, 2018, arXiv:1810.00394.Google Scholar
Chiang, T.-M., Klemm, A., Yau, S.-T., and Zaslow, E., ‘Local mirror symmetry: calculations and interpretations’, Adv. Theor. Math. Phys. 3 (1999), no. 3, 495–565.CrossRefGoogle Scholar
Choi, J., Katz, S., and Klemm, A., ‘The refined BPS index from stable pair invariants’, Comm. Math. Phys. 328 (2014), no. 3, 903–954.CrossRefGoogle Scholar
Coates, T. and Givental, A., ‘Quantum Riemann–Roch, Lefschetz and Serre’, Ann. of Math. 165 (2007), no. 1, 15–53.CrossRefGoogle Scholar
Coates, T. and Iritani, H., Gromov-Witten Invariants of Local ${\mathbb{P}}^2$ and Modular Forms, Preprint, 2018, arXiv:1804.03292Google Scholar
Diamond, F. and Shurman, J., A first course in modular forms, Graduate Texts in Mathematics, vol. 228, Springer-Verlag, New York, 2005.Google Scholar
Dijkgraaf, R., Mirror symmetry and elliptic curves, in The moduli space of curves (Texel Island, 1994), 1995, pp. 149–163.CrossRefGoogle Scholar
Eliashberg, Y., Givental, A., and Hofer, H., Introduction to symplectic field theory, Geom. Funct. Anal. Special Volume, Part II (2000), 560–673. GAFA 2000 (Tel Aviv, 1999).CrossRefGoogle Scholar
Eynard, B., Marino, M., and Orantin, N., ‘Holomorphic anomaly and matrix models’, J. High Energy Phys. 58 (2007).Google Scholar
Eynard, B. and Orantin, N., ‘Computation of open Gromov-Witten invariants for toric Calabi-Yau 3-folds by topological recursion, a proof of the BKMP conjecture’, Comm. Math. Phys. 337 (2015), no. 2, 483–567.CrossRefGoogle Scholar
Faber, C. and Pandharipande, R., ‘Hodge integrals and Gromov–Witten theory’, Invent. Math. 139 (2000), no. 1, 173–199.CrossRefGoogle Scholar
Faber, C. and Pandharipande, R., ‘Logarithmic series and Hodge integrals in the tautological ring’, 2000, pp. 215–252. With an appendix by Zagier, Don, Dedicated to William Fulton on the occasion of his 60th birthday.CrossRefGoogle Scholar
Fan, H., Wu, L., and You, F., ‘Higher genus relative Gromov–Witten theory and double ramification cycles’, Journal of the London Mathematical Society, available at https://londmathsoc.onlinelibrary.wiley.com/doi/pdf/10.1112/jlms.12417.Google Scholar
Fan, H., Wu, L., and You, F., ‘Structures in genus-zero relative Gromov–Witten theory’, J. Topol. 13 (2020), no. 1, 269–307.CrossRefGoogle Scholar
Fang, B., Liu, M.C.-C., and Zong, Z., On the remodelling conjecture for toric CalabiYau 3-orbifolds, Preprint, 2016, arXiv:1604.07123.Google Scholar
Fang, B., Ruan, Y., Zhang, Y., and Zhou, J., Open Gromov-Witten theory of ${K}_{{\mathbb{P}}^2}$, ${K}_{{\mathbb{P}}^1\times {\mathbb{P}}^1}$, ${K}_{W\mathbb{P}\left[1,1,2\right]}$, ${K}_{F_1}$and Jacobi forms, Comm. Math. Phys. 369 (2019), no. 2, 675–719.CrossRefGoogle Scholar
van Garrel, M., Graber, T., and Ruddat, H., ‘Local Gromov-Witten invariants are log invariants’, Adv. Math. 350 (2019), 860–876.CrossRefGoogle Scholar
Givental, A., ‘Equivariant Gromov-Witten invariants’, Internat. Math. Res. Notices 13 (1996), 613–663.CrossRefGoogle Scholar
Givental, A., ‘Gromov–Witten invariants and quantization of quadratic hamiltonians’, Moscow Mathematical Journal 1 (2001), no. 5, 551–568.CrossRefGoogle Scholar
Graber, T. and Pandharipande, R., ‘Localization of virtual classes’, Invent. Math. 135 (1999), no. 2, 487–518.CrossRefGoogle Scholar
Graber, T. and Vakil, R., ‘Relative virtual localization and vanishing of tautological classes on moduli spaces of curves’, Duke Math. J. 130 (2005), 1–37.CrossRefGoogle Scholar
Graefnitz, T., Tropical correspondence for smooth del Pezzo log Calabi-Yau pairs, Preprint, 2020, arXiv:2005.14018.Google Scholar
Guo, S., Janda, F., and Ruan, Y., Structure of higher genus Gromov-Witten invariants of quintic 3-folds, Preprint, 2018, arXiv:1812.11908.Google Scholar
Haghighat, B., Klemm, A., and Rauch, M., ‘Integrability of the holomorphic anomaly equations’, J. High Energy Phys. 10 (2008), 097, 37.Google Scholar
Hu, X., ‘Localized standard versus reduced formula and genus 1 local Gromov-Witten invariants’, Int. Math. Res. Not. IMRN 20 (2015), 9921–9990.CrossRefGoogle Scholar
Huang, M.-x., Kashani-Poor, A.-K., and Klemm, A., The $\varOmega$-deformed B-model for rigid $N=2$ theories, Ann. Henri Poincaré 14 (2013), no. 2, 425–497.CrossRefGoogle Scholar
Huang, M.-x. and Klemm, A., ‘Holomorphic anomaly in gauge theories and matrix models’, J. High Energy Phys. 9 (2007), 054, 33.Google Scholar
Huang, M.-x. and Klemm, A., ‘Direct integration for general backgrounds’, Adv. Theor. Math. Phys. 16 (2012), no. 3, 805–849.CrossRefGoogle Scholar
Huang, M.-x., Klemm, A., and Quackenbush, S., Topological string theory on compact Calabi-Yau: modularity and boundary conditions, Homological mirror symmetry, 2009, pp. 45–102.Google Scholar
Ionel, E.-N. and Parker, T.-H., ‘Relative Gromov-Witten invariants’, Ann. of Math. (2) 157 (2003), no. 1, 45–96.CrossRefGoogle Scholar
Joyce, D. and Song, Y., ‘A theory of generalized Donaldson-Thomas invariants’, Mem. Amer. Math. Soc. 217 (2012), no. 1020, iv+199.Google Scholar
Katz, E., Line-bundles on stacks of relative maps, Preprint, 2005, arXiv:0507322.Google Scholar
Katz, S., ‘Genus zero Gopakumar-Vafa invariants of contractible curves’, J. Differential Geom. 79 (2008), no. 2, 185–195.CrossRefGoogle Scholar
Kim, B., Lho, H., and Ruddat, H., The degeneration formula for stable log maps, Preprint, 2018, arXiv:1803.04210.Google Scholar
Klemm, A. and Zaslow, E., ‘Local mirror symmetry at higher genus’, in Winter School on Mirror Symmetry, Vector Bundles and Lagrangian Submanifolds (Cambridge, MA, 1999), 2001, pp. 183–207.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Stability structures, motivic Donaldson-Thomas invariants and cluster transformations, Preprint, 2008, arXiv:0811.2435.Google Scholar
Krefl, D. and Walcher, J., ‘Extended holomorphic anomaly in gauge theory’, Lett. Math. Phys. 95 (2011), no. 1, 67–88.CrossRefGoogle Scholar
Lho, H., Gromov-Witten invariants of Calabi-Yau manifolds with two Kähler parameters, Preprint, 2018, arXiv:1804.04399.CrossRefGoogle Scholar
Lho, H. and Pandharipande, R., ‘Stable quotients and the holomorphic anomaly equation’, Adv. Math. 332 (2018), 349–402.CrossRefGoogle Scholar
Lho, H. and Pandharipande, R., Crepant resolution and the holomorphic anomaly equation for $\left[{\mathbb{C}}^3/ {\mathbb{Z}}_3\right]$, Proc. Lond. Math. Soc. (3) 119 (2019), no. 3, 781–813.CrossRefGoogle Scholar
Lho, H. and Pandharipande, R., ‘Holomorphic anomaly equations for the formal quintic’, Peking Mathematical Journal 2 (2019), no. 1, 1–40.CrossRefGoogle Scholar
Li, A.-M. and Ruan, Y., ‘Symplectic surgery and Gromov-Witten invariants of Calabi-Yau 3-folds’, Invent. Math. 145 (2001), no. 1, 151–218.CrossRefGoogle Scholar
Li, J., ‘Stable morphisms to singular schemes and relative stable morphisms’, J. Differential Geom. 57 (2001), no. 509–578.CrossRefGoogle Scholar
Li, J., ‘A Degeneration formula of GW-invariants’, J. Differential Geom. 60 (2002), 199–293.CrossRefGoogle Scholar
Lian, B.H., Liu, K., and Yau, S.-T., ‘Mirror principle. I’, Asian J. Math. 1 (1997), no. 4, 729–763.CrossRefGoogle Scholar
Maier, R.S., ‘On rationally parametrized modular equations’, J. Ramanujan Math. Soc. 24 (2009), no. 1, 1–73.Google Scholar
Maier, R.S., ‘Nonlinear differential equations satisfied by certain classical modular forms’, Manuscripta Math. 134 (2011), no. 1–2, 1–42.CrossRefGoogle Scholar
Maulik, Nekrasov, Okounkov, and Pandharipande, ‘Gromov–Witten theory and Donaldson–Thomas theory, I’, Compos. Math. 142 (2006), no. 5, 1263–1285.CrossRefGoogle Scholar
Maulik, D. and Shen, J., Cohomological $\chi$-independence for moduli of one-dimensional sheaves and moduli of Higgs bundles, Preprint, 2020, arXiv:2012.06627.Google Scholar
Milanov, T., Ruan, Y., and Shen, Y., ‘Gromov-Witten theory and cycle-valued modular forms’, J. Reine Angew. Math. 735 (2018), 287–315.CrossRefGoogle Scholar
Mumford, D., ‘Towards an enumerative geometry of the moduli space of curves’, Arithmetic and geometry, Vol. II, 1983, pp. 271–328.CrossRefGoogle Scholar
Nekrasov, N. and Okounkov, A., ‘Membranes and sheaves’, Algebr. Geom. 3 (2016), no. 3, 320–369.CrossRefGoogle Scholar
Oberdieck, G. and Pixton, A., ‘Holomorphic anomaly equations and the Igusa cusp form conjecture’, Invent. Math. 213 (2018), no. 2, 507–587.CrossRefGoogle Scholar
Oberdieck, G. and Pixton, A., ‘Gromov-Witten theory of elliptic fibrations: Jacobi forms and holomorphic anomaly equations’, Geom. Topol. 23 (2019), no. 3, 1415–1489.CrossRefGoogle Scholar
Okounkov, A. and Pandharipande, R., ‘Gromov–Witten theory, Hurwitz theory, and completed cycles’, Ann. of Math. 163 (2006), 517–560.CrossRefGoogle Scholar
Okounkov, A. and Pandharipande, R., ‘Virasoro constraints for target curves’, Invent. Math. 163 (2006), 47–108.CrossRefGoogle Scholar
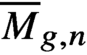Pandharipande, R., Pixton, A., and Zvonkine, D., Relations on ${\overline{M}}_{g,n}$ via $3$-spin structures, J. Amer. Math. Soc. 28 (2015), no. 1, 279–309.CrossRefGoogle Scholar
Pandharipande, R. and Thomas, R.P., ‘Curve counting via stable pairs in the derived category’, Invent. Math. 178 (2009), no. 2, 407–447.CrossRefGoogle Scholar
Wang, X., Finite generation and holomorphic anomaly equation for equivariant Gromov-Witten invariants of ${K}_{{\mathbb{P}}^1\times {\mathbb{P}}^1}$, Preprint, 2019, arXiv:1908.03691.Google Scholar
Wang, X., Quasi-modularity and Holomorphic Anomaly Equation for the Twisted Gromov-Witten Theory: $\mathbf{\mathcal{O}}(3)$ over ${\mathbb{P}}^2$, Acta Math. Sin. (Engl. Ser.) 35 (2019), no. 12, 1945–1962.CrossRefGoogle Scholar
Wu, L., ‘A remark on Gromov-Witten invariants of quintic threefold’, Adv. Math. 326 (2018), 241–313.CrossRefGoogle Scholar
Zagier, D., Elliptic modular forms and their applications, in The 1-2-3 of modular forms, 2008, pp. 1–103.CrossRefGoogle Scholar
Zagier, D. and Zinger, A., Some properties of hypergeometric series associated with mirror symmetry, in Modular forms and string duality, 2008, pp. 163–177.CrossRefGoogle Scholar
Zhou, J., Arithmetic Properties of Moduli Spaces and Topological String Partition Functions of Some Calabi-Yau Threefolds (2014). Ph.D. thesis, Harvard University, available at https://dash.harvard.edu/handle/1/12274581.Google Scholar