Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T04:42:04.607Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER GENUS GROMOV–WITTEN THEORY OF $\mathsf{Hilb}^{n}(\mathbb{C}^{2})$ AND 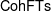$\mathsf{CohFTs}$ ASSOCIATED TO LOCAL CURVES

Part of: Projective and enumerative geometry Symplectic geometry, contact geometry

Published online by Cambridge University Press:  31 July 2019

RAHUL PANDHARIPANDE  and
HSIAN-HUA TSENG
RAHUL PANDHARIPANDE
Affiliation:
Department of Mathematics, ETH Zürich, Rämistrasse 101, 8092 Zürich, Switzerland; [email protected]
HSIAN-HUA TSENG
Affiliation:
Department of Mathematics, Ohio State University, 100 Math Tower, 231 West 18th Ave., Columbus, OH 43210, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the higher genus equivariant Gromov–Witten theory of the Hilbert scheme of $n$ points of 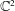$\mathbb{C}^{2}$. Since the equivariant quantum cohomology, computed by Okounkov and Pandharipande [Invent. Math. 179 (2010), 523–557], is semisimple, the higher genus theory is determined by an 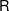$\mathsf{R}$-matrix via the Givental–Teleman classification of Cohomological Field Theories (CohFTs). We uniquely specify the required 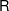$\mathsf{R}$-matrix by explicit data in degree $0$. As a consequence, we lift the basic triangle of equivalences relating the equivariant quantum cohomology of the Hilbert scheme 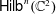$\mathsf{Hilb}^{n}(\mathbb{C}^{2})$ and the Gromov–Witten/Donaldson–Thomas correspondence for 3-fold theories of local curves to a triangle of equivalences in all higher genera. The proof uses the analytic continuation of the fundamental solution of the QDE of the Hilbert scheme of points determined by Okounkov and Pandharipande [Transform. Groups 15 (2010), 965–982]. The GW/DT edge of the triangle in higher genus concerns new CohFTs defined by varying the 3-fold local curve in the moduli space of stable curves. The equivariant orbifold Gromov–Witten theory of the symmetric product 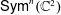$\mathsf{Sym}^{n}(\mathbb{C}^{2})$ is also shown to be equivalent to the theories of the triangle in all genera. The result establishes a complete case of the crepant resolution conjecture [Bryan and Graber, Algebraic Geometry–Seattle 2005, Part 1, Proceedings of Symposia in Pure Mathematics, 80 (American Mathematical Society, Providence, RI, 2009), 23–42; Coates et al., Geom. Topol. 13 (2009), 2675–2744; Coates & Ruan, Ann. Inst. Fourier (Grenoble) 63 (2013), 431–478].

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Secondary: 53D45: Gromov-Witten invariants, quantum cohomology, Frobenius manifolds
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 7 , 2019 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Bryan, J. and Graber, T., ‘The crepant resolution conjecture’, inAlgebraic Geometry–Seattle 2005, Part 1, Proceedings of Symposia in Pure Mathematics, 80 (American Mathematical Society, Providence, RI, 2009), 23–42.Google Scholar
Bryan, J. and Pandharipande, R., ‘The local Gromov–Witten theory of curves’, J. Amer. Math. Soc. 21 (2008), 101–136.Google Scholar
Cavalieri, R., ‘A topological quantum field theory of intersection numbers on moduli spaces of admissible covers’, Algebra Number Theory 1 (2007), 35–66.Google Scholar
Coates, T. and Givental, A., ‘Quantum Riemann–Roch, Lefschetz and Serre’, Ann. of Math. (2) 165 (2007), 15–53.Google Scholar
Coates, T., Iritani, H. and Tseng, H.-H., ‘Wall-crossings in toric Gromov–Witten theory. I. Crepant examples’, Geom. Topol. 13 (2009), 2675–2744.Google Scholar
Coates, T. and Ruan, Y., ‘Quantum cohomology and crepant resolutions: a conjecture’, Ann. Inst. Fourier (Grenoble) 63 (2013), 431–478.Google Scholar
Dubrovin, B., ‘Geometry of 2D topological filed theories’, inIntegrable Systems and Quantum Groups (Montecatini Terme, 1993), Lecture Notes in Mathematics, 1620 (Springer, Berlin, 1996), 120–348.Google Scholar
Faber, C. and Pagani, N., ‘The class of the bielliptic locus in genus 3’, Int. Math. Res. Not. IMRN 12 (2015), 3943–3961.Google Scholar
Faber, C. and Pandharipande, R., ‘Hodge integrals and Gromov–Witten theory’, Invent. Math. 139 (2000), 173–199.Google Scholar
Fulton, W. and Pandharipande, R., ‘Notes on stable maps and quantum cohomology’, inAlgebraic Geometry–Santa Cruz 1995, Part 2, Proceedings of Symposia in Applied Mathematics, 62 (American Mathematical Society, Providence, RI, 1997), 45–96.Google Scholar
Givental, A., ‘Elliptic Gromov–Witten invariants and the generalized mirror conjecture’, inIntegrable Systems and Algebraic Geometry (Kobe/Kyoto, 1997) (World Scientific Publishing, River Edge, NJ, 1998), 107–155.Google Scholar
Givental, A., ‘Gromov–Witten invariants and quantization of quadratic Hamiltonians’, Mosc. Math. J. 4 (2001), 551–568.Google Scholar
Givental, A., ‘Semisimple Frobenius structures at higher genus’, Int. Math. Res. Not. IMRN 23 (2001), 1265–1286.Google Scholar
Göttsche, L., ‘Hilbert schemes of points on surfaces’, inICM Proceedings, Vol. II (Higher Education Press, Beijing, China, 2002), 483–494.Google Scholar
Graber, T. and Pandharipande, R., ‘Localization of virtual classes’, Invent. Math. 135 (1999), 487–518.Google Scholar
Grojnowski, I., ‘Instantons and affine algebras I: the Hilbert scheme and vertex operators’, Math. Res. Lett. 3 (1996), 275–291.Google Scholar
Haiman, M., ‘Combinatorics, symmetric functions and Hilbert schemes’, inCurrent Developments in Mathematics 2002, Vol. 1 (International Press of Boston, Somerville, MA, USA, 2002), 39–111.Google Scholar
Haiman, M., ‘Notes on Macdonald polynomials and the geometry of Hilbert schemes’, inSymmetric Functions 2001: Surveys of Developments and Perspectives, Proceedings of the NATO Advanced Study Institute held in Cambridge, June 25–July 6, 2001 (ed. Fomin, S.) (Kluwer, Dordrecht, 2002), 1–64.Google Scholar
Ince, E. L., Ordinary Differential Equations (Dover Publications, New York, 1944).Google Scholar
Kontsevich, M. and Manin, Y., ‘Gromov–Witten classes, quantum cohomology, and enumerative geometry’, Comm. Math. Phys. 164 (1994), 525–562.Google Scholar
Lee, Y.-P. and Pandharipande, R., ‘Frobenius manifolds, Gromov–Witten theory, and Virasoro constraints’, Preprint available from the authors’ website: https://people.math.ethz.ch/∼rahul/Part1.ps.Google Scholar
Lehn, M., ‘Chern classes of tautological sheaves on Hilbert schemes of points on surfaces’, Invent. Math. 136 (1999), 157–207.Google Scholar
Macdonald, I., Symmetric Functions and Hall Polynomials, 2nd edn, Oxford Mathematical Monographs (Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1995), With contributions by A. Zelevinsky.Google Scholar
Manin, Y., Frobenius Manifolds, Quantum Cohomology, and Moduli Spaces, American Mathematical Society Colloquium Publications, 47 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Marian, A., Oprea, D., Pandharipande, R., Pixton, A. and Zvonkine, D., ‘The Chern character of the Verlinde bundle over the moduli space of stable curves’, J. Reine Angew. Math. 732 (2017), 147–163.Google Scholar
Maulik, D., Pandharipande, R. and Thomas, R., ‘Curves on K3 surfaces and modular forms’, J. Topol. 3 (2010), 937–996.Google Scholar
Mumford, D., ‘Towards an enumerative geometry of the moduli space of curves’, inArithmetics and Geometry, Vol. 2 (eds. Artin, M. and Tate, J.) (Birkhäuser, Boston, MA, USA, 1983), 271–328.Google Scholar
Nakajima, H., Lectures on Hilbert Schemes of Points on Surfaces, University Lecture Series, 18 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Okounkov, A. and Pandharipande, R., ‘Quantum cohomology of the Hilbert scheme of points in the plane’, Invent. Math. 179 (2010), 523–557.Google Scholar
Okounkov, A. and Pandharipande, R., ‘The quantum differential equation of the Hilbert scheme of points in the plane’, Transform. Groups 15 (2010), 965–982.Google Scholar
Okounkov, A. and Pandharipande, R., ‘The local Donaldson–Thomas theory of curves’, Geom. Topol. 14 (2010), 1503–1567.Google Scholar
Pandharipande, R., ‘Descendents for stable pairs on 3-folds’, inModern Geometry: A Celebration of the Work of Simon Donaldson, Proceedings of Symposia in Pure Mathematics, 99 (2018), 251–288.Google Scholar
Pandharipande, R., ‘Cohomological field theory calculations’, inProceedings of the ICM, Vol. 1 (World Scientific, Rio de Janeiro, 2018), 869–898.Google Scholar
Pandharipande, R. and Pixton, A., ‘GW/P descendent correspondence for toric 3-folds’, Geom. Topol. 18 (2014), 2747–2821.Google Scholar
Pandharipande, R., Pixton, A. and Zvonkine, D., ‘Relations on M g, n via 3-spin structures’, J. Amer. Math. Soc. 28 (2015), 279–309.Google Scholar
Pandharipande, R. and Thomas, R., ‘Counting curves via stable pairs in the derived category’, Invent. Math. 178 (2009), 407–447.Google Scholar
Russell, D. L. and Subiya, Y., ‘The problem of singular perturbations of linear ordinary differential equations at regular singular points, I’, Funkcial. Ekvac. 9 (1966), 207–218.Google Scholar
Russell, D. L. and Subiya, Y., ‘The problem of singular perturbations of linear ordinary differential equations at regular singular points, II’, Funkcial. Ekvac. 11 (1968), 175–184.Google Scholar
Schmitt, J. and van Zelm, J., ‘Intersections of loci of admissible covers with tautological classes’, Preprint, 2018, arXiv:1808.05817.Google Scholar
Teleman, C., ‘The structure of 2D semi-simple field theories’, Invent. Math. 188 (2012), 525–588.Google Scholar
Tseng, H.-H., ‘Orbifold quantum Riemann–Roch, Lefschetz and Serre’, Geom. Topol. 14 (2010), 1–81.Google Scholar
Wasow, W., Asymptotic Expansions for Ordinary Differential Equations, Pure and Applied Mathematics, XIV (Interscience Publishers John Wiley & Sons, Inc., New York-London-Sydney, 1965).Google Scholar
Whittaker, E. and Watson, G., A Course of Modern Analysis. An Introduction to the General Theory of Infinite Processes and of Analytic Functions; With an Account of the Principal Transcendental Functions, Reprint of the fourth (1927) edition, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1996.Google Scholar