Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T11:43:45.309Z Has data issue: false hasContentIssue false
  • English
  • Français

The fields of values of characters of degree not divisible by p

Part of: Representation theory of groups

Published online by Cambridge University Press:  15 February 2021

Gabriel Navarro  and
Pham Huu Tiep
Gabriel Navarro
Affiliation:
Department of Mathematics, Universitat de València, València, Spain; E-mail: [email protected]
Pham Huu Tiep
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ, USA; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

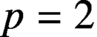We study the fields of values of the irreducible characters of a finite group of degree not divisible by a prime p. In the case where $p=2$, we fully characterise these fields. In order to accomplish this, we generalise the main result of [ILNT] to higher irrationalities. We do the same for odd primes, except that in this case the analogous results hold modulo a simple-to-state conjecture on the character values of quasi-simple groups.

MSC classification

Primary: 20C15: Ordinary representations and characters 20C33: Representations of finite groups of Lie type
Type
Algebra
Information
Forum of Mathematics, Pi , Volume 9 , 2021 , e2
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

Dedicated to Gunter Malle on the occasion of his 60th birthday

References

Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., An ATLAS of Finite Groups (Clarendon Press, Oxford, 1985).Google Scholar
Carter, R., Finite Groups of Lie type: Conjugacy Classes and Complex Characters (Wiley, Chichester, 1985).Google Scholar
Dade, E. C., ‘Blocks with cyclic defect groups’, Ann. of Math. 84 (1966), 20–48.CrossRefGoogle Scholar
Dade, E. C., ‘Counting characters in blocks with cyclic defect groups, I’, J. Algebra 186 (1996), 934–969.CrossRefGoogle Scholar
Digne, F. and Michel, J., Representations of Finite Groups of Lie Type, London Mathematical Society Student Texts, 21 (Cambridge University Press, Cambridge, 1991).Google Scholar
Fein, B. and Gordon, B., ‘Fields generated by characters of finite groups’, J. Lond. Math. Soc. 4 (1972), 735–740.CrossRefGoogle Scholar
The GAP Group, ‘GAP – groups, algorithms, and programming’, version 4.10.0 (2018). URL: http://www.gap-system.org.Google Scholar
Giannelli, E., ‘The Sylow restriction refinement of the McKay conjecture for symmetric and alternating groups’, Algebra Number Theory, 2021 (to appear).Google Scholar
Giannelli, E., Kleshchev, A. S., Navarro, G. and Tiep, P. H., ‘Restriction of odd degree characters and natural correspondences’, Int. Math. Res. Not. IMRN 2017 (20), 6089–6118.Google Scholar
Guralnick, R. M., Liebeck, M. W., O’Brien, E., Shalev, A. and Tiep, P. H, ‘Surjective word maps and Burnside’s ${p}^a{q}^b$ theorem’, Invent. Math. 213 (2018), 589–695.CrossRefGoogle Scholar
Geck, M. and Malle, G., The Character Theory of Finite Groups of Lie Type: A Guided Tour, Cambridge Studies in Advanced Mathematics (Cambridge University Press, 2020).CrossRefGoogle Scholar
Guralnick, R. M. and Tiep, P. H., ‘Low-dimensional representations of special linear groups in cross characteristic’, Proc. Lond. Math. Soc. 78 (1999), 116–138.CrossRefGoogle Scholar
Hoffman, P. N. and Humphreys, J. F., Projective Representations of the Symmetric Group (Clarendon Press, Oxford, 1992).Google Scholar
Isaacs, I. M., Liebeck, M., Navarro, G. and Tiep, P. H, ‘Fields of values of odd degree irreducible characters’, Adv. Math. 354 (2019), 106757.CrossRefGoogle Scholar
Isaacs, I. M, ‘Characters of solvable and symplectic groups’, Amer. J. Math. 85 (1973), 594–635.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (American Mathematical Society, Providence, RI, 2008).Google Scholar
Isaacs, I. M., Characters of Solvable Groups (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar
James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and Its Applications, 16 (Addison-Wesley, Reading, MA, 1981).Google Scholar
Kondrat’ev, A. S., ‘Normalizers of the Sylow $2$-subgroups in finite simple groups’, Math. Notes 78 (2005), 338–346.CrossRefGoogle Scholar
Liebeck, M. W., Saxl, J. and Seitz, G., ‘Subgroups of maximal rank in finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. 65 (1992), 297–325.CrossRefGoogle Scholar
Lübeck, F., ‘Character degrees and their multiplicities for some groups of Lie type of rank $<9$’, URL: http://www.math.rwth-aachen.de/~Frank.Luebeck/chev/DegMult/index.html.Google Scholar
Malle, G., ‘Height $0$ characters of finite groups of Lie type’, Represent. Theory 11 (2007), 192–220.CrossRefGoogle Scholar
Malle, G. and Späth, B., ‘Characters of odd degree’, Ann. of Math. 184 (2016), 869–908.CrossRefGoogle Scholar
Navarro, G., ‘The McKay conjecture and Galois automorphisms’, Ann. of Math. 160 (2004), 1129–1140.CrossRefGoogle Scholar
Navarro, G., Character Theory and the McKay Conjecture (Cambridge University Press, Cambridge, 2018).CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Rational irreducible characters and rational conjugacy classes in finite groups’, Trans. Amer. Math. Soc. 360 (2008), 2443–2465.CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Real groups and Sylow 2-subgroups’, Adv. Math. 299 (2016), 331–360.CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Irreducible representations of odd degree’, Math. Ann. 365 (2016), 1155–1185.CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Sylow subgroups, exponents, and character tables’, Trans. Amer. Math. Soc. 372 (2019), 4263–4291.CrossRefGoogle Scholar
Navarro, G., Tiep, P. H. and Vallejo, C., ‘McKay natural correspondences on characters’, Algebra Number Theory 8 (2014), 1839–1856.CrossRefGoogle Scholar
Olsson, J. B., ‘McKay numbers and heights of characters’, Math. Scand. 38 (1976), 25–42.CrossRefGoogle Scholar
Ruhstorfer, L., ‘The Navarro refinement of the McKay conjecture for finite groups of Lie type in defining characteristic’, Preprint, 2020, arXiv:1703.09006.Google Scholar
Schaeffer-Fry, A. A., ‘Actions of Galois automorphisms on Harish-Chandra series and Navarro’s self-normalizing Sylow $2$-subgroup conjecture’, Trans. Amer. Math. Soc. 372 (2019), 457–483.CrossRefGoogle Scholar
Schaeffer-Fry, A. A. and Taylor, J., ‘On self-normalising Sylow 2-subgroups in type $A$’, J. Lie Theory 28 (2018), 139–168.Google Scholar
Turull, A., ‘Strengthening the McKay conjecture to include local fields and local Schur indices’, J. Algebra 319 (2008), 4853–4868.CrossRefGoogle Scholar
Tiep, P. H. and Zalesskii, A. E., ‘Unipotent elements of finite groups of Lie type and realization fields of their complex representations’, J. Algebra 271 (2004), 327–390.CrossRefGoogle Scholar
Weintraub, S. H., Galois Theory, Universitext (Springer, New York 2009).CrossRefGoogle Scholar
Wilson, R. A., ‘The McKay conjecture is true for the sporadic simple groups’, J. Algebra 207 (1998), 294–305.CrossRefGoogle Scholar