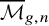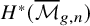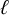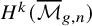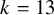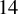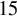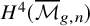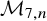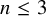1 Introduction
The moduli spaces of stable curves
![]() ${\overline {\mathcal {M}}}_{g,n}$
are smooth and proper over the integers, and this implies strong restrictions on the motivic structures, such as
${\overline {\mathcal {M}}}_{g,n}$
are smooth and proper over the integers, and this implies strong restrictions on the motivic structures, such as
![]() $\ell $
-adic Galois representations, that can appear in
$\ell $
-adic Galois representations, that can appear in
![]() $H^*({\overline {\mathcal {M}}}_{g,n})$
. Widely believed conjectures regarding analytic continuations and functional equations for L-functions lead to precise predictions, by Chenevier and Lannes, about which such structures can appear in degrees less than or equal to 22 [Reference Chenevier and Lannes10, Theorem F]. These predictions are consistent with all previously known results on
$H^*({\overline {\mathcal {M}}}_{g,n})$
. Widely believed conjectures regarding analytic continuations and functional equations for L-functions lead to precise predictions, by Chenevier and Lannes, about which such structures can appear in degrees less than or equal to 22 [Reference Chenevier and Lannes10, Theorem F]. These predictions are consistent with all previously known results on
![]() $H^*({\overline {\mathcal {M}}}_{g,n})$
. Recent work inspired by these predictions confirms their correctness in all degrees less than or equal to 12 [Reference Bergström, Faber and Payne4, Reference Canning, Larson and Payne8]. Here, we introduce new methods to systematically study the motivic structures in
$H^*({\overline {\mathcal {M}}}_{g,n})$
. Recent work inspired by these predictions confirms their correctness in all degrees less than or equal to 12 [Reference Bergström, Faber and Payne4, Reference Canning, Larson and Payne8]. Here, we introduce new methods to systematically study the motivic structures in
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for
$H^k({\overline {\mathcal {M}}}_{g,n})$
for
![]() $k> 12$
and confirm these predictions in degrees
$k> 12$
and confirm these predictions in degrees
![]() $13$
,
$13$
,
![]() $14$
and
$14$
and
![]() $15$
.
$15$
.
Throughout, we write
![]() $H^*(X)$
for the rational singular cohomology of a scheme or Deligne-Mumford stack X endowed with its associated Hodge structure or
$H^*(X)$
for the rational singular cohomology of a scheme or Deligne-Mumford stack X endowed with its associated Hodge structure or
![]() $\ell $
-adic Galois representation and
$\ell $
-adic Galois representation and
![]() $H^*(X)^{\mathrm {ss}}$
for its semi-simplification. Let
$H^*(X)^{\mathrm {ss}}$
for its semi-simplification. Let
![]() $\mathsf {L} := H^2(\mathbb {P}^1)$
and
$\mathsf {L} := H^2(\mathbb {P}^1)$
and
![]() ${\mathsf {S}}_{12} := H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
${\mathsf {S}}_{12} := H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
Theorem 1.1. For all g and n, we have
![]() $H^{13}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus \mathsf {L}{\mathsf {S}}_{12}$
and
$H^{13}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus \mathsf {L}{\mathsf {S}}_{12}$
and
![]() $H^{14}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus \mathsf {L}^{7}$
. Moreover, for
$H^{14}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus \mathsf {L}^{7}$
. Moreover, for
![]() $g \geq 2$
, we have
$g \geq 2$
, we have
![]() $H^{15} ({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus {\mathsf {L}}^2 {\mathsf {S}}_{12}$
.
$H^{15} ({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}} \cong \bigoplus {\mathsf {L}}^2 {\mathsf {S}}_{12}$
.
Theorem 1.1 confirms the predictions of Chenevier and Lannes for motivic weights
![]() $k \leq 15$
. Note that the Hodge structure on the cohomology of a smooth and proper Deligne–Mumford stack such as
$k \leq 15$
. Note that the Hodge structure on the cohomology of a smooth and proper Deligne–Mumford stack such as
![]() ${\overline {\mathcal {M}}}_{g,n}$
is semi-simple, so the semi-simplification in Theorem 1.1 is relevant only when considering
${\overline {\mathcal {M}}}_{g,n}$
is semi-simple, so the semi-simplification in Theorem 1.1 is relevant only when considering
![]() $\ell $
-adic Galois representations.
$\ell $
-adic Galois representations.
The proof of Theorem 1.1 uses the inductive structure of the boundary of the moduli space and the maps induced by tautological morphisms between moduli spaces, as do the proofs of the precursor results mentioned above. Recall that the collection of tautological rings
![]() $RH^*({\overline {\mathcal {M}}}_{g,n}) \subset H^*({\overline {\mathcal {M}}}_{g,n})$
is the smallest collection of subrings that is closed under pushforward and pullback for the tautological morphisms induced by gluing, forgetting and permuting marked points. For many inductive arguments, including those used here, it suffices to consider the operations that produce cohomology classes on moduli spaces of larger dimension from those on moduli spaces of smaller dimension.
$RH^*({\overline {\mathcal {M}}}_{g,n}) \subset H^*({\overline {\mathcal {M}}}_{g,n})$
is the smallest collection of subrings that is closed under pushforward and pullback for the tautological morphisms induced by gluing, forgetting and permuting marked points. For many inductive arguments, including those used here, it suffices to consider the operations that produce cohomology classes on moduli spaces of larger dimension from those on moduli spaces of smaller dimension.
Definition 1.2. A semi-tautological extension (STE) is a collection of subrings
![]() $S^*({\overline {\mathcal {M}}}_{g,n})$
of
$S^*({\overline {\mathcal {M}}}_{g,n})$
of
![]() $H^*({\overline {\mathcal {M}}}_{g,n})$
that contains the tautological subrings
$H^*({\overline {\mathcal {M}}}_{g,n})$
that contains the tautological subrings
![]() $RH^*({\overline {\mathcal {M}}}_{g,n})$
and is closed under pullback by forgetting and permuting marked points and under pushforward for gluing marked points.
$RH^*({\overline {\mathcal {M}}}_{g,n})$
and is closed under pullback by forgetting and permuting marked points and under pushforward for gluing marked points.
Examples of STEs include the trivial extension
![]() $RH^*$
, the full cohomology rings
$RH^*$
, the full cohomology rings
![]() $H^*$
and the collection of subrings generated by algebraic cycle classes. Not every STE is closed under the additional tautological operations induced by push-forward for forgetting marked points and pullback for gluing marked points. However, the main examples we study here are indeed closed under all of the tautological operations (see Proposition 2.4).
$H^*$
and the collection of subrings generated by algebraic cycle classes. Not every STE is closed under the additional tautological operations induced by push-forward for forgetting marked points and pullback for gluing marked points. However, the main examples we study here are indeed closed under all of the tautological operations (see Proposition 2.4).
Note that any intersection of STEs is an STE. An STE is finitely generated if it is the smallest STE that contains a given finite subset (or, equivalently, the union of finitely many
![]() $\mathbb {Q}$
-vector subspaces) of
$\mathbb {Q}$
-vector subspaces) of
![]() $\coprod _{g,n} H^*({\overline {\mathcal {M}}}_{g,n})$
. A finitely generated STE is suitable for combinatorial study via algebraic operations on decorated graphs. See [22, Reference Pixton31] for discussions of the graphical algebra underlying the tautological ring, and [Reference Payne and Willwacher24, Reference Payne and Willwacher25] for applications of such operadic methods, with not necessarily tautological decorations, to the weight spectral sequence for
$\coprod _{g,n} H^*({\overline {\mathcal {M}}}_{g,n})$
. A finitely generated STE is suitable for combinatorial study via algebraic operations on decorated graphs. See [22, Reference Pixton31] for discussions of the graphical algebra underlying the tautological ring, and [Reference Payne and Willwacher24, Reference Payne and Willwacher25] for applications of such operadic methods, with not necessarily tautological decorations, to the weight spectral sequence for
![]() ${\mathcal {M}}_{g,n}$
. Every STE that we consider is motivic, meaning that
${\mathcal {M}}_{g,n}$
. Every STE that we consider is motivic, meaning that
![]() $S^*({\overline {\mathcal {M}}}_{g,n}) \subset H^*({\overline {\mathcal {M}}}_{g,n})$
is a sub-Hodge structure and its base change to
$S^*({\overline {\mathcal {M}}}_{g,n}) \subset H^*({\overline {\mathcal {M}}}_{g,n})$
is a sub-Hodge structure and its base change to
![]() $\mathbb {Q}_\ell $
is preserved by the Galois action.
$\mathbb {Q}_\ell $
is preserved by the Galois action.
Theorem 1.3. For any fixed degree k, the STE generated by
contains
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
$H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
In particular, there is a finitely generated STE that contains
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
$H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
Corollary 1.4. For each k, there are only finitely many isomorphism classes of simple Hodge structures (respectively,
![]() $\ell $
-adic Galois representations) in
$\ell $
-adic Galois representations) in
![]() $\bigoplus _{g,n} H^k({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
.
$\bigoplus _{g,n} H^k({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
.
We developed the notion of STEs to study nontrivial extensions of tautological rings, such as the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
, but the same methods also yield new results on the tautological ring itself. We apply the explicit bounds in Theorem 1.3, together with new tools and results for small g, n and k to prove the following. At the level of
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
, but the same methods also yield new results on the tautological ring itself. We apply the explicit bounds in Theorem 1.3, together with new tools and results for small g, n and k to prove the following. At the level of
![]() $\mathbb {Q}$
-vector spaces, we identify
$\mathbb {Q}$
-vector spaces, we identify
![]() $H_k({\overline {\mathcal {M}}}_{g,n})$
with
$H_k({\overline {\mathcal {M}}}_{g,n})$
with
![]() $H^{2d_{g,n} - k}({\overline {\mathcal {M}}}_{g,n})$
, where
$H^{2d_{g,n} - k}({\overline {\mathcal {M}}}_{g,n})$
, where
![]() $d_{g,n} := 3g-3+n$
is the dimension of
$d_{g,n} := 3g-3+n$
is the dimension of
![]() ${\overline {\mathcal {M}}}_{g,n}$
. Similarly, when
${\overline {\mathcal {M}}}_{g,n}$
. Similarly, when
![]() $S^*$
is an STE, we write
$S^*$
is an STE, we write
![]() $S_k({\overline {\mathcal {M}}}_{g,n})$
for the
$S_k({\overline {\mathcal {M}}}_{g,n})$
for the
![]() $\mathbb {Q}$
-vector space
$\mathbb {Q}$
-vector space
![]() $S^{2d_{g,n} - k}({\overline {\mathcal {M}}}_{g,n})$
.
$S^{2d_{g,n} - k}({\overline {\mathcal {M}}}_{g,n})$
.
Theorem 1.5. The tautological ring
![]() $RH^*({\overline {\mathcal {M}}}_{g,n})$
contains
$RH^*({\overline {\mathcal {M}}}_{g,n})$
contains
-
1.
 $H^4({\overline {\mathcal {M}}}_{g,n}),$
for all g and n,
$H^4({\overline {\mathcal {M}}}_{g,n}),$
for all g and n, -
2.
 $H^6({\overline {\mathcal {M}}}_{g,n}),$
for
$H^6({\overline {\mathcal {M}}}_{g,n}),$
for
 $g \geq 10$
,
$g \geq 10$
, -
3.
 $H_{k}({\overline {\mathcal {M}}}_{g,n}),$
for even
$H_{k}({\overline {\mathcal {M}}}_{g,n}),$
for even
 $k \leq 14$
, for all g and n.
$k \leq 14$
, for all g and n.
Theorem 1.6. The STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
![]() $H_{13}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
$H_{13}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
Theorem 1.7. The STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15})$
contains
$H^{15}({\overline {\mathcal {M}}}_{1,15})$
contains
![]() $H_{15}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
$H_{15}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
Theorem 1.5(1) confirms a prediction of Arbarello and Cornalba from the 1990s; they proposed that their inductive method used to prove that
![]() $H^2({\overline {\mathcal {M}}}_{g,n})$
is tautological should also apply in degree 4 [Reference Arbarello and Cornalba1, p. 1]. Shortly thereafter, Polito confirmed that
$H^2({\overline {\mathcal {M}}}_{g,n})$
is tautological should also apply in degree 4 [Reference Arbarello and Cornalba1, p. 1]. Shortly thereafter, Polito confirmed that
![]() $H^4({\overline {\mathcal {M}}}_{g,n})$
is tautological for
$H^4({\overline {\mathcal {M}}}_{g,n})$
is tautological for
![]() $g \geq 8$
[Reference Polito32], but the general case remained open until now. Theorem 1.5(3) implies that
$g \geq 8$
[Reference Polito32], but the general case remained open until now. Theorem 1.5(3) implies that
![]() $H^k({\overline {\mathcal {M}}}_{g,n}) \cong \bigoplus \mathsf {L}^{k/2}$
for even
$H^k({\overline {\mathcal {M}}}_{g,n}) \cong \bigoplus \mathsf {L}^{k/2}$
for even
![]() $k \leq 14$
. The work of Chenevier and Lannes predicts that
$k \leq 14$
. The work of Chenevier and Lannes predicts that
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
should also be isomorphic to
$H^k({\overline {\mathcal {M}}}_{g,n})$
should also be isomorphic to
![]() $\bigoplus \mathsf {L}^{k/2}$
for
$\bigoplus \mathsf {L}^{k/2}$
for
![]() $k = 16, 18, 20$
. The Hodge and Tate conjectures then predict that these groups are generated by algebraic cycle classes. However, generation by algebraic cycle classes is an open problem except in the cases where
$k = 16, 18, 20$
. The Hodge and Tate conjectures then predict that these groups are generated by algebraic cycle classes. However, generation by algebraic cycle classes is an open problem except in the cases where
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
is known to be generated by tautological cycle classes.
$H^k({\overline {\mathcal {M}}}_{g,n})$
is known to be generated by tautological cycle classes.
By Theorems 1.6 and 1.7,
![]() $H_{13}({\overline {\mathcal {M}}}_{g,n})$
and
$H_{13}({\overline {\mathcal {M}}}_{g,n})$
and
![]() $H_{15}({\overline {\mathcal {M}}}_{g,n})$
lie in STEs generated by cohomology from genus
$H_{15}({\overline {\mathcal {M}}}_{g,n})$
lie in STEs generated by cohomology from genus
![]() $1$
moduli spaces. On the other hand,
$1$
moduli spaces. On the other hand,
![]() $H_{17}({\overline {\mathcal {M}}}_{g,n})$
requires genus
$H_{17}({\overline {\mathcal {M}}}_{g,n})$
requires genus
![]() $2$
data because
$2$
data because
![]() $W_{17}H^{17}({\mathcal {M}}_{2,14})\neq 0$
[Reference Faber and Pandharipande13].
$W_{17}H^{17}({\mathcal {M}}_{2,14})\neq 0$
[Reference Faber and Pandharipande13].
We note that any STE is top-heavy, in the sense that
![]() $\dim S^k({\overline {\mathcal {M}}}_{g,n}) \leq \dim S_k({\overline {\mathcal {M}}}_{g,n})$
for
$\dim S^k({\overline {\mathcal {M}}}_{g,n}) \leq \dim S_k({\overline {\mathcal {M}}}_{g,n})$
for
![]() $k \leq \dim {\overline {\mathcal {M}}}_{g,n}$
(cf. [Reference Petersen and Tommasi30]). Moreover, the dimensions in even and odd degrees are unimodal. This is because any STE contains
$k \leq \dim {\overline {\mathcal {M}}}_{g,n}$
(cf. [Reference Petersen and Tommasi30]). Moreover, the dimensions in even and odd degrees are unimodal. This is because any STE contains
![]() $RH^*$
and hence contains an ample class. Multiplication by a suitable power of the ample class gives an injection from
$RH^*$
and hence contains an ample class. Multiplication by a suitable power of the ample class gives an injection from
![]() $S^k({\overline {\mathcal {M}}}_{g,n})$
to
$S^k({\overline {\mathcal {M}}}_{g,n})$
to
![]() $S_k({\overline {\mathcal {M}}}_{g,n})$
.
$S_k({\overline {\mathcal {M}}}_{g,n})$
.
One could show that
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
is generated by tautological cycles in the remaining cases covered by Theorem 1.5(3) by showing that the pairing on
$H^k({\overline {\mathcal {M}}}_{g,n})$
is generated by tautological cycles in the remaining cases covered by Theorem 1.5(3) by showing that the pairing on
![]() $RH^k({\overline {\mathcal {M}}}_{g,n}) \times RH_k({\overline {\mathcal {M}}}_{g,n})$
is perfect, for example, using admcycles [Reference Delecroix, Schmitt and van Zelm11]. However, computational complexity prevents meaningful progress by brute force. Note that Petersen and Tommasi showed that this pairing is not perfect in general for
$RH^k({\overline {\mathcal {M}}}_{g,n}) \times RH_k({\overline {\mathcal {M}}}_{g,n})$
is perfect, for example, using admcycles [Reference Delecroix, Schmitt and van Zelm11]. However, computational complexity prevents meaningful progress by brute force. Note that Petersen and Tommasi showed that this pairing is not perfect in general for
![]() $k \geq 22$
[Reference Petersen28, Reference Petersen and Tommasi30]. Graber and Pandharipande had previously shown that
$k \geq 22$
[Reference Petersen28, Reference Petersen and Tommasi30]. Graber and Pandharipande had previously shown that
![]() $H^{22}({\overline {\mathcal {M}}}_{2,20})$
contains an algebraic cycle class that is not tautological [Reference Graber and Pandharipande17].
$H^{22}({\overline {\mathcal {M}}}_{2,20})$
contains an algebraic cycle class that is not tautological [Reference Graber and Pandharipande17].
Conjecture 1.8. The tautological ring
![]() $RH^*({\overline {\mathcal {M}}}_{g,n})$
contains
$RH^*({\overline {\mathcal {M}}}_{g,n})$
contains
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for even
$H^k({\overline {\mathcal {M}}}_{g,n})$
for even
![]() $k \leq 20$
.
$k \leq 20$
.
The results above show that Conjecture 1.8 is true for
![]() $k \leq 4$
, and for
$k \leq 4$
, and for
![]() $k = 6$
and
$k = 6$
and
![]() $g \geq 10$
. For
$g \geq 10$
. For
![]() $k \leq 14$
, the conjecture is true if and only if the pairing
$k \leq 14$
, the conjecture is true if and only if the pairing
![]() $RH^k({\overline {\mathcal {M}}}_{g,n}) \times RH_k({\overline {\mathcal {M}}}_{g,n})$
is perfect. The examples of Graber–Pandharipande and Petersen–Tommasi show that the conjectured bound of
$RH^k({\overline {\mathcal {M}}}_{g,n}) \times RH_k({\overline {\mathcal {M}}}_{g,n})$
is perfect. The examples of Graber–Pandharipande and Petersen–Tommasi show that the conjectured bound of
![]() $k \leq 20$
is the best possible. As further evidence for Conjecture 1.8, we note that the Arbarello–Cornalba induction together with known base cases implies the vanishing of
$k \leq 20$
is the best possible. As further evidence for Conjecture 1.8, we note that the Arbarello–Cornalba induction together with known base cases implies the vanishing of
![]() $H^{16,0}({\overline {\mathcal {M}}}_{g,n})$
and
$H^{16,0}({\overline {\mathcal {M}}}_{g,n})$
and
![]() $H^{18,0}({\overline {\mathcal {M}}}_{g,n})$
for all g and n, as recently observed by Fontanari [Reference Fontanari15].
$H^{18,0}({\overline {\mathcal {M}}}_{g,n})$
for all g and n, as recently observed by Fontanari [Reference Fontanari15].
The inductive arguments used to study
![]() $H^{k}({\overline {\mathcal {M}}}_{g,n})$
for all g and n rely on understanding base cases
$H^{k}({\overline {\mathcal {M}}}_{g,n})$
for all g and n rely on understanding base cases
![]() $H^{k'}({\overline {\mathcal {M}}}_{g',n'})$
, where
$H^{k'}({\overline {\mathcal {M}}}_{g',n'})$
, where
![]() $g'$
and
$g'$
and
![]() $n'$
are small relative to k. As k grows, more base cases are needed. With the exception of
$n'$
are small relative to k. As k grows, more base cases are needed. With the exception of
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
, all base cases required for previous work with
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
, all base cases required for previous work with
![]() $k \leq 12$
have been pure Hodge–Tate [Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4, Reference Canning and Larson6]. Substantial work went into establishing these base cases via point counts and other methods. When
$k \leq 12$
have been pure Hodge–Tate [Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4, Reference Canning and Larson6]. Substantial work went into establishing these base cases via point counts and other methods. When
![]() $k \geq 13$
, the problem becomes fundamentally more difficult, as an increasing number of the required base cases are not pure Hodge–Tate. In particular, previous techniques for handling base cases do not apply.
$k \geq 13$
, the problem becomes fundamentally more difficult, as an increasing number of the required base cases are not pure Hodge–Tate. In particular, previous techniques for handling base cases do not apply.
The advances presented here depend on a new technique for controlling the pure weight cohomology of
![]() ${\mathcal {M}}_{g,n}$
. A space X has the Chow–Künneth generation Property (CKgP) if the tensor product map on Chow groups
${\mathcal {M}}_{g,n}$
. A space X has the Chow–Künneth generation Property (CKgP) if the tensor product map on Chow groups
![]() $A_*(X) \otimes A_*(Y) \to A_*(X \times Y)$
is surjective for all Y. If X is smooth, proper and has the CKgP, then the cycle class map is an isomorphism. However, in several of the base cases needed for our arguments, the smooth and proper moduli space
$A_*(X) \otimes A_*(Y) \to A_*(X \times Y)$
is surjective for all Y. If X is smooth, proper and has the CKgP, then the cycle class map is an isomorphism. However, in several of the base cases needed for our arguments, the smooth and proper moduli space
![]() ${\overline {\mathcal {M}}}_{g,n}$
has odd cohomology and hence does not have the CKgP. Nevertheless, we show that the open moduli spaces
${\overline {\mathcal {M}}}_{g,n}$
has odd cohomology and hence does not have the CKgP. Nevertheless, we show that the open moduli spaces
![]() ${\mathcal {M}}_{g,n}$
do have the CKgP for the relevant pairs
${\mathcal {M}}_{g,n}$
do have the CKgP for the relevant pairs
![]() $(g,n)$
. To apply this in the proof of our main results, the key new technical statement is Lemma 4.3, which says that if X is smooth and has the CKgP, then
$(g,n)$
. To apply this in the proof of our main results, the key new technical statement is Lemma 4.3, which says that if X is smooth and has the CKgP, then
![]() $W_k H^k(X)$
is algebraic. This extension of the aforementioned result on the cycle class map to spaces that are not necessarily proper is essential for controlling the motivic structures that appear in
$W_k H^k(X)$
is algebraic. This extension of the aforementioned result on the cycle class map to spaces that are not necessarily proper is essential for controlling the motivic structures that appear in
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for
$H^k({\overline {\mathcal {M}}}_{g,n})$
for
![]() $k \geq 13$
. For example, using that
$k \geq 13$
. For example, using that
![]() ${\mathcal {M}}_{3,n}$
has the CKgP for
${\mathcal {M}}_{3,n}$
has the CKgP for
![]() $n \leq 11$
[Reference Canning and Larson5, Theorem 1.4], we determine the Hodge structures and Galois representations that appear in
$n \leq 11$
[Reference Canning and Larson5, Theorem 1.4], we determine the Hodge structures and Galois representations that appear in
![]() $H^*({\overline {\mathcal {M}}}_{3,n})$
, for
$H^*({\overline {\mathcal {M}}}_{3,n})$
, for
![]() $n \leq 11$
.
$n \leq 11$
.
Theorem 1.9. For
![]() $n \leq 11$
,
$n \leq 11$
,
![]() $H^*({\overline {\mathcal {M}}}_{3,n})^{\mathrm {ss}}$
is a polynomial in
$H^*({\overline {\mathcal {M}}}_{3,n})^{\mathrm {ss}}$
is a polynomial in
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() ${\mathsf {S}}_{12}$
.
${\mathsf {S}}_{12}$
.
Bergström and Faber recently used point counting techniques to compute the cohomology of
![]() ${\overline {\mathcal {M}}}_{3,n}$
as an
${\overline {\mathcal {M}}}_{3,n}$
as an
![]() $\mathbb {S}_n$
-equivariant Galois representation for
$\mathbb {S}_n$
-equivariant Galois representation for
![]() $n \leq 14$
. For
$n \leq 14$
. For
![]() $n \geq 9$
, these computations are conditional on the assumption that the only
$n \geq 9$
, these computations are conditional on the assumption that the only
![]() $\ell $
-adic Galois representations appearing are those from the list of Chenevier and Lannes [Reference Bergström and Faber3]. Theorem 1.9 unconditionally confirms the calculations of Bergström and Faber for
$\ell $
-adic Galois representations appearing are those from the list of Chenevier and Lannes [Reference Bergström and Faber3]. Theorem 1.9 unconditionally confirms the calculations of Bergström and Faber for
![]() $n = 9$
,
$n = 9$
,
![]() $10$
and
$10$
and
![]() $11$
.
$11$
.
In order to prove Theorems 1.1, 1.5(3) and 1.7, our inductive arguments require several base cases beyond what was already in the literature. In particular, we prove the following results in genus
![]() $7$
, which are also of independent interest.
$7$
, which are also of independent interest.
Theorem 1.10. For
![]() $n \leq 3$
, the moduli space
$n \leq 3$
, the moduli space
![]() ${\mathcal {M}}_{7,n}$
has the CKgP and
${\mathcal {M}}_{7,n}$
has the CKgP and
![]() $R^*({\mathcal {M}}_{7,n}) = A^*({\mathcal {M}}_{7,n})$
.
$R^*({\mathcal {M}}_{7,n}) = A^*({\mathcal {M}}_{7,n})$
.
Here,
![]() $R^*$
denotes the subring of the Chow ring
$R^*$
denotes the subring of the Chow ring
![]() $A^*$
generated by tautological cycle classes. Previous results proving that
$A^*$
generated by tautological cycle classes. Previous results proving that
![]() ${\mathcal {M}}_{g,n}$
has the CKgP and
${\mathcal {M}}_{g,n}$
has the CKgP and
![]() $R^*({\mathcal {M}}_{g,n}) = A^*({\mathcal {M}}_{g,n})$
for small g and n have primarily relied on corresponding results for Hurwitz spaces with marked points [Reference Canning and Larson5]. Unfortunately, the numerics for degree
$R^*({\mathcal {M}}_{g,n}) = A^*({\mathcal {M}}_{g,n})$
for small g and n have primarily relied on corresponding results for Hurwitz spaces with marked points [Reference Canning and Larson5]. Unfortunately, the numerics for degree
![]() $5$
covers prevented this technique from working with marked points. Here, we take a new approach to the pentagonal locus, using a modification of Mukai’s construction [Reference Mukai21] that includes markings.
$5$
covers prevented this technique from working with marked points. Here, we take a new approach to the pentagonal locus, using a modification of Mukai’s construction [Reference Mukai21] that includes markings.
2 Preliminaries
In this section, we establish notation and terminology that we will use throughout the paper and discuss a few basic examples of STEs. We also recall previously known facts about the cohomology groups of moduli spaces, especially in genus 0, 1 and 2, that will be used in the base cases of our inductive arguments.
2.1 Preliminaries on STEs
Recall that an STE is, by definition, closed under the tautological operations given by pushing forward from the boundary or pulling back from moduli spaces with fewer marked points. Let
![]() $\widetilde {\partial \mathcal {M}}_{g,n}$
denote the normalization of the boundary. The sequence
$\widetilde {\partial \mathcal {M}}_{g,n}$
denote the normalization of the boundary. The sequence
is right exact.
Let
![]() $\pi _i \colon {\mathcal {M}}_{g,n} \to {\mathcal {M}}_{g,n-1}$
be the tautological morphism forgetting the ith marking, and let
$\pi _i \colon {\mathcal {M}}_{g,n} \to {\mathcal {M}}_{g,n-1}$
be the tautological morphism forgetting the ith marking, and let
The following lemma is a cohomological analogue of the “filling criteria” in [Reference Canning and Larson5, Section 4].
We consider the partial order in which
![]() $(g', n') \prec (g, n)$
if
$(g', n') \prec (g, n)$
if
![]() $g' \leq g$
,
$g' \leq g$
,
![]() $2g' + n' \leq 2g + n$
and
$2g' + n' \leq 2g + n$
and
![]() $(g',n') \neq (g, n)$
. The moduli space
$(g',n') \neq (g, n)$
. The moduli space
![]() ${\overline {\mathcal {M}}}_{g,n}$
is stratified according to the topological types of stable curves, and each stratum of the boundary is a finite quotient of a product of moduli spaces
${\overline {\mathcal {M}}}_{g,n}$
is stratified according to the topological types of stable curves, and each stratum of the boundary is a finite quotient of a product of moduli spaces
![]() ${\mathcal {M}}_{g',n'}$
, such that
${\mathcal {M}}_{g',n'}$
, such that
![]() $(g',n') \prec (g,n)$
. Recall that we write
$(g',n') \prec (g,n)$
. Recall that we write
![]() $d_{g,n} := 3g - 3 + n$
.
$d_{g,n} := 3g - 3 + n$
.
Lemma 2.1. Let
![]() $S^*$
be an STE, and let
$S^*$
be an STE, and let
![]() $2g - 2 + n> 0$
. If the canonical map
$2g - 2 + n> 0$
. If the canonical map
is surjective for
![]() $(g',n',k') = (g, n, k)$
and all
$(g',n',k') = (g, n, k)$
and all
![]() $(g', n', k')$
satisfying
$(g', n', k')$
satisfying
then
![]() $S^k({\overline {\mathcal {M}}}_{g,n}) = H^k({\overline {\mathcal {M}}}_{g,n})$
.
$S^k({\overline {\mathcal {M}}}_{g,n}) = H^k({\overline {\mathcal {M}}}_{g,n})$
.
Proof. The proof is by induction on g and n. Consider the diagram

Here, we extend
![]() $S^*$
to
$S^*$
to
![]() $\widetilde {\partial {\mathcal {M}}_{g,n}}$
in the natural way, by summing over components, using the Künneth formula, and taking invariants under automorphisms of the dual graph. We claim that
$\widetilde {\partial {\mathcal {M}}_{g,n}}$
in the natural way, by summing over components, using the Künneth formula, and taking invariants under automorphisms of the dual graph. We claim that
![]() $\alpha $
is an isomorphism. By the Künneth formula, the domain of
$\alpha $
is an isomorphism. By the Künneth formula, the domain of
![]() $\alpha $
is a sum of tensor products of
$\alpha $
is a sum of tensor products of
![]() $S^{\ell }({\overline {\mathcal {M}}}_{\gamma ,\nu })$
with
$S^{\ell }({\overline {\mathcal {M}}}_{\gamma ,\nu })$
with
![]() $\ell \leq k - 2$
and
$\ell \leq k - 2$
and
![]() $(\gamma , \nu ) \prec (g,n)$
. Furthermore, by considering dimensions of the cycles involved, we must also have
$(\gamma , \nu ) \prec (g,n)$
. Furthermore, by considering dimensions of the cycles involved, we must also have
![]() $2d_{\gamma ,\nu } - \ell \leq 2d_{g,n} - k$
. This is because we must have
$2d_{\gamma ,\nu } - \ell \leq 2d_{g,n} - k$
. This is because we must have
![]() $k -2- \ell \leq 2(d_{g,n} - 1 - d_{\gamma ,\nu })$
, so that the degree of the other Künneth component does not exceed its real dimension. Now, suppose we are given
$k -2- \ell \leq 2(d_{g,n} - 1 - d_{\gamma ,\nu })$
, so that the degree of the other Künneth component does not exceed its real dimension. Now, suppose we are given
![]() $(g',n',k')$
that satisfy
$(g',n',k')$
that satisfy
Then
![]() $(g',n',k')$
satisfies (2.2), so
$(g',n',k')$
satisfies (2.2), so
![]() $S^{\ell }({\overline {\mathcal {M}}}_{\gamma , \nu }) = H^\ell ({\overline {\mathcal {M}}}_{\gamma ,\nu })$
by induction. This proves the claim.
$S^{\ell }({\overline {\mathcal {M}}}_{\gamma , \nu }) = H^\ell ({\overline {\mathcal {M}}}_{\gamma ,\nu })$
by induction. This proves the claim.
Next, by induction, we have
![]() $H^k({\overline {\mathcal {M}}}_{g,n-1}) = S^k({\overline {\mathcal {M}}}_{g,n-1})$
, so the image of
$H^k({\overline {\mathcal {M}}}_{g,n-1}) = S^k({\overline {\mathcal {M}}}_{g,n-1})$
, so the image of
is contained in
![]() $S^k({\overline {\mathcal {M}}}_{g,n})$
for all i. Hence,
$S^k({\overline {\mathcal {M}}}_{g,n})$
for all i. Hence,
![]() $\Phi ^k_{g,n}$
is contained in the image of
$\Phi ^k_{g,n}$
is contained in the image of
![]() $\phi $
. The tautological classes
$\phi $
. The tautological classes
![]() $RH^k({\mathcal {M}}_{g,n}) \subseteq W_k H^k({\mathcal {M}}_{g,n})$
are also contained in the image of
$RH^k({\mathcal {M}}_{g,n}) \subseteq W_k H^k({\mathcal {M}}_{g,n})$
are also contained in the image of
![]() $\phi $
by definition. Thus, the surjectivity of
$\phi $
by definition. Thus, the surjectivity of
implies that
![]() $\phi $
is surjective. Hence,
$\phi $
is surjective. Hence,
![]() $\beta $
is also surjective, as desired.
$\beta $
is also surjective, as desired.
In order to apply Lemma 2.1, we need results that help us understand generators for
![]() $W_kH^k({\mathcal {M}}_{g,n})/\left (\Phi ^k_{g,n} + RH^k({\mathcal {M}}_{g,n})\right )$
. This is the topic of Sections 3 and 4.
$W_kH^k({\mathcal {M}}_{g,n})/\left (\Phi ^k_{g,n} + RH^k({\mathcal {M}}_{g,n})\right )$
. This is the topic of Sections 3 and 4.
2.2 Pure cohomology in genus 1 and 2
On
![]() ${\mathcal {M}}_{0,n}$
, the only nonvanishing pure cohomology is
${\mathcal {M}}_{0,n}$
, the only nonvanishing pure cohomology is
![]() $W_0 H^0({\mathcal {M}}_{0,n})$
. Below, we present the complete classification of pure cohomology in genus
$W_0 H^0({\mathcal {M}}_{0,n})$
. Below, we present the complete classification of pure cohomology in genus
![]() $1$
, which is due to Getzler [Reference Getzler16]. In genus
$1$
, which is due to Getzler [Reference Getzler16]. In genus
![]() $2$
, we present a classification in low cohomological degree, following Petersen [Reference Petersen27].
$2$
, we present a classification in low cohomological degree, following Petersen [Reference Petersen27].
2.2.1 Genus 1
The following statement appeared in [Reference Pandharipande, Zvonkine and Petersen23, Proposition 7]; the proof there is omitted. Here, we include the proof (and corrected statement), which was explained to us by Petersen. Let
![]() ${\mathsf {S}}_{k+1}$
denote the weight k structure associated to the space of cusp forms of weight
${\mathsf {S}}_{k+1}$
denote the weight k structure associated to the space of cusp forms of weight
![]() $k+1$
for
$k+1$
for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. Let
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. Let
![]() $\pi \colon E \to {\mathcal {M}}_{1,1}$
be the universal curve, and let
$\pi \colon E \to {\mathcal {M}}_{1,1}$
be the universal curve, and let
![]() $\mathbb {V}$
be the local system
$\mathbb {V}$
be the local system
![]() $R^1\pi _*\mathbb {Q}$
. By the Eichler–Shimura correspondence, we have
$R^1\pi _*\mathbb {Q}$
. By the Eichler–Shimura correspondence, we have
![]() ${\mathsf {S}}_{k+1} = W_{k}H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes {k-1}})$
. We will see that the latter is identified with
${\mathsf {S}}_{k+1} = W_{k}H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes {k-1}})$
. We will see that the latter is identified with
![]() $W_k H^k({\mathcal {M}}_{1,k})$
. More generally, we have the following. Given a partition
$W_k H^k({\mathcal {M}}_{1,k})$
. More generally, we have the following. Given a partition
![]() $\lambda $
of n, let
$\lambda $
of n, let
![]() $V_\lambda $
be the associated Specht module representation of
$V_\lambda $
be the associated Specht module representation of
![]() $\mathbb {S}_n$
.
$\mathbb {S}_n$
.
Proposition 2.2. For
![]() $n\geq k,$
a basis for
$n\geq k,$
a basis for
![]() $W_kH^k({\mathcal {M}}_{1,n})$
is given by the
$W_kH^k({\mathcal {M}}_{1,n})$
is given by the
![]() $\binom {n-1}{k-1}$
pullbacks from
$\binom {n-1}{k-1}$
pullbacks from
![]() $W_kH^k({\mathcal {M}}_{1,A})$
, where A runs over all subsets of
$W_kH^k({\mathcal {M}}_{1,A})$
, where A runs over all subsets of
![]() $\{1,\ldots ,n\}$
of size k, such that
$\{1,\ldots ,n\}$
of size k, such that
![]() $1 \in A$
. Consequently, there is an
$1 \in A$
. Consequently, there is an
![]() $\mathbb {S}_n$
-equivariant isomorphism
$\mathbb {S}_n$
-equivariant isomorphism
For
![]() $n<k$
, we have
$n<k$
, we have
![]() $W_k H^k({\mathcal {M}}_{1,n})=0$
.
$W_k H^k({\mathcal {M}}_{1,n})=0$
.
Proof. Let
![]() $\pi \colon E\rightarrow {\mathcal {M}}_{1,1}$
denote the universal elliptic curve, and
$\pi \colon E\rightarrow {\mathcal {M}}_{1,1}$
denote the universal elliptic curve, and
![]() $\sigma \colon {\mathcal {M}}_{1,1} \to E$
the section. Associated to the open embedding
$\sigma \colon {\mathcal {M}}_{1,1} \to E$
the section. Associated to the open embedding
![]() ${\mathcal {M}}_{1,n}\hookrightarrow E^{n-1}$
, we have a right exact sequence
${\mathcal {M}}_{1,n}\hookrightarrow E^{n-1}$
, we have a right exact sequence
Since
![]() $f\colon E^{n-1}\rightarrow {\mathcal {M}}_{1,1}$
is smooth and proper, the Leray spectral sequence degenerates at
$f\colon E^{n-1}\rightarrow {\mathcal {M}}_{1,1}$
is smooth and proper, the Leray spectral sequence degenerates at
![]() $E_2$
, and by [Reference Deligne12, Proposition 2.16], we have a direct sum decomposition
$E_2$
, and by [Reference Deligne12, Proposition 2.16], we have a direct sum decomposition
By the Künneth formula, we have
Let
![]() $\mathbb {V}:=R^1\pi _*\mathbb {Q}$
, and note that
$\mathbb {V}:=R^1\pi _*\mathbb {Q}$
, and note that
![]() $R^0\pi _*\mathbb {Q} = \mathbb {Q}$
and
$R^0\pi _*\mathbb {Q} = \mathbb {Q}$
and
![]() $R^2\pi _*\mathbb {Q} = \mathbb {Q}(-1)$
.
$R^2\pi _*\mathbb {Q} = \mathbb {Q}(-1)$
.
Fix some p and
![]() $(i_2, \ldots , i_{n})$
with
$(i_2, \ldots , i_{n})$
with
![]() $p + i_2 + \cdots + i_{n} = k$
. If
$p + i_2 + \cdots + i_{n} = k$
. If
![]() $i_j = 2$
, then, we claim that
$i_j = 2$
, then, we claim that
lies in the image of the first map in (2.4). More precisely, let
![]() $\alpha _{j} \colon E^{n-2} \rightarrow E^{n-1}$
be the locus where the jth entry in
$\alpha _{j} \colon E^{n-2} \rightarrow E^{n-1}$
be the locus where the jth entry in
![]() $E^{n-1}$
agrees with the section
$E^{n-1}$
agrees with the section
![]() $\sigma \colon {\mathcal {M}}_{1,1} \to E$
. In other words,
$\sigma \colon {\mathcal {M}}_{1,1} \to E$
. In other words,
![]() $\alpha _j$
is defined by the fiber diagram
$\alpha _j$
is defined by the fiber diagram

If
![]() $i_j = 2,$
we have
$i_j = 2,$
we have
![]() $p + i_2 + \cdots + i_{j-1} + i_{j+1} + \cdots + i_{n} = k-2$
. Therefore, using the Leray spectral sequence for
$p + i_2 + \cdots + i_{j-1} + i_{j+1} + \cdots + i_{n} = k-2$
. Therefore, using the Leray spectral sequence for
![]() $E^{n-2} \to {\mathcal {M}}_{1,1}$
, there is a corresponding term
$E^{n-2} \to {\mathcal {M}}_{1,1}$
, there is a corresponding term
Then the pushforward
![]() $\alpha _{j*}\colon H^{k-2}(E^{n-2}) \to H^k(E^{n-1})$
sends the subspace on the left of (2.7) isomorphically onto the subspace on the left of (2.6), which proves the claim.
$\alpha _{j*}\colon H^{k-2}(E^{n-2}) \to H^k(E^{n-1})$
sends the subspace on the left of (2.7) isomorphically onto the subspace on the left of (2.6), which proves the claim.
It follows that
![]() $W_kH^k({\mathcal {M}}_{1,n})$
is generated by the terms
$W_kH^k({\mathcal {M}}_{1,n})$
is generated by the terms
![]() $W_k H^p({\mathcal {M}}_{1,1}, R^{i_2} \pi _*\mathbb {Q} \otimes \cdots \otimes R^{i_{n}}\pi _*\mathbb {Q})$
in
$W_k H^p({\mathcal {M}}_{1,1}, R^{i_2} \pi _*\mathbb {Q} \otimes \cdots \otimes R^{i_{n}}\pi _*\mathbb {Q})$
in
![]() $W_k H^k(E^{n-1})$
, where all
$W_k H^k(E^{n-1})$
, where all
![]() $i_j \leq 1$
. By [Reference Petersen26, Section 2], we have
$i_j \leq 1$
. By [Reference Petersen26, Section 2], we have
![]() $W_k H^p({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes q}) = 0$
unless
$W_k H^p({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes q}) = 0$
unless
![]() $p = 1$
and
$p = 1$
and
![]() $q = k-1$
, in which case
$q = k-1$
, in which case
![]() $W_k H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1}) = {\mathsf {S}}_{k+1}$
by Eichler–Shimura.
$W_k H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1}) = {\mathsf {S}}_{k+1}$
by Eichler–Shimura.
There are
![]() $\binom {n-1}{k-1}$
terms of the form
$\binom {n-1}{k-1}$
terms of the form
![]() $H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1})$
in (2.5) coming from choosing which
$H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1})$
in (2.5) coming from choosing which
![]() $k-1$
of the
$k-1$
of the
![]() $n-1$
indices have
$n-1$
indices have
![]() $i_j =1$
. Each of these terms is pulled back along the projection map
$i_j =1$
. Each of these terms is pulled back along the projection map
![]() $E^{n-1} \to E^{k-1}$
, which remembers the
$E^{n-1} \to E^{k-1}$
, which remembers the
![]() $k-1$
factors for which
$k-1$
factors for which
![]() $i_j = 1$
. Let A be the collection of indices j, such that
$i_j = 1$
. Let A be the collection of indices j, such that
![]() $i_j = 1$
together with
$i_j = 1$
together with
![]() $1$
. There is a commutative diagram
$1$
. There is a commutative diagram

It follows that
![]() $W_kH^k({\mathcal {M}}_{1,n})$
is generated by the pullbacks from
$W_kH^k({\mathcal {M}}_{1,n})$
is generated by the pullbacks from
![]() $W_kH^k({\mathcal {M}}_{1,A})$
as A ranges over all subsets of size k containing
$W_kH^k({\mathcal {M}}_{1,A})$
as A ranges over all subsets of size k containing
![]() $1$
. Finally, we note that there can be no relations among these
$1$
. Finally, we note that there can be no relations among these
![]() $\binom {n-1}{k-1}$
copies of
$\binom {n-1}{k-1}$
copies of
![]() $W_k H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1}) = {\mathsf {S}}_{k+1}$
since the image of the left-hand map of (2.4) lies in the subspace of type
$W_k H^1({\mathcal {M}}_{1,1}, \mathbb {V}^{\otimes k-1}) = {\mathsf {S}}_{k+1}$
since the image of the left-hand map of (2.4) lies in the subspace of type
![]() $\mathsf {L}^i {\mathsf {S}}_{k+1-2i}$
for
$\mathsf {L}^i {\mathsf {S}}_{k+1-2i}$
for
![]() $i \geq 1$
.
$i \geq 1$
.
We have now shown that
![]() $W_kH^k({\mathcal {M}}_{1,n}) = {\mathsf {S}}_{k+1} \otimes U$
for some
$W_kH^k({\mathcal {M}}_{1,n}) = {\mathsf {S}}_{k+1} \otimes U$
for some
![]() $\binom {n-1}{k-1}$
-dimensional vector space U. From the discussion above, it is not difficult to identify U as an
$\binom {n-1}{k-1}$
-dimensional vector space U. From the discussion above, it is not difficult to identify U as an
![]() $\mathbb {S}_n$
-representation. When
$\mathbb {S}_n$
-representation. When
![]() $n = k$
, the
$n = k$
, the
![]() $\mathbb {S}_k$
action on
$\mathbb {S}_k$
action on
![]() $W_kH^k({\mathcal {M}}_{1,k})$
is the sign representation. To identify U for
$W_kH^k({\mathcal {M}}_{1,k})$
is the sign representation. To identify U for
![]() $n> k$
, let
$n> k$
, let
![]() $\mathbb {S}_{n-1} \subset \mathbb {S}_n$
be the subgroup that fixes
$\mathbb {S}_{n-1} \subset \mathbb {S}_n$
be the subgroup that fixes
![]() $1$
. Since
$1$
. Since
![]() $W_kH^k({\mathcal {M}}_{1,n})$
is freely generated by the pullbacks from
$W_kH^k({\mathcal {M}}_{1,n})$
is freely generated by the pullbacks from
![]() $W_kH^k({\mathcal {M}}_{1,A})$
as A runs over subsets of size k containing
$W_kH^k({\mathcal {M}}_{1,A})$
as A runs over subsets of size k containing
![]() $1$
, we have
$1$
, we have
By the Pieri rule, we have
By the branching rule,
![]() $V_{n-k+1,1^{k-1}}$
is the unique
$V_{n-k+1,1^{k-1}}$
is the unique
![]() $\mathbb {S}_n$
representation whose restriction to
$\mathbb {S}_n$
representation whose restriction to
![]() $\mathbb {S}_{n-1}$
is the representation in (2.8).
$\mathbb {S}_{n-1}$
is the representation in (2.8).
Since
![]() ${\mathsf {S}}_{14} = 0$
, we have the following.
${\mathsf {S}}_{14} = 0$
, we have the following.
Corollary 2.3.
![]() $H^{13}({\overline {\mathcal {M}}}_{1,n})$
lies in the STE generated by
$H^{13}({\overline {\mathcal {M}}}_{1,n})$
lies in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
for all n.
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
for all n.
Let
![]() $S^*_\omega $
denote the STE generated by
$S^*_\omega $
denote the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Note that
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Note that
![]() $S^*_\omega $
is the STE generated by the class
$S^*_\omega $
is the STE generated by the class
![]() $\omega \in H^{11,0}({\overline {\mathcal {M}}}_{1,11})$
associated to the weight
$\omega \in H^{11,0}({\overline {\mathcal {M}}}_{1,11})$
associated to the weight
![]() $12$
cusp form for
$12$
cusp form for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
,that is, it is the smallest STE whose complexification contains
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
,that is, it is the smallest STE whose complexification contains
![]() $\omega $
. In [Reference Canning, Larson and Payne8], we showed that
$\omega $
. In [Reference Canning, Larson and Payne8], we showed that
![]() $S^*_\omega $
contains
$S^*_\omega $
contains
![]() $H^{11}({\overline {\mathcal {M}}}_{g,n})$
, and hence
$H^{11}({\overline {\mathcal {M}}}_{g,n})$
, and hence
![]() $H_{11}({\overline {\mathcal {M}}}_{g,n})$
, for all g and n. In this paper, we show that it also contains
$H_{11}({\overline {\mathcal {M}}}_{g,n})$
, for all g and n. In this paper, we show that it also contains
![]() $H_{13}({\overline {\mathcal {M}}}_{g,n})$
for all g and n (Theorem 1.6). In contrast with the system of tautological rings, an arbitrary STE need not be closed under pushforward along maps forgetting marked points or pullback to the boundary. Nevertheless, we have the following result for
$H_{13}({\overline {\mathcal {M}}}_{g,n})$
for all g and n (Theorem 1.6). In contrast with the system of tautological rings, an arbitrary STE need not be closed under pushforward along maps forgetting marked points or pullback to the boundary. Nevertheless, we have the following result for
![]() $S_{\omega }^*({\overline {\mathcal {M}}}_{g,n})$
.
$S_{\omega }^*({\overline {\mathcal {M}}}_{g,n})$
.
Proposition 2.4. The STE
![]() $S_{\omega }^*$
is closed under the tautological operations induced by pushforward for forgetting marked points and pullback for gluing marked points.
$S_{\omega }^*$
is closed under the tautological operations induced by pushforward for forgetting marked points and pullback for gluing marked points.
Proof. By [Reference Petersen26], all even cohomology in genus
![]() $1$
is represented by boundary strata. Therefore, any product of two odd degree classes can be written as a sum of boundary strata. It follows that every class in
$1$
is represented by boundary strata. Therefore, any product of two odd degree classes can be written as a sum of boundary strata. It follows that every class in
![]() $S_{\omega }^*({\overline {\mathcal {M}}}_{g,n})$
can be represented as a linear combination of decorated graphs, all of whose nontautological decorations are
$S_{\omega }^*({\overline {\mathcal {M}}}_{g,n})$
can be represented as a linear combination of decorated graphs, all of whose nontautological decorations are
![]() $H^{11}$
-classes on genus 1 vertices.
$H^{11}$
-classes on genus 1 vertices.
The pushforward of
![]() $H^{11}({\overline {\mathcal {M}}}_{1,n})$
along the maps forgetting marked points is zero. Since the tautological rings are closed under pushforward, it follows that
$H^{11}({\overline {\mathcal {M}}}_{1,n})$
along the maps forgetting marked points is zero. Since the tautological rings are closed under pushforward, it follows that
![]() $S_{\omega }^*$
is closed under pushforward.
$S_{\omega }^*$
is closed under pushforward.
By [Reference Canning, Larson and Payne8, Lemma 2.2], the image of
![]() $H^{11}({\overline {\mathcal {M}}}_{1,n})$
under pullback to the boundary lies in
$H^{11}({\overline {\mathcal {M}}}_{1,n})$
under pullback to the boundary lies in
![]() $S^*_{\omega }$
. By the excess intersection formula, and using the fact that
$S^*_{\omega }$
. By the excess intersection formula, and using the fact that
![]() $\psi $
-classes in genus 1 are boundary classes, it follows that the pullback of any such decorated graph in
$\psi $
-classes in genus 1 are boundary classes, it follows that the pullback of any such decorated graph in
![]() $S_\omega ^*$
to any boundary stratum is a sum of decorated graphs of the same form. In particular,
$S_\omega ^*$
to any boundary stratum is a sum of decorated graphs of the same form. In particular,
![]() $S_{\omega }^*$
is closed under pullback to the boundary, as required.
$S_{\omega }^*$
is closed under pullback to the boundary, as required.
Remark 2.5. More generally, the Hodge groups
![]() $H^{k,0}({\overline {\mathcal {M}}}_{1,k})$
correspond to the space of cusp forms for
$H^{k,0}({\overline {\mathcal {M}}}_{1,k})$
correspond to the space of cusp forms for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
of weight
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
of weight
![]() $k+1$
. Essentially the same argument shows that the STE generated by any subset of these cusp form spaces is closed under all of the tautological operations.
$k+1$
. Essentially the same argument shows that the STE generated by any subset of these cusp form spaces is closed under all of the tautological operations.
2.2.2 Genus 2
Here, we summarize what we need about the pure weight cohomology of
![]() ${\mathcal {M}}_{2,n}$
in low degrees, from [Reference Petersen28, Reference Petersen and Tommasi30].
${\mathcal {M}}_{2,n}$
in low degrees, from [Reference Petersen28, Reference Petersen and Tommasi30].
Proposition 2.6. Let
![]() $k\leq 10$
. Then
$k\leq 10$
. Then
![]() $W_{2k} H^{2k}({\mathcal {M}}_{2,n})=RH^{2k}({\mathcal {M}}_{2,n})$
.
$W_{2k} H^{2k}({\mathcal {M}}_{2,n})=RH^{2k}({\mathcal {M}}_{2,n})$
.
Proof. When
![]() $n<20$
, we have
$n<20$
, we have
![]() $H^{2k}({\overline {\mathcal {M}}}_{2,n})=RH^{2k}({\overline {\mathcal {M}}}_{2,n})$
by [Reference Petersen28, Theorem 3.8]. Hence,
$H^{2k}({\overline {\mathcal {M}}}_{2,n})=RH^{2k}({\overline {\mathcal {M}}}_{2,n})$
by [Reference Petersen28, Theorem 3.8]. Hence,
![]() $W_{2k} H^{2k}({\mathcal {M}}_{2,n})=RH^{2k}({\mathcal {M}}_{2,n})$
by restriction. For
$W_{2k} H^{2k}({\mathcal {M}}_{2,n})=RH^{2k}({\mathcal {M}}_{2,n})$
by restriction. For
![]() $n=20$
and
$n=20$
and
![]() $k\leq 10$
, the same result holds (see [Reference Petersen28, Remark 3.10]). For
$k\leq 10$
, the same result holds (see [Reference Petersen28, Remark 3.10]). For
![]() $n>20$
and
$n>20$
and
![]() $k \leq 10$
, all of
$k \leq 10$
, all of
![]() $W_{2k} H^{2k}({\mathcal {M}}_{2,n})$
is pulled back from
$W_{2k} H^{2k}({\mathcal {M}}_{2,n})$
is pulled back from
![]() $W_{2k} H^{2k}({\mathcal {M}}_{2,m})$
where
$W_{2k} H^{2k}({\mathcal {M}}_{2,m})$
where
![]() $m\leq 20$
(see Lemma 3.1, below). Because the tautological ring is closed under forgetful pullbacks, the lemma follows.
$m\leq 20$
(see Lemma 3.1, below). Because the tautological ring is closed under forgetful pullbacks, the lemma follows.
Applying Lemma 2.1 to the STE
![]() $RH^*$
immediately implies Conjecture 1.8 for
$RH^*$
immediately implies Conjecture 1.8 for
![]() $g = 2$
.
$g = 2$
.
Corollary 2.7. If
![]() $k \leq 10$
, then
$k \leq 10$
, then
![]() $H^{2k}({\overline {\mathcal {M}}}_{2,n}) = RH^{2k}({\overline {\mathcal {M}}}_{2,n})$
for all n.
$H^{2k}({\overline {\mathcal {M}}}_{2,n}) = RH^{2k}({\overline {\mathcal {M}}}_{2,n})$
for all n.
In odd degrees, there are restrictions on the possible motivic structures coming from the cohomology of local systems on the moduli space of principally polarized abelian surfaces.
Proposition 2.8. In the category of Galois representations, the pure weight cohomology of
![]() ${\mathcal {M}}_{2,n}$
in degrees 13 and 15 is of the form
${\mathcal {M}}_{2,n}$
in degrees 13 and 15 is of the form
Proof. For every k, the surjection
factors through
![]() $W_k H^k({\mathcal {M}}_{2,n}^{\operatorname {\mathrm {ct}}})$
. Here,
$W_k H^k({\mathcal {M}}_{2,n}^{\operatorname {\mathrm {ct}}})$
. Here,
![]() ${\mathcal {M}}_{2,n}^{\operatorname {\mathrm {ct}}}$
is the moduli space of genus
${\mathcal {M}}_{2,n}^{\operatorname {\mathrm {ct}}}$
is the moduli space of genus
![]() $2$
curves of compact type with n markings. By [Reference Petersen28, Theorem 2.1(i) and (ii)],
$2$
curves of compact type with n markings. By [Reference Petersen28, Theorem 2.1(i) and (ii)],
where
![]() $A^q$
and
$A^q$
and
![]() $B^q$
are local systems of weight q, given by direct sums of Tate twists of symplectic local systems. Moreover, the terms
$B^q$
are local systems of weight q, given by direct sums of Tate twists of symplectic local systems. Moreover, the terms
![]() $H^p(\operatorname {\mathrm {Sym}}^2 {\mathcal {M}}_{1,1},B^q)$
map to zero under restriction to
$H^p(\operatorname {\mathrm {Sym}}^2 {\mathcal {M}}_{1,1},B^q)$
map to zero under restriction to
![]() $H^k({\mathcal {M}}_{2,n})$
by [Reference Petersen28, Lemma 3.3].
$H^k({\mathcal {M}}_{2,n})$
by [Reference Petersen28, Lemma 3.3].
We now consider the terms
![]() $H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},A^q)$
. Let
$H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},A^q)$
. Let
![]() $\mathbb {V}$
be a Tate twist of a symplectic local system of weight q on
$\mathbb {V}$
be a Tate twist of a symplectic local system of weight q on
![]() ${\mathcal {M}}_2^{\operatorname {\mathrm {ct}}}$
. If q is odd, then
${\mathcal {M}}_2^{\operatorname {\mathrm {ct}}}$
. If q is odd, then
![]() $H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},\mathbb {V})$
vanishes because the hyperelliptic involution acts on the fibers of
$H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},\mathbb {V})$
vanishes because the hyperelliptic involution acts on the fibers of
![]() $\mathbb {V}$
by
$\mathbb {V}$
by
![]() $(-1)^q$
. When q is even, the possible Galois representations appearing in
$(-1)^q$
. When q is even, the possible Galois representations appearing in
![]() $H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},\mathbb {V})^{\mathrm {ss}}$
are determined by [Reference Petersen27, Theorem 2.1]. When
$H^p({\mathcal {M}}_{2}^{\operatorname {\mathrm {ct}}},\mathbb {V})^{\mathrm {ss}}$
are determined by [Reference Petersen27, Theorem 2.1]. When
![]() $p+q=13$
(respectively,
$p+q=13$
(respectively,
![]() $p+q=15)$
, the only possibility of pure weight is
$p+q=15)$
, the only possibility of pure weight is
![]() $\mathsf {L}{\mathsf {S}}_{12}$
(respectively,
$\mathsf {L}{\mathsf {S}}_{12}$
(respectively,
![]() ${\mathsf {L}}^2{\mathsf {S}}_{12})$
.
${\mathsf {L}}^2{\mathsf {S}}_{12})$
.
Corollary 2.9. On
![]() ${\overline {\mathcal {M}}}_{2,n}$
, in the category of Galois representations, we have
${\overline {\mathcal {M}}}_{2,n}$
, in the category of Galois representations, we have
Proof. For degree 13, consider the right exact sequence
By [Reference Canning, Larson and Payne8], the semi-simplification of the left-hand side is a sum of terms
![]() ${\mathsf {S}}_{12}$
. Proposition 2.8 shows that the semi-simplification of the right-hand side consists only of Tate twists of
${\mathsf {S}}_{12}$
. Proposition 2.8 shows that the semi-simplification of the right-hand side consists only of Tate twists of
![]() ${\mathsf {S}}_{12}$
. Thus, the semi-simplification of the middle term does, too.
${\mathsf {S}}_{12}$
. Thus, the semi-simplification of the middle term does, too.
Similarly, for degree
![]() $15$
, we consider the right exact sequence
$15$
, we consider the right exact sequence
The boundary divisors on
![]() ${\overline {\mathcal {M}}}_{2,n}$
are finite quotients of products of moduli spaces for genus at most
${\overline {\mathcal {M}}}_{2,n}$
are finite quotients of products of moduli spaces for genus at most
![]() $2$
. In particular, by the Künneth formula and vanishing of odd cohomology in degrees less than or equal to
$2$
. In particular, by the Künneth formula and vanishing of odd cohomology in degrees less than or equal to
![]() $9$
, we see that the left-hand side is a sum of terms of the form
$9$
, we see that the left-hand side is a sum of terms of the form
![]() $H^{13}({\overline {\mathcal {M}}}_{g',n'})$
or
$H^{13}({\overline {\mathcal {M}}}_{g',n'})$
or
![]() $H^2({\overline {\mathcal {M}}}_{g_1,n_1}) \otimes H^{11}({\overline {\mathcal {M}}}_{g_2,n_2})$
, where
$H^2({\overline {\mathcal {M}}}_{g_1,n_1}) \otimes H^{11}({\overline {\mathcal {M}}}_{g_2,n_2})$
, where
![]() $g', g_1, g_2 \leq 2$
. By the degree 13 result just proved, the semi-simplification of terms of the first kind is a sum of
$g', g_1, g_2 \leq 2$
. By the degree 13 result just proved, the semi-simplification of terms of the first kind is a sum of
![]() $\mathsf {L}{\mathsf {S}}_{12}$
. Meanwhile, we know
$\mathsf {L}{\mathsf {S}}_{12}$
. Meanwhile, we know
![]() $H^2({\overline {\mathcal {M}}}_{g_1,n_1})$
is pure Tate by [Reference Arbarello and Cornalba1] and
$H^2({\overline {\mathcal {M}}}_{g_1,n_1})$
is pure Tate by [Reference Arbarello and Cornalba1] and
![]() $H^{11}({\overline {\mathcal {M}}}_{g_2, n_2})^{\mathrm {ss}}$
is a sum of terms
$H^{11}({\overline {\mathcal {M}}}_{g_2, n_2})^{\mathrm {ss}}$
is a sum of terms
![]() ${\mathsf {S}}_{12}$
by [Reference Canning, Larson and Payne8]. Hence, the semi-simplification of terms of the second kind is also a sum of
${\mathsf {S}}_{12}$
by [Reference Canning, Larson and Payne8]. Hence, the semi-simplification of terms of the second kind is also a sum of
![]() $\mathsf {L}{\mathsf {S}}_{12}$
. To conclude, note that Proposition 2.8 shows that the semi-simplification of the right-hand side consists only of Tate twists of
$\mathsf {L}{\mathsf {S}}_{12}$
. To conclude, note that Proposition 2.8 shows that the semi-simplification of the right-hand side consists only of Tate twists of
![]() ${\mathsf {S}}_{12}$
, so the semi-simplification of the middle term does too.
${\mathsf {S}}_{12}$
, so the semi-simplification of the middle term does too.
Remark 2.10. See Lemma 8.1 for an analogous result in the category of Hodge structures.
3 Finite generation
Let
![]() $S^*$
be an STE. By Lemma 2.1,
$S^*$
be an STE. By Lemma 2.1,
![]() $S^k({\overline {\mathcal {M}}}_{g,n})$
contains
$S^k({\overline {\mathcal {M}}}_{g,n})$
contains
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n if and only if it surjects onto
$H^k({\overline {\mathcal {M}}}_{g,n})$
for all g and n if and only if it surjects onto
![]() $W_kH^k({\mathcal {M}}_{g,n})/ \big (\Phi ^k_{g,n} + RH^k({\mathcal {M}}_{g,n}) \big )$
for all g and n. Below we give a sufficient criterion for the vanishing of
$W_kH^k({\mathcal {M}}_{g,n})/ \big (\Phi ^k_{g,n} + RH^k({\mathcal {M}}_{g,n}) \big )$
for all g and n. Below we give a sufficient criterion for the vanishing of
![]() $W_kH^k({\mathcal {M}}_{g,n})/ \Phi ^k_{g,n}.$
The argument is similar to the proof of Proposition 2.2, using the Künneth decomposition of the Leray spectral sequence for the n-fold fiber product of the universal curve
$W_kH^k({\mathcal {M}}_{g,n})/ \Phi ^k_{g,n}.$
The argument is similar to the proof of Proposition 2.2, using the Künneth decomposition of the Leray spectral sequence for the n-fold fiber product of the universal curve
![]() $\mathcal {C}^n \to {\mathcal {M}}_g$
.
$\mathcal {C}^n \to {\mathcal {M}}_g$
.
We are grateful to Petersen for explaining how an earlier version of this lemma could be strengthened to the version presented here. This stronger version will also be useful for controlling some additional base cases in Section 7. To state it, we define the subspace
In other words,
![]() $\Psi ^k_{g,n}$
is generated by pullbacks from moduli spaces with fewer markings multiplied with
$\Psi ^k_{g,n}$
is generated by pullbacks from moduli spaces with fewer markings multiplied with
![]() $\psi $
-classes. Given a g-tuple of integers
$\psi $
-classes. Given a g-tuple of integers
![]() $\lambda = (\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _g \geq 0)$
, let
$\lambda = (\lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _g \geq 0)$
, let
![]() $\mathbb {V}_\lambda $
be the associated symplectic local system on
$\mathbb {V}_\lambda $
be the associated symplectic local system on
![]() ${\mathcal {M}}_g$
, as in [Reference Petersen, Tavakol and Yin29]. Let
${\mathcal {M}}_g$
, as in [Reference Petersen, Tavakol and Yin29]. Let
![]() $|\lambda | = \lambda _1 + \cdots + \lambda _g$
, which is the weight of the local system
$|\lambda | = \lambda _1 + \cdots + \lambda _g$
, which is the weight of the local system
![]() $\mathbb {V}_\lambda $
. When
$\mathbb {V}_\lambda $
. When
![]() $|\lambda | = n$
, as in the previous section, we write
$|\lambda | = n$
, as in the previous section, we write
![]() $V_{\lambda }$
for the irreducible
$V_{\lambda }$
for the irreducible
![]() $\mathbb {S}_n$
representation corresponding to
$\mathbb {S}_n$
representation corresponding to
![]() $\lambda $
.
$\lambda $
.
Lemma 3.1.
(a) If
![]() $g \geq 2$
, then
$g \geq 2$
, then
(b) Moreover, if
![]() $n> 0$
and
$n> 0$
and
![]() $n \geq k$
, then
$n \geq k$
, then
![]() $W_kH^k({\mathcal {M}}_{g,n}) = \Phi ^k_{g,n}$
.
$W_kH^k({\mathcal {M}}_{g,n}) = \Phi ^k_{g,n}$
.
Proof. (a) Let
![]() $\pi \colon \mathcal {C} \to {\mathcal {M}}_g$
be the universal curve. There is an open inclusion
$\pi \colon \mathcal {C} \to {\mathcal {M}}_g$
be the universal curve. There is an open inclusion
![]() ${\mathcal {M}}_{g,n} \subset \mathcal {C}^n$
, and hence restriction gives a surjection from
${\mathcal {M}}_{g,n} \subset \mathcal {C}^n$
, and hence restriction gives a surjection from
![]() $W_kH^k(\mathcal {C}^n)$
to
$W_kH^k(\mathcal {C}^n)$
to
![]() $W_kH^k({\mathcal {M}}_{g,n})$
. Given a subset
$W_kH^k({\mathcal {M}}_{g,n})$
. Given a subset
![]() $A \subset \{1, \ldots , n\}$
, let
$A \subset \{1, \ldots , n\}$
, let
![]() $\mathcal {C}^n \to \mathcal {C}^A$
be the projection onto the factors indexed by A. We consider the following three subspaces of
$\mathcal {C}^n \to \mathcal {C}^A$
be the projection onto the factors indexed by A. We consider the following three subspaces of
![]() $H^k(\mathcal {C}^n)$
:
$H^k(\mathcal {C}^n)$
:
-
•
 $\widetilde {\Phi }$
, the span of the pullbacks of
$\widetilde {\Phi }$
, the span of the pullbacks of
 $H^k(\mathcal {C}^{\{i\}^c})$
along projection
$H^k(\mathcal {C}^{\{i\}^c})$
along projection
 $\mathcal {C}^n \to \mathcal {C}^{\{i\}^c}$
$\mathcal {C}^n \to \mathcal {C}^{\{i\}^c}$
-
•
 $\widetilde {\Psi }$
, the span of
$\widetilde {\Psi }$
, the span of
 $\psi _i \cdot H^{k-2}(\mathcal {C}^{\{i\}^c})$
$\psi _i \cdot H^{k-2}(\mathcal {C}^{\{i\}^c})$
-
•
 $\widetilde {\Delta }$
, the span of
$\widetilde {\Delta }$
, the span of
 $\Delta _{ij} \cdot H^{k-2}(\mathcal {C}^{\{i, j\}^c})$
, where
$\Delta _{ij} \cdot H^{k-2}(\mathcal {C}^{\{i, j\}^c})$
, where
 $\Delta _{ij}$
denotes the pullback of the class of the diagonal in
$\Delta _{ij}$
denotes the pullback of the class of the diagonal in
 $H^2(\mathcal {C}^{\{i,j\}})$
.
$H^2(\mathcal {C}^{\{i,j\}})$
.
Note that
![]() $\widetilde {\Delta }$
lies in the kernel of
$\widetilde {\Delta }$
lies in the kernel of
![]() $H^k(\mathcal {C}^n) \to H^k({\mathcal {M}}_{g,n})$
, and the images of the weight k parts of
$H^k(\mathcal {C}^n) \to H^k({\mathcal {M}}_{g,n})$
, and the images of the weight k parts of
![]() $\widetilde {\Phi }$
and
$\widetilde {\Phi }$
and
![]() $\widetilde {\Psi }$
under
$\widetilde {\Psi }$
under
![]() $W_kH^k(\mathcal {C}^n) \to W_kH^k({\mathcal {M}}_{g,n})$
are the subspaces
$W_kH^k(\mathcal {C}^n) \to W_kH^k({\mathcal {M}}_{g,n})$
are the subspaces
![]() $\Phi ^k_{g,n}$
and
$\Phi ^k_{g,n}$
and
![]() $\Psi ^k_{g,n}$
, respectively. To prove part (a), it thus suffices to show that
$\Psi ^k_{g,n}$
, respectively. To prove part (a), it thus suffices to show that
We explain how (3.1) follows from [Reference Petersen, Tavakol and Yin29].
Since
![]() $f\colon \mathcal {C}^n \to {\mathcal {M}}_g$
is smooth and proper, the Leray spectral sequence degenerates at
$f\colon \mathcal {C}^n \to {\mathcal {M}}_g$
is smooth and proper, the Leray spectral sequence degenerates at
![]() $E_2$
, and by [Reference Deligne12, Proposition 2.16], we have a direct sum decomposition
$E_2$
, and by [Reference Deligne12, Proposition 2.16], we have a direct sum decomposition
Applying the Künneth formula, we obtain
 $$ \begin{align} H^k(\mathcal{C}^n) = \bigoplus_{\substack{p + q = k \\i_1 + \ldots+ i_n = q }} H^p\left({\mathcal{M}}_g, R^{i_1} \pi_* \mathbb{Q} \otimes \cdots \otimes R^{i_n} \pi_* \mathbb{Q} \right). \end{align} $$
$$ \begin{align} H^k(\mathcal{C}^n) = \bigoplus_{\substack{p + q = k \\i_1 + \ldots+ i_n = q }} H^p\left({\mathcal{M}}_g, R^{i_1} \pi_* \mathbb{Q} \otimes \cdots \otimes R^{i_n} \pi_* \mathbb{Q} \right). \end{align} $$
As observed in [Reference Petersen, Tavakol and Yin29, Section 5.2.2], the subspace
![]() $\widetilde {\Phi }$
corresponds to the span of the summands where some
$\widetilde {\Phi }$
corresponds to the span of the summands where some
![]() $i_s = 0$
. Meanwhile, modulo
$i_s = 0$
. Meanwhile, modulo
![]() $\widetilde {\Phi }$
, the subspace
$\widetilde {\Phi }$
, the subspace
![]() $\widetilde {\Psi }$
corresponds to the span of summands where some
$\widetilde {\Psi }$
corresponds to the span of summands where some
![]() $i_s = 2$
. This follows from the formulas for the projector
$i_s = 2$
. This follows from the formulas for the projector
![]() $\pi _2$
(which projects onto such summands) in [Reference Petersen, Tavakol and Yin29, Section 5.1]. Quotienting by
$\pi _2$
(which projects onto such summands) in [Reference Petersen, Tavakol and Yin29, Section 5.1]. Quotienting by
![]() $\widetilde {\Phi } + \widetilde {\Psi }$
thus leaves the term with
$\widetilde {\Phi } + \widetilde {\Psi }$
thus leaves the term with
![]() $i_1 = \ldots = i_n = 1$
. The local system
$i_1 = \ldots = i_n = 1$
. The local system
![]() $(R^1\pi _*\mathbb {Q})^{\otimes n}$
corresponds to the nth tensor power of the standard representation of
$(R^1\pi _*\mathbb {Q})^{\otimes n}$
corresponds to the nth tensor power of the standard representation of
![]() $\mathrm {Sp}_{2g}$
. It thus decomposes into a direct sum of irreducible local systems, as in [Reference Petersen, Tavakol and Yin29, Section 3.2]. As explained there, we have a natural projection
$\mathrm {Sp}_{2g}$
. It thus decomposes into a direct sum of irreducible local systems, as in [Reference Petersen, Tavakol and Yin29, Section 3.2]. As explained there, we have a natural projection
whose kernel is spanned by the image of the
![]() $\binom {n}{2}$
insertion maps
$\binom {n}{2}$
insertion maps
given by inserting the class of the symplectic form. Modulo other Künneth components, the class of the diagonal
![]() $\Delta _{i,j}$
is the class of the symplectic form in
$\Delta _{i,j}$
is the class of the symplectic form in
![]() $H^{1}(\mathcal {C}) \otimes H^1(\mathcal {C}) \subset H^2(\mathcal {C}^{\{i,j\}})$
. Summarizing, we have found
$H^{1}(\mathcal {C}) \otimes H^1(\mathcal {C}) \subset H^2(\mathcal {C}^{\{i,j\}})$
. Summarizing, we have found
and the kernel is spanned by
![]() $\widetilde {\Delta }$
. This establishes (3.1)
$\widetilde {\Delta }$
. This establishes (3.1)
(b) Now assume
![]() $n \geq k$
. If some
$n \geq k$
. If some
![]() $i_s = 2$
and
$i_s = 2$
and
![]() $i_1 + \cdots + i_n = k$
, we must have some other
$i_1 + \cdots + i_n = k$
, we must have some other
![]() $i_{s'} = 0$
. It follows that
$i_{s'} = 0$
. It follows that
![]() $\widetilde {\Psi } \subset \widetilde {\Phi }$
, and hence
$\widetilde {\Psi } \subset \widetilde {\Phi }$
, and hence
![]() $\Psi ^k_{g,n} \subset \Phi ^k_{g,n}$
. Thus, it suffices to see that the right-hand side of (a) vanishes when
$\Psi ^k_{g,n} \subset \Phi ^k_{g,n}$
. Thus, it suffices to see that the right-hand side of (a) vanishes when
![]() $n \geq k$
and
$n \geq k$
and
![]() $n> 0$
. This is immediate when
$n> 0$
. This is immediate when
![]() $n> k$
. Meanwhile, for the case
$n> k$
. Meanwhile, for the case
![]() $n =k$
, we have
$n =k$
, we have
![]() $H^0({\mathcal {M}}_g, \mathbb {V}_{\lambda }) = 0$
since
$H^0({\mathcal {M}}_g, \mathbb {V}_{\lambda }) = 0$
since
![]() $\mathbb {V}_{\lambda }$
is nontrivial.
$\mathbb {V}_{\lambda }$
is nontrivial.
We note a neat consequence of Lemma 3.1(a) in genus
![]() $2$
, which was also pointed out to us by Petersen.
$2$
, which was also pointed out to us by Petersen.
Lemma 3.2. Suppose n is odd. The STE generated by
![]() $H^k({\overline {\mathcal {M}}}_{2,n-1}), H^{k-2}({\overline {\mathcal {M}}}_{2,n-1})$
and
$H^k({\overline {\mathcal {M}}}_{2,n-1}), H^{k-2}({\overline {\mathcal {M}}}_{2,n-1})$
and
![]() $H^{k-2}({\overline {\mathcal {M}}}_{1,m})$
for
$H^{k-2}({\overline {\mathcal {M}}}_{1,m})$
for
![]() $m \leq n+2$
contains
$m \leq n+2$
contains
![]() $H^k({\overline {\mathcal {M}}}_{2,n})$
.
$H^k({\overline {\mathcal {M}}}_{2,n})$
.
Proof. The STE generated by
![]() $H^k({\overline {\mathcal {M}}}_{2,n-1}), H^{k-2}({\overline {\mathcal {M}}}_{2,n-1})$
and
$H^k({\overline {\mathcal {M}}}_{2,n-1}), H^{k-2}({\overline {\mathcal {M}}}_{2,n-1})$
and
![]() $H^{k-2}({\overline {\mathcal {M}}}_{1,m})$
for
$H^{k-2}({\overline {\mathcal {M}}}_{1,m})$
for
![]() $m \leq n+2$
contains all classes in
$m \leq n+2$
contains all classes in
![]() $H^{k}({\overline {\mathcal {M}}}_{2,n})$
that are pushed forward from the boundary, pulled back from less marked points or products of
$H^{k}({\overline {\mathcal {M}}}_{2,n})$
that are pushed forward from the boundary, pulled back from less marked points or products of
![]() $\psi $
classes with classes pulled back from less marked points. It, therefore, suffices to show that
$\psi $
classes with classes pulled back from less marked points. It, therefore, suffices to show that
![]() $W_kH^k({\mathcal {M}}_{2,n})/(\Phi ^k_{2,n} + \Psi ^k_{2,n}) = 0$
. By Lemma 3.1(a), this quotient is a sum of the pure cohomology of local systems of weight n. But on
$W_kH^k({\mathcal {M}}_{2,n})/(\Phi ^k_{2,n} + \Psi ^k_{2,n}) = 0$
. By Lemma 3.1(a), this quotient is a sum of the pure cohomology of local systems of weight n. But on
![]() ${\mathcal {M}}_2$
, the hyperelliptic involution acts on local systems of weight n by
${\mathcal {M}}_2$
, the hyperelliptic involution acts on local systems of weight n by
![]() $(-1)^n$
, so local systems of odd weight have no cohomology.
$(-1)^n$
, so local systems of odd weight have no cohomology.
Proof of Theorem 1.3.
Let
![]() $S^*$
be the STE generated by the cohomology groups listed in the statement of the theorem. By Lemma 2.1, it suffices to check that
$S^*$
be the STE generated by the cohomology groups listed in the statement of the theorem. By Lemma 2.1, it suffices to check that
![]() $S^*({\overline {\mathcal {M}}}_{g',n'})$
surjects onto
$S^*({\overline {\mathcal {M}}}_{g',n'})$
surjects onto
![]() $W_{k'}H^{k'}({\mathcal {M}}_{g',n'})/\left (\Phi ^{k'}_{g',n'} + RH^{k'}({\mathcal {M}}_{g',n'})\right )$
for all
$W_{k'}H^{k'}({\mathcal {M}}_{g',n'})/\left (\Phi ^{k'}_{g',n'} + RH^{k'}({\mathcal {M}}_{g',n'})\right )$
for all
![]() $(g', n', k')$
with
$(g', n', k')$
with
![]() $k' \leq k-2$
. By Lemma 3.1(b), the target vanishes when
$k' \leq k-2$
. By Lemma 3.1(b), the target vanishes when
![]() $n'> k'$
. By the vcd of
$n'> k'$
. By the vcd of
![]() ${\mathcal {M}}_{g',n'}$
, it also vanishes when
${\mathcal {M}}_{g',n'}$
, it also vanishes when
![]() $k'> 4g' - 4 + n'$
. Finally,
$k'> 4g' - 4 + n'$
. Finally,
![]() $H^{k'}({\mathcal {M}}_{g',n'})$
is tautological for
$H^{k'}({\mathcal {M}}_{g',n'})$
is tautological for
![]() $k' \leq \frac {2g'-2}{3}$
[Reference Wahl35].
$k' \leq \frac {2g'-2}{3}$
[Reference Wahl35].
Remark 3.3. One can prove analogues of Theorem 1.3 and Lemma 2.1 for homology. In particular, for each k, there is a finitely generated STE that contains
![]() $H_k({\overline {\mathcal {M}}}_{g,n})$
for all g and n, with explicit bounds on the generators.
$H_k({\overline {\mathcal {M}}}_{g,n})$
for all g and n, with explicit bounds on the generators.

Figure 1 The argument in the proof of Theorem 1.3 shows that
![]() $W_{17}H^{17}({\mathcal {M}}_{g,n})/(\Phi ^{17}_{g,n} + RH^{17}({\mathcal {M}}_{g,n}))$
vanishes for
$W_{17}H^{17}({\mathcal {M}}_{g,n})/(\Phi ^{17}_{g,n} + RH^{17}({\mathcal {M}}_{g,n}))$
vanishes for
![]() $(g,n)$
outside the gray shaded region. Note that this quotient does not vanish for
$(g,n)$
outside the gray shaded region. Note that this quotient does not vanish for
![]() $(g,n)$
equal to
$(g,n)$
equal to
![]() $(1,17)$
and
$(1,17)$
and
![]() $(2,14)$
, which are pictured by purple dots.
$(2,14)$
, which are pictured by purple dots.
4 The Chow–Künneth generation Property
In this section, we prove a key lemma about the cycle class map for spaces that have the following property.
Definition 4.1. Let X be a smooth algebraic stack of finite type over a field, stratified by quotient stacks. We say that X has the CKgP if for all algebraic stacks Y (of finite type, stratified by quotient stacks), the exterior product
is surjective.
For convenience, we record here several properties of the CKgP, all of which are proven in [Reference Canning and Larson5, Section 3.1].
Proposition 4.2. Let X be a smooth algebraic stack of finite type over a field, stratified by quotient stacks.
-
1. if
 $U\subset X$
is open and X has the CKgP, then U has the CKgP;
$U\subset X$
is open and X has the CKgP, then U has the CKgP; -
2. if
 $Y\rightarrow X$
is proper, surjective, representable by DM stacks, and Y has the CKgP, then X has the CKgP;
$Y\rightarrow X$
is proper, surjective, representable by DM stacks, and Y has the CKgP, then X has the CKgP; -
3. if X admits a finite stratification
 $X=\coprod _{S\in \mathcal {S}} S$
, such that each S has the CKgP, then X has the CKgP;
$X=\coprod _{S\in \mathcal {S}} S$
, such that each S has the CKgP, then X has the CKgP; -
4. if
 $V\rightarrow X$
is an affine bundle, then V has the CKgP if and only if X has the CKgP;
$V\rightarrow X$
is an affine bundle, then V has the CKgP if and only if X has the CKgP; -
5. if X has the CKgP, and
 $G\rightarrow X$
is a Grassmann bundle, then G has the CKgP;
$G\rightarrow X$
is a Grassmann bundle, then G has the CKgP; -
6. if
 $X = \operatorname {\mathrm {BGL}}_n, \operatorname {\mathrm {BSL}}_n$
or
$X = \operatorname {\mathrm {BGL}}_n, \operatorname {\mathrm {BSL}}_n$
or
 $\operatorname {\mathrm {BPGL}}_n$
, then X has the CKgP.
$\operatorname {\mathrm {BPGL}}_n$
, then X has the CKgP.
If X is smooth and proper and has the CKgP, then the cycle class map for X is an isomorphism [Reference Canning and Larson5, Lemma 3.11].
When X is smooth but not necessarily proper and has the CKgP, the cycle class map is not necessarily an isomorphism. Nevertheless, we have the following useful substitute (cf. [Reference Laterveer20, Reference Totaro33] for slightly different statements with similar proofs).
Lemma 4.3. Let X be an open substack of a smooth proper Deligne–Mumford stack
![]() $\overline {X}$
over the complex numbers. If X has the CKgP, then the cycle class map
$\overline {X}$
over the complex numbers. If X has the CKgP, then the cycle class map
is surjective. In particular, if k is odd, then
![]() $W_kH^k(X)=0$
, and if k is even, then
$W_kH^k(X)=0$
, and if k is even, then
![]() $W_k H^k(X)$
is pure Hodge–Tate.
$W_k H^k(X)$
is pure Hodge–Tate.
Proof. Set
![]() $d:=\dim \overline {X}$
and
$d:=\dim \overline {X}$
and
![]() $D:=\overline {X}\smallsetminus X$
. Let
$D:=\overline {X}\smallsetminus X$
. Let
![]() $\Delta \subset \overline {X}\times \overline {X}$
denote the diagonal. Because X has the CKgP, the exterior product map
$\Delta \subset \overline {X}\times \overline {X}$
denote the diagonal. Because X has the CKgP, the exterior product map
 $$\begin{align*}\bigoplus_{\ell=0}^{d} A^\ell(\overline{X})\otimes A^{d-\ell}(X)\rightarrow A^d(\overline{X}\times X) \end{align*}$$
$$\begin{align*}\bigoplus_{\ell=0}^{d} A^\ell(\overline{X})\otimes A^{d-\ell}(X)\rightarrow A^d(\overline{X}\times X) \end{align*}$$
is surjective. We have the excision exact sequence
It follows that we can write the class of the diagonal in
![]() $A^d(\overline {X} \times \overline {X})$
as
$A^d(\overline {X} \times \overline {X})$
as
where
![]() $\Gamma $
is supported on
$\Gamma $
is supported on
![]() $\overline {X}\times D$
and each
$\overline {X}\times D$
and each
![]() $\Delta ^\ell $
is a linear combination of cycles of the form
$\Delta ^\ell $
is a linear combination of cycles of the form
![]() $V_i^\ell \times W_i^{d-\ell }$
, where
$V_i^\ell \times W_i^{d-\ell }$
, where
![]() $V_i^{\ell }$
and
$V_i^{\ell }$
and
![]() $W_i^{d-\ell }$
are subvarieties of
$W_i^{d-\ell }$
are subvarieties of
![]() $\overline {X}$
of codimension
$\overline {X}$
of codimension
![]() $\ell $
and
$\ell $
and
![]() $d-\ell $
, respectively.
$d-\ell $
, respectively.
Let
![]() $p_1$
and
$p_1$
and
![]() $p_2$
be the projections of
$p_2$
be the projections of
![]() $\overline {X} \times \overline {X}$
to the first and second factors, respectively. Given a class
$\overline {X} \times \overline {X}$
to the first and second factors, respectively. Given a class
![]() $\Psi \in H^*(\overline {X} \times \overline {X})$
, we write
$\Psi \in H^*(\overline {X} \times \overline {X})$
, we write
![]() $\Psi _*\colon H^*(\overline {X}) \to H^*(\overline {X})$
for the associated correspondence, defined by
$\Psi _*\colon H^*(\overline {X}) \to H^*(\overline {X})$
for the associated correspondence, defined by
![]() $\Psi _*\alpha = p_{2*}(p_1^*\alpha \cdot \Psi )$
.
$\Psi _*\alpha = p_{2*}(p_1^*\alpha \cdot \Psi )$
.
Let
![]() $a\in W_k H^k(X)$
. Let
$a\in W_k H^k(X)$
. Let
![]() $\alpha $
be a lift of a in
$\alpha $
be a lift of a in
![]() $W_k H^k(\overline {X})=H^k(\overline {X})$
. Then
$W_k H^k(\overline {X})=H^k(\overline {X})$
. Then
First, we study
![]() $\Delta ^\ell _*\alpha = p_{2*}(p_1^*\alpha \cdot \Delta ^{\ell }).$
Note that
$\Delta ^\ell _*\alpha = p_{2*}(p_1^*\alpha \cdot \Delta ^{\ell }).$
Note that
![]() $p_1^*\alpha \cdot \Delta ^{\ell }$
vanishes for dimension reasons if
$p_1^*\alpha \cdot \Delta ^{\ell }$
vanishes for dimension reasons if
![]() $k+2\ell>2d$
. Furthermore, since
$k+2\ell>2d$
. Furthermore, since
![]() $p_2$
is of relative dimension d, the pushforward by
$p_2$
is of relative dimension d, the pushforward by
![]() $p_2$
of any cycle will vanish if
$p_2$
of any cycle will vanish if
![]() $k+2\ell <2d$
. Thus, the only nonzero terms occur when
$k+2\ell <2d$
. Thus, the only nonzero terms occur when
![]() $k=2d-2\ell $
. Moreover,
$k=2d-2\ell $
. Moreover,
![]() $\Delta ^{\ell }_*\alpha $
is a linear combination of the form
$\Delta ^{\ell }_*\alpha $
is a linear combination of the form
![]() $\sum c_i W_i^{d-\ell }$
, so it lies in the image of the cycle class map.
$\sum c_i W_i^{d-\ell }$
, so it lies in the image of the cycle class map.
Next, we study
![]() $\Gamma _*\alpha $
. It suffices to treat the case that
$\Gamma _*\alpha $
. It suffices to treat the case that
![]() $\Gamma $
is the class of a subvariety of
$\Gamma $
is the class of a subvariety of
![]() $\overline {X}\times \overline {X}$
contained in
$\overline {X}\times \overline {X}$
contained in
![]() $\overline {X}\times D$
, as it is a linear combination of such subvarieties. In this case, the map
$\overline {X}\times D$
, as it is a linear combination of such subvarieties. In this case, the map
![]() $p_2|_{\Gamma }\colon \Gamma \rightarrow \overline {X}$
factors through
$p_2|_{\Gamma }\colon \Gamma \rightarrow \overline {X}$
factors through
![]() $D\rightarrow \overline {X}$
. Thus,
$D\rightarrow \overline {X}$
. Thus,
![]() $\Gamma _*\alpha $
maps to zero under the restriction to
$\Gamma _*\alpha $
maps to zero under the restriction to
![]() $W_k H^k(X)$
because the correspondence map factors through the cohomology of the boundary D. Thus,
$W_k H^k(X)$
because the correspondence map factors through the cohomology of the boundary D. Thus,
![]() $\alpha |_{X}=a$
is in the image of the cycle class map.
$\alpha |_{X}=a$
is in the image of the cycle class map.
Remark 4.4. Essentially the same argument (only with
![]() $\mathbb {Q}_\ell $
-coefficients) gives a similar statement for the cycle class map to
$\mathbb {Q}_\ell $
-coefficients) gives a similar statement for the cycle class map to
![]() $\ell $
-adic étale cohomology over an arbitrary field.
$\ell $
-adic étale cohomology over an arbitrary field.
The first two authors have previously given many examples of moduli spaces
![]() ${\mathcal {M}}_{g,n}$
that have the CKgP and also satisfy
${\mathcal {M}}_{g,n}$
that have the CKgP and also satisfy
![]() $A^*({\mathcal {M}}_{g,n}) = R^*({\mathcal {M}}_{g,n})$
[Reference Canning and Larson5, Theorem 1.4]. For the inductive arguments in this paper, we need more base cases in genus
$A^*({\mathcal {M}}_{g,n}) = R^*({\mathcal {M}}_{g,n})$
[Reference Canning and Larson5, Theorem 1.4]. For the inductive arguments in this paper, we need more base cases in genus
![]() $7$
. In the next section, we prove that
$7$
. In the next section, we prove that
![]() ${\mathcal {M}}_{7,n}$
has the CKgP and
${\mathcal {M}}_{7,n}$
has the CKgP and
![]() $A^*({\mathcal {M}}_{7,n}) = R^*({\mathcal {M}}_{7,n})$
, for
$A^*({\mathcal {M}}_{7,n}) = R^*({\mathcal {M}}_{7,n})$
, for
![]() $n \leq 3$
. The table below records the previously known results from [Reference Canning and Larson5, Theorem 1.4] together with Theorem 1.10.
$n \leq 3$
. The table below records the previously known results from [Reference Canning and Larson5, Theorem 1.4] together with Theorem 1.10.
The following is a consequence of Lemma 4.3.
Proposition 4.5. For all
![]() $g\leq 7$
and
$g\leq 7$
and
![]() $n \leq c(g)$
as specified in Table 1, we have
$n \leq c(g)$
as specified in Table 1, we have
In particular, if k is odd and
![]() $n \leq c(g)$
, then
$n \leq c(g)$
, then
Table 1
![]() ${\mathcal {M}}_{g,n}$
has the CKgP and
${\mathcal {M}}_{g,n}$
has the CKgP and
![]() $A^*({\mathcal {M}}_{g,n})=R^*({\mathcal {M}}_{g,n})$
, for
$A^*({\mathcal {M}}_{g,n})=R^*({\mathcal {M}}_{g,n})$
, for
![]() $n \leq c(g)$
, by [Reference Canning and Larson5, Theorem 1.4] and Theorem 1.10.
$n \leq c(g)$
, by [Reference Canning and Larson5, Theorem 1.4] and Theorem 1.10.

Proof of Theorem 1.9, assuming Theorem 1.1.
By the hard Lefschetz theorem, it suffices to prove that
![]() $H^k({\overline {\mathcal {M}}}_{3,n})^{\mathrm {ss}}$
is a polynomial in
$H^k({\overline {\mathcal {M}}}_{3,n})^{\mathrm {ss}}$
is a polynomial in
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() ${\mathsf {S}}_{12}$
for fixed
${\mathsf {S}}_{12}$
for fixed
![]() $k\leq 17$
and
$k\leq 17$
and
![]() $n\leq 11$
. Consider the right exact sequence
$n\leq 11$
. Consider the right exact sequence
By Theorem 1.1 and [Reference Canning, Larson and Payne8, Theorems 1.1, 1.2 and Lemma 2.1], for
![]() $k'\leq 15$
,
$k'\leq 15$
,
![]() $H^{k'}({\overline {\mathcal {M}}}_{g',n'})^{\mathrm {ss}}$
is a polynomial in
$H^{k'}({\overline {\mathcal {M}}}_{g',n'})^{\mathrm {ss}}$
is a polynomial in
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() ${\mathsf {S}}_{12}$
for all
${\mathsf {S}}_{12}$
for all
![]() $g'\neq 1$
and all
$g'\neq 1$
and all
![]() $n'$
as well as for
$n'$
as well as for
![]() $g'=1$
and
$g'=1$
and
![]() $n'\leq 13$
. Since we assume
$n'\leq 13$
. Since we assume
![]() $n \leq 11$
, no
$n \leq 11$
, no
![]() ${\overline {\mathcal {M}}}_{1,n'}$
with
${\overline {\mathcal {M}}}_{1,n'}$
with
![]() $n' \geq 14$
appears as a factor in a component of the normalized boundary. It follows that,
$n' \geq 14$
appears as a factor in a component of the normalized boundary. It follows that,
![]() $H^{k-2}(\widetilde {\partial {\mathcal {M}}_{3,n}})^{\mathrm {ss}}$
is a polynomial in
$H^{k-2}(\widetilde {\partial {\mathcal {M}}_{3,n}})^{\mathrm {ss}}$
is a polynomial in
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() ${\mathsf {S}}_{12}$
. By [Reference Canning and Larson5, Theorem 1.4],
${\mathsf {S}}_{12}$
. By [Reference Canning and Larson5, Theorem 1.4],
![]() ${\mathcal {M}}_{3,n}$
has the CKgP and
${\mathcal {M}}_{3,n}$
has the CKgP and
![]() $A^*({\mathcal {M}}_{3,n}) = R^*({\mathcal {M}}_{3,n})$
for
$A^*({\mathcal {M}}_{3,n}) = R^*({\mathcal {M}}_{3,n})$
for
![]() $n \leq 11$
. Thus,
$n \leq 11$
. Thus,
![]() $W_k H^k({\mathcal {M}}_{3,n})=RH^k({\mathcal {M}}_{3,n})$
by Lemma 4.3. Hence,
$W_k H^k({\mathcal {M}}_{3,n})=RH^k({\mathcal {M}}_{3,n})$
by Lemma 4.3. Hence,
![]() $W_k H^k({\mathcal {M}}_{3,n})$
is pure Hodge–Tate, and the theorem follows.
$W_k H^k({\mathcal {M}}_{3,n})$
is pure Hodge–Tate, and the theorem follows.
5 The CKgP in genus 7 with at most three marked points
In order to prove Theorems 1.1, 1.5(3) for
![]() $k = 14$
and 1.7, we need more base cases in genus
$k = 14$
and 1.7, we need more base cases in genus
![]() $7$
. The required base cases are given by Theorem 1.10, which we now prove.
$7$
. The required base cases are given by Theorem 1.10, which we now prove.
In order to prove Theorem 1.10, we filter
![]() ${\mathcal {M}}_{7,n}$
by gonality:
${\mathcal {M}}_{7,n}$
by gonality:
Here,
![]() $\mathcal {M}^{k}_{7,n}$
is the locus parametrizing smooth curves C with n marked points that admit a map of degree at most k to
$\mathcal {M}^{k}_{7,n}$
is the locus parametrizing smooth curves C with n marked points that admit a map of degree at most k to
![]() $\mathbb {P}^1$
. Standard results from Brill–Noether theory show that the maximal gonality of a genus
$\mathbb {P}^1$
. Standard results from Brill–Noether theory show that the maximal gonality of a genus
![]() $7$
curve is
$7$
curve is
![]() $5$
. By Proposition 4.2(3), to show that
$5$
. By Proposition 4.2(3), to show that
![]() ${\mathcal {M}}_{7,n}$
has the CKgP, it suffices to show that each gonality stratum
${\mathcal {M}}_{7,n}$
has the CKgP, it suffices to show that each gonality stratum
has the CKgP. Moreover, to show that
![]() $A^*({\mathcal {M}}_{7,n})=R^*({\mathcal {M}}_{7,n})$
, it suffices to show for each k, that all classes supported on
$A^*({\mathcal {M}}_{7,n})=R^*({\mathcal {M}}_{7,n})$
, it suffices to show for each k, that all classes supported on
![]() $\mathcal {M}^k_{7,n}$
are tautological up to classes supported on
$\mathcal {M}^k_{7,n}$
are tautological up to classes supported on
![]() $\mathcal {M}^{k-1}_{7,n}$
. In other words, we must show that every class in
$\mathcal {M}^{k-1}_{7,n}$
. In other words, we must show that every class in
![]() $A^*({\mathcal {M}}_{7,n}^k \smallsetminus {\mathcal {M}}_{7,n}^{k-1})$
pushes forward to a class in
$A^*({\mathcal {M}}_{7,n}^k \smallsetminus {\mathcal {M}}_{7,n}^{k-1})$
pushes forward to a class in
![]() $A^*({\mathcal {M}}_{7,n} \smallsetminus \mathcal {M}^{k-1}_ {7,n})$
that is the restriction of a tautological class on
$A^*({\mathcal {M}}_{7,n} \smallsetminus \mathcal {M}^{k-1}_ {7,n})$
that is the restriction of a tautological class on
![]() ${\mathcal {M}}_{7,n}$
.
${\mathcal {M}}_{7,n}$
.
5.1 Hyperelliptic and trigonal loci
By [Reference Canning and Larson5, Lemma 9.9], if
![]() $n\leq 14$
, then
$n\leq 14$
, then
![]() $\mathcal {M}^3_{7,n}$
has the CKgP and all classes in
$\mathcal {M}^3_{7,n}$
has the CKgP and all classes in
![]() $A^*({\mathcal {M}}_{7,n})$
supported on
$A^*({\mathcal {M}}_{7,n})$
supported on
![]() $\mathcal {M}^3_{7,n}$
are tautological. Note that this includes the hyperelliptic locus.
$\mathcal {M}^3_{7,n}$
are tautological. Note that this includes the hyperelliptic locus.
5.2 The tetragonal locus
To study the tetragonal locus
![]() $\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
, we will use the Hurwitz stack
$\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
, we will use the Hurwitz stack
![]() $\mathcal {H}_{4,g,n}$
parametrizing degree
$\mathcal {H}_{4,g,n}$
parametrizing degree
![]() $4$
covers
$4$
covers
![]() $f\colon C\rightarrow \mathbb {P}^1$
, where C is a smooth curve of genus g with n marked points. There is a forgetful morphism
$f\colon C\rightarrow \mathbb {P}^1$
, where C is a smooth curve of genus g with n marked points. There is a forgetful morphism
Restricting to curves of gonality exactly
![]() $4$
, we obtain a proper morphism
$4$
, we obtain a proper morphism
with image
![]() ${\mathcal {M}}_{g,n}^4 \smallsetminus {\mathcal {M}}_{g,n}^3$
. To show that
${\mathcal {M}}_{g,n}^4 \smallsetminus {\mathcal {M}}_{g,n}^3$
. To show that
![]() $\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
has the CKgP, it suffices to show that
$\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
has the CKgP, it suffices to show that
![]() $\mathcal {H}_{4,7,n}^\Diamond $
has the CKgP by Proposition 4.2(2). We will do so by further stratifying
$\mathcal {H}_{4,7,n}^\Diamond $
has the CKgP by Proposition 4.2(2). We will do so by further stratifying
![]() $\mathcal {H}_{4,7,n}^\Diamond $
.
$\mathcal {H}_{4,7,n}^\Diamond $
.
In [Reference Canning and Larson6, Section 4.4], the first two authors studied a stratification of
![]() $\mathcal {H}_{4,7} := \mathcal {H}_{4,7,0}$
with no markings. Here, we carry out a similar analysis with marked points. The Casnati–Ekedahl structure theorem [Reference Casnati and Ekedahl9] associates to a point in
$\mathcal {H}_{4,7} := \mathcal {H}_{4,7,0}$
with no markings. Here, we carry out a similar analysis with marked points. The Casnati–Ekedahl structure theorem [Reference Casnati and Ekedahl9] associates to a point in
![]() $\mathcal {H}_{4,g}$
a rank
$\mathcal {H}_{4,g}$
a rank
![]() $3$
vector bundle E and a rank
$3$
vector bundle E and a rank
![]() $2$
vector bundle F on
$2$
vector bundle F on
![]() $\mathbb {P}^1$
, both of degree
$\mathbb {P}^1$
, both of degree
![]() $g+3$
, equipped with a canonical isomorphism
$g+3$
, equipped with a canonical isomorphism
![]() $\det E \cong \det F$
[Reference Canning and Larson7, Section 3]. Let
$\det E \cong \det F$
[Reference Canning and Larson7, Section 3]. Let
![]() $\mathcal {B}$
be the moduli stack of pairs of vector bundles
$\mathcal {B}$
be the moduli stack of pairs of vector bundles
![]() $(E, F)$
on
$(E, F)$
on
![]() $\mathbb {P}^1$
of degree
$\mathbb {P}^1$
of degree
![]() $g+3$
, together with an isomorphism of their determinants as in [Reference Canning and Larson7, Definition 5.2]. Let
$g+3$
, together with an isomorphism of their determinants as in [Reference Canning and Larson7, Definition 5.2]. Let
![]() $\pi \colon \mathcal {P} \to \mathcal {B}$
be the universal
$\pi \colon \mathcal {P} \to \mathcal {B}$
be the universal
![]() $\mathbb {P}^1$
-fibration, and let
$\mathbb {P}^1$
-fibration, and let
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {F}$
be the universal bundles on
$\mathcal {F}$
be the universal bundles on
![]() $\mathcal {P}$
. There is a natural morphism
$\mathcal {P}$
. There is a natural morphism
![]() $\mathcal {H}_{4,g} \to \mathcal {B}$
that sends a degree
$\mathcal {H}_{4,g} \to \mathcal {B}$
that sends a degree
![]() $4$
cover to its associated pair of vector bundles. Moreover, the Casnati–Ekedahl construction gives an embedding of the universal curve
$4$
cover to its associated pair of vector bundles. Moreover, the Casnati–Ekedahl construction gives an embedding of the universal curve
![]() $\mathcal {C}$
over
$\mathcal {C}$
over
![]() $\mathcal {H}_{4,g}$
into
$\mathcal {H}_{4,g}$
into
![]() $\mathbb {P} \mathcal {E}^{\vee }$
.
$\mathbb {P} \mathcal {E}^{\vee }$
.
Consider the natural commutative diagram

where
![]() $\mathcal {C}_n$
is the universal curve over
$\mathcal {C}_n$
is the universal curve over
![]() $\mathcal {H}_{4,g,n}$
. For each i, the map
$\mathcal {H}_{4,g,n}$
. For each i, the map
![]() $a \circ b \circ \sigma _i$
sends a pointed curve to the image of the ith marking under the Casnati–Ekedahl embedding. Taking the product of these maps for
$a \circ b \circ \sigma _i$
sends a pointed curve to the image of the ith marking under the Casnati–Ekedahl embedding. Taking the product of these maps for
![]() $i = 1, \ldots , n$
, we obtain a commutative diagram
$i = 1, \ldots , n$
, we obtain a commutative diagram

Lemma 5.1 (Lemma 10.5 of [Reference Canning and Larson5]).
Suppose
![]() $x \in A^*(\mathcal {H}_{4,g,n}^\Diamond )$
lies in the image of the map
$x \in A^*(\mathcal {H}_{4,g,n}^\Diamond )$
lies in the image of the map
![]() $A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(\mathcal {H}_{4,g,n}^\Diamond )$
. Then
$A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(\mathcal {H}_{4,g,n}^\Diamond )$
. Then
![]() $\beta ^{\prime }_{n*}x$
is tautological on
$\beta ^{\prime }_{n*}x$
is tautological on
![]() ${\mathcal {M}}_{g,n} \smallsetminus {\mathcal {M}}_{g,n}^3$
.
${\mathcal {M}}_{g,n} \smallsetminus {\mathcal {M}}_{g,n}^3$
.
The splitting types of the Casnati–Ekedahl bundles E and F induce a stratification on
![]() $\mathcal {H}_{4,7}$
. We write
$\mathcal {H}_{4,7}$
. We write
![]() $E = (e_1, e_2, e_3)$
and
$E = (e_1, e_2, e_3)$
and
![]() $F = (f_1, f_2)$
to indicate that the bundles have splitting types
$F = (f_1, f_2)$
to indicate that the bundles have splitting types
We will consider a stratification into three pieces
The three strata correspond to unions of splitting types of E and F. The possible splitting types are recorded in [Reference Canning and Larson6, Section 4.4]. The locus
![]() $Z_n$
is the set of covers with maximally unbalanced splitting types, and parametrizes hyperelliptic curves [Reference Canning and Larson6, Equation 4.5]. Its image in
$Z_n$
is the set of covers with maximally unbalanced splitting types, and parametrizes hyperelliptic curves [Reference Canning and Larson6, Equation 4.5]. Its image in
![]() ${\mathcal {M}}_{7,n}$
is contained in
${\mathcal {M}}_{7,n}$
is contained in
![]() ${\mathcal {M}}_{7,n}^3$
, which has the CKgP when
${\mathcal {M}}_{7,n}^3$
, which has the CKgP when
![]() $n\leq 14$
, as noted above. We will show that
$n\leq 14$
, as noted above. We will show that
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
have the CKgP and that
$Y_n$
have the CKgP and that
![]() $A^*((\mathbb {P} \mathcal {E}^{\vee })^n)$
surjects onto the Chow ring of their union, which is
$A^*((\mathbb {P} \mathcal {E}^{\vee })^n)$
surjects onto the Chow ring of their union, which is
![]() $\mathcal {H}_{4,7,n}^\Diamond $
. We start with
$\mathcal {H}_{4,7,n}^\Diamond $
. We start with
![]() $X_n$
.
$X_n$
.
Let
![]() $X_n\subset \mathcal {H}_{4,7,n}$
denote the locus of covers with splitting types
$X_n\subset \mathcal {H}_{4,7,n}$
denote the locus of covers with splitting types
![]() $E = (3, 3, 4)$
and
$E = (3, 3, 4)$
and
![]() $F = (5,5)$
, or
$F = (5,5)$
, or
![]() $E = (3, 3, 4)$
and
$E = (3, 3, 4)$
and
![]() $F = (4, 6)$
.
$F = (4, 6)$
.
Lemma 5.2. If
![]() $n \leq 3$
, then
$n \leq 3$
, then
![]() $X_n$
has the CKgP and
$X_n$
has the CKgP and
![]() $A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(X_n)$
is surjective.
$A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(X_n)$
is surjective.
Proof. Taking
![]() $f =4$
in [Reference Canning and Larson5, Definition 10.8], we have
$f =4$
in [Reference Canning and Larson5, Definition 10.8], we have
![]() $X_n = \mathcal {H}_{4,7,n}^4$
. The result then follows from [Reference Canning and Larson5, Lemmas 10.11 and 10.12] with
$X_n = \mathcal {H}_{4,7,n}^4$
. The result then follows from [Reference Canning and Larson5, Lemmas 10.11 and 10.12] with
![]() $g = 7$
and
$g = 7$
and
![]() $f = f_1 = 4$
.
$f = f_1 = 4$
.
Now let
![]() $Y_n\subset \mathcal {H}_{4,7,n}$
be the union
$Y_n\subset \mathcal {H}_{4,7,n}$
be the union
where
![]() $\Sigma _{2,n}$
parametrizes covers with splitting types
$\Sigma _{2,n}$
parametrizes covers with splitting types
![]() $E = (2, 4, 4)$
and
$E = (2, 4, 4)$
and
![]() $F = (4,6)$
, and
$F = (4,6)$
, and
![]() $\Sigma _{3,n}$
parametrizes covers with splitting types
$\Sigma _{3,n}$
parametrizes covers with splitting types
![]() $E = (2, 3, 5)$
and
$E = (2, 3, 5)$
and
![]() $F = (4,6)$
.
$F = (4,6)$
.
Recall that
![]() $\pi \colon \mathcal {P} \rightarrow \mathcal {B}$
is the structure map for the
$\pi \colon \mathcal {P} \rightarrow \mathcal {B}$
is the structure map for the
![]() $\mathbb {P}^1$
bundle
$\mathbb {P}^1$
bundle
![]() $\mathcal {P}$
. Let
$\mathcal {P}$
. Let
![]() $\gamma \colon \mathbb {P} \mathcal {E}^\vee \to \mathcal {P}$
denote the structure map and
$\gamma \colon \mathbb {P} \mathcal {E}^\vee \to \mathcal {P}$
denote the structure map and
![]() $\eta _i\colon (\mathbb {P} \mathcal {E}^\vee )^n \to \mathbb {P} \mathcal {E}^\vee $
denote the ith projection. Define
$\eta _i\colon (\mathbb {P} \mathcal {E}^\vee )^n \to \mathbb {P} \mathcal {E}^\vee $
denote the ith projection. Define
Then
![]() $z_i$
and
$z_i$
and
![]() $\zeta _i$
generate
$\zeta _i$
generate
![]() $A^*((\mathbb {P} \mathcal {E}^\vee )^n)$
as an algebra over
$A^*((\mathbb {P} \mathcal {E}^\vee )^n)$
as an algebra over
![]() $A^*(\mathcal {B})$
. Write
$A^*(\mathcal {B})$
. Write
![]() $\Sigma _{\ell } := \Sigma _{\ell , 0}$
.
$\Sigma _{\ell } := \Sigma _{\ell , 0}$
.
Lemma 5.3. For
![]() $\ell = 2,3$
and
$\ell = 2,3$
and
![]() $n \leq 3$
, there is a surjection
$n \leq 3$
, there is a surjection
induced by
![]() $\Sigma _{\ell ,n}\rightarrow \Sigma _\ell $
and restriction from
$\Sigma _{\ell ,n}\rightarrow \Sigma _\ell $
and restriction from
![]() $(\mathbb {P} \mathcal {E}^{\vee })^n$
. Moreover,
$(\mathbb {P} \mathcal {E}^{\vee })^n$
. Moreover,
![]() $\Sigma _{\ell ,n}$
has the CKgP.
$\Sigma _{\ell ,n}$
has the CKgP.
Proof. Let
![]() $\vec {e}$
and
$\vec {e}$
and
![]() $\vec {f}$
be the splitting types associated to
$\vec {f}$
be the splitting types associated to
![]() $\Sigma _{\ell }$
, and let
$\Sigma _{\ell }$
, and let
![]() $\mathcal {B}_{\vec {e}, \vec {f}} \subset \mathcal {B}$
be the locally closed substack that parametrizes pairs of bundles
$\mathcal {B}_{\vec {e}, \vec {f}} \subset \mathcal {B}$
be the locally closed substack that parametrizes pairs of bundles
![]() $(E, F)$
with locally constant splitting types
$(E, F)$
with locally constant splitting types
![]() $\vec {e}$
and
$\vec {e}$
and
![]() $\vec {f}$
. We write
$\vec {f}$
. We write
![]() $\mathcal {O}(\vec {e}) := \mathcal {O}(e_1) \oplus \cdots \oplus \mathcal {O}(e_k)$
. By construction,
$\mathcal {O}(\vec {e}) := \mathcal {O}(e_1) \oplus \cdots \oplus \mathcal {O}(e_k)$
. By construction,
![]() $\Sigma _{\ell ,n}$
is the preimage of
$\Sigma _{\ell ,n}$
is the preimage of
![]() $\mathcal {B}_{\vec {e}, \vec {f}}$
along
$\mathcal {B}_{\vec {e}, \vec {f}}$
along
![]() $\mathcal {H}_{4,7,n} \to \mathcal {B}$
. We, therefore, study the base change of (5.2) along
$\mathcal {H}_{4,7,n} \to \mathcal {B}$
. We, therefore, study the base change of (5.2) along
![]() $\mathcal {B}_{\vec {e}, \vec {f}} \to \mathcal {B}$
:
$\mathcal {B}_{\vec {e}, \vec {f}} \to \mathcal {B}$
:

We now recall the description of
![]() $\Sigma _\ell $
as an open substack of a vector bundle on
$\Sigma _\ell $
as an open substack of a vector bundle on
![]() $\mathcal {B}_{\vec {e}, \vec {f}}$
, as in [Reference Canning and Larson6, Lemma 3.10]. Let
$\mathcal {B}_{\vec {e}, \vec {f}}$
, as in [Reference Canning and Larson6, Lemma 3.10]. Let
be the open subset of equations that define a smooth curve, as in [Reference Canning and Larson6, Lemma 3.10]. Then
The stack
![]() $\mathcal {B}_{\vec {e}, \vec {f}}$
is the part obtained by forgetting U:
$\mathcal {B}_{\vec {e}, \vec {f}}$
is the part obtained by forgetting U:
As explained in [Reference Canning and Larson6, Equation 3.1], there is a product of stacks
![]() $\operatorname {\mathrm {BGL}}_n$
which is an affine bundle over
$\operatorname {\mathrm {BGL}}_n$
which is an affine bundle over
![]() $\mathrm {B}\!\operatorname {\mathrm {Aut}}(\mathcal {O}(\vec {e}))$
. As such,
$\mathrm {B}\!\operatorname {\mathrm {Aut}}(\mathcal {O}(\vec {e}))$
. As such,
![]() $\mathcal {B}_{\vec {e}, \vec {f}}$
has the CKgP by Proposition 4.2(4) and (5). It follows that
$\mathcal {B}_{\vec {e}, \vec {f}}$
has the CKgP by Proposition 4.2(4) and (5). It follows that
![]() $\Sigma _{\ell }$
also has the CKgP by Proposition 4.2(1) and (4).
$\Sigma _{\ell }$
also has the CKgP by Proposition 4.2(1) and (4).
Let us define the rank
![]() $2$
vector bundle
$2$
vector bundle
![]() $\mathcal {W} := \gamma ^*\mathcal {F}^\vee \otimes \mathcal {O}_{\mathbb {P} \mathcal {E}^\vee }(2)$
on
$\mathcal {W} := \gamma ^*\mathcal {F}^\vee \otimes \mathcal {O}_{\mathbb {P} \mathcal {E}^\vee }(2)$
on
![]() $\mathbb {P} \mathcal {E}^\vee $
. Write
$\mathbb {P} \mathcal {E}^\vee $
. Write
![]() $\mathcal {W}_{\vec {e},\vec {f}}$
for the restriction of
$\mathcal {W}_{\vec {e},\vec {f}}$
for the restriction of
![]() $\mathcal {W}$
to
$\mathcal {W}$
to
![]() $\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}}$
. The discussion above says that
$\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}}$
. The discussion above says that
![]() $\Sigma _{\ell }$
is an open substack of the vector bundle
$\Sigma _{\ell }$
is an open substack of the vector bundle
![]() $(\pi \circ \gamma )_*\mathcal {W}_{\vec {e},\vec {f}}$
on
$(\pi \circ \gamma )_*\mathcal {W}_{\vec {e},\vec {f}}$
on
![]() $\mathcal {B}_{\vec {e},\vec {f}}$
.
$\mathcal {B}_{\vec {e},\vec {f}}$
.
Next, we give a similar description with marked points. Consider the evaluation map
Pulling back to the fiber product
![]() $(\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
, we obtain
$(\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
, we obtain
 $$ \begin{align} \eta_j^*(\pi\circ\gamma)^*(\pi\circ\gamma)_*\mathcal{W}_{\vec{e},\vec{f}}\rightarrow \bigoplus_{i=1}^n\eta_i^*\mathcal{W}_{\vec{e},\vec{f}}. \end{align} $$
$$ \begin{align} \eta_j^*(\pi\circ\gamma)^*(\pi\circ\gamma)_*\mathcal{W}_{\vec{e},\vec{f}}\rightarrow \bigoplus_{i=1}^n\eta_i^*\mathcal{W}_{\vec{e},\vec{f}}. \end{align} $$
Note that
![]() $\eta _j^*(\pi \circ \gamma )^*(\pi \circ \gamma )_*\mathcal {W}_{\vec {e},\vec {f}}$
is independent of j. The kernel
$\eta _j^*(\pi \circ \gamma )^*(\pi \circ \gamma )_*\mathcal {W}_{\vec {e},\vec {f}}$
is independent of j. The kernel
![]() $\mathcal {Y}$
of (5.4) parametrizes tuples of n points on
$\mathcal {Y}$
of (5.4) parametrizes tuples of n points on
![]() $\mathbb {P} \mathcal {O}(\vec {e})^\vee $
together with a section of
$\mathbb {P} \mathcal {O}(\vec {e})^\vee $
together with a section of
that vanishes on the points. There is, therefore, a natural map
![]() $\Sigma _{\ell ,n} \hookrightarrow \mathcal {Y}$
defined by sending a pointed curve to the images of the points on
$\Sigma _{\ell ,n} \hookrightarrow \mathcal {Y}$
defined by sending a pointed curve to the images of the points on
![]() $\mathbb {P} \mathcal {O}(\vec {e})^\vee $
and the defining section of the curve. The kernel
$\mathbb {P} \mathcal {O}(\vec {e})^\vee $
and the defining section of the curve. The kernel
![]() $\mathcal {Y}$
is not locally free. Nevertheless, its restriction to the open substack
$\mathcal {Y}$
is not locally free. Nevertheless, its restriction to the open substack
![]() $U_n \subset (\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
where (5.4) is surjective is locally free.
$U_n \subset (\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
where (5.4) is surjective is locally free.
We claim that the map
![]() $\Sigma _{\ell ,n} \to \mathcal {Y}$
factors through
$\Sigma _{\ell ,n} \to \mathcal {Y}$
factors through
![]() $\mathcal {Y}|_{U_n}$
. To see this, suppose
$\mathcal {Y}|_{U_n}$
. To see this, suppose
![]() $C \subset \mathbb {P} \mathcal {O}(\vec {e})^\vee $
is the vanishing of a section of
$C \subset \mathbb {P} \mathcal {O}(\vec {e})^\vee $
is the vanishing of a section of
![]() $\gamma ^* \mathcal {O}(\vec {f})^\vee \otimes \mathcal {O}_{\mathbb {P} \mathcal {O}(\vec {e})^\vee }(2)$
and C is smooth and irreducible. By [Reference Canning and Larson5, Lemma 10.6], if
$\gamma ^* \mathcal {O}(\vec {f})^\vee \otimes \mathcal {O}_{\mathbb {P} \mathcal {O}(\vec {e})^\vee }(2)$
and C is smooth and irreducible. By [Reference Canning and Larson5, Lemma 10.6], if
![]() $n\leq 3$
, the evaluation map (5.4) is surjective at any tuple of n distinct points on C. It follows that the image of the composition
$n\leq 3$
, the evaluation map (5.4) is surjective at any tuple of n distinct points on C. It follows that the image of the composition
![]() $\Sigma _{\ell ,n} \rightarrow \mathcal {Y} \rightarrow (\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
is contained in
$\Sigma _{\ell ,n} \rightarrow \mathcal {Y} \rightarrow (\mathbb {P} \mathcal {E}^\vee |_{\mathcal {B}_{\vec {e},\vec {f}}})^n$
is contained in
![]() $U_n$
. Hence,
$U_n$
. Hence,
![]() $\Sigma _{\ell ,n} \hookrightarrow \mathcal {Y}|_{U_n}$
.
$\Sigma _{\ell ,n} \hookrightarrow \mathcal {Y}|_{U_n}$
.
In summary, we have a sequence of maps
each of which is an open inclusion, vector bundle or product of projective bundles. Since
![]() $\mathcal {B}_{\vec {e},\vec {f}}$
has the CKgP, it follows that
$\mathcal {B}_{\vec {e},\vec {f}}$
has the CKgP, it follows that
![]() $\Sigma _{\ell ,n}$
also has the CKgP by Proposition 4.2(1), (4) and (5). Moreover, we see that
$\Sigma _{\ell ,n}$
also has the CKgP by Proposition 4.2(1), (4) and (5). Moreover, we see that
is surjective. Finally, note that
![]() $\Sigma _{\ell ,n} \to \mathcal {B}_{\vec {e},\vec {f}}$
factors through
$\Sigma _{\ell ,n} \to \mathcal {B}_{\vec {e},\vec {f}}$
factors through
![]() $\Sigma _\ell $
, so
$\Sigma _\ell $
, so
![]() $A^*(\mathcal {B}_{\vec {e},\vec {f}}) \to A^*(\Sigma _{\ell ,n})$
factors through
$A^*(\mathcal {B}_{\vec {e},\vec {f}}) \to A^*(\Sigma _{\ell ,n})$
factors through
![]() $A^*(\Sigma _{\ell })$
. This proves the claim.
$A^*(\Sigma _{\ell })$
. This proves the claim.
Corollary 5.4. For
![]() $n \leq 3$
,
$n \leq 3$
,
![]() $\mathcal {H}_{4,7,n}^\Diamond $
has the CKgP. Hence,
$\mathcal {H}_{4,7,n}^\Diamond $
has the CKgP. Hence,
![]() $\mathcal {M}^4_{7,n}$
has the CKgP.
$\mathcal {M}^4_{7,n}$
has the CKgP.
Proof. We have
![]() $\mathcal {H}_{4,7,n}^\Diamond = X_n \sqcup Y_n$
. By Lemmas 5.2 and 5.3, each of these pieces has the CKgP. Note that
$\mathcal {H}_{4,7,n}^\Diamond = X_n \sqcup Y_n$
. By Lemmas 5.2 and 5.3, each of these pieces has the CKgP. Note that
![]() $\mathcal {H}^{\Diamond }_{4,7,n}$
maps properly onto
$\mathcal {H}^{\Diamond }_{4,7,n}$
maps properly onto
![]() $\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
, and
$\mathcal {M}^4_{7,n}\smallsetminus \mathcal {M}^3_{7,n}$
, and
![]() ${\mathcal {M}}_{7,n}^3$
has the CKgP. Thus, the result follows by Proposition 4.2(2)–(3).
${\mathcal {M}}_{7,n}^3$
has the CKgP. Thus, the result follows by Proposition 4.2(2)–(3).
The next step is to show that all classes in
![]() $A^*(\Sigma _{\ell ,n})$
are restrictions from
$A^*(\Sigma _{\ell ,n})$
are restrictions from
![]() $(\mathbb {P} \mathcal {E}^{\vee })^n$
.
$(\mathbb {P} \mathcal {E}^{\vee })^n$
.
Lemma 5.5. For
![]() $\ell = 2,3$
and
$\ell = 2,3$
and
![]() $n \leq 3$
, the restriction
$n \leq 3$
, the restriction
![]() $A^*((\mathbb {P} \mathcal {E}^{\vee })^n) \to A^*(\Sigma _{\ell ,n})$
is surjective.
$A^*((\mathbb {P} \mathcal {E}^{\vee })^n) \to A^*(\Sigma _{\ell ,n})$
is surjective.
Proof. Consider the following diagram:

The map
![]() $A^*(\mathcal {B}) \to A^*(\Sigma _{\ell })$
is surjective by [Reference Canning and Larson6, Lemma 4.2] for
$A^*(\mathcal {B}) \to A^*(\Sigma _{\ell })$
is surjective by [Reference Canning and Larson6, Lemma 4.2] for
![]() $\ell =2$
, and by [Reference Canning and Larson6, Lemma 4.3(1)] for
$\ell =2$
, and by [Reference Canning and Larson6, Lemma 4.3(1)] for
![]() $\ell = 3$
. Therefore, the bottom horizontal arrow is surjective. By Lemma 5.3, the right vertical arrow is also surjective. Hence, the top horizontal arrow is surjective.
$\ell = 3$
. Therefore, the bottom horizontal arrow is surjective. By Lemma 5.3, the right vertical arrow is also surjective. Hence, the top horizontal arrow is surjective.
Lemma 5.6. For
![]() $n \leq 3$
, the pullback map
$n \leq 3$
, the pullback map
![]() $A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(\mathcal {H}_{4,7,n}^\Diamond )$
is surjective.
$A^*((\mathbb {P} \mathcal {E}^\vee )^n) \to A^*(\mathcal {H}_{4,7,n}^\Diamond )$
is surjective.
Proof. First, we fix some notation. Let
denote the natural closed inclusion maps. Let
![]() $\phi \colon \mathcal {H}_{4,7,n}^\Diamond \to (\mathbb {P} \mathcal {E}^\vee )^n$
be the map from the top left to top right in diagram (5.2). We let
$\phi \colon \mathcal {H}_{4,7,n}^\Diamond \to (\mathbb {P} \mathcal {E}^\vee )^n$
be the map from the top left to top right in diagram (5.2). We let
![]() $\phi ':X_n\rightarrow (\mathbb {P} \mathcal {E}^{\vee })^n$
be the composite of the open inclusion
$\phi ':X_n\rightarrow (\mathbb {P} \mathcal {E}^{\vee })^n$
be the composite of the open inclusion
![]() $X_n \hookrightarrow \mathcal {H}_{4,7,n}^{\Diamond }$
and
$X_n \hookrightarrow \mathcal {H}_{4,7,n}^{\Diamond }$
and
![]() $\phi $
. Let
$\phi $
. Let
![]() $\psi :=\phi \circ \iota $
, and let
$\psi :=\phi \circ \iota $
, and let
![]() $\psi '$
be the composite of the open inclusion
$\psi '$
be the composite of the open inclusion
![]() $\Sigma _{2,n}\hookrightarrow Y_n$
and
$\Sigma _{2,n}\hookrightarrow Y_n$
and
![]() $\psi $
.
$\psi $
.
Consider the following commutative diagram, where the bottom row is exact

By Lemma 5.2,
![]() $\phi ^{\prime }*$
is surjective. It thus suffices to show that the image of
$\phi ^{\prime }*$
is surjective. It thus suffices to show that the image of
![]() $\iota _*$
is contained in the image of
$\iota _*$
is contained in the image of
![]() $\phi ^*$
. To do so, we consider another commutative diagram where the bottom row is exact
$\phi ^*$
. To do so, we consider another commutative diagram where the bottom row is exact

By Lemma 5.5,
![]() $\psi ^{\prime }*$
is surjective. Moreover, by the projection formula and Lemma 5.5, the image of
$\psi ^{\prime }*$
is surjective. Moreover, by the projection formula and Lemma 5.5, the image of
![]() $\jmath $
is generated as an
$\jmath $
is generated as an
![]() $A^*((\mathbb {P} \mathcal {E}^{\vee })^n)$
module by the fundamental class
$A^*((\mathbb {P} \mathcal {E}^{\vee })^n)$
module by the fundamental class
![]() $[\Sigma _{3,n}]\in A^*(Y_n)$
. Therefore, any class
$[\Sigma _{3,n}]\in A^*(Y_n)$
. Therefore, any class
![]() $\alpha \in A^*(Y_n)$
can be written as
$\alpha \in A^*(Y_n)$
can be written as
where
![]() $\alpha _i\in A^*((\mathbb {P} \mathcal {E}^\vee )^n)$
. By the projection formula,
$\alpha _i\in A^*((\mathbb {P} \mathcal {E}^\vee )^n)$
. By the projection formula,
where now the fundamental class
![]() $[\Sigma _{3,n}]$
is a class on
$[\Sigma _{3,n}]$
is a class on
![]() $\mathcal {H}^{\Diamond }_{4,7,n}$
. It thus suffices to show that the classes
$\mathcal {H}^{\Diamond }_{4,7,n}$
. It thus suffices to show that the classes
![]() $[Y_n]$
and
$[Y_n]$
and
![]() $[\Sigma _{3,n}]$
are in the image of
$[\Sigma _{3,n}]$
are in the image of
![]() $\phi ^*$
.
$\phi ^*$
.
By [Reference Canning and Larson6, Lemma 4.8],
![]() $[\overline {\Sigma _{\ell }}]$
is in the image of
$[\overline {\Sigma _{\ell }}]$
is in the image of
![]() $A^*(\mathcal {B}) \to A^*(\mathcal {H}_{4,7}^\Diamond )$
. Because
$A^*(\mathcal {B}) \to A^*(\mathcal {H}_{4,7}^\Diamond )$
. Because
![]() $[\Sigma _{3,n}]$
is the pullback of
$[\Sigma _{3,n}]$
is the pullback of
![]() $[\Sigma _3]$
along
$[\Sigma _3]$
along
![]() $A^*(\mathcal {H}_{4,7}^{\Diamond }) \to A^*(\mathcal {H}_{4,7,n}^{\Diamond })$
and
$A^*(\mathcal {H}_{4,7}^{\Diamond }) \to A^*(\mathcal {H}_{4,7,n}^{\Diamond })$
and
![]() $[Y_n]$
is the pullback of
$[Y_n]$
is the pullback of
![]() $[\overline {\Sigma _{2}}]$
, both
$[\overline {\Sigma _{2}}]$
, both
![]() $[\Sigma _{3,n}]$
and
$[\Sigma _{3,n}]$
and
![]() $[Y_n]$
are in the image of
$[Y_n]$
are in the image of
![]() $A^*(\mathcal {B})\to A^*(\mathcal {H}_{4,7,n}^{\Diamond })$
. Hence, they are in the image of
$A^*(\mathcal {B})\to A^*(\mathcal {H}_{4,7,n}^{\Diamond })$
. Hence, they are in the image of
![]() $\phi ^*$
.
$\phi ^*$
.
Recall that proper, surjective maps induce surjective maps on rational Chow groups. Since the map
![]() $\beta _n'\colon \mathcal {H}_{4,7,n}^\Diamond \to {\mathcal {M}}_{7,n} \smallsetminus {\mathcal {M}}_{7,n}^3$
is proper with image
$\beta _n'\colon \mathcal {H}_{4,7,n}^\Diamond \to {\mathcal {M}}_{7,n} \smallsetminus {\mathcal {M}}_{7,n}^3$
is proper with image
![]() ${\mathcal {M}}_{7,n}^4 \smallsetminus {\mathcal {M}}_{7,n}^3$
, every class supported on the tetragonal locus is the pushforward of a class from
${\mathcal {M}}_{7,n}^4 \smallsetminus {\mathcal {M}}_{7,n}^3$
, every class supported on the tetragonal locus is the pushforward of a class from
![]() $\mathcal {H}_{4,7,n}^\Diamond $
. Combining Lemmas 5.1 and 5.6, therefore, proves the following.
$\mathcal {H}_{4,7,n}^\Diamond $
. Combining Lemmas 5.1 and 5.6, therefore, proves the following.
Lemma 5.7. If
![]() $n \leq 3$
, then all classes supported on
$n \leq 3$
, then all classes supported on
![]() ${\mathcal {M}}_{7,n}^4 \smallsetminus {\mathcal {M}}_{7,n}^3$
are tautological.
${\mathcal {M}}_{7,n}^4 \smallsetminus {\mathcal {M}}_{7,n}^3$
are tautological.
5.3 The pentagonal locus
It remains to study the locus
![]() ${\mathcal {M}}_{7,n}^\circ = {\mathcal {M}}_{7,n} \smallsetminus {\mathcal {M}}_{7,n}^4$
of curves of gonality exactly
${\mathcal {M}}_{7,n}^\circ = {\mathcal {M}}_{7,n} \smallsetminus {\mathcal {M}}_{7,n}^4$
of curves of gonality exactly
![]() $5$
. Mukai showed that every curve in
$5$
. Mukai showed that every curve in
![]() ${\mathcal {M}}_{7}^{\circ }$
is realized as a linear section of the orthogonal Grassmannian in its spinor embedding
${\mathcal {M}}_{7}^{\circ }$
is realized as a linear section of the orthogonal Grassmannian in its spinor embedding
![]() $\operatorname {\mathrm {OG}}(5,10) \hookrightarrow \mathbb {P}^{15}$
[Reference Mukai21]. To take advantage of this construction, we first develop a few lemmas about the orthogonal Grassmannian.
$\operatorname {\mathrm {OG}}(5,10) \hookrightarrow \mathbb {P}^{15}$
[Reference Mukai21]. To take advantage of this construction, we first develop a few lemmas about the orthogonal Grassmannian.
5.3.1 The orthogonal Grassmannian
Let
![]() $\mathcal {V}$
be the universal rank
$\mathcal {V}$
be the universal rank
![]() $10$
bundle on
$10$
bundle on
![]() $\operatorname {\mathrm {BSO}}_{10}$
. The universal orthogonal Grassmannian is the quotient stack
$\operatorname {\mathrm {BSO}}_{10}$
. The universal orthogonal Grassmannian is the quotient stack
![]() $[\operatorname {\mathrm {OG}}(5, 10)/\mathrm {SO}_{10}]$
, which we think of as the orthogonal Grassmann bundle with structure map
$[\operatorname {\mathrm {OG}}(5, 10)/\mathrm {SO}_{10}]$
, which we think of as the orthogonal Grassmann bundle with structure map
![]() $\pi \colon \operatorname {\mathrm {OG}}(5,\mathcal {V}) \to \operatorname {\mathrm {BSO}}_{10}$
. By construction, the pullback of
$\pi \colon \operatorname {\mathrm {OG}}(5,\mathcal {V}) \to \operatorname {\mathrm {BSO}}_{10}$
. By construction, the pullback of
![]() $\mathcal {V}$
along
$\mathcal {V}$
along
![]() $\pi $
satisfies
$\pi $
satisfies
![]() $\pi ^* \mathcal {V} = \mathcal {U} \oplus \mathcal {U}^{\vee }$
where
$\pi ^* \mathcal {V} = \mathcal {U} \oplus \mathcal {U}^{\vee }$
where
![]() $\mathcal {U}$
is the universal rank
$\mathcal {U}$
is the universal rank
![]() $5$
subbundle on
$5$
subbundle on
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
.
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
.
Lemma 5.8. The stack
has the CKgP. Moreover, its Chow ring is freely generated by the Chern classes of
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Proof. Let
![]() $V = \mathrm {span}\{e_1, \ldots , e_{10}\}$
be a fixed
$V = \mathrm {span}\{e_1, \ldots , e_{10}\}$
be a fixed
![]() $10$
-dimensional vector space with quadratic form
$10$
-dimensional vector space with quadratic form
 $$\begin{align*}Q = \left(\begin{matrix} 0 & I_5 \\ I_5 & 0 \end{matrix}\right).\end{align*}$$
$$\begin{align*}Q = \left(\begin{matrix} 0 & I_5 \\ I_5 & 0 \end{matrix}\right).\end{align*}$$
Let
![]() $U = \mathrm {span}\{e_1, \ldots , e_5\}$
, which is an isotropic subspace. The stabilizer of
$U = \mathrm {span}\{e_1, \ldots , e_5\}$
, which is an isotropic subspace. The stabilizer of
![]() $\mathrm {SO}_{10}$
acting on
$\mathrm {SO}_{10}$
acting on
![]() $\operatorname {\mathrm {OG}}(5,10)$
at U is
$\operatorname {\mathrm {OG}}(5,10)$
at U is
 $$\begin{align*}\mathrm{Stab}_U = \left\{M = \left(\begin{matrix} A & B \\ 0 & D \end{matrix}\right) : M^TQM =Q\right\} \subset \mathrm{SO}_{10}. \end{align*}$$
$$\begin{align*}\mathrm{Stab}_U = \left\{M = \left(\begin{matrix} A & B \\ 0 & D \end{matrix}\right) : M^TQM =Q\right\} \subset \mathrm{SO}_{10}. \end{align*}$$
Expanding, we have
 $$\begin{align*}M^T Q M = \left(\begin{matrix} A^T & 0 \\ B^T & D^T \end{matrix}\right)\left(\begin{matrix} 0 & I_5 \\ I_5 & 0 \end{matrix}\right)\left(\begin{matrix} A & B \\ 0 & D \end{matrix}\right) = \left( \begin{matrix} 0 & A^TD \\ D^TA & B^TD + D^TB \end{matrix}\right).\end{align*}$$
$$\begin{align*}M^T Q M = \left(\begin{matrix} A^T & 0 \\ B^T & D^T \end{matrix}\right)\left(\begin{matrix} 0 & I_5 \\ I_5 & 0 \end{matrix}\right)\left(\begin{matrix} A & B \\ 0 & D \end{matrix}\right) = \left( \begin{matrix} 0 & A^TD \\ D^TA & B^TD + D^TB \end{matrix}\right).\end{align*}$$
Thus,
![]() $\mathrm {Stab}_U$
is defined by the conditions
$\mathrm {Stab}_U$
is defined by the conditions
![]() $D = (A^T)^{-1}$
and
$D = (A^T)^{-1}$
and
![]() $B^TD + D^TB = 0$
.
$B^TD + D^TB = 0$
.
Note that
![]() $\mathrm {Stab}_U$
is a maximal parabolic subgroup and
$\mathrm {Stab}_U$
is a maximal parabolic subgroup and
![]() $\operatorname {\mathrm {OG}}(5, 10) = \mathrm {SO}_{10}/\mathrm {Stab}_U$
. As such, the quotient
$\operatorname {\mathrm {OG}}(5, 10) = \mathrm {SO}_{10}/\mathrm {Stab}_U$
. As such, the quotient
![]() $[\operatorname {\mathrm {OG}}(5,10)/\mathrm {SO}_{10}]$
is equivalent to the classifying stack
$[\operatorname {\mathrm {OG}}(5,10)/\mathrm {SO}_{10}]$
is equivalent to the classifying stack
![]() $\mathrm {BStab}_U$
. To gain a better understanding of the latter, consider the group homomorphism
$\mathrm {BStab}_U$
. To gain a better understanding of the latter, consider the group homomorphism
 $$\begin{align*}\operatorname{\mathrm{GL}}_5 \hookrightarrow \mathrm{Stab}_U, \qquad A\mapsto \left(\begin{matrix} A & 0 \\ 0 & (A^T)^{-1}\end{matrix}\right).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{GL}}_5 \hookrightarrow \mathrm{Stab}_U, \qquad A\mapsto \left(\begin{matrix} A & 0 \\ 0 & (A^T)^{-1}\end{matrix}\right).\end{align*}$$
For fixed D, the condition
![]() $B^TD + D^TB = 0$
is linear in B. Specifically, it says that B lies in the
$B^TD + D^TB = 0$
is linear in B. Specifically, it says that B lies in the
![]() $(D^{T})^{-1}$
translation of the
$(D^{T})^{-1}$
translation of the
![]() $\mathbb {A}^{10}$
of skew symmetric
$\mathbb {A}^{10}$
of skew symmetric
![]() $5 \times 5$
matrices. In particular, the cosets of the subgroup
$5 \times 5$
matrices. In particular, the cosets of the subgroup
![]() $\operatorname {\mathrm {GL}}_5 \hookrightarrow \mathrm {Stab}_U$
are isomorphic to affine spaces
$\operatorname {\mathrm {GL}}_5 \hookrightarrow \mathrm {Stab}_U$
are isomorphic to affine spaces
![]() $\mathbb {A}^{10}$
. In other words, the induced map on classifying spaces
$\mathbb {A}^{10}$
. In other words, the induced map on classifying spaces
![]() $\operatorname {\mathrm {BGL}}_5 \to \mathrm {BStab}_U \cong \operatorname {\mathrm {OG}}(5, \mathcal {V})$
is an affine bundle. It follows that
$\operatorname {\mathrm {BGL}}_5 \to \mathrm {BStab}_U \cong \operatorname {\mathrm {OG}}(5, \mathcal {V})$
is an affine bundle. It follows that
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
has the CKgP by Proposition 4.2(4) and (5).
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
has the CKgP by Proposition 4.2(4) and (5).
Furthermore, by construction, the tautological subbundle
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
pulls back to the tautological rank
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
pulls back to the tautological rank
![]() $5$
bundle on
$5$
bundle on
![]() $\operatorname {\mathrm {BGL}}_5$
. It follows that
$\operatorname {\mathrm {BGL}}_5$
. It follows that
![]() $A^*(\mathrm {BStab}_U) \cong A^*(\mathrm {BGL}_5)$
and is freely generated by the Chern classes of the tautological bundle.
$A^*(\mathrm {BStab}_U) \cong A^*(\mathrm {BGL}_5)$
and is freely generated by the Chern classes of the tautological bundle.
Remark 5.9. There is also a natural map
![]() $\mathrm {Stab}_U \to \operatorname {\mathrm {GL}}_5$
that sends
$\mathrm {Stab}_U \to \operatorname {\mathrm {GL}}_5$
that sends
 $\left (\begin {matrix} A & B \\ 0 & D \end {matrix}\right )$
to A. The kernel of
$\left (\begin {matrix} A & B \\ 0 & D \end {matrix}\right )$
to A. The kernel of
![]() $\mathrm {Stab}_U \to \operatorname {\mathrm {GL}}_5$
is the subgroup
$\mathrm {Stab}_U \to \operatorname {\mathrm {GL}}_5$
is the subgroup
![]() $G \cong (\mathbb {G}_a)^{10}$
, where
$G \cong (\mathbb {G}_a)^{10}$
, where
![]() $A = I_5, D = I_5$
and
$A = I_5, D = I_5$
and
![]() $B + B^T = 0$
. This shows that
$B + B^T = 0$
. This shows that
![]() $\mathrm {Stab}_U$
is actually a semi-direct product
$\mathrm {Stab}_U$
is actually a semi-direct product
![]() $G \rtimes \operatorname {\mathrm {GL}}_5$
. The map
$G \rtimes \operatorname {\mathrm {GL}}_5$
. The map
![]() $\mathrm {BStab}_U \to \operatorname {\mathrm {BGL}}_5$
is a
$\mathrm {BStab}_U \to \operatorname {\mathrm {BGL}}_5$
is a
![]() $\mathrm {B}G$
-banded gerbe.
$\mathrm {B}G$
-banded gerbe.
Lemma 5.10. Let V be a rank
![]() $2\nu $
vector bundle with quadratic form on X.
$2\nu $
vector bundle with quadratic form on X.
-
1. The rational Chow ring of
 $\operatorname {\mathrm {OG}}(\nu , V)$
is generated over the Chow ring of X by the Chern classes of the tautological subbundle.
$\operatorname {\mathrm {OG}}(\nu , V)$
is generated over the Chow ring of X by the Chern classes of the tautological subbundle. -
2. If X has the CKgP, then
 $\operatorname {\mathrm {OG}}(\nu , V)$
has the CKgP.
$\operatorname {\mathrm {OG}}(\nu , V)$
has the CKgP.
Proof. The argument is very similar to that for Grassmannians in type A.
First consider the case when X is a point. The orthogonal Grassmannian
![]() $\operatorname {\mathrm {OG}}(\nu , 2\nu )$
is stratified by Schubert cells, each of which is isomorphic to an affine space. By Proposition 4.2(3), it follows that
$\operatorname {\mathrm {OG}}(\nu , 2\nu )$
is stratified by Schubert cells, each of which is isomorphic to an affine space. By Proposition 4.2(3), it follows that
![]() $\operatorname {\mathrm {OG}}(\nu , 2\nu )$
has the CKgP. Moreover, the fundamental classes of these cells are expressed in terms of the Chern classes of the tautological quotient or subbundle via a Giambelli formula [Reference Kresch and Tamvakis19, p. 1–2]. Note that this formula involves dividing by
$\operatorname {\mathrm {OG}}(\nu , 2\nu )$
has the CKgP. Moreover, the fundamental classes of these cells are expressed in terms of the Chern classes of the tautological quotient or subbundle via a Giambelli formula [Reference Kresch and Tamvakis19, p. 1–2]. Note that this formula involves dividing by
![]() $2$
, so it is important that we work with rational coefficients for this claim. In conclusion, the Chern classes of the tautological subbundle generate the Chow ring of
$2$
, so it is important that we work with rational coefficients for this claim. In conclusion, the Chern classes of the tautological subbundle generate the Chow ring of
![]() $\operatorname {\mathrm {OG}}(\nu , 2\nu )$
.
$\operatorname {\mathrm {OG}}(\nu , 2\nu )$
.
More generally, for a fiber bundle
![]() $f\colon \operatorname {\mathrm {OG}}(\nu , V) \to X$
, to prove (1), we stratify X into locally closed subsets
$f\colon \operatorname {\mathrm {OG}}(\nu , V) \to X$
, to prove (1), we stratify X into locally closed subsets
![]() $X_i$
over which V is trivial, such that
$X_i$
over which V is trivial, such that
![]() $\overline X_i \supset X_j$
for
$\overline X_i \supset X_j$
for
![]() $i \leq j$
and
$i \leq j$
and
![]() $X_i$
has codimension at least i. To check that the desired classes generate
$X_i$
has codimension at least i. To check that the desired classes generate
![]() $A^k(\operatorname {\mathrm {OG}}(\nu , V))$
for a given k, it suffices to show that they generate
$A^k(\operatorname {\mathrm {OG}}(\nu , V))$
for a given k, it suffices to show that they generate
![]() $A^k(f^{-1}(X_0 \cup X_1 \cup \cdots \cup X_k))$
.
$A^k(f^{-1}(X_0 \cup X_1 \cup \cdots \cup X_k))$
.
Over each piece of the stratification,
![]() $f^{-1}(X_i) = X_i \times \operatorname {\mathrm {OG}}(\nu , 2\nu )$
. Since
$f^{-1}(X_i) = X_i \times \operatorname {\mathrm {OG}}(\nu , 2\nu )$
. Since
![]() $\operatorname {\mathrm {OG}}(\nu ,2\nu )$
has the CKgP, the Chow ring of
$\operatorname {\mathrm {OG}}(\nu ,2\nu )$
has the CKgP, the Chow ring of
![]() $f^{-1}(X_i) = X_i \times \operatorname {\mathrm {OG}}(\nu , 2\nu )$
is generated by
$f^{-1}(X_i) = X_i \times \operatorname {\mathrm {OG}}(\nu , 2\nu )$
is generated by
![]() $A^*(X_i)$
and restrictions of the Chern classes from the tautological subbundle on
$A^*(X_i)$
and restrictions of the Chern classes from the tautological subbundle on
![]() $\operatorname {\mathrm {OG}}(\nu , V)$
. By excision and the push-pull formula, the Chow ring of any finite union
$\operatorname {\mathrm {OG}}(\nu , V)$
. By excision and the push-pull formula, the Chow ring of any finite union
![]() $f^{-1}(X_0) \cup f^{-1}(X_1) \cup \cdots \cup f^{-1}(X_k)$
is generated by the desired classes.
$f^{-1}(X_0) \cup f^{-1}(X_1) \cup \cdots \cup f^{-1}(X_k)$
is generated by the desired classes.
Finally, (2) follows from (1) exactly as in [Reference Canning and Larson5, Lemma 3.7].
Corollary 5.11. For any
![]() $n \geq 1$
, the n-fold fiber product
$n \geq 1$
, the n-fold fiber product
has the CKgP, and its Chow ring is generated by the Chern classes of the tautological subbundles
![]() $\mathcal {U}_1, \ldots , \mathcal {U}_n$
pulled back from each factor.
$\mathcal {U}_1, \ldots , \mathcal {U}_n$
pulled back from each factor.
Proof. The case
![]() $n = 1$
follows from Lemma 5.8. For
$n = 1$
follows from Lemma 5.8. For
![]() $n> 1$
, the n-fold fiber product is an orthogonal Grassmann bundle over the
$n> 1$
, the n-fold fiber product is an orthogonal Grassmann bundle over the
![]() $(n-1)$
-fold fiber product, so the claim follows from Lemma 5.10.
$(n-1)$
-fold fiber product, so the claim follows from Lemma 5.10.
Remark 5.12. By Proposition 4.2(2), the fact that
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
has the CKgP implies that
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
has the CKgP implies that
![]() $\operatorname {\mathrm {BSO}}_{10}$
also has the CKgP. It should be possible to show that
$\operatorname {\mathrm {BSO}}_{10}$
also has the CKgP. It should be possible to show that
![]() $\operatorname {\mathrm {BSO}}_{10}$
has the CKgP (with integral coefficients as well) using the calculation of its Chow ring by Field [Reference Field14]. If the calculation there holds over any field, it would show that
$\operatorname {\mathrm {BSO}}_{10}$
has the CKgP (with integral coefficients as well) using the calculation of its Chow ring by Field [Reference Field14]. If the calculation there holds over any field, it would show that
![]() $\operatorname {\mathrm {BSO}}_{10}$
has Totaro’s “weak Chow–Künneth Property,” which is equivalent to the CKgP by the proof of [Reference Totaro34, Theorem 4.1].
$\operatorname {\mathrm {BSO}}_{10}$
has Totaro’s “weak Chow–Künneth Property,” which is equivalent to the CKgP by the proof of [Reference Totaro34, Theorem 4.1].
5.3.2 Review of the Mukai construction
We first review Mukai’s construction and then explain how to modify it for pointed curves. The canonical model of a pentagonal genus
![]() $7$
curve
$7$
curve
![]() $C \subset \mathbb {P}^6$
lies on a
$C \subset \mathbb {P}^6$
lies on a
![]() $10$
-dimensional space of quadrics. The vector space W of these quadrics is defined by the exact sequence
$10$
-dimensional space of quadrics. The vector space W of these quadrics is defined by the exact sequence
For each
![]() $p \in C$
, the subspace
$p \in C$
, the subspace
![]() $W_p \subset W$
of quadrics that are singular at p is
$W_p \subset W$
of quadrics that are singular at p is
![]() $5$
-dimensional. It appears in the exact sequence (see [Reference Mukai21, Section 3])
$5$
-dimensional. It appears in the exact sequence (see [Reference Mukai21, Section 3])
Mukai shows that
![]() $W^\vee $
has a canonical quadratic form and
$W^\vee $
has a canonical quadratic form and
![]() $W_p^\perp $
is an isotropic subspace, so one obtains a map
$W_p^\perp $
is an isotropic subspace, so one obtains a map
![]() $C \to \operatorname {\mathrm {OG}}(5, W^\vee )$
via
$C \to \operatorname {\mathrm {OG}}(5, W^\vee )$
via
![]() $p \mapsto [W_p^\perp ] \in \operatorname {\mathrm {OG}}(5, W^\vee )$
[Reference Mukai21, Theorem 0.4].
$p \mapsto [W_p^\perp ] \in \operatorname {\mathrm {OG}}(5, W^\vee )$
[Reference Mukai21, Theorem 0.4].
Let
![]() $\operatorname {\mathrm {OG}}(5, 10) \hookrightarrow \mathbb {P} S^+$
be the spinor embedding, as in [Reference Mukai21, Section 1]. The composition
$\operatorname {\mathrm {OG}}(5, 10) \hookrightarrow \mathbb {P} S^+$
be the spinor embedding, as in [Reference Mukai21, Section 1]. The composition
realizes C as a linear section
![]() $C = \operatorname {\mathrm {OG}}(5,10) \cap \mathbb {P}^6 \subset \mathbb {P} S^+$
, and
$C = \operatorname {\mathrm {OG}}(5,10) \cap \mathbb {P}^6 \subset \mathbb {P} S^+$
, and
![]() $C \subset \mathbb {P}^6$
is canonically embedded [Reference Mukai21, Theorem 0.4]. Conversely, if a linear section
$C \subset \mathbb {P}^6$
is canonically embedded [Reference Mukai21, Theorem 0.4]. Conversely, if a linear section
![]() $\mathbb {P}^6 \cap \operatorname {\mathrm {OG}}(5, 10)$
is a smooth curve, then it is a canonically embedded pentagonal genus
$\mathbb {P}^6 \cap \operatorname {\mathrm {OG}}(5, 10)$
is a smooth curve, then it is a canonically embedded pentagonal genus
![]() $7$
curve [Reference Mukai21, Proposition 2.2]. This construction works in families, and Mukai proves that there is an equivalence of stacks
$7$
curve [Reference Mukai21, Proposition 2.2]. This construction works in families, and Mukai proves that there is an equivalence of stacks
where
![]() $\Delta \subset \operatorname {\mathrm {Gr}}(7, S^+)$
is the closed locus of linear subspaces
$\Delta \subset \operatorname {\mathrm {Gr}}(7, S^+)$
is the closed locus of linear subspaces
![]() $\mathbb {P}^6 \subset \mathbb {P} S^+$
whose intersection with
$\mathbb {P}^6 \subset \mathbb {P} S^+$
whose intersection with
![]() $\operatorname {\mathrm {OG}}(5, 10)$
is not a smooth curve [Reference Mukai21, Section 5].
$\operatorname {\mathrm {OG}}(5, 10)$
is not a smooth curve [Reference Mukai21, Section 5].
The spinor representation of
![]() $\mathrm {SO}_{10}$
corresponds to a rank
$\mathrm {SO}_{10}$
corresponds to a rank
![]() $16$
vector bundle
$16$
vector bundle
![]() $\mathcal {S}^+$
on the classifying stack
$\mathcal {S}^+$
on the classifying stack
![]() $\operatorname {\mathrm {BSO}}_{10}$
. Then, the equivalence (5.10) shows that
$\operatorname {\mathrm {BSO}}_{10}$
. Then, the equivalence (5.10) shows that
![]() ${\mathcal {M}}_7^\circ $
is an open substack of the Grassmann bundle
${\mathcal {M}}_7^\circ $
is an open substack of the Grassmann bundle
![]() $\operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
over
$\operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
over
![]() $\operatorname {\mathrm {BSO}}_{10}$
:
$\operatorname {\mathrm {BSO}}_{10}$
:

We note that the tautological subbundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $\operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
restricts to the dual of the Hodge bundle on
$\operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
restricts to the dual of the Hodge bundle on
![]() ${\mathcal {M}}_7^\circ $
. In other words, if
${\mathcal {M}}_7^\circ $
. In other words, if
![]() $f\colon \mathcal {C} \to {\mathcal {M}}_7^{\circ }$
is the universal curve, then
$f\colon \mathcal {C} \to {\mathcal {M}}_7^{\circ }$
is the universal curve, then
![]() $\alpha _0^*\mathcal {E} = (f_*\omega _f)^\vee $
. The universal version of the Mukai construction furnishes a map
$\alpha _0^*\mathcal {E} = (f_*\omega _f)^\vee $
. The universal version of the Mukai construction furnishes a map
![]() $\mathcal {C} \to \operatorname {\mathrm {OG}}(5, \mathcal {V})$
over
$\mathcal {C} \to \operatorname {\mathrm {OG}}(5, \mathcal {V})$
over
![]() $\operatorname {\mathrm {BSO}}_{10}$
.
$\operatorname {\mathrm {BSO}}_{10}$
.
5.3.3 The Mukai construction with markings
For
![]() $n \leq 4$
, we describe
$n \leq 4$
, we describe
![]() ${\mathcal {M}}_{7,n}^{\circ }$
in a similar fashion to (5.11) but this time as an open substack of a Grassmann bundle over
${\mathcal {M}}_{7,n}^{\circ }$
in a similar fashion to (5.11) but this time as an open substack of a Grassmann bundle over
![]() $\operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
. To do so, let
$\operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
. To do so, let
![]() $\iota \colon \operatorname {\mathrm {OG}}(5, \mathcal {V}) \hookrightarrow \mathbb {P} \mathcal {S}^+$
be the universal spinor embedding, and let
$\iota \colon \operatorname {\mathrm {OG}}(5, \mathcal {V}) \hookrightarrow \mathbb {P} \mathcal {S}^+$
be the universal spinor embedding, and let
![]() $\mathcal {L} := \iota ^*\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
. The embedding
$\mathcal {L} := \iota ^*\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
. The embedding
![]() $\iota $
is determined by an inclusion of vector bundles
$\iota $
is determined by an inclusion of vector bundles
![]() $\mathcal {L} \hookrightarrow \pi ^*\mathcal {S}^+$
on
$\mathcal {L} \hookrightarrow \pi ^*\mathcal {S}^+$
on
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
. On the n-fold fiber product
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
. On the n-fold fiber product
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
, let
$\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
, let
![]() $\mathcal {L}_i$
and
$\mathcal {L}_i$
and
![]() $\mathcal {U}_i$
denote the pullbacks of
$\mathcal {U}_i$
denote the pullbacks of
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {U}$
, respectively, from the ith factor. Let
$\mathcal {U}$
, respectively, from the ith factor. Let
![]() $\pi _n \colon \operatorname {\mathrm {OG}}(5, \mathcal {V})^n \to \operatorname {\mathrm {BSO}}_{10}$
be the structure map. Consider the sum of the inclusions
$\pi _n \colon \operatorname {\mathrm {OG}}(5, \mathcal {V})^n \to \operatorname {\mathrm {BSO}}_{10}$
be the structure map. Consider the sum of the inclusions
 $$ \begin{align} \bigoplus_{i=1}^n \mathcal{L}_i \xrightarrow{\phi_n} \pi_n^* \mathcal{S}^+. \end{align} $$
$$ \begin{align} \bigoplus_{i=1}^n \mathcal{L}_i \xrightarrow{\phi_n} \pi_n^* \mathcal{S}^+. \end{align} $$
Let
![]() $Z_n \subset \operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
be the open substack where
$Z_n \subset \operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
be the open substack where
![]() $\phi _n$
has rank n. In other words,
$\phi _n$
has rank n. In other words,
![]() $Z_n$
is the locus where the n points on
$Z_n$
is the locus where the n points on
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})$
have independent image under the spinor embedding.
$\operatorname {\mathrm {OG}}(5, \mathcal {V})$
have independent image under the spinor embedding.
Let
![]() $\mathcal {Q}_n$
be the cokernel of
$\mathcal {Q}_n$
be the cokernel of
![]() $\phi _n|_{Z_n}$
, which is a rank
$\phi _n|_{Z_n}$
, which is a rank
![]() $16 - n$
vector bundle on
$16 - n$
vector bundle on
![]() $Z_n$
. The fiber of
$Z_n$
. The fiber of
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
over
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
over
![]() $(p_1, \ldots , p_n) \in \operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
parametrizes linear spaces
$(p_1, \ldots , p_n) \in \operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
parametrizes linear spaces
![]() $\mathbb {P}^6 \subset \mathbb {P} S^+$
that contain the n points
$\mathbb {P}^6 \subset \mathbb {P} S^+$
that contain the n points
![]() $p_i$
. Thus, we can identify
$p_i$
. Thus, we can identify
![]() $\operatorname {\mathrm {Gr}}(7-n,\mathcal {Q}_n)$
with the locally closed substack
$\operatorname {\mathrm {Gr}}(7-n,\mathcal {Q}_n)$
with the locally closed substack
Lemma 5.13. For
![]() $n \leq 4$
, there is an open embedding
$n \leq 4$
, there is an open embedding
![]() $\alpha _n$
of
$\alpha _n$
of
![]() ${\mathcal {M}}_{7,n}^\circ $
in the Grassmann bundle
${\mathcal {M}}_{7,n}^\circ $
in the Grassmann bundle

Hence,
![]() ${\mathcal {M}}_{7,n}^{\circ }$
has the CKgP.
${\mathcal {M}}_{7,n}^{\circ }$
has the CKgP.
Proof. Let
![]() $f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve, and let
$f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve, and let
![]() $\sigma _i\colon {\mathcal {M}}_{7,n}^{\circ } \to \mathcal {C}$
be the ith section. The universal version of the Mukai construction gives a morphism
$\sigma _i\colon {\mathcal {M}}_{7,n}^{\circ } \to \mathcal {C}$
be the ith section. The universal version of the Mukai construction gives a morphism
![]() $\mathcal {C} \to \operatorname {\mathrm {OG}}(5, \mathcal {V})$
. Precomposing with each of the sections
$\mathcal {C} \to \operatorname {\mathrm {OG}}(5, \mathcal {V})$
. Precomposing with each of the sections
![]() $\sigma _i$
defines a map
$\sigma _i$
defines a map
![]() ${\mathcal {M}}_{7, n}^{\circ } \to \operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
over
${\mathcal {M}}_{7, n}^{\circ } \to \operatorname {\mathrm {OG}}(5,\mathcal {V})^n$
over
![]() $\operatorname {\mathrm {BSO}}_{10}$
. We claim that, for
$\operatorname {\mathrm {BSO}}_{10}$
. We claim that, for
![]() $n \leq 4$
, the images of
$n \leq 4$
, the images of
![]() $\sigma _1, \ldots , \sigma _n$
must be independent. Indeed, suppose the images of the sections in a fiber,
$\sigma _1, \ldots , \sigma _n$
must be independent. Indeed, suppose the images of the sections in a fiber,
![]() $p_1, \ldots , p_n \in C$
, are dependent under the canonical embedding. Then
$p_1, \ldots , p_n \in C$
, are dependent under the canonical embedding. Then
![]() $p_1 + \cdots + p_n$
would give a
$p_1 + \cdots + p_n$
would give a
![]() $g^1_n$
on C, but curves in
$g^1_n$
on C, but curves in
![]() ${\mathcal {M}}_{7,n}^{\circ }$
have no
${\mathcal {M}}_{7,n}^{\circ }$
have no
![]() $g^1_n$
for
$g^1_n$
for
![]() $n \leq 4$
by definition.
$n \leq 4$
by definition.
We also have the map
![]() ${\mathcal {M}}_{7,n}^{\circ } \to {\mathcal {M}}_7^\circ \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
that sends a curve to its span under the spinor embedding. Taking the product of these maps over
${\mathcal {M}}_{7,n}^{\circ } \to {\mathcal {M}}_7^\circ \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
that sends a curve to its span under the spinor embedding. Taking the product of these maps over
![]() $\operatorname {\mathrm {BSO}}_{10}$
yields a map
$\operatorname {\mathrm {BSO}}_{10}$
yields a map
This map sends a family of pointed curves
![]() $(C, p_1, \ldots , p_n)$
over a scheme T to the data of sections
$(C, p_1, \ldots , p_n)$
over a scheme T to the data of sections
![]() $p_i\colon T \to C \to \operatorname {\mathrm {OG}}(5, W^\vee )$
and the subbundle of the spinor representation of
$p_i\colon T \to C \to \operatorname {\mathrm {OG}}(5, W^\vee )$
and the subbundle of the spinor representation of
![]() $W^\vee $
determined by the span of the fibers of
$W^\vee $
determined by the span of the fibers of
![]() $C \subset \operatorname {\mathrm {OG}}(5, W^\vee ) \subset \mathbb {P} S^+$
over T. The map evidently factors through the locally closed locus in (5.13), which we identified with
$C \subset \operatorname {\mathrm {OG}}(5, W^\vee ) \subset \mathbb {P} S^+$
over T. The map evidently factors through the locally closed locus in (5.13), which we identified with
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. In fact, the image is precisely
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. In fact, the image is precisely
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \smallsetminus \Delta $
, where
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \smallsetminus \Delta $
, where
![]() $\Delta $
is the closed locus, such that
$\Delta $
is the closed locus, such that
![]() $\mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee )$
is not a family of smooth curves. Indeed, on the complement of
$\mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee )$
is not a family of smooth curves. Indeed, on the complement of
![]() $\Delta $
, an inverse map
$\Delta $
, an inverse map
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \smallsetminus \Delta \to {\mathcal {M}}_{7,n}^{\circ }$
is defined by sending
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \smallsetminus \Delta \to {\mathcal {M}}_{7,n}^{\circ }$
is defined by sending
![]() $(p_1, \ldots , p_n, \Lambda )$
to the curve
$(p_1, \ldots , p_n, \Lambda )$
to the curve
![]() $C = \mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee )$
together with the sections
$C = \mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee )$
together with the sections
![]() $p_i \in \mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee ) = C$
.
$p_i \in \mathbb {P} \Lambda \cap \operatorname {\mathrm {OG}}(5, W^\vee ) = C$
.
By Corollary 5.11, we know
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
has the CKgP. To complete the proof, apply Proposition 4.2(1) and (5).
$\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
has the CKgP. To complete the proof, apply Proposition 4.2(1) and (5).
We now identify the restrictions of the universal bundles on
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
and
$\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
and
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
to
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
to
![]() ${\mathcal {M}}_{7,n}^{\circ }$
along
${\mathcal {M}}_{7,n}^{\circ }$
along
![]() $\alpha _n$
.
$\alpha _n$
.
Lemma 5.14. Let
![]() $f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve, and let
$f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve, and let
![]() $\sigma _i$
denote the image of the ith section. The vector bundle
$\sigma _i$
denote the image of the ith section. The vector bundle
![]() $\alpha _n^*\, \mathcal {U}_i$
sits in an exact sequence
$\alpha _n^*\, \mathcal {U}_i$
sits in an exact sequence
In particular, all classes pulled back from
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
to
$\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
to
![]() ${\mathcal {M}}_{7,n}^\circ $
are tautological.
${\mathcal {M}}_{7,n}^\circ $
are tautological.
Proof. The composition of
![]() $\alpha _n$
with projection onto the ith factor of
$\alpha _n$
with projection onto the ith factor of
![]() $Z_n$
is the map that sends a pointed curve
$Z_n$
is the map that sends a pointed curve
![]() $(C, p_1, \ldots , p_n)$
to the image of
$(C, p_1, \ldots , p_n)$
to the image of
![]() $p_i$
under the canonical map from C to
$p_i$
under the canonical map from C to
![]() $\operatorname {\mathrm {OG}}(5, W^\vee ) \cong \operatorname {\mathrm {OG}}(5, 10)$
. By construction, the fiber at
$\operatorname {\mathrm {OG}}(5, W^\vee ) \cong \operatorname {\mathrm {OG}}(5, 10)$
. By construction, the fiber at
![]() $p_i$
of the universal rank
$p_i$
of the universal rank
![]() $5$
bundle on
$5$
bundle on
![]() $\operatorname {\mathrm {OG}}(5,10)$
is
$\operatorname {\mathrm {OG}}(5,10)$
is
![]() $W_p^\perp $
. Equation (5.14) is the relative version of (5.9). By Grothendieck–Riemann–Roch, the middle and right terms in (5.14) have tautological Chern classes. It follows that the Chern classes of
$W_p^\perp $
. Equation (5.14) is the relative version of (5.9). By Grothendieck–Riemann–Roch, the middle and right terms in (5.14) have tautological Chern classes. It follows that the Chern classes of
![]() $\alpha _n^*\mathcal {U}_i$
are also tautological. The last claim now follows from Corollary 5.11.
$\alpha _n^*\mathcal {U}_i$
are also tautological. The last claim now follows from Corollary 5.11.
Lemma 5.15. We have
![]() $c_1(\alpha _n^*\mathcal {L}_i) = -\psi _i$
in
$c_1(\alpha _n^*\mathcal {L}_i) = -\psi _i$
in
![]() $A^1({\mathcal {M}}_{7,n}^{\circ })$
.
$A^1({\mathcal {M}}_{7,n}^{\circ })$
.
Proof. Let
![]() $f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve. The line bundle
$f\colon \mathcal {C} \to {\mathcal {M}}_{7,n}^{\circ }$
be the universal curve. The line bundle
![]() $\alpha ^*\mathcal {L}_i$
is the pullback of
$\alpha ^*\mathcal {L}_i$
is the pullback of
![]() $\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
along the composition
$\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
along the composition
But the above composition also factors as
and
![]() $\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
restricts to
$\mathcal {O}_{\mathbb {P} \mathcal {S}^+}(-1)$
restricts to
![]() $\mathcal {O}_{\mathbb {P} (f_* \omega _f)^\vee }(-1)$
. Hence,
$\mathcal {O}_{\mathbb {P} (f_* \omega _f)^\vee }(-1)$
. Hence,
![]() $\alpha _n^*\mathcal {L}_i$
is
$\alpha _n^*\mathcal {L}_i$
is
![]() $\sigma _i^* \mathcal {O}_{\mathbb {P} (f_* \omega _f)^\vee }(-1) = (\sigma _i^*\omega _f)^\vee $
.
$\sigma _i^* \mathcal {O}_{\mathbb {P} (f_* \omega _f)^\vee }(-1) = (\sigma _i^*\omega _f)^\vee $
.
Lemma 5.16. Let
![]() $\mathcal {E}_n$
be the tautological rank
$\mathcal {E}_n$
be the tautological rank
![]() $7 - n$
subbundle on
$7 - n$
subbundle on
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. The pullback
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. The pullback
![]() $\alpha _n^*\mathcal {E}_n$
sits in an exact sequence
$\alpha _n^*\mathcal {E}_n$
sits in an exact sequence
 $$ \begin{align} 0 \rightarrow \bigoplus_{i=1}^n \alpha_n^*\mathcal{L}_i \rightarrow (f_*\omega_f)^\vee \rightarrow \alpha_n^*\mathcal{E}_n \rightarrow 0. \end{align} $$
$$ \begin{align} 0 \rightarrow \bigoplus_{i=1}^n \alpha_n^*\mathcal{L}_i \rightarrow (f_*\omega_f)^\vee \rightarrow \alpha_n^*\mathcal{E}_n \rightarrow 0. \end{align} $$
In particular, the Chern classes of
![]() $\alpha _n^* \mathcal {E}_n$
are tautological.
$\alpha _n^* \mathcal {E}_n$
are tautological.
Proof. Recall that we defined
![]() $\mathcal {Q}_n$
as the cokernel of (5.12). The map onto the second factor in (5.13),
$\mathcal {Q}_n$
as the cokernel of (5.12). The map onto the second factor in (5.13),
![]() $p\colon \operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
, sends a
$p\colon \operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n) \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
, sends a
![]() $7 - n$
dimensional subspace to its preimage under the quotient map
$7 - n$
dimensional subspace to its preimage under the quotient map
![]() $\mathcal {S}^+ \to \mathcal {Q}_n$
. Hence, there is an exact sequence on
$\mathcal {S}^+ \to \mathcal {Q}_n$
. Hence, there is an exact sequence on
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
 $$\begin{align*}0 \rightarrow \bigoplus_{i=1}^n \mathcal{L}_i \to p^* \mathcal{E} \to \mathcal{E}_n \rightarrow 0.\end{align*}$$
$$\begin{align*}0 \rightarrow \bigoplus_{i=1}^n \mathcal{L}_i \to p^* \mathcal{E} \to \mathcal{E}_n \rightarrow 0.\end{align*}$$
Then note that
![]() $\alpha _n^*p^*\mathcal {E}$
is the same as the pullback of
$\alpha _n^*p^*\mathcal {E}$
is the same as the pullback of
![]() $\mathcal {E}$
along
$\mathcal {E}$
along
![]() ${\mathcal {M}}_{7,n}^\circ \to {\mathcal {M}}_{7}^\circ \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
, which is the dual of the Hodge bundle. The last claim follows by combining the exact sequence (5.15) with Lemma 5.15.
${\mathcal {M}}_{7,n}^\circ \to {\mathcal {M}}_{7}^\circ \to \operatorname {\mathrm {Gr}}(7, \mathcal {S}^+)$
, which is the dual of the Hodge bundle. The last claim follows by combining the exact sequence (5.15) with Lemma 5.15.
Lemma 5.17. The Chow ring of
![]() ${\mathcal {M}}_{7,n}^{\circ }$
is generated by tautological classes.
${\mathcal {M}}_{7,n}^{\circ }$
is generated by tautological classes.
Proof. By Lemma 5.13, we know that
![]() ${\mathcal {M}}_{7,n}^\circ $
is an open substack of
${\mathcal {M}}_{7,n}^\circ $
is an open substack of
![]() $\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. The Chow ring of the latter is generated by pullbacks of classes from
$\operatorname {\mathrm {Gr}}(7 - n, \mathcal {Q}_n)$
. The Chow ring of the latter is generated by pullbacks of classes from
![]() $\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
and by the Chern classes of the tautological subbundle
$\operatorname {\mathrm {OG}}(5, \mathcal {V})^n$
and by the Chern classes of the tautological subbundle
![]() $\mathcal {E}_n$
. By Lemmas 5.14 and 5.16, respectively, both of these collections of classes restrict to tautological classes on
$\mathcal {E}_n$
. By Lemmas 5.14 and 5.16, respectively, both of these collections of classes restrict to tautological classes on
![]() ${\mathcal {M}}_{7,n}^\circ $
.
${\mathcal {M}}_{7,n}^\circ $
.
6 Applications to even cohomology
Here, we use the results from Sections 3, 4 and 5 to prove Theorem 1.5.
6.1 The degree 4 cohomology of
 ${\overline {\mathcal {M}}}_{g,n}$
is tautological
${\overline {\mathcal {M}}}_{g,n}$
is tautological
Proof of Theorem 1.5(1).
By [Reference Arbarello and Cornalba1], we know that
![]() $H^k({\overline {\mathcal {M}}}_{g,n})$
is tautological for
$H^k({\overline {\mathcal {M}}}_{g,n})$
is tautological for
![]() $k \leq 3$
. Therefore, using Theorem 1.3, we deduce that
$k \leq 3$
. Therefore, using Theorem 1.3, we deduce that
![]() $H^4({\overline {\mathcal {M}}}_{g,n})$
is contained in the STE generated by
$H^4({\overline {\mathcal {M}}}_{g,n})$
is contained in the STE generated by
![]() $H^4({\overline {\mathcal {M}}}_{g',n'})$
for
$H^4({\overline {\mathcal {M}}}_{g',n'})$
for
![]() $g' < 7$
and
$g' < 7$
and
![]() $n' \leq 4$
. By Proposition 4.5,
$n' \leq 4$
. By Proposition 4.5,
![]() $W_4H^4({\mathcal {M}}_{g',n'})$
is tautological for
$W_4H^4({\mathcal {M}}_{g',n'})$
is tautological for
![]() $g'$
and
$g'$
and
![]() $n'$
in this range, and it follows that
$n'$
in this range, and it follows that
![]() $H^4({\overline {\mathcal {M}}}_{g,n})$
is tautological.
$H^4({\overline {\mathcal {M}}}_{g,n})$
is tautological.
Proof of Theorem 1.5(2).
By Theorem 1.5(1) and [Reference Arbarello and Cornalba1], all classes in
![]() $H^6({\overline {\mathcal {M}}}_{g,n})$
that are pushed forward from the boundary are tautological. Also,
$H^6({\overline {\mathcal {M}}}_{g,n})$
that are pushed forward from the boundary are tautological. Also,
![]() $H^6({\mathcal {M}}_{g,n})$
is stable and hence tautological for
$H^6({\mathcal {M}}_{g,n})$
is stable and hence tautological for
![]() $g \geq 10$
[Reference Wahl35]. It follows that
$g \geq 10$
[Reference Wahl35]. It follows that
![]() $H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological for
$H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological for
![]() $g \geq 10$
.
$g \geq 10$
.
Remark 6.1. By Lemma 3.1, to show that
![]() $H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological for all g and n, it would suffice to show this for
$H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological for all g and n, it would suffice to show this for
![]() $g\leq 9$
and
$g\leq 9$
and
![]() $n\leq 6$
. In principle, this can be checked computationally as follows. By Theorem 1.5(3), we know that
$n\leq 6$
. In principle, this can be checked computationally as follows. By Theorem 1.5(3), we know that
![]() $H_6({\overline {\mathcal {M}}}_{g,n})$
is tautological for all g and n. Thus, if the intersection pairing
$H_6({\overline {\mathcal {M}}}_{g,n})$
is tautological for all g and n. Thus, if the intersection pairing
is perfect for
![]() $g\leq 9$
and
$g\leq 9$
and
![]() $n\leq 6$
, then
$n\leq 6$
, then
![]() $H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological. In principle, one could compute this pairing using the Sage package admcycles [Reference Delecroix, Schmitt and van Zelm11]. In practice, however, this computation is too memory intensive to carry out.
$H^6({\overline {\mathcal {M}}}_{g,n})$
is tautological. In principle, one could compute this pairing using the Sage package admcycles [Reference Delecroix, Schmitt and van Zelm11]. In practice, however, this computation is too memory intensive to carry out.
6.2 The low degree even homology of
 ${\overline {\mathcal {M}}}_{g,n}$
is tautological
${\overline {\mathcal {M}}}_{g,n}$
is tautological
Let
![]() $H_k^{BM}$
denote Borel–Moore homology with coefficients in
$H_k^{BM}$
denote Borel–Moore homology with coefficients in
![]() $\mathbb {Q}$
or
$\mathbb {Q}$
or
![]() $\mathbb {Q}_{\ell }$
, together with its mixed Hodge structure or Galois action. From the long exact sequence in Borel–Moore homology, we have a right exact sequence
$\mathbb {Q}_{\ell }$
, together with its mixed Hodge structure or Galois action. From the long exact sequence in Borel–Moore homology, we have a right exact sequence
for all k.
Proof of Theorem 1.5(3).
We now show that
![]() $H_k({\overline {\mathcal {M}}}_{g,n})$
is tautological for even
$H_k({\overline {\mathcal {M}}}_{g,n})$
is tautological for even
![]() $k \geq 14$
. For
$k \geq 14$
. For
![]() $g=0$
, we have
$g=0$
, we have
![]() $H^*({\overline {\mathcal {M}}}_{0,n}) = RH^*({\overline {\mathcal {M}}}_{0,n})$
[Reference Keel18]. For
$H^*({\overline {\mathcal {M}}}_{0,n}) = RH^*({\overline {\mathcal {M}}}_{0,n})$
[Reference Keel18]. For
![]() $g \geq 1$
, by [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
$g \geq 1$
, by [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
![]() $H_k^{BM}$
and
$H_k^{BM}$
and
![]() $H^k_c$
, we have:
$H^k_c$
, we have:
 $$ \begin{align*} H_k^{BM}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} k<2g \text{ and } n=0,1; \\ k<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} H_k^{BM}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} k<2g \text{ and } n=0,1; \\ k<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
Combining this with the exact sequence (6.1), we reduce inductively to the finitely many cases
![]() $k\geq 2g$
and
$k\geq 2g$
and
![]() $n=0,1$
or
$n=0,1$
or
![]() $k\geq 2g-2+n$
and
$k\geq 2g-2+n$
and
![]() $n\geq 2$
. When
$n\geq 2$
. When
![]() $g\geq 3$
, in all of these cases, with
$g\geq 3$
, in all of these cases, with
![]() $k\leq 14$
, we know that
$k\leq 14$
, we know that
![]() ${\mathcal {M}}_{g,n}$
has the CKgP and
${\mathcal {M}}_{g,n}$
has the CKgP and
![]() $A^*({\mathcal {M}}_{g,n})=R^*({\mathcal {M}}_{g,n})$
(see Table 1). By Proposition 4.5, it follows that
$A^*({\mathcal {M}}_{g,n})=R^*({\mathcal {M}}_{g,n})$
(see Table 1). By Proposition 4.5, it follows that
![]() $W_{-k}H^{BM}_k({\mathcal {M}}_{g,n})$
is tautological, so again, by induction and the exact sequence (6.1), we reduce to the cases of
$W_{-k}H^{BM}_k({\mathcal {M}}_{g,n})$
is tautological, so again, by induction and the exact sequence (6.1), we reduce to the cases of
![]() $g=1,2$
. When
$g=1,2$
. When
![]() $g=1$
, all even cohomology is tautological [Reference Petersen26]. When
$g=1$
, all even cohomology is tautological [Reference Petersen26]. When
![]() $g=2$
, we apply Corollary 2.7.
$g=2$
, we apply Corollary 2.7.
Corollary 6.2. As Hodge structures or Galois representations, we have
Proof. We proved
![]() $H_{14}({\overline {\mathcal {M}}}_{g,n})$
is tautological and hence algebraic. Applying Poincaré duality yields the corollary.
$H_{14}({\overline {\mathcal {M}}}_{g,n})$
is tautological and hence algebraic. Applying Poincaré duality yields the corollary.
7 The 13th and 15th homology of
 ${\overline {\mathcal {M}}}_{g,n}$
${\overline {\mathcal {M}}}_{g,n}$
In this section, we prove Theorems 1.6 and 1.7. As a corollary, we obtain restrictions on the Hodge structures and Galois representations appearing in
![]() $H_{13}({\overline {\mathcal {M}}}_{g,n})$
and
$H_{13}({\overline {\mathcal {M}}}_{g,n})$
and
![]() $H_{15}({\overline {\mathcal {M}}}_{g,n})$
.
$H_{15}({\overline {\mathcal {M}}}_{g,n})$
.
7.1 13th homology
As usual, we argue by induction on g and n. First, we must treat one extra base case.
Lemma 7.1. The group
![]() $H^{13}({\overline {\mathcal {M}}}_{2,11})$
is in the STE generated by
$H^{13}({\overline {\mathcal {M}}}_{2,11})$
is in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
Proof. We showed in [Reference Canning, Larson and Payne8] that
![]() $H^{11}({\overline {\mathcal {M}}}_{g,n})$
is in the STE generated by
$H^{11}({\overline {\mathcal {M}}}_{g,n})$
is in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
for all g and n. Next, we note that
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
for all g and n. Next, we note that
![]() ${\mathcal {M}}_{2,10}$
has the CKgP (see Table 1), so
${\mathcal {M}}_{2,10}$
has the CKgP (see Table 1), so
![]() $H^{13}({\overline {\mathcal {M}}}_{2,10})$
consists of classes pushed forward from the boundary by Proposition 4.5. In particular,
$H^{13}({\overline {\mathcal {M}}}_{2,10})$
consists of classes pushed forward from the boundary by Proposition 4.5. In particular,
![]() $H^{13}({\overline {\mathcal {M}}}_{2,10})$
also lies in this STE. The claim then follows from Lemma 3.2.
$H^{13}({\overline {\mathcal {M}}}_{2,10})$
also lies in this STE. The claim then follows from Lemma 3.2.
Proof of Theorem 1.6.
The proof is similar to that of Theorem 1.5(3). When
![]() $g=0$
, all odd cohomology vanishes [Reference Keel18], so we can assume
$g=0$
, all odd cohomology vanishes [Reference Keel18], so we can assume
![]() $g\geq 1$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
$g\geq 1$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
![]() $H_{13}^{BM}$
and
$H_{13}^{BM}$
and
![]() $H^{13}_c$
, we have that for
$H^{13}_c$
, we have that for
![]() $g\geq 1$
$g\geq 1$
 $$ \begin{align*} H^{BM}_{13}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} 13<2g \text{ and } n=0,1 \\ 13<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} H^{BM}_{13}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} 13<2g \text{ and } n=0,1 \\ 13<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
Combining this with the exact sequence (6.1), we reduce inductively to the finitely many cases where
![]() $13\geq 2g$
and
$13\geq 2g$
and
![]() $n=0,1$
or
$n=0,1$
or
![]() $13\geq 2g-2+n$
and
$13\geq 2g-2+n$
and
![]() $n\geq 2$
. All such cases except for
$n\geq 2$
. All such cases except for
![]() $(g,n)$
in
$(g,n)$
in
![]() $Z = \{ (2,11), (1,11),(1,12),(1,13)\}$
have the CKgP (see Table 1). By Proposition 4.5, it follows that
$Z = \{ (2,11), (1,11),(1,12),(1,13)\}$
have the CKgP (see Table 1). By Proposition 4.5, it follows that
![]() $W_{-13}H_{13}^{BM}({\mathcal {M}}_{g,n})=0$
for
$W_{-13}H_{13}^{BM}({\mathcal {M}}_{g,n})=0$
for
![]() $(g,n) \not \in Z$
. By induction and the exact sequence (6.1), we reduce to the exceptional cases of
$(g,n) \not \in Z$
. By induction and the exact sequence (6.1), we reduce to the exceptional cases of
![]() $(g,n) \in Z$
. The case
$(g,n) \in Z$
. The case
![]() $(g,n)=(2,11)$
follows from Lemma 7.1 and hard Lefschetz. The cases where
$(g,n)=(2,11)$
follows from Lemma 7.1 and hard Lefschetz. The cases where
![]() $g=1$
follow from Proposition 2.2 and induction on n.
$g=1$
follow from Proposition 2.2 and induction on n.
Following the proof strategy above, we obtain the following corollary.
Corollary 7.2. As Hodge structures or Galois representations, we have
for all g and n.
Proof. From the proof above, we see that
![]() $W_{-13}H_{13}^{BM}({\mathcal {M}}_{g,n})=0$
for
$W_{-13}H_{13}^{BM}({\mathcal {M}}_{g,n})=0$
for
![]() $(g,n)\notin Z$
, and so
$(g,n)\notin Z$
, and so
is surjective. Noting that pushforward along a gluing map just induces a Tate twist, by induction on g and n, we reduce to the cases
![]() $(g, n) \in Z$
. The case
$(g, n) \in Z$
. The case
![]() $(g,n)=(2,11)$
follows from Lemma 7.1 and hard Lefschetz. The cases where
$(g,n)=(2,11)$
follows from Lemma 7.1 and hard Lefschetz. The cases where
![]() $g=1$
follow from Proposition 2.2 and induction on n.
$g=1$
follow from Proposition 2.2 and induction on n.
7.2 15th homology
Again, we will argue by induction on g and n. We first need to treat two additional base cases in genus
![]() $2$
. The difficult one is with
$2$
. The difficult one is with
![]() $12$
markings.
$12$
markings.
Lemma 7.3.
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
is generated by classes pushed forward from the boundary. Hence,
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
is generated by classes pushed forward from the boundary. Hence,
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
is contained in the STE generated by
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
is contained in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
The proof of Lemma 7.3 involves calculating intersection pairings via decorated graphs. In order to simplify pictures for and language surrounding decorated graphs, we use the following conventions:
-
1. A white circle
 $\circ $
is a vertex of genus
$\circ $
is a vertex of genus
 $1$
$1$
-
2. A black circle
 $\bullet $
is a vertex of genus
$\bullet $
is a vertex of genus
 $0$
$0$
-
3. All markings that are not drawn elsewhere are understood to be on the leftmost genus
 $1$
vertex
$1$
vertex -
4. The decoration
 $\omega _i$
on a genus
$\omega _i$
on a genus
 $1$
vertex is shorthand for
$1$
vertex is shorthand for
 $f_i^*\omega $
, where
$f_i^*\omega $
, where
 $f_i\colon {\overline {\mathcal {M}}}_{1,12} \to {\overline {\mathcal {M}}}_{1,11}$
forgets the ith marking and
$f_i\colon {\overline {\mathcal {M}}}_{1,12} \to {\overline {\mathcal {M}}}_{1,11}$
forgets the ith marking and
 $\omega \in H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Similarly,
$\omega \in H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Similarly,
 $\omega _{ij}$
is shorthand for
$\omega _{ij}$
is shorthand for
 $f_{ij}^*\omega $
, where
$f_{ij}^*\omega $
, where
 $f_{ij} \colon {\overline {\mathcal {M}}}_{1,13} \to {\overline {\mathcal {M}}}_{1,11}$
forgets the ith and jth markings.
$f_{ij} \colon {\overline {\mathcal {M}}}_{1,13} \to {\overline {\mathcal {M}}}_{1,11}$
forgets the ith and jth markings. -
5. As we vary the decoration
 $\omega $
over
$\omega $
over
 $H^{11}({\overline {\mathcal {M}}}_{1,11}) \cong {\mathsf {S}}_{12}$
, pushforward along a map that glues e pairs of marked points determines a morphism
$H^{11}({\overline {\mathcal {M}}}_{1,11}) \cong {\mathsf {S}}_{12}$
, pushforward along a map that glues e pairs of marked points determines a morphism
 $\mathsf {L}^e {\mathsf {S}}_{12} \to H^{11+2e}({\overline {\mathcal {M}}}_{g,n})$
. We say that a collection of
$\mathsf {L}^e {\mathsf {S}}_{12} \to H^{11+2e}({\overline {\mathcal {M}}}_{g,n})$
. We say that a collection of
 $\omega $
-decorated graphs “is a basis for
$\omega $
-decorated graphs “is a basis for
 $H^k({\overline {\mathcal {M}}}_{g,n})$
” if the corresponding morphisms
$H^k({\overline {\mathcal {M}}}_{g,n})$
” if the corresponding morphisms
 $\mathsf {L}^e {\mathsf {S}}_{12} \to H^{k}({\overline {\mathcal {M}}}_{g,n})$
form a basis for
$\mathsf {L}^e {\mathsf {S}}_{12} \to H^{k}({\overline {\mathcal {M}}}_{g,n})$
form a basis for
 $\operatorname {\mathrm {Hom}}(\mathsf {L}^e{\mathsf {S}}_{12}, H^{k}({\overline {\mathcal {M}}}_{g,n}))$
and we have
$\operatorname {\mathrm {Hom}}(\mathsf {L}^e{\mathsf {S}}_{12}, H^{k}({\overline {\mathcal {M}}}_{g,n}))$
and we have
 $H^k({\overline {\mathcal {M}}}_{g,n}) \cong \operatorname {\mathrm {Hom}}(\mathsf {L}^e{\mathsf {S}}_{12}, H^{k}({\overline {\mathcal {M}}}_{g,n})) \otimes \mathsf {L}^e {\mathsf {S}}_{12}$
.
$H^k({\overline {\mathcal {M}}}_{g,n}) \cong \operatorname {\mathrm {Hom}}(\mathsf {L}^e{\mathsf {S}}_{12}, H^{k}({\overline {\mathcal {M}}}_{g,n})) \otimes \mathsf {L}^e {\mathsf {S}}_{12}$
.
Bergström and Faber’s implementation [Reference Bergström2] of the Getzler–Kapranov formula in genus
![]() $2$
shows that, viewed as Galois representations,
$2$
shows that, viewed as Galois representations,
In fact, we will produce
![]() $836$
independent maps
$836$
independent maps
![]() ${\mathsf {L}}^2{\mathsf {S}}_{12} \to H^{15}({\overline {\mathcal {M}}}_{2,12})$
that arise through pushforward from the boundary. From this, we will conclude that
${\mathsf {L}}^2{\mathsf {S}}_{12} \to H^{15}({\overline {\mathcal {M}}}_{2,12})$
that arise through pushforward from the boundary. From this, we will conclude that
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
is semi-simple and decomposes as a sum of these
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
is semi-simple and decomposes as a sum of these
![]() $836$
copies of
$836$
copies of
![]() ${\mathsf {L}}^2{\mathsf {S}}_{12}$
.
${\mathsf {L}}^2{\mathsf {S}}_{12}$
.
As discussed above, an
![]() $\omega $
-decorated graph with e edges represents a morphism
$\omega $
-decorated graph with e edges represents a morphism
![]() $\mathsf {L}^e {\mathsf {S}}_{12} \to H^{11 + 2e}({\overline {\mathcal {M}}}_{g,n})$
. In Figure 2, we list
$\mathsf {L}^e {\mathsf {S}}_{12} \to H^{11 + 2e}({\overline {\mathcal {M}}}_{g,n})$
. In Figure 2, we list
![]() $891$
such decorated graphs for
$891$
such decorated graphs for
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
and record particular Künneth components of their pullbacks to boundary divisors. We then argue that there are
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
and record particular Künneth components of their pullbacks to boundary divisors. We then argue that there are
![]() $55$
relations among these graphs, which allow us to conclude that there are
$55$
relations among these graphs, which allow us to conclude that there are
![]() $836$
independent graphs among them.
$836$
independent graphs among them.

Figure 2 Selected Künneth components of pullbacks of the
![]() $891$
classes to boundary divisors. In the chart, each row represents several rows of a block matrix. The number of rows in each group is listed to its left. The two half-edges glued to make a boundary divisor (pictured across the top) are labeled q on the left vertex and p on the right vertex.
$891$
classes to boundary divisors. In the chart, each row represents several rows of a block matrix. The number of rows in each group is listed to its left. The two half-edges glued to make a boundary divisor (pictured across the top) are labeled q on the left vertex and p on the right vertex.
Before proving Lemma 7.3, we require some explicit bases for
![]() $H^{13}({\overline {\mathcal {M}}}_{g,n})$
for small
$H^{13}({\overline {\mathcal {M}}}_{g,n})$
for small
![]() $g, n$
. Recall that Getzler [Reference Getzler16] showed that
$g, n$
. Recall that Getzler [Reference Getzler16] showed that
![]() $H^{13}({\overline {\mathcal {M}}}_{1,n})^{\mathrm {ss}} = \bigoplus \mathsf {L}{\mathsf {S}}_{12}$
for all n.
$H^{13}({\overline {\mathcal {M}}}_{1,n})^{\mathrm {ss}} = \bigoplus \mathsf {L}{\mathsf {S}}_{12}$
for all n.
Lemma 7.4. The following
![]() $11\ \omega $
-decorated graphs form a basis for
$11\ \omega $
-decorated graphs form a basis for
![]() $H^{13}({\overline {\mathcal {M}}}_{1,12})$
$H^{13}({\overline {\mathcal {M}}}_{1,12})$

Proof. Consider the block diagonal pairing against the basis for
![]() $H^{11}({\overline {\mathcal {M}}}_{1,12})$
given by the set of genus
$H^{11}({\overline {\mathcal {M}}}_{1,12})$
given by the set of genus
![]() $1$
vertices decorated by
$1$
vertices decorated by
![]() $\omega _2, \ldots , \omega _{12}$
.
$\omega _2, \ldots , \omega _{12}$
.
Lemma 7.5. The following
![]() $429\ \omega $
-decorated graphs form a basis for
$429\ \omega $
-decorated graphs form a basis for
![]() $H^{13}({\overline {\mathcal {M}}}_{1,13})$
$H^{13}({\overline {\mathcal {M}}}_{1,13})$

Above,
![]() $x, y$
are any two markings. In the last group of classes, i or j can be equal to y.
$x, y$
are any two markings. In the last group of classes, i or j can be equal to y.
Proof. Getzler [Reference Getzler16] proved that
![]() $H^{13}({\overline {\mathcal {M}}}_{1,13})^{\mathrm {ss}} = 429 \, \mathsf {L}{\mathsf {S}}_{12}$
, so it suffices to show that the images of these maps span. We know that
$H^{13}({\overline {\mathcal {M}}}_{1,13})^{\mathrm {ss}} = 429 \, \mathsf {L}{\mathsf {S}}_{12}$
, so it suffices to show that the images of these maps span. We know that
![]() $H^{13}({\overline {\mathcal {M}}}_{1,13})$
is pushed forward from the boundary by Proposition 2.2. Modulo classes of the first kind, the second two kinds are pulled back from
$H^{13}({\overline {\mathcal {M}}}_{1,13})$
is pushed forward from the boundary by Proposition 2.2. Modulo classes of the first kind, the second two kinds are pulled back from
![]() $H^{13}({\overline {\mathcal {M}}}_{1,12})$
. Pulling back the relations from
$H^{13}({\overline {\mathcal {M}}}_{1,12})$
. Pulling back the relations from
![]() $H^{13}({\overline {\mathcal {M}}}_{1,12})$
, we can ensure that a fixed marking, such as y in the first case or x in the next case, is on the genus
$H^{13}({\overline {\mathcal {M}}}_{1,12})$
, we can ensure that a fixed marking, such as y in the first case or x in the next case, is on the genus
![]() $0$
vertex.
$0$
vertex.
Lemma 7.6. Let
![]() $\{x, y, 1, \ldots , 12\}$
be a set of
$\{x, y, 1, \ldots , 12\}$
be a set of
![]() $14$
markings. The following
$14$
markings. The following
![]() $6,006\ \omega $
-decorated graphs form a basis for
$6,006\ \omega $
-decorated graphs form a basis for
![]() $H^{13}({\overline {\mathcal {M}}}_{1,14})$
$H^{13}({\overline {\mathcal {M}}}_{1,14})$

In the last grouping above,
![]() $i, j$
or k can equal y.
$i, j$
or k can equal y.
Proof. Getzler [Reference Getzler16] proved that
![]() $H^{13}({\overline {\mathcal {M}}}_{1,14})^{\mathrm {ss}}=6006\,\mathsf {L}{\mathsf {S}}_{12}$
, so it suffices to show that the images of these maps span. Modulo classes of the first and second kinds above, the last three kinds are pulled back from
$H^{13}({\overline {\mathcal {M}}}_{1,14})^{\mathrm {ss}}=6006\,\mathsf {L}{\mathsf {S}}_{12}$
, so it suffices to show that the images of these maps span. Modulo classes of the first and second kinds above, the last three kinds are pulled back from
![]() ${\overline {\mathcal {M}}}_{1,12}$
. Thus, using the relations on
${\overline {\mathcal {M}}}_{1,12}$
. Thus, using the relations on
![]() $H^{13}({\overline {\mathcal {M}}}_{1,12})$
, we can ensure that a fixed marking among those
$H^{13}({\overline {\mathcal {M}}}_{1,12})$
, we can ensure that a fixed marking among those
![]() $12$
is on the genus
$12$
is on the genus
![]() $0$
vertex.
$0$
vertex.
Lemma 7.7. The following
![]() $264\ \omega $
-decorated graphs form a basis for
$264\ \omega $
-decorated graphs form a basis for
![]() $H^{13}({\overline {\mathcal {M}}}_{2,12})$
$H^{13}({\overline {\mathcal {M}}}_{2,12})$

Proof. Bergström and Faber’s implementation [Reference Bergström2] of the Getzler–Kapranov formula in genus
![]() $2$
shows that, as Galois representations,
$2$
shows that, as Galois representations,
![]() $H^{13}({\overline {\mathcal {M}}}_{2,12})^{\mathrm {ss}} = 264 \, \mathsf {L}{\mathsf {S}}_{12}$
. Thus, it suffices to show that the above
$H^{13}({\overline {\mathcal {M}}}_{2,12})^{\mathrm {ss}} = 264 \, \mathsf {L}{\mathsf {S}}_{12}$
. Thus, it suffices to show that the above
![]() $264$
maps are independent. We verify this by computing their pullbacks to
$264$
maps are independent. We verify this by computing their pullbacks to
![]() $H^{13}({\overline {\mathcal {M}}}_{1,14})$
and using Lemma 7.6 to see that those maps are independent. Indeed, the pullback is given by the graph that replaces the rightmost genus
$H^{13}({\overline {\mathcal {M}}}_{1,14})$
and using Lemma 7.6 to see that those maps are independent. Indeed, the pullback is given by the graph that replaces the rightmost genus
![]() $1$
vertex with a genus
$1$
vertex with a genus
![]() $0$
vertex and adds two markings labeled
$0$
vertex and adds two markings labeled
![]() $x, y$
to that vertex.
$x, y$
to that vertex.
Remark 7.8. Theorem 1.6 says that
![]() $H_{13}({\overline {\mathcal {M}}}_{g,n})$
is contained in the STE generated by
$H_{13}({\overline {\mathcal {M}}}_{g,n})$
is contained in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Thus, it has a graphical presentation in which the generators are graphs of the sort appearing in Lemmas 7.4–7.7. In forthcoming work, we will show that
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
. Thus, it has a graphical presentation in which the generators are graphs of the sort appearing in Lemmas 7.4–7.7. In forthcoming work, we will show that
![]() $H^{13}({\overline {\mathcal {M}}}_{g,n})$
is also contained in this STE. There, we take a more systematic approach and provide a complete list of relations among the corresponding decorated graph generators.
$H^{13}({\overline {\mathcal {M}}}_{g,n})$
is also contained in this STE. There, we take a more systematic approach and provide a complete list of relations among the corresponding decorated graph generators.
Proof of Lemma 7.3.
Figure 2 represents a matrix with
![]() $891$
rows. We first show that the matrix has rank
$891$
rows. We first show that the matrix has rank
![]() $825$
and describe the
$825$
and describe the
![]() $66$
relations among the rows.
$66$
relations among the rows.
First, notice that the rows in A1 are the only rows with nonzero entries in the first column. Next, rows in A2, A3 and A4 have entries in column 2 that are independent from the other entries that appear in that column for later rows (by Lemma 7.5). This shows that the rows in A1 through A4 are independent and independent from the remaining five rows. Meanwhile, the bottom four rows are block upper triangular. This shows that the rank of the matrix is at least
![]() $825$
.
$825$
.
Meanwhile, it is not hard to check that the following
![]() $66$
relations exist among the rows:
$66$
relations exist among the rows:
To verify these relations, one needs to make use of known relations among tautological classes in
![]() $H^4({\overline {\mathcal {M}}}_{1,3})$
and
$H^4({\overline {\mathcal {M}}}_{1,3})$
and
![]() $H^2({\overline {\mathcal {M}}}_{1,2})$
and
$H^2({\overline {\mathcal {M}}}_{1,2})$
and
![]() $H^2({\overline {\mathcal {M}}}_{1,1})$
.
$H^2({\overline {\mathcal {M}}}_{1,1})$
.
Now, let

We claim
![]() $M_{ij} \neq 0$
. To see this, consider the intersection of
$M_{ij} \neq 0$
. To see this, consider the intersection of
![]() $M_{ij}$
with
$M_{ij}$
with
![]() $R_5(ik)$
for
$R_5(ik)$
for
![]() $k \neq j$
. The intersection of
$k \neq j$
. The intersection of
![]() $R_5(ik)$
with the first five terms in the above equation vanish, since there is no
$R_5(ik)$
with the first five terms in the above equation vanish, since there is no
![]() $H^{11}$
on a genus
$H^{11}$
on a genus
![]() $1$
vertex with less than
$1$
vertex with less than
![]() $11$
markings. Meanwhile, the intersection
$11$
markings. Meanwhile, the intersection
![]() $R_5(ij) \cdot R_5(ik)$
is nonzero using the usual rules for intersecting decorated graphs, as in [Reference Graber and Pandharipande17]. To see this, one should take the
$R_5(ij) \cdot R_5(ik)$
is nonzero using the usual rules for intersecting decorated graphs, as in [Reference Graber and Pandharipande17]. To see this, one should take the
![]() $\omega $
decoration on the
$\omega $
decoration on the
![]() ${\overline {\mathcal {M}}}_{1,11}$
vertex in
${\overline {\mathcal {M}}}_{1,11}$
vertex in
![]() $R_5(ij)$
to be dual to the decoration used on the
$R_5(ij)$
to be dual to the decoration used on the
![]() ${\overline {\mathcal {M}}}_{1,11}$
vertex in
${\overline {\mathcal {M}}}_{1,11}$
vertex in
![]() $R_5(ik)$
.
$R_5(ik)$
.
Finally, the
![]() $\mathbb {S}_{12}$
action on the symbols
$\mathbb {S}_{12}$
action on the symbols
![]() $M_{ij}$
is
$M_{ij}$
is
![]() $\mathrm {Ind}_{\mathbb {S}_{10}}^{\mathbb {S}_{12}}(V_{1^{10}}) = V_{2,1^{10}} \oplus V_{3,1^9}$
, which is a sum of irreducible representations of dimension
$\mathrm {Ind}_{\mathbb {S}_{10}}^{\mathbb {S}_{12}}(V_{1^{10}}) = V_{2,1^{10}} \oplus V_{3,1^9}$
, which is a sum of irreducible representations of dimension
![]() $11$
and
$11$
and
![]() $55$
. It follows that there are either
$55$
. It follows that there are either
![]() $11$
or
$11$
or
![]() $55$
relations among the
$55$
relations among the
![]() $M_{ij}$
. There cannot be only
$M_{ij}$
. There cannot be only
![]() $11$
relations among the
$11$
relations among the
![]() $M_{ij}$
because then there would be more than
$M_{ij}$
because then there would be more than
![]() $836$
independent copies of
$836$
independent copies of
![]() ${\mathsf {L}}^2{\mathsf {S}}_{12}$
in
${\mathsf {L}}^2{\mathsf {S}}_{12}$
in
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
, violating the dimension count (7.1). Hence, there must be exactly
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
, violating the dimension count (7.1). Hence, there must be exactly
![]() $55$
relations among the
$55$
relations among the
![]() $M_{ij}$
. This shows that the
$M_{ij}$
. This shows that the
![]() $891$
copies of
$891$
copies of
![]() ${\mathsf {L}}^2{\mathsf {S}}_{12}$
listed on the left of the table generate an
${\mathsf {L}}^2{\mathsf {S}}_{12}$
listed on the left of the table generate an
![]() $836$
-dimensional space, so they span all of
$836$
-dimensional space, so they span all of
![]() $H^{15}({\overline {\mathcal {M}}}_{2,12})$
.
$H^{15}({\overline {\mathcal {M}}}_{2,12})$
.
Remark 7.9. One could instead prove that the
![]() $891$
classes span a space of rank
$891$
classes span a space of rank
![]() $836$
by computing the pairing of this space against itself. By the argument above, the pairing must have rank
$836$
by computing the pairing of this space against itself. By the argument above, the pairing must have rank
![]() $836$
.
$836$
.
Finally, applying Lemma 3.2(a) together with Lemmas 7.3 and 7.7, and Corollary 2.3, we obtain one more base case.
Lemma 7.10.
![]() $H^{15}({\overline {\mathcal {M}}}_{2,13})$
lies in the STE generated by
$H^{15}({\overline {\mathcal {M}}}_{2,13})$
lies in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
.
Proof of Theorem 1.7.
The proof is similar to that of Theorem 1.6. When
![]() $g=0$
, all odd cohomology vanishes [Reference Keel18], so we can assume
$g=0$
, all odd cohomology vanishes [Reference Keel18], so we can assume
![]() $g\geq 1$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
$g\geq 1$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1] and the duality between
![]() $H_{15}^{BM}$
and
$H_{15}^{BM}$
and
![]() $H^{15}_c$
, we have that for
$H^{15}_c$
, we have that for
![]() $g\geq 1$
$g\geq 1$
 $$ \begin{align*} H^{BM}_{15}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} 15<2g \text{ and } n=0,1 \\ 15<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} H^{BM}_{15}({\mathcal{M}}_{g,n})=0 \text{ for } \begin{cases} 15<2g \text{ and } n=0,1 \\ 15<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
Combining this with the exact sequence (6.1), we reduce inductively to the finitely many cases
![]() $15\geq 2g$
and
$15\geq 2g$
and
![]() $n=0,1$
or
$n=0,1$
or
![]() $15\geq 2g-2+n$
and
$15\geq 2g-2+n$
and
![]() $n\geq 2$
. In such cases, when
$n\geq 2$
. In such cases, when
![]() $g\geq 3$
,
$g\geq 3$
,
![]() ${\mathcal {M}}_{g,n}$
has the CKgP, and so by induction and the exact sequence (6.1), we reduce to the cases where
${\mathcal {M}}_{g,n}$
has the CKgP, and so by induction and the exact sequence (6.1), we reduce to the cases where
![]() $g=1$
and
$g=1$
and
![]() $11\leq n \leq 14$
, or
$11\leq n \leq 14$
, or
![]() $g=2$
and
$g=2$
and
![]() $11\leq n\leq 13$
. When
$11\leq n\leq 13$
. When
![]() $g=2$
and
$g=2$
and
![]() $n=11$
, the result follows from hard Lefschetz and Lemma 7.1. When
$n=11$
, the result follows from hard Lefschetz and Lemma 7.1. When
![]() $g=2$
and
$g=2$
and
![]() $12\leq n\leq 13$
, the result follows from Lemmas 7.3 and 7.10. For
$12\leq n\leq 13$
, the result follows from Lemmas 7.3 and 7.10. For
![]() $g = 1$
, the claim follows from Proposition 2.2.
$g = 1$
, the claim follows from Proposition 2.2.
Corollary 7.11. As Hodge structures or Galois representations, we have
for all g and n.
Proof. The proof is similar to that of Corollary 7.2, using the additional input that
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15})^{\mathrm {ss}} \cong {\mathsf {S}}_{16} \oplus 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
by [Reference Getzler16, p. 491].
$H^{15}({\overline {\mathcal {M}}}_{1,15})^{\mathrm {ss}} \cong {\mathsf {S}}_{16} \oplus 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
by [Reference Getzler16, p. 491].
We expect that Theorem 1.7 can be improved as follows.
Conjecture 7.12. The STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
![]() $H^{15}({\overline {\mathcal {M}}}_{g,n})$
for
$H^{15}({\overline {\mathcal {M}}}_{g,n})$
for
![]() $g \geq 2$
.
$g \geq 2$
.
The proof of Theorem 1.1 in the next section shows that for
![]() $g\geq 2$
,
$g\geq 2$
,
![]() $H^{15}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
contains no copies of
$H^{15}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
contains no copies of
![]() ${\mathsf {S}}_{16}$
. Conjecture 7.12 is, therefore, equivalent to the assertion that the STE generated by
${\mathsf {S}}_{16}$
. Conjecture 7.12 is, therefore, equivalent to the assertion that the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15})$
contains
$H^{15}({\overline {\mathcal {M}}}_{1,15})$
contains
![]() $H^{15}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
$H^{15}({\overline {\mathcal {M}}}_{g,n})$
for all g and n.
8 Proof of Theorem 1.1
The first two statements of Theorem 1.1 follow immediately from Corollaries 6.2 and 7.2 by Poincaré duality. From Corollary 7.11, we can similarly conclude that
![]() $H^{15}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
is a direct sum of copies of
$H^{15}({\overline {\mathcal {M}}}_{g,n})^{\mathrm {ss}}$
is a direct sum of copies of
![]() ${\mathsf {L}}^2 {\mathsf {S}}_{12}$
and
${\mathsf {L}}^2 {\mathsf {S}}_{12}$
and
![]() ${\mathsf {S}}_{16}$
. To finish, it suffices to show that when
${\mathsf {S}}_{16}$
. To finish, it suffices to show that when
![]() $g\geq 2$
, no copies of
$g\geq 2$
, no copies of
![]() ${\mathsf {S}}_{16}$
appear.
${\mathsf {S}}_{16}$
appear.
Lemma 8.1. The STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
contains
![]() $H_{15}({\overline {\mathcal {M}}}_{2,n})$
for all n. Hence,
$H_{15}({\overline {\mathcal {M}}}_{2,n})$
for all n. Hence,
![]() $H^{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}} \cong \bigoplus {\mathsf {L}}^2{\mathsf {S}}_{12}$
, as Galois representations or Hodge structures.
$H^{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}} \cong \bigoplus {\mathsf {L}}^2{\mathsf {S}}_{12}$
, as Galois representations or Hodge structures.
Proof. When
![]() $g=2$
, as Galois representations, there are no copies of
$g=2$
, as Galois representations, there are no copies of
![]() ${\mathsf {S}}_{16}$
in
${\mathsf {S}}_{16}$
in
![]() $H^{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
by Corollary 2.9. This shows that
$H^{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
by Corollary 2.9. This shows that
![]() $H_{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
is a direct sum of copies of
$H_{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
is a direct sum of copies of
![]() $\mathsf {L}^{d_{2,n} - 13} {\mathsf {S}}_{12}$
in the category of Galois representations. But we know that
$\mathsf {L}^{d_{2,n} - 13} {\mathsf {S}}_{12}$
in the category of Galois representations. But we know that
![]() $H_{15}({\overline {\mathcal {M}}}_{g,n})$
lies in the STE generated by
$H_{15}({\overline {\mathcal {M}}}_{g,n})$
lies in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
and
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15})$
by Theorem 1.7. By considering the Galois representations involved, it follows that
$H^{15}({\overline {\mathcal {M}}}_{1,15})$
by Theorem 1.7. By considering the Galois representations involved, it follows that
![]() $H_{15}({\overline {\mathcal {M}}}_{2,n})$
lies in the STE generated by
$H_{15}({\overline {\mathcal {M}}}_{2,n})$
lies in the STE generated by
![]() $H^{11}({\overline {\mathcal {M}}}_{1,11})$
. In particular,
$H^{11}({\overline {\mathcal {M}}}_{1,11})$
. In particular,
![]() $H_{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
is a direct sum of copies of
$H_{15}({\overline {\mathcal {M}}}_{2,n})^{\mathrm {ss}}$
is a direct sum of copies of
![]() $\mathsf {L}^{d_{2,n} - 13} {\mathsf {S}}_{12}$
, either as Galois representations or Hodge structures. The second statement follows by Poincaré duality.
$\mathsf {L}^{d_{2,n} - 13} {\mathsf {S}}_{12}$
, either as Galois representations or Hodge structures. The second statement follows by Poincaré duality.
To show there are no copies of
![]() ${\mathsf {S}}_{16}$
when
${\mathsf {S}}_{16}$
when
![]() $g\geq 3$
, we will use a similar strategy to that of [Reference Canning, Larson and Payne8]. We study the first two maps in the weight
$g\geq 3$
, we will use a similar strategy to that of [Reference Canning, Larson and Payne8]. We study the first two maps in the weight
![]() $15$
complex:
$15$
complex:
Here,
![]() $\Gamma $
is a stable graph of genus g with n legs. The first map is the pullback to the normalization of the boundary
$\Gamma $
is a stable graph of genus g with n legs. The first map is the pullback to the normalization of the boundary
![]() $\widetilde {\partial {\mathcal {M}}_{g,n}}$
. The second map is explicitly described in [Reference Canning, Larson and Payne8, Section 4.1].
$\widetilde {\partial {\mathcal {M}}_{g,n}}$
. The second map is explicitly described in [Reference Canning, Larson and Payne8, Section 4.1].
Lemma 8.2. If
![]() $g\geq 3$
, then the pullback map
$g\geq 3$
, then the pullback map
![]() $\alpha $
in (8.1) is injective.
$\alpha $
in (8.1) is injective.
Proof. The map
![]() $\alpha $
is injective when
$\alpha $
is injective when
![]() $\mathrm {gr}^W_{15}H^{15}_c({\mathcal {M}}_{g,n})=0$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1], this holds whenever
$\mathrm {gr}^W_{15}H^{15}_c({\mathcal {M}}_{g,n})=0$
. By [Reference Bergström, Faber and Payne4, Proposition 2.1], this holds whenever
![]() $2g-2+n>15$
. When
$2g-2+n>15$
. When
![]() $2g-2+n\leq 15$
,
$2g-2+n\leq 15$
,
![]() ${\mathcal {M}}_{g,n}$
has the CKgP (see Table 1). The result follows from Proposition 4.5.
${\mathcal {M}}_{g,n}$
has the CKgP (see Table 1). The result follows from Proposition 4.5.
We now assume
![]() $g\geq 3$
, and we study the second map in (8.1) as a morphism of Hodge structures. In particular, we consider the
$g\geq 3$
, and we study the second map in (8.1) as a morphism of Hodge structures. In particular, we consider the
![]() $H^{15,0}$
part:
$H^{15,0}$
part:
 $$ \begin{align} \bigoplus_{|E(\Gamma)| = 1} H^{15,0}({\overline{\mathcal{M}}}_{\Gamma})^{\operatorname{\mathrm{Aut}}(\Gamma)} \xrightarrow{ \ \beta \ } \bigoplus_{|E(\Gamma)| = 2} \big(H^{15,0}({\overline{\mathcal{M}}}_{\Gamma}) \otimes \det E(\Gamma)\big)^{\operatorname{\mathrm{Aut}}(\Gamma)}. \end{align} $$
$$ \begin{align} \bigoplus_{|E(\Gamma)| = 1} H^{15,0}({\overline{\mathcal{M}}}_{\Gamma})^{\operatorname{\mathrm{Aut}}(\Gamma)} \xrightarrow{ \ \beta \ } \bigoplus_{|E(\Gamma)| = 2} \big(H^{15,0}({\overline{\mathcal{M}}}_{\Gamma}) \otimes \det E(\Gamma)\big)^{\operatorname{\mathrm{Aut}}(\Gamma)}. \end{align} $$
By Lemma 8.2, to prove the theorem in the category of Hodge structures, it suffices to show that
![]() $\beta $
is injective. The domain is a direct sum over graphs with one edge. If
$\beta $
is injective. The domain is a direct sum over graphs with one edge. If
![]() $\Gamma $
has one vertex and a loop, then
$\Gamma $
has one vertex and a loop, then
![]() $H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })=H^{15,0}({\overline {\mathcal {M}}}_{g-1,n+2})=0$
by induction on g. If
$H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })=H^{15,0}({\overline {\mathcal {M}}}_{g-1,n+2})=0$
by induction on g. If
![]() $\Gamma $
has two vertices with an edge connecting them, then by the Künneth formula, we have
$\Gamma $
has two vertices with an edge connecting them, then by the Künneth formula, we have
Assume
![]() $a\geq b$
. By induction, the above is nonvanishing only if
$a\geq b$
. By induction, the above is nonvanishing only if
![]() $b=1$
and
$b=1$
and
![]() $|A^c|\geq 14$
. Because
$|A^c|\geq 14$
. Because
![]() $g\geq 3$
, it follows that
$g\geq 3$
, it follows that
![]() $H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })=H^{15,0}({\overline {\mathcal {M}}}_{1,A^c\cup q})$
in this case. Let
$H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })=H^{15,0}({\overline {\mathcal {M}}}_{1,A^c\cup q})$
in this case. Let
![]() $\Gamma '$
be the graph obtained from
$\Gamma '$
be the graph obtained from
![]() $\Gamma $
by adding a loop on the genus
$\Gamma $
by adding a loop on the genus
![]() $g-1$
vertex and decreasing the genus accordingly, as in Figure 3. Then
$g-1$
vertex and decreasing the genus accordingly, as in Figure 3. Then
![]() $H^{15,0}({\overline {\mathcal {M}}}_{\Gamma '})$
has a summand
$H^{15,0}({\overline {\mathcal {M}}}_{\Gamma '})$
has a summand
![]() $H^{15,0}({\overline {\mathcal {M}}}_{1,A^c\cup q})$
, and the map
$H^{15,0}({\overline {\mathcal {M}}}_{1,A^c\cup q})$
, and the map
![]() $H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })\rightarrow H^{15,0}({\overline {\mathcal {M}}}_{\Gamma '})$
injects into that summand. This completes the proof of Theorem 1.1 in the category of Hodge structures.
$H^{15,0}({\overline {\mathcal {M}}}_{\Gamma })\rightarrow H^{15,0}({\overline {\mathcal {M}}}_{\Gamma '})$
injects into that summand. This completes the proof of Theorem 1.1 in the category of Hodge structures.

Figure 3 The graph
![]() $\Gamma $
on the left and
$\Gamma $
on the left and
![]() $\Gamma '$
on the right.
$\Gamma '$
on the right.
Finally, we explain how to deduce the result in the category of Galois representations from the result in the category of Hodge structures. To do so, we need one more lemma.
Lemma 8.3. Let
![]() $V \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
be the subspace of classes pushed forward from the boundary, and let
$V \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
be the subspace of classes pushed forward from the boundary, and let
![]() $W \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
be the image of
$W \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
be the image of
![]() $H^{15}_c({\mathcal {M}}_{1,15}) \to H^{15}({\overline {\mathcal {M}}}_{1,15})$
. Then there is a direct sum decomposition
$H^{15}_c({\mathcal {M}}_{1,15}) \to H^{15}({\overline {\mathcal {M}}}_{1,15})$
. Then there is a direct sum decomposition
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15}) = V \oplus W$
, as Hodge structures or as Galois representations. Moreover, we have
$H^{15}({\overline {\mathcal {M}}}_{1,15}) = V \oplus W$
, as Hodge structures or as Galois representations. Moreover, we have
![]() $W \cong {\mathsf {S}}_{16}$
and
$W \cong {\mathsf {S}}_{16}$
and
![]() $V^{\mathrm {ss}} \cong 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
.
$V^{\mathrm {ss}} \cong 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
.
Proof. There is an exact sequence
It thus suffices to show that the composition
is an isomorphism. The pairing
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15}) \times H^{15}({\overline {\mathcal {M}}}_{1,15}) \to \mathbb {Q}$
equips
$H^{15}({\overline {\mathcal {M}}}_{1,15}) \times H^{15}({\overline {\mathcal {M}}}_{1,15}) \to \mathbb {Q}$
equips
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15})$
with a nondegenerate bilinear form, under which the inclusion of W is dual to the quotient
$H^{15}({\overline {\mathcal {M}}}_{1,15})$
with a nondegenerate bilinear form, under which the inclusion of W is dual to the quotient
![]() $H^{15}({\overline {\mathcal {M}}}_{1,15}) \to W_{15} H^{15}({\mathcal {M}}_{1,15})$
. To show (8.3) is an isomorphism is, therefore, equivalent to showing that the restriction of the pairing to W with itself is full rank. This becomes clear in the category of Hodge structures: Since V has type
$H^{15}({\overline {\mathcal {M}}}_{1,15}) \to W_{15} H^{15}({\mathcal {M}}_{1,15})$
. To show (8.3) is an isomorphism is, therefore, equivalent to showing that the restriction of the pairing to W with itself is full rank. This becomes clear in the category of Hodge structures: Since V has type
![]() $H^{13,2} \oplus H^{2,13}$
and W has type
$H^{13,2} \oplus H^{2,13}$
and W has type
![]() $H^{15,0} \oplus H^{0,15}$
, the pairing between V and W is trivial, so W must be full rank on itself. This claim holds at the level of
$H^{15,0} \oplus H^{0,15}$
, the pairing between V and W is trivial, so W must be full rank on itself. This claim holds at the level of
![]() $\mathbb {Q}$
-vector spaces. Since all the maps above are also maps of Galois representations, we have a direct sum decomposition as Galois representations too.
$\mathbb {Q}$
-vector spaces. Since all the maps above are also maps of Galois representations, we have a direct sum decomposition as Galois representations too.
The identification of the remainder
![]() $V^{\mathrm {ss}} = 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
follows from [Reference Getzler16, p. 491].
$V^{\mathrm {ss}} = 186263\, {\mathsf {L}}^2{\mathsf {S}}_{12}$
follows from [Reference Getzler16, p. 491].
By Poincaré duality, to prove Theorem 1.1, it suffices to show that when
![]() $g \geq 2$
, there are no copies of
$g \geq 2$
, there are no copies of
![]() $\mathsf {L}^{d_{g,n}-15} {\mathsf {S}}_{16}$
in the right-hand side of Corollary 7.11. The proof of Theorem 1.7 exhibits
$\mathsf {L}^{d_{g,n}-15} {\mathsf {S}}_{16}$
in the right-hand side of Corollary 7.11. The proof of Theorem 1.7 exhibits
![]() $H^{2d_{g,n} - 15}({\overline {\mathcal {M}}}_{g,n})$
as a quotient of a direct sum of the form
$H^{2d_{g,n} - 15}({\overline {\mathcal {M}}}_{g,n})$
as a quotient of a direct sum of the form
where the map from each summand on the left is a composition of a forgetful pullback with a gluing pushforward. By Lemma 8.3, it suffices to show that, for each of these maps, the composition with the inclusion of
![]() $W \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
,
$W \subset H^{15}({\overline {\mathcal {M}}}_{1,15})$
,
vanishes. When we view (8.4) as a map of Hodge structures, we see that it vanishes, since we have already proved Theorem 1.1 in the category of Hodge structures. Thus, (8.4) vanishes as a map of
![]() $\mathbb {Q}$
-vector spaces, and so also as a map of Galois representations.
$\mathbb {Q}$
-vector spaces, and so also as a map of Galois representations.
Acknowledgements
We thank Jonas Bergström, Carel Faber, Rahul Pandharipande, Dan Petersen, Kartik Prasanna, Burt Totaro and Thomas Willwacher for helpful conversations related to this work. We especially thank Dan Petersen for his comments that led to an improved version of Lemma 3.1. S.C. was supported by a Hermann-Weyl-Instructorship from the Forschungsinstitut für Mathematik at ETH Zürich. This research was partially conducted during the period H.L. served as a Clay Research Fellow and as a guest of the Forschungsinstitut für Mathematik at ETH Zürich. S.P. was supported in part by National Science Foundation grants DMS–2302475 and DMS–2053261.
Competing interests
The authors have no competing interest to declare.