Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-12T19:48:49.744Z Has data issue: false hasContentIssue false
  • English
  • Français

THE EXACT MINIMUM NUMBER OF TRIANGLES IN GRAPHS WITH GIVEN ORDER AND SIZE

Part of: Graph theory

Published online by Cambridge University Press:  20 April 2020

HONG LIU ,
OLEG PIKHURKO  and
KATHERINE STADEN
HONG LIU
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, CoventryCV4 7AL, UK; [email protected], [email protected]
OLEG PIKHURKO
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, CoventryCV4 7AL, UK; [email protected], [email protected]
KATHERINE STADEN
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

What is the minimum number of triangles in a graph of given order and size? Motivated by earlier results of Mantel and Turán, Rademacher solved the first nontrivial case of this problem in 1941. The problem was revived by Erdős in 1955; it is now known as the Erdős–Rademacher problem. After attracting much attention, it was solved asymptotically in a major breakthrough by Razborov in 2008. In this paper, we provide an exact solution for all large graphs whose edge density is bounded away from 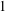$1$, which in this range confirms a conjecture of Lovász and Simonovits from 1975. Furthermore, we give a description of the extremal graphs.

MSC classification

Primary: 05C35: Extremal problems
Type
Discrete Mathematics
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Bollobás, B., ‘On complete subgraphs of different orders’, Math. Proc. Cambridge Philos. Soc. 79 (1976), 19–24.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B., ‘An approximate version of Sidorenko’s conjecture’, Geom. Funct. Anal. 20 (2010), 1354–1366.CrossRefGoogle Scholar
Conlon, D., Kim, J. H., Lee, C. and Lee, J., ‘Some advances on Sidorenko’s conjecture’, J. Lond. Math. Soc. 98 (2018), 593–608.CrossRefGoogle Scholar
Csikvári, P., ‘Note on the smallest root of the independence polynomial’, Combin. Probab. Comput. 22 (2013), 1–8.CrossRefGoogle Scholar
Erdős, P. and Simonovits, M., ‘Supersaturated graphs and hypergraphs’, Combinatorica 3 (1983), 181–192.CrossRefGoogle Scholar
Erdős, P., ‘Some theorems on graphs’, Riveon Lematematika 9 (1955), 13–17.Google Scholar
Erdős, P., ‘On a theorem of Rademacher–Turán’, Illinois. J. Maths 6 (1962), 122–127.CrossRefGoogle Scholar
Erdős, P., ‘Some recent results on extremal problems in graph theory. Results’, inTheory of Graphs (Internat. Sympos., Rome, 1966) (Gordon and Breach, New York, 1967), 117–123. (English); pp 124–130 (French).Google Scholar
Erdős, P. and Stone, A. H., ‘On the structure of linear graphs’, Bull. Amer. Math. Soc. (N.S.) 52 (1946), 1087–1091.CrossRefGoogle Scholar
Fisher, D. C., ‘Lower bounds on the number of triangles in a graph’, J. Graph Theory 13 (1989), 505–512.CrossRefGoogle Scholar
Glebov, R., Grzesik, A., Hu, P., Hubai, T., Král’, D. and Volec, J., ‘Densities of 3-vertex graphs’, Preprint, 2016, arXiv:1610.02446.Google Scholar
Goldwurm, M. and Santini, M., ‘Clique polynomials have a unique root of smallest modulus’, Inform. Process. Lett. 75 (2000), 127–132.CrossRefGoogle Scholar
Goodman, A. W., ‘On sets of acquaintances and strangers at any party’, Amer. Math. Monthly 66 (1959), 778–783.CrossRefGoogle Scholar
Harangi, V., ‘On the density of triangles and squares in regular finite and unimodular random graphs’, Combinatorica 33 (2013), 531–548.CrossRefGoogle Scholar
Hatami, H., ‘Graph norms and Sidorenko’s conjecture’, Israel J. Math. 175 (2010), 125–150.CrossRefGoogle Scholar
Hatami, H. and Norine, S., ‘Undecidability of linear inequalities in graph homomorphism densities’, J. Amer. Math. Soc. 24 (2011), 547–565.CrossRefGoogle Scholar
Hatami, H. and Norine, S., ‘On the boundary of the region defined by homomorphism densities’, J. Combin. 10 (2019), 203–219.Google Scholar
Huang, H., Linial, N., Naves, H., Peled, Y. and Sudakov, B., ‘On the 3-local profiles of graphs’, J. Graph Theory 76 (2014), 236–248.CrossRefGoogle Scholar
Kang, M., Makai, T. and Pikhurko, O., ‘Supersaturation problem for the bowtie’, Eur. J. Combin. (2017), in press, doi:10.1016/j.ejc.2020.103107.Google Scholar
Katona, G. O. H., ‘Intersection theorems for systems of finite sets’, Acta Math. Acad. Sci. Hung. 15 (1964), 329–337.CrossRefGoogle Scholar
Kim, J., Liu, H., Pikhurko, O. and Sharifzadeh, M., ‘Asymptotic structure for the clique density theorem’, Preprint, 2019, arXiv:1906.05942.Google Scholar
Kim, J. H., Lee, C. and Lee, J., ‘Two approaches to Sidorenko’s conjecture’, Trans. Amer. Math. Soc. 368 (2016), 5057–5074.CrossRefGoogle Scholar
Kruskal, J. B., ‘The number of simplices in a complex’, inMathematical Optimization Techniques (ed. Bellman, R.) (University California Press, Berkeley, 1963), 251–278.Google Scholar
Li, J. L. X. and Szegedy, B., ‘On the logarithmic calculus and Sidorenko’s conjecture’, Combinatorica (2011), to appear.Google Scholar
Lovász, L. and Simonovits, M., ‘On the number of complete subgraphs of a graph’, inProceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975) (Congressus Numerantium, No. XV, Winnipeg, Man, 1976), 431–441. Utilitas Math.Google Scholar
Lovász, L. and Simonovits, M., ‘On the number of complete subgraphs of a graph. II’, inStudies in Pure Mathematics (Birkhäuser, Basel, 1983), 459–495.CrossRefGoogle Scholar
Mantel, W., ‘Problem 28’, Winkundige Opgaven 10 (1907), 60–61.Google Scholar
Moon, J. W. and Moser, L., ‘On a problem of Turán’, Publ. Math. Inst. Hungar. Acad. Sci. 7 (1962), 283–287.Google Scholar
Mubayi, D., ‘Counting substructures I: color critical graphs’, Adv. Math. 225 (2010), 2731–2740.CrossRefGoogle Scholar
Nikiforov, V., ‘The number of cliques in graphs of given order and size’, Trans. Amer. Math. Soc. 363 (2011), 1599–1618.CrossRefGoogle Scholar
Nikiforov, V. S., ‘On a problem of P Erdős’, Annuaire Univ. Sofia Fac. Math. Méc. 71 (1976/77), 157–160.Google Scholar
Nikiforov, V. S. and Khadzhiivanov, N. G., ‘Solution of the problem of P. Erdős on the number of triangles in graphs with n vertices and [n 2/4] + l edges’, C. R. Acad. Bulgare Sci. 34 (1981), 969–970.Google Scholar
Nordhaus, E. A. and Stewart, B. M., ‘Triangles in an ordinary graph’, Canad. J. Math. 15 (1963), 33–41.CrossRefGoogle Scholar
Pikhurko, O. and Razborov, A., ‘Asymptotic structure of graphs with the minimum number of triangles’, Combin. Probab. Comput. 26 (2017), 138–160.CrossRefGoogle Scholar
Pikhurko, O. and Yilma, Z., ‘Supersaturation problem for color-critical graphs’, J. Combin. Theory B 123 (2017), 148–185.CrossRefGoogle Scholar
Razborov, A., ‘Flag algebras’, J. Symb. Logic 72 (2007), 1239–1282.CrossRefGoogle Scholar
Razborov, A., ‘On the minimal density of triangles in graphs’, Combin. Probab. Comput. 17 (2008), 603–618.CrossRefGoogle Scholar
Reiher, C., ‘The clique density theorem’, Ann. of Math. (2) 184 (2016), 683–707.CrossRefGoogle Scholar
Sidorenko, A. F., ‘A correlation inequality for bipartite graphs’, Graphs Combin. 9 (1993), 201–204.CrossRefGoogle Scholar
Simonovits, M., ‘A method for solving extremal problems in graph theory, stability problems’, inTheory of Graphs (Proc. Colloq., Tihany, 1966) (Academic Press, New York, 1968), 279–319.Google Scholar
Szegedy, B., ‘An information theoretic approach to Sidorenko’s conjecture’, Preprint, 2014, arXiv:1406.6738v3.Google Scholar
Turán, P., ‘On an extremal problem in graph theory (in Hungarian)’, Mat. Fiz. Lapok 48 (1941), 436–452.Google Scholar