Article contents
Brill-Noether theory for curves of a fixed gonality
Published online by Cambridge University Press: 08 January 2021
Abstract
We prove a generalisation of the Brill-Noether theorem for the variety of special divisors
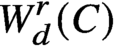 $W^r_d(C)$
on a general curve C of prescribed gonality. Our main theorem gives a closed formula for the dimension of
$W^r_d(C)$
on a general curve C of prescribed gonality. Our main theorem gives a closed formula for the dimension of
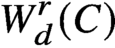 $W^r_d(C)$
. We build on previous work of Pflueger, who used an analysis of the tropical divisor theory of special chains of cycles to give upper bounds on the dimensions of Brill-Noether varieties on such curves. We prove his conjecture, that this upper bound is achieved for a general curve. Our methods introduce logarithmic stable maps as a systematic tool in Brill-Noether theory. A precise relation between the divisor theory on chains of cycles and the corresponding tropical maps theory is exploited to prove new regeneration theorems for linear series with negative Brill-Noether number. The strategy involves blending an analysis of obstruction theories for logarithmic stable maps with the geometry of Berkovich curves. To show the utility of these methods, we provide a short new derivation of lifting for special divisors on a chain of cycles with generic edge lengths, proved using different techniques by Cartwright, Jensen, and Payne. A crucial technical result is a new realisability theorem for tropical stable maps in obstructed geometries, generalising a well-known theorem of Speyer on genus
$W^r_d(C)$
. We build on previous work of Pflueger, who used an analysis of the tropical divisor theory of special chains of cycles to give upper bounds on the dimensions of Brill-Noether varieties on such curves. We prove his conjecture, that this upper bound is achieved for a general curve. Our methods introduce logarithmic stable maps as a systematic tool in Brill-Noether theory. A precise relation between the divisor theory on chains of cycles and the corresponding tropical maps theory is exploited to prove new regeneration theorems for linear series with negative Brill-Noether number. The strategy involves blending an analysis of obstruction theories for logarithmic stable maps with the geometry of Berkovich curves. To show the utility of these methods, we provide a short new derivation of lifting for special divisors on a chain of cycles with generic edge lengths, proved using different techniques by Cartwright, Jensen, and Payne. A crucial technical result is a new realisability theorem for tropical stable maps in obstructed geometries, generalising a well-known theorem of Speyer on genus
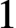 $1$
curves to arbitrary genus.
$1$
curves to arbitrary genus.
MSC classification
- Type
- Algebraic and Complex Geometry
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 11
- Cited by



