INTRODUCTION
Motivation
Understanding farm diversity in its multiple dimensions is decisive in the design of sound agricultural policies (Ruben and Pender, Reference Ruben and Pender2004), and in assessing the suitability of technological innovation to improve agricultural production (Giller et al., Reference Giller, Tittonell, Rufino, van Wijk, Zingore, Mapfumo, Adjei-Nsiah, Herrero, Chikowo, Corbeels, Rowe, Baijukya, Mwijage, Smith, Yeboah, van der Burg, Sanogo, Misiko, de Ridder, Karanja, Kaizzi, K'ungu, Mwale, Nwaga, Pacini and Vanlauwe2011; Tittonell et al., Reference Tittonell, Muriuki, Shepherd, Mugendi, Kaizzi, Okeyo, Verchot, Coe and Vanlauwe2010). Diversity of livelihoods and farmers’ strategies is one of the backbones of sustainability, as it is through diverse farm livelihoods that greater resilience against stresses and shocks may be ensured (Block and Webb, Reference Block and Webb2001; Ellis, Reference Ellis2000; Tesfaye et al., Reference Tesfaye, Perret and Kirsten2004). At regional level, sustainability targets call for a holistic perspective taking into account the whole range of farmers’ responses.
Researchers have used farm typologies to support their studies with various aims, such as building econometric models to predict farm structural change (Zimmermann et al., Reference Zimmermann, Heckelei and Pérez Domínguez2009), selecting case study farms for detailed analyses and modelling (Tittonell et al., Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005, Reference Tittonell, van Wijk, Herrero, Rufino, de Ridder and Giller2009), scaling-up of field and farm-level model results at regional level (Righi et al., Reference Righi, Dogliotti, Stefanini and Pacini2011b), prototyping crop management systems (Blazy et al., Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009), analysing agricultural trajectories (Iraizoz et al., Reference Iraizoz, Gorton and Davidova2007), conceptual investigation in rural sociology (van der Ploeg et al., Reference Van der Ploeg, Laurent, Blondeau and Bonnafous2009) and predicting household behaviour in wealth-based studies (Paumgarten and Shackleton, Reference Paumgarten and Shackleton2009).
In these cases, a major challenge of typology identification typically consists in the large variability of farm production systems, socio-economic circumstances and biophysical conditions, which are distinctive of the agricultural sector. Besides production and biophysical variables, there are a variety of other factors at the root of farm diversity, including household composition, technology and remittance income. Variable selection is a fundamental step in the process of farm data analysis since it can highly affect the resulting typology. The purpose for which the typology is being created should drive such process, and only the factors that have a proven impact on the relevant structural diversity should be selected. To this end, it is often beneficial and sometimes imperative to include local expert knowledge in the process of typology identification.
Considering that local expert knowledge is strongly contextual, can objective replicability be made compatible with the need to take local knowledge and contexts in due consideration? On the opposite end, the use of sophisticated statistical analysis may yield proper farm classifications but remain opaque to many stakeholders involved in the process of dealing with farm diversity. How can the results of statistical analyses be made easily readable for different stakeholders (including other researchers) dealing with the agricultural sector's extreme diversity?
The present paper attempts to address such questions by adopting a number of well-established multivariate techniques and combining them in a way that favours the integration of expert knowledge and communication to a vast range of stakeholders. We provide an application of this method to a sample of farms located in the mid-Zambezi Valley, Zimbabwe, as the starting point of a research for development intervention aimed at designing alternative, sustainable farming strategies.
Background and objectives
Methods for farm or household typology identification include: (i) conceptual categorization based on economic data (e.g. the farm typology relying on the European farm accountancy data network; Decision 85/377/EEC, 1985), on economic and environmental criteria (Andersen et al., Reference Andersen, Elbersen, Godeschalk and Verhoog2007), on socio-economic knowledge (Laurent et al., Reference Laurent, Cartier, Fabre, Mundler, Ponchelet and Remy1998; van der Ploeg et al., Reference Van der Ploeg, Laurent, Blondeau and Bonnafous2009), on a combination of socio-economic and agro-ecological aspects with production objectives (Tittonell et al., Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005), or on iterative abstractions based on contextualized reading of qualitative and quantitative data (Madsen and Adriansen, Reference Madsen and Adriansen2004); (ii) Statistical, non-parametric multivariate analysis (MVA) such as principal component analysis (PCA), multiple correspondence analysis, cluster analysis (CA) and factor analysis (Blazy et al., Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009; Gaspar et al., Reference Gaspar, Escribano, Mesías, Rodriguez de Ledesma and Pulido2008; Iraizoz et al., Reference Iraizoz, Gorton and Davidova2007; Solano et al., Reference Solano, Leon, Perez and Herrero2001); (iii) MVA techniques with parametric distributional assumptions, such as the mixture-of-distribution technique (Kostov and McErlean, Reference Kostov and McErlean2006); (iv) Participatory techniques such as wealth ranking and focus groups (Adams et al., Reference Adams, Evans, Mohammed and Farnsworth1997; Zingore et al., Reference Zingore, Murwira, Delve and Giller2007), in some cases corroborated by MVA techniques (e.g. Paumgarten and Shackleton, Reference Paumgarten and Shackleton2009; Tittonell et al., Reference Tittonell, Muriuki, Shepherd, Mugendi, Kaizzi, Okeyo, Verchot, Coe and Vanlauwe2010).
Each approach to farm typology identification has strengths and weaknesses. Quantitative identification and characterization methods based on multivariate descriptors are sometimes preferred to a priori approaches based on expert knowledge, due to the objective replicability built in their statistical foundations and to the possibility of making an efficient use of information (Iraizoz et al., Reference Iraizoz, Gorton and Davidova2007). Coherently with such considerations on reproducibility and efficiency, the methods used in this study are based on MVA techniques, in particular non-parametric techniques. We believe that, as compared to parametric approaches, non-parametric techniques hold a strong potential for facilitating the communication of results to non-technical end-users. Such potential for communicability of results is only partially addressed by MVA non-parametric studies in the literature (Blazy et al., Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009). In these studies, data reduction plays a key role: first, the original database is typically transformed by either PCA, multiple correspondence or factor analysis (or a combination of those) in order to select a smaller group of uncorrelated scores, then CA is applied for farm grouping. However, the use of factors or components from PCA, multiple correspondence and factor analysis to define the clusters makes it hard for non-technical stakeholders to understand what variables are principally responsible for the classification. Studies on typology identification are generally deficient in this sense, even if the problem is technically addressed by studying the weighting of correlations of the variables with the principal components (see e.g. Gaspar et al., Reference Gaspar, Escribano, Mesías, Rodriguez de Ledesma and Pulido2008). In many of these studies, the data obtained and especially the knowledge of the context where data were collected are often reduced in order to function as inputs in statistical measures (Madsen and Adriansen, Reference Madsen and Adriansen2004), so as to sometimes appear research-driven rather than problem-driven, imposing (especially those relying on CA) predetermined categories on reality.
The objectives of the present paper are (a) to present an application of multi-dimensional scaling (MDS) in combination with cluster analysis for farm typology identification, (b) to evaluate the statistical reliability of the method as compared to a parametric method based on a mixture model using latent class analysis along the lines of Kostov and McErlean (Reference Kostov and McErlean2006), (c) to compare the results of our approach with those of conceptual categorization and participatory methods and (d) to discuss relevant strengths and weaknesses of the method. The method outlined in the present paper was elaborated and applied during two EU projects in Africa and Latin America, with a total of 18 studies in 11 countries. For the sake of simplicity, the method will be presented and discussed in detail with reference to the application to a study area in north Zimbabwe, selected results will be shown for another area in western Kenya, but the general conclusions drawn about the method are borne out by evidence stemming from the whole set of applications.
MATERIALS AND METHOD
The study sites
The main steps of the method are illustrated in detail with reference to data on household characteristics from the Dande Communal Land, an area located in the mid-Zambezi Valley, northern Zimbabwe. Communal Lands are state lands used for small-scale farming and residential purposes in accordance with local traditional authority and/or the local rural district council regulations. The Dande Communal Land is characterized by former floodplains of the Zambezi river basin, at an average altitude of 400 m above sea level. It has a dry tropical climate, with low and very variable annual rainfall (on average between 450 and 650 mm/year) and a mean annual temperature of 25 °C. Two seasons are clearly defined: a rainy season from December to March and a long dry season from April to November. Settlements are found predominantly along the main rivers and the major activity is dryland farming of cotton, maize and sorghum (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011).
The mid-Zambezi Valley is an area of global importance for its biodiversity, which is hosted in a network of protected areas (e.g. national parks, safari areas), as well as in patches of the communal land. Rapid and extensive land-use and land-cover changes, however, are threatening this biodiversity. Such changes are driven by immigration and by changes in farming systems, notably the expansion of plough-based agriculture and cotton farming. Different farming systems affect the environment differently. The purpose of constructing a typology in the mid-Zambezi Valley was to develop a recommendation domain for the design of innovative, sustainable farming systems, highly productive while having a limited impact on the environment (in terms of area used for cropping, erosion, pollution by biocides, etc.).
To compare the combined application of MDS and cluster analysis with conceptual categorization and participatory methods, selected applications of the method are also presented for a typology of smallholder, subsistence-oriented mixed farming systems from western Kenya, which was previously developed based on participatory methods and conceptual categorizations (Tittonell et al., Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005).
Method
The method involves the following steps: (i) data collection, (ii) selection of variables for farm groupings, (iii) identification of farm groups, and (iv) characterization of representative farms and farm typology. In this section, the method is presented in detail. Concerning steps (iii) and (iv), the present method has been adapted from a methodology developed at the Plymouth Marine Laboratory for the analysis of change in marine communities (Clarke and Warwick, Reference Clarke and Warwick2001). The non-parametric MVAs in this study were performed with the software PRIMER 6 (Clark and Gorley, Reference Clarke and Gorley2006).
Data collection
The identification of the farm sample was the first important step of the analysis. The sample should be representative of the diversity of farms in the area. Depending on the characteristics of the farms, the sampling frame can be based on stratification, random selection or transects with exclusion rules. In the case of Zimbabwe, data were collected from 176 farms on a transect following an intensification gradient (i.e. increasing human density, cattle density and cotton production along that transect) of about 40 km, oriented north-west–west/south-east–east (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011). Along this gradient, wildlife population and tsetse population decrease, whilst human and livestock population, total cultivated surface and surface under cotton increase. Variables included in the farm surveys were selected by experts with an intimate knowledge of local farming systems.
Selection of variables for farm groupings: from classification to key variables
The selection of the variables for the farm groupings was performed in two successive steps. First, a list of classification variables was developed based on expert knowledge and data availability, taking into account the structure of the farming system and giving importance to the main sources of variability/diversity among the farms. Variables related to farm resources availability and management were chosen by experts and were considered as the starting point to design alternative, more sustainable farm strategies, which was the ultimate goal of the farm typology identification.
Quantitative as well as qualitative variables were included in the database. Qualitative variables are ordinal variables whose scores reproduce increasing levels of quality. In a second step, different sets of key variables were defined by reducing the number of classification variables with the aim of obtaining a meaningful differentiation of the farm samples for the purpose of delineating a typology. The selection of the final set of key variables was carried out based on expert knowledge supported by the use of PCA to identify highly correlated variables.
Identification of farm groups
All key variables were standardized as percentages to avoid the influence of different levels of variation due to the unit of measurement. The similarity matrix, which shows the degree of resemblance between each pair of objects (farms, in our case), was then calculated. We used the Bray–Curtis distance (a non-metric coefficient particularly common in ecology) for the quantitative and qualitative standardized variables (Bray and Curtis, Reference Bray and Curtis1957), and the Jaccard similarity coefficient for the binary variables (presence/absence variables in our case), defined as the size of the intersection divided by the size of the union of the sample sets (Jaccard, Reference Jaccard1901).
Usually, the availability of different types of variables (qualitative, quantitative and binary) is dealt with using data-reduction techniques such as PCA, multiple correspondence or factor analysis (e.g. Blazy et al., Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009; Gaspar et al., Reference Gaspar, Escribano, Mesías, Rodriguez de Ledesma and Pulido2008; Iraizoz et al., Reference Iraizoz, Gorton and Davidova2007; Solano et al., Reference Solano, Leon, Perez and Herrero2001; Tittonell et al., Reference Tittonell, Muriuki, Shepherd, Mugendi, Kaizzi, Okeyo, Verchot, Coe and Vanlauwe2010). In this paper instead, we decided to rule out any such database reduction prior to the application of MVA techniques, on the grounds that presenting the results of the classification of farms in the form of the original variables (standardized by percentage) would be more meaningful for MVA non-practitioners.
Alternatively, the joint processing of quali-quantitative and binary variables could be achieved for example by using the general similarity coefficient of Gower (Reference Gower1971) or by combining the use of the Bray–Curtis coefficient for quali-quantitative variables and the Sorensen–Dice coefficient for presence or absence variables (Dice, Reference Dice1945; Sørensen, Reference Sørensen1957). Instead, we decided not to combine datasets in such a manner and we chose to use the Jaccard coefficient for its straightforward logic of ‘simple matching’ similarity only adjusted by removing those variables which are jointly absent from all sample units.
The coefficients of the similarity matrix were used as inputs for the MVAs, which we carried out sequentially. First, we concentrated on the qualitative and quantitative variables, computing the Bray–Curtis coefficients, and thus forming the main groupings of farms. Then we turned to the presence/absence variables, computing the Jaccard coefficient conditional on belonging to each group, to check whether we could identify meaningful subgroups. We relegated the binary variables to such ancillary role because our analyses showed that their information content was modest and that they had no capacity of generating reasonable groupings of farms on their own.
Farm groups were generated by using a combination of the results of MDS and CA. Non-metric MDS (Kruskal, Reference Kruskal1964; Kruskal and Wish, Reference Kruskal and Wish1978) was performed with graphical representation in two- dimensional plots. MDS was used to construct a plot of the samples in a specified number of dimensions (normally two or three), which attempts to satisfy all the conditions imposed by the similarity matrix in terms of resemblance between each sample pair. The non-metric MDS algorithm is an iterative procedure, constructing the MDS plot by successively relocating the points (samples) until their positions satisfy, as closely as possible, the dissimilarity relations between samples. Relocation of sample points is done by regressing the interpoint distances from this plot on the corresponding dissimilarities. The MDS plot is interpreted in terms of the relative distances between samples since similarities are the only information used by non-metric MDS ordination. There is normally some distortion in the plot that is minimized by the MDS algorithm, which is captured by the stress value. The stress value is a goodness-of-fit measure depending on the difference between the distances of each couple of sample points on the MDS plot and the distance predicted from the fitted regression line corresponding to coefficients of dissimilarities. If such difference is equal to zero, the stress is zero. Instead, widely scattered points clearly lead to a large stress and this can be interpreted as measuring the difficulty involved in compressing the sample relationships into two (or a small number of) dimensions (Clarke and Warwick, Reference Clarke and Warwick2001).
Agglomerative hierarchical clustering was used to group the farm samples according to the group average link method (Clarke and Warwick, Reference Clarke and Warwick2001; Field et al., Reference Field, Clarke and Warwick1982). Groups of farms were identified by the superimposition of the clusters on the MDS plot at a chosen similarity level, which is a graphical facility of PRIMER. Such choice, which determines the number of clusters, was handled with a heuristic procedure, through a subjective inspection of the CA dendrogram (Kobrich et al., Reference Kobrich, Rehman and Khan2003) and supported by ‘analysis of similarities’ statistics (ANOSIM, Clarke, Reference Clarke1993).
The most representative farm groups, in terms of number of farm samples included, were selected for farm typology characterization. The choice of how to assemble groups at different similarity levels was statistically supported by ANOSIM, which is used to measure the dissimilarities within the groups, and guided by experts, who gave indications on the most plausible number of groups. The ANOSIM tests operate on the similarity matrix and constitute an approximate analogue of the standard analysis of variance tests. ANOSIM compares pairs of clusters on the basis of similarities between samples. It computes a statistical test (R) that lies in the interval (−1,1) and is a comparative measure of the degree of separation of the groups. The R statistic is equal to 1 only if all samples within a group are more similar to each other than any sample from different groups and is approximately zero if the similarities between and within groups are on average the same. A significance level is then calculated by referring the observed value of R to its permutation distribution (Clarke and Warwick, Reference Clarke and Warwick2001). However, ANOSIM is not a valid test of differences between groups generated by CA or other methods starting from the similarity matrix and should be applied to test the differences between groups defined a priori by an independent classification scheme (Clarke and Gorley, Reference Clarke and Gorley2006). We used ANOSIM in an explorative way to evaluate and compare the differences between the groups identified in order to support the selection of the most representative farm types in combination with MDS plot and expert knowledge.
Characterization of representative farms and farm typology
The last step of the methodology was the similarity percentages (SIMPER) analysis of the farm groups (Clarke, Reference Clarke1993). SIMPER analysis concentrates on Bray–Curtis similarities between samples and highlights the variables principally responsible for determining the sample groups in the cluster or ordination analyses. The SIMPER algorithm first computes the average similarity between all pairs of sample units within a group and then disaggregates this average into separate contributions from each variable. The variables whose values are all equal to zero within a group, although equal, do not give any contribution to the within-group similarity. The rate between within-group similarity and each variable's standard deviation holds a strong characterization power if the variable values are relatively constant within a group, so that standard deviation of its contribution is low, and the ratio between within-group similarity and standard deviation is high.
The average and modal variable values of the most representative farm groups were used to describe the farming structure using farm types. In this way, the resource endowment of each farm type was summarized by a virtual farm characterized by the average values of the whole group. The variables that provide the highest contributions to form the clusters according to SIMPER analysis were emphasized to characterize the farm types.
Further, in order to represent the farm population in a more realistic way, several representative farms were selected among the farm sample units. The process of selection of representative farms is straightforward as farms with average and modal values of the selected variables are placed in the middle of the farm groupings in the MDS plot. Whether virtual farms are able to realistically portray the farm types depends on specific features of each group and can be assessed by considering the relative differences of virtual and representative farms variables as well as by assessing such differences with the support of SIMPER statistics, e.g. by giving greater importance to virtual versus representative similarities for those variables with higher contribution to within-group similarity and with higher ratio between within-group similarity and standard deviation. Such assessment was carried out by local experts.
On the other hand, the number of farm types chosen by local experts as supported by ANOSIM results was refined after the SIMPER analysis by adding a constraint allowing for a minimum of 50% of within-group similarity. The latter constraint was posed in order to warrant that on average farms belonging to one type be rather similar than dissimilar to each other, given the key variables selected (Kobrich et al., Reference Kobrich, Rehman and Khan2003).
Comparison with latent-class-based classification
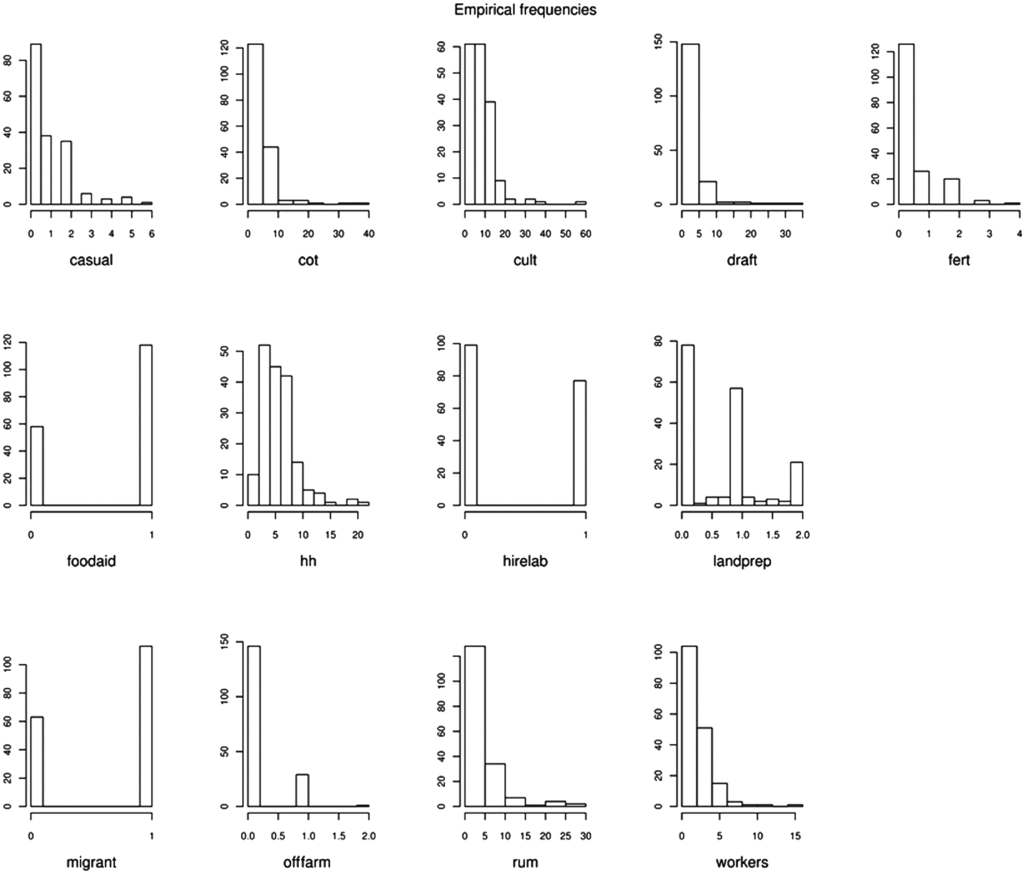
In order to evaluate the reliability of the method described above, we considered an explicitly parametric method based on latent class analysis, inspired by Kostov and McErlean (Reference Kostov and McErlean2006). Using the same set of variables of the mid-Zambezi Valley dataset as described above, we employed the mixed-mode latent class regression (mmlcr) package under R (R Development Core Team, 2009). This package was selected because it can handle different classes of distributions for the variables (which can be both quantitative – either continuous or discrete – and categorical). Indeed, the database of mid-Zambezi Valley contemplates such heterogeneity, as can be inferred from Figure 1. The package is built around the Expectation Maximization algorithm of Dempster et al. (Reference Dempster, Laird and Rubin1977).

Figure 1. Distributions of selected variables of the dataset of the mid-Zambezi Valley, Zimbabwe. Legend: casual: adults working sometimes as casual workers (no.), cot: cotton land (ha), cult: cultivated land (ha), draft: draft animals (no. of adult cattle + donkeys), fert: inorganic fertilizers and manure applications for cotton, maize and sorghum (no.), foodaid: food mainly produced and/or purchased (presence/absence), hh: household members (no.), hirelab: hired labour (presence/absence), landprep: land preparation (index), migrant: migrant settlers (presence/absence), offfarm: adults having off-farm employment (no.), rum: small ruminants (no.), workers: adults working (no.).
The procedure basically entails estimating a mixture model which gives, for each farm, the probability of belonging to each of a (predetermined) number of latent classes. With regard to the assumptions about the (marginal) distributions, which need to be assigned explicitly to each variable, the variables recording the number of adults having off-farm employment (‘offfarm’) and the index of land preparation (‘landprep’) were coded as multinomial, whereas all the remaining variables were coded as negative binomial.Footnote 1 We estimated models with three, four, five and six classes. For each class size, we ran 200 independent estimations each characterized by different, randomly selected initial conditions and generating a potentially different model. The models can be judged through the usual score functions, namely the Akaike Information Criterion (AIC) and the Bayes Information Criterion (BIC). For the best fitting models, according to AIC and BIC, we also computed the consistency of the resulting groups with the typology constructed non-parametrically with CA and MDS in the following way. For a given number of classes (3 to 6), the algorithm returns a vector of probabilities for each farm; we then used the highest probability to identify the class membership for each farm (this is known as the ‘maximum a posteriori’ principle). We then considered the best possible match between the groups of farms constructed with this method and with CA and MDS, computing the fraction of farms belonging to corresponding groups.
Comparison with conceptual categorization and participatory methods
Using the same set of variables of three farm samples in western Kenya as in Tittonell et al. (Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005), we applied the method based on CA and MDS as presented in the previous section. In Tittonell et al. (Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005), an initial approach to classify farms solely based on wealth ranking led to the identification of three farm types, but it resulted in poor discrimination of resource allocation patterns. Adding information on production goals, the main types of constraints faced by the household, position in the farm developmental cycle and main source of income improved the discrimination of farm types. Here, we compare the results obtained with MDS in combination with CA, reported through the corresponding plot, with the typology identified by Tittonell et al. (Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005).
RESULTS
Application of the method in the mid-Zambezi Valley
Data collection
Three transects oriented along the intensification gradient were sampled and 176 farms were sampled along the gradient. Every household that had at least one cultivated field on one of the transects was sampled. Heads of selected households were interviewed on 75 variables including location of the farm (GPS point), age of the head, composition of the household (including number of people working as casual workers for other farmers and number of external people hired), number of implements (plough, wheelbarrow, etc.), areas cultivated in different crops, planting dates for these crops, use of fertilizers and manure, mode of land preparation, mode of weeding, livestock number (disaggregated by species), destruction by wildlife.
Selection of variables for farm groupings
Selected classification variables are reported in Figure 1 together with corresponding histograms showing empirical distributions. From the initial complete list of 75 classification variables, 13 key variables were selected, three of which were presence/absence variables and the other 10 were quali-quantitative. Some key variables were calculated by condensing information from two or more classification variables; this was the case of the farm-level number of fertilizer applications and the farm-level land preparation index, which were calculated as the mean value of the number of fertilizer applications for the different crops weighed by their surface area and as the mean value of the land preparation index for the different crops weighed by their surface area, respectively. For each crop, the land preparation index value was set to zero when no tillage was used (i.e. digging of shallow planting holes by hand-hoe without previous land preparation), one when minimum tillage was used (i.e. opening of a furrow without soil inversion) and two when ploughing was used (i.e. land preparation with soil inversion).
Identification of farm groups
Figure 2 shows the two-dimensional MDS plot. The relative distances of one sample to another represent between-sample similarities. The stress value of the representation is 0.19. According to Clarke and Warwick (Reference Clarke and Warwick2001), a stress value between 0.1 and 0.2 gives a potentially useful two-dimensional picture, though for values at the upper end of the range, a cross check of the groupings should be made by superimposing CA groups of farms.

Figure 2. Superimposition of cluster groupings on the multi-dimensional scaling plot representing the farm sample of the mid-Zambezi Valley, Zimbabwe. The stress value of the representation is 0.19. Results were obtained after standardization by percentage of the variables and calculation of a similarity matrix based on the Bray–Curtis coefficient.
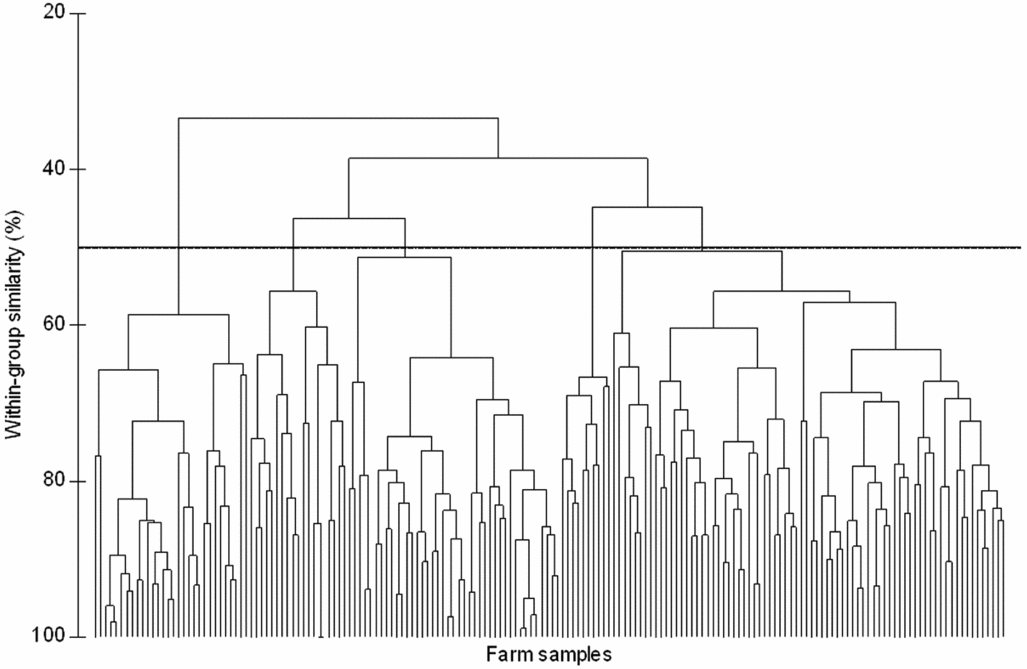
Using a cut-off value of 50% for within-group similarity for CA, five groups of farms were identified (Figure 3). The classification in five groups was favourably evaluated by local experts.

Figure 3. Cluster dendrogram grouping the sample farms of the mid-Zambezi Valley, Zimbabwe. Results were obtained after standardization by percentage of the variables and calculation of a similarity matrix based on the Bray–Curtis coefficient. Five groupings were identified at 50% of within-group similarity.
In Figure 2, the clusters are superimposed on the MDS plot. While the level of determination of membership of each farm sample to one of the five groups is made possible at higher detail thanks to the superimposition of clusters, inter-relations between the samples on a continuous scale are displayed thanks to the MDS configuration on the plot. Clusters are not imposed because the continuum of change is visible on the MDS plot. Besides, farms representative of the group and of boundary conditions can be easily identified and selected for further study or scaling-up of results by choosing farm samples at the centre and on the borders of the groups, respectively.
Some farms were positioned in the overlapping space between two different groupings when MDS and CA were combined: their attribution to groups was ambiguous (Figure 2). Allocating each farm to a single group (including those in the intersections) would be possible by checking their single membership on the CA dendrogram. However, it can be the case that in real-world conditions, single farms hold intermediate characteristics between different groups; these farms represent boundary conditions of groups and as such they were considered in our study. A further scrutiny was carried out on single groups based on dissimilarities of presence/absence variables calculated with the Jaccard coefficient. However, this analysis did not produce additional results in terms of identification of sub-groups, perhaps because of the low number of farm samples compared to the poor information content of binary variables.
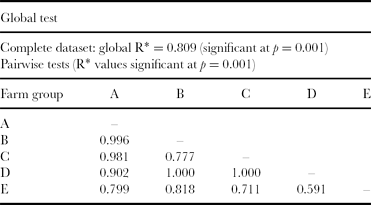
Table 1 reports the results of ANOSIM. The R statistics of each couple of identified groups is strongly significant for almost all of the group combinations, with lower but still significant dissimilarities between the couples C–E (R = 0.711) and E–D (R = 0.591). Overall, the ANOSIM confirmed the groups obtained in the preceding steps.
Table 1. Results from analysis of similarity (ANOSIM) of farm groups of the farm sample of the mid-Zambezi Valley, Zimbabwe.

*Test statistic comparatively measuring the degree of separation of the groups.
Characterization of representative farms and farm typology
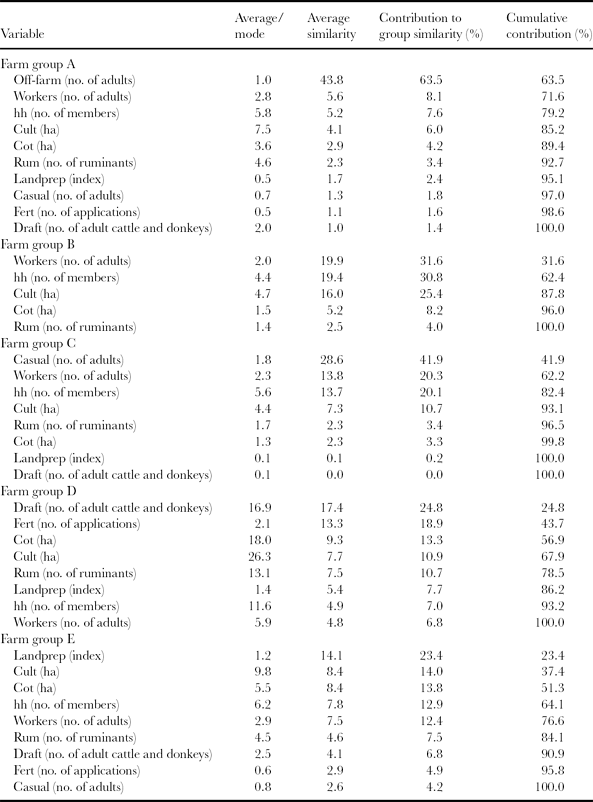
In Table 2, group average, average similarities, single and cumulative contribution to within-group similarity of each variable per group are reported for the mid-Zambezi Valley farm dataset. The first column can be used to support the selection of a representative farm among the farm samples as indicated by the average values of variables. Farm samples close to the centre of the groups in the MDS plot (Figure 2) hold values that are close to group averages. Such farms can be used as pilot (group representative) farms for detailed analyses. Furthermore, ‘virtual’ farms can be constructed based on averages of variables retrieved from SIMPER analysis or, in case of qualitative class variables, on corresponding modal values. Local experts identified five types of farms corresponding to the above identified groups: (a) farms receiving off-farm income and using (some sort of) animal draught power, (b) hand-hoe-based farms with family labour, (c) hand-hoe-based farms selling out a large part of their labour (casual work for other farms), (d) large commercial enterprises, mainly cotton-based, using large quantities of fertilizers and manure, and (e) farms using animal draught power and farming large cotton areas.
Table 2. Results of similarity percentage (SIMPER) analysis for the farm sample of the mid-Zambezi Valley, Zimbabwe (farm group average similarities: A = 68.9; B = 62. 9; C = 68.2; D = 70.3; E = 60.3).

This typology reveals the paramount importance of power/labour available at farm level – both human power/labour and animal draught power – in shaping the farms’ heterogeneity in the area, which corresponds to findings of previous studies (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011). Indeed, Table 2 shows that variables related to labour and animal draught power (also reflected in the index of land preparation) are the main variables contributing to the similarity of all the groups but farm group D. This illustrates the fact that the area under study can be considered an agricultural frontier, i.e. that the farming systems are limited by man/animal power more than by land (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011). It can also be observed from Figure 2 that farm groups A and D form quite distinct clouds of points whilst farm groups C, B and E overlap strongly. The continuum created by farm groups C, B and D illustrates the typical farm development pathway observed in the area: most farms start as a hand-hoe-based farms selling a large proportion of their labour (farm group C), develop progressively into a hand-hoe-based farm investing most of its available labour on farm activity, increasing its cultivated surface (particularly cotton) and investing in draught animals (farm group B), and later develop into a farm using animal draught power, with bigger surface under cultivation (mostly cotton, farm group D). However, this typical development pathway is inhibited in tsetse-infested areas, as cattle, a source of draught power, cannot be kept. Cotton is the cash crop permitting wealth accumulation and increasing production capacity, particularly in the form of purchase of draught animals and hiring of labour (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011). Farm groups A and D form distinct clouds on the MDS plot which illustrates their functional differences: the farming system represented by farm group A depends mostly on off-farm income (for hiring labour, purchasing inputs and acquiring draught animals) whilst the farming system represented by farm group D represents large commercial enterprises, which are very different from peasant farms that make up the other groups.
Comparison with latent class analysis
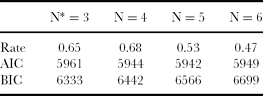
The results obtained using latent class analysis are summarized in Table 3 with reference to four models corresponding to 3, 4, 5 and 6 farm groups. AIC and BIC values of the four models are reported together with the resultant rate of consistency with the MDS/CA typology.
Table 3. Summary statistics for latent class analysis models of the dataset of the mid-Zambezi Valley, Zimbabwe, various N.
*Number of classes.
AIC-based ranking suggests N = 4 and N = 5 as the best choices (AIC values equal to 5944 and 5942, respectively), with N = 3 and N = 6 performing worse. This observation would support the evidence coming from the approach presented above and approved by experts. Besides, experts would reject any grouping with three classes (suggested by the BIC criterion) or less as corresponding groups would not lead to any useful typology due to low within-group similarity. A six-class model seems to be the least appropriate according to both criteria.
Consistency rates between latent class analysis and MDS/CA are considerably high for the N = 3 and N = 4 models (0.65 and 0.68, respectively) but decrease noticeably for the N = 5 and N = 6 models (0.53 and 0.47, respectively).
Comparison with expert-based and participatory methods
In Figure 4, a MDS plot representing the sample of western Kenya is reported where farms were labelled with symbols representing classes identified in a participatory approach (i.e. farmers’ self-ranking into wealth classes). The method produced farm groups that were able to capture variation while keeping in evidence the actual continuum that may exist between and within the groups. The distribution of wealth classes is well represented in the plot by a gradient of wealth, with wealthier farms (wealth class 1) located at the bottom of the plot and farms with low resource endowment at the top (wealth class 3). After excluding groups of farms composed by one or two individuals, five main groups were identified at 92% of within-group similarity by superimposing groups of farm individuals obtained from the corresponding cluster analysis dendrogram. Again, the composition of these groupings significantly matches the description of the five farm types obtained through conceptual categorization in Tittonell et al. (Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005). Farm group 1 is composed mainly of farms with high resource endowment (Wealth Class 1) and a few farms with medium endowment but all of them with significant access to off-farm income (Wealth Class 2, 3 farms out of 13), Farm group 2 comprises farms with high endowment and growing cash crops (all but one), Farm group 3 has farms with medium endowment marketing food crops (all but one), Farm group 4 represents farms with medium and low endowment practicing non-farm activities (and only 2 out of 16 belong to the wealthier class), and Farm group 5 is mainly composed of farms with low endowment and working as casual workers for wealthier farmers (9 out of 12). Such categorization allows going beyond the structural classification by asset endowment, towards a more functional typology of households that reveals livelihood strategies as well.

Figure 4. Superimposition of wealth ranking classes on the multi-dimensional scaling plot of the farm sample of western Kenya. The stress value of the representation is 0.06. Results were obtained after standardization by percentage of the variables and calculation of a similarity matrix based on the Bray–Curtis coefficient. Five main groups were identified at 92% of within-group similarity by superimposing farm groupings obtained from the corresponding cluster analysis dendrogram. Group compositions correspond to five types as identified with a conceptual categorization by Tittonell et al. (Reference Tittonell, Vanlauwe, Leffelaar, Rowe and Giller2005, Table 3). Legend: farm code letters, location codes, namely A: Aludeka, E: Emuhaia, S: Shinyalu.
DISCUSSION
The method has been implemented on two farm samples from African areas encompassing extensive land use, with small-scale and diffuse settlement patterns, characterized by complex interactions between the socio-economic and biophysical environments. This application allowed us to assess the potential of the method, its statistical reliability, its pertinence vis-à-vis local rural livelihood strategies and its strength and weaknesses with regard to other methods, as discussed below.
The potential of MDS for typology delineation
Methodologies similar to the one we used have been applied for classification in the field of ecology and biology (e.g. Catalán et al., Reference Catalán, Jiménez, Alconchel, Prieto and Muñoz2006; Selleslagh and Amara, Reference Selleslagh and Amara2008; Stergiou et al., Reference Stergiou, Moutopoulos, Soriguer, Puente, Lino, Zabala, Monteiro, Errazkin and Erzini2006) but, to the best of our knowledge, they have never been used in farming systems analysis. Besides the applications in Zimbabwe and Kenya presented in this study, the method has been applied to a total of 18 studies in 11 countries of Africa and Latin America, with datasets ranging from ad hoc field surveys to structured information from national statistical census (e.g. Righi et al., Reference Righi, Dogliotti, Stefanini and Pacini2011b, for the case of South Uruguay). The method has been shown to cope with such heterogeneity in data sources and to capture location-specific diversity in terms of farm structure (e.g. in Righi et al., Reference Righi, Cittadini, Mundet, San Martino, Sanz and Baltuska2011a, for the case of South Patagonia).
The outcomes of the method in all the studies were validated by local experts. Kobrich et al. (Reference Kobrich, Rehman and Khan2003) suggest that a good procedure to validate farm types is to contrast them with (expert-based) existing hypotheses about their structure, as well as with researchers’ perception about the variety of farming systems that have been observed empirically. Moreover, they argue that for classes to be meaningful, and useful, they have to be related to the purposes for which they are being created; therefore, the fact that they serve the purposes for which they are intended provides the most meaningful way of testing their conceptual validity. In the case of mid-Zambezi Valley, two experienced researchers from the area acted as experts. They were supported by a number of researchers and technicians in group discussions, assessed positively the five-group classification and described the corresponding farm types coherent with the purpose of the typology and previous studies (Baudron et al., Reference Baudron, Corbeels, Andersson, Sibanda and Giller2011).
Statistical reliability
Besides expert validation, the reliability of the method was tested in comparison to a mixture model using latent class analysis along the lines of Kostov and McErlean (Reference Kostov and McErlean2006). Within this analysis, the AIC criterion suggests N = 4 and N = 5 as optimal number of groups (with a slight preference for the five-group model). Concerning these two class sizes, the consistency rates of the (best fitting) estimates differ considerably, i.e. 0.68 for N = 4 versus 0.53 for N = 5, being lower than the value of the class size identified with MDS/CA and favourably evaluated by experts (i.e. 5). The model with four groups also fares well with respect to the BIC criterion. A farm typology consisting of four groups could also be obtained with MDS/CA (results not shown) by merging farm groups B and C of Figure 4 at a within-group similarity level of 52%. This alternative farm grouping could be considered for further analysis.
MDS versus current methods: relevance and robustness
In the case of western Kenya, farm groupings obtained with MDS and CA matched a classification based on wealth ranking and a conceptual categorization based on production goals, main types of constraints faced, position in the farm development cycle and main source of income (Figure 4). Our results, however, constituted an improvement in terms of objective reproducibility and of possibility of making efficient use of information. This is in line with what Iraizoz et al. (Reference Iraizoz, Gorton and Davidova2007) found regarding the descriptive strength of MVA techniques. Additional features of MVA techniques as compared to expert-based classifications are the graphical visualization of farm type groupings, the possibility of selecting candidate representative farms for in-depth analyses and the systematization of information through SIMPER analysis. Indeed, objective reproducibility is one noteworthy improvement over qualitative participatory methods such as wealth ranking. According to Adams et al. (Reference Adams, Evans, Mohammed and Farnsworth1997), the sensitivity of the wealth ranking method to the number, age, and gender of key informants or to the attributes of facilitators may jeopardize its reliability. Other limitations of wealth ranking are the inability to identify/quantify differences in specific dimensions of household wealth and in supporting meaningful cross-regional comparisons. On the other hand, the great strength of wealth ranking lies in its sensitivity to local contexts and its emphasis on local expertise (Chambers, Reference Chambers1994).
Several features of our method have the potential to improve effectiveness of statistical analyses in the field of farm typology identification. An example of such a potential as compared to current methods is again given by the study in western Kenya, where the typology based on wealth ranking and conceptual categorization was further developed and extended to six sub-regions of East Africa (Tittonell et al., Reference Tittonell, Muriuki, Shepherd, Mugendi, Kaizzi, Okeyo, Verchot, Coe and Vanlauwe2010). PCA and CA were used to identify non-correlated variables and to group households in homogeneous classes. However, in Tittonell et al. (Reference Tittonell, Muriuki, Shepherd, Mugendi, Kaizzi, Okeyo, Verchot, Coe and Vanlauwe2010), the clustering obtained was refined through reclassification of cases lying in fuzzy areas after examination of corresponding variables, which requires detailed field knowledge on the systems being analysed. This is one of the fields where the combined use of MDS and CA shown here could complement classical CA or qualitative approaches by representing the farm sample as a continuum on an MDS plot where clusters are superimposed. Although this represents a strength of the present approach, we recommend its use as complementary rather than alternative to other methods.
Towards a stakeholder-oriented approach: visualization and communication
In the context of this paper, stakeholder-orientation refers to the need to cooperate with the stakeholders during the analysis and to consider the knowledge of the context while taking into account the level of technical background required to correctly read and interpret the results. This is in line with findings by Blazy et al. (Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009) in the case of banana systems in Guadeloupe, where all the experts involved in the development of a farm typology with PCA and CA were scientists. Blazy et al. (Reference Blazy, Ozier-Lafontaine, Dorè, Thomas and Wery2009) report that it was not possible to bring on board professional actors, the process of farm type identification being unusual and time-consuming for professional actors like farmers. They conclude that their methodological framework would therefore be improved by collaboration with ergonomists and participatory research scientists to determine how to facilitate the participation of professional actors.
Different understanding of a farm typology between scientists and other stakeholders can result in an information imbalance that would lead to a research-driven (scientists’ perspective), instead of a problem-driven (farmers’ perspective) approach. In the applications of MDS and CA reported and cited in the present paper, the stakeholder understanding of the typology and the inclusion of local knowledge were promoted by working on two main aspects: the visualization of typology groupings (as compared to PCA and simple CA), and the exclusion of data reduction prior to the application of MDS and CA (as compared to methods implying reduction with PCA, correspondence or factor Analysis).
One major advantage of MDS as compared to PCA in visualizing farm groupings lies in the preservation of distances (representing dissimilarities between sample individuals) when the information is difficult to represent on a low number of dimensions (Clarke and Warwick, Reference Clarke and Warwick1994). Indeed, the ability of PCA to preserve distances is poor when the variation among sample individuals is distributed on multiple dimensions, which is instead a feature of MDS.
The level of agreement between CA and MDS is higher than that between CA and PCA, as the data input is the same for CA and MDS (similarity coefficients), which does not happen with PCA. In the present approach, the PCA is limited to a preliminary exploration of the multivariate data structure; therefore, it is useful to generate questions about variable selection to be addressed during further elicitation with the expert.
Concerning the visualization potential of the approach as compared to simple CA, the combined use of MDS and CA can account for fine distinctions between farm groupings in relatively homogeneous farm populations. According to Clarke and Warwick (Reference Clarke and Warwick2001), methods based on cluster analysis fail in graphically representing the two-way inter-relations within the sample on a continuous scale and, especially in non-dispersed populations, tend to impose a rather arbitrary grouping on what may be a continuum of change. CA groups the samples into discrete clusters but is not able to display a steady gradation in the database structure. In contrast, MDS is able to represent the farm sample as a continuum; this feature of MDS visualization is particularly important to visualize inter-relations among farms as witnessed by other studies in the literature. For instance, Madsen and Adriansen (Reference Madsen and Adriansen2004) reported that the best way to describe the relation between the different landowner types of a land-use study carried out in Denmark seemed to be the concept of continuum, because there was a gradual transition from one landowner type to the other. The description of landowner types in terms of continua could possibly be enhanced by displaying the continua of farms on an MDS plot with CA clusters superimposed.
To keep a straightforward communication with non-technical experts (e.g. farmers, technicians, etc.), we avoided any database reduction prior to the application of MDS and CA, assuming that presenting the results of the classification of farms in the form of the original variables would be more meaningful for MVA non-practitioners. In order to mitigate the effects of retaining non-reduced variables in terms of redundancy of information, we chose to use PCA to uncover highly correlated variables and help expert knowledge to avoid duplications, if any (Clarke and Gorley, Reference Clarke and Gorley2006).
Madsen and Adriansen (Reference Madsen and Adriansen2004) advocate the use of multi-methods encompassing qualitative and quantitative approaches to understand the use of rural space. Combined used of CA and MDS for the applications presented and cited in this paper showed a high visualization and communication potential. Although it is not possible to generalize this potential, in the areas under study and with corresponding stakeholders, combined use of CA and MDS proved to be able to supply entry points for facilitated stakeholder knowledge inclusion, and could be integrated in a multi-method framework together with more qualitative and participatory approaches.
CONCLUSIONS
In this paper, we aimed to bridge the recurrent gap in typology delineation between statistical soundness and the need to consider expert knowledge on the drivers of rural livelihood diversity. The additional application of MDS to classical non-parametric multivariate approaches based on cluster analysis is geared towards the incorporation of sensitivity to local peculiarities and expertise, typical of participatory methods, into an objectively reproducible MVA tool-kit. Indeed, the results of any classification process are influenced by its eventual purposes and by the variables chosen, which should ultimately both be defined by the local stakeholders. Hence, the inclusion of local knowledge in the classification process should be eased through the adoption of appropriate, stakeholder-oriented devices.
In conclusion, facilitating participatory identification of farm typologies, while retaining objectivity and replicability of sound statistical tools, is the main advantage of the method described here. Its main limitation, as compared to other approaches entailing variable reduction prior to clustering, is that redundancy of information is only partially taken into consideration. A further disadvantage of the method as compared to parametric methods is that the evidence gathered for a representative farm cannot trivially be scaled up to aggregate levels, given that strong assumptions on key variables distributions (such as normality) are typically not borne out by the data. However, the latter can be also considered as a potential advantage, in the sense that often variables from farm databases are not normally distributed, which poses limitations to the application of parametric methods.
In general, we believe that the method presented is an acceptable compromise between the need to guarantee the properties of replicability and objectivity ensured by statistical tools and the necessity to facilitate inclusion of expert knowledge within a multi-method framework. As far as sustainable development is a process determined by negotiations among local stakeholders, it is of vital importance that such stakeholders, including farmers, technicians and policymakers, are aware of the diversity of production and livelihood systems that can be put in place to realize transition pathways towards sustainability. With its focus on communication and visualization of results, the method described in the present paper aims at involving local stakeholders in the process of capturing heterogeneity of farming systems and at raising awareness of the diversity of possible solutions.
Acknowledgements
This study has been realized as part of the Project EULACIAS (INCO-dev), Sixth Framework Programme of the European Union, contract no. 0032387.