Stable finite element approximation of a Cahn–Hilliard–Stokes system coupled to an electric field

Abstract

We consider a fully practical finite element approximation of the Cahn–Hilliard–Stokes system:

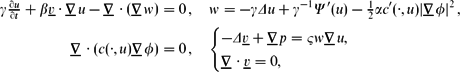$$\begin{align*} \gamma \tfrac{\partial u}{\partial t} + \beta v \cdot \nabla u - \nabla \cdot \left( \nabla w \right) & = 0 \,, \quad w= -\gamma \Delta u + \gamma ^{-1} \Psi ' (u) - \tfrac12 \alpha c'(\cdot,u) | \nabla \phi |^2\,, \\ \nabla \cdot (c(\cdot,u) \nabla \phi) & = 0\,,\quad \begin{cases} -\Delta v + \nabla p = \varsigma w \nabla u, \\ \nabla \cdot v = 0, \end{cases} \end{align*}$$

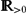subject to an initial condition u⁰(.) ∈ [−1, 1] on the conserved order parameter u ∈ [−1, 1], and mixed boundary conditions. Here, γ ∈ $\mathbb{R}_{>0}$ is the interfacial parameter, α ∈ 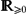$\mathbb{R}_{\geq0}$ is the field strength parameter, Ψ is the obstacle potential, c(⋅, u) is the diffusion coefficient, and c′(⋅, u) denotes differentiation with respect to the second argument. Furthermore, w is the chemical potential, φ is the electro-static potential, and (v, p) are the velocity and pressure. The system has been proposed to model the manipulation of morphologies in organic solar cells with the help of an applied electric field and kinetics.