Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Santos, M. L.
Campelo, A. D. S.
and
Almeida Júnior, D. S.
2017.
On the Decay Rates of Porous Elastic Systems.
Journal of Elasticity,
Vol. 127,
Issue. 1,
p.
79.
Almeida Júnior, D. S.
and
Ramos, A. J. A.
2017.
On the nature of dissipative Timoshenko systems at light of the second spectrum of frequency.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 68,
Issue. 6,
CAMPELO, A. D. S.
ALMEIDA JÚNIOR, D. S.
and
SANTOS, M. L.
2018.
Stability of weakly dissipative Reissner–Mindlin–Timoshenko plates: A sharp result.
European Journal of Applied Mathematics,
Vol. 29,
Issue. 2,
p.
226.
Chen, Zhijing
Liu, Wenjun
and
Chen, Dongqin
2019.
General Decay Rates for a Laminated Beam with Memory.
Taiwanese Journal of Mathematics,
Vol. 23,
Issue. 5,
Almeida Júnior, D S
Elishakoff, I
Ramos, A J A
and
Rosário Miranda, L G
2019.
The hypothesis of equal wave speeds for stabilization of Timoshenko beam is not necessary anymore: the time delay cases†.
IMA Journal of Applied Mathematics,
Vol. 84,
Issue. 4,
p.
763.
Liu, Wenjun
and
Zhao, Weifan
2019.
Stabilization of a Thermoelastic Laminated Beam with Past History.
Applied Mathematics & Optimization,
Vol. 80,
Issue. 1,
p.
103.
Feng, B.
Almeida, D. S.
dos Santos, M. J.
and
Rosário Miranda, L. G.
2020.
A new scenario for stability of nonlinear Bresse‐Timoshenko type systems with time dependent delay.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 100,
Issue. 2,
Liu, Wenjun
and
Zhao, Weifan
2021.
Exponential and polynomial decay for a laminated beam with Fourier’s law of heat conduction and possible absence of structural damping.
Frontiers of Mathematics in China,
Vol. 16,
Issue. 4,
p.
997.
Liu, Wenjun
and
Zhao, Weifan
2022.
Quasi-Stability and Attractor for a Laminated-Coleman-Gurtin Beam Without Structural Damping.
Acta Applicandae Mathematicae,
Vol. 180,
Issue. 1,
Ramos, A.J.A.
Araújo, A.L.A.
Campelo, A.D.S.
Freitas, M.M.
and
Veras, L.S.
2023.
Polynomial stabilization for thermoelastic Reissner–Mindlin–Timoshenko plates with structural damping.
Asymptotic Analysis,
Vol. 134,
Issue. 1-2,
p.
63.
Bchatnia, Ahmed
Chebbi, Sabrine
and
Hamouda, Makram
2024.
Nonlinear damping effects for the 2D Mindlin–Timoshenko system.
Arabian Journal of Mathematics,
Vol. 13,
Issue. 3,
p.
485.
Duan, Yu-Ying
and
Xiao, Ti-Jun
2025.
Rates of decay for locally damped porous-elastic systems with history via operator semigroups.
Semigroup Forum,
Vol. 110,
Issue. 1,
p.
162.
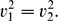 \begin{equation*}
v_{1}^{2}=v_{2}^{2}.
\end{equation*}
\begin{equation*}
v_{1}^{2}=v_{2}^{2}.
\end{equation*}