Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T21:07:22.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of standing waves for a class of quasilinear Schrödinger equations

Published online by Cambridge University Press:  24 May 2012

JIANQING CHEN ,
YONGQING LI  and
ZHI-QIANG WANG
JIANQING CHEN
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, P. R. China email: [email protected]
YONGQING LI
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, P. R. China email: [email protected]
ZHI-QIANG WANG
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, P. R. China email: [email protected] Department of Mathematics and Statistics, Utah State University, Logan, UT 84322, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the stability and instability of standing waves for the quasilinear Schrödinger equation of the form 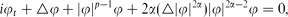which has been derived in many models from mathematical physics. We find the exact threshold depending upon the interplay of quasilinear and nonlinear terms that separates stability and instability. More precisely, we prove that for α ∈ 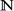and odd p ∈ 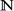, when 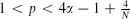, the standing wave is stable, and when 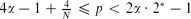(where 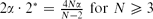for N ≥ 3 and 2 α ċ 2* = +∞ for N = 2), the standing wave is strongly unstable. Our results show that the quasilinear term 2 α(△|φ|2α)|φ|2α−2φ makes the standing waves more stable, which is consistent with the physical phenomena.

Keywords

Quasilinear Schrödinger equationsStanding wavesStabilityInstability
Type
Papers
Information
European Journal of Applied Mathematics , Volume 23 , Issue 5 , October 2012 , pp. 611 - 633
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Berestycki, H. & Cazenave, T. (1981) Instabilite des etats stationnaires dans les equations de schrodinger et de Klein-Gordon non linearires. C. R. Math. Acad. Sci. Paris 293, 489–492.Google Scholar
[2]Brihaye, Y. & Hartmann, B. (2006) Solitons on Nanotubes and Fullerenes as Solutions of a Modified Nonlinear Schrödinger Equation, Advances in Soliton Research, Nova Sci., Hauppauge, NY, pp. 135–151.Google Scholar
[3]Brizhik, L., Eremko, A., Piette, B. & Zakrzewski, W. J. (2001) Electron self-trapping in a discrete two-dimensional lattice. Physica D. 159, 71–90.CrossRefGoogle Scholar
[4]Brizhik, L., Eremko, A., Piette, B. & Zakrzewski, W. J. (2003) Static solutions of a D-dimensional modified nonlinear Schrödinger equation. Nonlinearity 16, 1481–1497.CrossRefGoogle Scholar
[5]Browder, F. E. (1965) Variational methods for nonlinear elliptic eigenvalue problems. Bull. Amer. Math. Soc. 71, 176–183.CrossRefGoogle Scholar
[6]Cazenave, T. (2005) Semilinear Schrödinger Equations, Courant Lecture Notes in Mathematics, Vol. 10, Courant Institute of Mathematical Sciences, Providence, RI.Google Scholar
[7]Cazenave, T. & Lions, P. L. (1982) Orbital stability of standing waves for some nonlinear Schrödinger equations. Comm. Math. Phys. 85, 549–561.CrossRefGoogle Scholar
[8]Chen, J. & Guo, B. (2009) Blow-up and strong instability result for a quasilinear Schrödinger equation. Appl. Math. Model 33, 4192–4200.CrossRefGoogle Scholar
[9]Chen, X. L. & Sudan, R. N. (1993) Necessary and sufficient conditions for self-focusing of short ultra-intense laser pulse in under dense plasma. Phys. Rev. Lett. 70, 2082–2085.CrossRefGoogle Scholar
[10]Colin, M. & Jeanjean, L. (2004) Solutions for a quasilinear Schrödinger equation: A dual approach. Nonlinear Anal. 56, 213–226.CrossRefGoogle Scholar
[11]Colin, M., Jeanjean, L. & Squassina, M. (2010) Stability and instability results for standing waves of quasilinear Schrödinger equations. Nonlinearity 23, 1353–1385.CrossRefGoogle Scholar
[12]de Bouard, A., Hayashi, N. & Saut, J. C. (1997) Global existence of small solutions to a relativistic nonlinear Schrödinger equation. Comm. Math. Phys. 189, 73–105.CrossRefGoogle Scholar
[13]Grillakis, M., Shatah, J. & Strauss, W. (1987) Stability theory of solitary waves in the presence of symmetry I. J. Funct. Anal. 74, 160–197.CrossRefGoogle Scholar
[14]Grillakis, M., Shatah, J. & Strauss, W. (1990) Stability theory of solitary waves in the presence of symmetry II. J. Funct. Anal. 94, 308–348.CrossRefGoogle Scholar
[15]Hartmann, B. & Zakrzewski, W. J. (2003) Electrons on hexagonal lattices and applications to nanotubes. Phys. Rev. B 68, 184302.CrossRefGoogle Scholar
[16]Hasse, R. W. (1980) A general method for the solution of nonlinear soliton and kink Schrödinger equations. Z. Physik B 37, 83–87.CrossRefGoogle Scholar
[17]Iliev, I. D. & Kirchev, K. P. (1993) Stability and instability of solitary waves for one-dimensional singular Schrödinger equations. Differ. Integral Equ. 6, 685–703.Google Scholar
[18]Jeanjean, L. & Le Coz, S. (2006) An existence and stability result for standing waves of nonlinear Schrödinger equations. Adv. Differ. Equ. 11, 813–840.Google Scholar
[19]Kenig, C. E., Ponce, G. & Vega, L. (2004) The Cauchy problem for quasilinear Schrödinger equations. Invent. Math. 158, 343–388.CrossRefGoogle Scholar
[20]Kurihura, S. (1981) Large amplitude quasi-solitons in superfluid film. J. Phys. Soc. Japan 50, 3262–3267.CrossRefGoogle Scholar
[21]Lange, H., Poppenperg, M. & Teismann, H. (1999) Nash–Moser methods for the solutions of quasilinear Schrödinger equations. Comm. Partial Differ. Equ. 24, 1399–1418.CrossRefGoogle Scholar
[22]Le Coz, S. (2008) A note on Berestycki-Cazenave's classical instability result for nonlinear Schrödinger equations. Adv. Nonlinear Stud. 8, 455–463.CrossRefGoogle Scholar
[23]Lions, P. L. (1984) The concentration-compactness principle in the calculus of variations. The locally compact case, parts 1 and 2. Ann. Inst. H. Poincaré Anal. Non Linéaire 1, 109–145; 223–283.CrossRefGoogle Scholar
[24]Liu, J. Q. & Wang, Z.-Q. (2003) Soliton solutions for quasilinear Schrödinger equations. Proc. Amer. Math. Soc. 131, 486–490.Google Scholar
[25]Liu, J. Q., Wang, Y. & Wang, Z.-Q. (2003) Soliton solutions for quasilinear Schrödinger equations, II. J. Differ. Equ. 187, 473–493.CrossRefGoogle Scholar
[26]Liu, J. Q., Wang, Y. & Wang, Z.-Q. (2004) Solutions for quasilinear Schrödinger equations via Nehari method. Comm. Partial Differ. Equ. 29, 879–901.CrossRefGoogle Scholar
[27]Liu, Y., Wang, X. P. & Wang, K. (2006) Instability of standing waves of the Schrödinger equations with inhomogeneous nonlinearity. Trans. Amer. Math. Soc. 358, 2105–2122.CrossRefGoogle Scholar
[28]Poppenberg, M. (2001) On the local well posedness of quasilinear Schrödinger equations in arbitrary space dimension. J. Differ. Equ. 172, 83–115.CrossRefGoogle Scholar
[29]Poppenberg, M., Schmitt, K. & Wang, Z.-Q. (2002) On the existence of soliton solutions to quasilinear Schrödinger equations. Calc. Var. Partial Differ. Equ. 14, 329–344.CrossRefGoogle Scholar
[30]Porkolab, M. & Goddman, M. V. (1976) Upper hybrid solitons and oscillating two-stream instabilities. Phys. Fluids 19, 872–881.CrossRefGoogle Scholar
[31]Shatah, J. & Strauss, W. (1985) Instability of nonlinear bound states. Comm. Math. Phys. 100, 173–190.CrossRefGoogle Scholar
[32]Spatschek, K. H. & Tagary, S. G. (1977) Nonlinear propagation of ion-cyclotron modes. Phys. Fluids 20, 1505–1509.CrossRefGoogle Scholar
[33]Strauss, W. (1977) Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55, 149–162.CrossRefGoogle Scholar
[34]Stuart, C. A. (2008) Lectures on the orbital stability of standing waves and application to the nonlinear Schrödinger equation. Milan J. Math. 76, 329–399.CrossRefGoogle Scholar
[35]Weinstein, M. I. (1983) Nonlinear Schrödinger equations and sharp interpolation estimates. Comm. Math. Phys. 87, 567–576.CrossRefGoogle Scholar
[36]Yu, M. Y. & Shuhla, P. K. (1977) On the formation of upper-hybrid solitons. Plasma Phys. 19, 889–893.CrossRefGoogle Scholar
[37]Zhang, J. (2002) Sharp conditions of global existence for nonlinear Schrödinger and Klein–Gordon equations. Nonlinear Anal. 48, 191–207.CrossRefGoogle Scholar