Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:47:28.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of patterns with arbitrary period for a Ginzburg-Landau equation with a mean field

Published online by Cambridge University Press:  01 April 2007

J. NORBURY ,
J. WEI  and
M. WINTER
J. NORBURY
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St. Giles', Oxford OX1 3LB, UK email: [email protected]
J. WEI
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong email: [email protected]
M. WINTER
Affiliation:
Department of Mathematical Sciences, Brunel University, Uxbridge UB8 3PH, UK email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following system of equations: 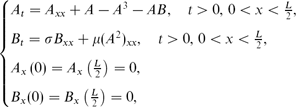where the spatial average ⟨ B ⟩ = 0 and μ > σ > 0. This system plays an important role as a Ginzburg-Landau equation with a mean field in several areas of the applied sciences and the steady-states of this system extend to periodic steady-states with period L on the real line which are observed in experiments. Our approach is by combining methods of nonlinear functional analysis such as nonlocal eigenvalue problems and the variational characterization of eigenvalues with Jacobi elliptic integrals. This enables us to give a complete classification of all stable steady-states for any positive L.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 18 , Issue 2 , April 2007 , pp. 129 - 151
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abramowitz, M. and Stegun, I. A. (1964) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Washington, National Bureau of Standards Applied Mathematics.Google Scholar
[2]Byrd, P. F. and Friedman, M. D. (1971) Handbook of elliptic integrals for engineers and scientists, Springer-Verlag.CrossRefGoogle Scholar
[3]Coullet, P. and Iooss, G. (1990) Instabilities of one-dimensional cellular patterns. Phys. Rev. Lett. 64, 866–869.CrossRefGoogle ScholarPubMed
[4]Cox, S. M. and Matthews, P. C. (2001) New instabilities in two-dimensional rotating convection and magnetoconvection. Physica D 149, 210–229.CrossRefGoogle Scholar
[5]Cross, M. C. and Hohenberg, P. C. (1993) Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112.CrossRefGoogle Scholar
[6]Doelman, A., Gardner, R. A., and Kaper, T. J. (2001) Large stable pulse solutions in reaction-diffusion equations, Indiana Univ. Math. J. 50, 443–507.CrossRefGoogle Scholar
[7]Doelman, A., Gardner, R. A., and Kaper, T. J. (2002) A stability index analysis of 1-D patterns of the Gray-Scott model, Mem. Amer. Math. Soc. 155, no. 737.Google Scholar
[8]Doelman, A., Hek, G. and Valkhoff, N. (2004) Stabilization by slow diffusion in a real Ginzburg-Landau system. J. Nonlinear Sci. 14, 237–278.CrossRefGoogle Scholar
[9]Fauve, S. (1998) Pattern forming instabilities, Hydrodynamics and nonlinear instabilities, Godrèche, C. and Manneville, P. ed., Cambridge University Press, 387–491.CrossRefGoogle Scholar
[10]Iron, D., Ward, M. J. and Wei, J. (2001) The stability of spike solutions to the one-dimensional Gierer-Meinhardt model. Physica D 150, 25–62.CrossRefGoogle Scholar
[11]Komarova, N. L. and Newell, A. C. (2000) Nonlinear dynamics of sand banks and sand waves. J. Fluid. Mech. 415, 285–321.CrossRefGoogle Scholar
[12]Lin, C.-S. and Ni, W.-M. (1988) On the diffusion coefficient of a semilinear Neumann problem. Calculus of variations and partial differential equations (Trento, 1986), Lecture Notes in Math. 1340, Springer, Berlin-New York, 160–174.CrossRefGoogle Scholar
[13]Matthews, P. C. and Cox, S. M. (2000) Pattern formation with a conservation law. Nonlinearity 13, 1293–1320.Google Scholar
[14]Mielke, A. (2002) The Ginzburg-Landau equation in its role as a modulation equation. Handbook of dynamical systems 2, North-Holland, Amsterdam, 759–834.Google Scholar
[15]Norbury, J., Wei, J. and Winter, M. (2002) Existence and stability of singular patterns in a Ginzburg-Landau equation coupled with a mean field. Nonlinearity 15, 2077–2096.CrossRefGoogle Scholar
[16]Riecke, H. (1992) Self-trapping of traveling-pulse wave pulses in binary mixture convection. Phys. Rev. Lett. 68, 301–304.CrossRefGoogle Scholar
[17]Riecke, H. (1996) Solitary waves under the influence of a long-wave mode. Physica D 92, 69–94.CrossRefGoogle Scholar
[18]Riecke, H. (1998) Localized structures in pattern-forming systems. Pattern formation in continuous and coupled systems, IMA Vol. Math. Appl. 115, Minneapolis, USA 215–229.Google Scholar
[19]Sandstede, B. and Scheel, A. (2005) Absolute inequalities of standing pulses. Nonlinearity 18, 331–378.CrossRefGoogle Scholar
[20]Ward, M. J. and Wei, J. (2002) Asymmetric Spike Patterns for the One-Dimensional Gierer-Meinhardt Model: Equilibria and Stability, Europ. J. Appl. Math. 13, No. 3, pp. 283–320.CrossRefGoogle Scholar
[21]Ward, M. J, and Wei, J. (2003) Hopf Bifurcations and Oscillatory Instabilities of Spike Solutions for the One-Dimensional Gierer-Meinhardt Model, Journal of Nonlinear Science 13, No. 2, pp. 209–264.CrossRefGoogle Scholar
[22]Wei, J. (1999) On single interior spike solutions of the Gierer-Meinhardt system: uniqueness and spectrum estimates. Euro. Jnl of Applied Mathematics 10, 353–378.CrossRefGoogle Scholar
[23]Wei, J. and Winter, M. (2003) Stability of monotone solutions for the shadow Gierer-Meinhardt system with finite diffusivity, Differential Integral Equations 16, 1153–1180.CrossRefGoogle Scholar
[24]Winterbottom, D. M., Matthews, P. C. and Cox, S. M. (2005) Oscillataory pattern formation with a conserved quantity. Nonlinearity 18, 1031–1056.CrossRefGoogle Scholar