Small Péclet-number mass transport to a finite strip: An advection–diffusion–reaction model of surface-based biosensors

Abstract

We consider two-dimensional mass transport to a finite absorbing strip in a uniform shear flow as a model of surface-based biosensors. The quantity of interest is the Sherwood number Sh, namely the dimensionless net flux onto the strip. Considering early-time absorption, it is a function of the Péclet number Pe and the Damköhler number Da, which, respectively, represent the characteristic magnitude of advection and reaction relative to diffusion. With a view towards modelling nanoscale biosensors, we consider the limit Pe«1. This singular limit is handled using matched asymptotic expansions, with an inner region on the scale of the strip, where mass transport is diffusively dominated, and an outer region at distances that scale as Pe^-1/2, where advection enters the dominant balance. At the inner region, the mass concentration possesses a point-sink behaviour at large distances, proportional to Sh. A rescaled concentration, normalised using that number, thus possesses a universal logarithmic divergence; its leading-order correction represents a uniform background concentration. At the outer region, where advection by the shear flow enters the leading-order balance, the strip appears as a point singularity. Asymptotic matching with the concentration field in that region provides the Sherwood number as

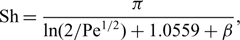$${\rm{Sh}} = {\pi \over {\ln (2/{\rm{P}}{{\rm{e}}^{1/2}}) + 1.0559 + \beta }},$$

wherein β is the background concentration. The latter is determined by the solution of the canonical problem governing the rescaled inner concentration, and is accordingly a function of Da alone. Using elliptic-cylinder coordinates, we have obtained an exact solution of the canonical problem, valid for arbitrary values of Da. It is supplemented by approximate solutions for both small and large Da values, representing the respective limits of reaction- and transport-limited conditions.