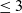Projective invariants of images

Abstract

The method of equivariant moving frames is employed to construct and completely classify the differential invariants for the action of the projective group on functions defined on the two-dimensional projective plane. While there are four independent differential invariants of order $\leq 3$, it is proved that the algebra of differential invariants is generated by just two of them through invariant differentiation. The projective differential invariants are, in particular, of importance in image processing applications.

The differential invariants pertaining to several basic planar transformation groups of geometric significance – Euclidean, similarity, equi-affine, affine, Möbius and projective – have played important roles in image processing over many years, see for instance [11] for a survey for developments through the early 1990s. Except for the Möbius group [10, 22], all the groups noted above are subgroups of the projective group, which governs the transformations of camera projections of three-dimensional objects and forms the focus of this note. Research has tended to concentrate on the induced action on planar curves, representing the outlines of (the projections of) objects [3, 5, 6]. One can, alternatively, study the action on the entire image. For us, this means a greyscale image, represented (in the continuum limit) by a smooth function $u=f(x,y)$ defined on some planar region $ \Omega \subset \mathbb{R}^2$ , often, but not necessarily, a rectangle. The group acts trivially on the dependent variable u, whose value (usually between $0 =$ black and $1=$ white) corresponds to the grey level of the pixel at position $(x,y) \in \Omega $ . Extensions of this analysis to colour images, where the dependent variable u is vector valued, will not be treated here, although our moving frame methods can be readily extended to this more general context.

Let $\mathbb{RP}^2$ be the real projective plane consisting of all lines passing through the origin in $\mathbb{R}^3$ . On the dense open subset containing those lines that do not lie in the x y plane, we can employ the inhomogeneous coordinates (x, y) to represent the line in the direction (x, y, 1). The standard action of the general linear group $\textrm{GL}(3,\mathbb{R})$ on $\mathbb{R}^3$ induces an action of the 8 dimensional projective linear group $\textrm{PSL}(3,\mathbb{R}) = \textrm{GL}(3,\mathbb{R})/\{\lambda \textrm{I} | 0 \ne \lambda \in \mathbb{R}\}$ on the lines in $\mathbb{RP}^2$ . We are thus interested in the induced intransitive action

(1) \begin{equation}\displaystyle{X = \frac{\alpha x+\beta y+\gamma }{\rho x+\sigma y+\tau },\ \ Y = \frac{\lambda x+\mu y+\nu }{\rho x+\sigma y+\tau },\ \ U = u,}\end{equation}

of $\textrm{PSL}(3,\mathbb{R})$ on the trivial bundle $M = \mathbb{RP}^2 \times \mathbb{R}$ . To avoid the overall scaling ambiguity, we impose the unimodularity condition

(2) \begin{equation}\Delta = \det\left(\begin{array}{c@{\quad}c@{\quad}c}\alpha & \beta & \gamma\\ \\[-9pt]\lambda & \mu & \nu\\ \\[-9pt]\rho & \sigma & \tau\end{array}\right) = 1\end{equation}

on the group parameters appearing in the coefficient matrix. This action coincides with the special case $n=0$ for the one-parameter family of actions of the general linear group $\textrm{GL}(3)$ that was studied in [20]. However, this particular case was not relevant to the main focus of that work – ternary forms in classical invariant theory – and so was not analysed.

The goal is to conduct a similar moving frame-based analysis, cf. [4, 9, 18, 19], of the differential invariants of the induced action of (1) on two-dimensional surfaces $S \subset M$ representing the graphs of functions $u=f(x,y)$ ; in other words, we have two independent variables and one dependent variable. We prolong the group action to the surface jet bundles $\displaystyle{\textrm{J}^{n} = \textrm{J}^{n}(M,2), n=0,1,2,\ldots}$ , [12], which are coordinatised by the independent variables x, y, along with the dependent variable $u = u_{00}$ and its derivatives:

(3) \begin{equation}u_{jk} = \textrm{D}_{x}^{\,j} \textrm{D}_{y}^{ k} u \qquad \textrm{for}\qquad 0 \leq j+k \leq n,\end{equation}

in which $\textrm{D}_{x},\textrm{D}_{y}$ denote the total derivative operators with respect to x, y, respectively. A smooth function of the jet coordinates, defined an open subset of $\textrm{J}^{n}$ , is known as a differential function. A projective differential invariant is a differential function that is unchanged by the prolonged projective group action. Note: When writing ‘differential invariant’ without qualification, we always mean an absolute differential invariant. Often these are ratios of two relative differential invariants having the same weight, see [13]. We begin by noting the obvious differential invariant of order 0

(4) \begin{equation}I_0 = u,\end{equation}

resulting from the intransitivity of the group action.

In local coordinates, the prolonged action is explicitly given by

(5) \begin{equation}u_{jk} \ \longmapsto\ U_{jk} = \textrm{D}_{X}^{ j} \textrm{D}_{Y}^{ k} U,\end{equation}

where

(6) $$\begin{gathered} {{\text{D}}_X} = \frac{{\rho x + \sigma y + \tau }}{\Delta }\left( {{\mkern 1mu} [(\mu \rho - \lambda \sigma )x + \mu \tau - \nu \sigma ]{{\text{D}}_x} + [{\mkern 1mu} (\mu \rho - \lambda \sigma )y - \lambda \tau + \nu \rho ]{{\text{D}}_y}} \right), \hfill \\ {{\text{D}}_Y} = \frac{{\rho x + \sigma y + \tau }}{\Delta }\left( {{\mkern 1mu} [(\alpha \sigma - \beta \rho )x - \beta \tau + \gamma \sigma ]{{\text{D}}_x} + [{\mkern 1mu} (\alpha \sigma - \beta \rho )y + \alpha \tau - \gamma \rho ]{{\text{D}}_y}} \right), \hfill \\ \end{gathered}$$

are the operators of implicit differentiation. They are dual to the transformed one-forms

(7) \begin{align}dX &= \frac{\bigl [{(\alpha \sigma - \beta \rho )y + \alpha \tau - \gamma \rho }\bigr ]dx+\bigl [{(\beta \rho - \alpha \sigma )x + \beta \tau - \gamma \sigma }\,\bigr ]dy}{({\rho x+\sigma y+\tau })^2}, \nonumber\\[3pt]dY &= \frac{\bigl [{(\lambda \sigma - \mu \rho )y + \lambda \tau - \nu \rho }\bigr ]dx+\bigl[{(\mu \rho - \lambda \sigma )x + \mu \tau - \nu \sigma }\bigr ]dy}{({\rho x+\sigma y+\tau })^2},\end{align}

which are obtained by differentiating the expressions for X, Y in (1). Duality means that the horizontal differential [13] of a differential function $F(x,u^{(u)})$ is given by

\begin{equation*}d_HF = (\textrm{D}_{x} F) dx + (\textrm{D}_{y} F) dy = (\textrm{D}_{X} F) dX + (\textrm{D}_{Y} F) dY.\end{equation*}

Let us construct the moving frame based on the cross-section

(8) \begin{equation}\mathcal{K} = \{ x=y=0,\ \ u_{x} = u_{yy}=1, u_{y}=u_{xx}=u_{xy}=u_{yyy}=0 \} \subset \textrm{J}^3.\end{equation}

We will not write out the explicit formulas for the transformed jet coordinates (5) during our implementation of the normalisation procedure but just display the results of the Mathematica calculation. At each stage, the successive partial normalisations of the group parameters are substituted into the remaining formulas before effecting the next round of normalisations. However, it is important that the prolonged transformation formulae be computed in advance, before any normalisation is implemented; an alternative strategy would be to employ the recursive normalisation algorithm developed in [16], which has the advantage of determining the formulas for the projective differential invariants in terms of differential invariants of its subgroups; this remains to be written down in detail.

First, setting $X=Y=0$ produces

(9) \begin{equation}{\gamma = - \alpha x-\beta y,\ \ \nu = - \lambda x-\mu y.}\end{equation}

Next, setting $\displaystyle{U_X=1,\ U_Y=0}$ , implies

(10) \begin{equation}{\alpha =({\rho x+\sigma y+\tau })\,u_x,\ \ \beta = ({\rho x+\sigma y+\tau })\,u_y.}\end{equation}

The second-order normalisations are done in two steps. First, setting $\displaystyle{U_{XX}=U_{XY}=0}$ yields

(11) \begin{equation}{\sigma = -\,\frac AC\,\rho,\qquad\tau = -\,\frac BC\,\rho,}\end{equation}

where

(12) \begin{align}A &= \mu ^2 ({u_y u_{xx} - 2 u_x u_{xy}}) + 2 \lambda \mu u_x u_{yy} - \lambda ^2u_y u_{yy},\nonumber\\[3pt]B &= \mu ^2 ({x u_x u_{xx} + 2 y u_x u_{xy}- y u_y u_{xx} + 2 u_x^2}) -2 \lambda \mu ({x u_y u_{xx} + y u_x u_{yy} + 2 u_xu_y})\nonumber\\[3pt] &\quad + \lambda ^2({- x u_x u_{yy} + 2 x u_y u_{xy} + y u_y u_{yy} + 2 u_y^2}),\nonumber\\[3pt]C &= \mu ^2 u_x u_{xx} - 2 \lambda \mu u_y u_{xx} + \lambda ^2({ 2 u_y u_{xy}- u_x u_{yy}}) .\end{align}

We then substitute these values and solve $\displaystyle{U_{YY}=1}$ for

(13) \begin{equation}\rho = -\,\frac{\mu ^2 u_x u_{xx} - 2 \lambda \mu u_y u_{xx} + \lambda ^2({ 2 u_y u_{xy}- u_x u_{yy}})}{2 ({\mu u_x - \lambda u_y }) \, \sqrt J}\,,\end{equation}

where

(14) \begin{equation}J = u_y^2 u_{xx} - 2 u_xu_y u_{xy} + u_x^2 u_{yy} .\end{equation}

Substituting (13) into (11) produces the slightly simpler formulas

(15) \begin{equation}{\sigma = \frac E{2 ({\mu u_x - \lambda u_y }) \, \sqrt J}\,,\ \ \tau = \frac F{2 ({\mu u_x - \lambda u_y }) \, \sqrt J}\,.}\end{equation}

where

(16) \begin{align}E &= \mu ^2 ({u_y u_{xx} - 2 u_x u_{xy}}) + 2 \lambda \mu u_x u_{yy} - \lambda ^2u_y u_{yy}, \nonumber\\[3pt]F &= \mu ^2 ({x u_x u_{xx} + 2 y u_x u_{xy}- y u_y u_{xx} + 2 u_x^2}) -2 \lambda \mu ({x u_y u_{xx} + y u_x u_{yy} + 2 u_xu_y}) \nonumber\\[3pt] &\quad + \lambda ^2({- x u_x u_{yy} + 2 x u_y u_{xy} + y u_y u_{yy} + 2 u_y^2}).\end{align}

We note that the second-order differential polynomial J given in (14) is a relative differential invariant, transforming under the projective action (1) according to

(17) \begin{equation}J \ \longmapsto\ W^2\, J,\qquad \textrm{where} \qquad W = \frac{({\rho x+\sigma y+\tau })^3}{ \Delta }\,.\end{equation}

The multiplier function $W^2$ is also known as the weight of J. We refer the reader to [8] and [21] for applications of J in image analysis. We are assuming $J > 0$ . If $J< 0$ , we can replace J by $- J$ in any square roots that appear or, alternatively, use its absolute value throughout. Also, as in most moving frame calculations in the literature, we ignore any discrete ambiguities caused by the change of sign in a square root, which are due to the local freeness of the prolonged group action, cf. [4]. (See [15] for a complete discussion of sign ambiguities in the case of Euclidean curves.)

The points where J vanishes define the singular subvariety $\mathcal{V} = \{ J = 0\}$ , where the orbits of the prolonged the action of $\textrm{PSL}(2)$ have less than maximal dimension, and are not covered by the moving frame constructed here. Isolated points where J vanishes can be handled by using a higher order moving frame. On the other hand, the functions for which $J \equiv 0$ are totally singular [14] and therefore do not admit a moving frame of any order. They can be explicitly characterised as follows.

Theorem 1. Let u(x, y) be a $\textrm{C}^{2}$ function with domain $D \subset \mathbb{R}^2$ that has non-zero gradient everywhere in its domain: $\nabla u = (u_x,u_y) \ne 0$ . Then u is a solution to the quasilinear partial differential equation

(18) \begin{equation}J = u_y^2 u_{xx} - 2 u_xu_y u_{xy} + u_x^2 u_{yy} =0\end{equation}

if and only if all its level curves $u(x,y) = c$ , for $c \in \mathbb{R}$ , are straight line segments or disjoint unions thereof.

Note that if $\nabla u \equiv 0$ on a connected open set, then u is constant and has no level curves there. Otherwise, isolated points and curves on which $\nabla u = 0$ will correspond to intersections, limit points and envelopes [2] of its level curves.

Remark: The second-order parabolic quasilinear partial differential equation (18) was analysed in [1], where it was shown to have vanishing Goursat invariant and hence infinitely many non-trivial (generalised) conservation laws and, in particular, infinitely many inequivalent Lagrangians.

Proof Let $(x_0,y_0) \in D$ . We assume, without loss of generality, that $u_y(x_0,y_0) \ne 0$ , and hence, by continuity, also in a neighbourhood of $(x_0,y_0)$ . Otherwise, we must have $u_x(x_0,y_0) \ne 0$ , and we can apply the following arguments with the roles of x and y reversed. The implicit function theorem implies that the level curve passing through $(x_0,y_0)$ can be locally parametrised by $y = y(x)$ . Then, differentiating the level curve equation

\begin{equation*}u({x,y(x)}) = c, \qquad \textrm{where} \qquad c \in \mathbb{R},\end{equation*}

twice with respect to x yields

$$\begin{align*}{u_x + u_y y_x = 0,\ \ u_{xx} + 2 u_{xy} y_x + u_{yy} y_x^2 + u_y y_{xx} =0.}\end{align*}$$

Combining the second and third equations produces

\begin{equation*}y_{xx} = -u_y^{-3} J.\end{equation*}

Thus, if u satisfies (18), then its level curve satisfies $y_{xx} = 0$ , and hence must be a straight line.

An alternative proof proceeds by noting that one can write J as multiple of a Jacobian determinant:

(19) \begin{equation}J = u_x^2\,\frac{\partial(u,u_y/u_x)}{\partial(x,y)} = u_x^3 \textrm{D}_{y}(u_y/u_x) - u_x^2 u_y \textrm{D}_{x}(u_y/u_x).\end{equation}

Thus, if (18) holds, then the functions u and $u_y/u_x$ are functionally dependent, so, locally, ${u_y}/{u_x} = h(u)$ for some scalar function h(u), or, equivalently,

(20) \begin{equation}u_y - h(u) u_x = 0.\end{equation}

Using the method of characteristics [17], one deduces that any solution to such a quasilinear first-order partial differential equation is constant on its characteristic curves, which, in this case, are straight lines.

In particular, if the solution to (18) is defined and has non-vanishing gradient for all $(x,y) \in \mathbb{R}^2$ , then its level curves corresponding to different values of c cannot cross, ¹ and hence must all be parallel straight lines. This implies:

Corollary 2. The only globally defined solutions to (18) are functions of the form $u = g(a x + b y )$ for $a,b\in \mathbb{R}$ and g(t) an arbitrary scalar function.

Of course, there are many locally defined solutions that are not of this special form.

Returning to our moving frame calculation, we now recall the unimodularity constraint (2) Under the normalisations accumulated so far (9, 10, 13, 15), this becomes

\begin{equation*}\Delta = \frac{({\mu u_x - \lambda u_y })}J = 1,\end{equation*}

which serves to constrain the values of $\lambda, \mu $ when we perform the final normalisation $\displaystyle{U_{YYY}=0}$ , which yields

(21) \begin{align}\lambda &= \frac{u_x K - 6 u_y^3 u_{xx}^2 + 18 u_xu_y^2 u_{xx}u_{xy}- 6 u_x^2u_y (u_{xx} u_{yy} + 2 u_{xy}^2) + 6 u_x^3 u_{xy}u_{yy}}{6 J^{5/3} }, \nonumber\\[3pt]\mu &= \frac{u_yK - 6 u_y^3 u_{xx}u_{xy} + 6 u_xu_y^2(u_{xx} u_{yy} + 2 u_{xy}^2)- 18 u_x^2u_yu_{xy} u_{yy} + 6 u_x^3 u_{yy}^2}{6 J^{5/3} },\end{align}

where

(22) \begin{equation}K = u_y^3 u_{xxx} - 3 u_xu_y^2 u_{xxy} + 3 u_x^2u_y u_{xyy} - u_x^3 u_{yyy}.\end{equation}

We remark that, despite its elegance and similarity to (14), the differential polynomial K in (22) is not a relative invariant, meaning that, under the group action (1), it does not transform to a multiple of itself. Third-order relative invariants will appear in the expressions for the (absolute) differential invariants below.

This completes our derivation of the moving frame based on the cross-section (8). The right equivariant moving frame map $\rho \colon \textrm{J}^3 \setminus \mathcal{V} \to \textrm{PSL}(3)$ is obtained by combining the preceding normalisation formulas (9, 10, 13, 15, 21), producing fairly long formulas for all the group parameters in terms of the third-order jet coordinates, which we will not write out in detail.

There are three functionally independent third-order (absolute) differential invariants, corresponding to the invariantisations of the remaining third-order jet coordinates:

\begin{equation*}{I_1 = \iota(u_{xxx}),\qquad I_2 = \iota(u_{xxy}),\qquad I_3 = \iota(u_{xyy}).}\end{equation*}

To obtain their explicit formulas, we merely substitute the moving frame normalisations (9, 10, 13, 15, 21) into the formulas for the unnormalised transformed third-order jet coordinates $U_{XXX},U_{XXY},U_{XYY}$ , respectively, to eliminate all the group parameters. The resulting expressions are the third-order differential invariants. First,

(23) \begin{equation}{\widehat{I}_1 = I_1 - \textstyle\frac{1}{2} I_3^2 = \displaystyle\frac{L_1}{2\, J^2},\quad I_2 = \frac{L_2}{54\, J^{9/2}},\quad I_3 = \frac{L_3}{12\, J^3}.}\end{equation}

The fact that $\widehat{I}_1,I_2,I_3$ are absolute differential invariants implies that their numerators $L_1,L_2,L_3$ are relative differential invariants of weights $W^4, W^9, W^6$ , respectively, where $W^2$ denotes the weight of J, cf. (17). The explicit formulas are as follows:

(24) \begin{align}L_1 &= u_x^2 (u_{xxy} u_{yyy} - u_{xyy} ^2) + u_x u_y (u_{xxy} u_{xyy} - u_{xxx} u_{yyy}) + u_y^2 (u_{xxx} u_{xyy} - u_{xxy} ^2) \nonumber\\[3pt]&\quad + 2 u_x\bigl({ u_{yy} ^2u_{xxx} - 3 u_{xy} u_{yy} u_{xxy} + (u_{xx} u_{yy} + 2 u_{xy} ^2) u_{xyy} - u_{xx} u_{xy} u_{yyy}}\bigr) \nonumber\\[3pt]&\quad + 2 u_y\bigl({ - u_{xy} u_{yy}u_{xxx} + (u_{xx} u_{yy} + 2 u_{xy} ^2) u_{xxy} - 3 u_{xx} u_{xy} u_{xyy} + u_{xx}^2 u_{yyy}}\bigr) -4 H^2,\end{align}

where

(25) \begin{equation}H = u_{xx} u_{yy} - u_{xy} ^2\end{equation}

is the Hessian of the function u, while

(26) \begin{equation}{L_2 = - K^3 + 18 J ^2 M_1 + 18 J M_2,\qquad L_3 = K^2 - 12 J^2 H + 12 J M_3,}\end{equation}

where

(27) \begin{align}M_1 &= \bigl [{u_y^3 (u_{xx} u_{yy} - 4 u_{xy} ^2) + 6 u_x u_y^2u_{xy} u_{yy} - 3 u_x^2 u_y u_{yy} ^2}\bigr ]u_{xxx} \nonumber\\[3pt] &\quad +\bigl [{6 u_y^3 u_{xx} u_{xy} - 9 u_x u_y^2u_{xx} u_{yy} + 3 u_x^3u_{yy} ^2}\bigr ]u_{xxy} \nonumber\\[3pt] &\quad + \bigl [\!{- 3 u_y^3 u_{xx}^2 + 9 u_x^2 u_yu_{xx} u_{yy} - 6 u_x^3u_{xy} u_{yy}}\bigr ]u_{xyy} \nonumber\\[3pt] &\quad + \bigl [{3 u_x u_y^2 u_{xx} ^2 - 6 u_x^2 u_yu_{xx} u_{xy} - u_x^3 (u_{xx} u_{yy} - 4 u_{xy} ^2)}\bigr ]u_{yyy},\nonumber\\[3pt] M_2 &= u_y^5(u_y u_{xy} - u_x u_{yy} ) u_{xxx}^2+ u_y^4(- u_y^2 u_{xx} - 4 u_x u_y u_{xy} + 5 u_x ^2u_{yy} ) u_{xxx}u_{xxy}\nonumber\\[3pt] &\quad + u_x u_y^3(u_y^2 u_{xx} + u_x u_y u_{xy} - 2 u_x ^2u_{yy} ) (2 u_{xxx}u_{xyy} + 3 u_{xxy}^2)\nonumber\\[3pt] &\quad + u_x^2 u_y^2(- u_y^2 u_{xx} + u_x ^2u_{yy} ) (u_{xxx}u_{yyy} + 9 u_{xxy}u_{xyy})\nonumber\\[3pt] &\quad + u_x^3 u_y(2 u_y^2 u_{xx} - u_x u_y u_{xy} - u_x ^2u_{yy} ) (3 u_{xyy}^2 + 2 u_{xxy}u_{yyy})\nonumber\\[3pt] &\quad + u_x^4(- 5 u_y^2 u_{xx} + 4 u_x u_y u_{xy} + u_x ^2u_{yy} ) u_{xyy}u_{yyy}+u_x^5(u_y u_{xx} - u_x u_{xy} ) u_{yyy}^2 ,\nonumber\\[3pt] M_3 &= (- u_y^3 u_{xy} + u_xu_y^2 u_{yy} )u_{xxx} + (u_y^3 u_{xx} + u_xu_y^2u_{xy} - 2 u_x^2u_y u_{yy} )u_{xxy}\nonumber\\[3pt] &\quad + (- 2 u_xu_y^2 u_{xx} + u_x^2u_yu_{xy} + u_x^3 u_{yy} )u_{xyy} + (u_x^2u_y u_{xx} - u_x^3 u_{xy} )u_{yyy}.\end{align}

Again, it is worth noting that, while J and $L_1,L_2,L_3$ are relative differential invariants, their individual summands are not, and neither are $H,K, M_1,M_2,M_3$ . The third-order relative differential invariant $L_3$ was found in [8]; the other two third-order relative differential invariants $L_1,L_2$ appear to be new.

There are five independent fourth-order differential invariants, given by invariantising the corresponding jet coordinates:

(28) \begin{equation}{I_4 = \iota(u_{xxxx}),\quad I_5 = \iota(u_{xxxy}),\quad I_6 = \iota(u_{xxyy}),\quad I_7 = \iota(u_{xyyy}),\quad I_8 = \iota(u_{yyyy}).}\end{equation}

As we will see, these can all be generated by invariantly differentiating the third-order differential invariants, which implies that the latter along with the order 0 differential invariant $I_0 = u$ form a generating set for the differential invariant algebra. To prove this, we use the symbolic moving frame calculus [4, 18] to construct the recurrence formulae that relate the invariantly differentiated and normalised differential invariants.

First, normalising the implicit differentiation operators (6) using the moving frame formulas yields the explicit formulas for the two invariant differential operators:

(29) $${\mathcal{D}_1} = \frac{{[{\mkern 1mu} {u_y}K + 6( - {u_y}{u_{xy}} + {u_x}{u_{yy}}){\mkern 1mu} J{\mkern 1mu} ]{\mkern 1mu} {{\text{D}}_x} + [ - {u_x}K + 6({u_y}{u_{xx}} - {u_x}{u_{xy}}){\mkern 1mu} J{\mkern 1mu} ]{\mkern 1mu} {{\text{D}}_y}}}{{6{J^2}}},{\mkern 1mu} {\mkern 1mu} {\mathcal{D}_2} = \frac{{ - {u_y}{{\text{D}}_x} + {u_x}{{\text{D}}_y}}}{{\sqrt J }}.$$

By definition, applying $\mathcal{D}_1, \mathcal{D}_2$ to any (absolute) differential invariant produces another differential invariant. (However, applying $\mathcal{D}_1$ or $\mathcal{D}_2$ to a relative differential invariant does not necessarily produce a relative differential invariant, see below.) According to the Lie–Tresse theorem, [4, 7], we can generate all the higher order differential invariants by applying these operators to a finite generating set of differential invariants. We note that the invariant differential operators do not commute; indeed, their commutator is given by

(30) \begin{equation}[{\mathcal{D}_1},{\mathcal{D}_2}]= \mathcal{D}_1\,\mathcal{D}_2 - \mathcal{D}_2\,\mathcal{D}_1 = Y\,\mathcal{D}_2, \qquad \textrm{where}\qquad Y = - \textstyle \frac{1}{6} I_8 + I_3\end{equation}

is the sole commutator invariant. The commutator (30) can also be straightforwardly deduced using the general symbolic moving frame calculus.

We begin by invariantly differentiating the order 0 invariant $I_0 = u$ :

(31) \begin{equation}{\mathcal{D}_1u = 1,\qquad \mathcal{D}_2u = 0,}\end{equation}

which are easy to check directly from the formula (29). The right-hand sides of (31) are trivially invariant since they are constant, and consequently not of any help. We also note

(32) \begin{equation}{\mathcal{D}_1J = \frac{K^2 + 6 J M_3 + 12 J^2H}{J^2}\,,\qquad \mathcal{D}_2J = \frac K{\sqrt J}\,,}\end{equation}

which are found by direct calculation. However, these are not relative differential invariants, and we will not make use of these formulas here.

We compute the higher order recurrence formulas by implementing the standard symbolic algorithm, [4, 20], in Mathematica. The starting point is the following basis for the infinitesimal generators of the projective action (1):

(33) \begin{align}\textbf{v}_1&=\partial_{x},\quad \textbf{v}_2=\partial_{y},\quad \textbf{v}_3=x \partial_{x},\quad \textbf{v}_4=y \partial_{y},\nonumber\\[3pt]\textbf{v}_5&=y \partial_{x},\quad \textbf{v}_6=x \partial_{y},\quad \textbf{v}_7=x^2 \partial_{x}+x y \partial_{y},\quad \textbf{v}_8=x y \partial_{x}+y^2 \partial_{y}.\end{align}

These are prolonged to the jet spaces and then used to write out the associated recurrence formulae. Leaving out the intermediate details, after solving for the Maurer–Cartan invariants, the third-order recurrence formulas take a relatively simple form:

(34) \begin{align}\mathcal{D}_1I_1\,{=}\,I_4 + \frac{1}{2} I_2I_7 - 3 I_2^2,&\quad \mathcal{D}_2I_1=I_5 + \frac{1}{2} I_2I_8 - \frac{9}{2} I_2I_3,\nonumber\\[3pt]\mathcal{D}_1I_2=I_5 + \frac{1}{3} I_3I_7 - \frac{5}{2} I_2I_3,&\quad \mathcal{D}_2I_2=I_6 + \frac{1}{3} I_3I_8 - I_1 - 3 I_3^2,\nonumber\\[3pt]\mathcal{D}_1I_3=I_6 - I_1 - I_3^2,&\quad \mathcal{D}_2I_3=I_7 - 3 I_2.\end{align}

Thus, we can generate all the fourth-order differential invariants (28) except $I_8$ by differentiating the third-order differential invariants. Since $I_8$ can be deduced from the commutator invariant Y, we can use the commutator trick, as in [20], to also generate it. Moreover, since the moving frame has order 3, a general theorem [4] implies that we can generate all differential invariants by invariantly differentiating the normalised differential invariants of order $\leq 4$ . The only differential invariant we cannot generate in this fashion is the trivial order 0 invariant $I_0 = u$ . We have thus proved that the four differential invariants $I_0,I_1,I_2,I_3$ of order $\leq 3$ generate the projective differential invariant algebra.

Further detailed analysis of the recurrence formulae can be used to reduce the number of generators to two.

Theorem 3. The differential invariant algebra for the projective action (1) on surfaces $S \subset \mathbb{RP}^2 \times \mathbb{R}$ is generated by the order 0 invariant $I_0 = u$ along with the third-order differential invariant $I_3$ , as given in (23, 26, 27).

Remark: This almost proves that $I_0,I_3$ form a minimal generating set. Indeed, by (31), we clearly cannot generate $I_3$ from $I_0$ . On the other hand, invariantly differentiating $I_3$ does not produce a differential invariant that explicitly depends on u, and hence we also clearly cannot generate $I_0$ from $I_3$ . However, there is the (remote) possibility that starting with some cleverly chosen differential invariant that depends on both u and the higher order invariants, one might be able to generate both $I_0$ and $I_3$ by combining its invariant derivatives. This seems extremely unlikely, but I am as yet unable to completely rule this out. On the other hand, if this were the case, one could start with the commutator trick to generate Y, as given in (30), in terms of the purported generator, and then proceed from there. But I find it hard to believe this strategy would be successful. Unfortunately, when dealing with more than one independent variable, there is no known criterion for proving that a generating set of differential invariants is minimal – unless it happens to consist of just one differential invariant!

Proof Starting with $I_3$ , we first apply the commutator trick referenced above to $I_3$ in order to generate the commutator invariant $Y= - \textstyle \frac{1}{6} I_8 + I_3$ , and hence $I_8$ , as a rational function of $I_3$ and its invariant derivatives. On the other hand, using the last two recurrence formulas (34) for the derivatives of $I_3$ , we can also generate the third-order differential invariants $I_6 - I_1$ and $I_7 - 3 I_2$ .

We now need the fourth-order recurrence formulas:

(35) \begin{align}\mathcal{D}_1I_4&=I_9 + \textstyle\frac{2}{3} I_5I_7 - 4 I_2 I_5 - 6 I_1^2,\nonumber\\[3pt]\mathcal{D}_2I_4&=I_{10} + \textstyle\frac{2}{3} I_5I_8 - 6 I_3I_5 - 6 I_1I_2,\nonumber\\[3pt]\mathcal{D}_1I_5&=I_{10} + \textstyle \frac{1}{2} I_6I_7 - \textstyle \frac{1}{2} I_3I_5 - 3 I_2I_6 - \textstyle \frac{1}{2} I_1I_7 - \frac{9}{2} I_1I_2,\nonumber\\[3pt]\mathcal{D}_2I_5&=I_{11} - I_4 - \textstyle\frac{9}{2} I_3 I_6 - \textstyle\frac{1}{2} I_1 I_8 + \textstyle \frac{1}{2} I_6 I_8 + \frac32 I_1 I_3 - \frac{9}{2} I_2^2,\nonumber\\[3pt]\mathcal{D}_1I_6&=I_{11} - I_3 I_6 + \textstyle \frac{1}{3} I_7^2 - 3 I_2 I_7 - 3 I_1 I_3,\nonumber\\[3pt]\mathcal{D}_2I_6&=I_{12} - 2 I_5 - 3 I_3I_7 - I_2I_8 + \textstyle\frac{1}{3} I_7I_8,\nonumber\\[3pt]\mathcal{D}_1I_7&=I_{12} - 3 I_3I_7 - I_2I_8 +\textstyle \frac{1}{6} I_7I_8,\nonumber\\[3pt]\mathcal{D}_2I_7&=I_{13} - 3 I_6 - 3 I_3I_8 +\textstyle \frac{1}{6} I_8^2 + \frac{9}{2} I_3^2,\nonumber\\[3pt]\mathcal{D}_1I_8&=I_{13} - 2 I_3I_8,\nonumber\\[3pt]\mathcal{D}_2I_8&=I_{14} - 4 I_7,\end{align}

where

(36) \begin{align}I_9 = \iota(u_{xxxxx}),&\quad I_{10} = \iota(u_{xxxxy}),&I_{11} = \iota(u_{xxxyy}),\nonumber\\[3pt]I_{12} = \iota(u_{xxyyy}),&\quad I_{13} = \iota(u_{xyyyy}),&\quad I_{14} = \iota(u_{yyyyy}),\end{align}

are the functionally independent fifth-order differential invariants. This allows us to compute

\begin{equation*}\mathcal{D}_2(I_7 - 3 I_2) - \mathcal{D}_1 I_8 = 3 I_1 - 6 I_6 + \bigl({\textstyle \frac{1}{6} I_8^2 - 2 I_3I_8 + \frac{27}2 I_3^2}\,\bigr).\end{equation*}

We have already shown how to generate the terms on the left-hand side and the terms in the parentheses by suitably combining invariant derivatives of $I_3$ , and hence the same holds for $I_1 - 2 I_6$ . But we also know how to generate $I_1 - I_6$ , and hence we can generate both $I_1$ and $I_6$ individually. Finally, we use the recurrence formulae (34, 35) to compute

(37) \begin{align}&\mathcal{D}_1I_6 - \mathcal{D}_2^2 I_1 - \mathcal{D}_1I_1 - \textstyle \frac{1}{3} \bigl({\mathcal{D}_2I_3}\bigr)^2 \nonumber\\[3pt]&\quad = - \textstyle \frac{1}{2} I_2\,\mathcal{D}_2\bigl({I_8 - 6 I_3}\bigr) + I_1 I_8 + 8 I_3 I_6 - \textstyle \frac{1}{6} I_3 I_8^2 - I_6 I_8 + 3 I_3^2 I_8 - \frac{27}{2} I_3^3 - 9 I_1 I_3.\end{align}

The right-hand side depends linearly on $I_2$ . Moreover, we already know how to express the left-hand side and all terms other than $I_2$ on the right-hand side in terms of $I_3$ and its invariant derivatives. Thus, assuming

(38) \begin{equation}\mathcal{D}_2({I_8 - 6 I_3}) \ne 0,\end{equation}

then we can solve (37) to express $I_2$ as a rational function of $I_3$ and its invariant derivatives. Since $I_8$ has order 4, while $I_3$ has order 3, and the invariant differential operator $\mathcal{D}_2$ is explicitly given in (29), it is easily checked that condition (38) holds for generic surfaces $u = f(x,y)$ . It would be of interest to classify those surfaces for which the non-degeneracy condition (38) fails.

We have thus generated both $I_1$ and $I_2$ from $I_3$ , thereby completing the proof of Theorem 1. The explicit formulas expressing them as rational combinations of the invariant derivatives of $I_3$ can be constructed by implementing the above manipulations. However, they are quite complicated and not especially enlightening, and thus will not be displayed.

Remark: The commutator trick used at the outset also requires that the surface be suitably generic. Applying the argument in [19], genericity fails when the surface is degenerate in the sense that there exist scalar functions $F_1(t), F_2(t)$ , such that, when evaluated on the surface, the differential invariant $I_3$ satisfies the equations

(39) \begin{equation}{\mathcal{D}_1 I_3 = F_1(I_3),\ \ \mathcal{D}_2 I_3 = F_2(I_3).}\end{equation}

It would also be of interest to classify such projectively degenerate surfaces.