Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-12T19:48:15.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-local effects in an integro-PDE model from population genetics

Published online by Cambridge University Press:  20 November 2015

F. LI ,
K. NAKASHIMA  and
W.-M. NI
F. LI
Affiliation:
Center for Partial Differential Equations, East China Normal University, Minhang, Shanghai 200241, People's Republic of China email: [email protected]
K. NAKASHIMA
Affiliation:
Tokyo University of Marine Science and Technology, 4-5-7 Konan, Minato-ku, Tokyo 108-8477, Japan email: [email protected]
W.-M. NI
Affiliation:
Center for Partial Differential Equations, East China Normal University, Minhang, Shanghai 200241, People's Republic of China email: [email protected] School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the following non-local problem: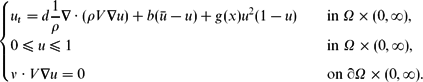

\begin{equation*}\begin{cases}\displaystyle u_t=d{1\over\rho}\nabla\cdot(\rho V\nabla u)+b(\bar{u}-u)+ g(x) u^2(1-u) &\displaystyle \quad \textrm{in} \; \Omega\times (0,\infty),\\[3pt]\displaystyle 0\leq u\leq 1 & \quad\displaystyle \textrm{in}\ \Omega\times (0,\infty),\\[3pt]\displaystyle \nu \cdot V\nabla u=0 &\displaystyle \quad \textrm{on} \; \partial\Omega\times (0,\infty).\vspace*{-2pt}\end{cases}\end{equation*}
This model, proposed by T. Nagylaki, describes the evolution of two alleles under the joint action of selection, migration, and partial panmixia – a non-local term, for the complete dominance case, where g(x) is assumed to change sign at least once to reflect the diversity of the environment. First, properties for general non-local problems are studied. Then, existence of non-trivial steady states, in terms of the diffusion coefficient d and the partial panmixia rate b, is obtained under different signs of the integral ∫Ωg(x)dx. Furthermore, stability and instability properties for non-trivial steady states, as well as the trivial steady states u ≡ 0 and u ≡ 1 are investigated. Our results illustrate how the non-local term – namely, the partial panmixia – helps the migration in this model.

Keywords

partial panmixianon-local effectsnon-trivial steady statesstability
Type
Papers
Information
European Journal of Applied Mathematics , Volume 28 , Issue 1 , February 2017 , pp. 1 - 41
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Brown, K. J. & Hess, P. (1990) Stability and uniqueness of positive solutions for a semi-linear elliptic boundary value problem. Differ. Integral Equ. 3 (2), 201–207.Google Scholar
[2] Coville, J. (2006) On uniqueness and monotonicity of solutions of non-local reaction diffusion equation. Ann. Mat. Pura Appl. (4) 185 (3), 461–485.Google Scholar
[3] Fleming, W. H. (1975) A selection-migration model in population genetics. J. Math. Biol. 2 (3), 219–233.Google Scholar
[4] Friedman, A. (1964) Partial Differential Equations of Parabolic Type, Prentice-Hall, Inc., Englewood Cliffs, N.J. Google Scholar
[5] Henry, D. (1981) Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics, Vol. 840, Springer-Verlag, Berlin-New York.CrossRefGoogle Scholar
[6] Hutson, V., Shen, W. & Vickers, G. T. (2008) Spectral theory for nonlocal dispersal with periodic or almost-periodic time dependence. Rocky Mt. J. Math. 38 (4), 1147–1175.Google Scholar
[7] Li, F., Nakashima, K. & Ni, W.-M. (2008) Stability from the point of view of diffusion, relaxation and spatial inhomogeneity. Discrete Contin. Dyn. Syst. 20 (2), 259–274.CrossRefGoogle Scholar
[8] Li, F. & Ni, W.-M. (2009) On the global existence and finite time blow-up of shadow systems. J. Differ. Equ. 247 (6), 1762–1776.Google Scholar
[9] Li, F. & Yip, N. (2014) Finite time blow-up of parabolic system with nonlocal terms. Indiana Univ. Math. J. 63 (3), 783–829.Google Scholar
[10] Lou, Y. & Nagylaki, T. (2002) A semilinear parabolic system for migration and selection in population gentics. J. Differ. Equ. 181 (2), 388–418.Google Scholar
[11] Lou, Y., Nagylaki, T. & Su, L. (2013) An integro-PDE model from population genetics. J. Differ. Equ. 254 (6), 2367–2392.Google Scholar
[12] Lou, Y., Ni, W.-M. & Su, L. (2010) An indefinite nonlinear diffusion problem in population genetics. II. Stability and multiplicity. Discrete Contin. Dyn. Syst. 27 (2), 643–655.Google Scholar
[13] Lunardi, A. (1995) Analytic Semigroups and Optimal Regularity in Parabolic Problems, Birkhäuser Verlag, Basel.Google Scholar
[14] Mora, X. (1983) Semilinear parabolic problems define semiflows on C k spaces. Trans. Amer. Math. Soc. 278 (1), 21–55.Google Scholar
[15] Nagylaki, T. (1975) Conditions for the existence of clines. Genetics 80 (3), 595–615.Google Scholar
[16] Nagylaki, T. (2011) The influence of partial panmixia on neutral models of spatial variation. Theor. Popul. Biol. 79 (1–2), 19–38.Google Scholar
[17] Nagylaki, T. (2012) Clines with partial panmixia. Theor. Popul. Biol. 81 (1), 45–68.Google Scholar
[18] Nagylaki, T. (2012) Clines with partial panmixia in an unbounded unidimensional habitat. Theor. Popul. Biol. 82 (1), 22–28.Google Scholar
[19] Nakashima, K., Ni, W.-M. & Su, L. (2010) An indefinite nonlinear diffusion problem in population genetics. I. Existence and limiting profiles. Discrete Contin. Dyn. Syst. 27 (2), 617–641.CrossRefGoogle Scholar
[20] Rawal, N. & Shen, W. (2012) Criteria for the existence and lower bounds of principal eigenvalues of time periodic nonlocal dispersal operators and applications. J. Dyn. Diff. Eqs. 24 (4), 927–954.CrossRefGoogle Scholar
[21] Senn, S. (1983) On a nonlinear elliptic eigenvalue problem with Neumann boundary conditions, with an application to population genetics. Commun. Partial Differ. Equ. 8 (11), 1199–1228.Google Scholar
[22] Shen, W. & Vickers, G. T. (2007) Spectral theory for general nonautonomous/random dispersal evolution operators. J. Differ. Equ. 235 (1), 262–297.Google Scholar
[23] Slatkin, M. (1973) Gene flow and selection in a cline. Genetics 75 (4), 73–756.Google Scholar
[24] Winkler, M. (2010) Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J. Differ. Equ. 248 (12), 2889–2905.Google Scholar