Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
EVANS, J. D.
GALAKTIONOV, V. A.
and
KING, J. R.
2007.
Source-type solutions of the fourth-order unstable thin film equation.
European Journal of Applied Mathematics,
Vol. 18,
Issue. 3,
p.
273.
Evans, J D
Galaktionov, V A
and
King, J R
2007.
Unstable sixth-order thin film equation: I. Blow-up similarity solutions.
Nonlinearity,
Vol. 20,
Issue. 8,
p.
1799.
Galaktionov, V. A.
2008.
On blow-up space jets for the Navier–Stokes equations in R3 with convergence to Euler equations.
Journal of Mathematical Physics,
Vol. 49,
Issue. 11,
Galaktionov, V.A.
2009.
Three types of self-similar blow-up for the fourth-orderp-Laplacian equation with source.
Journal of Computational and Applied Mathematics,
Vol. 223,
Issue. 1,
p.
326.
Galaktionov, V A
2009.
Five types of blow-up in a semilinear fourth-order reaction–diffusion equation: an analytic–numerical approach.
Nonlinearity,
Vol. 22,
Issue. 7,
p.
1695.
Cherniha, Roman
and
Myroniuk, Liliia
2010.
Lie symmetries and exact solutions of a class of thin film equations.
Journal of Physical Mathematics,
Vol. 2,
Issue. ,
p.
1.
Galaktionov, V. A.
2010.
Incomplete Self‐Similar Blow‐Up in a Semilinear Fourth‐Order Reaction‐Diffusion Equation.
Studies in Applied Mathematics,
Vol. 124,
Issue. 4,
p.
347.
Galaktionov, V. A.
2010.
Very Singular Solutions for Thin Film Equations with Absorption.
Studies in Applied Mathematics,
Vol. 124,
Issue. 1,
p.
39.
Hsu, Shu-Yu
2010.
Removable singularity of the polyharmonic equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 2,
p.
624.
EVANS, J. D.
and
GALAKTIONOV, V. A.
2011.
On continuous branches of very singular similarity solutions of a stable thin film equation. I – The Cauchy problem.
European Journal of Applied Mathematics,
Vol. 22,
Issue. 3,
p.
217.
Álvarez-Caudevilla, P.
and
Galaktionov, V. A.
2011.
Local bifurcation-branching analysis of global and “blow-up” patterns for a fourth-order thin film equation.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 18,
Issue. 5,
p.
483.
EVANS, J. D.
and
GALAKTIONOV, V. A.
2011.
On continuous branches of very singular similarity solutions of the stable thin film equation. II – Free-boundary problems.
European Journal of Applied Mathematics,
Vol. 22,
Issue. 3,
p.
245.
Lisini, Stefano
Matthes, Daniel
and
Savaré, Giuseppe
2012.
Cahn–Hilliard and thin film equations with nonlinear mobility as gradient flows in weighted-Wasserstein metrics.
Journal of Differential Equations,
Vol. 253,
Issue. 2,
p.
814.
Zhao, Xiaopeng
Zhang, Min
and
Liu, Changchun
2013.
Some properties of solutions for a fourth‐order parabolic equation.
Mathematical Methods in the Applied Sciences,
Vol. 36,
Issue. 2,
p.
169.
Álvarez-Caudevilla, Pablo
Evans, Jonathan D.
and
Galaktionov, Victor A.
2013.
The Cauchy Problem for a Tenth-Order Thin Film Equation I. Bifurcation of Oscillatory Fundamental Solutions.
Mediterranean Journal of Mathematics,
Vol. 10,
Issue. 4,
p.
1761.
Li, Yibao
and
Kim, Junseok
2013.
Numerical investigations on self-similar solutions of the nonlinear diffusion equation.
European Journal of Mechanics - B/Fluids,
Vol. 42,
Issue. ,
p.
30.
2014.
Blow-up for Higher-Order Parabolic, Hyperbolic, Dispersion and Schrodinger Equations.
p.
41.
Taranets, Roman M.
and
King, John R.
2014.
On an unstable thin-film equation in multi-dimensional domains.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 21,
Issue. 1,
p.
105.
Álvarez-Caudevilla, Pablo
and
Galaktionov, Victor A.
2015.
Well-posedness of the Cauchy problem for a fourth-order thin film equation via regularization approaches.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 121,
Issue. ,
p.
19.
Álvarez-Caudevilla, P.
D. Evans, J.
and
A. Galaktionov, V.
2015.
The Cauchy problem for a tenth-order thin film equation II.
Oscillatory source-type and fundamental similarity solutions.
Discrete & Continuous Dynamical Systems - A,
Vol. 35,
Issue. 3,
p.
807.
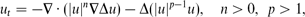 which contains a backward (unstable) diffusion term. Our main goal is a detailed study of the case of the first critical exponent
which contains a backward (unstable) diffusion term. Our main goal is a detailed study of the case of the first critical exponent
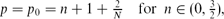 where N ≥ 1 is the space dimension. We show that the free-boundary problem with zero contact angle and zero-flux conditions admits continuous sets (branches) of blow-up self-similar solutions. For the Cauchy problem in RN × R+, we detect compactly supported blow-up patterns, which have infinitely many oscillations near interfaces and exhibit a “maximal” regularity there. As a key principle, we use the fact that, for small positive n, such solutions are close to the similarity solutions of the semilinear unstable limit Cahn-Hilliard equation
where N ≥ 1 is the space dimension. We show that the free-boundary problem with zero contact angle and zero-flux conditions admits continuous sets (branches) of blow-up self-similar solutions. For the Cauchy problem in RN × R+, we detect compactly supported blow-up patterns, which have infinitely many oscillations near interfaces and exhibit a “maximal” regularity there. As a key principle, we use the fact that, for small positive n, such solutions are close to the similarity solutions of the semilinear unstable limit Cahn-Hilliard equation
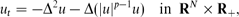 which are better understood and have been studied earlier [19]. We also discuss some general aspects of formation of self-similar blow-up singularities for other values of p.
which are better understood and have been studied earlier [19]. We also discuss some general aspects of formation of self-similar blow-up singularities for other values of p.