Article contents
Asymptotic behaviour of solutions of Fisher–KPP equation with free boundaries in time-periodic environment
Published online by Cambridge University Press: 25 March 2019
Abstract
We study a free boundary problem of the form: ut = uxx + f(t, u) (g(t) < x < h(t)) with free boundary conditions h′(t) = −ux(t, h(t)) – α(t) and g′(t) = −ux(t, g(t)) + β(t), where β(t) and α(t) are positive T-periodic functions, f(t, u) is a Fisher–KPP type of nonlinearity and T-periodic in t. This problem can be used to describe the spreading of a biological or chemical species in time-periodic environment, where free boundaries represent the spreading fronts of the species. We study the asymptotic behaviour of bounded solutions. There are two T-periodic functions α0(t) and α*(t; β) with 0 < α0 < α* which play key roles in the dynamics. More precisely, (i) in case 0 < β< α0 and 0 < α < α*, we obtain a trichotomy result: (i-1) spreading, that is, h(t) – g(t) → +∞ and u(t, ⋅ + ct) → 1 with 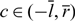 $c\in (-\overline{l},\overline{r})$, where
$c\in (-\overline{l},\overline{r})$, where 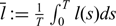 $ \overline{l}:=\frac{1}{T}\int_{0}^{T}l(s)ds$,
$ \overline{l}:=\frac{1}{T}\int_{0}^{T}l(s)ds$, 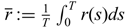 $\overline{r}:=\frac{1}{T}\int_{0}^{T}r(s)ds$, the T-periodic functions −l(t) and r(t) are the asymptotic spreading speeds of g(t) and h(t) respectively (furthermore, r(t) > 0 > −l(t) when 0 < β < α < α0; r(t) = 0 > −l(t) when 0 < β < α = α0;
$\overline{r}:=\frac{1}{T}\int_{0}^{T}r(s)ds$, the T-periodic functions −l(t) and r(t) are the asymptotic spreading speeds of g(t) and h(t) respectively (furthermore, r(t) > 0 > −l(t) when 0 < β < α < α0; r(t) = 0 > −l(t) when 0 < β < α = α0; 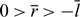 $0 \gt \overline{r} \gt -\overline{l}$ when 0 < β < α0 < α < α*); (i-2) vanishing, that is,
$0 \gt \overline{r} \gt -\overline{l}$ when 0 < β < α0 < α < α*); (i-2) vanishing, that is, 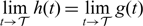 $\lim\limits_{t \to \mathcal {T}}h(t) = \lim\limits_{t \to \mathcal {T}}g(t)$ and
$\lim\limits_{t \to \mathcal {T}}h(t) = \lim\limits_{t \to \mathcal {T}}g(t)$ and 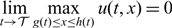 $\lim\limits_{t \to \mathcal {T}}\max\limits_{g(t)\leq x\leq h(t)} u(t,x)=0$, where
$\lim\limits_{t \to \mathcal {T}}\max\limits_{g(t)\leq x\leq h(t)} u(t,x)=0$, where 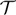 $\mathcal {T}$ is some positive constant; (i-3) transition, that is, g(t) → −∞, h(t) → −∞,
$\mathcal {T}$ is some positive constant; (i-3) transition, that is, g(t) → −∞, h(t) → −∞, 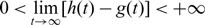 $0<\lim\limits_{t \to \infty}[h(t)-g(t)] \lt +\infty$ and u(t, ⋅) → V(t, ⋅), where V is a T-periodic solution with compact support. (ii) in case β ≥ α0 or α ≥ α*, vanishing happens for any solution.
$0<\lim\limits_{t \to \infty}[h(t)-g(t)] \lt +\infty$ and u(t, ⋅) → V(t, ⋅), where V is a T-periodic solution with compact support. (ii) in case β ≥ α0 or α ≥ α*, vanishing happens for any solution.
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
This research was sponsored by NSFC (No. 11701359, No. 11502141).
References
- 1
- Cited by


