1. Introduction
Vegetation patterns have been widely studied in recent years due to their importance as ecological indicators [Reference Chen, Kolokolnikov, Tzou and Gai10, Reference Gilad, von Hardenberg, Provenzale, Shachak and Meron16, Reference Klausmeier19, Reference Lei, Zhang and Zhou20, Reference Rietkerk, Boerlijst, van Langevelde, HilleRisLambers, van de Koppel, Kumar, Prins and de Roos32, Reference Rietkerk, Dekker, de Ruiter and van de Koppel33]. Changes in their structure, in fact, provide a valuable insight into ecological changes and illustrate the flexibility and resilience of an ecosystem [Reference Scheffer, Carpenter, Foley, Folke and Walker37, Reference Yizhaq, Gilad and Meron40]; vegetation patterns can therefore be used as early-warning indicators for desertification [Reference Rietkerk, Dekker, de Ruiter and van de Koppel33]. These patterns can appear in different forms depending on the type of terrain considered: while spots, gaps, and labyrinths can be observed on flat grounds, stripes and arced bands typically appear on sloped terrains. These types of patterns were observed as early as 1950 [Reference Macfadyen23] under different slope conditions [Reference Valentin, d’Herbès and Poesen38] and have been studied in numerous works including [Reference Consolo, Currò and Valenti11, Reference Deblauwe, Barbier, Couteron, Lejeune and Bogaert12, Reference Gandhi, Werner, Iams, Gowda and Silber15]. As reported by recent experimental work, this type of pattern appears also in other biological systems, such as fungi [Reference Allegrezza, Bonanomi, Zotti, Carteni, Moreno, Olivieri, Garbarino, Tesei, Giannino and Mazzoleni1]. Partial differential equations (PDE) have been widely used with the aim to reproduce experimental observations by linking the occurrence of such patterns to space-dependent factors [Reference Bastiaansen, Chirilus-Bruckner and Doelman2, Reference Bastiaansen and Doelman3, Reference Gandhi, Werner, Iams, Gowda and Silber15, Reference Rietkerk and van de Koppel34, Reference Valentin, d’Herbès and Poesen38]. Most models consist of two/three reaction-diffusion-advection equations accounting only for biomass and water interactions. While this assumption may result reasonably when approaching arid and semi-arid environments, aerial photographs and data collection show that these patterns can emerge also when water is not a scarce resource [Reference Bonanomi, Incerti, Stinca, Cartenì, Giannino and Mazzoleni6, Reference Leprun21, Reference Marasco, Iuorio, Cartenì, Bonanomi, Tartakovsky, Mazzoleni and Giannino26]. In such cases, further biological mechanisms should hence be included in the model in order to justify their emergence.
In this context, an ecological factor which has proven to play a crucial role in vegetation dynamics is the so-called autotoxicity, produced by plant litter decomposition [Reference Berg and McClaugherty4] and whose occurrence is related to the exposure to fragmented self-DNA [Reference Mazzoleni, Bonanomi, Giannino, Rietkerk, Dekker and Zucconi28, Reference Mazzoleni, Bonanomi, Incerti, Chiusano, Termolino, Mingo, Senatore, Giannino, Cartenì, Rietkerk and Lanzotti29]. In particular, the involvement of accumulated extracellular DNA in plant–soil negative feedback has been observed experimentally, providing further evidence of its importance in shaping plant communities [Reference Bonanomi, Zotti, Idbella, Termolino, De Micco and Mazzoleni7]. Mathematical models incorporating biomass-autotoxicity interactions have been increasingly studied in recent years in order to understand the impact of autotoxicity on several relevant ecological issues, such as species coexistence and biodiversity [Reference Bonanomi, Giannino and Mazzoleni5, Reference Mazzoleni, Bonanomi, Giannino, Incerti, Dekker and Rietkerk27, Reference Mazzoleni, Bonanomi, Giannino, Rietkerk, Dekker and Zucconi28]. Moreover, including explicit spatial components using reaction-diffusion-ODE models has allowed for an investigation of autotoxicity effects on plants’ spatial organisation, such as clonal rings [Reference Bonanomi, Incerti, Stinca, Cartenì, Giannino and Mazzoleni6, Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8], fairy rings [Reference Karst, Dralle and Thompson18, Reference Salvatori, Moreno, Zotti, Iuorio, Cartenì, Bonanomi, Mazzoleni and Giannino35] and vegetation patterns [Reference Marasco, Giannino and Iuorio25, Reference Marasco, Iuorio, Cartenì, Bonanomi, Tartakovsky, Mazzoleni and Giannino26]. Its influence on sloped patterns, however, has not been fully understood yet.
In this work, following the PDE model presented in [Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8], we consider a novel advection term with the aim to understand the effect of autotoxicity on the formation of arced bands on sloped terrains. Our analysis reveals the absence of Turing patterns; however, as suggested by our numerical investigation, the system supports the occurrence of travelling waves. In particular, focusing on one-dimensional sections of the emerging profiles, we observe that while travelling fronts arise when the effect of toxicity is neglected from the biomass dynamics, these fronts turn into pulses when the dynamics of these variables are coupled. These transient patterns often emerge in different kinds of biological and ecological systems and have therefore raised a considerable interest in the scientific community in the past few years (see, among others, [Reference Deng and Zhang13, Reference Doelman, Kaper and Zegeling14, Reference Iuorio and Veerman17, Reference Scheel36, Reference van Saarloos39]). This result is consistent with the current available literature results, since the presence of a slope induces a movement in the emergent pattern (see e.g. [Reference Carter and Doelman9, Reference Klausmeier19]). The structure of our model allows us to obtain an analytical result for the critical wave speed which is confirmed by numerical observations.
The paper is organised as follows: in Section 2, we introduce the model, which we subsequently analyse in Section 3. In particular, we investigate stability with respect to homogeneous and heterogeneous perturbations (which exclude the emergence of Turing patterns) and derive a formula for the asymptotic wave speed of travelling wave solutions. Numerical results aimed to visualise the system’s dynamics and support the existence of travelling waves as well as investigate the slope intensity on the height of the biomass peak are discussed in Section 4. We finally conclude our work with a discussion of the results and future research perspectives in Section 5.
2. The mathematical model
Our modelling framework consists of two partial differential equations (PDEs) describing the dynamics of biomass
![]() $B$
(
$B$
(
![]() $\textrm{kg} \cdot \textrm{m}^2$
) and toxicity
$\textrm{kg} \cdot \textrm{m}^2$
) and toxicity
![]() $T$
(
$T$
(
![]() $\textrm{kg} \cdot \textrm{m}^2$
) within a smooth domain
$\textrm{kg} \cdot \textrm{m}^2$
) within a smooth domain
![]() $\Omega \in \mathbb{R}^2$
. These variables are assumed to evolve as follows: biomass grows according to a growth rate
$\Omega \in \mathbb{R}^2$
. These variables are assumed to evolve as follows: biomass grows according to a growth rate
![]() $g$
inhibited by toxicity via a sensitivity coefficient
$g$
inhibited by toxicity via a sensitivity coefficient
![]() $s$
, dies with a mortality rate
$s$
, dies with a mortality rate
![]() $d$
and diffuses proportionally to the constant parameter
$d$
and diffuses proportionally to the constant parameter
![]() $D_B$
. In particular, we assume that (even in the absence of toxicity) the biomass dynamics follows a logistic law, i.e. the biomass growth is limited by resource abundance via a carrying capacity term given by
$D_B$
. In particular, we assume that (even in the absence of toxicity) the biomass dynamics follows a logistic law, i.e. the biomass growth is limited by resource abundance via a carrying capacity term given by
![]() $g/d$
. On the other hand, toxicity increases proportionally to the biomass death via a coefficient
$g/d$
. On the other hand, toxicity increases proportionally to the biomass death via a coefficient
![]() $c$
, decays at rate
$c$
, decays at rate
![]() $q$
, diffuses in the soil proportionally to
$q$
, diffuses in the soil proportionally to
![]() $D_T$
and additionally spreads with a velocity
$D_T$
and additionally spreads with a velocity
![]() $V_T$
in the downhill direction of the terrain whose slope is described by
$V_T$
in the downhill direction of the terrain whose slope is described by
![]() $m$
. The intensity of the total advection term is hence given by the product between these two quantities, which have been kept separate to emphasise their ecological derivation and to include an explicit space dependence linked with real topographical data in the future.
$m$
. The intensity of the total advection term is hence given by the product between these two quantities, which have been kept separate to emphasise their ecological derivation and to include an explicit space dependence linked with real topographical data in the future.
The above assumptions result in the following system of reaction-diffusion-advection equations:
A detailed description of the model parameters, together with their values and units, is illustrated in Table 1.
3. Analysis
In order to investigate the emergence of patterned structures as well as travelling waves, we first reduce equations (2.1a), (2.1b) to a suitable nondimensional form. To this aim, we rescale the model variables as follows
 \begin{equation} \begin{gathered} \tilde{t} = g \, t, \quad \tilde{x} = \sqrt{\frac{g}{D_B}} x, \quad \tilde{y} = \sqrt{\frac{g}{D_B}} y \\[5pt] \tilde{B} = \frac{d}{g} B, \quad \tilde{T} = s \, T. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \tilde{t} = g \, t, \quad \tilde{x} = \sqrt{\frac{g}{D_B}} x, \quad \tilde{y} = \sqrt{\frac{g}{D_B}} y \\[5pt] \tilde{B} = \frac{d}{g} B, \quad \tilde{T} = s \, T. \end{gathered} \end{equation}
Therefore, the corresponding nondimensional system is (we omit the tildes for the sake of readability)
where we have introduced the following nondimensional parameters:
The parameter
![]() $\alpha$
, representing the nondimensional production of
$\alpha$
, representing the nondimensional production of
![]() $T$
due to
$T$
due to
![]() $B$
, collects all the parameters contributing to the toxicity production; in particular, it describes the ratio between the biomass growth and death rates (
$B$
, collects all the parameters contributing to the toxicity production; in particular, it describes the ratio between the biomass growth and death rates (
![]() $g$
and
$g$
and
![]() $d$
, respectively) times the factors of conversion and sensitivity to toxicity (
$d$
, respectively) times the factors of conversion and sensitivity to toxicity (
![]() $c$
and
$c$
and
![]() $s$
, respectively). Moreover, we note that the parameter
$s$
, respectively). Moreover, we note that the parameter
![]() $\beta$
here coincides with
$\beta$
here coincides with
![]() $\gamma$
in [Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8] – coherently with the structure for the
$\gamma$
in [Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8] – coherently with the structure for the
![]() $T$
equation presented here – and represents the characteristic rate of toxicity dynamics relative to plant growth rate. In particular, for fixed values of
$T$
equation presented here – and represents the characteristic rate of toxicity dynamics relative to plant growth rate. In particular, for fixed values of
![]() $g$
this parameter can be interpreted as the nondimensional version of the toxicity decay rate. The parameter
$g$
this parameter can be interpreted as the nondimensional version of the toxicity decay rate. The parameter
![]() $\gamma$
represents the ratio between the lateral flow of the toxicity and the radial diffusion of the biomass, whereas
$\gamma$
represents the ratio between the lateral flow of the toxicity and the radial diffusion of the biomass, whereas
![]() $\delta$
corresponds to the ratio between the two diffusion coefficients. According to the ranges identified for the dimensional parameters in Table 1, we have that
$\delta$
corresponds to the ratio between the two diffusion coefficients. According to the ranges identified for the dimensional parameters in Table 1, we have that
3.1. Equilibria and stability
Equations (3.2a), (3.2b) admit two equilibria, obtained by solving
and discarding the one which does not satisfy the feasibility assumption
![]() $B \geq 0$
. These two equilibria are
$B \geq 0$
. These two equilibria are
 \begin{equation} \begin{aligned} (B_0,T_0) &= (0,0) \quad &\text{(bare soil)},\\[5pt] (B_c,T_c) &= \left ( \frac{-\beta + \sqrt{\beta (4\alpha +\beta )}}{2 \alpha }, \frac{2\alpha + \beta -\sqrt{\beta (4\alpha +\beta )}}{2 \alpha } \right ) \quad &\text{(coexistence)}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (B_0,T_0) &= (0,0) \quad &\text{(bare soil)},\\[5pt] (B_c,T_c) &= \left ( \frac{-\beta + \sqrt{\beta (4\alpha +\beta )}}{2 \alpha }, \frac{2\alpha + \beta -\sqrt{\beta (4\alpha +\beta )}}{2 \alpha } \right ) \quad &\text{(coexistence)}. \end{aligned} \end{equation}
The steady-state
![]() $(B_c,T_c)$
can also be written as
$(B_c,T_c)$
can also be written as
![]() $(\Gamma, 1-\Gamma )$
, with
$(\Gamma, 1-\Gamma )$
, with
We note that the coexistence steady-state is monotonic in
![]() $\beta$
; in particular,
$\beta$
; in particular,
![]() $B_c$
is increasing and
$B_c$
is increasing and
![]() $T_c$
is decreasing with respect to the parameter
$T_c$
is decreasing with respect to the parameter
![]() $\beta$
. This is consistent with the idea that the faster the toxicity is removed from the soil, the higher the biomass density and the lower the toxicity density, respectively. Conversely,
$\beta$
. This is consistent with the idea that the faster the toxicity is removed from the soil, the higher the biomass density and the lower the toxicity density, respectively. Conversely,
![]() $B_c$
is decreasing and
$B_c$
is decreasing and
![]() $T_c$
is increasing with respect to the parameter
$T_c$
is increasing with respect to the parameter
![]() $\alpha$
: as expected, in fact, higher values of the factors related to biomass which increase toxicity lead to higher toxicity and lower biomass at steady state (see Figure 1).
$\alpha$
: as expected, in fact, higher values of the factors related to biomass which increase toxicity lead to higher toxicity and lower biomass at steady state (see Figure 1).

Figure 1.
![]() $B$
(left panel) and
$B$
(left panel) and
![]() $T$
(right panel) components of the spatially homogeneous coexistence equilibria
$T$
(right panel) components of the spatially homogeneous coexistence equilibria
![]() $(B_c, T_C)$
as functions of
$(B_c, T_C)$
as functions of
![]() $\beta$
, for
$\beta$
, for
![]() $\alpha =6$
(dotted line),
$\alpha =6$
(dotted line),
![]() $\alpha =18$
(dashed line) and
$\alpha =18$
(dashed line) and
![]() $\alpha =30$
(solid line).
$\alpha =30$
(solid line).
![]() $B_c$
is increasing in
$B_c$
is increasing in
![]() $\beta$
and decreasing in
$\beta$
and decreasing in
![]() $\alpha$
, whereas
$\alpha$
, whereas
![]() $T_c$
is decreasing in
$T_c$
is decreasing in
![]() $\beta$
and increasing in
$\beta$
and increasing in
![]() $\alpha$
.
$\alpha$
.

Figure 2. Bifurcation diagram associated with equations (3.2a), (3.2b) with respect to parameter
![]() $\beta$
for
$\beta$
for
![]() $\alpha =18$
. The blue and purple lines correspond to
$\alpha =18$
. The blue and purple lines correspond to
![]() $B_0$
and
$B_0$
and
![]() $B_c$
, respectively. Solid (resp. dashed) lines represent stability (resp. instability) with respect to spatially homogeneous perturbations, respectively.
$B_c$
, respectively. Solid (resp. dashed) lines represent stability (resp. instability) with respect to spatially homogeneous perturbations, respectively.
3.1.1. Stability to homogeneous perturbations
The Jacobian matrix associated with equation (3.5) is given by
 \begin{equation} J= \begin{pmatrix} 1-2\,B_\ast -T_\ast\;\;\;\;\; & -B_\ast \\[5pt] 2 \, \alpha \, B_\ast\;\;\;\;\; & -\beta \end{pmatrix}, \end{equation}
\begin{equation} J= \begin{pmatrix} 1-2\,B_\ast -T_\ast\;\;\;\;\; & -B_\ast \\[5pt] 2 \, \alpha \, B_\ast\;\;\;\;\; & -\beta \end{pmatrix}, \end{equation}
where
![]() $(B_\ast, T_\ast )$
represents a generic equilibrium. We therefore have that (see also Figure 2)
$(B_\ast, T_\ast )$
represents a generic equilibrium. We therefore have that (see also Figure 2)
• The bare soil equilibrium is a saddle, since
 $J$
evaluated at
$J$
evaluated at
 $(B_0,T_0)$
admits the eigenvalues
$(B_0,T_0)$
admits the eigenvalues
 $\lambda _1=1,$
$\lambda _1=1,$
 $\lambda _2=-\beta$
.
$\lambda _2=-\beta$
.• The coexistence equilibrium is stable, since
 $J$
evaluated at
$J$
evaluated at
 $(B_c,T_c)$
satisfiesfor any
$(B_c,T_c)$
satisfiesfor any \begin{equation*} \begin {aligned} \textrm {tr}\,J \vert _{(B_c,T_c)} &= \frac {\beta (1-2 \alpha ) -\sqrt {\beta(4 \alpha +\beta )}}{2 \alpha } \lt 0, \\[5pt] \textrm {det}\,J \vert _{(B_c,T_c)} &= \frac {\beta \!\left (4 \alpha +\beta -\sqrt {\beta (4 \alpha +\beta )} \right )}{2 \alpha } \gt 0, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} \textrm {tr}\,J \vert _{(B_c,T_c)} &= \frac {\beta (1-2 \alpha ) -\sqrt {\beta(4 \alpha +\beta )}}{2 \alpha } \lt 0, \\[5pt] \textrm {det}\,J \vert _{(B_c,T_c)} &= \frac {\beta \!\left (4 \alpha +\beta -\sqrt {\beta (4 \alpha +\beta )} \right )}{2 \alpha } \gt 0, \end {aligned} \end{equation*}
 $\alpha, \, \beta \gt 0$
.
$\alpha, \, \beta \gt 0$
.
3.1.2. Stability to heterogeneous perturbations
In order to investigate the stability of the steady-states (3.6) with respect to heterogeneous perturbations, we introduce the following non-uniform infinitesimal perturbations:
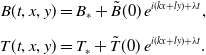 \begin{equation} \begin{aligned} B(t,x,y) &= B_\ast + \tilde{B}(0)\, e^{i (k x+ l y)+\lambda t}, \\[5pt] T(t,x,y) &= T_\ast + \tilde{T}(0)\, e^{i (k x+ l y)+\lambda t}. \\[5pt] \end{aligned} \end{equation}
\begin{equation} \begin{aligned} B(t,x,y) &= B_\ast + \tilde{B}(0)\, e^{i (k x+ l y)+\lambda t}, \\[5pt] T(t,x,y) &= T_\ast + \tilde{T}(0)\, e^{i (k x+ l y)+\lambda t}. \\[5pt] \end{aligned} \end{equation}
In particular, the norm of the spatial perturbation is defined as
![]() $h=\sqrt{k^2+l^2}$
.
$h=\sqrt{k^2+l^2}$
.
When we linearise equations (3.2a), (3.2b) around the abovementioned steady states, we obtain the following system for the perturbations
![]() $\tilde{B}$
,
$\tilde{B}$
,
![]() $\tilde{T}$
(again we omit the tildes for sake of simplicity):
$\tilde{T}$
(again we omit the tildes for sake of simplicity):
 \begin{equation} \begin{aligned} \lambda \, B &= (1-2\,B_\ast -T_\ast )\,B-B_\ast \,T-h^2 B, \\[5pt] \lambda \, T &= 2\, \alpha \,B_\ast \, B-\beta \, T+ i\, k\, \gamma \,T-\delta h^2\, T. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \lambda \, B &= (1-2\,B_\ast -T_\ast )\,B-B_\ast \,T-h^2 B, \\[5pt] \lambda \, T &= 2\, \alpha \,B_\ast \, B-\beta \, T+ i\, k\, \gamma \,T-\delta h^2\, T. \end{aligned} \end{equation}
Equation (3.10) is equivalent to an eigenvalue problem
![]() $J_h\, U = \lambda \, U$
, where
$J_h\, U = \lambda \, U$
, where
![]() $U=(B,T)$
and
$U=(B,T)$
and
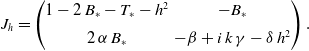 \begin{equation} J_h= \begin{pmatrix} 1-2\,B_\ast -T_\ast - h^2 & -B_\ast \\[5pt] 2 \, \alpha \, B_\ast & -\beta + i\, k\, \gamma -\delta \,h^2 \end{pmatrix}. \end{equation}
\begin{equation} J_h= \begin{pmatrix} 1-2\,B_\ast -T_\ast - h^2 & -B_\ast \\[5pt] 2 \, \alpha \, B_\ast & -\beta + i\, k\, \gamma -\delta \,h^2 \end{pmatrix}. \end{equation}
The characteristic polynomial, necessary to investigate the stability of (3.6), is given by
• The eigenvalues of
 $J_h$
evaluated at
$J_h$
evaluated at
 $(B_0,T_0)$
are
$(B_0,T_0)$
are
 $\lambda _1=1-h^2$
,
$\lambda _1=1-h^2$
,
 $\lambda _2=-\beta + i\, k\, \gamma -\delta \,h^2$
. Since this steady state is unstable with respect to homogeneous perturbations (see Section 3.1.1), no diffusion-driven instability occurs, and therefore, the stability character of the bare soil equilibrium is not relevant in the investigation of vegetation patterns. However, we observe that for
$\lambda _2=-\beta + i\, k\, \gamma -\delta \,h^2$
. Since this steady state is unstable with respect to homogeneous perturbations (see Section 3.1.1), no diffusion-driven instability occurs, and therefore, the stability character of the bare soil equilibrium is not relevant in the investigation of vegetation patterns. However, we observe that for
 $h$
such that
$h$
such that
 $h^2\lt 1$
the bare soil equilibrium retains its saddle structure, whereas for
$h^2\lt 1$
the bare soil equilibrium retains its saddle structure, whereas for
 $h$
such that
$h$
such that
 $h^2\gt 1$
it becomes stable (hence diffusion may induce a stabilising effect, as often expected).
$h^2\gt 1$
it becomes stable (hence diffusion may induce a stabilising effect, as often expected).• As for the coexistence equilibrium, we have that the trace and the determinant of
 $J_h$
evaluated at
$J_h$
evaluated at
 $(B_c,T_c)$
are(3.13)Equation (3.12) is solved by two roots given by
$(B_c,T_c)$
are(3.13)Equation (3.12) is solved by two roots given by \begin{equation} \begin{aligned} \textrm{tr}\,J_h &= -\beta -\Gamma -h^2(\delta +1)+ i\,k\,\gamma, \\[5pt] \textrm{det}\,J_h &= (h^2+\Gamma )(\beta +\delta \, h^2-i\,k\,\gamma )+2\,\alpha \,\Gamma ^2. \end{aligned} \end{equation}
(3.14)where
\begin{equation} \begin{aligned} \textrm{tr}\,J_h &= -\beta -\Gamma -h^2(\delta +1)+ i\,k\,\gamma, \\[5pt] \textrm{det}\,J_h &= (h^2+\Gamma )(\beta +\delta \, h^2-i\,k\,\gamma )+2\,\alpha \,\Gamma ^2. \end{aligned} \end{equation}
(3.14)where \begin{equation} \lambda _\pm =\frac 12 \left ( -\beta -\Gamma -h^2(\delta +1)+i\,k\,\gamma \right ) \pm \sqrt{X+i\,Y}, \end{equation}
(3.15)The real and imaginary part of the eigenvalues (3.14) can be written as
\begin{equation} \lambda _\pm =\frac 12 \left ( -\beta -\Gamma -h^2(\delta +1)+i\,k\,\gamma \right ) \pm \sqrt{X+i\,Y}, \end{equation}
(3.15)The real and imaginary part of the eigenvalues (3.14) can be written as \begin{equation} \begin{aligned} X &= (\beta - \Gamma +h^2(\delta -1))^2 - k^2\,\gamma ^2-8\,\alpha \,\Gamma ^2, \\[5pt] Y &= -2\,k\,\gamma \left ( \beta -\Gamma +h^2(\delta -1) \right ). \end{aligned} \end{equation}
(3.16a)
\begin{equation} \begin{aligned} X &= (\beta - \Gamma +h^2(\delta -1))^2 - k^2\,\gamma ^2-8\,\alpha \,\Gamma ^2, \\[5pt] Y &= -2\,k\,\gamma \left ( \beta -\Gamma +h^2(\delta -1) \right ). \end{aligned} \end{equation}
(3.16a) \begin{align} \textrm{Re}\,\lambda &= \frac 12 \left ( -\beta -\Gamma -h^2(\delta +1)+j\sqrt{\frac{X+\sqrt{X^2+Y^2}}{2}} \right ), \end{align}
(3.16b)
\begin{align} \textrm{Re}\,\lambda &= \frac 12 \left ( -\beta -\Gamma -h^2(\delta +1)+j\sqrt{\frac{X+\sqrt{X^2+Y^2}}{2}} \right ), \end{align}
(3.16b) \begin{align} \textrm{Im}\,\lambda &= \frac 12 \left ( \,k\,\gamma +j\, \textrm{sgn}(Y) \sqrt{\frac{\sqrt{X^2+Y^2}-X}{2}} \right ), \end{align}
\begin{align} \textrm{Im}\,\lambda &= \frac 12 \left ( \,k\,\gamma +j\, \textrm{sgn}(Y) \sqrt{\frac{\sqrt{X^2+Y^2}-X}{2}} \right ), \end{align}
where
 $j=\pm 1$
. In order for patterns to emerge, there must exist
$j=\pm 1$
. In order for patterns to emerge, there must exist
 $k$
,
$k$
,
 $l$
such that
$l$
such that
 $\textrm{Re}\,\lambda \gt 0$
[Reference Murray30]. It is already clear that this condition cannot be satisfied in the case
$\textrm{Re}\,\lambda \gt 0$
[Reference Murray30]. It is already clear that this condition cannot be satisfied in the case
 $j=-1$
; therefore, we focus our forthcoming analysis on the case
$j=-1$
; therefore, we focus our forthcoming analysis on the case
 $j=+1$
. Since the right-hand side of (3.16a) is given by the sum of a positive term (the square root) and a negative term (the rest), for this quantity to be positive it must beUsing the ranges determined for the nondimensional parameters in (3.4), we have that
$j=+1$
. Since the right-hand side of (3.16a) is given by the sum of a positive term (the square root) and a negative term (the rest), for this quantity to be positive it must beUsing the ranges determined for the nondimensional parameters in (3.4), we have that \begin{equation*} \sqrt {\frac {X+\sqrt {X^2+Y^2}}{2}} \gt \beta +\Gamma +h^2(\delta +1). \end{equation*}
\begin{equation*} \sqrt {\frac {X+\sqrt {X^2+Y^2}}{2}} \gt \beta +\Gamma +h^2(\delta +1). \end{equation*}
 $\textrm{Re}\,\lambda \lt 0$
for any
$\textrm{Re}\,\lambda \lt 0$
for any
 $h$
and for any
$h$
and for any
 $\alpha$
,
$\alpha$
,
 $\beta$
,
$\beta$
,
 $\delta$
in (3.4). Therefore, no Turing patterns can emerge.
$\delta$
in (3.4). Therefore, no Turing patterns can emerge.
3.2. Travelling waves
In this section, we consider the formation of travelling wave profiles, i.e. profiles which move through the spatial domain keeping constant shape and speed.
Extensive simulations of equations (2.1a), (2.1b) reveal that one-dimensional sections of compact initial data
![]() $B(0,x,y)$
and
$B(0,x,y)$
and
![]() $T(0,x,y)$
numerically evolve into travelling waves for a wide parameter range (see Figure 3, Section 4). In particular, the unstable nature of the trivial steady-state
$T(0,x,y)$
numerically evolve into travelling waves for a wide parameter range (see Figure 3, Section 4). In particular, the unstable nature of the trivial steady-state
![]() $(B_0, T_0)$
suggests we are in the presence of pulled fronts, where the linear spreading of small perturbations pulls the front into the linearly unstable bare soil steady-state [Reference Lewis, Li and Weinberger22, Reference Maini, McElwain and Leavesley24, Reference van Saarloos39]. The (nondimensional) asymptotic travelling speed of such structures
$(B_0, T_0)$
suggests we are in the presence of pulled fronts, where the linear spreading of small perturbations pulls the front into the linearly unstable bare soil steady-state [Reference Lewis, Li and Weinberger22, Reference Maini, McElwain and Leavesley24, Reference van Saarloos39]. The (nondimensional) asymptotic travelling speed of such structures
![]() $\tilde{c}_\infty$
therefore coincides with the linear spreading speed
$\tilde{c}_\infty$
therefore coincides with the linear spreading speed
![]() $\tilde{c}_\infty$
. In order to compute it, we introduce the characteristic polynomial of the Jacobian matrix associated with equations (3.2a), (3.2b) evaluated at
$\tilde{c}_\infty$
. In order to compute it, we introduce the characteristic polynomial of the Jacobian matrix associated with equations (3.2a), (3.2b) evaluated at
![]() $(B_0,T_0)$
focusing on one-dimensional domains:
$(B_0,T_0)$
focusing on one-dimensional domains:
where
 \begin{equation} \begin{aligned} \mathcal{A}_1 &\;:\!=\; k \, (k \, (1+\delta ) - i \, \gamma ) + \beta -1, \\[5pt] \mathcal{A}_0 &\;:\!=\; \left ( k^2-1 \right ) \left ( k \, (\delta \, k - i \, \gamma )+\beta \right ). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathcal{A}_1 &\;:\!=\; k \, (k \, (1+\delta ) - i \, \gamma ) + \beta -1, \\[5pt] \mathcal{A}_0 &\;:\!=\; \left ( k^2-1 \right ) \left ( k \, (\delta \, k - i \, \gamma )+\beta \right ). \end{aligned} \end{equation}
The dispersion relation, corresponding to the solution to
![]() $p_0(\lambda )=0$
with the largest real part, is given by
$p_0(\lambda )=0$
with the largest real part, is given by
The linear spreading speed
![]() $\tilde{c}_\infty$
is obtained by solving (see [Reference Murray30])
$\tilde{c}_\infty$
is obtained by solving (see [Reference Murray30])
Here,
![]() $k_0$
is a constant related to the asymptotic evaluation of the Fourier transform of the perturbation solving the linearised system via the method of steepest descents for
$k_0$
is a constant related to the asymptotic evaluation of the Fourier transform of the perturbation solving the linearised system via the method of steepest descents for
![]() $t \to \infty$
. Equation (3.20b), on the other hand, represents the assumption that such perturbation neither grows nor decays at the leading edge of the front.
$t \to \infty$
. Equation (3.20b), on the other hand, represents the assumption that such perturbation neither grows nor decays at the leading edge of the front.

Figure 3. Travelling arc moving uphill obtained by numerically simulating equations (2.1a), (2.1b) at four different time steps for biomass (
![]() $B$
), toxicity (
$B$
), toxicity (
![]() $T$
) (first and second row panels) and a one-dimensional cross-section obtained by cutting the profiles in the middle of the two-dimensional domain along the direction of the slope. The parameter values used for the simulation are taken from Table 1 together with
$T$
) (first and second row panels) and a one-dimensional cross-section obtained by cutting the profiles in the middle of the two-dimensional domain along the direction of the slope. The parameter values used for the simulation are taken from Table 1 together with
![]() $m=0.5$
,
$m=0.5$
,
![]() $q=0.01$
,
$q=0.01$
,
![]() $s=3$
,
$s=3$
,
![]() $D_T=1.2$
, and
$D_T=1.2$
, and
![]() $V_T=5$
.
$V_T=5$
.
Since
![]() $\tilde{c}_\infty \in \mathbb{R}$
, equation (3.20a) implies
$\tilde{c}_\infty \in \mathbb{R}$
, equation (3.20a) implies
![]() $k_0 = \dfrac{i \, \tilde{c}_\infty }{2}$
. Plugging this into equation (3.20b) (and focusing our attention on right-moving fronts, i.e. fronts with positive speed), we obtain
$k_0 = \dfrac{i \, \tilde{c}_\infty }{2}$
. Plugging this into equation (3.20b) (and focusing our attention on right-moving fronts, i.e. fronts with positive speed), we obtain
(This, in turn, leads to
![]() $k_0=i$
). We note that this coincides with the critical wave speed of a travelling wave solution to the Fisher-KPP equation (see e.g. [Reference Murray31]). Heuristically, this can be explained by the absence of toxicity at the leading edge of the front, which turns equation (3.2a) precisely into the Fisher-KPP equation.
$k_0=i$
). We note that this coincides with the critical wave speed of a travelling wave solution to the Fisher-KPP equation (see e.g. [Reference Murray31]). Heuristically, this can be explained by the absence of toxicity at the leading edge of the front, which turns equation (3.2a) precisely into the Fisher-KPP equation.
In order to compare this result with numerical simulations of the dimensional model (2.1a), (2.1b) and to facilitate the ecological interpretation of this quantity, we convert
![]() $\tilde{c}_\infty$
into its dimensional version
$\tilde{c}_\infty$
into its dimensional version
![]() $c_\infty$
by recalling that, due to equation (3.1), we have
$c_\infty$
by recalling that, due to equation (3.1), we have
![]() $\frac{dx}{dt} = \sqrt{D_B \, g} \, \frac{d\tilde{x}}{d\tilde{t}}$
, therefore
$\frac{dx}{dt} = \sqrt{D_B \, g} \, \frac{d\tilde{x}}{d\tilde{t}}$
, therefore
The right-moving front hence moves with constant shape and speed
![]() $\tilde{c}_\infty$
, which solely depends on the biomass growth rate and its diffusion coefficient. The presence of the slope, regulated by the parameter
$\tilde{c}_\infty$
, which solely depends on the biomass growth rate and its diffusion coefficient. The presence of the slope, regulated by the parameter
![]() $\gamma$
, induces the formation of a travelling arc (in the uphill direction) for
$\gamma$
, induces the formation of a travelling arc (in the uphill direction) for
![]() $\gamma \gt 0$
(see Figure 3), i.e. the ‘tail’ of the ring is disrupted by the downhill flow of toxicity. Turning off the effect induced by toxicity via the slope term by considering
$\gamma \gt 0$
(see Figure 3), i.e. the ‘tail’ of the ring is disrupted by the downhill flow of toxicity. Turning off the effect induced by toxicity via the slope term by considering
![]() $\gamma =0$
–representing a flat ground – substantially changes the structure of the emerging pattern: the travelling arc reduces to a ring symmetrically expanding in all directions and, depending on the intensity of the toxicity parameters, secondary travelling rings may form inside the primary ring (see Figure 4). In both cases, we recall that the stability analysis illustrated in Section 3.1.2 implies that, as
$\gamma =0$
–representing a flat ground – substantially changes the structure of the emerging pattern: the travelling arc reduces to a ring symmetrically expanding in all directions and, depending on the intensity of the toxicity parameters, secondary travelling rings may form inside the primary ring (see Figure 4). In both cases, we recall that the stability analysis illustrated in Section 3.1.2 implies that, as
![]() $t \to \infty$
, we have convergence to the uniform equilibrium
$t \to \infty$
, we have convergence to the uniform equilibrium
![]() $(B_c,T_c)$
.
$(B_c,T_c)$
.

Figure 4. Travelling ring obtained by numerically simulating equations (2.1a), (2.1b) at four different time steps for biomass (
![]() $B$
), toxicity (
$B$
), toxicity (
![]() $T$
) (first and second row panels) and a one-dimensional cross-section obtained by cutting the profiles in the middle of the symmetric two-dimensional domain. The parameter values used for the simulation are taken from Table 1 together with
$T$
) (first and second row panels) and a one-dimensional cross-section obtained by cutting the profiles in the middle of the symmetric two-dimensional domain. The parameter values used for the simulation are taken from Table 1 together with
![]() $m=0$
,
$m=0$
,
![]() $q=0.01$
,
$q=0.01$
,
![]() $s=3$
, and
$s=3$
, and
![]() $D_T=1.2$
.
$D_T=1.2$
.
4. Numerical simulations
In this section, we perform a series of numerical simulations of equations (2.1a), (2.1b) equipped with Neumann boundary conditions on a two-dimensional square domain
![]() $[0, L] \times [0, L]$
using the software Matlab. As for the initial conditions, we set
$[0, L] \times [0, L]$
using the software Matlab. As for the initial conditions, we set
where
![]() $B_i(x,y) = 0$
everywhere except for
$B_i(x,y) = 0$
everywhere except for
![]() $B_i(L/2,L/2)=0.5$
(
$B_i(L/2,L/2)=0.5$
(
![]() $\textrm{kg} \cdot{m}^{-2}$
) and
$\textrm{kg} \cdot{m}^{-2}$
) and
![]() $T_i(x,y)=0$
(
$T_i(x,y)=0$
(
![]() $\textrm{kg} \cdot{m}^{-2}$
) for all
$\textrm{kg} \cdot{m}^{-2}$
) for all
![]() $x, y$
. We note that from here on we focus on the dimensional model, as dimensional parameters and quantities are easier to interpret from the ecological viewpoint.
$x, y$
. We note that from here on we focus on the dimensional model, as dimensional parameters and quantities are easier to interpret from the ecological viewpoint.
In Figure 5, we investigate the influence of toxicity on the structure of the emerging travelling patterns by comparing the simulated one-dimensional profiles in the cases
![]() $s \gt 0$
(biomass dynamics affected by toxicity) and
$s \gt 0$
(biomass dynamics affected by toxicity) and
![]() $s=0$
(biomass and toxicity dynamics decoupled) on a sloped terrain at a fixed instant. We observe that, while in the first case a travelling pulse arises moving in the uphill direction, in the second case this pulse reduces to two fronts symmetrically travelling in an outward direction. The maximum peak reached by the biomass is also sensibly lower in the case
$s=0$
(biomass and toxicity dynamics decoupled) on a sloped terrain at a fixed instant. We observe that, while in the first case a travelling pulse arises moving in the uphill direction, in the second case this pulse reduces to two fronts symmetrically travelling in an outward direction. The maximum peak reached by the biomass is also sensibly lower in the case
![]() $s\gt 0$
; toxicity further influences this quantity via the slope parameter
$s\gt 0$
; toxicity further influences this quantity via the slope parameter
![]() $m$
, as investigated below (see Figure 6).
$m$
, as investigated below (see Figure 6).

Figure 5. Comparison between two one-dimensional cross sections of biomass profiles obtained by simulating equations (2.1a), (2.1b) with initial conditions as in (4.1) for
![]() $D_B=0.5$
,
$D_B=0.5$
,
![]() $g=0.6$
,
$g=0.6$
,
![]() $d=0.06$
,
$d=0.06$
,
![]() $c=0.6$
,
$c=0.6$
,
![]() $V=5$
,
$V=5$
,
![]() $D_T=1.2$
,
$D_T=1.2$
,
![]() $q=0.01$
,
$q=0.01$
,
![]() $m=0.5$
and
$m=0.5$
and
![]() $s=3$
(solid line) vs
$s=3$
(solid line) vs
![]() $s=0$
(dashed line). In the first case, a travelling pulse forms which moves along the slope direction, whereas in the second case, we have two travelling fronts symmetrically moving outwards.
$s=0$
(dashed line). In the first case, a travelling pulse forms which moves along the slope direction, whereas in the second case, we have two travelling fronts symmetrically moving outwards.

Figure 6. Variations in the peak of biomass (
![]() $B$
, left vertical axis, continuous line) and toxicity (
$B$
, left vertical axis, continuous line) and toxicity (
![]() $T$
, right vertical axis, dashed line) due to changes in slope (
$T$
, right vertical axis, dashed line) due to changes in slope (
![]() $m$
). The parameter values used for the simulation are taken from Table 1 with
$m$
). The parameter values used for the simulation are taken from Table 1 with
![]() $k=0.01$
,
$k=0.01$
,
![]() $s=3$
,
$s=3$
,
![]() $D_T=1.2$
, and
$D_T=1.2$
, and
![]() $V_T=5$
.
$V_T=5$
.
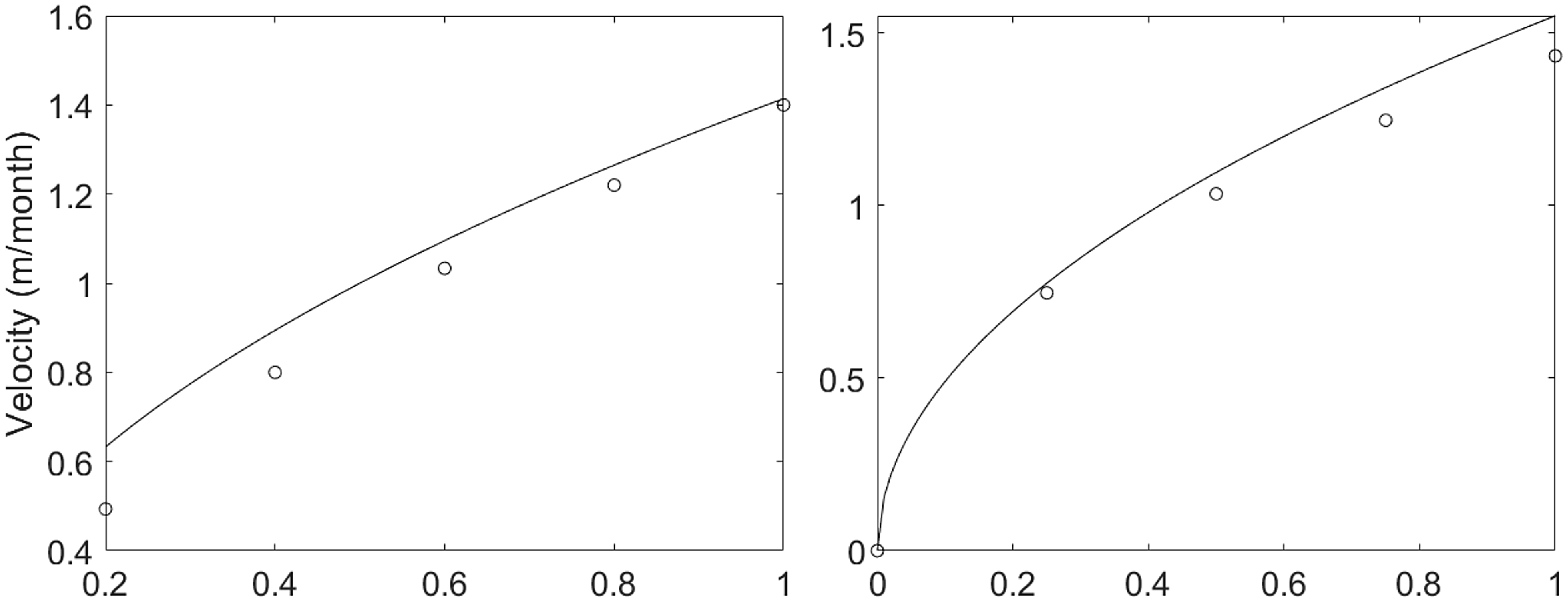
Figure 7. Analytical representation (equation (3.22), continuous line) and numerical simulations (circles) of the asymptotic travelling speed
![]() $c_\infty$
with respect to the biomass growth parameter
$c_\infty$
with respect to the biomass growth parameter
![]() $g$
(left panel) and the biomass diffusion parameter
$g$
(left panel) and the biomass diffusion parameter
![]() $D_B$
(right panel). The other parameter values used for the simulation are taken from Table 1 together with
$D_B$
(right panel). The other parameter values used for the simulation are taken from Table 1 together with
![]() $m=0.5$
,
$m=0.5$
,
![]() $k=0.01$
,
$k=0.01$
,
![]() $s=3$
,
$s=3$
,
![]() $D_T=1.2$
and
$D_T=1.2$
and
![]() $V_T=5$
.
$V_T=5$
.
The next step in our numerical investigation focuses on the influence of the toxicity on the arising travelling patterns via the slope parameter
![]() $m$
. First, we analyse the scenario of a sloped terrain represented by
$m$
. First, we analyse the scenario of a sloped terrain represented by
![]() $m\gt 0$
in Figure 3, which shows the evolution of the system’s dynamics at increasing time steps corresponding to 10, 50, 100 and 150 months. In this simulation, the slope coefficient
$m\gt 0$
in Figure 3, which shows the evolution of the system’s dynamics at increasing time steps corresponding to 10, 50, 100 and 150 months. In this simulation, the slope coefficient
![]() $m$
is set to
$m$
is set to
![]() $0.5$
, with the uphill direction corresponding to the right-hand side of the domain. The first two rows represent the accumulation of biomass and toxicity in the square grid, respectively. As expected, biomass starts growing radially until it is inhibited by the presence of toxicity which, due to the advection term in equations (2.1a), (2.1b), diffuses prominently in the downhill direction. This induces the emergence of a travelling arced shape of biomass. This behaviour is displayed also in the third row of Figure 3 via a one-dimensional horizontal section of the square numerical domain showing the evolution in time of both biomass and toxicity.
$0.5$
, with the uphill direction corresponding to the right-hand side of the domain. The first two rows represent the accumulation of biomass and toxicity in the square grid, respectively. As expected, biomass starts growing radially until it is inhibited by the presence of toxicity which, due to the advection term in equations (2.1a), (2.1b), diffuses prominently in the downhill direction. This induces the emergence of a travelling arced shape of biomass. This behaviour is displayed also in the third row of Figure 3 via a one-dimensional horizontal section of the square numerical domain showing the evolution in time of both biomass and toxicity.
An analogous temporal evolution of the system’s dynamics in the case of flat grounds (represented by the case
![]() $m=0$
) is shown in Figure 4. Here, the radial growth of the biomass is symmetrically affected by toxicity and hence not disrupted, leading to rings expanding in the two-dimensional domain. With the parameter values adopted in this simulation, secondary rings form within the primary ring as a result of the fact that, after some time, the toxicity removed from the centre of the domain creates the conditions for new biomass growth. This result is consistent with the findings presented in [Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8].
$m=0$
) is shown in Figure 4. Here, the radial growth of the biomass is symmetrically affected by toxicity and hence not disrupted, leading to rings expanding in the two-dimensional domain. With the parameter values adopted in this simulation, secondary rings form within the primary ring as a result of the fact that, after some time, the toxicity removed from the centre of the domain creates the conditions for new biomass growth. This result is consistent with the findings presented in [Reference Cartenì, Marasco, Bonanomi, Mazzoleni, Rietkerk and Giannino8].
Due to the importance of the slope intensity in the toxicity advection term, we evaluate numerically the dependence between the slope parameter
![]() $m$
and the height of the leading travelling pulse both for biomass and toxicity. As expected by the mathematical formulation, the higher the slope, the higher the advection which reduces, even if only slightly, the toxicity and its maximum peak (Figure 6). This decrease in the toxicity then induces a corresponding increase in the biomass peak of the main travelling pulse.
$m$
and the height of the leading travelling pulse both for biomass and toxicity. As expected by the mathematical formulation, the higher the slope, the higher the advection which reduces, even if only slightly, the toxicity and its maximum peak (Figure 6). This decrease in the toxicity then induces a corresponding increase in the biomass peak of the main travelling pulse.
Finally, as the asymptotic travelling speed
![]() $c_\infty$
was shown to depend only on
$c_\infty$
was shown to depend only on
![]() $D_B$
and
$D_B$
and
![]() $g$
(see equation (3.22)), we compare this expression with the numerically calculated velocity by varying both of these parameters. The numerical speed was calculated as the ratio of the number of pixels covered by the travelling peak to the number of timesteps (converted to m/month) with parameter values as in Table 1 and
$g$
(see equation (3.22)), we compare this expression with the numerically calculated velocity by varying both of these parameters. The numerical speed was calculated as the ratio of the number of pixels covered by the travelling peak to the number of timesteps (converted to m/month) with parameter values as in Table 1 and
![]() $k=0.01$
,
$k=0.01$
,
![]() $s=3$
,
$s=3$
,
![]() $D_T=1.2$
,
$D_T=1.2$
,
![]() $V_T=5$
. In both cases, numerical results are in good agreement with the analytical predictions (see Figure 7).
$V_T=5$
. In both cases, numerical results are in good agreement with the analytical predictions (see Figure 7).
5. Discussion and conclusion
In this work, we introduce and analyse a reaction-diffusion-advection model describing vegetation spatial distributions (in the form of arcs on slopes) observed in nature and also in environments where water is not limited. Our investigation allows us to confirm the ecologically feasible condition of the transient nature of such patterns. Moreover, thanks to the ecological constraints reflected by the model, we are able to compute the asymptotic speed of the corresponding emerging travelling waves. This expression does not depend on the slope coefficient
![]() $m$
, nor does the emergence of such a transient pattern.
$m$
, nor does the emergence of such a transient pattern.
Despite the fact that the slope (represented by the parameter
![]() $m$
) does not affect the biomass dynamics directly but only via the toxicity flow, the main effect produced by
$m$
) does not affect the biomass dynamics directly but only via the toxicity flow, the main effect produced by
![]() $m$
on the long-term dynamics consists of the height of the main travelling pulse of
$m$
on the long-term dynamics consists of the height of the main travelling pulse of
![]() $B$
(as shown in Figure 6). In fact, as
$B$
(as shown in Figure 6). In fact, as
![]() $m$
increases, the downhill flow of
$m$
increases, the downhill flow of
![]() $T$
accordingly increases, therefore reducing the maximum of
$T$
accordingly increases, therefore reducing the maximum of
![]() $T$
reached in the proximity of the
$T$
reached in the proximity of the
![]() $B$
peak. Consequently, the maximum biomass in the travelling pulse can reach a higher value – net of other relevant ecological factors not considered in our model, such as the ability of the root system to successfully establish.
$B$
peak. Consequently, the maximum biomass in the travelling pulse can reach a higher value – net of other relevant ecological factors not considered in our model, such as the ability of the root system to successfully establish.
Due to the ecological focus of our model, a natural next step consists of the comparison and validation with real-life data. In order to further increase potential connections with relevant ecological scenarios, a future extension we plan to consider is given by a space-dependent slope coefficient in our equations accounting for topographical differences in existing sloped profiles.
Financial support
AI acknowledges support from an FWF Hertha Firnberg Research Fellowship (T 1199-N) and is a member of Gruppo Nazionale per la Fisica Matematica, Istituto Nazionale di Alta Matematica (INdAM). FG and GT are members of Gruppo Nazionale per il Calcolo Scientifico, Istituto Nazionale di Alta Matematica (INdAM). GT was supported by the PRIN grant (Bando 2022) Numerical Optimization with Adaptive Accuracy and Applications to Machine Learning (Prot. 2022N3ZNAX).
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









































































