Article contents
Dynamic and stochastic propagation of the Brenier optimal mass transport
Published online by Cambridge University Press: 20 March 2019
Abstract
Similar to how Hopf–Lax–Oleinik-type formula yield variational solutions for Hamilton–Jacobi equations on Euclidean space, optimal mass transportations can sometimes provide variational formulations for solutions of certain mean-field games. We investigate here the particular case of transports that maximize and minimize the following ‘ballistic’ cost functional on phase space TM, which propagates Brenier’s transport along a Lagrangian L,
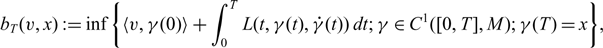 $$b_T(v, x):=\inf\left\{\langle v, \gamma (0)\rangle +\int_0^TL(t, \gamma (t), {\dot \gamma}(t))\, dt; \gamma \in C^1([0, T], M); \gamma(T)=x\right\}\!,$$
$$b_T(v, x):=\inf\left\{\langle v, \gamma (0)\rangle +\int_0^TL(t, \gamma (t), {\dot \gamma}(t))\, dt; \gamma \in C^1([0, T], M); \gamma(T)=x\right\}\!,$$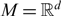 $M = \mathbb{R}^d$, and T >0. We also consider the stochastic counterpart:
$M = \mathbb{R}^d$, and T >0. We also consider the stochastic counterpart:
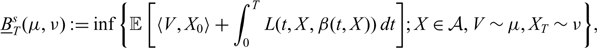 \begin{align*}
\underline{B}_T^s(\mu,\nu):=\inf\left\{\mathbb{E}\left[\langle V,X_0\rangle +\int_0^T L(t, X,\beta(t,X))\,dt\right]\!; X\in \mathcal{A}, V\sim\mu,X_T\sim \nu\right\}\!,
\end{align*}
\begin{align*}
\underline{B}_T^s(\mu,\nu):=\inf\left\{\mathbb{E}\left[\langle V,X_0\rangle +\int_0^T L(t, X,\beta(t,X))\,dt\right]\!; X\in \mathcal{A}, V\sim\mu,X_T\sim \nu\right\}\!,
\end{align*}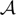 $\mathcal{A}$ is the set of stochastic processes satisfying dX = βX (t, X) dt + dWt, for some drift βX (t, X), and where Wt is σ(Xs: 0 ≤ s ≤ t)-Brownian motion. Both cases lead to Lax–Oleinik-type formulas on Wasserstein space that relate optimal ballistic transports to those associated with dynamic fixed-end transports studied by Bernard–Buffoni and Fathi–Figalli in the deterministic case, and by Mikami–Thieullen in the stochastic setting. While inf-convolution easily covers cost minimizing transports, this is not the case for total cost maximizing transports, which actually are sup-inf problems. However, in the case where the Lagrangian L is jointly convex on phase space, Bolza-type dualities – well known in the deterministic case but novel in the stochastic case – transform sup-inf problems to sup–sup settings. We also write Eulerian formulations and point to links with the theory of mean-field games.
$\mathcal{A}$ is the set of stochastic processes satisfying dX = βX (t, X) dt + dWt, for some drift βX (t, X), and where Wt is σ(Xs: 0 ≤ s ≤ t)-Brownian motion. Both cases lead to Lax–Oleinik-type formulas on Wasserstein space that relate optimal ballistic transports to those associated with dynamic fixed-end transports studied by Bernard–Buffoni and Fathi–Figalli in the deterministic case, and by Mikami–Thieullen in the stochastic setting. While inf-convolution easily covers cost minimizing transports, this is not the case for total cost maximizing transports, which actually are sup-inf problems. However, in the case where the Lagrangian L is jointly convex on phase space, Bolza-type dualities – well known in the deterministic case but novel in the stochastic case – transform sup-inf problems to sup–sup settings. We also write Eulerian formulations and point to links with the theory of mean-field games.
Keywords
- Type
- Papers
- Information
- European Journal of Applied Mathematics , Volume 30 , Special Issue 6: Applied Optimal Transport , December 2019 , pp. 1264 - 1299
- Copyright
- © Cambridge University Press 2019
Footnotes
This work is part of a Master’s thesis prepared by A. Barton under the supervision of N. Ghoussoub. It was partially supported by a grant from the Natural Sciences and Engineering Research Council of Canada.
References
- 2
- Cited by


