Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T13:44:19.233Z Has data issue: false hasContentIssue false
  • English
  • Français

Blow-up similarity solutions of the fourth-order unstable thin film equation

Published online by Cambridge University Press:  01 April 2007

J. D. EVANS ,
V. A. GALAKTIONOV  and
J. R. KING
J. D. EVANS
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK email: [email protected]
V. A. GALAKTIONOV
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK email: [email protected]
J. R. KING
Affiliation:
Theoretical Mechanics Section, University of Nottingham, Nottingham NG7 2RD, UK email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

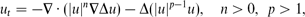We study blow-up behaviour of solutions of the fourth-order thin film equation which contains a backward (unstable) diffusion term. Our main goal is a detailed study of the case of the first critical exponent 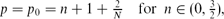where N ≥ 1 is the space dimension. We show that the free-boundary problem with zero contact angle and zero-flux conditions admits continuous sets (branches) of blow-up self-similar solutions. For the Cauchy problem in RN × R+, we detect compactly supported blow-up patterns, which have infinitely many oscillations near interfaces and exhibit a “maximal” regularity there. As a key principle, we use the fact that, for small positive n, such solutions are close to the similarity solutions of the semilinear unstable limit Cahn-Hilliard equation 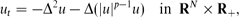which are better understood and have been studied earlier [19]. We also discuss some general aspects of formation of self-similar blow-up singularities for other values of p.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 18 , Issue 2 , April 2007 , pp. 195 - 231
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ansini, L., & Giacomelli, L. (2004) Doubly nonlinear thin-film equations on one space dimension. Arch. Ration. Mech. Anal. 173, 89–131.CrossRefGoogle Scholar
[2]Becker, J. & Grün, G. (2005) The thin-film equation: recent advances and some new perspectives. J. Phys.: Condens. Matter 17, S291–S307.Google Scholar
[3]Bernis, F. & Friedman, A. (1990) Higher order nonlinear degenerate parabolic equations. J. Differ. Equat. 83, 179–206.CrossRefGoogle Scholar
[4]Bernis, F. & McLeod, J. B. (1991) Similarity solutions of a higher order nonlinear diffusion equation. Nonl. Anal., TMA 17, 1039–1068.CrossRefGoogle Scholar
[5]Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source type solutions of a fourth order nonlinear degenerate parabolic equation. Nonl. Anal., TMA 18, 217–234.Google Scholar
[6]Bernoff, A. J. & Bertozzi, A. L. (1995) Singularities in a modified Kuramoto-Sivashinsky equation describing interface motion for phase transition. Physica D 85, 375–404.CrossRefGoogle Scholar
[7]Bertozzi, A. L. & Pugh, M. C. (1998) Long-wave instabilities and saturation in thin film equations. Comm. Pur. Appl. Math. LI, 625–651.3.0.CO;2-9>CrossRefGoogle Scholar
[8]Bertozzi, A. L. & Pugh, M. C. (2000) Finite-time blow-up of solutions of some long-wave unstable thin film equations. Indiana Univ. Math. J. 49, 1323–1366.CrossRefGoogle Scholar
[9]Bowen, M. & King, J. R. (2001) Moving boundary problems and non-uniqueness for the thin film equation. Euro J. Appl. Math. 12, 321–356.Google Scholar
[10]Carrillo, J. A. & Toscani, G. (2002) Long-time asymptotic behaviour for strong solutions of the thin film eqwuations. Comm. Math. Phys. 225, 551–571.CrossRefGoogle Scholar
[11]Chandrasekhar, S. (1981) Hydrodynamic and Hydromagnetic Stability. Dover, New York.Google Scholar
[12]Coddington, E. A. & Levinson, N. (1955) Theory of Ordinary Differential Equations. McGraw-Hill Book Company, Inc., New York/London.Google Scholar
[13]Egorov, Yu. V., Galaktionov, V. A., Kondratiev, V. A. & Pohozaev, S. I. (2000) On the necessary conditions of existence to a quasilinear inequality in the half-space. Comptes Rendus Acad. Sci. Paris, Série I 330, 93–98.Google Scholar
[14]Egorov, Yu. V., Galaktionov, V. A., Kondratiev, V. A. & Pohozaev, S. I. (2004) Asymptotic behaviour of global solutions to higher-order semilinear parabolic equations in the supercritical range. Adv. Differ. Equat. 9, 1009–1038.Google Scholar
[15]Eidelman, S. D. (1969) Parabolic Systems. North-Holland Publ. Comp., Amsterdam/London.Google Scholar
[16]Elliott, C. & Songmu, Z. (1986) On the Cahn-Hilliard equation. Arch. Rat. Mech. Anal. 96, 339–357.CrossRefGoogle Scholar
[17]Evans, J. D., Galaktionov, V. A. & King, J. R.Unstable sixth-order thin film equation. I. Blow-up similarity solutions; II. Global similarity patterns. Nonlinearity, to appear.Google Scholar
[18]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007) Source-type solutions for the fourth-order unstable thin film equation. Euro J. Appl. Math., in press.CrossRefGoogle Scholar
[19]Evans, J. D., Galaktionov, V. A. & Williams, J. F. (2006) Blow-up and global asymptotics of the limit unstable Cahn-Hilliard equation. SIAM J. Math. Anal. 38, 64–102.CrossRefGoogle Scholar
[20]Ferreira, R. & Bernis, F. (1997) Source-type solutions to thin-film equations in higher dimensions. Euro J. Appl. Math. 8, 507–534.CrossRefGoogle Scholar
[21]Galaktionov, V. A. (2004) Geometric Sturmian Theory of Nonlinear Parabolic Equations and Applications. Chapman & Hall/CRC, Boca Raton, Florida.CrossRefGoogle Scholar
[22]Galaktionov, V. A. (2006) On interfaces and oscillatory solutions of higher-order semilinear parabolic equations with nonlipschitz nonlinearities. Stud. Appl. Math. 117, 353–389.CrossRefGoogle Scholar
[23]Galaktionov, V. A. & Pohozaev, S. I. (2006) Blow-up and critical exponents for parabolic equations with non-divergent operators: dual porous medium and thin film operators. J. Evol. Equat. 6, 45–69.CrossRefGoogle Scholar
[24]Galaktionov, V. A. & Svirshchevskii, S. R. (2007) Exact Solution and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics. Chapman & Hall/CRC, Boca Raton, Florida.Google Scholar
[25]Galaktionov, V. A. & Vazquez, J. L. (2002) The problem of blow-up in nonlinear parabolic equations. Discr. Cont. Dyn. Syst. 8, 399–433.Google Scholar
[26]King, J. R. (2001) Two generalisations of the thin film equation. Math. Comput. Modelling 34, 737–756.CrossRefGoogle Scholar
[27]Krasnosel'skii, M. A. & Zabreiko, P. P. (1984) Geometrical Methods of Nonlinear Analysis. Springer-Verlag, Berlin/Tokyo.CrossRefGoogle Scholar
[28]Lions, J. L. (1969) Quelques méthodes de résolution des problèmes aux limites non linéaires, Dunod, Gauthier–Villars, Paris.Google Scholar
[29]Novick-Cohen, A. (1992) Blow-up and growth in the directional solidification of dilute binary alloys. Appl. Anal. 47, 241–257.Google Scholar
[30]Novick-Cohen, A. & Segel, L. A. (1984) Nonlinear aspects of the Cahn-Hilliard equation. Physica D 10, 277–298.CrossRefGoogle Scholar
[31]Slepčev, D. & Pugh, M. C. (2005) Self-similar blow-up of unstable thin-film equations. Indiana Univ. Math. J. 54, 1697–1738.CrossRefGoogle Scholar
[32]Samarskii, A. A., Galaktionov, V. A., Kurdyumov, S. P. & Mikhailov, A. P. (1995) Blow-up in Quasilinear Parabolic Equations. Walter de Gruyter, Berlin/New York.CrossRefGoogle Scholar
[33]Witelski, T. P., Bernoff, A. J. & Bertozzi, A. L. (2004) Blow-up and dissipation in a critical-case unstable thin film equation. Euro J. Appl. Math. 15, 223–256.CrossRefGoogle Scholar