Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:01:36.506Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dynamical Tide and Resonance Locking

Published online by Cambridge University Press:  20 June 2008

M.-J. Goupil ,
J.-P. Zahn  and
G.-J. Savonije
G.-J. Savonije*
Affiliation:
Astronomical Institute “Anton Pannekoek”, University of Amsterdam Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
*
[email protected]
Get access

Abstract

A general problem with the theory of stellar tides is that the observations indicate that the effectiveness in circularising binary orbits is much larger than predicted by current theories. A mechanism that may be at least part of the solution to this problem is resonance locking: prolonged enhanced tidal interaction when the tide is nearly resonant with a stellar oscillation mode. In these lectures we focus on the dynamical tide which takes into account that the tides can indeed excite non-radial oscillations in a star when the forcing period happens to be close to the period of a free oscillation mode of the star. Such resonant interaction can in principle speed-up the tidal evolution of a close binary. By including the Coriolis force in rotating stars the oscillation spectrum is enriched by rotational oscillation modes that can also be excited by the tides. Although the chances that the tides in a particular binary system happen to be close to a resonance with a free oscillation mode seem nevertheless slim, it appears that binary systems with a significant orbital eccentricity, and thus with several tidal harmonics, evolve through many resonances on timescales short compared to their main sequence (MS) lifetime. Stellar rotation, which is usually neglected in tidal calculations, plays an important role in that it is relatively easy to tidally spin a star up or down, whereby the forcing frequency (in the stellar frame) can move towards a resonance with a free oscillation mode of the star on relatively short timescales. Often this gives rise to resonance locking whereby the system remains nearly resonant, with enhanced tidal evolution, for a relatively long period. We will present the results of several numerical simulations, for both massive MS binaries and solar type binary systems in which resonance locking is studied in some detail.Note: in the following all numerically listed frequencies are normalised by the stellar break-up speed $\Omega_c=\sqrt{G\, M_s/R^3_s}$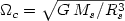, unless explicitly indicated otherwise.

Type
Research Article
Information
European Astronomical Society Publications Series , Volume 29: Tidal Effects in Stars, Planets and Disks , 2008 , pp. 91 - 125
Copyright
© EAS, EDP Sciences, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brouwer, D., & Clemence, G., 1961, Methods of Celestial Mechanics (Academic Press, New York)
Cowling, T., 1941, MNRAS, 267, 367 CrossRef
Darwin, G., 1879, Phil. Trans. R. Soc., 170, 1 CrossRef
De Cat, P., Aerts, C., De Ridder, J., et al., 2000, A&A, 355, 1015
De Cat, P., Telting, J. Aerts, C., & Mathias, P., 2001, A&A, 359, 539
Duquennoy, A., & Mayor, M., 1991, A&A, 248, 485
Eggleton, P.P., Kiseleva, L.G., & Hut, P., 1998, ApJ, 499, 853 CrossRef
Giuricin, G., Mardirossian, F., & Mezetti, M., 1984, A&A, 134, 365
Goldreich, P., & Tremaine, S., 1980, ApJ, 241, 425 CrossRef
Goodman, J., & Dickson, E., 1998, ApJ, 507, 938 CrossRef
Handler, G., Balona, L.A., Shobbrook, R.R., et al., 2002, MNRAS, 333, 261
Hut, P., 1981, A&A, 99, 126
Ivanov, P.B., & Papaloizou, J.C., 2004a, MNRAS, 347, 437 CrossRef
Ivanov, P.B., & Papaloizou, J.C., 2004b, MNRAS, 353, 1161 CrossRef
Lin, D., & Papaloizou, J.C., 1986, ApJ, 309, 846 CrossRef
Mathieu, R.D., Meibom, S., & Dolan, C.J., 2004, ApJ, 602, 121 CrossRef
Meibom, S., & Dolan, C.J., 2005, ApJ, 620, 970 CrossRef
Papaloizou, J., & Pringle, J., 1978, MNRAS, 182, 423 CrossRef
Papaloizou, J., & Savonije, G., 1997, MNRAS, 291, 651 CrossRef
Polfliet, R., & Smeyers, P., 1990, A&A, 237, 110
Pols, O., Tout, C., Eggleton, P., & Han, Z., 1995, MNRAS, 274, 964 CrossRef
Provost, J., Berthomieu, C., & Rocca, A., 1981, A&A, 94, 126
Quaintrell, H., Norton, A.J., Ash, T.D., et al., 2003, A&A, 401, 313
Savonije, G., & Papaloizou, J., 1984, MNRAS, 207, 685 CrossRef
Savonije, G., & Papaloizou, J., 1997, MNRAS, 291, 633 CrossRef
Savonije, G., & Witte, M., 2002, A&A, 386, 211
Terquem, C., Papaloizou, J., Nelson, R., & Lin, D., 1998, ApJ, 502, 788 CrossRef
Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H., 1989, Non-radial Oscillations of Stars (University of Tokyo Press)
Verbunt, F., & Phinney, E., 1995, A&A, 296, 709
Willems, B., & Aerts, C., 2002, A&A, 384, 441
Witte, M., & Savonije, G., 1999a, A&A, 341, 842
Witte, M., & Savonije, G., 1999b, A&A, 350, 129
Witte, M., & Savonije, G., 2001, A&A, 366, 840 PubMed
Witte, M., & Savonije, G., 2002, A&A, 386, 222
Zahn, J., 1966, Ann. d'Ap., 29, 313
Zahn, J., 1977, A&A, 57, 383 PubMed