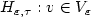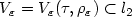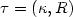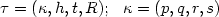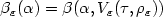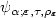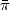Under regularity assumptions, we establish a sharp largedeviation principle for Hermitian quadratic forms ofstationary Gaussian processes. Our result is similar tothe well-known Bahadur-Rao theorem [2] on the samplemean. We also provide several examples of applicationsuch as the sharp large deviation properties ofthe Neyman-Pearson likelihood ratio test, of the sum of squares,of the Yule-Walkerestimator of the parameter of a stable autoregressive Gaussian process,and finally of the empirical spectral repartition function.

We study the LRT statistic for testing a single population i.i.d. model against a mixture of two populations with Markov regime.We prove that the LRT statistic converges to infinity in probability as the number of observations tends to infinity. This is a consequence of a convergence result of the LRT statistic for a subproblem where the parameters are restricted to a subset of the whole parameter set.

We observe an infinitely dimensional Gaussian random vector x = ξ + vwhereξ is a sequence of standard Gaussian variables and v ∈ l2 is anunknownmean. We consider the hypothesis testing problem H0 : v = 0versusalternatives $H_{\varepsilon,\tau}:v\in V_{\varepsilon}$ 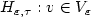for the sets $V_{\varepsilon}=V_{\varepsilon}(\tau,\rho_{\varepsilon})\subset l_2$ 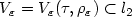.The sets Vε are l q -ellipsoidsof semi-axes ai = i-s R/ε with l p -ellipsoidof semi-axes bi = i-r pε/ε removed orsimilar Besov bodies Bq,t;s (R/ε) with Besovbodies Bp,h;r (pε/ε) removed. Here $\tau =(\kappa,R)$ 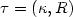or $\tau =(\kappa,h,t,R);\ \\kappa=(p,q,r,s)$ 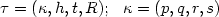are the parameters which define thesets Vε for given radii pε → 0,0 < p,q,h,t ≤ ∞, -∞ ≤ r,s ≤ ∞, R > 0; ε → 0 is theasymptotical parameter.We study the asymptotics of minimaxsecond kind errors $\beta_{\varepsilon}(\alpha)=\beta(\alpha, V_{\varepsilon}(\tau,\rho_{\varepsilon}))$ 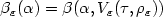and construct asymptotically minimax or minimax consistent families oftests $\psi_{\alpha;\varepsilon,\tau,\rho_{\varepsilon}}$ 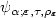, if it is possible.We describe the partition of the set of parameters κ into regions withdifferent types of asymptotics: classical, trivial, degenerate and Gaussian(of various types).Analogous rates have been obtained in a signal detectionproblem for continuous variant of white noise model: alternativescorrespond to Besov or Sobolev balls with Besov or Sobolev balls removed.The study is based on an extension of methods of constructions ofasymptotically least favorable priors.These methods are applicable to wide class of “convex separablesymmetrical" infinite-dimensional hypothesis testingproblems in white Gaussian noise model. Under some assumptionsthese methodsare based on the reduction of hypothesis testing problemto convex extreme problem: to minimize specially defined Hilbert normover convex sets of sequences $\bar{\pi}$ 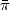of measures πi on thereal line. The study of this extreme problem allows to obtain differenttypes of Gaussian asymptotics.If necessary assumptions do not hold, then we obtain other types ofasymptotics.

We give limit theorems specifying weak andstrong rates of convergence associated to a quadratic extension of themartingale almost-sure central limit theorem. Some typical examples arediscussed to illustrate how to make use of them in statistic.

The p-values are often implicitly used as a measure of evidence for thehypotheses of the tests. This practice has been analyzed with different approaches. It is generallyaccepted for the one-sided hypothesis problem, but it is often criticized for the two-sided hypothesisproblem. We analyze this practice with a new approach to statistical inference. First we select gooddecision rules without using a loss function, we call them experts. Then we define a probabilitydistribution on the space of experts. The measure of evidence for a hypothesis is the inductiveprobability of experts that decide this hypothesis.

Let (Xt ) be a diffusion on the interval (l,r) and Δn a sequence of positive numbers tending to zero. We define J i as the integral between iΔn and (i + 1)Δn of X s .We give an approximation of the law of (J0,...,Jn-1)by means of a Euler scheme expansion for the process (Ji ). In some special cases, an approximation by anexplicit Gaussian ARMA(1,1) process is obtained.When Δn = n-1 we deduce from this expansion estimatorsof the diffusion coefficient of X based on (Ji ). These estimatorsare shown to be asymptotically mixed normal as n tends to infinity.

We define a notion of delta-variance maximization and show it implies epsilon-proximity in expactations.

Let YT = (Yt)t∈[0,T] be a real ergodic diffusion process which drift depends on an unkown parameter $\theta_{0}\in \mathbb{R}^{p}$ . Our aim is to estimate θ 0 from a discrete observation of the process YT , (Ykδ)k=0,n , for a fixed and small δ, as T = nδ goes to infinity. For that purpose, we adapt the Generalized Method of Moments (see Hansen) to the anticipative and approximate discrete-time trapezoidal scheme, and then to Simpson's.Under some general assumptions, the trapezoidal scheme (respectively Simpson's scheme) provides an estimation of θ 0 with a bias of order δ 2 (resp. δ 4). Moreover, this estimator is asymptotically normal. These results generalize Bergstrom's [1], which were obtained for a Gaussian diffusion process, which drift is linear in θ.